Sufficiency theorems for local minimizers of the multiple integrals of the calculus of variations
Published online by Cambridge University Press: 11 July 2007
Abstract
Let Ω ⊂ Rn be a bounded domain and let f : Ω × RN × RN×n → R. Consider the functional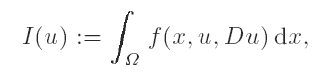 over the class of Sobolev functions W1,q(Ω;RN) (1 ≤ q ≤ ∞) for which the integral on the right is well defined. In this paper we establish sufficient conditions on a given function u0 and f to ensure that u0 provides an Lr local minimizer for I where 1 ≤ r ≤ ∞. The case r = ∞ is somewhat known and there is a considerable literature on the subject treating the case min(n, N) = 1, mostly based on the field theory of the calculus of variations. The main contribution here is to present a set of sufficient conditions for the case 1 ≤ r < ∞. Our proof is based on an indirect approach and is largely motivated by an argument of Hestenes relying on the concept of ‘directional convergence’.
over the class of Sobolev functions W1,q(Ω;RN) (1 ≤ q ≤ ∞) for which the integral on the right is well defined. In this paper we establish sufficient conditions on a given function u0 and f to ensure that u0 provides an Lr local minimizer for I where 1 ≤ r ≤ ∞. The case r = ∞ is somewhat known and there is a considerable literature on the subject treating the case min(n, N) = 1, mostly based on the field theory of the calculus of variations. The main contribution here is to present a set of sufficient conditions for the case 1 ≤ r < ∞. Our proof is based on an indirect approach and is largely motivated by an argument of Hestenes relying on the concept of ‘directional convergence’.
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 131 , Issue 1 , February 2001 , pp. 155 - 184
- Copyright
- Copyright © Royal Society of Edinburgh 2001
- 10
- Cited by

