Published online by Cambridge University Press: 15 September 2014
The frequency ratio of the allelomorphs of a Mendelian factor is only stable if selection favours the heterozygote: such factors, though occurring rarely, will accumulate in the stock, while those of opposite tendency will be eliminated.
The survival of a mutant gene although established in a mature and potent individual is to a very large extent a matter of chance ; only when a large number of individuals have become affected does selection, dependent on its contribution to the fitness of the organism, become of importance. This is so even for dominant mutants; for recessive mutants selection remains very small so long as the mutant form is an inconsiderable fraction of the interbreeding group.
The distribution of the frequency ratio for different factors may be calculated from the condition that this distribution is stable, as is that of velocities in the Theory of Gases : in the absence of selection the distribution of log 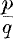 is given in fig. 1. Fig. 2 represents the case of steady decay in variance by the action of random survival (the Hagedoorn effect).
is given in fig. 1. Fig. 2 represents the case of steady decay in variance by the action of random survival (the Hagedoorn effect).
Fig. 3 shows the distribution in the somewhat artificial case of uniform genetic selection : this would be the distribution to be expected in the absence of dominance. Fig. 4 shows the asymmetrical distribution due to uniform genotypic selection with or without homogamy.
Under genotypic selection the dominance ratio for complete dominance comes to be exactly ⅓, in close agreement with the value obtained from human measurements.
The rate of mutation necessary to maintain the variance of the species may be calculated from these distributions. Very infrequent mutation will serve to counterbalance the effect of random survival; for equilibrium with selective action a much higher level is needed, though still mutation may be individually rare, especially in large populations.
It would seem that the supposition of genotypic selection balanced by occasional mutations fitted the facts deduced from the correlations of relatives in mankind.