Hostname: page-component-7dd5485656-g8tfn Total loading time: 0 Render date: 2025-10-29T22:20:23.488Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotically Corrected Person Fit Statistics for Multidimensional Constructs with Simple Structure and Mixed Item Types

Published online by Cambridge University Press:  01 January 2025

Maxwell Hong ,
Lizhen Lin  and
Ying Cheng
Maxwell Hong
Affiliation:
University of Notre Dame
Lizhen Lin
Affiliation:
University of Notre Dame
Ying Cheng*
Affiliation:
University of Notre Dame
*
Correspondence should be made to Ying Cheng, Department of Psychology, University of Notre Dame, 442 Corbett Family Hall, Notre Dame, IN46556, USA. Email: ycheng4@nd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Person fit statistics are frequently used to detect aberrant behavior when assuming an item response model generated the data. A common statistic, lz\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$l_z$$\end{document}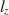, has been shown in previous studies to perform well under a myriad of conditions. However, it is well-known that lz\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$l_z$$\end{document} 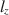does not follow a standard normal distribution when using an estimated latent trait. As a result, corrections of lz\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$l_z$$\end{document}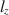, called lz∗\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$l_z^*$$\end{document}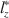, have been proposed in the literature for specific item response models. We propose a more general correction that is applicable to many types of data, namely survey or tests with multiple item types and underlying latent constructs, which subsumes previous work done by others. In addition, we provide corrections for multiple estimators of θ\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\theta $$\end{document}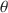, the latent trait, including MLE, MAP and WLE. We provide analytical derivations that justifies our proposed correction, as well as simulation studies to examine the performance of the proposed correction with finite test lengths. An applied example is also provided to demonstrate proof of concept. We conclude with recommendations for practitioners when the asymptotic correction works well under different conditions and also future directions.

Keywords

person fititem response theorylzAsymptoticsoutlier detectionmultidimensionalmixed item type

Information

Type
Theory and Methods
Information
Psychometrika , Volume 86 , Issue 2 , June 2021 , pp. 464 - 488
Copyright
Copyright © 2021 The Psychometric Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Ying Cheng is supported by the National Science Foundation Grant SES-1853166. The contribution of Lizhen Lin was supported by NSF grant DMS Career 1654579.

References

Albers, C. J., Meijer, R. R., Tendeiro, J. N. (2016). Derivation and applicability of asymptotic results for multiple subtests person-fit statistics. Applied Psychological Measurement, 40 (4) 274–288CrossRefGoogle ScholarPubMed
Baer, R. A., Ballenger, J, Berru, D, Wetter, M. W. (1997). Detection of random responding on the MMPI-A. Journal of Personality Assessment, 68 (1), 139–151CrossRefGoogle ScholarPubMed
Bedrick, E. J. (1997). Approximating the conditional distribution of person fit indexes for checking the rasch model. Psychometrika, 62, 191–199CrossRefGoogle Scholar
Berry, DTR, Wetter, M. W., Baer, R. A., Larsen, L, Clark, C, Monroe, K (1992). MMPI-2 random responding indices: Validation using a self-report methodology. Psychological Assessment, 4 (3), 340–345CrossRefGoogle Scholar
Bhattacharya, R, Lin, L, Victor, P A course in mathematical statistics and large sample theory, (2016). Berlin: SpringerCrossRefGoogle Scholar
Birnbaum, A. (1968). Some latent trait models and their use in inferring an examinees ability. In F. M. Lord & M. Novick (Eds.), Statistical theories of mental test scores (pp 397–472).Google Scholar
Casella, G. & Berger, R. (2001). Statistical Inference (No. 141). https://doi.org/10.1057/pt.2010.23CrossRefGoogle Scholar
Chalmers, R. P. (2012). mirt: A Multidimensional Item Response Theory Package for the R Environment. Journal of Statistical Software 48 (6). Retrieved from http://www.jstatsoft.org/v48/i06/ https://doi.org/10.18637/jss.v048.i06CrossRefGoogle Scholar
Cheng, Y, Yuan, K. H. (2010). The impact of fallible item parameter estimates on latent trait recovery. Psychometrika, 75, 280–291CrossRefGoogle ScholarPubMed
Conijn, J. M., Emons, W. H., Sijtsma, K (2014). Statistic lz-based person-fit methods for noncognitive multiscale measures. Applied Psychological Measurement, 38 (2), 122–136CrossRefGoogle Scholar
Conrad, K. J., Bezruczko, N, Chan, Y. F., Riley, B, Diamond, G, Dennis, M. L. (2010). Screening for atypical suicide risk with person fit statistics among people presenting to alcohol and other drug treatment. Drug and Alcohol Dependence, 106, 92–100CrossRefGoogle ScholarPubMed
Drasgow, F, Levine, M. V., McLaughlin, M. E. (1991). Appropriateness measurement for some multidimensional test batteries. Applied Psychological Measurement, 15 (2), 171–191CrossRefGoogle Scholar
Drasgow, F, Levine, M. V., Williams, E. A. (1985). Appropriateness measurement with polychotomous item response models and standardized indices. British Journal of Mathematical and Statistical Psychology, 38 (1), 67–86CrossRefGoogle Scholar
Goldberg, L. R. (1992). The development of markers for the big-five factor structure. Psychological Assessment, 4 (1), 26–42CrossRefGoogle Scholar
Goldberg, L. R., Kilkowski, J. M. (1985). The prediction of semantic consistency in self-descriptions. Characteristics of persons and of terms that affect the consistency of responses to synonym and antonym pairs. Journal of Personality and Social Psychology, 48 (1), 82–98CrossRefGoogle ScholarPubMed
Hong, M, Steedle, J. T., Cheng, Y (2019). Methods of detecting insufficient effort responding: Comparisons and practical recommendations. Educational and Psychological Measurement, 80 (2), 312–345CrossRefGoogle ScholarPubMed
Jeon, M, De Boeck, P (2019). Evaluation on types of invariance in studying extreme response bias with an IRTree approach. British Journal of Mathematical and Statistical Psychology, 72 (3), 517–537CrossRefGoogle ScholarPubMed
Karabatsos, G. (2003). Comparing the Aberrant Response Detection Performance of Thirty-Six Person-Fit Statistics., 16(4), 277–298. https://doi.org/10.1207/S15324818AME1604.CrossRefGoogle Scholar
Magis, D, Raîche, G, Béland, S (2012). A didactic presentation of snijders’s l z* index of person fit with emphasis on response model selection and ability estimation. Journal of Educational and Behavioral Statistics, 37 (1), 57–81CrossRefGoogle Scholar
Magnus, J, Neudecker, H Matrix differential calculus with applications in statistics and econometrics, (1988). New York: WileyGoogle Scholar
Meijer, R. R. (1996). Person-fit research: An introduction. Applied Measurement in Education, 9 (1), 1–2CrossRefGoogle Scholar
Meijer, R. R., Sijtsma, K (2001). Methodology review: Evaluating person fit. Applied Psychological Measurement, 25 (2), 107–135 Retrieved fromCrossRefGoogle Scholar
Molenaar, I. W., Hoijtink, H (1990). The many null distributions of person fit indices. Psychometrika, 55, 75–106CrossRefGoogle Scholar
Niessen, ASM, Meijer, R. R., Tendeiro, J. N. (2016). Detecting careless respondents in web-based questionnaires: Which method to use?. Journal of Research in Personality, 63, 1–11CrossRefGoogle Scholar
Reckase, M. (2009). Multidimensional Item Response Theory. https://doi.org/10.1007/978-0-387-89976-3.CrossRefGoogle Scholar
Reise, S. P. (1990). A comparison of item- and person-fit methods of assessing model-data fit in IRT. Applied Psychological Measurement, 14 (2), 127–137CrossRefGoogle Scholar
Rizopoulos, D. (2006). Itm: An R package for latent variable modeling and item response theory analyses. Journal of Statistical Software. https://doi.org/10.18637/jss.v017.i05.CrossRefGoogle Scholar
Rupp, A. A. (2013). A systematic review of the methodology for person fit research in item response theory: Lessons about generalizability of inferences from the design of simulation studies. Psychological Test and Assessment Modeling, 55 (1), 3–38Google Scholar
Samejima, F. (1969). Estimation of latent ability using a response pattern of graded scores (Vol. 35) (No. 1). https://doi.org/10.1007/BF02290599CrossRefGoogle Scholar
Shao, C, Li, J, Cheng, Y (2016). Detection of test speededness using change-point analysis. Psychometrika, 81 (4), 1118–1141CrossRefGoogle ScholarPubMed
Sinharay, S (2016). Asymptotically correct standardization of person-fit statistics beyond dichotomous items. Psychometrika, 81, 992–1013CrossRefGoogle ScholarPubMed
Sinharay, S (2016). Some remarks on applications of tests for detecting a change point to psychometric problems. Psychometrika, 82, 1–13Google ScholarPubMed
Snijders, TAB (2001). Asymptotic null distribution of person fit statistics with estimated person parameter. Psychometrika, 66 (3), 331–342CrossRefGoogle Scholar
Tendeiro, J. N. (2017). The lz(p)* person-fit statistic in an unfolding model context. Applied Psychological Measurement, 41 (1), 44–59CrossRefGoogle Scholar
Tendeiro, J. N., Meijer, R. R., Niessen, ASM (2016). Perfit: An R package for person-fit analysis in IRT. Journal of Statistical Software, 74 (5), 1–27CrossRefGoogle Scholar
von Davier, M, Molenaar, I. W. (2003). A person-fit index for polytomous rasch models, latent class models, and their mixture generalizations. Psychometrika, 68, 213–228CrossRefGoogle Scholar
Wang, C (2015). On latent trait estimation in multidimensional compensatory item response models. Psychometrika, 80, 428–449CrossRefGoogle ScholarPubMed
Warm, T. A. (1989). Weighted likelihood estimation of ability in item response theory. Psychometrika, 54, 427–450CrossRefGoogle Scholar
Yu, X, Cheng, Y (2019). A change-point analysis procedure based on weighted residuals to detect back random responding. Psychological Methods, 5, 658–674CrossRefGoogle Scholar
Zhang, J, Stout, W (1999). The theoretical detect index of dimensionality and its application to approximate simple structure. Psychometrika, 64, 213–249CrossRefGoogle Scholar
Supplementary material: File

Hong et al. supplementary material

Hong et al. supplementary material 1
Download Hong et al. supplementary material(File)
File 135.8 KB
Supplementary material: File

Hong et al. supplementary material

Hong et al. supplementary material 2
Download Hong et al. supplementary material(File)
File 429.5 KB
Supplementary material: File

Hong et al. supplementary material

Hong et al. supplementary material 3
Download Hong et al. supplementary material(File)
File 6.7 KB