An algorithm for assessing the correspondence of one or more attribute rating variables to a symmetric matrix of dissimilarities is presented. The algorithm is useful as an alternative to fitting property variables into a multidimensional scaling space. Rather than requiring a two step process of first deriving a multidimensional space and then fitting variables individually into the space, the algorithm directly assesses the correspondence of each variable to the symmetric matrix and permits a regression extension such that a set of variables can be considered simultaneously. The relation between the matrix and the variables is determined by evaluating pairs of pairs relations,\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\left( {\begin{array}{*{20}c} {\left( {\begin{array}{*{20}c} n\\ 2\\ \end{array} } \right)}\\ 2\\ \end{array} } \right)$$\end{document}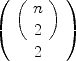. Though the algorithm requires only ordinal assumptions, the correspondence may be computed intervally also. Multiple ordinal regression is performed with the values derived from the matrix serving as the dependent variable and those derived from the attribute ratings serving as the independent variables. Standard multiple regression statistics for R-square, F, and t are calculated as well as measures of ordinal association between the vectors and the matrix.