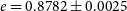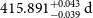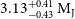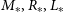1. Introduction
Since the first detection of a planet around a main-sequence star more than two decades ago (Mayor & Queloz Reference Mayor and Queloz1995), thousands of planetary systems have been found with astonishing diversity. The transit method has produced the most planet discoveries to date, mostly due to the overwhelming success of NASA’s Kepler mission (Borucki et al. Reference Borucki2010). Yet, a significant fraction of all planets has been found using the radial velocity (RV) technique, including many longer-period planets, for which ground-based Doppler searches have a natural advantage over short-lived space missions. The RV method also remains a valuable tool for the detection and characterisation of planets, as it yields the minimum mass of a planet and therefore nicely complements the transit method, which yields the size of a planet. Space-based transit searches such as Kepler (Borucki et al. Reference Borucki2010) or the Transiting Exoplanet Survey Satellite (TESS) (Ricker et al. Reference Ricker2015) also rely on ground-based RV follow-up observations to confirm their planet candidates, to determine their masses and hence densities, and to search for additional planets in these systems.
Slowly rotating solar-type and late-type stars are ideal targets for Doppler planet searches, as their spectra exhibit numerous sharp absorption lines. However, main-sequence stars more massive than about
![]() $1.5\,\textrm{M}_{{\odot}}$
are generally not suitable for precise RV measurements, due to their high temperatures and fast rotation rates (e.g. Galland et al. Reference Galland, Lagrange, Udry, Chelli, Pepe, Beuzit and Mayor2005). Consequently, the occurrence rate and distribution of planets as a function of stellar mass and metallicity for intermediate-mass stars are not as well established compared to planets around lower-mass stars (e.g. Johnson et al. Reference Johnson, Aller, Howard and Crepp2010; Reffert et al. Reference Reffert, Bergmann, Quirrenbach, Trifonov and Künstler2015; Jones et al. Reference Jones2016; Wittenmyer et al. Reference Wittenmyer, Jones, Zhao, Marshall, Butler, Tinney, Wang and Johnson2017a). In order to learn more about planetary systems around these intermediate-mass stars, several planet search programmes have been specifically targeting evolved stars of the same mass (often dubbed ‘retired A-stars’), as they do not suffer from these effects (e.g. Frink et al. Reference Frink, Mitchell, Quirrenbach, Fischer, Marcy and Butler2002; Sato et al. Reference Sato2003; Johnson et al. Reference Johnson2007; Niedzielski et al. Reference Niedzielski2007; Wittenmyer et al. Reference Wittenmyer, Endl, Wang, Johnson, Tinney and O’Toole2011; Jones et al. Reference Jones, Jenkins, Rojo and Melo2011).
$1.5\,\textrm{M}_{{\odot}}$
are generally not suitable for precise RV measurements, due to their high temperatures and fast rotation rates (e.g. Galland et al. Reference Galland, Lagrange, Udry, Chelli, Pepe, Beuzit and Mayor2005). Consequently, the occurrence rate and distribution of planets as a function of stellar mass and metallicity for intermediate-mass stars are not as well established compared to planets around lower-mass stars (e.g. Johnson et al. Reference Johnson, Aller, Howard and Crepp2010; Reffert et al. Reference Reffert, Bergmann, Quirrenbach, Trifonov and Künstler2015; Jones et al. Reference Jones2016; Wittenmyer et al. Reference Wittenmyer, Jones, Zhao, Marshall, Butler, Tinney, Wang and Johnson2017a). In order to learn more about planetary systems around these intermediate-mass stars, several planet search programmes have been specifically targeting evolved stars of the same mass (often dubbed ‘retired A-stars’), as they do not suffer from these effects (e.g. Frink et al. Reference Frink, Mitchell, Quirrenbach, Fischer, Marcy and Butler2002; Sato et al. Reference Sato2003; Johnson et al. Reference Johnson2007; Niedzielski et al. Reference Niedzielski2007; Wittenmyer et al. Reference Wittenmyer, Endl, Wang, Johnson, Tinney and O’Toole2011; Jones et al. Reference Jones, Jenkins, Rojo and Melo2011).
More than 100 planets have now been discovered orbiting giant stars, and except for the very few such systems discovered by Kepler (e.g. Quinn et al. Reference Quinn2015), all of these have been discovered via the RV technique. Notably, the first planet found to orbit a giant star,
![]() $\iota\textrm{Drab}$
, also happens to be on a very eccentric orbit with
$\iota\textrm{Drab}$
, also happens to be on a very eccentric orbit with
![]() $e = 0.71$
(Frink et al. Reference Frink, Mitchell, Quirrenbach, Fischer, Marcy and Butler2002; Kane et al. Reference Kane, Reffert, Henry, Fischer, Schwab, Clubb and Bergmann2010). More recently, planets on even more eccentric orbits were found around the K3III giant BD+48 740 (HIP 12684) with
$e = 0.71$
(Frink et al. Reference Frink, Mitchell, Quirrenbach, Fischer, Marcy and Butler2002; Kane et al. Reference Kane, Reffert, Henry, Fischer, Schwab, Clubb and Bergmann2010). More recently, planets on even more eccentric orbits were found around the K3III giant BD+48 740 (HIP 12684) with
![]() $e = 0.76$
(Adamów et al. Reference Adamów, Niedzielski, Villaver, Nowak and Wolszczan2012, Reference Adamów, Niedzielski, Kowalik, Villaver, Wolszczan, Maciejewski and Gromadzki2018), and around the K1III giant HD 76920 with
$e = 0.76$
(Adamów et al. Reference Adamów, Niedzielski, Villaver, Nowak and Wolszczan2012, Reference Adamów, Niedzielski, Kowalik, Villaver, Wolszczan, Maciejewski and Gromadzki2018), and around the K1III giant HD 76920 with
![]() $e = 0.86$
(Wittenmyer et al. Reference Wittenmyer2017b). The latter currently claims the title of being the most eccentric planet orbiting an evolved star and is the subject of this work.
$e = 0.86$
(Wittenmyer et al. Reference Wittenmyer2017b). The latter currently claims the title of being the most eccentric planet orbiting an evolved star and is the subject of this work.
Orbits with certain combinations of high eccentricities and longitudes of periastron produce RV curves that are essentially flat for the majority of the orbital period and only exhibit a narrow peak near periastron passage. However, because nearly all the information needed to determine the orbital parameters, including the RV semi-amplitude and thus the minimum mass of the planet, is contained in this short phase of the orbit, it is rather difficult from an observational point of view to obtain a good orbital solution for such systems. In their discovery paper, Wittenmyer et al. (Reference Wittenmyer2017b) pointed out that the periastron passage of HD 76920 b still needed better observational sampling in order to sufficiently constrain the orbital elements and minimum mass of the planet. We therefore planned a multi-site observing run and successfully filled in the gap in the phase coverage near periastron passage with RV measurements.
In this paper, we present the results of our observational campaign. We describe our multi-site observations and RV measurements in Sections 2 and 3, respectively. We then present newly computed stellar parameters in Section 4. In Section 5, we describe the orbit-fitting process and present our improved orbital solution. We also present an upper mass limit for HD 76920 b in Section 6, followed by a discussion of our findings in Section 7.
2. Observations
Between January and March 2018, we acquired 63 observations of HD 76920 using four different instruments. Firstly, 39 were taken at the University of Canterbury Mt John Observatory (UCMJO) in Lake Tekapo, New Zealand, using the 1-m McLellan telescope in conjunction with the HERCULES spectrograph (Hearnshaw et al. Reference Hearnshaw, Barnes, Kershaw, Frost, Graham, Ritchie and Nankivell2002). Of these, 19 were taken with a 100-
![]() $\mu$
m core diameter fibre (‘fibre 1’), corresponding to a resolving power of
$\mu$
m core diameter fibre (‘fibre 1’), corresponding to a resolving power of
![]() $R \sim 41\,000$
, and another 20 were taken with a different 100-
$R \sim 41\,000$
, and another 20 were taken with a different 100-
![]() $\mu$
m core diameter fibre with a 50-
$\mu$
m core diameter fibre with a 50-
![]() $\mu$
m micro-slit attached to its end (‘fibre 3’), corresponding to a resolving power of
$\mu$
m micro-slit attached to its end (‘fibre 3’), corresponding to a resolving power of
![]() $R \sim 70\,000$
. These observations are referred to below as MJ1 and MJ3, respectively.
$R \sim 70\,000$
. These observations are referred to below as MJ1 and MJ3, respectively.
A further eight observations were obtained with the CHIRON spectrograph (Tokovinin et al. Reference Tokovinin, Fischer, Bonati, Giguere, Moore, Schwab, Spronck and Szymkowiak2013) attached to the 1.5-m telescope at Cerro Tololo Inter-American Observatory (CTIO) in Chile. These new spectra were obtained using the ‘slit mode’, which delivers a resolving power of
![]() $R \sim 95\,000$
and a total system efficiency of
$R \sim 95\,000$
and a total system efficiency of
![]() $\sim$
2%. Both HERCULES and CHIRON employ the iodine-cell technique (e.g. Butler et al. Reference Butler, Marcy, Williams, McCarthy, Dosanjh and Vogt1996; Endl, Kürster, & Els Reference Endl, Kürster and Els2000), that is, during the observations a gas absorption cell containing molecular iodine (kept at a constant temperature of
$\sim$
2%. Both HERCULES and CHIRON employ the iodine-cell technique (e.g. Butler et al. Reference Butler, Marcy, Williams, McCarthy, Dosanjh and Vogt1996; Endl, Kürster, & Els Reference Endl, Kürster and Els2000), that is, during the observations a gas absorption cell containing molecular iodine (kept at a constant temperature of
![]() $50.0 \pm 0.1\ ^\circ\textrm{C}$
) is placed in the light path for wavelength calibration and for modelling of the instrumental profile.
$50.0 \pm 0.1\ ^\circ\textrm{C}$
) is placed in the light path for wavelength calibration and for modelling of the instrumental profile.
Finally, we also obtained 15 spectra using FIDEOS (Vanzi et al. Reference Vanzi2018) and one new spectrum using FEROS (Kaufer et al. Reference Kaufer, Stahl, Tubbesing, Nørregaard, Avila, Francois, Pasquini and Pizzella1999). These two high-resolution (
![]() $R \sim 43\,000$
and
$R \sim 43\,000$
and
![]() $R \sim 48\,000$
, respectively) spectrographs are located at La Silla Observatory in Chile and are attached to the ESO 1-m and 2.2-m telescopes, respectively. In addition, they are both fed by multiple optical fibres, allowing a simultaneous ThAr wavelength calibration during the science exposure for precision RVs.
$R \sim 48\,000$
, respectively) spectrographs are located at La Silla Observatory in Chile and are attached to the ESO 1-m and 2.2-m telescopes, respectively. In addition, they are both fed by multiple optical fibres, allowing a simultaneous ThAr wavelength calibration during the science exposure for precision RVs.
3. Radial Velocities
Raw-reduction of the HERCULES observations was performed with the latest version (v5.2.9) of the HERCULES Reduction Software Package (HRSP; Skuljan Reference Skuljan2004) and the pipeline described in Bergmann (Reference Bergmann2015). From the reduced spectra, we derived RVs using our version of the AUSTRAL Doppler code described by Endl et al. (Reference Endl, Kürster and Els2000). We used a high S/N, iodine-free spectrum of the K1III star
![]() $\nu$
Octantis as a template (Ramm et al. Reference Ramm2016). While this set-up has proven to deliver long-term RV precisions of about
$\nu$
Octantis as a template (Ramm et al. Reference Ramm2016). While this set-up has proven to deliver long-term RV precisions of about
![]() $4.5\,\text{ms}^{-1}$
(with short-term precision of
$4.5\,\text{ms}^{-1}$
(with short-term precision of
![]() $\lesssim 3\,\text{ms}^{-1}$
) for bright solar-type stars (Bergmann Reference Bergmann2015; Bergmann et al. Reference Bergmann2015), the fainter magnitude of HD 76920
$\lesssim 3\,\text{ms}^{-1}$
) for bright solar-type stars (Bergmann Reference Bergmann2015; Bergmann et al. Reference Bergmann2015), the fainter magnitude of HD 76920
![]() $(V=7.8)$
combined with poor seeing conditions for a majority of the nights resulted in single-shot uncertainties of typically
$(V=7.8)$
combined with poor seeing conditions for a majority of the nights resulted in single-shot uncertainties of typically
![]() $14.5\,\text{ms}^{-1}$
for the higher-resolution fibre, and
$14.5\,\text{ms}^{-1}$
for the higher-resolution fibre, and
![]() $16.5\,\text{ms}^{-1}$
for the lower-resolution fibre, which was preferred if the seeing was worse than about 3 arcsec.
$16.5\,\text{ms}^{-1}$
for the lower-resolution fibre, which was preferred if the seeing was worse than about 3 arcsec.
The CHIRON spectra were reduced with the observatory customised pipeline, which provides order by order extracted and wavelength-calibrated spectra for CHIRON users. The RVs were computed following the method described in Jones et al. (Reference Jones, Brahm, Wittenmyer, Drass, Jenkins, Melo, Vos and Rojo2017). We note that the new CHIRON velocities have larger uncertainties compared to those in Wittenmyer et al. (Reference Wittenmyer2017b), as the new spectra were obtained in ‘slit mode’, rather than in ‘fibre-slicer mode’ (
![]() $R \sim 80\,000$
). As a consequence, although the new data were taken at a slightly higher resolving power, the efficiency is drastically reduced (by a factor of
$R \sim 80\,000$
). As a consequence, although the new data were taken at a slightly higher resolving power, the efficiency is drastically reduced (by a factor of
![]() $\sim 3$
), when compared to ‘fibre-slicer mode’, directly translating into lower S/N data, and thus leading to larger RV uncertainties. We have also recomputed the ‘fibre-slicer mode’ CHIRON RVs published in Wittenmyer et al. (Reference Wittenmyer2017b), including the new data, which resulted in small but non-negligible changes.
$\sim 3$
), when compared to ‘fibre-slicer mode’, directly translating into lower S/N data, and thus leading to larger RV uncertainties. We have also recomputed the ‘fibre-slicer mode’ CHIRON RVs published in Wittenmyer et al. (Reference Wittenmyer2017b), including the new data, which resulted in small but non-negligible changes.
Finally, both FIDEOS and FEROS data were processed with the CERES code (Brahm, Jordán, & Espinoza Reference Brahm, Jordán and Espinoza2017a), including a re-reduction of the eight FEROS observations published in Wittenmyer et al. (Reference Wittenmyer2017b). CERES performs a standard échelle spectra reduction including bias subtraction, order tracing, optimal extraction, and wavelength calibration. The RVs for the two instruments were obtained from the cross-correlation function (CCF; Tonry & Davis Reference Tonry and Davis1979). In the case of FIDEOS, the template used for the CCF corresponds to a numerical binary mask as explained in Brahm et al. (Reference Brahm, Jordán and Espinoza2017a), while in the case of FEROS data we use a high S/N template, which is built by stacking all of the individual observed spectra (Jones et al. Reference Jones, Brahm, Wittenmyer, Drass, Jenkins, Melo, Vos and Rojo2017). The final velocities are obtained after correcting for the night drift (from the simultaneous calibration fibre) and barycentric velocity. Note that the newly computed FEROS RVs are superior to those presented in Wittenmyer et al. (Reference Wittenmyer2017b), where a much lower S/N template was used. All RVs used in this work and their corresponding uncertainties are summarised in Table A.1.
4. Stellar parameters
4.1. Spectroscopy
We computed the atmospheric parameters of HD 76920 using the ZASPE code (Brahm et al. Reference Brahm, Jordán, Hartman and Bakos2017b). For this purpose, we first combined all of the individual FEROS spectra. The co-added master spectrum is then compared to the ATLAS9 grid of stellar models (Castelli & Kurucz Reference Castelli and Kurucz2004), in carefully selected regions that are more sensitive to changes in the atmospheric parameters. This procedure is performed iteratively until we obtain the effective temperature (
![]() $T_{{\rm eff}}$
), the surface gravity (
$T_{{\rm eff}}$
), the surface gravity (
![]() $\log{g}$
), the stellar metallicity (
$\log{g}$
), the stellar metallicity (
![]() ${\rm [Fe/H]}$
), and the projected rotational velocity (
${\rm [Fe/H]}$
), and the projected rotational velocity (
![]() $v \sin{i}$
). Using these derived parameters, we then computed the corresponding spectral energy distribution (SED). For this, we used the BT-Settl-CIFIST models (Baraffe et al. Reference Baraffe, Homeier, Allard and Chabrier2015). From the SED, we computed synthetic magnitudes and we compared them to the observed ones, which are listed in Table 1. During this process, the stellar radius (
$v \sin{i}$
). Using these derived parameters, we then computed the corresponding spectral energy distribution (SED). For this, we used the BT-Settl-CIFIST models (Baraffe et al. Reference Baraffe, Homeier, Allard and Chabrier2015). From the SED, we computed synthetic magnitudes and we compared them to the observed ones, which are listed in Table 1. During this process, the stellar radius (
![]() $R_{\star}$
) and the visual extinction (
$R_{\star}$
) and the visual extinction (
![]() $A_V$
) are derived, and thus the stellar luminosity (
$A_V$
) are derived, and thus the stellar luminosity (
![]() $L_{\star}$
).
$L_{\star}$
).
Table 1. Stellar parameters of HD 76920

Finally, to obtain the stellar mass and evolutionary status of HD 76920, we compared the derived atmospheric parameters to the PARSEC evolutionary models (Bressan et al. Reference Bressan, Marigo, Girardi, Salasnich, Dal Cero, Rubele and Nanni2012). We found that HD 76920 has a mass of
![]() $M_{\star}\,= 1.0 \pm 0.2\,\textrm{M}_{\odot}$
, and that it is ascending the red-giant branch (RGB) phase. Figure 1 shows the position of HD 76920 in the HR diagram. For comparison, two different PARSEC isomass evolutionary tracks are overplotted. As can be seen, HD 76920 is located midway on its RGB ascent and is reaching the luminosity bump region. We note that no horizontal branch track (i.e. Helium burning core) crosses its position in the HR diagram. All derived atmospheric and physical parameters are listed in Table 1.
$M_{\star}\,= 1.0 \pm 0.2\,\textrm{M}_{\odot}$
, and that it is ascending the red-giant branch (RGB) phase. Figure 1 shows the position of HD 76920 in the HR diagram. For comparison, two different PARSEC isomass evolutionary tracks are overplotted. As can be seen, HD 76920 is located midway on its RGB ascent and is reaching the luminosity bump region. We note that no horizontal branch track (i.e. Helium burning core) crosses its position in the HR diagram. All derived atmospheric and physical parameters are listed in Table 1.
4.2. Asteroseismology
As an independent method, we used asteroseismology to derive the stellar mass from the TESS (Ricker et al. Reference Ricker2015) photometric data. The TESS mission observed HD 76920 in the long-cadence mode (30 min) in sectors 9, 10, and 11, adding up to a total of 3 492 individual photometric measurements. To obtain the light curve, we used the Python tool tesseract (Rojas et al., in preparation) using the autoap aperture. We removed the most deviant outliers using the clean.py tool and normalised each sector data independently by its median value. We also detrended the light curve using a linear fit, achieving a dispersion of 494.6 ppm. Figure 2 shows the resulting normalised TESS photometry of HD 76920. Then, we ran a generalised Lomb–Scargle (GLS, Zechmeister & Kürster Reference Zechmeister and Kürster2009) routine to obtain the power spectral density and search for asteroseismic power excess in order to measure
![]() $\nu_{\rm max}$
and
$\nu_{\rm max}$
and
![]() $\Delta\nu$
. We also corrected the background using a very wide Gaussian profile kernel. After this correction, we followed the method presented in Jones et al. (Reference Jones2018), which consists of convolving a Gaussian profile with a
$\Delta\nu$
. We also corrected the background using a very wide Gaussian profile kernel. After this correction, we followed the method presented in Jones et al. (Reference Jones2018), which consists of convolving a Gaussian profile with a
![]() $\sigma= 12\,\mu {\rm Hz}$
kernel around the power excess in order to find the peak that corresponds to
$\sigma= 12\,\mu {\rm Hz}$
kernel around the power excess in order to find the peak that corresponds to
![]() $\nu_{\rm max}$
. To obtain
$\nu_{\rm max}$
. To obtain
![]() $\Delta\nu$
, we convolved a Gaussian profile with a
$\Delta\nu$
, we convolved a Gaussian profile with a
![]() $\sigma= 1\,\mu {\rm Hz}$
kernel and we ran an autocorrelation routine. Using this procedure, we obtained
$\sigma= 1\,\mu {\rm Hz}$
kernel and we ran an autocorrelation routine. Using this procedure, we obtained
![]() $\nu_{\rm max} = 54.01 \pm 2.75\,\mu {\rm Hz}$
and
$\nu_{\rm max} = 54.01 \pm 2.75\,\mu {\rm Hz}$
and
![]() $\Delta\nu = 5.64 \pm 0.24\,\mu {\rm Hz}$
. From these values, and following the scaling relations presented in Kjeldsen & Bedding (Reference Kjeldsen and Bedding1995), we obtained a mass of
$\Delta\nu = 5.64 \pm 0.24\,\mu {\rm Hz}$
. From these values, and following the scaling relations presented in Kjeldsen & Bedding (Reference Kjeldsen and Bedding1995), we obtained a mass of
![]() $M_{\star}\,= 1.29 \pm 0.17\,\textrm{M}_{\odot}$
and a radius
$M_{\star}\,= 1.29 \pm 0.17\,\textrm{M}_{\odot}$
and a radius
![]() $R_{\star}\,= 9.07 \pm 0.63\,\textrm{R}_{\odot}$
. The corresponding 1-
$R_{\star}\,= 9.07 \pm 0.63\,\textrm{R}_{\odot}$
. The corresponding 1-
![]() $\sigma$
error bars were obtained from a bootstrap analysis. The asteroseismic mass and radius are in reasonably good agreement with the spectroscopic values.
$\sigma$
error bars were obtained from a bootstrap analysis. The asteroseismic mass and radius are in reasonably good agreement with the spectroscopic values.

Figure 1. HR diagram showing the position of HD 76920. The solid and dashed lines correspond to PARSEC models with
![]() $M_{\star} \, = 1.0\, \textrm{M}_{\odot}$
, for
$M_{\star} \, = 1.0\, \textrm{M}_{\odot}$
, for
![]() ${\rm [Fe/H]} \,= -0.24$
and
${\rm [Fe/H]} \,= -0.24$
and
![]() $-0.14\,\textrm{dex}$
, respectively.
$-0.14\,\textrm{dex}$
, respectively.

Figure 2. Normalised and detrended TESS photometry of HD 76920.
Table 2. Best-fit orbital solution and derived quantities for HD 76920 b

![]() $^\dagger$
A negative value for the square of the instrumental jitter indicates that the formal internal errors are overestimated and that the fitted instrumental jitter needs to be subtracted in quadrature in Equation (1).
$^\dagger$
A negative value for the square of the instrumental jitter indicates that the formal internal errors are overestimated and that the fitted instrumental jitter needs to be subtracted in quadrature in Equation (1).
![]() $^\dagger$
A negative value for the square of the instrumental jitter indicates that the formal internal errors are overestimated and that the fitted instrumental jitter needs to be subtracted in quadrature in Equation (1).
$^\dagger$
A negative value for the square of the instrumental jitter indicates that the formal internal errors are overestimated and that the fitted instrumental jitter needs to be subtracted in quadrature in Equation (1).
5. Orbital solution
Wittenmyer et al. (Reference Wittenmyer2017b) published 37 RVs of HD 76920 obtained with three different spectrographs. Of these, 17 were taken with UCLES (Diego et al. Reference Diego, Charalambous, Fish and Walker1990) installed at the 3.9-m Anglo-Australian Telescope (AAT), 12 were taken with CHIRON at the 1.5-m telescope at CTIO, and 8 were taken with FEROS installed at the 2.2-m telescope at La Silla.
We combined our 63 new RV measurements with the 12 re-reduced CHIRON RVs, the 8 newly reduced FEROS RVs, and the remaining 17 UCLES RVs from Wittenmyer et al. (Reference Wittenmyer2017b) and fitted a single Keplerian model to the combined dataset consisting of a total of 100 RVs. We used the emcee 2.2.1 package (Foreman-Mackey et al. Reference Foreman-Mackey, Hogg, Lang and Goodman2013), a pure-Python implementation of the Affine-Invariant Markov chain Monte Carlo (MCMC) Ensemble sampler (Goodman & Weare Reference Goodman and Weare2010), to obtain the best-fit parameters. We used logarithmic priors for P,
![]() $T_0$
, and K, that is, we fit in terms of
$T_0$
, and K, that is, we fit in terms of
![]() $\log{P}$
,
$\log{P}$
,
![]() $\log{T_0}$
, and
$\log{T_0}$
, and
![]() $\log{K}$
, and used uniform priors for all other parameters.Footnote a We deployed 32 walkers and ran 3 000 steps for the first burn-in phase until the walkers had explored the parameter space sufficiently. At the end of the first burn-in phase, walkers are re-sampled around the most probable position to reject bad samplings. We then continued with a second burn-in phase for another 3 000 steps. All parameters have clearly converged after the second burn-in phase. Finally, we collected the samples from the last 10 000 steps to calculate the maximum likelihood set of parameters and estimate the uncertainties. The random zero-point offsets between the different instrumental set-ups were included as additional free parameters in the fitting process. For consistency with the work of Wittenmyer et al. (Reference Wittenmyer2017b), we also added
$\log{K}$
, and used uniform priors for all other parameters.Footnote a We deployed 32 walkers and ran 3 000 steps for the first burn-in phase until the walkers had explored the parameter space sufficiently. At the end of the first burn-in phase, walkers are re-sampled around the most probable position to reject bad samplings. We then continued with a second burn-in phase for another 3 000 steps. All parameters have clearly converged after the second burn-in phase. Finally, we collected the samples from the last 10 000 steps to calculate the maximum likelihood set of parameters and estimate the uncertainties. The random zero-point offsets between the different instrumental set-ups were included as additional free parameters in the fitting process. For consistency with the work of Wittenmyer et al. (Reference Wittenmyer2017b), we also added
![]() $7\,\text{ms}^{-1}$
of stellar jitter in quadrature to the error bars, as is appropriate for this type of star (Kjeldsen & Bedding Reference Kjeldsen and Bedding1995), and as explained in Wittenmyer et al. (Reference Wittenmyer2016). Finally, following the method described by Baluev (Reference Baluev2009), we also included an ‘instrumental jitter’ term in the fitting, which acts to ensure that the uncertainties from the different instrumental set-ups do not introduce a spurious weighting of the RV points. This can happen if the internal error bars are overestimated or underestimated for some instruments. In our case, the internal error bars of the AAT and FIDEOS data seem to be substantially underestimated as indicated by the large positive values of the square of their instrumental jitter terms in Table 2, whereas the MJ1 error bars seem to be somewhat overestimated as indicated by the negative value of the square of their instrumental jitter term in Table 2. The total uncertainty for each RV measurement is thus given by:
$7\,\text{ms}^{-1}$
of stellar jitter in quadrature to the error bars, as is appropriate for this type of star (Kjeldsen & Bedding Reference Kjeldsen and Bedding1995), and as explained in Wittenmyer et al. (Reference Wittenmyer2016). Finally, following the method described by Baluev (Reference Baluev2009), we also included an ‘instrumental jitter’ term in the fitting, which acts to ensure that the uncertainties from the different instrumental set-ups do not introduce a spurious weighting of the RV points. This can happen if the internal error bars are overestimated or underestimated for some instruments. In our case, the internal error bars of the AAT and FIDEOS data seem to be substantially underestimated as indicated by the large positive values of the square of their instrumental jitter terms in Table 2, whereas the MJ1 error bars seem to be somewhat overestimated as indicated by the negative value of the square of their instrumental jitter term in Table 2. The total uncertainty for each RV measurement is thus given by:
where
![]() $\sigma_{\textrm{int}}$
is the internal error as reported in Table A.1,
$\sigma_{\textrm{int}}$
is the internal error as reported in Table A.1,
![]() $\sigma_{\textrm{st.jitt.}}$
is the stellar jitter, and
$\sigma_{\textrm{st.jitt.}}$
is the stellar jitter, and
![]() $\sigma_{\textrm{inst.jitt.}}$
is the instrumental jitter. The RMS around the combined fit is
$\sigma_{\textrm{inst.jitt.}}$
is the instrumental jitter. The RMS around the combined fit is
![]() $14.1\,\text{ms}^{-1}$
, and the weighted RMS is
$14.1\,\text{ms}^{-1}$
, and the weighted RMS is
![]() $11.7\,\text{ms}^{-1}$
. Figure 3 shows all data points together with our best-fit orbital solution, Figure 4 shows a phase-folded version of that plot, and Figure 5 shows a close-up view of the RV peak near periastron passage (again phase-folded with the orbital period). A corner plot of the posterior probability distributions of the parameters, generated from the last 10 000 steps and demonstrating that all parameters are well constrained, is shown in Figure A.1 in the appendix.
$11.7\,\text{ms}^{-1}$
. Figure 3 shows all data points together with our best-fit orbital solution, Figure 4 shows a phase-folded version of that plot, and Figure 5 shows a close-up view of the RV peak near periastron passage (again phase-folded with the orbital period). A corner plot of the posterior probability distributions of the parameters, generated from the last 10 000 steps and demonstrating that all parameters are well constrained, is shown in Figure A.1 in the appendix.

Figure 3. All available RV data together with our best-fit Keplerian orbital solution for HD 76920 b. The black points are the AAT data from Wittenmyer et al. (Reference Wittenmyer2017b), the red points are the re-reduced CHIRON and FEROS data, and the blue points are the CHIRON, FEROS, FIDEOS, and HERCULES data taken for this work. Error bars represent the total uncertainty given by Equation (1). The RMS about this fit is
![]() $14.1\,\text{ms}^{-1}$
.
$14.1\,\text{ms}^{-1}$
.

Figure 4. Same as Figure 3, but phase-folded on the orbital period. Data from different instruments/set-ups are shown in different colours: AAT— black, CHIRON— cyan, FEROS— green, FIDEOS— orange, MJ1— red, MJ3— blue.

Figure 5. Close-up view of the RV peak near periastron passage. Colour-coding is the same as in Figure 4.
In order to confirm our MCMC results, we also fitted a single Keplerian orbit using the IDL package RVLIN (Wright & Howard Reference Wright and Howard2009). Here, we estimated the corresponding uncertainties in the orbital parameters via the bootstrapping algorithm from the BOOTTRAN package (Wang et al. 2012) using 100 000 steps. Because the extra instrumental jitter term cannot be set as a free parameter, we used the modified error bars given by Equation (1) as input to the fitting. While the uncertainty estimates derived with the bootstrapping method are somewhat larger, the two sets of best-fit parameters are in good agreement. Both best-fit single-Keplerian orbital solutions and the corresponding parameter uncertainty estimates are summarised in Table 2.
For the calculation of the semi-major axis and minimum mass of the planet, we give the values using both the spectroscopic stellar mass of
![]() $M_* = 1.0 \pm 0.2\,\textrm{M}_{\odot}$
(see Section 4.1), as well as the asteroseismic mass of
$M_* = 1.0 \pm 0.2\,\textrm{M}_{\odot}$
(see Section 4.1), as well as the asteroseismic mass of
![]() $1.29 \pm 0.17\,\textrm{M}_{\odot}$
(see Section 4.2). For the rest of this work, we will adopt the spectroscopically derived stellar mass and radius unless otherwise mentioned. Note that the uncertainty in the semi-major axis is completely dominated by the uncertainty in stellar mass, which to a lesser extent also affects the uncertainty in the minimum mass of the planet. Note that Wittenmyer et al. (Reference Wittenmyer2017b) used a mass of
$1.29 \pm 0.17\,\textrm{M}_{\odot}$
(see Section 4.2). For the rest of this work, we will adopt the spectroscopically derived stellar mass and radius unless otherwise mentioned. Note that the uncertainty in the semi-major axis is completely dominated by the uncertainty in stellar mass, which to a lesser extent also affects the uncertainty in the minimum mass of the planet. Note that Wittenmyer et al. (Reference Wittenmyer2017b) used a mass of
![]() $1.17 \pm 0.20\,\textrm{M}_{\odot}$
, which has a comparable relative error. This leads us to believe that their uncertainty estimate for
$1.17 \pm 0.20\,\textrm{M}_{\odot}$
, which has a comparable relative error. This leads us to believe that their uncertainty estimate for
![]() $m_{\textrm{P}}\,\sin i$
is underestimated and may not include the uncertainty in stellar mass.
$m_{\textrm{P}}\,\sin i$
is underestimated and may not include the uncertainty in stellar mass.
We also searched for periodic signals in the residuals (Figure 6) but did not find any significant power, as can be seen in the GLS periodogram shown in Figure 7.

Figure 7. GLS periodogram of the residuals from the best-fit orbital solution shown in Figure 6.
6. Companion Upper Mass Limit
6.1. Astrometric limit
To better constrain the mass of HD 76920 b, we applied the method presented in Jones et al. (Reference Jones, Brahm, Wittenmyer, Drass, Jenkins, Melo, Vos and Rojo2017) (which is based on Sahlmann et al. Reference Sahlmann2011), to derive the orbital inclination angle, and thus its dynamical mass. To do this, we combined the orbital elements derived here with the Hipparcos Intermediate Astrometric Data (HIAD) obtained in van Leeuwen (Reference van Leeuwen2007b). This dataset comprises a total of 106 one-dimensional abscissa measurements (see Section 2.2.2 in van Leeuwen 2007a), with a mean uncertainty of
![]() $1.9\,\textrm{mas}$
. For this purpose, we first attempted to directly obtain a full 7-parameter orbital solution, solving for the inclination angle i and the longitude of the ascending node
$1.9\,\textrm{mas}$
. For this purpose, we first attempted to directly obtain a full 7-parameter orbital solution, solving for the inclination angle i and the longitude of the ascending node
![]() $\Omega$
, while keeping fixed the five parameters derived from the Keplerian fit (P, e,
$\Omega$
, while keeping fixed the five parameters derived from the Keplerian fit (P, e,
![]() $\omega$
, K,
$\omega$
, K,
![]() $T_0$
), and correcting for the five single-star parameters solution (
$T_0$
), and correcting for the five single-star parameters solution (
![]() $\alpha^{\star}$
,
$\alpha^{\star}$
,
![]() $\delta$
,
$\delta$
,
![]() $\mu_{\alpha^{\star}}$
,
$\mu_{\alpha^{\star}}$
,
![]() $\mu_{\delta}$
,
$\mu_{\delta}$
,
![]() $\varpi$
). Unfortunately, due to the small astrometric signal, in part due to the relatively small parallax (correspondingly large distance) of HD 76920 (
$\varpi$
). Unfortunately, due to the small astrometric signal, in part due to the relatively small parallax (correspondingly large distance) of HD 76920 (
![]() $\varpi = 5.41 \pm 0.03$
mas; Gaia Collaboration et al. 2018), and also because of the high eccentricity (a significant astrometric perturbation occurs only close to periastron passage), no significant solution was obtained. This basically means that the orbital solution does not improve the standard Hipparcos 5-parameter solution. However, we could still compute an upper mass limit for the companion by injecting synthetic astrometric signals induced by the companion at different inclination angles (the smaller the value of i, the larger the astrometric signal). Briefly, we generated synthetic datasets, keeping fixed the time of the individual epochs of the HIAD and computing the expected astrometric signal induced by the companion by propagating the orbital solution to the epoch of the HIAD observations. This was performed at decreasing inclination angles, while randomly selecting
$\varpi = 5.41 \pm 0.03$
mas; Gaia Collaboration et al. 2018), and also because of the high eccentricity (a significant astrometric perturbation occurs only close to periastron passage), no significant solution was obtained. This basically means that the orbital solution does not improve the standard Hipparcos 5-parameter solution. However, we could still compute an upper mass limit for the companion by injecting synthetic astrometric signals induced by the companion at different inclination angles (the smaller the value of i, the larger the astrometric signal). Briefly, we generated synthetic datasets, keeping fixed the time of the individual epochs of the HIAD and computing the expected astrometric signal induced by the companion by propagating the orbital solution to the epoch of the HIAD observations. This was performed at decreasing inclination angles, while randomly selecting
![]() $\Omega$
in the range 0–
$\Omega$
in the range 0–
![]() $360^{\circ}$
. For each synthetic dataset, we added Gaussian-distributed uncertainties with standard deviation equal to the median abscissa error (
$360^{\circ}$
. For each synthetic dataset, we added Gaussian-distributed uncertainties with standard deviation equal to the median abscissa error (
![]() $1.9\,\textrm{mas}$
in this case). Then, we solved the 7-parameter solution to the synthetic datasets until we recovered the simulated (i,
$1.9\,\textrm{mas}$
in this case). Then, we solved the 7-parameter solution to the synthetic datasets until we recovered the simulated (i,
![]() $\Omega$
) pairs. Figure 8 shows the resulting (
$\Omega$
) pairs. Figure 8 shows the resulting (
![]() $i, \Omega$
) values for a total of 100 synthetic datasets, with an input inclination angle of
$i, \Omega$
) values for a total of 100 synthetic datasets, with an input inclination angle of
![]() $0.6^{\circ}$
, which corresponds to an angular semi-major axis of
$0.6^{\circ}$
, which corresponds to an angular semi-major axis of
![]() $1.9\,\textrm{mas}$
. As can be seen, for such a low i-value, we are capable of recovering most of the synthetic signals with relatively good accuracy. We obtained a median of
$1.9\,\textrm{mas}$
. As can be seen, for such a low i-value, we are capable of recovering most of the synthetic signals with relatively good accuracy. We obtained a median of
![]() $i = 0.54^{\circ}$
with a standard deviation of
$i = 0.54^{\circ}$
with a standard deviation of
![]() $0.37^{\circ}$
. We also note that only in eight cases we obtained a reduced
$0.37^{\circ}$
. We also note that only in eight cases we obtained a reduced
![]() $\chi^2$
-value larger than for the Hipparcos 5-parameter solution. For comparison, we repeated this analysis for an inclination angle of
$\chi^2$
-value larger than for the Hipparcos 5-parameter solution. For comparison, we repeated this analysis for an inclination angle of
![]() $0.8^{\circ}$
(corresponding to
$0.8^{\circ}$
(corresponding to
![]() $a = 1.5\,\textrm{mas}$
). We obtained a standard deviation of
$a = 1.5\,\textrm{mas}$
). We obtained a standard deviation of
![]() $0.73^{\circ}$
, and already in 17% of the simulations the reduced
$0.73^{\circ}$
, and already in 17% of the simulations the reduced
![]() $\chi^2$
of the synthetic solution is larger than for the Hipparcos 5-parameter solution, showing how rapidly the detectability drops with the astrometric amplitude. In fact, only at inclination values of
$\chi^2$
of the synthetic solution is larger than for the Hipparcos 5-parameter solution, showing how rapidly the detectability drops with the astrometric amplitude. In fact, only at inclination values of
![]() $i < 0.3^{\circ}$
we obtained reduced
$i < 0.3^{\circ}$
we obtained reduced
![]() $\chi^2$
-values of the synthetic solution lower than for the Hipparcos 5-parameter model in
$\chi^2$
-values of the synthetic solution lower than for the Hipparcos 5-parameter model in
![]() $>99\%$
of the cases. Based on this analysis, we might adopt a lower i-value of
$>99\%$
of the cases. Based on this analysis, we might adopt a lower i-value of
![]() $\sim 0.4$
–
$\sim 0.4$
–
![]() $0.6^{\circ}$
, which corresponds to an upper mass limit for HD 76920 b of
$0.6^{\circ}$
, which corresponds to an upper mass limit for HD 76920 b of
![]() $\sim 0.4$
–
$\sim 0.4$
–
![]() $0.6\,\textrm{M}_\odot$
. Finally, we note that by considering an orbital inclination angle of
$0.6\,\textrm{M}_\odot$
. Finally, we note that by considering an orbital inclination angle of
![]() $90^{\circ}$
(edge-on orbit), the astrometric semi-major axis is only
$90^{\circ}$
(edge-on orbit), the astrometric semi-major axis is only
![]() $20\,\mu\textrm{as}$
, which is comparable to the Gaia precision (Gaia Collaboration et al. 2016). It would thus be very challenging to significantly detect such a small signal even in the Gaia data.
$20\,\mu\textrm{as}$
, which is comparable to the Gaia precision (Gaia Collaboration et al. 2016). It would thus be very challenging to significantly detect such a small signal even in the Gaia data.

Figure 8.
Upper panel: Inclination angles recovered from the 100 simulations, as a function of synthetic
![]() $\Omega$
values. The horizontal dashed line corresponds to the input value of i = 0.6 deg. Lower panel: same as the upper panel, but this time for the
$\Omega$
values. The horizontal dashed line corresponds to the input value of i = 0.6 deg. Lower panel: same as the upper panel, but this time for the
![]() $\Omega$
values. The dashed line corresponds to the one-to-one correlation.
$\Omega$
values. The dashed line corresponds to the one-to-one correlation.
6.2. Geometric limit
The method described in Section 6.1 does not place very stringent upper limits on the mass of the planet. It is therefore interesting to note that we can put a much lower limit on the planet’s mass from simple geometry. While the inclination is unknown, we know that there is no preferred orientation of the orbital plane with respect to the line of sight, in other words the inclination has an isotropic probability density function (pdf). This corresponds to a pdf that is flat in
![]() $\cos\,i$
, which makes it easy to draw from for a Monte Carlo simulation using random inclination angles. We used a sample size of
$\cos\,i$
, which makes it easy to draw from for a Monte Carlo simulation using random inclination angles. We used a sample size of
![]() $10^8$
and found a 3-
$10^8$
and found a 3-
![]() $\sigma$
(99.73% confidence) upper mass limit of
$\sigma$
(99.73% confidence) upper mass limit of
![]() $42.6\,\textrm{M}_{\textrm{J}}$
, corresponding to an inclination of
$42.6\,\textrm{M}_{\textrm{J}}$
, corresponding to an inclination of
![]() $4.2^{\circ}$
. Results for a number of confidence levels are summarised in Table 3.
$4.2^{\circ}$
. Results for a number of confidence levels are summarised in Table 3.
Table 3. Geometric upper mass limits and corresponding inclinations for HD 76920 b for different confidence levels

7. Summary and Discussion
We obtained 63 new RV measurements of HD 76920 from four different instruments around the time of the predicted periastron passage. The unusually high eccentricity of HD 76920 b means that
![]() $\sim 90\%$
of the peak-to-peak RV is traversed up and down in only
$\sim 90\%$
of the peak-to-peak RV is traversed up and down in only
![]() $\sim 14\%$
of the orbital period, and the RV curve is approximately flat for the remaining
$\sim 14\%$
of the orbital period, and the RV curve is approximately flat for the remaining
![]() $\sim 360$
days of the orbital period, making it difficult to determine precise orbital elements from an observational point of view. However, in order to constrain the orbital elements, it is essential to have good sampling of the non-flat parts of the orbit where the RV changes rapidly over time. As the orbital phase near periastron passage was not very well covered in their initial work, Wittenmyer et al. (Reference Wittenmyer2017b) suggested follow-up observations be carried out during the next periastron passage. Flexible scheduling of observing time during periastron passage on telescopes with high-resolution spectrographs is an effective way of confirming the nature of highly eccentric planets and determining their orbital properties and minimum mass to high precision. For example, HD 37605 b with an eccentricity of
$\sim 360$
days of the orbital period, making it difficult to determine precise orbital elements from an observational point of view. However, in order to constrain the orbital elements, it is essential to have good sampling of the non-flat parts of the orbit where the RV changes rapidly over time. As the orbital phase near periastron passage was not very well covered in their initial work, Wittenmyer et al. (Reference Wittenmyer2017b) suggested follow-up observations be carried out during the next periastron passage. Flexible scheduling of observing time during periastron passage on telescopes with high-resolution spectrographs is an effective way of confirming the nature of highly eccentric planets and determining their orbital properties and minimum mass to high precision. For example, HD 37605 b with an eccentricity of
![]() $e = 0.74$
or HD 45350 b with an eccentricity of
$e = 0.74$
or HD 45350 b with an eccentricity of
![]() $e = 0.76$
has been confirmed in this way (Cochran et al. Reference Cochran2004; Endl et al. Reference Endl, Cochran, Wittenmyer and Hatzes2006).
$e = 0.76$
has been confirmed in this way (Cochran et al. Reference Cochran2004; Endl et al. Reference Endl, Cochran, Wittenmyer and Hatzes2006).

Figure 9. Comparison of the best-fit model RV curve from this work (solid grey line) with the one from Wittenmyer et al. (Reference Wittenmyer2017b) (dashed grey line). The periastron passage happened about 3 days later than predicted by the orbital elements from Wittenmyer et al. (Reference Wittenmyer2017b).
We were fortunate enough to be granted access to the HERCULES, CHIRON, FEROS, and FIDEOS spectrographs during that period and hence managed to obtain near-continuous coverage of the corresponding RV peak. In hindsight, getting enough telescope time either side of the predicted periastron passage was particularly important because the periastron passage actually happened about 3 days later than predicted, or about
![]() $3.7$
-σ when we calculate the uncertainty on the time of periastron passage via bootstrapping based on the orbital elements given by Wittenmyer et al. (Reference Wittenmyer2017b) (see Figure 9). This highlights the importance and scientific value of small-to-medium size telescopes with high-resolution spectrographs to the exoplanet community (e.g. Swift et al. Reference Swift2015; Addison et al. Reference Addison2019), as it would have been near impossible to get enough time on larger telescopes at such short notice.
$3.7$
-σ when we calculate the uncertainty on the time of periastron passage via bootstrapping based on the orbital elements given by Wittenmyer et al. (Reference Wittenmyer2017b) (see Figure 9). This highlights the importance and scientific value of small-to-medium size telescopes with high-resolution spectrographs to the exoplanet community (e.g. Swift et al. Reference Swift2015; Addison et al. Reference Addison2019), as it would have been near impossible to get enough time on larger telescopes at such short notice.
Our best-fit orbital solution to the combined dataset from a total of five instruments (and six different operating modes) yielded an even higher than expected eccentricity of
![]() $e=0.88$
and an orbital period of
$e=0.88$
and an orbital period of
![]() $415.9\,\textrm{d}$
. We also found a RV semi-amplitude of
$415.9\,\textrm{d}$
. We also found a RV semi-amplitude of
![]() $178\,\text{ms}^{-1}$
and a semi-major axis of
$178\,\text{ms}^{-1}$
and a semi-major axis of
![]() $1.09\,\textrm{AU}$
. The new orbital solution corresponds to minimum mass of
$1.09\,\textrm{AU}$
. The new orbital solution corresponds to minimum mass of
![]() $3.1\,\textrm{M}_{\textrm{J}}$
for the planet that is about 20% lower than that reported by Wittenmyer et al. (Reference Wittenmyer2017b), mainly owing to our new lower stellar mass estimate. Formally, the RMS of the residuals from our fit is larger than in Wittenmyer et al. (Reference Wittenmyer2017b), partly because the individual uncertainties in and the scatter of the HERCULES data are about three times larger compared to the other instruments, and partly because we have effectively given different weights to the RV measurements during the fitting via the error treatment described in Section 5. In particular, note that the RMS of the AAT residuals from our best fit is now
$3.1\,\textrm{M}_{\textrm{J}}$
for the planet that is about 20% lower than that reported by Wittenmyer et al. (Reference Wittenmyer2017b), mainly owing to our new lower stellar mass estimate. Formally, the RMS of the residuals from our fit is larger than in Wittenmyer et al. (Reference Wittenmyer2017b), partly because the individual uncertainties in and the scatter of the HERCULES data are about three times larger compared to the other instruments, and partly because we have effectively given different weights to the RV measurements during the fitting via the error treatment described in Section 5. In particular, note that the RMS of the AAT residuals from our best fit is now
![]() $17.0\,\text{ms}^{-1}$
, which is of course expected as they now carry less weight compared to Wittenmyer et al. (Reference Wittenmyer2017b). More importantly though, due to the much improved phase coverage near periastron passage, the uncertainties in the orbital elements are now significantly reduced. Notably, the uncertainty in the orbital period was reduced by a factor of 5, and the uncertainty in the eccentricity was reduced by more than a factor of 3. In addition, we also estimated an upper mass limit of
$17.0\,\text{ms}^{-1}$
, which is of course expected as they now carry less weight compared to Wittenmyer et al. (Reference Wittenmyer2017b). More importantly though, due to the much improved phase coverage near periastron passage, the uncertainties in the orbital elements are now significantly reduced. Notably, the uncertainty in the orbital period was reduced by a factor of 5, and the uncertainty in the eccentricity was reduced by more than a factor of 3. In addition, we also estimated an upper mass limit of
![]() $0.4$
–
$0.4$
–
![]() $0.6\,\textrm{M}_\odot$
for the companion from Hipparcos astrometry, and a 3-
$0.6\,\textrm{M}_\odot$
for the companion from Hipparcos astrometry, and a 3-
![]() $\sigma$
upper mass limit of
$\sigma$
upper mass limit of
![]() $42.6\,\textrm{M}_{\textrm{J}}$
from geometric considerations.
$42.6\,\textrm{M}_{\textrm{J}}$
from geometric considerations.
7.1. Star–Planet interactions
Note that our value of the semi-major axis is slightly smaller than the one given by Wittenmyer et al. (Reference Wittenmyer2017b), while our eccentricity is slightly larger. However, this seemingly small difference means that the planet actually comes to within
![]() $2.4 \pm 0.3$
stellar radii from its host star’s surface at closest approach, or about one stellar radius closer than estimated by Wittenmyer et al. (Reference Wittenmyer2017b). Naturally, this makes the system a prime target for studies of star-planet interactions. Also note that we calculate the same value for the planet’s distance from the stellar surface at periastron in units of the stellar radius, independent of whether we use the spectroscopic or the asteroseismic stellar parameters.
$2.4 \pm 0.3$
stellar radii from its host star’s surface at closest approach, or about one stellar radius closer than estimated by Wittenmyer et al. (Reference Wittenmyer2017b). Naturally, this makes the system a prime target for studies of star-planet interactions. Also note that we calculate the same value for the planet’s distance from the stellar surface at periastron in units of the stellar radius, independent of whether we use the spectroscopic or the asteroseismic stellar parameters.
The orbital evolution is determined by the combined effect of tidally induced orbital decay and mass-loss-induced orbital expansion. Following the same procedure as in Villaver et al. (Reference Villaver, Livio, Mustill and Siess2014) and Wittenmyer et al. (Reference Wittenmyer2017b), we determined the planet’s orbit and eccentricity evolution as the star evolves up the RGB, and the tidal dissipation is dominated by motions in the star’s convective envelope (Zahn Reference Zahn1977). We have updated both the planetary and stellar parameters since Wittenmyer et al. (Reference Wittenmyer2017b). We use SSE stellar models (Hurley, Pols, & Tout Reference Hurley, Pols and Tout2000) with the asteroseismic mass of
![]() $1.3\, \textrm{M}_{\odot}$
and a Solar metallicity. We furthermore consider two values for the Reimers
$1.3\, \textrm{M}_{\odot}$
and a Solar metallicity. We furthermore consider two values for the Reimers
![]() $\eta$
mass-loss parameter (Reimers Reference Reimers1975): a standard value of
$\eta$
mass-loss parameter (Reimers Reference Reimers1975): a standard value of
![]() $\eta=0.6$
and an extreme case of
$\eta=0.6$
and an extreme case of
![]() $\eta=0.0$
(no mass loss). The latter means that the planet experiences only tidal decay on its orbit, not any orbital expansion owing to mass loss, and hence represents an optimal case for a maximum orbital decay owing to tidal forces.
$\eta=0.0$
(no mass loss). The latter means that the planet experiences only tidal decay on its orbit, not any orbital expansion owing to mass loss, and hence represents an optimal case for a maximum orbital decay owing to tidal forces.
In each case, the planet’s orbit undergoes only very minor decay before the planet is engulfed in the stellar envelope: for both
![]() $\eta=0.6$
and
$\eta=0.6$
and
![]() $\eta=0.0$
, the orbital eccentricity decays by only about
$\eta=0.0$
, the orbital eccentricity decays by only about
![]() $0.002$
before the star engulfs the planet. With no stellar mass loss (
$0.002$
before the star engulfs the planet. With no stellar mass loss (
![]() $\eta=0.0$
), the semi-major axis decays by
$\eta=0.0$
), the semi-major axis decays by
![]() $0.01\,\textrm{AU}$
, while with mass loss (
$0.01\,\textrm{AU}$
, while with mass loss (
![]() $\eta=0.6$
) the semi-major axis increases by
$\eta=0.6$
) the semi-major axis increases by
![]() $0.003\,\textrm{AU}$
. The planet enters the stellar envelope when the star has grown to a little over three times its present radius, some 50 Myr hence. Adopting the spectroscopic stellar mass of
$0.003\,\textrm{AU}$
. The planet enters the stellar envelope when the star has grown to a little over three times its present radius, some 50 Myr hence. Adopting the spectroscopic stellar mass of
![]() $1.0\, \textrm{M}_{\odot}$
does not qualitatively change the future evolution: the eccentricity decay is a little larger (0.004–0.005) and the remaining lifetime a little longer (
$1.0\, \textrm{M}_{\odot}$
does not qualitatively change the future evolution: the eccentricity decay is a little larger (0.004–0.005) and the remaining lifetime a little longer (
![]() $\sim 80\,\textrm{Myr}$
), but there are still no large changes to the orbit expected.
$\sim 80\,\textrm{Myr}$
), but there are still no large changes to the orbit expected.
7.2. Transit probability
Our updated orbital solution also leads to an even higher transit probability than the
![]() $10.3\%$
reported in Wittenmyer et al. (Reference Wittenmyer2017b). From the emcee best-fit orbital elements listed in Table 2, it follows that at inferior conjunction, which happens at a true anomaly of
$10.3\%$
reported in Wittenmyer et al. (Reference Wittenmyer2017b). From the emcee best-fit orbital elements listed in Table 2, it follows that at inferior conjunction, which happens at a true anomaly of
![]() $88.8^{\circ}$
and
$88.8^{\circ}$
and
![]() $5.06\,\textrm{d}$
after periastron passage, the star–planet separation is
$5.06\,\textrm{d}$
after periastron passage, the star–planet separation is
![]() $0.245\,\textrm{AU}$
, and the azimuthal component of the orbital velocity is
$0.245\,\textrm{AU}$
, and the azimuthal component of the orbital velocity is
![]() $60.7\,\textrm{kms}^{-1}$
. In order to calculate the probability, depth, and duration of a potential transit, we must first have an estimate of the planetary radius. We used the mass–radius relationship for the Jovian regime in form of the power law
$60.7\,\textrm{kms}^{-1}$
. In order to calculate the probability, depth, and duration of a potential transit, we must first have an estimate of the planetary radius. We used the mass–radius relationship for the Jovian regime in form of the power law
![]() $R_{pl} \propto m_P^{-0.04}$
as given by Chen & Kipping (Reference Chen and Kipping2017), with which we calculated the planet’s radius to be
$R_{pl} \propto m_P^{-0.04}$
as given by Chen & Kipping (Reference Chen and Kipping2017), with which we calculated the planet’s radius to be
![]() $0.96\,\textrm{R}_{\textrm{J}}$
. With that in hand, we calculated a relatively high transit probability of
$0.96\,\textrm{R}_{\textrm{J}}$
. With that in hand, we calculated a relatively high transit probability of
![]() $16.0\%$
, using Equation (5) from Kane & von Braun (Reference Kane and von Braun2008), with a duration of
$16.0\%$
, using Equation (5) from Kane & von Braun (Reference Kane and von Braun2008), with a duration of
![]() $2.2\,\textrm{d}$
and a transit depth of
$2.2\,\textrm{d}$
and a transit depth of
![]() $0.013\%$
or 130 ppm, assuming an inclination of
$0.013\%$
or 130 ppm, assuming an inclination of
![]() $i=90^{\circ}$
and ignoring limb-darkening effects. While the large stellar radius increases the transit probability, unfortunately it also decreases the transit depth, requiring a level of photometric precision that is extremely challenging for ground-based transit searches, albeit perhaps not impossible (e.g. Tregloan-Reed & Southworth Reference Tregloan-Reed and Southworth2013). However, TESS can technically achieve the required precision for a star of this magnitude (Ricker et al. Reference Ricker2015). HD 76920 has ecliptic coordinates of about
$i=90^{\circ}$
and ignoring limb-darkening effects. While the large stellar radius increases the transit probability, unfortunately it also decreases the transit depth, requiring a level of photometric precision that is extremely challenging for ground-based transit searches, albeit perhaps not impossible (e.g. Tregloan-Reed & Southworth Reference Tregloan-Reed and Southworth2013). However, TESS can technically achieve the required precision for a star of this magnitude (Ricker et al. Reference Ricker2015). HD 76920 has ecliptic coordinates of about
![]() $\lambda = 202.5^{\circ}$
and
$\lambda = 202.5^{\circ}$
and
![]() $\beta = -73.2^{\circ}$
and therefore lies about five degrees outside the southern TESS continuous viewing zone. However, by pure coincidence, this placed HD 76920 inside the sector that TESS was observing at the time of the next potential transit (sector 9), which we predicted to occur approximately between
$\beta = -73.2^{\circ}$
and therefore lies about five degrees outside the southern TESS continuous viewing zone. However, by pure coincidence, this placed HD 76920 inside the sector that TESS was observing at the time of the next potential transit (sector 9), which we predicted to occur approximately between
![]() $\textrm{JD}2458559.43\,\pm\,0.63$
and
$\textrm{JD}2458559.43\,\pm\,0.63$
and
![]() $\textrm{JD}2458561.66\,\pm\,0.63$
(UT 16.93–19.16 March 2019). We list predicted mid-transit times, as well as ingress and egress times for potential future transits in Table 4.
$\textrm{JD}2458561.66\,\pm\,0.63$
(UT 16.93–19.16 March 2019). We list predicted mid-transit times, as well as ingress and egress times for potential future transits in Table 4.
Table 4. Predicted windows for potential past and future transits of HD 76920 b

Unfortunately, due to it being an evolved star, HD 76920 presents a photometric variability at the 500-ppm level, which is significantly larger than the expected transit depth. However, before searching for a potential transit signal, we corrected the light curve using a Gaussian process (GP), following a similar procedure to that described in Jones et al. (Reference Jones2019). The fit was performed with the Juliet code (Espinoza, Kossakowski, & Brahm Reference Espinoza, Kossakowski and Brahm2019) using a Matérn kernel. To model the asteroseismic signal, we used a Gaussian prior with mean equal to the period corresponding to
![]() $\nu_{\max}$
, as derived in Section 4.2. Figure 10 shows the TESS light curve and the GP model.
$\nu_{\max}$
, as derived in Section 4.2. Figure 10 shows the TESS light curve and the GP model.
Finally, to determine if the planet transits on the predicted date, we compared the Bayesian evidence between a transit model and a non-transit model. As we found no significant difference, we assumed the simpler model, that is, the non-transit model. The GP-corrected light curve around the expected transit time is shown in Figure 11.

Figure 10. TESS light curve around the expected transit time, which is highlighted in light blue. The yellow line represents the Gaussian process fit.

Figure 11. GP-corrected TESS light curve of HD 76920. The expected transit time is highlighted in light blue.
7.3. Origin of the high eccentricity
The origin of Hot Jupiters and/or highly eccentric planets is usually explained via the Kozai–Lidov mechanism, whereby perturbations caused by a massive third body (i.e. a stellar companion) can cause oscillations between the planet’s eccentricity and inclination as long as its angular momentum component parallel to the orbital angular momentum of the two stars remains constant (Lidov Reference Lidov1962; Kozai Reference Kozai1962). However, as already noted by Wittenmyer et al. (Reference Wittenmyer2017b), there are no indications for additional massive companions in the RV data. Also, while the Gaia DR2 catalogue (Gaia Collaboration et al. 2016, 2018) lists two faint
![]() $(G \sim 21\,\textrm{mag})$
stellar objects (Gaia DR2 IDs 5224124753994137984 and 5224127812011479808) with compatible parallaxes within 5 arcmin from HD 76920, corresponding to a physical separation of
$(G \sim 21\,\textrm{mag})$
stellar objects (Gaia DR2 IDs 5224124753994137984 and 5224127812011479808) with compatible parallaxes within 5 arcmin from HD 76920, corresponding to a physical separation of
![]() $\lesssim 55\,000\,\textrm{AU}$
at a distance of
$\lesssim 55\,000\,\textrm{AU}$
at a distance of
![]() $d=184\,\textrm{pc}$
(Bailer-Jones et al. Reference Bailer-Jones, Rybizki, Fouesneau, Mantelet and Andrae2018), their respective proper motions and
$d=184\,\textrm{pc}$
(Bailer-Jones et al. Reference Bailer-Jones, Rybizki, Fouesneau, Mantelet and Andrae2018), their respective proper motions and
![]() $B-R$
colours are very different from the corresponding values for HD 76920, which rules them out as physically close companions. Furthermore, as also noted by Wittenmyer et al. (Reference Wittenmyer2017b), in the Kozai–Lidov scenario, planets like HD 76920 b are readily being engulfed by their host stars as they move up the RGB (Frewen & Hansen Reference Frewen and Hansen2016), and, according to simulations by Parker, Lichtenberg, & Quanz (Reference Parker, Lichtenberg and Quanz2017), free-floating planets are almost exclusively captured into much wider orbits
$B-R$
colours are very different from the corresponding values for HD 76920, which rules them out as physically close companions. Furthermore, as also noted by Wittenmyer et al. (Reference Wittenmyer2017b), in the Kozai–Lidov scenario, planets like HD 76920 b are readily being engulfed by their host stars as they move up the RGB (Frewen & Hansen Reference Frewen and Hansen2016), and, according to simulations by Parker, Lichtenberg, & Quanz (Reference Parker, Lichtenberg and Quanz2017), free-floating planets are almost exclusively captured into much wider orbits
![]() $(a > 100\,\textrm{AU})$
. This leaves planet–planet scattering as the most likely explanation for the highly eccentric orbit of HD 76920 b (e.g. Chatterjee et al. Reference Chatterjee, Ford, Matsumura and Rasio2008). In this scenario, a second planet of comparable mass would have either been ejected from the system as the result of a close encounter with HD 76920 b or at least pushed outwards into a long-period orbit that is beyond our current detection limits. A third option is that the second planet disappeared from the system because it was thrown towards the star and engulfed by it.
$(a > 100\,\textrm{AU})$
. This leaves planet–planet scattering as the most likely explanation for the highly eccentric orbit of HD 76920 b (e.g. Chatterjee et al. Reference Chatterjee, Ford, Matsumura and Rasio2008). In this scenario, a second planet of comparable mass would have either been ejected from the system as the result of a close encounter with HD 76920 b or at least pushed outwards into a long-period orbit that is beyond our current detection limits. A third option is that the second planet disappeared from the system because it was thrown towards the star and engulfed by it.
7.4. Additional considerations
The very high eccentricity of HD 76920 b not only makes it the most eccentric planet known to orbit an evolved star by some margin but also puts it in fifth place among all known exoplanets.Footnote b Its eccentricity is only surpassed by HD 4113 A b (
![]() $e=0.90$
) (Tamuz et al. Reference Tamuz2008), HD 7449 A b (
$e=0.90$
) (Tamuz et al. Reference Tamuz2008), HD 7449 A b (
![]() $e=0.92$
) (Dumusque et al. Reference Dumusque2011; Wittenmyer et al. Reference Wittenmyer, Clark, Zhao, Horner, Wang and Johns2019a), HD 80606 b (
$e=0.92$
) (Dumusque et al. Reference Dumusque2011; Wittenmyer et al. Reference Wittenmyer, Clark, Zhao, Horner, Wang and Johns2019a), HD 80606 b (
![]() $e=0.93$
) (Naef et al. Reference Naef2001; Moutou et al. Reference Moutou2009), and HD 20782 b (
$e=0.93$
) (Naef et al. Reference Naef2001; Moutou et al. Reference Moutou2009), and HD 20782 b (
![]() $e=0.97$
) (Jones et al. Reference Jones, Butler, Tinney, Marcy, Carter, Penny, McCarthy and Bailey2006; O’Toole et al. Reference O’Toole, Tinney, Jones, Butler, Marcy, Carter and Bailey2009; Kane et al. Reference Kane2016), all of which are gas giants orbiting solar mass main-sequence stars.
$e=0.97$
) (Jones et al. Reference Jones, Butler, Tinney, Marcy, Carter, Penny, McCarthy and Bailey2006; O’Toole et al. Reference O’Toole, Tinney, Jones, Butler, Marcy, Carter and Bailey2009; Kane et al. Reference Kane2016), all of which are gas giants orbiting solar mass main-sequence stars.
Several studies have highlighted the possibility that a RV curve produced by two low-eccentricity planets can be misinterpreted as being caused by one planet with medium to high eccentricity, especially for low signal-to-noise ratios
![]() $K/ \sigma$
, poor sampling, and/or if the two planets are in resonant orbits (e.g. Shen & Turner Reference Shen and Turner2008; Rodigas & Hinz Reference Rodigas and Hinz2009; Anglada-Escudé, López-Morales, & Chambers Reference Anglada-Escudé, López-Morales and Chambers2010; Wittenmyer et al. Reference Wittenmyer2012, Reference Wittenmyer2013, Reference Wittenmyer, Clark, Zhao, Horner, Wang and Johns2019a, b). However, given the large
$K/ \sigma$
, poor sampling, and/or if the two planets are in resonant orbits (e.g. Shen & Turner Reference Shen and Turner2008; Rodigas & Hinz Reference Rodigas and Hinz2009; Anglada-Escudé, López-Morales, & Chambers Reference Anglada-Escudé, López-Morales and Chambers2010; Wittenmyer et al. Reference Wittenmyer2012, Reference Wittenmyer2013, Reference Wittenmyer, Clark, Zhao, Horner, Wang and Johns2019a, b). However, given the large
![]() $K/ \sigma$
ratio, the dense sampling we have achieved around periastron passage, and the very high eccentricity (which is well outside the ‘danger zone’ as identified by Wittenmyer et al. (Reference Wittenmyer, Bergmann, Horner, Clark and Kane2019b), that is, the range of eccentricities that can be most easily mimicked by two near-circular planets), we are very confident that the results presented in this paper remove any possibly remaining doubts about the RV variations being caused by a single planetary companion in a highly eccentric orbit.
$K/ \sigma$
ratio, the dense sampling we have achieved around periastron passage, and the very high eccentricity (which is well outside the ‘danger zone’ as identified by Wittenmyer et al. (Reference Wittenmyer, Bergmann, Horner, Clark and Kane2019b), that is, the range of eccentricities that can be most easily mimicked by two near-circular planets), we are very confident that the results presented in this paper remove any possibly remaining doubts about the RV variations being caused by a single planetary companion in a highly eccentric orbit.
Acknowledgements
CB was supported by Australian Research Council Discovery Grant DP170103491. LV acknowledges support from CONICYT through projects Fondecyt n. 1171364 and Anillo ACT-1417. AZ is supported by CONICYT grant n. 2117053. SW thanks the Heising-Simons Foundation for their generous support. AJM acknowledges support from the Knut and Alice Wallenberg Foundation (project grant 2014.0017), the Swedish Research Council (starting grant 2017-04945), and the Walter Gyllenberg Foundation of the Royal Physiographic Society of Lund. RB acknowledges support from FONDECYT Project 11200751, from CORFO project N
![]() $^\circ$
14ENI2-26865, and from project IC120009 ‘Millennium Institute of Astrophysics (MAS)’ of the Millenium Science Initiative, Chilean Ministry of Economy. We are grateful for receiving a generous allocation of observing time at UCMJO. This research has made use of NASA’s Astrophysics Data System (ADS), and the SIMBAD database, operated at CDS, Strasbourg, France. This research has also made use of the Extrasolar Planets Encyclopaedia at http://www.exoplanet.eu. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. Finally, we would like to thank the anonymous referee for their insightful comments that helped noticeably to improve this manuscript.
$^\circ$
14ENI2-26865, and from project IC120009 ‘Millennium Institute of Astrophysics (MAS)’ of the Millenium Science Initiative, Chilean Ministry of Economy. We are grateful for receiving a generous allocation of observing time at UCMJO. This research has made use of NASA’s Astrophysics Data System (ADS), and the SIMBAD database, operated at CDS, Strasbourg, France. This research has also made use of the Extrasolar Planets Encyclopaedia at http://www.exoplanet.eu. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. Finally, we would like to thank the anonymous referee for their insightful comments that helped noticeably to improve this manuscript.
A Radial Velocity Data
B Corner plot of the fit parameters
Table A.1. Radial velocities for HD 76920. Note that the velocities shown have instrument-specific zero points, which are included in the fitting process and are given in Table 2. The AAT data were taken from Wittenmyer et al. (Reference Wittenmyer2017b).


Figure A.1. Corner plot of the posterior probability distributions of the 17 free parameters used in the emcee fitting. All numerical values shown are rounded to two decimal places.