1 ASTRONOMY IN THE GRAVITATIONAL WAVE ERA
The detection of gravitational waves (GWs) will rank as one of the major scientific achievements of this century. Their detection will open up a new observational window to the Universe, revealing dynamic sources of strong field relativistic gravity previously inaccessible through conventional astronomical instruments. Our understanding of space–time and matter under the most extreme conditions will be transformed.
Although there has been no direct detection of GWs to date, indirect evidence for their existence comes from high precision, Nobel-prize winning measurements of the pulsar PSR 1913+16 and its companion neutron star (NS; Hulse & Taylor Reference Hulse and Taylor1975; Weisberg & Taylor Reference Weisberg and Taylor1984). The GW emission that drives the system’s orbital decay is in agreement with the predictions of general relativity to better than 1% (Hartle Reference Hartle2003).
When such binary neutron star (BNS) systems eventually coalesce, they are predicted to emit copious amounts of GWs (Thorne Reference Thorne, Hawking and Israel1987). These sources will be prime targets for the new generation of GW detectors, led by Advanced LIGO (aLIGO; Aasi et al. Reference Aasi2015) which is set to begin observing during the second half of 2015 and Advanced Virgo (AdV) a year later (Acernese et al. Reference Acernese2015). At final sensitivity, these advanced detectors are expected to detect BNS mergers at a rate within the range 0.4–400 yr−1 (Abadie et al. Reference Abadie2010b). Compact Binary Coalescences (CBCs) consisting of at least one black hole (BH) are also targets for GW detectors; although there is compelling evidence for their existence (Barnard, Clark, & Kolb Reference Barnard, Clark and Kolb2008; Prestwich et al. Reference Prestwich2007), the event rates of these sources for aLIGO detection is not well known.
One realisation in the last decade is that coalescing systems of NS/NS or NS/BH events could be the progenitors of short-hard gamma-ray bursts (SGRBs); transient events routinely observed throughout the electromagnetic (EM) spectrum (Paczynski Reference Paczynski1986; Eichler et al. Reference Eichler, Livio, Piran and Schramm1989a; Narayan, Paczynski, & Piran Reference Narayan, Paczynski and Piran1992; Rezzolla et al. Reference Rezzolla, Giacomazzo, Baiotti, Granot, Kouveliotou and Aloy2011; Gehrels et al. Reference Gehrels2005; Berger et al. Reference Berger2005; Bloom et al. Reference Bloom2006). There exist other types of EM, neutrino, and cosmic ray emissions that may also be associated with GW events. These include long-duration gamma-ray bursts (LGRBs; Kobayashi & Mészáros Reference Kobayashi and Mészáros2003), short gamma-ray repeaters (Abbott et al. Reference Abbott2008b), supernovae (Fryer, Holz, & Hughes Reference Fryer, Holz and Hughes2002; Ott Reference Ott2009), fast radio bursts (FRBs; Zhang Reference Zhang2014) as well as others.
History has already shown that multi-wavelength astronomy can play an important role in unveiling new phenomena. In the last decade, X-ray, optical, and radio follow-ups have all transformed and revealed new processes in our understanding of gamma-ray bursts (GRBs); combining EM observations with those in the GW domain will too provide new insight into the internal engines and mechanisms at play in a multitude of different sources. A new generation of sensitive, wide-field telescopes, advancements in time domain astronomy and upgrades to neutrino and cosmic ray detectors can provide a coordinated network for discovery. The possible simultaneous detection of photons, neutrinos, or high energy particles with GWs would be a landmark moment for astrophysics, initiating a new era of multi-messenger Footnote 1 astronomy, for the first time including GW.
Maximising the potential offered by GW observations involves the development of a worldwide, multi-messenger network. Australian facilities are ideally placed to foster scientific exchanges in this new era and agreements have already been established. To conduct EM follow-up of GW triggers, memorandums of understanding (MoUs) have been signed between the LIGO/Virgo GW collaboration and a number of facilities either based in Australia or with strong Australian involvement; these include the following: The Anglo-Australian Telescope, the Australian Square Kilometer Array Pathfinder (ASKAP; Murphy et al. Reference Murphy2013), the Cherenkov Telescope Array (CTA; Acharya et al. Reference Acharya2013), The High Energy Stereoscopic System (H.E.S.S; Lennarz et al. Reference Lennarz, Chadwick, Domainko, Parsons, Rowell and Tam2013), IceCube (IceCube Collaboration et al. 2006), The Murchison Widefield Array (MWA; Tingay et al. Reference Tingay2013), and the SkyMapper (Keller et al. Reference Keller2007), The GW Optical Transient Observer (GOTOFootnote 2), and Zadko (Coward et al. Reference Coward2010) optical telescopes.
In this paper, we focus on the most probable multi-messenger observations from the advanced detector era; those associated with GRBs. Whilst doing so, we consider the contribution that the Australian facilities can make to the worldwide multi-messenger effort.
The structure of this paper is as follows: Section 2 describes GW astronomy. Sections 3 and 4 introduce SGRBs and LGRBs and describe how co-ordinated GW and multi-wavelength observations of these events can provide breakthrough science. Section 5 acts as a primer for those unfamiliar with the concepts and terminologies of detection and data analysis often used in the GW domain; this section is not designed to be exhaustive but to present some of the most important concepts in GW detection and data analysis. Section 6 discusses the expected rates and detection ranges for GW sources. The next two sections describe two of the strategies that form the basis for coordinated GW and EM observations in the GW era. Section 7 discusses EM triggered GW searches; these could likely yield the first coincident GW-EM event through archival GW data. Section 8 discusses the EM follow-up of GW Triggers; this strategy is highly challenging due to the large positional uncertainties of GW observations but the potential rewards for success are without doubt highly significant. Section 10 discusses the Australian facilities involved in the co-ordinated science programmes with aLIGO/AdV and we highlight the areas in which they could contribute in this new frontier. Finally, in Section 11 we discuss the role neutrino follow-up plays in GW detection.
2 GRAVITATIONAL WAVES: A NEW TYPE OF ASTRONOMY
GWs are produced by regions of space–time that are distorted by high-velocity bulk motions of matter. The timescale of the motions determine the frequency of the GW emission; ground-based detectors will target systems with masses in the range 1–103 M⊙, which emit in the 1 Hz–10 kHz band. This frequency range, covering the audio band, has motivated the characterisation of interferometric GW astronomy as ‘listening to the Universe’.
Instruments capable of achieving detections will begin observations in the second half of 2015. ALIGO, a pair of US-based interferometric detectors at Hanford and Livingston (USA; Aasi et al. Reference Aasi2015) will have its first observational science run (O1) in late-2015; a year later, it will be joined by the Italian AdV (Acernese et al. Reference Acernese2015; Accadia et al. Reference Accadia2012) for a second observing run (O2). The ‘advanced’ network of interferometric GW detectors will eventually have 10 times the sensitivity of the first generation instruments. The increased sensitivity translates into a factor 103 increase in observed volume, making detections expected rather than plausible.
Additional instruments are expected to eventually join the network. KAGRA, a Japanese detector, is envisioned to begin operation in 2018–19 (Somiya Reference Somiya2012) and LIGO-India is expected to be operational from 2020, reaching a design sensitivity at the same level as aLIGO by around 2022 (Aasi et al. Reference Aasi2013b).
The GW observations made by these instruments will differ from most conventional EM observations in several ways:
• GWs are not scattered or obscured by intervening material like dust so provide a window into the densest regions of the Universe.
• As GW detectors observe an amplitude rather than a flux, the measure of detectability follows an inverse relationship with distance rather than the conventional inverse square law. Therefore, number counts of a homogeneous distribution of standard-candle sources increases with distance, d, as, d 3, rather than, d 3/2.
• As GWs couple weakly to the detectors, even very local astronomical sources of GWs have to be highly energetic emitters of gravitational radiation.
• GW detectors are nearly omnidirectional, with a nearly 4π steradian sensitivity to astrophysical events with a greater than average response over more than 40% of the sky.
The first point implies that GW observations can allow us to view astrophysical phenomena inaccessible by other means. The gravitational window can therefore enable frontier explorations in the low to intermediate redshift universe (z ≲ 0.4) of sources that are electromagnetically invisible for much, or all, of their lives. The second point means that a factor 2 improvement in the sensitivity of a GW detector results in a factor 8 increase in the volume of the Universe being probed. The third point emphasises a detection bias for detecting the most highly energetic astrophysical events. The typical fluxes of GW sources are of order 1020 Jy, far greater than equivalent fluxes typically observed in the radio domain (μJy–Jy). The final point means that GW detectors are naturally survey instruments over a wide band of frequencies (10–5 000 Hz).
There are a number of types of EM counterparts that may be associated with GW emissions (Branchesi et al. Reference Branchesi2012; Mandel et al. Reference Mandel, Kelley, Ramirez-Ruiz, Griffin, Hanisch and Seaman2012). As some of these counterparts are quite speculative, this paper focuses on GW signals associated with GRBs. Other sources of simultaneous EM and GW emission include supernovae as well as multiple emission mechanisms from NSs; for a review of the latter, see the accompanying article in this series (Lasky Reference Lasky2015).
In the next few sections, we provide a summary of both SGRBs and LGRBs and the type of GW/EM associations that could be targeted in the GW era. Some of these predictions are based on solid foundations whilst some are more speculative. In considering the latter, we note that when a new window of observation has been opened in the past, the discoveries that transform our understanding of the Universe have often been the least expected.
3 MULTI-MESSENGER ASTRONOMY WITH SHORT GAMMA-RAY BURSTS
GWs from the merger of coalescing binary systems of NS/NS and NS/BHsFootnote 3 are confidently predicted to have observable EM counterparts. This expectation is a result of the connection between these events and SGRBs (e.g. Eichler et al. Reference Eichler, Livio, Piran and Schramm1989a; Gehrels et al. Reference Gehrels2005; Tanvir et al. Reference Tanvir, Levan, Fruchter, Hjorth, Hounsell, Wiersema and Tunnicliffe2013; Berger, Fong, & Chornock Reference Berger, Fong and Chornock2013). The evidence stems from a number of different channels. Firstly, the dynamic timescales of discs predicted from the merger of CBCs are consistent with the durations of SGRBs. Secondly, EM follow-ups of SGRBs have never provided an associated supernova. Thirdly, SGRB afterglows have been localised to galaxies harbouring older stellar populations with offsets of order tens of kpc from their galactic centers; this is consistent with post-natal kick velocities of 100s of km s−1, and also with the fainter and shorter lived afterglows expected from an ambient interstellar medium at a large offset. Finally, as is discussed in Section 3.4, the discovery of a faint EM transient called a kilonova has provided the strongest observational evidence to date of the SGRB/CBC association.
Conclusive proof of the CBC/SGRB association will be provided through GW observations. Coincident EM and GW observations of SGRBs could also provide a fascinating insight to the dominant mechanisms at the heart of GRBs. Low-latency GW pipelines could enable multi-wavelength follow-up measurements of the prompt emission, constraining both the underlying central engines and the emission mechanisms at work (Elliott et al. Reference Elliott2014). Later-time multi-wavelength follow-ups can provide insight through extensive coverage of the SGRB afterglow.
A number of EM counterparts have been predicted to accompany the inspiral and merger of NS/NS and NS/BH systems. In Figure 1, we show the likely outcomes of these mergers and in the following sections we will briefly review the most likely EM counterparts that could accompany CBCs.

Figure 1. A cartoon illustrating some of the possible scenarios for coalescing systems of NSs and BHs. Short-duration gamma-ray bursts (SGRBs) have been linked with the merger of compact objects (Berger et al. Reference Berger2005; Bloom et al. Reference Bloom2006) and could be accompanied by a fast radio burst (FRB; Thornton et al. Reference Thornton2013; Lorimer et al. Reference Lorimer, Karastergiou, McLaughlin and Johnston2013; Totani Reference Totani2013; Palaniswamy et al. Reference Palaniswamy, Wayth, Trott, McCallum, Tingay and Reynolds2014; Zhang Reference Zhang2014). If a stable magnetar is formed, the long-lived X-ray plateaus observed in many SGRBs could indicate a constant energy injection (Corsi & Mészáros Reference Corsi and Mészáros2009a; Rowlinson et al. Reference Rowlinson2010, Reference Rowlinson, O’Brien, Metzger, Tanvir and Levan2013; Zhang Reference Zhang2013; Gao et al. Reference Gao, Ding, Wu, Zhang and Dai2013a; Fan, Wu, & Wei Reference Fan, Wu and Wei2013); the possible collapse of a merger product to a BH could also result in an FRB (Falcke & Rezzolla Reference Falcke and Rezzolla2014; Zhang Reference Zhang2014). Figure adapted from Chu et al. 2015.
3.1 Prompt emission
During the final stages of the merger of a compact binary, the system is expected to launch a highly relativistic jet that interacts with itself and the surrounding medium (the fireball model for GRBs; e.g. Piran Reference Piran1999). Collisions of material moving at different velocities within the jet will lead to internal shocks, giving short-lived bursts of gamma-rays that we detect as the SGRB prompt emission. As the accretion timescale is expected to be < 2 s (Metzger, Piro, & Quataert Reference Metzger, Piro and Quataert2008), the GRBs associated with compact binary mergers are typically shorter in duration than those associated with core-collapse supernovae (explaining the observed distribution of GRBs; Kouveliotou et al. Reference Kouveliotou, Meegan, Fishman, Bhat, Briggs, Koshut, Paciesas and Pendleton1993). However, the division between these two populations is not easily identifiable from the prompt gamma-ray emission alone (e.g. Bromberg et al. Reference Bromberg, Nakar, Piran and Sari2013; Qin et al. Reference Qin2013).
A number of Fermi-LAT GRBs have shown > GeV emission (even at redshifts as distant as z ≈ 4). Two bursts were observed with gamma-ray photons reaching energies up to 94 GeV (GRB 130427A) and 62 GeV (GRB 131231A)—this supports the suggestion that the photon energies may extend higher than previously assumed (Bouvier et al. Reference Bouvier, Gilmore, Connaughton, Otte, Primack and Williams2011; Inoue et al. Reference Inoue, Granot and O’Brien2013). Significantly, these discoveries have not been limited to LGRBs, with SGRBs also showing high-energy photons and GeV emission often continuing for tens of seconds beyond the initial burst. The fact that Fermi-LAT discovered a photon of energy 31 GeV during the prompt phase of GRB 090510 (Ackermann et al. Reference Ackermann2010) is promising for co-ordinated observations between GW detectors and ground-based CTAs (Bartos et al. Reference Bartos2014) operating at > 10 GeV. Additionally, SGRBs with time-extended emission have recently been cited as promising targets for CTAs (Veres & Mészáros Reference Veres and Mészáros2014).
One exciting possibility is the observation of prompt optical flashes. So far, these emissions have only been observed in LGRBs (Racusin et al. Reference Racusin2008; Akerlof et al. Reference Akerlof1999; Vestrand et al. Reference Vestrand2014). An early optical emission correlated with the prompt gamma-rays could indicate a common origin related to the internal shocks (Vestrand et al. Reference Vestrand2005).
A number of studies have suggested that compact binary mergers could generate prompt coherent radio emission (e.g. Totani Reference Totani2013). Such mechanisms include excitation of the plasma surrounding a compact binary merger by GWs (Moortgat & Kuijpers Reference Moortgat, Kuijpers, Chen, Bloom, Madejski and Patrosian2005), from a dynamically generated magnetic field after the merger (Pshirkov & Postnov Reference Pshirkov and Postnov2010), or from the onset of the collision of the forward shock with the surrounding medium (Usov & Katz Reference Usov and Katz2000; Sagiv & Waxman Reference Sagiv and Waxman2002). However, the detectability of emission from these processes will be dependent upon the scattering by the surrounding environment (Macquart Reference Macquart2007). Nonetheless, these studies suggest compact binary mergers are an interesting contender for the progenitors of FRBs (Lorimer et al. Reference Lorimer, Bailes, McLaughlin, Narkevic and Crawford2007; Thornton et al. Reference Thornton2013), which are currently unknown.
3.2 Energy injection at late times
Plateaus and flares in X-ray light curves following GRBs are signatures of ongoing energy injection. This could be caused by late-time accretion onto a central BH (unlikely in the compact binary scenario; see discussion in Rowlinson et al. Reference Rowlinson, O’Brien, Metzger, Tanvir and Levan2013), or from ongoing energy injection from the spindown of a newly born NS. Indeed, recent studies (e.g. Giacomazzo & Perna Reference Giacomazzo and Perna2013; Zhang Reference Zhang2013; Lasky et al. Reference Lasky, Haskell, Ravi, Howell and Coward2014) have shown that the merger of two NSs could result in a supramassive NS; a star with a mass greater than the non-rotating maximum mass but supported from further collapse through rotation (Cook, Shapiro, & Teukolsky Reference Cook, Shapiro and Teukolsky1994).
Around 60% of X-ray afterglow light curves of SGRBs observed by the Swift satelliteFootnote 4 (Gehrels et al. Reference Gehrels2004) have shown plateaus lasting 100–10 000 s after the burst; these have been attributed to EM spin-down emissions from protomagnetars (Rowlinson et al. Reference Rowlinson2010, Reference Rowlinson, O’Brien, Metzger, Tanvir and Levan2013) formed via the merger of two NSs (Dai & Lu Reference Dai and Lu1998; Zhang & Mészáros Reference Zhang and Mészáros2001). Observations of the plateau phase can also be used to constrain the NS equation of state, with GW observations of the inspiral phase significantly aiding this endeavour (Lasky et al. Reference Lasky, Haskell, Ravi, Howell and Coward2014).
If the post-merger remnant is an NS, early optical afterglow as bright as 17th magnitude in R band (assuming a distance of ~ 300 Mpc; see Section 6.2) could be produced from dissipation of a wide-beamed protomagnetar wind Zhang (Reference Zhang2013). This magnetar wind could launch ejecta at relativistic speeds which would interact with the surrounding medium and produce a bright broadband afterglow from synchrotron radiation (Gao et al. Reference Gao, Ding, Wu, Zhang and Dai2013a).
GW emission may also accompany an afterglow plateau if a millisecond magnetar is born from the collision. Multiple mechanisms for generating such GWs exist in nascent NSs, including secular bar modes (e.g. Lai & Shapiro Reference Lai and Shapiro1995; Shibata & Karino Reference Shibata and Karino2004; Corsi & Mészáros Reference Corsi and Mészáros2009a), r-modes (Andersson Reference Andersson1998; Andersson & Kokkotas Reference Andersson and Kokkotas2001), and magnetic-field-induced stellar deformations (Cutler Reference Cutler2002; Haskell et al. Reference Haskell, Samuelsson, Glampedakis and Andersson2008; Dall’Osso et al. Reference Dall’Osso, Giacomazzo, Perna and Stella2015). Such emission could be observable by aLIGO out to ≲ 100 Mpc (Corsi & Mészáros Reference Corsi and Mészáros2009a; Fan et al. Reference Fan, Wu and Wei2013; Dall’Osso et al. Reference Dall’Osso, Giacomazzo, Perna and Stella2015). In fact, the X-ray light curve itself can be used to constrain the total GW emission from these systems (Lasky & Glampedakis, in preparation).
Some plateaus following SGRBs exhibit an extremely steep decay phase, commonly interpreted as the collapse of the nascent NS to a BH (Troja et al. Reference Troja2007; Lyons et al. Reference Lyons2010; Rowlinson et al. Reference Rowlinson2010, Reference Rowlinson, O’Brien, Metzger, Tanvir and Levan2013). Such collapse could potentially produce an FRB when the magnetic field lines snap as they cross the BH horizon (Falcke & Rezzolla Reference Falcke and Rezzolla2014; Zhang Reference Zhang2014), which is expected to occur ≲ 5 × 104 s after the merger (Ravi & Lasky Reference Ravi and Lasky2014). A low-latency GW trigger could enable prompt follow-ups to test this connection (Chu et al. Reference Chu, Howell, Rowlinson, Gao, Zhang, Tingay, Boer and Wen2015).
3.3 Afterglow
As the relativistic jet propagates, it collides with the medium surrounding the progenitor resulting in a forward shock travelling into the surrounding medium, and a reverse shock propagating back up the jet (e.g. Sari, Piran, & Halpern Reference Sari, Piran and Halpern1999; Rees & Meszaros Reference Rees and Meszaros1992). These shock fronts produce multi-wavelength synchrotron emission, initially peaking in the X-ray and moving through the different wavelengths to radio as it fades. The typical afterglow of GRBs is attributed to the forward shock emission and the brightness of this afterglow is dependent upon a number of parameters, including the density of the surrounding medium. Therefore, in a low-density environment, the forward shock component is expected to be relatively faint.
The multi-wavelength afterglows of SGRBs have been observed and are typically fainter than those of LGRBs (Berger Reference Berger2007; Gehrels et al. Reference Gehrels2008; Nysewander, Fruchter, & Pe’er Reference Nysewander, Fruchter and Pe’er2009; Kann et al. Reference Kann2011). This is consistent with SGRBs being less energetic than LGRBs and with their locations in lower density environments. The reverse shock has also been observed for SGRB 051221A (e.g. Soderberg et al. Reference Soderberg2006).
3.4 Kilonova
A ‘kilonova’ is been predicted to form after the merger of two NSs. This faint optical transient is powered by the radioactive decay of the ejected neutron rich matter (Li & Paczyński Reference Li and Paczyński1998; Rosswog Reference Rosswog2005; Metzger et al. Reference Metzger2010) and could reach around 21–23 mag in the optical and 21–24 mag in the near-infrared (NIR) for a source at 200 Mpc (Tanaka & Hotokezaka Reference Tanaka and Hotokezaka2013). Recent optical and NIR follow-up observations of GRB 130603B have provided the most conclusive evidence to date of this scenario, reinforcing the theory that compact object mergers are the progenitors of SGRBs (Tanvir et al. Reference Tanvir, Levan, Fruchter, Hjorth, Hounsell, Wiersema and Tunnicliffe2013; Berger et al. Reference Berger, Fong and Chornock2013). These observations have added significantly to other observational evidence in support of this scenario (Berger et al. Reference Berger2005; Bloom et al. Reference Bloom2006; Berger Reference Berger2009). Coincident EM and GW observations could confirm that SGRBs are indeed the result of coalescing compact binaries.
An additional prompt EM emission related to the kilonova mechanism has also recently been suggested by Metzger et al. (Reference Metzger, Bauswein, Goriely and Kasen2015). This has been inspired by studies that suggest a small fraction of the ejected neutron-rich matter can expand rapidly enough to avoid r-process capture (Bauswein, Goriely, & Janka Reference Bauswein, Goriely and Janka2013). The suggestion is that β-decay from free neutrons in the outermost layers of this ejecta could power optical emission on a timescale of hours after the merger, peaking at around magnitude 22 in the U-band for a source. For a source at 200 Mpc, this signal would peak at around magnitude 22 in the U-band and would act as a precursor to a kilonova.
4 LONG GAMMA-RAY BURSTS AS MULTI-MESSENGER TARGETS FOR GWS
LGRBs are amongst the most-luminous transient events in the Universe in terms of EM radiation per unit solid angle. These beamed emissions have been observed to last up to 104 s (Gendre et al. Reference Gendre2013; Greiner et al. Reference Greiner2015) and can radiate a total energy equivalent to that of the Sun in its entire 10 Gyr lifetime. The extreme luminosities allow LGRBs to be seen out to cosmological volumes, making them a probe of the high-redshift universe (z > 5).
The favoured scenario for these bursts is described by the collapsar model (Woosley, MacFadyen, & Heger Reference Woosley, MacFadyen and Heger1999) in which the inner part of a Wolf–Rayet star progenitor collapses to form a rapidly rotating BH. High angular momentum enables the infalling matter to form an accretion disk, which in turn provides the energy reservoir to power an ultra-relativistic jet that blasts its way through the stellar envelope. The observed radiation is explained through synchrotron and/or inverse Compton emission from the accelerated electrons in internal and external shocks. Some authors have suggested instead that the central engines may consist of magnetars (Usov Reference Usov1992; Duncan & Thompson Reference Duncan and Thompson1992; Bucciantini et al. Reference Bucciantini2009). There is observational evidence to support this scenario for at least a proportion of LGRBs (Metzger et al. Reference Metzger, Giannios, Thompson, Bucciantini and Quataert2011).
The connection between LGRBs with the collapse of massive stars (Woosley & Bloom Reference Woosley and Bloom2006; Hjorth Reference Hjorth2003; Stanek Reference Stanek2003) has been supported by afterglow observations in or near dense regions of active star formation; predominantly dwarf starburst field galaxies (Fruchter et al. Reference Fruchter2006). As mentioned earlier, their denser environments, as well as their higher emission energies, mean that the multi-wavelength afterglows of LGRBs are typically brighter than those that occur from SGRBs (Nysewander et al. Reference Nysewander, Fruchter and Pe’er2009; Kann et al. Reference Kann2011).
In terms of GW emissions from these events, a number of LGRBs have been associated with core-collapse supernova (Hjorth Reference Hjorth2003; Campana et al. Reference Campana2006). Modelling the GW emission from these supernovae is very complex, requiring a combination of general relativistic hydrodynamics, magnetic fields, rotation, neutrino transport, and nuclear physics (Ott Reference Ott2009). Simulations have so far provided a picture of a very complex and chaotic behaviour that includes shock formation and turbulence that create highly complex waveforms with multiple sharp bursts over ms durations. However, most scenarios suggest an event may have to be within tens of kpc for detection. As most LGRBs occur at cosmological distances, the vast majority of their GW signals will be out of reach for advanced detectors.
The requirement for rapid rotation to produce the disc in a GRB (Woosley & Janka Reference Woosley and Janka2005) allows for alternative emission mechanisms that could produce detectable GWs out to tens of Mpc (Fryer & New Reference Fryer and New2011). Fragmentation instabilities could be produced in the core or in the disc (Fryer et al. Reference Fryer, Holz and Hughes2002; Kobayashi & Mészáros Reference Kobayashi and Mészáros2003). Rapid rotation could also give rise to rotational instabilities in the protoneutron star remnant (Dimmelmeier et al. Reference Dimmelmeier, Ott, Marek and Janka2008; Corsi & Mészáros Reference Corsi and Mészáros2009a; Piro & Ott Reference Piro and Ott2011; Piro & Thrane Reference Piro and Thrane2012).
A number of studies have suggested there exists a sub-population of LGRBs known as low-luminosity GRBs (llGRBs). These events have isotropic equivalent gamma-ray luminosities 2–3 orders of magnitude below classical LGRBs (Coward Reference Coward2005; Murase et al. Reference Murase2006; Guetta & Della Valle Reference Guetta and Della Valle2007; Imerito et al. Reference Imerito2008; Howell & Coward Reference Howell and Coward2013) and have only been detected at low-z due to their lower energy emissions (the closest was GRB 980425 at z = 0.0085 or 36Mpc). As such, their rates have been predicted to be 2–3 orders of magnitude greater than LGRBs.
Observations have confirmed that both LGRBs and llGRBs produce supernovae, suggesting that the llGRBs may just be lower-energy events from the tail of the distribution. This has been a long going debate and attempts to address it have used statistical arguments (Soderberg et al. Reference Soderberg2006; Guetta & Della Valle Reference Guetta and Della Valle2007), fits to the peak flux distribution (Pian et al. Reference Pian2006), and simulation (Coward Reference Coward2005; Virgilii, Liang, & Zhang Reference Virgilii, Liang and Zhang2008). The suggestion that llGRBs could be just normal LGRBs viewed off-axis was discounted based on statistical arguments, as it would produce a far higher local rate density than expected from LGRBs and would require narrower opening angles for LGRBs than determined from the breaks in afterglow lightcurves (Daigne & Mochkovitch Reference Daigne and Mochkovitch2007).
Recently, an analysis of llGRB 060218 has suggested that the main difference in the two bursts arises from an extended low-mass envelope in llGRBs (Nakar Reference Nakar2015). The existence of such an envelope can smother the jet and drive a mildly relativistic shock resulting in a much lower luminosity than that produced by an ultra-relativistic jet that is able to penetrate through the bare progenitor star. Interestingly, the statistical arguments suggesting separate populations put forward by Howell & Coward (Reference Howell and Coward2013) can also support these two different scenarios. It is therefore possible that GW emission mechanisms could be driven by the same type of engine for both these classes.
5 GW SENSITIVITY AND NETWORKS
5.1 Instrument sensitivity
The output from a single GW detector consists of a time series data stream, s(t), composed of the detector response to a GW signal, h(t), and the detector noise n(t):
In general, h(t) will be a linear combination of the two orthogonal transverse polarizations, ![]() $h_{+,\times }$, weighted by the dimensionless detector antenna pattern functions for the two polarizations F +, ×:
$h_{+,\times }$, weighted by the dimensionless detector antenna pattern functions for the two polarizations F +, ×:
which describe the detector sensitivity to radiation of different polarisations, incident from different directions (Schutz & Tinto Reference Schutz and Tinto1987; Tinto Reference Tinto1987; Jaranowski, Krolak, & Schutz Reference Jaranowski, Krolak and Schutz1998). The angles, θ and ϕ, represent the direction to the source and ψ is the polarisation angle of the wave.
A GW detector can follow the phase of a GW signal, so the time series is generally represented in the frequency domain by the strain amplitude spectral density, ![]() $\tilde{h}(f)$. This quantity is defined through the power spectral density
$\tilde{h}(f)$. This quantity is defined through the power spectral density ![]() $S_{s}(f)=\tilde{s}^{*}(f)\tilde{s}(f)$, with
$S_{s}(f)=\tilde{s}^{*}(f)\tilde{s}(f)$, with ![]() $\tilde{s}(f)$ the Fourier transform of the time series. Similarly, one can define a signal power spectral density, Sh(f), and a noise power spectral density, Sn(f). The strain amplitude spectral density is given by
$\tilde{s}(f)$ the Fourier transform of the time series. Similarly, one can define a signal power spectral density, Sh(f), and a noise power spectral density, Sn(f). The strain amplitude spectral density is given by
with dimensions of Hz−1/2 (Thorne, Reference Thorne, Hawking and Israel1987). This quantity is often used in plots to display the sensitivity of GW interferometers.
5.2 GW detector networks
A single GW detector cannot determine the polarisation state or source direction of a transient signalFootnote 5. To obtain source localisation, a widely separated network of GW detectors is essential. Such a network may employ techniques such as coincidence analysis, in which individual events from different detectors are correlated in time (Arnaud et al., Reference Arnaud2002), or coherent analysis, in which synchronised detector outputs are merged before searching for a common pattern (Finn, Reference Finn2002). By effectively resolving the different times of arrival of GW events between members of a network, coherent network analysis enables a detector array to become an all-sky monitor with good angular resolution over all source directions.
Achieving good directional sensitivity is of paramount importance for GW/EM associations. For the sources considered in this review, directional sensitivity is determined through triangulation of arrival timesFootnote 6. To maximise the time delays, and hence improve directionality, it is advantageous that a network be as geographically widely separated as possible (Sathyaprakash, Reference Sathyaprakash2004) and as such, a number of detectors are planned to join the aLIGO/AdV network throughout the next decade.
The Japanese observatory KAGRAFootnote 7, should begin operations by around 2018–19 (Kuroda & the LCGT Collaboration, Reference Kuroda2010); at design sensitivity, this detector could improve the directional precision of a aLIGO/AdV network by a factor of 1.5–2 and the detection rate by a similar factor (Fairhurst, Reference Fairhurst2011; Chu et al., Reference Chu, Howell, Rowlinson, Gao, Zhang, Tingay, Boer and Wen2015). LIGO-India operating at aLIGO sensitivity will be added to the aLIGO/AdV network by 2022—by then, BNSs will be detectable out to ~ 200 Mpc and up to 400 events are possible per year (Abadie et al., Reference Abadie2010b). An Indian detector will improve the angular resolution sufficiently to increase the percentage of GW sources detected within 5 deg2 from 3–7% to 17% (Aasi et al., Reference Aasi2013b).
It has long been recognised that a GW detector in Australia would add the longest baseline to the proposed advanced detector network (e.g. Cavalier et al., Reference Cavalier2006; Blair et al., Reference Blair2008; Wen & Chen, Reference Wen and Chen2010). For example, adding an Australian detector to an aLIGO/AdV three detector network can reduce the error in solid angle to tens of arcminutes for high signal-to-noise ratio (SNR) signals (Wen & Schutz, Reference Wen, Schutz, Blair, Howell, Ju and Zhao2012), dramatically improving the ability to localise GW sources for multi-wavelength follow-up observations. This scenario could be realised when third-generation observatories such as the ‘Einstein gravitational wave Telescope’ (ET)Footnote 8 become a reality in the next decade (Hild, Chelkowski, & Freise, Reference Hild, Chelkowski and Freise2008; Hild et al., Reference Hild, Chelkowski, Freise, Franc, Morgado, Flaminio and DeSalvo2010, Reference Hild2011). The optimal site for a detector in the southern hemisphere been shown to be Western Australia (Schutz, Reference Schutz2011), the current home to an 80-m baseline prototype GW detectorFootnote 9.
5.3 The GW false alarm rate
The false alarm rate (FAR) is the rate that false positives appear above a given SNR threshold, and is dependent on the number of glitches (non-stationary transients) in the GW data stream. It is a critical measure as it determines whether a candidate should be considered for follow-up. For well-modelled sources, the background of false alarms is at a level close to that of Gaussian noise. For unmodelled sources—typically short-duration transients—the data quality has a greater effect on detection confidence. One therefore sets the threshold high enough so that noise generated false alarms are negligible. Given that the probability, P(h)dh, of observing an event with an amplitude in the range h to h + dh is given by a Gaussian distribution of standard deviation σ, the probability of obtaining a FAR greater than a given threshold, ρ, is
To be 99% confident that a GW has been detected, one can set an SNR ~ 8 which is equivalent to a FAR of 1 in 100 years of observation (3 × 10−10 Hz). To see this, one can approximate number of noise instances during that period. If the detector output sampling rate is 1 kHz and the output is processed through ~ 103 filters, in 100 years we get P(h|h > z) = (3 × 1015)−1, yielding ρ ~ 8 which is our required SNR (see Sathyaprakash & Schutz, Reference Sathyaprakash and Schutz2009, for a detailed discussion of this argument). For a network of three equivalent detectors combined SNR, ρc is given as
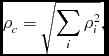 $$\begin{equation}
\rho _{c} = \sqrt{\sum _{i}{\rho ^{2}_{i}}},
\end{equation}$$
$$\begin{equation}
\rho _{c} = \sqrt{\sum _{i}{\rho ^{2}_{i}}},
\end{equation}$$
where ρi represents the SNR in the ith detector (Cutler & Flanagan, Reference Cutler and Flanagan1994). This shows that for a network of three equivalent detectors, to dismiss false alarms at a level 3 × 10−10 Hz requires ρc ~ 12.
6 GRAVITATIONAL WAVES FROM INSPIRALLING COMPACT OBJECTS
6.1 Detection of inspiralling compact objects
The expected GW signals from CBCs takes on the well-modelled chirp form shown in Figure 2. The figure shows how the signal increases in both amplitude and frequency towards merger; as it does so it sweeps across the sensitive bandwidth of advanced GW interferometric detectors.

Figure 2. Top: The predicted chirp waveform of a coalescing compact binary system 40 s before merger. As the signal increases in both amplitude and frequency towards merger, it will sweep across the sensitive bandwidth of advanced GW interferometric detectors. After the merger, the signal will show a ring down phase (not shown in this plot) which will take the form of an increasingly damped sinusoid. Bottom: The final 50 ms before merger.
For such well-modelled signals, the most efficient signal detection method to extract signals from noisy detector data is matched filtering, in which a template, representing the predicted waveform as a function of time is correlated with the output of a detector (Helstrom, Reference Helstrom1968). A matched signal will produce an output much greater than that expected for pure noise with an optimal SNR given as
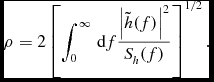 $$\begin{equation}
\rho = 2\left[ \int _{0}^\infty \, \mathrm{d}f\frac{ \left|\tilde{h}(f)\right|^2 }{S_h(f)} \right]^{1/2}.
\end{equation}$$
$$\begin{equation}
\rho = 2\left[ \int _{0}^\infty \, \mathrm{d}f\frac{ \left|\tilde{h}(f)\right|^2 }{S_h(f)} \right]^{1/2}.
\end{equation}$$
For well-modelled sources, matched filtering enhances the value of the signal by a factor ![]() $\sqrt{n}$, where n is the number of cycles used in the integration. As inspiralling systems approach merger, even though the rest frame GW amplitude will increase, the number of cycles in each frequency bin, n = f 2(df/dt)−1, gets smaller; therefore, the detected signal will decrease. This means that for inspiralling systems, rather than solely base the predicted amplitude of the radiation as a true indicator of the detectability, we include a measure of the observed cycles. The value of n increases with the compactness of the system as it approaches merger and if observed from a frequency of 10 Hz until merger, could produce n ~ 104 cycles—effectively improving the detectability by a factor of 100. However, to achieve such gains, a GW data-stream would have to be filtered by a large number of templates (of order ~ 104$–$105) in near real time—the significant challenges in both theoretical modelling and computational efficiency to achieve this cannot be underestimated.
$\sqrt{n}$, where n is the number of cycles used in the integration. As inspiralling systems approach merger, even though the rest frame GW amplitude will increase, the number of cycles in each frequency bin, n = f 2(df/dt)−1, gets smaller; therefore, the detected signal will decrease. This means that for inspiralling systems, rather than solely base the predicted amplitude of the radiation as a true indicator of the detectability, we include a measure of the observed cycles. The value of n increases with the compactness of the system as it approaches merger and if observed from a frequency of 10 Hz until merger, could produce n ~ 104 cycles—effectively improving the detectability by a factor of 100. However, to achieve such gains, a GW data-stream would have to be filtered by a large number of templates (of order ~ 104$–$105) in near real time—the significant challenges in both theoretical modelling and computational efficiency to achieve this cannot be underestimated.
One important aspect of well-modelled inspiralling systems is that a detection can be made tens of seconds before the merger if enough cycles can be detected to boost the SNR (Manzotti & Dietz, Reference Manzotti and Dietz2012; Cannon et al., Reference Cannon2012). Figure 2 illustrates this concept showing a chirp signal 40 s before the merger phase. This scenario could allow a low-latency alert to be sent out to EM facilities as near real-time as possible to catch a prompt EM signature; the combination of EM and GW data in this regime would provide valuable insight into the inner workings of such cataclysmic events.
It is also worth noting that GWs can provide an independent measure of luminosity distance, d L (Schutz, Reference Schutz1986). During the inspiral phase, the GW strain, and the rate of change of GW frequency are given as
where ![]() $\mathcal {M}_z=\left(1+z\right)\mathcal {M}$ is the redshifted chirp mass,
$\mathcal {M}_z=\left(1+z\right)\mathcal {M}$ is the redshifted chirp mass, ![]() $\mathcal {M} = \left( m_{1} m_{2} \right)^{3/5}/( m_{1} + m_{2})^{1/5}$, and m 1, m 2 are the component masses of the binary. Therefore, if one can determine the redshift through, for example, a galaxy association, one can measure the redshift–luminosity distance relation independent of the cosmic distance ladder. A recent series of papers has reinvigorated this topic by introducing novel methods for breaking the redshift-chirp mass degeneracy with future GW observations (Messenger & Read, Reference Messenger and Read2012; Taylor, Gair, & Mandel, Reference Taylor, Gair and Mandel2012; Taylor & Gair, Reference Taylor and Gair2012; Nissanke et al., Reference Nissanke, Holz, Dalal, Hughes, Sievers and Hirata2013; Messenger et al., Reference Messenger, Takami, Gossan, Rezzolla and Sathyaprakash2014).
$\mathcal {M} = \left( m_{1} m_{2} \right)^{3/5}/( m_{1} + m_{2})^{1/5}$, and m 1, m 2 are the component masses of the binary. Therefore, if one can determine the redshift through, for example, a galaxy association, one can measure the redshift–luminosity distance relation independent of the cosmic distance ladder. A recent series of papers has reinvigorated this topic by introducing novel methods for breaking the redshift-chirp mass degeneracy with future GW observations (Messenger & Read, Reference Messenger and Read2012; Taylor, Gair, & Mandel, Reference Taylor, Gair and Mandel2012; Taylor & Gair, Reference Taylor and Gair2012; Nissanke et al., Reference Nissanke, Holz, Dalal, Hughes, Sievers and Hirata2013; Messenger et al., Reference Messenger, Takami, Gossan, Rezzolla and Sathyaprakash2014).
Although matched filtering is the optimal strategy for Gaussian, stationary noise, high-amplitude transients due to instrumental and environmental artefacts can render GW data to be non-stationary and non-Gaussian. Therefore, one must employ robust methods that can reject instrumental artefacts and retain the true GW events.
One such method is the χ2 veto that is a powerful consistency test used to reject false alarms (Allen, Reference Allen2005). This method uses the fact that the quantity ρ is an integral over all frequencies and therefore not sensitive to the contributions from different frequency regions of the broadband signal. One can split the signal spectrum into n bins of equal SNR contribution, and draw a comparison with the expected value in each bin (based on the model template). A true GW event will have power accumulated approximately equally in each of n bins; a noise glitch will have power unevenly distributed and will yield a large χ2 value.
6.2 The detection range and rates of coalescing compact objects
In the GW domain, detector sensitivity is generally based on the detection range of BNSs—the most likely events for detection. The inspiral horizon distance, D H, is the distance to which an optimally orientated and located equal mass binary can be detected with a SNR equal to 8. For a system with reduced mass, ![]() $\mathcal {\mu } = \left( m_{1} m_{2} \right)/( m_{1} + m_{2})$, this distance is approximated as (Singer et al., Reference Singer2014)
$\mathcal {\mu } = \left( m_{1} m_{2} \right)/( m_{1} + m_{2})$, this distance is approximated as (Singer et al., Reference Singer2014)
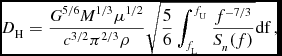 $$\begin{equation}
D_{\mathrm{H}} = \frac{G^{5/6}M^{1/3}\mu ^{1/2}}{c^{3/2}\pi ^{2/3}\rho }\sqrt{\frac{5}{6} \int ^{ f_{{\rm U}} }_{ f_{{\rm L}} } \frac{ f^{-7/3} }{S_{n}(f) } } \rm {d}f \,,
\end{equation}$$
$$\begin{equation}
D_{\mathrm{H}} = \frac{G^{5/6}M^{1/3}\mu ^{1/2}}{c^{3/2}\pi ^{2/3}\rho }\sqrt{\frac{5}{6} \int ^{ f_{{\rm U}} }_{ f_{{\rm L}} } \frac{ f^{-7/3} }{S_{n}(f) } } \rm {d}f \,,
\end{equation}$$
where G is Newton’s gravitational constant, c is the speed of light, M = m 1 + m 2 is the total of the system masses, Sn(f) the power spectral density of the detectors noise curve, and f the signal frequency. The lower limiting frequency of the integral, f L is equal to 10 Hz for aLIGO; the upper limiting frequency can be approximated by the last stable orbit of a Schwarzchild BH, ![]() $4400[\rm M_{\odot }/ (m_{1} + m_{2})]\,\rm {Hz}$.
$4400[\rm M_{\odot }/ (m_{1} + m_{2})]\,\rm {Hz}$.
To calculate approximate values of D H, a simpler approximation is given by
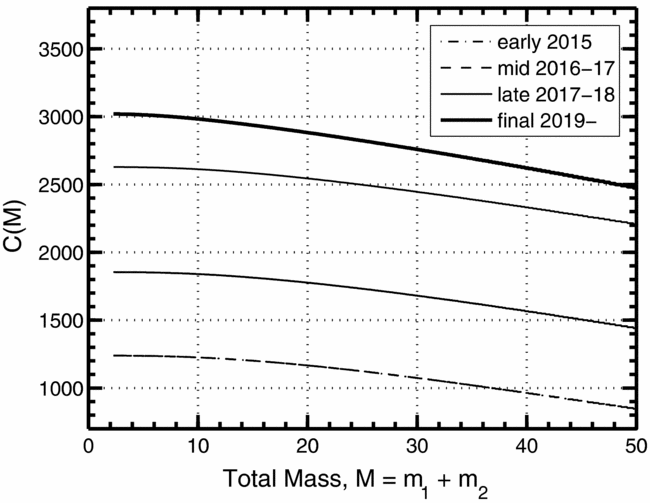
where C(M) gives the value of the integral over Sn(f) in Equation (8) for different M; these are calculated for different observing epochs using the sensitivity curves expected for early aLIGO configurationsFootnote 10. The values of C(M) can then be conveniently read off Figure 3 for the different observing runs of aLIGO/AdV. Tabulated values of C(M) are provided in Table A1.

Figure 3. To easily approximate the maximum detection ranges for different types of coalescing compact objects, values of C(M) given in Equation (9) are provided by the curves for different values of the combined masses. The curves represent the values of the integral in Equation (8) for the different values of upper frequency and for the different aLIGO observing scenarios as shown in Table 1.
An average range can be obtained by scaling D H by a factor 2.26 (Singer et al., Reference Singer2014). This range assumes a uniform distribution of source sky locations and orientations. A standard figure of merit used by aLIGO/AdV is the SenseMon Range which is the average detectable range for two 1.4 M⊙ NSs (Abadie et al., Reference Abadie2010a). An additional scaling is given through the association of a GRB with a face on merger which provides an on-source time in which to search for a GW event; this increases the sensitivity by a factor of 1.5 (and the corresponding rate of events by a factor 3; Schutz, Reference Schutz2011) in comparison with an all-sky/all-time search (Kochanek & Piran, Reference Kochanek and Piran1993); therefore, the average orientation average distance of 197 Mpc (see Table 1) becomes 300 Mpc. Thus, spatially and temporally coincident EM observations enable GW searches to dig deeper into the noise and therefore extend the detection horizon (Was et al., Reference Was, Sutton, Jones and Leonor2012).
Table 1. The expected observing scenarios for the aLIGO/AdV era based on Aasi et al. (Reference Aasi2013b). The available detectors are labelled: H: aLIGO-Handford; L: aLIGO-Livinstone; V: AdV. The aLIGO/AdV detectors will be at design sensitivity by 2019. The expected average ranges for NS/NS and NS/BH inspirals are given in Mpc as well as the horizon distances in parenthesis; these are calculated using Equation (8) along with the sensitivity noise curves for each of the different observing epochs given in https://dcc.ligo.org/LIGO-T1200307 and assuming masses of 1.4 M⊙ and 10 M⊙ for NSs and BHs, respectively. The detection rates are estimated using the calculated horizon distances along with Equation (19) of Kopparapu et al. (Reference Kopparapu, Hanna, Kalogera, O’Shaughnessy, González, Brady and Fairhurst2008) which is valid for horizon distances greater than 50 Mpc; we obtain estimates in agreement with upper range of the plausible estimates given in Abadie et al. (Reference Abadie2010b).

Table 1 shows that by 2016–2017 aLIGO/AdV will be accessible to NS/NS inspirals beyond the Coma cluster (100 Mpc). Beyond 2017, with rates of order 20 yr−1, detections can be expected. The estimates provided in Table 1 assume a realistic event rate estimates for CBC sources (Abadie et al., Reference Abadie2010b); corresponding numbers that assume plausible pessimistic rate estimates can be obtained by scaling the detection rate estimates down by an order of magnitude. Adopting the latter estimates, there is still a reasonable chance of an NS/NS inspiral and merger detection during 2017.
7 GRAVITATIONAL WAVES FROM BURST SOURCES
7.1 Detecting unmodelled burst sources
Transients that are not well modelled due to their highly complex emissions are also targets for GW detectors; many such unmodelled bursts could be associated with LGRBs.
All sky burst searches aim to cast the widest possible net and utilise signal processing algorithms that are as robust as possible; no assumptions are made on the time of arrival, the signals origin or direction. Detection algorithms typically look for signals above a background noise level that are consistent in across multiple detectors; such algorithms often use time–frequency domain methods that look for excesses in time–frequency maps. For example, X-PIPELINE combines data from arbitrary detectors in a network and searches for clusters of pixels with energies significantly greater than background (Sutton et al., Reference Sutton2010). Searches are best employed in networks of detectors using coherent analyses, as described in Section 5.2. By combining amplitude and phase information from separate detectors in a network, the combined GW signal will increase coherently while the uncorrelated noise can be eliminated. The coherent WaveBurst (cWB) is the primary analysis pipeline for identifying burst signals in low latency (Klimenko et al., Reference Klimenko, Mohanty, Rakhmanov and Mitselmakher2005).
7.2 The detection range and rates of burst events
For unmodelled burst sources, the detection strategies are independent of waveform morphology. Therefore, an effective sensitive rangeFootnote 11 for a narrow-band source can be estimated by considering the total energy emitted in GWs assuming a peak emission frequency, f 0, for a given SNR ρ (Sutton, Reference Sutton2013):
One can determine a convenient approximation of D Eff:
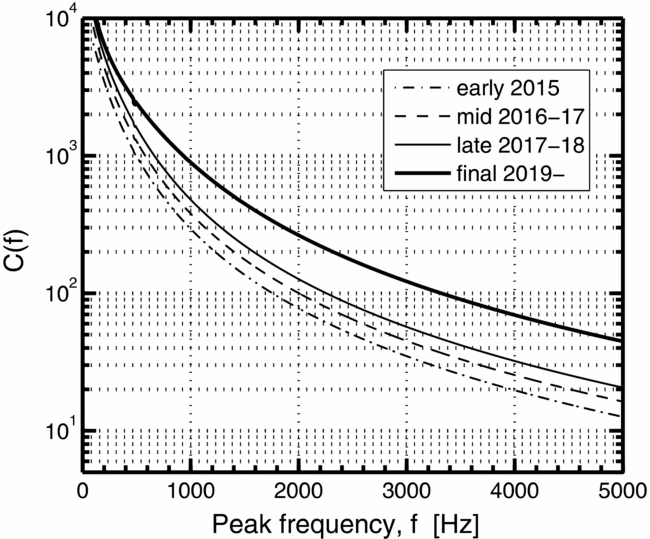
for which, as in Section 6.2, values of C B can be derived using the projected sensitivity noise curves for different epochs of observation for aLIGO. Values of C B can be read from Figure 4 for a given f 0; tabulated values of C B are provided in Table B1.

Figure 4. To easily approximate the maximum detection ranges for different types of GW burst events, the curves of the function CB(f) given in Equation (11) are provided for different values of the peak GW frequency. The curves represent the first two components of Equation (10) and are shown for different aLIGO observing scenarios as shown in Table 1.
Although there is significant uncertainty in these estimations, as will be discussed later in Section 8.1, such approximations can provide constraints on the global parameters of burst populations such as GRBs.
8 GW SEARCHES FROM EM TRIGGERS
GW interferometers typically continuously collect data from all sky directions. Opportunities exist for both close-to-real-time follow-ups of EM events as well as archival searches. In comparison with all-sky searches using just GW data from an entire science run (of the order of months), an EM triggered search can be conducted over a much smaller time window and sky location. There are a couple of significant advantages with this approach:
• A good sky-location enables a search on a portion of the sky with a known antenna pattern sensitivity; this information can allow one to improve the estimation of the GW source parameters.
• The on-source data is a window of data taken a short interval before and after the EM trigger timeFootnote 12. The statistical significance of a GW event in this data segment is determined through a comparison with off-source data taken in a period surrounding the on-source window (to represent the noise properties of the on-source segment). The EM trigger time places tighter temporal constraints on the on-source window in comparison with an all-sky all-time search pipeline (Section 7.1); a lower number of higher amplitude noise artefacts (non-stationary background noise) will be expected in a smaller interval. As shown by equation 4, this also allows the SNR threshold to be lowered.
Numerous archival searches have been carried out using first-generation instruments using events such as GRBs (Abadie et al., Reference Abadie2012b, Reference Abadie2012c; Aasi et al., Reference Aasi2014b) and activity from galactic magneters (Abadie et al., Reference Abadie2011). Although these searches have all produced null results in terms of GW detections, they have enabled the detection procedures for the advanced detector era to be refined as well as providing scientific results. The scientific outcomes of these studies provide an insight into the type of multi-messenger science that could be achieved through the greater detection ranges available in the advanced era. We will describe a few of these below.
8.1 GRB searches
A number of searches have been conducted using LIGO data for coincident GRB events (Abadie et al., Reference Abadie2012b, Reference Abadie2012c; Aasi et al., Reference Aasi2013a; Abbott et al., Reference Abbott2008c; Predoi et al., Reference Predoi and Hurley2012). The recent GRB search of Abadie et al. (Reference Abadie2012b) used 154 GRBs observed during the LIGO and Virgo science runs of 2009–2010 and used both modelled and unmodelled searches in a time-window around the recorded time of the GRB and from the same directions on the sky. For unmodelled bursts, the X-PIPELINE” method was used to conduct a coherent search, assuming an optimistic emission in GWs of order 10−2M⊙ and peak emission frequencies of 150 and 300 Hz. Modelled searches were conducted on the sample of short-duration GRBs by combining the data coherently and using template banks corresponding to probable parameters for coalescing systems of NSs and/or BHs (Harry & Fairhurst, Reference Harry and Fairhurst2011), also yielding exclusion distances—the distance beyond which the source must be to avoid detection. The median exclusion distances were 17 Mpc at 150 Hz for the unmodelled search and 16 Mpc for the modelled.
While no GW events were found, none of the observed GRBs fell within the exclusion distance; the closest to date was the llGRB 980425 at 36 Mpc (z ~ 0.0085). However, in the advanced detector era, null detections will yield exclusion distances useful to constrain models. For example, two llGRBs observed by Swift were at 145 Mpc (GRB 060218) and 264 Mpc (GRB 100316D). Such distances mean that some of the more extreme emission models can be put to the test using GW data.
As discussed earlier in Section 4, following the collapse of a massive star, long-lived ( ~ 10–1000 s) GW bursts may be produced from rotational instabilities in the protoneutron star remnant (Corsi & Mészáros, Reference Corsi and Mészáros2009a; Piro & Thrane, Reference Piro and Thrane2012; Piro & Ott, Reference Piro and Ott2011) or in the resulting accretion disk (van Putten, Reference van Putten2008; Piro & Pfahl, Reference Piro and Pfahl2007). In either case, the signal is expected to be narrow band with a slowly evolving frequency.
Specialised searches for long-lived GW transients associated with GRBs were conducted but have yielded no candidate detections (Aasi et al., Reference Aasi2013a). Sensitivity studies suggest that advanced detectors could detect such signals at distances of 44 Mpc (Thrane & Coughlin, Reference Thrane and Coughlin2014). There are significant theoretical uncertainties, but the rate of long-lived GW bursts may be sufficiently high for detections with advanced detectors (Piro & Thrane, Reference Piro and Thrane2012). EM counterparts might include jet-powered type II supernovae, a luminous red nova-like event, or an ‘un-nova’ (Piro & Thrane, Reference Piro and Thrane2012).
8.2 Individual GRB searches
GW searches based on the short-hard GRBs 051103 and 070201 were able to provide some insight into the hosts and emission mechanisms. In the case of GRB 051103, GW data supported evidence that this event was a giant flare of a Soft Gamma-ray Repeater (SGR) (Ofek et al., Reference Ofek2006; Frederiks et al., Reference Frederiks, Palshin, Aptekar, Golenetskii, Cline and Mazets2007; Hurley et al., Reference Hurley2010). Triangulation by the inter-planetary network (IPNFootnote 13) suggested that the bright short hard GRB 051103 was in the nearby M81 galaxy (3.6 Mpc). Whether it was from an SGRB (its duration was 0.17 s) or an SGR, giant flare was uncertain (Ofek et al., Reference Ofek2006; Hurley et al., Reference Hurley2010). The energy release, ~ 5 × 1048 erg assuming it occurred in M81, is a factor of 10 times brighter than the brightest SGR giant flare observed (SGR 1806-20; Hurley, Boggs, & Smith, Reference Hurley2005; Hurley et al., Reference Hurley2010). Given a typical SGRB energy release of ~ 1050 erg, for an SGRB origin to be compatible, the event could have been a background event to M81 or one would need to invoke a fainter population of short-hard GRBs (Lipunov et al., Reference Lipunov2005; Hurley et al., Reference Hurley2010).
Follow-up GW searches were performed for both modelled (assuming an inspiralling coalescing binary compact object) and unmodelled bursts (assuming events such as an associated star-quake in a magnetar) (Abadie et al., Reference Abadie2012c). Only the former signal would have been detectible at the distance of M81 (Levin & van Hoven, Reference Levin and van Hoven2011; Zink, Lasky, & Kokkotas, Reference Zink, Lasky and Kokkotas2012); the analysis and null result exclude a BNS merger in M81 as the progenitor with 98% confidence. If the event occurred in M81, the analysis supports the hypothesis of an SGR giant flare producing GRB 051103, which is therefore the most distant extragalactic magnetar observed. Similarly, the study of GRB 070201 (Abbott et al., Reference Abbott2008a) observed in M31, provided evidence that this burst did not result from a BNS merger from M31 and is likely to be an SGR giant flare. Given our understanding of SGR giant flares from our own Galaxy, it is statistically unlikely that both GRBs 051103 and 070201 were extragalactic SGR giant flares (Chapman, Priddey, & Tanvir, Reference Chapman, Priddey and Tanvir2009); hence, it is likely that one or both are classical SGRBs from background galaxies.
9 EM FOLLOW-UP OF GW TRIGGERS
There is no doubt that low-latency optical and radio follow-ups of GRB triggers revolutionised the field through the discovery of afterglows in the optical and radio (Costa et al., Reference Costa1997; Bloom et al., Reference Bloom1999). Similarly, the combination of GW emissions, with complementary EM observations would revolutionise the domain of transient phenomena.
One of the main challenges in achieving this will be the source localisations of the order 100 s of deg2 (Wen & Chen, Reference Wen and Chen2010; Fairhurst, Reference Fairhurst2011; Chu, Wen, & Blair, Reference Chu, Wen and Blair2012; Aasi et al., Reference Aasi2013b; Singer et al., Reference Singer2014; Essick et al., Reference Essick, Vitale, Katsavounidis, Vedovato and Klimenko2015). Although the nearly omnidirectional GW sensitivity would enable the detection of close EM sources that may be otherwise missed because of their beamed emissions, the large error regions make coordinated followups particularly challenging.
9.1 The GW detection pipeline
The main objective of the GW detection pipeline is to identify the most statistically significant GW triggers in the data stream, determine the most probable sky positions and relay the information to partner EM observational facilities as fast as possible—the general strategy was previously referred to as LOOC-UPFootnote 14 (Kanner et al., Reference Kanner2008; Shawhan, Reference Shawhan, Peck, Seaman and Comeron2012). The advanced detector era will see significant improvements in speed; and when a forth detector comes on line, coordinate reconstruction. The basic processes involved in sending out GW triggers to EM partners can be generalised as follows:
Low-latency data analysis: For well-modelled CBC signals, matched filtering (see Section 7.1) is applied to the data using a bank of templates; these are based on the most probable ranges of source parameters e.g. component masses, inclination angles etc. Events above a defined SNR are recorded as triggers. Unmodelled burst searches are also conducted using techniques that are designed to detect a wide range of signals.
Position reconstruction: Timing triangulation using the differences in the arrival times at each detector in a network can localise the source on the sky (Fairhurst, Reference Fairhurst2009). At the expense of speed, tighter confidence regions can be determined through more time intensive methods such as coherent analysis. The latter would be beneficial for the optical or radio follow-ups of GRB afterglows.
Host Galaxy identification: As the positional errors are typically larger than the FoV of most EM instruments (typically tens of square degrees), the probability of a successful follow-up can be improved by using catalogues of nearby galaxies and globular clusters to apply statistical weight on individual tiles (typically 0.4° × 0.4°) of an error box (Nuttall & Sutton, Reference Nuttall and Sutton2010; Fan, Messenger, & Heng, Reference Fan, Messenger and Heng2014; Bartos, Crotts, & Marka, Reference Bartos, Crotts and Marka2015). We note that the final aLIGO detection horizon will extend to regions beyond which typical galaxy catalogues have good completeness. Additionally, sources with large galactic offsets could prove problematic (Tunnicliffe et al., Reference Tunnicliffe2014).
FAR estimation: The statistical significance of a GW trigger is given through its FAR already discussed in Section 5.3. The FAR will identify high significance events that should be considered for follow-up. The FAR represents the average rate at which detector noise fluctuations create false positives with an equal or greater value than the detection statistic or SNR. The rate of background triggers it typically estimated by applying a number of artificial time-shifts of varying durations to the data streams of different detectors in a network around the time of the event—the time shifts remove any correlations from possible GW signals. By sampling different alignments of the statistical fluctuations, a measure of the background rate is obtained that sets the value of the FAR around any GW trigger. A typical FAR threshold adopted to send out alerts during O1 is around one event each month of livetimeFootnote 15
Send out VOEvent: To rapidly communicate the information required by EM facilities for follow-up the VOEventFootnote 16 standard will be adopted (Williams et al., Reference Williams, Barthelmy, Denny, Graham, Swinbank, Peck, Seaman and Comeron2012). This is recognised as the standard syntax for fast dissemination of machine-readable information on astrophysical transients. There are currently different implementations of the VOEvent Transport ProtocolFootnote 17 that have been adopted by NASA and ESA space-based observatories including Swift and Fermi and will be used by the Square Kilometer Array pathfinder telescopes, The Low Frequency Array (LOFAR), ASKAP, and MeerKAT. The technical content of a VOEvent alert sent out by aLIGO/AdV for a CBC event should include estimates of the FAR (in Hz), chirp mass the maximum distance (in Mpc); for burst events. content will include central frequency, duration and an estimate of the energy fluence at Earth. Rather than a singular RA/Dec position, the sky position of a GW source will be provided by way of a probability sky map which can be multimodal and non-Gaussian.
9.2 Communicating GW triggers for EM follow-up
If the search pipelines find a candidate signal, it is recorded in the GW Candidate event Database (GraceDBFootnote 18). If its FAR is above threshold, a series of VOEvents are issued. The initial VOEvent will contain only basic information such as the event time, FAR and the GW detectors that have recorded the event. Subsequent VOEvents will contain the information discussed above including skymaps which will provide the probability that the event came from a particular region of sky. The VOEvent will contain a link to the sky map provided in the HEALPixFootnote 19 format. The first skymap will be a rapid localisation skymap determined by the BAYESTARFootnote 20 pipeline (Singer et al., Reference Singer2014). This localisation information can be available within 10 s of seconds after detection (Singer, Reference Singer2015). After further analysis (of order hours), refined full parameter estimation skymaps will be provided using the more rigorous but computationally demanding stochastic samplers in the LALINFERENCE pipelineFootnote 21 that utilises detailed estimates of masses and spins (Berry et al., Reference Berry2015).
The morphology of the skymaps are dependent on the location of the source in the sky relative to the GW detector networks antenna pattern function. Some of the probability maps will consist of a single elongated arc which can cover several hundred square degrees, whilst others consist of two or more degenerate arcs. The degeneracy is a result of the two detector networks limited sensitivity to source polarisation (Schutz, Reference Schutz2011; Klimenko et al., Reference Klimenko2011). Figure 5 shows two example skymapsFootnote 22 typical of that expected from the period 2015–17 which will consist of a two detector network and later a third AdV at lower sensitivity (around 36 Mpc range as compared to around 100 Mpc for the aLIGO instruments). The plot shows both a single mode and a bimodal skymaps which will occur in almost equal numbers during this run.

Figure 5. Typical GW source skymaps expected from science runs between 2015 and 2017. The maps are Mollweide projections in geographical coordinates and show (a) two degenerate arcs totalling 820 deg2 (event ♯10405) and (b) a single elongated arc of 692 deg2 (event ♯790258). Both events have a network SNR of 12.7 and the true location of the events are shown by stars. The skymaps are taken from the website repository http://www.ligo.org/scientists/first2years/.
We note that for two-detector detections during this period both the BAYESTAR and stochastic sampler pipelines are expected to produce compatible localisation regions (Singer et al., Reference Singer2014; Berry et al., Reference Berry2015). For the case of 2016–17 with three-detectors in operation, triggers in all three instruments can provide confidence regions of tens of degrees, although this will occur in less than 17% of events (Singer et al., Reference Singer2014). If AdV records an SNR less than 4, as BAYESTAR only considers triggers above SNR = 4, it will ignore the third instrument; in this case the stochastic sampler could provide an improved estimate, with up to 50% smaller area, although within hours latency rather than seconds. By 2019, with aLIGO and AdV running at design sensitivity, up to 25% of coalescing binary sources are expected to be localised within 20 deg2 (Aasi et al., Reference Aasi2013b).
To fully exploit the scientific promise of rapid GW triggered follow-ups, the signal processing will have to be conducted as close to real time as possible (low latency). This a tremendously complex task and is highly computationally demanding. A number of pipelines have been proposed and tested (Abadie et al., Reference Abadie2012a; Buskulic et al., Reference Buskulic2010; Cannon et al., Reference Cannon2012); this has been a particular focus for Australian facilities (Luan et al., Reference Luan, Hooper, Wen and Chen2011; Hooper et al., Reference Hooper, Chung, Luan, Blair, Chen and Wen2012). Pipelines are presently able to make detections in under a minute (Urban, personal communication), but the effort to get this down to as low as possible will continue throughout the GW multi-messenger era.
10 AUSTRALIA’S ROLE IN GRAVITATIONAL WAVE ASTRONOMY
10.1 The first follow-up programme: 2009–2010
The first EM follow-up of GW triggers was performed during 2009–2010Footnote 23 using the low-latency pipelines cWB, Omega, and MBTA (see Abadie et al., Reference Abadie2012d). GW data from the LIGO/Virgo network was calibrated and sent to the LIGO computing centre at Caltech for analysis within a minute. Although triggers were generated within 6 min, additional manual checks were performed to further verify the data quality and conditions at each detector site—these latter steps extended the total latency to around 10–30 min for each alert. As mentioned in Section 10.1, the strategy in this pilot study was referred to as LOOC-UP (Kanner et al., Reference Kanner2008; Shawhan, Reference Shawhan, Peck, Seaman and Comeron2012).
A total of 10 EM instruments were employed for LOOK-UP including Swift, LOFAR, ROTSE, TAROT, QUEST, the Liverpool Telescope, PTF, and Pi of the Sky; Australian participation was provided in the optical through SkyMapper (Keller et al., Reference Keller2007) and the Zadko Telescope (Coward et al., Reference Coward2010). Both instruments responded to GW triggers at a rate of around one per week, with nine and five tiles per trigger respectively; in total eight alerts were followed up (Aasi et al., Reference Aasi2014a). The main latency bottleneck during LOOK-UP was the manual checks on data quality and conditions. To allow alerts to be sent out significantly faster, automation was highlighted as an important prerequisite for coincident detection in the advanced detector era.
10.2 Multi-messenger astrophysics during the advanced detector era
The number of Australian facilities with involvement has increased for the advanced detector era. In addition to Zadko and SkyMapper, a number of other instruments have MoUs with the aLIGO/AdV event follow-up programme. The full complement is given in Table 2, along with their relevant specifications.
Table 2. The properties of a selection of the Australian instruments with MoUs in place for aLIGO/AdV follow-ups [1] Tingay et al. (Reference Tingay2013); [2] Murphy et al. (Reference Murphy2013); [3] Tinney et al. (Reference Tinney, Moorwood and Iye2004); [4] Keller et al. (Reference Keller2007); [5] Coward et al. (Reference Coward2010); [6] http://goto-observatory.org/; [7] Lennarz et al. (Reference Lennarz, Chadwick, Domainko, Parsons, Rowell and Tam2013); [8] Acharya et al. (Reference Acharya2013); Bartos et al. (Reference Bartos2014). ♭ Approximated using Figure 5 of Funk, Hinton, & CTA Consortium (Reference Funk and Hinton2013a). † Sensitivity in survey mode based on Bartos et al. (Reference Bartos2014). Exposure time includes an estimate of the required slewing times to tile a 1000 deg2 area using convergent pointing mode.

In the following sections, starting from low-energy observational instruments up to high energy, we discuss these different facilities and their potential contribution towards the multi-messenger era. As discussed in Section 9.2, the greatest challenge that will face EM facilities will be contending with the large error regions which could often consist of two or more degenerate arcs—we cannot be certain of the exact error regions we will have to overcome. We can however consider two epochs in the following:
Early epoch: This epoch includes the early and mid observing runs from 2015 to 2017 as given in Table 1. The median error regions will be in the range 230–500 deg2 (Singer et al., Reference Singer2014)–we conservatively adopt the larger value of 500 deg2 for our approximations. Near the end of this epoch, as AdV joins the two aLIGO detectors, one could expect to observe less than 12% of sources within 20 deg2 (Aasi et al., Reference Aasi2013b), but it is safe to assume that the vast majority of the expected small sample of detections will have error regions of order 100 s of deg2.
Late epoch: During this epoch, aLIGO and AdV will be approaching design sensitivity. One can now expect of order 10–30% of the detections to be localised within 20 deg2 (Aasi et al., Reference Aasi2013b). Chu et al. (Reference Chu, Howell, Rowlinson, Gao, Zhang, Tingay, Boer and Wen2015) have shown that assuming a three detector aLIGO/AdV network 100% of sources can be localised within 50 deg2—we will therefore conservatively adopt this value. We note that the inclusion of KAGRA in 2018–19 could improve the situation in terms of localisation; Chu et al. (Reference Chu, Howell, Rowlinson, Gao, Zhang, Tingay, Boer and Wen2015) further show that including this detector to expand the aLIGO/AdV network will allow 100% of sources to be localised to within 30 deg2.
10.3 The radio domain
10.3.1 Radio facilities for follow-ups of GW events
Australian investment in radio facilities and infrastructure has been complemented in recent years by advances in high-speed computing. These new instruments promise a rich era of transient detection by virtue of their wide field-of-view (FoV), high sensitivity, and the ability to respond from sub-seconds up to within a minute. Two Australian facilities have signed MoUs with the aLIGO/AdV Event Follow-up programme: the MWA (Tingay et al., Reference Tingay2013) and ASKAP (Johnston et al., Reference Johnston2007).
The Murchison Widefield Array: The MWA is a low-frequency radio telescope operating between 80 and 300 MHz and located at the Murchison Radio-astronomy Observatory in Western Australia (Tingay et al., Reference Tingay2013). The very large FoV of 610 deg2 at 150 MHz and the use of electronic steering make this facility well suited for GW followups. The MWA can start collecting data within 10 s of receiving a GW announcement, and additional strategies can be used to survey larger FoVs at reduced sensitivity if needed (Chu et al., Reference Chu, Howell, Rowlinson, Gao, Zhang, Tingay, Boer and Wen2015). Processing at the start of aLIGO/AdV operation should produce results within 24 h; this latency could eventually be reduced to less than 1 h.
Australian Square Kilometre Array Pathfinder: ASKAP consists of an array of 36 × 12 m diameter antennas with phased-array feeds in Western Australia. The array can cover an instantaneous FoV of 30 deg2, with a resolution of 10–30 arcsec, 300-MHz bandwidth, and a frequency range of 0.7 to 1.8 GHz. Early science is expected to start in mid-2016. The ASKAP survey for Variables and Slow Transients, VAST (Murphy et al., Reference Murphy2013), is a survey science programme that will conduct both custom surveys and run commensally with other survey observations. The VAST pipeline will operate on an imaging cadence of 5–10 s at the fastest, down to cadences of minutes depending on the available supercomputing resources. Repeated observations of selected fields can allow longer cadences up to hours–months. Once completed, ASKAP will operate in autonomously mode with ToO response times of order minutes.
Another project that also will have the capability to perform EM follow-ups in the future will be the ASKAP survey for transients on timescales shorter than the correlator integration time. The Commensal Realtime ASKAP Fast Transient (CRAFT) Survey (Macquart et al., Reference Macquart, Bailes and Bhat2010) performs exactly this task with a commensal survey for fast ( < 5 s) transient sources, with ASKAP. The extragalactic burst detected by Lorimer et al. (Reference Lorimer, Bailes, McLaughlin, Narkevic and Crawford2007), with a 30 Jy pulse of 5 ms width, provided the first hint of the existence of a previously unknown class of astronomical objects waiting to be discovered. The CRAFT objective is to use the large FoV made available by ASKAP (30 deg2), combined with its excellent sensitivity and resolution, to provide a uniquely capable instrument for both the detection of fast transients and for providing accurate locations to a few arcseconds of those events.
10.3.2 Coordinated radio observations of GW triggers
For follow-ups in the radio band, the wide FoV of both MWA and ASKAP will be well suited to cover the large GW error region rapidly. The implementation of VOEvent triggering and the fast response times of both these instruments will have great benefits for prompt low-latency follow-ups. Once initial localisation has been achieved other radio telescopes such as the Australia Telescope Compact Array (ATCA) will be valuable for further follow-up. The ATCA has a broadband backend (CABB; Wilson et al., Reference Wilson2011) and a rapid response capability through the its Target of Opportunity and NAPA programmes.
During the early epoch, the larger FoV of MWA will be well suited for low-latency follow-ups as the large GW error region to be surveyed quickly (Chu et al., Reference Chu, Howell, Rowlinson, Gao, Zhang, Tingay, Boer and Wen2015); in fact, the delays of the low-latency GW analysis may end up dominating the timeline for the MWA, and could limit the types of signals that can be seen. If there is sufficient significance, then a prompt GW alert from before an NS merger could allow MWA to get on-source and prove any association between these events and FRBs. Other than FRBs, MWA will be sensitive to any prompt, coherent emission processes that could accompany SGRBs. A particular advantage of MWA’s low-frequency bandpass is that it any signal will be further delayed through dispersion as it propagates through the ionised intergalactic/interstellar medium. The advantages of this strategy for low-latency follow-ups are clear and have been discussed in Chu et al. (Reference Chu, Howell, Rowlinson, Gao, Zhang, Tingay, Boer and Wen2015); this additionally adds astrophysical information about the host galaxy and the intergalactic medium (e.g., Ioka, Reference Ioka2003; Macquart & Koay, Reference Macquart and Koay2013).
At shorter wavelengths, transient sources that could be accessible by ASKAP could include synchrotron radiation produced through ejected material being accelerated by a magnetar wind (Section 3.2) or through the reverse shock (Section 3.3). For ASKAP, early follow-ups will only be possible during the late epoch with error regions in the tens of deg2. Although prompt follow-up observations of early engine activity of GW triggers will be challenging for ASKAP during the early epoch, the 30 deg2 FoV can provide good coverage of GW error regions for later time follow-ups. In the GHz regime surveyed by ASKAP, there have been observations of late-time radio afterglow components from GRBs (see for example, Fong et al., Reference Fong2014) of order hours after the burst. The FoV of ASKAP means that this instrument could return to the same field multiple times to capture the early onset of the light curve to constrain properties of the merger and the local environment.
The observing strategy for CRAFT is to detect any dispersed transient in the total power signal (which is sensitive to the whole 30 deg2 FoV of the telescope) and, after detection, download the raw data from a circular buffer for correlation offline with high temporal resolution. Such a system is compatible with searches based on external triggers from GW detections, if the telescope happened to be pointing in the correct direction. The CRAFT project is 100% commensal and would be running continuously during all observations. For such a scheme to be successful, the GW trigger would need to be communicated to the ASKAP telescope before the circular buffer was overwritten; the current specification of the buffer is for 2 GB DIMMs, which can provide up to a 40 s buffer. However, the FoV of the ASKAP telescopes mean that such a detection is possible but not likely, and CRAFT is mostly likely to contribute with high time resolution observations during follow-up. The dispersion delay for a signal with a DM of a few 100 at 700 MHz (corresponding with a aLIGO range of 200–450 Mpc), compared to the arrival of the GW, would be of order 2–3 s. Even by the late epoch, we could not expect such triggering speeds on ASKAP, but for the lower frequency MWA or SKA-low, a longer dispersion delay ( ~ 40 s @150 MHz) would prove valuable for low-latency follow-ups.
The inclusion of the multi-messenger capability to detect and locate very short time scale signals will be an important and unique contribution from the Australian astronomical community. Signals on sub-second timescales would be expected from coherent emission processes at the frequencies covered by ASKAP (Cordes, Lazio, & McLaughlin, Reference Cordes, Lazio and McLaughlin2004), therefore would represent the direct detection of the GW event, not that of the following ‘fireball’. Recent analysis argues that these will be detectable out to very high redshifts (Lorimer et al., Reference Lorimer, Karastergiou, McLaughlin and Johnston2013; Macquart & Koay, Reference Macquart and Koay2013); however, the origins and actual physics involved are still so unsure all these arguments are purely conjectural and the answers will come from observations.
Event candidates detected by the ASKAP and MWA pipelines will eventually be distributed in near-real time using the VOEvent standard. The faster an EM counterpart can be communicated to the wider community, the greater the opportunity for observations at higher energies when optical/X-ray counterparts may still be detectable.
The significance of any apparent counterpart will have to undergo evaluation for false coincidences. The transient surveys carried out my MWA and ASKAP will be invaluable in this regard. For example, transients observed by the MWA can be evaluated by using a background rate of transient/variable objects (Bell et al., Reference Bell2014). Such rates can be determined though observations of the sky spanning thousands of deg2 over many cadences (minutes to years). In addition, for MWA sets of high-quality reference images taken as part of the GaLactic and Extragalactic All-sky MWA (GLEAM) survey (Wayth et al., Reference Wayth2015) can act as an important sky template for the study of transient radio sources. Overall, the rate of astrophysical radio transients is rather low compared to the optical sky (e.g. Metzger, Williams, & Berger, Reference Metzger, Williams and Berger2015; Rowlinson et al., in preparation), so that although care must be taken to eliminate instrumental artefacts (Frail et al., Reference Frail, Kulkarni, Ofek, Bower and Nakar2012), false coincidences will be rare and follow-up effort can be allocated accordingly.
ASKAP and MWA will be detecting and archiving large amounts of transient data with core use of such data for multi-wavelength/multi-messenger follow-up searches for counterparts. Therefore, Australian radio facilities can also make a contribution to supplying data for archival GW follow-up searches. Such transient searches will follow the same procedures as that of the burst searches for GRB triggers outlined in Section 8.1. GW data streams will be routinely archived allowing early searches around the time of EM triggers, followed by broader archival searches. An archival search can allow one to dig deeper into the GW data stream as an EM trigger provides information of both the sky location and the time of the event. As shown in Section 8, the FAR will increase with a longer on-source time window, making timing information important. One potential problem is that the timing differentials for different emission mechanisms will have to be well understood; at present, for most sources the expected emissions in the EM domain are quite uncertain. A particular challenge will be to set up automated classification algorithms to catalogue different category of source (e.g. Richards et al., Reference Richards, Starr, Butler, Bloom, Brewer, Crellin-Quick, Higgins, Kennedy and Rischard2011; Farrell, Murphy, & Lo, Reference Farrell, Murphy and Lo2015).
10.4 The optical domain
10.4.1 Coordinated observations of GW triggers with optical telescopes
In the optical, both deep, wide-field instruments and rapidly slewing robotic instruments will have an important role to play. Australia has four facilities that are registered as EM partners to aLIGO/AdV: SkyMapper and Zadko conducted follow-ups during the initial LIGO programme (2009–2010). The Australian facilities will be expanded to include the Anglo-Australian Telescope and a new telescope dedicated to GW follow-up, GOTO. We provide a snapshot of these facilities below:
The Anglo-Australian Telescope (AAT): AAT is a 4-m telescope located at Siding Spring Observatory in NSW, Australia. The AAT has a broad instrument suite, spanning low to high resolution single-object and multi-object optical spectroscopy, as well as NIR imaging and spectroscopy. The use of optical fibres allows its Two Degree Field (2dF) multi-object system to obtain up to 392 spectra simultaneously from objects within a 2 deg2 FoV. In terms of co-ordinated observations on GW targets, the smaller FoV of the AAT means that the most profitable scenario would be through followup observations of already localised EM signatures. Spectroscopy could be performed if the AAOmega and HERMES instruments were available; both these instruments are fed by the 2dF. This latter scenario would require a delay of up to 1 h to allow for counterpart confirmation and instrument fibre reconfiguration (Lidman, personal communication). Short exposures could be performed without guiding; longer exposures would require guiding but could be achieved using just two fibres (one guide and one object fibre). NIR imaging can also be conducted using the IRIS2 instrument (Tinney et al., Reference Tinney, Moorwood and Iye2004); this allows for imaging over a 7 arcmin2 FoV, long-slit spectroscopy and multi-object spectroscopy.
The GW Optical Transient Observer (GOTO): GOTO is a proposed network of robotic wide-field ( ~ 36–72 deg2) optical telescopes to be situated at La Palma, in the Canary Islands, and a yet-to-be-determined Australian site. Phase 1 of the project (denoted here as P1), supported primarily by Monash and Warwick Universities (as well as Leicester, Sheffield, and Armagh universities in the UK) will deploy a prototype with 18 deg2 FOV (half that of the full-scale instrument) beginning in late 2015, to demonstrate the feasibility of the approach. The full-scale instrument will be capable of surveying the entire sky every night and is intended to trigger on GW alerts in real time. A particular goal is to identify candidate transients rapidly in order to trigger other facilities for deeper photometric follow-up and spectroscopic characterisation. The initial configuration will consist of an ~ 18 deg2 FoV array in La Palma, Spain, capable of reaching 21 mag in 5 min (depending on moon phase). To cover the GW error areas in sufficient time, this initial configuration could image at a shallower 20–21 mag, allowing a few hundred degrees to be surveyed in around 30 min. The initial design is scalable and the final configuration will include a second instrument in Australia (denoted here as phase 2, or P2) with 36–72 deg2 instantaneous FoV (the larger value for two domes on each site) allowing rapid coverage of GW error ellipses (Steeghs & Galloway, personal communication).
The SkyMapper telescope: SkyMapper, located at the Siding Spring Observatory in Australia, is a 1.35-m fully autonomous optical telescope with a 5.7 deg2 FoV and equipped with a 268-million pixel CCD array. Its main role is to carry out the Southern Sky Survey (Schmidt et al., Reference Schmidt, Keller, Francis and Bessell2005; Keller et al., Reference Keller2007); however, a significant component of the SkyMapper science programme involves observations of optical transient phenomena. In particular, the SkyMapper Supernova Search, a low-redshift rolling optical survey commencing in 2015, is expected to discover a wide range of optical transients, including Type Ia supernovae for next generation cosmology. The GW follow-up programme will benefit from the team’s expertise in transient searches. GW triggers received by SkyMapper will take priority over other observations and images will be processed through the transient detection pipeline already developed for the supernova search. Whenever available, images taken as part of the Southern Sky Survey (2015–2018) will serve as pre-detection template. The significance of any optical counter part will be accessed using coincident rate calculated from the supernova search.
The Zadko Telescope: Zadko is a 1-m fully robotic instrument with a 23-arcmin FoV located in Gingin, Western Australia. Along with the TAROTFootnote 24 network of fast response telescopes, this instrument has operated successfully as part of a network (CADOR) undertaking automated optical follow up of Swift alerts (to m ≈ 21) since 2009. It has a core science theme of photometry of rapid time varying sources and it is the most successful Australian-operated facility for GRB afterglow light-curve studies. For GW follow-up, Zadko will be part of a larger network: the TAROT - Zadko - National Aures Observatory Network (TZA). The TAROT network comprises two identical 25-cm, 1.86 deg2 robotic telescopes located at Mt Calern in Southern France and ESO La Silla Observatory, Chile. All TAROT telescopes will share a common operating and data processing system. The Algerian National Observatory (Aures) may be operational from 2017 and will comprise of several 50–60 cm telescopes.
10.4.2 Coordinated optical observations of GW triggers
The relative sparsity of automated telescopes in the Southern hemisphere implies that instruments such as AAT, GOTO, SkyMapper, and Zadko can play an important role in GW follow-ups. This bias has been seen in the sky distribution of Swift triggered GRB optical afterglows (see for example, Figure 5 of Coward et al., Reference Coward2010). For the case of GRBs, this can hamper the sampling of light curves that last order ~ hours. Hence, both the longitude and latitude of the Australian optical facilities fill a niche space for follow-up.
In Figure 6, we examine the performance of the larger FoV Australian instruments shown in Table 2 (we have omitted AAT due to its smaller FoV) in terms of obtaining the optical afterglow of an SGRB associated with a NS/NS merger. The general formalism is given in Coward et al. (Reference Coward, Branchesi, Howell, Lasky and Böer2014) and considers a measure of the decay of the afterglow with time and a derived luminosity function. The plot is a good illustration of the capabilities of different instruments for rapid response follow-ups. The plot shows that in terms of GW follow-up of SGRBs associated with NS mergers, the first configuration of GOTO (assuming an exposure time of ~ 7.5 min for Phase 1 and 2 instruments) will be comparative with that of SkyMapper; both are well equipped for follow-ups and can achieve efficiencies of the order of 80–90% that of facilities such as BlackGEM (Ghosh & Nelemans, Reference Ghosh and Nelemans2015), Pan-STARRS (Hodapp et al., Reference Hodapp and Oschmann2004), and ZTF (Smith et al., Reference Smith, Ramsay, McLean and Takami2014). Zadko performs well in comparison to the fast response and wider FoV TAROT telescopes because of its sensitivity (TAROTs limit is 18 mag in the R-band and it has a FoV of 3.5 deg2).

Figure 6. A density plot of coincident GW-Optical detection efficiency to recover an SGRB (fading) optical afterglow in the imaging time versus telescope limiting magnitude plane. This plot, adapted from Coward et al. (Reference Coward, Branchesi, Howell, Lasky and Böer2014), shows the Australian optical instruments that have MoUs in place for aLIGO/AdV follow-ups. The total imaging time is the product of the number of tiles required to cover a uniform GW error box for a particular instruments FoV and exposure time. The efficiency, shown by the shaded regions is calculated by considering an optical afterglow luminosity function for SGRBs coupled with limiting magnitude and total imaging time of each instrument. We show results for two scenarios: early epoch (lhs: 500 deg2) and late epoch (rhs: 50 deg2). The Australian facilities Zadko and SkyMapper as well as GOTO (Phase 1, P1 and Phase 2, P2 which will include a second instrument in Australia), Pan-STARRS, BlackGEM and ZTF; three facilities expected to perform with high efficiency in follow-ups during the advanced detector era—their imaging [time/limiting magnitude] combinations result in their performance being far better the assumed parameter space shown for the late epoch. The efficiencies can be scaled by the expected detection rates and other caveats related to follow-up. We note that GOTO (both P1 and P2) and SkyMapper can make an important contributions to the follow-up programme in both epochs. Zadko can make a niche contribution during the latter stages of the advanced detector era as the error regions and detection rates improve.
We note here the coincident detection efficiencies considered in this section ignores a number of other factors including crowded star fields in the Galactic plane and Galactic dust obscuration. Other factors include expertise in dealing with false positives and the ability to apply optimum tiling strategies—it does however supply a gauge of how well Australian optical facilities can compete in this area.
Follow-up searches for optical r-process kilonova detections could also play an important role in the multi-messenger era. For a source at 200 Mpc, the predictions of Tanaka & Hotokezaka (Reference Tanaka and Hotokezaka2013) suggest that the flux should reach around 21–23 mag in the optical and 21–24 mag in the NIR JHK bands (in AB magnitudes). Although the AAT would seem well suited to NIR follow-ups, the small FoV of this instrument may make detections difficult for the large error box of a aLIGO/AdV network (10–100 deg2 ). However, this instrument could be useful as part of a hierarchical strategy, providing deep follow-up of targets obtained from a larger FoV telescope. The large FoV of SkyMapper is well suited but would require an event with m < 21 mag. The final configuration of GOTO ( m = 21 mag with a large FoV (18–38 deg2) suggests this facility could be efficient for follow-up. In fact, dedicated instruments with a wide FoV such as GOTO should play an important role in the multi-messenger era as the first stage of a coordinated follow-up strategy, refining positions for smaller FoV EM instruments.
10.4.3 Future instruments for GW follow-ups
Looking towards 2016 and beyond, there are other projects with Australian involvement that can contribute to the GW follow-up programme. A new imaging system optimised for low-surface brightness imaging, called HuntsmanFootnote 25, will be based at Siding Spring Observatory. The system consists of an array of Canon telephoto lens based upon the Dragonfly Telephoto Array design (Abraham & van Dokkum, Reference Abraham and van Dokkum2014). With multiple apertures, the system can be automatically configured for shallow imaging over large FoVs or else deep 2x3 deg2 imaging taken with multiple cadences. The response time for a trigger will be a few minutes. The shallow wide-field mode will have an initial FoV of 24 deg2 and will be available from early 2016. It will be upgraded to a field of at least 60 deg2. With 143 mm aperture lenses, the depths in the r′-band are approximately 18 AB mag with 9-min exposures for the shallow field; for 60-s exposures, the depth is 16.8 AB mag.
The ‘Deeper Wider Faster’ project will target simultaneous, fast cadenced observations with optical and radio facilities (Andreoni et al., in preparation). The same region of the sky will be observed in the time-domain with the Dark Energy Camera (DECam; Diehl & Dark Energy Survey Collaboration, Reference Diehl2012; Flaugher et al., Reference Flaugher, McLean, Ramsay and Takami2012), a wide-field optical imager mounted at the prime focus of the Blanco telescope at CTIO, along with the Parkes (Manchester et al., Reference Manchester2013) and Molonglo Observatory Synthesis Telescope (MOST; Mills, Reference Mills1981) in Australia and the Swift satellite. The programme takes advantage of the unique “deep, wide, and fast” capability of DECam reaching a depth of ~ 23.8 mag (g filter) in 20 s and readout time of 17 s with 62 CCDs covering a FoV of ~ 3 deg2 per pointing.
Optical and radio data can be processed and analysed in real time to trigger the UV and X-ray instruments mounted on Swift Footnote 26 to guarantee fast follow-up. These triggers allow other optical facilities to spectroscopically characterise the discovered transients via a rapid ToO request programme with the Gemini observatory.
‘Deeper Wider Faster’ aims to unveil the optical counterparts to FRBs, along with the discovery of rare and fast (evolving on timescales of seconds to hours) optical transients. Some of these fast transients could be associated with putative GW emitters, some of which have been discussed in Section 3: they include the shock breakouts of nearby core-collapse supernovae (e.g. Nakar & Sari, Reference Nakar and Sari2010), kilonovae (Metzger & Berger, Reference Metzger and Berger2012; Tanvir et al., Reference Tanvir, Levan, Fruchter, Hjorth, Hounsell, Wiersema and Tunnicliffe2013), GRB prompt/early optical emission (Vestrand et al., Reference Vestrand2014; Fox et al., Reference Fox2003), and ‘orphan’ GRBs (Ghirlanda et al., Reference Ghirlanda2015). Some models (e.g. Falcke & Rezzolla, Reference Falcke and Rezzolla2014) argue that FRBs themselves can generate GW radiation.
The programme has the capability to identify and reject contaminants in the search for EM counterparts to GWs, such as distant supernovae, stellar flares, tidal disruption events or uncatalogued Active Galactic Nuclei. The project is being led by Swinburne University and is setting up an MoU with the LIGO/Virgo GW collaboration to undertake EM follow-up.
10.5 Ground-based follow-ups in gamma-rays
10.5.1 Very high energy gamma-ray telescopes for the advanced GW detector era
At gamma-ray energies from the ground, follow-up observations are possible through Imaging Atmospheric Cherenkov Telescopes (IACTs). These instruments are able to detect gamma-ray photons in the few tens of GeV to 100 TeV range. They operate by imaging the very short (nanosecond duration) flashes of Cherenkov radiation that result from cascades of relativistic charged particles (known as air-showers) produced when very high-energy (VHE) gamma-rays strike the earth’s atmosphere. A particular target for these instruments will be gamma-rays from SGRBs which are expected as a result of the > GeV emission recorded by Fermi-LAT (see Section 4.1). There are two such facilities with active Australian participation: H.E.S.S. and CTA. A key feature of these telescopes is their huge instantaneous collection area ( > 104 m2). Flux sensitivities at least a factor 1 000 times better than Fermi-LAT can therefore be achieved over short observations (seconds to hours) in the ~ 20 to 100 GeV energy range where GRBs are likely to be detected from the ground (Funk et al., Reference Funk and Hinton2013a).
The High Energy Stereoscopic System (H.E.S.S.): H.E.S.S.Footnote 27 is an array of five Cherenkov telescopes (with 4 × 12 m and one 28 m diameter mirrors) located in Namibia for TeV or VHE gamma-ray astronomy. H.E.S.S. has been operational since 2004 with the fifth larger telescope joining in 2013. The latter instrument lowered the observable energy range from 100 GeV to a few tens of GeV and has a rapid slewing capability improving the mean time to go from a random observation position down to about 30 s (Lennarz et al., Reference Lennarz, Chadwick, Domainko, Parsons, Rowell and Tam2013).
The Cherenkov Telescope Array: CTA (Acharya et al., Reference Acharya2013)Footnote 28 is a next generation ground-based instrument that will improve over previous experiments such as H.E.S.S, VERITAS,Footnote 29 and MAGICFootnote 30 with increased sensitivity, angular resolution, FoV over a wider energy range. The project will consist of two arrays: a southern hemispheric array focusing on Galactic sources and a northern hemispheric array on extragalactic. These will be formed from Cherenkov telescopes of three different sizes; large (23 m diameter), medium (12 m) and small (6 m) size telescopes, offering wide area, and energy coverage. An Australian collaboration of six universities led by the University of Adelaide has committed to this project and will contribute expertise through the analysis of CTA data including contributions to the atmospheric calibration. Access to all levels of CTA data will enable Australian collaboration members to contribute towards the GW follow-up programme.
10.5.2 Coordinated observations of GW triggers at high-energy gamma-ray
The capabilities of H.E.S.S. for GW follow-ups has been demonstrated through prompt observations of GRB triggers since 2003— one of the prime targets for H.E.S.S., and even more so now with the lower-threshold 28-m telescope. The fastest follow-up observation was achieved within 7 min after the burst (GRB 070621; Aharonian et al., Reference Aharonian2009). In addition, one burst GRB060602B was fortuitously in the H.E.S.S. FoV on receipt of the trigger (although this may be a galactic transient) and also GRB 100621A was observed within 10 min.
The wide FoV of CTA will be highly beneficial for GW follow-up allowing the error region to be tiled reasonably rapidly (Bartos et al., Reference Bartos2014). CTA’s sensitivity (up to a factor 10 better than H.E.S.S.) is expected to guarantee high statistics studies of GRBs well into the multi-GeV regime on minute-wise timescales (Inoue et al., Reference Inoue, Granot and O’Brien2013). The CTA is designed to respond to GW alerts by triggering its lowest-threshold telescopes with an expected response of ⩾ 20 to 60 s (Acharya et al., Reference Acharya2013) allowing this instrument to make a contribution towards low-latency follow-ups. For GW sources within 200 Mpc, the highest-energy photons will not be effected by degradation by extragalactic background light; therefore the full array can be triggered.
For CTA, data processing for new transient sources can be conducted within 30 s of taking the data, thus providing the capacity for rapid alerts for GW search pipelines (as is presently done by GRB satellites). Additionally, online analysis can provide nearly real-time data on detections in the FoV; this would enable interesting sources coincident with a GW event to be scrutinised by lower energy instruments.
The direct detection of air shower particles at ground may also be a fruitful way to detect gamma-rays from GRBs (Bertou & Allard, Reference Bertou and Allard2005). Although designed to study the highest energy cosmic rays, the Pierre-Auger Observatory (PAOFootnote 31), which has Australian involvement, has considered this technique (Allard et al., Reference Allard, Parizot, Bertou, Beatty, Du Vernois, Nitz and Rodriguez2005). Using the detection rates from individual Cherenkov water tanks, a > 100 MeV fluence (erg cm−2) sensitivity just beyond that of the brightest Fermi-LAT GRBs so far observed may be achieved. To-date, there is no MoU agreement with PAO but planned upgrades to PAO may offer new opportunities to pursue this avenue. Finally, the High Altitude Water Cherenkov (HAWC) gamma-ray telescope has recently been completed. Its high density sampling of air shower particles at over 4000 m above sea level is expected to guarantee detection of at least a few GRBs per year in the > 100 GeV band based on Fermi-LAT detections (Abeysekara et al., Reference Abeysekara2015).
11 FOLLOW-UP BY NEUTRINO DETECTION
The IceCube detector at the South Pole was completed in December of 2010, and monitors a cubic kilometre of deep ice with over 5000 photomultipliers, which detect Cherenkov light emissions from relativistic particles. Neutrinos can travel to the Earth from vast distances and if they interact near, or in, the detector volume, the resulting leptons—muons, electrons, and taus can be detected. These particles will lose energy to particle showers, the daughter particles of which in turn will radiate Cherenkov light. The signature of a muon is a track—the muon may have a range of many kilometres, producing detected light in many modules along its path through the detector. Electrons will lose their energy rapidly, in a short distance (of order a few metres), and result in an approximately spherical pattern of light outflow from the interaction point. In both cases, there is sufficient information in the shape and magnitude of the timing distributions at the modules to allow for a reconstruction of the event arrival direction and energy; muons are resolvable to better than one degree, and cascades to approximately 10–20°.
In the first few years of full operation, IceCube has opened a new observation window on the Universe, with the detection of high-energy astrophysical neutrinos (IceCube Collaboration, 2013; Aartsen et al., Reference Aartsen2014a, Reference Aartsen2015b, Reference Aartsen2015a). These appear as an excess of events relative to expectations for atmospheric neutrinos, which are the background events made when cosmic rays interact with the Earth’s atmosphere. The highest energy events observed are around 1–2 PeV, and these are the most certain astrophysical events. For lower energy events, each has a probability of being an astrophysical signal relative to the background expectations, and, over many analyses, the equivalent of about 100 events are thought to be astrophysical. The most definitive events have energies in the hundreds of TeV range and above, with several events observed beyond 1 PeV. Possible sources for these neutrinos include particle acceleration environments in our own galaxy, and in other galaxies. The deep reach of neutrinos means that IceCube can probe particle acceleration processes out to redshifts of 1 and beyond. The ongoing goal of IceCube is to determine the sources and production mechanisms of the observed neutrinos, and finding a neutrino signal in coincidence with another messenger would yield critical information about the neutrino sources.
IceCube operates in full-sky coverage mode at near 100% uptime, making it ideal for followup studies of other messengers such as GW sources. If a GW signal is discovered, the already collected IceCube data from the discovery time may be retrieved and checked to see if any neutrinos were in coincidence. To this end, IceCube has formalised agreements with LIGO/Virgo for the joint analysis of data. The first analyses have been published, covering periods of joint operation from 2007 to 2010 (Aartsen et al., Reference Aartsen2014b). This joint analysis assigns significance to GW and neutrino events separately, and then these significances are combined. In this first analysis, no significant correlations are seen. Work is underway to analyse the full detector data that now exists, and to prepare for next-generation GW detectors coming online.
12 SUMMARY
The current network of interferometric GW detectors offer the very real prospect of providing an entirely new avenue for understanding the Universe. It is anticipated that a key capability to maximise scientific return from the detector network will be the ability to detect EM counterparts for GW sources.
One of the most promising EM sources for co-ordinated GW observations are GRBs. It is widely assumed that the progenitors of these events are cataclysmic sources, such as the collapse of massive stars and coalescing systems of compact binaries. These events are also detection targets for the GW domain. In this review, we focused on GRBs to consider some of the multi-messenger scenarios that may be possible with GWs.
Discovery possibilities are numerous and highly uncertain at this time. Coordinated GW observations of short-duration GRBs could yield conclusive proof of a connection with compact binary mergers. A low-latency detection of a coalescing compact object tens of seconds before the merger could allow fast response telescopes to be on-source at the time of the merger and thus observe the prompt and early emissions (Section 6.1). Such a scenario could be the key to unlocking mysteries such as the mechanisms behind long-lived X-ray plataus (Section 3.2) and the observed VHE gamma-ray emissions (Section 3.1) and to test if any connection with FRBs exists (Section 3.1 and Section 3.2). If instabilities exist in the collapse of massive stars, the enhanced GW emissions could be detected from a local population of llGRBs and coupled with EM or neutrino observations of the burst and an associated supernova (Section 4). Many other coordinated EM observations are possible with GW triggers at both early and late times. We should also be prepared for serendipitous discoveries.
While searches for such counterparts present technical challenges, past achievements in detecting counterparts for other types of transients in large error regions are encouraging (Singer et al., Reference Singer2015). Teams of observers with wide-field instruments across the EM spectrum are already preparing for EM-followups. Different follow-up techniques are being tested, including sophisticated tiling strategies and machine-learning approaches for screening of candidate counterparts.
At the same time, new wide-field radio facilities in Australia including ASKAP, MWA, and eventually SKA will offer an expanded ability to detect transient sources in very large fields (Section 10.3). These developing capabilities, coupled with Australia’s geographic advantage in terms of access to a large fraction of the Southern sky implies that ground-based followup in both the optical and radio seems particularly promising. Certainly, the geographic location is proven for telescopes like AAT, SkyMapper, and Zadko and in the future, GOTO (Section 10.4) can also capitalise. The energetics of GW sources suggest that Australian involvement in both high-energy gamma (Section 10.5) and neutrino observations (Section 11) could offer unique capabilities. Although extremely challenging, participation in this new era has the potential to place Australia at the forefront of arguably the most exciting discoveries for 21st century astronomy.
ACKNOWLEDGEMENTS
A number of people have aided this paper through valuable discussions and by providing information on the different featured EM facilities: we particularly wish to thank Chris Lidman (AAO), Paul OBrien, and Jim Hinton (CTA), Danny Steeghs (GOTO), Shami Chatterjee (VAST), Jeff Cooke (‘Deeper Wider Faster’). EJH acknowledges support from a UWA Research Fellowship. DC is supported by an Australian Research Council Future Fellowship (FT100100345). PDL is supported by the Australian Research Council Discovery Project (DP140102578). Part of this research was conducted by the Australian Research Council Centre of Excellence for All-sky Astrophysics (CAASTRO), through project number CE110001020. DLK was supported by NSF grant AST-1412421. The authors thank Marica Branchesi, the assigned reviewer for the LIGO Scientific Collaboration, for conducting a thorough review of the manuscript which included a number of insightful suggestions. We also acknowledge the anonymous referee who highlighted a number of areas that have benefited from improved clarity. This is LIGO document number LIGO-P1500153.
Table A1. The values of C(M) as given in Equation (8) for the sensitivities corresponding with the different observation runs of aLIGO/AdV. These data can be interpolated and used to calculate estimates of the gravitational wave detection ranges of coalescing compact objects.

Table B1. The values of C B(f) as given in Equation (10) for the sensitivities corresponding with the different observation runs of aLIGO/AdV. These data can be interpolated and used to calculate estimates of the gravitational wave detection ranges of burst sources of different peak frequencies.