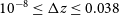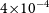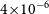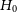1. Introduction
The power of Type Ia Supernovae (SNe Ia) as a probe of the expansion history of the universe comes from comparing the measured distances of the SNe to the distances expected for their redshift in different cosmological models (Riess et al. Reference Riess1998; Perlmutter et al. Reference Perlmutter1999; Wood-Vasey et al. Reference Wood-Vasey2007; Kessler et al. Reference Kessler2009; Betoule et al. Reference Betoule2014; Scolnic et al. Reference Scolnic2018; Dark Energy Survey 2019). Since the relative precision of spectroscopically measured redshifts is typically significantly greater than that of redshift-independent distances, much more effort has been spent on improving distance measurements than improving redshift measurements (e.g. Phillips Reference Phillips1993; Phillips et al. Reference Phillips, Lira, Suntzeff, Schommer, Hamuy and Maza1999; Goldhaber et al. Reference Goldhaber2001; Guy et al. Reference Guy2007; Jha, Riess, & Kirshner Reference Jha, Riess and Kirshner2007; Hicken et al. Reference Hicken2009; Kessler et al. Reference Kessler2009; Scolnic et al. Reference Scolnic2015; Kessler & Scolnic Reference Kessler and Scolnic2017; Brout et al. Reference Brout2019; Kessler et al. Reference Kessler2019; Lasker et al. Reference Lasker2019). This prioritisation is supported by the fact that redshift measurements, either from the host galaxies or SNe, are straightforward; small errors are usually expected to be random, shifting redshifts higher as often as lower. However, with samples of greater than 1000 SNe, systematic uncertainties are of paramount concern, and potential systematic biases in the redshift measurements must be considered (e.g. Huterer et al. Reference Huterer, Kim, Krauss and Broderick2004; Wojtak et al. Reference Wojtak, Davis and Wiis2015; Davis et al. Reference Davis, Hinton, Howlett and Calcino2019; Steinhardt, Sneppen, & Sen Reference Steinhardt, Sneppen and Sen2020; Mitra & Linder Reference Mitra and Linder2021). In this analysis, we perform a comprehensive review of the redshifts of individual SNe used in the latest samples for cosmological analyses and analyse potential biases due to issues with redshifts in the recovery of cosmological parameters.
Several recent papers have considered the impact of redshifts errors on supernova cosmology. For example, Steinhardt et al. (Reference Steinhardt, Sneppen and Sen2020) determined whether the source for each redshift in the Pantheon sample (Scolnic et al. Reference Scolnic2018) was either the host galaxy spectrum or SN spectrum, and found difference in cosmological parameters at a
${\sim}3\unicode{x03C3}$
level between the two subsets. Rameez & Sarkar (Reference Rameez and Sarkar2021) noted changes in the measured redshifts of sub-samples of large SN compilations that were larger than the reported uncertainties and questioned the repeatability of SN experiments. While here we show the effect of redshift errors on cosmological parameters remains small (relative to their current precision), we note that the redshifts came from a variety of sources, with many measurements having been over 20 yr ago. Old and/or inhomogeneous redshift measurements are not necessarily a problem, but these factors increase the potential for miscellaneous errors to be carried through different SN samples, so a comprehensive review is warranted. Achieving accurate redshifts for cosmological studies requires multiple stages, and in this paper we apply improvements at each stage except for performing new spectroscopic measurements.
Redshifts in the heliocentric frame are measured either from the SN spectrum, which is typically precise on the level of
$\unicode{x03C3}_z\sim0.005$
(a somewhat conservative estimation), or the host-galaxy spectrum, which is typically precise on the level of
$\unicode{x03C3}_z\sim0.0002$
(see Section 4). Host redshifts are preferred because the hosts have sharper spectral lines that result in a more accurate and precise redshift. However, it is essential for the correct host-galaxy to be associated with the SN (Gupta et al. Reference Gupta2016), else SNe will be misplaced on the Hubble diagram. Here we review the host galaxy assignment of all SNe where possible, and update heliocentric redshifts accordingly.
Once the heliocentric redshift is determined, we convert the redshift into the CMB frame. While the CMB conversion is standard, an unnecessary approximation has often been applied (see, e.g. Carr & Davis Reference Carr and Davis2021, and references therein) and we replace that with the exact correction (Section 5).
The final step to obtain accurate cosmological redshifts is applying the correction to account for the peculiar velocity of the source. We introduce a slightly improved technique of estimating peculiar velocities (that also better models the external bulk flow to arbitrary redshift) based on the existing 2M++ compilation (Carrick et al. Reference Carrick, Turnbull, Lavaux and Hudson2015). We apply this correction to all redshifts whereas previously, corrections had been applied only at low redshift, or with a biased model at large redshifts.
We thus release a comprehensive update to the redshifts of all publicly available Type Ia supernovae that make up the ‘Pantheon+’ sample. Unlike previous analyses, we do not isolate our work to redshifts of ‘cosmologically useful’ SNe (those that make it onto the Hubble diagram) since data cuts may be relaxed or otherwise altered in future analyses.
This paper is one of many that contribute to the Pantheon+ sample, culminating in the full cosmology analysis in Brout et al. (Reference Brout2022). This work is companion to Peterson et al. (Reference Peterson2021), that studies the effects of replacing host galaxy redshifts with average redshifts of host galaxy groups on Hubble diagram residuals, and provides group-averaged redshifts and group-centre coordinates which we also release here. In addition, Peterson et al. (Reference Peterson2021) studies the efficacy of using different peculiar velocity samples—including those derived in this work—on Hubble residuals. Brout et al. (Reference Brout2021) re-calibrates the many photometric systems of Pantheon+ and quantifies the systematic effects of photometric calibration on cosmological parameters. Scolnic et al. (Reference Scolnic2021) releases the 1701 updated light curves of 1550 unique SNe IaFootnote a used in the Pantheon+ w analysis and Supernovae and H0 for the Equation of State of dark energy (SH0ES)
$H_0$
analysis (Riess et al. Reference Riess2022). Peterson et al. (Reference Peterson2021), Scolnic et al. (Reference Scolnic2021) and Brout et al. (Reference Brout2021, Reference Brout2022) utilise the redshifts of this work, and we utilise the group-averaged redshifts from Peterson et al. (Reference Peterson2021) and distance moduli from Brout et al. (Reference Brout2022) in our analysis of the effects of the redshift updates. See https://PantheonPlusSH0ES.github.io for the other papers that contribute to Pantheon+.
In this work, the main improvements we implemented are detailed in the following sections:
-
Fixed coordinates and miscellaneous bookkeeping redshift errors (Section 2).
-
Updated heliocentric redshift values using the NASA/IPAC Extragalactic Database (NED) when better redshifts were available (Section 3).
-
Ensured all redshifts have uncertainty estimates (Section 4).
-
Used the exact redshift conversion when (a) going from heliocentric redshifts to the CMB frame, and (b) going from CMB frame to Hubble diagram redshift (Section 5). These respectively correct for (a) our Sun’s motion with respect to the CMB and (b) the host galaxy’s motion with respect to the CMB.
-
Provided improved peculiar velocity estimates that better represent the bulk flow at large distances (Section 6).
Next, we analyse the impact of each change on cosmological parameters in Section 7 and finally discuss and conclude in Section 8.
The Pantheon+ redshifts and accompanying data will be released as a machine readable Centre de Données astronomiques de Strasbourg (CDS) VizieR table with the publication of this work, and also on GitHub at https://github.com/PantheonPlusSH0ES/DataRelease which will log any possible updates. The light curves for each SN (see Scolnic et al. Reference Scolnic2021), which contain our updated redshifts and peculiar velocities, are also available at this GitHub. The peculiar velocity method developed for this paper is available at https://github.com/KSaid-1/pvhub.
2. Samples and bookkeeping
Our aim is to complete a comprehensive review of the redshifts assigned to every publicly available SN Ia used for cosmology and other SN Ia studies. We include primarily normal Type Ia supernovae along with various Ia subtypes, such as ‘1991T–like’ or just ‘peculiar’ (Li et al. Reference Li, Filippenko, Treffers, Riess, Hu and Qiu2001). The Pantheon+ sample is compiled of supernovae taken from a diverse array of samples, as listed in Table 1 and shown in Figure 1. The master list of our updated redshifts, which includes the SN and host coordinates; heliocentric, CMB, and cosmological (Hubble diagram) redshifts; and peculiar velocity values, can be found in Table 2. Including all of these quantities aids in the traceability of the redshifts (and hosts) and repeatability of the corrections.
Table 1. Description of sub-samples and list of changes.
$N_{\text{Tot}}$
is the number of Type Ia (including subtypes) supernova light curves in each sample. See Section 3 for the definition of ‘best NED redshift’. See dot points in Sections 2.2 and 3 for more detailed descriptions of the improvements.
aSNID vespasion: Pantheon ID was previously ‘vespesian’ (spelled with an e), and coordinates were mistakenly those of the supernova Obama (EGS11Oba) (Riess et al. Reference Riess2018). See new coordinates in Table 3.
bPSNJ1628383 from FSS shares the same host group as SN 2009eu. See entry in Table A2.
cThe DES sample contains 26 non-confirmed but highly probable SNe Ia spectroscopic classifications (type ‘SNIa?’ in Table 6 of Smith et al. Reference Smith2020a). Of these, 22 pass our cosmology sample quality cuts.
dUpdated with new OzDES redshifts and improved SN host association (M. Smith, private communication). The redshift of DES supernova 1280201 (DES15X3iv) was updated to the higher precision FSS measurement (ASASSN-15od).
eThe PS1MD redshift of 580104 was updated to the higher precision DES measurement (1261579; DES13X3woy).
fWe include only secure spectroscopic Type Ia classifications from SDSS, which excludes 41 SNe (type ‘SNIa?’, in Table 2 of Sako et al. Reference Sako2018), four of which were originally in Pantheon (2005gv, 2005kt, 2007oq, 2007ow) cf. 22/26 DES ‘SNIa?’ in our cosmology sample, implying the SDSS SNIa? are less secure. A further two SNe (2006lo, 2006md) in Pantheon were excluded due to being photometrically classified (type ‘zSNIa’ in Sako et al. Reference Sako2018).
References: (1) Gilliland et al. (Reference Gilliland, Nugent and Phillips1999); (2) Riess et al. (Reference Riess2001); (3) Suzuki et al. (Reference Suzuki2012); (4) Riess et al. (Reference Riess2018); (5) Chen et al. (Reference Chen2020); (6) Riess et al. (Reference Riess1999); (7) Hamuy et al. (Reference Hamuy1996); (8) Riess et al. (Reference Riess2004); (9) Riess et al. (Reference Riess2007); (10) Jha et al. (Reference Jha2006); (11) Jha et al. (Reference Jha, Riess and Kirshner2007) and references therein; (12) Milne et al. (Reference Milne2010); (13) Stritzinger et al. (Reference Stritzinger2010); (14) Tsvetkov & Elenin (Reference Tsvetkov and Elenin2010); (15) Zhang et al. (Reference Zhang2010); (16) Hsiao et al. (Reference Hsiao2015); (17) Krisciunas et al. (Reference Krisciunas, Suntzeff, Espinoza, Gonzalez, Miranda and Sanhueza2017a); (18) Burns et al. (Reference Burns2018); (19) Contreras et al. (Reference Contreras2010); (20) Gall et al. (Reference Gall2018); (21) Wee et al. (Reference Wee, Chakraborty, Wang and Penprase2018); (22) Burns et al. (Reference Burns2020); (23) Kawabata et al. (Reference Kawabata2020); (24) Stahl et al. (Reference Stahl2019); (25) Hicken et al. (Reference Hicken2012); (26) Brown et al. (Reference Brown, Breeveld, Holland, Kuin and Pritchard2014); (27) https://pbrown801.github.io/SOUSA/; (28) Krisciunas et al. (Reference Krisciunas2017b); (29) Ganeshalingam et al. (Reference Ganeshalingam2010); (30) Hicken et al. (Reference Hicken2009); (31) Guy et al. (Reference Guy2010); (32) Foley et al. (Reference Foley2018); (33) Scolnic et al. (Reference Scolnic2021); (34) Brout et al. (Reference Brout2019); (35) Smith et al. (Reference Smith2020a); (36) Scolnic et al. (Reference Scolnic2018); (37) Sako et al. (Reference Sako2018).
Figure 1. Distribution of Pantheon+ SNe across the sky. Many SNe are common between samples, but only one sample is picked to represent each SN. Redshifts from the host galaxies are represented by black-outlined solid symbols, and redshifts from supernova spectra are colour-outlined unfilled symbols. Several samples (generally at higher z i.e. SNLS, DES, PS1MD, HST) targeted small sky areas repeatedly, so many SNe are confined to small patches. These patches are visible where many lighter, unfilled symbols overlap (these groups obscure the underlying host galaxy redshifts which are always the majority).
2.1 Description of parameters
The relevant parameters for our study are the redshifts and peculiar velocities. The heliocentric redshift (
${z_{\text{hel}}}$
) is the ‘observed’ redshift.Footnote b We convert from
${z_{\text{hel}}}$
to the CMB frame redshift (
$z_{\text{CMB}}$
) using the standard formulae in Section 5 and emphasise that we do not approximate these transformations. CMB-frame redshift refers to the redshift after we correct for only our own peculiar velocity, that is we correct for the Planck-observed CMB dipole. The peculiar velocity (
${v_{\text{p}}}$
) and corresponding peculiar redshift (
${z_{\text{p}}}$
) refer to the motion of the distant galaxy that is in addition to the Hubble flow. The final Hubble-diagram redshift that is used for cosmology (
$z_{\text{HD}}$
) is the final stage, after we have corrected
$z_{\text{CMB}}$
for the peculiar velocity of the distant galaxy. The standard formulae are also given in Section 5, and the derivation of the peculiar velocities themselves is described in Section 6. Each of these parameters have uncertainties represented by
$\unicode{x03C3}$
. When the parameters come from the host galaxy group (from Peterson et al. Reference Peterson2021) instead of the individual host or SN, the symbol is preceded by ‘Group’.
2.2 Corrections and additions to previous data
Pantheon+ carries over the same SNe from Pantheon and includes many more SNe from FSS, DES, LOSS, SOUSA and CNIa0.02, as defined in Scolnic et al. (Reference Scolnic2021). Therefore, redshift and bookkeeping mistakes are carried over from Pantheon which were in turn carried over from their original sources, mostly from older SN compilations. After examining each of the samples listed in Table 1 we found and fixed various errors, and added improvements as follows:
-
GOODS+PANS and SCP had Right Ascension (RA) and Declination (Dec) listed as zeros. As a result, the heliocentric corrections had been made to the incorrect part of the sky. We assign coordinates from the original datasets (Riess et al. Reference Riess2004; Riess et al. Reference Riess2007; Suzuki et al. Reference Suzuki2012) and recompute
$z_{\text{CMB}}$
. -
We provide updates to DES redshifts from their 3-yr values (Smith et al. Reference Smith2020a) to their (previously unpublished) values that will be used in DES 5-yr cosmology. This includes reassigning uncertainty based on whether the redshift comes from the host or SN spectrum: 5
${\times 10^{-4}}$
and 5
${\times 10^{-3}}$
respectively. -
All SCP and GOODS+PANS SNe had redshift uncertainties set to 1
${\times 10^{-3}}$
regardless of redshift source, so we reassigned the uncertainties the same way as with DES. -
Six FSS SNe had coordinates that disagreed with both the NED entry and FSS-assigned-host by up to tens of degrees. We therefore correct the SN coordinates to the NED coordinates, as listed in Table 3.
-
One CfA4 SN had its location mistaken for a SN discovered around the same time. The record for 2008cm had the coordinates of SNF 20080514-002, but since the redshift was in agreement with the host of 2008cm, we update the SN coordinates using NED (Table 3).
-
We update the coordinates of CfA1 SN 1996C to those of SIMBAD because the NED coordinates are incorrect (Table 3).
-
Where we have identified the host of a SN, host coordinates are provided separately to SN coordinates. There was previously no record of SN hosts in Pantheon or some source catalogues. Heliocentric corrections are performed using host coordinates where possible.
-
Where an International Astronomical Union name (IAUC) for a SN exists, we record it alongside the internal ID (SNID). The IAUC links SNe that are common across samples that use different internal names. However, we recommend that in future, a dictionary of all names for a SN be implemented since SNe without an IAUC must be matched via position instead.
-
In collaboration with Peterson et al. (Reference Peterson2021), we include group-centre coordinates and group-average heliocentric redshifts, from which we derive group
$z_{\text{CMB}}$
, group
$z_{\text{HD}}$
and group
${v_{\text{p}}}{}$
(see Table 2).
Table 2. Master table of updated redshifts. Symbols are defined in Section 2.1. The full machine readable table is available online from VizieR and at https://github.com/PantheonPlusSH0ES/DataRelease. The online versions of this table include columns for peculiar velocity uncertainty and binary classifications for if a SN has an associated host, if the redshift is from a host and if the supernova has group values. All peculiar velocities have an uncertainty of 250
$\mathrm{km\,s}^{-1}$
, and all
${z_{\text{hel}}}$
share the same uncertainty as their corresponding
$z_{\text{CMB}}$
. Blank entries for group information mean the SN has no associated group, and blank IAUC entries mean there is no IAU name for the SN.
As a result of these changes, all SNe now have the same information: both the SNID and IAUC where applicable, both SN and host co-ordinates where applicable, redshifts in the heliocentric and CMB frame, and finally our updated peculiar velocities.
Table 3. Corrections to SN positions.
3. Reviewing heliocentric redshifts
The most accurate redshift for a SN—in the absence of a galaxy group average redshift—is that of its host galaxy, so it is imperative that the correct host is assigned. This is true at any redshift, but especially so at low redshift. In this work, we define the low-z sample as the
$\sim$
1000 galaxies with
$z\lesssim0.12$
(median
$z\sim 0.024$
). These are primarily the SNe that were not uniquely observed in the typical ‘high-z’ surveys of SNLS, DES, SDSS, PS1MD and HST, however some SNe in these surveys are low-z since they were also observed by the low-z surveys.
In the interest of thoroughly reassessing the redshifts of Pantheon+, we used Aladin (Bonnarel et al. Reference Bonnarel2000) to visually inspect Pan-STARRS images at every low-z (and occasionally moderate-z) SN location, to assign and record hosts. It is this requirement of visual inspection that makes our definition of low-z unique. We also used Dark Energy Camera Legacy Survey, SDSS and DES images where available, and for Dec
${\lesssim}-30{^{\circ}}$
we used mostly Digitized Sky Survey 2 images. For the hosts we identified, we chose the ‘best’ redshift according to a hierarchy of criteria outlined below. For the three low-z SNe we could not assign hosts—1996ab, 2007kg and 2008dx—we use the redshift given in the original classification reports. Apart from these three, there was ambiguity in only six low-z hosts (see discussion below). In addition the low-z sample for which we identified redshifts, we confirmed the coordinates and host names of all SDSS and FSS SNe.
Some redshifts in NED are supplied with a comment as to their origins, which contribute to picking the best redshift. The origins are either ‘from new data’ (i.e. the reference measured the redshift), ‘from reprocessed raw data’, or ‘from uncertain origins’. Most redshifts are from uncertain origins, usually because the sources re-record older redshifts, but also because some NED records do not report that the redshift is new.
The criteria for picking the best redshift are:
-
1. We use SDSS Data Release 13 (DR13) redshifts when they are available, as these are usually the most up-to-date measurement, have low uncertainty, and show stability in that earlier iterations of SDSS tend to converge on the DR13 values.
-
2. Next we consider other sources that include uncertainty estimates. Among these we choose the one that first satisfies, in order of decreasing priority:
-
(a) The most recent source that has taken new data and measured a new redshift.
-
(b) The most recent source that has reprocessed old data.
-
(c) The most recent source that has an uncertain origin. This may be original data, but may also be from a new publication that uses old redshifts because these often appear as new entries in NED. We endeavoured to avoid republished redshifts and quote the original source.
In the case of multiple redshifts satisfying any condition, we take the most precise redshift.
-
3. If none of the above criteria are satisfied we consider redshifts that lack an uncertainty estimate, but are not a SN redshift. In these cases, we set the uncertainty to 9
${\times 10^{-5}}$
(see Section 4). -
4. As the last resort we take the redshift derived from the original SN spectrum. In the cases where no redshift uncertainty is reported, we set the uncertainty to be 5
${\times 10^{-3}}$
(Section 4).
We examined all redshifts in the low-z sample except those that come from FSS. These redshifts were not updated because FSS adopt their own hierarchical approach to selecting redshifts in the literature (Foley et al. Reference Foley2018). Importantly, FSS measure new host redshifts for SNe previously without host redshifts. Thus, we assume this sample has the best existing redshift estimates already.
Out of 2285 unique SNe Ia, 990 heliocentric redshifts have been updated. This is mainly for low-z hosts, whose redshifts have been measured multiple times. Some notable cases:
-
All HST supernovae had
${z_{\text{hel}}}$
listed as
$z_{\text{CMB}}$
. In each case, we use the heliocentric redshifts given by the original publication and recompute
$z_{\text{CMB}}$
. -
SN 1992bk, 2000cp, 2008bf, 2008ff, 2009eu, 2014at and PSNJ1628383 each occurred in a group of galaxies so that a unique host could not be determined. The most accurate treatment of these cases, and in fact in general, is to average the redshifts of host-galaxy-group members, as in Peterson et al. (Reference Peterson2021), with more members giving a more accurate redshift. Figure 2 shows images for these six cases, with SN locations and potential hosts indicated. We set the group redshift uncertainty to the dispersion in group member redshifts. SN 1992bk is a good example of how the ‘directional light radius’ (DLR; see Gupta et al. Reference Gupta2016) might be used to exclude the smaller, less likely cluster galaxies from being considered as hosts. We do not use DLRs to determine the most likely host, and instead visually identify the most likely group members and take their average redshift, which gives a more accurate estimate of the Hubble-flow redshift than any single group member.
-
Some SNe had multiple unique SDSS redshift measurements from the same data release. The unique redshifts were averaged, and uncertainties estimated from the dispersion of redshift measurements, similar to the ambiguous host redshifts (see Table A1). The quoted redshift uncertainties are often less than the standard deviation of the measurements (despite the fact that standard deviations measured from small samples are typically underestimated) indicating that the redshift uncertainties may be underestimated; see discussion in Section 4.
-
There were many cases where a SN redshift was quoted in place of a more accurate host redshift, as seen in the discrepancies between the four different redshift sources Sako et al. (Reference Sako2018, Tables 1 and 9), Gupta et al. (Reference Gupta2011), and Östman et al. (Reference Östman2011). We examined every image of SDSS SNe to confirm the host, SN coordinates, and attempt to update the redshift using NED. In ambiguous host cases, we use the host coordinates published in Sako et al. (Reference Sako2018). In this way, we replace 81 SN redshifts with host redshifts.
-
Zheng et al. (Reference Zheng2008) noted in the first year SDSS SN data release that there was a systematic offset of 3
${\times 10^{-3}}$
between host redshifts and SN redshifts, and thus they applied the shift to SN redshifts to bring them in line with host redshifts. Sako et al. (Reference Sako2018) found a similar offset of
$(2.2\pm0.4){\times 10^{-3}}$
was present in their larger sample of SDSS SNe, however they did not apply the shift to the SN redshifts. We confirm that we see the same trend in the 81 SDSS SNe whose SN-z we replace with host-z. Unlike Sako et al. (Reference Sako2018), we do apply this systematic redshift shift of
$+2.2{\times 10^{-3}}$
to the remaining 46 SDSS SN-zs.Footnote c
Figure 2. All instances of an ambiguous host where redshifts of multiple likely hosts have been averaged (in each case all possible hosts are at approximately the same redshift). In all images, North is up and East to the left. Red crosses indicate the location of the SN, and green circles indicate the hosts used. Other objects in the images were not selected because they were stars, or were less likely host galaxies due to their size.
Table A2 shows the largest disagreements between new and old redshifts in decreasing level of disagreement, with justifications for the update. Since we expect updates from SN-z to host-z to be large, we focus on disagreements between host-zs.
4. Estimating redshift uncertainties
Ideally, each object would have an individual redshift uncertainty measurement based on its spectrum. However, many surveys (generally those at higher redshift) do not provide this information and instead give overall estimates of redshift uncertainties for typical classes of object (e.g. DES, PS1MD, SNLS; see Figure 3). There are several ways to estimate the redshift of an object: emission-line redshifting (e.g. Colless et al. Reference Colless2001), cross-correlation with templates (Tonry & Davis Reference Tonry and Davis1979), least-squares minimisation (Bolton et al. Reference Bolton2012), or from 21 cm H i emission profiles in radio (e.g. Springob et al. Reference Springob, Haynes, Giovanelli and Kent2005). Each method has its own way of estimating redshift uncertainty per spectrum, and the Pantheon+ sample has redshifts determined from each of these methods. For instance, SDSS uses least-squares minimisation, DES/OzDES uses cross-correlation, there are many galaxies with 21 cm H i redshifts (mostly from Springob et al. Reference Springob, Haynes, Giovanelli and Kent2005), and many more that are unspecified.
Figure 3. Uncertainty in redshift versus redshift. We observe a general upward trend with redshift as expected. Samples that use standard uncertainties have been highlighted with dashed lines. The standard uncertainty of 1.5
${\times 10^{-4}}$
is that of the 6dF redshifts in the low-z sample.
4.1 Typical uncertainties
More problematic than reporting only class-based uncertainties is the non-reporting of uncertainties. Some SN data releases did not include uncertainties (e.g. CSP, CfA), in which case the only way to obtain an uncertainty estimate is to instead use an original measurement of the redshift. Our aim is for every redshift to have an uncertainty estimate, so we must estimate uncertainties where none are reported. Despite identifying the best primary source according to the hierarchy above, a small number of sources did not provide uncertainties. With no information about the spectra themselves, we opt to set missing uncertainties to a typical value, according to whether they are host or SN redshifts.
We examine the redshift uncertainties of five surveys with redshifts in Pantheon+ or that provide their own galaxy redshift uncertainty statistics: the Two-degree Field Galaxy Redshift Survey (2dFGRS; Colless et al. Reference Colless2001), the WiggleZ Dark Energy Survey (Drinkwater et al. Reference Drinkwater2018), SDSS, DES/OzDES (Lidman et al. Reference Lidman2020) and the Digital Archive of H i 21 Centimeter Line Spectra from Springob et al. (Reference Springob, Haynes, Giovanelli and Kent2005). However, we defer the discussion of SDSS-measured redshifts to Section 4.2 as SDSS redshift uncertainties are consistently smaller than other optical estimates.
While each method of redshifting naturally provides a way of estimating uncertainty, the more common way to estimate uncertainty is by comparing multiple measurements of the same object. Each survey found:
-
2dFGRS: Over
$0<z<0.3$
, the RMS of multiple measurements was
$\unicode{x03C3}_z=2.8{\times 10^{-4}}$
. The authors found a slight upwards trend with redshift. -
WiggleZ: Over
$0<z<1.3$
, the standard deviation of multiple measurements ranged from
$\unicode{x03C3}_z=1.7{\times 10^{-4}}$
for the highest quality spectra to
$\unicode{x03C3}_z=2.7{\times 10^{-4}}$
for the lower quality but successfully redshifted spectra. The authors found no trend with redshift. -
OzDES: The collaboration opted to estimate uncertainties for classes of objects, assigning general SN host galaxies uncertainties of
$\unicode{x03C3}_z=1.5{\times 10^{-4}}$
, which the authors state is a lower bound.Footnote d
-
Springob et al. (Reference Springob, Haynes, Giovanelli and Kent2005) 21 cm Archive: Compared with optical, redshifts determined from the 21 cm line offer impressive precision. After reanalysing nearly 9000 nearby (
$-0.005<z<0.08$
) H i galaxies, the mean and median redshift uncertainty was 1.7
${\times 10^{-5}}$
and 1.2
${\times 10^{-5}}$
respectively.
For the Pantheon+ low-z sample, which has a mix of optical and radio redshifts from the literature, we find a median redshift uncertainty of 9
${\times 10^{-5}}$
, which is consistent with the above measurements. We also include in this test the 30 PS1MD and SNLS SNe whose host galaxies we find third party redshifts for, extending to
$z\sim0.50$
. We show in Figure 4 the distribution of the redshift uncertainties of this modified low-z sample. Since there remain 30 host galaxies that lack redshift uncertainties, all at low-z, we opt to assign the median uncertainty calculated from the rest of our low-z sample (see Table A3).
Figure 4. Comparison of SDSS DR13 redshift uncertainties and all other low-z SN uncertainties. SDSS DR13 has a tight distribution peaking around 1
${\times 10^{-5}}$
, while low-z is much broader due to its heterogeneous redshift sub-samples. Redshifts larger than 0.0006 have been collected into a single bin, as the maximum is 0.002 (Perlmutter et al. Reference Perlmutter1999). The spike in low-z at
$\unicode{x03C3}_z=0.00015$
is due to 6dF, while the SDSS spike at
$\unicode{x03C3}_z=0.0005$
corresponds to the uncertainty typically set for a redshift from emission/absorption lines in a SN spectrum.
Until now, we have discussed only host galaxy redshifts because these have been studied in detail. Estimating redshifts from SN spectra has had less attention. Like host galaxy redshifts, there are SN redshifts without uncertainty estimates. In these cases, we rely on a less concrete estimation of
$\unicode{x03C3}_z=0.005$
, based on the population of SN redshifts to date and expert opinion. We reiterate that this is a somewhat conservative but fair estimation. As an example, as given by SNID (Blondin & Tonry Reference Blondin and Tonry2007), the mean redshift uncertainty of the 51 supernovae with Type Ia SNID classifications from the CfA Supernova Group websiteFootnote e is
$\unicode{x03C3}_z=4.1{\times 10^{-3}}$
with a standard deviation of 1.7
${\times 10^{-3}}$
.
See Table A3 for a list of all SNe previously missing uncertainties.
4.2 Underestimated SDSS uncertainties
We noted in Section 3 that when multiple redshift measurements were available in SDSS, the dispersion in redshift values is usually higher than expected from their typical uncertainties of 1
${\times 10^{-5}}$
. This comparison indicates that typical SDSS redshift uncertainties are somewhat optimistic. We quantify this comparison by calculating both average uncertainty,
$\overline{\unicode{x03C3}_z}$
, and dispersion in z,
$\unicode{x03C3}(z)$
, for all multiply-measured objects in SDSS DR13. Only objects with two or more reliable redshifts are used.
The average uncertainty versus z dispersion for all multiply-measured objects is shown in Figure 5. We perform a linear fit to the objects with five or more measurements weighted by number of redshift measurements. Calculating standard deviation from few points is systematically biased low (grey points), so we exclude objects with two–four measurements. We also exclude dispersions above 0.01 since these dispersions are caused by multiple confident but disparate redshifts. Thus the fit was performed on 1000 of 31000 objects.
Figure 5. Standard deviation of multiple SDSS DR13 reliable redshift measurements of the same object against the average of their quoted uncertainties. We expect a slope of 1.0 (red dashed line) if the uncertainties are appropriate. The solid blue line is a linear fit to all data with five or more measurements and a dispersion of
$\unicode{x03C3}(z)<0.01$
, which shows that, consistently,
$\unicode{x03C3}(z)>\overline{\unicode{x03C3}_z}$
. Every point with
$\unicode{x03C3}(z)\gtrsim0.01$
is a catastrophic redshift failure caused by at least two distinct confident redshifts.
The uncertainty of 9
${\times 10^{-5}}$
that we apply to sources with no provided uncertainty reflects the mean dispersion of 9.5
${\times 10^{-5}}$
we calculate for repeated non-outlying SDSS measurements. Since we see a gradient of almost unity and a positive offset of roughly 3
${\times 10^{-5}}$
between dispersion and estimated uncertainty, increasing the SDSS uncertainties by this amount would be reasonable, and we test the impact of this increase in our cosmological analysis in Section 7.Footnote f
5. Combining redshifts multiplicatively
5.1 Heliocentric corrections
Most publicly available heliocentric corrections, including those currently in NED and Pantheon used a low-redshift approximation (although the approximation in NED will be corrected; see Carr & Davis Reference Carr and Davis2021). When performing the heliocentric correction, the low-redshift approximation assumes the observed redshift
${z_{\text{hel}}}$
is an additive combination of
$z_{\text{CMB}}$
and the redshift due to our Sun’s peculiar motion,
$z_{\text{Sun}}$
,
\begin{equation}{z_{\text{hel}}}={z_{\text{CMB}}^{\mathrm{+}}}+z_{\text{Sun}}.\end{equation}
However, the correct way to combine redshifts is to multiplicatively combine factors of
$(1+z)$
, so
\begin{equation}(1+{z_{\text{hel}}})=\left(1+{z_{\text{CMB}}^{\mathrm{\times}}}\right)(1+z_{\text{Sun}}).\end{equation}
This gives the correct CMB-frame redshift, which is
\begin{equation}{z_{\text{CMB}}^{\mathrm{\times}}} = \frac{1+{z_{\text{hel}}}}{1+z_{\text{Sun}}}-1.\end{equation}
The difference between using the additive approximation and the correct multiplicative equation is exactly
$z_{\text{CMB}}z_{\text{Sun}}$
. Since
$z_{\text{Sun}}$
is our own motion with respect to the CMB (our velocity
$v_{\text{CMB}}$
in the direction of the CMB dipole), it is of order
${10^{-3}}$
. Therefore, at low-z, the difference between
${z_{\text{CMB}}^{\mathrm{\times}}}$
and
${z_{\text{CMB}}^{\mathrm{+}}}$
appears almost negligible; however, by
$z\sim 1$
, the error is on the order of
${10^{-3}}$
, which is an order of magnitude larger than most reported statistical uncertainties in redshifts.
We have ensured that all sub-samples in the new Pantheon+ sample consistently use the multiplicative correction.
5.1.1 Which dipole to use?
The Pantheon sample mostly used the CMB dipole measured by the Cosmic Background Explorer (COBE) satellite (Fixsen et al. Reference Fixsen, Cheng, Gales, Mather, Shafer and Wright1996), in the direction of galactic longitude and latitude
$(l, b) = (264.14{^{\circ}}{}\pm0.30{^{\circ}}{}, 48.26{^{\circ}}{}\pm0.30{^{\circ}}{})$
with a velocity
${v_{\text{Sun}}^{\text{COBE}}} = 371\pm1\,\mathrm{km\,s}^{-1}$
.
We update the heliocentric correction to use the dipole measured by the Planck Collaboration (Planck Collaboration et al. Reference Collaboration2020),
$(l, b) = (264.021{^{\circ}}{}\pm0.011{^{\circ}}{}, 48.253{^{\circ}}{}\pm0.005{^{\circ}}{})$
with a velocity
${v_{\text{Sun}}^{\text{Planck}}} = 369.82\pm0.11\,\mathrm{km\,s}^{-1}$
. The difference in redshift between using the COBE dipole and the Planck dipole is at most
${\sim}{10^{-5}}$
, so this is a small change.
5.1.2 Calculating
$z_{\text{Sun}}$
The projection of the Sun’s peculiar velocity along the line of sight to an object is
\begin{equation} v_{\text{Sun}} = \boldsymbol{v}_{\text{Sun}}\cdot\hat{\boldsymbol{n}}_{\text{obj}} = {v_{\text{Sun}}^{\mathrm{max}}}\cos\alpha, \end{equation}
where
$\hat{\boldsymbol{n}}_{\text{obj}}$
is the object’s position vector, and
$\alpha$
is the angle separating the dipole direction and the object.
Since the Sun’s velocity is small (order of
${10^{2}}\,\mathrm{km\,s}^{-1}$
) compared to c, the low-z approximation
$z_{\text{Sun}} \approx -v_{\text{Sun}}/c$
is adequate, but we use the full special relativistic calculation
\begin{equation} z_{\text{Sun}} = \sqrt{\frac{1+({-}v_{\text{Sun}})/c}{1-({-}v_{\text{Sun}})/c}}-1,\end{equation}
because there is negligible computational advantage to the approximation. The minus signs before
$v_{\text{Sun}}$
have been left explicit to emphasise that at zero angular separation (
$\alpha=0$
in Equation (4)) the object should appear slightly blueshifted due the our velocity directly towards it.
5.2 Peculiar velocity corrections
The peculiar redshifts arising due to the peculiar velocities of the supernova host galaxies also need to be treated multiplicatively. Equation (2) becomes
\begin{equation}(1+{z_{\text{hel}}})=(1+z_{\text{HD}})(1+z_{\text{Sun}})(1+{z_{\text{p}}}{}).\end{equation}
Here we use the ‘Hubble diagram redshift’
$z_{\text{HD}}$
, which is the cosmological redshift we are interested in. This differs in our nomenclature from the CMB-frame redshift
$z_{\text{CMB}}$
, because
$z_{\text{CMB}}$
takes into account our motion but not the peculiar velocity of the source. Combined with Equation (2) we see
\begin{equation}z_{\text{HD}}=\frac{1+z_{\text{CMB}}}{1+{z_{\text{p}}}{}} -1.\end{equation}
Thus the Hubble diagram redshift requires knowledge of the SN host’s peculiar redshift
${z_{\text{p}}}$
, so we turn to how we derive peculiar velocities.
6. Updating peculiar velocity modelling
By applying the heliocentric-to-CMB correction we have accounted for the motion of our own solar system with respect to the CMB. However, we have not yet accounted for the peculiar velocity of the supernova’s host galaxy (
${v_{\text{p}}}{}$
). Removing the redshift due to the estimated peculiar velocity of the host galaxy leaves the cosmological redshift
$z_{\text{HD}}$
(Equation (7)), which is the redshift needed for the Hubble diagram.
In this section, we describe the methodology for computing the peculiar velocity for each host galaxy. Our treatment differs from the peculiar velocities used in Pantheon in the following ways:
-
We use the multiplicative equation for combining redshifts (Equation (6)).
-
We convert the predicted peculiar velocity field to redshift-space (Section 6.2).
-
Outside the measured peculiar velocity field we model the residual bulk flow as a decaying function, rather than a constant external velocity (Section 6.3).
-
We flip the
${v_{\text{p}}}$
sign convention used in the Pantheon sample (and effected the same change in the SuperNova ANAlysis software (SNANA, Kessler et al. Reference Kessler2009) as of version 11.02). Now,
${v_{\text{p}}}$
is positive when moving away from us, which is consistent with the sign of recession velocities.
The nominal set of peculiar velocities we derive here are examined in the companion paper Peterson et al. (Reference Peterson2021) in the context of the efficacy of different peculiar velocity samples, models and parameters of our own model on SN Hubble residuals.
6.1 Estimating peculiar velocities
The most precise way to estimate peculiar velocities is to measure the density field (e.g. through a redshift survey) and use that to predict the expected peculiar velocity field.Footnote g This is known as velocity field reconstruction. Importantly, this method does not use supernova distances, and therefore does not introduce correlations between the peculiar-velocity-corrected SN redshift and its measured distance. The reconstruction does require an assumed cosmological model, but the cosmological dependence is weak. We quantify the impact of these peculiar velocity corrections on cosmological parameters in Section 7.
In the linear regime, peculiar velocity is related to the gravitational acceleration via:
\begin{equation} v(r) = \frac{f}{4\pi}\int \mathrm{d}^3\boldsymbol{r}^\prime \unicode{x03B4}(\boldsymbol{r}^\prime) \frac{\boldsymbol{r}^\prime-\boldsymbol{r}}{|\boldsymbol{r}^\prime-\boldsymbol{r}|^3},\end{equation}
where f is the growth rate of the cosmic structure and
$\unicode{x03B4}(\boldsymbol{r})$
is the density contrast. This equation has two limitations:
-
Galaxy surveys do not measure the total matter density, so it is assumed that the observed galaxy density (
$\unicode{x03B4}_g$
) linearly traces the total density,
$\unicode{x03B4} = \unicode{x03B4}_g/b$
. Here b is the linear biasing parameter, which is different for different types of galaxies, and therefore has to be measured or marginalised over. -
The region over which we have a sufficient number density of measured galaxies to do reconstruction is smaller than the region for which we need to estimate peculiar velocities. This has been addressed by estimating the ‘external velocity’,
${\boldsymbol{V}_{\text{ext}}}$
, which arises due to structures outside the survey volume, and estimating how that would theoretically decay with distance (Section 6.3).
We use the velocity field reconstruction created by Carrick et al. (Reference Carrick, Turnbull, Lavaux and Hudson2015), which uses data from the 2M
$++$
compilation from Lavaux & Hudson (Reference Lavaux and Hudson2011). 2M
$++$
includes data from 2MRS (Huchra et al. Reference Huchra, Fairall and Woudt2005), 6dFGS (Jones et al. Reference Jones2009), and SDSS (Abazajian et al. Reference Abazajian2009) and extends to a radius of
$r_{\text{max}}=200\;{h}^{-1}\mathrm{Mpc}$
. One slice (
$SGZ=0$
) of the reconstructed density field is shown in Figure 6 in the supergalactic plane (
$SGX-SGY$
). Figure 7 shows the 2M
$++$
velocity field in redshift-space on a regular spatial grid.
Figure 6. Slice of the 2M
$++$
reconstructed density field plotted in the supergalactic plane (
$SGZ=0$
). White areas are regions for which data is missing, therefore the density reconstruction is uncertain.
Figure 7. 2M
$++$
velocity field plotted on a regular grid of redshift-space positions. Note the white regions in Figure 6 have been interpolated over to make a complete velocity field out to 200
${h}^{-1}\mathrm{Mpc}$
, which means those regions of the velocity field will have higher uncertainty than other regions.
A key model parameter to evaluate is
$\unicode{x03B2}\equiv f/b$
. The rate of growth is often parameterised by
$f={\Omega_{\text{m}}}^\gamma$
, where
$\gamma=0.55$
in the standard cosmological model,
$\Lambda$
CDM. Importantly, however,
$\unicode{x03B2}$
is determined empirically rather than computed from the
$\Lambda$
CDM model.
Both
$\unicode{x03B2}$
and
${\boldsymbol{V}_{\text{ext}}}$
are derived from a combination of density field reconstruction and observation. The reconstruction process delivers a normalised peculiar velocity field,
$v_{\rm p,recon.}(\boldsymbol{r})$
, which gives the directions and relative magnitudes of the peculiar velocities as a function of position. Predictions from this peculiar velocity field are compared with galaxies that have peculiar velocities derived from distance measures such as the Tully-Fisher relation or Fundamental Plane relation. The calibrated peculiar velocity field is
\begin{equation}v_{\rm p}(\boldsymbol{r}) = \unicode{x03B2} v_{\rm p,recon.}(\boldsymbol{r}) + V_{\text{ext}}(\boldsymbol{r}).\end{equation}
The parameter
$\unicode{x03B2}$
thus acts as a scaling of the normalised velocity field (subject to the sample of observed
${v_{\text{p}}}$
), and
${\boldsymbol{V}_{\text{ext}}}$
is the residual mean velocity.
Carrick et al. (Reference Carrick, Turnbull, Lavaux and Hudson2015) measured
$\unicode{x03B2}=0.431\pm0.021$
and an external velocity of
$|{\boldsymbol{V}_{\text{ext}}}{}| = 159\pm23\,\mathrm{km\,s}^{-1}$
in the direction of
$(l, b) = (304{^{\circ}}\pm11{^{\circ}}, 6{^{\circ}}\pm13{^{\circ}})$
. While we use the velocity field measured by Carrick et al. (Reference Carrick, Turnbull, Lavaux and Hudson2015), we use an updated value of
$\unicode{x03B2}=0.314^{+0.031}_{-0.047}$
derived in Said et al. (Reference Said, Colless, Magoulas, Lucey and Hudson2020), which gives a better fit when comparing SDSS Fundamental Plane peculiar velocities to the predicted peculiar velocity field. We confirm that this lower
$\unicode{x03B2}$
value results in a lower scatter in the supernova Hubble diagram, see Peterson et al. (Reference Peterson2021).
Carrick et al. (Reference Carrick, Turnbull, Lavaux and Hudson2015) estimated the peculiar velocity uncertainty to be 250
$\mathrm{km\,s}^{-1}$
for the galaxies (the particle velocity field) and 150
$\mathrm{km\,s}^{-1}$
for galaxy groups (the haloes). In other words, the uncertainty on an individual galaxy’s peculiar velocity is higher than the uncertainty on peculiar velocity of the group in which it resides. We note, however, that some regions of the reconstruction are less certain than others because of incomplete sampling. Unfortunately, sampling is not accounted for in current models, so we adopt the value of
$\unicode{x03C3}_{v_{\rm p}}=250$
$\mathrm{km\,s}^{-1}$
and leave a more precise estimate of the peculiar velocity uncertainty for future work.
6.2 Real vs redshift-space
Carrick et al. (Reference Carrick, Turnbull, Lavaux and Hudson2015) provide the velocity field in ‘real-space’, so the position and distance of a galaxy can be used to draw the peculiar velocity directly from the modelled velocity field. However, in supernova cosmology, the distance measured via the distance modulus should be independent of the redshift. This distance should not be used to predict the peculiar velocity to correct the redshift. Converting the observed redshift to distance (by assuming a cosmology) to estimate the peculiar velocity is valid, but less precise than using the redshift. We therefore convert the reconstructed velocity field of Carrick et al. (Reference Carrick, Turnbull, Lavaux and Hudson2015) to redshift-space. While we assume a cosmology for this conversion, any reasonable choice has a negligible effect on the velocity field. Thus we query the peculiar velocity model using the coordinates of each host galaxy or SN (RA, Dec,
$z_{\text{CMB}}$
), and Equation (9).
The conversion to redshift-space takes two steps. First, for each real-space grid point i we convert the real-space position,
$\boldsymbol{r}_i$
, into redshift position
$\boldsymbol{z}_i$
using the predicted peculiar velocity at that grid point,
$\boldsymbol{v}_{\text{p},i}$
. Second, we use inverse distance weighting to interpolate and adjust the irregularly-spaced grid in redshift-space to a regular grid. This process is described in more detail in Appendix B.
An alternative method is to integrate along the line of sight over real-space. This technique is used by the online toolFootnote h associated with Carrick et al. (Reference Carrick, Turnbull, Lavaux and Hudson2015), which was previously used to estimate the Pantheon peculiar velocities. Both methods agree very well, within the uncertainty, as seen in Figure 8. The mean difference is only 5 km s–1 (50 times smaller than the individual uncertainty).
Figure 8. The predicted peculiar velocity for a sample of 851 host galaxies using two different approaches. Each
${v_{\text{p}}}$
has an uncertainty of 250
$\mathrm{km\,s}^{-1}$
. We use the 2M++ velocity field converted from real-space to redshift-space whereas the method associated with Carrick et al. (Reference Carrick, Turnbull, Lavaux and Hudson2015) (previously used for Pantheon), integrates over real-space along the line of sight for each host galaxy. There are only negligible systematic differences between the results of these techniques, and all scatter is within 1
$\unicode{x03C3}$
.
6.3 Velocities beyond
$r_{\rm max}$
It is difficult to properly account for velocities outside
$r_{\rm max}$
because we do not have an adequate measurement of the density field to predict individual velocities precisely. However, we expect velocities to continue to behave largely according to the bulk flow trend beyond
$r_{\rm max}$
as a consequence of
$\Lambda$
CDM large scale structure. In standard
$\Lambda$
CDM a theoretical bulk flow magnitude of
${\sim}20\,\mathrm{km\,s}^{-1}$
is expected even for a sphere with radius
$z\sim1$
(grey dashed lines in Figure 9). Accordingly, peculiar velocities of galaxies outside
$r_{\rm max}$
should not be set to zero.
Figure 9. Top: Pantheon (original) peculiar velocities converted to redshift. The expected decay of peculiar velocity amplitude according to
$\Lambda$
CDM is over-plotted (grey dashed), outside the limit of the reconstruction at 200
${h}^{-1}\mathrm{Mpc}$
(
$z\approx0.067$
). The spurious increase in peculiar velocities as redshift increases is driven by the erroneous use of the low-redshift approximation (Equation (1)). The error term is plotted (red dashed) only for the four SNLS fields. Bottom: Pantheon+ (this work) peculiar velocities, converted to redshift, which are now well-behaved beyond low-redshift.
To ensure a smooth transition across
$r_{\rm max}$
we have chosen to model the bulk flow as a decaying function consistent with
$\Lambda$
CDM expectations, and in the direction of the bulk flow of the 200
${h}^{-1}\mathrm{Mpc}$
sphere. While there is a
$\Lambda$
CDM model dependence, the impact of this high-z correction on cosmological inferences is small both because the corrections are small (at most
${\sim}5 \times 10^{-4}$
when in the direction of the bulk flow), and because at high-z these peculiar redshifts represent a small fraction of the total redshift.
We note that there is a slight difference between
${\boldsymbol{V}_{\text{ext}}}$
and the bulk flow of the 200
${h}^{-1}\mathrm{Mpc}$
sphere. The bulk flow of the sphere is the average of the internal velocities (which is small but non-zero), plus the external velocity. We calculate the bulk flow at the 2M
$++$
maximum radius of 200
${h}^{-1}\mathrm{Mpc}$
to be
$182\pm23\,\mathrm{km\,s}^{-1}$
in the direction of
$(l, b) = (302{^{\circ}}\pm10{^{\circ}}, 2{^{\circ}}\pm9{^{\circ}})$
. At this large radius, the bulk flow is dominated by the external bulk flow (
$V_{\text{ext}} \approx 170$
km s–1: Said et al. Reference Said, Colless, Magoulas, Lucey and Hudson2020; Boruah, Hudson & Lavaux Reference Boruah, Hudson and Lavaux2020) plus a small contribution from the mean internal velocities.
Contrary to common expectations, the bulk flow should not necessarily converge on the direction of the CMB dipole. The observed CMB dipole is particular to our own motion, and is removed with the correction from the heliocentric to the CMB frame. Dramatic changes to the magnitude and direction of bulk flow direction become unlikely as we average over spheres that approach the scale of homogeneity. Therefore, we fix the direction of the decaying bulk flow in the direction of the 200
${h}^{-1}\mathrm{Mpc}$
sphere’s bulk flow.
The Pantheon sample peculiar velocities outside the velocity reconstruction suffered three main issues which can be seen in Figure 9. The most apparent issue is the increasing
${v_{\text{p}}}$
with redshift. We show that this artefact is caused by the low-z approximation of the heliocentric correction by plotting the error term (i.e. the difference between Equations (1) and (2)) for the four SNLS fields, as these stretch to high-z. This particular error also occurs for PS1MD and SDSS but is less visible since these surveys do not extend as far in redshift. Also visible in Figure 9 are the HST SNe with
${v_{\text{p}}}{}=0$
, and the somewhat random scatter around
$z\approx0.15$
which may have been due to assigning 2M++ peculiar velocities outside the 2M++ sphere. We show in the bottom panel of Figure 9 that these issues are now resolved.
7. Impact on cosmological parameters
To test the impact of these redshift updates on cosmological parameters we fit for
$H_0$
, and (separately) the dark energy equation of state w, in a flat-wCDM model for various different combinations of updates as listed in Table 4 and described below. We only report the changes in these parameters, relative to the nominal ‘Final’ set that includes all of the updates (updated
${z_{\text{hel}}}$
, exact formula for combining redshifts, and new peculiar velocities). The full Pantheon+ cosmology analysis is reported in Brout et al. (Reference Brout2022).
Table 4. Impact of different corrections, redshift samples, systematics, and uncertainties on cosmological parameters. We define the change in cosmological parameters to be the variation minus the nominal value (variation 5).
$N_{\rm SN}$
refers to the number of supernovae in each sample, which differ between variations depending on which supernovae pass or fail quality cuts as their redshifts change. The uncertainties (
$\unicode{x03C3}_{H_0}$
and
$\unicode{x03C3}_w$
) show only the uncertainty due to the supernova sample size and distance moduli uncertainties, not the expected precision of the measurement.
Figure 10. Difference in distance moduli for selected variations compared to the Final values (variation 5),
$\unicode{x03BC}_{\text{Final}}$
. Faint points are individual SNe, while dark points are binned in redshift. The grey shaded region represents the redshift range used to fit
$H_0$
. All deviations in the binned differences are within 1
$\unicode{x03C3}$
, where the uncertainty comes only from distance modulus uncertainty (and not absolute magnitude calibration). The largest changes come from the updates to
${z_{\text{hel}}}$
and next largest from the updates to
${v_{\text{p}}}$
.
In addition to combinations of redshift updates, we consider other redshift/sample variations for a total of 14 variations. Each variation is numbered, as listed in Table 4, and the same numbering is also included in each figure for easy reference. The variations we consider are:
-
(0) No corrections This is the original data without any redshift corrections.
-
(1–4) Partial corrections These variations are the permutations of (a) updating
${z_{\text{hel}}}$
; (b) combining redshifts multiplicatively,
${z_{\text{CMB}}^{\mathrm{\times}}}$
(as opposed to using the low-z additive approximation); (c) using our new peculiar velocities,
${v_{\text{p}}}$
. -
(5) All corrections The nominal Final data includes all redshift updates.
-
(6–7) Redshift source We consider first the subset of supernovae that have host-galaxy redshifts (1576 of the 1763 redshifts). Second, for the entire sample we replace host-galaxy redshifts with the redshift of the host galaxy’s group when available (186 of 1763 redshifts).
-
(8–11) Systematic offsets We consider two different forms of systematic redshift offsets: shifting the redshift by
$\pm \unicode{x03C3}_z$
(variations 8, 9), and by
$\pm 4{\times 10^{-5}}$
(as suggested by Calcino & Davis Reference Calcino and Davis2017; Brout et al. Reference Brout2019) (variations 10, 11). -
(12–13) Uncertainty changes The last test is how the size of redshift uncertainties affects cosmological parameters (as suggested by Steinhardt et al. Reference Steinhardt, Sneppen and Sen2020), so we scale all uncertainties up by a factor of 3 (variation 12), and only SDSS-measured redshift uncertainties by
$+3{\times 10^{-5}}$
(variation 13; see Section 4).
In addition, in Section 7.4 we discuss the sub-sample of SNe that lack host-z (187 SNe; the complement to variation 6), but we do not list this as a numbered variation due to the small number of SNe.
7.1 Dependence of distance modulus on redshift change
We analyse each variation independently, meaning that for each: each SN light curve is fit using the SALT2 model Guy et al. (Reference Guy2010) as derived in Brout et al. (Reference Brout2021) using SNANA (Kessler et al. Reference Kessler2009), biases are corrected following the BEAMS with Bias Correction (BBC) framework established in Kessler & Scolnic (Reference Kessler and Scolnic2017), and distance moduli
$\unicode{x03BC}$
are determined, all within the Pippin framework (Hinton & Brout Reference Hinton and Brout2020). The details of this process are given in Brout et al. (Reference Brout2022). The resulting distance moduli changes can be seen in Figure 10.
The total number of supernovae in each variation changes slightly due to various reasons. When we restrict the redshift range for fitting
$H_0$
and w, some borderline-redshift supernovae are shifted in and out of the sample due to redshift changes. However, shifting redshifts also affects the light curve fit parameters. The quality cuts we apply are to these fit parameters (among others) and also their errors. A redshift shift can therefore also shift a supernova in or out of the sample. For example, a light curve parameter may pass the cut with the shifted redshift, or the fit may be poorer at the shifted redshift.
We expect
$\unicode{x03BC}$
to change when a supernova redshift changes because the duration of a light curve (stretch) is affected by time-dilation and its colour is affected by K-corrections, both of which are dependent on the measured heliocentric redshift (but not the peculiar velocity correction); the theoretical basis for these variations is explained in Huterer et al. (Reference Huterer, Kim, Krauss and Broderick2004). However, the distance modulus of a supernova may also change between sample variations without changing the redshift. The procedure for deriving distance moduli for a supernova sample (e.g. using BBC; Kessler & Scolnic Reference Kessler and Scolnic2017) determines the peak magnitude (
$m_B$
) from the light curve, the global parameters
$\alpha$
and
$\unicode{x03B2}$
that adjust the stretch (
$x_1$
) and colour (c) of the supernovae, and a correction term for selection biases (
$\unicode{x03B4}\unicode{x03BC}_{\text{bias}}$
), according to a modified version of the Tripp relation (Tripp Reference Tripp1998), following Kessler et al. (Reference Kessler2019),Footnote i
\begin{equation}\unicode{x03BC} = m_B-M+\alpha x_1 - \unicode{x03B2} c -\unicode{x03B4}\unicode{x03BC}_{\text{bias}}.\end{equation}
Therefore the distance modulus may change even if the redshift is not altered since the calibration of
$\alpha$
,
$\unicode{x03B2}$
and absolute magnitude (M) depend on the sample as a whole. This explains the slight changes in distance moduli for variation 6 (the host-z sample), in which we do not alter any redshifts.
The dependence of the change in a supernova’s
$\unicode{x03BC}$
between variations on the change in z is demonstrated in Figure 11, which shows that the two are strongly correlated (see also Huterer et al. Reference Huterer, Kim, Krauss and Broderick2004). This correlation results in a cancellation that reduces the impact of redshift uncertainties, particularly at mid-range redshifts (around
$z\sim0.5$
). This can be seen in the solid lines in Figure 11, which show the slope (d
$\unicode{x03BC}/\textit{d}z$
) of the Hubble diagram at different redshifts. At mid-range redshifts the slope is the same as the degeneracy direction between redshift change and distance modulus change. Thus uncertainties in redshift essentially cancel out at these redshifts, as they cause points to be shifted along the magnitude-redshift relation instead of deviating from it. This may be particularly helpful for supernova cosmology using photometric redshifts whose uncertainties are larger than spectroscopic redshifts (Chen et al. Reference Chen2022).
Figure 11. Change in distance modulus versus change in redshift (circles), and
$\unicode{x03BC}(z)$
derivatives d
$\unicode{x03BC}$
/dz for given redshifts (black lines). The largest changes occurred due to amending
${z_{\text{hel}}}$
. The black lines represent the purely theoretical
$\Delta\unicode{x03BC}$
that would occur on the Hubble diagram given the
$\Delta z$
on the horizontal axis (in other words, the slope of the Hubble diagram at those redshifts). The positive trend demonstrates that a change in redshift is partially cancelled the corresponding change in
$\unicode{x03BC}$
(see discussion in Section 7.1). This trend is seen in each variation.
For a simplified assessment of how redshift changes impact cosmology, it is natural to simply use the published
$\unicode{x03BC}$
values, and shift the redshifts (as was done in Davis et al. Reference Davis, Hinton, Howlett and Calcino2019; Steinhardt et al. Reference Steinhardt, Sneppen and Sen2020). For the low-z sample, we show using the large, transparent symbols in Figure 12 that this gives a reasonable approximation to the full analysis that uses recalculated
$\unicode{x03BC}$
values (smaller symbols). The main difference of not recalculating
$\unicode{x03BC}$
is less cancellation of the effect of systematic redshift changes. At intermediate redshifts one might expect that neglecting the cancellation in d
$\unicode{x03BC}$
/dz may overestimate the deviation due to redshift shifts. Interestingly, we find that when fitting for w without re-deriving
$\unicode{x03BC}$
the change in w often becomes slightly larger (e.g. variations 0–2) but in some cases (e.g. variations 8–9, shifting the redshifts by 1
$\unicode{x03C3}_z$
) we find the shift in w goes in the opposite direction (likely due to
$\unicode{x03C3}_z$
increasing with z). Overall we find that doing approximate cosmology fits by changing z without changing
$\unicode{x03BC}$
gives reasonable results, but for precision cosmology one should refit
$\unicode{x03BC}$
whenever
${z_{\text{hel}}}$
changes.
Figure 12. The impact on inferences of
$H_0$
and w due to changes in the redshifts. The regular symbols are the nominal results while the faint, larger symbols come from not recalculating
$\unicode{x03BC}$
after changing redshift so that the partial cancellations seen in Figure 11 are not present. The descriptions on the left hand side and variation numbers on the right hand side both correspond to the descriptions in Table 4. The
$H_0$
fit uses the redshift range
$0.0233<z_{\text{HD}}<0.15$
, while the w fit uses the range
$z_{\text{HD}}>0.01$
, where the maximum redshift of the sample is 2.26. The uncertainties in both
$H_0$
and w only represent the statistical uncertainty from the SN magnitude uncertainties—they do not contain any uncertainty from distance ladder calibration nor intrinsic dispersion in SN magnitudes. All variations are small, showing that the cosmology results are robust to small changes in redshift and there is no indication of systematic redshift errors biasing previous results.
7.2 Fitting
$H_0$
We first fit
$H_0$
using the method in Riess et al. (Reference Riess2016), that compares the distance modulus data to a low-redshift approximation of the recession velocity.Footnote j The only free parameter in this fit is
$H_0$
.
For this fit we focus on only the low-redshift regime of
$0.0233<z_{\text{HD}}<0.15$
, which is the standard range used by previous supernova cosmology analyses such as Riess et al. (Reference Riess2016); Riess et al. (Reference Riess2018). In the Final dataset this redshift range contains 512 SNe of which only 17 lack host galaxy redshifts.
When calculating the uncertainties we only consider the statistical uncertainties in the distance moduli of the supernovae, not the uncertainties in the absolute magnitude calibration. Thus the uncertainties in
$H_0$
in Figure 12 reflect the size of shifts due only to redshift/sample variations and not the size of uncertainties in the
$H_0$
measurements (for example the current uncertainty on
$H_0$
from SN cosmology is about 5 times larger).
The results are shown in Table 4 and Figure 12, where we see that the redshift improvements we have made have a small impact on the value of
$H_0$
relative to the uncertainty from the SH0ES
$H_0$
measurement with uncertainty of
$1.0\, \mathrm{km\,s}^{-1}\mathrm{Mpc}^{-1}$
(Riess et al. Reference Riess2022). We define the difference in cosmological parameters for each variation to be the variation minus the Final value, that is
$\Delta H_0 = H_0^n - H_0^{\text{Final}}$
for variation n. Applying all updates to the original redshifts results in
$\Delta H_0 = -0.12\,\mathrm{km\,s}^{-1}\mathrm{Mpc}^{-1}$
. The largest redshift variations, that is shifting all redshifts by their
$1\unicode{x03C3}$
uncertainties (variations 8 and 9) result in
$|\Delta H_0|\leq0.2\,\mathrm{km\,s}^{-1}\mathrm{Mpc}^{-1}$
.
7.3 Fitting wCDM
We also evaluate the impact of the redshift updates on the best fit parameters in the flat-wCDM model. This model has two free parameters: the matter density
${\Omega_{\text{m}}}$
, and the equation of state of dark energy w, but we implement a Planck-like prior on the matter density of
${\Omega_{\text{m}}}=0.311\pm0.010$
so we can isolate the impact on w. We marginalise over absolute magnitude and
$H_0$
, and we fit over the redshift range
$z_{\text{HD}}>0.01$
. To estimate the changes in w we use the fast minimisation routine wFit in SNANA (Kessler et al. Reference Kessler2009) which outputs marginalised cosmology parameters w and
$\Omega_M$
; the complete fit with a thorough covariance analysis can be found in Brout et al. (Reference Brout2022).
The results are shown in Table 4 and Figure 12; changes in w are smaller than the statistical uncertainty of
$\lesssim$
0.03 given in the full Pantheon+ w measurement from Brout et al. (Reference Brout2022) and the uncertainty of 0.04 from Pantheon (Scolnic et al. Reference Scolnic2018). Applying all updates to the original redshifts results in
$\Delta w = 0.003$
. The largest redshift variations, that is shifting all redshifts by their
$1\unicode{x03C3}$
uncertainties (variations 8 and 9) result in
$|\Delta w|\leq0.015$
.
7.4 SN-z vs host-z
Using the original Pantheon sample, Steinhardt et al. (Reference Steinhardt, Sneppen and Sen2020) find a statistically significant shift in the cosmological parameters derived for the subset of SNe that have redshifts measured from the supernova (SN-z) and those that have host-galaxy redshifts (host-z). Here we revisit this analysis with our updated data.
There are several important differences between Steinhardt et al. (Reference Steinhardt, Sneppen and Sen2020) and our analysis: (1) Steinhardt et al. (Reference Steinhardt, Sneppen and Sen2020) fit all wCDM parameters simultaneously, (2) our definition of the SN-z sample is stricter than their not-host-z, in that we allow host emission-lines in SN-dominated spectra to be assigned to the host-z sample, and (3) our allocation of SN-z particularly for PS1MD and SDSS SNe differs from theirs. We expect the SDSS classifications to differ because, as we addressed in Section 3, we updated 81 SN-zs to host-zs (and further, applied the
$+2.2{\times 10^{-3}}$
systematic offset to the remaining SN-zs as determined in Sako et al. Reference Sako2018). However, the reason for the PS1MD classification differences are unclear; our classifications come directly from reported redshift uncertainties (SN-z have uncertainties of 0.01 and host-z 0.001).
We find that restricting the data to only those SNe with host-z (variation 6 in Table 4 and Figure 12) gives
$\Delta H_0=0.05\pm0.20\,\mathrm{km\,s}^{-1}\mathrm{Mpc}^{-1}$
(i.e.
$0.3\unicode{x03C3}$
) relative to the nominal Final dataset. By contrast, when we restrict the data to the SN-z sample (of which only 17 are in the redshift range of the
$H_0$
fit), we find
$\Delta H_0=-2.8\pm1.3\,\mathrm{km\,s}^{-1}\mathrm{Mpc}^{-1}$
.
These results are broadly consistent with Steinhardt et al. (Reference Steinhardt, Sneppen and Sen2020), who found that
$\Delta H_0= 0.45\pm 0.25\,\mathrm{km\,s}^{-1}\mathrm{Mpc}^{-1}$
for the host-z sample and
$\Delta H_0=-0.96\pm0.50\,\mathrm{km\,s}^{-1}\mathrm{Mpc}^{-1}$
for the SN-z sample. The significance of the shift in the host-z sample is lower in our case, which is likely due to the greater proportion of host-z redshifts in our sample and the corrections we have implemented to the SN-z based on the systematic offset correction determined by Sako et al. (Reference Sako2018). On the other hand, the
$H_0$
shift we find in the SN-z sample is larger than Steinhardt et al. (Reference Steinhardt, Sneppen and Sen2020), but our results are of similar significance (approximately
$2\unicode{x03C3}$
in each case) since we have fewer SNe in the SN-z sample.
Increasing the redshift range over which we fit for
$H_0$
adds some model dependence, but allows us to include more of the SN-z sample. When we do so the deviation from the nominal dataset vanishes, with the results from SN-z alone agreeing with the result from host-z alone (within
$1\unicode{x03C3}$
) for all
$z_{\rm max}\gtrsim 0.25$
. Figure 13 shows the impact of including or excluding SN-z from our fit for
$H_0$
, as a function of redshift range used in the fit. The impact is small, with
$|\Delta H_0|\lesssim 0.05\,\mathrm{km\,s}^{-1}\mathrm{Mpc}^{-1}$
.
Figure 13. The dependence of
$H_0$
on the redshift-range we fit over. The horizontal axis shows the maximum redshift used in the fit, keeping the minimum redshift as
$z_{\text{HD}}=0.0233$
. Red shows the Final sample, and blue shows the host-z sample in order to demonstrate the impact of excluding SNe that only have SN-z. As redshift increases the cosmological model dependence becomes increasingly important so the grey shading shows the range of
$H_0$
values from fitting with
$0.25<{\Omega_{\text{m}}}<0.35$
in the flat-
$\Lambda$
CDM model (
${\Omega_{\text{m}}}=0.35$
being the lower edge). At the nominal upper redshift limit of
$z_{\rm max}=0.15$
the statistical variance of the sample (black error bar) remains larger than the uncertainty due to even this quite wide range of
${\Omega_{\text{m}}}$
.
As expected, Figure 13 shows that as we increase the maximum redshift in our
$H_0$
fit the cosmological model-dependence becomes increasingly apparent. The
$v_{\rm approx}(z,q_0,j_0)$
equation in Section 7.2 is a good approximation to the full equation
$v(z)=c\int_0^z\frac{dz}{E(z)}$
where
$E(z)\equiv H(z)/H_0$
, as long as
${\Omega_{\text{m}}}\sim0.3$
for the flat-
$\Lambda$
CDM model. Over the nominal redshift range of
$0.0233<z_{\text{HD}}<0.15$
(black point) a shift of
$\Delta{\Omega_{\text{m}}}\pm0.05$
results in
$\Delta H_0\mp0.2\,\mathrm{km\,s}^{-1}\mathrm{Mpc}^{-1}$
, showing the cosmological model-dependence is still sub-dominant to the sampling uncertainties on
$H_0$
(which is the purpose of using the restricted redshift range).
For the equation of state of dark energy, the host-z only case (6) shows a shift of
$\Delta w = -0.022\pm0.048$
. This is the largest impact on w of any variation, albeit still insignificant (
$0.6\unicode{x03C3}$
). Using only SN-z gives
$\Delta w=0.25\pm0.16$
. The reason for this shift can be seen in Figure 10, where the SN-z sample shows a systematic positive offset in
$\Delta \unicode{x03BC}$
at low redshift, but a negative offset at high redshift. Any shift with a redshift dependence will have an impact on w whereas a constant shift would mainly affect
$H_0$
.
Given these results, in Section 8 we discuss whether SN-z samples should be included in cosmological fits.
7.5 Redshift systematics and uncertainty values
As expected, some of the largest changes in
$H_0$
and w occur when we add a systematic shift to all redshifts in the sample (variations 8–11). However, even when we shift the redshifts systematically by their uncertainties (variations 8–9) the impact is only
$|\Delta H_0|\sim 0.2\pm0.2\,\mathrm{km\,s}^{-1}\mathrm{Mpc}^{-1}$
and
$|\Delta w|\sim0.015\pm0.045$
, smaller than the sample uncertainties in each case.
Changing the size of the uncertainties on the redshifts has a negligible impact on the cosmological parameters (variations 12–13).
8. Discussion and conclusions
Motivated in part by the fact that a systematic error in redshift could affect standard candle derivations of
$H_0$
, especially if it were at low redshift, we have reviewed and revised the redshifts for the Pantheon+ supernova sample. This includes fixing bookkeeping errors, updating heliocentric redshifts when available, adding uncertainty estimates, converting from the heliocentric to the CMB-frame redshifts without using the low-z additive approximation, updating peculiar velocity estimates at all redshifts, and correcting the peculiar velocities from large-scale flow predictions at large redshifts.
These curated redshifts are the ones that should be used in the future for all supernova cosmology analyses using these data. They are available at the CDS VizieR database and also https://github.com/PantheonPlusSH0ES/DataRelease, and the code that generated the peculiar velocity predictions can be found at https://github.com/KSaid-1/pvhub.
We found that these redshift updates do not have a large impact on cosmological results. This fortunate circumstance arises for a few reasons. Firstly, errors at high-z are relatively unimportant, because the relative uncertainty in redshift decreases as redshift increases. That is compounded by the fact that a particular
$\Delta z$
corresponds to a much smaller distance difference at high-z than at low-z. Furthermore the
$\Delta\unicode{x03BC}$
versus
$\Delta z$
correlation we mentioned in Section 7.1 and Figure 11 reduces the impact of redshift errors, especially near
$z\sim0.5$
. Thus at high-z even a large error in redshift gives a small error in expected magnitude.
Secondly, for the SNe at very low redshifts (
$z<0.01$
) that are used to calibrate the SN Ia absolute magnitude, the redshifts are not used—they are replaced by the brightness of another standard candle (TRGB or Cepheids), that acts as an anchor.
Finally, many potential systematic redshift errors (for example due to the approximate heliocentric to CMB-frame conversion) are only systematic if the sample covers a small area of the sky. The low-z supernova sample (
$z\lesssim0.15$
), for which redshift errors could have a large impact, is spread across most of the sky (see Figure 1). We also confirmed in Section 6.1 that the new peculiar velocities do not systematically differ from those previously predicted. Thus the updates to the redshifts of Pantheon+ mostly caused random shifts, predominantly via updating
${z_{\text{hel}}}$
and
${v_{\text{p}}}$
. Across the whole sample the root-mean-square deviation of all the redshift changes was
${\sim}3 \times 10^{-3}$
, however the mean redshift change was an order of magnitude smaller (
${\sim}4 \times 10^{-4}$
). Within the redshift range
$0.0233<z_{\text{HD}}<0.15$
, RMS
$(\Delta z_{\text{HD}})\sim 1{\times 10^{-3}}$
and the mean redshift change was
${\sim}1 \times 10^{-4}$
. The mean change is actually almost completely frame and redshift-range independent, but is smaller for the
$H_0$
sample because, unlike for the mean
${z_{\text{hel}}}$
of the full sample, it does not account for repeat observations of the same SNe originally being assigned different
${z_{\text{hel}}}$
. This resulting impact on
$H_0$
is consistent with that predicted by (Davis et al. Reference Davis, Hinton, Howlett and Calcino2019, see the green dashed line in their Figure 4).
We compared the cosmological results with and without the sample that has only supernova redshifts in Section 7.4). As in previous studies (e.g. Steinhardt et al. Reference Steinhardt, Sneppen and Sen2020), we found differences in the results from these sub-samples, the most significant of which was a
$2\unicode{x03C3}$
deviation in
$H_0$
for the SN-z sub-sample. While it is possible this is a statistical fluctuation with so few SNe in the SN-z sample, there are reasons to expect a systematic offset from the host-z sample. When host galaxies lack redshifts it is usually because they are faint and/or low-mass, and SNe Ia properties are correlated with their hosts’ properties (e.g. Sullivan et al. Reference Sullivan2006; Smith et al. Reference Smith2020b; Wiseman et al. Reference Wiseman2020). Therefore the SN-z sample could represent a physically different subset of SNe that is not accounted for in, for example, SALT2 modelling. Alternatively, a slight bias could arise if, for example, supernova spectral templates do not fully account for the blueshift due to the velocity of the visible side of the supernova’s photosphere.
Given the greater uncertainty in supernova redshifts compared to host-galaxy redshifts, and the potential for bias (as seen with SDSS SNe in Zheng et al. Reference Zheng2008; Sako et al. Reference Sako2018), one could consider removing all supernovae that lack a host redshift from cosmology samples. This would reduce the cosmologically useful sample size slightly, and thus sacrifice a small amount of precision for potentially greater accuracy. At
$z<0.15$
approximately 3% of the Type Ia supernova sample lacks host galaxy redshifts, but that proportion increases to approximately 10% at high redshift. Excluding the SN-z excludes a different proportion of the supernova population as a function of redshift. While this effect should be monitored for future cosmological studies (and should motivate further follow-up efforts to get host-z), we have shown here that the impact of including or excluding the SN-z sample remains small relative to the uncertainties in the measurement (Figure 13).
Finally, we have also made sure all supernova redshifts now have estimated uncertainties. As noted by Steinhardt et al. (Reference Steinhardt, Sneppen and Sen2020), uncertainties are important because sampling from a symmetric redshift uncertainty systematically prefers a larger
$\unicode{x03BC}$
for a given redshift due to the sublinear nature of the
$\unicode{x03BC}(z)$
relation. This would effectively reduce the gradient of the
$\unicode{x03BC}(z)$
relation at low-z and cause samples with large uncertainties (such SN-z) to prefer a smaller
$H_0$
. Furthermore, the precision of redshift indirectly affects one of the largest systematic uncertainties in SNe Ia analyses: the determination of their intrinsic scatter. If the precision is not correctly measured, more or less scatter will be attributed to the intrinsic variation of SN Ia distances, which could bias the modelling used to determine accurate distances. Additionally, the precision and accuracy of redshifts must be known accurately when using SNe Ia to measure growth-of-structure. In that case, instead of applying peculiar velocities to SNe from an external model, one uses SNe Ia to measure peculiar velocities.
Most of the uncertainties we provide are based on the precision of a particular survey or sample. A better method for determining uncertainties would be to estimate them on a spectrum-by-spectrum basis. However, we tested the impact of changing the uncertainties (see Figure 12) and it had a negligible affect on the cosmological results, so we conclude that the uncertainties we provide are sufficient for current data.
While new surveys and datasets will continue to come online over the next decade, the sample presented here will not easily be replaced due to its utility for measuring
$H_0$
, which is rate-limited by the number of SNe in the very-nearby universe and will take another 30 yr to re-accumulate. Because of that importance, in this work we endeavour to provide an updated and homogeneously treated set of supernova redshifts that we hope will be useful to the community.
Acknowledgement
The authors thank A. Whitford, C. Chang, Y. Lai, A. Glanville and L. Rauf for assisting in visual inspection of host galaxies and performing redshift checks in NED (Section 3). We also thank C. Howlett, M. Colless, and M. Hudson for useful discussions on peculiar velocities and M. Smith for insights into SN host galaxies. TMD is the recipient of an Australian Research Council Australian Laureate Fellowship (project number FL180100168) funded by the Australian Government. DS is supported by DOE grant DE-SC0010007, DE-SC0021962 and the David and Lucile Packard Foundation. DS is supported in part by the National Aeronautics and Space Administration under Contract No. NNG17PX03C issued through the Roman Science Investigation Teams Programme.
This work has made use of the NASA/IPAC Extragalactic Database, which is funded by the National Aeronautics and Space Administration and operated by the California Institute of Technology. This work was also supported by resources provided by the University of Chicago Research Computing Center, and based in part on data acquired at the Anglo-Australian Telescope. We acknowledge the traditional custodians of the land on which the AAT stands, the Gamilaraay people, and pay our respects to elders past and present.
Appendix A. Supplementary Data Tables
Table A1. Averaging of multiple SDSS redshifts.
Table A2. Heliocentric redshift update discrepancies
$\geq$
$1\times10^{-3}$
. Discrepancies that arise from SN redshifts are generally not included (unless they are particularly large or unusual) since they are routinely larger than
$1\times10^{-3}$
.
aMissing heliocentric redshift, so these cases are actually CMB-frame redshift discrepancies.
bThis host was assigned by FSS because it is the closest and largest of the three nearby galaxies but we do not attempt to pick a unique host (see Figure 2).
Table A3. Supernovae previously without redshift uncertainties. The uncertainty is assigned to be
$5\times10^{-3}$
if the redshift is measured directly from a SN spectrum without host emission, and
$9\times10^{-5}$
if not.
a2002hu is the only exception, which is a host redshift we have inflated the uncertainty on due to particularly ambiguous reporting of redshifts.
bRedshift independently measured by Chen et al. (Reference Chen2020), but redshift uncertainties have not been released at the time of writing.
Appendix B. Converting real-space velocities to redshift-space velocities
Here we detail how we transfer the 2M
$++$
velocity reconstruction from real space to redshift space. The purpose of this transformation is so that we do not need to convert redshifts to distances in order to estimate their peculiar velocities.
B.1 Scaling the 2M++ real-space grid
As in Equation (9), the peculiar velocity grid must be scaled from the normalised reconstruction to best match observed peculiar velocities from the Tully-Fisher and Fundamental Plane relations. Each real-space grid point is scaled by
$\unicode{x03B2}$
and adjusted by
${\boldsymbol{V}_{\text{ext}}}$
:
\begin{equation} \boldsymbol{v}_{\text{p}} = \unicode{x03B2} \boldsymbol{v}_{\text{p,recon.}} + {\boldsymbol{V}_{\text{ext}}},\end{equation}
where
$\boldsymbol{v}_{\text{p}} = (v_X, v_Y, v_Z)$
are the new scaled velocities at real-space grid points
$\boldsymbol{r}=(X, Y, Z)$
. The projected line of sight velocity for each grid point is
\begin{equation} v_{\text{proj.}} = \boldsymbol{v}_{\text{p}}\cdot\hat{\boldsymbol{r}}\end{equation}
B.2 Converting to supergalactic coordinates in real-space
The 2M++ real-space grid is in galactic Cartesian coordinates, so we transform to supergalactic Cartesian coordinates by rotating via
\begin{equation} R = \begin{pmatrix} -\sin(l) & \;\;\,\cos(l) & \;\;\, 0 \\ -\sin(b)\cos(l) & -\sin(b)\sin(l) & \;\;\,\cos(b) \\ \;\;\,\cos(b)\cos(l) & \;\;\,\cos(b)\sin(l) & -\sin(b) \end{pmatrix},\end{equation}
so that the positive z-direction (now SGZ) is in the direction of the supergalactic north pole,
$(l,b)=(47.37{^{\circ}},6.32{^{\circ}})$
(Lahav et al. Reference Lahav, Santiago, Webster, Strauss, Davis, Dressler and Huchra2000). With
$\boldsymbol{r}_{\text{SG}}=(SGX,SGY,SGZ)$
and
$\boldsymbol{v}_{\text{SG}}=(v_{SGX},v_{SGY},v_{SGZ})$
,
\begin{equation} \boldsymbol{r}_{\text{SG}}^{\text{T}} = R\boldsymbol{r}^{\text{T}},\end{equation}
and
\begin{equation} \boldsymbol{v}_{\text{SG}}^{\text{T}} = R\boldsymbol{v}_{\text{p}}^{\text{T}}.\end{equation}
The projected line of sight velocity using supergalactic coordinates in real-space is
\begin{equation} v_{\text{SG,proj.}} = \boldsymbol{v}_{\text{SG}}\cdot\hat{\boldsymbol{r}}_{\text{SG}}\end{equation}
B.3 Converting to redshift-space
The distance to any grid point is
\begin{equation} D = \sqrt{\boldsymbol{r}\cdot\boldsymbol{r}} = \sqrt{\boldsymbol{r}_{\text{SG}}\cdot\boldsymbol{r}_{\text{SG}}} =\sqrt{{SGX}^2 +{SGY}^2 +{SGZ}^2}.\end{equation}
We then adjust the redshift of each grid point by its associated peculiar redshift via
\begin{equation} z = [(1+\bar{z})(1+z_{\text{p}}) -1],\end{equation}
where
$\bar{z}$
is the cosmological redshift corresponding to D in
${h}^{-1}\mathrm{Mpc}$
using
$H_0=100h\,\mathrm{km\,s}^{-1}\mathrm{Mpc}^{-1}$
(making it independent of
$H_0$
),
$\Omega_m = 0.3$
(the same value used in the reconstruction process), and
$z_p \approx v_{\text{SG,proj.}}/c$
. The redshift-space position vector is then the real-space position vector converted to redshift by the ratio of z to D,
\begin{equation}\boldsymbol{z}= \frac{z}{D} \boldsymbol{r}_{\text{SG}}.\end{equation}
However, the grid points are now irregularly spaced. Thus, the final step is to use inverse distance weighting to interpolate and adjust the irregularly-spaced grid to a regular grid.
Open access
