1 INTRODUCTION
The state of matter at the interior of core-collapse supernovae as well as in the core of proto-neutron stars (PNS) can reach extreme conditions, in terms of temperatures up to several 1011 K (1.16 × 1010K ≃ 1 MeV), densities in excess of normal nuclear matter density and large isospin asymmetry. The associated supernova phase diagram, i.e. the thermodynamic conditions obtained during a core-collapse supernova, is shown in Figure 1(a) for a selected example simulation. Central densities and maximum temperatures may vary on the order of 10–20% depending on the stellar progenitor. The EOS for supernova simulations must cover such an extended three-dimensional domain illustrated in Figure 1(a), where presently first-principle EOS are not available. Instead, model EOS are being developed for supernova studies. These combine several domains with different degrees of freedom, e.g., heavy nuclei at low temperatures, inhomogeneous nuclear matter composed of light and heavy nuclei together with unbound nucleons, and homogeneous matter at high temperatures and densities. In this article, we reflect on the role of the EOS in core-collapse supernovae explored in spherically symmetric simulations. To this end, accurate three-flavour Boltzmann neutrino transport, developed by Mezzacappa & Bruenn (Reference Mezzacappa and Bruenn1993b, Reference Mezzacappa and Bruenn1993a, Reference Mezzacappa and Bruenn1993c), is employed in the fully self-consistent general relativistic radiation-hydrodynamics framework of Liebendörfer et al. (Reference Liebendörfer2004). In general, accurate neutrino transport is essential for the prediction of the neutrino signal for core-collapse supernova events, as was observed from SN1987A (cf. Bionta et al. Reference Bionta1987; Hirata et al. Reference Hirata1988) which marked a benchmark for current supernova modelling. The latter already confirmed that neutrinos from the next galactic event will be the potentially observable signal, from which we will learn not only details about the stellar explosion but also about the state of matter at the supernova interior which is hidden otherwise, e.g., for electromagnetic radiation by the stellar mantle.
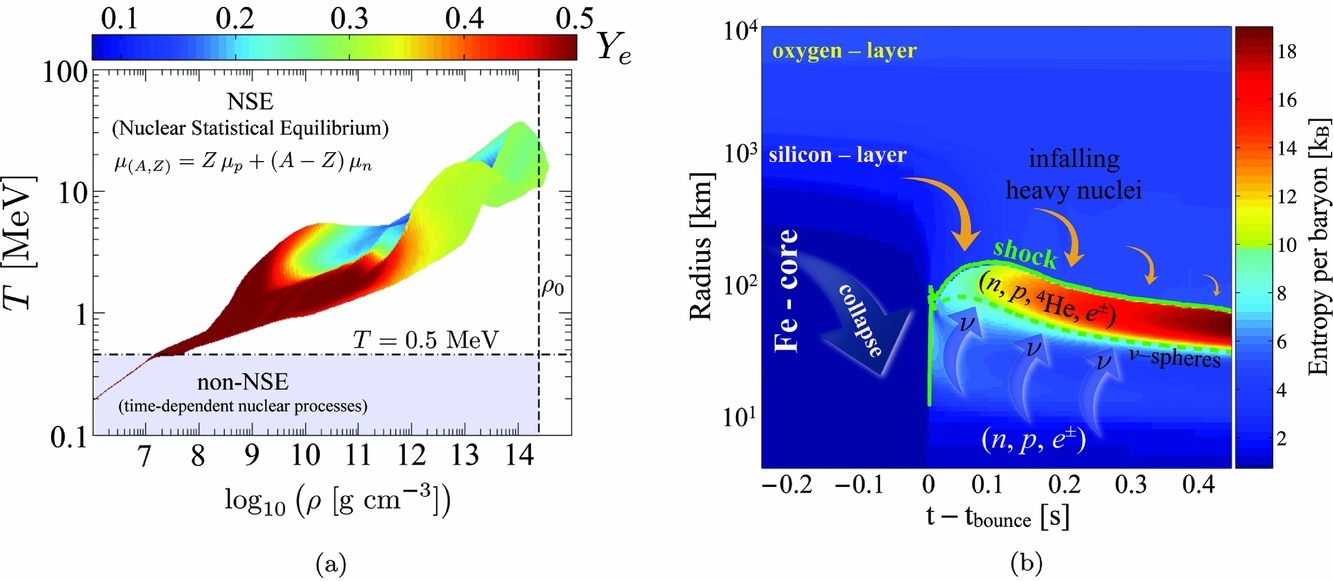
Figure 1. Supernova phase diagram (colour coding is due to the electron fraction Y e) in graph (a) and space-time diagram of the supernova evolution (colour coding is due to the entropy per baryon) in graph (b), both obtained from the spherically symmetric core-collapse supernova simulation of the massive progenitor star of 18 M⊙ published in Fischer (Reference Fischer2016a). (a) Temperature-density domain of a supernova evolution. (b) Space-time diagram of the supernova evolution.
1.1. Supernova phenomenology
PNS are the central object of core-collapse supernovae. The latter are being triggered from the initial implosion of the stellar core of stars more massive than about 8 M⊙. The core collapse proceeds until normal nuclear matter density is reached, when nuclei dissolve into homogeneous matter. The highly repulsive nature of the short-range nuclear force balances gravity such that the core bounces back with the formation of a hydrodynamics shock wave which propagates quickly out of the stellar core, as illustrated in Figure 1(b) (thick solid green line). The shock stalls at around 100–200 km due to the continuous photodisintegration of infalling heavy nuclei from above and the launch of the νe-burst associated with the shock propagation across the neutrinosphere of last scattering (see thick dashed green line in Figure 1(b)). Consequently, the shock turns into an accretion front.
The supernova explosion, i.e., the revival of the shock wave and the subsequent ejection of the stellar mantle that surrounds the PNS, is due to the liberation of energy from the PNS interior to a thin layer of accumulated material at the PNS surface (for recent reviews, cf. Janka et al. Reference Janka, Langanke, Marek, Martínez-Pinedo and Müller2007; Janka Reference Janka2012). Several scenarios have been explored. Besides the magneto-rotational mechanism of LeBlanc & Wilson (Reference LeBlanc and Wilson1970) (for recent works, cf. Takiwaki, Kotake, & Sato Reference Takiwaki, Kotake and Sato2009; Winteler et al. Reference Winteler, Käppeli, Perego, Arcones, Vasset, Nishimura, Liebendörfer and Thielemann2012; Mösta et al. Reference Mösta2014, Reference Mösta, Ott, Radice, Roberts, Schnetter and Haas2015) and the dumping of sound waves developed by Burrows et al. (Reference Burrows, Livne, Dessart, Ott and Murphy2006)—yet not confirmed by other groups—the neutrino-heating mechanism of Bethe & Wilson (Reference Bethe and Wilson1985) has been demonstrated to lead to supernova explosions for a variety of massive progenitor stars (cf. Müller, Janka, & Marek Reference Müller, Janka and Marek2012; Takiwaki, Kotake, & Suwa Reference Takiwaki, Kotake and Suwa2012; Bruenn et al. Reference Bruenn2013; Melson, Janka, & Marek Reference Melson, Janka and Marek2015; Lentz et al. Reference Lentz2015; Roberts et al. Reference Roberts, Ott, Haas, O’Connor, Diener and Schnetter2016). However, in the framework of multi-dimensional simulations, accurate Boltzmann neutrino transport cannot be employed due to the current computational limitations. Instead, approximate neutrino transport schemes are commonly used, whose range of applicability is currently being debated (cf. Sumiyoshi et al. Reference Sumiyoshi, Takiwaki, Matsufuru and Yamada2015). Another issue of multi-dimensional supernova simulations with approximate neutrino transport may be related to the rather sparse neutrino phase-space resolution used, again, due to the current computational limitations.
Besides the aforementioned three scenarios for the onset of the supernova explosion, another mechanism was discovered by Sagert et al. (Reference Sagert2009) due to the phase transition at high densities from ordinary nuclear matter to the quark gluon plasma. The latter was being treated within the simple but powerful thermodynamic bag model. During the phase transition, a large amount of latent heat is released in a highly dynamical fashion, which in turn triggers the onset of the supernova explosion even in spherically symmetric simulations (for details, see also Fischer et al. Reference Fischer2011). Moreover, it leaves an observable millisecond burst in the neutrino signal (for details, see Dasgupta et al. Reference Dasgupta2010). These milestones demonstrate the sensitivity of EOS uncertainties related to our understanding of core-collapse supernovae and suffice the need of a more elaborate understanding of the EOS at high densities including better constraints in particular.
Once the supernova explosion proceeds, mass accretion ceases at the PNS surface and the nascent PNS deleptonises via the emission of neutrinos of all flavors on a timescale on the order of 10–30 s. This phase of the supernova evolution is mildly independent from details of the explosion mechanism. This has been explored in Fischer et al. (Reference Fischer, Whitehouse, Mezzacappa, Thielemann and Liebendörfer2010) and Hüdepohl et al. (Reference Hüdepohl, Müller, Janka, Marek and Raffelt2010) within the first self-consistent dynamical simulations based on accurate three-flavour Boltzmann neutrino transport in spherical symmetry. These aforementioned studies confirmed that the PNS settles into a quasi-static state (Pons et al. Reference Pons, Reddy, Prakash, Lattimer and Miralles1999) with a wind outflow developing from the PNS surface. This happens once the accretion funnels are quenched during the explosion phase and convection/SASI in the gain region cease.
This is associated with the thick layer of low-density material accumulated at the PNS surface, which is subject to convection and dynamical modes before the supernova explosion onset, falling into the gravitational potential as mass accretion ceases. Also, PNS convection affects the PNS deleptonisation, which was studied in Roberts et al. (Reference Roberts, Shen, Cirigliano, Pons, Reddy and Woosley2012b) and Mirizzi et al. (Reference Mirizzi, Tamborra, Janka, Saviano, Scholberg, Bollig, Hüdepohl and Chakraborty2016). Recently, it has been realised in sophisticated multi-dimensional long-term supernova simulations, with neutrino transport employed, that the beginning of the PNS deleptonisation may be delayed by several seconds due to prevailing accretion flows onto the PNS surface (cf. Müller Reference Müller2015; Bruenn et al. Reference Bruenn2016).
1.2. Supernova EOS
During the past years, constraints for model EOS for astrophysical applications have become increasingly stronger. Chiral effective field theory (EFT) (cf. Hebeler & Schwenk Reference Hebeler and Schwenk2010; Hebeler et al. Reference Hebeler, Lattimer, Pethick and Schwenk2010; Holt, Kaiser, & Weise Reference Holt, Kaiser and Weise2012; Sammarruca et al. Reference Sammarruca, Chen, Coraggio, Itaco and Machleidt2012; Tews et al. Reference Tews, Krüger, Hebeler and Schwenk2013; Krüger et al. Reference Krüger, Tews, Hebeler and Schwenk2013; Coraggio et al. Reference Coraggio, Holt, Itaco, Machleidt and Sammarruca2013, and references therein) is the ab-initio approach to the nuclear many-body problem of dilute neutron matter. It provides constraints up to normal nuclear matter density. Moreover, massive neutron stars with about 2 M⊙ were observed by Antoniadis et al. (Reference Antoniadis2013) and Demorest et al. (Reference Demorest, Pennucci, Ransom, Roberts and Hessels2010), recently reviewed by Fonseca et al. (Reference Fonseca2016), at high precision. Therefore, it requires sufficient stiffness at supersaturation densities. This finding challenges the appearance of additional particle degrees of freedom, e.g., hyperons and quarks. These tend to soften the EOS at supersaturation density. Note that this constraint ruled out the studies of Sagert et al. (Reference Sagert2009) and Fischer et al. (Reference Fischer2011) since their hadron-quark hybrid EOS yield maximum neutron star massesFootnote 1 much below 2 M⊙. On the other hand, the attempt of Fischer et al. (Reference Fischer, Hempel, Sagert, Suwa and Schaffner-Bielich2014) to construct a hybrid EOS based on the thermodynamic bag model in agreement with this constraint did not yield supernova explosions.
The large variety of conditions which are covered by the supernova EOS is illustrated in Figure 1(a). At temperatures below ~0.5 MeV, time-dependent nuclear reactions determine the composition. There heavy nuclei dominate, being the ash from the advanced nuclear burning stages of the progenitor star. With increasing temperature, towards T ≃ 0.5 MeV, complete chemical and thermal equilibrium known as NSE (nuclear statistical equilibrium) is achieved. In NSE, the nuclear composition is determined from the three independent variables: temperature T, rest-mass density ρ (or baryon number density, n B Footnote 2 ), and electron fraction Y e . With increasing density, these nuclei become heavier while their abundance decreases simultaneously. At normal nuclear matter density, ρ0 ≃ 2.5 × 1014 g cm−3 (n 0 ≃ 0.15 fm−3), as well as above temperatures of about 5–10 MeV, nuclei dissolve at the liquid–gas phase transition into homogeneous nuclear matter composed of quasi-free nucleons (for details, cf. Typel et al. Reference Typel, Röpke, Klähn, Blaschke and Wolter2010; Hempel et al. Reference Hempel, Schaffner-Bielich, Typel and Röpke2011; Röpke et al. Reference Röpke, Bastian, Blaschke, Klähn, Typel and Wolter2013).
The role of the EOS in core-collapse supernova simulations was explored in the multi-dimensional framework by Marek, Janka, & Müller (Reference Marek, Janka and Müller2009), Suwa et al. (Reference Suwa, Takiwaki, Kotake, Fischer, Liebendörfer and Sato2013), and recently by Nagakura et al. (Reference Nagakura2017), where neutrino-driven supernova explosions were the subjects of investigation. It was found that such explosions are favoured for soft EOS, e.g., Lattimer & Swesty (Reference Lattimer and Swesty1991) with an earlier onset of shock revival and generally higher explosion energies, in comparison to stiff EOS, e.g., Shen et al. (Reference Shen, Toki, Oyamatsu and Sumiyoshi1998). In failed core-collapse supernova explosions in spherical symmetry, EOS studies focused mainly on the dynamics and the neutrino signal up to the formation of the black hole (cf. Sumiyoshi et al. Reference Sumiyoshi, Yamada, Suzuki and Chiba2006; Fischer et al. Reference Fischer, Whitehouse, Mezzacappa, Thielemann and Liebendörfer2009; O’Connor & Ott Reference O’Connor and Ott2011; Steiner, Hempel, & Fischer Reference Steiner, Hempel and Fischer2013). Recently, the role of the nuclear symmetry energy in supernova simulations has been reviewed in Fischer et al. (Reference Fischer, Hempel, Sagert, Suwa and Schaffner-Bielich2014). This is an important nuclear matter property that is recently becoming more tightly constrained by experiments, nuclear theory and observations (for a summary of the current nuclear symmetry energy constraints, cf. Lattimer & Lim Reference Lattimer and Lim2013; Tews et al. Reference Tews, Lattimer, Ohnishi and Kolomeitsev2016).
2 HEAVY NUCLEI AT LOW TEMPERATURES
The domain of heavy nuclei can be sub-divided into two physically distinct conditions, i.e., where temperatures T < 0.5 MeV—time-dependent thermonuclear processes determine the nuclear composition—and T > 0.5 MeV where NSE is reached.
2.1. Small nuclear reaction networks
In the regime of low densities and low temperatures (T < 0.5 MeV), small nuclear reaction networks are commonly used which include about 14–50 nuclear species as explained in Thielemann et al. (Reference Thielemann, Brachwitz, Höflich, Martinez-Pinedo and Nomoto2004) (the implementation of the network into our supernova model is discussed in Fischer et al. Reference Fischer, Whitehouse, Mezzacappa, Thielemann and Liebendörfer2010). Even though they cannot accurately account for the evolution of Y e—matter is nearly isospin symmetric with Y e ≃ 0.5 [see the region below the horizontal dash-dotted line in Figure 1(a)]—they are sufficient for the nuclear energy generation. This domain, where time-dependent nuclear processes determine the evolution, corresponds to the outer core of the stellar progenitor, with the nuclear composition of dominantly silicon, sulphur as well as carbon and oxygen. In some cases, even parts of the hydrogen-rich helium envelope are taken into account, in particular in simulations of supernova explosions in order to be able to follow the shock evolution for tens of seconds through parts of the stellar envelope. However, during the early post-bounce evolution prior to the supernova explosion onset, the stellar envelope remains nearly unaffected by the dynamics in the supernova core [see Figure 1(b) above 103 km].
2.2. NSE
Towards the stellar core, the temperature increases above T = 0.5 MeV where NSE is fulfilled and where the relation μ(A, Z) = Zμp + (A − Z)μn between the chemical potential of nucleus μ(A, Z), with atomic mass A and charge Z, and the chemical potentials of neutron μn and proton μp holds. The NSE conditions found in the collapsing stellar core feature a broad distribution of nuclei with a pronounced peak around the iron-group, at low densities [see Figure 2(a)]. These nuclei can be classified within the NSE average, including nuclear shell effects as discussed in Hempel & Schaffner-Bielich (Reference Hempel and Schaffner-Bielich2010). This method extends beyond the commonly used single-nucleus approximation, which is marked by the crosses in Figure 2. Note also that with increasing density, the nuclear distribution shifts towards heavier nuclear species, moreover, it broadens with increasing temperature as illustrated in Figure 2(b). At high temperatures, around T ≃ 5 − 10 MeV, heavy nuclei dissolve via photodisintegration and (in)homogeneous nuclear matter forms, as shown in Figure 2(c). It will be discussed further in Section 3.
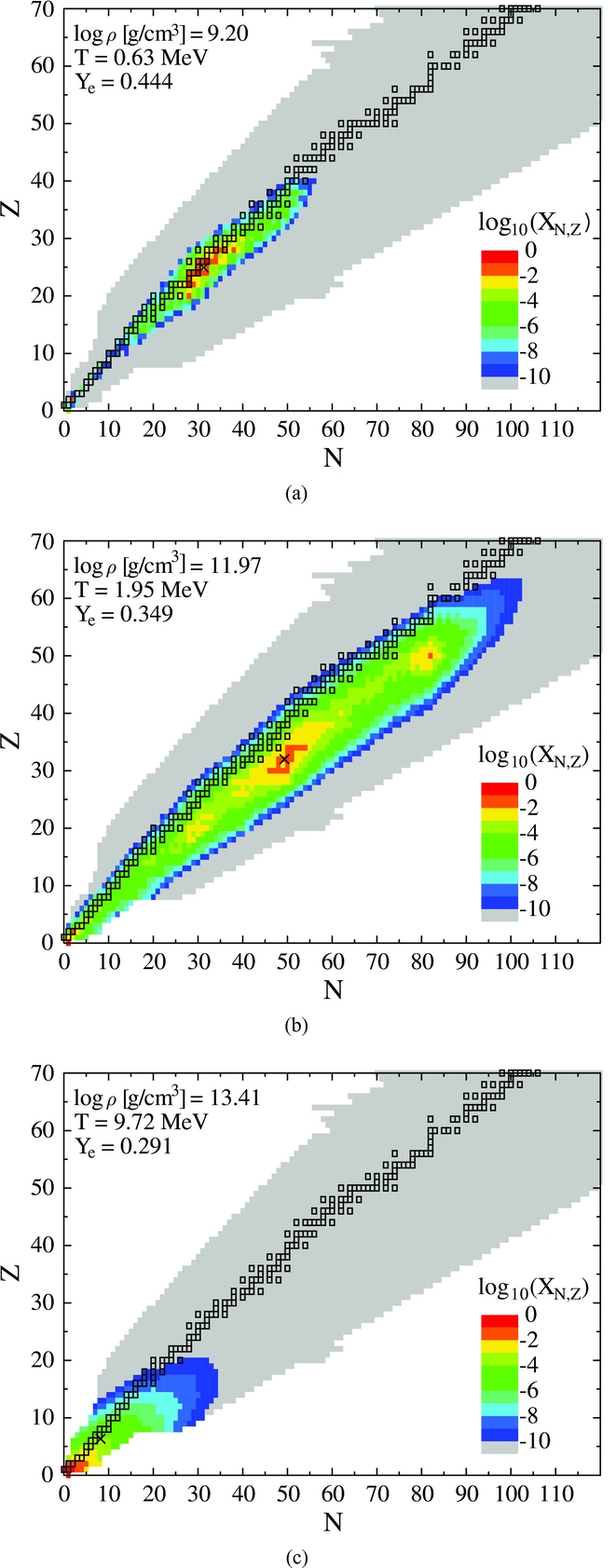
Figure 2. Nuclear composition in the chart of nuclides (neutron number N vs. proton number Z) based on the modified NSE approach of Hempel & Schaffner-Bielich (Reference Hempel and Schaffner-Bielich2010), obtained from the central conditions of the core-collapse evolution of Hempel et al. (Reference Hempel, Fischer, Schaffner-Bielich and Liebendörfer2012).
2.3. Weak interactions with heavy nuclei
Heavy nuclei with nuclear charge Z and mass A, are subject to fast electron captures, that are described collectively via the average composition as follows:
This process deleptonises stellar matter as the final-state neutrinos escape freely. As a consequence, the entropy per particle remains low during the entire stellar core collapse (cf. Bethe et al. Reference Bethe, Brown, Applegate and Lattimer1979; van Riper & Lattimer Reference van Riper and Lattimer1981), as illustrated in Figure 1(b). Electron capture rates commonly employed in supernova studies were developed by Bruenn (Reference Bruenn1985) with a crudely simplified description of the Gamow window. Improved rates were provided by Juodagalvis et al. (Reference Juodagalvis, Langanke, Hix, Martínez-Pinedo and Sampaio2010), based on large-scale nuclear shell-model calculations including several 1 000 nuclear species. A detailed comparison of both electron-capture rates and their impact on the collapse dynamics and neutrino signal can be found in Langanke et al. (Reference Langanke2003) and Hix et al. (Reference Hix, Messer, Mezzacappa, Liebendörfer, Sampaio, Langanke, Dean and Martínez-Pinedo2003). The rates of Juodagalvis et al. (Reference Juodagalvis, Langanke, Hix, Martínez-Pinedo and Sampaio2010) are averaged over the NSE composition and provided to the community as a table.
In addition to electron captures, coherent neutrino-nucleus scattering is taken into account following Bruenn (Reference Bruenn1985):
for all flavours. This channel is essential for neutrino trapping once neutrinos are being produced with sufficiently high energies via (1). Inelastic neutrino-nucleus scattering rates were provided in Langanke et al. (Reference Langanke2008). Moreover, heavy nuclei in the collapsing stellar core can exist at excited states, due to temperatures reached on the order of 0.5 MeV up to few MeV. The subsequent nuclear de-excitation process via the emission of neutrino-antineutrino pairs,
can be understood in a similar fashion as the neutral-current process (2). The original idea, pointed out by Fuller & Meyer (Reference Fuller and Meyer1991), would potentially contribute to the losses during stellar collapse. In fact, in Fischer, Langanke, & Martínez-Pinedo (Reference Fischer, Langanke and Martínez-Pinedo2013), it was confirmed that process (3) is the leading source of heavy lepton-flavour neutrinos as well as
![]() $\bar{\nu }_{\text{e}}$
during stellar core collapse. However, the neutrino fluxes remain small, compared to those of νe (see Figure 3 top panel), and the neutrino energies are low, on the order of few MeV (see Figure 3 bottom panel). Hence, the overall impact of nuclear de-excitations is negligible on the collapse dynamics and the neutrino signal. Instead, the stellar core collapse is dominated by nuclear electron captures and losses associated with νe (see Figure 3).
$\bar{\nu }_{\text{e}}$
during stellar core collapse. However, the neutrino fluxes remain small, compared to those of νe (see Figure 3 top panel), and the neutrino energies are low, on the order of few MeV (see Figure 3 bottom panel). Hence, the overall impact of nuclear de-excitations is negligible on the collapse dynamics and the neutrino signal. Instead, the stellar core collapse is dominated by nuclear electron captures and losses associated with νe (see Figure 3).

Figure 3. Supernova neutrino signal, luminosities (top panel) and mean energies (bottom panel) for all flavours, sampled in the co-moving frame of reference at 1 000 km. The supernova simulations were published in Fischer (Reference Fischer2016a), launched from the 18 M⊙ progenitor of Woosley, Heger, & Weaver (Reference Woosley, Heger and Weaver2002).
2.4. Heavy nuclear structures at high density
With increasing density, nuclei become heavier, as long as the temperatures are not too high which would enable efficient photodisintegration. This situation as well as the relevant density range is illustrated in Figure 4, for matter in β-equilibrium at two selected temperatures, based on the Thomas–Fermi approximation of Shen et al. (Reference Shen, Toki, Oyamatsu and Sumiyoshi1998). A detailed comparison between different nuclear approaches was performed in Shen, Horowitz, & Teige (Reference Shen, Horowitz and Teige2011). Comparing the Thomas–Fermi approximation of Shen et al. (Reference Shen, Toki, Oyamatsu and Sumiyoshi1998), compressible liquid drop model with Skyrme interactions by Lattimer & Swesty (Reference Lattimer and Swesty1991) and the virial EOS with nucleons and nuclei of Shen, Horowitz, & Teige (Reference Shen, Horowitz and Teige2010b) (combined with the RMF (RMF) EOS of Shen, Horowitz, & Teige Reference Shen, Horowitz and Teige2010a), qualitative agreement was found for the gross properties, e.g., pressure, entropy, nuclear abundances, average nuclear mass, and charge, comparing the three models.

Figure 4. Composition of heavy nuclear structures, average mass number as well as charge (top panel), and mass fraction, for matter in β-equilibrium at two selected temperatures, based on the Thomas–Fermi approximation of Shen et al. (Reference Shen, Toki, Oyamatsu and Sumiyoshi1998). The increasing neutron excess visible is due to the continuously decreasing Y e with increasing density in β-equilibrium.
Note that at the density range where these nuclear structures appear (see Figure 4), all protons in the system are consumed into heavy nuclei, such that effectively only free neutrons exist besides heavy and light nuclei. The latter aspect will be further discussed below in Section 4. The situation illustrated in Figure 4 corresponds to the liquid–gas phase transition at finite temperatures and large isospin asymmetry (note the very low proton abundances of Y p = 0.01 − 0.1 in β-equilibrium in this density domain).
It has long been realised that the formation of the heavy nuclear structures sketched in Figure 4 via spherical heavy nuclei, are due to the competition of the attractive long-range nuclear force and Coulomb repulsion (cf. Watanabe et al. Reference Watanabe, Sato, Yasuoka and Ebisuzaki2003, Reference Watanabe, Sonoda, Maruyama, Sato, Yasuoka and Ebisuzaki2009; Newton & Stone Reference Newton and Stone2009; Giménez Molinelli et al. Reference Molinelli, Nichols, López and Dorso2014; Schneider et al. Reference Schneider, Berry, Briggs, Caplan and Horowitz2014, and references therein). Due to surface effects, these structures form shapes, e.g., spaghetti, lasagna, and meat balls, denoted collectively as ‘nuclear pasta’. The conditions where nuclear pasta phases exist are listed in Table 1 at two selected values of Y e, based on the detailed three-dimensional Skyrme–Hartree–Fock calculations of Newton & Stone (Reference Newton and Stone2009). Comparing the density ranges of Table 1 for Y e = 0.05 and Figure 4, it becomes clear that only towards high density nuclear pasta appears, where at low densities spherical heavy nuclei exist. The reason why the heavy structures dissolve already below ρ = 1014 g cm−3 in Figure 4 is due to the even lower Y e in β-equilibrium, which is assumed in Figure 4. This points to the very sensitive dependence of nuclear pasta phases on temperature and Y e. Moreover, it has been realised that the neutrino mean free path is modified in nuclear pasta. Detailed molecular dynamics simulations of the neutrino response from coherent neutrino scattering were conduced in Horowitz, Pérez-García, & Piekarewicz (Reference Horowitz, Pérez-García and Piekarewicz2004a) and Horowitz et al. (Reference Horowitz, Pérez-García, Carriere, Berry and Piekarewicz2004b). An alternative approach has been developed in Alcain, Giménez Molinelli, & Dorso (Reference Alcain, Giménez Molinelli and Dorso2014).
Table 1. Selected conditions for the presence of nuclear pasta, in terms of two values of Y e and the density range, from calculations based on Newton & Stone (Reference Newton and Stone2009). T melt marks the approximate melting temperatures.

Note that this phase is relevant for the post-bounce supernova evolution prior to the explosion onset, since temperatures in this density range exceed T = 5 MeV and hence pasta melts (see Figure 4). However, the situation changes during the later PNS deleptonisation, after the supernova explosion onset when the temperature decreases continuously. Even though the structure of the PNS is not affected by the presence of such heavy nuclear structures, neutrino interactions may well modify the timescale on which neutrinos diffuse out of the PNS interior. Therefore, the very first detailed supernova simulations with sophisticated neutrino transport and an effective description of coherent neutrino-pasta scattering have been presented recently in Horowitz et al. (Reference Horowitz, Berry, Caplan, Fischer, Lin, Newton, O’Connor and Roberts2016). These results show qualitatively the role of nuclear pasta, i.e. an extended deleptonisation and cooling time of the PNS, once pasta phases form.
3 INHOMOGENEOUS NUCLEAR MATTER
During the core collapse evolution temperature and density rise continuously, which eventually leads to the transition to inhomogeneous matter with light and heavy nuclear clusters [corresponding to the transition from Figure 2(b)–(c)]. The conditions for this transition are obtained already before core bounce, and they remain during the entire post-bounce evolution, located between the supernova shock and the PNS surface [see the region of high entropy in Figure 1(b)]. This corresponds to the conditions where neutrinos decouple from matter and hence a ‘good’ treatment of weak processes and nuclear medium is essential. Weak reactions with heavy nuclei play only a sub-dominant role. Heavy nuclei dissociate due to the high temperatures and weak processes with free nucleons are significantly faster.
3.1. Weak processes
Here we distinguish electronic charged-current processes,
neutral-current elastic scattering on nucleons (N),
inelastic scattering on electrons and positrons,
and pair processes,
where
![]() $\nu \in \lbrace \nu _{\text{e}},\bar{\nu }_{\text{e}},\nu _{\mu /\tau },\bar{\nu }_{\mu /\tau }\rbrace$
and N ∈ {n, p} else notified otherwise. In Buras et al. (Reference Buras, Janka, Keil, Raffelt and Rampp2003), additional inelastic scattering processes have been considered, in analogy to the process (7b),
$\nu \in \lbrace \nu _{\text{e}},\bar{\nu }_{\text{e}},\nu _{\mu /\tau },\bar{\nu }_{\mu /\tau }\rbrace$
and N ∈ {n, p} else notified otherwise. In Buras et al. (Reference Buras, Janka, Keil, Raffelt and Rampp2003), additional inelastic scattering processes have been considered, in analogy to the process (7b),
which are relevant at high densities and temperatures where a large trapped ν e component exists. Recently, in Fischer (Reference Fischer2016b), the inverse neutron decay has been implemented,
Reactions (4) and (10) are known as Urca processes. Together with (5), they are typically treated in supernova simulations within the zero-momentum transfer approximation of Bruenn (Reference Bruenn1985). Inelastic contributions as well as corrections from weak magnetism are taken into account effectively in present supernova studies, following Horowitz (Reference Horowitz2002), which also takes into account the strangeness contents in the baryons via a strangeness axial-vector coupling constant, g
S
, which effectively reduces the axial-vector coupling constant, g
A
− g
S
. The currently accepted value for the nucleon strangeness contents, deduced from deep-inelastic proton-scattering experiments, relates to values of g
S
≃ 0.1 (cf. Hobbs, Alberg & Miller Reference Hobbs, Alberg and Miller2016, and references therein). Note that weak magnetism enhances the opacity for ν while it suppresses the opacity for
![]() $\bar{\nu }$
. It leads to the non-negligible enhancement of spectral differences between ν and
$\bar{\nu }$
. It leads to the non-negligible enhancement of spectral differences between ν and
![]() $\bar{\nu }$
, in particular for the heavy lepton flavour neutrinos where it is the leading cause, besides neutrino electron/positron scattering (6). The pair processes (7a) and (7b) do not distinguish between ν and
$\bar{\nu }$
, in particular for the heavy lepton flavour neutrinos where it is the leading cause, besides neutrino electron/positron scattering (6). The pair processes (7a) and (7b) do not distinguish between ν and
![]() $\bar{\nu }$
, i.e., both are produced with identical spectra.
$\bar{\nu }$
, i.e., both are produced with identical spectra.
For the processes (4) and (10), it is important to treat these weak interactions consistently with the underlying nuclear EOS, which was pointed out by Martínez-Pinedo et al. (Reference Martínez-Pinedo, Fischer, Lohs and Huther2012) and Roberts, Reddy, & Shen (Reference Roberts, Reddy and Shen2012a) based on the mean-field description of Reddy, Prakash, & Lattimer (Reference Reddy, Prakash and Lattimer1998). The associated medium modification, △U = U
n − U
p, defines the difference between neutron and proton single particle potentials (i.e. vector self-energies within the RMF framework as was discussed in, e.g., Hempel Reference Hempel2015). They depend on the nuclear symmetry energy △U∝E
sym(T, ρ) which has a strong density dependence. A detailed comparison between neutron matter and symmetric matter EOS can be found in Typel et al. (Reference Typel, Wolter, Röpke and Blaschke2014). Moreover, it was confirmed in detailed supernova simulations that E
sym determines the spectral difference between νe and
![]() $\bar{\nu }_{\text{e}}$
; however, with relevance only during the PNS deleptonisation after the supernova explosion onset has been launched. This is related to the energy scales involved. Note the Q-values for processes (4): Q = ±Q
0 ± △U, for νe (+) and
$\bar{\nu }_{\text{e}}$
; however, with relevance only during the PNS deleptonisation after the supernova explosion onset has been launched. This is related to the energy scales involved. Note the Q-values for processes (4): Q = ±Q
0 ± △U, for νe (+) and
![]() $\bar{\nu }_{\text{e}}(-)$
. Q
0 denotes the vacuum Q-value of the processes, Q
0 = m
n − m
p = 1.2935 MeV, being the neutron-to-proton rest mass difference. At low densities, the energetics of the processes (4) is determined by Q
0, since △U ≪ Q
0. With increasing density, the medium modifications start to dominate when △U ≳ Q
0.
$\bar{\nu }_{\text{e}}(-)$
. Q
0 denotes the vacuum Q-value of the processes, Q
0 = m
n − m
p = 1.2935 MeV, being the neutron-to-proton rest mass difference. At low densities, the energetics of the processes (4) is determined by Q
0, since △U ≪ Q
0. With increasing density, the medium modifications start to dominate when △U ≳ Q
0.
In order to determine (U n, U p), it is essential for supernova simulations to employ model EOS with a ‘good’ low-density behaviour. Here, the ab-initio approach is chiral EFT of dilute neutron matter. Figure 5 illustrates the chiral EFT results from Krüger et al. (Reference Krüger, Tews, Hebeler and Schwenk2013) together with a selection of RMF model EOS (DD2–IUFSU) and the non-relativistic EOS (LS180 and LS220), which were and still are commonly used in supernova simulations. Details about these EOS and a table that lists a selection of nuclear matter properties can be found in Fischer et al. (Reference Fischer, Hempel, Sagert, Suwa and Schaffner-Bielich2014). Important here is the maximum neutron star mass constraint of 2 M⊙ (not fulfilled by FSUgold, IUFSU, and LS180) and the constraint of the nuclear symmetry energy and its slope parameter at nuclear saturation density (fulfilled by DD2 and SFHo, for details cf. Lattimer & Lim Reference Lattimer and Lim2013). Moreover, from Figure 5, it becomes evident that the RMF model with density-dependent couplings DD2 of Typel et al. (Reference Typel, Röpke, Klähn, Blaschke and Wolter2010) is in quantitative agreement with chiral EFT. The other two EOS in good agreement with chiral EFT are the EOS of Steiner et al. (Reference Steiner, Hempel and Fischer2013), SFHo and SFHx, which were developed in accordance with neutron star radii deduced from the analysis of low-mass X-ray binaries by Steiner, Lattimer, & Brown (Reference Steiner, Lattimer and Brown2010). All other EOS, including the quark matter EOS of Fischer et al. (Reference Fischer, Hempel, Sagert, Suwa and Schaffner-Bielich2014) based on the thermodynamic bag model (QB139α S 0.7—we will come back to quark matter EOS in more details in Section 5), violate the chiral EFT constraint, besides the aforementioned conflicts with the other constraints.
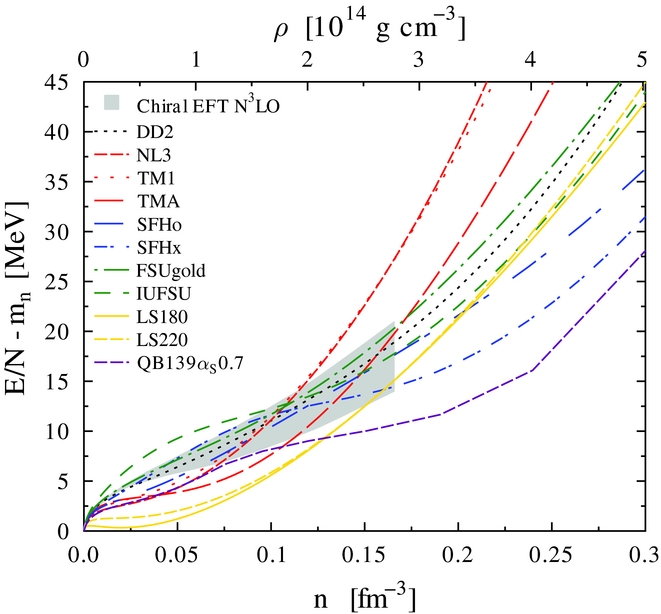
Figure 5. Neutron matter energy per particle for a selection of supernova model EOS, in comparison to the chiral EFT constraint of Krüger et al. (Reference Krüger, Tews, Hebeler and Schwenk2013). See text for details. (Figure adopted from Fischer et al. Reference Fischer, Hempel, Sagert, Suwa and Schaffner-Bielich2014).
In addition to the mean-field effects, which modify the charged-current processes, nuclear many-body correlations suppress the charged-current absorption rates and neutral-current neutrino scattering processes (5) with increasing density, for which the expressions of Burrows & Sawyer (Reference Burrows and Sawyer1998) and Burrows & Sawyer (Reference Burrows and Sawyer1999) are commonly employed in supernova studies. Recently, Horowitz et al. (Reference Horowitz, Caballero, Lin, O’Connor and Schwenk2017) reviewed many-body correlations for the neutral-current neutrino-nucleon scattering processes. The authors provide a useful fit for the vector response function, in combination with the Random Phase Approximation at high densities (see also Reddy et al. Reference Reddy, Prakash, Lattimer and Pons1999; Roberts & Reddy Reference Roberts and Reddy2017, and references therein) and the virial EOS for the low-density part.
Reaction rates for pair processes are provided in Bruenn (Reference Bruenn1985), where as N–N-bremsstrahlung rates were developed in Hannestad & Raffelt (Reference Hannestad and Raffelt1998) based on the vacuum 1π-exchange framework developed by Friman & Maxwell (Reference Friman and Maxwell1979). Recently, Fischer (Reference Fischer2016b) extended this treatment of the vacuum 1π-exchange for N–N-bremsstrahlung by taking into account the leading-order medium modifications, i.e., dressing of the πNN-vertex. Based on the Fermi-liquid theory, expressions have been derived that can be implemented into supernova simulations. In analogy, Bartl et al. (Reference Bartl, Bollig, Janka and Schwenk2016) describe such medium modifications at the level of chiral EFT.
The annihilation of trapped
![]() $\nu _{\text{e}}\bar{\nu }_{\text{e}}$
pairs processes of (7b) couples electron and heavy lepton flavour neutrinos, at high temperatures and densities. This channel reduces the difference of the luminosities and average energies of both flavours. Reaction rates were implemented in Buras et al. (Reference Buras, Janka, Keil, Raffelt and Rampp2003) and Fischer et al. (Reference Fischer, Whitehouse, Mezzacappa, Thielemann and Liebendörfer2009). Moreover, the highly inelastic neutrino-electron(positron) scattering (6) thermalises the neutrino spectra. Expressions for weak rates can be found, e.g., in Mezzacappa & Bruenn (Reference Mezzacappa and Bruenn1993c).
$\nu _{\text{e}}\bar{\nu }_{\text{e}}$
pairs processes of (7b) couples electron and heavy lepton flavour neutrinos, at high temperatures and densities. This channel reduces the difference of the luminosities and average energies of both flavours. Reaction rates were implemented in Buras et al. (Reference Buras, Janka, Keil, Raffelt and Rampp2003) and Fischer et al. (Reference Fischer, Whitehouse, Mezzacappa, Thielemann and Liebendörfer2009). Moreover, the highly inelastic neutrino-electron(positron) scattering (6) thermalises the neutrino spectra. Expressions for weak rates can be found, e.g., in Mezzacappa & Bruenn (Reference Mezzacappa and Bruenn1993c).
3.2. Post-bounce supernova dynamics and neutrino emission
Reaction (4) is responsible for the launch of the νe-burst (top central panel in Figure 3), which is associated with the propagation of the bounce shock across the neutrinospheres of last scattering [see Figure 1(b)] between 5–20 ms after core bounce. Weak equilibrium is re-established as matter is shock heated, associated with the sudden rise of the temperature. This highly non-equilibrium phenomenon is essential for the following supernova evolution as it determines a major source of losses, several 1053 erg s−1, being partly responsible for the dynamic bounce shock turning into a standing accretion front [see Figure 1(b)]. Moreover, only slightly before core bounce, when positrons exist, all other neutrino flavours are being produced mainly via electron-positron annihilation as well as via nucleon–nucleon bremsstrahlung [pair processes (7a)]. The luminosities of
![]() $\bar{\nu }_{\text{e}}$
and heavy-lepton flavour neutrinos rise accordingly (see Figure 3). The luminosities of all heavy lepton flavour neutrinos rise somewhat faster than those of
$\bar{\nu }_{\text{e}}$
and heavy-lepton flavour neutrinos rise accordingly (see Figure 3). The luminosities of all heavy lepton flavour neutrinos rise somewhat faster than those of
![]() $\bar{\nu }_{\text{e}}$
, since the latter are coupled more strongly to matter via the charged-current channel [see the second process of (4)]. This feature will eventually allow us to probe the neutrino mass hierarchy via the neutrino signal rise time from the neutrino observation of the next galactic supernova event (details can be found in Serpico et al. Reference Serpico, Chakraborty, Fischer, Hüdepohl, Janka and Mirizzi2012).
$\bar{\nu }_{\text{e}}$
, since the latter are coupled more strongly to matter via the charged-current channel [see the second process of (4)]. This feature will eventually allow us to probe the neutrino mass hierarchy via the neutrino signal rise time from the neutrino observation of the next galactic supernova event (details can be found in Serpico et al. Reference Serpico, Chakraborty, Fischer, Hüdepohl, Janka and Mirizzi2012).
The later post-bounce evolution is determined by mass accretion onto the standing shock [see Figure 1(b)], during which the average neutrino energy hierarchy is determined by the different coupling strengths to matter (see bottom panel in Figure 3). Consequently, each neutrino species has their own neutrinosphere radius R
ν of last (in)elastic collision where the following hierarchy holds:
![]() $R_{\nu _{\text{e}}}>R_{\bar{\nu }_{\text{e}}}>R_{\nu _{\mu /\tau }}\gtrsim R_{\bar{\nu }_{\mu /\tau }}$
. The electron (anti)neutrinos decouple in a thick layer of low-density material accumulated at the PNS surface, powered by the charged-current processes (4). Consequently, their luminosity can be approximated by the accretion luminosity as follows (cf. Janka et al. Reference Janka, Langanke, Marek, Martínez-Pinedo and Müller2007; Janka Reference Janka2012):
$R_{\nu _{\text{e}}}>R_{\bar{\nu }_{\text{e}}}>R_{\nu _{\mu /\tau }}\gtrsim R_{\bar{\nu }_{\mu /\tau }}$
. The electron (anti)neutrinos decouple in a thick layer of low-density material accumulated at the PNS surface, powered by the charged-current processes (4). Consequently, their luminosity can be approximated by the accretion luminosity as follows (cf. Janka et al. Reference Janka, Langanke, Marek, Martínez-Pinedo and Müller2007; Janka Reference Janka2012):
 $$\begin{eqnarray}
L_{\nu _{\text{e}}} \propto 10^{52} \left(\frac{{M}}{1.5 \rm M_{\odot }} \right) \left(\frac{\dot{m}}{0.4 \rm \frac{M_{\odot }}{{\rm s}}} \right) \left(\frac{100 \rm km}{R_{\nu _e}}\right) \frac{\rm erg}{\rm s},
\end{eqnarray}$$
$$\begin{eqnarray}
L_{\nu _{\text{e}}} \propto 10^{52} \left(\frac{{M}}{1.5 \rm M_{\odot }} \right) \left(\frac{\dot{m}}{0.4 \rm \frac{M_{\odot }}{{\rm s}}} \right) \left(\frac{100 \rm km}{R_{\nu _e}}\right) \frac{\rm erg}{\rm s},
\end{eqnarray}$$
with a typical mass enclosed inside the PNS M and radius associated with the neutrinospehere
![]() $R_{\nu _{\text{e}}}$
as well as mass accretion rate
$R_{\nu _{\text{e}}}$
as well as mass accretion rate
![]() $\dot{m}$
. On the other hand, the heavy lepton neutrino flavours are determined by diffusion in the absence of charged-current processes.
$\dot{m}$
. On the other hand, the heavy lepton neutrino flavours are determined by diffusion in the absence of charged-current processes.
The process of neutrino decoupling from matter is neutrino transport problem. Accurate three-flavour Boltzmann neutrino transport has been developed for spherically symmetric supernova models in Mezzacappa & Bruenn (Reference Mezzacappa and Bruenn1993a) and Liebendörfer et al. (Reference Liebendörfer2004). It leads to the establishment of a large cooling layer towards high densities at the PNS surface, where dQ/dt < 0Footnote 3 , as illustrated in Figure 6. It corresponds to the domain where high energy neutrinos decouple from matter, while the low energy spectrum is still thermalised with the medium. At low densities, between the standing shock at around 109 g cm−3, these low energy neutrinos deposit parts of their energy via absorption processes into the medium. There, a heating layer establishes where dQ/dt > 0. However, since most weak interaction rates have a strong dependence on the neutrino energy, the integrated heating rates are significantly smaller than the cooling at higher density, besides the smaller mass enclosed in the heating layer than in the cooling layer. These are the two main reasons why spherically symmetric supernova explosions could not be obtained for the massive progenitor stars that develop an extended mass accretion period, typically for stars with initial mass above around 10 M⊙. The success of the neutrino-heating mechanism in multi-dimensional simulations is attributed to the development of convection which allows material to remain effectively longer in the heating region, which increased the neutrino-heating efficiency. However, it should be mentioned that up to now only neutrino transport approximation schemes have been employed in multi-dimensional supernova studies. Note further that the situation is different for the low progenitor mass range, between 8 and10 M⊙. Such stars develop either oxygen-neon cores (cf. Nomoto Reference Nomoto1987; Jones et al. Reference Jones2013), leading to electron-capture supernovae as explored in Kitaura, Janka, & Hillebrandt (Reference Kitaura, Janka and Hillebrandt2006) and Fischer et al. (Reference Fischer, Whitehouse, Mezzacappa, Thielemann and Liebendörfer2010), or “tiny” iron-cores as was explored recently in Melson et al. (Reference Melson, Janka and Marek2015). In both cases, the special structure of the stellar core, i.e., sharp density gradient separating core and envelope, leads to fast shock expansions and explosions even in spherical symmetric supernova simulations with low explosion energies ~1050 erg and small amount of nickel ejected (for details, see Wanajo et al. Reference Wanajo, Nomoto, Janka, Kitaura and Müller2009). Similar core structures are obtained from binary stellar evolution. This was explored in Tauris et al. (Reference Tauris, Langer, Moriya, Podsiadlowski, Yoon and Blinnikov2013) and Tauris, Langer, & Podsiadlowski (Reference Tauris, Langer and Podsiadlowski2015), leading to so-called ultra-stripped progenitors of the secondary star that has undergone major mass transfer during the common-envelope evolution.
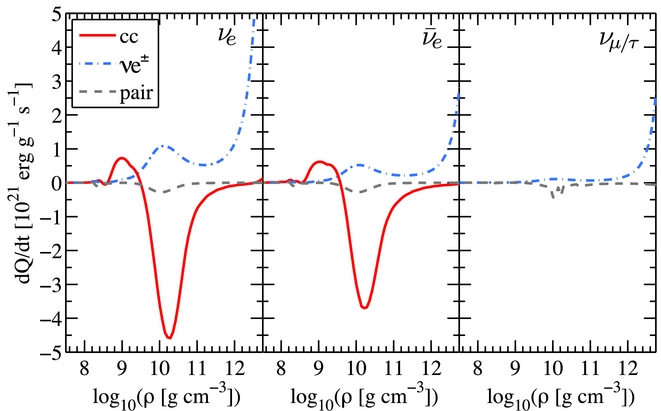
Figure 6. Integrated neutrino heating (dQ/dt > 0) and cooling (dQ/dt < 0) rates of the different channels charged-current (cc) processes (4), neutrino-electron and positron scattering (νe ±) processes (6), and the sum of all pair reactions (pair) processes (7a). The data are from the reference supernova simulation of Fischer (Reference Fischer2016a) as illustrated in Figure 1(b) at about 300 ms post bounce, and the density domain corresponds to the region between PNS surface at around 15–20 km and the standing bounce shock around 80 km.
4 ROLE OF LIGHT NUCLEAR CLUSTERS
With the recent advance regarding the improved description of medium modified nuclei (cf. Röpke et al. Reference Röpke, Bastian, Blaschke, Klähn, Typel and Wolter2013), particular interest has been devoted to the question about light nuclear clusters (see also Bastian et al. Reference Bastian2016, for a recent discussion about light clusters in heavy-ion collision experiments as tracers of early flow). It concerns nuclei with mass numbers A = 2 − 4. About their role on the supernova dynamics and the neutrino signal has long been speculated.
Within the ‘classical’ nuclear setup for supernova EOS, e.g., based on Lattimer & Swesty (Reference Lattimer and Swesty1991) and Shen et al. (Reference Shen, Toki, Oyamatsu and Sumiyoshi1998), the simplified nuclear composition includes free nucleons, α particle, and a single representative heavy nucleus with average mass and charge, (n, p, α, 〈A, Z〉). Hence, the question about the role of light clusters, others than α particles, could not be attributed. A first attempt to include all light clusters was given by Sumiyoshi & Röpke (Reference Sumiyoshi and Röpke2008) where the quantum statistical approach of Röpke, Münchow, & Schulz (Reference Röpke, Münchow and Schulz1982) has been used. Based on the concept of the excluded volume, already used in the ‘classical’ EOS, an advanced supernova EOS was developed by Hempel & Schaffner-Bielich (Reference Hempel and Schaffner-Bielich2010) with the inclusion of a detailed nuclear composition. The conditions where light clusters with A = 2 − 4 are abundant corresponds to the region of high entropy between the neutrinospheres and the bounce shock, see Figure 1(b), denoted here collectively via 4He.
There are two crucial aspects related to light clusters: (a) modification of the nuclear EOS and (b) the inclusion of a large variety of weak processes (cf. right column of Table (1) in Fischer et al. Reference Fischer, Martínez-Pinedo, Hempel, Huther, Röpke, Typel and Lohs2016) in addition to the standard weak processes (1)–(10).
4.1. EOS with light clusters
The consistent description of the nuclear medium with light clusters as explicit degrees of freedom reduces the abundance of the free nucleons and 4He, in the domain where light clusters are abundant. This is illustrated in Figure 7 (middle panel) at selected conditions found during the early PNS deleptonisation shortly after the supernova explosion onset—temperature and Y
e profiles are shown in the top panel, with respect to the baryon density. Here, we compare the medium-modified NSE approach of Hempel & Schaffner-Bielich (Reference Hempel and Schaffner-Bielich2010) including the complete abundances of all nuclear clusters (red lines) with those of the same approach where only 4He is considered as light nuclear cluster (blue lines). Note that the latter case corresponds to the ‘classical’ supernova EOS composition that was commonly employed in numerous supernova simulations. It becomes evident that not only the abundance of 4He is largely overestimated, also the abundances of neutrons and protons are overestimated. Note further that the region where light clusters and free protons are equally abundant, corresponds to the supernova cooling region (see Figure 6). Hence, this urges the need for the systematic comparison of EOS based on the ‘full’ composition and only simplified nuclear composition (n, p, α, 〈A, Z〉), in supernova simulations in much greater detail, especially within multi-dimensional framework. In particular, we find that weak reactions with protons, most relevant for the charged-current
![]() $\bar{\nu }_{\text{e}}$
-opacity, are off by a factor greater than two, since the reaction rates scale with the number density of protons. The magnitude of the differences in spherically symmetric supernova simulations is illustrated in Figure 8, where we compare the modified NSE approach of Hempel & Schaffner-Bielich (Reference Hempel and Schaffner-Bielich2010) with ‘all’ nuclear clusters included with the simplified composition (n, p, α, 〈A, Z〉). In particular, the luminosity and average energy of
$\bar{\nu }_{\text{e}}$
-opacity, are off by a factor greater than two, since the reaction rates scale with the number density of protons. The magnitude of the differences in spherically symmetric supernova simulations is illustrated in Figure 8, where we compare the modified NSE approach of Hempel & Schaffner-Bielich (Reference Hempel and Schaffner-Bielich2010) with ‘all’ nuclear clusters included with the simplified composition (n, p, α, 〈A, Z〉). In particular, the luminosity and average energy of
![]() $\bar{\nu }_e$
are overestimated when considering the simplified composition. Moreover, the rise time of the neutrino signal (for details about the role of the neutrino rise time can be found in Serpico et al. Reference Serpico, Chakraborty, Fischer, Hüdepohl, Janka and Mirizzi2012), in particular for
$\bar{\nu }_e$
are overestimated when considering the simplified composition. Moreover, the rise time of the neutrino signal (for details about the role of the neutrino rise time can be found in Serpico et al. Reference Serpico, Chakraborty, Fischer, Hüdepohl, Janka and Mirizzi2012), in particular for
![]() $\bar{\nu }_{\text{e}}$
and heavy-lepton flavour neutrinos, is suppressed with (n, p, α, 〈A, Z〉), being related to the suppression of N–N-bremsstrahlung processes. This may have implications for the appearance of prompt convection, which occurs on a short timescale on the order of few tens of milliseconds after core bounce. The potential impact remains to be explored in multi-dimensional simulations.
$\bar{\nu }_{\text{e}}$
and heavy-lepton flavour neutrinos, is suppressed with (n, p, α, 〈A, Z〉), being related to the suppression of N–N-bremsstrahlung processes. This may have implications for the appearance of prompt convection, which occurs on a short timescale on the order of few tens of milliseconds after core bounce. The potential impact remains to be explored in multi-dimensional simulations.
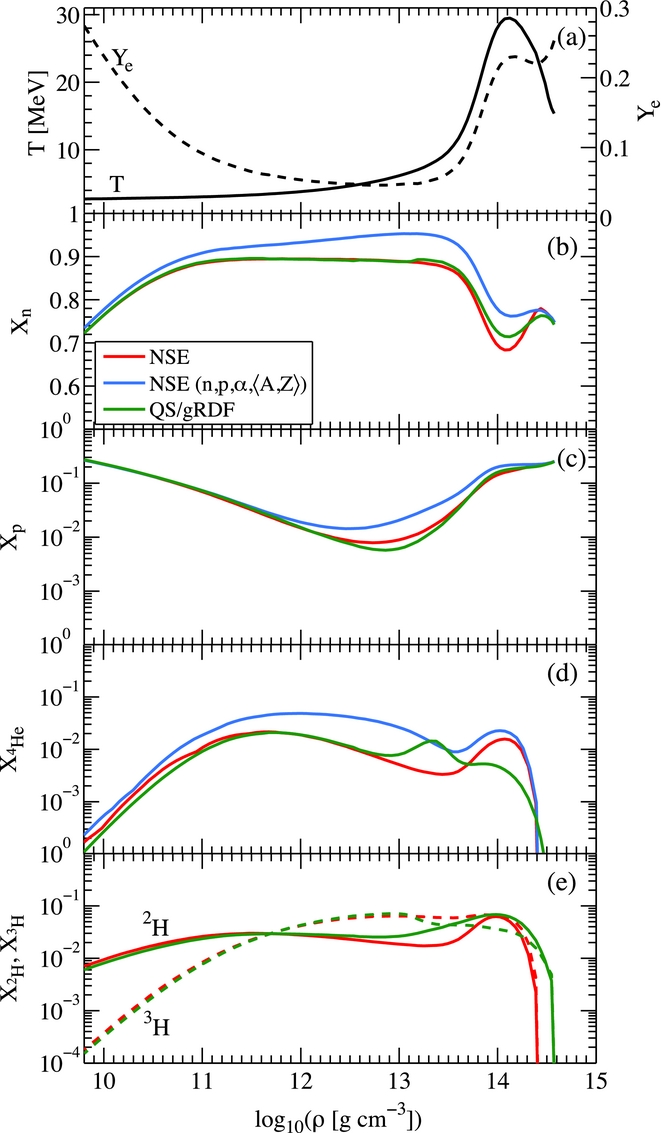
Figure 7. Abundances of the supernova composition of neutrons and protons (b--c) and selected light clusters (d--e). The thermodynamic conditions in terms of temperature and electron fraction Ye, shown in graph (a), correspond to the early PNS deleptonization phase shortly after the supernova explosion onset has been launched when the abundance of light nuclear clusters with A = 2 − 3 is maximum relative to those of protons (data obtained from Fischer et al. Reference Fischer, Martínez-Pinedo, Hempel, Huther, Röpke, Typel and Lohs2016).
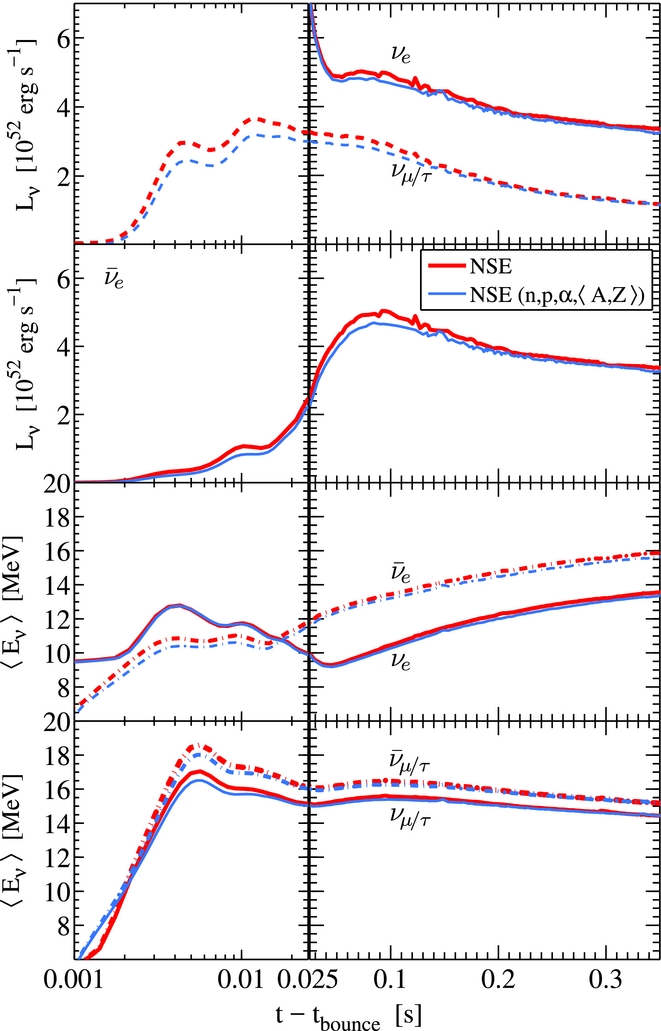
Figure 8. Neutrino luminosities and average energies sampled in the co-moving frame of reference at 1 000 km, comparing simulations where ‘all’ nuclear clusters are included based on the modified NSE approach of Hempel & Schaffner-Bielich (Reference Hempel and Schaffner-Bielich2010) (same as shown in Figure 3) with the simplified composition (n, p, α, 〈A, Z〉).
In Figure 7, we also compare the modified NSE of Hempel & Schaffner-Bielich (Reference Hempel and Schaffner-Bielich2010) with the more sophisticated approaches for the description of in-medium nuclear clusters, i.e. the generalised RMF approach (gRDF) of Typel et al. (Reference Typel, Röpke, Klähn, Blaschke and Wolter2010). The latter is based on in-medium nuclear properties, e.g., binding energies obtained within first-principle quantum statistical calculations of Röpke (Reference Röpke2009) and Röpke (Reference Röpke2011). There it becomes evident that the modified NSE approach provides a sufficient description of the growth properties, such as the particle densities, of light nuclear clusters as illustrated in Figure 7 (c). However, the caveat is at high densities, ρ > 1014 g cm−3, where the geometric excluded volume of the modified NSE fails to properly describe the dissolving of nuclear states into the mean field. Modified NSE provides an inaccurate description of the phase transition to homogeneous matter with over- and underestimated abundances of the light clusters, depending on density and temperature.
4.2. Weak processes with light clusters
The inclusion of self-consistent weak rates with these light clusters is a much more subtle problem. Unlike for nuclear electron captures (1), where average rates are employed, here rates with individual nuclei must be taken into account. It is common to focus on the most abundant species, 2H, 3H, and 3He. In Table 2, we provide a list of all weak reactions with these light nuclei A = 2 − 3, that were considered in the study of Fischer et al. (Reference Fischer, Martínez-Pinedo, Hempel, Huther, Röpke, Typel and Lohs2016).
Table 2. Weak processes with light clusters A = 2 − 3, separated into spallation (top) and scattering reactions (bottom).

Cross-sections
![]() $\sigma _{\nu ^2\text{H}}$
for spallation reactions with 2H, (1) and (2) in Table 2, are provided by Nakamura et al. (Reference Nakamura, Sato, Gudkov and Kubodera2001). They also provide cross-sections for inelastic neutrino scattering on deuteron, (12) in Table 2. In Fischer et al. (Reference Fischer, Martínez-Pinedo, Hempel, Huther, Röpke, Typel and Lohs2016), it has been realised that these cross-sections are related to the electron and positron capture reactions (3) and (4) in Table 2 via the following replacements:
$\sigma _{\nu ^2\text{H}}$
for spallation reactions with 2H, (1) and (2) in Table 2, are provided by Nakamura et al. (Reference Nakamura, Sato, Gudkov and Kubodera2001). They also provide cross-sections for inelastic neutrino scattering on deuteron, (12) in Table 2. In Fischer et al. (Reference Fischer, Martínez-Pinedo, Hempel, Huther, Röpke, Typel and Lohs2016), it has been realised that these cross-sections are related to the electron and positron capture reactions (3) and (4) in Table 2 via the following replacements:
regarding initial-state and final-state phase space occupations of nucleons N and deuteron, as well as the following transformations for the differential cross-sections,
assuming relativistic electrons/positrons. Moreover, cross-sections for the spallation reactions with 3H, (5) and (6) in Table 2, were calculated in Arcones et al. (Reference Arcones, Martínez-Pinedo, O’Connor, Schwenk, Janka, Horowitz and Langanke2008) based on the random phase approximation. In Fischer et al. (Reference Fischer, Martínez-Pinedo, Hempel, Huther, Röpke, Typel and Lohs2016), we realised that the processes (7) and (8) in Table 2 are significantly more important than the spallation reactions, with three nucleons in the final-state. Cross-sections can be given as follows:
where
with Fermi constant G
F and B(GT) = 5.97, known experimentally from the triton decay. Electron and positron energies are related to the νe and
![]() $\bar{\nu }_{\text{e}}$
energies via,
$\bar{\nu }_{\text{e}}$
energies via,
![]() $E_{\text{e}^-}=E_{\nu _{\text{e}}} + Q_0$
and
$E_{\text{e}^-}=E_{\nu _{\text{e}}} + Q_0$
and
![]() $E_{\text{e}^+}=E_{\bar{\nu }_{\text{e}}} - Q_0$
. The vacuum Q-value, Q
0 = 0.529 MeV, is the restmass difference between 3He and 3H. Figure 9 compares the cross-sections of all these charged-current weak processes, for A = 2 (top panel) and A = 3 (bottom panel) in comparison to those of the Urca processes (4), where
$E_{\text{e}^+}=E_{\bar{\nu }_{\text{e}}} - Q_0$
. The vacuum Q-value, Q
0 = 0.529 MeV, is the restmass difference between 3He and 3H. Figure 9 compares the cross-sections of all these charged-current weak processes, for A = 2 (top panel) and A = 3 (bottom panel) in comparison to those of the Urca processes (4), where
with vector and axial vector coupling constants g
V
= 1.0 and g
A
= 1.26. Here we relate electron(positron) and νe(
![]() $\bar{\nu }_{\text{e}}$
) energies with the vacuum Q-value Q
0 = 1.2935 MeV.
$\bar{\nu }_{\text{e}}$
) energies with the vacuum Q-value Q
0 = 1.2935 MeV.
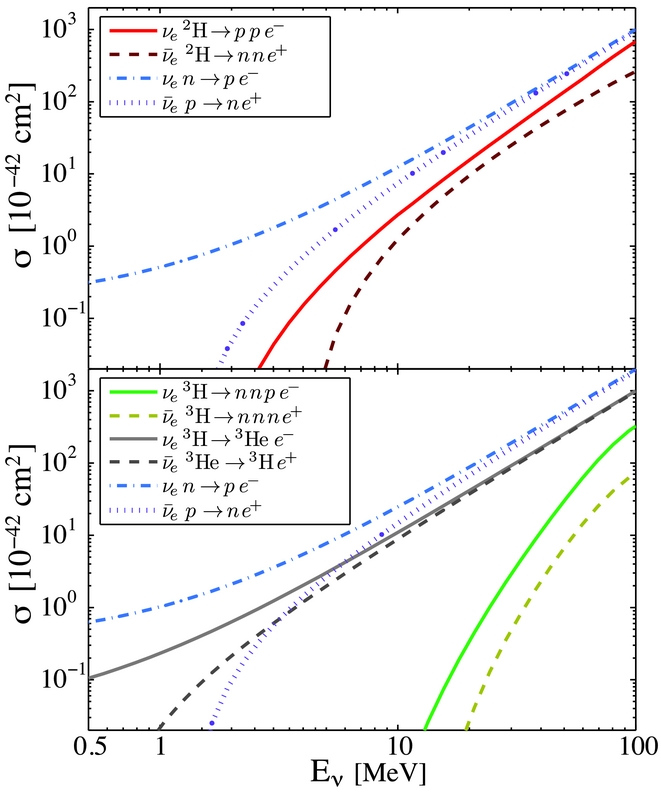
Figure 9. Charged current cross sections for νe- and
![]() $\bar{\nu }_{\text{e}}$
-absorption on light nuclei with A = 2 (top panel) and A = 3 (bottom panel), in comparison to those of the Urca processes (4) for charged current reactions.
$\bar{\nu }_{\text{e}}$
-absorption on light nuclei with A = 2 (top panel) and A = 3 (bottom panel), in comparison to those of the Urca processes (4) for charged current reactions.
When turning these cross-sections into reaction rates, the following two aspects are essential: (i) the vacuum cross-sections, including those of Nakamura et al. (Reference Nakamura, Sato, Gudkov and Kubodera2001), introduced above have to be ‘mapped’ into medium-modified cross-sections. The procedure therefore has been introduced in Fischer et al. (Reference Fischer, Martínez-Pinedo, Hempel, Huther, Röpke, Typel and Lohs2016) based on the mean-field treatment with single-particle energies and effective nucleon masses, (ii) the phase space of the contributing particles has to be taken into account properly (detailed expressions are provided as well in Fischer et al. Reference Fischer, Martínez-Pinedo, Hempel, Huther, Röpke, Typel and Lohs2016). If this is done accurately, then detailed balance is fulfilled (unlike was done in Furusawa et al. Reference Furusawa, Nagakura, Sumiyoshi and Yamada2013), and the impact from weak interactions with light nuclear clusters on the supernova neutrino signal and dynamics was found to be negligible in Fischer et al. (Reference Fischer, Martínez-Pinedo, Hempel, Huther, Röpke, Typel and Lohs2016). The reason for this is illustrated at the example of the mean-free paths in Figure 10—neutral-current scattering (top panel) and the charged-current absorption processes (bottom panel)Footnote 4 , comparing processes with free nucleons and reactions with light clusters with A = 2 − 4. Note that elastic scattering with light clusters is based on the coherent description of Bruenn (Reference Bruenn1985). The mean free paths, including the neutrino distribution functions, are obtained in detailed core-collapse supernova simulations with Boltzmann neutrino transport of Fischer et al. (Reference Fischer, Martínez-Pinedo, Hempel, Huther, Röpke, Typel and Lohs2016), including all these reactions with light clusters (for definitions of mean free path as well as neutrinospheres of last scattering, cf. Fischer et al. Reference Fischer, Martínez-Pinedo, Hempel and Liebendörfer2012).
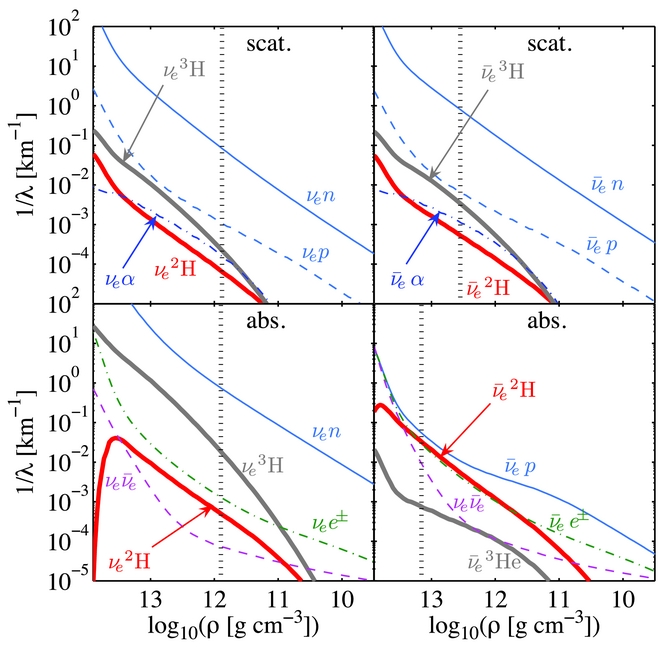
Figure 10. Mean-free paths for νe (left panel) and
![]() $\bar{\nu }_{\text{e}}$
-reactions (right panel) with light nuclei with A = 2 − 4, for neutral-current scattering (top) and charged-current absorption (bottom). The conditions are shown in Figure 7. (Figure adopted from Fischer et al. Reference Fischer, Martínez-Pinedo, Hempel, Huther, Röpke, Typel and Lohs2016).
$\bar{\nu }_{\text{e}}$
-reactions (right panel) with light nuclei with A = 2 − 4, for neutral-current scattering (top) and charged-current absorption (bottom). The conditions are shown in Figure 7. (Figure adopted from Fischer et al. Reference Fischer, Martínez-Pinedo, Hempel, Huther, Röpke, Typel and Lohs2016).
For the νe, scattering and absorption reactions with free neutrons are the dominating channels by orders of magnitude over those with any light nucleus. This is due to the high abundance of free neutrons in comparison with any other nuclear species (see Figure 7). Moreover, the total opacity is dominated by charged-current absorption on neutrons (see Figure 10). The situation is similar for
![]() $\bar{\nu }_{\text{e}}$
, for which the neutral current channel is also dominated by scattering on neutrons. Nevertheless,
$\bar{\nu }_{\text{e}}$
, for which the neutral current channel is also dominated by scattering on neutrons. Nevertheless,
![]() $\bar{\nu }_e$
-absorption on protons dominates less strictly over the absorption on 2H, however, at increasing density. There, the mean-free path for
$\bar{\nu }_e$
-absorption on protons dominates less strictly over the absorption on 2H, however, at increasing density. There, the mean-free path for
![]() $\bar{\nu }_e$
-absorption on 2H is comparable to other inelastic processes, e.g.,
$\bar{\nu }_e$
-absorption on 2H is comparable to other inelastic processes, e.g.,
![]() $\bar{\nu }_{\text{e}}$
scattering on electrons and positrons as well as N–N-bremsstrahlung. Note that in Figure 10 the labels
$\bar{\nu }_{\text{e}}$
scattering on electrons and positrons as well as N–N-bremsstrahlung. Note that in Figure 10 the labels
![]() $\nu _{\text{e}}\bar{\nu }_{\text{e}}$
correspond to the sum of all pair processes (7a).
$\nu _{\text{e}}\bar{\nu }_{\text{e}}$
correspond to the sum of all pair processes (7a).
Weak reactions with A = 3 have in general a negligible role. In Figure 10, we show only processes (7) and (8) of Table 2, which exceed the break-up reactions with 3H by orders of magnitude. The difference to Arcones et al. (Reference Arcones, Martínez-Pinedo, O’Connor, Schwenk, Janka, Horowitz and Langanke2008) may be due to the lack of final-state blocking contributions. Even though ν
e
-absorption on 3H exceeds ν
e
-absorption on 2H, it still lacks short by at least one order of magnitude ν
e
-absorption on neutrons. The largely suppressed
![]() $\bar{\nu }_e$
-absorption on 3He is due to the low abundance of 3He. Note also the region of relevance here, illustrated by black vertical dashed lines in Figure 10, which mark the locations of the average neutrinospheres of last inelastic (bottom panels) and the effective neutrinospheres (top panels).
$\bar{\nu }_e$
-absorption on 3He is due to the low abundance of 3He. Note also the region of relevance here, illustrated by black vertical dashed lines in Figure 10, which mark the locations of the average neutrinospheres of last inelastic (bottom panels) and the effective neutrinospheres (top panels).
The conditions of Figure 10 correspond to the early PNS deleptonisation phase at about 1 s after the supernova explosion onset has been launched, when the thick layer of accumulated material at the PNS surface from the mass accretion phase falls into the gravitational potential of the PNS. This is the moment of maximum impact of weak processes with light clusters, when the abundance of 2H and 3H exceed the one of protons maximally. However, the temperatures are already somewhat lower than during the post-bounce mass accretion period prior to the supernova explosion onset. Therefore, Fischer et al. (Reference Fischer, Martínez-Pinedo, Hempel, Huther, Röpke, Typel and Lohs2016) performed supernova simulations based on three-flavour Boltzmann neutrino transport, including in addition to the standard weak processes (1)–(10) also all weak processes with light clusters with A = 2 − 3 shown in Table 2. It was found that the impact of weak processes with light clusters on the overall supernova dynamics and the neutrino signal is negligible during the mass accretion phase as well as during the PNS deleptonisation phase.
Finally, when comparing the density domain where nuclear pasta may exists in Figure 4 with the one where light nuclei are abundant in Figure 7, it becomes evident that both overlap towards high densities. It is therefore important to develop sophisticated models for nuclear pasta that take the presence of light nuclear clusters into account consistently.
5 HOMOGENEOUS MATTER AT SUPERSATURATION DENSITY
With increasing density, the EOS becomes less and less constrained by nuclear physics. The ab-initio approach to the nuclear many-body problem of dilute neutron matter, chiral EFT, breaks down around normal nuclear matter density ρ0 Footnote 5 . It is also well known that (heavy) nuclear clusters dissolve due to the Pauli exclusion principle into homogeneous matter, composed of neutrons and protons (cf. Hempel et al. Reference Hempel, Schaffner-Bielich, Typel and Röpke2011; Röpke et al. Reference Röpke, Bastian, Blaschke, Klähn, Typel and Wolter2013; Furusawa & Mishustin Reference Furusawa and Mishustin2017).
5.1. Excluded volume approach
In order to explore the uncertainties of the supersaturation density EOS in simulations of core-collapse supernovae, the geometric excluded volume mechanism has been employed in Fischer (Reference Fischer2016a) based on the formalism developed in Typel (Reference Typel2016). There, the available volume of the nucleons V N is suppressed via V N = Vϕ, where V is the total volume of the system. Thereby, the density functional ϕ has the following Gaussian type:
 $$\begin{eqnarray}
\phi (n_{\rm B};\rm v) = \left\lbrace \begin{array}{l l}1 & (n_{\rm B}\le n_0) \\
& \\
\exp \left\lbrace -\frac{\text{v}\vert \text{v} \vert }{2}\left(n_{\rm B}-n_0\right)^2\right\rbrace & (n_{\rm B}>n_0) \end{array} \right.
\end{eqnarray}$$
$$\begin{eqnarray}
\phi (n_{\rm B};\rm v) = \left\lbrace \begin{array}{l l}1 & (n_{\rm B}\le n_0) \\
& \\
\exp \left\lbrace -\frac{\text{v}\vert \text{v} \vert }{2}\left(n_{\rm B}-n_0\right)^2\right\rbrace & (n_{\rm B}>n_0) \end{array} \right.
\end{eqnarray}$$
for both neutrons and protons, in order to ensure a smooth behaviour above saturation density. Based on the choice of the excluded volume parameter, v, additional stiffening is provided to the EOS for v > 0 or softening for v < 0 at supersaturation density. The reference case corresponds to v = 0, for which the modified NSE approach of Hempel & Schaffner-Bielich (Reference Hempel and Schaffner-Bielich2010) is selected together with the RMF parameterisation DD2 of Typel et al. (Reference Typel, Röpke, Klähn, Blaschke and Wolter2010), henceforth denoted as HS(DD2), while HS(DD2-EV) denote EOS with excluded volume modifications. Even though DD2 is already rather stiff at supersaturation density, in particular, in view of the symmetric matter flow constraint obtained from the detailed analysis of heavy-ion collisions by Danielewicz, Lacey, & Lynch (Reference Danielewicz, Lacey and Lynch2002), an even stiffer EOS cannot be ruled out a priori for supernova matter (i.e., at large isospin asymmetry).
It is important to note that within the approach (18), nuclear saturation properties remain unmodified, i.e., the saturation density n 0 and the symmetry energy at n 0 is J = 31.67 MeV. On the other hand, quantities which relate to derivatives are modified, e.g., the (in)compressibility modulus (a summary of present constraints are given in Stone, Stone, & Moszkowski Reference Stone, Stone and Moszkowski2014) varies from K ≃ 541 MeV to K ≃ 201 MeV for the two selected values of v = +8.0 fm3 and v = -3.0 fm3, respectively, compared to the reference case K ≃ 243 MeV (for v = 0). Further details are given in Typel (Reference Typel2016) and Fischer (Reference Fischer2016a).
Figure 11 shows the resulting pressures as a function of density (restmass density ρ at the bottom scale and baryon density n B at the top scale) for the two extreme choices, v = +8.0 fm−3 and v = -3.0 fm−3 (units are skipped in the Figure’s legend for simplicity). These values are selected such that causality is obtained (see the sound speed in the inlay of Figure 11) for the relevant supernova densities and maximum neutron star masses are in agreement with the current constraint of about 2 M⊙. Only for v = +8.0 fm−3, the sound speed exceeds the speed of light, however, at densities far above the central densities reached in the core-collapse simulations which will be further discussed below.
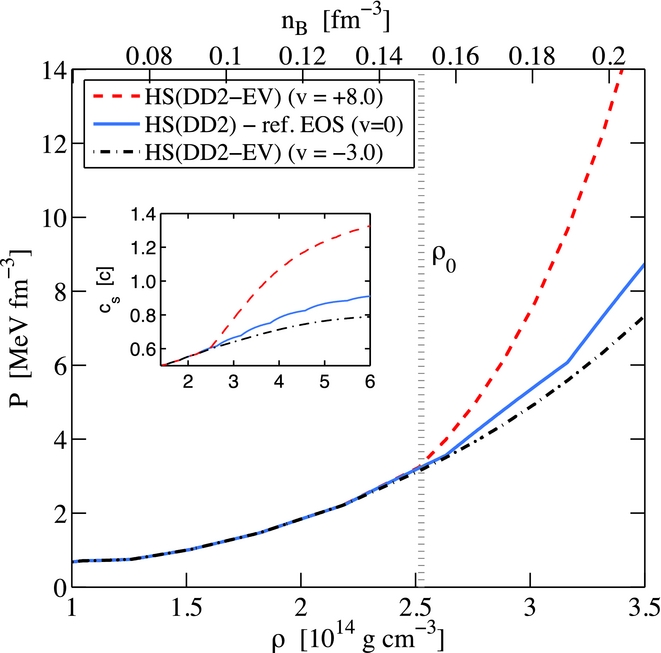
Figure 11. High density behaviour of the supernova EOS, at selected temperature of T = 5 MeV and electron fraction Y e = 0.3, comparing the reference treatment (v = 0) with the modified excluded volume approach with additional stiffening for v = +8.0 fm−3 and softening for v = -3.0 fm−3 above supersaturation density (ρ > ρ0). (Figure adopted from Fischer Reference Fischer2016a).
The central conditions found during the supernova evolutions are illustrated in Figure 12, in terms of density and temperature. In comparison to the reference case, significantly higher(lower) central densities and temperatures are obtained for the soft(stiff) modification of HS(DD2) with v = -3.0 fm−3(v = +8.0 fm−3). The central density reaches 4.25 × 1014 g cm−3 for v = -3.0 fm−3 in comparison to only 3.0 × 1014 g cm−3 for v = +8.0 fm−3, at about 500 ms post bounce. However, it was realised in Fischer (Reference Fischer2016a) that despite such large variation of the central conditions, the overall impact on the supernova dynamics and neutrino signal is negligible (see Figures (4) and (5) in Fischer Reference Fischer2016a). This is because the post-bounce dynamics is determined dominantly at low densities (inhomogeneous nuclear matter, region of high entropy in Figure 1(b)) and the supersaturation density domain of the PNS is generally small, ~0.05–0.1 M⊙ of the total enclosed baryonic mass of PNS with ~1.4–1.8 M⊙ that result from supernova simulations launched from progenitors in the mass range of ~10–30 M⊙ (cf. Ugliano et al. Reference Ugliano, Janka, Marek and Arcones2012).
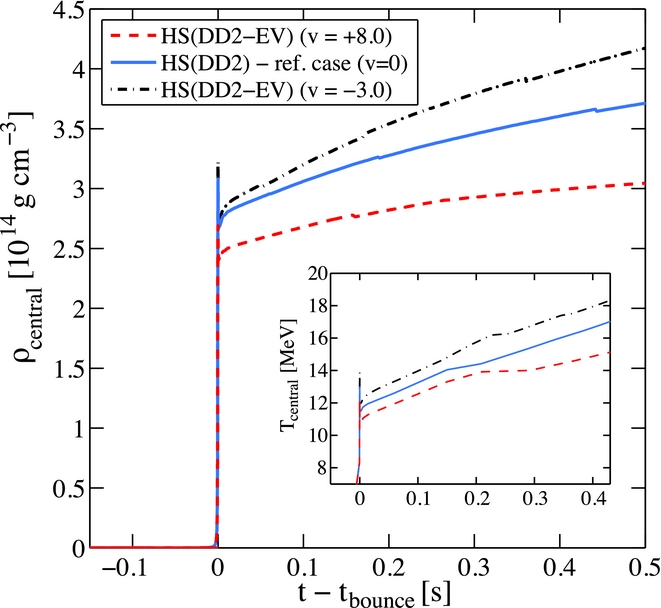
Figure 12. Supernova evolution of central density and temperature comparing reference EOS HS(DD2) and variations due the excluded volume approach (see text for details). The dynamical evolution of the reference case is illustrated in Figure 1 and the neutrino signal is shown in Figure 3. (Figure adopted from Fischer Reference Fischer2016a).
5.2. Phase transition to quark matter
Another similarly uncertain aspect of the EOS at supersaturation density is the question of a possible phase transition from nuclear matter, with hadrons as degrees of freedom, to the deconfined quark gluon plasma with quarks and gluons as the new degrees of freedom. This has long been explored in the context of cold neutron stars. In general, medium properties of quark matter have long been studied (cf. Bender et al. Reference Bender, Poulis, Roberts, Schmidt and Thomas1998; Roberts & Schmidt Reference Roberts and Schmidt2000; Buballa Reference Buballa2005; Alford, Blaschke, & Drago Reference Alford2007; Klähn et al. Reference Klähn, Blaschke, Sandin, Fuchs, Faessler, Grigorian, Röpke and Trümper2007; Ayriyan et al. Reference Ayriyan, Alvarez-Castillo, Benic, Blaschke, Grigorian and Typel2017a; Pagliara & Schaffner-Bielich Reference Pagliara and Schaffner-Bielich2008; McLerran & Pisarski Reference McLerran and Pisarski2007; Sagert et al. Reference Sagert2009; Pagliara, Hempel, & Schaffner-Bielich Reference Pagliara, Hempel and Schaffner-Bielich2009; Blaschke et al. Reference Blaschke, Sandin, Klähn and Berdermann2009; Klähn et al. Reference Klähn, Roberts, Chang, Chen and Liu2010b; Klähn, Blaschke, & Lastowiecki Reference Klähn, Blaschke and Lastowiecki2012; Chen et al. Reference Chen, Baldo, Burgio and Schulze2011; Fischer et al. Reference Fischer2011; Weissenborn, Chatterjee, & Schaffner-Bielich Reference Weissenborn, Chatterjee and Schaffner-Bielich2012; Bonanno & Sedrakian Reference Bonanno and Sedrakian2012; Blaschke et al. Reference Blaschke, Buballa, Dubinin, Röpke and Zablocki2014; Klähn, Łastowiecki, & Blaschke Reference Klähn, Łastowiecki and Blaschke2013; Kurkela et al. Reference Kurkela, Fraga, Schaffner-Bielich and Vuorinen2014; Beisitzer, Stiele, & Schaffner-Bielich Reference Beisitzer, Stiele and Schaffner-Bielich2014, and references therein). First-principle calculations of Quantum Chromodynamics (QCD)—the theory of strongly interacting matter—are possible by means of conducting large-scale numerical studies (cf. Fodor & Katz Reference Fodor and Katz2004; Ratti, Thaler, & Weise Reference Ratti, Thaler and Weise2006), however, only at vanishing density. They predict a smooth cross-over transition from hadronic matter to deconfined quark matter, for a temperature of T = 154 ± 9 MeV at μB ≃ 0 (cf. Borsányi et al. Reference Borsányi, Fodor, Katz, Krieg, Ratti and Szabó2012; Bazavov et al. Reference Bazavov2012a, Reference Bazavov2012b; Borsányi et al. Reference Borsányi, Fodor, Hoelbling, Katz, Krieg and Szabó2014, and references therein). Consequently, in astrophysics studies associated with high baryon densities, the two-phase approach is commonly used based on a hadronic EOS and a different EOS for quark matter at high density. It results in first-order phase transition for which Maxwell or Gibbs constructions are commonly employed. Alternatively, pasta-phases arise when taking into account finite-size effects (Yasutake et al. Reference Yasutake, Łastowiecki, Benić, Blaschke, Maruyama and Tatsumi2014). To this end, Ayriyan et al. (Reference Ayriyan, Alvarez-Castillo, Benic, Blaschke, Grigorian and Typel2017a) studied the appearance of such phases and the associated stability of hybrid stars.
It is important to note that perturbative QCD is valid only in the limit of asymptotic freedom where quarks are no longer strongly coupled (Kurkela et al. Reference Kurkela, Fraga, Schaffner-Bielich and Vuorinen2014), which automatically excludes astrophysical applications. Hence, in the interior of neutron stars and supernovae, where generally densities are encountered far below the asymptotic limit, effective quark matter models have been commonly employed, e.g., the thermodynamic bag model of Farhi & Jaffe (Reference Farhi and Jaffe1984) and models based on the Nambu–Jona–Lasinio (NJL) approach developed by Nambu & Jona-Lasinio (Reference Nambu and Jona-Lasinio1961), see also Klevansky (Reference Klevansky1992) and Buballa (Reference Buballa2005).
In simulations of core-collapse supernovae, the thermodynamic bag model has been employed in the detailed studies of Nakazato, Sumiyoshi, & Yamada (Reference Nakazato, Sumiyoshi and Yamada2008) and Sagert et al. (Reference Sagert2009). The latter study assumed low onset densities for the quark-hadron phase transition—tuned via the bag constant as free parameter—which are realised in the core of canonical supernovae launched from progenitors with initial masses in the range of 10–20 M⊙. It was found that the thermodynamically unstable region between the stable hadron and quark phases results in the collapse of the PNS, which launches a shock wave that in turn triggers the supernova explosion onset in otherwise non-exploding models in spherical symmetry (for details, see Fischer et al. Reference Fischer2011). It also releases a millisecond neutrino burst of all neutrino flavours, which was found to be observable with the current generation of neutrino detectors (details can be found in Dasgupta et al. Reference Dasgupta2010). Unfortunately, these detailed studies violate several ‘solid’ constraints, e.g., maximum neutron star masses are far below the current value of 2 M⊙, and chiral physics is largely violated. All this urges the need to develop more elaborate phenomenological quark matter EOS, being consistent with current constraints. This marks a major task due to the generally three-dimensional dependencies of supernova matter in terms of temperature, baryon, and isospin densities. Moreover, also the development of weak processes in deconfined quark matter, consistent with the underlying quark-matter EOS, is a major undertaken (for some recent progress, cf., Berdermann et al. Reference Berdermann, Blaschke, Fischer and Kachanovich2016, and references therein).
It has been demonstrated recently in Klähn & Fischer (Reference Klähn and Fischer2015) that the thermodynamic bag model and the NJL approach can be understood as limiting solutions of QCD’s in-medium Dyson–Schwinger gap equations (see also Bashir et al. Reference Bashir2012; Cloet & Roberts Reference Cloet and Roberts2014; Chang, Roberts, & Tandy Reference Chang, Roberts and Tandy2011; Roberts Reference Roberts2012; Roberts & Schmidt Reference Roberts and Schmidt2000; Chen et al. Reference Chen2008, Reference Chen, Baldo, Burgio and Schulze2011, Reference Chen, Wei, Baldo, Burgio and Schulze2015; Klähn et al. Reference Klähn, Roberts, Chang, Chen and Liu2010a). Based on the newly developed model vBag of Klähn & Fischer (Reference Klähn and Fischer2015), it has been realised that repulsive vector interaction provides the necessary stiffness for the EOS at high densities in order to yield massive hybrid stars with maximum masses in agreement with the current constraint of 2 M⊙. Higher order vector repulsion terms were explored in the non-local NJL model of Benic et al. (Reference Benic, Blaschke, Alvarez-Castillo, Fischer and Typel2015). This work has been complemented recently in Kaltenborn, Bastian, & Blaschke (Reference Kaltenborn, Bastian and Blaschke2017), providing a relativistic density functional approach to quark matter that implements a confinement mechanism for quarks and allows extensions to finite temperatures. Both aforementioned articles studied the physical case of massive hybrid stars which lead to the ‘twin’ phenomenon (see also Haensel, Potekhin, & Yakovlev Reference Haensel, Potekhin and Yakovlev2007; Read et al. Reference Read, Lackey, Owen and Friedman2009; Zdunik & Haensel Reference Zdunik and Haensel2013; Alford, Han, & Prakash Reference Alford, Han and Prakash2013, and references therein). It relates to the existence of two families of compact stellar objects with similar-to-equal masses but different radii, linked in the mass-radius diagram via a disconnected (i.e., thermodynamically unstable) branch (cf. Alvarez-Castillo & Blaschke Reference Alvarez-Castillo and Blaschke2017). This interesting situation is part of the science case of the NICER (Neutron Star Interior Composition Explorer)Footnote 6 NASA mission, which aims at deducing radii of massive neutron stars at high precision of 0.5 km. See also Alvarez-Castillo et al. (Reference Alvarez-Castillo, Ayriyan, Benic, Blaschke, Grigorian and Typel2016a) and Ayriyan et al. (Reference Ayriyan, Alvarez-Castillo, Benic, Blaschke, Grigorian and Typel2017b) for a recent Bayesian analysis of constraints on EOS with high-mass twin property using fictitious radius data, that could be provided in the near future, e.g., by NICER and similar missions. Moreover, recent developments point towards a universality condition for the hadron-quark phase transition (cf. Alvarez-Castillo et al. Reference Alvarez-Castillo, Benic, Blaschke, Han and Typel2016b).
In Klähn, Fischer, & Hempel (Reference Klähn, Fischer and Hempel2017a), vBag was extended to finite temperature and arbitrary isospin asymmetry. Figure 13 illustrates the resulting phase diagram for matter in β-equilibriumFootnote 7 , for a well selected model parameter B χ (chiral bag constant) which defines chiral symmetry restoration—marked in Figure 13 by ρχ—being in agreement with pion mass and decay constant. Onset densities for the first-order phase transition from the selected underlying hadronic EOS, here HS(DD2), is marked as ρH in Figure 13. Moreover, in contrast to the standard NJL-approach, here (de)confinement is taken into account via a phenomenological parameter (B dc) which is determined by the underlying hadronic EOS, being equal to the hadronic pressure at the chiral transition (for details, see Klähn et al. Reference Klähn, Fischer and Hempel2017a). Hence, it becomes medium dependent, B dc(T, μ Q ), where T and μ Q are temperature and charge chemical potential (the latter referring to isospin asymmetry), respectively. Consequently, additional terms appear which add to the EOS in order to ensure thermodynamic consistency, related to derivatives of B dc with respect to T and μ Q .
Figure 13. vBag phase diagram for matter in β-equilibrium for the quark matter model developed in Klähn & Fischer (Reference Klähn and Fischer2015), with the two parameters B χ and B dc, in comparison to the standard NJL approach (B dc = 0). (Figure adopted from Klähn et al. Reference Klähn, Fischer, Cierniak and Hempel2017b).
The canonical approach for constructing phase transitions based on the two-phase approach, i.e., setting B dc = 0 (also illustrated in Figure 13) corresponds to the standard NJL approach commonly used in neutron star studies. It results in significantly higher transition densities for the quark-hadron phase transition. Moreover, this concept leads to the problem that chiral symmetry is (at least partly) restored while matter remains in the confined phase. At present, one can only speculate about the existence of such phase as the currently running heavy-ion collision experiment at NICA (cf. the NICA white paper Blaschke et al. Reference Blaschke2016, and selected contributions therein) in Dubna (Russia) has not reported any scientific results yet, the low-energy fixed-target experiment at the Relativistic Heavy-Ion Collider (RHIC) in Brookhaven (USA) is expected to produce first results in 2018/2019, and the future Facility for Antiproton and Ion research (FAIR) at the GSI in Darmstadt (Germany) is still under construction. The science runs, in particular, experiments related to the compressed baryonic matter physics (cf. the CBM physics book Friman et al. Reference Friman, Höhne, Knoll, Leupold, Randrup, Rapp and Senger2011), will help to shed light onto the phase structure of the entire phase diagram at high densities and lower temperatures.
6 SUMMARY
In this review article, we summarised selected highlights of EOS developments in simulations of core-collapse supernovae. It covers the entire domain relevant for supernova studies, which can be classified as follows:
-
1. Low temperatures: Typically below T ≃ 5 MeV, heavy nuclei exist—the treatment of weak processes with heavy nuclei, electron captures, neutrino nucleus scattering, and nuclear (de)excitations, are relevant during stellar core collapse. Once heavy nuclei dissociate due to high temperatures as matter is being shock heated early post bounce, weak interactions with heavy nuclei become less important. Towards high densities and low temperatures on the order of few MeV, nuclei become very heavy with Z ≃ 20 − 35 and A ≃ 200 − 400 (the size of these structures depends on the conditions and the nuclear model). This marks the liquid–gas phase transition at arbitrary isospin asymmetry and in the presence of Coulomb repulsion, where structures shape known collectively as nuclear ‘pasta’ phases.
-
2. Intermediate densities and temperatures: in the domain between ρ ≃ 109 − 1013 g cm−3 and at T ≃ 5 − 10 MeV, inhomogeneous nuclear matter exists. Here, chiral EFT provides the constraint for dilute neutron matter. However, at arbitrary isospin asymmetry (i.e., with finite abundance of protons) nuclear clusters form. Then, the cluster-virial EOS (cf. Röpke et al. Reference Röpke, Bastian, Blaschke, Klähn, Typel and Wolter2013) can provide the constraint at low densities, with particular challenge regarding the extensions to large A (see also Bastian et al. Reference Bastian2016, regarding the production of light clusters in heavy-ion collisions). Inhomogeneous matter corresponds to the shock-heated region at the PNS surface with high entropies per baryon, where in particular light nuclear clusters exist in addition to the unbound nucleons.
Light nuclear clusters—play a two-fold role, they modify the nuclear EOS in terms of abundances of the free nucleons and single-particle properties and weak processes with light clusters modify the neutrino transport directly. The latter aspect turns out to be subleading since, taking medium modifications and the particle phase space correctly into account, the leading opacity is due to the Urca and other inelastic processes. This may be slightly modified in multi-dimensional supernova simulations when convection brings high-entropy material down into the cooling layer, which would potentially increase the abundance of light clusters. This will enhance reaction rates with light clusters. However, this remains to be shown in multi-dimensional simulations with neutrino transport which employ the weak processes listed in Table 2. In any case, it is essential to employ nuclear EOS in supernova simulations that treat the nuclear composition, including all nuclear clusters, consistently. Model EOS with simplified nuclear composition (n, p, α, 〈A, Z〉) should be banished from use in supernova studies (for recent efforts, cf. Furusawa et al. Reference Furusawa, Togashi, Nagakura, Sumiyoshi, Yamada, Suzuki and Takano2017).
-
3. At ρ ≳ ρ0 and/or high temperatures: the transition to homogeneous nuclear matter takes place—composed of free nucleons. The EoS constraints that apply for the state of matter at supersaturation densities are summarised in Klähn et al. (Reference Klähn2006). Of particular importance is the maximum mass of compact stars as predicted by a given EoS model since recent precise measurements of pulsar masses ~2 M⊙ allow to exclude EoS which do not possess sufficient stiffness at ρ ≫ ρ0. This challenges in particular the appearance of additional degrees of freedom, e.g., strangeness at the hadronic sector in form of hyperons (cf. Sumiyoshi et al. Reference Sumiyoshi, Ishizuka, Ohnishi, Yamada and Suzuki2009; Bonanno & Sedrakian Reference Bonanno and Sedrakian2012; Weissenborn et al. Reference Weissenborn, Chatterjee and Schaffner-Bielich2012; Bednarek et al. Reference Bednarek, Haensel, Zdunik, Bejger and Mańka2012; Nakazato et al. Reference Nakazato, Furusawa, Sumiyoshi, Ohnishi, Yamada and Suzuki2012) as well as the transition to quark matter. Both aspects tend to soften the EOS at ρ ≫ ρ0. Moreover, the status of the flow constraint by Danielewicz et al. (Reference Danielewicz, Lacey and Lynch2002) is debated. It is desirable to perform direct comparisons with data on directed and elliptic flow from heavy-ion collision experiments for given model EOS. To this end, advanced simulation programmes have to be employed. These would apply in particular in the low-energy region starting from SIS and AGS energies to the NICA and FAIR domain. The recently developed event simulation programme THESEUS which is based on a three-fluid hydrodynamics model, provides an appropriate tool for studying these questions and for comparing flow patterns of EOS with and without QCD phase transitions (see Batyuk et al. Reference Batyuk2016).
A detailed review of the presently available EOS has been provided in Oertel et al. (Reference Oertel, Hempel, Klähn and Typel2017), with a slightly different focus. However, some of the aspects discussed here are being explored in Oertel et al. (Reference Oertel, Hempel, Klähn and Typel2017) as well.
ACKNOWLEDGEMENTS
The authors acknowledge support from the Polish National Science Center (NCN) under grant numbers UMO-2016/23/B/ST2/00720 (TF), UMO-2011/02/A/ST2/00306 (DB), and UMO-2014/13/B/ST9/02621 (NUB and MC). DB and GR acknowledge support by the MEPhI Academic Excellence Project under contract No. 02.a03.21.0005. WN was supported by the Research Corporation for Science Advancement through the Cottrell College Science Award no. 22741. GMP and ST are partially supported by the DFG through grant SFB1245. This work was supported in part by the COST Actions MP1304 ‘NewCompStar’, CA15213 ‘THOR’, and CA16117 ‘ChETEC’.
A APPENDIX: NEUTRINO HEATING AND COOLING RATES
For νe from electron capture, the change in the entropy per nucleon, s, of matter with temperature T is given in Bruenn (Reference Bruenn1985) as followsFootnote 8 :
with chemical potentials of electrons μe, protons μp, and neutrons μn. In (A1), the last term accounts for the change in composition due to electron captures and has been determined assuming thermodynamical equilibrium.
![]() $\text{d}Q_{\rm \text{cc}}/\text{d}t\vert _{\rm net}$
is the net energy exchange rate between neutrinos and matter, defined to be negative when neutrino emission dominates. It can be determined from the electron neutrino emissivity, j(E), and opacity, χ(E), for nuclear electron captures (1) as well as the Urca processes (4) according to Bruenn (Reference Bruenn1985) and Mezzacappa & Bruenn (Reference Mezzacappa and Bruenn1993b) as follows:
$\text{d}Q_{\rm \text{cc}}/\text{d}t\vert _{\rm net}$
is the net energy exchange rate between neutrinos and matter, defined to be negative when neutrino emission dominates. It can be determined from the electron neutrino emissivity, j(E), and opacity, χ(E), for nuclear electron captures (1) as well as the Urca processes (4) according to Bruenn (Reference Bruenn1985) and Mezzacappa & Bruenn (Reference Mezzacappa and Bruenn1993b) as follows:
 $$\begin{eqnarray}
&& \left.\frac{\text{d}Q_{\rm cc}}{\text{d}t}\right|_{\rm net} = \frac{2\pi }{n_{\rm B}} \int \text{d}E E^3 d(\cos \theta ) \nonumber\\
&& \quad\,\times \; \biggr \lbrace \chi (E) f_{\nu _{\text{e}}} (E,\theta ) - j(E) \left(1-f_{\nu _{\text{e}}}(E,\theta )\right)\biggr \rbrace,
\end{eqnarray}$$
$$\begin{eqnarray}
&& \left.\frac{\text{d}Q_{\rm cc}}{\text{d}t}\right|_{\rm net} = \frac{2\pi }{n_{\rm B}} \int \text{d}E E^3 d(\cos \theta ) \nonumber\\
&& \quad\,\times \; \biggr \lbrace \chi (E) f_{\nu _{\text{e}}} (E,\theta ) - j(E) \left(1-f_{\nu _{\text{e}}}(E,\theta )\right)\biggr \rbrace,
\end{eqnarray}$$
with baryon density n
B. Expression (A2) takes into account the full phase-space dependence of all contributing particles, including final-state blocking of νe expressed here via the phase-space distribution function
![]() $f_{\nu _{\text{e}}}$
depending on neutrino energy E and lateral momentum angle θ. For a definition of the neutrino phase-space setup, see Figure 1 in Mezzacappa & Bruenn (Reference Mezzacappa and Bruenn1993b).
$f_{\nu _{\text{e}}}$
depending on neutrino energy E and lateral momentum angle θ. For a definition of the neutrino phase-space setup, see Figure 1 in Mezzacappa & Bruenn (Reference Mezzacappa and Bruenn1993b).
For neutrino-pair production (7a), we have
where dQ
pair/dt|net is determined from the neutrino-pair emission and absorption kernels,
![]() $\mathcal {R}^{\rm emi/abs}$
, as follows:
$\mathcal {R}^{\rm emi/abs}$
, as follows:
 $$\begin{eqnarray}
&&\hspace*{-1pc} \left.\frac{\text{d}Q_{\rm pair}}{\text{d}t}\right|_{\rm net} = \frac{(2\pi )^2}{n_{\rm B}} \int \text{d}E E^2 \text{d}(\cos \theta ) \, \text{d}\bar{E} \bar{E}^2 \text{d}(\cos \bar{\theta }) \nonumber \\
&&\hspace*{-1pc} \quad \times (E+\bar{E})\biggr \lbrace f_{\nu }(E,\theta ) f_{\bar{\nu }}(\bar{E},\bar{\theta })\,\mathcal {R}^{\rm abs}(E+\bar{E},\theta ,\bar{\theta }) \nonumber \\
&&\hspace*{-1pc} \quad -\, \left(1-f_{\nu }(E,\theta )\right)\left(1-f_{\bar{\nu }}(\bar{E},\bar{\theta })\right)\mathcal {R}^{\text{emi}}(E+\bar{E},\theta ,\bar{\theta })\biggr \rbrace,
\end{eqnarray}$$
$$\begin{eqnarray}
&&\hspace*{-1pc} \left.\frac{\text{d}Q_{\rm pair}}{\text{d}t}\right|_{\rm net} = \frac{(2\pi )^2}{n_{\rm B}} \int \text{d}E E^2 \text{d}(\cos \theta ) \, \text{d}\bar{E} \bar{E}^2 \text{d}(\cos \bar{\theta }) \nonumber \\
&&\hspace*{-1pc} \quad \times (E+\bar{E})\biggr \lbrace f_{\nu }(E,\theta ) f_{\bar{\nu }}(\bar{E},\bar{\theta })\,\mathcal {R}^{\rm abs}(E+\bar{E},\theta ,\bar{\theta }) \nonumber \\
&&\hspace*{-1pc} \quad -\, \left(1-f_{\nu }(E,\theta )\right)\left(1-f_{\bar{\nu }}(\bar{E},\bar{\theta })\right)\mathcal {R}^{\text{emi}}(E+\bar{E},\theta ,\bar{\theta })\biggr \rbrace,
\end{eqnarray}$$
taking into account the corresponding neutron and antineutrino phase-space occupations, f
ν(E, θ) and
![]() $f_{\bar{\nu }}(\bar{E}, \bar{\theta })$
, respectively.
$f_{\bar{\nu }}(\bar{E}, \bar{\theta })$
, respectively.
Finally, for inelastic ν scattering with electrons and positrons (6), we have
with
![]() $\text{d}Q_{\nu \text{e}^\pm }/\text{d}t\vert _{\rm net}$
being related to the ν scattering kernels by a similar expression to equation (A4).
$\text{d}Q_{\nu \text{e}^\pm }/\text{d}t\vert _{\rm net}$
being related to the ν scattering kernels by a similar expression to equation (A4).

















