INTRODUCTION
Direct CO2 analysis allows one to process small (tens of µg C) radiocarbon (14C) samples more efficiently, when CO2-producing devices are coupled with accelerator mass spectrometers (AMS) (Ruff et al. Reference Ruff, Wacker, Gäggeler, Suter, Synal and Szidat2007). Direct CO2 analysis requires a gas interface that effectively handles and injects the gas into the ion source. The applications of direct CO2 analysis often do not require as high precision as graphite analysis, but these applications need to process large numbers of small-size samples. Biomedical studies of 14C-labeled compounds and compound-specific radiocarbon analysis represent such applications that rely on efficient separation and collection of many small fractions (van Duijn et al. Reference Van Duijn, Sandman, Grossouw, Mocking, Coulier and Vaes2014; Bosch et al. Reference Bosch, Andersson, Kruså, Bandh, Hovorková and Klánová2015). Radiocarbon analysis of aerosol samples also requires direct CO2 analysis when the sample mass is small and medium precision is acceptable (Agrios et al. Reference Agrios, Salazar, Zhang, Uglietti, Battaglia and Luginbühl2015). Depending on the injection technique, the interfaces can be classified as non-continuous flow (non-CF) and continuous-flow (CF) interfaces.
Non-CF interfaces extract the CO2 from the carrier gas, for example, by collecting the CO2 onto an absorber; then the gas is recovered, mixed with a suitable carrier gas and is efficiently injected into the ion source (Wacker et al. Reference Wacker, Fahrni, Hajdas, Molnar, Synal, Szidat and Zhang2013). These interfaces are popular (Bard et al. Reference Bard, Tuna, Fagault, Bonvalot, Wacker, Fahrni and Synal2015; Zhang et al. Reference Zhang, Liu, Salazar, Li, Zotter and Zhang2014; Hoffmann et al. Reference Hoffmann, Friedrich, Kromer and Fahrni2017) due to their capacity to separate the CO2 from carrier gases that induce ionization suppression (e.g. O2) or with excessive flow rates. The process of handling and moving the gas is fairly complicated; thus, the cost of the interface increases due to the need of multiple parts. Moreover, real-time analysis is impossible due to the trapping step. Another disadvantage is that the absorber material not only traps the analyte, but also external CO2. This adds small quantities of constant and cross contamination into the sample. On the other hand, CF interfaces bypass the trapping step and are more compatible with real-time analysis. In practice, all CF interfaces have to control the carrier flow and the dead volume of the tubings in order to directly inject the CO2. In summary, non-CF interfaces can better control the gas mixing at the cost of complicated set up, potential contamination and losing online real-time detection.
From practical and scientific point of views, it is very important to understand the effect of the gas flow on the ionization yield. For CF interfaces coupled to a MICADAS AMS, it has been shown that the overall ionization yield is maximum (4.5-8%) when the carbon mass flow is ∼ 2 µg C/min (Agrios et al. Reference Agrios, Salazar and Szidat2017). Higher than 4% yields have been reached at ∼ 4 µg C/min (Welte et al. Reference Welte, Wacker, Hattendorf, Christl, Koch, Synal and Günther2016; Welte et al. Reference Welte, Wacker, Hattendorf, Christl and Koch2017) depending on the ion source conditions. For non-CF interfaces, even higher efficiencies (6-11%) have been reached at ∼ 1.5 µg C/min (Fahrni et al. Reference Fahrni, Wacker, Synal and Szidat2013) and 8% yield at 1.5 µL CO2/min (1.3 µg C/min) (Xu et al. Reference Xu, Dougans, Freeman, Maden and Loger2007). Above these carbon flows, the ionization yield decreases due to ionization suppression. It is easy to determine the carbon mass flow (
![]() $˙ m$
) with Equation (1), if the CO2 mass/volume concentration (C) is spatially uniform and constant, and the carrier
$˙ m$
) with Equation (1), if the CO2 mass/volume concentration (C) is spatially uniform and constant, and the carrier
volumetric flow (
![]() $˙ V$
) is known. However, in many CF applications, the CO2 is injected in the form of a pulse and its spatial concentration approximates to a Gaussian distribution. Since the CO2 injection rate is changing in time, understanding the ion signal is complicated. In this work, we present a low-cost CF interface with large dead volume for hyphenating an elemental analyzer with the gas ion source of a MICADAS (Szidat et al. Reference Szidat, Salazar, Vogel, Battaglia, Wacker, Synal and Türler2014); and develop a theoretical-mathematical model to predict carbon mass flow during CF injection. Our hypothesis is that it is possible to determine a real-time or instantaneous carbon mass flow by calculating the concentration profile of the injected CO2 peak. This mass flow should govern the intensity and efficiency of the ionization in a similar fashion as non-CF interfaces.
$˙ V$
) is known. However, in many CF applications, the CO2 is injected in the form of a pulse and its spatial concentration approximates to a Gaussian distribution. Since the CO2 injection rate is changing in time, understanding the ion signal is complicated. In this work, we present a low-cost CF interface with large dead volume for hyphenating an elemental analyzer with the gas ion source of a MICADAS (Szidat et al. Reference Szidat, Salazar, Vogel, Battaglia, Wacker, Synal and Türler2014); and develop a theoretical-mathematical model to predict carbon mass flow during CF injection. Our hypothesis is that it is possible to determine a real-time or instantaneous carbon mass flow by calculating the concentration profile of the injected CO2 peak. This mass flow should govern the intensity and efficiency of the ionization in a similar fashion as non-CF interfaces.
EXPERIMENTAL
Figure 1 shows our interface for CF hyphenation of an elemental analyzer (EA) model Vario MICRO (Elementar, Germany) with the ion source of a MICADAS AMS (Szidat et al. Reference Szidat, Salazar, Vogel, Battaglia, Wacker, Synal and Türler2014). In the “CN” mode, the EA combusts the sample and releases the peaks corresponding to N2, CO2 and other gases in sequence by thermal desorption using helium as gas carrier at 135 cm3/min. The peaks are detected with a thermal conductivity detector (TCD). The EA is connected to the gas interface through a 1/16” stainless steel tubing (inner diameter = 0.75 mm, length = 5 m). Figure 1b shows our modified “CN” method which releases the CO2 at warmer temperature than normal conditions in order to create a sharp peak. The pressure at the head valve of the helium bottle is lower than normal conditions (1.2 bar relative to ambient pressure). In the beginning of the run, the split valve is closed and all the flow enters the dead volume (flexible bellow tube size: L = 30 cm, 50 cm3), exiting to the vent through the purge valve while a small fraction still reaches the ion source, keeping the lines flushed. The flow is controlled by a mass flow controller (MFC) model MCW500 (Alicat, USA) and by a restriction tube at point “1” (1/16” tubing, i.d. = 0.1 mm, L = 80 mm). The MFC is set to a medium flow of 75 cm3/min at 150 s to guarantee the CO2 residence time inside the dead-volume to be long enough (60 s). This residence time can be measured with a non-dispersive infrared (NDIR) detector tuned for CO2 (Sunset Laboratory, USA) which can be mounted before or after the dead volume as indicated by the points “1” and “2” of Figure 1a. After 210 s, the MICADAS data acquisition is started and at ∼270 s, the control program searches for the CO2 peak height from the recorded TCD signal. The end time (tend = 300 s) is the end of the loading protocol, when the CO2 peak is almost at the end of the dead volume. At tend, the purge valve is closed and the split valve is opened. This new arrangement directs some of the carrier flow to the split vent at a rate controlled by the needle valve, keeping the dead volume pressurized around a desired value. This pressurization assures that an overpressure is maintained at the splitting “Tee” and the CO2 does not flush back into the split vent. At tend, the MFC is set to deliver a flow into the ion source of 1–5 cm3/min depending on the capillary i.d. and the pressure of the dead volume. All the steps before tend belong to the CO2 loading into the dead volume while all the later steps regard to the ion source injection protocol. tend defines t = 0 for Figures 3–4 (see below).

Figure 1 Scheme of the experimental method. (a) Experimental set up with a green trace line indicating the CO2 loading path, (b) Elemental analyzer conditions during CO2 loading. At tend, the pneumatic valves split the inflow, (c) Picture of the dead volume. (Please see electronic version for color figures.)

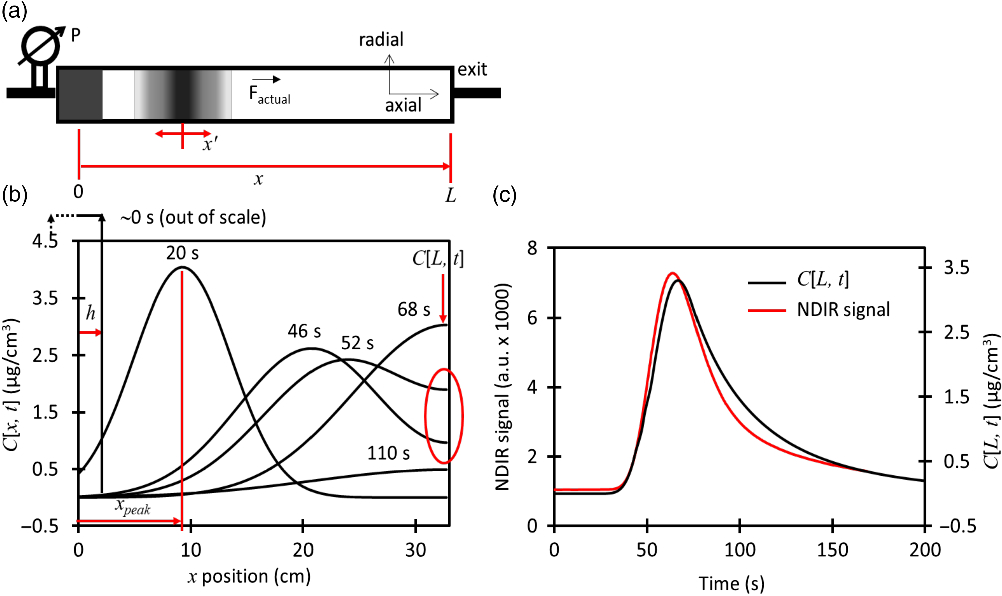
Figure 2 Illustration of the mathematical model during the high flow (75 cm3/min) loading. (a) Scheme of the dead volume with a CO2 peak that starts at the entrance and then diffuses and drifts during 20 s, (b) Calculations of the CO2 concentration showing how the peak drifts at several time steps. Wall reflection at the exit is highlighted with a red circle, (c) Calculation of the CO2 concentration at the exit of the dead volume as a function of time (C[L,t]) compared to the measured signal of a NDIR detector.

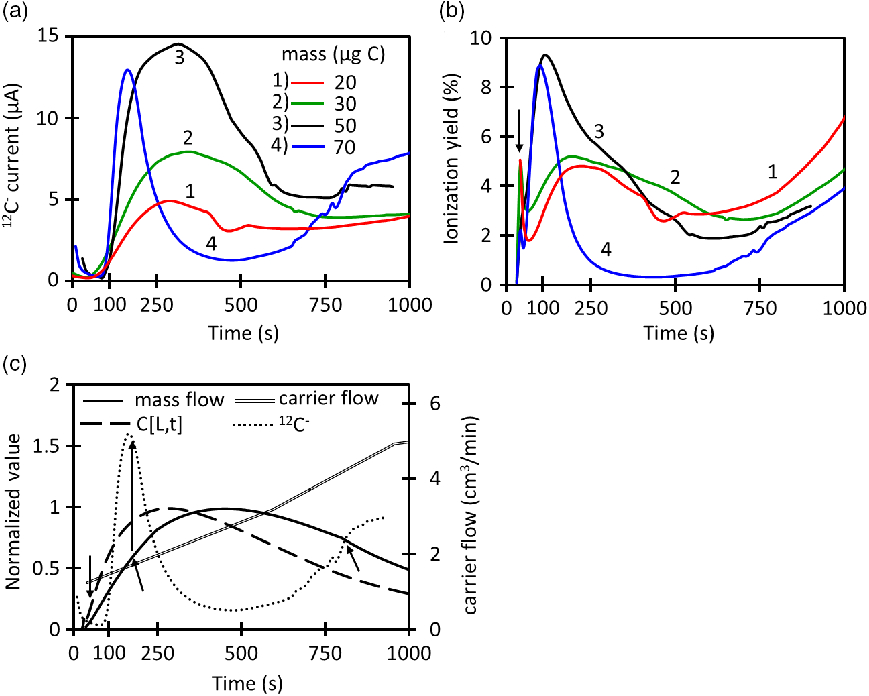
Figure 3 Time evolution and quality parameters of ionization using the whole protocol (CO2 loading and injection) for the dead-volume CF interface with a capillary i.d. of 0.18 mm. (a) Ion current signal, (b) Ionization yield, (c) Overlap of calculated CO2 concentration, mass flow and ion current for 70 µg C normalized to these conditions:C[L,t] = 1.1 µg C/mL, 12C– = 3.3 µA and
![]() $\˙ m$
= 3.5 µg C/min.
$\˙ m$
= 3.5 µg C/min.

Figure 4 Summary of the empirical and calculated data for 3 different injection capillaries as a function of the injected mass. (a) maximum ion current, (b) average ionization efficiency, (c) calculated CO2 concentration, and (d) calculated mass flow. The arrows indicate the onset of ionization suppression.
The control program of the interface is written in Visual Basic 2017 (community edition). It commands all the valves, involved devices and their respective software in real-time. The program controls the MICADAS and the EA by TCP commands. Both valves are shut-off valves with pneumatic actuation. Without pneumatic pressure, the split valve is in the open state and the purge valve is in the close state. In this way, both valves can share a single pneumatic feed. The pneumatic feed is delivered by a single valve DVI 205M (Pfeiffer, USA) connected to a home-made power relay which is controlled by a small signal from an ARDUINO board model MEGA 2560 (Arduino, Italy). The MFC hardware comes with the option for serial communication and control. The R program (R Core Team 2013) was employed to develop the algorithm and mathematical models. Later, those algorithms were implemented in a Visual Basic program, so it could track and display the calculated mass flow in real time. This method enables the system to be simple and low-cost but also it is able to carry out the loading and injection protocols automatically.
Aliquots of D-(+)-sucrose (Sigma Aldrich, USA) standard solution at 10 µg C/µL in ultra-pure water (18 MΩ·cm, TOC < 2ppb) are deposited in aluminum caps (Elementar, Germany) which are closed and set in the EA autosampler. The standards are solid crystals of sodium acetate (fossil; p.a., Merck, Germany), C5, C6 and C7 from IAEA and Oxalic Acid II (Oxa II) from NIST (SRM 4990c). The MICADAS is operated at 135ºC Cs temperature, 128 W power for the Cs reservoir heater and at a background pressure in the ionizer chamber of 2 × 10–6 mbar during gas injection.
RESULTS AND DISCUSSION
Mathematical Model
We developed an algorithm that tracks the CO2 peak along the dead volume and calculates the carbon mass flow at the exit or position L. The model is illustrated in Figure 2 and described in detail in the supplemental materials.
The CO2 peak with mass (m) starts as a disk with half width (h) and cross section area (A) determined by the container’s inner diameter. The initial CO2 concentration (C 0 ) is uniform in the axial and radial directions as defined by Equation (2). The axial speed is calculated, during the loading
and injection protocols, from the measured standard flow corrected by the pressure and the cross section area of the dead volume. The CO2 drift (x peak ) is illustrated in Figure 2a and 2b in which the center of the peak is moved until certain axial position at the same speed of the carrier gas during a small amount of time (dt = 1 s) each time.
The concentration profile along the whole axial coordinate is broadened using Equation (3) which is based on the error function (erf) and takes in account initial width, time (t), Diffusivity (D), axial position and gas reflection when encountering a wall at a distance (L) (Crank Reference Crank1975). We use a pressure-dependent diffusivity as determined for helium-CO2 mixtures by (Bogatyrev and Nezovitina Reference Bogatyrev and Nezovitina2012) at 25°C. The concentration profile relative to the axial direction is calculated with a travelling coordinate x’, where x’ = 0 at the peak center located at x peak position. The coordinates are transformed by Equation (4). Wall or boundary reflection is useful to realistically simulate the moment
when the peak reaches the end of the dead volume located at position L and is impeded to enter the injecting capillary. We observed that the series n = –1 to 1 was enough to approximate our results, although it should be noted that the original form of Equation (3) is an infinite series with n = –∞ to +∞ (Crank Reference Crank1975). We assume that diffusion, wall reflection and mass loss are the only factors that change the concentration profile in the axial direction. The concentration profile in the radial direction is kept uniform during the whole simulation. In this work, the ratio of dead volume length to disk initial width h is ∼12 and the length to inner diameter ratio is ∼12. Our assumptions will not work for neither small L/h nor L/i.d. ratios where there is gas mixing instead of lateral diffusion. Figure 2b illustrates how the concentration profile changes in time and in axial position. The red circle highlights how the wall reflection affects the CO2 concentration peak tail at the exit of the dead volume (C[L,t]). Equation (5) gives the real-time mass flow as the product of the instantaneous CO2 concentration in µg C/cm3 with the carrier flow in cm3/min as explained in Equation (1).
The mass inside the dead volume is calculated by numerical integration of Equation (3) with respect to volume for the whole range x = –h to L. The integration volume element is converted into axial units using
![]() $dV = {\it{A}}\,\,dx$
. The mass loss is the product of the mass flow delivered into the capillary during the interval dt. Then, C
0
is corrected to account for mass loss, the peak is let to drift again during dt and the algorithm is repeated. When the CO2 peak reaches the end position, the drift value is kept constant at x
peak
= L but time t continues increasing. The theory can be tested at high flow by carrying out the CO2 loading protocol without splitting the flow, letting the CO2 escape through the purge valve and including a non-dispersive infrared (NDIR) detector connected to the purge vent at position “2”. The dynamic response of this detector is linear for all the range of concentrations used in this work. The medium flow is kept constant at 75 cm3/min until the whole peak is detected. The theory is not tested for the injection protocol because of the lack of sensitivity of the NDIR detector at low flows. Figure 2c shows a very good agreement between the shape of the calculated CO2 concentration C[L,t] at the exit of the dead volume with the NDIR signal. We are not able to calibrate the NDIR signal to instantaneous concentrations, thus we cannot prove the accuracy of the model. Nevertheless, the calculated C[L,t] value seems to be reliable.
$dV = {\it{A}}\,\,dx$
. The mass loss is the product of the mass flow delivered into the capillary during the interval dt. Then, C
0
is corrected to account for mass loss, the peak is let to drift again during dt and the algorithm is repeated. When the CO2 peak reaches the end position, the drift value is kept constant at x
peak
= L but time t continues increasing. The theory can be tested at high flow by carrying out the CO2 loading protocol without splitting the flow, letting the CO2 escape through the purge valve and including a non-dispersive infrared (NDIR) detector connected to the purge vent at position “2”. The dynamic response of this detector is linear for all the range of concentrations used in this work. The medium flow is kept constant at 75 cm3/min until the whole peak is detected. The theory is not tested for the injection protocol because of the lack of sensitivity of the NDIR detector at low flows. Figure 2c shows a very good agreement between the shape of the calculated CO2 concentration C[L,t] at the exit of the dead volume with the NDIR signal. We are not able to calibrate the NDIR signal to instantaneous concentrations, thus we cannot prove the accuracy of the model. Nevertheless, the calculated C[L,t] value seems to be reliable.
Empirical Results
Figure 3a shows how the 12C– current signal changes during continuous-flow (CF) injection with the dead-volume interface coupled to the EA. A maximum current of 14.4 µA is reached during the time evolution of the 50 µg C injection. The maximum current for 50 µg C is the highest within the group of masses evaluated. Higher masses like 70 µg C produce the curve “4” in which the current starts to increase but suffers a sudden drop at 120 s that lasts until ∼800 s where the signal starts to recover again. This behavior reflects the ionization suppression which has been observed before for CF injection into AMS ion sources (Agrios et al. Reference Agrios, Salazar and Szidat2017). Equation (6) is used to calculate the instantaneous ionization efficiency at the low-energy side of the AMS where I is the ion current signal (µC/s), F is Faraday’s constant (96485 C/mol),
![]() $˙ m$
is the instantaneous mass flow (µg C/s) and M
C
is molar mass of carbon (12.011 g/mol). The ion current is recorded continuously and is only limited by the recording frequency of the detector (0.1 Hz). Hence, it is possible to calculate an “instantaneous” mass flow and ionization yield at any given moment. Figure 3b shows the ionization yield for the same group of
$˙ m$
is the instantaneous mass flow (µg C/s) and M
C
is molar mass of carbon (12.011 g/mol). The ion current is recorded continuously and is only limited by the recording frequency of the detector (0.1 Hz). Hence, it is possible to calculate an “instantaneous” mass flow and ionization yield at any given moment. Figure 3b shows the ionization yield for the same group of
injected masses as Figure 3a. The yield for 50 µg C reaches higher values than lower masses and the strong ionization suppression for 70 µg C is reflected in its reduction in ionization yield. The general behavior of the current and ionization yield are illustrated in Figure 3b and 3c for 70 µg C. In the beginning of the injection (< 50 s), the MFC flow reading is very low; however, the actual flow going into the ion source is higher. Momentarily, the actual flow is driven by the dead volume pressure due to the position of the MFC. This causes an underestimation of the mass flow (
![]() $˙ m$
) that lasts until the system equilibrates at ∼50 s. As consequence, the actual
$˙ m$
) that lasts until the system equilibrates at ∼50 s. As consequence, the actual
![]() $˙ m$
creates a small current (I) that in comparison with the underestimated
$˙ m$
creates a small current (I) that in comparison with the underestimated
![]() $˙ m$
translates into an artificial ionization yield peak as indicated with an arrow. After 100 s, the ion current is triggered when the mass flow is around 1 µg C/min. The onset of the current suppression and its recovering points occur when
$˙ m$
translates into an artificial ionization yield peak as indicated with an arrow. After 100 s, the ion current is triggered when the mass flow is around 1 µg C/min. The onset of the current suppression and its recovering points occur when
![]() $˙ m$
is ∼2.0 µg C/min as indicated by the arrows. In this case,
$˙ m$
is ∼2.0 µg C/min as indicated by the arrows. In this case,
![]() $˙ m$
reaches a maximum of 3.5 µg C/min. This suggests that the ionization suppression is reversible and only appears when the instantaneous
$˙ m$
reaches a maximum of 3.5 µg C/min. This suggests that the ionization suppression is reversible and only appears when the instantaneous
![]() $˙ m$
is higher than an onset value. The mass flow never reaches the suppression onset for relatively low masses (20–50 µg C), so their current signals are not affected. It should further be noted that the CO2 concentrationC[L,t] starts to rapidly increase earlier than
$˙ m$
is higher than an onset value. The mass flow never reaches the suppression onset for relatively low masses (20–50 µg C), so their current signals are not affected. It should further be noted that the CO2 concentrationC[L,t] starts to rapidly increase earlier than
![]() $˙ m$
. This is because, in the beginning of injection, the front of the CO2 peak is located at the end of the dead volume (L), hence C[L,t] is already increasing. However, the carrier flow is very low (1.3 cm3/mL), thus the estimated
$˙ m$
. This is because, in the beginning of injection, the front of the CO2 peak is located at the end of the dead volume (L), hence C[L,t] is already increasing. However, the carrier flow is very low (1.3 cm3/mL), thus the estimated
![]() $˙ m$
is also low at this moment. Later, the carrier flow slowly increases, reaching 3.2 cm3/mL at 600 s and after a quick increment, it reaches 5 cm3/mL at 900 s. The same flow increment pattern is used for all measurements with the exception of Table 1 and this pattern is intended to keep the dead volume pressure relatively constant. The maximum value of C[L,t] and
$˙ m$
is also low at this moment. Later, the carrier flow slowly increases, reaching 3.2 cm3/mL at 600 s and after a quick increment, it reaches 5 cm3/mL at 900 s. The same flow increment pattern is used for all measurements with the exception of Table 1 and this pattern is intended to keep the dead volume pressure relatively constant. The maximum value of C[L,t] and
![]() $˙ m$
time plots change proportionally with the mass, but they all have the same shape and width (see example in Figure 3c).
$˙ m$
time plots change proportionally with the mass, but they all have the same shape and width (see example in Figure 3c).
Table 1 Radiocarbon analysis of grains of standard materials showing the St. dev. as the standard deviation of the repeated measurement (n = 2), uncertainty as the average counting statistics uncertainty at 1-σ level and accuracy as the relative difference to the nominal value.

The long increasing tails of the ionization yield starting at 750 s occur when the CO2 concentration is decreasing but the carrier flow is increasing rapidly.
![]() $˙ m$
is the product ofC[L,t] and flow, consequently,
$˙ m$
is the product ofC[L,t] and flow, consequently,
![]() $˙ m$
decays slowly. The ion current tail is not following the fast decay of the CO2 concentration, but it is variating more with the long tail of
$˙ m$
decays slowly. The ion current tail is not following the fast decay of the CO2 concentration, but it is variating more with the long tail of
![]() $˙ m$
. However, the variation of the ion current is not perfectly governed by
$˙ m$
. However, the variation of the ion current is not perfectly governed by
![]() $˙ m$
. Our model estimation is based on perfect cylindrical tubing, but the dead volume has irregular geometry and can suffer of turbulent flows due to the considerable volume of the pressure gauge and the irregular shape of the dead volume walls as shown in Figure 1. The CO2 that is trapped in the turbulent flow and irregular geometries is released at a later time, increasing even more the tail of the ion current signal. These non-ideal situation creates inaccuracies in our mathematical model.
$˙ m$
. Our model estimation is based on perfect cylindrical tubing, but the dead volume has irregular geometry and can suffer of turbulent flows due to the considerable volume of the pressure gauge and the irregular shape of the dead volume walls as shown in Figure 1. The CO2 that is trapped in the turbulent flow and irregular geometries is released at a later time, increasing even more the tail of the ion current signal. These non-ideal situation creates inaccuracies in our mathematical model.
Figure 4 summarizes the data presented in Figure 3 for three different capillary sizes. Similar as in Figure 3, ionization suppression is observed for all capillaries, when the instantaneous
![]() $˙ m$
reaches the onset value. Figures 4a and 4b show how the maximum current and average ionization efficiency increase with the mass until reaching a maximum from where the signals start to be suppressed. The average ionization efficiency is defined as the average instantaneous ionization efficiency for the time range of 50–750 s. All capillaries reach similar levels of maximum current, however, the biggest capillary (0.18 mm) can reach higher efficiencies. On the other hand, the mass working-range for the largest capillary is comparatively narrow. This means that it is better to use large capillaries for small masses. The mass range can be extended by using lower carrier flows during injection of high masses because this avoids the mass flow to reach the suppression onset as it is done for Table 1. In the other hand, high carrier flows should be used for lower masses. Figure 4c indicates that the ionization suppression starts at different CO2 concentrations and the CO2 concentration at the onset is very different for each capillary. On the contrary, Figure 4d shows that the onset of ionization suppression falls in a narrow range (2.0–2.3 µg C/min) for all capillaries. This reflects that the signal for this type of interface and ion source is not controlled by the CO2 concentration alone, but by the mass flow.
$˙ m$
reaches the onset value. Figures 4a and 4b show how the maximum current and average ionization efficiency increase with the mass until reaching a maximum from where the signals start to be suppressed. The average ionization efficiency is defined as the average instantaneous ionization efficiency for the time range of 50–750 s. All capillaries reach similar levels of maximum current, however, the biggest capillary (0.18 mm) can reach higher efficiencies. On the other hand, the mass working-range for the largest capillary is comparatively narrow. This means that it is better to use large capillaries for small masses. The mass range can be extended by using lower carrier flows during injection of high masses because this avoids the mass flow to reach the suppression onset as it is done for Table 1. In the other hand, high carrier flows should be used for lower masses. Figure 4c indicates that the ionization suppression starts at different CO2 concentrations and the CO2 concentration at the onset is very different for each capillary. On the contrary, Figure 4d shows that the onset of ionization suppression falls in a narrow range (2.0–2.3 µg C/min) for all capillaries. This reflects that the signal for this type of interface and ion source is not controlled by the CO2 concentration alone, but by the mass flow.
Preliminary results are shown in Table 1 using the whole automatized protocol, but quantifying the CO2 using the height of the EA peak and limiting the maximum mass flow to 2.0 µg C/min by decreasing the carrier volumetric flow setting on real time. For this range of masses, the typical precision for non-CF interfaces using Oxa II is ca. 0.6–0.8% (Hoffmann et al. Reference Hoffmann, Friedrich, Kromer and Fahrni2017; Tuna et al. Reference Tuna, Fagault, Bonvalot, Capano and Bard2018). Although the results are comparable with non-CF works, Table 1 just represents a proof-of-concept due to the small number of repetitions. Further statistical characterization including constant and cross contamination shall be carried out in future.
In general, our CF interface gives 4–6% optimum ionization yields which are lower than the optimum yields reported for non-CF interfaces. We should mention that our Cs vaporization temperature (135°C) is much lower than for other studies. Hoffmann et al. (Reference Hoffmann, Friedrich, Kromer and Fahrni2017) used 160°C to achieve 4–6% yields. Fahrni et al. (Reference Fahrni, Wacker, Synal and Szidat2013) obtained a 6% yield at 150°C. Nevertheless, we think that at similar source conditions non-CF interfaces should be just slightly more efficient, because they work at nearly steady-state conditions and at low carrier flows (<1.4 cm3/min). In contrast, for our CF interface, the carrier flow is much higher and the carbon mass flow is continuously changing. Our data suggests that the higher carrier flow range (1–5 cm3/min) has small detrimental impact on the ionization yield comparing with non-CF yields. High carrier flows increase the background gas, interfering with the Cs+ beam; but perhaps at the same time, this cools down the Ti surface which increases the CO2 absorption. The optimal carbon mass flows from previous studies (Fahrni et al. Reference Fahrni, Wacker, Synal and Szidat2013; Hoffmann et al. Reference Hoffmann, Friedrich, Kromer and Fahrni2017) and from our results are in the same range; the ionization mechanism is therefore more governed by the amount of CO2 that is fed onto the Ti surface per unit time (independently of the type of injection flow or capillary size), if the Cs+ beam density is kept constant.
ACKNOWLEDGMENTS
We thank René Schraner and Michael Battaglia for their technical support for the construction of the experimental setup.
SUPPLEMENTARY MATERIAL
To view supplementary material for this article, please visit https://doi.org/10.1017/RDC.2019.93