Hostname: page-component-cb9f654ff-lqqdg Total loading time: 0 Render date: 2025-08-12T13:34:26.975Z Has data issue: false hasContentIssue false
  • English
  • Français

An automata-theoretic approach to the study of the intersectionof two submonoids of a free monoid

Published online by Cambridge University Press:  03 June 2008

Laura Giambruno  and
Antonio Restivo
Laura Giambruno
Affiliation:
Dipartimento di Matematica e Applicazioni, Università di Palermo, via Archirafi 34, 90123 Palermo, Italy; lgiambr;restivo@math.unipa.it
Antonio Restivo
Affiliation:
Dipartimento di Matematica e Applicazioni, Università di Palermo, via Archirafi 34, 90123 Palermo, Italy; lgiambr;restivo@math.unipa.it
Get access

Abstract

We investigate the intersection of two finitely generated submonoidsof the free monoid on a finite alphabet. To this purpose, weconsider automata that recognize such submonoids and we study theproduct automata recognizing their intersection. By using automatamethods we obtain a new proof of a result of Karhumäki on thecharacterization of the intersection of two submonoids ofrank two, in the case of prefix (or suffix) generators. In a moregeneral setting, for an arbitrary number of generators, we provethat if H and K are two finitely generated submonoids generatedby prefix sets such that the product automaton associated to $H \capK$ 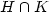has a given special property then $\widetilde{rk}(H \cap K) \leq\widetilde{rk}(H) \widetilde{rk}(K)$ 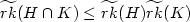where $\widetilde{rk}(L)=\max(0,rk(L)-1)$ 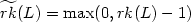for any submonoid L.

Keywords

Automatafree monoidsrankintersection of submonoids

Information

Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 42 , Issue 3: JM'06 , July 2008 , pp. 503 - 524
Copyright
© EDP Sciences, 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

J. Berstel and D. Perrin. Theory of Codes. Academic Press (1985).
Bruyére, V., Derencourt, D., Latteux, M.. The meet operation in the lattice of codes. Theoretical Computer Science 191 (1998) 117–129. CrossRef
Clement, J., Duval, J., G.Guaiana, D. Perrin, G. Rindone. Paarsing with a finite dictionary. Theoretical Computer Science 340 (2005) 432–442. CrossRef
H.Cormen, E. Leiserson, L. Rivest. Introduction to Algorithms. The MIT Press (1990).
J.E. Hopcroft, J.D. Ullman. Introduction to Automata Theory, Languages and Computation. Addison-Weisley Publishing Company (1979).
A.G. Howson. On the intersection of finitely generated free groups. J. London Math. Soc. 29 (1954) 428–434.
J. Karhumäki. A note on intersection of free submonoids of a free monoid. Semigroup Forum 29 (1984) 183–205.
M. Latteux and J. Leguy. On the composition of morphism and inverse morphisms. Lecture Notes in Computer Science 154 (1983) 420–432.
J. Meakin and P. Weil. Sugroups of free groups: a contribution to the Hanna Neumann conjecture. Geometriae Dedicata 94 (2002) 33–43.
H. Neumann. On intersections of finitely generated subgroups of free groups. Publ. Math. Debrecen 4 (1956) 186–189.
W.D. Neumann. On intersections of finitely generated subgroups of free groups. Lect. Notes Math. 1456 (1990) 161–170.
B. Tilson. The intersection of free submonoids of a free monoid is free. Semigroup Forum 4 (1972) 345–350.