Hostname: page-component-cb9f654ff-qc88w Total loading time: 0 Render date: 2025-08-08T18:13:32.893Z Has data issue: false hasContentIssue false
  • English
  • Français

Deciding whether a relation defined inPresburger logiccan be defined in weaker logics

Published online by Cambridge University Press:  18 January 2008

Christian Choffrut
Christian Choffrut*
Affiliation:
LIAFA, Université de Paris 7, 2 place Jussieu, 75251 Paris Cedex 05; cc@liafa.jussieu.fr
Get access

Abstract

We consider logics on $\mathbb{Z}$ 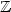and $\mathbb{N}$ 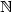which are weaker than Presburger arithmetic and we settle the following decision problem: given a k-ary relation on $\mathbb{Z}$ 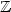and $\mathbb{N}$ 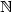which are first order definable inPresburger arithmetic, are they definable in theseweaker logics? These logics, intuitively,are obtained by considering modulo and threshold counting predicates for differences of two variables.

Keywords

Presburger arithmeticfirst order logicdecidability

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Carton, O., Choffrut, C. and Grigorieff, S.. Decision problems for rational relations. RAIRO-Theor. Inf. Appl. 40 (2006) 255–275. CrossRef
C. Choffrut and M. Goldwurm. Timed automata with periodic clock constraints. J. Algebra Lang. Comput. 5 (2000) 371–404.
S. Eilenberg. Automata, Languages and Machines, volume A. Academic Press (1974).
S. Eilenberg and M.-P. Schützenbeger. Rational sets in commutative monoids. J. Algebra 13 (1969) 173–191.
S. Ginsburg and E.H. Spanier. Bounded regular sets. Proc. Amer. Math. Soc. 17 (1966) 1043–1049.
M. Koubarakis. Complexity results for first-order theories of temporal constraints. KR (1994) 379–390.
H. Läuchli and C. Savioz. Monadic second order definable relations on the binary tree. J. Symbolic Logic 52 (1987) 219–226.
A. Muchnik. Definable criterion for definability in presburger arithmentic and its application (1991). Preprint in russian.
P. Péladeau. Logically defined subsets of ${\mathbb{N}}^k$ . Theoret. Comput. Sci. 93 (1992) 169–193.
J.-E. Pin. Varieties of formal languages. Plenum Publishing Co., New-York (1986). (Traduction de Variétés de langages formels.)
J. Sakarovitch. Eléments de théorie des automates. Vuibert Informatique (2003).
A. Schrijver. Theory of Linear and Integer Programming. John Wiley & sons (1998).
C. Smoryński. Logical Number Theory I: An Introduction. Springer Verlag (1991).