Hostname: page-component-cb9f654ff-fg9bn Total loading time: 0 Render date: 2025-08-09T03:24:31.611Z Has data issue: false hasContentIssue false
  • English
  • Français

Automata, Borel functions and real numbers in Pisot base

Published online by Cambridge University Press:  24 April 2007

Benoit Cagnard  and
Pierre Simonnet
Benoit Cagnard
Affiliation:
UMR CNRS 6134, université de Corse, BP 52, 20250 CORTE, France; cagnard@univ-corse.fr; simonnet@univ-corse.fr
Pierre Simonnet
Affiliation:
UMR CNRS 6134, université de Corse, BP 52, 20250 CORTE, France; cagnard@univ-corse.fr; simonnet@univ-corse.fr
Get access

Abstract

This note is about functions ƒ : Aω → Bω whose graph is recognized by a Büchi finite automaton on the product alphabet A x B. These functions are Baire class 2 in the Baire hierarchy of Borel functionsand it is decidable whether such function are continuous or not.In 1920 W. Sierpinski showed that a function $f : \mathbb{ R}\rightarrow \mathbb{R} $ 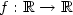is Baire class 1 if and only if both theovergraph and the undergraph of f are Fσ . We show thatsuch characterization is also true for functions on infinite wordsif we replace the real ordering by the lexicographical orderingon Bω . From this we deduce that it is decidable whethersuch function are of Baire class 1 or not. We extend this resultto real functions definable by automata in Pisot base.

Keywords

Borel setBorel functionautomatasequentialmachine.

Information

Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 41 , Issue 1: Real Numbers , January 2007 , pp. 27 - 44
Copyright
© EDP Sciences, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Avizienis, A., Signed-digit number representation for fast parallel aritmetic. IRE Trans. Electronic Comput. 10 (1961) 389–400. CrossRef
J.R. Büchi, On a decision method in restricted second order arithmetic, in Methodology and Philosophy of Science. Stanford Univ. Press, Calif. (1962) 1–11.
Choffrut, C., Pelibossian, H. and Simonnet, P., Decision issues on functions realized by finite automata. J. Automata Languages Combin. 4 (1999) 171–182.
A. Edgar, Classics On Fractals. Studies in non linearity. Westview Press (2004).
S. Eilenberg, Automata, Languages and Machines, Vol. A. Academic Press, New York London (1974).
Ercegovac, M.D. and Lang, T., On-the-fly convertion of redundant into conventional representations. IEEE Trans. Comput. 36 (1987) 895–897. CrossRef
Finkel, O., On the topological complexity of infinitary rational relations. Theor. Inform. Appl. 37 (2003) 105–113. CrossRef
Finkel, O., Undecidability of topological and arithmetical properties of infinitary rational relations. Theor. Inform. Appl. 37 (2003) 115–126. CrossRef
G. Flory, Topologie, Analyse. Vuibert (1976).
C. Frougny and J . Sakarovitch, Synchronized relations of finite and infinite words. Theoret. Comput. Sci. (1993) 45–82.
C. Frougny and B. Solomyak, On representation of integers in linear numeration systems, in Ergodic Theory of Zd -Actions. New Brunswick, New Jersey (1996) 345–368.
Frougny, C., On-the-fly algorithms and sequential machines. IEEE Trans. Comput. 49 (2000) 859–863. CrossRef
C. Frougny, Numeration Systems. Chapter 7 of M. Lothaire, Algebraic Combinatorics on Words. Cambridge University Press (2002).
Gire, F., Two decidability problems for infinite words. Inform. Proc. Lett. 22 (1986) 135–140. CrossRef
A.S. Kechris, Classical Descriptive Set Theory. Springer-Verlag (1995).
Kornerup, P., Digit-set convertions: Generalizations and applications. IEEE Trans. Comput. 43 (1994) 622–629. CrossRef
Landweber, L.H., Decision problem for ω-automata. Math. Systems. Theory 3 (1969) 376–384. CrossRef
B. Maurey and J.P. Tacchi, Ludwig Scheeffer et les extensions du Théorème des Accroissements Finis, in Séminaire du Luxembourg, Travaux mathématiques, fascicule XIII (2002) 1–60.
J.M. Muller, Arithmétique des ordinateurs. Masson, Paris (1989).
D. Perrin and J.-E. Pin, Infinite words, Automata, Semigroups, Logic and Games. Pure Appl. Mathematics Series 141, Academic Press, Elsevier (2004).
Prieur, C., How to decide continuity of rationnal functions on infinite words. Theoret. Comput. Sci. 250 (2001) 71–82. CrossRef
Prieur, C., How to decide continuity of rationnal functions on infinite words (Errata). Theoret. Comput. Sci. 276 (2002) 445–447. CrossRef
Saint Raymond, J., Fonctions boréliennes sur un quotient. Bull. Soc. Math. France 100 (1976) 141–147.
J. Sakarovitch, Éléments de théorie des automates. Vuibert informatique (2003).
Sierpinski, W., Sur les fonctions de première classe. C. R. Acad. Sci. Paris 170 (1920) 919–922.