No CrossRef data available.
Article contents
Unique decipherability in the additive monoid of sets of numbers
Published online by Cambridge University Press: 13 May 2011
Abstract
Sets of integers form a monoid, where the product of two sets Aand B is defined as the set containing a+b for all $a\in A$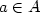
and$b\in B$
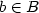. We give a characterization of when a family of finitesets is a code in this monoid, that is when the sets do not satisfyany nontrivial relation. We also extend this result for someinfinite sets, including all infinite rational sets.
Information
- Type
- Research Article
- Information
- Copyright
- © EDP Sciences, 2011
References
J. Berstel and D. Perrin, Theory of Codes. Academic Press (1985).
Ch. Choffrut and J. Karhumäki, Unique decipherability in the monoid of languages: an application of rational relations, in Proceedings of the Fourth International Computer Science Symposium in Russia (2009) 71–79.
R. Gilmer, Commutative Semigroup Rings. University of Chicago Press (1984).
J.-Y. Kao, J. Shallit and Z. Xu, The frobenius problem in a free monoid, in Proceedings of the 25th International Symposium on Theoretical Aspects of Computer Science (2008) 421–432.
Karhumäki, J. and Lisovik, L.P., The equivalence problem of finite substitutions on $ab\sp*c$
, with applications. Int. J. Found. Comput. Sci. 14 (2003) 699–710.
CrossRef
, with applications. Int. J. Found. Comput. Sci. 14 (2003) 699–710.
CrossRefKunc, M., The power of commuting with finite sets of words. Theor. Comput. Syst. 40 (2007) 521–551.
CrossRef
D. Perrin, Codes conjugués. Inform. Control. 20 (1972) 222–231.
J.L. Ramírez Alfonsín, The Diophantine Frobenius Problem. Oxford University Press (2005).