Article contents
THE MODAL LOGIC OF SET-THEORETIC POTENTIALISM AND THE POTENTIALIST MAXIMALITY PRINCIPLES
Published online by Cambridge University Press: 04 October 2019
Abstract
We analyze the precise modal commitments of several natural varieties of set-theoretic potentialism, using tools we develop for a general model-theoretic account of potentialism, building on those of Hamkins, Leibman and Löwe [14], including the use of buttons, switches, dials and ratchets. Among the potentialist conceptions we consider are: rank potentialism (true in all larger 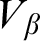 $V_\beta $), Grothendieck–Zermelo potentialism (true in all larger
$V_\beta $), Grothendieck–Zermelo potentialism (true in all larger 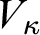 $V_\kappa $ for inaccessible cardinals
$V_\kappa $ for inaccessible cardinals 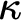 $\kappa $), transitive-set potentialism (true in all larger transitive sets), forcing potentialism (true in all forcing extensions), countable-transitive-model potentialism (true in all larger countable transitive models of ZFC), countable-model potentialism (true in all larger countable models of ZFC), and others. In each case, we identify lower bounds for the modal validities, which are generally either S4.2 or S4.3, and an upper bound of S5, proving in each case that these bounds are optimal. The validity of S5 in a world is a potentialist maximality principle, an interesting set-theoretic principle of its own. The results can be viewed as providing an analysis of the modal commitments of the various set-theoretic multiverse conceptions corresponding to each potentialist account.
$\kappa $), transitive-set potentialism (true in all larger transitive sets), forcing potentialism (true in all forcing extensions), countable-transitive-model potentialism (true in all larger countable transitive models of ZFC), countable-model potentialism (true in all larger countable models of ZFC), and others. In each case, we identify lower bounds for the modal validities, which are generally either S4.2 or S4.3, and an upper bound of S5, proving in each case that these bounds are optimal. The validity of S5 in a world is a potentialist maximality principle, an interesting set-theoretic principle of its own. The results can be viewed as providing an analysis of the modal commitments of the various set-theoretic multiverse conceptions corresponding to each potentialist account.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © Association for Symbolic Logic, 2022
References
BIBLIOGRAPHY
- 20
- Cited by


