Article contents
ABSTRACTIONIST CATEGORIES OF CATEGORIES
Published online by Cambridge University Press: 07 May 2015
Abstract
If 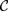 ${\cal C}$ is a category whose objects are themselves categories, and
${\cal C}$ is a category whose objects are themselves categories, and 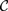 ${\cal C}$ has a rich enough structure, it is known that we can recover the internal structure of the categories in
${\cal C}$ has a rich enough structure, it is known that we can recover the internal structure of the categories in 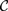 ${\cal C}$ entirely in terms of the arrows in
${\cal C}$ entirely in terms of the arrows in 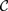 ${\cal C}$. In this sense, the internal structure of the categories in a rich enough category of categories is visible in the structure of the category of categories itself.
${\cal C}$. In this sense, the internal structure of the categories in a rich enough category of categories is visible in the structure of the category of categories itself.
In this paper, we demonstrate that this result follows as a matter of logic – given one starts from the right definitions. This is demonstrated by first producing an abstraction principle whose abstracts are functors, and then actually recovering the internal structure of the individual categories that intuitively stand at the sources and targets of these functors by examining the way these functors interact. The technique used in this construction will be useful elsewhere, and involves providing an abstract corresponding not to every object of some given family, but to all the relevant mappings of some family of objects.
This construction should settle, in particular, questions about whether categories of categories qualify as autonomous mathematical objects – categories of categories are perfectly acceptable autonomous objects and thus, in particular, suitable for foundational purposes.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2015
References
BIBLIOGRAPHY
- 1
- Cited by

