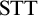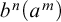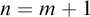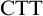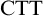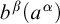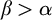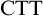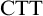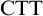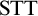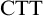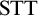Standard Type Theory,
![]() ${\textrm {STT}}$
, tells us that
${\textrm {STT}}$
, tells us that
![]() $b^n(a^m)$
is well-formed iff
$b^n(a^m)$
is well-formed iff
![]() $n=m+1$
. However, Linnebo and Rayo Reference Linnebo and Rayo[23] have advocated the use of Cumulative Type Theory,
$n=m+1$
. However, Linnebo and Rayo Reference Linnebo and Rayo[23] have advocated the use of Cumulative Type Theory,
![]() $\textrm {CTT}$
, which has more relaxed type-restrictions: according to
$\textrm {CTT}$
, which has more relaxed type-restrictions: according to
![]() $\textrm {CTT}$
,
$\textrm {CTT}$
,
![]() $b^\beta (a^\alpha )$
is well-formed iff
$b^\beta (a^\alpha )$
is well-formed iff
![]() $\beta>\alpha $
. Other philosophers, including Williamson [Reference Williamson44, pp. 237–238], Krämer [Reference Krämer21, p. 527], and Florio and Jones [Reference Florio and Jones10], have since expressed sympathy for cumulative types.
$\beta>\alpha $
. Other philosophers, including Williamson [Reference Williamson44, pp. 237–238], Krämer [Reference Krämer21, p. 527], and Florio and Jones [Reference Florio and Jones10], have since expressed sympathy for cumulative types.
We set ourselves against cumulative type theory. We begin our case by arguing against Linnebo and Rayo’s claim that
![]() $\textrm {CTT}$
sheds new philosophical light on set theory: in Section 2 we highlight some important mathematical differences between
$\textrm {CTT}$
sheds new philosophical light on set theory: in Section 2 we highlight some important mathematical differences between
![]() $\textrm {CTT}$
and set theory, and in Section 3 we explore the philosophical consequences of these differences. Then, in Section 4, we push our case against
$\textrm {CTT}$
and set theory, and in Section 3 we explore the philosophical consequences of these differences. Then, in Section 4, we push our case against
![]() $\textrm {CTT}$
further, by arguing that the type-restrictions it imposes are unjustifiable. This marks an important difference between
$\textrm {CTT}$
further, by arguing that the type-restrictions it imposes are unjustifiable. This marks an important difference between
![]() $\textrm {CTT}$
and
$\textrm {CTT}$
and
![]() ${\textrm {STT}}$
: a Fregean semantics justifies
${\textrm {STT}}$
: a Fregean semantics justifies
![]() ${\textrm {STT}}$
’s type-restrictions (see Section 5), and this Fregean semantics also provides us with a principled way to resist Linnebo and Rayo’s Semantic Argument for
${\textrm {STT}}$
’s type-restrictions (see Section 5), and this Fregean semantics also provides us with a principled way to resist Linnebo and Rayo’s Semantic Argument for
![]() $\textrm {CTT}$
(see Section 6). We end, in Section 7, by examining an alternative approach to cumulative types due to Florio and Jones Reference Florio and Jones[10]; we argue that their theory is best seen as a misleadingly formulated version of
$\textrm {CTT}$
(see Section 6). We end, in Section 7, by examining an alternative approach to cumulative types due to Florio and Jones Reference Florio and Jones[10]; we argue that their theory is best seen as a misleadingly formulated version of
![]() ${\textrm {STT}}$
.
${\textrm {STT}}$
.
1 Formal type theories
We start by outlining the formalisms of
![]() ${\textrm {STT}}$
and
${\textrm {STT}}$
and
![]() $\textrm {CTT}$
. For simplicity of exposition, in this paper we focus on monadic type theories. (We also only consider un-ramified type theories.)
$\textrm {CTT}$
. For simplicity of exposition, in this paper we focus on monadic type theories. (We also only consider un-ramified type theories.)
1.1
 ${\textrm {STT}}$
${\textrm {STT}}$
![]() ${\textrm {STT}}$
has a countable infinity of types,
${\textrm {STT}}$
has a countable infinity of types,
![]() $0 \leq n < \omega $
. The type of a term is indicated with a numerical superscript:
$0 \leq n < \omega $
. The type of a term is indicated with a numerical superscript:
![]() $a^n$
is a type n term. We have constants and variables of every type. Atomic formulas are made by combining a type
$a^n$
is a type n term. We have constants and variables of every type. Atomic formulas are made by combining a type
![]() $n\mathord {+}1$
term with a type n term:
$n\mathord {+}1$
term with a type n term:
![]() $b^n(a^m)$
is well-formed iff
$b^n(a^m)$
is well-formed iff
![]() $n = m + 1$
. Intuitively,
$n = m + 1$
. Intuitively,
![]() $b^{n+1}(a^n)$
applies a type
$b^{n+1}(a^n)$
applies a type
![]() $n\mathord {+}1$
entity to a type n entity, where an entity is of type n iff it is a value of a type n variable; however, exactly what this intuitive gloss amounts to will depend on your preferred interpretation of the types (see Sections 4 and 5).
$n\mathord {+}1$
entity to a type n entity, where an entity is of type n iff it is a value of a type n variable; however, exactly what this intuitive gloss amounts to will depend on your preferred interpretation of the types (see Sections 4 and 5).
Every type of variable can be bound by quantifiers. We here present the rules for
![]() $\forall $
; the rules for
$\forall $
; the rules for
![]() $\exists $
are the obvious duals. For all types n, the following inferences are licensed, provided that (i) all expressions are well-formed and (ii)
$\exists $
are the obvious duals. For all types n, the following inferences are licensed, provided that (i) all expressions are well-formed and (ii)
![]() $b^n$
does not occur in any undischarged assumptions on which
$b^n$
does not occur in any undischarged assumptions on which
![]() $\phi (b^n)$
depends:
$\phi (b^n)$
depends:

To ensure that each level of the type hierarchy is well-populated, we have the following scheme, for each type n:
-
 ${{STT}}$
-Comprehension.
${{STT}}$
-Comprehension.
 $\exists z^{n+1}\forall x^n(z^{n+1}(x^n)\leftrightarrow \phi (x^n))$
, whenever
$\exists z^{n+1}\forall x^n(z^{n+1}(x^n)\leftrightarrow \phi (x^n))$
, whenever
 $\phi (x^n)$
is well-formed and does not contain
$\phi (x^n)$
is well-formed and does not contain
 $z^{n+1}$
.
$z^{n+1}$
.
![]() ${\textrm {STT}}$
has the usual stock of logical devices: quantifiers, connectives, and the identity sign,
${\textrm {STT}}$
has the usual stock of logical devices: quantifiers, connectives, and the identity sign,
![]() $=$
. The identity sign can be flanked by a pair of terms of any type, but they must be terms of the same type; so
$=$
. The identity sign can be flanked by a pair of terms of any type, but they must be terms of the same type; so
![]() $a^m=b^n$
is well-formed iff
$a^m=b^n$
is well-formed iff
![]() $m=n$
. Identity is governed by the following scheme, for each type n:
$m=n$
. Identity is governed by the following scheme, for each type n:
We can treat this as an axiom scheme or an explicit definition. But, either way,
![]() $x^n=y^n$
is typically ambiguous: there is not a single identity relation that applies across all the types, but a different relation for each type.
$x^n=y^n$
is typically ambiguous: there is not a single identity relation that applies across all the types, but a different relation for each type.
1.2
 $\textrm {CTT}$
$\textrm {CTT}$
Linnebo and Rayo Reference Linnebo and Rayo[23] ask us to consider an alternative, cumulative, type theory,
![]() $\textrm {CTT}$
. This type theory was formally developed by Degen and Johannsen Reference Degen and Johannsen[7]. (We discuss a different approach to cumulation, due to Florio and Jones Reference Florio and Jones[10], in Section 7.) The basic thought behind
$\textrm {CTT}$
. This type theory was formally developed by Degen and Johannsen Reference Degen and Johannsen[7]. (We discuss a different approach to cumulation, due to Florio and Jones Reference Florio and Jones[10], in Section 7.) The basic thought behind
![]() $\textrm {CTT}$
is that the entities cumulate as you ascend through the types. Let us see how this is implemented.
$\textrm {CTT}$
is that the entities cumulate as you ascend through the types. Let us see how this is implemented.
First,
![]() $\textrm {CTT}$
relaxes
$\textrm {CTT}$
relaxes
![]() ${\textrm {STT}}$
’s syntax. In
${\textrm {STT}}$
’s syntax. In
![]() ${\textrm {STT}}$
,
${\textrm {STT}}$
,
![]() $b^n(a^m)$
is well-formed iff
$b^n(a^m)$
is well-formed iff
![]() $n = m +1$
. But, if the types cumulate, then everything at level
$n = m +1$
. But, if the types cumulate, then everything at level
![]() $0$
reappears at level
$0$
reappears at level
![]() $1$
; so, since
$1$
; so, since
![]() $c^2(a^1)$
is meaningful,
$c^2(a^1)$
is meaningful,
![]() $c^2(a^0)$
should be too. More generally,
$c^2(a^0)$
should be too. More generally,
![]() $\textrm {CTT}$
allows that
$\textrm {CTT}$
allows that
![]() $b^\beta (a^\alpha )$
is well-formed iff
$b^\beta (a^\alpha )$
is well-formed iff
![]() $\beta> \alpha $
. And note that we use ‘
$\beta> \alpha $
. And note that we use ‘
![]() $\alpha $
’ and ‘
$\alpha $
’ and ‘
![]() $\beta $
’ rather than ‘n’ and ‘m’ here: if the types cumulate, we will want to be able to consider transfinite types, and so we must allow ourselves a transfinite stock of type-indices. (One obvious way to do this is to stipulate that the type-indices are von Neumann’s ordinals, but the only important constraint is that the type-indices be well-ordered.)Footnote
1
$\beta $
’ rather than ‘n’ and ‘m’ here: if the types cumulate, we will want to be able to consider transfinite types, and so we must allow ourselves a transfinite stock of type-indices. (One obvious way to do this is to stipulate that the type-indices are von Neumann’s ordinals, but the only important constraint is that the type-indices be well-ordered.)Footnote
1
Second,
![]() $\textrm {CTT}$
has rather permissive inference rules for quantifiers. (Again, we only outline the rules for
$\textrm {CTT}$
has rather permissive inference rules for quantifiers. (Again, we only outline the rules for
![]() $\forall $
.) For all types
$\forall $
.) For all types
![]() $\beta \geq \alpha $
, the following inferences are licensed, provided that (i) all expressions are well-formed and (ii)
$\beta \geq \alpha $
, the following inferences are licensed, provided that (i) all expressions are well-formed and (ii)
![]() $b^\beta $
does not occur in any undischarged assumption on which
$b^\beta $
does not occur in any undischarged assumption on which
![]() $\phi (b^\beta )$
depends:Footnote
2
$\phi (b^\beta )$
depends:Footnote
2

These rules are intuitively sound, given the idea of cumulation: every type
![]() $\alpha $
entity is a type
$\alpha $
entity is a type
![]() $\beta \geq \alpha $
entity too; so if
$\beta \geq \alpha $
entity too; so if
![]() $\phi $
holds of every type
$\phi $
holds of every type
![]() $\beta $
entity, then
$\beta $
entity, then
![]() $\phi $
holds of each type
$\phi $
holds of each type
![]() $\alpha $
entity.
$\alpha $
entity.
Third, to ensure that each successor-level of the type hierarchy is well-populated,
![]() $\textrm {CTT}$
has a Comprehension scheme, for each type
$\textrm {CTT}$
has a Comprehension scheme, for each type
![]() $\alpha $
:Footnote
3
$\alpha $
:Footnote
3
-
 ${CTT}$
-Comprehension.
${CTT}$
-Comprehension.
 $\exists z^{\alpha +1}\forall x^\alpha (z^{\alpha +1}(x^\alpha )\leftrightarrow \phi (x^\alpha ))$
, whenever
$\exists z^{\alpha +1}\forall x^\alpha (z^{\alpha +1}(x^\alpha )\leftrightarrow \phi (x^\alpha ))$
, whenever
 $\phi (x^\alpha )$
is well-formed and does not contain
$\phi (x^\alpha )$
is well-formed and does not contain
 $z^{\alpha +1}$
.
$z^{\alpha +1}$
.
Fourth,
![]() $\textrm {CTT}$
has an infinitary inference rule for each limit type
$\textrm {CTT}$
has an infinitary inference rule for each limit type
![]() $\lambda $
:Footnote
4
$\lambda $
:Footnote
4

Intuitively, this guarantees that nothing essentially ‘new’ happens at limit types, so that any type
![]() $\lambda $
entity is an entity of some type
$\lambda $
entity is an entity of some type
![]() $\alpha < \lambda $
.
$\alpha < \lambda $
.
So far, we have identified entities across types quite freely. However, Linnebo and Rayo [Reference Linnebo and Rayo23, pp. 281–283] retain the rule that a strict identity claim,
![]() $x^\alpha =y^\beta $
, is well-formed iff
$x^\alpha =y^\beta $
, is well-formed iff
![]() $\alpha =\beta $
. To deal with cross-type identity, they explicitly define a new sign,
$\alpha =\beta $
. To deal with cross-type identity, they explicitly define a new sign,
![]() $\mathrel {\equiv }$
, for any types
$\mathrel {\equiv }$
, for any types
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
and where
$\beta $
and where
![]() $\gamma = \max (\alpha , \beta )+1$
:Footnote
5
$\gamma = \max (\alpha , \beta )+1$
:Footnote
5
This definition is typically ambiguous: it defines different relations for different
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. But all of these relations behave like identity: if
$\beta $
. But all of these relations behave like identity: if
![]() $\phi (a^\alpha )$
and
$\phi (a^\alpha )$
and
![]() $\phi (b^\beta )$
are both well-formed, then
$\phi (b^\beta )$
are both well-formed, then
![]() $\phi (a^\alpha )$
and
$\phi (a^\alpha )$
and
![]() $a^\alpha \equiv b^\beta $
together entail
$a^\alpha \equiv b^\beta $
together entail
![]() $\phi (b^\beta )$
.Footnote
6
Now we can prove the following theorem scheme, for all
$\phi (b^\beta )$
.Footnote
6
Now we can prove the following theorem scheme, for all
![]() $\alpha \leq \beta $
:Footnote
7
$\alpha \leq \beta $
:Footnote
7
-
Type-Raising Scheme.
 $\forall x^\alpha \exists y^\beta \phantom {(}x^\alpha \equiv y^\beta $
$\forall x^\alpha \exists y^\beta \phantom {(}x^\alpha \equiv y^\beta $
So, if
![]() $\alpha \leq \beta $
, then every type
$\alpha \leq \beta $
, then every type
![]() $\alpha $
entity is a type
$\alpha $
entity is a type
![]() $\beta $
entity, in the sense of ‘is’ expressed by
$\beta $
entity, in the sense of ‘is’ expressed by
![]() $\mathrel {\equiv }$
.
$\mathrel {\equiv }$
.
We also provide another (typically ambiguous) explicit definition, where
![]() $\gamma = \max (\alpha , \beta )+1$
:Footnote
8
$\gamma = \max (\alpha , \beta )+1$
:Footnote
8
This membership-like notion applies
![]() $b^\beta $
to
$b^\beta $
to
![]() $a^\alpha $
, but is well-formed for every
$a^\alpha $
, but is well-formed for every
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. So
$\beta $
. So
![]() $a^\alpha \mathrel {\varepsilon } b^\beta $
allows us to simulate
$a^\alpha \mathrel {\varepsilon } b^\beta $
allows us to simulate
![]() $b^\beta (a^\alpha )$
, even when
$b^\beta (a^\alpha )$
, even when
![]() $\alpha \geq \beta $
.
$\alpha \geq \beta $
.
If we provide no further axioms, though, then
![]() $\mathrel {\varepsilon }$
can be ill-founded. To rule this out, we lay down two final schemes, for all
$\mathrel {\varepsilon }$
can be ill-founded. To rule this out, we lay down two final schemes, for all
![]() $\alpha , \beta $
:Footnote
9
$\alpha , \beta $
:Footnote
9
-
Type-Founded.
 $\forall a^\alpha \forall b^{\beta +1}(a^\alpha \mathrel {\varepsilon } b^{\beta +1} \rightarrow \exists x^\beta \ a^\alpha \mathrel {\equiv } x^\beta )$
$\forall a^\alpha \forall b^{\beta +1}(a^\alpha \mathrel {\varepsilon } b^{\beta +1} \rightarrow \exists x^\beta \ a^\alpha \mathrel {\equiv } x^\beta )$
-
Type-Base.

This completes the list of axioms and inference rules for
![]() $\textrm {CTT}$
.
$\textrm {CTT}$
.
It is worth making a brief observation about syntax. In moving from
![]() ${\textrm {STT}}$
to
${\textrm {STT}}$
to
![]() $\textrm {CTT}$
, we are asked to relax
$\textrm {CTT}$
, we are asked to relax
![]() ${\textrm {STT}}$
’s syntax:
${\textrm {STT}}$
’s syntax:
![]() $b^\beta (a^\alpha )$
is well-formed iff
$b^\beta (a^\alpha )$
is well-formed iff
![]() $\beta> \alpha $
. There is an obvious way to relax this further, whilst retaining a typed theory: allow that
$\beta> \alpha $
. There is an obvious way to relax this further, whilst retaining a typed theory: allow that
![]() $b^\beta (a^\alpha )$
is well-formed for any
$b^\beta (a^\alpha )$
is well-formed for any
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. However, this further relaxation would have no real effect. As just noted,
$\beta $
. However, this further relaxation would have no real effect. As just noted,
![]() $\textrm {CTT}$
can simulate
$\textrm {CTT}$
can simulate
![]() $b^\beta (a^\alpha )$
using the formula
$b^\beta (a^\alpha )$
using the formula
![]() $a^\alpha \mathrel {\varepsilon } b^\beta $
, where the latter is defined using the more stringent type-restrictions. Consequently, we can be largely indifferent on whether to use the stringent type-restrictions, so that
$a^\alpha \mathrel {\varepsilon } b^\beta $
, where the latter is defined using the more stringent type-restrictions. Consequently, we can be largely indifferent on whether to use the stringent type-restrictions, so that
![]() $b^\beta (a^\alpha )$
is well-formed iff
$b^\beta (a^\alpha )$
is well-formed iff
![]() $\beta> \alpha $
, or the more liberal type-restrictions, so that
$\beta> \alpha $
, or the more liberal type-restrictions, so that
![]() $b^\beta (a^\alpha )$
is well-formed for any
$b^\beta (a^\alpha )$
is well-formed for any
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. In what follows, we will tend to adopt the stringent type-restrictions, but we will revisit this in Section 4.
$\beta $
. In what follows, we will tend to adopt the stringent type-restrictions, but we will revisit this in Section 4.
For each type-index
![]() $\tau $
, the theory
$\tau $
, the theory
![]() ${{\textrm {CTT}^{\tau }}}$
has a countable infinity of distinct variables of every type
${{\textrm {CTT}^{\tau }}}$
has a countable infinity of distinct variables of every type
![]() $< \tau $
, and no variables of any type
$< \tau $
, and no variables of any type
![]() $\geq \tau $
. We refer to the cumulative type theories in general as ‘
$\geq \tau $
. We refer to the cumulative type theories in general as ‘
![]() $\textrm {CTT}$
’, using ‘
$\textrm {CTT}$
’, using ‘
![]() ${{\textrm {CTT}^{\tau }}}$
’ with the superscript when it is important to pay attention to the bound.
${{\textrm {CTT}^{\tau }}}$
’ with the superscript when it is important to pay attention to the bound.
2 The sets-from-types theorem
Degen and Johannsen Reference Degen and Johannsen[7] and Linnebo and Rayo Reference Linnebo and Rayo[23] note that
![]() $\textrm {CTT}$
interprets an iterative set theory. In this section, we present a strengthened version of their formal results. We discuss its philosophical significance in Section 3. For ease of exposition, we will consider set theories without urelements (and similar type theories); we could accommodate urelements if we liked, but it would complicate our discussion without adding any real insight.
$\textrm {CTT}$
interprets an iterative set theory. In this section, we present a strengthened version of their formal results. We discuss its philosophical significance in Section 3. For ease of exposition, we will consider set theories without urelements (and similar type theories); we could accommodate urelements if we liked, but it would complicate our discussion without adding any real insight.
2.1 The interpretation
We will focus on a ‘pure’ version of
![]() ${{\textrm {CTT}^{\tau }}}$
, which we call
${{\textrm {CTT}^{\tau }}}$
, which we call
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
. This augments
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
. This augments
![]() ${{\textrm {CTT}^{\tau }}}$
with principles guaranteeing that there is exactly one type
${{\textrm {CTT}^{\tau }}}$
with principles guaranteeing that there is exactly one type
![]() $0$
entity, and that coextensive entities at higher-types are identical. (For details, see Appendix B.2.) The set theory that
$0$
entity, and that coextensive entities at higher-types are identical. (For details, see Appendix B.2.) The set theory that
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
can interpret is
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
can interpret is
![]() ${\textrm {Zr}}$
, i.e., Zermelo set theory together with the principle that the sets are arranged into well-ordered ranks. This theory omits Replacement, and so is strictly weaker than
${\textrm {Zr}}$
, i.e., Zermelo set theory together with the principle that the sets are arranged into well-ordered ranks. This theory omits Replacement, and so is strictly weaker than
![]() ${\textrm {ZF}}$
. (For more details, see Appendix B; note that
${\textrm {ZF}}$
. (For more details, see Appendix B; note that
![]() ${\textrm {ZF}}$
=
${\textrm {ZF}}$
=
![]() ${\textrm {Zr}}$
+ Replacement.)
${\textrm {Zr}}$
+ Replacement.)
To interpret
![]() ${\textrm {Zr}}$
with
${\textrm {Zr}}$
with
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
, we first define a translation. For each
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
, we first define a translation. For each
![]() ${\textrm {Zr}}$
-formula
${\textrm {Zr}}$
-formula
![]() $\phi $
, let
$\phi $
, let
![]() ${{\phi }^{(\kappa )}}$
be the formula which results by replacing each ‘
${{\phi }^{(\kappa )}}$
be the formula which results by replacing each ‘
![]() $\in $
’ with ‘
$\in $
’ with ‘
![]() $\mathrel {\varepsilon }$
’, each ‘
$\mathrel {\varepsilon }$
’, each ‘
![]() $=$
’ with ‘
$=$
’ with ‘
![]() $\mathrel {\equiv }$
’, and superscripting each variable with
$\mathrel {\equiv }$
’, and superscripting each variable with
![]() $\kappa $
. For example, the Axiom of
$\kappa $
. For example, the Axiom of
![]() ${\textrm {Powersets}^{(\kappa )}}$
is:
${\textrm {Powersets}^{(\kappa )}}$
is:
Now we can prove the following result (see Appendix B, Theorem 13):Footnote 10
-
The Sets-from-Types Theorem.
 ${\textrm {CTT}^{\tau }_{\textrm {p}}} \vdash {{\textrm {Zr}^{(\kappa )}}}$
, for any limit
${\textrm {CTT}^{\tau }_{\textrm {p}}} \vdash {{\textrm {Zr}^{(\kappa )}}}$
, for any limit
 $\kappa> \omega $
with
$\kappa> \omega $
with
 $\kappa + 2 < \tau $
.
$\kappa + 2 < \tau $
.
Otherwise put:
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
proves the translations of all theorems of
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
proves the translations of all theorems of
![]() ${\textrm {Zr}}$
.
${\textrm {Zr}}$
.
2.2 Differences between
 ${\textrm {Zr}}$
and
${\textrm {Zr}}$
and
 ${\textrm {Zr}}^{\boldsymbol{(\kappa )}}$
${\textrm {Zr}}^{\boldsymbol{(\kappa )}}$
The proof of the Sets-from-Types Theorem involves establishing a tight association between two notions: an entity’s type, as in
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
and
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
and
![]() $\textrm {Zr}^{(\kappa )}$
, and a set’s rank, as in
$\textrm {Zr}^{(\kappa )}$
, and a set’s rank, as in
![]() ${\textrm {Zr}}$
. This sort of connection leads Linnebo and Rayo [Reference Linnebo and Rayo23, p. 289] to claim that ‘there is no deep mathematical difference between the ideological hierarchy of type theory and the ontological hierarchy of set theory’.
${\textrm {Zr}}$
. This sort of connection leads Linnebo and Rayo [Reference Linnebo and Rayo23, p. 289] to claim that ‘there is no deep mathematical difference between the ideological hierarchy of type theory and the ontological hierarchy of set theory’.
Whether to describe them as ‘deep’ may be a matter of taste, but it is worth noting three mathematical differences between
![]() ${\textrm {Zr}}$
, on the one hand, and
${\textrm {Zr}}$
, on the one hand, and
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
and
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
and
![]() $\textrm {Zr}^{(\kappa )}$
, on the other.Footnote
11
We summarize the differences in the following table:
$\textrm {Zr}^{(\kappa )}$
, on the other.Footnote
11
We summarize the differences in the following table:

We will now explain these three differences.
Concerning (1). The notion of rank is explicitly defined within
![]() ${\textrm {Zr}}$
itself, much as it is within
${\textrm {Zr}}$
itself, much as it is within
![]() ${\textrm {ZF}}$
.Footnote
12
By contrast, the notion of type is metatheoretic for both
${\textrm {ZF}}$
.Footnote
12
By contrast, the notion of type is metatheoretic for both
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
and
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
and
![]() $\textrm {Zr}^{(\kappa )}$
. Every variable carries a type-index, and these type-indices are supplied externally. Indeed, when we take the very first step of describing the syntax of
$\textrm {Zr}^{(\kappa )}$
. Every variable carries a type-index, and these type-indices are supplied externally. Indeed, when we take the very first step of describing the syntax of
![]() ${{\textrm {CTT}^{\tau }}}$
, we assume as given all the type-indices
${{\textrm {CTT}^{\tau }}}$
, we assume as given all the type-indices
![]() $< \tau $
.
$< \tau $
.
Concerning (2).
![]() ${\textrm {Zr}}$
is essentially untyped. It has exactly one kind of variable, which ranges over all sets of all ranks. By contrast, every variable in
${\textrm {Zr}}$
is essentially untyped. It has exactly one kind of variable, which ranges over all sets of all ranks. By contrast, every variable in
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
and
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
and
![]() $\textrm {Zr}^{(\kappa )}$
carries a type-index, and
$\textrm {Zr}^{(\kappa )}$
carries a type-index, and
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
’s quantifier rules indicate that type
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
’s quantifier rules indicate that type
![]() $\alpha $
variables range only over entities of type
$\alpha $
variables range only over entities of type
![]() $\leq \alpha $
. These theories have no untyped variables; that is, they have no variables which range over all entities of all types. (Note that, despite our use of the phrase ‘ranging over’, this difference shows up at the level of the formal theories, prior to interpretation. Indeed, none of the differences depend upon any semantic considerations.)
$\leq \alpha $
. These theories have no untyped variables; that is, they have no variables which range over all entities of all types. (Note that, despite our use of the phrase ‘ranging over’, this difference shows up at the level of the formal theories, prior to interpretation. Indeed, none of the differences depend upon any semantic considerations.)
Concerning (3). Clearly,
![]() ${\textrm {Zr}}$
is recursively axiomatized (see Appendix B.1). However, neither
${\textrm {Zr}}$
is recursively axiomatized (see Appendix B.1). However, neither
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
nor
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
nor
![]() $\textrm {Zr}^{(\kappa )}$
is recursively axiomatizable, thanks to the intrinsically infinitary Limit-rules. Indeed, Limit
$\textrm {Zr}^{(\kappa )}$
is recursively axiomatizable, thanks to the intrinsically infinitary Limit-rules. Indeed, Limit
![]() $^\omega $
makes these theories arithmetically complete, since it simulates Hilbert’s
$^\omega $
makes these theories arithmetically complete, since it simulates Hilbert’s
![]() $\omega $
-rule.Footnote
13
$\omega $
-rule.Footnote
13
2.3 Mathematical foundations
We will now explain why these three differences are mathematically significant. In brief: the differences show that
![]() ${\textrm {Zr}}$
is expressively richer but deductively weaker than
${\textrm {Zr}}$
is expressively richer but deductively weaker than
![]() $\textrm {Zr}^{(\kappa )}$
; this makes
$\textrm {Zr}^{(\kappa )}$
; this makes
![]() ${\textrm {Zr}}$
much more suitable as a framework for considering mathematical foundations.
${\textrm {Zr}}$
much more suitable as a framework for considering mathematical foundations.
Differences (1) and (2) show that
![]() ${\textrm {Zr}}$
is expressively richer than
${\textrm {Zr}}$
is expressively richer than
![]() $\textrm {Zr}^{(\kappa )}$
. To see this, consider how we might formulate questions about the height of a hierarchy. In the case of
$\textrm {Zr}^{(\kappa )}$
. To see this, consider how we might formulate questions about the height of a hierarchy. In the case of
![]() ${\textrm {Zr}}$
, we might ask a specific question like: Should we countenance a strongly inaccessible rank? That question is formulated within the object language of
${\textrm {Zr}}$
, we might ask a specific question like: Should we countenance a strongly inaccessible rank? That question is formulated within the object language of
![]() ${\textrm {Zr}}$
, and this is possible because
${\textrm {Zr}}$
, and this is possible because
![]() ${\textrm {Zr}}$
’s untyped variables range over all the sets, whatever their rank. So, whilst
${\textrm {Zr}}$
’s untyped variables range over all the sets, whatever their rank. So, whilst
![]() ${\textrm {Zr}}$
does not settle whether there are any sets of strongly inaccessible rank, it does allow us to formulate the claim that there are, and tells us that any such sets obey Extensionality and Separation (for example). In the case of
${\textrm {Zr}}$
does not settle whether there are any sets of strongly inaccessible rank, it does allow us to formulate the claim that there are, and tells us that any such sets obey Extensionality and Separation (for example). In the case of
![]() ${\textrm {CTT}_{\textrm {p}}}$
, the analogous question about the height of a type-hierarchy would be: Should we countenance a strongly inaccessible type-index? But this question is, of course, formulated within a metalanguage. After all, each
${\textrm {CTT}_{\textrm {p}}}$
, the analogous question about the height of a type-hierarchy would be: Should we countenance a strongly inaccessible type-index? But this question is, of course, formulated within a metalanguage. After all, each
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
has variables of all and only the types
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
has variables of all and only the types
![]() $< \tau $
, and
$< \tau $
, and
![]() $\textrm {Zr}^{(\kappa )}$
has variables of all and only the types
$\textrm {Zr}^{(\kappa )}$
has variables of all and only the types
![]() $\leq \kappa +2 < \tau $
,Footnote
14
so neither theory allows us to formulate questions about entities of type
$\leq \kappa +2 < \tau $
,Footnote
14
so neither theory allows us to formulate questions about entities of type
![]() $\tau $
; they literally lack the vocabulary for doing so.
$\tau $
; they literally lack the vocabulary for doing so.
Difference (3), however, shows that
![]() ${\textrm {Zr}}$
is deductively weaker than
${\textrm {Zr}}$
is deductively weaker than
![]() $\textrm {Zr}^{(\kappa )}$
. This is obvious—one is arithmetically complete, the other is not—but let us draw out a couple of consequences. The Sets-from-Types Theorem tells us that
$\textrm {Zr}^{(\kappa )}$
. This is obvious—one is arithmetically complete, the other is not—but let us draw out a couple of consequences. The Sets-from-Types Theorem tells us that
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
interprets
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
interprets
![]() ${\textrm {Zr}}$
. However, this interpretation is not faithful, i.e., some non-theorems of
${\textrm {Zr}}$
. However, this interpretation is not faithful, i.e., some non-theorems of
![]() ${\textrm {Zr}}$
become theorems of
${\textrm {Zr}}$
become theorems of
![]() $\textrm {Zr}^{(\kappa )}$
under interpretation; nor is the interpretation mutual, i.e.,
$\textrm {Zr}^{(\kappa )}$
under interpretation; nor is the interpretation mutual, i.e.,
![]() ${\textrm {Zr}}$
cannot interpret
${\textrm {Zr}}$
cannot interpret
![]() $\textrm {Zr}^{(\kappa )}$
.Footnote
15
$\textrm {Zr}^{(\kappa )}$
.Footnote
15
This combination of expressive richness with deductive weakness makes
![]() ${\textrm {Zr}}$
much more suitable as a framework for mathematical foundations than
${\textrm {Zr}}$
much more suitable as a framework for mathematical foundations than
![]() $\textrm {Zr}^{(\kappa )}$
or
$\textrm {Zr}^{(\kappa )}$
or
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
.Footnote
16
Concerning expressive strength: if our hierarchy is to serve as any kind of mathematical foundation, then questions about the height of the hierarchy will be of pressing importance; but only
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
.Footnote
16
Concerning expressive strength: if our hierarchy is to serve as any kind of mathematical foundation, then questions about the height of the hierarchy will be of pressing importance; but only
![]() ${\textrm {Zr}}$
provides a suitable framework for raising such questions. Concerning deductive weakness: any adequate foundational theory must be recursively axiomatizable since, as Gödel [Reference Gödel and Feferman18, p. 45] put it, only recursively axiomatizable theories can leave no doubt regarding whether a putative proof is a proof, so that ‘the highest possible degree of exactness is obtained’; but only
${\textrm {Zr}}$
provides a suitable framework for raising such questions. Concerning deductive weakness: any adequate foundational theory must be recursively axiomatizable since, as Gödel [Reference Gödel and Feferman18, p. 45] put it, only recursively axiomatizable theories can leave no doubt regarding whether a putative proof is a proof, so that ‘the highest possible degree of exactness is obtained’; but only
![]() ${\textrm {Zr}}$
is recursively axiomatized.
${\textrm {Zr}}$
is recursively axiomatized.
2.4 Gödel on ‘superfluous restrictions’ in type theory
We just quoted Gödel on mathematical foundations. Having made the quoted remarks, Gödel went on to make a more famous claim:
the system of axioms for the theory of aggregates, as presented by Zermelo, Fraenkel, and von Neumann…is nothing else but a natural generalization of the theory of types, or rather, what becomes of the theory of types if certain superfluous restrictions are removed.Footnote 17
He continued by outlining the ‘superfluous restrictions’ thus:Footnote 18
-
(i) ‘
 $a \in b$
’ is meaningful iff the type of ‘b’ is exactly one greater than that of ‘a’;
$a \in b$
’ is meaningful iff the type of ‘b’ is exactly one greater than that of ‘a’; -
(ii) each class (of any type) can contain classes of exactly one type; and
-
(iii) only finite types are allowed.
Whilst explicitly disavowing exegetical aims, Linnebo and Rayo [Reference Linnebo and Rayo23, pp. 273–274, 278] motivate
![]() $\textrm {CTT}$
by suggesting that
$\textrm {CTT}$
by suggesting that
![]() $\textrm {CTT}$
arises from
$\textrm {CTT}$
arises from
![]() ${\textrm {STT}}$
simply by lifting these ‘superfluous restrictions’.
${\textrm {STT}}$
simply by lifting these ‘superfluous restrictions’.
Certainly
![]() $\textrm {CTT}$
lifts restrictions (i)–(iii). But
$\textrm {CTT}$
lifts restrictions (i)–(iii). But
![]() ${\textrm {Zr}}$
also lifts these restrictions, and in a different way. Moreover, it is this latter way which we find in Gödel’s Reference Gödel and Feferman[18] lecture. On each of points (1)–(3) from Section 2.2, Gödel sides against the use of anything like
${\textrm {Zr}}$
also lifts these restrictions, and in a different way. Moreover, it is this latter way which we find in Gödel’s Reference Gödel and Feferman[18] lecture. On each of points (1)–(3) from Section 2.2, Gödel sides against the use of anything like
![]() $\textrm {Zr}^{(\kappa )}$
.
$\textrm {Zr}^{(\kappa )}$
.
Concerning (1). Gödel [Reference Gödel and Feferman18, p. 47] is clear that the theory which arises by removing
![]() ${\textrm {STT}}$
’s ‘superfluous restrictions’ will supply its own ‘types’.Footnote
19
${\textrm {STT}}$
’s ‘superfluous restrictions’ will supply its own ‘types’.Footnote
19
Concerning (2). Gödel [Reference Gödel and Feferman18, p. 49] complains that, in
![]() ${\textrm {STT}}$
, we have to formulate ‘the logical axioms for each type separately’, and he states that the theory which removes
${\textrm {STT}}$
, we have to formulate ‘the logical axioms for each type separately’, and he states that the theory which removes
![]() ${\textrm {STT}}$
’s ‘superfluous restrictions’ will avoid this complaint. Such a theory will therefore employ an untyped variable, which can range over all entities.
${\textrm {STT}}$
’s ‘superfluous restrictions’ will avoid this complaint. Such a theory will therefore employ an untyped variable, which can range over all entities.
Concerning (3). As already noted, Gödel [Reference Gödel and Feferman18, p. 45 and 48] insists that an adequate formalization of the foundations of mathematics must be recursively axiomatizable, and explicitly remarks that such theories are necessarily arithmetically incomplete.
Gödel, then, seems never to have envisaged theories like
![]() $\textrm {Zr}^{(\kappa )}$
or
$\textrm {Zr}^{(\kappa )}$
or
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
.Footnote
20
Rather, Gödel’s suggestion was that removing
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
.Footnote
20
Rather, Gödel’s suggestion was that removing
![]() ${\textrm {STT}}$
’s ‘superfluous restrictions’ led to
${\textrm {STT}}$
’s ‘superfluous restrictions’ led to
![]() ${\textrm {ZFU}}$
, by the simple stipulation that the ‘type’ of x is
${\textrm {ZFU}}$
, by the simple stipulation that the ‘type’ of x is
![]() $\alpha $
iff
$\alpha $
iff
![]() $x \in V_{\alpha +1} \setminus V_\alpha $
, with these segments of the set hierarchy defined directly within
$x \in V_{\alpha +1} \setminus V_\alpha $
, with these segments of the set hierarchy defined directly within
![]() ${\textrm {ZFU}}$
in the (now) familiar fashion.Footnote
21
That is, Gödel simply identified a set’s ‘type’ with (what we now call) its rank, and advocated the use of recursively axiomatized theories whose untyped variables range over all the sets (of all ranks).
${\textrm {ZFU}}$
in the (now) familiar fashion.Footnote
21
That is, Gödel simply identified a set’s ‘type’ with (what we now call) its rank, and advocated the use of recursively axiomatized theories whose untyped variables range over all the sets (of all ranks).
3 The (in)significance of the Sets-from-Types Theorem
We have noted the important mathematical differences between
![]() ${\textrm {Zr}}$
and
${\textrm {Zr}}$
and
![]() $\textrm {Zr}^{(\kappa )}$
. We will now show how these differences undermine the philosophical significance of the Sets-from-Types Theorem. In broad brush strokes: Linnebo and Rayo think that the Sets-from-Types Theorem sheds important new light on set theory; we disagree, since
$\textrm {Zr}^{(\kappa )}$
. We will now show how these differences undermine the philosophical significance of the Sets-from-Types Theorem. In broad brush strokes: Linnebo and Rayo think that the Sets-from-Types Theorem sheds important new light on set theory; we disagree, since
![]() $\textrm {Zr}^{(\kappa )}$
and
$\textrm {Zr}^{(\kappa )}$
and
![]() ${\textrm {Zr}}$
and importantly distinct.
${\textrm {Zr}}$
and importantly distinct.
3.1 Elsa’s worries
To reconstruct Linnebo and Rayo’s [Reference Linnebo and Rayo23, pp. 289–294, Reference Linnebo and Rayo24, p. 178] intended use of the Sets-from-Types Theorem, we will introduce a character, Elsa. Elsa wants to use
![]() ${\textrm {Zr}}$
to talk about the hierarchy of sets, but she has some ontological worries. Following post-Quinean orthodoxy, Elsa draws a sharp distinction between a theory’s ontology and its ideology. In general, Elsa thinks that if a theory is coherent, then that is enough to guarantee the good standing of its ideology: roughly, Elsa thinks that a theory’s ideology merely provides you with a way of talking about objects, and there is no standard beyond coherence by which to judge ways of talking. Now, Elsa is certain that
${\textrm {Zr}}$
to talk about the hierarchy of sets, but she has some ontological worries. Following post-Quinean orthodoxy, Elsa draws a sharp distinction between a theory’s ontology and its ideology. In general, Elsa thinks that if a theory is coherent, then that is enough to guarantee the good standing of its ideology: roughly, Elsa thinks that a theory’s ideology merely provides you with a way of talking about objects, and there is no standard beyond coherence by which to judge ways of talking. Now, Elsa is certain that
![]() ${\textrm {Zr}}$
is coherent, and so she has no reservations about its ideology. But,
${\textrm {Zr}}$
is coherent, and so she has no reservations about its ideology. But,
![]() ${\textrm {Zr}}$
also postulates a rich ontology of sets, and Elsa insists that the mere coherence of a theory is not enough to guarantee the existence of its ontological commitments. So, Elsa worries: What guarantees that there are enough sets?
${\textrm {Zr}}$
also postulates a rich ontology of sets, and Elsa insists that the mere coherence of a theory is not enough to guarantee the existence of its ontological commitments. So, Elsa worries: What guarantees that there are enough sets?
Linnebo and Rayo have a sequence of recommendations for Elsa. First, they will introduce Elsa to the type hierarchy, in the form of
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
, whose coherence can be assumed (at least, in this context). The question arises of how Elsa should think about ontology/ideology in the type-theoretic context. Quantification over type
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
, whose coherence can be assumed (at least, in this context). The question arises of how Elsa should think about ontology/ideology in the type-theoretic context. Quantification over type
![]() $0$
entities is just first-order quantification; so Elsa should think that theorizing at type
$0$
entities is just first-order quantification; so Elsa should think that theorizing at type
![]() $0$
introduces ontological commitments. However, Elsa can perhaps be encouraged to think that theorizing at higher types simply gives us sophisticated ways to talk about the objects at type
$0$
introduces ontological commitments. However, Elsa can perhaps be encouraged to think that theorizing at higher types simply gives us sophisticated ways to talk about the objects at type
![]() $0$
, and so only introduces ideological commitments. If Elsa agrees to think in this way, then she will map her dichotomy between ontology and ideology onto the dichotomy between type
$0$
, and so only introduces ideological commitments. If Elsa agrees to think in this way, then she will map her dichotomy between ontology and ideology onto the dichotomy between type
![]() $0$
and type
$0$
and type
![]() $> 0$
.Footnote
22
Having done this, she will regard
$> 0$
.Footnote
22
Having done this, she will regard
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
as ontologically unproblematic: it posits just one object (i.e., one type
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
as ontologically unproblematic: it posits just one object (i.e., one type
![]() $0$
entity). Granted, she may regard
$0$
entity). Granted, she may regard
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
as ideologically profligate, but she thinks that its coherence guarantees the good standing of its ideology. Consequently, Elsa should have no worries about using
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
as ideologically profligate, but she thinks that its coherence guarantees the good standing of its ideology. Consequently, Elsa should have no worries about using
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
. Now, via the Set-from-Types Theorem, Elsa can use
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
. Now, via the Set-from-Types Theorem, Elsa can use
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
to obtain
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
to obtain
![]() $\textrm {Zr}^{(\kappa )}$
. So, according to Linnebo and Rayo, Elsa will have no reason to worry about using
$\textrm {Zr}^{(\kappa )}$
. So, according to Linnebo and Rayo, Elsa will have no reason to worry about using
![]() $\textrm {Zr}^{(\kappa )}$
in place of
$\textrm {Zr}^{(\kappa )}$
in place of
![]() ${\textrm {Zr}}$
.
${\textrm {Zr}}$
.
Having come this far, Linnebo and Rayo [Reference Linnebo and Rayo23, p. 290] hope that Elsa might now be brought to share their view, that ‘the two hierarchies’—the ‘ideological’ hierarchy of
![]() $\textrm {Zr}^{(\kappa )}$
and the ‘ontological’ hierarchy of
$\textrm {Zr}^{(\kappa )}$
and the ‘ontological’ hierarchy of
![]() ${\textrm {Zr}}$
—‘constitute different perspectives on the same subject-matter.’ But we do not need to consider that further step. We think that Elsa should balk at the line of reasoning given in the previous paragraph.
${\textrm {Zr}}$
—‘constitute different perspectives on the same subject-matter.’ But we do not need to consider that further step. We think that Elsa should balk at the line of reasoning given in the previous paragraph.
3.2 Ontology relocated
The immediate problem is that
![]() ${\textrm {Zr}}$
and
${\textrm {Zr}}$
and
![]() $\textrm {Zr}^{(\kappa )}$
are importantly different theories. One of the differences, mentioned in Section 2.3, is that Elsa can ask about the height of her set-hierarchy within the object-language of
$\textrm {Zr}^{(\kappa )}$
are importantly different theories. One of the differences, mentioned in Section 2.3, is that Elsa can ask about the height of her set-hierarchy within the object-language of
![]() ${\textrm {Zr}}$
, whereas she can only ask about the height of a type-hierarchy within a metalanguage. But, as we will now show, this basic issue—of object language versus metalanguage—completely undermines the dialectical force of Linnebo and Rayo’s line of reasoning.
${\textrm {Zr}}$
, whereas she can only ask about the height of a type-hierarchy within a metalanguage. But, as we will now show, this basic issue—of object language versus metalanguage—completely undermines the dialectical force of Linnebo and Rayo’s line of reasoning.
Recall: Elsa wants to use
![]() ${\textrm {Zr}}$
, but worries: What guarantees that enough sets exist? Linnebo and Rayo recommend that Elsa invoke the Sets-from-Types Theorem. Specifically, they encourage Elsa to fix some limit
${\textrm {Zr}}$
, but worries: What guarantees that enough sets exist? Linnebo and Rayo recommend that Elsa invoke the Sets-from-Types Theorem. Specifically, they encourage Elsa to fix some limit
![]() $\kappa> \omega $
with
$\kappa> \omega $
with
![]() $\kappa + 2 < \tau $
, then work in
$\kappa + 2 < \tau $
, then work in
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
to obtain
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
to obtain
![]() $\textrm {Zr}^{(\kappa )}$
.
$\textrm {Zr}^{(\kappa )}$
.
Inevitably, though, this discussion of
![]() $\kappa $
and
$\kappa $
and
![]() $\tau $
takes place within some metatheory which we use to describe
$\tau $
takes place within some metatheory which we use to describe
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
. After all, as noted in Sections 2.2–2.3,
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
. After all, as noted in Sections 2.2–2.3,
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
’s types are supplied externally. So, if Elsa is to follow Linnebo and Rayo’s recommendation, she will have to countenance a suitably large index,
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
’s types are supplied externally. So, if Elsa is to follow Linnebo and Rayo’s recommendation, she will have to countenance a suitably large index,
![]() $\tau $
, in the metatheory, so that she can both describe
$\tau $
, in the metatheory, so that she can both describe
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
and obtain
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
and obtain
![]() $\textrm {Zr}^{(\kappa )}$
.
$\textrm {Zr}^{(\kappa )}$
.
At this point, though, Elsa will simply want to ask: What guarantees that any suitable
![]() $\tau $
exists? Such an entity would have to stand at the head of a vast sequence of type-indices. Well then: What guarantees that enough type-indices exist? Her ontological worries about sets have not have been addressed; they have just become worries about the ontology postulated within the metatheory.
$\tau $
exists? Such an entity would have to stand at the head of a vast sequence of type-indices. Well then: What guarantees that enough type-indices exist? Her ontological worries about sets have not have been addressed; they have just become worries about the ontology postulated within the metatheory.
3.3 Ideological-bootstrapping
This elementary problem undermines Linnebo and Rayo’s way of dealing with Elsa. However, it is worth considering one possible line of response, via (what we call) ideological-bootstrapping. This idea is independently interesting, and it will buy Linnebo and Rayo some slack, but not enough slack to save their argumentative strategy.
To define
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
, we must be given the type-index
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
, we must be given the type-index
![]() $\tau $
. In the previous subsection, we imagined Elsa worrying about whether
$\tau $
. In the previous subsection, we imagined Elsa worrying about whether
![]() $\tau $
exists. But—so this line of reply runs—Elsa is mistakenly assuming here that
$\tau $
exists. But—so this line of reply runs—Elsa is mistakenly assuming here that
![]() $\tau $
must be a type
$\tau $
must be a type
![]() $0$
entity. Instead,
$0$
entity. Instead,
![]() $\tau $
could be a higher-type entity, supplied by some ideologically-rich but ontologically-innocent theory,
$\tau $
could be a higher-type entity, supplied by some ideologically-rich but ontologically-innocent theory,
![]() ${\textrm {CTT}^{\sigma }_{\textrm {p}}}$
. In turn,
${\textrm {CTT}^{\sigma }_{\textrm {p}}}$
. In turn,
![]() $\sigma $
might be some higher-type entity, supplied by some theory
$\sigma $
might be some higher-type entity, supplied by some theory
![]() ${\textrm {CTT}^{\rho }_{\textrm {p}}}$
. And so on.Footnote
23
${\textrm {CTT}^{\rho }_{\textrm {p}}}$
. And so on.Footnote
23
The hope is that, somehow, considering a sequence of such theories will sooth away Elsa’s ontological concerns. But, however exactly this line of response is meant to work, it will require that
![]() $\tau> \sigma > \rho > \ldots $
. After all, Elsa’s worries kick in as soon as the syntax of
$\tau> \sigma > \rho > \ldots $
. After all, Elsa’s worries kick in as soon as the syntax of
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
is laid down; so her worries clearly cannot be addressed by starting with some theory
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
is laid down; so her worries clearly cannot be addressed by starting with some theory
![]() ${\textrm {CTT}^{\sigma }_{\textrm {p}}}$
with
${\textrm {CTT}^{\sigma }_{\textrm {p}}}$
with
![]() $\sigma \geq \tau $
.
$\sigma \geq \tau $
.
This simple observation dictates the form that the attempted reply must take. We are being asked to imagine a sequence of theories,
![]() ${\textrm {CTT}^{\tau _1}_{\textrm {p}}}$
, …,
${\textrm {CTT}^{\tau _1}_{\textrm {p}}}$
, …,
![]() ${\textrm {CTT}^{\tau _n}_{\textrm {p}}}$
, as follows:
${\textrm {CTT}^{\tau _n}_{\textrm {p}}}$
, as follows:
-
(a)
 $\tau _1$
is so small that Elsa has no serious qualms about its existence.
$\tau _1$
is so small that Elsa has no serious qualms about its existence. -
(b) As we move along the sequence, the ideology strictly increases (i.e.,
 $\tau _i < \tau _{i+1}$
), but the earlier theory proves the existence of an entity which indexes the terms of the next theory (i.e., each
$\tau _i < \tau _{i+1}$
), but the earlier theory proves the existence of an entity which indexes the terms of the next theory (i.e., each
 ${\textrm {CTT}^{\tau _i}_{\textrm {p}}}$
proves the existence of something with order-type
${\textrm {CTT}^{\tau _i}_{\textrm {p}}}$
proves the existence of something with order-type
 $\tau _{i+1}> \tau _i$
).
$\tau _{i+1}> \tau _i$
). -
(c)
 ${\textrm {CTT}^{\tau _n}_{\textrm {p}}}$
proves
${\textrm {CTT}^{\tau _n}_{\textrm {p}}}$
proves
 $\textrm {Zr}^{(\kappa )}$
, for some suitable
$\textrm {Zr}^{(\kappa )}$
, for some suitable
 $\kappa $
.
$\kappa $
.
Call this response ideological-bootstrapping, since ideologically weaker theories are used to define ideologically richer theories at step (b).Footnote 24
(Note that we have assumed that the sequence of theories is finite. To explain why, suppose someone instead suggests this: If Elsa has accepted the existence of an
![]() $\omega $
-sequence of theories
$\omega $
-sequence of theories
![]() ${\textrm {CTT}^{\tau _1}_{\textrm {p}}}$
,
${\textrm {CTT}^{\tau _1}_{\textrm {p}}}$
,
![]() ${\textrm {CTT}^{\tau _2}_{\textrm {p}}}$
, …, then Elsa can bootstrap her way to their limit,
${\textrm {CTT}^{\tau _2}_{\textrm {p}}}$
, …, then Elsa can bootstrap her way to their limit,
![]() ${\textrm {CTT}^{\tau _\omega }_{\textrm {p}}}$
. This suggestion is spurious. If some
${\textrm {CTT}^{\tau _\omega }_{\textrm {p}}}$
. This suggestion is spurious. If some
![]() ${\textrm {CTT}^{\tau _i}_{\textrm {p}}}$
is sufficient to introduce an entity with order-type
${\textrm {CTT}^{\tau _i}_{\textrm {p}}}$
is sufficient to introduce an entity with order-type
![]() $\tau _\omega $
, then we can simply take
$\tau _\omega $
, then we can simply take
![]() ${\textrm {CTT}^{\tau _\omega }_{\textrm {p}}}$
as the
${\textrm {CTT}^{\tau _\omega }_{\textrm {p}}}$
as the
![]() $i\mathord {+}1^{\textrm {th}}$
theory. The important case is when none of the theories
$i\mathord {+}1^{\textrm {th}}$
theory. The important case is when none of the theories
![]() ${\textrm {CTT}^{\tau _i}_{\textrm {p}}}$
suffices to introduce anything with order-type
${\textrm {CTT}^{\tau _i}_{\textrm {p}}}$
suffices to introduce anything with order-type
![]() $\tau _\omega $
. But in this case, Elsa will worry whether ‘taking the limit’ is ontologically innocent; for, by assumption, she has not found any ontologically innocent theory which supplies
$\tau _\omega $
. But in this case, Elsa will worry whether ‘taking the limit’ is ontologically innocent; for, by assumption, she has not found any ontologically innocent theory which supplies
![]() $\tau _\omega $
.)
$\tau _\omega $
.)
Ideological-bootstrapping might work in specific circumstances. For example, suppose Elsa is comfortable with the existence of
![]() $\omega +\omega + 3$
, and so has no concerns with the specification of
$\omega +\omega + 3$
, and so has no concerns with the specification of
![]() ${\textrm {CTT}^{\omega +\omega +3}_{\textrm {p}}}$
. Invoking the Sets-from-Types Theorem,
${\textrm {CTT}^{\omega +\omega +3}_{\textrm {p}}}$
. Invoking the Sets-from-Types Theorem,
![]() ${\textrm {CTT}^{\omega +\omega +3}_{\textrm {p}}}$
proves
${\textrm {CTT}^{\omega +\omega +3}_{\textrm {p}}}$
proves
![]() ${\textrm {Zr}}^{(\omega +\omega )}$
. This allows Elsa to simulate the set-theoretic hierarchy up to
${\textrm {Zr}}^{(\omega +\omega )}$
. This allows Elsa to simulate the set-theoretic hierarchy up to
![]() $V_{\omega +\omega }$
. Living within
$V_{\omega +\omega }$
. Living within
![]() $V_{\omega +\omega }$
, Elsa can find an uncountable A well-ordered by some relation
$V_{\omega +\omega }$
, Elsa can find an uncountable A well-ordered by some relation
![]() $<$
.Footnote
25
Using this, Elsa can define a theory
$<$
.Footnote
25
Using this, Elsa can define a theory
![]() ${\textrm {CTT}^{A}_{\textrm {p}}}$
, whose type indices are the members of A as ordered by
${\textrm {CTT}^{A}_{\textrm {p}}}$
, whose type indices are the members of A as ordered by
![]() $<$
. Since A is uncountable,
$<$
. Since A is uncountable,
![]() ${\textrm {CTT}^{A}_{\textrm {p}}}$
is straightforwardly richer than
${\textrm {CTT}^{A}_{\textrm {p}}}$
is straightforwardly richer than
![]() ${\textrm {CTT}^{\omega + \omega + 3}_{\textrm {p}}}$
. Moreover, using
${\textrm {CTT}^{\omega + \omega + 3}_{\textrm {p}}}$
. Moreover, using
![]() ${\textrm {CTT}^{A}_{\textrm {p}}}$
, Elsa can simulate a much larger chunk of the set-theoretic hierarchy than
${\textrm {CTT}^{A}_{\textrm {p}}}$
, Elsa can simulate a much larger chunk of the set-theoretic hierarchy than
![]() $V_{\omega +\omega }$
; living within that chunk of the hierarchy, she can find larger well-orders; these can be used to supply the indices for some further development of
$V_{\omega +\omega }$
; living within that chunk of the hierarchy, she can find larger well-orders; these can be used to supply the indices for some further development of
![]() ${\textrm {CTT}_{\textrm {p}}}\ldots $
and so on. This seems like a case where ideological-bootstrapping might genuinely achieve something.
${\textrm {CTT}_{\textrm {p}}}\ldots $
and so on. This seems like a case where ideological-bootstrapping might genuinely achieve something.
Nevertheless, there are hard limits on what ideological-bootstrapping can achieve. In the simplest case, suppose Elsa insists on starting with
![]() ${\textrm {CTT}^{n}_{\textrm {p}}}$
, for some finite n, because she is uncertain whether there are infinitely many entities. Since
${\textrm {CTT}^{n}_{\textrm {p}}}$
, for some finite n, because she is uncertain whether there are infinitely many entities. Since
![]() ${\textrm {CTT}^{n}_{\textrm {p}}}$
only yields (surrogates for) finite well-orders, no amount of ideological-boostrapping from this starting point will allow Elsa to obtain any infinite well-order. So, whenever Linnebo and Rayo try to describe any theory
${\textrm {CTT}^{n}_{\textrm {p}}}$
only yields (surrogates for) finite well-orders, no amount of ideological-boostrapping from this starting point will allow Elsa to obtain any infinite well-order. So, whenever Linnebo and Rayo try to describe any theory
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
such that
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
such that
![]() $\tau $
is infinite, Elsa will worry whether the theory itself even exists.
$\tau $
is infinite, Elsa will worry whether the theory itself even exists.
The shape of this problem is quite general. Say that
![]() $\kappa $
is a hereditary-point iff
$\kappa $
is a hereditary-point iff
![]() $\kappa $
is an infinite cardinal and everything in
$\kappa $
is an infinite cardinal and everything in
![]() $V_\kappa $
is strictly smaller than
$V_\kappa $
is strictly smaller than
![]() $\kappa $
(so
$\kappa $
(so
![]() $\omega $
is the first hereditary-point).Footnote
26
When
$\omega $
is the first hereditary-point).Footnote
26
When
![]() $\kappa $
is a hereditary-point, it is in principle impossible to ideologically-bootstrap your way from below
$\kappa $
is a hereditary-point, it is in principle impossible to ideologically-bootstrap your way from below
![]() $\kappa $
to above
$\kappa $
to above
![]() $\kappa $
, since every entity below level
$\kappa $
, since every entity below level
![]() $\kappa $
is strictly smaller than
$\kappa $
is strictly smaller than
![]() $\kappa $
itself.
$\kappa $
itself.
This problem is especially pertinent, given two facts about hereditary-points and
![]() ${\textrm {ZF}}$
. First,
${\textrm {ZF}}$
. First,
![]() ${\textrm {ZF}}$
proves that there are proper-class-many hereditary-points; but, since any hereditary-point after
${\textrm {ZF}}$
proves that there are proper-class-many hereditary-points; but, since any hereditary-point after
![]() $\omega $
would be pretty enormous, it is not unreasonable to wonder whether any exist; and ideological-bootstrapping cannot quiet such qualms.Footnote
27
Second, the standard models of
$\omega $
would be pretty enormous, it is not unreasonable to wonder whether any exist; and ideological-bootstrapping cannot quiet such qualms.Footnote
27
Second, the standard models of
![]() ${\textrm {ZF}}$
are the
${\textrm {ZF}}$
are the
![]() $V_\kappa $
such that
$V_\kappa $
such that
![]() $\kappa $
is strongly inaccessible; and every strongly inaccessible cardinal is a hereditary-point; so ideological-bootstrapping cannot possibly address any ontological worries that an Elsa-like character might have about the existence of any standard model of
$\kappa $
is strongly inaccessible; and every strongly inaccessible cardinal is a hereditary-point; so ideological-bootstrapping cannot possibly address any ontological worries that an Elsa-like character might have about the existence of any standard model of
![]() ${\textrm {ZF}}$
.
${\textrm {ZF}}$
.
The argument of Section 3.2 therefore stands essentially unchanged. Linnebo and Rayo are mistaken to think that cumulative type theories can help us to overcome ontological worries, since the very existence of the (syntactically individuated) theories themselves requires a rich ontology in the metatheory.
4 CTT: superfluous type-restrictions
In Section 2.4, we discussed Gödel’s claim that
![]() ${\textrm {STT}}$
’s type-restrictions were ‘superfluous’. We should now make explicit something which we there left implicit: these type-restrictions are superfluous given Gödel’s aims. Specifically, Gödel wanted to establish a foundational, ‘formal system which avoids the logical paradoxes and retains all [of] mathematics’ [Reference Gödel and Feferman18, p. 46]. Given those aims,
${\textrm {STT}}$
’s type-restrictions were ‘superfluous’. We should now make explicit something which we there left implicit: these type-restrictions are superfluous given Gödel’s aims. Specifically, Gödel wanted to establish a foundational, ‘formal system which avoids the logical paradoxes and retains all [of] mathematics’ [Reference Gödel and Feferman18, p. 46]. Given those aims,
![]() $\textrm {CTT}$
’s type-restrictions are just as superfluous as
$\textrm {CTT}$
’s type-restrictions are just as superfluous as
![]() ${\textrm {STT}}$
’s; it is best to follow Gödel, and work with something like
${\textrm {STT}}$
’s; it is best to follow Gödel, and work with something like
![]() ${\textrm {Zr}}$
, with its untyped variables.
${\textrm {Zr}}$
, with its untyped variables.
All of this is compatible with the idea that, given alternative aims,
![]() ${\textrm {STT}}$
’s or
${\textrm {STT}}$
’s or
![]() $\textrm {CTT}$
’s type-restrictions might not be superfluous, but deeply important. As we will show in this section, though,
$\textrm {CTT}$
’s type-restrictions might not be superfluous, but deeply important. As we will show in this section, though,
![]() $\textrm {CTT}$
’s type-restrictions are inevitably ‘superfluous restrictions’, in the sense that any semantics for
$\textrm {CTT}$
’s type-restrictions are inevitably ‘superfluous restrictions’, in the sense that any semantics for
![]() $\textrm {CTT}$
also licenses the use of an untyped variable and allows the ‘types’ to be defined internally. (Cf. points (1) and (2) from Section 2.2.) So, in a slogan:
$\textrm {CTT}$
also licenses the use of an untyped variable and allows the ‘types’ to be defined internally. (Cf. points (1) and (2) from Section 2.2.) So, in a slogan:
![]() $\textrm {CTT}$
’s type-restrictions are superfluous, on any semantics.
$\textrm {CTT}$
’s type-restrictions are superfluous, on any semantics.
We will unpack the details in a moment. First, we should explain the phrase ‘a semantics for
![]() $\textrm {CTT}$
’. As we are using that phrase, a semantics for
$\textrm {CTT}$
’. As we are using that phrase, a semantics for
![]() $\textrm {CTT}$
is a general framework within which to provide models of
$\textrm {CTT}$
is a general framework within which to provide models of
![]() $\textrm {CTT}$
, rather than a specific model of some
$\textrm {CTT}$
, rather than a specific model of some
![]() ${{\textrm {CTT}^{\tau }}}$
. (Compare the idea of ‘the possible worlds semantics for modal language’.) So, in providing a semantics for
${{\textrm {CTT}^{\tau }}}$
. (Compare the idea of ‘the possible worlds semantics for modal language’.) So, in providing a semantics for
![]() $\textrm {CTT}$
, we fix the meaning of phrases like ‘a model of
$\textrm {CTT}$
, we fix the meaning of phrases like ‘a model of
![]() $\textrm {CTT}$
’ and ‘an entity of type
$\textrm {CTT}$
’ and ‘an entity of type
![]() $\alpha $
’; the latter will be the sort of entity which, according to the semantics, can be the value of a type
$\alpha $
’; the latter will be the sort of entity which, according to the semantics, can be the value of a type
![]() $\alpha $
variable.
$\alpha $
variable.
4.1 The abstract argument for introducing untyped variables
Our argument begins with an uncontentious point: the stringently-stated rules for
![]() $\textrm {CTT}$
tell us that
$\textrm {CTT}$
tell us that
![]() $y^\beta (x^\alpha )$
is well-formed iff
$y^\beta (x^\alpha )$
is well-formed iff
![]() $\beta> \alpha $
; but these rules are needlessly stringent, on any given semantics.
$\beta> \alpha $
; but these rules are needlessly stringent, on any given semantics.
To see this, fix some semantics for
![]() $\textrm {CTT}$
, and let
$\textrm {CTT}$
, and let
![]() $\beta \leq \alpha $
. The formula
$\beta \leq \alpha $
. The formula
![]() $x^\alpha \mathrel {\varepsilon } y^\beta $
is well-formed according to
$x^\alpha \mathrel {\varepsilon } y^\beta $
is well-formed according to
![]() $\textrm {CTT}$
. So, for any model
$\textrm {CTT}$
. So, for any model
![]() $\mathcal {M}$
and any type
$\mathcal {M}$
and any type
![]() $\alpha $
entity
$\alpha $
entity
![]() $a^\alpha $
and type
$a^\alpha $
and type
![]() $\beta $
entity
$\beta $
entity
![]() $b^\beta $
from
$b^\beta $
from
![]() $\mathcal {M}$
, either
$\mathcal {M}$
, either
![]() $\mathcal {M} \models a^\alpha \mathrel {\varepsilon } b^\beta $
or
$\mathcal {M} \models a^\alpha \mathrel {\varepsilon } b^\beta $
or
![]() $\mathcal {M} \models \lnot a^\alpha \mathrel {\varepsilon } b^\beta $
. (Note: what exactly this comes to will depend on the details of the semantics; but we are proceeding abstractly for now and want to consider any semantics for
$\mathcal {M} \models \lnot a^\alpha \mathrel {\varepsilon } b^\beta $
. (Note: what exactly this comes to will depend on the details of the semantics; but we are proceeding abstractly for now and want to consider any semantics for
![]() $\textrm {CTT}$
.) Now, as explained in Section 1.2, the formula
$\textrm {CTT}$
.) Now, as explained in Section 1.2, the formula
![]() $x^\alpha \mathrel {\varepsilon } y^\beta $
perfectly simulates the formula
$x^\alpha \mathrel {\varepsilon } y^\beta $
perfectly simulates the formula
![]() $y^\beta (x^\alpha )$
; that is, it perfectly simulates the notion of applying a type
$y^\beta (x^\alpha )$
; that is, it perfectly simulates the notion of applying a type
![]() $\beta $
entity to a type
$\beta $
entity to a type
![]() $\alpha $
entity. So we could have allowed
$\alpha $
entity. So we could have allowed
![]() $y^\beta (x^\alpha )$
to count as well-formed, even though
$y^\beta (x^\alpha )$
to count as well-formed, even though
![]() $\beta \ngtr \alpha $
. So,
$\beta \ngtr \alpha $
. So,
![]() $\textrm {CTT}$
’s stringently-stated type-restrictions are needlessly stringent.
$\textrm {CTT}$
’s stringently-stated type-restrictions are needlessly stringent.
To be clear, this is not an objection to
![]() $\textrm {CTT}$
’s type-restrictions. We are really just repackaging a point we made in Section 1.2, and also made by Linnebo and Rayo [Reference Linnebo and Rayo23, pp. 282–283], that we can liberalise
$\textrm {CTT}$
’s type-restrictions. We are really just repackaging a point we made in Section 1.2, and also made by Linnebo and Rayo [Reference Linnebo and Rayo23, pp. 282–283], that we can liberalise
![]() $\textrm {CTT}$
’s stringently-stated formation rules, and allow that
$\textrm {CTT}$
’s stringently-stated formation rules, and allow that
![]() $y^\beta (x^\alpha )$
is well-formed for any type-indices
$y^\beta (x^\alpha )$
is well-formed for any type-indices
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. From a purely formal point of view, this changes almost nothing. So, in what follows, we will simply allow that
$\beta $
. From a purely formal point of view, this changes almost nothing. So, in what follows, we will simply allow that
![]() $\textrm {CTT}$
counts every formula
$\textrm {CTT}$
counts every formula
![]() $y^\beta (x^\alpha )$
as well-formed.
$y^\beta (x^\alpha )$
as well-formed.
Significantly, though,
![]() $\textrm {CTT}$
still lacks untyped variables. But, for exactly the same reason, this is also needlessly stringent, on any given semantics.
$\textrm {CTT}$
still lacks untyped variables. But, for exactly the same reason, this is also needlessly stringent, on any given semantics.
To see this, fix some semantics for (liberally formulated)
![]() $\textrm {CTT}$
. Now
$\textrm {CTT}$
. Now
![]() $y^\beta (x^\alpha )$
is well-formed for any
$y^\beta (x^\alpha )$
is well-formed for any
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. So, for any model
$\beta $
. So, for any model
![]() $\mathcal {M}$
and any type
$\mathcal {M}$
and any type
![]() $\alpha $
entity
$\alpha $
entity
![]() $a^\alpha $
and type
$a^\alpha $
and type
![]() $\beta $
entity
$\beta $
entity
![]() $b^\beta $
from that model, either
$b^\beta $
from that model, either
![]() $\mathcal {M} \models b^\beta (a^\alpha )$
or
$\mathcal {M} \models b^\beta (a^\alpha )$
or
![]() $\mathcal {M} \models \lnot b^\beta (a^\alpha )$
. That is, any model assigns a truth value to the application of any entity to any entity, whatever their types might happen to be. So we could have allowed the untyped atomic formula,
$\mathcal {M} \models \lnot b^\beta (a^\alpha )$
. That is, any model assigns a truth value to the application of any entity to any entity, whatever their types might happen to be. So we could have allowed the untyped atomic formula,
![]() $y(x)$
, to count as well-formed: whatever specific values the variables take, the formula would just amount to applying some entity to some entity, which is exactly what the semantics allows.
$y(x)$
, to count as well-formed: whatever specific values the variables take, the formula would just amount to applying some entity to some entity, which is exactly what the semantics allows.
The upshot is that any semantics for
![]() $\textrm {CTT}$
also licenses the use of untyped variables. This time, though, we do have an objection to
$\textrm {CTT}$
also licenses the use of untyped variables. This time, though, we do have an objection to
![]() $\textrm {CTT}$
’s type-restrictions. Whereas stringently-formulated
$\textrm {CTT}$
’s type-restrictions. Whereas stringently-formulated
![]() $\textrm {CTT}$
can simulate any typed-formula
$\textrm {CTT}$
can simulate any typed-formula
![]() $y^\beta (x^\alpha )$
, via
$y^\beta (x^\alpha )$
, via
![]() $x^\alpha \mathrel {\varepsilon } y^\beta $
, it lacks the technical resources to simulate the untyped-formula
$x^\alpha \mathrel {\varepsilon } y^\beta $
, it lacks the technical resources to simulate the untyped-formula
![]() $y(x)$
. Untyped variables have to be added by hand. But, once we have added them, we will have moved from a typed to an untyped theory; if we choose to retain ‘typed’ variables, then they will just behave as restricted untyped variables.
$y(x)$
. Untyped variables have to be added by hand. But, once we have added them, we will have moved from a typed to an untyped theory; if we choose to retain ‘typed’ variables, then they will just behave as restricted untyped variables.
Of course, if there had been no consistent way to introduce untyped variables, then
![]() $\textrm {CTT}$
’s type-restrictions would have been far from superfluous. But, in this sort of a context, theories like
$\textrm {CTT}$
’s type-restrictions would have been far from superfluous. But, in this sort of a context, theories like
![]() ${\textrm {Zr}}$
provide us with a clear method for consistently introducing untyped variables.Footnote
28
Moreover, they also provide us with a paradigm for how to define the notion of ‘type’ (i.e., rank) within the theory. So
${\textrm {Zr}}$
provide us with a clear method for consistently introducing untyped variables.Footnote
28
Moreover, they also provide us with a paradigm for how to define the notion of ‘type’ (i.e., rank) within the theory. So
![]() $\textrm {CTT}$
’s type-restrictions are genuinely superfluous.Footnote
29
$\textrm {CTT}$
’s type-restrictions are genuinely superfluous.Footnote
29
4.2 Illustration: the class semantics
The argument of the previous subsection is very abstract. To make it more concrete, in this subsection and the next, we will consider two specific semantics in detail: the class semantics, and the plural semantics. Just as our abstract argument predicts, both semantics clearly license the use of untyped variables.
(To avoid any unfortunate misunderstandings: we offer these semantics merely as illustrations. When we say that no semantics could justify the adoption of
![]() $\textrm {CTT}$
’s type-restrictions, we are not making an inductive inference from these two examples; that conclusion was established by the abstract argument of Section 4.1.)
$\textrm {CTT}$
’s type-restrictions, we are not making an inductive inference from these two examples; that conclusion was established by the abstract argument of Section 4.1.)
We start by considering the class semantics. To define a model for
![]() $\textrm {CTT}$
within this semantics, we first specify some suitable set of urelements, U. We then stipulate that the type
$\textrm {CTT}$
within this semantics, we first specify some suitable set of urelements, U. We then stipulate that the type
![]() $\alpha $
entities are the members of
$\alpha $
entities are the members of
![]() $U_{\alpha +1}$
, where we define:
$U_{\alpha +1}$
, where we define:
Finally, we offer a general clause governing the semantics of atomic sentences:
-
‘
 $b^\beta (a^\alpha )$
’ is true iff the referent of ‘
$b^\beta (a^\alpha )$
’ is true iff the referent of ‘
 $a^\alpha $
’ is a member of the referent of ‘
$a^\alpha $
’ is a member of the referent of ‘
 $b^\beta $
’.
$b^\beta $
’.
Uncontroversially,
![]() $\textrm {CTT}$
is sound for the class semantics. A stringently-typed formula like ‘
$\textrm {CTT}$
is sound for the class semantics. A stringently-typed formula like ‘
![]() $b^2(a^0)$
’ will be true (in a model) iff the referent of ‘
$b^2(a^0)$
’ will be true (in a model) iff the referent of ‘
![]() $a^0$
’ is a member of the referent of ‘
$a^0$
’ is a member of the referent of ‘
![]() $b^2$
’. A liberally-typed formula like ‘
$b^2$
’. A liberally-typed formula like ‘
![]() $b^0(a^2)$
’ will also be true (in a model) iff the referent of ‘
$b^0(a^2)$
’ will also be true (in a model) iff the referent of ‘
![]() $a^2$
’ is a member of the referent of ‘
$a^2$
’ is a member of the referent of ‘
![]() $b^0$
’; and this will inevitably be false, since the latter is guaranteed to be an urelement, i.e., an individual without members.
$b^0$
’; and this will inevitably be false, since the latter is guaranteed to be an urelement, i.e., an individual without members.
Our semantic clause for atomic sentences employed type restrictions. However, on the class semantics, the type-restrictions are straightforwardly superfluous. We can easily offer a similar semantic clause for untyped terms:
-
‘
 $b(a)$
’ is true iff the referent of ‘a’ is a member of the referent of ‘b’.
$b(a)$
’ is true iff the referent of ‘a’ is a member of the referent of ‘b’.
Otherwise put: there is no barrier to introducing untyped variables, whose values can be any individual or class. Of course, given the old paradoxes, we will have to take care in introducing untyped variables. However, as we have already discussed,
![]() ${\textrm {Zr}}$
-like theories show us how to do this safely.
${\textrm {Zr}}$
-like theories show us how to do this safely.
4.3 Illustration: the plural semantics
The class semantics concerns a class-hierarchy built from a basis of individuals. The plural semantics concerns a plural-hierarchy built from a similar basis.Footnote
30
In a little more detail, we use the phrase ‘plural
![]() $^*$
’ as a catch-all for whatever we find at any level in the plural hierarchy, i.e., any object, any objects, any objectses, …, any objects(es)
$^*$
’ as a catch-all for whatever we find at any level in the plural hierarchy, i.e., any object, any objects, any objectses, …, any objects(es)
![]() $^\alpha $
….Footnote
31
We then offer this general clause governing the semantics for atomic sentences:
$^\alpha $
….Footnote
31
We then offer this general clause governing the semantics for atomic sentences:
-
‘
 $b^\beta (a^\alpha )$
’ is true iff what ‘
$b^\beta (a^\alpha )$
’ is true iff what ‘
 $b^\beta $
’ refers to includes what ‘
$b^\beta $
’ refers to includes what ‘
 $a^\alpha $
’ refers to.Footnote
32
$a^\alpha $
’ refers to.Footnote
32
So ‘
![]() $b^2(a^0)$
’ is true iff what ‘
$b^2(a^0)$
’ is true iff what ‘
![]() $b^2$
’ refers to includes what ‘
$b^2$
’ refers to includes what ‘
![]() $a^0$
’ refers to; and ‘
$a^0$
’ refers to; and ‘
![]() $b^0(a^2)$
’ is true iff what ‘
$b^0(a^2)$
’ is true iff what ‘
![]() $b^0$
’ refers to includes what ‘
$b^0$
’ refers to includes what ‘
![]() $a^2$
’ refers to. But equally, the semantic clause applies perfectly well to untyped terms:
$a^2$
’ refers to. But equally, the semantic clause applies perfectly well to untyped terms:
-
‘
 $b(a)$
’ is true iff what ‘b’ refers to includes what ‘a’ refers to.
$b(a)$
’ is true iff what ‘b’ refers to includes what ‘a’ refers to.
Again: there is no barrier to introducing untyped variables, whose values can be any plural
![]() $^*$
.
$^*$
.
As before, care must be taken to preserve consistency. But we know how to take care: roughly stated, we just need to do for plurals
![]() $^*$
what
$^*$
what
![]() ${\textrm {Zr}}$
does for classes/sets. In more detail, instead of setting up a plural
${\textrm {Zr}}$
does for classes/sets. In more detail, instead of setting up a plural
![]() $^*$
-hierarchy using type-restricted variables with externally supplied type-indices, we can reason about plurals
$^*$
-hierarchy using type-restricted variables with externally supplied type-indices, we can reason about plurals
![]() $^*$
using an untyped variable, with the plurals
$^*$
using an untyped variable, with the plurals
![]() $^*$
arranged into a cumulative hierarchy according to their rank (with ‘rank’ defined within the theory, using our untyped variable). And this work has been carried out carefully: Oliver and Smiley [Reference Oliver and Smiley28, chap. 15] and Florio and Linnebo [Reference Florio and Linnebo11, sec. 12.6] both present consistent plural logics featuring untyped variables. Indeed, Florio and Linnebo develop their untyped plural logic precisely by starting with the
$^*$
arranged into a cumulative hierarchy according to their rank (with ‘rank’ defined within the theory, using our untyped variable). And this work has been carried out carefully: Oliver and Smiley [Reference Oliver and Smiley28, chap. 15] and Florio and Linnebo [Reference Florio and Linnebo11, sec. 12.6] both present consistent plural logics featuring untyped variables. Indeed, Florio and Linnebo develop their untyped plural logic precisely by starting with the
![]() $\textrm {CTT}$
on the plural semantics, and then collapsing the types in the way that we have described.
$\textrm {CTT}$
on the plural semantics, and then collapsing the types in the way that we have described.
5
 ${\textrm {STT}}$
: type-restrictions justified
${\textrm {STT}}$
: type-restrictions justified
We have argued that
![]() $\textrm {CTT}$
’s type-restrictions are inevitably superfluous. They are unnecessary for the aim of providing a foundational theory for mathematics, and they cannot be justified semantically, since any semantics for
$\textrm {CTT}$
’s type-restrictions are inevitably superfluous. They are unnecessary for the aim of providing a foundational theory for mathematics, and they cannot be justified semantically, since any semantics for
![]() $\textrm {CTT}$
will permit the introduction of an untyped variable.
$\textrm {CTT}$
will permit the introduction of an untyped variable.
In this section, we will show that
![]() ${\textrm {STT}}$
’s type-restrictions are not similarly superfluous. We can justify the adoption of
${\textrm {STT}}$
’s type-restrictions are not similarly superfluous. We can justify the adoption of
![]() ${\textrm {STT}}$
’s type-restrictions by invoking the Fregean semantics. Indeed, on this semantics, a formula is intelligible iff it is well-formed in
${\textrm {STT}}$
’s type-restrictions by invoking the Fregean semantics. Indeed, on this semantics, a formula is intelligible iff it is well-formed in
![]() ${\textrm {STT}}$
.
${\textrm {STT}}$
.
5.1 Against referentialism
In Sections 4.2 and 4.3, we used the class and plural semantics to illustrate our objection to
![]() $\textrm {CTT}$
. Both of these semantics are referentialist. By this we mean that both semantics treat every type of term as a type of referring term: every type of term performs the same semantic role—referring—and all that changes is what they refer to—individuals, classes/plurals
$\textrm {CTT}$
. Both of these semantics are referentialist. By this we mean that both semantics treat every type of term as a type of referring term: every type of term performs the same semantic role—referring—and all that changes is what they refer to—individuals, classes/plurals
![]() $^*$
, or something else.Footnote
33
$^*$
, or something else.Footnote
33
The class and plural semantics render
![]() $\textrm {CTT}$
’s type-restrictions superfluous, precisely because they are referentialist. After all, if every type of term performs the same kind of semantic role as every other type of term, then every type of term can be meaningfully substituted for every other type of term. In that case, as we argued in Section 4.1, the semantics will also allows us to introduce an untyped variable. It follows, immediately, that any semantics which might justify
$\textrm {CTT}$
’s type-restrictions superfluous, precisely because they are referentialist. After all, if every type of term performs the same kind of semantic role as every other type of term, then every type of term can be meaningfully substituted for every other type of term. In that case, as we argued in Section 4.1, the semantics will also allows us to introduce an untyped variable. It follows, immediately, that any semantics which might justify
![]() ${\textrm {STT}}$
’s type-restrictions will have to be non-referentialist; in other words, it will have to assign different kinds of semantic role to different types of term.
${\textrm {STT}}$
’s type-restrictions will have to be non-referentialist; in other words, it will have to assign different kinds of semantic role to different types of term.
Now, at one time, this might have seemed like an impossible demand. According to the old Quinean [Reference Prior30, pp. 66–68] orthodoxy, we can only quantify into the position of a referring term; so type theory—which allows us to bind variables of every type—must be given a referentialist semantics. Fortunately, times have changed, and philosophers are increasingly willing to accept quantification into other kinds of position.Footnote
34
In what follows, we will simply assume that the old Quinean orthodoxy is mistaken, and will present a particular non-referentialist semantics—the Fregean semantics—which justifies
![]() ${\textrm {STT}}$
’s type-restrictions.
${\textrm {STT}}$
’s type-restrictions.
5.2 Conceptual but referentialist semantics
The Fregean semantics is a variety of conceptual semantics. On a conceptual semantics, type theories are theories of predication:Footnote
35
‘
![]() $a^0$
’ is a name which refers to an object; ‘
$a^0$
’ is a name which refers to an object; ‘
![]() $b^1$
’ is a first-level predicate which expresses a property of objects (a type 1 property);Footnote
36
‘
$b^1$
’ is a first-level predicate which expresses a property of objects (a type 1 property);Footnote
36
‘
![]() $c^2$
’ is a second-level predicate which expresses a property of properties of objects (a type 2 property); and so on.
$c^2$
’ is a second-level predicate which expresses a property of properties of objects (a type 2 property); and so on.
This way of characterising conceptual semantics is schematic, and we get different versions of the semantics when we supply different accounts of what it means for a predicate to express a property. On one view of predication, predicates ‘express’ properties in the sense that they refer to properties, just as names refer to objects. To illustrate, take the following sentence:
-
(1) Socrates pontificates
According to this view of predication, ‘pontificates’ refers to the property Pontification.Footnote 37 Clearly, combining this account of predication with the conceptual semantics yields another brand of referentialism. Every type of term is still referential; all that changes is whether it refers to an ordinary individual (like Socrates) or to something within a property-hierarchy (like Pontification). We then have the following semantic clause for atomic sentences:
-
‘
 $b^\beta (a^\alpha )$
’ is true iff the referent of ‘
$b^\beta (a^\alpha )$
’ is true iff the referent of ‘
 $a^\alpha $
’ instantiates the referent of ‘
$a^\alpha $
’ instantiates the referent of ‘
 $b^\beta $
’
$b^\beta $
’
This allows us to make sense of ‘
![]() $b^\beta (a^\alpha )$
’, for any types
$b^\beta (a^\alpha )$
’, for any types
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. For example, ‘
$\beta $
. For example, ‘
![]() $b^0(a^0)$
’ is true iff the referent of ‘
$b^0(a^0)$
’ is true iff the referent of ‘
![]() $a^0$
’ instantiates the referent of ‘
$a^0$
’ instantiates the referent of ‘
![]() $b^0$
’. Now, admittedly, this formula would correspond to something slightly peculiar in natural language. If ‘
$b^0$
’. Now, admittedly, this formula would correspond to something slightly peculiar in natural language. If ‘
![]() $a^0$
’ referred to Socrates, and ‘
$a^0$
’ referred to Socrates, and ‘
![]() $b^0$
’ referred to Plato, then we might try to render ‘
$b^0$
’ referred to Plato, then we might try to render ‘
![]() $b^0(a^0)$
’ as:
$b^0(a^0)$
’ as:
-
(2) Socrates Plato
This is scarcely grammatical English. Still, for referentialists about predication, (2) is intelligible: it says that Socrates instantiates Plato. Indeed, precisely this point is made by Magidor Reference Magidor[27], who insists that (2) is perfectly meaningful and trivially false. We are not agreeing with Magidor here, but we do think that referentialists about predication should agree with her. Moreover, and as in Section 4.1, referentialists about predication will ultimately find type-restrictions superfluous; nothing will prevent them from introducing untyped variables and insisting that ‘
![]() $b(a)$
’ is true iff the referent of ‘a’ instantiates the referent of ‘b’.
$b(a)$
’ is true iff the referent of ‘a’ instantiates the referent of ‘b’.
5.3 Fregean semantics
There is, however, a non-referentialist version of the conceptual semantics: it is a Fregean semantics.
Unlike referentialists, Fregeans do not think that predicates refer to properties (not, at least, in anything like the sense that a name ‘refers’).Footnote 38 Rather, they think that the role of a predicate is to say something of an object; for example, ‘pontificates’ says of an object that it pontificates. This is the sense in which Fregeans think that predicates are ‘incomplete’, and they indicate this by writing their predicates with gaps. So rather than writing the predicate in (1) as ‘pontificates’, they write it as ‘x pontificates’, where ‘x’ marks a gap for a name to go. We can then say that sentence (1) is true iff ‘x pontificates’ says something true of the referent of ‘Socrates’, i.e., iff Socrates pontificates.Footnote 39
From this Fregean perspective, (2) is not just ungrammatical, but unintelligible. We arrive at it by taking (1) and replacing its predicate, ‘x pontificates’, with a referring name, ‘Plato’. Names and predicates are made to work together, but two names cannot work together in the same way. It is not within a name’s remit to say anything of an object; names just refer to objects. And that is why (2) is a meaningless string: neither name says anything of the referent of the other (let alone something true or false).
Now consider the following sentence:
-
(3) Someone pontificates
This sentence is not made by combining a predicate with a name. Instead, it is made by combining two predicates, ‘x pontificates’ and ‘Someone Y’. Crucially, though, these are two different types of predicates: ‘x pontificates’ is a first-level predicate, meaning that ‘x’ marks a gap for a name; ‘Someone Y’ is a second-level predicate, meaning that ‘Y’ marks a gap for a first-level predicate. Just as first-level predicates play a different kind of semantic role from the names they can take as input, second-level predicates play a different kind of semantic role from the first-level predicates that they can take as input. We might describe this role thus: a second-level predicate says something of things said of objects. This means that (3) is true/false iff ‘Someone Y’ says something true/false of what ‘x pontificates’ says of objects. Specifically: ‘Someone Y’ says something true of what ‘x pontificates’ says of objects iff ‘x pontificates’ says something true of someone; and it says something false of what ‘x pontificates’ says of objects iff ‘x pontificates’ says something false of everyone.
Again, from this Fregean perspective, it is easy to see that we cannot meaningfully substitute a name for the first-level predicate in (3). Attempting to do this would yield:
-
(4) Someone Plato
This string is not just ungrammatical, but meaningless. To be meaningful, the input to ‘Someone Y’ must be the kind of expression that says something of objects. But ‘Plato’ refers to an object, rather than saying anything of objects (let alone something true of someone or false of everyone). So, if we try to plug ‘Plato’ into the argument-place of ‘Someone Y’, we end up with garbage.Footnote 40
The crucial point is that, on the Fregean semantics, different types of term play different types of semantic role: ‘
![]() $a^0$
’ is a name which refers to an object; ‘
$a^0$
’ is a name which refers to an object; ‘
![]() $b^1$
’ is a first-level predicate which says something of objects; ‘
$b^1$
’ is a first-level predicate which says something of objects; ‘
![]() $c^2$
’ is a second-level predicate which says something of things said of objects; and so on. And rather than having a single semantic clause which applies to all atomic sentences, we have different clauses for different types of predication:
$c^2$
’ is a second-level predicate which says something of things said of objects; and so on. And rather than having a single semantic clause which applies to all atomic sentences, we have different clauses for different types of predication:
-
‘
 $b^1(a^0)$
’ is true iff ‘
$b^1(a^0)$
’ is true iff ‘
 $b^1$
’ says something true of the referent of ‘
$b^1$
’ says something true of the referent of ‘
 $a^0$
’
$a^0$
’ -
‘
 $c^2(b^1)$
’ is true iff ‘
$c^2(b^1)$
’ is true iff ‘
 $c^2$
’ says something true of what ‘
$c^2$
’ says something true of what ‘
 $b^1$
’ says of objects
$b^1$
’ says of objects -
 $\ldots $
$\ldots $
These semantic clauses allow us to make sense of ‘
![]() $b^n(a^m)$
’ iff
$b^n(a^m)$
’ iff
![]() $n=m+1$
. This is how the Fregean semantics justifies
$n=m+1$
. This is how the Fregean semantics justifies
![]() ${\textrm {STT}}$
’s type-restrictions: a formula is intelligible on the Fregean semantics iff it is well-formed in
${\textrm {STT}}$
’s type-restrictions: a formula is intelligible on the Fregean semantics iff it is well-formed in
![]() ${\textrm {STT}}$
.
${\textrm {STT}}$
.
For the same reason, the Fregean semantics also prohibits the introduction of untyped variables. Untyped variables would need to be able to take any entity of any type as their values. But, on the Fregean semantics, there is no one sense in which different types of entity could be the ‘value’ of a variable; the sense in which an object is the value of a type 0 variable is incommensurable with the sense in which a type 1 property is the value of a type 1 variable.
To be clear, we are not trying to argue here that anyone should adopt the Fregean semantics.Footnote
41
Our point here is just that
![]() ${\textrm {STT}}$
’s type-restrictions, unlike
${\textrm {STT}}$
’s type-restrictions, unlike
![]() $\textrm {CTT}$
’s, are justified by at least one semantics.Footnote
42
$\textrm {CTT}$
’s, are justified by at least one semantics.Footnote
42
5.4 ‘Cumulative types’ as ambiguous
We have just argued that the Fregean semantics prohibits the introduction of untyped variables. But what it cannot prohibit, of course, is the introduction of ambiguous variables, which sometimes behave as one type, and sometimes behave as another. And in fact, this provides the Fregeans with one way of starting to make sense of
![]() $\textrm {CTT}$
. Specifically, they can treat
$\textrm {CTT}$
. Specifically, they can treat
![]() $a^0$
as an ambiguous term: in
$a^0$
as an ambiguous term: in
![]() $b^1(a^0)$
, it behave as a name, and so refers to an object; in
$b^1(a^0)$
, it behave as a name, and so refers to an object; in
![]() $c^2(a^0)$
, it behaves as a first-level predicate, and so says something of an object.
$c^2(a^0)$
, it behaves as a first-level predicate, and so says something of an object.
If that is how we are to read formulas like
![]() $c^2(a^0)$
, though, then they no longer represent any departure from
$c^2(a^0)$
, though, then they no longer represent any departure from
![]() ${\textrm {STT}}$
. Working in
${\textrm {STT}}$
. Working in
![]() ${\textrm {STT}}$
, we can introduce an injective type-raising function,
${\textrm {STT}}$
, we can introduce an injective type-raising function,
![]() $\mathord {\uparrow }$
, from objects to type
$\mathord {\uparrow }$
, from objects to type
![]() $1$
properties; so
$1$
properties; so
![]() $a^0$
is an object, but
$a^0$
is an object, but
![]() $\mathord {\uparrow } a^0$
is a type
$\mathord {\uparrow } a^0$
is a type
![]() $1$
property (We also lay down rules to ensure that
$1$
property (We also lay down rules to ensure that
![]() $\mathord {\uparrow } a^0$
behaves as a suitable surrogate for ‘the
$\mathord {\uparrow } a^0$
behaves as a suitable surrogate for ‘the
![]() $a^1$
such that
$a^1$
such that
![]() $a^1 \mathrel {\equiv } a^0$
’; for details, see §C.) To avoid ambiguity, we can then rewrite
$a^1 \mathrel {\equiv } a^0$
’; for details, see §C.) To avoid ambiguity, we can then rewrite
![]() $c^2(a^0)$
as
$c^2(a^0)$
as
![]() $c^2(\mathord {\uparrow } a^0)$
, which is now well-formed according to
$c^2(\mathord {\uparrow } a^0)$
, which is now well-formed according to
![]() ${\textrm {STT}}$
’s type-restrictions.
${\textrm {STT}}$
’s type-restrictions.
This idea can be extended across all finite types. The result is
![]() ${\textrm {STT}_{\uparrow }}$
, which augments
${\textrm {STT}_{\uparrow }}$
, which augments
![]() ${\textrm {STT}}$
with a theory of type-raising functions, like
${\textrm {STT}}$
with a theory of type-raising functions, like
![]() $\mathord {\uparrow }$
, whilst retaining
$\mathord {\uparrow }$
, whilst retaining
![]() ${\textrm {STT}}$
’s type-restrictions. We can then prove the following strong result:
${\textrm {STT}}$
’s type-restrictions. We can then prove the following strong result:
![]() ${\textrm {CTT}^{\omega }}$
and
${\textrm {CTT}^{\omega }}$
and
![]() ${\textrm {STT}_{\uparrow }}$
are definitionally equivalent (where
${\textrm {STT}_{\uparrow }}$
are definitionally equivalent (where
![]() ${\textrm {CTT}^{\omega }}$
is the fragment of
${\textrm {CTT}^{\omega }}$
is the fragment of
![]() $\textrm {CTT}$
which uses all and only finite type indices; for details, see Appendix C).
$\textrm {CTT}$
which uses all and only finite type indices; for details, see Appendix C).
There is, however, an important limitation to this equivalence result. Since entities do not really cumulate in
![]() ${\textrm {STT}_{\uparrow }}$
,
${\textrm {STT}_{\uparrow }}$
,
![]() ${\textrm {STT}_{\uparrow }}$
cannot accommodate transfinite types, and so cannot recapture any transfinite uses of
${\textrm {STT}_{\uparrow }}$
cannot accommodate transfinite types, and so cannot recapture any transfinite uses of
![]() $\textrm {CTT}$
. This is significant, because Linnebo and Rayo’s main argument for
$\textrm {CTT}$
. This is significant, because Linnebo and Rayo’s main argument for
![]() $\textrm {CTT}$
invokes transfinite types (see Section 6). For this reason, Linnebo and Rayo must have intended
$\textrm {CTT}$
invokes transfinite types (see Section 6). For this reason, Linnebo and Rayo must have intended
![]() $\textrm {CTT}$
to be taken at face-value, rather than as a disguised form of
$\textrm {CTT}$
to be taken at face-value, rather than as a disguised form of
![]() ${\textrm {STT}_{\uparrow }}$
. Unfortunately for them, though, nothing could justify
${\textrm {STT}_{\uparrow }}$
. Unfortunately for them, though, nothing could justify
![]() $\textrm {CTT}$
’s type-restrictions, taken at face-value; that was the lesson of Section 4.
$\textrm {CTT}$
’s type-restrictions, taken at face-value; that was the lesson of Section 4.
6 The semantic argument
We have established an important difference between
![]() $\textrm {CTT}$
and
$\textrm {CTT}$
and
![]() ${\textrm {STT}}$
: nothing could justify
${\textrm {STT}}$
: nothing could justify
![]() $\textrm {CTT}$
’s type-restrictions, but the Fregean semantics can justify
$\textrm {CTT}$
’s type-restrictions, but the Fregean semantics can justify
![]() ${\textrm {STT}}$
’s type-restrictions. In this section, we will respond to Linnebo and Rayo’s Semantic Argument for
${\textrm {STT}}$
’s type-restrictions. In this section, we will respond to Linnebo and Rayo’s Semantic Argument for
![]() $\textrm {CTT}$
. This argument is designed to show that
$\textrm {CTT}$
. This argument is designed to show that
![]() ${\textrm {STT}}$
is semantically unstable, and that restoring stability pushes us to
${\textrm {STT}}$
is semantically unstable, and that restoring stability pushes us to
![]() $\textrm {CTT}$
. We will not present any new objections to
$\textrm {CTT}$
. We will not present any new objections to
![]() $\textrm {CTT}$
in this section; our aim is simply to explain how an advocate of the Fregean semantics should reply to Linnebo and Rayo.
$\textrm {CTT}$
in this section; our aim is simply to explain how an advocate of the Fregean semantics should reply to Linnebo and Rayo.
6.1 Naïve Optimism and Naïve Union
Linnebo and Rayo introduce us to two notions:
-
• A
 $\beta $
-order language is a language which contains variables of all (and only) the types
$\beta $
-order language is a language which contains variables of all (and only) the types
 $\alpha < \beta $
.Footnote
43
$\alpha < \beta $
.Footnote
43
-
• A generalized semantic theory for a language is ‘a theory of all possible interpretations the language might take’ [Reference Linnebo and Rayo23, p. 275]. In particular, a generalized semantic theory for a
 $\beta $
-order language provides an interpretation which allows any type
$\beta $
-order language provides an interpretation which allows any type
 $\alpha $
entity to be the value of a variable
$\alpha $
entity to be the value of a variable
 $x^\alpha $
, for each
$x^\alpha $
, for each
 $\alpha < \beta $
.Footnote
44
$\alpha < \beta $
.Footnote
44
These notions are connected by two formal results Linnebo and Rayo [Reference Linnebo and Rayo23, Appendix B]:
-
Blocker Theorem. No language can provide a generalized semantic theory for itself.
-
Enabler Theorem. For any
 $\beta $
, let
$\beta $
, let
 $\beta ^* = \beta + 2$
if
$\beta ^* = \beta + 2$
if
 $\beta $
is a limit and
$\beta $
is a limit and
 $\beta ^* = \beta +1$
otherwise; then a
$\beta ^* = \beta +1$
otherwise; then a
 $\beta ^*$
-order language can provide a generalized semantic theory for a
$\beta ^*$
-order language can provide a generalized semantic theory for a
 $\beta $
-order language.
$\beta $
-order language.
The Blocker Theorem holds by familiar, liar-like reasoning. Moreover, as Florio and Shapiro [Reference Florio and Shapiro12, pp. 162–163] note, it shows that these two principles are jointly inconsistent:
-
Naïve Optimism. Any language can be given a generalized semantic theory.
-
Naïve Union. For any languages, there is a union language, which combines all the expressions of those languages.
To see the problem: by Naïve Union, there is a language,
![]() $\mathscr {U}$
, which is the union of all languages; by Naïve Optimism,
$\mathscr {U}$
, which is the union of all languages; by Naïve Optimism,
![]() $\mathscr {U}$
can be given a generalized semantic theory in some language
$\mathscr {U}$
can be given a generalized semantic theory in some language
![]() $\mathscr {G}$
; by the Blocker Theorem,
$\mathscr {G}$
; by the Blocker Theorem,
![]() $\mathscr {G}$
is not a sub-language of
$\mathscr {G}$
is not a sub-language of
![]() $\mathscr {U}$
; but this contradicts the fact that
$\mathscr {U}$
; but this contradicts the fact that
![]() $\mathscr {U}$
is the union of all languages, including
$\mathscr {U}$
is the union of all languages, including
![]() $\mathscr {G}$
.
$\mathscr {G}$
.
6.2 Linnebo and Rayo’s Semantic Argument
Linnebo and Rayo avoid contradiction by restricting Naïve Union as follows:
-
Limited Union. For any limit
 $\lambda $
, if there is a
$\lambda $
, if there is a
 $\beta $
-order language for every
$\beta $
-order language for every
 $\beta < \lambda $
, then there is also a
$\beta < \lambda $
, then there is also a
 $\lambda $
-order language.Footnote
45
$\lambda $
-order language.Footnote
45
Having restricted Naïve Union in this way, Linnebo and Rayo’s [Reference Linnebo and Rayo23, pp. 275–281] Semantic Argument for
![]() $\textrm {CTT}$
now gets going. Here is a very brief summary. Suppose we start with an ordinary first-order language. By Naïve Optimism, this language has a generalized semantic theory. By the Blocker Theorem, this generalized semantic theory cannot be given in a first-order language; but, by the Enabler Theorem, it can be given in a second-order language. Naïve Optimism now requires that this second-order language has a generalized semantic theory; as before, the Blocker and Enabler theorems will lead us to provide this semantics in a third-order language. This process repeats, running through every finite order. At this point, Limited Union kicks in, giving us an
$\textrm {CTT}$
now gets going. Here is a very brief summary. Suppose we start with an ordinary first-order language. By Naïve Optimism, this language has a generalized semantic theory. By the Blocker Theorem, this generalized semantic theory cannot be given in a first-order language; but, by the Enabler Theorem, it can be given in a second-order language. Naïve Optimism now requires that this second-order language has a generalized semantic theory; as before, the Blocker and Enabler theorems will lead us to provide this semantics in a third-order language. This process repeats, running through every finite order. At this point, Limited Union kicks in, giving us an
![]() $\omega $
-order language which combines all of the finite orders into a single language. To present a generalized semantic theory for this language, Naïve Optimism and the Blocker and Enabler Theorems push us up to an
$\omega $
-order language which combines all of the finite orders into a single language. To present a generalized semantic theory for this language, Naïve Optimism and the Blocker and Enabler Theorems push us up to an
![]() $\omega \mathord {+}2$
-order language. And there is now no stopping us: Naïve Optimism, Limited Union and the two theorems keep pushing us to countenance languages of higher and higher orders. Moreover, when we supply the semantics for variables of some limit type
$\omega \mathord {+}2$
-order language. And there is now no stopping us: Naïve Optimism, Limited Union and the two theorems keep pushing us to countenance languages of higher and higher orders. Moreover, when we supply the semantics for variables of some limit type
![]() $\lambda $
, the only plausible option is to allow them to take all entities of all types
$\lambda $
, the only plausible option is to allow them to take all entities of all types
![]() $<\lambda $
as values. And this requires that at least some of our types be cumulative.
$<\lambda $
as values. And this requires that at least some of our types be cumulative.
6.3 Rebutting the semantic argument
We agree with the following conditional: if we accept both Naïve Optimism and Limited Union, then there is good reason to embrace
![]() $\textrm {CTT}$
. Our response is to reject Naïve Optimism (and to insist on Naïve Union). However, we will show that our stance is more principled that Linnebo and Rayo’s.
$\textrm {CTT}$
. Our response is to reject Naïve Optimism (and to insist on Naïve Union). However, we will show that our stance is more principled that Linnebo and Rayo’s.
Linnebo and Rayo [Reference Linnebo and Rayo23, p. 280] motivate Limited Union as follows: whenever you are ‘prepared to countenance languages of order
![]() $\beta $
for every
$\beta $
for every
![]() $\beta < \lambda $
’, you ‘should also countenance languages of order
$\beta < \lambda $
’, you ‘should also countenance languages of order
![]() $\lambda $
’, since ‘they would be made up entirely of vocabulary that had been previously deemed legitimate’. This line of reasoning is compelling. However, it clearly generalizes, to provide a motivation for Naïve Union. After all: whenever you are prepared to countenance some languages, you should also countenance their union, for that union would be made up entirely of vocabulary that had been previously deemed legitimate. In short: the only motivation Linnebo and Rayo offer for Limited Union is really a motivation for Naïve Union.
$\lambda $
’, since ‘they would be made up entirely of vocabulary that had been previously deemed legitimate’. This line of reasoning is compelling. However, it clearly generalizes, to provide a motivation for Naïve Union. After all: whenever you are prepared to countenance some languages, you should also countenance their union, for that union would be made up entirely of vocabulary that had been previously deemed legitimate. In short: the only motivation Linnebo and Rayo offer for Limited Union is really a motivation for Naïve Union.
Of course, Naïve Union is inconsistent with Naïve Optimism. So, if there were a stellar argument in favour of Naïve Optimism, we could see the retreat from Naïve Union to Limited Union as a simple instance of the heuristic that, on encountering a contradiction, we should aim to get as close as we can to what we initially wanted, without falling into inconsistency.Footnote
46
Regrettably, though, Linnebo and Rayo provide no argument for Naïve Optimism. So, prima facie, an equally good instance of that heuristic would be to accept Naïve Union and instead restrict Naïve Optimism. This threatens to leave us with a deadlock, between those who want to restrict Naïve Union (and so embrace
![]() $\textrm {CTT}$
), and those who want to restrict Naïve Optimism (and so might reject
$\textrm {CTT}$
), and those who want to restrict Naïve Optimism (and so might reject
![]() $\textrm {CTT}$
).
$\textrm {CTT}$
).
Fortunately, the argument of Section 5 provides a principled way to break the deadlock: if we are working with a Fregean semantics for the types, then we should restrict Naïve Optimism. Specifically, we should replace Naïve Optimism with the following:
-
Finite Optimism. Any language of any finite order can be given a generalized semantic theory.
To be clear: the motivation for this restriction is not simply to avoid contradiction. (As far as restoring formal consistency goes, Finite Optimism is serious overkill.) Rather, Finite Optimism expresses the exact amount of optimism which is even coherent on the Fregean semantics. Since Fregean types cannot cumulate, we cannot make any sense of the idea of an
![]() $\omega \mathord {+}2$
-order language on the Fregean semantics. Finite Optimism and Naïve Union push us to countenance an
$\omega \mathord {+}2$
-order language on the Fregean semantics. Finite Optimism and Naïve Union push us to countenance an
![]() $\omega $
-order language, like
$\omega $
-order language, like
![]() ${\textrm {STT}}$
itself, but we are pushed no further. Otherwise put:
${\textrm {STT}}$
itself, but we are pushed no further. Otherwise put:
![]() ${\textrm {STT}}$
is the principled limit on Fregean types.
${\textrm {STT}}$
is the principled limit on Fregean types.
7 Partially cumulative types
In this paper, we have critically discussed
![]() $\textrm {CTT}$
, which is the approach to cumulative types favoured by Linnebo and Rayo. In this final section, we will discuss an alternative approach to cumulative types, due to Florio and Jones [Reference Florio and Jones10, sec. 5].
$\textrm {CTT}$
, which is the approach to cumulative types favoured by Linnebo and Rayo. In this final section, we will discuss an alternative approach to cumulative types, due to Florio and Jones [Reference Florio and Jones10, sec. 5].
![]() $\textrm {CTT}$
is cumulative in two senses: first,
$\textrm {CTT}$
is cumulative in two senses: first,
![]() $b^\beta (a^\alpha )$
is well-formed whenever
$b^\beta (a^\alpha )$
is well-formed whenever
![]() $\beta> \alpha $
; second, the values of
$\beta> \alpha $
; second, the values of
![]() $x^\beta $
include all of the values of
$x^\beta $
include all of the values of
![]() $x^\alpha $
, whenever
$x^\alpha $
, whenever
![]() $\beta \geq \alpha $
. Florio and Jones’ cumulative type theory—call it
$\beta \geq \alpha $
. Florio and Jones’ cumulative type theory—call it
![]() ${\textrm {FJT}}$
—is cumulative only in the first of these senses. Indeed, for them, no type
${\textrm {FJT}}$
—is cumulative only in the first of these senses. Indeed, for them, no type
![]() $\alpha $
entity is a type
$\alpha $
entity is a type
![]() $\beta $
entity, when
$\beta $
entity, when
![]() $\alpha \neq \beta $
. As we will see, this difference between
$\alpha \neq \beta $
. As we will see, this difference between
![]() $\textrm {CTT}$
and
$\textrm {CTT}$
and
![]() ${\textrm {FJT}}$
is a double-edged sword: on the one hand, it provides Florio and Jones with the means to defend
${\textrm {FJT}}$
is a double-edged sword: on the one hand, it provides Florio and Jones with the means to defend
![]() ${\textrm {FJT}}$
from the argument we offered against
${\textrm {FJT}}$
from the argument we offered against
![]() $\textrm {CTT}$
in Section 4; on the other hand, it leaves so little distance between
$\textrm {CTT}$
in Section 4; on the other hand, it leaves so little distance between
![]() ${\textrm {FJT}}$
and
${\textrm {FJT}}$
and
![]() ${\textrm {STT}}$
, that
${\textrm {STT}}$
, that
![]() ${\textrm {FJT}}$
is best seen as a misleadingly formulated version of
${\textrm {FJT}}$
is best seen as a misleadingly formulated version of
![]() ${\textrm {STT}}$
.
${\textrm {STT}}$
.
7.1
 ${\textrm {FJT}}$
${\textrm {FJT}}$
Since entities do not cumulate up the types in
![]() ${\textrm {FJT}}$
, its quantifier rules must be more restrictive than
${\textrm {FJT}}$
, its quantifier rules must be more restrictive than
![]() $\textrm {CTT}$
’s (see Section 1.2). Indeed,
$\textrm {CTT}$
’s (see Section 1.2). Indeed,
![]() ${\textrm {FJT}}$
has exactly the same quantifier rules as
${\textrm {FJT}}$
has exactly the same quantifier rules as
![]() ${\textrm {STT}}$
(see Section 1.1). Consequently, in
${\textrm {STT}}$
(see Section 1.1). Consequently, in
![]() ${\textrm {FJT}}$
, you cannot generalize about everything that has a type
${\textrm {FJT}}$
, you cannot generalize about everything that has a type
![]() $2$
property by writing
$2$
property by writing
![]() $\forall x^1(a^2(x^1) \rightarrow \phi (x^1))$
.Footnote
47
In
$\forall x^1(a^2(x^1) \rightarrow \phi (x^1))$
.Footnote
47
In
![]() ${\textrm {FJT}}$
, that formula generalizes over every type 1 property that has
${\textrm {FJT}}$
, that formula generalizes over every type 1 property that has
![]() $a^2$
, but it says nothing about any objects that have it. To cover everything that might have
$a^2$
, but it says nothing about any objects that have it. To cover everything that might have
![]() $a^2$
, we must conjoin that formula with
$a^2$
, we must conjoin that formula with
![]() $\forall x^0(a^2(x^0) \rightarrow \phi (x^0))$
. Indeed, to generalize over everything that might have a type n property, we will need n conjuncts. This is illustrated by Florio and Jones [Reference Florio and Linnebo11, p. 55] version of Comprehension:
$\forall x^0(a^2(x^0) \rightarrow \phi (x^0))$
. Indeed, to generalize over everything that might have a type n property, we will need n conjuncts. This is illustrated by Florio and Jones [Reference Florio and Linnebo11, p. 55] version of Comprehension:
-
 ${FJT}$
-Comprehension.
${FJT}$
-Comprehension.
 $\exists z^n\bigwedge _{i < n}\forall x^i (z^n(x^i) \leftrightarrow \phi _i(x^i))$
, for each
$\exists z^n\bigwedge _{i < n}\forall x^i (z^n(x^i) \leftrightarrow \phi _i(x^i))$
, for each
 $n> 0$
, whenever each
$n> 0$
, whenever each
 $\phi _i(x^i)$
is well-formed and does not contain
$\phi _i(x^i)$
is well-formed and does not contain
 $z^n$
.
$z^n$
.
The various
![]() $\phi _i$
s need have nothing in common, so this is an instance of
$\phi _i$
s need have nothing in common, so this is an instance of
![]() ${\textrm {FJT}}$
-Comprehension:
${\textrm {FJT}}$
-Comprehension:
As Florio and Jones [Reference Florio and Jones10, p. 61] observe, this entails
![]() $\forall x^0 \forall y^1\phantom {)} x^0 \mathrel {\not \equiv } y^1$
, where
$\forall x^0 \forall y^1\phantom {)} x^0 \mathrel {\not \equiv } y^1$
, where
![]() $\mathrel {\equiv }$
is defined as before. More generally, in
$\mathrel {\equiv }$
is defined as before. More generally, in
![]() ${\textrm {FJT}}$
, if
${\textrm {FJT}}$
, if
![]() $n \neq m$
then
$n \neq m$
then
![]() $\forall x^n \forall y^m\phantom {(}x^n\mathrel {\not \equiv } y^m$
. So
$\forall x^n \forall y^m\phantom {(}x^n\mathrel {\not \equiv } y^m$
. So
![]() ${\textrm {FJT}}$
contradicts
${\textrm {FJT}}$
contradicts
![]() $\textrm {CTT}$
’s Type-Raising principle (see Section 1.2).
$\textrm {CTT}$
’s Type-Raising principle (see Section 1.2).
7.2
 ${\textrm {FJT}}$
is finitary
${\textrm {FJT}}$
is finitary
In formulating
![]() ${\textrm {FJT}}$
-Comprehension, we have reverted to using natural numbers as type indices, rather than allowing that types might be transfinite (contrast the formulation of
${\textrm {FJT}}$
-Comprehension, we have reverted to using natural numbers as type indices, rather than allowing that types might be transfinite (contrast the formulation of
![]() $\textrm {CTT}$
-Comprehension in Section 1.2). We have done this for a simple reason: formulating
$\textrm {CTT}$
-Comprehension in Section 1.2). We have done this for a simple reason: formulating
![]() ${\textrm {FJT}}$
-Comprehension for a transfinite type,
${\textrm {FJT}}$
-Comprehension for a transfinite type,
![]() $\beta $
, would require infinitary conjunction:
$\beta $
, would require infinitary conjunction:
But
![]() ${\textrm {FJT}}$
does not allow for infinitary conjunction. Consequently,
${\textrm {FJT}}$
does not allow for infinitary conjunction. Consequently,
![]() ${\textrm {FJT}}$
cannot comprehend any transfinite types.Footnote
48
${\textrm {FJT}}$
cannot comprehend any transfinite types.Footnote
48
Much of our discussion of
![]() $\textrm {CTT}$
focussed on the Sets-from-Types Theorem (see Section 2–3). However, due to its finitary nature,
$\textrm {CTT}$
focussed on the Sets-from-Types Theorem (see Section 2–3). However, due to its finitary nature,
![]() ${\textrm {FJT}}$
cannot establish any similar result. Indeed, if we add surrogates for purity and extensionality to
${\textrm {FJT}}$
cannot establish any similar result. Indeed, if we add surrogates for purity and extensionality to
![]() ${\textrm {FJT}}$
, the resulting theory is decidable.Footnote
49
${\textrm {FJT}}$
, the resulting theory is decidable.Footnote
49
7.3 Interpreting
 ${\textrm {FJT}}$
’s types
${\textrm {FJT}}$
’s types
Having discussed the Sets-from-Types Theorem, we then argued that
![]() $\textrm {CTT}$
’s type-restrictions cannot be justified semantically (see Section 4). We began with Linnebo and Rayo [Reference Linnebo and Rayo23, pp. 282–283] observation that, even if we stuck with the stringent formation rules for
$\textrm {CTT}$
’s type-restrictions cannot be justified semantically (see Section 4). We began with Linnebo and Rayo [Reference Linnebo and Rayo23, pp. 282–283] observation that, even if we stuck with the stringent formation rules for
![]() $\textrm {CTT}$
, we could always apply
$\textrm {CTT}$
, we could always apply
![]() $b^\beta $
to
$b^\beta $
to
![]() $a^\alpha $
in
$a^\alpha $
in
![]() $\textrm {CTT}$
with the formula
$\textrm {CTT}$
with the formula
![]() $a^\alpha \mathrel {\varepsilon } b^\beta $
, which is defined as follows (where
$a^\alpha \mathrel {\varepsilon } b^\beta $
, which is defined as follows (where
![]() $\gamma = \max (\alpha , \beta )+1$
):
$\gamma = \max (\alpha , \beta )+1$
):
We then argued that, since every type of entity can be applied to every type of entity in
![]() $\textrm {CTT}$
, there can be no barrier to introducing untyped variables.
$\textrm {CTT}$
, there can be no barrier to introducing untyped variables.
This line of argument is not straightforwardly applicable to
![]() ${\textrm {FJT}}$
. Since entities do not cumulate up the types in
${\textrm {FJT}}$
. Since entities do not cumulate up the types in
![]() ${\textrm {FJT}}$
,
${\textrm {FJT}}$
,
![]() $b^n$
is not identical to any entity of type
$b^n$
is not identical to any entity of type
![]() $k \neq n$
. So, as Florio and Jones [Reference Florio and Jones10, sec. 7] stress, it is doubtful whether
$k \neq n$
. So, as Florio and Jones [Reference Florio and Jones10, sec. 7] stress, it is doubtful whether
![]() $a^m \mathrel {\varepsilon } b^n$
, i.e.,
$a^m \mathrel {\varepsilon } b^n$
, i.e.,
![]() $(\exists x^{k} \mathrel {\equiv } b^n) x^{k}(a^m)$
with
$(\exists x^{k} \mathrel {\equiv } b^n) x^{k}(a^m)$
with
![]() $k = \max (m,n)+1$
, provides us with a way of applying
$k = \max (m,n)+1$
, provides us with a way of applying
![]() $b^n$
to
$b^n$
to
![]() $a^m$
in
$a^m$
in
![]() ${\textrm {FJT}}$
.
${\textrm {FJT}}$
.
Nonetheless, we are still left with the question of how to justify the type-restrictions imposed by
![]() ${\textrm {FJT}}$
. Florio and Jones [Reference Florio and Jones10, pp. 45–47] explicitly intend to provide
${\textrm {FJT}}$
. Florio and Jones [Reference Florio and Jones10, pp. 45–47] explicitly intend to provide
![]() ${\textrm {FJT}}$
with some version of the conceptual semantics, but it is unclear which version they could have in mind. The referentialist version that we discussed in Section 5.2 licenses the use of an untyped variable; the Fregean version that we discussed in Section 5.3 justifies
${\textrm {FJT}}$
with some version of the conceptual semantics, but it is unclear which version they could have in mind. The referentialist version that we discussed in Section 5.2 licenses the use of an untyped variable; the Fregean version that we discussed in Section 5.3 justifies
![]() ${\textrm {STT}}$
’s type-restrictions; so it seems that neither of these versions of the conceptual semantics could serve their purpose.
${\textrm {STT}}$
’s type-restrictions; so it seems that neither of these versions of the conceptual semantics could serve their purpose.
In fact, appearances are somewhat misleading here. It is true that, when
![]() ${\textrm {FJT}}$
is taken at face value, the Fregean semantics cannot justify its type-restrictions. However, it turns out that the Fregean semantics can make good sense of
${\textrm {FJT}}$
is taken at face value, the Fregean semantics cannot justify its type-restrictions. However, it turns out that the Fregean semantics can make good sense of
![]() ${\textrm {FJT}}$
, if its terms are interpreted as being systematically ambiguous, in the following way: in ‘
${\textrm {FJT}}$
, if its terms are interpreted as being systematically ambiguous, in the following way: in ‘
![]() $c^2(b^1)$
’, ‘
$c^2(b^1)$
’, ‘
![]() $c^2$
’ expresses a type
$c^2$
’ expresses a type
![]() $2$
property, but in ‘
$2$
property, but in ‘
![]() $c^2(a^0)$
’, it expresses a type
$c^2(a^0)$
’, it expresses a type
![]() $1$
property. (Compare the interpretation of
$1$
property. (Compare the interpretation of
![]() $\textrm {CTT}$
in
$\textrm {CTT}$
in
![]() ${\textrm {STT}_{\uparrow }}$
of Section 5.4.)Footnote
50
${\textrm {STT}_{\uparrow }}$
of Section 5.4.)Footnote
50
This ambiguity can easily be handled by augmenting
![]() ${\textrm {STT}}$
with a theory of type-lowering relations. We start by introducing a type-lowering relation,
${\textrm {STT}}$
with a theory of type-lowering relations. We start by introducing a type-lowering relation,
![]() $\triangleright $
, from type
$\triangleright $
, from type
![]() $2$
to type
$2$
to type
![]() $1$
. We then read ‘
$1$
. We then read ‘
![]() $c^2(b^1)$
’ verbatim, but treat ‘
$c^2(b^1)$
’ verbatim, but treat ‘
![]() $c^2(a^0)$
’ as shorthand for ‘
$c^2(a^0)$
’ as shorthand for ‘
![]() $\forall x^1 (c^2\triangleright x^1\rightarrow x^1(a^0))$
’. This latter formula is perfectly well-formed according to
$\forall x^1 (c^2\triangleright x^1\rightarrow x^1(a^0))$
’. This latter formula is perfectly well-formed according to
![]() ${\textrm {STT}}$
’s type-constraints, and the idea can be extended across all types. The resulting theory is
${\textrm {STT}}$
’s type-constraints, and the idea can be extended across all types. The resulting theory is
![]() ${\textrm {STT}_{\triangleright }}$
. We can then prove that
${\textrm {STT}_{\triangleright }}$
. We can then prove that
![]() ${\textrm {FJT}}$
and
${\textrm {FJT}}$
and
![]() ${\textrm {STT}_{\triangleright }}$
are definitionally equivalent. (For details and proof, see Appendix D.)
${\textrm {STT}_{\triangleright }}$
are definitionally equivalent. (For details and proof, see Appendix D.)
We think that
![]() ${\textrm {FJT}}$
is best understood as a (somewhat misleading) formulation of
${\textrm {FJT}}$
is best understood as a (somewhat misleading) formulation of
![]() ${\textrm {STT}_{\triangleright }}$
. To begin with, there is no obvious reason to resist this interpretation of
${\textrm {STT}_{\triangleright }}$
. To begin with, there is no obvious reason to resist this interpretation of
![]() ${\textrm {FJT}}$
. Linnebo and Rayo had a clear technical reason for refusing to interpret
${\textrm {FJT}}$
. Linnebo and Rayo had a clear technical reason for refusing to interpret
![]() $\textrm {CTT}$
via
$\textrm {CTT}$
via
![]() ${\textrm {STT}_{\uparrow }}$
: the major selling point of
${\textrm {STT}_{\uparrow }}$
: the major selling point of
![]() $\textrm {CTT}$
was meant to be its ability to accommodate transfinite types (see Section 6). But, as we saw in Section 7.2,
$\textrm {CTT}$
was meant to be its ability to accommodate transfinite types (see Section 6). But, as we saw in Section 7.2,
![]() ${\textrm {FJT}}$
is just as limited to finite types as
${\textrm {FJT}}$
is just as limited to finite types as
![]() ${\textrm {STT}}$
. So
${\textrm {STT}}$
. So
![]() ${\textrm {FJT}}$
, like
${\textrm {FJT}}$
, like
![]() ${\textrm {STT}}$
, cannot go beyond Finite Optimism.
${\textrm {STT}}$
, cannot go beyond Finite Optimism.
Not only is there no reason for Florio and Jones to resist the interpretation of
![]() ${\textrm {FJT}}$
as
${\textrm {FJT}}$
as
![]() ${\textrm {STT}_{\triangleright }}$
, there is good reason for them adopt it. Their Reference Florio and Jones[10] main aim is to argue that cumulative type theories can accommodate absolute generality. However, as we will now show,
${\textrm {STT}_{\triangleright }}$
, there is good reason for them adopt it. Their Reference Florio and Jones[10] main aim is to argue that cumulative type theories can accommodate absolute generality. However, as we will now show,
![]() ${\textrm {FJT}}$
can accommodate absolute generality iff it is taken as a mere notational variant of
${\textrm {FJT}}$
can accommodate absolute generality iff it is taken as a mere notational variant of
![]() ${\textrm {STT}_{\triangleright }}$
.
${\textrm {STT}_{\triangleright }}$
.
7.4
 ${\textrm {STT}}$
accommodates absolute generality
${\textrm {STT}}$
accommodates absolute generality
We start by explaining how
![]() ${\textrm {STT}}$
accommodates absolute generality.
${\textrm {STT}}$
accommodates absolute generality.
In traditional set-theoretic semantics, domains are taken to be sets. In
![]() ${\textrm {STT}}$
, we can think of them as properties. For example, we can think of a domain of objects as a type 1 property,
${\textrm {STT}}$
, we can think of them as properties. For example, we can think of a domain of objects as a type 1 property,
![]() $d^1$
, and we can say that
$d^1$
, and we can say that
![]() $x^0$
is in that domain iff
$x^0$
is in that domain iff
![]() $d^1(x^0)$
. As Williamson Reference Williamson[43] clearly explains, there is a real advantage to thinking of domains in this type-theoretic way. There is no set of all objects, and so if we think of domains as sets, unrestricted quantification over all objects is impossible. But
$d^1(x^0)$
. As Williamson Reference Williamson[43] clearly explains, there is a real advantage to thinking of domains in this type-theoretic way. There is no set of all objects, and so if we think of domains as sets, unrestricted quantification over all objects is impossible. But
![]() ${\textrm {STT}}$
straightforwardly supplies a type
${\textrm {STT}}$
straightforwardly supplies a type
![]() $1$
property,
$1$
property,
![]() $U^1$
, held by all objects, i.e.:Footnote
51
$U^1$
, held by all objects, i.e.:Footnote
51
(Nothing special is signified by our use of a capitalized ‘U’ here; it simply aids readability.)
Whilst
![]() $U^1$
includes all the objects, one might worry that it is still restricted, since it includes no type
$U^1$
includes all the objects, one might worry that it is still restricted, since it includes no type
![]() $1$
properties. But, in the context of
$1$
properties. But, in the context of
![]() ${\textrm {STT}}$
, this worry is toothless; no sense can be made of this idea in
${\textrm {STT}}$
, this worry is toothless; no sense can be made of this idea in
![]() ${\textrm {STT}}$
. To regard
${\textrm {STT}}$
. To regard
![]() $U^1$
as restricted, we would have to be able to make sense of the idea of a more inclusive domain, which contains both objects and properties.Footnote
52
But that is incoherent in
$U^1$
as restricted, we would have to be able to make sense of the idea of a more inclusive domain, which contains both objects and properties.Footnote
52
But that is incoherent in
![]() ${\textrm {STT}}$
. To say ‘d contains both objects and properties’ is to say
${\textrm {STT}}$
. To say ‘d contains both objects and properties’ is to say
![]() $\exists x^0\exists y^1(d(x^0) \land d(y^1))$
, which is just ungrammatical in
$\exists x^0\exists y^1(d(x^0) \land d(y^1))$
, which is just ungrammatical in
![]() ${\textrm {STT}}$
. For
${\textrm {STT}}$
. For
![]() $d(x^0)$
to be grammatical, d must be type
$d(x^0)$
to be grammatical, d must be type
![]() $1$
; for
$1$
; for
![]() $d(y^1)$
to be grammatical, d must be type
$d(y^1)$
to be grammatical, d must be type
![]() $2$
; but every term has a unique type.
$2$
; but every term has a unique type.
Suppose, then, we introduce suitably typed domains,
![]() $d^1$
and
$d^1$
and
![]() $d^2$
. In
$d^2$
. In
![]() ${\textrm {STT}}$
, these domains are incommensurable, to use Williamson’s [Reference Williamson43, p. 458] phrase. This does not mean that
${\textrm {STT}}$
, these domains are incommensurable, to use Williamson’s [Reference Williamson43, p. 458] phrase. This does not mean that
![]() $d^1$
and
$d^1$
and
![]() $d^2$
have different members; it means that we cannot even express the idea that they have the same (or different) members. We might put this by saying that, in
$d^2$
have different members; it means that we cannot even express the idea that they have the same (or different) members. We might put this by saying that, in
![]() ${\textrm {STT}}$
, we cannot articulate a univocal notion of Thing or Entity which applies to both objects and properties. (We can still talk about ‘type
${\textrm {STT}}$
, we cannot articulate a univocal notion of Thing or Entity which applies to both objects and properties. (We can still talk about ‘type
![]() $0$
entities’, ‘type
$0$
entities’, ‘type
![]() $1$
entities’, etc., but we cannot think of ‘entity’ as a recurring categorematic component in these constructions.) So, if a first-order quantifier quantifies over all objects, then it quantifies over absolutely every thing it makes sense to imagine that it might quantify over.
$1$
entities’, etc., but we cannot think of ‘entity’ as a recurring categorematic component in these constructions.) So, if a first-order quantifier quantifies over all objects, then it quantifies over absolutely every thing it makes sense to imagine that it might quantify over.
We can put the same point slightly differently by drawing on Florio and Jones’ [Reference Florio and Jones10, p. 49] explication of unrestrictedness: ‘an unrestricted domain is a domain such that true universal quantification over it precludes there from being absolutely any counterexamples whatsoever.’Footnote
53
This informal explication can be converted into a formal definition in
![]() ${\textrm {STT}}$
. To say that ‘everything melted’ is true over the domain things in the freezer is just to say that
${\textrm {STT}}$
. To say that ‘everything melted’ is true over the domain things in the freezer is just to say that
![]() $\forall x(x \mbox{ is in the freezer }\rightarrow x \textrm { melted})$
. More generally, to say that
$\forall x(x \mbox{ is in the freezer }\rightarrow x \textrm { melted})$
. More generally, to say that
![]() $\forall x^{n-1} y^{n}(x^{n-1})$
is true over domain
$\forall x^{n-1} y^{n}(x^{n-1})$
is true over domain
![]() $d^{n}$
is just to say
$d^{n}$
is just to say
![]() $\forall x^{n-1}(d^{n}(x^{n-1}) \rightarrow y^{n}(x^{n-1}))$
. To say that there are absolutely no counterexamples to this restricted generalization is to say that the generalization still holds good even when we lift the restriction, and return to
$\forall x^{n-1}(d^{n}(x^{n-1}) \rightarrow y^{n}(x^{n-1}))$
. To say that there are absolutely no counterexamples to this restricted generalization is to say that the generalization still holds good even when we lift the restriction, and return to
![]() $\forall x^{n-1} y^{n}(x^{n-1})$
. And finally, to say that there are absolutely no counterexamples to any true quantification over
$\forall x^{n-1} y^{n}(x^{n-1})$
. And finally, to say that there are absolutely no counterexamples to any true quantification over
![]() $d^{n}$
is just to generalize over all
$d^{n}$
is just to generalize over all
![]() $y^{n}$
. Assembling this, we obtain, for all
$y^{n}$
. Assembling this, we obtain, for all
![]() $n> 0$
:
$n> 0$
:
-
(1)
 $d^{n}$
is unrestricted
$d^{n}$
is unrestricted
 $\mathrel {\textrm {iff}_{\textrm {df}}}$
$\mathrel {\textrm {iff}_{\textrm {df}}}$
 $$ \begin{align*}\forall y^{n}(\forall x^{n-1}(d^{n}(x^{n-1})\rightarrow y^{n}(x^{n-1}))\rightarrow \forall x^{n-1}y^{n}(x^{n-1})).\end{align*} $$
$$ \begin{align*}\forall y^{n}(\forall x^{n-1}(d^{n}(x^{n-1})\rightarrow y^{n}(x^{n-1}))\rightarrow \forall x^{n-1}y^{n}(x^{n-1})).\end{align*} $$
This definition is adequate because, in
![]() ${\textrm {STT}}$
, only generalizations of the form
${\textrm {STT}}$
, only generalizations of the form
![]() $\forall x^{n-1} y^{n}(x^{n-1})$
can be true over
$\forall x^{n-1} y^{n}(x^{n-1})$
can be true over
![]() $d^{n}$
. And
$d^{n}$
. And
![]() $U^1$
, as introduced at the start of this subsection, is unrestricted according to (1): since
$U^1$
, as introduced at the start of this subsection, is unrestricted according to (1): since
![]() $\forall x^0U^1(x^0)$
, if
$\forall x^0U^1(x^0)$
, if
![]() $\forall x^0(U^1(x^0)\rightarrow y^1(x^0))$
, it immediately follows that
$\forall x^0(U^1(x^0)\rightarrow y^1(x^0))$
, it immediately follows that
![]() $\forall x^0 y^1(x^0)$
. More generally, within
$\forall x^0 y^1(x^0)$
. More generally, within
![]() ${\textrm {STT}}$
, it is obvious that
${\textrm {STT}}$
, it is obvious that
![]() $d^{n}$
is unrestricted iff
$d^{n}$
is unrestricted iff
![]() $\forall x^{n-1} d^{n}(x^{n-1})$
.
$\forall x^{n-1} d^{n}(x^{n-1})$
.
7.5 Absolute generality in
 ${\textrm {FJT}}$
${\textrm {FJT}}$
We have seen that
![]() ${\textrm {STT}}$
can accommodate absolute generality. So, if we read
${\textrm {STT}}$
can accommodate absolute generality. So, if we read
![]() ${\textrm {FJT}}$
as a (misleadingly formulated) notational variant of
${\textrm {FJT}}$
as a (misleadingly formulated) notational variant of
![]() ${\textrm {STT}_{\triangleright }}$
, then
${\textrm {STT}_{\triangleright }}$
, then
![]() ${\textrm {FJT}}$
can equally accommodate absolute generality. But, as we will now show,
${\textrm {FJT}}$
can equally accommodate absolute generality. But, as we will now show,
![]() ${\textrm {FJT}}$
cannot accommodate absolute generality if it is taken at face-value.
${\textrm {FJT}}$
cannot accommodate absolute generality if it is taken at face-value.
To establish this, we will assume in what follows that
![]() ${\textrm {FJT}}$
is to be taken at face-value, so that
${\textrm {FJT}}$
is to be taken at face-value, so that
![]() $d^2(y^1)$
and
$d^2(y^1)$
and
![]() $d^2(x^0)$
apply the very same type
$d^2(x^0)$
apply the very same type
![]() $2$
property to
$2$
property to
![]() $y^1$
and
$y^1$
and
![]() $x^0$
. (That assumption will remain in force until we explicitly lift it in Section 7.7.) So understood,
$x^0$
. (That assumption will remain in force until we explicitly lift it in Section 7.7.) So understood,
![]() ${\textrm {FJT}}$
allows type
${\textrm {FJT}}$
allows type
![]() $2$
properties to serve as domains containing both objects and type 1 properties. In fact,
$2$
properties to serve as domains containing both objects and type 1 properties. In fact,
![]() ${\textrm {FJT}}$
delivers a domain,
${\textrm {FJT}}$
delivers a domain,
![]() $U^2$
, which contains all type
$U^2$
, which contains all type
![]() $1$
properties and all objects, i.e., such that:Footnote
54
$1$
properties and all objects, i.e., such that:Footnote
54
But now first-order quantification becomes a form of restricted quantification: in a clear sense,
![]() $U^1$
is a restriction of
$U^1$
is a restriction of
![]() $U^2$
, since
$U^2$
, since
![]() $U^2$
contains everything in
$U^2$
contains everything in
![]() $U^1$
, and more besides.Footnote
55
$U^1$
, and more besides.Footnote
55
The point here is that
![]() ${\textrm {FJT}}$
does treat objects and type
${\textrm {FJT}}$
does treat objects and type
![]() $1$
properties as a species of a single genus. Indeed, for each
$1$
properties as a species of a single genus. Indeed, for each
![]() $n>0$
, we can think of Thing
$n>0$
, we can think of Thing
![]() $^{n}$
as the property
$^{n}$
as the property
![]() $U^{n}$
such that
$U^{n}$
such that
![]() $\bigwedge _{m < n} \forall x^mU^{n}(x^m)$
. So in
$\bigwedge _{m < n} \forall x^mU^{n}(x^m)$
. So in
![]() ${\textrm {FJT}}$
, it makes sense, and is true, to say that first-order quantifiers quantify over some things but not others.Footnote
56
${\textrm {FJT}}$
, it makes sense, and is true, to say that first-order quantifiers quantify over some things but not others.Footnote
56
Again, we can make the same point in terms of Florio and Jones’ idea that
![]() $d^n$
is unrestricted iff there are absolutely no counterexamples to any universal generalization which is true over
$d^n$
is unrestricted iff there are absolutely no counterexamples to any universal generalization which is true over
![]() $d^n$
. Applied to
$d^n$
. Applied to
![]() ${\textrm {FJT}}$
, this does not quite yield a simple definition of unrestrictedness,Footnote
57
but it does yield a schematic necessary condition for unrestrictedness: if
${\textrm {FJT}}$
, this does not quite yield a simple definition of unrestrictedness,Footnote
57
but it does yield a schematic necessary condition for unrestrictedness: if
![]() $d^{n}$
is unrestricted, and
$d^{n}$
is unrestricted, and
![]() $y^{m}$
is true of everything in
$y^{m}$
is true of everything in
![]() $d^{n}$
that it can be meaningfully applied to, then
$d^{n}$
that it can be meaningfully applied to, then
![]() $y^m$
is true of absolutely everything it can be meaningfully applied to. Formalizing this intuitive idea, we obtain the following, for all
$y^m$
is true of absolutely everything it can be meaningfully applied to. Formalizing this intuitive idea, we obtain the following, for all
![]() $m,n> 0$
:
$m,n> 0$
:
-
(2)
 $d^{n}$
is unrestricted
$d^{n}$
is unrestricted
 $\rightarrow $
$\rightarrow $
 $\qquad\qquad\phantom{sssssss}\forall y^{m}(\bigwedge _{i < \min (m, n)}\forall x^{i}(d^{n}(x^{i})\rightarrow y^{m}(x^{i}))\rightarrow \bigwedge _{i < m}\forall x^{i} y^{m}(x^{i})).$
$\qquad\qquad\phantom{sssssss}\forall y^{m}(\bigwedge _{i < \min (m, n)}\forall x^{i}(d^{n}(x^{i})\rightarrow y^{m}(x^{i}))\rightarrow \bigwedge _{i < m}\forall x^{i} y^{m}(x^{i})).$
This makes
![]() $U^1$
restricted, since
$U^1$
restricted, since
![]() ${\textrm {FJT}}$
yields an
${\textrm {FJT}}$
yields an
![]() $H^2$
which applies to every object but to no type
$H^2$
which applies to every object but to no type
![]() $1$
property, i.e., such that:Footnote
58
$1$
property, i.e., such that:Footnote
58
Clearly
![]() $\forall x^0(U^1(x^{0}) \rightarrow H^2(x^0))$
, but
$\forall x^0(U^1(x^{0}) \rightarrow H^2(x^0))$
, but
![]() $\lnot \forall x^1 H^2(x^1)$
; so
$\lnot \forall x^1 H^2(x^1)$
; so
![]() $U^1$
is restricted by (2).Footnote
59
A similar argument shows that every domain of every type is restricted in
$U^1$
is restricted by (2).Footnote
59
A similar argument shows that every domain of every type is restricted in
![]() ${\textrm {FJT}}$
.Footnote
60
(And the same style of argument shows that no domain is unrestricted in
${\textrm {FJT}}$
.Footnote
60
(And the same style of argument shows that no domain is unrestricted in
![]() $\textrm {CTT}$
.)Footnote
61
$\textrm {CTT}$
.)Footnote
61
7.6 Florio and Jones on (R=U)
Our argument that every domain is restricted in
![]() ${\textrm {FJT}}$
was based on Florio and Jones’ own explication of unrestrictedness. But they thought that
${\textrm {FJT}}$
was based on Florio and Jones’ own explication of unrestrictedness. But they thought that
![]() ${\textrm {FJT}}$
could accommodate absolute generality. In this subsection, we will lay out their reasoning, and explain why it was mistaken.
${\textrm {FJT}}$
could accommodate absolute generality. In this subsection, we will lay out their reasoning, and explain why it was mistaken.
Alongside their explication of unrestrictedness, Florio and Jones [Reference Florio and Jones10, p. 51] introduce a further notion: a domain is Russellian for a generalization
![]() $\forall v Fv$
iff it coincides with the range of significance of the predicate F, i.e., the range of things that F can be meaningfully applied to. They then propose [Reference Florio and Jones10, pp. 51–53]:
$\forall v Fv$
iff it coincides with the range of significance of the predicate F, i.e., the range of things that F can be meaningfully applied to. They then propose [Reference Florio and Jones10, pp. 51–53]:
-
(R=U) A domain is Russellian iff it is unrestricted.
Here is the idea behind (R=U): a counterexample to
![]() $\forall v Fv$
would be something of which F is false; but F does not say anything (whether true or false) of the things which fall outside of its range of significance; so if
$\forall v Fv$
would be something of which F is false; but F does not say anything (whether true or false) of the things which fall outside of its range of significance; so if
![]() $\forall v Fv$
is true over d, and d is Russellian for
$\forall v Fv$
is true over d, and d is Russellian for
![]() $\forall v Fv$
, then there cannot be any counterexamples to
$\forall v Fv$
, then there cannot be any counterexamples to
![]() $\forall v Fv$
; so d is unrestricted for
$\forall v Fv$
; so d is unrestricted for
![]() $\forall v Fv$
.
$\forall v Fv$
.
Florio and Jones [Reference Florio and Jones10, pp. 57–58] attempt to use (R=U) as follows. The domain
![]() $U^1$
is Russellian for the generalization
$U^1$
is Russellian for the generalization
![]() $\forall x^0 a^1(x^0)$
: after all, type 1 terms express type 1 properties, and type 1 properties apply meaningfully only to objects.Footnote
62
So if we read
$\forall x^0 a^1(x^0)$
: after all, type 1 terms express type 1 properties, and type 1 properties apply meaningfully only to objects.Footnote
62
So if we read
![]() $\forall x^0 a^1(x^0)$
as a quantification over
$\forall x^0 a^1(x^0)$
as a quantification over
![]() $U^1$
, then by (R=U) it is unrestricted. Whilst
$U^1$
, then by (R=U) it is unrestricted. Whilst
![]() $U^1$
is a strict sub-domain of
$U^1$
is a strict sub-domain of
![]() $U^2$
, none of the extra entities in
$U^2$
, none of the extra entities in
![]() $U^2$
fall within
$U^2$
fall within
![]() $a^1$
’s range of significance.
$a^1$
’s range of significance.
Our basic problem with (R=U) is quite simple: there is a fundamental mismatch between the R and the U. Unrestrictedness is normally understood in absolute terms: either a domain is absolutely unrestricted, or it is not. By contrast, Florio and Jones’ notion of Russellianness is a relative matter: a domain is not just Russellian full stop; it is only ever Russellian for a generalization
![]() $\forall v Fv$
. This basic problem can be overcome in
$\forall v Fv$
. This basic problem can be overcome in
![]() ${\textrm {STT}}$
, but not in
${\textrm {STT}}$
, but not in
![]() ${\textrm {FJT}}$
.
${\textrm {FJT}}$
.
In
![]() ${\textrm {STT}}$
, a property
${\textrm {STT}}$
, a property
![]() $d^{n}$
can (meaningfully) be a domain for, and only for, generalizations of the form
$d^{n}$
can (meaningfully) be a domain for, and only for, generalizations of the form
![]() $\forall x^{n-1} y^{n}(x^{n-1})$
. After all, if we attempt to relativize the generalization
$\forall x^{n-1} y^{n}(x^{n-1})$
. After all, if we attempt to relativize the generalization
![]() $\forall y^{m}(x^i)$
to
$\forall y^{m}(x^i)$
to
![]() $d^{n}$
, obtaining
$d^{n}$
, obtaining
![]() $\forall x^i(d^{n}(x^i) \rightarrow y^{m}(x^i))$
, then the result is grammatical in
$\forall x^i(d^{n}(x^i) \rightarrow y^{m}(x^i))$
, then the result is grammatical in
![]() ${\textrm {STT}}$
iff
${\textrm {STT}}$
iff
![]() $n = m = i+1$
. Consequently, the relativity involved in Russellianness can be safely ignored: it would not even make sense to say that
$n = m = i+1$
. Consequently, the relativity involved in Russellianness can be safely ignored: it would not even make sense to say that
![]() $d^{n}$
is Russellian for
$d^{n}$
is Russellian for
![]() $\forall x^{m-1} y^{m}(x^{m-1})$
when
$\forall x^{m-1} y^{m}(x^{m-1})$
when
![]() $n\neq m$
. Indeed, since the range of significance of any type n property in
$n\neq m$
. Indeed, since the range of significance of any type n property in
![]() ${\textrm {STT}}$
is always exactly the type
${\textrm {STT}}$
is always exactly the type
![]() $n\mathord {-}1$
entities, we can say that
$n\mathord {-}1$
entities, we can say that
![]() $d^{n}$
is Russellian
$d^{n}$
is Russellian
![]() $\mathrel {\textrm {iff}_{\textrm {df}}} \forall x^{n-1} d^{n}(x^{n-1})$
. Using (1) from Section 7.4, we can then prove (R=U) for
$\mathrel {\textrm {iff}_{\textrm {df}}} \forall x^{n-1} d^{n}(x^{n-1})$
. Using (1) from Section 7.4, we can then prove (R=U) for
![]() ${\textrm {STT}}$
.
${\textrm {STT}}$
.
In
![]() ${\textrm {FJT}}$
, by contrast, a property
${\textrm {FJT}}$
, by contrast, a property
![]() $d^n$
can (meaningfully) be a domain for generalizations
$d^n$
can (meaningfully) be a domain for generalizations
![]() $\forall x^i y^m(x^i)$
with
$\forall x^i y^m(x^i)$
with
![]() $n \neq m$
, so we cannot simply ignore the relativity in Russellianess. Let us, then, try to accommodate it. Officially, a domain is supposed to be Russellian for a generalization. However, since the range of significance of any type m property in
$n \neq m$
, so we cannot simply ignore the relativity in Russellianess. Let us, then, try to accommodate it. Officially, a domain is supposed to be Russellian for a generalization. However, since the range of significance of any type m property in
![]() ${\textrm {FJT}}$
is always exactly the type
${\textrm {FJT}}$
is always exactly the type
![]() $k < m$
entities, all that really matters is the type of the predicate used in the generalization. This leads to an explicitly relativized notion of Russellianness as follows:
$k < m$
entities, all that really matters is the type of the predicate used in the generalization. This leads to an explicitly relativized notion of Russellianness as follows:
-
(3)
 $d^{n}$
is
$d^{n}$
is
 ${m}$
-Russellian
${m}$
-Russellian
 $\mathrel {\textrm {iff}_{\textrm {df}}}$
all and only the type
$\mathrel {\textrm {iff}_{\textrm {df}}}$
all and only the type
 $k < m$
entities have
$k < m$
entities have
 $d^{n}$
$d^{n}$
i.e.,
 ${\bigl (\bigwedge _{k < m}\kern-1pt\forall y^k \bigvee _{i < n} (\exists x^i \kern-2pt\mathrel {\equiv }\kern-2pt y^k)d^{n}(x^i)\kern-1pt\bigr ) \kern1pt{\land}\kern1pt \bigl (\bigwedge _{i < n}\kern-1.5pt\forall x^{i}(d^{n}(x^{i}) \kern0.5pt{\rightarrow} \bigvee _{k < m}\kern-1pt\exists y^{k} x^{i} \kern-2pt\mathrel {\equiv }\kern-2pt y^{k}\kern-1pt)\kern-1pt\bigr )\kern-1pt.}$
${\bigl (\bigwedge _{k < m}\kern-1pt\forall y^k \bigvee _{i < n} (\exists x^i \kern-2pt\mathrel {\equiv }\kern-2pt y^k)d^{n}(x^i)\kern-1pt\bigr ) \kern1pt{\land}\kern1pt \bigl (\bigwedge _{i < n}\kern-1.5pt\forall x^{i}(d^{n}(x^{i}) \kern0.5pt{\rightarrow} \bigvee _{k < m}\kern-1pt\exists y^{k} x^{i} \kern-2pt\mathrel {\equiv }\kern-2pt y^{k}\kern-1pt)\kern-1pt\bigr )\kern-1pt.}$
The first conjunct captures the idea that every type
![]() $k < m$
entity has
$k < m$
entity has
![]() $d^{n}$
; it says that every type
$d^{n}$
; it says that every type
![]() $k < m$
entity is an entity in
$k < m$
entity is an entity in
![]() $d^{n}$
. The second conjunct captures the idea that only the type
$d^{n}$
. The second conjunct captures the idea that only the type
![]() $k < m$
entities have
$k < m$
entities have
![]() $d^{n}$
; it says that every (type
$d^{n}$
; it says that every (type
![]() $i < n$
) entity in
$i < n$
) entity in
![]() $d^{n}$
is a type
$d^{n}$
is a type
![]() $k < m$
entity.Footnote
63
This definition allows us (meaningfully) to ask whether
$k < m$
entity.Footnote
63
This definition allows us (meaningfully) to ask whether
![]() $d^{n}$
is m-Russellian, for any n and m. Furthermore, if
$d^{n}$
is m-Russellian, for any n and m. Furthermore, if
![]() $n < m$
, then
$n < m$
, then
![]() $d^{n}$
is not m-Russellian. In particular,
$d^{n}$
is not m-Russellian. In particular,
![]() $U^1$
is not
$U^1$
is not
![]() $2$
-Russellian. However,
$2$
-Russellian. However,
![]() $U^1$
is
$U^1$
is
![]() $1$
-Russellian. So, in
$1$
-Russellian. So, in
![]() ${\textrm {FJT}}$
, Russellianness is significantly relativized.
${\textrm {FJT}}$
, Russellianness is significantly relativized.
To make sense of (R=U) in
![]() ${\textrm {FJT}}$
, then, Florio and Jones must relativize the notion of unrestrictedness, so that it matches the relativity in Russellianness. Tacitly, they do exactly this, describing domains as unrestricted for certain generalizations [Reference Florio and Jones10, e.g., pp. 52–53]. Florio and Jones do not define this relative sense of ‘unrestricted’, but we can easily provide a definition on their behalf. To say that
${\textrm {FJT}}$
, then, Florio and Jones must relativize the notion of unrestrictedness, so that it matches the relativity in Russellianness. Tacitly, they do exactly this, describing domains as unrestricted for certain generalizations [Reference Florio and Jones10, e.g., pp. 52–53]. Florio and Jones do not define this relative sense of ‘unrestricted’, but we can easily provide a definition on their behalf. To say that
![]() $d^{n}$
is unrestricted with regard to type m is, presumably, to say this: if
$d^{n}$
is unrestricted with regard to type m is, presumably, to say this: if
![]() $y^{m}$
is true of everything in
$y^{m}$
is true of everything in
![]() $d^{n}$
that it can be meaningfully applied to, then it is true of absolutely everything it can be meaningfully applied to. Formalizing this, we obtain the following, for all
$d^{n}$
that it can be meaningfully applied to, then it is true of absolutely everything it can be meaningfully applied to. Formalizing this, we obtain the following, for all
![]() $m,n>0$
:
$m,n>0$
:
-
(4)
 $d^{n}$
is
$d^{n}$
is
 $m\textrm {-unrestricted} \mathrel {\textrm {iff}_{\textrm {df}}}$
$m\textrm {-unrestricted} \mathrel {\textrm {iff}_{\textrm {df}}}$
-
 $\qquad\qquad\forall y^{m}(\bigwedge _{i < \min (m, n)}\forall x^{i}(d^{n}(x^{i})\rightarrow y^{m}(x^{i}))\rightarrow \bigwedge _{i < m}\forall x^{i} y^{m}(x^{i})).$
$\qquad\qquad\forall y^{m}(\bigwedge _{i < \min (m, n)}\forall x^{i}(d^{n}(x^{i})\rightarrow y^{m}(x^{i}))\rightarrow \bigwedge _{i < m}\forall x^{i} y^{m}(x^{i})).$
Indeed, this just turns (2), which is a schematic necessary condition on unrelativized unrestrictedness, into a definition of relativized m-unrestrictedness.
We can now understand (R=U) thus: a domain is m-Russellian iff it is m-unrestricted. But so understood, (R=U) is false:
![]() $U^2$
is
$U^2$
is
![]() $1$
-unrestricted but not
$1$
-unrestricted but not
![]() $1$
-Russellian, with
$1$
-Russellian, with
![]() $U^2$
as given in Section 7.5. Moreover, we do not need any principle like (R=U) to determine whether a given domain is m-unrestricted; we can just use definition (4). For example, it is clear from (4) that
$U^2$
as given in Section 7.5. Moreover, we do not need any principle like (R=U) to determine whether a given domain is m-unrestricted; we can just use definition (4). For example, it is clear from (4) that
![]() $U^1$
is
$U^1$
is
![]() $1$
-unrestricted but
$1$
-unrestricted but
![]() $2$
-restricted. More generally,
$2$
-restricted. More generally,
![]() $d^{n}$
is m-unrestricted iff both
$d^{n}$
is m-unrestricted iff both
![]() $n \geq m$
and
$n \geq m$
and
![]() $\bigwedge _{i < m}\forall x^i d^{n}(x^i)$
.
$\bigwedge _{i < m}\forall x^i d^{n}(x^i)$
.
The only remaining question is whether the salient notion of unrestrictedness in
![]() ${\textrm {FJT}}$
is the absolute notion governed by (2), or the relative notion defined by (4). We think it is completely clear that the relevant notion is the absolute one. After all, the debate here is about absolute generality. It would be false advertising to enter that debate, promising to vindicate unrestricted quantification, and then only deliver relatively unrestricted quantification. To emphasise this point, return to the example of
${\textrm {FJT}}$
is the absolute notion governed by (2), or the relative notion defined by (4). We think it is completely clear that the relevant notion is the absolute one. After all, the debate here is about absolute generality. It would be false advertising to enter that debate, promising to vindicate unrestricted quantification, and then only deliver relatively unrestricted quantification. To emphasise this point, return to the example of
![]() $U^1$
: evidently,
$U^1$
: evidently,
![]() $U^1$
is
$U^1$
is
![]() $1$
-unrestricted but
$1$
-unrestricted but
![]() $2$
-restricted, as defined by (4). Precisely because
$2$
-restricted, as defined by (4). Precisely because
![]() $U^1$
is
$U^1$
is
![]() $2$
-restricted, though, there is a clear sense in which
$2$
-restricted, though, there is a clear sense in which
![]() $U^1$
is restricted simpliciter. In particular, with
$U^1$
is restricted simpliciter. In particular, with
![]() $H^2$
as given at the end of Section 7.5, everything which is
$H^2$
as given at the end of Section 7.5, everything which is
![]() $U^1$
is
$U^1$
is
![]() $H^2$
, i.e.,
$H^2$
, i.e.,
![]() $\forall x^0(U^1(x^0) \rightarrow H^2(x^0))$
, but some entities are not
$\forall x^0(U^1(x^0) \rightarrow H^2(x^0))$
, but some entities are not
![]() $H^2$
, in that
$H^2$
, in that
![]() $\exists x^1 \lnot H^2(x^1)$
.
$\exists x^1 \lnot H^2(x^1)$
.
Indeed, this is exactly where Florio and Jones [Reference Florio and Jones10, p. 57] go wrong. They recognise that you can find a type
![]() $1$
entity not in
$1$
entity not in
![]() $U^1$
, but say: ‘it does not entail that F is meaningfully predicable of that entity’, where
$U^1$
, but say: ‘it does not entail that F is meaningfully predicable of that entity’, where
![]() $\forall x^0 F (x^0)$
is the generalization under consideration. However,
$\forall x^0 F (x^0)$
is the generalization under consideration. However,
![]() ${\textrm {FJT}}$
has precisely that entailment when F’s type is
${\textrm {FJT}}$
has precisely that entailment when F’s type is
![]() $> 1$
, as in the case of
$> 1$
, as in the case of
![]() $F = H^2$
.
$F = H^2$
.
7.7
 ${\textrm {FJT}}$
: the case for ambiguity
${\textrm {FJT}}$
: the case for ambiguity
It might be helpful to end our discussion of
![]() ${\textrm {FJT}}$
by summarizing our case for reading it as a mere notational variant of
${\textrm {FJT}}$
by summarizing our case for reading it as a mere notational variant of
![]() ${\textrm {STT}_{\triangleright }}$
.
${\textrm {STT}_{\triangleright }}$
.
First. We see no reason not to read
![]() ${\textrm {FJT}}$
in this way. Linnedo and Rayo could not read
${\textrm {FJT}}$
in this way. Linnedo and Rayo could not read
![]() ${\textrm {CTT}^{\omega }}$
as a notational variant of
${\textrm {CTT}^{\omega }}$
as a notational variant of
![]() ${\textrm {STT}_{\uparrow }}$
, because they wanted to extend
${\textrm {STT}_{\uparrow }}$
, because they wanted to extend
![]() ${\textrm {CTT}^{\omega }}$
into the transfinite. But
${\textrm {CTT}^{\omega }}$
into the transfinite. But
![]() ${\textrm {FJT}}$
is as finitary as
${\textrm {FJT}}$
is as finitary as
![]() ${\textrm {STT}_{\uparrow }}$
.
${\textrm {STT}_{\uparrow }}$
.
Second. If we take
![]() ${\textrm {FJT}}$
at face-value, then it is unclear how we should interpret it. Florio and Jones explicitly intended to give
${\textrm {FJT}}$
at face-value, then it is unclear how we should interpret it. Florio and Jones explicitly intended to give
![]() ${\textrm {FJT}}$
a conceptual semantics, but we know of no version of that semantics which could justify
${\textrm {FJT}}$
a conceptual semantics, but we know of no version of that semantics which could justify
![]() ${\textrm {FJT}}$
’s type-restrictions, taken at face-value.
${\textrm {FJT}}$
’s type-restrictions, taken at face-value.
Third. If we take
![]() ${\textrm {FJT}}$
at face-value, then it cannot accommodate absolute generality. However, if we read
${\textrm {FJT}}$
at face-value, then it cannot accommodate absolute generality. However, if we read
![]() ${\textrm {FJT}}$
as a notational variant of
${\textrm {FJT}}$
as a notational variant of
![]() ${\textrm {STT}_{\triangleright }}$
, then it can supply absolutely unrestricted domains.
${\textrm {STT}_{\triangleright }}$
, then it can supply absolutely unrestricted domains.
8 Conclusion
In this paper, we have argued for four main claims:
-
(a)
 $\textrm {CTT}$
cannot be used to close the gap between an ideological hierarchy of types and an ontological hierarchy of sets (Section 2 and 3).
$\textrm {CTT}$
cannot be used to close the gap between an ideological hierarchy of types and an ontological hierarchy of sets (Section 2 and 3). -
(b)
 $\textrm {CTT}$
’s type-restrictions are superfluous, on any semantics (Section 4).
$\textrm {CTT}$
’s type-restrictions are superfluous, on any semantics (Section 4). -
(c)
 ${\textrm {STT}}$
’s type-restrictions can be justified by a Fregean semantics, which also provides us with a way to resist Linnebo and Rayo’s Semantic Argument in favour of
${\textrm {STT}}$
’s type-restrictions can be justified by a Fregean semantics, which also provides us with a way to resist Linnebo and Rayo’s Semantic Argument in favour of
 $\textrm {CTT}$
(Sections 5 and 6).
$\textrm {CTT}$
(Sections 5 and 6). -
(d)
 ${\textrm {FJT}}$
is best understood as a misleading formulation of
${\textrm {FJT}}$
is best understood as a misleading formulation of
 ${\textrm {STT}_{\triangleright }}$
(Section 7).
${\textrm {STT}_{\triangleright }}$
(Section 7).
We start with (a). The Sets-from-Types Theorem allows us to simulate
![]() ${\textrm {Zr}}$
within
${\textrm {Zr}}$
within
![]() $\textrm {CTT}$
. But deep mathematical differences remain between
$\textrm {CTT}$
. But deep mathematical differences remain between
![]() ${\textrm {Zr}}$
and and
${\textrm {Zr}}$
and and
![]() $\textrm {Zr}^{(\kappa )}$
, rendering
$\textrm {Zr}^{(\kappa )}$
, rendering
![]() $\textrm {Zr}^{(\kappa )}$
unsuitable as a framework for mathematical foundations. Furthermore, the Sets-from-Types Theorem cannot allay any ontological worries we might have about set theory:
$\textrm {Zr}^{(\kappa )}$
unsuitable as a framework for mathematical foundations. Furthermore, the Sets-from-Types Theorem cannot allay any ontological worries we might have about set theory:
![]() $\textrm {CTT}$
’s type-indices are supplied externally, and so the Sets-from-Types Theorem merely shunts our ontological worries into the metalanguage.
$\textrm {CTT}$
’s type-indices are supplied externally, and so the Sets-from-Types Theorem merely shunts our ontological worries into the metalanguage.
Next is (b).
![]() $\textrm {CTT}$
is a remarkably relaxed type theory: it allows us to apply every type of entity to every type of entity. But it still retains the constraint that all of its variables are typed and, in
$\textrm {CTT}$
is a remarkably relaxed type theory: it allows us to apply every type of entity to every type of entity. But it still retains the constraint that all of its variables are typed and, in
![]() $\textrm {CTT}$
, that type-restriction is superfluous. Once every type of entity can be applied to every type of entity, there can be no barrier to introducing untyped variables.
$\textrm {CTT}$
, that type-restriction is superfluous. Once every type of entity can be applied to every type of entity, there can be no barrier to introducing untyped variables.
We come now to (c). The strict type-restrictions imposed by
![]() ${\textrm {STT}}$
can be justified by the Fregean semantics. On this semantics, different types of term play fundamentally different types of semantic role, so that they cannot be meaningfully intersubstituted. Moreover, this semantics yields a principled reason to reject Naïve Optimism, a crucial premise in Linnebo and Rayo’s Semantic Argument.
${\textrm {STT}}$
can be justified by the Fregean semantics. On this semantics, different types of term play fundamentally different types of semantic role, so that they cannot be meaningfully intersubstituted. Moreover, this semantics yields a principled reason to reject Naïve Optimism, a crucial premise in Linnebo and Rayo’s Semantic Argument.
We end with (d). Florio and Jones’
![]() ${\textrm {FJT}}$
was meant to be a partially cumulative type theory, but we argue it is best understood as a notational variant of
${\textrm {FJT}}$
was meant to be a partially cumulative type theory, but we argue it is best understood as a notational variant of
![]() ${\textrm {STT}_{\triangleright }}$
: taking
${\textrm {STT}_{\triangleright }}$
: taking
![]() ${\textrm {FJT}}$
at face-value leaves it unable to accommodate absolute generality; whereas
${\textrm {FJT}}$
at face-value leaves it unable to accommodate absolute generality; whereas
![]() ${\textrm {STT}_{\triangleright }}$
—which is definitionally equivalent to
${\textrm {STT}_{\triangleright }}$
—which is definitionally equivalent to
![]() ${\textrm {FJT}}$
—provides absolutely unrestricted domains of quantification.
${\textrm {FJT}}$
—provides absolutely unrestricted domains of quantification.
A Elementary facts about CTT
The remainder of this paper comprises technical appendices, covering the formal results mentioned in the main text. We will start with some elementary observations about
![]() $\textrm {CTT}$
. As mentioned in Section 1.2, for each ordinal
$\textrm {CTT}$
. As mentioned in Section 1.2, for each ordinal
![]() $\tau $
, we have a theory
$\tau $
, we have a theory
![]() ${{\textrm {CTT}^{\tau }}}$
.Footnote
64
Recall that we have explicitly defined
${{\textrm {CTT}^{\tau }}}$
.Footnote
64
Recall that we have explicitly defined
![]() $\mathrel {\equiv }$
and
$\mathrel {\equiv }$
and
![]() $\mathrel {\varepsilon }$
, for any types
$\mathrel {\varepsilon }$
, for any types
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
and where
$\beta $
and where
![]() $\gamma = \max (\alpha , \beta )+1$
:
$\gamma = \max (\alpha , \beta )+1$
:
 $$ \begin{align*} a^\alpha \mathrel{\equiv} b^\beta & \mathrel{\textrm{iff}_{\textrm{df}}} \forall x^{\gamma}(x^{\gamma}(a^\alpha) \leftrightarrow x^\gamma(b^\beta))\\ a^\alpha \mathrel{\varepsilon} b^\beta & \mathrel{\textrm{iff}_{\textrm{df}}} (\exists x^{\gamma} \mathrel{\equiv} b^\beta)x^{\gamma}(a^\alpha). \end{align*} $$
$$ \begin{align*} a^\alpha \mathrel{\equiv} b^\beta & \mathrel{\textrm{iff}_{\textrm{df}}} \forall x^{\gamma}(x^{\gamma}(a^\alpha) \leftrightarrow x^\gamma(b^\beta))\\ a^\alpha \mathrel{\varepsilon} b^\beta & \mathrel{\textrm{iff}_{\textrm{df}}} (\exists x^{\gamma} \mathrel{\equiv} b^\beta)x^{\gamma}(a^\alpha). \end{align*} $$
In what follows, we will frequently invoke the following simple facts about
![]() $\mathrel {\equiv }$
and
$\mathrel {\equiv }$
and
![]() $\mathrel {\varepsilon }$
; crudely, they allow us to move seamlessly between different type-levels:
$\mathrel {\varepsilon }$
; crudely, they allow us to move seamlessly between different type-levels:
Lemma 1. If
![]() $\alpha \leq \beta $
and
$\alpha \leq \beta $
and
![]() $\beta + 1 < \tau $
, then
$\beta + 1 < \tau $
, then
![]() ${{\textrm {CTT}^{\tau }}}$
proves:
${{\textrm {CTT}^{\tau }}}$
proves:
![]() $\forall a^\alpha \exists b^\beta \phantom {)}a^\alpha \mathrel {\equiv } b^\beta $
$\forall a^\alpha \exists b^\beta \phantom {)}a^\alpha \mathrel {\equiv } b^\beta $
Proof. By
![]() ${\forall {\textrm {I}}^{\beta +1}_{\beta +1}}$
, we have
${\forall {\textrm {I}}^{\beta +1}_{\beta +1}}$
, we have
![]() $\forall x^{\beta +1}(x^{\beta +1}(a^\alpha ) \leftrightarrow x^{\beta +1}(a^\alpha ))$
, i.e.,
$\forall x^{\beta +1}(x^{\beta +1}(a^\alpha ) \leftrightarrow x^{\beta +1}(a^\alpha ))$
, i.e.,
![]() $a^\alpha \mathrel {\equiv } a^\alpha $
; so
$a^\alpha \mathrel {\equiv } a^\alpha $
; so
![]() $\forall a^\alpha \exists b^\beta \ a^\alpha \mathrel {\equiv } b^\beta $
by
$\forall a^\alpha \exists b^\beta \ a^\alpha \mathrel {\equiv } b^\beta $
by
![]() ${\exists {\textrm {I}}^{\beta }_{\alpha }}$
followed by
${\exists {\textrm {I}}^{\beta }_{\alpha }}$
followed by
![]() ${\forall {\textrm {I}}^{\alpha }_{\alpha }}$
.□
${\forall {\textrm {I}}^{\alpha }_{\alpha }}$
.□
Lemma 2. For any
![]() $\phi $
, and any
$\phi $
, and any
![]() $\alpha , \beta , \gamma $
with
$\alpha , \beta , \gamma $
with
![]() $\max (\alpha , \beta , \gamma ) + 2 < \tau $
,
$\max (\alpha , \beta , \gamma ) + 2 < \tau $
,
![]() ${{\textrm {CTT}^{\tau }}}$
proves:
${{\textrm {CTT}^{\tau }}}$
proves:
-
(1) if
 $a^\alpha \mathrel {\equiv } b^\beta $
and
$a^\alpha \mathrel {\equiv } b^\beta $
and
 $\phi (a^\alpha )$
, then
$\phi (a^\alpha )$
, then
 $\phi (b^\beta )$
, when this is well-formed
$\phi (b^\beta )$
, when this is well-formed -
(2) if
 $a^\alpha \mathrel {\equiv } b^\beta \mathrel {\equiv } c^\gamma $
, then
$a^\alpha \mathrel {\equiv } b^\beta \mathrel {\equiv } c^\gamma $
, then
 $a^\alpha \mathrel {\equiv } c^\gamma $
$a^\alpha \mathrel {\equiv } c^\gamma $
-
(3) if
 $a^\alpha \mathrel {\equiv } b^\beta $
and
$a^\alpha \mathrel {\equiv } b^\beta $
and
 $a^\alpha \mathrel {\varepsilon } c^\gamma $
, then
$a^\alpha \mathrel {\varepsilon } c^\gamma $
, then
 $b^\beta \mathrel {\varepsilon } c^\gamma $
$b^\beta \mathrel {\varepsilon } c^\gamma $
-
(4) if
 $a^\alpha \mathrel {\equiv } b^\beta $
and
$a^\alpha \mathrel {\equiv } b^\beta $
and
 $c^\gamma \mathrel {\varepsilon } a^\alpha $
, then
$c^\gamma \mathrel {\varepsilon } a^\alpha $
, then
 $c^\gamma \mathrel {\varepsilon } b^\beta $
$c^\gamma \mathrel {\varepsilon } b^\beta $
Proof.
(1) Suppose
![]() $a^\alpha \mathrel {\equiv } b^\beta $
and
$a^\alpha \mathrel {\equiv } b^\beta $
and
![]() $\phi (a^\alpha )$
. Let
$\phi (a^\alpha )$
. Let
![]() $\delta = \max (\alpha , \beta )$
; by
$\delta = \max (\alpha , \beta )$
; by
![]() $\textrm {CTT}$
-Comprehension there is some
$\textrm {CTT}$
-Comprehension there is some
![]() $c^{\delta +1}$
such that
$c^{\delta +1}$
such that
![]() $\forall x^{\delta }(c^{\delta +1}(x^{\delta }) \leftrightarrow \phi (x^{\delta }))$
. Since
$\forall x^{\delta }(c^{\delta +1}(x^{\delta }) \leftrightarrow \phi (x^{\delta }))$
. Since
![]() $\phi (a^\alpha )$
, by
$\phi (a^\alpha )$
, by
![]() ${\forall {\textrm {E}}^{\delta }_{\alpha }}$
we have that
${\forall {\textrm {E}}^{\delta }_{\alpha }}$
we have that
![]() $c^{\delta +1}(a^\alpha )$
. Since
$c^{\delta +1}(a^\alpha )$
. Since
![]() $a^\alpha \mathrel {\equiv } b^\beta $
, i.e.,
$a^\alpha \mathrel {\equiv } b^\beta $
, i.e.,
![]() $\forall z^{\delta +1}(z^{\delta +1}(a^\alpha ) \leftrightarrow z^{\delta +1}(b^\beta ))$
, by
$\forall z^{\delta +1}(z^{\delta +1}(a^\alpha ) \leftrightarrow z^{\delta +1}(b^\beta ))$
, by
![]() ${\forall {\textrm {E}}^{\delta +1}_{\delta +1}}$
we have that
${\forall {\textrm {E}}^{\delta +1}_{\delta +1}}$
we have that
![]() $c^{\delta +1}(b^\beta )$
. Now
$c^{\delta +1}(b^\beta )$
. Now
![]() $\phi (b^\beta )$
by
$\phi (b^\beta )$
by
![]() ${\forall {\textrm {E}}^{\delta }_{\beta }}$
.
${\forall {\textrm {E}}^{\delta }_{\beta }}$
.
(2)–(4) We leave these to the reader. They are not completely immediate consequences of (1), since the definitions of
![]() $\mathrel {\equiv }$
and
$\mathrel {\equiv }$
and
![]() $\mathrel {\varepsilon }$
are typically ambiguous.□
$\mathrel {\varepsilon }$
are typically ambiguous.□
Lemma 3. If
![]() $\max (\alpha , \beta ) + 2 < \tau $
, then
$\max (\alpha , \beta ) + 2 < \tau $
, then
![]() ${{\textrm {CTT}^{\tau }}}$
proves:
${{\textrm {CTT}^{\tau }}}$
proves:
![]() $a^\alpha \mathrel {\varepsilon } b^{\beta +1} \leftrightarrow (\exists x^\beta \mathrel {\equiv } a^\alpha ) b^{\beta +1}(x^\beta )$
$a^\alpha \mathrel {\varepsilon } b^{\beta +1} \leftrightarrow (\exists x^\beta \mathrel {\equiv } a^\alpha ) b^{\beta +1}(x^\beta )$
It is worth emphasising that Type-Founded and Type-Basis are independent from
![]() $\textrm {CTT}$
’s other axioms. To show this, we begin by building an ill-founded set-theoretic structure,
$\textrm {CTT}$
’s other axioms. To show this, we begin by building an ill-founded set-theoretic structure,
![]() $\mathcal {A}$
. Let
$\mathcal {A}$
. Let
![]() $\textbf {a} = \{\emptyset , \textbf {a}\}$
; now define:
$\textbf {a} = \{\emptyset , \textbf {a}\}$
; now define:
So
![]() $A_2 = \{\emptyset , \{\emptyset \}, \{\textbf {a}\}, \textbf {a}\}$
. Let
$A_2 = \{\emptyset , \{\emptyset \}, \{\textbf {a}\}, \textbf {a}\}$
. Let
![]() $\mathcal {A}$
be the structure whose domain is A and which interprets
$\mathcal {A}$
be the structure whose domain is A and which interprets
![]() $\in $
verbatim; evidently,
$\in $
verbatim; evidently,
![]() $\mathcal {A}$
is ill-founded. Using a slight tweak of the class semantics of Section 4.2, we now create a model,
$\mathcal {A}$
is ill-founded. Using a slight tweak of the class semantics of Section 4.2, we now create a model,
![]() $\mathcal {M}$
, of
$\mathcal {M}$
, of
![]() ${\textrm {CTT}^{\omega }}$
without Type-Founded. We start by defining a ranking function
${\textrm {CTT}^{\omega }}$
without Type-Founded. We start by defining a ranking function
![]() $\rho : A \longrightarrow \mathbb {N}$
on
$\rho : A \longrightarrow \mathbb {N}$
on
![]() $\mathcal {A}$
as follows:
$\mathcal {A}$
as follows:
So
![]() $\rho (\{\emptyset \}) = 2$
. Now we stipulate that
$\rho (\{\emptyset \}) = 2$
. Now we stipulate that
![]() $\mathcal {M}$
’s type n entities are all those
$\mathcal {M}$
’s type n entities are all those
![]() $c \in A$
such that
$c \in A$
such that
![]() $\rho (c) \leq n$
, and applications are stipulated to hold as follows, for all
$\rho (c) \leq n$
, and applications are stipulated to hold as follows, for all
![]() $m < n$
and all
$m < n$
and all
![]() $b, c \in A$
:
$b, c \in A$
:
It is easy to confirm that
![]() $\mathcal {M}$
models
$\mathcal {M}$
models
![]() ${\textrm {CTT}^{\omega }}$
without Type-Founded. But, by construction,
${\textrm {CTT}^{\omega }}$
without Type-Founded. But, by construction,
![]() $c^m \mathrel {\equiv } c^n$
whenever
$c^m \mathrel {\equiv } c^n$
whenever
![]() $\min (m, n) \geq \rho (c)$
. So
$\min (m, n) \geq \rho (c)$
. So
![]() $\textbf {a}^2(\textbf {a}^1)$
with
$\textbf {a}^2(\textbf {a}^1)$
with
![]() $\textbf {a}^2 \mathrel {\equiv } \textbf {a}^1$
, and hence
$\textbf {a}^2 \mathrel {\equiv } \textbf {a}^1$
, and hence
![]() $\textbf {a}^1 \mathrel {\varepsilon } \textbf {a}^1$
. So
$\textbf {a}^1 \mathrel {\varepsilon } \textbf {a}^1$
. So
![]() $\mathcal {M}$
violates Type-Founded. Admittedly, Type-Basis holds in
$\mathcal {M}$
violates Type-Founded. Admittedly, Type-Basis holds in
![]() $\mathcal {M}$
, but we can violate it with a similar construction: start with a Quine atom
$\mathcal {M}$
, but we can violate it with a similar construction: start with a Quine atom
![]() $\textbf {b} = \{\textbf {b}\}$
; let
$\textbf {b} = \{\textbf {b}\}$
; let
![]() $B_0 = \textbf {b}$
and
$B_0 = \textbf {b}$
and
![]() $B_{n+1} = \wp (B_n)$
; define
$B_{n+1} = \wp (B_n)$
; define
![]() $\rho (c) = n$
iff
$\rho (c) = n$
iff
![]() $c \in B_n \setminus B_{n-1}$
; and note that
$c \in B_n \setminus B_{n-1}$
; and note that
![]() $\textbf {b}^0 \mathrel {\varepsilon } \textbf {b}^0$
.
$\textbf {b}^0 \mathrel {\varepsilon } \textbf {b}^0$
.
B Obtaining
 ${\textrm {Zr}}$
in
${\textrm {Zr}}$
in
 ${\textrm {CTT}_{\textrm {p}}}$
${\textrm {CTT}_{\textrm {p}}}$
In Section 2, we stated the Sets-from-Types Theorem. In this appendix, we prove that result. We also introduce the interpreting theory,
![]() ${\textrm {CTT}_{\textrm {p}}}$
, and the interpreted theory,
${\textrm {CTT}_{\textrm {p}}}$
, and the interpreted theory,
![]() ${\textrm {Zr}}$
, and discuss how
${\textrm {Zr}}$
, and discuss how
![]() ${\textrm {CTT}_{\textrm {p}}}$
deals with Replacement.
${\textrm {CTT}_{\textrm {p}}}$
deals with Replacement.
B.1 The theory
 ${\textrm {Zr}}$
${\textrm {Zr}}$
The set theory which we simulate is
![]() ${\textrm {Zr}}$
. We can think of
${\textrm {Zr}}$
. We can think of
![]() ${\textrm {Zr}}$
as arising by adding to
${\textrm {Zr}}$
as arising by adding to
![]() ${\textrm {Z}}$
the principle that the sets are arranged in well-ordered levels;
${\textrm {Z}}$
the principle that the sets are arranged in well-ordered levels;
![]() ${\textrm {Zr}}$
is therefore strictly stronger than
${\textrm {Zr}}$
is therefore strictly stronger than
![]() ${\textrm {Z}}$
and strictly weaker than
${\textrm {Z}}$
and strictly weaker than
![]() ${\textrm {ZF}}$
.Footnote
65
We follow Button’s Reference Button[5] formulation of
${\textrm {ZF}}$
.Footnote
65
We follow Button’s Reference Button[5] formulation of
![]() ${\textrm {Zr}}$
, starting with a core of definitions:
${\textrm {Zr}}$
, starting with a core of definitions:
Definition 4. Say that h is a history, written Hist
![]() $(h)$
, iff
$(h)$
, iff
![]() $(\forall a \in h)\forall x(x \in a \leftrightarrow (\exists c \in h)x \subseteq c \in a)$
. Say that s is a level, written Lev
$(\forall a \in h)\forall x(x \in a \leftrightarrow (\exists c \in h)x \subseteq c \in a)$
. Say that s is a level, written Lev
![]() $(s)$
, iff
$(s)$
, iff
![]() $\exists h({{{Hist}}}(h) \land \forall x(x \in s \leftrightarrow \exists c(x \subseteq c \in h)))$
.Footnote
66
$\exists h({{{Hist}}}(h) \land \forall x(x \in s \leftrightarrow \exists c(x \subseteq c \in h)))$
.Footnote
66
Using these definitions, we can consider some axioms:
-
Extensionality
 $\forall a \forall b (\forall x(x \in a \leftrightarrow x \in b) \rightarrow a =b)$
$\forall a \forall b (\forall x(x \in a \leftrightarrow x \in b) \rightarrow a =b)$
-
Separation
 $\forall a \exists b \forall x(x \in b \leftrightarrow (\phi (x) \land x \in a))$
, for every
$\forall a \exists b \forall x(x \in b \leftrightarrow (\phi (x) \land x \in a))$
, for every
 $\phi $
not containing b
$\phi $
not containing b
-
Stratification
 $\forall a (\exists s \supseteq a){\textit{Lev}}(s)$
$\forall a (\exists s \supseteq a){\textit{Lev}}(s)$
-
Endless
 $\forall a \exists b\ a \in b$
$\forall a \exists b\ a \in b$
-
Infinity
 $\exists a(\exists x\ x \in a \land (\forall x \in a)\exists y(x \in y \in a))$
$\exists a(\exists x\ x \in a \land (\forall x \in a)\exists y(x \in y \in a))$
The theory
![]() ${\textrm {LT}}$
has, as axioms, Extensionality, all instances of Separation, and Stratification, which serves as a principle of foundation. The theory
${\textrm {LT}}$
has, as axioms, Extensionality, all instances of Separation, and Stratification, which serves as a principle of foundation. The theory
![]() ${\textrm {Zr}}$
adds Endless and Infinity to
${\textrm {Zr}}$
adds Endless and Infinity to
![]() ${\textrm {LT}}$
. In what follows, these next two results will be extremely useful:Footnote
67
${\textrm {LT}}$
. In what follows, these next two results will be extremely useful:Footnote
67
Lemma 5. Extensionality + Separation proves: if
![]() ${\textit{Lev}}(s)$
, then
${\textit{Lev}}(s)$
, then
![]() $s = \{x : \exists r({\textit{Lev}}(r) \land x \subseteq r \in s)\}$
.
$s = \{x : \exists r({\textit{Lev}}(r) \land x \subseteq r \in s)\}$
.
Theorem 6. Extensionality + Separation proves: the levels are well-ordered by
![]() $\in $
, i.e.:
$\in $
, i.e.:
-
(1)
 $\exists s({\textit{Lev}}(s) \land \phi (s)) \rightarrow \exists s({\textit{Lev}}(s) \land \phi (s) \land \lnot (\exists r \in s)({\textit{Lev}}(r) \land \phi (r)))$
$\exists s({\textit{Lev}}(s) \land \phi (s)) \rightarrow \exists s({\textit{Lev}}(s) \land \phi (s) \land \lnot (\exists r \in s)({\textit{Lev}}(r) \land \phi (r)))$
-
(2)
 $\forall s\forall t(({\textit{Lev}}(s) \land {\textit{Lev}}(t)) \rightarrow (s \in t \lor s = t \lor t \in s))$
$\forall s\forall t(({\textit{Lev}}(s) \land {\textit{Lev}}(t)) \rightarrow (s \in t \lor s = t \lor t \in s))$
This last result allows us to define the rank of a, written
![]() $\textrm {rank}(a)$
, within
$\textrm {rank}(a)$
, within
![]() ${\textrm {LT}}$
, in terms of the
${\textrm {LT}}$
, in terms of the
![]() $\in $
-least level with a as a subset.
$\in $
-least level with a as a subset.
B.2 The theory
 ${\textrm {CTT}_{\textrm {p}}}$
${\textrm {CTT}_{\textrm {p}}}$
The theory
![]() ${\textrm {CTT}_{\textrm {p}}}$
extends
${\textrm {CTT}_{\textrm {p}}}$
extends
![]() $\textrm {CTT}$
with two new principles.Footnote
68
First, we add a version of ‘extensionality’, for all
$\textrm {CTT}$
with two new principles.Footnote
68
First, we add a version of ‘extensionality’, for all
![]() $\alpha \leq \beta $
:
$\alpha \leq \beta $
:
-
Type-Ext.
 $\forall a^{\alpha +1} \forall b^{\beta +1}([\forall x^\alpha (a^{\alpha +1}(x^\alpha ) \rightarrow b^{\beta +1}(x^\alpha )) \land {}$
$\forall a^{\alpha +1} \forall b^{\beta +1}([\forall x^\alpha (a^{\alpha +1}(x^\alpha ) \rightarrow b^{\beta +1}(x^\alpha )) \land {}$
 $\quad\forall x^\beta (b^{\beta +1}(x^\beta ) \rightarrow (\exists y^\alpha \mathrel {\equiv } x^\beta )a^{\alpha +1}(y^\alpha ))] \rightarrow a^{\alpha +1} \mathrel {\equiv } b^{\beta +1}).$
$\quad\forall x^\beta (b^{\beta +1}(x^\beta ) \rightarrow (\exists y^\alpha \mathrel {\equiv } x^\beta )a^{\alpha +1}(y^\alpha ))] \rightarrow a^{\alpha +1} \mathrel {\equiv } b^{\beta +1}).$
Second, to achieve ‘purity’, we add an axiom stating that there is exactly one object:
-
Type-Purity.
 $\forall x^0\forall y^0\ x^0 = y^0$
$\forall x^0\forall y^0\ x^0 = y^0$
Note that, modulo
![]() $\textrm {CTT}$
’s other axioms, Type-Founded follows from Type-Ext and Type-Purity.
$\textrm {CTT}$
’s other axioms, Type-Founded follows from Type-Ext and Type-Purity.
To begin our simulation of
![]() ${\textrm {Zr}}$
within
${\textrm {Zr}}$
within
![]() ${\textrm {CTT}_{\textrm {p}}}$
, we will show that
${\textrm {CTT}_{\textrm {p}}}$
, we will show that
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
proves
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
proves
![]() ${\textrm {Extensionality}^{(\kappa )}}$
and
${\textrm {Extensionality}^{(\kappa )}}$
and
![]() ${\textrm {Separation}^{(\kappa )}}$
.
${\textrm {Separation}^{(\kappa )}}$
.
Lemma 7.
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}} \vdash {\textrm {Extensionality}^{(\kappa )}}$
, whenever
${\textrm {CTT}^{\tau }_{\textrm {p}}} \vdash {\textrm {Extensionality}^{(\kappa )}}$
, whenever
![]() $\kappa + 2 < \tau $
.
$\kappa + 2 < \tau $
.
Proof. Suppose
![]() $\kappa $
is a limit (the proof is easier when
$\kappa $
is a limit (the proof is easier when
![]() $\kappa $
is a successor). Without loss of generality, fix
$\kappa $
is a successor). Without loss of generality, fix
![]() $\alpha \leq \beta < \kappa $
and suppose
$\alpha \leq \beta < \kappa $
and suppose
![]() $\forall x^\kappa (x^\kappa \mathrel {\varepsilon } a^\alpha \leftrightarrow x^\kappa \mathrel {\varepsilon } b^\beta )$
.
$\forall x^\kappa (x^\kappa \mathrel {\varepsilon } a^\alpha \leftrightarrow x^\kappa \mathrel {\varepsilon } b^\beta )$
.
Using Lemma 1, find
![]() $a^{\alpha +1} \mathrel {\equiv } a^\alpha $
and
$a^{\alpha +1} \mathrel {\equiv } a^\alpha $
and
![]() $b^{\beta +1} \mathrel {\equiv } b^\beta $
. Suppose
$b^{\beta +1} \mathrel {\equiv } b^\beta $
. Suppose
![]() $a^{\alpha +1}(x^\alpha )$
. So
$a^{\alpha +1}(x^\alpha )$
. So
![]() $x^\alpha \mathrel {\varepsilon } a^{\alpha +1}$
by Lemma 3; by Lemma 1 there is
$x^\alpha \mathrel {\varepsilon } a^{\alpha +1}$
by Lemma 3; by Lemma 1 there is
![]() $x^\kappa \mathrel {\equiv } x^\alpha $
, and
$x^\kappa \mathrel {\equiv } x^\alpha $
, and
![]() $x^\kappa \mathrel {\varepsilon } a^{\alpha }$
by Lemma 2; so
$x^\kappa \mathrel {\varepsilon } a^{\alpha }$
by Lemma 2; so
![]() $x^\kappa \mathrel {\varepsilon } b^\beta $
, and now
$x^\kappa \mathrel {\varepsilon } b^\beta $
, and now
![]() $b^{\beta +1}(x^\alpha )$
by Lemmas 2 and 3. Similar reasoning shows: if
$b^{\beta +1}(x^\alpha )$
by Lemmas 2 and 3. Similar reasoning shows: if
![]() $b^{\beta +1}(x^\beta )$
then
$b^{\beta +1}(x^\beta )$
then
![]() $(\exists y^\alpha \mathrel {\equiv } x^\beta )a^{\alpha +1}(y^\alpha )$
. By Type-Ext,
$(\exists y^\alpha \mathrel {\equiv } x^\beta )a^{\alpha +1}(y^\alpha )$
. By Type-Ext,
![]() $a^{\alpha +1} \mathrel {\equiv } b^{\beta +1}$
; hence
$a^{\alpha +1} \mathrel {\equiv } b^{\beta +1}$
; hence
![]() $a^\alpha \mathrel {\equiv } b^\beta $
by Lemma 2. Generalizing, for any
$a^\alpha \mathrel {\equiv } b^\beta $
by Lemma 2. Generalizing, for any
![]() $\alpha , \beta < \kappa $
:
$\alpha , \beta < \kappa $
:
Now
![]() ${\textrm {Extensionality}^{(\kappa )}}$
holds, using Limit
${\textrm {Extensionality}^{(\kappa )}}$
holds, using Limit
![]() $^\kappa $
twice.□
$^\kappa $
twice.□
Lemma 8.
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}} \vdash {\textrm {Separation}^{(\kappa )}}$
, whenever
${\textrm {CTT}^{\tau }_{\textrm {p}}} \vdash {\textrm {Separation}^{(\kappa )}}$
, whenever
![]() $\kappa + 2 < \tau $
.
$\kappa + 2 < \tau $
.
Proof. Suppose
![]() $\kappa $
is a limit (the proof is easier when
$\kappa $
is a limit (the proof is easier when
![]() $\kappa $
is a successor). Fix
$\kappa $
is a successor). Fix
![]() $\alpha < \kappa $
and
$\alpha < \kappa $
and
![]() $\phi $
such that
$\phi $
such that
![]() $\phi (x^\kappa )$
is well-formed. Fix
$\phi (x^\kappa )$
is well-formed. Fix
![]() $a^\alpha $
and find
$a^\alpha $
and find
![]() $a^{\alpha +1} \mathrel {\equiv } a^\alpha $
by Lemma 1. Using
$a^{\alpha +1} \mathrel {\equiv } a^\alpha $
by Lemma 1. Using
![]() $\textrm {CTT}$
-Comprehension, fix
$\textrm {CTT}$
-Comprehension, fix
![]() $b^{\alpha +1}$
such that:
$b^{\alpha +1}$
such that:
Suppose
![]() $z^\kappa \mathrel {\varepsilon } b^{\alpha +1}$
; by Lemma 3 there is
$z^\kappa \mathrel {\varepsilon } b^{\alpha +1}$
; by Lemma 3 there is
![]() $z^\alpha \mathrel {\equiv } z^\kappa $
such that
$z^\alpha \mathrel {\equiv } z^\kappa $
such that
![]() $b^{\alpha +1}(z^\alpha )$
; so using the biconditional,
$b^{\alpha +1}(z^\alpha )$
; so using the biconditional,
![]() $\phi (z^\kappa ) \land z^\kappa \mathrel {\varepsilon } a^{\alpha +1}$
. Conversely, suppose
$\phi (z^\kappa ) \land z^\kappa \mathrel {\varepsilon } a^{\alpha +1}$
. Conversely, suppose
![]() $\phi (z^\kappa ) \land z^\kappa \mathrel {\varepsilon } a^{\alpha +1}$
; by Type-Founded there is
$\phi (z^\kappa ) \land z^\kappa \mathrel {\varepsilon } a^{\alpha +1}$
; by Type-Founded there is
![]() $z^\alpha \mathrel {\equiv } z^\kappa $
, and
$z^\alpha \mathrel {\equiv } z^\kappa $
, and
![]() $(\forall x^\kappa \mathrel {\equiv } z^\alpha )(\phi (x^\kappa ) \land x^{\kappa } \mathrel {\varepsilon } a^{\alpha +1})$
by Lemma 2; so
$(\forall x^\kappa \mathrel {\equiv } z^\alpha )(\phi (x^\kappa ) \land x^{\kappa } \mathrel {\varepsilon } a^{\alpha +1})$
by Lemma 2; so
![]() $b^{\alpha +1}(z^\alpha )$
, and
$b^{\alpha +1}(z^\alpha )$
, and
![]() $z^\kappa \mathrel {\varepsilon } b^{\alpha +1}$
by Lemma 3. Summarizing:
$z^\kappa \mathrel {\varepsilon } b^{\alpha +1}$
by Lemma 3. Summarizing:
![]() $z^\kappa \mathrel {\varepsilon } b^{\alpha +1} \leftrightarrow (\phi (z^\kappa ) \land z^\kappa \mathrel {\varepsilon } a^{\alpha +1})$
. By Lemma 1 there is
$z^\kappa \mathrel {\varepsilon } b^{\alpha +1} \leftrightarrow (\phi (z^\kappa ) \land z^\kappa \mathrel {\varepsilon } a^{\alpha +1})$
. By Lemma 1 there is
![]() $b^\kappa \mathrel {\equiv } b^{\alpha +1}$
. Generalizing and using Lemma 2, for any
$b^\kappa \mathrel {\equiv } b^{\alpha +1}$
. Generalizing and using Lemma 2, for any
![]() $\alpha < \kappa $
:
$\alpha < \kappa $
:
Now
![]() ${\textrm {Separation}^{(\kappa )}}$
follows by the Limit
${\textrm {Separation}^{(\kappa )}}$
follows by the Limit
![]() $^\kappa $
-rule.□
$^\kappa $
-rule.□
Consequently,
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
proves Lemma
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
proves Lemma
![]() ${\textrm {5}}^{(\kappa )}$
and Theorem
${\textrm {5}}^{(\kappa )}$
and Theorem
![]() ${\textrm {6}^{(\kappa )}}$
. The latter result states that the
${\textrm {6}^{(\kappa )}}$
. The latter result states that the
![]() ${\textit{Lev}}^{(\kappa )}$
s are well-ordered by
${\textit{Lev}}^{(\kappa )}$
s are well-ordered by
![]() $\mathrel {\varepsilon }$
. Here, ‘
$\mathrel {\varepsilon }$
. Here, ‘
![]() ${\textit{Lev}}^{(\kappa )}$
’ is the obvious translation of the definition of ‘
${\textit{Lev}}^{(\kappa )}$
’ is the obvious translation of the definition of ‘
![]() ${\textit{Lev}}$
’; we also call these levels
${\textit{Lev}}$
’; we also call these levels
![]() $^{(\kappa )}$
. In what follows, we also write things like
$^{(\kappa )}$
. In what follows, we also write things like
![]() $x^\kappa \subseteq ^{(\kappa )} y^\kappa $
for
$x^\kappa \subseteq ^{(\kappa )} y^\kappa $
for
![]() $(\forall v^\kappa \mathrel {\varepsilon } x^\kappa )v^\kappa \mathrel {\varepsilon } y^\kappa $
.
$(\forall v^\kappa \mathrel {\varepsilon } x^\kappa )v^\kappa \mathrel {\varepsilon } y^\kappa $
.
Our next goal is to show that
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
simulates our set-theoretic principle of foundation, i.e., Stratification. We first need a small subsidiary lemma, which says (roughly) that any subset of a low-typed entity is itself low-typed:
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
simulates our set-theoretic principle of foundation, i.e., Stratification. We first need a small subsidiary lemma, which says (roughly) that any subset of a low-typed entity is itself low-typed:
Lemma 9.
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}} \vdash \forall a^\alpha (\forall b^\kappa \subseteq ^{(\kappa )} a^\alpha )\exists x^\alpha \ b^\kappa \mathrel {\equiv } x^\alpha $
, whenever
${\textrm {CTT}^{\tau }_{\textrm {p}}} \vdash \forall a^\alpha (\forall b^\kappa \subseteq ^{(\kappa )} a^\alpha )\exists x^\alpha \ b^\kappa \mathrel {\equiv } x^\alpha $
, whenever
![]() $\kappa + 2 < \tau $
.
$\kappa + 2 < \tau $
.
Proof. Suppose
![]() $\alpha $
and
$\alpha $
and
![]() $\kappa $
are limits (the proof is easier otherwise). Let
$\kappa $
are limits (the proof is easier otherwise). Let
![]() $\beta < \kappa $
, and fix
$\beta < \kappa $
, and fix
![]() $b^\beta \subseteq ^{(\kappa )} a^\alpha $
; it suffices to show that
$b^\beta \subseteq ^{(\kappa )} a^\alpha $
; it suffices to show that
![]() $\exists x^\alpha \ b^\beta \mathrel {\equiv } x^\alpha $
, since we can then use Limit
$\exists x^\alpha \ b^\beta \mathrel {\equiv } x^\alpha $
, since we can then use Limit
![]() $^\kappa $
to establish the result.
$^\kappa $
to establish the result.
If
![]() $\beta \leq \alpha $
, Lemma 1 immediately tells us that
$\beta \leq \alpha $
, Lemma 1 immediately tells us that
![]() $\exists x^\alpha \ b^\beta \mathrel {\equiv } x^\alpha $
. Suppose instead that
$\exists x^\alpha \ b^\beta \mathrel {\equiv } x^\alpha $
. Suppose instead that
![]() $\beta> \alpha $
. Fix
$\beta> \alpha $
. Fix
![]() $\gamma < \alpha $
, and suppose there is some
$\gamma < \alpha $
, and suppose there is some
![]() $a^{\gamma +1} \mathrel {\equiv } a^\alpha $
. Using Lemma 1, let
$a^{\gamma +1} \mathrel {\equiv } a^\alpha $
. Using Lemma 1, let
![]() $b^{\beta +1} \mathrel {\equiv } b^\beta $
. By
$b^{\beta +1} \mathrel {\equiv } b^\beta $
. By
![]() $\textrm {CTT}$
-Comprehension, there is
$\textrm {CTT}$
-Comprehension, there is
![]() $c^{\gamma +1}$
such that:
$c^{\gamma +1}$
such that:
Using Lemmas 1–3: if
![]() $b^{\beta +1}(v^\beta )$
, then
$b^{\beta +1}(v^\beta )$
, then
![]() $v^\beta \mathrel {\varepsilon } a^{\gamma +1}$
since
$v^\beta \mathrel {\varepsilon } a^{\gamma +1}$
since
![]() $b^\beta \subseteq ^{(\kappa )} a^{\gamma +1}$
, so that there is
$b^\beta \subseteq ^{(\kappa )} a^{\gamma +1}$
, so that there is
![]() $y^\gamma \mathrel {\equiv } v^\beta $
; now
$y^\gamma \mathrel {\equiv } v^\beta $
; now
![]() $b^{\beta +1}(y^\gamma )$
, so that
$b^{\beta +1}(y^\gamma )$
, so that
![]() $c^{\gamma +1}(y^\gamma )$
. Generalizing,
$c^{\gamma +1}(y^\gamma )$
. Generalizing,
![]() $\forall v^\beta (b^{\beta +1}(v^\beta ) \rightarrow (\exists y^\gamma \mathrel {\equiv } v^\beta )c^{\gamma +1}(y^\gamma ))$
. By Type-Ext,
$\forall v^\beta (b^{\beta +1}(v^\beta ) \rightarrow (\exists y^\gamma \mathrel {\equiv } v^\beta )c^{\gamma +1}(y^\gamma ))$
. By Type-Ext,
![]() $c^{\gamma +1} \mathrel {\equiv } b^{\beta +1} \mathrel {\equiv } b^\beta $
. Summarizing all this, we have established the following conditional, for each
$c^{\gamma +1} \mathrel {\equiv } b^{\beta +1} \mathrel {\equiv } b^\beta $
. Summarizing all this, we have established the following conditional, for each
![]() $\gamma < \alpha $
:
$\gamma < \alpha $
:
Now, for reductio, suppose that
![]() $\forall x^\alpha \ b^\beta \mathrel {\not \equiv } x^\alpha $
. Then
$\forall x^\alpha \ b^\beta \mathrel {\not \equiv } x^\alpha $
. Then
![]() $\forall x^{\gamma +1}\ b^\beta \mathrel {\not \equiv } x^{\gamma +1}$
for all
$\forall x^{\gamma +1}\ b^\beta \mathrel {\not \equiv } x^{\gamma +1}$
for all
![]() $\gamma < \alpha $
. So, by the relevant conditional,
$\gamma < \alpha $
. So, by the relevant conditional,
![]() $\forall x^{\gamma +1}\ a^\alpha \mathrel {\not \equiv } x^{\gamma +1}$
. By the Limit
$\forall x^{\gamma +1}\ a^\alpha \mathrel {\not \equiv } x^{\gamma +1}$
. By the Limit
![]() $^\alpha $
-rule,
$^\alpha $
-rule,
![]() $\forall x^\alpha \ a^\alpha \mathrel {\not \equiv } x^\alpha $
, a contradiction. Discharging the reductio,
$\forall x^\alpha \ a^\alpha \mathrel {\not \equiv } x^\alpha $
, a contradiction. Discharging the reductio,
![]() $\exists x^\alpha \ b^\beta \mathrel {\equiv } x^\alpha $
, as required.□
$\exists x^\alpha \ b^\beta \mathrel {\equiv } x^\alpha $
, as required.□
Lemma 10.
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}} \vdash {\textrm {Stratification}^{(\kappa )}}$
, whenever
${\textrm {CTT}^{\tau }_{\textrm {p}}} \vdash {\textrm {Stratification}^{(\kappa )}}$
, whenever
![]() $\kappa + 2 < \tau $
.
$\kappa + 2 < \tau $
.
Proof. We will show that, for each
![]() $\beta \leq \kappa $
,
$\beta \leq \kappa $
,
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
proves
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
proves
![]() $\forall a^\beta (\exists s^\beta \supseteq ^{(\kappa )} a^\beta ){\textit{Lev}}^{(\kappa )}(s^\beta )$
. This is an induction on
$\forall a^\beta (\exists s^\beta \supseteq ^{(\kappa )} a^\beta ){\textit{Lev}}^{(\kappa )}(s^\beta )$
. This is an induction on
![]() $\beta $
in the metatheory, where our induction hypothesis is that for each
$\beta $
in the metatheory, where our induction hypothesis is that for each
![]() $\alpha < \beta $
we have established
$\alpha < \beta $
we have established
![]() $\forall a^\alpha (\exists s^\alpha \supseteq ^{(\kappa )} a^\alpha ){\textit{Lev}}^{(\kappa )}(s^\alpha )$
$\forall a^\alpha (\exists s^\alpha \supseteq ^{(\kappa )} a^\alpha ){\textit{Lev}}^{(\kappa )}(s^\alpha )$
Induction case when
![]() $\beta = 0$
. By Type-Founded,
$\beta = 0$
. By Type-Founded,
![]() . So
. So
![]() ${{\textit{Hist}}}^\kappa (a^0)$
and
${{\textit{Hist}}}^\kappa (a^0)$
and
![]() ${\textit{Lev}}^{(\kappa )}(a^0)$
, vacuously. So
${\textit{Lev}}^{(\kappa )}(a^0)$
, vacuously. So
![]() $\forall a^0(\exists s^0 \supseteq ^{(\kappa )} a^0){\textit{Lev}}^{(\kappa )}(s^0)$
.
$\forall a^0(\exists s^0 \supseteq ^{(\kappa )} a^0){\textit{Lev}}^{(\kappa )}(s^0)$
.
Induction case when
![]() $\beta $
is a limit. Applying Lemmas 1–2 to our induction hypothesis, we have
$\beta $
is a limit. Applying Lemmas 1–2 to our induction hypothesis, we have
![]() $\forall a^\alpha (\exists s^\beta \supseteq ^{(\kappa )} a^\alpha ){\textit{Lev}}^{(\kappa )}(s^\beta )$
. Now
$\forall a^\alpha (\exists s^\beta \supseteq ^{(\kappa )} a^\alpha ){\textit{Lev}}^{(\kappa )}(s^\beta )$
. Now
![]() $\forall a^\beta (\exists s^\beta \supseteq ^{(\kappa )} a^\beta ){\textit{Lev}}^{(\kappa )}(s^\beta )$
, by the Limit
$\forall a^\beta (\exists s^\beta \supseteq ^{(\kappa )} a^\beta ){\textit{Lev}}^{(\kappa )}(s^\beta )$
, by the Limit
![]() $^\beta $
-rule.
$^\beta $
-rule.
Induction case when
![]() $\beta = \alpha + 1$
. Using
$\beta = \alpha + 1$
. Using
![]() $\textrm {CTT}$
-Comprehension twice, find
$\textrm {CTT}$
-Comprehension twice, find
![]() $h^{\beta }$
and
$h^{\beta }$
and
![]() $s^{\beta }$
such that
$s^{\beta }$
such that
Combining these with the induction hypothesis, we obtain:
Next, applying
![]() ${\forall {\textrm {E}}^{\kappa }_{\alpha }}$
and
${\forall {\textrm {E}}^{\kappa }_{\alpha }}$
and
![]() ${\forall {\textrm {I}}^{\alpha }_{\alpha }}$
to Lemma
${\forall {\textrm {I}}^{\alpha }_{\alpha }}$
to Lemma
![]() ${\textrm {5}^{(\kappa )}}$
gives:
${\textrm {5}^{(\kappa )}}$
gives:
i.e.,
![]() $h^\beta $
is a history
$h^\beta $
is a history
![]() $^{(\kappa )}$
. So
$^{(\kappa )}$
. So
![]() $s^\beta $
is a level
$s^\beta $
is a level
![]() $^{(\kappa )}$
, by (3). Moreover, for any
$^{(\kappa )}$
, by (3). Moreover, for any
![]() $a^{\beta }$
, we have
$a^{\beta }$
, we have
![]() $a^\beta \subseteq ^{(\kappa )} s^\beta $
by (2) and Lemmas 1–3. So
$a^\beta \subseteq ^{(\kappa )} s^\beta $
by (2) and Lemmas 1–3. So
![]() $\forall a^{\beta }(\exists s^{\beta }\supseteq ^{(\kappa )} a^\alpha ){\textit{Lev}}^{(\kappa )}(s^{\beta })$
.□
$\forall a^{\beta }(\exists s^{\beta }\supseteq ^{(\kappa )} a^\alpha ){\textit{Lev}}^{(\kappa )}(s^{\beta })$
.□
We have now established
![]() ${\textrm {LT}^{(\kappa )}}$
. To obtain
${\textrm {LT}^{(\kappa )}}$
. To obtain
![]() ${\textrm {Zr}^{(\kappa )}}$
, we need just two straightforward results, which we leave to the reader (they hold using
${\textrm {Zr}^{(\kappa )}}$
, we need just two straightforward results, which we leave to the reader (they hold using
![]() $\textrm {CTT}$
-Comprehension, Lemmas 1–3, and the Limit-rule).
$\textrm {CTT}$
-Comprehension, Lemmas 1–3, and the Limit-rule).
Lemma 11.
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}} \vdash {{\textrm {Endless}^{(\kappa )}}}$
, whenever
${\textrm {CTT}^{\tau }_{\textrm {p}}} \vdash {{\textrm {Endless}^{(\kappa )}}}$
, whenever
![]() $\kappa + 2 < \tau $
and
$\kappa + 2 < \tau $
and
![]() $\kappa $
is a limit.
$\kappa $
is a limit.
Lemma 12.
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}} \vdash {{\textrm {Infinity}^{(\kappa )}}}$
, whenever
${\textrm {CTT}^{\tau }_{\textrm {p}}} \vdash {{\textrm {Infinity}^{(\kappa )}}}$
, whenever
![]() $\kappa> \omega $
and
$\kappa> \omega $
and
![]() $\kappa + 2 < \tau .$
$\kappa + 2 < \tau .$
Assembling Lemmas 7–12, we have the Sets-from-Types Theorem:
Theorem 13.
![]() ${\textrm {CTT}^{\tau }_{\textrm {p}}} \vdash {\textrm {Zr}^{(\kappa )}}$
for any limit
${\textrm {CTT}^{\tau }_{\textrm {p}}} \vdash {\textrm {Zr}^{(\kappa )}}$
for any limit
![]() $\kappa> \omega $
with
$\kappa> \omega $
with
![]() $\kappa + 2 < \tau $
.
$\kappa + 2 < \tau $
.
B.3 Replacement, and semantic considerations
We mentioned that
![]() ${\textrm {Zr}}$
sits strictly between
${\textrm {Zr}}$
sits strictly between
![]() ${\textrm {Z}}$
and
${\textrm {Z}}$
and
![]() ${\textrm {ZF}}$
. Specifically,
${\textrm {ZF}}$
. Specifically,
![]() ${\textrm {Zr}}$
does not include Replacement. To settle the status of Replacement with regard to
${\textrm {Zr}}$
does not include Replacement. To settle the status of Replacement with regard to
![]() ${\textrm {CTT}_{\textrm {p}}}$
,Footnote
69
we will move from proof theory to semantics, linking models of
${\textrm {CTT}_{\textrm {p}}}$
,Footnote
69
we will move from proof theory to semantics, linking models of
![]() ${\textrm {CTT}_{\textrm {p}}}$
with models of
${\textrm {CTT}_{\textrm {p}}}$
with models of
![]() ${\textrm {LT}}$
. (Recall that
${\textrm {LT}}$
. (Recall that
![]() ${\textrm {LT}}$
is the subtheory of
${\textrm {LT}}$
is the subtheory of
![]() ${\textrm {Zr}}$
whose axioms are Extensionality, Separation and Stratification.)
${\textrm {Zr}}$
whose axioms are Extensionality, Separation and Stratification.)
In considering models of
![]() ${\textrm {LT}}$
, we restrict our attention to transitive models.Footnote
70
Recall that a structure
${\textrm {LT}}$
, we restrict our attention to transitive models.Footnote
70
Recall that a structure
![]() $\mathcal {A}$
in the signature of set theory is transitive iff both
$\mathcal {A}$
in the signature of set theory is transitive iff both
![]() $(\forall x \in A)x\subseteq A$
, and
$(\forall x \in A)x\subseteq A$
, and
![]() $(\forall a \in A)(\forall b \in A)(a \in b \leftrightarrow a \in ^{\mathcal {A}} b)$
. So membership and subsethood are absolute for transitive models. Also recall that being a (von Neumann) ordinal is absolute for transitive models,Footnote
71
and so is the notion of a set’s (ordinal) rank. (Recall from Appendix B.1 that we can define a set’s rank within
$(\forall a \in A)(\forall b \in A)(a \in b \leftrightarrow a \in ^{\mathcal {A}} b)$
. So membership and subsethood are absolute for transitive models. Also recall that being a (von Neumann) ordinal is absolute for transitive models,Footnote
71
and so is the notion of a set’s (ordinal) rank. (Recall from Appendix B.1 that we can define a set’s rank within
![]() ${\textrm {LT}}$
, and hence within
${\textrm {LT}}$
, and hence within
![]() ${\textrm {Zr}}$
.) Where
${\textrm {Zr}}$
.) Where
![]() $\mathcal {A}$
is a transitive model of
$\mathcal {A}$
is a transitive model of
![]() ${{\textrm {LT}}}$
, let
${{\textrm {LT}}}$
, let
![]() ${\textit{Ord}({\mathcal {A}})}$
be the least ordinal not in A itself.
${\textit{Ord}({\mathcal {A}})}$
be the least ordinal not in A itself.
Whilst we consider only transitive models of
![]() ${\textrm {LT}}$
, we will entertain non-standard models. A transitive model
${\textrm {LT}}$
, we will entertain non-standard models. A transitive model
![]() $\mathcal {A} \models {{\textrm {LT}}}$
is standard iff for any
$\mathcal {A} \models {{\textrm {LT}}}$
is standard iff for any
![]() $\alpha < {{\textit{Ord}({\mathcal {A}})}}$
, every subset of
$\alpha < {{\textit{Ord}({\mathcal {A}})}}$
, every subset of
![]() $\{x \in A : {\textrm {rank}}(x) \leq \alpha \}$
is itself in
$\{x \in A : {\textrm {rank}}(x) \leq \alpha \}$
is itself in
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Given any model
![]() $\mathcal {M} \models {\textrm {CTT}^{\tau }_{\textrm {p}}}$
with
$\mathcal {M} \models {\textrm {CTT}^{\tau }_{\textrm {p}}}$
with
![]() $\kappa + 2 < \tau $
, we can easily turn it into a transitive set-theoretic model,
$\kappa + 2 < \tau $
, we can easily turn it into a transitive set-theoretic model,
![]() ${\textbf {L}^{\kappa }\mathcal {M}}$
, as follows: let
${\textbf {L}^{\kappa }\mathcal {M}}$
, as follows: let
![]() ${\textbf {L}^{\kappa }\mathcal {M}}$
’s domain comprise all the type
${\textbf {L}^{\kappa }\mathcal {M}}$
’s domain comprise all the type
![]() $\kappa $
entities from
$\kappa $
entities from
![]() $\mathcal {M}$
; and let
$\mathcal {M}$
; and let
![]() ${{\textbf {L}^{\kappa }\mathcal {M}}} \models a \in b$
iff
${{\textbf {L}^{\kappa }\mathcal {M}}} \models a \in b$
iff
![]() $\mathcal {M} \models a \mathrel {\varepsilon } b$
.
$\mathcal {M} \models a \mathrel {\varepsilon } b$
.
Lemma 14. When
![]() $\kappa + 2 < \tau $
: if
$\kappa + 2 < \tau $
: if
![]() $\mathcal {M} \models {\textrm {CTT}^{\tau }_{\textrm {p}}}$
, then
$\mathcal {M} \models {\textrm {CTT}^{\tau }_{\textrm {p}}}$
, then
![]() ${\textbf {L}^{\kappa }\mathcal {M}}$
is isomorphic to a unique transitive model of
${\textbf {L}^{\kappa }\mathcal {M}}$
is isomorphic to a unique transitive model of
![]() ${\textrm {LT}}$
.
${\textrm {LT}}$
.
Proof. By Lemmas 7–10,
![]() ${{\textbf {L}^{\kappa }\mathcal {M}}} \models {{\textrm {LT}}}$
. The type indices are well-ordered. By the Limit-rule, Type-Founded, Type-Purity and Lemma 7,
${{\textbf {L}^{\kappa }\mathcal {M}}} \models {{\textrm {LT}}}$
. The type indices are well-ordered. By the Limit-rule, Type-Founded, Type-Purity and Lemma 7,
![]() ${\textbf {L}^{\kappa }\mathcal {M}}$
’s membership relation is extensional and well-founded. Now use Mostowski’s Collapsing Lemma.□
${\textbf {L}^{\kappa }\mathcal {M}}$
’s membership relation is extensional and well-founded. Now use Mostowski’s Collapsing Lemma.□
We can also move in the opposite direction, from transitive models of
![]() ${\textrm {LT}}$
to models of
${\textrm {LT}}$
to models of
![]() ${\textrm {CTT}_{\textrm {p}}}$
. In effect, we follow the class-semantics of Section 4.2, but tweaked to ban urelements and to allow for non-standard models of
${\textrm {CTT}_{\textrm {p}}}$
. In effect, we follow the class-semantics of Section 4.2, but tweaked to ban urelements and to allow for non-standard models of
![]() ${\textrm {CTT}_{\textrm {p}}}$
, where a model of
${\textrm {CTT}_{\textrm {p}}}$
, where a model of
![]() ${\textrm {CTT}_{\textrm {p}}}$
is standard iff for any entities of any type
${\textrm {CTT}_{\textrm {p}}}$
is standard iff for any entities of any type
![]() $\alpha $
(other than the greatest) in the model, some type
$\alpha $
(other than the greatest) in the model, some type
![]() $\alpha \mathord {+}1$
property in the model applies exactly to those entities.Footnote
72
Still, the basic plan is simple: start with a transitive model of
$\alpha \mathord {+}1$
property in the model applies exactly to those entities.Footnote
72
Still, the basic plan is simple: start with a transitive model of
![]() ${\textrm {LT}}$
; treat entities of different rank as being of different types; and read membership as ‘application’.
${\textrm {LT}}$
; treat entities of different rank as being of different types; and read membership as ‘application’.
Unfortunately, there is a small wrinkle in implementing this plan, thanks to an irritating mismatch between the types of
![]() ${\textrm {CTT}_{\textrm {p}}}$
and a set’s rank. To illustrate:
${\textrm {CTT}_{\textrm {p}}}$
and a set’s rank. To illustrate:
![]() ${\textrm {CTT}_{\textrm {p}}}$
’s Limit-rule means that every type
${\textrm {CTT}_{\textrm {p}}}$
’s Limit-rule means that every type
![]() $\omega $
entity is of some finite type, but the ordinal
$\omega $
entity is of some finite type, but the ordinal
![]() $\omega $
has rank
$\omega $
has rank
![]() $\omega $
. To deal with this wrinkle, we define a function which (in effect) tells us how to map from ranks to types:
$\omega $
. To deal with this wrinkle, we define a function which (in effect) tells us how to map from ranks to types:
 $$ \begin{align*} \alpha^* &= \begin{cases} \alpha&\mbox{if } \alpha < \omega\\ \alpha+1&\mbox{if } \alpha \geq \omega. \end{cases} \end{align*} $$
$$ \begin{align*} \alpha^* &= \begin{cases} \alpha&\mbox{if } \alpha < \omega\\ \alpha+1&\mbox{if } \alpha \geq \omega. \end{cases} \end{align*} $$
We can now implement our plan. Where
![]() $\mathcal {A}$
is a transitive model of
$\mathcal {A}$
is a transitive model of
![]() ${\textrm {LT}}$
, define
${\textrm {LT}}$
, define
![]() ${\textbf {C}\mathcal {A}}$
as follows. Its denizens are just the members of A, and if
${\textbf {C}\mathcal {A}}$
as follows. Its denizens are just the members of A, and if
![]() ${{\textrm {rank}}}(x) = \alpha $
then x is treated as a type
${{\textrm {rank}}}(x) = \alpha $
then x is treated as a type
![]() $\beta $
entity for all
$\beta $
entity for all
![]() $\alpha ^* \leq \beta < {{\textit{Ord}({\mathcal {A}})}}^*$
. Then, we stipulate that
$\alpha ^* \leq \beta < {{\textit{Ord}({\mathcal {A}})}}^*$
. Then, we stipulate that
![]() ${{\textbf {C}\mathcal {A}}} \models y^{\alpha }(x^{\alpha })$
iff
${{\textbf {C}\mathcal {A}}} \models y^{\alpha }(x^{\alpha })$
iff
![]() $\mathcal {A} \models x \in y$
.
$\mathcal {A} \models x \in y$
.
Lemma 15. Let
![]() $\mathcal {A} \models {{\textrm {LT}}}$
be transitive. Then
$\mathcal {A} \models {{\textrm {LT}}}$
be transitive. Then
![]() ${{\textbf {C}\mathcal {A}}} \models {\textrm {CTT}^{{{\textit{Ord}({\mathcal {A}})}}^{*}}_{\textrm {p}}}$
. Moreover,
${{\textbf {C}\mathcal {A}}} \models {\textrm {CTT}^{{{\textit{Ord}({\mathcal {A}})}}^{*}}_{\textrm {p}}}$
. Moreover,
![]() $\mathcal {A}$
is standard iff
$\mathcal {A}$
is standard iff
![]() ${\textbf {C}\mathcal {A}}$
is standard.
${\textbf {C}\mathcal {A}}$
is standard.
Proof sketch. The quantifier-rules and Limit-rules are obviously sound. When
![]() $\mathrel {\equiv }$
and
$\mathrel {\equiv }$
and
![]() $\mathrel {\varepsilon }$
are well-defined
$\mathrel {\varepsilon }$
are well-defined
![]() ${\textrm {CTT}^{{\textit{Ord}({\mathcal {A}})^{*}}}}$
-expressions,Footnote
73
distinct entities
${\textrm {CTT}^{{\textit{Ord}({\mathcal {A}})^{*}}}}$
-expressions,Footnote
73
distinct entities
![]() $a^{\alpha }$
and
$a^{\alpha }$
and
![]() $b^\beta $
are distinguished by
$b^\beta $
are distinguished by
![]() $\{a^\alpha \}^{\alpha +1}$
, so
$\{a^\alpha \}^{\alpha +1}$
, so
![]() $\mathrel {\equiv }^{{{\textbf {C}\mathcal {A}}}}$
is identity and
$\mathrel {\equiv }^{{{\textbf {C}\mathcal {A}}}}$
is identity and
![]() $\mathrel {\varepsilon }^{{{\textbf {C}\mathcal {A}}}}$
is membership. Type-Base and Type-Purity now hold, as
$\mathrel {\varepsilon }^{{{\textbf {C}\mathcal {A}}}}$
is membership. Type-Base and Type-Purity now hold, as
![]() $\mathcal {A}$
has exactly one rank-
$\mathcal {A}$
has exactly one rank-
![]() $0$
object, and it is empty. Type-Ext follows from Extensionality and simple reasoning about ranks. For
$0$
object, and it is empty. Type-Ext follows from Extensionality and simple reasoning about ranks. For
![]() $\textrm {CTT}$
-Comprehension, fix
$\textrm {CTT}$
-Comprehension, fix
![]() $\phi $
and
$\phi $
and
![]() $\alpha $
with
$\alpha $
with
![]() $\alpha +1 < {{\textit{Ord}({\mathcal {A}})}}^*$
; we will show that:
$\alpha +1 < {{\textit{Ord}({\mathcal {A}})}}^*$
; we will show that:
Let
![]() $\beta ^* = {\alpha +1}$
; note that
$\beta ^* = {\alpha +1}$
; note that
![]() $\beta \in A$
, as
$\beta \in A$
, as
![]() $\mathcal {A}$
is transitive. Fix
$\mathcal {A}$
is transitive. Fix
![]() $s \in A$
such that
$s \in A$
such that
![]() $\mathcal {A}$
thinks that s is the
$\mathcal {A}$
thinks that s is the
![]() $\in $
-least level with
$\in $
-least level with
![]() $\beta $
as a subset. By Separation on s in
$\beta $
as a subset. By Separation on s in
![]() $\mathcal {A}$
, there is some
$\mathcal {A}$
, there is some
![]() $c \in A$
of rank
$c \in A$
of rank
![]() $\leq \beta $
which serves as a witnessing value for
$\leq \beta $
which serves as a witnessing value for
![]() $z^{\alpha +1}$
when regarded as an entity of type
$z^{\alpha +1}$
when regarded as an entity of type
![]() $\alpha +1$
. Finally, the remark about standardness is immediate from the construction.□
$\alpha +1$
. Finally, the remark about standardness is immediate from the construction.□
We now have the means to move between transitive models of
![]() ${\textrm {LT}}$
and models of
${\textrm {LT}}$
and models of
![]() ${\textrm {CTT}_{\textrm {p}}}$
. Recalling that
${\textrm {CTT}_{\textrm {p}}}$
. Recalling that
![]() ${\textrm {LT}}$
is strictly weaker than
${\textrm {LT}}$
is strictly weaker than
![]() ${\textrm {ZF}}$
, we can now settle the status of Replacement, in
${\textrm {ZF}}$
, we can now settle the status of Replacement, in
![]() ${\textrm {CTT}_{\textrm {p}}}$
, by using some well-known facts concerning models of
${\textrm {CTT}_{\textrm {p}}}$
, by using some well-known facts concerning models of
![]() ${\textrm {ZF}}$
:
${\textrm {ZF}}$
:
Theorem 16. Fix
![]() $\kappa> \omega $
such that
$\kappa> \omega $
such that
![]() $\kappa + 2 < \tau $
:
$\kappa + 2 < \tau $
:
-
(1) If
 $\kappa $
is strongly inaccessible, every model of
$\kappa $
is strongly inaccessible, every model of
 ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
satisfies
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
satisfies
 ${{\textrm {ZF}}^{(\kappa )}}$
.
${{\textrm {ZF}}^{(\kappa )}}$
. -
(2) If
 $\kappa $
is not strongly inaccessible, there are models of
$\kappa $
is not strongly inaccessible, there are models of
 ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
which violate
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
which violate
 ${{\textrm {ZF}}^{(\kappa )}}$
, and any model of
${{\textrm {ZF}}^{(\kappa )}}$
, and any model of
 ${\textrm {CTT}^{\tau }_{\textrm {p}}}$
which satisfies
${\textrm {CTT}^{\tau }_{\textrm {p}}}$
which satisfies
 ${{\textrm {ZF}}^{(\kappa )}}$
is non-standard.
${{\textrm {ZF}}^{(\kappa )}}$
is non-standard.
Proof.
(1) Let
![]() $\kappa $
be strongly inaccessible with
$\kappa $
be strongly inaccessible with
![]() $\mathcal {M} \models {\textrm {CTT}^{\tau }_{\textrm {p}}}$
. Using Theorem 13 and Lemma 14, obtain a transitive model
$\mathcal {M} \models {\textrm {CTT}^{\tau }_{\textrm {p}}}$
. Using Theorem 13 and Lemma 14, obtain a transitive model
![]() $\mathcal {A} \cong {\textbf {L}^{\kappa }\mathcal {M}} \models {\textrm {Zr}}$
. To show that
$\mathcal {A} \cong {\textbf {L}^{\kappa }\mathcal {M}} \models {\textrm {Zr}}$
. To show that
![]() $\mathcal {M} \models {{\textrm {ZF}}^{(\kappa )}}$
, it suffices to show that
$\mathcal {M} \models {{\textrm {ZF}}^{(\kappa )}}$
, it suffices to show that
![]() $\mathcal {A} \models \textrm {Replacement}$
. So: fix
$\mathcal {A} \models \textrm {Replacement}$
. So: fix
![]() $a \in A$
and suppose
$a \in A$
and suppose
![]() $\mathcal {A} \models (\forall x \in a)\exists !y \phi (x,y)$
. Working outside
$\mathcal {A} \models (\forall x \in a)\exists !y \phi (x,y)$
. Working outside
![]() $\mathcal {A}$
, let
$\mathcal {A}$
, let
Since
![]() $\mathcal {A}$
is transitive and
$\mathcal {A}$
is transitive and
![]() $\kappa $
is strongly inaccessible,
$\kappa $
is strongly inaccessible,
![]() $\beta \in A$
. So also
$\beta \in A$
. So also
![]() $\{c : \mathcal {A} \models (\exists x \in a)\phi (x,c)\} \in A$
, by Separation in
$\{c : \mathcal {A} \models (\exists x \in a)\phi (x,c)\} \in A$
, by Separation in
![]() $\mathcal {A}$
on what
$\mathcal {A}$
on what
![]() $\mathcal {A}$
thinks is a level with
$\mathcal {A}$
thinks is a level with
![]() $\beta $
as a subset.
$\beta $
as a subset.
(2) Here are two general facts about the
![]() $V_\alpha $
hierarchy:
$V_\alpha $
hierarchy:
 $$ \begin{align*} V_\kappa \models {{\mbox{ZF }}}&\mbox{ iff } \kappa \mbox{ is strongly inaccessible}\\ V_{\kappa}\models {{\mbox{LT }}}&\mbox{ iff } \kappa> 0. \end{align*} $$
$$ \begin{align*} V_\kappa \models {{\mbox{ZF }}}&\mbox{ iff } \kappa \mbox{ is strongly inaccessible}\\ V_{\kappa}\models {{\mbox{LT }}}&\mbox{ iff } \kappa> 0. \end{align*} $$
So suppose
![]() $\kappa> \omega $
is not strongly inaccessible. Fix
$\kappa> \omega $
is not strongly inaccessible. Fix
![]() $\sigma $
such that
$\sigma $
such that
![]() $\sigma ^* \geq \tau $
. Now,
$\sigma ^* \geq \tau $
. Now,
![]() $V_\sigma $
is a transitive model of
$V_\sigma $
is a transitive model of
![]() ${\textrm {LT}}$
and Ord
${\textrm {LT}}$
and Ord
![]() ${{({V_\sigma })}} = \sigma $
. Using Lemma 15, obtain
${{({V_\sigma })}} = \sigma $
. Using Lemma 15, obtain
![]() ${{\textbf {C}V_{\sigma }}} \models {\textrm {CTT}^{\tau }_{\textrm {p}}}$
. By construction,
${{\textbf {C}V_{\sigma }}} \models {\textrm {CTT}^{\tau }_{\textrm {p}}}$
. By construction,
![]() ${\textbf {L}^{\kappa }{\textbf {C}V_{\sigma }}} = V_{\kappa }$
. Since
${\textbf {L}^{\kappa }{\textbf {C}V_{\sigma }}} = V_{\kappa }$
. Since
![]() $V_{\kappa } \nvDash \textrm {Replacement}$
, also
$V_{\kappa } \nvDash \textrm {Replacement}$
, also
![]() ${{\textbf {C}V_{\sigma }}} \nvDash {{\textrm {Replacement}^{(\kappa )}}}$
.
${{\textbf {C}V_{\sigma }}} \nvDash {{\textrm {Replacement}^{(\kappa )}}}$
.
For the second clause: suppose
![]() $\mathcal {M} \models {\textrm {CTT}^{\tau }_{\textrm {p}}}$
and
$\mathcal {M} \models {\textrm {CTT}^{\tau }_{\textrm {p}}}$
and
![]() $\mathcal {M} \models {{\textrm {ZF}}^{(\kappa )}}$
, with
$\mathcal {M} \models {{\textrm {ZF}}^{(\kappa )}}$
, with
![]() $\kappa $
not strongly inaccessible. Use Lemma 14 to obtain a unique transitive model
$\kappa $
not strongly inaccessible. Use Lemma 14 to obtain a unique transitive model
![]() $\mathcal {A} \cong {{\textbf {L}^{\kappa }\mathcal {M}}}$
. Since
$\mathcal {A} \cong {{\textbf {L}^{\kappa }\mathcal {M}}}$
. Since
![]() $\mathcal {A} \models {\textrm {ZF}}$
but
$\mathcal {A} \models {\textrm {ZF}}$
but
![]() ${\textit{Ord}({\mathcal {A}})}$
is not strongly inaccessible,
${\textit{Ord}({\mathcal {A}})}$
is not strongly inaccessible,
![]() $\mathcal {A}$
is non-standard.□
$\mathcal {A}$
is non-standard.□
C Definitional equivalence for
 ${{\textrm {CTT}}^{\omega }}$
${{\textrm {CTT}}^{\omega }}$
In Section 5.4, we stated that
![]() ${\textrm {CTT}^{\omega }}$
is definitionally equivalent to
${\textrm {CTT}^{\omega }}$
is definitionally equivalent to
![]() ${\textrm {STT}_{\uparrow }}$
. In this appendix, we define
${\textrm {STT}_{\uparrow }}$
. In this appendix, we define
![]() ${\textrm {STT}_{\uparrow }}$
, and prove the equivalence.
${\textrm {STT}_{\uparrow }}$
, and prove the equivalence.
![]() ${\textrm {STT}_{\uparrow }}$
augments
${\textrm {STT}_{\uparrow }}$
augments
![]() ${\textrm {STT}}$
with a new function symbol,
${\textrm {STT}}$
with a new function symbol,
![]() $\mathord {\uparrow }$
, for each n, which takes a type n entity as input and outputs a type
$\mathord {\uparrow }$
, for each n, which takes a type n entity as input and outputs a type
![]() $n\mathord {+}1$
entity.Footnote
74
So, for example,
$n\mathord {+}1$
entity.Footnote
74
So, for example,
![]() $b^2(\mathord {\uparrow } a^0)$
and
$b^2(\mathord {\uparrow } a^0)$
and
![]() $c^5(\mathord {\uparrow }\mathord {\uparrow } b^2)$
are well-formed.
$c^5(\mathord {\uparrow }\mathord {\uparrow } b^2)$
are well-formed.
![]() ${\textrm {STT}_{\uparrow }}$
retains
${\textrm {STT}_{\uparrow }}$
retains
![]() ${\textrm {STT}}$
-Comprehension; this holds for formulas containing
${\textrm {STT}}$
-Comprehension; this holds for formulas containing
![]() $\mathord {\uparrow }$
.
$\mathord {\uparrow }$
.
![]() ${\textrm {STT}_{\uparrow }}$
then has axioms ensuring that
${\textrm {STT}_{\uparrow }}$
then has axioms ensuring that
![]() $\mathord {\uparrow }$
is injective, preserves property-possession, and delivers well-foundedness:
$\mathord {\uparrow }$
is injective, preserves property-possession, and delivers well-foundedness:
-
Up-Inject.
 $\forall x^n \forall y^n(\mathord {\uparrow } x^n = \mathord {\uparrow } y^n \rightarrow x^n = y^n)$
$\forall x^n \forall y^n(\mathord {\uparrow } x^n = \mathord {\uparrow } y^n \rightarrow x^n = y^n)$
-
Up-Possess.
 $\forall x^n \forall y^{n+1}(\mathord {\uparrow } y^{n+1}(\mathord {\uparrow } x^n) \leftrightarrow y^{n+1}(x^n))$
$\forall x^n \forall y^{n+1}(\mathord {\uparrow } y^{n+1}(\mathord {\uparrow } x^n) \leftrightarrow y^{n+1}(x^n))$
-
Up-Founded.
 $\forall x^{n+1}\forall y^{n+1}(\mathord {\uparrow } y^{n+1}(x^{n+1}) \rightarrow \exists z^n\ x^{n+1} = \mathord {\uparrow } z^n)$
$\forall x^{n+1}\forall y^{n+1}(\mathord {\uparrow } y^{n+1}(x^{n+1}) \rightarrow \exists z^n\ x^{n+1} = \mathord {\uparrow } z^n)$
-
Up-Base.
 $\forall x^0\forall y^0 \lnot \mathord {\uparrow } y^0(x^0)$
$\forall x^0\forall y^0 \lnot \mathord {\uparrow } y^0(x^0)$
For readability, where
![]() $m> n$
, we write
$m> n$
, we write
![]() $\mathord {\uparrow }_{m}a^n$
for the result of applying
$\mathord {\uparrow }_{m}a^n$
for the result of applying
![]() $m - n$
instances of
$m - n$
instances of
![]() $\mathord {\uparrow }$
to
$\mathord {\uparrow }$
to
![]() $a^n$
, yielding a type m entity; so
$a^n$
, yielding a type m entity; so
![]() $\mathord {\uparrow }_{4} a^0$
abbreviates
$\mathord {\uparrow }_{4} a^0$
abbreviates
![]() $\mathord {\uparrow }\mathord {\uparrow }\mathord {\uparrow }\mathord {\uparrow } a^0$
, and
$\mathord {\uparrow }\mathord {\uparrow }\mathord {\uparrow }\mathord {\uparrow } a^0$
, and
![]() $c^5(\mathord {\uparrow }_{4}b^2)$
abbreviates
$c^5(\mathord {\uparrow }_{4}b^2)$
abbreviates
![]() $c^5(\mathord {\uparrow }\mathord {\uparrow } b^2)$
. Simple induction, which we leave to the reader, shows that
$c^5(\mathord {\uparrow }\mathord {\uparrow } b^2)$
. Simple induction, which we leave to the reader, shows that
![]() ${\textrm {STT}_{\uparrow }}$
proves generalizations of our new axioms; specifically, for each
${\textrm {STT}_{\uparrow }}$
proves generalizations of our new axioms; specifically, for each
![]() $m> n$
:
$m> n$
:
-
•
 $\forall x^n \forall y^n(\mathord {\uparrow }_{m} x^n = \mathord {\uparrow }_{m} y^n \rightarrow x^n = y^n)$
$\forall x^n \forall y^n(\mathord {\uparrow }_{m} x^n = \mathord {\uparrow }_{m} y^n \rightarrow x^n = y^n)$
-
•
 $\forall x^n \forall y^{n+1}(\mathord {\uparrow }_{m+1} y^{n+1}(\mathord {\uparrow }_{m} x^n) \leftrightarrow y^{n+1}(x^n))$
$\forall x^n \forall y^{n+1}(\mathord {\uparrow }_{m+1} y^{n+1}(\mathord {\uparrow }_{m} x^n) \leftrightarrow y^{n+1}(x^n))$
-
•
 $\forall x^{m}\forall y^{n+1}(\mathord {\uparrow }_{m+1}y^{n+1}(x^{m}) \rightarrow \exists z^n\ x^{m} = \mathord {\uparrow }_{m}z^n)$
$\forall x^{m}\forall y^{n+1}(\mathord {\uparrow }_{m+1}y^{n+1}(x^{m}) \rightarrow \exists z^n\ x^{m} = \mathord {\uparrow }_{m}z^n)$
-
•
 $\forall x^n\forall y^0 \lnot \mathord {\uparrow }_{n+1} y^0(x^n)$
.
$\forall x^n\forall y^0 \lnot \mathord {\uparrow }_{n+1} y^0(x^n)$
.
To prove that
![]() ${\textrm {STT}_{\uparrow }}$
and
${\textrm {STT}_{\uparrow }}$
and
![]() ${\textrm {CTT}^{\omega }}$
are definitionally equivalent (Theorem 23), we first define an interpretation, I, from
${\textrm {CTT}^{\omega }}$
are definitionally equivalent (Theorem 23), we first define an interpretation, I, from
![]() ${\textrm {CTT}^{\omega }}$
to
${\textrm {CTT}^{\omega }}$
to
![]() ${\textrm {STT}_{\uparrow }}$
. This preserves the interpretation of all logical symbols, including
${\textrm {STT}_{\uparrow }}$
. This preserves the interpretation of all logical symbols, including
![]() $=$
; its only non-trivial action is as follows:Footnote
75
$=$
; its only non-trivial action is as follows:Footnote
75
Observe that if
![]() $n = m + 1$
, then
$n = m + 1$
, then
![]() $[y^n(x^m)]^I$
is just
$[y^n(x^m)]^I$
is just
![]() $y^n(x^m)$
. Here is a very simple fact about the relationship between
$y^n(x^m)$
. Here is a very simple fact about the relationship between
![]() $\mathord {\uparrow }$
and the interpretations of
$\mathord {\uparrow }$
and the interpretations of
![]() $\mathrel {\varepsilon }$
and
$\mathrel {\varepsilon }$
and
![]() $\mathrel {\equiv }$
, which holds just by unpacking some definitions (the proof is left to the reader):
$\mathrel {\equiv }$
, which holds just by unpacking some definitions (the proof is left to the reader):
Lemma 17. Where
![]() $i = \max (m, n)$
,
$i = \max (m, n)$
,
![]() ${\textrm {STT}_{\uparrow }}$
proves:
${\textrm {STT}_{\uparrow }}$
proves:
-
(1)
 $[x^m \mathrel {\equiv } y^n]^I \leftrightarrow \mathord {\uparrow }_{i} x^m = \mathord {\uparrow }_{i}y^n$
$[x^m \mathrel {\equiv } y^n]^I \leftrightarrow \mathord {\uparrow }_{i} x^m = \mathord {\uparrow }_{i}y^n$
-
(2)
 $[x^m \mathrel {\varepsilon } y^n]^I \leftrightarrow \mathord {\uparrow }_{i+1}y^n(\mathord {\uparrow }_{i}x^m)$
$[x^m \mathrel {\varepsilon } y^n]^I \leftrightarrow \mathord {\uparrow }_{i+1}y^n(\mathord {\uparrow }_{i}x^m)$
We now have one substantial result:
Lemma 18. The I-interpretations of
![]() ${\forall {\textrm {E}}^{n}_{m}}$
and
${\forall {\textrm {E}}^{n}_{m}}$
and
![]() ${\forall {\textrm {I}}^{n}_{m}}$
are admissible in
${\forall {\textrm {I}}^{n}_{m}}$
are admissible in
![]() ${\textrm {STT}_{\uparrow }}$
${\textrm {STT}_{\uparrow }}$
Proof. We start with
![]() ${\forall {\textrm {E}}^{n}_{m}}$
. Suppose that both
${\forall {\textrm {E}}^{n}_{m}}$
. Suppose that both
![]() $\phi (x^n)$
and
$\phi (x^n)$
and
![]() $\phi (a^m)$
are well-formed in
$\phi (a^m)$
are well-formed in
![]() ${\textrm {CTT}^{\omega }}$
. Working in
${\textrm {CTT}^{\omega }}$
. Working in
![]() ${\textrm {STT}_{\uparrow }}$
, suppose
${\textrm {STT}_{\uparrow }}$
, suppose
![]() $\forall x^n\phi ^I(x^n)$
. If
$\forall x^n\phi ^I(x^n)$
. If
![]() $m = n$
, then
$m = n$
, then
![]() $\phi ^I(a^m)$
follows by ordinary
$\phi ^I(a^m)$
follows by ordinary
![]() $\forall $
E in
$\forall $
E in
![]() ${\textrm {STT}_{\uparrow }}$
. So consider the case when
${\textrm {STT}_{\uparrow }}$
. So consider the case when
![]() $m < n$
. The variable
$m < n$
. The variable
![]() $x^n$
cannot occur in any identity-claim, e.g.
$x^n$
cannot occur in any identity-claim, e.g.
![]() $x^n = c^n$
, since
$x^n = c^n$
, since
![]() $a^m = c^n$
is ill-formed in
$a^m = c^n$
is ill-formed in
![]() ${\textrm {CTT}^{\omega }}$
; so
${\textrm {CTT}^{\omega }}$
; so
![]() $\phi $
must have this kind of shape (illustratively):
$\phi $
must have this kind of shape (illustratively):
with
![]() $i < m < n < k$
; note that
$i < m < n < k$
; note that
![]() $i < m$
, since
$i < m$
, since
![]() $\phi (a^m)$
is well-formed in
$\phi (a^m)$
is well-formed in
![]() ${\textrm {CTT}^{\omega }}$
. Now
${\textrm {CTT}^{\omega }}$
. Now
![]() $\phi ^I$
is:
$\phi ^I$
is:
Using
![]() ${\textrm {STT}_{\uparrow }}'$
s rule
${\textrm {STT}_{\uparrow }}'$
s rule
![]() $\forall \textrm {E}^n$
, we can infer
$\forall \textrm {E}^n$
, we can infer
![]() $\phi ^I(\mathord {\uparrow }_{n} a^m)$
, i.e.:
$\phi ^I(\mathord {\uparrow }_{n} a^m)$
, i.e.:
Simplifying, and using generalized Up-Possess, we obtain:
which is precisely
![]() $\phi ^I(a^m)$
, as required.
$\phi ^I(a^m)$
, as required.
The admissibility of
![]() ${\forall {\textrm {I}}^{n}_{m}}$
under interpretation follows straightforwardly. Given
${\forall {\textrm {I}}^{n}_{m}}$
under interpretation follows straightforwardly. Given
![]() $\phi ^I(b^n)$
, with
$\phi ^I(b^n)$
, with
![]() $b^n$
suitably arbitrary: infer
$b^n$
suitably arbitrary: infer
![]() $\forall x^n\phi ^I(x^n)$
using
$\forall x^n\phi ^I(x^n)$
using
![]() ${\textrm {STT}_{\uparrow }}$
’s rule
${\textrm {STT}_{\uparrow }}$
’s rule
![]() $\forall \textrm {I}^n$
; with
$\forall \textrm {I}^n$
; with
![]() $a^m$
suitably arbitrary, infer
$a^m$
suitably arbitrary, infer
![]() $\phi ^I(a^m)$
using
$\phi ^I(a^m)$
using
![]() ${\forall {\textrm {I}}^{n}_{m}}$
under interpretation; finally, infer
${\forall {\textrm {I}}^{n}_{m}}$
under interpretation; finally, infer
![]() $\forall x^m\phi ^I(x^m)$
using
$\forall x^m\phi ^I(x^m)$
using
![]() ${\textrm {STT}_{\uparrow }}$
’s rule
${\textrm {STT}_{\uparrow }}$
’s rule
![]() $\forall \textrm {I}^m$
.□
$\forall \textrm {I}^m$
.□
It is now easy to prove that I is an interpretation:
Lemma 19.
![]() $I : {\textrm {CTT}^{\omega }} \longrightarrow {{\textrm {STT}_{\uparrow }}}$
is an interpretation.
$I : {\textrm {CTT}^{\omega }} \longrightarrow {{\textrm {STT}_{\uparrow }}}$
is an interpretation.
Proof. We simply check all inference rules and axioms. Lemma 18 deals with the quantifier-rules, and no Limit-rules apply since we are considering
![]() ${\textrm {CTT}^{\omega }}$
.
${\textrm {CTT}^{\omega }}$
.
![]() ${\textrm {CTT}^{\omega }}$
-Comprehension. If
${\textrm {CTT}^{\omega }}$
-Comprehension. If
![]() $\phi (x^n)$
is an
$\phi (x^n)$
is an
![]() ${\textrm {CTT}^{\omega }}$
-formula, then
${\textrm {CTT}^{\omega }}$
-formula, then
![]() $\phi ^I(x^n)$
is an
$\phi ^I(x^n)$
is an
![]() ${\textrm {STT}_{\uparrow }}$
-formula; now use
${\textrm {STT}_{\uparrow }}$
-formula; now use
![]() ${\textrm {STT}_{\uparrow }}$
-Comprehension.
${\textrm {STT}_{\uparrow }}$
-Comprehension.
Type-Founded. Suppose
![]() $[a^m \mathrel {\varepsilon } b^{n+1}]^I$
i.e.
$[a^m \mathrel {\varepsilon } b^{n+1}]^I$
i.e.
![]() $\mathord {\uparrow }_{i+1}b^{n+1}(\mathord {\uparrow }_{i}a^m)$
with
$\mathord {\uparrow }_{i+1}b^{n+1}(\mathord {\uparrow }_{i}a^m)$
with
![]() $i = \max (m, n+1)$
by Lemma 17.2. By generalized Up-Founded, there is
$i = \max (m, n+1)$
by Lemma 17.2. By generalized Up-Founded, there is
![]() $z^{n}$
such that
$z^{n}$
such that
![]() $\mathord {\uparrow }_{i}a^m = \mathord {\uparrow }_{i} z^n$
, i.e.,
$\mathord {\uparrow }_{i}a^m = \mathord {\uparrow }_{i} z^n$
, i.e.,
![]() $[a^m \mathrel {\equiv } z^n]^I$
by Lemma 17.1.
$[a^m \mathrel {\equiv } z^n]^I$
by Lemma 17.1.
Type-Base. By generalized Up-Base,
![]() $\lnot \mathord {\uparrow }_{n+1} y^0(x^n)$
; so
$\lnot \mathord {\uparrow }_{n+1} y^0(x^n)$
; so
![]() by Lemma 17.2.□
by Lemma 17.2.□
We now switch to working in
![]() ${\textrm {CTT}^{\omega }}$
. It will help if we allow ourselves the use of a definite description operator,
${\textrm {CTT}^{\omega }}$
. It will help if we allow ourselves the use of a definite description operator,
![]() , within
, within
![]() ${\textrm {CTT}^{\omega }}$
. (This is harmless since, by standard Russellian techniques, this can always be eliminated from any formula.)Footnote
76
Now, by Type-Raising in
${\textrm {CTT}^{\omega }}$
. (This is harmless since, by standard Russellian techniques, this can always be eliminated from any formula.)Footnote
76
Now, by Type-Raising in
![]() ${\textrm {CTT}^{\omega }}$
, for any type n and each
${\textrm {CTT}^{\omega }}$
, for any type n and each
![]() $x^n$
there is a unique
$x^n$
there is a unique
![]() $x^{n+1}$
such that
$x^{n+1}$
such that
![]() $x^n \mathrel {\equiv } x^{n+1}$
; we will denote this in
$x^n \mathrel {\equiv } x^{n+1}$
; we will denote this in
![]() ${\textrm {CTT}^{\omega }}$
using
${\textrm {CTT}^{\omega }}$
using
![]() $\mathord {\Uparrow } x^n$
, i.e.,
$\mathord {\Uparrow } x^n$
, i.e.,
![]() . As before, we write
. As before, we write
![]() ${\mathord {\Uparrow }_{n}} a^m$
for the result of applying
${\mathord {\Uparrow }_{n}} a^m$
for the result of applying
![]() $n-m$
instances of
$n-m$
instances of
![]() $\mathord {\Uparrow }$
to
$\mathord {\Uparrow }$
to
![]() $a^m$
, yielding a type n entity. We now define an interpretation, J, from
$a^m$
, yielding a type n entity. We now define an interpretation, J, from
![]() ${\textrm {STT}_{\uparrow }}$
to
${\textrm {STT}_{\uparrow }}$
to
![]() ${\textrm {CTT}^{\omega }}$
, with these actions:Footnote
77
${\textrm {CTT}^{\omega }}$
, with these actions:Footnote
77
 $$ \begin{align*} [y^{n+1}(x^n)]^J &:= y^{n+1}(x^n)\\ [\mathord{\uparrow} x^n]^J &:= \mathord{\Uparrow} x^n. \end{align*} $$
$$ \begin{align*} [y^{n+1}(x^n)]^J &:= y^{n+1}(x^n)\\ [\mathord{\uparrow} x^n]^J &:= \mathord{\Uparrow} x^n. \end{align*} $$
Lemma 20.
![]() $J : {{\textrm {STT}_{\uparrow }}} \longrightarrow {\textrm {CTT}^{\omega }}$
is an interpretation.
$J : {{\textrm {STT}_{\uparrow }}} \longrightarrow {\textrm {CTT}^{\omega }}$
is an interpretation.
Proof.
![]() ${\textrm {CTT}^{\omega }}$
-Comprehension immediately licenses
${\textrm {CTT}^{\omega }}$
-Comprehension immediately licenses
![]() ${\textrm {STT}_{\uparrow }}$
-Comprehension. For Up-Inject, suppose
${\textrm {STT}_{\uparrow }}$
-Comprehension. For Up-Inject, suppose
![]() $\mathord {\Uparrow } x^n = \mathord {\Uparrow } y^n$
, i.e.,
$\mathord {\Uparrow } x^n = \mathord {\Uparrow } y^n$
, i.e.,
![]() ; so
; so
![]() $x^n \mathrel {\equiv } y^n$
by Lemma 2, and hence
$x^n \mathrel {\equiv } y^n$
by Lemma 2, and hence
![]() $x^n = y^n$
. Similarly, Up-Possess holds by Lemma 2. And Up-Founded and Up-Base hold via Type-Founded and Type-Base.□
$x^n = y^n$
. Similarly, Up-Possess holds by Lemma 2. And Up-Founded and Up-Base hold via Type-Founded and Type-Base.□
It only remains to show that I and J together yield a definitional equivalence.
Lemma 21.
![]() ${\textrm {CTT}^{\omega }}$
proves this scheme:
${\textrm {CTT}^{\omega }}$
proves this scheme:
![]() $[[y^n(x^m)]^I]^J \leftrightarrow y^n(x^m)$
.
$[[y^n(x^m)]^I]^J \leftrightarrow y^n(x^m)$
.
Proof. Note that
![]() $[[y^n(x^m)]^I]^J\, \textrm {iff}\ [y^n(\mathord {\uparrow }_{n-1}x^m)]^J\, \textrm {iff}\ y^n({\mathord {\Uparrow }_{n-1}} x^m)\ \textrm {iff}\ y^n(x^m)$
, using Lemma 2 for the final biconditional.□
$[[y^n(x^m)]^I]^J\, \textrm {iff}\ [y^n(\mathord {\uparrow }_{n-1}x^m)]^J\, \textrm {iff}\ y^n({\mathord {\Uparrow }_{n-1}} x^m)\ \textrm {iff}\ y^n(x^m)$
, using Lemma 2 for the final biconditional.□
Lemma 22.
![]() ${\textrm {STT}_{\uparrow }}$
proves these schemes:
${\textrm {STT}_{\uparrow }}$
proves these schemes:
![]() $[[y^{n+1}(x^n)]^J]^I \leftrightarrow y^{n+1}(x^n)$
and
$[[y^{n+1}(x^n)]^J]^I \leftrightarrow y^{n+1}(x^n)$
and
![]() $[[\mathord {\uparrow } x^n]^J]^I = \mathord {\uparrow } x^n$
.
$[[\mathord {\uparrow } x^n]^J]^I = \mathord {\uparrow } x^n$
.
Proof. The first scheme is trivial. For the second:

□
Assembling Lemmas 19–22, we obtain:
Theorem 23.
![]() ${\textrm {STT}_{\uparrow }}$
and
${\textrm {STT}_{\uparrow }}$
and
![]() ${\textrm {CTT}^{\omega }}$
are definitionally equivalent
${\textrm {CTT}^{\omega }}$
are definitionally equivalent
D Definitional equivalence for
 ${\textrm {FJT}}$
${\textrm {FJT}}$
In Section 7, we stated that
![]() ${\textrm {FJT}}$
is definitionally equivalent to
${\textrm {FJT}}$
is definitionally equivalent to
![]() ${\textrm {STT}_{\triangleright }}$
. In this appendix, we define
${\textrm {STT}_{\triangleright }}$
. In this appendix, we define
![]() ${\textrm {STT}_{\triangleright }}$
and prove the equivalence.
${\textrm {STT}_{\triangleright }}$
and prove the equivalence.
The guiding idea is to simulate
![]() ${\textrm {FJT}}$
by using a version of
${\textrm {FJT}}$
by using a version of
![]() ${\textrm {STT}}$
with this sort of behaviour: for all types
${\textrm {STT}}$
with this sort of behaviour: for all types
![]() $1 < m < n$
, each type n entity
$1 < m < n$
, each type n entity
![]() $a^n$
projects downwards to some type m entity
$a^n$
projects downwards to some type m entity
![]() $\mathord {\downarrow _m}a^n$
; we can then simulate an application
$\mathord {\downarrow _m}a^n$
; we can then simulate an application
![]() $a^n(x^{m-1})$
by instead considering
$a^n(x^{m-1})$
by instead considering
![]() $\mathord {\downarrow _m}a^n(x^{m-1})$
. However, there is a small snag: we are treating
$\mathord {\downarrow _m}a^n(x^{m-1})$
. However, there is a small snag: we are treating
![]() $\mathord {\downarrow _m}$
as functional; but, if we assume no version of extensionality, then we will have no way to decide whether
$\mathord {\downarrow _m}$
as functional; but, if we assume no version of extensionality, then we will have no way to decide whether
![]() $a^2$
should project downwards to
$a^2$
should project downwards to
![]() $b^1$
or
$b^1$
or
![]() $c^1$
, if
$c^1$
, if
![]() $b^1$
and
$b^1$
and
![]() $c^1$
are coextensional. The snag can be avoided by using a relational (rather than function) version of downward-projection. What follows spells this out rigorously.
$c^1$
are coextensional. The snag can be avoided by using a relational (rather than function) version of downward-projection. What follows spells this out rigorously.
We define
![]() ${\textrm {STT}_{\triangleright }}$
by augmenting
${\textrm {STT}_{\triangleright }}$
by augmenting
![]() ${\textrm {STT}}$
as follows. For each
${\textrm {STT}}$
as follows. For each
![]() $n> 0$
, we have a relational constant,
$n> 0$
, we have a relational constant,
![]() $\triangleright $
, expressing the downward-projecting relation from a type
$\triangleright $
, expressing the downward-projecting relation from a type
![]() $n\mathord {+}1$
entity to a type n entity. So we write e.g.
$n\mathord {+}1$
entity to a type n entity. So we write e.g.
![]() $e^4 \triangleright d^3$
or
$e^4 \triangleright d^3$
or
![]() $b^1 \triangleright a^0$
;Footnote
78
when convenient, we may write
$b^1 \triangleright a^0$
;Footnote
78
when convenient, we may write
![]() $d^3 \triangleleft e^4$
or
$d^3 \triangleleft e^4$
or
![]() $a^0 \triangleleft b^1$
instead. We introduce some useful abbreviations:
$a^0 \triangleleft b^1$
instead. We introduce some useful abbreviations:
 $$ \begin{align*} a^n \approx b^n & \mathrel{\textrm{iff}_{\textrm{df}}} \forall x^{n-1}(a^n(x^{n-1}) \leftrightarrow b^n(x^{n-1})), \textrm{when}\ n>0\\ a^n \mathrel{\blacktriangledown} b^n & \mathrel{\textrm{iff}_{\textrm{df}}} \forall x^{n-1}(a^n \triangleright x^{n-1} \leftrightarrow b^n \triangleright x^{n-1}), \textrm{when}\ n >1\\ a^1 \mathrel{\blacktriangledown} b^1 & \mathrel{\textrm{iff}_{\textrm{df}}} a^1 = a^1. \end{align*} $$
$$ \begin{align*} a^n \approx b^n & \mathrel{\textrm{iff}_{\textrm{df}}} \forall x^{n-1}(a^n(x^{n-1}) \leftrightarrow b^n(x^{n-1})), \textrm{when}\ n>0\\ a^n \mathrel{\blacktriangledown} b^n & \mathrel{\textrm{iff}_{\textrm{df}}} \forall x^{n-1}(a^n \triangleright x^{n-1} \leftrightarrow b^n \triangleright x^{n-1}), \textrm{when}\ n >1\\ a^1 \mathrel{\blacktriangledown} b^1 & \mathrel{\textrm{iff}_{\textrm{df}}} a^1 = a^1. \end{align*} $$
So
![]() $a^n \approx b^n$
tells us that
$a^n \approx b^n$
tells us that
![]() $a^n$
and
$a^n$
and
![]() $b^n$
are coextensive, and
$b^n$
are coextensive, and
![]() $a^n \mathrel {\blacktriangledown } b^n$
tells us that
$a^n \mathrel {\blacktriangledown } b^n$
tells us that
![]() $a^n$
and
$a^n$
and
![]() $b^n$
project downwards to exactly the same entities. The special stipulation for
$b^n$
project downwards to exactly the same entities. The special stipulation for
![]() $a^1 \mathrel {\blacktriangledown } b^1$
is needed as
$a^1 \mathrel {\blacktriangledown } b^1$
is needed as
![]() ${\textrm {STT}_{\triangleright }}$
has no relational constant
${\textrm {STT}_{\triangleright }}$
has no relational constant
![]() $\triangleright $
expressing a relation from a type
$\triangleright $
expressing a relation from a type
![]() $1$
entity to a type
$1$
entity to a type
![]() $0$
entity, and so will hold vacuously. We concatenate chains of conjunctions; so we may write e.g.,
$0$
entity, and so will hold vacuously. We concatenate chains of conjunctions; so we may write e.g.,
![]() $a^2 \triangleleft d^3 \triangleright b^2 \approx c^2$
in place of
$a^2 \triangleleft d^3 \triangleright b^2 \approx c^2$
in place of
![]() $(d^3 \triangleright a^2 \land d^3 \triangleright b^2 \land b^2 \approx c^2)$
.
$(d^3 \triangleright a^2 \land d^3 \triangleright b^2 \land b^2 \approx c^2)$
.
![]() ${\textrm {STT}_{\triangleright }}$
retains the
${\textrm {STT}_{\triangleright }}$
retains the
![]() ${\textrm {STT}}$
-Comprehension scheme for type
${\textrm {STT}}$
-Comprehension scheme for type
![]() $1$
entities, i.e.,
$1$
entities, i.e.,
![]() $\exists z^1 \forall x^0(z^1(x^0) \leftrightarrow \phi (x^0))$
; but for each
$\exists z^1 \forall x^0(z^1(x^0) \leftrightarrow \phi (x^0))$
; but for each
![]() $n> 1$
, it has an augmented scheme:Footnote
79
$n> 1$
, it has an augmented scheme:Footnote
79
-
 ${\textrm {STT}_{\triangleright }}$
-Comprehension.
${\textrm {STT}_{\triangleright }}$
-Comprehension.
 $\forall y^n (\exists z^{n+1} \triangleright y^n) \forall x^n(z^{n+1}(x^n)\leftrightarrow \phi (x^n))$
, for any formula
$\forall y^n (\exists z^{n+1} \triangleright y^n) \forall x^n(z^{n+1}(x^n)\leftrightarrow \phi (x^n))$
, for any formula
 $\phi (x^n)$
not containing
$\phi (x^n)$
not containing
 $z^{n+1}$
.
$z^{n+1}$
.
For each
![]() $n> 0$
,
$n> 0$
,
![]() ${\textrm {STT}_{\triangleright }}$
also has these axioms:
${\textrm {STT}_{\triangleright }}$
also has these axioms:
-
Down
 $_\exists $
.
$_\exists $
.
 $\forall z^{n+1}\exists x^n\phantom {)}z^{n+1} \triangleright x^n$
$\forall z^{n+1}\exists x^n\phantom {)}z^{n+1} \triangleright x^n$
-
Down
 $_{{Sim}}$
.
$_{{Sim}}$
.
 $\forall z^{n+1}\forall x^{n}\forall y^n(x^n \triangleleft z^{n+1} \triangleright y^n \rightarrow x^n \approx y^n \mathrel {\blacktriangledown } x^{n})$
$\forall z^{n+1}\forall x^{n}\forall y^n(x^n \triangleleft z^{n+1} \triangleright y^n \rightarrow x^n \approx y^n \mathrel {\blacktriangledown } x^{n})$
-
Down
 $_{{Max}}$
.
$_{{Max}}$
.
 $\forall z^{n+1}\forall x^{n}\forall y^{n}(z^{n+1} \triangleright x^n \approx y^n \mathrel {\blacktriangledown } x^{n} \rightarrow z^{n+1} \triangleright y^{n})$
$\forall z^{n+1}\forall x^{n}\forall y^{n}(z^{n+1} \triangleright x^n \approx y^n \mathrel {\blacktriangledown } x^{n} \rightarrow z^{n+1} \triangleright y^{n})$
So Down
![]() $_\exists $
says that all entities of types
$_\exists $
says that all entities of types
![]() $\geq 2$
project downwards; Down
$\geq 2$
project downwards; Down
![]() $_{\textrm {Sim}}$
says that if
$_{\textrm {Sim}}$
says that if
![]() $z^{n+1}$
projects to two entities
$z^{n+1}$
projects to two entities
![]() $x^n$
and
$x^n$
and
![]() $y^n$
, then
$y^n$
, then
![]() $x^n$
and
$x^n$
and
![]() $y^n$
apply and project to exactly the same entities; and Down
$y^n$
apply and project to exactly the same entities; and Down
![]() $_{\textrm {Max}}$
says that if
$_{\textrm {Max}}$
says that if
![]() $z^{n+1}$
projects to some entity
$z^{n+1}$
projects to some entity
![]() $x^n$
, then
$x^n$
, then
![]() $z^{n+1}$
also projects to any
$z^{n+1}$
also projects to any
![]() $y^n$
which applies and projects to exactly the same entities as
$y^n$
which applies and projects to exactly the same entities as
![]() $x^n$
. These axioms ensure that
$x^n$
. These axioms ensure that
![]() $\triangleright $
-chains are always equivalent, in a strong sense which is brought out by these next two lemmas:
$\triangleright $
-chains are always equivalent, in a strong sense which is brought out by these next two lemmas:
Lemma 24.
![]() ${\textrm {STT}_{\triangleright }}$
proves this scheme (with
${\textrm {STT}_{\triangleright }}$
proves this scheme (with
![]() $n> 0$
). If
$n> 0$
). If
![]() $a^{n+1} \triangleright x^n$
and
$a^{n+1} \triangleright x^n$
and
![]() $b^{n+1} \triangleright x^n$
for some
$b^{n+1} \triangleright x^n$
for some
![]() $x^n$
, then
$x^n$
, then
![]() $a^{n+1} \mathrel {\blacktriangledown } b^{n+1}$
.
$a^{n+1} \mathrel {\blacktriangledown } b^{n+1}$
.
Proof. Suppose
![]() $a^{n+1} \triangleright x^n$
and
$a^{n+1} \triangleright x^n$
and
![]() $b^{n+1} \triangleright x^n$
. If
$b^{n+1} \triangleright x^n$
. If
![]() $a^{n+1} \triangleright y^n$
, then
$a^{n+1} \triangleright y^n$
, then
![]() $x^n \approx y^n \mathrel {\blacktriangledown } x^n$
by Down
$x^n \approx y^n \mathrel {\blacktriangledown } x^n$
by Down
![]() $_{\textrm {Sim}}$
, so
$_{\textrm {Sim}}$
, so
![]() $b^{n+1} \triangleright y^n$
by Down
$b^{n+1} \triangleright y^n$
by Down
![]() $_{\textrm {Max}}$
; similarly if
$_{\textrm {Max}}$
; similarly if
![]() $b^{n+1} \triangleright y^n$
then
$b^{n+1} \triangleright y^n$
then
![]() $a^{n+1} \triangleright y^n$
.□
$a^{n+1} \triangleright y^n$
.□
Lemma 25.
![]() ${\textrm {STT}_{\triangleright }}$
proves this scheme (with
${\textrm {STT}_{\triangleright }}$
proves this scheme (with
![]() $n> 0$
). Given any
$n> 0$
). Given any
![]() $\triangleright $
-chains:
$\triangleright $
-chains:
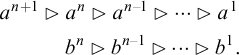 $$ \begin{align*} a^{n+1} \triangleright {}&a^{n} \triangleright a^{n-1} \triangleright \cdots \triangleright a^{1}\\ &b^{n} \triangleright b^{n-1} \triangleright \cdots \triangleright b^{1}. \end{align*} $$
$$ \begin{align*} a^{n+1} \triangleright {}&a^{n} \triangleright a^{n-1} \triangleright \cdots \triangleright a^{1}\\ &b^{n} \triangleright b^{n-1} \triangleright \cdots \triangleright b^{1}. \end{align*} $$
-
(1) If
 $a^{n+1} \triangleright b^{n}$
, then
$a^{n+1} \triangleright b^{n}$
, then
 $\bigwedge _{1 \leq i \leq n} a^{i} \approx b^{i} \mathrel {\blacktriangledown } a^{i}$
.
$\bigwedge _{1 \leq i \leq n} a^{i} \approx b^{i} \mathrel {\blacktriangledown } a^{i}$
. -
(2) If there is m such that
 $1 \leq m \leq n$
and
$1 \leq m \leq n$
and
 $b^m \mathrel {\blacktriangledown } a^m$
and
$b^m \mathrel {\blacktriangledown } a^m$
and
 $\bigwedge _{m \leq i \leq n} a^{i} \approx b^{i}$
, then
$\bigwedge _{m \leq i \leq n} a^{i} \approx b^{i}$
, then
 $\bigwedge _{m \leq i \leq n} b^{i} \mathrel {\blacktriangledown } a^{i}$
and
$\bigwedge _{m \leq i \leq n} b^{i} \mathrel {\blacktriangledown } a^{i}$
and
 $a^{n+1} \triangleright b^{n}$
.
$a^{n+1} \triangleright b^{n}$
.
Proof.
(1) From Down
![]() $_{\textrm {Sim}}$
, by induction.
$_{\textrm {Sim}}$
, by induction.
(2) By assumption,
![]() $a^{m+1} \triangleright a^m \approx b^m \mathrel {\blacktriangledown } a^m$
, so
$a^{m+1} \triangleright a^m \approx b^m \mathrel {\blacktriangledown } a^m$
, so
![]() $a^{m+1} \triangleright b^m$
by Down
$a^{m+1} \triangleright b^m$
by Down
![]() $_{\textrm {Max}}$
; so
$_{\textrm {Max}}$
; so
![]() $b^{m+1} \mathrel {\blacktriangledown } a^{m+1}$
by Lemma 24. This establishes a base case; the rest follows by induction. Now
$b^{m+1} \mathrel {\blacktriangledown } a^{m+1}$
by Lemma 24. This establishes a base case; the rest follows by induction. Now
![]() $a^{n+1} \triangleright b^{n}$
by Down
$a^{n+1} \triangleright b^{n}$
by Down
![]() $_{\textrm {Max}}$
.□
$_{\textrm {Max}}$
.□
We will use these results to prove that
![]() ${\textrm {STT}_{\triangleright }}$
and
${\textrm {STT}_{\triangleright }}$
and
![]() ${\textrm {FJT}}$
are definitionally equivalent (Theorem 31). We first define an interpretation, I, to take us from
${\textrm {FJT}}$
are definitionally equivalent (Theorem 31). We first define an interpretation, I, to take us from
![]() ${\textrm {FJT}}$
to
${\textrm {FJT}}$
to
![]() ${\textrm {STT}_{\triangleright }}$
:Footnote
80
${\textrm {STT}_{\triangleright }}$
:Footnote
80
Note that if
![]() $m + 1 = n$
, then
$m + 1 = n$
, then
![]() $[y^n(x^m)]^I$
is just
$[y^n(x^m)]^I$
is just
![]() $y^n(x^m)$
.
$y^n(x^m)$
.
Lemma 26.
![]() $I : {{\textrm {FJT}}} \longrightarrow {{\textrm {STT}_{\triangleright }}}$
is an interpretation
$I : {{\textrm {FJT}}} \longrightarrow {{\textrm {STT}_{\triangleright }}}$
is an interpretation
Proof. For all
![]() $0 \leq i < n$
, let
$0 \leq i < n$
, let
![]() $\phi _i$
be
$\phi _i$
be
![]() ${\textrm {FJT}}$
-formulas not containing
${\textrm {FJT}}$
-formulas not containing
![]() $z^n$
or
$z^n$
or
![]() $z^j$
or
$z^j$
or
![]() $y^j$
for any
$y^j$
for any
![]() $0 \leq j < n$
. (No generality is lost here, as we can relabel variables as necessary.) By multiple successive applications of
$0 \leq j < n$
. (No generality is lost here, as we can relabel variables as necessary.) By multiple successive applications of
![]() ${\textrm {STT}_{\triangleright }}$
-Comprehension, there are
${\textrm {STT}_{\triangleright }}$
-Comprehension, there are
![]() $z^1 \triangleleft z^2 \triangleleft \cdots \triangleleft z^n$
such that
$z^1 \triangleleft z^2 \triangleleft \cdots \triangleleft z^n$
such that
![]() $\forall x^i(z^{i+1}(x^i) \leftrightarrow \phi _i^I(x^i))$
, for each
$\forall x^i(z^{i+1}(x^i) \leftrightarrow \phi _i^I(x^i))$
, for each
![]() $0 \leq i < n$
. By Lemma 25.1, for each
$0 \leq i < n$
. By Lemma 25.1, for each
![]() $0 \leq i < n$
, we have:
$0 \leq i < n$
, we have:
 $$ \begin{align*} \forall x^i(\forall y^{n-1}\cdots \forall y^{i+1}(z^{n} \triangleright y^{n-1} \triangleright \cdots \triangleright y^{i+1} \rightarrow y^{i+1}(x^i)) &\leftrightarrow \phi_i^I(x^i))\\ \textrm{i.e.,}\ \forall x^i([z^{n}(x^i)]^I &\leftrightarrow \phi_i^I(x^i)). \end{align*} $$
$$ \begin{align*} \forall x^i(\forall y^{n-1}\cdots \forall y^{i+1}(z^{n} \triangleright y^{n-1} \triangleright \cdots \triangleright y^{i+1} \rightarrow y^{i+1}(x^i)) &\leftrightarrow \phi_i^I(x^i))\\ \textrm{i.e.,}\ \forall x^i([z^{n}(x^i)]^I &\leftrightarrow \phi_i^I(x^i)). \end{align*} $$
Conjoining these biconditionals and applying
![]() $\exists $
I, we obtain
$\exists $
I, we obtain
![]() $[\exists z^{n}\bigwedge _{i < n}\forall x^i(z^n(x^i) \leftrightarrow \phi _i(x^i))]^I$
, i.e., an arbitrary instance of
$[\exists z^{n}\bigwedge _{i < n}\forall x^i(z^n(x^i) \leftrightarrow \phi _i(x^i))]^I$
, i.e., an arbitrary instance of
![]() $[{\textrm {FJT}}\text{-}\textrm {Comprehension}]^I$
.□
$[{\textrm {FJT}}\text{-}\textrm {Comprehension}]^I$
.□
We now switch to working in
![]() ${\textrm {FJT}}$
. We introduce another abbreviation, for a bounded version of coextensiveness, whenever
${\textrm {FJT}}$
. We introduce another abbreviation, for a bounded version of coextensiveness, whenever
![]() $k \leq \min (m,n)$
:
$k \leq \min (m,n)$
:
Note the bound is
![]() $i < k$
. We now define an interpretation, J, from
$i < k$
. We now define an interpretation, J, from
![]() ${\textrm {STT}_{\triangleright }}$
to
${\textrm {STT}_{\triangleright }}$
to
![]() ${\textrm {FJT}}$
:Footnote
81
${\textrm {FJT}}$
:Footnote
81
 $$ \begin{align*} [y^{n+1}(x^n)]^J &:= y^{n+1}(x^n)\\ [y^{n+1} \triangleright x^n]^J &:= y^{n+1} \approxeq_{n} x^{n}. \end{align*} $$
$$ \begin{align*} [y^{n+1}(x^n)]^J &:= y^{n+1}(x^n)\\ [y^{n+1} \triangleright x^n]^J &:= y^{n+1} \approxeq_{n} x^{n}. \end{align*} $$
Lemma 27.
![]() ${\textrm {FJT}}$
proves the following schemes, where well-formed:
${\textrm {FJT}}$
proves the following schemes, where well-formed:
-
(1) If
 $a^{m} \approxeq _{k} c^l$
and
$a^{m} \approxeq _{k} c^l$
and
 $b^{n} \approxeq _{k} c^l$
, then
$b^{n} \approxeq _{k} c^l$
, then
 $a^m \approxeq _{k} b^n$
.
$a^m \approxeq _{k} b^n$
. -
(2)
 $a^m \approxeq _{k} b^n$
iff
$a^m \approxeq _{k} b^n$
iff
 $\forall x^k(a^{m} \approxeq _{k} x^k \leftrightarrow b^{n} \approxeq _{k} x^k)$
.
$\forall x^k(a^{m} \approxeq _{k} x^k \leftrightarrow b^{n} \approxeq _{k} x^k)$
. -
(3)
 $a^n \approxeq _{n-1} b^n$
iff
$a^n \approxeq _{n-1} b^n$
iff
 $[a^n \mathrel {\blacktriangledown } b^n]^J$
, noting here that we must have
$[a^n \mathrel {\blacktriangledown } b^n]^J$
, noting here that we must have
 $n> 1$
.
$n> 1$
.
Proof. (1) Trivial.
(2) Left-to-right. Suppose
![]() $a^{m} \approxeq _{k} b^{n}$
; if
$a^{m} \approxeq _{k} b^{n}$
; if
![]() $a^{m} \approxeq _{k} c^k$
, then
$a^{m} \approxeq _{k} c^k$
, then
![]() $b^{n} \approxeq _{k} c^k$
by (1), and conversely. Right-to-left. Suppose
$b^{n} \approxeq _{k} c^k$
by (1), and conversely. Right-to-left. Suppose
![]() $\forall x^k(a^{m} \approxeq _{k} x^k \leftrightarrow b^{n} \approxeq _{k} v^k)$
; by
$\forall x^k(a^{m} \approxeq _{k} x^k \leftrightarrow b^{n} \approxeq _{k} v^k)$
; by
![]() ${\textrm {FJT}}$
-Comprehension, there is some
${\textrm {FJT}}$
-Comprehension, there is some
![]() $c^k \approxeq _{k} a^{m}$
; so
$c^k \approxeq _{k} a^{m}$
; so
![]() $b^{n} \approxeq _{k} c^k$
, and now
$b^{n} \approxeq _{k} c^k$
, and now
![]() $a^{n} \approxeq _{k} b^{n}$
by (1).
$a^{n} \approxeq _{k} b^{n}$
by (1).
(3) Using (2), since
![]() $[a^{n} \mathrel {\blacktriangledown } b^{n}]^J$
is
$[a^{n} \mathrel {\blacktriangledown } b^{n}]^J$
is
![]() $\forall x^{n-1}(a^{n} \approxeq _{n-1} x^{n-1} \leftrightarrow b^{n} \approxeq _{n} x^{n-1})$
.□
$\forall x^{n-1}(a^{n} \approxeq _{n-1} x^{n-1} \leftrightarrow b^{n} \approxeq _{n} x^{n-1})$
.□
Lemma 28.
![]() $J : {{\textrm {STT}_{\triangleright }}} \longrightarrow {{\textrm {FJT}}}$
is an interpretation.
$J : {{\textrm {STT}_{\triangleright }}} \longrightarrow {{\textrm {FJT}}}$
is an interpretation.
Proof.
For Down
![]() $_\exists $
. Fix
$_\exists $
. Fix
![]() $z^{n+1}$
; by
$z^{n+1}$
; by
![]() ${\textrm {FJT}}$
-Comprehension there is some
${\textrm {FJT}}$
-Comprehension there is some
![]() $x^n \approxeq _{n} z^{n+1}$
, i.e.,
$x^n \approxeq _{n} z^{n+1}$
, i.e.,
![]() $[z^{n+1} \triangleright x^{n}]^J$
.
$[z^{n+1} \triangleright x^{n}]^J$
.
For Down
![]() $_{{Sim}}$
. Suppose
$_{{Sim}}$
. Suppose
![]() $[x^n \triangleleft z^{n+1} \triangleright y^n]^J$
, i.e.,
$[x^n \triangleleft z^{n+1} \triangleright y^n]^J$
, i.e.,
![]() $x^n \approxeq _{n} z^{n+1} \approxeq _{n} x^n$
; so
$x^n \approxeq _{n} z^{n+1} \approxeq _{n} x^n$
; so
![]() $x^n \approxeq _{n} y^n$
by Lemma 27.1. In particular,
$x^n \approxeq _{n} y^n$
by Lemma 27.1. In particular,
![]() $x^n \approx y^n$
, so
$x^n \approx y^n$
, so
![]() $[x^n \approx y^n]^J$
. Moreover, if
$[x^n \approx y^n]^J$
. Moreover, if
![]() $n> 1$
then
$n> 1$
then
![]() $x^n \approxeq _{n-1} y^n$
, so that
$x^n \approxeq _{n-1} y^n$
, so that
![]() $[x^n \mathrel {\blacktriangledown } y^n]^J$
by Lemma 27.3; if
$[x^n \mathrel {\blacktriangledown } y^n]^J$
by Lemma 27.3; if
![]() $n = 1$
then
$n = 1$
then
![]() $[x^n \mathrel {\blacktriangledown } y^n]^J$
vacuously.
$[x^n \mathrel {\blacktriangledown } y^n]^J$
vacuously.
For Down
![]() $_{{Max}}$
. Suppose
$_{{Max}}$
. Suppose
![]() $[z^{n+1} \triangleright x^{n} \approx y^{n} \mathrel {\blacktriangledown } x^n]^J$
, i.e.,
$[z^{n+1} \triangleright x^{n} \approx y^{n} \mathrel {\blacktriangledown } x^n]^J$
, i.e.,
![]() $z^{n+1} \approxeq _{n} x^n \approx y^{n} \approxeq _{n-1} x^{n}$
, using Lemma 27.3. So
$z^{n+1} \approxeq _{n} x^n \approx y^{n} \approxeq _{n-1} x^{n}$
, using Lemma 27.3. So
![]() $y^{n} \approxeq _{n} x^{n}$
, and hence
$y^{n} \approxeq _{n} x^{n}$
, and hence
![]() $z^{n+1} \approxeq _{n} y^{n}$
by Lemma 27.1, i.e.,
$z^{n+1} \approxeq _{n} y^{n}$
by Lemma 27.1, i.e.,
![]() $[z^{n+1} \triangleright y^{n}]^J$
.
$[z^{n+1} \triangleright y^{n}]^J$
.
For
![]() ${\textrm {STT}_{\triangleright }}$
-Comprehension. Let
${\textrm {STT}_{\triangleright }}$
-Comprehension. Let
![]() $\phi $
be any
$\phi $
be any
![]() ${\textrm {STT}_{\triangleright }}$
-formula not containing
${\textrm {STT}_{\triangleright }}$
-formula not containing
![]() $z^{n+1}$
(but which may contain
$z^{n+1}$
(but which may contain
![]() $y^n$
). Fix
$y^n$
). Fix
![]() $y^n$
; by
$y^n$
; by
![]() ${\textrm {FJT}}$
-Comprehension, there is
${\textrm {FJT}}$
-Comprehension, there is
![]() $z^{n+1}$
such that:
$z^{n+1}$
such that:
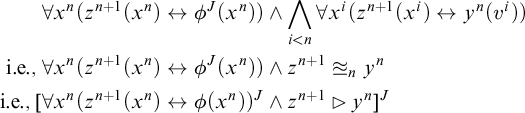 $$ \begin{align*} \forall x^n(z^{n+1}(x^n) \leftrightarrow \phi^J(x^n)) &\land \bigwedge_{i < n}\forall x^i(z^{n+1}(x^i) \leftrightarrow y^n(v^i))\\ \textrm{i.e.,}\ \forall x^n(z^{n+1}(x^n) \leftrightarrow \phi^J(x^n)) &\land z^{n+1} \approxeq_{n} y^n\\ \textrm{i.e.,}\ [\forall x^n(z^{n+1}(x^n) \leftrightarrow \phi(x^n))^J &\land z^{n+1} \triangleright y^n]^J \end{align*} $$
$$ \begin{align*} \forall x^n(z^{n+1}(x^n) \leftrightarrow \phi^J(x^n)) &\land \bigwedge_{i < n}\forall x^i(z^{n+1}(x^i) \leftrightarrow y^n(v^i))\\ \textrm{i.e.,}\ \forall x^n(z^{n+1}(x^n) \leftrightarrow \phi^J(x^n)) &\land z^{n+1} \approxeq_{n} y^n\\ \textrm{i.e.,}\ [\forall x^n(z^{n+1}(x^n) \leftrightarrow \phi(x^n))^J &\land z^{n+1} \triangleright y^n]^J \end{align*} $$
So we have arbitrary instances of
![]() $[{{\textrm {STT}_{\triangleright }}}\textrm {-Comprehension}]^J$
.□
$[{{\textrm {STT}_{\triangleright }}}\textrm {-Comprehension}]^J$
.□
It only remains to show that I and J characterise a definitional equivalence.
Lemma 29.
![]() ${\textrm {FJT}}$
proves this scheme:
${\textrm {FJT}}$
proves this scheme:
![]() $[[y^n(x^m)]^I]^J \leftrightarrow y^n(x^m)$
.
$[[y^n(x^m)]^I]^J \leftrightarrow y^n(x^m)$
.
Proof. Note that the following are equivalent:
-
(1)
 $[[y^n(x^m)]^I]^J$
$[[y^n(x^m)]^I]^J$
-
(2)
 $[\forall y^{n-1}\cdots \forall y^{m+1}(y^n \triangleright y^{n-1} \triangleright \cdots \triangleright y^{m+1} \rightarrow y^{m+1}(x^m))]^J$
$[\forall y^{n-1}\cdots \forall y^{m+1}(y^n \triangleright y^{n-1} \triangleright \cdots \triangleright y^{m+1} \rightarrow y^{m+1}(x^m))]^J$
-
(3)
 $\forall y^{n-1}\cdots \forall y^{m+1}(y^n \approxeq _{n-1} y^{n-1} \approxeq _{n-2} \cdots \approxeq _{m+1} y^{m+1} \rightarrow y^{m+1}(x^m))$
$\forall y^{n-1}\cdots \forall y^{m+1}(y^n \approxeq _{n-1} y^{n-1} \approxeq _{n-2} \cdots \approxeq _{m+1} y^{m+1} \rightarrow y^{m+1}(x^m))$
-
(4)
 $y^n(x^m)$
$y^n(x^m)$
The last equivalence uses Lemma 27.1, and repeated instances of
![]() ${\textrm {FJT}}$
-Comprehension to provide a chain
${\textrm {FJT}}$
-Comprehension to provide a chain
![]() $y^n \approxeq _{n-1} a^{n-1} \approxeq _{n-2} \cdots \approxeq _{m+1} a^{m+1}$
.□
$y^n \approxeq _{n-1} a^{n-1} \approxeq _{n-2} \cdots \approxeq _{m+1} a^{m+1}$
.□
Lemma 30.
![]() ${\textrm {STT}_{\triangleright }}$
proves these schemes:
${\textrm {STT}_{\triangleright }}$
proves these schemes:
![]() $[[y^{n+1}(x^n)]^J]^I \leftrightarrow y^{n+1}(x^n)$
and
$[[y^{n+1}(x^n)]^J]^I \leftrightarrow y^{n+1}(x^n)$
and
![]() $[[y^{n+1} \triangleright x^n]^J]^I \leftrightarrow y^{n+1} \triangleright x^n$
.
$[[y^{n+1} \triangleright x^n]^J]^I \leftrightarrow y^{n+1} \triangleright x^n$
.
Proof. The first scheme is trivial. For the second, note that the following are equivalent:
-
(1)
 $[[y^{n+1} \triangleright x^n]^J]^I$
$[[y^{n+1} \triangleright x^n]^J]^I$
-
(2)
 $[\bigwedge _{i < n}\forall v^i(y^{n+1}(v^i) \leftrightarrow x^n(v^i))]^I$
$[\bigwedge _{i < n}\forall v^i(y^{n+1}(v^i) \leftrightarrow x^n(v^i))]^I$
-
(3)
 $\bigwedge _{i < n}\forall v^i(\forall y^n \forall y^{n-1}\cdots \forall y^{i+1}(y^{n+1} \triangleright y^{n} \triangleright y^{n-1} \triangleright \cdots \triangleright y^{i+1} \rightarrow y^{i+1}(v^i)) \leftrightarrow {}$
$\bigwedge _{i < n}\forall v^i(\forall y^n \forall y^{n-1}\cdots \forall y^{i+1}(y^{n+1} \triangleright y^{n} \triangleright y^{n-1} \triangleright \cdots \triangleright y^{i+1} \rightarrow y^{i+1}(v^i)) \leftrightarrow {}$
 $\forall x^{n-1} \cdots \forall x^{i+1}(x^n \triangleright x^{n-1} \triangleright \cdots \triangleright x^{i+1} \rightarrow x^{i+1}(v^i)))$
$\forall x^{n-1} \cdots \forall x^{i+1}(x^n \triangleright x^{n-1} \triangleright \cdots \triangleright x^{i+1} \rightarrow x^{i+1}(v^i)))$
-
(4)
 $y^{n+1} \triangleright x^n$
$y^{n+1} \triangleright x^n$
For the last equivalence, first note that repeated use of Down
![]() $_\exists $
gives us chains:
$_\exists $
gives us chains:
Using Lemma 25.1 twice, (3) is equivalent to:
-
(
 $3^{\prime }$
)
$3^{\prime }$
)
 $a^n \approx x^n \land a^{n-1} \approx b^{n-1} \land \cdots \land a^1 \approx b^1$
$a^n \approx x^n \land a^{n-1} \approx b^{n-1} \land \cdots \land a^1 \approx b^1$
Now Lemma 25.1 yields (4)
![]() $\Rightarrow $
(3
$\Rightarrow $
(3
![]() $'$
), and Lemma 25.2 gives (3
$'$
), and Lemma 25.2 gives (3
![]() $'$
)
$'$
)
![]() $\Rightarrow $
(4).□
$\Rightarrow $
(4).□
Assembling Lemmas 26–30, we obtain:
Theorem 31.
![]() ${\textrm {STT}_{\triangleright }}$
and
${\textrm {STT}_{\triangleright }}$
and
![]() ${\textrm {FJT}}$
are definitionally equivalent
${\textrm {FJT}}$
are definitionally equivalent
Acknowledgements
Thanks to Neil Barton, Salvatore Florio, Peter Fritz, Luca Incurvati, Stephan Krämer, Øystein Linnebo, Nicholas Jones, Agustín Rayo, Thomas Schindler, Lukas Skiba, and an anonymous referee for Review of Symbolic Logic.