Article contents
COMPLETENESS FOR COUNTER-DOXA CONDITIONALS – USING RANKING SEMANTICS
Published online by Cambridge University Press: 30 October 2018
Abstract
Standard conditionals 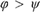 $\varphi > \psi$, by which I roughly mean variably strict conditionals à la Stalnaker and Lewis, are trivially true for impossible antecedents. This article investigates three modifications in a doxastic setting. For the neutral conditional, all impossible-antecedent conditionals are false, for the doxastic conditional they are only true if the consequent is absolutely necessary, and for the metaphysical conditional only if the consequent is ‘model-implied’ by the antecedent. I motivate these conditionals logically, and also doxastically by properties of conditional belief and belief revision. For this I show that the Lewisian hierarchy of conditional logics can be reproduced within ranking semantics, provided we slightly stretch the notion of a ranking function. Given this, acceptance of a conditional can be interpreted as a conditional belief. The epistemic and the neutral conditional deviate from Lewis’ weakest system
$\varphi > \psi$, by which I roughly mean variably strict conditionals à la Stalnaker and Lewis, are trivially true for impossible antecedents. This article investigates three modifications in a doxastic setting. For the neutral conditional, all impossible-antecedent conditionals are false, for the doxastic conditional they are only true if the consequent is absolutely necessary, and for the metaphysical conditional only if the consequent is ‘model-implied’ by the antecedent. I motivate these conditionals logically, and also doxastically by properties of conditional belief and belief revision. For this I show that the Lewisian hierarchy of conditional logics can be reproduced within ranking semantics, provided we slightly stretch the notion of a ranking function. Given this, acceptance of a conditional can be interpreted as a conditional belief. The epistemic and the neutral conditional deviate from Lewis’ weakest system 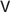 $V$, in that ID (
$V$, in that ID (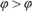 $\varphi > \varphi$) or even CN (
$\varphi > \varphi$) or even CN (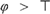 $\varphi > \top$) are dropped, and new axioms appear. The logic of the metaphysical conditional is completely axiomatised by
$\varphi > \top$) are dropped, and new axioms appear. The logic of the metaphysical conditional is completely axiomatised by 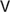 $V$ to which we add the known Kripke axioms T5 for the outer modality. Related completeness results for variations of the ranking semantics are obtained as corollaries.
$V$ to which we add the known Kripke axioms T5 for the outer modality. Related completeness results for variations of the ranking semantics are obtained as corollaries.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2018
References
BIBLIOGRAPHY
- 10
- Cited by

