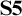1 Introduction
Modal expressions such as might and must can be used epistemically, for instance when one says that the Twin Prime Conjecture might be true and it might be false. When used in this way, they are known as epistemic modals and have been widely discussed in the recent literature, both in formal semantics and in philosophy. Challenges have been issued to the classic contextualist approach (Kratzer, Reference Kratzer1977, Reference Kratzer2012; DeRose, Reference DeRose1991) which aim to motivate relativist (MacFarlane, Reference MacFarlane2014), dynamic (Veltman, Reference Veltman1996; Willer, Reference Willer2013), probabilistic (Swanson, Reference Swanson2006; Moss, Reference Moss2015) and expressivist (Yalcin, Reference Yalcin2007; Charlow, Reference Charlow2015) accounts.
Despite the recent flurry of interest, however, no general logical framework is available for reasoning involving epistemic modality. In this paper, we present such a framework. Technically, the framework is obtained by extending bilateral systems—that is, systems in which formulae are decorated with signs for assertion and rejection (Rumfitt, Reference Rumfitt2000)—with a marker for the speech act of weak assertion (Incurvati & Schlöder, Reference Incurvati and Schlöder2019). Philosophically, the framework is developed from an inferentialist perspective. It respects well-known constraints on the acceptability of inference rules and hence provides the basis for an account of epistemic modality according to which the meanings of epistemic modals is given by their inferential role.
Although the logical framework is motivated from an inferentialist standpoint, it has the resources to account for several phenomena surrounding epistemic modality that have featured prominently in the recent literature. We focus here on Yalcin sentences (Yalcin, Reference Yalcin2007), i.e. sentences like It is raining and it might not be raining, and related phenomena. We show that, when supplemented with an inferentialist account of supposition, the logical framework predicts that Yalcin sentences are infelicitous and remain so under supposition. By appealing to the notion of supposability, our explanation may be extended to generalizations of Yalcin sentences due to Santorio (Reference Santorio2017) and Mandelkern (Reference Mandelkern2019).Footnote 1
We begin by making a case for developing a logical framework for reasoning about epistemic modality using the tools of proof-theoretic semantics (§2). We then present the logical framework, which we dub epistemic multilateral logic (§3). We give a model theory for epistemic multilateral logic and prove that the logic is sound and complete with respect to this model theory (§4). We apply our framework, suitably extended with an account of supposition, to Yalcin sentences and generalized Yalcin sentences (§5). One remarkable feature of epistemic multilateral logic is that it extends classical logic, unlike several current approaches to epistemic modality. Indeed, epistemic multilateral logic extends the modal logic
![]() $\mathbf {S5}$
. Issues for systems dealing with epistemic modality that extend
$\mathbf {S5}$
. Issues for systems dealing with epistemic modality that extend
![]() $\mathbf {S5}$
have been recently discussed by Schulz (Reference Schulz2010) and Bledin & Lando (Reference Bledin and Lando2018). We argue that these issues can be dealt with by distinguishing between two notions of proof-theoretic consequence in epistemic multilateral logic (§6). We conclude by outlining some directions for future work (§7).
$\mathbf {S5}$
have been recently discussed by Schulz (Reference Schulz2010) and Bledin & Lando (Reference Bledin and Lando2018). We argue that these issues can be dealt with by distinguishing between two notions of proof-theoretic consequence in epistemic multilateral logic (§6). We conclude by outlining some directions for future work (§7).
2 Inferentialism, bilateralism and multilateralism
Reasoning involving epistemic modality is widespread. For instance, suppose that one believes that Jane must be at the party. Then, it seems, one can conclude that Jane is at the party (von Fintel & Gillies, Reference von Fintel and Gillies2010). This is an instance of an inference pattern one may call epistemic weakening. But another commonly recognized inference allows us to conclude Jane must be at the party from Jane is at the party. It has been argued (see, e.g., Schulz, Reference Schulz2010) that this latter inference, an instance of epistemic strengthening, is importantly different in its logical status from epistemic weakening. Our proof theory will enable us to trace the difference precisely. In particular, it will allow us to distinguish between derivations that clearly preserve evidence (such as those formalizing epistemic weakening) and those for which this is more controversial but can nonetheless be taken to preserve commitment (such as those formalizing epistemic strengthening). This is an advantage of a proof-theoretic approach: by inspecting the rules featuring in a given derivation, one can determine which style of reasoning it employs and hence the epistemic properties it preserves. Current accounts of epistemic modality are presented in a model-theoretic framework, and a proof theory for epistemic modality is at present not available.
We aim to repair the situation. We will develop a proof theory for epistemic modality from an inferentialist perspective. Inferentialism is the view that the meaning of an expression is given by its role in inferences. In the case of a logical expression, it has often been contended that its inferential role can be captured by its introduction and elimination rules in a natural deduction system. Thus, logical inferentialism is the view that the meaning of logical constants is given by such rules.
Logical inferentialism faces the problem that not every pair of introduction and elimination rules seems to confer a coherent meaning on the logical constant involved. Arthur Prior (Reference Prior1960) first raised the problem by exhibiting the connective
![]() $\mathsf {tonk}$
.
$\mathsf {tonk}$
.

Adding
![]() $\mathsf {tonk}$
to a logical system makes it trivial: any sentence follows from any sentence whatsoever. Prior concluded that this sinks logical inferentialism. Inferentialists reacted by formulating criteria for the admissibility of inference rules which would rule out problematic constants such as
$\mathsf {tonk}$
to a logical system makes it trivial: any sentence follows from any sentence whatsoever. Prior concluded that this sinks logical inferentialism. Inferentialists reacted by formulating criteria for the admissibility of inference rules which would rule out problematic constants such as
![]() $\mathsf {tonk}$
. One prominent such criterion is harmony, the requirement that, for any given constant, there should be a certain balance between its introduction and elimination rules. We will present a natural deduction system for epistemic modality which complies with the harmony constraint and other standard proof-theoretic constraints.
$\mathsf {tonk}$
. One prominent such criterion is harmony, the requirement that, for any given constant, there should be a certain balance between its introduction and elimination rules. We will present a natural deduction system for epistemic modality which complies with the harmony constraint and other standard proof-theoretic constraints.
In many cases, for instance when dealing with modal vocabulary, it is not straightforward to satisfy these constraints, witness the search for suitable natural deduction rules for the modal logics
![]() $\mathbf {S4}$
and
$\mathbf {S4}$
and
![]() $\mathbf {S5}$
(see, e.g., Poggiolesi & Restall, Reference Poggiolesi, Restall, Restall and Russell2012; Read, Reference Read2015). Rather than being a hindrance, however, proof-theoretic constraints serve to narrow down the range of options available when developing a system for epistemic modality. This represents a further advantage of the proof-theoretic approach over the model-theoretic one, which is instead presented with several competing candidates, all of which appear plausible given the linguistic data.
$\mathbf {S5}$
(see, e.g., Poggiolesi & Restall, Reference Poggiolesi, Restall, Restall and Russell2012; Read, Reference Read2015). Rather than being a hindrance, however, proof-theoretic constraints serve to narrow down the range of options available when developing a system for epistemic modality. This represents a further advantage of the proof-theoretic approach over the model-theoretic one, which is instead presented with several competing candidates, all of which appear plausible given the linguistic data.
The situation here should be familiar from the debate over the underdetermination of theory by data in the philosophy of science. Model-theoretic semantics is typically pursued in a bottom-up fashion by surveying a wide range of data and attempting to define truth-conditions as appropriate generalizations that account for these data. Without any further constraints, it is wildly underdetermined what these truth-conditions should be. Proof-theoretic semantics, by contrast, proceeds in a top-down manner by developing a theory which satisfies a number of theoretical constraints (such as harmony) and testing whether the theory matches the data. We adopt the methodology of proof-theoretic semantics here. In §3, we develop an account of epistemic modality which satisfies the proof-theoretic constraints but is otherwise motivated only by simple data involving epistemic modals. We test it against more involved data in §5 and §6.
Besides seemingly ruling out
![]() $\mathsf {tonk}$
, however, proof-theoretic constraints appear to sanction an intuitionistic logic, since the rules for classical negation in standard natural deduction systems do not seem to be harmonious.Footnote
2
However, this is so because standard natural deduction systems only deal with asserted content: so-called bilateral systems—systems in which rejected content is also countenanced—are classical and satisfy the harmony constraint. Taking the rules of these systems to be meaning-determining leads to bilateralism, the view that the meaning of the logical constants is given by conditions on assertion and rejection. Here, assertion and rejection are speech acts expressing attitudes: assertion expresses assent, rejection expresses dissent. Importantly, rejection is, contra Frege (Reference Frege1919), distinct from, and not reducible to, the assertion of a negation.
$\mathsf {tonk}$
, however, proof-theoretic constraints appear to sanction an intuitionistic logic, since the rules for classical negation in standard natural deduction systems do not seem to be harmonious.Footnote
2
However, this is so because standard natural deduction systems only deal with asserted content: so-called bilateral systems—systems in which rejected content is also countenanced—are classical and satisfy the harmony constraint. Taking the rules of these systems to be meaning-determining leads to bilateralism, the view that the meaning of the logical constants is given by conditions on assertion and rejection. Here, assertion and rejection are speech acts expressing attitudes: assertion expresses assent, rejection expresses dissent. Importantly, rejection is, contra Frege (Reference Frege1919), distinct from, and not reducible to, the assertion of a negation.
Nonetheless, in standard bilateral systems (Smiley, Reference Smiley1996; Rumfitt, Reference Rumfitt2000), rejection and negative assertion have the same inference potential. That is, one can pass from the rejection of a proposition to its negative assertion, and vice versa. This is clearly encapsulated by the rules for negation of standard bilateral systems (see, e.g., Rumfitt, Reference Rumfitt2000), using
![]() $+\hspace {-0.1em}$
and
$+\hspace {-0.1em}$
and
![]() $\ominus \hspace {-0.08em}$
as, respectively, markers for assertion and rejection.
$\ominus \hspace {-0.08em}$
as, respectively, markers for assertion and rejection.

Although these rules are harmonious, they appear not to match certain important linguistic data about rejection. For the presence of these rules means that in standard bilateral systems rejection is strong: from the rejection of p it is always possible to infer the assertion of not p. However, linguistic evidence suggests that this is not always possible: rejections can be weak. Consider, for instance, the following dialogue, based on Grice (Reference Grice1991):
-
(1) Alice: X or Y will win the election.
Bob: No, X or Y or Z will win.
Bob is here rejecting what Alice said: he is expressing dissent from X or Y will win the election. But Bob’s rejection is weak. It would be mistaken to infer that he is assenting to neither X nor Y will win the election. His utterance leaves open the possibility that X will win the election or that Y will.
In Incurvati & Schlöder (Reference Incurvati and Schlöder2017) we develop a bilateral logic in which rejection is weak. In this logic, however, the rules for negation are, on the face of it, not harmonious. The issue can be addressed by extending the bilateralist approach to a multilateralist one. In Incurvati & Schlöder (Reference Incurvati and Schlöder2019) we present evidence for the existence of a speech act of weak assertion, linguistically realized using perhaps in otherwise assertoric contexts. Thus, in uttering (2a) in standard contexts one performs the familiar assertion (henceforth strong assertion) of it is raining. By contrast, an utterance of (2b) serves to realize the weak assertion of it is raining.
-
(2) a. It is raining.
b. Perhaps it is raining.
Strong assertion, rejection and weak assertion can be embedded within a Stalnakerian model of conversation. Stalnaker takes the essential effect of strongly asserting p to be that of proposing the addition of p to the common ground. In Incurvati & Schlöder (Reference Incurvati and Schlöder2017) we argue that the essential effect of rejecting p is to prevent the addition of p to the common ground (which is not the same as proposing to add not p to it). And in Incurvati & Schlöder (Reference Incurvati and Schlöder2019) we argue that the essential effect of weakly asserting p is to prevent the addition of not p to the common ground.
In the next section, we present a multilateral system involving weak assertion, strong assertion and (weak) rejection. Before doing so, however, we should clarify how consequence is best understood within a multilateral setting. Consider, for instance, the inference from the strong assertion of not A to the rejection of A. The validity of this inference does not mean that anyone strongly asserting not A is also explicitly rejecting A (see Dutilh Novaes, Reference Dutilh Novaes2015 for a similar point). Nor does it mean that anyone assenting to not A is also in the cognitive state of dissenting from A: since arbitrarily many further attitudes follow from assent to any given proposition (e.g. by disjunction introduction), this notion of consequence would imply that anyone who expresses a single attitude towards a single proposition must have unboundedly many attitudes to unboundedly many propositions. This is implausible (Harman, Reference Harman1986; Restall, Reference Restall, Hájek, Valdés-Villanueva and Westersthl2005).
Properly understood, the multilateralist notion of consequence is social. The proof rules determine which attitudes one is committed to have (see also Searle & Vanderveken, Reference Searle and Vanderveken1985; Dutilh Novaes, Reference Dutilh Novaes2015; Incurvati & Schlöder, Reference Incurvati and Schlöder2017). Someone who explicitly assents to not A need not also hold the attitude of dissent towards A, since she may fail to draw the inference licensed by (
![]() $+\hspace {-0.1em}\neg $
E.). Nevertheless, we may say that she is committed to dissenting from A, since if the inference is pointed out to her, she must dissent from A or admit to a mistake.
$+\hspace {-0.1em}\neg $
E.). Nevertheless, we may say that she is committed to dissenting from A, since if the inference is pointed out to her, she must dissent from A or admit to a mistake.
3 Epistemic multilateral logic
We are now ready to present epistemic multilateral logic (
![]() $\mathsf {EML}$
), a multilateral system for reasoning about epistemic modality. As in standard bilateral systems, in
$\mathsf {EML}$
), a multilateral system for reasoning about epistemic modality. As in standard bilateral systems, in
![]() $\mathsf {EML}$
formulae are signed. More specifically, the language
$\mathsf {EML}$
formulae are signed. More specifically, the language
![]() $\mathcal {L}_{EML}$
of
$\mathcal {L}_{EML}$
of
![]() $\mathsf {EML}$
is characterized as follows. We have a countable infinity of propositional atoms
$\mathsf {EML}$
is characterized as follows. We have a countable infinity of propositional atoms
![]() $p_1, \ldots , p_n$
. We then say that A is a sentence of
$p_1, \ldots , p_n$
. We then say that A is a sentence of
![]() $\mathcal {L}_{EML}$
if it belongs to the smallest class containing the propositional atoms and closed under applications of the unary connective
$\mathcal {L}_{EML}$
if it belongs to the smallest class containing the propositional atoms and closed under applications of the unary connective
![]() $\neg $
, the binary connective
$\neg $
, the binary connective
![]() $\wedge $
and the operator
$\wedge $
and the operator
![]() $\Diamond $
. We define
$\Diamond $
. We define
![]() $A \rightarrow B$
in the usual classical way, that is as
$A \rightarrow B$
in the usual classical way, that is as
![]() $\neg (A \wedge \neg B)$
. Moreover, we define
$\neg (A \wedge \neg B)$
. Moreover, we define
![]() $\Box A$
as
$\Box A$
as
![]() $\neg \Diamond \neg A$
. Finally, we say that
$\neg \Diamond \neg A$
. Finally, we say that
![]() $\varphi $
is a signed formula if it is obtained by prefixing a sentence of
$\varphi $
is a signed formula if it is obtained by prefixing a sentence of
![]() $\mathcal {L}_{EML}$
with one of
$\mathcal {L}_{EML}$
with one of
![]() $+\hspace {-0.1em}$
,
$+\hspace {-0.1em}$
,
![]() $\ominus \hspace {-0.08em}$
and
$\ominus \hspace {-0.08em}$
and
![]() $\oplus \hspace {-0.08em}$
. These are force-markers and stand, respectively, for strong assertion, (weak) rejection and weak assertion.
$\oplus \hspace {-0.08em}$
. These are force-markers and stand, respectively, for strong assertion, (weak) rejection and weak assertion.
![]() $\mathcal {L}_{EML}$
also includes a symbol
$\mathcal {L}_{EML}$
also includes a symbol
![]() $\perp $
, but this will be considered neither a sentence nor a (0-place) connective, as is sometimes the case, but a punctuation mark indicating that a logical dead end has been reached (see Tennant, Reference Tennant, Gabbay and Wansing1999; Rumfitt, Reference Rumfitt2000). In general, we use lowercase Greek letters for signed formulae and uppercase Latin letters for unsigned sentences.
$\perp $
, but this will be considered neither a sentence nor a (0-place) connective, as is sometimes the case, but a punctuation mark indicating that a logical dead end has been reached (see Tennant, Reference Tennant, Gabbay and Wansing1999; Rumfitt, Reference Rumfitt2000). In general, we use lowercase Greek letters for signed formulae and uppercase Latin letters for unsigned sentences.
3.1 Proof theory
The proof theory of
![]() $\mathsf {EML}$
is formulated by means of natural deduction rules. We briefly discuss the rules as described in Incurvati & Schlöder (Reference Incurvati and Schlöder2019).
$\mathsf {EML}$
is formulated by means of natural deduction rules. We briefly discuss the rules as described in Incurvati & Schlöder (Reference Incurvati and Schlöder2019).
For conjunction, we simply take the standard rules and prefix each sentence with the strong assertion sign.

The rules say that from two strongly asserted propositions one can infer the strong assertion of their conjunction, and that from a strongly asserted conjunction one can infer the strong assertion of either conjunct.
Linguistic analysis reveals that weakly asserting a proposition has the same consequences as rejecting its negation (see Incurvati & Schlöder, Reference Incurvati and Schlöder2019). Hence, the weak assertion of A and the rejection of not A should be interderivable. Linguistic analysis also shows that rejecting a proposition has the same consequences as weakly asserting its negation. Thus, the rejection of A and the weak assertion of not A should be interderivable too. This licenses the following rules for negation.


The rules for the epistemic possibility operator are based on two observations. The first is that uttering perhaps A has the same consequences as uttering it might be that A. It follows that the weak assertion of A and the strong assertion of
![]() $\Diamond A$
should be interderivable.
$\Diamond A$
should be interderivable.

The second observation is that uttering perhaps A has the same consequences as uttering perhaps it might be that A. It follows that the weak assertion of A and the weak assertion of
![]() $\Diamond A$
should be interderivable too.
$\Diamond A$
should be interderivable too.

The rules for
![]() $\neg $
and
$\neg $
and
![]() $\Diamond $
are clearly harmonious, since the elimination rules are the inverses of the corresponding introduction rules. They are also simple and pure in Dummett’s (Reference Dummett1991, p. 257) sense: only one logical constant features in them and this constant occurs only once.
$\Diamond $
are clearly harmonious, since the elimination rules are the inverses of the corresponding introduction rules. They are also simple and pure in Dummett’s (Reference Dummett1991, p. 257) sense: only one logical constant features in them and this constant occurs only once.
We have presented the operational rules of
![]() $\mathsf {EML}$
—that is, rules for the introduction and elimination of its operators. But we are not quite finished yet. For in multilateral systems (just as in bilateral systems) we also need rules that specify how the speech-act markers interact. Such rules are known as coordination principles and are needed to validate mixed inferences—inferences involving propositions that are uttered with different forces and are therefore prefixed by different signs. One example, involving strong assertion and rejection, is the seemingly valid pattern of inference that allows one to conclude the rejection of p from the strong assertion of if p, then q and the rejection of q (see Smiley, Reference Smiley1996). Another example, involving weak and strong assertion, is the inference pattern of weak modus ponens, which allows one to conclude the weak assertion of q from the weak assertion of p and the strong assertion of if p, then q (see Incurvati & Schlöder, Reference Incurvati and Schlöder2019). That is, from if p, then q and perhaps p one may infer perhaps q.
$\mathsf {EML}$
—that is, rules for the introduction and elimination of its operators. But we are not quite finished yet. For in multilateral systems (just as in bilateral systems) we also need rules that specify how the speech-act markers interact. Such rules are known as coordination principles and are needed to validate mixed inferences—inferences involving propositions that are uttered with different forces and are therefore prefixed by different signs. One example, involving strong assertion and rejection, is the seemingly valid pattern of inference that allows one to conclude the rejection of p from the strong assertion of if p, then q and the rejection of q (see Smiley, Reference Smiley1996). Another example, involving weak and strong assertion, is the inference pattern of weak modus ponens, which allows one to conclude the weak assertion of q from the weak assertion of p and the strong assertion of if p, then q (see Incurvati & Schlöder, Reference Incurvati and Schlöder2019). That is, from if p, then q and perhaps p one may infer perhaps q.
As in standard bilateral systems, the rules coordinating strong assertion and rejection characterize these speech acts as contraries.

(Rejection) states that strong assertion and rejection are incompatible: it is absurd to both propose and prevent the addition of the same proposition to the common ground. (SR
![]() $_1$
) says that if, in the presence of one’s extant commitments, strongly asserting a proposition leads to absurdity, then one is already committed to preventing the addition of that proposition to the common ground. A similar reading of (SR
$_1$
) says that if, in the presence of one’s extant commitments, strongly asserting a proposition leads to absurdity, then one is already committed to preventing the addition of that proposition to the common ground. A similar reading of (SR
![]() $_2$
) is available. The conjunction of (SR
$_2$
) is available. The conjunction of (SR
![]() $_1$
) and (SR
$_1$
) and (SR
![]() $_2$
) is known as the Smileian reductio principle, after Smiley (Reference Smiley1996).
$_2$
) is known as the Smileian reductio principle, after Smiley (Reference Smiley1996).
The remaining coordination principles characterize weak assertion as subaltern to its strong counterpart. We write
![]() $+\vdots$
for a derivation in which all premisses and undischarged assumptions are strongly asserted sentences, i.e. formulae of the form
$+\vdots$
for a derivation in which all premisses and undischarged assumptions are strongly asserted sentences, i.e. formulae of the form
![]() $+\hspace {-0.1em} A$
. Since
$+\hspace {-0.1em} A$
. Since
![]() $\bot $
is treated as a punctuation mark, in (Weak Inference) we distinguish between the case in which one infers
$\bot $
is treated as a punctuation mark, in (Weak Inference) we distinguish between the case in which one infers
![]() $+\hspace {-0.1em} B$
in the subderivation and the case in which one infers
$+\hspace {-0.1em} B$
in the subderivation and the case in which one infers
![]() $\bot $
. In the former case, (Weak Inference) allows one to conclude
$\bot $
. In the former case, (Weak Inference) allows one to conclude
![]() $+\hspace {-0.1em} B$
; in the latter case, it allows one to conclude
$+\hspace {-0.1em} B$
; in the latter case, it allows one to conclude
![]() $\bot $
.Footnote
3
$\bot $
.Footnote
3

(Assertion) ensures that in performing the strong assertion of a proposition, one is committed to dissenting from its negation. (Weak Inference) ensures that weak assertion is closed under strongly asserted implication and hence that inferences like if p then q; perhaps p; therefore perhaps q are valid. For if one’s evidential situation sanctions perhaps p and one knows that any situation where p is the case is also a situation where q is the case, then one is entitled to conclude perhaps q.
The restrictions on the subderivation of (Weak Inference) are due to the specificity problem (Incurvati & Schlöder, Reference Incurvati and Schlöder2017). As noted by Imogen Dickie (Reference Dickie2010), a correct strong assertion of A requires there being evidence for A. By contrast, the speech act of weak rejection is ‘messy’ in that it makes unspecific demands about evidence: a weak rejection of A may be correct because there is evidence against A, but may also be correct because of the (mere) absence of evidence for A (Incurvati & Schlöder, Reference Incurvati and Schlöder2017). This means the following for the justification of (Weak Inference). Suppose that in the base context one’s evidential status sanctions perhaps A. To apply (Weak Inference), one then considers the hypothetical situation in which A is the case and attempts to derive B. In the hypothetical situation in which A is the case, there may be evidence that is not available in the base context (e.g. evidence for A). Thus, in the subderivation of (Weak Inference), one may not use rejected premisses from the base context that one rejects for lack of evidence. Due to the unspecificity of weak rejection, this means that one may not use any premisses that are weakly rejected. Since
![]() $\oplus $
switches with
$\oplus $
switches with
![]() $\ominus $
and
$\ominus $
and
![]() $\oplus $
switches with
$\oplus $
switches with
![]() $+\hspace {-0.1em}\Diamond $
, one may also not use any weakly asserted premisses or apply
$+\hspace {-0.1em}\Diamond $
, one may also not use any weakly asserted premisses or apply
![]() $\Diamond $
-Eliminations to strongly asserted premisses.Footnote
4
$\Diamond $
-Eliminations to strongly asserted premisses.Footnote
4
3.2 Derived rules
This concludes the exposition of the proof theory of
![]() $\mathsf {EML}$
, and we use
$\mathsf {EML}$
, and we use
![]() $\vdash $
to denote derivability in
$\vdash $
to denote derivability in
![]() $\mathsf {EML}$
. To simplify the presentation in the remainder of the paper, however, it will be useful to present some additional derived rules of
$\mathsf {EML}$
. To simplify the presentation in the remainder of the paper, however, it will be useful to present some additional derived rules of
![]() $\mathsf {EML}$
, characterizing the behavior of the primitive connectives under some of the speech acts not covered by the basic rules and the behavior of the defined connectives. This will also serve to give a flavour of how derivations in
$\mathsf {EML}$
, characterizing the behavior of the primitive connectives under some of the speech acts not covered by the basic rules and the behavior of the defined connectives. This will also serve to give a flavour of how derivations in
![]() $\mathsf {EML}$
work.
$\mathsf {EML}$
work.
We begin with a rule which specifies how to introduce the strong assertion of a negation.
Proposition 3.1. The following rule is derivable in
![]() $\mathsf {EML}$
.
$\mathsf {EML}$
.

Proof.
![]() $\mathsf {EML}$
derives (
$\mathsf {EML}$
derives (
![]() $+\hspace {-0.1em}\neg $
I.) as follows.
$+\hspace {-0.1em}\neg $
I.) as follows.

□
Next, we have rules specifying the behavior of conjunction under weak assertion.Footnote 5
Proposition 3.2. The following rules are derivable in
![]() $\mathsf {EML}$
.
$\mathsf {EML}$
.

Proof.
![]() $\mathsf {EML}$
derives (
$\mathsf {EML}$
derives (
![]() $\oplus \hspace {-0.08em}\land $
I.
$\oplus \hspace {-0.08em}\land $
I.
![]() $_1$
) as follows.
$_1$
) as follows.

The case of (
![]() $\oplus \hspace {-0.08em}\land $
I.
$\oplus \hspace {-0.08em}\land $
I.
![]() $_2$
) is analogous. (
$_2$
) is analogous. (
![]() $\oplus \hspace {-0.08em}\land $
E.
$\oplus \hspace {-0.08em}\land $
E.
![]() $_1$
) follows from (Weak Inference):
$_1$
) follows from (Weak Inference):

(
![]() $\oplus \hspace {-0.08em}\land $
E.
$\oplus \hspace {-0.08em}\land $
E.
![]() $_2$
) is analogous. □
$_2$
) is analogous. □
Note that these derived rules are applicable in arbitrary proof contexts, even when their premisses are derived using
![]() $\Diamond $
-Elimination rules. While the derivations make use of (
$\Diamond $
-Elimination rules. While the derivations make use of (
![]() $+\hspace {-0.1em}\neg $
I.) and (Weak Inference)—rules that disallow
$+\hspace {-0.1em}\neg $
I.) and (Weak Inference)—rules that disallow
![]() $\Diamond $
-Eliminations—the applications of (
$\Diamond $
-Eliminations—the applications of (
![]() $+\hspace {-0.1em}\neg $
I.) and (Weak Inference) occur within self-contained subderivations and hence are correct irrespective of the wider proof context.
$+\hspace {-0.1em}\neg $
I.) and (Weak Inference) occur within self-contained subderivations and hence are correct irrespective of the wider proof context.
3.2.1 The material conditional
As mentioned, we are taking the conditional
![]() $A \rightarrow B$
to be defined as
$A \rightarrow B$
to be defined as
![]() $\neg (A \wedge \neg B)$
. Given the classicality of our calculus (to be shown below), this means that the conditional will be material. The following rules for strongly asserted conditionals can be derived.
$\neg (A \wedge \neg B)$
. Given the classicality of our calculus (to be shown below), this means that the conditional will be material. The following rules for strongly asserted conditionals can be derived.

Proof. (
![]() $+\hspace {-0.1em}\rightarrow $
I.) is derivable as follows.
$+\hspace {-0.1em}\rightarrow $
I.) is derivable as follows.

And (
![]() $+\hspace {-0.1em}\rightarrow $
E.) is derivable as follows:
$+\hspace {-0.1em}\rightarrow $
E.) is derivable as follows:

□
In addition, one can derive the rule of weak modus ponens (WMP).

Proof.

□
By (
![]() $+\hspace {-0.1em}\Diamond $
I.) and (
$+\hspace {-0.1em}\Diamond $
I.) and (
![]() $+\hspace {-0.1em}\Diamond $
E.), (WMP) entails the derivability of epistemic modus ponens (EMP).
$+\hspace {-0.1em}\Diamond $
E.), (WMP) entails the derivability of epistemic modus ponens (EMP).

3.2.2 Necessity modal
![]() $\Box A$
is defined as
$\Box A$
is defined as
![]() $\neg \Diamond \neg A$
. The following are derived rules for
$\neg \Diamond \neg A$
. The following are derived rules for
![]() $\Box $
:
$\Box $
:

Proof. (
![]() $+\hspace {-0.1em}\Box $
I.) is derivable as follows:
$+\hspace {-0.1em}\Box $
I.) is derivable as follows:

(
![]() $+\hspace {-0.1em}\Box $
E.) is derivable as follows:
$+\hspace {-0.1em}\Box $
E.) is derivable as follows:

□
Note that the derivability of (
![]() $+\hspace {-0.1em}\Box $
I.) does not imply that
$+\hspace {-0.1em}\Box $
I.) does not imply that
![]() $+\hspace {-0.1em} (A\rightarrow \Box A)$
, since the derivation of
$+\hspace {-0.1em} (A\rightarrow \Box A)$
, since the derivation of
![]() $+\hspace {-0.1em} \neg \Diamond \neg A$
from
$+\hspace {-0.1em} \neg \Diamond \neg A$
from
![]() $+\hspace {-0.1em} A$
uses a
$+\hspace {-0.1em} A$
uses a
![]() $\Diamond $
-Elimination rule, which rules out an application of (
$\Diamond $
-Elimination rule, which rules out an application of (
![]() $+\hspace {-0.1em}\rightarrow $
I.). In fact, there is no derivation of
$+\hspace {-0.1em}\rightarrow $
I.). In fact, there is no derivation of
![]() $+\hspace {-0.1em} (A\rightarrow \Box A)$
in
$+\hspace {-0.1em} (A\rightarrow \Box A)$
in
![]() $\mathsf {EML}$
, as shown by the soundness of
$\mathsf {EML}$
, as shown by the soundness of
![]() $\mathsf {EML}$
with respect to
$\mathsf {EML}$
with respect to
![]() $\mathbf {S5}$
modulo an appropriate translation (see §4).
$\mathbf {S5}$
modulo an appropriate translation (see §4).
3.3 Classicality
We now show that, in a defined sense, the logic of strong assertion extends classical logic (in much the same way that normal modal logics extend classical logic).
Let
![]() $\sigma : \text {At} \rightarrow \text {wff}_{\text {EML}}$
be any mapping from propositional atoms to formulae in the language
$\sigma : \text {At} \rightarrow \text {wff}_{\text {EML}}$
be any mapping from propositional atoms to formulae in the language
![]() $\mathcal {L}_{EML}$
of
$\mathcal {L}_{EML}$
of
![]() $\mathsf {EML}$
. If A is a formula in the language
$\mathsf {EML}$
. If A is a formula in the language
![]() $\mathcal {L}_{PL}$
of propositional logic, write
$\mathcal {L}_{PL}$
of propositional logic, write
![]() $\sigma [A]$
for the
$\sigma [A]$
for the
![]() $\mathcal {L}_{EML}$
-formula that results from replacing every atom p in A with
$\mathcal {L}_{EML}$
-formula that results from replacing every atom p in A with
![]() $\sigma (p)$
. Moreover, let
$\sigma (p)$
. Moreover, let
![]() $\models ^{\text {CPL}}$
be the consequence relation of classical propositional logic. We have:
$\models ^{\text {CPL}}$
be the consequence relation of classical propositional logic. We have:
Theorem 3.3 (Supra-Classicality).
Let
![]() $\Gamma $
be a set of
$\Gamma $
be a set of
![]() $\mathcal {L}_{PL}$
-formulae and A an
$\mathcal {L}_{PL}$
-formulae and A an
![]() $\mathcal {L}_{PL}$
-formula. If
$\mathcal {L}_{PL}$
-formula. If
![]() $\Gamma \models ^{\text {CPL}} A$
, then
$\Gamma \models ^{\text {CPL}} A$
, then
![]() $\{+\hspace {-0.1em} \sigma [B] \mid B \in \Gamma \} \vdash +\hspace {-0.1em}\sigma [A]$
.
$\{+\hspace {-0.1em} \sigma [B] \mid B \in \Gamma \} \vdash +\hspace {-0.1em}\sigma [A]$
.
Proof. Since
![]() $\mathsf {EML}$
validates modus ponens, it suffices to show that the strongly asserted versions of the axioms of the propositional calculus are theorems of
$\mathsf {EML}$
validates modus ponens, it suffices to show that the strongly asserted versions of the axioms of the propositional calculus are theorems of
![]() $\mathsf {EML}$
. That is, for arbitrary A, B and C in
$\mathsf {EML}$
. That is, for arbitrary A, B and C in
![]() $\mathcal {L}_{EML}$
, we have:
$\mathcal {L}_{EML}$
, we have:
 $$ \begin{align*} \begin{array}{l} \vdash +\hspace{-0.1em}(A \rightarrow \neg\neg A),\\ \vdash +\hspace{-0.1em}(\neg\neg A\rightarrow A),\\ \vdash +\hspace{-0.1em}((A \rightarrow B) \rightarrow (\neg B \rightarrow \neg A)),\\ \vdash +\hspace{-0.1em}((A \rightarrow (B \rightarrow C)) \rightarrow ((A \rightarrow B) \rightarrow (A \rightarrow C))),\\ \vdash +\hspace{-0.1em}((A \rightarrow (B \rightarrow C)) \rightarrow (B \rightarrow (A \rightarrow C))),\\ \vdash +\hspace{-0.1em}(A \rightarrow (B \rightarrow A)). \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l} \vdash +\hspace{-0.1em}(A \rightarrow \neg\neg A),\\ \vdash +\hspace{-0.1em}(\neg\neg A\rightarrow A),\\ \vdash +\hspace{-0.1em}((A \rightarrow B) \rightarrow (\neg B \rightarrow \neg A)),\\ \vdash +\hspace{-0.1em}((A \rightarrow (B \rightarrow C)) \rightarrow ((A \rightarrow B) \rightarrow (A \rightarrow C))),\\ \vdash +\hspace{-0.1em}((A \rightarrow (B \rightarrow C)) \rightarrow (B \rightarrow (A \rightarrow C))),\\ \vdash +\hspace{-0.1em}(A \rightarrow (B \rightarrow A)). \end{array} \end{align*} $$
These are easy to check (see Incurvati & Schlöder, Reference Incurvati and Schlöder2019). □
Together with the Soundness result (Theorem 4.1) we will prove in §4, this yields the following corollary.
Corollary 3.4 (Classicality).
Let
![]() $\Gamma $
be a set of
$\Gamma $
be a set of
![]() $\mathcal {L}_{PL}$
-formulae and A an
$\mathcal {L}_{PL}$
-formulae and A an
![]() $\mathcal {L}_{PL}$
-formula.
$\mathcal {L}_{PL}$
-formula.
![]() $\Gamma \models ^{\text {CPL}} A$
iff
$\Gamma \models ^{\text {CPL}} A$
iff
![]() $\{+\hspace {-0.1em} B \mid B \in \Gamma \} \vdash +\hspace {-0.1em} A$
.
$\{+\hspace {-0.1em} B \mid B \in \Gamma \} \vdash +\hspace {-0.1em} A$
.
Proof. The left-to-right direction follows from Theorem 3.3. The right-to-left direction is a corollary of
![]() $\mathbf {S5}$
-Soundness (Theorem 4.1): if
$\mathbf {S5}$
-Soundness (Theorem 4.1): if
![]() $\{+\hspace {-0.1em} B \mid B \in \Gamma \} \vdash +\hspace {-0.1em} A$
, then
$\{+\hspace {-0.1em} B \mid B \in \Gamma \} \vdash +\hspace {-0.1em} A$
, then
![]() $\{\Box B \mid B \in \Gamma \} \models ^{\mathbf {S5}} \Box A$
, which for propositional
$\{\Box B \mid B \in \Gamma \} \models ^{\mathbf {S5}} \Box A$
, which for propositional
![]() $\Gamma $
and A entails
$\Gamma $
and A entails
![]() $\Gamma \models ^{\text {CPL}} A$
, since all worlds in an
$\Gamma \models ^{\text {CPL}} A$
, since all worlds in an
![]() $\mathbf {S5}$
-model are models of classical propositional logic. □
$\mathbf {S5}$
-model are models of classical propositional logic. □
3.4
 $\mathsf {EML}$
extends
$\mathsf {EML}$
extends
 $\mathbf {S5}$
$\mathbf {S5}$
We now show that
![]() $\mathsf {EML}$
extends
$\mathsf {EML}$
extends
![]() $\mathbf {S5}$
, i.e. that the logic of strong assertion validates every
$\mathbf {S5}$
, i.e. that the logic of strong assertion validates every
![]() $\mathbf {S5}$
-valid argument. To this end, we shall prove that if A is an
$\mathbf {S5}$
-valid argument. To this end, we shall prove that if A is an
![]() $\mathbf {S5}$
-tautology, then its strongly asserted counterpart is a theorem of
$\mathbf {S5}$
-tautology, then its strongly asserted counterpart is a theorem of
![]() $\mathsf {EML}$
. That is:
$\mathsf {EML}$
. That is:
Theorem 3.5. If
![]() $\models ^{\mathbf {S5}} A$
, then
$\models ^{\mathbf {S5}} A$
, then
![]() $\vdash +\hspace {-0.1em} A$
.
$\vdash +\hspace {-0.1em} A$
.
This will yield the desired result.
Corollary 3.6. If
![]() $\Gamma \models ^{\mathbf {S5}} A$
, then
$\Gamma \models ^{\mathbf {S5}} A$
, then
![]() $\{+\hspace {-0.1em} B \mid B \in \Gamma \} \vdash +\hspace {-0.1em} A$
.
$\{+\hspace {-0.1em} B \mid B \in \Gamma \} \vdash +\hspace {-0.1em} A$
.
Proof. If
![]() $\Gamma \models ^{\mathbf {S5}} A$
, then there is a finite
$\Gamma \models ^{\mathbf {S5}} A$
, then there is a finite
![]() $\Gamma '$
such that
$\Gamma '$
such that
![]() $\models ^{\mathbf {S5}} \bigwedge _{B\in \Gamma '} B \rightarrow A$
. By Theorem 3.5,
$\models ^{\mathbf {S5}} \bigwedge _{B\in \Gamma '} B \rightarrow A$
. By Theorem 3.5,
![]() $\vdash +\hspace {-0.1em} (\bigwedge _{B\in \Gamma '} B \rightarrow A)$
. Since the (
$\vdash +\hspace {-0.1em} (\bigwedge _{B\in \Gamma '} B \rightarrow A)$
. Since the (
![]() $+\hspace {-0.1em}\rightarrow $
E.) rule is derivable in
$+\hspace {-0.1em}\rightarrow $
E.) rule is derivable in
![]() $\mathsf {EML}$
, it follows that
$\mathsf {EML}$
, it follows that
![]() $\{+\hspace {-0.1em} B \mid B \in \Gamma \} \vdash +\hspace {-0.1em} A$
. □
$\{+\hspace {-0.1em} B \mid B \in \Gamma \} \vdash +\hspace {-0.1em} A$
. □
Towards the proof of Theorem 3.5, we first prove a technical lemma.
Lemma 3.7. The following rule is derivable in
![]() $\mathsf {EML}$
.
$\mathsf {EML}$
.

Proof.

□
We are now ready to prove the main result of this section.
Proof of Theorem 3.5
![]() $\mathsf {EML}$
proves all substitution-instances of classical tautologies (Theorem 3.3). Moreover, by the (
$\mathsf {EML}$
proves all substitution-instances of classical tautologies (Theorem 3.3). Moreover, by the (
![]() $+\hspace {-0.1em}\Box $
I.) rule, we have that if
$+\hspace {-0.1em}\Box $
I.) rule, we have that if
![]() $\vdash +\hspace {-0.1em} A$
then also
$\vdash +\hspace {-0.1em} A$
then also
![]() $\vdash +\hspace {-0.1em}\Box A$
. Thus, it suffices to show that the
$\vdash +\hspace {-0.1em}\Box A$
. Thus, it suffices to show that the
![]() $\mathbf {KT5}$
axioms are derivable in
$\mathbf {KT5}$
axioms are derivable in
![]() $\mathsf {EML}$
.
$\mathsf {EML}$
.
Axiom
![]() $\mathbf {K}$
can be written on the signature
$\mathbf {K}$
can be written on the signature
![]() $\{\neg ,\land ,\Diamond \}$
as
$\{\neg ,\land ,\Diamond \}$
as
The following derivation witnesses
![]() $\vdash +\hspace {-0.1em} \neg (\neg \Diamond (A\land \neg B) \land \neg \Diamond \neg A \land \Diamond \neg B)$
:
$\vdash +\hspace {-0.1em} \neg (\neg \Diamond (A\land \neg B) \land \neg \Diamond \neg A \land \Diamond \neg B)$
:

Axiom
![]() $\mathbf {T}$
follows immediately from (
$\mathbf {T}$
follows immediately from (
![]() $+\hspace {-0.1em}\Box $
E.) and (
$+\hspace {-0.1em}\Box $
E.) and (
![]() $+\hspace {-0.1em}\rightarrow $
I.), as the derivation of (
$+\hspace {-0.1em}\rightarrow $
I.), as the derivation of (
![]() $+\hspace {-0.1em}\Box $
E.) does not involve
$+\hspace {-0.1em}\Box $
E.) does not involve
![]() $\Diamond $
-Elimination rules.
$\Diamond $
-Elimination rules.
Axiom
![]() $\mathbf {5}$
can be written on the signature
$\mathbf {5}$
can be written on the signature
![]() $\{\neg ,\land ,\Diamond \}$
as
$\{\neg ,\land ,\Diamond \}$
as
![]() $\neg (\Diamond A \land \Diamond \neg \Diamond A)$
. The following derivation witnesses
$\neg (\Diamond A \land \Diamond \neg \Diamond A)$
. The following derivation witnesses
![]() $\vdash +\hspace {-0.1em} \neg (\Diamond A \land \Diamond \neg \Diamond A)$
:
$\vdash +\hspace {-0.1em} \neg (\Diamond A \land \Diamond \neg \Diamond A)$
:

□
The derivations of Axioms K and 5 make use of
![]() $\Diamond $
-Elimination rules, but we can apply these axioms within (Weak Inference) by assuming them and then discharging them. To wit, suppose that from
$\Diamond $
-Elimination rules, but we can apply these axioms within (Weak Inference) by assuming them and then discharging them. To wit, suppose that from
![]() $+\hspace {-0.1em} A$
we can infer
$+\hspace {-0.1em} A$
we can infer
![]() $+\hspace {-0.1em} B$
using Axiom K. Then the following application of (Weak Inference) is, strictly speaking, incorrect.
$+\hspace {-0.1em} B$
using Axiom K. Then the following application of (Weak Inference) is, strictly speaking, incorrect.

But we may still derive
![]() $\oplus \hspace {-0.08em} B$
from
$\oplus \hspace {-0.08em} B$
from
![]() $\oplus \hspace {-0.08em} A$
as follows.
$\oplus \hspace {-0.08em} A$
as follows.

Here, the application of (Weak Inference) is licit since it uses
![]() $+\hspace {-0.1em} (K)$
as a dischargeable assumption. If this application of (Weak Inference) occurs within another application of (Weak Inference), one can defer the derivation of
$+\hspace {-0.1em} (K)$
as a dischargeable assumption. If this application of (Weak Inference) occurs within another application of (Weak Inference), one can defer the derivation of
![]() $+\hspace {-0.1em} (K)$
to the outermost proof level. Clearly, this method generalizes to uses of Axiom 5 within applications of (Weak Inference). So we will use the S5 axioms freely from now on. In general, if
$+\hspace {-0.1em} (K)$
to the outermost proof level. Clearly, this method generalizes to uses of Axiom 5 within applications of (Weak Inference). So we will use the S5 axioms freely from now on. In general, if
![]() $+\hspace {-0.1em} A$
is a theorem—if one can show it from no side premisses, even when using
$+\hspace {-0.1em} A$
is a theorem—if one can show it from no side premisses, even when using
![]() $\Diamond $
-Eliminations—one may use
$\Diamond $
-Eliminations—one may use
![]() $+\hspace {-0.1em} A$
even in proof contexts that disallow
$+\hspace {-0.1em} A$
even in proof contexts that disallow
![]() $\Diamond $
-Eliminations by assuming
$\Diamond $
-Eliminations by assuming
![]() $+\hspace {-0.1em} A$
, conditionalizing on A and deriving
$+\hspace {-0.1em} A$
, conditionalizing on A and deriving
![]() $+\hspace {-0.1em} A$
at the outermost proof level.
$+\hspace {-0.1em} A$
at the outermost proof level.
4 Model theory for epistemic multilateral logic
We have motivated epistemic multilateral logic from an inferentialist perspective and have therefore focused on the proof theory so far. We now proceed to provide a model theory for the logic. We do this by providing a translation of epistemic multilateral logic into modal logic and showing that the result is sound and complete with respect to
![]() $\mathbf {S5}$
.
$\mathbf {S5}$
.
4.1 Soundness
We begin with the translation. The idea is to translate strong assertion with necessity, rejection with possible falsity, and weak assertion with possibility, but note that this is a translation only in the technical sense: it is not intended to provide the intended interpretation of the force-markers. Formally, we define a mapping
![]() $\tau $
from
$\tau $
from
![]() $\mathcal {L}_{EML}$
-formulae to formulae in the language
$\mathcal {L}_{EML}$
-formulae to formulae in the language
![]() $\mathcal {L}_{ML}$
of modal logic.
$\mathcal {L}_{ML}$
of modal logic.
 $$ \begin{align*}\tau(\varphi) = \begin{cases} \Box\psi\text{, if }\varphi = +\hspace{-0.1em}\psi\\ \Diamond\neg\psi\text{, if }\varphi = \ominus\hspace{-0.08em}\psi\\ \Diamond\psi\text{, if }\varphi = \oplus\hspace{-0.08em}\psi \end{cases}\end{align*} $$
$$ \begin{align*}\tau(\varphi) = \begin{cases} \Box\psi\text{, if }\varphi = +\hspace{-0.1em}\psi\\ \Diamond\neg\psi\text{, if }\varphi = \ominus\hspace{-0.08em}\psi\\ \Diamond\psi\text{, if }\varphi = \oplus\hspace{-0.08em}\psi \end{cases}\end{align*} $$
If
![]() $\Gamma $
is a set of
$\Gamma $
is a set of
![]() $\mathcal {L}_{EML}$
-formulae, we write
$\mathcal {L}_{EML}$
-formulae, we write
![]() $\tau [\Gamma ]$
for
$\tau [\Gamma ]$
for
![]() $\{\tau (\varphi ): \varphi \in \Gamma \}$
.
$\{\tau (\varphi ): \varphi \in \Gamma \}$
.
We now prove that, under this translation,
![]() $\mathsf {EML}$
is sound with respect to
$\mathsf {EML}$
is sound with respect to
![]() $\mathbf {S5}$
. That is:
$\mathbf {S5}$
. That is:
Theorem 4.1 (Soundness).
Let
![]() $\Gamma $
be a set of
$\Gamma $
be a set of
![]() $\mathcal {L}_{EML}$
-formulae. If
$\mathcal {L}_{EML}$
-formulae. If
![]() $\Gamma \vdash \varphi $
then
$\Gamma \vdash \varphi $
then
![]() $\tau [\Gamma ] \models ^{\mathbf {S5}} \tau (\varphi )$
.
$\tau [\Gamma ] \models ^{\mathbf {S5}} \tau (\varphi )$
.
The main challenge is to show that the restrictions on (Weak Inference) are effective in ensuring the soundness of the calculus. To this end, let
![]() $\mathsf {EML}^+$
be the calculus of
$\mathsf {EML}^+$
be the calculus of
![]() $\mathsf {EML}$
plus the derivable rules for conjunction under weak assertion, which we recall for convenience.
$\mathsf {EML}$
plus the derivable rules for conjunction under weak assertion, which we recall for convenience.

Since these are derivable in
![]() $\mathsf {EML}$
, the soundness of
$\mathsf {EML}$
, the soundness of
![]() $\mathsf {EML}$
is equivalent to the soundness of
$\mathsf {EML}$
is equivalent to the soundness of
![]() $\mathsf {EML}^+$
. We use
$\mathsf {EML}^+$
. We use
![]() $\vdash ^+$
to denote derivability in
$\vdash ^+$
to denote derivability in
![]() $\mathsf {EML}^+$
and write
$\mathsf {EML}^+$
and write
![]() $\Gamma \vdash ^+_D \varphi $
to indicate that the derivation D witnesses the existence of this derivability relation between
$\Gamma \vdash ^+_D \varphi $
to indicate that the derivation D witnesses the existence of this derivability relation between
![]() $\Gamma $
and
$\Gamma $
and
![]() $\varphi $
.
$\varphi $
.
Now let
![]() $\mathsf {EML}^-$
be the calculus of
$\mathsf {EML}^-$
be the calculus of
![]() $\mathsf {EML}^+$
without (Weak Inference) and write
$\mathsf {EML}^+$
without (Weak Inference) and write
![]() $\vdash ^-$
for the resulting derivability relation. By inspecting the proofs of (
$\vdash ^-$
for the resulting derivability relation. By inspecting the proofs of (
![]() $+\hspace {-0.1em}\rightarrow $
E.) and (WMP), one can see that (
$+\hspace {-0.1em}\rightarrow $
E.) and (WMP), one can see that (
![]() $+\hspace {-0.1em}\rightarrow $
E.) and (WMP) are derivable in
$+\hspace {-0.1em}\rightarrow $
E.) and (WMP) are derivable in
![]() $\mathsf {EML}^-$
. (The conditional proof rule (
$\mathsf {EML}^-$
. (The conditional proof rule (
![]() $+\hspace {-0.1em}\rightarrow $
I.) is not derivable in
$+\hspace {-0.1em}\rightarrow $
I.) is not derivable in
![]() $\mathsf {EML}^-$
, but this does not matter for present purposes.)
$\mathsf {EML}^-$
, but this does not matter for present purposes.)
Now, it is straightforward to show that
![]() $\mathsf {EML}^-$
is sound with respect to
$\mathsf {EML}^-$
is sound with respect to
![]() $\mathbf {S5}$
modulo the translation
$\mathbf {S5}$
modulo the translation
![]() $\tau $
.
$\tau $
.
Theorem 4.2 (Pre-Soundness).
Let
![]() $\Gamma $
be a set of
$\Gamma $
be a set of
![]() $\mathcal {L}_{EML}$
-formulae and
$\mathcal {L}_{EML}$
-formulae and
![]() $\varphi $
an
$\varphi $
an
![]() $\mathcal {L}_{EML}$
-formula. If
$\mathcal {L}_{EML}$
-formula. If
![]() $\Gamma \vdash ^- \varphi $
then
$\Gamma \vdash ^- \varphi $
then
![]() $\tau [\Gamma ] \models ^{\mathbf {S5}} \tau (\varphi )$
.
$\tau [\Gamma ] \models ^{\mathbf {S5}} \tau (\varphi )$
.
The proof is a standard induction on the length of derivations and is therefore omitted. Next, we prove the soundness of the full calculus. First, we need an auxiliary definition and a technical lemma. The following definition provides the tools to rewrite a proof D not involving
![]() $\Diamond $
-Eliminations to a proof where
$\Diamond $
-Eliminations to a proof where
![]() $\Diamond $
s only occur in sentences that translate back to S5-tautologies.
$\Diamond $
s only occur in sentences that translate back to S5-tautologies.
Definition 1. Suppose
![]() $\Gamma \vdash ^+_D \varphi $
where D does not use
$\Gamma \vdash ^+_D \varphi $
where D does not use
![]() $\Diamond $
-Elimination rules,
$\Diamond $
-Elimination rules,
![]() $\Gamma $
contains only strongly asserted formulae and D uses all premisses in
$\Gamma $
contains only strongly asserted formulae and D uses all premisses in
![]() $\Gamma $
(in particular, then,
$\Gamma $
(in particular, then,
![]() $\Gamma $
is finite).
$\Gamma $
is finite).
Construct a mapping
![]() $\pi ^D$
as follows: for each formula Z that occurs anywhere in D pick an unused (in D) propositional atom
$\pi ^D$
as follows: for each formula Z that occurs anywhere in D pick an unused (in D) propositional atom
![]() $c_Z$
and let
$c_Z$
and let
![]() $\pi ^{D}(+\hspace {-0.1em} Z) = +\hspace {-0.1em} c_Z$
,
$\pi ^{D}(+\hspace {-0.1em} Z) = +\hspace {-0.1em} c_Z$
,
![]() $\pi ^{D}(\ominus \hspace {-0.08em} Z) = \ominus \hspace {-0.08em} c_Z$
and
$\pi ^{D}(\ominus \hspace {-0.08em} Z) = \ominus \hspace {-0.08em} c_Z$
and
![]() $\pi ^{D}(\oplus \hspace {-0.08em} Z) = \oplus \hspace {-0.08em} c_z$
(this is easily possible, since D is finite).
$\pi ^{D}(\oplus \hspace {-0.08em} Z) = \oplus \hspace {-0.08em} c_z$
(this is easily possible, since D is finite).
Let
![]() $\Sigma ^D$
be the set containing exactly the following formulae. For any formulae X and Y occurring anywhere in D:
$\Sigma ^D$
be the set containing exactly the following formulae. For any formulae X and Y occurring anywhere in D:
-
a.
 $+\hspace {-0.1em}(c_{\neg X} \rightarrow \neg c_X)$
and
$+\hspace {-0.1em}(c_{\neg X} \rightarrow \neg c_X)$
and
 $+\hspace {-0.1em}(\neg c_X \rightarrow c_{\neg X})$
.
$+\hspace {-0.1em}(\neg c_X \rightarrow c_{\neg X})$
. -
b.
 $+\hspace {-0.1em}(c_{\neg \neg X} \rightarrow c_X)$
and
$+\hspace {-0.1em}(c_{\neg \neg X} \rightarrow c_X)$
and
 $+\hspace {-0.1em}(c_X \rightarrow c_{\neg \neg X})$
.
$+\hspace {-0.1em}(c_X \rightarrow c_{\neg \neg X})$
. -
c.
 $+\hspace {-0.1em}(c_{X \land Y} \rightarrow (c_X \land c_Y))$
and
$+\hspace {-0.1em}(c_{X \land Y} \rightarrow (c_X \land c_Y))$
and
 $+\hspace {-0.1em}((c_X \land c_Y) \rightarrow c_{X \land Y})$
.
$+\hspace {-0.1em}((c_X \land c_Y) \rightarrow c_{X \land Y})$
. -
d.
 $+\hspace {-0.1em} (c_X \rightarrow c_{\Diamond X})$
.
$+\hspace {-0.1em} (c_X \rightarrow c_{\Diamond X})$
. -
e.
 $+\hspace {-0.1em}(\Diamond c_{\Diamond X} \rightarrow c_{\Diamond X})$
.
$+\hspace {-0.1em}(\Diamond c_{\Diamond X} \rightarrow c_{\Diamond X})$
.
Note that all formulae in
![]() $\Sigma ^D$
substitute to S5-tautologies under the map
$\Sigma ^D$
substitute to S5-tautologies under the map
![]() $c_X \mapsto X$
(i.e. the inverse of
$c_X \mapsto X$
(i.e. the inverse of
![]() $\pi ^D$
). The following lemma shows that these added assumptions suffice to rewrite the proof D under the translation
$\pi ^D$
). The following lemma shows that these added assumptions suffice to rewrite the proof D under the translation
![]() $\pi ^D$
.
$\pi ^D$
.
Lemma 4.3. Suppose
![]() $\Gamma \vdash ^+_D \varphi $
where D does not use
$\Gamma \vdash ^+_D \varphi $
where D does not use
![]() $\Diamond $
-Elimination rules and
$\Diamond $
-Elimination rules and
![]() $\Gamma $
contains only strongly asserted formulae. Then there is a derivation
$\Gamma $
contains only strongly asserted formulae. Then there is a derivation
![]() $D'$
such that
$D'$
such that
![]() $\pi ^D[\Gamma ] \cup \Sigma ^D \vdash ^+_{D'} \pi ^D(\varphi )$
and
$\pi ^D[\Gamma ] \cup \Sigma ^D \vdash ^+_{D'} \pi ^D(\varphi )$
and
![]() $D'$
contains no more applications of (Weak Inference) than D.
$D'$
contains no more applications of (Weak Inference) than D.
Proof. We show by induction on the length n of D that every derivation D can be rewritten to a derivation
![]() $D'$
as in the Lemma. The base case
$D'$
as in the Lemma. The base case
![]() $n=1$
is trivial since if D has length
$n=1$
is trivial since if D has length
![]() $1$
, then
$1$
, then
![]() $\varphi \in \Gamma $
and hence also
$\varphi \in \Gamma $
and hence also
![]() $\pi ^D(\varphi ) \in \pi ^D[\Gamma ]$
.
$\pi ^D(\varphi ) \in \pi ^D[\Gamma ]$
.
So let D be a derivation of length
![]() $n> 1$
. By the induction hypothesis, we know that all proper subderivations of D can be rewritten as required for the Lemma. Hence, it suffices to show that the last rule applied in D can be rewritten as well. In the induction steps we will use derivations E that are proper subderivations of D. Without loss of generality, we can assume that
$n> 1$
. By the induction hypothesis, we know that all proper subderivations of D can be rewritten as required for the Lemma. Hence, it suffices to show that the last rule applied in D can be rewritten as well. In the induction steps we will use derivations E that are proper subderivations of D. Without loss of generality, we can assume that
![]() $\pi ^E \subseteq \pi ^D$
for all such cases, i.e. that
$\pi ^E \subseteq \pi ^D$
for all such cases, i.e. that
![]() $\pi ^E(\varphi ) = \pi ^D(\varphi )$
for all
$\pi ^E(\varphi ) = \pi ^D(\varphi )$
for all
![]() $\varphi $
occurring in E. (If
$\varphi $
occurring in E. (If
![]() $\pi ^E$
is different, one only needs to apply an appropriate substitution.) In particular, this means that
$\pi ^E$
is different, one only needs to apply an appropriate substitution.) In particular, this means that
![]() $\Sigma ^E \subseteq \Sigma ^D$
. Also, we usually write
$\Sigma ^E \subseteq \Sigma ^D$
. Also, we usually write
![]() $+\hspace {-0.1em} c_X$
(
$+\hspace {-0.1em} c_X$
(
![]() $\ominus \hspace {-0.08em} c_X$
,
$\ominus \hspace {-0.08em} c_X$
,
![]() $\oplus \hspace {-0.08em} c_X)$
for
$\oplus \hspace {-0.08em} c_X)$
for
![]() $\pi ^D(+\hspace {-0.1em} X)$
(
$\pi ^D(+\hspace {-0.1em} X)$
(
![]() $\pi ^D(\ominus \hspace {-0.08em} X)$
,
$\pi ^D(\ominus \hspace {-0.08em} X)$
,
![]() $\pi ^D(\oplus \hspace {-0.08em} X)$
).
$\pi ^D(\oplus \hspace {-0.08em} X)$
).
The coordination principles require no rewriting aside from substituting
![]() $c_X$
for X.
$c_X$
for X.
-
• If the last rule applied in D is (Assertion) to conclude
 $\oplus \hspace {-0.08em} X$
, then there is a shorter derivation E such that
$\oplus \hspace {-0.08em} X$
, then there is a shorter derivation E such that
 $\Gamma \vdash ^+_E +\hspace {-0.1em} X$
. By the induction hypothesis, there is an
$\Gamma \vdash ^+_E +\hspace {-0.1em} X$
. By the induction hypothesis, there is an
 $E'$
such that
$E'$
such that
 $\pi ^D[\Gamma ] \cup \Sigma ^D \vdash ^+_{E'} +\hspace {-0.1em} c_X$
.We then obtain
$\pi ^D[\Gamma ] \cup \Sigma ^D \vdash ^+_{E'} +\hspace {-0.1em} c_X$
.We then obtain
 $D'$
from
$D'$
from
 $E'$
by a final application of (Assertion) to derive
$E'$
by a final application of (Assertion) to derive
 $\oplus \hspace {-0.08em} c_X$
from
$\oplus \hspace {-0.08em} c_X$
from
 $+\hspace {-0.1em} c_X$
. Thus,
$+\hspace {-0.1em} c_X$
. Thus,
 $\pi ^D[\Gamma ] \vdash ^+ \pi ^D(+\hspace {-0.1em} X)$
.
$\pi ^D[\Gamma ] \vdash ^+ \pi ^D(+\hspace {-0.1em} X)$
. -
• (Weak Inference), (Rejection), (SR
 $_1$
) and (SR
$_1$
) and (SR
 $_2$
) can be immediately transformed like (Assertion).
$_2$
) can be immediately transformed like (Assertion).
The other rules require some work and use the premisses added to
![]() $\Sigma ^D$
. We only show a selection of cases, since the method is uniform.
$\Sigma ^D$
. We only show a selection of cases, since the method is uniform.
-
• The clauses (a.), (b.) and (c.) of the construction of
 $\Sigma ^D$
can be used to translate applications of
$\Sigma ^D$
can be used to translate applications of
 $(+\hspace {-0.1em}\land $
I.),
$(+\hspace {-0.1em}\land $
I.),
 $(+\hspace {-0.1em}\land $
E.), (
$(+\hspace {-0.1em}\land $
E.), (
 $\oplus \hspace {-0.08em}\land $
I.), (
$\oplus \hspace {-0.08em}\land $
I.), (
 $\oplus \hspace {-0.08em}\land $
E.),
$\oplus \hspace {-0.08em}\land $
E.),
 $(\ominus \hspace {-0.08em}\neg $
E.),
$(\ominus \hspace {-0.08em}\neg $
E.),
 $(\ominus \hspace {-0.08em}\neg $
I.), (
$(\ominus \hspace {-0.08em}\neg $
I.), (
 $\oplus \hspace {-0.08em}\neg $
I.) and (
$\oplus \hspace {-0.08em}\neg $
I.) and (
 $\oplus \hspace {-0.08em}\neg $
E.). This is easy to check: the formulae in
$\oplus \hspace {-0.08em}\neg $
E.). This is easy to check: the formulae in
 $\Sigma ^D$
in combination with (
$\Sigma ^D$
in combination with (
 $+\hspace {-0.1em}\rightarrow $
E.) and (WMP) allow us to make the appropriate inferences. To illustrate the method, we cover the (
$+\hspace {-0.1em}\rightarrow $
E.) and (WMP) allow us to make the appropriate inferences. To illustrate the method, we cover the (
 $\ominus \hspace {-0.08em}\neg $
E.) case: if D concludes with an application of (
$\ominus \hspace {-0.08em}\neg $
E.) case: if D concludes with an application of (
 $\ominus \hspace {-0.08em}\neg $
E.) to move from
$\ominus \hspace {-0.08em}\neg $
E.) to move from
 $\ominus \hspace {-0.08em}\neg Z$
to
$\ominus \hspace {-0.08em}\neg Z$
to
 $\oplus \hspace {-0.08em} Z$
, there is a derivation E such that
$\oplus \hspace {-0.08em} Z$
, there is a derivation E such that
 $\pi ^D[\Gamma ]\cup \Sigma ^D \vdash ^+_E \ominus \hspace {-0.08em} c_{\neg Z}$
. Then obtain
$\pi ^D[\Gamma ]\cup \Sigma ^D \vdash ^+_E \ominus \hspace {-0.08em} c_{\neg Z}$
. Then obtain
 $\pi ^D[\Gamma ]\cup \Sigma ^D \vdash ^+ \oplus \hspace {-0.08em} c_Z$
as follows:
$\pi ^D[\Gamma ]\cup \Sigma ^D \vdash ^+ \oplus \hspace {-0.08em} c_Z$
as follows:
-
• It is left to treat applications of (
 $\oplus \hspace {-0.08em}\Diamond $
I.) and (
$\oplus \hspace {-0.08em}\Diamond $
I.) and (
 $+\hspace {-0.1em}\Diamond $
I.) in D. So suppose first that D concludes with an application of (
$+\hspace {-0.1em}\Diamond $
I.) in D. So suppose first that D concludes with an application of (
 $\oplus \hspace {-0.08em}\Diamond $
I.) to move from
$\oplus \hspace {-0.08em}\Diamond $
I.) to move from
 $\oplus \hspace {-0.08em} Z$
to
$\oplus \hspace {-0.08em} Z$
to
 $\oplus \hspace {-0.08em}\Diamond Z$
. By the induction hypothesis, there is a derivation E such that
$\oplus \hspace {-0.08em}\Diamond Z$
. By the induction hypothesis, there is a derivation E such that
 $\pi ^D[\Gamma ]\cup \Sigma ^D \vdash ^+_E \oplus \hspace {-0.08em} c_Z$
. We then obtain
$\pi ^D[\Gamma ]\cup \Sigma ^D \vdash ^+_E \oplus \hspace {-0.08em} c_Z$
. We then obtain
 $\pi ^D[\Gamma ]\cup \Sigma ^D \vdash ^+ \oplus \hspace {-0.08em} c_{\Diamond Z}$
as follows:
$\pi ^D[\Gamma ]\cup \Sigma ^D \vdash ^+ \oplus \hspace {-0.08em} c_{\Diamond Z}$
as follows:
 $+\hspace {-0.1em}\Diamond $
I.) to move from
$+\hspace {-0.1em}\Diamond $
I.) to move from
 $\oplus \hspace {-0.08em} Z$
to
$\oplus \hspace {-0.08em} Z$
to
 $+\hspace {-0.1em}\Diamond Z$
. By the induction hypothesis, there is a derivation E such that
$+\hspace {-0.1em}\Diamond Z$
. By the induction hypothesis, there is a derivation E such that
 $\pi ^D[\Gamma ]\cup \Sigma ^D \vdash ^+_E \oplus \hspace {-0.08em} c_Z$
. We then obtain
$\pi ^D[\Gamma ]\cup \Sigma ^D \vdash ^+_E \oplus \hspace {-0.08em} c_Z$
. We then obtain
 $\pi ^D[\Gamma ]\cup \Sigma ^D \vdash ^+ +\hspace {-0.1em} c_{\Diamond Z}$
as follows:
$\pi ^D[\Gamma ]\cup \Sigma ^D \vdash ^+ +\hspace {-0.1em} c_{\Diamond Z}$
as follows:
This concludes the induction. □
Note that no applications of (Weak Inference) were added when translating D to
![]() $D'$
, since (WMP) and (
$D'$
, since (WMP) and (
![]() $+\hspace {-0.1em}\rightarrow $
E.) can be derived in
$+\hspace {-0.1em}\rightarrow $
E.) can be derived in
![]() $\mathsf {EML}^+$
from (
$\mathsf {EML}^+$
from (
![]() $\oplus \hspace {-0.08em}\land $
E.) without using (Weak Inference).
$\oplus \hspace {-0.08em}\land $
E.) without using (Weak Inference).
Now we are ready to prove the Soundness of the full calculus.
Proof of Theorem 4.1
We prove the statement of the theorem for
![]() $\vdash ^+$
, which immediately entails the theorem. Without loss of generality, we may assume that
$\vdash ^+$
, which immediately entails the theorem. Without loss of generality, we may assume that
![]() $\Gamma $
contains only strongly asserted formulae: if it contains
$\Gamma $
contains only strongly asserted formulae: if it contains
![]() $\ominus \hspace {-0.08em} A$
, one can substitute with
$\ominus \hspace {-0.08em} A$
, one can substitute with
![]() $+\hspace {-0.1em}\Diamond \neg A$
, and if it contains
$+\hspace {-0.1em}\Diamond \neg A$
, and if it contains
![]() $\oplus \hspace {-0.08em} A$
, one can substitute with
$\oplus \hspace {-0.08em} A$
, one can substitute with
![]() $+\hspace {-0.1em}\Diamond A$
.
$+\hspace {-0.1em}\Diamond A$
.
The proof proceeds by induction on the number n of times that (Weak Inference) is applied in a derivation. The base case
![]() $n=0$
is exactly Theorem 4.2.
$n=0$
is exactly Theorem 4.2.
Suppose that Soundness holds for all derivations D in which (Weak Inference) is applied less than n times. We want to show that derivations with n applications are sound. Let D be a derivation with n applications of (Weak Inference) and consider any subderivation
![]() $D'$
that ends in one such application. Note that we do not need to treat applications of (Weak Inference) to conclude
$D'$
that ends in one such application. Note that we do not need to treat applications of (Weak Inference) to conclude
![]() $\bot $
, since they are equivalent to the case in which B is
$\bot $
, since they are equivalent to the case in which B is
![]() $p\land \neg p$
for an arbitrary p. Thus, the local proof context is this:
$p\land \neg p$
for an arbitrary p. Thus, the local proof context is this:

In this situation,
![]() $D'$
does not use
$D'$
does not use
![]() $\Diamond $
-Elimination rules, and there is a finite subset
$\Diamond $
-Elimination rules, and there is a finite subset
![]() $\Gamma ' \subseteq \Gamma $
such that all formulae in
$\Gamma ' \subseteq \Gamma $
such that all formulae in
![]() $\Gamma '$
are signed by
$\Gamma '$
are signed by
![]() $+$
, such that
$+$
, such that
![]() $\Gamma ',+\hspace {-0.1em} A \vdash ^+_{D'} +\hspace {-0.1em} B$
and
$\Gamma ',+\hspace {-0.1em} A \vdash ^+_{D'} +\hspace {-0.1em} B$
and
![]() $\Gamma ' \vdash ^+ \oplus \hspace {-0.08em} A$
. To conclude the proof, it suffices to show that
$\Gamma ' \vdash ^+ \oplus \hspace {-0.08em} A$
. To conclude the proof, it suffices to show that
![]() $\tau [\Gamma '] \models ^{\mathbf {S5}} \tau (\oplus B)$
.
$\tau [\Gamma '] \models ^{\mathbf {S5}} \tau (\oplus B)$
.
For readability we will henceforth omit mentioning
![]() $\tau $
, so that, say,
$\tau $
, so that, say,
![]() $\Gamma ' \models ^{\mathbf {S5}} +\hspace {-0.1em} A$
is understood to stand for
$\Gamma ' \models ^{\mathbf {S5}} +\hspace {-0.1em} A$
is understood to stand for
![]() $\tau [\Gamma ']\models ^{\mathbf {S5}} \tau (+\hspace {-0.1em} A)$
. Since
$\tau [\Gamma ']\models ^{\mathbf {S5}} \tau (+\hspace {-0.1em} A)$
. Since
![]() $D'$
contains less than n applications of (Weak Inference), by the induction hypothesis we have that
$D'$
contains less than n applications of (Weak Inference), by the induction hypothesis we have that
and that
The proof that
![]() $\Gamma ' \models ^{\mathbf {S5}} \Diamond B$
now proceeds in two steps.
$\Gamma ' \models ^{\mathbf {S5}} \Diamond B$
now proceeds in two steps.
-
i. We show that
 $\Gamma ' \models ^{\mathbf {S5}} \oplus \hspace {-0.08em} B$
if A and B are
$\Gamma ' \models ^{\mathbf {S5}} \oplus \hspace {-0.08em} B$
if A and B are
 $\mathcal {L}_{PL}$
-formulae and
$\mathcal {L}_{PL}$
-formulae and
 $\Gamma '$
can be split in
$\Gamma '$
can be split in
 $\Gamma ' = \Delta \cup \Theta $
such that: for all
$\Gamma ' = \Delta \cup \Theta $
such that: for all
 $+\hspace {-0.1em} C \in \Delta $
, C is an
$+\hspace {-0.1em} C \in \Delta $
, C is an
 $\mathcal {L}_{PL}$
-formula; and for all
$\mathcal {L}_{PL}$
-formula; and for all
 $+\hspace {-0.1em} D \in \Theta $
,
$+\hspace {-0.1em} D \in \Theta $
,
 $D = \Diamond X \rightarrow X$
for some
$D = \Diamond X \rightarrow X$
for some
 $\mathcal {L}_{PL}$
-formula X.
$\mathcal {L}_{PL}$
-formula X. -
ii. By Lemma 4.3, any other application of (Weak Inference) can be reduced to (i.).
So, first assume that A and B are
![]() $\mathcal {L}_{PL}$
-formulae and
$\mathcal {L}_{PL}$
-formulae and
![]() $\Gamma ' = \Delta \cup \Theta $
as above. We need to show that for any model
$\Gamma ' = \Delta \cup \Theta $
as above. We need to show that for any model
![]() $V = \langle W^V,R^V,V^V,w^V \rangle $
of
$V = \langle W^V,R^V,V^V,w^V \rangle $
of
![]() $\Gamma '$
, we have that
$\Gamma '$
, we have that
![]() $V, w^V \Vdash \Diamond B$
, where
$V, w^V \Vdash \Diamond B$
, where
![]() $\Vdash $
is the usual satisfaction relation for worlds in modal logic. Assume for reductio that there is a counterexample, i.e. a V with
$\Vdash $
is the usual satisfaction relation for worlds in modal logic. Assume for reductio that there is a counterexample, i.e. a V with
![]() $V,w^{V} \Vdash \Box \neg B$
. By the induction hypothesis and in particular (I2), we also have that
$V,w^{V} \Vdash \Box \neg B$
. By the induction hypothesis and in particular (I2), we also have that
![]() $V,w^V \Vdash \Diamond A$
. It follows that
$V,w^V \Vdash \Diamond A$
. It follows that
![]() $V,w^V \Vdash \Diamond (A\land \neg B)$
. Let
$V,w^V \Vdash \Diamond (A\land \neg B)$
. Let
![]() $v \in W^{V}$
be a witness, i.e.
$v \in W^{V}$
be a witness, i.e.
![]() $V,v \Vdash A \land \neg B$
. Note that for all
$V,v \Vdash A \land \neg B$
. Note that for all
![]() $+\hspace {-0.1em} C \in \Delta $
we have that
$+\hspace {-0.1em} C \in \Delta $
we have that
![]() $V,v^{V} \Vdash C$
, since
$V,v^{V} \Vdash C$
, since
![]() $V,w^{V} \Vdash \Box C$
.
$V,w^{V} \Vdash \Box C$
.
Now consider the model
![]() $V'$
such that:
$V'$
such that:
![]() $W^{V'} = \{v\}$
,
$W^{V'} = \{v\}$
,
![]() $V^{V'}(v) = V^{V}(v)$
,
$V^{V'}(v) = V^{V}(v)$
,
![]() $R^{V'} = \{(v,v)\}$
,
$R^{V'} = \{(v,v)\}$
,
![]() $w^{V'} = v$
. Note that all C with
$w^{V'} = v$
. Note that all C with
![]() $+\hspace {-0.1em} C \in \Delta $
are assumed to be
$+\hspace {-0.1em} C \in \Delta $
are assumed to be
![]() $\mathcal {L}_{PL}$
-formulae. That is, the fact that
$\mathcal {L}_{PL}$
-formulae. That is, the fact that
![]() $V,v^V \Vdash C$
is dependent only on the valuation
$V,v^V \Vdash C$
is dependent only on the valuation
![]() $V(v)$
and not on any other worlds in
$V(v)$
and not on any other worlds in
![]() $W^V$
. Thus it is also the case that
$W^V$
. Thus it is also the case that
![]() $V',w^{V'} \Vdash C$
for all C with
$V',w^{V'} \Vdash C$
for all C with
![]() $+\hspace {-0.1em} C \in \Delta $
. For the same reason,
$+\hspace {-0.1em} C \in \Delta $
. For the same reason,
![]() $V',w^{V'} \Vdash A \land \neg B$
. Also note that, since
$V',w^{V'} \Vdash A \land \neg B$
. Also note that, since
![]() $V'$
has precisely one world,
$V'$
has precisely one world,
![]() $V',w^{V'} \Vdash \Diamond X$
iff
$V',w^{V'} \Vdash \Diamond X$
iff
![]() $V',w^{V'} \Vdash X$
. So
$V',w^{V'} \Vdash X$
. So
![]() $V',w^{V'} \Vdash \Diamond X \rightarrow X$
for any X. Thus
$V',w^{V'} \Vdash \Diamond X \rightarrow X$
for any X. Thus
![]() $V' \Vdash \Theta $
.
$V' \Vdash \Theta $
.
Hence
![]() $V',w^{V'} \Vdash \Gamma '$
. By construction,
$V',w^{V'} \Vdash \Gamma '$
. By construction,
![]() $V',w^{V'} \Vdash \Box A$
and
$V',w^{V'} \Vdash \Box A$
and
![]() $V', w^{V'} \Vdash \neg \Box B$
. So
$V', w^{V'} \Vdash \neg \Box B$
. So
![]() $V'$
is a countermodel to
$V'$
is a countermodel to
![]() $\Gamma '\cup \{+\hspace {-0.1em} A\} \models ^{\mathbf {S5}} +\hspace {-0.1em} B$
, but this is true by induction (I1). Contradiction. Thus there is no such V. This shows (i.).
$\Gamma '\cup \{+\hspace {-0.1em} A\} \models ^{\mathbf {S5}} +\hspace {-0.1em} B$
, but this is true by induction (I1). Contradiction. Thus there is no such V. This shows (i.).
For (ii.), we relax our assumption so that A, B and the formulae in
![]() $\Gamma '$
may be arbitrary. By Lemma 4.3, we have a derivation
$\Gamma '$
may be arbitrary. By Lemma 4.3, we have a derivation
![]() $D''$
such that
$D''$
such that
![]() $\pi ^{D'}[\Gamma '] \cup \Sigma ^{D'}, +\hspace {-0.1em} c_A \vdash ^+_{D''} +\hspace {-0.1em} c_B$
(writing
$\pi ^{D'}[\Gamma '] \cup \Sigma ^{D'}, +\hspace {-0.1em} c_A \vdash ^+_{D''} +\hspace {-0.1em} c_B$
(writing
![]() $+\hspace {-0.1em} c_A$
for
$+\hspace {-0.1em} c_A$
for
![]() $\pi ^{D'}(+\hspace {-0.1em} A)$
and same for B).
$\pi ^{D'}(+\hspace {-0.1em} A)$
and same for B).
Note that since
![]() $\pi ^{D'}$
maps everything to
$\pi ^{D'}$
maps everything to
![]() $\mathcal {L}_{PL}$
-formulae, the elements of
$\mathcal {L}_{PL}$
-formulae, the elements of
![]() $\pi ^{D'}[\Gamma '] \cup \Sigma ^{D'}$
are as described in (i):
$\pi ^{D'}[\Gamma '] \cup \Sigma ^{D'}$
are as described in (i):
![]() $\pi ^{D'}[\Gamma '] \cup \Sigma ^{D'} = \Delta \cup \Theta $
with
$\pi ^{D'}[\Gamma '] \cup \Sigma ^{D'} = \Delta \cup \Theta $
with
![]() $\Theta $
being exactly all formulae added in clause (e.) in the construction of
$\Theta $
being exactly all formulae added in clause (e.) in the construction of
![]() $\Sigma ^{D'}$
(Definition 1). Thus we obtain
$\Sigma ^{D'}$
(Definition 1). Thus we obtain
![]() $\pi ^{D'}[\Gamma '], \Sigma ^{D'} \models ^{\mathbf {S5}} \Diamond c_B$
by the argument of (i). Note that the argument of (i) rests on the induction hypothesis, but this is still licit here since
$\pi ^{D'}[\Gamma '], \Sigma ^{D'} \models ^{\mathbf {S5}} \Diamond c_B$
by the argument of (i). Note that the argument of (i) rests on the induction hypothesis, but this is still licit here since
![]() $D''$
does not contain more applications of (Weak Inference) than
$D''$
does not contain more applications of (Weak Inference) than
![]() $D'$
(by Lemma 4.3).
$D'$
(by Lemma 4.3).
Now let
![]() $\Sigma = (\pi ^D)^{-1}[\Sigma ^{D'}]$
. Since
$\Sigma = (\pi ^D)^{-1}[\Sigma ^{D'}]$
. Since
![]() $\mathbf {S5}$
is closed under uniform substitution,
$\mathbf {S5}$
is closed under uniform substitution,
![]() $\Gamma '\cup \Sigma \models ^{\mathbf {S5}} \Diamond B$
. But
$\Gamma '\cup \Sigma \models ^{\mathbf {S5}} \Diamond B$
. But
![]() $\Sigma $
contains only
$\Sigma $
contains only
![]() $\mathbf {S5}$
-tautologies (by inspection of Definition 1). Hence
$\mathbf {S5}$
-tautologies (by inspection of Definition 1). Hence
![]() $\Gamma ' \models ^{\mathbf {S5}} \Diamond B$
.□
$\Gamma ' \models ^{\mathbf {S5}} \Diamond B$
.□
It is worth noting why the argument above does not work for the rules excluded from (Weak Inference), i.e. (
![]() $+\hspace {-0.1em}\Diamond $
E.) and (
$+\hspace {-0.1em}\Diamond $
E.) and (
![]() $\oplus \hspace {-0.08em}\Diamond $
E.). The reason is that translating these rules in the proof of Lemma 4.3 would require us to add
$\oplus \hspace {-0.08em}\Diamond $
E.). The reason is that translating these rules in the proof of Lemma 4.3 would require us to add
![]() $+\hspace {-0.1em} (c_{\Diamond Z} \rightarrow c_Z)$
to
$+\hspace {-0.1em} (c_{\Diamond Z} \rightarrow c_Z)$
to
![]() $\Sigma ^D$
in Definition 1. This, however, does not substitute to an
$\Sigma ^D$
in Definition 1. This, however, does not substitute to an
![]() $\mathbf {S5}$
-tautology, so the final step in the soundness proof would fail.
$\mathbf {S5}$
-tautology, so the final step in the soundness proof would fail.
4.2 Completeness
We now show that, modulo the translation
![]() $\tau $
defined above,
$\tau $
defined above,
![]() $\mathsf {EML}$
is also complete with respect to
$\mathsf {EML}$
is also complete with respect to
![]() $\mathbf {S5}$
.
$\mathbf {S5}$
.
Theorem 4.4 (Completeness).
Let
![]() $\Gamma $
be a set of
$\Gamma $
be a set of
![]() $\mathcal {L}_{EML}$
-formulae and
$\mathcal {L}_{EML}$
-formulae and
![]() $\varphi $
an
$\varphi $
an
![]() $\mathcal {L}_{EML}$
-formula. If
$\mathcal {L}_{EML}$
-formula. If
![]() $\tau [\Gamma ] \models ^{\mathbf {S5}} \tau (\varphi )$
then
$\tau [\Gamma ] \models ^{\mathbf {S5}} \tau (\varphi )$
then
![]() $\Gamma \vdash \varphi $
.
$\Gamma \vdash \varphi $
.
This is shown by a model existence theorem. The construction of a canonical term model has to respect the difference between derivations that use
![]() $\Diamond $
-Eliminations and those that do not. To this end, we need some additional definitions. We write
$\Diamond $
-Eliminations and those that do not. To this end, we need some additional definitions. We write
![]() $\vdash ^*$
to denote provability in
$\vdash ^*$
to denote provability in
![]() $\mathsf {EML}$
without the rules for
$\mathsf {EML}$
without the rules for
![]() $\Diamond $
-Elimination. We say that a set
$\Diamond $
-Elimination. We say that a set
![]() $\Gamma $
is S-consistent if
$\Gamma $
is S-consistent if
![]() $\Gamma $
contains only strongly asserted formulae and
$\Gamma $
contains only strongly asserted formulae and
![]() $\Gamma \not \vdash ^* \bot $
. And we say that
$\Gamma \not \vdash ^* \bot $
. And we say that
![]() $\Gamma $
is S-inconsistent if it contains only strongly asserted formulae and
$\Gamma $
is S-inconsistent if it contains only strongly asserted formulae and
![]() $\Gamma \vdash ^* \bot $
. Note that there are inconsistent S-consistent sets, e.g.
$\Gamma \vdash ^* \bot $
. Note that there are inconsistent S-consistent sets, e.g.
![]() $\{+\hspace {-0.1em} p, +\hspace {-0.1em}\Diamond \neg p\}$
.
$\{+\hspace {-0.1em} p, +\hspace {-0.1em}\Diamond \neg p\}$
.
In the typical canonical construction, one takes maximally consistent sets of formulae to be the worlds. We will instead take maximally S-consistent sets of formulae. In the construction, we shall use the following technical lemmas.
Lemma 4.5. If
![]() $\Gamma \cup \{+\hspace {-0.1em} A\}$
is S-inconsistent, then
$\Gamma \cup \{+\hspace {-0.1em} A\}$
is S-inconsistent, then
![]() $\Gamma \vdash ^* +\hspace {-0.1em}\neg A$
.
$\Gamma \vdash ^* +\hspace {-0.1em}\neg A$
.
Proof. This is just another way to write (
![]() $+\hspace {-0.1em}\neg $
I.). □
$+\hspace {-0.1em}\neg $
I.). □
Lemma 4.6. If
![]() $\Gamma $
contains only strongly asserted formulae and
$\Gamma $
contains only strongly asserted formulae and
![]() $\Gamma \vdash +\hspace {-0.1em}((\bigwedge _{i < n} \neg B_i) \rightarrow \neg A)$
, then
$\Gamma \vdash +\hspace {-0.1em}((\bigwedge _{i < n} \neg B_i) \rightarrow \neg A)$
, then
![]() $\Gamma \vdash +\hspace {-0.1em} \Diamond A\rightarrow (\bigvee _{i < n}\Diamond B_i)$
.
$\Gamma \vdash +\hspace {-0.1em} \Diamond A\rightarrow (\bigvee _{i < n}\Diamond B_i)$
.
Proof. This follows from the fact that
![]() $\mathsf {EML}$
extends classical logic (Theorem 3.3) and proves all
$\mathsf {EML}$
extends classical logic (Theorem 3.3) and proves all
![]() $\mathbf {S5}$
axioms (Theorem 3.5). □
$\mathbf {S5}$
axioms (Theorem 3.5). □
Now we are ready to demonstrate a model existence result.
Theorem 4.7 (Model Existence).
Let
![]() $\Gamma $
be a set of
$\Gamma $
be a set of
![]() $\mathcal {L}_{EML}$
-formulae. If
$\mathcal {L}_{EML}$
-formulae. If
![]() $\Gamma $
is consistent, then there is an
$\Gamma $
is consistent, then there is an
![]() $\mathbf {S5}$
-model M such that
$\mathbf {S5}$
-model M such that
![]() $M \models \tau [\Gamma ]$
.
$M \models \tau [\Gamma ]$
.
Proof. Let
![]() $Cl^+\hspace {-0.1em}(\Gamma )$
consists of all strongly asserted formulae in the closure of
$Cl^+\hspace {-0.1em}(\Gamma )$
consists of all strongly asserted formulae in the closure of
![]() $\Gamma $
under derivability
$\Gamma $
under derivability
![]() $\vdash $
in
$\vdash $
in
![]() $\mathsf {EML}$
. Concisely,
$\mathsf {EML}$
. Concisely,
![]() $Cl^+\hspace {-0.1em}(\Gamma ) = \{+\hspace {-0.1em} A \mid \Gamma \vdash +\hspace {-0.1em} A\}$
. Moreover, let
$Cl^+\hspace {-0.1em}(\Gamma ) = \{+\hspace {-0.1em} A \mid \Gamma \vdash +\hspace {-0.1em} A\}$
. Moreover, let
![]() $\mathcal {E} = \{\Delta \mid \Delta $
is a maximal S-consistent extension of
$\mathcal {E} = \{\Delta \mid \Delta $
is a maximal S-consistent extension of
![]() $Cl^+\hspace {-0.1em}(\Gamma )\}$
and define a model
$Cl^+\hspace {-0.1em}(\Gamma )\}$
and define a model
![]() $M = \langle W,R,V\rangle $
as follows.
$M = \langle W,R,V\rangle $
as follows.
-
•
 $W = \mathcal {E}$
.
$W = \mathcal {E}$
. -
•
 $wRv$
iff (for all
$wRv$
iff (for all
 $+\hspace {-0.1em} A \in v : +\hspace {-0.1em}\Diamond A \in w$
).
$+\hspace {-0.1em} A \in v : +\hspace {-0.1em}\Diamond A \in w$
). -
•
 $V(w) = \{p \mid +\hspace {-0.1em} p \in w\}$
.
$V(w) = \{p \mid +\hspace {-0.1em} p \in w\}$
.
Now we show by induction on the complexity of sentences A that:
![]() $+\hspace {-0.1em} A \in w$
iff
$+\hspace {-0.1em} A \in w$
iff
![]() $M,w \Vdash A$
. The cases for atomic A and
$M,w \Vdash A$
. The cases for atomic A and
![]() $A = B \land C$
are straightforward, so we only cover negation and the modal.
$A = B \land C$
are straightforward, so we only cover negation and the modal.
-
• If
 $+\hspace {-0.1em} \neg A \in w$
, then
$+\hspace {-0.1em} \neg A \in w$
, then
 $+\hspace {-0.1em} A \notin w$
. By the induction hypothesis,
$+\hspace {-0.1em} A \notin w$
. By the induction hypothesis,
 $M, w \not \Vdash A$
. Thus
$M, w \not \Vdash A$
. Thus
 $M,w \Vdash \neg A$
. Conversely, if
$M,w \Vdash \neg A$
. Conversely, if
 $M,w \Vdash \neg A$
, then
$M,w \Vdash \neg A$
, then
 $M,w \not \Vdash A$
, so
$M,w \not \Vdash A$
, so
 $+\hspace {-0.1em} A\notin w$
by the induction hypothesis. Since w is a maximally S-consistent set, this means that
$+\hspace {-0.1em} A\notin w$
by the induction hypothesis. Since w is a maximally S-consistent set, this means that
 $+\hspace {-0.1em} A$
is S-inconsistent with w. By Lemma 4.5,
$+\hspace {-0.1em} A$
is S-inconsistent with w. By Lemma 4.5,
 $+\hspace {-0.1em} \neg A \in w$
.
$+\hspace {-0.1em} \neg A \in w$
. -
• Suppose
 $+\hspace {-0.1em}\Diamond A \in w$
. We first show that
$+\hspace {-0.1em}\Diamond A \in w$
. We first show that
 $+\hspace {-0.1em} A$
is S-consistent with
$+\hspace {-0.1em} A$
is S-consistent with
 $Cl^+\hspace {-0.1em}(\Gamma )$
. Towards a contradiction, assume
$Cl^+\hspace {-0.1em}(\Gamma )$
. Towards a contradiction, assume
 $+\hspace {-0.1em} A$
is S-inconsistent with
$+\hspace {-0.1em} A$
is S-inconsistent with
 $Cl^+\hspace {-0.1em}(\Gamma )$
. That is,
$Cl^+\hspace {-0.1em}(\Gamma )$
. That is,
 $Cl^+\hspace {-0.1em}(\Gamma ) \vdash +\hspace {-0.1em}\neg A$
by Lemma 4.5. Because
$Cl^+\hspace {-0.1em}(\Gamma ) \vdash +\hspace {-0.1em}\neg A$
by Lemma 4.5. Because
 $Cl^+\hspace {-0.1em}(\Gamma )$
is closed under
$Cl^+\hspace {-0.1em}(\Gamma )$
is closed under
 $\vdash $
, this means that
$\vdash $
, this means that
 $+\hspace {-0.1em}\neg \Diamond A \in Cl^+\hspace {-0.1em}(\Gamma )$
by (
$+\hspace {-0.1em}\neg \Diamond A \in Cl^+\hspace {-0.1em}(\Gamma )$
by (
 $+\hspace {-0.1em}\Box $
I.). But then
$+\hspace {-0.1em}\Box $
I.). But then
 $+\hspace {-0.1em}\Diamond A$
is S-inconsistent with
$+\hspace {-0.1em}\Diamond A$
is S-inconsistent with
 $Cl^+\hspace {-0.1em}(\Gamma )$
, hence
$Cl^+\hspace {-0.1em}(\Gamma )$
, hence
 $+\hspace {-0.1em}\Diamond A \notin w$
. Contradiction.
$+\hspace {-0.1em}\Diamond A \notin w$
. Contradiction.This establishes that there is a world (i.e. a maximally S-consistent extension of
 $Cl^+\hspace {-0.1em}(\Gamma )$
) that contains
$Cl^+\hspace {-0.1em}(\Gamma )$
) that contains
 $+\hspace {-0.1em} A$
. We now show that one such world v is accessible from w, i.e. that
$+\hspace {-0.1em} A$
. We now show that one such world v is accessible from w, i.e. that
 $wRv$
.
$wRv$
.Let
 $\{B_i \mid i \in \omega \}$
be the sentences such that
$\{B_i \mid i \in \omega \}$
be the sentences such that
 $+\hspace {-0.1em}\Diamond B_i \notin w$
. We need a v such that
$+\hspace {-0.1em}\Diamond B_i \notin w$
. We need a v such that
 $+\hspace {-0.1em} A \in v$
and for all i,
$+\hspace {-0.1em} A \in v$
and for all i,
 $+\hspace {-0.1em} B_i \notin v$
. Note that if
$+\hspace {-0.1em} B_i \notin v$
. Note that if
 $+\hspace {-0.1em}\Diamond B_i \notin w$
, then
$+\hspace {-0.1em}\Diamond B_i \notin w$
, then
 $+\hspace {-0.1em}\Diamond B_i$
is S-inconsistent with w, so
$+\hspace {-0.1em}\Diamond B_i$
is S-inconsistent with w, so
 $+\hspace {-0.1em}\neg \Diamond B_i \in w$
. In particular also
$+\hspace {-0.1em}\neg \Diamond B_i \in w$
. In particular also
 $+\hspace {-0.1em} \neg B_i \in w$
since
$+\hspace {-0.1em} \neg B_i \in w$
since
 $Cl^+\hspace {-0.1em}(\Gamma )$
contains Axiom T. Thus,
$Cl^+\hspace {-0.1em}(\Gamma )$
contains Axiom T. Thus,
 $Cl^+\hspace {-0.1em}(\Gamma ) \cup \{+\hspace {-0.1em} \neg B_i \mid i \in \omega \}$
is S-consistent, since it is a subset of w.
$Cl^+\hspace {-0.1em}(\Gamma ) \cup \{+\hspace {-0.1em} \neg B_i \mid i \in \omega \}$
is S-consistent, since it is a subset of w.Now, if
 $Cl^+\hspace {-0.1em}(\Gamma ) \cup \{+\hspace {-0.1em} \neg B_i \mid i \in \omega \} \cup \{+\hspace {-0.1em} A\}$
is S-consistent, there is a v as needed. Towards a contradiction, assume this set is S-inconsistent. By Lemma 4.5, this means that
$Cl^+\hspace {-0.1em}(\Gamma ) \cup \{+\hspace {-0.1em} \neg B_i \mid i \in \omega \} \cup \{+\hspace {-0.1em} A\}$
is S-consistent, there is a v as needed. Towards a contradiction, assume this set is S-inconsistent. By Lemma 4.5, this means that
 $Cl^+\hspace {-0.1em}(\Gamma ) \cup \{+\hspace {-0.1em} \neg B_i \mid i \in \omega \} \vdash ^* +\hspace {-0.1em}\neg A$
. It follows by (
$Cl^+\hspace {-0.1em}(\Gamma ) \cup \{+\hspace {-0.1em} \neg B_i \mid i \in \omega \} \vdash ^* +\hspace {-0.1em}\neg A$
. It follows by (
 $+\hspace {-0.1em}\rightarrow $
I.) that there is a finite set of
$+\hspace {-0.1em}\rightarrow $
I.) that there is a finite set of
 $B_i$
s (with all
$B_i$
s (with all
 $i < n$
, without loss of generality) such that
$i < n$
, without loss of generality) such that
 $Cl^+\hspace {-0.1em}(\Gamma ) \vdash +\hspace {-0.1em}((\bigwedge _{i<n}\neg B_i) \rightarrow \neg A)$
. By Lemma 4.6,
$Cl^+\hspace {-0.1em}(\Gamma ) \vdash +\hspace {-0.1em}((\bigwedge _{i<n}\neg B_i) \rightarrow \neg A)$
. By Lemma 4.6,
 $\Gamma \vdash +\hspace {-0.1em} \Diamond A\rightarrow (\bigvee _{i < n}\Diamond B_i)$
. Since
$\Gamma \vdash +\hspace {-0.1em} \Diamond A\rightarrow (\bigvee _{i < n}\Diamond B_i)$
. Since
 $\Diamond A \in w$
this means that
$\Diamond A \in w$
this means that
 $+\hspace {-0.1em}(\bigvee _{i < n}\Diamond B_i)\in w$
. But we saw that for any
$+\hspace {-0.1em}(\bigvee _{i < n}\Diamond B_i)\in w$
. But we saw that for any
 $i<n$
,
$i<n$
,
 $+\hspace {-0.1em}\neg \Diamond B_i \in w$
. Hence w is S-inconsistent. Contradiction.
$+\hspace {-0.1em}\neg \Diamond B_i \in w$
. Hence w is S-inconsistent. Contradiction.Thus, there is a
 $v \in W$
with
$v \in W$
with
 $+\hspace {-0.1em} A \in v$
and
$+\hspace {-0.1em} A \in v$
and
 $wRv$
. By the induction hypothesis,
$wRv$
. By the induction hypothesis,
 $M,v \Vdash A$
. Thus,
$M,v \Vdash A$
. Thus,
 $M,w \Vdash \Diamond A$
.
$M,w \Vdash \Diamond A$
.Conversely, suppose
 $M,w \Vdash \Diamond A$
. Then there is a v,
$M,w \Vdash \Diamond A$
. Then there is a v,
 $wRv$
such that
$wRv$
such that
 $M,v \Vdash A$
. By the induction hypothesis,
$M,v \Vdash A$
. By the induction hypothesis,
 $+\hspace {-0.1em} A \in v$
. By definition of R,
$+\hspace {-0.1em} A \in v$
. By definition of R,
 $+\hspace {-0.1em}\Diamond A \in w$
.
$+\hspace {-0.1em}\Diamond A \in w$
.
Let
![]() $w \in W$
be arbitrary. Without loss of generality, we can write
$w \in W$
be arbitrary. Without loss of generality, we can write
![]() $\Gamma $
with all formulae signed by
$\Gamma $
with all formulae signed by
![]() $+$
(see the proof of Theorem 4.1). Since
$+$
(see the proof of Theorem 4.1). Since
![]() $\Gamma \subseteq w$
, it follows that
$\Gamma \subseteq w$
, it follows that
![]() $M,w \Vdash \varphi $
for each
$M,w \Vdash \varphi $
for each
![]() $\varphi \in \tau [\Gamma ]$
.
$\varphi \in \tau [\Gamma ]$
.
It remains to show that
![]() $\langle W,R,V\rangle $
is an
$\langle W,R,V\rangle $
is an
![]() $\mathbf {S5}$
model. This follows from the fact that the
$\mathbf {S5}$
model. This follows from the fact that the
![]() $\mathbf {KT5}$
axioms are contained in
$\mathbf {KT5}$
axioms are contained in
![]() $Cl^+\hspace {-0.1em}(\Gamma )$
.□
$Cl^+\hspace {-0.1em}(\Gamma )$
.□
Intuitively, the reason why the worlds of the term model may denote inconsistent sets of formulae is as follows. The inference
![]() $+\hspace {-0.1em} A \vdash +\hspace {-0.1em}\Box A$
must be excluded when computing maximal consistent sets. That is, if we were taking consistent sets (instead of S-consistent sets) as the worlds of the term model, then whenever
$+\hspace {-0.1em} A \vdash +\hspace {-0.1em}\Box A$
must be excluded when computing maximal consistent sets. That is, if we were taking consistent sets (instead of S-consistent sets) as the worlds of the term model, then whenever
![]() $+\hspace {-0.1em} A \in w$
for some consistent w, it would also be the case that
$+\hspace {-0.1em} A \in w$
for some consistent w, it would also be the case that
![]() $+\hspace {-0.1em}\Box A \in w$
. But such sets are not useful as worlds in a canonical model, since they can only see themselves according to the definition of R in the canonical model construction. The notion of S-consistency takes care of this issue.
$+\hspace {-0.1em}\Box A \in w$
. But such sets are not useful as worlds in a canonical model, since they can only see themselves according to the definition of R in the canonical model construction. The notion of S-consistency takes care of this issue.
One may also wonder why the same argument does not work when we weaken the demand that
![]() $\Gamma $
be consistent in the statement of Theorem 4.7 to
$\Gamma $
be consistent in the statement of Theorem 4.7 to
![]() $\Gamma $
being merely S-consistent. The stronger assumption of consistency is used in the step for
$\Gamma $
being merely S-consistent. The stronger assumption of consistency is used in the step for
![]() $+\hspace {-0.1em}\Diamond A$
in the induction on the complexity of sentences in the proof of the theorem. For this step of the proof relies on the fact that
$+\hspace {-0.1em}\Diamond A$
in the induction on the complexity of sentences in the proof of the theorem. For this step of the proof relies on the fact that
![]() $Cl^+\hspace {-0.1em}(\Gamma )$
is closed under the derivability relation in the full
$Cl^+\hspace {-0.1em}(\Gamma )$
is closed under the derivability relation in the full
![]() $\mathsf {EML}$
calculus and in particular under (
$\mathsf {EML}$
calculus and in particular under (
![]() $+\hspace {-0.1em}\Box $
I.). But if we were to allow inconsistent S-consistent
$+\hspace {-0.1em}\Box $
I.). But if we were to allow inconsistent S-consistent
![]() $\Gamma $
, then closure under the full
$\Gamma $
, then closure under the full
![]() $\mathsf {EML}$
calculus would result in the trivial theory. Thus, only consistent
$\mathsf {EML}$
calculus would result in the trivial theory. Thus, only consistent
![]() $\Gamma $
have a canonical model (but the worlds in this canonical model may be inconsistent sets).
$\Gamma $
have a canonical model (but the worlds in this canonical model may be inconsistent sets).
4.3 Some corollaries
The following is a noteworthy corollary of the completeness theorem.
Proposition 4.8. For any
![]() $\mathcal {L}_{ML}$
-formula A and set of
$\mathcal {L}_{ML}$
-formula A and set of
![]() $\mathcal {L}_{ML}$
-formulae
$\mathcal {L}_{ML}$
-formulae
![]() $\Gamma $
,
$\Gamma $
,
![]() $\{\Box B \mid B\in \Gamma \} \models ^{\mathbf {S5}} \Box A$
iff
$\{\Box B \mid B\in \Gamma \} \models ^{\mathbf {S5}} \Box A$
iff
![]() $\{+\hspace {-0.1em} B \mid B \in \Gamma \} \vdash +\hspace {-0.1em} A$
.
$\{+\hspace {-0.1em} B \mid B \in \Gamma \} \vdash +\hspace {-0.1em} A$
.
Proof. Immediate from Soundness and Completeness. □
That is, the
![]() $\mathsf {EML}$
logic of strong assertion is the logic that preserves
$\mathsf {EML}$
logic of strong assertion is the logic that preserves
![]() $\mathbf {S5}$
-validity. Schulz (Reference Schulz2010, p. 389) noted the same result about Yalcin’s (Reference Yalcin2007) informational consequence (IC). That is,
$\mathbf {S5}$
-validity. Schulz (Reference Schulz2010, p. 389) noted the same result about Yalcin’s (Reference Yalcin2007) informational consequence (IC). That is,
![]() $\Gamma \models ^{\text {IC}} A$
iff
$\Gamma \models ^{\text {IC}} A$
iff
![]() $\{\Box B \mid B\in \Gamma \} \models ^{\mathbf {S5}} \Box A$
. Thus, we may conclude, the logic of strong assertion coincides with informational consequence.
$\{\Box B \mid B\in \Gamma \} \models ^{\mathbf {S5}} \Box A$
. Thus, we may conclude, the logic of strong assertion coincides with informational consequence.
There is a caveat, however. Yalcin’s semantics includes a conditional
![]() $\rightarrow $
that is not a material conditional, but a version of a restricted strict conditional (Yalcin, Reference Yalcin2007, p. 998). Clearly, then, Yalcin’s informational consequence only preserves
$\rightarrow $
that is not a material conditional, but a version of a restricted strict conditional (Yalcin, Reference Yalcin2007, p. 998). Clearly, then, Yalcin’s informational consequence only preserves
![]() $\mathbf {S5}$
-validity on the signature
$\mathbf {S5}$
-validity on the signature
![]() $\{\neg ,\land ,\Diamond \}$
. Hence the
$\{\neg ,\land ,\Diamond \}$
. Hence the
![]() $\mathsf {EML}$
logic of strong assertion only corresponds to the nonimplicative fragment of informational consequence. In either logic, however, the material conditional is definable from
$\mathsf {EML}$
logic of strong assertion only corresponds to the nonimplicative fragment of informational consequence. In either logic, however, the material conditional is definable from
![]() $\neg $
and
$\neg $
and
![]() $\land $
.
$\land $
.
Now, since in
![]() $\mathbf {S5}$
tautological truths are validities, Proposition 4.8 entails that the strongly asserted theorems of
$\mathbf {S5}$
tautological truths are validities, Proposition 4.8 entails that the strongly asserted theorems of
![]() $\mathsf {EML}$
are exactly the
$\mathsf {EML}$
are exactly the
![]() $\mathbf {S5}$
-tautologies. This shows the converse direction of Theorem 3.5 to establish Theorem 4.9).
$\mathbf {S5}$
-tautologies. This shows the converse direction of Theorem 3.5 to establish Theorem 4.9).
Theorem 4.9.
![]() $\models ^{\mathbf {S5}} A$
iff
$\models ^{\mathbf {S5}} A$
iff
![]() $\vdash +\hspace {-0.1em} A$
.
$\vdash +\hspace {-0.1em} A$
.
From these results, we also obtain two corollaries about the logic of rejection in
![]() $\mathsf {EML}$
.
$\mathsf {EML}$
.
Proposition 4.10. For any
![]() $\mathcal {L}_{ML}$
-formula A and finite set of
$\mathcal {L}_{ML}$
-formula A and finite set of
![]() $\mathcal {L}_{ML}$
-formulae
$\mathcal {L}_{ML}$
-formulae
![]() $\Gamma $
,
$\Gamma $
,
![]() $\{\Box B \mid B\in \Gamma \} \models ^{\mathbf {S5}} \Box A$
iff
$\{\Box B \mid B\in \Gamma \} \models ^{\mathbf {S5}} \Box A$
iff
![]() $\ominus \hspace {-0.08em} A\vdash \ominus \hspace {-0.08em}\bigwedge _{B \in \Gamma } B$
.
$\ominus \hspace {-0.08em} A\vdash \ominus \hspace {-0.08em}\bigwedge _{B \in \Gamma } B$
.
Proposition 4.11. For any
![]() $\mathcal {L}_{ML}$
-formula A,
$\mathcal {L}_{ML}$
-formula A,
![]() $\Box A\models ^{\mathbf {S5}} \bot $
iff
$\Box A\models ^{\mathbf {S5}} \bot $
iff
![]() $\vdash \ominus \hspace {-0.08em} A$
.
$\vdash \ominus \hspace {-0.08em} A$
.
Proposition 4.11 mentions
![]() $\Box A$
, whereas Theorem 4.9 does not. This difference is due to the fact that
$\Box A$
, whereas Theorem 4.9 does not. This difference is due to the fact that
![]() $\models ^{\mathbf {S5}} A$
iff
$\models ^{\mathbf {S5}} A$
iff
![]() $\models ^{\mathbf {S5}} \Box A$
, whereas, in general, it is not the case that
$\models ^{\mathbf {S5}} \Box A$
, whereas, in general, it is not the case that
![]() $A \models ^{\mathbf {S5}} \bot $
iff
$A \models ^{\mathbf {S5}} \bot $
iff
![]() $\Box A\models ^{\mathbf {S5}} \bot $
. A counterexample to the latter is obtained by letting A be
$\Box A\models ^{\mathbf {S5}} \bot $
. A counterexample to the latter is obtained by letting A be
![]() $p \land \Diamond \neg p$
.
$p \land \Diamond \neg p$
.
But what is the relation of
![]() $\mathsf {EML}$
to the consequence relation
$\mathsf {EML}$
to the consequence relation
![]() $\models ^{\mathbf {S5}}$
with premisses? We can approximate this relation from below by considering
$\models ^{\mathbf {S5}}$
with premisses? We can approximate this relation from below by considering
![]() $\vdash ^*$
, the derivability relation of
$\vdash ^*$
, the derivability relation of
![]() $\mathsf {EML}$
without rules for
$\mathsf {EML}$
without rules for
![]() $\Diamond $
-Elimination.
$\Diamond $
-Elimination.
Proposition 4.12. Let
![]() $\Gamma $
be a set of
$\Gamma $
be a set of
![]() $\mathcal {L}_{ML}$
-formulae and A an
$\mathcal {L}_{ML}$
-formulae and A an
![]() $\mathcal {L}_{ML}$
-formula. If
$\mathcal {L}_{ML}$
-formula. If
![]() $\{+\hspace {-0.1em} B \mid B \in \Gamma \} \vdash ^* +\hspace {-0.1em} A$
, then
$\{+\hspace {-0.1em} B \mid B \in \Gamma \} \vdash ^* +\hspace {-0.1em} A$
, then
![]() $\Gamma \models ^{\mathbf {S5}} A$
.
$\Gamma \models ^{\mathbf {S5}} A$
.
Proof. Since derivations in
![]() $\mathsf {EML}$
are finite, we may suppose that
$\mathsf {EML}$
are finite, we may suppose that
![]() $\Gamma $
is finite. Assume that
$\Gamma $
is finite. Assume that
![]() $\{+\hspace {-0.1em} B \mid B \in \Gamma \} \vdash ^* +\hspace {-0.1em} A$
. By (
$\{+\hspace {-0.1em} B \mid B \in \Gamma \} \vdash ^* +\hspace {-0.1em} A$
. By (
![]() $+\hspace {-0.1em}\rightarrow $
I.), this means that
$+\hspace {-0.1em}\rightarrow $
I.), this means that
![]() $\vdash ^* +\hspace {-0.1em} \left(\left(\bigwedge _{B\in \Gamma } B\right) \rightarrow A\right)$
. By Theorem 4.9,
$\vdash ^* +\hspace {-0.1em} \left(\left(\bigwedge _{B\in \Gamma } B\right) \rightarrow A\right)$
. By Theorem 4.9,
![]() $\models ^{\mathbf {S5}} \Box \left(\left(\bigwedge _{B\in \Gamma } B\right) \rightarrow A\right)$
, which entails
$\models ^{\mathbf {S5}} \Box \left(\left(\bigwedge _{B\in \Gamma } B\right) \rightarrow A\right)$
, which entails
![]() $\models ^{\mathbf {S5}} (\bigwedge _{B\in \Gamma } B) \rightarrow A$
by Axiom T and modus ponens. □
$\models ^{\mathbf {S5}} (\bigwedge _{B\in \Gamma } B) \rightarrow A$
by Axiom T and modus ponens. □
However, we used
![]() $\Diamond $
-Elimination rules to derive Axioms K and 5. Nonetheless, one can recapture S5 using the derivability relation
$\Diamond $
-Elimination rules to derive Axioms K and 5. Nonetheless, one can recapture S5 using the derivability relation
![]() $\vdash ^{**}$
that results from adding to
$\vdash ^{**}$
that results from adding to
![]() $\vdash ^*$
the following restricted rule of
$\vdash ^*$
the following restricted rule of
![]() $\Diamond $
-Elimination.
$\Diamond $
-Elimination.

The restriction serves to recover the Necessitation rule in the proof of the following theorem.
Theorem 4.13. Let
![]() $\Gamma $
be a set of
$\Gamma $
be a set of
![]() $\mathcal {L}_{ML}$
-formulae and A an
$\mathcal {L}_{ML}$
-formulae and A an
![]() $\mathcal {L}_{ML}$
-formula. It is the case that
$\mathcal {L}_{ML}$
-formula. It is the case that
![]() $\{+\hspace {-0.1em} B \mid B \in \Gamma \} \vdash ^{**} +\hspace {-0.1em} A$
iff
$\{+\hspace {-0.1em} B \mid B \in \Gamma \} \vdash ^{**} +\hspace {-0.1em} A$
iff
![]() $\Gamma \models ^{\mathbf {S5}} A$
.
$\Gamma \models ^{\mathbf {S5}} A$
.
Proof. We first prove the right-to-left direction. Inspection of the proofs in §3.4 reveals that
![]() $\vdash ^{**}$
derives all S5 axioms. Furthermore, the following derivation shows that
$\vdash ^{**}$
derives all S5 axioms. Furthermore, the following derivation shows that
![]() $\vdash ^{**}$
satisfies a version of the Necessitation rule, i.e. that if
$\vdash ^{**}$
satisfies a version of the Necessitation rule, i.e. that if
![]() $\emptyset \vdash ^{**} +\hspace {-0.1em} A$
, then
$\emptyset \vdash ^{**} +\hspace {-0.1em} A$
, then
![]() $\emptyset \vdash ^{**} +\hspace {-0.1em}\Box A$
.
$\emptyset \vdash ^{**} +\hspace {-0.1em}\Box A$
.

The application of (
![]() $\oplus \hspace {-0.08em}\Diamond $
E.*) is legitimate here, since the (SR
$\oplus \hspace {-0.08em}\Diamond $
E.*) is legitimate here, since the (SR
![]() $_2$
) derivation uses no premisses or assumptions other than the one being discharged and
$_2$
) derivation uses no premisses or assumptions other than the one being discharged and
![]() $+\hspace {-0.1em} A$
(which is a theorem by assumption.)
$+\hspace {-0.1em} A$
(which is a theorem by assumption.)
Now, since
![]() $\Gamma \models ^{\mathbf {S5}} A$
and S5 is complete with respect to its model theory, there is a natural deduction proof of A that requires only the premisses
$\Gamma \models ^{\mathbf {S5}} A$
and S5 is complete with respect to its model theory, there is a natural deduction proof of A that requires only the premisses
![]() $\Gamma $
, the S5 Axioms, the Necessitation rule and modus ponens. By the above, this proof can be performed in
$\Gamma $
, the S5 Axioms, the Necessitation rule and modus ponens. By the above, this proof can be performed in
![]() $\vdash ^{**}$
to derive
$\vdash ^{**}$
to derive
![]() $+\hspace {-0.1em} A$
from
$+\hspace {-0.1em} A$
from
![]() $\{+\hspace {-0.1em} B \mid B \in \Gamma \}$
. This concludes the right-to-left direction.
$\{+\hspace {-0.1em} B \mid B \in \Gamma \}$
. This concludes the right-to-left direction.
For left-to-right direction, the proof of Proposition 4.12 works, but the following step is nontrivial:
-
(*) Assume that
 $\{+\hspace {-0.1em} B \mid B \in \Gamma \} \vdash ^{**} +\hspace {-0.1em} A$
. By (
$\{+\hspace {-0.1em} B \mid B \in \Gamma \} \vdash ^{**} +\hspace {-0.1em} A$
. By (
 $+\hspace {-0.1em}\rightarrow $
I.), this means that
$+\hspace {-0.1em}\rightarrow $
I.), this means that
 $\vdash ^{**} +\hspace {-0.1em} \left(\left(\bigwedge _{B\in \Gamma } B\right) \rightarrow A\right)$
.
$\vdash ^{**} +\hspace {-0.1em} \left(\left(\bigwedge _{B\in \Gamma } B\right) \rightarrow A\right)$
.
It is not clear that (
![]() $+\hspace {-0.1em}\rightarrow $
I.) can be applied here, since under
$+\hspace {-0.1em}\rightarrow $
I.) can be applied here, since under
![]() $\vdash ^{**}$
one may apply the rule (
$\vdash ^{**}$
one may apply the rule (
![]() $\oplus \hspace {-0.08em}\Diamond $
E.*), and we have not established that this rule is permitted in (
$\oplus \hspace {-0.08em}\Diamond $
E.*), and we have not established that this rule is permitted in (
![]() $+\hspace {-0.1em}\rightarrow $
I.). To see that the step (*) is nonetheless correct here, note that any occurrence of (
$+\hspace {-0.1em}\rightarrow $
I.). To see that the step (*) is nonetheless correct here, note that any occurrence of (
![]() $\oplus \hspace {-0.08em}\Diamond $
E.*) can only be in an (SR
$\oplus \hspace {-0.08em}\Diamond $
E.*) can only be in an (SR
![]() $_2$
) subderivation that establishes
$_2$
) subderivation that establishes
![]() $+\hspace {-0.1em} X$
for some sentence X. Let R be the set of all
$+\hspace {-0.1em} X$
for some sentence X. Let R be the set of all
![]() $+\hspace {-0.1em} X$
that are established this way anywhere in the proof. Then the following version of (*) is obviously correct, as all subderivations using (
$+\hspace {-0.1em} X$
that are established this way anywhere in the proof. Then the following version of (*) is obviously correct, as all subderivations using (
![]() $\oplus \hspace {-0.08em}\Diamond $
E.*) can be replaced by a premiss from R.
$\oplus \hspace {-0.08em}\Diamond $
E.*) can be replaced by a premiss from R.
-
Assume that
 $\{+\hspace {-0.1em} B \mid B \in \Gamma \} \vdash ^{**} +\hspace {-0.1em} A$
. By (
$\{+\hspace {-0.1em} B \mid B \in \Gamma \} \vdash ^{**} +\hspace {-0.1em} A$
. By (
 $+\hspace {-0.1em}\rightarrow $
I.), this means that
$+\hspace {-0.1em}\rightarrow $
I.), this means that
 $R \vdash ^{**} +\hspace {-0.1em} \left(\left(\bigwedge _{B\in \Gamma } B\right) \rightarrow A\right)$
.
$R \vdash ^{**} +\hspace {-0.1em} \left(\left(\bigwedge _{B\in \Gamma } B\right) \rightarrow A\right)$
.
But all members of R are theorems under
![]() $\vdash ^{**}$
, since they can be established by a Smileian reductio that does not require any side premisses. Thus the step (*) is correct. □
$\vdash ^{**}$
, since they can be established by a Smileian reductio that does not require any side premisses. Thus the step (*) is correct. □
5 Yalcin sentences and their generalizations
5.1 Yalcin sentences
Yalcin (Reference Yalcin2007) famously observed that sentences of the form p and it might not be that p sound bad even when occurring in certain embedded environments, such as suppositions, in which Moore-paradoxical sentences (p and I don’t believe that p) sound fine. The following proof in EML shows
![]() $+\hspace {-0.1em} p \land \Diamond \neg p$
to be absurd.
$+\hspace {-0.1em} p \land \Diamond \neg p$
to be absurd.

This proof shows that uttering the sentence p and it might not be that p immediately commits one to having incompatible attitudes (namely, assent to p and dissent from p), which is absurd. Thus it also explains why suppose that p and might not p sounds odd, as to suppose p and it might not be that p is to suppose something manifestly absurd. This is the argument we give in Incurvati & Schlöder (Reference Incurvati and Schlöder2019), but we can clarify why precisely it is absurd to suppose p and it might not be that p.
To formalize supposition, we add a new primitive force-marker
![]() $\mathcal {S}$
to our language. In English, supposition refers both to an attitude and to its expression (Green, Reference Green2000, pp. 377–378). That is, the speech act of supposing that A expresses the attitude of supposing that A. Accordingly,
$\mathcal {S}$
to our language. In English, supposition refers both to an attitude and to its expression (Green, Reference Green2000, pp. 377–378). That is, the speech act of supposing that A expresses the attitude of supposing that A. Accordingly,
![]() $\mathcal {S}A$
stands for the speech act of supposing A, performed through locutions such as suppose that A, and expresses the attitude of supposing A.
$\mathcal {S}A$
stands for the speech act of supposing A, performed through locutions such as suppose that A, and expresses the attitude of supposing A.
Following Stalnaker (Reference Stalnaker2014), pp. 150–151, we take the supposition of A to consists in a proposal to add A to the common ground, but to do so temporarily.Footnote
6
In supposing that A, one is not committing to A, but is probing what happens if one were to commit to A. That is, one is checking what the consequences would be of adding A to the common ground.Footnote
7
For this process to work as desired, the internal logic of supposition must be the same as the logic of strong assertion. This sanctions the coordination principle (
![]() $\mathcal {S}$
-Inference), which states that the suppositional consequences of a suppositional context mirror the strongly assertoric consequences of the corresponding strongly assertoric context.Footnote
8
$\mathcal {S}$
-Inference), which states that the suppositional consequences of a suppositional context mirror the strongly assertoric consequences of the corresponding strongly assertoric context.Footnote
8

This coordination principle immediately implies that suppose p and might not p is absurd. For as shown above,
![]() $+\hspace {-0.1em} p\land \Diamond \neg p$
entails incompatible attitudes, which is absurd. By (
$+\hspace {-0.1em} p\land \Diamond \neg p$
entails incompatible attitudes, which is absurd. By (
![]() $\mathcal {S}$
-Inference), this means that supposing p and might not p is absurd as well, i.e. one derives
$\mathcal {S}$
-Inference), this means that supposing p and might not p is absurd as well, i.e. one derives
![]() $\bot $
from
$\bot $
from
![]() $\mathcal {S}(p\land \Diamond \neg p)$
.
$\mathcal {S}(p\land \Diamond \neg p)$
.
The absurdity of suppose p and might not p does not quite explain its infelicity, since not all absurd suppositions sound bad. One may felicitously suppose certain logical contradictions. For instance, someone not familiar with the derivability of Peirce’s Law in classical logic may felicitously suppose its negation. However, to see that the negation of Peirce’s Law is absurd requires a complex argument. By contrast, anyone grasping the meaning of and and not will immediately recognize the absurdity of, say, p and not p. This explains why p and not p sounds bad and continues to do so in embedded contexts. The same holds for p and might not p: its absurdity can be immediately inferred by applying the meaning-conferring rules of and, not and might. This absurdity is therefore manifest to anyone who grasps the meaning of these expressions, which explains why suppose p and might not p is infelicitous.
In addition to explaining the infelicity of Yalcin sentences under suppose, our account has the resources to explain why Moore sentences sound bad in ordinary contexts but cease to do so in suppositional ones. For while strongly asserting p and I do not believe that p is improper, it is not absurd in the sense of
![]() $+\hspace {-0.1em} p \land \neg Bp$
entailing
$+\hspace {-0.1em} p \land \neg Bp$
entailing
![]() $\perp $
. In our view, uttering a Moore sentence is infelicitous because it violates one of the preparatory conditions of strong assertion, e.g. that one should know or believe what one strongly asserts. But such preparatory conditions do not factor into the commitments undertaken by a strong assertion. Thus, the violation of these preparatory conditions does not proof-theoretically reduce to the speaker having both strongly asserted and rejected the same proposition. Hence, suppose that p and I do not believe that p is not predicted to be absurd. Since supposition and strong assertion have different preparatory conditions—in particular, one need not believe what one supposes—suppose that p and I do not believe that p is not predicted to be improper either.
$\perp $
. In our view, uttering a Moore sentence is infelicitous because it violates one of the preparatory conditions of strong assertion, e.g. that one should know or believe what one strongly asserts. But such preparatory conditions do not factor into the commitments undertaken by a strong assertion. Thus, the violation of these preparatory conditions does not proof-theoretically reduce to the speaker having both strongly asserted and rejected the same proposition. Hence, suppose that p and I do not believe that p is not predicted to be absurd. Since supposition and strong assertion have different preparatory conditions—in particular, one need not believe what one supposes—suppose that p and I do not believe that p is not predicted to be improper either.
The rule (
![]() $\mathcal {S}$
-Inference) is sufficient to explain the relevant data about Yalcin sentences, but to give a complete account of supposition further rules may need to be added. For our present project, there are more immediate concerns.
$\mathcal {S}$
-Inference) is sufficient to explain the relevant data about Yalcin sentences, but to give a complete account of supposition further rules may need to be added. For our present project, there are more immediate concerns.
5.2 Generalized Yalcin sentences
Paolo Santorio (Reference Santorio2017) observed that sentences like (3) seem to sound as bad as the original Yalcin sentences, and continue to do so when embedded under suppose.
-
(3) (If p, then it might be that q) and (if p, then
 $\neg $
q).
$\neg $
q).
We have seen that there are good reasons to treat Yalcin sentences as semantically contradictory. But then, Santorio argues, one should also treat sentences like (3) as semantically contradictory. However, it is difficult to find a conditional
![]() $>$
and a consequence relation
$>$
and a consequence relation
![]() $\models $
such that
$\models $
such that
![]() $p>\Diamond q \land p>\neg q \models \bot $
. This is because if
$p>\Diamond q \land p>\neg q \models \bot $
. This is because if
![]() $>$
can be vacuous, then the incompatibility of
$>$
can be vacuous, then the incompatibility of
![]() $\Diamond q$
and
$\Diamond q$
and
![]() $\neg q$
does not force us to conclude
$\neg q$
does not force us to conclude
![]() $\perp $
, but only that p satisfies the vacuity-condition for
$\perp $
, but only that p satisfies the vacuity-condition for
![]() $>$
.
$>$
.
Santorio (Reference Santorio2017) succeeds in defining such a
![]() $>$
and
$>$
and
![]() $\models $
, but we want to offer a different diagnosis of the problem posed by (3), one which does not require adopting a revised notion of consequence. Observe that an utterance of (4), which does not contain an epistemic modal, already sounds odd.
$\models $
, but we want to offer a different diagnosis of the problem posed by (3), one which does not require adopting a revised notion of consequence. Observe that an utterance of (4), which does not contain an epistemic modal, already sounds odd.
-
(4) (If p, then q) and (if p, then
 $\neg $
q).
$\neg $
q).
The reason why (3) and (4) both sound odd seems to be similar. To wit, both utterances appear to prompt one to suppose that p, i.e. to consider what follows should p be the case—but to do so is absurd, given the information the utterances contain. That is, we will argue that (3) and (4) sound bad for the same reason that (5a) and (5b) sound bad—their antecedents cannot be supposed.
-
(5) a. If (p and not p), then q.
b. If (p and it might not be p), then q.
We propose to explain the infelicitousness of (3), (4) and (5) by using a notion of supposability based on our characterization of supposition
![]() $\mathcal {S}$
. We have followed Stalnaker in taking the supposition of A to be a proposal to temporarily update the common ground with A. The supposability of A in a given context is the possibility of supposing A in that context.
$\mathcal {S}$
. We have followed Stalnaker in taking the supposition of A to be a proposal to temporarily update the common ground with A. The supposability of A in a given context is the possibility of supposing A in that context.
Definition 2. Let A and C be a
![]() $\mathcal {L}_{ML}$
-formulae. We say that A is supposable in (context) C if
$\mathcal {L}_{ML}$
-formulae. We say that A is supposable in (context) C if
![]() $\mathcal {S}(C\land A) \not \vdash \bot $
.
$\mathcal {S}(C\land A) \not \vdash \bot $
.
As we explain below, a strong assertion of an indicative conditional pragmatically presupposes the supposability of the conditional’s antecedent in a context C that corresponds to the current common ground updated with the strong assertion’s content. So, in the case of (3), the supposability of p is to be checked with respect to a context C that contains at least
![]() $(p> \neg q) \land (p> \Diamond q)$
. But we have that
$(p> \neg q) \land (p> \Diamond q)$
. But we have that
![]() $\mathcal {S} (p \land (p> \neg q) \land (p> \Diamond q)) \vdash \bot $
(assuming that
$\mathcal {S} (p \land (p> \neg q) \land (p> \Diamond q)) \vdash \bot $
(assuming that
![]() $>$
satisfies modus ponens), so the presupposition fails.
$>$
satisfies modus ponens), so the presupposition fails.
Why should the indicative conditional have such a presupposition? Following Stalnaker (Reference Stalnaker1978), the pragmatic presuppositions of a strong assertion include all the information that can be inferred from the performance of the strong assertion itself. In particular, a strong assertion presupposes that the context is such that its essential effect (i) changes the context in a nontrivial and well-defined way and (ii) everyone in the conversation can compute this change. Now, when one proposes to update the common ground with a conditional, one proposes to change it in such a way that if the antecedent is added to the common ground, its consequent should be added too. Everyone must be able to compute what this change amounts to, as this is what they base their decision to accept or reject the update proposal on. Thus, everyone must be able to consider the common ground updated with the conditional and then temporarily (for the purpose of deliberation) add the conditional’s antecedent and arrive at a well-defined result. This may be seen as a discoursive analogue of the Ramsey test. Hence, strong assertions of conditional content pragmatically presuppose that the conditional’s antecedent is supposable in the context of the current common ground updated with the assertion’s content. But this presupposition cannot be met for the conditionals (3), (4) and (5). Many have claimed that conditionals presuppose, in some sense, that their antecedents are possible (Gillies, Reference Gillies2010; Mandelkern & Romoli, Reference Mandelkern and Romoli2017; Crespo, Karawani, & Veltman, Reference Crespo, Karawani, Veltman, Ball and Rabern2018). Our argument shows that supposability is the right way to specify what kind of possibility should be meant here, at least within the Stalnakerian framework.
One might reply that our pragmatic explanation is not general enough. For Santorio’s generalized Yalcin sentence (3) also sounds bad when the conditionals it contains are read as subjunctives. And, the reply goes, the assertion of a subjunctive conditional does not have the supposability presupposition associated with the assertion of its indicative counterpart. While indicative conditionals change the common ground in a way that can be evaluated by provisionally updating the common ground with their antecedents, subjunctive conditionals change the common ground in a way that can be evaluated by provisionally revising the common ground with their antecedent (Stalnaker, Reference Stalnaker, Harper, Stalnaker and Pearce1968). Thus, the strong assertion of a subjunctive conditional does not presuppose that its antecedent be supposable in the common ground updated with the strong assertion’s content, since some of this content might be revised in order to suppose the antecedent.
The reply is unsuccessful. Although the assertion of a subjunctive does not have the same supposability presupposition as the assertion of the corresponding indicative, it does have a supposability presupposition. And this presupposition cannot be met when Santorio’s (3) is read as a subjunctive conditional. In particular, since not all information in the common ground is up for revision when considering a subjunctive antecedent, the assertion of a subjunctive conditional presupposes that its antecedent be supposable in C, where C is the nonrevisable part of the common ground updated with the conditional. Now consider the strong assertion (if it were p, then q) and (if it were p, then not q). Clearly, p is not supposable in the context
![]() $C'$
that results from updating C with the strong assertion, since
$C'$
that results from updating C with the strong assertion, since
![]() $\mathcal {S}(C' \land p) \vdash \mathcal {S}(p\land \neg p)$
, which entails
$\mathcal {S}(C' \land p) \vdash \mathcal {S}(p\land \neg p)$
, which entails
![]() $\bot $
. The same goes for (if it were p, then q) and (if it were p, then it might be that not q): p is not supposable in the context
$\bot $
. The same goes for (if it were p, then q) and (if it were p, then it might be that not q): p is not supposable in the context
![]() $C'$
that results from updating C with this strong assertion, since
$C'$
that results from updating C with this strong assertion, since
![]() $\mathcal {S}( p\land C') \vdash \mathcal {S}(p\land \Diamond \neg p)$
, which entails
$\mathcal {S}( p\land C') \vdash \mathcal {S}(p\land \Diamond \neg p)$
, which entails
![]() $\bot $
.
$\bot $
.
One may wonder how this pragmatic explanation of the infelicity of generalized Yalcin sentences can account for their infelicity when embedded under suppose. After all, the special problem raised by Yalcin sentences is that, unlike Moore sentences, they continue to sound bad under suppose and similar environments. This, the usual story goes, precludes a pragmatic explanation of their infelicity similar to the one given for Moore sentences, since pragmatic inferences are suspended under suppose.
This story overplays the power of suppose to suspend pragmatic inferences: although the pragmatic inferences used to explain the infelicity of Moore sentences are suspended under suppose, it does not follow that all such inferences are. The pragmatic inference used to explain the infelicity of Moore sentences is suspended under supposition because while it seems a preparatory condition for strong assertion that one ought to believe what one strongly asserts, there is no analogue preparatory condition for supposition. By contrast, the pragmatic inference we outlined in the previous paragraphs clearly goes through under supposition. In particular, just as the actual update of the common ground with a conditional is only well-defined if its antecedent is supposable in the right context C, so is the temporary update with the same conditional only well-defined if its antecedent is supposable in C. That is, this supposability requirement—unlike the requirement that one ought to believe the content of the speech act—is shared by strong assertions and suppositions of conditionals alike.
There are some further generalized Yalcin sentences that we can explain using this suppositional strategy. Matthew Mandelkern (Reference Mandelkern2019) observed that sentences like (6a) and (6b) seem to sound as bad as the original Yalcin sentences.
-
(6) #a. (p and it might not be that p) or (q and it might not be that q)
#b. might (p and it might not be that p)
However, on our account such sentences are not absurd: there are models of
![]() $\mathsf {EML}$
in which (7a) and (7b) hold and hence neither sentence entails
$\mathsf {EML}$
in which (7a) and (7b) hold and hence neither sentence entails
![]() $\bot $
(on the assumption that neither A nor B are classical contradictions).
$\bot $
(on the assumption that neither A nor B are classical contradictions).
-
(7) a. +((A
 $\land \Diamond \neg $
A)
$\land \Diamond \neg $
A)
 $\lor $
(B
$\lor $
(B
 $\land \Diamond \neg $
B)).
$\land \Diamond \neg $
B)).b. +
 $\Diamond $
(A
$\Diamond $
(A
 $\land \Diamond \neg $
A).
$\land \Diamond \neg $
A).
Similarly to Santorio’s cases, Mandelkern’s cases can only be accounted for semantically by making substantial revisions to classical logic. Any attempt to add further rules to
![]() $\mathsf {EML}$
so that (7a) and (7b) entail
$\mathsf {EML}$
so that (7a) and (7b) entail
![]() $\bot $
would trivialize the epistemic possibility modal.
$\bot $
would trivialize the epistemic possibility modal.
Theorem 5.1. Suppose that one of the following is the case.
-
(a)
 $+\hspace {-0.1em} ((A\land \Diamond \neg A)\lor (B\land \Diamond \neg B)) \vdash \bot $
for all
$+\hspace {-0.1em} ((A\land \Diamond \neg A)\lor (B\land \Diamond \neg B)) \vdash \bot $
for all
 $A, B$
.
$A, B$
. -
(b)
 $+\hspace {-0.1em}\Diamond (A\land \Diamond \neg A) \vdash \bot $
for all A.
$+\hspace {-0.1em}\Diamond (A\land \Diamond \neg A) \vdash \bot $
for all A.
Then for any A,
![]() $+\hspace {-0.1em} \Diamond A \vdash +\hspace {-0.1em} A$
.
$+\hspace {-0.1em} \Diamond A \vdash +\hspace {-0.1em} A$
.
Proof. Suppose that (a) is the case, letting A be p and B be
![]() $\neg p$
. That is, we have that
$\neg p$
. That is, we have that
![]() $+\hspace {-0.1em} ((p \land \Diamond \neg p) \lor (\neg p \land \Diamond p)) \vdash \bot $
. By Smileian reductio, this means that
$+\hspace {-0.1em} ((p \land \Diamond \neg p) \lor (\neg p \land \Diamond p)) \vdash \bot $
. By Smileian reductio, this means that
![]() $\vdash \ominus \hspace {-0.08em} ((p \land \Diamond \neg p) \lor (\neg p \land \Diamond p))$
, which by (
$\vdash \ominus \hspace {-0.08em} ((p \land \Diamond \neg p) \lor (\neg p \land \Diamond p))$
, which by (
![]() $\oplus \hspace {-0.08em}\neg $
I.) means that
$\oplus \hspace {-0.08em}\neg $
I.) means that
![]() $\vdash \oplus \hspace {-0.08em} \neg ((p \land \Diamond \neg p) \lor (\neg p \land \Diamond p))$
.
$\vdash \oplus \hspace {-0.08em} \neg ((p \land \Diamond \neg p) \lor (\neg p \land \Diamond p))$
.
By De Morgan,
![]() $\neg ((p \land \Diamond \neg p) \lor (\neg p \land \Diamond p))$
can be written as
$\neg ((p \land \Diamond \neg p) \lor (\neg p \land \Diamond p))$
can be written as
![]() $(\neg p \lor \neg \Diamond \neg p) \land (p \lor \neg \Diamond p)$
, which is classically equivalent to
$(\neg p \lor \neg \Diamond \neg p) \land (p \lor \neg \Diamond p)$
, which is classically equivalent to
![]() $\neg \Diamond \neg p \lor \neg \Diamond p$
. This sentence can be rewritten as
$\neg \Diamond \neg p \lor \neg \Diamond p$
. This sentence can be rewritten as
![]() $\Diamond p \rightarrow \Box p$
. Hence, (a) implies that
$\Diamond p \rightarrow \Box p$
. Hence, (a) implies that
![]() $\vdash \oplus \hspace {-0.08em} (\Diamond p \rightarrow \Box p)$
. But then, we can derive
$\vdash \oplus \hspace {-0.08em} (\Diamond p \rightarrow \Box p)$
. But then, we can derive
![]() $+\hspace {-0.1em} p$
from
$+\hspace {-0.1em} p$
from
![]() $+\hspace {-0.1em}\Diamond p$
as follows.
$+\hspace {-0.1em}\Diamond p$
as follows.

For the second part, suppose that (b) is the case, letting A be
![]() $\neg p$
. That is, we have that
$\neg p$
. That is, we have that
![]() $+\hspace {-0.1em} \Diamond (\neg p \land \Diamond p) \vdash \bot $
. By Smileian reductio, this means that
$+\hspace {-0.1em} \Diamond (\neg p \land \Diamond p) \vdash \bot $
. By Smileian reductio, this means that
![]() $\vdash \ominus \hspace {-0.08em} \Diamond (\neg p \land \Diamond p)$
. By (
$\vdash \ominus \hspace {-0.08em} \Diamond (\neg p \land \Diamond p)$
. By (
![]() $\oplus \hspace {-0.08em}\neg $
I.), this is equivalent to
$\oplus \hspace {-0.08em}\neg $
I.), this is equivalent to
![]() $\vdash \oplus \hspace {-0.08em}\neg \Diamond (\neg p \land \Diamond p)$
. By Lemma 3.7, it follows that
$\vdash \oplus \hspace {-0.08em}\neg \Diamond (\neg p \land \Diamond p)$
. By Lemma 3.7, it follows that
![]() $\vdash +\hspace {-0.1em} \neg (\neg p \land \neg \Diamond p)$
, which by Classicality is equivalent to
$\vdash +\hspace {-0.1em} \neg (\neg p \land \neg \Diamond p)$
, which by Classicality is equivalent to
![]() $\vdash +\hspace {-0.1em} \Diamond p\rightarrow p$
.□
$\vdash +\hspace {-0.1em} \Diamond p\rightarrow p$
.□
One might take issue with Lemma 3.7 here, but inspection of the proof of the lemma shows that it rests on well-motivated assumptions. Challenging the application of (Weak Inference) in the proof of (a) would not help, since the proof of (b) does not require this principle. Thus, we cannot semantically account for these generalized cases without giving up on classical logic. Mandelkern’s (Reference Mandelkern2019) account avoids these results by denying the universal validity of the relevant classically valid transformations (e.g. the application of De Morgan in the above proof).
Instead of making deep revisions to our semantics, we again provide a pragmatic explanation of the relevant data. We explain the infelicitousness of (6a) by taking the strong assertion of A or B to presuppose the supposability of A and the supposability of B. And we explain the infelicitousness of (6b) by taking the strong assertion of might A to pragmatically presuppose the supposability of A. The pragmatic inferences from A or B and might A to supposability are evinced by the felicitousness of sequences like the following.
-
(8) a. It is either p or q. So suppose that it in fact the case that p. b. It might be that p. So suppose that it in fact the case that p.
At this point, one might suggest taking the inferences from A or B and might A to supposability to be not pragmatic, but semantic. In particular, one might identify the meaning of might with supposability and the meaning of A or B with might A and might B.Footnote 9 However, supposition can be counterfactual, so having asserted not A one may go on to suppose that A, possibly just for the sake of argument. By contrast, having asserted not A, it is a mistake to also assert might A. Thus might cannot be identified with supposability.
Pragmatically explaining the data in (6) has also an empirical advantage over Mandelkern’s (Reference Mandelkern2019) own semantic approach. He claims that the infelicitousness of (6a) is explained by the fact that Yalcin sentences are classical contradictions and that disjunctions of classical contradictions are themselves classical contradictions. But now consider (9).
-
(9) (p and it might not be that p) or q.
If q is true, then according to the usual truth-functional meaning of disjunction (which Mandelkern does not dispute), (9) is true, since it has a true disjunct. However, (9) sounds odd. Thus Mandelkern would seem to need some further mechanism to explain the oddity of (9), e.g. our pragmatic presupposition or another principle entailing that disjunctions one of whose disjuncts is a classical contradiction sound generally bad. But then, any such mechanism would also account for the infelicitousness of (6). Hence, the more parsimonious approach is to stick with classical consequence and explain both (6) and (9) pragmatically, as we have done.
6 Consequence, credence and commitment
Moritz Schulz (Reference Schulz2010) presented an objection to informational consequence (and hence
![]() $\mathsf {EML}$
’s notion of consequence) as an account of logical consequence. Schulz argues that, in situations of uncertainty, it may be rational to assign a high credence to A but a low credence to it must be the case that A. This is because one’s evidence for A need not rule out not A and hence need not be evidence for must A. Consider, for instance, a situation in which one sees that the lights are on. On the basis of this evidence, one might (rationally) assign a high credence to (10a). However, says Schulz, one cannot rule out that they forgot to switch off the lights. Hence one must assign a low credence to (10b).
$\mathsf {EML}$
’s notion of consequence) as an account of logical consequence. Schulz argues that, in situations of uncertainty, it may be rational to assign a high credence to A but a low credence to it must be the case that A. This is because one’s evidence for A need not rule out not A and hence need not be evidence for must A. Consider, for instance, a situation in which one sees that the lights are on. On the basis of this evidence, one might (rationally) assign a high credence to (10a). However, says Schulz, one cannot rule out that they forgot to switch off the lights. Hence one must assign a low credence to (10b).
-
(10) a. They are at home.
b. They must be at home.
However, in
![]() $\mathsf {EML}$
,
$\mathsf {EML}$
,
![]() $+\hspace {-0.1em}\Box A$
is derivable from
$+\hspace {-0.1em}\Box A$
is derivable from
![]() $+\hspace {-0.1em} A$
and hence (10b) follows from (10a), at least assuming the obvious formalization of these sentences. Thus, Schulz continues,
$+\hspace {-0.1em} A$
and hence (10b) follows from (10a), at least assuming the obvious formalization of these sentences. Thus, Schulz continues,
![]() $\mathsf {EML}$
-consequence, like informational consequence
$\mathsf {EML}$
-consequence, like informational consequence
clearly violates a reasonable constraint on logical consequence: If a rational and logically omniscient subject’s credence function P is such that
![]() $P (\phi ) = t$
, and
$P (\phi ) = t$
, and
![]() $\phi \models \psi $
, then
$\phi \models \psi $
, then
![]() $P(\psi ) \geq t$
, i.e. if we assign to a statement
$P(\psi ) \geq t$
, i.e. if we assign to a statement
![]() $\phi $
subjective probability t, and we are certain that
$\phi $
subjective probability t, and we are certain that
![]() $\psi $
follows logically from
$\psi $
follows logically from
![]() $\phi $
, then we should assign to
$\phi $
, then we should assign to
![]() $\psi $
a subjective probability at least as high as t. After all, we know that the former cannot hold without the latter. (Schulz, Reference Schulz2010, p. 388)
$\psi $
a subjective probability at least as high as t. After all, we know that the former cannot hold without the latter. (Schulz, Reference Schulz2010, p. 388)
Schulz concludes that epistemic strengthening (the inference from A to must A) is invalid.
More recently, Justin Bledin and Tamar Lando (Reference Bledin and Lando2018) have considered cases similar to (10). One goes as follows. It is the run-up to the 1980 US elections and, according to the polls, Reagan will win by a landslide, Carter will come second and Anderson will be third by a wide margin. On the basis of this evidence, you come to believe (11a). But given that you cannot rule out that Carter will win, it would seem wrong for you to believe (11b) on the basis of the same evidence.
-
(11) a. Carter will not win the election
b. It is not the case that Carter might win the election
However, in
![]() $\mathsf {EML}$
,
$\mathsf {EML}$
,
![]() $+\hspace {-0.1em} \neg \Diamond A$
is derivable from
$+\hspace {-0.1em} \neg \Diamond A$
is derivable from
![]() $+\hspace {-0.1em} \neg A$
—an inference step also known as Łukasiewicz’s principle. Unlike Schulz, however, Bledin and Lando do not conclude that the relevant inference should be regarded as invalid. Rather, they say that philosophers face a choice between rejecting Łukasiewicz’s principle, rejecting Justification with Risk—i.e. the claim that there are cases in which one can justifiably believe
$+\hspace {-0.1em} \neg A$
—an inference step also known as Łukasiewicz’s principle. Unlike Schulz, however, Bledin and Lando do not conclude that the relevant inference should be regarded as invalid. Rather, they say that philosophers face a choice between rejecting Łukasiewicz’s principle, rejecting Justification with Risk—i.e. the claim that there are cases in which one can justifiably believe
![]() $\neg A$
but not
$\neg A$
but not
![]() $\neg \Diamond A$
—and rejecting Single-Premiss Closure—i.e. the principle that if one is justified in believing
$\neg \Diamond A$
—and rejecting Single-Premiss Closure—i.e. the principle that if one is justified in believing
![]() $\phi $
and one comes to believe that
$\phi $
and one comes to believe that
![]() $\psi $
by competently deducing
$\psi $
by competently deducing
![]() $\psi $
from
$\psi $
from
![]() $\phi $
, then one is justified in believing
$\phi $
, then one is justified in believing
![]() $\psi $
(a nonprobabilistic variant of Schulz’s constraint).
$\psi $
(a nonprobabilistic variant of Schulz’s constraint).
Bledin and Lendo present some arguments to the effect that Łukasiewicz’s principle and Justification with Risk hold. A philosopher persuaded by those arguments, they conclude, needs to give up Single-Premise Closure. However, Bledin and Lando do not offer any positive reason for thinking that Single Premise Closure does not hold.
There is a familiar strategy for dealing with this sort of cases. According to this strategy, we should give up Justification with Risk (or its equivalent for epistemic strengthening) and explain away the troublesome cases by appealing to the idea that, when the possibility of error is made salient, this brings about a change of context (DeRose, Reference DeRose1991) or of the standards of precision in play (Moss, Reference Moss2019). Thus, in the Schulz case (10), one should assign a high credence to they are at home because one sees that the lights are on. When the possibility that they forgot to switch off the lights is raised, one should not assign a high credence to they must be at home. But then, in those circumstances, one should not assign a high credence to they are at home either.
However, under Schulz’s assumptions that epistemic modals can be assigned probabilities and that probabilities obey the classical probability calculus, one can show that this response is inadequate. In particular, it follows from these assumptions that Schulz’s constraint on logical consequence is incompatible with any logic of epistemic modality which treats not p and it might be that p as a contradiction. For if
![]() $\neg p \land \Diamond p \models \bot $
, then according to Schulz’s constraint,
$\neg p \land \Diamond p \models \bot $
, then according to Schulz’s constraint,
![]() $P(\neg p \land \Diamond p) \leq P(\bot ) = 0$
. Since probabilities are positive,
$P(\neg p \land \Diamond p) \leq P(\bot ) = 0$
. Since probabilities are positive,
![]() $P(\neg p \land \Diamond p) = 0$
. Thus, if one believes that it might be that p, i.e.
$P(\neg p \land \Diamond p) = 0$
. Thus, if one believes that it might be that p, i.e.
![]() $P(\Diamond p) = 1$
, it follows that
$P(\Diamond p) = 1$
, it follows that
![]() $P(\neg p) = 0$
, i.e.
$P(\neg p) = 0$
, i.e.
![]() $P(p) = 1$
by the law of total probability.Footnote
10
Schulz himself (Reference Schulz2010, § 3) favors a pragmatic explanation of Yalcin sentences. According to this explanation, when you strongly assert A, you rule out all not-A worlds. Thus, in it is raining and it might not be raining, the domain of the epistemic modal in the second conjunct is restricted to rain-worlds. So there is no way, once you have strongly asserted that it is raining, that you can also strongly assert that it might not be. However, this explanation predicts that it might not be raining and it is raining should be felicitous, which does not appear to be the case.
$P(p) = 1$
by the law of total probability.Footnote
10
Schulz himself (Reference Schulz2010, § 3) favors a pragmatic explanation of Yalcin sentences. According to this explanation, when you strongly assert A, you rule out all not-A worlds. Thus, in it is raining and it might not be raining, the domain of the epistemic modal in the second conjunct is restricted to rain-worlds. So there is no way, once you have strongly asserted that it is raining, that you can also strongly assert that it might not be. However, this explanation predicts that it might not be raining and it is raining should be felicitous, which does not appear to be the case.
So what are the options for the defender of informational consequence, who wants to insist that Yalcin sentences are, indeed, contradictions? She could try to develop a nonclassical probability calculus (see Williams, Reference Williams, Hájek and Hitchcock2016 for a survey). Or she could reject Schulz’s constraint on logical consequences and hence, arguably, also Single-Premiss Closure. We explore the former option in ongoing work. Here we exploit features of
![]() $\mathsf {EML}$
and our proof-theoretic approach to show that the prospects for the latter option are brighter than they might appear at first sight.
$\mathsf {EML}$
and our proof-theoretic approach to show that the prospects for the latter option are brighter than they might appear at first sight.
Bledin & Lando (Reference Bledin and Lando2018, p. 19) argue that, even if they reject the principle of Single-Premiss Closure, defenders of informational consequence can still accept the principle restricted to nonmodal formulae. However, there are inferences involving epistemic modals that are compatible with Schulz’s constraint and hence satisfy Single-Premiss Closure. A case in point is epistemic weakening (that is, the inference from must A to A). Epistemic weakening satisfies Schulz’s constraint: the credence rationally assigned to A can never be lower than the credence assigned to must A. For, if Schulz is correct, one’s evidence for must A is evidence that rules out not A, and evidence that rules out not A is also evidence for A. Thus, the portion of informational consequence that respects Schulz’s constraint is not exhausted by its nonmodal fragment.
Our proof-theoretic account allows us to isolate an evidence-preserving fragment of informational consequence that validates more inferences than merely the nonmodal ones. This is the fragment
![]() $\vdash ^*$
of
$\vdash ^*$
of
![]() $\mathsf {EML}$
consequence that one obtains by removing the
$\mathsf {EML}$
consequence that one obtains by removing the
![]() $\Diamond $
-Elimination rules from
$\Diamond $
-Elimination rules from
![]() $\mathsf {EML}$
. By inspecting the proofs of epistemic strengthening and epistemic weakening, one finds that the former is not derivable in
$\mathsf {EML}$
. By inspecting the proofs of epistemic strengthening and epistemic weakening, one finds that the former is not derivable in
![]() $\vdash ^*$
, whereas the latter is. The rules for
$\vdash ^*$
, whereas the latter is. The rules for
![]() $\Diamond $
-Elimination are also required to derive that
$\Diamond $
-Elimination are also required to derive that
![]() $+\hspace {-0.1em} (p\land \Diamond \neg p) \vdash \bot $
, which we demonstrated to be incompatible with Schulz’s constraint as well (again, assuming the classical probability calculus).
$+\hspace {-0.1em} (p\land \Diamond \neg p) \vdash \bot $
, which we demonstrated to be incompatible with Schulz’s constraint as well (again, assuming the classical probability calculus).
As we note in Incurvati & Schlöder (Reference Incurvati and Schlöder2019, pp. 760–762), the use of
![]() $\Diamond $
-Elimination means that there may be a loss of specificity when going from the premisses of an inference to the conclusion. That is to say, we can go from specific premisses to an unspecific conclusion, which may result in a loss of evidence. This is the reason why we restricted the subderivation in (Weak Inference) to cases in which the
$\Diamond $
-Elimination means that there may be a loss of specificity when going from the premisses of an inference to the conclusion. That is to say, we can go from specific premisses to an unspecific conclusion, which may result in a loss of evidence. This is the reason why we restricted the subderivation in (Weak Inference) to cases in which the
![]() $\Diamond $
-Elimination rules are not applied. This suggests that while
$\Diamond $
-Elimination rules are not applied. This suggests that while
![]() $\mathsf {EML}$
does not preserve evidence, the fragment
$\mathsf {EML}$
does not preserve evidence, the fragment
![]() $\vdash ^*$
does.
$\vdash ^*$
does.
But if inference in
![]() $\mathsf {EML}$
does not preserve evidence, why think that this is a suitable notion of inference at all? We contend that even if inference in
$\mathsf {EML}$
does not preserve evidence, why think that this is a suitable notion of inference at all? We contend that even if inference in
![]() $\mathsf {EML}$
does not preserve evidence, it does preserve commitment. As mentioned in §2, a derivation in
$\mathsf {EML}$
does not preserve evidence, it does preserve commitment. As mentioned in §2, a derivation in
![]() $\mathsf {EML}$
computes which attitudes someone is committed to in virtue of their having the attitudes in the premisses. In speech act terms, a derivation in
$\mathsf {EML}$
computes which attitudes someone is committed to in virtue of their having the attitudes in the premisses. In speech act terms, a derivation in
![]() $\mathsf {EML}$
computes what someone is committed to accepting in the common ground given the public stances that they have taken on the acceptability of certain propositions into the common ground. This is compatible with consequence in
$\mathsf {EML}$
computes what someone is committed to accepting in the common ground given the public stances that they have taken on the acceptability of certain propositions into the common ground. This is compatible with consequence in
![]() $\mathsf {EML}$
not preserving evidence and hence with the failure of Singe-Premise Closure.
$\mathsf {EML}$
not preserving evidence and hence with the failure of Singe-Premise Closure.
7 Conclusion and further work
We have described a general framework for the proof-theoretic study of epistemic modality. We have restricted our presentation to the interaction of epistemic modality with the classical Boolean connectives. In ongoing work, we apply the strategy of placing principled proof-theoretic constraints on the rules governing epistemic modal operators to problems going beyond these connectives.
Several authors have noted that principles like classical reductio fail in the presence of epistemic vocabulary (e.g. Bledin, Reference Bledin2014): it might not be raining and it is raining sound contradictory, but it is mistaken to apply classical reductio to derive it is not raining from it might not be raining. In
![]() $\mathsf {EML}$
, reductio is only applicable when certain proof-theoretic restrictions are met, which gives one the tools to account for these problems. But the problems of epistemic modality are not confined to propositional logic. In §5, we outlined some possible extensions of
$\mathsf {EML}$
, reductio is only applicable when certain proof-theoretic restrictions are met, which gives one the tools to account for these problems. But the problems of epistemic modality are not confined to propositional logic. In §5, we outlined some possible extensions of
![]() $\mathsf {EML}$
to the study of indicative conditionals and the concept of supposition. In addition, there are well-known puzzles regarding the interaction of quantifiers and epistemic modals (Aloni, Reference Aloni2001, Reference Aloni2005), recently brought to renewed attention by Ninan (Reference Ninan2018). Naïve applications of first-order logic to epistemic modality license defective inferences like every card might be a losing card; therefore, the winning card might be a losing card. EML opens up the strategy of blocking such inferences via proof-theoretic restrictions on the use of epistemic modals under quantification.
$\mathsf {EML}$
to the study of indicative conditionals and the concept of supposition. In addition, there are well-known puzzles regarding the interaction of quantifiers and epistemic modals (Aloni, Reference Aloni2001, Reference Aloni2005), recently brought to renewed attention by Ninan (Reference Ninan2018). Naïve applications of first-order logic to epistemic modality license defective inferences like every card might be a losing card; therefore, the winning card might be a losing card. EML opens up the strategy of blocking such inferences via proof-theoretic restrictions on the use of epistemic modals under quantification.
Acknowledgments
We are grateful to two anonymous referees and our editor at The Review of Symbolic Logic for comments on previous versions of this material. This work has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 758540) within the project From the Expression of Disagreement to New Foundations for Expressivist Semantics.