Article contents
MODELS OF POSITIVE TRUTH
Published online by Cambridge University Press: 26 December 2018
Abstract
This paper is a follow-up to [4], in which a mistake in [6] (which spread also to [9]) was corrected. We give a strenghtening of the main result on the semantical nonconservativity of the theory of PT− with internal induction for total formulae 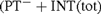 ${(\rm{P}}{{\rm{T}}^ - } + {\rm{INT}}\left( {{\rm{tot}}} \right)$, denoted by PT− in [9]). We show that if to PT− the axiom of internal induction for all arithmetical formulae is added (giving
${(\rm{P}}{{\rm{T}}^ - } + {\rm{INT}}\left( {{\rm{tot}}} \right)$, denoted by PT− in [9]). We show that if to PT− the axiom of internal induction for all arithmetical formulae is added (giving 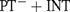 ${\rm{P}}{{\rm{T}}^ - } + {\rm{INT}}$), then this theory is semantically stronger than
${\rm{P}}{{\rm{T}}^ - } + {\rm{INT}}$), then this theory is semantically stronger than 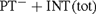 ${\rm{P}}{{\rm{T}}^ - } + {\rm{INT}}\left( {{\rm{tot}}} \right)$. In particular the latter is not relatively truth definable (in the sense of [11]) in the former. Last but not least, we provide an axiomatic theory of truth which meets the requirements put forward by Fischer and Horsten in [9]. The truth theory we define is based on Weak Kleene Logic instead of the Strong one.
${\rm{P}}{{\rm{T}}^ - } + {\rm{INT}}\left( {{\rm{tot}}} \right)$. In particular the latter is not relatively truth definable (in the sense of [11]) in the former. Last but not least, we provide an axiomatic theory of truth which meets the requirements put forward by Fischer and Horsten in [9]. The truth theory we define is based on Weak Kleene Logic instead of the Strong one.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2018
References
BIBLIOGRAPHY
- 5
- Cited by

