Article contents
TWO (OR THREE) NOTIONS OF FINITISM
Published online by Cambridge University Press: 20 January 2010
Abstract
Finitism is given an interpretation based on two ideas about strings (sequences of symbols): a replacement principle extracted from Hilbert’s work and a counting principle inspired by Tait. These principles are used to justify an equational arithmetic 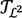 based on the algebra of lower elementary functions. The extension of this algebra to Grzegorczyk’s class ɛ2 can be justified by means of an additional finitistic choice principle, thus obtaining a second equational theory
based on the algebra of lower elementary functions. The extension of this algebra to Grzegorczyk’s class ɛ2 can be justified by means of an additional finitistic choice principle, thus obtaining a second equational theory 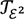 . It is unknown whether
. It is unknown whether 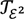 is strictly stronger than
is strictly stronger than 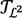 since ɛ2 may coincide with the class of lower elementary functions.
since ɛ2 may coincide with the class of lower elementary functions.
If the objects of arithmetic are taken to be binary numerals instead of tally numerals, then it becomes possible to provide a finitistic justification for a theory 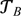 that may be incomparable to
that may be incomparable to 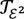 (neither of the two includes the other). I conclude by suggesting that the equational theory of Kalmar elementary functions is a strict upper bound for finitistic arithmetic.
(neither of the two includes the other). I conclude by suggesting that the equational theory of Kalmar elementary functions is a strict upper bound for finitistic arithmetic.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2010
References
BIBLIOGRAPHY
- 5
- Cited by

