Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Welch, P. D.
2009.
Games for Truth.
The Bulletin of Symbolic Logic,
Vol. 15,
Issue. 4,
p.
410.
Cantini, Andrea
2010.
Hartry Field, Saving Truth from Paradox.
Erkenntnis,
Vol. 72,
Issue. 3,
p.
417.
McGee, Vann
2010.
Field’s logic of truth.
Philosophical Studies,
Vol. 147,
Issue. 3,
p.
421.
Ripley, David
2010.
Book Reviews.
Studia Logica,
Vol. 94,
Issue. 1,
p.
139.
WELCH, P. D.
2011.
TRUTH, LOGICAL VALIDITY AND DETERMINATENESS: A COMMENTARY ON FIELD’SSAVING TRUTH FROM PARADOX.
The Review of Symbolic Logic,
Vol. 4,
Issue. 3,
p.
348.
MARTIN, DONALD A.
2011.
FIELD’S SAVING TRUTH FROM PARADOX: SOME THINGS IT DOESN’T DO.
The Review of Symbolic Logic,
Vol. 4,
Issue. 3,
p.
339.
HORSTEN, LEON
LEIGH, GRAHAM E.
LEITGEB, HANNES
and
WELCH, PHILIP
2012.
REVISION REVISITED.
The Review of Symbolic Logic,
Vol. 5,
Issue. 4,
p.
642.
Heck, Richard G.
2012.
More on ‘A Liar Paradox’.
Thought: A Journal of Philosophy,
Vol. 1,
Issue. 4,
p.
270.
Bacon, Andrew
2013.
Non-classical Metatheory for Non-classical Logics.
Journal of Philosophical Logic,
Vol. 42,
Issue. 2,
p.
335.
Welch, P.D.
2014.
Turing's Legacy.
p.
493.
WELCH, P. D.
2014.
SOME OBSERVATIONS ON TRUTH HIERARCHIES.
The Review of Symbolic Logic,
Vol. 7,
Issue. 1,
p.
1.
Schindler, Thomas
2015.
A Disquotational Theory of Truth as Strong as Z 2 − $Z_{2}^{-}$.
Journal of Philosophical Logic,
Vol. 44,
Issue. 4,
p.
395.
Bacon, Andrew
2015.
Paradoxes of Logical Equivalence and Identity.
Topoi,
Vol. 34,
Issue. 1,
p.
89.
Rivello, Edoardo
2015.
Periodicity and Reflexivity in Revision Sequences.
Studia Logica,
Vol. 103,
Issue. 6,
p.
1279.
Welch, P. D.
2015.
Turing’s Revolution.
p.
161.
Rossi, Lorenzo
2016.
Adding a Conditional to Kripke’s Theory of Truth.
Journal of Philosophical Logic,
Vol. 45,
Issue. 5,
p.
485.
Jenny, Matthias
2017.
Classicality Lost: K3 and LP after the Fall.
Thought: A Journal of Philosophy,
Vol. 6,
Issue. 1,
p.
43.
Gupta, Anil
and
Standefer, Shawn
2017.
Conditionals in Theories of Truth.
Journal of Philosophical Logic,
Vol. 46,
Issue. 1,
p.
27.
Welch, P. D.
2019.
Rethinking Revision.
Journal of Philosophical Logic,
Vol. 48,
Issue. 1,
p.
137.
Priest, Graham
2019.
Graham Priest on Dialetheism and Paraconsistency.
Vol. 18,
Issue. ,
p.
575.
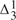 -CA0 (second-order number theory with a
-CA0 (second-order number theory with a 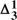 -comprehension axiom scheme) is insufficient. We briefly consider his claim to have produced a ‘revenge-immune’ solution to the semantic paradoxes by introducing this conditional. We remark that the notion of a ‘determinately true’ operator can be introduced in other settings.
-comprehension axiom scheme) is insufficient. We briefly consider his claim to have produced a ‘revenge-immune’ solution to the semantic paradoxes by introducing this conditional. We remark that the notion of a ‘determinately true’ operator can be introduced in other settings.
