Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-23T06:02:36.677Z Has data issue: false hasContentIssue false
  • English
  • Français

VARIETIES OF DE MORGAN MONOIDS: COVERS OF ATOMS

Published online by Cambridge University Press:  26 January 2019

T. MORASCHINI ,
J. G. RAFTERY  and
J. J. WANNENBURG
T. MORASCHINI*
Affiliation:
Institute of Computer Science, Academy of Sciences of the Czech Republic
J. G. RAFTERY*
Affiliation:
Department of Mathematics and Applied Mathematics, University of Pretoria
J. J. WANNENBURG*
Affiliation:
Department of Mathematics and Applied Mathematics, University of Pretoria; DST-NRF Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS)
*
*INSTITUTE OF COMPUTER SCIENCE ACADEMY OF SCIENCES OF THE CZECH REPUBLIC POD VODÁRENSKOU VĚŽÍ 2, 182 07 PRAGUE 8, CZECH REPUBLIC E-mail: moraschini@cs.cas.cz
†DEPARTMENT OF MATHEMATICS AND APPLIED MATHEMATICS UNIVERSITY OF PRETORIA, PRIVATE BAG X20, HATFIELD PRETORIA 0028, SOUTH AFRICA E-mail: james.raftery@up.ac.za
‡DEPARTMENT OF MATHEMATICS AND APPLIED MATHEMATICS UNIVERSITY OF PRETORIA, PRIVATE BAG X20, HATFIELD PRETORIA 0028, AND DST-NRF CENTRE OF EXCELLENCE IN MATHEMATICAL AND STATISTICAL SCIENCES (COE-MASS) SOUTH AFRICA E-mail: jamie.wannenburg@up.ac.za
Get access Rights & Permissions [Opens in a new window]

Abstract

The variety DMM of De Morgan monoids has just four minimal subvarieties. The join-irreducible covers of these atoms in the subvariety lattice of DMM are investigated. One of the two atoms consisting of idempotent algebras has no such cover; the other has just one. The remaining two atoms lack nontrivial idempotent members. They are generated, respectively, by 4-element De Morgan monoids C4 and D4, where C4 is the only nontrivial 0-generated algebra onto which finitely subdirectly irreducible De Morgan monoids may be mapped by noninjective homomorphisms. The homomorphic preimages of C4 within DMM (together with the trivial De Morgan monoids) constitute a proper quasivariety, which is shown to have a largest subvariety U. The covers of the variety 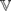(C4) within U are revealed here. There are just ten of them (all finitely generated). In exactly six of these ten varieties, all nontrivial members have C4 as a retract. In the varietal join of those six classes, every subquasivariety is a variety—in fact, every finite subdirectly irreducible algebra is projective. Beyond U, all covers of 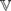(C4) [or of 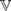(D4)] within DMM are discriminator varieties. Of these, we identify infinitely many that are finitely generated, and some that are not. We also prove that there are just 68 minimal quasivarieties of De Morgan monoids.

Keywords

Primary 03B4706D9906F05Secondary 03G2506D30De Morgan monoidSugihara monoidDunn monoidresiduated latticerelevance logic
Type
Research Article
Information
The Review of Symbolic Logic , Volume 13 , Issue 2 , June 2020 , pp. 338 - 374
Copyright
Copyright © Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Anderson, A. R. & Belnap, N. D. Jr. (1975). Entailment: The Logic of Relevance and Necessity, Vol. 1. Princeton, NJ: Princeton University Press.Google Scholar
Bergman, C. (2012). Universal Algebra. Fundamentals and Selected Topics. Boca Raton, FL: CRC Press.Google Scholar
Bergman, C. & McKenzie, R. (1990). Minimal varieties and quasivarieties. Journal of the Australian Mathematical Society Series A, 48, 133–147.CrossRefGoogle Scholar
Blok, W. J., Köhler, P., & Pigozzi, D. (1984). On the structure of varieties with equationally definable principal congruences II. Algebra Universalis, 18, 334–379.CrossRefGoogle Scholar
Blok, W. J. & Pigozzi, D. (1989). Algebraizable Logics. Memoirs of the American Mathematical Society, Vol. 396. Providence, RI: American Mathematical Society.Google Scholar
Burris, S. & Sankappanavar, H. P. (1981). A Course in Universal Algebra. Graduate Texts in Mathematics. New York: Springer-Verlag.Google Scholar
Dunn, J. M. (1966). The Algebra of Intensional Logics. Ph.D. Thesis, University of Pittsburgh.Google Scholar
Dunn, J. M. (1970). Algebraic completeness results for R-mingle and its extensions. Journal of Symbolic Logic, 35, 1–13.CrossRefGoogle Scholar
Fried, E. & Kiss, E. W. (1983). Connection between congruence-lattices and polynomial properties. Algebra Universalis, 17, 227–262.CrossRefGoogle Scholar
Galatos, N. (2005). Minimal varieties of residuated lattices. Algebra Universalis, 52, 215–239.CrossRefGoogle Scholar
Galatos, N., Jipsen, P., Kowalski, T., & Ono, H. (2007). Residuated Lattices. An Algebraic Glimpse at Substructural Logics. Studies in Logic and the Foundations of Mathematics, Vol. 151. Amsterdam: Elsevier.Google Scholar
Galatos, N. & Raftery, J. G. (2012). A category equivalence for odd Sugihara monoids and its applications. Journal of Pure and Applied Algebra, 216, 2177–2192.CrossRefGoogle Scholar
Galatos, N. & Raftery, J. G. (2015). Idempotent residuated structures: Some category equivalences and their applications. Transactions of the American Mathematical Society, 367, 3189–3223.CrossRefGoogle Scholar
Gorbunov, V. A. (1976). Lattices of quasivarieties. Algebra and Logic, 15, 275–288.CrossRefGoogle Scholar
Hart, J., Rafter, L., & Tsinakis, C. (2002). The structure of commutative residuated lattices. International Journal of Algebra and Computation, 12, 509–524.CrossRefGoogle Scholar
Jónsson, B. (1967). Algebras whose congruence lattices are distributive. Mathematica Scandinavica, 21, 110–121.CrossRefGoogle Scholar
Jońsson, B. (1972). Topics in Universal Algebra. Lecture Notes in Mathematics, Vol. 250. Berlin and New York: Springer-Verlag.CrossRefGoogle Scholar
Jónsson, B. (1995). Congruence distributive varieties. Mathematica Japonicae, 42, 353–401.Google Scholar
Meyer, R. K. (1972). Conservative extension in relevant implication. Studia Logica, 31, 39–46.CrossRefGoogle Scholar
Meyer, R. K. (1973). On conserving positive logics. Notre Dame Journal of Formal Logic, 14, 224–236.CrossRefGoogle Scholar
Meyer, R. K. (1986). Sentential constants in R and R¬. Studia Logica, 45, 301–327.CrossRefGoogle Scholar
Meyer, R. K., Dunn, J. M., & Leblanc, H. (1974). Completeness of relevant quantification theories. Notre Dame Journal of Formal Logic, 15, 97–121.CrossRefGoogle Scholar
Moraschini, T., Raftery, J. G., & Wannenburg, J. J. Varieties of De Morgan monoids: Minimality and irreducible algebras. Journal of Pure and Applied Algebra, in preparation. https://doi.org/10.1016/j.jpaa.2018.09.015.Google Scholar
Olson, J. S. & Raftery, J. G. (2007). Positive Sugihara monoids. Algebra Universalis, 57, 75–99.CrossRefGoogle Scholar
Slaney, J. K. (1985). 3088 varieties: A solution to the Ackermann constant problem. Journal of Symbolic Logic, 50, 487–501.CrossRefGoogle Scholar
Slaney, J. K. (1989). On the structure of De Morgan monoids with corollaries on relevant logic and theories. Notre Dame Journal of Formal Logic, 30, 117–129.CrossRefGoogle Scholar
Slaney, J. K. (1993). Sentential constants in systems near R. Studia Logica, 52, 443–455.CrossRefGoogle Scholar
Urquhart, A. (1984). The undecidability of entailment and relevant implication. Journal of Symbolic Logic, 49, 1059–1073.CrossRefGoogle Scholar
Wroński, A. (1974). The degree of completeness of some fragments of the intuitionistic propositional logic. Reports on Mathematical Logic, 2, 55–62.Google Scholar