Hostname: page-component-7dd5485656-6kn8j Total loading time: 0 Render date: 2025-10-31T12:00:04.615Z Has data issue: false hasContentIssue false
  • English
  • Français

Phase Transition at the Metric Elastic Universe

Published online by Cambridge University Press:  25 May 2016

Alexander Gusev
Alexander Gusev*
Affiliation:
Department of General Relativity and Astronomy, Kazan State University, 18, Lenin str., Kazan, 420008, Russia

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

At the last time the concept of the curved space-time as the some medium with stress tensor σαβ on the right part of Einstein equation is extensively studied in the frame of the Sakharov - Wheeler metric elasticity(Sakharov (1967), Wheeler (1970)). The physical cosmology pre- dicts a different phase transitions (Linde (1990), Guth (1991)). In the frame of Relativistic Theory of Finite Deformations (RTFD) (Gusev (1986)) the transition from the initial state 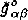of the Universe (Minkowskian's vacuum, quasi-vacuum(Gliner (1965), Zel'dovich (1968)) to the final state 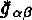of the Universe(Friedmann space, de Sitter space) has the form of phase transition(Gusev (1989) which is connected with different space-time symmetry of the initial and final states of Universe(from the point of view of isometric group Gn of space). In the RTFD (Gusev (1983), Gusev (1989)) the space-time is described by deformation tensor 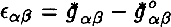of the three-dimensional surfaces, and the Einstein's equations are viewed as the constitutive relations between the deformations ∊αβ and stresses σαβ. The vacuum state of Universe have the visible zero physical characteristics and one is unsteady relatively quantum and topological deformations (Gunzig & Nardone (1989), Guth (1991)). Deformations of vacuum state, identifying with empty Mikowskian's space are described the deformations tensor ∊αβ, where 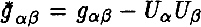the metrical tensor of deformation state of 3-geometry on the hypersurface, which is ortogonaled to the four-velocity 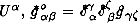is the 3 -geometry of initial state, 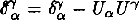is a projection tensor.

Information

Type
Part II: Contributed Papers
Information
Symposium - International Astronomical Union , Volume 168: Examining the Big Bang and the Diffuse Background Radiations , 1996 , pp. 569 - 570
Copyright
Copyright © Kluwer 1996 

References

Gliner, E.B., (1965), Zhurnal eksper. i teoretich. fiziki., 49, p.542.Google Scholar
Gunzig, E., Nardone, P., (1989), Int. J. Theor. Phys., 28, p.943.CrossRefGoogle Scholar
Gusev, A.V., (1983), Proc. Kazan Astr. Observatory, 47, p.126.Google Scholar
Gusev, A.V., (1986), Proc. Kazan Astr. Observatory, 50, p.33.Google Scholar
Gusev, A.V., (1989), Proc. Kazan Astr. Observatory, 52, p.114.Google Scholar
Guth, A.H., (1991), Physica Scripta, 36, p.237.CrossRefGoogle Scholar
Hoyle, F., Barbidge, G., Narlikar, J.V. (1993), Ap. J, 410, p.437.Google Scholar
Landau, L.D., Lifshitz, E.M., (1976), Statisticheskay fizika, Moscow, Nauka.Google Scholar
Linde, A.D., (1990), Elementary Particle Physics and Inflationary Cosmology, Moscow, Nauka.Google Scholar
Misner, C.W., Thorne, K.S. and Wheeler, J. A., (1973), Gravitation, San Francisco, Freeman.Google Scholar
Prigogine, I. et al, (1988), Proc. Nat. Acad. Sci. USA, 85, p.7428.CrossRefGoogle Scholar
Sakharov, A.D., (1967), Dokl. Akad. Nauk USSR, 177, p.70.Google Scholar
Zel'dovich, Ya.B., (1968), Usp. Phys. Nauk, 95, p.209.CrossRefGoogle Scholar