1. The use of string multiphonics in my compositions
Ever since the early 1990s timbre has played a very important role in my work. Experimental playing techniques, noise and combinations of individual instrumental sounds with other unrelated instruments have been of particular interest to me. A parallel line of inquiry, which I began to pursue in 1982, was my work with microtonality. This meant that natural harmonics began to play a large role in my compositions for string instruments (both for the airy heights characteristic of the higher harmonics and for the microtonal deviations such as the natural seventh). At the time, there was already a well-established body of knowledge about woodwind multiphonics, and in collaborations with performers such as Peter Veale (then the oboist in Ensemble Recherche), the flutist Normisa Pereira da Silva and the clarinettist Diego Montes (both members of the Thürmchen Ensemble) I began using woodwind multiphonics often and prominently in my compositions.
Figure 1: Caspar Johannes Walter, durchscheinende Etüde VIII/d (1991), 3rd movement, bars 87–89, © 1991 Thürmchen Verlag.
See video example: https://vimeo.com/359731910
My work as a performer began with the founding of the Thürmchen Ensemble in 1992. Experiments on the cello, especially in the area of natural harmonics, led me to expand conventional playing techniques. High natural harmonics that produce an extreme shift in register and special harmonic relationships when the player transitions from harmonic finger pressure to a normal stopped note are a characteristic element of my elegia, composed in 1992, from the cycle glissando, elegia e capriccio for cello solo.
Figure 2: elegia from glissando, elegia e capriccio (1992–95) for cello solo, beginning, © 1995 Thürmchen Verlag.
See video example: https://vimeo.com/359731935
The guiding compositional principle was to create the maximum change in the sounding result with minimal movement of the fingers of the left hand. In order to explore the different ways to exploit all the possible positions of the natural harmonics I constructed a table of the natural harmonics.
Figure 3: Table of natural harmonics, from the early 1990s
In practising compositions employing many high harmonics it is unavoidable that multiphonics will occur when the attack of a complicated harmonic is slightly off (the 13th partial played in the position slightly higher than a minor sixth above the open string right at the beginning of elegia in Figure 2 is a good example of such a passage). This can be avoided by being more exacting with the articulation. But these ‘mistakes’ are in themselves interesting, beautiful sounds. After detailed observations it became clear that these sonorities are a combination of a possible range of natural harmonics whose nodal points were very close together.
First use of string multiphonics (1994–2009)
The first compositions that deliberately employed these sorts of pure multiphonicsFootnote 1 based on natural harmonics were my Klavierquartett and the Höhlentrio for 3 cellos (both 1994).
Figure 4: Caspar Johannes Walter, Klavierquartett (1994), bars 142–152, © 1994 Thürmchen Verlag.
See video example: https://vimeo.com/359731951
The preface to the first version of the Höhlentrio introduces 28 different playing techniques and includes the following explanation for a pure multiphonic, not only describing the way multiphonics are used in this composition but also providing a roadmap for possible extensions of the technique:
= ‘Multiphonic’ on a harmonic fingering.
A complicated natural harmonic (e.g. 7th or 8th harmonic) is fingered and is attacked with a somewhat greater than normal bow pressure at a larger distance away from the bridge than normal (perhaps also with a slower bow speed) so that a spectrum of overtones of the open string (or the stopped note in the case of artificial harmonics) sounds. The overtones of the finger that is lightly stopping the string at the node can also augment the spectrum of the fundamental (to achieve this, the finger of the left hand may need to be pressed down more firmly – half-harmonic pressure). In this way, noticeable beatings can occur under the right circumstances.
Figure 5: Caspar Johannes Walter, Höhlentrio (2nd version, 1994/95), bars 18–21, © 1995 Thürmchen Verlag.
See video example: https://vimeo.com/359731969
In the same piece, a second type of multiphonic is introduced: the left hand stops a node on the ‘wrong’ side of the bow between the bow and the bridge close to the point of contact of the bow on the string, yielding a sound similar to an overblown bass clarinet multiphonic.
Figure 6: Caspar Johannes Walter, Höhlentrio (2nd version, 1994/95), bars 22–27, © 1995 Thürmchen Verlag.
See video example: https://vimeo.com/359731978
My compositions in the mid-1990s and early 2000s make extensive use of both types of string multiphonics: pure multiphonics for all string instruments, at least in the finger positions a minor sixth and a tritone above the open string; and the ‘bass-clarinet-like’ multiphonics on the lower strings of the violin, viola and cello with the left hand stopping the string on the other side of the bow. The notation and explanation for the last technique can, for example, be found in the preface to Drei Ansichten (1997/99):
= play with the bow on ‘the wrong side of the fingers’ (between the finger stopping the string and the nut). By applying heavy bow pressure, a multiphonic similar to a bass clarinet multiphonic should emerge.
Examples of both types of multiphonics can be found in my chamber music and ensemble works, schwierig genug, den Ernst zu begreifen (1995), Spuk I (1995), Eine Musik für Werner K (1997/99), weg von der Null (1999), Angst und Ahnung (2002, this piece also features multiphonics in the solo voice part), Fünf Ohren (2003) and metrische Dissonanzen (2009) as well as in the solo parts of the orchestral compositions such as Lebenslinie for violin, cello and orchestra (2002), and Zeichnung for violin, 4 solo percussionists and orchestra (2003/04).
The cello trio Flattergeist (2007) represents a special case. Here a new type of cello multiphonic was introduced: plucking on both sides above and below a glass resting on the string. I was especially interested in the tripartite relationship between the open string, the sound on the section of the string between the glass and the bridge, and the sound on the other section of the string between the glass and the nut always created a pitch structure that consisted of relationships from the undertone series. This was in marked contrast to the overtone relationships found in pure multiphonics. Particularly when performing glissando gestures with the glass (this technique yields pizzicati with an especially beautiful, long sustain), this undertone structure leads to a completely novel harmonic texture.
Figure 7: Caspar Johannes Walter, Flattergeist (2007), bars 106–110, © 2007 Thürmchen Verlag.
See video example: https://vimeo.com/359731995
Systematic use of string and piano multiphonics (after 2009)
Over the years, I became more involved with identifying the pitches contained in a given pure multiphonic and why they occurred. It became clear that the number of the partials of the harmonic spectrum heard in a given multiphonic followed some sort of general rule. In my ‘favourite’ multiphonic, fingered somewhat higher that the minor sixth, there is a central pitch that can be sounded in isolation: the 13th partial. As a ‘normal’ natural harmonic, it would be fingered exactly there, at the 5th node of the 13th harmonic. In the multiphonic, the partials 8, 5 and 3 were predictably present. In my ‘second favourite’ multiphonic on the tritone, it behaved similarly. Depending on whether it was a somewhat larger or smaller tritone, the central pitch was the 10th or 11th partial. In the multiphonic, the partials 7, 4 and 3 were present. These configurations of numbers (3,5,8,13–3,4,7,10–3,4,7,11) were familiar to me from my work with chords based on difference tones, in which two core pitches are combined with the sums and differences of these core pitches. 13 and 3 are the sum and difference of 5 and 8. With a centre of 4 and 7, the sum is 11 and the difference is 3; with a centre of 3 and 7, it is 10 and 4.
Based on these observations, I began a detailed investigation of these structures in the summer of 2008 and arrived at a procedure that I later termed the fraction windowing algorithm, which allowed me to predict the sound of a multiphonic based on the point of contact of the finger with the string. This is not to say that empirical work with physical instruments was not an essential part of the project: one especially nice moment was when I was able to uncover a mistake in my logic while checking the results on a Bösendorfer 200 grand piano (for this heavily theoretical research project, I chose the piano as the reference for a vibrating string rather than my instrument, the cello, as everything is much clearer and less prone to errors on the piano).
Building on these investigations into the mathematical structure of pure multiphonics, I decided to shift the focus of my compositional work to the piano. Unlike string instruments every model of grand piano is different, so it was important to investigate the differences and similarities between various makes of piano (subsequently I have made alternative versions of the same piece for Steinway D, Steinway B, Bechstein, Bösendorfer and others). It is also important not to damage the instruments with techniques performed directly on the strings so I use adjustable protective strips, playing with gloves, or frames with a protective gauze net containing markings, which can be securely attached to the piano frame.
The first piece of this kind, versunkene Form, was written as a compulsory piece for the Bechstein Piano Competition in 2009. The commission specified the exact instrument (a Bechstein concert grand). I chose multiphonics and harmonics that were easy to find on a ‘map’ of the inside of the piano and to simplify the performer's task, I provided extensive diagrams and video tutorials.
Figure 8: Caspar Johannes Walter, versunkene Form (2009), bars 13–15, © 2009 Thürmchen Verlag.
See video example: https://vimeo.com/359732013
While versunkene Form does not require any sort of preparation of the piano, Aus dem Leben der Amöben (2010) for three clarinets and piano uses a series of rubber strips that can be adjusted to fit different models of pianos and can be installed in a few minutes. The harmonics or multiphonics are fingered by pressing down on rubber strips stretched over the strings, which are attached to moveable guide rails that are clamped to the piano frame.
Figure 9: Instructions for the preparation of the piano for Aus dem Leben der Amöben.
The piano technician for the WDR was so impressed by the protective gauze frame insert for Interferenzen (2010), a piece in which four percussionists play the inside of the piano, that she allowed us to use WDR's best concert grand piano for the world premiere. The gauze net stretched over the frame rests less than a millimetre over the strings; it serves as a surface to place markings and to protect the strings from the moisture on the players’ fingers. Removing the frame took less than a minute and left no traces; the same instrument was used to play Janáček's Concertino directly after my piece.
Figure 10: The frame insert for Interferenzen.
Additional multiphonic types (after 2013)
Eisklänge (2012) features a new type of multiphonic, in this case for the clarinet: multiphonics performed on ‘half’ of the clarinet (just the upper joint) with the end of the tube covered by the player's free hand. These extremely soft and delicate sounds are used here due to their similarity to different piano sounds, multiphonics, harmonics and noises.
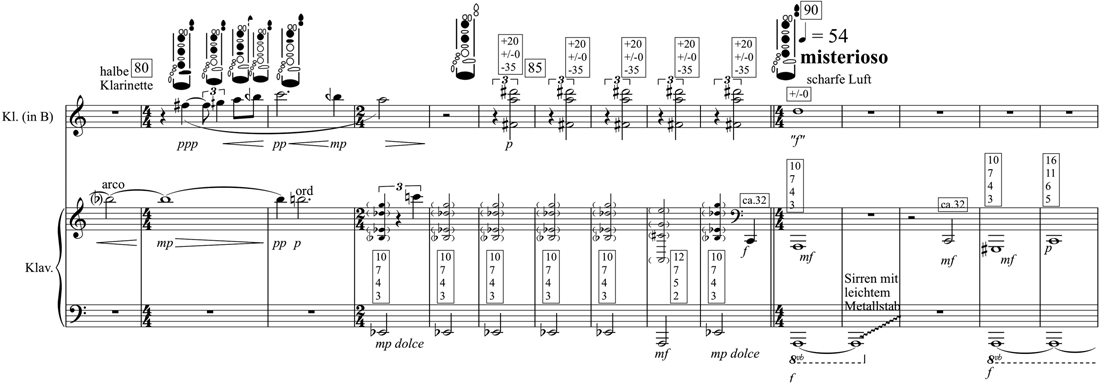
Figure 11: Caspar Johannes Walter, Eisklänge (2012), bars 79–94, © 2012 Thürmchen Verlag.
See video example: https://vimeo.com/359732036
Such composite sounds can also be generated by a single instrument; I call these hybrid multiphonics. split tones 3 (2014) uses two types of these hybrid multiphonics simultaneously. In Figure 12 the pure multiphonics discussed above are juxtaposed with a hybrid multiphonic in the cello as well as the piano part. The square notehead in the middle of the senza tempo bar in the piano part indicates a note prepared with an elastic mass of pressure-sensitive adhesive putty (Blu Tack) so that, in addition to a clear harmonic, a percussive attack (similar in sound to a temple block) can be heard whose pitch can be adjusted by modifying the mass and the position of the adhesive on the string. The last sound in the cello alternates between a relatively harsh overbowed sound, in which the pitch where the bow makes contact with the string can be heard, and a very faint, pale sound, centred around the pitch fingered by the left hand; in the transitional phase when the bow pressure is reduced, both extremely disparate timbres sound simultaneously. I have termed such multiphonics string split tones (analogous to the split tones on brass instruments where, by modifying the embouchure, a multiphonic is produced that lies between two partials).
Figure 12: Caspar Johannes Walter, split tones 3 (2nd version, 2014), bars 42–44, © 2014 Thürmchen Verlag.
See video example: https://vimeo.com/359732052
These cello split tones can be found in bars 63–65 of Figure 13 in their stable form, while the piano part exhibits a series of different sound types: in bars 57–58, ‘as if’ notes generated by heavily muting very low clusters at different positions; in bars 58–59 and 66, the player scrapes with the fingernail (or a plectrum) on the wrapping of a bass string in a manner that yields a precisely pitched glissando; and bars 59–60 again feature the hybrid prepared piano multiphonics.
Figure 13: Caspar Johannes Walter, split tones 3 (2nd version, 2014), bars 57–67, © 2014 Thürmchen Verlag.
See video example: https://vimeo.com/359732067
These types of sounds are found across the entire split tone cycle: split tone 1 (2013) for cello solo introduced the split-tone multiphonic into the repertoire of multiphonics, and the piano parts in split tones 2 (2013/14) for clarinet and two pianos weave a web of scraping sounds, harmonics, pure multiphonics and hybrid piano preparation multiphonics.
Another exciting and fertile area for the investigation of string multiphonics is artificial pure multiphonics (based on artificial harmonics), which can also be played as a glissando. As the interest in string multiphonics has increased dramatically in recent years, there are now many performers who are experimenting with these techniques. David Eggert showed me how it was possible to play good sounding glissando multiphonics with a tritone artificial harmonic fingering by keeping the bow position very far away from the bridge (in this position, the bow makes contact at the crest of the second wave of the central tone instead of the first wave nearer to the bridge). I wrote a duo for the multiphonic specialist Ellen Fallowfield that uses these sounds.
Figure 14: Caspar Johannes Walter, multiphonic objects gliding through 43-tone space (2014), bars 11–18, © 2014 Thürmchen Verlag.
See video example: https://vimeo.com/359732087
After working with the above types, I began experimenting with pure multiphonics that contained very high partials. I noticed that a two-voice counterpoint consisting of a new fundamental and a very prominent high partial emerges from a high natural harmonic or pure multiphonic when the finger of the left is pressed down while maintaining constant bow pressure and bow position. These dyads can span a range of almost four octaves. In my cycle black rotation I worked with these sort of sound complexes. Both sonorities approach E7, in one case as the 12th partial of string I and in the second case as the 18th partial of string II. When the finger is pressed down, the E7 harmonic has a tendency to shift to a quasi-harmonic pitch that is as close as possible to E7. In the following example, the E7 on string I becomes a somewhat sharp F#7 which is the 8th partial of the fingered F#4. On string II, it becomes a very low E@7, which is the 12th partial of the fingered A@4. Depending on how the bow is articulated, the E7 can also shift to other useable partials. I assume that the string does not tend to continue sounding the E7 when the finger is depressed because this frequency would then represent a complicated partial of the fingered pitch: on string I, the 7th partial (the 8th or even the 10th partial is much easier to make sound here); and on string II, it would be the 13th partial (here the 12th partial is clearly more stable). See Figure 15. As these sounds are relatively difficult to control, I have mostly used them as prerecorded material mixed with live instruments in my compositions (see Figure 16).
Figure 15: The development of quasi-harmonic dyads from high pure multiphonics.
See video example: https://vimeo.com/359732120
Figure 16: Caspar Johannes Walter, black rotation 2, bars 8–16, © 2018 Delirium Edition.
See video example: https://vimeo.com/359732133
Pedal steel guitar
The pure multiphonics on the piano can be transferred to other stringed instruments. In the course of my research on Harry Partch at the Universities of the Arts in Basel and Bern, I acquired a pedal steel guitar so that I could recreate the tuning and playing techniques used on Partch's 10-string adapted guitar. The steel strings and the technique of playing with a glass slide where the guitar is played flat in a horizonal position are exactly the same as the Partch model. Using the seven freely adjustable pedals, it is even possible to switch between U-tonality and O-tonality tunings (similar to Partch's compositions). The pedal steel guitar is capable of playing extraordinarily clear pure multiphonics that can be shifted in pitch using the slide or pedals. Schwebende Symmetrien (2015) combines these sorts of multiphonics with multiphonics in the piano and the strings (Figures 17 and 18).
Figure 17: Caspar Johannes Walter, Schwebende Symmetrien (2015), overview of the sounds played on the pedal steel guitar, © 2015 Caspar Johannes Walter.
Figure 18: Caspar Johannes Walter, Schwebende Symmetrien (2015), bars 140–147, © 2015 Thürmchen Verlag.
See video example: https://vimeo.com/359732152
Harp
The harp also lends itself to the exploration of harmonics and pure multiphonics. On the lower metal-bound strings partials up to at least the 12th are playable as harmonics, and multiphonics offering many microtonal possibilities as the strings can be easily retuned and then transposed twice using the pedals. In Enharmonische Utopien II (2017), I was able to explore a wide field of enharmonic relationships in quasi just intonation by only retuning six strings. A somewhat noisy passage featuring very low multiphonics can be seen in Figure 19.
Figure 19: Caspar Johannes Walter, Enharmonische Utopien II (2017), bars 68–77, © 2017 Thürmchen Verlag.
See video example: https://vimeo.com/359732174
In 2018 I extended these harmonic ideas and focused more intensively on the harp. In collaboration with Alice Belugou we developed a scordatura that gave rise to a field of quasi just intervals in three dimensions (fifths, thirds and natural sevenths) that could be performed using the pedals, as harmonics, and also in multiphonics. This tuning system was even able to integrate quarter tones into the context of just intonation.
Figure 20: harp scordatura for cubic relationships II, This is what they call a Comma (both 2018) and the cycle Flatterecho I–III (2019).
In Figure 21 retuned strings, harmonics and multiphonics on the harp provide reference pitches for a vocal ensemble, making it possible to perform very fine enharmonic modulations in complex harmonic textures.
Figure 21: Caspar Johannes Walter, cubic relationships II (2018), bars 29–32, © 2018 Thürmchen Verlag.
See video example: https://vimeo.com/359732196
The solo passage from Flatterecho I for harp and two miniature loudspeakers, in Figure 22, demonstrates an alien dissonant musical language built from the harp techniques discussed above.
Figure 22: Caspar Johannes Walter, Flatterecho I (2019), bars 77–81, © 2019 Thürmchen Verlag.
See video example: https://vimeo.com/359732213
As a fascinating example of an instrumental technique that skirts the conventional ideal of instrumental sound, focused on a full sound and a source of concrete, non-tempered harmonic structures, multiphonics have shaped many more of my compositions than those mentioned in this text. Given the growing interest in multiphonics and the practicalities of how to perform them from the younger generation of performers, an open exchange of theoretical, artistic and practical information is sure to be helpful. I hope this text can be part of this evolving project.
2. Mathematics: the fraction windowing algorithm and continued fractions
Several years ago,Footnote 2 when I began to study the structure of the frequencies present in multiphonics on vibrating strings,Footnote 3 it occurred to me that the partials (integer multiples of the frequency of the fundamental pitch of the string) in a given multiphonic seemed to follow some sort of orderly mathematical structure. Often it was the case that it was possible to discern a four-note chord by ear; these chords consisted of two central frequencies and two additional pitches that represented the sum and the difference of these central frequencies. Adjacent to such a multiphonic, the point of contact on the string for two further multiphonics can be found. In these neighbouring multiphonics, the sum tone of the first multiphonic becomes one of the central tones (accordingly, the partial numbers increase). By continuing these processes step by step, I determined that the location of points of contact for multiphonics, represented as fractions of the total string length, can be mapped across the entire length of the string. I then developed an algorithm to compute all the possible sounds in an idealised system (the actual limitations imposed by various parameters in a physical system were not considered in this model): the fraction windowing algorithm. The ‘multiphonic maps’ of piano strings, which were based on this algorithm, have since become an important basis for composing and performing music with these sorts of multiphonics. By running the algorithm backwards it is also possible to find the point of contact for a multiphonic when only two of the sounding components are known.
A large number of apps that are designed to illustrate various phenomena in the areas of microtonality, pitch systems and rhythmic theory are available on my website.Footnote 4 The app Piano Multiphonic CalculatorFootnote 5 is based on the fraction windowing algorithm and calculates multiphonics on piano strings in which two given partials of the fundamental are present. These two partials are entered as integers; the app then calculates where on the string the multiphonic containing both these partials as its highest partials is located. Running the fraction windowing algorithm backwards calculates all of the natural harmonics (including all corresponding nodes), yielding a series of nodes of partials that approach the location of the two given highest partials. These are the exact harmonics that can potentially sound as components of the multiphonic. Two such multiphonics can be entered into the calculator simultaneously (One and Two; coloured red and blue in the calculator), which makes it possible to investigate interferences between multiphonics.Footnote 6
This is a useful practical tool for composers and performers when working with these multiphonics. A video comparing the multiphonic simulation of the app with real multiphonics and showing how to operate the app can be found here: https://vimeo.com/359735538
The fraction windowing algorithm is a mathematical tool that does not take into consideration the physical limitations of instruments, such as the fact that it possible to hear very high partials in the sound depending on the material the string is made of, how it is excited, its length, thickness and tension.
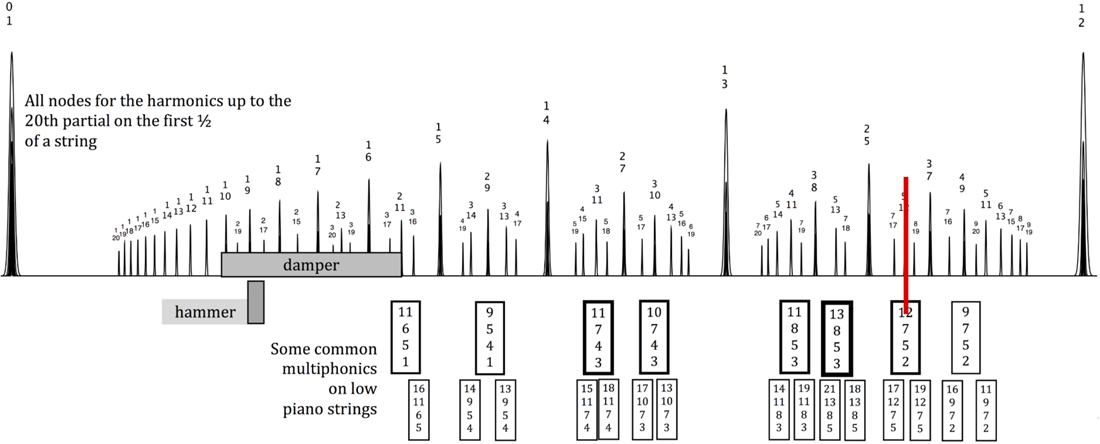
Figure 23: Multiphonic ‘map’ on the piano, screenshot from the app ‘Piano Multiphonic Calculator’: the point of contact for the multiphonic at 5/12 is marked with a solid bar extending below the map.
The rules of the fraction windowing algorithm
In choosing the name ‘fraction windowing algorithm’ I imagined that a number lies on a visible section of the continuous number line. This is the window. The frame of the window is initially defined by the natural number below the number inputted into the algorithm and the next highest natural number. These are the first two sides of the window frame (the stiles) and also the first two elements of the sequence. Now, as a third element, a bar is inserted between adjacent panes of glass (a muntin): to do this the mediant (Farey sum)Footnote 7 of the first two elements is calculated. This yields two window openings. A comparison of the number inputted with the last element of the sequence of fractions (the position of the last vertical bar that divided the window) determines in which of the two window openings the inputted number lies. Between the two visible frames’ boundaries (the last vertical bar and one of the two previous sides of the frame) a further mediant will be calculated, and the procedure will be continued until the number inputted is reached (when a fraction has been inputted) or the desired level of precision has been reached for a fractional approximation. Each new fraction in the sequence is always the simplest possible fraction between the active sides of the frame (these are the next vertical bars dividing the window above or below the inputted fraction), that is to say the fraction with the smallest denominator: in musical terms, the one with the lowest pitch. In this procedure, each point on the number line – every point on the string – can be represented or approximated mathematically.
Taking the natural numbersFootnote 8 as the starting point for the procedure, a sequence of fractions is generated. The initial two natural numbers in the form of 
${N \over 1}$ and 
$\textstyle{{N + 1} \over 1}$ are the first two sides (the frame boundaries) of the window. When applying the algorithm to the calculation of multiphonics on a vibrating string, these are 0 and 1 in the form 
${0 \over 1}$ and 
${1 \over 1}$ representing the beginning and end of the string. Each subsequent fraction of the sequence is the mediant of the two current frame sides. The third fraction in the sequence given these two initial terms is thus 
${{2N + 1} \over 2}$ (for a vibrating string, the result would be 
${1 \over 2}$).
Depending which section of the window is closed in the next step, the fractions that define the currently visible frame now become the active frame boundaries. The next fraction in the sequence is found between these two frame boundaries. In each case, one of the frame boundaries is the last term in the sequence of fractions; the second frame boundary may be the penultimate or earlier term. In the case of a regular convergence (alternating from below and above the inputted number), it is always the last two fractions. In a stepwise approach from one side (what I call mutation), the frame boundaries are the last fraction and not the penultimate, but rather an earlier term in the sequence that is still an active frame boundary: it is the window frame on the other side of the last vertical bar that is closest.
Figure 24: Fraction windowing approaching 5/12.
An extension of the fraction windowing algorithm
Running the algorithm backwards, using a subtraction procedure,Footnote 9 one can calculate the numerators of two fractions whose denominators are known. Between any two natural numbers, there are always exactly two of these pairs of fractions arranged symmetrically about the halfway position of the two natural numbers that form the frame boundaries (in the case of our string with a range of 0 to 1, the halfway point is 
${1 \over 2}$, and examples of a symmetrical pairs would be 
${1 \over 3}$, 
${2 \over 5}\; $ and 
${2 \over 3}$, 
${3 \over 5}$).
This extension is useful in a musical context. As the denominator corresponds to the pitch of the partial present in a multiphonic, this variation of the algorithm makes it possible to calculate the point on a vibrating string to touch so that these two given partials are present in the multiphonic; other pitches of the multiphonic can also be calculated using this procedure.
Fraction windowing algorithm and continued fractions
A side effect of the fraction windowing algorithm is that it is a simple and powerful tool for approximating rational and irrational numbers with fractions. Others have pointed out that my fraction windowing algorithm is actually a type of continued fraction and that continued fractions are even more effective when trying to identify a good fractional approximation. This is true: the sequence of fractions associated with a fractional approximation derived from a continued fraction is shorter than or at most the same length (in the case of sequences of Fibonacci fractionsFootnote 10 that lack mutations) as the sequence of fractions generated by the fraction windowing algorithm. Nevertheless, I was left with an uneasy feeling because the continued fractions skip over some good approximations that the fraction windowing algorithm includes, or these are only present if adjacent fractional approximation are included in the sequence. Thus, the sequence seems to be less homogeneous than the one generated by the fraction windowing algorithm. All in all, the sequence of fractional approximation derived from a continued fraction is made up exclusively of fractions derived from the fraction windowing algorithm, but the continued fraction method excluded some of these fractions, which represent the pitches that have the potential to sound as a component of a multiphonic. I felt that this was an unfortunate omission. It is a nice property of the fraction windowing algorithm that it is able to represent an audible sound result in numbers that can be explained as a logically consistent structure. Perhaps continued fractions would also be able accomplish this, as they are so closely related to the fraction windowing algorithm in terms of their internal mathematical structure.
This discrepancy (as well as the structures of numbers in general) continued to be of interest to me so, in the summer of 2017, I began to work more intensively on continued fractions. I am not a mathematician, nor do I have an overview of research in this area, so it is quite likely that the ideas formulated here are already well-established in the mathematical literature. However, in the course of my research, I was unable to find many relevant sources.Footnote 11 Here I have tried to provide a starting point for a discussion in the form of a collection of continued fraction examples, which will allow someone who is familiar with the material to simply and quickly follow my line of reasoning. An essential goal of my investigation was to find a type of continued fraction that includes all the fractions generated by my fraction windowing algorithm and no other fractions and then to make a classification of several variant types until I identified such a type (type 10).
In comparison to the fraction windowing algorithm, the inner workings of continued fractions reveal their affinity to music. Not only in the DNA of multiphonics, but also in the principle of combination tones with their sum and difference tones (and the harmonic consonances that they imply), and even in several aspects related to the handling of rhythm (in rhythmical morphing, the construction of intermediate states between two patterns) the mediants of two fractions are a decisive criteria of the inner structure. In these areas, the powerful mathematic tool of the continued fraction has the potential to open a wide field of applications. A quasi artistic approach to continued fractions per se, such as the construction of Sisyphus loops detailed above, allows us to go deeper into compositional thinking in a totally new way.
By using the two mentioned apps, it is possible, on the one hand, to explore the world of continued fractions in the way discussed above and, on the other hand, to make these abstract mathematical structures audible in the fascinating pitch structures of the string multiphonics. It is to be hoped that these tools will help us form a more detailed picture of string multiphonics, so that these will no longer be used only as exotic sound objects, but will become part of a mature musical language in which these sounds with all their different parameters are capable of creating rich and complicated relationships. The structures of numbers that can also be used to represent musical sounds are intrinsically fascinating both for musicians and mathematicians; I am interested in receiving feedback as to whether mathematicians have more succinctly formulated the ideas I have outlined.
Translated by Carter Williams
