Published online by Cambridge University Press: 07 April 2004
A superconducting metallic film bolometer in contactwith thermal bath of temperature T 0, is biased by a (i)constant current $I_{\mathrm{b} }$  , or by (ii) the constantvoltage $U_{\mathrm{b}}$
, or by (ii) the constantvoltage $U_{\mathrm{b}}$ 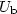 . The absorption of the time-dependentpower of a phonon beam W(t) elevates temperature of the film to $T(t)>T_{\mathrm{0}}$
. The absorption of the time-dependentpower of a phonon beam W(t) elevates temperature of the film to $T(t)>T_{\mathrm{0}}$  . The thermal contact of the bolometer withthe environment is characterized by the thermal conductance G,and it depends on $[T^{n}(t)-T_{\mathrm{0}}^{n}]$
. The thermal contact of the bolometer withthe environment is characterized by the thermal conductance G,and it depends on $[T^{n}(t)-T_{\mathrm{0}}^{n}]$  ( $n=4{-}6$
( $n=4{-}6$  ). Forboth above methods of bias, we derive ordinarynonautonomous nonlinear differential equations of the first order.These equations are numerically solved. The knowledge of W(t)allows one to calculate (i) $U_{\mathrm{b} }(t)$
). Forboth above methods of bias, we derive ordinarynonautonomous nonlinear differential equations of the first order.These equations are numerically solved. The knowledge of W(t)allows one to calculate (i) $U_{\mathrm{b} }(t)$  or (ii) $I_{\mathrm{b}}(t)$
or (ii) $I_{\mathrm{b}}(t)$  . The inverse problem of calculation of W(t)from known (i) $U_{\mathrm{b}}(t)$
. The inverse problem of calculation of W(t)from known (i) $U_{\mathrm{b}}(t)$ 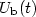 or (ii) $I_{\mathrm{b}}(t)$
or (ii) $I_{\mathrm{b}}(t)$  isalso solved. Using W(t) calculated in computer experiments, weobtained the bolometer signal, and compared it with results ofreal experiments performed on GaAs in which $I_{\mathrm{b}}$
isalso solved. Using W(t) calculated in computer experiments, weobtained the bolometer signal, and compared it with results ofreal experiments performed on GaAs in which $I_{\mathrm{b}}$ 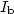 isfixed, and U is measured. Comparison of calculated results withresults obtained for the linearized model shows that thenonlinearity is essential for the correct description of metallicsuperconducting film bolometer response.
isfixed, and U is measured. Comparison of calculated results withresults obtained for the linearized model shows that thenonlinearity is essential for the correct description of metallicsuperconducting film bolometer response.