No CrossRef data available.
Article contents
Symbolic Specialization of Rewriting Logic Theories with Presto
Published online by Cambridge University Press: 11 February 2022
Abstract
This paper introduces 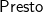 $\tt{{Presto}}$, a symbolic partial evaluator for Maude’s rewriting logic theories that can improve system analysis and verification. In
$\tt{{Presto}}$, a symbolic partial evaluator for Maude’s rewriting logic theories that can improve system analysis and verification. In 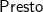 $\tt{{Presto}}$, the automated optimization of a conditional rewrite theory
$\tt{{Presto}}$, the automated optimization of a conditional rewrite theory 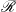 $\mathcal{R}$ (whose rules define the concurrent transitions of a system) is achieved by partially evaluating, with respect to the rules of
$\mathcal{R}$ (whose rules define the concurrent transitions of a system) is achieved by partially evaluating, with respect to the rules of 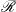 $\mathcal{R}$, an underlying, companion equational logic theory
$\mathcal{R}$, an underlying, companion equational logic theory 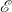 $\mathcal{E}$ that specifies the algebraic structure of the system states of
$\mathcal{E}$ that specifies the algebraic structure of the system states of 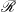 $\mathcal{R}$. This can be particularly useful for specializing an overly general equational theory
$\mathcal{R}$. This can be particularly useful for specializing an overly general equational theory 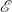 $\mathcal{E}$ whose operators may obey complex combinations of associativity, commutativity, and/or identity axioms, when being plugged into a host rewrite theory
$\mathcal{E}$ whose operators may obey complex combinations of associativity, commutativity, and/or identity axioms, when being plugged into a host rewrite theory 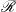 $\mathcal{R}$ as happens, for instance, in protocol analysis, where sophisticated equational theories for cryptography are used.
$\mathcal{R}$ as happens, for instance, in protocol analysis, where sophisticated equational theories for cryptography are used.  $\tt{{Presto}}$ implements different unfolding operators that are based on folding variant narrowing (the symbolic engine of Maude’s equational theories). When combined with an appropriate abstraction algorithm, they allow the specialization to be adapted to the theory termination behavior and bring significant improvement while ensuring strong correctness and termination of the specialization. We demonstrate the effectiveness of
$\tt{{Presto}}$ implements different unfolding operators that are based on folding variant narrowing (the symbolic engine of Maude’s equational theories). When combined with an appropriate abstraction algorithm, they allow the specialization to be adapted to the theory termination behavior and bring significant improvement while ensuring strong correctness and termination of the specialization. We demonstrate the effectiveness of  $\tt{{Presto}}$ in several examples of protocol analysis where it achieves a significant speed-up. Actually, the transformation provided by
$\tt{{Presto}}$ in several examples of protocol analysis where it achieves a significant speed-up. Actually, the transformation provided by  $\tt{{Presto}}$ may cut down an infinite folding variant narrowing space to a finite one, and moreover, some of the costly algebraic axioms and rule conditions may be eliminated as well. As far as we know, this is the first partial evaluator for Maude that respects the semantics of functional, logic, concurrent, and object-oriented computations.
$\tt{{Presto}}$ may cut down an infinite folding variant narrowing space to a finite one, and moreover, some of the costly algebraic axioms and rule conditions may be eliminated as well. As far as we know, this is the first partial evaluator for Maude that respects the semantics of functional, logic, concurrent, and object-oriented computations.
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
Footnotes
This research was partially supported by TAILOR, a project funded by EU Horizon 2020 research and innovation programme under GA No 952215, grant RTI2018-094403-B-C32 funded by MCIN/AEI/10.13039/501100011033 and by ”ERDF A way of making Europe”, and by Generalitat Valenciana under grant PROMETEO/2019/098. Julia Sapiña has been supported by the Generalitat Valenciana APOSTD/2019/127 grant.


