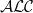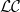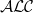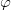1 Introduction
Preferential approaches to common sense reasoning by Kraus et al. (Reference Kraus, Lehmann and Magidor1990), Pearl (Reference Pearl1990), Lehmann and Magidor (Reference Lehmann and Magidor1992), Benferhat et al. (Reference Benferhat, Cayrol, Dubois, Lang and Prade1993), have been extended to description logics (DLs) to deal with inheritance with exceptions in ontologies, by allowing for non-strict inclusions, called typicality or defeasible inclusions, with different preferential semantics, for example, by Giordano et al. (Reference Giordano, Gliozzi, Olivetti and Pozzato2007) and Britz et al. (Reference Britz, Heidema, Meyer, Press and Sidney2008), and closure constructions, for example, by Casini and Straccia (Reference Casini, Straccia, Janhunen and Niemelä2010); Casini and Straccia (Reference Casini and Straccia2013a) and Giordano et al. (Reference Giordano, Gliozzi, Olivetti and Pozzato2015).
In recent work, a concept-wise multipreference semantics has been proposed by Giordano and Theseider Dupré (Reference Giordano and Theseider Dupré2020) as a semantics for ranked DL knowledge bases (KBs), that is KBs in which defeasible or typicality inclusions of the form
![]() ${\bf T}(C) \sqsubseteq D$
(meaning “the typical C’s are D’s” or “normally C’s are D’s”) are given a rank, a natural number, representing their strength, where T is a typicality operator (Giordano et al. Reference Giordano, Gliozzi, Olivetti and Pozzato2007), that singles out the typical instances of concept C. The concept-wise multipreference semantics takes into account preferences with respect to different concepts, and integrates them into a single global preference relation, which is used in the evaluation of defeasible inclusions. Answer set programming (ASP) and, in particular, the asprin framework for answer set preferences, by Brewka et al. (Reference Brewka, Delgrande, Romero and Schaub2015), is exploited to achieve defeasible reasoning under the multipreference approach for
${\bf T}(C) \sqsubseteq D$
(meaning “the typical C’s are D’s” or “normally C’s are D’s”) are given a rank, a natural number, representing their strength, where T is a typicality operator (Giordano et al. Reference Giordano, Gliozzi, Olivetti and Pozzato2007), that singles out the typical instances of concept C. The concept-wise multipreference semantics takes into account preferences with respect to different concepts, and integrates them into a single global preference relation, which is used in the evaluation of defeasible inclusions. Answer set programming (ASP) and, in particular, the asprin framework for answer set preferences, by Brewka et al. (Reference Brewka, Delgrande, Romero and Schaub2015), is exploited to achieve defeasible reasoning under the multipreference approach for
![]() ${\mathcal{EL}}^{+}_{\bot}$
(Baader et al. Reference Baader, Brandt, Lutz, Kaelbling and Saffiotti2005).
${\mathcal{EL}}^{+}_{\bot}$
(Baader et al. Reference Baader, Brandt, Lutz, Kaelbling and Saffiotti2005).
The multipreferential semantics has been extended by Giordano and Theseider Dupré (Reference Giordano and Theseider Dupré2021b) to weighted KBs, in which typicality inclusions have a real (positive or negative) weight, representing plausibility or implausibility. The multipreference semantics has been exploited to provide a preferential interpretation to Multilayer Perceptrons (MLPs, Haykin Reference Haykin1999), an approach previously considered by Giordano et al. (Reference Giordano, Gliozzi, Theseider Dupré, Calimeri, Perri and Zumpano2020); Giordano et al. (Reference Giordano, Gliozzi and Theseider Dupré2022) for self-organizing maps (SOMs, Kohonen et al. 2001). In both cases, considering the domain of all input stimuli presented to the network during training (or in the generalization phase), one can build a semantic interpretation describing the input–output behavior of the network as a multipreference interpretation, where preferences are associated to concepts. For MLPs, based on the fuzzy multipreference semantics for weighted KBs, a deep neural network can actually be regarded as a weighted conditional KB (Giordano and Theseider Dupré Reference Giordano and Theseider Dupré2021b). This rises the issue of defining proof methods for reasoning with weighted conditional KBs.
Undecidability results for fuzzy DLs with general inclusion axioms by Cerami and Straccia (Reference Cerami and Straccia2011) and Borgwardt and Peñaloza (Reference Borgwardt, Peñaloza and Press2012) motivate the investigation of many-valued approximations of fuzzy multipreference entailment. We then restrict to the case of finitely many-valued DLs, studied by García-Cerdaña et al. (2010), Bobillo and Straccia (Reference Bobillo and Straccia2011), Bobillo et al. (Reference Bobillo, Delgado, Gómez-Romero and Straccia2012), Borgwardt and Peñaloza (Reference Borgwardt and Peñaloza2013), and reconsider the fuzzy multipreference semantics based on the notions of coherent, faithful, and
![]() $\varphi$
-coherent model of a defeasible KB (Giordano and Theseider Dupré Reference Giordano and Theseider Dupré2021b; Giordano Reference Giordano2021a; Giordano Reference Giordano2021b). The last notion is suitable to characterize the stationary states of MLPs and is related to the previously introduced notions of multipreferential interpretation.
$\varphi$
-coherent model of a defeasible KB (Giordano and Theseider Dupré Reference Giordano and Theseider Dupré2021b; Giordano Reference Giordano2021a; Giordano Reference Giordano2021b). The last notion is suitable to characterize the stationary states of MLPs and is related to the previously introduced notions of multipreferential interpretation.
We consider the finitely many-valued Gödel DL
![]() $G_n \mathcal{ALC}$
, and the finitely many-valued Łukasiewicz DL,
$G_n \mathcal{ALC}$
, and the finitely many-valued Łukasiewicz DL,
![]() $\unicode{x0141}_n \mathcal{ALC}$
, and develop their extension with typicality and a semantic closure construction based on coherent, faithful, and
$\unicode{x0141}_n \mathcal{ALC}$
, and develop their extension with typicality and a semantic closure construction based on coherent, faithful, and
![]() $\varphi_n$
-coherent interpretations to deal with weighted KBs. For the boolean fragment
$\varphi_n$
-coherent interpretations to deal with weighted KBs. For the boolean fragment
![]() $\mathcal{LC}$
of
$\mathcal{LC}$
of
![]() $\mathcal{ALC}$
, which neither contains roles, nor universal and existential restrictions, we develop an ASP approach for deciding
$\mathcal{ALC}$
, which neither contains roles, nor universal and existential restrictions, we develop an ASP approach for deciding
![]() $\varphi_n$
-coherent entailment from weighted KBs in the finitely many-valued case. In particular, we develop an ASP encoding of a weighted KB and exploit asprin (see Brewka et al. Reference Brewka, Delgrande, Romero and Schaub2015) for defeasible reasoning, to prove typicality properties of a weighted conditional KB. From the soundness and completeness of the encoding, we also get a
$\varphi_n$
-coherent entailment from weighted KBs in the finitely many-valued case. In particular, we develop an ASP encoding of a weighted KB and exploit asprin (see Brewka et al. Reference Brewka, Delgrande, Romero and Schaub2015) for defeasible reasoning, to prove typicality properties of a weighted conditional KB. From the soundness and completeness of the encoding, we also get a
![]() $\Pi^p_2$
complexity upper bound for
$\Pi^p_2$
complexity upper bound for
![]() $\varphi_n$
-coherent entailment.
$\varphi_n$
-coherent entailment.
As a proof of concept, we experiment our approach over weighted KBs corresponding to some of the trained multilayer feedforward networks considered by Thrun et al. (Reference Thrun1991). We exploit ASP to verify some properties of the network expressed as typicality properties in the finite many-valued case. This is a step towards explainability of the black-box, in view of a trustworthy, reliable, and explainable AI (Adadi and Berrada Reference Adadi and Berrada2018; Guidotti et al. Reference Guidotti, Monreale, Ruggieri, Turini, Giannotti and Pedreschi2019; Arrieta et al. Reference Arrieta, Rodrguez, Ser, Bennetot, Tabik, Barbado, Garca, Gil-Lopez, Molina, Benjamins, Chatila and Herrera2020), and of an integrated use of symbolic reasoning and neural models.
2 Finitely many-valued
 $\boldsymbol{\mathcal{ALC}}$
$\boldsymbol{\mathcal{ALC}}$
Fuzzy DLs have been widely studied in the literature for representing vagueness in DLs, for example, by Straccia (Reference Straccia2005), Stoilos et al. (Reference Stoilos, Stamou, Tzouvaras, Pan and Horrocks2005), Lukasiewicz and Straccia (Reference Lukasiewicz and Straccia2009), Borgwardt and Peñaloza (Reference Borgwardt, Peñaloza and Press2012), Bobillo and Straccia (Reference Bobillo and Straccia2018), based on the idea that concepts and roles can be interpreted as fuzzy sets and fuzzy relations.
In fuzzy logic formulas have a truth degree from a truth space
![]() $\cal S$
, usually [0, 1], as in mathematical fuzzy logic (Cintula et al. 2011) or
$\cal S$
, usually [0, 1], as in mathematical fuzzy logic (Cintula et al. 2011) or
![]() $\{0, \frac{1}{n},\ldots, \frac{n-1}{n}, \frac{n}{n}\}$
, for an integer
$\{0, \frac{1}{n},\ldots, \frac{n-1}{n}, \frac{n}{n}\}$
, for an integer
![]() $n \geq 1$
.
$n \geq 1$
.
![]() $\cal S$
may as well be a complete lattice or a bilattice.
$\cal S$
may as well be a complete lattice or a bilattice.
The finitely many-valued case is also well studied for DLs (García-Cerdaña et al. 2010; Bobillo and Straccia Reference Bobillo and Straccia2011; Bobillo et al. Reference Bobillo, Delgado, Gómez-Romero and Straccia2012; Borgwardt and Peñaloza Reference Borgwardt and Peñaloza2013), and, in the following, we will consider a finitely many-valued extension of
![]() $\mathcal{ALC}$
with typicality.
$\mathcal{ALC}$
with typicality.
The basic
![]() $\mathcal{ALC}$
syntax features a set
$\mathcal{ALC}$
syntax features a set
![]() ${N_C}$
of concept names, a set
${N_C}$
of concept names, a set
![]() ${N_R}$
of role names and a set
${N_R}$
of role names and a set
![]() ${N_I}$
of individual names. The set of
${N_I}$
of individual names. The set of
![]() $\mathcal{ALC}$
concepts can be defined inductively:
$\mathcal{ALC}$
concepts can be defined inductively:
-
–
 $A \in N_C$
,
$A \in N_C$
,
 $\top$
and
$\top$
and
 $\bot$
are concepts;
$\bot$
are concepts; -
– if C and D are concepts, and
 $r \in N_R$
, then
$r \in N_R$
, then
 $C \sqcap D,\; C \sqcup D,\; \neg C, \; \forall r.C,\; \exists r.C$
are concepts.
$C \sqcap D,\; C \sqcup D,\; \neg C, \; \forall r.C,\; \exists r.C$
are concepts.
We assume the truth space to be
![]() ${\cal C}_n= \{0, \frac{1}{n},\ldots, \frac{n-1}{n}, \frac{n}{n}\}$
, for an integer
${\cal C}_n= \{0, \frac{1}{n},\ldots, \frac{n-1}{n}, \frac{n}{n}\}$
, for an integer
![]() $n \geq 1$
. A finitely many-valued interpretation for
$n \geq 1$
. A finitely many-valued interpretation for
![]() $\mathcal{ALC}$
is a pair
$\mathcal{ALC}$
is a pair
![]() $I=\langle \Delta, \cdot^I \rangle$
where:
$I=\langle \Delta, \cdot^I \rangle$
where:
![]() $\Delta$
is a non-empty domain and
$\Delta$
is a non-empty domain and
![]() $\cdot^I$
is an interpretation function that assigns to each
$\cdot^I$
is an interpretation function that assigns to each
![]() $a \in N_I$
a value
$a \in N_I$
a value
![]() $a^I \in\Delta$
, to each
$a^I \in\Delta$
, to each
![]() $A\in N_C$
a function
$A\in N_C$
a function
![]() $A^I : \Delta \rightarrow {\cal C}_n $
, to each
$A^I : \Delta \rightarrow {\cal C}_n $
, to each
![]() $r \in N_R$
a function
$r \in N_R$
a function
![]() $r^I: \Delta \times \Delta \rightarrow {\cal C}_n $
. A domain element
$r^I: \Delta \times \Delta \rightarrow {\cal C}_n $
. A domain element
![]() $x \in \Delta$
belongs to the extension of concept name A to some degree
$x \in \Delta$
belongs to the extension of concept name A to some degree
![]() $A^I(x)$
in
$A^I(x)$
in
![]() ${\cal C}_n$
. The interpretation function
${\cal C}_n$
. The interpretation function
![]() $\cdot^I$
is extended to complex concepts as follows:
$\cdot^I$
is extended to complex concepts as follows:
![]() $\top^I(x)=1$
,
$\top^I(x)=1$
,
![]() $\bot^I(x)=0$
,
$\bot^I(x)=0$
,
![]() $(\neg C)^I(x)= \ominus C^I(x)$
,
$(\neg C)^I(x)= \ominus C^I(x)$
,
![]() $(\exists r.C)^I(x) = sup_{y \in \Delta} \; r^I(x,y) \otimes C^I(y)$
,
$(\exists r.C)^I(x) = sup_{y \in \Delta} \; r^I(x,y) \otimes C^I(y)$
,
![]() $(C \sqcup D)^I(x) =C^I(x) \oplus D^I(x)$
$(C \sqcup D)^I(x) =C^I(x) \oplus D^I(x)$
![]() $(\forall r.C)^I (x) = inf_{y \in \Delta} \; r^I(x,y) \rhd C^I(y)$
,
$(\forall r.C)^I (x) = inf_{y \in \Delta} \; r^I(x,y) \rhd C^I(y)$
,
![]() $(C \sqcap D)^I(x) =C^I(x) \otimes D^I(x),$
$(C \sqcap D)^I(x) =C^I(x) \otimes D^I(x),$
where
![]() $x \in \Delta$
and
$x \in \Delta$
and
![]() $\otimes$
,
$\otimes$
,
![]() $\oplus$
,
$\oplus$
,
![]() $\rhd $
, and
$\rhd $
, and
![]() $\ominus$
are arbitrary but fixed t-norm, s-norm, implication function, and negation function (Lukasiewicz and Straccia Reference Lukasiewicz and Straccia2009). In particular, in this paper we consider two finitely many-valued DLs based on
$\ominus$
are arbitrary but fixed t-norm, s-norm, implication function, and negation function (Lukasiewicz and Straccia Reference Lukasiewicz and Straccia2009). In particular, in this paper we consider two finitely many-valued DLs based on
![]() $\mathcal{ALC}$
, the finitely many-valued Łukasiewicz DL
$\mathcal{ALC}$
, the finitely many-valued Łukasiewicz DL
![]() $\mathcal{ALC}$
(
$\mathcal{ALC}$
(
![]() $\unicode{x0141}_n \mathcal{ALC}$
in the following) as well as the finitely many-valued Gödel DL
$\unicode{x0141}_n \mathcal{ALC}$
in the following) as well as the finitely many-valued Gödel DL
![]() $\mathcal{ALC}$
, extended with a standard involutive negation
$\mathcal{ALC}$
, extended with a standard involutive negation
![]() $ \ominus a = 1-a$
(
$ \ominus a = 1-a$
(
![]() $G_n \mathcal{ALC}$
in the following). Such logics are defined along the lines of the finitely many-valued DL
$G_n \mathcal{ALC}$
in the following). Such logics are defined along the lines of the finitely many-valued DL
![]() $\cal SROIQ$
by Bobillo and Straccia (Reference Bobillo and Straccia2011), the logic GZ
$\cal SROIQ$
by Bobillo and Straccia (Reference Bobillo and Straccia2011), the logic GZ
![]() $\cal SROIQ$
by Bobillo et al. (Reference Bobillo, Delgado, Gómez-Romero and Straccia2012), and the logic
$\cal SROIQ$
by Bobillo et al. (Reference Bobillo, Delgado, Gómez-Romero and Straccia2012), and the logic
![]() $\mathcal{ALC}^*(S)$
by García-Cerdaña et al. (2010), where
$\mathcal{ALC}^*(S)$
by García-Cerdaña et al. (2010), where
![]() $*$
is a divisible finite t-norm over a chain of n elements.
$*$
is a divisible finite t-norm over a chain of n elements.
Specifically, in an
![]() $\unicode{x0141}_n \mathcal{ALC}$
interpretation, we let:
$\unicode{x0141}_n \mathcal{ALC}$
interpretation, we let:
![]() $a \otimes b= \max\{a+b-1,0\}$
,
$a \otimes b= \max\{a+b-1,0\}$
,
![]() $a \oplus b= \min\{a+b,1\}$
,
$a \oplus b= \min\{a+b,1\}$
,
![]() $a \rhd b= \min\{1- a+b,1\}$
, and
$a \rhd b= \min\{1- a+b,1\}$
, and
![]() $ \ominus a = 1-a$
. In a
$ \ominus a = 1-a$
. In a
![]() $G_n \mathcal{ALC}$
interpretation, we let:
$G_n \mathcal{ALC}$
interpretation, we let:
![]() $a \otimes b= \min\{a,b\}$
,
$a \otimes b= \min\{a,b\}$
,
![]() $a \oplus b= \max\{a,b\}$
,
$a \oplus b= \max\{a,b\}$
,
![]() $a \rhd b= 1$
if
$a \rhd b= 1$
if
![]() $a \leq b$
and b otherwise; and
$a \leq b$
and b otherwise; and
![]() $ \ominus a = 1-a$
.
$ \ominus a = 1-a$
.
The interpretation function
![]() $\cdot^I$
is also extended to
$\cdot^I$
is also extended to
![]() $\mathcal{ALC}$
concept inclusions of the form
$\mathcal{ALC}$
concept inclusions of the form
![]() $C \sqsubseteq D$
(where C and D are
$C \sqsubseteq D$
(where C and D are
![]() $\mathcal{ALC}$
concepts), and to
$\mathcal{ALC}$
concepts), and to
![]() $\mathcal{ALC}$
assertions of the form C(a) and r(a,b) (where C is an
$\mathcal{ALC}$
assertions of the form C(a) and r(a,b) (where C is an
![]() $\mathcal{ALC}$
concept,
$\mathcal{ALC}$
concept,
![]() $r\in N_R$
,
$r\in N_R$
,
![]() $a,b \in N_I$
), as follows:
$a,b \in N_I$
), as follows:
![]() $(C \sqsubseteq D)^I= inf_{x \in \Delta} C^I(x) \rhd D^I(x)$
,
$(C \sqsubseteq D)^I= inf_{x \in \Delta} C^I(x) \rhd D^I(x)$
,
![]() $(C(a))^I=C^I(a^I)$
,
$(C(a))^I=C^I(a^I)$
,
![]() $(R(a,b))^I=R^I(a^I,b^I)$
.
$(R(a,b))^I=R^I(a^I,b^I)$
.
A
![]() $G_n \mathcal{ALC}$
(
$G_n \mathcal{ALC}$
(
![]() $\unicode{x0141}_n \mathcal{ALC}$
) knowledge base K is a pair
$\unicode{x0141}_n \mathcal{ALC}$
) knowledge base K is a pair
![]() $({\cal T}, {\cal A})$
where
$({\cal T}, {\cal A})$
where
![]() ${\cal T}$
is a TBox and
${\cal T}$
is a TBox and
![]() ${\cal A}$
an ABox. A TBox
${\cal A}$
an ABox. A TBox
![]() ${\cal T}$
is a set of
${\cal T}$
is a set of
![]() $G_n \mathcal{ALC}$
(
$G_n \mathcal{ALC}$
(
![]() $\unicode{x0141}_n \mathcal{ALC}$
) concept inclusions of the form
$\unicode{x0141}_n \mathcal{ALC}$
) concept inclusions of the form
![]() $C \sqsubseteq D \;\theta\; \alpha$
, where
$C \sqsubseteq D \;\theta\; \alpha$
, where
![]() $C \sqsubseteq D$
is an
$C \sqsubseteq D$
is an
![]() $\mathcal{ALC}$
concept inclusion,
$\mathcal{ALC}$
concept inclusion,
![]() $\theta \in \{\geq,\leq,>,<\}$
and
$\theta \in \{\geq,\leq,>,<\}$
and
![]() $\alpha \in [0,1]$
. An ABox
$\alpha \in [0,1]$
. An ABox
![]() ${\cal A}$
is a set of
${\cal A}$
is a set of
![]() $G_n \mathcal{ALC}$
(
$G_n \mathcal{ALC}$
(
![]() $\unicode{x0141}_n \mathcal{ALC}$
) assertions of the form
$\unicode{x0141}_n \mathcal{ALC}$
) assertions of the form
![]() $C(a) \; \theta \alpha$
or
$C(a) \; \theta \alpha$
or
![]() $r(a,b) \; \theta \alpha$
, where C is an
$r(a,b) \; \theta \alpha$
, where C is an
![]() $\mathcal{ALC}$
concept,
$\mathcal{ALC}$
concept,
![]() $r\in N_R$
,
$r\in N_R$
,
![]() $a,b \in N_I$
,
$a,b \in N_I$
,
![]() $\theta \in \{{\geq,}\leq,>,<\}$
and
$\theta \in \{{\geq,}\leq,>,<\}$
and
![]() $\alpha \in [0,1]$
. The notions of satisfiability of a KB in a many-valued interpretation and of
$\alpha \in [0,1]$
. The notions of satisfiability of a KB in a many-valued interpretation and of
![]() $G_n \mathcal{ALC}$
(
$G_n \mathcal{ALC}$
(
![]() $\unicode{x0141}_n \mathcal{ALC}$
) entailment are defined as follows:
$\unicode{x0141}_n \mathcal{ALC}$
) entailment are defined as follows:
Definition 1 (Satisfiability and entailment for
![]() $G_n \mathcal{ALC}$
and
$G_n \mathcal{ALC}$
and
![]() $\unicode{x0141}_n \mathcal{ALC}$
) A
$\unicode{x0141}_n \mathcal{ALC}$
) A
![]() $G_n \mathcal{ALC}$
(
$G_n \mathcal{ALC}$
(
![]() $\unicode{x0141}_n \mathcal{ALC}$
) interpretation I satisfies a
$\unicode{x0141}_n \mathcal{ALC}$
) interpretation I satisfies a
![]() $G_n \mathcal{ALC}$
(
$G_n \mathcal{ALC}$
(
![]() $\unicode{x0141}_n \mathcal{ALC}$
) axiom E, as follows:
$\unicode{x0141}_n \mathcal{ALC}$
) axiom E, as follows:
-
– I satisfies axiom
 $C \sqsubseteq D \;\theta\; \alpha$
if
$C \sqsubseteq D \;\theta\; \alpha$
if
 $(C \sqsubseteq D)^I \theta\; \alpha$
;
$(C \sqsubseteq D)^I \theta\; \alpha$
; -
– I satisfies assertion
 $C(a) \; \theta \; \alpha$
if
$C(a) \; \theta \; \alpha$
if
 $C^I(a^I) \theta\; \alpha$
;
$C^I(a^I) \theta\; \alpha$
; -
– I satisfies assertion
 $r(a,b) \; \theta \; \alpha$
if
$r(a,b) \; \theta \; \alpha$
if
 $r^I(a^I,b^I) \theta\; \alpha$
.
$r^I(a^I,b^I) \theta\; \alpha$
.
Given a
![]() $G_n \mathcal{ALC}$
(
$G_n \mathcal{ALC}$
(
![]() $\unicode{x0141}_n \mathcal{ALC}$
) knowledge base
$\unicode{x0141}_n \mathcal{ALC}$
) knowledge base
![]() $K=({\cal T}, {\cal A})$
, a
$K=({\cal T}, {\cal A})$
, a
![]() $G_n \mathcal{ALC}$
(
$G_n \mathcal{ALC}$
(
![]() $\unicode{x0141}_n \mathcal{ALC}$
) interpretation I satisfies
$\unicode{x0141}_n \mathcal{ALC}$
) interpretation I satisfies
![]() ${\cal T}$
(resp.
${\cal T}$
(resp.
![]() ${\cal A}$
) if I satisfies all inclusions in
${\cal A}$
) if I satisfies all inclusions in
![]() ${\cal T}$
(resp. all assertions in
${\cal T}$
(resp. all assertions in
![]() ${\cal A}$
). A
${\cal A}$
). A
![]() $G_n \mathcal{ALC}$
(
$G_n \mathcal{ALC}$
(
![]() $\unicode{x0141}_n \mathcal{ALC}$
) interpretation I is a
$\unicode{x0141}_n \mathcal{ALC}$
) interpretation I is a
![]() $G_n \mathcal{ALC}$
(
$G_n \mathcal{ALC}$
(
![]() $\unicode{x0141}_n \mathcal{ALC}$
) model of K if I satisfies
$\unicode{x0141}_n \mathcal{ALC}$
) model of K if I satisfies
![]() ${\cal T}$
and
${\cal T}$
and
![]() ${\cal A}$
. A
${\cal A}$
. A
![]() $G_n \mathcal{ALC}$
(
$G_n \mathcal{ALC}$
(
![]() $\unicode{x0141}_n \mathcal{ALC}$
) axiom E is entailed by knowledge base K, written
$\unicode{x0141}_n \mathcal{ALC}$
) axiom E is entailed by knowledge base K, written
![]() $K \models_{G_n \mathcal{ALC}} E$
(resp.
$K \models_{G_n \mathcal{ALC}} E$
(resp.
![]() $K \models_{\unicode{x0141}_n \mathcal{ALC}} E$
), if for all
$K \models_{\unicode{x0141}_n \mathcal{ALC}} E$
), if for all
![]() $G_n \mathcal{ALC}$
(
$G_n \mathcal{ALC}$
(
![]() $\unicode{x0141}_n \mathcal{ALC}$
) models
$\unicode{x0141}_n \mathcal{ALC}$
) models
![]() $I=+\langle \Delta, \cdot^I\rangle$
of K, I satisfies E.
$I=+\langle \Delta, \cdot^I\rangle$
of K, I satisfies E.
3 Finitely many-valued
 $\boldsymbol{\mathcal{ALC}}$
with typicality
$\boldsymbol{\mathcal{ALC}}$
with typicality
In this section, we consider an extension of finitely many-valued
![]() $\mathcal{ALC}$
with typicality concepts, based on a preferential semantics, first introduced by Giordano and Theseider Dupré (Reference Giordano and Theseider Dupré2021b) for weighted
$\mathcal{ALC}$
with typicality concepts, based on a preferential semantics, first introduced by Giordano and Theseider Dupré (Reference Giordano and Theseider Dupré2021b) for weighted
![]() $\mathcal{EL}^{\bot}$
knowledge bases (we adopt an equivalent slight reformulation of the semantics by Giordano Reference Giordano2021b). The idea is similar to the extension of
$\mathcal{EL}^{\bot}$
knowledge bases (we adopt an equivalent slight reformulation of the semantics by Giordano Reference Giordano2021b). The idea is similar to the extension of
![]() $\mathcal{ALC}$
with typicality in the two-valued case by Giordano et al. (Reference Giordano, Gliozzi, Olivetti and Pozzato2007), but the degree of membership of domain individuals in a concept C is used to identify the typical elements of C. The extension allows for the definition of typicality inclusions of the form
$\mathcal{ALC}$
with typicality in the two-valued case by Giordano et al. (Reference Giordano, Gliozzi, Olivetti and Pozzato2007), but the degree of membership of domain individuals in a concept C is used to identify the typical elements of C. The extension allows for the definition of typicality inclusions of the form
![]() ${\bf T}(C) \sqsubseteq D \;\theta \; \alpha$
. For instance,
${\bf T}(C) \sqsubseteq D \;\theta \; \alpha$
. For instance,
![]() ${\bf T}(C) \sqsubseteq D \geq \alpha$
means that typical C-elements are D-elements with degree greater than
${\bf T}(C) \sqsubseteq D \geq \alpha$
means that typical C-elements are D-elements with degree greater than
![]() $\alpha$
. In the two-valued case, a typicality inclusion
$\alpha$
. In the two-valued case, a typicality inclusion
![]() ${\bf T}(C) \sqsubseteq D$
corresponds to a KLM conditional implication
${\bf T}(C) \sqsubseteq D$
corresponds to a KLM conditional implication
![]() $C \mathrel{{\scriptstyle\mid\!\sim}} D$
by Kraus et al. (Reference Kraus, Lehmann and Magidor1990), Lehmann and Magidor (Reference Lehmann and Magidor1992). As in the two-valued case, nesting of the typicality operator is not allowed.
$C \mathrel{{\scriptstyle\mid\!\sim}} D$
by Kraus et al. (Reference Kraus, Lehmann and Magidor1990), Lehmann and Magidor (Reference Lehmann and Magidor1992). As in the two-valued case, nesting of the typicality operator is not allowed.
Note that, in a many-valued
![]() $\mathcal{ALC}$
interpretation
$\mathcal{ALC}$
interpretation
![]() $I= \langle \Delta, \cdot^I \rangle$
, the degree of membership
$I= \langle \Delta, \cdot^I \rangle$
, the degree of membership
![]() $C^I(x)$
of domain elements x in a concept C induces a preference relation
$C^I(x)$
of domain elements x in a concept C induces a preference relation
![]() $<_C$
on
$<_C$
on
![]() $\Delta$
:
$\Delta$
:
For a finitely many-valued
![]() $\mathcal{ALC}$
interpretation
$\mathcal{ALC}$
interpretation
![]() $I= \langle \Delta, \cdot^I \rangle$
, each preference relation
$I= \langle \Delta, \cdot^I \rangle$
, each preference relation
![]() $<_{C}$
has the properties of preference relations in KLM-style ranked interpretations by Lehmann and Magidor (Reference Lehmann and Magidor1992), that is,
$<_{C}$
has the properties of preference relations in KLM-style ranked interpretations by Lehmann and Magidor (Reference Lehmann and Magidor1992), that is,
![]() $<_{C}$
is a modular and well-founded strict partial order. Let us recall that
$<_{C}$
is a modular and well-founded strict partial order. Let us recall that
![]() $<_{C}$
is well-founded if there is no infinite descending chain of domain elements;
$<_{C}$
is well-founded if there is no infinite descending chain of domain elements;
![]() $<_{C}$
is modular if, for all
$<_{C}$
is modular if, for all
![]() $x,y,z \in \Delta$
,
$x,y,z \in \Delta$
,
![]() $x <_{C} y$
implies (
$x <_{C} y$
implies (
![]() $x <_{C} z$
or
$x <_{C} z$
or
![]() $z <_{C} y$
). Well-foundedness holds for the induced preference
$z <_{C} y$
). Well-foundedness holds for the induced preference
![]() $<_C$
defined by condition (1) as we have assumed the truth space to be
$<_C$
defined by condition (1) as we have assumed the truth space to be
![]() ${\cal C}_n$
. We will denote
${\cal C}_n$
. We will denote
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
and
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
and
![]() $G_n \mathcal{ALC} {\bf T}$
the extensions of
$G_n \mathcal{ALC} {\bf T}$
the extensions of
![]() $\unicode{x0141}_n \mathcal{ALC}$
and
$\unicode{x0141}_n \mathcal{ALC}$
and
![]() $G_n \mathcal{ALC}$
with typicality.
$G_n \mathcal{ALC}$
with typicality.
Each relation
![]() $<_C$
has the properties of a preference relation in KLM rational interpretations, also called ranked interpretations. As many-valued interpretations induce multiple preferences, they can be regarded as multipreferential interpretations, which have also been studied in the two-valued case, for example, by Giordano and Theseider Dupré (Reference Giordano and Theseider Dupré2020), Delgrande and Rantsoudis (Reference Delgrande and Rantsoudis2020), Giordano and Gliozzi (Reference Giordano and Gliozzi2021), Casini et al. (Reference Casini, Meyer and Varzinczak2021).
$<_C$
has the properties of a preference relation in KLM rational interpretations, also called ranked interpretations. As many-valued interpretations induce multiple preferences, they can be regarded as multipreferential interpretations, which have also been studied in the two-valued case, for example, by Giordano and Theseider Dupré (Reference Giordano and Theseider Dupré2020), Delgrande and Rantsoudis (Reference Delgrande and Rantsoudis2020), Giordano and Gliozzi (Reference Giordano and Gliozzi2021), Casini et al. (Reference Casini, Meyer and Varzinczak2021).
The preference relation
![]() $<_C$
captures the relative typicality of domain elements wrt concept C and may then be used to identify the typical C-elements. We regard typical C-elements as the domain elements x that are preferred with respect to
$<_C$
captures the relative typicality of domain elements wrt concept C and may then be used to identify the typical C-elements. We regard typical C-elements as the domain elements x that are preferred with respect to
![]() $<_C$
among the ones such that
$<_C$
among the ones such that
![]() $C^I(x) \neq 0$
. Let
$C^I(x) \neq 0$
. Let
![]() $C^I_{>0}$
be the crisp set containing all domain elements x such that
$C^I_{>0}$
be the crisp set containing all domain elements x such that
![]() $C^I(x)>0$
, that is,
$C^I(x)>0$
, that is,
![]() $C^I_{>0}= \{x \in \Delta \mid C^I(x)>0 \}$
. One can provide a (two-valued) interpretation of typicality concepts
$C^I_{>0}= \{x \in \Delta \mid C^I(x)>0 \}$
. One can provide a (two-valued) interpretation of typicality concepts
![]() ${\bf T}(C)$
with respect to an interpretation I as:
${\bf T}(C)$
with respect to an interpretation I as:
where
![]() $\min_<(S)= \{u: u \in S$
and
$\min_<(S)= \{u: u \in S$
and
![]() $\nexists z \in S$
s.t.
$\nexists z \in S$
s.t.
![]() $z < u \}$
. When
$z < u \}$
. When
![]() $({\bf T}(C))^I(x)=1$
, x is said to be a typical C-element in I. Note that, if
$({\bf T}(C))^I(x)=1$
, x is said to be a typical C-element in I. Note that, if
![]() $C^I(x)>0$
for some
$C^I(x)>0$
for some
![]() $x \in \Delta$
,
$x \in \Delta$
,
![]() $\min_{<_C} (C^I_{>0}) \neq \emptyset$
. This generalizes the property that, in the crisp case,
$\min_{<_C} (C^I_{>0}) \neq \emptyset$
. This generalizes the property that, in the crisp case,
![]() $C^I\neq \emptyset$
implies
$C^I\neq \emptyset$
implies
![]() $({\bf T}(C))^I\neq \emptyset$
.
$({\bf T}(C))^I\neq \emptyset$
.
Definition 2
(
![]() $G_n \mathcal{ALC} {\bf T}$
(
$G_n \mathcal{ALC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) interpretation) A
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) interpretation) A
![]() $G_n \mathcal{ALC} {\bf T}$
(
$G_n \mathcal{ALC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) interpretation
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) interpretation
![]() $I= \langle \Delta, \cdot^I \rangle$
is a finitely many-valued
$I= \langle \Delta, \cdot^I \rangle$
is a finitely many-valued
![]() $G_n \mathcal{ALC}$
(
$G_n \mathcal{ALC}$
(
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) interpretation over
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) interpretation over
![]() ${\cal C}_n$
, extended by interpreting typicality concepts as in (2).
${\cal C}_n$
, extended by interpreting typicality concepts as in (2).
A many-valued interpretation
![]() $I= \langle \Delta, \cdot^I \rangle$
implicitly defines a multipreferential interpretation, where any concept C is associated to a relation
$I= \langle \Delta, \cdot^I \rangle$
implicitly defines a multipreferential interpretation, where any concept C is associated to a relation
![]() $<_C$
. The notions of satisfiability in
$<_C$
. The notions of satisfiability in
![]() $G_n \mathcal{ALC} {\bf T}$
(
$G_n \mathcal{ALC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
), model of a
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
), model of a
![]() $G_n \mathcal{ALC} {\bf T}$
(
$G_n \mathcal{ALC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) knowledge base, and
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) knowledge base, and
![]() $G_n \mathcal{ALC} {\bf T}$
(
$G_n \mathcal{ALC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) entailment are defined similarly as for
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) entailment are defined similarly as for
![]() $\unicode{x0141}_n \mathcal{ALC}$
and
$\unicode{x0141}_n \mathcal{ALC}$
and
![]() $G_n \mathcal{ALC}$
in Section 2.
$G_n \mathcal{ALC}$
in Section 2.
3.1 Weighted KBs and closure construction for finitely many values
In this section we introduce the notion of weighted
![]() $G_n \mathcal{ALC} {\bf T}$
(
$G_n \mathcal{ALC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) knowledge base allowing for weighted defeasible inclusions, namely, typicality inclusions with a real-valued weight, as introduced for
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) knowledge base allowing for weighted defeasible inclusions, namely, typicality inclusions with a real-valued weight, as introduced for
![]() $\cal EL$
by Giordano and Theseider Dupré (Reference Giordano and Theseider Dupré2021b).
$\cal EL$
by Giordano and Theseider Dupré (Reference Giordano and Theseider Dupré2021b).
A weighted
![]() $G_n \mathcal{ALC} {\bf T}$
knowledge base K, over a set
$G_n \mathcal{ALC} {\bf T}$
knowledge base K, over a set
![]() ${\cal C}= \{C_1, \ldots, C_k\}$
of distinguished
${\cal C}= \{C_1, \ldots, C_k\}$
of distinguished
![]() $G_n \mathcal{ALC}$
concepts, is a tuple
$G_n \mathcal{ALC}$
concepts, is a tuple
![]() $\langle {\cal T}, {\cal T}_{C_1}, \ldots, {\cal T}_{C_k}, {\cal A} \rangle$
, where
$\langle {\cal T}, {\cal T}_{C_1}, \ldots, {\cal T}_{C_k}, {\cal A} \rangle$
, where
![]() ${\cal T}$
is a set of
${\cal T}$
is a set of
![]() $G_n \mathcal{ALC}$
inclusion axioms,
$G_n \mathcal{ALC}$
inclusion axioms,
![]() ${\cal A}$
is a set of
${\cal A}$
is a set of
![]() $G_n \mathcal{ALC}$
assertions, and
$G_n \mathcal{ALC}$
assertions, and
![]() ${\cal T}_{C_i}=\{(d^i_h,w^i_h)\}$
is a set of all weighted typicality inclusions
${\cal T}_{C_i}=\{(d^i_h,w^i_h)\}$
is a set of all weighted typicality inclusions
![]() $d^i_h= {\bf T}(C_i) \sqsubseteq D_{i,h}$
for
$d^i_h= {\bf T}(C_i) \sqsubseteq D_{i,h}$
for
![]() $C_i$
, indexed by h, where each inclusion
$C_i$
, indexed by h, where each inclusion
![]() $d^i_h$
has weight
$d^i_h$
has weight
![]() $w^i_h$
, a real number, and
$w^i_h$
, a real number, and
![]() $C_i$
and
$C_i$
and
![]() $D_{i,h}$
are
$D_{i,h}$
are
![]() $G_n \mathcal{ALC}$
concepts. The typicality operator is assumed to occur only on the left hand side of a weighted typicality inclusion, and we call distinguished concepts those concepts
$G_n \mathcal{ALC}$
concepts. The typicality operator is assumed to occur only on the left hand side of a weighted typicality inclusion, and we call distinguished concepts those concepts
![]() $C_i$
occurring on the l.h.s. of some typicality inclusion
$C_i$
occurring on the l.h.s. of some typicality inclusion
![]() ${\bf T}(C_i) \sqsubseteq D$
. The definition of a weighted
${\bf T}(C_i) \sqsubseteq D$
. The definition of a weighted
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
knowledge base is similar. Let us consider the following example.
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
knowledge base is similar. Let us consider the following example.
Example 1 Consider the weighted
![]() $G_n \mathcal{ALC} {\bf T}$
knowledge base
$G_n \mathcal{ALC} {\bf T}$
knowledge base
![]() $K =\langle {\cal T}, {\cal T}_{Bird}, {\cal T}_{Penguin},$
$K =\langle {\cal T}, {\cal T}_{Bird}, {\cal T}_{Penguin},$
![]() $ {\cal A} \rangle$
, over the set of distinguished concepts
$ {\cal A} \rangle$
, over the set of distinguished concepts
![]() ${\cal C}=\{{Bird, Penguin}\}$
, with
${\cal C}=\{{Bird, Penguin}\}$
, with
![]() $ {\cal T}$
containing, for instance, the inclusion
$ {\cal T}$
containing, for instance, the inclusion
![]() ${Black \sqcap Red \sqsubseteq \bot \geq 1}$
.
${Black \sqcap Red \sqsubseteq \bot \geq 1}$
.
The weighted TBox
![]() ${\cal T}_{Bird} $
contains the weighted defeasible inclusions:
${\cal T}_{Bird} $
contains the weighted defeasible inclusions:
![]() $(d_1)$
$(d_1)$
![]() ${{\bf T}(Bird) \sqsubseteq Fly}$
, +20
${{\bf T}(Bird) \sqsubseteq Fly}$
, +20
![]() $(d_2)$
$(d_2)$
![]() ${{\bf T}(Bird) \sqsubseteq Has\_Wings}$
, +50
${{\bf T}(Bird) \sqsubseteq Has\_Wings}$
, +50
![]() $(d_3)$
$(d_3)$
![]() ${{\bf T}(Bird) \sqsubseteq Has\_Feather}$
, +50.
${{\bf T}(Bird) \sqsubseteq Has\_Feather}$
, +50.
and
![]() ${\cal T}_{Penguin}$
contains the weighted defeasible inclusions:
${\cal T}_{Penguin}$
contains the weighted defeasible inclusions:
![]() $(d_4)$
$(d_4)$
![]() ${{\bf T}(Penguin) \sqsubseteq Bird}$
, +100
${{\bf T}(Penguin) \sqsubseteq Bird}$
, +100
![]() $(d_5)$
$(d_5)$
![]() ${{\bf T}(Penguin) \sqsubseteq Fly}$
, - 70
${{\bf T}(Penguin) \sqsubseteq Fly}$
, - 70
![]() $(d_6)$
$(d_6)$
![]() ${{\bf T}(Penguin) \sqsubseteq Black}$
, +50.
${{\bf T}(Penguin) \sqsubseteq Black}$
, +50.
That is, a bird normally has wings, has feathers and flies, but having wings and feather (both with weight 50) for a bird is more plausible than flying (weight 20), although flying is regarded as being plausible; and so on. Given Abox
![]() ${\cal A}$
in which Reddy is red, has wings, has feather and flies (all with degree 1) and Opus has wings and feather (with degree 1), is black with degree 0.8 and does not fly, considering the weights of defeasible inclusions, we expect Reddy to be more typical than Opus as a bird, but less typical as a penguin.
${\cal A}$
in which Reddy is red, has wings, has feather and flies (all with degree 1) and Opus has wings and feather (with degree 1), is black with degree 0.8 and does not fly, considering the weights of defeasible inclusions, we expect Reddy to be more typical than Opus as a bird, but less typical as a penguin.
In previous work, Giordano and Theseider Dupré (Reference Giordano and Theseider Dupré2021b) introduced a semantics of a weighted
![]() ${\cal EL}$
knowledge bases through a semantic closure construction, similar in spirit to the rational closure by Lehmann and Magidor (Reference Lehmann and Magidor1992), to the lexicographic closure by Lehmann (Reference Lehmann1995), and related to c-representations by Kern-Isberner (Reference Kern-Isberner2001), but based on multiple preferences. Here, the same construction is extended to weighted
${\cal EL}$
knowledge bases through a semantic closure construction, similar in spirit to the rational closure by Lehmann and Magidor (Reference Lehmann and Magidor1992), to the lexicographic closure by Lehmann (Reference Lehmann1995), and related to c-representations by Kern-Isberner (Reference Kern-Isberner2001), but based on multiple preferences. Here, the same construction is extended to weighted
![]() $G_n \mathcal{ALC} {\bf T}$
(
$G_n \mathcal{ALC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) knowledge bases, by considering the notions of coherent, faithful, and
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) knowledge bases, by considering the notions of coherent, faithful, and
![]() $\varphi$
-coherent interpretations. The construction allows a subset of the
$\varphi$
-coherent interpretations. The construction allows a subset of the
![]() $G_n \mathcal{ALC} {\bf T}$
(
$G_n \mathcal{ALC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) interpretations to be selected, those in which the preference relations
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) interpretations to be selected, those in which the preference relations
![]() $<_{C_i}$
coherently or faithfully represent the defeasible part of the knowledge base K.
$<_{C_i}$
coherently or faithfully represent the defeasible part of the knowledge base K.
Let
![]() ${\cal T}_{C_i}=\{(d^i_h,w^i_h)\}$
be the set of weighted typicality inclusions
${\cal T}_{C_i}=\{(d^i_h,w^i_h)\}$
be the set of weighted typicality inclusions
![]() $d^i_h= {\bf T}(C_i) \sqsubseteq D_{i,h}$
associated to the distinguished concept
$d^i_h= {\bf T}(C_i) \sqsubseteq D_{i,h}$
associated to the distinguished concept
![]() $C_i$
, and let
$C_i$
, and let
![]() $I=\langle \Delta, \cdot^I \rangle$
be a
$I=\langle \Delta, \cdot^I \rangle$
be a
![]() $G_n \mathcal{ALC} {\bf T}$
(
$G_n \mathcal{ALC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) interpretation. In the two-valued case, we would associate to each domain element
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) interpretation. In the two-valued case, we would associate to each domain element
![]() $x \in \Delta$
and each distinguished concept
$x \in \Delta$
and each distinguished concept
![]() $C_i$
, a weight
$C_i$
, a weight
![]() $W_i(x)$
of x wrt
$W_i(x)$
of x wrt
![]() $C_i$
in I, by summing the weights of the defeasible inclusions satisfied by x. However, as I is a many-valued interpretation, we need to consider, for all inclusions
$C_i$
in I, by summing the weights of the defeasible inclusions satisfied by x. However, as I is a many-valued interpretation, we need to consider, for all inclusions
![]() ${\bf T}(C_i) \sqsubseteq D_{i,h} \in {\cal T}_{C_i}$
, the degree of membership of x in
${\bf T}(C_i) \sqsubseteq D_{i,h} \in {\cal T}_{C_i}$
, the degree of membership of x in
![]() $D_{i,h}$
. For each domain element
$D_{i,h}$
. For each domain element
![]() $x \in \Delta$
and distinguished concept
$x \in \Delta$
and distinguished concept
![]() $C_i$
, the weight
$C_i$
, the weight
![]() $W_i(x)$
of x wrt
$W_i(x)$
of x wrt
![]() $C_i$
in a
$C_i$
in a
![]() $G_n \mathcal{ALC} {\bf T}$
(
$G_n \mathcal{ALC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) interpretation
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) interpretation
![]() $I=\langle \Delta, \cdot^I \rangle$
is:
$I=\langle \Delta, \cdot^I \rangle$
is:
where
![]() $-\infty$
is added at the bottom of
$-\infty$
is added at the bottom of
![]() ${\mathbb{R}}$
. The value of
${\mathbb{R}}$
. The value of
![]() $W_i(x) $
is
$W_i(x) $
is
![]() $- \infty $
when x is not a C-element (i.e.,
$- \infty $
when x is not a C-element (i.e.,
![]() $C_i^I(x)=0$
). Otherwise,
$C_i^I(x)=0$
). Otherwise,
![]() $C_i^I(x) >0$
and the higher is the sum
$C_i^I(x) >0$
and the higher is the sum
![]() $W_i(x) $
, the more typical is the element x relative to the defeasible properties of
$W_i(x) $
, the more typical is the element x relative to the defeasible properties of
![]() $C_i$
.
$C_i$
.
Example 2 Let us consider again Example 1. Let I be an
![]() $G_n \mathcal{ALC} {\bf T}$
interpretation such that
$G_n \mathcal{ALC} {\bf T}$
interpretation such that
![]() ${Fly^I(red}$
-
${Fly^I(red}$
-
![]() ${dy)}$
${dy)}$
![]() ${= (Has\_Wings)^I (reddy)= (Has\_Feather)^I (reddy)={\mathit{1}}}$
and
${= (Has\_Wings)^I (reddy)= (Has\_Feather)^I (reddy)={\mathit{1}}}$
and
![]() ${Red^I(reddy) ={\mathit{1}} }$
, and
${Red^I(reddy) ={\mathit{1}} }$
, and
![]() ${Black}^I (reddy)={\mathit{0}}$
. Suppose further that
${Black}^I (reddy)={\mathit{0}}$
. Suppose further that
![]() ${Fly^I(opus) = {\mathit{0}}}$
and
${Fly^I(opus) = {\mathit{0}}}$
and
![]() ${ (Has\_Wings)^I (opus)= } $
${ (Has\_Wings)^I (opus)= } $
![]() $ {=(Has\_Feather)^I }$
$ {=(Has\_Feather)^I }$
![]() ${(opus)={\mathit{1}} }$
and
${(opus)={\mathit{1}} }$
and
![]() ${ Black^I(opus) ={\mathit{0.8}}}$
. Considering the weights of typicality inclusions for
${ Black^I(opus) ={\mathit{0.8}}}$
. Considering the weights of typicality inclusions for
![]() ${Bird}$
,
${Bird}$
,
![]() ${W_{Bird}(reddy)= {\mathit{20}}+{\mathit{50}}+{\mathit{50}}={\mathit{120}}}$
and
${W_{Bird}(reddy)= {\mathit{20}}+{\mathit{50}}+{\mathit{50}}={\mathit{120}}}$
and
![]() ${W_{Bird}(opus)=}$
${W_{Bird}(opus)=}$
![]() ${={\mathit{0}}+{\mathit{50}}+{\mathit{50}}={\mathit{100}}}$
. This suggests that Reddy should be more typical as a bird than Opus. On the other hand, if we suppose that
${={\mathit{0}}+{\mathit{50}}+{\mathit{50}}={\mathit{100}}}$
. This suggests that Reddy should be more typical as a bird than Opus. On the other hand, if we suppose that
![]() ${Bird^I(reddy)={\mathit{1}}}$
and
${Bird^I(reddy)={\mathit{1}}}$
and
![]() ${Bird^I(opus)={\mathit{0.8}}}$
, then
${Bird^I(opus)={\mathit{0.8}}}$
, then
![]() ${W_{Penguin}}$
${W_{Penguin}}$
![]() ${(reddy)}$
${(reddy)}$
![]() $ {= {\mathit{100}}-{\mathit{70}}={\mathit{30}}}$
and
$ {= {\mathit{100}}-{\mathit{70}}={\mathit{30}}}$
and
![]() ${W_{Penguin}(opus)= }$
${W_{Penguin}(opus)= }$
![]() ${{\mathit{0.8}} \times {\mathit{100}}+{\mathit{0.8}} \times {\mathit{50}}}$
${{\mathit{0.8}} \times {\mathit{100}}+{\mathit{0.8}} \times {\mathit{50}}}$
![]() ${={\mathit{120}}}$
, and Reddy should be less typical as a penguin than Opus.
${={\mathit{120}}}$
, and Reddy should be less typical as a penguin than Opus.
In previous work, a notion of coherence is introduced by Giordano and Theseider Dupré (Reference Giordano and Theseider Dupré2021b) to force an agreement between the preference relations
![]() $<_{C_i}$
induced by a fuzzy interpretation I, for distinguished concepts
$<_{C_i}$
induced by a fuzzy interpretation I, for distinguished concepts
![]() $C_i$
, and the weights
$C_i$
, and the weights
![]() $W_i(x)$
computed, for each
$W_i(x)$
computed, for each
![]() $x \in \Delta$
, from the knowledge base K, given the interpretation I. In the many-valued case, this leads to the following definition of coherent multipreference model of a weighted
$x \in \Delta$
, from the knowledge base K, given the interpretation I. In the many-valued case, this leads to the following definition of coherent multipreference model of a weighted
![]() $G_n \mathcal{ALC} {\bf T}$
(
$G_n \mathcal{ALC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) knowledge base.
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) knowledge base.
Definition 3
(Coherent multipreference model of a weighted
![]() $G_n \mathcal{ALC} {\bf T}$
/
$G_n \mathcal{ALC} {\bf T}$
/
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
KB) Let
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
KB) Let
![]() $K=\langle {\cal T},$
$K=\langle {\cal T},$
![]() $ {\cal T}_{C_1}, \ldots,$
$ {\cal T}_{C_1}, \ldots,$
![]() $ {\cal T}_{C_k}, {\cal A} \rangle$
be a weighted
$ {\cal T}_{C_k}, {\cal A} \rangle$
be a weighted
![]() $G_n \mathcal{ALC} {\bf T}$
(
$G_n \mathcal{ALC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) knowledge base over
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) knowledge base over
![]() ${\cal C }$
. A coherent multipreference model (cm-model) of K is a
${\cal C }$
. A coherent multipreference model (cm-model) of K is a
![]() $G_n \mathcal{ALC} {\bf T}$
(
$G_n \mathcal{ALC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) interpretation
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) interpretation
![]() $I=\langle \Delta, \cdot^I \rangle$
s.t.:
$I=\langle \Delta, \cdot^I \rangle$
s.t.:
![]() $\bullet$
I satisfies the inclusions in
$\bullet$
I satisfies the inclusions in
![]() $ {\cal T}$
and the assertions in
$ {\cal T}$
and the assertions in
![]() ${\cal A}$
;
${\cal A}$
;
![]() $\bullet$
for all
$\bullet$
for all
![]() $C_i\in {\cal C}$
, the preference
$C_i\in {\cal C}$
, the preference
![]() $<_{C_i}$
is coherent to
$<_{C_i}$
is coherent to
![]() $ {\cal T}_{C_i}$
, that is, for all
$ {\cal T}_{C_i}$
, that is, for all
![]() $x,y \in \Delta$
,
$x,y \in \Delta$
,
In a similar way, one can define a faithful multipreference model (fm-model) of K by replacing the coherence condition (4) with a faithfulness condition: for all
![]() $x,y \in \Delta$
,
$x,y \in \Delta$
,
The weaker notion of faithfulness allows to define a larger class of multipreference models of a weighted KB, compared to the class of coherent models. This allows a larger class of monotone non-decreasing activation functions in neural network models to be captured, whose activation function is monotonically non-decreasing (we refer to the work by Giordano and Theseider Dupré (Reference Giordano and Theseider Dupré2021b) and by Giordano (Reference Giordano2021b).
4
 $\boldsymbol\varphi$
-coherent models with finitely many values
$\boldsymbol\varphi$
-coherent models with finitely many values
In this section we consider another notion of coherence of a many-valued interpretation I wrt a KB, that we call
![]() $\varphi$
-coherence, where
$\varphi$
-coherence, where
![]() $\varphi$
is a function from
$\varphi$
is a function from
![]() $\mathbb{R}$
to the interval [0,1], that is,
$\mathbb{R}$
to the interval [0,1], that is,
![]() $\varphi: {\mathbb{R}} \rightarrow [0,1]$
.
$\varphi: {\mathbb{R}} \rightarrow [0,1]$
.
![]() $\varphi$
-coherent models have been first introduced by Giordano (Reference Giordano2021a) in the definition of a gradual argumentation semantics. Let us consider
$\varphi$
-coherent models have been first introduced by Giordano (Reference Giordano2021a) in the definition of a gradual argumentation semantics. Let us consider
![]() $\varphi$
-coherent
$\varphi$
-coherent
![]() $G_n \mathcal{ALC} {\bf T}$
(
$G_n \mathcal{ALC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) interpretations.
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) interpretations.
Definition 4
(
![]() $\varphi$
-coherence) Let
$\varphi$
-coherence) Let
![]() $K=\langle {\cal T},$
$K=\langle {\cal T},$
![]() $ {\cal T}_{C_1}, \ldots,$
$ {\cal T}_{C_1}, \ldots,$
![]() $ {\cal T}_{C_k}, {\cal A} \rangle$
be a weighted
$ {\cal T}_{C_k}, {\cal A} \rangle$
be a weighted
![]() $G_n \mathcal{ALC} {\bf T}$
(
$G_n \mathcal{ALC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) knowledge base, and
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) knowledge base, and
![]() $\varphi: {\mathbb{R} } \rightarrow [0,1]$
. A
$\varphi: {\mathbb{R} } \rightarrow [0,1]$
. A
![]() $G_n \mathcal{ALC} {\bf T}$
(
$G_n \mathcal{ALC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) interpretation
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) interpretation
![]() $I=\langle \Delta, \cdot^I \rangle$
is
$I=\langle \Delta, \cdot^I \rangle$
is
![]() $\varphi$
-coherent if, for all concepts
$\varphi$
-coherent if, for all concepts
![]() $C_i \in {\cal C}$
and
$C_i \in {\cal C}$
and
![]() $x\in \Delta$
,
$x\in \Delta$
,
 \begin{align}C_i^I(x)= \varphi \left(\sum_{h} w_h^i \; D_{i,h}^I(x)\right),\end{align}
\begin{align}C_i^I(x)= \varphi \left(\sum_{h} w_h^i \; D_{i,h}^I(x)\right),\end{align}
where
![]() ${\cal T}_{C_i}=\{({\bf T}(C_i) \sqsubseteq D_{i,h},w^i_h)\}$
is the set of weighted conditionals for
${\cal T}_{C_i}=\{({\bf T}(C_i) \sqsubseteq D_{i,h},w^i_h)\}$
is the set of weighted conditionals for
![]() $C_i$
. A
$C_i$
. A
![]() $\varphi$
-coherent multipreference model (
$\varphi$
-coherent multipreference model (
![]() $\varphi $
-coherent model) of a knowledge base K, is defined as a coherent model in Definition 3, but replacing the notion of coherence in condition (4) with the notion of
$\varphi $
-coherent model) of a knowledge base K, is defined as a coherent model in Definition 3, but replacing the notion of coherence in condition (4) with the notion of
![]() $\varphi$
-coherence (6).
$\varphi$
-coherence (6).
The relationships between the three semantics (Giordano Reference Giordano2021a) extend to the finite many-valued case as follows.
Proposition 1 Let K be a weighted
![]() $G_n \mathcal{ALC} {\bf T}$
(
$G_n \mathcal{ALC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) knowledge base and
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) knowledge base and
![]() $\varphi: {\mathbb{R}} \rightarrow [0,1]$
. (1) if
$\varphi: {\mathbb{R}} \rightarrow [0,1]$
. (1) if
![]() $\varphi$
is a monotonically non-decreasing function, a
$\varphi$
is a monotonically non-decreasing function, a
![]() $\varphi$
-coherent multipreference model I of K is also a faithful model of K; (2) if
$\varphi$
-coherent multipreference model I of K is also a faithful model of K; (2) if
![]() $\varphi$
is a monotonically increasing function, a
$\varphi$
is a monotonically increasing function, a
![]() $\varphi$
-coherent multipreference model I of K is also a coherent model of K.
$\varphi$
-coherent multipreference model I of K is also a coherent model of K.
To see that the set of equations defined by (6) allow to characterize the stationary states of multilayer perceptrons (MLPs), let us consider (Haykin Reference Haykin1999) the model of a neuron as an information-processing unit in an (artificial) neural network. The basic elements are the following: (1) a set of synapses or connecting links, each one characterized by a weight. We let
![]() $x_j$
be the signal at the input of synapse j connected to neuron i, and
$x_j$
be the signal at the input of synapse j connected to neuron i, and
![]() $w_{ij}$
the related synaptic weight; (2) the adder for summing the input signals to the neuron, weighted by the respective synapses weights:
$w_{ij}$
the related synaptic weight; (2) the adder for summing the input signals to the neuron, weighted by the respective synapses weights:
![]() $\sum^n_{j=1} w_{ij} x_j$
; (3) an activation function for limiting the amplitude of the output of the neuron (here, we assume, to the interval [0,1]). A neuron i can be described by the following pair of equations:
$\sum^n_{j=1} w_{ij} x_j$
; (3) an activation function for limiting the amplitude of the output of the neuron (here, we assume, to the interval [0,1]). A neuron i can be described by the following pair of equations:
![]() $u_i= \sum^n_{j=1} w_{ij} x_j $
and
$u_i= \sum^n_{j=1} w_{ij} x_j $
and
![]() $y_i=\varphi(u_i + b_i)$
where
$y_i=\varphi(u_i + b_i)$
where
![]() $x_1, \ldots, x_n$
are the input signals and
$x_1, \ldots, x_n$
are the input signals and
![]() $w_{i1}, \ldots,$
$w_{i1}, \ldots,$
![]() $ w_{in} $
are the weights of neuron i;
$ w_{in} $
are the weights of neuron i;
![]() $b_i$
is the bias,
$b_i$
is the bias,
![]() $\varphi$
the activation function, and
$\varphi$
the activation function, and
![]() $y_i$
is the output signal of neuron i. By adding a new synapse with input
$y_i$
is the output signal of neuron i. By adding a new synapse with input
![]() $x_0=+1$
and synaptic weight
$x_0=+1$
and synaptic weight
![]() $w_{i0}=b_i$
, one can write:
$w_{i0}=b_i$
, one can write:
![]() $u_i= \sum^n_{j=0} w_{ij} x_j $
, and
$u_i= \sum^n_{j=0} w_{ij} x_j $
, and
![]() $y_i=\varphi(u_i)$
, where
$y_i=\varphi(u_i)$
, where
![]() $u_i$
is called the induced local field of the neuron.
$u_i$
is called the induced local field of the neuron.
A neural network
![]() $\mathcal{N}$
can then be seen as “a directed graph consisting of nodes with interconnecting synaptic and activation links” (Haykin Reference Haykin1999). Nodes in the graph are the neurons (the processing units) and the weight
$\mathcal{N}$
can then be seen as “a directed graph consisting of nodes with interconnecting synaptic and activation links” (Haykin Reference Haykin1999). Nodes in the graph are the neurons (the processing units) and the weight
![]() $w_{ij}$
on the edge from node j to node i represents the strength of the connection between unit j and unit i.
$w_{ij}$
on the edge from node j to node i represents the strength of the connection between unit j and unit i.
A mapping of a neural network to a conditional KB can be defined in a simple way (Giordano and Theseider Dupré Reference Giordano and Theseider Dupré2021b), associating a concept name
![]() $C_i$
with each unit i in the network and by introducing, for each synaptic connection from neuron h to neuron i with weight
$C_i$
with each unit i in the network and by introducing, for each synaptic connection from neuron h to neuron i with weight
![]() $w_{ih}$
, a conditional
$w_{ih}$
, a conditional
![]() ${\bf T}(C_i) \sqsubseteq C_h$
with weight
${\bf T}(C_i) \sqsubseteq C_h$
with weight
![]() $w_h^i=w_{ih}$
. If we assume that
$w_h^i=w_{ih}$
. If we assume that
![]() $\varphi$
is the activation function of all units in the network
$\varphi$
is the activation function of all units in the network
![]() $\mathcal{N}$
and we consider the infinite-valued fuzzy logic with truth space
$\mathcal{N}$
and we consider the infinite-valued fuzzy logic with truth space
![]() ${\cal S} = [0,1]$
, then the solutions of equations (6) characterize the stationary states of MLPs, where
${\cal S} = [0,1]$
, then the solutions of equations (6) characterize the stationary states of MLPs, where
![]() $C_i^I(x)$
corresponds to the activation of neuron i for some input stimulus x, each
$C_i^I(x)$
corresponds to the activation of neuron i for some input stimulus x, each
![]() $D_{i,h}^I(x)$
corresponds to the input signal
$D_{i,h}^I(x)$
corresponds to the input signal
![]() $x_h$
, and
$x_h$
, and
![]() $\sum_{h} w_h^i \; D_{i,h}^I(x)$
corresponds to the induced local field of neuron i.
$\sum_{h} w_h^i \; D_{i,h}^I(x)$
corresponds to the induced local field of neuron i.
Notice that, when the truth space is the finite set
![]() ${\cal C}_n$
, for
${\cal C}_n$
, for
![]() $n\geq 1$
, the notion of
$n\geq 1$
, the notion of
![]() $\varphi$
-coherence may fail to characterize all the stationary states of a network, simply as there may be stationary states such that the activity values of units fall outside
$\varphi$
-coherence may fail to characterize all the stationary states of a network, simply as there may be stationary states such that the activity values of units fall outside
![]() ${\cal C}_n$
. In the next section, we will consider an approximation
${\cal C}_n$
. In the next section, we will consider an approximation
![]() $\varphi_n$
of the function
$\varphi_n$
of the function
![]() $\varphi$
over
$\varphi$
over
![]() ${\cal C}_n$
, with the idea to capture an approximated behavior of the network based on the finite many-valued semantics of a weighted conditional KB, and to construct a preferential model for properties verification.
${\cal C}_n$
, with the idea to capture an approximated behavior of the network based on the finite many-valued semantics of a weighted conditional KB, and to construct a preferential model for properties verification.
For a weighted
![]() $G_n \mathcal{ALC} {\bf T}$
(
$G_n \mathcal{ALC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) knowledge base K, a notion of coherent/faithful/
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) knowledge base K, a notion of coherent/faithful/
![]() $\varphi$
-coherent entailment can be defined in a natural way. As for concept-wise entailment in the two-valued case (Giordano et al. Reference Giordano, Gliozzi, Olivetti and Pozzato2015), we restrict our consideration to canonical models, that is, models which are large enough to contain all the relevant domain elements with their different valuations. Informally, a canonical
$\varphi$
-coherent entailment can be defined in a natural way. As for concept-wise entailment in the two-valued case (Giordano et al. Reference Giordano, Gliozzi, Olivetti and Pozzato2015), we restrict our consideration to canonical models, that is, models which are large enough to contain all the relevant domain elements with their different valuations. Informally, a canonical
![]() $\varphi$
-coherent model of K is a
$\varphi$
-coherent model of K is a
![]() $\varphi$
-coherent model of K that contains a domain element for each possible valuation of concepts which is present in any
$\varphi$
-coherent model of K that contains a domain element for each possible valuation of concepts which is present in any
![]() $\varphi$
-coherent model of K. Similarly for coherent and faithful models.
$\varphi$
-coherent model of K. Similarly for coherent and faithful models.
Definition 5 (Canonical coherent/faithful/
![]() $\varphi$
-coherent model of) Given a weighted
$\varphi$
-coherent model of) Given a weighted
![]() $G_n \mathcal{LC} {\bf T}$
(
$G_n \mathcal{LC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{LC} {\bf T}$
) knowledge base K,
$\unicode{x0141}_n \mathcal{LC} {\bf T}$
) knowledge base K,
![]() $I=(\Delta, \cdot^I)$
is a canonical coherent/faithful/
$I=(\Delta, \cdot^I)$
is a canonical coherent/faithful/
![]() $\varphi$
-coherent model of K if: (i) I is a coherent/faithful/
$\varphi$
-coherent model of K if: (i) I is a coherent/faithful/
![]() $\varphi$
-coherent model of K and, (ii) for each coherent/faithful/
$\varphi$
-coherent model of K and, (ii) for each coherent/faithful/
![]() $\varphi$
-coherent model
$\varphi$
-coherent model
![]() $J=(\Delta^J, \cdot^J)$
of K and each
$J=(\Delta^J, \cdot^J)$
of K and each
![]() $y \in \Delta^J$
, there is an element
$y \in \Delta^J$
, there is an element
![]() $z \in \Delta$
such that
$z \in \Delta$
such that
![]() $B^I(z)=B^J(y)$
, for all concept names B occurring in K.
$B^I(z)=B^J(y)$
, for all concept names B occurring in K.
A result concerning the existence of canonical
![]() $\varphi$
-coherent models, for weighted KBs having at least a
$\varphi$
-coherent models, for weighted KBs having at least a
![]() $\varphi$
-coherent model, can be found in the supplementary material for the paper, Appendix A. Let us define entailment.
$\varphi$
-coherent model, can be found in the supplementary material for the paper, Appendix A. Let us define entailment.
Definition 6 (coherent/faithful/
![]() $\varphi$
-coherent entailment) Given a weighted
$\varphi$
-coherent entailment) Given a weighted
![]() $G_n \mathcal{ALC} {\bf T}$
(
$G_n \mathcal{ALC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) knowledge base K, a
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) knowledge base K, a
![]() $G_n \mathcal{ALC} {\bf T}$
(
$G_n \mathcal{ALC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) axiom E is coherently/faithfully/
$\unicode{x0141}_n \mathcal{ALC} {\bf T}$
) axiom E is coherently/faithfully/
![]() $\varphi$
-coherently entailed from K if, for all canonical coherent/ faithful/
$\varphi$
-coherently entailed from K if, for all canonical coherent/ faithful/
![]() $\varphi$
-coherent models
$\varphi$
-coherent models
![]() $I=\langle \Delta, \cdot^I \rangle$
of K, I satisfies E.
$I=\langle \Delta, \cdot^I \rangle$
of K, I satisfies E.
The properties of faithful entailment in the fuzzy case have been studied by Giordano (Reference Giordano2021b). Faithful entailment is well-behaved: it deals with specificity and irrelevance; it is not subject to inheritance blocking; it satisfies most of the KLM properties of a preferential consequence relation (Kraus et al. Reference Kraus, Lehmann and Magidor1990; Lehmann and Magidor Reference Lehmann and Magidor1992), depending on their fuzzy reformulation and on the chosen combination functions.
In the next section, we restrict our consideration to the boolean fragment
![]() $\mathcal{LC}$
of
$\mathcal{LC}$
of
![]() $\mathcal{ALC}$
(with neither roles, nor universal nor existential restrictions), which is sufficient to encode MLPs as weighted KBs and to formulate boolean properties of the network. We consider the finitely many-valued logics
$\mathcal{ALC}$
(with neither roles, nor universal nor existential restrictions), which is sufficient to encode MLPs as weighted KBs and to formulate boolean properties of the network. We consider the finitely many-valued logics
![]() $G_n \mathcal{LC} {\bf T}$
and
$G_n \mathcal{LC} {\bf T}$
and
![]() $\unicode{x0141}_n \mathcal{LC} {\bf T}$
, and exploit ASP and asprin for defeasible reasoning in
$\unicode{x0141}_n \mathcal{LC} {\bf T}$
, and exploit ASP and asprin for defeasible reasoning in
![]() $G_n \mathcal{LC} {\bf T}$
and
$G_n \mathcal{LC} {\bf T}$
and
![]() $\unicode{x0141}_n \mathcal{LC} {\bf T}$
under an approximation
$\unicode{x0141}_n \mathcal{LC} {\bf T}$
under an approximation
![]() $\varphi_n$
of
$\varphi_n$
of
![]() $\varphi$
.
$\varphi$
.
5 ASP and asprin for reasoning in
 $\boldsymbol{G}_{\boldsymbol{n}} \boldsymbol{\mathcal{LC}} \boldsymbol{{\bf T}}$
and
$\boldsymbol{G}_{\boldsymbol{n}} \boldsymbol{\mathcal{LC}} \boldsymbol{{\bf T}}$
and
 $\boldsymbol{\unicode{x0141}}_{\boldsymbol{n}} \boldsymbol{\mathcal{LC} {\bf T}}$
:
$\boldsymbol{\unicode{x0141}}_{\boldsymbol{n}} \boldsymbol{\mathcal{LC} {\bf T}}$
:
 $\boldsymbol\varphi_{\boldsymbol{n}}$
-coherence and verification of MLPs
$\boldsymbol\varphi_{\boldsymbol{n}}$
-coherence and verification of MLPs
Given a monotonically non-decreasing function
![]() $\varphi: {\mathbb{R}} \rightarrow [0,1]$
, and an integer
$\varphi: {\mathbb{R}} \rightarrow [0,1]$
, and an integer
![]() $n>1$
, let function
$n>1$
, let function
![]() $\varphi_n: {\mathbb{R}} \rightarrow {\cal C}_n$
be defined as follows:
$\varphi_n: {\mathbb{R}} \rightarrow {\cal C}_n$
be defined as follows:
 \begin{align} \varphi_n(x) & = \left\{\begin{array}{ll} 0 & \mbox{if } \varphi(x) \leq \frac{1}{2n} \\[4pt] \frac{i}{n} & \mbox{if } \frac{2i -1}{2n} < \varphi(x) \leq \frac{2i +1}{2n}, \mbox{ for } 0<i<n \\[4pt] 1 & \mbox{if } \frac{2n -1}{2n} < \varphi(x) \end{array}\right.\end{align}
\begin{align} \varphi_n(x) & = \left\{\begin{array}{ll} 0 & \mbox{if } \varphi(x) \leq \frac{1}{2n} \\[4pt] \frac{i}{n} & \mbox{if } \frac{2i -1}{2n} < \varphi(x) \leq \frac{2i +1}{2n}, \mbox{ for } 0<i<n \\[4pt] 1 & \mbox{if } \frac{2n -1}{2n} < \varphi(x) \end{array}\right.\end{align}
![]() $\varphi_n(x)$
approximates
$\varphi_n(x)$
approximates
![]() $\varphi(x)$
to the nearest value in
$\varphi(x)$
to the nearest value in
![]() ${\cal C}_n$
. The notions of
${\cal C}_n$
. The notions of
![]() $\varphi_n$
-coherence,
$\varphi_n$
-coherence,
![]() $\varphi_n$
-coherent model, canonical
$\varphi_n$
-coherent model, canonical
![]() $\varphi_n$
-coherent model,
$\varphi_n$
-coherent model,
![]() $\varphi_n$
-coherent entailment can be defined as in Definitions 4 and 6, by replacing
$\varphi_n$
-coherent entailment can be defined as in Definitions 4 and 6, by replacing
![]() $\varphi$
with
$\varphi$
with
![]() $\varphi_n$
. The above-mentioned result concerning the existence of canonical models also extends to canonical
$\varphi_n$
. The above-mentioned result concerning the existence of canonical models also extends to canonical
![]() $\varphi_n$
-coherent models of weighted KBs (see Proposition 4 in the supplementary material for the paper, Appendix A).
$\varphi_n$
-coherent models of weighted KBs (see Proposition 4 in the supplementary material for the paper, Appendix A).
In the following, we formulate the problem of
![]() $\varphi_n$
-coherent entailment from a weighted
$\varphi_n$
-coherent entailment from a weighted
![]() $G_n \mathcal{LC} {\bf T}$
(
$G_n \mathcal{LC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{LC} {\bf T}$
) knowledge base as a problem of computing preferred answer sets of an ASP program. Verifying
$\unicode{x0141}_n \mathcal{LC} {\bf T}$
) knowledge base as a problem of computing preferred answer sets of an ASP program. Verifying
![]() $\varphi_n$
-coherent entailment of a typicality inclusion
$\varphi_n$
-coherent entailment of a typicality inclusion
![]() ${\bf T}(C) \sqsubseteq D \; \theta \;\alpha$
from a weighted knowledge base K (a subsumption problem), would require considering all typical C-elements in all possible canonical
${\bf T}(C) \sqsubseteq D \; \theta \;\alpha$
from a weighted knowledge base K (a subsumption problem), would require considering all typical C-elements in all possible canonical
![]() $\varphi_n$
-coherent models of K, and checking whether they are all instances of D with a degree d such that
$\varphi_n$
-coherent models of K, and checking whether they are all instances of D with a degree d such that
![]() $d \theta \alpha$
. We reformulate this problem as a problem of generating answer sets representing
$d \theta \alpha$
. We reformulate this problem as a problem of generating answer sets representing
![]() $\varphi_n$
-coherent models of the KB, and then selecting preferred answer sets, where a distinguished domain element
$\varphi_n$
-coherent models of the KB, and then selecting preferred answer sets, where a distinguished domain element
![]() $aux_C$
is intended to represent a typical C-element. For the selection of preferred answer sets, the ones maximizing the degree of membership of
$aux_C$
is intended to represent a typical C-element. For the selection of preferred answer sets, the ones maximizing the degree of membership of
![]() $aux_C$
in concept C, we use asprin by Brewka et al. (Reference Brewka, Delgrande, Romero and Schaub2015). Our proof method is sound and complete for the computation of
$aux_C$
in concept C, we use asprin by Brewka et al. (Reference Brewka, Delgrande, Romero and Schaub2015). Our proof method is sound and complete for the computation of
![]() $\varphi_n$
-coherent entailment.
$\varphi_n$
-coherent entailment.
Given a weighted
![]() $G_n \mathcal{LC} {\bf T}$
(
$G_n \mathcal{LC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{LC} {\bf T}$
) knowledge base
$\unicode{x0141}_n \mathcal{LC} {\bf T}$
) knowledge base
![]() $K=\langle {\cal T},$
$K=\langle {\cal T},$
![]() $ {\cal T}_{C_1}, \ldots,$
$ {\cal T}_{C_1}, \ldots,$
![]() $ {\cal T}_{C_k}, {\cal A} \rangle$
, we let
$ {\cal T}_{C_k}, {\cal A} \rangle$
, we let
![]() $\Pi_{K,n}$
be the representation of K in Datalog, where:
$\Pi_{K,n}$
be the representation of K in Datalog, where:
![]() ${val(v)}$
holds for each value v in
${val(v)}$
holds for each value v in
![]() $\{0,1, \ldots, n\}$
, which is intended to represent the value
$\{0,1, \ldots, n\}$
, which is intended to represent the value
![]() $\frac{v}{n}$
in
$\frac{v}{n}$
in
![]() ${\cal C}_n$
;
${\cal C}_n$
;
![]() ${nom(a)}$
,
${nom(a)}$
,
![]() ${cls(A)}$
Footnote 1
, are used for
${cls(A)}$
Footnote 1
, are used for
![]() ${a \in N_I}$
,
${a \in N_I}$
,
![]() ${A \in N_C}$
. We also have
${A \in N_C}$
. We also have
![]() ${nom(auxc)}$
Footnote 2
.
${nom(auxc)}$
Footnote 2
.
Boolean concepts
![]() $C \sqcap D$
,
$C \sqcap D$
,
![]() $C \sqcup D$
,
$C \sqcup D$
,
![]() $\neg C$
are represented as and(C’,D’), or(C’,D’), neg(C’), where C’ and D’ are terms representing concepts C and D;
$\neg C$
are represented as and(C’,D’), or(C’,D’), neg(C’), where C’ and D’ are terms representing concepts C and D;
![]() ${subTyp(C',D',w')} $
represents a defeasible inclusion
${subTyp(C',D',w')} $
represents a defeasible inclusion
![]() $( {T(C) \sqsubseteq D} , w)$
, where w’ is an integer corresponding to
$( {T(C) \sqsubseteq D} , w)$
, where w’ is an integer corresponding to
![]() $w \times 10^k$
, for w approximated to k decimal places. The concepts of interest, to be considered for limiting grounding in the rules introduced later, are represented (1) with assertions concept(C’), where C’ is the term for boolean concepts C occurring in K or in the formula to be verified (see later); (2) with rules implying that subconcepts are also of interest, for example:
$w \times 10^k$
, for w approximated to k decimal places. The concepts of interest, to be considered for limiting grounding in the rules introduced later, are represented (1) with assertions concept(C’), where C’ is the term for boolean concepts C occurring in K or in the formula to be verified (see later); (2) with rules implying that subconcepts are also of interest, for example:
![]() $ {concept(A) \leftarrow concept(and(A,B)). } $
$ {concept(A) \leftarrow concept(and(A,B)). } $
![]() $\Pi_{K,n}$
also contains the set of rules for generating
$\Pi_{K,n}$
also contains the set of rules for generating
![]() $\varphi_n$
-coherent models of K. The valuation is encoded by a set of atoms of the form
$\varphi_n$
-coherent models of K. The valuation is encoded by a set of atoms of the form
![]() ${inst(x,A,v)}$
, meaning that
${inst(x,A,v)}$
, meaning that
![]() $\frac{v}{n} \in C_n$
is the degree of membership of x in A. The rule:
$\frac{v}{n} \in C_n$
is the degree of membership of x in A. The rule:
![]() $ {\mathit{1}\{inst(X,A, V) : val(V)\}\mathit{1} \ \leftarrow cls(A), nom(X). } $
$ {\mathit{1}\{inst(X,A, V) : val(V)\}\mathit{1} \ \leftarrow cls(A), nom(X). } $
generates alternative answer sets, corresponding to interpretations of each constant
![]() ${x}$
(either a named individual or
${x}$
(either a named individual or
![]() $aux_C$
), with different values v corresponding to a membership degree
$aux_C$
), with different values v corresponding to a membership degree
![]() $\frac{v}{n} \in {\cal C}_n$
in each atomic concept A.
$\frac{v}{n} \in {\cal C}_n$
in each atomic concept A.
The valuation of complex boolean concepts D is encoded by introducing a predicate
![]() ${eval(D, X, V)}$
to determine the membership degree V of element X in D. A rule is introduced for each boolean operator to encode its semantics. For
${eval(D, X, V)}$
to determine the membership degree V of element X in D. A rule is introduced for each boolean operator to encode its semantics. For
![]() $G_n \mathcal{LC} {\bf T}$
, the
$G_n \mathcal{LC} {\bf T}$
, the
![]() ${eval}$
predicate encodes the semantics of
${eval}$
predicate encodes the semantics of
![]() $\sqcap$
,
$\sqcap$
,
![]() $\sqcup$
and
$\sqcup$
and
![]() $\neg$
, based on Gödel logic t-norm, s-norm and on involutive negation as follows:
$\neg$
, based on Gödel logic t-norm, s-norm and on involutive negation as follows:
![]() $ {eval(A, X, V) \leftarrow cls(A), inst(X,A,V)}$
.
$ {eval(A, X, V) \leftarrow cls(A), inst(X,A,V)}$
.
![]() $ {eval(and(A, B), X, V) \leftarrow concept(and(A, B)), eval(A,X,V\mathit{1}), eval(B,X,V\mathit{1}),}$
$ {eval(and(A, B), X, V) \leftarrow concept(and(A, B)), eval(A,X,V\mathit{1}), eval(B,X,V\mathit{1}),}$
![]() $ {min(V\mathit{1}, V\mathit{2},V). } $
$ {min(V\mathit{1}, V\mathit{2},V). } $
![]() $ {eval(or(A, B), X, V) \leftarrow concept(or(A, B)), eval(A,X,V\mathit{1}), eval(B,X,V\mathit{1}), }$
$ {eval(or(A, B), X, V) \leftarrow concept(or(A, B)), eval(A,X,V\mathit{1}), eval(B,X,V\mathit{1}), }$
![]() $ { max(V\mathit{1}, V\mathit{2},V). } $
$ { max(V\mathit{1}, V\mathit{2},V). } $
![]() $ {eval(neg( A), X, V) \leftarrow concept(neg (A)), eval(A,X,V\mathit{1}), V= n-V\mathit{1}, } $
$ {eval(neg( A), X, V) \leftarrow concept(neg (A)), eval(A,X,V\mathit{1}), V= n-V\mathit{1}, } $
where the predicates
![]() ${\min}$
and
${\min}$
and
![]() ${\max}$
are suitably defined. A similar evaluation function
${\max}$
are suitably defined. A similar evaluation function
![]() ${eval}$
can be defined for Łukasiewicz combination functions.
${eval}$
can be defined for Łukasiewicz combination functions.
To guarantee the satisfiability of
![]() $G_n \mathcal{LC} {\bf T}$
axioms (assertions and inclusions) a set of constraints is added. For instance, for the assertion
$G_n \mathcal{LC} {\bf T}$
axioms (assertions and inclusions) a set of constraints is added. For instance, for the assertion
![]() $C(a) \geq \alpha$
we add the constraint
$C(a) \geq \alpha$
we add the constraint
![]() ${\bot \leftarrow eval(C',a,V), V < n\alpha ,}$
${\bot \leftarrow eval(C',a,V), V < n\alpha ,}$
where
![]() ${C'}$
is the term representing concept C, while for a strict
${C'}$
is the term representing concept C, while for a strict
![]() $G_n \mathcal{LC} {\bf T}$
inclusion
$G_n \mathcal{LC} {\bf T}$
inclusion
![]() $E \sqsubseteq D \geq \alpha$
we add the constraint
$E \sqsubseteq D \geq \alpha$
we add the constraint
![]() ${\bot \leftarrow eval(E',X,V\mathit{1}), eval(D',X,V\mathit{2}), V\mathit{1}>V\mathit{2}, V\mathit{2} < \alpha,}$
${\bot \leftarrow eval(E',X,V\mathit{1}), eval(D',X,V\mathit{2}), V\mathit{1}>V\mathit{2}, V\mathit{2} < \alpha,}$
and similarly for other axioms and for the
![]() $\unicode{x0141}_n \mathcal{LC} {\bf T}$
case. An answer set represents a
$\unicode{x0141}_n \mathcal{LC} {\bf T}$
case. An answer set represents a
![]() $\varphi_n$
-coherent interpretation if the following constraint is satisfied:
$\varphi_n$
-coherent interpretation if the following constraint is satisfied:
![]() ${\bot \leftarrow nom(X), dcls(Ci), eval(Ci,X,V), weight(X,Ci,W), valphi(n,W,V\mathit{1}), V != V\mathit{1},}$
${\bot \leftarrow nom(X), dcls(Ci), eval(Ci,X,V), weight(X,Ci,W), valphi(n,W,V\mathit{1}), V != V\mathit{1},}$
where
![]() ${dcls(Ci)}$
is included in
${dcls(Ci)}$
is included in
![]() $\Pi_{K,n}$
for each distinguished class
$\Pi_{K,n}$
for each distinguished class
![]() $C_i \in {\cal C}$
. Given that the weights
$C_i \in {\cal C}$
. Given that the weights
![]() $w_h^i$
are approximated to k decimal places, argument W for
$w_h^i$
are approximated to k decimal places, argument W for
![]() ${weight}$
corresponds to the integer
${weight}$
corresponds to the integer
![]() $n \times W_i(x) \times 10^k$
, and valphi(n,W,V1) is defined (see below) to correspond to
$n \times W_i(x) \times 10^k$
, and valphi(n,W,V1) is defined (see below) to correspond to
![]() $ V1 = n \times \varphi_n(W_i(x))) = n \times \varphi_n(W/(n \times 10^k)) $
again representing
$ V1 = n \times \varphi_n(W_i(x))) = n \times \varphi_n(W/(n \times 10^k)) $
again representing
![]() ${\cal C}_n$
with
${\cal C}_n$
with
![]() $\{0,1, \ldots, n\}$
. Predicate
$\{0,1, \ldots, n\}$
. Predicate
![]() ${weight}$
(for the weighted sum) could, in principle, be defined as follows:
${weight}$
(for the weighted sum) could, in principle, be defined as follows:
![]() $ {weight(X,C,W) \leftarrow dcls(C),nom(X),}$
$ {weight(X,C,W) \leftarrow dcls(C),nom(X),}$
![]() $ {W = \#sum\{ Wi*V,D : cls(D),eval(D,X,V), subTyp(C,D,Wi) \}.} $
$ {W = \#sum\{ Wi*V,D : cls(D),eval(D,X,V), subTyp(C,D,Wi) \}.} $
but, for grounding reasons, it can be better defined with a rule for each distinguished class; such rules can be generated, for each distinguished concept
![]() $C_i$
, from the set of weighted typicality inclusions
$C_i$
, from the set of weighted typicality inclusions
![]() $ {\cal T}_{C_i}$
. In particular, given
$ {\cal T}_{C_i}$
. In particular, given
![]() ${\cal T}_{C_i}=\{({\bf T}(C_i) \sqsubseteq D_{i,h},w^i_h), h=1,\ldots,k\}$
, the following rule is introduced:
${\cal T}_{C_i}=\{({\bf T}(C_i) \sqsubseteq D_{i,h},w^i_h), h=1,\ldots,k\}$
, the following rule is introduced:
![]() $ { weight(X,Ci',W) \leftarrow nom(X), W = Wi\mathit{1} * Vi\mathit{1} + \ldots + Wik * Vik,}$
$ { weight(X,Ci',W) \leftarrow nom(X), W = Wi\mathit{1} * Vi\mathit{1} + \ldots + Wik * Vik,}$
![]() $ { subTyp(Ci',Di\mathit{1}',Wi\mathit{1}), eval(Di\mathit{1}',X,Vi\mathit{1}), \ldots , }$
$ { subTyp(Ci',Di\mathit{1}',Wi\mathit{1}), eval(Di\mathit{1}',X,Vi\mathit{1}), \ldots , }$
![]() $ { subTyp(Ci',Dik',Wik), eval(Dik',X,Vik), }$
$ { subTyp(Ci',Dik',Wik), eval(Dik',X,Vik), }$
where
![]() $ {Ci'}$
,
$ {Ci'}$
,
![]() $ {Di\mathit{1}'}$
,
$ {Di\mathit{1}'}$
,
![]() $\ldots$
,
$\ldots$
,
![]() $ {Dik'}$
are the terms representing concepts
$ {Dik'}$
are the terms representing concepts
![]() $ {C_i}$
,
$ {C_i}$
,
![]() $ {D_{i,\mathit{1}}}$
,
$ {D_{i,\mathit{1}}}$
,
![]() $\ldots$
,
$\ldots$
,
![]() $ {D_{i,k}}$
.
$ {D_{i,k}}$
.
Predicate valphi can be defined with rules such as:
![]() ${valphi(n,W,\mathit{0}) \leftarrow num(W),W < k_\mathit{1}.}$
${valphi(n,W,\mathit{0}) \leftarrow num(W),W < k_\mathit{1}.}$
![]() ${valphi(n,W,\mathit{1}) \leftarrow num(W),W>= k_\mathit{1}, W < k_\mathit{2}.}$
${valphi(n,W,\mathit{1}) \leftarrow num(W),W>= k_\mathit{1}, W < k_\mathit{2}.}$
![]() $\ldots$
$\ldots$
![]() ${valphi(n,W,n) \leftarrow num(W),W > k_{n-\mathit{1}},}$
${valphi(n,W,n) \leftarrow num(W),W > k_{n-\mathit{1}},}$
where:
![]() $ { num(W) \leftarrow nom(X),weight(X,C,W),dcls(C)}$
$ { num(W) \leftarrow nom(X),weight(X,C,W),dcls(C)}$
is used for limiting grounding of the previous rules, and
![]() $k_1, \ldots, k_{n-1}$
can be precomputed to be:
$k_1, \ldots, k_{n-1}$
can be precomputed to be:
![]() $k_1 = \lfloor w \rfloor$
where w is such that
$k_1 = \lfloor w \rfloor$
where w is such that
![]() $\varphi(w/(n \times 10^k)) = 1/2n$
,
$\varphi(w/(n \times 10^k)) = 1/2n$
,
![]() $k_2 = \lfloor w \rfloor$
where w is such that
$k_2 = \lfloor w \rfloor$
where w is such that
![]() $\varphi(w/(n \times 10^k)) = 3/2n$
,
$\varphi(w/(n \times 10^k)) = 3/2n$
,
![]() $\ldots$
$\ldots$
![]() $k_{n-1} = \lfloor w \rfloor$
where w is such that
$k_{n-1} = \lfloor w \rfloor$
where w is such that
![]() $\varphi(w/(n \times 10^k)) = (2n-1)/2n$
.
$\varphi(w/(n \times 10^k)) = (2n-1)/2n$
.
The program
![]() $\Pi(K,n,C,D,\theta, \alpha)$
associated to the
$\Pi(K,n,C,D,\theta, \alpha)$
associated to the
![]() $G_n \mathcal{LC} {\bf T}$
(
$G_n \mathcal{LC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{LC} {\bf T}$
) knowledge base K and a typicality subsumption
$\unicode{x0141}_n \mathcal{LC} {\bf T}$
) knowledge base K and a typicality subsumption
![]() ${\bf T}(C) \sqsubseteq D \; \theta \; \alpha$
is composed of two parts,
${\bf T}(C) \sqsubseteq D \; \theta \; \alpha$
is composed of two parts,
![]() $\Pi(K,n,C,D,$
$\Pi(K,n,C,D,$
![]() $\theta , \alpha)= \Pi_{K,n} \cup \Pi_{C,D, \theta \alpha}$
. We have already introduced the first one.
$\theta , \alpha)= \Pi_{K,n} \cup \Pi_{C,D, \theta \alpha}$
. We have already introduced the first one.
![]() $\Pi_{C,D,n,\theta,\alpha}$
contains the facts
$\Pi_{C,D,n,\theta,\alpha}$
contains the facts
![]() $ {nom(aux_C)}$
and
$ {nom(aux_C)}$
and
![]() $ {auxtc(aux_C,C')}$
and the rules:
$ {auxtc(aux_C,C')}$
and the rules:
![]() ${ok \leftarrow eval(D', aux_C,V), V \theta \alpha n. }$
${ok \leftarrow eval(D', aux_C,V), V \theta \alpha n. }$
![]() ${notok \leftarrow not \;ok ,}$
${notok \leftarrow not \;ok ,}$
where
![]() ${ok}$
is intended to represent that
${ok}$
is intended to represent that
![]() $aux_C$
satisfies the property that its membership degree V in concept D is such that
$aux_C$
satisfies the property that its membership degree V in concept D is such that
![]() $V \theta \alpha$
holds.
$V \theta \alpha$
holds.
Given a query
![]() ${\bf T}(C) \sqsubseteq D \; \theta \alpha$
, we have to verify that, in all canonical
${\bf T}(C) \sqsubseteq D \; \theta \alpha$
, we have to verify that, in all canonical
![]() $\varphi_n$
-coherent models of the
$\varphi_n$
-coherent models of the
![]() $G_n \mathcal{LC} {\bf T}$
(
$G_n \mathcal{LC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{LC} {\bf T}$
) knowledge base, all typical C-elements are D-elements with a certain degree v (representing
$\unicode{x0141}_n \mathcal{LC} {\bf T}$
) knowledge base, all typical C-elements are D-elements with a certain degree v (representing
![]() $v/n \in {\cal{C}}_n$
) such that
$v/n \in {\cal{C}}_n$
) such that
![]() $ v \theta \alpha n$
. This verification is accomplished by generating answer sets corresponding to the
$ v \theta \alpha n$
. This verification is accomplished by generating answer sets corresponding to the
![]() $\varphi_n$
-coherent models of the KB, and by selecting the preferred ones, in which the distinguished element
$\varphi_n$
-coherent models of the KB, and by selecting the preferred ones, in which the distinguished element
![]() $aux_C$
represents a typical C-element.
$aux_C$
represents a typical C-element.
Given two answer sets S and S’ of
![]() $\Pi(K,n,C,D,\theta , \alpha)$
, S is preferred to S’ if the membership degree of
$\Pi(K,n,C,D,\theta , \alpha)$
, S is preferred to S’ if the membership degree of
![]() $aux_C$
in concept C is higher in S than in S’, that is: if
$aux_C$
in concept C is higher in S than in S’, that is: if
![]() ${eval(C',aux_C,v\mathit{1})}$
holds in S and
${eval(C',aux_C,v\mathit{1})}$
holds in S and
![]() ${eval(C',aux_C,v\mathit{2})}$
holds in S’, then
${eval(C',aux_C,v\mathit{2})}$
holds in S’, then
![]() $v1 > v2$
.
$v1 > v2$
.
This condition is encoded directly into a preference program for asprin as follows. One such program requires defining when an answer set S is preferred to S’ according to a preference P (optimal solutions wrt such a preference can then be required with an
![]() $ {\#optimize}$
directive). This is done by defining a predicate better(P) for the case where P is of the type being defined, using predicates holds and holds’ to check whether atoms hold in S and S’, respectively. In this case the preference program, defining a “concept wise” preference, is simply as follows:
$ {\#optimize}$
directive). This is done by defining a predicate better(P) for the case where P is of the type being defined, using predicates holds and holds’ to check whether atoms hold in S and S’, respectively. In this case the preference program, defining a “concept wise” preference, is simply as follows:
![]() $ {\#program ~ preference(cwise).}$
$ {\#program ~ preference(cwise).}$
![]() $ { better(P) \leftarrow preference(P,cwise), holds(auxtc(auxc,C)), betterwrt(C).} $
$ { better(P) \leftarrow preference(P,cwise), holds(auxtc(auxc,C)), betterwrt(C).} $
![]() $ { betterwrt(C) \leftarrow holds(eval(C,auxc,V\mathit{1})),holds'(eval(C,auxc,V\mathit{2})),V\mathit{1}>V\mathit{2}. } $
$ { betterwrt(C) \leftarrow holds(eval(C,auxc,V\mathit{1})),holds'(eval(C,auxc,V\mathit{2})),V\mathit{1}>V\mathit{2}. } $
The query
![]() ${\bf T}(C) \sqsubseteq D \; \theta \; \alpha$
is entailed from the knowledge base K if, in all (maximally) preferred answer sets,
${\bf T}(C) \sqsubseteq D \; \theta \; \alpha$
is entailed from the knowledge base K if, in all (maximally) preferred answer sets,
![]() $aux_C$
is an instance of concept D with a membership degree v (representing
$aux_C$
is an instance of concept D with a membership degree v (representing
![]() $v/n \in {\cal{C}}_n$
) such that
$v/n \in {\cal{C}}_n$
) such that
![]() $v \theta \alpha n$
holds; that is, if
$v \theta \alpha n$
holds; that is, if
![]() ${ok}$
holds in all preferred answer sets, or, equivalently,
${ok}$
holds in all preferred answer sets, or, equivalently,
![]() ${notok}$
does not hold in any of them. In fact, we can prove that this corresponds to verifying that D is satisfied in all
${notok}$
does not hold in any of them. In fact, we can prove that this corresponds to verifying that D is satisfied in all
![]() $<_C$
-minimal C-elements in all canonical
$<_C$
-minimal C-elements in all canonical
![]() $\varphi_n$
-coherent models of the KB:
$\varphi_n$
-coherent models of the KB:
Proposition 2 Given a
![]() $G_n \mathcal{LC} {\bf T}$
(
$G_n \mathcal{LC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{LC} {\bf T}$
) knowledge base K, the query
$\unicode{x0141}_n \mathcal{LC} {\bf T}$
) knowledge base K, the query
![]() ${\bf T}(C) \sqsubseteq D \; \theta \; \alpha$
is falsified in some canonical
${\bf T}(C) \sqsubseteq D \; \theta \; \alpha$
is falsified in some canonical
![]() $\varphi_n$
-coherent model of K if and only if there is a preferred answer set S of the program
$\varphi_n$
-coherent model of K if and only if there is a preferred answer set S of the program
![]() $\Pi(K,C,D,n,\theta,\alpha)$
containing
$\Pi(K,C,D,n,\theta,\alpha)$
containing
![]() $eval(D',aux_C,v)$
such that
$eval(D',aux_C,v)$
such that
![]() $v \theta \alpha n$
does not hold (and then containing
$v \theta \alpha n$
does not hold (and then containing
![]() ${notok}$
).
${notok}$
).
The proof can be found in the supplementary material for the paper, Appendix B. It exploits the existence of
![]() $\varphi_n$
-coherent canonical models, for KBs having a
$\varphi_n$
-coherent canonical models, for KBs having a
![]() $\varphi_n$
-coherent model (Proposition 4 in Appendix A). Appendix B also contains a proof of the following upper bound on the complexity of
$\varphi_n$
-coherent model (Proposition 4 in Appendix A). Appendix B also contains a proof of the following upper bound on the complexity of
![]() $\varphi_n$
-coherent entailment.
$\varphi_n$
-coherent entailment.
Proposition 3
![]() $\varphi_n$
-coherent entailment from a weighted
$\varphi_n$
-coherent entailment from a weighted
![]() $G_n \mathcal{LC} {\bf T}$
(
$G_n \mathcal{LC} {\bf T}$
(
![]() $\unicode{x0141}_n \mathcal{LC} {\bf T}$
) knowledge base is in
$\unicode{x0141}_n \mathcal{LC} {\bf T}$
) knowledge base is in
![]() $\Pi^p_2$
.
$\Pi^p_2$
.
As a proof of concept, the approach has been experimented for the weighted
![]() $G_n \mathcal{LC} {\bf T}$
KBs corresponding to two of the trained multilayer feedforward network for the MONK’s problems (Thrun et al. Reference Thrun1991), namely, the network for problem 1 and the second network for problem 3. The networks have 17 non-independent binary inputs, corresponding to values of 6 inputs having 2 to 4 possible values; such inputs are features of a robot, for example, head shape and body shape being round, square or octagon, and jacket color being red, yellow, green or blue. The network for problem 1 (Figure 1) has 3 hidden units (h1,h2,h3) and an output unit (o); the one for problem 3 has 2 hidden units.
$G_n \mathcal{LC} {\bf T}$
KBs corresponding to two of the trained multilayer feedforward network for the MONK’s problems (Thrun et al. Reference Thrun1991), namely, the network for problem 1 and the second network for problem 3. The networks have 17 non-independent binary inputs, corresponding to values of 6 inputs having 2 to 4 possible values; such inputs are features of a robot, for example, head shape and body shape being round, square or octagon, and jacket color being red, yellow, green or blue. The network for problem 1 (Figure 1) has 3 hidden units (h1,h2,h3) and an output unit (o); the one for problem 3 has 2 hidden units.

Fig. 1. The network for MONK’s problem 1, with some of the weights after training (using 3 decimal digits), two of the corresponding typicality inclusions and their ASP representation.
In the two problems, the trained networks learned to classify inputs satisfying two formulae, respectively, F1 and F3, which are boolean combinations of the inputs. In particular, F1 is
![]() ${jacket\_color\_red \ or \ head\_shape = body\_shape}$
and, in terms of the classes
${jacket\_color\_red \ or \ head\_shape = body\_shape}$
and, in terms of the classes
![]() ${i{\mathit {1}}, \ldots , i{\mathit {17}}}$
corresponding to the binary inputs, it is:
${i{\mathit {1}}, \ldots , i{\mathit {17}}}$
corresponding to the binary inputs, it is:
![]() ${F{\mathit {1}} \equiv i{\mathit {12}} \sqcup (i{\mathit {1}} \sqcap i{\mathit {4}}) \sqcup (i{\mathit {2}} \sqcap i{\mathit {5}}) \sqcup (i{\mathit {3}} \sqcap i{\mathit {6}}) }$
${F{\mathit {1}} \equiv i{\mathit {12}} \sqcup (i{\mathit {1}} \sqcap i{\mathit {4}}) \sqcup (i{\mathit {2}} \sqcap i{\mathit {5}}) \sqcup (i{\mathit {3}} \sqcap i{\mathit {6}}) }$
(
![]() ${i{\mathit {12}}}$
is
${i{\mathit {12}}}$
is
![]() ${jacket\_color\_red}$
,
${jacket\_color\_red}$
,
![]() ${i{\mathit {1}}}$
is
${i{\mathit {1}}}$
is
![]() ${head\_shape\_round}$
,
${head\_shape\_round}$
,
![]() ${i{\mathit {4}}}$
is
${i{\mathit {4}}}$
is
![]() ${body\_shape\_round}$
, etc.).
${body\_shape\_round}$
, etc.).
The approach described above has been applied, using values 0 and 1 as possible values for classes associated with input nodes, rather than all values in
![]() ${\cal C}_n$
. The networks are feedforward, then for a choice of values for input nodes, there is only one choice of values in
${\cal C}_n$
. The networks are feedforward, then for a choice of values for input nodes, there is only one choice of values in
![]() ${\cal C}_n$
for non-input nodes satisfying the constraint for
${\cal C}_n$
for non-input nodes satisfying the constraint for
![]() $\varphi_n$
-coherent interpretations (then the number of answer sets of
$\varphi_n$
-coherent interpretations (then the number of answer sets of
![]() $\Pi(K,C,D,n,\theta,\alpha)$
is given by the possible combinations of input values and does not depend on n).
$\Pi(K,C,D,n,\theta,\alpha)$
is given by the possible combinations of input values and does not depend on n).
For the trained network for problem 1, the formula
![]() ${\bf T}(o) \sqsubseteq F1 \geq 1$
can be verified, for example, for
${\bf T}(o) \sqsubseteq F1 \geq 1$
can be verified, for example, for
![]() $n=5$
; o is the concept name associated with the output unit. That is, the
$n=5$
; o is the concept name associated with the output unit. That is, the
![]() $G_5 \mathcal{LC} {\bf T}$
knowledge base entails that the typical o-elements satisfy F1. The formula can also be verified for
$G_5 \mathcal{LC} {\bf T}$
knowledge base entails that the typical o-elements satisfy F1. The formula can also be verified for
![]() $n=1,3,9$
with minor variations on the running times (all below 10 s). This result is explainable (also for n=1), as an input was classified by the network as class member if the output was
$n=1,3,9$
with minor variations on the running times (all below 10 s). This result is explainable (also for n=1), as an input was classified by the network as class member if the output was
![]() $\geq 0.5$
and, for problem 1, the network learned the concept with 100% accuracy.
$\geq 0.5$
and, for problem 1, the network learned the concept with 100% accuracy.
Stronger variants of F1 have also been considered, to check that the network learned F1 but not such variants. For the following variants with one less disjunct:
![]() ${F{\mathit {1}}' \equiv i{\mathit {12}} \sqcup (i{\mathit {1}} \sqcap i{\mathit {4}}) \sqcup (i{\mathit {2}} \sqcap i{\mathit {5}}) }$
${F{\mathit {1}}' \equiv i{\mathit {12}} \sqcup (i{\mathit {1}} \sqcap i{\mathit {4}}) \sqcup (i{\mathit {2}} \sqcap i{\mathit {5}}) }$
![]() ${F{\mathit {1}}'' \equiv (i{\mathit {1}} \sqcap i{\mathit {4}}) \sqcup (i{\mathit {2}} \sqcap i{\mathit {5}}) \sqcup (i{\mathit {3}} \sqcap i{\mathit {6}}) }$
${F{\mathit {1}}'' \equiv (i{\mathit {1}} \sqcap i{\mathit {4}}) \sqcup (i{\mathit {2}} \sqcap i{\mathit {5}}) \sqcup (i{\mathit {3}} \sqcap i{\mathit {6}}) }$
the formulae
![]() ${\bf T}(o) \sqsubseteq F{1}' \geq 1$
and
${\bf T}(o) \sqsubseteq F{1}' \geq 1$
and
![]() ${\bf T}(o) \sqsubseteq F{1}'' \geq 1$
are indeed not entailed for
${\bf T}(o) \sqsubseteq F{1}'' \geq 1$
are indeed not entailed for
![]() $n=1,3,5,9$
.
$n=1,3,5,9$
.
An important issue in analyzing a trained network is also associating a meaning to hidden nodes. The following formulae have been verified for
![]() $n=1,3,5,9$
for hidden nodes
$n=1,3,5,9$
for hidden nodes
![]() ${h{\mathit {1}},h{\mathit {2}},h{\mathit {3}}}$
:
${h{\mathit {1}},h{\mathit {2}},h{\mathit {3}}}$
:
![]() ${\bf T}(h1) \sqsubseteq i12 \sqcup (\neg i1 \sqcap \neg i4) \geq 1$
${\bf T}(h1) \sqsubseteq i12 \sqcup (\neg i1 \sqcap \neg i4) \geq 1$
![]() ${\bf T}(h2) \sqsubseteq i12 \sqcup (\neg i3 \sqcap \neg i6) \geq 1$
${\bf T}(h2) \sqsubseteq i12 \sqcup (\neg i3 \sqcap \neg i6) \geq 1$
![]() ${\bf T}(h3) \sqsubseteq \neg i12 \sqcup (i2 \sqcup i5) \geq 1.$
${\bf T}(h3) \sqsubseteq \neg i12 \sqcup (i2 \sqcup i5) \geq 1.$
In problem 3, there was noise (some misclassifications) in the training set. Then the accuracy of the trained network is not 100%. However, the trained network produces no false positives. Therefore, the formula
![]() ${\bf T}(o) \sqsubseteq F3 \geq 1$
can be verified for
${\bf T}(o) \sqsubseteq F3 \geq 1$
can be verified for
![]() $n=1,3,5,9$
, where F3 is
$n=1,3,5,9$
, where F3 is
![]() ${(jacket\_color\_red \ and \ holding\_sword) \ or \ (not \ jacket\_color\_blue \ and \ not }$
${(jacket\_color\_red \ and \ holding\_sword) \ or \ (not \ jacket\_color\_blue \ and \ not }$
![]() ${body\_shape\_octagon)}$
. Since there are false negatives, the formula
${body\_shape\_octagon)}$
. Since there are false negatives, the formula
![]() ${\bf T}(\neg o) \sqsubseteq \neg F3 \geq 1$
is not entailed for
${\bf T}(\neg o) \sqsubseteq \neg F3 \geq 1$
is not entailed for
![]() $n=1$
but, for instance, it is for
$n=1$
but, for instance, it is for
![]() $n=5$
.
$n=5$
.
6 Conclusions
The “concept-wise” multipreference semantics (both in the two-valued and in the fuzzy case) has recently been proposed as a logical semantics of MLPs by Giordano and Theseider Dupré (Reference Giordano and Theseider Dupré2021b). In this paper we consider weighted conditional
![]() $\mathcal{ALC}$
knowledge bases in the finitely many-valued case, under a coherent, a faithful, and a
$\mathcal{ALC}$
knowledge bases in the finitely many-valued case, under a coherent, a faithful, and a
![]() $\varphi$
-coherent semantics, the last one being suitable to characterize the stationary states of MLPs. For the boolean fragment
$\varphi$
-coherent semantics, the last one being suitable to characterize the stationary states of MLPs. For the boolean fragment
![]() $\mathcal{LC}$
of
$\mathcal{LC}$
of
![]() $\mathcal{ALC}$
we exploit ASP and asprin, see Brewka et al. (Reference Brewka, Delgrande, Romero and Schaub2015), for reasoning under
$\mathcal{ALC}$
we exploit ASP and asprin, see Brewka et al. (Reference Brewka, Delgrande, Romero and Schaub2015), for reasoning under
![]() $\varphi$
-coherent entailment, by restricting to canonical models of the KB. We have proven soundness and completeness of ASP encoding for the finitely many-valued case and provided an upper complexity bound. As a proof of concept, we have experimented the proposed approach for checking properties of some trained neural networks for the MONK’s problems, see Thrun et al. (Reference Thrun1991).
$\varphi$
-coherent entailment, by restricting to canonical models of the KB. We have proven soundness and completeness of ASP encoding for the finitely many-valued case and provided an upper complexity bound. As a proof of concept, we have experimented the proposed approach for checking properties of some trained neural networks for the MONK’s problems, see Thrun et al. (Reference Thrun1991).
Undecidability results for fuzzy DLs with general inclusion axioms (Cerami and Straccia Reference Cerami and Straccia2011; Borgwardt and Peñaloza Reference Borgwardt, Peñaloza and Press2012), motivate the investigation of many-valued approximations of fuzzy multipreference entailment. The choice of
![]() $\mathcal{LC}$
is motivated by the fact it is sufficient to encode a neural network as a weighted KB as well as to formulate boolean properties of the network. This work is a first step towards the definition of proof methods for reasoning from weighted KBs under a finitely many-valued preferential semantics in more expressive or lightweight DLs. For
$\mathcal{LC}$
is motivated by the fact it is sufficient to encode a neural network as a weighted KB as well as to formulate boolean properties of the network. This work is a first step towards the definition of proof methods for reasoning from weighted KBs under a finitely many-valued preferential semantics in more expressive or lightweight DLs. For
![]() $\mathcal{EL}^{\bot}$
, the two-valued case has been studied in previous work by Giordano and Theseider Dupré (Reference Giordano and Theseider Dupré2021a).
$\mathcal{EL}^{\bot}$
, the two-valued case has been studied in previous work by Giordano and Theseider Dupré (Reference Giordano and Theseider Dupré2021a).
The encoding of a neural network as a conditional KB opens the possibility of combining empirical knowledge with elicited knowledge, for example, in the form of strict inclusions and definitions. Much work has been devoted, in recent years, to the combination of neural networks and symbolic reasoning (see the survey by Lamb et al. Reference Lamb, d’Avila Garcez, Gori, Prates, Avelar and Vardi2020), leading to the definition of new computational models and to extensions of logic programming languages with neural predicates. The relationships between normal logic programs and connectionist network have been investigated by d’Avila Garcez and Zaverucha (Reference d’Avila Garcez and Zaverucha1999) and by Hitzler et al. (Reference Hitzler, Hölldobler and Seda2004). A correspondence between neural networks and gradual argumentation semantics has been recently investigated by Potyka (Reference Potyka2021) by studying the semantic properties and the convergence conditions of a MLP-based bipolar semantics. The correspondence between neural network models and fuzzy systems has been first investigated by Kosko (Reference Kosko1992) in his seminal work. A fuzzy extension of preferential logics has been studied by Casini and Straccia (Reference Casini and Straccia2013b) based on rational closure.
While using preferential logic for the verification of properties of neural networks is a general (model agnostic) approach, first proposed for SOMs by Giordano et al. (Reference Giordano, Gliozzi, Theseider Dupré, Calimeri, Perri and Zumpano2020); Giordano et al. (Reference Giordano, Gliozzi and Theseider Dupré2022), whether it is possible to extend the logical encoding of MLPs as weighted conditional KBs to other network models is a subject for future investigation. The development of a temporal extension of weighted conditional KBs to capture the transient behavior of MLPs is also an interesting direction to extend this work.
Supplementary material
To view supplementary material for this article, please visit http://doi.org/10.1017/S1471068422000163.