1 Introduction
Answer set programming (ASP) is a declarative problem-solving formalism that emerged in the area of logic programming and nonmonotonic reasoning (Gelfond and Lifschitz (Reference Gelfond and Lifschitz1991); Eiter et al. (Reference Eiter, Ianni, Krennwallner, Tessaris, Franconi, Eiter, Gutiérrez, Handschuh, Rousset and Schmidt2009); Brewka et al. (Reference Brewka, Eiter and Truszczynski2011)). Thanks to its solid theoretical foundations and the availability of efficient implementations (see Gebser et al. (Reference Gebser, Leone, Maratea, Perri, Ricca and Schaub2018) for a survey), ASP is recognized as a powerful tool for knowledge representation and reasoning (KRR) and has become widely used in AI.
Rules represent the basic linguistic construct in ASP. A rule has the form
![]() $Head\leftarrow Body$
, where the
$Head\leftarrow Body$
, where the
![]() $Body$
is a logic conjunction in which negation may appear, and
$Body$
is a logic conjunction in which negation may appear, and
![]() $Head$
can be either an atomic formula or a logic disjunction; a rule is interpreted according to common sense principles: roughly, its intuitive semantics corresponds to an implication. Rules featuring an atomic formula in the head and an empty body are used to represent information known to be certainly true and are indeed called facts. In ASP, a computational problem is typically solved by modeling it via a logic program consisting of a collection of rules along with a set of facts representing the instance at hand and then by making use of an ASP system that determines existing solutions by computing the intended models, called answer sets. The latter are computed according to the so-called answer set semantics. Answer sets correspond one-to-one to the solutions of the given instance of the modeled problem; if a program has no answer sets, the corresponding problem instance has no solutions.
$Head$
can be either an atomic formula or a logic disjunction; a rule is interpreted according to common sense principles: roughly, its intuitive semantics corresponds to an implication. Rules featuring an atomic formula in the head and an empty body are used to represent information known to be certainly true and are indeed called facts. In ASP, a computational problem is typically solved by modeling it via a logic program consisting of a collection of rules along with a set of facts representing the instance at hand and then by making use of an ASP system that determines existing solutions by computing the intended models, called answer sets. The latter are computed according to the so-called answer set semantics. Answer sets correspond one-to-one to the solutions of the given instance of the modeled problem; if a program has no answer sets, the corresponding problem instance has no solutions.
The majority of currently available ASP systems relies on the traditional “ground & solve” workflow, which is based on two consecutive steps. First, a grounding step (also called an instantiation step) transforms the input program into a semantically equivalent “ground” program, that is, a propositional program without first-order variables. Then, in a subsequent solving step, algorithms are applied on this ground program to compute the corresponding answer sets. There are other systems, which, instead, are based on approaches that interleave grounding and solving or rely on intermediate translations like the ones presented in Bomanson et al. (Reference Bomanson, Janhunen and Weinzierl2019), Dal Palù et al. (Reference Dal Palù, Dovier, Pontelli and Rossi2009), and Lefèvre et al. (Reference Lefèvre, Béatrix, STéphan and Garcia2017).
In the latest years, emerging application contexts, such as real-time motion tracking (Suchan et al. (Reference Suchan, Bhatt, Walega and Schultz2018)), content distribution (Beck et al. (Reference Beck, Bierbaumer, Dao-tran, Eiter, Hellwagner and Schekotihin2017)), robotics (Saribatur et al. (Reference Saribatur, Patoglu and Erdem2019)), artificial players in videogames (Calimeri et al. (Reference Calimeri, Germano, Ianni, Pacenza, Perri, Zangari, Benzmüller, Ricca, Parent and Roman2018)), and sensor network configuration (Dodaro et al. (Reference Dodaro, Eiter, Ogris and Schekotihin2020)), have been posing new challenges for ASP systems. Most of the above applications require to show high reactivity while performing the repeated execution of reasoning tasks over rapidly changing input data. Each repeated execution is commonly called “shot,” hence the terminology “multi-shot” reasoning. In the context of multi-shot reasoning, the naïve approach of starting ASP systems at hand from scratch at each execution significantly impacts on performance and is impracticable when shots are needed at a very high pace and/or over a high volume of input data.
Lately, many efforts have been spent by the scientific community to define proper incremental evaluation techniques that save and reuse knowledge built across shots, thus making ASP systems and general rule-based systems evolve toward more efficient multi-shot solutions, such as the works of Motik et al. (Reference Motik, Nenov, Piro and Horrocks2019), Gebser et al. (Reference Gebser, Kaminski, Kaufmann and Schaub2019), Dell’Aglio et al. (Reference Dell’Aglio, Valle, Van Harmelen and Bernstein2017), Valle et al. (Reference Valle, Ceri, Barbieri, Braga and Campi2008), Mileo et al. (Reference Mileo, Abdelrahman, Policarpio and Hauswirth2013), Gebser et al. (Reference Gebser, Kaminski, Kaufmann and Schaub2019), Calimeri et al. (Reference Calimeri, Ianni, Pacenza, Perri and Zangari2019), Ianni et al. (Reference Ianni, Pacenza and Zangari2020), and Beck et al. (Reference Beck, Bierbaumer, Dao-tran, Eiter, Hellwagner and Schekotihin2017).
In this work, we present Incremental-DLV2, a new incremental ASP reasoner that represents the evolution of DLV2 of Alviano et al. (Reference Alviano, Calimeri, Dodaro, Fuscá, Leone, Perri, Ricca, Veltri and Zangari2017) toward multi-shot reasoning. DLV2 is a novel version of one of the first and more widespread ASP systems, namely, DLV (Leone et al. (Reference Leone, Pfeifer, Faber, Eiter, Gottlob, Perri and Scarcello2006)); the new system has been re-implemented from scratch and encompasses the outcome of the latest research effort on both grounding and solving areas. Just as DLV and DLV2, Incremental-DLV2 entirely embraces the declarative nature of ASP; furthermore, it contributes to research in multi-shot solving with the introduction and management of a form of incremental grounding, which is fully transparent to users of the system. This is achieved via the overgrounding techniques presented in Calimeri et al. (Reference Calimeri, Ianni, Pacenza, Perri and Zangari2019) and Ianni et al. (Reference Ianni, Pacenza and Zangari2020). The overgrounding approach makes, at each shot, the instantiation effort directly proportional to the number of unseen facts, up to the point that the grounding computational effort might be close to none when all input facts have been already seen in previous shots. Notably, overgrounded programs are increasingly larger across shots: as this could negatively impact on the solving step, Incremental-DLV2 properly selects only a smaller yet equivalent portion of the current overgrounded program to be considered during solving.
In the remainder of the manuscript, we first provide an overview of the incremental grounding techniques, which the system relies on, in Section 2; then, we illustrate the system architecture and its computational workflow in Section 3; furthermore, we describe its usage and its applicability in Section 4, while we assess the performance of the system in some practically relevant domains in Section 5. Eventually, we discuss related work in Section 6, and we conclude by commenting about future work in Section 7.
2 Overview of overgrounding techniques
In the following, we give an overview of the approach adopted by the system to efficiently manage the grounding task in multi-shot contexts. We assume that the reader is familiar with the basic logic programming terminology, including the notions of predicate, atom, literal, rule, head, body, and refer to the literature for a detailed and systematic description of the ASP language and semantics (Calimeri et al. (Reference Calimeri, Faber, Gebser, Ianni, Kaminski, Krennwallner, Leone, Maratea, Ricca and Schaub2020)).
As mentioned, ASP solvers generally deal with a non-ground ASP program
![]() $P$
, made of a set of universally quantified rules, and a set of input facts
$P$
, made of a set of universally quantified rules, and a set of input facts
![]() $F$
. A traditional ASP system performs two separate steps to determine the corresponding models, that is, the answer sets of
$F$
. A traditional ASP system performs two separate steps to determine the corresponding models, that is, the answer sets of
![]() $P$
and
$P$
and
![]() $F$
, denoted
$F$
, denoted
![]() $AS(P\cup F)$
. The first step is called instantiation (or grounding) and consists of the generation of a logic program
$AS(P\cup F)$
. The first step is called instantiation (or grounding) and consists of the generation of a logic program
![]() $gr(P,F)$
, obtained by properly replacing first-order variables with constants. Second, the solving step is responsible for computing the answer sets
$gr(P,F)$
, obtained by properly replacing first-order variables with constants. Second, the solving step is responsible for computing the answer sets
![]() $AS(gr(P,F))$
. Grounding modules are typically geared toward building
$AS(gr(P,F))$
. Grounding modules are typically geared toward building
![]() $gr(P,F)$
as a smaller and optimized version of the theoretical instantiation
$gr(P,F)$
as a smaller and optimized version of the theoretical instantiation
![]() $grnd(P,F)$
, which is classically defined via the Herbrand base.
$grnd(P,F)$
, which is classically defined via the Herbrand base.
When building
![]() $gr(P,F)$
, it is implicitly assumed a “one-shot” context: the instantiation procedure is performed once and for all. Hence, state-of-the-art grounders adopt ad hoc strategies in order to heavily reduce the size of
$gr(P,F)$
, it is implicitly assumed a “one-shot” context: the instantiation procedure is performed once and for all. Hence, state-of-the-art grounders adopt ad hoc strategies in order to heavily reduce the size of
![]() $gr(P,F)$
. In other words,
$gr(P,F)$
. In other words,
![]() $gr(P,F)$
is shaped on the basis of the problem instance at hand, still keeping its semantics. Basic equivalence is guaranteed as
$gr(P,F)$
is shaped on the basis of the problem instance at hand, still keeping its semantics. Basic equivalence is guaranteed as
![]() $gr$
is built in a way such that
$gr$
is built in a way such that
![]() $AS(P \cup F) = AS(grnd(P,F)) = AS(gr(P,F))$
.
$AS(P \cup F) = AS(grnd(P,F)) = AS(gr(P,F))$
.
Based on the information about the structure of the program and the given input facts, the generation of a significant number of useless ground rules can be avoided: for instance, rules having a definitely false literal in the body can be eliminated. Moreover, while producing a ground rule, on-the-fly simplification strategies can be applied; for example, certainly true literals can be removed from rule bodies. For an overview of grounding optimizations, the reader can refer to Gebser et al. (Reference Gebser, Kaminski, König, Schaub, Delgrande and Faber2011), Calimeri et al. (Reference Calimeri, Fuscá, Perri and Zangari2017), and Calimeri et al. (Reference Calimeri, Ianni, Pacenza, Perri and Zangari2019).
However, this optimization process makes
![]() $gr(P,F)$
“tailored” for the
$gr(P,F)$
“tailored” for the
![]() $P \cup F$
input only. Assuming that
$P \cup F$
input only. Assuming that
![]() $P$
is kept fixed, it is not guaranteed that, for a future different input
$P$
is kept fixed, it is not guaranteed that, for a future different input
![]() $F'$
, we will have
$F'$
, we will have
![]() $gr(P,F) = AS(P \cup F')$
. Nonetheless, it might be desirable to maintain
$gr(P,F) = AS(P \cup F')$
. Nonetheless, it might be desirable to maintain
![]() $gr(P,F)$
and incrementally modify it, with as little effort as possible, in order to regain equivalence for a subsequent shot with input set of facts
$gr(P,F)$
and incrementally modify it, with as little effort as possible, in order to regain equivalence for a subsequent shot with input set of facts
![]() $F'$
.
$F'$
.
In this scenario it is crucial to limit as much as possible the regeneration of parts of the ground programs which were already evaluated at the previous step; at the same time, given that the set of input facts is possibly different from any other shot, shaping the produced ground program cannot be strongly optimized and tailored to
![]() $F'$
as in the “one-shot” scenario. As a consequence, it is desirable that the instantiation process takes into account facts from both the current and the previous shots. In this respect, Calimeri et al. (Reference Calimeri, Ianni, Pacenza, Perri and Zangari2019) and Ianni et al. (Reference Ianni, Pacenza and Zangari2020) proposed overgrounding techniques to efficiently perform incremental instantiations.
$F'$
as in the “one-shot” scenario. As a consequence, it is desirable that the instantiation process takes into account facts from both the current and the previous shots. In this respect, Calimeri et al. (Reference Calimeri, Ianni, Pacenza, Perri and Zangari2019) and Ianni et al. (Reference Ianni, Pacenza and Zangari2020) proposed overgrounding techniques to efficiently perform incremental instantiations.
The basic idea of the technique, originally introduced by Calimeri et al. (Reference Calimeri, Ianni, Pacenza, Perri and Zangari2019), is to maintain an overgrounded program
![]() $G$
.
$G$
.
![]() $G$
is monotonically enlarged across shots, in order to be semantics-preserving with respect to new input facts. Interestingly, the overgrounded version of
$G$
is monotonically enlarged across shots, in order to be semantics-preserving with respect to new input facts. Interestingly, the overgrounded version of
![]() $G$
resulting at a given iteration
$G$
resulting at a given iteration
![]() $i$
is semantics-preserving for all the set of input facts at a previous iteration
$i$
is semantics-preserving for all the set of input facts at a previous iteration
![]() $i'$
(
$i'$
(
![]() $1 \leq i' \leq i$
), still producing the correct answer sets. More formally, for each
$1 \leq i' \leq i$
), still producing the correct answer sets. More formally, for each
![]() $i', (1\leq i' \leq i)$
, we have
$i', (1\leq i' \leq i)$
, we have
![]() $AS(G \cup F_{i'}) = AS(P \cup F_{i'})$
After some iterations,
$AS(G \cup F_{i'}) = AS(P \cup F_{i'})$
After some iterations,
![]() $G$
converges to a propositional theory that is general enough to be reused together with large families of possible future inputs, without requiring further updates. In order to achieve the above property,
$G$
converges to a propositional theory that is general enough to be reused together with large families of possible future inputs, without requiring further updates. In order to achieve the above property,
![]() $G$
is adjusted from one shot to another by adding new ground rules and avoiding specific input-dependent simplifications. This virtually eliminates the need for grounding activities in later iterations, at the price of potentially increasing the burden of the solver (sub)systems, which are supposed to deal with larger ground programs.
$G$
is adjusted from one shot to another by adding new ground rules and avoiding specific input-dependent simplifications. This virtually eliminates the need for grounding activities in later iterations, at the price of potentially increasing the burden of the solver (sub)systems, which are supposed to deal with larger ground programs.
Overgrounding with tailoring, proposed by Ianni et al. (Reference Ianni, Pacenza and Zangari2020), has been introduced with the aim of overcoming such limitations by keeping the principle that
![]() $G$
grows monotonically from one shot to another, yet adopting fine-tuned techniques that allow to reduce the number of additions to
$G$
grows monotonically from one shot to another, yet adopting fine-tuned techniques that allow to reduce the number of additions to
![]() $G$
at each step. More in detail, in the overgrounding with tailoring approach, new rules added to
$G$
at each step. More in detail, in the overgrounding with tailoring approach, new rules added to
![]() $G$
are subject to simplifications, which cause the length of individual rules and the overall size of the overgrounded program to be reduced, but desimplifications are applied whenever necessary in order to maintain compatibility with input facts.
$G$
are subject to simplifications, which cause the length of individual rules and the overall size of the overgrounded program to be reduced, but desimplifications are applied whenever necessary in order to maintain compatibility with input facts.
In the following, we illustrate how the two techniques behave across subsequent shots with the help of a proper example.
Example 2.1.
Let us consider the program
![]() $P_{ex}$
:
$P_{ex}$
:
Let us assume at shot
![]() $1$
to have the input facts
$1$
to have the input facts
![]() $F_1 = \{ e(3,1),\ e(1,2),\ q(3) \}$
. In the standard overgrounding approach, we start from
$F_1 = \{ e(3,1),\ e(1,2),\ q(3) \}$
. In the standard overgrounding approach, we start from
![]() $F_1$
and generate, in a bottom-up way, new rules by iterating through positive body-head dependencies, obtaining the ground program
$F_1$
and generate, in a bottom-up way, new rules by iterating through positive body-head dependencies, obtaining the ground program
![]() $G_1$
:
$G_1$
:
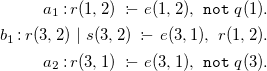 \begin{align*} a_1 : r(1,2) \ :\!\!- \ e(1,2),\ {\mathtt {not}}\ q(1). \\ b_1 : r(3,2) \ |\ s(3,2) \ :\!\!- \ e(3,1),\ r(1,2). \\ a_2 : r(3,1) \ :\!\!- \ e(3,1),\ {\mathtt {not}}\ q(3). \end{align*}
\begin{align*} a_1 : r(1,2) \ :\!\!- \ e(1,2),\ {\mathtt {not}}\ q(1). \\ b_1 : r(3,2) \ |\ s(3,2) \ :\!\!- \ e(3,1),\ r(1,2). \\ a_2 : r(3,1) \ :\!\!- \ e(3,1),\ {\mathtt {not}}\ q(3). \end{align*}
In the overgrounding with tailoring, rules that have no chance of firing along with definitely true atoms are simplified, thus obtaining a simplified program
![]() $G'_1$
:
$G'_1$
:
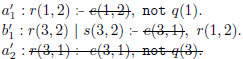
![]() $G'_1$
can be seen as less general and “re-usable” than
$G'_1$
can be seen as less general and “re-usable” than
![]() $G_1$
:
$G_1$
:
![]() $a'_1$
is simplified on the assumption that
$a'_1$
is simplified on the assumption that
![]() $e(1,2)$
will be always true, and
$e(1,2)$
will be always true, and
![]() $a'_2$
is deleted on the assumption that
$a'_2$
is deleted on the assumption that
![]() $q(3)$
is always true.
$q(3)$
is always true.
One might want to adapt
![]() $G'_1$
to be compatible with different sets of input facts, but this requires the additional effort of retracting no longer valid simplifications. In turn, enabling simplifications could improve solving performance since a smaller overgrounded program is built.
$G'_1$
to be compatible with different sets of input facts, but this requires the additional effort of retracting no longer valid simplifications. In turn, enabling simplifications could improve solving performance since a smaller overgrounded program is built.
Let us now assume that the shot
![]() $2$
requires
$2$
requires
![]() $P_{ex}$
to be evaluated over a different set of input facts
$P_{ex}$
to be evaluated over a different set of input facts
![]() $F_2 = \{ e(3,1),\ e(1,4),\ q(1) \}$
. Note that, with respect to
$F_2 = \{ e(3,1),\ e(1,4),\ q(1) \}$
. Note that, with respect to
![]() $F_1$
,
$F_1$
,
![]() $F_2$
features the additions
$F_2$
features the additions
![]() $F^+ = \{ e(1,4), q(1) \}$
and the deletions
$F^+ = \{ e(1,4), q(1) \}$
and the deletions
![]() $F^- = \{ e(1,2), q(3)\}$
. In the standard overgrounding approach, since no simplification is done,
$F^- = \{ e(1,2), q(3)\}$
. In the standard overgrounding approach, since no simplification is done,
![]() $G_1$
can be easily adapted to the new input
$G_1$
can be easily adapted to the new input
![]() $F_2$
by incrementally augmenting it according to
$F_2$
by incrementally augmenting it according to
![]() $F^+$
; this turns into adding the following rules
$F^+$
; this turns into adding the following rules
![]() $\Delta G_1 = \{b_2, a_3\}$
, thus obtaining
$\Delta G_1 = \{b_2, a_3\}$
, thus obtaining
![]() $G_2$
:
$G_2$
:
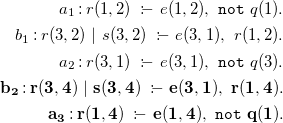 \begin{align*} a_1 : r(1,2) \ :\!\!- \ e(1,2),\ {\mathtt {not}}\ q(1). \\ b_1 : r(3,2) \ |\ s(3,2) \ :\!\!- \ e(3,1),\ r(1,2). \\ a_2 : r(3,1) \ :\!\!- \ e(3,1),\ {\mathtt {not}}\ q(3).\\ \mathbf{b_2 : r(3,4) \ |\ s(3,4) \ :\!\!- \ e(3,1),\ r(1,4).} \\ \mathbf{a_3 : r(1,4) \ :\!\!- \ e(1,4),\ {\mathtt {not}}\ q(1).} \end{align*}
\begin{align*} a_1 : r(1,2) \ :\!\!- \ e(1,2),\ {\mathtt {not}}\ q(1). \\ b_1 : r(3,2) \ |\ s(3,2) \ :\!\!- \ e(3,1),\ r(1,2). \\ a_2 : r(3,1) \ :\!\!- \ e(3,1),\ {\mathtt {not}}\ q(3).\\ \mathbf{b_2 : r(3,4) \ |\ s(3,4) \ :\!\!- \ e(3,1),\ r(1,4).} \\ \mathbf{a_3 : r(1,4) \ :\!\!- \ e(1,4),\ {\mathtt {not}}\ q(1).} \end{align*}
![]() $G_2$
is equivalent to
$G_2$
is equivalent to
![]() $P$
, when evaluated over
$P$
, when evaluated over
![]() $F_1$
or
$F_1$
or
![]() $F_2$
. Furthermore,
$F_2$
. Furthermore,
![]() $G_2$
enjoys the property of being compatible as it is, with every possible subset of
$G_2$
enjoys the property of being compatible as it is, with every possible subset of
![]() $F_1 \cup F_2$
. In the case of overgrounding with tailoring,
$F_1 \cup F_2$
. In the case of overgrounding with tailoring,
![]() $G'_1$
needs to be re-adapted by undoing no longer valid simplifications. In particular, rule
$G'_1$
needs to be re-adapted by undoing no longer valid simplifications. In particular, rule
![]() $a_2$
, previously deleted since
$a_2$
, previously deleted since
![]() $q(3) \in F_1$
, is now restored, given that
$q(3) \in F_1$
, is now restored, given that
![]() $q(3) \not \in F_2$
; moreover, rule
$q(3) \not \in F_2$
; moreover, rule
![]() $a'_1$
is reverted to its un-simplified version
$a'_1$
is reverted to its un-simplified version
![]() $a_1$
, since
$a_1$
, since
![]() $e(1,2) \not \in F_2$
.
$e(1,2) \not \in F_2$
.
![]() $b'_1$
is left unchanged, as reasons that led to simplify
$b'_1$
is left unchanged, as reasons that led to simplify
![]() $b_1$
into
$b_1$
into
![]() $b'_1$
are still valid (i.e.,
$b'_1$
are still valid (i.e.,
![]() $e(3,1)$
, featured in
$e(3,1)$
, featured in
![]() $F_1$
, still appears in
$F_1$
, still appears in
![]() $F_2$
).
$F_2$
).
The so-called desimplification step applied to
![]() $G'_1$
thus produces the following ground program:
$G'_1$
thus produces the following ground program:
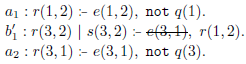
A further incremental step then generates new ground rules
![]() $b_2$
and
$b_2$
and
![]() $a_3$
, based on the presence of new facts
$a_3$
, based on the presence of new facts
![]() $F^+$
. Only newly generated rules are subject to simplifications according to
$F^+$
. Only newly generated rules are subject to simplifications according to
![]() $F_2$
. In particular,
$F_2$
. In particular,
![]() $e(3,1)$
is simplified from the body of
$e(3,1)$
is simplified from the body of
![]() $b_2$
, obtaining
$b_2$
, obtaining
![]() $b'_2$
;
$b'_2$
;
![]() $a_3$
is eliminated (i.e., an empty version
$a_3$
is eliminated (i.e., an empty version
![]() $a'_3$
is generated) since
$a'_3$
is generated) since
![]() $not\ q(1)$
is false; The resulting program
$not\ q(1)$
is false; The resulting program
![]() $G'_2$
is as follows:
$G'_2$
is as follows:
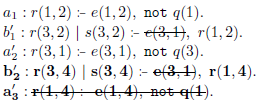
It is worth noting that
![]() $G'_2$
maintains the same semantics of
$G'_2$
maintains the same semantics of
![]() $P_{ex}$
, when either
$P_{ex}$
, when either
![]() $F_1$
or
$F_1$
or
![]() $F_2$
are given as input facts, but the semantics is not preserved with all possible subsets of
$F_2$
are given as input facts, but the semantics is not preserved with all possible subsets of
![]() $F_1 \cup F_2$
.
$F_1 \cup F_2$
.
If a third shot is requested over the input facts
![]() $F_3 = \{ e(1,4),\ e(3,1),\ e(1,2)\}$
, we observe that
$F_3 = \{ e(1,4),\ e(3,1),\ e(1,2)\}$
, we observe that
![]() $G_2$
does not need any further incremental update, as all facts in
$G_2$
does not need any further incremental update, as all facts in
![]() $F_3$
already appeared at previous steps; hence,
$F_3$
already appeared at previous steps; hence,
![]() $G_3 = G_2$
.
$G_3 = G_2$
.
Concerning
![]() $G'_2$
, the desimplification step reinstates
$G'_2$
, the desimplification step reinstates
![]() $a'_3$
while no additional rules are generated in the incremental step. This leads to the ground program
$a'_3$
while no additional rules are generated in the incremental step. This leads to the ground program
![]() $G'_3$
:
$G'_3$
:
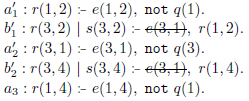
3 The Incremental-DLV2 system
In this section, we present the Incremental-DLV2 system, an incremental ASP reasoner stemming as a natural evolution of DLV2 of Alviano et al. (Reference Alviano, Calimeri, Dodaro, Fuscá, Leone, Perri, Ricca, Veltri and Zangari2017) toward multi-shot incremental reasoning. We first provide the reader with a general overview of the computational workflow and then discuss some insights about the main computational stages.
3.1 Computational workflow
Incremental-DLV2 is built upon a proper integration of the overgrounding-based incremental grounder
![]() ${I}^2$
-DLV, presented by Ianni et al. (Reference Ianni, Pacenza and Zangari2020), into DLV2. Coherently with its roots, Incremental-DLV2 fully complies with the declarative nature of ASP; among all the requirements, an important feature is that all means for enabling efficient multi-shot incremental reasoning are mostly transparent to the user. Incremental-DLV2 adapts the traditional ground & solve pipeline that we briefly recalled in Section 2 to the new incremental context. The grounding step of Incremental-DLV2 is based on overgrounding with tailoring; furthermore, in order to reduce the impact of a ground program that grows across steps, the solving phase selectively processes only a smaller, equivalent subset of the current overgrounded program.
${I}^2$
-DLV, presented by Ianni et al. (Reference Ianni, Pacenza and Zangari2020), into DLV2. Coherently with its roots, Incremental-DLV2 fully complies with the declarative nature of ASP; among all the requirements, an important feature is that all means for enabling efficient multi-shot incremental reasoning are mostly transparent to the user. Incremental-DLV2 adapts the traditional ground & solve pipeline that we briefly recalled in Section 2 to the new incremental context. The grounding step of Incremental-DLV2 is based on overgrounding with tailoring; furthermore, in order to reduce the impact of a ground program that grows across steps, the solving phase selectively processes only a smaller, equivalent subset of the current overgrounded program.
Figure 1 provides a high-level picture of the internal workflow of the system. When Incremental-DLV2 is started, it keeps itself alive in a listening state waiting for commands. Commands refer to high-level operations to be executed on demand, as detailed in Section 4.
![]() ${I}^2$
-DLV acts as OverGrounder module and enables incrementality in the computation on the grounding side, while the integrated Solver sub-system currently relies on the same non-incremental solving algorithms adopted in DLV2. Differently from DLV2, in Incremental-DLV2, both the grounding and the solving sub-systems are kept alive across the shots; while
${I}^2$
-DLV acts as OverGrounder module and enables incrementality in the computation on the grounding side, while the integrated Solver sub-system currently relies on the same non-incremental solving algorithms adopted in DLV2. Differently from DLV2, in Incremental-DLV2, both the grounding and the solving sub-systems are kept alive across the shots; while
![]() ${I}^2$
-DLV was already designed to this extent, the Solver module has been modified to remain alive as well. The updates in the solver and the tighter coupling of the two sub-systems pave the way to further steps toward a fully integrated incremental solving.
${I}^2$
-DLV was already designed to this extent, the Solver module has been modified to remain alive as well. The updates in the solver and the tighter coupling of the two sub-systems pave the way to further steps toward a fully integrated incremental solving.
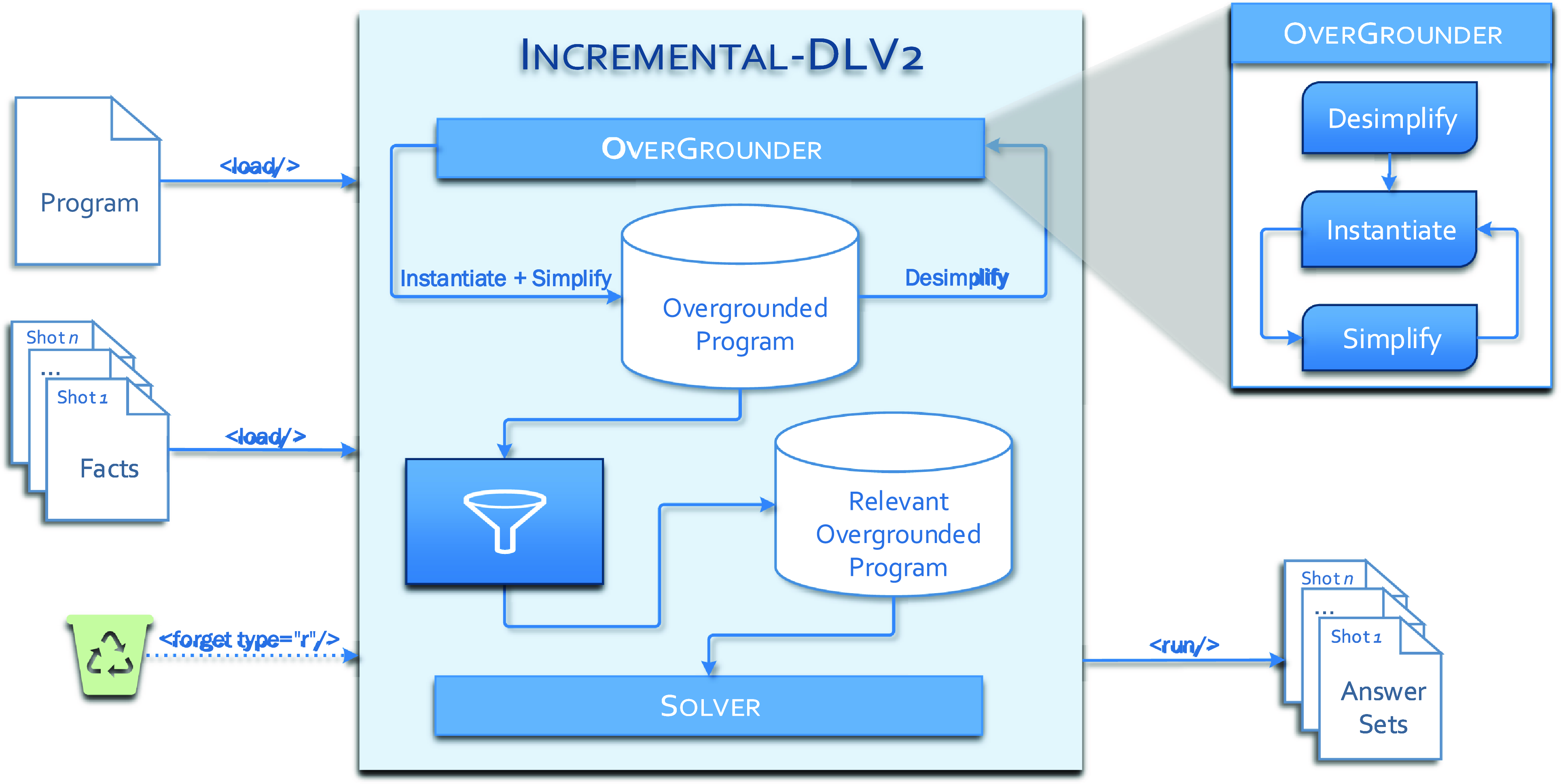
Fig 1. Incremental-DLV2 architecture.
Multi-shot reasoning is performed by loading a fixed program
![]() $P$
at first and then a set of facts
$P$
at first and then a set of facts
![]() $F_{i}$
for each shot
$F_{i}$
for each shot
![]() $i$
. According to the techniques described in Section 2, the OverGrounder module maintains across all shots a monotonically growing propositional program
$i$
. According to the techniques described in Section 2, the OverGrounder module maintains across all shots a monotonically growing propositional program
![]() $G$
. Such program is updated at each shot
$G$
. Such program is updated at each shot
![]() $i$
with the new ground rules generated on the basis of facts in
$i$
with the new ground rules generated on the basis of facts in
![]() $F_i$
that were never seen in previous shots; then, an internal component efficiently manages ad hoc internal data structures, updated from shot to shot, that allow to keep track and select a relevant, yet smaller, portion of
$F_i$
that were never seen in previous shots; then, an internal component efficiently manages ad hoc internal data structures, updated from shot to shot, that allow to keep track and select a relevant, yet smaller, portion of
![]() $G$
to be passed to the Solver module. On the basis of such “relevant” portion, the Solver module is then able to compute the answer sets of
$G$
to be passed to the Solver module. On the basis of such “relevant” portion, the Solver module is then able to compute the answer sets of
![]() $AS(P \cup F_i)$
for the shot
$AS(P \cup F_i)$
for the shot
![]() $i$
. Note that “relevant” is here used in the sense of “sufficient to keep equivalence with
$i$
. Note that “relevant” is here used in the sense of “sufficient to keep equivalence with
![]() $P \cup F_i$
.” Eventually, once the answer sets are provided as output, the internal data structures of the Solver module are cleaned up from shot-dependent information, so to be ready for the subsequent evaluations.
$P \cup F_i$
.” Eventually, once the answer sets are provided as output, the internal data structures of the Solver module are cleaned up from shot-dependent information, so to be ready for the subsequent evaluations.

Fig 2. Simplified version of the incremental algorithm IncrInst.
3.2 Implementation details
The evaluation order taking place in the OverGrounder module is carried out by considering direct and indirect dependencies among predicates in
![]() $P$
. Connected components in the obtained dependency graph are identified once and for all before at the beginning of the first shot: then, the incremental grounding process takes place on a per component basis, following a chosen order. We report an abstract version of our IncrInst algorithm in Figure 2, where, for the sake of simplicity, we assume the input program
$P$
. Connected components in the obtained dependency graph are identified once and for all before at the beginning of the first shot: then, the incremental grounding process takes place on a per component basis, following a chosen order. We report an abstract version of our IncrInst algorithm in Figure 2, where, for the sake of simplicity, we assume the input program
![]() $P$
forms a single component.
$P$
forms a single component.
At shot
![]() $i$
, a new overgrounded program
$i$
, a new overgrounded program
![]() $G' = DG \cup {N\!R}$
is obtained from
$G' = DG \cup {N\!R}$
is obtained from
![]() $G$
by iteratively repeating, until fixed point, a Desimpl step, followed by an Instantiate and Simplify step, which we call
$G$
by iteratively repeating, until fixed point, a Desimpl step, followed by an Instantiate and Simplify step, which we call
![]() $\Delta {INST}$
. A set
$\Delta {INST}$
. A set
![]() $AF$
of accumulated atoms keeps track of possibly true ground atoms found across shots; the set
$AF$
of accumulated atoms keeps track of possibly true ground atoms found across shots; the set
![]() $N\!R$
keeps track of newly added rules whose heads can be used to build additional ground rules at the current shot, while
$N\!R$
keeps track of newly added rules whose heads can be used to build additional ground rules at the current shot, while
![]() $DG$
is a “desimplified” version of
$DG$
is a “desimplified” version of
![]() $G$
.
$G$
.
The Desimplstep properly undoes all simplifications applied on
![]() $G$
at previous shots that are no longer valid according to
$G$
at previous shots that are no longer valid according to
![]() $F_i$
. This step relies on the meta-data collected during the previous simplifications: intuitively, meta-data keep record of the “reasons” that led to simplifications, such as deleted rules and/or literals. As a result of this phase, deleted rules might be reinstated, simplified rules might be lengthened, and new additions to
$F_i$
. This step relies on the meta-data collected during the previous simplifications: intuitively, meta-data keep record of the “reasons” that led to simplifications, such as deleted rules and/or literals. As a result of this phase, deleted rules might be reinstated, simplified rules might be lengthened, and new additions to
![]() $N\!R$
could be triggered.
$N\!R$
could be triggered.
The following
![]() $\Delta {INST}$
step incrementally processes each rule
$\Delta {INST}$
step incrementally processes each rule
![]() $r \in P$
, possibly producing new additions to
$r \in P$
, possibly producing new additions to
![]() $N\!R$
. The
$N\!R$
. The
![]() $getInstances$
function generates all the new ground instances
$getInstances$
function generates all the new ground instances
![]() $I_r$
of a rule
$I_r$
of a rule
![]() $r$
by finding substitutions for the variables of
$r$
by finding substitutions for the variables of
![]() $r$
obtained by properly combining head atoms of
$r$
obtained by properly combining head atoms of
![]() $DG$
and of
$DG$
and of
![]() $N\!R$
.
$N\!R$
.
The instantiation of a rule relies on a version of the classic semi-naïve strategy of Ullman (Reference Ullman1988). The reader may see the work Faber et al. (Reference Faber, Leone and Perri2012) for details about a specialized implementation for ASP. The rules of
![]() $P$
are processed according to an order induced by predicate dependencies.
$P$
are processed according to an order induced by predicate dependencies.
Then we simplify
![]() $I_r$
to
$I_r$
to
![]() $I'_r$
. In particular, this step processes rules in
$I'_r$
. In particular, this step processes rules in
![]() $I_r$
to check if some can be simplified or even eliminated (see Section 2), still guaranteeing semantics. On the grounding side, all ground rules in
$I_r$
to check if some can be simplified or even eliminated (see Section 2), still guaranteeing semantics. On the grounding side, all ground rules in
![]() $I_r$
are stored in their complete and non-simplified version along with information (i.e., meta-data) regarding body literals that were simplified and regarding deleted rules, for example, those rules containing a certainly false literal in their body. Then
$I_r$
are stored in their complete and non-simplified version along with information (i.e., meta-data) regarding body literals that were simplified and regarding deleted rules, for example, those rules containing a certainly false literal in their body. Then
![]() $I'_r$
is added to
$I'_r$
is added to
![]() $N\!R$
.
$N\!R$
.
It must be noted that
![]() $DG$
is subject only to additions and desimplifications, while simplifications are allowed only on the newly added rules
$DG$
is subject only to additions and desimplifications, while simplifications are allowed only on the newly added rules
![]() $N\!R$
. Further details on the tailored overgrounding process can be found in Ianni et al. (Reference Ianni, Pacenza and Zangari2020).
$N\!R$
. Further details on the tailored overgrounding process can be found in Ianni et al. (Reference Ianni, Pacenza and Zangari2020).
Once these two phases are over, the obtained ground rules are used to update the overgrounded program
![]() $G$
; meta-data related to the occurred simplifications are maintained in order to undo no longer valid simplifications in later shots.
$G$
; meta-data related to the occurred simplifications are maintained in order to undo no longer valid simplifications in later shots.
Note that
![]() $G$
is cumulatively computed across the shots and kept in memory, ready to be re-adapted and possibly enlarged, yet becoming more generally applicable to a wider class of sets of input facts; this comes at the price of a generally larger memory footprint. Moreover, when fed to the Solver module, the size of
$G$
is cumulatively computed across the shots and kept in memory, ready to be re-adapted and possibly enlarged, yet becoming more generally applicable to a wider class of sets of input facts; this comes at the price of a generally larger memory footprint. Moreover, when fed to the Solver module, the size of
![]() $G$
can highly influence performance. In order to mitigate the latter issue, Incremental-DLV2 makes use of the aforementioned meta-data for identifying a smaller yet equivalent ground program, which is in turn given as input to the Solver module in place of the whole
$G$
can highly influence performance. In order to mitigate the latter issue, Incremental-DLV2 makes use of the aforementioned meta-data for identifying a smaller yet equivalent ground program, which is in turn given as input to the Solver module in place of the whole
![]() $G$
.
$G$
.
Furthermore, to mitigate memory consumption, the system has been endowed with a simple forgetting strategy that, upon request, removes all rules accumulated in
![]() $G$
so far, while still keeping atoms stored; this will cause the overgrounded program to be computed from scratch from the next shot on, but allows one to instantly reduce the memory footprint of the system. Other finer-grained forgetting strategies for overgrounded programs are presented in Calimeri et al. (Reference Calimeri, Ianni, Pacenza, Perri, Zangari, Gebser and Sergey2024).
$G$
so far, while still keeping atoms stored; this will cause the overgrounded program to be computed from scratch from the next shot on, but allows one to instantly reduce the memory footprint of the system. Other finer-grained forgetting strategies for overgrounded programs are presented in Calimeri et al. (Reference Calimeri, Ianni, Pacenza, Perri, Zangari, Gebser and Sergey2024).
4 System usage
Incremental-DLV2 can be executed either remotely or locally. In case of a remote execution, clients can request for a connection specified via an IP address and a port number, corresponding to the connection coordinates at which the system is reachable. Once a connection is established, the system creates a working session and waits for incoming XML statements specifying which tasks have to be accomplished. The system manages the given commands in the order they are provided. The possible commands are Load, Run, Forget, Reset, and Exit.
The system works on the assumption that a fixed program
![]() $P$
can be loaded once at the beginning of the system’s life-cycle; multiple set of facts, each representing a specific shot, can be repeatedly loaded; a shot
$P$
can be loaded once at the beginning of the system’s life-cycle; multiple set of facts, each representing a specific shot, can be repeatedly loaded; a shot
![]() $k$
composed of facts
$k$
composed of facts
![]() $F_k$
can be run – that is, one can ask the system to compute
$F_k$
can be run – that is, one can ask the system to compute
![]() $AS(P \cup F_k)$
. Of course,
$AS(P \cup F_k)$
. Of course,
![]() $P$
can possibly also contain facts, which will be assumed to be fixed across shots, in contrast with the set
$P$
can possibly also contain facts, which will be assumed to be fixed across shots, in contrast with the set
![]() $F_k$
, which can vary from shot to shot.
$F_k$
, which can vary from shot to shot.
The available commands are detailed next:
Load. A load tag can be formed in order to request to load a program or a set of facts from a file. The attribute path can be used to specify a string, representing a file path containing what has to be loaded. Multiple load commands can be provided: rules files are accumulated to form a unique program, and similarly, facts are also accumulated. For instance, with the following commands, the system is asked to load four files:

Assuming the first two loaded files contain rules while the latter two contain facts, the system composes a fixed program
![]() $P$
consisting of all rule files and stores all loaded facts, which together compose the first shot’s input
$P$
consisting of all rule files and stores all loaded facts, which together compose the first shot’s input
![]() $F_1$
. Note that the set of rules can be loaded only at the beginning of the system’s activity, while input facts can be loaded at any time.
$F_1$
. Note that the set of rules can be loaded only at the beginning of the system’s activity, while input facts can be loaded at any time.
Run. The <run/> command requests to compute the answer sets of the loaded program together with the collected facts. As a side effect, incremental grounding takes place, thus updating the current overgrounded program
![]() $G_P$
.
$G_P$
.
After a run command is executed, all so far loaded facts are assumed to be no longer true. Future loading of rule files after the first run is discarded, as
![]() $P$
is assumed to be fixed; conversely, one expects further loading of facts forming subsequent shots’ inputs.
$P$
is assumed to be fixed; conversely, one expects further loading of facts forming subsequent shots’ inputs.
Forget. Since
![]() $G_P$
tends to be continuously enlarged, forgetting can be used to save memory by dropping off parts of the accumulated ground program. Incremental-DLV2 features a form of forgetting, which is accessible either as a command or using program annotations.
$G_P$
tends to be continuously enlarged, forgetting can be used to save memory by dropping off parts of the accumulated ground program. Incremental-DLV2 features a form of forgetting, which is accessible either as a command or using program annotations.
With the command ![]() , it is possible to request the “forgetting” (i.e., removal) of accumulated atoms or rules along the shots. More in detail, mode can be either r or p to enable the so-called “rule-based forgetting” or “predicate-based forgetting,” respectively (see Calimeri et al. (Reference Calimeri, Ianni, Pacenza, Perri, Zangari, Gebser and Sergey2024)). The rule-based forgetting removes all ground rules composing the so far accumulated overgrounded program
, it is possible to request the “forgetting” (i.e., removal) of accumulated atoms or rules along the shots. More in detail, mode can be either r or p to enable the so-called “rule-based forgetting” or “predicate-based forgetting,” respectively (see Calimeri et al. (Reference Calimeri, Ianni, Pacenza, Perri, Zangari, Gebser and Sergey2024)). The rule-based forgetting removes all ground rules composing the so far accumulated overgrounded program
![]() $G_P$
, whereas the predicate-based forgetting removes all ground rules and accumulated atoms of all predicates appearing either in rule bodies or heads. Overgrounding is started from scratch at the next shot. Note that the forget command allows to choose in which shot forgetting happens, but one cannot select which parts of
$G_P$
, whereas the predicate-based forgetting removes all ground rules and accumulated atoms of all predicates appearing either in rule bodies or heads. Overgrounding is started from scratch at the next shot. Note that the forget command allows to choose in which shot forgetting happens, but one cannot select which parts of
![]() $G_P$
must be removed.
$G_P$
must be removed.
Alternatively, forgetting can be managed by adding annotations within
![]() $P$
. Annotations consist of meta-data embedded in comments (see Calimeri et al. (Reference Calimeri, Fuscá, Perri and Zangari2017)) and allow to specify which predicates or rules have to be forgotten at each shot. Syntactically, all annotations start with the prefix “
$P$
. Annotations consist of meta-data embedded in comments (see Calimeri et al. (Reference Calimeri, Fuscá, Perri and Zangari2017)) and allow to specify which predicates or rules have to be forgotten at each shot. Syntactically, all annotations start with the prefix “
![]() $\%@$
” and end with a dot (“
$\%@$
” and end with a dot (“
![]() $.$
”). The idea is borrowed from Java and Python annotations, having no direct effect on the code they annotate, yet allowing the programmer to inspect the annotated code at runtime, thus changing the code behavior at will. In order to apply the predicate-based forgetting type after each shot over some specific predicates, the user can include in the loaded logic program an annotation of the following form:
$.$
”). The idea is borrowed from Java and Python annotations, having no direct effect on the code they annotate, yet allowing the programmer to inspect the annotated code at runtime, thus changing the code behavior at will. In order to apply the predicate-based forgetting type after each shot over some specific predicates, the user can include in the loaded logic program an annotation of the following form:
forcing the system to forget all the atoms featuring the predicate p of arity n. To forget more than one predicate, the user can simply specify more than one annotation of this type. Furthermore, an annotation in the form:
can be used in the logic program before a rule to express that all ground instances of such a rule have to be dropped at each shot. The user can annotate more than one rule; each one needs to be preceded by the annotation.
Service commands. Further appropriate service commands allow managing the behavior of the system. The <reset/> command requests to hard reset all internal data structures, including
![]() $P$
and
$P$
and
![]() $G_P$
, and restarts the computation from scratch, while the <exit/> command requests to close the working session and to stop the system.
$G_P$
, and restarts the computation from scratch, while the <exit/> command requests to close the working session and to stop the system.
The default reasoning task of Incremental-DLV2 is the search for just one answer set; it is possible to compute all the existing answer sets with a dedicated switch (option -n0). Alternatively, the system can perform grounding only and output just the current overgrounded program, which can be piped to a solver module of choice (option ![]() ).
).
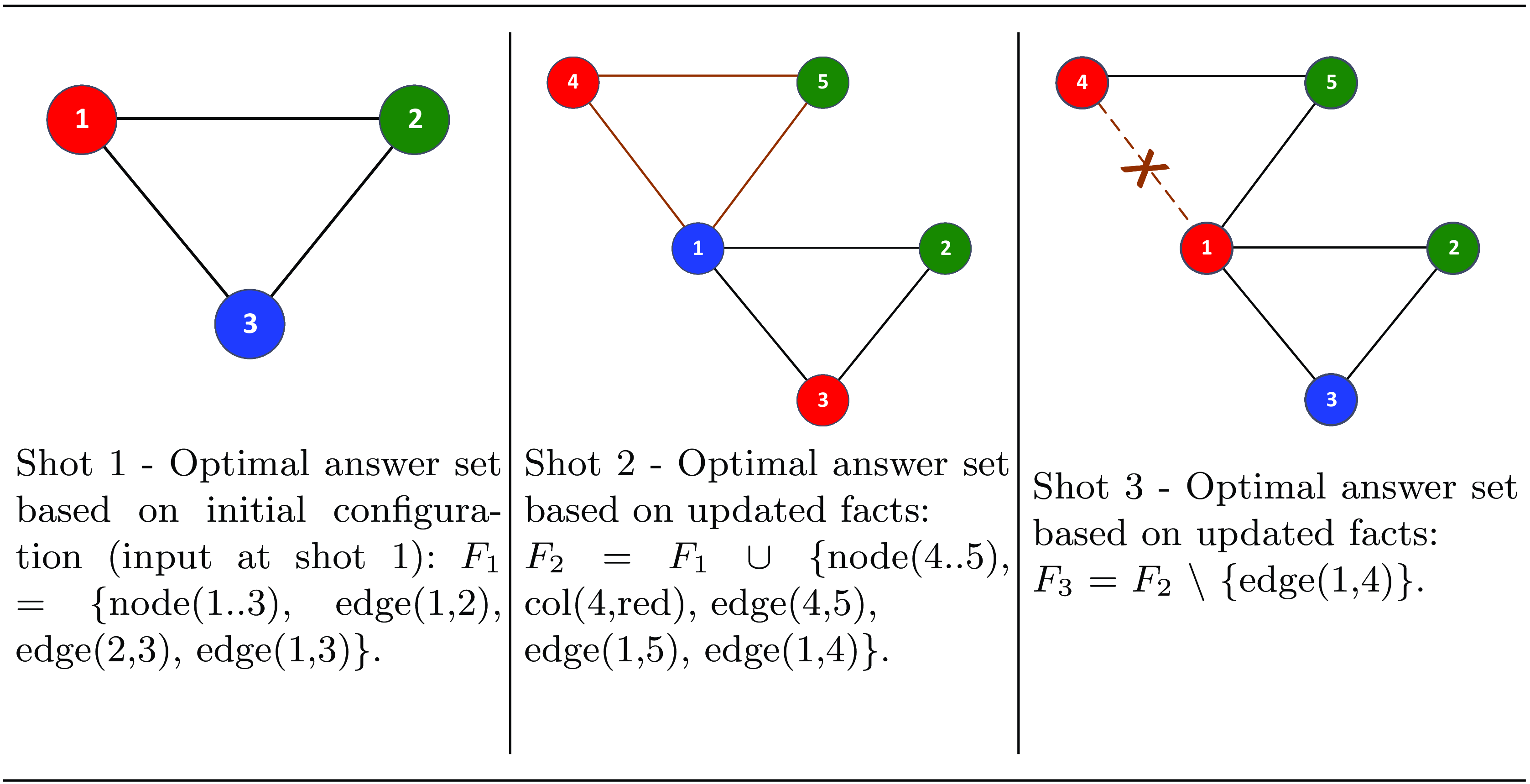
Fig 3. An example of multi-shot reasoning task based on Incremental-DLV2: compute 3-coloring for graphs featuring a structure that changes over time.
We illustrate next how the system works when properly executed for a multi-shot reasoning task; to this aim, we make use of an example over dynamic graphs, that is, graphs whose shape changes over time. Dynamic graphs have practical relevance in many real-world scenarios, for example, communication networks, VLSI design, graphics, assembly planning, IoT, etc. (see Demetrescu et al. (Reference Demetrescu, Finocchi, Italiano, Mehta and Sahni2004); He et al. (Reference He, Tang and Zeh2014); Wang et al. (Reference Wang, Yuan, Ma and Wang2019); Adi et al. (Reference Adi, Sihombing, Siregar, Yanris, Sianturi, Purba, Tamba, Simatupang, Arifuddin, Subairi and Prasetya2021)); for the sake of presentation, we will consider here a simple setting based on the classical NP-hard 3-coloring problem (Lawler (Reference Lawler1976)) in a dynamic setting. Given a graph
![]() $G(V,E)$
, the problem is to assign each node
$G(V,E)$
, the problem is to assign each node
![]() $v\in V$
with exactly one color out of a set of
$v\in V$
with exactly one color out of a set of
![]() $3$
(say, red, green, and blue), so that any pair of adjacent nodes never gets the same color. If the structure of a given graph instance
$3$
(say, red, green, and blue), so that any pair of adjacent nodes never gets the same color. If the structure of a given graph instance
![]() $G$
is specified by means of facts over predicates
$G$
is specified by means of facts over predicates
![]() $node$
and
$node$
and
![]() $edge$
, then the following program
$edge$
, then the following program
![]() $P_{3col}$
encodes the problem in ASP:
$P_{3col}$
encodes the problem in ASP:
Here,
![]() $r_1$
is a “guessing” rule, expressing that each node must be assigned with one of the three available colors, whereas
$r_1$
is a “guessing” rule, expressing that each node must be assigned with one of the three available colors, whereas
![]() $r_2$
is a strong constraint that filters out all candidate solutions that assign two adjacent nodes with the same color. We refer here to an optimization version of the problem, in which some preferences over admissible solutions are given; this can be easily expressed via the following weak constraints (see Calimeri et al. (Reference Calimeri, Faber, Gebser, Ianni, Kaminski, Krennwallner, Leone, Maratea, Ricca and Schaub2020) for details on the linguistic features of ASP):
$r_2$
is a strong constraint that filters out all candidate solutions that assign two adjacent nodes with the same color. We refer here to an optimization version of the problem, in which some preferences over admissible solutions are given; this can be easily expressed via the following weak constraints (see Calimeri et al. (Reference Calimeri, Faber, Gebser, Ianni, Kaminski, Krennwallner, Leone, Maratea, Ricca and Schaub2020) for details on the linguistic features of ASP):
In this case, rules
![]() $r_3$
and
$r_3$
and
![]() $r_4$
express preferences for colors to be assigned to nodes
$r_4$
express preferences for colors to be assigned to nodes
![]() $1$
and
$1$
and
![]() $2$
: more in detail, color red is preferred for node
$2$
: more in detail, color red is preferred for node
![]() $1$
, while color green is preferred for node
$1$
, while color green is preferred for node
![]() $2$
.
$2$
.
Let us consider the setting in which it is needed to reason on a graph whose structure changes over time, that is, at each shot, nodes and edges can be added or removed.
We show the behavior of the system across three possible shots where input facts change (see Figure 3). Assuming that rules
![]() $r_1$
,
$r_1$
,
![]() $r_2$
,
$r_2$
,
![]() $r_3$
,
$r_3$
,
![]() $r_4$
are contained in a file 3-col.asp, the command
$r_4$
are contained in a file 3-col.asp, the command ![]() has issued to Incremental-DLV2 to load the program. Let f1.asp be a file containing the input facts for the first shot:
has issued to Incremental-DLV2 to load the program. Let f1.asp be a file containing the input facts for the first shot:
By issuing the commands ![]() and <run/>, the system finds the unique optimum answer set that assigns nodes
and <run/>, the system finds the unique optimum answer set that assigns nodes
![]() $1,2,3$
with colors red, green, and blue, respectively, and internally stores the overgrounded program
$1,2,3$
with colors red, green, and blue, respectively, and internally stores the overgrounded program
![]() $G_{3col}$
reported below, in which barred atoms represent occurred simplifications:
$G_{3col}$
reported below, in which barred atoms represent occurred simplifications:

At this point, facts in f1.asp are no longer assumed to be true, and the system is ready for a further shot. Suppose that now a further file f2.asp containing the facts for the second shot is loaded (Figure 3, middle column):
two new nodes connected to each other are added and connected also to node
![]() $1$
, while coloring for node
$1$
, while coloring for node
![]() $4$
is already known to be red. If now another
$4$
is already known to be red. If now another
![]() $\lt$
run/
$\lt$
run/
![]() $\gt$
command is issued, thanks to the overgrounding-based instantiation strategy, the system only generates further ground rules due to newly added nodes and edges and adds them to
$\gt$
command is issued, thanks to the overgrounding-based instantiation strategy, the system only generates further ground rules due to newly added nodes and edges and adds them to
![]() $G_{3col}$
:
$G_{3col}$
:
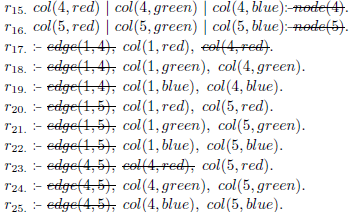
Notably, simplifications made at shot 1 remain valid since all facts in shot
![]() $1$
are also facts of shot
$1$
are also facts of shot
![]() $2$
. Finally, suppose that in the third shot, the system loads a file f3.asp containing the facts (Figure 3, right column):
$2$
. Finally, suppose that in the third shot, the system loads a file f3.asp containing the facts (Figure 3, right column):
The input graph is updated by removing the edge between nodes
![]() $1$
and
$1$
and
![]() $4$
. Now, no new fact results as unseen in previous shots: hence, no additional ground rules are generated, and no grounding effort is needed; the only update in
$4$
. Now, no new fact results as unseen in previous shots: hence, no additional ground rules are generated, and no grounding effort is needed; the only update in
![]() $G_{3col}$
consists of the desimplification of
$G_{3col}$
consists of the desimplification of
![]() $edge(1,4)$
in rules
$edge(1,4)$
in rules
![]() $r_{17}$
,
$r_{17}$
,
![]() $r_{18}$
, and
$r_{18}$
, and
![]() $r_{19}$
:
$r_{19}$
:

The unique optimum answer set now consists of coloring nodes
![]() $1,2,3,4,5$
in red, green, blue, red, green, respectively. It is worth noting that the savings in computational time, obtained by properly reusing ground rules generated at previous shots, occur with no particular assumption made in advance about possible incoming input facts. Moreover, the management of the incremental computation is completely automated and transparent to the user, who is not required to define a priori what is fixed and what might change.
$1,2,3,4,5$
in red, green, blue, red, green, respectively. It is worth noting that the savings in computational time, obtained by properly reusing ground rules generated at previous shots, occur with no particular assumption made in advance about possible incoming input facts. Moreover, the management of the incremental computation is completely automated and transparent to the user, who is not required to define a priori what is fixed and what might change.
5 Experimental analysis
In this section, we discuss the performance of Incremental-DLV2 when executing multi-shot reasoning tasks in real-world scenarios.
5.1 Benchmarks
We considered a collection of real-world problems that have been already used for testing incremental reasoners. A brief description of each benchmark follows. The full logic programs, instances, and experimental settings can be found at https://dlv.demacs.unical.it/incremental.
5.1.1 Pac-Man (Calimeri et al. (Reference Calimeri, Germano, Ianni, Pacenza, Perri, Zangari, Benzmüller, Ricca, Parent and Roman2018))
This domain models the well-known real-time game Pac-Man. Here, a logic program
![]() $P_{pac}$
describes the decision-making process of an artificial player guiding the Pac-Man in a real implementation. The logic program
$P_{pac}$
describes the decision-making process of an artificial player guiding the Pac-Man in a real implementation. The logic program
![]() $P_{pac}$
is repeatedly executed together with different inputs describing the current status of the game board. The game map is of size
$P_{pac}$
is repeatedly executed together with different inputs describing the current status of the game board. The game map is of size
![]() $30 \times 30$
and includes the current position of enemy ghosts, the position of pellets, of walls, and any other relevant game information. Several parts of
$30 \times 30$
and includes the current position of enemy ghosts, the position of pellets, of walls, and any other relevant game information. Several parts of
![]() $P_{pac}$
are “grounding-intensive,” like the ones describing the distances between different positions in the game map. These make use of a predicate
$P_{pac}$
are “grounding-intensive,” like the ones describing the distances between different positions in the game map. These make use of a predicate
![]() $distance(X_1,Y_1, X_2, Y_2,D)$
, where
$distance(X_1,Y_1, X_2, Y_2,D)$
, where
![]() $D$
represents the distance between points
$D$
represents the distance between points
![]() $(X_1,Y_1)$
and
$(X_1,Y_1)$
and
![]() $(X_2,Y_2)$
, obtained by taking into account the shape of the labyrinth in the game map.
$(X_2,Y_2)$
, obtained by taking into account the shape of the labyrinth in the game map.
5.1.2 Content caching (Ianni et al. (Reference Ianni, Pacenza and Zangari2020))
This domain is obtained from the multimedia video streaming context (see Beck et al. (Reference Beck, Bierbaumer, Dao-tran, Eiter, Hellwagner and Schekotihin2017)). In this scenario, one of the common problems is to decide the caching policy of a given video content, depending on variables like the number and the current geographic distribution of viewers. The caching policy is managed via a logic program
![]() $P_{cc}$
. In particular, policy rules are encoded in the answer sets
$P_{cc}$
. In particular, policy rules are encoded in the answer sets
![]() $AS(P_{cc} \cup E)$
, where
$AS(P_{cc} \cup E)$
, where
![]() $E$
encodes a continuous stream of events describing the evolving popularity level of the content at hand. This application has been originally designed in the LARS framework of Beck et al. (Reference Beck, Dao-tran and Eiter2018), using time window operators in order to quantify over past events. We adapted the available LARS specification according to the conversion method presented by Beck et al. (Reference Beck, Bierbaumer, Dao-tran, Eiter, Hellwagner and Schekotihin2017) to obtain
$E$
encodes a continuous stream of events describing the evolving popularity level of the content at hand. This application has been originally designed in the LARS framework of Beck et al. (Reference Beck, Dao-tran and Eiter2018), using time window operators in order to quantify over past events. We adapted the available LARS specification according to the conversion method presented by Beck et al. (Reference Beck, Bierbaumer, Dao-tran, Eiter, Hellwagner and Schekotihin2017) to obtain
![]() $P_{cc}$
as a plain logic program under answer set semantics; events over
$P_{cc}$
as a plain logic program under answer set semantics; events over
![]() $30\,000$
time points were converted to corresponding sets of input facts. This category of stream-reasoning applications can be quite challenging, depending on the pace of events and the size of time windows.
$30\,000$
time points were converted to corresponding sets of input facts. This category of stream-reasoning applications can be quite challenging, depending on the pace of events and the size of time windows.
5.1.3 Photo-voltaic system (Calimeri et al. (Reference Calimeri, Manna, Mastria, Morelli, Perri and Zangari2021))
We consider here a stream-reasoning scenario in which an intelligent monitoring system (IMS) for a photo-voltaic system (PVS) is used to promptly detect major grid malfunctions. We consider a PVS composed of a grid of
![]() $60 \times 60$
solar panels interconnected via cables; each panel continuously produces a certain amount of energy to be transferred to a central energy accumulator directly or via a path between neighbor panels across the grid. The amount of energy produced is tracked and sent to the IMS. An ASP program is repeatedly executed over streamed data readings with the aim of identifying situations to be alerted for and thus prompting the necessity of maintenance interventions. Notably, this domain causes a more intensive computational effort on the grounding side with respect to the solving side as the logic program at hand does not feature disjunction and is stratified.
$60 \times 60$
solar panels interconnected via cables; each panel continuously produces a certain amount of energy to be transferred to a central energy accumulator directly or via a path between neighbor panels across the grid. The amount of energy produced is tracked and sent to the IMS. An ASP program is repeatedly executed over streamed data readings with the aim of identifying situations to be alerted for and thus prompting the necessity of maintenance interventions. Notably, this domain causes a more intensive computational effort on the grounding side with respect to the solving side as the logic program at hand does not feature disjunction and is stratified.

Fig 4. Incremental-DLV2 against DLV2: performance in multi-shot contexts.
5.2 Setting
We compared the herein presented Incremental-DLV2 system against the DLV2 system. Both systems were run in single-threaded mode. Experiments have been performed on a NUMA machine equipped with two
![]() $2.8$
GHz AMD Opteron
$2.8$
GHz AMD Opteron
![]() $6320$
CPUs, with
$6320$
CPUs, with
![]() $16$
cores and
$16$
cores and
![]() $128$
GB of RAM. Differently from Incremental-DLV2, DLV2 is restarted, that is, executed from scratch, at each shot in order to evaluate the given program on the current facts. For each domain, we choose two different measures: we track the total accumulated time and the maximum memory peak per shot. Figure 4 plots the chosen measures against the number of shots for all benchmarks; the
$128$
GB of RAM. Differently from Incremental-DLV2, DLV2 is restarted, that is, executed from scratch, at each shot in order to evaluate the given program on the current facts. For each domain, we choose two different measures: we track the total accumulated time and the maximum memory peak per shot. Figure 4 plots the chosen measures against the number of shots for all benchmarks; the
![]() $X$
axis diagrams data in the shot execution order.
$X$
axis diagrams data in the shot execution order.
5.3 Execution times
When observing execution times, a clear advantage is experienced by Incremental-DLV2 over all considered domains.
The Pac-Man benchmark is characterized by the need for computing all distances between all positions (
![]() $30 \times 30$
) in the game map, which is fixed, and hence Incremental-DLV2 is able to compute them only once at the first shot, which is the most time expensive. At each shot after the first, there is a net gain in grounding times stabilizing at an approximate speedup factor of 4.6; furthermore, given the nature of the available instances, which encode a real game, it turns out that, for a large part of the overgrounded program, the simplifications performed are preserved when moving toward the next shots. Hence, Incremental-DLV2 gains from the low need for desimplifications, while still avoiding to burden the Solver module too much as it is fed with highly simplified versions of the ground program.
$30 \times 30$
) in the game map, which is fixed, and hence Incremental-DLV2 is able to compute them only once at the first shot, which is the most time expensive. At each shot after the first, there is a net gain in grounding times stabilizing at an approximate speedup factor of 4.6; furthermore, given the nature of the available instances, which encode a real game, it turns out that, for a large part of the overgrounded program, the simplifications performed are preserved when moving toward the next shots. Hence, Incremental-DLV2 gains from the low need for desimplifications, while still avoiding to burden the Solver module too much as it is fed with highly simplified versions of the ground program.
In the Content Caching scenario, reasoning is performed on a time window spanning over the last 1000 time ticks. Thus, instances are so that for the first
![]() $1000$
shots, the input facts span over a time window of less than
$1000$
shots, the input facts span over a time window of less than
![]() $1000$
ticks, and consequently, they are a superset of inputs coming from previous shots; then, from shot
$1000$
ticks, and consequently, they are a superset of inputs coming from previous shots; then, from shot
![]() $1000$
on, possible input facts do not change anymore. This implies that, basically, from shot to shot the whole overgrounded program is just monotonically enriched with new ground rules, yet keeping the simplifications performed in previous shots, up to the point that nothing new has to be instantiated after shot
$1000$
on, possible input facts do not change anymore. This implies that, basically, from shot to shot the whole overgrounded program is just monotonically enriched with new ground rules, yet keeping the simplifications performed in previous shots, up to the point that nothing new has to be instantiated after shot
![]() $1000$
. While Incremental-DLV2 cumulative time performance exhibits a linear growth, the DLV2 behavior worsens as instances become larger. Indeed, early shots require a little computational effort, and thus DLV2 takes advantage of the lack of the multi-shot machinery overhead, although the computing times of the two systems are very close. However, in later shots, the picture overturns: the growth of DLV2 times starts accelerating after a few hundred shots, up to the point that, from shot
$1000$
. While Incremental-DLV2 cumulative time performance exhibits a linear growth, the DLV2 behavior worsens as instances become larger. Indeed, early shots require a little computational effort, and thus DLV2 takes advantage of the lack of the multi-shot machinery overhead, although the computing times of the two systems are very close. However, in later shots, the picture overturns: the growth of DLV2 times starts accelerating after a few hundred shots, up to the point that, from shot
![]() $1000$
on, as the task to be executed is almost the same across all shots, Incremental-DLV2 significantly outperforms DLV2, as it basically saves the whole grounding time thanks to the overgrounding technique. It is also worth noting that Incremental-DLV2 scales definitely better, as the growth of the execution time is always almost linear; on the other hand, the DLV2 cumulative execution time has a quadratic like trend at the very start and becomes linear only when the effort for requested tasks stabilizes after shot
$1000$
on, as the task to be executed is almost the same across all shots, Incremental-DLV2 significantly outperforms DLV2, as it basically saves the whole grounding time thanks to the overgrounding technique. It is also worth noting that Incremental-DLV2 scales definitely better, as the growth of the execution time is always almost linear; on the other hand, the DLV2 cumulative execution time has a quadratic like trend at the very start and becomes linear only when the effort for requested tasks stabilizes after shot
![]() $1000$
, converging to a speedup factor in favor of Incremental-DLV2 of around 1.6.
$1000$
, converging to a speedup factor in favor of Incremental-DLV2 of around 1.6.
In the case of the PVS benchmark, both systems show a linear growth in cumulated time; still, Incremental-DLV2 clearly outperforms DLV2, with a speedup factor of slightly less than 2. The corresponding logic program is stratified and features a recursive component that is “activated” at each shot; hence, the hard part of the computation is carried out during the grounding phase, which, also given the nature of the available instances, still remains significant in later shots, differently from the other domains.
5.4 Memory usage
Some additional considerations deserve to be done about memory usage. Indeed, as it is expected because of the incremental grounding strategy herein adopted, the memory footprint is definitely higher for Incremental-DLV2, in all considered domains. However, interestingly, it can be noted that in all cases the memory usage trend shows an asymptotic “saturation” behavior: after a certain number of shots the memory usage basically stays constant; hence, the price to pay in terms of memory footprint is not only counterbalanced by the gain in terms of performance, but it also happens to not “explode.” We also observe that in the Content Caching and PVS benchmarks the memory usage increases along the shots, while it reaches a sort of plateau in the Pac-Man benchmark. Indeed, in this latter domain, a large amount of information, useful in all shots, is inferred only at the first shot and then kept in memory, but with some redundancy. As a result, the memory usage in this benchmark domain is high at the beginning of the shot series, but it stays almost unchanged later. On the other hand, DLV2 makes a good job in generating, from scratch, a compact ground program for each shot. Although the results show a fairly reasonable memory usage, as mentioned before, memory-limiting and rule-forgetting policies added on top of existing algorithms can help in mitigating the memory footprint of Incremental-DLV2, especially in scenarios where memory caps are imposed.
6 Related work
6.1 Theoretical foundations of incremental grounding in ASP
The theoretical foundations and algorithms at the basis of Incremental-DLV2 were laid out by Calimeri et al. (Reference Calimeri, Ianni, Pacenza, Perri and Zangari2019) and Ianni et al. (Reference Ianni, Pacenza and Zangari2020). The two contributions propose, respectively, a notion of embedding and tailored embedding. Embeddings are families of ground programs, which enjoy a number of desired properties. Given
![]() $P \cup F$
, an embedding
$P \cup F$
, an embedding
![]() $E$
is such that
$E$
is such that
![]() $AS(P \cup F) = AS(E)$
;
$AS(P \cup F) = AS(E)$
;
![]() $E$
must be such that it embeds (
$E$
must be such that it embeds (
![]() $E \vdash r$
) all
$E \vdash r$
) all
![]() $r \in ground(P \cup F)$
.
$r \in ground(P \cup F)$
.
The
![]() $\vdash$
operator is similar to the operator
$\vdash$
operator is similar to the operator
![]() $\models$
that is applied to interpretations and enjoys similar model theoretical properties. Intuitively, given interpretation
$\models$
that is applied to interpretations and enjoys similar model theoretical properties. Intuitively, given interpretation
![]() $I$
and rule
$I$
and rule
![]() $r$
with head
$r$
with head
![]() $h_r$
and positive body
$h_r$
and positive body
![]() $b_r$
, it is known that
$b_r$
, it is known that
![]() $I \models r$
whenever
$I \models r$
whenever
![]() $I \models h_r$
or
$I \models h_r$
or
![]() $I \not \models b_r$
, thus enforcing an implicative dependency between
$I \not \models b_r$
, thus enforcing an implicative dependency between
![]() $b_r$
and
$b_r$
and
![]() $h_r$
. A similar implicative dependency is enforced on the structure of ground programs qualified as embeddings:
$h_r$
. A similar implicative dependency is enforced on the structure of ground programs qualified as embeddings:
![]() $E \vdash r$
whenever
$E \vdash r$
whenever
![]() $r \in E$
or whenever, for some atom
$r \in E$
or whenever, for some atom
![]() $b \in b_r$
,
$b \in b_r$
,
![]() $E$
does not embed any rule having
$E$
does not embed any rule having
![]() $b$
in its head. Embeddings are closed under intersection, and the unique minimal embedding can be computed in a bottom-up fashion by an iterated fixed-point algorithm. An overgrounded program
$b$
in its head. Embeddings are closed under intersection, and the unique minimal embedding can be computed in a bottom-up fashion by an iterated fixed-point algorithm. An overgrounded program
![]() $G$
of
$G$
of
![]() $P \cup F$
is such that
$P \cup F$
is such that
![]() $G \cup F$
is an embedding of
$G \cup F$
is an embedding of
![]() $P \cup F$
.
$P \cup F$
.
Ianni et al. (Reference Ianni, Pacenza and Zangari2020) extend the notion of embedding to tailored embeddings. Tailored embeddings are families of ground programs, equivalent to some
![]() $P \cup F$
, which allow the possibility of including in the ground program itself a simplified version
$P \cup F$
, which allow the possibility of including in the ground program itself a simplified version
![]() $r'$
of a rule
$r'$
of a rule
![]() $r \in ground(P)$
. A tailored embedding is such that
$r \in ground(P)$
. A tailored embedding is such that
![]() $T \Vdash r$
for each
$T \Vdash r$
for each
![]() $r \in ground(P \cup F)$
. The operator
$r \in ground(P \cup F)$
. The operator
![]() $\Vdash$
takes into account the possibility of simplifications and deletion of rules. The presence of simplified rules might lead to ground programs, which are not comparable under plain set containment; however, tailored embeddings are closed under a generalized notion of containment, and the least tailored embedding can be computed using a bottom-up fixed-point algorithm. Importantly, an overgrounded program with tailoring
$\Vdash$
takes into account the possibility of simplifications and deletion of rules. The presence of simplified rules might lead to ground programs, which are not comparable under plain set containment; however, tailored embeddings are closed under a generalized notion of containment, and the least tailored embedding can be computed using a bottom-up fixed-point algorithm. Importantly, an overgrounded program with tailoring
![]() $G$
obtained by the IncrInst algorithm at shot
$G$
obtained by the IncrInst algorithm at shot
![]() $i$
with input facts
$i$
with input facts
![]() $F_i$
, is such that
$F_i$
, is such that
![]() $G \cup F_i$
is a tailored embedding of
$G \cup F_i$
is a tailored embedding of
![]() $P \cup F_i$
, and thus
$P \cup F_i$
, and thus
![]() $AS(G \cup F_i) = AS(P \cup F_i)$
.
$AS(G \cup F_i) = AS(P \cup F_i)$
.
It is worth highlighting that embeddings and tailored embeddings can be seen as families of relativized hyperequivalent logic programs in the sense of Truszczynski and Woltran (Reference Truszczynski and Woltran2009). Indeed, given logic programs
![]() $P$
and
$P$
and
![]() $Q$
, these are said to be hyperequivalent relatively to a finite family of programs
$Q$
, these are said to be hyperequivalent relatively to a finite family of programs
![]() $\mathcal{F}$
iff
$\mathcal{F}$
iff
![]() $AS(P \cup F) = AS(Q \cup F)$
for each
$AS(P \cup F) = AS(Q \cup F)$
for each
![]() $F \in \mathcal{F}$
. A member
$F \in \mathcal{F}$
. A member
![]() $G$
of a sequence of overgrounded programs is characterized by being equivalent to a program
$G$
of a sequence of overgrounded programs is characterized by being equivalent to a program
![]() $P$
relative to (part of) a finite set of inputs
$P$
relative to (part of) a finite set of inputs
![]() $F_1, \ldots , F_n$
, similarly to hyperequivalent programs relative to finite sets of inputs. Conditions in which a form of equivalence is preserved under simplifications, possibly changing the simplified program signature w.r.t. the original program, were studied by Saribatur and Woltran (Reference Saribatur and Woltran2023).
$F_1, \ldots , F_n$
, similarly to hyperequivalent programs relative to finite sets of inputs. Conditions in which a form of equivalence is preserved under simplifications, possibly changing the simplified program signature w.r.t. the original program, were studied by Saribatur and Woltran (Reference Saribatur and Woltran2023).
6.2 Other ASP systems with incremental features
The ASP system clingo (Gebser et al. (Reference Gebser, Kaminski, Kaufmann and Schaub2019)) represents the main contribution related to multi-shot reasoning in ASP. clingo allows to procedurally control which and how parts of the logic program have to be incremented, updated and taken into account among consecutive shots. This grants designers of logic programs a great flexibility; however, the approach requires specific knowledge about how the system internally holds its computation and about how the domain at hand is structured. It must in fact be noted that the notion of “incrementality” in clingo is intended in a constructive manner as the management of parts of the logic program that can be built in incremental layers. Conversely, in the approach proposed in this paper, the ability of using procedural directives is purposely avoided, in favor of a purely declarative approach. Incrementality is herein intended as an internal process to the ASP system, which works on a fixed input program.
The Stream Reasoning system Ticker of Beck et al. (Reference Beck, Bierbaumer, Dao-tran, Eiter, Hellwagner and Schekotihin2017) represents an explicit effort toward a more general approach to ASP incremental reasoning. Ticker implements the LARS stream-reasoning formal framework of Beck et al. (Reference Beck, Dao-tran and Eiter2018). The input language of LARS allows window operators, which enable reasoning on streams of data under ASP semantics. Ticker implements a fragment of LARS, with no disjunction and no constraints/odd-cycle negation loops, by using back-end incremental truth maintenance techniques.
Among approaches that integrate tightly grounding and solving, it is worth mentioning lazy grounding (see Dal Palù et al. (Reference Dal Palù, Dovier, Pontelli and Rossi2009); Lefèvre et al. (Reference Lefèvre, Béatrix, STéphan and Garcia2017); Bomanson et al. (Reference Bomanson, Janhunen and Weinzierl2019)). Note that overgrounding is essentially orthogonal to lazy grounding techniques, since these latter aim at blending grounding tasks within the solving step for reducing memory consumption; rather, our focus is on making grounding times negligible on repeated evaluations by explicitly allowing the usage of more memory, while still keeping a loose coupling between the two evaluation steps.
6.3 Incrementality in datalog
The issue of incremental reasoning on ASP logic programs is clearly related to the problem of maintaining views expressed in Datalog. In this respect, Motik et al. (Reference Motik, Nenov, Piro and Horrocks2019) proposed the so-called delete/rederive techniques, which aim at updating materialized views. In this approach, no redundancy is allowed, that is, updated views reflect only currently true logical assertions: this differs from the overgrounding idea, which aims to materialize bigger portions of logic programs, which can possibly support true logic assertions. Hu et al. (Reference Hu, Motik and Horrocks2022) extended further the idea, by proposing a general method in which modular parts of a Datalog view can be attached to ad hoc incremental maintenance algorithms. For instance, one can plug in the general framework a special incremental algorithm for updating transitive closure patterns, etc.
7 Future work and conclusions
As future work is concerned, we plan to further extend the incremental evaluation capabilities of Incremental-DLV2, by making the solving phase connected in a tighter way with grounding, in the multi-shot setting. Moreover, in order to limit the impact of memory consumption, we intend to study new forgetting strategies to be automatic, carefully timed, and more fine-grained than the basic ones currently implemented. Besides helping at properly managing the memory footprint, such strategies can have a positive impact also on performance; think, for instance, of scenarios where input highly varies across different shots: from a certain point in time on, it is very likely that only a small subset of the whole amount of accumulated rules will actually play a role in computing answer sets. As a consequence, accumulating rules and atoms may easily lead to a worsening in both time and memory performance: here, proper forgetting techniques can help at selectively dropping the part of the overgrounded program that constitutes a useless burden, thus allowing to enjoy the advantages of overgrounding at a much lower cost. A variant of this approach has been proposed by Calimeri et al. (Reference Calimeri, Ianni, Pacenza, Perri, Zangari, Gebser and Sergey2024). Investigating the relationship between overgrounded programs and the notion of relativized hyperequivalence of Truszczynski and Woltran (Reference Truszczynski and Woltran2009), possibly under semantics other than the answer set one, deserves further research.
Funding statement
This work has been partially supported by the Italian MIUR Ministry and the Presidency of the Council of Ministers under the project “Declarative Reasoning over Streams” under the “PRIN” 2017 call (CUP
![]() $H24I17000080001$
, project 2017M9C25L_001); by the Italian Ministry of Economic Development (MISE) under the PON project “MAP4ID - Multipurpose Analytics Platform 4 Industrial Data,” N. F/190138/01-03/X44; and by European Union under the National Recovery and Resilience Plan (NRRP) funded by the Italian MUR Ministry with the project Future Artificial Intelligence Research (FAIR, PE0000013), Spoke 9. Francesco Calimeri is a member of the Gruppo Nazionale Calcolo Scientifico-Istituto Nazionale di Alta Matematica (GNCS-INdAM).
$H24I17000080001$
, project 2017M9C25L_001); by the Italian Ministry of Economic Development (MISE) under the PON project “MAP4ID - Multipurpose Analytics Platform 4 Industrial Data,” N. F/190138/01-03/X44; and by European Union under the National Recovery and Resilience Plan (NRRP) funded by the Italian MUR Ministry with the project Future Artificial Intelligence Research (FAIR, PE0000013), Spoke 9. Francesco Calimeri is a member of the Gruppo Nazionale Calcolo Scientifico-Istituto Nazionale di Alta Matematica (GNCS-INdAM).
Competing interests
Francesco Calimeri is CEO and sole director of the Italian limited liability company DLVSystem Srl and owns shares of the company; Simona Perri owns shares of DLVSystem Srl; other authors declare none. DLVSystem Srl is a spin-off company of the University of Calabria. A shorter version of this paper has been presented at PPDP 2022: 24th International Symposium on Principles and Practice of Declarative Programming.






