Before I moved to the field of human genetics, I was working on quantitative trait locus mapping in experimental populations of plants and animals. That is why I did not know the name Nick Martin until the second last year of my PhD candidature. Toward the end of my PhD candidature, it was clear to me that I should find a postdoc position somewhere, but Australia was not quite on my radar until the year 2006 when I had a three months’ visit in Western Australia. Then, I started thinking about the possibility of moving to Australia. A few Google searches brought my attention to the research groups led by Professors Nicholas Martin, Grant Montgomery and Peter Visscher. I joined Peter’s lab in September 2008 to start my academic career in human genetics.
I might have seen Nick at my job interview seminar at Queensland Institute of Medical Research (renamed QIMR Berghofer Medical Research Institute in 2013), but from memory, we met for the first time when Peter introduced me to him in his office. The conversation was short but impressive, not least because of the old-fashioned computer on his desk. I was also impressed later on when I often saw him working in the office on Sunday afternoons, which, believe me, is not common in Australia.
In the year 2009, I was working with Peter (and Mike Goddard from Melbourne) on a project aiming to estimate the proportion of variance in human height explained by all single-nucleotide polymorphisms (SNPs) that are common in European populations (Yang et al., Reference Yang, Benyamin, McEvoy, Gordon, Henders, Nyholt and Visscher2010). At that time, there was confusion about the genetic architecture of common traits and diseases like height and obesity largely because of the observation that genetic loci identified from published genome-wide association studies (GWASs) only accounted for a small fraction of heritability for almost all the traits studied, leading to the ‘missing heritability’ puzzle and criticisms of the failure of GWAS as an experimental design (Manolio et al., Reference Manolio, Collins, Cox, Goldstein, Hindorff, Hunter and Visscher2009; McClellan & King, Reference McClellan and King2010).
In GWAS, each SNP is tested for association with a trait of interest one by one across the genome to search for genomic loci responsible for the trait variation in a population. Because of the large number of tests performed (typically from 100,000 to millions depending on the coverage of the SNP array and whether the SNP data have been imputed to a reference panel with whole-genome sequence data), a correction for multiple testing is needed to avoid false-positive discoveries, for example, a p value threshold of 5 × 10-8 is often used to claim significant findings from GWASs. This means that if the effect size of an SNP is small and the GWAS sample size is not sufficiently large, we would not have enough power to detect it at a genome-wide significance level. Hence, one critical question was how much proportion of the trait variance is accounted for by the SNPs that did not reach genome-wide significance level. This might be achieved by fitting the effects of all SNPs jointly as random effects in a mixed linear model.
The model was appealing, but how about the data? It was not like these days when we can easily get access to GWAS datasets of 10,000s or even 100,000s individuals from public resources such as the dbGaP and the UK Biobank (Bycroft et al., Reference Bycroft, Freeman, Petkova, Band, Elliott, Sharp and Marchini2018). GWASs with only a few thousand or even a hundred individuals were not uncommon at that time. Our model attempts to estimate the aggregated effect of many SNPs, which is equivalent to a classical additive genetic model y = g + e with g being the total additive genetic value of an individual captured by all SNPs and e being the residual (Yang et al., Reference Yang, Benyamin, McEvoy, Gordon, Henders, Nyholt and Visscher2010). Estimating the variance of g and thereby the heritability captured by all SNPs, that is, the SNP-based heritability 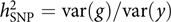 $$h_{{\rm{SNP}}}^2 = {\rm{var}}\left( g \right)/{\rm{var}}\left( y \right)$$
, requires a correlation matrix of g (also known as the genetic relationship matrix or GRM). We did not want to include any related individuals in the model because otherwise we could not distinguish whether the estimated var(g) was captured by the SNPs or by the pedigree relatedness reconstructed from SNP data. The latter is more complex and can contain variance components due to common environmental effects that are shared among close relatives and rare genetic variations not tagged by array SNPs. The precision of the estimate of var(g) (often measured by the standard error or SE), however, is inversely proportional to the variability of the off-diagonal elements of the GRM (Visscher et al., Reference Visscher, Hemani, Vinkhuyzen, Chen, Lee, Wray and Yang2014). Because the model uses only unrelated individuals, the variance of the off-diagonal elements of the GRM is small so that a relatively large sample size (at least much larger than those used in pedigree-based heritability analyses) is required to obtain an estimate of
$$h_{{\rm{SNP}}}^2 = {\rm{var}}\left( g \right)/{\rm{var}}\left( y \right)$$
, requires a correlation matrix of g (also known as the genetic relationship matrix or GRM). We did not want to include any related individuals in the model because otherwise we could not distinguish whether the estimated var(g) was captured by the SNPs or by the pedigree relatedness reconstructed from SNP data. The latter is more complex and can contain variance components due to common environmental effects that are shared among close relatives and rare genetic variations not tagged by array SNPs. The precision of the estimate of var(g) (often measured by the standard error or SE), however, is inversely proportional to the variability of the off-diagonal elements of the GRM (Visscher et al., Reference Visscher, Hemani, Vinkhuyzen, Chen, Lee, Wray and Yang2014). Because the model uses only unrelated individuals, the variance of the off-diagonal elements of the GRM is small so that a relatively large sample size (at least much larger than those used in pedigree-based heritability analyses) is required to obtain an estimate of 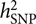 $$h_{{\rm{SNP}}}^2$$
with useful precision.
$$h_{{\rm{SNP}}}^2$$
with useful precision.
We started with an analysis in a dataset with ~2500 unrelated people and the estimate of 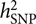 $$h_{{\rm{SNP}}}^2$$
for height was somewhere between 0.4 and 0.5. We were all very excited about it, but the SE and thus the confidence interval of the estimate was too wide to make any convincing conclusion. Fortunately, we heard from Nick that there was an additional batch of data that would be available soon, which pushed the sample size up to ~4000. We finally obtained an estimate of 0.45 (SE = 0.08), which was significantly larger than the proportion of variance accounted for by SNPs passing genome-wide significance level (~10%) reported by a GWAS meta-analysis of ~180,000 individuals in 2010 (Lango Allen et al., Reference Lango Allen, Estrada, Lettre, Berndt, Weedon, Rivadeneira and Hirschhorn2010).
$$h_{{\rm{SNP}}}^2$$
for height was somewhere between 0.4 and 0.5. We were all very excited about it, but the SE and thus the confidence interval of the estimate was too wide to make any convincing conclusion. Fortunately, we heard from Nick that there was an additional batch of data that would be available soon, which pushed the sample size up to ~4000. We finally obtained an estimate of 0.45 (SE = 0.08), which was significantly larger than the proportion of variance accounted for by SNPs passing genome-wide significance level (~10%) reported by a GWAS meta-analysis of ~180,000 individuals in 2010 (Lango Allen et al., Reference Lango Allen, Estrada, Lettre, Berndt, Weedon, Rivadeneira and Hirschhorn2010).
The implication of this study is profound. It suggests that a large proportion of the heritability for height can be explained by all common SNPs so that the heritability is not missing. GWASs at that time were not very successful mainly because of many genetic variants, each with an effect too small to reach the stringent genome-wide significance threshold. This suggests that the genetic architecture for height (and possibly for many other common traits and diseases) is likely to be polygenic and that more associations would be discovered in GWASs with larger sample sizes. These findings and implications have been corroborated by many studies in recent years. The paper on this work, entitled ‘Common SNPs explain a large proportion of the heritability for human height’, was eventually published in Nature Genetics in 2010 and has received >3000 citations in the past 10 years. The method has now been implemented in a widely software tool GCTA (Yang et al., Reference Yang, Lee, Goddard and Visscher2011).
This study would have not been possible without the critical contribution from Nick. The amazing human genetic resources established by the team led by Nick and the critical mass of researchers in human genetics in Brisbane directly and indirectly because of him had laid the foundation for scientific ideas like this to evolve and to be implemented. His generosity in data sharing and vision in human genetics have always inspired me.


