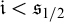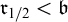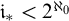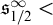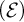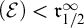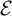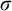1 Introduction
Given
![]() $S,X \in [\omega ]^\omega $
, we say that S splits X if
$S,X \in [\omega ]^\omega $
, we say that S splits X if
![]() $|X \cap S| = |X \setminus S | = \aleph _0$
. The splitting number
$|X \cap S| = |X \setminus S | = \aleph _0$
. The splitting number
![]() $\mathfrak {s}$
is the least size of a splitting family
$\mathfrak {s}$
is the least size of a splitting family
![]() $\mathcal {S}\subseteq [\omega ]^\omega $
, that is, every infinite subset of
$\mathcal {S}\subseteq [\omega ]^\omega $
, that is, every infinite subset of
![]() $\omega $
is split by a member of
$\omega $
is split by a member of
![]() $\mathcal {S}$
. For
$\mathcal {S}$
. For
![]() $X \in [\omega ]^\omega $
and
$X \in [\omega ]^\omega $
and
![]() $0<n<\omega $
, define the initial density of X up to n as
$0<n<\omega $
, define the initial density of X up to n as
![]() $d_n(X)=\frac {|X\cap n|}{n}$
. In case of convergence of
$d_n(X)=\frac {|X\cap n|}{n}$
. In case of convergence of
![]() $d_n(X)$
, call
$d_n(X)$
, call
![]() $d(X)=\lim _{n \to \infty } d_n(X)$
the asymptotic density or just the density of X. In [Reference Brendle, Halbeisen, Klausner, Lischka and Shelah5] the following variants of
$d(X)=\lim _{n \to \infty } d_n(X)$
the asymptotic density or just the density of X. In [Reference Brendle, Halbeisen, Klausner, Lischka and Shelah5] the following variants of
![]() $\mathfrak {s}$
were introduced by using the notion of asymptotic density to characterize different intersection properties of infinite sets.
$\mathfrak {s}$
were introduced by using the notion of asymptotic density to characterize different intersection properties of infinite sets.
Definition 1.1. Let
![]() $S,X \in [\omega ]^{\omega }$
.
$S,X \in [\omega ]^{\omega }$
.
-
• S bisects X, written as
 $S |_{1/2} X$
, if
$S |_{1/2} X$
, if  $$\begin{align*}\lim_{n \to \infty} \frac{|S \cap X \cap n|}{|X\cap n|}= \lim_{n \to \infty} \frac{d_n(S\cap X)}{d_n(X)}= \frac{1}{2}. \end{align*}$$
$$\begin{align*}\lim_{n \to \infty} \frac{|S \cap X \cap n|}{|X\cap n|}= \lim_{n \to \infty} \frac{d_n(S\cap X)}{d_n(X)}= \frac{1}{2}. \end{align*}$$
-
• For
 $0< \epsilon < 1/2$
,
$0< \epsilon < 1/2$
,
 $S\ \epsilon $
-almost bisects X, written as
$S\ \epsilon $
-almost bisects X, written as
 $S \, |_{1/2 \pm \epsilon } \, X$
, if for all but finitely many
$S \, |_{1/2 \pm \epsilon } \, X$
, if for all but finitely many
 $n \in \omega $
, we have
$n \in \omega $
, we have  $$\begin{align*}\frac{|S \cap X \cap n|}{|X\cap n|}= \frac{d_n(S\cap X)}{d_n(X)} \in \left(\frac{1}{2}- \epsilon, \frac{1}{2}+ \epsilon\right). \end{align*}$$
$$\begin{align*}\frac{|S \cap X \cap n|}{|X\cap n|}= \frac{d_n(S\cap X)}{d_n(X)} \in \left(\frac{1}{2}- \epsilon, \frac{1}{2}+ \epsilon\right). \end{align*}$$
-
• S weakly bisects X, written as
 $S \, |_{1/2}^{w} \, X$
, if for any
$S \, |_{1/2}^{w} \, X$
, if for any
 $\epsilon>0$
, for infinitely many
$\epsilon>0$
, for infinitely many
 $n\in \omega ,$
we have
$n\in \omega ,$
we have  $$\begin{align*}\frac{|S \cap X \cap n|}{|X\cap n|}= \frac{d_n(S\cap X)}{d_n(X)} \in \left(\frac{1}{2}- \epsilon, \frac{1}{2}+ \epsilon\right). \end{align*}$$
$$\begin{align*}\frac{|S \cap X \cap n|}{|X\cap n|}= \frac{d_n(S\cap X)}{d_n(X)} \in \left(\frac{1}{2}- \epsilon, \frac{1}{2}+ \epsilon\right). \end{align*}$$
-
• S cofinally bisects X, written as
 $S \, |_{1/2}^{\infty } \, X$
, if for infinitely many
$S \, |_{1/2}^{\infty } \, X$
, if for infinitely many
 $n\in \omega $
, we have
$n\in \omega $
, we have  $$\begin{align*}\frac{|S \cap X \cap n|}{|X\cap n|}= \frac{d_n(S\cap X)}{d_n(X)} = \frac{1}{2}. \end{align*}$$
$$\begin{align*}\frac{|S \cap X \cap n|}{|X\cap n|}= \frac{d_n(S\cap X)}{d_n(X)} = \frac{1}{2}. \end{align*}$$
Definition 1.2. We say a family
![]() $\mathcal {S}$
of infinite sets is
$\mathcal {S}$
of infinite sets is
 $$\begin{align*}\left\{ \begin{array}{c} \text{bisecting} \\ \epsilon\text{-almost bisecting} \\ \text{weakly bisecting} \\ \text{cofinally bisecting} \end{array} \right. \end{align*}$$
$$\begin{align*}\left\{ \begin{array}{c} \text{bisecting} \\ \epsilon\text{-almost bisecting} \\ \text{weakly bisecting} \\ \text{cofinally bisecting} \end{array} \right. \end{align*}$$
if for each
![]() $X \in [\omega ]^\omega $
, there is some
$X \in [\omega ]^\omega $
, there is some
![]() $S \in \mathcal {S}$
such that
$S \in \mathcal {S}$
such that
 $$\begin{align*}\left\{ \begin{array}{c} S\ \text{bisects} X \\ S\ \epsilon\text{-almost bisects X} \\ S \text{weakly bisects X} \\ S \text{cofinally bisects X} \end{array} \right. \end{align*}$$
$$\begin{align*}\left\{ \begin{array}{c} S\ \text{bisects} X \\ S\ \epsilon\text{-almost bisects X} \\ S \text{weakly bisects X} \\ S \text{cofinally bisects X} \end{array} \right. \end{align*}$$
and denote the least cardinality of such a family by
![]() $\mathfrak {s}_{1/2}, \mathfrak {s}_{1/2 \pm \epsilon }, \mathfrak {s}_{1/2}^{w}, \mathfrak {s}_{1/2}^{\infty }$
, respectively.
$\mathfrak {s}_{1/2}, \mathfrak {s}_{1/2 \pm \epsilon }, \mathfrak {s}_{1/2}^{w}, \mathfrak {s}_{1/2}^{\infty }$
, respectively.
Let
![]() $\mathcal {N}$
denote the ideal of Lebesgue null sets,
$\mathcal {N}$
denote the ideal of Lebesgue null sets,
![]() $\mathcal {M}$
the ideal of meager sets,
$\mathcal {M}$
the ideal of meager sets,
![]() $\mathfrak {d}$
the dominating number, and
$\mathfrak {d}$
the dominating number, and
![]() $\mathfrak {b}$
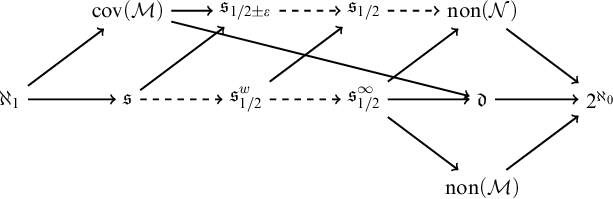
the unbounding number (see [Reference Blass2] for information on these concepts). Figure 1 shows the relations already proved between these new cardinals and other well-known cardinal characteristics. The proofs of these results are in [Reference Brendle, Halbeisen, Klausner, Lischka and Shelah5].
$\mathfrak {b}$
the unbounding number (see [Reference Blass2] for information on these concepts). Figure 1 shows the relations already proved between these new cardinals and other well-known cardinal characteristics. The proofs of these results are in [Reference Brendle, Halbeisen, Klausner, Lischka and Shelah5].

Figure 1 Inequalities between
![]() $\mathfrak {s}_{1/2}, \mathfrak {s}_{1/2 \pm \epsilon }, \mathfrak {s}_{1/2}^{w}, \mathfrak {s}_{1/2}^{\infty }$
and other well-known cardinal characteristics.
$\mathfrak {s}_{1/2}, \mathfrak {s}_{1/2 \pm \epsilon }, \mathfrak {s}_{1/2}^{w}, \mathfrak {s}_{1/2}^{\infty }$
and other well-known cardinal characteristics.
![]() $\dashrightarrow $
means
$\dashrightarrow $
means
![]() $\leq $
, and
$\leq $
, and
![]() $\rightarrow $
means
$\rightarrow $
means
![]() $\leq $
, consistently
$\leq $
, consistently
![]() $<$
.
$<$
.
The cardinals defined in Definition 1.2 also have their dual version. Recall that the reaping number
![]() $\mathfrak {r}$
is the dual of
$\mathfrak {r}$
is the dual of
![]() $\mathfrak {s}$
, and it is the least size of a reaping family
$\mathfrak {s}$
, and it is the least size of a reaping family
![]() $\mathcal {R} \subseteq [\omega ]^\omega $
, that is, no single infinite set splits all members of
$\mathcal {R} \subseteq [\omega ]^\omega $
, that is, no single infinite set splits all members of
![]() $\mathcal {R}$
.
$\mathcal {R}$
.
Definition 1.3. We say a family
![]() $\mathcal {R}$
of infinite sets is
$\mathcal {R}$
of infinite sets is
 $$\begin{align*}\left\{ \begin{array}{c} 1/2\text{-reaping} \\ \epsilon\text{-almost } 1/2\text{-reaping} \\ \text{weakly } 1/2\text{-reaping} \\ \text{cofinally } 1/2\text{-reaping} \end{array} \right. \end{align*}$$
$$\begin{align*}\left\{ \begin{array}{c} 1/2\text{-reaping} \\ \epsilon\text{-almost } 1/2\text{-reaping} \\ \text{weakly } 1/2\text{-reaping} \\ \text{cofinally } 1/2\text{-reaping} \end{array} \right. \end{align*}$$
if there is no
![]() $X \in [\omega ]^\omega $
such that for all
$X \in [\omega ]^\omega $
such that for all
![]() $R \in \mathcal {R}$
$R \in \mathcal {R}$
 $$\begin{align*}\left\{ \begin{array}{c} X\text{ bisects } R \\ X\ \epsilon\text{-almost bisects }R \\ X \text{ weakly bisects }R \\ X \text{ cofinally bisects }R \end{array} \right. \end{align*}$$
$$\begin{align*}\left\{ \begin{array}{c} X\text{ bisects } R \\ X\ \epsilon\text{-almost bisects }R \\ X \text{ weakly bisects }R \\ X \text{ cofinally bisects }R \end{array} \right. \end{align*}$$
and denote the least cardinality of such a family by
![]() $\mathfrak {r}_{1/2}, \mathfrak {r}_{1/2 \pm \epsilon }, \mathfrak {r}_{1/2}^{w}, \mathfrak {r}_{1/2}^{\infty }$
, respectively.
$\mathfrak {r}_{1/2}, \mathfrak {r}_{1/2 \pm \epsilon }, \mathfrak {r}_{1/2}^{w}, \mathfrak {r}_{1/2}^{\infty }$
, respectively.
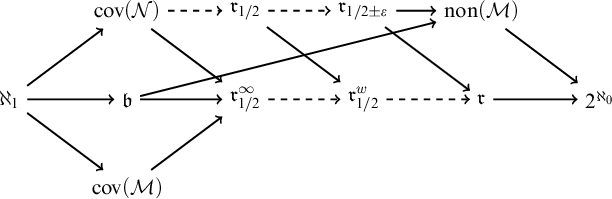
Figure 2 shows the inequalities already proved between these new variants of
![]() $\mathfrak {r}$
and other well-known cardinal characteristics. The proofs of these results are also in [Reference Brendle, Halbeisen, Klausner, Lischka and Shelah5].
$\mathfrak {r}$
and other well-known cardinal characteristics. The proofs of these results are also in [Reference Brendle, Halbeisen, Klausner, Lischka and Shelah5].

Figure 2 Dual diagram.
![]() $\dashrightarrow $
means
$\dashrightarrow $
means
![]() $\leq $
, and
$\leq $
, and
![]() $\rightarrow $
means
$\rightarrow $
means
![]() $\leq $
, consistently
$\leq $
, consistently
![]() $<$
.
$<$
.
It is consistently true that
![]() $\mathfrak {s}_{1/2}< \mathfrak {d}$
since this holds in any model of Con
$\mathfrak {s}_{1/2}< \mathfrak {d}$
since this holds in any model of Con
![]() $($
non
$($
non
![]() $(\mathcal {N}) < \mathfrak {d})$
, for example, the Laver model. However, the problem about Con(
$(\mathcal {N}) < \mathfrak {d})$
, for example, the Laver model. However, the problem about Con(
![]() $\mathfrak {d}<\mathfrak {s}_{1/2}$
) remained open until it was solved recently in [Reference Farkas, Klausner and Lischka6]. They also proved the dual problem Con
$\mathfrak {d}<\mathfrak {s}_{1/2}$
) remained open until it was solved recently in [Reference Farkas, Klausner and Lischka6]. They also proved the dual problem Con
![]() $(\mathfrak {r}_{1/2} < \mathfrak {b})$
. However, different methods were used to prove each result. Independently, we demonstrated that the same inequalities hold using a different and shorter argument. This is developed in Section 2. We use just one method to prove Con(
$(\mathfrak {r}_{1/2} < \mathfrak {b})$
. However, different methods were used to prove each result. Independently, we demonstrated that the same inequalities hold using a different and shorter argument. This is developed in Section 2. We use just one method to prove Con(
![]() $\mathfrak {d}<\mathfrak {s}_{1/2}$
), Con
$\mathfrak {d}<\mathfrak {s}_{1/2}$
), Con
![]() $(\mathfrak {r}_{1/2} < \mathfrak {b})$
, and even a stronger result which is Con(
$(\mathfrak {r}_{1/2} < \mathfrak {b})$
, and even a stronger result which is Con(
![]() $\mathfrak {i}<\mathfrak {s}_{1/2}$
). Recall that
$\mathfrak {i}<\mathfrak {s}_{1/2}$
). Recall that
![]() $\mathfrak {i}$
stands for the independence number (see below), and it is known that
$\mathfrak {i}$
stands for the independence number (see below), and it is known that
![]() $\mathfrak {d}\leq \mathfrak {i}$
.
$\mathfrak {d}\leq \mathfrak {i}$
.
We also investigate relations between these new cardinal characteristics and the cardinal characteristics associated with the ideal
![]() $\mathcal {E}$
, which is the
$\mathcal {E}$
, which is the
![]() $\sigma $
-ideal generated by closed sets of measure zero. In Section 3, we show that
$\sigma $
-ideal generated by closed sets of measure zero. In Section 3, we show that
![]() $\mathfrak {s}_{1/2}^{\infty } \leq $
non
$\mathfrak {s}_{1/2}^{\infty } \leq $
non
![]() $(\mathcal {E})$
and cov
$(\mathcal {E})$
and cov
![]() $(\mathcal {E}) \leq \mathfrak {r}_{1/2}^{\infty }$
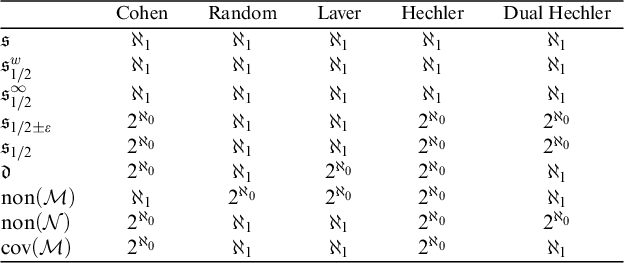
. Besides, we also prove that the strict inequalities are consistent using the Hechler and Dual Hechler model. By the results in Sections 2 and 3, we know the behavior of these cardinals in these models (see Table 1).
$(\mathcal {E}) \leq \mathfrak {r}_{1/2}^{\infty }$
. Besides, we also prove that the strict inequalities are consistent using the Hechler and Dual Hechler model. By the results in Sections 2 and 3, we know the behavior of these cardinals in these models (see Table 1).
In [Reference Brendle, Halbeisen, Klausner, Lischka and Shelah5], it was also introduced the following variant of the independence number
![]() $\mathfrak {i}$
, the least cardinality of a maximal independent family. Recall that a family
$\mathfrak {i}$
, the least cardinality of a maximal independent family. Recall that a family
![]() $\mathcal {I}$
of subsets of
$\mathcal {I}$
of subsets of
![]() $\omega $
is called independent if for any disjoint finite subfamilies
$\omega $
is called independent if for any disjoint finite subfamilies
![]() $\mathcal {A}, \mathcal {B} \subseteq \mathcal {I}$
, the set
$\mathcal {A}, \mathcal {B} \subseteq \mathcal {I}$
, the set
is infinite.
Definition 1.4. A set
![]() $X\in [\omega ]^\omega $
is moderate if
$X\in [\omega ]^\omega $
is moderate if
![]() $\underline {d}(X):=\liminf _{n\to \infty } d_n(X)>0$
as well as
$\underline {d}(X):=\liminf _{n\to \infty } d_n(X)>0$
as well as
![]() $\bar {d}(X):=\limsup _{n\to \infty }d_n(X)<1$
.
$\bar {d}(X):=\limsup _{n\to \infty }d_n(X)<1$
.
Definition 1.5. We say that a family
![]() $\mathcal {I} \subseteq [\omega ]^\omega $
is
$\mathcal {I} \subseteq [\omega ]^\omega $
is
![]() $*$
-independent if for any set
$*$
-independent if for any set
![]() ${X \in \mathcal {I}}$
, we have that X is moderate and for any finite subfamily
${X \in \mathcal {I}}$
, we have that X is moderate and for any finite subfamily
![]() $\mathcal {F}\subseteq \mathcal {I}$
, the following holds:
$\mathcal {F}\subseteq \mathcal {I}$
, the following holds:
 $$\begin{align*}\lim_{n \to \infty} \left( \frac{d_n(\bigcap_{E\in \mathcal{F}} E )}{\prod_{E\in \mathcal{F}} d_n(E) } \right) = 1. \end{align*}$$
$$\begin{align*}\lim_{n \to \infty} \left( \frac{d_n(\bigcap_{E\in \mathcal{F}} E )}{\prod_{E\in \mathcal{F}} d_n(E) } \right) = 1. \end{align*}$$
We denote the least cardinality of a maximal
![]() $*$
-independent family by
$*$
-independent family by
![]() $\mathfrak {i}_{*}$
$\mathfrak {i}_{*}$
In [Reference Brendle, Halbeisen, Klausner, Lischka and Shelah5, Theorem 3.8], it was proved that
![]() $\mathfrak {r}_{1/2}\leq \mathfrak {i}_{*}$
. Moreover, they constructed a model in which
$\mathfrak {r}_{1/2}\leq \mathfrak {i}_{*}$
. Moreover, they constructed a model in which
![]() $\mathfrak {r}_{1/2}$
is strictly smaller than
$\mathfrak {r}_{1/2}$
is strictly smaller than
![]() $\mathfrak {i}_{*}$
. However, it is not known whether there are upper bounds for
$\mathfrak {i}_{*}$
. However, it is not known whether there are upper bounds for
![]() $\mathfrak {i}_{*}$
aside from
$\mathfrak {i}_{*}$
aside from
![]() $2^{\aleph _0}$
. We prove that
$2^{\aleph _0}$
. We prove that
![]() $\mathfrak {i}_{*}$
is consistently different from the continuum. In Section 4, we show that Con(
$\mathfrak {i}_{*}$
is consistently different from the continuum. In Section 4, we show that Con(
![]() $\mathfrak {i}_{*}<2^{\aleph _0}$
) holds in the Cohen model, assuming continuum hypothesis (CH) in the ground model. This solves question six raised in [Reference Brendle, Halbeisen, Klausner, Lischka and Shelah5].
$\mathfrak {i}_{*}<2^{\aleph _0}$
) holds in the Cohen model, assuming continuum hypothesis (CH) in the ground model. This solves question six raised in [Reference Brendle, Halbeisen, Klausner, Lischka and Shelah5].
Table 1 Behavior of
![]() $\mathfrak {s}_{1/2}, \mathfrak {s}_{1/2 \pm \epsilon }, \mathfrak {s}_{1/2}^{w}, \mathfrak {s}_{1/2}^{\infty }$
and other well-known cardinal characteristics in some models obtained using classical forcing notions.
$\mathfrak {s}_{1/2}, \mathfrak {s}_{1/2 \pm \epsilon }, \mathfrak {s}_{1/2}^{w}, \mathfrak {s}_{1/2}^{\infty }$
and other well-known cardinal characteristics in some models obtained using classical forcing notions.

2
 $\sigma $
-centered forcing
$\sigma $
-centered forcing
Let us review the notion of
![]() $\sigma $
-centered forcing.
$\sigma $
-centered forcing.
Definition 2.1. Let
![]() $\mathbb {P}$
be a forcing notion. A subset
$\mathbb {P}$
be a forcing notion. A subset
![]() $\mathcal {P}\subseteq \mathbb {P}$
is called centered if for all finite
$\mathcal {P}\subseteq \mathbb {P}$
is called centered if for all finite
![]() $F \subseteq \mathcal {P}$
there is
$F \subseteq \mathcal {P}$
there is
![]() $q\in \mathbb {P}$
such that
$q\in \mathbb {P}$
such that
![]() $q\leq p$
for all
$q\leq p$
for all
![]() $p \in F$
.
$p \in F$
.
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\sigma $
-centered if there are centered sets
$\sigma $
-centered if there are centered sets
![]() $\mathcal {P}_i$
such that
$\mathcal {P}_i$
such that
![]() $\mathbb {P}= \bigcup _{i\in \omega }\mathcal {P}_i$
.
$\mathbb {P}= \bigcup _{i\in \omega }\mathcal {P}_i$
.
Fix
![]() $0<\epsilon <1/2$
. We prove that
$0<\epsilon <1/2$
. We prove that
![]() $\mathfrak {s}_{1/2\pm \epsilon }$
cannot decrease under iterations of
$\mathfrak {s}_{1/2\pm \epsilon }$
cannot decrease under iterations of
![]() $\sigma $
-centered forcing. First, we deal with the single step iteration.
$\sigma $
-centered forcing. First, we deal with the single step iteration.
Lemma 2.2. Let
![]() $\mathbb {P}$
be a
$\mathbb {P}$
be a
![]() $\sigma $
-centered forcing notion. Let
$\sigma $
-centered forcing notion. Let
![]() $\dot {x}$
be a
$\dot {x}$
be a
![]() $\mathbb {P}$
-name for an element of
$\mathbb {P}$
-name for an element of
![]() $[\omega ]^\omega $
. There are sets
$[\omega ]^\omega $
. There are sets
![]() $\{X_i\}_{i\in \omega }$
such that for all
$\{X_i\}_{i\in \omega }$
such that for all
![]() $A \in [\omega ]^\omega $
, if for all
$A \in [\omega ]^\omega $
, if for all
![]() $i\in \omega $
, there are infinitely many
$i\in \omega $
, there are infinitely many
![]() $n \in \omega $
such that
$n \in \omega $
such that
 $$\begin{align*}\frac{d_n(X_i \cap A)}{d_n(A)} \not\in (1/2 - \epsilon, \epsilon + 1/2). \end{align*}$$
$$\begin{align*}\frac{d_n(X_i \cap A)}{d_n(A)} \not\in (1/2 - \epsilon, \epsilon + 1/2). \end{align*}$$
Then
 $$\begin{align*}\Vdash \exists^\infty n \in \omega \left(\frac{d_n(\dot{x} \cap A)}{d_n(A)} \not\in (1/2 - \epsilon, \epsilon + 1/2) \right). \end{align*}$$
$$\begin{align*}\Vdash \exists^\infty n \in \omega \left(\frac{d_n(\dot{x} \cap A)}{d_n(A)} \not\in (1/2 - \epsilon, \epsilon + 1/2) \right). \end{align*}$$
Proof. Let
![]() $\mathbb {P}= \bigcup _{i\in \omega } \mathcal {P}_i$
, where the
$\mathbb {P}= \bigcup _{i\in \omega } \mathcal {P}_i$
, where the
![]() $\mathcal {P}_i$
are centered. Fix
$\mathcal {P}_i$
are centered. Fix
![]() $i \in \omega $
. Note that for each
$i \in \omega $
. Note that for each
![]() $n \in \omega $
, there is
$n \in \omega $
, there is
![]() $y \in \mathcal {P}(\{0, ..., n-1\})$
such that no
$y \in \mathcal {P}(\{0, ..., n-1\})$
such that no
![]() $p\in \mathcal {P}_i$
forces
$p\in \mathcal {P}_i$
forces
Otherwise, for every
![]() $y \in \mathcal {P}(\{0, ..., n-1\})$
, there is a condition
$y \in \mathcal {P}(\{0, ..., n-1\})$
, there is a condition
![]() $p_y\in \mathcal {P}_i$
such that
$p_y\in \mathcal {P}_i$
such that
![]() $p_y \Vdash \dot {x} \cap n \neq y$
. Since
$p_y \Vdash \dot {x} \cap n \neq y$
. Since
![]() $\mathcal {P}_i$
is centered, there exists
$\mathcal {P}_i$
is centered, there exists
![]() $p\in \mathbb {P}$
such that
$p\in \mathbb {P}$
such that
![]() $p \leq p_y$
for all
$p \leq p_y$
for all
![]() $y \in \mathcal {P}(\{0, ..., n-1\})$
, then
$y \in \mathcal {P}(\{0, ..., n-1\})$
, then
![]() $p \Vdash \dot {x} \cap n \neq y$
for all
$p \Vdash \dot {x} \cap n \neq y$
for all
![]() $y \in \mathcal {P}(\{0, ..., n-1\})$
, which is a contradiction. By König’s lemma, there is
$y \in \mathcal {P}(\{0, ..., n-1\})$
, which is a contradiction. By König’s lemma, there is
![]() $X_i \subset \omega $
such that for all
$X_i \subset \omega $
such that for all
![]() $n \in \omega $
no
$n \in \omega $
no
![]() $p\in \mathcal {P}_i$
forces
$p\in \mathcal {P}_i$
forces
Let A be an infinite subset of
![]() $\omega $
, and suppose that for all
$\omega $
, and suppose that for all
![]() $i\in \omega $
, there are infinitely many
$i\in \omega $
, there are infinitely many
![]() $n \in \omega $
such that
$n \in \omega $
such that
 $$\begin{align*}\frac{d_n(X_i \cap A)}{d_n(A)} \not\in (1/2 - \epsilon, \epsilon + 1/2). \end{align*}$$
$$\begin{align*}\frac{d_n(X_i \cap A)}{d_n(A)} \not\in (1/2 - \epsilon, \epsilon + 1/2). \end{align*}$$
Fix
![]() $m \in \omega $
and a condition
$m \in \omega $
and a condition
![]() $p \in \mathbb {P}$
. There is
$p \in \mathbb {P}$
. There is
![]() $\mathcal {P}_i$
such that
$\mathcal {P}_i$
such that
![]() $p \in \mathcal {P}_i$
. Also, there is
$p \in \mathcal {P}_i$
. Also, there is
![]() $n>m$
such that
$n>m$
such that
 $$\begin{align*}\frac{d_n(X_i \cap A)}{d_n(A)} \not\in (1/2 - \epsilon, \epsilon + 1/2). \end{align*}$$
$$\begin{align*}\frac{d_n(X_i \cap A)}{d_n(A)} \not\in (1/2 - \epsilon, \epsilon + 1/2). \end{align*}$$
By (1), there is
![]() $q\leq p$
such that
$q\leq p$
such that
Therefore,
 $$\begin{align*}q \Vdash \frac{d_n(\dot{x} \cap A)}{d_n(A)} = \frac{d_n(X_i \cap A)}{d_n(A)} \not\in (1/2 - \epsilon, \epsilon + 1/2). \end{align*}$$
$$\begin{align*}q \Vdash \frac{d_n(\dot{x} \cap A)}{d_n(A)} = \frac{d_n(X_i \cap A)}{d_n(A)} \not\in (1/2 - \epsilon, \epsilon + 1/2). \end{align*}$$
By the previous paragraph, the set
![]() $D_m=\{ q\in \mathbb {P} \, | \, $
. There is
$D_m=\{ q\in \mathbb {P} \, | \, $
. There is
![]() $n>m$
such that
$n>m$
such that
![]() $ q \Vdash \frac {d_n(\dot {x} \cap A)}{d_n(A)} \not \in (1/2 - \epsilon , \epsilon + 1/2) \}$
is dense. Then
$ q \Vdash \frac {d_n(\dot {x} \cap A)}{d_n(A)} \not \in (1/2 - \epsilon , \epsilon + 1/2) \}$
is dense. Then
 $$\begin{align*}\Vdash \exists^\infty n \in \omega \left(\frac{d_n(\dot{x} \cap A)}{d_n(A)} \not\in (1/2 - \epsilon, \epsilon + 1/2) \right).\\[-41pt] \end{align*}$$
$$\begin{align*}\Vdash \exists^\infty n \in \omega \left(\frac{d_n(\dot{x} \cap A)}{d_n(A)} \not\in (1/2 - \epsilon, \epsilon + 1/2) \right).\\[-41pt] \end{align*}$$
Let us say a partial order has property
![]() $(\star )$
if it shares the property exhibited in Lemma 2.2. Note that any forcing notion that has this property does not decrease
$(\star )$
if it shares the property exhibited in Lemma 2.2. Note that any forcing notion that has this property does not decrease
![]() $\mathfrak {s}_{1/2\pm \epsilon }$
. We use a classical argument to prove that
$\mathfrak {s}_{1/2\pm \epsilon }$
. We use a classical argument to prove that
![]() $(\star )$
is preserved under finite support iteration (fsi) of ccc forcing notions.
$(\star )$
is preserved under finite support iteration (fsi) of ccc forcing notions.
Lemma 2.3. Let
![]() $\delta $
be a limit ordinal. Let
$\delta $
be a limit ordinal. Let
![]() $(\mathbb {P}_\alpha , \dot {\mathbb {Q}}_{\alpha } : \alpha < \delta )$
be an fsi of ccc forcing notions. Assume that
$(\mathbb {P}_\alpha , \dot {\mathbb {Q}}_{\alpha } : \alpha < \delta )$
be an fsi of ccc forcing notions. Assume that
![]() $\mathbb {P}_\alpha $
has property
$\mathbb {P}_\alpha $
has property
![]() $(\star )$
for all
$(\star )$
for all
![]() $\alpha <\delta $
. Then also
$\alpha <\delta $
. Then also
![]() $\mathbb {P}_\delta $
has property
$\mathbb {P}_\delta $
has property
![]() $(\star )$
.
$(\star )$
.
Proof. No new reals arise in limit stages of uncountable cofinality so that the lemma vacuously holds if cf
![]() $(\delta )>\omega $
. Hence assume cf
$(\delta )>\omega $
. Hence assume cf
![]() $(\delta )=\omega $
. To simplify notation, suppose
$(\delta )=\omega $
. To simplify notation, suppose
![]() $\delta =\omega $
.
$\delta =\omega $
.
Let
![]() $\dot {x}$
be a
$\dot {x}$
be a
![]() $\mathbb {P}_\omega $
-name for an element of
$\mathbb {P}_\omega $
-name for an element of
![]() $[\omega ]^\omega $
. Fix
$[\omega ]^\omega $
. Fix
![]() $m \in \omega $
. Work in
$m \in \omega $
. Work in
![]() $V^{\mathbb {P}_m}$
for the moment. There is a decreasing sequence of conditions
$V^{\mathbb {P}_m}$
for the moment. There is a decreasing sequence of conditions
![]() $p_k=p_{m,k}$
in the remainder forcing
$p_k=p_{m,k}$
in the remainder forcing
![]() $\mathbb {P}_\omega \setminus \mathbb {P}_m$
such that
$\mathbb {P}_\omega \setminus \mathbb {P}_m$
such that
![]() $p_k$
decides the k-th element of
$p_k$
decides the k-th element of
![]() $\dot {x}$
. Say
$\dot {x}$
. Say
Let
![]() $X_m=\{l_k \,| \, k\in \omega \}$
. Work in the ground model V. We have a
$X_m=\{l_k \,| \, k\in \omega \}$
. Work in the ground model V. We have a
![]() $\mathbb {P}_m$
-name
$\mathbb {P}_m$
-name
![]() $\dot {x}_m$
for
$\dot {x}_m$
for
![]() $X_m$
. Since
$X_m$
. Since
![]() $\mathbb {P}_m$
has property
$\mathbb {P}_m$
has property
![]() $(\star )$
, we can find
$(\star )$
, we can find
![]() $X_{m,i}$
,
$X_{m,i}$
,
![]() $i\in \omega $
which satisfy what property
$i\in \omega $
which satisfy what property
![]() $(\star )$
said for
$(\star )$
said for
![]() $\dot {x}_m$
. Now, fix
$\dot {x}_m$
. Now, fix
![]() $A\in [\omega ]^\omega $
. We claim that if for all
$A\in [\omega ]^\omega $
. We claim that if for all
![]() $i,m\in \omega $
, there are infinitely many
$i,m\in \omega $
, there are infinitely many
![]() $n \in \omega $
such that
$n \in \omega $
such that
 $$\begin{align*}\frac{d_n(X_{m,i} \cap A)}{d_n(A)} \not\in (1/2 - \epsilon, \epsilon + 1/2) \end{align*}$$
$$\begin{align*}\frac{d_n(X_{m,i} \cap A)}{d_n(A)} \not\in (1/2 - \epsilon, \epsilon + 1/2) \end{align*}$$
then
 $$\begin{align*}\Vdash \exists^\infty n \in \omega \left(\frac{d_n(\dot{x} \cap A)}{d_n(A)} \not\in (1/2 - \epsilon, \epsilon + 1/2) \right). \end{align*}$$
$$\begin{align*}\Vdash \exists^\infty n \in \omega \left(\frac{d_n(\dot{x} \cap A)}{d_n(A)} \not\in (1/2 - \epsilon, \epsilon + 1/2) \right). \end{align*}$$
To see this, let
![]() $p \in \mathbb {P}_\omega $
and
$p \in \mathbb {P}_\omega $
and
![]() $n\in \omega $
. Fix m such that
$n\in \omega $
. Fix m such that
![]() $p \in \mathbb {P}_m$
and work in
$p \in \mathbb {P}_m$
and work in
![]() $V^{\mathbb {P}_m}$
. We know that there is
$V^{\mathbb {P}_m}$
. We know that there is
![]() $j> n$
such that
$j> n$
such that
 $$\begin{align*}p_{m,j} \Vdash \frac{d_{j}(\dot{x} \cap A)}{d_{j}(A)} = \frac{d_{j}(X_m \cap A)}{d_{j}(A)} \not\in (1/2 - \epsilon, \epsilon + 1/2). \end{align*}$$
$$\begin{align*}p_{m,j} \Vdash \frac{d_{j}(\dot{x} \cap A)}{d_{j}(A)} = \frac{d_{j}(X_m \cap A)}{d_{j}(A)} \not\in (1/2 - \epsilon, \epsilon + 1/2). \end{align*}$$
Now work in the ground model V. By strengthening
![]() $p\in \mathbb {P}_n$
, if necessary, we may assume p decides
$p\in \mathbb {P}_n$
, if necessary, we may assume p decides
![]() $p_{m,j}$
. Then
$p_{m,j}$
. Then
 $$\begin{align*}q= p^\frown p_{m,j} \Vdash \frac{d_{j}(\dot{x} \cap A)}{d_{j}(A)} \not\in (1/2 - \epsilon, \epsilon + 1/2).\\[-41pt] \end{align*}$$
$$\begin{align*}q= p^\frown p_{m,j} \Vdash \frac{d_{j}(\dot{x} \cap A)}{d_{j}(A)} \not\in (1/2 - \epsilon, \epsilon + 1/2).\\[-41pt] \end{align*}$$
Let
![]() $\mathbb {P}$
be a forcing notion, and let
$\mathbb {P}$
be a forcing notion, and let
![]() $\dot {x}$
be a
$\dot {x}$
be a
![]() $\mathbb {P}$
-name for an element of
$\mathbb {P}$
-name for an element of
![]() $[\omega ]^\omega $
. We say that
$[\omega ]^\omega $
. We say that
![]() $\dot {x}$
is a
$\dot {x}$
is a
![]() $\epsilon $
-bisecting real if for all
$\epsilon $
-bisecting real if for all
![]() $y\in [\omega ]^\omega $
, we have that
$y\in [\omega ]^\omega $
, we have that
![]() $\Vdash $
“
$\Vdash $
“
![]() $\dot {x} \epsilon $
-almost bisects y”. Lemmas 2.2 and 2.3 immediately imply the following.
$\dot {x} \epsilon $
-almost bisects y”. Lemmas 2.2 and 2.3 immediately imply the following.
Corollary 2.4. Iterations of
![]() $\sigma $
-centered forcing do not add
$\sigma $
-centered forcing do not add
![]() $\epsilon $
-bisecting reals.
$\epsilon $
-bisecting reals.
We proceed to prove the consistency results. We use the Hechler forcing which is a
![]() $\sigma $
-centered forcing. For the purposes of the next section, we use a slightly different representation of Hechler forcing.
$\sigma $
-centered forcing. For the purposes of the next section, we use a slightly different representation of Hechler forcing.
Definition 2.5. We define Hechler forcing
![]() $\mathbb {D}$
as the set of all pairs
$\mathbb {D}$
as the set of all pairs
![]() $(s, \phi )$
such that
$(s, \phi )$
such that
![]() $s\in \omega ^{<\omega }$
and
$s\in \omega ^{<\omega }$
and
![]() $\phi : \omega ^{<\omega } \rightarrow \omega $
. The order is given by
$\phi : \omega ^{<\omega } \rightarrow \omega $
. The order is given by
![]() $(t, \psi ) \leq (s, \phi )$
if
$(t, \psi ) \leq (s, \phi )$
if
![]() $t \supseteq s$
,
$t \supseteq s$
,
![]() $\psi $
dominates
$\psi $
dominates
![]() $\phi $
everywhere, that is,
$\phi $
everywhere, that is,
![]() $\phi (x)\leq \psi (x)$
for all
$\phi (x)\leq \psi (x)$
for all
![]() $x\in \omega ^{<\omega }$
, and
$x\in \omega ^{<\omega }$
, and
![]() $t(i) \geq \phi (t\upharpoonright i)$
for all
$t(i) \geq \phi (t\upharpoonright i)$
for all
![]() $i \in |t| \setminus |s|$
.
$i \in |t| \setminus |s|$
.
Alternatively, one can use the tree Hechler forcing
![]() $\mathbb {D}_T$
which consists of nonempty trees
$\mathbb {D}_T$
which consists of nonempty trees
![]() $T\subseteq \omega ^{<\omega }$
such that for any
$T\subseteq \omega ^{<\omega }$
such that for any
![]() $s\in T$
beyond the stem,
$s\in T$
beyond the stem,
![]() $s^\frown n$
belongs to T for almost all
$s^\frown n$
belongs to T for almost all
![]() $n\in \omega $
. The forcing is ordered by inclusion. It is easy to see that
$n\in \omega $
. The forcing is ordered by inclusion. It is easy to see that
![]() $\mathbb {D}_T$
and
$\mathbb {D}_T$
and
![]() $\mathbb {D}$
are forcing equivalent.
$\mathbb {D}$
are forcing equivalent.
Corollary 2.6. Con
![]() $( \mathfrak {d}< \mathfrak {s}_{1/2\pm \epsilon } )$
$( \mathfrak {d}< \mathfrak {s}_{1/2\pm \epsilon } )$
Proof. Fix
![]() $\kappa> \aleph _1$
. Let
$\kappa> \aleph _1$
. Let
![]() $\mathbb {C}_\kappa $
be an fsi of Cohen forcing of length
$\mathbb {C}_\kappa $
be an fsi of Cohen forcing of length
![]() $\kappa $
. Then
$\kappa $
. Then
![]() $V^{\mathbb {C}_\kappa } \models $
cov
$V^{\mathbb {C}_\kappa } \models $
cov
![]() $(\mathcal {M}) = \mathfrak {s}_{1/2\pm \epsilon } = \kappa $
. Denote
$(\mathcal {M}) = \mathfrak {s}_{1/2\pm \epsilon } = \kappa $
. Denote
![]() $M= V^{\mathbb {C}_\kappa }$
. Now, let
$M= V^{\mathbb {C}_\kappa }$
. Now, let
![]() $\mathbb {D}_{\aleph _1}$
be an fsi of Hechler forcing of length
$\mathbb {D}_{\aleph _1}$
be an fsi of Hechler forcing of length
![]() $\aleph _1$
over M. Then
$\aleph _1$
over M. Then
![]() $M^{\mathbb {D}_{\aleph _1}} \models \mathfrak {d} = \aleph _1$
because
$M^{\mathbb {D}_{\aleph _1}} \models \mathfrak {d} = \aleph _1$
because
![]() $\aleph _1$
dominating reals are added. By Lemmas 2.3 and 2.2,
$\aleph _1$
dominating reals are added. By Lemmas 2.3 and 2.2,
![]() $\mathbb {D}_{\aleph _1}$
has property
$\mathbb {D}_{\aleph _1}$
has property
![]() $(\star )$
, so
$(\star )$
, so
![]() $M^{\mathbb {D}_{\aleph _1}} \models \mathfrak {s}_{1/2\pm \epsilon }=\kappa $
.
$M^{\mathbb {D}_{\aleph _1}} \models \mathfrak {s}_{1/2\pm \epsilon }=\kappa $
.
Corollary 2.7. Con
![]() $( \mathfrak {r}_{1/2\pm \epsilon } < \mathfrak {b} )$
$( \mathfrak {r}_{1/2\pm \epsilon } < \mathfrak {b} )$
Proof. Fix
![]() $\kappa> \aleph _1$
and assume CH in the ground model. Let
$\kappa> \aleph _1$
and assume CH in the ground model. Let
![]() $\mathbb {D}_{\kappa }$
be an fsi of Hechler forcing of length
$\mathbb {D}_{\kappa }$
be an fsi of Hechler forcing of length
![]() $\kappa $
. It is known that
$\kappa $
. It is known that
![]() $V^{\mathbb {D}_\kappa } \models \mathfrak {b}=\kappa $
. Besides, the set
$V^{\mathbb {D}_\kappa } \models \mathfrak {b}=\kappa $
. Besides, the set
![]() $V \cap [\omega ]^\omega $
remains an
$V \cap [\omega ]^\omega $
remains an
![]() $\epsilon $
-almost reaping family in
$\epsilon $
-almost reaping family in
![]() $V^{\mathbb {D}_\kappa }$
by Corollary 2.4. Thus
$V^{\mathbb {D}_\kappa }$
by Corollary 2.4. Thus
![]() $V^{\mathbb {D}_\kappa } \models \mathfrak {r}_{1/2\pm \epsilon }= \aleph _1$
.
$V^{\mathbb {D}_\kappa } \models \mathfrak {r}_{1/2\pm \epsilon }= \aleph _1$
.
We can obtain a stronger result than Corollary 2.6 using a variation of Mathias forcing.
Definition 2.8. Let
![]() $\mathcal {F}$
be a filter over
$\mathcal {F}$
be a filter over
![]() $\omega $
. Mathias forcing with
$\omega $
. Mathias forcing with
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() $\mathbb {M}_{\mathcal {F}}$
, consists of all pairs
$\mathbb {M}_{\mathcal {F}}$
, consists of all pairs
![]() $(s,A)$
, where s is a finite subset of
$(s,A)$
, where s is a finite subset of
![]() $\omega $
, and
$\omega $
, and
![]() $A \in \mathcal {F}$
. The order is given by
$A \in \mathcal {F}$
. The order is given by
![]() $(t,B)\leq (s,A)$
if
$(t,B)\leq (s,A)$
if
![]() $s\subseteq t$
,
$s\subseteq t$
,
![]() $B\subseteq A$
and
$B\subseteq A$
and
![]() $t \setminus s \subseteq A$
. It generically adds a new real m with
$t \setminus s \subseteq A$
. It generically adds a new real m with
![]() $m=\bigcup \{s:(s,A)\in G$
for some
$m=\bigcup \{s:(s,A)\in G$
for some
![]() $A\}$
, where G denotes an
$A\}$
, where G denotes an
![]() $\mathbb {M}_{\mathcal {F}}$
-generic filter over V. It is known that m is a pseudo-intersection of
$\mathbb {M}_{\mathcal {F}}$
-generic filter over V. It is known that m is a pseudo-intersection of
![]() $\mathcal {F}$
. Note that
$\mathcal {F}$
. Note that
![]() $\mathbb {M}_{\mathcal {F}}$
is a
$\mathbb {M}_{\mathcal {F}}$
is a
![]() $\sigma $
-centered forcing.
$\sigma $
-centered forcing.
The following proposition is a known result about independent families (see exercises (A12) and (A13) in chapter VIII of [Reference Kunen8]).
Proposition 2.9. Let
![]() $\mathcal {I}$
be an independent family. There is a filter
$\mathcal {I}$
be an independent family. There is a filter
![]() $\mathcal {F}$
over
$\mathcal {F}$
over
![]() $\omega $
such that
$\omega $
such that
where
![]() $\dot {m}$
is an
$\dot {m}$
is an
![]() $\mathbb {M}_{\mathcal {F}}$
-name of the generic real, and for all
$\mathbb {M}_{\mathcal {F}}$
-name of the generic real, and for all
![]() $x \subseteq \omega $
with
$x \subseteq \omega $
with
![]() $x \not \in \mathcal {I}$
, we have
$x \not \in \mathcal {I}$
, we have
Proof. Denote as
![]() $\mathcal {I}^\star $
the set of finite Boolean combinations of
$\mathcal {I}^\star $
the set of finite Boolean combinations of
![]() $\mathcal {I}$
. Consider a filter
$\mathcal {I}$
. Consider a filter
![]() $\mathcal {F}$
over
$\mathcal {F}$
over
![]() $\omega $
such that
$\omega $
such that
and
![]() $\mathcal {F}$
is maximal with this property. Let
$\mathcal {F}$
is maximal with this property. Let
![]() $\dot {m}$
be an
$\dot {m}$
be an
![]() $\mathbb {M}_{\mathcal {F}}$
-name of the generic real. Consider
$\mathbb {M}_{\mathcal {F}}$
-name of the generic real. Consider
![]() $I \in \mathcal {I}^\star $
. For each
$I \in \mathcal {I}^\star $
. For each
![]() $n \in \omega $
, we define
$n \in \omega $
, we define
 $$\begin{align*}B_n &:= \{ (s,A) \, | \, \text{ there is }m>n \text{ such that }m \in s \cap I \} \\C_n&:= \{ (s,A) \, | \, \text{ there is }m>n \text{ such that }m \in I \text{ but }m \not\in s \cup A \}. \end{align*}$$
$$\begin{align*}B_n &:= \{ (s,A) \, | \, \text{ there is }m>n \text{ such that }m \in s \cap I \} \\C_n&:= \{ (s,A) \, | \, \text{ there is }m>n \text{ such that }m \in I \text{ but }m \not\in s \cup A \}. \end{align*}$$
It is easy to check that
![]() $B_n$
and
$B_n$
and
![]() $C_n$
are dense sets. Therefore,
$C_n$
are dense sets. Therefore,
![]() $\Vdash _{\mathbb {M}_{\mathcal {F}}} \text {"} I \cap \dot {m} \text { is infinite"}$
and
$\Vdash _{\mathbb {M}_{\mathcal {F}}} \text {"} I \cap \dot {m} \text { is infinite"}$
and
![]() $\Vdash _{\mathbb {M}_{\mathcal {F}}} \text {"} I \cap \omega \setminus \dot {m} \text { is infinite"}$
. Now, consider
$\Vdash _{\mathbb {M}_{\mathcal {F}}} \text {"} I \cap \omega \setminus \dot {m} \text { is infinite"}$
. Now, consider
![]() $x \subseteq \omega $
such that
$x \subseteq \omega $
such that
![]() $x \not \in \mathcal {I}$
. If
$x \not \in \mathcal {I}$
. If
![]() $\{x\}\cup \mathcal {I}$
is not an independent family, then there is nothing to do. Thus, suppose that
$\{x\}\cup \mathcal {I}$
is not an independent family, then there is nothing to do. Thus, suppose that
![]() $\{x\}\cup \mathcal {I}$
is an independent family. If
$\{x\}\cup \mathcal {I}$
is an independent family. If
![]() $x \in \mathcal {F}$
, then
$x \in \mathcal {F}$
, then
![]() $\Vdash _{\mathbb {M}_{\mathcal {F}}} \dot {m} \subseteq ^{\star } x$
. If
$\Vdash _{\mathbb {M}_{\mathcal {F}}} \dot {m} \subseteq ^{\star } x$
. If
![]() $x \not \in \mathcal {F}$
, then there is
$x \not \in \mathcal {F}$
, then there is
![]() $y \in \mathcal {F}$
and
$y \in \mathcal {F}$
and
![]() $I \in \mathcal {I}^\star $
such that
$I \in \mathcal {I}^\star $
such that
![]() $y \cap x \cap I$
is finite. Since
$y \cap x \cap I$
is finite. Since
![]() $\Vdash _{\mathbb {M}_{\mathcal {F}}} \dot {m} \subseteq ^{\star } y$
, then
$\Vdash _{\mathbb {M}_{\mathcal {F}}} \dot {m} \subseteq ^{\star } y$
, then
![]() $\Vdash _{\mathbb {M}_{\mathcal {F}}} \text {"}\dot {m} \cap x \cap I \text { is finite"}$
.
$\Vdash _{\mathbb {M}_{\mathcal {F}}} \text {"}\dot {m} \cap x \cap I \text { is finite"}$
.
Corollary 2.10. Con
![]() $( \mathfrak {i}< \mathfrak {s}_{1/2\pm \epsilon } )$
$( \mathfrak {i}< \mathfrak {s}_{1/2\pm \epsilon } )$
Proof. Fix
![]() $\kappa> \aleph _1$
. Let
$\kappa> \aleph _1$
. Let
![]() $\mathbb {C}_\kappa $
be an fsi of Cohen forcing of length
$\mathbb {C}_\kappa $
be an fsi of Cohen forcing of length
![]() $\kappa $
. Then
$\kappa $
. Then
![]() $V^{\mathbb {C}_\kappa } \models $
cov
$V^{\mathbb {C}_\kappa } \models $
cov
![]() $(\mathcal {M}) = \mathfrak {s}_{1/2\pm \epsilon } = \kappa $
. Denote
$(\mathcal {M}) = \mathfrak {s}_{1/2\pm \epsilon } = \kappa $
. Denote
![]() $M= V^{\mathbb {C}_\kappa }$
. Let
$M= V^{\mathbb {C}_\kappa }$
. Let
![]() $\mathcal {I}_0 \in M$
be a countable independent family. Build in M an iterated forcing construction
$\mathcal {I}_0 \in M$
be a countable independent family. Build in M an iterated forcing construction
![]() $\mathbb {P}=(\mathbb {P}_\alpha , \dot {\mathbb {Q}}_\alpha : \alpha < \omega _1)$
such that
$\mathbb {P}=(\mathbb {P}_\alpha , \dot {\mathbb {Q}}_\alpha : \alpha < \omega _1)$
such that
![]() $\Vdash _\alpha \text {"}\mathcal {I}_0 \cup \{\dot {m}_\beta : \beta < \alpha \} \text { is an independent family"}$
, where
$\Vdash _\alpha \text {"}\mathcal {I}_0 \cup \{\dot {m}_\beta : \beta < \alpha \} \text { is an independent family"}$
, where
![]() $\{\dot {m}_\beta : \beta < \alpha \} $
are the
$\{\dot {m}_\beta : \beta < \alpha \} $
are the
![]() $\mathbb {P}_\alpha $
-names of generic reals added by
$\mathbb {P}_\alpha $
-names of generic reals added by
![]() $\mathbb {P}_\alpha $
, and
$\mathbb {P}_\alpha $
, and
![]() $\Vdash _\alpha \text {"}\dot {\mathbb {Q}}_\alpha $
is a Mathias forcing with
$\Vdash _\alpha \text {"}\dot {\mathbb {Q}}_\alpha $
is a Mathias forcing with
![]() $\dot {\mathcal {F}}_\alpha $
”, where
$\dot {\mathcal {F}}_\alpha $
”, where
![]() $\dot {\mathcal {F}}_\alpha $
is a
$\dot {\mathcal {F}}_\alpha $
is a
![]() $\mathbb {P}_\alpha $
-name of the filter given by Proposition 2.9 with the family
$\mathbb {P}_\alpha $
-name of the filter given by Proposition 2.9 with the family
![]() $\mathcal {I}_0 \cup \{\dot {m}_\beta : \beta < \alpha \}$
. Work in
$\mathcal {I}_0 \cup \{\dot {m}_\beta : \beta < \alpha \}$
. Work in
![]() $M^{\mathbb {P}}$
. Denote as
$M^{\mathbb {P}}$
. Denote as
![]() $\mathcal {I}$
the family
$\mathcal {I}$
the family
![]() $\mathcal {I}_0 \cup \{m_\beta : \beta < \omega _1\}$
. By Proposition 2.9,
$\mathcal {I}_0 \cup \{m_\beta : \beta < \omega _1\}$
. By Proposition 2.9,
![]() $\mathcal {I}$
is a maximal independent family. Then,
$\mathcal {I}$
is a maximal independent family. Then,
![]() $M^{\mathbb {P}} \models \mathfrak {i}=\aleph _1$
. Note that
$M^{\mathbb {P}} \models \mathfrak {i}=\aleph _1$
. Note that
![]() $\mathbb {P}$
has property (
$\mathbb {P}$
has property (
![]() $\star $
) because of Lemmas 2.2 and 2.3. Therefore,
$\star $
) because of Lemmas 2.2 and 2.3. Therefore,
![]() $M^{\mathbb {P}} \models \mathfrak {s}_{1/2\pm \epsilon } = \kappa $
.
$M^{\mathbb {P}} \models \mathfrak {s}_{1/2\pm \epsilon } = \kappa $
.
3 Relations with the cardinal characteristics associated with
 $\mathcal {E}$
$\mathcal {E}$
Recall that the ideal
![]() $\mathcal {E}$
is the
$\mathcal {E}$
is the
![]() $\sigma $
-ideal generated by closed sets of measure zero. By definition, we have that non
$\sigma $
-ideal generated by closed sets of measure zero. By definition, we have that non
![]() $(\mathcal {E})$
is smaller than non
$(\mathcal {E})$
is smaller than non
![]() $(\mathcal {N})$
and non
$(\mathcal {N})$
and non
![]() $(\mathcal {M})$
. In [Reference Brendle, Halbeisen, Klausner, Lischka and Shelah5], they prove that
$(\mathcal {M})$
. In [Reference Brendle, Halbeisen, Klausner, Lischka and Shelah5], they prove that
![]() $\mathfrak {s}_{1/2}^{\infty }$
is also smaller than these two cardinals. It turns out that
$\mathfrak {s}_{1/2}^{\infty }$
is also smaller than these two cardinals. It turns out that
![]() $\mathfrak {s}_{1/2}^{\infty }\leq $
non
$\mathfrak {s}_{1/2}^{\infty }\leq $
non
![]() $(\mathcal {E})$
.
$(\mathcal {E})$
.
Proposition 3.1. Let X be an infinite subset of
![]() $\omega $
. Consider the set
$\omega $
. Consider the set
Then
![]() $[\omega ]^\omega \setminus B(X)$
belongs to
$[\omega ]^\omega \setminus B(X)$
belongs to
![]() $\mathcal {E}$
.
$\mathcal {E}$
.
Proof. Let
![]() $\{x_i\}_{i\in \omega }$
be an increasing enumeration of X. For each
$\{x_i\}_{i\in \omega }$
be an increasing enumeration of X. For each
![]() $m\in \omega $
consider the set
$m\in \omega $
consider the set
![]() $ B_{2m} := \{ B \subseteq \{x_1, ..., x_{2m} \} \, | \, |B|=m \}$
, and for each
$ B_{2m} := \{ B \subseteq \{x_1, ..., x_{2m} \} \, | \, |B|=m \}$
, and for each
![]() $B\in B_{2m}$
consider the function
$B\in B_{2m}$
consider the function
![]() $f_B: \{x_1, ..., x_{2m} \} \rightarrow \{0,1\}$
where
$f_B: \{x_1, ..., x_{2m} \} \rightarrow \{0,1\}$
where
![]() $f_B(x_i)=1$
if and only if
$f_B(x_i)=1$
if and only if
![]() $x_i\in B$
. Denote as
$x_i\in B$
. Denote as
![]() $[f_B]$
the open set generated by
$[f_B]$
the open set generated by
![]() $f_B$
. Define
$f_B$
. Define
![]() $A_{2m}:= \bigcup _{B \in B_{2m}} [f_B]$
. Note that Y cofinally bisects X if and only if there are infinitely many m such that
$A_{2m}:= \bigcup _{B \in B_{2m}} [f_B]$
. Note that Y cofinally bisects X if and only if there are infinitely many m such that
![]() $Y\in A_{2m}$
. Thus,
$Y\in A_{2m}$
. Thus,
Therefore
![]() $[\omega ]^\omega \setminus B(X)$
is a countable union of closed sets. Furthermore, it is already shown in [Reference Brendle, Halbeisen, Klausner, Lischka and Shelah5] that
$[\omega ]^\omega \setminus B(X)$
is a countable union of closed sets. Furthermore, it is already shown in [Reference Brendle, Halbeisen, Klausner, Lischka and Shelah5] that
![]() $[\omega ]^\omega \setminus B(X)$
is a set of measure zero, so
$[\omega ]^\omega \setminus B(X)$
is a set of measure zero, so
![]() $[\omega ]^\omega \setminus B(X)$
is a countable union of closed sets of measure zero.
$[\omega ]^\omega \setminus B(X)$
is a countable union of closed sets of measure zero.
Corollary 3.2.
![]() $\mathfrak {s}_{1/2}^{\infty } \leq $
non
$\mathfrak {s}_{1/2}^{\infty } \leq $
non
![]() $(\mathcal {E})$
and cov
$(\mathcal {E})$
and cov
![]() $(\mathcal {E}) \leq \mathfrak {r}_{1/2}^{\infty }$
.
$(\mathcal {E}) \leq \mathfrak {r}_{1/2}^{\infty }$
.
To prove the consistency of
![]() $\mathfrak {s}_{1/2}^{\infty } <$
non
$\mathfrak {s}_{1/2}^{\infty } <$
non
![]() $(\mathcal {E})$
and cov
$(\mathcal {E})$
and cov
![]() $(\mathcal {E}) < \mathfrak {r}_{1/2}^{\infty }$
, we work with new objects called good block sequences instead of infinite subsets of
$(\mathcal {E}) < \mathfrak {r}_{1/2}^{\infty }$
, we work with new objects called good block sequences instead of infinite subsets of
![]() $\omega $
.
$\omega $
.
Definition 3.3. We say that a sequence
![]() $\mathcal {A}=(A_n : n \in \omega )$
of finite subsets of
$\mathcal {A}=(A_n : n \in \omega )$
of finite subsets of
![]() $\omega $
is a block sequence if
$\omega $
is a block sequence if
![]() $\max (A_n)<\min (A_{n+1})$
. We say that a set
$\max (A_n)<\min (A_{n+1})$
. We say that a set
![]() $B \in [\omega ]^\omega $
splits
$B \in [\omega ]^\omega $
splits
![]() $\mathcal {A}$
if both
$\mathcal {A}$
if both
![]() $\{n \in \omega \, | \, A_n \subseteq B \}$
and
$\{n \in \omega \, | \, A_n \subseteq B \}$
and
![]() $\{n \in \omega \, | \, A_n \cap B = \emptyset \}$
are infinite.
$\{n \in \omega \, | \, A_n \cap B = \emptyset \}$
are infinite.
Definition 3.4. Let
![]() $\mathcal {A}=(A_n : n \in \omega )$
be a block sequence. We say that
$\mathcal {A}=(A_n : n \in \omega )$
be a block sequence. We say that
![]() $\mathcal {A}$
is a good block sequence if there is a recursive function
$\mathcal {A}$
is a good block sequence if there is a recursive function
![]() $f \in \omega ^\omega $
such that
$f \in \omega ^\omega $
such that
![]() $|A_n|=f(n)$
.
$|A_n|=f(n)$
.
There are two cardinal characteristics associated with the previous notions.
 $$\begin{align*}\mathfrak{fs}&= \min\{ | \mathcal{F} | \, | \, \mathcal{F} \subseteq [\omega]^\omega \text{ and every block sequence is split by a member of } \mathcal{F} \}. \\\mathfrak{fs}_{g}&= \min\{ | \mathcal{F} | \, | \, \mathcal{F} \subseteq [\omega]^\omega \text{ and every good block sequence is split by a member of }\mathcal{F} \}. \end{align*}$$
$$\begin{align*}\mathfrak{fs}&= \min\{ | \mathcal{F} | \, | \, \mathcal{F} \subseteq [\omega]^\omega \text{ and every block sequence is split by a member of } \mathcal{F} \}. \\\mathfrak{fs}_{g}&= \min\{ | \mathcal{F} | \, | \, \mathcal{F} \subseteq [\omega]^\omega \text{ and every good block sequence is split by a member of }\mathcal{F} \}. \end{align*}$$
Kamburelis and Węglorz showed that
![]() $\mathfrak {fs} = \max \{ \mathfrak {b}, \mathfrak {s} \}$
(see [Reference Kamburelis and Węglorz7]). These cardinals also have their dual version.
$\mathfrak {fs} = \max \{ \mathfrak {b}, \mathfrak {s} \}$
(see [Reference Kamburelis and Węglorz7]). These cardinals also have their dual version.
 $$\begin{align*}\mathfrak{fr}&= \min\{ | \mathcal{F} | \, | \, \mathcal{F} \text{ consists of block sequences and no single} A\in [\omega]^\omega \text{ splits}\\& \qquad\qquad \text{all members of } \mathcal{F} \}. \\\mathfrak{fr}_{g}&= \min\{ | \mathcal{F} | \, | \, \mathcal{F} \text{ consists of good block sequences and no single } A\in [\omega]^\omega \text{ splits}\\& \qquad\qquad \text{all members of } \mathcal{F} \}. \end{align*}$$
$$\begin{align*}\mathfrak{fr}&= \min\{ | \mathcal{F} | \, | \, \mathcal{F} \text{ consists of block sequences and no single} A\in [\omega]^\omega \text{ splits}\\& \qquad\qquad \text{all members of } \mathcal{F} \}. \\\mathfrak{fr}_{g}&= \min\{ | \mathcal{F} | \, | \, \mathcal{F} \text{ consists of good block sequences and no single } A\in [\omega]^\omega \text{ splits}\\& \qquad\qquad \text{all members of } \mathcal{F} \}. \end{align*}$$
In [Reference Brendle3], Jörg Brendle showed that
![]() $\mathfrak {fr} = \min \{ \mathfrak {d}, \mathfrak {r} \}$
. There is a relation with
$\mathfrak {fr} = \min \{ \mathfrak {d}, \mathfrak {r} \}$
. There is a relation with
![]() $\mathfrak {s}_{1/2}^{\infty }$
and
$\mathfrak {s}_{1/2}^{\infty }$
and
![]() $\mathfrak {r}_{1/2}^{\infty }$
.
$\mathfrak {r}_{1/2}^{\infty }$
.
Proposition 3.5. Let
![]() $A, B$
be infinite subsets of
$A, B$
be infinite subsets of
![]() $\omega $
. Let
$\omega $
. Let
![]() $\{a_i\}_{i \geq 1}$
be the increasing enumeration of A. Define
$\{a_i\}_{i \geq 1}$
be the increasing enumeration of A. Define
![]() $A_n=\{a_{\sum _{i\leq n}2^i}, ..., a_{(\sum _{i \leq n+1} 2^i ) -1} \}$
and consider the block sequence
$A_n=\{a_{\sum _{i\leq n}2^i}, ..., a_{(\sum _{i \leq n+1} 2^i ) -1} \}$
and consider the block sequence
![]() $\mathcal {A}=(A_n : n \in \omega )$
. Note that
$\mathcal {A}=(A_n : n \in \omega )$
. Note that
![]() $\mathcal {A}$
is a good block sequence because
$\mathcal {A}$
is a good block sequence because
![]() $|A_n|=2^{n+1}$
. We have that if B splits
$|A_n|=2^{n+1}$
. We have that if B splits
![]() $\mathcal {A}$
then B cofinally bisects A.
$\mathcal {A}$
then B cofinally bisects A.
Proof. Assume that B splits
![]() $\mathcal {A}$
. To see that B cofinally bisects A it suffices to show that both
$\mathcal {A}$
. To see that B cofinally bisects A it suffices to show that both
![]() $\{n\in \omega \, | \, \frac {d_n(B\cap A)}{d_n(A)}\geq 1/2 \}$
and
$\{n\in \omega \, | \, \frac {d_n(B\cap A)}{d_n(A)}\geq 1/2 \}$
and
![]() $\{n\in \omega \, | \, \frac {d_n(B\cap A)}{d_n(A)}\leq 1/2 \}$
are infinite. Fix
$\{n\in \omega \, | \, \frac {d_n(B\cap A)}{d_n(A)}\leq 1/2 \}$
are infinite. Fix
![]() $n\in \omega $
. There are
$n\in \omega $
. There are
![]() $m_1,m_2>n$
such that
$m_1,m_2>n$
such that
![]() $A_{m_1} \subseteq B$
and
$A_{m_1} \subseteq B$
and
![]() $A_{m_2} \cap B = \emptyset $
. Letting
$A_{m_2} \cap B = \emptyset $
. Letting
![]() $K_1:=a_{(\sum _{i \leq m_1+1} 2^i )+1}$
and
$K_1:=a_{(\sum _{i \leq m_1+1} 2^i )+1}$
and
![]() $K_2:=a_{(\sum _{i \leq m_2+1} 2^i )+1}$
, we have
$K_2:=a_{(\sum _{i \leq m_2+1} 2^i )+1}$
, we have
 $$\begin{align*}\kern-12pt \frac{d_{K_1}(B\cap A)}{d_{K_1}(A)} \geq \frac{2^{m_1+1}}{\sum_{i \leq m_1+1} 2^i } \geq \frac{1}{2} \text{ and } \frac{d_{K_2}(B\cap A)}{d_{K_2}(A)} \leq \frac{\sum_{i \leq m_2} 2^i}{\sum_{i \leq m_2+1} 2^i } \leq \frac{1}{2}.\\[-41pt] \end{align*}$$
$$\begin{align*}\kern-12pt \frac{d_{K_1}(B\cap A)}{d_{K_1}(A)} \geq \frac{2^{m_1+1}}{\sum_{i \leq m_1+1} 2^i } \geq \frac{1}{2} \text{ and } \frac{d_{K_2}(B\cap A)}{d_{K_2}(A)} \leq \frac{\sum_{i \leq m_2} 2^i}{\sum_{i \leq m_2+1} 2^i } \leq \frac{1}{2}.\\[-41pt] \end{align*}$$
As an immediate consequence, we get the following.
Corollary 3.6.
![]() $\mathfrak {s}_{1/2}^{\infty } \leq \mathfrak {fs}_{g} \leq \mathfrak {fs}$
and
$\mathfrak {s}_{1/2}^{\infty } \leq \mathfrak {fs}_{g} \leq \mathfrak {fs}$
and
![]() $\mathfrak {fr} \leq \mathfrak {fr}_{g} \leq \mathfrak {r}_{1/2}^{\infty }$
.
$\mathfrak {fr} \leq \mathfrak {fr}_{g} \leq \mathfrak {r}_{1/2}^{\infty }$
.
Now, we are going to prove that
![]() $\mathfrak {fs}_{g}=\aleph _1$
in the Hechler model. The proof is analogous to the classical proof that shows that Hechler forcing preserves
$\mathfrak {fs}_{g}=\aleph _1$
in the Hechler model. The proof is analogous to the classical proof that shows that Hechler forcing preserves
![]() $\omega $
-splitting families (see, e.g., [Reference Brendle4, Theorem 3.13]).
$\omega $
-splitting families (see, e.g., [Reference Brendle4, Theorem 3.13]).
Lemma 3.7. Assume
![]() $\dot {\mathcal {A}}=(\dot {A}_n : n \in \omega )$
is a
$\dot {\mathcal {A}}=(\dot {A}_n : n \in \omega )$
is a
![]() $\mathbb {D}$
-name of a good block sequence. There are good block sequences
$\mathbb {D}$
-name of a good block sequence. There are good block sequences
![]() $\mathcal {A}_i=(A_j^i : j \in \omega )$
,
$\mathcal {A}_i=(A_j^i : j \in \omega )$
,
![]() $i\in \omega $
, such that whenever
$i\in \omega $
, such that whenever
![]() $B \in [\omega ]^\omega $
splits all
$B \in [\omega ]^\omega $
splits all
![]() $\mathcal {A}_i$
, then
$\mathcal {A}_i$
, then
Proof. Let
![]() $p\in \mathbb {D}$
. There are
$p\in \mathbb {D}$
. There are
![]() $r \leq p $
and
$r \leq p $
and
![]() $f\in \omega ^\omega $
a recursive function such that
$f\in \omega ^\omega $
a recursive function such that
![]() $r \Vdash |\dot {A}_n|=f(n)$
. Since we are going to work below r, to simplify the notation, we can assume
$r \Vdash |\dot {A}_n|=f(n)$
. Since we are going to work below r, to simplify the notation, we can assume
For
![]() $s\in \omega ^{<\omega }$
,
$s\in \omega ^{<\omega }$
,
![]() $i\in \omega $
, and
$i\in \omega $
, and
![]() $0<n\leq f(i)$
, say that s favors that k is the n-th element of
$0<n\leq f(i)$
, say that s favors that k is the n-th element of
![]() $\dot {A}_i$
if there is no condition with first coordinate s which forces that “k is not the n-th element of
$\dot {A}_i$
if there is no condition with first coordinate s which forces that “k is not the n-th element of
![]() $\dot {A}_i$
”. Define the rank rk
$\dot {A}_i$
”. Define the rank rk
![]() $_n^i(s)$
by recursion on the ordinals, as follows:
$_n^i(s)$
by recursion on the ordinals, as follows:
-
• rk
 $_n^i(s)=0$
if for some
$_n^i(s)=0$
if for some
 $k \in \omega $
, s favors that k is the n-th element of
$k \in \omega $
, s favors that k is the n-th element of
 $\dot {A}_i$
.
$\dot {A}_i$
. -
• for
 $\alpha>0$
: rk
$\alpha>0$
: rk
 $_n^i(s)=\alpha $
if there is no
$_n^i(s)=\alpha $
if there is no
 $\beta < \alpha $
such that rk
$\beta < \alpha $
such that rk
 $_n^i(s)=\beta $
and there are infinitely many l such that rk
$_n^i(s)=\beta $
and there are infinitely many l such that rk
 $_n^i(s^\frown l)<\alpha $
.
$_n^i(s^\frown l)<\alpha $
.
Clearly, rk
![]() $_n^i(s)$
must be a countable ordinal or undefined (in which case we write rk
$_n^i(s)$
must be a countable ordinal or undefined (in which case we write rk
![]() $_n^i(s) = \infty $
). We show the latter never happens.
$_n^i(s) = \infty $
). We show the latter never happens.
Claim 3.8. rk
![]() $_n^i(s) < \omega _1$
for all
$_n^i(s) < \omega _1$
for all
![]() $s\in \omega ^{<\omega }$
,
$s\in \omega ^{<\omega }$
,
![]() $i \in \omega $
, and
$i \in \omega $
, and
![]() $n<f(i)$
.
$n<f(i)$
.
Proof. Assume rk
![]() $_n^i(s)=\infty $
. Notice that for any t, if rk
$_n^i(s)=\infty $
. Notice that for any t, if rk
![]() $_n^i(t) = \infty $
, then rk
$_n^i(t) = \infty $
, then rk
![]() $_n^i(t^\frown l) = \infty $
for almost all
$_n^i(t^\frown l) = \infty $
for almost all
![]() $l \in \omega $
. This allows us to recursively construct a function
$l \in \omega $
. This allows us to recursively construct a function
![]() $\phi : \omega ^{<\omega } \rightarrow \omega $
such that whenever
$\phi : \omega ^{<\omega } \rightarrow \omega $
such that whenever
![]() $t \supset s$
and
$t \supset s$
and
![]() $t(i) \geq \phi (t\upharpoonright i)$
for all
$t(i) \geq \phi (t\upharpoonright i)$
for all
![]() $i \in |t|\setminus |s|$
, then rk
$i \in |t|\setminus |s|$
, then rk
![]() $_n^i(t)=\infty $
.
$_n^i(t)=\infty $
.
Consider the condition
![]() $(s, \phi )$
. Find
$(s, \phi )$
. Find
![]() $(t, \psi ) \leq (s, \phi )$
and
$(t, \psi ) \leq (s, \phi )$
and
![]() $k \in \omega $
such that
$k \in \omega $
such that
![]() $(t, \psi )$
forces that k is the n-th element of
$(t, \psi )$
forces that k is the n-th element of
![]() $\dot {A}_i$
. Then rk
$\dot {A}_i$
. Then rk
![]() $_n^i(t)=0$
. However, by the preceding paragraph, rk
$_n^i(t)=0$
. However, by the preceding paragraph, rk
![]() $_n^i(t)=\infty $
, a contradiction.
$_n^i(t)=\infty $
, a contradiction.
We continue the proof of the lemma. Consider the function
![]() $F(i)= \sum _{j< i} f(j)$
. Let
$F(i)= \sum _{j< i} f(j)$
. Let
![]() $s\in \omega ^{<\omega }$
. We make a recursive construction on the rank to get the block sequences we need. Given
$s\in \omega ^{<\omega }$
. We make a recursive construction on the rank to get the block sequences we need. Given
![]() $s\in \omega ^{<\omega }$
, there are three cases we need to consider.
$s\in \omega ^{<\omega }$
, there are three cases we need to consider.
-
Case 0. There infinitely many
 $(n,i)$
such that rk
$(n,i)$
such that rk
 $_n^i(s)=0$
. It is easy to check that this actually implies rk
$_n^i(s)=0$
. It is easy to check that this actually implies rk
 $_n^i(s)=0$
for all
$_n^i(s)=0$
for all
 $(n,i)$
.
$(n,i)$
. -
Case 1. There is
 $(n,i) \in \omega \times \omega $
such that rk
$(n,i) \in \omega \times \omega $
such that rk
 $_n^i(s)=1$
. This constitutes our base case for the recursive construction.
$_n^i(s)=1$
. This constitutes our base case for the recursive construction. -
Case 2. There is some
 $1<\alpha <\omega _1$
and
$1<\alpha <\omega _1$
and
 $(n,i) \in \omega \times \omega $
such that rk
$(n,i) \in \omega \times \omega $
such that rk
 $_n^i(s)=\alpha $
.
$_n^i(s)=\alpha $
.
Let us begin the construction.
-
Case 0. Let
 $s\in \omega ^{<\omega }$
be such that rk
$s\in \omega ^{<\omega }$
be such that rk
 $_n^i(s)=0$
for infinitely many
$_n^i(s)=0$
for infinitely many
 $(n,i)$
, or equivalently, rk
$(n,i)$
, or equivalently, rk
 $_n^i(s)=0$
for all
$_n^i(s)=0$
for all
 $(n,i)$
. For all
$(n,i)$
. For all
 $m \in \omega $
, we can find a finite sequence of finite sets
$m \in \omega $
, we can find a finite sequence of finite sets
 $\mathcal {B}_m=(B_i^m : i<m )$
such that s favors that
$\mathcal {B}_m=(B_i^m : i<m )$
such that s favors that
 $\mathcal {B}_m$
are the first m blocks of
$\mathcal {B}_m$
are the first m blocks of
 $\dot {\mathcal {A}}$
. Fix
$\dot {\mathcal {A}}$
. Fix
 $i<\omega $
. Choose one block of the collection
$i<\omega $
. Choose one block of the collection
 $\{B_i^m\}_{m> i}$
such that its maximum element coincides with
$\{B_i^m\}_{m> i}$
such that its maximum element coincides with
 $\min \{ \max (B_i^m) \, | \, m \in \omega \}$
, and denote this block as
$\min \{ \max (B_i^m) \, | \, m \in \omega \}$
, and denote this block as
 $B_i$
. We denote the collection
$B_i$
. We denote the collection
 $(B_i : i< \omega )$
as
$(B_i : i< \omega )$
as
 $\mathcal {A}_s$
. Note that
$\mathcal {A}_s$
. Note that
 $\mathcal {A}_s$
is a good block sequence.
$\mathcal {A}_s$
is a good block sequence. -
Case 1. Let
 $(n,i) \in \omega \times \omega $
and
$(n,i) \in \omega \times \omega $
and
 $s\in \omega ^{<\omega }$
such that rk
$s\in \omega ^{<\omega }$
such that rk
 $_n^i(s)=1$
. There are infinitely many
$_n^i(s)=1$
. There are infinitely many
 $l\in \omega $
such that rk
$l\in \omega $
such that rk
 $_n^i(s^\frown l)=0$
. For each such l, we may find
$_n^i(s^\frown l)=0$
. For each such l, we may find
 ${A_l \in [\omega ]^{F(i)+n}}$
such that
${A_l \in [\omega ]^{F(i)+n}}$
such that
 $s ^\frown l$
favors that
$s ^\frown l$
favors that
 $A_l$
are the first
$A_l$
are the first
 $(F(i)+n)$
-th elements of
$(F(i)+n)$
-th elements of
 $\bigcup \dot {\mathcal {A}}$
. Define:
$\bigcup \dot {\mathcal {A}}$
. Define:  $$\begin{align*}i_s:= \max \{j \in \omega \, | \, \{a_j : a_j \text{ is the }j\text{-th element of some }A_l \} \text{ is finite} \}. \end{align*}$$
$$\begin{align*}i_s:= \max \{j \in \omega \, | \, \{a_j : a_j \text{ is the }j\text{-th element of some }A_l \} \text{ is finite} \}. \end{align*}$$
Then there is
 $A \in [\omega ]^{i_s}$
such that the set
$A \in [\omega ]^{i_s}$
such that the set
 $\{ l \, | \, A \text { are the first }i_s\text {-th elements} \text{of } A_l \}$
is infinite. We denote this set as
$\{ l \, | \, A \text { are the first }i_s\text {-th elements} \text{of } A_l \}$
is infinite. We denote this set as
 $A_{s,n}^i$
. We can construct a block sequence
$A_{s,n}^i$
. We can construct a block sequence
 $\mathcal {A}_{s,n}^i$
such that
$\mathcal {A}_{s,n}^i$
such that-
•
 $\mathcal {A}_{s,n}^i \subseteq [\omega ]^{F(i)+n-i_s}$
, so it is a good block sequence. Note that we must have
$\mathcal {A}_{s,n}^i \subseteq [\omega ]^{F(i)+n-i_s}$
, so it is a good block sequence. Note that we must have
 $i_s < F(i)+n$
because rk
$i_s < F(i)+n$
because rk
 $_n^i(s)>0$
.
$_n^i(s)>0$
. -
• For each
 $l\in \omega $
, there is
$l\in \omega $
, there is
 $l^\prime> l$
and
$l^\prime> l$
and
 $D \in \mathcal {A}_{s,n}^i$
such that
$D \in \mathcal {A}_{s,n}^i$
such that
 $s ^\frown l^\prime $
favors that
$s ^\frown l^\prime $
favors that
 $A_{s,n}^i \cup D$
are the first
$A_{s,n}^i \cup D$
are the first
 $(F(i)+n)$
-th elements of
$(F(i)+n)$
-th elements of
 $\bigcup \dot {\mathcal {A}}$
.
$\bigcup \dot {\mathcal {A}}$
.
Note that s favors that
 $A_{s,n}^i$
are the first
$A_{s,n}^i$
are the first
 $i_s$
-th elements of
$i_s$
-th elements of
 $\bigcup \dot {\mathcal {A}}$
.
$\bigcup \dot {\mathcal {A}}$
. -
-
Case 2. Let
 $(n,i) \in \omega \times \omega $
and
$(n,i) \in \omega \times \omega $
and
 $s\in \omega ^{<\omega }$
such that rk
$s\in \omega ^{<\omega }$
such that rk
 $_n^i(s)=\alpha>1$
. There are infinitely many
$_n^i(s)=\alpha>1$
. There are infinitely many
 $l\in \omega $
such that
$l\in \omega $
such that
 $0<$
rk
$0<$
rk
 $_n^i(s^\frown l)<\alpha $
. For each
$_n^i(s^\frown l)<\alpha $
. For each
 $s^\frown l$
, there exist a set
$s^\frown l$
, there exist a set
 $A_{s^\frown l,n}^i$
and a natural number
$A_{s^\frown l,n}^i$
and a natural number
 $i_{s^\frown l}$
such that
$i_{s^\frown l}$
such that
 $s^\frown l$
favors that
$s^\frown l$
favors that
 $A_{s^\frown l,n}^i$
are the first
$A_{s^\frown l,n}^i$
are the first
 $i_{s^\frown l}$
elements of
$i_{s^\frown l}$
elements of
 $\bigcup \dot {\mathcal {A}}$
. Also, there is a block sequence
$\bigcup \dot {\mathcal {A}}$
. Also, there is a block sequence
 $\mathcal {A}_{s^\frown l,n}^i$
. Define: Then there is
$\mathcal {A}_{s^\frown l,n}^i$
. Define: Then there is $$\begin{align*}i_s:= \max \{j \in \omega \, | \, \{a_i : a_i \text{ is the} j\text{-th element of some }A_{s^\frown l,n}^i \} \text{ is finite} \}. \end{align*}$$
$$\begin{align*}i_s:= \max \{j \in \omega \, | \, \{a_i : a_i \text{ is the} j\text{-th element of some }A_{s^\frown l,n}^i \} \text{ is finite} \}. \end{align*}$$
 $A \in [\omega ]^{i_s}$
such that the set
$A \in [\omega ]^{i_s}$
such that the set
 $\{ l \, | \, A \text { are the first} i_s\text {-th elements} \text{of } A_{s^\frown l,n}^i \}$
is infinite. We denote this set as
$\{ l \, | \, A \text { are the first} i_s\text {-th elements} \text{of } A_{s^\frown l,n}^i \}$
is infinite. We denote this set as
 $A_{s,n}^i$
. Also, choose a number
$A_{s,n}^i$
. Also, choose a number
 $m\leq F(i)+n$
such that the set
$m\leq F(i)+n$
such that the set
 $\{ l \, | \, A_{s,n}^i \text { are the first }i_s\text {-th elements of} A_{s^\frown l,n}^i \text {and } m=|A_{s^\frown l,n}^i \setminus A_{s,n}^i| \}$
is infinite. We can construct a block sequence
$\{ l \, | \, A_{s,n}^i \text { are the first }i_s\text {-th elements of} A_{s^\frown l,n}^i \text {and } m=|A_{s^\frown l,n}^i \setminus A_{s,n}^i| \}$
is infinite. We can construct a block sequence
 $\mathcal {A}_{s,n}^i$
such that
$\mathcal {A}_{s,n}^i$
such that
-
•
 $\mathcal {A}_{s,n}^i \subseteq [\omega ]^{m}$
, so it is a good block sequence. Note that
$\mathcal {A}_{s,n}^i \subseteq [\omega ]^{m}$
, so it is a good block sequence. Note that
 $m>0$
since rk
$m>0$
since rk
 $_n^i(s)>0$
and the maximality of
$_n^i(s)>0$
and the maximality of
 $i_s$
.
$i_s$
. -
• For each
 $l\in \omega $
, there is
$l\in \omega $
, there is
 $l^\prime> l$
and
$l^\prime> l$
and
 $D \in \mathcal {A}_{s,n}^i$
such that
$D \in \mathcal {A}_{s,n}^i$
such that
 $D = A_{s^\frown l^\prime ,n}^i \setminus A_{s,n}^i$
.
$D = A_{s^\frown l^\prime ,n}^i \setminus A_{s,n}^i$
.
Note that s favors that
 $A_{s,n}^i$
are the first
$A_{s,n}^i$
are the first
 $i_s$
-th elements of
$i_s$
-th elements of
 $\bigcup \dot {\mathcal {A}}$
.
$\bigcup \dot {\mathcal {A}}$
. -
We claim that if B splits all
![]() $\mathcal {A}_s$
and all
$\mathcal {A}_s$
and all
![]() $\mathcal {A}_{s,n}^i$
, then
$\mathcal {A}_{s,n}^i$
, then
![]() $\Vdash B \text { splits } \dot {\mathcal {A}}$
. Let
$\Vdash B \text { splits } \dot {\mathcal {A}}$
. Let
![]() $(s, \phi )$
be a condition and let
$(s, \phi )$
be a condition and let
![]() $m\in \omega $
. We need to find
$m\in \omega $
. We need to find
![]() $(t,\psi ) \leq (s, \phi )$
and
$(t,\psi ) \leq (s, \phi )$
and
![]() $m_1,m_2\geq m$
such that
$m_1,m_2\geq m$
such that
![]() $(t,\psi )$
forces that
$(t,\psi )$
forces that
![]() $\dot {A}_{m_1} \subseteq B$
and
$\dot {A}_{m_1} \subseteq B$
and
![]() $\dot {A}_{m_2} \cap B = \emptyset $
. Since the construction of
$\dot {A}_{m_2} \cap B = \emptyset $
. Since the construction of
![]() $m_1$
and
$m_1$
and
![]() $m_2$
is analogous, it suffices to produce the former.
$m_2$
is analogous, it suffices to produce the former.
-
Case 0. There are infinitely many
 $(n,i)$
such that rk
$(n,i)$
such that rk
 $_n^i(s)=0$
. Since B splits
$_n^i(s)=0$
. Since B splits
 $\mathcal {A}_s$
, there is
$\mathcal {A}_s$
, there is
 $n>m$
such that
$n>m$
such that
 $B_n \in \mathcal {A}_s $
and
$B_n \in \mathcal {A}_s $
and
 $B_n \subseteq B$
. By definition of
$B_n \subseteq B$
. By definition of
 $\mathcal {A}_s$
, s favors that
$\mathcal {A}_s$
, s favors that
 $B_n$
is the n-th block of
$B_n$
is the n-th block of
 $\dot {\mathcal {A}}$
. Therefore, there is
$\dot {\mathcal {A}}$
. Therefore, there is
 $(t,\psi ) \leq (s, \phi ) $
such that
$(t,\psi ) \leq (s, \phi ) $
such that
 $(t,\psi ) \Vdash \dot {A}_n = B_n \subseteq B$
.
$(t,\psi ) \Vdash \dot {A}_n = B_n \subseteq B$
.
Now, suppose that rk
![]() $_n^i(s)>0$
for all but finitely many
$_n^i(s)>0$
for all but finitely many
![]() $(n,i)$
. Choose
$(n,i)$
. Choose
![]() $i\geq m$
such that rk
$i\geq m$
such that rk
![]() $_n^i(s)>0$
for all
$_n^i(s)>0$
for all
![]() $0<n\leq f(i)$
. There are two cases.
$0<n\leq f(i)$
. There are two cases.
-
Case 1. Suppose that rk
 $_{f(i)}^i(s) =1 $
. Since B splits
$_{f(i)}^i(s) =1 $
. Since B splits
 $\mathcal {A}_{s,f(i)}^i$
, we can find
$\mathcal {A}_{s,f(i)}^i$
, we can find
 $l\geq \phi (s)$
and
$l\geq \phi (s)$
and
 $D\in \mathcal {A}_{s,f(i)}^i$
such that
$D\in \mathcal {A}_{s,f(i)}^i$
such that-
•
 $D \subseteq B$
and
$D \subseteq B$
and
 $s ^\frown l$
favors that
$s ^\frown l$
favors that
 $A_{s,f(i)}^i \cup D$
are the first
$A_{s,f(i)}^i \cup D$
are the first
 $(F(i)+f(i))$
-th elements of
$(F(i)+f(i))$
-th elements of
 $\bigcup \dot {\mathcal {A}}$
.
$\bigcup \dot {\mathcal {A}}$
.
Note that
 $|A_{s,f(i)}^i|=i_s \leq F(i)$
because rk
$|A_{s,f(i)}^i|=i_s \leq F(i)$
because rk
 $_n^i(s)>0$
for all
$_n^i(s)>0$
for all
 $0<n\leq f(i)$
, thus
$0<n\leq f(i)$
, thus
 $s ^\frown l$
favors that D contains the i-th block of
$s ^\frown l$
favors that D contains the i-th block of
 $\dot {\mathcal {A}}$
. Therefore, there is
$\dot {\mathcal {A}}$
. Therefore, there is
 $(r,\psi ) \leq (s, \phi ) $
such that
$(r,\psi ) \leq (s, \phi ) $
such that  $$\begin{align*}(r,\psi) \Vdash \dot{A}_i \subseteq D \subseteq B. \end{align*}$$
$$\begin{align*}(r,\psi) \Vdash \dot{A}_i \subseteq D \subseteq B. \end{align*}$$
-
-
Case 2. Suppose that rk
 $_{f(i)}^i(s) = \alpha> 1$
. Since B splits
$_{f(i)}^i(s) = \alpha> 1$
. Since B splits
 $\mathcal {A}_{s,f(i)}^i$
, we can find
$\mathcal {A}_{s,f(i)}^i$
, we can find
 $l_1\geq \phi (s)$
and
$l_1\geq \phi (s)$
and
 $D_1\in \mathcal {A}_{s,f(i)}^i$
such that
$D_1\in \mathcal {A}_{s,f(i)}^i$
such that-
•
 $1\leq $
rk
$1\leq $
rk
 $_{f(i)}^i(s^\frown l_1) <$
rk
$_{f(i)}^i(s^\frown l_1) <$
rk
 $_{f(i)}^i(s)$
$_{f(i)}^i(s)$
-
•
 $D_1 \subseteq B$
and
$D_1 \subseteq B$
and
 $D_1 = A_{s^\frown l_1,f(i)}^i \setminus A_{s,f(i)}^i$
.
$D_1 = A_{s^\frown l_1,f(i)}^i \setminus A_{s,f(i)}^i$
.
Repeating this argument, we can extend s to
 $s^\frown l_1 ^{\frown ... \frown } l_k=t$
and find finite sets
$s^\frown l_1 ^{\frown ... \frown } l_k=t$
and find finite sets
 $D_1, ..., D_k$
such that
$D_1, ..., D_k$
such that-
•
 $t(i)\geq \phi (t\upharpoonright i)$
for all
$t(i)\geq \phi (t\upharpoonright i)$
for all
 $i \in |t| \setminus |s|$
, and rk
$i \in |t| \setminus |s|$
, and rk
 $_{f(i)}^i(t)=1$
.
$_{f(i)}^i(t)=1$
. -
•
 $D_j \subseteq B$
and
$D_j \subseteq B$
and
 $D_j = A_{s^\frown l_1 ^{\frown ... \frown } l_j,f(i)}^i \setminus A_{l_1 ^{\frown ... \frown } l_{j-1},f(i)}^i$
.
$D_j = A_{s^\frown l_1 ^{\frown ... \frown } l_j,f(i)}^i \setminus A_{l_1 ^{\frown ... \frown } l_{j-1},f(i)}^i$
.
Finally, since rk
 $_{f(i)}^i(t)=1$
and B splits
$_{f(i)}^i(t)=1$
and B splits
 $\mathcal {A}_{t,f(i)}^i$
, we can find
$\mathcal {A}_{t,f(i)}^i$
, we can find
 $l\geq \phi (t)$
and
$l\geq \phi (t)$
and
 $D\in \mathcal {A}_{t,f(i)}^i$
such that
$D\in \mathcal {A}_{t,f(i)}^i$
such that-
•
 $D \subseteq B$
and
$D \subseteq B$
and
 $t ^\frown l$
favors that
$t ^\frown l$
favors that
 $A_{t,f(i)}^i \cup D$
are the first
$A_{t,f(i)}^i \cup D$
are the first
 $(F(i)+f(i))$
-th elements of
$(F(i)+f(i))$
-th elements of
 $\bigcup \dot {\mathcal {A}}$
.
$\bigcup \dot {\mathcal {A}}$
.
Note that
 $|A_{s,f(i)}^i|=i_s \leq F(i)$
because rk
$|A_{s,f(i)}^i|=i_s \leq F(i)$
because rk
 $_n^i(s)>0$
for all
$_n^i(s)>0$
for all
 $0<n\leq f(i)$
. Also, by construction,
$0<n\leq f(i)$
. Also, by construction,
 $A_{t,f(i)}^i = D_1 \cup ... \cup D_k \cup A_{s,f(i)}^i $
, thus
$A_{t,f(i)}^i = D_1 \cup ... \cup D_k \cup A_{s,f(i)}^i $
, thus
 $t ^\frown l$
favors that
$t ^\frown l$
favors that
 $D_1 \cup ... \cup D_k \cup D$
contains the i-th block of
$D_1 \cup ... \cup D_k \cup D$
contains the i-th block of
 $\dot {\mathcal {A}}$
. Therefore, there is
$\dot {\mathcal {A}}$
. Therefore, there is
 $(r,\psi ) \leq (s, \phi ) $
such that
$(r,\psi ) \leq (s, \phi ) $
such that  $$\begin{align*}(r,\psi) \Vdash \dot{A}_i \subseteq D_1 \cup ... \cup D_k \cup D \subseteq B.\\[-31pt] \end{align*}$$
$$\begin{align*}(r,\psi) \Vdash \dot{A}_i \subseteq D_1 \cup ... \cup D_k \cup D \subseteq B.\\[-31pt] \end{align*}$$
-
Let us say a partial order has property
![]() $(\star \star )$
if it shares the property exhibited in Lemma 3.7. That is, given a name of a good block sequence
$(\star \star )$
if it shares the property exhibited in Lemma 3.7. That is, given a name of a good block sequence
![]() $\dot {\mathcal {A}}=(\dot {A}_n : n \in \omega )$
, there are good block sequences
$\dot {\mathcal {A}}=(\dot {A}_n : n \in \omega )$
, there are good block sequences
![]() $\mathcal {A}_i=(A_j^i : j \in \omega )$
,
$\mathcal {A}_i=(A_j^i : j \in \omega )$
,
![]() $i\in \omega $
in the ground model such that for all
$i\in \omega $
in the ground model such that for all
![]() $B \in [\omega ]^\omega $
, if B splits all
$B \in [\omega ]^\omega $
, if B splits all
![]() $\mathcal {A}_i$
, then
$\mathcal {A}_i$
, then
![]() $\Vdash B \text { splits } \dot {\mathcal {A}}$
. This property is preserved under fsi of ccc forcing notions.
$\Vdash B \text { splits } \dot {\mathcal {A}}$
. This property is preserved under fsi of ccc forcing notions.
Lemma 3.9. Let
![]() $\delta $
be a limit ordinal. Let
$\delta $
be a limit ordinal. Let
![]() $(\mathbb {P}_\alpha , \dot {\mathbb {Q}}_{\alpha } : \alpha < \delta )$
be an fsi of ccc forcing notions. Assume that
$(\mathbb {P}_\alpha , \dot {\mathbb {Q}}_{\alpha } : \alpha < \delta )$
be an fsi of ccc forcing notions. Assume that
![]() $\mathbb {P}_\alpha $
has property
$\mathbb {P}_\alpha $
has property
![]() $(\star \star )$
for all
$(\star \star )$
for all
![]() $\alpha <\delta $
. Then also
$\alpha <\delta $
. Then also
![]() $\mathbb {P}_\delta $
has property
$\mathbb {P}_\delta $
has property
![]() $(\star \star )$
.
$(\star \star )$
.
Proof. No new reals arise in limit stages of uncountable cofinality so that the lemma vacuously holds if cf
![]() $(\delta )>\omega $
. Hence assume cf
$(\delta )>\omega $
. Hence assume cf
![]() $(\delta )=\omega $
. To simplify notation, suppose
$(\delta )=\omega $
. To simplify notation, suppose
![]() $\delta =\omega $
.
$\delta =\omega $
.
Let
![]() $\dot {\mathcal {A}}=(\dot {A}_n : n \in \omega )$
be a
$\dot {\mathcal {A}}=(\dot {A}_n : n \in \omega )$
be a
![]() $\mathbb {P}_\omega $
-name of a good block sequence. Fix
$\mathbb {P}_\omega $
-name of a good block sequence. Fix
![]() $m \in \omega $
. Work in
$m \in \omega $
. Work in
![]() $V^{\mathbb {P}_m}$
for the moment. There is a decreasing sequence of conditions
$V^{\mathbb {P}_m}$
for the moment. There is a decreasing sequence of conditions
![]() $p_k=p_{m,k}$
in the remainder forcing
$p_k=p_{m,k}$
in the remainder forcing
![]() $\mathbb {P}_\omega \setminus \mathbb {P}_m$
such that
$\mathbb {P}_\omega \setminus \mathbb {P}_m$
such that
![]() $p_k$
decides the k-th block of
$p_k$
decides the k-th block of
![]() $\dot {\mathcal {A}}$
. Say
$\dot {\mathcal {A}}$
. Say
![]() $p_k \Vdash B_k= \dot {A}_k$
. Let
$p_k \Vdash B_k= \dot {A}_k$
. Let
![]() $\mathcal {A}_m=(B_n: n \in \omega )$
.
$\mathcal {A}_m=(B_n: n \in \omega )$
.
Work in the ground model V. We have a
![]() $\mathbb {P}_m$
-name
$\mathbb {P}_m$
-name
![]() $\dot {\mathcal {A}}_m$
for
$\dot {\mathcal {A}}_m$
for
![]() $\mathcal {A}_m$
. Since
$\mathcal {A}_m$
. Since
![]() $\mathbb {P}_m$
has property
$\mathbb {P}_m$
has property
![]() $(\star \star )$
, there are good block sequences
$(\star \star )$
, there are good block sequences
![]() $\mathcal {A}_{m,i}$
,
$\mathcal {A}_{m,i}$
,
![]() $i\in \omega $
, such that whenever
$i\in \omega $
, such that whenever
![]() $B \in [\omega ]^\omega $
splits all
$B \in [\omega ]^\omega $
splits all
![]() $\mathcal {A}_{m,i}$
, then
$\mathcal {A}_{m,i}$
, then
![]() $\Vdash B \text { splits } \dot {\mathcal {A}}_m$
.
$\Vdash B \text { splits } \dot {\mathcal {A}}_m$
.
Now, fix
![]() $B\in [\omega ]^\omega $
. We claim that if
$B\in [\omega ]^\omega $
. We claim that if
![]() $B \in [\omega ]^\omega $
splits all
$B \in [\omega ]^\omega $
splits all
![]() $\mathcal {A}_{m,i}$
for all
$\mathcal {A}_{m,i}$
for all
![]() $i,m\in \omega $
, then
$i,m\in \omega $
, then
![]() $\Vdash B \text { splits } \dot {\mathcal {A}}$
.
$\Vdash B \text { splits } \dot {\mathcal {A}}$
.
To see this, let
![]() $p \in \mathbb {P}_\omega $
and
$p \in \mathbb {P}_\omega $
and
![]() $n\in \omega $
. We need to find
$n\in \omega $
. We need to find
![]() $q \leq p$
and
$q \leq p$
and
![]() $m_1,m_2\geq n$
such that q forces that
$m_1,m_2\geq n$
such that q forces that
![]() $\dot {A}_{m_1} \subseteq B$
and
$\dot {A}_{m_1} \subseteq B$
and
![]() $\dot {A}_{m_2} \cap B = \emptyset $
. Since the construction of
$\dot {A}_{m_2} \cap B = \emptyset $
. Since the construction of
![]() $m_1$
and
$m_1$
and
![]() $m_2$
is analogous, it suffices to produce the former. Fix m such that
$m_2$
is analogous, it suffices to produce the former. Fix m such that
![]() $p \in \mathbb {P}_m$
and work in
$p \in \mathbb {P}_m$
and work in
![]() $V^{\mathbb {P}_m}$
. We know that B splits
$V^{\mathbb {P}_m}$
. We know that B splits
![]() $\mathcal {A}_m$
. Thus there is
$\mathcal {A}_m$
. Thus there is
![]() $k> n$
such that
$k> n$
such that
![]() $B_k\subseteq B$
and
$B_k\subseteq B$
and
Now work in the ground model V. By strengthening
![]() $p\in \mathbb {P}_n$
, if necessary, we may assume p decides
$p\in \mathbb {P}_n$
, if necessary, we may assume p decides
![]() $p_k$
and
$p_k$
and
![]() $B_k$
. Then
$B_k$
. Then
Corollary 3.10.
![]() $V^{\mathbb {D}_\kappa }\models \aleph _1 =\mathfrak {s}_{1/2}^{\infty } =\mathfrak {fs}_{g} < \mathfrak {fs} = \kappa $
, where
$V^{\mathbb {D}_\kappa }\models \aleph _1 =\mathfrak {s}_{1/2}^{\infty } =\mathfrak {fs}_{g} < \mathfrak {fs} = \kappa $
, where
![]() $\mathbb {D}_\kappa $
is an fsi of Hechler forcing of length
$\mathbb {D}_\kappa $
is an fsi of Hechler forcing of length
![]() $\kappa> \aleph _1$
.
$\kappa> \aleph _1$
.
Proof. Let
![]() $c_\alpha $
,
$c_\alpha $
,
![]() $\alpha < \omega _1$
denote the Cohen reals added by the first
$\alpha < \omega _1$
denote the Cohen reals added by the first
![]() $\aleph _1$
many Hechler reals. It is easy to see that every countable family of good block sequences in
$\aleph _1$
many Hechler reals. It is easy to see that every countable family of good block sequences in
![]() $V^{\mathbb {D}_{\aleph _1}}$
is split by some
$V^{\mathbb {D}_{\aleph _1}}$
is split by some
![]() $c_\alpha $
. By the previous lemmas,
$c_\alpha $
. By the previous lemmas,
![]() $\mathbb {D}_\kappa $
has property
$\mathbb {D}_\kappa $
has property
![]() $(\star \star )$
, so every good block sequence in
$(\star \star )$
, so every good block sequence in
![]() $V^{\mathbb {D}_{\kappa }}$
is split by
$V^{\mathbb {D}_{\kappa }}$
is split by
![]() $\{c_\alpha \}_{\alpha <\omega _1}$
. Therefore, by Corollary 3.6, we get
$\{c_\alpha \}_{\alpha <\omega _1}$
. Therefore, by Corollary 3.6, we get
![]() $V^{\mathbb {D}_\kappa }\models \aleph _1 = \mathfrak {fs}_{g} =\mathfrak {s}_{1/2}^{\infty }$
. Besides, since
$V^{\mathbb {D}_\kappa }\models \aleph _1 = \mathfrak {fs}_{g} =\mathfrak {s}_{1/2}^{\infty }$
. Besides, since
![]() $\mathfrak {fs} = \max \{ \mathfrak {b}, \mathfrak {s} \}$
, we have
$\mathfrak {fs} = \max \{ \mathfrak {b}, \mathfrak {s} \}$
, we have
![]() $V^{\mathbb {D}_\kappa }\models \mathfrak {b}=\mathfrak {fs} = \kappa $
.
$V^{\mathbb {D}_\kappa }\models \mathfrak {b}=\mathfrak {fs} = \kappa $
.
To prove that we can obtain models where
![]() $\mathfrak {s}_{1/2}^{\infty } <$
non
$\mathfrak {s}_{1/2}^{\infty } <$
non
![]() $(\mathcal {E})$
and cov
$(\mathcal {E})$
and cov
![]() $(\mathcal {E}) < \mathfrak {r}_{1/2}^{\infty }$
, we need the following theorem.
$(\mathcal {E}) < \mathfrak {r}_{1/2}^{\infty }$
, we need the following theorem.
Theorem 3.11.
-
1. If cov
 $(\mathcal {M}) = \mathfrak {d}$
, then cov
$(\mathcal {M}) = \mathfrak {d}$
, then cov
 $(\mathcal {E}) = \max \{$
cov
$(\mathcal {E}) = \max \{$
cov
 $(\mathcal {M})$
, cov
$(\mathcal {M})$
, cov
 $(\mathcal {N}) \}$
.
$(\mathcal {N}) \}$
. -
2. If non
 $(\mathcal {M})=\mathfrak {b}$
, then non
$(\mathcal {M})=\mathfrak {b}$
, then non
 $(\mathcal {E})=\min \{$
non
$(\mathcal {E})=\min \{$
non
 $(\mathcal {M})$
, non
$(\mathcal {M})$
, non
 $(\mathcal {N}) \}$
.
$(\mathcal {N}) \}$
.
Proof. See [Reference Bartoszynski and Judah1, Theorem 2.6.9].
Corollary 3.12. Con
![]() $( \mathfrak {s}_{1/2}^{\infty } <$
non
$( \mathfrak {s}_{1/2}^{\infty } <$
non
![]() $(\mathcal {E}) ) $
.
$(\mathcal {E}) ) $
.
Proof. Let
![]() $\kappa>\aleph _1$
. By Corollary 3.10,
$\kappa>\aleph _1$
. By Corollary 3.10,
![]() $V^{\mathbb {D}_\kappa }\models \mathfrak {s}_{1/2}^{\infty }= \aleph _1$
. Furthermore, it is known that
$V^{\mathbb {D}_\kappa }\models \mathfrak {s}_{1/2}^{\infty }= \aleph _1$
. Furthermore, it is known that
![]() $V^{\mathbb {D}_\kappa }\models $
non
$V^{\mathbb {D}_\kappa }\models $
non
![]() $(\mathcal {M}) = \mathfrak {b} =$
non
$(\mathcal {M}) = \mathfrak {b} =$
non
![]() $(\mathcal {N}) = \kappa $
, then
$(\mathcal {N}) = \kappa $
, then
![]() $V^{\mathbb {D}_\kappa }\models $
non
$V^{\mathbb {D}_\kappa }\models $
non
![]() $(\mathcal {E})= \kappa $
by Theorem 3.11.
$(\mathcal {E})= \kappa $
by Theorem 3.11.
Corollary 3.13. Con
![]() $($
cov
$($
cov
![]() $(\mathcal {E}) < \mathfrak {r}_{1/2}^{\infty } )$
.
$(\mathcal {E}) < \mathfrak {r}_{1/2}^{\infty } )$
.
Proof. Fix
![]() $\kappa> \aleph _1$
. Let
$\kappa> \aleph _1$
. Let
![]() $\mathbb {C}_\kappa $
be an fsi of Cohen forcing of length
$\mathbb {C}_\kappa $
be an fsi of Cohen forcing of length
![]() $\kappa $
. Because of
$\kappa $
. Because of
![]() $\mathfrak {fr}=\min \{\mathfrak {d},\mathfrak {r}\}$
and Corollary 3.6, we have
$\mathfrak {fr}=\min \{\mathfrak {d},\mathfrak {r}\}$
and Corollary 3.6, we have
![]() $V^{\mathbb {C}_\kappa } \models \kappa =$
cov
$V^{\mathbb {C}_\kappa } \models \kappa =$
cov
![]() $(\mathcal {M}) = \mathfrak {d}=\mathfrak {r} = \mathfrak {fr} = \mathfrak {fr}_g = \mathfrak {r}_{1/2}^\infty $
. Denote
$(\mathcal {M}) = \mathfrak {d}=\mathfrak {r} = \mathfrak {fr} = \mathfrak {fr}_g = \mathfrak {r}_{1/2}^\infty $
. Denote
![]() $M= V^{\mathbb {C}_\kappa }$
. Now, let
$M= V^{\mathbb {C}_\kappa }$
. Now, let
![]() $\mathbb {D}_{\aleph _1}$
be an fsi of Hechler forcing of length
$\mathbb {D}_{\aleph _1}$
be an fsi of Hechler forcing of length
![]() $\aleph _1$
over M. Then
$\aleph _1$
over M. Then
![]() $M^{\mathbb {D}_{\aleph _1}} \models \mathfrak {d} =$
cov
$M^{\mathbb {D}_{\aleph _1}} \models \mathfrak {d} =$
cov
![]() $(\mathcal {M}) =$
cov
$(\mathcal {M}) =$
cov
![]() $(\mathcal {N}) = \aleph _1$
because
$(\mathcal {N}) = \aleph _1$
because
![]() $\aleph _1$
dominating reals are added. Hence
$\aleph _1$
dominating reals are added. Hence
![]() $M^{\mathbb {D}_{\aleph _1}} \models \aleph _1 =$
cov
$M^{\mathbb {D}_{\aleph _1}} \models \aleph _1 =$
cov
![]() $(\mathcal {E})$
by Theorem 3.11. Also,
$(\mathcal {E})$
by Theorem 3.11. Also,
![]() $M^{\mathbb {D}_{\aleph _1}} \models \kappa = \mathfrak {fr}_g = \mathfrak {r}_{1/2}^{\infty } $
because
$M^{\mathbb {D}_{\aleph _1}} \models \kappa = \mathfrak {fr}_g = \mathfrak {r}_{1/2}^{\infty } $
because
![]() $\mathbb {D}_{\aleph _1}$
has property
$\mathbb {D}_{\aleph _1}$
has property
![]() $(\star \star )$
.
$(\star \star )$
.
4
 $*$
-independent families
$*$
-independent families
We show that there exists a maximal
![]() $*$
-independent family of size
$*$
-independent family of size
![]() $\aleph _1$
in the Cohen model. The proof uses similar ideas as [Reference Brendle, Halbeisen, Klausner, Lischka and Shelah5, Lemma 3.16], but there are more technical details to deal with. First, since any member of an independent family is moderate, we have to construct sets with this property. The following lemmas will help us in achieving this objective.
$\aleph _1$
in the Cohen model. The proof uses similar ideas as [Reference Brendle, Halbeisen, Klausner, Lischka and Shelah5, Lemma 3.16], but there are more technical details to deal with. First, since any member of an independent family is moderate, we have to construct sets with this property. The following lemmas will help us in achieving this objective.
Lemma 4.1. If
![]() $R,S \subseteq \omega $
,
$R,S \subseteq \omega $
,
![]() $0<\epsilon <1$
and
$0<\epsilon <1$
and
![]() $m\leq l$
are such that
$m\leq l$
are such that
then
Proof. First suppose that
![]() $l < \frac {2m}{\epsilon }$
. Note that
$l < \frac {2m}{\epsilon }$
. Note that
 $$\begin{align*}\frac{|(R \cap m) \cup (S\cap [m,l) )|}{l} &= \frac{|R \cap m |}{l} + \frac{|S\cap [m,l )|}{l } \\&\leq \frac{m}{l}(1-\epsilon) + \frac{l-m}{l} \\&= 1- \epsilon\frac{m}{l} \\&<1 - \frac{\epsilon^2}{2}. \end{align*}$$
$$\begin{align*}\frac{|(R \cap m) \cup (S\cap [m,l) )|}{l} &= \frac{|R \cap m |}{l} + \frac{|S\cap [m,l )|}{l } \\&\leq \frac{m}{l}(1-\epsilon) + \frac{l-m}{l} \\&= 1- \epsilon\frac{m}{l} \\&<1 - \frac{\epsilon^2}{2}. \end{align*}$$
For the lower bound, we get
 $$\begin{align*}\frac{|(R \cap m) \cup (S\cap [m,l) )|}{l} &= \frac{|R \cap m |}{l} + \frac{|S\cap [m,l )|}{l } \\ &\geq \frac{m}{l}(\epsilon) \\ &> \frac{\epsilon^2}{2}. \end{align*}$$
$$\begin{align*}\frac{|(R \cap m) \cup (S\cap [m,l) )|}{l} &= \frac{|R \cap m |}{l} + \frac{|S\cap [m,l )|}{l } \\ &\geq \frac{m}{l}(\epsilon) \\ &> \frac{\epsilon^2}{2}. \end{align*}$$
Now, suppose this were false for some
![]() $l^{\star } \geq \frac {2m}{\epsilon }$
. Then, without loss of generality,
$l^{\star } \geq \frac {2m}{\epsilon }$
. Then, without loss of generality,
Since
we get
But then
implies
 $$\begin{align*}\frac{|S \cap l^{\star}|}{l^{\star}} = \frac{|(S \cap m) \cup (S\cap [m,l^{\star}) ) |}{l^{\star}} & \displaystyle> \frac{m}{l^{\star}}(\epsilon) + 1-\frac{\epsilon^2}{2} - \frac{m}{l^{\star}}(1-\epsilon) \\&= 1-\frac{\epsilon^2}{2} + \frac{2m}{l^{\star}}(\epsilon) - \frac{m}{l^{\star}} \\& > 1-\frac{\epsilon^2}{2} - \frac{m}{l^{\star}} \\&\geq 1- \epsilon, \end{align*}$$
$$\begin{align*}\frac{|S \cap l^{\star}|}{l^{\star}} = \frac{|(S \cap m) \cup (S\cap [m,l^{\star}) ) |}{l^{\star}} & \displaystyle> \frac{m}{l^{\star}}(\epsilon) + 1-\frac{\epsilon^2}{2} - \frac{m}{l^{\star}}(1-\epsilon) \\&= 1-\frac{\epsilon^2}{2} + \frac{2m}{l^{\star}}(\epsilon) - \frac{m}{l^{\star}} \\& > 1-\frac{\epsilon^2}{2} - \frac{m}{l^{\star}} \\&\geq 1- \epsilon, \end{align*}$$
which is a contradiction.
Lemma 4.2. If
![]() $R,S \subseteq \omega $
are disjoint finite sets of sizes r and s, respectively,
$R,S \subseteq \omega $
are disjoint finite sets of sizes r and s, respectively,
![]() $s=c\cdot r$
for some
$s=c\cdot r$
for some
![]() $c>1$
,
$c>1$
,
![]() $q_0,q_1 \in (0,1)$
and
$q_0,q_1 \in (0,1)$
and
![]() $A\subseteq R$
,
$A\subseteq R$
,
![]() $B\subseteq S$
such that
$B\subseteq S$
such that
 $$\begin{align*}q_0 \leq \frac{|B|}{|S|} \leq q_1 \end{align*}$$
$$\begin{align*}q_0 \leq \frac{|B|}{|S|} \leq q_1 \end{align*}$$
then
 $$\begin{align*}q_0 - \frac{1}{c} \leq \frac{|A \cup B |}{|R \cup S|} \leq q_1 + \frac{1}{c}. \end{align*}$$
$$\begin{align*}q_0 - \frac{1}{c} \leq \frac{|A \cup B |}{|R \cup S|} \leq q_1 + \frac{1}{c}. \end{align*}$$
Proof. Same proof as [Reference Brendle, Halbeisen, Klausner, Lischka and Shelah5, Lemma 3.14].
Corollary 4.3. Let
![]() $k\in \omega $
and
$k\in \omega $
and
![]() $0< \epsilon _0 < 1$
. Let
$0< \epsilon _0 < 1$
. Let
![]() $Z, W \subseteq \omega $
be such that
$Z, W \subseteq \omega $
be such that
![]() $Z\subseteq k$
and
$Z\subseteq k$
and
![]() $\epsilon _0 < \underline {d}(W) \leq \bar {d}(W) < 1-\epsilon _0$
. Denote
$\epsilon _0 < \underline {d}(W) \leq \bar {d}(W) < 1-\epsilon _0$
. Denote
![]() $Z \cup (W\cap [k,l))$
by
$Z \cup (W\cap [k,l))$
by
![]() $Z_l$
. Then, there exists
$Z_l$
. Then, there exists
![]() $k^\prime \in \omega $
such that for any
$k^\prime \in \omega $
such that for any
![]() $l \geq k^\prime $
, we have
$l \geq k^\prime $
, we have
Proof. Let
![]() $\delta>0$
be such that
$\delta>0$
be such that
![]() $\epsilon _0 < \delta \leq \underline {d}(W) \leq \bar {d}(W) \leq 1- \delta < 1-\epsilon _0$
. First, notice that
$\epsilon _0 < \delta \leq \underline {d}(W) \leq \bar {d}(W) \leq 1- \delta < 1-\epsilon _0$
. First, notice that
 $$\begin{align*}\begin{array}{c} \displaystyle\limsup_{n \to \infty} \frac{|W \cap n|}{n} = \limsup_{n \to \infty} \frac{|W \cap [k,n)|}{n-k} \\ \displaystyle\liminf_{n \to \infty} \frac{|W \cap n|}{n} = \liminf_{n \to \infty} \frac{|W \cap [k,n)|}{n-k} \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{c} \displaystyle\limsup_{n \to \infty} \frac{|W \cap n|}{n} = \limsup_{n \to \infty} \frac{|W \cap [k,n)|}{n-k} \\ \displaystyle\liminf_{n \to \infty} \frac{|W \cap n|}{n} = \liminf_{n \to \infty} \frac{|W \cap [k,n)|}{n-k} \end{array} \end{align*}$$
then, there is
![]() $N>0$
such that for all
$N>0$
such that for all
![]() $l>N$
, we have
$l>N$
, we have
Thus, for any
![]() $l>N$
, we can apply Lemma 4.2 to
$l>N$
, we can apply Lemma 4.2 to
![]() $R:= k$
,
$R:= k$
,
![]() $S:=[k,l)$
,
$S:=[k,l)$
,
![]() $A:= Z$
,
$A:= Z$
,
![]() $B:=W\cap [k,l)$
,
$B:=W\cap [k,l)$
,
![]() $q_0:= \delta $
, and
$q_0:= \delta $
, and
![]() $q_1:=1-\delta $
to obtain
$q_1:=1-\delta $
to obtain
where
![]() $c=(l-k)/k$
. Choose
$c=(l-k)/k$
. Choose
![]() $k^\prime $
large enough to guarantee
$k^\prime $
large enough to guarantee
![]() $\epsilon _0 <\delta -\frac {1}{c}$
.
$\epsilon _0 <\delta -\frac {1}{c}$
.
Corollary 4.4. Let
![]() $k\in \omega $
and
$k\in \omega $
and
![]() $0< q < 1$
. Let
$0< q < 1$
. Let
![]() $Z, W \subseteq \omega $
be such that
$Z, W \subseteq \omega $
be such that
![]() $Z\subseteq k$
and
$Z\subseteq k$
and
![]() $d(W)=q$
. Denote
$d(W)=q$
. Denote
![]() $Z \cup (W\cap [k,l))$
by
$Z \cup (W\cap [k,l))$
by
![]() $Z_l$
. Then, for all
$Z_l$
. Then, for all
![]() $\delta>0$
, there exists
$\delta>0$
, there exists
![]() $k^\prime \in \omega $
such that for any
$k^\prime \in \omega $
such that for any
![]() $l \geq k^\prime $
, we have
$l \geq k^\prime $
, we have
Proof. Same proof as Corollary 4.3.
Second, to get a maximal
![]() $*$
-independent family, we make a recursive construction in which we have to extend an
$*$
-independent family, we make a recursive construction in which we have to extend an
![]() $*$
-independent family already constructed. The following lemmas will help us with this.
$*$
-independent family already constructed. The following lemmas will help us with this.
Lemma 4.5. Let
![]() $k\in \omega $
and
$k\in \omega $
and
![]() $0<\epsilon <1$
. Let
$0<\epsilon <1$
. Let
![]() $\mathcal {B}=\{B_i\}_{i< n}$
be an
$\mathcal {B}=\{B_i\}_{i< n}$
be an
![]() $*$
-independent family and Z a finite subset of
$*$
-independent family and Z a finite subset of
![]() $\omega $
such that for all
$\omega $
such that for all
![]() $E \subseteq n$
, we have
$E \subseteq n$
, we have
 $$\begin{align*}\displaystyle \frac{d_{k}(\bigcap_{i \in E} B_i \cap Z)}{\prod_{i\in E}d_{k}(B_i)d_{k}(Z)} \in \left( 1-\epsilon, 1+ \epsilon \right). \end{align*}$$
$$\begin{align*}\displaystyle \frac{d_{k}(\bigcap_{i \in E} B_i \cap Z)}{\prod_{i\in E}d_{k}(B_i)d_{k}(Z)} \in \left( 1-\epsilon, 1+ \epsilon \right). \end{align*}$$
Also, let
![]() $W \subseteq \omega $
and
$W \subseteq \omega $
and
![]() $k^\prime \in \omega $
such that
$k^\prime \in \omega $
such that
-
•
 $\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap W)}{\prod _{i\in E}d_{l}(B_i)d_{l}(W)}, \frac {\prod _{i\in E}d_{l}(B_i)d_{l}(W)}{d_{l}(\bigcap _{i \in E} B_i \cap W)} \in \left ( 1-\epsilon , 1+ \epsilon \right )$
for all
$\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap W)}{\prod _{i\in E}d_{l}(B_i)d_{l}(W)}, \frac {\prod _{i\in E}d_{l}(B_i)d_{l}(W)}{d_{l}(\bigcap _{i \in E} B_i \cap W)} \in \left ( 1-\epsilon , 1+ \epsilon \right )$
for all
 $k \leq l \leq k^\prime $
.
$k \leq l \leq k^\prime $
. -
•
 $\displaystyle \frac {|W \cap k|}{|Z \cap k|}, \frac {|Z \cap k|}{|W \cap k|} \in \left ( 1-\epsilon , 1+ \epsilon \right )$
.
$\displaystyle \frac {|W \cap k|}{|Z \cap k|}, \frac {|Z \cap k|}{|W \cap k|} \in \left ( 1-\epsilon , 1+ \epsilon \right )$
.
Then, if we define
![]() $Z^\prime :=Z \cup (W\cap [k, k^\prime ))$
, the following holds:
$Z^\prime :=Z \cup (W\cap [k, k^\prime ))$
, the following holds:
 $$\begin{align*}\displaystyle \frac{d_{l}(\bigcap_{i \in E} B_i \cap Z^\prime)}{\prod_{i\in E}d_{l}(B_i)d_{l}(Z^\prime)} \in \left( 1-15\epsilon, 1+ 15\epsilon \right) \end{align*}$$
$$\begin{align*}\displaystyle \frac{d_{l}(\bigcap_{i \in E} B_i \cap Z^\prime)}{\prod_{i\in E}d_{l}(B_i)d_{l}(Z^\prime)} \in \left( 1-15\epsilon, 1+ 15\epsilon \right) \end{align*}$$
for all
![]() $E \subseteq n$
and for all
$E \subseteq n$
and for all
![]() $k \leq l \leq k^\prime $
.
$k \leq l \leq k^\prime $
.
Proof. Fix
![]() $E \subseteq n$
. For any
$E \subseteq n$
. For any
![]() $k \leq l \leq k^\prime $
, we have
$k \leq l \leq k^\prime $
, we have
 $$\begin{align*}\frac{d_{l}(\bigcap_{i \in E} B_i \cap Z^\prime)}{\prod_{i\in E}d_{l}(B_i)d_{l}(Z^\prime)} &= \frac{1}{\prod_{i\in E}d_{l}(B_i)}\frac{|\bigcap_{i \in E} B_i \cap Z\cap k|+|\bigcap_{i \in E} B_i \cap W \cap [k,l)|}{|Z\cap k|+|W\cap [k,l)|} \\&\leq \left(1+ \epsilon \right)\left( \frac{ |W \cap l |}{ |\bigcap_{i \in E} B_i \cap W \cap l|} \right)\\& \quad \times \left( \frac{|\bigcap_{i \in E} B_i \cap Z \cap k|+|\bigcap_{i \in E} B_i \cap W \cap [k ,l)|}{|Z\cap k|+|W\cap [k,l)|} \right) \\&= \left(1+ \epsilon\right)\left(\frac{|W\cap l|}{ |Z\cap k|+|W\cap [k,l)|} \right)\\& \quad \times \left( \frac{|\bigcap_{i \in E} B_i \cap Z \cap k|+|\bigcap_{i \in E} B_i \cap W \cap [k,l)|}{|\bigcap_{i \in E} B_i \cap W \cap l|} \right) \\&= \left(1+ \epsilon\right)\left(\frac{|W\cap k|+ l^\prime}{ |Z\cap k|+l^\prime} \right) \left( \frac{|\bigcap_{i \in E} B_i \cap Z \cap k|+l^{\prime\prime}}{|\bigcap_{i \in E} B_i \cap W \cap k|+l^{\prime\prime}} \right), \end{align*}$$
$$\begin{align*}\frac{d_{l}(\bigcap_{i \in E} B_i \cap Z^\prime)}{\prod_{i\in E}d_{l}(B_i)d_{l}(Z^\prime)} &= \frac{1}{\prod_{i\in E}d_{l}(B_i)}\frac{|\bigcap_{i \in E} B_i \cap Z\cap k|+|\bigcap_{i \in E} B_i \cap W \cap [k,l)|}{|Z\cap k|+|W\cap [k,l)|} \\&\leq \left(1+ \epsilon \right)\left( \frac{ |W \cap l |}{ |\bigcap_{i \in E} B_i \cap W \cap l|} \right)\\& \quad \times \left( \frac{|\bigcap_{i \in E} B_i \cap Z \cap k|+|\bigcap_{i \in E} B_i \cap W \cap [k ,l)|}{|Z\cap k|+|W\cap [k,l)|} \right) \\&= \left(1+ \epsilon\right)\left(\frac{|W\cap l|}{ |Z\cap k|+|W\cap [k,l)|} \right)\\& \quad \times \left( \frac{|\bigcap_{i \in E} B_i \cap Z \cap k|+|\bigcap_{i \in E} B_i \cap W \cap [k,l)|}{|\bigcap_{i \in E} B_i \cap W \cap l|} \right) \\&= \left(1+ \epsilon\right)\left(\frac{|W\cap k|+ l^\prime}{ |Z\cap k|+l^\prime} \right) \left( \frac{|\bigcap_{i \in E} B_i \cap Z \cap k|+l^{\prime\prime}}{|\bigcap_{i \in E} B_i \cap W \cap k|+l^{\prime\prime}} \right), \end{align*}$$
where
![]() $l^\prime =|W\cap [k,l)|$
and
$l^\prime =|W\cap [k,l)|$
and
![]() $l^{\prime \prime }=|\bigcap _{i \in E} B_i \cap W \cap [k,l)|$
. We have four cases:
$l^{\prime \prime }=|\bigcap _{i \in E} B_i \cap W \cap [k,l)|$
. We have four cases:
![]() $|W\cap k|\leq |Z\cap k|$
and
$|W\cap k|\leq |Z\cap k|$
and
![]() $|\bigcap _{i \in E} B_i \cap W \cap k| \geq |\bigcap _{i \in E} B_i \cap Z \cap k|$
. In this case, we get
$|\bigcap _{i \in E} B_i \cap W \cap k| \geq |\bigcap _{i \in E} B_i \cap Z \cap k|$
. In this case, we get
 $$\begin{align*}\left(\frac{|W\cap k|+ l^\prime}{ |Z\cap k|+l^\prime} \right) \left( \frac{|\bigcap_{i \in E} B_i \cap Z \cap k|+l^{\prime\prime}}{|\bigcap_{i \in E} B_i \cap W \cap k|+l^{\prime\prime}} \right) \leq 1. \end{align*}$$
$$\begin{align*}\left(\frac{|W\cap k|+ l^\prime}{ |Z\cap k|+l^\prime} \right) \left( \frac{|\bigcap_{i \in E} B_i \cap Z \cap k|+l^{\prime\prime}}{|\bigcap_{i \in E} B_i \cap W \cap k|+l^{\prime\prime}} \right) \leq 1. \end{align*}$$
![]() $|W\cap k|\geq |Z\cap k|$
and
$|W\cap k|\geq |Z\cap k|$
and
![]() $|\bigcap _{i \in E} B_i \cap W \cap k|\leq |\bigcap _{i \in E} B_i \cap Z \cap k|$
. Note that
$|\bigcap _{i \in E} B_i \cap W \cap k|\leq |\bigcap _{i \in E} B_i \cap Z \cap k|$
. Note that
 $$ \begin{align} \displaystyle \frac{|W\cap k |}{ |Z \cap k|} \frac{|\bigcap_{i \in E} B_i \cap Z \cap k |}{|\bigcap_{i \in E} B_i \cap W \cap k |} = \frac{\prod_{i\in E}d_{k}(B_i) |W\cap k|}{|\bigcap_{i \in E} B_i \cap W \cap k| } \frac{|\bigcap_{i \in E} B_i \cap Z \cap k|}{\prod_{i\in E}d_{k}(B_i) |Z\cap k|} \leq \left(1+ \epsilon \right)^2. \end{align} $$
$$ \begin{align} \displaystyle \frac{|W\cap k |}{ |Z \cap k|} \frac{|\bigcap_{i \in E} B_i \cap Z \cap k |}{|\bigcap_{i \in E} B_i \cap W \cap k |} = \frac{\prod_{i\in E}d_{k}(B_i) |W\cap k|}{|\bigcap_{i \in E} B_i \cap W \cap k| } \frac{|\bigcap_{i \in E} B_i \cap Z \cap k|}{\prod_{i\in E}d_{k}(B_i) |Z\cap k|} \leq \left(1+ \epsilon \right)^2. \end{align} $$
Therefore, in this case, we get
 $$\begin{align*}&\left(\frac{|W\cap k|+ l^\prime}{ |Z\cap k|+l^\prime} \right) \left( \frac{|\bigcap_{i \in E} B_i \cap Z \cap k|+l^{\prime\prime}}{|\bigcap_{i \in E} B_i \cap W \cap k|+l^{\prime\prime}} \right)\\& \quad \leq \left(\frac{|W\cap k|}{ |Z\cap k|} \right) \left( \frac{|\bigcap_{i \in E} B_i \cap Z \cap k|}{|\bigcap_{i \in E} B_i \cap W \cap k|} \right) \leq \left(1+ \epsilon \right)^2. \end{align*}$$
$$\begin{align*}&\left(\frac{|W\cap k|+ l^\prime}{ |Z\cap k|+l^\prime} \right) \left( \frac{|\bigcap_{i \in E} B_i \cap Z \cap k|+l^{\prime\prime}}{|\bigcap_{i \in E} B_i \cap W \cap k|+l^{\prime\prime}} \right)\\& \quad \leq \left(\frac{|W\cap k|}{ |Z\cap k|} \right) \left( \frac{|\bigcap_{i \in E} B_i \cap Z \cap k|}{|\bigcap_{i \in E} B_i \cap W \cap k|} \right) \leq \left(1+ \epsilon \right)^2. \end{align*}$$
![]() $|W\cap k|\geq |Z\cap k|$
and
$|W\cap k|\geq |Z\cap k|$
and
![]() $|\bigcap _{i \in E} B_i \cap W \cap k|\geq |\bigcap _{i \in E} B_i \cap Z \cap k|$
. In this case, we have
$|\bigcap _{i \in E} B_i \cap W \cap k|\geq |\bigcap _{i \in E} B_i \cap Z \cap k|$
. In this case, we have
 $$\begin{align*}\left(\frac{|W\cap k|+ l^\prime}{ |Z\cap k|+l^\prime} \right) \left( \frac{|\bigcap_{i \in E} B_i \cap Z \cap k|+l^{\prime\prime}}{|\bigcap_{i \in E} B_i \cap W \cap k|+l^{\prime\prime}} \right) \leq \frac{|W\cap k|}{ |Z\cap k|} \leq 1+ \epsilon. \end{align*}$$
$$\begin{align*}\left(\frac{|W\cap k|+ l^\prime}{ |Z\cap k|+l^\prime} \right) \left( \frac{|\bigcap_{i \in E} B_i \cap Z \cap k|+l^{\prime\prime}}{|\bigcap_{i \in E} B_i \cap W \cap k|+l^{\prime\prime}} \right) \leq \frac{|W\cap k|}{ |Z\cap k|} \leq 1+ \epsilon. \end{align*}$$
![]() $|W\cap k|\leq |Z\cap k|$
and
$|W\cap k|\leq |Z\cap k|$
and
![]() $|\bigcap _{i \in E} B_i \cap W \cap k|\leq |\bigcap _{i \in E} B_i \cap Z \cap k|$
. Note that in (2), we also get
$|\bigcap _{i \in E} B_i \cap W \cap k|\leq |\bigcap _{i \in E} B_i \cap Z \cap k|$
. Note that in (2), we also get
 $$\begin{align*}\frac{|\bigcap_{i \in E} B_i \cap Z \cap k|}{|\bigcap_{i \in E} B_i \cap W \cap k| } \leq (1+\epsilon)^2 \frac{|Z \cap k|}{|W \cap k|} \leq (1+ \epsilon)^3. \end{align*}$$
$$\begin{align*}\frac{|\bigcap_{i \in E} B_i \cap Z \cap k|}{|\bigcap_{i \in E} B_i \cap W \cap k| } \leq (1+\epsilon)^2 \frac{|Z \cap k|}{|W \cap k|} \leq (1+ \epsilon)^3. \end{align*}$$
Thus, in this case, we have
 $$\begin{align*}\left(\frac{|W\cap k|+ l^\prime}{ |Z\cap k|+l^\prime} \right) \left( \frac{|\bigcap_{i \in E} B_i \cap Z \cap k|+l^{\prime\prime}}{|\bigcap_{i \in E} B_i \cap W \cap k|+l^{\prime\prime}} \right) \leq \frac{|\bigcap_{i \in E} B_i \cap Z \cap k|}{|\bigcap_{i \in E} B_i \cap W \cap k| } \leq (1+ \epsilon)^3. \end{align*}$$
$$\begin{align*}\left(\frac{|W\cap k|+ l^\prime}{ |Z\cap k|+l^\prime} \right) \left( \frac{|\bigcap_{i \in E} B_i \cap Z \cap k|+l^{\prime\prime}}{|\bigcap_{i \in E} B_i \cap W \cap k|+l^{\prime\prime}} \right) \leq \frac{|\bigcap_{i \in E} B_i \cap Z \cap k|}{|\bigcap_{i \in E} B_i \cap W \cap k| } \leq (1+ \epsilon)^3. \end{align*}$$
To summarize, we get
 $$\begin{align*}\displaystyle \frac{d_{l}(\bigcap_{i \in E} B_i \cap Z^\prime)}{\prod_{i\in E}d_{l}(B_i)d_{l}(Z^\prime)} \leq (1+\epsilon)^4 \leq 1+ 15\epsilon. \end{align*}$$
$$\begin{align*}\displaystyle \frac{d_{l}(\bigcap_{i \in E} B_i \cap Z^\prime)}{\prod_{i\in E}d_{l}(B_i)d_{l}(Z^\prime)} \leq (1+\epsilon)^4 \leq 1+ 15\epsilon. \end{align*}$$
In a similar way, we have the lower bound.
Lemma 4.6. Let
![]() $k\in \omega $
and
$k\in \omega $
and
![]() $0<\epsilon <1$
. Let
$0<\epsilon <1$
. Let
![]() $\mathcal {B}=\{B_i\}_{i< n}$
be an
$\mathcal {B}=\{B_i\}_{i< n}$
be an
![]() $*$
-independent family and Z a subset of k. Let W be a subset of
$*$
-independent family and Z a subset of k. Let W be a subset of
![]() $\omega $
such that
$\omega $
such that
![]() $\mathcal {B} \cup \{W\}$
is an
$\mathcal {B} \cup \{W\}$
is an
![]() $*$
-independent family. Denote
$*$
-independent family. Denote
![]() $Z \cup (W\cap [k, l))$
by
$Z \cup (W\cap [k, l))$
by
![]() $Z_l$
. Then, there exists
$Z_l$
. Then, there exists
![]() $k^\prime \in \omega $
such that for all
$k^\prime \in \omega $
such that for all
![]() $E \subseteq n$
and
$E \subseteq n$
and
![]() $l \geq k^\prime $
, we have
$l \geq k^\prime $
, we have
 $$\begin{align*}\displaystyle \frac{d_{l}(\bigcap_{i \in E} B_i \cap Z_l)}{\prod_{i\in E}d_{l}(B_i)d_{l}(Z_l)} \in \left( 1- \epsilon, 1+ \epsilon \right). \end{align*}$$
$$\begin{align*}\displaystyle \frac{d_{l}(\bigcap_{i \in E} B_i \cap Z_l)}{\prod_{i\in E}d_{l}(B_i)d_{l}(Z_l)} \in \left( 1- \epsilon, 1+ \epsilon \right). \end{align*}$$
Proof. First, note that
 $$\begin{align*}\displaystyle \lim_{l \to \infty} \frac{d_{l}(\bigcap_{i \in E} B_i \cap W)}{\prod_{i\in E}d_{l}(B_i)d_{l}(W)} = \displaystyle \lim_{l \to \infty} \frac{ |\bigcap_{i \in E} B_i \cap W \cap [k, l)| }{\prod_{i\in E}d_{l}(B_i) |W \cap [k, l)|} \end{align*}$$
$$\begin{align*}\displaystyle \lim_{l \to \infty} \frac{d_{l}(\bigcap_{i \in E} B_i \cap W)}{\prod_{i\in E}d_{l}(B_i)d_{l}(W)} = \displaystyle \lim_{l \to \infty} \frac{ |\bigcap_{i \in E} B_i \cap W \cap [k, l)| }{\prod_{i\in E}d_{l}(B_i) |W \cap [k, l)|} \end{align*}$$
for any
![]() $E\subseteq n$
. Therefore, there is
$E\subseteq n$
. Therefore, there is
![]() $N\in \omega $
such that for all
$N\in \omega $
such that for all
![]() $E\subseteq n$
and
$E\subseteq n$
and
![]() $l>N$
, we have
$l>N$
, we have
 $$\begin{align*}\displaystyle \frac{|\bigcap_{i \in E} B_i \cap W \cap [k,l)|}{\prod_{i\in E}d_{l}(B_i) |W \cap [k, l)|} \in \left( 1-\frac{\epsilon}{2}, 1+ \frac{\epsilon}{2} \right). \end{align*}$$
$$\begin{align*}\displaystyle \frac{|\bigcap_{i \in E} B_i \cap W \cap [k,l)|}{\prod_{i\in E}d_{l}(B_i) |W \cap [k, l)|} \in \left( 1-\frac{\epsilon}{2}, 1+ \frac{\epsilon}{2} \right). \end{align*}$$
Choose some
![]() $k^\prime> N$
. For the upper bound, we have
$k^\prime> N$
. For the upper bound, we have
 $$\begin{align*}\begin{array}{ll} \displaystyle \frac{d_{k^\prime}(\bigcap_{i \in E} B_i \cap Z_{k^\prime})}{\prod_{i\in E}d_{k^\prime}(B_i)d_{k^\prime}(Z_{k^\prime})} & \leq \displaystyle\frac{ k + |\bigcap_{i \in E} B_i \cap W \cap [k,k^\prime)| }{\prod_{i\in E}d_{k^\prime}(B_i) |W \cap [k, k^\prime)|} \\ \\ & \leq \displaystyle \frac{k(1+ \frac{\epsilon}{2})}{|\bigcap_{i \in E} B_i \cap W \cap [k, k^\prime)|} + 1+ \frac{\epsilon}{2}. \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{ll} \displaystyle \frac{d_{k^\prime}(\bigcap_{i \in E} B_i \cap Z_{k^\prime})}{\prod_{i\in E}d_{k^\prime}(B_i)d_{k^\prime}(Z_{k^\prime})} & \leq \displaystyle\frac{ k + |\bigcap_{i \in E} B_i \cap W \cap [k,k^\prime)| }{\prod_{i\in E}d_{k^\prime}(B_i) |W \cap [k, k^\prime)|} \\ \\ & \leq \displaystyle \frac{k(1+ \frac{\epsilon}{2})}{|\bigcap_{i \in E} B_i \cap W \cap [k, k^\prime)|} + 1+ \frac{\epsilon}{2}. \end{array} \end{align*}$$
For the lower bound, we have
 $$\begin{align*}\begin{array}{ll} \displaystyle \frac{d_{k^\prime}(\bigcap_{i \in E} B_i \cap Z_{k^\prime})}{\prod_{i\in E}d_{k^\prime}(B_i)d_{k^\prime}(Z_{k^\prime})} & \geq \displaystyle\frac{ |\bigcap_{i \in E} B_i \cap W \cap [k, k^\prime)| }{\prod_{i\in E}d_{k^\prime}(B_i) (k+|W \cap [k, k^\prime)|)} \\ \\ & \geq \displaystyle\frac{ (1- \frac{\epsilon}{2}) \prod_{i\in E}d_{k^\prime}(B_i) ||W \cap [k, k^\prime)| }{\prod_{i\in E}d_{k^\prime}(B_i) (k+|W \cap [k, k^\prime)|)} \\ \\ &= \displaystyle \left(1-\frac{\epsilon}{2}\right) \frac{1}{1+\frac{k}{|W \cap [k, k^\prime)|}}. \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{ll} \displaystyle \frac{d_{k^\prime}(\bigcap_{i \in E} B_i \cap Z_{k^\prime})}{\prod_{i\in E}d_{k^\prime}(B_i)d_{k^\prime}(Z_{k^\prime})} & \geq \displaystyle\frac{ |\bigcap_{i \in E} B_i \cap W \cap [k, k^\prime)| }{\prod_{i\in E}d_{k^\prime}(B_i) (k+|W \cap [k, k^\prime)|)} \\ \\ & \geq \displaystyle\frac{ (1- \frac{\epsilon}{2}) \prod_{i\in E}d_{k^\prime}(B_i) ||W \cap [k, k^\prime)| }{\prod_{i\in E}d_{k^\prime}(B_i) (k+|W \cap [k, k^\prime)|)} \\ \\ &= \displaystyle \left(1-\frac{\epsilon}{2}\right) \frac{1}{1+\frac{k}{|W \cap [k, k^\prime)|}}. \end{array} \end{align*}$$
Since the collection of subsets of
![]() $ \{0, ..., n-1\}$
is finite, we can choose
$ \{0, ..., n-1\}$
is finite, we can choose
![]() $k^\prime $
sufficiently large as to guarantee
$k^\prime $
sufficiently large as to guarantee
![]() $(1-\frac {\epsilon }{2}) \frac {1}{1+\frac {k}{|W \cap [k, k^\prime )|}}\geq 1-\epsilon $
and
$(1-\frac {\epsilon }{2}) \frac {1}{1+\frac {k}{|W \cap [k, k^\prime )|}}\geq 1-\epsilon $
and
![]() $\frac {k(1+ \epsilon /2)}{|\bigcap _{i \in E} B_i \cap W \cap [k, k^\prime )|} \leq \frac {\epsilon }{2}$
for all
$\frac {k(1+ \epsilon /2)}{|\bigcap _{i \in E} B_i \cap W \cap [k, k^\prime )|} \leq \frac {\epsilon }{2}$
for all
![]() $E \subseteq n$
.
$E \subseteq n$
.
Finally, the following lemmas will help us to construct a finite set that satisfies the conditions of all aforementioned lemmas.
Lemma 4.7. Let
![]() $\mathcal {B}=\{B_i\}_{i< n}$
be an
$\mathcal {B}=\{B_i\}_{i< n}$
be an
![]() $*$
-independent family. Then, for every rational number
$*$
-independent family. Then, for every rational number
![]() $0<q<1$
, there exists an infinite set
$0<q<1$
, there exists an infinite set
![]() $X_q$
such that
$X_q$
such that
-
•
 $d(X_q)=q$
$d(X_q)=q$
-
•
 $\mathcal {B} \cup \{X_q\}$
is an
$\mathcal {B} \cup \{X_q\}$
is an
 $*$
-independent family.
$*$
-independent family.
Proof. First, for each function
![]() $f:n \rightarrow \{-1,1\}$
, we define
$f:n \rightarrow \{-1,1\}$
, we define
where
![]() $B_i^1:=B_i$
and
$B_i^1:=B_i$
and
![]() $B_i^{-1}:=\omega \setminus B_i$
. Note that the collection
$B_i^{-1}:=\omega \setminus B_i$
. Note that the collection
![]() $\{ \mathcal {B}_f \, | \, f \in \{-1,1\}^n \}$
is a partition of
$\{ \mathcal {B}_f \, | \, f \in \{-1,1\}^n \}$
is a partition of
![]() $\omega $
. Fix a function
$\omega $
. Fix a function
![]() $f \in \{-1,1\}^n$
. Let
$f \in \{-1,1\}^n$
. Let
![]() $\{d_j\}_{j\in \omega }$
be an increasing enumeration of
$\{d_j\}_{j\in \omega }$
be an increasing enumeration of
![]() $\mathcal {B}_f$
. Let
$\mathcal {B}_f$
. Let
![]() $\frac {a}{b}$
be the irreducible fraction of q, and let A be a set containing exactly a residue classes modulo b. Define
$\frac {a}{b}$
be the irreducible fraction of q, and let A be a set containing exactly a residue classes modulo b. Define
It is easy to show that
 $\displaystyle \lim _{l \to \infty } \frac {|X_f \cap l|}{|\mathcal {B}_f \cap l |} = \frac {a}{b}$
. Now, define
$\displaystyle \lim _{l \to \infty } \frac {|X_f \cap l|}{|\mathcal {B}_f \cap l |} = \frac {a}{b}$
. Now, define
Let us see that
![]() $X_q$
satisfies the conditions of the lemma. It suffices to show that for any
$X_q$
satisfies the conditions of the lemma. It suffices to show that for any
![]() $E \subseteq n$
, we have
$E \subseteq n$
, we have
 $$\begin{align*}\lim_{l \to \infty}\frac{|\bigcap_{i \in E} B_i \cap X_q \cap l |}{|\bigcap_{i \in E} B_i \cap l |} = \frac{a}{b}. \end{align*}$$
$$\begin{align*}\lim_{l \to \infty}\frac{|\bigcap_{i \in E} B_i \cap X_q \cap l |}{|\bigcap_{i \in E} B_i \cap l |} = \frac{a}{b}. \end{align*}$$
Let E be a subset of n. Consider the set
![]() $G:=\{ f \in \{-1,1\}^n \,| \, f(i)=1 \text { for all} i \in E \} $
. Note that
$G:=\{ f \in \{-1,1\}^n \,| \, f(i)=1 \text { for all} i \in E \} $
. Note that
Also, given
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $N\in \omega $
such that for all
$N\in \omega $
such that for all
![]() $l>N$
, we have
$l>N$
, we have
 $$\begin{align*}\frac{|X_f \cap l|}{|\mathcal{B}_f \cap l |} \in \left( \frac{a}{b}- \epsilon, \frac{a}{b}+\epsilon \right) \end{align*}$$
$$\begin{align*}\frac{|X_f \cap l|}{|\mathcal{B}_f \cap l |} \in \left( \frac{a}{b}- \epsilon, \frac{a}{b}+\epsilon \right) \end{align*}$$
for all
![]() $f\in G$
. Thus, for
$f\in G$
. Thus, for
![]() $l>N$
, we get
$l>N$
, we get
 $$\begin{align*}\begin{array}{ll} \displaystyle\frac{|\bigcap_{i \in E} B_i \cap X_q \cap l |}{|\bigcap_{i \in E} B_i \cap l |} &\displaystyle= \sum_{f \in G} \frac{|\mathcal{B}_f \cap X_q \cap l|}{ |\bigcap_{i \in E} B_i \cap l |} \\ \\ &\displaystyle= \sum_{f \in G} \frac{|X_f \cap l|}{|\bigcap_{i \in E} B_i \cap l |} = \sum_{f \in G} \frac{|X_f \cap l|}{|\mathcal{B}_f \cap l |}\frac{|\mathcal{B}_f \cap l |}{|\bigcap_{i \in E} B_i \cap l |} \\ \\ &\displaystyle\leq \left( \frac{a}{b} + \epsilon\right)\sum_{f \in G}\frac{|\mathcal{B}_f \cap l |}{|\bigcap_{i \in E} B_i \cap l |} = \left( \frac{a}{b} + \epsilon\right). \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{ll} \displaystyle\frac{|\bigcap_{i \in E} B_i \cap X_q \cap l |}{|\bigcap_{i \in E} B_i \cap l |} &\displaystyle= \sum_{f \in G} \frac{|\mathcal{B}_f \cap X_q \cap l|}{ |\bigcap_{i \in E} B_i \cap l |} \\ \\ &\displaystyle= \sum_{f \in G} \frac{|X_f \cap l|}{|\bigcap_{i \in E} B_i \cap l |} = \sum_{f \in G} \frac{|X_f \cap l|}{|\mathcal{B}_f \cap l |}\frac{|\mathcal{B}_f \cap l |}{|\bigcap_{i \in E} B_i \cap l |} \\ \\ &\displaystyle\leq \left( \frac{a}{b} + \epsilon\right)\sum_{f \in G}\frac{|\mathcal{B}_f \cap l |}{|\bigcap_{i \in E} B_i \cap l |} = \left( \frac{a}{b} + \epsilon\right). \end{array} \end{align*}$$
In a similar way, we get
![]() $\left ( \frac {a}{b} - \epsilon \right ) \leq \frac {|\bigcap _{i \in E} B_i \cap X_q \cap l |}{|\bigcap _{i \in E} B_i \cap l |}$
.
$\left ( \frac {a}{b} - \epsilon \right ) \leq \frac {|\bigcap _{i \in E} B_i \cap X_q \cap l |}{|\bigcap _{i \in E} B_i \cap l |}$
.
Lemma 4.8. Let
![]() $k\in \omega $
,
$k\in \omega $
,
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $\epsilon _0>0$
. Let
$\epsilon _0>0$
. Let
![]() $\mathcal {B}=\{B_i\}_{i< n}$
be an
$\mathcal {B}=\{B_i\}_{i< n}$
be an
![]() $*$
-independent family and Z a subset of k such that for all
$*$
-independent family and Z a subset of k such that for all
![]() $E \subseteq n$
, we have
$E \subseteq n$
, we have
 $$\begin{align*}\displaystyle \frac{d_{k}(\bigcap_{i \in E} B_i \cap Z)}{\prod_{i\in E}d_{k}(B_i)d_{k}(Z)} \in \left( 1-\epsilon, 1+ \epsilon \right). \end{align*}$$
$$\begin{align*}\displaystyle \frac{d_{k}(\bigcap_{i \in E} B_i \cap Z)}{\prod_{i\in E}d_{k}(B_i)d_{k}(Z)} \in \left( 1-\epsilon, 1+ \epsilon \right). \end{align*}$$
Besides, for every
![]() $m \geq k$
, there is a finite set
$m \geq k$
, there is a finite set
![]() $Z_m \subseteq m$
such that
$Z_m \subseteq m$
such that
-
•
 $Z_m \cap k = Z$
$Z_m \cap k = Z$
-
•
 $\epsilon _0 \leq \frac {|Z_m \cap l|}{l} \leq 1- \epsilon _0 $
for all
$\epsilon _0 \leq \frac {|Z_m \cap l|}{l} \leq 1- \epsilon _0 $
for all
 $k \leq l \leq m$
.
$k \leq l \leq m$
. -
•
 $\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap Z_m)}{\prod _{i\in E}d_{l}(B_i)d_{l}(Z_m)} \in \left ( 1-\epsilon , 1+ \epsilon \right )$
for all
$\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap Z_m)}{\prod _{i\in E}d_{l}(B_i)d_{l}(Z_m)} \in \left ( 1-\epsilon , 1+ \epsilon \right )$
for all
 $k \leq l \leq m$
.
$k \leq l \leq m$
.
Let W be an infinite subset of
![]() $\omega $
such that
$\omega $
such that
![]() $\epsilon _0 \leq \frac {|W \cap l|}{l} \leq 1- \epsilon _0$
for all
$\epsilon _0 \leq \frac {|W \cap l|}{l} \leq 1- \epsilon _0$
for all
![]() $l>k$
. Then, there exists
$l>k$
. Then, there exists
![]() $k^\prime> k$
and a finite set
$k^\prime> k$
and a finite set
![]() $Z^\prime \subseteq k^\prime $
such that
$Z^\prime \subseteq k^\prime $
such that
-
•
 $Z^\prime \cap k = Z$
.
$Z^\prime \cap k = Z$
. -
•
 $\displaystyle \frac {\epsilon _0^2}{2} \leq \frac {|Z^\prime \cap l|}{l} \leq 1- \frac {\epsilon _0^2}{2} $
for all
$\displaystyle \frac {\epsilon _0^2}{2} \leq \frac {|Z^\prime \cap l|}{l} \leq 1- \frac {\epsilon _0^2}{2} $
for all
 $k \leq l < k^\prime $
.
$k \leq l < k^\prime $
. -
•
 $\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap Z^\prime )}{\prod _{i\in E}d_{l}(B_i)d_{l}(Z^\prime )} \in \left ( 1-15\epsilon , 1+ 15\epsilon \right )$
for all
$\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap Z^\prime )}{\prod _{i\in E}d_{l}(B_i)d_{l}(Z^\prime )} \in \left ( 1-15\epsilon , 1+ 15\epsilon \right )$
for all
 $k \leq l < k^\prime $
and any
$k \leq l < k^\prime $
and any
 $E \subseteq n$
.
$E \subseteq n$
. -
•
 $\displaystyle \epsilon _0 \leq \frac {|Z^\prime \cap k^\prime |}{k^\prime } \leq 1- \epsilon _0 $
$\displaystyle \epsilon _0 \leq \frac {|Z^\prime \cap k^\prime |}{k^\prime } \leq 1- \epsilon _0 $
-
•
 $\displaystyle \frac {d_{k^\prime }(\bigcap _{i \in E} B_i \cap Z^\prime )}{\prod _{i\in E}d_{k^\prime }(B_i)d_{k^\prime }(Z^\prime )} \in \left ( 1- \epsilon , 1+ \epsilon \right )$
for any
$\displaystyle \frac {d_{k^\prime }(\bigcap _{i \in E} B_i \cap Z^\prime )}{\prod _{i\in E}d_{k^\prime }(B_i)d_{k^\prime }(Z^\prime )} \in \left ( 1- \epsilon , 1+ \epsilon \right )$
for any
 $E \subseteq n$
.
$E \subseteq n$
. -
•
 $\displaystyle \frac {|Z^\prime \cap k^\prime |}{|W \cap k^\prime |}, \frac {|W \cap k^\prime |}{|Z^\prime \cap k^\prime |} \in (1 -\epsilon , 1 + \epsilon ).$
$\displaystyle \frac {|Z^\prime \cap k^\prime |}{|W \cap k^\prime |}, \frac {|W \cap k^\prime |}{|Z^\prime \cap k^\prime |} \in (1 -\epsilon , 1 + \epsilon ).$
Proof. First, note that there exists some rational
![]() $\delta>0$
such that for any q rational number such that
$\delta>0$
such that for any q rational number such that
![]() $\epsilon _0 \leq q \leq 1- \epsilon _0,$
we have
$\epsilon _0 \leq q \leq 1- \epsilon _0,$
we have
In fact, it is easy to prove that any
![]() $\delta < \frac {\epsilon _0 \epsilon }{2+\epsilon }$
satisfies the previous inequality. Now, consider a finite collection of intervals with rational center
$\delta < \frac {\epsilon _0 \epsilon }{2+\epsilon }$
satisfies the previous inequality. Now, consider a finite collection of intervals with rational center
![]() $\mathcal {I}_0= \{( q_j - \delta , q_j + \delta ) \}_{j < J}$
such that
$\mathcal {I}_0= \{( q_j - \delta , q_j + \delta ) \}_{j < J}$
such that
![]() $\epsilon _0 < q_j < 1-\epsilon _0$
and
$\epsilon _0 < q_j < 1-\epsilon _0$
and
![]() $[\epsilon _0,1-\epsilon _0] \subseteq \bigcup \mathcal {I}_0 $
. Let
$[\epsilon _0,1-\epsilon _0] \subseteq \bigcup \mathcal {I}_0 $
. Let
![]() $X_{q_j}$
be the sets which are given by Lemma 4.7. Let
$X_{q_j}$
be the sets which are given by Lemma 4.7. Let
![]() $k_0 \in \omega $
such that for any
$k_0 \in \omega $
such that for any
![]() $E \subseteq n$
,
$E \subseteq n$
,
![]() $ j < J$
and for all
$ j < J$
and for all
![]() $l \geq k_0,$
we have
$l \geq k_0,$
we have
-
•
 $ \displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap X_{q_j})}{\prod _{i\in E}d_{l}(B_i)d_{l}(X_{q_j})}, \frac {\prod _{i\in E}d_{l}(B_i)d_{l}(X_{q_j})}{d_{l}(\bigcap _{i \in E} B_i \cap X_{q_j})} \in \left ( 1- \epsilon , 1+ \epsilon \right ) $
$ \displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap X_{q_j})}{\prod _{i\in E}d_{l}(B_i)d_{l}(X_{q_j})}, \frac {\prod _{i\in E}d_{l}(B_i)d_{l}(X_{q_j})}{d_{l}(\bigcap _{i \in E} B_i \cap X_{q_j})} \in \left ( 1- \epsilon , 1+ \epsilon \right ) $
-
•
 $\displaystyle \frac {|X_{q_j}\cap l|}{l} \in \left ( q_j - \delta , q_j + \delta \right ) $
$\displaystyle \frac {|X_{q_j}\cap l|}{l} \in \left ( q_j - \delta , q_j + \delta \right ) $
-
•
 $\displaystyle \epsilon _0 < \frac {|X_{q_j}\cap l|}{l} < 1-\epsilon _0. $
$\displaystyle \epsilon _0 < \frac {|X_{q_j}\cap l|}{l} < 1-\epsilon _0. $
Besides, there is a finite set
![]() $Z_{k_0}\subseteq k_0$
such that
$Z_{k_0}\subseteq k_0$
such that
-
•
 $Z_{k_0} \cap k = Z$
$Z_{k_0} \cap k = Z$
-
•
 $\epsilon _0 \leq \frac {|Z_{k_0} \cap l|}{l} \leq 1- \epsilon _0 $
for all
$\epsilon _0 \leq \frac {|Z_{k_0} \cap l|}{l} \leq 1- \epsilon _0 $
for all
 $k \leq l \leq k_0$
.
$k \leq l \leq k_0$
. -
•
 $\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap Z_{k_0} )}{\prod _{i\in E}d_{l}(B_i)d_{l}(Z_{k_0} )} \in \left ( 1-\epsilon , 1+ \epsilon \right )$
for all
$\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap Z_{k_0} )}{\prod _{i\in E}d_{l}(B_i)d_{l}(Z_{k_0} )} \in \left ( 1-\epsilon , 1+ \epsilon \right )$
for all
 $k \leq l \leq k_0 $
.
$k \leq l \leq k_0 $
.
Also, there is some
![]() $j< J$
such that
$j< J$
such that
![]() $\frac {|Z_{k_0} \cap k_0 |}{k_0} \in \left (q_j-\delta , q_j + \delta \right )$
. Denote this rational as
$\frac {|Z_{k_0} \cap k_0 |}{k_0} \in \left (q_j-\delta , q_j + \delta \right )$
. Denote this rational as
![]() $r_1$
. Then, we get
$r_1$
. Then, we get
 $$\begin{align*}1 - \epsilon \leq \frac{r_1-\delta}{r_1+\delta} \leq \frac{|X_{r_1}\cap k_0 |}{ |Z_{k_0} \cap k_0 | } , \frac{|Z_{k_0} \cap k_0 |}{|X_{r_1}\cap k_0 |} \leq \frac{r_1+\delta}{r_1-\delta} \leq 1 + \epsilon. \end{align*}$$
$$\begin{align*}1 - \epsilon \leq \frac{r_1-\delta}{r_1+\delta} \leq \frac{|X_{r_1}\cap k_0 |}{ |Z_{k_0} \cap k_0 | } , \frac{|Z_{k_0} \cap k_0 |}{|X_{r_1}\cap k_0 |} \leq \frac{r_1+\delta}{r_1-\delta} \leq 1 + \epsilon. \end{align*}$$
Denote
![]() $Z_{k_0} \cup (X_{r_1} \cap [k_0, l))$
by
$Z_{k_0} \cup (X_{r_1} \cap [k_0, l))$
by
![]() $Z_l^1$
. Therefore, we can apply Lemmas 4.1, 4.5, and 4.6 and Corollaries 4.3 and 4.4 with
$Z_l^1$
. Therefore, we can apply Lemmas 4.1, 4.5, and 4.6 and Corollaries 4.3 and 4.4 with
![]() $Z_{k_0}$
and
$Z_{k_0}$
and
![]() $X_{r_1}$
to find
$X_{r_1}$
to find
![]() $k_1$
such that
$k_1$
such that
-
•
 $\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap Z_{l}^1)}{\prod _{i\in E}d_{l}(B_i)d_{l}(Z_{l}^1)} \in \left ( 1-15\epsilon , 1+ 15\epsilon \right )$
for all
$\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap Z_{l}^1)}{\prod _{i\in E}d_{l}(B_i)d_{l}(Z_{l}^1)} \in \left ( 1-15\epsilon , 1+ 15\epsilon \right )$
for all
 $k_0 \leq l < k_1$
.
$k_0 \leq l < k_1$
. -
•
 $\displaystyle \frac {\epsilon _0^2}{2} \leq \frac {|Z_l^1 \cap l|}{l} \leq 1- \frac {\epsilon _0^2}{2} $
for all
$\displaystyle \frac {\epsilon _0^2}{2} \leq \frac {|Z_l^1 \cap l|}{l} \leq 1- \frac {\epsilon _0^2}{2} $
for all
 $k \leq l < k_1$
$k \leq l < k_1$
-
•
 $\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap Z_{l}^1)}{\prod _{i\in E}d_{l}(B_i)d_{l}(Z_{l}^1)} \in \left ( 1- \epsilon , 1+ \epsilon \right )$
for all
$\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap Z_{l}^1)}{\prod _{i\in E}d_{l}(B_i)d_{l}(Z_{l}^1)} \in \left ( 1- \epsilon , 1+ \epsilon \right )$
for all
 $l \geq k_1$
$l \geq k_1$
-
•
 $\displaystyle \epsilon _0 \leq \frac {|Z_l^1 \cap l|}{l} \leq 1- \epsilon _0 $
for all
$\displaystyle \epsilon _0 \leq \frac {|Z_l^1 \cap l|}{l} \leq 1- \epsilon _0 $
for all
 $l \geq k_1$
$l \geq k_1$
-
•
 $\displaystyle \frac {|Z_{l}^1 \cap l|}{l} \in \left (r_1 -\delta , r_1 + \delta \right )$
for all
$\displaystyle \frac {|Z_{l}^1 \cap l|}{l} \in \left (r_1 -\delta , r_1 + \delta \right )$
for all
 $l \geq k_1.$
$l \geq k_1.$
If there is
![]() $l \geq k_1$
such that
$l \geq k_1$
such that
![]() $\frac {|W \cap l|}{l}\in \left (r_1 -\delta , r_1 + \delta \right )$
, then we have the result with
$\frac {|W \cap l|}{l}\in \left (r_1 -\delta , r_1 + \delta \right )$
, then we have the result with
![]() $Z^\prime := Z_l^1$
and
$Z^\prime := Z_l^1$
and
![]() $k^\prime =l$
. Otherwise, there is
$k^\prime =l$
. Otherwise, there is
![]() $k_1^\prime>k_1$
such that
$k_1^\prime>k_1$
such that
for all
![]() $l\geq k_1^\prime $
. Without loss of generality, we can assume that
$l\geq k_1^\prime $
. Without loss of generality, we can assume that
![]() $\frac {|W \cap l|}{l} < r_1 -\delta $
for all
$\frac {|W \cap l|}{l} < r_1 -\delta $
for all
![]() $l>k_1^\prime $
. Now, define
$l>k_1^\prime $
. Now, define
![]() $r_2:= r_1 - \frac {\delta }{2}$
. Note that
$r_2:= r_1 - \frac {\delta }{2}$
. Note that
![]() $r_2> \epsilon _0$
since
$r_2> \epsilon _0$
since
![]() $ \frac {|W \cap k_1^\prime |}{k_1^\prime } \geq \epsilon _0$
. Consider the set
$ \frac {|W \cap k_1^\prime |}{k_1^\prime } \geq \epsilon _0$
. Consider the set
![]() $X_{r_2}$
given by Lemma 4.7. Since there is
$X_{r_2}$
given by Lemma 4.7. Since there is
![]() $\delta ^\prime $
such that
$\delta ^\prime $
such that
![]() $(r_1- \delta ^\prime , r_1 + \delta ^\prime ) \subseteq \left (r_2 -\delta , r_2 + \delta \right )$
, by Corollary 4.4, there is some
$(r_1- \delta ^\prime , r_1 + \delta ^\prime ) \subseteq \left (r_2 -\delta , r_2 + \delta \right )$
, by Corollary 4.4, there is some
![]() $k_1^{\prime \prime } \geq k_1^\prime $
such that for all
$k_1^{\prime \prime } \geq k_1^\prime $
such that for all
![]() $l \geq k_1^{\prime \prime }$
$l \geq k_1^{\prime \prime }$
Besides, if
![]() $k_1^{\prime \prime }$
is large enough, we can ask that for any
$k_1^{\prime \prime }$
is large enough, we can ask that for any
![]() $E \subseteq n$
and for all
$E \subseteq n$
and for all
![]() $l \geq k_1^{\prime \prime }$
$l \geq k_1^{\prime \prime }$
-
•
 $ \displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap X_{r_2})}{\prod _{i\in E}d_{l}(B_i)d_{l}(X_{r_2})}, \frac {\prod _{i\in E}d_{l}(B_i)d_{l}(X_{r_2})}{d_{l}(\bigcap _{i \in E} B_i \cap X_{r_2})} \in \left ( 1- \epsilon , 1+ \epsilon \right ) $
$ \displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap X_{r_2})}{\prod _{i\in E}d_{l}(B_i)d_{l}(X_{r_2})}, \frac {\prod _{i\in E}d_{l}(B_i)d_{l}(X_{r_2})}{d_{l}(\bigcap _{i \in E} B_i \cap X_{r_2})} \in \left ( 1- \epsilon , 1+ \epsilon \right ) $
-
•
 $\displaystyle \frac {|X_{r_2}\cap l|}{l} \in \left ( r_2 - \delta , r_2 + \delta \right ) $
$\displaystyle \frac {|X_{r_2}\cap l|}{l} \in \left ( r_2 - \delta , r_2 + \delta \right ) $
-
•
 $\displaystyle \epsilon _0 < \frac {|X_{r_2}\cap l|}{l} < 1-\epsilon _0. $
$\displaystyle \epsilon _0 < \frac {|X_{r_2}\cap l|}{l} < 1-\epsilon _0. $
Then, we get
 $$\begin{align*}1 - \epsilon \leq \frac{r_2-\delta}{r_2+\delta} \leq \frac{|X_{r_2}\cap k_1^{\prime\prime} |}{ |Z_{k_1^{\prime\prime}}^1 \cap k_1^{\prime\prime} | } , \frac{|Z_{k_1^{\prime\prime}}^1 \cap k_1^{\prime\prime} |}{|X_{r_2}\cap k_1^{\prime\prime} |} \leq \frac{r_2+\delta}{r_2-\delta} \leq 1 + \epsilon. \end{align*}$$
$$\begin{align*}1 - \epsilon \leq \frac{r_2-\delta}{r_2+\delta} \leq \frac{|X_{r_2}\cap k_1^{\prime\prime} |}{ |Z_{k_1^{\prime\prime}}^1 \cap k_1^{\prime\prime} | } , \frac{|Z_{k_1^{\prime\prime}}^1 \cap k_1^{\prime\prime} |}{|X_{r_2}\cap k_1^{\prime\prime} |} \leq \frac{r_2+\delta}{r_2-\delta} \leq 1 + \epsilon. \end{align*}$$
Denote
![]() $Z_{k_1^{\prime \prime }}^1 \cup (X_{r_2} \cap [k_1^{\prime \prime }, l))$
by
$Z_{k_1^{\prime \prime }}^1 \cup (X_{r_2} \cap [k_1^{\prime \prime }, l))$
by
![]() $Z_l^2$
. Therefore, we can apply again Lemmas 4.1, 4.5, and 4.6 and Corollaries 4.3 and 4.4 with
$Z_l^2$
. Therefore, we can apply again Lemmas 4.1, 4.5, and 4.6 and Corollaries 4.3 and 4.4 with
![]() $Z_{k_1^{\prime \prime }}^1 $
and
$Z_{k_1^{\prime \prime }}^1 $
and
![]() $X_{r_2}$
to find
$X_{r_2}$
to find
![]() $k_2$
such that
$k_2$
such that
-
•
 $\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap Z_{l}^2)}{\prod _{i\in E}d_{l}(B_i)d_{l}(Z_{l}^2)} \in \left ( 1-15\epsilon , 1+ 15\epsilon \right )$
for all
$\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap Z_{l}^2)}{\prod _{i\in E}d_{l}(B_i)d_{l}(Z_{l}^2)} \in \left ( 1-15\epsilon , 1+ 15\epsilon \right )$
for all
 $k_1^{\prime \prime } \leq l < k_2$
.
$k_1^{\prime \prime } \leq l < k_2$
. -
•
 $\displaystyle \frac {\epsilon _0^2}{2} \leq \frac {|Z_l^2 \cap l|}{l} \leq 1- \frac {\epsilon _0^2}{2} $
for all
$\displaystyle \frac {\epsilon _0^2}{2} \leq \frac {|Z_l^2 \cap l|}{l} \leq 1- \frac {\epsilon _0^2}{2} $
for all
 $k_1^{\prime \prime } \leq l < k_2$
$k_1^{\prime \prime } \leq l < k_2$
-
•
 $\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap Z_{l}^2)}{\prod _{i\in E}d_{l}(B_i)d_{l}(Z_{l}^2)} \in \left ( 1- \epsilon , 1+ \epsilon \right )$
for all
$\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap Z_{l}^2)}{\prod _{i\in E}d_{l}(B_i)d_{l}(Z_{l}^2)} \in \left ( 1- \epsilon , 1+ \epsilon \right )$
for all
 $l \geq k_2$
$l \geq k_2$
-
•
 $\displaystyle \epsilon _0 \leq \frac {|Z_l^2 \cap l|}{l} \leq 1- \epsilon _0 $
for all
$\displaystyle \epsilon _0 \leq \frac {|Z_l^2 \cap l|}{l} \leq 1- \epsilon _0 $
for all
 $l \geq k_2$
$l \geq k_2$
-
•
 $\displaystyle \frac {|Z_{l}^2 \cap l|}{l} \in \left (r_2 -\delta , r_2 + \delta \right )$
for all
$\displaystyle \frac {|Z_{l}^2 \cap l|}{l} \in \left (r_2 -\delta , r_2 + \delta \right )$
for all
 $l \geq k_2$
.
$l \geq k_2$
.
If there is
![]() $l \geq k_2$
such that
$l \geq k_2$
such that
![]() $\frac {|W \cap l|}{l}\in \left (r_2 -\delta , r_2 + \delta \right )$
, then we have the result with
$\frac {|W \cap l|}{l}\in \left (r_2 -\delta , r_2 + \delta \right )$
, then we have the result with
![]() ${Z^\prime := Z_l^2}$
and
${Z^\prime := Z_l^2}$
and
![]() $k^\prime =l$
. Otherwise,
$k^\prime =l$
. Otherwise,
![]() $\frac {|W \cap l|}{l} < r_2 -\delta $
for all
$\frac {|W \cap l|}{l} < r_2 -\delta $
for all
![]() $l \geq k_2$
. Then, define
$l \geq k_2$
. Then, define
![]() ${r_3= r_2 - \frac {\delta }{2}}$
and repeat the previous step. This construction has an ending because
${r_3= r_2 - \frac {\delta }{2}}$
and repeat the previous step. This construction has an ending because
![]() ${\epsilon _0 \leq \frac {|W \cap l|}{l} \leq 1- \epsilon _0}$
for all
${\epsilon _0 \leq \frac {|W \cap l|}{l} \leq 1- \epsilon _0}$
for all
![]() $l>k$
.
$l>k$
.
Now, we are ready to begin the proof.
Theorem 4.9. Assume CH in the ground model and let
![]() $\kappa \geq \aleph _2$
with
$\kappa \geq \aleph _2$
with
![]() $\kappa =\kappa ^{\aleph _0}$
. Let
$\kappa =\kappa ^{\aleph _0}$
. Let
![]() $\mathbb {C}$
be the Cohen forcing, then
$\mathbb {C}$
be the Cohen forcing, then
![]() $V^{\mathbb {C}_{\kappa }} \models $
“There is a maximal
$V^{\mathbb {C}_{\kappa }} \models $
“There is a maximal
![]() $*$
-independent family of size
$*$
-independent family of size
![]() $\aleph _1$
”.
$\aleph _1$
”.
Proof. It suffices to consider what happens when forcing with just
![]() $\mathbb {C}=$
Fn
$\mathbb {C}=$
Fn
![]() $(2,\omega )$
because we are going to build a maximal
$(2,\omega )$
because we are going to build a maximal
![]() $*$
-independent family of size
$*$
-independent family of size
![]() $\aleph _1$
that is preserved by Cohen forcing, and a new real added by
$\aleph _1$
that is preserved by Cohen forcing, and a new real added by
![]() $\mathbb {C}_{\kappa }$
is already added by a countable fragment which is isomorphic to Cohen forcing. Let
$\mathbb {C}_{\kappa }$
is already added by a countable fragment which is isomorphic to Cohen forcing. Let
![]() $\mathcal {A}_0=\{A_n \subseteq [\omega ]^\omega \, | \, n \in \omega \}$
be an
$\mathcal {A}_0=\{A_n \subseteq [\omega ]^\omega \, | \, n \in \omega \}$
be an
![]() $*$
-independent family. Fix an enumeration
$*$
-independent family. Fix an enumeration
![]() $\{(p_\alpha , \dot {X}_{\alpha }) \, | \, \omega \leq \alpha \leq \omega _1 \}$
of all pairs
$\{(p_\alpha , \dot {X}_{\alpha }) \, | \, \omega \leq \alpha \leq \omega _1 \}$
of all pairs
![]() $(p, \dot {X})$
such that
$(p, \dot {X})$
such that
![]() $p\in \mathbb {C}$
and
$p\in \mathbb {C}$
and
![]() $\dot {X}$
is a nice name for a subset of
$\dot {X}$
is a nice name for a subset of
![]() $\omega $
. Note that since
$\omega $
. Note that since
![]() $V\models $
CH, there are just
$V\models $
CH, there are just
![]() $\aleph _1$
many nice names for subsets of
$\aleph _1$
many nice names for subsets of
![]() $\omega $
in V.
$\omega $
in V.
We now construct a maximal
![]() $*$
-independent family
$*$
-independent family
![]() $\mathcal {A}$
from
$\mathcal {A}$
from
![]() $\mathcal {A}_0$
as follows. Let
$\mathcal {A}_0$
as follows. Let
![]() $\omega \leq \alpha < \omega _1$
and assume we have already defined set
$\omega \leq \alpha < \omega _1$
and assume we have already defined set
![]() $A_\beta $
for all
$A_\beta $
for all
![]() $\beta <\alpha $
. Below, we will construct
$\beta <\alpha $
. Below, we will construct
![]() $A_\alpha \subseteq \omega $
such that the following two properties hold:
$A_\alpha \subseteq \omega $
such that the following two properties hold:
-
(i) The family
 $\{A_\beta \, | \, \beta \leq \alpha \}$
is
$\{A_\beta \, | \, \beta \leq \alpha \}$
is
 $*$
-independent.
$*$
-independent. -
(ii) If there is a rational number
 $\epsilon _0>0$
and
$\epsilon _0>0$
and
 $N\in \omega $
in the ground model such that then there exists
$N\in \omega $
in the ground model such that then there exists $$\begin{align*} &p_\alpha \Vdash \text{"}\epsilon_0 < d_l(\dot{X}_\alpha) < 1-\epsilon_0 \text{ for all }l\geq N,\\ & \quad \text{and } \{A_\beta \, | \, \beta < \alpha \} \cup \{ \dot{X}_\alpha \}\text{ is } *\text{-independent",} \end{align*}$$
$$\begin{align*} &p_\alpha \Vdash \text{"}\epsilon_0 < d_l(\dot{X}_\alpha) < 1-\epsilon_0 \text{ for all }l\geq N,\\ & \quad \text{and } \{A_\beta \, | \, \beta < \alpha \} \cup \{ \dot{X}_\alpha \}\text{ is } *\text{-independent",} \end{align*}$$
 $\epsilon ^\prime < \epsilon _0$
and a sequence of intervals of
$\epsilon ^\prime < \epsilon _0$
and a sequence of intervals of
 $\omega $
,
$\omega $
,
 $\mathcal {I}_\alpha =\{ I_j \}_{j \in \omega }$
, with
$\mathcal {I}_\alpha =\{ I_j \}_{j \in \omega }$
, with
 $\max I_j < \min I_{j+1}$
, such that
$\max I_j < \min I_{j+1}$
, such that
-
(a)
 $|I_n \cap A_\alpha |> (1-\epsilon ^\prime )| (\max I_n +1) \cap A_\alpha |$
.
$|I_n \cap A_\alpha |> (1-\epsilon ^\prime )| (\max I_n +1) \cap A_\alpha |$
. -
(b) For all
 $m\in \omega $
, the set is dense below
$m\in \omega $
, the set is dense below $$\begin{align*}D^\alpha_{m}:=\{ q \in \mathbb{C} \, | \, \exists n \geq m : q \Vdash A_\alpha \cap I_n = \dot{X}_{\alpha} \cap I_n \} \end{align*}$$
$$\begin{align*}D^\alpha_{m}:=\{ q \in \mathbb{C} \, | \, \exists n \geq m : q \Vdash A_\alpha \cap I_n = \dot{X}_{\alpha} \cap I_n \} \end{align*}$$
 $p_\alpha $
.
$p_\alpha $
.
-
We first show that the family
![]() $\mathcal {A}=\{A_\beta \, | \, \beta < \omega _1 \}$
constructed this way is a maximal
$\mathcal {A}=\{A_\beta \, | \, \beta < \omega _1 \}$
constructed this way is a maximal
![]() $*$
-independent family in
$*$
-independent family in
![]() $V^{\mathbb {C}}$
. Clearly,
$V^{\mathbb {C}}$
. Clearly,
![]() $\mathcal {A}$
is an
$\mathcal {A}$
is an
![]() $*$
-independent family. Suppose it were not maximal. Then, there is a condition p and a nice name
$*$
-independent family. Suppose it were not maximal. Then, there is a condition p and a nice name
![]() $\dot {X}$
for a subset of
$\dot {X}$
for a subset of
![]() $\omega $
such that
$\omega $
such that
By strengthening p, we can assume that there is a rational number
![]() $\epsilon _0$
and
$\epsilon _0$
and
![]() $N\in \omega $
such that
$N\in \omega $
such that
for
![]() $l \geq N$
. This is possible since
$l \geq N$
. This is possible since
![]() $\Vdash $
“
$\Vdash $
“
![]() $\dot {X}$
is moderate”. Let
$\dot {X}$
is moderate”. Let
![]() $\alpha $
be such that
$\alpha $
be such that
![]() $(p,\dot {X})=(p_\alpha , \dot {X}_\alpha )$
, so
$(p,\dot {X})=(p_\alpha , \dot {X}_\alpha )$
, so
By property (ii), there exist
![]() $\epsilon ^\prime < \epsilon _0$
and a sequence of intervals of
$\epsilon ^\prime < \epsilon _0$
and a sequence of intervals of
![]() $\omega $
,
$\omega $
,
![]() $\mathcal {I}_\alpha =\{ I_n \}_{n \in \omega }$
, such that
$\mathcal {I}_\alpha =\{ I_n \}_{n \in \omega }$
, such that
![]() $|I_n \cap A_\alpha |> (1-\epsilon ^\prime )| (\max I_n +1) \cap A_\alpha |$
. Let
$|I_n \cap A_\alpha |> (1-\epsilon ^\prime )| (\max I_n +1) \cap A_\alpha |$
. Let
![]() $\epsilon = \frac {1-\epsilon ^\prime }{1-\epsilon _0} - 1$
. Find a condition
$\epsilon = \frac {1-\epsilon ^\prime }{1-\epsilon _0} - 1$
. Find a condition
![]() $q\leq p_\alpha $
and
$q\leq p_\alpha $
and
![]() $M \in \omega $
such that for all
$M \in \omega $
such that for all
![]() $n\geq M$
$n\geq M$
 $$ \begin{align} q\Vdash \frac{d_n(A_\alpha \cap \dot{X}_\alpha) }{d_n(A_\alpha) \cdot d_n(\dot{X}_\alpha) } \in ( 1- \epsilon, 1+ \epsilon ). \end{align} $$
$$ \begin{align} q\Vdash \frac{d_n(A_\alpha \cap \dot{X}_\alpha) }{d_n(A_\alpha) \cdot d_n(\dot{X}_\alpha) } \in ( 1- \epsilon, 1+ \epsilon ). \end{align} $$
Consider an interval
![]() $I_m$
such that
$I_m$
such that
![]() $\min I_m> N, M$
. Now by the density of
$\min I_m> N, M$
. Now by the density of
![]() $D^\alpha _{m}$
, we can find
$D^\alpha _{m}$
, we can find
![]() $r \leq q$
and some
$r \leq q$
and some
![]() $n\geq m$
such that
$n\geq m$
such that
![]() $r \Vdash A_\alpha \cap I_n = \dot {X}_{\alpha } \cap I_n$
. Denote j as
$r \Vdash A_\alpha \cap I_n = \dot {X}_{\alpha } \cap I_n$
. Denote j as
![]() $\max I_n +1$
. We have
$\max I_n +1$
. We have
 $$\begin{align*} r \Vdash \frac{d_{j}(A_\alpha \cap \dot{X}_\alpha) }{ d_{j}(\dot{X}_\alpha) \cdot d_{j}(A_\alpha) } &= \frac{|A_\alpha \cap \dot{X}_\alpha \cap j|}{ \frac{|\dot{X}_\alpha \cap j | }{j} \cdot |A_\alpha \cap j | } \\ &\geq \frac{|A_\alpha \cap \dot{X}_\alpha \cap j|}{ (1-\epsilon_0) \cdot |A_\alpha \cap j | } \\ & \geq \frac{|A_\alpha \cap \dot{X}_\alpha \cap I_n|}{ (1-\epsilon_0) \cdot |A_\alpha \cap j | } = \frac{|A_\alpha \cap I_n|}{ (1-\epsilon_0) \cdot |A_\alpha \cap j | }> \frac{1-\epsilon^\prime}{1- \epsilon_0} = 1 + \epsilon, \end{align*}$$
$$\begin{align*} r \Vdash \frac{d_{j}(A_\alpha \cap \dot{X}_\alpha) }{ d_{j}(\dot{X}_\alpha) \cdot d_{j}(A_\alpha) } &= \frac{|A_\alpha \cap \dot{X}_\alpha \cap j|}{ \frac{|\dot{X}_\alpha \cap j | }{j} \cdot |A_\alpha \cap j | } \\ &\geq \frac{|A_\alpha \cap \dot{X}_\alpha \cap j|}{ (1-\epsilon_0) \cdot |A_\alpha \cap j | } \\ & \geq \frac{|A_\alpha \cap \dot{X}_\alpha \cap I_n|}{ (1-\epsilon_0) \cdot |A_\alpha \cap j | } = \frac{|A_\alpha \cap I_n|}{ (1-\epsilon_0) \cdot |A_\alpha \cap j | }> \frac{1-\epsilon^\prime}{1- \epsilon_0} = 1 + \epsilon, \end{align*}$$
which contradicts Equation (3).
Now, we are going to show that we can construct such an
![]() $A_\alpha $
satisfying the properties (i) and (ii) for
$A_\alpha $
satisfying the properties (i) and (ii) for
![]() $\omega \leq \alpha < \omega _1$
. We only have to consider those
$\omega \leq \alpha < \omega _1$
. We only have to consider those
![]() $\alpha $
such that
$\alpha $
such that
![]() $\dot {X}_\alpha $
satisfies the assumption in property (ii), since finding an
$\dot {X}_\alpha $
satisfies the assumption in property (ii), since finding an
![]() $A_\alpha $
with property (i) is straightforward. Therefore, assume that there is a rational number
$A_\alpha $
with property (i) is straightforward. Therefore, assume that there is a rational number
![]() $\epsilon _0>0$
and
$\epsilon _0>0$
and
![]() $N\in \omega $
in the ground model such that
$N\in \omega $
in the ground model such that
and consider
![]() $\epsilon ^\prime < \epsilon _0$
. Let
$\epsilon ^\prime < \epsilon _0$
. Let
![]() $\{ B_n \, | \, n<\omega \}$
be an enumeration of
$\{ B_n \, | \, n<\omega \}$
be an enumeration of
![]() $\{A_\beta \, | \, \beta < \alpha \}$
. We further pick some strictly decreasing sequence of real numbers
$\{A_\beta \, | \, \beta < \alpha \}$
. We further pick some strictly decreasing sequence of real numbers
![]() $\{\delta _n\}_{n\in \omega }$
with
$\{\delta _n\}_{n\in \omega }$
with
![]() $\delta _0<1$
and
$\delta _0<1$
and
![]() $\lim _{n \to \infty } \delta _n =0$
, and let
$\lim _{n \to \infty } \delta _n =0$
, and let
![]() $\{q_n \, | \, n \in \omega \}$
be some sequence enumerating all conditions below
$\{q_n \, | \, n \in \omega \}$
be some sequence enumerating all conditions below
![]() $p_\alpha $
infinitely often. By induction on
$p_\alpha $
infinitely often. By induction on
![]() $n<\omega $
, we will construct conditions
$n<\omega $
, we will construct conditions
![]() $r_n \leq q_n^\prime \leq q_n$
, a strictly increasing of natural numbers
$r_n \leq q_n^\prime \leq q_n$
, a strictly increasing of natural numbers
![]() $\{k_n\}_{n \in \omega }$
and initial segments
$\{k_n\}_{n \in \omega }$
and initial segments
![]() $Z_n=A_\alpha \cap k_n$
of
$Z_n=A_\alpha \cap k_n$
of
![]() $A_\alpha $
such that the following statementsFootnote
1
will hold:
$A_\alpha $
such that the following statementsFootnote
1
will hold:
![]() $*$
-Independence:
$*$
-Independence:
-
C1.
 $\displaystyle \frac {d_{k_n}(\bigcap _{i \in E} B_i \cap Z_n)}{\prod _{i\in E}d_{k_n}(B_i)d_{k_n}(Z_n)} \in \left ( 1-\frac {\delta _n}{15}, 1+ \frac {\delta _n}{15} \right )$
for all
$\displaystyle \frac {d_{k_n}(\bigcap _{i \in E} B_i \cap Z_n)}{\prod _{i\in E}d_{k_n}(B_i)d_{k_n}(Z_n)} \in \left ( 1-\frac {\delta _n}{15}, 1+ \frac {\delta _n}{15} \right )$
for all
 $E \subseteq \{0, ..., n \}$
.
$E \subseteq \{0, ..., n \}$
. -
C2.
 $\displaystyle q_n^\prime \Vdash \displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap \dot {X}_\alpha )}{\prod _{i\in E}d_{l}(B_i)d_{l}(\dot {X}_\alpha )} \in \left ( 1-\frac {\delta _n}{15}, 1+ \frac {\delta _n}{15} \right )$
and
$\displaystyle q_n^\prime \Vdash \displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap \dot {X}_\alpha )}{\prod _{i\in E}d_{l}(B_i)d_{l}(\dot {X}_\alpha )} \in \left ( 1-\frac {\delta _n}{15}, 1+ \frac {\delta _n}{15} \right )$
and
 $\displaystyle q_n^\prime \Vdash \displaystyle \frac {\prod _{i\in E}d_{l}(B_i)d_{l}(\dot {X}_\alpha )}{d_{l}(\bigcap _{i \in E} B_i \cap \dot {X}_\alpha )} \in \left ( 1-\frac {\delta _n}{15}, 1+ \frac {\delta _n}{15} \right )$
for all
$\displaystyle q_n^\prime \Vdash \displaystyle \frac {\prod _{i\in E}d_{l}(B_i)d_{l}(\dot {X}_\alpha )}{d_{l}(\bigcap _{i \in E} B_i \cap \dot {X}_\alpha )} \in \left ( 1-\frac {\delta _n}{15}, 1+ \frac {\delta _n}{15} \right )$
for all
 $l\geq k_n$
and
$l\geq k_n$
and
 $E \subseteq \{0, ..., n \}$
.
$E \subseteq \{0, ..., n \}$
. -
C3.
 $\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap Z_{n+1})}{\prod _{i\in E}d_{l}(B_i)d_{l}(Z_{n+1})} \in \left ( 1-\delta _n, 1+ \delta _n \right )$
for all
$\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap Z_{n+1})}{\prod _{i\in E}d_{l}(B_i)d_{l}(Z_{n+1})} \in \left ( 1-\delta _n, 1+ \delta _n \right )$
for all
 $k_n \leq l \leq k_{n+1}$
and
$k_n \leq l \leq k_{n+1}$
and
 $E \subseteq \{0, ..., n \}$
.
$E \subseteq \{0, ..., n \}$
.
Moderate:
-
C4.
 $ \epsilon ^\prime \leq \displaystyle d_{k_n}(Z_n) \leq 1-\epsilon ^\prime $
.
$ \epsilon ^\prime \leq \displaystyle d_{k_n}(Z_n) \leq 1-\epsilon ^\prime $
. -
C5.
 $ \frac {(\epsilon ^\prime )^2}{2} \leq \displaystyle d_{l}(Z_{n+1}) \leq 1-\frac {(\epsilon ^\prime )^2}{2}$
for all
$ \frac {(\epsilon ^\prime )^2}{2} \leq \displaystyle d_{l}(Z_{n+1}) \leq 1-\frac {(\epsilon ^\prime )^2}{2}$
for all
 $k_n \leq l \leq k_{n+1}$
with
$k_n \leq l \leq k_{n+1}$
with
 $n>0$
.
$n>0$
.
For the construction:
-
C6. For every
 $m \geq k_n$
, there is a finite set
$m \geq k_n$
, there is a finite set
 $Y_m \subseteq m$
such that
$Y_m \subseteq m$
such that-
•
 $Y_m \cap k_n = Z_n$
$Y_m \cap k_n = Z_n$
-
•
 $\epsilon ^\prime \leq \frac {|Y_m \cap l|}{l} \leq 1- \epsilon ^\prime $
for all
$\epsilon ^\prime \leq \frac {|Y_m \cap l|}{l} \leq 1- \epsilon ^\prime $
for all
 $k_n \leq l \leq m$
.
$k_n \leq l \leq m$
. -
•
 $\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap Y_m)}{\prod _{i\in E}d_{l}(B_i)d_{l}(Y_m)} \in \left ( 1-\frac {\delta _n}{15}, 1+ \frac {\delta _n}{15} \right )$
for all
$\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap Y_m)}{\prod _{i\in E}d_{l}(B_i)d_{l}(Y_m)} \in \left ( 1-\frac {\delta _n}{15}, 1+ \frac {\delta _n}{15} \right )$
for all
 $k_n \leq l \leq m$
.
$k_n \leq l \leq m$
.
-
Intervals: There is
![]() $k_n^\prime \geq k_n$
such that
$k_n^\prime \geq k_n$
such that
-
C7.
 $\displaystyle |Z_{n+1} \cap [k_n^\prime , k_{n+1}) |> (1-\epsilon ^\prime )|Z_{n+1} \cap k_{n+1} |$
$\displaystyle |Z_{n+1} \cap [k_n^\prime , k_{n+1}) |> (1-\epsilon ^\prime )|Z_{n+1} \cap k_{n+1} |$
-
C8.
 $\displaystyle r_n \Vdash Z_{n+1} \cap [k_n^\prime , k_{n+1}) = \dot {X}_\alpha \cap [k_n^\prime , k_{n+1}) $
.
$\displaystyle r_n \Vdash Z_{n+1} \cap [k_n^\prime , k_{n+1}) = \dot {X}_\alpha \cap [k_n^\prime , k_{n+1}) $
.
It is clear that (C1)–(C8) taken together for all
![]() $n<\omega $
imply that
$n<\omega $
imply that
![]() $A_\alpha := \bigcup _{n<\omega } Z_n$
is moderate and satisfies the properties (i) and (ii) with the intervals
$A_\alpha := \bigcup _{n<\omega } Z_n$
is moderate and satisfies the properties (i) and (ii) with the intervals
![]() $I_n:=[k_n^\prime , k_{n+1})$
. Now, we are going to begin our construction.
$I_n:=[k_n^\prime , k_{n+1})$
. Now, we are going to begin our construction.
For
![]() $n=0$
, choose any
$n=0$
, choose any
![]() $k_0$
,
$k_0$
,
![]() $q^\prime _0 \leq q_0$
and
$q^\prime _0 \leq q_0$
and
![]() $Z_0$
such that (C1), (C2), (C4), and (C6) hold. There is nothing to show yet for (C3), (C5), (C7), and (C8).
$Z_0$
such that (C1), (C2), (C4), and (C6) hold. There is nothing to show yet for (C3), (C5), (C7), and (C8).
Now assume that we have obtained
![]() $k_n \in \omega $
,
$k_n \in \omega $
,
![]() $q_n^\prime \leq q_n$
and
$q_n^\prime \leq q_n$
and
![]() $Z_n$
such that (C1), (C2), (C4), and (C6) hold for n. We will construct
$Z_n$
such that (C1), (C2), (C4), and (C6) hold for n. We will construct
![]() $r_n \leq q_n^\prime $
,
$r_n \leq q_n^\prime $
,
![]() $k_{n+1} \in \omega $
,
$k_{n+1} \in \omega $
,
![]() $q_{n+1}^\prime \leq q_{n+1}$
and
$q_{n+1}^\prime \leq q_{n+1}$
and
![]() $Z_{n+1}$
such that (C3), (C5), (C7), and (C8) hold for n and (C1), (C2), (C4), and (C6) hold for
$Z_{n+1}$
such that (C3), (C5), (C7), and (C8) hold for n and (C1), (C2), (C4), and (C6) hold for
![]() $n+1$
. First, note that
$n+1$
. First, note that
![]() $Z_{n}$
,
$Z_{n}$
,
![]() $\frac {\delta _n}{15}$
, and
$\frac {\delta _n}{15}$
, and
![]() $\epsilon ^\prime $
satisfy the conditions of Lemma 4.8 since (C1) and (C6) hold for n. Then, we can find
$\epsilon ^\prime $
satisfy the conditions of Lemma 4.8 since (C1) and (C6) hold for n. Then, we can find
![]() $k_n^\prime \geq k_n$
, a condition
$k_n^\prime \geq k_n$
, a condition
![]() $q_n^{\prime \prime } \leq q_n^\prime $
, and a finite set
$q_n^{\prime \prime } \leq q_n^\prime $
, and a finite set
![]() $Z_n^\prime \subseteq k_n^\prime $
such that
$Z_n^\prime \subseteq k_n^\prime $
such that
-
•
 $Z^\prime _n \cap k_n = Z_n$
.
$Z^\prime _n \cap k_n = Z_n$
. -
•
 $\displaystyle \frac {(\epsilon ^\prime )^2}{2} \leq \frac {|Z^\prime _n \cap l|}{l} \leq 1- \frac {(\epsilon ^\prime )^2}{2} $
for all
$\displaystyle \frac {(\epsilon ^\prime )^2}{2} \leq \frac {|Z^\prime _n \cap l|}{l} \leq 1- \frac {(\epsilon ^\prime )^2}{2} $
for all
 $k_n \leq l < k^\prime _n$
.
$k_n \leq l < k^\prime _n$
. -
•
 $\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap Z^\prime _n)}{\prod _{i\in E}d_{l}(B_i)d_{l}(Z^\prime _n)} \in \left ( 1- \delta _n, 1+ \delta _n \right )$
for all
$\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap Z^\prime _n)}{\prod _{i\in E}d_{l}(B_i)d_{l}(Z^\prime _n)} \in \left ( 1- \delta _n, 1+ \delta _n \right )$
for all
 $k_n \leq l < k^\prime _n$
and for any
$k_n \leq l < k^\prime _n$
and for any
 $E \subseteq n$
.
$E \subseteq n$
. -
•
 $\displaystyle \epsilon ^\prime \leq \frac {|Z^\prime _n \cap k^\prime _n|}{k^\prime _n} \leq 1- \epsilon ^\prime $
$\displaystyle \epsilon ^\prime \leq \frac {|Z^\prime _n \cap k^\prime _n|}{k^\prime _n} \leq 1- \epsilon ^\prime $
-
•
 $\displaystyle \frac {d_{k^\prime _n}(\bigcap _{i \in E} B_i \cap Z^\prime _n)}{\prod _{i\in E}d_{k^\prime _n}(B_i)d_{k^\prime }(Z^\prime _n)} \in \left ( 1- \frac {\delta _n}{15}, 1+ \frac {\delta _n}{15} \right )$
for any
$\displaystyle \frac {d_{k^\prime _n}(\bigcap _{i \in E} B_i \cap Z^\prime _n)}{\prod _{i\in E}d_{k^\prime _n}(B_i)d_{k^\prime }(Z^\prime _n)} \in \left ( 1- \frac {\delta _n}{15}, 1+ \frac {\delta _n}{15} \right )$
for any
 $E \subseteq n$
.
$E \subseteq n$
. -
•
 $q_n^{\prime \prime } \Vdash \displaystyle \frac {|Z^\prime _n \cap k^\prime _n|}{|\dot {X}_\alpha \cap k^\prime _n|}, \frac {|\dot {X}_\alpha \cap k^\prime _n|}{|Z^\prime _n \cap k^\prime _n|} \in \left (1 -\frac {\delta _n}{15}, 1 + \frac {\delta _n}{15}\right )$
.
$q_n^{\prime \prime } \Vdash \displaystyle \frac {|Z^\prime _n \cap k^\prime _n|}{|\dot {X}_\alpha \cap k^\prime _n|}, \frac {|\dot {X}_\alpha \cap k^\prime _n|}{|Z^\prime _n \cap k^\prime _n|} \in \left (1 -\frac {\delta _n}{15}, 1 + \frac {\delta _n}{15}\right )$
.
Now, find a condition
![]() $q_{n+1}^\prime \leq q_{n+1}$
and
$q_{n+1}^\prime \leq q_{n+1}$
and
![]() $k_n^{\prime \prime } \geq k_n^\prime $
such that for all
$k_n^{\prime \prime } \geq k_n^\prime $
such that for all
![]() $E \subseteq \{0, ..., n+1\}$
, we have that
$E \subseteq \{0, ..., n+1\}$
, we have that
 $$\begin{align*}\displaystyle q_{n+1}^\prime \Vdash \frac{d_{l}(\bigcap_{i \in E} B_i \cap \dot{X}_\alpha)}{\prod_{i\in E}d_{l}(B_i)d_{l}(\dot{X}_\alpha)} \in \left( 1-\frac{\delta_{n+1}}{15}, 1+ \frac{\delta_{n+1}}{15} \right) \end{align*}$$
$$\begin{align*}\displaystyle q_{n+1}^\prime \Vdash \frac{d_{l}(\bigcap_{i \in E} B_i \cap \dot{X}_\alpha)}{\prod_{i\in E}d_{l}(B_i)d_{l}(\dot{X}_\alpha)} \in \left( 1-\frac{\delta_{n+1}}{15}, 1+ \frac{\delta_{n+1}}{15} \right) \end{align*}$$
and
 $$\begin{align*}\displaystyle q_{n+1}^\prime \Vdash \frac{\prod_{i\in E}d_{l}(B_i)d_{l}(\dot{X}_\alpha)}{d_{l}(\bigcap_{i \in E} B_i \cap \dot{X}_\alpha)} \in \left( 1-\frac{\delta_{n+1}}{15}, 1+ \frac{\delta_{n+1}}{15} \right) \end{align*}$$
$$\begin{align*}\displaystyle q_{n+1}^\prime \Vdash \frac{\prod_{i\in E}d_{l}(B_i)d_{l}(\dot{X}_\alpha)}{d_{l}(\bigcap_{i \in E} B_i \cap \dot{X}_\alpha)} \in \left( 1-\frac{\delta_{n+1}}{15}, 1+ \frac{\delta_{n+1}}{15} \right) \end{align*}$$
for all
![]() $l\geq k_n^{\prime \prime }$
. This is possible since the assumption in property (ii) is true. This implies that (C2) holds for
$l\geq k_n^{\prime \prime }$
. This is possible since the assumption in property (ii) is true. This implies that (C2) holds for
![]() $n+1$
. Next, we find
$n+1$
. Next, we find
![]() $r_n \leq q_n^{\prime \prime }$
and a sufficiently large
$r_n \leq q_n^{\prime \prime }$
and a sufficiently large
![]() $k_{n+1}> k_n^{\prime \prime }$
such that for all
$k_{n+1}> k_n^{\prime \prime }$
such that for all
![]() $E \subseteq \{0, ..., n+1\}$
, we have
$E \subseteq \{0, ..., n+1\}$
, we have
 $$ \begin{align} \displaystyle r_n \Vdash \displaystyle \frac{d_{k_{n+1}}(\bigcap_{i \in E} B_i \cap (Z_n^\prime \cup (\dot{X}_\alpha \cap [k_n^\prime, k_{n+1}))) )}{\prod_{i\in E}d_{k_{n+1}}(B_i)d_{k_{n+1}}(Z_n^\prime \cup (\dot{X}_\alpha \cap [k_n^\prime, k_{n+1})))} \in \left( 1- \frac{\delta_{n+1}}{15}, 1+ \frac{\delta_{n+1}}{15} \right) \end{align} $$
$$ \begin{align} \displaystyle r_n \Vdash \displaystyle \frac{d_{k_{n+1}}(\bigcap_{i \in E} B_i \cap (Z_n^\prime \cup (\dot{X}_\alpha \cap [k_n^\prime, k_{n+1}))) )}{\prod_{i\in E}d_{k_{n+1}}(B_i)d_{k_{n+1}}(Z_n^\prime \cup (\dot{X}_\alpha \cap [k_n^\prime, k_{n+1})))} \in \left( 1- \frac{\delta_{n+1}}{15}, 1+ \frac{\delta_{n+1}}{15} \right) \end{align} $$
 $$ \begin{align} \displaystyle r_n \Vdash \epsilon_0 \leq \frac{\dot{X}_\alpha \cap [k_n^\prime, k_{n+1})}{k_{n+1}-k_n^\prime} \leq 1- \epsilon_0 \end{align} $$
$$ \begin{align} \displaystyle r_n \Vdash \epsilon_0 \leq \frac{\dot{X}_\alpha \cap [k_n^\prime, k_{n+1})}{k_{n+1}-k_n^\prime} \leq 1- \epsilon_0 \end{align} $$
and
Besides, we can assume that
![]() $r_n$
decides
$r_n$
decides
![]() $\dot {X}_\alpha \cap k_{n+1}$
. Specifically, there is
$\dot {X}_\alpha \cap k_{n+1}$
. Specifically, there is
![]() $X_n \subseteq [k_n^\prime , k_{n+1})$
such that
$X_n \subseteq [k_n^\prime , k_{n+1})$
such that
![]() $r_n \Vdash X_n=\dot {X}_\alpha \cap [k_n^\prime , k_{n+1})$
. All this is also possible because of the assumption in property (ii), Lemma 4.6, and the following is forced:
$r_n \Vdash X_n=\dot {X}_\alpha \cap [k_n^\prime , k_{n+1})$
. All this is also possible because of the assumption in property (ii), Lemma 4.6, and the following is forced:
 $$\begin{align*}\begin{array}{rl} \displaystyle \limsup\limits_{l\rightarrow \infty} \frac{|\dot{X}_\alpha \cap l|}{l} &= \displaystyle \limsup\limits_{l\rightarrow \infty} \frac{|\dot{X}_\alpha \cap [k_n^\prime, l)|}{l-k_n^\prime} \\ \displaystyle \liminf\limits_{l\rightarrow \infty} \frac{|\dot{X}_\alpha \cap l|}{l} &= \displaystyle \liminf\limits_{l\rightarrow \infty} \frac{|\dot{X}_\alpha \cap [k_n^\prime, l)|}{l-k_n^\prime}. \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{rl} \displaystyle \limsup\limits_{l\rightarrow \infty} \frac{|\dot{X}_\alpha \cap l|}{l} &= \displaystyle \limsup\limits_{l\rightarrow \infty} \frac{|\dot{X}_\alpha \cap [k_n^\prime, l)|}{l-k_n^\prime} \\ \displaystyle \liminf\limits_{l\rightarrow \infty} \frac{|\dot{X}_\alpha \cap l|}{l} &= \displaystyle \liminf\limits_{l\rightarrow \infty} \frac{|\dot{X}_\alpha \cap [k_n^\prime, l)|}{l-k_n^\prime}. \end{array} \end{align*}$$
Let
![]() $Z_{n+1}:=Z_n^\prime \cup X_n$
. Note that (C7) and (C8) hold for n, and (C1) holds for
$Z_{n+1}:=Z_n^\prime \cup X_n$
. Note that (C7) and (C8) hold for n, and (C1) holds for
![]() $n+1$
by definition of
$n+1$
by definition of
![]() $Z_{n+1}$
. Let us see that the remaining conditions hold. Consider W such that
$Z_{n+1}$
. Let us see that the remaining conditions hold. Consider W such that
![]() $r_n \Vdash W=\dot {X}_\alpha \cap k_{n+1}$
.
$r_n \Vdash W=\dot {X}_\alpha \cap k_{n+1}$
.
-
Condition (C5). By construction
 $ \frac {(\epsilon ^\prime )^2}{2} \leq \frac {|Z_n^\prime \cap l|}{l} \leq 1- \frac {(\epsilon ^\prime )^2}{2} $
for
$ \frac {(\epsilon ^\prime )^2}{2} \leq \frac {|Z_n^\prime \cap l|}{l} \leq 1- \frac {(\epsilon ^\prime )^2}{2} $
for
 $k_n \leq l < k_n^\prime $
and
$k_n \leq l < k_n^\prime $
and
 $\displaystyle \epsilon ^\prime \leq \frac {|Z^\prime _n \cap k^\prime _n|}{k^\prime _n} \leq 1- \epsilon ^\prime $
. Since for any l with
$\displaystyle \epsilon ^\prime \leq \frac {|Z^\prime _n \cap k^\prime _n|}{k^\prime _n} \leq 1- \epsilon ^\prime $
. Since for any l with $$\begin{align*}\epsilon^\prime \leq \frac{|W \cap k_n^\prime|}{k_n^\prime}, \frac{|W \cap l|}{l} \leq 1-\epsilon^\prime \end{align*}$$
$$\begin{align*}\epsilon^\prime \leq \frac{|W \cap k_n^\prime|}{k_n^\prime}, \frac{|W \cap l|}{l} \leq 1-\epsilon^\prime \end{align*}$$
 $k_n^\prime \leq l \leq k_{n+1}$
, by Lemma 4.1, we get Thus (C5) holds for n.
$k_n^\prime \leq l \leq k_{n+1}$
, by Lemma 4.1, we get Thus (C5) holds for n. $$\begin{align*}\frac{(\epsilon^\prime)^2}{2} \leq \displaystyle d_{l}(Z_{n+1}) \leq 1- \frac{(\epsilon^\prime)^2}{2}. \end{align*}$$
$$\begin{align*}\frac{(\epsilon^\prime)^2}{2} \leq \displaystyle d_{l}(Z_{n+1}) \leq 1- \frac{(\epsilon^\prime)^2}{2}. \end{align*}$$
-
Condition (C4). Note that by Equation (5) and (C8) for n, we have
Thus, we can apply Lemma 4.2 to $$\begin{align*}\epsilon_0 \leq \frac{X_n}{k_{n+1}-k_n^\prime} \leq 1-\epsilon_0. \end{align*}$$
$$\begin{align*}\epsilon_0 \leq \frac{X_n}{k_{n+1}-k_n^\prime} \leq 1-\epsilon_0. \end{align*}$$
 $R:= k_n^\prime $
,
$R:= k_n^\prime $
,
 $S:=[k_n^\prime , k_{n+1})$
,
$S:=[k_n^\prime , k_{n+1})$
,
 $A=Z_n^\prime $
, and
$A=Z_n^\prime $
, and
 $B=X_n$
to obtain where
$B=X_n$
to obtain where $$\begin{align*}\epsilon_0 - \frac{1}{c} \leq \frac{Z_{n}^\prime\cup X_n}{k_n^\prime \cup [k_n^\prime, k_{n+1})} = d_{k_{n+1}}(Z_{n+1}) \leq 1-\epsilon_0 + \frac{1}{c}, \end{align*}$$
$$\begin{align*}\epsilon_0 - \frac{1}{c} \leq \frac{Z_{n}^\prime\cup X_n}{k_n^\prime \cup [k_n^\prime, k_{n+1})} = d_{k_{n+1}}(Z_{n+1}) \leq 1-\epsilon_0 + \frac{1}{c}, \end{align*}$$
 $c=\frac {k_{n+1}-k_n^\prime }{k_n^\prime }$
. Note that we can choose
$c=\frac {k_{n+1}-k_n^\prime }{k_n^\prime }$
. Note that we can choose
 $k_{n+1}$
sufficiently large as to guarantee
$k_{n+1}$
sufficiently large as to guarantee
 $\epsilon ^\prime < \epsilon _0 - \frac {1}{c}$
, so (C4) holds for
$\epsilon ^\prime < \epsilon _0 - \frac {1}{c}$
, so (C4) holds for
 $n+1$
.
$n+1$
.
-
Condition (C6). Let
 $l \geq k_{n+1}$
. Let
$l \geq k_{n+1}$
. Let
 $X_l$
be any finite set that is a witness of
$X_l$
be any finite set that is a witness of
 $\dot {X}_\alpha \cap [k_n^\prime , l)$
, that is, there is a condition
$\dot {X}_\alpha \cap [k_n^\prime , l)$
, that is, there is a condition
 $r \leq r_n$
such that
$r \leq r_n$
such that
 $r \Vdash X_l = \dot {X}_\alpha \cap [k_n^\prime , l)$
. Then, by the previous arguments,
$r \Vdash X_l = \dot {X}_\alpha \cap [k_n^\prime , l)$
. Then, by the previous arguments,
 $Y_l:= Z_n^\prime \cup X_l = Z_{n+1} \cup X_l \setminus X_n$
satisfies the inequalities of the condition (C6). Thus (C6) holds for
$Y_l:= Z_n^\prime \cup X_l = Z_{n+1} \cup X_l \setminus X_n$
satisfies the inequalities of the condition (C6). Thus (C6) holds for
 $n+1$
.
$n+1$
. -
Condition (C3). By construction, we already have
for all $$\begin{align*}\displaystyle \frac{d_{l}(\bigcap_{i \in E} B_i \cap Z_{n+1})}{\prod_{i\in E}d_{l}(B_i)d_{l}(Z_{n+1})} \in \left( 1- \delta_n, 1+ \delta_n \right) \end{align*}$$
$$\begin{align*}\displaystyle \frac{d_{l}(\bigcap_{i \in E} B_i \cap Z_{n+1})}{\prod_{i\in E}d_{l}(B_i)d_{l}(Z_{n+1})} \in \left( 1- \delta_n, 1+ \delta_n \right) \end{align*}$$
 $k_n \leq l < k^\prime _n$
and
$k_n \leq l < k^\prime _n$
and
 $E \subseteq \{0, ..., n\}$
. Besides, by (C2) and (C8) for n, we have
$E \subseteq \{0, ..., n\}$
. Besides, by (C2) and (C8) for n, we have -
•
 $\displaystyle \frac {d_{k_n^\prime }(\bigcap _{i \in E} B_i \cap Z_n^\prime )}{\prod _{i\in E}d_{k_n^\prime }(B_i)d_{k_n^\prime }(Z_n^\prime )} \in \left ( 1-\frac {\delta _n}{15}, 1+ \frac {\delta _n}{15} \right )$
for any
$\displaystyle \frac {d_{k_n^\prime }(\bigcap _{i \in E} B_i \cap Z_n^\prime )}{\prod _{i\in E}d_{k_n^\prime }(B_i)d_{k_n^\prime }(Z_n^\prime )} \in \left ( 1-\frac {\delta _n}{15}, 1+ \frac {\delta _n}{15} \right )$
for any
 $E \subseteq \{0, ..., n\}$
.
$E \subseteq \{0, ..., n\}$
. -
•
 $\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap W)}{\prod _{i\in E}d_{l}(B_i)d_{l}(W)}, \frac {\prod _{i\in E}d_{l}(B_i)d_{l}(W)}{d_{l}(\bigcap _{i \in E} B_i \cap W)} \in \left ( 1-\frac {\delta _n}{15}, 1+ \frac {\delta _n}{15} \right ) $
for
$\displaystyle \frac {d_{l}(\bigcap _{i \in E} B_i \cap W)}{\prod _{i\in E}d_{l}(B_i)d_{l}(W)}, \frac {\prod _{i\in E}d_{l}(B_i)d_{l}(W)}{d_{l}(\bigcap _{i \in E} B_i \cap W)} \in \left ( 1-\frac {\delta _n}{15}, 1+ \frac {\delta _n}{15} \right ) $
for
 $l \geq k_n^\prime $
and
$l \geq k_n^\prime $
and
 $E \subseteq \{0, ..., n\}$
.
$E \subseteq \{0, ..., n\}$
. -
•
 $\displaystyle \frac {|Z^\prime _n \cap k^\prime _n|}{|W \cap k^\prime _n|}, \frac {|W \cap k^\prime _n|}{|Z^\prime _n \cap k^\prime _n|} \in \left (1 -\frac {\delta _n}{15}, 1 + \frac {\delta _n}{15}\right )$
.
$\displaystyle \frac {|Z^\prime _n \cap k^\prime _n|}{|W \cap k^\prime _n|}, \frac {|W \cap k^\prime _n|}{|Z^\prime _n \cap k^\prime _n|} \in \left (1 -\frac {\delta _n}{15}, 1 + \frac {\delta _n}{15}\right )$
.
 $Z_n^\prime $
and W to get for
$Z_n^\prime $
and W to get for $$\begin{align*}\displaystyle \frac{d_{l}(\bigcap_{i \in E} B_i \cap Z_{n+1})}{\prod_{i\in E}d_{l}(B_i)d_{l}(Z_{n+1})} \in \left( 1- \delta_n, 1+ \delta_n \right) \end{align*}$$
$$\begin{align*}\displaystyle \frac{d_{l}(\bigcap_{i \in E} B_i \cap Z_{n+1})}{\prod_{i\in E}d_{l}(B_i)d_{l}(Z_{n+1})} \in \left( 1- \delta_n, 1+ \delta_n \right) \end{align*}$$
 $k_n^\prime \leq l \leq k_{n+1} $
and
$k_n^\prime \leq l \leq k_{n+1} $
and
 $E \subseteq \{0, ..., n\}$
. Therefore, (C3) holds for
$E \subseteq \{0, ..., n\}$
. Therefore, (C3) holds for
 $(n)$
.
$(n)$
.
-
The previous proof relies on the countability of Cohen forcing to construct a maximal
![]() $*$
-independent family. However, it is not known whether there exists a purely combinatorial condition on maximal
$*$
-independent family. However, it is not known whether there exists a purely combinatorial condition on maximal
![]() $*$
-independent families which implies Cohen indestructibility. It would be interesting to determine whether such a condition exists.
$*$
-independent families which implies Cohen indestructibility. It would be interesting to determine whether such a condition exists.
Acknowledgments
I am grateful to Jörg Brendle for guiding me during this research. His ideas and suggestions contributed to the development of this article.