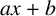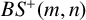1 Introduction
C*-algebras associated to correspondences have been actively studied ever since they were introduced by Pimsner [Reference Pimsner28]. Originally promoted as simultaneous generalizations of Cuntz–Krieger algebras and crossed products by
$\mathbb {Z}$
, Pimsner algebras have found many other applications and stimulated much research over the past three decades. The construction uses the tensor powers of a correspondence over a C*-algebra of coefficients to produce a C*-algebra of left creation operators (the Toeplitz–Pimsner algebra) and a distinguished quotient of it (the Cuntz–Pimsner algebra). Pimsner’s approach also relies on viewing these algebras as universal objects for a class of representations of the correspondence. For the details, in addition to the original reference, see also [Reference Fowler and Raeburn13, Reference Katsura19]. The construction appeared independently in [Reference Abadie, Eilers and Exel1] under the further assumption that the correspondence is a Hilbert bimodule.
Partly guided by Arveson’s theory of product systems of Hilbert spaces, Fowler [Reference Neal27] proposed a generalization of Pimsner’s construction for generalized systems of tensor products of correspondences over semigroups (product systems, for short). The definition of a reduced Toeplitz algebra generated by left creation operators on the Fock module of a product system is entirely analogous to the case of a single correspondence, for which the relevant semigroup is
$\mathbb {N}$
. However, complications arose when trying to identify a convenient class of representations of the product system that was useful to study the reduced Toeplitz algebra from a universal C*-algebra point of view. This was the case even for semigroup C*-algebras, which arise from product systems of one-dimensional correspondences; essentially, the reason is that some crucial properties of representations are automatic for
$\mathbb {N}$
but need to be specified explicitly in general to keep things tractable.
With the theory of semigroup C*-algebras available at the time, the construction of a universal Toeplitz algebra associated to a product system could only proceed under further assumptions; broadly, that the semigroup arises from a quasi-lattice order in the sense of Nica and that the product system is compactly aligned. It was only under these assumptions, or slight generalizations thereof, that a workable theory was developed in analogy to Pimsner’s.
The past 15 years have seen significant advances in the understanding of semigroup C*-algebras beyond the quasi-lattice or right least common multiple (LCM) conditions. This has been largely the result of seminal work of Xin Li [Reference Li23], which takes into account the structure of constructible right ideals of the semigroup. Naturally, these advances are now beginning to permeate the study of C*-algebras of general product systems, notably through the techniques developed in [Reference Sehnem29]. This provides the context for the present work, in which we study product systems of correspondences over monoids that embed in a group.
In this paper, we are primarily interested in the structure of the (reduced) Toeplitz algebra
${\mathcal {T}_{\lambda }}(\mathcal {E})$
of a product system
$\mathcal {E}$
over a general group-embeddable monoid P. Our main goal is to study nuclearity and exactness of
${\mathcal {T}_{\lambda }}(\mathcal {E})$
in terms of the underlying coefficient algebra beyond the case of compactly aligned product systems over right LCM monoids. For compactly aligned product systems over right LCM monoids, an analysis of these structural properties is carried out in [Reference Kakariadis, Katsoulis, Laca and Li18]. For single correspondences, nuclearity (respectively exactness) of the Toeplitz algebra was shown to be equivalent to nuclearity (respectively exactness) of the coefficient algebra in the work of Katsura [Reference Katsura19] (see also [Reference Dykema and Shlyakhtenko10]). For similar structural results at the level of Cuntz–Pimsner-type C*-algebras of product systems over Ore monoids, we mention the work of Albandik and Meyer [Reference Albandik and Meyer3], and pioneering work of Murphy on C*-algebras associated to abelian semigroups of endomorphisms [Reference Murphy26].
This paper is organized as follows. We begin Section 2 with a very brief introduction to Toeplitz C*-algebras of product systems. We then give the definition of Fock covariant representations and of a universal Toeplitz algebra, and discuss a filtration of C*-algebras indexed by the collection of finite families of constructible ideals that are closed under intersection. In Section 3, we consider tensor products of product systems. Our motivation is a result in the setting of Toeplitz algebras of correspondences that establishes existence of canonical isomorphisms
${\mathcal {T}_{\lambda }}(\mathcal {E})\otimes _{\mu }B\cong {\mathcal {T}_{\lambda }}(\mathcal {E}\otimes _{\mu } B)$
, where
$\mu $
denotes either the minimal or maximal norm. We show that an isomorphism
${\mathcal {T}_{\lambda }}(\mathcal {E})\otimes _{\min }B\cong {\mathcal {T}_{\lambda }}(\mathcal {E}\otimes _{\min } B)$
always exists and discuss what happens with the maximal norm in relation to universal Toeplitz algebras.
The independence condition for monoids introduced by Li [Reference Li23] is relevant in our work and we review it in Section 4. We discuss related properties in the setting of product systems that allow us to give a simplified characterization of Fock covariant representations. When P embeds in a group G, we analyse the fixed point algebra
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
for the canonical gauge coaction of G in a similar fashion as for Toeplitz algebras of single correspondences in the work of Katsura [Reference Katsura19] and of compactly aligned product systems in the work of Fowler [Reference Neal27]. We give sufficient conditions for nuclearity of the fixed point algebra
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
for the gauge coaction in terms of subalgebras associated to constructible right ideals of P. In many cases, these conditions are also necessary, Theorem 4.6. In Theorem 4.7, we give sufficient conditions for exactness of
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
.
Section 5 contains our main results. We show that if
$\mathcal {E}=(\mathcal {E}_p)_{p\in P}$
is a product system with coefficient algebra A for which the left action on
$\mathcal {E}_p$
contains the compact operators for each
$p\in P$
, then
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
is nuclear if and only if A is nuclear provided that
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
is spanned in a certain precise sense by elements associated to symmetric words in P; see Theorem 5.4. The main idea is that these conditions imply that each of the building blocks of
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
corresponding to a constructible right ideal of P is a quotient of an ideal in A. The analogous statement about exactness is proved in Theorem 5.6. We observe that the left action on
$\mathcal {E}_p$
contains the compact operators for all
$p\in P$
whenever
$\mathcal {E}=(\mathcal {E}_p)_{p\in P}$
is a product system of Hilbert bimodules.
In Section 6, we give several examples of monoids for which every full product system such that the left action contains the compact operators automatically satisfies the conditions in our main theorem. These include abelian monoids,
$ax+b$
-monoids of integral domains and Baumslag–Solitar monoids
$BS^+(m,n)$
. In the case where
$\gcd (m,n) =1$
, we give an embedding of
$BS^+(m,n)$
into an amenable group; it is possible that this is known, but we have found no reference for it. In any case, it is of independent interest.
2 Product systems and Fock covariance
2.1 Notation and basic notions
Let A and B be
$\mathrm {C}^{*}$
-algebras. A correspondence
$\mathcal {E}\colon A\leadsto B$
is a Hilbert B-module
$\mathcal {E}$
with a nondegenerate left action of A implemented by a
${}^{*}$
- homomorphism
$\phi \colon A\to {\mathbb B}(\mathcal {E})$
. We say that
$\mathcal {E}$
is a Hilbert
$A,B$
-bimodule if the left action of A is induced from a left A-valued inner product
${\langle }{\!\langle {\cdot }\,\vert \,\mathopen {}{\cdot }\rangle \!}{\rangle }$
on
$\mathcal {E}$
that is compatible with the right B-valued inner product
${\langle }{{\cdot }\,\vert \,\mathopen {}{\cdot }}{\rangle }$
in the sense that
${\langle }{\!\langle {\xi }\,\vert \,\mathopen {}{\eta }\rangle \!}{\rangle }\zeta =\xi {\langle }{{\eta }\,\vert \,\mathopen {}{\zeta }}{\rangle }$
for all
$\xi ,\eta ,\zeta \in \mathcal {E}$
. We say that
$\mathcal {E}$
is full if
${\langle }{{\mathcal {E}}\,\vert \,\mathopen {}{\mathcal {E}}}{\rangle }=A$
.
Let P be a semigroup with identity e. A product system over P of A-correspondences consists of:
-
(i) a correspondence
$\mathcal {E}_p\colon A\leadsto A$
for each
$p\in P$
, where
$\mathcal {E}_e=A$
is the identity correspondence over A; -
(ii) correspondence isomorphisms
$\mu _{p,q}\colon \mathcal {E}_p\otimes _A\mathcal {E}_q\overset {\cong }{\rightarrow }\mathcal {E}_{pq}$
, also called multiplication maps, for all
$p,q\in P$
;
$\mu _{e,p}$
on
$A\otimes _A\mathcal {E}_p$
is left multiplication
$\varphi _p\colon A\to {\mathbb B}(\mathcal {E}_p)$
, while
$\mu _{p,e}$
is the right action of A on
$\mathcal {E}_p$
.
The multiplication maps are associative, that is, the following diagram commutes for all
$p, q, r\in P$
:
We say that
$\mathcal {E}$
is full if
$\mathcal {E}_p$
is full for all
$p\in P$
. If each
$\mathcal {E}_p$
is a Hilbert A-bimodule, we speak of a product system of Hilbert bimodules.
A representation of a product system
$\mathcal {E}=(\mathcal {E}_p)_{p\in P}$
in a
$\mathrm {C}^{*}$
-algebra B consists of linear maps
$\psi _p\colon \mathcal {E}_p\rightarrow B$
, for all
$p\in P\setminus \{e\},$
and a
${}^{*}$
-homomorphism
$\psi _e\colon A\rightarrow B$
, satisfying:
-
(R1)
$\psi _p(\xi )\psi _q(\eta )=\psi _{pq}(\xi \eta )$
for all
$p,q\in P$
,
$\xi \in \mathcal {E}_p$
and
$\eta \in \mathcal {E}_q$
; -
(R2)
$\psi _p(\xi )^*\psi _p(\eta )=\psi _e({\langle }{{\xi }\,\vert \,\mathopen {}{\eta }}{\rangle })$
for all
$p\in P$
and
$\xi , \eta \in \mathcal {E}_p$
.
If
$\psi _e$
is faithful, we say that
$\psi $
is injective. In this case, the relation (R2) implies that
$\|\psi _p(\xi )\|=\|\xi \|$
for all
$\xi \in \mathcal {E}_p$
and
$p\in P$
.
The reduced Toeplitz algebra
${\mathcal {T}_{\lambda }}(\mathcal {E})$
of
$\mathcal {E}$
is defined as follows. Let
$\mathcal {E}^+ = \bigoplus _p \mathcal {E}_p$
be the Fock correspondence and let
$\phi $
be the Fock representation of
$\mathcal {E}$
on
$\mathcal {E}^+$
given by left-creation operators
$\phi _p(\xi )$
for
$\xi \in \mathcal {E}_p$
defined on fibres by
$\phi _p(\xi ) \eta = \xi \otimes \eta $
. In particular,
$\phi _e$
implements left multiplication by A. These operators satisfy relations (R1) and (R2), and hence give a representation of
$\mathcal {E}$
; see [Reference Neal27, page 340]. By definition,
${\mathcal {T}_{\lambda }}(\mathcal {E})$
is the C*-algebra generated by the image of
$\phi $
inside the algebra of adjointable operators on
$\mathcal {E}^+$
.
We need to consider the universal C*-algebra
${\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}$
of representations of
$\mathcal {E}$
satisfying relations (R1) and (R2). This was introduced by Fowler in [Reference Neal27], who referred to it as the Toeplitz algebra of
$\mathcal {E}$
. We believe that a Toeplitz algebra ought to reflect further properties of the reduced Toeplitz C*-algebra
${\mathcal {T}_{\lambda }}(\mathcal {E})$
. Thus, we refer to
${\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}$
simply as the universal C*-algebra of representations of
$\mathcal {E}$
and reserve the term Toeplitz for a C*-algebra whose representations satisfy a further set of relations derived from the Fock representation. To illustrate the issue, we point out that it is generally accepted that the Toeplitz C*-algebra of the monoid
$\mathbb {N}^2$
is generated by two commuting isometries S and T that also satisfy
$S^*T = TS^*$
, and that omitting this last condition produces a universal C*-algebra that is much larger than the intended target [Reference Murphy25].
2.2 Fock covariance
As in many situations involving concrete C*-algebras of operators, it is very useful here to have an abstract presentation of a universal object in terms of generators and relations that single out a class of representations. The concrete C*-algebra is then a canonical image of the universal one, and faithfulness depends on a type of amenability. In the case of compactly aligned product systems over quasi-lattice ordered semigroups, this was achieved in [Reference Neal27] by considering Nica–Toeplitz covariant representations. Our next aim is to come up with such a presentation suitable for
${\mathcal {T}_{\lambda }}(\mathcal {E})$
when
$\mathcal {E}$
is a product system over a group-embeddable monoid. The idea is to add more relations to the presentation in relations (R1) and (R2) of
${\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}$
.
Recall from [Reference Dor-On, Kakariadis, Katsoulis, Laca and Li9, Proposition 4.1] that if P embeds in a group G, then the reduced Toeplitz algebra
${\mathcal {T}_{\lambda }}(\mathcal {E})$
has a canonical gauge coaction of G determined by
$$ \begin{align*} \phi _p(\xi) \mapsto \phi _p(\xi) \otimes u_p, \quad p \in P,\quad \xi\in \mathcal{E}_p, \end{align*} $$
where
$u_p$
denotes the canonical generator of
$C^*(G)$
associated to p.
Let
$\psi ^u$
denote the universal representation of
$\mathcal {E}$
in
${\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}$
and recall from [Reference Neal27] that the map
$\tilde {\delta }:\psi ^u(\xi _p) \mapsto \psi ^u(\xi _p) \otimes u_p$
determines a natural gauge coaction of G on the universal C*-algebra
${\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}$
for representations of
$\mathcal {E}$
. The spectral subspace of
$\tilde \delta $
corresponding to
$g\in G$
is
$$ \begin{align*} {\mathrm{C}^{*}_{\mathrm{rep}}(\mathcal{E})}^g := \{ a\in {\mathrm{C}^{*}_{\mathrm{rep}}(\mathcal{E})} \mid \tilde\delta(a) = a\otimes u_g\}. \end{align*} $$
The spectral subspace corresponding to the identity
$e\in G$
is the fixed point algebra
${\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}^G= \{ a\in {\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})} \mid \tilde \delta (a) = a\otimes u_e\}$
.
There is also a compatible (normal) gauge coaction
$\delta : {\mathcal {T}_{\lambda }}(\mathcal {E}) \to {\mathcal {T}_{\lambda }}(\mathcal {E})\otimes C^*_r(G)$
. See for example [Reference Dor-On, Kakariadis, Katsoulis, Laca and Li9]. The fixed-point algebra of this coaction,
$$ \begin{align*}{\mathcal{T}_{\lambda}}(\mathcal{E})^G := \{ a\in {\mathcal{T}_{\lambda}}(\mathcal{E}) \mid \tilde\delta(a) = a\otimes \lambda_g\},\end{align*} $$
is the key to our definition of a universal Toeplitz algebra for
$\mathcal {E}$
.
Definition 2.1. (Fock covariance) We say that a representation
$\psi $
of
$\mathcal {E}$
is Fock covariant if the restriction of the associated representation of
${\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}$
to the fixed point algebra
${\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}^G$
of the gauge coaction factors through the fixed point algebra
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
.
Following [Reference Laca and Sehnem20], we define the universal Toeplitz algebra of
$\mathcal {E}$
, denoted by
$\mathcal {T}_u(\mathcal {E})$
, to be the universal C*-algebra for Fock covariant representations. We write
${\phi ^u :\mathcal {E} \to \mathcal {T}_u(\mathcal {E})}$
for the universal Fock covariant representation. Obviously, the Fock representation
$\phi $
itself is Fock covariant and this gives a canonical homomorphism of
$\mathcal {T}_u(\mathcal {E})$
onto
${\mathcal {T}_{\lambda }}(\mathcal {E})$
that restricts to an isomorphism
$\mathcal {T}_u(\mathcal {E})^G\cong {\mathcal {T}_{\lambda }}(\mathcal {E})^G$
.
We give a C*-algebraic characterization of Fock covariance in Proposition 2.8 below. Before we can state it, we need to consider certain subalgebras of
${\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}$
and of
$\mathcal {T}_u(\mathcal {E})$
defined using constructible right ideals of P, in analogy to what is done for semigroup C*-algebras [Reference Li23]. It is convenient to use the notation from [Reference Laca and Sehnem20, Section 2], which we review next. By a word on P, we mean a sequence
$\alpha = (p_1, p_2, \ldots , p_{2k-1}, p_{2k})$
consisting of an even number of elements of P. We use
${\mathcal W}$
to denote the set of all such words and
${\mathcal W}^k$
to denote the words of half-length k. For each word
${\alpha = (p_1, p_2, \ldots , p_{2k-1}, p_{2k}) \in {\mathcal W}^k}$
, we let
$\tilde {\alpha } = (p_{2k}, p_{2k-1}, \ldots ,p_2, p_1)$
be the reverse word and define 
; we say that the word
$\alpha $
is neutral if
$\dot \alpha =e$
. The iterated quotient set is the finite set
The constructible right ideal corresponding to
$\alpha \in {\mathcal W}$
is the subset
$K(\alpha )$
of P defined by
Let 
denote the collection of constructible right ideals; it is a semilattice under intersections [Reference Li23, Section 2]; see also [Reference Laca and Sehnem20, Section 2] for more details.
For each neutral word
$\alpha = (p_1, p_2, \ldots , p_{2k-1}, p_{2k})$
and elements
$\xi _{p_j} \in \mathcal {E}_{p_j}$
for
${j = 1, 2, \ldots , 2k}$
, we consider products of the form
$$ \begin{align*} \psi^u(\xi_{p_1})^* \psi^u(\xi_{p_2}) \cdots \psi^u(\xi_{p_{2k-1}})^* \psi^u(\xi_{p_{2k}}), \end{align*} $$
where
$\psi ^u$
is the universal representation of
$\mathcal {E}$
in
${\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}$
.
Lemma 2.2. Let P be a submonoid of a group G and let
$\mathcal {E} = (\mathcal {E}_p)_{p\in P}$
be a product system of correspondences over the
$\mathrm {C}^{*}$
-algebra A. Then, for each
$S\in {\mathfrak J}$
, the space
is a C*-subalgebra of
${\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}^G$
and:
-
(1)
$\phi ({\tilde {\mathcal I}}(\emptyset ) )= (0)$
if
$\emptyset \in {\mathfrak J}$
; -
(2)
${\tilde {\mathcal I}}(R) {\tilde {\mathcal I}}(S) \subset {\tilde {\mathcal I}}(R\cap S)$
for
$R,S \in {\mathfrak J}$
; -
(3)
${\tilde {\mathcal I}}(P) =A$
.
Proof. By definition,
${\tilde {\mathcal I}}(S)$
is a closed subspace of
${\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}$
. To see that it is
$*$
-closed, notice that the adjoint of the spanning element
$\psi ^u(\xi _{p_1})^* \psi ^u(\xi _{p_2}) \cdots \psi ^u(\xi _{p_{2k-1}})^* \psi ^u(\xi _{p_{2k}})$
, corresponding to a word
$\alpha = (p_1, p_2, \ldots , p_{2k-1}, p_{2k})$
satisfying
$\dot \alpha =e$
and
$K(\alpha ) = S$
, is precisely another spanning element corresponding to the word
$\tilde \alpha $
, which satisfies
$\dot {\tilde \alpha } = \dot {\alpha }^{-1} = e$
and
$K(\tilde \alpha )=K(\alpha )$
by for example [Reference Laca and Sehnem20, Lemma 2.5(4)].
Suppose now R and S are constructible ideals in P and let
$\alpha =(p_i)$
and
$\beta = (q_j)$
be neutral words satisfying
$K(\alpha ) = R$
and
$K(\beta ) = S$
. A typical spanning element of
${\tilde {\mathcal I}}(R) {\tilde {\mathcal I}}(S)$
is a product of the form
$$ \begin{align*} \psi^u(\xi_{p_1})^* \psi^u(\xi_{p_2}) \cdots \psi^u(\xi_{p_{2k-1}})^* \psi^u(\xi_{p_{2k}}) \psi^u(\xi_{q_1})^* \psi^u(\xi_{q_2}) \cdots \psi^u(\xi_{q_{2l-1}})^* \psi^u(\xi_{q_{2l}}), \end{align*} $$
which corresponds to the concatenation
$\alpha \beta {\kern-1pt}={\kern-1pt}(p_1, \ldots , q_{2l}) {\kern-1pt}\in{\kern-1pt} {\mathcal W}^{k+l}$
. Since
${(\alpha \beta )\dot {} {\kern-1pt}={\kern-1pt} \dot \alpha \dot \beta {\kern-1pt}={\kern-1pt}e}$
and
$K(\alpha \beta ) = K(\alpha ) \cap K(\beta ) = R\cap S$
, by for example [Reference Laca and Sehnem20, Lemma 2.5(4)], we conclude that part (2) holds. Setting
$R = S$
in part (2) now shows that
${\tilde {\mathcal I}}(S)$
is closed under multiplication.
For part (3), let
$\alpha =(p_i)$
be a neutral word with
$K(\alpha )=P$
and let
$\xi _{p_j}\in \mathcal {E}_{p_j}$
for
${j=1, \ldots, 2k}$
. We show by induction on k that there exists
$a\in A$
such that
$$ \begin{align} \psi^u(\xi_{p_1})^* \psi^u(\xi_{p_2}) \cdots \psi^u(\xi_{p_{2k-1}})^* \psi^u(\xi_{p_{2k}})=a. \end{align} $$
Indeed, for
$k=1$
, we must have
$\alpha =(p,p)$
and the conclusion follows because
$\psi ^u$
satisfies axiom (R2) of the definition of a representation of
$\mathcal {E}$
. Suppose the claim holds for words of length up to
$k-1$
and let
$\alpha = (p_1, p_2, \ldots , p_{2k-1}, p_{2k})$
. Since
$e\in K(\alpha )\subset p_{2k}^{-1}p_{2k-1} P\cap P$
, there exists
$r\in P$
such that
$p_{2k}=p_{2k-1}r$
, and hence
$\psi ^u(\xi _{p_{2k-1}})^*\psi ^u(\xi _{p_{2k}})= \psi ^u (\eta )$
for some
$\eta \in \mathcal {E}_r$
. Using this and relation (R1), we can condense the last three factors in (2-1), obtaining
$$ \begin{align*} \psi^u(\xi_{p_{1}})^* \cdots \psi^u(\xi_{p_{2k-2}}) \psi^u(\xi_{p_{2k-1}})^* \psi^u(\xi_{p_{2k}})= \psi^u(\xi_{p_{1}})^* \cdots \psi^u(\xi_{p_{2k-2}}\eta), \end{align*} $$
where the right-hand side has length
$k-1$
and is thus in A by the induction hypothesis. This completes the proof of part (3) and of the proposition.
Corollary 2.3. The projection of the Fock space onto the direct summand
$\mathcal {E}_e=A$
induces conditional expectations
$E_{A,u}\colon \mathcal {T}_u(\mathcal {E})\to A$
and
$E_{A,r}\colon {\mathcal {T}_{\lambda }}(\mathcal {E})\to A$
that factor through the corresponding conditional expectations onto
$\mathcal {T}_u(\mathcal {E})^G\cong {\mathcal {T}_{\lambda }}(\mathcal {E})^G$
and vanish on
${\tilde {\mathcal I}}(S)$
for all
$S\in {\mathfrak J}\setminus \{P\}.$
Proof. This follows from Lemma 2.2(3).
Lemma 2.4. Let P be a submonoid of a group G and let
$\mathcal {E}$
be a product system over P. For each finite
$\cap $
-closed subcollection
${\mathcal C}$
of constructible right ideals, define
Then:
-
(1)
${\tilde {\mathfrak A}}({\mathcal C})$
is a C*-algebra (that is, the linear span is already closed); -
(2) if
${\mathcal C}_1 \subset {\mathcal C}_2$
, then
${\tilde {\mathfrak A}}({\mathcal C}_1)$
is an ideal in
$ {\tilde {\mathfrak A}}( {\mathcal C}_2)$
; -
(3)
$\{{\tilde {\mathfrak A}}({\mathcal C})\}_{\mathcal C}$
is an increasing system of C*-subalgebras indexed by the set of finite
$\cap $
-closed subcollections
${\mathcal C}$
of
${\mathfrak J}$
, partially ordered by inclusion, whose union is dense in
${\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}^G$
; -
(4) for each maximal element
$\bar {S}$
of
${\mathcal C}$
, the sequence is exact.
$$ \begin{align*} 0\to {\tilde{\mathfrak A}}({\mathcal C}\setminus\{\bar{S}\} ) \to{\tilde{\mathfrak A}}({\mathcal C})\to{\tilde{\mathcal I}}(\bar{S})/({\tilde{\mathcal I}}(\bar{S})\cap{\tilde{\mathfrak A}}({\mathcal C}\setminus\{\bar{S}\}))\to 0 \end{align*} $$
Proof. It is clear that
${\tilde {\mathfrak A}}({\mathcal C}_1) \subset {\tilde {\mathfrak A}}({\mathcal C}_2) $
whenever
${\mathcal C}_1 \subset {\mathcal C}_2$
and that
${\tilde {\mathfrak A}}({\mathcal C}) \subset {\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}^G $
. Since
${\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}^G$
is generated by products corresponding to neutral words,
$\bigcup _{\mathcal C} {\tilde {\mathfrak A}}({\mathcal C})$
is dense in
${\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}^G$
.
Let
${\mathcal C}$
be a finite
$\cap $
-closed collection of constructible right ideals of P. We show that
${\tilde {\mathfrak A}}({\mathcal C}) $
is a
$\mathrm {C}^{*}$
-subalgebra of
$\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})$
. The proof is by induction on
$|{\mathcal C}|$
. If
$|{\mathcal C}|=1$
, then
${\tilde {\mathfrak A}}({\mathcal C})={\tilde {\mathcal I}}({S})$
, which is a
$\mathrm {C}^{*}$
-algebra by Lemma 2.2. Let
$n\geq 1$
and suppose
$\sum _{\substack {S\in {\mathcal C}'}}{\tilde {\mathcal I}}(S)$
is a
$\mathrm {C}^{*}$
-algebra, whenever
${\mathcal C}'\subset {\mathfrak J}$
is a finite
$\cap $
-closed subcollection of
${\mathfrak J}$
with
$|{\mathcal C}'|=n$
. Assume
$|{\mathcal C}|=n+1$
and let
$\bar {S}$
be a maximal element of
${\mathcal C}$
. Set 
. Then,
$|{\mathcal C}'|=n$
and
${\mathcal C}'$
is still closed under intersection because by removing the maximal element
$\bar {S}$
, we have not removed any intersection of elements of
${\mathcal C}'$
. By the induction hypothesis,
${\tilde {\mathfrak A}}({\mathcal C}')$
is a
$\mathrm {C}^{*}$
-algebra. Moreover,
${\tilde {\mathfrak A}}({\mathcal C}')$
is a closed ideal in
${\tilde {\mathfrak A}}({\mathcal C})$
because
${\tilde {\mathcal I}}(\bar {S}){\tilde {\mathcal I}}(S)\subseteq {\tilde {\mathcal I}}(\bar {S}\cap S)$
for every S in
${\mathcal C}'$
by Lemma 2.2, and
$\bar {S}\cap S$
has to be in
${\mathcal C}'$
. Thus,
$\sum _{\substack {S\in {\mathcal C}}}{\tilde {\mathcal I}}(S)={\tilde {\mathcal I}}(\bar {S})+{\tilde {\mathfrak A}}({\mathcal C}')$
is a
$\mathrm {C}^{*}$
-algebra by for example [Reference Murphy24, Theorem 3.1.7]. Since
${\tilde {\mathfrak A}}({\mathcal C}')$
is a closed ideal in
${\tilde {\mathfrak A}}({\mathcal C})$
, we have
${\tilde {\mathfrak A}}({\mathcal C})/{\tilde {\mathfrak A}}({\mathcal C}')\cong {\tilde {\mathcal I}}(\bar {S})/({\tilde {\mathcal I}}(\bar {S})\cap {\tilde {\mathfrak A}}({\mathcal C}'))$
, which proves that the given sequence is exact.
We also define the analogous subalgebras at the level of
${\mathcal {T}_{\lambda }}(\mathcal {E})^G \cong \mathcal {T}_u(\mathcal {E})^G$
, namely
and
These are the images in
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
of
${\tilde {\mathcal I}}(S)$
and
${\tilde {\mathfrak A}}({\mathcal C})$
from Lemmas 2.2 and 2.4; and it is clear that the analogues of both lemmas also hold at the level of
$ {\mathcal {T}_{\lambda }}(\mathcal {E})^G$
.
Remark 2.5. Along the lines indicated in [Reference Sehnem29, Remark 3.11] for the fixed point algebra of the covariance algebra of a product system, here too, the fixed point algebra
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
of the reduced Toeplitz algebra does not depend on the specific group G. This is important because it implies that the notion of Fock covariance from Definition 2.1 is intrinsic to the product system itself. To see why, recall from the proof of [Reference Dor-On, Kakariadis, Katsoulis, Laca and Li9, Proposition 4.1] that
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
is the closed linear span of the set of elements of the form
$$ \begin{align*} \phi (\xi_{p_1})^* \phi (\xi_{p_2}) \cdots \phi (\xi_{p_{2k-1}})^* \phi (\xi_{p_{2k}}) \quad \text{with } p_1^{-1} p_2 \cdots p_{2k-1}^{-1} p_{2k} = e. \end{align*} $$
By [Reference Laca and Sehnem20, Lemma 2.9], this set does not depend on the specific G into which P embeds because when
$K(\alpha ) = \emptyset $
for a neutral word in P, the product vanishes by Lemma 2.2(1).
2.3 Coaction on
$\mathcal {T}_u(\mathcal {E})$
To conclude that the gauge coaction
$\tilde \delta $
of G on
${\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}$
passes to the universal Toeplitz C*-algebra, we verify next that the ideal of
${\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}$
generated by the kernel of the restriction of the Fock representation to
${\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}^G$
is gauge invariant.
Lemma 2.6 (Compare with [Reference Sehnem29, Lemma 3.3]).
Let
$\tilde \phi $
be the representation of
${\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}$
obtained from the Fock representation
$\phi $
of
$\mathcal {E}$
by the universal property. Let 
and let
$J^{\phi }\mathrel {\triangleleft }\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})$
be the ideal generated by
$J_e^{\phi }$
. Then,
$$ \begin{align*} J^{\phi }=\bigoplus_{\substack{g\in G}}\mathrm{C}^{*}_{\mathrm{rep}}(\mathcal{E})^gJ_e^{\phi }=\bigoplus_{\substack{g\in G}}J^{\phi }\cap \mathrm{C}^{*}_{\mathrm{rep}}(\mathcal{E})^g, \end{align*} $$
where
$\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})^g$
denotes the spectral subspace at g relative to the gauge coaction of G on
${\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}$
.
Proof. We begin by proving the first equality. To do this, it suffices to show that
$J_e^{\phi } \mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})^g\subseteq \mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})^g J_e^{\phi }$
for each
$g\in G$
. So fix g, and take
$c_g\in \mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})^g $
and
$b\in J_e^{\phi }$
. Since
$\tilde {\phi }$
is a
${}^{*}$
-homomorphism,
$bc_g$
belongs to the kernel of the Fock representation. So,
$c_g^*b^*bc_g\in \ker \tilde {\phi }\cap \mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})^G$
. Therefore,
$bc_g\in \mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})^gJ_e^{\phi }$
by [Reference Pimsner28, Lemma 3.5] (view
$\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})^g$
as a correspondence over
$\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})^G$
). Using the first equality and the contractive projection from
$\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})$
onto
$\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})^g$
, we deduce that
$J^{\phi }\cap \mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})^g=\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})^gJ_e^{\phi }$
and hence the second equality also holds.
As a consequence of the previous lemma, we have the following lemma.
Lemma 2.7 (Compare with [Reference Sehnem29, Lemma 3.4]).
Let
$q_{\mathrm {cov}}\colon \mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})/ J^{\phi } \to \mathcal {T}_u(\mathcal {E})$
be the quotient map. There is a full nondegenerate coaction
$$ \begin{align*}\delta _u\colon \mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})/ J^{\phi }\rightarrow \mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})/ J^{\phi }\otimes \mathrm {C}^{*}(G)\end{align*} $$
satisfying
$\delta _u\circ q_{\mathrm {cov}}=(q_{\mathrm {cov}}\otimes \mathrm {id}_{\mathrm {C}^{*}(G)})\circ \widetilde {\delta }$
, where
$\widetilde {\delta }$
stands for the coaction of G on
$\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})$
. Moreover, the spectral subspace for
$\delta _u$
at
$g\in G$
is canonically isomorphic to
$\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})^g/\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})^gJ_e^{\phi }.$
Proof. The proof follows as in [Reference Sehnem29, Lemma 3.4].
Proposition 2.8. Let
$\psi \colon \mathcal {E} \to B$
be a representation of the product system
$\mathcal {E}$
in the C*-algebra B, and denote by
$\tilde \psi $
the corresponding homomorphism of
${\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}$
onto the C*-algebra generated by
$\psi (\mathcal {E})$
. Then,
$\psi $
is Fock covariant if and only if for every
${\mathcal C}$
, the restriction
$\tilde \psi : {\tilde {\mathfrak A}}({\mathcal C}) \to B$
factors through
${\mathfrak A}({\mathcal C}) := \tilde \phi ({\tilde {\mathfrak A}}({\mathcal C}))$
(image of
${\tilde {\mathfrak A}}({\mathcal C})$
in the Fock representation).
Proof. The ‘only if’ direction is clear because
${\tilde {\mathfrak A}}({\mathcal C}) \subset {\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})}^G$
. We prove that a representation
$\psi $
of
$\mathcal {E}$
is Fock covariant whenever its restriction
$\tilde {\psi }\restriction _{{\tilde {\mathfrak A}}({\mathcal C})}$
factors through the Fock representation for every finite
$\cap $
-closed
${\mathcal C}\subset {\mathfrak J}$
. It suffices to show that
$\tilde {\psi }$
vanishes on 
. By Lemma 2.4,
$\mathrm {C}^{*}_{\mathrm {rep}}(\mathcal {E})^G=\lim _{{\mathcal C}} {\tilde {\mathfrak A}}({\mathcal C})$
. Thus,
$J_e^{\phi }=\lim _{{\mathcal C}}J_e^{\phi }\cap {\tilde {\mathfrak A}}({\mathcal C})$
by for example [Reference Adji, Laca, Nilsen and Raeburn2, Lemma 1.3]. Since
$\tilde {\psi }$
vanishes on
$J_e^{\phi }\cap {\tilde {\mathfrak A}}({\mathcal C})$
for every
${\mathcal C}$
by assumption, we conclude that
$\psi $
is covariant.
3 Tensor products
Suppose that
$\mathcal {E} = (\mathcal {E}_p)_{p\in P}$
is a product system of correspondences over a C*-algebra A and that B is another C*-algebra, and choose a norm
$\mu $
on the algebraic tensor product
$A \odot B$
. Then, the system of algebraic tensor products
$\mathcal {E} \odot B = \{ \mathcal {E}_p\odot B\}_{p\in P}$
can be completed to a product system
$\mathcal {E}\otimes _{\mu } B=(\mathcal {E}_p\otimes _\mu B)_{p\in P}$
over
$A\otimes _\mu B$
with the inner product and the norm on
$\mathcal {E}_p \odot B$
determined by the norm
$\mu $
on
$A\otimes _\mu B$
via
$$ \begin{align*} \langle\xi\otimes b, \eta\otimes c\rangle = \langle\xi, \eta\rangle \otimes \langle b, c\rangle \quad \text{for }\xi,\eta \in \mathcal{E}_p \text{ and } b,c\in B. \end{align*} $$
Motivated by the case of single correspondences and also of C*-algebras associated to Fell bundles, in this section, we investigate the relationships between
$\mathcal {T}_u(\mathcal {E})\otimes _{\max }B$
and
$\mathcal {T}_u(\mathcal {E}\otimes _{\max } B)$
, and similarly between
${\mathcal {T}_{\lambda }}(\mathcal {E})\otimes _{\min } B$
and
${\mathcal {T}_{\lambda }}(\mathcal {E}\otimes _{\min } B)$
. For a single correspondence, there are canonical isomorphisms
${\mathcal {T}_{\lambda }}(\mathcal {E})\otimes _{\max }B\cong {\mathcal {T}_{\lambda }}(\mathcal {E}\otimes _{\max } B)$
and
${\mathcal {T}_{\lambda }}(\mathcal {E})\otimes _{\min }B\cong {\mathcal {T}_{\lambda }}(\mathcal {E}\otimes _{\min } B)$
; see (the proof of) [Reference Brown and Ozawa4, Lemma 4.6.24]. We prove below that the canonical isomorphism at the level of minimal tensor products and reduced Toeplitz algebras always exists in the setting of product systems, Proposition 3.2. However, complications arise from both the more general structure of the semigroup and of the product system. So, at the level of maximal tensor products and universal Toeplitz algebras, we are only able to establish the existence of a canonical homomorphism from
$\mathcal {T}_u(\mathcal {E})\otimes _{\max }B$
onto
$\mathcal {T}_u(\mathcal {E}\otimes _{\max } B)$
, Proposition 3.3.
Initially, we consider the more general situation of the external tensor product of two product systems, regarded as a product system over the direct product of monoids with coefficients in the minimal tensor product of the coefficient algebras.
Suppose that A and B are C*-algebras,
$\mathcal {X}$
is a Hilbert A-module and
$\mathcal {Y}$
is a Hilbert B-module. Recall that the exterior tensor product
$\mathcal {X}\otimes _{\min } \mathcal {Y}$
is the completion of the algebraic tensor product of
$\mathcal {X}$
and
$\mathcal {Y}$
, with respect of the norm arising from the sesquilinear form with values in
$A\otimes _{\min } B$
defined on elementary tensors by
$$ \begin{align*} \langle\xi_1\otimes \eta_1, \xi_2\otimes \eta_2\rangle = \langle\xi_1, \xi_2\rangle \otimes \langle \eta_1, \eta_2\rangle \in A\otimes_{\min} B. \end{align*} $$
The fact that the above sesquilinear form is actually an inner product is proven in [Reference Lance21, page 34]; there it is also shown that
$\mathcal {X}\otimes _{\min } \mathcal {Y}$
admits a (natural) right module action by
$A\otimes _{\min } B$
and so it becomes a Hilbert
$A\otimes _{\min } B$
-module. Furthermore, there is a
$*$
-injection
$$ \begin{align*} j \colon {\mathbb B}(\mathcal{X})\otimes_{\min} {\mathbb B}(\mathcal{Y})\longrightarrow {\mathbb B}(\mathcal{X}\otimes_{\min} \mathcal{Y}); s\otimes t \longmapsto j(s\otimes t), \end{align*} $$
with
$j(s\otimes t) (\xi \otimes \eta )= s\xi \otimes t \eta $
,
$\xi \in \mathcal {X},\ \eta \in \mathcal {Y}$
. (For a proof of this fact, see [Reference Lance21, pages 35–37].) The existence of the injection j easily implies that if
$\mathcal {X}$
and
$\mathcal {Y}$
are C*-correspondences over A and B, respectively, then
$\mathcal {X}\otimes _{\min } \mathcal {Y}$
becomes an
$A\otimes _{\min } B$
-correspondence.
Proposition 3.1. Let
$\mathcal {X}$
and
$\mathcal {Y}$
be product systems over monoids P and Q with coefficient C*-algebras A and B, respectively. Then there is a product system
$\mathcal {X} \otimes _{\min } \mathcal {Y}$
over the monoid
$P\times Q$
with coefficient C*-algebra
$A\otimes _{\min } B$
in which the fibre over
$(p,q)$
is
$ \mathcal {X}_p\otimes \mathcal {Y}_q $
and the multiplication is given by
$$ \begin{align*} (\xi_1\otimes \eta_1)_{(p_1,q_1)} (\xi_2\otimes \eta_2)_{(p_2, q_2)} = (\xi_1 \xi_2)_{p_1p_2} \otimes (\eta_1 \eta_2)_{q_1q_2}. \end{align*} $$
This gives a canonical isomorphism of Fock modules,
$$ \begin{align*} (\mathcal{X} \otimes_{\min} \mathcal{Y})^+ \cong \mathcal{X}^+ \otimes_{\min} \mathcal{Y}^+ \end{align*} $$
and a spatial isomorphism of reduced Toeplitz algebras,
$$ \begin{align*} {\mathcal{T}_{\lambda}}(\mathcal{X} \otimes_{\min} \mathcal{Y}) \cong {\mathcal{T}_{\lambda}}(\mathcal{X}) \otimes_{\min} {\mathcal{T}_{\lambda}}(\mathcal{Y}). \end{align*} $$
Proof. It follows from the previous discussion that each fibre
$(\mathcal {X}\otimes _{\min }\mathcal {Y})_{p,q}$
,
$p,q \in P$
, is an
$A\otimes _{\min } B$
-correspondence. The balanced tensor product
$$ \begin{align*} (\mathcal{X}\otimes_{\min} \mathcal{Y})_{p_1,q_1}\underset{A\otimes_{\min} B}{\otimes}(\mathcal{X}\otimes_{\min} \mathcal{Y})_{p_2,q_2} \end{align*} $$
with respect to
$A\otimes B$
corresponds to the tensor product of balanced tensors
$$ \begin{align*} (\mathcal{X}_{p_1}\underset{A}{\otimes} \mathcal{X}_{p_2}) \otimes (\mathcal{Y}_{q_1}\underset{B}{\otimes} \mathcal{Y}_{q_2}). \end{align*} $$
Hence, if we define a multiplication on
$\mathcal {X}\otimes _{\min } \mathcal {Y}$
by
$$ \begin{align*} (\xi_1\otimes \eta_1)_{(p_1,q_1)} (\xi_2\otimes \eta_2)_{(p_2, q_2)} = (\xi_1 \xi_2) \otimes (\eta_1 \eta_2) \in \mathcal{X}_{p_1 p_2} \otimes \mathcal{Y}_{q_1q_2}, \end{align*} $$
with
$\xi _i \in \mathcal {X}_{p_i}$
,
$\eta _i \in \mathcal {X}_{q_i},\ i=1,2$
, then this multiplication is associative and therefore
$\mathcal {X}\otimes _{\min } \mathcal {Y}$
becomes a product system.
It is easy to see now that there is an isometric isomorphism of right-Hilbert
$A\otimes B$
Fock bimodules
$$ \begin{align*} (\mathcal{X} \otimes_{\min} \mathcal{Y})^+ \cong \mathcal{X}^+ \otimes_{\min} \mathcal{Y}^+. \end{align*} $$
Since for all elementary tensors
$\xi _i \otimes \eta _i\in \mathcal {X}_{p_i} \otimes _{\min } \mathcal {Y}_{q_i}$
for
$i =1,2$
,
$$ \begin{align*} L_{\xi_1 \otimes \eta_1} (\xi_2 \otimes \eta_2) &= (\xi_1 \otimes \eta_1) \underset{A\otimes B}{\otimes} (\xi_2 \otimes \eta_2) = (\xi_1 \underset{A}{\otimes} \xi_2) \otimes (\eta_1 \underset{ B}{\otimes} \eta_2)\\ &= L_{\xi_1} \xi_2 \otimes L_{\eta_1} \eta_2 = (L_{\xi_1} \otimes L_{\eta_1} ) ( \xi_2 \otimes \eta_2), \end{align*} $$
the map
$$ \begin{align*} L_{\xi_1 \otimes \eta_1} \mapsto L_{\xi_1} \otimes_{\min} L_{\eta_1} \end{align*} $$
extends to the required isomorphism of reduced Toeplitz algebras.
Proposition 3.2. Let
$\mathcal {E}$
be a product system over a monoid P with coefficient algebra A and let B be a C*-algebra. Then, there are canonical isomorphisms
${\mathcal {E}^+ \otimes B \cong (\mathcal {E}\otimes B)^+}$
and
$$ \begin{align*} {\mathcal{T}_{\lambda}}(\mathcal{E}) \otimes_{\min} B \cong {\mathcal{T}_{\lambda}}(\mathcal{E} \otimes_{\min} B). \end{align*} $$
Proof. The result follows from Proposition 3.1 with
$\mathcal {X} =\mathcal {E}$
,
$\mathcal {Y} =B$
and
$Q =\{e\}$
, so that
$P\times Q \cong P$
and
${\mathcal {T}_{\lambda }}(\mathcal {Y}) =B$
.
Proposition 3.3. Suppose
$\mathcal {E} = (\mathcal {E}_p)_{p\in P}$
is a product system over the monoid P with coefficient algebra A and let B be a C*-algebra. Then, there is a (canonical) homomorphism
$$ \begin{align*} \pi : \mathcal{T}_u(\mathcal{E})\otimes_{\max}B \rightarrow \mathcal{T}_u(\mathcal{E}\otimes_{\max}B), \end{align*} $$
such that
$\pi : T_\xi \otimes b \mapsto T_{\xi \otimes b} $
for
$\xi \in \mathcal {E}_p$
and
$b \in B$
.
Proof. Assume first that B is unital. Then, the map that sends
$\xi \in \mathcal {E}_p$
to
$T_{\xi \otimes 1} \in \mathcal {T}_u(\mathcal {E}\otimes _{\max }B)$
for each
$p\in P$
is a Fock covariant representation of
$\mathcal {E}$
that commutes with the representation
$b\mapsto 1 \otimes b$
of B in the multiplier algebra
$\mathcal M (\mathcal {T}_u(\mathcal {E}\otimes _{\max }B))$
. The universal property of the maximal tensor product then gives a homomorphism
$\pi : \mathcal {T}_u(\mathcal {E})\otimes _{\max }B \to \mathcal M(\mathcal {T}_u(\mathcal {E}\otimes _{\max }B))$
whose image is generated by the products
$T_{\xi \otimes 1} (1 \otimes b) = T_{\xi \otimes b}$
and hence is contained in
$\mathcal {T}_u(\mathcal {E}\otimes _{\max }B)$
.
In the case where B is not unital, let
$(u_\lambda )_{\lambda \in \Lambda }$
be an approximate identity for B, and for
$p\in P$
and
$\xi \in \mathcal {E}_p$
, let
$T_{\xi \otimes 1}\in M(\mathcal {T}_u(\mathcal {E}\otimes _{\max }B))$
be the limit of the net
$(\phi _p(\xi \otimes u_\lambda ))_{\lambda \in \Lambda }$
in the strict topology of
$M(\mathcal {T}_u(\mathcal {E}\otimes _{\max }B))$
. As above, the map
$\xi \mapsto T_{\xi \otimes 1}$
is a Fock covariant representation of
$\mathcal {E}$
that commutes with the representation
$b\mapsto 1 \otimes b$
of B, and hence induces a homomorphism
$\pi : \mathcal {T}_u(\mathcal {E})\otimes _{\max }B \to \mathcal {T}_u(\mathcal {E}\otimes _{\max }B)$
as in the statement.
Proposition 3.4. Let
$\mathcal {E} = (\mathcal {E}_p)_{p\in P}$
be a product system over the monoid P with coefficient algebra A and let B be a C*-algebra. The following are equivalent:
-
(1) the homomorphism
$\pi \colon \mathcal {T}_u(\mathcal {E})\otimes _{\max }B \rightarrow \mathcal {T}_u(\mathcal {E}\otimes _{\max }B)$
is an isomorphism; -
(2) the composition of
$\pi $
with the Fock representation of
$\mathcal {T}_u(\mathcal {E}\otimes _{\max }B)$
is faithful on
$\mathcal {T}_u(\mathcal {E})^G \otimes _{\max }B$
.
Proof. (1)
$\implies $
(2) is obvious because the Fock representation of
$\mathcal {T}_u(\mathcal {E}\otimes _{\max }B)$
is faithful on
$\mathcal {T}_u(\mathcal {E}\otimes _{\max }B)^G$
. Suppose part (2) holds. Then,
$\pi $
restricts to an isomorphism
$\mathcal {T}_u(\mathcal {E})^G\otimes _{\max }B \cong \mathcal {T}_u(\mathcal {E}\otimes _{\max }B)^G$
. It follows that the representation of
$\mathcal {E}\otimes B$
in
$\mathcal {T}_u(\mathcal {E})^G\otimes _{\max }B $
that identifies elementary tensors is Fock covariant, and hence it induces a homomorphism
$\mathcal {T}_u(\mathcal {E}\otimes _{\max }B)\to \mathcal {T}_u(\mathcal {E})^G\otimes _{\max }B $
by the universal property. This is the inverse of
$\pi $
.
Corollary 3.5. Let
$\mathcal {E} = (\mathcal {E}_p)_{p\in P}$
be a product system over the monoid P with coefficient C*-algebra A. Suppose that A is nuclear. Then, the following are equivalent:
-
(1) the homomorphism
$\pi \colon \mathcal {T}_u(\mathcal {E})\otimes _{\max }B \rightarrow \mathcal {T}_u(\mathcal {E}\otimes B)$
is an isomorphism for every C*-algebra B; -
(2)
$\mathcal {T}_u(\mathcal {E})^G$
is nuclear.
If, in addition,
$\mathcal {T}_u(\mathcal {E}\otimes B)\cong {\mathcal {T}_{\lambda }}(\mathcal {E}\otimes B)$
canonically for every C*-algebra B (for example, if G is amenable), the above conditions are equivalent to:
-
(3)
${\mathcal {T}_{\lambda }}(\mathcal {E})$
is nuclear.
Proof. If
$\pi $
is an isomorphism for every C*-algebra B, restriction to the fixed point algebra
$\mathcal {T}_u(\mathcal {E})^G\otimes _{\max }B$
implies that
$\mathcal {T}_u(\mathcal {E})^G\otimes _{\max }B\cong \mathcal {T}_u(E\otimes B)^G$
canonically for every C*-algebra B. Then, the assumption combined with Proposition 3.2 yields
$$ \begin{align*}\mathcal{T}_u(\mathcal{E})^G\otimes_{\max}B\cong \mathcal{T}_u(E\otimes B)^G\cong{\mathcal{T}_{\lambda}}(\mathcal{E}\otimes B)^G\cong \mathcal{T}_u(\mathcal{E})^G\otimes_{\min}B\end{align*} $$
canonically for every C*-algebra B, proving that
$\mathcal {T}_u(\mathcal {E})^G$
is nuclear.
Conversely, suppose
$\mathcal {T}_u(\mathcal {E})^G$
is nuclear. Then, using again Proposition 3.2, we have for every C*-algebra B that
$$ \begin{align*}\mathcal{T}_u(\mathcal{E})^G\otimes_{\max}B\cong\mathcal{T}_u(\mathcal{E})^G\otimes_{\min}B\cong {\mathcal{T}_{\lambda}}(\mathcal{E})^G\otimes_{\min}B\cong {\mathcal{T}_{\lambda}}(\mathcal{E}\otimes B)^G\cong \mathcal{T}_u(\mathcal{E}\otimes B)^G\end{align*} $$
canonically. Proposition 3.4 gives that
$\pi $
is an isomorphism.
Remark 3.6. Notice that when G is amenable, the equivalence between conditions
$(2)$
and
$(3)$
in Corollary 3.5 follows from a general result on C*-algebras associated to Fell bundles; see [Reference Exel12, Proposition 25.10]. Under the assumption that A is nuclear, condition
$(1)$
in Corollary 3.5 always holds if
$\mathcal {E}$
is a single correspondence or, more generally, a compactly aligned product system over a right LCM monoid. We do not know if Corollary 3.5
$(1)$
automatically holds for arbitrary product systems (over group embeddable monoids).
4 Independence and the fixed point algebra
Recall from [Reference Li23, Definition 2.26] that a monoid P is said to satisfy independence when no constructible right ideal of P can be written as a finite union of proper sub-ideals. Equivalently, P satisfies independence if and only if the projections
${\{\chi _S\mid S\in {\mathfrak J}\}}$
in
$\mathcal {B}(\ell ^2(P))$
corresponding to characteristic functions on constructible right ideals of P form a linearly independent set. In this case, the Fock covariance condition for the canonical product system over P is equivalent to a condition involving single right ideals in
${\mathfrak J}$
, rather than subcollections of them. Motivated by this observation, we consider product systems
$\mathcal {E}$
such that
$$ \begin{align} {\mathfrak A}({\mathcal C})=\bigoplus_{\substack{S\in{\mathcal C}}}{\mathcal I}(S) \quad \text{for every finite }\cap\text{-closed } {\mathcal C}\subset{\mathfrak J}. \end{align} $$
Proposition 4.1. Let P be a submonoid of a group and let
$\mathcal {E}$
be a product system over P. If a representation
$\psi $
of
$\mathcal {E}$
in a
$\mathrm {C}^{*}$
-algebra B is Fock covariant, then the restriction of
$\tilde {\psi }$
to
${\tilde {\mathcal I}}(S)$
factors through the Fock representation
$\tilde {\phi }$
for every
$S\in {\mathfrak J}$
. The converse holds if
$\mathcal {E}$
satisfies (4-1).
Proof. The first assertion follows easily from Proposition 2.8 with
${\mathcal C} = \{S\}$
. For the converse, assume (4-1) holds and let
$\psi $
be a representation of
$\mathcal {E}$
in B such that
$\tilde {\psi }\restriction _{{\tilde {\mathcal I}}(S)}$
factors through the Fock representation for every
$S\in {\mathfrak J}$
. To show that
$\psi $
is Fock covariant, by Proposition 2.8, all we need to prove is that
$\tilde {\psi }\restriction _{{\tilde {\mathfrak A}}({\mathcal C})}$
factors through the Fock representation for every finite
$\cap $
-closed subcollection
${\mathcal C}\subseteq {\mathfrak J}$
. Specifically, we need to show that
$\tilde {\psi }(b)=0$
for each
$b\in {\tilde {\mathfrak A}}({\mathcal C})$
such that
$\tilde {\phi }(b)=0$
. By Lemma 2.4, we can write
$b=\sum _{\substack {S\in {\mathcal C}}}b_S$
with
$b_S\in {\tilde {\mathcal I}}(S)$
for each
$S\in {\mathcal C}$
. It follows that
$$ \begin{align*} 0=\tilde{\phi }(b)=\sum_{\substack{S\in{\mathcal C}}}\tilde{\phi }(b_S). \end{align*} $$
However, then
$\tilde {\phi }(b_S)=0$
for each
$S\in {\mathcal C}$
by (4-1). By assumption,
$\tilde {\psi }\restriction _{{\tilde {\mathcal I}}(S)}$
factors through
$\tilde {\phi }$
and thus
$\tilde {\psi }(b_S)=0$
, which proves that
$\tilde {\psi }(b)=0$
, as desired.
4.1 Sufficient conditions and examples
Next, we observe that the property (4-1) for product systems is consistent with independence for monoids.
Proposition 4.2 [Reference Cuntz, Echterhoff, Li and Yu8, see Proposition 5.6.22].
Let P be a submonoid of a group G. Then, the canonical product system over P with one-dimensional fibres satisfies (4-1) if and only if P satisfies independence.
Proposition 4.3. Let P be a submonoid of a group G and assume that P satisfies independence. Suppose further that the family
${\mathfrak J}$
of constructible right ideals of P has the following property: given
$S_1,S_2\in {\mathfrak J}$
with
$S_1\subsetneq S_2$
and
$s_1\in S_1$
, there exists
${s_2\in S_2\setminus S_1}$
such that
$s_2\leq s_1$
. Then, every product system over P satisfies (4-1).
Proof. First, we claim that if S,
$S_i$
,
$i=1,\ldots , n$
are in
${\mathfrak J}$
, and
$S\setminus (\bigcup _{\substack {j}}S_j)\neq \emptyset $
, then for every
$s\in \bigcup ^n_{\substack {j=1}}S\cap S_j$
, there exists
$\bar {s}\in S\setminus (\bigcup ^n_{\substack {j=1}}S_j)$
with
$\bar {s}\leq s$
. We prove the claim by induction on n. This is just the hypothesis on the family
${\mathfrak J}$
of ideals of P if
$n=1$
. Assume the claim holds for
$n\geq 1$
fixed. Let S,
$S_j$
,
$j=1,\ldots ,n+1$
be constructible right ideals of P and suppose that
$$ \begin{align*} S\setminus\bigg(\bigcup^{n+1}_{\substack{j=1}}S_j\bigg)\neq\emptyset. \end{align*} $$
Take
$s{\kern-1pt}\in{\kern-1pt} \bigcup ^{n+1}_{\substack {j=1}}S{\kern-1pt}\cap{\kern-1pt} S_j $
and let
$i{\kern-1pt}\in{\kern-1pt} \{1,\ldots ,n+1\}$
be such that
$s{\kern-1pt}\in{\kern-1pt} S{\kern-1pt}\cap{\kern-1pt} S_i$
. Let
${s'\in S\setminus (S\cap S_i)}$
with
$s'\leq s$
. If
$s'\in S\setminus (\bigcup ^{n+1}_{\substack {j=1}}S_j)$
, we are done. Otherwise,
$s'\in \bigcup _{\substack {i\neq j}}S\cap S_j$
and we can apply the induction hypothesis to find
$\bar {s}\in S\setminus \bigcup _{\substack {j\neq i}} S_j$
with
$\bar {s}\leq s'\leq s$
. Because
$s'\not \in S_i$
and
$S_i$
is a right ideal,
$\bar {s}$
cannot lie in
$S_i$
as well. Thus,
$\bar {s}\leq s$
with
$\bar {s}$
in
$S\setminus (\bigcup ^{n+1}_{\substack {j=1}}S_j)$
. This completes the proof of the claim.
Now, let
$b=\sum _{\substack {S\in {\mathcal C}}}b_S\in {\tilde {\mathfrak A}}({\mathcal C})$
with
$\tilde {\phi }(b)=0$
in
$\mathcal {B}(\mathcal {E}^+)$
. We claim that
$\tilde {\phi }(b_S)=0$
for every
$S\in {\mathcal C}$
. Let
$\bar {S}$
be a maximal element of
${\mathcal C}$
and choose
$\bar s \in \bar {S} \setminus \bigcup _{\substack {\bar {S}\neq S\in {\mathcal C}}}S$
. It follows that, for all
$S\in {\mathcal C}\setminus \{\bar {S}\}$
,
$\tilde {\phi }(b_S)=0$
on the direct summand
$\mathcal {E}_{\bar {s}}\subseteq \mathcal {E}^+$
because
$\bar {s}\not \in S$
. Thus,
$\tilde {\phi }(b_{\bar {S}})$
must vanish on
$\mathcal {E}_{\bar {s}}$
whenever
$\bar {s}\not \in \bigcup _{\substack {\bar {S}\neq S\in {\mathcal C}}}S$
. By the first part of the proof, if
$s\in \bar {S}\cap \bigcup _{\substack {\bar {S}\neq S\in {\mathcal C}}}S$
, we can find
$\bar {s}\in \bar {S}\setminus (\bar {S}\cap \bigcup _{\substack {\bar {S}\neq S\in {\mathcal C}}}S)$
with
$\bar {s}\leq s$
. Using the correspondence isomorphism
$\mathcal {E}_{s}\cong \mathcal {E}_{\bar {s}}\otimes \mathcal {E}_{\bar {s}^{-1}s}$
, we deduce that
$\tilde {\phi }(b_{\bar {S}})=0$
on
$\mathcal {E}_s$
. So
$\tilde {\phi }(b_{\bar {S}})=0$
. Proceeding with this argument, we conclude that
$\tilde {\phi }(b_S)=0$
for each
$S\in {\mathcal C}$
. So
$\mathcal {E}$
satisfies independence as asserted.
A left-cancellative monoid P is said to be right LCM if the intersection of any two principal right ideals is either a principal right ideal or is empty.
Corollary 4.4. Let
$P\subseteq G$
and suppose that P is right LCM. Then, every product system over P satisfies (4-1).
Proof. Let P be a right LCM submonoid of a group G. Then, every constructible right ideal of P is principal and P satisfies independence by [Reference Cuntz, Echterhoff, Li and Yu8, Lemma 5.6.31]. Let
$S_1$
and
$S_2$
be nonempty right ideals of P such that
$S_1\subsetneq S_2$
. We can write
$S_1=pP$
and
${S_2=qP}$
with
$p,q\in P$
such that
$q < p$
. For every
$s_1 \in S_1$
, we may choose 
, which clearly satisfies
$s_2 < p \leq s_1$
. The result follows by Proposition 4.3.
4.2 Exactness and nuclearity in terms of subalgebras
Suppose that P is a submonoid of a group G and let S be a constructible right ideal in P. The family
of all constructible right ideals contained in S is
$\cap $
-closed, but in most cases is infinite. Since
${\mathfrak J}_{\subset S}$
is relevant to the study of nuclearity and exactness of
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
, we introduce in Theorem 4.6 a stronger version of condition (4-1) that takes it into account. Let
$\mathcal {E}$
be a product system over P and define
Even when
${\mathfrak J}_{\subset S}$
is infinite,
$$ \begin{align*} {\mathfrak A}({\mathfrak J}_{\subset S})= \lim_{{\mathcal C}\Subset {\mathfrak J}_{\subset S}} {\mathfrak A}({\mathcal C}). \end{align*} $$
Lemma 4.5. Let P be a submonoid of a group G and let
$\mathcal {E}$
be a product system over P. Then,
${\mathfrak A}({\mathfrak J}_{\subset S})$
and
${\mathfrak A}({\mathfrak J}_{\subset S}\setminus \{S\})$
are ideals in
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
, and the sequence
$$ \begin{align} 0\to {\mathfrak A}({\mathfrak J}_{\subset S}\setminus\{S\})\to{\mathfrak A}({\mathfrak J}_{\subset S})\to{\mathcal I}(S)/({\mathcal I}(S)\cap{\mathfrak A}({\mathfrak J}_{\subset S}\setminus\{S\}))\to 0 \end{align} $$
is exact.
Proof. Since the constructible right ideal S is maximal (in fact largest) in
${\mathfrak J}_{\subset S}$
, the statement follows as in part (4) of Lemma 2.4.
Theorem 4.6. Let P be a submonoid of a group G and let
$\mathcal {E}$
be a product system over P. Suppose that for each constructible right ideal
$S\in {\mathfrak J}$
, the
$\mathrm {C}^{*}$
-algebra
${\mathcal I}(S)$
is nuclear. Then, the fixed point algebra
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
of the gauge coaction is nuclear. The converse holds if
$$ \begin{align} {\mathcal I}(S)\cap{\mathfrak A}({\mathfrak J}_{\subset S}\setminus\{S\}) = (0) \quad \text{for all } S\in {\mathfrak J}. \end{align} $$
Proof. Suppose first that
${\mathcal I}(S)$
is nuclear for every
$S\in {\mathfrak J}.$
An induction argument on
$|{\mathcal C}|$
combined with Lemma 2.4 shows that
${\mathfrak A}({\mathcal C})$
is nuclear for every finite
$\cap $
-closed collection
${\mathcal C}$
of constructible right ideals of P. Since
${\mathcal {T}_{\lambda }}(\mathcal {E})^G=\lim _{{\mathcal C}}{\mathfrak A}({\mathcal C})$
, it follows that
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
is nuclear.
Assume now that (4-3) holds, so that the exact sequence (4-2) reads
$$ \begin{align*}0\to {\mathfrak A}({\mathfrak J}_{\subset S}\setminus\{S\})\to{\mathfrak A}({\mathfrak J}_{\subset S})\to{\mathcal I}(S)\to 0. \end{align*} $$
If
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
is nuclear, then
${\mathfrak A}({\mathfrak J}_{\subset S})$
is nuclear because it is an ideal in
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
; but then
${\mathcal I}(S)$
is nuclear because it is a quotient of
${\mathfrak A}({\mathfrak J}_{\subset S})$
by Lemma 4.5.
Since exactness passes to subalgebras, it is clear that
${\mathcal I}(S)$
is exact for every
$S\in {\mathfrak J}$
provided that
$\mathcal {T}_u(E)^G$
is exact. To prove the converse, we need (4-1).
Theorem 4.7. Let P be a submonoid of a group G and let
$\mathcal {E}$
be a product system over P. Suppose that
$\mathcal {E}$
satisfies (4-1) and that the
$\mathrm {C}^{*}$
-algebra
${\mathcal I}(S)$
is exact for every constructible right ideal
$S\in {\mathfrak J}$
. Then,
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
is exact.
Proof. Suppose that
${\mathcal I}(S)$
is exact for every
$S\in {\mathfrak J}$
and let
${\mathcal C}\subset {\mathfrak J}$
be a finite
$\cap $
-closed collection of constructible right ideals. By (4-1), we have
${\mathcal I}(\bar {S})\cap {\mathfrak A}({\mathcal C}\setminus \{\bar {S}\})=(0)$
when
$\bar {S}$
is a maximal element in
${\mathcal C}$
. Hence, the analogue of the exact sequence of Lemma 2.4(4) at the level of
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
splits. Since exactness is preserved by taking split extensions, an induction argument on
$|{\mathcal C}|$
shows that
${\mathfrak A}({\mathcal C})$
is exact for every finite
$\cap $
-closed collection
${\mathcal C}$
of constructible right ideals. Since exactness is preserved by taking direct limits, it follows that
${\mathcal {T}_{\lambda }}(\mathcal {E})^G=\lim _{{\mathcal C}}{\mathfrak A}({\mathcal C})$
is exact.
Condition (4-3) implies Condition (4-1), and both are satisfied by right LCM monoids. If we apply Theorem 4.6 to a compactly aligned product system over a right LCM monoid, we recover a key result that is embedded in the proof of [Reference Kakariadis, Katsoulis, Laca and Li18, Theorem 6.11].
Corollary 4.8 (Compare with [Reference Kakariadis, Katsoulis, Laca and Li18, Theorem 6.11]).
Let P be a right LCM submonoid of G and let
$\mathcal {E}$
be a compactly aligned product system over P with coefficient algebra A. Then, the fixed point algebra
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
of the gauge coaction is nuclear (respectively exact) if and only if A is nuclear (respectively exact).
Proof. If
$\mathcal {E}$
is compactly aligned, for every
$p\in P$
, the C*-subalgebra
${\mathcal I}(pP)$
corresponding to
$S=pP$
is the algebra of compact operators
${\mathbb K}(\mathcal {E}_p)$
. This is nuclear (respectively exact) if and only if A is, because
${\mathbb K}(\mathcal {E}_p)$
is Morita equivalent to an ideal in A. The conclusion now follows from Theorems 4.6 and 4.7.
5 Main results
We wish to apply the results in the previous section to a class of product systems for which the left action of the coefficient algebra contains the compact operators. Central to our approach is the set
${\mathcal W}_{\mathrm {{sym}}}$
of symmetric words. Recall that a word
$\beta \in {\mathcal W}$
is symmetric if it has the form
$\beta =\tilde \alpha \alpha $
for
$\alpha \in {\mathcal W}$
, where
$\tilde {\alpha }$
is the reverse of
$\alpha $
.
Notation 5.1. We denote by
$\langle {\mathcal W}_{\mathrm {{sym}}}\rangle $
the smallest subcollection of words in
${\mathcal W}$
containing all symmetric words that is closed under concatenation and under conjugation by words in
${\mathcal W}$
, in the sense that if
$\alpha \in {\mathcal W}$
and
$\beta \in \langle {\mathcal W}_{\mathrm {{sym}}}\rangle $
, then
$\tilde {\alpha }\beta \alpha \in \langle {\mathcal W}_{\mathrm {{sym}}}\rangle .$
Given a constructible right ideal
$S\in {\mathfrak J}$
, we denote by
$\langle {\mathcal W}_{\mathrm {{sym}}}\rangle (S)$
, the collection of words
$\beta \in \langle {\mathcal W}_{\mathrm {{sym}}}\rangle $
such that
$K(\beta )=S.$
Notice that every word in
$\langle {\mathcal W}_{\mathrm {{sym}}}\rangle $
is neutral. Further, given a word
$\beta =(p_1,p_2,\ldots , p_{2l-1},p_{2l})\in {\mathcal W}$
, we let
Lemma 5.2. Let P be a submonoid of a group and let
$\mathcal {E}=(\mathcal {E}_p)_{p\in P}$
be a product system over P with coefficients in a
$\mathrm {C}^{*}$
-algebra A. Suppose that
$\varphi _p(A)\supset {\mathbb K}(\mathcal {E}_p)$
for all
$p\in P$
and let
$\beta \in \langle {\mathcal W}_{\mathrm {{sym}}}\rangle $
. Then, for each
$b\in {\mathcal I}(\beta )$
, there exists
$a\in A$
such that
$b = \varphi _s(a)$
as operators on
$\mathcal {E}_s$
for every
$s\in K(\beta )$
.
Proof. The result is true if
$\beta =(p,p)$
for
$p\in P$
because then,
$\phi (\xi _p)^*\phi (\eta _p)=\phi ({\langle }{{\xi _p}\,\vert \,\mathopen {}{\eta _p}}{\rangle })$
for every
$\xi _p, \eta _p\in \mathcal {E}_p$
. Suppose
$\beta \in {\mathcal W}$
has the form
$\beta =(p,q,q,p).$
Let
$\xi _1,\xi _2\in \mathcal {E}_p$
and
$\eta _1,\eta _2\in \mathcal {E}_q.$
We show that there exists
$a \in A$
such that
$$ \begin{align*} \phi (\xi_1)^* \phi (\eta_1) \phi (\eta_2)^*\phi (\xi_2)\zeta_s=\varphi_s(a)\zeta_s \end{align*} $$
for all
$\zeta _s\in \mathcal {E}_s$
and
$s\in K(\beta )$
.
Let
$c\in A$
be such that
$\varphi _s(c)=\phi (\eta _1) \phi (\eta _2)^*$
on
$\mathcal {E}_s$
for all
$s\in qP$
. If
$s\in K(\beta )$
, then
$ps\in qP$
and
$$ \begin{align*} \phi (\xi_1)^* \phi (\eta_1) \phi (\eta_2)^*\phi (\xi_2)\zeta_s=\phi (\xi_1)^* \varphi_{ps}(c)\phi (\xi_2)\zeta_s=\varphi_s({\langle}{{\xi_1}\,\vert\,\mathopen{}{\varphi_p(c)\xi_2}}{\rangle})\zeta_s. \end{align*} $$
Setting 
, we see that
$\phi (\xi _1)^* \phi (\eta _1) \phi (\eta _2)^*\phi (\eta _2)\zeta _s=\varphi _s(a)\zeta _s$
for all
$\zeta _s\in \mathcal {E}_s$
and all
$s\in K(\beta )$
, as needed.
To establish the statement, consider the collection of neutral words
$\beta $
such that for all
$b\in {\mathcal I}(\beta )$
, there exists
$a\in A$
with
$\varphi _s(a)=b$
on
$\mathcal {E}_s$
for all
$s\in K(\beta )$
. To show that this collection contains
$\langle {\mathcal W}_{\mathrm {{sym}}}\rangle $
, it suffices to show that it is closed under concatenation and conjugation by words of the form
$(p,q)$
with
$p,q\in P$
. Indeed, that it is closed under concatenation follows because
$K(\beta _1\beta _2)=K(\beta _1)\cap K(\beta _2)$
whenever
$\beta _1,\beta _2\in {\mathcal W}$
are neutral words and because the diagonal action of A on the Fock space is multiplicative. That the collection is closed under concatenation by words of the form
$(p,q)$
with
$p,q\in P$
follows as in the first part of the proof.
Proposition 5.3. Let P be a submonoid of a group and let
$\mathcal {E}=(\mathcal {E}_p)_{p\in P}$
be a product system over P with coefficients in a
$\mathrm {C}^{*}$
-algebra A. Suppose that
$\varphi _p(A)\supset {\mathbb K}(\mathcal {E}_p)$
for all
$p\in P$
. Let
$\emptyset \neq S\in {\mathfrak J}$
and suppose that
$$ \begin{align} {\mathcal I}(S)\subset{\operatorname{\overline {span}}}\{bQ_S\mid b\in {\mathcal I}(\beta),\ \beta\in \langle{\mathcal W}_{\mathrm{{sym}}}\rangle, \ K(\beta)\supset S\}, \end{align} $$
where
$Q_S$
denotes the orthogonal projection of the Fock space
$\mathcal {E}^+$
onto
$\bigoplus _{p\in S}\mathcal {E}_p$
. Then, there exists an ideal
$I_S\mathrel {\triangleleft } A$
such that the
${}^{*}$
- homomorphism
$\phi _S$
from A into the algebra of adjointable operators on
$\bigoplus _{s\in S}\mathcal {E}_s$
obtained by the restriction of the Fock representation induces a surjective
${}^{*}$
- homomorphism
$\phi _S\restriction _{I_S}\colon I_S\to {\mathcal I}(S)$
. In particular, if A is nuclear (respectively exact), then so is
${\mathcal I}(S)$
.
Proof. Let
$\phi _S$
be the
${}^{*}$
- homomorphism from A into the algebra of adjointable operators on
$\bigoplus _{s\in S}\mathcal {E}_s$
obtained by compressing the Fock representation with the projection onto
$\bigoplus _{s\in S}\mathcal {E}_s$
. By Lemma 5.2 for every
$\beta \in \langle {\mathcal W}_{\mathrm {{sym}}}\rangle $
and
$b\in {\mathcal I}(\beta )$
, there exists
$a\in A$
such that
$\phi _{K(\beta )}(a)=b$
. Then, Assumption (5-1) implies that
$\phi _S(A)\supset {\mathcal I}(S)$
.
Define 
Then,
$I_S$
is an ideal of A because
$\phi $
is a representation of
$\mathcal {E}$
. We conclude that
$\phi _S\restriction _{I_S}\colon I_S\to {\mathcal I}(S)$
is a surjective
${}^{*}$
-homomorphism. Since ideals of nuclear
$\mathrm {C}^{*}$
-algebras are also nuclear and nuclearity passes to quotients, we obtain that nuclearity of A implies that of
${\mathcal I}(S).$
Theorem 5.4. Let P be a submonoid of a group G and let
$\mathcal {E}=(\mathcal {E}_p)_{p\in P}$
be a product system over P with coefficients in a
$\mathrm {C}^{*}$
-algebra A. Suppose that
$\varphi _p(A)\supset {\mathbb K}(\mathcal {E}_p)$
for all
$p\in P$
and that every nontrivial constructible right ideal
$ S$
of P satisfies (5-1). Then, the following are equivalent:
-
(1) the coefficient algebra A is nuclear;
-
(2) the fixed point algebra
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
is nuclear.
If, in addition, G is amenable, then
$\mathcal {T}_u(\mathcal {E}) \cong {\mathcal {T}_{\lambda }}(\mathcal {E})$
and these conditions are also equivalent to:
-
(3) the Toeplitz algebra
${\mathcal {T}_{\lambda }}(\mathcal {E})$
is nuclear.
Proof. Suppose first A is nuclear. By Proposition 5.3,
${\mathcal I}(S)$
is nuclear for every
$S\in {\mathfrak J}$
. By Theorem 4.6,
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
is nuclear.
Suppose now that
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
is nuclear. The compression of the Fock representation with the projection onto the direct summand
$\mathcal {E}_e=A$
yields a
${}^{*}$
-homomorphism from
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
onto A. Hence, A is nuclear.
If G is any group containing P, the topological G-grading of
${\mathcal {T}_{\lambda }}(\mathcal {E})$
induced by the canonical normal gauge coaction of G gives
${\mathcal {T}_{\lambda }}(\mathcal {E})$
the structure of reduced
$\mathrm {C}^{*}$
-algebra of a Fell bundle over G. Since the fixed point algebra
${\mathcal {T}_{\lambda }}(\mathcal {E})^G\cong \mathcal {T}_u(\mathcal {E})^G$
is the range of the conditional expectation of the gauge coaction, (3) implies (2). Suppose now G is amenable, in which case,
$\mathcal {T}_u(\mathcal {E}) \cong {\mathcal {T}_{\lambda }}(\mathcal {E})$
because their Fell bundle is amenable. If
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
is nuclear, then
${\mathcal {T}_{\lambda }}(\mathcal {E})$
is nuclear by [Reference Exel12, Proposition 25.10]. This shows that in this case, (3) is equivalent to (1) and (2), completing the proof.
Remark 5.5. Theorem 5.4 gives conditions under which nuclearity passes from the coefficient algebra A to the Toeplitz algebra
${\mathcal {T}_{\lambda }}(\mathcal {E})$
. What makes this possible is that the fixed point algebra
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
that appears in the intermediate step does not depend on the group in which P is embedded; see Remark 2.5. So all it takes is to find an embedding of P in an amenable group. Examples show that such embeddings may exist even in cases when the obvious embeddings of P are into nonamenable groups.
When the group G is exact,
${\mathcal {T}_{\lambda }}(\mathcal {E})$
is exact if and only if the fixed point algebra
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
is exact by [Reference Exel12, Proposition 25.12]. This focuses our attention on exactness of
${\mathcal {T}_{\lambda }}(\mathcal {E})^G$
, for which we have the following result, which is independent from exactness of G.
6 Examples
In this section, we exhibit several classes of monoids for which every product system of full correspondences, such that the left action of the coefficient algebra contains the compact operators, automatically satisfies the assumptions of Theorem 5.4. Most of the monoids we consider embed into amenable groups, so that Theorem 5.4 tells us that
${\mathcal {T}_{\lambda }}(\mathcal {E})$
is nuclear if and only if the coefficient algebra A is nuclear. In all our examples, the monoids embed into exact groups, so that Theorem 5.6 implies that
${\mathcal {T}_{\lambda }}(\mathcal {E})$
is exact if and only if A is exact. We emphasize that the results in this section apply to the class of product systems arising from the framework initially introduced by Exel as a generalization of the crossed product construction for single endomorphisms [Reference Exel11], and developed by Larsen for abelian semigroups of endomorphisms, provided that the left action contains the compact operators [Reference Larsen22]. This is the case when the action of P on A consists of injective endomorphisms with hereditary range (Example 6.1); in fact, these examples were our original motivation behind Theorem 5.4.
Example 6.1. Let A be a unital
$\mathrm {C}^{*}$
-algebra and let
$\alpha \colon P\to \mathrm {End}(A)$
be an action of P on A by injective endomorphisms with hereditary range. For each
$p\in P$
, let 
, with the left action of A given by multiplication and the right action implemented by
$\alpha _p$
. When equipped with the A-valued inner product 
each
$A_{\alpha _p}$
is a correspondence over A and
$A_\alpha =(A_{\alpha _p})_{p\in P}$
is a product system over P, where the correspondence isomorphism
$\mu _{p,q}$
is determined on an elementary tensor by
$\mu _{p,q}(a\alpha _p(1)\otimes b\alpha _q(1))=a\alpha _p(b)\alpha _{pq}(1).$
6.1 Abelian monoids
Theorem 6.2. Let P be an abelian cancellative monoid and A be a
$\mathrm {C}^{*}$
-algebra. Let
$\mathcal {E}=(\mathcal {E}_p)_{p\in P}$
be a product system over P with coefficient algebra A such that
${\varphi _p(A)\supset {\mathbb K}(\mathcal {E}_p)}$
for all
$p\in P$
. Suppose in addition that
$\mathcal {E}_p$
is full for each
$p\in P$
. Then,
$\mathcal {E}$
satisfies the assumptions of Theorem 5.4, and hence
${\mathcal {T}_{\lambda }}(\mathcal {E})$
is nuclear if and only if A is nuclear.
Proof. By assumption, P embeds in an abelian (hence amenable) group and
$\varphi (A)$
contains the compacts by assumption, so we only need to verify that (5-1) holds for
$\mathcal {E}$
.
First, we observe that since
$\mathcal {E}$
is full and P is abelian,
$$ \begin{align} {\mathcal I}((p,q))=\phi (\mathcal{E}_{p})^*\phi (\mathcal{E}_{q})=\phi (\mathcal{E}_{sp})^*\phi (\mathcal{E}_{sq})= \phi (\mathcal{E}_{ps})^*\phi (\mathcal{E}_{qs})={\mathcal I}((ps,qs)) \end{align} $$
for all
$p,q\in P$
. Given a not necessarily neutral word
$\beta =(p_1,p_2,p_3,p_4)\in {\mathcal W}^2$
, we let 
; then,
$\dot {\beta '}=\dot {\beta }, K(\beta ')=K(\beta )$
and (6-1) implies that
${\mathcal I}(\beta )\subset {\mathcal I}(\beta ')$
. Notice that the second letter coincides with the third one.
Assume as induction hypothesis that for some fixed
$l\geq 3$
and for every word
$\sigma \in {\mathcal W}^s$
with
$s\leq l$
, there exists
$\sigma '\in {\mathcal W}^s$
with
$\dot {\sigma '}=\dot {\sigma }$
,
$K(\sigma ')=K(\sigma )$
and
$\mathcal {I}(\sigma )\subset \mathcal {I}(\sigma ')$
such that every even letter
$q_{2j}$
in
$\sigma '$
coincides with the subsequent letter
$q_{2j+1}$
. Let
$\beta =(p_1,p_2,\ldots ,p_{2l+1}, p_{2l+2})\in {\mathcal W}^{l+1}$
be a word of even length
$l+1$
. Write
$\beta =\sigma (p_{2l+1},p_{2l+2})$
with
$\sigma =(p_1, \ldots , p_{2l-1},p_{2l})\in {\mathcal W}^l$
and let
$\sigma '=(q_1,\ldots , q_{2l})\in {\mathcal W}^l$
be as in the induction hypothesis for
$\sigma $
. Then,
$$ \begin{align*} \dot{\beta}=\dot{\sigma'}p_{2l+1}^{-1}p_{2l}, \quad K(\beta)=K(\dot{\sigma'}p_{2l+1}^{-1}p_{2l+2})\quad \text{and}\quad {\mathcal I}(\beta)\subset {\mathcal I}(\sigma'(p_{2l+1},p_{2l+2})). \end{align*} $$
Set
$$ \begin{align*} \beta'&=(q_1p_{2l+1},q_2p_{2l+1},\ldots,q_{2l-1}p_{2l+1},q_{2l}p_{2l+1},p_{2l+1}q_{2l},p_{2l+2}q_{2l})\\ &= (\sigma'\cdot p_{2l+1}) ((p_{2l+1},p_{2l+2})\cdot q_{2l}). \end{align*} $$
That is,
$\beta '\in {\mathcal W}^{l+1}$
is the concatenation of the word obtained by multiplying each letter of
$\sigma '$
by
$p_{2l+1}$
on the right, with the word
$(p_{2l+1}q_{2l},p_{2l+2}q_{2l})$
. Then,
$\beta '$
satisfies
$$ \begin{align*} \dot{\beta'}=\dot{\beta}, \quad K(\beta')=K(\sigma'(p_{2l+1},p_{2l+2}))=K(\beta),\end{align*} $$
and again by (6-1),
$$ \begin{align*} {\mathcal I}(\beta)\subset {\mathcal I}(\sigma'(p_{2l+1},p_{2l}))\subset{\mathcal I}(\beta'). \end{align*} $$
Moreover, since P is abelian,
$q_{2l}p_{2l+1} = p_{2l+1}q_{2l}$
and thus every even letter of
$\beta '$
coincides with the subsequent letter. This proves that the induction hypothesis holds for words of even length
$l+1$
, and hence by induction, it also holds for words of arbitrary length.
Now, let
$\beta $
be a neutral word. Then there exists a neutral word
$\beta '$
, with the same even length as
$\beta $
, such that
$K(\beta ')=K(\beta ), {\mathcal I}(\beta )\subset {\mathcal I}(\beta ')$
and every even letter in
$\beta '$
coincides with the subsequent letter. Because
$\beta '$
is neutral, it follows in addition that the first and last letters of
$\beta '$
are the same. Hence, we may view
$\beta '$
as a word in
$\langle {\mathcal W}_{\mathrm {{sym}}}\rangle $
by adding letters that equal the identity element e, if necessary. This shows that
$\mathcal {E}$
satisfies (5-1), and thus all the assumptions of Theorem 5.4 are satisfied. By the equivalence of parts (1) and (3) in Theorem 5.4,
${\mathcal {T}_{\lambda }}(\mathcal {E})$
is nuclear if and only if A is nuclear, completing the proof.
6.2 ax+b monoids
Suppose now R is an integral domain and let
$R^\times $
denote the multiplicative monoid of nonzero elements of R. Let
$R\rtimes R^\times $
be the
$ax+b$
-monoid of R, in which the operation is
$(b,a) (d,c) = (b+ad,ac) $
.
Theorem 6.3. Let
$R\rtimes R^\times $
be the
$ax+b$
-monoid of the integral domain R and let A be a
$\mathrm {C}^{*}$
-algebra. Let
$\mathcal {E}=(\mathcal {E}_p)_{p\in P}$
be a product system over
$R\rtimes R^\times $
with coefficient algebra A such that
$\varphi _p(A)\supset {\mathbb K}(\mathcal {E}_p)$
for all
$p\in R\rtimes R^\times $
. Suppose in addition that
$\mathcal {E}_p$
is full for each
$p\in R\rtimes R^\times $
. Then,
$\mathcal {E}$
satisfies the assumptions of Theorem 5.4, so that
${\mathcal {T}_{\lambda }}(\mathcal {E})$
is nuclear if and only if A is nuclear.
Proof. Let
$K = (R^\times )^{-1} R$
be the fraction field of R. Then,
$R\rtimes R^\times $
embeds in the group
$K\rtimes K^*$
, which is amenable. Left multiplication by A contains the compacts by assumption, so we only need to verify that the inclusion (5-1) holds.
Notice that since
$\{(a,1)\mid a\in R\}$
is an abelian submonoid of
$R\rtimes R^\times $
, it follows as in the proof of Theorem 6.2 that
$$ \begin{align*} {\mathcal I}(\beta)\subset{\operatorname{\overline {span}}}\{b\mid b\in {\mathcal I}(\beta'), \ \beta'\in {\mathcal W}_{\mathrm{{sym}}}(R\rtimes\{1\}), K(\beta')=K(\beta)\} \end{align*} $$
in the case where
$b_i=1$
for all
$i=1,\ldots , 2l$
. Also, in the case where
$b_i=1$
for all i except for
$i=1$
and
$i=2l$
, we have
$b_1=b_{2l}$
and
$$ \begin{align*} \mathcal{I}(\beta)\subset\tilde{\phi }(\mathcal{E}_{(0,b_1)})^*\mathcal{I}(\tilde{\beta})\tilde{\phi }(\mathcal{E}_{(0,b_1)}), \end{align*} $$
where
$\tilde {\beta }=((a_1,1), (a_2,1),\ldots , (a_{2l-1},1),(a_{2l},1))$
. Since
$\tilde {\beta }$
is neutral because
$\beta $
is, we obtain that
$$ \begin{align*} {\mathcal I}(\beta)\subset{\operatorname{\overline {span}}}\{b\mid b\in {\mathcal I}(\beta'),\ \beta'\in{\mathcal W}_{\mathrm{{sym}}}s(R\rtimes R^\times), K(\beta')=K(\beta)\}. \end{align*} $$
The general case follows from the above if we show that for every word
$\beta \in {\mathcal W}$
(not necessarily neutral), there exist
$\tilde {\beta }\in {\mathcal W}^l(R\rtimes \{1\})$
and
$c_1, c_{2l}\in R^\times $
such that
$\dot {\beta }=(0,c_1)^{-1}\dot {\tilde {\beta }}(0,c_{2l})$
,
$K(\beta )\subset K(((0,c_1),e)\tilde {\beta }(e,(0,c_{2l})))$
and
$$ \begin{align*}\mathcal {I}(\beta )\subset \tilde {\phi }(\mathcal {E}_{(0,c_1)})^*\mathcal {I} (\tilde {\beta })\tilde {\phi }(\mathcal {E}_{(0,b_1)})Q_{K(\beta )}. \end{align*} $$
To do so, we begin by proving by induction that given a word
$\beta =(p_1,p_2,\ldots , p_{2l-1}, p_{2l}) \in {\mathcal W}^l$
in
$R\rtimes R^\times $
, with
$p_i=(a_i,b_i)\in R\rtimes R^\times $
for each
$i=1, \ldots , 2l$
, there exists a word
$\beta '=(q_1,q_2,\ldots , q_{2l-1},q_{2l})\in {\mathcal W}^l,$
where
$q_i=(c_i,d_i)$
for
$i=1,\ldots , 2l$
, with
$\dot {\beta '}=\dot {\beta }$
,
$K(\beta ')=K(\beta )$
and
${\mathcal I}(\beta )\subset {\mathcal I}(\beta ')$
such that for every even letter
$q_{2j}$
in
$\beta '$
, its coordinate
$d_{2j}$
coincides with the corresponding coordinate
$d_{2j+1}$
in the subsequent letter
$q_{2j+1}$
.
As in the proof of Theorem 6.2, we have that for all
$a_1, a_2\in R$
and
$b_1,b_2\in R^\times $
,
$$ \begin{align*}{\mathcal I}(((a_1,b_1),(a_2,b_2)))={\mathcal I}(((da_1,db_1),(da_2,db_2)))\end{align*} $$
for all
$d\in R^\times $
since
$\mathcal {E}_{(0,d)}$
is full. So, given a word
$\beta =(p_1,p_2,p_3,p_4)\in {\mathcal W}^2$
with
$p_i=(a_i,b_i)\in R\rtimes R^\times $
, we let 
; then,
$\dot {\beta '}=\dot {\beta }, K(\beta ')=K(\beta )$
and
${\mathcal I}(\beta )\subset {\mathcal I}(\beta ')$
. In addition, if we write
$\beta '=(q_1,q_2,q_3,q_4)$
and
$q_i=(c_i,d_i)\in R\rtimes R^\times $
, we see that
$d_2=d_3$
because R is commutative, so that
$\beta '$
has the desired properties.
Assume as induction hypothesis that for some fixed
$l\geq 3$
and for every word
${\sigma \in {\mathcal W}^s}$
with
$s\leq l$
, there exists
$\sigma '\in {\mathcal W}^s$
with
$\dot {\sigma '}=\dot {\sigma }$
,
$K(\sigma ')=K(\sigma )$
and
$\mathcal {I}(\sigma )\subset \mathcal {I}(\sigma ')$
such that the second coordinate of every even letter
$q_{2j}$
in
$\sigma '$
coincides with the second coordinate in the subsequent letter
$q_{2j+1}$
. Let
${\beta =(p_1,p_2,\ldots ,p_{2l+1}, p_{2l+2})\in {\mathcal W}^{l+1}}$
be a word of even length
$l+1$
. Proceeding as in the proof of Theorem 6.2, we write
$\beta =\sigma (p_{2l+1},p_{2l+2})$
with
$\sigma =(p_1, \ldots , p_{2l-1},p_{2l})\in {\mathcal W}^l$
and let
$\sigma '=(q_1,\ldots , q_{2l})\in {\mathcal W}^l$
with
$q_i=(c_i,d_i)\in R\rtimes R^\times $
be as in the induction hypothesis for
$\sigma $
. Putting
$$ \begin{align*} \beta'&= ((0,b_{2l+1})\cdot\sigma') ((0,d_{2l})\cdot(p_{2l+1},p_{2l+2})), \end{align*} $$
we see that
$\beta '$
satisfies the required properties, so that the induction hypothesis also holds for
$\beta $
. Hence, it also holds for every word in
${\mathcal W}(R\rtimes R^\times )$
.
Now, let
$\beta =(p_1,p_2,\ldots , p_{2l-1}, p_{2l}) \in {\mathcal W}^l$
. We write
$p_i=(a_i,b_i)\in R\rtimes R^\times $
for
$i=1, \ldots , 2l$
. By the above, we may assume that
$b_{2i}=b_{2i+1}$
for
$1\leq i\leq l-1.$
Using that
$\phi (\mathcal {E}_{(a,b)})=\phi (\mathcal {E}_{(a,1)})\phi (\mathcal {E}_{(0,b)})$
on the Fock space and that for all
$b\in R^\times $
, the left action of A on
$\mathcal {E}_{(0,b)}$
contains the compact operators, we deduce that
${\mathcal I}(\beta )\subset {\mathcal I}(\beta ')Q(\beta ),$
where
$\beta '=(q_1,q_2,\ldots , q_{2l})$
is the word whose first and last letters coincide with those of
$\beta $
, and
$q_i=(a_i,1)$
for
$i=2,3,\ldots , 2l-1$
. Since
$\beta '$
, in turn, satisfies
${{\mathcal I}(\beta ')={\mathcal I} (((0,b_1),e)\tilde {\beta }(e,(0,b_{2l})))}$
where
$\tilde {\beta }=((a_1,1),(a_2,1),\ldots , (a_{2l},1))\in {\mathcal W}(R\rtimes \{1\}),$
the conclusion now follows as in Theorem 6.2.
6.3 Baumslag–Solitar monoids
For each pair of nonzero integers
$m,n$
, the Baumslag–Solitar group
$BS(m,n)$
is the group with presentation
The presentation can be restated without using negative exponents, so that it makes sense for monoids. Thus, when
$m,n \geq 1$
, the Baumslag–Solitar monoid is the monoid with presentation
and when
$m\geq 1$
and
$n\leq -1$
, it is the monoid with presentation
The cases where
$m\leq -1$
,
$n\leq -1$
and
$m\leq -1$
,
$n\geq 1$
can be reduced to the two above by exchanging m and n. We thus assume that we are either in
Case 1:
$m \geq 1$
,
$n \geq 1$
or in
Case 2:
$m\geq 1$
,
$n\leq -1$
.
Every element p in
$BS^+(m,n)$
has a unique normal form
$$ \begin{align*} p=b^{c_0}ab^{c_1}a\cdots b^{c_{k-1}}a b^{c_k}, \end{align*} $$
in which
$k \in \mathbb {N}$
and
$0\leq c_i\leq |n|-1 $
for
$0\leq i\leq k-1$
with
$c_k\in \mathbb {N}$
in Case 1 and
${c_k\in \mathbb {Z}}$
in Case 2, except that
$c_0 \geq 0$
always. This is obtained by pushing powers of b to the right using
$ b^na \rightsquigarrow ab^m $
until the normal form is achieved; see for example [Reference Spielberg30, Section 2]. Here, k is the number of a terms in any expression of p; it is called the height of p and is denoted 
. The stem of p is the product 
, so that
$p=\mathrm {stem}(p)b^{c_k}$
.
Using the normal form for elements of
$BS(m,n)$
, one can show that the monoid
$BS^+(m,n)$
embeds canonically in the group
$BS(m,n)$
as the submonoid generated by a and b. The pair
$(BS(m,n),BS^+(m,n))$
is a weak quasi-lattice order, that is,
$BS^+(m,n)$
is a group-embeddable right LCM monoid with no nontrivial invertible elements.
Remark 6.4. Recall from [Reference an Huef, Raeburn and Tolich16, Lemma 5.5] that if p and q have a common upper bound in
$BS^+(m,n)$
(that is, if
$pBS^+(m,n)\cap qBS^+(m,n)\neq \emptyset $
) and
$\theta (p)\leq \theta (q)$
, then
$\mathrm {stem}(p)$
is a prefix of
$\mathrm {stem}(q)$
. This is useful in the proof of the next result.
We are now ready to show that every full product system over a Baumslag–Solitar monoid with
$m,n\geq 1$
such that the left action contains the compact operators automatically satisfies the assumptions in Theorem 5.4. For the case where
$m\geq 1$
,
$n\leq -1$
, see Remark 6.6.
Theorem 6.5. Suppose
$m,n\geq 1$
and let
$\mathcal {E}=(\mathcal {E}_p)_{p\in BS^+(m,n)}$
be a product system over the Baumslag–Solitar monoid
$BS^+(m,n)$
with coefficient algebra A such that
${\varphi _p(A)\supset {\mathbb K}(\mathcal {E}_p)}$
for all
$p\in BS^+(m,n)$
. Suppose in addition that
$\mathcal {E}_p$
is full for each
$p\in BS^+(m,n)$
. Then,
$\mathcal {E}$
satisfies the assumptions of Theorem 5.4 and the following hold:
-
(1)
${\mathcal {T}_{\lambda }}(\mathcal {E})$
is exact if and only if A is exact; -
(2) if
$\gcd (m,n) =1$
, then
${\mathcal {T}_{\lambda }}(\mathcal {E})$
is nuclear if and only if A is nuclear. The result is valid without the assumption
$\gcd (m,n) =1$
; see Remark 6.6(2) below.
Proof. Let
$\beta =(p_1,p_2,\ldots , p_{2l})\in {\mathcal W}^l$
be a neutral word in
$BS^+(m,n).$
We prove by induction on l that there exists
$\beta '\in \langle {\mathcal W}_{\mathrm {{sym}}}\rangle $
, with even length at most l,
$K(\beta )\subset K(\beta ')$
and
${\mathcal I}(\beta )\subset {\mathcal I}(\beta ')Q_{K(\beta )}.$
First, notice that because
$\phi (\mathcal {E}_p)^*\phi (\mathcal {E}_p)\subset \phi ({\langle }{{\mathcal {E}_p}\,\vert \,\mathopen {}{\mathcal {E}_p}}{\rangle })$
, using Remark 6.4, we may assume that for each
$1\leq i\leq l$
, one of the letters
$p_{2i-1}$
or
$p_{2i}$
has height zero, and hence belongs to
$\langle b\rangle ^+$
. By the same reasoning, we may assume that the letter of positive height starts with a in normal form.
Now, let
$\beta $
be as above with
$l=2$
, say
$\beta =(p_1,p_2,p_3,p_4)$
. Since
$\beta $
is neutral, we must have either
$\theta (p_2)=\theta (p_3)=0$
or
$\theta (p_1)=\theta (p_4)=0.$
Case 1:
$\theta (p_2)=\theta (p_3)=0$
. In this case,
$\beta =(p_1, b^{k_1}, b^{k_2}, p_4)$
with
$k_1, k_2\in \mathbb {N}$
. If
$k_2\geq k_1$
, we use that the action of A on
$\mathcal {E}_{b^{k_1}}$
contains the compact operators to conclude that
$$ \begin{align*} {\mathcal I}(\beta)\subset {\mathcal I}(\beta')Q(\beta), \end{align*} $$
where
$\beta '=(b^{k_2-k_1}p_1, p_4)$
is neutral with
$K(\beta )\subset K(\beta ')$
. Similarly in the case where
$k_1\geq k_2$
, we get
${\mathcal I}(\beta )\subset {\mathcal I}(\beta ')Q(\beta )$
, with
$\beta '=(p_1, b^{k_1-k_2}p_4)$
.
Case 2:
$\theta (p_1)=\theta (p_4)=0$
. In this case,
$\beta =(b^{k_1}, p_2, p_3, b^{k_2})$
with
$k_1, k_2\in \mathbb {N}$
. Since
$\beta $
is neutral, we obtain
$p_2p_3^{-1}=b^{k_1-k_2}.$
In the case where
$k_1\geq k_2$
, we use that
$p_2=b^{k_1-k_2}p_3$
and that the left action of A on
$\mathcal {E}_{p_3}$
contains the compact operators to get that
${\mathcal I}(\beta )\subset {\mathcal I}(\beta ')Q_{K(\beta )}$
with
$\beta '=(b^{k_1}, b^{k_1})$
. Similarly, in the case where
$k_1-k_2<0$
, we see that
$p_3=b^{k_2-k_1}p_2$
, and so
${\mathcal I}(\beta )\subset {\mathcal I}(\beta ')Q_{K(\beta )}$
with
$\beta '=(k_2,k_2).$
Suppose
$\beta =(p_1,p_2,\ldots , p_{2l+1}, p_{2l})\in {\mathcal W}$
is a neutral word in
$BS^+(m,n)$
as above with even length
$l+1\geq 3$
. We separate the proof into two cases.
Case 1:
$\theta (p_1)>0$
. In this case, there must be
$1\leq i\leq l$
such that
${\theta (p_{2i})=\theta (p_{2i+1})=0}$
because
$\beta $
is neutral. Then, we proceed as in Case 1 above to find a neutral word
$\beta _l\in {\mathcal W}^l$
such that
$K(\beta )\subset K(\beta _l)$
and
${\mathcal I}(\beta )={\mathcal I}(\beta _l)Q_{K(\beta )}.$
By induction, there exists
${\beta '\in \langle {\mathcal W}_{\mathrm {{sym}}}\rangle }$
with
$K(\beta )\subset K(\beta _l)\subset K(\beta ') $
and
${\mathcal I}(\beta )\subset {\mathcal I}(\beta _l)Q_{K(\beta )}\subset {\mathcal I}(\beta ')Q_{K(\beta )}$
, as desired.
Case 2:
$\theta (p_1)=0$
. In this case, there must be
$1\leq i\leq l$
such that
${\theta (p_{2i})\neq 0}$
and
$\theta (p_{2i+1})\neq 0$
. Write
$\beta $
as the concatenation
$\beta =\sigma _1\beta _1\sigma _2$
, where
$\sigma _1\in {\mathcal W}^{i-1}$
,
${\sigma _2\in {\mathcal W}^{l-i}}$
and
$\beta _1=(p_{2i-1},p_{2i}, p_{2i+1},p_{2i+2})$
. It follows from our assumptions on
$\beta $
that
${\theta (p_{2i-1})=0=\theta (p_{2i+2}).}$
If either
$\theta (p_{2i-2})=0$
or
$\theta (p_{2i+3})=0$
, we proceed as in the proof of Case 1.
Suppose
$\theta (p_{2i-2})\neq 0$
. Let
$k\geq 0$
be such that
$p_{2i-1}=b^k$
. Using the relations in
$BS^+(m,n)$
, we can find a positive power
$c\in \mathbb {N}$
such that
$b^cp_{2i-3}=p_{2i-3}'b^d$
for some
$p^{\prime }_{2i-3}\in BS^+(m,n)$
and some
$d\geq k$
. Then, we use that
$$ \begin{align*}{\mathcal I}((p_{2i-3},p_{2i-2}))\subset {\mathcal I}((b^cp_{2i-3},b^cp_{2i-2})),\end{align*} $$
that
$\phi (\mathcal {E}_{p_{2i-3}'b^{d}})=\phi (\mathcal {E}_{p_{2i-3}'b^{d-k}})\phi (\mathcal {E}_{b^k})$
and that the action of A on
$\mathcal {E}_{b^k}$
contains the compact operators to get a neutral word
$\beta _l$
of even length l such that
$K(\beta )\subset K(\beta _l)$
and
${\mathcal I}(\beta )\subset {\mathcal I}(\beta _l)Q_{K(\beta )}.$
Again by induction, there exists
$\beta '\in \langle {\mathcal W}_{\mathrm {{sym}}}\rangle $
with
$K(\beta )\subset K(\beta _l)\subset K(\beta ') $
and
${\mathcal I}(\beta )\subset {\mathcal I}(\beta _l)Q_{K(\beta )}\subset {\mathcal I}(\beta ')Q_{K(\beta )}$
as required. This gives the case when the last letter of
$\sigma _1$
has positive height. The case when the first letter of
$\sigma _2$
has positive height follows from this by taking adjoints.
Part (1) now follows from Theorem 5.6 and [Reference Exel12, Proposition 25.12] because
$BS(m,n)$
is a one-relator group and hence is exact by [Reference Guentner14, Theorem 2.1]. Part (2) follows from Theorem 5.4 because when
$\gcd (m,n) =1$
, there is an embedding of
$B^+(m,n)$
into an amenable group G by Proposition 6.7 below.
Remark 6.6. (1) In the case where
$m\geq 1$
,
$n\leq -1$
, every two elements
$p,q\in B^+(m,n)$
with a common upper bound in
$BS^+(m,n)$
are comparable. See for example [Reference an Huef, Nucinkis, Sehnem and Yang15, Proposition 5.11]. Hence, every product system over
$B^+(m,n)$
is automatically compactly aligned and so Corollary 4.8 applies.
(2) After a first version of this paper was circulated, in which we proved that for relatively prime m and n, the monoid
$BS^+(m,n)$
embeds in an (amenable) group of upper triangular matrices, we learned from Xin Li that in [Reference Chen5, Section 4.2.1], it is proved that every Baumslag–Solitar monoid embeds in an amenable group; see also [Reference Chen and Li6]. As an immediate consequence, we see that Theorem 6.5(2) is valid without assuming
$\gcd (m,n) =1$
.
6.4 An embedding of
$BS^+(m,n)$
in an amenable group for
$\gcd (m,n) =1$
We include here for easy reference the proof that
$BS^+(m,n)$
embeds in the upper triangular
$2\times 2$
matrices in the relatively prime case.
Proposition 6.7. For every
$m,n \geq 1$
, there is a unique monoid homomorphism
$$ \begin{align*} \pi: BS^+(m,n) \to M_n^+(\mathbb{Z}) \subset \operatorname{GL}_2(\mathbb{Q}) \end{align*} $$
such that
$$ \begin{align*} a \mapsto A := \begin{pmatrix}n&0\\0&m\end{pmatrix}\quad\text{and}\quad b\mapsto B:= \begin{pmatrix}1&1\\0&1\end{pmatrix}. \end{align*} $$
If
$\gcd (m,n) =1$
, then
$\pi $
is an embedding of
$BS^+(m,n)$
into the subgroup of
$\operatorname {GL}_2(\mathbb {Q})$
generated by A and B, which is amenable.
Proof. For
$k,l \in \mathbb {N}$
, we compute
$AB^k = (\begin {smallmatrix}{n}&{kn}\\ 0&{m}\end {smallmatrix})$
and
$B^l A = (\begin {smallmatrix}{n}&{lm}\\ 0&{m}\end {smallmatrix})$
.
Let
$d:=\gcd (m,n)$
, and set
$k = m/d$
and
$l = n/d$
; then
$$ \begin{align*} AB^{m/d} = \begin{pmatrix}n&mn/d\\0&m\end{pmatrix} = B^{n/d}A. \end{align*} $$
If
$m,n$
are relatively prime, this is exactly the relation defining
$BS^+(m,n)$
. In general, write
$B^m = (B^{m/d})^d$
and move the d blocks
$B^{m/d}$
one by one using the above relation to obtain the relation defining
$B^+(m,n)$
.
Suppose now that the word
$p(a,b)$
in a and b representing an element of
$B^+(m,n)$
is in (R) normal form. The (R) normal form is the one obtained by pushing every possible b to the right until the substitution
$ b^na \rightsquigarrow ab^m $
can no longer be applied. Specifically,
$$ \begin{align*} p(a,b) = b^{j_0} ab^{j_1} a b^{j_2} a \cdots ab^{j_\ell} \end{align*} $$
with
$0\leq j_i < n$
for each
$i = 0,1, 2, \ldots , \ell -1$
and
$j_\ell \in \mathbb {Z}$
(in fact,
$j_\ell \in \mathbb {N}$
in Case 1), where
$\ell $
is the number of a terms in
$p(a,b)$
. The corresponding product of matrices is
$$ \begin{align*} p(A,B) = \begin{pmatrix}n^\ell& j_0 m^{\ell} + n j_1 m^{\ell-1} + \cdots +n^{\ell -1}j_{\ell -1} m + n^{\ell} j_\ell \\0&{m^\ell}\end{pmatrix}. \end{align*} $$
Assume now that there exist two different normal forms p and
$p'$
(necessarily corresponding to two different elements of
$BS^+(m,n)$
that produce the same matrix
$p(A,B) = p'(A,B)$
). Then,
$p(A,B)_{1,1} = p'(A,B)_{1,1}$
implies that
$\ell = \ell '$
. If we then take
$p(A,B)_{1,2} = p'(A,B)_{1,2}$
modulo n,
$$ \begin{align*} (j_0 - j^{\prime}_0) m^\ell = 0 \ (\text{mod } n). \end{align*} $$
Assuming
$\gcd (m,n) =1$
, we see that
$j_0 - j^{\prime }_0 =0\ (\text {mod } n)$
, and hence,
$j_0 =j^{\prime }_0$
because both
$j_0$
and
$j^{\prime }_0$
are between
$0$
and
$n-1$
. We can then factor out the first power of B and the first A in both p and
$p'$
. This gives two different shorter normal forms in
$BS^+(m,n)$
(in the a-length) that produce the same matrix. Iterating this procedure, we arrive at a contradiction. We conclude that the representation is an embedding when
$d=1$
.
The subgroup of
$\operatorname {GL}_2(\mathbb {Q})$
generated by the matrices A and B is contained in the group of upper triangular matrices, which is solvable, and hence amenable.
Remark 6.8. If
$\gcd (m,n) \neq 1$
, then the representation
$\pi $
given in the proposition is not an embedding of
$BS^+(m,n)$
into matrices. Indeed, as seen above, the matrices satisfy
$AB^{m/d} = B^{n/d}A$
, but since
$n/d <n$
, both
$ab^{m/d}$
and
$b^{n/d}a$
are in normal form, and hence are different in
$BS^+(m,n)$
. If we factor A as
$$ \begin{align*} A := \begin{pmatrix}d&0\\0&{d}\end{pmatrix} \begin{pmatrix}n/d&0\\ 0&{m/d}\end{pmatrix} \end{align*} $$
and use a slight modification of the proof of the lemma, we see that the image of
$\pi $
is isomorphic to
$BS^+(m/d,n/d)$
. The case
$m=n= d$
presents an extreme failure of embeddability; indeed
$$ \begin{align*} A := \begin{pmatrix}d&0\\0&{d}\end{pmatrix}\quad\text{and}\quad B:= \begin{pmatrix}1&1\\0&{1}\end{pmatrix} \end{align*} $$
commute and generate a copy of
$\mathbb {N}^2$
.
Acknowledgements
We are thankful for the hospitality extended to us by Marek Ptak at Uniwersytet Rolinczy. At the later stages, we received the preprint [Reference Kakariadis and Paraskevas17] which also deals with Fock covariance for product systems; the overlap is limited because the main concern there is with Hao–Ng type theorems, while the main results here are about nuclearity and exactness. We would like to thank Xin Li for pointing out the references [Reference Chen5, Reference Chen and Li6], and the anonymous referee for many helpful suggestions.
Open access
