1 Introduction
At least since Tarski’s 1936 article on logical notions, logic has often been understood as the subject studying those notions which are “invariant under all possible one-one transformations of the world onto itself” [Reference Tarski29, p. 149]. Tarski’s view was inspired by Felix Klein’s 1872 Erlanger Programm, and expresses very neatly the philosophical idea of logic as the discipline with the most general character. While, for instance, metric geometry studies notions that are invariant under transformations that preserve distances, and topology studies notions invariant under continuous maps, logic deals with notions which are invariant under arbitrary bijections. Formally, this led to the technical definition of logics as consequence relations which are additionally closed under uniform substitutions.
As a matter of fact, Tarski’s approach can be seen as a key step in the transition from the “symbolic” algebraic logic of the nineteenth century (exemplified by the works of Boole, De Morgan, Jevons, Peirce, etc.) to the contemporary field of abstract algebraic logic. Using the general notion of logic as a closure operator on the term algebra, Rasiowa made the first steps into the “mathematical” version of algebraic logic, and in particular she developed in An Algebraic Approach to Non-Classical Logics [Reference Rasiowa27] a general theory of algebraization for implicative logics. Finally, the algebraic approach was put in its contemporary formulation by Blok and Pigozzi, who introduced in Algebraizable Logics [Reference Blok and Pigozzi4] the notion of algebraizable logics and developed their general theory.
In recent years, however, there has been an increasing interest into systems which do possess a logical nature but fail nonetheless to be closed under uniform substitution in Tarski’s original strong sense. The field of modal logic is particularly rich of such examples: Buss’ pure provability logic [Reference Buss6], public announcement logic (
![]() $ \mathtt {PAL} $
) [Reference Holliday, Hoshi, Icard, Ditmarsch, Lang and Ju19, Reference Holliday, Hoshi and Icard20], and other epistemic logics are all examples of this behaviour. Furthermore, propositional logics based on team semantics, such as inquisitive [Reference Ciardelli and Roelofsen12] and dependence logic [Reference Yang and Väänänen30], also do not satisfy Tarski’s requirement of closure under uniform substitution. We believe that this state of affairs is not a mistake requiring correction, but that it rather reflects the increasing plurality of logics and their aptness for applications. At the same time, however, the anomalous behaviour of these logical systems prevented so far a uniform abstract study, and did not allow for immediately applying facts and results from abstract algebraic logic, thus forcing scholars to reprove abstract results in these settings, or adapt standard techniques to their specific situation.
$ \mathtt {PAL} $
) [Reference Holliday, Hoshi, Icard, Ditmarsch, Lang and Ju19, Reference Holliday, Hoshi and Icard20], and other epistemic logics are all examples of this behaviour. Furthermore, propositional logics based on team semantics, such as inquisitive [Reference Ciardelli and Roelofsen12] and dependence logic [Reference Yang and Väänänen30], also do not satisfy Tarski’s requirement of closure under uniform substitution. We believe that this state of affairs is not a mistake requiring correction, but that it rather reflects the increasing plurality of logics and their aptness for applications. At the same time, however, the anomalous behaviour of these logical systems prevented so far a uniform abstract study, and did not allow for immediately applying facts and results from abstract algebraic logic, thus forcing scholars to reprove abstract results in these settings, or adapt standard techniques to their specific situation.
Motivated by these facts, we propose in this article a generalisation of the notion of algebraizable logic which breaks apart from Tarski’s original view of logics as being invariant under all substitutions. In other words, we want to study consequence operators that are invariant under some substitutions, but not necessarily all. We introduce the notion of weak logic, generalising previous definitions of Ciardelli and Roelofsen [Reference Ciardelli and Roelofsen12] and Punčochář [Reference Punčochář24], as a consequence relation which is invariant under all substitutions which map atomic variables to atomic variables. In other words, we relax Tarski’s constraint of invariance under arbitrary substitutions and we require that it holds only with respect to these so-called atomic substitutions (cf. Section 3 below).
We proceed in this article as follows. In Sections 3–6 we develop at length the key aspects of the theory of algebraizable weak logics. In Section 3 we define weak logics and introduce what we call expanded algebras as their corresponding algebraic notion. In Section 4 we introduce the notions of loose and strict algebraizability for weak logics and we show that the (loose or strict) equivalent algebraic semantics of a weak logic is unique, thus mirroring the classical result by Blok and Pigozzi for standard algebraizable logics. Then, in Section 5, we study the relation between a weak logic and its schematic fragment of consequences invariant under arbitrary substitutions. In particular, we provide a characterisation of the algebraizability of weak logics in terms of the algebraizability of their schematic fragment. Additionally, we introduce the notion of standard companion and generalise to this setting previous results from [Reference Almeida1, Reference Bezhanishvili, Grilletti and Quadrellaro3]. Finally, in Section 6 we develop on these results and we prove a version of Blok and Pigozzi’s Isomorphism Theorem for strictly algebraizable weak logics. These sections thus establish the fundamentals of the theory of algebraizable weak logics and show that several key results from the field of abstract algebraic logic carry on to the setting without uniform substitution. On a partially separate line of inquiry, in Section 7 we take a small excursus explaining how to adapt the usual matrix semantics of propositional logics to the setting of weak logics. We show that (similarly to the standard setting) every weak logic admits a matrix semantics, and we describe the class of reduced models of (strictly) algebraizable weak logics. We put our abstract framework to the test in Section 8, where we apply it to the specific case of inquisitive and dependence logics. In particular, we build on previous results from [Reference Bezhanishvili, Grilletti and Quadrellaro3, Reference Ciardelli, Iemhoff and Yang11, Reference Quadrellaro26] to show that the classical version of inquisitive and dependence logic is strictly algebraizable, while their intuitionistic versions are only loosely so. To our eyes, this indicates a significant difference between the classical version of inquisitive and dependence logic—which can essentially be recasted as a theory over their schematic fragment—and their intuitionistic counterparts, which do not admit such reformulation.
Together with these results on inquisitive and dependence logic, we regard as the main contribution of the present work the fact that it provides a framework for reasoning about logical systems lacking uniform substitution. In particular, this work relates several algebraic studies on inquisitive logic [Reference Bezhanishvili, Grilletti and Holliday2, Reference Bezhanishvili, Grilletti and Quadrellaro3, Reference Punčochář24, Reference Punčochář25], dependence logic [Reference Quadrellaro26], and polyatomic logics [Reference Almeida1], by showcasing all the algebraic semantics from these works as instances of what we call core semantics in the present article. Given the increasing popularity of logics without uniform substitution in the logic literature, we hope that our approach will be useful to researchers working in these areas also in the future.
2 Preliminaries
We recall in this section some basic facts concerning logics, algebras, and model theory. We also fix some notation that we shall follow throughout the rest of the article. The following general context sets the framework of our work.
Context 2.1. Throughout this article we always let
![]() $\mathsf {Var}$
be a set of variables and we let
$\mathsf {Var}$
be a set of variables and we let
![]() $\mathcal {L}$
be an algebraic (i.e., purely functional) signature (unless we specify otherwise). We denote by
$\mathcal {L}$
be an algebraic (i.e., purely functional) signature (unless we specify otherwise). We denote by
![]() $\mathsf {Fm}_{\mathcal {L}}$
both the set of first-order terms over
$\mathsf {Fm}_{\mathcal {L}}$
both the set of first-order terms over
![]() $\mathsf {Var}$
in the signature
$\mathsf {Var}$
in the signature
![]() $\mathcal {L}$
and the term algebra in the signature
$\mathcal {L}$
and the term algebra in the signature
![]() $\mathcal {L}$
over
$\mathcal {L}$
over
![]() $\mathsf {Var}$
. We omit the index
$\mathsf {Var}$
. We omit the index
![]() $\mathcal {L}$
when it is clear from the context. Notice that, since we are often dealing with propositional logical systems, we often refer to elements of
$\mathcal {L}$
when it is clear from the context. Notice that, since we are often dealing with propositional logical systems, we often refer to elements of
![]() $\mathsf {Fm}_{\mathcal {L}}$
also as (propositional) formulas in the language
$\mathsf {Fm}_{\mathcal {L}}$
also as (propositional) formulas in the language
![]() $\mathcal {L}$
. These should not be confused with the first-order formulas in the signature
$\mathcal {L}$
. These should not be confused with the first-order formulas in the signature
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
Given the language
![]() $\mathcal {L}$
, we recall the standard abstract Tarskian definition of (propositional) logic. We refer the reader to [Reference Font16, Section 1] for more on consequence relations and logics, and for slight variations of these definitions.
$\mathcal {L}$
, we recall the standard abstract Tarskian definition of (propositional) logic. We refer the reader to [Reference Font16, Section 1] for more on consequence relations and logics, and for slight variations of these definitions.
Definition 2.2. A (finitary) consequence relation is a relation
![]() $\vdash \; \subseteq \: \wp (\mathsf {Fm})\times \mathsf {Fm}$
such that, for all
$\vdash \; \subseteq \: \wp (\mathsf {Fm})\times \mathsf {Fm}$
such that, for all
![]() $\Gamma \subseteq \mathsf {Fm}$
:
$\Gamma \subseteq \mathsf {Fm}$
:
-
(1)
 $\Gamma \vdash \phi $
for all
$\Gamma \vdash \phi $
for all
 $\phi \in \Gamma $
;
$\phi \in \Gamma $
; -
(2) if
 $\Gamma \vdash \phi $
for all
$\Gamma \vdash \phi $
for all
 $\phi \in \Delta $
, and
$\phi \in \Delta $
, and
 $\Delta \vdash \psi $
, then
$\Delta \vdash \psi $
, then
 $\Gamma \vdash \psi $
;
$\Gamma \vdash \psi $
; -
(3) if
 $\Gamma \vdash \phi $
and
$\Gamma \vdash \phi $
and
 $\Gamma \subseteq \Delta $
, then
$\Gamma \subseteq \Delta $
, then
 $\Delta \vdash \phi $
;
$\Delta \vdash \phi $
; -
(4) if
 $\Gamma \vdash \phi ,$
then there is some
$\Gamma \vdash \phi ,$
then there is some
 $\Delta \subseteq \Gamma $
such that
$\Delta \subseteq \Gamma $
such that
 $|\Delta | < \aleph _0$
and
$|\Delta | < \aleph _0$
and
 $\Delta \vdash \phi $
.
$\Delta \vdash \phi $
.
Remark 2.3. Condition 2.2(3) already follows from Condition 2.2(1) together with Condition 2.2(2) (cf. also [Reference Font16, p. 14]), but we include it to make explicit the fact that we always assume consequence relations (and logics) to be monotone. Differently, Condition 2.2(4) is not always required in the definition of consequence relation and it essentially restricts the focus to the finitary ones. This reflects our elementary approach to the subject, as Condition 2.2(4) allows us to translate propositional systems into first-order logic and to avoid the use of infinitary logical systems lacking compactness. We stress that this requirement is not necessary, and it is possible to study consequence relations and propositional logics where this condition fails. We refer the interested reader to [Reference Font16] for discussions of Condition 2.2(4) and also for an (algebraic) treatment of non-finitary propositional logics.
Definition 2.4. A substitution is an endomorphism
![]() $\sigma : \mathsf {Fm} \to \mathsf {Fm}$
of the
$\sigma : \mathsf {Fm} \to \mathsf {Fm}$
of the
![]() $\mathcal {L}$
-term algebra. We denote by
$\mathcal {L}$
-term algebra. We denote by
![]() $\mathsf {Subst}(\mathcal {L})$
the set of all substitutions in the language
$\mathsf {Subst}(\mathcal {L})$
the set of all substitutions in the language
![]() $\mathcal {L}$
. If
$\mathcal {L}$
. If
![]() $x_1,\dots , x_n\in \mathsf {Var}$
and
$x_1,\dots , x_n\in \mathsf {Var}$
and
![]() $\phi _1,\dots ,\phi _n$
are arbitrary
$\phi _1,\dots ,\phi _n$
are arbitrary
![]() $\mathcal {L}$
-formulas, we denote by
$\mathcal {L}$
-formulas, we denote by
![]() $\Gamma [\phi _1 \dots \phi _n/x_1 \dots x_n]$
the result of simultaneously substituting each
$\Gamma [\phi _1 \dots \phi _n/x_1 \dots x_n]$
the result of simultaneously substituting each
![]() $\phi _i$
for all occurrences of
$\phi _i$
for all occurrences of
![]() $x_i$
in the formulas in
$x_i$
in the formulas in
![]() $\Gamma $
.
$\Gamma $
.
Definition 2.5 (Logic).
A consequence relation
![]() $\vdash $
is closed under uniform substitution if
$\vdash $
is closed under uniform substitution if
![]() $\Gamma \vdash \phi $
entails
$\Gamma \vdash \phi $
entails
![]() $ \sigma [\Gamma ] \vdash \sigma (\phi )$
for all substitutions
$ \sigma [\Gamma ] \vdash \sigma (\phi )$
for all substitutions
![]() $\sigma \in \mathsf {Subst}(\mathcal {L})$
. A (standard) logic is a consequence relation
$\sigma \in \mathsf {Subst}(\mathcal {L})$
. A (standard) logic is a consequence relation
![]() $\vdash $
which is closed under uniform substitution.
$\vdash $
which is closed under uniform substitution.
Example 2.6. Obvious examples of standard logics are the classical propositional logic
![]() $\mathtt {CPC}$
and the intuitionistic propositional logic
$\mathtt {CPC}$
and the intuitionistic propositional logic
![]() $\mathtt {IPC}$
. Non-examples of logics in this sense are first-order logic, as it is not a consequence relation of the propositional term algebra, infinitary logics, and higher-order systems.
$\mathtt {IPC}$
. Non-examples of logics in this sense are first-order logic, as it is not a consequence relation of the propositional term algebra, infinitary logics, and higher-order systems.
In the context of abstract algebraic logic, one is often interested in the algebraic semantics of a propositional logic
![]() $\vdash $
. This is provided by algebras, i.e., first-order structures in some purely functional language
$\vdash $
. This is provided by algebras, i.e., first-order structures in some purely functional language
![]() $\mathcal {L}$
. We first fix some notation concerning first-order models.
$\mathcal {L}$
. We first fix some notation concerning first-order models.
Notation 2.7. Let
![]() $\mathcal {L}$
be a first-order language, not necessarily functional. We use Latin letters
$\mathcal {L}$
be a first-order language, not necessarily functional. We use Latin letters
![]() $A, B, \dots $
both to denote first-order
$A, B, \dots $
both to denote first-order
![]() $\mathcal {L}$
-structures and their underlying domain. When confusion may arise, we also write
$\mathcal {L}$
-structures and their underlying domain. When confusion may arise, we also write
![]() $\mathsf {dom}(A)$
to refer to the underlying universe of A. For all function symbols
$\mathsf {dom}(A)$
to refer to the underlying universe of A. For all function symbols
![]() $f \in \mathcal {L}$
and all relation symbols
$f \in \mathcal {L}$
and all relation symbols
![]() $R \in \mathcal {L}$
, we write
$R \in \mathcal {L}$
, we write
![]() $f^{A}$
and
$f^{A}$
and
![]() $R^{A}$
for their interpretation in A. We use the same notations for symbols and their interpretation when it does not cause confusion. If
$R^{A}$
for their interpretation in A. We use the same notations for symbols and their interpretation when it does not cause confusion. If
![]() $t(\bar {x})$
is a term in the language
$t(\bar {x})$
is a term in the language
![]() $\mathcal {L}$
(i.e., a propositional formula), we usually call its interpretation
$\mathcal {L}$
(i.e., a propositional formula), we usually call its interpretation
![]() $t^{A}$
a polynomial. If
$t^{A}$
a polynomial. If
![]() $X\subseteq A$
, we write
$X\subseteq A$
, we write
![]() $\langle X\rangle $
for the substructure of A generated by X. The symbol
$\langle X\rangle $
for the substructure of A generated by X. The symbol
![]() $\models $
refers to the standard satisfaction symbol from first-order logic. We usually denote classes of structures by boldface font—both for arbitrary collections
$\models $
refers to the standard satisfaction symbol from first-order logic. We usually denote classes of structures by boldface font—both for arbitrary collections
![]() $(\mathbf {Q}, \mathbf {K}, \dots )$
and designated ones, e.g., the class of all Heyting algebras
$(\mathbf {Q}, \mathbf {K}, \dots )$
and designated ones, e.g., the class of all Heyting algebras
![]() $\mathbf {HA}$
or the class of all Boolean algebras
$\mathbf {HA}$
or the class of all Boolean algebras
![]() $ \mathbf {BA}$
.
$ \mathbf {BA}$
.
We assume the reader is familiar with the usual constructions from model theory and universal algebra, and refer to [Reference Burris and Sankappanavar5, Reference Chang and Keisler9] for background. We recall in particular the following notions of maps, as we shall need them in the rest of the article.
Definition 2.8. Let
![]() $h:A \to B$
be a function between two
$h:A \to B$
be a function between two
![]() $\mathcal {L}$
-structures A and B, for some first-order language
$\mathcal {L}$
-structures A and B, for some first-order language
![]() $\mathcal {L}$
. We define the following notions:
$\mathcal {L}$
. We define the following notions:
-
(1) we say that h is a homomorphism if for every function symbol
 $f\in \mathcal {L}$
we have and for every relation symbol
$f\in \mathcal {L}$
we have and for every relation symbol $$\begin{align*}h(f(a_1,\dots,a_n)) = f(h(a_1),\dots, h(a_n)) \end{align*}$$
$$\begin{align*}h(f(a_1,\dots,a_n)) = f(h(a_1),\dots, h(a_n)) \end{align*}$$
 $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,  $$\begin{align*}A\models R(a_1,\dots,a_n) \; \Longrightarrow\; B\models R(h(a_1),\dots, h(a_n));\end{align*}$$
$$\begin{align*}A\models R(a_1,\dots,a_n) \; \Longrightarrow\; B\models R(h(a_1),\dots, h(a_n));\end{align*}$$
-
(2) we say that h is a strong homomorphism if it is a homomorphism and, additionally, we have that
 $R^B= h[R^A]$
for every relation symbol
$R^B= h[R^A]$
for every relation symbol
 $R\in \mathcal {L}$
;
$R\in \mathcal {L}$
; -
(3) we say that h is a strict homomorphism if it is a homomorphism and, for every relation symbol
 $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,  $$\begin{align*}A\models R(a_1,\dots,a_n) \; \Longleftrightarrow\; B\models R(h(a_1),\dots, h(a_n));\end{align*}$$
$$\begin{align*}A\models R(a_1,\dots,a_n) \; \Longleftrightarrow\; B\models R(h(a_1),\dots, h(a_n));\end{align*}$$
-
(4) we say that h is an embedding if it is an injective strict homomorphism.
We write
![]() $A{\leqslant } B$
if A is a substructure of B, i.e., if the identity map
$A{\leqslant } B$
if A is a substructure of B, i.e., if the identity map
![]() $\mathsf {id}:A\to B$
is an embedding. We write
$\mathsf {id}:A\to B$
is an embedding. We write
![]() $A \cong B$
if A is isomorphic to B. We say that B is a homomorphic image of A if there is a surjective homomorphism
$A \cong B$
if A is isomorphic to B. We say that B is a homomorphic image of A if there is a surjective homomorphism
![]() $h:A\twoheadrightarrow B$
; we say that B is a strong (resp. strict) homomorphic image of A if h is a strong (resp. strict) homomorphism.
$h:A\twoheadrightarrow B$
; we say that B is a strong (resp. strict) homomorphic image of A if h is a strong (resp. strict) homomorphism.
Remark 2.9. We briefly explain the rationale behind the different versions of homomorphism. The notion of homomorphism from Definition 2.8 is standard from the literature in model theory and universal algebra (cf. [Reference Chang and Keisler9, pp. 70–71] and [Reference Burris and Sankappanavar5, p. 203]). The notion of strong homomorphism comes from [Reference Chang and Keisler9, p. 321] and is motivated by the following observation. Let A be an
![]() $\mathcal {L}$
-structure and let
$\mathcal {L}$
-structure and let
![]() $\mathcal {L}'$
consists of the functional symbols from
$\mathcal {L}'$
consists of the functional symbols from
![]() $\mathcal {L}$
. If
$\mathcal {L}$
. If
![]() $\theta $
is a congruence of the algebraic reduct of A we can consider the quotient
$\theta $
is a congruence of the algebraic reduct of A we can consider the quotient
![]() $\mathcal {L}'$
-structure
$\mathcal {L}'$
-structure
![]() $A/\theta $
and expand it to an
$A/\theta $
and expand it to an
![]() $\mathcal {L}$
-structure by letting
$\mathcal {L}$
-structure by letting
![]() $R^{A/\theta }=R^A/\theta $
for all relational symbols
$R^{A/\theta }=R^A/\theta $
for all relational symbols
![]() $R\in \mathcal {L}$
. Then, the projection map induced by this quotient is a strong homomorphism. Finally, we take the notion of strict homomorphism from [Reference Casanovas, Dellunde and Jansana7, Reference Dellunde and Jansana14], and we stress that strict homomorphisms correspond to those quotients which are additionally compatible with the relational part of the vocabulary from
$R\in \mathcal {L}$
. Then, the projection map induced by this quotient is a strong homomorphism. Finally, we take the notion of strict homomorphism from [Reference Casanovas, Dellunde and Jansana7, Reference Dellunde and Jansana14], and we stress that strict homomorphisms correspond to those quotients which are additionally compatible with the relational part of the vocabulary from
![]() $\mathcal {L}$
, in the sense that, if
$\mathcal {L}$
, in the sense that, if
![]() $(a_i,b_i)\in \theta $
for all
$(a_i,b_i)\in \theta $
for all
![]() $1{\leqslant } i {\leqslant } n$
, then for every relational symbol
$1{\leqslant } i {\leqslant } n$
, then for every relational symbol
![]() $R\in \mathcal {L}$
we have that
$R\in \mathcal {L}$
we have that
![]() $A\models R(a_1,\dots ,a_n)$
if and only if
$A\models R(a_1,\dots ,a_n)$
if and only if
![]() $A\models R(b_1,\dots ,b_n)$
. In this article we will mostly be dealing with strong homomorphisms, but we will consider strict homomorphisms in Section 7.
$A\models R(b_1,\dots ,b_n)$
. In this article we will mostly be dealing with strong homomorphisms, but we will consider strict homomorphisms in Section 7.
Notation 2.10. Let
![]() $\mathbf {K}$
be any class of first-order structures. We denote by
$\mathbf {K}$
be any class of first-order structures. We denote by
![]() $\mathbb {I}(\mathbf {K})$
its closure under isomorphic copies, by
$\mathbb {I}(\mathbf {K})$
its closure under isomorphic copies, by
![]() $\mathbb {S}(\mathbf {K})$
its closure under substructures, by
$\mathbb {S}(\mathbf {K})$
its closure under substructures, by
![]() $\mathbb {P}(\mathbf {K})$
its closure under (direct) products, and by
$\mathbb {P}(\mathbf {K})$
its closure under (direct) products, and by
![]() $\mathbb {P}_{\mathrm {U}}(\mathbf {K})$
its closure under ultraproducts. Finally, we write
$\mathbb {P}_{\mathrm {U}}(\mathbf {K})$
its closure under ultraproducts. Finally, we write
![]() $\mathbb {H}(\mathbf {K})$
for its closure under strong homomorphic images, and
$\mathbb {H}(\mathbf {K})$
for its closure under strong homomorphic images, and
![]() $\mathbb {H}_{\mathrm {s}}(\mathbf {K})$
for its closure under strict homomorphic images.
$\mathbb {H}_{\mathrm {s}}(\mathbf {K})$
for its closure under strict homomorphic images.
Definition 2.11. A class of algebras
![]() $\mathbf {K}$
is a quasivariety if it is closed under the operators
$\mathbf {K}$
is a quasivariety if it is closed under the operators
![]() $\mathbb {I}$
,
$\mathbb {I}$
,
![]() $\mathbb {S}$
,
$\mathbb {S}$
,
![]() $\mathbb {P}$
,
$\mathbb {P}$
,
![]() $\mathbb {P}_{\mathrm {U}} $
, i.e., if it is closed under isomorphic copies, subalgebras, products, and ultraproducts. A class of algebras
$\mathbb {P}_{\mathrm {U}} $
, i.e., if it is closed under isomorphic copies, subalgebras, products, and ultraproducts. A class of algebras
![]() $\mathbf {K}$
is a variety if it is closed under
$\mathbf {K}$
is a variety if it is closed under
![]() $\mathbb {H}$
,
$\mathbb {H}$
,
![]() $\mathbb {S,}$
and
$\mathbb {S,}$
and
![]() $\mathbb {P}$
, i.e., if it is closed under homomorphic images, subalgebras, and products. We denote by
$\mathbb {P}$
, i.e., if it is closed under homomorphic images, subalgebras, and products. We denote by
![]() $\mathbb {Q}(\mathbf {K})$
and
$\mathbb {Q}(\mathbf {K})$
and
![]() $\mathbb {V}(\mathbf {K})$
the quasivariety and the variety generated by
$\mathbb {V}(\mathbf {K})$
the quasivariety and the variety generated by
![]() $\mathbf {K}$
, respectively.
$\mathbf {K}$
, respectively.
Crucially, the closure of a class of structures under (some of) the operators
![]() $\mathbb {I}$
,
$\mathbb {I}$
,
![]() $\mathbb {S}$
,
$\mathbb {S}$
,
![]() $\mathbb {P}$
,
$\mathbb {P}$
,
![]() $\mathbb {P}_{\mathrm {U}} $
,
$\mathbb {P}_{\mathrm {U}} $
,
![]() $\mathbb {H}$
is related to conditions pertaining its axiomatisability. Most famously, it is a fundamental result by Keisler and Shelah that a class of structures
$\mathbb {H}$
is related to conditions pertaining its axiomatisability. Most famously, it is a fundamental result by Keisler and Shelah that a class of structures
![]() $\mathbf {K}$
is elementary (i.e., first-order axiomatisable) if and only if
$\mathbf {K}$
is elementary (i.e., first-order axiomatisable) if and only if
![]() $\mathbf {K}$
is closed under ultraproducts. In this work we are concerned with less general definability conditions. We introduce them by focusing on three special subclasses of first-order formulas.
$\mathbf {K}$
is closed under ultraproducts. In this work we are concerned with less general definability conditions. We introduce them by focusing on three special subclasses of first-order formulas.
Notation 2.12. We write
![]() $\bar {x}$
as a shorthand for a sequence of variables
$\bar {x}$
as a shorthand for a sequence of variables
![]() $(x_0,\dots ,x_n)$
. Also, as we often deal with equational classes of structures, we abide to the usual convention from universal algebra to distinguish the syntactical equality symbol, written
$(x_0,\dots ,x_n)$
. Also, as we often deal with equational classes of structures, we abide to the usual convention from universal algebra to distinguish the syntactical equality symbol, written
![]() $\approx $
, from the semantical equality symbol, which we denote by
$\approx $
, from the semantical equality symbol, which we denote by
![]() $=$
. To help the reader to distinguish when we talk of first-order formulas from when we deal with propositional ones, we use lowercase Greek symbols
$=$
. To help the reader to distinguish when we talk of first-order formulas from when we deal with propositional ones, we use lowercase Greek symbols
![]() $\phi ,\psi ,\dots $
for the latter and uppercase Greek symbols
$\phi ,\psi ,\dots $
for the latter and uppercase Greek symbols
![]() $\Phi ,\Psi ,\dots $
for the former.
$\Phi ,\Psi ,\dots $
for the former.
Definition 2.13. Let
![]() $\mathcal {L}$
be an arbitrary first-order signature, not necessarily functional. Then we define the following types of formulas:
$\mathcal {L}$
be an arbitrary first-order signature, not necessarily functional. Then we define the following types of formulas:
-
(1) an equation is a formula of the form
 $\varepsilon \approx \delta $
, where
$\varepsilon \approx \delta $
, where
 $\varepsilon $
and
$\varepsilon $
and
 $\delta $
are two
$\delta $
are two
 $\mathcal {L}$
-terms;
$\mathcal {L}$
-terms; -
(2) a quasiequation is a formula of the form
 $\bigwedge _{i{\leqslant } n} (\varepsilon _i\approx \delta _i) \to \varepsilon \approx \delta $
, for some
$\bigwedge _{i{\leqslant } n} (\varepsilon _i\approx \delta _i) \to \varepsilon \approx \delta $
, for some
 $n<\omega $
, where all
$n<\omega $
, where all
 $\varepsilon _i,\delta _i$
and
$\varepsilon _i,\delta _i$
and
 $\varepsilon ,\delta $
are
$\varepsilon ,\delta $
are
 $\mathcal {L}$
-terms;
$\mathcal {L}$
-terms; -
(3) a basic Horn formula is a formula of the form
 $\bigvee _{1{\leqslant } i{\leqslant } n}\Psi _i$
, where every
$\bigvee _{1{\leqslant } i{\leqslant } n}\Psi _i$
, where every
 $\Psi _i$
is either an atomic or a negated atomic formula, and at most one
$\Psi _i$
is either an atomic or a negated atomic formula, and at most one
 $\Psi _i$
is atomic;
$\Psi _i$
is atomic; -
(4) a basic Horn formula is strict if exactly one of its disjuncts is atomic;
-
(5) a universal Horn formula is a formula of the form
for some $$\begin{align*}\forall x_1 \dots \forall x_m \; \big( \bigwedge_{1{\leqslant} i{\leqslant} \ell} \Phi_i(\bar{x}) \big) \end{align*}$$
$$\begin{align*}\forall x_1 \dots \forall x_m \; \big( \bigwedge_{1{\leqslant} i{\leqslant} \ell} \Phi_i(\bar{x}) \big) \end{align*}$$
 $m,\ell <\omega $
, and where each
$m,\ell <\omega $
, and where each
 $\Phi _i$
for
$\Phi _i$
for
 $1{\leqslant } i{\leqslant } m$
is a basic Horn formula;
$1{\leqslant } i{\leqslant } m$
is a basic Horn formula;
-
(6) a universal Horn formulas is strict if all the basic Horn formulas
 $\Phi _i$
occurring in it are strict.
$\Phi _i$
occurring in it are strict.
The following classical results relate the closure under the operators
![]() $\mathbb {I}$
,
$\mathbb {I}$
,
![]() $\mathbb {S}$
,
$\mathbb {S}$
,
![]() $\mathbb {P}$
,
$\mathbb {P}$
,
![]() $\mathbb {P}_{\mathrm {U}} $
,
$\mathbb {P}_{\mathrm {U}} $
,
![]() $\mathbb {H}$
with different definability conditions. We refer the reader to [Reference Burris and Sankappanavar5, I: Theorem 2.23, Theorem 2.25; II: Theorem 11.9] for their proofs. Facts (1) and (2) are also known, respectively, as Birkhoff’s Theorem and Maltsev’s Theorem.
$\mathbb {H}$
with different definability conditions. We refer the reader to [Reference Burris and Sankappanavar5, I: Theorem 2.23, Theorem 2.25; II: Theorem 11.9] for their proofs. Facts (1) and (2) are also known, respectively, as Birkhoff’s Theorem and Maltsev’s Theorem.
Fact 2.14. Let
![]() $\mathcal {L}$
be an algebraic signature and
$\mathcal {L}$
be an algebraic signature and
![]() $\mathbf {K}$
a class of
$\mathbf {K}$
a class of
![]() $\mathcal {L}$
-algebras, then:
$\mathcal {L}$
-algebras, then:
-
(1)
 $\mathbf {K}$
is a variety if and only if it is axiomatised by equations;
$\mathbf {K}$
is a variety if and only if it is axiomatised by equations; -
(2)
 $\mathbf {K}$
is a quasivariety if and only if it is axiomatised by quasiequations.
$\mathbf {K}$
is a quasivariety if and only if it is axiomatised by quasiequations.
Moreover, if
![]() $\mathcal {L}$
is any first-order signature and
$\mathcal {L}$
is any first-order signature and
![]() $\mathbf {K}$
is a class of
$\mathbf {K}$
is a class of
![]() $\mathcal {L}$
-structures, then:
$\mathcal {L}$
-structures, then:
-
(3)
 $\mathbf {K}$
is closed under
$\mathbf {K}$
is closed under
 $\mathbb {I}$
,
$\mathbb {I}$
,
 $\mathbb {S}$
,
$\mathbb {S}$
,
 $\mathbb {P,}$
and
$\mathbb {P,}$
and
 $\mathbb {P}_{\mathrm {U}} $
if and only if it is axiomatised by universal Horn sentences.
$\mathbb {P}_{\mathrm {U}} $
if and only if it is axiomatised by universal Horn sentences.
In the light of the previous results, it is convenient to fix some shorthand notation to talk about (fragments of) first-order theories, and their classes of models.
Notation 2.15. Let
![]() $\mathcal {L}$
be an arbitrary first-order language. If T is a set of first-order sentences in
$\mathcal {L}$
be an arbitrary first-order language. If T is a set of first-order sentences in
![]() $\mathcal {L}$
, we write
$\mathcal {L}$
, we write
![]() $\mathrm {Mod}(T)$
for the class of all
$\mathrm {Mod}(T)$
for the class of all
![]() $\mathcal {L}$
-structures A such that
$\mathcal {L}$
-structures A such that
![]() $A \models T$
. We write
$A \models T$
. We write
![]() $\mathrm {Mod}(\mathcal {L})$
for the class of all
$\mathrm {Mod}(\mathcal {L})$
for the class of all
![]() $\mathcal {L}$
-structures. Notice that, if T is a set of formulas (e.g., a set of equations or quasiequations), then
$\mathcal {L}$
-structures. Notice that, if T is a set of formulas (e.g., a set of equations or quasiequations), then
![]() $\mathrm {Mod}(T)$
is the class of structures which models the sentences
$\mathrm {Mod}(T)$
is the class of structures which models the sentences
![]() $\forall x_1\dots \forall x_n (\Phi (\bar {x}))$
, for every
$\forall x_1\dots \forall x_n (\Phi (\bar {x}))$
, for every
![]() $\Phi \in T$
. On the other hand, let
$\Phi \in T$
. On the other hand, let
![]() $\mathbf {K}$
be a class of
$\mathbf {K}$
be a class of
![]() $\mathcal {L}$
-structures. Then we write
$\mathcal {L}$
-structures. Then we write
![]() $\mathrm {Th}_{\mathrm {fol}}(\mathbf {K})$
for the set of all
$\mathrm {Th}_{\mathrm {fol}}(\mathbf {K})$
for the set of all
![]() $\mathcal {L}$
-sentences true in
$\mathcal {L}$
-sentences true in
![]() $\mathbf {K}$
;
$\mathbf {K}$
;
![]() $\mathrm {Th}_{\mathrm {h}}(\mathbf {K})$
for the set of all universal Horn sentences true in
$\mathrm {Th}_{\mathrm {h}}(\mathbf {K})$
for the set of all universal Horn sentences true in
![]() $\mathbf {K}$
;
$\mathbf {K}$
;
![]() $\mathrm {Th}_{\mathrm {qe}}(\mathbf {K})$
for the set of all quasiequations true in
$\mathrm {Th}_{\mathrm {qe}}(\mathbf {K})$
for the set of all quasiequations true in
![]() $\mathbf {K}$
; and, finally,
$\mathbf {K}$
; and, finally,
![]() $\mathrm {Th}_{\mathrm {e}}(\mathbf {K})$
for the set of all equations true in
$\mathrm {Th}_{\mathrm {e}}(\mathbf {K})$
for the set of all equations true in
![]() $\mathbf {K}$
. We also write
$\mathbf {K}$
. We also write
![]() $\mathsf {Eq}_{\mathcal {L}}$
for the set of all equations in
$\mathsf {Eq}_{\mathcal {L}}$
for the set of all equations in
![]() $\mathcal {L}$
, and
$\mathcal {L}$
, and
![]() $\mathsf {QEq}_{\mathcal {L}}$
for the set of all quasiequations in
$\mathsf {QEq}_{\mathcal {L}}$
for the set of all quasiequations in
![]() $\mathcal {L}$
—we omit the index
$\mathcal {L}$
—we omit the index
![]() $\mathcal {L}$
when it is clear from the context.
$\mathcal {L}$
when it is clear from the context.
Finally, we conclude this preliminary section by recalling what is the propositional consequence relation induced by a class of algebras.
Notation 2.16. Recall that
![]() $\mathsf {Fm}_{\mathcal {L}}$
is the term algebra in the language
$\mathsf {Fm}_{\mathcal {L}}$
is the term algebra in the language
![]() $\mathcal {L}$
. A (propositional) assignment is a homomorphism
$\mathcal {L}$
. A (propositional) assignment is a homomorphism
![]() $h:\mathsf {Fm}_{\mathcal {L}}\to A$
, where A is an
$h:\mathsf {Fm}_{\mathcal {L}}\to A$
, where A is an
![]() $\mathcal {L}$
-structure. We denote the family of all assignments into A as
$\mathcal {L}$
-structure. We denote the family of all assignments into A as
![]() $\mathsf {Hom}(\mathsf {Fm},A)$
. If
$\mathsf {Hom}(\mathsf {Fm},A)$
. If
![]() $h:\mathsf {Fm}_{\mathcal {L}}\to A$
is an assignment and
$h:\mathsf {Fm}_{\mathcal {L}}\to A$
is an assignment and
![]() $\alpha \approx \beta $
an equation, then we often write simply
$\alpha \approx \beta $
an equation, then we often write simply
![]() $h(\alpha \approx \beta )$
for the formula
$h(\alpha \approx \beta )$
for the formula
![]() $h(\alpha )\approx h(\beta )$
.
$h(\alpha )\approx h(\beta )$
.
Definition 2.17. Let
![]() $\mathbf {K}$
be a class of
$\mathbf {K}$
be a class of
![]() $\mathcal {L}$
-algebras and let
$\mathcal {L}$
-algebras and let
![]() $\Theta \cup \{\varepsilon \approx \delta \}\subseteq \mathsf {Eq}$
a set of equations, then the equational consequence relative to
$\Theta \cup \{\varepsilon \approx \delta \}\subseteq \mathsf {Eq}$
a set of equations, then the equational consequence relative to
![]() $\mathbf {K}$
is defined as follows:
$\mathbf {K}$
is defined as follows:
 $$ \begin{align*} \Theta \models_{\mathbf{K}} \varepsilon\approx \delta \Longleftrightarrow & \text{ for all } A \in \mathbf{K}, \, h\in \mathsf{Hom}(\mathsf{Fm},A), \\ & \text{ if } h(\varepsilon_i)= h(\delta_i) \text{ for all } \varepsilon_i\approx \delta_i\in \Theta, \text{ then } h(\varepsilon)= h(\delta). \end{align*} $$
$$ \begin{align*} \Theta \models_{\mathbf{K}} \varepsilon\approx \delta \Longleftrightarrow & \text{ for all } A \in \mathbf{K}, \, h\in \mathsf{Hom}(\mathsf{Fm},A), \\ & \text{ if } h(\varepsilon_i)= h(\delta_i) \text{ for all } \varepsilon_i\approx \delta_i\in \Theta, \text{ then } h(\varepsilon)= h(\delta). \end{align*} $$
And we write
![]() $\models _{\mathbf {K}} \bigwedge _{i{\leqslant } n} \varepsilon _i\approx \delta _i \to \varepsilon \approx \delta $
if
$\models _{\mathbf {K}} \bigwedge _{i{\leqslant } n} \varepsilon _i\approx \delta _i \to \varepsilon \approx \delta $
if
![]() $ \bigwedge _{i{\leqslant } n} \varepsilon _i\approx \delta _i \models _{\mathbf {K}} \varepsilon \approx \delta $
. We often write
$ \bigwedge _{i{\leqslant } n} \varepsilon _i\approx \delta _i \models _{\mathbf {K}} \varepsilon \approx \delta $
. We often write
![]() $A \models \bigwedge _{i{\leqslant } n} \varepsilon _i\approx \delta _i \to \varepsilon \approx \delta $
in place of
$A \models \bigwedge _{i{\leqslant } n} \varepsilon _i\approx \delta _i \to \varepsilon \approx \delta $
in place of
![]() $\models _{\{A \}} \bigwedge _{i{\leqslant } n} \varepsilon _i\approx \delta _i \to \varepsilon \approx \delta $
. The related notions for equations are defined analogously.
$\models _{\{A \}} \bigwedge _{i{\leqslant } n} \varepsilon _i\approx \delta _i \to \varepsilon \approx \delta $
. The related notions for equations are defined analogously.
Remark 2.18. Notice that, in Definition 2.17, we can assume without loss of generality that
![]() $\mathbf {K}$
is a quasivariety, since by Fact 2.14 the validity of quasiequations is preserved under the operations
$\mathbf {K}$
is a quasivariety, since by Fact 2.14 the validity of quasiequations is preserved under the operations
![]() $\mathbb {I}$
,
$\mathbb {I}$
,
![]() $\mathbb {S}$
,
$\mathbb {S}$
,
![]() $\mathbb {P}$
,
$\mathbb {P}$
,
![]() $\mathbb {P}_{\mathrm {U}}$
. Then, if the set of formulas
$\mathbb {P}_{\mathrm {U}}$
. Then, if the set of formulas
![]() $\Theta $
is finite, we have that
$\Theta $
is finite, we have that
![]() $ \Theta \models _{\mathbf {K}} \varepsilon \approx \delta $
is equivalent to
$ \Theta \models _{\mathbf {K}} \varepsilon \approx \delta $
is equivalent to
![]() $\mathbf {K}\models \forall x_1\dots \forall x_n (\bigwedge \Theta \to \varepsilon \approx \delta )$
. This shows that, when the set of premises
$\mathbf {K}\models \forall x_1\dots \forall x_n (\bigwedge \Theta \to \varepsilon \approx \delta )$
. This shows that, when the set of premises
![]() $\Theta $
is finite, then the consequence relation
$\Theta $
is finite, then the consequence relation
![]() $\models _{\mathbf {K}}$
can be encoded by the consequence relation from first-order logic. Notice that this ultimately justifies the notational conventions from Definition 2.17 above. If the relation
$\models _{\mathbf {K}}$
can be encoded by the consequence relation from first-order logic. Notice that this ultimately justifies the notational conventions from Definition 2.17 above. If the relation
![]() $\models _{\mathbf {K}}$
is not finitary this does not need to be the case: one needs to work with so-called generalised quasivarieties instead, and replace the consequence relation from first-order logic by the consequence relation of some suitable infinitary logic. Given our present interest in finitary logical systems we will not expand on this issue, and we simply refer the interested reader to [Reference Font16].
$\models _{\mathbf {K}}$
is not finitary this does not need to be the case: one needs to work with so-called generalised quasivarieties instead, and replace the consequence relation from first-order logic by the consequence relation of some suitable infinitary logic. Given our present interest in finitary logical systems we will not expand on this issue, and we simply refer the interested reader to [Reference Font16].
3 Weak logics and expanded algebras
In this section we introduce weak logics as a generalisation of propositional logical systems and we provide several examples of them. Alongside, we define expanded algebras and core semantics to provide an algebraic interpretation to these logics.
3.1 Weak logics
We start by introducing the notion of weak logical systems, which is the key object of interest of the present work. As we are interested in logical systems which are not necessarily closed under uniform substitution, we firstly identify the restricted class of atomic substitutions.
Definition 3.1. An atomic substitution is a substitution
![]() $\sigma \in \mathsf {Subst}(\mathcal {L})$
such that
$\sigma \in \mathsf {Subst}(\mathcal {L})$
such that
![]() $\sigma [\mathsf {Var}] \subseteq \mathsf {Var}$
. We denote by
$\sigma [\mathsf {Var}] \subseteq \mathsf {Var}$
. We denote by
![]() $\mathsf {At}(\mathcal {L})$
the set of all atomic substitutions in
$\mathsf {At}(\mathcal {L})$
the set of all atomic substitutions in
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
Definition 3.2 (Weak logic).
A weak logic is a (finitary) consequence relation
![]() $\Vdash $
such that, for all atomic substitutions
$\Vdash $
such that, for all atomic substitutions
![]() $\sigma \in \mathsf {At}(\mathcal {L})$
,
$\sigma \in \mathsf {At}(\mathcal {L})$
,
![]() $\Gamma \Vdash \phi $
entails
$\Gamma \Vdash \phi $
entails
![]() $\sigma [\Gamma ] \Vdash \sigma (\phi )$
.
$\sigma [\Gamma ] \Vdash \sigma (\phi )$
.
Remark 3.3. A weak logic is thus a consequence relation which is closed under atomic substitution. Intuitively, this principle reifies the least prerequisite a consequence relation must satisfy in order to be characterizable as a logic: the validity of the consequences in a weak logic can depend on the logical complexity of its formulas, but not on the specific variables that occur in them. Philosophically, this can be interpreted as a weakening of the Bolzanian–Tarskian notion of logicality.
Obviously, standard logics are weak logics. More poignantly, there are several examples of weak logics which are not standard logics and that have been extensively studied in the literature. Their existence and recognition constitutes the main motivation behind our interest for this class of consequence relations and for the abstract results of this article.
Example 3.4.
![]() $ \mathtt {PAL} $
[Reference Holliday, Hoshi, Icard, Ditmarsch, Lang and Ju19] is an example of a modal logic that is not closed under uniform substitution [Reference Holliday, Hoshi and Icard20]. However, it can be shown that
$ \mathtt {PAL} $
[Reference Holliday, Hoshi, Icard, Ditmarsch, Lang and Ju19] is an example of a modal logic that is not closed under uniform substitution [Reference Holliday, Hoshi and Icard20]. However, it can be shown that
![]() $\mathtt {PAL}$
is closed under atomic substitution [Reference Holliday, Hoshi and Icard20, Section 2.1] and it is therefore a weak logic. Introducing the proper syntax and semantics of
$\mathtt {PAL}$
is closed under atomic substitution [Reference Holliday, Hoshi and Icard20, Section 2.1] and it is therefore a weak logic. Introducing the proper syntax and semantics of
![]() $\mathtt {PAL}$
is out of scope of this article, but we mention the following example from [Reference Holliday, Hoshi and Icard20] to provide the reader with some intuition why uniform substitution fails. Given a set of agents A, the language of
$\mathtt {PAL}$
is out of scope of this article, but we mention the following example from [Reference Holliday, Hoshi and Icard20] to provide the reader with some intuition why uniform substitution fails. Given a set of agents A, the language of
![]() $\mathtt {PAL}$
extends the basic modal language with operators
$\mathtt {PAL}$
extends the basic modal language with operators
![]() $K_i$
, for all
$K_i$
, for all
![]() $i \in A$
, and
$i \in A$
, and
![]() $\langle \phi \rangle $
for any formula
$\langle \phi \rangle $
for any formula
![]() $\phi $
. The sentence
$\phi $
. The sentence
![]() $K_i \phi $
should be read as “agent i knows that
$K_i \phi $
should be read as “agent i knows that
![]() $\phi $
” and
$\phi $
” and
![]() $\langle \phi \rangle \psi $
as “after the truthful announcement of
$\langle \phi \rangle \psi $
as “after the truthful announcement of
![]() $\phi $
to all agents,
$\phi $
to all agents,
![]() $\psi $
holds.” Let the atoms of the language stand for facts—that is, sentences that can be truly uttered at any time. Consider then the principle:
$\psi $
holds.” Let the atoms of the language stand for facts—that is, sentences that can be truly uttered at any time. Consider then the principle:
The schema (⋆) is valid for facts, but in general does not hold if we substitute p with a sentence talking about the epistemic state of an agent. Let
![]() $\phi $
be the sentence “Ljubljana became the capital of an independent Slovenia in 1991, and agent j does not know this,” with translation
$\phi $
be the sentence “Ljubljana became the capital of an independent Slovenia in 1991, and agent j does not know this,” with translation
![]() $c \land \lnot K_j c$
. Now substituting
$c \land \lnot K_j c$
. Now substituting
![]() $\phi $
for p in (⋆) gives us a Moorean sentence—after truthfully announcing
$\phi $
for p in (⋆) gives us a Moorean sentence—after truthfully announcing
![]() $\phi $
, agent j learns that “Ljubljana became the capital of an independent Slovenia in 1991,” and thus the conclusion
$\phi $
, agent j learns that “Ljubljana became the capital of an independent Slovenia in 1991,” and thus the conclusion
![]() $\langle \phi \rangle \phi $
is no longer truthful.
$\langle \phi \rangle \phi $
is no longer truthful.
Example 3.5. Logics based on team semantics, such as inquisitive and dependence logics [Reference Ciardelli, Iemhoff and Yang11, Reference Ciardelli and Roelofsen12, Reference Yang and Väänänen30], offer a rich supply of examples of weak logics. In Section 8 we will focus particularly on
![]() $\mathtt {InqB}$
,
$\mathtt {InqB}$
,
![]() $\mathtt {InqB}^\otimes $
,
$\mathtt {InqB}^\otimes $
,
![]() $\mathtt {InqI,}$
and
$\mathtt {InqI,}$
and
![]() $\mathtt {InqI}^\otimes $
, namely, the classical and the intuitionistic versions of inquisitive and dependence logic. However, already now we can provide a conceptual motivation why
$\mathtt {InqI}^\otimes $
, namely, the classical and the intuitionistic versions of inquisitive and dependence logic. However, already now we can provide a conceptual motivation why
![]() $\mathtt {InqB}$
is not closed under uniform substitution. One of the main goals of
$\mathtt {InqB}$
is not closed under uniform substitution. One of the main goals of
![]() $\mathtt {InqB}$
is to serve as a basis for a uniform treatment of both truth-conditional statements and questions in natural language. To that end, the intended semantics of
$\mathtt {InqB}$
is to serve as a basis for a uniform treatment of both truth-conditional statements and questions in natural language. To that end, the intended semantics of
![]() $\mathtt {InqB}$
must establish when a piece of information supports a statement or settles a question rather than their truth conditions. We call the evidence an information state and represent it as a set of possible worlds.
$\mathtt {InqB}$
must establish when a piece of information supports a statement or settles a question rather than their truth conditions. We call the evidence an information state and represent it as a set of possible worlds.
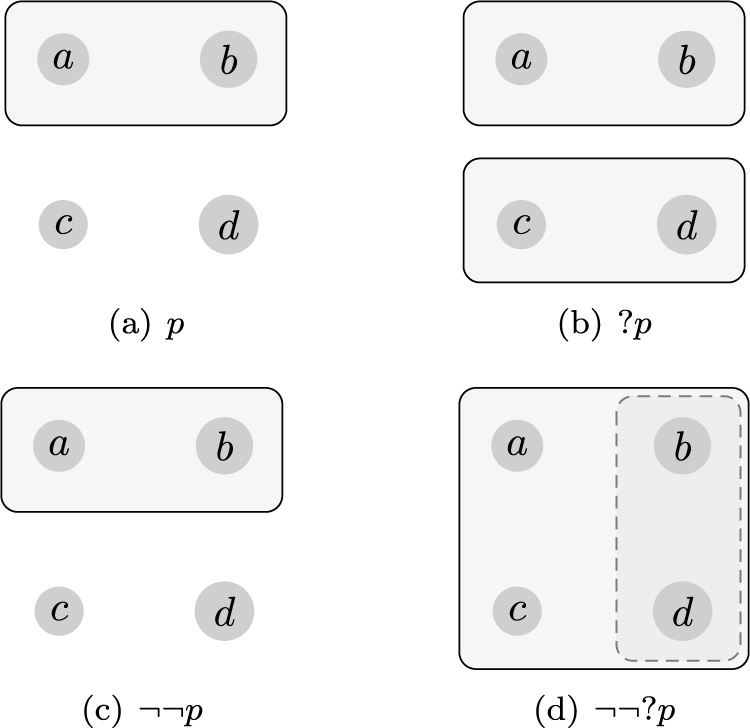
Let p be an arbitrary statement without inquisitive content, e.g., “It is raining in Glasgow.” Assume that p holds in the possible worlds a and b, i.e., the information state
![]() $\{a,b\}$
supports p (see Figure 1). We form the polar question
$\{a,b\}$
supports p (see Figure 1). We form the polar question
![]() $?p$
—“Is it raining in Glasgow?”, and model it as the set of alternatives
$?p$
—“Is it raining in Glasgow?”, and model it as the set of alternatives
![]() $\{a , b\}$
and
$\{a , b\}$
and
![]() $\{c,d\}$
. Let’s check the validity of
$\{c,d\}$
. Let’s check the validity of
![]() $\textit {double negation elimination}$
(DNE)—
$\textit {double negation elimination}$
(DNE)—
![]() $\lnot \lnot q \to q$
; we interpret negation as the complement of the union of alternatives. Thus any information state supporting
$\lnot \lnot q \to q$
; we interpret negation as the complement of the union of alternatives. Thus any information state supporting
![]() $\lnot \lnot p$
will support the statement p as well (Figure 1(c)). However, this is not the case for questions—e.g., the state
$\lnot \lnot p$
will support the statement p as well (Figure 1(c)). However, this is not the case for questions—e.g., the state
![]() $\{b,d\}$
supports
$\{b,d\}$
supports
![]() $\lnot \lnot ?p$
, but does not settle
$\lnot \lnot ?p$
, but does not settle
![]() $?p$
as the possible worlds b and d do not agree on a same answer. Hence we can conclude that the schema DNE is valid only for statements without inquisitive content, i.e., for propositional atoms.
$?p$
as the possible worlds b and d do not agree on a same answer. Hence we can conclude that the schema DNE is valid only for statements without inquisitive content, i.e., for propositional atoms.

Figure 1 Double-negation elimination for statements and polar questions.
Actually,
![]() $\mathtt {InqB}$
is a concrete example of a wider class of weak logics—a double negation atoms logic or
$\mathtt {InqB}$
is a concrete example of a wider class of weak logics—a double negation atoms logic or
![]() $\mathtt {DNA}$
-logic. A
$\mathtt {DNA}$
-logic. A
![]() $\mathtt {DNA}$
-logic (also negative variant of an intermediate logic [Reference Ciardelli10, Reference Miglioli, Moscato, Ornaghi, Quazza and Usberti22]) is a set of formulas
$\mathtt {DNA}$
-logic (also negative variant of an intermediate logic [Reference Ciardelli10, Reference Miglioli, Moscato, Ornaghi, Quazza and Usberti22]) is a set of formulas
![]() $\mathtt {L}^\neg =\{ \phi [\neg p_0,\dots ,\neg p_n/p_0,\dots ,p_n] : \phi \in \mathtt {L} \}$
, where
$\mathtt {L}^\neg =\{ \phi [\neg p_0,\dots ,\neg p_n/p_0,\dots ,p_n] : \phi \in \mathtt {L} \}$
, where
![]() $\mathtt {L}$
is an intermediate logic, namely, a logic comprised between
$\mathtt {L}$
is an intermediate logic, namely, a logic comprised between
![]() $\mathtt {IPC}$
and
$\mathtt {IPC}$
and
![]() $\mathtt {CPC}$
. It can be proved (see, e.g., [Reference Ciardelli10, Proposition 3.2.15]) that
$\mathtt {CPC}$
. It can be proved (see, e.g., [Reference Ciardelli10, Proposition 3.2.15]) that
![]() $\mathtt {DNA}$
-logics are closed under atomic substitutions. However, for any
$\mathtt {DNA}$
-logics are closed under atomic substitutions. However, for any
![]() $\mathtt {DNA}$
-logic
$\mathtt {DNA}$
-logic
![]() $\mathtt {L}\neq \mathtt {CPC}$
it is the case that
$\mathtt {L}\neq \mathtt {CPC}$
it is the case that
![]() $\neg \neg p\to p\in \mathtt {L}^\neg $
, but
$\neg \neg p\to p\in \mathtt {L}^\neg $
, but
![]() $(\neg \neg ( p \lor \lnot p) \to p \lor \lnot p) \notin \mathtt {L}^\neg $
, showing that
$(\neg \neg ( p \lor \lnot p) \to p \lor \lnot p) \notin \mathtt {L}^\neg $
, showing that
![]() $\mathtt {DNA}$
-logics are not standard logics. We also notice that
$\mathtt {DNA}$
-logics are not standard logics. We also notice that
![]() $\mathtt {DNA}$
-logics can be further generalised to
$\mathtt {DNA}$
-logics can be further generalised to
![]() $\chi $
-logics, defined in [Reference Quadrellaro26], which provide yet another non-trivial example of weak logics.
$\chi $
-logics, defined in [Reference Quadrellaro26], which provide yet another non-trivial example of weak logics.
We briefly mention the following natural notions, although we will not use them in the rest of the article. If
![]() $\Vdash $
is a weak logic we know that it is at least closed under all atomic substitutions
$\Vdash $
is a weak logic we know that it is at least closed under all atomic substitutions
![]() $\sigma \in \mathsf {At}(\mathcal {L})$
, but in general there could be more substitutions for which the logic
$\sigma \in \mathsf {At}(\mathcal {L})$
, but in general there could be more substitutions for which the logic
![]() $\Vdash $
is closed. We call such substitutions admissible for
$\Vdash $
is closed. We call such substitutions admissible for
![]() $\Vdash $
.
$\Vdash $
.
Definition 3.6 (Admissible substitutions).
Let
![]() $\Vdash $
be a weak logic. The set of admissible substitutions
$\Vdash $
be a weak logic. The set of admissible substitutions
![]() $\mathsf {AS}(\Vdash )$
is the set of all substitutions
$\mathsf {AS}(\Vdash )$
is the set of all substitutions
![]() $\sigma $
such that, for all sets of formulas
$\sigma $
such that, for all sets of formulas
![]() $\Gamma \cup \{ \phi \} \subseteq \mathsf {Fm}$
,
$\Gamma \cup \{ \phi \} \subseteq \mathsf {Fm}$
,
![]() $ \Gamma \Vdash \phi $
entails
$ \Gamma \Vdash \phi $
entails
![]() $ \sigma [\Gamma ] \Vdash \sigma (\phi )$
.
$ \sigma [\Gamma ] \Vdash \sigma (\phi )$
.
Remark 3.7. As noticed above, we immediately have that
![]() $\mathsf {At}(\mathcal {L}) \subseteq \mathsf {AS}(\Vdash )$
. However, in stark contrast with the set of atomic substitutions, determining the set of admissible substitutions of a weak logic is in principle much harder. An example of such a characterization can be given for the case of inquisitive logic
$\mathsf {At}(\mathcal {L}) \subseteq \mathsf {AS}(\Vdash )$
. However, in stark contrast with the set of atomic substitutions, determining the set of admissible substitutions of a weak logic is in principle much harder. An example of such a characterization can be given for the case of inquisitive logic
![]() $\mathtt {InqB}$
: one can in fact verify that
$\mathtt {InqB}$
: one can in fact verify that
![]() $\sigma \in \mathsf {AS}(\mathtt {InqB}) $
if and only if
$\sigma \in \mathsf {AS}(\mathtt {InqB}) $
if and only if
![]() $\sigma $
is a classical substitution, namely, if for all
$\sigma $
is a classical substitution, namely, if for all
![]() $p\in \mathsf {Var}$
,
$p\in \mathsf {Var}$
,
![]() $\sigma (p)\equiv _{\mathtt {InqB}}\psi ,$
where
$\sigma (p)\equiv _{\mathtt {InqB}}\psi ,$
where
![]() $\psi $
is a disjunction-free formula.
$\psi $
is a disjunction-free formula.
Even if in weak logics we cannot freely substitute formulas in place of variables, we often want to consider the subset of formulas for which this is possible. We refer to this subset as the core of a logic.
Definition 3.8 (Core of a logic).
The core of a weak logic
![]() $\Vdash $
is the set
$\Vdash $
is the set
![]() $\mathsf {core}(\Vdash )$
of all formulas
$\mathsf {core}(\Vdash )$
of all formulas
![]() $\psi \in \mathsf {Fm}$
such that for all sets of formulas
$\psi \in \mathsf {Fm}$
such that for all sets of formulas
![]() $\Gamma \cup \{\phi \}$
we have that
$\Gamma \cup \{\phi \}$
we have that
where
![]() $x\in \mathsf {Var}$
is any atomic variable.
$x\in \mathsf {Var}$
is any atomic variable.
Remark 3.9. Equivalently, we can say that
![]() $\psi $
is a core formula of
$\psi $
is a core formula of
![]() $\Vdash $
if and only if for all
$\Vdash $
if and only if for all
![]() $x \in \mathsf {Var}$
the substitution
$x \in \mathsf {Var}$
the substitution
![]() $\sigma $
such that
$\sigma $
such that
![]() $\sigma {\restriction } \mathsf {Var} \setminus \{x \} = \mathsf {id}_{\mathsf {Var}}$
and
$\sigma {\restriction } \mathsf {Var} \setminus \{x \} = \mathsf {id}_{\mathsf {Var}}$
and
![]() $\sigma (x) = \psi $
is admissible. Clearly, we always have that
$\sigma (x) = \psi $
is admissible. Clearly, we always have that
![]() $\mathsf {Var} \subseteq \mathsf {core}(\Vdash )$
.
$\mathsf {Var} \subseteq \mathsf {core}(\Vdash )$
.
3.2 Expanded algebras
In order to make sense of weak logics from an algebraic perspective, we need to refine the usual algebraic semantics from abstract algebraic logic in order to handle the failure of uniform substitution. To this end, we introduce expanded algebras as the expansion of standard algebras by an extra predicate symbol.
Definition 3.10 (Expanded algebra).
Let A be an
![]() $\mathcal {L}$
-algebra and P a unary predicate, an expanded algebra is a structure in the language
$\mathcal {L}$
-algebra and P a unary predicate, an expanded algebra is a structure in the language
![]() $\mathcal {L} \cup \{P\}$
. We denote
$\mathcal {L} \cup \{P\}$
. We denote
![]() $P^A$
also by
$P^A$
also by
![]() $\mathsf {core}(A)$
and we refer to it as the core of the expanded algebra A.
$\mathsf {core}(A)$
and we refer to it as the core of the expanded algebra A.
Remark 3.11. Essentially, expanded algebras are first-order structures with exactly one predicate symbol of arity 1, and arbitrary many functional symbols. Since the relational part of the language consists of only one predicate, we always assume without loss of generality that it consists of the same symbol, so that we always regard any two expanded
![]() $\mathcal {L}$
-algebras as structures in the same vocabulary. When the signature
$\mathcal {L}$
-algebras as structures in the same vocabulary. When the signature
![]() $\mathcal {L}$
is clear from the context we talk simply of algebras and expanded algebras. Notice that algebras augmented by a single predicate symbol often appear in abstract algebraic logic as matrices (cf. [Reference Font16, Chapter 4]). The key difference between expanded algebras and matrices is in the role played by the additional predicate symbol. In fact, in the context of expanded algebras the predicate identifies the core of the algebra, which we use to restrict the possible interpretation of the atomic formulas (cf. 3.17 below). Differently, in the context of logical matrices, the predicate rather identifies a designated “truth set.” We will consider in Section 7 a matrix-like approach to weak logics which unifies these two points of views.
$\mathcal {L}$
is clear from the context we talk simply of algebras and expanded algebras. Notice that algebras augmented by a single predicate symbol often appear in abstract algebraic logic as matrices (cf. [Reference Font16, Chapter 4]). The key difference between expanded algebras and matrices is in the role played by the additional predicate symbol. In fact, in the context of expanded algebras the predicate identifies the core of the algebra, which we use to restrict the possible interpretation of the atomic formulas (cf. 3.17 below). Differently, in the context of logical matrices, the predicate rather identifies a designated “truth set.” We will consider in Section 7 a matrix-like approach to weak logics which unifies these two points of views.
Since expanded algebras are first-order structures, we can apply the definition of maps from Definition 2.8 in their setting. We recall that a strong homomorphism
![]() $h:A\to B$
of two expanded algebras is an
$h:A\to B$
of two expanded algebras is an
![]() $\mathcal {L}$
-algebra homomorphism such that
$\mathcal {L}$
-algebra homomorphism such that
![]() $h[\mathsf {core}(A)]=\mathsf {core}(B)$
. We recall from Notation 2.10 that
$h[\mathsf {core}(A)]=\mathsf {core}(B)$
. We recall from Notation 2.10 that
![]() $\mathbb {H}(\mathbf {K})$
indicates the closure of
$\mathbb {H}(\mathbf {K})$
indicates the closure of
![]() $\mathbf {K}$
under images by strong homomorphisms. We can then extend the notions of quasivarieties and varieties to the setting of expanded algebras.
$\mathbf {K}$
under images by strong homomorphisms. We can then extend the notions of quasivarieties and varieties to the setting of expanded algebras.
Definition 3.12. A class of expanded algebras
![]() $\mathbf {K}$
is a quasivariety if it is closed under
$\mathbf {K}$
is a quasivariety if it is closed under
![]() $\mathbb {I}$
,
$\mathbb {I}$
,
![]() $\mathbb {S}$
,
$\mathbb {S}$
,
![]() $\mathbb {P,}$
and
$\mathbb {P,}$
and
![]() $\mathbb {P}_{\mathrm {U}}$
. A class of expanded algebras
$\mathbb {P}_{\mathrm {U}}$
. A class of expanded algebras
![]() $\mathbf {K}$
is a variety if it is closed under
$\mathbf {K}$
is a variety if it is closed under
![]() $\mathbb {H}$
,
$\mathbb {H}$
,
![]() $\mathbb {S,}$
and
$\mathbb {S,}$
and
![]() $\mathbb {P}$
. We denote by
$\mathbb {P}$
. We denote by
![]() $\mathbb {Q}(\mathbf {K})$
the quasivariety generated by
$\mathbb {Q}(\mathbf {K})$
the quasivariety generated by
![]() $\mathbf {K}$
and by
$\mathbf {K}$
and by
![]() $\mathbb {V}(\mathbf {K})$
the variety generated by
$\mathbb {V}(\mathbf {K})$
the variety generated by
![]() $\mathbf {K}$
.
$\mathbf {K}$
.
Notation 3.13. Let
![]() $\mathbf {K}$
be a class of expanded
$\mathbf {K}$
be a class of expanded
![]() $\mathcal {L}$
-algebras, then we write
$\mathcal {L}$
-algebras, then we write
![]() $\mathbf {K}\restriction \mathcal {L}$
for the class of its
$\mathbf {K}\restriction \mathcal {L}$
for the class of its
![]() $\mathcal {L}$
-reducts. If it is clear from the context, we also write
$\mathcal {L}$
-reducts. If it is clear from the context, we also write
![]() $\mathbf {K}$
for
$\mathbf {K}$
for
![]() $\mathbf {K}\restriction \mathcal {L}$
.
$\mathbf {K}\restriction \mathcal {L}$
.
Remark 3.14. We notice the following: if
![]() $\mathbf {K}$
is a quasivariety of expanded
$\mathbf {K}$
is a quasivariety of expanded
![]() $\mathcal {L}$
-algebras, then its
$\mathcal {L}$
-algebras, then its
![]() $\mathcal {L}$
-reducts
$\mathcal {L}$
-reducts
![]() $\mathbf {K}\restriction \mathcal {L}$
form a quasivariety of
$\mathbf {K}\restriction \mathcal {L}$
form a quasivariety of
![]() $\mathcal {L}$
-algebras. However, if
$\mathcal {L}$
-algebras. However, if
![]() $\mathbf {K}$
is a quasivariety of
$\mathbf {K}$
is a quasivariety of
![]() $\mathcal {L}$
-algebras, then it is not the case that an arbitrary expansion
$\mathcal {L}$
-algebras, then it is not the case that an arbitrary expansion
![]() $\mathbf {K}'$
of the algebras in
$\mathbf {K}'$
of the algebras in
![]() $\mathbf {K}$
gives rise to a quasivariety of expanded algebras. To obtain a quasivariety of expanded algebras we need to consider the generated quasivariety
$\mathbf {K}$
gives rise to a quasivariety of expanded algebras. To obtain a quasivariety of expanded algebras we need to consider the generated quasivariety
![]() $\mathbb {Q}(\mathbf {K}')$
. We shall consider in Section 4.3 later some cases when this additional step is not necessary, namely, the case when a quasivariety of algebras determines uniquely a quasivariety of expanded algebras.
$\mathbb {Q}(\mathbf {K}')$
. We shall consider in Section 4.3 later some cases when this additional step is not necessary, namely, the case when a quasivariety of algebras determines uniquely a quasivariety of expanded algebras.
Crucially, expanded algebras allow us to define a more fine-grained consequence relation than the one we introduced in Definition 2.17. The key idea is to use the core of the algebra to restrict the possible valuation of the atomic variables of the language. To our knowledge, the idea of restricting the possible valuations of the atomic variables to a specific subset of an algebra first appeared in [Reference Bezhanishvili, Grilletti and Holliday2].
Definition 3.15. The expanded term algebra in the signature
![]() $\mathcal {L}$
is the structure
$\mathcal {L}$
is the structure
![]() $\mathsf {Fm}_{\mathcal {L}}$
augmented with
$\mathsf {Fm}_{\mathcal {L}}$
augmented with
![]() $\mathsf {core}(\mathsf {Fm}_{\mathcal {L}})=\mathsf {Var}$
. We often write
$\mathsf {core}(\mathsf {Fm}_{\mathcal {L}})=\mathsf {Var}$
. We often write
![]() $ (\mathsf {Fm},\mathsf {Var}) $
and omit the index
$ (\mathsf {Fm},\mathsf {Var}) $
and omit the index
![]() $\mathcal {L}$
and its signature operations when the language is clear from the context. A homomorphism from
$\mathcal {L}$
and its signature operations when the language is clear from the context. A homomorphism from
![]() $\mathsf {Fm}_{\mathcal {L}}$
to an expanded
$\mathsf {Fm}_{\mathcal {L}}$
to an expanded
![]() $\mathcal {L}$
-algebra A is a core assignment, i.e., it is a homomorphism
$\mathcal {L}$
-algebra A is a core assignment, i.e., it is a homomorphism
![]() $h:\mathsf {Fm}_{\mathcal {L}}\to A$
such that
$h:\mathsf {Fm}_{\mathcal {L}}\to A$
such that
![]() $h(x)\in \mathsf {core}(A)$
for all
$h(x)\in \mathsf {core}(A)$
for all
![]() $x\in \mathsf {Var}$
. We write
$x\in \mathsf {Var}$
. We write
![]() $\mathsf {Hom}^c(\mathsf {Fm}_{\mathcal {L}},A)$
for the set of core assignments from
$\mathsf {Hom}^c(\mathsf {Fm}_{\mathcal {L}},A)$
for the set of core assignments from
![]() $\mathsf {Fm}_{\mathcal {L}}$
to A.
$\mathsf {Fm}_{\mathcal {L}}$
to A.
Remark 3.16. We notice that, alternatively, one could also consider the expansion of the term algebra
![]() $\mathsf {Fm}$
with the core defined by letting
$\mathsf {Fm}$
with the core defined by letting
![]() $\mathsf {core}(\mathsf {Fm}_{\mathcal {L}})=\mathsf {core}(\Vdash )$
. This means that the endomorphisms of the term algebra are all the admissible substitutions of
$\mathsf {core}(\mathsf {Fm}_{\mathcal {L}})=\mathsf {core}(\Vdash )$
. This means that the endomorphisms of the term algebra are all the admissible substitutions of
![]() $\Vdash $
, and not only the atomic substitutions. As this makes only for a minor generalisation of our results, we stick to the former definition and always consider the atomic formulas as the underlying core of the term algebra.
$\Vdash $
, and not only the atomic substitutions. As this makes only for a minor generalisation of our results, we stick to the former definition and always consider the atomic formulas as the underlying core of the term algebra.
Definition 3.17 (Core semantics).
Let
![]() $\mathbf {K}$
be a class of expanded algebras and
$\mathbf {K}$
be a class of expanded algebras and
![]() $\Theta \cup \{\varepsilon \approx \delta \}$
a set of equations, then the equational core-consequence relation relative to
$\Theta \cup \{\varepsilon \approx \delta \}$
a set of equations, then the equational core-consequence relation relative to
![]() $\mathbf {K}$
is defined as follows:
$\mathbf {K}$
is defined as follows:
 $$ \begin{align*} \Theta \models^c_{\mathbf{K}} \varepsilon\approx \delta \Longleftrightarrow & \text{ for all } A \in \mathbf{K},\, h\in \mathsf{Hom}^c(\mathsf{Fm},A), \\ & \text{ if } h(\epsilon_i)= h(\delta_i) \text{ for all } \epsilon_i\approx \delta_i\in \Theta, \text{ then } h(\varepsilon)= h(\delta). \end{align*} $$
$$ \begin{align*} \Theta \models^c_{\mathbf{K}} \varepsilon\approx \delta \Longleftrightarrow & \text{ for all } A \in \mathbf{K},\, h\in \mathsf{Hom}^c(\mathsf{Fm},A), \\ & \text{ if } h(\epsilon_i)= h(\delta_i) \text{ for all } \epsilon_i\approx \delta_i\in \Theta, \text{ then } h(\varepsilon)= h(\delta). \end{align*} $$
We then write
![]() $\models ^c_{\mathbf {K}} \bigwedge _{i{\leqslant } n} \varepsilon _i\approx \delta _i \to \varepsilon \approx \delta $
if
$\models ^c_{\mathbf {K}} \bigwedge _{i{\leqslant } n} \varepsilon _i\approx \delta _i \to \varepsilon \approx \delta $
if
![]() $ \bigwedge _{i{\leqslant } n} \varepsilon _i\approx \delta _i \models ^c_{\mathbf {K}} \varepsilon \approx \delta $
. We usually write
$ \bigwedge _{i{\leqslant } n} \varepsilon _i\approx \delta _i \models ^c_{\mathbf {K}} \varepsilon \approx \delta $
. We usually write
![]() $A \models ^c \bigwedge _{i{\leqslant } n} \varepsilon _i\approx \delta _i \to \varepsilon \approx \delta $
in place of
$A \models ^c \bigwedge _{i{\leqslant } n} \varepsilon _i\approx \delta _i \to \varepsilon \approx \delta $
in place of
![]() $\models ^c_{\{A \}} \bigwedge _{i{\leqslant } n} \varepsilon _i\approx \delta _i \to \varepsilon \approx \delta $
. The related notions for equations are defined analogously.
$\models ^c_{\{A \}} \bigwedge _{i{\leqslant } n} \varepsilon _i\approx \delta _i \to \varepsilon \approx \delta $
. The related notions for equations are defined analogously.
Remark 3.18. Crucially, if
![]() $\Theta $
is a finite set of equations
$\Theta $
is a finite set of equations
![]() $\{\varepsilon _i\approx \delta _i : i{\leqslant } n\}$
, then we have that
$\{\varepsilon _i\approx \delta _i : i{\leqslant } n\}$
, then we have that
![]() $ \bigwedge _{i{\leqslant } n} \varepsilon _i\approx \delta _i \models ^c_{\mathbf {K}} \varepsilon \approx \delta $
holds if and only if
$ \bigwedge _{i{\leqslant } n} \varepsilon _i\approx \delta _i \models ^c_{\mathbf {K}} \varepsilon \approx \delta $
holds if and only if
 $$\begin{align*}\mathbf{K} \models \forall x_0,\dots ,\forall x_m \Big( \bigwedge_{i{\leqslant} m} \mathsf{core}(x_i) \land \bigwedge_{i{\leqslant} n} \varepsilon_i\approx \delta_i \to \varepsilon \approx \delta \Big), \end{align*}$$
$$\begin{align*}\mathbf{K} \models \forall x_0,\dots ,\forall x_m \Big( \bigwedge_{i{\leqslant} m} \mathsf{core}(x_i) \land \bigwedge_{i{\leqslant} n} \varepsilon_i\approx \delta_i \to \varepsilon \approx \delta \Big), \end{align*}$$
where all variables from
![]() $\Theta \cup \{\varepsilon \approx \delta \} $
are from
$\Theta \cup \{\varepsilon \approx \delta \} $
are from
![]() $x_0,\dots , x_m$
. In other words, when
$x_0,\dots , x_m$
. In other words, when
![]() $\Theta $
is finite the core semantics over a class of expanded algebra can be encoded in terms of the standard first-order consequence relation
$\Theta $
is finite the core semantics over a class of expanded algebra can be encoded in terms of the standard first-order consequence relation
![]() $\models $
, exactly as in the case of the relation
$\models $
, exactly as in the case of the relation
![]() $\models _{\mathbf {K}}$
. As we stressed in Remark 2.18, if the relation
$\models _{\mathbf {K}}$
. As we stressed in Remark 2.18, if the relation
![]() $\models ^c_{\mathbf {K}}$
is not finitary, then one could provide a similar translation into a suitable infinitary logic and replace quasivarieties by generalised quasivarieties.
$\models ^c_{\mathbf {K}}$
is not finitary, then one could provide a similar translation into a suitable infinitary logic and replace quasivarieties by generalised quasivarieties.
By Definition 3.17, in core semantics atomic variables are always assigned to core elements and, as a result of this feature, arbitrary formulas are always interpreted inside the subalgebra generated by the core. This motivates the interest in core-generated structures and in quasivarieties which are generated by these structures.
Definition 3.19. An expanded algebra A is core-generated if
![]() $A = \langle \mathsf {core}(A) \rangle $
. If
$A = \langle \mathsf {core}(A) \rangle $
. If
![]() $\mathbf {Q}$
is a class of algebras, we write
$\mathbf {Q}$
is a class of algebras, we write
![]() $\mathbf {Q}_{\mathrm {CG}}$
for its subclass of core-generated structures. A quasivariety
$\mathbf {Q}_{\mathrm {CG}}$
for its subclass of core-generated structures. A quasivariety
![]() $\mathbf {Q}$
of expanded algebras is core-generated if it is generated by its subclass of core-generated expanded algebras, i.e.,
$\mathbf {Q}$
of expanded algebras is core-generated if it is generated by its subclass of core-generated expanded algebras, i.e.,
![]() $\mathbf {Q}=\mathbb {Q}(\mathbf {Q}_{\mathrm {CG}})$
. Similarly, a variety
$\mathbf {Q}=\mathbb {Q}(\mathbf {Q}_{\mathrm {CG}})$
. Similarly, a variety
![]() $\mathbf {V}$
of expanded algebras is core-generated if
$\mathbf {V}$
of expanded algebras is core-generated if
![]() $\mathbf {V} = \mathbb {V}(\mathbf {V}_{\mathrm {CG}})$
.
$\mathbf {V} = \mathbb {V}(\mathbf {V}_{\mathrm {CG}})$
.
The next proposition shows that unrestricted substitutions interact nicely with core-generated quasivarieties in core semantics. In a sense, the next result shows that core semantics in core-generated classes of structures approximates as much as possible the standard consequence relations defined over quasivarieties.
Lemma 3.20. Let A be a core-generated expanded algebra and let
![]() $h\in \mathsf {Hom}(\mathsf {Fm},A)$
, then there are a core assignment
$h\in \mathsf {Hom}(\mathsf {Fm},A)$
, then there are a core assignment
![]() $g\in \mathsf {Hom}^c(\mathsf {Fm},A)$
and a substitution
$g\in \mathsf {Hom}^c(\mathsf {Fm},A)$
and a substitution
![]() $\sigma $
such that
$\sigma $
such that
![]() $h(\phi )=g(\sigma (\phi ))$
for all
$h(\phi )=g(\sigma (\phi ))$
for all
![]() $\phi \in \mathsf {Fm}$
.
$\phi \in \mathsf {Fm}$
.
Proof. Let
![]() $(x_i)_{i<\omega }$
be an enumeration of
$(x_i)_{i<\omega }$
be an enumeration of
![]() $\mathsf {Var}$
. Since A is core-generated, we have that for all
$\mathsf {Var}$
. Since A is core-generated, we have that for all
![]() $x_i\in \mathsf {Var}$
there is a polynomial
$x_i\in \mathsf {Var}$
there is a polynomial
![]() $t_i$
such that
$t_i$
such that
![]() $h(x_i) = t_i(a^i_0,\dots ,a^i_{n_i})$
with
$h(x_i) = t_i(a^i_0,\dots ,a^i_{n_i})$
with
![]() $a^i_j\in \mathsf {core}(A)$
for all
$a^i_j\in \mathsf {core}(A)$
for all
![]() $j{\leqslant } n_i$
. Let now
$j{\leqslant } n_i$
. Let now
![]() $\{ y^i_j : i<\omega , \; j{\leqslant } n_i \}$
be another enumeration of
$\{ y^i_j : i<\omega , \; j{\leqslant } n_i \}$
be another enumeration of
![]() $\mathsf {Var}$
and define
$\mathsf {Var}$
and define
![]() $g \in \mathsf {Hom}^c(\mathsf {Fm},A)$
such that
$g \in \mathsf {Hom}^c(\mathsf {Fm},A)$
such that
![]() $g(y^i_j) = a^i_j$
for all
$g(y^i_j) = a^i_j$
for all
![]() $ i<\omega $
,
$ i<\omega $
,
![]() $j{\leqslant } n_i$
. In particular, this means that for all formulas
$j{\leqslant } n_i$
. In particular, this means that for all formulas
![]() $\psi (x_0, \dots , x_m)\in \mathsf {Fm}$
we have
$\psi (x_0, \dots , x_m)\in \mathsf {Fm}$
we have
By construction we have that g is a core assignment. Let
![]() $\sigma $
be the substitution defined by letting
$\sigma $
be the substitution defined by letting
![]() $\sigma (x_i) = t_i(y^i_0,\dots ,y^i_{n_i})$
for all
$\sigma (x_i) = t_i(y^i_0,\dots ,y^i_{n_i})$
for all
![]() $x_i\in \mathsf {Var}$
, then from the display above we derive that
$x_i\in \mathsf {Var}$
, then from the display above we derive that
![]() $h(\phi )=g(\sigma (\phi ))$
for all
$h(\phi )=g(\sigma (\phi ))$
for all
![]() $\phi \in \mathsf {Fm}$
.
$\phi \in \mathsf {Fm}$
.
Proposition 3.21. Let
![]() $\mathbf {Q}$
be a core-generated quasivariety of expanded algebras, then
$\mathbf {Q}$
be a core-generated quasivariety of expanded algebras, then
![]() $\sigma (\Theta ) \models ^c_{\mathbf {Q}} \sigma (\varepsilon \approx \delta )$
for all
$\sigma (\Theta ) \models ^c_{\mathbf {Q}} \sigma (\varepsilon \approx \delta )$
for all
![]() $\sigma \in \mathsf {Subst}(\mathcal {L})$
holds if and only if
$\sigma \in \mathsf {Subst}(\mathcal {L})$
holds if and only if
![]() $ \Theta \models _{\mathbf {Q}} \varepsilon \approx \delta $
.
$ \Theta \models _{\mathbf {Q}} \varepsilon \approx \delta $
.
Proof. We consider the left-to-right direction. Suppose that
![]() $\Theta \not \models _{\mathbf {Q}} \varepsilon \approx \delta $
. Since
$\Theta \not \models _{\mathbf {Q}} \varepsilon \approx \delta $
. Since
![]() $\mathbf {Q}$
is core-generated, there is a core-generated expanded algebra
$\mathbf {Q}$
is core-generated, there is a core-generated expanded algebra
![]() $A \in \mathbf {Q}$
and some
$A \in \mathbf {Q}$
and some
![]() $h\in \mathsf {Hom}(\mathsf {Fm},A)$
such that
$h\in \mathsf {Hom}(\mathsf {Fm},A)$
such that
![]() $A\models h(\Theta )$
and
$A\models h(\Theta )$
and
![]() $A\not \models h(\varepsilon ) \approx h(\delta )$
(recall Definition 2.17). From Lemma 3.20 it follows that there is a core assignment
$A\not \models h(\varepsilon ) \approx h(\delta )$
(recall Definition 2.17). From Lemma 3.20 it follows that there is a core assignment
![]() $g\in \mathsf {Hom}^c(\mathsf {Fm},A)$
and a substitution
$g\in \mathsf {Hom}^c(\mathsf {Fm},A)$
and a substitution
![]() $\sigma $
such that
$\sigma $
such that
![]() $h(\phi )=g(\sigma (\phi ))$
for all
$h(\phi )=g(\sigma (\phi ))$
for all
![]() $\phi \in \mathsf {Fm}$
. Then it follows that
$\phi \in \mathsf {Fm}$
. Then it follows that
![]() $A \models g(\sigma [\Theta ])$
but
$A \models g(\sigma [\Theta ])$
but
![]() $A \not \models g(\sigma (\varepsilon \approx \delta ))$
, whence
$A \not \models g(\sigma (\varepsilon \approx \delta ))$
, whence
![]() $\sigma (\Theta ) \not \models ^c_{\mathbf {Q}} \sigma (\varepsilon \approx \delta )$
.
$\sigma (\Theta ) \not \models ^c_{\mathbf {Q}} \sigma (\varepsilon \approx \delta )$
.
We consider the right-to-left direction. Suppose that
![]() $\sigma (\Theta ) \not \models ^c_{\mathbf {Q}} \sigma (\varepsilon \approx \delta )$
, thus we can find an algebra
$\sigma (\Theta ) \not \models ^c_{\mathbf {Q}} \sigma (\varepsilon \approx \delta )$
, thus we can find an algebra
![]() $A\in \mathbf {Q}$
and an assignment
$A\in \mathbf {Q}$
and an assignment
![]() $h \in \mathsf {Hom}^c(\mathsf {Fm}, A)$
such that
$h \in \mathsf {Hom}^c(\mathsf {Fm}, A)$
such that
![]() $A \models h(\sigma [\Theta ])$
and
$A \models h(\sigma [\Theta ])$
and
![]() $A \not \models h(\sigma (\varepsilon \approx \delta ))$
. Then we have that
$A \not \models h(\sigma (\varepsilon \approx \delta ))$
. Then we have that
![]() $h \circ \sigma \in \mathsf {Hom}(\mathsf {Fm},A)$
, whence
$h \circ \sigma \in \mathsf {Hom}(\mathsf {Fm},A)$
, whence
![]() $ \Theta \not \models _{\mathbf {Q}} \varepsilon \approx \delta $
.
$ \Theta \not \models _{\mathbf {Q}} \varepsilon \approx \delta $
.
Since core semantics only looks at the substructure
![]() $\langle \mathsf {core}(A) \rangle $
of an expanded algebra A, it make sense to consider extensions of A that preserve the core.
$\langle \mathsf {core}(A) \rangle $
of an expanded algebra A, it make sense to consider extensions of A that preserve the core.
Definition 3.22. We say that B is a core superalgebra of A if
![]() $ B\in \mathrm {Mod}(\mathcal {L})$
,
$ B\in \mathrm {Mod}(\mathcal {L})$
,
![]() $A {\leqslant } B$
(i.e., A is a subalgebra of B) and
$A {\leqslant } B$
(i.e., A is a subalgebra of B) and
![]() $\mathsf {core}(A) = \mathsf {core}(B)$
. If
$\mathsf {core}(A) = \mathsf {core}(B)$
. If
![]() $\mathbf {K}$
is class of expanded algebras, we write
$\mathbf {K}$
is class of expanded algebras, we write
![]() $\mathbb {C}(\mathbf {K}) $
for the class of all core superalgebras of elements of
$\mathbb {C}(\mathbf {K}) $
for the class of all core superalgebras of elements of
![]() $\mathbf {K}$
.
$\mathbf {K}$
.
The next lemma and the following proposition establish some fundamental facts about the relation
![]() $\models ^c$
. Importantly, they show that the validity of quasiequations is preserved both under the operators
$\models ^c$
. Importantly, they show that the validity of quasiequations is preserved both under the operators
![]() $\mathbb {I}$
,
$\mathbb {I}$
,
![]() $\mathbb {S}$
,
$\mathbb {S}$
,
![]() $\mathbb {P}$
,
$\mathbb {P}$
,
![]() $\mathbb {P}_{\mathrm {U}} $
, and also under the core superstructure operator
$\mathbb {P}_{\mathrm {U}} $
, and also under the core superstructure operator
![]() $\mathbb {C}$
from Definition 3.22. Additionally, we also show that equations are preserved under strong homomorphisms. The following lemma is essentially a rephrasing of Remark 3.18.
$\mathbb {C}$
from Definition 3.22. Additionally, we also show that equations are preserved under strong homomorphisms. The following lemma is essentially a rephrasing of Remark 3.18.
Lemma 3.23. Let
![]() $\mathbf {K}$
be a class of expanded algebras, let
$\mathbf {K}$
be a class of expanded algebras, let
![]() $\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i\to \varepsilon \approx \delta $
be a quasiequation, and let V be all the variables occurring in it, then
$\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i\to \varepsilon \approx \delta $
be a quasiequation, and let V be all the variables occurring in it, then
Proof. This follows immediately from the fact that an assignment
![]() $h\in \mathsf {Hom}(\mathsf {Fm}, A)$
is a core assignment if and only if
$h\in \mathsf {Hom}(\mathsf {Fm}, A)$
is a core assignment if and only if
![]() $h(x)\in \mathsf {core}(A)$
for all
$h(x)\in \mathsf {core}(A)$
for all
![]() $x\in \mathsf {Var}$
.
$x\in \mathsf {Var}$
.
Proposition 3.24. Let
![]() $\mathbf {K}$
be a class of expanded algebras, then the following hold:
$\mathbf {K}$
be a class of expanded algebras, then the following hold:
-
(1) let
 $\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \varepsilon \approx \delta $
be a quasi-equation, then for all
$\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \varepsilon \approx \delta $
be a quasi-equation, then for all
 $\mathbb {O}\in \{ \mathbb {I}, \mathbb {S},\mathbb {P},\mathbb {P}_{\mathrm {U}}, \mathbb {C} \}$
we have that
$\mathbb {O}\in \{ \mathbb {I}, \mathbb {S},\mathbb {P},\mathbb {P}_{\mathrm {U}}, \mathbb {C} \}$
we have that  $$ \begin{align*} \{\varepsilon_i \approx \delta_i : i {\leqslant} n \}\models^c_{\mathbf{K}} \varepsilon \approx \delta \; \Longrightarrow \; \{\varepsilon_i \approx \delta_i : i {\leqslant} n \} \models^c_{\mathbb{O}(\mathbf{K})} \varepsilon \approx \delta; \end{align*} $$
$$ \begin{align*} \{\varepsilon_i \approx \delta_i : i {\leqslant} n \}\models^c_{\mathbf{K}} \varepsilon \approx \delta \; \Longrightarrow \; \{\varepsilon_i \approx \delta_i : i {\leqslant} n \} \models^c_{\mathbb{O}(\mathbf{K})} \varepsilon \approx \delta; \end{align*} $$
-
(2) if
 $\models ^c_{\mathbf {K}} \varepsilon \approx \delta $
, then
$\models ^c_{\mathbf {K}} \varepsilon \approx \delta $
, then
 $ \models ^c_{\mathbb {H}(\mathbf {K})} \varepsilon \approx \delta $
.
$ \models ^c_{\mathbb {H}(\mathbf {K})} \varepsilon \approx \delta $
.
Proof. For Claim (1) recall that the validity of universal Horn formulas is preserved by the operators
![]() $\mathbb {O}\in \{ \mathbb {I}, \mathbb {S},\mathbb {P},\mathbb {P}_{\mathrm {U}} \}$
. Then Lemma 3.23 implies that the validity of formulas in core semantics is preserved by
$\mathbb {O}\in \{ \mathbb {I}, \mathbb {S},\mathbb {P},\mathbb {P}_{\mathrm {U}} \}$
. Then Lemma 3.23 implies that the validity of formulas in core semantics is preserved by
![]() $\mathbb {O}\in \{ \mathbb {I}, \mathbb {S},\mathbb {P},\mathbb {P}_{\mathrm {U}} \}$
. Preservation of validity by
$\mathbb {O}\in \{ \mathbb {I}, \mathbb {S},\mathbb {P},\mathbb {P}_{\mathrm {U}} \}$
. Preservation of validity by
![]() $\mathbb {C}$
follows immediately by the definitions of core semantics and core superstructure. Claim (2) is immediate by the definition of core semantics and the fact that, if
$\mathbb {C}$
follows immediately by the definitions of core semantics and core superstructure. Claim (2) is immediate by the definition of core semantics and the fact that, if
![]() $B\in \mathbb {H}(\mathbf {K})$
, then there is
$B\in \mathbb {H}(\mathbf {K})$
, then there is
![]() $A\in \mathbf {K}$
and a surjective homomorphism
$A\in \mathbf {K}$
and a surjective homomorphism
![]() $h:A\to B$
such that
$h:A\to B$
such that
![]() $\mathsf {core}(B)=h[\mathsf {core}(A)]$
.
$\mathsf {core}(B)=h[\mathsf {core}(A)]$
.
We conclude this section by showing a version of Maltsev’s Theorem for the setting of core-generated quasivarieties, i.e., we prove that every core-generated quasivariety is axiomatised by its validities under core semantics.
Definition 3.25. We define the following notions.
-
(1) For any set T of quasiequations (or equations), we let
 $\mathrm {Mod}^c(T)$
be the class of expanded algebras A such that
$\mathrm {Mod}^c(T)$
be the class of expanded algebras A such that
 $A \models ^c T$
and
$A \models ^c T$
and
 $\mathrm {Mod}_{\mathrm {CG}}^c(T)$
for its subclass of core-generated models.
$\mathrm {Mod}_{\mathrm {CG}}^c(T)$
for its subclass of core-generated models. -
(2) For any class
 $\mathbf {K}$
of expanded algebras, we denote by
$\mathbf {K}$
of expanded algebras, we denote by
 $\mathrm {Th}_{\mathrm {qe}}^c(\mathbf {K})$
the set of all quasiequations true in
$\mathrm {Th}_{\mathrm {qe}}^c(\mathbf {K})$
the set of all quasiequations true in
 $\mathbf {K}$
under core semantics, and we denote by
$\mathbf {K}$
under core semantics, and we denote by
 $\mathrm {Th}_{\mathrm {e}}^c(\mathbf {K})$
the set of all equations true in
$\mathrm {Th}_{\mathrm {e}}^c(\mathbf {K})$
the set of all equations true in
 $\mathbf {K}$
under core semantics.
$\mathbf {K}$
under core semantics.
The following proposition is an immediate corollary of Maltsev’s Theorem (cf. Fact 2.14) and Proposition 3.21.
Proposition 3.26. Let
![]() $\mathbf {Q}$
be a quasivariety of expanded algebras and let A be a core-generated expanded algebra. Then
$\mathbf {Q}$
be a quasivariety of expanded algebras and let A be a core-generated expanded algebra. Then
![]() $A \in \mathbf {Q}_{\mathrm {CG}}$
if and only if
$A \in \mathbf {Q}_{\mathrm {CG}}$
if and only if
![]() $A \models ^c \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q})$
.
$A \models ^c \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q})$
.
Proof. The direction from left-to-right follows immediately by the definition of
![]() $\mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q})$
. We consider the direction from right-to-left. Let A be core-generated and suppose
$\mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q})$
. We consider the direction from right-to-left. Let A be core-generated and suppose
![]() $A\notin \mathbf {Q}_{\mathrm {CG}}$
. It follows that
$A\notin \mathbf {Q}_{\mathrm {CG}}$
. It follows that
![]() $A\notin \mathbf {Q}$
and so by Maltsev’s Theorem
$A\notin \mathbf {Q}$
and so by Maltsev’s Theorem
![]() $A \not \models \mathrm {Th}_{\mathrm {qe}}(\mathbf {Q})$
. Let
$A \not \models \mathrm {Th}_{\mathrm {qe}}(\mathbf {Q})$
. Let
![]() $\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \alpha \approx \beta \in \mathrm {Th}_{\mathrm {qe}}(\mathbf {Q})$
be such that
$\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \alpha \approx \beta \in \mathrm {Th}_{\mathrm {qe}}(\mathbf {Q})$
be such that
![]() $A\not \models \bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \alpha \approx \beta $
. By Proposition 3.21 it follows that there is a substitution
$A\not \models \bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \alpha \approx \beta $
. By Proposition 3.21 it follows that there is a substitution
![]() $\sigma $
such that
$\sigma $
such that
![]() $A\not \models ^c \sigma (\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \alpha \approx \beta )$
. Now, since the relation
$A\not \models ^c \sigma (\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \alpha \approx \beta )$
. Now, since the relation
![]() $\models _{\mathbf {Q}}$
is closed under uniform substitution, it follows in particular that
$\models _{\mathbf {Q}}$
is closed under uniform substitution, it follows in particular that
![]() $\sigma (\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \alpha \approx \beta ) \in \mathrm {Th}_{\mathrm {qe}}(\mathbf {Q})$
. Moreover, since obviously
$\sigma (\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \alpha \approx \beta ) \in \mathrm {Th}_{\mathrm {qe}}(\mathbf {Q})$
. Moreover, since obviously
![]() $\mathrm {Th}_{\mathrm {qe}}(\mathbf {Q})\subseteq \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}) $
, we obtain that
$\mathrm {Th}_{\mathrm {qe}}(\mathbf {Q})\subseteq \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}) $
, we obtain that
![]() $\sigma (\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \alpha \approx \beta ) \in \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q})$
. We conclude that
$\sigma (\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \alpha \approx \beta ) \in \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q})$
. We conclude that
![]() $A \not \models ^c \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q})$
.
$A \not \models ^c \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q})$
.
4 Algebraizability of weak logics
In this section we use quasivarieties of expanded algebras to provide three different notions of algebraizability for the setting of weak logics, which we, respectively, call loose algebraizability, strict algebraizability, and fixed-point algebraizability. We proceed as follows: firstly, we review the notion of algebraizability for the setting of standard logics in Section 4.1, then in Section 4.2 we introduce the loose notion of algebraizability for weak logics, in Section 4.3 we consider the strict version of algebraizability for weak logics, and finally in Section 4.4 we focus on the very specific notion of fixed-point algebraizability.
4.1 Algebraizability of standard logics
We first review in this section the notion of algebraizability for the setting of standard logics. Recall that we denote by
![]() $\mathsf {Fm}$
and
$\mathsf {Fm}$
and
![]() $\mathsf {Eq,}$
respectively, the set of formulas and equations in the signature
$\mathsf {Eq,}$
respectively, the set of formulas and equations in the signature
![]() $\mathcal {L}$
. We shall refer to two maps, called transformers [Reference Font16], that allow us to translate formulas into equations and vice versa.
$\mathcal {L}$
. We shall refer to two maps, called transformers [Reference Font16], that allow us to translate formulas into equations and vice versa.
Definition 4.1. A pair of transformers in the language
![]() $\mathcal {L}$
is a pair of functions
$\mathcal {L}$
is a pair of functions
![]() $\tau : \mathsf {Fm} \to \wp (\mathsf {Eq})$
and
$\tau : \mathsf {Fm} \to \wp (\mathsf {Eq})$
and
![]() $\Delta : \mathsf {Eq} \to \wp (\mathsf {Fm})$
. We say that
$\Delta : \mathsf {Eq} \to \wp (\mathsf {Fm})$
. We say that
![]() $\tau $
and
$\tau $
and
![]() $\Delta $
are structural if for all substitutions
$\Delta $
are structural if for all substitutions
![]() $\sigma \in \mathsf {Subst}(\mathcal {L})$
,
$\sigma \in \mathsf {Subst}(\mathcal {L})$
,
![]() $\tau (\sigma (\phi )) = \sigma (\tau (\phi ))$
and
$\tau (\sigma (\phi )) = \sigma (\tau (\phi ))$
and
![]() $\sigma (\Delta (\varepsilon ,\delta )) = \Delta (\sigma (\varepsilon ,\delta ))$
, where we let
$\sigma (\Delta (\varepsilon ,\delta )) = \Delta (\sigma (\varepsilon ,\delta ))$
, where we let
![]() $\sigma (\varepsilon ,\delta ) = (\sigma (\varepsilon ),\sigma (\delta ))$
. We say that the transformers
$\sigma (\varepsilon ,\delta ) = (\sigma (\varepsilon ),\sigma (\delta ))$
. We say that the transformers
![]() $\tau , \Delta $
are finitary if for all
$\tau , \Delta $
are finitary if for all
![]() $\phi \in \mathsf {Fm}$
and
$\phi \in \mathsf {Fm}$
and
![]() $\varepsilon \approx \delta \in \mathsf {Eq}$
,
$\varepsilon \approx \delta \in \mathsf {Eq}$
,
![]() $|\tau (\phi )|<\aleph _0$
and
$|\tau (\phi )|<\aleph _0$
and
![]() $|\Delta (\varepsilon ,\delta )|<\aleph _0$
. For any set of formulas
$|\Delta (\varepsilon ,\delta )|<\aleph _0$
. For any set of formulas
![]() $\Gamma \subseteq \mathsf {Fm}$
, we let
$\Gamma \subseteq \mathsf {Fm}$
, we let
![]() $\tau (\Gamma ) = \bigcup _{\phi \in \Gamma } \tau (\phi )$
and for all set of equations
$\tau (\Gamma ) = \bigcup _{\phi \in \Gamma } \tau (\phi )$
and for all set of equations
![]() $\Theta \subseteq \mathsf {Eq}$
we let
$\Theta \subseteq \mathsf {Eq}$
we let
![]() $\Delta (\Theta ) = \bigcup _{\varepsilon \approx \delta \in \Theta }\Delta (\varepsilon ,\delta )$
.
$\Delta (\Theta ) = \bigcup _{\varepsilon \approx \delta \in \Theta }\Delta (\varepsilon ,\delta )$
.
The following notion of algebraizability was introduced by Blok and Pigozzi in their seminal article [Reference Blok and Pigozzi4]. We write
![]() $\Gamma _0 \equiv _{\mathbf {K}} \Gamma _1$
as a shorthand for
$\Gamma _0 \equiv _{\mathbf {K}} \Gamma _1$
as a shorthand for
![]() $\Gamma _0 \vDash _{\mathbf {K}} \Gamma _1$
and
$\Gamma _0 \vDash _{\mathbf {K}} \Gamma _1$
and
![]() $\Gamma _1 \vDash _{\mathbf {K}} \Gamma _0$
.
$\Gamma _1 \vDash _{\mathbf {K}} \Gamma _0$
.
Definition 4.2 (Algebraizability).
A (standard) logic
![]() $\vdash $
is algebraizable if there are a quasivariety of (standard) algebras
$\vdash $
is algebraizable if there are a quasivariety of (standard) algebras
![]() $\mathbf {Q}$
and structural transformers
$\mathbf {Q}$
and structural transformers
![]() $\tau : \mathsf {Fm} \to \wp (\mathsf {Eq})$
and
$\tau : \mathsf {Fm} \to \wp (\mathsf {Eq})$
and
![]() $\Delta : \mathsf {Eq} \to \wp (\mathsf {Fm})$
such that
$\Delta : \mathsf {Eq} \to \wp (\mathsf {Fm})$
such that
If these conditions are met, we then say that
![]() $\mathbf {Q}$
is an equivalent algebraic semantics of
$\mathbf {Q}$
is an equivalent algebraic semantics of
![]() $\vdash $
, and that
$\vdash $
, and that
![]() $(\mathbf {Q},\tau ,\Delta )$
witnesses the algebraizability of
$(\mathbf {Q},\tau ,\Delta )$
witnesses the algebraizability of
![]() $\vdash $
.
$\vdash $
.
Remark 4.3. The restriction to quasivarieties of algebras stems from the fact that we are exclusively considering finitary consequence relations
![]() $\vdash $
. See [Reference Font16, Section 3] for an extension of this definition to generalised quasivarieties and non-finitary logics.
$\vdash $
. See [Reference Font16, Section 3] for an extension of this definition to generalised quasivarieties and non-finitary logics.
We recall the following two important facts about algebraizability. We refer the reader to [Reference Font16, Proposition 3.12, Theorem 3.37] for a proof of these results.
Fact 4.4. Let
![]() $\vdash $
be a standard logic, then:
$\vdash $
be a standard logic, then:
It is a key property of algebraizability that the equivalent algebraic semantics of a standard logic is unique. See [Reference Font16] for a proof of this result.
Fact 4.5. If the tuples
![]() $(\mathbf {Q}_0, \tau _0, \Delta _0)$
and
$(\mathbf {Q}_0, \tau _0, \Delta _0)$
and
![]() $(\mathbf {Q}_1, \tau _1, \Delta _1)$
both witness the algebraizability of a standard logic
$(\mathbf {Q}_1, \tau _1, \Delta _1)$
both witness the algebraizability of a standard logic
![]() $\vdash $
, then:
$\vdash $
, then:
-
(1)
 $\mathbf {Q}_0= \mathbf {Q}_1$
;
$\mathbf {Q}_0= \mathbf {Q}_1$
; -
(2)
 $\Delta _0(\varepsilon ,\delta ) \dashv \vdash \Delta _1(\varepsilon ,\delta )$
, for all
$\Delta _0(\varepsilon ,\delta ) \dashv \vdash \Delta _1(\varepsilon ,\delta )$
, for all
 $\varepsilon \approx \delta \in \mathsf {Eq}$
;
$\varepsilon \approx \delta \in \mathsf {Eq}$
; -
(3)
 $\tau _0(\phi ) \equiv _{\mathbf {Q}_i} \tau _1(\phi )$
with
$\tau _0(\phi ) \equiv _{\mathbf {Q}_i} \tau _1(\phi )$
with
 $i\in \{0,1\}$
, for all
$i\in \{0,1\}$
, for all
 $\phi \in \mathsf {Fm}$
.
$\phi \in \mathsf {Fm}$
.
4.2 Loose algebraizability of weak logics
By using the core consequence relation
![]() $\models ^c$
in place of the standard one
$\models ^c$
in place of the standard one
![]() $\models $
, we can provide a first version of the notion of algebraizability in the setting of weak logics. Obviously, we write
$\models $
, we can provide a first version of the notion of algebraizability in the setting of weak logics. Obviously, we write
![]() $\Gamma _0 \equiv ^c_{\mathbf {K}} \Gamma _1$
as a shorthand for
$\Gamma _0 \equiv ^c_{\mathbf {K}} \Gamma _1$
as a shorthand for
![]() $\Gamma _0 \models ^c_{\mathbf {K}} \Gamma _1$
and
$\Gamma _0 \models ^c_{\mathbf {K}} \Gamma _1$
and
![]() $\Gamma _1 \models ^c_{\mathbf {K}} \Gamma _0$
.
$\Gamma _1 \models ^c_{\mathbf {K}} \Gamma _0$
.
Definition 4.6. A weak logic
![]() $\Vdash $
is loosely algebraizable if there is a core-generated quasivariety of expanded algebras
$\Vdash $
is loosely algebraizable if there is a core-generated quasivariety of expanded algebras
![]() $\mathbf {Q}$
and two structural transformers
$\mathbf {Q}$
and two structural transformers
![]() $\tau : \mathsf {Fm} \to \wp (\mathsf {Eq})$
and
$\tau : \mathsf {Fm} \to \wp (\mathsf {Eq})$
and
![]() $\Delta : \mathsf {Eq} \to \wp (\mathsf {Fm})$
such that
$\Delta : \mathsf {Eq} \to \wp (\mathsf {Fm})$
such that
If these conditions are met, we then say that
![]() $\mathbf {Q}$
is a loose algebraic semantics of
$\mathbf {Q}$
is a loose algebraic semantics of
![]() $\Vdash $
, and that the tuple
$\Vdash $
, and that the tuple
![]() $(\mathbf {Q},\tau ,\Delta )$
witnesses the loose algebraizability of
$(\mathbf {Q},\tau ,\Delta )$
witnesses the loose algebraizability of
![]() $\Vdash $
.
$\Vdash $
.
To show this definition is indeed robust, we adapt the proof of the uniqueness of the equivalent algebraic semantic of standard logics [Reference Font16, Theorem 3.17] to the case of loosely algebraizable weak logics. In the light of the following theorem, we often refer to the tuple
![]() $(\mathbf {Q}, \tau , \Delta )$
witnessing the loose algebraizability of the weak logic
$(\mathbf {Q}, \tau , \Delta )$
witnessing the loose algebraizability of the weak logic
![]() $\Vdash $
as the equivalent loose algebraic semantics of
$\Vdash $
as the equivalent loose algebraic semantics of
![]() $\Vdash $
.
$\Vdash $
.
Theorem 4.7. If both the tuples
![]() $(\mathbf {Q}_0, \tau _0, \Delta _0)$
and
$(\mathbf {Q}_0, \tau _0, \Delta _0)$
and
![]() $(\mathbf {Q}_1, \tau _1, \Delta _1)$
witness the algebraizability of
$(\mathbf {Q}_1, \tau _1, \Delta _1)$
witness the algebraizability of
![]() $\Vdash $
, then:
$\Vdash $
, then:
-
(1)
 $\mathbf {Q}_0= \mathbf {Q}_1$
;
$\mathbf {Q}_0= \mathbf {Q}_1$
; -
(2)
 , for all
, for all
 $\varepsilon \approx \delta \in \mathsf {Eq}$
;
$\varepsilon \approx \delta \in \mathsf {Eq}$
; -
(3)
 $\tau _0(\phi )\equiv ^c_{\mathbf {Q}_i}\tau _1(\phi ) $
with
$\tau _0(\phi )\equiv ^c_{\mathbf {Q}_i}\tau _1(\phi ) $
with
 $i\in \{0,1\}$
, for all
$i\in \{0,1\}$
, for all
 $\phi \in \mathsf {Fm}$
.
$\phi \in \mathsf {Fm}$
.
Proof. Notice that the two witnesses of algebraizability give rise to two different consequence relations, which we shall denote by
![]() $\models ^0_{\mathbf {Q}_0}$
and
$\models ^0_{\mathbf {Q}_0}$
and
![]() $\models ^1_{\mathbf {Q}_1}$
.
$\models ^1_{\mathbf {Q}_1}$
.
Clause (2): ![]() , for all
, for all
![]() $\varepsilon \approx \delta \in \mathsf {Eq}$
. We prove
$\varepsilon \approx \delta \in \mathsf {Eq}$
. We prove
![]() $\Delta _0(\varepsilon ,\delta ) \Vdash \Delta _1(\varepsilon ,\delta ) $
. Let
$\Delta _0(\varepsilon ,\delta ) \Vdash \Delta _1(\varepsilon ,\delta ) $
. Let
![]() $\phi \in \Delta _1(\varepsilon ,\delta ) $
, then we clearly have that
$\phi \in \Delta _1(\varepsilon ,\delta ) $
, then we clearly have that
Now, we have that
![]() $\varnothing \models ^1_{\mathbf {Q}_1} \varepsilon \approx \varepsilon $
, hence by
$\varnothing \models ^1_{\mathbf {Q}_1} \varepsilon \approx \varepsilon $
, hence by
![]() $\phi \in \Delta _1(\varepsilon ,\varepsilon )$
and 4.6(W2), we obtain
$\phi \in \Delta _1(\varepsilon ,\varepsilon )$
and 4.6(W2), we obtain
Moreover, it also follows that
![]() $\varepsilon \approx \delta \models ^0_{\mathbf {Q}_0} \phi (\varepsilon ,\varepsilon )\approx \phi (\varepsilon ,\delta )$
, hence by 4.6(W2),
$\varepsilon \approx \delta \models ^0_{\mathbf {Q}_0} \phi (\varepsilon ,\varepsilon )\approx \phi (\varepsilon ,\delta )$
, hence by 4.6(W2),
Finally, by (a)–(c), it follows that
![]() $\Delta _0(\varepsilon ,\delta ) \Vdash \phi (\varepsilon ,\delta ) $
, hence
$\Delta _0(\varepsilon ,\delta ) \Vdash \phi (\varepsilon ,\delta ) $
, hence
![]() $\Delta _0(\varepsilon ,\delta ) \Vdash \Delta _1(\varepsilon ,\delta ) $
. The converse direction is proven analogously.
$\Delta _0(\varepsilon ,\delta ) \Vdash \Delta _1(\varepsilon ,\delta ) $
. The converse direction is proven analogously.
Clause (1):
![]() $\mathbf {Q}_0= \mathbf {Q}_1$
. We first prove that
$\mathbf {Q}_0= \mathbf {Q}_1$
. We first prove that
![]() $\mathbf {Q}_0$
and
$\mathbf {Q}_0$
and
![]() $\mathbf {Q}_1$
satisfy the same quasiequations under core semantics. We show only that
$\mathbf {Q}_1$
satisfy the same quasiequations under core semantics. We show only that
![]() $\mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}_0) \subseteq \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}_1)$
, as the other direction follows analogously. Let
$\mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}_0) \subseteq \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}_1)$
, as the other direction follows analogously. Let
![]() $\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \varepsilon \approx \delta \in \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}_0) $
, then it follows that
$\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \varepsilon \approx \delta \in \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}_0) $
, then it follows that
![]() $\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \models ^0_{\mathbf {Q}_0} \varepsilon \approx \delta $
and this yields that
$\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \models ^0_{\mathbf {Q}_0} \varepsilon \approx \delta $
and this yields that
![]() $ \bigcup _{i{\leqslant } n} \Delta _0(\varepsilon _i,\delta _i) \Vdash \Delta _0(\varepsilon , \delta )$
by 4.6(W2). By point (3) above, it follows that
$ \bigcup _{i{\leqslant } n} \Delta _0(\varepsilon _i,\delta _i) \Vdash \Delta _0(\varepsilon , \delta )$
by 4.6(W2). By point (3) above, it follows that
![]() $\bigcup _{i{\leqslant } n} \Delta _1(\varepsilon _i,\delta _i) \Vdash \Delta _1 (\varepsilon , \delta ) $
, hence by 4.6(W2) we get
$\bigcup _{i{\leqslant } n} \Delta _1(\varepsilon _i,\delta _i) \Vdash \Delta _1 (\varepsilon , \delta ) $
, hence by 4.6(W2) we get
![]() $\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \models ^1_{\mathbf {Q}_1} \varepsilon \approx \delta $
. The latter entails
$\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \models ^1_{\mathbf {Q}_1} \varepsilon \approx \delta $
. The latter entails
![]() $\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \varepsilon \approx \delta \in \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}_1) $
and thus
$\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \varepsilon \approx \delta \in \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}_1) $
and thus
![]() $\mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}_0)\subseteq \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}_1)$
. By reasoning analogously we obtain that
$\mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}_0)\subseteq \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}_1)$
. By reasoning analogously we obtain that
![]() $\mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}_1)\subseteq \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}_0) $
, hence
$\mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}_1)\subseteq \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}_0) $
, hence
![]() $\mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}_0)= \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}_1) $
. It then follows by Proposition 3.26 above that
$\mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}_0)= \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q}_1) $
. It then follows by Proposition 3.26 above that
![]() $(\mathbf {Q}_0)_{\mathrm {CG}}=(\mathbf {Q}_1)_{\mathrm {CG}}$
and since both
$(\mathbf {Q}_0)_{\mathrm {CG}}=(\mathbf {Q}_1)_{\mathrm {CG}}$
and since both
![]() $\mathbf {Q}_0 $
and
$\mathbf {Q}_0 $
and
![]() $\mathbf {Q}_1 $
are core-generated we conclude that
$\mathbf {Q}_1 $
are core-generated we conclude that
![]() $\mathbf {Q}_0=\mathbf {Q}_1$
.
$\mathbf {Q}_0=\mathbf {Q}_1$
.
Clause (3):
![]() $\tau _0(\phi )\equiv ^c_{\mathbf {Q}_i}\tau _1(\phi ) $
with
$\tau _0(\phi )\equiv ^c_{\mathbf {Q}_i}\tau _1(\phi ) $
with
![]() $i\in \{0,1\}$
, for all
$i\in \{0,1\}$
, for all
![]() $\phi \in \mathsf {Fm}$
. By Clause (1), it suffices to prove that
$\phi \in \mathsf {Fm}$
. By Clause (1), it suffices to prove that
![]() $\tau _0(\phi ) \equiv _{\mathbf {Q}_0}^0 \tau _1(\phi )$
. By 4.6(W3), we have
$\tau _0(\phi ) \equiv _{\mathbf {Q}_0}^0 \tau _1(\phi )$
. By 4.6(W3), we have ![]() and by Clause (2) this is equivalent to
and by Clause (2) this is equivalent to ![]() . It then follows by 4.6(W2) that
. It then follows by 4.6(W2) that
![]() $\tau _0(\phi ) \equiv _{\mathbf {Q}_0}^0 \tau _1(\phi )$
.
$\tau _0(\phi ) \equiv _{\mathbf {Q}_0}^0 \tau _1(\phi )$
.
We have thus established that every algebraizable weak logic has a unique equivalent algebraic semantics, up to equivalence under the core consequence relation. We conclude this section by proving an analogue of Fact 4.4 for weak logics.
Proposition 4.8. Let
![]() $\Vdash $
be a weak logic, then:
$\Vdash $
be a weak logic, then:
Proof. We prove (1). Suppose
![]() $\Vdash $
is a weak logic and let
$\Vdash $
is a weak logic and let
![]() $(\mathbf {Q}, \tau , \Delta )$
satisfy 4.6(W1) and 4.6(W4). We verify that 4.6(W2) and 4.6(W3) hold as well. By 4.6(W4)
$(\mathbf {Q}, \tau , \Delta )$
satisfy 4.6(W1) and 4.6(W4). We verify that 4.6(W2) and 4.6(W3) hold as well. By 4.6(W4)
![]() $\Theta \models ^c_{\mathbf {Q}} \varepsilon \approx \delta $
is equivalent to
$\Theta \models ^c_{\mathbf {Q}} \varepsilon \approx \delta $
is equivalent to
![]() $\tau [\Delta (\Theta )]\models ^c_{\mathbf {Q}}\tau (\Delta (\varepsilon ,\delta )) $
, which by 4.6(W1) is equivalent to
$\tau [\Delta (\Theta )]\models ^c_{\mathbf {Q}}\tau (\Delta (\varepsilon ,\delta )) $
, which by 4.6(W1) is equivalent to
![]() $\Delta (\Theta )\Vdash \Delta (\varepsilon ,\delta ) $
, proving 4.6(W2). Also, for any formula
$\Delta (\Theta )\Vdash \Delta (\varepsilon ,\delta ) $
, proving 4.6(W2). Also, for any formula
![]() $\phi $
, we have that
$\phi $
, we have that
![]() $ \tau (\phi )\equiv ^c_{\mathbf {Q}} \tau (\phi )$
, hence by 4.6(W4)
$ \tau (\phi )\equiv ^c_{\mathbf {Q}} \tau (\phi )$
, hence by 4.6(W4)
![]() $\tau [\Delta ( \tau (\phi ))]\equiv ^c_{\mathbf {Q}} \tau (\phi )$
and by 4.6(W1)
$\tau [\Delta ( \tau (\phi ))]\equiv ^c_{\mathbf {Q}} \tau (\phi )$
and by 4.6(W1) ![]() , proving 4.6(W3). If
, proving 4.6(W3). If
![]() $(\mathbf {Q}, \tau , \Delta )$
satisfies 4.6(W2) and 4.6(W3), then we proceed analogously.
$(\mathbf {Q}, \tau , \Delta )$
satisfies 4.6(W2) and 4.6(W3), then we proceed analogously.
We prove (2). For any
![]() $\phi \in \mathsf {Fm}$
, we have by 4.6(W3) that
$\phi \in \mathsf {Fm}$
, we have by 4.6(W3) that ![]() , thus by
, thus by
![]() $\Vdash $
being finitary there is some
$\Vdash $
being finitary there is some
![]() $\tau _0(\phi )\subseteq \tau (\phi ) $
such that
$\tau _0(\phi )\subseteq \tau (\phi ) $
such that
![]() $|\tau _0(\phi )|<\aleph _0$
and
$|\tau _0(\phi )|<\aleph _0$
and ![]() . Moreover, for any equation
. Moreover, for any equation
![]() $\varepsilon \approx \delta \in \mathsf {Eq}$
, we have by 4.6(W4) that
$\varepsilon \approx \delta \in \mathsf {Eq}$
, we have by 4.6(W4) that
![]() $\varepsilon \approx \delta \equiv ^c_{\mathbf {Q}} \tau [ \Delta (\varepsilon ,\delta )]$
, so we obtain by finitarity a finite subset
$\varepsilon \approx \delta \equiv ^c_{\mathbf {Q}} \tau [ \Delta (\varepsilon ,\delta )]$
, so we obtain by finitarity a finite subset
![]() $\Delta _0(\varepsilon ,\delta ) \subseteq \Delta (\varepsilon ,\delta )$
such that
$\Delta _0(\varepsilon ,\delta ) \subseteq \Delta (\varepsilon ,\delta )$
such that
![]() $\varepsilon \approx \delta \equiv ^c_{\mathbf {Q}} \tau [ \Delta _0(\varepsilon ,\delta )]$
. Finally, it follows by the choice of
$\varepsilon \approx \delta \equiv ^c_{\mathbf {Q}} \tau [ \Delta _0(\varepsilon ,\delta )]$
. Finally, it follows by the choice of
![]() $\tau _0,\Delta _0$
that
$\tau _0,\Delta _0$
that ![]() , hence
, hence
![]() $\tau (\phi )\equiv ^c_{\mathbf {Q}} \tau _0(\phi )$
. Similarly, from
$\tau (\phi )\equiv ^c_{\mathbf {Q}} \tau _0(\phi )$
. Similarly, from
![]() $\tau [ \Delta (\varepsilon ,\delta )] \equiv ^c_{\mathbf {Q}} \tau [ \Delta _0(\varepsilon ,\delta )]$
we obtain
$\tau [ \Delta (\varepsilon ,\delta )] \equiv ^c_{\mathbf {Q}} \tau [ \Delta _0(\varepsilon ,\delta )]$
we obtain ![]() . Thus
. Thus
![]() $\tau _0,\Delta _0,$
and
$\tau _0,\Delta _0,$
and
![]() $\mathbf {Q}$
witness the algebraizability of
$\mathbf {Q}$
witness the algebraizability of
![]() $\Vdash $
.
$\Vdash $
.
Remark 4.9. As witnessed by the previous results, loose algebraizability satisfies the same uniqueness property of standard algebraizability. However, we believe this is too weak of a notion, as it does not really meet the fundamental intuition behind algebraizability. In fact, in contrast to the matrix semantics of logics (which we shall explore later in Section 7), the fundamental aspect of algebraizability is that it allows us to translate logical systems into equational consequences defined by classes of algebras, and not by arbitrary first-order structures containing relations. We will achieve this by considering strict algebraizability in the next section.
4.3 Strict algebraizability of weak logics
We introduce strict algebraizability as a refined notion of algebraizability for weak logical systems. As we mentioned in Remark 4.9, the problem with loose algebraizability is that it relates weak logics to (universal Horn) classes of first-order structures, and not really to algebras. To overcome this issue, we need to look for ways in which one can, so to speak, eliminate the core predicate
![]() $\mathsf {core}(A)$
. The key idea is to restrict attention to classes of expanded algebras in which the core is already definable in the functional part of the signature. Furthermore, since we are dealing with quasivarieties and we want the validity of formulas to be preserved by the operators
$\mathsf {core}(A)$
. The key idea is to restrict attention to classes of expanded algebras in which the core is already definable in the functional part of the signature. Furthermore, since we are dealing with quasivarieties and we want the validity of formulas to be preserved by the operators
![]() $\mathbb {I}$
,
$\mathbb {I}$
,
![]() $\mathbb {S}$
,
$\mathbb {S}$
,
![]() $\mathbb {P,}$
and
$\mathbb {P,}$
and
![]() $\mathbb {P}_{\mathrm {U}}$
, we exclusively consider definability by means of equations. We make this explicit in the following definitions.
$\mathbb {P}_{\mathrm {U}}$
, we exclusively consider definability by means of equations. We make this explicit in the following definitions.
Notation 4.10. If A is an
![]() $\mathcal {L}$
-algebra and
$\mathcal {L}$
-algebra and
![]() $\Sigma (x)$
a set of equations in the variable x, we let
$\Sigma (x)$
a set of equations in the variable x, we let
![]() $\Sigma (A)=\{a\in A : A \models \varepsilon (a) \approx \delta (a) \text { for all } \varepsilon \approx \delta \in \Sigma \}$
.
$\Sigma (A)=\{a\in A : A \models \varepsilon (a) \approx \delta (a) \text { for all } \varepsilon \approx \delta \in \Sigma \}$
.
Definition 4.11. An expanded algebra A is said to have an equationally definable core if there is a finite set of equations
![]() $\Sigma $
in the variable x such that
$\Sigma $
in the variable x such that
![]() $\mathsf {core}(A)=\Sigma (A)$
. A class of expanded algebras
$\mathsf {core}(A)=\Sigma (A)$
. A class of expanded algebras
![]() $\mathbf {K}$
is said to have a (uniformly) equationally definable core if there is a finite set of equations
$\mathbf {K}$
is said to have a (uniformly) equationally definable core if there is a finite set of equations
![]() $\Sigma $
such that
$\Sigma $
such that
![]() $\mathsf {core}(A)=\Sigma (A)$
for all
$\mathsf {core}(A)=\Sigma (A)$
for all
![]() $A \in \mathbf {K}$
.
$A \in \mathbf {K}$
.
The key reason that explains our interest in quasivarieties of expanded algebras with an equationally definable core is that, given an algebra A and a finite set of equations
![]() $\Sigma $
, there is a unique way to expand A into an expanded algebra with core defined by
$\Sigma $
, there is a unique way to expand A into an expanded algebra with core defined by
![]() $\Sigma $
. As the following proposition shows, this provides us with a canonical expansion of
$\Sigma $
. As the following proposition shows, this provides us with a canonical expansion of
![]() $\mathbf {Q}$
into a quasivariety of expanded algebras with core defined by
$\mathbf {Q}$
into a quasivariety of expanded algebras with core defined by
![]() $\Sigma $
.
$\Sigma $
.
Proposition 4.12. Let
![]() $\mathbf {Q}$
be a quasivariety of
$\mathbf {Q}$
be a quasivariety of
![]() $\mathcal {L}$
-algebras and
$\mathcal {L}$
-algebras and
![]() $\Sigma (x)$
a finite set of equations, then the class of structures
$\Sigma (x)$
a finite set of equations, then the class of structures
![]() $(A,\mathsf {core}(A))$
with
$(A,\mathsf {core}(A))$
with
![]() $A\in \mathbf {Q}$
and
$A\in \mathbf {Q}$
and
![]() $ \mathsf {core}(A)=\Sigma (A) $
is a quasivariety of expanded algebras.
$ \mathsf {core}(A)=\Sigma (A) $
is a quasivariety of expanded algebras.
Proof. Let
![]() $\mathbf {Q}$
be a quasivariety of
$\mathbf {Q}$
be a quasivariety of
![]() $\mathcal {L}$
-algebras and let
$\mathcal {L}$
-algebras and let
![]() $\mathbf {K}$
be the class of structures
$\mathbf {K}$
be the class of structures
![]() $(A,\mathsf {core}(A))$
with
$(A,\mathsf {core}(A))$
with
![]() $A\in \mathbf {Q}$
and
$A\in \mathbf {Q}$
and
![]() $ \mathsf {core}(A)=\Sigma (A) $
. Let
$ \mathsf {core}(A)=\Sigma (A) $
. Let
![]() $\{\alpha _i\approx \beta _i : i{\leqslant } n\}$
enumerate all equations in
$\{\alpha _i\approx \beta _i : i{\leqslant } n\}$
enumerate all equations in
![]() $\Sigma $
. Then consider the formulas
$\Sigma $
. Then consider the formulas

Clearly, both
![]() $\Psi $
and each
$\Psi $
and each
![]() $\Phi _i$
are universal Horn sentences, thus by Fact 2.14 they are preserved by the quasivariety operators
$\Phi _i$
are universal Horn sentences, thus by Fact 2.14 they are preserved by the quasivariety operators
![]() $\mathbb {I}$
,
$\mathbb {I}$
,
![]() $\mathbb {S}$
,
$\mathbb {S}$
,
![]() $\mathbb {P,}$
and
$\mathbb {P,}$
and
![]() $\mathbb {P}_{\mathrm {U}}$
. It follows that
$\mathbb {P}_{\mathrm {U}}$
. It follows that
![]() $\mathsf {core}(A)=\Sigma (A)$
for all
$\mathsf {core}(A)=\Sigma (A)$
for all
![]() $A\in \mathbb {Q}(\mathbf {K})$
, and thus that
$A\in \mathbb {Q}(\mathbf {K})$
, and thus that
![]() $\mathbf {K}$
is already a quasivariety.
$\mathbf {K}$
is already a quasivariety.
Remark 4.13. Crucially, the previous proposition cannot be extended to varieties of expanded algebras. In particular, if
![]() $\mathbf {K}$
is a class of expanded algebras with
$\mathbf {K}$
is a class of expanded algebras with
![]() $\mathsf {core}(A)=\Sigma (A)$
for all
$\mathsf {core}(A)=\Sigma (A)$
for all
![]() $A\in \mathbf {K}$
, it is not necessarily the case that
$A\in \mathbf {K}$
, it is not necessarily the case that
![]() $\mathsf {core}(A)=\Sigma (A)$
for all
$\mathsf {core}(A)=\Sigma (A)$
for all
![]() $A\in \mathbb {H}(\mathbf {K})$
. For example, consider the equation
$A\in \mathbb {H}(\mathbf {K})$
. For example, consider the equation
![]() $x\approx \neg x$
, let A be any Boolean algebra with size
$x\approx \neg x$
, let A be any Boolean algebra with size
![]() $|A|{\geqslant } 2$
and let B be the trivial one-element Boolean algebra. Clearly, there is a surjective homomorphism
$|A|{\geqslant } 2$
and let B be the trivial one-element Boolean algebra. Clearly, there is a surjective homomorphism
![]() $h:A\twoheadrightarrow B$
and, at the same time, we also have that
$h:A\twoheadrightarrow B$
and, at the same time, we also have that
![]() $\Sigma (B)=B$
and
$\Sigma (B)=B$
and
![]() $\Sigma (A)=\emptyset $
, showing that
$\Sigma (A)=\emptyset $
, showing that
![]() $\mathsf {core}(B)\neq h(\mathsf {core}(A))$
. This shows that we cannot replace quasivarieties by varieties in the statement of Proposition 4.12. We shall see later that this is possible in the restricted setting of fixed-point algebraizability.
$\mathsf {core}(B)\neq h(\mathsf {core}(A))$
. This shows that we cannot replace quasivarieties by varieties in the statement of Proposition 4.12. We shall see later that this is possible in the restricted setting of fixed-point algebraizability.
It is easy to find concrete examples of quasivarieties of expanded algebras whose core is equationally definable. We list here some examples which are determined by some very basic equations.
Example 4.14. Let M be a monoid in
![]() $\mathcal {L}=(\cdot ,e)$
and define
$\mathcal {L}=(\cdot ,e)$
and define
![]() $\mathsf {core}(M) = \{a \in M : a^n = e^M \}$
, then M is an expanded algebra with core defined by
$\mathsf {core}(M) = \{a \in M : a^n = e^M \}$
, then M is an expanded algebra with core defined by
![]() $\Sigma =\{ x^n\approx e \}$
.
$\Sigma =\{ x^n\approx e \}$
.
Example 4.15. Let
![]() $\mathbf {HA}$
be the variety of Heyting algebras and for all
$\mathbf {HA}$
be the variety of Heyting algebras and for all
![]() $A\in \mathbf {HA}$
let
$A\in \mathbf {HA}$
let
![]() $\mathsf {core}(A) = A_\neg =\{ x\in A : A \models x \approx \neg \neg x \}$
, i.e., the core of A is its subset of regular elements. Let
$\mathsf {core}(A) = A_\neg =\{ x\in A : A \models x \approx \neg \neg x \}$
, i.e., the core of A is its subset of regular elements. Let
![]() $\mathbf {ML}$
be the variety of all Medvedev algebras, then
$\mathbf {ML}$
be the variety of all Medvedev algebras, then
![]() $\mathbf {ML}$
is generated by its subclass of core-generated Heyting algebras A with core
$\mathbf {ML}$
is generated by its subclass of core-generated Heyting algebras A with core
![]() $A_\neg $
(cf. [Reference Bezhanishvili, Grilletti and Holliday2, Reference Bezhanishvili, Grilletti and Quadrellaro3] and Fact 8.16 below). As we shall see in Section 8, this class plays an important role in the semantics of classical inquisitive propositional logic.
$A_\neg $
(cf. [Reference Bezhanishvili, Grilletti and Holliday2, Reference Bezhanishvili, Grilletti and Quadrellaro3] and Fact 8.16 below). As we shall see in Section 8, this class plays an important role in the semantics of classical inquisitive propositional logic.
We define the strict version of algebraizability for weak logics by requiring that the core-generated algebras corresponding to a weak logic
![]() $\Vdash $
have the core defined by a finite set of equations
$\Vdash $
have the core defined by a finite set of equations
![]() $\Sigma $
. This definition is significantly stronger than the one we introduced in the previous section, and it essentially rephrases the weak logic
$\Sigma $
. This definition is significantly stronger than the one we introduced in the previous section, and it essentially rephrases the weak logic
![]() $\Vdash $
in terms of the relative consequence relation
$\Vdash $
in terms of the relative consequence relation
![]() $\models _{\mathbf {Q}}$
of the corresponding quasivariety of algebras.
$\models _{\mathbf {Q}}$
of the corresponding quasivariety of algebras.
Definition 4.16. A weak logic
![]() $\Vdash $
is strictly algebraizable if it is loosely algebraized (in the sense of Definition 4.6) by
$\Vdash $
is strictly algebraizable if it is loosely algebraized (in the sense of Definition 4.6) by
![]() $(\mathbf {Q},\tau ,\Delta )$
and, additionally, there is a finite set of equations
$(\mathbf {Q},\tau ,\Delta )$
and, additionally, there is a finite set of equations
![]() $\Sigma $
defining the core of the expanded algebras in
$\Sigma $
defining the core of the expanded algebras in
![]() $\mathbf {Q}$
. We then say that
$\mathbf {Q}$
. We then say that
![]() $\Vdash $
is strictly algebraized by
$\Vdash $
is strictly algebraized by
![]() $(\mathbf {Q},\Sigma ,\tau ,\Delta )$
and call
$(\mathbf {Q},\Sigma ,\tau ,\Delta )$
and call
![]() $(\mathbf {Q},\Sigma ,\tau ,\Delta )$
its (equivalent) strict algebraic semantics.
$(\mathbf {Q},\Sigma ,\tau ,\Delta )$
its (equivalent) strict algebraic semantics.
We can then strengthen Theorem 4.7 to the present context of core-generated quasivarieties with a definable core.
Theorem 4.17. If both the tuples
![]() $(\mathbf {Q}_0, \Sigma _0, \tau _0, \Delta _0)$
and
$(\mathbf {Q}_0, \Sigma _0, \tau _0, \Delta _0)$
and
![]() $(\mathbf {Q}_1, \Sigma _1, \tau _1, \Delta _1)$
witness the strict algebraizability of
$(\mathbf {Q}_1, \Sigma _1, \tau _1, \Delta _1)$
witness the strict algebraizability of
![]() $\Vdash $
, then:
$\Vdash $
, then:
-
(1)
 $\mathbf {Q}_0= \mathbf {Q}_1$
;
$\mathbf {Q}_0= \mathbf {Q}_1$
; -
(2)
 $\Sigma _0 \equiv _{\mathbf {Q}_i} \Sigma _1 $
with
$\Sigma _0 \equiv _{\mathbf {Q}_i} \Sigma _1 $
with
 $i\in \{0,1\}$
;
$i\in \{0,1\}$
; -
(3)
 $\Delta _0(\varepsilon ,\delta ) \dashv \Vdash \Delta _1(\varepsilon ,\delta ) $
, for all
$\Delta _0(\varepsilon ,\delta ) \dashv \Vdash \Delta _1(\varepsilon ,\delta ) $
, for all
 $\varepsilon \approx \delta \in \mathsf {Eq}$
;
$\varepsilon \approx \delta \in \mathsf {Eq}$
; -
(4)
 $\tau _0(\phi )\equiv ^c_{\mathbf {Q}_i}\tau _1(\phi ) $
with
$\tau _0(\phi )\equiv ^c_{\mathbf {Q}_i}\tau _1(\phi ) $
with
 $i\in \{0,1\}$
, for all
$i\in \{0,1\}$
, for all
 $\phi \in \mathsf {Fm}$
.
$\phi \in \mathsf {Fm}$
.
Proof. Clauses (1), (3), and (4) follow immediately from Theorem 4.7, so we prove (2). We write
![]() $\mathsf {core}_0(A)$
and
$\mathsf {core}_0(A)$
and
![]() $\mathsf {core}_1(A)$
for the core predicates induced by
$\mathsf {core}_1(A)$
for the core predicates induced by
![]() $\Sigma _0$
and
$\Sigma _0$
and
![]() $\Sigma _1$
on A, respectively. First, notice that by (1) we have
$\Sigma _1$
on A, respectively. First, notice that by (1) we have
![]() $\mathbf {Q}_0 = \mathbf {Q}_1$
, so let
$\mathbf {Q}_0 = \mathbf {Q}_1$
, so let
![]() $\mathbf {Q} = \mathbf {Q}_i$
,
$\mathbf {Q} = \mathbf {Q}_i$
,
![]() $i \in \{0,1\}$
. Let
$i \in \{0,1\}$
. Let
![]() $\alpha _0\approx \beta _0\in \Sigma _0$
, then
$\alpha _0\approx \beta _0\in \Sigma _0$
, then
![]() $\models ^{0}_{\mathbf {Q}} \alpha _0\approx \beta _0$
hence by 4.6(W2) we obtain
$\models ^{0}_{\mathbf {Q}} \alpha _0\approx \beta _0$
hence by 4.6(W2) we obtain
![]() $\varnothing \Vdash \Delta _0(\alpha _0,\beta _0)$
and thus
$\varnothing \Vdash \Delta _0(\alpha _0,\beta _0)$
and thus
![]() $\varnothing \Vdash \Delta _1(\alpha _0,\beta _0)$
. It follows that
$\varnothing \Vdash \Delta _1(\alpha _0,\beta _0)$
. It follows that
![]() $\models _{\mathbf {Q}}^{1}\alpha _0\approx \beta _0$
, meaning that
$\models _{\mathbf {Q}}^{1}\alpha _0\approx \beta _0$
, meaning that
![]() $(A,\mathsf {core}_1(A)) \models \alpha _0\approx \beta _0$
. Since this holds for all equations
$(A,\mathsf {core}_1(A)) \models \alpha _0\approx \beta _0$
. Since this holds for all equations
![]() $\alpha _0\approx \beta _0\in \Sigma _0$
, it follows that
$\alpha _0\approx \beta _0\in \Sigma _0$
, it follows that
![]() $\mathsf {core}_1(A) \subseteq \mathsf {core}_0(A)$
. The other direction is proven analogously.
$\mathsf {core}_1(A) \subseteq \mathsf {core}_0(A)$
. The other direction is proven analogously.
The following corollary follows immediately from Proposition 4.8.
Corollary 4.18. Let
![]() $\Vdash $
be a standard logic, then:
$\Vdash $
be a standard logic, then:
4.4 Fixed-point algebraizability of weak logics
We introduce a third alternative definition of algebraizability for weak logics, which can be seen as a refinement of strict algebraizability. We first define the following notion of selector term, essentially from [Reference Almeida1].
Notation 4.19. Let
![]() $t(x)$
be unary
$t(x)$
be unary
![]() $\mathcal {L}$
-term, then we define recursively
$\mathcal {L}$
-term, then we define recursively
![]() $t^1(x)=t(x)$
and
$t^1(x)=t(x)$
and
![]() $t^{n+1}(x)=t(t^n(x))$
for all
$t^{n+1}(x)=t(t^n(x))$
for all
![]() $1\leq n < \omega $
.
$1\leq n < \omega $
.
Definition 4.20. Let
![]() $\mathbf {Q}$
be a quasivariety of
$\mathbf {Q}$
be a quasivariety of
![]() $\mathcal {L}$
-algebras and
$\mathcal {L}$
-algebras and
![]() $\delta (x)$
be a unary term in
$\delta (x)$
be a unary term in
![]() $\mathcal {L}$
, then we say that
$\mathcal {L}$
, then we say that
![]() $\delta (x)$
is a selector term for
$\delta (x)$
is a selector term for
![]() $\mathbf {Q}$
if
$\mathbf {Q}$
if
![]() $\mathbf {Q}\models \delta (x) \approx \delta ^2(x)$
.
$\mathbf {Q}\models \delta (x) \approx \delta ^2(x)$
.
Remark 4.21. Selector terms essentially identify the fixed points of polynomials in
![]() $\mathbf {Q}$
. If there is some
$\mathbf {Q}$
. If there is some
![]() $n<\omega $
such that for all
$n<\omega $
such that for all
![]() $m<\omega $
we have
$m<\omega $
we have
![]() $\delta ^{n+m}(x)=\delta ^{n}(x)$
, then in particular we obtain
$\delta ^{n+m}(x)=\delta ^{n}(x)$
, then in particular we obtain
for all
![]() $A\in \mathbf {Q}$
. Thus
$A\in \mathbf {Q}$
. Thus
![]() $\delta ^{n}$
is a selector term for
$\delta ^{n}$
is a selector term for
![]() $\mathbf {Q}$
.
$\mathbf {Q}$
.
Definition 4.22. A weak logic
![]() $\Vdash $
is fixed-point algebraizable if it is strictly algebraized by a tuple
$\Vdash $
is fixed-point algebraizable if it is strictly algebraized by a tuple
![]() $(\mathbf {Q},\Sigma ,\tau ,\Delta )$
(as in Definition 4.16) and, additionally,
$(\mathbf {Q},\Sigma ,\tau ,\Delta )$
(as in Definition 4.16) and, additionally,
![]() $\Sigma =\{ x\approx \delta (x) \}$
for some selector term
$\Sigma =\{ x\approx \delta (x) \}$
for some selector term
![]() $\delta (x)$
.
$\delta (x)$
.
The key idea in the previous definition is that the core of the expanded algebras corresponding to the logic
![]() $\Vdash $
is not simply defined by a finite set of equations, but by one single equation characterising it as the set of fixed points of a certain polynomial. The main motivation lies in the fact that fixed-point algebraizability behaves very well in the context of varieties, as the following result shows (this is essentially [Reference Grilletti, Quadrellaro, Özgün and Zinova18, Theorem 19] and [Reference Almeida1, Theorem 3.14]).
$\Vdash $
is not simply defined by a finite set of equations, but by one single equation characterising it as the set of fixed points of a certain polynomial. The main motivation lies in the fact that fixed-point algebraizability behaves very well in the context of varieties, as the following result shows (this is essentially [Reference Grilletti, Quadrellaro, Özgün and Zinova18, Theorem 19] and [Reference Almeida1, Theorem 3.14]).
Proposition 4.23. Let
![]() $\mathbf {V}$
be a variety of
$\mathbf {V}$
be a variety of
![]() $\mathcal {L}$
-algebras and
$\mathcal {L}$
-algebras and
![]() $\Sigma (x)=\{\delta (x)\approx x\}$
for some selector term
$\Sigma (x)=\{\delta (x)\approx x\}$
for some selector term
![]() $\delta $
, then the class of structures
$\delta $
, then the class of structures
![]() $(A,\mathsf {core}(A))$
with
$(A,\mathsf {core}(A))$
with
![]() $A\in \mathbf {V}$
and
$A\in \mathbf {V}$
and
![]() $ \mathsf {core}(A)=\Sigma (A) $
is a variety of expanded algebras.
$ \mathsf {core}(A)=\Sigma (A) $
is a variety of expanded algebras.
Proof. Let
![]() $\mathbf {V}$
be a variety of
$\mathbf {V}$
be a variety of
![]() $\mathcal {L}$
-algebras and let
$\mathcal {L}$
-algebras and let
![]() $\mathbf {K}$
be the class of structures
$\mathbf {K}$
be the class of structures
![]() $(A,\mathsf {core}(A))$
with
$(A,\mathsf {core}(A))$
with
![]() $A\in \mathbf {V}$
and
$A\in \mathbf {V}$
and
![]() $ \mathsf {core}(A)=\Sigma (A) $
. By Proposition 4.12 it follows that
$ \mathsf {core}(A)=\Sigma (A) $
. By Proposition 4.12 it follows that
![]() $\mathbf {K}$
is a quasivariety. We show that
$\mathbf {K}$
is a quasivariety. We show that
![]() $\mathbf {K}$
is also closed under homomorphic images. Let
$\mathbf {K}$
is also closed under homomorphic images. Let
![]() $A\in \mathbf {V}$
and consider a surjective homomorphism
$A\in \mathbf {V}$
and consider a surjective homomorphism
![]() $h:A\to B$
, it suffices to show that
$h:A\to B$
, it suffices to show that
![]() $\mathsf {core}(B)=h[\mathsf {core}(A)]$
. Since
$\mathsf {core}(B)=h[\mathsf {core}(A)]$
. Since
![]() $\mathsf {core}(A)=\Sigma (A)$
and
$\mathsf {core}(A)=\Sigma (A)$
and
![]() $\mathsf {core}(B)=\Sigma (B)$
, it follows from the fact that homomorphic images preserve the validity of equations that
$\mathsf {core}(B)=\Sigma (B)$
, it follows from the fact that homomorphic images preserve the validity of equations that
![]() $h[\mathsf {core}(A)]\subseteq \mathsf {core}(B)$
. Consider now some
$h[\mathsf {core}(A)]\subseteq \mathsf {core}(B)$
. Consider now some
![]() $b\in \mathsf {core}(B)$
and notice that since h is surjective there is some
$b\in \mathsf {core}(B)$
and notice that since h is surjective there is some
![]() $a\in A$
with
$a\in A$
with
![]() $h(a)=b$
. Then we have that
$h(a)=b$
. Then we have that
![]() $h(\delta (a))=\delta (h(a))=h(a)$
, given that
$h(\delta (a))=\delta (h(a))=h(a)$
, given that
![]() $h(a)=b\in \mathsf {core}(B)=\Sigma (B)$
. Since
$h(a)=b\in \mathsf {core}(B)=\Sigma (B)$
. Since
![]() $\delta $
is a selector term, we have
$\delta $
is a selector term, we have
![]() $A\models \delta (a)\approx \delta ^2(a)$
and so
$A\models \delta (a)\approx \delta ^2(a)$
and so
![]() $\delta (a) \in \mathsf {core}(A)$
and
$\delta (a) \in \mathsf {core}(A)$
and
![]() $b \in h[\mathsf {core}(A)]$
.
$b \in h[\mathsf {core}(A)]$
.
Remark 4.24. We notice that most of our examples of algebraizable weak logics are actually fixed-point algebraizable. However, in the present work we shall not focus on the special features of fixed-point algebraizability, as our interest is rather in the more general properties of loose and strict algebraizability. We refer the reader to [Reference Almeida1] for an in-depth study of logics arising from selector terms.
5 Schematic fragment and standard companions
We start in this section to investigate the relation between the loose and the strict version of algebraizability. In particular, we introduce the notion of schematic fragment of a weak logic and relate the algebraizability of a weak logic to the standard algebraizability of its schematic fragment.
5.1 The schematic fragment of a weak logic
Given a weak logic
![]() $\Vdash $
, it is natural to ask if we can associate to it to some specific standard logical system. The study of negative variants of intermediate logics led to the notion of schematic fragment, which was originally introduced in [Reference Miglioli, Moscato, Ornaghi, Quazza and Usberti22, p. 545] (under the name of standardization) and further investigated in [Reference Bezhanishvili, Grilletti and Quadrellaro3, Reference Ciardelli and Roelofsen12]. Here we generalise it to arbitrary weak logics.
$\Vdash $
, it is natural to ask if we can associate to it to some specific standard logical system. The study of negative variants of intermediate logics led to the notion of schematic fragment, which was originally introduced in [Reference Miglioli, Moscato, Ornaghi, Quazza and Usberti22, p. 545] (under the name of standardization) and further investigated in [Reference Bezhanishvili, Grilletti and Quadrellaro3, Reference Ciardelli and Roelofsen12]. Here we generalise it to arbitrary weak logics.
Definition 5.1 (Schematic fragment).
Let
![]() $\Vdash $
be a weak logic, we define its schematic fragment
$\Vdash $
be a weak logic, we define its schematic fragment
![]() $\mathrm {Schm}(\Vdash )$
as follows:
$\mathrm {Schm}(\Vdash )$
as follows:
and we then also write
![]() $\Gamma \Vdash _{\mathrm {s}}\phi $
if
$\Gamma \Vdash _{\mathrm {s}}\phi $
if
![]() $(\Gamma ,\phi )\in \mathrm {Schm}(\Vdash )$
.
$(\Gamma ,\phi )\in \mathrm {Schm}(\Vdash )$
.
It is clear from the definition that
![]() $\mathrm {Schm}(\Vdash )$
is the largest standard logic contained in
$\mathrm {Schm}(\Vdash )$
is the largest standard logic contained in
![]() $\Vdash $
. We use the schematic fragment of a weak logic to relate loose and strict algebraizability to standard algebraizability. To this end, we first introduce the following notion of (finite) representability of a weak logic.
$\Vdash $
. We use the schematic fragment of a weak logic to relate loose and strict algebraizability to standard algebraizability. To this end, we first introduce the following notion of (finite) representability of a weak logic.
Notation 5.2. Let
![]() $\Gamma \subseteq \mathsf {Fm}$
be a set of formulas, we let
$\Gamma \subseteq \mathsf {Fm}$
be a set of formulas, we let
![]() $\mathsf {At}[\Gamma ]$
be the closure of
$\mathsf {At}[\Gamma ]$
be the closure of
![]() $\Gamma $
under all atomic substitutions
$\Gamma $
under all atomic substitutions
![]() $\sigma \in \mathsf {At}(\mathcal {L})$
. If
$\sigma \in \mathsf {At}(\mathcal {L})$
. If
![]() $\Theta $
is a set of equations we similarly denote by
$\Theta $
is a set of equations we similarly denote by
![]() $\mathsf {At}[\Theta ]$
the closure of
$\mathsf {At}[\Theta ]$
the closure of
![]() $\Theta $
under atomic substitutions.
$\Theta $
under atomic substitutions.
Definition 5.3. We say that a weak logic
![]() $\Vdash $
is representable if there is a set of formulas
$\Vdash $
is representable if there is a set of formulas
![]() $\Lambda $
in one variable such that for all
$\Lambda $
in one variable such that for all
![]() $\Gamma \cup \{\phi \} \subseteq \mathsf {Fm}$
,
$\Gamma \cup \{\phi \} \subseteq \mathsf {Fm}$
,
We say that
![]() $\Vdash $
is finitely representable if the condition above holds for some finite set
$\Vdash $
is finitely representable if the condition above holds for some finite set
![]() $\Lambda \subseteq \mathsf {Fm}$
.
$\Lambda \subseteq \mathsf {Fm}$
.
Proposition 5.4. If a weak logic
![]() $\Vdash $
is loosely algebraized by
$\Vdash $
is loosely algebraized by
![]() $(\mathbf {Q},\tau ,\Delta )$
, then its schematic fragment
$(\mathbf {Q},\tau ,\Delta )$
, then its schematic fragment
![]() $\mathrm {Schm}(\Vdash )$
is algebraized by
$\mathrm {Schm}(\Vdash )$
is algebraized by
![]() $(\mathbf {Q},\tau ,\Delta )$
as well.
$(\mathbf {Q},\tau ,\Delta )$
as well.
Proof. Let
![]() $(\mathbf {Q},\tau ,\Delta )$
witness the loose algebraizability of
$(\mathbf {Q},\tau ,\Delta )$
witness the loose algebraizability of
![]() $\Vdash $
. In particular
$\Vdash $
. In particular
![]() $\mathbf {Q}$
is a core-generated quasivariety of expanded algebra, and thus the collection of its algebraic reducts
$\mathbf {Q}$
is a core-generated quasivariety of expanded algebra, and thus the collection of its algebraic reducts
![]() $\mathbf {Q}\restriction \mathcal {L}$
is a quasivariety of algebras. We claim that
$\mathbf {Q}\restriction \mathcal {L}$
is a quasivariety of algebras. We claim that
![]() $(\mathbf {Q}\restriction \mathcal {L},\tau ,\Delta )$
witnesses the algebraizability of
$(\mathbf {Q}\restriction \mathcal {L},\tau ,\Delta )$
witnesses the algebraizability of
![]() $\mathrm {Schm}(\Vdash )$
. Notice that by Fact 4.4 it suffices to verify that
$\mathrm {Schm}(\Vdash )$
. Notice that by Fact 4.4 it suffices to verify that
![]() $(\mathbf {Q}\restriction \mathcal {L}, \tau , \Delta )$
satisfies 4.2(A1) and 4.2(A4). Firstly, we consider 4.2(A1):
$(\mathbf {Q}\restriction \mathcal {L}, \tau , \Delta )$
satisfies 4.2(A1) and 4.2(A4). Firstly, we consider 4.2(A1):
 $$ \begin{align*} \Gamma \Vdash_{\mathrm{s}} \phi &\Longleftrightarrow \forall \sigma \in \mathsf{Subst}(\mathcal{L}),\; \sigma[\Gamma] \Vdash \sigma(\phi) & \text{(by definition)} \\ &\Longleftrightarrow \forall \sigma \in \mathsf{Subst}(\mathcal{L}),\;\tau(\sigma[\Gamma]) \models^c_{\mathbf{Q}\restriction\mathcal{L}} \tau(\sigma(\phi)) & \text{(by 4.6(W2))} \\ &\Longleftrightarrow \forall \sigma \in \mathsf{Subst}(\mathcal{L}),\;\sigma(\tau[\Gamma]) \models^c_{\mathbf{Q}\restriction\mathcal{L}} \sigma(\tau(\phi)) & (\text{by structurality of } \tau) \\ &\Longleftrightarrow \tau[\Gamma] \models_{\mathbf{Q}\restriction\mathcal{L}} \tau(\phi) & \text{(by Proposition~3.21).} \end{align*} $$
$$ \begin{align*} \Gamma \Vdash_{\mathrm{s}} \phi &\Longleftrightarrow \forall \sigma \in \mathsf{Subst}(\mathcal{L}),\; \sigma[\Gamma] \Vdash \sigma(\phi) & \text{(by definition)} \\ &\Longleftrightarrow \forall \sigma \in \mathsf{Subst}(\mathcal{L}),\;\tau(\sigma[\Gamma]) \models^c_{\mathbf{Q}\restriction\mathcal{L}} \tau(\sigma(\phi)) & \text{(by 4.6(W2))} \\ &\Longleftrightarrow \forall \sigma \in \mathsf{Subst}(\mathcal{L}),\;\sigma(\tau[\Gamma]) \models^c_{\mathbf{Q}\restriction\mathcal{L}} \sigma(\tau(\phi)) & (\text{by structurality of } \tau) \\ &\Longleftrightarrow \tau[\Gamma] \models_{\mathbf{Q}\restriction\mathcal{L}} \tau(\phi) & \text{(by Proposition~3.21).} \end{align*} $$
Next, consider 4.2(A4). To this end, suppose that
![]() $\tau (\Delta (x,y)) \not \equiv _{\mathbf {Q}\restriction \mathcal {L}} x \approx y$
, then by Proposition 3.21 and the fact that
$\tau (\Delta (x,y)) \not \equiv _{\mathbf {Q}\restriction \mathcal {L}} x \approx y$
, then by Proposition 3.21 and the fact that
![]() $\mathbf {Q}$
is core-generated, we get that there exists a substitution
$\mathbf {Q}$
is core-generated, we get that there exists a substitution
![]() $\sigma $
such that
$\sigma $
such that
![]() $\sigma (\tau (\Delta (x,y))) \not \equiv ^c_{\mathbf {Q}} \sigma (x \approx y)$
. Then, we obtain by the structurality of
$\sigma (\tau (\Delta (x,y))) \not \equiv ^c_{\mathbf {Q}} \sigma (x \approx y)$
. Then, we obtain by the structurality of
![]() $\tau $
and
$\tau $
and
![]() $\Delta $
that
$\Delta $
that
![]() $\tau (\Delta (\sigma (x), \sigma (y))) \not \equiv ^c_{\mathbf {Q}} \sigma (x) \approx \sigma (y)$
, contradicting the algebraizability of
$\tau (\Delta (\sigma (x), \sigma (y))) \not \equiv ^c_{\mathbf {Q}} \sigma (x) \approx \sigma (y)$
, contradicting the algebraizability of
![]() $\Vdash $
. This completes the proof.
$\Vdash $
. This completes the proof.
The following theorem allows us to relate loose and strict algebraizability of weak logics to the standard algebraizability of their schematic fragment.
Theorem 5.5. For a weak logic
![]() $\Vdash $
, the following are equivalent:
$\Vdash $
, the following are equivalent:
-
(1)
 $\Vdash $
is strictly algebraizable;
$\Vdash $
is strictly algebraizable; -
(2)
 $\Vdash $
is loosely algebraizable and
$\Vdash $
is loosely algebraizable and
 $\Vdash $
is finitely representable;
$\Vdash $
is finitely representable; -
(3)
 $\mathrm {Schm}(\Vdash )$
is algebraizable and
$\mathrm {Schm}(\Vdash )$
is algebraizable and
 $\Vdash $
is finitely representable.
$\Vdash $
is finitely representable.
Proof. We first show that (1) entails (2). By definition, if
![]() $\Vdash $
is strictly algebraizable, then it is also loosely algebraizable. We show that it is also finitely representable. Let
$\Vdash $
is strictly algebraizable, then it is also loosely algebraizable. We show that it is also finitely representable. Let
![]() $(\mathbf {Q},\Sigma ,\tau ,\Delta )$
be the strict algebraic semantics of
$(\mathbf {Q},\Sigma ,\tau ,\Delta )$
be the strict algebraic semantics of
![]() $\Vdash $
. In particular we have that
$\Vdash $
. In particular we have that
![]() $\mathsf {core}(A)=\Sigma (A)$
for all
$\mathsf {core}(A)=\Sigma (A)$
for all
![]() $A\in \mathbf {Q}$
. We then have the following equivalences:
$A\in \mathbf {Q}$
. We then have the following equivalences:
 $$ \begin{align*} &\Gamma \Vdash\phi \Longleftrightarrow \tau[\Gamma] \models^c_{\mathbf{Q}} \tau(\phi) & \text{(by 4.6(W1))} \\ & \Longleftrightarrow \tau[\Gamma] \cup \mathsf{At}[\Sigma] \models_{\mathbf{Q}} \tau(\phi) & \text{(by Lemma~3.23)} \\ & \Longleftrightarrow \forall \sigma \in \mathsf{Subst}(\mathcal{L}),\; \sigma(\tau(\Gamma)) \cup \sigma(\mathsf{At}[\Sigma]) \models^c_{\mathbf{Q}} \sigma(\tau(\phi))& \text{(by Proposition~3.21)} \\ & \Longleftrightarrow \forall \sigma \in \mathsf{Subst}(\mathcal{L}),\; \tau(\sigma(\Gamma)) \cup \sigma(\mathsf{At}(\Sigma)) \models^c_{\mathbf{Q}} \tau(\sigma(\phi))& (\text{by structurality of} \tau) \\ & \Longleftrightarrow \forall \sigma \in \mathsf{Subst}(\mathcal{L}),\; \sigma[\Gamma] \cup \Delta(\sigma(\mathsf{At}(\Sigma))) \Vdash \sigma(\phi) & \text{(by 4.6(W2) and 4.6(W3))} \\ & \Longleftrightarrow \forall \sigma \in \mathsf{Subst}(\mathcal{L}),\; \sigma[\Gamma] \cup \sigma(\mathsf{At}(\Delta(\Sigma))) \Vdash \sigma(\phi) & (\text{by structurality of } \Delta) \\ & \Longleftrightarrow \Gamma \cup \mathsf{At}(\Delta(\Sigma)) \Vdash_{\mathrm{s}} \phi, & \end{align*} $$
$$ \begin{align*} &\Gamma \Vdash\phi \Longleftrightarrow \tau[\Gamma] \models^c_{\mathbf{Q}} \tau(\phi) & \text{(by 4.6(W1))} \\ & \Longleftrightarrow \tau[\Gamma] \cup \mathsf{At}[\Sigma] \models_{\mathbf{Q}} \tau(\phi) & \text{(by Lemma~3.23)} \\ & \Longleftrightarrow \forall \sigma \in \mathsf{Subst}(\mathcal{L}),\; \sigma(\tau(\Gamma)) \cup \sigma(\mathsf{At}[\Sigma]) \models^c_{\mathbf{Q}} \sigma(\tau(\phi))& \text{(by Proposition~3.21)} \\ & \Longleftrightarrow \forall \sigma \in \mathsf{Subst}(\mathcal{L}),\; \tau(\sigma(\Gamma)) \cup \sigma(\mathsf{At}(\Sigma)) \models^c_{\mathbf{Q}} \tau(\sigma(\phi))& (\text{by structurality of} \tau) \\ & \Longleftrightarrow \forall \sigma \in \mathsf{Subst}(\mathcal{L}),\; \sigma[\Gamma] \cup \Delta(\sigma(\mathsf{At}(\Sigma))) \Vdash \sigma(\phi) & \text{(by 4.6(W2) and 4.6(W3))} \\ & \Longleftrightarrow \forall \sigma \in \mathsf{Subst}(\mathcal{L}),\; \sigma[\Gamma] \cup \sigma(\mathsf{At}(\Delta(\Sigma))) \Vdash \sigma(\phi) & (\text{by structurality of } \Delta) \\ & \Longleftrightarrow \Gamma \cup \mathsf{At}(\Delta(\Sigma)) \Vdash_{\mathrm{s}} \phi, & \end{align*} $$
and thus
![]() $\Lambda =\Delta (\Sigma )$
witnesses the fact that
$\Lambda =\Delta (\Sigma )$
witnesses the fact that
![]() $\Vdash $
is finitely representable.
$\Vdash $
is finitely representable.
The direction from (2) to (3) follows immediately by Proposition 5.4.
Finally, we show that (3) entails (1). Suppose that
![]() $\mathrm {Schm}(\Vdash )$
is algebraized by
$\mathrm {Schm}(\Vdash )$
is algebraized by
![]() $(\mathbf {Q}, \tau , \Delta )$
and that
$(\mathbf {Q}, \tau , \Delta )$
and that
![]() $\Vdash $
is finitely represented via a set of formulas
$\Vdash $
is finitely represented via a set of formulas
![]() $\Lambda $
. Let
$\Lambda $
. Let
![]() $\mathsf {core}(A)=\tau [\Lambda ](A)$
for all
$\mathsf {core}(A)=\tau [\Lambda ](A)$
for all
![]() $A\in \mathbf {Q}$
and consider
$A\in \mathbf {Q}$
and consider
![]() $\mathbf {Q'} := \mathbb {Q}(\{\langle \mathsf {core}(A) \rangle : A \in \mathbf {Q}\})$
, i.e.,
$\mathbf {Q'} := \mathbb {Q}(\{\langle \mathsf {core}(A) \rangle : A \in \mathbf {Q}\})$
, i.e.,
![]() $\mathbf {Q'}$
is the quasivariety of expanded algebras generated by the algebras of the form
$\mathbf {Q'}$
is the quasivariety of expanded algebras generated by the algebras of the form
![]() $\langle \mathsf {core}(A) \rangle $
, for
$\langle \mathsf {core}(A) \rangle $
, for
![]() $A \in \mathbf {Q}$
. We then derive the following equivalences:
$A \in \mathbf {Q}$
. We then derive the following equivalences:
 $$ \begin{align*} \Gamma \Vdash \phi &\iff \Gamma \cup \mathsf{At}[\Lambda] \Vdash_{\mathrm{s}} \phi & \text{(by assumption)} \\ &\iff \tau[\Gamma] \cup \tau[\mathsf{At}[\Lambda]] \models_{\mathbf{Q}} \tau(\phi)& \text{(by 4.2(A1))} \\ &\iff \tau[\Gamma] \models_{\mathbf{Q}}^c \tau(\phi). & \text{(by Lemma~3.23)} \\ &\iff \tau[\Gamma] \models_{\mathbf{Q}'}^c \tau(\phi), & \text{(by Proposition~3.24)} \end{align*} $$
$$ \begin{align*} \Gamma \Vdash \phi &\iff \Gamma \cup \mathsf{At}[\Lambda] \Vdash_{\mathrm{s}} \phi & \text{(by assumption)} \\ &\iff \tau[\Gamma] \cup \tau[\mathsf{At}[\Lambda]] \models_{\mathbf{Q}} \tau(\phi)& \text{(by 4.2(A1))} \\ &\iff \tau[\Gamma] \models_{\mathbf{Q}}^c \tau(\phi). & \text{(by Lemma~3.23)} \\ &\iff \tau[\Gamma] \models_{\mathbf{Q}'}^c \tau(\phi), & \text{(by Proposition~3.24)} \end{align*} $$
which establish 4.6(W1). We next verify that 4.6(W4) holds as well. Suppose that
![]() $\tau (\Delta (x,y)) \not \equiv ^c_{\mathbf {Q'}} x \approx y$
, then since
$\tau (\Delta (x,y)) \not \equiv ^c_{\mathbf {Q'}} x \approx y$
, then since
![]() $\mathsf {core}(A)=\tau [\Lambda ](A)$
we obtain that
$\mathsf {core}(A)=\tau [\Lambda ](A)$
we obtain that
which contradicts the fact that
![]() $\mathrm {Schm}(\Vdash )$
is algebraized by
$\mathrm {Schm}(\Vdash )$
is algebraized by
![]() $(\mathbf {Q}, \tau , \Delta )$
.
$(\mathbf {Q}, \tau , \Delta )$
.
The following corollary is an immediate consequence of the proofs of the previous theorem and lemma.
Corollary 5.6. A weak logic
![]() $\Vdash $
is strictly algebraized by
$\Vdash $
is strictly algebraized by
![]() $(\mathbf {Q},\Sigma ,\tau ,\Delta )$
if and only if it is represented by
$(\mathbf {Q},\Sigma ,\tau ,\Delta )$
if and only if it is represented by
![]() $\Delta [\Sigma ]$
and
$\Delta [\Sigma ]$
and
![]() $\mathrm {Schm}(\Vdash )$
is algebraized by
$\mathrm {Schm}(\Vdash )$
is algebraized by
![]() $(\mathbf {Q},\tau ,\Delta )$
.
$(\mathbf {Q},\tau ,\Delta )$
.
5.2 The lattice of standard companions
The previous results established that, if
![]() $\Vdash $
is strictly algebraizable, then there is a finite set
$\Vdash $
is strictly algebraizable, then there is a finite set
![]() $\Lambda $
witnessing its finite representability. Essentially, this means that the consequences in
$\Lambda $
witnessing its finite representability. Essentially, this means that the consequences in
![]() $\Vdash $
can be encoded as logical consequences in its schematic fragment
$\Vdash $
can be encoded as logical consequences in its schematic fragment
![]() $\Vdash _{\mathrm {s}}$
, modulo the set of formulas
$\Vdash _{\mathrm {s}}$
, modulo the set of formulas
![]() $\Lambda $
. However, the schematic fragment of
$\Lambda $
. However, the schematic fragment of
![]() $\Vdash $
is not necessarily the only standard logic which bears this property. We study what are the standard logics that, up to
$\Vdash $
is not necessarily the only standard logic which bears this property. We study what are the standard logics that, up to
![]() $\Lambda $
, share the same consequences.
$\Lambda $
, share the same consequences.
Definition 5.7. Let
![]() $\Vdash $
be a strictly algebraizable weak logic which is finitely representable by
$\Vdash $
be a strictly algebraizable weak logic which is finitely representable by
![]() $\Lambda $
and with strict algebraic semantics
$\Lambda $
and with strict algebraic semantics
![]() $(\mathbf {Q},\Sigma ,\tau ,\Delta )$
. A standard logic
$(\mathbf {Q},\Sigma ,\tau ,\Delta )$
. A standard logic
![]() $\vdash $
is a standard companion of
$\vdash $
is a standard companion of
![]() $\Vdash $
if the following conditions hold:
$\Vdash $
if the following conditions hold:
-
(1)
 $\Gamma \Vdash \phi \; \Longleftrightarrow \; \Gamma \cup \mathsf {At}[\Lambda ] \vdash \phi $
;
$\Gamma \Vdash \phi \; \Longleftrightarrow \; \Gamma \cup \mathsf {At}[\Lambda ] \vdash \phi $
; -
(2)
 $\vdash $
is algebraized by a quasivariety
$\vdash $
is algebraized by a quasivariety
 $\mathbf {K}$
together with the transformers
$\mathbf {K}$
together with the transformers
 $\tau $
and
$\tau $
and
 $\Delta $
.
$\Delta $
.
We denote by
![]() $\mathrm {St}(\Vdash )$
the family of all standard companions of
$\mathrm {St}(\Vdash )$
the family of all standard companions of
![]() $\Vdash $
.
$\Vdash $
.
Remark 5.8. We provide some explanations of the previous definition. Condition 5.7(1) is essentially the same condition of representability from Definition 5.3, but with respect to an arbitrary standard logic. Thus Condition 5.7(1) identifies those standard logics that, up to
![]() $\Lambda $
, deliver the same weak logic
$\Lambda $
, deliver the same weak logic
![]() $\Vdash $
. However, this condition by itself is quite weak, and thus we focus on logics that satisfy also condition 5.7(2), i.e., that can be algebraized via the same transformers
$\Vdash $
. However, this condition by itself is quite weak, and thus we focus on logics that satisfy also condition 5.7(2), i.e., that can be algebraized via the same transformers
![]() $\tau $
and
$\tau $
and
![]() $\Delta $
as
$\Delta $
as
![]() $\Vdash $
. Notice that, in the specific cases of polyatomic logics and negative variants, these families had already been identified and studied in [Reference Almeida1, Reference Bezhanishvili, Grilletti and Quadrellaro3], respectively.
$\Vdash $
. Notice that, in the specific cases of polyatomic logics and negative variants, these families had already been identified and studied in [Reference Almeida1, Reference Bezhanishvili, Grilletti and Quadrellaro3], respectively.
Our underlying intuition is that the family of standard companions defined above must give rise to a corresponding notion on the side of quasivarieties of algebras.
Definition 5.9. Let
![]() $\mathbf {Q}$
be a core-generated quasivariety of expanded algebras with core defined by a finite set of equations
$\mathbf {Q}$
be a core-generated quasivariety of expanded algebras with core defined by a finite set of equations
![]() $\Sigma (x)$
. Let
$\Sigma (x)$
. Let
![]() $\mathbf {K}$
be an arbitrary quasivariety of algebras (in the same signature as
$\mathbf {K}$
be an arbitrary quasivariety of algebras (in the same signature as
![]() $\mathbf {Q}$
), then we say that
$\mathbf {Q}$
), then we say that
![]() $\mathbf {K}$
is a standard companion of
$\mathbf {K}$
is a standard companion of
![]() $\mathbf {Q}$
if, for all
$\mathbf {Q}$
if, for all
![]() $A\in \mathbf {K}$
, we have
$A\in \mathbf {K}$
, we have
![]() $ \langle \Sigma (A) \rangle \in \mathbf {Q}$
.
$ \langle \Sigma (A) \rangle \in \mathbf {Q}$
.
Lemma 5.10. Let
![]() $\Vdash $
be a weak logic strictly algebraized by
$\Vdash $
be a weak logic strictly algebraized by
![]() $(\mathbf {Q},\Sigma ,\tau ,\Delta )$
, and let
$(\mathbf {Q},\Sigma ,\tau ,\Delta )$
, and let
![]() $\vdash $
be a standard logic. Then
$\vdash $
be a standard logic. Then
![]() $\vdash \in \mathrm {St}(\Vdash )$
if and only if
$\vdash \in \mathrm {St}(\Vdash )$
if and only if
![]() $\vdash $
is algebraized by
$\vdash $
is algebraized by
![]() $(\mathbf {K},\tau ,\Delta )$
for some
$(\mathbf {K},\tau ,\Delta )$
for some
![]() $\mathbf {K}$
standard companion of
$\mathbf {K}$
standard companion of
![]() $\mathbf {Q}$
.
$\mathbf {Q}$
.
Proof. We first prove the left-to-right direction. Since
![]() $\vdash \in \mathrm {St}(\Vdash )$
we have by definition that
$\vdash \in \mathrm {St}(\Vdash )$
we have by definition that
![]() $\vdash $
is algebraized by some
$\vdash $
is algebraized by some
![]() $(\mathbf {K},\tau ,\Delta )$
, where
$(\mathbf {K},\tau ,\Delta )$
, where
![]() $\tau $
and
$\tau $
and
![]() $\Delta $
also witness the strict algebraizability of
$\Delta $
also witness the strict algebraizability of
![]() $\Vdash $
. In particular, notice that by the strict algebraizability of
$\Vdash $
. In particular, notice that by the strict algebraizability of
![]() $\Vdash $
and Corollary 5.6 we have that
$\Vdash $
and Corollary 5.6 we have that
![]() $\Vdash $
is represented by
$\Vdash $
is represented by
![]() $\Delta [\Sigma ]$
over its schematic fragment, i.e., that
$\Delta [\Sigma ]$
over its schematic fragment, i.e., that
![]() $\Lambda =\Delta [\Sigma ]$
. Now, we consider
$\Lambda =\Delta [\Sigma ]$
. Now, we consider
![]() $\mathbf {K}$
as a class of expanded algebras with core
$\mathbf {K}$
as a class of expanded algebras with core
![]() $\Sigma (A)$
for all
$\Sigma (A)$
for all
![]() $A\in \mathbf {K}$
and we let
$A\in \mathbf {K}$
and we let
![]() $\mathbf {C}=\mathbb {Q}(\{ \langle \Sigma (A)\rangle : A\in \mathbf {K} \})$
. Clearly, we have by Proposition 3.26 that
$\mathbf {C}=\mathbb {Q}(\{ \langle \Sigma (A)\rangle : A\in \mathbf {K} \})$
. Clearly, we have by Proposition 3.26 that
![]() $\Theta \models ^c_{\mathbf {C}}\varepsilon \approx \delta $
holds if and only if
$\Theta \models ^c_{\mathbf {C}}\varepsilon \approx \delta $
holds if and only if
![]() $\Theta \models ^c_{\mathbf {K}}\varepsilon \approx \delta $
does. Also, we have by strict algebraizability of
$\Theta \models ^c_{\mathbf {K}}\varepsilon \approx \delta $
does. Also, we have by strict algebraizability of
![]() $\Vdash $
and
$\Vdash $
and
![]() $\vdash $
that
$\vdash $
that
![]() $\Theta \models ^c_{\mathbf {K}}\varepsilon \approx \delta $
is equivalent to
$\Theta \models ^c_{\mathbf {K}}\varepsilon \approx \delta $
is equivalent to
![]() $\Theta \models ^c_{\mathbf {Q}}\varepsilon \approx \delta $
, since
$\Theta \models ^c_{\mathbf {Q}}\varepsilon \approx \delta $
, since
![]() $\vdash \in \mathrm {St}(\Vdash )$
and
$\vdash \in \mathrm {St}(\Vdash )$
and
![]() $\Lambda =\Delta [\Sigma ]$
. Thus we obtain that
$\Lambda =\Delta [\Sigma ]$
. Thus we obtain that
![]() $\mathrm {Th}_{\mathrm {qe}}^c(\mathbf {C})=\mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q})$
and so by Proposition 3.26
$\mathrm {Th}_{\mathrm {qe}}^c(\mathbf {C})=\mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q})$
and so by Proposition 3.26
![]() $\mathbf {C}=\mathbf {Q}$
, proving that
$\mathbf {C}=\mathbf {Q}$
, proving that
![]() $\mathbf {K}$
is a standard companion of
$\mathbf {K}$
is a standard companion of
![]() $\mathbf {Q}$
.
$\mathbf {Q}$
.
We consider the right-to-left direction. Suppose
![]() $\vdash $
is algebraized by
$\vdash $
is algebraized by
![]() $(\mathbf {K},\tau ,\Delta )$
and let
$(\mathbf {K},\tau ,\Delta )$
and let
![]() $\mathbf {K}$
be a standard companion of
$\mathbf {K}$
be a standard companion of
![]() $\mathbf {Q}$
, we show that
$\mathbf {Q}$
, we show that
![]() $\vdash $
is a standard companion of
$\vdash $
is a standard companion of
![]() $\Vdash $
. We view
$\Vdash $
. We view
![]() $\mathbf {K}$
also as a quasivariety of expanded algebras by letting,
$\mathbf {K}$
also as a quasivariety of expanded algebras by letting,
![]() $\mathsf {core}(A)=\Sigma (A)$
for each
$\mathsf {core}(A)=\Sigma (A)$
for each
![]() $A\in \mathbf {K}$
. We have the following equivalences:
$A\in \mathbf {K}$
. We have the following equivalences:
 $$ \begin{align*} \Gamma \Vdash \phi & \Longleftrightarrow \tau(\Gamma) \models^c_{\mathbf{Q}} \tau(\phi) & \text{(by 4.6(W1))} \\ & \Longleftrightarrow \tau(\Gamma) \models^c_{\mathbf{K}} \tau(\phi) & \text{(by Definition~5.9 and Proposition~3.26)} \\ & \Longleftrightarrow \tau(\Gamma) \cup \mathsf{At}[\Sigma] \models_{\mathbf{K}} \tau(\phi) & \text{(by Lemma~3.23)} \\ & \Longleftrightarrow \Gamma \cup \Delta(\mathsf{At}[\Sigma]) \vdash \phi & \text{(by 4.2(A2) and 4.2(A3))} \\ & \Longleftrightarrow \Gamma \cup \mathsf{At}(\Delta[\Sigma]) \vdash \phi & (\text{by structurality of } \Delta) \end{align*} $$
$$ \begin{align*} \Gamma \Vdash \phi & \Longleftrightarrow \tau(\Gamma) \models^c_{\mathbf{Q}} \tau(\phi) & \text{(by 4.6(W1))} \\ & \Longleftrightarrow \tau(\Gamma) \models^c_{\mathbf{K}} \tau(\phi) & \text{(by Definition~5.9 and Proposition~3.26)} \\ & \Longleftrightarrow \tau(\Gamma) \cup \mathsf{At}[\Sigma] \models_{\mathbf{K}} \tau(\phi) & \text{(by Lemma~3.23)} \\ & \Longleftrightarrow \Gamma \cup \Delta(\mathsf{At}[\Sigma]) \vdash \phi & \text{(by 4.2(A2) and 4.2(A3))} \\ & \Longleftrightarrow \Gamma \cup \mathsf{At}(\Delta[\Sigma]) \vdash \phi & (\text{by structurality of } \Delta) \end{align*} $$
and thus, since
![]() $\Lambda =\Delta [\Sigma ]$
(as we argued in the previous direction), it follows that
$\Lambda =\Delta [\Sigma ]$
(as we argued in the previous direction), it follows that
![]() $\vdash $
is a standard companion of
$\vdash $
is a standard companion of
![]() $\Vdash $
. This completes our proof.
$\Vdash $
. This completes our proof.
The correspondence provided by the previous lemma motivates the following definition. Intuitively, while the schematic fragment identifies the greatest standard logic contained in a weak logic, the following notion characterises the greatest quasivariety with core defined by
![]() $\Sigma $
and which has the same core-generated substructures of a quasivariety
$\Sigma $
and which has the same core-generated substructures of a quasivariety
![]() $\mathbf {Q}$
. The following definition essentially refines the notion of core superalgebra (Definition 3.22) in the setting with equationally definable core.
$\mathbf {Q}$
. The following definition essentially refines the notion of core superalgebra (Definition 3.22) in the setting with equationally definable core.
Definition 5.11. We say that B is a
![]() $\Sigma $
-superalgebra of A if
$\Sigma $
-superalgebra of A if
![]() $A {\leqslant } B$
and
$A {\leqslant } B$
and
![]() $\Sigma (A) = \Sigma (B)$
. If
$\Sigma (A) = \Sigma (B)$
. If
![]() $\mathbf {Q}$
is a class of algebras, then we write
$\mathbf {Q}$
is a class of algebras, then we write
![]() $\mathbb {C}_{\Sigma }(\mathbf {Q}) $
for the class of all
$\mathbb {C}_{\Sigma }(\mathbf {Q}) $
for the class of all
![]() $\Sigma $
-superalgebras of elements of
$\Sigma $
-superalgebras of elements of
![]() $\mathbf {Q}$
.
$\mathbf {Q}$
.
Lemma 5.12. Suppose
![]() $\mathbf {K}$
is a quasivariety of expanded algebras with core defined by
$\mathbf {K}$
is a quasivariety of expanded algebras with core defined by
![]() $\Sigma $
, then
$\Sigma $
, then
![]() $\mathbb {C}_\Sigma (\mathbf {K})$
is also a quasivariety of expanded algebras.
$\mathbb {C}_\Sigma (\mathbf {K})$
is also a quasivariety of expanded algebras.
Proof. We notice that
![]() $A\in \mathbb {C}_\Sigma (\mathbf {K})$
if and only if
$A\in \mathbb {C}_\Sigma (\mathbf {K})$
if and only if
![]() $A\models \forall x(\mathsf {core}(x)\leftrightarrow \bigwedge \Sigma (x))$
, which can be rephrased by means of Horn formulas as in Proposition 4.12. Also, for all quasiequations
$A\models \forall x(\mathsf {core}(x)\leftrightarrow \bigwedge \Sigma (x))$
, which can be rephrased by means of Horn formulas as in Proposition 4.12. Also, for all quasiequations
![]() $\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \varepsilon \approx \delta \in \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {K})$
we have that this is equivalent to saying
$\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \varepsilon \approx \delta \in \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {K})$
we have that this is equivalent to saying
where these are also Horn formulas. It follows immediately by Fact 2.14 that
![]() $\mathbb {C}_\Sigma (\mathbf {K})$
is closed under
$\mathbb {C}_\Sigma (\mathbf {K})$
is closed under
![]() $ \mathbb {I} $
,
$ \mathbb {I} $
,
![]() $ \mathbb {S} $
,
$ \mathbb {S} $
,
![]() $ \mathbb {P} $
, and
$ \mathbb {P} $
, and
![]() $ \mathbb {P}_{\mathrm {U}} $
.
$ \mathbb {P}_{\mathrm {U}} $
.
We conclude this section with the following characterisation of the family of standard companions of a strictly algebraizable weak logic
![]() $\Vdash $
. This generalises the previous results from [Reference Almeida1, Reference Bezhanishvili, Grilletti and Quadrellaro3] to our abstract setting.
$\Vdash $
. This generalises the previous results from [Reference Almeida1, Reference Bezhanishvili, Grilletti and Quadrellaro3] to our abstract setting.
Notation 5.13. Let
![]() $\tau :\mathsf {Fm}\to \mathsf {Eq}$
and let
$\tau :\mathsf {Fm}\to \mathsf {Eq}$
and let
![]() $\mathbf {Q}$
be a quasivariety, then we write
$\mathbf {Q}$
be a quasivariety, then we write
![]() $\mathsf {Log}_\tau (\mathbf {Q})$
for the set of all pairs
$\mathsf {Log}_\tau (\mathbf {Q})$
for the set of all pairs
![]() $(\Gamma ,\phi )$
such that
$(\Gamma ,\phi )$
such that
![]() $\tau (\Gamma )\models _{\mathbf {Q}} \tau (\phi )$
.
$\tau (\Gamma )\models _{\mathbf {Q}} \tau (\phi )$
.
Theorem 5.14. Let
![]() $\Vdash $
be a weak logic algebraized by
$\Vdash $
be a weak logic algebraized by
![]() $(\mathbf {Q},\Sigma ,\tau ,\Delta )$
, then
$(\mathbf {Q},\Sigma ,\tau ,\Delta )$
, then
![]() $\mathrm {St}(\Vdash )$
with the subset ordering
$\mathrm {St}(\Vdash )$
with the subset ordering
![]() $\subseteq $
forms a bounded lattice with maximum element
$\subseteq $
forms a bounded lattice with maximum element
![]() $\mathrm {Schm}(\Vdash )$
and minimum element
$\mathrm {Schm}(\Vdash )$
and minimum element
![]() $\mathsf {Log}_\tau (\mathbb {C}_\Sigma (\mathbf {Q}))$
.
$\mathsf {Log}_\tau (\mathbb {C}_\Sigma (\mathbf {Q}))$
.
Proof. Let
![]() $\vdash _0,\vdash _1 \in \mathrm {St}(\Vdash )$
, then
$\vdash _0,\vdash _1 \in \mathrm {St}(\Vdash )$
, then
![]() $\vdash _0\cap \vdash _1$
is a standard logic and it is straightforward to verify that
$\vdash _0\cap \vdash _1$
is a standard logic and it is straightforward to verify that
![]() $\vdash _0\cap \vdash _1\in \mathrm {St}(\Vdash )$
. Similarly, if
$\vdash _0\cap \vdash _1\in \mathrm {St}(\Vdash )$
. Similarly, if
![]() $\vdash _0,\vdash _1 \in \mathrm {St}(\Vdash )$
and they are algebraized, respectively, by
$\vdash _0,\vdash _1 \in \mathrm {St}(\Vdash )$
and they are algebraized, respectively, by
![]() $(\mathbf {K}_0,\tau ,\Delta )$
and
$(\mathbf {K}_0,\tau ,\Delta )$
and
![]() $(\mathbf {K}_1,\tau ,\Delta )$
, then
$(\mathbf {K}_1,\tau ,\Delta )$
, then
![]() $\mathbf {K}_0\cap \mathbf {K}_1$
is a quasivariety, and the logic
$\mathbf {K}_0\cap \mathbf {K}_1$
is a quasivariety, and the logic
![]() $\vdash _2$
defined by letting
$\vdash _2$
defined by letting
is the supremum of
![]() $\vdash _0$
and
$\vdash _0$
and
![]() $\vdash _1$
in
$\vdash _1$
in
![]() $\mathrm {St}(\Vdash )$
. This shows that
$\mathrm {St}(\Vdash )$
. This shows that
![]() $(\mathrm {St}(\Vdash ), \subseteq )$
is a lattice.
$(\mathrm {St}(\Vdash ), \subseteq )$
is a lattice.
We show that
![]() $\mathrm {Schm}(\Vdash )$
is maximal in
$\mathrm {Schm}(\Vdash )$
is maximal in
![]() $\mathrm {St}(\Vdash )$
. Recall that, by Corollary 5.6, we have that
$\mathrm {St}(\Vdash )$
. Recall that, by Corollary 5.6, we have that
![]() $\mathrm {Schm}(\Vdash )=\mathsf {Log}_\tau (\mathbf {Q})$
. Suppose now that
$\mathrm {Schm}(\Vdash )=\mathsf {Log}_\tau (\mathbf {Q})$
. Suppose now that
![]() $\vdash \;\in \mathrm {St}(\Vdash )$
then by monotonicity
$\vdash \;\in \mathrm {St}(\Vdash )$
then by monotonicity
![]() $\Gamma \vdash \phi $
entails
$\Gamma \vdash \phi $
entails
![]() $\Gamma \cup \Lambda \vdash \phi $
, and thus we have
$\Gamma \cup \Lambda \vdash \phi $
, and thus we have
![]() $\Gamma \Vdash \phi $
. This shows that
$\Gamma \Vdash \phi $
. This shows that
![]() $\vdash \;\subseteq \; \Vdash $
. Since
$\vdash \;\subseteq \; \Vdash $
. Since
![]() $\vdash $
and
$\vdash $
and
![]() $\mathrm {Schm}(\Vdash )$
are both closed under uniform substitution, it follows that
$\mathrm {Schm}(\Vdash )$
are both closed under uniform substitution, it follows that
![]() $\vdash \subseteq \mathrm {Schm}(\Vdash )$
.
$\vdash \subseteq \mathrm {Schm}(\Vdash )$
.
We show that
![]() $\mathsf {Log}_\tau (\mathbb {C}_\Sigma (\mathbf {Q}))$
is minimal in
$\mathsf {Log}_\tau (\mathbb {C}_\Sigma (\mathbf {Q}))$
is minimal in
![]() $\mathrm {St}(\Vdash )$
. If
$\mathrm {St}(\Vdash )$
. If
![]() $\vdash \; \in \mathrm {St}(\Vdash )$
, then by Lemma 5.10
$\vdash \; \in \mathrm {St}(\Vdash )$
, then by Lemma 5.10
![]() $\vdash $
is algebraized by
$\vdash $
is algebraized by
![]() $(\mathbf {K},\tau ,\Delta )$
, for some standard companion
$(\mathbf {K},\tau ,\Delta )$
, for some standard companion
![]() $\mathbf {K}$
of
$\mathbf {K}$
of
![]() $\mathbf {Q}$
. By Definition 5.11, it follows that
$\mathbf {Q}$
. By Definition 5.11, it follows that
![]() $\mathbf {K}\subseteq \mathbb {C}_{\Sigma }(\mathbf {Q})$
and so
$\mathbf {K}\subseteq \mathbb {C}_{\Sigma }(\mathbf {Q})$
and so
![]() $\mathsf {Log}_\tau (\mathbb {C}_\Sigma (\mathbf {Q}))\subseteq \mathsf {Log}_\tau (\mathbf {K})=\; \vdash $
.
$\mathsf {Log}_\tau (\mathbb {C}_\Sigma (\mathbf {Q}))\subseteq \mathsf {Log}_\tau (\mathbf {K})=\; \vdash $
.
Remark 5.15. We notice that, if
![]() $\Vdash $
is fixed-point algebraized by
$\Vdash $
is fixed-point algebraized by
![]() $(\mathbf {Q},\Sigma ,\tau ,\Delta )$
with
$(\mathbf {Q},\Sigma ,\tau ,\Delta )$
with
![]() $\Sigma =\{x\approx \delta (x)\}$
as in Definition 4.22, then
$\Sigma =\{x\approx \delta (x)\}$
as in Definition 4.22, then
![]() $\Theta \models ^c_{\mathbf {Q}} \alpha \approx \beta $
if and only if
$\Theta \models ^c_{\mathbf {Q}} \alpha \approx \beta $
if and only if
![]() $\sigma _{\delta }(\Theta )\models \sigma _{\delta }(\alpha )\approx \sigma _{\delta }(\beta )$
, where
$\sigma _{\delta }(\Theta )\models \sigma _{\delta }(\alpha )\approx \sigma _{\delta }(\beta )$
, where
![]() $\sigma _{\delta }$
is the substitution
$\sigma _{\delta }$
is the substitution
![]() $\sigma _{\delta }(x)=\delta (x)$
for all
$\sigma _{\delta }(x)=\delta (x)$
for all
![]() $x\in \mathsf {Var}$
. Then, since
$x\in \mathsf {Var}$
. Then, since
![]() $\Vdash _{\mathrm {s}}$
is the logic
$\Vdash _{\mathrm {s}}$
is the logic
![]() $\mathsf {Log}_\tau (\mathbf {Q})$
, we obtain that
$\mathsf {Log}_\tau (\mathbf {Q})$
, we obtain that
![]() $\Gamma \Vdash \phi $
if and only if
$\Gamma \Vdash \phi $
if and only if
![]() $\sigma _{\delta }(\Gamma )\Vdash _{\mathrm {s}} \sigma _{\delta }(\phi )$
. This correspondence showcases a special case where the equations identifying the core of the expanded algebra induce a translation between a logic and its schematic fragment. We refer the reader to [Reference Almeida1] for an in-depth study of such translations and to [Reference Almeida1, Reference Moraschini23] for the relation between such translations and corresponding adjunctions between quasivarieties of algebras.
$\sigma _{\delta }(\Gamma )\Vdash _{\mathrm {s}} \sigma _{\delta }(\phi )$
. This correspondence showcases a special case where the equations identifying the core of the expanded algebra induce a translation between a logic and its schematic fragment. We refer the reader to [Reference Almeida1] for an in-depth study of such translations and to [Reference Almeida1, Reference Moraschini23] for the relation between such translations and corresponding adjunctions between quasivarieties of algebras.
5.3 Example of bridge theorem: Deduction theorem
As stressed by Font in [Reference Font16, p. 160], “Bridge theorems and transfer theorems are the ultimate justification of abstract algebraic logic.” We show that this motivation remains applicable in our modified setting of weak logics. The key observation is that, in virtue of Theorem 5.5, we do not have to come up with novel algebraic descriptions of logical properties, but we can rely on the established characterisation of such properties for standard logics.
To showcase a concrete example, we look at one bridge theorem for strictly algebraizable weak logics, i.e., we consider the case of strictly algebraizable logics with a deduction–detachment theorem. We start by recalling the definition of this property and the standard bridge theorem relating logics with the deduction–detachment theorem and quasivarieties with the so-called EDPRC property.
Definition 5.16. A weak (or standard) logic
![]() $\Vdash $
has the deduction–detachment theorem (DDT) if there is a finite set of formulas
$\Vdash $
has the deduction–detachment theorem (DDT) if there is a finite set of formulas
![]() $I(x,y)$
such that, for every set of formulas
$I(x,y)$
such that, for every set of formulas
![]() $\Gamma $
,
$\Gamma $
,
Definition 5.17. A quasivariety
![]() $\mathbf {K}$
has equationally definable principal relative congruences (EDPRC) if there is a finite set of equations
$\mathbf {K}$
has equationally definable principal relative congruences (EDPRC) if there is a finite set of equations
![]() $\Theta (x, y, z, v)$
such that, for every
$\Theta (x, y, z, v)$
such that, for every
![]() $A\in \mathbf {K}$
and
$A\in \mathbf {K}$
and
![]() $a,b,c,d\in A$
,
$a,b,c,d\in A$
,
where
![]() $\mathrm {Cn}_{\mathbf {K}}(c,d) $
is the
$\mathrm {Cn}_{\mathbf {K}}(c,d) $
is the
![]() $\mathbf {K}$
-congruence of A induced by the equation
$\mathbf {K}$
-congruence of A induced by the equation
![]() $c\approx d$
, i.e., the smallest congruence
$c\approx d$
, i.e., the smallest congruence
![]() $\theta $
of A such that
$\theta $
of A such that
![]() $(c,d)\in \theta $
and
$(c,d)\in \theta $
and
![]() $A/\theta \in \mathbf {K}$
(cf. Notation 6.3).
$A/\theta \in \mathbf {K}$
(cf. Notation 6.3).
The following result, due to Blok and Pigozzi, is one classical bridge theorem from abstract algebraic logic. We refer the reader to [Reference Font16, Theorem 3.85] for a proof of this result.
Fact 5.18 (Blok–Pigozzi).
Let
![]() $\vdash $
be a standard algebraizable logic with equivalent algebraic semantics
$\vdash $
be a standard algebraizable logic with equivalent algebraic semantics
![]() $\mathbf {Q}$
, then
$\mathbf {Q}$
, then
![]() $\vdash $
has a deduction–detachment theorem if and only if
$\vdash $
has a deduction–detachment theorem if and only if
![]() $\mathbf {Q}$
has EDPRC.
$\mathbf {Q}$
has EDPRC.
In the case of a strictly algebraizable weak logic
![]() $\Vdash $
, finite representability allows us to transfer the property of having the DDT from
$\Vdash $
, finite representability allows us to transfer the property of having the DDT from
![]() $\Vdash $
to
$\Vdash $
to
![]() $\Vdash _{\mathrm {s}}$
. More precisely, we can prove the following proposition.
$\Vdash _{\mathrm {s}}$
. More precisely, we can prove the following proposition.
Proposition 5.19. Let
![]() $\Vdash $
be a strictly algebraizable weak logic, then
$\Vdash $
be a strictly algebraizable weak logic, then
![]() $\Vdash $
has DDT if and only of
$\Vdash $
has DDT if and only of
![]() $\Vdash _{\mathrm {s}}$
has DDT, witnessed by the same finite set of formulas
$\Vdash _{\mathrm {s}}$
has DDT, witnessed by the same finite set of formulas
![]() $I(x,y)$
.
$I(x,y)$
.
Proof. We first prove the right-to-left direction. Suppose
![]() $\Vdash _{\mathrm {s}}$
has DDT, and notice that since
$\Vdash _{\mathrm {s}}$
has DDT, and notice that since
![]() $\Vdash $
is strictly algebraizable then it is finitely represented by a set of formulas
$\Vdash $
is strictly algebraizable then it is finitely represented by a set of formulas
![]() $\Lambda $
(by Theorem 5.5). We have the following equivalences:
$\Lambda $
(by Theorem 5.5). We have the following equivalences:
 $$ \begin{align*} \Gamma\cup \{\phi\}\Vdash \psi &\Longleftrightarrow \Gamma\cup \{\phi\}\cup \mathsf{At}[\Lambda]\Vdash_{\mathrm{s}} \psi & \text{(by representability)} \\ &\Longleftrightarrow \Gamma\cup \mathsf{At}[\Lambda]\Vdash_{\mathrm{s}} I(\phi,\psi) & \text{(by assumption)} \\ &\Longleftrightarrow \Gamma \Vdash I(\phi,\psi), & \text{(by representability)} \end{align*} $$
$$ \begin{align*} \Gamma\cup \{\phi\}\Vdash \psi &\Longleftrightarrow \Gamma\cup \{\phi\}\cup \mathsf{At}[\Lambda]\Vdash_{\mathrm{s}} \psi & \text{(by representability)} \\ &\Longleftrightarrow \Gamma\cup \mathsf{At}[\Lambda]\Vdash_{\mathrm{s}} I(\phi,\psi) & \text{(by assumption)} \\ &\Longleftrightarrow \Gamma \Vdash I(\phi,\psi), & \text{(by representability)} \end{align*} $$
which establish that
![]() $\Vdash $
has DDT.
$\Vdash $
has DDT.
Consider now the left-to-right direction. We assume that
![]() $\Vdash $
has DDT and that this is witnessed by the finite set of formulas
$\Vdash $
has DDT and that this is witnessed by the finite set of formulas
![]() $I(x,y)$
, then:
$I(x,y)$
, then:
 $$ \begin{align*} \Gamma\cup \{\phi\}\Vdash_{\mathrm{s}} \psi &\Longleftrightarrow \forall\sigma\in\mathsf{Subst}(\mathcal{L}), \; \sigma(\Gamma\cup \{\phi\})\Vdash \sigma(\psi) & \text{(by Definition~5.1)} \\ &\Longleftrightarrow \forall\sigma\in\mathsf{Subst}(\mathcal{L}), \; \sigma(\Gamma)\Vdash I(\sigma(\phi),\sigma(\psi)) & \text{(by assumption)} \\ &\Longleftrightarrow \Gamma \Vdash_{\mathrm{s}} I(\phi,\psi), & \text{(by Definition~5.1)} \end{align*} $$
$$ \begin{align*} \Gamma\cup \{\phi\}\Vdash_{\mathrm{s}} \psi &\Longleftrightarrow \forall\sigma\in\mathsf{Subst}(\mathcal{L}), \; \sigma(\Gamma\cup \{\phi\})\Vdash \sigma(\psi) & \text{(by Definition~5.1)} \\ &\Longleftrightarrow \forall\sigma\in\mathsf{Subst}(\mathcal{L}), \; \sigma(\Gamma)\Vdash I(\sigma(\phi),\sigma(\psi)) & \text{(by assumption)} \\ &\Longleftrightarrow \Gamma \Vdash_{\mathrm{s}} I(\phi,\psi), & \text{(by Definition~5.1)} \end{align*} $$
which proves our claim.
Corollary 5.20. Let
![]() $\Vdash $
be a strictly algebraizable weak logic with equivalent algebraic semantics
$\Vdash $
be a strictly algebraizable weak logic with equivalent algebraic semantics
![]() $\mathbf {Q}$
, then
$\mathbf {Q}$
, then
![]() $\Vdash $
has DDT if and only if
$\Vdash $
has DDT if and only if
![]() $\mathbf {Q}$
has EDPRC.
$\mathbf {Q}$
has EDPRC.
Remark 5.21. The previous result provides one example where one can obtain results about strictly algebraizable weak logics by investigating their schematic fragments. In particular, we did not need to come up with a novel algebraic characterisation for the presence of a deduction–detachment theorem in a strictly algebraizable weak logic
![]() $\Vdash $
, and we could simply rely on Theorem 5.5 and the classical bridge theorem by Blok and Pigozzi. This shows that strict algebraizability provides an especially strong and well-behaved notion in the setting of weak logics. We point out that we ascribe the underlying reason of this phenomena to the validity of a strong version of the Isomorphism Theorem in the case of strict algebraizability (in contrast to loose algebraizability). We shall investigate this in Section 6.3.
$\Vdash $
, and we could simply rely on Theorem 5.5 and the classical bridge theorem by Blok and Pigozzi. This shows that strict algebraizability provides an especially strong and well-behaved notion in the setting of weak logics. We point out that we ascribe the underlying reason of this phenomena to the validity of a strong version of the Isomorphism Theorem in the case of strict algebraizability (in contrast to loose algebraizability). We shall investigate this in Section 6.3.
6 The isomorphism theorem
Blok and Pigozzi’s isomorphism theorem [Reference Font16, Section 3.5] is possibly the most important single result on algebraizability, as it relates the algebraizability of a logic to the existence, for every algebra, of an isomorphism between the lattice of deductive filters of the logic and the lattice of its relative congruences. We consider in this section analogues of this result for the setting of algebraizable weak logics. Firstly, in Section 6.1 we recall the isomorphism theorem for standard algebraizable logic. In Section 6.2 we provide a partial analogue of this result for loosely algebraizable weak logics, and then in Section 6.3 we prove a stronger result for the case of strictly algebraizable weak logics.
6.1 Standard algebraizable logics
We start by providing some preliminary definitions needed to state Blok and Pigozzi’s result. We first recall the notion of deductive filter and fix some notation for algebraic congruences.
Definition 6.1. For any algebra A and standard logic
![]() $\vdash $
, we say that
$\vdash $
, we say that
![]() $F\subseteq A$
is a deductive filter of
$F\subseteq A$
is a deductive filter of
![]() $\vdash $
on A if:
$\vdash $
on A if:
and we let
![]() $\mathsf {Fi}_{\vdash }(A)$
be the set of all deductive filters of
$\mathsf {Fi}_{\vdash }(A)$
be the set of all deductive filters of
![]() $\vdash $
on A.
$\vdash $
on A.
Remark 6.2. We notice that
![]() $\mathsf {Fi}_{\vdash }(A)$
is closed under arbitrary intersections and thus that it forms a complete lattice under the subset ordering. Moreover, if F is a deductive filter and h is an endomorphism of A, then
$\mathsf {Fi}_{\vdash }(A)$
is closed under arbitrary intersections and thus that it forms a complete lattice under the subset ordering. Moreover, if F is a deductive filter and h is an endomorphism of A, then
![]() $h^{-1}(F)$
is also a deductive filter. We denote by
$h^{-1}(F)$
is also a deductive filter. We denote by
![]() $\mathsf {Fi}^+_{\vdash }(A)$
the lattice expansion
$\mathsf {Fi}^+_{\vdash }(A)$
the lattice expansion
![]() $(\mathsf {Fi}_{\vdash }, \subseteq , \{ h^{-1} : h \in \mathsf {End}(\mathcal {L}) \})$
. We refer the reader to [Reference Font16, Section 2.3] for proofs of these facts.
$(\mathsf {Fi}_{\vdash }, \subseteq , \{ h^{-1} : h \in \mathsf {End}(\mathcal {L}) \})$
. We refer the reader to [Reference Font16, Section 2.3] for proofs of these facts.
Notation 6.3. Given any algebra A we let
![]() $\mathsf {Con}(A)$
be the set of all congruences
$\mathsf {Con}(A)$
be the set of all congruences
![]() $\theta $
over A, and
$\theta $
over A, and
![]() $\mathsf {Con}_{\mathbf {Q}}(A)$
be the set of all
$\mathsf {Con}_{\mathbf {Q}}(A)$
be the set of all
![]() $\mathbf {Q}$
-congruences of A, i.e., those congruences
$\mathbf {Q}$
-congruences of A, i.e., those congruences
![]() $\theta $
over A such that
$\theta $
over A such that
![]() $A/\theta \in \mathbf {Q}$
.
$A/\theta \in \mathbf {Q}$
.
Remark 6.4. Similarly to the case of deductive filters,
![]() $\mathsf {Con}_{\mathbf {Q}}(A)$
is closed under arbitrary intersections and therefore it is also a lattice under the subset ordering. Additionally, it is possible to verify that
$\mathsf {Con}_{\mathbf {Q}}(A)$
is closed under arbitrary intersections and therefore it is also a lattice under the subset ordering. Additionally, it is possible to verify that
![]() $\mathsf {Con}_{\mathbf {Q}}(A)$
is closed under inverse endomorphisms of A. We then write
$\mathsf {Con}_{\mathbf {Q}}(A)$
is closed under inverse endomorphisms of A. We then write
![]() $\mathsf {Con}^+_{\mathbf {Q}}(A)$
for this lattice expansion, i.e.,
$\mathsf {Con}^+_{\mathbf {Q}}(A)$
for this lattice expansion, i.e.,
![]() $\mathsf {Con}^+_{\mathbf {Q}}(A)=(\mathsf {Con}_{\mathbf {Q}}(A), \subseteq , \{h^{-1} : h \in \mathsf {End}(A)\})$
.
$\mathsf {Con}^+_{\mathbf {Q}}(A)=(\mathsf {Con}_{\mathbf {Q}}(A), \subseteq , \{h^{-1} : h \in \mathsf {End}(A)\})$
.
Finally, we introduce syntactical and semantical theories as follows.
Definition 6.5. If
![]() $\vdash $
is a standard logic, then we denote by
$\vdash $
is a standard logic, then we denote by
![]() $\mathsf {Th}(\vdash )$
the set of all (syntactic) theories over
$\mathsf {Th}(\vdash )$
the set of all (syntactic) theories over
![]() $\vdash $
, i.e., all sets
$\vdash $
, i.e., all sets
![]() $\Gamma \subseteq \mathsf {Fm}$
such that
$\Gamma \subseteq \mathsf {Fm}$
such that
![]() $\Gamma \vdash \phi $
entails
$\Gamma \vdash \phi $
entails
![]() $\phi \in \Gamma $
. If
$\phi \in \Gamma $
. If
![]() $\mathbf {Q}$
is a quasivariety, then
$\mathbf {Q}$
is a quasivariety, then
![]() $\mathsf {Th}(\models _{\mathbf {Q}})$
denotes the set of (semantical) theories over
$\mathsf {Th}(\models _{\mathbf {Q}})$
denotes the set of (semantical) theories over
![]() $\mathbf {Q}$
, i.e., the sets of equations
$\mathbf {Q}$
, i.e., the sets of equations
![]() $\Theta \subseteq \mathsf {Eq}$
such that
$\Theta \subseteq \mathsf {Eq}$
such that
![]() $\Theta \models _{\mathbf {Q}} \alpha \approx \beta $
entails
$\Theta \models _{\mathbf {Q}} \alpha \approx \beta $
entails
![]() $\alpha \approx \beta \in \Theta $
.
$\alpha \approx \beta \in \Theta $
.
Remark 6.6. We notice that
![]() $\mathsf {Th}(\vdash )$
forms a lattice under the subset relation, and that it is additionally closed under inverse substitutions. We refer by
$\mathsf {Th}(\vdash )$
forms a lattice under the subset relation, and that it is additionally closed under inverse substitutions. We refer by
![]() $\mathsf {Th}^+(\vdash )$
to the lattice expansion
$\mathsf {Th}^+(\vdash )$
to the lattice expansion
![]() $(\mathsf {Th}(\vdash ), \subseteq , \{ \sigma ^{-1} : \sigma \in \mathsf {Subst}(\mathcal {L}) \} )$
. Similarly, also
$(\mathsf {Th}(\vdash ), \subseteq , \{ \sigma ^{-1} : \sigma \in \mathsf {Subst}(\mathcal {L}) \} )$
. Similarly, also
![]() $\mathsf {Th}(\models _{\mathbf {Q}})$
forms a lattice under the subset ordering and is closed under inverse substitutions. We let
$\mathsf {Th}(\models _{\mathbf {Q}})$
forms a lattice under the subset ordering and is closed under inverse substitutions. We let
![]() $\mathsf {Th}^+(\models _{\mathbf {Q}})=(\mathsf {Th}(\models _{\mathbf {Q}}), \subseteq , \{ \sigma ^{-1} : \sigma \in \mathsf {Subst}(\mathcal {L}) \} )$
. These properties follow from the fact that the syntactic theories over
$\mathsf {Th}^+(\models _{\mathbf {Q}})=(\mathsf {Th}(\models _{\mathbf {Q}}), \subseteq , \{ \sigma ^{-1} : \sigma \in \mathsf {Subst}(\mathcal {L}) \} )$
. These properties follow from the fact that the syntactic theories over
![]() $\vdash $
are exactly the deductive filters of
$\vdash $
are exactly the deductive filters of
![]() $\vdash $
over
$\vdash $
over
![]() $\mathsf {Fm}$
, and that, under the identification of equations and pairs of formulas, the semantic theories over
$\mathsf {Fm}$
, and that, under the identification of equations and pairs of formulas, the semantic theories over
![]() $\models _{\mathbf {Q}}$
are the
$\models _{\mathbf {Q}}$
are the
![]() $\mathbf {Q}$
-congruences of
$\mathbf {Q}$
-congruences of
![]() $\mathsf {Fm}$
.
$\mathsf {Fm}$
.
Blok and Pigozzi’s isomorphism theorem for standard logics provides a criterion to determine if a logic is algebraized by a quasivariety based on their associated lattices of filters and congruences. For a proof of the following theorem we refer the reader to [Reference Font16, Section 3.5].
Fact 6.7 (Isomorphism theorem).
Let
![]() $\vdash $
be a standard logic and
$\vdash $
be a standard logic and
![]() $\mathbf {Q}$
a quasivariety, then the following are equivalent:
$\mathbf {Q}$
a quasivariety, then the following are equivalent:
-
(1)
 $\vdash $
is algebraizable with equivalent algebraic semantics
$\vdash $
is algebraizable with equivalent algebraic semantics
 $\mathbf {Q}$
;
$\mathbf {Q}$
; -
(2)
 $\mathsf {Fi}^+_{\vdash }(A) \cong \mathsf {Con}^+_{\mathbf {Q}}(A)$
, for any algebra A;
$\mathsf {Fi}^+_{\vdash }(A) \cong \mathsf {Con}^+_{\mathbf {Q}}(A)$
, for any algebra A; -
(3)
 $\mathsf {Th}^+(\vdash ) \cong \mathsf {Th}^+(\models _{\mathbf {Q}})$
.
$\mathsf {Th}^+(\vdash ) \cong \mathsf {Th}^+(\models _{\mathbf {Q}})$
.
Remark 6.8. We clarify what are the underlying witnesses in the previous theorem (cf. [Reference Font16, p. 150]). On the one hand, let
![]() $\vdash $
be an algebraizable logic with equivalent algebraic semantics
$\vdash $
be an algebraizable logic with equivalent algebraic semantics
![]() $(\mathbf {Q},\tau ,\Delta )$
. Then the associated isomorphism
$(\mathbf {Q},\tau ,\Delta )$
. Then the associated isomorphism
![]() $\mathsf {Fi}^+_{\vdash }(A) \cong \mathsf {Con}^+_{\mathbf {Q}}(A)$
is given by the following map from filters to congruences:
$\mathsf {Fi}^+_{\vdash }(A) \cong \mathsf {Con}^+_{\mathbf {Q}}(A)$
is given by the following map from filters to congruences:

and the following map from congruences to filters:

which can be shown to be inverse of each other. On the other hand, suppose
![]() $\Omega :\mathsf {Th}^+(\vdash ) \cong \mathsf {Th}^+(\models _{\mathbf {Q}})$
is an isomorphism. Then the two transformers
$\Omega :\mathsf {Th}^+(\vdash ) \cong \mathsf {Th}^+(\models _{\mathbf {Q}})$
is an isomorphism. Then the two transformers
![]() $\tau $
and
$\tau $
and
![]() $\Delta $
are defined as follows:
$\Delta $
are defined as follows:
 $$ \begin{align*} \tau(x)&=\sigma_x(\Omega(\mathrm{Cn}_{\vdash}(x)))\\ \Delta(x,y)&= \sigma_{x,y}( \Omega^{-1}(\mathrm{Cn}_{\mathbf{Q}}(x\approx y) ) ), \end{align*} $$
$$ \begin{align*} \tau(x)&=\sigma_x(\Omega(\mathrm{Cn}_{\vdash}(x)))\\ \Delta(x,y)&= \sigma_{x,y}( \Omega^{-1}(\mathrm{Cn}_{\mathbf{Q}}(x\approx y) ) ), \end{align*} $$
where
![]() $\mathrm {Cn}_{\vdash }$
and
$\mathrm {Cn}_{\vdash }$
and
![]() $\mathrm {Cn}_{\mathbf {Q}}$
denote, respectively, the closure consequence operators on the logic
$\mathrm {Cn}_{\mathbf {Q}}$
denote, respectively, the closure consequence operators on the logic
![]() $\vdash $
and the quasivariety
$\vdash $
and the quasivariety
![]() $\mathbf {Q}$
,
$\mathbf {Q}$
,
![]() $\sigma _x$
is the substitution sending every variable to x, and
$\sigma _x$
is the substitution sending every variable to x, and
![]() $\sigma _{x,y}$
is the substitution sending every variable but y to x and y to itself.
$\sigma _{x,y}$
is the substitution sending every variable but y to x and y to itself.
6.2 Loosely algebraizable weak logics
We prove in this section a (partial) version of the isomorphism theorem for loosely algebraizable weak logics. To this end, we start by introducing a version of deductive filters and congruences relative to core semantics.
Definition 6.9. For any expanded algebra A and weak logic
![]() $\Vdash $
, we say that
$\Vdash $
, we say that
![]() $F\subseteq A$
is a core filter of
$F\subseteq A$
is a core filter of
![]() $\Vdash $
over A if:
$\Vdash $
over A if:
and we denote the set of core filters of A with respect to
![]() $\Vdash $
by
$\Vdash $
by
![]() $\mathsf {Fi}_{\Vdash }(A)$
.
$\mathsf {Fi}_{\Vdash }(A)$
.
Remark 6.10. If A is an expanded algebra and
![]() $\mathbf {Q}$
a quasivariety of algebras in the same algebraic signature of A, then we write
$\mathbf {Q}$
a quasivariety of algebras in the same algebraic signature of A, then we write
![]() $\mathsf {Con}(A)$
and
$\mathsf {Con}(A)$
and
![]() $\mathsf {Con}_{\mathbf {Q}}(A)$
also for the congruences and the
$\mathsf {Con}_{\mathbf {Q}}(A)$
also for the congruences and the
![]() $\mathbf {Q}$
-congruences of A, respectively. Notice that, if A is an expanded algebra and
$\mathbf {Q}$
-congruences of A, respectively. Notice that, if A is an expanded algebra and
![]() $\theta $
a congruence of its algebraic reduct, then the structure
$\theta $
a congruence of its algebraic reduct, then the structure
![]() $A/\theta $
is simply the quotient of the algebraic reduct of A by
$A/\theta $
is simply the quotient of the algebraic reduct of A by
![]() $\theta $
with
$\theta $
with
![]() $\mathsf {core}(A/\theta )=\mathsf {core}(A)/\theta $
. This corresponds to viewing
$\mathsf {core}(A/\theta )=\mathsf {core}(A)/\theta $
. This corresponds to viewing
![]() $A/\theta $
as a strong homomorphic image of A (cf. Definition 2.8 and Remark 2.9).
$A/\theta $
as a strong homomorphic image of A (cf. Definition 2.8 and Remark 2.9).
Definition 6.11. Given an expanded algebra A and a quasivariety
![]() $\mathbf {Q}$
of expanded algebras, a congruence
$\mathbf {Q}$
of expanded algebras, a congruence
![]() $\theta \in \mathsf {Con}(A)$
is said to be a core
$\theta \in \mathsf {Con}(A)$
is said to be a core
![]() $\mathbf {Q}$
-congruence if
$\mathbf {Q}$
-congruence if
![]() $A/\theta \in \mathbf {Q}$
. We write
$A/\theta \in \mathbf {Q}$
. We write
![]() $\mathsf {Con}^c_{\mathbf {Q}}(A)$
for the set of all core
$\mathsf {Con}^c_{\mathbf {Q}}(A)$
for the set of all core
![]() $\mathbf {Q}$
-congruences over A.
$\mathbf {Q}$
-congruences over A.
Remark 6.12. Similarly to Remarks 6.2 and 6.4, it is possible to verify that both
![]() $\mathsf {Fi}_{\Vdash }(A)$
and
$\mathsf {Fi}_{\Vdash }(A)$
and
![]() $\mathsf {Con}^c_{\mathbf {Q}}(A)$
are closed under arbitrary intersections, and thus form complete lattices under the subset ordering.
$\mathsf {Con}^c_{\mathbf {Q}}(A)$
are closed under arbitrary intersections, and thus form complete lattices under the subset ordering.
Lemma 6.13. Let
![]() $\mathbf {Q}$
be a quasivariety of expanded algebras and let A be a core-generated expanded algebra, then:
$\mathbf {Q}$
be a quasivariety of expanded algebras and let A be a core-generated expanded algebra, then:
-
(1) if
 $G\subseteq A$
is a core filter of
$G\subseteq A$
is a core filter of
 $\Vdash $
, it is a deductive filter of its schematic fragment
$\Vdash $
, it is a deductive filter of its schematic fragment
 $\Vdash _{\mathrm {s}}$
;
$\Vdash _{\mathrm {s}}$
; -
(2) if
 $\theta $
is a core
$\theta $
is a core
 $\mathbf {Q}$
-congruence of A, then it is also a
$\mathbf {Q}$
-congruence of A, then it is also a
 $\mathbf {Q}\restriction \mathcal {L}$
-congruence.
$\mathbf {Q}\restriction \mathcal {L}$
-congruence.
Proof. Clause (2) follows immediately from the definition of core
![]() $\mathbf {Q}$
-congruence. We thus consider clause (1). Let
$\mathbf {Q}$
-congruence. We thus consider clause (1). Let
![]() $G\subseteq A$
be a core filter of
$G\subseteq A$
be a core filter of
![]() $\Vdash $
, and let
$\Vdash $
, and let
![]() $\Gamma \Vdash _{\mathrm {s}} \phi $
,
$\Gamma \Vdash _{\mathrm {s}} \phi $
,
![]() $h[\Gamma ]\subseteq G$
for some
$h[\Gamma ]\subseteq G$
for some
![]() $h\in \mathsf {Hom}(\mathsf {Fm},A)$
. Now, since A is core-generated, by Lemma 3.20 we can find a substitution
$h\in \mathsf {Hom}(\mathsf {Fm},A)$
. Now, since A is core-generated, by Lemma 3.20 we can find a substitution
![]() $\sigma $
and a core assignment g, such that
$\sigma $
and a core assignment g, such that
![]() $g(\sigma (x))=h(x)$
for all
$g(\sigma (x))=h(x)$
for all
![]() $x\in \mathsf {Var}$
. In particular, it follows that
$x\in \mathsf {Var}$
. In particular, it follows that
![]() $g[\sigma [\Gamma ]]\subseteq G$
. Now, since
$g[\sigma [\Gamma ]]\subseteq G$
. Now, since
![]() $\Gamma \Vdash _{\mathrm {s}} \phi $
, it follows by uniform substitution that
$\Gamma \Vdash _{\mathrm {s}} \phi $
, it follows by uniform substitution that
![]() $\sigma [\Gamma ]\Vdash _{\mathrm {s}} \sigma (\phi )$
and therefore
$\sigma [\Gamma ]\Vdash _{\mathrm {s}} \sigma (\phi )$
and therefore
![]() $\sigma [\Gamma ]\Vdash \sigma (\phi )$
. Now, since g is a core assignment and G a core filter with
$\sigma [\Gamma ]\Vdash \sigma (\phi )$
. Now, since g is a core assignment and G a core filter with
![]() $g[\sigma [\Gamma ]]\subseteq G$
, it follows that
$g[\sigma [\Gamma ]]\subseteq G$
, it follows that
![]() $g(\sigma (\phi ))\in G$
, whence
$g(\sigma (\phi ))\in G$
, whence
![]() $h(\phi )\in G$
. This shows that G is a deductive filter with respect to
$h(\phi )\in G$
. This shows that G is a deductive filter with respect to
![]() $\Vdash _{\mathrm {s}}$
.
$\Vdash _{\mathrm {s}}$
.
Lemma 6.14. Let
![]() $\mathbf {Q}$
be a quasivariety of expanded algebras, A be a core-generated expanded algebra, and let h be a strong endomorphism of A, then the following hold:
$\mathbf {Q}$
be a quasivariety of expanded algebras, A be a core-generated expanded algebra, and let h be a strong endomorphism of A, then the following hold:
-
(1) if F is a core filter of
 $\Vdash $
, then
$\Vdash $
, then
 $h^{-1}(F)$
is also a core filter;
$h^{-1}(F)$
is also a core filter; -
(2) if
 $\theta \in \mathsf {Con}^c_{\mathbf {Q}}(A)$
then
$\theta \in \mathsf {Con}^c_{\mathbf {Q}}(A)$
then
 $h^{-1}(\theta )\in \mathsf {Con}^c_{\mathbf {Q}}(A)$
.
$h^{-1}(\theta )\in \mathsf {Con}^c_{\mathbf {Q}}(A)$
.
Therefore,
![]() $\mathsf {Fi}_{\Vdash }(A)$
and
$\mathsf {Fi}_{\Vdash }(A)$
and
![]() $\mathsf {Con}^c_{\mathbf {Q}}(A)$
are two lattices commuting with all inverse strong endomorphisms of A.
$\mathsf {Con}^c_{\mathbf {Q}}(A)$
are two lattices commuting with all inverse strong endomorphisms of A.
Proof. We already pointed out in Remark 6.12 that
![]() $\mathsf {Fi}_{\Vdash }(A)$
and
$\mathsf {Fi}_{\Vdash }(A)$
and
![]() $\mathsf {Con}^c_{\mathbf {Q}}(A)$
are (complete) lattices under the subset ordering, whence we simply prove (1) and (2).
$\mathsf {Con}^c_{\mathbf {Q}}(A)$
are (complete) lattices under the subset ordering, whence we simply prove (1) and (2).
We prove (1). Suppose
![]() $\Gamma \Vdash \phi $
and let
$\Gamma \Vdash \phi $
and let
![]() $ g\in \mathsf {Hom}^c(\mathsf {Fm}, A) $
be such that
$ g\in \mathsf {Hom}^c(\mathsf {Fm}, A) $
be such that
![]() $g[\Gamma ]\subseteq h^{-1}(F)$
. Then
$g[\Gamma ]\subseteq h^{-1}(F)$
. Then
![]() $h(g[\Gamma ])\subseteq F$
and, since
$h(g[\Gamma ])\subseteq F$
and, since
![]() $h\circ g\in \mathsf {Hom}^c(\mathsf {Fm}, A)$
, it follows that
$h\circ g\in \mathsf {Hom}^c(\mathsf {Fm}, A)$
, it follows that
![]() $h(g[\phi ])\subseteq F$
and thus
$h(g[\phi ])\subseteq F$
and thus
![]() $g(\phi )\in h^{-1}(F)$
.
$g(\phi )\in h^{-1}(F)$
.
We prove (2). The fact that
![]() $h^{-1}(\theta )\in \mathsf {Con}(A)$
follows from Remark 6.4. We next show that
$h^{-1}(\theta )\in \mathsf {Con}(A)$
follows from Remark 6.4. We next show that
![]() $A/h^{-1}(\theta )\in \mathbf {Q}$
. Consider a quasiequation
$A/h^{-1}(\theta )\in \mathbf {Q}$
. Consider a quasiequation
![]() $\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \alpha \approx \beta \in \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q})$
. Since
$\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \alpha \approx \beta \in \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q})$
. Since
![]() $A/\theta \in \mathbf {Q}$
we have that
$A/\theta \in \mathbf {Q}$
we have that
![]() $A/\theta \models ^c \bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \alpha \approx \beta $
. Now, let
$A/\theta \models ^c \bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \alpha \approx \beta $
. Now, let
![]() $g\in \mathsf {Hom}^c(\mathsf {Fm}, A) $
be such that
$g\in \mathsf {Hom}^c(\mathsf {Fm}, A) $
be such that
![]() $g(\varepsilon _i)/h^{-1}(\theta ) = g(\delta _i)/h^{-1}(\theta )$
for all
$g(\varepsilon _i)/h^{-1}(\theta ) = g(\delta _i)/h^{-1}(\theta )$
for all
![]() $i{\leqslant } n$
, then it follows that
$i{\leqslant } n$
, then it follows that
![]() $h\circ g(\varepsilon _i)/\theta = h\circ g(\delta _i)/\theta $
for all
$h\circ g(\varepsilon _i)/\theta = h\circ g(\delta _i)/\theta $
for all
![]() $i{\leqslant } n$
. Since h is a strong endomorphism of A we obtain that
$i{\leqslant } n$
. Since h is a strong endomorphism of A we obtain that
![]() $h\circ g(\alpha )/\theta = h\circ g(\beta )/\theta $
. It then follows that
$h\circ g(\alpha )/\theta = h\circ g(\beta )/\theta $
. It then follows that
![]() $ g(\alpha )/h^{-1}(\theta ) = g(\beta )/h^{-1}(\theta )$
. This shows that
$ g(\alpha )/h^{-1}(\theta ) = g(\beta )/h^{-1}(\theta )$
. This shows that
![]() $A/h^{-1}(\theta )\models ^c \bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \alpha \approx \beta $
and so
$A/h^{-1}(\theta )\models ^c \bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \alpha \approx \beta $
and so
![]() $A/h^{-1}(\theta )\models ^c \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q})$
. Finally, notice that since A is core generated, also
$A/h^{-1}(\theta )\models ^c \mathrm {Th}_{\mathrm {qe}}^c(\mathbf {Q})$
. Finally, notice that since A is core generated, also
![]() $A/h^{-1}(\theta )$
is core generated, and thus we have from Proposition 3.26 that
$A/h^{-1}(\theta )$
is core generated, and thus we have from Proposition 3.26 that
![]() $A/h^{-1}(\theta ) \in \mathbf {Q}$
. We conclude that
$A/h^{-1}(\theta ) \in \mathbf {Q}$
. We conclude that
![]() $h^{-1}(\theta )\in \mathsf {Con}^c_{\mathbf {Q}}(A)$
.
$h^{-1}(\theta )\in \mathsf {Con}^c_{\mathbf {Q}}(A)$
.
As expanded algebras augment standard algebras with an additional core predicate, we now expand
![]() $\mathsf {Fi}^+_{\vdash }(A) $
and
$\mathsf {Fi}^+_{\vdash }(A) $
and
![]() $ \mathsf {Con}^+_{\mathbf {Q}}(A)$
in a similar way to capture core filters and congruences.
$ \mathsf {Con}^+_{\mathbf {Q}}(A)$
in a similar way to capture core filters and congruences.
Definition 6.15. Let
![]() $\Vdash $
be a weak logic and let
$\Vdash $
be a weak logic and let
![]() $\mathbf {Q}$
be a quasivariety of expanded algebras, for any core-generated expanded algebra A, we write
$\mathbf {Q}$
be a quasivariety of expanded algebras, for any core-generated expanded algebra A, we write
![]() $\overline {\mathsf {Fi}}_{\Vdash }(A) $
for the structure
$\overline {\mathsf {Fi}}_{\Vdash }(A) $
for the structure
and we write
![]() $\overline {\mathsf {Con}}_{\mathbf {Q}}(A) $
for the structure
$\overline {\mathsf {Con}}_{\mathbf {Q}}(A) $
for the structure
where
![]() $\mathsf {sEnd}(A)$
is the set of all strong endomorphisms of the expanded algebra A (recall Definition 2.8).
$\mathsf {sEnd}(A)$
is the set of all strong endomorphisms of the expanded algebra A (recall Definition 2.8).
Remark 6.16. The key intuition in the context of weak logics is to consider together arbitrary filters and core filters, and to consider together arbitrary
![]() $\mathbf {Q}$
-congruences and core
$\mathbf {Q}$
-congruences and core
![]() $\mathbf {Q}$
-congruences. This is possible because of Lemma 6.13, which makes sure that core filters are deductive filters, and that core congruences are congruences. Then, by Lemma 6.14, we additionally have that strict endomorphisms also preserve core filters and core congruences.
$\mathbf {Q}$
-congruences. This is possible because of Lemma 6.13, which makes sure that core filters are deductive filters, and that core congruences are congruences. Then, by Lemma 6.14, we additionally have that strict endomorphisms also preserve core filters and core congruences.
Theorem 6.17. Let
![]() $\Vdash $
be a weak logic and suppose it is loosely algebraized by
$\Vdash $
be a weak logic and suppose it is loosely algebraized by
![]() $(\mathbf {Q},\tau ,\Delta )$
, then for every core-generated expanded algebra A there is an isomorphism
$(\mathbf {Q},\tau ,\Delta )$
, then for every core-generated expanded algebra A there is an isomorphism
![]() $\Omega :\overline {\mathsf {Fi}}_{\Vdash }(A) \cong \overline {\mathsf {Con}}_{\mathbf {Q}}(A)$
.
$\Omega :\overline {\mathsf {Fi}}_{\Vdash }(A) \cong \overline {\mathsf {Con}}_{\mathbf {Q}}(A)$
.
Proof. Firstly, we define the following map from filters to congruences:

and the following map from congruences to filters:

Now, notice that since
![]() $\Vdash $
is loosely algebraized by
$\Vdash $
is loosely algebraized by
![]() $(\mathbf {Q},\tau ,\Delta )$
, then it follows from Proposition 5.4 that also
$(\mathbf {Q},\tau ,\Delta )$
, then it follows from Proposition 5.4 that also
![]() $\Vdash _{\mathrm {s}}$
is algebraized by
$\Vdash _{\mathrm {s}}$
is algebraized by
![]() $(\mathbf {Q},\tau ,\Delta )$
. Since the two maps above are exactly the same that occur in the proof of the isomorphism theorem for standard logics (cf. Remark 6.8), it follows immediately that they describe an isomorphism
$(\mathbf {Q},\tau ,\Delta )$
. Since the two maps above are exactly the same that occur in the proof of the isomorphism theorem for standard logics (cf. Remark 6.8), it follows immediately that they describe an isomorphism
![]() $\mathsf {Fi}^+_{\Vdash _{\mathrm {s}}}(A) \cong \mathsf {Con}^+_{\mathbf {Q}}(A)$
. Thus, it suffices to show that
$\mathsf {Fi}^+_{\Vdash _{\mathrm {s}}}(A) \cong \mathsf {Con}^+_{\mathbf {Q}}(A)$
. Thus, it suffices to show that
![]() $\theta _{(-)}$
sends core filters to core congruences, and that
$\theta _{(-)}$
sends core filters to core congruences, and that
![]() $F_{(-)}$
sends core congruences to core filters.
$F_{(-)}$
sends core congruences to core filters.
First, let G be a core filter over A, we show that
![]() $\theta _G$
is a core-
$\theta _G$
is a core-
![]() $\mathbf {Q}$
-congruence of A. Consider
$\mathbf {Q}$
-congruence of A. Consider
![]() $A/\theta _G$
and notice that this is well-defined because
$A/\theta _G$
and notice that this is well-defined because
![]() $\theta _G$
is a congruence. Now, consider the expansion of
$\theta _G$
is a congruence. Now, consider the expansion of
![]() $A/\theta _G$
defined by letting
$A/\theta _G$
defined by letting
![]() $\mathsf {core}(A/\theta _G)=\mathsf {core}(A)/\theta _G$
, we claim that
$\mathsf {core}(A/\theta _G)=\mathsf {core}(A)/\theta _G$
, we claim that
![]() $(A/\theta _G, \mathsf {core}(A)/\theta _G)\in \mathbf {Q}$
. Let
$(A/\theta _G, \mathsf {core}(A)/\theta _G)\in \mathbf {Q}$
. Let
![]() $\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \models ^c_{\mathbf {Q}} \alpha \approx \beta $
and suppose
$\bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \models ^c_{\mathbf {Q}} \alpha \approx \beta $
and suppose
![]() $h\in \mathsf {Hom}^c(\mathsf {Fm},A/\theta _G)$
is such that
$h\in \mathsf {Hom}^c(\mathsf {Fm},A/\theta _G)$
is such that
![]() $h(\epsilon _i)=h(\delta _i)$
for all
$h(\epsilon _i)=h(\delta _i)$
for all
![]() $i{\leqslant } n$
. By algebraizability we have that
$i{\leqslant } n$
. By algebraizability we have that
![]() $\bigcup _{i{\leqslant } n}\Delta (\varepsilon _i \approx \delta _i) \Vdash \Delta (\alpha ,\beta )$
and so
$\bigcup _{i{\leqslant } n}\Delta (\varepsilon _i \approx \delta _i) \Vdash \Delta (\alpha ,\beta )$
and so
![]() $h(\Delta (\alpha ,\beta ))\subseteq G$
. It follows that
$h(\Delta (\alpha ,\beta ))\subseteq G$
. It follows that
![]() $(h(\alpha ),h(\beta ))\in \theta _G$
and so
$(h(\alpha ),h(\beta ))\in \theta _G$
and so
![]() $A/\theta _G\models ^c \alpha \approx \beta $
. This shows that
$A/\theta _G\models ^c \alpha \approx \beta $
. This shows that
![]() $(A/\theta _G, \mathsf {core}(A)/\theta _G)\models ^c \bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \alpha \approx \beta $
. Since
$(A/\theta _G, \mathsf {core}(A)/\theta _G)\models ^c \bigwedge _{i{\leqslant } n} \varepsilon _i \approx \delta _i \to \alpha \approx \beta $
. Since
![]() $\mathbf {Q}$
is a core-generated quasivariety of expanded algebras, it follows from Proposition 3.26 that
$\mathbf {Q}$
is a core-generated quasivariety of expanded algebras, it follows from Proposition 3.26 that
![]() $(A/\theta _G, \mathsf {core}(A)/\theta _G)\in \mathbf {Q}$
. We conclude that the map
$(A/\theta _G, \mathsf {core}(A)/\theta _G)\in \mathbf {Q}$
. We conclude that the map
![]() $\theta _{(-)}$
sends core filters to core-
$\theta _{(-)}$
sends core filters to core-
![]() $\mathbf {Q}$
-congruences.
$\mathbf {Q}$
-congruences.
Next, we show that for any core-
![]() $\mathbf {Q}$
-congruence
$\mathbf {Q}$
-congruence
![]() $\theta $
over A the filter
$\theta $
over A the filter
![]() $F_\theta $
is a core filter. Suppose
$F_\theta $
is a core filter. Suppose
![]() $\Gamma \Vdash \phi $
and
$\Gamma \Vdash \phi $
and
![]() $ h\in \mathsf {Hom}^c(\mathsf {Fm}, A) $
is such that
$ h\in \mathsf {Hom}^c(\mathsf {Fm}, A) $
is such that
![]() $h[\Gamma ]\subseteq F_\theta $
. Then, we have by definition that
$h[\Gamma ]\subseteq F_\theta $
. Then, we have by definition that
![]() $\tau ^A(c)\subseteq \theta $
for every
$\tau ^A(c)\subseteq \theta $
for every
![]() $c\in h[\Gamma ]$
. By algebraizability, notice that we have
$c\in h[\Gamma ]$
. By algebraizability, notice that we have
![]() $\tau (\Gamma )\models ^c_{\mathbf {Q}}\tau (\phi )$
, thus we obtain
$\tau (\Gamma )\models ^c_{\mathbf {Q}}\tau (\phi )$
, thus we obtain
![]() $h(\tau (\phi ))=\tau ^A(h(\phi ))\subseteq \theta $
and so
$h(\tau (\phi ))=\tau ^A(h(\phi ))\subseteq \theta $
and so
![]() $h(\phi )\in F_\theta $
. This shows that
$h(\phi )\in F_\theta $
. This shows that
![]() $F_\theta $
is a core deductive filter and completes the proof.
$F_\theta $
is a core deductive filter and completes the proof.
Exactly as in the standard setting, it is possible to specialise the previous isomorphism to the specific case of filters and congruences of the (expanded) algebra of formulas
![]() $\mathsf {Fm}$
. We first define syntactic and semantic theories in the setting of weak logics.
$\mathsf {Fm}$
. We first define syntactic and semantic theories in the setting of weak logics.
Definition 6.18. If
![]() $\Vdash $
is a weak logic then we denote by
$\Vdash $
is a weak logic then we denote by
![]() $\mathsf {Th}(\Vdash )$
the set of all (syntactic) theories over
$\mathsf {Th}(\Vdash )$
the set of all (syntactic) theories over
![]() $\Vdash $
, i.e., all sets
$\Vdash $
, i.e., all sets
![]() $\Gamma \subseteq \mathsf {Fm}$
such that if
$\Gamma \subseteq \mathsf {Fm}$
such that if
![]() $\Gamma \Vdash \phi $
then
$\Gamma \Vdash \phi $
then
![]() $\phi \in \Gamma $
. If
$\phi \in \Gamma $
. If
![]() $\mathbf {Q}$
is a core-generated quasivariety of expanded algebras, then
$\mathbf {Q}$
is a core-generated quasivariety of expanded algebras, then
![]() $\mathsf {Th}(\models ^c_{\mathbf {Q}})$
denotes the set of (semantical) core theories over
$\mathsf {Th}(\models ^c_{\mathbf {Q}})$
denotes the set of (semantical) core theories over
![]() $\mathbf {Q}$
, i.e., those sets of equations
$\mathbf {Q}$
, i.e., those sets of equations
![]() $\Theta \subseteq \mathsf {Eq}$
such that
$\Theta \subseteq \mathsf {Eq}$
such that
![]() $\Theta \models ^c_{\mathbf {Q}} \alpha \approx \beta $
entails
$\Theta \models ^c_{\mathbf {Q}} \alpha \approx \beta $
entails
![]() $\alpha \approx \beta \in \Theta $
.
$\alpha \approx \beta \in \Theta $
.
Remark 6.19. It is straightforward to verify that, for
![]() $\Vdash $
a weak logic, the syntactic theories from Definition 6.18 are exactly the core filters of
$\Vdash $
a weak logic, the syntactic theories from Definition 6.18 are exactly the core filters of
![]() $\Vdash $
over
$\Vdash $
over
![]() $(\mathsf {Fm},\mathsf {Var})$
. Similarly, if
$(\mathsf {Fm},\mathsf {Var})$
. Similarly, if
![]() $\mathbf {Q}$
is a quasivariety of expanded algebras, then the semantical core theories over
$\mathbf {Q}$
is a quasivariety of expanded algebras, then the semantical core theories over
![]() $\mathbf {Q}$
are exactly the core congruences of
$\mathbf {Q}$
are exactly the core congruences of
![]() $(\mathsf {Fm},\mathsf {Var})$
. Since
$(\mathsf {Fm},\mathsf {Var})$
. Since
![]() $(\mathsf {Fm},\mathsf {Var})$
is a core-generated algebra, we obtain as in Definition 6.15 an expanded lattice
$(\mathsf {Fm},\mathsf {Var})$
is a core-generated algebra, we obtain as in Definition 6.15 an expanded lattice
![]() $\overline {\mathsf {Th}}(\Vdash ) $
defined by
$\overline {\mathsf {Th}}(\Vdash ) $
defined by
and an expanded lattice
![]() $\overline {\mathsf {Th}}(\models ^c_{\mathbf {Q}}) $
defined by
$\overline {\mathsf {Th}}(\models ^c_{\mathbf {Q}}) $
defined by
This clearly corresponds to the fact that theories over
![]() $\Vdash $
are also theories in
$\Vdash $
are also theories in
![]() $\Vdash _{\mathrm {s}}$
, and theories over
$\Vdash _{\mathrm {s}}$
, and theories over
![]() $\models ^c_{\mathbf {Q}}$
are also theories over
$\models ^c_{\mathbf {Q}}$
are also theories over
![]() $\models _{\mathbf {Q}}$
. Additionally, since the strong endomorphisms of
$\models _{\mathbf {Q}}$
. Additionally, since the strong endomorphisms of
![]() $(\mathsf {Fm},\mathsf {Var})$
are exactly the atomic substitutions, it follows from Lemma 6.14 that inverse atomic substitutions preserve elements in
$(\mathsf {Fm},\mathsf {Var})$
are exactly the atomic substitutions, it follows from Lemma 6.14 that inverse atomic substitutions preserve elements in
![]() $\mathsf {Th}(\Vdash )$
and
$\mathsf {Th}(\Vdash )$
and
![]() $\mathsf {Th}(\models ^c_{\mathbf {Q}})$
.
$\mathsf {Th}(\models ^c_{\mathbf {Q}})$
.
Corollary 6.20. Let
![]() $\Vdash $
be a weak logic and suppose it is loosely algebraized by
$\Vdash $
be a weak logic and suppose it is loosely algebraized by
![]() $(\mathbf {Q},\tau ,\Delta )$
, then there is an isomorphism
$(\mathbf {Q},\tau ,\Delta )$
, then there is an isomorphism
![]() $\Omega :\overline {\mathsf {Th}}(\Vdash ) \cong \overline {\mathsf {Th}}(\models ^c_{\mathbf {Q}})$
.
$\Omega :\overline {\mathsf {Th}}(\Vdash ) \cong \overline {\mathsf {Th}}(\models ^c_{\mathbf {Q}})$
.
Remark 6.21. A key aspect of Blok and Pigozzi’s isomorphism theorem (Fact 6.7) is that one can recover the two transformers
![]() $\tau $
and
$\tau $
and
![]() $\Delta $
from the isomorphism between
$\Delta $
from the isomorphism between
![]() $\mathsf {Fi}^+_{\vdash }(A)$
and
$\mathsf {Fi}^+_{\vdash }(A)$
and
![]() $\mathsf {Con}^+_{\mathbf {Q}}(A)$
, thus showing algebraizability. We indicate however that this fact is not as clear in the setting of loose algebraizability. In fact, in the proof of the isomorphism theorem (cf. Remark 6.8 and [Reference Font16, Section 3.5]) the two transformers are defined as follows:
$\mathsf {Con}^+_{\mathbf {Q}}(A)$
, thus showing algebraizability. We indicate however that this fact is not as clear in the setting of loose algebraizability. In fact, in the proof of the isomorphism theorem (cf. Remark 6.8 and [Reference Font16, Section 3.5]) the two transformers are defined as follows:
 $$ \begin{align*} \tau(x)&=\sigma_x(\Omega(\mathrm{Cn}_{\vdash}(x)))\\ \Delta(x,y)&= \sigma_{x,y}( \Omega^{-1}(\mathrm{Cn}_{\mathbf{Q}}(x\approx y) ) ), \end{align*} $$
$$ \begin{align*} \tau(x)&=\sigma_x(\Omega(\mathrm{Cn}_{\vdash}(x)))\\ \Delta(x,y)&= \sigma_{x,y}( \Omega^{-1}(\mathrm{Cn}_{\mathbf{Q}}(x\approx y) ) ), \end{align*} $$
where
![]() $\mathrm {Cn}_{\vdash }$
and
$\mathrm {Cn}_{\vdash }$
and
![]() $\mathrm {Cn}_{\mathbf {Q}}$
denote, respectively, the closure consequence operators on the logic
$\mathrm {Cn}_{\mathbf {Q}}$
denote, respectively, the closure consequence operators on the logic
![]() $\vdash $
and the quasivariety
$\vdash $
and the quasivariety
![]() $\mathbf {Q}$
, while
$\mathbf {Q}$
, while
![]() $\sigma _x$
is a substitution sending every variable to x, and
$\sigma _x$
is a substitution sending every variable to x, and
![]() $\sigma _{x,y}$
is one sending every variable but y to x and y to itself. If one simply mimics this proof in the setting of weak logics and lets, for example,
$\sigma _{x,y}$
is one sending every variable but y to x and y to itself. If one simply mimics this proof in the setting of weak logics and lets, for example,
where
![]() $\mathrm {Cn}_{\Vdash }$
is the closure consequence operator of the weak logic
$\mathrm {Cn}_{\Vdash }$
is the closure consequence operator of the weak logic
![]() $\Vdash $
, then crucially it could be that structurality fails. In fact, we could have that
$\Vdash $
, then crucially it could be that structurality fails. In fact, we could have that
![]() $x\Vdash \delta (x)$
but also
$x\Vdash \delta (x)$
but also
![]() $\phi \not \Vdash \delta (\phi )$
, witnessing the failure of uniform substitution. Let
$\phi \not \Vdash \delta (\phi )$
, witnessing the failure of uniform substitution. Let
![]() $\sigma $
be the substitution sending every variable to
$\sigma $
be the substitution sending every variable to
![]() $\phi $
, then we have
$\phi $
, then we have
and therefore we obtain
![]() $\Omega (\mathrm {Cn}_{\Vdash }(\sigma ( \mathrm {Cn}_{\Vdash }(x))))\neq \Omega (\mathrm {Cn}_{\Vdash }(\sigma (x))).$
Clearly, we have that
$\Omega (\mathrm {Cn}_{\Vdash }(\sigma ( \mathrm {Cn}_{\Vdash }(x))))\neq \Omega (\mathrm {Cn}_{\Vdash }(\sigma (x))).$
Clearly, we have that
![]() $\Omega (\mathrm {Cn}_{\Vdash }(\sigma (x)))= \Omega (\mathrm {Cn}_{\Vdash }(\phi ))$
, simply by the definition of
$\Omega (\mathrm {Cn}_{\Vdash }(\sigma (x)))= \Omega (\mathrm {Cn}_{\Vdash }(\phi ))$
, simply by the definition of
![]() $\sigma $
. Assume additionally that
$\sigma $
. Assume additionally that
![]() $\Omega $
commutes with closure operators and substitution, i.e., that
$\Omega $
commutes with closure operators and substitution, i.e., that
for all sets of formulas
![]() $\Gamma $
and substitutions
$\Gamma $
and substitutions
![]() $\sigma $
(and where
$\sigma $
(and where
![]() $\mathrm {Cn}^c_{\mathbf {Q}}$
refers the closure operator associated with the core semantics of a quasivariety of core-generated expanded algebras
$\mathrm {Cn}^c_{\mathbf {Q}}$
refers the closure operator associated with the core semantics of a quasivariety of core-generated expanded algebras
![]() $\mathbf {Q}$
). Then we obtain
$\mathbf {Q}$
). Then we obtain
 $$ \begin{align*} \Omega(\mathrm{Cn}_{\Vdash}(\sigma( \mathrm{Cn}_{\Vdash}(x)))) &= \mathrm{Cn}^c_{\mathbf{Q}}( \sigma(\Omega (\mathrm{Cn}_{\Vdash}( \mathrm{Cn}_{\Vdash}(x)) ) ) ) \\ &= \mathrm{Cn}^c_{\mathbf{Q}}( \sigma(\Omega (\mathrm{Cn}_{\Vdash}(x)) ) )\\ & = \mathrm{Cn}^c_{\mathbf{Q}}( \sigma\sigma_x(\Omega (\mathrm{Cn}_{\Vdash}(x)) ) )\\ & = \mathrm{Cn}^c_{\mathbf{Q}}( \tau(\phi)) \end{align*} $$
$$ \begin{align*} \Omega(\mathrm{Cn}_{\Vdash}(\sigma( \mathrm{Cn}_{\Vdash}(x)))) &= \mathrm{Cn}^c_{\mathbf{Q}}( \sigma(\Omega (\mathrm{Cn}_{\Vdash}( \mathrm{Cn}_{\Vdash}(x)) ) ) ) \\ &= \mathrm{Cn}^c_{\mathbf{Q}}( \sigma(\Omega (\mathrm{Cn}_{\Vdash}(x)) ) )\\ & = \mathrm{Cn}^c_{\mathbf{Q}}( \sigma\sigma_x(\Omega (\mathrm{Cn}_{\Vdash}(x)) ) )\\ & = \mathrm{Cn}^c_{\mathbf{Q}}( \tau(\phi)) \end{align*} $$
and therefore
![]() $\mathrm {Cn}^c_{\mathbf {Q}}( \tau (\phi ))\neq \Omega (\mathrm {Cn}_{\Vdash }(\phi ))$
. This indicates that the usual proof of the isomorphism theorem does not work in the setting of loosely algebraizable weak logics. We leave it as a pointer for future works to establish if there is a version of the isomorphism theorem in the setting of loosely algebraizable weak logics.
$\mathrm {Cn}^c_{\mathbf {Q}}( \tau (\phi ))\neq \Omega (\mathrm {Cn}_{\Vdash }(\phi ))$
. This indicates that the usual proof of the isomorphism theorem does not work in the setting of loosely algebraizable weak logics. We leave it as a pointer for future works to establish if there is a version of the isomorphism theorem in the setting of loosely algebraizable weak logics.
6.3 Strictly algebraizable weak logics
In contrast to Remark 6.21, in the case of strictly algebraizable weak logics, we can use the fact that they are finitely representable to derive a full version of the isomorphism theorem. We first recall some preliminary definitions, which we employed informally already in Remark 6.21.
Definition 6.22 (Closure operators).
Let A be an expanded algebra,
![]() $\Vdash $
a weak logic, and
$\Vdash $
a weak logic, and
![]() $\mathbf {Q}$
a core-generated quasivariety of expanded algebras. We denote by
$\mathbf {Q}$
a core-generated quasivariety of expanded algebras. We denote by
![]() $ \mathrm {Cn}_{\Vdash } $
the closure operator on A defined by letting
$ \mathrm {Cn}_{\Vdash } $
the closure operator on A defined by letting
![]() $\mathrm {Cn}_{\Vdash }(X)$
be the smallest core filter of A with respect to
$\mathrm {Cn}_{\Vdash }(X)$
be the smallest core filter of A with respect to
![]() $\Vdash $
that contains
$\Vdash $
that contains
![]() $X\subseteq A$
. Similarly, we denote by
$X\subseteq A$
. Similarly, we denote by
![]() $\mathrm {Cn}^c_{\mathbf {Q}}$
the closure operator on
$\mathrm {Cn}^c_{\mathbf {Q}}$
the closure operator on
![]() $A^2$
defined by letting
$A^2$
defined by letting
![]() $ \mathrm {Cn}^c_{\mathbf {Q}} (R)$
be the smallest congruence in
$ \mathrm {Cn}^c_{\mathbf {Q}} (R)$
be the smallest congruence in
![]() $\mathsf {Con}^c_{\mathbf {Q}}(A)$
containing
$\mathsf {Con}^c_{\mathbf {Q}}(A)$
containing
![]() $R\subseteq A^2$
.
$R\subseteq A^2$
.
Remark 6.23. Recall that, in the expanded term algebra
![]() $(\mathsf {Fm},\mathsf {Var})$
, the core filters coincide exactly with the syntactical theories and the core congruences coincide with the semantical theories. In this case we recover the more intuitive definition of the closure operators
$(\mathsf {Fm},\mathsf {Var})$
, the core filters coincide exactly with the syntactical theories and the core congruences coincide with the semantical theories. In this case we recover the more intuitive definition of the closure operators
![]() $\mathrm {Cn}_{\Vdash } $
and
$\mathrm {Cn}_{\Vdash } $
and
![]() $\mathrm {Cn}^c_{\mathbf {Q}}$
, namely, for
$\mathrm {Cn}^c_{\mathbf {Q}}$
, namely, for
![]() $\Theta \subseteq \mathsf {Eq}$
and
$\Theta \subseteq \mathsf {Eq}$
and
![]() $\Gamma \subseteq \mathsf {Fm}$
,
$\Gamma \subseteq \mathsf {Fm}$
,
 $$ \begin{align*} \mathrm{Cn}_{\Vdash}(\Gamma)&=\{\phi\in \mathsf{Fm} : \Gamma\Vdash \phi \}\\ \mathrm{Cn}^c_{\mathbf{Q}} (\Theta)&=\{\alpha\approx\beta \in \mathsf{Eq} : \Theta\models^c_{\mathbf{Q}} \alpha\approx\beta \}. \end{align*} $$
$$ \begin{align*} \mathrm{Cn}_{\Vdash}(\Gamma)&=\{\phi\in \mathsf{Fm} : \Gamma\Vdash \phi \}\\ \mathrm{Cn}^c_{\mathbf{Q}} (\Theta)&=\{\alpha\approx\beta \in \mathsf{Eq} : \Theta\models^c_{\mathbf{Q}} \alpha\approx\beta \}. \end{align*} $$
In the context of strictly algebraizable weak logics, it is also convenient to work with the following notions of
![]() $\Lambda $
-filters and
$\Lambda $
-filters and
![]() $\Sigma $
-congruences.
$\Sigma $
-congruences.
Definition 6.24. Let
![]() $\Lambda $
be a set of formulas in
$\Lambda $
be a set of formulas in
![]() $\mathsf {Fm}$
, then for any algebra A and standard logic
$\mathsf {Fm}$
, then for any algebra A and standard logic
![]() $\vdash $
, we say that
$\vdash $
, we say that
![]() $F\subseteq A$
is a
$F\subseteq A$
is a
![]() $\Lambda $
-filter over A with respect to
$\Lambda $
-filter over A with respect to
![]() $\vdash $
if
$\vdash $
if
We denote the set of
![]() $\Lambda $
-filters of A with respect to
$\Lambda $
-filters of A with respect to
![]() $\vdash $
by
$\vdash $
by
![]() $\Lambda \mathsf {Fi}_{\vdash }(A)$
. Similarly, we let
$\Lambda \mathsf {Fi}_{\vdash }(A)$
. Similarly, we let
![]() $\Lambda \mathsf {Th}(\vdash ) $
be the set of all syntactical theories
$\Lambda \mathsf {Th}(\vdash ) $
be the set of all syntactical theories
![]() $\Gamma $
over
$\Gamma $
over
![]() $\vdash $
such that
$\vdash $
such that
![]() $\mathsf {At}[\Lambda ] \subseteq \Gamma $
.
$\mathsf {At}[\Lambda ] \subseteq \Gamma $
.
Definition 6.25. Given an expanded algebra A, a quasivariety of expanded algebras
![]() $\mathbf {Q,}$
and a finite set of equations in one variable
$\mathbf {Q,}$
and a finite set of equations in one variable
![]() $\Sigma $
, a congruence
$\Sigma $
, a congruence
![]() $\theta \in \mathsf {Con}_{\mathbf {Q}\restriction \mathcal {L}}(A)$
is said to be a
$\theta \in \mathsf {Con}_{\mathbf {Q}\restriction \mathcal {L}}(A)$
is said to be a
![]() $\Sigma $
-congruence if
$\Sigma $
-congruence if
![]() $\Sigma (a)\subseteq \theta $
for all
$\Sigma (a)\subseteq \theta $
for all
![]() $a\in \mathsf {core}(A)$
. We write
$a\in \mathsf {core}(A)$
. We write
![]() $\Sigma \mathsf {Con}_{\mathbf {Q}\restriction \mathcal {L}}(A)$
for the set of all
$\Sigma \mathsf {Con}_{\mathbf {Q}\restriction \mathcal {L}}(A)$
for the set of all
![]() $\mathbf {Q}\restriction \mathcal {L}$
-congruences of A which are also
$\mathbf {Q}\restriction \mathcal {L}$
-congruences of A which are also
![]() $\Sigma $
-congruences. Similarly, we let
$\Sigma $
-congruences. Similarly, we let
![]() $\Sigma \mathsf {Th}(\models _{\mathbf {Q}})$
denote the set of all semantical theories
$\Sigma \mathsf {Th}(\models _{\mathbf {Q}})$
denote the set of all semantical theories
![]() $\Theta $
such that
$\Theta $
such that
![]() $ \mathsf {At}[\Sigma ]\subseteq \Theta $
.
$ \mathsf {At}[\Sigma ]\subseteq \Theta $
.
Remark 6.26. It is clear from the definition of
![]() $\Lambda $
-filters and the monotonicity of
$\Lambda $
-filters and the monotonicity of
![]() $\vdash $
that the
$\vdash $
that the
![]() $\Lambda $
-filters of
$\Lambda $
-filters of
![]() $\vdash $
on A are a special kind of deductive filters of
$\vdash $
on A are a special kind of deductive filters of
![]() $\vdash $
. Similarly,
$\vdash $
. Similarly,
![]() $\Sigma $
-congruences are clearly a special kind of congruences. The set of
$\Sigma $
-congruences are clearly a special kind of congruences. The set of
![]() $\Lambda $
-filters as well as that of
$\Lambda $
-filters as well as that of
![]() $\Sigma $
-congruences are closed under arbitrary intersections and hence form complete lattices under the subset relation, but, crucially, they are not necessarily closed under arbitrary inverse endomorphisms.
$\Sigma $
-congruences are closed under arbitrary intersections and hence form complete lattices under the subset relation, but, crucially, they are not necessarily closed under arbitrary inverse endomorphisms.
Lemma 6.27. Let
![]() $\Vdash $
be a weak logic. If
$\Vdash $
be a weak logic. If
![]() $\Vdash $
is represented by a set of formulas
$\Vdash $
is represented by a set of formulas
![]() $\Lambda $
then
$\Lambda $
then
![]() $\mathsf {Fi}_{\Vdash }(A)=\Lambda \mathsf {Fi}_{\Vdash _{\mathrm {s}}}(A)$
for any core-generated expanded algebra A. Moreover, if
$\mathsf {Fi}_{\Vdash }(A)=\Lambda \mathsf {Fi}_{\Vdash _{\mathrm {s}}}(A)$
for any core-generated expanded algebra A. Moreover, if
![]() $\mathsf {Th}(\Vdash )=\Lambda \mathsf {Th}(\Vdash _{\mathrm {s}})$
, then
$\mathsf {Th}(\Vdash )=\Lambda \mathsf {Th}(\Vdash _{\mathrm {s}})$
, then
![]() $\Vdash $
is represented by
$\Vdash $
is represented by
![]() $\Lambda $
.
$\Lambda $
.
Proof. We prove the first claim. Suppose
![]() $\Vdash $
is represented by
$\Vdash $
is represented by
![]() $\Lambda $
. Let
$\Lambda $
. Let
![]() $F\in \mathsf {Fi}_{\Vdash }(A)$
,
$F\in \mathsf {Fi}_{\Vdash }(A)$
,
![]() $\Gamma \cup \mathsf {At}[\Lambda ]\Vdash _{\mathrm {s}}\phi ,$
and
$\Gamma \cup \mathsf {At}[\Lambda ]\Vdash _{\mathrm {s}}\phi ,$
and
![]() $h\in \mathsf {Hom}(\mathsf {Fm}, A) $
be such that
$h\in \mathsf {Hom}(\mathsf {Fm}, A) $
be such that
![]() $h[\Gamma ]\subseteq F$
. By the representability of
$h[\Gamma ]\subseteq F$
. By the representability of
![]() $\Vdash $
we have that
$\Vdash $
we have that
![]() $\Gamma \Vdash \phi $
. Since A is core-generated, by Lemma 3.20 there are a core-assignment
$\Gamma \Vdash \phi $
. Since A is core-generated, by Lemma 3.20 there are a core-assignment
![]() $g\in \mathsf {Hom}^c(\mathsf {Fm}, A) $
and a substitution
$g\in \mathsf {Hom}^c(\mathsf {Fm}, A) $
and a substitution
![]() $\sigma \in \mathsf {Subst}(\mathcal {L})$
such that
$\sigma \in \mathsf {Subst}(\mathcal {L})$
such that
![]() $h[\Gamma \cup \{\phi \}]=g[\sigma (\Gamma \cup \{\phi \})]$
. It follows that
$h[\Gamma \cup \{\phi \}]=g[\sigma (\Gamma \cup \{\phi \})]$
. It follows that
![]() $g[\sigma (\Gamma )]\subseteq F$
and so, since
$g[\sigma (\Gamma )]\subseteq F$
and so, since
![]() $\Gamma \Vdash \phi $
, we obtain from the definition of core filters that
$\Gamma \Vdash \phi $
, we obtain from the definition of core filters that
![]() $h(\phi )=g(\sigma (\phi ))\in F$
. This shows that
$h(\phi )=g(\sigma (\phi ))\in F$
. This shows that
![]() $\mathsf {Fi}_{\Vdash }(A)\subseteq \Lambda \mathsf {Fi}_{\Vdash _{\mathrm {s}}}(A)$
.
$\mathsf {Fi}_{\Vdash }(A)\subseteq \Lambda \mathsf {Fi}_{\Vdash _{\mathrm {s}}}(A)$
.
Conversely, let
![]() $F\in \Lambda \mathsf {Fi}_{\Vdash _{\mathrm {s}}}(A)$
. Suppose
$F\in \Lambda \mathsf {Fi}_{\Vdash _{\mathrm {s}}}(A)$
. Suppose
![]() $\Gamma \Vdash \phi $
and let
$\Gamma \Vdash \phi $
and let
![]() $h\in \mathsf {Hom}^c(\mathsf {Fm}, A) $
be such that
$h\in \mathsf {Hom}^c(\mathsf {Fm}, A) $
be such that
![]() $h[\Gamma ]\subseteq F$
. By representability we obtain that
$h[\Gamma ]\subseteq F$
. By representability we obtain that
![]() $\Gamma \cup \mathsf {At}[\Lambda ]\Vdash _{\mathrm {s}} \phi $
, thus it follows from
$\Gamma \cup \mathsf {At}[\Lambda ]\Vdash _{\mathrm {s}} \phi $
, thus it follows from
![]() $F\in \Lambda \mathsf {Fi}_{\Vdash _{\mathrm {s}}}(A)$
that
$F\in \Lambda \mathsf {Fi}_{\Vdash _{\mathrm {s}}}(A)$
that
![]() $h(\phi )\in F$
. This shows that
$h(\phi )\in F$
. This shows that
![]() $\Lambda \mathsf {Fi}_{\Vdash _{\mathrm {s}}}(A)\subseteq \mathsf {Fi}_{\Vdash }(A)$
and thus proves that
$\Lambda \mathsf {Fi}_{\Vdash _{\mathrm {s}}}(A)\subseteq \mathsf {Fi}_{\Vdash }(A)$
and thus proves that
![]() $\mathsf {Fi}_{\Vdash }(A)=\Lambda \mathsf {Fi}_{\Vdash _{\mathrm {s}}}(A)$
.
$\mathsf {Fi}_{\Vdash }(A)=\Lambda \mathsf {Fi}_{\Vdash _{\mathrm {s}}}(A)$
.
We now prove the second claim. Suppose we have that
![]() $\mathsf {Th}(\Vdash )=\Lambda \mathsf {Th}(\Vdash _{\mathrm {s}})$
. Then, for any
$\mathsf {Th}(\Vdash )=\Lambda \mathsf {Th}(\Vdash _{\mathrm {s}})$
. Then, for any
![]() $\psi \in \mathsf {Fm}$
we have that
$\psi \in \mathsf {Fm}$
we have that
 $$ \begin{align*} \mathrm{Cn}_{\Vdash}(\psi) &= \mathrm{Cn}_{\Vdash_{\mathrm{s}}}(\mathrm{Cn}_{\Vdash}(\psi) \cup \mathsf{At}[\Lambda]); \\ \mathrm{Cn}_{\Vdash_{\mathrm{s}}}(\psi\cup \mathsf{At}[\Lambda]) &= \mathrm{Cn}_{\Vdash}(\mathrm{Cn}_{\Vdash_{\mathrm{s}}}(\psi \cup \mathsf{At}[\Lambda])). \end{align*} $$
$$ \begin{align*} \mathrm{Cn}_{\Vdash}(\psi) &= \mathrm{Cn}_{\Vdash_{\mathrm{s}}}(\mathrm{Cn}_{\Vdash}(\psi) \cup \mathsf{At}[\Lambda]); \\ \mathrm{Cn}_{\Vdash_{\mathrm{s}}}(\psi\cup \mathsf{At}[\Lambda]) &= \mathrm{Cn}_{\Vdash}(\mathrm{Cn}_{\Vdash_{\mathrm{s}}}(\psi \cup \mathsf{At}[\Lambda])). \end{align*} $$
Therefore, it follows from the first equality (and monotonicity of the consequence operators) that
![]() $\mathrm {Cn}_{\Vdash _{\mathrm {s}}}(\psi \cup \mathsf {At}[\Lambda ])\subseteq \mathrm {Cn}_{\Vdash }(\psi )$
, and it follows from the second equality that
$\mathrm {Cn}_{\Vdash _{\mathrm {s}}}(\psi \cup \mathsf {At}[\Lambda ])\subseteq \mathrm {Cn}_{\Vdash }(\psi )$
, and it follows from the second equality that
![]() $\mathrm {Cn}_{\Vdash }(\psi ) \subseteq \mathrm {Cn}_{\Vdash _{\mathrm {s}}}(\psi \cup \mathsf {At}[\Lambda ])$
. This yields that
$\mathrm {Cn}_{\Vdash }(\psi ) \subseteq \mathrm {Cn}_{\Vdash _{\mathrm {s}}}(\psi \cup \mathsf {At}[\Lambda ])$
. This yields that
![]() $\mathrm {Cn}_{\Vdash }(\psi ) = \mathrm {Cn}_{\Vdash _{\mathrm {s}}}(\psi \cup \mathsf {At}[\Lambda ])$
. Finally, we derive the following equivalences:
$\mathrm {Cn}_{\Vdash }(\psi ) = \mathrm {Cn}_{\Vdash _{\mathrm {s}}}(\psi \cup \mathsf {At}[\Lambda ])$
. Finally, we derive the following equivalences:
 $$ \begin{align*} \Gamma \Vdash\phi & \Longleftrightarrow \mathrm{Cn}_{\Vdash}(\phi)\subseteq \mathrm{Cn}_{\Vdash}(\Gamma) \\ & \Longleftrightarrow \mathrm{Cn}_{\Vdash_{\mathrm{s}}}(\phi\cup\mathsf{At}[\Lambda])\subseteq \mathrm{Cn}_{\Vdash_{\mathrm{s}}}(\Gamma\cup\mathsf{At}[\Lambda]) \\ & \Longleftrightarrow \Gamma \cup \mathsf{At}[\Lambda] \Vdash_{\mathrm{s}} \phi, \end{align*} $$
$$ \begin{align*} \Gamma \Vdash\phi & \Longleftrightarrow \mathrm{Cn}_{\Vdash}(\phi)\subseteq \mathrm{Cn}_{\Vdash}(\Gamma) \\ & \Longleftrightarrow \mathrm{Cn}_{\Vdash_{\mathrm{s}}}(\phi\cup\mathsf{At}[\Lambda])\subseteq \mathrm{Cn}_{\Vdash_{\mathrm{s}}}(\Gamma\cup\mathsf{At}[\Lambda]) \\ & \Longleftrightarrow \Gamma \cup \mathsf{At}[\Lambda] \Vdash_{\mathrm{s}} \phi, \end{align*} $$
which prove the representability of
![]() $\Vdash $
via
$\Vdash $
via
![]() $\Lambda $
.
$\Lambda $
.
Lemma 6.28. Let
![]() $\mathbf {Q}$
be a core-generated quasivariety with core defined by a set of equations
$\mathbf {Q}$
be a core-generated quasivariety with core defined by a set of equations
![]() $\Sigma $
, then
$\Sigma $
, then
![]() $\mathsf {core}(A)=\Sigma (A)$
entails
$\mathsf {core}(A)=\Sigma (A)$
entails
![]() $\mathsf {Con}^c_{\mathbf {Q}}(A)=\Sigma \mathsf {Con}_{\mathbf {Q}\restriction \mathcal {L}}(A)$
for any core-generated expanded algebra A.
$\mathsf {Con}^c_{\mathbf {Q}}(A)=\Sigma \mathsf {Con}_{\mathbf {Q}\restriction \mathcal {L}}(A)$
for any core-generated expanded algebra A.
Proof. Suppose that
![]() $\mathsf {core}(A)=\Sigma (A)$
for all
$\mathsf {core}(A)=\Sigma (A)$
for all
![]() $A\in \mathbf {Q}$
. First, let
$A\in \mathbf {Q}$
. First, let
![]() $\theta \in \mathsf {Con}^c_{\mathbf {Q}}(A) $
, then it follows that
$\theta \in \mathsf {Con}^c_{\mathbf {Q}}(A) $
, then it follows that
![]() $A/\theta \in \mathbf {Q}$
and so that
$A/\theta \in \mathbf {Q}$
and so that
![]() $\mathsf {core}(A/\theta )= \Sigma [A/\theta ]$
. This yields
$\mathsf {core}(A/\theta )= \Sigma [A/\theta ]$
. This yields
![]() $\Sigma (a)\subseteq \theta $
for all
$\Sigma (a)\subseteq \theta $
for all
![]() $a\in \mathsf {core}(A)$
, showing that
$a\in \mathsf {core}(A)$
, showing that
![]() $\theta \in \Sigma \mathsf {Con}_{\mathbf {Q}\restriction \mathcal {L}}(A) $
. Conversely, suppose
$\theta \in \Sigma \mathsf {Con}_{\mathbf {Q}\restriction \mathcal {L}}(A) $
. Conversely, suppose
![]() $\theta \in \Sigma \mathsf {Con}_{\mathbf {Q}\restriction \mathcal {L}}(A)$
, then in particular
$\theta \in \Sigma \mathsf {Con}_{\mathbf {Q}\restriction \mathcal {L}}(A)$
, then in particular
![]() $A/\theta \in \mathbf {Q}\restriction \mathcal {L}$
. Since
$A/\theta \in \mathbf {Q}\restriction \mathcal {L}$
. Since
![]() $\mathbf {Q}$
has core defined by the set of equations
$\mathbf {Q}$
has core defined by the set of equations
![]() $\Sigma $
, the unique expansion of
$\Sigma $
, the unique expansion of
![]() $A/\theta $
which belongs to
$A/\theta $
which belongs to
![]() $\mathbf {Q}$
is
$\mathbf {Q}$
is
![]() $(A/\theta , \Sigma (A/\theta ))\in \mathbf {Q}$
. It follows that
$(A/\theta , \Sigma (A/\theta ))\in \mathbf {Q}$
. It follows that
![]() $\mathsf {core}(A/\theta )=\Sigma (A/\theta )$
and so that
$\mathsf {core}(A/\theta )=\Sigma (A/\theta )$
and so that
![]() $\theta \in \mathsf {Con}^c_{\mathbf {Q}}(A)$
.
$\theta \in \mathsf {Con}^c_{\mathbf {Q}}(A)$
.
We use the previous lemmas to obtain the following isomorphism theorem for strictly algebraizable weak logics. This result displays how the setting of strict algebraizability better reproduces the original approach from Blok and Pigozzi in the context of logics without uniform substitutions.
Theorem 6.29. Let
![]() $\Vdash $
be a weak logic and
$\Vdash $
be a weak logic and
![]() $\mathbf {Q}$
a core-generated quasivariety of expanded algebras with core defined by a finite set of equations
$\mathbf {Q}$
a core-generated quasivariety of expanded algebras with core defined by a finite set of equations
![]() $\Sigma $
. The following statements are equivalent:
$\Sigma $
. The following statements are equivalent:
-
(1)
 $\Vdash $
is strictly algebraized by
$\Vdash $
is strictly algebraized by
 $(\mathbf {Q},\Sigma , \tau ,\Delta )$
.
$(\mathbf {Q},\Sigma , \tau ,\Delta )$
. -
(2) There is a finite set of formulas
 $\Lambda $
such that, for every core-generated expanded algebra A, it holds that
$\Lambda $
such that, for every core-generated expanded algebra A, it holds that
 $\mathsf {Fi}_{\Vdash }(A)=\Lambda \mathsf {Fi}_{\Vdash _{\mathrm {s}}}(A)$
and
$\mathsf {Fi}_{\Vdash }(A)=\Lambda \mathsf {Fi}_{\Vdash _{\mathrm {s}}}(A)$
and
 $\mathsf {Con}^c_{\mathbf {Q}}(A)=\Sigma \mathsf {Con}_{\mathbf {Q}\restriction \mathcal {L}}(A)$
. Moreover, there is an isomorphism
$\mathsf {Con}^c_{\mathbf {Q}}(A)=\Sigma \mathsf {Con}_{\mathbf {Q}\restriction \mathcal {L}}(A)$
. Moreover, there is an isomorphism
 $\Omega :\overline {\mathsf {Fi}}_{\Vdash }(A) \cong \overline {\mathsf {Con}}_{\mathbf {Q}}(A)$
.
$\Omega :\overline {\mathsf {Fi}}_{\Vdash }(A) \cong \overline {\mathsf {Con}}_{\mathbf {Q}}(A)$
. -
(3) There is a finite set of formulas
 $\Lambda $
such that
$\Lambda $
such that
 $\mathsf {Th}(\Vdash )=\Lambda \mathsf {Th}(\Vdash _{\mathrm {s}})$
and
$\mathsf {Th}(\Vdash )=\Lambda \mathsf {Th}(\Vdash _{\mathrm {s}})$
and
 $\mathsf {Th}(\models ^c_{\mathbf {Q}})=\Sigma \mathsf {Th}(\models _{\mathbf {Q}})$
. Moreover, there is an isomorphism
$\mathsf {Th}(\models ^c_{\mathbf {Q}})=\Sigma \mathsf {Th}(\models _{\mathbf {Q}})$
. Moreover, there is an isomorphism
 $\Omega :\overline {\mathsf {Th}}(\Vdash ) \cong \overline {\mathsf {Th}}(\models ^c_{\mathbf {Q}})$
.
$\Omega :\overline {\mathsf {Th}}(\Vdash ) \cong \overline {\mathsf {Th}}(\models ^c_{\mathbf {Q}})$
.
Proof. Direction from (1) to (2) follows immediately from Theorem 6.17 and Lemmas 6.27 and 6.28. Direction from (2) to (3) follows from Remark 6.19. It remains to show that (3) entails (1).
Firstly, notice that the isomorphism
![]() $\Omega :\overline {\mathsf {Th}}(\Vdash ) \cong \overline {\mathsf {Th}}(\models ^c_{\mathbf {Q}})$
induces an isomorphism
$\Omega :\overline {\mathsf {Th}}(\Vdash ) \cong \overline {\mathsf {Th}}(\models ^c_{\mathbf {Q}})$
induces an isomorphism
![]() $\mathsf {Th}^+(\Vdash _{\mathrm {s}}) \cong \mathsf {Th}^+(\models _{\mathbf {Q}})$
, thus by the standard isomorphism theorem it immediately follows that
$\mathsf {Th}^+(\Vdash _{\mathrm {s}}) \cong \mathsf {Th}^+(\models _{\mathbf {Q}})$
, thus by the standard isomorphism theorem it immediately follows that
![]() $\Vdash _{\mathrm {s}}$
is algebraized by
$\Vdash _{\mathrm {s}}$
is algebraized by
![]() $(\mathbf {Q},\tau ,\Delta )$
, where
$(\mathbf {Q},\tau ,\Delta )$
, where
 $$ \begin{align*} \tau(x)&=\sigma_x(\Omega(\mathrm{Cn}_{\Vdash_{\mathrm{s}}}(x)))\\ \Delta(x,y)&= \sigma_{x,y}( \Omega^{-1}(\mathrm{Cn}_{\mathbf{Q}\restriction\mathcal{L}}(x\approx y) ) ), \end{align*} $$
$$ \begin{align*} \tau(x)&=\sigma_x(\Omega(\mathrm{Cn}_{\Vdash_{\mathrm{s}}}(x)))\\ \Delta(x,y)&= \sigma_{x,y}( \Omega^{-1}(\mathrm{Cn}_{\mathbf{Q}\restriction\mathcal{L}}(x\approx y) ) ), \end{align*} $$
as in Remark 6.8. In particular,
![]() $\sigma _x$
is the substitution sending every variable to x, and
$\sigma _x$
is the substitution sending every variable to x, and
![]() $\sigma _{x,y}$
is the substitution sending every variable but y to x and y to itself. Now, since
$\sigma _{x,y}$
is the substitution sending every variable but y to x and y to itself. Now, since
![]() $\Omega $
is an isomorphism, the least syntactic theory in
$\Omega $
is an isomorphism, the least syntactic theory in
![]() $\Vdash $
must be mapped to the least theory in core semantics, i.e.,
$\Vdash $
must be mapped to the least theory in core semantics, i.e.,
![]() $\Omega (\mathrm {Cn}_{\Vdash }(\emptyset ))=\mathrm {Cn}^c_{\mathbf {Q}}(\emptyset )$
. By assumption, we have that
$\Omega (\mathrm {Cn}_{\Vdash }(\emptyset ))=\mathrm {Cn}^c_{\mathbf {Q}}(\emptyset )$
. By assumption, we have that
![]() $\mathrm {Cn}_{\Vdash }(\emptyset )=\mathrm {Cn}_{\Vdash _{\mathrm {s}}}(\mathsf {At}[\Lambda ])$
and
$\mathrm {Cn}_{\Vdash }(\emptyset )=\mathrm {Cn}_{\Vdash _{\mathrm {s}}}(\mathsf {At}[\Lambda ])$
and
![]() $\mathrm {Cn}^c_{\mathbf {Q}}(\emptyset )=\mathrm {Cn}_{\mathbf {Q}\restriction \mathcal {L}}(\mathsf {At}[\Sigma ])$
, thus we obtain that
$\mathrm {Cn}^c_{\mathbf {Q}}(\emptyset )=\mathrm {Cn}_{\mathbf {Q}\restriction \mathcal {L}}(\mathsf {At}[\Sigma ])$
, thus we obtain that
![]() $\Omega (\mathrm {Cn}_{\Vdash _{\mathrm {s}}}(\mathsf {At}[\Lambda ]))=\mathrm {Cn}_{\mathbf {Q}\restriction \mathcal {L}}(\mathsf {At}[\Sigma ])$
. Let
$\Omega (\mathrm {Cn}_{\Vdash _{\mathrm {s}}}(\mathsf {At}[\Lambda ]))=\mathrm {Cn}_{\mathbf {Q}\restriction \mathcal {L}}(\mathsf {At}[\Sigma ])$
. Let
![]() $\sigma _\delta $
the substitution sending x to
$\sigma _\delta $
the substitution sending x to
![]() $\delta $
and
$\delta $
and
![]() $\sigma _{\alpha ,\beta }$
the substitution sending x to
$\sigma _{\alpha ,\beta }$
the substitution sending x to
![]() $\alpha $
and y to
$\alpha $
and y to
![]() $\beta $
. Then we obtain that
$\beta $
. Then we obtain that
 $$ \begin{align*} \sigma_x\left(\Omega\left(\mathrm{Cn}_{\Vdash_{\mathrm{s}}}\left(\bigcup_{\delta\in\mathsf{At}[\Lambda]}\sigma_{\delta}(x)\right)\right)\right) &= \sigma_x\left(\mathrm{Cn}_{\mathbf{Q}\restriction\mathcal{L}}\left(\bigcup_{\alpha\approx\beta\in\mathsf{At}[\Sigma]}\sigma_{\alpha,\beta}(x\approx y)\right)\right)\\ &\subseteq \mathrm{Cn}_{\mathbf{Q}\restriction\mathcal{L}}\left(\sigma_x \left(\bigcup_{\alpha\approx\beta\in\mathsf{At}[\Sigma]}\sigma_{\alpha,\beta}(x\approx y)\right)\right) \end{align*} $$
$$ \begin{align*} \sigma_x\left(\Omega\left(\mathrm{Cn}_{\Vdash_{\mathrm{s}}}\left(\bigcup_{\delta\in\mathsf{At}[\Lambda]}\sigma_{\delta}(x)\right)\right)\right) &= \sigma_x\left(\mathrm{Cn}_{\mathbf{Q}\restriction\mathcal{L}}\left(\bigcup_{\alpha\approx\beta\in\mathsf{At}[\Sigma]}\sigma_{\alpha,\beta}(x\approx y)\right)\right)\\ &\subseteq \mathrm{Cn}_{\mathbf{Q}\restriction\mathcal{L}}\left(\sigma_x \left(\bigcup_{\alpha\approx\beta\in\mathsf{At}[\Sigma]}\sigma_{\alpha,\beta}(x\approx y)\right)\right) \end{align*} $$
as
![]() $\sigma _x$
is an atomic substitution. It follows that
$\sigma _x$
is an atomic substitution. It follows that
![]() $\Sigma \models _{\mathbf {Q}\restriction \mathcal {L}} \tau (\Lambda )$
. Similarly, we have
$\Sigma \models _{\mathbf {Q}\restriction \mathcal {L}} \tau (\Lambda )$
. Similarly, we have
 $$ \begin{align*} \sigma_{x,y}\left( \Omega^{-1}\left(\mathrm{Cn}_{\mathbf{Q}\restriction\mathcal{L}}\left(\bigcup_{\alpha\approx\beta\in\mathsf{At}[\Sigma]}\sigma_{\alpha,\beta}(x\approx y)\right) \right) \right) &= \sigma_{x,y}\left(\mathrm{Cn}_{\Vdash_{\mathrm{s}}}\left(\bigcup_{\delta\in\mathsf{At}[\Lambda]}\sigma_{\delta}(x)\right)\right) \\ &\subseteq \mathrm{Cn}_{\Vdash_{\mathrm{s}}} \left(\sigma_{x,y}\left(\bigcup_{\delta\in\mathsf{At}[\Lambda]}\sigma_{\delta}(x)\right)\right), \end{align*} $$
$$ \begin{align*} \sigma_{x,y}\left( \Omega^{-1}\left(\mathrm{Cn}_{\mathbf{Q}\restriction\mathcal{L}}\left(\bigcup_{\alpha\approx\beta\in\mathsf{At}[\Sigma]}\sigma_{\alpha,\beta}(x\approx y)\right) \right) \right) &= \sigma_{x,y}\left(\mathrm{Cn}_{\Vdash_{\mathrm{s}}}\left(\bigcup_{\delta\in\mathsf{At}[\Lambda]}\sigma_{\delta}(x)\right)\right) \\ &\subseteq \mathrm{Cn}_{\Vdash_{\mathrm{s}}} \left(\sigma_{x,y}\left(\bigcup_{\delta\in\mathsf{At}[\Lambda]}\sigma_{\delta}(x)\right)\right), \end{align*} $$
which shows that
![]() $\Lambda \Vdash _{\mathrm {s}} \Delta (\Sigma )$
. By the algebraizability of
$\Lambda \Vdash _{\mathrm {s}} \Delta (\Sigma )$
. By the algebraizability of
![]() $\Vdash _{\mathrm {s}}$
and
$\Vdash _{\mathrm {s}}$
and
![]() $\Sigma \models _{\mathbf {Q}\restriction \mathcal {L}} \tau (\Lambda )$
this entails that
$\Sigma \models _{\mathbf {Q}\restriction \mathcal {L}} \tau (\Lambda )$
this entails that
![]() $\tau (\Lambda )\equiv _{\mathbf {Q}\restriction \mathcal {L}}\Sigma $
and
$\tau (\Lambda )\equiv _{\mathbf {Q}\restriction \mathcal {L}}\Sigma $
and
![]() $\Delta (\Sigma )\Vdash _{\mathrm {s}}\Lambda $
,
$\Delta (\Sigma )\Vdash _{\mathrm {s}}\Lambda $
,
![]() $\Lambda \Vdash _{\mathrm {s}}\Delta (\Sigma )$
. Also, from the assumption that
$\Lambda \Vdash _{\mathrm {s}}\Delta (\Sigma )$
. Also, from the assumption that
![]() $\mathsf {Th}(\Vdash )=\Lambda \mathsf {Th}(\Vdash _{\mathrm {s}})$
and Lemma 6.27 we also obtain that
$\mathsf {Th}(\Vdash )=\Lambda \mathsf {Th}(\Vdash _{\mathrm {s}})$
and Lemma 6.27 we also obtain that
![]() $\Lambda $
witnesses the finite representability of
$\Lambda $
witnesses the finite representability of
![]() $\Vdash $
. We finally conclude from Corollary 5.6 that
$\Vdash $
. We finally conclude from Corollary 5.6 that
![]() $\Vdash $
is strictly algebraized by
$\Vdash $
is strictly algebraized by
![]() $(\mathbf {Q},\Sigma , \tau ,\Delta )$
.
$(\mathbf {Q},\Sigma , \tau ,\Delta )$
.
7 Aside: Matrix semantics
In the previous sections we have focused on loosely and strictly algebraizable weak logics, thus extending the notion of algebraizability to the setting of logics without uniform substitution. However, in the setting of abstract algebraic logic, algebraizability makes only for one of several properties, and it could be seen as the concept carving out the most well-behaved family of logical systems. On the converse direction, in this section we work towards an increased level of generality and we study the matrix semantics of arbitrary weak logics. In fact, while not every logic is algebraizable, it can be shown that every logic admits a matrix semantics (see, e.g., [Reference Font16, Theorem 4.16]). Furthermore, Dellunde and Jansana [Reference Dellunde and Jansana14] provided a characterisation of the class of matrices of a (possibly infinitary) logic in terms of some model-theoretic results for first-order logic without equality. We show in this section that similar results can be proved in the context of weak logics. We prove in Section 7.1 that every weak logic is complete with respect to a suitable class of so-called bimatrices, and we show in Section 7.2 that Dellunde and Jansana’s results are still applicable in our setting.
7.1 Completeness of matrix semantics
We briefly recall the matrix semantics for standard logics. Intuitively, the idea is to work with first-order structures with a predicate
![]() $\mathsf {truth}(A)$
which encodes the “truth set” of the algebra A.
$\mathsf {truth}(A)$
which encodes the “truth set” of the algebra A.
Definition 7.1. A (logical) matrix of type
![]() $\mathcal {L}$
is a pair
$\mathcal {L}$
is a pair
![]() $(A ,\mathsf {truth}(A)),$
where A is an
$(A ,\mathsf {truth}(A)),$
where A is an
![]() $\mathcal {L}$
-algebra and
$\mathcal {L}$
-algebra and
![]() $\mathsf {truth}(A) \subseteq \mathsf {dom}(A)$
.
$\mathsf {truth}(A) \subseteq \mathsf {dom}(A)$
.
Matrices induce a consequence relation over propositional formulas analogously as classes of algebras do. However, notice that here we work directly with propositional formulas (i.e., terms in the language
![]() $\mathcal {L}$
) and not with equations. This corresponds to the fact that these logics do not necessarily correspond to quasiequational theories over classes of algebras.
$\mathcal {L}$
) and not with equations. This corresponds to the fact that these logics do not necessarily correspond to quasiequational theories over classes of algebras.
Notation 7.2. For notational convenience, in this section we denote logics and weak logics by
![]() $L, L_0,L_1,\dots $
. We then write
$L, L_0,L_1,\dots $
. We then write
![]() $\Gamma \vdash _{L}\phi $
if
$\Gamma \vdash _{L}\phi $
if
![]() $(\Gamma ,\phi )\in L$
. If L is a weak logic, then we write
$(\Gamma ,\phi )\in L$
. If L is a weak logic, then we write
![]() $\Gamma \Vdash _{L}\phi $
if
$\Gamma \Vdash _{L}\phi $
if
![]() $(\Gamma ,\phi )\in L$
.
$(\Gamma ,\phi )\in L$
.
Definition 7.3. Let
![]() $\mathbf {K}$
be a class of
$\mathbf {K}$
be a class of
![]() $\mathcal {L}$
-matrices and let
$\mathcal {L}$
-matrices and let
![]() $\Gamma \cup \{ \phi \}$
be a set of propositional formulas, then we let
$\Gamma \cup \{ \phi \}$
be a set of propositional formulas, then we let
 $$ \begin{align*} \Gamma \models_{\mathbf{K} } \phi \Longleftrightarrow & \text{ for all } A \in \mathbf{K}, \; h\in \mathsf{Hom}(\mathsf{Fm},A), \\ & \text{ if } h[\Gamma]\subseteq \mathsf{truth}(A) \text{, then } h(\phi)\in \mathsf{truth}(A). \end{align*} $$
$$ \begin{align*} \Gamma \models_{\mathbf{K} } \phi \Longleftrightarrow & \text{ for all } A \in \mathbf{K}, \; h\in \mathsf{Hom}(\mathsf{Fm},A), \\ & \text{ if } h[\Gamma]\subseteq \mathsf{truth}(A) \text{, then } h(\phi)\in \mathsf{truth}(A). \end{align*} $$
Given a logic L, we say that
![]() $(A,\mathsf {truth}(A))$
is a model of L and write
$(A,\mathsf {truth}(A))$
is a model of L and write
![]() $(A,\mathsf {truth}(A)) \models L$
if, for every
$(A,\mathsf {truth}(A)) \models L$
if, for every
![]() $\Gamma \cup \{\phi \} \subseteq \mathcal {L}$
,
$\Gamma \cup \{\phi \} \subseteq \mathcal {L}$
,
![]() $\Gamma \vdash _L \phi $
entails
$\Gamma \vdash _L \phi $
entails
![]() $\Gamma \models _{\{A\}} \phi $
. We often abbreviate this latter expression by
$\Gamma \models _{\{A\}} \phi $
. We often abbreviate this latter expression by
![]() $\models _{\{A\}}\Gamma $
.
$\models _{\{A\}}\Gamma $
.
We refer the reader to [Reference Font16, Section 4] for a detailed study of matrix semantics in the context of standard propositional logics. In particular, [Reference Font16, Theorem 4.16] states that every logic is complete with respect to a class of matrices. We show that one can obtain the same result in the setting of weak logics. First, we extend the matrix semantics to the setting of weak logics by introducing a further predicate, i.e., by viewing them as structures in an algebraic language
![]() $\mathcal {L}$
augmented by two unary predicates, one for the core set of A and one for the truth set of A.
$\mathcal {L}$
augmented by two unary predicates, one for the core set of A and one for the truth set of A.
Definition 7.4. The tuple
![]() $(A,\mathsf {truth}(A),\mathsf {core}(A))$
is a (logical) bimatrix of type
$(A,\mathsf {truth}(A),\mathsf {core}(A))$
is a (logical) bimatrix of type
![]() $\mathcal {L}$
if A is an
$\mathcal {L}$
if A is an
![]() $\mathcal {L}$
-algebra,
$\mathcal {L}$
-algebra,
![]() $\mathsf {truth}(A)\subseteq \mathsf {dom}(A)$
and
$\mathsf {truth}(A)\subseteq \mathsf {dom}(A)$
and
![]() $\mathsf {core}(A) \subseteq \mathsf {dom}(A)$
.
$\mathsf {core}(A) \subseteq \mathsf {dom}(A)$
.
Notation 7.5. As in the case of expanded algebras, we write
![]() $\mathsf {Hom}^c(\mathsf {Fm},A)$
for the set of all assignments
$\mathsf {Hom}^c(\mathsf {Fm},A)$
for the set of all assignments
![]() $h: \mathsf {Fm} \to A$
such that
$h: \mathsf {Fm} \to A$
such that
![]() $h[\mathsf {Var}] \subseteq \mathsf {core}(A)$
.
$h[\mathsf {Var}] \subseteq \mathsf {core}(A)$
.
Bimatrices induce a consequence relation analogous to that of expanded algebras by restricting attention to assignments over core elements.
Definition 7.6. Let
![]() $\mathbf {K}$
be a class of
$\mathbf {K}$
be a class of
![]() $\mathcal {L}$
-bimatrices and let
$\mathcal {L}$
-bimatrices and let
![]() $\Gamma \cup \{ \phi \}$
be a set of propositional formulas, then we let
$\Gamma \cup \{ \phi \}$
be a set of propositional formulas, then we let
 $$ \begin{align*} \Gamma \models^c_{\mathbf{K} } \phi \Longleftrightarrow & \text{ for all } A \in \mathbf{K}, \; h\in \mathsf{Hom}^c(\mathsf{Fm},A), \\ & \text{ if } h[\Gamma]\subseteq \mathsf{truth}(A) \text{, then } h(\phi)\in \mathsf{truth}(A). \end{align*} $$
$$ \begin{align*} \Gamma \models^c_{\mathbf{K} } \phi \Longleftrightarrow & \text{ for all } A \in \mathbf{K}, \; h\in \mathsf{Hom}^c(\mathsf{Fm},A), \\ & \text{ if } h[\Gamma]\subseteq \mathsf{truth}(A) \text{, then } h(\phi)\in \mathsf{truth}(A). \end{align*} $$
Given a weak logic L, we say that
![]() $(A,\mathsf {truth}(A),\mathsf {core}(A))$
is a model of L, and write
$(A,\mathsf {truth}(A),\mathsf {core}(A))$
is a model of L, and write
![]() ${(A, \mathsf {truth}(A),\mathsf {core}(A)) \models L}$
if, for every
${(A, \mathsf {truth}(A),\mathsf {core}(A)) \models L}$
if, for every
![]() $\Gamma \cup \{\phi \} \subseteq \mathcal {L}$
,
$\Gamma \cup \{\phi \} \subseteq \mathcal {L}$
,
![]() $\Gamma \vdash _L \phi $
entails
$\Gamma \vdash _L \phi $
entails
![]() $\Gamma \models ^c_{\{A\} } \phi $
. For set of formulas
$\Gamma \models ^c_{\{A\} } \phi $
. For set of formulas
![]() $\Gamma $
and a bimatrix A, we write
$\Gamma $
and a bimatrix A, we write
![]() $A\models ^c \Gamma $
if
$A\models ^c \Gamma $
if
![]() $\models ^c_{\{A\}}\Gamma $
.
$\models ^c_{\{A\}}\Gamma $
.
Thus, the main intuition behind bimatrices is the same of expanded algebras: we add a new predicate specifying the core of the matrix, in order to consider only the assignments sending atomic formulas to elements of the core. As shown by the following proposition, bimatrices give rise to several weak logics. As we stressed already before (cf. Remark 2.3), the finitary requirement in the following definition is not necessary per se, but we need it as we are focusing on finitary logical systems.
Definition 7.7. Let
![]() $\mathbf {K}$
be a class of
$\mathbf {K}$
be a class of
![]() $\mathcal {L}$
-bimatrices, then
$\mathcal {L}$
-bimatrices, then
![]() $\mathsf {Log}(\mathbf {K})$
is the set of all pairs
$\mathsf {Log}(\mathbf {K})$
is the set of all pairs
![]() $(\Gamma ,\phi )$
with
$(\Gamma ,\phi )$
with
![]() $\Gamma \cup \{\phi \}\subseteq \mathsf {Fm}$
such that
$\Gamma \cup \{\phi \}\subseteq \mathsf {Fm}$
such that
![]() $\Gamma _0 \models ^c_{\mathbf {K}} \phi $
for some finite
$\Gamma _0 \models ^c_{\mathbf {K}} \phi $
for some finite
![]() $\Gamma _0\subseteq \Gamma $
. We say that a weak logic L is complete with respect to
$\Gamma _0\subseteq \Gamma $
. We say that a weak logic L is complete with respect to
![]() $\mathbf {K}$
if
$\mathbf {K}$
if
![]() $L=\mathsf {Log}(\mathbf {K})$
.
$L=\mathsf {Log}(\mathbf {K})$
.
Proposition 7.8. Let
![]() $\mathbf {K}$
be a class of bimatrices, then
$\mathbf {K}$
be a class of bimatrices, then
![]() $\mathsf {Log}(\mathbf {K})$
is a weak logic.
$\mathsf {Log}(\mathbf {K})$
is a weak logic.
Proof. Let
![]() $L=\mathsf {Log}(\mathbf {K})$
, then Conditions (1)–(3) from the definition of consequence relation (Definition 2.2) are immediately valid by Definition 7.6. Additionally, if
$L=\mathsf {Log}(\mathbf {K})$
, then Conditions (1)–(3) from the definition of consequence relation (Definition 2.2) are immediately valid by Definition 7.6. Additionally, if
![]() $\Gamma \Vdash _{L}\phi $
, then by definition there is some finite
$\Gamma \Vdash _{L}\phi $
, then by definition there is some finite
![]() $\Gamma _0\subseteq \Gamma $
such that
$\Gamma _0\subseteq \Gamma $
such that
![]() $\Gamma _0 \models ^c_{\mathbf {K}} \phi $
, and therefore
$\Gamma _0 \models ^c_{\mathbf {K}} \phi $
, and therefore
![]() $\Gamma _0\Vdash _{L}\phi $
, which shows that L is also finitary.
$\Gamma _0\Vdash _{L}\phi $
, which shows that L is also finitary.
Finally, we show that L is closed under atomic substitutions. Suppose
![]() $\Gamma \models ^c_{\mathbf {K}} \phi $
but
$\Gamma \models ^c_{\mathbf {K}} \phi $
but
![]() $\sigma [\Gamma ] \not \models ^c_{\mathbf {K}} \sigma (\phi )$
for some atomic substitution
$\sigma [\Gamma ] \not \models ^c_{\mathbf {K}} \sigma (\phi )$
for some atomic substitution
![]() $\sigma $
. Then there are a bimatrix
$\sigma $
. Then there are a bimatrix
![]() $M\in \mathbf {K}$
and a core assignment
$M\in \mathbf {K}$
and a core assignment
![]() $h:\mathsf {Fm}\to M$
such that
$h:\mathsf {Fm}\to M$
such that
![]() $h[\sigma [\Gamma ]]\subseteq \mathsf {truth}(M)$
but
$h[\sigma [\Gamma ]]\subseteq \mathsf {truth}(M)$
but
![]() $h(\sigma (\phi ))\notin \mathsf {truth}(M)$
. Now, since h is a core assignment and
$h(\sigma (\phi ))\notin \mathsf {truth}(M)$
. Now, since h is a core assignment and
![]() $\sigma $
an atomic substitution, it follows that
$\sigma $
an atomic substitution, it follows that
![]() $h\circ \sigma \in \mathsf {Hom}^c(\mathsf {Fm},A)$
, contradicting
$h\circ \sigma \in \mathsf {Hom}^c(\mathsf {Fm},A)$
, contradicting
![]() $ \Gamma \models ^c_M \phi $
.
$ \Gamma \models ^c_M \phi $
.
By the previous proposition we have that every class of bimatrices determines a weak logic. Additionally, we can also show that every weak logic is complete with respect to a class of bimatrices.
Definition 7.9. For every weak logic
![]() $\Vdash $
and every set of propositional formulas
$\Vdash $
and every set of propositional formulas
![]() $\Gamma \subseteq \mathsf {Fm}$
, we let
$\Gamma \subseteq \mathsf {Fm}$
, we let
![]() $M^\Gamma _\Vdash $
be the bimatrix with domain
$M^\Gamma _\Vdash $
be the bimatrix with domain
![]() $\mathsf {dom}(M^\Gamma _\Vdash ) = \mathsf {Fm}$
and predicates
$\mathsf {dom}(M^\Gamma _\Vdash ) = \mathsf {Fm}$
and predicates
![]() $\mathsf {truth}(M^\Gamma _\Vdash ) = \mathrm {Cn}_{\Vdash }(\Gamma )$
and
$\mathsf {truth}(M^\Gamma _\Vdash ) = \mathrm {Cn}_{\Vdash }(\Gamma )$
and
![]() $\mathsf {core}(M^\Gamma _\Vdash ) = \mathsf {Var}$
. We let
$\mathsf {core}(M^\Gamma _\Vdash ) = \mathsf {Var}$
. We let
![]() $\mathbf {M}_\Vdash $
be the class of all bimatrices
$\mathbf {M}_\Vdash $
be the class of all bimatrices
![]() $M^\Gamma _\Vdash $
for
$M^\Gamma _\Vdash $
for
![]() $\Gamma \subseteq \mathsf {Fm}$
.
$\Gamma \subseteq \mathsf {Fm}$
.
Theorem 7.10. Every weak logic
![]() $\Vdash $
is complete with respect to the class
$\Vdash $
is complete with respect to the class
![]() $\mathbf {M}_\Vdash $
.
$\mathbf {M}_\Vdash $
.
Proof. We need to show that
![]() $\Vdash \; = \mathsf {Log}(\mathbf {K})$
. Firstly, suppose towards contradiction that
$\Vdash \; = \mathsf {Log}(\mathbf {K})$
. Firstly, suppose towards contradiction that
![]() $\Gamma \Vdash \phi $
but
$\Gamma \Vdash \phi $
but
![]() $\Gamma \not \models ^c_{\mathbf {M}_\Vdash } \phi $
. Then there is a bimatrix
$\Gamma \not \models ^c_{\mathbf {M}_\Vdash } \phi $
. Then there is a bimatrix
![]() $M^\Delta _\Vdash $
and a core assignment
$M^\Delta _\Vdash $
and a core assignment
![]() $h: \mathsf {Fm} \to M^\Delta _\Vdash $
such that
$h: \mathsf {Fm} \to M^\Delta _\Vdash $
such that
![]() $h[\Gamma ] \subseteq \mathsf {truth}(M^\Delta _\Vdash )$
and
$h[\Gamma ] \subseteq \mathsf {truth}(M^\Delta _\Vdash )$
and
![]() $h(\phi ) \notin \mathsf {truth}(M^\Delta _\Vdash )$
. Consider now the substitution
$h(\phi ) \notin \mathsf {truth}(M^\Delta _\Vdash )$
. Consider now the substitution
![]() $\sigma $
defined letting
$\sigma $
defined letting
![]() $\sigma (x)=h(x)$
for all
$\sigma (x)=h(x)$
for all
![]() $x\in \mathsf {Var}$
. Notice in particular that this is well-defined because the domain of
$x\in \mathsf {Var}$
. Notice in particular that this is well-defined because the domain of
![]() $M^\Delta _\Vdash $
is
$M^\Delta _\Vdash $
is
![]() $\mathsf {Fm}$
. Since h is a core assignment and
$\mathsf {Fm}$
. Since h is a core assignment and
![]() $\mathsf {core}(M^\Gamma _\Vdash ) = \mathsf {Var}$
, it follows that
$\mathsf {core}(M^\Gamma _\Vdash ) = \mathsf {Var}$
, it follows that
![]() $\sigma $
is an atomic substitution, thus we obtain that
$\sigma $
is an atomic substitution, thus we obtain that
![]() $\sigma (\Gamma )\Vdash \sigma (\phi )$
. Now, since
$\sigma (\Gamma )\Vdash \sigma (\phi )$
. Now, since
![]() $h[\Gamma ] \subseteq \mathsf {truth}(M^\Delta _\Vdash )$
it follows in particular that
$h[\Gamma ] \subseteq \mathsf {truth}(M^\Delta _\Vdash )$
it follows in particular that
![]() $\Delta \Vdash \sigma (\Gamma )$
and so by transitivity
$\Delta \Vdash \sigma (\Gamma )$
and so by transitivity
![]() $\Delta \Vdash \sigma (\phi )$
. Since
$\Delta \Vdash \sigma (\phi )$
. Since
![]() $\sigma (\phi )=h(\phi )\notin \mathsf {truth}(M^\Delta _\Vdash )$
, this contradicts the definition of
$\sigma (\phi )=h(\phi )\notin \mathsf {truth}(M^\Delta _\Vdash )$
, this contradicts the definition of
![]() $\mathsf {truth}(M^\Delta _\Vdash )$
. It follows that
$\mathsf {truth}(M^\Delta _\Vdash )$
. It follows that
![]() $\Gamma \models ^c_{\mathbf {M}_\Vdash } \phi $
.
$\Gamma \models ^c_{\mathbf {M}_\Vdash } \phi $
.
Conversely, suppose
![]() $\Gamma \models ^c_{\mathbf {M}_\Vdash } \phi $
and let
$\Gamma \models ^c_{\mathbf {M}_\Vdash } \phi $
and let
![]() $\mathsf {id}_{\mathsf {Fm}}: \mathsf {Fm} \to M^\Gamma _\Vdash $
be the identity map. Then clearly
$\mathsf {id}_{\mathsf {Fm}}: \mathsf {Fm} \to M^\Gamma _\Vdash $
be the identity map. Then clearly
![]() $\mathsf {id}_{\mathsf {Fm}}[\mathsf {Var}] \subseteq \mathsf {Var}$
and
$\mathsf {id}_{\mathsf {Fm}}[\mathsf {Var}] \subseteq \mathsf {Var}$
and
![]() $\mathsf {id}_{\mathsf {Fm}}[\Gamma ] \subseteq \mathsf {truth}(M^\Gamma _\Vdash )$
. Since
$\mathsf {id}_{\mathsf {Fm}}[\Gamma ] \subseteq \mathsf {truth}(M^\Gamma _\Vdash )$
. Since
![]() $\Gamma \models ^c_{\mathbf {M}_\Vdash } \phi $
we then obtain
$\Gamma \models ^c_{\mathbf {M}_\Vdash } \phi $
we then obtain
![]() $\phi =\mathsf {id}_{\mathsf {Fm}}(\phi )\in \mathsf {truth}(M^\Gamma _\Vdash )$
, showing
$\phi =\mathsf {id}_{\mathsf {Fm}}(\phi )\in \mathsf {truth}(M^\Gamma _\Vdash )$
, showing
![]() $\phi \in \mathrm {Cn}_{\Vdash }(\Gamma )$
and thus
$\phi \in \mathrm {Cn}_{\Vdash }(\Gamma )$
and thus
![]() $\Gamma \Vdash \phi $
.
$\Gamma \Vdash \phi $
.
7.2 Connections to model theory without equality
In the previous section we have established that every class of bimatrices defines a weak logic and, conversely, that every weak logic is complete with respect to a class of bimatrices. Here we next consider what is exactly the class of all bimatrices defined by a weak logic L, i.e., the class of all bimatrices M for which
![]() $M\models ^c \Gamma $
entails
$M\models ^c \Gamma $
entails
![]() $M\models ^c \phi $
whenever
$M\models ^c \phi $
whenever
![]() $\Gamma \Vdash _{L} \phi $
. In the standard context this issue was first considered by Czelakowski [Reference Czelakowski13], who characterized the class of all matrices which are models of a logic. Here we follow however the later work of Dellunde and Jansana in [Reference Dellunde and Jansana14], which provided a novel proof of Czelakowski’s result by employing the fact that (finitary) propositional logics can be translated into Horn theories without equality. We start by reviewing this translation, which is essentially a generalisation of what we already considered in Remark 3.18.
$\Gamma \Vdash _{L} \phi $
. In the standard context this issue was first considered by Czelakowski [Reference Czelakowski13], who characterized the class of all matrices which are models of a logic. Here we follow however the later work of Dellunde and Jansana in [Reference Dellunde and Jansana14], which provided a novel proof of Czelakowski’s result by employing the fact that (finitary) propositional logics can be translated into Horn theories without equality. We start by reviewing this translation, which is essentially a generalisation of what we already considered in Remark 3.18.
Proposition 7.11. Let
![]() $\mathcal {L}$
be an algebraic language,
$\mathcal {L}$
be an algebraic language,
![]() $\Gamma \cup \phi \subseteq \mathsf {Fm}$
and
$\Gamma \cup \phi \subseteq \mathsf {Fm}$
and
![]() $|\Gamma |<\aleph _0$
, then we can translate the consequence relations from Definitions 7.3 and 7.6 as follows:
$|\Gamma |<\aleph _0$
, then we can translate the consequence relations from Definitions 7.3 and 7.6 as follows:
-
(a) let
 $\mathbf {K}$
be a class of matrices then:
$\mathbf {K}$
be a class of matrices then:  $$\begin{align*}\Gamma \models_{\mathbf{K}} \phi \; \Longleftrightarrow \; \mathbf{K} \models \forall x_0,\dots,\forall x_n \Big ( \bigwedge_{\gamma\in \Gamma} \mathsf{truth}(\gamma(\bar{x})) \to \mathsf{truth}(\phi(\bar{x}) )\Big ); \end{align*}$$
$$\begin{align*}\Gamma \models_{\mathbf{K}} \phi \; \Longleftrightarrow \; \mathbf{K} \models \forall x_0,\dots,\forall x_n \Big ( \bigwedge_{\gamma\in \Gamma} \mathsf{truth}(\gamma(\bar{x})) \to \mathsf{truth}(\phi(\bar{x}) )\Big ); \end{align*}$$
-
(b) let
 $\mathbf {K}$
be a class of bimatrices, then:
$\mathbf {K}$
be a class of bimatrices, then:  $$\begin{align*}\Gamma &\models^c_{\mathbf{K}} \phi \; \Longleftrightarrow \; \mathbf{K} \models \forall x_0,\dots,\forall x_n \Big ( \bigwedge_{\gamma\in \Gamma} \mathsf{truth}(\gamma(\bar{x})) \land \bigwedge_{i{\leqslant} n} \mathsf{core}(x_i) \to \mathsf{truth}(\phi(\bar{x}))\Big ). \end{align*}$$
$$\begin{align*}\Gamma &\models^c_{\mathbf{K}} \phi \; \Longleftrightarrow \; \mathbf{K} \models \forall x_0,\dots,\forall x_n \Big ( \bigwedge_{\gamma\in \Gamma} \mathsf{truth}(\gamma(\bar{x})) \land \bigwedge_{i{\leqslant} n} \mathsf{core}(x_i) \to \mathsf{truth}(\phi(\bar{x}))\Big ). \end{align*}$$
Proof. This follows immediately from the definition of
![]() $\models _{\mathbf {K}}$
and
$\models _{\mathbf {K}}$
and
![]() $\models ^c_{\mathbf {K}}$
.
$\models ^c_{\mathbf {K}}$
.
It follows from the previous proposition that standard logics in the language
![]() $\mathcal {L}$
can be encoded by Horn theories in
$\mathcal {L}$
can be encoded by Horn theories in
![]() $\mathcal {L}\cup \{\mathsf {truth}\}$
, while weak logics can be encoded in
$\mathcal {L}\cup \{\mathsf {truth}\}$
, while weak logics can be encoded in
![]() $\mathcal {L}\cup \{\mathsf {truth},\mathsf {core}\}$
. This motivates the following definitions.
$\mathcal {L}\cup \{\mathsf {truth},\mathsf {core}\}$
. This motivates the following definitions.
Notation 7.12. Let
![]() $\Gamma \cup \{\phi \}\subseteq \mathsf {Fm}$
, then we write
$\Gamma \cup \{\phi \}\subseteq \mathsf {Fm}$
, then we write
![]() $\Phi (\Gamma ,\phi )$
for the first-order formula
$\Phi (\Gamma ,\phi )$
for the first-order formula
 $$\begin{align*}\forall x_0,\dots,\forall x_n \Big ( \bigwedge_{\gamma\in \Gamma} \mathsf{truth}(\gamma(\bar{x})) \land \bigwedge_{i{\leqslant} n} \mathsf{core}(x_i) \to \mathsf{truth}(\phi(\bar{x}))\Big ).\end{align*}$$
$$\begin{align*}\forall x_0,\dots,\forall x_n \Big ( \bigwedge_{\gamma\in \Gamma} \mathsf{truth}(\gamma(\bar{x})) \land \bigwedge_{i{\leqslant} n} \mathsf{core}(x_i) \to \mathsf{truth}(\phi(\bar{x}))\Big ).\end{align*}$$
Definition 7.13. Let
![]() $\Vdash $
be a weak logic, then we let
$\Vdash $
be a weak logic, then we let
![]() $\mathsf {Horn}(\Vdash ) $
be the Horn theory obtained by letting
$\mathsf {Horn}(\Vdash ) $
be the Horn theory obtained by letting
![]() $\Phi (\Gamma ,\phi )\in \mathsf {Horn}(\Vdash )$
whenever
$\Phi (\Gamma ,\phi )\in \mathsf {Horn}(\Vdash )$
whenever
![]() $\Gamma \Vdash \phi $
. We write
$\Gamma \Vdash \phi $
. We write
![]() $\mathrm {Mod}(\Vdash )$
for the class of structures
$\mathrm {Mod}(\Vdash )$
for the class of structures
![]() $\mathrm {Mod}(\mathsf {Horn}(\Vdash ))$
.
$\mathrm {Mod}(\mathsf {Horn}(\Vdash ))$
.
While Czelakowski’s original approach in [Reference Czelakowski13] was specifically tailored to logical matrices, Dellunde and Jansana considered arbitrary model classes axiomatized by Horn theories without equality, thus making it possible to apply their results to the setting of bimatrices and expanded algebras. We recall from Notation 2.10 that the operator
![]() $\mathbb {H}_{\mathrm {s}}$
refers to the closure under strict homomorphic images, and thus
$\mathbb {H}_{\mathrm {s}}$
refers to the closure under strict homomorphic images, and thus
![]() $\mathbb {H}^{-1}_{\mathrm {s}}(\mathbf {K})$
is the class of all structures A that are preimages of some strict homomorphism of some structure in
$\mathbb {H}^{-1}_{\mathrm {s}}(\mathbf {K})$
is the class of all structures A that are preimages of some strict homomorphism of some structure in
![]() $\mathbf {K}$
. We stress that Dellunde and Jansana’s results (from [Reference Dellunde and Jansana14]) hold in the setting without the equality symbol. In particular, when in the rest of this section we consider Horn formulas, we always restrict attention to Horn formulas not containing the equality symbol. For clarity, we introduce the following notation.
$\mathbf {K}$
. We stress that Dellunde and Jansana’s results (from [Reference Dellunde and Jansana14]) hold in the setting without the equality symbol. In particular, when in the rest of this section we consider Horn formulas, we always restrict attention to Horn formulas not containing the equality symbol. For clarity, we introduce the following notation.
Notation 7.14. We write
![]() $\mathcal {L}^{-}$
to refer to a fixed first-order language without the equality symbol
$\mathcal {L}^{-}$
to refer to a fixed first-order language without the equality symbol
![]() $\approx $
. Also, we write
$\approx $
. Also, we write
![]() $\mathcal {L}^{-}$
for the collections of all (first-order) formulas in this language (which clearly do not contain the equality symbol).
$\mathcal {L}^{-}$
for the collections of all (first-order) formulas in this language (which clearly do not contain the equality symbol).
Fact 7.15 (Dellunde and Jansana).
Let
![]() $\mathbf {K}$
be a class of
$\mathbf {K}$
be a class of
![]() $\mathcal {L}^{-}$
-structures, then the following are equivalent:
$\mathcal {L}^{-}$
-structures, then the following are equivalent:
-
(1)
 $\mathbf {K}$
is axiomatised by strict universal Horn formulas in
$\mathbf {K}$
is axiomatised by strict universal Horn formulas in
 $\mathcal {L}^{-}$
;
$\mathcal {L}^{-}$
; -
(2)
 $\mathbf {K}$
is closed under
$\mathbf {K}$
is closed under
 $\mathbb {H}_{\mathrm {s}}^{-1},\mathbb {H}_{\mathrm {s}},\mathbb {S},\mathbb {P}, \mathbb {P}_{\mathrm {U}} $
and contains a trivial structure;
$\mathbb {H}_{\mathrm {s}}^{-1},\mathbb {H}_{\mathrm {s}},\mathbb {S},\mathbb {P}, \mathbb {P}_{\mathrm {U}} $
and contains a trivial structure; -
(3)
 $\mathbf {K}=\mathbb {H}_{\mathrm {s}}^{-1}\mathbb {H}_{\mathrm {s}}\mathbb {S}\mathbb {P} \mathbb {P}_{\mathrm {U}}(\mathbf {K}_0) $
for some class
$\mathbf {K}=\mathbb {H}_{\mathrm {s}}^{-1}\mathbb {H}_{\mathrm {s}}\mathbb {S}\mathbb {P} \mathbb {P}_{\mathrm {U}}(\mathbf {K}_0) $
for some class
 $\mathbf {K}_0$
of
$\mathbf {K}_0$
of
 $\mathcal {L}$
-structures containing a trivial structure.
$\mathcal {L}$
-structures containing a trivial structure.
As we mentioned in Fact 2.14, the validity of Horn formulas is always preserved under the operators
![]() $\mathbb {I},\mathbb {S},\mathbb {P}, \mathbb {P}_{\mathrm {U}} $
. From the previous theorem it follows that strict Horn formulas in a language without equality are also preserved under the operators
$\mathbb {I},\mathbb {S},\mathbb {P}, \mathbb {P}_{\mathrm {U}} $
. From the previous theorem it follows that strict Horn formulas in a language without equality are also preserved under the operators
![]() $ \mathbb {H}_{\mathrm {s}}^{-1} $
and
$ \mathbb {H}_{\mathrm {s}}^{-1} $
and
![]() $ \mathbb {H}_{\mathrm {s}} $
. From this fact and the previous theorem we immediately obtain as a corollary the following characterization of the class of models
$ \mathbb {H}_{\mathrm {s}} $
. From this fact and the previous theorem we immediately obtain as a corollary the following characterization of the class of models
![]() $\mathrm {Mod}(\Vdash )$
, where
$\mathrm {Mod}(\Vdash )$
, where
![]() $\Vdash =\mathsf {Log}(\mathbf {K}) $
for some class of bimatrices
$\Vdash =\mathsf {Log}(\mathbf {K}) $
for some class of bimatrices
![]() $\mathbf {K}$
.
$\mathbf {K}$
.
Corollary 7.16. Let
![]() $\mathbf {K}$
be a class of bimatrices and let
$\mathbf {K}$
be a class of bimatrices and let
![]() $T=\mathsf {Horn}(\mathsf {Log}(\mathbf {K}) )$
, then:
$T=\mathsf {Horn}(\mathsf {Log}(\mathbf {K}) )$
, then:
where
![]() $\mathbf {K}'$
is
$\mathbf {K}'$
is
![]() $\mathbf {K}$
together with some trivial bimatrices.
$\mathbf {K}$
together with some trivial bimatrices.
Notice that, by Theorem 7.10, every weak logic
![]() $\Vdash $
is complete with respect to a class of bimatrices
$\Vdash $
is complete with respect to a class of bimatrices
![]() $\mathbf {M}_\Vdash $
and so the previous theorem applies to all weak logics
$\mathbf {M}_\Vdash $
and so the previous theorem applies to all weak logics
![]() $\Vdash $
and provides us with a characterization of the class of all bimatrices defined by
$\Vdash $
and provides us with a characterization of the class of all bimatrices defined by
![]() $\Vdash $
.
$\Vdash $
.
Importantly, however, one can see that the class of all matrices
![]() $\mathrm {Mod}(T)$
above does not meet the intuition about the “right” semantics of a (weak) logic, and will contain several pathological examples. For example, in the case of the standard logic
$\mathrm {Mod}(T)$
above does not meet the intuition about the “right” semantics of a (weak) logic, and will contain several pathological examples. For example, in the case of the standard logic
![]() $\mathtt {CPC}$
, the class
$\mathtt {CPC}$
, the class
![]() $\mathrm {Mod}(\mathtt {CPC})$
is not the class of Boolean algebras, but rather the class
$\mathrm {Mod}(\mathtt {CPC})$
is not the class of Boolean algebras, but rather the class
![]() $\mathbb {H}_{\mathrm {s}}^{-1}(\mathbf {BA})$
, where here we identify
$\mathbb {H}_{\mathrm {s}}^{-1}(\mathbf {BA})$
, where here we identify
![]() $\mathbf {BA}$
with the class of expansions
$\mathbf {BA}$
with the class of expansions
![]() $(B,\{1\})$
such that B is a Boolean algebra (for example, the so-called “benzene ring” is a matrix model of
$(B,\{1\})$
such that B is a Boolean algebra (for example, the so-called “benzene ring” is a matrix model of
![]() $\mathtt {CPC}$
, but it is not a Boolean algebra, cf. [Reference Font16, Example 4.79]). In order to identify the non-pathological models of a propositional logic, Dellunde and Jansana focused in [Reference Dellunde and Jansana14] on the so-called reduced structures. Since they work at the general level of model theory without equality, it is again straightforward to adapt their results to our current setting of bimatrices.
$\mathtt {CPC}$
, but it is not a Boolean algebra, cf. [Reference Font16, Example 4.79]). In order to identify the non-pathological models of a propositional logic, Dellunde and Jansana focused in [Reference Dellunde and Jansana14] on the so-called reduced structures. Since they work at the general level of model theory without equality, it is again straightforward to adapt their results to our current setting of bimatrices.
Definition 7.17. Let
![]() $\mathcal {L}$
be any first-order language, M an
$\mathcal {L}$
be any first-order language, M an
![]() $\mathcal {L}$
-structure, and
$\mathcal {L}$
-structure, and
![]() $X\subseteq M$
, then we write
$X\subseteq M$
, then we write
![]() $\mathcal {L}(X)$
for the set of all
$\mathcal {L}(X)$
for the set of all
![]() $\mathcal {L}$
-formulas with parameters in X.
$\mathcal {L}$
-formulas with parameters in X.
Definition 7.18. Let M be a first-order structure,
![]() $D \subseteq M,$
and
$D \subseteq M,$
and
![]() $\bar {a}\in M^{<\omega }$
, we let the type without equality of
$\bar {a}\in M^{<\omega }$
, we let the type without equality of
![]() $\bar {a}$
over D in M be the following set of equality-free formulas:
$\bar {a}$
over D in M be the following set of equality-free formulas:
Then, the Leibniz congruence is the relation
![]() $\sim _*$
on
$\sim _*$
on
![]() $ A $
defined by letting, for
$ A $
defined by letting, for
![]() $a,b \in M$
,
$a,b \in M$
,
A model M is reduced if the Leibniz congruence
![]() $\sim _*$
over M is the identity.
$\sim _*$
over M is the identity.
Remark 7.19. As shown in [Reference Dellunde and Jansana14],
![]() $\sim _*$
is the largest non-trivial congruence relation on M, meaning that it is the largest congruence
$\sim _*$
is the largest non-trivial congruence relation on M, meaning that it is the largest congruence
![]() $\theta $
over its algebraic reduct such that, for any relation symbol
$\theta $
over its algebraic reduct such that, for any relation symbol
![]() $R\in \mathcal {L}$
, if
$R\in \mathcal {L}$
, if
![]() $(a_i,b_i)\in \theta $
for all
$(a_i,b_i)\in \theta $
for all
![]() $1{\leqslant } i {\leqslant } n$
then
$1{\leqslant } i {\leqslant } n$
then
![]() $A\models R(a_1,\dots ,a_n)$
if and only if
$A\models R(a_1,\dots ,a_n)$
if and only if
![]() $A\models R(b_1,\dots ,b_n)$
. As we stressed already in Remark 2.9, the projections induced by congruences respecting this conditions are always strict homomorphisms. Additionally, since
$A\models R(b_1,\dots ,b_n)$
. As we stressed already in Remark 2.9, the projections induced by congruences respecting this conditions are always strict homomorphisms. Additionally, since
![]() $\sim _*$
is the greatest such congruence, any strict homomorphism from
$\sim _*$
is the greatest such congruence, any strict homomorphism from
![]() $M/\sim _*$
onto some further structure N must be the identity.
$M/\sim _*$
onto some further structure N must be the identity.
Notation 7.20. Let M be an
![]() $\mathcal {L}^{-}$
-structure and let
$\mathcal {L}^{-}$
-structure and let
![]() $\sim _*$
be the Leibniz congruence over M, then we write
$\sim _*$
be the Leibniz congruence over M, then we write
![]() $M^*$
for the quotient structure
$M^*$
for the quotient structure
![]() $M/\sim _*$
. For any class operator
$M/\sim _*$
. For any class operator
![]() $\mathbb {O} $
, we let
$\mathbb {O} $
, we let
![]() $\mathbb {O}^*(C):=\{A^* : A\in \mathbb {O}(C)\}$
, and for any class
$\mathbb {O}^*(C):=\{A^* : A\in \mathbb {O}(C)\}$
, and for any class
![]() $\mathbf {K}$
we let
$\mathbf {K}$
we let
![]() $\mathbf {K}^*=\{ A^* : A\in \mathbf {K}\}$
. Finally, we let
$\mathbf {K}^*=\{ A^* : A\in \mathbf {K}\}$
. Finally, we let
![]() $\mathrm {Mod}^*(T)=\{A^* : A\in \mathrm {Mod}(T) \}$
.
$\mathrm {Mod}^*(T)=\{A^* : A\in \mathrm {Mod}(T) \}$
.
Remark 7.21. By Fact 7.15, the validity of (strict) universal Horn formulas in a language without equality is closed by
![]() $\mathbb {H}_{\mathrm {s}}$
, and thus
$\mathbb {H}_{\mathrm {s}}$
, and thus
![]() $\mathrm {Mod}^*(T)\subseteq \mathrm {Mod}(T)$
.
$\mathrm {Mod}^*(T)\subseteq \mathrm {Mod}(T)$
.
From Fact 7.15, one immediately obtains the following theorem [Reference Dellunde and Jansana14, Theorem 18] and corollary. Notice that our formulation differs from the original one as Dellunde and Jansana assume that closure operators are already closed under isomorphic copies.
Fact 7.22 (Dellunde and Jansana).
Let
![]() $\mathbf {K}$
be a class of reduced
$\mathbf {K}$
be a class of reduced
![]() $\mathcal {L}^{-}$
-structures, then the following are equivalent:
$\mathcal {L}^{-}$
-structures, then the following are equivalent:
-
(1)
 $\mathbf {K}$
is the class of reduced models of an
$\mathbf {K}$
is the class of reduced models of an
 $\mathcal {L}^{-}$
-universal Horn theory;
$\mathcal {L}^{-}$
-universal Horn theory; -
(2)
 $\mathbf {K}$
is closed under the operators
$\mathbf {K}$
is closed under the operators
 $\mathbb {I}^*, \mathbb {S}^*,\mathbb {P}^*, \mathbb {P}^*_{\mathrm {U}} $
;
$\mathbb {I}^*, \mathbb {S}^*,\mathbb {P}^*, \mathbb {P}^*_{\mathrm {U}} $
; -
(3)
 $\mathbf {K}=\mathbb {I}^*\mathbb {S}^*\mathbb {P}^* \mathbb {P}^*_{\mathrm {U}}(\mathbf {K}_0) $
for some class
$\mathbf {K}=\mathbb {I}^*\mathbb {S}^*\mathbb {P}^* \mathbb {P}^*_{\mathrm {U}}(\mathbf {K}_0) $
for some class
 $\mathbf {K}_0$
of
$\mathbf {K}_0$
of
 $\mathcal {L}^{-}$
-structures.
$\mathcal {L}^{-}$
-structures.
Corollary 7.23. Let
![]() $\mathbf {K}$
be a class of reduced bimatrices,
$\mathbf {K}$
be a class of reduced bimatrices,
![]() $T=\mathsf {Horn}(\mathsf {Log}(\mathbf {K}))$
, then:
$T=\mathsf {Horn}(\mathsf {Log}(\mathbf {K}))$
, then:
Thus, since every weak logic is complete with respect to a class of bimatrices, the previous corollary provides us with a characterization of the class of reduced bimatrices defined by any weak logic
![]() $\Vdash $
. We conclude our abstract study of matrix semantics by showing that, in the case of a loosely algebraizable weak logic
$\Vdash $
. We conclude our abstract study of matrix semantics by showing that, in the case of a loosely algebraizable weak logic
![]() $\Vdash $
, its reduced core-generated bimatrices coincide with the core-generated expanded algebras of its equivalent algebraic semantics. We first define these notions and notice that Proposition 3.21 easily extends to this setting.
$\Vdash $
, its reduced core-generated bimatrices coincide with the core-generated expanded algebras of its equivalent algebraic semantics. We first define these notions and notice that Proposition 3.21 easily extends to this setting.
Definition 7.24. Let M be a bimatrix, we say that M is core-generated if
![]() $M=\langle \mathsf {core}(M)\rangle $
. We then write
$M=\langle \mathsf {core}(M)\rangle $
. We then write
![]() $\mathrm {Mod}_{\mathrm {CG}}(\Vdash )$
for the subclass of
$\mathrm {Mod}_{\mathrm {CG}}(\Vdash )$
for the subclass of
![]() $\mathrm {Mod}(\Vdash )$
consisting only of core-generated structures. We then let
$\mathrm {Mod}(\Vdash )$
consisting only of core-generated structures. We then let
![]() $\mathrm {Mod}^*_{\mathrm {CG}}(\Vdash )=(\mathrm {Mod}(\Vdash ))^*$
.
$\mathrm {Mod}^*_{\mathrm {CG}}(\Vdash )=(\mathrm {Mod}(\Vdash ))^*$
.
Proposition 7.25. Let A be a core-generated bimatrix, then
![]() $\sigma (\Theta ) \models ^c_{\{ A \}} \sigma (\varepsilon \approx \delta )$
for all
$\sigma (\Theta ) \models ^c_{\{ A \}} \sigma (\varepsilon \approx \delta )$
for all
![]() $\sigma \in \mathsf {Subst}(\mathcal {L})$
holds if and only if
$\sigma \in \mathsf {Subst}(\mathcal {L})$
holds if and only if
![]() $ \Theta \models _{\{A\}} \varepsilon \approx \delta $
.
$ \Theta \models _{\{A\}} \varepsilon \approx \delta $
.
We can then characterise the reduced, core-generated bimatrices of a loosely algebraizable weak logics
![]() $\Vdash $
by directly applying the standard version of this result. We recall the following classical result from [Reference Font16, Theorem 4.60].
$\Vdash $
by directly applying the standard version of this result. We recall the following classical result from [Reference Font16, Theorem 4.60].
Fact 7.26. Let
![]() $\vdash $
be an algebraizable standard logic with equivalent algebraic semantics
$\vdash $
be an algebraizable standard logic with equivalent algebraic semantics
![]() $(\mathbf {Q},\tau ,\Delta )$
. Then
$(\mathbf {Q},\tau ,\Delta )$
. Then
![]() $(A,\mathsf {truth}(A))\in \mathrm {Mod}^*(\vdash )$
if and only if
$(A,\mathsf {truth}(A))\in \mathrm {Mod}^*(\vdash )$
if and only if
![]() $A\in \mathbf {Q}$
and
$A\in \mathbf {Q}$
and
![]() $\mathsf {truth}(A)=\{a\in A : A\models \tau ^A(a)\}$
.
$\mathsf {truth}(A)=\{a\in A : A\models \tau ^A(a)\}$
.
Corollary 7.27. Let
![]() $\Vdash $
be a loosely algebraizable weak logic with equivalent algebraic semantics
$\Vdash $
be a loosely algebraizable weak logic with equivalent algebraic semantics
![]() $(\mathbf {Q},\tau ,\Delta )$
. Then
$(\mathbf {Q},\tau ,\Delta )$
. Then
![]() $(A,\mathsf {truth}(A),\mathsf {core}(A))\in \mathrm {Mod}_{\mathrm {CG}}^*(\Vdash )$
if and only if
$(A,\mathsf {truth}(A),\mathsf {core}(A))\in \mathrm {Mod}_{\mathrm {CG}}^*(\Vdash )$
if and only if
![]() $(A,\mathsf {core}(A))\in \mathbf {Q}_{\mathrm {CG}}$
and
$(A,\mathsf {core}(A))\in \mathbf {Q}_{\mathrm {CG}}$
and
![]() $\mathsf {truth}(A)=\{a\in A : A\models \tau ^A(a)\}$
.
$\mathsf {truth}(A)=\{a\in A : A\models \tau ^A(a)\}$
.
Proof. Firstly, notice that if
![]() $\Vdash $
is loosely algebraized by
$\Vdash $
is loosely algebraized by
![]() $(\mathbf {Q},\tau ,\Delta )$
, then by Proposition 5.4 we have that
$(\mathbf {Q},\tau ,\Delta )$
, then by Proposition 5.4 we have that
![]() $\Vdash _{\mathrm {s}}$
is also algebraized by
$\Vdash _{\mathrm {s}}$
is also algebraized by
![]() $(\mathbf {Q},\tau ,\Delta )$
.
$(\mathbf {Q},\tau ,\Delta )$
.
Suppose now that
![]() $(A,\mathsf {truth}(A),\mathsf {core}(A))\in \mathrm {Mod}_{\mathrm {CG}}^*(\Vdash )$
, then it follows by Proposition 7.25 that
$(A,\mathsf {truth}(A),\mathsf {core}(A))\in \mathrm {Mod}_{\mathrm {CG}}^*(\Vdash )$
, then it follows by Proposition 7.25 that
![]() $(A,\mathsf {truth}(A))\in \mathrm {Mod}(\Vdash _{\mathrm {s}})$
. We claim that
$(A,\mathsf {truth}(A))\in \mathrm {Mod}(\Vdash _{\mathrm {s}})$
. We claim that
![]() $(A,\mathsf {truth}(A))$
is also reduced. If
$(A,\mathsf {truth}(A))$
is also reduced. If
![]() $a,b\in A$
are distinct elements, then since
$a,b\in A$
are distinct elements, then since
![]() $\Vdash _{\mathrm {s}}$
is algebraized by
$\Vdash _{\mathrm {s}}$
is algebraized by
![]() $(\mathbf {Q},\tau ,\Delta )$
we have that
$(\mathbf {Q},\tau ,\Delta )$
we have that
![]() $A\models a\not \approx b$
is equivalent to
$A\models a\not \approx b$
is equivalent to
![]() $A\not \models \Delta ^A(a,b)$
. But then we have that
$A\not \models \Delta ^A(a,b)$
. But then we have that
![]() $\Delta (x,a)\in \text {tp}^-_M(a/A)$
but
$\Delta (x,a)\in \text {tp}^-_M(a/A)$
but
![]() $\Delta (x,a)\notin \text {tp}^-_M(b/A)$
, showing that
$\Delta (x,a)\notin \text {tp}^-_M(b/A)$
, showing that
![]() $(A,\mathsf {truth}(A))$
is reduced. It thus follows that
$(A,\mathsf {truth}(A))$
is reduced. It thus follows that
![]() $(A,\mathsf {truth}(A))\in \mathrm {Mod}^*(\Vdash _{\mathrm {s}})$
. So, by Fact 7.26 and the fact that A is core-generated, we then conclude that
$(A,\mathsf {truth}(A))\in \mathrm {Mod}^*(\Vdash _{\mathrm {s}})$
. So, by Fact 7.26 and the fact that A is core-generated, we then conclude that
![]() $(A,\mathsf {core}(A))\in \mathbf {Q}_{\mathrm {CG}}$
and
$(A,\mathsf {core}(A))\in \mathbf {Q}_{\mathrm {CG}}$
and
![]() $\mathsf {truth}(A)=\{a\in A : A\models \tau ^A(a)\}$
.
$\mathsf {truth}(A)=\{a\in A : A\models \tau ^A(a)\}$
.
Conversely, suppose that
![]() $(A,\mathsf {core}(A))\in \mathbf {Q}_{\mathrm {CG}}$
and
$(A,\mathsf {core}(A))\in \mathbf {Q}_{\mathrm {CG}}$
and
![]() $\mathsf {truth}(A)=\{a\in A : A\models \tau ^A(a)\}$
. By Fact 7.26 and the fact that
$\mathsf {truth}(A)=\{a\in A : A\models \tau ^A(a)\}$
. By Fact 7.26 and the fact that
![]() $\Vdash _{\mathrm {s}}$
is algebraized by
$\Vdash _{\mathrm {s}}$
is algebraized by
![]() $(\mathbf {Q},\tau ,\Delta )$
, we have that
$(\mathbf {Q},\tau ,\Delta )$
, we have that
![]() $(A,\mathsf {truth}(A))\in \mathrm {Mod}^*(\Vdash _{\mathrm {s}})$
. Also, since
$(A,\mathsf {truth}(A))\in \mathrm {Mod}^*(\Vdash _{\mathrm {s}})$
. Also, since
![]() $(A,\mathsf {core}(A))$
is core-generated, it follows from Proposition 7.25 that
$(A,\mathsf {core}(A))$
is core-generated, it follows from Proposition 7.25 that
![]() $(A,\mathsf {truth}(A),\mathsf {core}(A))\in \mathrm {Mod}_{\mathrm {CG}}^*(\Vdash )$
. This concludes our proof.
$(A,\mathsf {truth}(A),\mathsf {core}(A))\in \mathrm {Mod}_{\mathrm {CG}}^*(\Vdash )$
. This concludes our proof.
8 Application: Inquisitive and dependence logics
We turn in this section to one application of the abstract machinery that we studied, i.e., the case of (propositional) inquisitive and dependence logics. These logical systems make for two interesting examples of logics where uniform substitution fails, and which have also been studied from the algebraic point of view. In particular, an algebraic semantics for the classical version of inquisitive logic
![]() $\mathtt {InqB}$
was introduced in [Reference Bezhanishvili, Grilletti and Holliday2] (although some preliminary inquiry into the subject was provided already in [Reference Roelofsen28]) and further investigated in [Reference Bezhanishvili, Grilletti and Quadrellaro3]. Such semantics was later generalised in [Reference Quadrellaro26] to the intuitionistic logic
$\mathtt {InqB}$
was introduced in [Reference Bezhanishvili, Grilletti and Holliday2] (although some preliminary inquiry into the subject was provided already in [Reference Roelofsen28]) and further investigated in [Reference Bezhanishvili, Grilletti and Quadrellaro3]. Such semantics was later generalised in [Reference Quadrellaro26] to the intuitionistic logic
![]() $\mathtt {InqI}$
, and to both the classical and intuitionistic version of dependence logic
$\mathtt {InqI}$
, and to both the classical and intuitionistic version of dependence logic
![]() $\mathtt {InqB}^\otimes $
and
$\mathtt {InqB}^\otimes $
and
![]() $\mathtt {InqI}^\otimes $
. Since these logical systems do not satisfy the rule of uniform substitution, it has so far been an open question whether they are in any sense unique—as a matter of fact, another (similar) semantics to
$\mathtt {InqI}^\otimes $
. Since these logical systems do not satisfy the rule of uniform substitution, it has so far been an open question whether they are in any sense unique—as a matter of fact, another (similar) semantics to
![]() $\mathtt {InqI}$
was suggested independently in [Reference Punčochář25]. The notion of algebraizability of weak logics that we have introduced in this article provides us with a framework to make sense of this question. In this section, we build on these previous works and relate them to the notion of algebraizability from the present article. Our main result is that the classical versions of inquisitive and dependence logic
$\mathtt {InqI}$
was suggested independently in [Reference Punčochář25]. The notion of algebraizability of weak logics that we have introduced in this article provides us with a framework to make sense of this question. In this section, we build on these previous works and relate them to the notion of algebraizability from the present article. Our main result is that the classical versions of inquisitive and dependence logic
![]() $\mathtt {InqB}$
and
$\mathtt {InqB}$
and
![]() $\mathtt {InqB}^\otimes $
are strictly algebraizable, while their intuitionistic versions
$\mathtt {InqB}^\otimes $
are strictly algebraizable, while their intuitionistic versions
![]() $\mathtt {InqI}$
and
$\mathtt {InqI}$
and
![]() $\mathtt {InqI}^\otimes $
are only loosely so.
$\mathtt {InqI}^\otimes $
are only loosely so.
8.1 Inquisitive and dependence logic
We introduce in this section the intuitionistic and classical propositional variants of inquisitive and dependence logic. We refer the reader to [Reference Ciardelli and Roelofsen12, Reference Miglioli, Moscato, Ornaghi, Quazza and Usberti22] for the original presentation of classical propositional inquisitive logic, to [Reference Yang and Väänänen30] for classical propositional dependence logic, and to [Reference Ciardelli, Iemhoff and Yang11] for their intuitionistic versions. We make explicit in the following remark the language in which we formulate these logics. Notice that while our presentation follows essentially [Reference Ciardelli, Iemhoff and Yang11], our notation is as in [Reference Quadrellaro26].
Context 8.1. We let
![]() $\mathcal {L}_{\mathtt {IPC}}$
be the propositional language
$\mathcal {L}_{\mathtt {IPC}}$
be the propositional language
![]() $\mathcal {L}_{\mathtt {IPC}}=\{ \land , \lor , \rightarrow , \bot , \top \}$
, i.e.,
$\mathcal {L}_{\mathtt {IPC}}=\{ \land , \lor , \rightarrow , \bot , \top \}$
, i.e.,
![]() $\mathcal {L}_{\mathtt {IPC}}$
is simply the usual language of propositional intuitionistic logic. With some abuse of notation, we denote by
$\mathcal {L}_{\mathtt {IPC}}$
is simply the usual language of propositional intuitionistic logic. With some abuse of notation, we denote by
![]() $\mathcal {L}_{\mathtt {IPC}}$
also the set of all propositional formulas recursively built from
$\mathcal {L}_{\mathtt {IPC}}$
also the set of all propositional formulas recursively built from
![]() $\mathsf {Var}$
in this syntax. Also, we let
$\mathsf {Var}$
in this syntax. Also, we let
![]() $\mathcal {L}_{\mathtt {IPC}}^\otimes $
be the propositional language
$\mathcal {L}_{\mathtt {IPC}}^\otimes $
be the propositional language
![]() $\mathcal {L}_{\mathtt {IPC}}^\otimes =\{ \land , \lor , \otimes , \rightarrow , \bot ,\top \}$
, namely, the expansion of
$\mathcal {L}_{\mathtt {IPC}}^\otimes =\{ \land , \lor , \otimes , \rightarrow , \bot ,\top \}$
, namely, the expansion of
![]() $\mathcal {L}_{\mathtt {IPC}}$
by a novel tensor disjunction operation
$\mathcal {L}_{\mathtt {IPC}}$
by a novel tensor disjunction operation
![]() $\otimes $
. We denote by
$\otimes $
. We denote by
![]() $\mathcal {L}_{\mathtt {IPC}}^\otimes $
also the set of all propositional formulas recursively built from
$\mathcal {L}_{\mathtt {IPC}}^\otimes $
also the set of all propositional formulas recursively built from
![]() $\mathsf {Var}$
in the syntax
$\mathsf {Var}$
in the syntax
![]() $\mathcal {L}_{\mathtt {IPC}}^\otimes $
.
$\mathcal {L}_{\mathtt {IPC}}^\otimes $
.
Notation 8.2. We define the inquisitive operation ![]() . We treat negation as a defined operation and we define it by
. We treat negation as a defined operation and we define it by ![]() . Also, we write
. Also, we write
![]() $\phi \leftrightarrow \psi $
as an abbreviation for
$\phi \leftrightarrow \psi $
as an abbreviation for
![]() $\phi \to \psi \land \psi \to \phi $
.
$\phi \to \psi \land \psi \to \phi $
.
Definition 8.3. A formula of
![]() $\mathcal {L}_{\mathtt {IPC}}^\otimes $
is standard if it does not contain the symbol
$\mathcal {L}_{\mathtt {IPC}}^\otimes $
is standard if it does not contain the symbol
![]() $\vee $
. We write
$\vee $
. We write
![]() $\mathcal {L}_{\mathtt {CL}}$
for the signature
$\mathcal {L}_{\mathtt {CL}}$
for the signature
![]() $\mathcal {L}_{\mathtt {CL}}=\{ \land , \to , \bot ,\top \}$
and for the set of formulas determined by it. Similarly, we write
$\mathcal {L}_{\mathtt {CL}}=\{ \land , \to , \bot ,\top \}$
and for the set of formulas determined by it. Similarly, we write
![]() $\mathcal {L}_{\mathtt {CL}}^\otimes $
for the signature
$\mathcal {L}_{\mathtt {CL}}^\otimes $
for the signature
![]() $\mathcal {L}_{\mathtt {CL}}^\otimes =\{ \land , \to , \otimes , \bot ,\top \}$
and for its corresponding set of formulas.
$\mathcal {L}_{\mathtt {CL}}^\otimes =\{ \land , \to , \otimes , \bot ,\top \}$
and for its corresponding set of formulas.
We recall briefly the standard semantics of inquisitive and dependence logic, i.e., their team (or state) semantics. Intuitively, while in the standard semantics of classical propositional logic a formula is evaluated by a truth-table, i.e., by an assignment of atomic variables into
![]() $\{0,1\}$
, in the classical version of team semantics it is evaluated by a set of such assignments. Similarly, while in the standard semantics of intuitionistic propositional logic a formula is evaluated at a node of a poset, in the intuitionistic version of team semantics it is evaluated by a set of such nodes. We make this idea precise via the following definitions from [Reference Ciardelli, Iemhoff and Yang11].
$\{0,1\}$
, in the classical version of team semantics it is evaluated by a set of such assignments. Similarly, while in the standard semantics of intuitionistic propositional logic a formula is evaluated at a node of a poset, in the intuitionistic version of team semantics it is evaluated by a set of such nodes. We make this idea precise via the following definitions from [Reference Ciardelli, Iemhoff and Yang11].
Definition 8.4. A Kripke frame is a partial order
![]() $\mathfrak {F}=(W, R)$
. A Kripke model is a pair
$\mathfrak {F}=(W, R)$
. A Kripke model is a pair
![]() $\mathfrak {M}=(\mathfrak {F},V)$
, where
$\mathfrak {M}=(\mathfrak {F},V)$
, where
![]() $\mathfrak {F}$
is a Kripke frame and
$\mathfrak {F}$
is a Kripke frame and
![]() $V:W\rightarrow \wp (\mathsf {Var})$
is a valuation of atomic formulas such that, if
$V:W\rightarrow \wp (\mathsf {Var})$
is a valuation of atomic formulas such that, if
![]() $p\in V(w)$
and
$p\in V(w)$
and
![]() $wRv$
, then
$wRv$
, then
![]() $p\in V(v)$
. We say that a Kripke frame (resp. model)
$p\in V(v)$
. We say that a Kripke frame (resp. model)
![]() $\mathfrak {F}=(W, R)$
is classical if R is the identity relation.
$\mathfrak {F}=(W, R)$
is classical if R is the identity relation.
Definition 8.5. Let
![]() $\mathfrak {M}=(W,R,V)$
be a Kripke model. A team is a subset
$\mathfrak {M}=(W,R,V)$
be a Kripke model. A team is a subset
![]() $t\subseteq W$
of the set of possible worlds. A team s is an extension of a team t if
$t\subseteq W$
of the set of possible worlds. A team s is an extension of a team t if
![]() $s\subseteq R[t]$
.
$s\subseteq R[t]$
.
Remark 8.6. Crucially, an element in a Kripke model
![]() $(\mathfrak {F},V)$
is essentially a classical assignment, and we write
$(\mathfrak {F},V)$
is essentially a classical assignment, and we write
![]() $w(p)=1$
if and only if
$w(p)=1$
if and only if
![]() $p\in V(w)$
(when the underlying valuation V is clear from the context). This reflects the main underlying intuition that teams are essentially sets of assignments.
$p\in V(w)$
(when the underlying valuation V is clear from the context). This reflects the main underlying intuition that teams are essentially sets of assignments.
We can next define the team semantics of the formulas in
![]() $ \mathcal {L}_{\mathtt {IPC}}^\otimes $
, and thus of the classical and inquisitive variant of inquisitive and dependence logic.
$ \mathcal {L}_{\mathtt {IPC}}^\otimes $
, and thus of the classical and inquisitive variant of inquisitive and dependence logic.
Definition 8.7. Let
![]() $\mathfrak {M}=(W,R,V)$
be a Kripke model. The notion of a formula
$\mathfrak {M}=(W,R,V)$
be a Kripke model. The notion of a formula
![]() $\phi \in \mathcal {L}_{\mathtt {IPC}}^\otimes $
being true in a team
$\phi \in \mathcal {L}_{\mathtt {IPC}}^\otimes $
being true in a team
![]() $t\subseteq W$
is defined as follows:
$t\subseteq W$
is defined as follows:
 $$ \begin{align*} \begin{array}{l @{\hspace{1em}\Longleftrightarrow\hspace{1em}} l} \mathfrak{M},t\models p & {}\forall w\in t \ ( w(p)=1), \\ \mathfrak{M},t\models \bot & t=\varnothing,\\ \mathfrak{M},t\models \psi \lor \chi & \mathfrak{M},t\models \psi \text{ or } \mathfrak{M},t\models \chi,\\ \mathfrak{M},t\models \psi \land \chi & \mathfrak{M},t\models \psi \text{ and } \mathfrak{M},t\models \chi,\\ \mathfrak{M},t\models \psi \otimes \chi & \exists s,r\subseteq t \text{ such that } s\cup r = t \text{ and } \mathfrak{M},s\models \psi, \mathfrak{M},r\models \chi, \\ \mathfrak{M},t\models \psi \rightarrow \chi & \forall s \ ( \text{if }s\subseteq R[t] \text{ and } \mathfrak{M},s\models\psi \text{ then } \mathfrak{M},s\models \chi ).\\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l @{\hspace{1em}\Longleftrightarrow\hspace{1em}} l} \mathfrak{M},t\models p & {}\forall w\in t \ ( w(p)=1), \\ \mathfrak{M},t\models \bot & t=\varnothing,\\ \mathfrak{M},t\models \psi \lor \chi & \mathfrak{M},t\models \psi \text{ or } \mathfrak{M},t\models \chi,\\ \mathfrak{M},t\models \psi \land \chi & \mathfrak{M},t\models \psi \text{ and } \mathfrak{M},t\models \chi,\\ \mathfrak{M},t\models \psi \otimes \chi & \exists s,r\subseteq t \text{ such that } s\cup r = t \text{ and } \mathfrak{M},s\models \psi, \mathfrak{M},r\models \chi, \\ \mathfrak{M},t\models \psi \rightarrow \chi & \forall s \ ( \text{if }s\subseteq R[t] \text{ and } \mathfrak{M},s\models\psi \text{ then } \mathfrak{M},s\models \chi ).\\ \end{array} \end{align*} $$
If
![]() $\Gamma $
is a set of formulas, then we write
$\Gamma $
is a set of formulas, then we write
![]() $\mathfrak {M},t\models \Gamma $
if
$\mathfrak {M},t\models \Gamma $
if
![]() $\mathfrak {M},t\models \phi $
for all
$\mathfrak {M},t\models \phi $
for all
![]() $\phi \in \Gamma $
. Also, we write
$\phi \in \Gamma $
. Also, we write
![]() $\mathfrak {M}\models \phi $
if
$\mathfrak {M}\models \phi $
if
![]() $\mathfrak {M},t\models \phi $
for all
$\mathfrak {M},t\models \phi $
for all
![]() $t\subseteq W$
and we write
$t\subseteq W$
and we write
![]() $\mathfrak {F}\models \phi $
if
$\mathfrak {F}\models \phi $
if
![]() $(\mathfrak {F},V)\models \phi $
for all valuations V over W.
$(\mathfrak {F},V)\models \phi $
for all valuations V over W.
Definition 8.8. We define the following logical systems:
-
(a) the system
 $\Vdash _{\mathtt {InqI}}$
of intuitionistic inquisitive logic is the consequence relation in the language
$\Vdash _{\mathtt {InqI}}$
of intuitionistic inquisitive logic is the consequence relation in the language
 $\mathcal {L}_{\mathtt {IPC}}$
over the class of all Kripke models
$\mathcal {L}_{\mathtt {IPC}}$
over the class of all Kripke models
 $\mathfrak {M}$
, namely,
$\mathfrak {M}$
, namely,  $$ \begin{align*} \Gamma \Vdash_{\mathtt{InqI}} \phi \; \Longleftrightarrow & \; \mathfrak{M},t \models \Gamma \text{ entails } \mathfrak{M},t\models \phi \\ &\text{ for all Kripke models } \mathfrak{M} \text{ and teams } t\subseteq \mathfrak{M}; \end{align*} $$
$$ \begin{align*} \Gamma \Vdash_{\mathtt{InqI}} \phi \; \Longleftrightarrow & \; \mathfrak{M},t \models \Gamma \text{ entails } \mathfrak{M},t\models \phi \\ &\text{ for all Kripke models } \mathfrak{M} \text{ and teams } t\subseteq \mathfrak{M}; \end{align*} $$
-
(b) the system
 $\Vdash _{\mathtt {InqB}}$
of classical inquisitive logic is the consequence relation in the language
$\Vdash _{\mathtt {InqB}}$
of classical inquisitive logic is the consequence relation in the language
 $\mathcal {L}_{\mathtt {IPC}}$
over the class of all classical Kripke models
$\mathcal {L}_{\mathtt {IPC}}$
over the class of all classical Kripke models
 $\mathfrak {M}$
, namely,
$\mathfrak {M}$
, namely,  $$ \begin{align*} \Gamma \Vdash_{\mathtt{InqB}} \phi \; \Longleftrightarrow &\; \mathfrak{M},t\models \Gamma \text{ entails } \mathfrak{M},t\models \phi \\ &\text{ for all classical Kripke models } \mathfrak{M} \text{ and teams } t\subseteq \mathfrak{M}; \end{align*} $$
$$ \begin{align*} \Gamma \Vdash_{\mathtt{InqB}} \phi \; \Longleftrightarrow &\; \mathfrak{M},t\models \Gamma \text{ entails } \mathfrak{M},t\models \phi \\ &\text{ for all classical Kripke models } \mathfrak{M} \text{ and teams } t\subseteq \mathfrak{M}; \end{align*} $$
-
(c) the system
 $\Vdash _{\mathtt {InqI}^\otimes }$
of intuitionistic dependence logic is the consequence relation in the language
$\Vdash _{\mathtt {InqI}^\otimes }$
of intuitionistic dependence logic is the consequence relation in the language
 $\mathcal {L}_{\mathtt {IPC}}^\otimes $
over the class of all Kripke models
$\mathcal {L}_{\mathtt {IPC}}^\otimes $
over the class of all Kripke models
 $\mathfrak {M}$
, namely,
$\mathfrak {M}$
, namely,  $$ \begin{align*} \Gamma \Vdash_{\mathtt{InqI}^\otimes} \phi \; \Longleftrightarrow \; &\; \mathfrak{M},t\models \Gamma \text{ entails } \mathfrak{M},t \models \phi \\ & \text{ for all Kripke models } \mathfrak{M} \text{ and teams } t\subseteq \mathfrak{M}; \end{align*} $$
$$ \begin{align*} \Gamma \Vdash_{\mathtt{InqI}^\otimes} \phi \; \Longleftrightarrow \; &\; \mathfrak{M},t\models \Gamma \text{ entails } \mathfrak{M},t \models \phi \\ & \text{ for all Kripke models } \mathfrak{M} \text{ and teams } t\subseteq \mathfrak{M}; \end{align*} $$
-
(d) the system
 $\Vdash _{\mathtt {InqB}^\otimes }$
of classical dependence logic is the consequence relation in the language
$\Vdash _{\mathtt {InqB}^\otimes }$
of classical dependence logic is the consequence relation in the language
 $\mathcal {L}_{\mathtt {IPC}}^\otimes $
over the class of all classical Kripke models
$\mathcal {L}_{\mathtt {IPC}}^\otimes $
over the class of all classical Kripke models
 $\mathfrak {M}$
, namely,
$\mathfrak {M}$
, namely,  $$ \begin{align*} \Gamma \Vdash_{\mathtt{InqB}^\otimes} \phi \; \Longleftrightarrow \; & \mathfrak{M},t\models \Gamma \text{ entails } \mathfrak{M},t \models \phi \\ & \text{for all classical Kripke models } \mathfrak{M} \text{ and teams } t\subseteq \mathfrak{M}. \end{align*} $$
$$ \begin{align*} \Gamma \Vdash_{\mathtt{InqB}^\otimes} \phi \; \Longleftrightarrow \; & \mathfrak{M},t\models \Gamma \text{ entails } \mathfrak{M},t \models \phi \\ & \text{for all classical Kripke models } \mathfrak{M} \text{ and teams } t\subseteq \mathfrak{M}. \end{align*} $$
Remark 8.9. Notice that in [Reference Ciardelli, Iemhoff and Yang11] the previous systems were introduced simply as the sets of validities of the consequence relations from Definition 8.8. However this does not really make a difference, since these logics are all finitary and satisfy the deduction theorem. In particular, the fact that each of the previous consequence relations is finitary follows from [Reference Ciardelli, Iemhoff and Yang11, Corollary 4.22], while the deduction theorem is essentially [Reference Ciardelli, Iemhoff and Yang11, Proposition 4.3]. It then follows that, for any
![]() $L\in \{ \mathtt {InqB},\mathtt {InqB}^\otimes ,\mathtt {InqI}, \mathtt {InqI}^\otimes \}$
,
$L\in \{ \mathtt {InqB},\mathtt {InqB}^\otimes ,\mathtt {InqI}, \mathtt {InqI}^\otimes \}$
,
showing that each consequence relation
![]() $\Vdash _{L} $
is determined by its set of validities.
$\Vdash _{L} $
is determined by its set of validities.
The next proposition makes it explicit that these logics are proper examples of weak logics. The failure of uniform substitution in these logics has been pointed out since their introduction in [Reference Ciardelli, Iemhoff and Yang11, Reference Ciardelli and Roelofsen12, Reference Yang and Väänänen30]. We provide details of the following proposition (which essentially develops Example 3.5) for completeness of exposition, and since the lack of uniform substitution provides the key motivation of our abstract work.
Proposition 8.10. Let
![]() $L\in \{ \mathtt {InqB},\mathtt {InqB}^\otimes ,\mathtt {InqI}, \mathtt {InqI}^\otimes \}$
, then
$L\in \{ \mathtt {InqB},\mathtt {InqB}^\otimes ,\mathtt {InqI}, \mathtt {InqI}^\otimes \}$
, then
![]() $\Vdash _{L}$
is a weak logic, and it is not closed under uniform substitution.
$\Vdash _{L}$
is a weak logic, and it is not closed under uniform substitution.
Proof. Let
![]() $L\in \{ \mathtt {InqB},\mathtt {InqB}^\otimes ,\mathtt {InqI}, \mathtt {InqI}^\otimes \}$
, then the fact that
$L\in \{ \mathtt {InqB},\mathtt {InqB}^\otimes ,\mathtt {InqI}, \mathtt {InqI}^\otimes \}$
, then the fact that
![]() $\Vdash _{L}$
satisfies Conditions (1)–(3) from Definition 2.2 follows from the definition of the semantic consequence relation
$\Vdash _{L}$
satisfies Conditions (1)–(3) from Definition 2.2 follows from the definition of the semantic consequence relation
![]() $\models $
from Definition 8.7. Condition (4) follows from Remark 8.9 (thus in particular from [Reference Ciardelli, Iemhoff and Yang11, Corollary 4.22]). Finally, the fact that
$\models $
from Definition 8.7. Condition (4) follows from Remark 8.9 (thus in particular from [Reference Ciardelli, Iemhoff and Yang11, Corollary 4.22]). Finally, the fact that
![]() $\Vdash _{L}$
is closed under atomic substitution is immediate to verify using the team semantics from above.
$\Vdash _{L}$
is closed under atomic substitution is immediate to verify using the team semantics from above.
It remains to show that
![]() $\Vdash _{L}$
is not closed under uniform substitution. We prove this rigorously only for
$\Vdash _{L}$
is not closed under uniform substitution. We prove this rigorously only for
![]() $\mathtt {InqB}$
and
$\mathtt {InqB}$
and
![]() $\mathtt {InqB}^\otimes $
and mention an example that applies also to
$\mathtt {InqB}^\otimes $
and mention an example that applies also to
![]() $\mathtt {InqI}$
and
$\mathtt {InqI}$
and
![]() $ \mathtt {InqI}^\otimes $
below in Remark 8.11. Suppose thus
$ \mathtt {InqI}^\otimes $
below in Remark 8.11. Suppose thus
![]() $L\in \{ \mathtt {InqB},\mathtt {InqB}^\otimes \}$
, we formalize the model that we sketched in Example 3.5. Let
$L\in \{ \mathtt {InqB},\mathtt {InqB}^\otimes \}$
, we formalize the model that we sketched in Example 3.5. Let
![]() $\mathfrak {F}=(\{a,b,c,d\},=)$
be a classical Kripke frame, let
$\mathfrak {F}=(\{a,b,c,d\},=)$
be a classical Kripke frame, let
![]() $V:\mathsf {Var}\to \wp (\mathfrak {F})$
be a valuation such that
$V:\mathsf {Var}\to \wp (\mathfrak {F})$
be a valuation such that
![]() $V(p)=\{a,b\}$
and let
$V(p)=\{a,b\}$
and let
![]() $\mathfrak {M}=(\mathfrak {F},V)$
.
$\mathfrak {M}=(\mathfrak {F},V)$
.
Firstly, we use the team semantics from Definition 8.7 to show that
![]() $\mathfrak {M},\{b,d\}\models \neg \neg ?p$
. Suppose on the contrary that there is a team
$\mathfrak {M},\{b,d\}\models \neg \neg ?p$
. Suppose on the contrary that there is a team
![]() $t \subseteq \{b,d\}$
such that
$t \subseteq \{b,d\}$
such that
![]() $\mathfrak {M},t\models \neg ?p$
. Then, we have in particular that either
$\mathfrak {M},t\models \neg ?p$
. Then, we have in particular that either
![]() $\mathfrak {M},\{b\}\not \models ?p$
or
$\mathfrak {M},\{b\}\not \models ?p$
or
![]() $\mathfrak {M},\{d\}\not \models ?p$
, which are clearly false. We thus conclude that
$\mathfrak {M},\{d\}\not \models ?p$
, which are clearly false. We thus conclude that
![]() $\mathfrak {M},\{b,d\}\models \neg \neg ?p$
. Additionally, we notice that
$\mathfrak {M},\{b,d\}\models \neg \neg ?p$
. Additionally, we notice that
![]() $\mathfrak {M},\{b,d\}\not \models ?p$
. In fact,
$\mathfrak {M},\{b,d\}\not \models ?p$
. In fact,
![]() $\mathfrak {M},\{b,d\}\not \models p$
since
$\mathfrak {M},\{b,d\}\not \models p$
since
![]() $d(p)=0$
, and
$d(p)=0$
, and
![]() $\mathfrak {M},\{b,d\}\not \models \neg p$
since
$\mathfrak {M},\{b,d\}\not \models \neg p$
since
![]() $b(p)=1$
. This shows that
$b(p)=1$
. This shows that
![]() $\neg \neg ?p \not \Vdash _{\mathtt {InqB}} ?p $
and
$\neg \neg ?p \not \Vdash _{\mathtt {InqB}} ?p $
and
![]() $\neg \neg ?p \not \Vdash _{\mathtt {InqB}^\otimes } ?p $
.
$\neg \neg ?p \not \Vdash _{\mathtt {InqB}^\otimes } ?p $
.
However, suppose that
![]() $(\mathfrak {M},t)\models \neg \neg p$
for some classical Kripke model
$(\mathfrak {M},t)\models \neg \neg p$
for some classical Kripke model
![]() $\mathfrak {M}=(W,R,V)$
and
$\mathfrak {M}=(W,R,V)$
and
![]() $t\subseteq W$
. Then for every
$t\subseteq W$
. Then for every
![]() $w\in t$
we have
$w\in t$
we have
![]() $(\mathfrak {M},\{w\})\not \models \neg p$
, which entails that
$(\mathfrak {M},\{w\})\not \models \neg p$
, which entails that
![]() $w(p)=1$
for all
$w(p)=1$
for all
![]() $w\in t$
, and thus that
$w\in t$
, and thus that
![]() $(\mathfrak {M},t)\models p$
. In other words, we proved that
$(\mathfrak {M},t)\models p$
. In other words, we proved that
![]() $\neg \neg p \Vdash _{L} p$
in any of the logics
$\neg \neg p \Vdash _{L} p$
in any of the logics
![]() $L\in \{ \mathtt {InqB},\mathtt {InqB}^\otimes \}$
. We conclude that
$L\in \{ \mathtt {InqB},\mathtt {InqB}^\otimes \}$
. We conclude that
![]() $\mathtt {InqB}$
and
$\mathtt {InqB}$
and
![]() $\mathtt {InqB}^\otimes $
are not closed under the substitution
$\mathtt {InqB}^\otimes $
are not closed under the substitution
![]() $p\mapsto ?p$
.
$p\mapsto ?p$
.
Remark 8.11. We mention a counterexample to uniform substitution that applies to all
![]() $L\in \{ \mathtt {InqB},\mathtt {InqB}^\otimes ,\mathtt {InqI}, \mathtt {InqI}^\otimes \}$
. One can verify that:
$L\in \{ \mathtt {InqB},\mathtt {InqB}^\otimes ,\mathtt {InqI}, \mathtt {InqI}^\otimes \}$
. One can verify that:
but the result of the substitution
![]() $p\mapsto q\lor r$
is not a validity of these logics:
$p\mapsto q\lor r$
is not a validity of these logics:
We refer the reader to [Reference Ciardelli, Iemhoff and Yang11, 4.5] for an explanation of this fact and a lengthier discussion of the failure of uniform substitution in propositional inquisitive and dependence logic.
8.2 Strict algebraizability of
 $\mathtt {InqB}$
and
$\mathtt {InqB}$
and
 $\mathtt {InqB}^\otimes $
$\mathtt {InqB}^\otimes $
We prove in this section the strict algebraizability of the classical versions of inquisitive and dependence logic. We recall some important facts and definitions.
Definition 8.12. A Heyting algebra H is a bounded distributive lattice with an operation
![]() $\to $
such that, for all
$\to $
such that, for all
![]() $a,b,c\in H$
,
$a,b,c\in H$
,
where
![]() ${\leqslant }$
is the lattice order. The negation of
${\leqslant }$
is the lattice order. The negation of
![]() $a\in H$
is
$a\in H$
is
![]() $\neg a:= a\to \bot $
. An element
$\neg a:= a\to \bot $
. An element
![]() $a\in H$
is regular if
$a\in H$
is regular if
![]() $a = \neg \neg a $
. We write
$a = \neg \neg a $
. We write
![]() $H_\neg $
for the subset of regular elements of H, and we say that a Heyting algebra H is regular if
$H_\neg $
for the subset of regular elements of H, and we say that a Heyting algebra H is regular if
![]() $H=\langle H_\neg \rangle $
. We say that a variety
$H=\langle H_\neg \rangle $
. We say that a variety
![]() $\mathbf {V}$
of Heyting algebras is regularly generated if it is core-generated with
$\mathbf {V}$
of Heyting algebras is regularly generated if it is core-generated with
![]() $\mathsf {core}(H)=H_\neg $
for all
$\mathsf {core}(H)=H_\neg $
for all
![]() $H\in \mathbf {V}$
.
$H\in \mathbf {V}$
.
Remark 8.13. We recall that an intermediate logic is a standard logic
![]() $\mathtt {L}$
such that
$\mathtt {L}$
such that
![]() $\mathtt {IPC}\subseteq \mathtt {L}\subseteq \mathtt {CPC}$
, where
$\mathtt {IPC}\subseteq \mathtt {L}\subseteq \mathtt {CPC}$
, where
![]() $\mathtt {IPC}$
denotes the intuitionistic propositional calculus, and
$\mathtt {IPC}$
denotes the intuitionistic propositional calculus, and
![]() $\mathtt {CPC}$
the classical propositional calculus. Every intermediate logic
$\mathtt {CPC}$
the classical propositional calculus. Every intermediate logic
![]() $\mathtt {L}$
is algebraized by the variety of Heyting algebras
$\mathtt {L}$
is algebraized by the variety of Heyting algebras
![]() $\mathrm {Var}(\mathtt {L})$
defined by
$\mathrm {Var}(\mathtt {L})$
defined by
and by the transformers
![]() $(\tau , \Delta )$
given by
$(\tau , \Delta )$
given by
![]() $\tau (\phi )=(\phi \approx 1)$
and
$\tau (\phi )=(\phi \approx 1)$
and
![]() $\Delta (\alpha ,\beta )=\alpha \leftrightarrow \beta $
(cf. [Reference Font16, Example 3.34]).
$\Delta (\alpha ,\beta )=\alpha \leftrightarrow \beta $
(cf. [Reference Font16, Example 3.34]).
The following two definitions are less standard. First, we recall the
![]() $\mathtt {DNA}$
-logics from Example 3.5. Negative variants were originally considered in [Reference Miglioli, Moscato, Ornaghi, Quazza and Usberti22].
$\mathtt {DNA}$
-logics from Example 3.5. Negative variants were originally considered in [Reference Miglioli, Moscato, Ornaghi, Quazza and Usberti22].
Definition 8.14. Let
![]() $\mathtt {L}$
be an intermediate logic, then its negative variant
$\mathtt {L}$
be an intermediate logic, then its negative variant
![]() $\mathtt {L}^\neg $
is the set of formulas
$\mathtt {L}^\neg $
is the set of formulas
![]() $\mathtt {L}^\neg =\{ \phi [\neg p_0,\dots ,\neg p_n/p_0,\dots ,p_n] : \phi \in \mathcal {L}_{\mathtt {IPC}} \text { and } \vdash _{\mathtt {L}} \phi \}$
. A
$\mathtt {L}^\neg =\{ \phi [\neg p_0,\dots ,\neg p_n/p_0,\dots ,p_n] : \phi \in \mathcal {L}_{\mathtt {IPC}} \text { and } \vdash _{\mathtt {L}} \phi \}$
. A
![]() $\mathtt {DNA}$
-logic is the negative variant of some intermediate logic.
$\mathtt {DNA}$
-logic is the negative variant of some intermediate logic.
Additionally, we recall Medvedev’s logic of finite problems, which was originally introduced by Medvedev in [Reference Medvedev21]. This is an intermediate logic defined in terms of validity in a specific class of Kripke frames. We direct the reader to [Reference Chagrov and Zakharyaschev8, Section 2.2] for details about the Kripke semantics of intermediate logics.
Definition 8.15. We recall that the intermediate logic
![]() $\mathtt {ML}$
, known as Medvedev’s logic of finite problems, is the logic of all Kripke frames of the form
$\mathtt {ML}$
, known as Medvedev’s logic of finite problems, is the logic of all Kripke frames of the form
![]() $(\wp ^+(s),\supseteq )$
, where s is a finite set and
$(\wp ^+(s),\supseteq )$
, where s is a finite set and
![]() $\wp ^+(s)=\wp (s){\setminus }\{\emptyset \}$
.
$\wp ^+(s)=\wp (s){\setminus }\{\emptyset \}$
.
The next fact collects together some results by Ciardelli [Reference Ciardelli10] on the schematic variant of
![]() $\mathtt {InqB}$
, and the characterization of regularly generated varieties from [Reference Bezhanishvili, Grilletti and Quadrellaro3]. From these it is then immediate to prove the strict algebraizability of
$\mathtt {InqB}$
, and the characterization of regularly generated varieties from [Reference Bezhanishvili, Grilletti and Quadrellaro3]. From these it is then immediate to prove the strict algebraizability of
![]() $\mathtt {InqB}$
.
$\mathtt {InqB}$
.
Fact 8.16.
-
(1)
 $\mathtt {ML}^\neg =\mathtt {InqB}$
and
$\mathtt {ML}^\neg =\mathtt {InqB}$
and
 $\mathrm {Schm}(\mathtt {InqB})=\mathtt {ML}$
.
$\mathrm {Schm}(\mathtt {InqB})=\mathtt {ML}$
. -
(2)
 $\mathrm {Var}(\mathtt {ML})$
is regularly generated.
$\mathrm {Var}(\mathtt {ML})$
is regularly generated. -
(3) Let
 $\tau (\phi )=(\phi \approx 1)$
for all
$\tau (\phi )=(\phi \approx 1)$
for all
 $\phi \in \mathsf {Fm}$
, then for all
$\phi \in \mathsf {Fm}$
, then for all
 $\Gamma \cup \{ \phi \} \subseteq \mathcal {L}_{\mathtt {IPC}}$
,
$\Gamma \cup \{ \phi \} \subseteq \mathcal {L}_{\mathtt {IPC}}$
,
 $\Gamma \Vdash _{\mathtt {InqB}} \phi $
is equivalent to
$\Gamma \Vdash _{\mathtt {InqB}} \phi $
is equivalent to
 $ \tau (\Gamma ) \models ^c_{\mathrm {Var}(\mathtt {ML})} \tau (\phi )$
, where
$ \tau (\Gamma ) \models ^c_{\mathrm {Var}(\mathtt {ML})} \tau (\phi )$
, where
 $\mathsf {core}(H)=H_\neg $
for all
$\mathsf {core}(H)=H_\neg $
for all
 $H\in \mathrm {Var}(\mathtt {ML})$
.
$H\in \mathrm {Var}(\mathtt {ML})$
.
Proof. Considering Clause (1), both
![]() $\mathtt {ML}^\neg =\mathtt {InqB}$
and
$\mathtt {ML}^\neg =\mathtt {InqB}$
and
![]() $\mathrm {Schm}(\mathtt {InqB})=\mathtt {ML}$
were proved by Ciardelli in [Reference Ciardelli10]. Clause (2) follows immediately from (1) together with Proposition 4.17 from [Reference Bezhanishvili, Grilletti and Quadrellaro3]. Clause (3) is essentially the main algebraic completeness result for inquisitive logic shown in [Reference Bezhanishvili, Grilletti and Holliday2] (and later in [Reference Bezhanishvili, Grilletti and Quadrellaro3]). However, in these articles completeness is formulated with respect to the intermediate logics
$\mathrm {Schm}(\mathtt {InqB})=\mathtt {ML}$
were proved by Ciardelli in [Reference Ciardelli10]. Clause (2) follows immediately from (1) together with Proposition 4.17 from [Reference Bezhanishvili, Grilletti and Quadrellaro3]. Clause (3) is essentially the main algebraic completeness result for inquisitive logic shown in [Reference Bezhanishvili, Grilletti and Holliday2] (and later in [Reference Bezhanishvili, Grilletti and Quadrellaro3]). However, in these articles completeness is formulated with respect to the intermediate logics
![]() $\mathtt {KP}$
and
$\mathtt {KP}$
and
![]() $\mathtt {ND}$
, thus we explain how to obtain completeness with respect to
$\mathtt {ND}$
, thus we explain how to obtain completeness with respect to
![]() $\mathrm {Var}(\mathtt {ML})$
as stated in (3). Firstly, by Theorem 3.32 in [Reference Bezhanishvili, Grilletti and Quadrellaro3] we have that
$\mathrm {Var}(\mathtt {ML})$
as stated in (3). Firstly, by Theorem 3.32 in [Reference Bezhanishvili, Grilletti and Quadrellaro3] we have that
![]() $\Gamma \models _{\mathtt {InqB}} \phi $
is equivalent to
$\Gamma \models _{\mathtt {InqB}} \phi $
is equivalent to
![]() $ \Gamma \models ^c_{\mathrm {Var}(\mathtt {ND})} \phi $
, where
$ \Gamma \models ^c_{\mathrm {Var}(\mathtt {ND})} \phi $
, where
![]() $\mathtt {ND}$
is a specific intermediate logic and
$\mathtt {ND}$
is a specific intermediate logic and
![]() $\mathsf {core}(H)=H_\neg $
for all
$\mathsf {core}(H)=H_\neg $
for all
![]() $H\in \mathrm {Var}(\mathtt {ND})$
. Additionally, it follows from [Reference Bezhanishvili, Grilletti and Quadrellaro3, Theorem 5.9] that
$H\in \mathrm {Var}(\mathtt {ND})$
. Additionally, it follows from [Reference Bezhanishvili, Grilletti and Quadrellaro3, Theorem 5.9] that
![]() $\mathtt {ND}$
and
$\mathtt {ND}$
and
![]() $\mathtt {ML}$
contain the same regularly generated Heyting algebras. It then follows from Proposition 3.26 that
$\mathtt {ML}$
contain the same regularly generated Heyting algebras. It then follows from Proposition 3.26 that
![]() $\Gamma \Vdash _{\mathtt {InqB}} \phi $
is equivalent to
$\Gamma \Vdash _{\mathtt {InqB}} \phi $
is equivalent to
![]() $\Gamma \models ^c_{\mathrm {Var}(\mathtt {ML})} \phi $
.
$\Gamma \models ^c_{\mathrm {Var}(\mathtt {ML})} \phi $
.
Theorem 8.17.
![]() $\mathtt {InqB}$
is strictly algebraizable.
$\mathtt {InqB}$
is strictly algebraizable.
Proof. Let
![]() $\tau (\phi )= \phi \approx 1$
,
$\tau (\phi )= \phi \approx 1$
,
![]() $\Delta (x,y)=x\leftrightarrow y,$
and
$\Delta (x,y)=x\leftrightarrow y,$
and
![]() $\Sigma =\{ x\approx \neg \neg x \}$
. We prove that
$\Sigma =\{ x\approx \neg \neg x \}$
. We prove that
![]() $(\mathrm {Var}(\mathtt {ML}), \Sigma , \tau ,\Delta )$
strictly algebraizes
$(\mathrm {Var}(\mathtt {ML}), \Sigma , \tau ,\Delta )$
strictly algebraizes
![]() $\mathtt {InqB}$
. Firstly, by Fact 8.16(2) above we have that
$\mathtt {InqB}$
. Firstly, by Fact 8.16(2) above we have that
![]() $\mathrm {Var}(\mathtt {ML})$
is core-generated with core defined by
$\mathrm {Var}(\mathtt {ML})$
is core-generated with core defined by
![]() $\Sigma $
. Then, by Proposition 4.8 it suffices to show that
$\Sigma $
. Then, by Proposition 4.8 it suffices to show that
![]() $(\mathrm {Var}(\mathtt {ML}), x\approx \neg \neg x, \phi \approx 1, x\leftrightarrow y)$
satisfies 4.6(W1) and 4.6(W4). By Fact 8.16(3), Condition 4.6(W1) follows immediately. Moreover, for all
$(\mathrm {Var}(\mathtt {ML}), x\approx \neg \neg x, \phi \approx 1, x\leftrightarrow y)$
satisfies 4.6(W1) and 4.6(W4). By Fact 8.16(3), Condition 4.6(W1) follows immediately. Moreover, for all
![]() $H\in \mathrm {Var}(\mathtt {ML}) $
and
$H\in \mathrm {Var}(\mathtt {ML}) $
and
![]() $x,y\in H$
, we have that
$x,y\in H$
, we have that
![]() $x=y$
if and only if
$x=y$
if and only if
![]() $x{\leqslant } y$
and
$x{\leqslant } y$
and
![]() $y{\leqslant } x$
. This is equivalent to
$y{\leqslant } x$
. This is equivalent to
![]() $H\models x\to y \approx 1 $
and
$H\models x\to y \approx 1 $
and
![]() $H\models y\to x\approx 1$
. It follows that
$H\models y\to x\approx 1$
. It follows that
![]() $x\approx y\equiv ^c_{\mathrm {Var}(\mathtt {ML})} \{x\to y\approx 1, y\to x\approx 1 \}$
, showing that 4.6(W4) holds. It follows that
$x\approx y\equiv ^c_{\mathrm {Var}(\mathtt {ML})} \{x\to y\approx 1, y\to x\approx 1 \}$
, showing that 4.6(W4) holds. It follows that
![]() $\mathtt {InqB}$
is strictly algebraizable.
$\mathtt {InqB}$
is strictly algebraizable.
To extend the previous theorem to dependence logic, we firstly need to introduce a suitable notion of dependence algebras. We refer the reader to [Reference Burris and Sankappanavar5, p. 57] for the definition of subdirectly irreducible algebra.
Definition 8.18. An
![]() $\mathtt {InqB}^\otimes $
-algebra A is a structure in the signature
$\mathtt {InqB}^\otimes $
-algebra A is a structure in the signature
![]() $\mathcal {L}_{\mathtt {IPC}}^\otimes $
satisfying the following conditions:
$\mathcal {L}_{\mathtt {IPC}}^\otimes $
satisfying the following conditions:
-
(a)
 $A{ \upharpoonright } \{\lor ,\land ,\to , \bot \} \in \mathrm {Var}(\mathtt {ML}) $
;
$A{ \upharpoonright } \{\lor ,\land ,\to , \bot \} \in \mathrm {Var}(\mathtt {ML}) $
; -
(b)
 $A_\neg { \upharpoonright } \{\otimes ,\land ,\to , \bot \} \in \mathbf {BA}$
;
$A_\neg { \upharpoonright } \{\otimes ,\land ,\to , \bot \} \in \mathbf {BA}$
; -
(c)
 $ A \models \forall x \forall y \forall z \; (x \otimes (y \lor z) \approx (x\otimes y) \lor (x\otimes z)) $
;
$ A \models \forall x \forall y \forall z \; (x \otimes (y \lor z) \approx (x\otimes y) \lor (x\otimes z)) $
; -
(d)
 $ A \models \forall x \forall y \forall z \forall k \; ((x\to z) \to (y \to k) \approx (x\otimes y) \to (z\otimes k)) $
;
$ A \models \forall x \forall y \forall z \forall k \; ((x\to z) \to (y \to k) \approx (x\otimes y) \to (z\otimes k)) $
;
we then let
![]() $ \mathsf {InqBAlg^\otimes } $
be the variety of all
$ \mathsf {InqBAlg^\otimes } $
be the variety of all
![]() $\mathtt {InqB}^\otimes $
-algebras and
$\mathtt {InqB}^\otimes $
-algebras and
![]() $ \mathsf {InqBAlg^\otimes _{FRSI}} $
be its subclass of finite, regular, and subdirectly irreducible elements.
$ \mathsf {InqBAlg^\otimes _{FRSI}} $
be its subclass of finite, regular, and subdirectly irreducible elements.
Remark 8.19. Our definition is essentially from [Reference Quadrellaro26, Definition 2.2], with the difference that here we assume that the equations hold in the full algebra and not only in the subalgebra generated by the core. Since our results deal with core semantics and core-generated structure, this does not affect the validity of the results from [Reference Quadrellaro26].
The previous class of algebras was shown to provide a sound and complete semantics for
![]() $\mathtt {InqB}^\otimes $
. We recall the following fact from [Reference Quadrellaro26, Theorem 2.15, Theorem 3.20] and use it to show that
$\mathtt {InqB}^\otimes $
. We recall the following fact from [Reference Quadrellaro26, Theorem 2.15, Theorem 3.20] and use it to show that
![]() $\mathtt {InqB}^\otimes $
is strictly algebraizable. Notice that, since
$\mathtt {InqB}^\otimes $
is strictly algebraizable. Notice that, since
![]() $A{ \upharpoonright } \{\lor ,\land ,\to , \bot \} \in \mathrm {Var}(\mathtt {ML}) $
, for
$A{ \upharpoonright } \{\lor ,\land ,\to , \bot \} \in \mathrm {Var}(\mathtt {ML}) $
, for
![]() $A\in \mathsf {InqBAlg^\otimes }$
, it follows that the notion of regular elements and the subset
$A\in \mathsf {InqBAlg^\otimes }$
, it follows that the notion of regular elements and the subset
![]() $A_\neg $
are well defined in this context.
$A_\neg $
are well defined in this context.
Fact 8.20. Let
![]() $\tau (\phi )=(\phi \approx 1)$
for all
$\tau (\phi )=(\phi \approx 1)$
for all
![]() $\phi \in \mathsf {Fm}$
, then for all
$\phi \in \mathsf {Fm}$
, then for all
![]() $\Gamma \cup \{ \phi \} \subseteq \mathcal {L}_{\mathtt {IPC}}^\otimes $
, we have
$\Gamma \cup \{ \phi \} \subseteq \mathcal {L}_{\mathtt {IPC}}^\otimes $
, we have
![]() $\Gamma \Vdash _{\mathtt {InqB}^\otimes } \phi $
if and only if
$\Gamma \Vdash _{\mathtt {InqB}^\otimes } \phi $
if and only if
![]() $ \tau (\Gamma ) \models ^c_{\mathsf {InqBAlg^\otimes _{FRSI}}} \tau (\phi )$
, where
$ \tau (\Gamma ) \models ^c_{\mathsf {InqBAlg^\otimes _{FRSI}}} \tau (\phi )$
, where
![]() $\mathsf {core}(A)=A_\neg $
for all
$\mathsf {core}(A)=A_\neg $
for all
![]() $A\in \mathsf {InqBAlg^\otimes _{FRSI}}$
.
$A\in \mathsf {InqBAlg^\otimes _{FRSI}}$
.
Theorem 8.21.
![]() $\mathtt {InqB}^\otimes $
is strictly algebraizable.
$\mathtt {InqB}^\otimes $
is strictly algebraizable.
Proof. This follows from Fact 8.20 analogously to Theorem 8.17, by choosing for equivalent algebraic semantics the variety
![]() $ \mathbb {V}(\mathsf {InqBAlg^\otimes _{FRSI}})$
, the transformers
$ \mathbb {V}(\mathsf {InqBAlg^\otimes _{FRSI}})$
, the transformers
![]() $\tau (\phi ):= \phi \approx 1$
and
$\tau (\phi ):= \phi \approx 1$
and
![]() $\Delta (x,y)=x\rightarrow y \land y\rightarrow x$
, and the finite set of formulas defining the core
$\Delta (x,y)=x\rightarrow y \land y\rightarrow x$
, and the finite set of formulas defining the core
![]() $\Sigma =\{ x\approx \neg \neg x \}$
.
$\Sigma =\{ x\approx \neg \neg x \}$
.
8.3 Loose algebraizability of
 $\mathtt {InqI}$
and
$\mathtt {InqI}$
and
 $\mathtt {InqI}^\otimes $
$\mathtt {InqI}^\otimes $
We show in this section that
![]() $\mathtt {InqI}$
and
$\mathtt {InqI}$
and
![]() $\mathtt {InqI}^\otimes $
are both loosely algebraizable, but they are not strictly so. The loose algebraizability of these logics is essentially a corollary of the algebraic completeness result from [Reference Quadrellaro26]. We start by introducing the algebraic semantics for
$\mathtt {InqI}^\otimes $
are both loosely algebraizable, but they are not strictly so. The loose algebraizability of these logics is essentially a corollary of the algebraic completeness result from [Reference Quadrellaro26]. We start by introducing the algebraic semantics for
![]() $\mathtt {InqI}$
and
$\mathtt {InqI}$
and
![]() $\mathtt {InqI}^\otimes $
described in [Reference Quadrellaro26]. As in Definition 8.18 we slightly modify the definitions from [Reference Quadrellaro26] so that the equations defining
$\mathtt {InqI}^\otimes $
described in [Reference Quadrellaro26]. As in Definition 8.18 we slightly modify the definitions from [Reference Quadrellaro26] so that the equations defining
![]() $\mathtt {InqI}$
-algebras and
$\mathtt {InqI}$
-algebras and
![]() $\mathtt {InqI}^\otimes $
-algebra are valid in the entire structure and not only in the subalgebra generated by the core. As stressed in Remark 8.19, this does not affect the validity of the completeness results from [Reference Quadrellaro26].
$\mathtt {InqI}^\otimes $
-algebra are valid in the entire structure and not only in the subalgebra generated by the core. As stressed in Remark 8.19, this does not affect the validity of the completeness results from [Reference Quadrellaro26].
Definition 8.22. A Brouwerian semilattice B is a bounded join-semilattice with an additional operation
![]() $\to $
such that, for all
$\to $
such that, for all
![]() $a,b,c\in B$
,
$a,b,c\in B$
,
and we write BS for the class of all Browerian semilattices.
Definition 8.23. An
![]() $\mathtt {InqI}$
-algebra A is an expanded algebra in the signature
$\mathtt {InqI}$
-algebra A is an expanded algebra in the signature
![]() $\mathcal {L}_{\mathtt {IPC}}$
satisfying the following conditions:
$\mathcal {L}_{\mathtt {IPC}}$
satisfying the following conditions:
-
(a)
 $A{ \upharpoonright } \{\lor ,\land ,\to , \bot \} \in \mathbf {HA} $
;
$A{ \upharpoonright } \{\lor ,\land ,\to , \bot \} \in \mathbf {HA} $
; -
(b)
 $\mathsf {core}(A) { \upharpoonright } \{\land ,\to , \bot \}\in \mathbf {BS} $
;
$\mathsf {core}(A) { \upharpoonright } \{\land ,\to , \bot \}\in \mathbf {BS} $
; -
(c)
 $A\models \forall x \forall y \forall a \; (\mathsf {core}(a) \to (a \rightarrow (x \lor y) \approx (a \rightarrow x)\lor (a \rightarrow y)))$
;
$A\models \forall x \forall y \forall a \; (\mathsf {core}(a) \to (a \rightarrow (x \lor y) \approx (a \rightarrow x)\lor (a \rightarrow y)))$
;
and we then write
![]() $ \mathsf {InqIAlg} $
for the class of all
$ \mathsf {InqIAlg} $
for the class of all
![]() $\mathtt {InqI}$
-algebras.
$\mathtt {InqI}$
-algebras.
Definition 8.24. An
![]() $\mathtt {InqI}^\otimes $
-algebra A is an expanded algebra in the signature
$\mathtt {InqI}^\otimes $
-algebra A is an expanded algebra in the signature
![]() $\mathcal {L}_{\mathtt {IPC}}^\otimes $
satisfying the following conditions:
$\mathcal {L}_{\mathtt {IPC}}^\otimes $
satisfying the following conditions:
-
(a)
 $A{ \upharpoonright } \{\lor ,\land ,\to , \bot \} \in \mathbf {HA} $
;
$A{ \upharpoonright } \{\lor ,\land ,\to , \bot \} \in \mathbf {HA} $
; -
(b)
 $\mathsf {core}(A) { \upharpoonright } \{\land ,\otimes \to , \bot \}\in \mathbf {HA} $
;
$\mathsf {core}(A) { \upharpoonright } \{\land ,\otimes \to , \bot \}\in \mathbf {HA} $
; -
(c)
 $A\models \forall x \forall y \forall a \; (\mathsf {core}(a) \to (a \rightarrow (x \lor y) \approx (a \rightarrow x)\lor (a \rightarrow y)))$
;
$A\models \forall x \forall y \forall a \; (\mathsf {core}(a) \to (a \rightarrow (x \lor y) \approx (a \rightarrow x)\lor (a \rightarrow y)))$
; -
(d)
 $ A \models \forall x \forall y \forall z \; (x \otimes (y \lor z) \approx (x\otimes y) \lor (x\otimes z)) $
;
$ A \models \forall x \forall y \forall z \; (x \otimes (y \lor z) \approx (x\otimes y) \lor (x\otimes z)) $
; -
(e)
 $ A \models \forall x \forall y \forall z \forall k \; ((x\to z) \to (y \to k) \approx (x\otimes y) \to (z\otimes k)) $
;
$ A \models \forall x \forall y \forall z \forall k \; ((x\to z) \to (y \to k) \approx (x\otimes y) \to (z\otimes k)) $
;
and we then write
![]() $ \mathsf {InqIAlg^\otimes } $
for the class of all
$ \mathsf {InqIAlg^\otimes } $
for the class of all
![]() $\mathtt {InqI}^\otimes $
-algebras.
$\mathtt {InqI}^\otimes $
-algebras.
We next recall the algebraic completeness result for intuitionistic inquisitive and dependence logic. This follows immediately from [Reference Quadrellaro26, Proposition 2.15]. From this, it is immediately to show that both
![]() $\mathtt {InqI}$
and
$\mathtt {InqI}$
and
![]() $\mathtt {InqI}^\otimes $
are loosely algebraizable.
$\mathtt {InqI}^\otimes $
are loosely algebraizable.
Fact 8.25. Let
![]() $\tau :\mathsf {Fm}\to \mathsf {Eq}$
be defined by
$\tau :\mathsf {Fm}\to \mathsf {Eq}$
be defined by
![]() $\tau (x)=(x\approx 1)$
, then the following completeness results hold:
$\tau (x)=(x\approx 1)$
, then the following completeness results hold:
-
(1) For all
 $\Gamma \cup \{ \phi \} \subseteq \mathcal {L}_{\mathtt {IPC}}$
,
$\Gamma \cup \{ \phi \} \subseteq \mathcal {L}_{\mathtt {IPC}}$
,
 $\Gamma \Vdash _{\mathtt {InqI}} \phi $
if and only if
$\Gamma \Vdash _{\mathtt {InqI}} \phi $
if and only if
 $ \tau (\Gamma )\models ^c_{\mathsf {InqIAlg}} \tau (\phi ).$
$ \tau (\Gamma )\models ^c_{\mathsf {InqIAlg}} \tau (\phi ).$
-
(2) For all
 $\Gamma \cup \{ \phi \} \subseteq \mathcal {L}_{\mathtt {IPC}}^\otimes $
,
$\Gamma \cup \{ \phi \} \subseteq \mathcal {L}_{\mathtt {IPC}}^\otimes $
,
 $\Gamma \Vdash _{\mathtt {InqI}^\otimes } \phi $
if and only if
$\Gamma \Vdash _{\mathtt {InqI}^\otimes } \phi $
if and only if
 $ \tau (\Gamma ) \models ^c_{\mathsf {InqIAlg^\otimes }}\tau (\phi ).$
$ \tau (\Gamma ) \models ^c_{\mathsf {InqIAlg^\otimes }}\tau (\phi ).$
Theorem 8.26.
![]() $\mathtt {InqI}$
and
$\mathtt {InqI}$
and
![]() $\mathtt {InqI}^\otimes $
are loosely algebraizable.
$\mathtt {InqI}^\otimes $
are loosely algebraizable.
Proof. Consider the logic
![]() $\mathtt {InqI}$
. Let
$\mathtt {InqI}$
. Let
![]() $\mathbf {Q}$
be the quasivariety of expanded algebras generated by
$\mathbf {Q}$
be the quasivariety of expanded algebras generated by
![]() $\mathsf {InqIAlg}_{\mathrm {CG}}$
, i.e.,
$\mathsf {InqIAlg}_{\mathrm {CG}}$
, i.e.,
![]() $ \mathbf {Q}= \mathbb {Q}(\mathsf {InqIAlg}_{\mathrm {CG}}) $
,
$ \mathbf {Q}= \mathbb {Q}(\mathsf {InqIAlg}_{\mathrm {CG}}) $
,
![]() $\tau (\phi )=(\phi \approx 1),$
and
$\tau (\phi )=(\phi \approx 1),$
and
![]() $\Delta (\alpha ,\beta )=(\alpha \to \beta )\land (\beta \to \alpha )$
. Notice that, since every
$\Delta (\alpha ,\beta )=(\alpha \to \beta )\land (\beta \to \alpha )$
. Notice that, since every
![]() $H\in \mathbf {Q}{ \upharpoonright } \{\lor ,\land ,\to , \bot \}$
is a Heyting algebra, it follows that
$H\in \mathbf {Q}{ \upharpoonright } \{\lor ,\land ,\to , \bot \}$
is a Heyting algebra, it follows that
![]() $\tau (\Delta (\alpha ,\beta ))=\alpha \leftrightarrow \beta \approx 1$
is equivalent to
$\tau (\Delta (\alpha ,\beta ))=\alpha \leftrightarrow \beta \approx 1$
is equivalent to
![]() $\alpha \approx \beta $
. This establishes 4.6(W4). Moreover, we have by the algebraic completeness 8.25(1) and by Proposition 3.24 that
$\alpha \approx \beta $
. This establishes 4.6(W4). Moreover, we have by the algebraic completeness 8.25(1) and by Proposition 3.24 that
which establishes 4.6(W1). It follows from Proposition 4.8 that
![]() $(\mathbf {Q},\tau ,\Delta )$
loosely algebraizes
$(\mathbf {Q},\tau ,\Delta )$
loosely algebraizes
![]() $\mathtt {InqI}$
. The loose algebraizability of
$\mathtt {InqI}$
. The loose algebraizability of
![]() $\mathtt {InqI}^\otimes $
follows analogously.
$\mathtt {InqI}^\otimes $
follows analogously.
While the loose algebraizability of
![]() $\mathtt {InqI}$
and
$\mathtt {InqI}$
and
![]() $\mathtt {InqI}^\otimes $
follows straightforwardly from [Reference Quadrellaro26], the fact that they are not strictly algebraizabile is substantially more subtle. In principle, to show that a logic is not strictly algebraizable one should test infinitely many finite sets of equations to see whether any of them defines the core of the algebras in the corresponding quasivariety of expanded algebras, which is clearly a no-go. However, the failure of strict algebraizability in
$\mathtt {InqI}^\otimes $
follows straightforwardly from [Reference Quadrellaro26], the fact that they are not strictly algebraizabile is substantially more subtle. In principle, to show that a logic is not strictly algebraizable one should test infinitely many finite sets of equations to see whether any of them defines the core of the algebras in the corresponding quasivariety of expanded algebras, which is clearly a no-go. However, the failure of strict algebraizability in
![]() $\mathtt {InqI}$
and
$\mathtt {InqI}$
and
![]() $\mathtt {InqI}^\otimes $
is witnessed by a simpler pattern. Namely, we can find two inquisitive (dependence) algebras
$\mathtt {InqI}^\otimes $
is witnessed by a simpler pattern. Namely, we can find two inquisitive (dependence) algebras
![]() $H,K$
which have the same algebraic reduct, but different cores. Clearly, if a logic is strictly algebraizable this cannot happen, as the core is uniquely determined by a finite set of equations
$H,K$
which have the same algebraic reduct, but different cores. Clearly, if a logic is strictly algebraizable this cannot happen, as the core is uniquely determined by a finite set of equations
![]() $\Sigma $
. We make this intuition precise in the following proof.
$\Sigma $
. We make this intuition precise in the following proof.
Theorem 8.27.
![]() $\mathtt {InqI}$
and
$\mathtt {InqI}$
and
![]() $\mathtt {InqI}^\otimes $
are not strictly algebraizable.
$\mathtt {InqI}^\otimes $
are not strictly algebraizable.
Proof. We prove this for
![]() $\mathtt {InqI}$
, as the proof easily adapts to
$\mathtt {InqI}$
, as the proof easily adapts to
![]() $\mathtt {InqI}^\otimes $
. Firstly, notice that if
$\mathtt {InqI}^\otimes $
. Firstly, notice that if
![]() $(\mathbf {Q},\Sigma ,\tau ,\Delta )$
strictly algebraizes
$(\mathbf {Q},\Sigma ,\tau ,\Delta )$
strictly algebraizes
![]() $\mathtt {InqI}$
, then clearly
$\mathtt {InqI}$
, then clearly
![]() $(\mathbf {Q},\tau ,\Delta )$
is also a witness of its loose algebraizability. It then follows from Theorems 8.26 and 4.7 that
$(\mathbf {Q},\tau ,\Delta )$
is also a witness of its loose algebraizability. It then follows from Theorems 8.26 and 4.7 that
![]() $\mathbf {Q}= \mathbb {Q}(\mathsf {InqIAlg}_{\mathrm {CG}})$
. Now, by directly checking the definition of
$\mathbf {Q}= \mathbb {Q}(\mathsf {InqIAlg}_{\mathrm {CG}})$
. Now, by directly checking the definition of
![]() $\mathtt {InqI}$
-algebras from Definition 8.23 (or, alternatively, by applying the categorical duality between finite Kripke frames and finite, well-connected, core-generated,
$\mathtt {InqI}$
-algebras from Definition 8.23 (or, alternatively, by applying the categorical duality between finite Kripke frames and finite, well-connected, core-generated,
![]() $\mathtt {InqI}$
-algebras from [Reference Quadrellaro26]), one can verify that the expanded algebras
$\mathtt {InqI}$
-algebras from [Reference Quadrellaro26]), one can verify that the expanded algebras
![]() $H_0$
and
$H_0$
and
![]() $H_2$
from Figure 2 (with circles indicating which elements are in the core) belong to
$H_2$
from Figure 2 (with circles indicating which elements are in the core) belong to
![]() $\mathsf {InqIAlg}_{\mathrm {CG}}$
. Furthermore, since
$\mathsf {InqIAlg}_{\mathrm {CG}}$
. Furthermore, since
![]() $H_1{\leqslant } H_2$
, it also follows that
$H_1{\leqslant } H_2$
, it also follows that
![]() $H_1\in \mathbb {Q}(\mathsf {InqIAlg}_{\mathrm {CG}})$
. Crucially,
$H_1\in \mathbb {Q}(\mathsf {InqIAlg}_{\mathrm {CG}})$
. Crucially,
![]() $H_0$
and
$H_0$
and
![]() $H_1$
have the same algebraic reduct but different subsets of core elements. In particular, assuming that
$H_1$
have the same algebraic reduct but different subsets of core elements. In particular, assuming that
![]() $(\mathbf {Q},\Sigma ,\tau ,\Delta )$
strictly algebraizes
$(\mathbf {Q},\Sigma ,\tau ,\Delta )$
strictly algebraizes
![]() $\mathtt {InqI}$
, we obtain that
$\mathtt {InqI}$
, we obtain that
![]() $\mathsf {core}(H_0)=\Sigma (H_0)=\Sigma (H_1)=\mathsf {core}(H_1)$
, contradicting the fact that
$\mathsf {core}(H_0)=\Sigma (H_0)=\Sigma (H_1)=\mathsf {core}(H_1)$
, contradicting the fact that
![]() $\mathsf {core}(H_0)\neq \mathsf {core}(H_1)$
. It follows that
$\mathsf {core}(H_0)\neq \mathsf {core}(H_1)$
. It follows that
![]() $\mathtt {InqI}$
is not strictly algebraizable. The same argument also works for
$\mathtt {InqI}$
is not strictly algebraizable. The same argument also works for
![]() $\mathtt {InqI}^\otimes $
, as it suffices to notice that the core subsets of
$\mathtt {InqI}^\otimes $
, as it suffices to notice that the core subsets of
![]() $H_0,H_1$
, and
$H_0,H_1$
, and
![]() $H_2$
can all be expanded to form Heyting algebras with an additional disjunction
$H_2$
can all be expanded to form Heyting algebras with an additional disjunction
![]() $\otimes $
, which additionally satisfies the axioms from Definition 8.24 (this is done in full generality in [Reference Quadrellaro26, Section 4.3]).
$\otimes $
, which additionally satisfies the axioms from Definition 8.24 (this is done in full generality in [Reference Quadrellaro26, Section 4.3]).

Figure 2 The inquisitive (dependence) algebras from Theorem 8.27.
Corollary 8.28.
![]() $\mathtt {InqI}$
and
$\mathtt {InqI}$
and
![]() $\mathtt {InqI}^\otimes $
are not finitely representable.
$\mathtt {InqI}^\otimes $
are not finitely representable.
Question 8.29. We notice that in the proof of Theorem 8.27 we were in a sense lucky, i.e., we proved the impossibility of strict algebraizability by showcasing two expanded algebras with the same algebraic reduct and different cores. Must such situation always happen whenever a weak logic is loosely algebraizable, but not strictly so? More precisely, consider the following properties of a weak logic
![]() $\Vdash $
:
$\Vdash $
:
-
(i)
 $\Vdash $
is loosely algebraized by a tuple
$\Vdash $
is loosely algebraized by a tuple
 $(\mathbf {Q},\tau ,\Delta )$
;
$(\mathbf {Q},\tau ,\Delta )$
; -
(ii)
 $\Vdash $
is not strictly algebraizable;
$\Vdash $
is not strictly algebraizable; -
(iii) if
 $A\restriction \mathcal {L} = B\restriction \mathcal {L}$
then
$A\restriction \mathcal {L} = B\restriction \mathcal {L}$
then
 $\mathsf {core}(A)=\mathsf {core}(B)$
.
$\mathsf {core}(A)=\mathsf {core}(B)$
.
Is it possible to find a weak logic
![]() $\Vdash $
which satisfies the properties (i)–(iii) from above?
$\Vdash $
which satisfies the properties (i)–(iii) from above?
Question 8.30. We notice that the argument for the loose algebraizability of
![]() $\mathtt {InqI}$
and
$\mathtt {InqI}$
and
![]() $\mathtt {InqI}^\otimes $
easily generalises to the entire class of intermediate inquisitive (and dependence) logics from [Reference Quadrellaro26]. Now, as mentioned in Fact 8.16, the schematic fragment of
$\mathtt {InqI}^\otimes $
easily generalises to the entire class of intermediate inquisitive (and dependence) logics from [Reference Quadrellaro26]. Now, as mentioned in Fact 8.16, the schematic fragment of
![]() $\mathtt {InqB}$
is
$\mathtt {InqB}$
is
![]() $\mathtt {ML}$
. Moreover, as pointed out in [Reference Ferguson and Punčochář15], it is a corollary of the main result from [Reference Grilletti17] that the schematic fragment of
$\mathtt {ML}$
. Moreover, as pointed out in [Reference Ferguson and Punčochář15], it is a corollary of the main result from [Reference Grilletti17] that the schematic fragment of
![]() $\mathtt {InqI}$
is
$\mathtt {InqI}$
is
![]() $\mathtt {ML}$
as well. In other words, all the intermediate inquisitive logics
$\mathtt {ML}$
as well. In other words, all the intermediate inquisitive logics
![]() $\mathtt {L}$
have the same schematic fragment
$\mathtt {L}$
have the same schematic fragment
![]() $\mathtt {ML}$
. It thus follows from our Theorem 5.5 that the strictly algebraizable intermediate inquisitive logics are exactly those obtained by closure under modus ponens of sets of the form
$\mathtt {ML}$
. It thus follows from our Theorem 5.5 that the strictly algebraizable intermediate inquisitive logics are exactly those obtained by closure under modus ponens of sets of the form
![]() $\mathtt {ML} \cup \mathsf {At}[\Lambda ]$
, for some finite set of formulas
$\mathtt {ML} \cup \mathsf {At}[\Lambda ]$
, for some finite set of formulas
![]() $\Lambda \subseteq \mathcal {L}_{\mathtt {IPC}}$
in one variable. Is it possible to refine this characterisation? For example, can one provide a semantical characterisation of the intermediate inquisitive and dependence logics which are strictly algebraizable? We leave this and the previous question as pointers for future investigations.
$\Lambda \subseteq \mathcal {L}_{\mathtt {IPC}}$
in one variable. Is it possible to refine this characterisation? For example, can one provide a semantical characterisation of the intermediate inquisitive and dependence logics which are strictly algebraizable? We leave this and the previous question as pointers for future investigations.
Acknowledgments
The authors would like to thank Tommaso Moraschini for useful discussions and pointers to the literature, Fan Yang and Fredrik Nordvall Forsberg for their valuable comments and remarks to an early draft of this article, and one anonymous reviewer for their careful reading of the article and their many very useful suggestions.
Funding
The second author was supported by grant 336283 of the Academy of Finland and Research Funds of the University of Helsinki, and by an InDam postdoc scholarship.