1 Introduction
Throughout this paper we work over the field of complex numbers
$\mathbb {C}$
. We denote by
$\mathbb {N}$
the set of positive integers.
In the process of running minimal model program (MMP, for short), it is important to control the singularities that occur on the variety produced in each step. There are three types of steps in MMP: divisorial contractions, flips, and Mori fiber spaces. In the first two cases, the singularities on the resulting variety are not worse than those on the original variety (more precisely, the minimal log discrepancy of the resulting variety is no less than that of the original variety). However, in the last case, for a Mori fiber space
$f:X\rightarrow Z$
, it is much more complicated to understand the singularities on Z. McKernan conjectured that in this case the singularities on Z are bounded in terms of those on X.
Conjecture 1.1 (McKernan).
Fix a positive integer d and a real number
$\epsilon>0$
. There exists
$\delta>0$
depending only on d and
$\epsilon $
satisfying the following. Assume
-
(1) X is an
$\epsilon $
-lc variety of dimension d, -
(2)
$f:X\rightarrow Z$
is a Fano fibration (i.e., a contraction with
$-K_X$
being ample over Z), and -
(3)
$K_Z$
is
$\mathbb {Q}$
-Cartier.
Then Z is
$\delta $
-lc.
For a Fano fibration
$X\to Z$
where X is a threefold with only terminal singularities, Mori and Prokhorov [Reference Mori and Prokhorov18] proved that Z is
$1$
-lc. The toric case of McKernan’s conjecture was confirmed by Alexeev and Borisov [Reference Alexeev and Borisov1].
Shokurov proposed a more general conjecture which implies McKernan’s conjecture. Before stating this conjecture, we recall some background. Let
$\pi :(X,B)\rightarrow Z$
be an lc-trivial fibration (see Definition 2.5). For example,
$\pi :X\rightarrow Z$
is a contraction between normal varieties and
$(X,B)$
is an lc pair with
$K_X+B\sim _{\mathbb {R}} 0/Z$
. By constructions of Kawamata [Reference Kawamata15, Reference Kawamata16] and Ambro [Reference Ambro3], we have the so-called canonical bundle formula
$$ \begin{align*}K_X+B\sim_{\mathbb{R}} \pi^*(K_Z+B_Z+M_Z),\end{align*} $$
where
$B_Z$
is the discriminant part and
$M_Z$
is the moduli part (see Definition 2.7). The moduli part
$M_Z$
is determined up to
$\mathbb {R}$
-linear equivalence and thus can be represented by different
$\mathbb {R}$
-divisors. A projective variety F is said to be of Fano type if there exists a boundary
$\Delta $
on F such that
$(F,\Delta )$
is a klt pair and
$-(K_F+\Delta )$
is ample. We are now ready to state Shokurov’s conjecture.
Conjecture 1.2 (Shokurov, cf. [Reference Han, Jiang and Luo13, Conjecture 1.5]).
Fix a positive integer d and a real number
$\epsilon>0$
. There exists
$\delta>0$
depending only on d and
$\epsilon $
satisfying the following. Let
$\pi :(X,B)\rightarrow Z$
be an lc-trivial fibration and
$z\in Z$
a codimension
$\geqslant 1$
point such that
-
(1)
$\dim X - \dim Z=d$
, -
(2)
$\operatorname {\mathrm {mld}}(X/Z\ni z,B)\geqslant \epsilon $
, and -
(3) the generic fiber of
$\pi $
is of Fano type.
Then we can choose
$M_Z\geqslant 0$
representing the moduli part such that
$\operatorname {\mathrm {mld}}(Z\ni z, B_Z+M_Z)\geqslant \delta $
.
Here we denote by
$\operatorname {\mathrm {mld}}(X/Z\ni z,B)$
(resp.
$\operatorname {\mathrm {mld}}(Z\ni z,B_Z+M_Z)$
) the infimum of the log discrepancy of E with respect to
$(X,B)$
(resp.
$(Z,B_Z+M_Z)$
) where E runs over all prime divisors over X (resp. Z) whose image on Z is the closure
$\overline {z}$
of z.
Shokurov’s conjecture contains more information about singularities on Fano type fibrations than McKernan’s conjecture. One of its consequences is that given a Fano fibration
$X\to Z$
where X is
$\epsilon $
-lc, the multiplicities of fibers over codimension 1 points on Z are bounded from above in terms of
$\epsilon $
and the relative dimension. As a related result, Mori and Prokhorov [Reference Mori and Prokhorov19] showed that if
$X\rightarrow Z$
is a del Pezzo fibration from a terminal threefold onto a smooth curve, then the multiplicity of an irreducible fiber is at most 6.
Remark 1.3. (a) With a slightly stronger condition
$$ \begin{align*}(\text{2'})~ (X,B) \text{ is an } \epsilon\text{-lc pair,}\end{align*} $$
Birkar [Reference Birkar5] proved Conjecture 1.2 when either
$\dim X-\dim Z=1$
or
$(F,\operatorname {\mathrm {Supp}} B|_F)$
is log bounded where F is a general fiber of
$\pi $
. Combining the main results in [Reference Birkar6, Reference Birkar7], the conjecture under condition (2’) holds when the coefficients of the horizontal part of B are bounded from below by a fixed positive number.
(b) Birkar and Chen [Reference Birkar and Chen10] proved a modified version of Conjecture 1.2 under condition (2’) in the toric setting, which implies the boundedness of multiplicities of fibers over codimension 1 points for toric Fano fibrations.
(c) Very recently, Conjecture 1.2 was proved by Birkar [Reference Birkar8] under condition (2’).
In results mentioned in Remark 1.3, the existence of
$\delta $
was proved but the explicit value of
$\delta $
was not given. When
$\dim X-\dim Z=1$
and
$\epsilon \geqslant 1$
, Han, Jiang and Luo [Reference Han, Jiang and Luo13] gave the optimal value of
$\delta =\epsilon -1/2$
in Conjecture 1.2.
In this paper, we give the optimal value of
$\delta $
in Conjecture 1.2 for the case that
$0<\epsilon \leqslant 1$
and
$\dim X-\dim Z=1$
.
Theorem 1.4. Fix a real number
$0<\epsilon \leqslant 1$
. Let
$\pi :(X,B)\rightarrow Z$
be an lc-trivial fibration and
$z\in Z$
a codimension
$\geqslant 1$
point such that
-
(1)
$\dim X - \dim Z=1$
, -
(2)
$\operatorname {\mathrm {mld}}(X/Z\ni z,B)\geqslant \epsilon $
, and -
(3) the geometric generic fiber of
$\pi $
is a rational curve.
Then we can choose
$M_Z\geqslant 0$
representing the moduli part such that
$\operatorname {\mathrm {mld}}(Z\ni z, B_Z+M_Z) \geqslant \delta ,$
where
$$ \begin{align*} \delta=\frac{(2n+1)\epsilon-1}{2n(n+1)},\quad \text{when } \epsilon\in \left[\frac{1}{n+1},\frac{1}{n}\right] \text{ for some } n\in \mathbb{N}. \end{align*} $$
In particular,
$\delta \geqslant \epsilon ^2/2$
and the equality holds if and only if
$\epsilon =1/n$
for some
$n\in \mathbb {N}$
.
Remark 1.5. (a) The value of
$\delta $
in Theorem 1.4 is optimal by Example 1.6.
(b) As the geometric generic fiber of
$\pi $
is a rational curve, the condition that
$\pi :(X,B)\rightarrow Z$
is an lc-trivial fibration is equivalent to the following condition:
$\pi :X\rightarrow Z$
is a contraction between normal varieties with an lc sub-pair
$(X,B)$
such that
$K_X+B\sim _{\mathbb {R}} 0/Z$
and B is effective over generic point of Z (see [Reference Han, Jiang and Luo13, Remark 2.13]).
Example 1.6. Let
$\epsilon =\frac {p}{q}$
be a rational number such that
$\frac {1}{n+1}\leqslant \epsilon \leqslant \frac {1}{n}$
, where
$p,q,n\in \mathbb {N}$
. Let
$Z=\mathbb A^1$
with coordinate t and let
$X=Z \times \mathbb P^1$
with homogeneous coordinates
$x,y$
. Let
$\pi :X\rightarrow Z$
be the projection and let z be the origin of Z. Let B be the
$\mathbb {Q}$
-divisor
$$ \begin{align*}\frac{1}{qn(n+1)}\cdot \left(t^{q(2n+1)-p}x^{2qn(n+1)}+y^{2qn(n+1)}=0\right)+\frac{qn-p}{q(n+1)}\cdot (t=0).\end{align*} $$
Then
$K_X+B\sim _{\mathbb Q} 0/Z$
. By Lemma A.3 we have
$$ \begin{align*}\operatorname{\mathrm{mld}}(X/Z\ni z,B)=\epsilon \quad \text{ and }\quad \operatorname{\mathrm{lct}}(X/Z\ni z,B; \pi^*z)= \frac{(2n+1)\epsilon-1}{2n(n+1)}.\end{align*} $$
So the coefficient of z in the discriminant divisor
$B_Z$
is equal to
$$ \begin{align*}1-\frac{(2n+1)\epsilon-1}{2n(n+1)}.\end{align*} $$
As a corollary, we have the following global version of Theorem 1.4 which involves less technical notations.
Corollary 1.7. Fix a real number
$0<\epsilon \leqslant 1$
. Let
$(X,B)$
be a pair and
$\pi :X\rightarrow Z$
a contraction between normal varieties such that
-
(1)
$\dim X-\dim Z=1$
, -
(2)
$a(E,X,B)\geqslant \epsilon $
for any prime divisor E over X with
$\pi (\operatorname {\mathrm {center}}_X(E))\neq Z$
, -
(3)
$K_X+B\sim _{\mathbb R} 0/Z$
, and -
(4) the geometric generic fiber of
$\pi $
is a rational curve.
Then we can choose
$M_Z\geqslant 0$
representing the moduli part such that
$(Z,B_Z+M_Z)$
is
$\delta $
-lc, where
$\delta $
is as in Theorem 1.4.
Applying Corollary 1.7, we give an effective value of
$\delta $
in a more general form of Conjecture 1.1 when the relative dimension is 1.
Corollary 1.8. Fix a real number
$0<\epsilon \leqslant 1$
. Let
$\pi :X\rightarrow Z$
be a contraction between normal varieties such that
-
(1)
$\dim X - \dim Z=1$
, -
(2) X is
$\epsilon $
-lc, and -
(3)
$-K_X$
is big and nef over Z.
Then
-
(1) Z is
$\delta $
-lc if
$K_Z$
is
$\mathbb {Q}$
-Cartier, and -
(2) for any codimension 1 point
$z\in Z$
, the multiplicity of each component of
$\pi ^*z$
is bounded from above by
$1/\delta $
, where
$\delta $
is as in Theorem 1.4.
Following the idea in [Reference Han, Jiang and Luo13], we may reduce Theorem 1.4 to the case that
$\pi :X\rightarrow Z$
is a
$\mathbb {P}^1$
-bundle over a smooth curve, and finally reduce to a local problem of estimating the log canonical threshold of a smooth curve with respect to a pair on a smooth surface. Then we solve this local problem by proving the following theorem.
Theorem 1.9. Fix a real number
$0<\epsilon \leqslant 1$
. Let
$(X,B)$
be a pair with a closed point
$P\in X$
such that X is a smooth surface and
$\operatorname {\mathrm {mld}}(X\ni P,B)\geqslant \epsilon $
. Let C be a smooth curve on X passing through P such that
$\operatorname {\mathrm {mult}}_C B \leqslant 1-\epsilon $
and the local intersection number
$(B'\cdot C)_P\leqslant 2$
, where
$B'=B-\operatorname {\mathrm {mult}}_C B \cdot C$
. Then
$$ \begin{align*}\operatorname{\mathrm{lct}}(X\ni P,B;C)\geqslant \delta,\end{align*} $$
where
$\delta $
is as in Theorem 1.4.
The idea of the proof of Theorem 1.9 is as follows. Let
$\Gamma _+(B+tC)$
be the Newton polytope of
$B+tC$
(see Definition 3.1), which depends on the choice of local coordinates of
$X\ni P$
. One can show that
$$ \begin{align} \text{if }(X,B+tC)\text{ is lc near } P, \text{ then } \textbf{1}=(1,1)\in \Gamma_+(B+tC) \end{align} $$
(see Lemma 3.3). However, in general the converse of (1.1) does not hold. For example, let
$X=\mathbb A^2$
with coordinates
$x,y$
and
$B=(x^2+2xy+y^2=0)$
; then
$\textbf {1}\in \Gamma _+(B)$
while
$(X,B)$
is not lc. The key point is that, by making use of [Reference Kawakita14, Theorem 1] we can pick suitable local coordinates such that the converse of (1.1) holds. Then
$$ \begin{align*}\operatorname{\mathrm{lct}}(X\ni P,B;C)=\sup\{t>0\mid \textbf{1}\in \Gamma_+(B+tC)\}\end{align*} $$
and hence we can estimate its lower bound by combinatorics.
2 Preliminaries
We will freely use the standard notations and definitions in [Reference Kollár and Mori17, Reference Birkar, Cascini, Hacon and Mckernan9].
2.1 Sub-pairs and singularities
A contraction
$\pi :X\rightarrow Z$
is a projective morphism of varieties with
$\pi _*\mathcal {O}_X=\mathcal {O}_Z$
.
Definition 2.1 (cf. [Reference Han, Jiang and Luo13, Definition 2.4]).
A sub-pair
$(X,B)$
consists of a normal variety X and an
$\mathbb {R}$
-divisor B on X such that
$K_X+B$
is
$\mathbb {R}$
-Cartier. A sub-pair
$(X,B)$
is called a pair if B is effective.
A relative sub-pair
$(X/Z\ni z,B)$
consists of a sub-pair
$(X,B)$
, a contraction
$\pi :X\rightarrow Z$
and a (not necessarily closed) point
$z\in Z$
. A relative sub-pair
$(X/Z\ni z,B)$
is called a relative pair if B is effective. In the case that
$Z=X$
,
$z=x$
and
$\pi $
is the identity morphism, we will use
$(X\ni x,B)$
instead of
$(X/Z\ni z,B)$
.
Definition 2.2 (cf. [Reference Han, Jiang and Luo13, Definition 2.5]).
Let
$(X,B)$
be a sub-pair and E a prime divisor over X, that is, a prime divisor on a normal variety Y with a birational morphism
$g:Y\rightarrow X$
. We may write
$K_Y+B_Y:=g^*(K_X+B)$
. Then the center of E is defined as the image of E on X under the morphism g and the log discrepancy
$a(E,X,B)$
of E with respect to
$(X,B)$
is defined as
$1-\operatorname {\mathrm {mult}}_E B_Y$
.
Let
$(X/Z\ni z,B)$
be a relative sub-pair with contraction
$\pi :X\rightarrow Z$
. The minimal log discrepancy of
$(X/Z\ni z,B)$
is defined as
$$ \begin{align*} \operatorname{\mathrm{mld}}(X/Z\ni z,B):=\inf\{a(E,X,B) \mid E \text{is a prime divisor over} X \text{ with } \pi(\operatorname{\mathrm{center}}_X(E))=\overline{z}\}. \end{align*} $$
Definition 2.3 (cf. [Reference Han, Jiang and Luo13, Definition 2.7]).
A relative sub-pair
$(X/Z\ni z,B)$
is said to be
$\epsilon $
-lc (resp.
$\epsilon $
-klt, lc, klt) if
$\operatorname {\mathrm {mld}}(X/Z\ni z,B)\geqslant \epsilon $
(resp.
$>\epsilon $
,
$\geqslant 0$
,
$> 0$
). A sub-pair
$(X,B)$
is said to be
$\epsilon $
-lc (resp.
$\epsilon $
-klt, lc, klt) if
$(X\ni x,B)$
is so for any codimension
$\geqslant 1$
point
$x\in X$
. In the case when
$B=0$
, we also say X is
$\epsilon $
-lc (resp.
$\epsilon $
-klt, lc, klt). We remark that
$(X/Z\ni z,B)$
is lc if and only if
$(X,B)$
is lc over some neighborhood of
$z\in Z$
(see [Reference Han, Jiang and Luo13, Lemma 2.8]).
Definition 2.4 (cf. [Reference Han, Jiang and Luo13, Definition 2.10]).
Let
$(X/Z\ni z,B)$
be a relative sub-pair with contraction
$\pi :X\rightarrow Z$
and let D be an effective
$\mathbb {R}$
-Cartier
$\mathbb {R}$
-divisor on X. The log canonical threshold of D with respect to
$(X/Z\ni z,B)$
is defined as
$$ \begin{align*}\operatorname{\mathrm{lct}}(X/Z\ni z,B;D):=\sup\{t\geqslant 0\mid (X/Z\ni z,B+tD) \text{ is lc}\}.\end{align*} $$
If
$z\in Z$
is a codimension 1 point, then its closure
$\overline {z}$
is a Cartier divisor on some neighborhood U of z. We define
$$ \begin{align*}\operatorname{\mathrm{lct}}(X/Z\ni z,B;\pi^*\overline{z}):=\sup\{t\geqslant 0\mid (X/Z\ni z,B+t\pi^*\overline{z}) \text{ is lc over }U\}.\end{align*} $$
This definition is independent of the choice of U.
2.2 b-divisors
Let X be a normal variety. A birational model over X is a normal variety Y with a birational morphism
$Y\to X$
.
A b-
$\mathbb {R}$
-divisor
$\textbf {D}$
(or b-divisor for short) over X is a collection of
$\mathbb {R}$
-divisors
$\textbf {D}_Y$
for each birational model Y over X, such that for any birational morphism
$\sigma :Y_1\rightarrow Y_2/X$
we have
$\sigma _*\textbf {D}_{Y_1}=\textbf {D}_{Y_2}$
.
We say that a b-divisor
$\textbf {D}$
is b-semiample (resp. b-nef, b-abundant) if there is a birational model
$Y_0$
over X such that
$\textbf {D}_{Y_0}$
is a semiample (resp. nef, abundant)
$\mathbb {R}$
-Cartier
$\mathbb {R}$
-divisor and for any birational morphism
$\sigma :Y\rightarrow Y_0/X$
we have
$\textbf {D}_{Y}=\sigma ^* \textbf {D}_{Y_0}$
.
2.3 Canonical bundle formula
Definition 2.5 (cf. [Reference Ambro2, Definition 2.1], [Reference Fujino and Gongyo11, Definition 3.2]).
An lc-trivial fibration
$\pi :(X,B)\rightarrow Z$
consists of a contraction
$\pi :X\rightarrow Z$
between normal varieties and a sub-pair
$(X,B)$
such that
-
(1)
$(X/Z\ni \eta ,B)$
is lc, where
$\eta $
is the generic point of Z; -
(2)
$\operatorname {\mathrm {rank}} \pi _* \mathscr {O}_X(\lceil -B_{<1} \rceil )=1$
, where
$B_{<1}:=\sum _{b_i<1} b_i B_i$
for
$B=\sum b_i B_i$
with prime divisors
$B_i$
’s; -
(3)
$K_X+B \sim _{\mathbb {R}} 0/Z$
, that is, there is an
$\mathbb {R}$
-Cartier
$\mathbb {R}$
-divisor L on Z such that
$K_X+B\sim _{\mathbb {R}} \pi ^*L$
.
Remark 2.6 (cf. [Reference Han, Jiang and Luo13, Remark 2.13]).
If the geometric generic fiber of
$\pi $
is a rational curve, the second condition is equivalent to B being effective over the generic point of Z.
Definition 2.7 [Reference Kawamata15, Reference Kawamata16].
Let
$\pi :(X,B)\rightarrow Z$
be an lc-trivial fibration. Then
$K_X+B\sim _{\mathbb {R}} \pi ^* L$
for some
$\mathbb {R}$
-Cartier
$\mathbb {R}$
-divisor L on Z. For any prime divisor D on Z, denote
$$ \begin{align*}b_D:=\operatorname{\mathrm{lct}}(X/Z\ni \eta_D, B; \pi^*\overline{\eta_D})\end{align*} $$
where
$\eta _D$
is the generic point of D. We set
$B_Z=\sum _D (1-b_D)D$
where D runs over all prime divisors on Z. We set
$M_Z=L-K_Z-B_Z$
, which is determined up to
$\mathbb {R}$
-linear equivalence since L is so. Then we have the so-called canonical bundle formula
$$ \begin{align*}K_X+B\sim_{\mathbb{R}} \pi^*(K_Z+B_Z+M_Z).\end{align*} $$
The part
$B_Z$
is called the discriminant part and the part
$M_Z$
is called the moduli part. We remark that
$B_Z$
is effective if B is so.
Let
$\sigma : Z'\rightarrow Z$
be a birational morphism from a normal variety
$Z'$
and let
$X'$
be the resolution of the main component of
$X\times _Z Z'$
with induced morphism
$\tau :X'\rightarrow X$
and
$\pi ':X'\rightarrow Z'$
. Write
$K_{X'}+B'=\tau ^*(K_X+B)$
, then
$K_{X'}+B'\sim _{\mathbb {R}} \pi ^{\prime *} \sigma ^* L$
. Similarly we can define the discriminant part
$B_{Z'}$
and the moduli part
$M_{Z'}$
for the contraction
$(X',B')\rightarrow Z'$
. One can check that
$\sigma _* B_{Z'}=B_Z$
and
$\sigma _* M_{Z'}=M_Z$
. Hence there exist b-divisors
$\textbf {B}$
and
$\textbf {M}$
such that
$\textbf {B}_{Z'}=B_{Z'}$
and
$\textbf {M}_{Z'}=M_{Z'}$
for any birational model
$Z'$
over Z, which are called the discriminant b-divisor and the moduli b-divisor respectively.
Assume additionally that
$X, Z$
are projective, B is a
$\mathbb {Q}$
-divisor and B is effective over the generic point of Z. It is known that the moduli b-divisor
$\textbf {M}$
is b-nef and b-abundant ([Reference Kawamata16, 3, 11]). It was conjectured ([Reference Prokhorov and Shokurov20, Conjecture 7.13]) that
$\textbf {M}$
is b-semiample. This conjecture was confirmed when the geometric generic fiber of
$\pi $
is a rational curve.
Theorem 2.8 [Reference Prokhorov and Shokurov20, Theorem 8.1], cf. [Reference Han, Jiang and Luo13, Theorem 2.14].
Let
$\pi :(X,B)\rightarrow Z$
be an lc-trivial fibration such that
$X, Z$
are projective, B is a
$\mathbb {Q}$
-divisor,
$\dim X-\dim Z=1$
and the geometric generic fiber of
$\pi $
is a rational curve. Then the moduli b-divisor
$\mathbf {M}$
is b-semiample.
3 Log canonical thresholds on smooth surfaces
In this section, we use Newton diagrams to study the local problem on estimating the lower bound of the log canonical threshold of a smooth curve with respect to a pair on a smooth surface germ, which will play a key role in the proof of Theorem 1.4.
3.1 Newton diagrams
In this subsection we collect some basic definitions and facts about Newton diagrams.
Definition 3.1. Let
$f\in \mathbb {C}[[x,y]]$
be a nonzero power series in two variables. We may write
$$ \begin{align*}f=\sum_{(p,q)\in \mathbb{Z}_{\geqslant 0}} c_{p,q} x^p y^q.\end{align*} $$
Define the Newton polytope
$\Gamma _+(f)$
of f as the convex hull in
$\mathbb {R}^2$
of
$$ \begin{align*}\bigcup_{c_{p,q}\neq 0} (p,q)+\mathbb{R}_{\geqslant 0}^2\end{align*} $$
and define the Newton diagram
$\Gamma (f)$
of f as the boundary of
$\Gamma _+(f)$
. Then
$\Gamma (f)$
is the union of 1-dimensional faces of
$\Gamma _+(f)$
(including two noncompact faces).
Let
$X\ni P$
be a germ of smooth surface with local coordinates
$(x,y)$
and let B be an effective
$\mathbb {R}$
-divisor on X. Write
$B=\sum _i b_i B_i$
where each
$b_i$
is a positive real number and each
$B_i$
is a prime divisor. The completion of
$B_i$
along P is defined by
$(f_i=0)$
for some
$f_i\in \mathbb {C}[[x,y]]$
. We define the Newton polytope
$\Gamma _+(B)$
of B as
$\sum _i b_i\cdot \Gamma _+(f_i)$
and define the Newton diagram
$\Gamma (B)$
as the boundary of
$\Gamma _+(B)$
. Note that the definition of
$\Gamma _+(B)$
and
$\Gamma (B)$
do not depend on the choice of
$f_i$
up to a unit in
$\mathbb {C}[[x,y]]$
, but depend on the choice of local coordinates.
Definition 3.2. Let B be an effective
$\mathbb {R}$
-divisor on a germ of smooth surface
$X\ni P$
with local coordinates
$(x,y)$
and let S be a 1-dimensional face of
$\Gamma (B)$
. If S is a compact face, it has a normal vector with positive coordinates. Write its two vertices as
$(p_1,q_1)$
and
$(p_2,q_2)$
with
$p_1<p_2$
and
$q_1>q_2$
. We call
$(p_1,q_1)$
the left vertex of S and call
$(p_2,q_2)$
the right vertex of S. If S is a noncompact face, it is parallel to either x-axis or y-axis. So we may write S as either
$(p_1+\mathbb {R}_{\geqslant 0},q_1)$
or
$(p_2,q_2+\mathbb {R}_{\geqslant 0})$
. In the former (resp. latter) case we call
$(p_1,q_1)$
(resp.
$(0,+\infty )$
) the left vertex of S and call
$(+\infty ,0)$
(resp.
$(p_2,q_2)$
) the right vertex of S.
Notation. We write
$\langle , \rangle $
for the inner product of
$\mathbb {R}^2$
. For any
$\textbf {v}\in \mathbb {R}_{\geqslant 0}^2$
and any subset
$S\subseteq \mathbb {R}_{\geqslant 0}^2$
, we denote
$$ \begin{align*}\langle \textbf{v}, S \rangle:=\inf\{\langle \textbf{v}, \textbf{p} \rangle\mid \textbf{p} \in S\}.\end{align*} $$
Next we recall some facts about weighted blow-ups. Let
$X\ni P$
be a germ of smooth surface with local coordinates
$(x,y)$
and let
$\textbf {w}=(w_1,w_2)$
with two coprime positive integers
$w_1,w_2$
. Denote by
$E_{\textbf {w}}$
the exceptional divisor obtained by the weighted blow up
$\sigma :Y\rightarrow X$
at
$P\in X$
with
$\operatorname {\mathrm {wt}}(x,y)=(w_1,w_2)$
. Then
$$ \begin{align*}a(E_{\textbf{w}},X,0)=w_1+w_2=\langle \textbf{w},\textbf{1}\rangle,\end{align*} $$
where we write
$\textbf {1}$
for the vector
$(1,1)$
and write
$\langle , \rangle $
for the inner product of
$\mathbb {R}^2$
. Let B be an effective
$\mathbb {R}$
-divisor on X. Then
$$ \begin{align*}\operatorname{\mathrm{mult}}_{E_{\textbf{w}}} \sigma^*B=\langle \textbf{w}, \Gamma(B) \rangle.\end{align*} $$
Therefore,
$$ \begin{align} a(E_{\textbf{w}},X,B)=\langle \textbf{w},\textbf{1}\rangle-\langle \textbf{w},\Gamma(B)\rangle. \end{align} $$
Lemma 3.3. With the above notations, if
$\operatorname {\mathrm {mld}}(X\ni P, B)\geqslant 0$
, then
$\mathbf {1} \in \Gamma _+(B)$
.
Proof. If
$\textbf {1}\notin \Gamma _+(B)$
, there exists a 1-dimensional face of
$\Gamma (B)$
with normal vector
$\textbf {e}=(e_1,e_2)$
such that
$e_1,e_2\geqslant 0$
and
$e_1+e_2< \langle \textbf {e},\Gamma (B) \rangle $
. After some small perturbations, we may suppose that
$e_1,e_2$
are positive rational numbers and the above inequality still holds. Multiplying with some positive rational number, we may suppose that
$e_1,e_2$
are coprime positive integers. Let
$E_{\textbf {e}}$
be the exceptional divisor obtained by the weighted blow up at
$P\in X$
with
$\operatorname {\mathrm {wt}}(x,y)=(e_1,e_2)$
. Then
$a(E_{\textbf {e}},X,B)<0$
by (3.1), which contradicts our hypothesis.
Lemma 3.4. Let t be a non-negative real number and let
$B,D$
be two effective
$\mathbb {R}$
-divisors on a germ of smooth surface
$X \ni P$
with local coordinates
$(x,y)$
. Assume
$\Gamma (D)$
has only two vertices
$(p,0)$
and
$(0,q)$
, where
$p,q$
are positive numbers. Let S be a 1-dimensional face of
$\Gamma (B+tD)$
with left vertex
$(p_1,q_1)$
and right vertex
$(p_2,q_2)$
, where
$p_1,q_1,p_2,q_2$
are non-negative real numbers or
$+\infty $
.
-
1. If
$(q_1-q_2)/(p_2-p_1)>q/p$
, then
$S-(0,tq)$
is a face of
$\Gamma (B)$
. -
2. If
$(q_1-q_2)/(p_2-p_1)<q/p$
, then
$S-(tp,0)$
is a face of
$\Gamma (B)$
. -
3. If
$(q_1-q_2)/(p_2-p_1)=q/p$
, denote
$(p^{\prime }_1,q^{\prime }_1)=(p_1,q_1-tq)$
and
$(p^{\prime }_2,q^{\prime }_2)=(p_2-tp,q_2)$
, then the line segment connecting
$(p^{\prime }_1,q^{\prime }_1)$
and
$(p^{\prime }_2,q^{\prime }_2)$
is a face of
$\Gamma (B)$
(or a vertex of
$\Gamma (B)$
when these two points coincide). Moreover we have where
$$ \begin{align*}\langle\mathbf{v},\Gamma(B)\rangle=p^{\prime}_1q+q^{\prime}_1p=p^{\prime}_2q+q^{\prime}_2p,\end{align*} $$
$\mathbf {v}=(q,p)$
.
Proof. The Newton diagram
$\Gamma (B+tD)$
is obtained by gluing the 1-dimensional faces of
$\Gamma (B)$
and
$t\cdot \Gamma (D)$
, suitably displaced such that the slopes of faces are more and more gentle form left to right (cf. [Reference Greuel, Lossen and Shustin12, Chapter II, Remark 2.17.1]). See the figure below. The lemma follows directly from this fact.
Lemma 3.5. Let t be a non-negative real number and let
$B,D$
be two effective
$\mathbb {R}$
-divisors on a germ of smooth surface
$X \ni P$
with local coordinates
$(x,y)$
. Assume
$\Gamma (D)$
has only one vertex
$(p,0)$
(resp.
$(0,q)$
), where p (resp. q) is a positive number. Let S be a 1-dimensional face of
$\Gamma (B+tD)$
. Then
$S-(tp,0)$
(resp.
$S-(0,tq)$
) is a face of
$\Gamma (B)$
.
Proof. The lemma follows directly from the fact that
$\Gamma _+(B+tD)=\Gamma _+(B)+t\cdot \Gamma _+(D)$
.
Let
$X\ni P$
be a germ of smooth surface with local coordinates
$(x,y)$
and let C be a smooth curve on X passing through P. The completion of C along P is defined by
$(g=0)$
for some
$g\in \mathbb {C} [[x,y]]$
. Since C is smooth, after possibly switching x and y, we may suppose that the term x appears in the expression of g with nonzero coefficient. Therefore
$\Gamma (C)$
has either one vertex
$(1,0)$
or two vertices
$(1,0)$
and
$(0,b)$
, where b is a positive integer. In the former case, we also say
$\Gamma (C)$
has two vertices
$(1,0)$
and
$(0,+\infty )$
.
Lemma 3.6. Let B be an effective
$\mathbb {R}$
-divisor on a germ of smooth surface
$X \ni P$
with coordinates
$(x,y)$
and let C be a smooth curve passing through P. Suppose that
$C \nsubseteq \operatorname {\mathrm {Supp}} B$
and
$\Gamma (C)$
has two vertices
$(1,0)$
and
$(0,b)$
, where b is a positive integer or
$+\infty $
. Then the local intersection number of B and C at P
$$ \begin{align*}(B\cdot C)_P\geqslant \langle \mathbf{b}, \Gamma(B) \rangle\end{align*} $$
where
$\mathbf {b}=(b,1)$
. Here we use the convention that
$+\infty \cdot 0=0$
.
Proof. We may suppose that B is a prime divisor with its completion defined by
$(f=0)$
for some
$f\in \mathbb {C}[[x,y]]$
. Indeed, for the general case
$B=\sum _i b_iB_i$
, since
$(B\cdot C)_P=\sum _i b_i(B_i\cdot C)_P$
and
$\Gamma _+(B)=\sum _i b_i\cdot \Gamma _+(B_i)$
, it suffices to show the lemma for each
$B_i$
.
If b is a positive integer, by [Reference Greuel, Lossen and Shustin12, Chapter I, Theorem 3.3] there exists
$y(t)\in t\cdot \mathbb {C}[[t]]$
such that
$\varphi :t\mapsto (t^b,y(t))$
is a parametrization of C. As C is smooth, the multiplicity of
$y(t)$
at 0 is 1. For any term
$x^py^q$
appearing in the expression of f with nonzero coefficient, the multiplicity of
$\varphi ^*(x^py^q)=t^{pb}\cdot y(t)^q$
at 0 is
$pb+q\geqslant \langle \textbf {b},\Gamma (B)\rangle $
. Therefore
$(B\cdot C)_P\geqslant \langle \textbf {b} ,\Gamma (B)\rangle $
.
If
$b=+\infty $
, then
$\varphi :t\mapsto (0,t)$
is a parametrization of C. Since
$C \nsubseteq \operatorname {\mathrm {Supp}} B$
, there exists a non-negative integer I such that
$y^{I}$
appears in the expression of f with nonzero coefficient. Then
$$ \begin{align*}(B\cdot C)_P= \min\{I\mid (0,I)\in \Gamma_+(B)\}= \langle \textbf{b},\Gamma(B)\rangle,\end{align*} $$
where
$\textbf {b}=(+\infty ,1)$
.
3.2 Proof of Theorem 1.9
In this subsection we give the proof of Theorem 1.9.
Lemma 3.7. Let
$(X,B)$
be a pair with a codimension 2 point
$x\in X$
such that
$(X\ni x,B)$
is lc. Let D be a prime divisor on X. Denote
$t=\operatorname {\mathrm {lct}}(X\ni x,B;D)$
. If
$\operatorname {\mathrm {mult}}_D B+t<1$
, then
$\operatorname {\mathrm {mld}}(X\ni x, B+tD)=0$
.
Proof. As
$(X\ni x, B+tD)$
is lc, after shrinking X near x, we may suppose that
$(X,B+tD)$
is an lc pair. Let
$f:Y\rightarrow X$
be a log resolution of
$(X,B+D)$
. We may write
$$ \begin{align*}K_Y+\sum_i (1-a(E_i,X,B+tD))E_i+B_Y+tD_Y=f^*(K_X+B+tD)\end{align*} $$
where
$B_Y$
,
$D_Y$
are the strict transforms of
$B,D$
on Y respectively and
$E_i$
runs over all exceptional prime divisors on Y over X. Shrinking X near x, we may suppose that
$x \in \operatorname {\mathrm {center}}_X(E_i)$
for each
$E_i$
, which implies that
$\operatorname {\mathrm {center}}_X(E_i)=\overline {x}$
(i.e., the closure of x) since x is a codimension 2 point and
$E_i$
is exceptional over X.
We claim that
$a(E_i,X,B+tD)=0$
for some
$E_i$
. Indeed, if this is not the case,
$a(E_i,X,B+tD)>0$
for all
$E_i$
. Take
$t'$
such that
$0<t'-t\ll 1$
, then
$a(E_i,X,B+t'D)>0$
for all
$E_i$
and coefficients in
$B_Y+t'D_Y$
are at most 1 since
$\operatorname {\mathrm {mult}}_D B+t<1$
. Therefore, as
$B_Y+D_Y+\sum _i E_i$
is simple normal crossing and as
$$ \begin{align*}K_Y+\sum_i (1-a(E_i,X,B+t'D))E_i+B_Y+t'D_Y=f^*(K_X+B+t'D),\end{align*} $$
we deduce that
$(X,B+t'D)$
is lc. Hence
$\operatorname {\mathrm {lct}}(X\ni P,B;D)\geqslant t'>t$
, which leads to a contradiction.
By the above claim, there is
$E_i$
such that
$a(E_i,X,B+tD)=0$
. Note that
$(X,B+tD)$
is lc and
$\operatorname {\mathrm {center}}_X(E_i)=\overline {x}$
, we have
$\operatorname {\mathrm {mld}}(X\ni x, B+tD)=0$
.
Proof of Theorem 1.9.
Suppose that
$\frac {1}{n+1}\leqslant \epsilon \leqslant \frac {1}{n}$
for some
$n\in \mathbb {N}$
. Let
$t=\operatorname {\mathrm {lct}}(X\ni P,B;C)$
. We need to show that
$$ \begin{align*}t\geqslant \frac{(2n+1)\epsilon-1}{2n(n+1)}.\end{align*} $$
If
$t\geqslant \epsilon $
, there is nothing further to prove. So we may suppose that
$t<\epsilon $
. Then
$\operatorname {\mathrm {mld}}(X\ni P, B+tC)=0$
by Lemma 3.7. By [Reference Kawakita14, Theorem 1], there are local coordinates
$x,y$
and two coprime positive integers
$w_1,w_2$
such that
$$ \begin{align} a(E_{\textbf{w}},X,B+tC)=\operatorname{\mathrm{mld}}(X\ni P, B+tC)=0, \end{align} $$
where
$E_{\textbf {w}}$
is the exceptional divisor obtained by the weighted blow up at
$P\in X$
with
$\operatorname {\mathrm {wt}}(x,y)=(w_1,w_2)$
. For any
$\mathbb R$
-divisor D on X, we denote by
$\Gamma (D)$
its Newton diagram with respect to local coordinates
$(x,y)$
(see Definition 3.1).
From (3.1) and (3.2) we deduce that
$$ \begin{align} \langle \textbf{w},\textbf{1}\rangle=\langle \textbf{w},\Gamma(B+tC)\rangle, \end{align} $$
where
$\textbf {w}=(w_1,w_2)$
. On the other hand,
$\textbf {1}\in \Gamma _+(B+tC)$
by Lemma 3.3. This implies that
$$ \begin{align*}\textbf{1}\in\Gamma(B+tC).\end{align*} $$
Claim 3.8. If
$\mathbf {1}$
lies in a noncompact 1-dimensional face F of
$\Gamma (B+tC)$
, then
$\mathbf {1}$
is a vertex of F.
Proof. Without loss of generality, we may suppose that F is parallel to y-axis. We may write
$F=(1,s+\mathbb {R}_{\geqslant 0})$
since
$\textbf {1}\in F$
. If
$\textbf {1}$
is not the vertex of F, then
$0\leqslant s<1$
. It follows that
$w_1+sw_2<w_1+w_2$
, which contradicts (3.3).
Take S to be the unique 1-dimensional face of
$\Gamma (B+tC)$
such that
$\textbf {1}\in S$
and
$\textbf {1}$
is not the right vertex of S (see Definition 3.2 for the definition of right vertex). Then S is not parallel to y-axis by the above claim. We denote the left (resp. right) vertex of S by
$(p_1,q_1)$
(resp.
$(p_2,q_2)$
). The slope of S is defined to be
$$ \begin{align*}\operatorname{\mathrm{slope}}(S):=(q_1-q_2)/(p_2-p_1).\end{align*} $$
Then
$\operatorname {\mathrm {slope}}(S)$
is a non-negative real number (since S is not parallel to y-axis, the slope
$<+\infty $
).
Since C is a smooth curve passing through P, after possibly switching x and y, we may suppose that
$\Gamma (C)$
has two vertices
$(1,0)$
and
$(0,b)$
, where b is a positive integer or
$+\infty $
(see the argument before Lemma 3.6). Denote
$a=\operatorname {\mathrm {mult}}_C B$
. Then
$a\leqslant 1-\epsilon $
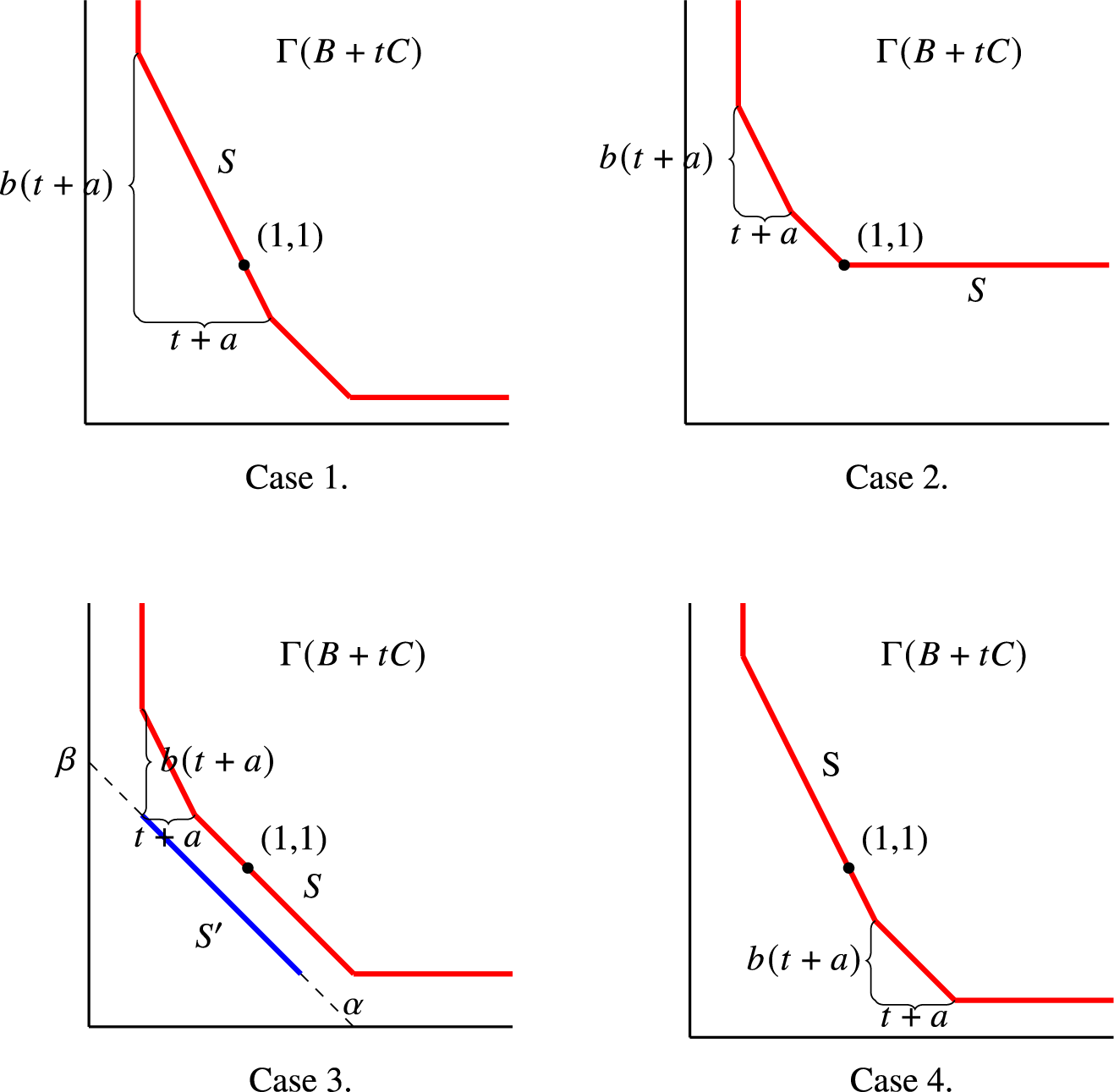
. We divide the rest of the proof into four cases based on the slope of S. The situation of these four cases is illustrated in Figure 1.
$\operatorname {\mathrm {slope}}(S)=b$
. Then
$0<b=\operatorname {\mathrm {slope}}(S)<+\infty $
. It follows from
$\textbf {1} \in S$
that
$$ \begin{align} b+1=bp_2+q_2. \end{align} $$
Let
$\textbf {b}=(b,1)$
and
$E_{\textbf {b}}$
be the exceptional divisor obtained by the weighted blow up
$\sigma :Y\rightarrow X$
at
$P\in X$
with
$\operatorname {\mathrm {wt}}(x,y)=(b,1)$
. Applying Lemma 3.4(3), we deduce that
$$ \begin{align*}\langle \textbf{b}, \Gamma(B) \rangle=b(p_2-t)+q_2.\end{align*} $$
By (3.1) we have
$$ \begin{align*}a(E_{\textbf{b}},X,B)=\langle \textbf{b},\textbf{1}\rangle-\langle \textbf{b},\Gamma(B) \rangle=b+1-[b(p_2-t)+q_2]=tb,\end{align*} $$
where the last equality follows from (3.4). As
$\operatorname {\mathrm {mld}}(X\ni P, B)\geqslant \epsilon $
, we have
$t\geqslant \epsilon /b$
.
We deduce that
$$ \begin{align} b(p_2-t-a)+q_2= \langle \textbf{b}, \Gamma(B-aC)\rangle\leqslant 2, \end{align} $$
where the equality follows from Lemma 3.4(3) (taking
$B=B-aC,~ D=C, ~t=t+a$
in Lemma 3.4) and the inequality follows from Lemma 3.6 and the condition that
$(B-aC\cdot C)_P\leqslant 2$
. Combining (3.4) and (3.5), we get
$$ \begin{align*}t\geqslant 1-a-\frac{1}{b}\geqslant \epsilon-\frac{1}{b}.\end{align*} $$
Therefore
$t\geqslant \max \{\epsilon /b,\epsilon -1/b\}.$
If
$b\geqslant 2n+1$
, then
$$ \begin{align*}t\geqslant\epsilon-\frac{1}{b}\geqslant\epsilon-\frac{1}{2n+1}=\frac{(2n+1)\epsilon-1}{2n+1} \geqslant \frac{(2n+1)\epsilon-1}{2n(n+1)}.\end{align*} $$
Otherwise
$b\leqslant 2n$
, then
$$ \begin{align*}t\geqslant \frac{\epsilon}{b}\geqslant \frac{\epsilon}{2n}=\frac{(n+1)\epsilon}{2n(n+1)}\geqslant \frac{(n+1)\epsilon+(n\epsilon-1)}{2n(n+1)}=\frac{(2n+1)\epsilon-1}{2n(n+1)}\end{align*} $$
where the third inequality follows from
$ \epsilon \leqslant 1/n$
.
$\operatorname {\mathrm {slope}}(S)=0$
. By Claim 3.8, 1 is a vertex of S, so we may write
$S=(1+\mathbb {R}_{\geqslant 0},1)$
. Then
$(1-t+\mathbb {R}_{\geqslant 0},1)$
is a face of
$\Gamma (B)$
by Lemma 3.4(2) when
$b<+\infty $
and by Lemma 3.5 when
$b=+\infty $
. Denote
$\textbf {s}=(1-t,1)$
. Let
$\textbf {p}=(1,N)$
and
$E_{\textbf {p}}$
be the exceptional divisor obtained by the weighted blow up at
$P\in X$
with
$\operatorname {\mathrm {wt}}(x,y)=(1,N)$
, where N is a sufficiently large integer. We claim that
$$ \begin{align} \langle \textbf{p},\Gamma(B) \rangle=\langle \textbf{p},\textbf{s}\rangle. \end{align} $$
Indeed, as
$(1-t+\mathbb {R}_{\geqslant 0},1)$
is a face of
$\Gamma (B)$
, for any vertex
$\textbf {v}=(v_1,v_2)\neq \textbf {s}$
of
$\Gamma (B)$
, we have
$v_2>1$
, which implies that
$$ \begin{align*}\langle \textbf{p}, \textbf{v} \rangle=v_1+Nv_2>(1-t)+N=\langle \textbf{p}, \textbf{s} \rangle\end{align*} $$
since N is sufficiently large and the number of vertices of
$\Gamma (B)$
is finite. So the equality (3.6) holds. Then we have
$$ \begin{align*} \epsilon\leqslant a(E_{\textbf{p}},X,B) &=\langle \textbf{p},\textbf{1} \rangle-\langle \textbf{p},\Gamma(B) \rangle=\langle \textbf{p},\textbf{1} \rangle-\langle \textbf{p},\textbf{s}\rangle\\ &=(1+N)-((1-t)+N)=t. \end{align*} $$
It follows that
$$ \begin{align*}t\geqslant\epsilon\geqslant \frac{(2n+1)\epsilon-1}{2n(n+1)}.\end{align*} $$
$0<\operatorname {\mathrm {slope}}(S)<b$
. Denote
$S'=S-(t+a,0)$
. Then
$S'$
is a compact 1-dimensional face of
$\Gamma (B-aC)$
by Lemma 3.4(2) when
$b<+\infty $
and by Lemma 3.5 when
$b=+\infty $
. Denote the intersection point of the line through
$S'$
with x-axis (resp. y-axis) by
$(\alpha ,0)$
(resp.
$(0,\beta )$
), where
$\alpha $
and
$\beta $
are positive real numbers. Then
$\beta /\alpha < b$
. As
$\textbf {1}\in S=S'+(t+a,0)$
, one has
$$ \begin{align} \beta\geqslant 1\quad \text{ and }\quad t=1+\alpha/\beta-\alpha-a. \end{align} $$
Note that
$\Gamma _+(B-aC)$
is contained in the convex hull of the union of
$(\alpha ,0)+\mathbb {R}_{\geqslant 0}^2$
and
$(0,\beta )+\mathbb {R}_{\geqslant 0}^2$
. So we have
$$ \begin{align} \beta=\min\{\beta,b\alpha\}\leqslant \langle \textbf{b},\Gamma(B-aC)\rangle\leqslant 2, \end{align} $$
where
$\textbf {b}=(b,1)$
and the last inequality follows from Lemma 3.6 and
$(B-aC\cdot C)_P\leqslant 2$
.
For any
$\textbf {e}=(e_1,e_2)\in \mathbb {N}^2$
with
$e_1,e_2$
coprime, we have
$$ \begin{align*}a(E_{\textbf{e}},X,B-aC)=e_1+e_2-\langle \textbf{e}, \Gamma(B-aC) \rangle\leqslant e_1+e_2-\min\{\alpha e_1,\beta e_2\},\end{align*} $$
where
$E_{\textbf {e}}$
is the exceptional divisor obtained by the weighted blow up
$\sigma :Y\rightarrow X$
at
$P\in X$
with
$\operatorname {\mathrm {wt}}(x,y)=(e_1,e_2)$
. Since
$\operatorname {\mathrm {mult}}_{E_{\textbf {e}}} \sigma ^* C=\min \{e_1,be_2\}$
and
$\beta /\alpha <b$
, one has
$$ \begin{align} \epsilon\leqslant a(E_{\textbf{e}},X,B) \leqslant \begin{cases} e_1+e_2-\alpha e_1- ae_1, & \text{if } e_1/e_2 \leqslant \beta/\alpha,\\ e_1+e_2-\beta e_2- ae_1, & \text{if } \beta/\alpha\leqslant e_1/e_2\leqslant b, \\ e_1+e_2-\beta e_2- abe_2, & \text{if } e_1/e_2\geqslant b. \end{cases} \end{align} $$
Define a piece-wise linear function f on
$\mathbb {R}_{\geqslant 0}^2$
by
$$ \begin{align*}f(r_1,r_2) := \begin{cases} r_1+r_2-\alpha r_1- ar_1, & \text{if } r_1/r_2 \leqslant \beta/\alpha,\\ r_1+r_2-\beta r_2- ar_1, & \text{if } r_1/r_2\geqslant \beta/\alpha, \\ \end{cases} \end{align*} $$
for any
$(r_1,r_2)\in \mathbb {R}_{\geqslant 0}^2$
. Here we use the convention that
$r_1/0=+\infty \geqslant \beta /\alpha $
. By (3.9) one has
$f(e_1,e_2)\geqslant \epsilon $
for any
$(e_1,e_2)\in \mathbb {N}^2$
such that
$e_1/e_2\leqslant b$
. In particular,
$f(b,1)\geqslant \epsilon $
if
$b<+\infty $
.
Claim.
$f(e_1,e_2)\geqslant \epsilon $
for any
$e_1\in \mathbb {N}$
and
$e_2\in \mathbb {Z}_{\geqslant 0}$
.
Proof. If
$e_2=0$
, then
$f(e_1,e_2)=(1-a)e_1\geqslant \epsilon e_1\geqslant \epsilon $
. So we may suppose that
$e_2>0$
. Since the claim has been confirmed when
$e_1/e_2\leqslant b$
, we may suppose that
$b<+\infty $
and
$e_1>be_2$
. Then
$f(e_1,e_2)=(1-a)e_1+(1-\beta )e_2$
since
$b> \beta /\alpha $
.
If
$e_1<b$
, then
$e_2<e_1/b<1$
, which implies that
$e_2\leqslant 0$
and contradicts our hypothesis. So we may assume that
$e_1\geqslant b$
. Then
$$ \begin{align*}f(e_1,e_2)\geqslant f(e_1,e_1/b)=f(b,1)\cdot e_1/b\geqslant \epsilon,\end{align*} $$
where the first inequality follows from
$1-\beta \leqslant 0$
(see (3.7)) and
$e_2<e_1/b$
.
By (3.7) we have
$t=f(1,\alpha /\beta )$
. By Lemma 3.9 below, there exist
$k\in \mathbb {N}$
and
$l\in \mathbb Z_{\geqslant 0}$
such that
$$ \begin{align*}\frac{\epsilon-|k\alpha/\beta-l| }{k}\geqslant \frac{(2n+1)\epsilon-1}{2n(n+1)}.\end{align*} $$
We claim that
$$ \begin{align*}f(k,k\alpha/\beta)\geqslant f(k,l)-|k\alpha/\beta-l|.\end{align*} $$
Indeed, if
$l\geqslant k\alpha /\beta $
, then
$$ \begin{align*}f(k,l)=k+l-\alpha k-ak=f(k,k\alpha/\beta)+(l-k\alpha/\beta);\end{align*} $$
Otherwise
$l\leqslant k\alpha /\beta $
, then
$$ \begin{align*} f(k,l)=k+l-\beta l -ak=& f(k,k\alpha/\beta)+(\beta-1)(k\alpha/\beta-l)\\ \leqslant & f(k,k\alpha/\beta)+(k\alpha/\beta-l), \end{align*} $$
where the inequality follows from
$1\leqslant \beta \leqslant 2$
(see (3.7) and (3.8)).
Therefore we have
$$ \begin{align*}t=f(1,\alpha/\beta)=\frac{f(k,k\alpha/\beta)}{k}\geqslant \frac{f(k,l)-|k\alpha/\beta-l| }{k}\geqslant \frac{\epsilon-|k\alpha/\beta-l| }{k}\geqslant \frac{(2n+1)\epsilon-1}{2n(n+1)}.\end{align*} $$
$\operatorname {\mathrm {slope}}(S)>b$
. Then
$0<b<\operatorname {\mathrm {slope}}(S)<+\infty $
. Denote
$S'=S-(0,b(t+a))$
. By Lemma 3.4(1)
$S'$
is a compact 1-dimensional face of
$\Gamma (B-aC)$
. Denote the intersection point of the line through
$S'$
with x-axis (resp. y-axis) by
$(\alpha ,0)$
(resp.
$(0,\beta )$
), where
$\alpha $
and
$\beta $
are positive real numbers. Then
$\beta> b\alpha $
and
$\Gamma _+(B-aC)$
is contained in the convex hull of the union of
$(\alpha ,0)+\mathbb {R}_{\geqslant 0}^2$
and
$(0,\beta )+\mathbb {R}_{\geqslant 0}^2$
. Recall that
$\textbf {1}\in S$
and
$\textbf {1}$
in not the right vertex of S, the x-coordinate of the right vertex of
$S'$
is larger than 1, which implies that
$\alpha>1$
. Since
$(B-aC\cdot C)_P\leqslant 2$
, by Lemma 3.6 one has
$$ \begin{align*}b\alpha=\min\{\beta,b\alpha\}\leqslant \langle\textbf{b},\Gamma(B-aC)\rangle\leqslant 2,\end{align*} $$
where
$\textbf {b}=(b,1)$
. Therefore
$b=1$
. After switching x and y, we have
$0<\operatorname {\mathrm {slope}}(S)<1=b$
and hence we can reduce this to Case 3 (note that the condition that
$\textbf {1}$
is not the right vertex of S may not be satisfied after switching x and y; fortunately this condition is not used in the proof for Case 3). This finishes the proof of Theorem 1.9.
Figure 1 Four cases.
Lemma 3.9. Let
$x,\epsilon $
be two real numbers so that
$x\geqslant 0$
and
$\frac {1}{n+1}\leqslant \epsilon \leqslant \frac {1}{n}$
for some
$n\in \mathbb {N}$
. Then there exist
$k\in \mathbb {N}$
and
$l\in \mathbb Z_{\geqslant 0}$
such that
$$ \begin{align*}\frac{\epsilon-|kx-l| }{k}\geqslant \frac{(2n+1)\epsilon-1}{2n(n+1)}.\end{align*} $$
Proof. Without loss of generality, we may suppose that
$0\leqslant x<1$
. If
$x=0$
, we can take
$k=1$
and
$l=0$
, then we are done. So we may suppose that
$0<x<1$
.
We construct two finite sequences as follows. Set
$r_{-1}=1$
,
$r_0=x$
,
$a_{-1}=0$
and
$a_{0}=1$
. For
$i\geqslant 1$
, assuming that
$r_{i-2}, r_{i-1}, a_{i-2},a_{i-1}$
have been defined, we define
$r_i$
by
$r_{i-2}=b_{i}r_{i-1}+r_{i}$
where
$b_i$
is the positive integer such that
$0\leqslant r_{i}<r_{i-1}$
and we define
$a_i=a_{i-2}+b_i a_{i-1}$
. If either
$r_i=0$
or
$a_i\geqslant n+1$
, we terminate the sequence and set m to be i. Note that the sequence will stop because
$a_i> a_{i-1}$
for
$i\geqslant 2$
. Moreover, by definition we have
$m\geqslant 1$
and
$a_i$
is a positive integer for
$0\leqslant i\leqslant m$
.
Claim. For
$i=-1,0,\cdots ,m$
, we have
$$ \begin{align*}a_i x \equiv \begin{cases} r_i ~(\operatorname{\mathrm{mod}} 1), & \text{if } i \text{ is even,} \\ -r_i~(\operatorname{\mathrm{mod}} 1), & \text{if } i \text{ is odd.} \end{cases} \end{align*} $$
Proof of the claim.
By definition we have
$r_{-1}=1-a_{-1} x$
and
$r_0=a_0 x$
. Suppose that the claim holds for
$i-2$
and
$i-1$
. If i is even, then
$$ \begin{align*} r_i &=r_{i-2}-b_i r_{i-1}\\ &\equiv a_{i-2}x-b_i(-a_{i-1}x) ~(\operatorname{\mathrm{mod}} 1)\\ & =(a_{i-2}+b_ia_{i-1})x=a_i x. \end{align*} $$
If i is odd, then
$$ \begin{align*} r_i&=r_{i-2}-b_i r_{i-1}\\ &\equiv -a_{i-2}x-b_i a_{i-1}x ~(\operatorname{\mathrm{mod}} 1)\\ &=-(a_{i-2}+b_ia_{i-1})x=-a_i x.\\[-37pt] \end{align*} $$
Claim.
$a_ir_{i-1}+a_{i-1}r_i=1$
for
$i=0,\cdots ,m$
.
Proof of the claim.
By definition we have
$a_{0}r_{-1}+a_{-1}r_0=1$
. Suppose that the claim holds for
$i-1$
. Then
$$ \begin{align*} &a_ir_{i-1}+a_{i-1}r_i\\& \quad =(a_{i-2}+b_ia_{i-1})r_{i-1}+a_{i-1}(r_{i-2}-b_ir_{i-1})\\& \quad =a_{i-2}r_{i-1}+a_{i-1}r_{i-2}=1.\\[-37pt] \end{align*} $$
If
$a_m\leqslant n$
, by definition we have
$r_m=0$
, so
$a_mx$
is an integer. Taking
$k=a_m$
and
$l=a_mx$
, we have
$$ \begin{align*}\frac{\epsilon-|kx-l| }{k}=\frac{\epsilon-0}{a_m}\geqslant \frac{\epsilon}{n}>\frac{(2n+1)\epsilon-1}{2n(n+1)}.\end{align*} $$
If
$a_m\geqslant n+1$
, by definition we have
$a_{m-1}\leqslant n$
. We claim that
$$ \begin{align} \left(\frac{1}{a_{m-1}}+\frac{1}{a_m}\right)\epsilon-\frac{1}{a_{m-1}a_{m}}\geqslant \left(\frac{1}{n}+\frac{1}{n+1}\right)\epsilon-\frac{1}{n(n+1)}. \end{align} $$
Indeed, the left side minus the right side of (3.10) is equal to
$$ \begin{align*} &\left(\frac{1}{a_{m-1}}-\frac{1}{n}\right)\epsilon-\frac{1}{a_ma_{m-1}}-\left(\frac{1}{n+1}-\frac{1}{a_m}\right)\epsilon+\frac{1}{n(n+1)}\\& \quad = \left(\frac{1}{a_{m-1}}-\frac{1}{n}\right)\epsilon-\frac{1}{a_ma_{m-1}}+\frac{1}{na_m}-\left(\frac{1}{n+1}-\frac{1}{a_m}\right)\epsilon+\frac{1}{n(n+1)}-\frac{1}{na_m}\\& \quad = \left(\frac{1}{a_{m-1}}-\frac{1}{n}\right)\left(\epsilon-\frac{1}{a_m}\right)+\left(\frac{1}{n+1}-\frac{1}{a_m}\right)\left(\frac{1}{n}-\epsilon\right)\geqslant 0. \end{align*} $$
By (3.10) and the fact that
$a_mr_{m-1}+a_{m-1}r_m=1$
, we have
$$ \begin{align*}\left(\frac{1}{a_{m-1}}+\frac{1}{a_m}\right)\epsilon-\frac{a_mr_{m-1}+a_{m-1}r_m}{a_{m-1}a_{m}}\geqslant \left(\frac{1}{n}+\frac{1}{n+1}\right)\epsilon-\frac{1}{n(n+1)},\end{align*} $$
which is equivalent to
$$ \begin{align*}\frac{\epsilon-r_{m-1}}{a_{m-1}}+\frac{\epsilon-r_{m}}{a_{m}}\geqslant \frac{(2n+1)\epsilon-1}{n(n+1)}.\end{align*} $$
So we have
$$ \begin{align*}\text{either }\quad \frac{\epsilon-r_{m-1}}{a_{m-1}}\geqslant \frac{(2n+1)\epsilon-1}{2n(n+1)}\quad \text{ or } \quad \frac{\epsilon-r_{m}}{a_{m}}\geqslant \frac{(2n+1)\epsilon-1}{2n(n+1)}.\end{align*} $$
In the former case we take
$k=a_{m-1}$
and in the latter case we take
$k=a_m$
. This completes the proof of Lemma 3.9.
4 Proofs of main theorems
Making a small modification to the proof of [Reference Han, Jiang and Luo13, Theorem 1.10] and applying Theorem 1.9, we obtain the proof of the following proposition.
Proposition 4.1. Let
$\pi :(X,B)\rightarrow Z$
be an lc-trivial fibration and
$z\in Z$
a codimension
$1$
point such that
-
(1)
$\dim X - \dim Z=1$
, -
(2)
$\operatorname {\mathrm {mld}}(X/Z\ni z,B)\geqslant \epsilon $
where
$0<\epsilon \leqslant 1$
, and -
(3) the geometric generic fiber of
$\pi $
is a rational curve.
Then
$\operatorname {\mathrm {lct}}(X/Z\ni z,B; \pi ^*\overline {z})\geqslant \delta $
, where
$\delta $
is as in Theorem 1.4. In particular, if B is effective, then the multiplicity of each component of
$\pi ^*z$
is bounded from above by
$1/\delta $
.
Proof. If
$\operatorname {\mathrm {mld}}(X/Z\ni z,B)> 1$
, by [Reference Han, Jiang and Luo13, Theorem 1.10],
$$ \begin{align*}\operatorname{\mathrm{lct}}(X/Z\ni z,B; \pi^*\overline{z})\geqslant \operatorname{\mathrm{mld}}(X/Z\ni z,B)-\frac{1}{2}> \frac{1}{2}.\end{align*} $$
It is easy to check that
$\delta \leqslant \frac {1}{2}$
where
$\delta $
is as in Theorem 1.4 when
$0<\epsilon \leqslant 1$
. So we may assume that
$\operatorname {\mathrm {mld}}(X/Z\ni z,B)\leqslant 1$
.
By the same argument as that in the proof of [Reference Han, Jiang and Luo13, Theorem 1.10], we can reduce the problem to the case when
$\dim X=2$
. So from now on we suppose that X is a surface and Z is a curve.
First we consider the case when X is smooth and B is effective. Since the geometric generic fiber of
$\pi $
is a rational curve, we can run an MMP on
$K_X$
over Z and reach a minimal ruled surface
$\pi ':X'\to Z$
, that is, a
$\mathbb {P}^1$
-bundle over Z. Denote by
$\phi :X\to X'$
the induced morphism and denote
$B'=\phi _*B$
. As
$K_X+B\sim 0/Z$
, we have
$K_X+B=\phi ^*(K_{X'}+B')$
, which implies that
$$ \begin{align*}\operatorname{\mathrm{mld}}(X'/Z\ni z,B')=\operatorname{\mathrm{mld}}(X/Z\ni z,B) \quad \text{and}\quad \operatorname{\mathrm{lct}}(X'/Z\ni z,B'; \pi^{\prime*}z)=\operatorname{\mathrm{lct}}(X/Z\ni z,B; \pi^*z).\end{align*} $$
Replacing
$\pi :X\to Z$
by
$\pi ':X'\to Z$
, we may assume that
$\pi : X\rightarrow Z$
is a
$\mathbb {P}^1$
-bundle over a curve. Then
$F:=\pi ^*z\cong \mathbb {P}^1$
. Applying the adjunction formula we obtain
$K_X\cdot F=-2$
. As
$(K_X+B)\cdot F=0$
and
$F\cdot F=0$
, we have
$B'\cdot F=2$
, where
$B'=B-\operatorname {\mathrm {mult}}_F B\cdot F$
. Therefore, for any closed point
$P\in F$
, the local intersection number
$(B'\cdot F)_P\leqslant 2$
. Moreover, as
$\operatorname {\mathrm {mld}}(X/Z\ni z,B)\geqslant \epsilon $
, one has
$\operatorname {\mathrm {mult}}_F B\leqslant 1-\epsilon $
and
$\operatorname {\mathrm {mld}}(X\ni P,B)\geqslant \epsilon $
. Applying Theorem 1.9, we deduce that
$\operatorname {\mathrm {lct}}(X\ni P, B;F)\geqslant \delta $
for any closed point
$P\in F$
, where
$\delta $
is as in Theorem 1.4. It follows that
$\operatorname {\mathrm {lct}}(X/Z\ni z,B; \pi ^*z)\geqslant \delta $
.
Next we treat the general case. Let
$f:W\rightarrow X$
be a log resolution of
$(X,B+\pi ^*z)$
. We may write
$K_W+B_W=f^*(K_X+B)$
. Then
$\operatorname {\mathrm {mld}}(W/Z\ni z,B_W)=\operatorname {\mathrm {mld}}(X/Z\ni z,B)$
. So we have
$$ \begin{align} \epsilon\leqslant \operatorname{\mathrm{mld}}(W/Z\ni z,B_W) \leqslant 1, \end{align} $$
which implies that
$(W/Z\ni z,B_W)$
is lc. Hence
$B_W\leqslant 1$
(i.e., coefficients of
$B_W$
are at most 1) after possibly shrinking Z near z. We claim that
$$ \begin{align} \text{there is a prime divisor } C_0\subseteq \operatorname{\mathrm{Supp}} f^*\pi^*z \text{ such that } \operatorname{\mathrm{mult}}_{C_0} B_W\geqslant 0. \end{align} $$
Indeed, if this is not the case, since
$B_W\leqslant 1$
and
$B_W$
is a simple normal crossing divisor, one has
$\operatorname {\mathrm {mld}}(W/Z\ni z,B_W)> 1$
, which is in contradiction with (4.1).
We may write
$B_W=D-G$
where
$D,G\geqslant 0$
have no common components. Then
$$ \begin{align*}K_W+D=K_W+B_W+G\sim_{\mathbb{R}} G/Z.\end{align*} $$
We claim that any
$(K_W+D)$
-MMP/Z is also a
$K_W$
-MMP/Z. Indeed, if E is a curve on W such that its image on Z is a point and
$E\cdot (K_W+D)<0$
, then
$E\cdot G<0$
and hence
$E\subseteq \operatorname {\mathrm {Supp}} G$
. So
$E\nsubseteq \operatorname {\mathrm {Supp}} D$
and
$E\cdot D\geqslant 0$
. It follows that
$E\cdot K_W <0$
.
By Remark 2.6, B is effective over the generic point of Z. So we may assume that
$\operatorname {\mathrm {Supp}} G\subseteq \operatorname {\mathrm {Supp}} f^*\pi ^* z$
after possibly shrinking Z near z. By (4.2), there exists a prime divisor
$C_0 \subseteq \operatorname {\mathrm {Supp}} f^*\pi ^* z$
but
$C_0 \nsubseteq \operatorname {\mathrm {Supp}} G$
. Hence G is very exceptional over Z (see [Reference Birkar4, Definition 3.1]). By [Reference Birkar4, Theorem 3.5], we may run a
$(K_W+D)$
-MMP/Z and reach a model Y such that
$G_Y=0$
with the induced maps
$g:W\rightarrow Y$
and
$h:Y\rightarrow Z$
. As this MMP is also a
$K_W$
-MMP/Z, Y is a smooth surface. Since
$K_W+B_W=K_W+D-G\sim _{\mathbb {R}} 0/Z$
, by the negativity lemma, one has
$g^*(K_Y+D_Y)=K_W+B_W$
. Hence
$$ \begin{align*}\operatorname{\mathrm{mld}}(Y/Z\ni z,D_Y)=\operatorname{\mathrm{mld}}(X/Z\ni z,B)=\epsilon\end{align*} $$
and
$$ \begin{align*}\operatorname{\mathrm{lct}}(Y/Z\ni z,D_Y;h^*z)=\operatorname{\mathrm{lct}}(X/Z\ni z,B;\pi^*z).\end{align*} $$
Replacing
$(X,B)$
by
$(Y,D_Y)$
, we can reduce the general case to the case when X is smooth and B is effective, which has been solved.
Proof of Theorem 1.4.
By the same argument as that in the proof of [Reference Han, Jiang and Luo13, Theorem 1.7], Theorem 1.4 follows from Proposition 4.1.
Proof of Corollary 1.7.
By the same argument as that in the proof of [Reference Han, Jiang and Luo13, Corollary 1.8], Corollary 1.7 follows from Proposition 4.1.
Proof of Corollary 1.8.
The case when
$\epsilon =1$
is solved in [Reference Han, Jiang and Luo13, Theorem 1.4]. So we may suppose that
$\epsilon <1$
. By the relative basepoint-free theorem [Reference Kollár and Mori17, Theorem 3.24],
$-K_X$
is semiample over Z. Take a large integer N such that
$1/N\leqslant 1-\epsilon $
and
$-NK_X$
is free over Z. Let H be a general effective divisor such that
$H\sim -NK_X/Z$
and let
$B=\frac {1}{N} H$
. Then
$K_X+B\sim _{\mathbb {Q}} 0/Z$
and
$(X,B)$
is an
$\epsilon $
-lc pair. By Corollary 1.7, we can choose
$M_Z\geqslant 0$
representing the moduli part so that
$(Z,B_Z+M_Z)$
is
$\delta $
-lc, where
$\delta $
is as in Theorem 1.4. Since
$B\geqslant 0$
, one has
$B_Z\geqslant 0$
. Hence Z is
$\delta $
-lc. The last statement of Corollary 1.8 follows from the last statement of Proposition 4.1.
A Proof of the lemma in Example 1.6
In this appendix we will prove the lemma used in Example 1.6.
Lemma A.1. Let
$X=\mathbb A^2$
with coordinates
$x,y$
. Let B be the
$\mathbb R$
-divisor
$$ \begin{align*}\lambda\cdot (x^m+y^n=0)+\mu\cdot (x=0)\end{align*} $$
where
$n,m\in \mathbb N$
and
$0\leqslant \lambda , \mu \leqslant 1$
, such that
$(X,B)$
is lc. Then
$$ \begin{align*}\operatorname{\mathrm{mld}}(X\ni 0, B)=\inf\big\{p_1+p_2-\min\{(\lambda m+\mu)p_1,\mu p_1 +\lambda n p_2\} \mid (p_1,p_2)\in \mathbb N^2 \big\}.\end{align*} $$
Proof. Denote
$B_1=\lambda \cdot (x^m+y^n=0)$
and
$B_2=\mu \cdot (x=0)$
. Then
$B=B_1+B_2$
. For any
$\textbf {p}=(p_1,p_2)\in \mathbb N^2$
with
$p_1,p_2$
coprime, denote by
$E_{\textbf {p}}$
the toric divisor over X corresponding to the ray
$\mathbb R_{\geqslant 0}\cdot \textbf {p}$
. Then
$$ \begin{align*}a(E_{\textbf{p}},X,B)=p_1+p_2-\min\{(\lambda m+\mu)p_1,\mu p_1 +\lambda n p_2\}.\end{align*} $$
So it suffices to show that there exists a toric divisor F over X with
$\text {center}_{X} F=0$
such that
$a(F,X,B)=\operatorname {\mathrm {mld}}(X\ni 0, B)$
.
Let
$g=\gcd (n,m)$
and
$(n',m')=(n,m)/g$
. Let
$\sigma : Y\rightarrow X$
be the weighted blow up at
$0$
with
$\operatorname {\mathrm {wt}}(x,y)=(n',m')$
. Then
$Y\subset X\times \mathbb P^1_{z,w}$
is defined by
$(x^{m'}w=y^{n'}z)$
and the exceptional divisor E on Y is isomorphic to
$\mathbb P^1_{z,w}$
. Denote
$P_1=[0:1]$
and
$P_2=[1:0]$
on E. Then
$Y\setminus \{P_1,P_2\}$
is smooth. Denote by
$B^{\prime }_1,B^{\prime }_2$
the birational transform of
$B_1,B_2$
on Y. Then we can write
$$ \begin{align*}K_Y+e E + B^{\prime}_1+B^{\prime}_2=\sigma^*(K_X+B).\end{align*} $$
Moreover,
$(\operatorname {\mathrm {Supp}} B^{\prime }_1)|_E$
is defined by
$(z^g+w^g=0)$
on E. Hence
$P_1,P_2\notin E \cap \operatorname {\mathrm {Supp}} B^{\prime }_1$
and E meets
$\operatorname {\mathrm {Supp}} B^{\prime }_1$
transversally. It follows that
$$ \begin{align*}\operatorname{\mathrm{mld}}(X\ni 0, B)=\min\{a(E,X,B),~ \operatorname{\mathrm{mld}}(Y\ni P_1,e E+B^{\prime}_2),~\operatorname{\mathrm{mld}}(Y\ni P_2,e E+B^{\prime}_2)\}.\end{align*} $$
Since
$\sigma :Y\rightarrow X$
is a toric morphism and
$E,B^{\prime }_2$
are toric divisors on Y, there exists a toric divisor
$F_i$
over Y with
$\text {center}_Y F_i=P_i$
such that
$$ \begin{align*}\operatorname{\mathrm{mld}}(Y\ni P_i,e E+B^{\prime}_2)=a(F_i,Y,e E+B^{\prime}_2)=a(F_i,X,B)\end{align*} $$
for
$i=1,2$
. This finishes the proof of the lemma.
Lemma A.2. Let
$X=\mathbb A^2$
with coordinates
$x,y$
. Let C be the curve
$(x=0)$
and B the
$\mathbb R$
-divisor
$\lambda \cdot (x^m+y^n=0)$
, where
$0\leqslant \lambda \leqslant 1$
and
$n,m\in \mathbb N$
such that
$\lambda n\geqslant 1$
and
$\frac {1}{n}+\frac {1}{m}\geqslant \lambda $
. Then
$$ \begin{align*}\operatorname{\mathrm{lct}}(X\ni 0,B; C)= 1-\lambda m +\frac{m}{n}.\end{align*} $$
Proof. By [Reference Han, Jiang and Luo13, Proposition 3.2],
$$ \begin{align*}\operatorname{\mathrm{lct}}(X\ni0,0;B+tC)=\min\{\frac{n+m}{\lambda nm+tn},\frac{1}{t},\frac{1}{\lambda}\}\end{align*} $$
for any
$t\geqslant 0$
. The lemma follows from the fact that
$$ \begin{align*}\operatorname{\mathrm{lct}}(X\ni 0,B; C)=\sup\{t\geqslant 0\mid \operatorname{\mathrm{lct}}(X\ni0,0;B+tC)\geqslant 1\}.\\[-37pt] \end{align*} $$
Lemma A.3. Let
$\epsilon =\frac {p}{q}$
be a rational number such that
$\frac {1}{n+1}\leqslant \epsilon \leqslant \frac {1}{n}$
, where
$p,q,n\in \mathbb {N}$
. Let
$X=\mathbb A^2$
with coordinates
$x,y$
. Let
$C=(x=0)$
and
$$ \begin{align*}B=\frac{1}{qn(n+1)}\cdot \left(x^{q(2n+1)-p}+y^{2qn(n+1)}=0\right)+\frac{qn-p}{q(n+1)}\cdot(x=0).\end{align*} $$
Then we have
$$ \begin{align*}\operatorname{\mathrm{mult}}_C B\leqslant 1-\epsilon, \quad \operatorname{\mathrm{mld}}(X\ni 0,B)=\epsilon \quad \text{ and }\quad \operatorname{\mathrm{lct}}(X\ni 0,B; C)= \frac{(2n+1)\epsilon-1}{2n(n+1)}.\end{align*} $$
Proof. The assertion on
$\operatorname {\mathrm {mult}}_C B$
can be checked directly. The assertion on the log canonical threshold follows from Lemma A.2 by direct calculation. Next we will treat the assertion on the minimal log discrepancy. By Lemma A.1, we have
$$ \begin{align*} \operatorname{\mathrm{mld}}(X\ni 0, B)&=\inf\big\{p_1+p_2-\min\{\frac{n-\epsilon}{n+1}p_1+2p_2,\frac{n+1-\epsilon}{n}p_1\}\mid p_1,p_2\in \mathbb N\big\}\\ &=\inf\big\{\max\{\frac{\epsilon+1}{n+1} p_1-p_2,\frac{\epsilon-1}{n}p_1+p_2\}\mid p_1,p_2\in \mathbb N\big\}. \end{align*} $$
Denote
$$ \begin{align*}k:=\frac{(2n+1)-\epsilon}{2n(n+1)}\end{align*} $$
and define a piece-wise linear function f on
$\mathbb R_{\geqslant 0}^2$
by
$$ \begin{align*}f(r_1,r_2) := \begin{cases} \frac{\epsilon+1}{n+1} r_1-r_2, & \text{if } \frac{r_2}{r_1} \leqslant k,\\ \frac{\epsilon-1}{n}r_1+r_2, & \text{if } \frac{r_2}{r_1} \geqslant k, \\ \end{cases} \end{align*} $$
for any
$r_1,r_2\in \mathbb R_{\geqslant 0}$
. Then we have
$$ \begin{align*}\operatorname{\mathrm{mld}}(X\ni 0, B)=\inf\{f(p_1,p_2)\mid p_1,p_2\in \mathbb N\}.\end{align*} $$
By the definition of f, for any
$r_1,r_2,r^{\prime }_1\in \mathbb R_{\geqslant 0}$
, we have
$$ \begin{align*}f(r_1,r_2)\leqslant f(r^{\prime}_1,r_2)\quad \text{ if } r_2/r_1\leqslant k \text{ and } r^{\prime}_1\geqslant r_1\end{align*} $$
and
$$ \begin{align*}f(r_1,r_2)\leqslant f(r^{\prime}_1,r_2) \quad \text{ if } r_2/r_1\geqslant k \text{ and } r^{\prime}_1\leqslant r_1.\end{align*} $$
It is easy to check that
$$ \begin{align*}\frac{1}{n+1}\leqslant k\leqslant \frac{1}{n} \quad \text{and}\quad \frac{2}{2n+2}\leqslant k\leqslant \frac{2}{2n+1}.\end{align*} $$
By direct calculation, we have
$f(n,1)=f(n+1,1)=\epsilon $
and
$$ \begin{align*}f(2n+1,2)=\frac{\epsilon-1}{n}(2n+1)+2\geqslant \epsilon \quad \text{ as } \epsilon\geqslant \frac{1}{n+1}.\end{align*} $$
For any
$(p_1,p_2)\in \mathbb N^2$
, there are the following three cases.
-
(1)
$p_2=1$
. If
$p_1\leqslant n$
, then
$f(p_1,1)\geqslant f(n,1)=\epsilon $
; otherwise
$p_1\geqslant n+1$
, then
$f(p_1,1)\geqslant f(n+1,1)=\epsilon $
. -
(2)
$p_2=2$
. If
$p_1\leqslant 2n+1$
, then
$f(p_1,2)\geqslant f(2n+1,2)\geqslant \epsilon $
; otherwise
$p_1\geqslant 2n+2$
, then
$f(p_1,2)\geqslant f(2n+2,2)=2\epsilon $
. -
(3)
$p_2\geqslant 3$
. Let
$p^{\prime }_1=p_2/k$
, then by calculation
$$ \begin{align*}f(p^{\prime}_1,p_2)=\frac{(2n+1)\epsilon-1}{(2n+1)-\epsilon}\cdot p_2.\end{align*} $$
One can check that
$f(p^{\prime }_1,p_2)\geqslant \epsilon $
when
$p_2\geqslant 3$
and
$\epsilon \geqslant 1/(n+1)$
. So, either
$p_1\leqslant p^{\prime }_1$
or
$p_1\geqslant p^{\prime }_1$
, we have
$f(p_1,p_2)\geqslant f(p^{\prime }_1,p_2)\geqslant \epsilon $
.
Therefore,
$$ \begin{align*}\operatorname{\mathrm{mld}}(X\ni 0, B)=\inf\{f(p_1,p_2)\mid p_1,p_2\in \mathbb N\}=\epsilon.\\[-37pt] \end{align*} $$
Acknowledgments
The author would like to thank Caucher Birkar for his valuable comments and constant support. This work was partially done at Tsinghua University. It was completed at Sun Yat-sen University with support from the start-up fund from Sun Yat-sen University.
Competing interests
The author has no competing interests to declare.
Financial support
The author was supported by the start-up fund from Sun Yat-sen University.
Open access
