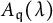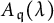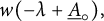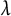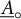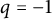1 Introduction
In the 1930s, Gelfand proposed a program in abstract harmonic analysis that allows the solution of difficult problems in numerous areas of mathematics through algebraic means. Attach an algebraic problem to the problem you wish to solve, decompose the algebraic problem into simpler (possibly infinitely many) problems, solve the simpler problems, reassemble the solutions to get an answer to the attached algebraic problem, and then transfer the solution to the original problem. To realize Gelfand’s program, the Unitary Dual Problem (classify the irreducible unitary representations of a group) must be solved.
In [Reference WignerWig39], Wigner studied unitary representations of the Lorentz group. In [Reference MackeyMac58], Mackey built on Wigner’s ideas to show how to build unitary representations of G from unitary representations of a normal subgroup N and
$G/N$
. In [Reference DufloDuf82], Duflo built on Mackey’s ideas to show how to describe the unitary dual of an algebraic Lie group in terms of unitary duals of smaller reductive Lie groups. Thus, we wish to find the unitary dual of a real reductive Lie group.
In [Reference VoganVog84], Vogan showed that
$A_{\mathfrak {q}}(\lambda )$
’s are unitarizable (see [Reference Salamanca-RibaSR99, p. 529] for the definition of
$A_{\mathfrak {q}}(\lambda )$
). In [Reference Salamanca-RibaSR99], Salmanca-Riba showed that any Hermitian representation of a real reductive Lie group with strongly regular infinitesimal character is unitary if and only if it is isomorphic to some
$A_{\mathfrak {q}}(\lambda )$
. Thus, finding the unitary dual of a real reductive Lie group is reduced to classifying unitary representations whose infinitesimal character is not strongly regular, hence representations of singular infinitesimal character are of particular importance.
In [Reference YeeYee05], the signature character of the canonical invariant Hermitian form on an arbitrary Hermitian irreducible Verma module was determined. The formula is complicated. In [Reference YeeYee19], the formula is simplified in the case where the infinitesimal character is regular: for the compact real form and infinitesimal character in alcoves of the form
$w(-\lambda + \underline {A}_\circ ),$
where
$\lambda \in \Lambda ^+$
is regular, the signature character of the canonical invariant Hermitian form on the irreducible Verma module is the “negative” of a Hall–Littlewood polynomial summand evaluated at
$q=-1$
times a version of the Weyl denominator. For general alcoves, the signature character is a sum of Hall–Littlewood polynomial summands evaluated at
$q=-1$
times a version of the Weyl denominator. (For other real forms, signature characters can be expressed using Hall–Littlewood polynomials as well.) We show in this article that the simplification extends also to the case where
$\lambda $
is singular.
The ultimate objective is a classification of irreducible unitary Harish-Chandra modules. Since the results of this article address representations of singular infinitesimal character, the results suggest that a classification of irreducible unitary Harish-Chandra modules of singular infinitesimal character is achievable.
The contents of the article are as follows. Section 2 establishes notation used in this article. Section 3 reviews key ideas of [Reference YeeYee05, Reference YeeYee19] on signature characters of invariant Hermitian forms on irreducible Verma modules. Section 4 reviews the affine Hecke algebra and Hall–Littlewood polynomials. Section 5 discusses alcove paths. In Sections 6 and 7, for compact real forms, we prove the relationship between signature characters at singular infinitesimal character and Hall–Littlewood polynomial summands for alcoves that are “translations” of the fundamental alcove. Section 8 shows that for general alcoves, the signature character is a sum of Hall–Littlewood polynomial summands evaluated at
$q=-1$
times a version of the Weyl denominator. Section 9 gives formulas for real forms that are not compact.
2 Notation
Notation 2.1. We use the following notation in this article:
-
–
$\mathfrak {g}_0$
is a real semisimple Lie algebra with Cartan decomposition
$\mathfrak {g}_0 = \mathfrak {k}_0 \oplus \mathfrak {p}_0$
and corresponding Cartan involution
$\theta .$
-
– Omitting the subscript
$0$
denotes complexification. -
–
$\mathfrak {h}_0 = \mathfrak {t}_0 \oplus \mathfrak {a}_0$
is the Cartan decomposition of a
$\theta $
-stable Cartan subalgebra. -
–
$\mathfrak {b} = \mathfrak {h} \oplus \mathfrak {n}$
is a Borel subalgebra of
$\mathfrak {g.}$
-
–
$\Delta (\mathfrak {g},\mathfrak {h})$
is the set of roots corresponding to
$\mathfrak {h}$
and
$\Delta ^+(\mathfrak {g},\mathfrak {h})$
the set of positive roots corresponding to
$\mathfrak {b.}$
-
–
$\rho $
is one half the sum of the positive roots and
$\rho ^\vee $
is one half the sum of the positive coroots. -
–
$\Pi = \{ \alpha _1, \ldots , \alpha _m \}$
is the set of simple roots corresponding to
$\Delta ^+(\mathfrak {g},\mathfrak {h})$
and
$\{\alpha _{0,1},\ldots , \alpha _{0,a}\}$
are the roots for which
$\alpha _{0,i}^\vee $
are the highest coroots for the simple components of
$\mathfrak {g.}$
-
–
$s_i = s_{\alpha _i}$
and
$S = \{ s_1, \ldots , s_m \}.$
-
–
$\Lambda _r$
is the root lattice and
$\Lambda $
is the weight lattice. -
–
$\{\lambda _1, \ldots , \lambda _m \}$
are the fundamental weights. -
– W is the Weyl group with long element
$w_0.$
-
– For dominant
$\lambda \in \mathfrak {h}^*, W_\lambda $
is the stabilizer with long element
$w_0^\lambda $
and
$W^\lambda $
is the set of minimal length coset representatives of
$W / W_\lambda .$
-
–
$\Delta _\lambda (\mathfrak {g},\mathfrak {h}) = \{ \alpha \in \Delta (\mathfrak {g},\mathfrak {h}) : (\lambda , \alpha ^\vee ) = 0 \}$
.
$\Delta _\lambda ^+(\mathfrak {g},\mathfrak {h}) = \Delta _\lambda (\mathfrak {g},\mathfrak {h}) \cap \Delta ^+(\mathfrak {g},\mathfrak {h})$
. -
– For
$\lambda \in \mathfrak {h}^*, M(\lambda ) = U(\mathfrak {g}) \otimes _{U(\mathfrak {b})} \mathbb {C}_{\lambda - \rho }$
is the Verma module of highest weight
$\lambda - \rho $
with generator
$v_{\lambda -\rho .}$
-
– For
$\alpha \in \Delta (\mathfrak {g},\mathfrak {h})$
and
$n \in \mathbb {Z}$
,
$H_{\alpha ,n} = \{ \lambda \in \mathrm {Span}_{\mathbb {R}} \Pi : (\lambda , \alpha ^\vee ) = n \}$
an affine hyperplane and the corresponding affine reflection of
$\mathrm {Span}_{\mathbb {R}} \Pi $
is
$s_{\alpha ,n.}$
-
–
$W_a$
is the (dual) affine Weyl group generated by the
$s_{\alpha ,n.}$
-
–
$H_{\alpha ,n}^+ = \{ \lambda \in \mathrm {Span}_{\mathbb {R}} \Pi : (\lambda , \alpha ^\vee )> n \}$
and
$H_{\alpha ,n}^- = \{ \lambda \in \mathrm {Span}_{\mathbb {R}} \Pi : (\lambda , \alpha ^\vee ) < n \}.$
-
–
$A_\circ = (\cap _{\alpha \in \Pi } H_{\alpha ,0}^- ) \cap ( \cap _{i=1}^a H_{\alpha _{0,i},-1}^+ )$
and
$\underline {A}_\circ = ( \cap _{\alpha \in \Pi } H_{\alpha ,0}^+ ) \cap ( \cap _{i=1}^a H_{\alpha _{0,i},1}^- ).$
-
–
$\mathfrak {C}_0 = \cap _{\alpha \in \Pi } H_{\alpha ,0}^-$
and let
$\underline {\mathfrak {C}}_0 = \cap _{\alpha \in \Pi } H_{\alpha ,0.}^+$
-
–
$\bar {\cdot }: W_a \to W$
is the group homomorphism induced by the semidirect product structure
$W_a = \Lambda _r \rtimes W$
. Then,
$\bar {s}_{\alpha ,k} =s_\alpha $
. -
–
$S_a = S \cup \{ s_{\alpha _{0,i}, -1} : 1 \leq i \leq a \}$
and
$\underline {S}_a = S \cup \{ s_{\alpha _{0,i},1}: 1 \leq i \leq a \}.$
-
–
$\Delta _i(\mathfrak {g},\mathfrak {h}) = \{ \alpha \in \Delta (\mathfrak {g},\mathfrak {h}) : \alpha \text { is imaginary}\}$
,
$\Delta _i^+(\mathfrak {g},\mathfrak {h}) = \Delta _i(\mathfrak {g},\mathfrak {h}) \cap \Delta ^+(\mathfrak {g},\mathfrak {h})$
,
$\Pi _i$
is the set of simple roots of
$\Delta _i(\mathfrak {g},\mathfrak {h})$
corresponding to
$\Delta _i^+(\mathfrak {g},\mathfrak {h}).$
-
–
$W_i$
is the group generated by
$s_\alpha $
’s, where
$\alpha \in \Delta _i(\mathfrak {g},\mathfrak {h}).$
-
–
$H_{\alpha ,n}^i = \{ \lambda \in i\mathfrak {h}_0^*: (\lambda ,\alpha ^\vee ) = n \}$
,
$H_{\alpha ,n}^{i,+}= \{\lambda \in i\mathfrak {h}_0^* : (\lambda , \alpha ^\vee )> n \}$
, and
$H_{\alpha ,n}^{i,-} := \{\lambda \in i\mathfrak {h}_0^* : (\lambda , \alpha ^\vee ) < n \}.$
-
–
$H_{\alpha ,n}^{\mathfrak {t},i} = \{ \lambda _{\mathfrak {t}} \in i\mathfrak {t}_0^* : (\lambda _{\mathfrak {t}}, \alpha ^\vee ) = n \}$
,
$H_{\alpha ,n}^{\mathfrak {t},i,+} = \{ \lambda _{\mathfrak {t}} \in i\mathfrak {t}_0^* : (\lambda _{\mathfrak {t}}, \alpha ^\vee )> n \}$
,
$H_{\alpha ,n}^{\mathfrak {t},i,-} = \{ \lambda _{\mathfrak {t}} \in i\mathfrak {t}_0^* : (\lambda _{\mathfrak {t}}, \alpha ^\vee ) < n \}.$
-
–
$\mathfrak {C}_0^{\mathfrak {t},i} = \cap _{\alpha \in \Pi _i} H_{\alpha ,0}^{\mathfrak {t},i,-}$
,
$A_\circ ^{\mathfrak {t},i} = (\cap _{\alpha \in \Pi _i} H_{\alpha ,0}^{\mathfrak {t},i,-} ) \cap ( \cap _{j=1}^{a_i} H_{\alpha _{0,j}^i,-1}^{\mathfrak {t},i,+} )$
, where
$\{ \alpha _{0,j}^i : 1 \leq j \leq a_i \} = \{ \alpha \in \Delta _i^+(\mathfrak {g}, \mathfrak {h}): \alpha ^\vee \text { is a highest coroot for a simple component of } \Delta _i(\mathfrak {g},\mathfrak {h}) \}$
, and
$\underline {A}_\circ ^{\mathfrak {t},i} = (\cap _{\alpha \in \Pi _i} H_{\alpha ,0}^{\mathfrak {t},i,+} ) \cap ( \cap _{j=1}^{a_i} H_{\alpha _{0,j}^i,1}^{\mathfrak {t},i,-} ).$
-
–
$\lambda = \lambda _{\mathfrak {t}} + \lambda _{\mathfrak {a}}$
is the decomposition of
$\lambda \in \mathfrak {h}^*$
under
$\mathfrak {h}^* = \mathfrak {t}^* \oplus \mathfrak {a}^*.$
-
–
$\Lambda _i^{\mathfrak {t}} = \{ \lambda _{\mathfrak {t}} \in i\mathfrak {t}_0^* : (\lambda _{\mathfrak {t}}, \alpha ^\vee ) \in \mathbb {Z} \, \forall \, \alpha \in \Delta _i(\mathfrak {g},\mathfrak {h}) \}.$
-
–
$(\Lambda _i^{\mathfrak {t}})^+ = \{ \lambda _{\mathfrak {t}} \in \Lambda _i^{\mathfrak {t}} : (\lambda _{\mathfrak {t}}, \alpha ^\vee ) \in \mathbb {Z}^{\geq 0} \, \forall \, \alpha \in \Delta _i^+(\mathfrak {g},\mathfrak {h}) \}$
. -
–
$\Lambda _r^i$
is the lattice of imaginary roots.
3 Signature characters of invariant Hermitian forms on irreducible Verma modules
In this section, we review key points on signature characters of invariant Hermitian forms on irreducible Verma modules from [Reference YeeYee05, Reference YeeYee19] and provide some corrections and clarifications on the material.
Definition 3.1. Let V be a representation of
$\mathfrak {g}$
. Then, a Hermitian form
$\left < \cdot , \cdot \right>: V \times V \to \mathbb {C}$
is an invariant Hermitian form if
$$ \begin{align*}\left < X\cdot v, w \right> + \left < v, \bar{X} \cdot w \right> = 0\end{align*} $$
for all
$v, w \in V$
and all
$X \in \mathfrak {g}$
.
Definition 3.2. Given
$\mu \in \mathfrak {h}^*$
, the complex conjugate
$\bar {\mu }$
of
$\mu $
is defined by
$\bar {\mu }(H) = \overline {\mu (\bar {H})}$
.
$\mu $
is real if
$\bar {\mu }= \mu $
, imaginary if
$\bar {\mu } = - \mu $
, and complex if it is neither real nor imaginary.
Definition 3.3. Given
$\mu \in \mathfrak {h}^*$
,
$\theta \mu \in \mathfrak {h}^*$
is defined by
$(\theta \mu )(H) = \mu ( \theta ^{-1}(H))$
.
Proposition 3.4. The Verma module
$M(\lambda )$
admits a nontrivial invariant Hermitian form if
$\mathfrak {h}$
is maximally compact,
$\theta ( \Delta ^+(\mathfrak {g},\mathfrak {h}) ) = \Delta ^+( \mathfrak {g}, \mathfrak {h} )$
, and
$\lambda $
is imaginary. Nontrivial invariant Hermitian forms on Verma modules are unique up to a nonzero real scalar.
For the remainder of the article, assume that
$\mathfrak {h}$
is maximally compact and
$\theta ( \Delta ^+(\mathfrak {g},\mathfrak {h})) = \Delta ^+( \mathfrak {g}, \mathfrak {h} )$
.
Definition 3.5. Suppose
$M(\lambda )$
admits a nontrivial invariant Hermitian form. Then, the invariant Hermitian form
$\left < \cdot , \cdot \right>_\lambda $
on
$M(\lambda )$
such that
$\left < v_{\lambda -\rho }, v_{\lambda -\rho }\right>_\lambda = 1$
is the Shapovalov form, the canonical invariant Hermitian form on
$M(\lambda )$
.
Proposition 3.6. (For more details, see [Reference YeeYee05, p. 644])
By the Shapovalov Determinant Formula, the Shapovalov form is degenerate precisely when the imaginary highest weight
$\lambda $
lies on affine hyperplanes of the form
$H_{\alpha ,n} := \{ \mu \in \mathrm {Span}_{\mathbb {R}} \Pi : (\mu , \alpha ^\vee ) = n \},$
where
$\alpha \in \Delta ^+(\mathfrak {g},\mathfrak {h})$
and
$n \in \mathbb {Z}^+$
. Such
$H_{\alpha ,n}$
are called reducibility hyperplanes. The radical of the Shapovalov form on a Verma module is its unique maximal proper submodule.
Given
$\mu , \nu \in \Lambda _r^+$
, by invariance, the
$\lambda -\mu $
weight space is orthogonal to the
$\lambda - \nu $
weight space if
$\nu \neq -\bar {\mu } = \theta (\mu )$
. The Shapovalov form pairs the
$\lambda -\mu $
and
$\lambda - \theta (\mu )$
weight spaces. For
$M(\lambda )$
irreducible and
$\mu \neq \theta (\mu )$
(i.e.,
$\mu $
not imaginary), the Shapovalov form on
$M(\lambda )_{\lambda -\mu -\rho } +M(\lambda )_{\lambda -\theta \mu - \rho }$
may be represented by a matrix of the form
$\left ( \begin {array}{cc} 0 & A \\ \bar {A}^t & 0 \end {array} \right )$
which has signature
$(p,p)$
. Thus, we make the following definition.
Definition 3.7. Let
$M( \lambda )$
be irreducible. For
$\mu \in \Lambda _r^+$
imaginary, let the signature of the Shapovalov form on
$M(\lambda )_{\lambda - \mu -\rho }$
be
$(p(\mu ), q(\mu ) )$
. The signature character of the Shapovalov form is
$$ \begin{align*}ch_s M(\lambda) = \sum_{\substack{\mu \in \Lambda_r^+ \\ \text{imaginary}}} (p(\mu)-q(\mu))e^{\lambda-\mu -\rho}.\end{align*} $$
For highest weights in any connected region of imaginary weights avoiding reducibility hyperplanes, the Shapovalov form remains non-degenerate as the highest weight varies over the region. Thus, the signature of the Shapovalov form cannot change in such a region. This philosophy was first introduced in [Reference VoganVog84]. Wallach determined the signature character for the largest such region, which we call the Wallach region, by an asymptotic argument. We postpone the definition of the Wallach region until after we describe the connected regions where signatures stay the same.
The form of the reducibility hyperplanes suggests that a formula for signature characters of the Shapovalov form on irreducible Verma modules should be indexed by alcoves of the (dual) affine Weyl group since those alcoves have walls of the form
$H_{\alpha ,n}$
, where
$\alpha \in \Delta ^+(\mathfrak {g},\mathfrak {h})$
and
$n \in \mathbb {Z}$
. (Alcoves of the affine Weyl group are in one-to-one correspondence with elements of the affine Weyl group.) However, alcoves of the affine Weyl group form a partition of
$\mathrm {Span}_{\mathbb {R}} \Pi $
while we wish to partition imaginary weights
$i \mathfrak {h}_0^*$
by the
$H_{\alpha ,n}$
.
For
$\mathfrak {h}_0 \theta $
-stable, a root
$\alpha \in \Delta (\mathfrak {g},\mathfrak {h})$
is imaginary-valued on
$\mathfrak {t}_0$
and real-valued on
$\mathfrak {a}_0$
(see [Reference KnappKna02, p. 386]). A root
$\alpha $
is imaginary if it vanishes on
$\mathfrak {a}_0$
and real if it vanishes on
$\mathfrak {t}_0$
. If
$\alpha $
is supported on both
$\mathfrak {t}_0$
and
$\mathfrak {a}_0$
, then
$\alpha $
is complex. Since
$\mathfrak {h}$
is maximally compact, therefore there are no real roots. Note that
$\theta \alpha = - \bar {\alpha }$
and
$\theta \mathfrak {g}_\alpha = \mathfrak {g}_{\theta \alpha }$
. For
$\alpha $
imaginary,
$\theta \mathfrak {g}_\alpha = \mathfrak {g}_\alpha $
so that
$\mathfrak {g}_\alpha = \mathfrak {g}_\alpha \cap \mathfrak {k} \oplus \mathfrak {g}_\alpha \cap \mathfrak {p}$
. Since
$\mathfrak {g}_\alpha $
is one-dimensional, either
$\mathfrak {g}_\alpha = \mathfrak {g}_\alpha \cap \mathfrak {k}$
or
$\mathfrak {g}_\alpha = \mathfrak {g}_\alpha \cap \mathfrak {p}$
. The imaginary root
$\alpha $
is said to be compact in the former case and noncompact in the latter case. (For more details, see [Reference YeeYee05, p. 642].)
The decomposition
$\mathfrak {h} = \mathfrak {t} \oplus \mathfrak {a}$
is both direct and orthogonal with respect to the Killing form (see [Reference KnappKna02, p. 359]). Thus,
$\mathfrak {h}^* = \mathfrak {t}^* \oplus \mathfrak {a}^*$
is an orthogonal decomposition with respect to the form induced by the Killing form. For
$\lambda \in \mathfrak {h}^*$
, write
$\lambda = \lambda _{\mathfrak {t}} + \lambda _{\mathfrak {a}}$
under this decomposition.
Given a root
$\alpha $
and an integer n, define
$H_{\alpha ,n}^i = \{\lambda \in i\mathfrak {h}_0^* : (\lambda , \alpha ^\vee ) = n \}$
. If
$\alpha $
is an imaginary root and
$\lambda \in i\mathfrak {h}_0^*$
, then
$(\lambda , \alpha ^\vee ) = (\lambda _{\mathfrak {t}} + \lambda _{\mathfrak {a}}, \alpha ^\vee ) = (\lambda _{\mathfrak {t}}, \alpha ^\vee )$
. Thus, for
$\alpha $
imaginary,
$$ \begin{align*}H_{\alpha,n}^i = \{\lambda \in i\mathfrak{h}_0^* : (\lambda, \alpha^\vee) = n \} = \{ \lambda_{\mathfrak{t}} \in i \mathfrak{t}_0^* : (\lambda_{\mathfrak{t}}, \alpha^\vee) = n \} \oplus i \mathfrak{a}_0^*,\end{align*} $$
which has codimension
$1$
in
$i\mathfrak {h}_0^*$
. Therefore, for
$\alpha $
imaginary,
$H_{\alpha ,n}^i$
divides
$i\mathfrak {h}_0^*$
into two halves:
$H_{\alpha ,n}^{i,+} := \{\lambda \in i\mathfrak {h}_0^* : (\lambda , \alpha ^\vee )> n \}$
and
$H_{\alpha ,n}^{i,-} := \{\lambda \in i\mathfrak {h}_0^* : (\lambda , \alpha ^\vee ) < n \}$
. Let
$H_{\alpha ,n}^{\mathfrak {t},i} = \{ \lambda _{\mathfrak {t}} \in i \mathfrak {t}_0^* : (\lambda _{\mathfrak {t}}, \alpha ^\vee ) = n \}$
, let
$H_{\alpha ,n}^{\mathfrak {t},i,+} = \{ \lambda _{\mathfrak {t}} \in i \mathfrak {t}_0^* : (\lambda _{\mathfrak {t}}, \alpha ^\vee )> n \}$
, and let
$H_{\alpha ,n}^{\mathfrak {t},i,-} = \{ \lambda _{\mathfrak {t}} \in i \mathfrak {t}_0^* : (\lambda _{\mathfrak {t}}, \alpha ^\vee ) < n \}$
. Then, for
$\alpha $
imaginary,
$H_{\alpha ,n}^i = H_{\alpha ,n}^{\mathfrak {t},i} \oplus i \mathfrak {a}_0^*$
,
$H_{\alpha ,n}^{i,+} = H_{\alpha ,n}^{\mathfrak {t},i,+} \oplus i \mathfrak {a}_0^*$
, and
$H_{\alpha ,n}^{i,-} = H_{\alpha ,n}^{\mathfrak {t},i,-} \oplus i \mathfrak {a}_0^*$
.
Let
$\alpha $
be a complex root. Then, given
$\lambda \in i\mathfrak {h}_0^*$
,
$(\lambda , (\alpha ^\vee )_{\mathfrak {t}} ) \in \mathbb {R}$
while
$(\lambda , (\alpha ^\vee )_{\mathfrak {a}}) \in i\mathbb {R}$
. Therefore,
$$ \begin{align*}H_{\alpha,n}^i = \{ \lambda \in i \mathfrak{h}_0^* : (\lambda, (\alpha^\vee)_{\mathfrak{t}} ) = n \text{ and } (\lambda, (\alpha^\vee)_{\mathfrak{a}}) = 0 \},\end{align*} $$
which has codimension
$2$
in
$i\mathfrak {h}_0^*$
. Therefore, for
$\alpha $
complex,
$i\mathfrak {h}_0^* \setminus H_{\alpha ,n}^i$
is connected. Thus, crossing
$H_{\alpha ,n}^i$
, where
$\alpha $
is complex, does not change the signature character. (Note that this was also shown in Section 3 of [Reference YeeYee05] by considering the Jantzen filtration.)
Let
$\Delta _i(\mathfrak {g},\mathfrak {h}) = \{ \alpha \in \Delta (\mathfrak {g},\mathfrak {h}) : \alpha \text { is imaginary}\}$
,
$\Delta _i^+(\mathfrak {g},\mathfrak {h}) = \Delta _i(\mathfrak {g},\mathfrak {h}) \cap \Delta ^+(\mathfrak {g},\mathfrak {h})$
, and
$\Pi _i$
be the simple roots of
$\Delta _i(\mathfrak {g},\mathfrak {h})$
corresponding to
$\Delta _i^+(\mathfrak {g},\mathfrak {h})$
. See Section 6 of [Reference YeeYee05] for more information on
$\Delta _i(\mathfrak {g},\mathfrak {h})$
and
$\Pi _i$
.
Definition 3.8. Define the Wallach region to be
$$ \begin{align*} \left[ \left(\cap_{\alpha \in \Pi_i} H_{\alpha,1}^{\mathfrak{t},i,-} \right) \cap \left( \cap_{j=1}^{a_i} H_{\alpha_{0,j}^i, 1}^{\mathfrak{t},i,-} \right) \right] \oplus i\mathfrak{a}_0^* \end{align*} $$
where
$\{ \alpha _{0,j}^i : 1 \leq j \leq a_i \} = \{ \alpha \in \Delta _i^+(\mathfrak {g}, \mathfrak {h}): \alpha ^\vee \text { is a highest coroot for a simple } \text {component } \text{of }\Delta _i(\mathfrak {g},\mathfrak {h})\}$
.
Theorem 3.9 [Reference WallachWal84, Lemma 2.3] reformulated in [Reference YeeYee05, Theorems 2.10 and 6.12]
If
$\lambda \in \mathfrak {h}^*$
is in the Wallach region and
$M(\lambda )$
is irreducible, then
$$ \begin{align*} ch_s M( \lambda )|_{\mathfrak{a}} &= e^{\lambda|_{\mathfrak{a}}} \qquad \text{and}\\ ch_s M( \lambda )|_{\mathfrak{t}} &= \frac{e^{(\lambda-\rho)|_{\mathfrak{t}}}}{\prod_{\alpha \in \Delta^+(\mathfrak{p},\mathfrak{t})} ( 1 - e^{-\alpha}) \prod_{\alpha \in \Delta^+(\mathfrak{k}, \mathfrak{t})} (1+e^{-\alpha})}. \end{align*} $$
Let
$W_i$
be the Weyl group corresponding to
$\Delta _i(\mathfrak {g},\mathfrak {h})$
and
$W_a^i$
be the corresponding (dual) affine Weyl group generated by
$s_{\alpha ,n}$
, where
$\alpha \in \Delta _i(\mathfrak {g},\mathfrak {h})$
and
$n \in \mathbb {Z}$
. Then, the action of
$W_a^i$
on
$i\mathfrak {t}_0^*$
divides
$i\mathfrak {t}_0^*$
into alcoves. Let
$A_\circ ^{\mathfrak {t},i} = \left (\cap _{\alpha \in \Pi _i} H_{\alpha ,0}^{\mathfrak {t},i,-} \right ) \cap \left ( \cap _{j=1}^{a_i} H_{\alpha _{0,j}^i,-1}^{\mathfrak {t},i,+} \right )$
. Let
$\underline {A}_\circ ^{\mathfrak {t},i} = \left (\cap _{\alpha \in \Pi _i} H_{\alpha ,0}^{\mathfrak {t},i,+} \right ) \cap \left ( \cap _{j=1}^{a_i} H_{\alpha _{0,j}^i,1}^{\mathfrak {t},i,-} \right )$
.
Definition 3.10. For an alcove A under the action of
$W_a^i$
on
$i\mathfrak {t}_0^*$
, let
$$ \begin{align*}R^A(\lambda ) = \sum_{\substack{\mu \in \Lambda_r^+ \\ \text{imaginary}}} c_\mu^A e^{\lambda - \mu - \rho}\end{align*} $$
be such that
$R^A(\lambda ) = ch_s M( \lambda )$
for
$\lambda \in A \oplus i\mathfrak {a}_0^*$
, where
$M(\lambda )$
is irreducible.
The philosophy for determining
$R^A$
is to calculate how it changes as you cross a reducibility hyperplane corresponding to an imaginary root, and then to use induction on a notion of distance to the region where Wallach computed the signature character. This philosophy was introduced in [Reference VoganVog84]. If you cross one reducibility hyperplane at a time, then the Jantzen filtration at the point of crossing only has two levels. Thus, by Proposition 3.3 of [Reference VoganVog84], the signature changes at a crossing point by the signature of the radical (
$M(\lambda -n\alpha ),$
where the reducibility hyperplane is
$H_{\alpha ,n}$
). Thus, we have the following.
Lemma 3.11. [Reference YeeYee05, Propositions 3.2]
Let A and
$A'$
be adjacent alcoves of
$i\mathfrak {t}_0^*$
under the action of
$W_a^i$
separated by the reducibility hyperplane
$H_{\alpha ,n}^{\mathfrak {t},i}$
, where
$\alpha \in \Delta ^+( \mathfrak {g}, \mathfrak {h})$
is imaginary. Then,
$$ \begin{align*}R^A(\lambda) = R^{A'}(\lambda)+ 2\varepsilon(A, A') R^{A-n\alpha}(\lambda - n \alpha),\end{align*} $$
where
$\varepsilon (A, A') = \pm 1$
.
In [Reference YeeYee05], it was shown that
$\varepsilon (A,A')$
depends only on the separating hyperplane and the Weyl chamber containing the alcoves.
Definition 3.12. For
$\gamma \in \Delta _i^+(\mathfrak {g},\mathfrak {h})$
,
$n \in \mathbb {Z}^+$
, and
$w \in W_i$
, let
$\varepsilon ( H_{\gamma ,n}^{\mathfrak {t},i}, w ) = \varepsilon (A, A'),$
where A and
$ A'$
are adjacent alcoves of
$i\mathfrak {t}_0^*$
(under the action of
$W_a^i$
) separated by
$H_{\gamma ,n}^{\mathfrak {t},i}$
,
$A \subset H_{\gamma ,n}^{\mathfrak {t},i,+}$
,
$A' \subset H_{\gamma ,n}^{\mathfrak {t},i,-}$
, and A and
$A'$
are contained in
$w \mathfrak {C}_0^{\mathfrak {t},i}$
, where
$\mathfrak {C}_0^{\mathfrak {t},i} = \cap _{\alpha \in \Pi _i} H_{\alpha ,0}^{\mathfrak {t},i,-}$
.
Let superscript and subscript i’s denote that an object is associated with the imaginary roots
$\Delta _i(\mathfrak {g},\mathfrak {h})$
. Then, we have the following.
Proposition 3.13. [Reference YeeYee19, Theorem 4.11]
Let
$\gamma \in \Delta _i^+(\mathfrak {g},\mathfrak {h})$
,
$n \in \mathbb {Z}^+$
and let
$\gamma $
hyperplanes be positive on
$w\mathfrak {C}_0^{\mathfrak {t},i}$
, where
$w \in W_i$
. Then,
$$ \begin{align*}\varepsilon( H_{\gamma,n}^{\mathfrak{t},i}, w ) = \left \{ \begin{array}{ll} -1 & \qquad \begin{array}{@{}l} \text{if }\theta \text{ does not fix any element of} \\ \text{the component of } \Pi \text{ containing } \gamma \end{array} \\[3pt] \epsilon( n \gamma ) (-1)^{\frac{1}{2}( \ell_i( w ) - \ell_i( s_\gamma w) -1) } & \qquad \text{otherwise,} \end{array} \right.\end{align*} $$
where
$\epsilon $
is the
$\mathbb {Z}_2$
-grading on the lattice of imaginary imaginary roots arising from
$\epsilon (\alpha ) = 1$
if
$\alpha $
is a compact root and
$\epsilon ( \alpha ) = -1$
if
$\alpha $
is a noncompact root.
By induction on distance to the Wallach region (see [Reference YeeYee05] for details), we obtain the following.
Theorem 3.14. [Reference YeeYee19, Corollary 4.15]
Let
$\Pi = \Pi _1 \cup \Pi _2$
, where
$\Pi _1$
consists of the components of
$\Pi $
such that
$\theta $
fixes some element and
$\Pi _2$
consists of the components of
$\Pi $
such that
$\theta $
does not fix any element. Let
$\mathfrak {g} = \mathfrak {g}_1 \oplus \mathfrak {g}_2$
and
$\mathfrak {h}^* = \mathfrak {h}_1^* \oplus \mathfrak {h}_2^*$
be the corresponding decompositions of
$\mathfrak {g}$
and
$\mathfrak {h}^*$
, respectively. Use superscript and subscript
$1$
’s and
$2$
’s to denote objects corresponding to
$\mathfrak {g}_1$
and
$\mathfrak {g}_2$
, respectively. Thus, let
$W = W_1 \times W_2$
,
$W_i = (W_1)_i \times (W_2)_i$
, and
$W_a^i = (W_1)_a^i \times (W_2)_a^i$
. Let
$\mu = \mu _1 + \mu _2 \in \mathfrak {h}_1^* \oplus \mathfrak {h}_2^*$
be imaginary and
$M(\mu )$
be irreducible. Let
$(\mu _j)_{\mathfrak {t}_j}$
belong to the alcove
$A_{(j)}$
under the action of
$(W_j)_a^i$
on
$i(\mathfrak {t}_j)_0^*$
,
$j=1,2$
. Let
$A_{(j)} \subset w_j (\mathfrak {C}_j)_0^{\mathfrak {t}_j,i}$
, where
$w_j \in (W_j)_i$
. Let
$A_{(1)} = C_0^1 \stackrel {r_1^{(1)}} {\to } C_1^1 \stackrel {r_2^{(1)}}{\to } \cdots \stackrel {r_{\ell _1}^{(1)}}{\to } C_{\ell _1}^1 = w_1 (A_1)_\circ ^{\mathfrak {t}_1,i}$
be an alcove path (i.e.,
$C_{i-1}^1$
is adjacent to
$C_i^1$
and
$C_i^1 = r_i^{(1)} C_{i-1}^1$
for
$1 \leq i \leq \ell _1$
) that stays in the Weyl chamber
$w_1 (\mathfrak {C}_1)_0^{\mathfrak {t}_1,i}$
. Let
$A_{(2)} = C_0^2 \stackrel {r_1^{(2)}} {\to } C_1^2 \stackrel {r_2^{(2)}}{\to } \cdots \stackrel {r_{\ell _2}^{(2)}}{\to } C_{\ell _2}^2 = w_2 (A_2)_\circ ^{\mathfrak {t}_2,i}$
be an alcove path that stays in the Weyl chamber
$w_2 (\mathfrak {C}_2)_0^{\mathfrak {t}_2,i}$
. Then,
$$ \begin{align*}ch_s M( \mu ) |_{\mathfrak{a}} = e^{(\mu-\rho)|_{\mathfrak{a}}}\end{align*} $$
and
$$ \begin{align*}ch_s M( \mu ) |_{\mathfrak{t}} = \left( ch_s M( \mu_1 ) |_{\mathfrak{t}_1} \right) \left( ch_s M( \mu_2 ) |_{\mathfrak{t}_2} \right),\end{align*} $$
where
$$ \begin{align*} & ch_s M( \mu_1 )|_{\mathfrak{t}_1} = \\ & \frac{e^{-\rho_1} \displaystyle{ \sum_{\substack{I = \{i_1 < \cdots < i_k\} \subset \{1, \ldots, \ell_1\} \\ w_1> \bar{r}_{i_1}^{(1)} w_1 > \bar{r}_{i_1}^{(1)}\bar{r}_{i_2}^{(1)} w_1 > \cdots > \bar{r}_{i_1}^{(1)} \dots \bar{r}_{i_k}^{(1)} w_1 }}} \epsilon( \nu(I) ) (-1)^{\frac{1}{2} ( \ell_i(w_1) - \ell_i( \chi(I)w_1 ) - |I| )} 2^{|I|} e^{\mu_1|_{\mathfrak{t}_1} - \nu(I)}} {\prod_{\alpha \in \Delta^+( \mathfrak{p}_1, \mathfrak{t}_1 )} (1 - e^{-\alpha}) \prod_{\alpha \in \Delta^+(\mathfrak{k}_1, \mathfrak{t}_1)}( 1 + e^{-\alpha})}, \end{align*} $$
where
$\nu (I) \in \Lambda _r^+$
is defined by
$\mu - \nu (I) = \bar {r}_{i_1}^{(1)} \dots \bar {r}_{i_k}^{(1)} r_{i_k}^{(1)} \dots r_{i_1}^{(1)} \mu $
and
$\chi (I)$
by
$\chi (I) = \bar {r}_{i_1}^{(1)} \dots \bar {r}_{i_k}^{(1)}$
, and
$$ \begin{align*}ch_s M( \mu_2 )|_{\mathfrak{t}_2} = \frac{e^{-\rho_2} \displaystyle{ \sum_{\substack{I = \{i_1 < \cdots < i_k\} \subset \{1, \ldots, \ell_2\} \\ w_2> \bar{r}_{i_1}^{(2)} w_2 > \bar{r}_{i_1}^{(2)}\bar{r}_{i_2}^{(2)} w_2 > \cdots > \bar{r}_{i_1}^{(2)} \dots \bar{r}_{i_k}^{(2)} w_2 }}} (-1)^{|I|} 2^{|I|} e^{\mu_2|_{\mathfrak{t}_2} - \nu(I)}} {\prod_{\alpha \in \Delta^+( \mathfrak{p}_2, \mathfrak{t}_2 )} (1 - e^{-\alpha}) \prod_{\alpha \in \Delta^+(\mathfrak{k}_2, \mathfrak{t}_2)}( 1 + e^{-\alpha})}.\end{align*} $$
We will show for the compact real form that
$ch_s M( \mu _1 ) |_{\mathfrak {t}_1}$
is equal to a sum of “negatives” of Hall–Littlewood polynomial summands evaluated at
$q=-1$
times a version of the Weyl denominator. Signature characters for other real forms may also be expressed in terms of Hall–Littlewood polynomial summands.
4 Hall–Littlewood polynomials
Hall–Littlewood polynomials are symmetric functions which specialize to Schur functions at
$q=0$
and monomial symmetric functions at
$q=1$
. Here, we review the theory required to define these polynomials.
Definition 4.1. Let
$\mathbb {K} = \mathbb {Z}(q^{\frac {1}{2}})$
. The Hecke algebra
$\mathcal {H}$
is the
$\mathbb {K}$
-algebra with basis
$\{\tilde {T}_w\}_{w \in W}$
such that for
$s \in S$
and
$w \in W$
,
$$ \begin{align*}\tilde{T}_s\tilde{T}_w = \left \{ \begin{array}{ll} \tilde{T}_{sw} & \qquad \text{if } \ell(sw)> \ell(w) \\ \tilde{T}_{sw} + (q^{\frac{1}{2}} - q^{-\frac{1}{2}}) \tilde{T}_w & \qquad \text{if } \ell(sw) < \ell(w). \end{array} \right.\end{align*} $$
Definition 4.2. Let
$u = q^{\frac {1}{2}} - q^{-\frac {1}{2}}$
. Define the
$\tilde {R}$
polynomials by
$\tilde {R}_{x,w} = 0$
if
$x \not \leq w$
. Otherwise,
$\tilde {R}_{x,w} \in \mathbb {Z}[u]$
is defined by
$$ \begin{align*}\tilde{T}_{w^{-1}}^{-1} = \sum_{x \leq w} \tilde{R}_{x,w}(u) \tilde{T}_x.\end{align*} $$
The
$\tilde {R}$
polynomials satisfy for
$s \in S$
,
$w \in W,$
where
$ws < w$
$$ \begin{align*}\tilde{R}_{x,w} = \left \{ \begin{array}{ll} \tilde{R}_{xs,ws} & \qquad \text{if } xs < x \\ \tilde{R}_{xs,ws} + u \tilde{R}_{x,ws} & \qquad \text{if } xs> x. \end{array} \right.\end{align*} $$
To define the affine Hecke algebra, we need to define the extended affine Weyl group. The weight lattice
$\Lambda $
is stable under the action of the Weyl group. Therefore, we can define the following.
Definition 4.3. The extended affine Weyl group is
$$ \begin{align*}W_e = W \ltimes \Lambda.\end{align*} $$
The action of the extended affine Weyl group on the set of alcoves is not free. Letting
$\Omega $
be the stabilizer of
$\underline {A}_\circ $
in
$W_e$
,
$\Omega \cong \Lambda / \Lambda _r$
, where the isomorphism is realized by sending
$g \in \Omega $
to
$g(0)+\Lambda _r$
. We have
$W_e \cong W_a \rtimes \Omega $
and so every
$w \in W_e$
is equal to
$vg,$
where
$v \in W_a$
and
$g \in \Omega $
. Define the length function on
$W_e$
by
$\ell (w) = \ell (v)$
.
We now define the affine Hecke algebra.
Definition 4.4. The affine Hecke algebra
$\mathcal {H}_a$
is the
$\mathbb {K}$
-algebra with
$\mathbb {K}$
-basis
$\{\tilde {T}_w\}_{w \in W_e}$
satisfying the relations
$$ \begin{align*} \tilde{T}_v \tilde{T}_w &= \tilde{T}_{vw} && \text{if } \ell(vw) = \ell(v)+\ell(w) \\ \tilde{T}_s^2 &= (q^{\frac{1}{2}} - q^{-\frac{1}{2}}) \tilde{T}_s + \tilde{T}_1 && \text{for }s \in \underline{S}_a. \end{align*} $$
Definition 4.5. For
$\mu \in \Lambda ,$
let
$\tau _\mu \in W_e$
be translation by
$\mu $
:
$\tau _\mu (\nu ) = \nu + \mu $
. For
$\mu \in \Lambda ^+$
, let
$$ \begin{align*}\tilde{X}^\mu := \tilde{T}_{\tau_\mu}.\end{align*} $$
For
$\mu \in \Lambda $
, there are
$\mu _1, \mu _2 \in \Lambda ^+$
such that
$\mu = \mu _1 - \mu _2$
. Let
$$ \begin{align*}\tilde{X}^\mu := \tilde{X}^{\mu_1}(\tilde{X}^{\mu_2})^{-1}.\end{align*} $$
The
$\tilde {X}^\mu $
’s satisfy the following Bernstein relations.
Proposition 4.6. [Reference RamRam06, Proposition 3.2]
-
(a)
$\tilde {X}^\mu \tilde {X}^\lambda = \tilde {X}^\lambda \tilde {X}^\mu $
. -
(b) If
$(\lambda , \alpha _i^\vee ) = 0$
, then
$\tilde {T}_{s_i} \tilde {X}^\lambda = \tilde {X}^\lambda \tilde {T}_{s_i}$
. -
(c) If
$(\lambda , \alpha _i^\vee ) = 1$
, then
$\tilde {T}_{s_i} \tilde {X}^{s_i \lambda } \tilde {T}_{s_i} = \tilde {X}^\lambda $
. -
(d)
$\tilde {T}_{s_i} \tilde {X}^\lambda = \tilde {X}^{s_i \lambda } + (q^{ \frac {1}{2}} - q^{-\frac {1}{2}}) \frac {\tilde {X}^\lambda - \tilde {X}^{s_i \lambda }}{1-\tilde {X}^{-\alpha _i}}$
.
Definition 4.7. [Reference RamRam06, p. 151]
Let
$$ \begin{align*}\tilde{\mathbf{1}}_0 = \frac{1}{W_0(q^{-1})} \sum_{w \in W} q^{-\ell(w)/2} \tilde{T}_{w^{-1}}^{-1} = \frac{1}{W_0(q)} \sum_{w \in W} q^{\ell(w)/2} \tilde{T}_w,\end{align*} $$
where
$W_0(t) = \sum _{w \in W} t^{\ell (w)}$
is the Poincaré polynomial of W.
Note that
$$ \begin{align} \tilde{T}_{w^{-1}}^{-1} \tilde{\mathbf{1}}_0 = q^{-\ell(w)/2} \tilde{\mathbf{1}}_0. \end{align} $$
We now define Hall–Littlewood polynomials.
Definition 4.8. Given
$\lambda \in \Lambda $
, let
$W_\lambda $
be the stabilizer of
$\lambda $
and
$W^\lambda $
the set of minimal length coset representatives of
$W / W_\lambda $
. Then,
$P_\lambda (X; q^{-1}) \in \mathbb {K}[\Lambda ]^W$
defined by
$$ \begin{align*}P_\lambda(X; q^{-1}) \tilde{\mathbf{1}}_0 = \left( \sum_{w \in W^\lambda} q^{-\ell(w)/2} \tilde{T}_{w^{-1}}^{-1} \right) \tilde{X}^\lambda \tilde{\mathbf{1}}_0\end{align*} $$
is a Hall–Littlewood polynomial or Macdonald spherical function.
Definition 4.9. Given
$\lambda \in \Lambda ^+$
and
$w \in W$
, a Hall–Littlewood polynomial summand of
$P_\lambda (X;q^{-1})$
is the polynomial
$P^w_\lambda (X; q^{-1})$
defined by
$$ \begin{align*}P_\lambda^w(X; q^{-1})\tilde{\mathbf{1}}_0 = q^{-\ell(w)/2} \tilde{T}_{w^{-1}}^{-1} \tilde{X}^\lambda \tilde{\mathbf{1}}_0.\end{align*} $$
We will relate Hall–Littlewood polynomial summands to signature characters of irreducible Verma modules.
Lemma 4.10. Let
$\lambda \in \Lambda ^+$
and
$w \in W$
. Let z be the minimal length coset representative of
$w W_\lambda $
. Then,
$$ \begin{align*}P_\lambda^w(X; q^{-1}) = q^{\ell(z)-\ell(w)} P_\lambda^z(X; q^{-1} ).\end{align*} $$
Proof Let
$w = zx$
so that
$x \in W_\lambda $
. Note that
$\ell (w) = \ell (z) + \ell (x)$
. Since
$\lambda $
is dominant, therefore,
$W_\lambda $
is a standard parabolic subgroup of W so that it is generated by some subset of S. Then,
$$ \begin{align*} P_\lambda^w(X; q^{-1})\tilde{\mathbf{1}}_0 &= q^{-\ell(w)/2} \tilde{T}_{w^{-1}} ^{-1} \tilde{X}^\lambda \tilde{\mathbf{1}}_0 \\ &= q^{-\ell(w)/2} \tilde{T}_{z^{-1}}^{-1} \tilde{T}_{x^{-1}}^{-1} \tilde{X}^\lambda \tilde{\mathbf{1}}_0 \\ &= q^{-\ell(w)/2} \tilde{T}_{z^{-1}}^{-1} \tilde{X}^\lambda \tilde{T}_{x^{-1}}^{-1} \tilde{\mathbf{1}}_0 \qquad \text{since } \tilde{T}_{s_i} \tilde{X}^\lambda = \tilde{X}^\lambda \tilde{T}_{s_i} \text{ for } (\lambda, \alpha_i^\vee) = 0 \\ &= q^{-\ell(w)/2-\ell(x)/2} \tilde{T}_{z^{-1}}^{-1} \tilde{X}^\lambda \tilde{\mathbf{1}}_0 \\ &= q^{-\ell(w)/2-\ell(w)/2 + \ell(z)/2} \tilde{T}_{z^{-1}}^{-1} \tilde{X}^\lambda \tilde{\mathbf{1}}_0 \\ &= q^{\ell(z) - \ell(w)} q^{-\ell(z)/2}\tilde{T}_{z^{-1}}^{-1} \tilde{X}^\lambda \tilde{\mathbf{1}}_0 \\ &= q^{\ell(z)-\ell(w)} P_\lambda^z(X;q^{-1}) \tilde{\mathbf{1}}_0. \end{align*} $$
5 Alcove walks and Hall–Littlewood polynomials
In this section, we discuss alcove walks and a formula for Hall–Littlewood polynomials in terms of alcove walks. Ram’s alcove walks [Reference RamRam06] originate from the work of Gaussent–Littelmann [Reference Gaussent and LittelmannGL05] and Lenart–Postnikov [Reference Lenart and PostnikovLP07, Reference Lenart and PostnikovLP08] on a discrete version of Littelmann paths. We follow the presentation of [Reference LenartLen11] for much of this material. For a more detailed account of alcove walks, please see [Reference RamRam06].
Definition 5.1. Distinct alcoves A and B are adjacent if they share a common alcove wall.
Definition 5.2. An alcove path from the alcove A to the alcove B is a sequence of alcoves
$A = A_0 \stackrel {R_1}{\to } A_1 \stackrel {R_2}{\to } \cdots \stackrel {R_\ell }{\to } A_\ell = B,$
where for
$1 \leq i \leq \ell A_{i-1}$
and
$A_i$
are adjacent and the
$R_i$
are the affine reflections such that
$A_i = R_i A_{i-1}$
.
Definition 5.3. An alcove walk from A to B is a sequence
$(A_0 = A, F_1, A_1, \ldots , F_\ell , A_\ell = B, F_\infty ),$
where the
$A_i$
are alcoves and each
$F_i$
is a codimension one common face of
$A_{i-1}$
and
$A_i$
and
$F_\infty $
is a vertex of the last alcove
$A_\ell $
.
Unlike an alcove path, for an alcove walk,
$A_{i-1}$
might equal
$A_i$
. Thus, we have the following.
Definition 5.4. For an alcove walk
$(A_0 = A, F_1, A_1, \ldots , F_\ell , A_\ell = B, F_\infty )$
, if
$A_{i-1} = A_i$
, then i is called a folding position of the walk. The fold is positive (respectively negative) if both
$A_{i-1}$
and
$A_i$
lie on the positive (respectively negative) side of the affine hyperplane containing
$F_i$
. If there are no folding positions, then the walk is said to be unfolded. If all of the folds of an alcove walk are positive, then it is said to be positively folded.
Definition 5.5. For an alcove walk
$(A_0 = A, F_1, A_1, \ldots , F_\ell , A_\ell = B, F_\infty )$
, let
$\phi _i$
be the folding operator defined by sending the alcove walk to
$(A_0, F_1, A_1, \ldots , A_{i-1}, F_i' = F_i, A_i', F_{i+1}', \ldots , F_\ell ', A_\ell ', F_\infty '),$
where for
$j \geq i, F_j' = R_i F_j$
and
$A_j' = R_i A_j$
, where
$R_i$
is the affine reflection through the hyperplane containing
$F_i$
. The folding operator
$\phi _i$
leaves
$A_0, \ldots , A_{i-1}$
alone and reflects the remaining tail of the walk through the affine hyperplane containing
$F_i$
.
Lenart observed that any two folding operators commute with each other.
Definition 5.6. Let
$\{j_1, \ldots , j_s \}$
be the set of folding positions of an alcove walk
$\Psi $
. Then, the unfold operator defined by
$$ \begin{align*}\mathrm{unfold}(\Psi) = \phi_{j_1} \dots \phi_{j_s} (\Psi)\end{align*} $$
produces an unfolded alcove walk.
Notation 5.7. Fix
$\lambda \in \Lambda ^+$
and let
$A_0 = \underline {A}_\circ \stackrel {R_1} {\to } A_1 \stackrel {R_2}{\to } \cdots \stackrel {R_\ell }{\to } \lambda + \underline {A}_\circ $
be a minimal length alcove path from
$\underline {A}_\circ $
to
$\lambda + \underline {A}_\circ $
. Then, for
$J = \{ j_1 < \cdots < j_s \} \subset \{1, \ldots , \ell \}$
define
$$ \begin{align*} \phi(J) &= \bar{R}_{j_1} \dots \bar{R}_{j_s} \qquad \text{and} \\ \mu(J) &= R_{j_1} \dots R_{j_s} (\lambda). \end{align*} $$
Theorem 5.8. [Reference SchwerSch06, Theorem 5.5] and [Reference RamRam06, Theorem 4.2], as formulated as Theorem 2.7 of [Reference LenartLen11]
Fix
$\lambda \in \Lambda ^+$
and let
$A_0 = \underline {A}_\circ \stackrel {R_1} {\to } A_1 \stackrel {R_2}{\to } \cdots \stackrel {R_\ell }{\to } \lambda + \underline {A}_\circ $
be a minimal length alcove path from
$\underline {A}_\circ $
to
$\lambda + \underline {A}_\circ $
. Then,
$$ \begin{align*}P_\lambda(X; q^{-1} ) = \sum_{w \in W^\lambda} \sum_{\substack{J = \{ j_1 < \cdots < j_s \} \subset \{1, \ldots, \ell \} \\ w> w\bar{R}_{j_1} > \cdots > w \bar{R}_{j_1} \dots \bar{R}_{j_s}}} q^{-\frac{1}{2}( \ell(w) + \ell( w \phi(J)) - |J|)} (1-q^{-1})^{|J|}\tilde{X}^{w\mu(J)}.\end{align*} $$
Also, we have the following.
Theorem 5.9. Fix
$\lambda \in \Lambda ^+$
and let
$A_0 = \underline {A}_\circ \stackrel {R_1} {\to } A_1 \stackrel {R_2}{\to } \cdots \stackrel {R_\ell }{\to } \lambda + \underline {A}_\circ $
be a minimal length alcove path from
$\underline {A}_\circ $
to
$\lambda + \underline {A}_\circ $
. Then, for
$w \in W,$
$$ \begin{align*}P_\lambda^w(X;q^{-1}) = \sum_{\substack{J = \{ j_1 < \cdots < j_s \} \subset \{1, \ldots, \ell \} \\ w> w\bar{R}_{j_1} > \cdots > w \bar{R}_{j_1} \cdots \bar{R}_{j_s}}} q^{-\frac{1}{2}( \ell(w) + \ell( w \phi(J)) - |J|)} (1-q^{-1})^{|J|}\tilde{X}^{w\mu(J)}.\end{align*} $$
Proof Note that Ram proved Theorem 3.3 of [Reference RamRam06] for all
$w \in W$
and not just
$w \in W^\lambda $
.
The Bruhat order condition in the index of the summation is Lenart’s formulation of positive folding of an alcove path, Proposition 2.5 of [Reference LenartLen11]. We review the proof [Reference LenartLen] using the notation of the above theorem to show that it holds for
$w \in W$
and not just
$w \in W^\lambda $
. Let
$\beta _i$
be the root orthogonal to the common wall of
$A_{i-1}$
and
$A_i$
pointing from
$A_{i-1}$
to
$A_i$
. If you multiply the whole path by w and then fold in positions
$j_1, \ldots , j_s$
before i, then the root
$\beta _i$
is mapped to
$\gamma _i = w \bar {R}_{j_1} \dots \bar {R}_{j_s} \beta _i$
. If you then fold at position i, whether the folding is positive or negative is given by the sign of
$\gamma _i$
: the folding is positive if
$\gamma _i < 0$
and it is negative if
$\gamma _i> 0$
. Expressed in terms of Bruhat order, the folding is positive if
$w\bar {R}_{j_1} \dots \bar {R}_{j_s} \bar {R}_i < w \bar {R}_{j_1} \dots \bar {R}_{j_s}$
and it is negative if
$w\bar {R}_{j_1} \dots \bar {R}_{j_s} \bar {R}_i> w \bar {R}_{j_1} \dots \bar {R}_{j_s}$
. Note that Lenart restricted his attention to
$w \in W^\lambda $
because they index a summation formula, Theorem 2.7 of [Reference LenartLen11], for
$P_\lambda (X;t)$
.
We will use the above theorem to relate signature characters of invariant Hermitian forms on irreducible Verma modules to summands of Hall–Littlewood polynomials.
6 Preliminary results for comparing signature characters and Hall–Littlewood polynomial summands
To begin, we show how a path for computing a Hall–Littlewood polynomial gives rise to a path for computing a signature character.
Definition 6.1. Let
$\Lambda _i^{\mathfrak {t}} = \{ \lambda _{\mathfrak {t}} \in i\mathfrak {t}_0^* : (\lambda _{\mathfrak {t}}, \alpha ^\vee ) \in \mathbb {Z} \, \forall \, \alpha \in \Delta _i(\mathfrak {g},\mathfrak {h}) \}$
. Let
$(\Lambda _i^{\mathfrak {t}})^+ = \{ \lambda _{\mathfrak {t}} \in \Lambda _i^{\mathfrak {t}} : (\lambda _{\mathfrak {t}}, \alpha ^\vee ) \in \mathbb {Z}^{\geq 0} \, \forall \, \alpha \in \Delta _i^+(\mathfrak {g},\mathfrak {h}) \}$
.
Lemma 6.2. Let
$\lambda _{\mathfrak {t}} \in (\Lambda _i^{\mathfrak {t}})^+$
,
$(W_i)_{\lambda _{\mathfrak {t}}}$
be the stabilizer of
$\lambda _{\mathfrak {t}}$
in
$W_i$
, let
$w_0^i$
be the long element of
$W_i$
, and let
$w_0^{i,\lambda _{\mathfrak {t}}}$
be the long element of
$(W_i)_{\lambda _{\mathfrak {t}}}$
. Let
$A_0 = \underline {A}_\circ ^{\mathfrak {t},i} \stackrel {R_1}{\to } A_1 \stackrel {R_2}{\to } \cdots \stackrel {R_\ell }{\to } A_\ell = \lambda _{\mathfrak {t}} + \underline {A}_\circ ^{\mathfrak {t},i}$
be a minimal length alcove path (in
$i\mathfrak {t}_0^*$
) from
$\underline {A}_\circ ^{\mathfrak {t},i}$
to
$\lambda _{\mathfrak {t}} + \underline {A}_\circ ^{\mathfrak {t},i}$
. Then:
-
(1) The path may be chosen to end in a minimal length path from
$\lambda _{\mathfrak {t}}+ w_0^{i,\lambda _{\mathfrak {t}}} w_0^i \underline {A}_\circ ^{\mathfrak {t},i}$
to
$\lambda _{\mathfrak {t}} + \underline {A}_\circ ^{\mathfrak {t},i}$
, where the alcoves in the path are of the form
$\lambda _{\mathfrak {t}} + x \underline {A}_\circ ^{\mathfrak {t},i}$
, where the
$x \in W_i$
come from a
$W_i$
-reduced expression for
$w_0^{i,\lambda _{\mathfrak {t}}} w_0^i$
. -
(2) Assume a path has been chosen as in (1). Let
$C_0 \stackrel {r_1}{\to } C_1 \stackrel {r_2}{\to } \cdots \stackrel {r_\ell }{\to } C_\ell $
be the alcove path (in
$i\mathfrak {t}_0^*$
) defined by
$C_i = w( -\lambda _{\mathfrak {t}} + A_i),$
where
$w \in W_i$
. Then, the path from
$C_0$
to
$C_{\ell - \ell _i(w_0^{i,\lambda _{\mathfrak {t}}} w_0^i)}$
stays in the Weyl chamber
$w w_0^{i,\lambda _{\mathfrak {t}}} \mathfrak {C}_0^{\mathfrak {t},i}$
. The affine hyperplanes crossed on the path from
$C_{\ell -\ell _i(w_0^{i,\lambda _{\mathfrak {t}}} w_0^i)}$
to
$C_\ell $
are
$H_{\alpha ,0}^{\mathfrak {t},i}$
, where
$\alpha \in w (\Delta _i^+(\mathfrak {g},\mathfrak {h}) \setminus (\Delta _i)_{\lambda _{\mathfrak {t}}}^+ ( \mathfrak {g}, \mathfrak {h})),$
where
$(\Delta _i)_{\lambda _{\mathfrak {t}}}^+ ( \mathfrak {g}, \mathfrak {h})) = \{ \alpha \in \Delta _i^+(\mathfrak {g},\mathfrak {h}) : (\lambda _{\mathfrak {t}},\alpha ) = 0 \}$
. -
(3) Suppose
$\theta $
fixes some element of every component of
$\Pi $
and the path
$C_0 \stackrel {r_1}{\to } C_1 \stackrel {r_2}{\to } \cdots \stackrel {r_\ell }{\to } C_\ell $
is a path as chosen in (2). Then, for
$\mu \in \underline {A}_\circ ^{\mathfrak {t},i}$
and
$\lambda _{\mathfrak {a}} \in i \mathfrak {a}_0^*$
,
$$ \begin{align*}ch_s M(w(-\lambda_{\mathfrak{t}} + \mu)+\lambda_{\mathfrak{a}})|_{\mathfrak{a}} = e^{(\lambda_{\mathfrak{a}}-\rho) |_{\mathfrak{a}}}\end{align*} $$
where
$$ \begin{align*} & ch_s M( w(-\lambda_{\mathfrak{t}} + \mu) + \lambda_{\mathfrak{a}} )|_{\mathfrak{t}} = \\ &\hskip-21pt \frac{e^{(w\mu-\rho)|_{\mathfrak{t}}} \displaystyle{ \sum_{\substack{I = \{i_1 < \cdots < i_k\} \subset \{1, \ldots, \ell - \ell_i(w_0^{i,\lambda_{\mathfrak{t}}} w_0^i) \} \\ w w_0^{i,\lambda_{\mathfrak{t}}}> \bar{r}_{i_1} w w_0^{i,\lambda_{\mathfrak{t}}} > \cdots > \bar{r}_{i_1} \dots \bar{r}_{i_k} w w_0^{i,\lambda_{\mathfrak{t}}} }} \begin{array}{l} \epsilon( \nu(I) ) (-1)^{\frac{1}{2} ( \ell_i(w w_0^{i,\lambda_{\mathfrak{t}}}) - \ell_i( \chi(I)w w_0^{i,\lambda_{\mathfrak{t}}}) - |I| )} \\ \times 2^{|I|} e^{w(-\lambda_{\mathfrak{t}}) - \nu(I)} \end{array} }} {\prod_{\alpha \in \Delta^+( \mathfrak{p}, \mathfrak{t} )} (1 - e^{-\alpha}) \prod_{\alpha \in \Delta^+(\mathfrak{k}, \mathfrak{t})}( 1 + e^{-\alpha})}, \end{align*} $$
$\chi (I) = \bar {r}_{i_1} \dots \bar {r}_{i_k}$
,
$\lambda - \nu (I) = \bar {r}_{i_1} \dots \bar {r}_{i_k} r_{i_k} \dots r_{i_1} \lambda $
, and
$\epsilon $
is the
$\mathbb {Z}_2$
-grading on the
$\mathbb {Z}$
-span of the imaginary roots.
-
(4) Suppose
$C_0 \stackrel {r_1}{\to } C_1 \stackrel {r_2}{\to } \dots \stackrel {r_\ell }{\to } C_\ell $
is a path as chosen in (2). For
$I \subset \{ 1, 2, \ldots , \ell - \ell _i( w_0^{i,\lambda _{\mathfrak {t}}} w_0^i) \}$
,
$$ \begin{align*}\chi(I)w = w \phi(I).\end{align*} $$
-
(5) Suppose
$C_0 \stackrel {r_1}{\to } C_1 \stackrel {r_2}{\to } \dots \stackrel {r_\ell }{\to } C_\ell $
is a path as chosen in (2). For
$I \subset \{ 1, 2, \ldots , \ell - \ell _i( w_0^{i,\lambda _{\mathfrak {t}}} w_0^i) \}$
,
$$ \begin{align*}w(-\lambda_{\mathfrak{t}}) - \nu(I) = -w \mu(I).\end{align*} $$
-
(6) Suppose
$C_0 \stackrel {r_1}{\to } C_1 \stackrel {r_2}{\to } \dots \stackrel {r_\ell }{\to } C_\ell $
is a path as chosen in (2). For
$J = I \cup \bar {J,}$
where
$I \subset \{ 1, 2, \ldots , \ell - \ell _i(w_0^{i,\lambda _{\mathfrak {t}}} w_0^i)\}$
and
$\bar {J} \subset \{ \ell - \ell _i(w_0^{i,\lambda _{\mathfrak {t}}} w_0^i)+1, \ell - \ell _i(w_0^{i,\lambda _{\mathfrak {t}}} w_0^i)+ 2, \dots , \ell \}$
,
$$ \begin{align*}w\mu(I) = w\mu(J).\end{align*} $$
Proof (1) The hyperplanes separating
$\underline {A}_\circ ^{\mathfrak {t},i}$
and
$\lambda _{\mathfrak {t}} + \underline {A}_\circ ^{\mathfrak {t},i}$
are
$\{ H_{\alpha ,n}^{\mathfrak {t},i} : \alpha \in \Delta _i^+(\mathfrak {g},\mathfrak {h}) \setminus (\Delta _i)_{\lambda _{\mathfrak {t}}}^+(\mathfrak {g},\mathfrak {h}), 1 \leq n \leq (\lambda _{\mathfrak {t}}, \alpha ^\vee ) \}$
. The hyperplanes separating
$\lambda _{\mathfrak {t}} + \underline {A}_\circ ^{\mathfrak {t},i}$
and
$\lambda _{\mathfrak {t}} + w_0^{i,\lambda _{\mathfrak {t}}} w_0^i \underline {A}_\circ ^{\mathfrak {t},i}$
are
$\{ H_{\alpha ,(\lambda _{\mathfrak {t}},\alpha ^\vee )}^{\mathfrak {t},i} : \alpha \in \Delta _i^+(\mathfrak {g},h) \setminus (\Delta _i)_{\lambda _{\mathfrak {t}}}^+(\mathfrak {g}, \mathfrak {h}) \}$
. The hyperplanes separating
$\underline {A}_\circ ^{\mathfrak {t},i}$
and
$\lambda _{\mathfrak {t}} + w_0^{i, \lambda _{\mathfrak {t}}} w_0^i \underline {A}_\circ ^{\mathfrak {t},i}$
are
$\{ H_{\alpha ,n}^{\mathfrak {t},i}: \alpha \in \Delta _i^+(\mathfrak {g},\mathfrak {h}) \setminus (\Delta _i)_{\lambda _{\mathfrak {t}}}^+(\mathfrak {g},\mathfrak {h}) \text { and } 1 \leq n \leq (\lambda _{\mathfrak {t}}, \alpha ^\vee ) -1 \}$
. Therefore, a minimal length path from
$\underline {A}_\circ ^{\mathfrak {t},i}$
to
$\lambda _{\mathfrak {t}} + \underline {A}_\circ ^{\mathfrak {t},i}$
may be chosen so that the last
$\ell _i(w_0^{i,\lambda _{\mathfrak {t}}} w_0^i) + 1$
alcoves traverse a minimal length path from
$\lambda _{\mathfrak {t}} + w_0^{i,\lambda _{\mathfrak {t}}} w_0^i \underline {A}_\circ ^{\mathfrak {t},i}$
to
$\lambda _{\mathfrak {t}} + \underline {A}_\circ ^{\mathfrak {t}, i}$
.
(2) The hyperplanes separating the alcoves
$-\lambda _{\mathfrak {t}} +A_0 = -\lambda _{\mathfrak {t}} + \underline {A}_\circ ^{\mathfrak {t},i}$
and
$-\lambda _{\mathfrak {t}} + A_{\ell -\ell _i(w_0^{i, \lambda _{\mathfrak {t}}} w_0^i)} = w_0^{i,\lambda _{\mathfrak {t}}} w_0^i \underline {A}_\circ ^ {\mathfrak {t},i}$
are
$\{ H_{\alpha ,n} : \alpha \in \Delta _i^+(\mathfrak {g},\mathfrak {h}) \setminus (\Delta _i)_{\lambda _{\mathfrak {t}}}^+( \mathfrak {g}, \mathfrak {h}) \text { and } -(\lambda _{\mathfrak {t}},\alpha ^\vee ) + 1 \leq n \leq -1 \}$
. Since all of the indices are strictly negative, therefore the alcoves
$-\lambda + A_i$
stay in the same Weyl chamber for
$1 \leq i \leq \ell - \ell _i(w_0^{i,\lambda _{\mathfrak {t}}} w_0^i)$
. Observe that
$w(-\lambda _{\mathfrak {t}} + A_{\ell - \ell _i( w_0^{i,\lambda _{\mathfrak {t}}} w_0^i)}) = w w_0^{i,\lambda _{\mathfrak {t}}} w_0^i \underline {A}_\circ \subset w w_0^{i,\lambda _{\mathfrak {t}}} \mathfrak {C}_0^{\mathfrak {t},i}$
. Therefore, the path from
$C_0$
to
$C_{\ell - \ell _i( w w_0^{i,\lambda _{\mathfrak {t}}})}$
stays in the Weyl chamber
$w w_0^{i,\lambda _{\mathfrak {t}}} \mathfrak {C}_0^{\mathfrak {t},i}$
. The hyperplanes separating
$-\lambda _{\mathfrak {t}} + A_{\ell - \ell _i(w_0^{i, \lambda _{\mathfrak {t}}} w_0^i)}$
to
$-\lambda _{\mathfrak {t}} + A_\ell $
are
$H_{\alpha ,0}^{\mathfrak {t},i}$
, where
$\alpha \in \Delta _i^+(\mathfrak {g},\mathfrak {h}) \setminus (\Delta _i)_{\lambda _{\mathfrak {t}}}^+(\mathfrak {g}, \mathfrak {h})$
, giving the final statement.
(3) The path from
$C_0$
to
$C_{\ell -\ell _i(w_0^{i,\lambda _{\mathfrak {t}}} w_0^i)}$
stays in the Weyl chamber
$w w_0^{i,\lambda _{\mathfrak {t}}} \mathfrak {C}_0^{\mathfrak {t},i}$
. From
$C_{\ell - \ell _i(w_0^{i,\lambda _{\mathfrak {t}}} w_0^i )}$
to
$C_\ell $
, the path does not cross any reducibility hyperplanes, so the hyperplane crossings do not alter the signature character. Thus, for the purpose of computing signature characters, we can truncate our path to end in
$C_{\ell - \ell _i(w_0^{i,\lambda _{\mathfrak {t}}} w_0^i)}$
. Then, we have the stated formula by Theorem 3.14.
(4)–(6) follow from the proof of Proposition 6.20 of [Reference YeeYee19].
Definition 6.3. The Bruhat graph is the directed graph
$\Gamma _{(W,S)}$
with vertices W and edges
$E_{W,S} := \{ (x,y) \in W \times W : x^{-1} y = s_\alpha \text { for some } \alpha \in \Delta (\mathfrak {g},\mathfrak {h}) \text { and } \ell (x) < \ell (y) \}$
.
We need the following result of Dyer.
Lemma 6.4. [Reference DyerDye87, Lemma 1.20]
If
$(x,y)$
is an edge in the Bruhat graph,
$s \in S$
, and
$y \neq xs$
, then
$(xs, ys)$
is an edge in the Bruhat graph.
Lemma 6.5. If
$z \in (W_i)_{\lambda _{\mathfrak {t}}}$
, then z permutes
$\Delta _i^+(\mathfrak {g},\mathfrak {h}) \setminus (\Delta _i)^+_{\lambda _{\mathfrak {t}}}(\mathfrak {g},\mathfrak {h})$
.
Proof This is stated without proof on page 344 of [Reference Nelsen and RamNR03] and page 285 of [Reference YeeYee19]. If
$\alpha \in \Delta _i^+(\mathfrak {g},\mathfrak {h}) \setminus (\Delta _i)_{\lambda _{\mathfrak {t}}}^+(\mathfrak {g},\mathfrak {h})$
, then expressing
$\alpha $
as a sum of simple roots the sum contains some simple root
$\beta $
not in
$(\Delta _i)^+_{\lambda _{\mathfrak {t}}}(\mathfrak {g},\mathfrak {h})$
. Since z changes roots by some linear combination of roots in
$(\Delta _i)^+_{\lambda _{\mathfrak {t}}}(\mathfrak {g},\mathfrak {h})$
,
$z\alpha $
written as a sum of simple roots still contains
$\beta $
, hence
$z\alpha \in \Delta _i^+(\mathfrak {g}, \mathfrak {h}) \setminus (\Delta _i)^+_{\lambda _{\mathfrak {t}}}(\mathfrak {g},\mathfrak {h})$
.
Remark 6.6. Note that this generalizes the fact that
$s_\alpha $
permutes
$\Delta ^+( \mathfrak {g}, \mathfrak {h}) \setminus \{ \alpha \}$
for
$\alpha $
simple.
Lemma 6.7. Let
$A_0 = \underline {A}_\circ ^{\mathfrak {t},i} \stackrel {R_1}{\to } A_1 \stackrel {R_2} {\to } \cdots \stackrel {R_\ell } {\to } A_\ell = \lambda _{\mathfrak {t}} + \underline {A}_\circ ^{ \mathfrak {t},i}$
and
$C_0 \stackrel {r_1}{\to } C_1 \stackrel {r_2}{\to } \cdots \stackrel {r_{\ell - \ell _i(w_0^{i,\lambda _{\mathfrak {t}}} w_0^i )}}{\to } C_{\ell - \ell _i(w_0^{i,\lambda _{\mathfrak {t}}} w_0^i )}$
, where
$C_i= w(-\lambda _{\mathfrak {t}} +A_i)$
(
$w \in W_i$
) be paths as chosen in parts (1) and (2) of Lemma 6.2. Then, for
$I = \{ i_1 < i_2 < \cdots < i_k \} \subset \{ 1, 2, \ldots , \ell - \ell _i(w_0^{i,\lambda _{\mathfrak {t}}} w_0^i) \}$
and
$z \in (W_i)_{\lambda _{\mathfrak {t}}}$
,
$$ \begin{align*}w z> \bar{r}_{i_1} w z > \cdots > \bar{r}_{i_1} \dots \bar{r}_{i_k} w z \text{ if and only if } w > w \bar{R}_{i_1} > \cdots > w \bar{R}_{i_1} \dots \bar{R}_{i_k}.\end{align*} $$
Proof Since
$\bar {r}_i = w \bar {R}_i w^{-1}$
, therefore
$$ \begin{align*}w z> \bar{r}_{i_1} w z > \cdots > \bar{r}_{i_1} \dots \bar{r}_{i_k} w z \iff w z > w\bar{R}_{i_1} z > \cdots > w \bar{R}_{i_1} \dots \bar{R}_{i_k} z.\end{align*} $$
For
$z \in (W_i)_{\lambda _{\mathfrak {t}}}$
, let
$x = w \bar {R}_{i_1} \dots \bar {R}_{i_j}z$
and
$y = w \bar {R}_{i_1} \dots \bar {R}_{i_{j-1}}z$
so that
$x^{-1}y = z^{-1} \bar {R}_{i_j} z$
. Since
$R_{i_j}$
comes from the chosen minimal length path from
$\underline {A}_\circ ^{\mathfrak {t},i}$
to
$\lambda +\underline {A}_\circ ^{\mathfrak {t},i}$
, therefore
$\bar {R}_{i_j} = s_\alpha $
for some
$\alpha \in \Delta _i^+(\mathfrak {g},\mathfrak {h}) \setminus (\Delta _i)_{\lambda _{\mathfrak {t}}}^+( \mathfrak {g}, \mathfrak {h} )$
. Then,
$x^{-1}y = z^{-1} \bar {R}_{i_j}z$
is also some
$s_\beta $
for some
$\beta \in \Delta _i^+(\mathfrak {g},\mathfrak {h}) \setminus (\Delta _i)_{\lambda _{\mathfrak {t}}}^+(\mathfrak {g},\mathfrak {h})$
by Lemma 6.5 since
$z \in (W_i)_{\lambda _{\mathfrak {t}}}$
. Therefore,
$y \neq xs$
for any simple
$s \in (W_i)_{\lambda _{\mathfrak {t}}}$
(here simple means
$W_i$
-simple). Recall that
$(W_i)_{\lambda _{\mathfrak {t}}}$
is a standard parabolic subgroup of
$W_i$
. Thus, by repeated usage of Lemma 6.4,
$(x,y)$
is an edge in the Bruhat graph (of
$W_i$
) if and only if
$(xz',yz')$
is an edge in the Bruhat graph (of
$W_i$
) for
$z' \in (W_i)_{\lambda _{\mathfrak {t}}}$
. This proves the lemma.
Proposition 6.8. Recall that for an alcove A under the action of
$W_a^i$
on
$i \mathfrak {t}_0^*$
,
$R^A(\lambda ) = \sum _{\substack {\mu \in \Lambda _r^+ \\ \text {imaginary}}} c^A_\mu e^{\lambda -\mu -\rho }$
is such that for
$\lambda \in A \oplus i\mathfrak {a}_0^*$
with
$M(\lambda )$
irreducible,
$ch_s M( \lambda ) = R^A(\lambda )$
. Let
$\lambda _{\mathfrak {t}} \in (\Lambda _i^{\mathfrak {t}})^+$
,
$w \in W_i$
be a minimal length coset representative of
$W_i / (W_i)_{\lambda _{\mathfrak {t}}}$
,
$\lambda _{\mathfrak {a}} \in i \mathfrak {a}_0^*$
, and
$z \in w(W_i )_{\lambda _{\mathfrak {t}}}$
. Then,
$R^{w(-\lambda _{\mathfrak {t}}+ \underline {A}_\circ ^{\mathfrak {t},i})} = R^{z(-\lambda _{\mathfrak {t}} + \underline {A}_\circ ^{\mathfrak {t},i})}$
so that for
$\mu \in \underline {A}_\circ ^{\mathfrak {t},i}$
,
$$ \begin{align*}ch_s M( w(-\lambda_{\mathfrak{t}} + \mu) + \lambda_{\mathfrak{a}} ) = e^{w\mu - z\mu} ch_s M( z(-\lambda_{\mathfrak{t}}+\mu) + \lambda_{\mathfrak{a}}).\end{align*} $$
Proof For
$z \in w (W_i)_{\lambda _{\mathfrak {t}}}$
,
$w(-\lambda _{\mathfrak {t}}) = z(-\lambda _{\mathfrak {t}})$
. Therefore,
$w(-\lambda _{\mathfrak {t}} + \underline {A}_\circ ^{\mathfrak {t},i})$
and
$z(-\lambda +\underline {A}_\circ ^{\mathfrak {t},i})$
are separated by hyperplanes passing through
$w(-\lambda _{\mathfrak {t}})$
. From Lemma 6.2,
$z(-\lambda _{\mathfrak {t}}+\underline {A}_\circ ^{\mathfrak {t},i}) \subset zw_0^{i,\lambda _{\mathfrak {t}}} \mathfrak {C}_0^{\mathfrak {t},i}$
for each
$z \in w (W_i)_{ \lambda _{\mathfrak {t}}}$
so the Weyl chambers containing each of the alcoves is distinct. Therefore,
$w(-\lambda _{\mathfrak {t}} + \underline {A}_\circ ^{\mathfrak {t},i})$
and
$z(-\lambda _{\mathfrak {t}}+\underline {A}_\circ ^{\mathfrak {t}, i})$
are separated only by Weyl chamber walls which are not reducibility hyperplanes. Therefore,
$R^{w(-\lambda _{\mathfrak {t}}+\underline {A}_\circ ^{\mathfrak {t},i})} = R^{z( -\lambda _{\mathfrak {t}}+ \underline {A}_\circ ^{\mathfrak {t},i})}$
and the proposition follows.
7 Using natural orders to relate signature characters of invariant Hermitian forms on Verma modules and Hall–Littlewood polynomial summands
In this section, we suppose that
$\mathfrak {g}_0$
is compact. Thus,
$\mathfrak {h} = \mathfrak {t}$
and all roots are imaginary.
$W=W_i$
,
$\mathfrak {C}_0 = \mathfrak {C}_0^{\mathfrak {t},i}$
,
$A_\circ = A_\circ ^{\mathfrak {t},i}$
, and so on. In this section, we show that
$ch_s M(w(-\lambda +\mu ))$
for
$\lambda \in \Lambda ^+$
and
$\mu \in \underline {A}_\circ $
is equal to the “negative” of a Hall–Littlewood polynomial summand evaluated at
$q=-1$
times a version of the Weyl denominator, whether
$\lambda $
is regular or singular.
We need to use Dyer’s work on natural orders (also called reflection orders) and R polynomials.
Notation 7.1. Let
$T = \cup _{w \in W} wSw^{-1}$
be the set of reflections of W.
Notation 7.2. For a subgroup
$W'$
of W, let
$S(W') = \{ t \in T : N(t) \cap W' = \{ t \} \},$
where
$N(w) = \{ t \in T : \ell (wt) < \ell (w) \}$
.
Definition 7.3. A subgroup
$W'$
of W is a reflection subgroup if
$W' = \left < W' \cap T \right>$
.
Definition 7.4. [Reference DyerDye87, Definition 6.15]
A natural order or reflection order on T is a partial order
$\preceq $
such that for any dihedral reflection subgroup
$W'$
of W, either
$$ \begin{align*}r \prec rsr \prec \cdots \prec srs \prec s \quad \text{or} \quad s \prec srs \prec \cdots \prec rsr \prec r,\end{align*} $$
where
$\{r,s\} = S(W')$
. Note that
$r \prec rsr \prec \cdots \prec srs \prec s$
means
$$ \begin{align*}\left \lbrace \begin{array}{lcl} \overbrace{rs \cdots r}^{2m+1} & \preceq & \overbrace{rs\cdots r}^{2n+1} \qquad 1 \leq 2m+1 \leq 2n+1 \leq ord(rs) \\ \overbrace{sr \cdots s}^{2m+1} & \preceq & \overbrace{sr\cdots s}^{2n+1} \qquad 1 \leq 2m+1 \leq 2n+1 \leq ord(rs) \\ \overbrace{rs \cdots r}^{2m+1} & \preceq & \overbrace{sr\cdots s}^{2n+1} \qquad 1 \leq 2m+1, 2n+1 \leq ord(rs). \end{array} \right. \end{align*} $$
Proposition 7.5 [Reference DyerDye87, Remark 6.16]
-
(1) A natural order on T is a total order.
-
(2) The reverse of a natural order is also a natural order.
-
(3)
$t_1 \prec t_2 \prec \cdots \prec t_{\ell (w_0)}$
is a natural order if and only if there is a reduced expression
$w_0 = s_{i_1} \dots s_{i_{ \ell (w_0)}}$
such that
$t_j = s_{i_1} s_{i_2} \dots s_{i_{j -1}} s_{i_j} s_{i_{j-1}} \dots s_{i_2} s_{i_1}$
.
Dyer shows in [Reference DyerDye87] that natural orders may be related to
$\tilde {R}$
polynomials in the following way.
Definition 7.6 [Reference DyerDye87, 6.22]
For a natural order
$\preceq $
on T, we define:
-
(1) Let
$C_1$
be the edge set of the Bruhat graph of
$(W,S)$
,
$$ \begin{align*}C_1 := \{ (x, y) \in W \times W : x < y, y = xs_\alpha \text{ for some } \alpha \in \Delta^+(\mathfrak{g},\mathfrak{h}) \}.\end{align*} $$
-
(2) For
$n \in \mathbb {Z}^+$
and
$x, y \in W$
, let
$C_n(x,y)$
be
$$ \begin{align*}C_n(x,y) = \{ (x_0, \ldots, x_n ) \in W^{n+1} : (x_{i-1},x_i) \in C_1 \text{ for } 1 \leq i \leq n, x_0 = x, x_n = y \}.\end{align*} $$
Note that
$C_n(x,y)$
corresponds to the set of paths of length n from x to y in the Bruhat graph. -
(3) Let
$C^\prec _n(x,y)$
be defined by
$$ \begin{align*}C^\prec_n (x,y ) = \{ (x_0, \ldots, x_n) \in C_n(x,y) : x_0^{-1} x_1 \prec x_1^{-1} x_2 \prec \cdots \prec x_{n-1}^{-1}x_n \}.\end{align*} $$
For
$x,y \in W$
, define
$r^\prec _{x,y}(u) \in \mathbb {Z}[u]$
by
$$ \begin{align*}r^\prec_{x,,y}(u) = \sum_{n \geq 0} \# C^\prec_n(x,y) u^n.\end{align*} $$
Theorem 7.7. [Reference DyerDye87, Theorem 6.23]
Given
$\preceq $
a natural order on the reflections of W, for all
$x,y \in W$
,
$$ \begin{align*}r^\prec_{x,y}(u ) = \tilde{R}_{x,y} (u).\end{align*} $$
(Recall that the
$\tilde {R}$
polynomials were defined in Definition 4.2.)
Fix paths
$A_0 = \underline {A}_\circ \stackrel {R_1}{\to } \cdots \stackrel {R_\ell }{\to } A_\ell = \lambda + \underline {A}_\circ $
and
$C_0 \stackrel {r_1}{\to } \cdots \stackrel {r_\ell }{\to } C_\ell $
as in parts (1) and (2) of Lemma 6.2.
Notation 7.8. Let
$w \in W$
and
$I = \{ i_1 < \cdots < i_k \} \subset \{1,2, \ldots , \ell - \ell (w_0^\lambda w_0) \}$
be such that
$w w_0^\lambda> \bar {r}_{i_1}w w_0^\lambda > \cdots > \bar {r}_{i_1} \dots \bar {r}_{i_k} w w_0^\lambda $
, which is equivalent to
$w> w \bar {R}_{i_1} > \cdots > w \bar {R}_{i_1} \dots \bar {R}_{i_k}$
by Lemma 6.7. Let
$$ \begin{align*}c_w(I) := (-1)^{\frac{1}{2}( \ell(w w_0^\lambda) - \ell(\chi(I)w w_0^\lambda) -|I|)} 2^{|I|} = (-1)^{\frac{1}{2}( \ell(w w_0^\lambda) - \ell(w \phi(I) w_0^\lambda) -|I|)} 2^{|I|}.\end{align*} $$
Let
$$ \begin{align*}p_w(I) := \sum_{ \substack{ J = I \cup \bar{J} \\ \bar{J} = \{i_{k+1} < \cdots < i_r \} \subset \{\ell- \ell(w_0^\lambda w_0) + 1, \dots, \ell \} \\ w\phi(I)> w \phi(I) \bar{R}_{i_{k+1}} > \cdots > w \phi(I) \bar{R}_{i_{k+1}} \dots \bar{R}_{i_r} }} (-1)^{\frac{1}{2}( \ell(w)+ \ell(w\phi(J)) - |J|) } 2^{|J|}.\end{align*} $$
Then,
$c_w(I)$
and
$p_w(I)$
are parts of summands appearing in
$ch_s M(w(-\lambda + \underline {A}_\circ ) )$
and
$P_\lambda ^w(X;-1)$
, respectively.
Notation 7.9. See the notation above. Let
$r_w(I)$
be such that
$p_w(I) = c_w(I) r_w(I)$
. That is,
$$ \begin{align*} & r_w(I) := \\ &\sum_{ \substack{\bar{J} = \{i_{k+1} < \cdots < i_r \} \subset \{\ell- \ell(w_0^\lambda w_0) + 1, \ldots, \ell \} \\ w\phi(I)> w \phi(I) \bar{R}_{i_{k+1}} > \cdots > w \phi(I) \bar{R}_{i_{k+1}} \dots \bar{R}_{i_r} }} (-1)^{\frac{1}{2}( \ell(w) - \ell(w w_0^\lambda) + \ell(w \phi(I \cup \bar{J})) + \ell(w \phi(I) w_0^\lambda) )} (-2i)^{|\bar{J}|}.\end{align*} $$
We show that for
$w \in W^\lambda $
,
$r_w(I) = 1$
. First, recall this result for
$\lambda $
regular:
Proposition 7.10. [Reference YeeYee19, Theorem 7.7 and Lemma 7.8]
If
$\lambda $
is regular and
$w \in W$
, then in the setup of notations 7.8 and 7.9,
$r_w(I) = 1$
.
Proof We sketch the proof of this result.
When
$\lambda $
is regular, the path from
$A_0$
to
$A_\ell $
ends in a path from
$A_{\ell - \ell (w_0)} = \lambda + w_0 \underline {A}_\circ $
to
$A_\ell = \lambda + \underline {A}_\circ $
coming from a reduced expression for
$w_0$
. Then, the reduced expression gives us a natural order
$\preceq $
on T:
$$ \begin{align*}\bar{R}_\ell \prec \bar{R}_{\ell-1} \prec \cdots \prec \bar{R}_{\ell- \ell(w_0)+2} \prec \bar{R}_{\ell-\ell(w_0)+1}.\end{align*} $$
In the setup of notation 7.8, let
$x = w \phi (I)$
. For some
$\bar {J} = \{ i_{k+1} < \cdots < i_r \},$
let
$y = x_0 = w \bar {R}_{i_1} \dots \bar {R}_{i_k} \bar {R}_{i_{k+1}} \dots \bar {R}_{i_r}$
,
$x_1 = w \bar {R}_{i_1} \dots \bar {R}_{i_k} \bar {R}_{i_{k+1}} \dots \bar {R}_{i_{r-1}}$
,
$\ldots $
,
$x = x_{|\bar {J}|} = w \phi (I) = w \bar {R}_{i_1} \dots \bar {R}_{i_k}$
.
$$ \begin{align*}x_0^{-1} x_1 = \bar{R}_{i_r}, x_1^{-1} x_2 = \bar{R}_{i_{r-1}}, \ldots, x_{|\bar{J}|-1}^{-1} x_{|\bar{J}|} = \bar{R}_{i_{k+1}}.\end{align*} $$
Thus, the condition
$i_{k+1} < i_{k+2} < \cdots < i_r$
in the formula for
$r_w(I)$
is equivalent to the condition
$x_0^{-1} x_1 \prec x_1^{-1} x_2 \prec \cdots \prec x_{|\bar {J}|-1}^{-1} x_{|\bar {J}|}$
in the definition of
$C_{|J|}^\prec (y,x)$
. Thus,
$$ \begin{align*} r_w(I) &= \sum_{ \substack{\bar{J} = \{i_{k+1} < \cdots < i_r \} \subset \{\ell- \ell(w_0) + 1, \ldots, \ell \} \\ w\phi(I)> w \phi(I) \bar{R}_{i_{k+1}} > \cdots > w \phi(I) \bar{R}_{i_{k+1}} \dots \bar{R}_{i_r} }} (-1)^{\frac{1}{2}( \ell(w \phi(I \cup \bar{J})) + \ell(w \phi(I) )} (-2i)^{|\bar{J}|} \\ &= \sum_{y \leq x} \sum_{n \geq 0} \sum_{(x_0,x_1, \ldots, x_n) \in C_n^\prec(y,x)} (-2i)^n i^{\ell(x)+ \ell(y)} \\ &= \sum_{y \leq x} r_{y,x}^\prec (-2i) i^{\ell(x)+ \ell(y)} \\ &= \sum_{y \leq x} \tilde{R}_{y,x}(-2i) i^{\ell(x)+\ell(y)} \qquad \text{by Theorem 7.7} \\ &= 1 \qquad \text{by Lemma 7.8 of [Yee19].} \end{align*} $$
We now turn to proving
$r_w(I) = 1$
for
$w \in W^\lambda $
when
$\lambda $
is singular.
Lemma 7.11. In the setup of 7.8 and 7.9, if w and
$x := \chi (I)w = w \phi (I)$
are in
$W^\lambda $
, then
$r_w(I) = 1$
.
Proof
$$ \begin{align*} &r_w(I)= \\ &\quad \sum_{ \substack{\bar{J} = \{i_{k+1} < \cdots < i_r \} \subset \{\ell- \ell(w_0^\lambda w_0) + 1, \ldots, \ell \} \\ w\phi(I)> w \phi(I) \bar{R}_{i_{k+1}} > \cdots > w \phi(I) \bar{R}_{i_{k+1}} \dots \bar{R}_{i_r} }} (-1)^{\frac{1}{2}( \ell(w) - \ell(w w_0^\lambda) + \ell(w \phi(I \cup \bar{J})) + \ell(w \phi(I) w_0^\lambda) )} (-2i)^{|\bar{J}|} \\ &= \sum_{ \substack{\bar{J} = \{i_{k+1} < \cdots < i_r \} \subset \{\ell- \ell(w_0^\lambda w_0) + 1, \dots, \ell \} \\ w\phi(I)> w \phi(I) \bar{R}_{i_{k+1}} > \cdots > w \phi(I) \bar{R}_{i_{k+1}} \dots \bar{R}_{i_r} }} (-1)^{\frac{1}{2}( \ell(w \phi(I \cup \bar{J})) + \ell(w \phi(I) ))} (-2i)^{|\bar{J}|}. \end{align*} $$
The reflections
$\bar {R}_i$
when
$i \in \{\ell - \ell (w_0^\lambda w_0) + 1, \ldots , \ell \}$
correspond to
$\{ s_\alpha : \alpha \in \Delta ^+(\mathfrak {g},\mathfrak {h}) \setminus \Delta _\lambda ^+(\mathfrak {g},\mathfrak {h})\}$
. Unlike the regular case where all reflections appear in
$\bar {R}_{\ell - \ell (w_0)+1}, \ldots , \bar {R}_\ell $
, there are limitations in the reflections appearing in the tail of the path. However, the summation in the formula for
$r_w(I)$
gives all elements of
$C_n^\prec (y,x)$
for the following reason.
First, by Remark 6.27 of [Reference DyerDye87], there is a natural order
$$ \begin{align*}\bar{R}_\ell \prec \bar{R}_{\ell-1} \prec \cdots \prec \bar{R}_{\ell - \ell(w_0^\lambda w_0)+1} \prec S_1 \prec \cdots \prec S_s,\end{align*} $$
where
$\{ S_1, \ldots , S_s \} = \{ s_\alpha : \alpha \in \Delta _\lambda ^+(\mathfrak {g}, \mathfrak {h}) \}$
. Since
$x = w \phi (I) \in W^\lambda $
, therefore
$xS_i> x$
. Therefore, if
$(x_0, x_1, \ldots , x_n) \in C_n^\prec (y,x)$
, then
$x_{n-1}^{-1} x_n$
must be some
$\bar {R}_i$
. Since the other
$x_{j-1}^{-1} x_j$
must be smaller than that
$\bar {R}_i$
, therefore they must also be of the form
$\bar {R}_i$
, not
$S_i$
. Thus,
$$ \begin{align*} r_w(I) &= \sum_{ \substack{\bar{J} = \{i_{k+1} < \cdots < i_r \} \subset \{\ell- \ell(w_0^\lambda w_0) + 1, \dots, \ell \} \\ w\phi(I)> w \phi(I) \bar{R}_{i_{k+1}} > \cdots > w \phi(I) \bar{R}_{i_{k+1}} \dots \bar{R}_{i_r} }} (-1)^{\frac{1}{2}( \ell(w \phi(I \cup \bar{J})) + \ell(w \phi(I) ))} (-2i)^{|\bar{J}|} \\ &= \sum_{y \leq x} \sum_{n \geq 0} \sum_{(x_0,x_1, \ldots, x_n) \in C_n^\prec(y,x)} (-2i)^n i^{\ell(x)+ \ell(y)} \\ &= \sum_{y \leq x} r_{y,x}^\prec (-2i) i^{\ell(x)+ \ell(y)} \\ &= \sum_{y \leq x} \tilde{R}_{y,x}(-2i) i^{\ell(x)+\ell(y)} \qquad \text{by Theorem 7.7} \\ &= 1 \qquad \text{by Lemma 7.8 of [Yee19].} \end{align*} $$
Lemma 7.12. In the setup of notations 7.8, 7.9, and 5.7, let
$w \in W^\lambda $
,
$x = w\phi (I)$
, and
$x \in z W_\lambda $
, where
$z \in W^\lambda $
. Then,
$$ \begin{align*}r_x(\{\}) = (-1)^{\ell(x)-\ell(z)} r_w(I).\end{align*} $$
Proof We have
$$ \begin{align*} \ell(w w_0^\lambda) &= \ell(w) + \ell(w_0^\lambda) \\ \ell(xw_0^\lambda) &= \ell(z) + \ell(w_0^\lambda) - ( \ell(x) - \ell(z)) = 2 \ell(z) - \ell(x)+ \ell(w_0^\lambda). \end{align*} $$
Then,
$$ \begin{align*} & (-1)^{\ell(x)-\ell(z)} r_w(I)= \\ &\quad \sum_{ \substack{\bar{J} = \{i_{k+1} < \cdots < i_r \} \subset \{\ell- \ell(w_0^\lambda w_0) + 1, \dots, \ell \} \\ w\phi(I)> w \phi(I) \bar{R}_{i_{k+1}} > \cdots > w \phi(I) \bar{R}_{i_{k+1}} \dots \bar{R}_{i_r} }} \begin{array}{l} (-1)^{\frac{1}{2}( 2\ell(x) - 2\ell(z) + \ell(w) -\ell(w w_0^\lambda) + \ell(w \phi(I \cup \bar{J})) + \ell( x w_0^\lambda ))} \\ \times (-2i)^{|\bar{J}|} \end{array} \\ & = \sum_{ \substack{\bar{J} = \{i_{k+1} < \cdots < i_r \} \subset \{\ell- \ell(w_0^\lambda w_0) + 1, \dots, \ell \} \\ w\phi(I)> w \phi(I) \bar{R}_{i_{k+1}} > \cdots > w \phi(I) \bar{R}_{i_{k+1}} \dots \bar{R}_{i_r} }} \begin{array}{l} (-1)^{\frac{1}{2}( 2\ell(x) -2\ell(z) - \ell( w_0^\lambda) + \ell(x \phi(\bar{J})) + 2\ell(z) - \ell(x) + \ell( w_0^\lambda ))} \\ \times (-2i)^{|\bar{J}|} \end{array} \\ & = \sum_{ \substack{\bar{J} = \{i_{k+1} < \cdots < i_r \} \subset \{\ell- \ell(w_0^\lambda w_0) + 1, \dots, \ell \} \\ x> x \bar{R}_{i_{k+1}} > \cdots > x \bar{R}_{i_{k+1}} \dots \bar{R}_{i_r} }} (-1)^{\frac{1}{2}( \ell(x) + \ell(x \phi(\bar{J})))} (-2i)^{|\bar{J}|} \\ & = r_x(\{\}). \end{align*} $$
Thus, to show that
$r_w(I)=1$
for
$w \in W^\lambda $
, we are reduced to showing that
$r_x(\{\}) = (-1)^{\ell (x)-\ell (z)}$
.
Lemma 7.13. For
$x \in z W_\lambda $
, where
$z \in W^\lambda $
,
$$ \begin{align*}r_x(\{\}) = (-1)^{\ell(x)-\ell(z)}.\end{align*} $$
Proof In the summation for
$P_\lambda ^x(X; -1)$
,
$\{ \}$
is the only subset
$I \subset \{1, \ldots , \ell - \ell (w_0^\lambda w_0) \}$
such that
$x \mu (I) = x \lambda $
. In the summation for
$P_\lambda ^z(X; -1)$
,
$\{ \}$
is the only subset
$I \subset \{1, \ldots , \ell - \ell (w_0^\lambda w_0 ) \}$
such that
$z \mu (I) = z \lambda = x \lambda $
. Since
$P_\lambda ^x( X; -1) = (-1)^{\ell (x)-\ell (z)}P_\lambda ^z(X;-1)$
by Lemma 4.10, therefore
$$ \begin{align*}p_x(\{\}) = (-1)^{\ell(x)-\ell(z)} p_z( \{\}).\end{align*} $$
Therefore,
$$ \begin{align*}c_x( \{ \} ) r_x( \{\}) = (-1)^{\ell(x)-\ell(z)} c_z(\{ \}) r_z(\{\}).\end{align*} $$
By Lemma 7.11,
$r_z( \{\}) = 1$
. Also,
$c_z(\{\}) = (-1)^{ \frac {1}{2}(\ell (z w_0^\lambda ) - \ell (z w_0^\lambda ))} = 1$
and
$c_x(\{\}) = (-1)^{ \frac {1}{2}(\ell (x w_0^\lambda ) - \ell (x w_0^\lambda ))} = 1$
. Therefore,
$r_x( \{ \} ) = (-1)^{\ell (x)-\ell (z)}$
.
Thus, by Lemma 7.12, we obtain the following.
Proposition 7.14. In the setup of notations 7.8, 7.9, and 5.7, for
$w \in W^\lambda $
,
$$ \begin{align*}r_w(I) = 1.\end{align*} $$
Therefore, by this proposition and by Lemmas 6.2 and 6.7 and Proposition 6.8, we obtain the following.
Theorem 7.15. Let
$\mathfrak {g}_0$
be compact. Then, for
$\lambda \in \Lambda ^+$
,
$\mu \in \underline {A}_\circ $
,
$w \in W$
with
$w \in zW_\lambda $
for
$z \in W^\lambda $
,
$$ \begin{align*} ch_s M( w(-\lambda + \mu)) &= e^{w \mu - z\mu} ch_s M( z(-\lambda+\mu) ) \\ &= \frac{e^{w\mu-\rho}}{\prod_{\alpha \in \Delta^+(\mathfrak{g},\mathfrak{h})}( 1 + e^{-\alpha})} \Phi( P_\lambda^z(X;-1)), \end{align*} $$
where the linear map
$\Phi $
satisfies
$\Phi ( \tilde {X}^\nu ) = e^{-\nu }$
and
$P_\lambda ^z( X; q^{-1}) \tilde {\mathbf {1}}_0 = q^{-\ell (z)/2} \tilde {T}_{z^{-1}}^{-1} \tilde {X}^\lambda \tilde {\mathbf {1}}_0$
is a Hall–Littlewood polynomial summand. Also,
$$ \begin{align*}ch_s M(w (-\lambda) - \mu ) &= e^{-\mu - w\mu} ch_s M(w(-\lambda+ \mu)) \\ &= \frac{e^{-\mu -\rho}}{\prod_{\alpha \in \Delta^+(\mathfrak{g},\mathfrak{h})}(1+e^{-\alpha})} \Phi( P^z_\lambda( X; -1 ) ).\end{align*} $$
Proof We only need to prove the final statement, which follows from the proof of Theorem 7.9 of [Reference YeeYee19].
8 Formula for alcoves of the form
$w(-\lambda + x \underline {A}_\circ )$
In the previous section, we saw that for the compact real form, signature characters for alcoves of the form
$w(-\lambda + \underline {A}_\circ )$
are “negatives” of Hall–Littlewood polynomial summands evaluated at
$q = -1$
times a version of the Weyl denominator (for both regular and singular
$\lambda $
). In this section, we show that for the compact real form and alcoves of the form
$w(-\lambda + x \underline {A}_\circ )$
, signature characters are sums of “negatives” of Hall–Littlewood polynomial summands evaluated at
$q = -1$
times a version of the Weyl denominator.
Throughout this section,
$\mathfrak {g}_0$
is compact.
Theorem 8.1. Let
$\mathfrak {g}_0$
be compact,
$\lambda \in \Lambda ^+$
, and
$w,x \in W$
. For
$y \in W$
, let
$y \in y'W_\lambda $
, where
$y' \in W^\lambda $
. Then, for
$\mu \in \underline {A}_\circ $
,
$$ \begin{align*}ch_s M(w(-\lambda + x \mu)) = \frac{e^{wx\mu - \rho}}{\prod_{\beta \in \Delta^+(\mathfrak{g},\mathfrak{h})} ( 1 + e^{-\beta})} \sum_{y' \in W^\lambda} c^{w,\lambda}_{y',x} \Phi( P^{y'}_{\lambda} ( X; -1 ) ),\end{align*} $$
where the constants
$c^{w,\lambda }_{y',x} \in \mathbb {Z}$
are defined by
-
(1)
$c^{w,\lambda }_{y',1} = \delta _{y',w';}$
-
(2)
$c^{w,\lambda }_{y', xs_\alpha } = c^{w,\lambda }_{y',x}$
for
$xs_\alpha> x,$
where
$\alpha $
is simple if
$x\alpha \in \Delta _\lambda (\mathfrak {g},\mathfrak {h});$
-
(3)
$c^{w,\lambda }_{y', xs_\alpha } = c^{w,\lambda }_{y',x}$
for
$xs_\alpha> x,$
where
$\alpha $
is simple if
$x\alpha \not \in \Delta _\lambda (\mathfrak {g},\mathfrak {h})$
and
$w < wxs_\alpha x^{-1}$
; -
(4)
$c^{w,\lambda }_{y', xs_\alpha } = c^{w,\lambda }_{y',x}+ 2(-1)^{\frac {1}{2} (\ell (w) - \ell (wxs_\alpha x^{-1}) -1)} c^{wxs_\alpha x^{-1},\lambda }_{y',x}$
for
$xs_\alpha> x,$
where
$\alpha $
is simple if
$x\alpha \not \in \Delta _\lambda (\mathfrak {g},\mathfrak {h})$
and
$w> wxs_\alpha x^{-1}.$
Proof This follows from Theorem 7.15 and the fact that for adjacent alcoves A and
$A'$
,
$R^A = R^{A'}$
if the separating hyperplane is not a reducibility hyperplane, and
$R^A(\mu ) = R^{A'}(\mu ) + 2 \varepsilon ( A, A') R^{A - n \gamma }(\mu - n \gamma )$
if the separating hyperplane is the reducibility hyperplane
$H_{\gamma ,n}$
. See the proof of Theorem 8.1 in [Reference YeeYee19] for more details.
9 The noncompact case
In Theorem 3.14, observe that the signature character for a noncompact real form differs from the signature character for the compact real form by multiplication by a sign for each weight space depending on whether the weight differs from the highest weight by a compact or noncompact element of the root lattice.
Recall
$\epsilon $
the
$\mathbb {Z}_2$
-grading of the lattice of imaginary roots. Denote the lattice of imaginary roots by
$\Lambda _r^i$
. Extend
$\epsilon $
to the formal series
$\mathbb {Z}[[\Lambda _r^i]]$
.
Notation 9.1. Let
$\xi = \sum _{\mu \in \Lambda _r^i} a_\mu e^\mu \in \mathbb {Z}[[\Lambda _r^i]]$
. Then,
$$ \begin{align*}\epsilon(\xi) := \sum_{\mu \in \Lambda_r^i} \epsilon(\mu) a_\mu e^\mu.\end{align*} $$
We then have the following.
Theorem 9.2. Let
$\Pi = \Pi _1 \cup \Pi _2,$
where
$\Pi _1$
consists of the components of
$\Pi $
for which
$\theta $
fixes some element and
$\Pi _2$
consists of the components of
$\Pi $
for which
$\theta $
does not fix any element. Let
$\mathfrak {g} = \mathfrak {g}_1 \oplus \mathfrak {g}_2$
and
$\mathfrak {h}^* = \mathfrak {h}_1^* \oplus \mathfrak {h}_2^*$
be the corresponding decompositions of
$\mathfrak {g}$
and
$\mathfrak {h}^*$
, respectively. Let
$W_i = (W_1)_i \times (W_2)_i$
and
$W_a^i = (W_1)_a^i \times (W_2)_a^i$
. Let subscript and superscript
$1$
’s and
$2$
’s refer to objects corresponding to
$\mathfrak {g}_1$
and
$\mathfrak {g}_2$
, respectively. Let
$\lambda = \lambda _{(1)} + \lambda _{(2)} \in ((\Lambda _1)_i^{\mathfrak {t}_1})^+ \oplus ((\Lambda _2)_i^{\mathfrak {t}_2})^+$
, let
$\mu _1 \in (\underline {A}_1)_\circ ^{\mathfrak {t}_1,i}$
,
$\mu _2 \in (\underline {A}_2)_\circ ^{\mathfrak {t}_2,i}$
, and let
$\mu = \mu _1 + \mu _2$
. Let
$w = (w_1, w_2 ) \in W_i = (W_1)_i \times (W_2)_i$
. Let
$w_1' \in ((W_1)_i)^{\lambda _{(1)}}$
be such that
$w_1 \in w_1' ((W_1)_i) _{\lambda _{(1)}}$
. Let
$w_2 (-\lambda _{(2)} + \mu _2)$
belong to the alcove
$A_{(2)}$
under the action of
$(W_2)_a^i$
on
$i(\mathfrak {t}_2)_0^*$
. Let
$A_{(2)} =C_0^2 \stackrel {r_1^{(2)}}{\to } C_1^2 \stackrel {r_2^{(2)}}{\to } C_2^2 \stackrel {r_3^{(2)}}{\to } \dots \stackrel {r_{\ell _2}^{(2)}}{\to } C_{\ell _2}^2 = w_2 (A_2)_\circ ^{\mathfrak {t}_2,i}$
be an alcove path that stays in the Weyl chamber
$w_2 (\mathfrak {C}_2)_0^{\mathfrak {t}_2,i}$
. Let
$\nu \in i\mathfrak {a}_0^*$
. Then,
$$ \begin{align*}ch_s M( w (-\lambda + \mu) + \nu ) |_{\mathfrak{a}} = e^{\nu}\end{align*} $$
and
$$ \begin{align*}ch_s M( w(-\lambda + \mu) + \nu) |_{\mathfrak{t}} = \left( ch_s M( w_1( -\lambda_{(1)} + \mu_1) ) |_{\mathfrak{t}_1} \right) \left( ch_s M( w_2 ( -\lambda_{(2)} + \mu_2) ) |_{\mathfrak{t}_2} \right),\end{align*} $$
where
$$ \begin{align*} ch_s M( w_1(-\lambda_{(1)}+\mu_1) )|_{\mathfrak{t}_1} &= \frac{e^{w_1( - \lambda_{(1)}+ \mu_1) -\rho_1}}{ \prod_{\alpha \in \Delta^+(\mathfrak{p}_1,\mathfrak{t}_1)} (1-e^{-\alpha}) \prod_{\alpha \in \Delta^+( \mathfrak{k}_1, \mathfrak{t}_1 )} (1+e^{-\alpha})} \\ & \quad \times \epsilon\left( e^{w_1\lambda_{(1)}} \Phi(P_{\lambda_{(1)}}^{w_1'}(X;-1)) \right), \end{align*} $$
where
$P_{\lambda _{(1)}}^{w_1'}(X;-1)$
is a Hall–Littlewood polynomial summand for
$(W_1)_i$
and
$$ \begin{align*} & ch_s M( w_2(-\lambda_{(2)}+\mu_2) )|_{\mathfrak{t}_2} \\ & = \frac{e^{-\rho_2} \sum_{\substack{I = \{i_1 < \cdots < i_k\} \subset \{1, \ldots, \ell_2\} \\ w_2> \bar{r}_{i_1}^{(2)} w_2 > \bar{r}_{i_1}^{(2)}\bar{r}_{i_2}^{(2)} w_2 > \cdots > \bar{r}_{i_1}^{(2)} \dots \bar{r}_{i_k}^{(2)} w_2 }} (-1)^{|I|} 2^{|I|} e^{(w_2(-\lambda_{(2)}+\mu_2))|_{\mathfrak{t}_2} - \nu(I)}} {\prod_{\alpha \in \Delta^+( \mathfrak{p}_2, \mathfrak{t}_2 )} (1 - e^{-\alpha}) \prod_{\alpha \in \Delta^+(\mathfrak{k}_2, \mathfrak{t}_2)}( 1 + e^{-\alpha})}. \end{align*} $$
Also,
$$ \begin{align*} ch_s M( w_1(-\lambda_{(1)})-\mu_1) )|_{\mathfrak{t}_1} &= \frac{e^{w_1( - \lambda_{(1)})- \mu_1 -\rho_1}}{ \prod_{\alpha \in \Delta^+(\mathfrak{p}_1,\mathfrak{t}_1)} (1-e^{-\alpha}) \prod_{\alpha \in \Delta^+( \mathfrak{k}_1, \mathfrak{t}_1 )} (1+e^{-\alpha})} \\ &\quad \times \epsilon\left( e^{w_1\lambda_{(1)}} \Phi(P_{\lambda_{(1)}}^{w_1'}(X;-1)) \right). \end{align*} $$
Theorem 9.3. Use the notation and setting of Theorem 9.2. Let
$w, x=(x_1, x_2) \in W_i$
. For
$y \in (W_1)_i$
, let
$y' \in ((W_1)_i)^{\lambda _{(1)}}$
be such that
$y \in y'((W_1)_i)_{\lambda _{(1)}}$
. Let
$w_2 (-\lambda _{(2)} + x_2 \mu _2)$
belong to the alcove
$A_{(2)}$
under the action of
$(W_2)_a^i$
on
$i(\mathfrak {t}_2)_0^*$
. Let
$A_{(2)} =C_0^2 \stackrel {r_1^{(2)}}{\to } C_1^2 \stackrel {r_2^{(2)}}{\to } C_2^2 \stackrel {r_3^{(2)}}{\to } \dots \stackrel {r_{\ell _2}^{(2)}}{\to } C_{\ell _2}^2 = w_2 (A_2)_\circ ^{\mathfrak {t}_2,i}$
be an alcove path that stays in the Weyl chamber
$w_2 (\mathfrak {C}_2)_0^{\mathfrak {t}_2,i}$
. Let
$\nu \in i\mathfrak {a}_0^*$
. Then,
$$ \begin{align*}ch_s M( w (-\lambda + x \mu) + \nu) |_{\mathfrak{a}} = e^{\nu}\end{align*} $$
and
$$ \begin{align*} & ch_s M( w(-\lambda + x\mu) + \nu) |_{\mathfrak{t}} \\ &\quad = \left( ch_s M( w_1( -\lambda_{(1)} + x_1 \mu_1) ) |_{\mathfrak{t}_1} \right) \left( ch_s M( w_2 ( -\lambda_{(2)} + x_2\mu_2) ) |_{\mathfrak{t}_2} \right),\end{align*} $$
where
$$ \begin{align*} & ch_s M(w_1(-\lambda_{(1)} + x_1 \mu_1 ) )|_{\mathfrak{t}_1} \\ &\quad = e^{w_1 x_1\mu_1 - \rho_1} \sum_{y' \in (W_1)_i^{\lambda_{(1)}}} \begin{array}[t]{l} {c}^{w_1,\lambda_{(1)}}_{y',x_1} \frac{e^{-y' \lambda_{(1)}}}{\prod_{\beta \in \Delta^+(\mathfrak{p}_1,\mathfrak{t}_1)}(1-e^{-\beta}) \prod_{\beta \in \Delta^+(\mathfrak{k}_1,\mathfrak{t}_1)}(1+e^{-\beta})} \\ \times \epsilon\left( e^{y'\lambda_{(1)}} \Phi( P_{\lambda_{(1)}}^{y'}(X;-1)) \right) \end{array} \end{align*} $$
(the constants
$c^{w_1,\lambda _{(1)}}_{y',x_1}$
are as defined in Theorem 8.1 except for
$(W_1)_i$
rather than W and
$P_{\lambda _{(1)}}^{y'} (X;q^{-1})$
is a Hall–Littlewood polynomial summand for
$(W_1)_i$
) and
$$ \begin{align*} & ch_s M( w_2(-\lambda_{(2)}+x_2 \mu_2) )|_{\mathfrak{t}_2} \\ & = \frac{e^{-\rho_2} \displaystyle{ \sum_{\substack{I = \{i_1 < \cdots < i_k\} \subset \{1, \ldots, \ell_2\} \\ w_2> \bar{r}_{i_1}^{(2)} w_2 > \bar{r}_{i_1}^{(2)}\bar{r}_{i_2}^{(2)} w_2 > \cdots > \bar{r}_{i_1}^{(2)} \dots \bar{r}_{i_k}^{(2)} w_2 }}} (-1)^{|I|} 2^{|I|} e^{(w_2(-\lambda_{(2)}+x_2 \mu_2))|_{\mathfrak{t}_2} - \nu(I)}} {\prod_{\alpha \in \Delta^+( \mathfrak{p}_2, \mathfrak{t}_2 )} (1 - e^{-\alpha}) \prod_{\alpha \in \Delta^+(\mathfrak{k}_2, \mathfrak{t}_2)}( 1 + e^{-\alpha})}. \end{align*} $$
Acknowledgements
We would like to thank Dan Ursu for writing an extremely useful computer program. Modifications of his computer program led us to conjecture that the Hall–Littlewood formulas of [Reference YeeYee19] extend to the singular case. We would also like to thank the referees for very helpful suggestions.
Open access
