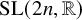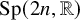1 Introduction
In this paper we study representations of the fundamental group
![]() $\Gamma _g$
of a closed oriented surface of genus
$\Gamma _g$
of a closed oriented surface of genus
![]() $g\geq 2$
into semi-simple Lie groups. Our goal is to characterize a special class of representations into
$g\geq 2$
into semi-simple Lie groups. Our goal is to characterize a special class of representations into
![]() $\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
, maximal representations, by the existence of an equivariant fibration of the projective model for the symmetric space associated to
$\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
, maximal representations, by the existence of an equivariant fibration of the projective model for the symmetric space associated to
![]() $\operatorname {\mathrm {SL}}(2n,\mathbb {R})$
, restricting to a fibration of the symmetric space associated to
$\operatorname {\mathrm {SL}}(2n,\mathbb {R})$
, restricting to a fibration of the symmetric space associated to
![]() $\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
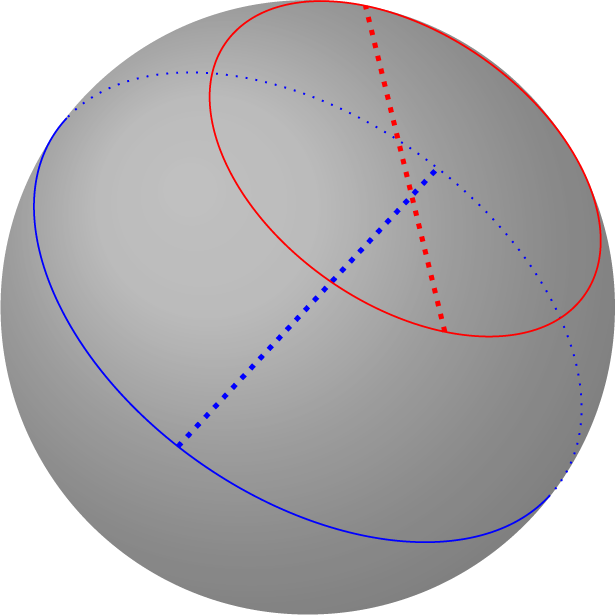
. To illustrate these ideas we begin by discussing quasi-Fuchsian representations in
$\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
. To illustrate these ideas we begin by discussing quasi-Fuchsian representations in
![]() $\operatorname {\mathrm {SL}}(2,\mathbb {C})$
.
$\operatorname {\mathrm {SL}}(2,\mathbb {C})$
.
1.1 Fibrations of
 $\mathbb {H}^3$
by geodesics
$\mathbb {H}^3$
by geodesics
Let
![]() $\rho :\Gamma _g\to \operatorname {\mathrm {SL}}(2,\mathbb {C})$
be the composition of a Fuchsian, that is, discrete and faithful, representation and the inclusion
$\rho :\Gamma _g\to \operatorname {\mathrm {SL}}(2,\mathbb {C})$
be the composition of a Fuchsian, that is, discrete and faithful, representation and the inclusion
![]() $\operatorname {\mathrm {SL}}(2,\mathbb {R})\subset \operatorname {\mathrm {SL}}(2,\mathbb {C})$
. The locally symmetric space
$\operatorname {\mathrm {SL}}(2,\mathbb {R})\subset \operatorname {\mathrm {SL}}(2,\mathbb {C})$
. The locally symmetric space
![]() $\mathbb {H}^3/\rho (\Gamma _g)$
is a fiber bundle over
$\mathbb {H}^3/\rho (\Gamma _g)$
is a fiber bundle over
![]() $S_g$
whose fibers are geodesics. One can construct such a fibration by taking the geodesics orthogonal to the totally geodesic copy of
$S_g$
whose fibers are geodesics. One can construct such a fibration by taking the geodesics orthogonal to the totally geodesic copy of
![]() $\mathbb {H}^2$
in
$\mathbb {H}^2$
in
![]() $\mathbb {H}^3$
preserved by the action of
$\mathbb {H}^3$
preserved by the action of
![]() $\operatorname {\mathrm {SL}}(2,\mathbb {R})$
. This fibration extends to a fibration of an open domain in
$\operatorname {\mathrm {SL}}(2,\mathbb {R})$
. This fibration extends to a fibration of an open domain in
![]() $\mathbb {H}^3 \cup \partial \mathbb {H}^3$
.
$\mathbb {H}^3 \cup \partial \mathbb {H}^3$
.
Such a fibration is described by
![]() $\rho $
-equivariant map
$\rho $
-equivariant map
![]() $u:\widetilde {S_g}\to \mathcal {G}$
where
$u:\widetilde {S_g}\to \mathcal {G}$
where
![]() $\mathcal {G}$
is the space of geodesics in
$\mathcal {G}$
is the space of geodesics in
![]() $\mathbb {H}^3$
. We say that an immersion
$\mathbb {H}^3$
. We say that an immersion
![]() $u:\widetilde {S_g}\to \mathcal {G}$
is fitting if the corresponding geodesics locally define a smooth fibration of
$u:\widetilde {S_g}\to \mathcal {G}$
is fitting if the corresponding geodesics locally define a smooth fibration of
![]() $\mathbb {H}^3\cup \partial \mathbb {H}^3$
.
$\mathbb {H}^3\cup \partial \mathbb {H}^3$
.
Let
![]() $\rho :\Gamma _g\to \operatorname {\mathrm {SL}}(2,\mathbb {C})$
be nearly Fuchsian, that is, suppose that it admits an equivariant immersion
$\rho :\Gamma _g\to \operatorname {\mathrm {SL}}(2,\mathbb {C})$
be nearly Fuchsian, that is, suppose that it admits an equivariant immersion
![]() $h:\widetilde {S_g}\to \mathbb {H}^3$
with principal curvature in
$h:\widetilde {S_g}\to \mathbb {H}^3$
with principal curvature in
![]() $(-1,1)$
. Epstein showed that the locally symmetric space
$(-1,1)$
. Epstein showed that the locally symmetric space
![]() $\mathbb {H}^3/\rho (\Gamma _g)$
admits a fibration described by the fitting immersion
$\mathbb {H}^3/\rho (\Gamma _g)$
admits a fibration described by the fitting immersion
![]() $\mathcal {G}h$
that associates to
$\mathcal {G}h$
that associates to
![]() $x\in \widetilde {S_g}$
the geodesic orthogonal to
$x\in \widetilde {S_g}$
the geodesic orthogonal to
![]() $h(\widetilde {S_g})$
at
$h(\widetilde {S_g})$
at
![]() $h(x)$
[Reference EpsteinEps86]. The map
$h(x)$
[Reference EpsteinEps86]. The map
![]() $\mathcal {G}h$
is sometimes referred to as the Gauss map of h.
$\mathcal {G}h$
is sometimes referred to as the Gauss map of h.
Nearly Fuchsian representations are quasi-Fuchsian, that is, are quasi-isometric embeddings [Reference EpsteinEps86]. We generalize this fact to any representation that admits an equivariant fitting immersion.
Theorem 1.1. Let
![]() $\rho :\Gamma _g\to \operatorname {\mathrm {SL}}(2,\mathbb {C})$
be a representation that admits an equivariant fitting immersion
$\rho :\Gamma _g\to \operatorname {\mathrm {SL}}(2,\mathbb {C})$
be a representation that admits an equivariant fitting immersion
![]() $u:\widetilde {S_g}\to \mathcal {G}$
. The representation
$u:\widetilde {S_g}\to \mathcal {G}$
. The representation
![]() $\rho $
is quasi-Fuchsian.
$\rho $
is quasi-Fuchsian.
This theorem is a consequence of Theorem 5.4. There may a priori exist representations with equivariant fitting maps that are not nearly Fuchsian, see Remark A.4. However, Theorem 1.1 does not provide a characterization of quasi-Fuchsian representations in general because of the following result.
Theorem 1.2 (Theorem A.5)
For a genus g large enough, there exist quasi-Fuchsian representations
![]() $\rho :\Gamma _g\to S_g$
that admit no equivariant fitting immersions
$\rho :\Gamma _g\to S_g$
that admit no equivariant fitting immersions
![]() $u:\widetilde {S_g}\to \mathcal {G}$
.
$u:\widetilde {S_g}\to \mathcal {G}$
.
As a corollary we prove that there exist quasi-Fuchsian representations that are not nearly Fuchsian.
1.2 Fibrations of a convex set
Let
![]() $V=\mathbb {R}^{2n}$
. We denote by
$V=\mathbb {R}^{2n}$
. We denote by
![]() $S^2V$
be the space of symmetric tensors in
$S^2V$
be the space of symmetric tensors in
![]() $V\otimes V$
, or equivalently the space of symmetric bilinear forms on
$V\otimes V$
, or equivalently the space of symmetric bilinear forms on
![]() $V^*$
. Let
$V^*$
. Let
![]() $S^2V^{>0}$
be the convex cone of positive tensors, that is, tensors that define positive symmetric bilinear forms on
$S^2V^{>0}$
be the convex cone of positive tensors, that is, tensors that define positive symmetric bilinear forms on
![]() $V^*$
.
$V^*$
.
The projective convex domain
![]() $\mathbb {P}(S^2V^{>0})$
is the projective model for the symmetric space
$\mathbb {P}(S^2V^{>0})$
is the projective model for the symmetric space
![]() $\mathbb {X}_{\operatorname {\mathrm {SL}}}=\operatorname {\mathrm {SL}}(2n,\mathbb {R})/\operatorname {\mathrm {SO}}(2n,\mathbb {R})$
. We study fibrations of this convex domain by projective codimension
$\mathbb {X}_{\operatorname {\mathrm {SL}}}=\operatorname {\mathrm {SL}}(2n,\mathbb {R})/\operatorname {\mathrm {SO}}(2n,\mathbb {R})$
. We study fibrations of this convex domain by projective codimension
![]() $2$
subspaces.
$2$
subspaces.
A codimension
![]() $2$
projective subspace of
$2$
projective subspace of
![]() $\mathbb {P}(S^2V)$
corresponds to a dimension
$\mathbb {P}(S^2V)$
corresponds to a dimension
![]() $2$
subspace of the dual vector space
$2$
subspace of the dual vector space
![]() $S^2V^*$
, that can be interpreted as the space of quadrics on V. We will write
$S^2V^*$
, that can be interpreted as the space of quadrics on V. We will write
![]() $\mathcal {Q}=S^2V^*$
. A plane in
$\mathcal {Q}=S^2V^*$
. A plane in
![]() $\mathcal {Q}$
is called a pencil of quadrics and we will denote by
$\mathcal {Q}$
is called a pencil of quadrics and we will denote by
![]() $\operatorname {\mathrm {Gr}}_2(\mathcal {Q})$
the space of such planes. Let
$\operatorname {\mathrm {Gr}}_2(\mathcal {Q})$
the space of such planes. Let
![]() $\operatorname {\mathrm {Gr}}_2^{\text {mix}}(\mathcal {Q})$
be the set of mixed pencils, that is, pencils P whose corresponding codimension
$\operatorname {\mathrm {Gr}}_2^{\text {mix}}(\mathcal {Q})$
be the set of mixed pencils, that is, pencils P whose corresponding codimension
![]() $2$
projective subspace intersects nontrivially the convex domain
$2$
projective subspace intersects nontrivially the convex domain
![]() $\mathbb {P}(S^2V^{>0})$
, or equivalently the pencils that do not contain any nonzero semi-positive quadric (in other words the signature of all quadrics of the pencil is mixed).
$\mathbb {P}(S^2V^{>0})$
, or equivalently the pencils that do not contain any nonzero semi-positive quadric (in other words the signature of all quadrics of the pencil is mixed).
In this setting, in a way that is analog as for immersions in the space
![]() $\mathcal {G}$
of geodesics in
$\mathcal {G}$
of geodesics in
![]() $\mathbb {H}^3$
, we say that an immersion
$\mathbb {H}^3$
, we say that an immersion
![]() $u:S\to \operatorname {\mathrm {Gr}}^{\text {mix}}_2(\mathcal {Q})$
from a surface S is fitting is the corresponding codimension two subsets define locally a smooth fibration of the closure
$u:S\to \operatorname {\mathrm {Gr}}^{\text {mix}}_2(\mathcal {Q})$
from a surface S is fitting is the corresponding codimension two subsets define locally a smooth fibration of the closure
![]() $\mathbb {P}(S^2V^{\geq 0})$
of the convex domain
$\mathbb {P}(S^2V^{\geq 0})$
of the convex domain
![]() $\mathbb {P}(S^2V^{> 0})$
. As in
$\mathbb {P}(S^2V^{> 0})$
. As in
![]() $\mathbb {H}^3$
one can construct examples of such maps by taking the Gauss map of some totally geodesic surfaces in
$\mathbb {H}^3$
one can construct examples of such maps by taking the Gauss map of some totally geodesic surfaces in
![]() $\operatorname {\mathrm {SL}}(2n,\mathbb {R})/\operatorname {\mathrm {SO}}(2n,\mathbb {R})$
, see Proposition 7.1.
$\operatorname {\mathrm {SL}}(2n,\mathbb {R})/\operatorname {\mathrm {SO}}(2n,\mathbb {R})$
, see Proposition 7.1.
Let
![]() $\rho :\Gamma \to \operatorname {\mathrm {SL}}(2n,\mathbb {R})$
be a representation and
$\rho :\Gamma \to \operatorname {\mathrm {SL}}(2n,\mathbb {R})$
be a representation and
![]() $u:\widetilde {S_g}\to \text {Gr}_2^{\text {mix}}(\mathcal {Q})$
a
$u:\widetilde {S_g}\to \text {Gr}_2^{\text {mix}}(\mathcal {Q})$
a
![]() $\rho $
-equivariant fitting immersion, then u is an embedding and defines a fibration of an open domain in
$\rho $
-equivariant fitting immersion, then u is an embedding and defines a fibration of an open domain in
![]() $\mathbb {P}(S^2V^{\geq 0})$
that contains
$\mathbb {P}(S^2V^{\geq 0})$
that contains
![]() $\mathbb {P}(S^2V^{> 0})$
, see Proposition 5.5.
$\mathbb {P}(S^2V^{> 0})$
, see Proposition 5.5.
Moreover let
![]() $\text {Gr}_2^{(n,n)}(\mathcal {Q})\subset \text {Gr}_2(\mathcal {Q}) $
be the set of pencils of quadrics P such that every non zero
$\text {Gr}_2^{(n,n)}(\mathcal {Q})\subset \text {Gr}_2(\mathcal {Q}) $
be the set of pencils of quadrics P such that every non zero
![]() $q\in P$
has signature
$q\in P$
has signature
![]() $(n,n)$
, or equivalently the pencils containing no degenerate nonzero quadric.
$(n,n)$
, or equivalently the pencils containing no degenerate nonzero quadric.
Theorem 1.3. Let
![]() $\rho :\Gamma _g\to \operatorname {\mathrm {SL}}(2n,\mathbb {R})$
be a representation that admits an equivariant fitting immersion
$\rho :\Gamma _g\to \operatorname {\mathrm {SL}}(2n,\mathbb {R})$
be a representation that admits an equivariant fitting immersion
![]() $u:\widetilde {N}\to \text {Gr}_2^{(n,n)}(\mathcal {Q})$
. The representation
$u:\widetilde {N}\to \text {Gr}_2^{(n,n)}(\mathcal {Q})$
. The representation
![]() $\rho $
is
$\rho $
is
![]() $\lbrace n\rbrace $
-Anosov.
$\lbrace n\rbrace $
-Anosov.
This theorem can be generalized by replacing
![]() $S_g$
by a closed manifold of some dimension d and considering equivariant maps into
$S_g$
by a closed manifold of some dimension d and considering equivariant maps into
![]() $\text {Gr}_d(\mathcal {Q})$
, see Theorem 5.4.
$\text {Gr}_d(\mathcal {Q})$
, see Theorem 5.4.
In order to show this result we introduce the notion of a fitting flow. Let
![]() $\mathcal {E}$
be the tautological rank
$\mathcal {E}$
be the tautological rank
![]() $2$
vector bundle over
$2$
vector bundle over
![]() $\text {Gr}_2(\mathcal {Q})$
, that is,
$\text {Gr}_2(\mathcal {Q})$
, that is,
Let
![]() $\pi :\mathcal {E}\to \mathcal {Q}$
be the tautological projection, that is, the projection onto the second factor. The pullback
$\pi :\mathcal {E}\to \mathcal {Q}$
be the tautological projection, that is, the projection onto the second factor. The pullback
![]() $u^*\mathbb {S} \mathcal {E}$
of the circle bundle
$u^*\mathbb {S} \mathcal {E}$
of the circle bundle
![]() $\mathbb {S} \mathcal {E}$
for a map
$\mathbb {S} \mathcal {E}$
for a map
![]() $u:S\to \text {Gr}^{\text {mix}}_2(\mathcal {Q})$
is the space of pairs
$u:S\to \text {Gr}^{\text {mix}}_2(\mathcal {Q})$
is the space of pairs
![]() $(x,H)$
where
$(x,H)$
where
![]() $x\in S$
and H is a co-oriented projective hyperplane in
$x\in S$
and H is a co-oriented projective hyperplane in
![]() $\mathbb {P}(S^2V)$
containing the codimension
$\mathbb {P}(S^2V)$
containing the codimension
![]() $2$
projective subspace associated to
$2$
projective subspace associated to
![]() $u(x)$
. Note that a co-oriented projective hyperplane intersecting
$u(x)$
. Note that a co-oriented projective hyperplane intersecting
![]() $\mathbb {P}(S^2V^{>0})$
defines a half-space in the convex set
$\mathbb {P}(S^2V^{>0})$
defines a half-space in the convex set
![]() $\mathbb {P}(S^2V^{\geq 0})$
$\mathbb {P}(S^2V^{\geq 0})$
A fitting flow for the map
![]() $u:S\to \text {Gr}^{\text {mix}}_d(\mathcal {Q})$
is a flow
$u:S\to \text {Gr}^{\text {mix}}_d(\mathcal {Q})$
is a flow
![]() $\Phi $
on this circle bundle
$\Phi $
on this circle bundle
![]() $ u^*\mathbb {S}\mathcal {E}$
over S such that along flow lines the corresponding projective half-spaces in
$ u^*\mathbb {S}\mathcal {E}$
over S such that along flow lines the corresponding projective half-spaces in
![]() $\mathbb {P}(S^2V^{\geq 0})$
are nested, see Definition 4.1.
$\mathbb {P}(S^2V^{\geq 0})$
are nested, see Definition 4.1.
We show that a fitting immersion always admits a smooth fitting flow, see Proposition 4.8, that flow lines must exist between the fibers over any pair of points in S and must be quasi-geodesic, see Proposition 4.5. Finally we use the nestedness of the half-spaces when following a flow line to show uniform contraction occuring in projective space that is sufficient to imply that the representation is Anosov, using an argument similar to the criterion on nested multicones from Bochi-Potrie-Sambarino [Reference BochiBPS19].
1.3 Maximal representations in
 $\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
$\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
Let us now focus on representations into the group
![]() $\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
of linear transformations of
$\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
of linear transformations of
![]() $\mathbb {R}^{2n}$
preserving a symplectic form.
$\mathbb {R}^{2n}$
preserving a symplectic form.
Maximal representations of a closed surface group in
![]() $\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
are representation whose Toledo invariant takes its maximal possible value [Reference Burger, Iozzi and WienhardBIW11]. Equivalently maximal representations can be characterized as positive representations [Reference Burger, Iozzi and WienhardBIW03], or again equivalently as representations that admit an equivariant continuous and transverse map
$\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
are representation whose Toledo invariant takes its maximal possible value [Reference Burger, Iozzi and WienhardBIW11]. Equivalently maximal representations can be characterized as positive representations [Reference Burger, Iozzi and WienhardBIW03], or again equivalently as representations that admit an equivariant continuous and transverse map
![]() $\xi _\rho ^n:\partial \Gamma \to \mathcal {L}_n$
having a specific homotopy type, with
$\xi _\rho ^n:\partial \Gamma \to \mathcal {L}_n$
having a specific homotopy type, with
![]() $\mathcal {L}_n$
the space of Lagrangians in
$\mathcal {L}_n$
the space of Lagrangians in
![]() $(\mathbb {R}^{2n},\omega )$
, see Theorem 2.5.
$(\mathbb {R}^{2n},\omega )$
, see Theorem 2.5.
Maximal representations form connected components of the space of representations, and such representations are all discrete and faithful [Reference Burger, Iozzi and WienhardBIW03]. The space of maximal representations is therefore called a higher rank Teichmüller space. The classical Teichmüller space as well as some higher rank Teichmüller spaces, can be interpreted as spaces of geometric structures. For instance, Hitchin representations in
![]() $\operatorname {\mathrm {SL}}(3,\mathbb {R})$
can be interpreted as spaces of convex projective structures on the considered surface. Maximal representations in
$\operatorname {\mathrm {SL}}(3,\mathbb {R})$
can be interpreted as spaces of convex projective structures on the considered surface. Maximal representations in
![]() $\operatorname {\mathrm {Sp}}(4,\mathbb {R})$
or
$\operatorname {\mathrm {Sp}}(4,\mathbb {R})$
or
![]() $\operatorname {\mathrm {SO}}_o(2,n)$
can be interpreted as spaces of projective or photon structures on a bundle over the surface that admit a special fibration [Reference Collier, Tholozan and ToulisseCTT19]. In these two examples these structures modeled on flag manifolds can be interpreted as a part of a natural compactification of the locally symmetric space associated with the representation. In the present paper we focus on the locally symmetric structures and ask the following:
$\operatorname {\mathrm {SO}}_o(2,n)$
can be interpreted as spaces of projective or photon structures on a bundle over the surface that admit a special fibration [Reference Collier, Tholozan and ToulisseCTT19]. In these two examples these structures modeled on flag manifolds can be interpreted as a part of a natural compactification of the locally symmetric space associated with the representation. In the present paper we focus on the locally symmetric structures and ask the following:
Question 1.4. Can maximal representations be characterized by the existence of some fibration of the associated locally symmetric space?
We provide some affirmative answer to this question. In order to study the symmetric space for
![]() $\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
we embed it into the projective model for the symmetric space of
$\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
we embed it into the projective model for the symmetric space of
![]() $\operatorname {\mathrm {SL}}(2n,\mathbb {R})$
.
$\operatorname {\mathrm {SL}}(2n,\mathbb {R})$
.
1.4 Characterization of maximal representations
The symmetric space
![]() $\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
associated to
$\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
associated to
![]() $\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
can be identified with a totally geodesic submanifold of
$\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
can be identified with a totally geodesic submanifold of
![]() $\mathbb {X}_{\operatorname {\mathrm {SL}}}$
. Let
$\mathbb {X}_{\operatorname {\mathrm {SL}}}$
. Let
![]() $\operatorname {\mathrm {Gr}}^\omega _2(\mathcal {Q})\subset \operatorname {\mathrm {Gr}}^{(n,n)}_2(\mathcal {Q})$
be the set of pencils P such that every nonzero
$\operatorname {\mathrm {Gr}}^\omega _2(\mathcal {Q})\subset \operatorname {\mathrm {Gr}}^{(n,n)}_2(\mathcal {Q})$
be the set of pencils P such that every nonzero
![]() $q\in P$
is positive on some Lagrangian and negative on some other Lagrangian in
$q\in P$
is positive on some Lagrangian and negative on some other Lagrangian in
![]() $\mathbb {R}^{2n}$
. We show that the projectivization of the codimension
$\mathbb {R}^{2n}$
. We show that the projectivization of the codimension
![]() $2$
projective subspace of
$2$
projective subspace of
![]() $\mathbb {P}(S^2V)$
corresponding to any
$\mathbb {P}(S^2V)$
corresponding to any
![]() $P\in \operatorname {\mathrm {Gr}}^\omega _2(\mathcal {Q})$
intersects transversely the totally geodesic symmetric subspace
$P\in \operatorname {\mathrm {Gr}}^\omega _2(\mathcal {Q})$
intersects transversely the totally geodesic symmetric subspace
![]() $\mathbb {X}_{\operatorname {\mathrm {Sp}}}\subset \mathbb {P}(S^2V^{>0})$
, see Lemma 7.4.
$\mathbb {X}_{\operatorname {\mathrm {Sp}}}\subset \mathbb {P}(S^2V^{>0})$
, see Lemma 7.4.
The set
![]() $\operatorname {\mathrm {Gr}}^\omega _2(\mathcal {Q})$
is open in
$\operatorname {\mathrm {Gr}}^\omega _2(\mathcal {Q})$
is open in
![]() $\operatorname {\mathrm {Gr}}_2(\mathcal {Q})$
, but we show that it is disconnected. We select a special union of connected components that we denote by
$\operatorname {\mathrm {Gr}}_2(\mathcal {Q})$
, but we show that it is disconnected. We select a special union of connected components that we denote by
![]() $\operatorname {\mathrm {Gr}}_2^{\max } (\mathcal {Q})$
and we show the following:
$\operatorname {\mathrm {Gr}}_2^{\max } (\mathcal {Q})$
and we show the following:
Theorem 1.5 (Theorem 6.5)
Let
![]() $\rho :\Gamma _g\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
be a representation. If it admits a
$\rho :\Gamma _g\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
be a representation. If it admits a
![]() $\rho $
-equivariant fitting immersion
$\rho $
-equivariant fitting immersion
![]() $u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
it is maximal for some orientation of
$u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
it is maximal for some orientation of
![]() $S_g$
.
$S_g$
.
If a representation
![]() $\rho :\Gamma _g\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
admits an equivariant fitting immersion
$\rho :\Gamma _g\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
admits an equivariant fitting immersion
![]() $u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}^{(n,n)}_2(\mathcal {Q})$
the image of u lies necessarily in
$u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}^{(n,n)}_2(\mathcal {Q})$
the image of u lies necessarily in
![]() $\operatorname {\mathrm {Gr}}^\omega _2(\mathcal {Q})$
. We then use that the homotopy type of the boundary map of
$\operatorname {\mathrm {Gr}}^\omega _2(\mathcal {Q})$
. We then use that the homotopy type of the boundary map of
![]() $\rho $
is determined by the connected component of
$\rho $
is determined by the connected component of
![]() $\operatorname {\mathrm {Gr}}^\omega _2(\mathcal {Q})$
in which the image of u lies to define
$\operatorname {\mathrm {Gr}}^\omega _2(\mathcal {Q})$
in which the image of u lies to define
![]() $\operatorname {\mathrm {Gr}}_2^{\max } (\mathcal {Q})$
and to prove this theorem, see Section 6.1.
$\operatorname {\mathrm {Gr}}_2^{\max } (\mathcal {Q})$
and to prove this theorem, see Section 6.1.
For
![]() $n=2$
using results of [Reference Collier, Tholozan and ToulisseCTT19] we show a converse to this statement, which therefore provides a characterization of maximal representations, see Corollary B.5. We compare this characterization with the one from Collier-Tholozan-Toulisse in Remark B.6. For
$n=2$
using results of [Reference Collier, Tholozan and ToulisseCTT19] we show a converse to this statement, which therefore provides a characterization of maximal representations, see Corollary B.5. We compare this characterization with the one from Collier-Tholozan-Toulisse in Remark B.6. For
![]() $n\geq 3$
we prove a weaker converse to this theorem. We construct equivariant maps
$n\geq 3$
we prove a weaker converse to this theorem. We construct equivariant maps
![]() $u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
for maximal representations that locally define a fibration of
$u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
for maximal representations that locally define a fibration of
![]() $\mathbb {P}(S^2V^{\geq 0})$
but are only continuous and not smooth.
$\mathbb {P}(S^2V^{\geq 0})$
but are only continuous and not smooth.
Theorem 1.6 (Theorem 6.5)
A representation
![]() $\rho :\Gamma _g\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
is maximal if and only if it admits a
$\rho :\Gamma _g\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
is maximal if and only if it admits a
![]() $\rho $
-equivariant continuous map of pencils that admits an equivariant fitting flow:
$\rho $
-equivariant continuous map of pencils that admits an equivariant fitting flow:
A continuous equivariant map
![]() $u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{{\max }}(\mathcal {Q})$
for a representation
$u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{{\max }}(\mathcal {Q})$
for a representation
![]() $\rho :\Gamma _g\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
with a fitting flow defines a
$\rho :\Gamma _g\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
with a fitting flow defines a
![]() $\rho $
-equivariant continuous fibration of
$\rho $
-equivariant continuous fibration of
![]() $\mathbb {P}(S^2V^{\geq 0})$
, but also of
$\mathbb {P}(S^2V^{\geq 0})$
, but also of
![]() $\mathbb {X}_{\operatorname {\mathrm {Sp}}}\subset \mathbb {P}(S^2V^{>0})$
as
$\mathbb {X}_{\operatorname {\mathrm {Sp}}}\subset \mathbb {P}(S^2V^{>0})$
as
![]() $\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
intersects the fibers transversely. Thus u defines a continuous fibration of the locally symmetric space
$\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
intersects the fibers transversely. Thus u defines a continuous fibration of the locally symmetric space
![]() $\mathbb {X}_{\operatorname {\mathrm {Sp}}}/\rho (\Gamma _g)$
.
$\mathbb {X}_{\operatorname {\mathrm {Sp}}}/\rho (\Gamma _g)$
.
The space of rank one elements of
![]() $\mathbb {P}(S^2V^{\geq 0})$
can naturally be identified with
$\mathbb {P}(S^2V^{\geq 0})$
can naturally be identified with
![]() $\mathbb {P}(V)$
. Such a map u defines a continuous
$\mathbb {P}(V)$
. Such a map u defines a continuous
![]() $\rho $
-equivariant fibration of a domain in projective space, that is equal to the domain of discontinuity in projective space constructed by Guichard-Wienhard [Reference Guichard and WienhardGW12]. The quotient of this domain inherits a
$\rho $
-equivariant fibration of a domain in projective space, that is equal to the domain of discontinuity in projective space constructed by Guichard-Wienhard [Reference Guichard and WienhardGW12]. The quotient of this domain inherits a
![]() $(\operatorname {\mathrm {Sp}}(2n,\mathbb {R}),\mathbb {RP}^{2n-1})$
-structure, a contact projective structure. Theorem 1.6 implies the following characterization of the contact projective structures corresponding to maximal representations.
$(\operatorname {\mathrm {Sp}}(2n,\mathbb {R}),\mathbb {RP}^{2n-1})$
-structure, a contact projective structure. Theorem 1.6 implies the following characterization of the contact projective structures corresponding to maximal representations.
Corollary 1.7. A contact projective structure on a fiber bundle M with fiber F over
![]() $S_g$
corresponds to a maximal representation by the construction of Guichard-Wienhard if and only if, up to homeomorphisms of M that stabilize
$S_g$
corresponds to a maximal representation by the construction of Guichard-Wienhard if and only if, up to homeomorphisms of M that stabilize
![]() $\pi _1(F)$
and act trivially on
$\pi _1(F)$
and act trivially on
![]() $\pi _1(M)/\pi _1(F)\simeq \Gamma _g$
, the fibers are mapped via the developing map onto the bases of maximal pencils of quadrics parametrized by a continuous map that admits an equivariant fitting flow.
$\pi _1(M)/\pi _1(F)\simeq \Gamma _g$
, the fibers are mapped via the developing map onto the bases of maximal pencils of quadrics parametrized by a continuous map that admits an equivariant fitting flow.
In order to construct continuous maps that admits a fitting flow for maximal representations, we show how to associate to a pair of transverse Lagrangians a quadric on
![]() $\mathbb {R}^{2n}$
.
$\mathbb {R}^{2n}$
.
1.5 Organization of the paper
This paper begins with a recall of some facts about maximal and Anosov representations in Section 2.
The main definitions are introduced in Section 3 where fibrations of a projective convex set by projective subspaces are discussed, more precisely fibrations of the projective model for the symmetric space of
![]() $\operatorname {\mathrm {SL}}(2n,\mathbb {R})$
.
$\operatorname {\mathrm {SL}}(2n,\mathbb {R})$
.
In Section 4 we introduce the notion of fitting flows.
In Section 5 we discuss how the existence of an equivariant continuous map with a fitting flow implies the Anosov property, Theorem 5.4, and describes a fibration of a domain of discontinuity in projective space.
In Section 6 we focus on representations into
![]() $\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
and prove Theorem 6.5, which is the characterization of maximal representations by the existence of a locally fitting map of maximal pencils of quadrics that admits a fitting flow.
$\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
and prove Theorem 6.5, which is the characterization of maximal representations by the existence of a locally fitting map of maximal pencils of quadrics that admits a fitting flow.
In Section 7 we prove two propositions relative to the symmetric space of
![]() $\operatorname {\mathrm {SL}}(2n,\mathbb {R})$
and
$\operatorname {\mathrm {SL}}(2n,\mathbb {R})$
and
![]() $\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
.
$\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
.
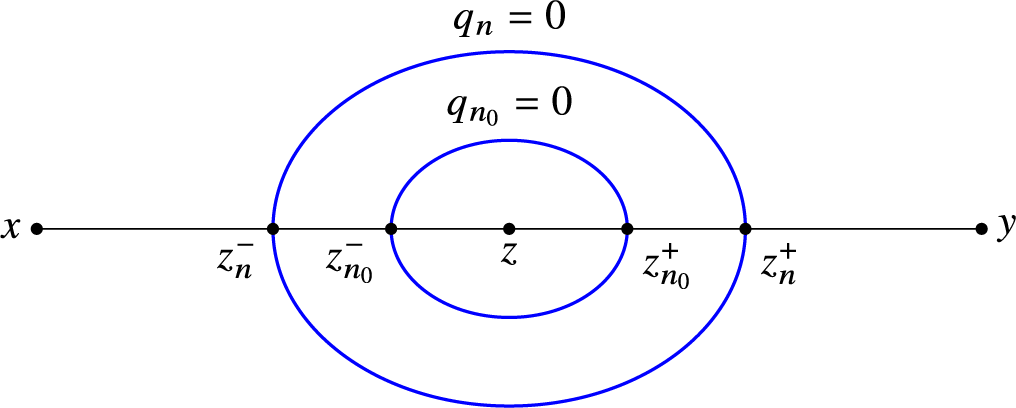
In Appendix A we discuss fibrations of the hyperbolic
![]() $3$
-space with geodesic fibers.
$3$
-space with geodesic fibers.
In Appendix B we show how spacelike surfaces in
![]() $\mathbb {H}^{2,2}$
with a bound on their principal curvatures define a fitting immersion of pencils.
$\mathbb {H}^{2,2}$
with a bound on their principal curvatures define a fitting immersion of pencils.
2 Maximal and Anosov representations
2.1 Maximal representations
Let us fix a symplectic form
![]() $\omega $
on
$\omega $
on
![]() $\mathbb {R}^{2n}$
, that is, a nondegenerated bilinear antisymmetric pairing. A symplectic basis of
$\mathbb {R}^{2n}$
, that is, a nondegenerated bilinear antisymmetric pairing. A symplectic basis of
![]() $\mathbb {R}^{2n}$
is a basis
$\mathbb {R}^{2n}$
is a basis
![]() $(x_1,\cdots , x_n,y_1,\cdots , y_n)$
in which:
$(x_1,\cdots , x_n,y_1,\cdots , y_n)$
in which:
 $$ \begin{align*}\omega= \sum_{i=1}^n x_i^*\wedge y_i^*.\end{align*} $$
$$ \begin{align*}\omega= \sum_{i=1}^n x_i^*\wedge y_i^*.\end{align*} $$
We define
![]() $\operatorname {\mathrm {Gr}}_n(\mathbb {R}^{2n})$
as the space of n-dimensional subspaces of
$\operatorname {\mathrm {Gr}}_n(\mathbb {R}^{2n})$
as the space of n-dimensional subspaces of
![]() $\mathbb {R}^{2n}$
. A Lagrangian in
$\mathbb {R}^{2n}$
. A Lagrangian in
![]() $(\mathbb {R}^{2n},\omega )$
is an element
$(\mathbb {R}^{2n},\omega )$
is an element
![]() $\ell \in \operatorname {\mathrm {Gr}}_n(\mathbb {R}^{2n})$
such that
$\ell \in \operatorname {\mathrm {Gr}}_n(\mathbb {R}^{2n})$
such that
![]() $\omega $
restricted to
$\omega $
restricted to
![]() $\ell $
is equal to zero. We denote by
$\ell $
is equal to zero. We denote by
![]() $\mathcal {L}_n$
the space of Lagrangians in
$\mathcal {L}_n$
the space of Lagrangians in
![]() $(\mathbb {R}^{2n},\omega )$
. We say that two Lagrangians are transverse if their intersection is trivial.
$(\mathbb {R}^{2n},\omega )$
. We say that two Lagrangians are transverse if their intersection is trivial.
Let
![]() $\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
be the subgroup of elements in
$\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
be the subgroup of elements in
![]() $\operatorname {\mathrm {SL}}(2n,\mathbb {R})$
that preserves
$\operatorname {\mathrm {SL}}(2n,\mathbb {R})$
that preserves
![]() $\omega $
. This group acts transitively on
$\omega $
. This group acts transitively on
![]() $\mathcal {L}_n$
, as well as on the space of pairs of transverse Lagrangians. Given a triple
$\mathcal {L}_n$
, as well as on the space of pairs of transverse Lagrangians. Given a triple
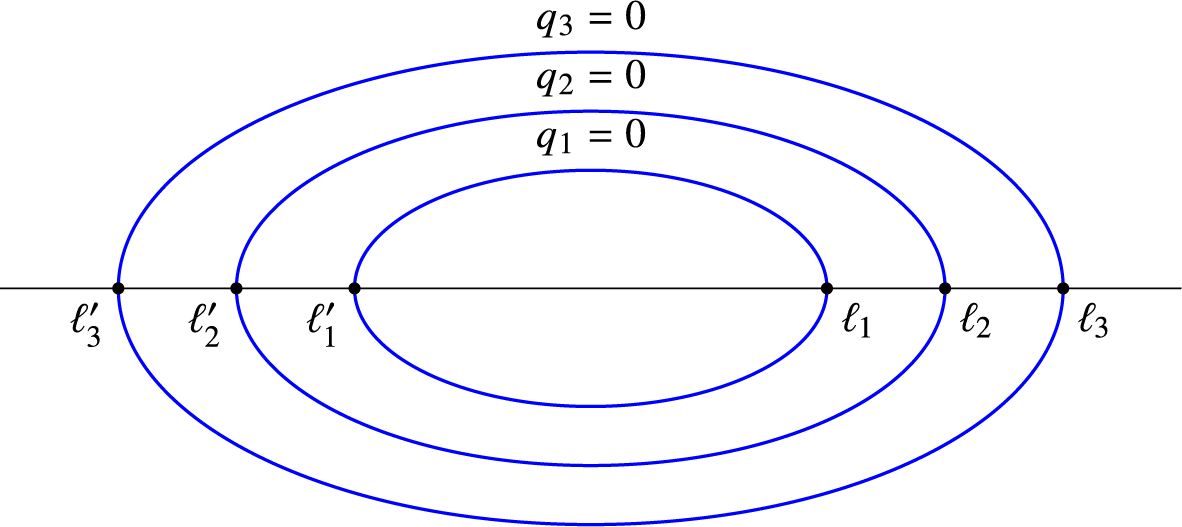
![]() $(\ell _1,\ell _2,\ell _3)$
of transverse Lagrangians, one can find a symplectic basis such that for some
$(\ell _1,\ell _2,\ell _3)$
of transverse Lagrangians, one can find a symplectic basis such that for some
![]() $(\epsilon _i)\in \lbrace 1,-1\rbrace $
:
$(\epsilon _i)\in \lbrace 1,-1\rbrace $
:
The sum of the
![]() $(\epsilon _i)$
is an invariant of the triple of flags that is called the Maslov index
$(\epsilon _i)$
is an invariant of the triple of flags that is called the Maslov index
![]() $M(\ell _1,\ell _2,\ell _3)$
. These facts can be found in [Reference Lion and VergneLV13, Section 1.5.7]. The group
$M(\ell _1,\ell _2,\ell _3)$
. These facts can be found in [Reference Lion and VergneLV13, Section 1.5.7]. The group
![]() $\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
acts transitively on the space of triples of transverse Lagrangians with a given Maslov index. We say that
$\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
acts transitively on the space of triples of transverse Lagrangians with a given Maslov index. We say that
![]() $(\ell _1,\ell _2,\ell _3)$
is maximal if the Maslov index of the triple is equal to n.
$(\ell _1,\ell _2,\ell _3)$
is maximal if the Maslov index of the triple is equal to n.
The Lie group
![]() $\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
is of Hermitian type and tube type. Hence it admits a special class in its continuous cohomology group
$\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
is of Hermitian type and tube type. Hence it admits a special class in its continuous cohomology group
![]() $[\tau ]\in H^2_c(\operatorname {\mathrm {Sp}}(2n,\mathbb {R}),\mathbb {Z})$
. Let
$[\tau ]\in H^2_c(\operatorname {\mathrm {Sp}}(2n,\mathbb {R}),\mathbb {Z})$
. Let
![]() $S_g$
be a closed oriented surface of genus
$S_g$
be a closed oriented surface of genus
![]() $g\geq 2$
. The fundamental class of
$g\geq 2$
. The fundamental class of
![]() $S_g$
defines a cohomology class
$S_g$
defines a cohomology class
![]() $[S_g]\in H^2(\pi _1(S_g),\mathbb {Z})\simeq \mathbb {Z}$
. Given a representation
$[S_g]\in H^2(\pi _1(S_g),\mathbb {Z})\simeq \mathbb {Z}$
. Given a representation
![]() $\rho :\pi _1(S_g)\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
one can consider the pullback of this class
$\rho :\pi _1(S_g)\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
one can consider the pullback of this class
![]() $\rho ^*[\tau ]=T(\rho )[S_g]$
. The integer
$\rho ^*[\tau ]=T(\rho )[S_g]$
. The integer
![]() $T(\rho )$
is called the Toledo number of
$T(\rho )$
is called the Toledo number of
![]() $\rho $
.
$\rho $
.
The Toledo number can take only finitely many values as the space of representations can only have finitely many connected components. More precisely:
Lemma 2.1 [Reference Burger, Iozzi and WienhardBIW11]
Let
![]() $\rho :\pi _1(S_g)\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
, the Toledo number satisfies:
$\rho :\pi _1(S_g)\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
, the Toledo number satisfies:
Such a representation is called maximal if its Toledo number is equal to
![]() $(2g-2)n$
.
$(2g-2)n$
.
2.2 Anosov representations
Let
![]() $\Gamma $
be a finitely generated group. Anosov representations are representations with some exponential gaps between singular values.
$\Gamma $
be a finitely generated group. Anosov representations are representations with some exponential gaps between singular values.
Fix a word metric
![]() $|\cdot |$
on
$|\cdot |$
on
![]() $\Gamma $
and a scalar product on
$\Gamma $
and a scalar product on
![]() $\mathbb {R}^{2n}$
allowing us to define the singular values
$\mathbb {R}^{2n}$
allowing us to define the singular values
![]() $\sigma _1(g)\geq \sigma _2(g)\geq \cdots \geq \sigma _{2n}(g)$
of
$\sigma _1(g)\geq \sigma _2(g)\geq \cdots \geq \sigma _{2n}(g)$
of
![]() $g\in \operatorname {\mathrm {SL}}(2n,\mathbb {R})$
as the eigenvalues of
$g\in \operatorname {\mathrm {SL}}(2n,\mathbb {R})$
as the eigenvalues of
![]() $\sqrt {g^tg}$
. The following definition is independent of these choices.
$\sqrt {g^tg}$
. The following definition is independent of these choices.
Definition 2.2 [Reference BochiBPS19]
We say that a representation
![]() $\rho :\Gamma \to \operatorname {\mathrm {SL}}(2n,\mathbb {R})$
is
$\rho :\Gamma \to \operatorname {\mathrm {SL}}(2n,\mathbb {R})$
is
![]() $\lbrace n\rbrace $
-Anosov if there exist
$\lbrace n\rbrace $
-Anosov if there exist
![]() $A,B>0$
such that for all
$A,B>0$
such that for all
![]() $\gamma \in \Gamma $
:
$\gamma \in \Gamma $
:
If a group admits an Anosov representation, it must be Gromov hyperbolic [Reference BochiBPS19]. We denote by
![]() $\partial \Gamma $
its Gromov boundary. Anosov representations come with boundary maps.
$\partial \Gamma $
its Gromov boundary. Anosov representations come with boundary maps.
Theorem 2.3 [Reference Guéritaud, Guichard, Kassel and WienhardGGKW17, Theorem 1.1]
Let
![]() $\rho :\Gamma \to \operatorname {\mathrm {SL}}(2n,\mathbb {R})$
be
$\rho :\Gamma \to \operatorname {\mathrm {SL}}(2n,\mathbb {R})$
be
![]() $\lbrace n\rbrace $
-Anosov. There exists a unique
$\lbrace n\rbrace $
-Anosov. There exists a unique
![]() $\rho $
-equivariant continuous map
$\rho $
-equivariant continuous map
![]() $\xi ^n_\rho :\partial \Gamma \to \operatorname {\mathrm {Gr}}_n(\mathbb {R}^{2n})$
such that:
$\xi ^n_\rho :\partial \Gamma \to \operatorname {\mathrm {Gr}}_n(\mathbb {R}^{2n})$
such that:
-
• for all distinct
 $x,y\in \partial \Gamma $
,
$x,y\in \partial \Gamma $
,
 $\xi ^n_\rho (x)\oplus \xi ^n_\rho (y)=\mathbb {R}^{2n}$
(transverse),
$\xi ^n_\rho (x)\oplus \xi ^n_\rho (y)=\mathbb {R}^{2n}$
(transverse), -
• for all
 $\gamma \in \Gamma $
that admit an attracting fixed point
$\gamma \in \Gamma $
that admit an attracting fixed point
 $\gamma ^+\in \partial \Gamma $
,
$\gamma ^+\in \partial \Gamma $
,
 $\xi ^n_\rho (\gamma ^+)$
is the attracting fixed point of the action of
$\xi ^n_\rho (\gamma ^+)$
is the attracting fixed point of the action of
 $\rho (\gamma )$
on
$\rho (\gamma )$
on
 $\operatorname {\mathrm {Gr}}_{n}(\mathbb {R}^{2n})$
(dynamic preserving),
$\operatorname {\mathrm {Gr}}_{n}(\mathbb {R}^{2n})$
(dynamic preserving),
If moreover
![]() $\rho (\Gamma )\subset \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
, then
$\rho (\Gamma )\subset \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
, then
![]() $\xi ^n_\rho (x)$
is a Lagrangian for all
$\xi ^n_\rho (x)$
is a Lagrangian for all
![]() $x\in \partial \Gamma $
.
$x\in \partial \Gamma $
.
The fact that
![]() $\xi ^n_\rho (x)$
is a Lagrangian is a consequence of the fact that an attracting fixed n-dimensional subspace for an element
$\xi ^n_\rho (x)$
is a Lagrangian is a consequence of the fact that an attracting fixed n-dimensional subspace for an element
![]() $g\in \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
is necessarily Lagrangian, and every
$g\in \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
is necessarily Lagrangian, and every
![]() $x\in \partial \Gamma $
is a limit of attracting fixed points
$x\in \partial \Gamma $
is a limit of attracting fixed points
![]() $\gamma ^+$
of elements
$\gamma ^+$
of elements
![]() $\gamma \in \Gamma $
.
$\gamma \in \Gamma $
.
Maximal representations have been characterized in [Reference Burger, Iozzi, Labourie and WienhardBILW05], [Reference Burger, Iozzi and WienhardBIW03]:
Theorem 2.4. A representation
![]() $\rho :\pi _1(S_g)\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
is maximal if and only if it is
$\rho :\pi _1(S_g)\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
is maximal if and only if it is
![]() $\lbrace n\rbrace $
-Anosov and for one and hence any positively oriented triple
$\lbrace n\rbrace $
-Anosov and for one and hence any positively oriented triple
![]() $(x,y,z)\in \partial \pi _1(S)$
the triple
$(x,y,z)\in \partial \pi _1(S)$
the triple
![]() $(\xi ^n_\rho (x),\xi ^n_\rho (y),\xi ^n_\rho (z))$
is a maximal triple of Lagrangians.
$(\xi ^n_\rho (x),\xi ^n_\rho (y),\xi ^n_\rho (z))$
is a maximal triple of Lagrangians.
One can also characterize maximal representations among
![]() $\lbrace n\rbrace $
-Anosov representations by looking at the homotopy type of their boundary map. The fundamental group of the space of Lagrangians
$\lbrace n\rbrace $
-Anosov representations by looking at the homotopy type of their boundary map. The fundamental group of the space of Lagrangians
![]() $\mathcal {L}_n$
is isomorphic to
$\mathcal {L}_n$
is isomorphic to
![]() $\mathbb {Z}$
[Reference WiggermanWig98] where a generator is:
$\mathbb {Z}$
[Reference WiggermanWig98] where a generator is:
 $$ \begin{align*}\tau:\theta\in \mathbb{S}^1\mapsto \langle \cos\left(\frac{\theta}{2}\right)x_1+\sin\left(\frac{\theta}{2}\right)y_1, x_2,\cdots, x_n\rangle\in \mathcal{L}_n.\end{align*} $$
$$ \begin{align*}\tau:\theta\in \mathbb{S}^1\mapsto \langle \cos\left(\frac{\theta}{2}\right)x_1+\sin\left(\frac{\theta}{2}\right)y_1, x_2,\cdots, x_n\rangle\in \mathcal{L}_n.\end{align*} $$
Theorem 2.5. A representation
![]() $\rho :\pi _1(S_g)\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
is maximal if and only if it is
$\rho :\pi _1(S_g)\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
is maximal if and only if it is
![]() $\lbrace n\rbrace $
-Anosov and the free homotopy type of the curve
$\lbrace n\rbrace $
-Anosov and the free homotopy type of the curve
![]() $\xi ^n_\rho $
is equal to
$\xi ^n_\rho $
is equal to
![]() $n[\tau ]$
.
$n[\tau ]$
.
Remark 2.6. In Theorem 2.4 and hence also in Theorem 2.5, one can relax the assumption that
![]() $\rho $
is
$\rho $
is
![]() $\lbrace n\rbrace $
-Anosov. In [Reference Burger, Iozzi and WienhardBIW03, Theorem 8] it is shown that it is sufficient to assume that
$\lbrace n\rbrace $
-Anosov. In [Reference Burger, Iozzi and WienhardBIW03, Theorem 8] it is shown that it is sufficient to assume that
![]() $\rho $
admits an equivariant, continuous and transverse map
$\rho $
admits an equivariant, continuous and transverse map
![]() $\xi ^n_\rho : \partial \Gamma \to \mathcal {L}_n$
satisfying the additional property of sending positive triples to maximal triples.
$\xi ^n_\rho : \partial \Gamma \to \mathcal {L}_n$
satisfying the additional property of sending positive triples to maximal triples.
Proof. Let
![]() $\rho :\pi _1(S_g)\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
be
$\rho :\pi _1(S_g)\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
be
![]() $\lbrace n\rbrace $
-Anosov. Let
$\lbrace n\rbrace $
-Anosov. Let
![]() $(x,y,z)$
be a positively oriented triple in
$(x,y,z)$
be a positively oriented triple in
![]() $\partial \pi _1(S_g)$
. Up to changing the symplectic basis, we can assume that for some
$\partial \pi _1(S_g)$
. Up to changing the symplectic basis, we can assume that for some
![]() $(\epsilon _i)\in \lbrace -1,1\rbrace $
:
$(\epsilon _i)\in \lbrace -1,1\rbrace $
:
Here the Maslov index of the triple
![]() $(\xi ^n_\rho (x),\xi ^n_\rho (y),\xi ^n_\rho (z))$
is equal to the sum of the
$(\xi ^n_\rho (x),\xi ^n_\rho (y),\xi ^n_\rho (z))$
is equal to the sum of the
![]() $(\epsilon _i)$
.
$(\epsilon _i)$
.
Consider the following curve:
 $$ \begin{align*}\tau_0:\theta\mapsto \langle \cos\left(\frac{\theta}{2}\right)x_1+\epsilon_1\sin\left(\frac{\theta}{2}\right)y_1,\cdots, \cos\left(\frac{\theta}{2}\right)x_n+ \epsilon_n\sin\left(\frac{\theta}{2}\right)y_n\rangle.\end{align*} $$
$$ \begin{align*}\tau_0:\theta\mapsto \langle \cos\left(\frac{\theta}{2}\right)x_1+\epsilon_1\sin\left(\frac{\theta}{2}\right)y_1,\cdots, \cos\left(\frac{\theta}{2}\right)x_n+ \epsilon_n\sin\left(\frac{\theta}{2}\right)y_n\rangle.\end{align*} $$
This loop is homotopic to the concatenation of the loops
![]() $\tau _i$
for
$\tau _i$
for
![]() $1\leq i\leq n$
:
$1\leq i\leq n$
:
 $$ \begin{align*}\tau_i:\theta\mapsto \langle x_1, x_2,\cdots , \cos\left(\frac{\theta}{2}\right)x_i+ \epsilon_i\sin\left(\frac{\theta}{2}\right)y_i, \cdots , x_n\rangle.\end{align*} $$
$$ \begin{align*}\tau_i:\theta\mapsto \langle x_1, x_2,\cdots , \cos\left(\frac{\theta}{2}\right)x_i+ \epsilon_i\sin\left(\frac{\theta}{2}\right)y_i, \cdots , x_n\rangle.\end{align*} $$
These loops are homotopic to
![]() $\tau $
or its inverse depending on the sign of
$\tau $
or its inverse depending on the sign of
![]() $\epsilon _i$
. The homotopy type of
$\epsilon _i$
. The homotopy type of
![]() $\tau _0$
is hence equal to
$\tau _0$
is hence equal to
![]() $(\epsilon _1+\epsilon _2+\cdots +\epsilon _n)[\tau ]$
. Moreover the set of Lagrangians transverse to a given Lagrangian is contractible, so one can homotope
$(\epsilon _1+\epsilon _2+\cdots +\epsilon _n)[\tau ]$
. Moreover the set of Lagrangians transverse to a given Lagrangian is contractible, so one can homotope
![]() $\tau _0$
on the intervals
$\tau _0$
on the intervals
![]() $[0,\frac {\pi }{2}]$
,
$[0,\frac {\pi }{2}]$
,
![]() $[\frac {\pi }{2}, \pi ]$
and
$[\frac {\pi }{2}, \pi ]$
and
![]() $[\pi ,2\pi ]$
to coincide with
$[\pi ,2\pi ]$
to coincide with
![]() $\xi ^n_\rho $
. Hence the free homotopy class of
$\xi ^n_\rho $
. Hence the free homotopy class of
![]() $\xi ^n_\rho $
is equal to the one of
$\xi ^n_\rho $
is equal to the one of
![]() $\tau _0$
, which is equal to
$\tau _0$
, which is equal to
![]() $M(\xi ^n_\rho (x),\xi ^n_\rho (y),\xi ^n_\rho (z))[\tau ]$
. We therefore deduce that
$M(\xi ^n_\rho (x),\xi ^n_\rho (y),\xi ^n_\rho (z))[\tau ]$
. We therefore deduce that
![]() $\rho $
is maximal if and only if it is
$\rho $
is maximal if and only if it is
![]() $\lbrace n\rbrace $
-Anosov and
$\lbrace n\rbrace $
-Anosov and
![]() $[\xi ^n_\rho ]=n[\tau ]$
.
$[\xi ^n_\rho ]=n[\tau ]$
.
3 An invariant convex domain and its fibrations
In this section we define globally fitting maps and fitting immersions, which are maps that parametrize fibrations of the projective model for the symmetric space of
![]() $\operatorname {\mathrm {SL}}(2n,\mathbb {R})$
by projective subspaces of codimension d.
$\operatorname {\mathrm {SL}}(2n,\mathbb {R})$
by projective subspaces of codimension d.
3.1 Pencils of quadrics
Let V be a finite even-dimensional vector space with a fixed volume form. Let
![]() $S^2V$
be the space of symmetric bilinear tensors on V, which we interpret as maps
$S^2V$
be the space of symmetric bilinear tensors on V, which we interpret as maps
![]() $V^*\to V$
. The dual space
$V^*\to V$
. The dual space
![]() $\mathcal {Q}=S^2V^*$
is the space of symmetric bilinear forms on V, or the space of quadrics on V, that we interpret as maps
$\mathcal {Q}=S^2V^*$
is the space of symmetric bilinear forms on V, or the space of quadrics on V, that we interpret as maps
![]() $V\to V^*$
.
$V\to V^*$
.
We denote by
![]() $S^2V^{\geq 0}$
and
$S^2V^{\geq 0}$
and
![]() $S^2V^{>0}$
respectively the space of semi-positive and positive symmetric tensors, that is, elements
$S^2V^{>0}$
respectively the space of semi-positive and positive symmetric tensors, that is, elements
![]() $s\in S^2V$
that define respectively a semi-positive and positive symmetric bilinear form on
$s\in S^2V$
that define respectively a semi-positive and positive symmetric bilinear form on
![]() $V^*$
. The Lie group
$V^*$
. The Lie group
![]() $\operatorname {\mathrm {SL}}(V)$
acts on
$\operatorname {\mathrm {SL}}(V)$
acts on
![]() $S^2V$
, and preserves the properly convex set
$S^2V$
, and preserves the properly convex set
![]() $\mathbb {P}(S^2V^{\geq 0})$
. The convex domain
$\mathbb {P}(S^2V^{\geq 0})$
. The convex domain
![]() $\mathbb {P}(S^2V^{>0})$
is a projective model for the symmetric space associated to
$\mathbb {P}(S^2V^{>0})$
is a projective model for the symmetric space associated to
![]() $\operatorname {\mathrm {SL}}(V)$
.
$\operatorname {\mathrm {SL}}(V)$
.
The Grassmannian of d-dimensional linear subspaces of
![]() $\mathcal {Q}$
will be denoted by
$\mathcal {Q}$
will be denoted by
![]() $\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
. An element of
$\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
. An element of
![]() $\operatorname {\mathrm {Gr}}_2(\mathcal {Q})$
is usually called a pencil of quadrics on V. We will here also call elements of
$\operatorname {\mathrm {Gr}}_2(\mathcal {Q})$
is usually called a pencil of quadrics on V. We will here also call elements of
![]() $\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
pencils of quadrics.
$\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
pencils of quadrics.
To an element
![]() $P\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
one can associate its annihilator, or dual, codimension d subspace
$P\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
one can associate its annihilator, or dual, codimension d subspace
![]() $P^\circ \subset S^2V$
. This dual space can be described as the space of symmetric tensors
$P^\circ \subset S^2V$
. This dual space can be described as the space of symmetric tensors
![]() $s\in S^2V$
on which one has
$s\in S^2V$
on which one has
![]() $q(s)=\operatorname {\mathrm {Tr}}(q\circ s)=0$
for all
$q(s)=\operatorname {\mathrm {Tr}}(q\circ s)=0$
for all
![]() $q\in P$
. Note that the projectivization
$q\in P$
. Note that the projectivization
![]() $\mathbb {P}(P^\circ )$
also has codimension d in
$\mathbb {P}(P^\circ )$
also has codimension d in
![]() $\mathbb {P}(S^2V)$
.
$\mathbb {P}(S^2V)$
.
The subspace
![]() $\mathbb {P}(P^\circ )$
does not necessarily intersect the convex
$\mathbb {P}(P^\circ )$
does not necessarily intersect the convex
![]() $\mathbb {P}(S^2V^{>0})$
.
$\mathbb {P}(S^2V^{>0})$
.
Definition 3.1. We say that a pencil
![]() $P\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
is mixed if
$P\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
is mixed if
![]() $P^\circ $
contains a positive element, that is, if
$P^\circ $
contains a positive element, that is, if
![]() $P^\circ \cap S^2V^{>0}\neq \lbrace 0\rbrace $
. We call the set of mixed pencils
$P^\circ \cap S^2V^{>0}\neq \lbrace 0\rbrace $
. We call the set of mixed pencils
![]() $\operatorname {\mathrm {Gr}}_d^{{\operatorname {\mathrm {mix}}}}(\mathcal {Q})$
.
$\operatorname {\mathrm {Gr}}_d^{{\operatorname {\mathrm {mix}}}}(\mathcal {Q})$
.
Proposition 3.2. A pencil
![]() $P\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
is mixed if and only if there is no semi-positive quadric
$P\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
is mixed if and only if there is no semi-positive quadric
![]() $0\neq q\in P$
.
$0\neq q\in P$
.
Morally this proposition is a consequence of the fact that the dual of the cone of positive elements
![]() $S^2V^{>0}$
is the cone of semi-positive bilinear forms in
$S^2V^{>0}$
is the cone of semi-positive bilinear forms in
![]() $\mathcal {Q}$
, in the sense that
$\mathcal {Q}$
, in the sense that
![]() $S^2V^{>0}$
is the set of tensors s such that
$S^2V^{>0}$
is the set of tensors s such that
![]() $q(s)>0$
for all semi-positive
$q(s)>0$
for all semi-positive
![]() $q\in \mathcal {Q}$
.
$q\in \mathcal {Q}$
.
Proof. Fix
![]() $P\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
and suppose that there is a positive element
$P\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
and suppose that there is a positive element
![]() $s\in E^\circ $
. We write s as a finite sum of positive rank one elements of the form
$s\in E^\circ $
. We write s as a finite sum of positive rank one elements of the form
![]() $v_i\otimes v_i$
with
$v_i\otimes v_i$
with
![]() $v_i\in V$
nonzero for
$v_i\in V$
nonzero for
![]() $i\in I$
in a finite set. Indeed s defines a positive bilinear form on
$i\in I$
in a finite set. Indeed s defines a positive bilinear form on
![]() $V^*$
and hence is a sum of rank one symmetric positive bilinear forms. Let
$V^*$
and hence is a sum of rank one symmetric positive bilinear forms. Let
![]() $q\in P$
be a semi-positive element. One has
$q\in P$
be a semi-positive element. One has
![]() $q(s)=0$
since
$q(s)=0$
since
![]() $s\in P^\circ $
but
$s\in P^\circ $
but
![]() $q(v_i\otimes v_i)=q(v_i,v_i)\geq 0$
since q is positive and hence for all
$q(v_i\otimes v_i)=q(v_i,v_i)\geq 0$
since q is positive and hence for all
![]() $i\in I$
,
$i\in I$
,
![]() $q(v_i,v_i)=0$
.
$q(v_i,v_i)=0$
.
Note that for all
![]() $v\in V$
nonzero we can choose a decomposition of s such that v is one of the
$v\in V$
nonzero we can choose a decomposition of s such that v is one of the
![]() $v_i$
, since
$v_i$
, since
![]() $s-\epsilon v\otimes v$
is still positive for
$s-\epsilon v\otimes v$
is still positive for
![]() $\epsilon $
small enough.
$\epsilon $
small enough.
We proved that
![]() $q(v,v)=0$
for all
$q(v,v)=0$
for all
![]() $v\in V$
so q is necessarily equal to
$v\in V$
so q is necessarily equal to
![]() $0$
. Hence P does not contain any nonzero semi-positive element.
$0$
. Hence P does not contain any nonzero semi-positive element.
Now suppose that
![]() $P^\circ $
is disjoint from the cone
$P^\circ $
is disjoint from the cone
![]() $S^2V^{>0}$
, so there must be a hyperplane H in
$S^2V^{>0}$
, so there must be a hyperplane H in
![]() $S^2V$
containing
$S^2V$
containing
![]() $P^\circ $
and disjoint from
$P^\circ $
and disjoint from
![]() $S^2V^{>0}$
. This hyperplane corresponds to
$S^2V^{>0}$
. This hyperplane corresponds to
![]() $\langle q\rangle ^\circ $
for some nonzero
$\langle q\rangle ^\circ $
for some nonzero
![]() $q\in P$
. This element has the property that
$q\in P$
. This element has the property that
![]() $q(s)\neq 0$
for all
$q(s)\neq 0$
for all
![]() $s\in S^2V^{>0}$
. Up to exchanging q by
$s\in S^2V^{>0}$
. Up to exchanging q by
![]() $-q$
one can assume that
$-q$
one can assume that
![]() $q(s)>0$
on
$q(s)>0$
on
![]() $S^2V^{>0}$
, so
$S^2V^{>0}$
, so
![]() $q(s)\geq 0$
on
$q(s)\geq 0$
on
![]() $S^2V^{\geq 0}$
. In particular for all
$S^2V^{\geq 0}$
. In particular for all
![]() $v\in V$
, one has
$v\in V$
, one has
![]() $q(v\otimes v)=q(v,v)\geq 0$
, so q is semi-positive.
$q(v\otimes v)=q(v,v)\geq 0$
, so q is semi-positive.
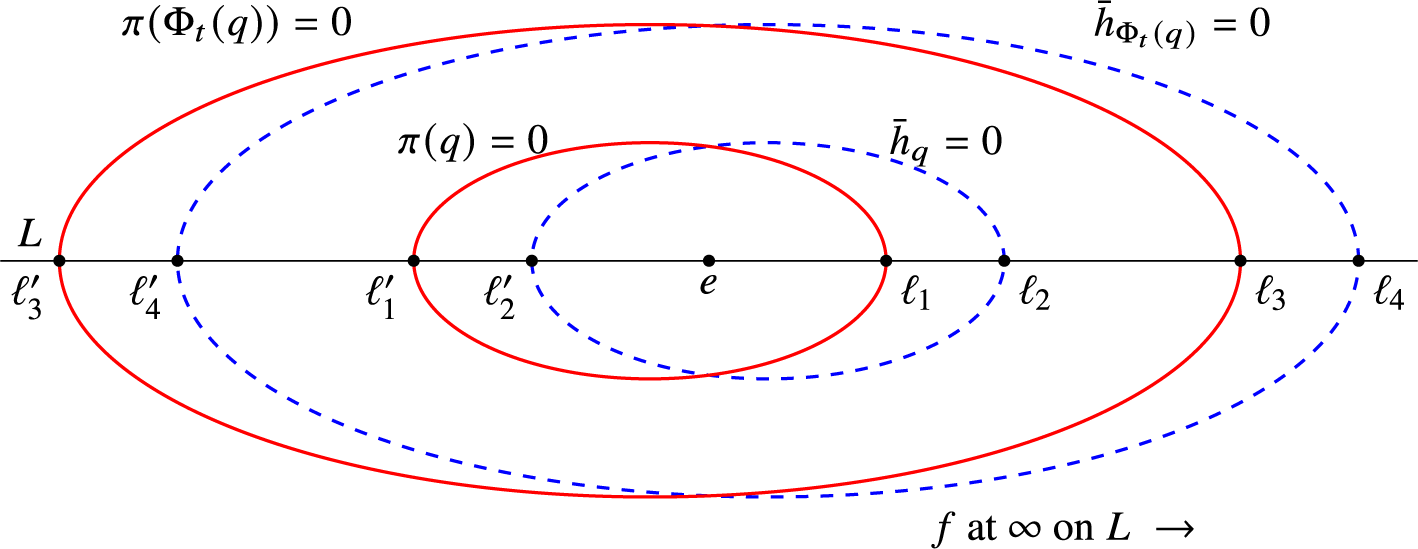
3.2 Fitting pairs
To a pencil
![]() $P\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
we associate the codimension d projective subspace
$P\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
we associate the codimension d projective subspace
![]() $\mathbb {P}(P^\circ )$
, and its intersection
$\mathbb {P}(P^\circ )$
, and its intersection
![]() $\mathbb {P}(P^\circ \cap S^2V^{\geq 0})$
in the convex set
$\mathbb {P}(P^\circ \cap S^2V^{\geq 0})$
in the convex set
![]() $\mathbb {P}(S^2V^{\geq 0})$
.
$\mathbb {P}(S^2V^{\geq 0})$
.
Definition 3.3. We say that two elements
![]() $P_1, P_2\in \operatorname {\mathrm {Gr}}^{\text {mix}}_d(\mathcal {Q})$
form a fitting pair if the associated subspaces
$P_1, P_2\in \operatorname {\mathrm {Gr}}^{\text {mix}}_d(\mathcal {Q})$
form a fitting pair if the associated subspaces
![]() $\mathbb {P}(P_1^\circ \cap S^2V^{\geq 0})$
and
$\mathbb {P}(P_1^\circ \cap S^2V^{\geq 0})$
and
![]() $\mathbb {P}(P_2^\circ \cap S^2V^{\geq 0})$
are disjoint.
$\mathbb {P}(P_2^\circ \cap S^2V^{\geq 0})$
are disjoint.
The structure of the convex set
![]() $\mathbb {P}(S^2V^{\geq 0})$
is involved, but the set of its extreme points
$\mathbb {P}(S^2V^{\geq 0})$
is involved, but the set of its extreme points
![]() $S^2\mathbb {P}(V)\subset \mathbb {P}(S^2V^{\geq 0})$
is the projectivization of the set of rank one tensors, which is in one-to-one correspondence with
$S^2\mathbb {P}(V)\subset \mathbb {P}(S^2V^{\geq 0})$
is the projectivization of the set of rank one tensors, which is in one-to-one correspondence with
![]() $\mathbb {P}(V)$
. Here the rank of a symmetric tensor is also the rank of the corresponding map
$\mathbb {P}(V)$
. Here the rank of a symmetric tensor is also the rank of the corresponding map
![]() $V^*\to V$
. The extreme points of a closed properly convex subset C of projective space are the points
$V^*\to V$
. The extreme points of a closed properly convex subset C of projective space are the points
![]() $x\in C$
such that if
$x\in C$
such that if
![]() $s\subset C$
is a projective segment containing it, x is an endpoint of s. We show that the condition of being a fitting pair can be checked by looking only at
$s\subset C$
is a projective segment containing it, x is an endpoint of s. We show that the condition of being a fitting pair can be checked by looking only at
![]() $\mathbb {P}(V)$
.
$\mathbb {P}(V)$
.
Given a symmetric bilinear form
![]() $q\in \mathcal {Q}$
, we will write respectively
$q\in \mathcal {Q}$
, we will write respectively
![]() $\lbrace q=0\rbrace $
,
$\lbrace q=0\rbrace $
,
![]() $\lbrace q>0\rbrace $
and
$\lbrace q>0\rbrace $
and
![]() $\lbrace q\geq 0\rbrace \subset \mathbb {P}(V)$
the set of lines that are respectively null, positive and non-negative for q.
$\lbrace q\geq 0\rbrace \subset \mathbb {P}(V)$
the set of lines that are respectively null, positive and non-negative for q.
Proposition 3.4. Let
![]() $P_1,P_2\in \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_d(\mathcal {Q})$
be two mixed pencils.
$P_1,P_2\in \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_d(\mathcal {Q})$
be two mixed pencils.
-
(i)
 $(P_1,P_2)$
form a fitting pair,
$(P_1,P_2)$
form a fitting pair, -
(ii) there exist
 $q_1\in P_1$
and
$q_1\in P_1$
and
 $q_2\in P_2$
such that
$q_2\in P_2$
such that
 $q_2-q_1$
is positive,
$q_2-q_1$
is positive, -
(iii) there exist
 $q_1\in P_1$
and
$q_1\in P_1$
and
 $q_2\in P_2$
such that
$q_2\in P_2$
such that
 $\lbrace q_1\geq 0\rbrace \subset \lbrace q_2> 0\rbrace $
.
$\lbrace q_1\geq 0\rbrace \subset \lbrace q_2> 0\rbrace $
.
In order to prove this statement, the key fact that we will prove and use is that the convex set
![]() $\mathbb {P}(S^2V^{\geq 0})$
does not have any segment as a face, that is, the intersection of this convex with any hyperplane intersecting trivially the interior
$\mathbb {P}(S^2V^{\geq 0})$
does not have any segment as a face, that is, the intersection of this convex with any hyperplane intersecting trivially the interior
![]() $\mathbb {P}(S^2V^{> 0})$
is never a nontrivial segment.
$\mathbb {P}(S^2V^{> 0})$
is never a nontrivial segment.
The set
![]() $\lbrace q=0\rbrace $
is identified via the identification
$\lbrace q=0\rbrace $
is identified via the identification
![]() $\mathbb {P}(V)\simeq S^2\mathbb {P}(V)\subset \mathbb {P}(S^2V)$
with the intersection
$\mathbb {P}(V)\simeq S^2\mathbb {P}(V)\subset \mathbb {P}(S^2V)$
with the intersection
![]() $\langle q\rangle ^\circ \cap S^2\mathbb {P}(V)$
.
$\langle q\rangle ^\circ \cap S^2\mathbb {P}(V)$
.
Lemma 3.5. For all linear hyperplane H in
![]() $S^2V$
the extreme points of
$S^2V$
the extreme points of
![]() $\mathbb {P}(H\cap S^2V^{\geq 0})$
are also extreme points of
$\mathbb {P}(H\cap S^2V^{\geq 0})$
are also extreme points of
![]() $\mathbb {P}(S^2V^{\geq 0})$
. In particular:
$\mathbb {P}(S^2V^{\geq 0})$
. In particular:
Furthermore if
![]() $H=\langle q\rangle ^\circ $
for
$H=\langle q\rangle ^\circ $
for
![]() $q\in \mathcal {Q}$
,
$q\in \mathcal {Q}$
,
![]() $H\cap S^2V=S^2\lbrace q=0\rbrace $
.
$H\cap S^2V=S^2\lbrace q=0\rbrace $
.
Recall that the Krein–Milman theorem states that the convex Hull of the extreme points of a closed convex set C in a finite dimensional vector space is equal to C.
Proof. Let f be a face of
![]() $\mathbb {P}(S^2V^{\geq 0})$
, that is, the intersection of
$\mathbb {P}(S^2V^{\geq 0})$
, that is, the intersection of
![]() $\mathbb {P}(S^2V^{\geq 0})$
with a projective hyperplane corresponding to
$\mathbb {P}(S^2V^{\geq 0})$
with a projective hyperplane corresponding to
![]() $[q]\in \mathbb {P}(S^2V^*)=\mathbb {P}(\mathcal {Q})$
not intersecting
$[q]\in \mathbb {P}(S^2V^*)=\mathbb {P}(\mathcal {Q})$
not intersecting
![]() $\mathbb {P}(S^2V^{>0})$
trivially. It is the intersection of this convex with a projective hyperplane corresponding to
$\mathbb {P}(S^2V^{>0})$
trivially. It is the intersection of this convex with a projective hyperplane corresponding to
![]() $[q]\in \mathbb {P}(S^2V^*)=\mathbb {P}(\mathcal {Q})$
. The fact that this hyperplane intersects
$[q]\in \mathbb {P}(S^2V^*)=\mathbb {P}(\mathcal {Q})$
. The fact that this hyperplane intersects
![]() $\mathbb {P}(S^2V^{>0})$
trivially implies that there is a lift
$\mathbb {P}(S^2V^{>0})$
trivially implies that there is a lift
![]() $q\in \mathcal {Q}$
that is a semi-positive element, by Proposition 3.2. Let
$q\in \mathcal {Q}$
that is a semi-positive element, by Proposition 3.2. Let
![]() $W\subset V$
be the vector subspace of isotropic vectors for q. The corresponding face is equal to
$W\subset V$
be the vector subspace of isotropic vectors for q. The corresponding face is equal to
![]() $\mathbb {P}(S^2W^{\geq 0})$
.
$\mathbb {P}(S^2W^{\geq 0})$
.
Hence faces of
![]() $\mathbb {P}(S^2V^{\geq 0})$
are of the form
$\mathbb {P}(S^2V^{\geq 0})$
are of the form
![]() $\mathbb {P}(S^2W^{\geq 0})$
for
$\mathbb {P}(S^2W^{\geq 0})$
for
![]() $W\subset V$
a linear subspace. This has dimension
$W\subset V$
a linear subspace. This has dimension
![]() $0$
or at least
$0$
or at least
![]() $2$
, and therefore no face is a segment.
$2$
, and therefore no face is a segment.
Suppose that for some general projective hyperplane, some extreme point
![]() $[s]$
of
$[s]$
of
![]() $\mathbb {P}(H\cap S^2V^{\geq 0})$
is not an extreme point of
$\mathbb {P}(H\cap S^2V^{\geq 0})$
is not an extreme point of
![]() $\mathbb {P}(S^2V^{\geq 0})$
, then it belongs to the interior of a face of
$\mathbb {P}(S^2V^{\geq 0})$
, then it belongs to the interior of a face of
![]() $\mathbb {P}(S^2V^{\geq 0})$
, that has dimension at least
$\mathbb {P}(S^2V^{\geq 0})$
, that has dimension at least
![]() $2$
as stated previously. The intersection of this face with H contains therefore an open segment containing s, so s is not an extreme point of
$2$
as stated previously. The intersection of this face with H contains therefore an open segment containing s, so s is not an extreme point of
![]() $H\cap \mathbb {P}(S^2V^{\geq 0})$
.
$H\cap \mathbb {P}(S^2V^{\geq 0})$
.
Proof of Proposition 3.4
Let us prove that
![]() $(i)$
implies
$(i)$
implies
![]() $(ii)$
. The set
$(ii)$
. The set
![]() $P_1^\circ \cap P_2^\circ $
is disjoint from
$P_1^\circ \cap P_2^\circ $
is disjoint from
![]() $\mathbb {P}(S^2V^{\geq 0})$
if and only if there exists an element in
$\mathbb {P}(S^2V^{\geq 0})$
if and only if there exists an element in
![]() $P_1+P_2$
that belongs to the dual of
$P_1+P_2$
that belongs to the dual of
![]() $\mathbb {P}(S^2V^{\geq 0})$
, that is, if there exists a positive bilinear form
$\mathbb {P}(S^2V^{\geq 0})$
, that is, if there exists a positive bilinear form
![]() $q\in P_1+P_2$
. This form can be written as
$q\in P_1+P_2$
. This form can be written as
![]() $q=q_1-q_2$
with
$q=q_1-q_2$
with
![]() $q_1\in P_1$
and
$q_1\in P_1$
and
![]() $q_2\in P_2$
, therefore
$q_2\in P_2$
, therefore
![]() $(i)$
implies
$(i)$
implies
![]() $(ii)$
.
$(ii)$
.
Moreover
![]() $(ii)$
implies
$(ii)$
implies
![]() $(iii)$
. Indeed, if
$(iii)$
. Indeed, if
![]() $q_2-q_1$
is positive then
$q_2-q_1$
is positive then
![]() $\lbrace q_1\geq 0\rbrace \subset \lbrace q_2> 0\rbrace $
.
$\lbrace q_1\geq 0\rbrace \subset \lbrace q_2> 0\rbrace $
.
It only remains to show that
![]() $(iii)$
implies
$(iii)$
implies
![]() $(i)$
. Lemma 3.5 implies that:
$(i)$
. Lemma 3.5 implies that:
Hence
![]() $q_2\in P_2\subset \mathcal {Q}=S^2V^*$
is positive on the cone
$q_2\in P_2\subset \mathcal {Q}=S^2V^*$
is positive on the cone
![]() $\langle q_1\rangle ^\circ \cap S^2V^{\geq 0}\subset S^2V$
and therefore
$\langle q_1\rangle ^\circ \cap S^2V^{\geq 0}\subset S^2V$
and therefore
![]() $\mathbb {P}(P_2^\circ )$
does not intersect
$\mathbb {P}(P_2^\circ )$
does not intersect
![]() $\mathbb {P}(\langle q_1\rangle ^\circ \cap S^2V^{\geq 0})$
.
$\mathbb {P}(\langle q_1\rangle ^\circ \cap S^2V^{\geq 0})$
.
3.3 Fitting directions
The space
![]() $\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
inherits the structure of a smooth manifold. A chart around a point
$\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
inherits the structure of a smooth manifold. A chart around a point
![]() $P\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
can be constructed given a subspace Q such that
$P\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
can be constructed given a subspace Q such that
![]() $P\oplus Q=\mathcal {Q}$
. We denote by
$P\oplus Q=\mathcal {Q}$
. We denote by
![]() $U_Q\subset \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
the open set of elements transverse to Q. Every element of
$U_Q\subset \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
the open set of elements transverse to Q. Every element of
![]() $U_Q$
can be written uniquely as the graph
$U_Q$
can be written uniquely as the graph
![]() $\lbrace x+u(x)|x\in P\rbrace $
for some linear map
$\lbrace x+u(x)|x\in P\rbrace $
for some linear map
![]() $u:P\to Q$
. Hence
$u:P\to Q$
. Hence
![]() $U_Q$
can be identified with the vector space
$U_Q$
can be identified with the vector space
![]() $\operatorname {\mathrm {Hom}}(P,Q)$
.
$\operatorname {\mathrm {Hom}}(P,Q)$
.
The tangent space
![]() $T_P\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
can be naturally identified with
$T_P\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
can be naturally identified with
![]() $\operatorname {\mathrm {Hom}}(P,\mathcal {Q}/P)$
, so that for each chart
$\operatorname {\mathrm {Hom}}(P,\mathcal {Q}/P)$
, so that for each chart
![]() $U_Q$
containing P, the tangent space identifies with the tangent space in the chart via the identification
$U_Q$
containing P, the tangent space identifies with the tangent space in the chart via the identification
![]() $\operatorname {\mathrm {Hom}}(P,Q)\simeq \operatorname {\mathrm {Hom}}(P,\mathcal {Q}/P)$
.
$\operatorname {\mathrm {Hom}}(P,Q)\simeq \operatorname {\mathrm {Hom}}(P,\mathcal {Q}/P)$
.
Because of the identification
![]() $T_{P}\operatorname {\mathrm {Gr}}_d(\mathcal {Q})\simeq T_{P^\circ }\operatorname {\mathrm {Gr}}_{N-d}(\mathcal {Q}^*)$
where
$T_{P}\operatorname {\mathrm {Gr}}_d(\mathcal {Q})\simeq T_{P^\circ }\operatorname {\mathrm {Gr}}_{N-d}(\mathcal {Q}^*)$
where
![]() $N=\dim (\mathcal {Q})$
, to such an element
$N=\dim (\mathcal {Q})$
, to such an element
![]() $\mathrm {v}$
corresponds an element:
$\mathrm {v}$
corresponds an element:
Let
![]() $\mathrm {v}^\circ \in T_P\operatorname {\mathrm {Gr}}_d(\mathcal {Q}^*)$
, that we see as an element of
$\mathrm {v}^\circ \in T_P\operatorname {\mathrm {Gr}}_d(\mathcal {Q}^*)$
, that we see as an element of
![]() $\operatorname {\mathrm {Hom}}(P^\circ ,\mathcal {Q}/P^\circ )$
. Let
$\operatorname {\mathrm {Hom}}(P^\circ ,\mathcal {Q}/P^\circ )$
. Let
![]() $(P^\circ _t)_{t\geq 0}$
be a curve of elements of
$(P^\circ _t)_{t\geq 0}$
be a curve of elements of
![]() $\operatorname {\mathrm {Gr}}_{N-d}(\mathcal {Q}^*)$
with
$\operatorname {\mathrm {Gr}}_{N-d}(\mathcal {Q}^*)$
with
![]() $P^\circ _0=P^\circ $
and derivative
$P^\circ _0=P^\circ $
and derivative
![]() $\mathrm {v}^\circ $
at
$\mathrm {v}^\circ $
at
![]() $t=0$
. One can interpret
$t=0$
. One can interpret
![]() $\operatorname {\mathrm {Ker}}(\mathrm {v}^\circ )$
as the set of vectors in
$\operatorname {\mathrm {Ker}}(\mathrm {v}^\circ )$
as the set of vectors in
![]() $P^\circ $
which remain in
$P^\circ $
which remain in
![]() $P^\circ _t$
at first order around
$P^\circ _t$
at first order around
![]() $t=0$
. More precisely the lines
$t=0$
. More precisely the lines
![]() $[s]$
in
$[s]$
in
![]() $\operatorname {\mathrm {Ker}}(\mathrm {v}^\circ )$
are exactly the ones such that for any Riemannian metric on
$\operatorname {\mathrm {Ker}}(\mathrm {v}^\circ )$
are exactly the ones such that for any Riemannian metric on
![]() $\mathbb {P}(V)$
and any such curve
$\mathbb {P}(V)$
and any such curve
![]() $(P^\circ _t)_{t>0}$
one has
$(P^\circ _t)_{t>0}$
one has
![]() $d(\mathbb {P} (P^\circ _t ),[s])=o(t)$
close to
$d(\mathbb {P} (P^\circ _t ),[s])=o(t)$
close to
![]() $t=0$
.
$t=0$
.
We will call fitting directions in the Grassmannian
![]() $\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
the tangent directions such that if
$\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
the tangent directions such that if
![]() $(P_t)\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
moves in this direction, the corresponding codimension d subspaces
$(P_t)\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
moves in this direction, the corresponding codimension d subspaces
![]() $\mathbb {P}\left (P_t^\circ \cap S^2V^{\geq 0}\right )$
are disjoint from
$\mathbb {P}\left (P_t^\circ \cap S^2V^{\geq 0}\right )$
are disjoint from
![]() $\mathbb {P}\left (P_0^\circ \cap S^2V^{\geq 0}\right )$
, at order one, see Proposition 3.7.
$\mathbb {P}\left (P_0^\circ \cap S^2V^{\geq 0}\right )$
, at order one, see Proposition 3.7.
Definition/Proposition 3.6. We say that a vector
![]() $\mathrm {v}\in T_P\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
is fitting if one of the following equivalent statements holds:
$\mathrm {v}\in T_P\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
is fitting if one of the following equivalent statements holds:
-
•
 $\operatorname {\mathrm {Ker}}(\mathrm {v}^\circ )\subset P^\circ $
intersects trivially
$\operatorname {\mathrm {Ker}}(\mathrm {v}^\circ )\subset P^\circ $
intersects trivially
 $S^2V^{\geq 0}$
,
$S^2V^{\geq 0}$
, -
•
 $\operatorname {\mathrm {Im}}(\mathrm {v})\subset \mathcal {Q}/P$
contains
$\operatorname {\mathrm {Im}}(\mathrm {v})\subset \mathcal {Q}/P$
contains
 $[q]$
where q is a positive element.
$[q]$
where q is a positive element.
We now check that these two statements in the definition are indeed equivalent.
Proof. We first show that
![]() $\operatorname {\mathrm {Ker}}(\mathrm {v}^\circ )=\operatorname {\mathrm {Im}}(\mathrm {v})^\circ $
, where we use the natural identification
$\operatorname {\mathrm {Ker}}(\mathrm {v}^\circ )=\operatorname {\mathrm {Im}}(\mathrm {v})^\circ $
, where we use the natural identification
![]() $(\mathcal {Q}/P)^*\simeq P^\circ $
.
$(\mathcal {Q}/P)^*\simeq P^\circ $
.
We prove this by writing an equation that relates
![]() $\mathrm {v}$
and
$\mathrm {v}$
and
![]() $\mathrm {v}^\circ $
. By definition,
$\mathrm {v}^\circ $
. By definition,
![]() $\operatorname {\mathrm {Tr}}(qs)=0$
for
$\operatorname {\mathrm {Tr}}(qs)=0$
for
![]() $q\in P$
and
$q\in P$
and
![]() $s\in P^\circ $
. Let us fix
$s\in P^\circ $
. Let us fix
![]() $q\in P$
and
$q\in P$
and
![]() $s\in P^\circ $
and choose some representatives
$s\in P^\circ $
and choose some representatives
![]() $\overline {\mathrm {v}(s)}\in S^2V$
and
$\overline {\mathrm {v}(s)}\in S^2V$
and
![]() $\overline {\mathrm {v}^\circ (q)}\in \mathcal {Q}$
for
$\overline {\mathrm {v}^\circ (q)}\in \mathcal {Q}$
for
![]() $\mathrm {v}(s)\in S^2V/P^\circ $
and
$\mathrm {v}(s)\in S^2V/P^\circ $
and
![]() $\mathrm {v}^\circ (q)\in \mathcal {Q}/P$
. If
$\mathrm {v}^\circ (q)\in \mathcal {Q}/P$
. If
![]() $(P_t)$
is a smooth curve with
$(P_t)$
is a smooth curve with
![]() $P_0=P$
and with derivative
$P_0=P$
and with derivative
![]() $\mathrm {v}$
at
$\mathrm {v}$
at
![]() $t=0$
,
$t=0$
,
![]() $s+t\overline {\mathrm {v}^\circ (p)}+o(t)\in P_t$
and
$s+t\overline {\mathrm {v}^\circ (p)}+o(t)\in P_t$
and
![]() $q+t\overline {\mathrm {v}(q)}+o(t)\in P^\circ _t$
. Hence we get:
$q+t\overline {\mathrm {v}(q)}+o(t)\in P^\circ _t$
. Hence we get:
An element
![]() $s\in P^\circ $
satisfies
$s\in P^\circ $
satisfies
![]() $s\in \operatorname {\mathrm {Ker}}(\mathrm {v}^\circ )$
if and only if
$s\in \operatorname {\mathrm {Ker}}(\mathrm {v}^\circ )$
if and only if
![]() $\operatorname {\mathrm {Tr}}(\overline {\mathrm {v}(q)}s)=0$
for all
$\operatorname {\mathrm {Tr}}(\overline {\mathrm {v}(q)}s)=0$
for all
![]() $q\in \mathcal {Q}$
, hence if and only if the corresponding linear form on
$q\in \mathcal {Q}$
, hence if and only if the corresponding linear form on
![]() $Q/P$
belongs to
$Q/P$
belongs to
![]() $\operatorname {\mathrm {Im}}(\mathrm {v})^\circ $
.
$\operatorname {\mathrm {Im}}(\mathrm {v})^\circ $
.
Now we prove the equivalence of the two definitions. If there exists
![]() $[q]\in \operatorname {\mathrm {Im}}(\mathrm {v})$
with q positive, then for any
$[q]\in \operatorname {\mathrm {Im}}(\mathrm {v})$
with q positive, then for any
![]() $s\in \operatorname {\mathrm {Ker}}(\mathrm {v}^\circ )$
,
$s\in \operatorname {\mathrm {Ker}}(\mathrm {v}^\circ )$
,
![]() $\operatorname {\mathrm {Tr}}(q\circ s)=0$
. Hence s is not a positive tensor. Therefore
$\operatorname {\mathrm {Tr}}(q\circ s)=0$
. Hence s is not a positive tensor. Therefore
![]() $\operatorname {\mathrm {Ker}}(\mathrm {v}^\circ )\subset P^\circ $
intersects trivially
$\operatorname {\mathrm {Ker}}(\mathrm {v}^\circ )\subset P^\circ $
intersects trivially
![]() $S^2V^{\geq 0}$
.
$S^2V^{\geq 0}$
.
Conversely if
![]() $\operatorname {\mathrm {Ker}}(\mathrm {v}^\circ )$
intersects trivially
$\operatorname {\mathrm {Ker}}(\mathrm {v}^\circ )$
intersects trivially
![]() $S^2V^{\geq 0}$
, there exists
$S^2V^{\geq 0}$
, there exists
![]() $q\in \mathcal {Q}$
that do not vanish on
$q\in \mathcal {Q}$
that do not vanish on
![]() $S^2V^{\geq 0}$
, that is, q is positive. The class
$S^2V^{\geq 0}$
, that is, q is positive. The class
![]() $[q]\in \mathcal {Q}/P$
belongs to
$[q]\in \mathcal {Q}/P$
belongs to
![]() $\operatorname {\mathrm {Im}}(\mathrm {v})$
.
$\operatorname {\mathrm {Im}}(\mathrm {v})$
.
Fitting directions are related to fitting pairs. More precisely:
Proposition 3.7. A vector
![]() $\mathrm {v}\in T_P\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
is fitting if and only if, for every
$\mathrm {v}\in T_P\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
is fitting if and only if, for every
![]() $\mathcal {C}^1$
curve
$\mathcal {C}^1$
curve
![]() $\gamma :[0,1]\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
with
$\gamma :[0,1]\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
with
![]() $\gamma _0=P$
and
$\gamma _0=P$
and
![]() $\gamma ^{\prime }_0=\mathrm {v}$
, the pair
$\gamma ^{\prime }_0=\mathrm {v}$
, the pair
![]() $(\gamma _t,\gamma _0)$
is fitting for all
$(\gamma _t,\gamma _0)$
is fitting for all
![]() $t>0$
small enough.
$t>0$
small enough.
Moreover in this case for any Riemannian metric on
![]() $\mathbb {P}(S^2V)$
there exists an
$\mathbb {P}(S^2V)$
there exists an
![]() $\epsilon>0$
such that for any
$\epsilon>0$
such that for any
![]() $t>0$
small enough the Riemannian distance between
$t>0$
small enough the Riemannian distance between
![]() $\mathbb {P}(\gamma _0^\circ \cap S^2V^{\geq 0})$
and
$\mathbb {P}(\gamma _0^\circ \cap S^2V^{\geq 0})$
and
![]() $\mathbb {P}(\gamma _t^\circ \cap S^2V^{\geq 0})$
is greater than
$\mathbb {P}(\gamma _t^\circ \cap S^2V^{\geq 0})$
is greater than
![]() $\epsilon t$
.
$\epsilon t$
.
Proof. Let us fix a complement H of
![]() $P^\circ $
in
$P^\circ $
in
![]() $S^2V$
. Let
$S^2V$
. Let
![]() $N=\dim (\mathcal {Q})=\frac {n(n+1)}{2}$
. We identify a neighborhood of
$N=\dim (\mathcal {Q})=\frac {n(n+1)}{2}$
. We identify a neighborhood of
![]() $P^\circ \subset \operatorname {\mathrm {Gr}}_{N-d}(\mathcal {Q})$
with
$P^\circ \subset \operatorname {\mathrm {Gr}}_{N-d}(\mathcal {Q})$
with
![]() $\operatorname {\mathrm {Hom}}(P^\circ ,H)$
. If there exists a nonzero element
$\operatorname {\mathrm {Hom}}(P^\circ ,H)$
. If there exists a nonzero element
![]() $s\in \operatorname {\mathrm {Ker}}(\mathrm {v}^\circ )\cap S^2V^{\geq 0}$
, one can consider the curve where
$s\in \operatorname {\mathrm {Ker}}(\mathrm {v}^\circ )\cap S^2V^{\geq 0}$
, one can consider the curve where
![]() $\gamma _t$
corresponds to
$\gamma _t$
corresponds to
The nonzero element
![]() $s \in S^2V^{\geq 0}$
belongs to
$s \in S^2V^{\geq 0}$
belongs to
![]() $P^\circ =\gamma _0^\circ $
and
$P^\circ =\gamma _0^\circ $
and
![]() $\gamma _t^\circ $
hence the pair
$\gamma _t^\circ $
hence the pair
![]() $(\gamma _0, \gamma _t)$
is not fitting for any
$(\gamma _0, \gamma _t)$
is not fitting for any
![]() $t>0$
.
$t>0$
.
In general the element corresponding to
![]() $\gamma _t$
is equal for t close to
$\gamma _t$
is equal for t close to
![]() $0$
to the element of
$0$
to the element of
![]() $\operatorname {\mathrm {Gr}}_{N-d}(\mathcal {Q})$
which is the graph of the map
$\operatorname {\mathrm {Gr}}_{N-d}(\mathcal {Q})$
which is the graph of the map
![]() $P^\circ \to H$
:
$P^\circ \to H$
:
The pair
![]() $(\gamma _o, \gamma _t)$
is fitting if and only if
$(\gamma _o, \gamma _t)$
is fitting if and only if
![]() $\operatorname {\mathrm {Ker}}(\mathrm {v})\cap S^2V^{\geq 0}=\lbrace 0\rbrace $
, hence if
$\operatorname {\mathrm {Ker}}(\mathrm {v})\cap S^2V^{\geq 0}=\lbrace 0\rbrace $
, hence if
![]() $\mathrm {v}$
is fitting.
$\mathrm {v}$
is fitting.
In this case the distance between
![]() $\mathbb {P}(\gamma _0^\circ \cap S^2V^{\geq 0})$
and
$\mathbb {P}(\gamma _0^\circ \cap S^2V^{\geq 0})$
and
![]() $\mathbb {P}(\gamma _t^\circ \cap S^2V^{\geq 0})$
grows at least linearly in t for t close to
$\mathbb {P}(\gamma _t^\circ \cap S^2V^{\geq 0})$
grows at least linearly in t for t close to
![]() $0$
.
$0$
.
Fitting vectors can be thought of analogs of spacelike vectors in a pseudo-Riemannian manifold of signature
![]() $(d,N)$
for some
$(d,N)$
for some
![]() $N>0$
. For instance, the set of spacelike vectors is the union of a family of cones parametrized by
$N>0$
. For instance, the set of spacelike vectors is the union of a family of cones parametrized by
![]() $\mathbb {S}^{d-1}$
, and so is the set of fitting vectors, as shown in the following proposition. This analogy is also emphasized by Remark A.3 and Theorem B.1.
$\mathbb {S}^{d-1}$
, and so is the set of fitting vectors, as shown in the following proposition. This analogy is also emphasized by Remark A.3 and Theorem B.1.
For a vector space W we write
![]() $\mathbb {S} W=(W\setminus \lbrace 0\rbrace )/\mathbb {R}_{>0}$
$\mathbb {S} W=(W\setminus \lbrace 0\rbrace )/\mathbb {R}_{>0}$
Proposition 3.8. The set of fitting vectors in
![]() $T_P\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
is equal to the union:
$T_P\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
is equal to the union:
Here
![]() $C_{[q]}$
is the convex open cone of elements
$C_{[q]}$
is the convex open cone of elements
![]() $\mathrm {v}\in T_P\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
such that there exists a positive element in the class
$\mathrm {v}\in T_P\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
such that there exists a positive element in the class
![]() $\mathrm {v}(q)\in \mathcal {Q}/P$
.
$\mathrm {v}(q)\in \mathcal {Q}/P$
.
Recall that we use the identification
![]() $\mathrm {v}\in T_P\operatorname {\mathrm {Gr}}_d(\mathcal {Q})\simeq \text {Hom}(P,\mathcal {Q}/P)$
.
$\mathrm {v}\in T_P\operatorname {\mathrm {Gr}}_d(\mathcal {Q})\simeq \text {Hom}(P,\mathcal {Q}/P)$
.
Proof. Because of the second part of Definition 3.6 a vector is well-fitting if and only if it belongs to
![]() $C_{[q]}$
for some
$C_{[q]}$
for some
![]() $[q]\in P$
. We just check that the sets
$[q]\in P$
. We just check that the sets
![]() $C_{[q]}$
are indeed open convex cones.
$C_{[q]}$
are indeed open convex cones.
Let us fix a complement H of P in
![]() $\mathcal {Q}$
to identify
$\mathcal {Q}$
to identify
![]() $T_P\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
with
$T_P\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
with
![]() $\operatorname {\mathrm {Hom}}(P,H)$
. If
$\operatorname {\mathrm {Hom}}(P,H)$
. If
![]() $\mathrm {v}_1,\mathrm {v}_2$
lie in
$\mathrm {v}_1,\mathrm {v}_2$
lie in
![]() $C_{[q]}$
and if
$C_{[q]}$
and if
![]() $\lambda ,\mu \in \mathbb {R}_{>0}$
, then for some
$\lambda ,\mu \in \mathbb {R}_{>0}$
, then for some
![]() $q_1,q_2\in P$
one has
$q_1,q_2\in P$
one has
![]() $\mathrm {v}_1(q)+q_1$
and
$\mathrm {v}_1(q)+q_1$
and
![]() $\mathrm {v}_2(q)+q_2$
positive. Therefore
$\mathrm {v}_2(q)+q_2$
positive. Therefore
![]() $(\lambda \mathrm {v}_1+\mu \mathrm {v}_2)(q)+\lambda q_1+\mu q_2$
is positive so
$(\lambda \mathrm {v}_1+\mu \mathrm {v}_2)(q)+\lambda q_1+\mu q_2$
is positive so
![]() $\lambda \mathrm {v}_1+\mu \mathrm {v}_2$
belongs to
$\lambda \mathrm {v}_1+\mu \mathrm {v}_2$
belongs to
![]() $C_{[q]}$
.
$C_{[q]}$
.
3.4 Fibration of a convex set and globally fitting maps
We consider continuous and smooth fibrations of the
![]() $\operatorname {\mathrm {SL}}(V)$
-invariant convex set
$\operatorname {\mathrm {SL}}(V)$
-invariant convex set
![]() $\mathbb {P}(S^2V^{\geq 0})$
by projective codimension d subspaces. Let M be a connected manifold of dimension d. We are interested in continuous injective maps, or smooth immersions
$\mathbb {P}(S^2V^{\geq 0})$
by projective codimension d subspaces. Let M be a connected manifold of dimension d. We are interested in continuous injective maps, or smooth immersions
![]() $u:M\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
.
$u:M\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
.
We write
![]() $u^\circ (x)=(u(x))^\circ $
. The map u determines a collection of projective subsets of codimension d:
$u^\circ (x)=(u(x))^\circ $
. The map u determines a collection of projective subsets of codimension d:
Note here that for any linear subspace
![]() $A\subset V$
the projective codimension of
$A\subset V$
the projective codimension of
![]() $P(A)$
in
$P(A)$
in
![]() $\mathbb {P}(V)$
is equal to the codimension of A in V.
$\mathbb {P}(V)$
is equal to the codimension of A in V.
If the image of u contains only mixed elements, then all the submanifolds in (1) are nonempty.
Definition 3.9. We call a continuous map
![]() $u:M\to \operatorname {\mathrm {Gr}}_d^{{\operatorname {\mathrm {mix}}}}(\mathcal {Q})$
a globally fitting map if the subsets in the collection (1) are disjoint.
$u:M\to \operatorname {\mathrm {Gr}}_d^{{\operatorname {\mathrm {mix}}}}(\mathcal {Q})$
a globally fitting map if the subsets in the collection (1) are disjoint.
A continuous map
![]() $u:M\to \operatorname {\mathrm {Gr}}_d^{{\operatorname {\mathrm {mix}}}}(\mathcal {Q})$
is a locally fitting map if for all
$u:M\to \operatorname {\mathrm {Gr}}_d^{{\operatorname {\mathrm {mix}}}}(\mathcal {Q})$
is a locally fitting map if for all
![]() $x\in M$
there is a neighborhood
$x\in M$
there is a neighborhood
![]() $U\subset M$
of x such that
$U\subset M$
of x such that
![]() $u_{|U}$
is a globally fitting map.
$u_{|U}$
is a globally fitting map.
Since
![]() $\dim (M)=d$
, the invariance of domain implies that the sets (1) for a globally fitting map form a fibration for all
$\dim (M)=d$
, the invariance of domain implies that the sets (1) for a globally fitting map form a fibration for all
![]() $x\in M$
of a neighborhood in
$x\in M$
of a neighborhood in
![]() $\mathbb {P}(S^2V^{\geq 0})$
of
$\mathbb {P}(S^2V^{\geq 0})$
of
![]() $\mathbb {P}\left (u^\circ (x)\cap S^2V^{\geq 0}\right )$
.
$\mathbb {P}\left (u^\circ (x)\cap S^2V^{\geq 0}\right )$
.
We now consider immersions from a manifold M of dimension d whose tangent directions are all fitting.
Definition 3.10. A smooth immersion
![]() $u:M\to \operatorname {\mathrm {Gr}}_d^{{\operatorname {\mathrm {mix}}}}(\mathcal {Q})$
is a fitting immersion if
$u:M\to \operatorname {\mathrm {Gr}}_d^{{\operatorname {\mathrm {mix}}}}(\mathcal {Q})$
is a fitting immersion if
![]() $\mathrm {d}u(v)$
is fitting for all
$\mathrm {d}u(v)$
is fitting for all
![]() $v\in TM$
.
$v\in TM$
.
Remark 3.11. In Appendix A.1 we discuss the simpler case when the pencils are hermitian pecils of quadrics on
![]() $\mathbb {C}^2$
. In this cases, fitting immersions are fibrations of
$\mathbb {C}^2$
. In this cases, fitting immersions are fibrations of
![]() $\mathbb {H}^3$
by geodesics.
$\mathbb {H}^3$
by geodesics.
Because of proposition 3.7, fitting immersions are locally fitting maps.
The following proposition is the infinitesimal equivalent of Proposition 3.4. We write the statement in a way to emphasize this analogy.
Consider the tautological rank d vector bundle
![]() $\operatorname {\mathrm {pr}}:\mathcal {E}\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
. The fiber at
$\operatorname {\mathrm {pr}}:\mathcal {E}\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
. The fiber at
![]() $P\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
of bundle
$P\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
of bundle
![]() $\mathcal {E}$
is identified with the vector subspace
$\mathcal {E}$
is identified with the vector subspace
![]() $P\subset \mathcal {Q}$
. Since all the fibers are naturally identified with subsets of
$P\subset \mathcal {Q}$
. Since all the fibers are naturally identified with subsets of
![]() $\mathcal {Q}$
, there is a tautological projection
$\mathcal {Q}$
, there is a tautological projection
![]() $\pi :\mathcal {E}\to \mathcal {Q}$
such that for
$\pi :\mathcal {E}\to \mathcal {Q}$
such that for
![]() $(P,q)$
in the tautological bundle, that is,
$(P,q)$
in the tautological bundle, that is,
![]() $P\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
and
$P\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
and
![]() $q\in P$
with
$q\in P$
with
![]() $q\in P$
,
$q\in P$
,
![]() $\pi (P,q)=q$
. We still denote by
$\pi (P,q)=q$
. We still denote by
![]() $\pi :u^*\mathcal {E}\to \mathcal {Q}$
the corresponding projection with a slight abuse of notations.
$\pi :u^*\mathcal {E}\to \mathcal {Q}$
the corresponding projection with a slight abuse of notations.
Note that that an element in
![]() $T\mathcal {Q}$
is a pair
$T\mathcal {Q}$
is a pair
![]() $(q, \dot {q})\in T_q\mathcal {Q}$
and we say that it is positive if the symmetric bilinear form
$(q, \dot {q})\in T_q\mathcal {Q}$
and we say that it is positive if the symmetric bilinear form
![]() $\dot {q}\in \mathcal {Q}$
is positive.
$\dot {q}\in \mathcal {Q}$
is positive.
Proposition 3.12. Given an immersion
![]() $u:M\to \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_d(\mathcal {Q})$
, let
$u:M\to \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_d(\mathcal {Q})$
, let
![]() $x_0\in M$
. The following are equivalent:
$x_0\in M$
. The following are equivalent:
-
(i) the manifolds
 $\left (\mathbb {P}(u^\circ (x))\right )_{x\in M}$
define locally a smooth fibration of an open neighborhood of
$\left (\mathbb {P}(u^\circ (x))\right )_{x\in M}$
define locally a smooth fibration of an open neighborhood of
 $\mathbb {P}\left (u^\circ (x_0)\cap S^2V^{\geq 0}\right )$
,
$\mathbb {P}\left (u^\circ (x_0)\cap S^2V^{\geq 0}\right )$
, -
(ii) for all
 $v\in T_{x_0}M$
,
$v\in T_{x_0}M$
,
 $\mathrm {d}u(v)$
is fitting,
$\mathrm {d}u(v)$
is fitting, -
(iii) for all
 $v\in T_{x_0}M$
there exists
$v\in T_{x_0}M$
there exists
 $\mathrm {w}\in T\mathcal {E}$
such that
$\mathrm {w}\in T\mathcal {E}$
such that
 $\mathrm {d}\operatorname {\mathrm {pr}}(\mathrm {w})=\mathrm {d}u(v)$
and
$\mathrm {d}\operatorname {\mathrm {pr}}(\mathrm {w})=\mathrm {d}u(v)$
and
 $\mathrm {d}\pi (\mathrm {w})\in T\mathcal {Q}$
is positive.
$\mathrm {d}\pi (\mathrm {w})\in T\mathcal {Q}$
is positive.
Proof. Note that since M has dimension d and
![]() $u^\circ (x_0)$
has codimension d, the statement
$u^\circ (x_0)$
has codimension d, the statement
![]() $(i)$
is equivalent to having for any Riemannian distance
$(i)$
is equivalent to having for any Riemannian distance
![]() $d_R$
on
$d_R$
on
![]() $\mathbb {P}(S^2V)$
and
$\mathbb {P}(S^2V)$
and
![]() $d_M$
on M, for some
$d_M$
on M, for some
![]() $\epsilon>0$
when x is close to
$\epsilon>0$
when x is close to
![]() $x_0$
:
$x_0$
:
Proposition 3.7 shows that the fitting condition is equivalent to having this distance growing linearly, hence the statements
![]() $(i)$
and
$(i)$
and
![]() $(ii)$
are equivalent.
$(ii)$
are equivalent.
A pair
![]() $(P,q_0)\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})\times \mathcal {Q}$
correspond to an element in
$(P,q_0)\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})\times \mathcal {Q}$
correspond to an element in
![]() $\mathcal {E}$
if and only if
$\mathcal {E}$
if and only if
![]() $q_0\in P$
. A pair
$q_0\in P$
. A pair
![]() $\left (\mathrm {v},\dot {q}\right )\in T_P\operatorname {\mathrm {Gr}}_d(\mathcal {Q})\times T_q\mathcal {Q}$
can be written as
$\left (\mathrm {v},\dot {q}\right )\in T_P\operatorname {\mathrm {Gr}}_d(\mathcal {Q})\times T_q\mathcal {Q}$
can be written as
![]() $\left (\mathrm {d}\operatorname {\mathrm {pr}}(\mathrm {w}),\mathrm {d}\pi (\mathrm {w})\right )$
for some
$\left (\mathrm {d}\operatorname {\mathrm {pr}}(\mathrm {w}),\mathrm {d}\pi (\mathrm {w})\right )$
for some
![]() $\mathrm {w}\in T\mathcal {E}$
if and only if
$\mathrm {w}\in T\mathcal {E}$
if and only if
![]() $\dot {q}$
belongs to the class defined by
$\dot {q}$
belongs to the class defined by
![]() $\mathrm {v}(q_0)$
.
$\mathrm {v}(q_0)$
.
Let us show this last claim. Let H be a complement of P in
![]() $\mathcal {Q}$
let
$\mathcal {Q}$
let
![]() $u:[0,1]\to \operatorname {\mathrm {Hom}}(P,H)$
and
$u:[0,1]\to \operatorname {\mathrm {Hom}}(P,H)$
and
![]() $q:[0,1]\to \mathcal {Q}$
be smooth curves with derivative
$q:[0,1]\to \mathcal {Q}$
be smooth curves with derivative
![]() $\mathrm {v}$
and
$\mathrm {v}$
and
![]() $\dot {q}$
at
$\dot {q}$
at
![]() $q=0$
and such that
$q=0$
and such that
![]() $q(t)$
belongs to the graph of
$q(t)$
belongs to the graph of
![]() $u(t)$
for
$u(t)$
for
![]() $t\in [0,1]$
. For some smooth curve
$t\in [0,1]$
. For some smooth curve
![]() $\tilde {q}:[0,1]\to P$
with
$\tilde {q}:[0,1]\to P$
with
![]() $\tilde {q}(0)=q_0$
and all
$\tilde {q}(0)=q_0$
and all
![]() $t\in [0,1]$
:
$t\in [0,1]$
:
Differentiating this at
![]() $t=0$
and we get exactly
$t=0$
and we get exactly
![]() $\mathrm {v}(q_0)+\tilde {q}'(0)=\dot {q}$
, so
$\mathrm {v}(q_0)+\tilde {q}'(0)=\dot {q}$
, so
![]() $\dot {q}$
belongs to the class defined by
$\dot {q}$
belongs to the class defined by
![]() $\mathrm {v}(q_0)$
, since
$\mathrm {v}(q_0)$
, since
![]() $\tilde {q}'(0)\in P$
. Reciprocally if this holds, one can construct such a curve
$\tilde {q}'(0)\in P$
. Reciprocally if this holds, one can construct such a curve
![]() $\tilde {q}$
, so the pair corresponds to an element of
$\tilde {q}$
, so the pair corresponds to an element of
![]() $T\mathcal {E}$
.
$T\mathcal {E}$
.
We conclude that
![]() $(iii)$
is equivalent to the second characterization of fitting vectors in Definition 3.6: one can find such a positive lift
$(iii)$
is equivalent to the second characterization of fitting vectors in Definition 3.6: one can find such a positive lift
![]() $\mathrm {w}$
if and only if one can find a class in
$\mathrm {w}$
if and only if one can find a class in
![]() $\operatorname {\mathrm {Im}}(\mathrm {v})$
that contains a positive element.
$\operatorname {\mathrm {Im}}(\mathrm {v})$
that contains a positive element.
In Proposition 7.1 we show how to construct some examples of fitting maps from a totally geodesic immersion in the symmetric space.
Remark 3.13. The definition of a fitting immersion and the previous two propositions can be generalized to the more general setup when
![]() $S^2V$
is replaced by a vector space W and
$S^2V$
is replaced by a vector space W and
![]() $S^2V^{\geq 0}$
is replaced by a closed proper convex cone C in W. In this setup positive quadrics should be replaced by elements in the dual cone of C in
$S^2V^{\geq 0}$
is replaced by a closed proper convex cone C in W. In this setup positive quadrics should be replaced by elements in the dual cone of C in
![]() $W^*$
.
$W^*$
.
4 Fitting flows
In this section we define the notion of a fitting flow, and study the consequence of the existence of such a flow. We show next that such flows always exist for fitting immersions. In this section let us fix a map
![]() $u:M\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
.
$u:M\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
.
4.1 Definition and application of fitting flows
The pullback
![]() $u^*\mathcal {E}$
of the tautological bundle
$u^*\mathcal {E}$
of the tautological bundle
![]() $\operatorname {\mathrm {pr}}:\mathcal {E}\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
defines a rank d vector bundle over M. We define the sphere bundle
$\operatorname {\mathrm {pr}}:\mathcal {E}\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
defines a rank d vector bundle over M. We define the sphere bundle
![]() $\mathbb {S}u^*\mathcal {E}$
as the quotient of the vector bundle
$\mathbb {S}u^*\mathcal {E}$
as the quotient of the vector bundle
![]() $u^*\mathcal {E}$
by the action of positive scalars.
$u^*\mathcal {E}$
by the action of positive scalars.
Recall that M has dimension d. We consider flows on
![]() $\mathbb {S}u^*\mathcal {E}$
so that some form of contraction occurs along the flow lines. We denote also by
$\mathbb {S}u^*\mathcal {E}$
so that some form of contraction occurs along the flow lines. We denote also by
![]() $\operatorname {\mathrm {pr}}$
the bundle maps
$\operatorname {\mathrm {pr}}$
the bundle maps
![]() $u^*\mathcal {E}\to M$
,
$u^*\mathcal {E}\to M$
,
![]() $\mathbb {S} u^*\mathcal {E}\to M$
, with a slight abuse of notations.
$\mathbb {S} u^*\mathcal {E}\to M$
, with a slight abuse of notations.
The fiber at
![]() $P\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
of the bundle
$P\in \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
of the bundle
![]() $\mathcal {E}$
is identified with the vector subspace
$\mathcal {E}$
is identified with the vector subspace
![]() $P\subset \mathcal {Q}$
. Recall that there is a natural projection
$P\subset \mathcal {Q}$
. Recall that there is a natural projection
![]() $\pi :\mathcal {E}\to \mathcal {Q}$
defined by
$\pi :\mathcal {E}\to \mathcal {Q}$
defined by
![]() $\pi (P,q)=q$
. We still denote by
$\pi (P,q)=q$
. We still denote by
![]() $\pi :u^*\mathcal {E}\to \mathcal {Q}$
the corresponding projection with a slight abuse of notations.
$\pi :u^*\mathcal {E}\to \mathcal {Q}$
the corresponding projection with a slight abuse of notations.
Definition 4.1. A fitting flow for a continuous map
![]() $u:M\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
is a continuous flow
$u:M\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
is a continuous flow
![]() $(\Phi _t)_{t\in \mathbb {R}}$
on
$(\Phi _t)_{t\in \mathbb {R}}$
on
![]() $\mathbb {S} u^*\mathcal {E}$
such that
$\mathbb {S} u^*\mathcal {E}$
such that
one can choose representatives q of
![]() $[q]$
and
$[q]$
and
![]() $q'$
of
$q'$
of
![]() $[q']=\Phi _t([q])$
such that
$[q']=\Phi _t([q])$
such that
![]() $\pi (q')-\pi (q)\in \mathcal {Q}$
is positive.
$\pi (q')-\pi (q)\in \mathcal {Q}$
is positive.
Note that the last condition is equivalent to asking that
![]() $\lbrace \pi (q)\geq 0\rbrace \subset \lbrace \pi (q')> 0\rbrace $
in
$\lbrace \pi (q)\geq 0\rbrace \subset \lbrace \pi (q')> 0\rbrace $
in
![]() $\mathbb {RP}^{2n-1}$
. Along such flows, the associated quadric hypersurfaces are nested into one another. In particular if u admits a fitting flow it is locally a fitting map.
$\mathbb {RP}^{2n-1}$
. Along such flows, the associated quadric hypersurfaces are nested into one another. In particular if u admits a fitting flow it is locally a fitting map.
Lemma 4.2. Let
![]() $u:M\to \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_d(\mathcal {Q})$
be a continuous map that admits a fitting flow. The projection to
$u:M\to \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_d(\mathcal {Q})$
be a continuous map that admits a fitting flow. The projection to
![]() $\operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_d(\mathcal {Q})$
of the flow lines of the fitting flow are embedded.
$\operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_d(\mathcal {Q})$
of the flow lines of the fitting flow are embedded.
Proof. Assume by contradiction that for some
![]() $t_0>0$
and
$t_0>0$
and
![]() $q\in \mathbb {S} u^*\mathcal {E}$
one has
$q\in \mathbb {S} u^*\mathcal {E}$
one has
![]() $u(x)=\operatorname {\mathrm {pr}}(q)=\operatorname {\mathrm {pr}}(\Phi _{t_0}(q))$
. The fact that the flow is fitting implies that for some
$u(x)=\operatorname {\mathrm {pr}}(q)=\operatorname {\mathrm {pr}}(\Phi _{t_0}(q))$
. The fact that the flow is fitting implies that for some
![]() $\lambda>0$
,
$\lambda>0$
,
![]() $\lambda \pi (\Phi _{t_0}(q))-\pi (q)\in \mathcal {Q}$
is positive. This positive quadric belongs to
$\lambda \pi (\Phi _{t_0}(q))-\pi (q)\in \mathcal {Q}$
is positive. This positive quadric belongs to
![]() $u(x)$
, contradicting the fact that
$u(x)$
, contradicting the fact that
![]() $u(x)\in \operatorname {\mathrm {Gr}}_d^{{\operatorname {\mathrm {mix}}}}(\mathcal {Q})$
by Proposition 3.2.
$u(x)\in \operatorname {\mathrm {Gr}}_d^{{\operatorname {\mathrm {mix}}}}(\mathcal {Q})$
by Proposition 3.2.
Some fitting flows can be constructed by taking a geodesic flow on M for some Riemannian metric and identifying
![]() $u^*\mathcal {E}$
with the tangent bundle to M. In general the projections of the flow lines of a fitting flow satisfy the following topological property, which is clearly satisfied for geodesic flows.
$u^*\mathcal {E}$
with the tangent bundle to M. In general the projections of the flow lines of a fitting flow satisfy the following topological property, which is clearly satisfied for geodesic flows.
Lemma 4.3. Let
![]() $u:M\to \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_d(\mathcal {Q})$
be a continuous map equipped with a fitting flow
$u:M\to \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_d(\mathcal {Q})$
be a continuous map equipped with a fitting flow
![]() $\Phi $
in a neighborhood of
$\Phi $
in a neighborhood of
![]() $x\in M$
. For
$x\in M$
. For
![]() $t>0$
small enough the sphere
$t>0$
small enough the sphere
![]() $S_t:[q]\in \mathbb {S} u^*\mathcal {E}_{|x}\mapsto p\circ \Phi _t([q])\in M$
is homotopic to a generator of the homology of
$S_t:[q]\in \mathbb {S} u^*\mathcal {E}_{|x}\mapsto p\circ \Phi _t([q])\in M$
is homotopic to a generator of the homology of
![]() $U\setminus \lbrace x\rbrace $
for any open neighborhood U of x in M that is diffeomorphic to
$U\setminus \lbrace x\rbrace $
for any open neighborhood U of x in M that is diffeomorphic to
![]() $\mathbb {R}^d$
.
$\mathbb {R}^d$
.
The proof relies on the fact the dimension of M is equal to d, and hence the manifolds
![]() $\mathbb {P}(u^\circ (x)\cap S^2V^{\geq 0})$
locally define a fibration of
$\mathbb {P}(u^\circ (x)\cap S^2V^{\geq 0})$
locally define a fibration of
![]() $\mathbb {P}(S^2V^{\geq 0})$
.
$\mathbb {P}(S^2V^{\geq 0})$
.
Proof. Let
![]() $P=u(x)$
. Let
$P=u(x)$
. Let
![]() $s_0\in P^\circ \subset S^2V$
be a positive tensor, which exists since the pencil P is assumed to be in
$s_0\in P^\circ \subset S^2V$
be a positive tensor, which exists since the pencil P is assumed to be in
![]() $\operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_d(\mathcal {Q})$
. Let
$\operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_d(\mathcal {Q})$
. Let
![]() $P'\in \operatorname {\mathrm {Gr}}_d(S^2V)$
be a supplement of
$P'\in \operatorname {\mathrm {Gr}}_d(S^2V)$
be a supplement of
![]() $P^\circ $
. Since u is continuous for all y close enough to x the vector subspace
$P^\circ $
. Since u is continuous for all y close enough to x the vector subspace
![]() $u^\circ (y)$
is transverse to
$u^\circ (y)$
is transverse to
![]() $P'$
, therefore there exists a unique vector
$P'$
, therefore there exists a unique vector
![]() $\phi (y)\in P'$
such that:
$\phi (y)\in P'$
such that:
This defines a continuous map
![]() $\phi $
from a neighborhood U of
$\phi $
from a neighborhood U of
![]() $x\in M$
to
$x\in M$
to
![]() $P'$
.
$P'$
.
Let
![]() $[q]\in \mathbb {S} u^*\mathcal {E}_x$
. For all t such that
$[q]\in \mathbb {S} u^*\mathcal {E}_x$
. For all t such that
![]() $s\circ \Phi _t(q)\in U$
, the linear form
$s\circ \Phi _t(q)\in U$
, the linear form
![]() $\pi \left (\Phi _t(q)\right )\in \mathcal {Q}=S^2V^*$
vanishes on
$\pi \left (\Phi _t(q)\right )\in \mathcal {Q}=S^2V^*$
vanishes on
![]() $\phi \left ( s\circ \Phi _t(q)\right )\in S^2V$
since this point belongs to
$\phi \left ( s\circ \Phi _t(q)\right )\in S^2V$
since this point belongs to
![]() $u^\circ (\operatorname {\mathrm {pr}}\circ \Phi _t(q))$
. Moreover
$u^\circ (\operatorname {\mathrm {pr}}\circ \Phi _t(q))$
. Moreover
![]() $\pi \left (\Phi _t(q)\right )-\pi (q)$
is a positive bilinear form since
$\pi \left (\Phi _t(q)\right )-\pi (q)$
is a positive bilinear form since
![]() $\Phi $
is a fitting flow.
$\Phi $
is a fitting flow.
In particular
![]() $\pi (q)\in \mathcal {Q}=S^2V^*$
is always negative on
$\pi (q)\in \mathcal {Q}=S^2V^*$
is always negative on
![]() $\phi \left ( \operatorname {\mathrm {pr}}\circ \Phi _t(q)\right )\in S^2V$
. Hence for t small enough
$\phi \left ( \operatorname {\mathrm {pr}}\circ \Phi _t(q)\right )\in S^2V$
. Hence for t small enough
![]() $[\phi \circ S_t]:\mathbb {S} u^*\mathcal {E}_x \to \mathbb {S} P'$
has the same degree as
$[\phi \circ S_t]:\mathbb {S} u^*\mathcal {E}_x \to \mathbb {S} P'$
has the same degree as
![]() $[\pi ]: \mathbb {S} u^*\mathcal {E}_x \to \mathbb {S} P^{\prime *}\simeq \mathbb {S} P$
which associates to
$[\pi ]: \mathbb {S} u^*\mathcal {E}_x \to \mathbb {S} P^{\prime *}\simeq \mathbb {S} P$
which associates to
![]() $[q]\in \mathbb {S} u^*\mathcal {E}_x $
the class
$[q]\in \mathbb {S} u^*\mathcal {E}_x $
the class
![]() $[\pi (q)]\in \mathbb {S} P$
. The map
$[\pi (q)]\in \mathbb {S} P$
. The map
![]() $[\pi ]$
is a diffeomorphism, so in particular
$[\pi ]$
is a diffeomorphism, so in particular
![]() $1=|\deg ([\pi ])|=|\deg (\phi )\deg (S_t)|$
. Hence
$1=|\deg ([\pi ])|=|\deg (\phi )\deg (S_t)|$
. Hence
![]() $S_t$
is a generator of the homotopy group of
$S_t$
is a generator of the homotopy group of
![]() $U\setminus \lbrace x\rbrace $
.
$U\setminus \lbrace x\rbrace $
.
Remark 4.4. In particular for an immersion
![]() $u:M\to \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_d(\mathcal {Q})$
that admits a fitting flow, choosing continuously an orientation of the pencils
$u:M\to \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_d(\mathcal {Q})$
that admits a fitting flow, choosing continuously an orientation of the pencils
![]() $u(x)$
for
$u(x)$
for
![]() $x\in M$
is equivalent to choosing an orientation of M.
$x\in M$
is equivalent to choosing an orientation of M.
Let
![]() $M=\widetilde {N}$
where N is compact and
$M=\widetilde {N}$
where N is compact and
![]() $\Gamma =\pi _1(N)$
. Let
$\Gamma =\pi _1(N)$
. Let
![]() $\rho :\Gamma \to \operatorname {\mathrm {SL}}(V)$
be a representation. Recall that a
$\rho :\Gamma \to \operatorname {\mathrm {SL}}(V)$
be a representation. Recall that a
![]() $(C,D)$
-quasi-geodesic in a metric space
$(C,D)$
-quasi-geodesic in a metric space
![]() $(X,d)$
is a curve
$(X,d)$
is a curve
![]() $\gamma :\mathbb {R}\to X$
such that for all
$\gamma :\mathbb {R}\to X$
such that for all
![]() $t_1,t_2\in \mathbb {R}$
:
$t_1,t_2\in \mathbb {R}$
:
Proposition 4.5. Let
![]() $u:\widetilde {N}\to \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_d(\mathcal {Q})$
be a
$u:\widetilde {N}\to \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_d(\mathcal {Q})$
be a
![]() $\rho $
-equivariant continuous map that admits a
$\rho $
-equivariant continuous map that admits a
![]() $\rho $
-equivariant fitting flow
$\rho $
-equivariant fitting flow
![]() $\Phi $
. There exist
$\Phi $
. There exist
![]() $C,D>0$
such that the projection to
$C,D>0$
such that the projection to
![]() $\widetilde {N}$
of the flow lines of
$\widetilde {N}$
of the flow lines of
![]() $\Phi $
are
$\Phi $
are
![]() $(C,D)$
-quasi-geodesics. Moreover for every
$(C,D)$
-quasi-geodesics. Moreover for every
![]() $(x,y)\in \widetilde {N}^2$
there exists a flow line whose projection to
$(x,y)\in \widetilde {N}^2$
there exists a flow line whose projection to
![]() $\widetilde {N}$
starts at x and ends at y.
$\widetilde {N}$
starts at x and ends at y.
In the previous statement one can consider any fixed Riemannian metric on the compact space
![]() $\mathbb {S} u^*\mathcal {E}/\rho (\Gamma )$
.
$\mathbb {S} u^*\mathcal {E}/\rho (\Gamma )$
.
Remark 4.6. Note that since there exists a flow line between any pair of points in
![]() $\widetilde {N}$
, the map u is necessarily a globally fitting map.
$\widetilde {N}$
, the map u is necessarily a globally fitting map.
In this proof we will use the Hilbert distance
![]() $d_H$
on the properly convex domain
$d_H$
on the properly convex domain
![]() $\mathbb {P}(S^2V^{>0})$
. It is defined which is defined using the cross ratio as
$\mathbb {P}(S^2V^{>0})$
. It is defined which is defined using the cross ratio as
![]() $d_H([s_1],[s_2])=\log \left (\text {cr}\left ([s^-],[s_1],[s_2],[s^+]\right )\right )$
where
$d_H([s_1],[s_2])=\log \left (\text {cr}\left ([s^-],[s_1],[s_2],[s^+]\right )\right )$
where
![]() $[s_1],[s_2]\in \mathbb {P}(S^2V^{>0})$
and
$[s_1],[s_2]\in \mathbb {P}(S^2V^{>0})$
and
![]() $[s^-]$
,
$[s^-]$
,
![]() $[s^+]$
are the intersection of the projective line through
$[s^+]$
are the intersection of the projective line through
![]() $[s_1]$
and
$[s_1]$
and
![]() $[s_2]$
with the boundary of the domain
$[s_2]$
with the boundary of the domain
![]() $\mathbb {P}(S^2V^{>0})$
. If the closure in
$\mathbb {P}(S^2V^{>0})$
. If the closure in
![]() $\mathbb {P}(S^2V)$
of two sets
$\mathbb {P}(S^2V)$
of two sets
![]() $A,B\subset \mathbb {P}(S^2V^{>0})$
are disjoint, then the two sets are at positive distance for the Hilbert distance. Indeed for every Riemannian metric
$A,B\subset \mathbb {P}(S^2V^{>0})$
are disjoint, then the two sets are at positive distance for the Hilbert distance. Indeed for every Riemannian metric
![]() $d_{\mathbb {S}}$
on the compact manifold
$d_{\mathbb {S}}$
on the compact manifold
![]() $\mathbb {P}(S^2V)$
, the Hilbert distance between any two points in
$\mathbb {P}(S^2V)$
, the Hilbert distance between any two points in
![]() $\mathbb {P}(S^2V^{>0})$
is bounded from below by some uniform multiple of
$\mathbb {P}(S^2V^{>0})$
is bounded from below by some uniform multiple of
![]() $d_{\mathbb {S}}$
.
$d_{\mathbb {S}}$
.
Proof. For all
![]() $[q]\in \mathbb {S} u^*\mathcal {E}$
we consider the convex
$[q]\in \mathbb {S} u^*\mathcal {E}$
we consider the convex
![]() $\mathbb {P}(\langle \pi (q)\rangle ^\circ \cap S^2V^{>0})$
.
$\mathbb {P}(\langle \pi (q)\rangle ^\circ \cap S^2V^{>0})$
.
We choose a continuous and
![]() $\rho $
-equivariant map
$\rho $
-equivariant map
![]() $\sigma :\mathbb {S} u^*\mathcal {E}\to \mathbb {P}(S^2V^{>0})$
with the property that
$\sigma :\mathbb {S} u^*\mathcal {E}\to \mathbb {P}(S^2V^{>0})$
with the property that
![]() $\sigma ([q])\in \mathbb {P}(\langle \pi (q)\rangle ^\circ \cap S^2V^{>0})$
for all
$\sigma ([q])\in \mathbb {P}(\langle \pi (q)\rangle ^\circ \cap S^2V^{>0})$
for all
![]() $[q]\in \mathbb {S} u^*\mathcal {E}$
. One can always find such a choice, as it amounts to finding a section of an open ball bundle over a compact set. Indeed
$[q]\in \mathbb {S} u^*\mathcal {E}$
. One can always find such a choice, as it amounts to finding a section of an open ball bundle over a compact set. Indeed
![]() $\mathbb {P}(\langle \pi (q)\rangle ^\circ \cap S^2V^{>0})$
is a nonempty convex set of codimension
$\mathbb {P}(\langle \pi (q)\rangle ^\circ \cap S^2V^{>0})$
is a nonempty convex set of codimension
![]() $1$
that forms an open ball for all
$1$
that forms an open ball for all
![]() $[q]\in \mathbb {S} u^*\mathcal {E}$
.
$[q]\in \mathbb {S} u^*\mathcal {E}$
.
We fix a
![]() $\Gamma $
-invariant Riemannian metric g on
$\Gamma $
-invariant Riemannian metric g on
![]() $\mathbb {S} u^*\mathcal {E}$
with associated distance
$\mathbb {S} u^*\mathcal {E}$
with associated distance
![]() $d_g$
. We set
$d_g$
. We set
![]() $C_1$
to be the supremum of
$C_1$
to be the supremum of
![]() $d_H\left (\sigma ([q_1]),\sigma ([q_2])\right )$
for all
$d_H\left (\sigma ([q_1]),\sigma ([q_2])\right )$
for all
![]() $[q_1],[q_2]\in \mathbb {S} u^*\mathcal {E}$
such that
$[q_1],[q_2]\in \mathbb {S} u^*\mathcal {E}$
such that
![]() $d_g([q_1],[q_2])\leq 1$
, which exists since
$d_g([q_1],[q_2])\leq 1$
, which exists since
![]() $\Gamma $
acts cocompactly on
$\Gamma $
acts cocompactly on
![]() $\widetilde {N}$
. The following inequality follows for all
$\widetilde {N}$
. The following inequality follows for all
![]() $[q_1],[q_2]\in \mathbb {S} u^*\mathcal {E}$
from the triangular inequality:
$[q_1],[q_2]\in \mathbb {S} u^*\mathcal {E}$
from the triangular inequality:
Let n be the unique integer
![]() $d_g([q_1],[q_2])\leq n< d_g([q_1],[q_2])+1$
. One can find elements
$d_g([q_1],[q_2])\leq n< d_g([q_1],[q_2])+1$
. One can find elements
![]() $x_0=[q_1], x_1,\cdots , x_n=[q_2]$
in
$x_0=[q_1], x_1,\cdots , x_n=[q_2]$
in
![]() $\mathbb {S} u^*\mathcal {E}$
such that for all
$\mathbb {S} u^*\mathcal {E}$
such that for all
![]() $1\leq i\leq n$
one has
$1\leq i\leq n$
one has
![]() $d_g(x_{i-1},x_i)\leq 1$
. The triangular inequality for the Hilbert distance implies that:
$d_g(x_{i-1},x_i)\leq 1$
. The triangular inequality for the Hilbert distance implies that:
We now set
![]() $C_2$
to be the supremum of
$C_2$
to be the supremum of
![]() $d_H\left (\sigma ([q_1]),\sigma (\Phi _t([q]))\right )$
for all
$d_H\left (\sigma ([q_1]),\sigma (\Phi _t([q]))\right )$
for all
![]() $[q_1]\in \mathbb {S} u^*\mathcal {E}$
and
$[q_1]\in \mathbb {S} u^*\mathcal {E}$
and
![]() $0\leq t\leq 1$
. Similarly we get the following inequality for all
$0\leq t\leq 1$
. Similarly we get the following inequality for all
![]() $[q]\in \mathbb {S} u^*\mathcal {E}$
and
$[q]\in \mathbb {S} u^*\mathcal {E}$
and
![]() $t\geq 0$
:
$t\geq 0$
:
Let K be a compact fundamental domain for the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\mathbb {S} u^*\mathcal {E}$
and let
$\mathbb {S} u^*\mathcal {E}$
and let
![]() $\epsilon $
be the infimum of the Hilbert distance for any
$\epsilon $
be the infimum of the Hilbert distance for any
![]() $[q]\in K$
between
$[q]\in K$
between
![]() $\mathbb {P}\left (\langle \pi (q)\rangle ^\circ \cap S^2V^{>0}\right )$
and
$\mathbb {P}\left (\langle \pi (q)\rangle ^\circ \cap S^2V^{>0}\right )$
and
![]() $\mathbb {P}\left (\langle \pi (\Phi _1(q))\rangle ^\circ \cap S^2V^{>0}\right )$
. Since the flow is fitting, the closures of these two sets in
$\mathbb {P}\left (\langle \pi (\Phi _1(q))\rangle ^\circ \cap S^2V^{>0}\right )$
. Since the flow is fitting, the closures of these two sets in
![]() $\mathbb {P}(S^2V)$
are disjoint for any
$\mathbb {P}(S^2V)$
are disjoint for any
![]() $[q]$
, and hence their Hilbert distance is positive. Since K is compact, the infimum
$[q]$
, and hence their Hilbert distance is positive. Since K is compact, the infimum
![]() $\epsilon $
is also positive.
$\epsilon $
is also positive.
The Hilbert distance between
![]() $\sigma (q)$
and
$\sigma (q)$
and
![]() $\sigma (\Phi _t(q))$
for
$\sigma (\Phi _t(q))$
for
![]() $t>0$
and
$t>0$
and
![]() $q\in \mathbb {S} u^*\mathcal {E}$
is greater than
$q\in \mathbb {S} u^*\mathcal {E}$
is greater than
![]() $\epsilon (t-1)$
. Indeed for all integer
$\epsilon (t-1)$
. Indeed for all integer
![]() $0\leq n\leq t$
the projective segment between
$0\leq n\leq t$
the projective segment between
![]() $\sigma (q)$
and
$\sigma (q)$
and
![]() $\sigma (\Phi _t(q))$
, which is a geodesic for the Hilbert distance, intersects
$\sigma (\Phi _t(q))$
, which is a geodesic for the Hilbert distance, intersects
![]() $\mathbb {P}\left (\langle \pi (\Phi _n(q))\rangle ^\circ \cap S^2V^{>0}\right ) $
in exactly one point
$\mathbb {P}\left (\langle \pi (\Phi _n(q))\rangle ^\circ \cap S^2V^{>0}\right ) $
in exactly one point
![]() $x_n$
. Hence the Hilbert distance between
$x_n$
. Hence the Hilbert distance between
![]() $x_n$
and
$x_n$
and
![]() $x_{n+1}$
for
$x_{n+1}$
for
![]() $0\leq n\leq t-1$
is at least
$0\leq n\leq t-1$
is at least
![]() $\epsilon $
.
$\epsilon $
.
Putting all of these inequalities together we get that for all
![]() $t\geq 0$
and
$t\geq 0$
and
![]() $[q]\in \mathbb {S} u^*\mathcal {E}$
:
$[q]\in \mathbb {S} u^*\mathcal {E}$
:
Hence the flow lines are quasi-isometric embeddings.
We now check that flow lines exist between any pair of points. Let
![]() $x\in M$
. Given
$x\in M$
. Given
![]() $t\in \mathbb {R}$
we consider the d-sphere
$t\in \mathbb {R}$
we consider the d-sphere
![]() $S_t:q\in \mathbb {S} u^*\mathcal {E}_{|x}\mapsto \Phi _t(q)\in u^*\mathcal {E}$
. Suppose that some
$S_t:q\in \mathbb {S} u^*\mathcal {E}_{|x}\mapsto \Phi _t(q)\in u^*\mathcal {E}$
. Suppose that some
![]() $y\in M$
, avoids the sphere
$y\in M$
, avoids the sphere
![]() $S_t$
for all
$S_t$
for all
![]() $t>0$
. Consider a curve
$t>0$
. Consider a curve
![]() $\eta $
between x and y. The homological intersection between this segment and the spheres
$\eta $
between x and y. The homological intersection between this segment and the spheres
![]() $S_t$
in
$S_t$
in
![]() $M\setminus \lbrace x,y\rbrace $
is constant, and is equal to zero for t large enough since the spheres
$M\setminus \lbrace x,y\rbrace $
is constant, and is equal to zero for t large enough since the spheres
![]() $S_t$
are then uniformly far from x. However for t small enough, the homotopy class of
$S_t$
are then uniformly far from x. However for t small enough, the homotopy class of
![]() $S_t$
is the one of any small sphere encircling x by Lemma 4.3. This leads to a contradiction since such a sphere will have homological intersection equal to
$S_t$
is the one of any small sphere encircling x by Lemma 4.3. This leads to a contradiction since such a sphere will have homological intersection equal to
![]() $1$
or
$1$
or
![]() $-1$
with the curve
$-1$
with the curve
![]() $\eta $
. Hence there exists a flow line joining any pair of points.
$\eta $
. Hence there exists a flow line joining any pair of points.
As a consequence, we get the following.
Corollary 4.7. Let
![]() $u:\widetilde {N}\to \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_d(\mathcal {Q})$
be a
$u:\widetilde {N}\to \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_d(\mathcal {Q})$
be a
![]() $\rho $
-equivariant continuous map that admits an equivariant fitting flow, then it is an embedding. In particular it is a globally fitting map. Moreover
$\rho $
-equivariant continuous map that admits an equivariant fitting flow, then it is an embedding. In particular it is a globally fitting map. Moreover
![]() $ \rho :\Gamma \to \operatorname {\mathrm {SL}}(V)$
is a quasi-isometric embedding.
$ \rho :\Gamma \to \operatorname {\mathrm {SL}}(V)$
is a quasi-isometric embedding.
Proof. Since there are flow lines between any pair of points in
![]() $\widetilde {N}$
, for every
$\widetilde {N}$
, for every
![]() $x \neq y\in M$
one can find
$x \neq y\in M$
one can find
![]() $q\in u(x)$
and
$q\in u(x)$
and
![]() $q'\in u(y)$
such that
$q'\in u(y)$
such that
![]() $q-q'$
is positive. Since the pencils
$q-q'$
is positive. Since the pencils
![]() $u(x)$
and
$u(x)$
and
![]() $u(y)$
are mixed, one cannot have
$u(y)$
are mixed, one cannot have
![]() $q-q'\in u(x)=u(y)$
so
$q-q'\in u(x)=u(y)$
so
![]() $u(x)\neq u(y)$
. Furthermore the pair
$u(x)\neq u(y)$
. Furthermore the pair
![]() $(u(x),u(y))$
is a fitting pair for all
$(u(x),u(y))$
is a fitting pair for all
![]() $x \neq y\in M$
, hence u is a globally fitting map by Proposition 3.4.
$x \neq y\in M$
, hence u is a globally fitting map by Proposition 3.4.
For any
![]() $\Gamma $
-invariant Riemannian metric g on
$\Gamma $
-invariant Riemannian metric g on
![]() $\mathbb {S} \mathcal {E}$
, any map
$\mathbb {S} \mathcal {E}$
, any map
![]() $\sigma $
as the proof of Proposition 4.5 is a quasi-isometric embedding. Indeed let
$\sigma $
as the proof of Proposition 4.5 is a quasi-isometric embedding. Indeed let
![]() $\delta $
be the maximum of
$\delta $
be the maximum of
![]() $d_g(x,x')$
or
$d_g(x,x')$
or
![]() $d_H(\sigma (x),\sigma (x'))$
for any
$d_H(\sigma (x),\sigma (x'))$
for any
![]() $x,x'$
in the same fiber of
$x,x'$
in the same fiber of
![]() $\operatorname {\mathrm {pr}}:\mathbb {S} \mathcal {E}\to \widetilde {N}$
. For every
$\operatorname {\mathrm {pr}}:\mathbb {S} \mathcal {E}\to \widetilde {N}$
. For every
![]() $x,y\in \mathbb {S} \mathcal {E}$
one can find
$x,y\in \mathbb {S} \mathcal {E}$
one can find
![]() $x',y'$
in the same fibers respectively as
$x',y'$
in the same fibers respectively as
![]() $x,y$
and in the same flow line for
$x,y$
and in the same flow line for
![]() $\Phi $
. Hence for the constants
$\Phi $
. Hence for the constants
![]() $C,D$
from Proposition 4.5:
$C,D$
from Proposition 4.5:
Hence
![]() $\rho $
is a quasi-isometric embedding.
$\rho $
is a quasi-isometric embedding.
4.2 Existence of fitting flows
We now prove that the existence of a fitting flow is guaranteed on compacts for fitting immersions. It is not clear if it is the case in general for locally fitting maps.
Proposition 4.8. Let M be a manifold of dimension d.
-
(i) A fitting immersion
 $u:M\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
admits a fitting flow.
$u:M\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
admits a fitting flow. -
(ii) An equivariant fitting immersion
 $u:M\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
for a representation
$u:M\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
for a representation
 $\rho :\Gamma \to \operatorname {\mathrm {SL}}(V)$
, and a proper action of
$\rho :\Gamma \to \operatorname {\mathrm {SL}}(V)$
, and a proper action of
 $\Gamma $
on M admits a
$\Gamma $
on M admits a
 $\rho $
-equivariant fitting flow.
$\rho $
-equivariant fitting flow.
Recall that
![]() $\operatorname {\mathrm {pr}}:\mathcal {E}\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
is the bundle map and
$\operatorname {\mathrm {pr}}:\mathcal {E}\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
is the bundle map and
![]() $\pi :\mathcal {E}\to \mathcal {Q}$
is the tautological map.
$\pi :\mathcal {E}\to \mathcal {Q}$
is the tautological map.
In order to construct the fitting flow we construct the vector field W on
![]() $\mathbb {S} u^*\mathcal {E}$
that generates the flow. This first step of the proof uses crucially the hypothesis that
$\mathbb {S} u^*\mathcal {E}$
that generates the flow. This first step of the proof uses crucially the hypothesis that
![]() $\dim (M)=d$
.
$\dim (M)=d$
.
Lemma 4.9. Let
![]() $u:M\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
be a fitting immersion with
$u:M\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
be a fitting immersion with
![]() $\dim (M)=d$
. For every
$\dim (M)=d$
. For every
![]() $x\in M$
and any
$x\in M$
and any
![]() $q\in u(x)$
, there exists a lift
$q\in u(x)$
, there exists a lift
![]() $\mathrm {w}\in T_{(u(x),q)}u^*\mathcal {E}$
such that
$\mathrm {w}\in T_{(u(x),q)}u^*\mathcal {E}$
such that
![]() $\mathrm {d}\pi (\mathrm {w})\in T\mathcal {Q}$
is positive.
$\mathrm {d}\pi (\mathrm {w})\in T\mathcal {Q}$
is positive.
We say that an element
![]() $(q,\dot {q})\in T\mathcal {Q}$
is positive if
$(q,\dot {q})\in T\mathcal {Q}$
is positive if
![]() $\dot {q}\in \mathcal {Q}$
is positive. Given any quadric in the pencil
$\dot {q}\in \mathcal {Q}$
is positive. Given any quadric in the pencil
![]() $u(x)$
, we want to find an infinitesimal direction in which to move this quadric as well as the pencil containing it inside the image of u so that the derivative of the quadrics is positive.
$u(x)$
, we want to find an infinitesimal direction in which to move this quadric as well as the pencil containing it inside the image of u so that the derivative of the quadrics is positive.
This lemma is an inverse of point
![]() $(iii)$
of Proposition 3.12: here we fix an element
$(iii)$
of Proposition 3.12: here we fix an element
![]() $q\in u(x)$
whereas before we were fixing a
$q\in u(x)$
whereas before we were fixing a
![]() $v\in TM$
. In order to construct this inverse we will use the fact that a continuous odd map between spheres of equal dimensions must have odd degree [Reference HatcherHat02, Proposition 2B.6] and therefore it must be surjective, as any nonsurjective map into a sphere is contractible.
$v\in TM$
. In order to construct this inverse we will use the fact that a continuous odd map between spheres of equal dimensions must have odd degree [Reference HatcherHat02, Proposition 2B.6] and therefore it must be surjective, as any nonsurjective map into a sphere is contractible.
Proof. Let us fix
![]() $x\in M$
. We construct a continuous map:
$x\in M$
. We construct a continuous map:
We require that this map satisfies
![]() $\lambda \phi (v)=\phi (\lambda v)$
for all
$\lambda \phi (v)=\phi (\lambda v)$
for all
![]() $v\in T_xM\setminus \lbrace 0\rbrace $
and
$v\in T_xM\setminus \lbrace 0\rbrace $
and
![]() $\lambda \in \mathbb {R}$
. Note that in particular
$\lambda \in \mathbb {R}$
. Note that in particular
![]() $\phi $
defines an odd map:
$\phi $
defines an odd map:
We furthermore construct a lift:
In other words we assume that
![]() $\psi (v)\in T_{\phi (v)}(u^*\mathcal {E})$
for
$\psi (v)\in T_{\phi (v)}(u^*\mathcal {E})$
for
![]() $v\in T_xM\setminus \lbrace 0\rbrace $
. We require that
$v\in T_xM\setminus \lbrace 0\rbrace $
. We require that
![]() $\psi (\lambda v)=\lambda (\mathrm {d}m_\lambda )(\psi (v))$
for all
$\psi (\lambda v)=\lambda (\mathrm {d}m_\lambda )(\psi (v))$
for all
![]() $v\in T_xM\setminus \lbrace 0\rbrace $
and
$v\in T_xM\setminus \lbrace 0\rbrace $
and
![]() $\lambda \in \mathbb {R}$
where
$\lambda \in \mathbb {R}$
where
![]() $m_\lambda :u^*\mathcal {E}\to u^*\mathcal {E}$
is the multiplication by
$m_\lambda :u^*\mathcal {E}\to u^*\mathcal {E}$
is the multiplication by
![]() $\lambda $
. We require
$\lambda $
. We require
![]() $\mathrm {d}\pi (\psi (v))\in T\mathcal {Q}$
to be positive for all
$\mathrm {d}\pi (\psi (v))\in T\mathcal {Q}$
to be positive for all
![]() $v\in T_xM\setminus \lbrace 0\rbrace $
.
$v\in T_xM\setminus \lbrace 0\rbrace $
.
Finally we will make this construction so that in addition
![]() $\mathrm {d}\operatorname {\mathrm {pr}}\left ( \psi (v)\right )=v$
for
$\mathrm {d}\operatorname {\mathrm {pr}}\left ( \psi (v)\right )=v$
for
![]() $v\in T_xM\setminus \lbrace 0\rbrace $
, but this property will be only used during the construction.
$v\in T_xM\setminus \lbrace 0\rbrace $
, but this property will be only used during the construction.
The following diagram illustrates the situation.

If we can construct such continuous maps, the fact that
![]() $\overline {\phi }$
is an odd map between two spheres of the same dimension implies that it is homotopically nontrivial and therefore surjective. In particular for all
$\overline {\phi }$
is an odd map between two spheres of the same dimension implies that it is homotopically nontrivial and therefore surjective. In particular for all
![]() $[q]\in \mathbb {S}\mathcal {E}_{u(x)}\simeq \mathbb {S} u(x)$
there exists a
$[q]\in \mathbb {S}\mathcal {E}_{u(x)}\simeq \mathbb {S} u(x)$
there exists a
![]() $v\in T_xM$
such that
$v\in T_xM$
such that
![]() $\phi (v)=q$
. The element
$\phi (v)=q$
. The element
![]() $\mathrm {w}=\psi (v)$
then satisfies the required conditions, so this finishes the proof.
$\mathrm {w}=\psi (v)$
then satisfies the required conditions, so this finishes the proof.
Now let us construct the maps
![]() $\phi $
and
$\phi $
and
![]() $\psi $
. We first show that for all
$\psi $
. We first show that for all
![]() $v\in T_xM\setminus \lbrace 0\rbrace $
we can define
$v\in T_xM\setminus \lbrace 0\rbrace $
we can define
![]() $\phi (v)$
and
$\phi (v)$
and
![]() $\psi (v)$
, and then we explain how to glue these maps together to get a continuous map.
$\psi (v)$
, and then we explain how to glue these maps together to get a continuous map.
Since u is a fitting immersion, the point
![]() $(iii)$
of Proposition 3.12 implies that given
$(iii)$
of Proposition 3.12 implies that given
![]() $v_0\in T_xM$
one can construct
$v_0\in T_xM$
one can construct
![]() $\phi (v_0)\in u^*\mathcal {E}_{x}$
and
$\phi (v_0)\in u^*\mathcal {E}_{x}$
and
![]() $\psi (v_0)\in T_{\phi (v_0)} u^*\mathcal {E}$
such that
$\psi (v_0)\in T_{\phi (v_0)} u^*\mathcal {E}$
such that
![]() $\mathrm {d}\pi (\psi (v_0))$
is positive and
$\mathrm {d}\pi (\psi (v_0))$
is positive and
![]() $\mathrm {d}\operatorname {\mathrm {pr}}\left ( \psi (v_0)\right )=v_0$
.
$\mathrm {d}\operatorname {\mathrm {pr}}\left ( \psi (v_0)\right )=v_0$
.
Note that the condition that
![]() $\mathrm {d}\pi (\psi (v))$
is positive is an open condition and the condition that
$\mathrm {d}\pi (\psi (v))$
is positive is an open condition and the condition that
![]() $\mathrm {d}\operatorname {\mathrm {pr}}\left ( \psi (v)\right )=v$
requires that
$\mathrm {d}\operatorname {\mathrm {pr}}\left ( \psi (v)\right )=v$
requires that
![]() $\psi $
is a section of an affine sub-bundle. Hence for every
$\psi $
is a section of an affine sub-bundle. Hence for every
![]() $v\in T_xM\setminus \lbrace 0\rbrace $
we can find a small neighborhood
$v\in T_xM\setminus \lbrace 0\rbrace $
we can find a small neighborhood
![]() $\mathcal {S}$
in a sphere in
$\mathcal {S}$
in a sphere in
![]() $T_xM$
containing
$T_xM$
containing
![]() $v_0$
on which we can define
$v_0$
on which we can define
![]() $\phi $
and a lift
$\phi $
and a lift
![]() $\psi $
such that
$\psi $
such that
![]() $\mathrm {d}\pi (\psi (v))$
is positive and
$\mathrm {d}\pi (\psi (v))$
is positive and
![]() $\mathrm {d}\operatorname {\mathrm {pr}}\left ( \psi (v)\right )=v$
for all
$\mathrm {d}\operatorname {\mathrm {pr}}\left ( \psi (v)\right )=v$
for all
![]() $v\in \mathcal {S}$
. We take
$v\in \mathcal {S}$
. We take
![]() $\mathcal {S}$
small enough so that it does not contain any antipodal pair of points.
$\mathcal {S}$
small enough so that it does not contain any antipodal pair of points.
We define U to be the set of nonzero elements
![]() $\lambda v$
for all
$\lambda v$
for all
![]() $\lambda \in \mathbb {R}$
and
$\lambda \in \mathbb {R}$
and
![]() $v\in \mathcal {S}$
, and we extend
$v\in \mathcal {S}$
, and we extend
![]() $\phi $
and
$\phi $
and
![]() $\psi $
to U in a homogeneous way. We define
$\psi $
to U in a homogeneous way. We define
![]() $\phi $
on U so that
$\phi $
on U so that
![]() $\phi _i(\lambda v)=\lambda \phi _i(v)$
for all
$\phi _i(\lambda v)=\lambda \phi _i(v)$
for all
![]() $\lambda \in \mathbb {R}$
nonzero and
$\lambda \in \mathbb {R}$
nonzero and
![]() $v\in \mathcal {S}$
. We set
$v\in \mathcal {S}$
. We set
![]() $\psi (\lambda v)=\lambda (\mathrm {d}m_\lambda ) \psi _i(v)$
for
$\psi (\lambda v)=\lambda (\mathrm {d}m_\lambda ) \psi _i(v)$
for
![]() $\lambda \in \mathbb {R}$
, where
$\lambda \in \mathbb {R}$
, where
![]() $m_\lambda $
is the multiplication by
$m_\lambda $
is the multiplication by
![]() $\lambda $
on
$\lambda $
on
![]() $u^*\mathcal {E}_x$
. Note that
$u^*\mathcal {E}_x$
. Note that
![]() $\mathrm {d}\pi \left (\psi _i(\lambda v)\right )=\lambda ^2\mathrm {d}\pi \left (\psi _i(v)\right )$
is positive and
$\mathrm {d}\pi \left (\psi _i(\lambda v)\right )=\lambda ^2\mathrm {d}\pi \left (\psi _i(v)\right )$
is positive and
![]() $\mathrm {d}\operatorname {\mathrm {pr}}\left ( \psi _i( \lambda v)\right )=\lambda v$
for all
$\mathrm {d}\operatorname {\mathrm {pr}}\left ( \psi _i( \lambda v)\right )=\lambda v$
for all
![]() $\lambda v\in U$
. Indeed
$\lambda v\in U$
. Indeed
![]() $\pi \circ m_\lambda =\lambda \pi $
so
$\pi \circ m_\lambda =\lambda \pi $
so
![]() $\mathrm {d}\pi \circ \mathrm {d}m_\lambda =\lambda \mathrm {d}\pi $
and
$\mathrm {d}\pi \circ \mathrm {d}m_\lambda =\lambda \mathrm {d}\pi $
and
![]() $p\circ m_\lambda =p$
so
$p\circ m_\lambda =p$
so
![]() $\mathrm {d}\operatorname {\mathrm {pr}}\circ \mathrm {d}m_\lambda =\mathrm {d}\operatorname {\mathrm {pr}}$
.
$\mathrm {d}\operatorname {\mathrm {pr}}\circ \mathrm {d}m_\lambda =\mathrm {d}\operatorname {\mathrm {pr}}$
.
We therefore can construct an open cover
![]() $\lbrace U_i\rbrace _{i\in I}$
of
$\lbrace U_i\rbrace _{i\in I}$
of
![]() $T_xM$
and continuous maps
$T_xM$
and continuous maps
![]() $\phi _i:U_i\to \mathbb {S} u^*\mathcal {E}\subset u^*\mathcal {E}$
, and lifts
$\phi _i:U_i\to \mathbb {S} u^*\mathcal {E}\subset u^*\mathcal {E}$
, and lifts
![]() $\psi _i:U_i\to Tu^*\mathcal {E}$
such that
$\psi _i:U_i\to Tu^*\mathcal {E}$
such that
![]() $\mathrm {d}\pi (\psi _i(v))$
is positive and
$\mathrm {d}\pi (\psi _i(v))$
is positive and
![]() $\mathrm {d}\operatorname {\mathrm {pr}}\left ( \psi _i(v)\right )=v$
for any
$\mathrm {d}\operatorname {\mathrm {pr}}\left ( \psi _i(v)\right )=v$
for any
![]() $i\in I$
and
$i\in I$
and
![]() $v\in U_i$
. The
$v\in U_i$
. The
![]() $U_i$
can be assumed invariant by scalar multiplication, and
$U_i$
can be assumed invariant by scalar multiplication, and
![]() $\phi $
and
$\phi $
and
![]() $\psi $
satisfy the aforementioned homogeneity conditions.
$\psi $
satisfy the aforementioned homogeneity conditions.
We now glue these maps together. Let
![]() $\chi _i:U_i\to [0,1]$
for
$\chi _i:U_i\to [0,1]$
for
![]() $i\in I$
be a family of functions that forms a locally finite partition of the unit. We define:
$i\in I$
be a family of functions that forms a locally finite partition of the unit. We define:
Let us check that
![]() $\phi (v)$
is always nonzero. This is where we use that
$\phi (v)$
is always nonzero. This is where we use that
![]() $\mathrm {d}\operatorname {\mathrm {pr}}\left ( \psi _i(v)\right )=v$
for
$\mathrm {d}\operatorname {\mathrm {pr}}\left ( \psi _i(v)\right )=v$
for
![]() $i\in I$
, and we also use that the fitting immersion u is defining a smooth fibration of the cone
$i\in I$
, and we also use that the fitting immersion u is defining a smooth fibration of the cone
![]() $S^2 V^{>0}$
. Let
$S^2 V^{>0}$
. Let
![]() $\gamma :\mathbb {R} \to M$
be a curve such that
$\gamma :\mathbb {R} \to M$
be a curve such that
![]() $\gamma (0)=x$
and
$\gamma (0)=x$
and
![]() $\gamma '(0)=v$
. For all
$\gamma '(0)=v$
. For all
![]() $t\in \mathbb {R}$
the intersection
$t\in \mathbb {R}$
the intersection
![]() $ u^\circ (\gamma (t))\cap S^2V^{>0}$
is a nonempty convex set, so we can construct a section
$ u^\circ (\gamma (t))\cap S^2V^{>0}$
is a nonempty convex set, so we can construct a section
![]() $s:t\in \mathbb {R} \mapsto S^2V^{>0}$
of the fibration, that is, such that for all
$s:t\in \mathbb {R} \mapsto S^2V^{>0}$
of the fibration, that is, such that for all
![]() $t\in \mathbb {R}$
,
$t\in \mathbb {R}$
,
![]() $s(t)\in u^\circ (\gamma (t))$
.
$s(t)\in u^\circ (\gamma (t))$
.
Let us fix
![]() $i\in I$
. Let
$i\in I$
. Let
![]() $q:\mathbb {R}\to \mathbb {S} u^*\mathcal {E}$
be such that
$q:\mathbb {R}\to \mathbb {S} u^*\mathcal {E}$
be such that
![]() $q'(0)=\psi (v)$
, which implies that
$q'(0)=\psi (v)$
, which implies that
![]() $p\circ q(t)$
is equal to
$p\circ q(t)$
is equal to
![]() $\gamma (t)$
at the first order around
$\gamma (t)$
at the first order around
![]() $t=0$
since
$t=0$
since
![]() $\gamma '(0)=\mathrm {d}\operatorname {\mathrm {pr}}\left (\psi (v)\right )=v$
. Since
$\gamma '(0)=\mathrm {d}\operatorname {\mathrm {pr}}\left (\psi (v)\right )=v$
. Since
![]() $s(t)\in u^\circ (\gamma (t))$
, one has
$s(t)\in u^\circ (\gamma (t))$
, one has
![]() $ \pi (q(t))\cdot s(t)=0$
at the first order around
$ \pi (q(t))\cdot s(t)=0$
at the first order around
![]() $t=0$
. Taking the first derivative at
$t=0$
. Taking the first derivative at
![]() $t=0$
of this equation we get:
$t=0$
of this equation we get:
Since
![]() $\mathrm {d}\pi (\psi _i(v) )$
is positive and
$\mathrm {d}\pi (\psi _i(v) )$
is positive and
![]() $s(0)$
is a positive tensor:
$s(0)$
is a positive tensor:
Hence for all
![]() $i\in I$
,
$i\in I$
,
![]() $\pi (\phi _i(v))\cdot s'(0)<0$
and therefore
$\pi (\phi _i(v))\cdot s'(0)<0$
and therefore
![]() $\pi (\phi (v))\cdot s'(0)<0$
. In particular
$\pi (\phi (v))\cdot s'(0)<0$
. In particular
![]() $\phi (v)$
does not vanish.
$\phi (v)$
does not vanish.
In order to glue the
![]() $\psi _i$
we need to be careful since the vectors
$\psi _i$
we need to be careful since the vectors
![]() $\psi _i(v)$
do not belong to the same fiber of the tangent bundle
$\psi _i(v)$
do not belong to the same fiber of the tangent bundle
![]() $Tu^*\mathcal {E}$
. Let
$Tu^*\mathcal {E}$
. Let
![]() $\Sigma $
be the following map:
$\Sigma $
be the following map:
Given
![]() $v\in \mathbb {S} T_xM$
we set:
$v\in \mathbb {S} T_xM$
we set:
This combination still satisfies that
![]() $\mathrm {d}\pi (\psi )$
is positive, indeed:
$\mathrm {d}\pi (\psi )$
is positive, indeed:
Note that we also get the following:
 $$ \begin{align*}\mathrm{d}\operatorname{\mathrm{pr}}(\psi(v))=\sum_{i\in I}\chi_i(v)\mathrm{d}\operatorname{\mathrm{pr}}(\psi_i(v))=\left(\sum_{i\in I}\chi_i(v)\right)v=v.\end{align*} $$
$$ \begin{align*}\mathrm{d}\operatorname{\mathrm{pr}}(\psi(v))=\sum_{i\in I}\chi_i(v)\mathrm{d}\operatorname{\mathrm{pr}}(\psi_i(v))=\left(\sum_{i\in I}\chi_i(v)\right)v=v.\end{align*} $$
This concludes the construction of
![]() $\phi $
and
$\phi $
and
![]() $\psi $
, and hence this concludes the proof.
$\psi $
, and hence this concludes the proof.
To prove Proposition 4.8 we use the directions
![]() $\mathrm {w}$
from Lemma 4.9 and we glue these vectors into a vector field using once again a partition of the unit. We construct the vector field
$\mathrm {w}$
from Lemma 4.9 and we glue these vectors into a vector field using once again a partition of the unit. We construct the vector field
![]() $W:\mathbb {S} u^*\mathcal {E}\to T\mathbb {S} u^*\mathcal {E}$
in a similar manner as
$W:\mathbb {S} u^*\mathcal {E}\to T\mathbb {S} u^*\mathcal {E}$
in a similar manner as
![]() $\psi :\mathbb {S} TM\to T\mathbb {S} u^*\mathcal {E}$
. Morally “
$\psi :\mathbb {S} TM\to T\mathbb {S} u^*\mathcal {E}$
. Morally “
![]() $W=\psi \circ \phi ^{-1}$
,” but the map
$W=\psi \circ \phi ^{-1}$
,” but the map
![]() $\phi $
constructed previously is not a priori bijective.
$\phi $
constructed previously is not a priori bijective.
Proof of Proposition 4.8
We construct a continuous vector field
![]() $\mathrm {W}$
over
$\mathrm {W}$
over
![]() $u^*\mathcal {E}$
, except the zero section that is homogeneous, that is, such that for all
$u^*\mathcal {E}$
, except the zero section that is homogeneous, that is, such that for all
![]() $x\in M$
and non zero
$x\in M$
and non zero
![]() $q\in u(x)$
one has
$q\in u(x)$
one has
![]() $W_{\lambda q}=\mathrm {d}(m_\lambda )W_q$
for all
$W_{\lambda q}=\mathrm {d}(m_\lambda )W_q$
for all
![]() $\lambda \in \mathbb {R}^{> 0}$
, where
$\lambda \in \mathbb {R}^{> 0}$
, where
![]() $m_\lambda $
is the multiplication by
$m_\lambda $
is the multiplication by
![]() $\lambda $
on
$\lambda $
on
![]() $\mathcal {E}$
. Such a vector field defines a vector field
$\mathcal {E}$
. Such a vector field defines a vector field
![]() $\overline {W}$
on
$\overline {W}$
on
![]() $\mathbb {S} u^*\mathcal {E}$
. We require moreover that
$\mathbb {S} u^*\mathcal {E}$
. We require moreover that
![]() $\mathrm {d}\pi (W)$
is always positive.
$\mathrm {d}\pi (W)$
is always positive.
Given any nonzero
![]() $q_0\in u^*\mathcal {E}$
, Lemma 4.9 provides the existence of some
$q_0\in u^*\mathcal {E}$
, Lemma 4.9 provides the existence of some
![]() $\mathrm {w}_0\in T_{(u(x),q)}\mathcal {E}$
for all
$\mathrm {w}_0\in T_{(u(x),q)}\mathcal {E}$
for all
![]() $(x,q)\in u^*\mathcal {E}$
such that:
$(x,q)\in u^*\mathcal {E}$
such that:
-
(i)
 $\mathrm {d}\operatorname {\mathrm {pr}}(\mathrm {w}_0)\in \mathrm {d}u(T_xM)$
,
$\mathrm {d}\operatorname {\mathrm {pr}}(\mathrm {w}_0)\in \mathrm {d}u(T_xM)$
, -
(ii)
 $\mathrm {d}\pi (\mathrm {w}_0)$
is positive.
$\mathrm {d}\pi (\mathrm {w}_0)$
is positive.
Property
![]() $(i)$
implies that
$(i)$
implies that
![]() $\mathrm {w}_0$
defines a vector in
$\mathrm {w}_0$
defines a vector in
![]() $T_{x,q_0}u^*\mathcal {E}$
. For each such
$T_{x,q_0}u^*\mathcal {E}$
. For each such
![]() $q_0$
one can find a neighborhood U of it in
$q_0$
one can find a neighborhood U of it in
![]() $u^*\mathcal {E}$
that is invariant by the
$u^*\mathcal {E}$
that is invariant by the
![]() $\mathbb {R}^{> 0}$
-action, and on which one can define a map W satisfying
$\mathbb {R}^{> 0}$
-action, and on which one can define a map W satisfying
![]() $(i)$
as well as the homogeneity condition
$(i)$
as well as the homogeneity condition
![]() $W_{\lambda q}=\mathrm {d}(m_\lambda )W_q$
. Condition
$W_{\lambda q}=\mathrm {d}(m_\lambda )W_q$
. Condition
![]() $(ii)$
being an open condition invariant by the action of
$(ii)$
being an open condition invariant by the action of
![]() $m_\lambda $
it is satisfied automatically for U small enough.
$m_\lambda $
it is satisfied automatically for U small enough.
Using a partition of the unit as in Lemma 4.9 we construct the desired vector field on
![]() $u^*\mathcal {E}$
. Note that both property
$u^*\mathcal {E}$
. Note that both property
![]() $(i)$
and the homogeneity are preserved by linear combinations, and
$(i)$
and the homogeneity are preserved by linear combinations, and
![]() $(ii)$
is preserved by positive combinations.
$(ii)$
is preserved by positive combinations.
Finally note that the collection
![]() $U_i$
as well as the partition of the unity can be chosen to be
$U_i$
as well as the partition of the unity can be chosen to be
![]() $\rho $
-equivariant, so that the vector field W is also
$\rho $
-equivariant, so that the vector field W is also
![]() $\rho $
-equivariant, and hence also the fitting flow
$\rho $
-equivariant, and hence also the fitting flow
![]() $\Phi $
.
$\Phi $
.
5 The Anosov property and fibrations
In this section we show that the existence of an equivariant map of pencils that admits a fitting flow implies that the representation is Anosov. Moreover we describe the domain that is fibered in
![]() $\mathbb {RP}^{2n-1}$
. Finally we apply this to show that some quasi-Fuchsian representations do not admit equivariant maps that admit a fitting flow.
$\mathbb {RP}^{2n-1}$
. Finally we apply this to show that some quasi-Fuchsian representations do not admit equivariant maps that admit a fitting flow.
5.1 The Anosov property
In order to show that a uniform contraction is taking place along the flow lines of the fitting flow, we define a way to measure the distance between two quadric hypersurfaces nested into one another. The characterization of Anosov representations that we use is similar to the characterization in terms of inclusion of multicones from [Reference BochiBPS19].
Let
![]() $\mathbb {S}\mathcal {Q}^{{\operatorname {\mathrm {mix}}}}$
be the set of quadrics that are not semi-positive or semi-negative up to a positive scalar.
$\mathbb {S}\mathcal {Q}^{{\operatorname {\mathrm {mix}}}}$
be the set of quadrics that are not semi-positive or semi-negative up to a positive scalar.
If we fix an affine chart of L so that
![]() $\ell _1,\ell _2,\ell _2',\ell _1'$
correspond to the real numbers
$\ell _1,\ell _2,\ell _2',\ell _1'$
correspond to the real numbers
![]() $x_1'< x_2'\leq x_2< x_1$
, the cross ratio
$x_1'< x_2'\leq x_2< x_1$
, the cross ratio
![]() $[\ell _1,\ell _2,\ell _2',\ell _1']$
is defined as:
$[\ell _1,\ell _2,\ell _2',\ell _1']$
is defined as:
 $$ \begin{align}[\ell_1,\ell_2,\ell_2',\ell_1']=\frac{x_2-x_1'}{x_2-x_2'}\times\frac{x_1-x_2'}{x_1-x_1'}. \end{align} $$
$$ \begin{align}[\ell_1,\ell_2,\ell_2',\ell_1']=\frac{x_2-x_1'}{x_2-x_2'}\times\frac{x_1-x_2'}{x_1-x_1'}. \end{align} $$
Another equivalent definition, if we take nonzero representatives
![]() $v_1,v_2,v_2',v_1'$
of
$v_1,v_2,v_2',v_1'$
of
![]() $\ell _1,\ell _2,\ell _2',\ell _1'$
:
$\ell _1,\ell _2,\ell _2',\ell _1'$
:
 $$ \begin{align*}[\ell_1,\ell_2,\ell_2',\ell_1']=\frac{v_2\wedge v_1'}{v_2\wedge v_2'}\times\frac{v_1\wedge v_2'}{v_1\wedge v_1'} .\end{align*} $$
$$ \begin{align*}[\ell_1,\ell_2,\ell_2',\ell_1']=\frac{v_2\wedge v_1'}{v_2\wedge v_2'}\times\frac{v_1\wedge v_2'}{v_1\wedge v_1'} .\end{align*} $$
This expression makes sense as
![]() $\bigwedge ^2 L\simeq \mathbb {R}$
, and it is independent of the chosen identification. The equivalence betweens these formulations is due to the fact that if
$\bigwedge ^2 L\simeq \mathbb {R}$
, and it is independent of the chosen identification. The equivalence betweens these formulations is due to the fact that if
![]() $v_1=e_1+x_1e_2$
and
$v_1=e_1+x_1e_2$
and
![]() $v_2=e_1+x_2e_2$
then
$v_2=e_1+x_2e_2$
then
![]() $v_2\wedge v_1=(x_2-x_1)e_2\wedge e_1$
.
$v_2\wedge v_1=(x_2-x_1)e_2\wedge e_1$
.
Definition/Proposition 5.1. Let
![]() $[q_1],[q_2]\in \mathbb {S}\mathcal {Q}^{\operatorname {\mathrm {mix}}}$
be such that for some choice of representatives, the difference
$[q_1],[q_2]\in \mathbb {S}\mathcal {Q}^{\operatorname {\mathrm {mix}}}$
be such that for some choice of representatives, the difference
![]() $q_2-q_1$
is positive. For every projective line L intersecting
$q_2-q_1$
is positive. For every projective line L intersecting
![]() $\lbrace q_1> 0\rbrace $
and
$\lbrace q_1> 0\rbrace $
and
![]() $\lbrace q_2< 0\rbrace $
we can define
$\lbrace q_2< 0\rbrace $
we can define
![]() $\ell _1$
and
$\ell _1$
and
![]() $\ell _1'$
are the zeros of
$\ell _1'$
are the zeros of
![]() $q_1$
on L and
$q_1$
on L and
![]() $\ell ^{\prime }_1$
and
$\ell ^{\prime }_1$
and
![]() $\ell _2'$
and the zeros of
$\ell _2'$
and the zeros of
![]() $q_2$
on L so that the points
$q_2$
on L so that the points
![]() $\ell _1,\ell _2,\ell _2',\ell _1'\in \mathbb {P}(V)$
are cyclically in this order on L. We define the cross-ratio distance
$\ell _1,\ell _2,\ell _2',\ell _1'\in \mathbb {P}(V)$
are cyclically in this order on L. We define the cross-ratio distance
![]() $\text {cr}([q_2],[q_1])\in [1, \infty )$
between
$\text {cr}([q_2],[q_1])\in [1, \infty )$
between
![]() $[q_2]$
and
$[q_2]$
and
![]() $[q_1]$
as the minimum of the cross ratio
$[q_1]$
as the minimum of the cross ratio
![]() $[\ell _1,\ell _2,\ell _2',\ell _1']$
for any such projective line L, which is well defined and in
$[\ell _1,\ell _2,\ell _2',\ell _1']$
for any such projective line L, which is well defined and in
![]() $(1,\infty )$
.
$(1,\infty )$
.
We now verify that this minimum exists and is in
![]() $(1,\infty )$
.
$(1,\infty )$
.
Proof. First note that the assumption
![]() $q_2-q_1$
is positive implies that
$q_2-q_1$
is positive implies that
![]() $\lbrace q_1\geq 0 \rbrace \subset \lbrace q_2>0\rbrace $
and
$\lbrace q_1\geq 0 \rbrace \subset \lbrace q_2>0\rbrace $
and
![]() $\lbrace q_2\leq 0 \rbrace \subset \lbrace q_1<0\rbrace $
. If L intersects
$\lbrace q_2\leq 0 \rbrace \subset \lbrace q_1<0\rbrace $
. If L intersects
![]() $\lbrace q_1>0\rbrace $
and
$\lbrace q_1>0\rbrace $
and
![]() $\lbrace q_1< 0 \rbrace $
then the quadratic forms
$\lbrace q_1< 0 \rbrace $
then the quadratic forms
![]() $q_1$
and
$q_1$
and
![]() $q_2$
are both positive on some points and negative on some points of L, and hence they both admit exactly two zeroes on L. These zeroes, denoted respectively
$q_2$
are both positive on some points and negative on some points of L, and hence they both admit exactly two zeroes on L. These zeroes, denoted respectively
![]() $\ell _1$
,
$\ell _1$
,
![]() $\ell _1'$
for
$\ell _1'$
for
![]() $q_1$
and
$q_1$
and
![]() $\ell _2$
,
$\ell _2$
,
![]() $\ell _2'$
for
$\ell _2'$
for
![]() $q_2$
are in the following cyclic order on L up to exchanging
$q_2$
are in the following cyclic order on L up to exchanging
![]() $\ell _1$
and
$\ell _1$
and
![]() $\ell _1'$
:
$\ell _1'$
:
![]() $(\ell _1,\ell _2,\ell _2',\ell _1')$
. One can refer to Figure 1 where
$(\ell _1,\ell _2,\ell _2',\ell _1')$
. One can refer to Figure 1 where
![]() $\lbrace q_i>0\rbrace $
is the interior of the corresponding ellipse.
$\lbrace q_i>0\rbrace $
is the interior of the corresponding ellipse.

Figure 1 Illustration of Proposition 5.2.
Consider the compact space X of projective lines L intersecting
![]() $\lbrace q_1\geq 0\rbrace $
and
$\lbrace q_1\geq 0\rbrace $
and
![]() $\lbrace q_2\leq 0\rbrace $
. For every such line we can define the lines
$\lbrace q_2\leq 0\rbrace $
. For every such line we can define the lines
![]() $\ell _1,\ell _1'$
and
$\ell _1,\ell _1'$
and
![]() $\ell _2, \ell _2'$
as in previously where
$\ell _2, \ell _2'$
as in previously where
![]() $\ell _1,\ell _1'\neq \ell _2,\ell _2'$
but eventually
$\ell _1,\ell _1'\neq \ell _2,\ell _2'$
but eventually
![]() $\ell _1=\ell _1'$
or
$\ell _1=\ell _1'$
or
![]() $\ell _2=\ell _2'$
which occur respectively exactly if L intersects trivially
$\ell _2=\ell _2'$
which occur respectively exactly if L intersects trivially
![]() $\lbrace q_1>0\rbrace $
or
$\lbrace q_1>0\rbrace $
or
![]() $\lbrace q_2>0\rbrace $
. Indeed in these cases the quadratic forms
$\lbrace q_2>0\rbrace $
. Indeed in these cases the quadratic forms
![]() $q_i$
are semi-positive or semi negative on L and hence have a double zero. By looking at the formula (2) on an affine chart such that
$q_i$
are semi-positive or semi negative on L and hence have a double zero. By looking at the formula (2) on an affine chart such that
![]() $x_1'< x_2'\leq x_2< x_1$
we see the cross ratio
$x_1'< x_2'\leq x_2< x_1$
we see the cross ratio
![]() $[\ell _1,\ell _2,\ell _2',\ell _1']$
is in
$[\ell _1,\ell _2,\ell _2',\ell _1']$
is in
![]() $(1,\infty ]$
. This ratio is finite if and only if
$(1,\infty ]$
. This ratio is finite if and only if
![]() $\ell _1\neq \ell _1'$
and
$\ell _1\neq \ell _1'$
and
![]() $\ell _2\neq \ell _2'$
which occurs exactly when L belongs to the interior of X, that is, when L intersects
$\ell _2\neq \ell _2'$
which occurs exactly when L belongs to the interior of X, that is, when L intersects
![]() $\lbrace q_1> 0\rbrace $
and
$\lbrace q_1> 0\rbrace $
and
![]() $\lbrace q_2< 0\rbrace $
. Finally note that this ratio depends continuously on
$\lbrace q_2< 0\rbrace $
. Finally note that this ratio depends continuously on
![]() $L\in X$
and that the interior of X is nonempty since
$L\in X$
and that the interior of X is nonempty since
![]() $q_1$
and
$q_1$
and
![]() $q_2$
are mixed. Therefore the minimum on X is well defined in
$q_2$
are mixed. Therefore the minimum on X is well defined in
![]() $ (1,\infty )$
and is reached on the interior of X.
$ (1,\infty )$
and is reached on the interior of X.
The logarithm of this quantity satisfies a reversed triangular inequality.
Proposition 5.2. Let
![]() $[q_1],[q_2],[q_3]\in \mathbb {S}\mathcal {Q}^{\operatorname {\mathrm {mix}}}$
be such that
$[q_1],[q_2],[q_3]\in \mathbb {S}\mathcal {Q}^{\operatorname {\mathrm {mix}}}$
be such that
![]() $q_3-q_2$
and
$q_3-q_2$
and
![]() $q_2-q_1$
are positive. Then:
$q_2-q_1$
are positive. Then:
We illustrate this proposition and its proof in Figure 1. This figure illustrates 3 quadrics of signature
![]() $(1,2)$
in
$(1,2)$
in
![]() $\mathbb {RP}^2$
. In these pictures the quadrics are positive on the inside of the ellipse they define.
$\mathbb {RP}^2$
. In these pictures the quadrics are positive on the inside of the ellipse they define.
Proof. Pick any projective line that crosses
![]() $\lbrace q_1>0\rbrace $
and
$\lbrace q_1>0\rbrace $
and
![]() $\lbrace q_3<0\rbrace $
. Let the intersections of L with the zeroes of
$\lbrace q_3<0\rbrace $
. Let the intersections of L with the zeroes of
![]() $q_1$
,
$q_1$
,
![]() $q_2$
and
$q_2$
and
![]() $q_3$
be respectively
$q_3$
be respectively
![]() $(\ell _1,\ell _2,\ell _3,\ell _3',\ell _2',\ell _1')$
, counted with multiplicity and cyclically ordered. We fix an affine chart for L such that this tuple corresponds to the tuple
$(\ell _1,\ell _2,\ell _3,\ell _3',\ell _2',\ell _1')$
, counted with multiplicity and cyclically ordered. We fix an affine chart for L such that this tuple corresponds to the tuple
![]() $x_3'< x_2'<x_1'\leq x_1<x_2<x_3$
of real numbers. This yields the following:
$x_3'< x_2'<x_1'\leq x_1<x_2<x_3$
of real numbers. This yields the following:
 $$ \begin{align*}[\ell_1,\ell_3,\ell_3',\ell_1']& =\frac{x_3-x_1'}{x_3-x_3'}\times\frac{x_1-x_3'}{x_1-x_1'} .\\
[\ell_1,\ell_3,\ell_3',\ell_1']& = \left( \frac{x_3-x_1'}{x_3-x_2'}\times\frac{x_1-x_2'}{x_1-x_1'}\right)\times \left(\frac{x_3-x_2'}{x_3-x_3'}\times\frac{x_1-x_3'}{x_1-x_2'}\right) .\end{align*} $$
$$ \begin{align*}[\ell_1,\ell_3,\ell_3',\ell_1']& =\frac{x_3-x_1'}{x_3-x_3'}\times\frac{x_1-x_3'}{x_1-x_1'} .\\
[\ell_1,\ell_3,\ell_3',\ell_1']& = \left( \frac{x_3-x_1'}{x_3-x_2'}\times\frac{x_1-x_2'}{x_1-x_1'}\right)\times \left(\frac{x_3-x_2'}{x_3-x_3'}\times\frac{x_1-x_3'}{x_1-x_2'}\right) .\end{align*} $$
Note that if
![]() $B>A>0$
, for all
$B>A>0$
, for all
![]() $c>0$
one has
$c>0$
one has
![]() $\frac {A}{B}\leq \frac {A+c}{B+c}$
and respectively
$\frac {A}{B}\leq \frac {A+c}{B+c}$
and respectively
![]() $\frac {B+c}{A+c}\leq \frac {B}{A}$
. Hence, due to the ordering of the tuple, we have the following inequalities by setting respectively
$\frac {B+c}{A+c}\leq \frac {B}{A}$
. Hence, due to the ordering of the tuple, we have the following inequalities by setting respectively
![]() $A=x_2-x_1'$
,
$A=x_2-x_1'$
,
![]() $B=x_2-x_2'$
,
$B=x_2-x_2'$
,
![]() $c=x_3-x_2$
and
$c=x_3-x_2$
and
![]() $A=x_1-x_2'$
,
$A=x_1-x_2'$
,
![]() $B=x_1-x_3'$
,
$B=x_1-x_3'$
,
![]() $c=x_2-x_1$
:
$c=x_2-x_1$
:
 $$ \begin{align*}\frac{x_2-x_1'}{x_2-x_2'}\leq \frac{x_3-x_1'}{x_3-x_2'}\;,\;\frac{x_2-x_3'}{x_2-x_2'} \leq \frac{x_1-x_3'}{x_1-x_2'}.\end{align*} $$
$$ \begin{align*}\frac{x_2-x_1'}{x_2-x_2'}\leq \frac{x_3-x_1'}{x_3-x_2'}\;,\;\frac{x_2-x_3'}{x_2-x_2'} \leq \frac{x_1-x_3'}{x_1-x_2'}.\end{align*} $$
Hence we obtain:
 $$ \begin{align*}\text{cr}([q_2],[q_1])\leq [\ell_1,\ell_2,\ell_2',\ell_1']&=\frac{x_2-x_1'}{x_2-x_2'}\times\frac{x_1-x_2'}{x_1-x_1'} \leq \frac{x_3-x_1'}{x_3-x_2'}\times\frac{x_1-x_2'}{x_1-x_1'} .\\\text{cr}([q_3],[q_2])\leq [\ell_2,\ell_3,\ell_3',\ell_2']&=\frac{x_3-x_2'}{x_3-x_3'}\times\frac{x_2-x_3'}{x_2-x_2'} \leq \frac{x_3-x_2'}{x_3-x_3'}\times\frac{x_1-x_3'}{x_1-x_2'}.\end{align*} $$
$$ \begin{align*}\text{cr}([q_2],[q_1])\leq [\ell_1,\ell_2,\ell_2',\ell_1']&=\frac{x_2-x_1'}{x_2-x_2'}\times\frac{x_1-x_2'}{x_1-x_1'} \leq \frac{x_3-x_1'}{x_3-x_2'}\times\frac{x_1-x_2'}{x_1-x_1'} .\\\text{cr}([q_3],[q_2])\leq [\ell_2,\ell_3,\ell_3',\ell_2']&=\frac{x_3-x_2'}{x_3-x_3'}\times\frac{x_2-x_3'}{x_2-x_2'} \leq \frac{x_3-x_2'}{x_3-x_3'}\times\frac{x_1-x_3'}{x_1-x_2'}.\end{align*} $$
Hence one has
![]() $[\ell _1,\ell _3,\ell _3',\ell _1']\geq \text {cr}([q_2],[q_1])\text {cr}([q_3],[q_2])$
for every such projective line L.
$[\ell _1,\ell _3,\ell _3',\ell _1']\geq \text {cr}([q_2],[q_1])\text {cr}([q_3],[q_2])$
for every such projective line L.
Therefore
![]() $\text {cr}([q_3],[q_1])\geq \text {cr}([q_3],[q_2])\text {cr}([q_2],[q_1])$
.
$\text {cr}([q_3],[q_1])\geq \text {cr}([q_3],[q_2])\text {cr}([q_2],[q_1])$
.
A sequence of quadrics such that the cross ratio distance between the first and last quadric goes to
![]() $+\infty $
satisfies that the intersection of all half-spaces determined by the quadrics is a projective subspace.
$+\infty $
satisfies that the intersection of all half-spaces determined by the quadrics is a projective subspace.
Proposition 5.3. Let
![]() $(q_n)_{n\in \mathbb {N}}$
be a sequence of quadrics such that
$(q_n)_{n\in \mathbb {N}}$
be a sequence of quadrics such that
![]() $q_{n+1}-q_n$
is positive for all
$q_{n+1}-q_n$
is positive for all
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $\text {cr}([q_{n}],[q_0])$
goes to
$\text {cr}([q_{n}],[q_0])$
goes to
![]() $+\infty $
. Then
$+\infty $
. Then
![]() $\bigcap _{n\in \mathbb {N}} \lbrace q_n\leq 0\rbrace \subset \mathbb {P}(V)$
is a projective subspace.
$\bigcap _{n\in \mathbb {N}} \lbrace q_n\leq 0\rbrace \subset \mathbb {P}(V)$
is a projective subspace.
This proposition is proven in [Reference Bochi and GourmelonBG09]. We write a version of the argument here for the sake of completeness. We illustrate this proposition with quadrics of signature
![]() $(1,2)$
in
$(1,2)$
in
![]() $\mathbb {RP}^2$
in Figure 2.
$\mathbb {RP}^2$
in Figure 2.

Figure 2 Illustration of Proposition 5.3.
Proof. The intersection
![]() $I=\bigcap _{n\in \mathbb {N}} \lbrace q_n\leq 0\rbrace $
is a compact nonempty subset. Let
$I=\bigcap _{n\in \mathbb {N}} \lbrace q_n\leq 0\rbrace $
is a compact nonempty subset. Let
![]() $x\neq y\in I$
and let L be the projective line from x to y. Suppose that there exists
$x\neq y\in I$
and let L be the projective line from x to y. Suppose that there exists
![]() $z\in L$
such that
$z\in L$
such that
![]() $z\notin I$
. Without any loss of generality one can assume that the open interval
$z\notin I$
. Without any loss of generality one can assume that the open interval
![]() $S\subset L$
bounded by
$S\subset L$
bounded by
![]() $x,y$
and containing z does not intersect I. Indeed one can otherwise replace
$x,y$
and containing z does not intersect I. Indeed one can otherwise replace
![]() $x,y$
by the points on
$x,y$
by the points on
![]() $L\cap I$
closest to z on both sides.
$L\cap I$
closest to z on both sides.
Since
![]() $z\notin I$
there exist
$z\notin I$
there exist
![]() $n_0\in \mathbb {N}$
such that
$n_0\in \mathbb {N}$
such that
![]() $q_{n_0}$
is positive on z. For
$q_{n_0}$
is positive on z. For
![]() $n\geq n_0$
, let
$n\geq n_0$
, let
![]() $z_1,z_2$
be the two intersections of L with the zeroes of
$z_1,z_2$
be the two intersections of L with the zeroes of
![]() $q_n$
so that the points
$q_n$
so that the points
![]() $(x,z_n^-,z,z_n^+,y)$
are cyclically ordered. The sequences
$(x,z_n^-,z,z_n^+,y)$
are cyclically ordered. The sequences
![]() $(z_n^-)$
and
$(z_n^-)$
and
![]() $(z_n^+)$
are monotonic in S and must converge to x and y since
$(z_n^+)$
are monotonic in S and must converge to x and y since
![]() $S\cap I=\emptyset $
. The value of
$S\cap I=\emptyset $
. The value of
![]() $\text {cr}([q_{n_0}],[q_n])$
is bounded from above by the cross ratio
$\text {cr}([q_{n_0}],[q_n])$
is bounded from above by the cross ratio
![]() $[z_{n_0}^+,z_n^+,z_n^-,z_{n_0}^-]$
, which in turn converges to the cross ratio
$[z_{n_0}^+,z_n^+,z_n^-,z_{n_0}^-]$
, which in turn converges to the cross ratio
![]() $[z_{n_0}^+,x,y,z_{n_0}^-]<\infty $
when n goes to
$[z_{n_0}^+,x,y,z_{n_0}^-]<\infty $
when n goes to
![]() $+\infty $
. This contradicts the fact that
$+\infty $
. This contradicts the fact that
![]() $\text {cr}([q_{n}],[q_0])$
goes to
$\text {cr}([q_{n}],[q_0])$
goes to
![]() $+\infty $
. Hence for every pair of points in I, the associated projective line is contained in I. In particular I is a projective subspace.
$+\infty $
. Hence for every pair of points in I, the associated projective line is contained in I. In particular I is a projective subspace.

Figure 3 Illustration of the proof of Theorem 5.4.
Let
![]() $\operatorname {\mathrm {Gr}}_d^{(n,n)}(\mathcal {Q})\subset \operatorname {\mathrm {Gr}}_d^{\text {mix}}(\mathcal {Q})$
be the open subset of
$\operatorname {\mathrm {Gr}}_d^{(n,n)}(\mathcal {Q})\subset \operatorname {\mathrm {Gr}}_d^{\text {mix}}(\mathcal {Q})$
be the open subset of
![]() $\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
of pencils P such that for all
$\operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
of pencils P such that for all
![]() $q\in P$
nonzero, q has signature
$q\in P$
nonzero, q has signature
![]() $(n,n)$
. We now apply the previous results to prove that representations that admit an equivariant fitting immersion in this open set, and more generally a fitting map with a fitting flow, are Anosov. For examples of such immersions, see Proposition 7.1. Here again
$(n,n)$
. We now apply the previous results to prove that representations that admit an equivariant fitting immersion in this open set, and more generally a fitting map with a fitting flow, are Anosov. For examples of such immersions, see Proposition 7.1. Here again
![]() $M=\widetilde {N}$
for a compact N,
$M=\widetilde {N}$
for a compact N,
![]() $\Gamma =\pi _1(N)$
and
$\Gamma =\pi _1(N)$
and
![]() $\rho :\Gamma \to \operatorname {\mathrm {SL}}(V)$
is a representation.
$\rho :\Gamma \to \operatorname {\mathrm {SL}}(V)$
is a representation.
Theorem 5.4. Let
![]() $u:\widetilde {N}\to \operatorname {\mathrm {Gr}}_d^{(n,n)}(\mathcal {Q})$
be a continuous
$u:\widetilde {N}\to \operatorname {\mathrm {Gr}}_d^{(n,n)}(\mathcal {Q})$
be a continuous
![]() $\rho $
-equivariant map that admits an equivariant fitting flow. The representation
$\rho $
-equivariant map that admits an equivariant fitting flow. The representation
![]() $\rho $
is
$\rho $
is
![]() $\lbrace n\rbrace $
-Anosov, and for any
$\lbrace n\rbrace $
-Anosov, and for any
![]() $q\in \mathbb {S} u^*\mathcal {E}$
, the limit map
$q\in \mathbb {S} u^*\mathcal {E}$
, the limit map
![]() $\xi ^n_\rho (\zeta )\in \operatorname {\mathrm {Gr}}_n(\mathbb {R}^{2n})$
at the limit
$\xi ^n_\rho (\zeta )\in \operatorname {\mathrm {Gr}}_n(\mathbb {R}^{2n})$
at the limit
![]() $\zeta \in \partial \Gamma $
of the flow line
$\zeta \in \partial \Gamma $
of the flow line
![]() $(\Phi _t(q))$
is the following projective subspace:
$(\Phi _t(q))$
is the following projective subspace:
Note that the flow lines of an equivariant fitting flow are quasi-geodesics by Proposition 4.5, and
![]() $\mathbb {S}u^*\mathcal {E}$
is quasi-isometric to
$\mathbb {S}u^*\mathcal {E}$
is quasi-isometric to
![]() $\Gamma $
, hence the limit point
$\Gamma $
, hence the limit point
![]() $\zeta $
is well-defined.
$\zeta $
is well-defined.
Proof. The flat V-bundle over
![]() $\mathbb {S} u^*\mathcal {E}$
associated with
$\mathbb {S} u^*\mathcal {E}$
associated with
![]() $\rho $
admits a continuous splitting
$\rho $
admits a continuous splitting
![]() $E\oplus F$
where for
$E\oplus F$
where for
![]() $q\in \mathbb {S} u^*\mathcal {E}$
:
$q\in \mathbb {S} u^*\mathcal {E}$
:
 $$ \begin{align*}\mathbb{P}\left(E_q\right) &=\bigcap_{t\geq 0} \lbrace \pi(\Phi_{-t}(q))\geq 0\rbrace,\\\mathbb{P}\left(F_q\right) &=\bigcap_{t\geq 0} \lbrace \pi(\Phi_{t}(q))\leq 0\rbrace.\end{align*} $$
$$ \begin{align*}\mathbb{P}\left(E_q\right) &=\bigcap_{t\geq 0} \lbrace \pi(\Phi_{-t}(q))\geq 0\rbrace,\\\mathbb{P}\left(F_q\right) &=\bigcap_{t\geq 0} \lbrace \pi(\Phi_{t}(q))\leq 0\rbrace.\end{align*} $$
This defines transverse vector subspaces by Proposition 5.3 since
![]() $\text {cr}(\Phi _t(q),q)$
and
$\text {cr}(\Phi _t(q),q)$
and
![]() $\text {cr}(-\Phi _{-t}(q),-q)$
go to
$\text {cr}(-\Phi _{-t}(q),-q)$
go to
![]() $+\infty $
when t goes to
$+\infty $
when t goes to
![]() $+\infty $
. Moreover the quadrics in the pencils in the image of u are of signature
$+\infty $
. Moreover the quadrics in the pencils in the image of u are of signature
![]() $(n,n)$
, one must have
$(n,n)$
, one must have
![]() $\dim (E_q)=\dim (F_q)=n$
so this splitting is well-defined. This splitting is preserved by
$\dim (E_q)=\dim (F_q)=n$
so this splitting is well-defined. This splitting is preserved by
![]() $\Phi $
.
$\Phi $
.
We now construct a metric h on this flat V-bundle over
![]() $\mathbb {S} u^*\mathcal {E}$
. Given
$\mathbb {S} u^*\mathcal {E}$
. Given
![]() $q\in \mathbb {S} u^*\mathcal {E}$
we define the symmetric bilinear form
$q\in \mathbb {S} u^*\mathcal {E}$
we define the symmetric bilinear form
![]() $h_q$
on
$h_q$
on
![]() $V=E_q\oplus F_q$
so that this sum is orthogonal and
$V=E_q\oplus F_q$
so that this sum is orthogonal and
![]() $h_q$
is equal to
$h_q$
is equal to
![]() $\pi (q)\in \mathcal {Q}$
on
$\pi (q)\in \mathcal {Q}$
on
![]() $E_q$
and
$E_q$
and
![]() $-\pi (q)\in \mathcal {Q}$
on
$-\pi (q)\in \mathcal {Q}$
on
![]() $F_q$
. Note that by definition of
$F_q$
. Note that by definition of
![]() $E_q$
and
$E_q$
and
![]() $F_q$
,
$F_q$
,
![]() $h_q$
is positive.
$h_q$
is positive.
We also introduce an auxiliary symmetric bilinear form
![]() $\bar {h}$
of signature
$\bar {h}$
of signature
![]() $(n,n)$
on this flat V-bundle over
$(n,n)$
on this flat V-bundle over
![]() $\mathbb {S} u^*\mathcal {E}$
so that the sum
$\mathbb {S} u^*\mathcal {E}$
so that the sum
![]() $E_q\oplus F_q$
is orthogonal and
$E_q\oplus F_q$
is orthogonal and
![]() $\bar {h}_q$
is equal to
$\bar {h}_q$
is equal to
![]() $\pi (q)\in \mathcal {Q}$
on
$\pi (q)\in \mathcal {Q}$
on
![]() $E_q$
and on
$E_q$
and on
![]() $F_q$
.
$F_q$
.
Our first step is to compare the quadric
![]() $\bar {h}_q$
with
$\bar {h}_q$
with
![]() $\pi (q)$
. Let L be a projective line intersecting
$\pi (q)$
. Let L be a projective line intersecting
![]() $\mathbb {P}(E_q)$
at some e and
$\mathbb {P}(E_q)$
at some e and
![]() $\mathbb {P}(F_q)$
at some f. In Figure 3, we illustrate some
$\mathbb {P}(F_q)$
at some f. In Figure 3, we illustrate some
![]() $\mathbb {RP}^2\subset \mathbb {RP}^{2n-1}$
containing the projective line L. Let
$\mathbb {RP}^2\subset \mathbb {RP}^{2n-1}$
containing the projective line L. Let
![]() $\ell _1,\ell ^{\prime }_1$
be the zeroes of
$\ell _1,\ell ^{\prime }_1$
be the zeroes of
![]() $\pi (q)$
on L and
$\pi (q)$
on L and
![]() $\ell _2,\ell ^{\prime }_2$
be the zeroes of
$\ell _2,\ell ^{\prime }_2$
be the zeroes of
![]() $\bar {h}_q$
on L, so that
$\bar {h}_q$
on L, so that
![]() $\ell _1,\ell _2$
lie in the same connected component of
$\ell _1,\ell _2$
lie in the same connected component of
![]() $L\setminus \lbrace e,f\rbrace $
. Since N is compact, there exists a maximum
$L\setminus \lbrace e,f\rbrace $
. Since N is compact, there exists a maximum
![]() $\delta <\infty $
for all
$\delta <\infty $
for all
![]() $q\in \mathbb {S} u^*\mathcal {E}$
and all such projective line L of the quantity
$q\in \mathbb {S} u^*\mathcal {E}$
and all such projective line L of the quantity
![]() $|\log \left ([\ell _1,\ell _2,f,e]\right )|$
.
$|\log \left ([\ell _1,\ell _2,f,e]\right )|$
.
Now we turn our attention to the contraction properties of
![]() $\Phi $
. Let
$\Phi $
. Let
![]() $t>0$
be a real number and let
$t>0$
be a real number and let
![]() $q\in \mathbb {S} u^*\mathcal {E}$
. Let
$q\in \mathbb {S} u^*\mathcal {E}$
. Let
![]() $v\in E_q$
and
$v\in E_q$
and
![]() $w\in F_q$
. We are interested in the following ratio:
$w\in F_q$
. We are interested in the following ratio:
 $$ \begin{align*}R=\frac{h_{\Phi_t(q)}(v)h_q(w)}{h_{\Phi_t(q)}(w)h_q(v)}.\end{align*} $$
$$ \begin{align*}R=\frac{h_{\Phi_t(q)}(v)h_q(w)}{h_{\Phi_t(q)}(w)h_q(v)}.\end{align*} $$
Let
![]() $e,f$
be the lines generated by
$e,f$
be the lines generated by
![]() $v,w$
and L be the projective line joining them. Let
$v,w$
and L be the projective line joining them. Let
![]() $\ell _1,\ell ^{\prime }_1$
be the zeroes of
$\ell _1,\ell ^{\prime }_1$
be the zeroes of
![]() $\pi (q)$
on L,
$\pi (q)$
on L,
![]() $\ell _2,\ell ^{\prime }_2$
the zeroes of
$\ell _2,\ell ^{\prime }_2$
the zeroes of
![]() $\bar {h}_q$
on L,
$\bar {h}_q$
on L,
![]() $\ell _3,\ell ^{\prime }_3$
be the zeroes of
$\ell _3,\ell ^{\prime }_3$
be the zeroes of
![]() $\pi (\Phi _t(q))$
on L and finally
$\pi (\Phi _t(q))$
on L and finally
![]() $\ell _4,\ell ^{\prime }_4$
the zeroes of
$\ell _4,\ell ^{\prime }_4$
the zeroes of
![]() $h_{\Phi _t(q)}$
on L. We assume that
$h_{\Phi _t(q)}$
on L. We assume that
![]() $\ell _1,\ell _2,\ell _3,\ell _4$
all lie on the same component of
$\ell _1,\ell _2,\ell _3,\ell _4$
all lie on the same component of
![]() $L\setminus \lbrace e,f\rbrace $
.
$L\setminus \lbrace e,f\rbrace $
.
The cross ratio
![]() $[\ell _2,\ell _4,f,e]$
is equal to
$[\ell _2,\ell _4,f,e]$
is equal to
![]() $R^{\frac {1}{2}}$
. Indeed
$R^{\frac {1}{2}}$
. Indeed
![]() $\ell _2$
is generated by
$\ell _2$
is generated by
![]() $h^{\frac {1}{2}}_q(w)v+h^{\frac {1}{2}}_q(v)w$
and
$h^{\frac {1}{2}}_q(w)v+h^{\frac {1}{2}}_q(v)w$
and
![]() $\ell _4$
is generated by
$\ell _4$
is generated by
![]() $h^{\frac {1}{2}}_{\Phi _t(q)}(w)v+h^{\frac {1}{2}}_{\Phi _t(q)}(v)w$
, up to changing
$h^{\frac {1}{2}}_{\Phi _t(q)}(w)v+h^{\frac {1}{2}}_{\Phi _t(q)}(v)w$
, up to changing
![]() $\ell _i$
by
$\ell _i$
by
![]() $\ell _i'$
for
$\ell _i'$
for
![]() $1\leq i\leq 4$
. Hence:
$1\leq i\leq 4$
. Hence:
 $$ \begin{align*}[\ell_2,\ell_4,f,e]=\frac{\left( h^{\frac{1}{2}}_{q}(w)v+h^{\frac{1}{2}}_{q}(v)w\right)\wedge w}{\left( h^{\frac{1}{2}}_{q}(w)v+h^{\frac{1}{2}}_{q}(v)w\right)\wedge v}\times \frac{\left( h^{\frac{1}{2}}_{\Phi_t(q)}(w)v+h^{\frac{1}{2}}_{\Phi_t(q)}(v)w\right)\wedge v}{\left( h^{\frac{1}{2}}_{\Phi_t(q)}(w)v+h^{\frac{1}{2}}_{\Phi_t(q)}(v)w\right)\wedge w}=R^{\frac{1}{2}}.\end{align*} $$
$$ \begin{align*}[\ell_2,\ell_4,f,e]=\frac{\left( h^{\frac{1}{2}}_{q}(w)v+h^{\frac{1}{2}}_{q}(v)w\right)\wedge w}{\left( h^{\frac{1}{2}}_{q}(w)v+h^{\frac{1}{2}}_{q}(v)w\right)\wedge v}\times \frac{\left( h^{\frac{1}{2}}_{\Phi_t(q)}(w)v+h^{\frac{1}{2}}_{\Phi_t(q)}(v)w\right)\wedge v}{\left( h^{\frac{1}{2}}_{\Phi_t(q)}(w)v+h^{\frac{1}{2}}_{\Phi_t(q)}(v)w\right)\wedge w}=R^{\frac{1}{2}}.\end{align*} $$
However due to our comparison of
![]() $\pi (q)$
and
$\pi (q)$
and
![]() $\bar {h}_q$
one has:
$\bar {h}_q$
one has:
Therefore
![]() $[\ell _2,\ell _4,f,e]/[\ell _1,\ell _3,f,e]\geq e^{-2\delta }$
. Hence
$[\ell _2,\ell _4,f,e]/[\ell _1,\ell _3,f,e]\geq e^{-2\delta }$
. Hence
![]() $R^{\frac {1}{2}}>e^{-2\delta }[\ell _1,\ell _3,f,e]$
. This last cross ratio is larger than:
$R^{\frac {1}{2}}>e^{-2\delta }[\ell _1,\ell _3,f,e]$
. This last cross ratio is larger than:
Since
![]() $\Phi $
is a fitting flow and since N is compact, there exist
$\Phi $
is a fitting flow and since N is compact, there exist
![]() $\alpha>0$
such that
$\alpha>0$
such that
![]() $\text {cr}\left (\pi (\Phi _1(q)),\pi (q)\right )\geq e^\alpha $
for all
$\text {cr}\left (\pi (\Phi _1(q)),\pi (q)\right )\geq e^\alpha $
for all
![]() $q\in \mathbb {S} u^*\mathcal {E}$
. Hence by the triangular inequality from Proposition 5.2, for all
$q\in \mathbb {S} u^*\mathcal {E}$
. Hence by the triangular inequality from Proposition 5.2, for all
![]() $t>0$
:
$t>0$
:
Hence we get the following estimate:
 $$ \begin{align*}\frac{h_{\Phi_t(q)}(v)h_q(w)}{h_{\Phi_t(q)}(w)h_q(v)}\geq e^{2\alpha t-4\delta-2\alpha} .\end{align*} $$
$$ \begin{align*}\frac{h_{\Phi_t(q)}(v)h_q(w)}{h_{\Phi_t(q)}(w)h_q(v)}\geq e^{2\alpha t-4\delta-2\alpha} .\end{align*} $$
This implies that the splitting
![]() $V=E_q\oplus F_q$
is
$V=E_q\oplus F_q$
is
![]() $\lbrace n\rbrace $
-contracting in the sense of [Reference BochiBPS19] with respect to the flow
$\lbrace n\rbrace $
-contracting in the sense of [Reference BochiBPS19] with respect to the flow
![]() $\Phi $
for the metric h. Moreover
$\Phi $
for the metric h. Moreover
![]() $\Gamma $
acts cocompactly on
$\Gamma $
acts cocompactly on
![]() $\mathbb {S} u^*\mathcal {E}$
and every geodesic in
$\mathbb {S} u^*\mathcal {E}$
and every geodesic in
![]() $\Gamma $
is at uniform distance from a flow line of
$\Gamma $
is at uniform distance from a flow line of
![]() $\Phi $
. The domination of this splitting implies an exponential gap for the singular values [Reference BochiBPS19, Theorem 2.2], which implies that
$\Phi $
. The domination of this splitting implies an exponential gap for the singular values [Reference BochiBPS19, Theorem 2.2], which implies that
![]() $\rho $
is
$\rho $
is
![]() $\lbrace n\rbrace $
-Anosov. The vector subspace
$\lbrace n\rbrace $
-Anosov. The vector subspace
![]() $\xi _\rho ^n(\zeta )$
is the contracted subspace
$\xi _\rho ^n(\zeta )$
is the contracted subspace
![]() $F_q$
.
$F_q$
.
5.2 Fibered domain of discontinuity
Such an equivariant map into the space of pencils that admits a fitting flow induces a fibration of the Guichard-Wienhard domain of discontinuity.
Recall that
![]() $u^o(x)\subset S^2V$
is the annihilator subspace of
$u^o(x)\subset S^2V$
is the annihilator subspace of
![]() $u(x)\subset \mathcal {Q}=\left (S^2V\right )^*$
.
$u(x)\subset \mathcal {Q}=\left (S^2V\right )^*$
.
Proposition 5.5. Let N be a compact manifold of dimension d with fundamental group
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $\rho :\Gamma \to \operatorname {\mathrm {SL}}(V)$
and
$\rho :\Gamma \to \operatorname {\mathrm {SL}}(V)$
and
![]() $u:\widetilde {N}\to \operatorname {\mathrm {Gr}}^{(n,n)}_d(\mathcal {Q})$
be a
$u:\widetilde {N}\to \operatorname {\mathrm {Gr}}^{(n,n)}_d(\mathcal {Q})$
be a
![]() $\rho $
-equivariant continuous map that admits an equivariant fitting flow
$\rho $
-equivariant continuous map that admits an equivariant fitting flow
![]() $\Phi $
on
$\Phi $
on
![]() $\mathbb {S} u^*\mathcal {E}$
. The union of
$\mathbb {S} u^*\mathcal {E}$
. The union of
![]() $\mathbb {P}(u^\circ (x)\cap S^2V^{>0})$
for
$\mathbb {P}(u^\circ (x)\cap S^2V^{>0})$
for
![]() $x\in \widetilde {N}$
covers all of
$x\in \widetilde {N}$
covers all of
![]() $\mathbb {P}(S^2V^{>0})$
, and the closure of this union intersects the space of rank one points
$\mathbb {P}(S^2V^{>0})$
, and the closure of this union intersects the space of rank one points
![]() $\mathbb {P}(V)\simeq S^2\mathbb {P}(V)\subset \mathbb {P}(S^2V^{\geq 0})$
exactly at the domain of discontinuity for
$\mathbb {P}(V)\simeq S^2\mathbb {P}(V)\subset \mathbb {P}(S^2V^{\geq 0})$
exactly at the domain of discontinuity for
![]() $\lbrace n\rbrace $
-Anosov representations considered by Guichard-Wienhard [Reference Guichard and WienhardGW12]:
$\lbrace n\rbrace $
-Anosov representations considered by Guichard-Wienhard [Reference Guichard and WienhardGW12]:
 $$ \begin{align} \Omega=\mathbb{P}(V)\setminus \bigcup_{\zeta\in \partial \Gamma} \mathbb{P}(\xi^n_\rho(\zeta)). \end{align} $$
$$ \begin{align} \Omega=\mathbb{P}(V)\setminus \bigcup_{\zeta\in \partial \Gamma} \mathbb{P}(\xi^n_\rho(\zeta)). \end{align} $$
The intersection of
![]() $\mathbb {P}(u^\circ (x)\cap S^2V^{>0})$
with the set of rank one points for
$\mathbb {P}(u^\circ (x)\cap S^2V^{>0})$
with the set of rank one points for
![]() $x\in \widetilde {N}$
defines a fibration over
$x\in \widetilde {N}$
defines a fibration over
![]() $\widetilde {N}$
of
$\widetilde {N}$
of
![]() $\Omega $
.
$\Omega $
.
In this argument we will use the Hilbert distance on
![]() $\mathbb {P}(S^2V^{>0})$
already introduced for the proof of Proposition 4.5. For a subset
$\mathbb {P}(S^2V^{>0})$
already introduced for the proof of Proposition 4.5. For a subset
![]() $A\subset \mathbb {P}(V)$
we write
$A\subset \mathbb {P}(V)$
we write
![]() $S^2 A\subset \mathbb {P}(S^2V)$
the corresponding set of rank one lines.
$S^2 A\subset \mathbb {P}(S^2V)$
the corresponding set of rank one lines.
Proving first that
![]() $\mathbb {P}(S^2V^{>0})$
is fully covered helps us proving that the Guichard -Wienhard domain is also fully covered.
$\mathbb {P}(S^2V^{>0})$
is fully covered helps us proving that the Guichard -Wienhard domain is also fully covered.
Proof. Let us first prove that all of
![]() $\mathbb {P}(S^2V^{>0})$
is covered by the union of
$\mathbb {P}(S^2V^{>0})$
is covered by the union of
![]() $\mathbb {P}(u^\circ (x)\cap S^2V^{>0})$
for
$\mathbb {P}(u^\circ (x)\cap S^2V^{>0})$
for
![]() $x\in \widetilde {N}$
. We fix a Riemannian metric on N that defines a Riemannian metric g on
$x\in \widetilde {N}$
. We fix a Riemannian metric on N that defines a Riemannian metric g on
![]() $\widetilde {N}$
, with associated distance
$\widetilde {N}$
, with associated distance
![]() $d_g$
. Since u is globally fitting, see Remark 4.6, for all
$d_g$
. Since u is globally fitting, see Remark 4.6, for all
![]() $x\in \widetilde {N}$
there exists a neighborhood U of
$x\in \widetilde {N}$
there exists a neighborhood U of
![]() $\mathbb {P}(u^\circ (x)\cap S^2V^{\geq 0})$
in
$\mathbb {P}(u^\circ (x)\cap S^2V^{\geq 0})$
in
![]() $\mathbb {P}(S^2V^{\geq 0})$
that is covered by the manifolds
$\mathbb {P}(S^2V^{\geq 0})$
that is covered by the manifolds
![]() $\mathbb {P}(u^\circ (y)\cap S^2V^{\geq 0})$
for y in the ball for
$\mathbb {P}(u^\circ (y)\cap S^2V^{\geq 0})$
for y in the ball for
![]() $d_g$
of radius
$d_g$
of radius
![]() $1$
centered at
$1$
centered at
![]() $0$
, by Proposition 3.12, part (i).
$0$
, by Proposition 3.12, part (i).
This neighborhood contains an
![]() $\epsilon $
-neighborhood of
$\epsilon $
-neighborhood of
![]() $\mathbb {P}(u^\circ (x)\cap S^2V^{> 0})$
for the Hilbert metric on
$\mathbb {P}(u^\circ (x)\cap S^2V^{> 0})$
for the Hilbert metric on
![]() $\mathbb {P}(S^2V^{>0})$
for some
$\mathbb {P}(S^2V^{>0})$
for some
![]() $\epsilon>0$
. Since N is compact, this
$\epsilon>0$
. Since N is compact, this
![]() $\epsilon>0$
can be chosen independently of x.
$\epsilon>0$
can be chosen independently of x.
Now let us fix some
![]() $x_0\in \widetilde {N}$
and some
$x_0\in \widetilde {N}$
and some
![]() $[s_0]\in \mathbb {P}(u^\circ (x_0)\cap S^2V^{> 0})$
. Given any
$[s_0]\in \mathbb {P}(u^\circ (x_0)\cap S^2V^{> 0})$
. Given any
![]() $[s']\in \mathbb {P}(S^2V^{> 0})$
one can find a finite sequence
$[s']\in \mathbb {P}(S^2V^{> 0})$
one can find a finite sequence
![]() $s_0,s_1,\cdots , s_k=s'$
in
$s_0,s_1,\cdots , s_k=s'$
in
![]() $S^2V^{>0}$
so that the Hilbert distance between
$S^2V^{>0}$
so that the Hilbert distance between
![]() $[s_i]$
and
$[s_i]$
and
![]() $[s_{i+1}]$
is less than
$[s_{i+1}]$
is less than
![]() $\epsilon $
for all
$\epsilon $
for all
![]() $0\leq i< k$
. By induction, and since the Riemannian metric
$0\leq i< k$
. By induction, and since the Riemannian metric
![]() $d_g$
is complete, one can construct for all
$d_g$
is complete, one can construct for all
![]() $1\leq i\leq k$
a point
$1\leq i\leq k$
a point
![]() $x_i\in \widetilde {N}$
such that
$x_i\in \widetilde {N}$
such that
![]() $[s_i]\in \mathbb {P}(u^\circ (x_i)\cap S^2V^{> 0})$
and
$[s_i]\in \mathbb {P}(u^\circ (x_i)\cap S^2V^{> 0})$
and
![]() $d_H(x_{i-1},x_i)\leq 1$
. Therefore the manifolds
$d_H(x_{i-1},x_i)\leq 1$
. Therefore the manifolds
![]() $\mathbb {P}(u^\circ (x)\cap S^2V^{> 0})$
cover all of
$\mathbb {P}(u^\circ (x)\cap S^2V^{> 0})$
cover all of
![]() $\mathbb {P}(S^2V^{>0})$
.
$\mathbb {P}(S^2V^{>0})$
.
Now let us consider the fibered domain in projective space. We first prove that the fibers are contained in the domain
![]() $S^2\Omega $
. Consider a rank one line
$S^2\Omega $
. Consider a rank one line
![]() $[s]\in S^2\mathbb {P}(\xi ^n_\rho (x))$
for some
$[s]\in S^2\mathbb {P}(\xi ^n_\rho (x))$
for some
![]() $\zeta \in \partial \Gamma $
. Suppose that p belongs to
$\zeta \in \partial \Gamma $
. Suppose that p belongs to
![]() $u^\circ (x)$
for some
$u^\circ (x)$
for some
![]() $x\in \widetilde {N}$
. There exists a flow line
$x\in \widetilde {N}$
. There exists a flow line
![]() $(\Phi _t([q]))_{t\geq 0}$
starting at
$(\Phi _t([q]))_{t\geq 0}$
starting at
![]() $\operatorname {\mathrm {pr}}([q])=x$
and converging to
$\operatorname {\mathrm {pr}}([q])=x$
and converging to
![]() $\zeta \in \partial \Gamma \simeq \partial \widetilde {N}$
by Proposition 4.5. Theorem 5.4 implies that
$\zeta \in \partial \Gamma \simeq \partial \widetilde {N}$
by Proposition 4.5. Theorem 5.4 implies that
![]() $\pi (q)\in \mathcal {Q}$
must be negative on
$\pi (q)\in \mathcal {Q}$
must be negative on
![]() $\xi ^2_\rho (\zeta )$
and hence p cannot belong to
$\xi ^2_\rho (\zeta )$
and hence p cannot belong to
![]() $u^\circ (x)$
.
$u^\circ (x)$
.
Conversely let us prove that every point in
![]() $S^2\Omega $
is covered by some fiber. Fix a point
$S^2\Omega $
is covered by some fiber. Fix a point
![]() $x\in \widetilde {N}$
and take any rank one point
$x\in \widetilde {N}$
and take any rank one point
![]() $[s]\in S^2\Omega $
in the Guichard-Wienhard domain of discontinuity. There exists a sequence
$[s]\in S^2\Omega $
in the Guichard-Wienhard domain of discontinuity. There exists a sequence
![]() $(x_n)$
such that
$(x_n)$
such that
![]() $[s]$
belongs to the limit of
$[s]$
belongs to the limit of
![]() $\mathbb {P}(u^\circ (x_n)\cap S^2V^{\geq 0})$
, since these manifolds cover
$\mathbb {P}(u^\circ (x_n)\cap S^2V^{\geq 0})$
, since these manifolds cover
![]() $\mathbb {P}(S^2V^{>0})$
. We consider some
$\mathbb {P}(S^2V^{>0})$
. We consider some
![]() $[q_n]\in \mathbb {S}\mathcal {E}_x$
such that
$[q_n]\in \mathbb {S}\mathcal {E}_x$
such that
![]() $\Phi _t([q_n])\in \mathbb {S}\mathcal {E}_{x_n}$
for some
$\Phi _t([q_n])\in \mathbb {S}\mathcal {E}_{x_n}$
for some
![]() $t_n>0$
, which exist by Proposition 4.5. If
$t_n>0$
, which exist by Proposition 4.5. If
![]() $t_n$
diverges when n varies, then the set
$t_n$
diverges when n varies, then the set
![]() $\mathbb {P}(u^\circ (x_n)\cap S^2\mathbb {P}(V))$
becomes arbitrarily close to
$\mathbb {P}(u^\circ (x_n)\cap S^2\mathbb {P}(V))$
becomes arbitrarily close to
![]() $S^2\mathbb {P}(\xi ^n_\rho (\zeta _n))$
where
$S^2\mathbb {P}(\xi ^n_\rho (\zeta _n))$
where
![]() $\zeta _n$
is the limit when t goes to
$\zeta _n$
is the limit when t goes to
![]() $+\infty $
of
$+\infty $
of
![]() $\Phi _t([q_n])$
. This would contradict the fact that
$\Phi _t([q_n])$
. This would contradict the fact that
![]() $[s]\in S^2\Omega $
, as in this case
$[s]\in S^2\Omega $
, as in this case
![]() $[s]\in \mathbb {P}(\xi _\rho ^n(\zeta ))$
where
$[s]\in \mathbb {P}(\xi _\rho ^n(\zeta ))$
where
![]() $\zeta $
is a limit point of
$\zeta $
is a limit point of
![]() $(\zeta _n)$
. Hence the sequence
$(\zeta _n)$
. Hence the sequence
![]() $(x_n)$
is bounded and therefore converges up to subsequence to some
$(x_n)$
is bounded and therefore converges up to subsequence to some
![]() $x_\infty \in \widetilde {N}$
, and
$x_\infty \in \widetilde {N}$
, and
![]() $[s]\in \mathbb {P}(u^\circ (x_\infty ))$
.
$[s]\in \mathbb {P}(u^\circ (x_\infty ))$
.
6 Fitting maps and maximal representations
Let us consider representations
![]() $\rho :\Gamma \to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
. We prove our main result, which is the characterization of maximal representations in terms of maps of pencils. The first part introduces
$\rho :\Gamma \to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
. We prove our main result, which is the characterization of maximal representations in terms of maps of pencils. The first part introduces
![]() $\omega $
-regular pencils, as well as a connected component of the space of
$\omega $
-regular pencils, as well as a connected component of the space of
![]() $\omega $
-regular pencils. We then state the characterization, and then present the construction of a map of pencils with a fitting flow for any maximal representation. This construction relies on a map from the space of pairs of Lagrangians to the space of quadrics.
$\omega $
-regular pencils. We then state the characterization, and then present the construction of a map of pencils with a fitting flow for any maximal representation. This construction relies on a map from the space of pairs of Lagrangians to the space of quadrics.
Throughout this section we set
![]() $d=2$
, and consider the case when
$d=2$
, and consider the case when
![]() $N=S_g$
is a surface.
$N=S_g$
is a surface.
6.1 Definition of maximal pencils
We say that a quadric q in
![]() $\left (\mathbb {R}^{2n},\omega \right )$
is
$\left (\mathbb {R}^{2n},\omega \right )$
is
![]() $\omega $
-regular if it is positive on some Lagrangian
$\omega $
-regular if it is positive on some Lagrangian
![]() $\ell _1$
and negative on some Lagrangian
$\ell _1$
and negative on some Lagrangian
![]() $\ell _2$
. Note that if
$\ell _2$
. Note that if
![]() $\ell _1,\ell _2$
are only assumed to be n dimensional subspaces, this condition is exactly the condition of having signature
$\ell _1,\ell _2$
are only assumed to be n dimensional subspaces, this condition is exactly the condition of having signature
![]() $(n,n)$
. We call
$(n,n)$
. We call
![]() $\operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
the space of pencils hose nonzero elements are all
$\operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
the space of pencils hose nonzero elements are all
![]() $\omega $
-regular, which is an open subset of
$\omega $
-regular, which is an open subset of
![]() $\operatorname {\mathrm {Gr}}_2^{{(n,n)}}(\mathcal {Q})$
. These pencils have in particular the property that the corresponding subsets of
$\operatorname {\mathrm {Gr}}_2^{{(n,n)}}(\mathcal {Q})$
. These pencils have in particular the property that the corresponding subsets of
![]() $\mathbb {P}(S^2V)$
intersect transversely the symmetric space of
$\mathbb {P}(S^2V)$
intersect transversely the symmetric space of
![]() $\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
, see Lemma 7.4.
$\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
, see Lemma 7.4.
Remark 6.1. If a locally fitting map
![]() $u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{{(n,n)}}(\mathcal {Q})$
admits a fitting flow which is equivariant with respect to a representation
$u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{{(n,n)}}(\mathcal {Q})$
admits a fitting flow which is equivariant with respect to a representation
![]() $\rho :\Gamma \to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
, the image of u must lie in
$\rho :\Gamma \to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
, the image of u must lie in
![]() $\operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
as
$\operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
as
![]() $\rho $
is
$\rho $
is
![]() $\lbrace n\rbrace $
-Anosov by Theorem 5.4, and the limit map of
$\lbrace n\rbrace $
-Anosov by Theorem 5.4, and the limit map of
![]() $\lbrace n\rbrace $
-Anosov representations in
$\lbrace n\rbrace $
-Anosov representations in
![]() $\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
takes values in the space of Lagrangians. This last fact is a consequence of the fact that an attractive fixed n-dimensional subspace of an element in
$\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
takes values in the space of Lagrangians. This last fact is a consequence of the fact that an attractive fixed n-dimensional subspace of an element in
![]() $\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
is necessarily Lagrangian, see, for instance, [Reference Guichard and WienhardGW12].
$\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
is necessarily Lagrangian, see, for instance, [Reference Guichard and WienhardGW12].
There are nonmaximal representations admitting equivariant fitting immersions, for instance almost-Fuchsian representations in
![]() $\operatorname {\mathrm {SL}}(2,\mathbb {C})\subset \operatorname {\mathrm {Sp}}(4,\mathbb {R})$
, see Appendix A. In order to obtain the maximality property, we need to restrict ourselves to the correct union of connected component of
$\operatorname {\mathrm {SL}}(2,\mathbb {C})\subset \operatorname {\mathrm {Sp}}(4,\mathbb {R})$
, see Appendix A. In order to obtain the maximality property, we need to restrict ourselves to the correct union of connected component of
![]() $\operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
.
$\operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
.
Let
![]() $P\in \operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
be a pencil, and fix an orientation for P. Recall that
$P\in \operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
be a pencil, and fix an orientation for P. Recall that
![]() $\mathcal {L}_n$
in the space of Lagrangians in
$\mathcal {L}_n$
in the space of Lagrangians in
![]() $\mathbb {R}^{2n}$
. We construct a “boundary map” for an
$\mathbb {R}^{2n}$
. We construct a “boundary map” for an
![]() $\omega $
-regular pencil of quadrics, defined up to homotopy. Before defining this map, note the following:
$\omega $
-regular pencil of quadrics, defined up to homotopy. Before defining this map, note the following:
Lemma 6.2. Let
![]() $q\in \mathcal {Q}$
be an
$q\in \mathcal {Q}$
be an
![]() $\omega $
-regular element. The set of Lagrangians
$\omega $
-regular element. The set of Lagrangians
![]() $\ell $
such that q is positive on
$\ell $
such that q is positive on
![]() $\ell $
is homeomorphic to an open ball.
$\ell $
is homeomorphic to an open ball.
Proof. There exist some
![]() $\ell _+\in \mathcal {L}_n$
on which q is positive. Moreover there exist some
$\ell _+\in \mathcal {L}_n$
on which q is positive. Moreover there exist some
![]() $\ell _-\in \mathcal {L}_n$
on which q is negative.
$\ell _-\in \mathcal {L}_n$
on which q is negative.
Every Lagrangian
![]() $\ell $
on which q is positive must be transverse to
$\ell $
on which q is positive must be transverse to
![]() $\ell _-$
, hence it can be written as the graph
$\ell _-$
, hence it can be written as the graph
![]() $\lbrace x+u(x)\mid x\in \ell _+\rbrace $
of some linear map
$\lbrace x+u(x)\mid x\in \ell _+\rbrace $
of some linear map
![]() $u:\ell _+\to \ell _-$
, and one has for all
$u:\ell _+\to \ell _-$
, and one has for all
![]() $v\in \ell ^+$
:
$v\in \ell ^+$
:
Since
![]() $q(v,v)>0$
and
$q(v,v)>0$
and
![]() $q(u(v),u(v))<0$
, for all
$q(u(v),u(v))<0$
, for all
![]() $0<\lambda <1$
:
$0<\lambda <1$
:
We can identify the elements of
![]() $\mathcal {L}_n$
transverse to
$\mathcal {L}_n$
transverse to
![]() $\ell _-$
as the vector subspace of the space of maps
$\ell _-$
as the vector subspace of the space of maps
![]() $u:\ell _+\to \ell _-$
. We just proved that in this chart the set of elements on which q is positive is open and star-shaped, hence it is an open ball.
$u:\ell _+\to \ell _-$
. We just proved that in this chart the set of elements on which q is positive is open and star-shaped, hence it is an open ball.
We now define the “boundary map” of the pencil.
Proposition 6.3. Let
![]() $P\in \operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
. There exists a continuous map
$P\in \operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
. There exists a continuous map
![]() $\xi _P:\mathbb {S} P\to \mathcal {L}_n$
such that for all
$\xi _P:\mathbb {S} P\to \mathcal {L}_n$
such that for all
![]() $[q]\in \mathbb {S} P$
,
$[q]\in \mathbb {S} P$
,
![]() $q>0$
on
$q>0$
on
![]() $\xi _P([q])$
. Moreover any two such maps are homotopic, so the free homotopy type
$\xi _P([q])$
. Moreover any two such maps are homotopic, so the free homotopy type
![]() $[\xi _P]$
is well defined.
$[\xi _P]$
is well defined.
Proof. A map
![]() $\xi _P$
is exactly a section of the bundle
$\xi _P$
is exactly a section of the bundle
![]() $\lbrace ([q],\ell )\mid q_{\mid \ell }>0\rbrace \to \mathbb {S} P$
, which is a fiber bundle whose fibers are open balls. Such sections always exist and are unique up to homotopy.
$\lbrace ([q],\ell )\mid q_{\mid \ell }>0\rbrace \to \mathbb {S} P$
, which is a fiber bundle whose fibers are open balls. Such sections always exist and are unique up to homotopy.
We say that a pencil is maximal for some orientation if
![]() $[\xi _P]=n[\tau ]$
, where
$[\xi _P]=n[\tau ]$
, where
![]() $[\tau ]$
is the generator of
$[\tau ]$
is the generator of
![]() $\pi _1(\mathcal {L}_n)$
introduced in Section 2.2. We denote by
$\pi _1(\mathcal {L}_n)$
introduced in Section 2.2. We denote by
![]() $\operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
the space of pencils that are maximal for some orientation. This is a union of connected components of
$\operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
the space of pencils that are maximal for some orientation. This is a union of connected components of
![]() $\operatorname {\mathrm {Gr}}^\omega _2(\mathcal {Q})$
as the homotopy type
$\operatorname {\mathrm {Gr}}^\omega _2(\mathcal {Q})$
as the homotopy type
![]() $[\xi _P]$
is locally invariant for
$[\xi _P]$
is locally invariant for
![]() $P\in \operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
.
$P\in \operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
.
Remark 6.4. The previous discussion allows us to distinguish several connected components of the open subspace
![]() $\operatorname {\mathrm {Gr}}^\omega _2(\mathcal {Q})$
by looking at the homotopy type of the boundary map
$\operatorname {\mathrm {Gr}}^\omega _2(\mathcal {Q})$
by looking at the homotopy type of the boundary map
![]() $\xi _P$
.
$\xi _P$
.
As a recall we have the following inclusions:
All these inclusions are open, and the inclusion
![]() $Gr_2^{\max }(\mathcal {Q})\subset \operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
is a union of connected components.
$Gr_2^{\max }(\mathcal {Q})\subset \operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
is a union of connected components.
6.2 Statement of the characterization
We obtain the following characterization of maximal representations in terms of the existence of locally fitting maps that admit a fitting flow.
Theorem 6.5. A representation
![]() $\rho :\Gamma _g\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
admits a
$\rho :\Gamma _g\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
admits a
![]() $\rho $
-equivariant locally fitting map
$\rho $
-equivariant locally fitting map
![]() $u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
that admits a
$u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
that admits a
![]() $\rho $
-invariant fitting flow if and only if it is maximal for some orientation of
$\rho $
-invariant fitting flow if and only if it is maximal for some orientation of
![]() $S_g$
.
$S_g$
.
In this case the orientation of
![]() $S_g$
for which
$S_g$
for which
![]() $\rho $
is maximal is induced by the orientation of the maximal pencils
$\rho $
is maximal is induced by the orientation of the maximal pencils
![]() $u(x)$
for
$u(x)$
for
![]() $x\in \widetilde {S_g}$
and Lemma 4.3.
$x\in \widetilde {S_g}$
and Lemma 4.3.
In particular if a representation
![]() $\rho $
admits an equivariant fitting immersion
$\rho $
admits an equivariant fitting immersion
![]() $u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
then it is maximal because of Proposition 4.8. This theorem leaves the following question open:
$u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
then it is maximal because of Proposition 4.8. This theorem leaves the following question open:
Question 6.6. Given a maximal representation
![]() $\rho :\Gamma _g\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
, is there always an equivariant fitting immersion
$\rho :\Gamma _g\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
, is there always an equivariant fitting immersion
![]() $u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
?
$u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
?
We show in Section B that this is true for
![]() $\operatorname {\mathrm {Sp}}(4,\mathbb {R})$
, and in this case there exists a fitting immersion whose image lies in a single special
$\operatorname {\mathrm {Sp}}(4,\mathbb {R})$
, and in this case there exists a fitting immersion whose image lies in a single special
![]() $\operatorname {\mathrm {Sp}}(4,\mathbb {R})$
-orbit of
$\operatorname {\mathrm {Sp}}(4,\mathbb {R})$
-orbit of
![]() $\operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
.
$\operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
.
The following Lemma shows one direction of Theorem 6.5, the other direction is proven by Lemma 6.13.
Lemma 6.7. Let
![]() $\rho :\Gamma _g\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
be a representation that admits an equivariant continuous map
$\rho :\Gamma _g\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
be a representation that admits an equivariant continuous map
![]() $u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
that admits an equivariant fitting flow. Then
$u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
that admits an equivariant fitting flow. Then
![]() $\rho $
is maximal for some orientation of
$\rho $
is maximal for some orientation of
![]() $S_g$
.
$S_g$
.
Recall that the limit map of
![]() $\lbrace n\rbrace $
-Anosov representations in
$\lbrace n\rbrace $
-Anosov representations in
![]() $\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
takes values in the space of Lagrangians, see Remark 6.1.
$\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
takes values in the space of Lagrangians, see Remark 6.1.
Proof. We first apply Theorem 5.4 which shows that
![]() $\rho $
is
$\rho $
is
![]() $\lbrace n\rbrace $
-Anosov. Let
$\lbrace n\rbrace $
-Anosov. Let
![]() $x\in \widetilde {S_g}$
, we prove that the homotopy type of the boundary curve
$x\in \widetilde {S_g}$
, we prove that the homotopy type of the boundary curve
![]() $\xi ^n_\rho $
is the same as the homotopy type
$\xi ^n_\rho $
is the same as the homotopy type
![]() $[\xi _{u(x)}]$
from Proposition 6.3. We consider the map
$[\xi _{u(x)}]$
from Proposition 6.3. We consider the map
![]() $\zeta _\infty $
that associates to
$\zeta _\infty $
that associates to
![]() $[q]\in \mathbb {S} u^*\mathcal {E}_{x}$
the limit of
$[q]\in \mathbb {S} u^*\mathcal {E}_{x}$
the limit of
![]() $\Phi _t([q])$
in
$\Phi _t([q])$
in
![]() $\partial \Gamma $
. This map is homotopic in
$\partial \Gamma $
. This map is homotopic in
![]() $\widetilde {S_g}\cup \partial \Gamma \setminus \lbrace x\rbrace $
to the map
$\widetilde {S_g}\cup \partial \Gamma \setminus \lbrace x\rbrace $
to the map
![]() $\zeta _{1}$
that associates the projection
$\zeta _{1}$
that associates the projection
![]() $p(\Phi _{1})$
. Hence by Lemma 4.3,
$p(\Phi _{1})$
. Hence by Lemma 4.3,
![]() $\zeta _1$
defines a diffeomorphism of degree
$\zeta _1$
defines a diffeomorphism of degree
![]() $1$
between the circle
$1$
between the circle
![]() $\mathbb {S} u(x)$
with its maximal orientation and the boundary
$\mathbb {S} u(x)$
with its maximal orientation and the boundary
![]() $\partial \Gamma $
for the induced orientation.
$\partial \Gamma $
for the induced orientation.
The map
![]() $\xi ^n_\rho \circ \zeta _\infty $
has the homotopy type
$\xi ^n_\rho \circ \zeta _\infty $
has the homotopy type
![]() $[\xi _{u(x)}]$
associated to
$[\xi _{u(x)}]$
associated to
![]() $u(x)$
: it defines a boundary map as in Proposition 6.3. The fact that
$u(x)$
: it defines a boundary map as in Proposition 6.3. The fact that
![]() $\rho $
is maximal is then a consequence of the characterization of maximal representations from Theorem 2.5. Indeed
$\rho $
is maximal is then a consequence of the characterization of maximal representations from Theorem 2.5. Indeed
![]() $u(x)\in \operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
implies that
$u(x)\in \operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
implies that
![]() $[\xi _{u(x)}]=n[\tau ]$
, and we already know that the degree of
$[\xi _{u(x)}]=n[\tau ]$
, and we already know that the degree of
![]() $\zeta _\infty $
is equal to the degree of
$\zeta _\infty $
is equal to the degree of
![]() $\zeta _1$
which is equal to
$\zeta _1$
which is equal to
![]() $1$
.
$1$
.
6.3 Construction of a fitting flow
In this section we study special quadrics in
![]() $\mathbb {R}^{2n}$
associated to pairs of transverse Lagrangians. These objects will allow us to construct fitting continuous embeddings of pencils.
$\mathbb {R}^{2n}$
associated to pairs of transverse Lagrangians. These objects will allow us to construct fitting continuous embeddings of pencils.
Definition 6.8. Let
![]() $\ell _1$
,
$\ell _1$
,
![]() $\ell _2$
be two transverse Lagrangians in
$\ell _2$
be two transverse Lagrangians in
![]() $\mathbb {R}^{2n}$
. We define
$\mathbb {R}^{2n}$
. We define
![]() $q_{\ell _1,\ell _2}$
to be the symmetric bilinear form on
$q_{\ell _1,\ell _2}$
to be the symmetric bilinear form on
![]() $\mathbb {R}^{2n}$
such that if
$\mathbb {R}^{2n}$
such that if
![]() $\pi _1,\pi _2$
are the projections on
$\pi _1,\pi _2$
are the projections on
![]() $\ell _1,\ell _2$
associated to the direct sum
$\ell _1,\ell _2$
associated to the direct sum
![]() $\ell _1\oplus \ell _2=V$
:
$\ell _1\oplus \ell _2=V$
:
Note that
![]() $q_{\ell _2,\ell _1}=-q_{\ell _1,\ell _2}$
.
$q_{\ell _2,\ell _1}=-q_{\ell _1,\ell _2}$
.
Remark 6.9. In particular
![]() $q_{\ell _1,\ell _2}$
is characterized by the fact that
$q_{\ell _1,\ell _2}$
is characterized by the fact that
![]() $\ell _1$
and
$\ell _1$
and
![]() $\ell _2$
are isotropic and for all
$\ell _2$
are isotropic and for all
![]() $v\in \ell _1,w\in \ell _2$
:
$v\in \ell _1,w\in \ell _2$
:
Maximal triples of Lagrangians can be characterized as follows:
Lemma 6.10. A triple of Lagrangians
![]() $(\ell _1,\ell _2,\ell _3)$
is maximal if and only if
$(\ell _1,\ell _2,\ell _3)$
is maximal if and only if
![]() $q_{\ell _1,\ell _3}$
is positive on
$q_{\ell _1,\ell _3}$
is positive on
![]() $\ell _2$
.
$\ell _2$
.
Proof. Let us write
![]() $\ell _1,\ell _2,\ell _3$
as in Section 2.1 for some symplectic basis:
$\ell _1,\ell _2,\ell _3$
as in Section 2.1 for some symplectic basis:
The form
![]() $q_{\ell _1,\ell _3}$
can be written in this basis as:
$q_{\ell _1,\ell _3}$
can be written in this basis as:
 $$ \begin{align*}q_{\ell_1,\ell_3}=\frac{1}{2}\sum_{i=1}^n x_i^*\otimes y_i^* +y_i^*\otimes x_i^*.\end{align*} $$
$$ \begin{align*}q_{\ell_1,\ell_3}=\frac{1}{2}\sum_{i=1}^n x_i^*\otimes y_i^* +y_i^*\otimes x_i^*.\end{align*} $$
This form is positive on
![]() $\ell _2$
if and only if all of the
$\ell _2$
if and only if all of the
![]() $\epsilon _i$
are positive, and hence if the triple is maximal.
$\epsilon _i$
are positive, and hence if the triple is maximal.
These quadrics have also the following remarkable properties for maximal quadruples of Lagrangians.
A quadruple of Lagrangians
![]() $(\ell _1,\ell _2,\ell _3,\ell _4)$
is called maximal if each cyclic oriented subtriple is maximal.
$(\ell _1,\ell _2,\ell _3,\ell _4)$
is called maximal if each cyclic oriented subtriple is maximal.
Lemma 6.11. Let
![]() $(\ell _1,\ell _2,\ell _3,\ell _4)$
be a maximal quadruple of Lagrangians. The bilinear form
$(\ell _1,\ell _2,\ell _3,\ell _4)$
be a maximal quadruple of Lagrangians. The bilinear form
![]() $q_{\ell _4,\ell _3}-q_{\ell _1,\ell _2}$
is positive. In particular the zero set of these quadrics define two disjoint quadric hypersurfaces in
$q_{\ell _4,\ell _3}-q_{\ell _1,\ell _2}$
is positive. In particular the zero set of these quadrics define two disjoint quadric hypersurfaces in
![]() $\mathbb {P}(\mathbb {R}^{2n})$
.
$\mathbb {P}(\mathbb {R}^{2n})$
.
Note that a triple of Lagrangians
![]() $(\ell _1,\ell _2,\ell _3)$
is maximal if and only if corresponding linear map
$(\ell _1,\ell _2,\ell _3)$
is maximal if and only if corresponding linear map
![]() $u\in \operatorname {\mathrm {Hom}}(\ell _1,\ell _3)$
whose graph is equal to
$u\in \operatorname {\mathrm {Hom}}(\ell _1,\ell _3)$
whose graph is equal to
![]() $\ell _2$
is such that
$\ell _2$
is such that
![]() $\omega (\cdot , u(\cdot ))$
is positive on
$\omega (\cdot , u(\cdot ))$
is positive on
![]() $\ell _1$
.
$\ell _1$
.
Proof. Let us prove the first part of the statement. Since
![]() $(\ell _4,\ell _1,\ell _3)$
is a maximal triple of Lagrangians,
$(\ell _4,\ell _1,\ell _3)$
is a maximal triple of Lagrangians,
![]() $\ell _1$
can be written as the graph of some linear map
$\ell _1$
can be written as the graph of some linear map
![]() $u_1:\ell _4\to \ell _3$
such that
$u_1:\ell _4\to \ell _3$
such that
![]() $\omega \left (\cdot ,u_1(\cdot )\right )$
is a positive bilinear form on
$\omega \left (\cdot ,u_1(\cdot )\right )$
is a positive bilinear form on
![]() $\ell _4$
. Similarly since
$\ell _4$
. Similarly since
![]() $(\ell _4,\ell _2,\ell _3)$
is a maximal triple of Lagrangians,
$(\ell _4,\ell _2,\ell _3)$
is a maximal triple of Lagrangians,
![]() $\ell _2$
can be written as the graph of some linear map
$\ell _2$
can be written as the graph of some linear map
![]() $u_2:\ell _4\to \ell _3$
such that
$u_2:\ell _4\to \ell _3$
such that
![]() $\omega \left (\cdot ,u_2(\cdot )\right )$
is a positive bilinear form on
$\omega \left (\cdot ,u_2(\cdot )\right )$
is a positive bilinear form on
![]() $\ell _4$
.
$\ell _4$
.
Let
![]() ${v}\in \mathbb {R}^{2n}$
, it can be decomposed uniquely as
${v}\in \mathbb {R}^{2n}$
, it can be decomposed uniquely as
![]() ${v}={v}_1+{v}_2$
with
${v}={v}_1+{v}_2$
with
![]() ${v}_1\in \ell _1$
and
${v}_1\in \ell _1$
and
![]() ${v}_2\in \ell _2$
. Moreover there exist some unique
${v}_2\in \ell _2$
. Moreover there exist some unique
![]() $x,y\in \ell _4$
such that
$x,y\in \ell _4$
such that
![]() ${v}_1=x+u_1(x)$
and
${v}_1=x+u_1(x)$
and
![]() ${v}_2=y+u_2(y)$
. The vector
${v}_2=y+u_2(y)$
. The vector
![]() ${v}$
decomposes therefore as
${v}$
decomposes therefore as
![]() ${v}=x+y+u_1(x)+u_2(y)$
. One computes that:
${v}=x+y+u_1(x)+u_2(y)$
. One computes that:
 $$\begin{align*} q_{\ell_4,\ell_3}({v},{v})-q_{\ell_1,\ell_2}({v},{v})&=\omega\left(x+y,u_1(x)+u_2(y)\right)-\omega\left(x+u_1(x),y+u_2(y)\right),\\ &=\omega\left(x,u_1(x)\right)+\omega\left(y,u_2(y)\right)+2\omega\left(y,u_1(x)\right). \end{align*}$$
$$\begin{align*} q_{\ell_4,\ell_3}({v},{v})-q_{\ell_1,\ell_2}({v},{v})&=\omega\left(x+y,u_1(x)+u_2(y)\right)-\omega\left(x+u_1(x),y+u_2(y)\right),\\ &=\omega\left(x,u_1(x)\right)+\omega\left(y,u_2(y)\right)+2\omega\left(y,u_1(x)\right). \end{align*}$$
Finally the fact that
![]() $(\ell _1,\ell _2,\ell _3)$
forms a maximal triple implies that the bilinear form
$(\ell _1,\ell _2,\ell _3)$
forms a maximal triple implies that the bilinear form
![]() $\omega \left (\cdot ,\widetilde {u_2}(\cdot )\right )$
is positive on
$\omega \left (\cdot ,\widetilde {u_2}(\cdot )\right )$
is positive on
![]() $\ell _1$
, where
$\ell _1$
, where
![]() $\widetilde {u_2}\in \operatorname {\mathrm {Hom}}(\ell _1,\ell _3)$
corresponding to
$\widetilde {u_2}\in \operatorname {\mathrm {Hom}}(\ell _1,\ell _3)$
corresponding to
![]() $u_2$
. In particular for all nonzero
$u_2$
. In particular for all nonzero
![]() $x\in \ell _4$
:
$x\in \ell _4$
:
However note that by definition
![]() $x+u_1(x)+\widetilde {u_2}(x+u_1(x))=x+u_2(x)$
and in particular
$x+u_1(x)+\widetilde {u_2}(x+u_1(x))=x+u_2(x)$
and in particular
![]() $\widetilde {u_2}(x+u_1(x))=(u_2-u_1)(x)$
. Hence the symmetric bilinear form
$\widetilde {u_2}(x+u_1(x))=(u_2-u_1)(x)$
. Hence the symmetric bilinear form
![]() $\omega \left (\cdot ,(u_2-u_1)(\cdot )\right )$
is positive on
$\omega \left (\cdot ,(u_2-u_1)(\cdot )\right )$
is positive on
![]() $\ell _4$
.
$\ell _4$
.
In particular for
![]() $y\neq 0$
the previous expression is strictly greater than the following
$y\neq 0$
the previous expression is strictly greater than the following
![]() $\omega \left (x,u_1(x)\right )+\omega \left (y,u_1(y)\right )+2\omega \left (y,u_1(x)\right )$
, which is non-negative since
$\omega \left (x,u_1(x)\right )+\omega \left (y,u_1(y)\right )+2\omega \left (y,u_1(x)\right )$
, which is non-negative since
![]() $\omega \left (\cdot ,u_1(\cdot )\right )$
is positive. In the case when
$\omega \left (\cdot ,u_1(\cdot )\right )$
is positive. In the case when
![]() $y=0$
, this last inequality is strict for
$y=0$
, this last inequality is strict for
![]() $x\neq 0$
. Otherwise the previous inequality
$x\neq 0$
. Otherwise the previous inequality
![]() $\omega \left (y,(u_2-u_1)(y)\right )>0$
is strict. Therefore for
$\omega \left (y,(u_2-u_1)(y)\right )>0$
is strict. Therefore for
![]() ${v}\neq 0$
,
${v}\neq 0$
,
![]() $q_{\ell _4,\ell _3}({v},{v})-q_{\ell _1,\ell _2}({v},{v})>0$
.
$q_{\ell _4,\ell _3}({v},{v})-q_{\ell _1,\ell _2}({v},{v})>0$
.
We now state an infinitesimal version of Lemma 6.11 that we will use in Section B.
Lemma 6.12. Let
![]() $\ell ^+,\ell ^-:[0,1]\to \mathcal {L}_n$
be smooth and such that
$\ell ^+,\ell ^-:[0,1]\to \mathcal {L}_n$
be smooth and such that
![]() $\ell _0^+=\ell ^+(0)$
and
$\ell _0^+=\ell ^+(0)$
and
![]() $\ell _0^-=\ell ^-(0)$
are transverse and the linear maps
$\ell _0^-=\ell ^-(0)$
are transverse and the linear maps
![]() $\dot {u}^+\in \operatorname {\mathrm {Hom}}(\ell ^+_0,\ell ^-_0)$
and
$\dot {u}^+\in \operatorname {\mathrm {Hom}}(\ell ^+_0,\ell ^-_0)$
and
![]() $\dot {u}^-\in \operatorname {\mathrm {Hom}}(\ell ^+_0,\ell ^+_0)$
corresponding to
$\dot {u}^-\in \operatorname {\mathrm {Hom}}(\ell ^+_0,\ell ^+_0)$
corresponding to
![]() $(\ell ^+)'(0)$
and
$(\ell ^+)'(0)$
and
![]() $(\ell ^-)'(0)$
are such that
$(\ell ^-)'(0)$
are such that
![]() $\omega (\cdot , \dot {u}^+(\cdot ))$
and
$\omega (\cdot , \dot {u}^+(\cdot ))$
and
![]() $\omega (\dot {u}^-(\cdot ), \cdot )$
are positive respectively on
$\omega (\dot {u}^-(\cdot ), \cdot )$
are positive respectively on
![]() $\ell ^+_0$
and
$\ell ^+_0$
and
![]() $\ell ^-_0$
. The derivative at
$\ell ^-_0$
. The derivative at
![]() $t=0$
of
$t=0$
of
![]() $q_{\ell ^+(t), \ell ^-(t)}$
is positive.
$q_{\ell ^+(t), \ell ^-(t)}$
is positive.
Proof. The proof is similar to the previous one. Let
![]() $u^+(t)\in \operatorname {\mathrm {Hom}}(\ell ^+_0,\ell ^-_0)$
and
$u^+(t)\in \operatorname {\mathrm {Hom}}(\ell ^+_0,\ell ^-_0)$
and
![]() $u^-(t)\in \operatorname {\mathrm {Hom}}(\ell ^-_0,\ell ^+_0)$
be the linear maps whose graph is equal to
$u^-(t)\in \operatorname {\mathrm {Hom}}(\ell ^-_0,\ell ^+_0)$
be the linear maps whose graph is equal to
![]() $\ell ^+(t)$
and
$\ell ^+(t)$
and
![]() $\ell ^-(t)$
respectively. Let
$\ell ^-(t)$
respectively. Let
![]() ${v}\in \mathbb {R}^{2n}$
. The derivative of the evaluation of
${v}\in \mathbb {R}^{2n}$
. The derivative of the evaluation of
![]() $q_t=q_{\ell ^+(t), \ell ^-(t)}$
to
$q_t=q_{\ell ^+(t), \ell ^-(t)}$
to
![]() ${v}$
can be written in term of the derivative
${v}$
can be written in term of the derivative
![]() $\dot {{v}}_t^+$
,
$\dot {{v}}_t^+$
,
![]() $\dot {{v}}_t^-$
of the vectors
$\dot {{v}}_t^-$
of the vectors
![]() ${v}_t^+\in \ell _+(t)$
,
${v}_t^+\in \ell _+(t)$
,
![]() ${v}_t^-\in \ell _-(t)$
such that
${v}_t^-\in \ell _-(t)$
such that
![]() ${v}={v}_t^++{v}_t^-$
:
${v}={v}_t^++{v}_t^-$
:
One has
![]() $\dot {{v}}^+_0=-\dot {{v}}^-_0$
since
$\dot {{v}}^+_0=-\dot {{v}}^-_0$
since
![]() ${v}=v^+_t+v^-_t$
does not vary with t. The fact that
${v}=v^+_t+v^-_t$
does not vary with t. The fact that
![]() $v^+_t\in \ell _+(t)$
for all t implies that
$v^+_t\in \ell _+(t)$
for all t implies that
![]() $\dot {{v}}^+_0$
can be written
$\dot {{v}}^+_0$
can be written
![]() ${w}^++\dot {u}^+({{v}}_0^+)$
with
${w}^++\dot {u}^+({{v}}_0^+)$
with
![]() ${w}^+\in \ell ^+_0$
. Similarly
${w}^+\in \ell ^+_0$
. Similarly
![]() $\dot {{v}}^-_0$
can be written
$\dot {{v}}^-_0$
can be written
![]() ${w}^-+\dot {u}^-({{v}}_0^+)$
with
${w}^-+\dot {u}^-({{v}}_0^+)$
with
![]() ${w}^-\in \ell ^-_0$
. Note that
${w}^-\in \ell ^-_0$
. Note that
![]() $\omega (v_0^+,w^+)=0$
as they belong to the same Lagrangian
$\omega (v_0^+,w^+)=0$
as they belong to the same Lagrangian
![]() $\ell ^+_0$
. Similarly
$\ell ^+_0$
. Similarly
![]() $\omega (v_0^-,w^-)=0$
and hence:
$\omega (v_0^-,w^-)=0$
and hence:
This is positive by our assumption.
We now construct an equivariant continuous map that admits a well-fitting flow.
Proposition 6.13. Let
![]() $\rho :\Gamma _g\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
be a maximal representation. There exists a continuous map
$\rho :\Gamma _g\to \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
be a maximal representation. There exists a continuous map
![]() $u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
that admits a fitting flow.
$u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
that admits a fitting flow.
We prove this lemma using some averaging argument, where the basic building blocks are the quadrics associated to pairs of Lagrangians in the limit curve. This construction is not unique, as we start by fixing a hyperbolic metric.
Proof. Fix a hyperbolic metric on
![]() $S_g$
. Since
$S_g$
. Since
![]() $S_g$
is oriented it admits an associated complex structure J. For
$S_g$
is oriented it admits an associated complex structure J. For
![]() $v\in T^1_x\widetilde {S_g}$
write
$v\in T^1_x\widetilde {S_g}$
write
![]() $\ell _v=\xi ^n_\rho (\zeta _v)$
where
$\ell _v=\xi ^n_\rho (\zeta _v)$
where
![]() $\zeta _v\in \partial \Gamma $
is the limit point of the geodesic with initial derivative v. We furthermore define:
$\zeta _v\in \partial \Gamma $
is the limit point of the geodesic with initial derivative v. We furthermore define:
These quadrics for a fixed
![]() $x\in \widetilde {S_g}$
do not in general define a pencil of quadrics. We therefore define the following quadric associated to
$x\in \widetilde {S_g}$
do not in general define a pencil of quadrics. We therefore define the following quadric associated to
![]() $v\in T_x\widetilde {S_g}$
:
$v\in T_x\widetilde {S_g}$
:
Here we take the integral for the measure
![]() $\lambda $
on
$\lambda $
on
![]() $T^1_x\widetilde {S}$
induced by the hyperbolic metric. For each
$T^1_x\widetilde {S}$
induced by the hyperbolic metric. For each
![]() $x\in \widetilde {S}$
, we consider the pencil
$x\in \widetilde {S}$
, we consider the pencil
![]() $u(x)= \lbrace q_v |v\in T\widetilde {S_g}\rbrace \in \operatorname {\mathrm {Gr}}_2(\mathcal {Q})$
which is well defined since
$u(x)= \lbrace q_v |v\in T\widetilde {S_g}\rbrace \in \operatorname {\mathrm {Gr}}_2(\mathcal {Q})$
which is well defined since
![]() $q_v$
depends linearly on
$q_v$
depends linearly on
![]() $v\in T_xS$
.
$v\in T_xS$
.
First we check that these pencils are in
![]() $\operatorname {\mathrm {Gr}}_2^{(n,n)}(\mathcal {Q})$
, by proving that they are actually
$\operatorname {\mathrm {Gr}}_2^{(n,n)}(\mathcal {Q})$
, by proving that they are actually
![]() $\omega $
-regular.
$\omega $
-regular.
Let
![]() $v\in T^1_x\widetilde {S_g}$
be nonzero for some
$v\in T^1_x\widetilde {S_g}$
be nonzero for some
![]() $x\in \widetilde {S_g}$
. For all
$x\in \widetilde {S_g}$
. For all
![]() $w\in T_x\widetilde {S_g}$
if
$w\in T_x\widetilde {S_g}$
if
![]() $\langle w,v\rangle> 0$
, the triple
$\langle w,v\rangle> 0$
, the triple
![]() $(\zeta _{-Jw},\zeta _v,\zeta _{Jw})$
is positively oriented and hence
$(\zeta _{-Jw},\zeta _v,\zeta _{Jw})$
is positively oriented and hence
![]() $(\ell _{-Jw},\ell _v,\ell _{Jw})$
is maximal and hence
$(\ell _{-Jw},\ell _v,\ell _{Jw})$
is maximal and hence
![]() $q^\circ _w$
is negative on
$q^\circ _w$
is negative on
![]() $\ell _v$
. If
$\ell _v$
. If
![]() $\langle w,v\rangle <0$
, the triple
$\langle w,v\rangle <0$
, the triple
![]() $(\ell _{Jw},\ell _v,\ell _{-Jw})$
is maximal and hence
$(\ell _{Jw},\ell _v,\ell _{-Jw})$
is maximal and hence
![]() $q^\circ _w$
is positive on
$q^\circ _w$
is positive on
![]() $\ell _v$
. Hence
$\ell _v$
. Hence
![]() $q_v$
is negative on
$q_v$
is negative on
![]() $\ell _v$
, and by a similar argument
$\ell _v$
, and by a similar argument
![]() $q_v$
is positive on
$q_v$
is positive on
![]() $\ell _{-v}$
, which are Lagrangians. In particular
$\ell _{-v}$
, which are Lagrangians. In particular
![]() $q_v$
is
$q_v$
is
![]() $\omega $
-regular for all
$\omega $
-regular for all
![]() $v\in T^1_x\widetilde {S_g}$
, and so
$v\in T^1_x\widetilde {S_g}$
, and so
![]() $u(x)$
is
$u(x)$
is
![]() $\omega $
-regular.
$\omega $
-regular.
We consider the geodesic flow on
![]() $u^*\mathbb {S} \mathcal {E}\simeq T^1\widetilde {S_g}$
, and we prove that this flow is fitting. Let
$u^*\mathbb {S} \mathcal {E}\simeq T^1\widetilde {S_g}$
, and we prove that this flow is fitting. Let
![]() $t>0$
,
$t>0$
,
![]() $x\in \widetilde {S_g}$
and
$x\in \widetilde {S_g}$
and
![]() $v\in T^1_x\widetilde {S_g}$
. Let
$v\in T^1_x\widetilde {S_g}$
. Let
![]() $(y,v')$
be the image of
$(y,v')$
be the image of
![]() $(x,v)$
by the geodesic flow at time t, and let
$(x,v)$
by the geodesic flow at time t, and let
![]() $\phi :T^1_x\widetilde {S_g}\to T^1_y\widetilde {S_g}$
be the identification given by the parallel transport along the geodesic between x and y.
$\phi :T^1_x\widetilde {S_g}\to T^1_y\widetilde {S_g}$
be the identification given by the parallel transport along the geodesic between x and y.
Let
![]() $w\in T^1_x\widetilde {S}$
be such that
$w\in T^1_x\widetilde {S}$
be such that
![]() $\langle w,v\rangle>0$
. The following quadruple is positive
$\langle w,v\rangle>0$
. The following quadruple is positive
![]() $(\zeta _{Jw},\zeta _{-Jw}, \zeta _{-J\phi (w)}, \zeta _{J\phi (w)})$
due to the negative curvature of the metric we put on
$(\zeta _{Jw},\zeta _{-Jw}, \zeta _{-J\phi (w)}, \zeta _{J\phi (w)})$
due to the negative curvature of the metric we put on
![]() $\widetilde {S_g}$
, see Figure 4. Hence the corresponding quadruple of Lagrangians is maximal. Therefore
$\widetilde {S_g}$
, see Figure 4. Hence the corresponding quadruple of Lagrangians is maximal. Therefore
![]() $q_{\phi (w)}^\circ -q_{w}^\circ $
is positive by Lemma 6.11. When
$q_{\phi (w)}^\circ -q_{w}^\circ $
is positive by Lemma 6.11. When
![]() $\langle w,v\rangle <0$
, the following quadruple is positive
$\langle w,v\rangle <0$
, the following quadruple is positive
![]() $(\zeta _{-Jw}, \zeta _{Jw},\zeta _{J\phi (w)}, \zeta _{-J\phi (w) })$
and therefore
$(\zeta _{-Jw}, \zeta _{Jw},\zeta _{J\phi (w)}, \zeta _{-J\phi (w) })$
and therefore
![]() $q_{\phi (w)}^\circ -q_{w}^\circ $
is negative. Hence:
$q_{\phi (w)}^\circ -q_{w}^\circ $
is negative. Hence:

Figure 4 Proof of Lemma 6.13.
We therefore have proven that the geodesic flow for the fixed hyperbolic metric is a fitting flow on
![]() $ T^1\widetilde {S_g}\simeq \mathbb {S} u^{\mathcal {E}}$
.
$ T^1\widetilde {S_g}\simeq \mathbb {S} u^{\mathcal {E}}$
.
Finally as in the proof of Lemma 6.7 the homotopy type of
![]() $\xi ^n_\rho $
is equal to the homotopy type of
$\xi ^n_\rho $
is equal to the homotopy type of
![]() $\xi _{u(x)}$
for all
$\xi _{u(x)}$
for all
![]() $x\in \widetilde {S_g}$
. Hence these pencils are in
$x\in \widetilde {S_g}$
. Hence these pencils are in
![]() $\operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
.
$\operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
.
Remark 6.14. These pencils always lie in the same connected component of
![]() $\operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
. Indeed one can construct such a pencil
$\operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
. Indeed one can construct such a pencil
![]() $u(x)\in \operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
given any maximal continuous map
$u(x)\in \operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
given any maximal continuous map
![]() $\xi $
from
$\xi $
from
![]() $\partial \widetilde {S_g}$
into the space of Lagrangians. The space of such maximal continuous maps being path connected, any two such pencils can be joined by a path in
$\partial \widetilde {S_g}$
into the space of Lagrangians. The space of such maximal continuous maps being path connected, any two such pencils can be joined by a path in
![]() $\operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
. It is not clear if
$\operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
. It is not clear if
![]() $\operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
only contains this connected component.
$\operatorname {\mathrm {Gr}}_2^{\max }(\mathcal {Q})$
only contains this connected component.
7 Geometry of the symmetric space
In this section we prove Proposition 7.1 and Lemma 7.4 which are two facts independent from the main results of the paper. We show how to construct fitting immersions of pencils using totally geodesic surfaces in the symmetric space
![]() $\mathbb {P}(S^2V^{>0})$
as in [Reference DavaloDav23]. We then prove that the codimension d submanifolds corresponding to pencils in
$\mathbb {P}(S^2V^{>0})$
as in [Reference DavaloDav23]. We then prove that the codimension d submanifolds corresponding to pencils in
![]() $\operatorname {\mathrm {Gr}}^\omega _d(\mathcal {Q})$
intersect transversely the symmetric space of
$\operatorname {\mathrm {Gr}}^\omega _d(\mathcal {Q})$
intersect transversely the symmetric space of
![]() $\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
embedded in
$\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
embedded in
![]() $\mathbb {P}(S^2V^{>0})$
.
$\mathbb {P}(S^2V^{>0})$
.
Given an immersion
![]() $h:M\to \mathbb {P}(S^2V^{>0})$
from a manifold M of dimension d we define its Gauss map
$h:M\to \mathbb {P}(S^2V^{>0})$
from a manifold M of dimension d we define its Gauss map
![]() $\mathcal {G}h :M\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
, that associates to
$\mathcal {G}h :M\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
, that associates to
![]() $x\in M$
the pencil P associated with the codimension d projective subspace of
$x\in M$
the pencil P associated with the codimension d projective subspace of
![]() $\text {Gr}_d(\mathcal {Q})$
orthogonal to
$\text {Gr}_d(\mathcal {Q})$
orthogonal to
![]() $\mathrm {d}h(TM)$
at
$\mathrm {d}h(TM)$
at
![]() $h(x)$
, for the
$h(x)$
, for the
![]() $\operatorname {\mathrm {SL}}(V)$
-invariant Riemannian metric on
$\operatorname {\mathrm {SL}}(V)$
-invariant Riemannian metric on
![]() $\mathbb {P}(S^2V)$
.
$\mathbb {P}(S^2V)$
.
The invariant Riemannian metric of the symmetric space associated to
![]() $\operatorname {\mathrm {SL}}(V)$
can be described by a natural identification between
$\operatorname {\mathrm {SL}}(V)$
can be described by a natural identification between
![]() $\mathbb {P}(S^2V^{>0})$
and its dual cone
$\mathbb {P}(S^2V^{>0})$
and its dual cone
![]() $\mathbb {P}(S^2(V^*)^{>0})$
. We therefore reformulate the definition of
$\mathbb {P}(S^2(V^*)^{>0})$
. We therefore reformulate the definition of
![]() $\mathcal {G}h$
as follows.
$\mathcal {G}h$
as follows.
We first identify
![]() $\mathbb {P}(S^2V^{>0})$
with
$\mathbb {P}(S^2V^{>0})$
with
![]() $\mathbb {P}(S^2(V^*)^{>0})$
via the map
$\mathbb {P}(S^2(V^*)^{>0})$
via the map
![]() $[X]\mapsto [X^{-1}]$
. Note as once again we view elements of
$[X]\mapsto [X^{-1}]$
. Note as once again we view elements of
![]() $S^2V$
and
$S^2V$
and
![]() $S^2(V^*)=\mathcal {Q}$
respectively as maps
$S^2(V^*)=\mathcal {Q}$
respectively as maps
![]() $V^*\to V$
and
$V^*\to V$
and
![]() $V\to V^*$
. An immersion
$V\to V^*$
. An immersion
![]() $h:M\to \mathbb {P}(S^2V^{>0})$
hence defines a dual immersion
$h:M\to \mathbb {P}(S^2V^{>0})$
hence defines a dual immersion
![]() $h^*:M\to \mathbb {P}(S^2(V^*)^{>0})$
. Fixing a volume form on V and
$h^*:M\to \mathbb {P}(S^2(V^*)^{>0})$
. Fixing a volume form on V and
![]() $V^*$
allows us to lift this map to a map
$V^*$
allows us to lift this map to a map
![]() $\overline {h}^*$
into the space of elements in
$\overline {h}^*$
into the space of elements in
![]() $S^2(V^*)^{>0}$
whose corresponding map
$S^2(V^*)^{>0}$
whose corresponding map
![]() $V\to V^*$
has determinant
$V\to V^*$
has determinant
![]() $1$
. We define
$1$
. We define
![]() $\mathcal {G}h(x)=\mathrm {d}\overline {h}^*(T_xM)\subset S^2V^*=\mathcal {Q}$
.
$\mathcal {G}h(x)=\mathrm {d}\overline {h}^*(T_xM)\subset S^2V^*=\mathcal {Q}$
.
Proposition 7.1. Let
![]() $h:M\to \mathbb {P}(S^2V^{>0})$
be a totally geodesic immersion. Suppose that the image of the Gauss map
$h:M\to \mathbb {P}(S^2V^{>0})$
be a totally geodesic immersion. Suppose that the image of the Gauss map
![]() $\mathcal {G}h :M\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
contains only regular pencils, that is, pencils containing only nondegenerate quadrics. The immersion
$\mathcal {G}h :M\to \operatorname {\mathrm {Gr}}_d(\mathcal {Q})$
contains only regular pencils, that is, pencils containing only nondegenerate quadrics. The immersion
![]() $\mathcal {G}h $
is then a fitting immersion. If h is complete it is a globally fitting map.
$\mathcal {G}h $
is then a fitting immersion. If h is complete it is a globally fitting map.
This proposition can be applied for instance to the totally geodesic surface associated to any representation of
![]() $\operatorname {\mathrm {SL}}(2,\mathbb {R})$
into
$\operatorname {\mathrm {SL}}(2,\mathbb {R})$
into
![]() $\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
. This can also be applied to the totally geodesic immersion of
$\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
. This can also be applied to the totally geodesic immersion of
![]() $\mathbb {H}^3$
induced by the inclusion
$\mathbb {H}^3$
induced by the inclusion
![]() $\operatorname {\mathrm {SL}}(2,\mathbb {C})\subset \operatorname {\mathrm {Sp}}(4,\mathbb {R})$
.
$\operatorname {\mathrm {SL}}(2,\mathbb {C})\subset \operatorname {\mathrm {Sp}}(4,\mathbb {R})$
.
Remark 7.2. The fibration of a domain of
![]() $\mathbb {P}(V)$
induced by the fitting map in this proposition is a particular case of Theorem 6.3 from [Reference DavaloDav23].
$\mathbb {P}(V)$
induced by the fitting map in this proposition is a particular case of Theorem 6.3 from [Reference DavaloDav23].
Note that if
![]() $d\geq 2$
, the signature
$d\geq 2$
, the signature
![]() $(a,b)$
of the quadrics of a regular pencil must satisfy
$(a,b)$
of the quadrics of a regular pencil must satisfy
![]() $a=b$
since
$a=b$
since
![]() $\mathbb {S}^{d-1}$
is connected. Hence the condition that the pencils are regular can be replaced in this case by the condition that the pencils belong to
$\mathbb {S}^{d-1}$
is connected. Hence the condition that the pencils are regular can be replaced in this case by the condition that the pencils belong to
![]() $\operatorname {\mathrm {Gr}}_d^{(n,n)}(\mathcal {Q})$
where
$\operatorname {\mathrm {Gr}}_d^{(n,n)}(\mathcal {Q})$
where
![]() $\dim (V)=2n$
.
$\dim (V)=2n$
.
As a corollary one can construct fitting immersions for some representations that factor through
![]() $\operatorname {\mathrm {SL}}(2,\mathbb {R})$
. Indeed if one has a representation
$\operatorname {\mathrm {SL}}(2,\mathbb {R})$
. Indeed if one has a representation
![]() $\iota :\operatorname {\mathrm {SL}}(2,\mathbb {R})\to \operatorname {\mathrm {SL}}(V)$
there exists a
$\iota :\operatorname {\mathrm {SL}}(2,\mathbb {R})\to \operatorname {\mathrm {SL}}(V)$
there exists a
![]() $\iota $
-equivariant totally geodesic map
$\iota $
-equivariant totally geodesic map
![]() $h:\mathbb {H}^2\to \operatorname {\mathrm {SL}}(V)$
, see Proposition 7.1.
$h:\mathbb {H}^2\to \operatorname {\mathrm {SL}}(V)$
, see Proposition 7.1.
Proof. Let
![]() $\gamma :\mathbb {R}\to M$
be a geodesic for the metric induced by h. Recall that
$\gamma :\mathbb {R}\to M$
be a geodesic for the metric induced by h. Recall that
![]() $\overline {h}(\gamma (t))$
for
$\overline {h}(\gamma (t))$
for
![]() $t\in \mathbb {R}$
is an element of
$t\in \mathbb {R}$
is an element of
![]() $S^2V$
, and hence it defines a positive symmetric endomorphism of
$S^2V$
, and hence it defines a positive symmetric endomorphism of
![]() $V^*$
and as such it is diagonalizable in an orthonormal basis with positive coefficients. We write the representative of
$V^*$
and as such it is diagonalizable in an orthonormal basis with positive coefficients. We write the representative of
![]() $h(\gamma (o))$
with determinant
$h(\gamma (o))$
with determinant
![]() $1$
in a basis
$1$
in a basis
![]() $(e_i)_{i\in I}$
such that for some
$(e_i)_{i\in I}$
such that for some
![]() $\lambda ^i\in \mathbb {R}$
, for all
$\lambda ^i\in \mathbb {R}$
, for all
![]() $t\in \mathbb {R}$
:
$t\in \mathbb {R}$
:
The dual immersion can be written as:
The element
![]() $q_t\in \mathcal {Q}$
corresponding to
$q_t\in \mathcal {Q}$
corresponding to
![]() $(\overline {h}^*\circ \gamma )'(t)$
is the symmetric bilinear form:
$(\overline {h}^*\circ \gamma )'(t)$
is the symmetric bilinear form:
The derivative of
![]() $(q_t)$
at
$(q_t)$
at
![]() $t=0$
equals:
$t=0$
equals:
This is a positive bilinear form if and only if all the
![]() $\lambda _i$
are nonzero, which is the case if and only if the bilinear forms
$\lambda _i$
are nonzero, which is the case if and only if the bilinear forms
![]() $q_t$
are nondegenerate, that is, if the image of
$q_t$
are nondegenerate, that is, if the image of
![]() $\mathcal {G}h$
contains only regular pencils. In this case, the positivity of the derivative of
$\mathcal {G}h$
contains only regular pencils. In this case, the positivity of the derivative of
![]() $(q_t)$
implies that the geodesic flow on
$(q_t)$
implies that the geodesic flow on
![]() $\mathbb {S}TM$
induces a fitting flow on
$\mathbb {S}TM$
induces a fitting flow on
![]() $\mathcal {G}h^*\mathbb {S}\mathcal {E}$
, so
$\mathcal {G}h^*\mathbb {S}\mathcal {E}$
, so
![]() $\mathcal {G}h$
is a fitting immersion.
$\mathcal {G}h$
is a fitting immersion.
If moreover h is complete, it is
![]() $\rho $
-equivariant for the discrete and faithful action of some closed surface group
$\rho $
-equivariant for the discrete and faithful action of some closed surface group
![]() $\Gamma $
. Hence Corollary 4.7 implies that h is a globally fitting map.
$\Gamma $
. Hence Corollary 4.7 implies that h is a globally fitting map.
Let us fix a symplectic form
![]() $\omega $
on
$\omega $
on
![]() $V=\mathbb {R}^{2n}$
. Let
$V=\mathbb {R}^{2n}$
. Let
![]() $\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
be the subset of
$\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
be the subset of
![]() $\mathbb {P}(S^2V^{>0})$
consisting of tensors
$\mathbb {P}(S^2V^{>0})$
consisting of tensors
![]() $[q^{-1}]$
that are compatible with
$[q^{-1}]$
that are compatible with
![]() $\omega $
, that is, such that for some complex structure J on
$\omega $
, that is, such that for some complex structure J on
![]() $\mathbb {R}^{2n}$
, the bilinear form
$\mathbb {R}^{2n}$
, the bilinear form
![]() $q+i\omega $
is a J-hermitian metric on V. Recall that
$q+i\omega $
is a J-hermitian metric on V. Recall that
![]() $q:V\to V^*$
is a bilinear form, and
$q:V\to V^*$
is a bilinear form, and
![]() $q^{-1}:V^*\to V$
is a tensor.
$q^{-1}:V^*\to V$
is a tensor.
The space
![]() $\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
is a copy of the symmetric space associated to
$\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
is a copy of the symmetric space associated to
![]() $\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
, which is a totally geodesic subspace of the symmetric space associated to the Lie group
$\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
, which is a totally geodesic subspace of the symmetric space associated to the Lie group
![]() $\operatorname {\mathrm {SL}}(2n,\mathbb {R})$
whose model is
$\operatorname {\mathrm {SL}}(2n,\mathbb {R})$
whose model is
![]() $\mathbb {P}(S^2V^{>0})$
. However it is not a projective subset: the closure of the projective convex hull of
$\mathbb {P}(S^2V^{>0})$
. However it is not a projective subset: the closure of the projective convex hull of
![]() $\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
in
$\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
in
![]() $\mathbb {P}(S^2V^{>0})$
is equal to
$\mathbb {P}(S^2V^{>0})$
is equal to
![]() $\mathbb {P}(S^2V^{\geq 0})$
since it contains all the extreme points of
$\mathbb {P}(S^2V^{\geq 0})$
since it contains all the extreme points of
![]() $\mathbb {P}(S^2V^{\geq 0})$
, that is, the rank one elements
$\mathbb {P}(S^2V^{\geq 0})$
, that is, the rank one elements
![]() $S^2\mathbb {P}(\mathbb {R}^{2n})$
.
$S^2\mathbb {P}(\mathbb {R}^{2n})$
.
Indeed, we can write matrices of the form
![]() $\text {Diag}(\lambda , 1, \cdots , 1,\lambda ^{-1})\in \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
for any
$\text {Diag}(\lambda , 1, \cdots , 1,\lambda ^{-1})\in \operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
for any
![]() $\lambda \in \mathbb {R}_{>0}$
and such that the first basis spans any fixed line
$\lambda \in \mathbb {R}_{>0}$
and such that the first basis spans any fixed line
![]() $\ell \in \mathbb {RP}^{2n-1}$
, one can observe that the closure of the orbit of any point of
$\ell \in \mathbb {RP}^{2n-1}$
, one can observe that the closure of the orbit of any point of
![]() $\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
by these elements contains the rank one point corresponding to
$\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
by these elements contains the rank one point corresponding to
![]() $\ell $
. Hence the closure of
$\ell $
. Hence the closure of
![]() $\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
contains all rank one points.
$\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
contains all rank one points.
The intersection of
![]() $\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
with a general linear subspace is not necessarily transverse. However it is the case for some special subspaces.
$\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
with a general linear subspace is not necessarily transverse. However it is the case for some special subspaces.
Definition 7.3. We say that an element
![]() $q\in \mathcal {Q}$
is
$q\in \mathcal {Q}$
is
![]() $\omega $
-regular if for some Lagrangians
$\omega $
-regular if for some Lagrangians
![]() $\ell ^+$
,
$\ell ^+$
,
![]() $\ell ^-$
the bilinear form q is positive on
$\ell ^-$
the bilinear form q is positive on
![]() $\ell ^+$
and negative on
$\ell ^+$
and negative on
![]() $\ell ^-$
.
$\ell ^-$
.
We denote by
![]() $\operatorname {\mathrm {Gr}}^\omega _d(\mathcal {Q})$
the set of pencils whose nonzero elements are
$\operatorname {\mathrm {Gr}}^\omega _d(\mathcal {Q})$
the set of pencils whose nonzero elements are
![]() $\omega $
-regular.
$\omega $
-regular.
In particular an
![]() $\omega $
-regular pencil q has signature
$\omega $
-regular pencil q has signature
![]() $(n,n)$
.
$(n,n)$
.
Lemma 7.4. Let
![]() $P\in \operatorname {\mathrm {Gr}}^\omega _2(\mathcal {Q})$
be an
$P\in \operatorname {\mathrm {Gr}}^\omega _2(\mathcal {Q})$
be an
![]() $\omega $
-regular pencil, that is, such that all its nonzero elements are
$\omega $
-regular pencil, that is, such that all its nonzero elements are
![]() $\omega $
-regular. The space
$\omega $
-regular. The space
![]() $\mathbb {P}(P^\circ )$
intersects transversely the manifold
$\mathbb {P}(P^\circ )$
intersects transversely the manifold
![]() $\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
in a codimension
$\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
in a codimension
![]() $2$
submanifold.
$2$
submanifold.
Proof. Let
![]() $q\in \mathcal {Q}$
be
$q\in \mathcal {Q}$
be
![]() $\omega $
-regular, and let
$\omega $
-regular, and let
![]() $x\in \mathbb {X}_{\operatorname {\mathrm {Sp}}}\cap \mathbb {P}(\langle q\rangle ^\circ )$
be an intersection point. Up to acting by
$x\in \mathbb {X}_{\operatorname {\mathrm {Sp}}}\cap \mathbb {P}(\langle q\rangle ^\circ )$
be an intersection point. Up to acting by
![]() $\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
, one can assume that
$\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
, one can assume that
![]() $x=[X^{-1}]\in \mathbb {P}(S^2V)$
where X is the bilinear form whose associated matrix in some symplectic basis is:
$x=[X^{-1}]\in \mathbb {P}(S^2V)$
where X is the bilinear form whose associated matrix in some symplectic basis is:
 $$ \begin{align*}\begin{pmatrix} I_n & 0\\ 0 & I_n \end{pmatrix}.\end{align*} $$
$$ \begin{align*}\begin{pmatrix} I_n & 0\\ 0 & I_n \end{pmatrix}.\end{align*} $$
The annihilator
![]() $(T\mathbb {X}_{\operatorname {\mathrm {Sp}}})^\circ \subset S^2V$
of the tangent space to
$(T\mathbb {X}_{\operatorname {\mathrm {Sp}}})^\circ \subset S^2V$
of the tangent space to
![]() $\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
at this point, viewed as a linear subspace of
$\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
at this point, viewed as a linear subspace of
![]() $\mathcal {Q}$
can be identified with the space of following symmetric matrices where A is symmetric and B is antisymmetric:
$\mathcal {Q}$
can be identified with the space of following symmetric matrices where A is symmetric and B is antisymmetric:
 $$ \begin{align*}\begin{pmatrix} A & B\\ -B & A \end{pmatrix}.\end{align*} $$
$$ \begin{align*}\begin{pmatrix} A & B\\ -B & A \end{pmatrix}.\end{align*} $$
Suppose that the intersection is not transverse, that is, that q can be written in this form. Let
![]() $\ell ^+$
and
$\ell ^+$
and
![]() $\ell ^-$
be Lagrangians on which q is respectively positive and negative. Since the maximal compact
$\ell ^-$
be Lagrangians on which q is respectively positive and negative. Since the maximal compact
![]() $U(n)$
acts transitively on the space of Lagrangians one can assume that
$U(n)$
acts transitively on the space of Lagrangians one can assume that
![]() $\ell ^+=\langle x_1,\cdots ,x_n\rangle $
. Let
$\ell ^+=\langle x_1,\cdots ,x_n\rangle $
. Let
![]() $\ell _0^-=\langle y_1,\cdots ,y_n\rangle $
be its orthogonal for the fixed euclidean metric. The Lagrangian
$\ell _0^-=\langle y_1,\cdots ,y_n\rangle $
be its orthogonal for the fixed euclidean metric. The Lagrangian
![]() $\ell ^-$
is transverse to
$\ell ^-$
is transverse to
![]() $\ell ^+$
so for some symmetric matrix U, one can view
$\ell ^+$
so for some symmetric matrix U, one can view
![]() $\ell ^-$
as the image of:
$\ell ^-$
as the image of:
The fact that q is positive on
![]() $\ell ^+$
implies that A is positive. The fact that q is negative on
$\ell ^+$
implies that A is positive. The fact that q is negative on
![]() $\ell ^-$
implies that the following is negative:
$\ell ^-$
implies that the following is negative:
But A and
![]() $UAU$
are both positive and the bracket
$UAU$
are both positive and the bracket
![]() $[B,U]$
has trace zero so it cannot be negative. Hence the intersection must be transverse.
$[B,U]$
has trace zero so it cannot be negative. Hence the intersection must be transverse.
Proposition 7.5. A tangent vector in
![]() $T\mathbb {X}_{\operatorname {\mathrm {Sp}}} \subset T\mathbb {P}(S^2(V^*)^{>0})$
is
$T\mathbb {X}_{\operatorname {\mathrm {Sp}}} \subset T\mathbb {P}(S^2(V^*)^{>0})$
is
![]() $\omega $
-regular if and only if the corresponding element of
$\omega $
-regular if and only if the corresponding element of
![]() $\mathcal {Q}$
is nondegenerate.
$\mathcal {Q}$
is nondegenerate.
Proof. Given
![]() $\mathrm {v}\in T\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
one can write the corresponding element
$\mathrm {v}\in T\mathbb {X}_{\operatorname {\mathrm {Sp}}}$
one can write the corresponding element
![]() $q\in \mathcal {Q}$
for some symplectic basis
$q\in \mathcal {Q}$
for some symplectic basis
![]() $(x_1,\cdots x_n,y_1,\cdots y_n)$
as:
$(x_1,\cdots x_n,y_1,\cdots y_n)$
as:
 $$ \begin{align*}\sum_{i=1}^n \lambda_i(x_i^*\otimes x_i^*-y_i^*\otimes y_i^*).\end{align*} $$
$$ \begin{align*}\sum_{i=1}^n \lambda_i(x_i^*\otimes x_i^*-y_i^*\otimes y_i^*).\end{align*} $$
This bilinear form is regular if and only if all the
![]() $\lambda _i$
are nonzero. Else we can assume that
$\lambda _i$
are nonzero. Else we can assume that
![]() $\lambda _i>0$
up to exchanging
$\lambda _i>0$
up to exchanging
![]() $x_i$
by
$x_i$
by
![]() $y_i$
and
$y_i$
and
![]() $y_i$
by
$y_i$
by
![]() $-x_i$
in the symplectic basis. Then the bilinear form is positive on the Lagrangian
$-x_i$
in the symplectic basis. Then the bilinear form is positive on the Lagrangian
![]() $\langle x_1,\cdots , x_n\rangle $
and negative on the Lagrangian
$\langle x_1,\cdots , x_n\rangle $
and negative on the Lagrangian
![]() $\langle y_1,\cdots , y_n\rangle $
.
$\langle y_1,\cdots , y_n\rangle $
.
A Immersions in the space of geodesics in
 $\mathbb {H}^3$
$\mathbb {H}^3$
A.1 The space of geodesics
In this section we set
![]() $V=\mathbb {C}^2$
, and restrict ourselves to pencils of Hermitian quadrics. Note that we can see this way
$V=\mathbb {C}^2$
, and restrict ourselves to pencils of Hermitian quadrics. Note that we can see this way
![]() $\operatorname {\mathrm {SL}}(2,\mathbb {C})$
as a subgroup of
$\operatorname {\mathrm {SL}}(2,\mathbb {C})$
as a subgroup of
![]() $\operatorname {\mathrm {Sp}}(4,\mathbb {R})\simeq \operatorname {\mathrm {Sp}}(V,\omega )$
for
$\operatorname {\mathrm {Sp}}(4,\mathbb {R})\simeq \operatorname {\mathrm {Sp}}(V,\omega )$
for
![]() $\omega $
the real part of a volume form on
$\omega $
the real part of a volume form on
![]() $\mathbb {C}^2$
. The results of this Section serve as an illustration of the previously introduced notions of fitting pairs and fitting directions.
$\mathbb {C}^2$
. The results of this Section serve as an illustration of the previously introduced notions of fitting pairs and fitting directions.
Let
![]() $\mathcal {H}\subset \mathcal {Q}$
be the subset of Hermitian bilinear forms on
$\mathcal {H}\subset \mathcal {Q}$
be the subset of Hermitian bilinear forms on
![]() $V=\mathbb {C}^2$
. A Hermitian form
$V=\mathbb {C}^2$
. A Hermitian form
![]() $q\in \mathcal {H}$
that is not semi-positive or semi-negative is of Hermitian signature
$q\in \mathcal {H}$
that is not semi-positive or semi-negative is of Hermitian signature
![]() $(1,1)$
, and hence its zero set in
$(1,1)$
, and hence its zero set in
![]() $\mathbb {CP}^1$
is a circle.
$\mathbb {CP}^1$
is a circle.
Let
![]() $S^2V=S^2_hV\oplus S^2_aV$
be the eigenspace decomposition for the operator
$S^2V=S^2_hV\oplus S^2_aV$
be the eigenspace decomposition for the operator
![]() $J\otimes J$
where J is the complex conjugation. Here
$J\otimes J$
where J is the complex conjugation. Here
![]() $S^2_hV$
is the
$S^2_hV$
is the
![]() $4$
-dimensional eigenspace associated to
$4$
-dimensional eigenspace associated to
![]() $1$
and
$1$
and
![]() $S^2_aV=\mathcal {H}^\circ $
, the
$S^2_aV=\mathcal {H}^\circ $
, the
![]() $6$
-dimensional space associated to
$6$
-dimensional space associated to
![]() $-1$
. The intersection of
$-1$
. The intersection of
![]() $\mathbb {P}(S^2_hV)$
with the space of positive tensors is the projective Klein model for
$\mathbb {P}(S^2_hV)$
with the space of positive tensors is the projective Klein model for
![]() $\mathbb {H}^3$
.
$\mathbb {H}^3$
.
The annihilator of a pencil
![]() $P\in \operatorname {\mathrm {Gr}}_2^{{\operatorname {\mathrm {mix}}}}(\mathcal {H})$
, that is, a plane
$P\in \operatorname {\mathrm {Gr}}_2^{{\operatorname {\mathrm {mix}}}}(\mathcal {H})$
, that is, a plane
![]() $P\subset \mathcal {H}$
such that no nonzero vectors are semi-positive, is equal to
$P\subset \mathcal {H}$
such that no nonzero vectors are semi-positive, is equal to
![]() $P^\circ =\mathcal {H}^\circ \oplus H$
where H is a plane in
$P^\circ =\mathcal {H}^\circ \oplus H$
where H is a plane in
![]() $S^2_hV$
, which in turns corresponds to a geodesic in
$S^2_hV$
, which in turns corresponds to a geodesic in
![]() $\mathbb {H}^3$
in the projective Klein model.
$\mathbb {H}^3$
in the projective Klein model.
A pencil of quadrics
![]() $P\in \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_2(\mathcal {H})$
vanishes completely on two points in
$P\in \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_2(\mathcal {H})$
vanishes completely on two points in
![]() $\mathbb {CP}^1$
, as in Figure 5 where the zero set of three elements of the pencil are depicted. The space of mixed pencils in
$\mathbb {CP}^1$
, as in Figure 5 where the zero set of three elements of the pencil are depicted. The space of mixed pencils in
![]() $\mathcal {H}$
can be identified with the space
$\mathcal {H}$
can be identified with the space
![]() $\mathcal {G}$
of unoriented geodesics in
$\mathcal {G}$
of unoriented geodesics in
![]() $\mathbb {H}^3$
.
$\mathbb {H}^3$
.

Figure 5 Three Hermitian quadrics in a pencil and the corresponding geodesic in
![]() $\mathbb {H}^3$
.
$\mathbb {H}^3$
.
Remark A.1. The space
![]() $\mathcal {G}$
is a
$\mathcal {G}$
is a
![]() $\operatorname {\mathrm {SL}}(2,\mathbb {C})$
-homogeneous space. Note that however the larger spaces
$\operatorname {\mathrm {SL}}(2,\mathbb {C})$
-homogeneous space. Note that however the larger spaces
![]() $P\in \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_2(\mathcal {Q})$
or
$P\in \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_2(\mathcal {Q})$
or
![]() $P\in \operatorname {\mathrm {Gr}}^{{\omega }}_2(\mathcal {Q})$
from the rest of the paper are not
$P\in \operatorname {\mathrm {Gr}}^{{\omega }}_2(\mathcal {Q})$
from the rest of the paper are not
![]() $\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
or
$\operatorname {\mathrm {Sp}}(2n,\mathbb {R})$
or
![]() $\operatorname {\mathrm {SL}}(2n,\mathbb {R})$
homogeneous spaces.
$\operatorname {\mathrm {SL}}(2n,\mathbb {R})$
homogeneous spaces.
Two pencils in
![]() $\mathcal {H}$
form a fitting pair if and only if we can find a circle in each of the pencils that are disjoint. This is possible if and only if the two corresponding geodesics in
$\mathcal {H}$
form a fitting pair if and only if we can find a circle in each of the pencils that are disjoint. This is possible if and only if the two corresponding geodesics in
![]() $\mathbb {H}^3$
are disjoint, with disjoint endpoints. A fitting pair of pencils is illustrated in Figure 6.
$\mathbb {H}^3$
are disjoint, with disjoint endpoints. A fitting pair of pencils is illustrated in Figure 6.

Figure 6 Two disjoint geodesics in
![]() $\mathbb {H}^3$
and disjoint circles in
$\mathbb {H}^3$
and disjoint circles in
![]() $\mathbb {CP}^1$
between their endpoints.
$\mathbb {CP}^1$
between their endpoints.
The space
![]() $\mathcal {G}$
of unoriented geodesics in
$\mathcal {G}$
of unoriented geodesics in
![]() $\mathbb {H}^3$
admits a pseudo-Riemannian metric of signature
$\mathbb {H}^3$
admits a pseudo-Riemannian metric of signature
![]() $(2,2)$
: we now compare the notion of fitting vectors with the notion of spacelike vectors. The tangent space at a geodesic with endpoints
$(2,2)$
: we now compare the notion of fitting vectors with the notion of spacelike vectors. The tangent space at a geodesic with endpoints
![]() $(x,y)\in \mathbb {CP}^1$
can be identified with
$(x,y)\in \mathbb {CP}^1$
can be identified with
![]() $T_x\mathbb {CP}^1\times T_y\mathbb {CP}^1$
. The choice of a point in the geodesic provides an identification
$T_x\mathbb {CP}^1\times T_y\mathbb {CP}^1$
. The choice of a point in the geodesic provides an identification
![]() $\phi :T_x\mathbb {CP}^1\to T_y\mathbb {CP}^1$
and a metric
$\phi :T_x\mathbb {CP}^1\to T_y\mathbb {CP}^1$
and a metric
![]() $q_0$
on
$q_0$
on
![]() $T_y\mathbb {CP}^1$
. Taking a different point in the geodesic means replacing
$T_y\mathbb {CP}^1$
. Taking a different point in the geodesic means replacing
![]() $\phi $
by
$\phi $
by
![]() $\lambda \phi $
and
$\lambda \phi $
and
![]() $q_0$
by
$q_0$
by
![]() $\lambda ^{-1} q_0$
for some
$\lambda ^{-1} q_0$
for some
![]() $\lambda \in R_{>0}$
.
$\lambda \in R_{>0}$
.
Hence we can consider the pseudo Riemannian metric that is invariant by the action of the isometry group of
![]() $\mathbb {H}^3$
:
$\mathbb {H}^3$
:
For this metric a vector
![]() $(v,w)\in T_x\mathbb {CP}^1\times T_y\mathbb {CP}^1$
is spacelike if and only if
$(v,w)\in T_x\mathbb {CP}^1\times T_y\mathbb {CP}^1$
is spacelike if and only if
![]() $q_0(\phi (v),w)>0$
.
$q_0(\phi (v),w)>0$
.
Proposition A.2. A pair of geodesics is a fitting pair if and only if the corresponding geodesics are disjoint.
A tangent vector
![]() $(v,w)$
to
$(v,w)$
to
![]() $\mathcal {G}\simeq \operatorname {\mathrm {Gr}}_2(\mathcal {H})$
is fitting if and only if
$\mathcal {G}\simeq \operatorname {\mathrm {Gr}}_2(\mathcal {H})$
is fitting if and only if
![]() $\phi (v)$
and w are not positively anti-colinear, that is, there are no
$\phi (v)$
and w are not positively anti-colinear, that is, there are no
![]() $\lambda ,\mu \in \mathbb {R}^{\geq 0}$
such that
$\lambda ,\mu \in \mathbb {R}^{\geq 0}$
such that
![]() $\lambda \phi (v)=- \mu w$
.
$\lambda \phi (v)=- \mu w$
.
Remark A.3. In particular spacelike vectors are fitting, but not all fitting vectors are spacelike.
Proof. Let
![]() $P_1,P_2\in \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_2(\mathcal {H})$
. One has
$P_1,P_2\in \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_2(\mathcal {H})$
. One has
![]() $\mathbb {P}(S_a^2V)\cap \mathbb {P}(S^2V^{\geq 0})=\emptyset $
. Hence the subsets
$\mathbb {P}(S_a^2V)\cap \mathbb {P}(S^2V^{\geq 0})=\emptyset $
. Hence the subsets
![]() $\mathbb {P}(P_1^\circ \cap S^2V^{\geq 0})$
and
$\mathbb {P}(P_1^\circ \cap S^2V^{\geq 0})$
and
![]() $\mathbb {P}(P_2^\circ \cap S^2V^{\geq 0})$
for
$\mathbb {P}(P_2^\circ \cap S^2V^{\geq 0})$
for
![]() $P_1,P_2\in \operatorname {\mathrm {Gr}}_2^{{\operatorname {\mathrm {mix}}}}(\mathcal {H})$
are disjoint if and only if the corresponding geodesics are disjoint.
$P_1,P_2\in \operatorname {\mathrm {Gr}}_2^{{\operatorname {\mathrm {mix}}}}(\mathcal {H})$
are disjoint if and only if the corresponding geodesics are disjoint.
Let
![]() $(v,w)$
be a tangent vector to
$(v,w)$
be a tangent vector to
![]() $\gamma \in \mathcal {G}$
and let
$\gamma \in \mathcal {G}$
and let
![]() $\gamma _t$
be a curve in
$\gamma _t$
be a curve in
![]() $\mathcal {G}$
with this derivative at
$\mathcal {G}$
with this derivative at
![]() $t=0$
. If
$t=0$
. If
![]() $\phi (v)$
and w are not nonpositively colinear, the distance between
$\phi (v)$
and w are not nonpositively colinear, the distance between
![]() $\gamma =\gamma _0$
and
$\gamma =\gamma _0$
and
![]() $\gamma _t$
is greater than
$\gamma _t$
is greater than
![]() $\epsilon t$
for some
$\epsilon t$
for some
![]() $\epsilon>0$
and t small enough. Indeed there exist
$\epsilon>0$
and t small enough. Indeed there exist
![]() $z\in T_x\mathbb {CP}^1$
such that
$z\in T_x\mathbb {CP}^1$
such that
![]() $q_0(\phi (z),\phi (x)),q_0(\phi (z),w)\geq 0$
, and the totally geodesic disk in
$q_0(\phi (z),\phi (x)),q_0(\phi (z),w)\geq 0$
, and the totally geodesic disk in
![]() $\mathbb {H}^3$
through
$\mathbb {H}^3$
through
![]() $x,y$
normal to z at x contains
$x,y$
normal to z at x contains
![]() $\gamma _0$
while being at distance
$\gamma _0$
while being at distance
![]() $\epsilon t$
to
$\epsilon t$
to
![]() $\gamma _t$
.
$\gamma _t$
.
Hence the distance between the subsets
![]() $\mathbb {P}(P_0^\circ \cap S^2V^{\geq 0})$
and
$\mathbb {P}(P_0^\circ \cap S^2V^{\geq 0})$
and
![]() $\mathbb {P}(P_t^\circ \cap S^2V^{\geq 0})$
is also greater than
$\mathbb {P}(P_t^\circ \cap S^2V^{\geq 0})$
is also greater than
![]() $\epsilon 't$
for some
$\epsilon 't$
for some
![]() $\epsilon '>0$
and all t small enough. Therefore by Proposition 3.7 this direction is fitting.
$\epsilon '>0$
and all t small enough. Therefore by Proposition 3.7 this direction is fitting.
Conversely if If
![]() $\phi (v)$
and w are nonpositively colinear, then there is such a curve
$\phi (v)$
and w are nonpositively colinear, then there is such a curve
![]() $\gamma _t$
such that the corresponding geodesics all have a common point. Therefore by Proposition 3.7 this direction is not fitting.
$\gamma _t$
such that the corresponding geodesics all have a common point. Therefore by Proposition 3.7 this direction is not fitting.
Remark A.4. If S is a surface in
![]() $\mathbb {H}^3$
with principal curvature in
$\mathbb {H}^3$
with principal curvature in
![]() $(-1,1)$
, then the set of normal geodesics forms spacelike surface, for the pseudo-Riemannian structure on the space of geodesics described in Section A.1. The corresponding map
$(-1,1)$
, then the set of normal geodesics forms spacelike surface, for the pseudo-Riemannian structure on the space of geodesics described in Section A.1. The corresponding map
![]() $\mathcal {G}u:S\to \mathcal {G}$
is called the Gauss map. Nearly Fuchsian representations are representations of a closed surface group
$\mathcal {G}u:S\to \mathcal {G}$
is called the Gauss map. Nearly Fuchsian representations are representations of a closed surface group
![]() $\Gamma _g$
admitting an equivariant surface with principal curvature in
$\Gamma _g$
admitting an equivariant surface with principal curvature in
![]() $(-1,1)$
. They are a priori a larger class of representations than almost Fuchsian representations, for which the equivariant surface with principal curvature in
$(-1,1)$
. They are a priori a larger class of representations than almost Fuchsian representations, for which the equivariant surface with principal curvature in
![]() $(-1,1)$
is required to be minimal.
$(-1,1)$
is required to be minimal.
The space
![]() $\mathcal {G}$
also admits a special
$\mathcal {G}$
also admits a special
![]() $\operatorname {\mathrm {SL}}_2(\mathbb {C})$
-invariant symplectic structure. An immersion in
$\operatorname {\mathrm {SL}}_2(\mathbb {C})$
-invariant symplectic structure. An immersion in
![]() $\mathcal {G}$
is locally the Gauss map of an immersion with principal curvature in
$\mathcal {G}$
is locally the Gauss map of an immersion with principal curvature in
![]() $(-1,1)$
if and only if it is spacelike and Lagrangian for this symplectic structure [Reference Emam and SeppiES22]. Therefore if the fitting immersion is not Lagrangian, it does not come as the Gauss map of a surface in
$(-1,1)$
if and only if it is spacelike and Lagrangian for this symplectic structure [Reference Emam and SeppiES22]. Therefore if the fitting immersion is not Lagrangian, it does not come as the Gauss map of a surface in
![]() $\mathbb {H}^3$
. Hence there could be representations admitting fitting immersions that are not nearly Fuchsian.
$\mathbb {H}^3$
. Hence there could be representations admitting fitting immersions that are not nearly Fuchsian.
A.2 A quasi-Fuchsian representation with no fitting immersions
Having a representation that is Anosov is not sufficient to ensure that there exist an equivariant fitting immersion. We show that there are quasi-Fuchsian representations that admit no such immersions of Hermitian pencils of quadrics. We use here the notations from Section A.1.
Theorem A.5. There exists a quasi-Fuchsian representation
![]() $\rho :\Gamma _g\to \operatorname {\mathrm {SL}}(2,\mathbb {C})$
for some genus g large enough that admits no
$\rho :\Gamma _g\to \operatorname {\mathrm {SL}}(2,\mathbb {C})$
for some genus g large enough that admits no
![]() $\rho $
-equivariant fitting immersion
$\rho $
-equivariant fitting immersion
![]() $u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{{\operatorname {\mathrm {mix}}}}(\mathcal {H})=\mathcal {G}$
.
$u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{{\operatorname {\mathrm {mix}}}}(\mathcal {H})=\mathcal {G}$
.
Moreover it also admits no continuous map
![]() $u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{{\operatorname {\mathrm {mix}}}}(\mathcal {H})=\mathcal {G}$
that admits a
$u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}_2^{{\operatorname {\mathrm {mix}}}}(\mathcal {H})=\mathcal {G}$
that admits a
![]() $\rho $
-equivariant fitting flow.
$\rho $
-equivariant fitting flow.
A particular corollary is the following result on Nearly Fuchsian representations, introduced in Remark A.4.
Corollary A.6. There exist quasi-Fuchsian representations that are not nearly Fuchsian.
Almost Fuchsian representations were already known to not contain all quasi-Fuchsian representations see for instance [Reference Huang and WangHW15], but a recent result of Nguyen, Schlenker and Seppi [Reference Nguyen, Schlenker and SeppiNSS25] proves that nearly Fuchsian representations are not all almost Fuchsian, making this corollary new.
Here
![]() $V=\mathbb {C}^2$
and if
$V=\mathbb {C}^2$
and if
![]() $\rho :\Gamma _g \to \operatorname {\mathrm {SL}}(2,\mathbb {C})\subset \operatorname {\mathrm {Sp}}(4,\mathbb {R})$
, the Guichard-Wienhard domain of discontinuity
$\rho :\Gamma _g \to \operatorname {\mathrm {SL}}(2,\mathbb {C})\subset \operatorname {\mathrm {Sp}}(4,\mathbb {R})$
, the Guichard-Wienhard domain of discontinuity
![]() $\Omega _\rho $
, mentioned in Proposition 5.5 corresponds to the pullback in
$\Omega _\rho $
, mentioned in Proposition 5.5 corresponds to the pullback in
![]() $\mathbb {RP}^3=\mathbb {P}_{\mathbb {R}}(\mathbb {C}^2)$
, of a domain of discontinuity
$\mathbb {RP}^3=\mathbb {P}_{\mathbb {R}}(\mathbb {C}^2)$
, of a domain of discontinuity
![]() $\Omega _\rho ^0\subset \mathbb {CP}^1=\mathbb {P}_{\mathbb {C}}(\mathbb {C}^2)$
. This domain is the complement in
$\Omega _\rho ^0\subset \mathbb {CP}^1=\mathbb {P}_{\mathbb {C}}(\mathbb {C}^2)$
. This domain is the complement in
![]() $\mathbb {CP}^1$
of the limit set of
$\mathbb {CP}^1$
of the limit set of
![]() $\rho $
.
$\rho $
.
Since
![]() $\Gamma _g$
is a surface group, this domain in
$\Gamma _g$
is a surface group, this domain in
![]() $\mathbb {CP}^1$
is the union of two topological disks, and hence for each
$\mathbb {CP}^1$
is the union of two topological disks, and hence for each
![]() $x\in \widetilde {S_g}$
the geodesic corresponding to
$x\in \widetilde {S_g}$
the geodesic corresponding to
![]() $u(x)$
has one endpoint in each of these discs. This fact will be used in the proof of Theorem A.5.
$u(x)$
has one endpoint in each of these discs. This fact will be used in the proof of Theorem A.5.
Another ingredient of the proof of Theorem A.5 is the following.
Proposition A.7 [Reference Huang and WangHW15, Corollary 3.5]
Given any
![]() $\mathcal {C}^1$
embedded circle
$\mathcal {C}^1$
embedded circle
![]() $\gamma $
in
$\gamma $
in
![]() $\mathbb {CP}^1$
, and any
$\mathbb {CP}^1$
, and any
![]() $\epsilon>0$
, there exists a quasi-Fuchsian representation
$\epsilon>0$
, there exists a quasi-Fuchsian representation
![]() $\rho :\Gamma _g\to \operatorname {\mathrm {SL}}(2,\mathbb {C})$
for some genus g large enough whose limit set has Hausdorff distance at most
$\rho :\Gamma _g\to \operatorname {\mathrm {SL}}(2,\mathbb {C})$
for some genus g large enough whose limit set has Hausdorff distance at most
![]() $\epsilon $
with
$\epsilon $
with
![]() $\gamma $
.
$\gamma $
.
Proof of Theorem A.5
We consider the Jordan curve
![]() $\gamma $
from Figure 7. Let
$\gamma $
from Figure 7. Let
![]() $x,y,z$
be as in the figure. We consider a quasi-Fuchsian representation of
$x,y,z$
be as in the figure. We consider a quasi-Fuchsian representation of
![]() $\Gamma _g$
for a genus large enough such that its limit set
$\Gamma _g$
for a genus large enough such that its limit set
![]() $\Lambda $
contains
$\Lambda $
contains
![]() $x,z$
and is close enough to
$x,z$
and is close enough to
![]() $\gamma $
using Proposition A.7. More precisely let
$\gamma $
using Proposition A.7. More precisely let
![]() $s_x$
and
$s_x$
and
![]() $s_z$
be the open arcs of the circle of
$s_z$
be the open arcs of the circle of
![]() $\mathbb {CP}^1$
passing through
$\mathbb {CP}^1$
passing through
![]() $x,y,z$
respectively between
$x,y,z$
respectively between
![]() $x,y$
and
$x,y$
and
![]() $y,z$
and let I be the interior of the Jordan curve
$y,z$
and let I be the interior of the Jordan curve
![]() $\Lambda $
. We require that the union
$\Lambda $
. We require that the union
![]() $U_x$
of all the connected component of
$U_x$
of all the connected component of
![]() $I\setminus s_z$
whose closure contain x is disjoint from the union
$I\setminus s_z$
whose closure contain x is disjoint from the union
![]() $U_z$
of all the connected component of
$U_z$
of all the connected component of
![]() $I\setminus s_x$
whose closure contain z. These two disjoint sets are illustrated for the curve
$I\setminus s_x$
whose closure contain z. These two disjoint sets are illustrated for the curve
![]() $\gamma $
as the two gray regions.
$\gamma $
as the two gray regions.

Figure 7 A Jordan curve in
![]() $\mathbb {CP}^1$
.
$\mathbb {CP}^1$
.
Let
![]() $\rho :\Gamma _g\to \operatorname {\mathrm {SL}}(2,\mathbb {C})$
then be such a quasi-Fuchsian representation. Suppose that it admits an equivariant continuous map
$\rho :\Gamma _g\to \operatorname {\mathrm {SL}}(2,\mathbb {C})$
then be such a quasi-Fuchsian representation. Suppose that it admits an equivariant continuous map
![]() $u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_2(\mathcal {H})$
with an equivariant fitting flow
$u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}^{{\operatorname {\mathrm {mix}}}}_2(\mathcal {H})$
with an equivariant fitting flow
![]() $\Phi $
on
$\Phi $
on
![]() $\mathbb {S} u^*\mathcal {E}$
. By Proposition 4.5 there exists a flow line
$\mathbb {S} u^*\mathcal {E}$
. By Proposition 4.5 there exists a flow line
![]() $(\Phi _t(q))_{t\in \mathbb {R}}$
such that its projection
$(\Phi _t(q))_{t\in \mathbb {R}}$
such that its projection
![]() $\gamma :\mathbb {R}\to \widetilde {S_g}$
is a quasi-geodesic between the points of
$\gamma :\mathbb {R}\to \widetilde {S_g}$
is a quasi-geodesic between the points of
![]() $\partial \Gamma $
corresponding to x and z in the limit set.
$\partial \Gamma $
corresponding to x and z in the limit set.
For all
![]() $t\in \mathbb {R}$
, let
$t\in \mathbb {R}$
, let
![]() $x_t\in \mathbb {CP}^1$
be the endpoint of the geodesic corresponding to
$x_t\in \mathbb {CP}^1$
be the endpoint of the geodesic corresponding to
![]() $u(\gamma (t))$
that belongs to the interior of the Jordan curve
$u(\gamma (t))$
that belongs to the interior of the Jordan curve
![]() $\Lambda $
. When t goes to
$\Lambda $
. When t goes to
![]() $+\infty $
,
$+\infty $
,
![]() $x_t$
converges to z and it converges to x for t going to
$x_t$
converges to z and it converges to x for t going to
![]() $-\infty $
. Moreover
$-\infty $
. Moreover
![]() $x_t$
always belong to the circle determined by
$x_t$
always belong to the circle determined by
![]() $\Phi _t(q)$
.
$\Phi _t(q)$
.
There exists a
![]() $t_0\in \mathbb {R}$
such that y belongs to the circle
$t_0\in \mathbb {R}$
such that y belongs to the circle
![]() $\Phi _{t_0}(q)$
. Note that this great circle splits
$\Phi _{t_0}(q)$
. Note that this great circle splits
![]() $\mathbb {CP}^1$
in two parts, one containing x and
$\mathbb {CP}^1$
in two parts, one containing x and
![]() $s_x$
and one containing z and
$s_x$
and one containing z and
![]() $s_z$
. In particular
$s_z$
. In particular
![]() $(x_t)_{t\geq t_0}$
must lie in
$(x_t)_{t\geq t_0}$
must lie in
![]() $U_z$
and
$U_z$
and
![]() $(x_t)_{t\leq t_0}$
must lie in
$(x_t)_{t\leq t_0}$
must lie in
![]() $U_x$
, leading to a contradiction. Hence no such map u can exist.
$U_x$
, leading to a contradiction. Hence no such map u can exist.
B Fitting immersions and spacelike immersions for
 $\operatorname {\mathrm {Sp}}(4,\mathbb {R})$
$\operatorname {\mathrm {Sp}}(4,\mathbb {R})$
In this section we explain how the data of a maximal immersion into the Pseudo-Riemannian space
![]() $\mathbb {H}^{2,2}$
with principal curvature in
$\mathbb {H}^{2,2}$
with principal curvature in
![]() $(-1,1)$
induces a fitting immersion. Combining this with a result from Collier-Tholozan-Toulisse we show that our characterization of maximal representations can be improved in
$(-1,1)$
induces a fitting immersion. Combining this with a result from Collier-Tholozan-Toulisse we show that our characterization of maximal representations can be improved in
![]() $\operatorname {\mathrm {Sp}}(4,\mathbb {R})$
.
$\operatorname {\mathrm {Sp}}(4,\mathbb {R})$
.
Note first that one has the following exceptional isomorphism:
This isomorphism comes from the fact that
![]() $\operatorname {\mathrm {PSp}}(4,\mathbb {R})$
preserves a subspace of dimension
$\operatorname {\mathrm {PSp}}(4,\mathbb {R})$
preserves a subspace of dimension
![]() $5$
of
$5$
of
![]() $\Lambda ^2\mathbb {R}^4$
, as well as a symmetric bilinear form of signature
$\Lambda ^2\mathbb {R}^4$
, as well as a symmetric bilinear form of signature
![]() $(2,3)$
on this subspace. Hence
$(2,3)$
on this subspace. Hence
![]() $\operatorname {\mathrm {PSp}}(4,\mathbb {R})$
acts naturally on the pseudo-Riemannian symmetric space with constant negative sectional curvature
$\operatorname {\mathrm {PSp}}(4,\mathbb {R})$
acts naturally on the pseudo-Riemannian symmetric space with constant negative sectional curvature
![]() $\mathbb {H}^{2,2}$
, which consists of vectors of norm
$\mathbb {H}^{2,2}$
, which consists of vectors of norm
![]() $-1$
in
$-1$
in
![]() $\mathbb {R}^{2,3}$
. The space of Lagrangians
$\mathbb {R}^{2,3}$
. The space of Lagrangians
![]() $\mathcal {L}$
in
$\mathcal {L}$
in
![]() $\mathbb {R}^4$
is naturally identified with the space of isotropic lines
$\mathbb {R}^4$
is naturally identified with the space of isotropic lines
![]() $\operatorname {\mathrm {Ein}}^{1,2}$
in
$\operatorname {\mathrm {Ein}}^{1,2}$
in
![]() $\mathbb {R}^{2,3}$
.
$\mathbb {R}^{2,3}$
.
To a pointed totally geodesic spacelike plane
![]() $(p,P)$
in
$(p,P)$
in
![]() $\mathbb {H}^{2,2}$
one can associate an element in a special G-orbit of
$\mathbb {H}^{2,2}$
one can associate an element in a special G-orbit of
![]() $\operatorname {\mathrm {Gr}}^{\max }_2(\mathcal {Q})$
. For every geodesic in this plane passing through the base point, we consider the endpoints
$\operatorname {\mathrm {Gr}}^{\max }_2(\mathcal {Q})$
. For every geodesic in this plane passing through the base point, we consider the endpoints
![]() $\ell _1,\ell _2\in \mathcal {L}\simeq \operatorname {\mathrm {Ein}}^{1,2}$
, and the space generated by all such quadrics
$\ell _1,\ell _2\in \mathcal {L}\simeq \operatorname {\mathrm {Ein}}^{1,2}$
, and the space generated by all such quadrics
![]() $q_{\ell _1,\ell _2}$
forms a plane which is an element of
$q_{\ell _1,\ell _2}$
forms a plane which is an element of
![]() $\operatorname {\mathrm {Gr}}^\omega _2(\mathcal {Q})$
. Indeed for some symplectic basis
$\operatorname {\mathrm {Gr}}^\omega _2(\mathcal {Q})$
. Indeed for some symplectic basis
![]() $(x_1,x_2,y_1,y_2)$
the Lagrangians corresponding to the boundary of the spacelike plane P are for
$(x_1,x_2,y_1,y_2)$
the Lagrangians corresponding to the boundary of the spacelike plane P are for
![]() $\theta \in [0,2\pi ]$
:
$\theta \in [0,2\pi ]$
:
 $$ \begin{align*}\ell(\theta)=\langle \cos\left(\frac{\theta}{2}\right)x_1+\sin\left(\frac{\theta}{2}\right)y_1,\cos\left(\frac{\theta}{2}\right)x_2+\sin\left(\frac{\theta}{2}\right)y_2 \rangle.\end{align*} $$
$$ \begin{align*}\ell(\theta)=\langle \cos\left(\frac{\theta}{2}\right)x_1+\sin\left(\frac{\theta}{2}\right)y_1,\cos\left(\frac{\theta}{2}\right)x_2+\sin\left(\frac{\theta}{2}\right)y_2 \rangle.\end{align*} $$
The corresponding quadric
![]() $q_{\ell (0),\ell (\pi )}$
for
$q_{\ell (0),\ell (\pi )}$
for
![]() $\theta =0$
in the basis
$\theta =0$
in the basis
![]() $(x_1,y_1,x_2,y_2)$
is equal to:
$(x_1,y_1,x_2,y_2)$
is equal to:
 $$ \begin{align*}\begin{pmatrix} 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0 \end{pmatrix}.\end{align*} $$
$$ \begin{align*}\begin{pmatrix} 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0 \end{pmatrix}.\end{align*} $$
Let
![]() $R_\theta $
be the following rotation matrix:
$R_\theta $
be the following rotation matrix:
 $$ \begin{align*}\begin{pmatrix} \cos(\theta) & \sin(\theta) \\ -\sin(\theta) & \cos(\theta) \end{pmatrix}.\end{align*} $$
$$ \begin{align*}\begin{pmatrix} \cos(\theta) & \sin(\theta) \\ -\sin(\theta) & \cos(\theta) \end{pmatrix}.\end{align*} $$
The corresponding quadric
![]() $q_{\ell (\theta ),\ell (\theta +\pi )}$
in the basis
$q_{\ell (\theta ),\ell (\theta +\pi )}$
in the basis
![]() $(x_1,y_1,x_2,y_2)$
is equal to:
$(x_1,y_1,x_2,y_2)$
is equal to:
 $$ \begin{align*}\begin{pmatrix} R_{\frac{\theta}{2}} & 0\\ 0 & R_{\frac{\theta}{2}} \end{pmatrix}q_{\ell(0),\ell(\pi)}\begin{pmatrix} R_{-{\frac{\theta}{2}}} & 0\\ 0 & R_{-{\frac{\theta}{2}}} \end{pmatrix}.\end{align*} $$
$$ \begin{align*}\begin{pmatrix} R_{\frac{\theta}{2}} & 0\\ 0 & R_{\frac{\theta}{2}} \end{pmatrix}q_{\ell(0),\ell(\pi)}\begin{pmatrix} R_{-{\frac{\theta}{2}}} & 0\\ 0 & R_{-{\frac{\theta}{2}}} \end{pmatrix}.\end{align*} $$
Hence
![]() $q_{\ell (\theta ),\ell (\theta +\pi )}$
is equal to:
$q_{\ell (\theta ),\ell (\theta +\pi )}$
is equal to:
 $$ \begin{align*}\begin{pmatrix} \sin(\theta) & \cos(\theta) & 0 & 0\\ \cos(\theta) & -\sin(\theta) & 0 & 0\\ 0 & 0 & \sin(\theta) & \cos(\theta)\\ 0 & 0 & \cos(\theta) & -\sin(\theta) \end{pmatrix}.\end{align*} $$
$$ \begin{align*}\begin{pmatrix} \sin(\theta) & \cos(\theta) & 0 & 0\\ \cos(\theta) & -\sin(\theta) & 0 & 0\\ 0 & 0 & \sin(\theta) & \cos(\theta)\\ 0 & 0 & \cos(\theta) & -\sin(\theta) \end{pmatrix}.\end{align*} $$
These quadrics span a plane in
![]() $\mathcal {Q}$
when
$\mathcal {Q}$
when
![]() $\theta $
varies, and these quadrics are
$\theta $
varies, and these quadrics are
![]() $\omega $
-regular so this plane is in
$\omega $
-regular so this plane is in
![]() $\operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
.
$\operatorname {\mathrm {Gr}}_2^\omega (\mathcal {Q})$
.
We define the Gauss map
![]() $\mathcal {G}u:S\to \operatorname {\mathrm {Gr}}^{\max }_2(\mathcal {Q})$
of a spacelike immersion
$\mathcal {G}u:S\to \operatorname {\mathrm {Gr}}^{\max }_2(\mathcal {Q})$
of a spacelike immersion
![]() $u:S\to \mathbb {H}^{2,2}$
as the map that associates to
$u:S\to \mathbb {H}^{2,2}$
as the map that associates to
![]() $x\in S$
the pencils corresponding to the pointed totally geodesic spacelike plane
$x\in S$
the pencils corresponding to the pointed totally geodesic spacelike plane
![]() $(u(x),P)$
where
$(u(x),P)$
where
![]() $T_{u(x)}P=\mathrm {d}u(T_xS)$
. Let
$T_{u(x)}P=\mathrm {d}u(T_xS)$
. Let
![]() $\mathrm{I\!I}_u$
be the second fundamental form of the immersion u.
$\mathrm{I\!I}_u$
be the second fundamental form of the immersion u.
Theorem B.1. Let
![]() $u:S\to \mathbb {H}^{2,2}$
be a spacelike immersion such that for all
$u:S\to \mathbb {H}^{2,2}$
be a spacelike immersion such that for all
![]() $v\in TS$
,
$v\in TS$
,
![]() $\lVert \mathrm{I\!I}_u(v,v)\rVert <\lVert v\rVert ^2$
. The Gauss map
$\lVert \mathrm{I\!I}_u(v,v)\rVert <\lVert v\rVert ^2$
. The Gauss map
![]() $\mathcal {G}u:S\to \operatorname {\mathrm {Gr}}^{\max }_2(\mathcal {Q})$
is a fitting immersion.
$\mathcal {G}u:S\to \operatorname {\mathrm {Gr}}^{\max }_2(\mathcal {Q})$
is a fitting immersion.
Let S be a spacelike surface in
![]() $\mathbb {H}^{2,n}$
. Let
$\mathbb {H}^{2,n}$
. Let
![]() $\gamma :[0,1]\to S$
be a geodesic for the induced metric on S parametrized with unit speed and let
$\gamma :[0,1]\to S$
be a geodesic for the induced metric on S parametrized with unit speed and let
![]() $V:[0,1]\to TS$
be the unit orthogonal vector field to
$V:[0,1]\to TS$
be the unit orthogonal vector field to
![]() $\gamma '$
in S along
$\gamma '$
in S along
![]() $\gamma $
. We denote by
$\gamma $
. We denote by
![]() $V^+, V^-:[0,1]\to \operatorname {\mathrm {Ein}}^{1,2}$
the endpoints of the geodesic rays starting respectively at V and
$V^+, V^-:[0,1]\to \operatorname {\mathrm {Ein}}^{1,2}$
the endpoints of the geodesic rays starting respectively at V and
![]() $-V$
. Up to changing the sign of V one can assume that
$-V$
. Up to changing the sign of V one can assume that
![]() $(V^+,\gamma ^+,V^-)$
is a maximal triple where
$(V^+,\gamma ^+,V^-)$
is a maximal triple where
![]() $\gamma ^+$
is the endpoint of the geodesic ray starting at
$\gamma ^+$
is the endpoint of the geodesic ray starting at
![]() $\gamma '$
.
$\gamma '$
.
We say that an immersed curve
![]() $c:\mathbb {R}\to \operatorname {\mathrm {Ein}}^{1,2}$
is spacelike if the tangent vectors to one and hence any lift of c to
$c:\mathbb {R}\to \operatorname {\mathrm {Ein}}^{1,2}$
is spacelike if the tangent vectors to one and hence any lift of c to
![]() $\mathbb {R}^{2,n+1}$
is spacelike. At every point
$\mathbb {R}^{2,n+1}$
is spacelike. At every point
![]() $p\in \mathbb {H}^{2,2}$
, the set of tangent vectors of space type decomposes into two cones, a positive and a negative cone. One can make such a global continuous choice of positive cones on all of
$p\in \mathbb {H}^{2,2}$
, the set of tangent vectors of space type decomposes into two cones, a positive and a negative cone. One can make such a global continuous choice of positive cones on all of
![]() $\operatorname {\mathrm {Ein}}^{1,2}$
, and this choice is preserved by the action of
$\operatorname {\mathrm {Ein}}^{1,2}$
, and this choice is preserved by the action of
![]() $\operatorname {\mathrm {SO}}_o(2,n+1)$
, but not
$\operatorname {\mathrm {SO}}_o(2,n+1)$
, but not
![]() $\operatorname {\mathrm {SO}}(2,n+1)$
. We say that a spacelike curve is positive if its derivative lies in the positive cones, and negative if it lies in the other cones.
$\operatorname {\mathrm {SO}}(2,n+1)$
. We say that a spacelike curve is positive if its derivative lies in the positive cones, and negative if it lies in the other cones.
The identification of
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\operatorname {\mathrm {Ein}}^{1,2}$
via the isomorphism
$\operatorname {\mathrm {Ein}}^{1,2}$
via the isomorphism
![]() $\operatorname {\mathrm {PSp}}(4,\mathbb {R})\simeq \operatorname {\mathrm {SO}}_o(2,3)$
identifies a point
$\operatorname {\mathrm {PSp}}(4,\mathbb {R})\simeq \operatorname {\mathrm {SO}}_o(2,3)$
identifies a point
![]() $p\in \operatorname {\mathrm {Ein}}^{1,2}$
with
$p\in \operatorname {\mathrm {Ein}}^{1,2}$
with
![]() $\ell \in \mathcal {L}$
and identifies the positive cone of vectors of spacelike type at
$\ell \in \mathcal {L}$
and identifies the positive cone of vectors of spacelike type at
![]() $p\in \operatorname {\mathrm {Ein}}^{1,2}$
with the cone of
$p\in \operatorname {\mathrm {Ein}}^{1,2}$
with the cone of
![]() $T_\ell \mathcal {L}\simeq \operatorname {\mathrm {Hom}}(\ell , \mathbb {R}^4/\ell )$
of elements
$T_\ell \mathcal {L}\simeq \operatorname {\mathrm {Hom}}(\ell , \mathbb {R}^4/\ell )$
of elements
![]() $u\in \operatorname {\mathrm {Hom}}(\ell , \mathbb {R}^4/\ell )$
such that
$u\in \operatorname {\mathrm {Hom}}(\ell , \mathbb {R}^4/\ell )$
such that
![]() $\omega (\cdot , u(\cdot ))$
is positive definite on
$\omega (\cdot , u(\cdot ))$
is positive definite on
![]() $\ell $
.
$\ell $
.
Remark B.2. This last identification is a consequence of the fact that the boundary of these cones are exactly the directions
![]() $v\in T_\ell \operatorname {\mathrm {Ein}}^{1,2}\simeq T_\ell \mathcal {L}$
tangent to the locus of flags that are not transverse, that is, in generic position, with
$v\in T_\ell \operatorname {\mathrm {Ein}}^{1,2}\simeq T_\ell \mathcal {L}$
tangent to the locus of flags that are not transverse, that is, in generic position, with
![]() $\ell $
. Note that changing the choice of positive cones in
$\ell $
. Note that changing the choice of positive cones in
![]() $T\operatorname {\mathrm {Ein}}^{1,2}$
amounts to changing the symplectic form
$T\operatorname {\mathrm {Ein}}^{1,2}$
amounts to changing the symplectic form
![]() $\omega $
to
$\omega $
to
![]() $-\omega $
.
$-\omega $
.
Lemma B.3. Suppose that
![]() $\lVert \mathrm{I\!I}_u(V,\gamma ')\rVert \leq 1$
, then the curves
$\lVert \mathrm{I\!I}_u(V,\gamma ')\rVert \leq 1$
, then the curves
![]() $V^+,V^-:[0,1]\to \operatorname {\mathrm {Ein}}^{1,2}$
are respectively spacelike positive and spacelike negative, up to reversing the choice of positive cones.
$V^+,V^-:[0,1]\to \operatorname {\mathrm {Ein}}^{1,2}$
are respectively spacelike positive and spacelike negative, up to reversing the choice of positive cones.
Note that in this lemma
![]() $\mathrm{I\!I}_u(V,\gamma ')$
is timelike, so its norm is the timelike norm that we see as a positive number.
$\mathrm{I\!I}_u(V,\gamma ')$
is timelike, so its norm is the timelike norm that we see as a positive number.
Proof. We fix a orthogonal basis
![]() $(e_i)$
of
$(e_i)$
of
![]() $\mathbb {R}^{2,n+1}$
such that
$\mathbb {R}^{2,n+1}$
such that
![]() $e_1$
and
$e_1$
and
![]() $e_2$
have norm
$e_2$
have norm
![]() $1$
and
$1$
and
![]() $e_i$
for
$e_i$
for
![]() $i\geq 3$
have norm
$i\geq 3$
have norm
![]() $-1$
. Without any loss of generality we suppose that
$-1$
. Without any loss of generality we suppose that
![]() $\gamma (0)=e_3$
,
$\gamma (0)=e_3$
,
![]() $\gamma '(0)=e_1$
and
$\gamma '(0)=e_1$
and
![]() $V(0)=e_2$
. Let d be the flat connection on
$V(0)=e_2$
. Let d be the flat connection on
![]() $\mathbb {R}^{2,n}$
and let
$\mathbb {R}^{2,n}$
and let
![]() $\nabla $
be the Levi-Civita connection on
$\nabla $
be the Levi-Civita connection on
![]() $u(S)$
for the induced spacelike metric. We view V as a vector field along the curve
$u(S)$
for the induced spacelike metric. We view V as a vector field along the curve
![]() $\gamma $
. For t close to
$\gamma $
. For t close to
![]() $0$
we have
$0$
we have
![]() $V(t)=V(0)+tdV(0)$
and along the curve
$V(t)=V(0)+tdV(0)$
and along the curve
![]() $\gamma $
we have
$\gamma $
we have
![]() $dV=\nabla V+ \mathrm{I\!I}_{\mathbb {H}^{2,n}}(V,\gamma ')+\mathrm{I\!I}_u(V,\gamma ')$
. Here the second fundamental form of
$dV=\nabla V+ \mathrm{I\!I}_{\mathbb {H}^{2,n}}(V,\gamma ')+\mathrm{I\!I}_u(V,\gamma ')$
. Here the second fundamental form of
![]() $\mathbb {H}^{2,n}$
inside
$\mathbb {H}^{2,n}$
inside
![]() $\mathbb {R}^{2,n+1}$
is equal to
$\mathbb {R}^{2,n+1}$
is equal to
![]() $\mathrm{I\!I}_{\mathbb {H}^{2,n}}(v_1,v_2)=\langle v_1,v_2\rangle v_0$
for
$\mathrm{I\!I}_{\mathbb {H}^{2,n}}(v_1,v_2)=\langle v_1,v_2\rangle v_0$
for
![]() $v_1,v_2\in T_{v_0}\mathbb {H}^{2,n}$
. Note also that since
$v_1,v_2\in T_{v_0}\mathbb {H}^{2,n}$
. Note also that since
![]() $\gamma $
is a geodesic and V an orthogonal unit vector field along
$\gamma $
is a geodesic and V an orthogonal unit vector field along
![]() $\gamma $
,
$\gamma $
,
![]() $\nabla V=0$
.
$\nabla V=0$
.
Hence
![]() $V(t)=e_2+t\mathrm{I\!I}_u(V,\gamma ')+o(t)$
. Since V has norm
$V(t)=e_2+t\mathrm{I\!I}_u(V,\gamma ')+o(t)$
. Since V has norm
![]() $1$
, we can write a representative of the isotropic line
$1$
, we can write a representative of the isotropic line
![]() $V^+(t)$
as
$V^+(t)$
as
![]() $v^+(t)=V(t)+\gamma (t)$
. Therefore:
$v^+(t)=V(t)+\gamma (t)$
. Therefore:
This curve is spacelike since
![]() $e_2$
is spacelike of norm
$e_2$
is spacelike of norm
![]() $1$
and the (timelike) norm of
$1$
and the (timelike) norm of
![]() $\mathrm{I\!I}_u(V,\gamma ')$
is strictly less than
$\mathrm{I\!I}_u(V,\gamma ')$
is strictly less than
![]() $1$
. The same holds for
$1$
. The same holds for
![]() $V^-$
,
$V^-$
,
![]() $v^-(t)=-V(t)+\gamma (t)$
, and we get:
$v^-(t)=-V(t)+\gamma (t)$
, and we get:
Now we check that these two tangent directions lie in different families of cones,:
 $$ \begin{align*}(v^+)'(0)&=e_1+\mathrm{I\!I}_u(V,\gamma')\in (e_2+e_3)^\perp\simeq T_{[e_2+e_3]}\operatorname{\mathrm{Ein}}^{1,2},\\(v^-)'(0)&=e_1-\mathrm{I\!I}_u(V,\gamma')\in (-e_2+e_3)^\perp\simeq T_{[-e_2+e_3]}\operatorname{\mathrm{Ein}}^{1,2}.\end{align*} $$
$$ \begin{align*}(v^+)'(0)&=e_1+\mathrm{I\!I}_u(V,\gamma')\in (e_2+e_3)^\perp\simeq T_{[e_2+e_3]}\operatorname{\mathrm{Ein}}^{1,2},\\(v^-)'(0)&=e_1-\mathrm{I\!I}_u(V,\gamma')\in (-e_2+e_3)^\perp\simeq T_{[-e_2+e_3]}\operatorname{\mathrm{Ein}}^{1,2}.\end{align*} $$
For that we move continuously the second vector by the rotation of angle
![]() $\theta $
in the plane
$\theta $
in the plane
![]() $\langle e_1,e_2\rangle $
. When
$\langle e_1,e_2\rangle $
. When
![]() $\theta =\pi $
, the vector
$\theta =\pi $
, the vector
![]() $(v^-)'(0)$
is sent to:
$(v^-)'(0)$
is sent to:
This vector is in the opposite cone of spacelike vectors to
![]() $(v^+)'(0)$
, hence
$(v^+)'(0)$
, hence
![]() $(v^-)'(0)$
and
$(v^-)'(0)$
and
![]() $(v^+)'(0)$
belong to opposite families of cones of spacelike vectors. The curves
$(v^+)'(0)$
belong to opposite families of cones of spacelike vectors. The curves
![]() $V^+$
,
$V^+$
,
![]() $V^-$
are hence spacelike with one being positive and one negative.
$V^-$
are hence spacelike with one being positive and one negative.
Proof of Theorem B.1
The Gauss map
![]() $\mathcal {G}u:S\to \operatorname {\mathrm {Gr}}^{\max }_2(\mathcal {Q})$
comes with an identification between
$\mathcal {G}u:S\to \operatorname {\mathrm {Gr}}^{\max }_2(\mathcal {Q})$
comes with an identification between
![]() $u^*\mathcal {E}$
and
$u^*\mathcal {E}$
and
![]() $TS$
,
$TS$
,
![]() $\mathcal {E}$
being the tautological bundle over
$\mathcal {E}$
being the tautological bundle over
![]() $\operatorname {\mathrm {Gr}}^{\max }_2(\mathcal {Q})$
. We consider the geodesic flow
$\operatorname {\mathrm {Gr}}^{\max }_2(\mathcal {Q})$
. We consider the geodesic flow
![]() $\Phi $
on
$\Phi $
on
![]() $\mathbb {S} TS$
for the metric induced by u.
$\mathbb {S} TS$
for the metric induced by u.
Lemma B.3 implies that the curves
![]() $V^+$
and
$V^+$
and
![]() $V^-$
are spacelike. Up to exchanging the positive cones and negative cones, we can assume that for all starting point
$V^-$
are spacelike. Up to exchanging the positive cones and negative cones, we can assume that for all starting point
![]() $\gamma (0)$
and tangent vector
$\gamma (0)$
and tangent vector
![]() $\gamma '(0)$
, the associated curve
$\gamma '(0)$
, the associated curve
![]() $V^+$
is positive and
$V^+$
is positive and
![]() $V^-$
is negative. Hence the corresponding curves of Lagrangians
$V^-$
is negative. Hence the corresponding curves of Lagrangians
![]() $\ell ^+,\ell ^-$
in
$\ell ^+,\ell ^-$
in
![]() $\mathbb {R}^4$
satisfy the hypothesis of Lemma 6.12.
$\mathbb {R}^4$
satisfy the hypothesis of Lemma 6.12.
In particular the derivative of the associated quadrics along this flow is positive so
![]() $\Phi $
is a fitting flow. Since u admits a fitting flow it is in particular a well-fitting immersion.
$\Phi $
is a fitting flow. Since u admits a fitting flow it is in particular a well-fitting immersion.
The existence of a maximal spacelike immersion was proven by Collier-Tholozan-Toulisse and a bound of its second fundamental form is a consequence of a result from Cheng.
Theorem B.4 [Reference Collier, Tholozan and ToulisseCTT19],[Reference ChengChe93]
Every maximal representation
![]() $\rho :\Gamma _g\to \operatorname {\mathrm {SO}}_o(2,3)$
admits a unique
$\rho :\Gamma _g\to \operatorname {\mathrm {SO}}_o(2,3)$
admits a unique
![]() $\rho $
-equivariant maximal spacelike immersion
$\rho $
-equivariant maximal spacelike immersion
![]() $u:\widetilde {S_g}\to \mathbb {H}^{2,2}$
. Moreover it is an embedding and for all
$u:\widetilde {S_g}\to \mathbb {H}^{2,2}$
. Moreover it is an embedding and for all
![]() $v\in TS$
,
$v\in TS$
,
![]() $\lVert \mathrm{I\!I}_u(v,v)\rVert < \lVert v\rVert ^2$
.
$\lVert \mathrm{I\!I}_u(v,v)\rVert < \lVert v\rVert ^2$
.
The bound on the second fundamental form is a consequence of a maximal principle, see [Reference Labourie and ToulisseLT22, Corollary 5.2]. Note that in this reference it is written that the square norm of
![]() $\mathrm{I\!I}_u$
is at most
$\mathrm{I\!I}_u$
is at most
![]() $2$
, but since u is maximal it implies that the principal values are at most equal to
$2$
, but since u is maximal it implies that the principal values are at most equal to
![]() $1$
.
$1$
.
Putting together Theorem B.1, Theorem B.4 and Theorem 6.5 we obtain:
Corollary B.5. Every maximal representation
![]() $\rho :\Gamma _g\to \operatorname {\mathrm {Sp}}(4,\mathbb {R})$
admits a fitting immersion
$\rho :\Gamma _g\to \operatorname {\mathrm {Sp}}(4,\mathbb {R})$
admits a fitting immersion
![]() $u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}^{\max }_2(\mathcal {Q})$
that is
$u:\widetilde {S_g}\to \operatorname {\mathrm {Gr}}^{\max }_2(\mathcal {Q})$
that is
![]() $\rho $
-equivariant. This characterizes representations which are maximal for some orientation of
$\rho $
-equivariant. This characterizes representations which are maximal for some orientation of
![]() $S_g$
.
$S_g$
.
Remark B.6. Note that a maximal spacelike surface in
![]() $\mathbb {H}^{2,2}$
always defines a fibration of the space of photons and of the symmetric space of
$\mathbb {H}^{2,2}$
always defines a fibration of the space of photons and of the symmetric space of
![]() $\operatorname {\mathrm {Sp}}(4,\mathbb {R})$
, without assuming any bound on the second fundamental form. In this case however the bound is useful to deduce that the fibration extends to a fibration of the symmetric space of
$\operatorname {\mathrm {Sp}}(4,\mathbb {R})$
, without assuming any bound on the second fundamental form. In this case however the bound is useful to deduce that the fibration extends to a fibration of the symmetric space of
![]() $\operatorname {\mathrm {SL}}(4,\mathbb {R})$
.
$\operatorname {\mathrm {SL}}(4,\mathbb {R})$
.
Acknowledgments
I would like to thank Andrea Seppi for the helpful discussions during my stay in Grenoble that helped me a lot on this project. I would like to thank also Beatrice Pozzetti for discussing this topic and giving feedback. The author was funded through the DFG Emmy Noether project 427903332 of B. Pozzetti and the RTG 2229 “Asymptotic Invariants and Limits of Groups and Spaces,” and partially by the European Union via the ERC 101124349 “GENERATE.”
Views and opinions expressed are however those of the authors only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them.