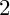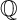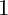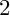1 Introduction
A well-known result of Shafarevich [Reference Shafarevich28] states that the number of isomorphism classes of elliptic curves over a given number field that have good reduction outside a finite set of primes is finite. The online tables by Cremona [Reference Cremona7] exhibit all elliptic curves over the rational field of conductors up to
$500,000$
, together with additional arithmetic data such as the torsion subgroup and the Mordell–Weil rank. In [Reference Cremona and Lingham8], Cremona and Lingham give an explicit algorithm to find all elliptic curves over a number field with good reduction outside a given finite set of primes.
We remark that all results concerning explicit classifications of elliptic curves over
$\mathbb Q$
with bad reduction outside a finite set of primes S target the case when S consists of at most two primes. In what follows, we give a short overview of such known results. Such elliptic curves were completely classified when
$S=\{2\}$
by Ogg [Reference Ogg21], and when
$S=\{3\}$
by Hadano [Reference Hadano11]. Setzer [Reference Setzer27] classified all elliptic curves with prime conductor and a rational point of order
$2$
. Ivorra [Reference Ivorra14] classified elliptic curves over
$\mathbb Q$
of conductor
$2^kp$
, where p is an odd prime, with a rational point of order
$2$
. Bennett, Vatsal, and Yazdani [Reference Bennett, Vatsal and Yazdani1] classified all elliptic curves over
$\mathbb Q$
with a rational
$3$
-torsion point and good reduction outside the set
$\{3,p\}$
, for a fixed prime p. Furthermore, Howe [Reference Howe12], Sadek [Reference Sadek26], and Dąbrowski-Jędrzejak [Reference Dąbrowski and Jędrzejak9] studied the classification of elliptic curves over
$\mathbb Q$
with good reduction outside two distinct primes and with a rational point of fixed order
$\geq 4$
. In addition, Best and Matschke [Reference Best and Matschke2] presented a database of elliptic curves with good reduction outside the first six primes.
Shafarevich [Reference Shafarevich28] conjectured that for each number field K, finite set of places S, and integer
$g\ge 2$
, there are only finitely many K-isomorphism classes of curves of genus g over K with good reduction outside S. The proof was sketched by him in the hyperelliptic case (for details, see the papers by Parshin and Oort [Reference Oort and Popp22], [Reference Parshin23]). Merriman and Smart [Reference Merriman and Smart19] determined all curves of genus
$2$
with a rational Weierstrass point and with good reduction away from
$2$
, up to an equivalence relation which is coarser than the relation of isogeny between the associated Jacobian varieties. Smart [Reference Smart29] produced an explicit list of all genus
$2$
curves with good reduction away from
$2$
by transforming the problem into the problem of solving some S-unit equations. Rowan [Reference Rowan25] adapted the latter method in order to produce examples of genus
$2$
curves with good reduction away from the prime
$3$
. Recently, infinitely many examples of genus
$2$
curves over quadratic fields were presented when S is empty; more precisely, the authors furnished examples of genus
$2$
curves defined over the rational field that attain everywhere good reduction after a quadratic base change [Reference Dąbrowski and Sadek10]. Genus
$2$
Curve Search Results from LMFDB [Reference Booker, Sijsling, Sutherland, Voight and Yasaki3, Reference Cremona7] give many (probably not all) genus
$2$
curves with absolute discriminant up to
$10^6$
, together with additional arithmetic information. An expository paper by Poonen [Reference Poonen and Cohen24] contains some potential relevant projects.
It can be seen that genus 2 curves with good reduction away from an odd prime have not been studied thoroughly in literature. In this article, we are interested in genus
$2$
curves C with
$\mathbb Q$
-rational Weierstrass points. We attempt to extend the existing lists of genus 2 curves in [Reference Merriman and Smart19], [31], to include curves with bad reduction at only one prime different from
$2$
. The aim of this article is to find explicitly genus 2 curves with
$\mathbb Q$
-rational Weierstrass points and with odd prime absolute discriminant. We assemble lists of such genus 2 curves, analogous to existing lists of elliptic curves with bad reduction at only one odd prime.
In this work, we consider genus 2 curves C that can be described by globally minimal Weierstrass equations over
${\mathbb Q}$
of the form
$y^2+Q(x)y=P(x)$
, where
$\deg Q(x)\le 2$
and
$P(x)$
is monic of degree
$5$
. Moreover, we assume that these curves possess at least two
${\mathbb Q}$
-rational Weierstrass points. This implies that they can be described by integral equations of the form
$y^2=xf(x)$
, where
$f(x)$
is monic of degree
$4$
. Moreover, the latter equation may be assumed to be minimal at every prime except at
$2$
. It turns out that if
$f(x)$
is reducible, then the absolute discriminant of C can never be an odd prime, except when
$f(x)=(x-b)g(x)$
and
$g(x)$
is irreducible. We show that there are many (conjecturally, infinitely many) genus
$2$
curves C defined by
$y^2=x(x-b)g(x)$
(with
$g(x)$
irreducible) and such that the discriminant of C is
$\pm p$
, where p is an odd prime. Let us give two families of such curves. In fact, we prove in §7 that these are the only families of such curves.
-
(i) Let
$f(t) = 256t^4 - 2,064t^3 + 4,192t^2 + 384t - 1,051$
. The hyperelliptic curve
$C_t$
defined by the (non-minimal) equation has discriminant
$$\begin{align*}y^2 = x(x+1)(x^3+64tx^2+64(t+4)x+256),\qquad t\in{\mathbb Z}, \end{align*}$$
$\pm p$
for some odd prime p if and only if
$f(t)=\pm p$
. One can easily check that for
$0 < t < 100$
,
$f(t)$
is a prime exactly when and for such values of t, the discriminant
$$ \begin{align*}t\in\{3,4,5,7,13,20,26,31,40,42,43,46,48,51, 55,82,83,90,98\},\end{align*} $$
$\Delta _{C_t}=f(t)$
. For instance, one has
$\Delta _{C_3}=2,837$
,
$\Delta _{C_4}=997$
,
$\Delta _{C_5}=7,669$
,
$\Delta _{C_7}=113,749$
,
$\Delta _{C_{13}}=3,489,397$
, and
$\Delta _{C_{20}}=26,131,429$
.
-
(ii) Let
$g(t) = 256t^4 + 768t^3 - 800t^2 - 2,064t - 6,343$
. The hyperelliptic curve
$C_t$
given by the (non-minimal) equation has discriminant
$$ \begin{align*}y^2 = x(x-4)(x^3+(4t+1)x^2-4(4t+5)x+64), \qquad t\in{\mathbb Z}, \end{align*} $$
$\pm p$
for some odd prime p if and only if
$g(t)=\pm p$
. For
$0 < t < 100$
,
$g(t)$
is a prime exactly when and for such values of t,
$$ \begin{align*}t\in\{3,6,10,12,13,18,23,25,27,31,35,44,51, 58,74,80,82,93,95\},\end{align*} $$
$\Delta _{C_t}=g(t)$
is an odd prime, for example,
$\Delta _{C_3}=21,737$
,
$\Delta _{C_6}=450,137$
,
$\Delta _{C_{10}}=3,221,017$
,
$\Delta _{C_{12}}=6,489,209$
,
$\Delta _{C_{13}}=8,830,537$
, and
$\Delta _{C_{18}}=31,050,137$
.
Conjecturally, each of the above two families contains infinitely many genus
$2$
curves of prime discriminant. Such a statement follows from the above discussion, and a classical conjecture by Bouniakovsky [Reference Bouniakovsky5] concerning prime values of irreducible polynomials
$f(x)\in \mathbb Z[x]\colon $
if the set of values
$f(\mathbb Z^{+})$
has no common divisor larger than
$1$
, then
$|f(x)|$
represents infinitely many prime numbers. It is not difficult to give examples with very large discriminants, for instance,
$f(49,983)=\Delta _{C_{49,983}}=1,597,567,383,051,905,525,717$
and
$f(69,945)=\Delta _{C_{69,945}}=6,126,558,731,378,331,096,629$
are primes, where
$f(t) = 256t^4 - 2,064t^3 + 4,192t^2 + 384t - 1,051$
, and
$C_t$
belongs to the family (i) above.
In §8, we give two explicit (conjecturally, infinite) families of genus
$2$
curves with absolute prime discriminant described by
$y^2=xf(x)$
, with
$f(x)$
an irreducible monic polynomial. We remark that the fact that we are looking for Weierstrass equations with odd prime absolute discriminant describing these curves implies that these Weierstrass equations are globally minimal.
It is worth mentioning that the families of genus
$2$
curves that we obtain in this work can be seen as the genus-2 analogue to the famous Neumann–Setzer families of elliptic curves over the rationals [Reference Setzer27]. We recall that a Neumann–Setzer elliptic curve possesses a rational point of order
$2$
and its discriminant is an odd prime. Moreover, these elliptic curves may be described by the following globally minimal Weierstrass equation
$$ \begin{align*}y^2+xy=x^3+\frac{1}{4}(t-1)x^2-x,\qquad t\equiv 1 \textrm{ mod }4,\end{align*} $$
where the discriminant is an odd prime p if and only if
$t^2+64=p$
; hence, it is conjectured that there are infinitely many such curves.
Our explicit families of genus
$2$
curves with odd prime (or odd square-free) discriminants lead to abelian surfaces (Jacobians) with trivial endomorphisms, and may be useful when testing the paramodular conjecture of Brumer and Kramer. If C is such a curve, then the conjecture of Brumer and Kramer predicts the existence of a cuspidal, nonlift Siegel paramodular newform f of degree
$2$
, weight
$2$
, and level
$N_C$
with rational Hecke eigenvalues, such that
$L(\text {Jac}(C),s) = L(f,s,\text {spin})$
. The interested reader may consult [Reference Brumer and Kramer6].
2 Preliminaries on genus
$2$
curves
Let C be a smooth projective curve of genus
$2$
over a perfect field K. Let
$\sigma $
be the hyperelliptic involution of C. Given a generator x of the subfield of
$K(C)$
fixed by
$\sigma $
over K, and
$y\in K(C)$
such that
$K(C)=K(x)[y]$
, a Weierstrass equation E of C is given by
$$\begin{align*}E\colon y^2+Q(x)y=P(x),\qquad P(x),Q(x)\in K[x],\; \deg Q(x)\le 3,\;\deg P(x)\le 6.\end{align*}$$
If
$E'\colon v^2+Q'(u)v=P'(u)$
is another Weierstrass equation describing C, then there exist
$\Big ( \begin {array}{cc} a & b \\ c & d \\ \end {array} \Big )\in \operatorname {GL}_2(K) $
,
$e\in K\setminus \{0\}$
,
$H(x)\in K[x]$
such that
$$\begin{align*}u=\frac{ax+b}{cx+d},\qquad v=\frac{ey+H(x)}{(cx+d)^3}.\end{align*}$$
If
$\operatorname {char} K\ne 2$
, then we define the discriminant
$\Delta _E$
of the Weierstrass equation E to be
$$\begin{align*}\Delta_E=2^{-12}\operatorname{disc}(4P(x)+Q(x)^2).\end{align*}$$
One has
$\Delta _E\ne 0$
if and only if E describes a smooth curve. Moreover,
$$ \begin{align} \Delta_{E'}=e^{20}(ad-bc)^{-30}\Delta_{E} \end{align} $$
(see, e.g., [Reference Liu17, §2]).
Assuming, moreover, that K is a discrete valuation field with discrete valuation
$\nu $
and ring of integers
${\mathcal O}_K$
, E is said to be an integral Weierstrass equation of C if both
$P(x),Q(x)\in {\mathcal O}_K[x]$
. This implies that
$\Delta _E\in {\mathcal O}_K.$
A Weierstrass equation E describing C is said to be minimal if E is integral and
$\nu (\Delta _E)$
is the smallest valuation among all integral Weierstrass equations describing C. In the latter case,
$\nu (\Delta _E)$
is the discriminant of C over
${\mathcal O}_K$
.
If K is a number field with ring of integers
${\mathcal O}_K$
, then a Weierstrass model E describing C is integral if
$P(x),Q(x)\in {\mathcal O}_K[x].$
A Weierstrass equation E is globally minimal if it is minimal over
${\mathcal O}_{K_{\mathfrak p}}$
for every prime ideal
$\mathfrak p$
of
${\mathcal O}_K$
, where
$K_{\mathfrak p}$
is the completion of K at
$\mathfrak p$
. Globally, minimal Weierstrass equations do not exist in general, yet if K has class number one, then C has a globally minimal Weierstrass equation (see [Reference Liu17, Remarque 6]). In the latter case, the discriminant of a globally minimal Weierstrass equation describing C is the discriminant of C.
One notices that since we will be looking for Weierstrass equations with odd prime absolute discriminant, it follows that these equations are globally minimal; hence, the corresponding discriminants are minimal.
3 Rational Weierstrass points
In this section, we assume that C is a smooth projective genus
$2$
curve defined over a number field K of class number one. We assume, moreover, that C possesses a K-rational Weierstrass point. It follows that C can be described by a Weierstrass equation of the form
$$ \begin{align} E\colon y^2+Q(x)y=P(x), \qquad\textrm{where }P(x),Q(x)\in K[x] \end{align} $$
and
$\deg Q(x)\le 2$
, and
$P(x)$
is monic of degree 5.
Moreover, such an equation is unique up to a change of coordinates of the form
$x\mapsto u^2 x+r$
,
$y\mapsto u^5y+H(x)$
where
$u\in K\setminus \{0\}$
,
$r\in K$
, and
$H(x)\in K[x]$
is of degree at most
$2$
(see [Reference Lockart18, Prop. 1.2]).
Throughout this paper, we will assume that C is defined over
${\mathbb Q}$
by a globally minimal Weierstrass equation E of the form in (3.1). After the following transformation
$x\mapsto x$
and
$y\mapsto y+Q(x)/2$
, then C is described by
$4y^2=4P(x)+Q(x)^2$
. Now, using the transformation
$x\mapsto x/2^2$
,
$y\mapsto y/2^5$
, an integral Weierstrass equation describing C is
$E'\colon y^2=G(x)$
where
$G(x)\in {\mathbb Z}[x]$
is monic of degree
$5$
and
$\Delta _{E'}=2^{40}\Delta _E$
.
Lemma 3.1. Let C be a smooth projective curve of genus
$2$
defined over
${\mathbb Q}$
by a globally minimal Weierstrass equation of the form
$y^2+Q(x)y=P(x)$
, where
$\deg Q(x)\le 2$
and
$P(x)$
is monic of degree 5, with odd discriminant
$\Delta $
. Assume, moreover, that C has at least two
${\mathbb Q}$
-rational Weierstrass points. Then C can be described by a Weierstrass equation of the form
$E\colon y^2=xF(x)$
, where
$F(x)\in {\mathbb Z}[x]$
is a monic polynomial of degree
$4$
, and
$\Delta _E=2^{40}\Delta $
. In particular, E is minimal over every p-adic ring
${\mathbb Z}_p$
except when
$p=2$
.
Proof. This follows from the argument above together with the fact that one of the rational Weierstrass points is sent to infinity, while the other point is sent to
$(0,0)\in C({\mathbb Q})$
via a translation map. We notice that all the transformations used do not change minimality at odd primes.
Let C be a smooth projective curve of genus
$2$
defined by a Weierstrass equation of the form
$E\colon y^2=P(x)$
, where
$P(x)\in {\mathbb Z}[x]$
is of degree
$5$
(not necessarily monic). The Igusa invariants
$J_{2i}$
,
$1\le i\le 5$
, associated with E were defined in [Reference Igusa13, §4]. In fact, these invariants can be defined for any Weierstrass equation describing C (see [Reference Liu16]). These invariants can be used to identify the reduction type of C at a given prime p (see [Reference Igusa13], [Reference Liu15]). For instance, the following result is [Reference Liu15, Théorème 1].
Theorem 3.2. Let C be a smooth projective curve of genus
$2$
defined by the Weierstrass equation
$y^2+Q(x)y=P(x)$
over
${\mathbb Q}$
. Then C has potential good reduction at the prime p if and only if
$J_{2i}^5/J_{10}^i\in {\mathbb Z}_p$
, for every
$1\le i\le 5$
, where
${\mathbb Z}_p$
is the ring of p-adic integers.
One remarks that if C does not have potential good reduction at a prime p, then C does not have good reduction at p.
4 Curves with six rational Weierstrass points
We assume that C is a smooth projective curve of genus
$2$
over
${\mathbb Q}$
. If C has six
${\mathbb Q}$
-rational Weierstrass points, then C may be described by a Weierstrass equation of the form
$$ \begin{align*}E\colon y^2=x(x-b_1)(x-b_2)(x-b_3)(x-b_4),\qquad b_i\in{\mathbb Z},\,i=1,2,3,4.\end{align*} $$
Theorem 4.1. Let C be a smooth projective curve of genus
$2$
defined over
${\mathbb Q}$
. Assume that C has six
${\mathbb Q}$
-rational Weierstrass points. If C is described by a globally minimal Weierstrass equation E such that
$|\Delta _E|$
is of the form
$2^ap^b$
, where p is an odd prime,
$a\ge 0$
,
$b\ge 1$
, then C is isomorphic to one of the following curves described by the following Weierstrass equations:
$$ \begin{align*} &E_0\ \colon\ y^2 = x (x-1) (x+1) (x-2) (x+2),\qquad \Delta_{E_0}=2^{18} \times 3^4,\\ &E_1\ \colon\ y^2 = x (x-3) (x+3) (x-6) (x+6),\qquad \Delta_{E_1}=2^{18} \times 3^{14}. \end{align*} $$
Proof. The curve C can be described by an integral Weierstrass equation of the form
$E\colon y^2=x(x-b_1)(x-b_2)(x-b_3)(x-b_4)$
, where E is minimal at every odd prime. The discriminant
$\Delta _{E}$
of E is described by
$$\begin{align*}\Delta_{E}=2^8b_1^2 (b_1 - b_2)^2 b_2^2 (b_1 - b_3)^2 (b_2 - b_3)^2 b_3^2 (b_1 - b_4)^2 (b_2 - b_4)^2 (b_3 - b_4)^2 b_4^2.\end{align*}$$
Now, we assume that
$\Delta _{E}=2^mp^{n}$
, where
$m\ge 8$
,
$n\ge 1$
.
We claim that at least two of the
$b_i$
’s are even. Assume on the contrary that
$b_1 = \pm p^{\alpha _1}$
,
$b_2 = \pm p^{\alpha _2}$
, and
$b_3 = \pm p^{\alpha _3}$
(
$\alpha _1 \geq \alpha _2 \geq \alpha _3 \geq 0$
) are all odd. Then
$|b_1 - b_2| = 2^{s_1}p^{l_1}$
,
$|b_1 - b_3| = 2^{s_2}p^{l_2}$
, and
$|b_2 - b_3| = 2^{s_3}p^{l_3}$
, with
$s_i \geq 1$
,
$i=1,2,3$
. If all
$b_i$
’s are of the same sign, then using Catalan’s conjecture (Mihăilescu’s theorem), we obtain
$\alpha _1 = \alpha _2 + 2 = \alpha _3 +2$
and
$\alpha _2 = \alpha _3 +2$
, a contradiction. Now, if some
$b_i$
and
$b_j$
are of opposite signs, then we obtain
$\alpha _i = \alpha _j$
; in particular, it follows that
$\alpha _1 = \alpha _2 = \alpha _3$
. This will imply that two of
$b_i$
’s are equal, which is a contradiction.
This justifies considering the following subcases:
(i) In case two of the
$b_i$
’s are even, we may assume without loss of generality that
$b_1=\pm 2^{c_1}p^{d_1},b_2=\pm 2^{c_2}p^{d_2}$
,
$b_3=\pm p^{d_3}$
, and
$b_4=\pm p^{d_4}$
, with
$c_1\ge c_2>0$
. Elementary, but long case-by-case calculations show that necessarily we have
$d_1=d_2=d_3=d_4=d$
; in particular,
$b_3=-b_4$
. Now, it is easy to check that
$p=3$
and
$c_1=c_2=1$
; in particular,
$b_1=-b_2$
. Hence,
$b_1=2\times 3^d$
,
$b_2=-2 \times 3^d$
,
$b_3=3^d$
, and
$b_4=-3^d$
, which leads to the Weierstrass equation
$E_d\colon y^2 = x (x-2 \times 3^d) (x+2 \times 3^d) (x-3^d) (x+3^d)$
. A straight forward change of variables yields that the Weierstrass equations
$E_d$
and
$E_{d+2}$
describe two isomorphic genus
$2$
hyperelliptic curves; hence, we only obtain two non-isomorphic genus
$2$
curves
$C_0$
and
$C_1$
in the latter family described by
$E_0$
and
$E_1$
with minimal discriminants
$2^{18} \times 3^4$
and
$2^{18} \times 3^{14}$
, respectively.
(ii) We assume now without loss of generality that
$b_1=\pm 2^{c_1}p^{d_1},b_2=\pm 2^{c_2}p^{d_2}$
,
$b_3=\pm 2^{c_3} p^{d_3}$
, and
$b_4=\pm p^{d_4}$
, with
$c_1\ge c_2\geq c_3>0$
. Again, long case-by-case calculations show that necessarily we have
$d_1=d_2=d_3=d_4=d$
. In this case, we obtain
$b_1=2^{3} \times 3^d$
,
$b_2=-2^{2} \times 3^d$
,
$b_3=2 \times 3^d$
, and
$b_4=-3^d$
, which leads to the curves
$C^{\prime }_d$
described by the Weierstrass equations
$ y^2 = x (x-2^{3} \times 3^d) (x+2^{2} \times 3^d) (x-2 \times 3^d) (x+ 3^d)$
. Again, it is easily seen that the curves
$C^{\prime }_{d}$
and
$C^{\prime }_{d+2}$
are isomorphic. Moreover, using the function IsIsomorphic(,) in MAGMA, we can verify that the curves
$C_0$
and
$C^{\prime }_0$
are isomorphic, and that the curves
$C_1$
and
$ C^{\prime }_1$
are isomorphic.
(iii) We assume now without loss of generality that
$b_1=\pm 2^{c_1}p^{d_1},b_2=\pm 2^{c_2}p^{d_2}$
,
$b_3=\pm 2^{c_3} p^{d_3}$
, and
$b_4=\pm 2^{c_4} p^{d_4}$
, with
$c_1\ge c_2\geq c_3 \geq c_4>0$
. Again, long case-by-case calculations show that necessarily we have
$d_1=d_2=d_3=d_4=d$
. In this case, we obtain
$b_1=2^{t+3} \times 3^d$
,
$b_2=-2^{t+2} \times 3^d$
,
$b_3=2^{t+1} \times 3^d$
, and
$b_4=-2^t \times 3^d$
, which leads to the curves
$C_{t,d}$
described by
$y^2 = x (x-2^{t+3} \times 3^d) (x+2^{t+2} \times 3^d) (x-2^{t+1} \times 3^d) (x+ 2^t \times 3^d)$
. Now, the curves
$C_{t,d}$
and
$C_{t,d+2}$
are isomorphic. Moreover, we may check using the function IsIsomorphic(,) that the curves
$C_{t,d}$
and
$C_{t+1,d}$
are isomorphic. Therefore, we obtain only two non-isomorphic curves
$C_{1,0}$
and
$C_{1,1}$
. Finally, in a similar fashion, one notices that
$C_0$
and
$C_{1,0}$
are isomorphic, and the genus
$2$
curves
$C_1$
and
$ C_{1,1}$
are isomorphic.
Remark 4.2. One sees easily that none of the curves C described in Theorem 4.1 can be described by a globally minimal Weierstrass equation whose discriminant is square-free. This holds because
$\Delta _{E}$
is always a square. Moreover, if C is a curve that is described by neither
$E_0$
nor
$E_1$
, and C has bad reduction at exactly two primes, then both primes must be odd.
Corollary 4.3. Let C be a smooth projective curve of genus
$2$
defined over
${\mathbb Q}$
. Assume that C has six
${\mathbb Q}$
-rational Weierstrass points. If C is described by a globally minimal Weierstrass equation E, then
$|\Delta _E|$
can never be a power of a prime. In other words, C cannot have bad reduction at exactly one prime.
Proof. Theorem 4.1 asserts that if C has bad reduction at exactly one prime, then this prime must be
$2$
. However, according to [Reference Merriman and Smart19, §6.1], there is no such curve with bad reduction only at
$2$
.
5 Curves with exactly four rational Weierstrass points
We assume that C is a smooth projective curve of genus
$2$
over
${\mathbb Q}$
described by a globally minimal Weierstrass equation of the form
$E\colon y^2+Q(x)y=P(x)$
,
$P(x),Q(x)\in {\mathbb Z}[x]$
,
$\deg Q(x)\le 2$
, and
$P(x)$
is monic of degree
$5$
. If C has exactly four
${\mathbb Q}$
-rational Weierstrass points, then C may be described by a Weierstrass equation of the form
$$ \begin{align*}E'\colon y^2 = x(x-b_1)(x-b_2)(x^2+b_3x+b_4),\quad b_i\in{\mathbb Z},\;i=1,2,3,4,\end{align*} $$
with
$\Delta _{E'}=2^{40}\Delta _E$
(see Lemma 3.1).
Theorem 5.1. Let C be a smooth projective curve of genus
$2$
defined over
${\mathbb Q}$
. Assume that C has exactly four
${\mathbb Q}$
-rational Weierstrass points. If C is described by a globally minimal Weierstrass equation of the form
$E\colon y^2+Q(x)y=P(x)$
,
$\deg Q(x)\le 2$
and
$P(x)$
is monic of degree
$5$
, then
$|\Delta _E|$
is never an odd prime.
Proof. In accordance with Lemma 3.1, C is described by
$E'\colon y^2 = x(x-b_1)(x-b_2)(x^2+b_3x+b_4)$
,
$b_i\in {\mathbb Z}$
, and
$x^2+b_3x+b_4$
is irreducible. Moreover,
$\Delta _{E'}=2^{40}\Delta _E$
; hence,
$E'$
is minimal at every odd prime. We have the following explicit formula for the discriminant of
$E'$
:
$$ \begin{align} \Delta_{E'} = 2^8 b_1^2(b_1-b_2)^2b_2^2(b_3^2-4b_4)b_4^2(b_1^2+b_1b_3+b_4)^2 (b_2^2+b_2b_3+b_4)^2. \end{align} $$
We now assume that
$\Delta _{E'}=\pm 2^{40}p$
, where p is an odd prime. It follows that:
-
(a)
$b_1=\pm 2^a$
,
$b_2=\pm 2^b$
,
$b_1-b_2=\pm 2^c$
,
$b_4=\pm 2^d$
, -
(b)
$b_3^2-4b_4=\pm 2^e p$
(note that
$b_3^2-4b_4$
is the only non-square factor, and hence it is the only one that can be divisible by p), -
(c)
$b_1^2+b_1b_3+b_4=\pm 2^f$
,
$b_2^2+b_2b_3+b_4=\pm 2^g$
,
where
$a,b,c,d,e,f,g$
are nonnegative integers such that
$2a+2b+2c+2d+e+2f+2g=32$
. We will consider the following three cases.
(i)
$a=b=0$
. Then necessarily,
$b_1=-b_2$
,
$c=1$
, and combining the equations (c), we obtain
$b_4=\pm 2^{f-1} \pm 2^{g-1} -1$
and
$b_3=\pm 2^{f-1} \pm 2^{g-1}$
. The first one gives
$1\pm 2^d = \pm 2^{f-1} \pm 2^{g-1}$
.
If
$d\geq 1$
, then
$f=1$
(and, therefore,
$g=d+1$
) or
$g=1$
(and, therefore,
$f=d+1$
). In this case,
$b_3$
is odd, and hence
$e=0$
, and we obtain
$4d+6=32$
, which is impossible.
If
$d=0$
, then
$\pm 2^{f-1} \pm 2^{g-1} = 1 \pm 2^d = 2$
or
$0$
. In the first case,
$f=g=1$
and
$b_3=0$
or
$\pm 2$
, and there are no p satisfying (b). In the second case,
$f=g\geq 1$
, and
$b_3=0$
or
$\pm 2^f$
. In the last case, (b) implies
$e=2$
,
$4f=28$
, and hence
$p=2^{12} \pm 1$
, which is not a prime.
(ii)
$a=0$
,
$b\geq 1$
. Then, necessarily,
$b=1$
and
$c=0$
. We obtain a contradiction, considering carefully all possible tuples
$(d,e,f,g)$
satisfying
$2d+e+2f+2g=30$
, and combining the equations (b) and (c).
(iii)
$a, b\geq 1$
. Then
$a=b$
,
$b_1=-b_2$
, and
$c=a+1$
. We have
$2a+2b+2c = 6a+2$
; hence, we have five cases to consider:
$a=b\leq 5$
. For each such a, we consider
$d\geq 0$
, and try to find e, f, and g using (b) and (c). None of these cases lead to genus
$2$
curve E with odd prime value of
$|\Delta _E|$
. We omit the details.
6 Curves with exactly two rational Weierstrass points and a quadratic Weierstrass point
Let C be a smooth projective curve of genus
$2$
over
${\mathbb Q}$
described by a globally minimal Weierstrass equation of the form
$E\colon y^2+Q(x)y=P(x)$
,
$P(x),Q(x)\in {\mathbb Z}[x]$
,
$\deg Q(x)\le 2$
, and
$P(x)$
is monic of degree
$5$
. If C has exactly two
${\mathbb Q}$
-rational Weierstrass points and a quadratic Weierstrass point, then Lemma 3.1 implies that C is described by a Weierstrass equation of the form
$$ \begin{align*}E'\colon y^2 = x(x^2+a_1x+a_2)(x^2+b_1x+b_2),\quad a_i, b_i\in{\mathbb Z},\end{align*} $$
where both
$x^2+a_1x+a_2$
and
$x^2+b_1x+b_2$
are irreducible, and
$\Delta _{E'}=2^{40}\Delta _E.$
Theorem 6.1. Let C be a smooth projective curve of genus 2 defined over
${\mathbb Q}$
. Assume that C has exactly two
${\mathbb Q}$
-rational Weierstrass points and a quadratic Weierstrass point. If C is described by a globally minimal Weierstrass equation of the form
$E\colon y^2+Q(x)y=P(x)$
,
$\deg Q(x)\le 2$
and
$ P(x)$
is monic of degree
$5$
, then
$|\Delta _E|$
is never an odd prime.
Proof. As seen above, C can be described by an integral Weierstrass equation
$E'\colon y^2=x(x^2+a_1x+a_2)(x^2+b_1x+b_2)$
with
$\Delta _{E'}=2^{40}\Delta _E$
. In particular,
$E'$
is minimal at every odd prime. We have the following explicit formula for the discriminant of E:
$$ \begin{align} \Delta_{E'} = 2^8(a_1^2-4a_2)a_2^2(b_1^2-4b_2)b_2^2K^2, \end{align} $$
where
$K=a_2^2-a_1a_2b_1+a_2b_1^2+a_1^2b_2-2a_2b_2-a_1b_1b_2+b_2^2$
. We assume that
$\Delta _{E'}=\pm 2^{40}p$
, where p is an odd prime. It is clear that
$|a_2|=2^a$
and
$|b_2|=2^b$
, with
$a,b\geq 0$
. Therefore, we can assume without loss of generality that
$$ \begin{align} |a_1^2-4a_2|=2^c \end{align} $$
and
$$ \begin{align} |b_1^2-4b_2|=2^dp, \end{align} $$
where
$c,d\geq 0$
. Note that K is necessarily a power of
$2$
. We will solve systems of these equations, controlling the condition
$2a+2b+c+d+2v_2(K)=32$
, where
$v_2$
is the
$2$
-valuation. We will consider the following four cases, with many subcases.
(i)
$a+2=c$
, and both a and c are even. Note that
$(a,c)\in \{(0,2), (2,4), (4,6), (6,8), (8,10), (10,12)\}$
.
(ii)
$a+2=c$
, and both a and c are odd. Note that
$(a,c)\in \{(1,3), (3,5), (5,7), (7,9), (9,11)\}$
.
(iii)
$a+2>c$
, then necessarily c is even. Using (6.2), we obtain that
$a+2-c = 1$
or
$3$
. This gives rise to the following
$11$
pairs
$(a,c)$
:
(iiia)
$(1,2)$
,
$(3,4)$
,
$(5,6)$
,
$(7,8)$
,
$(9,10)$
,
(iiib)
$(1,0)$
,
$(3,2)$
,
$(5,4)$
,
$(7,6)$
,
$(9,8)$
,
$(11,10)$
.
(iv)
$a+2<c$
, then necessarily a is even. Using (6.2), we obtain that
$c-a-2 = 1$
or
$3$
. This yields the following
$10$
pairs
$(a,c)$
:
(iva)
$(0,3)$
,
$(2,5)$
,
$(4,7)$
,
$(6,9)$
,
$(8,11)$
,
(ivb)
$(0,5)$
,
$(2,7)$
,
$(4,9)$
,
$(6,11)$
,
$(8,13)$
.
The general strategy of the proof is as follows:
-
• Fix a pair
$(a,c)$
as above (we have
$32$
such pairs). -
• We have
$a_2=\pm 2^a$
, and hence we can calculate
$a_1$
using (6.2). -
• Now consider
$b_2=\pm 2^b$
, for all nonnegative integers b satisfying
$2a+2b+c\leq 32$
. Then, of course,
$d+2v_2(K) \leq 32-2a-2b-c$
. -
• For each triple
$(a,b,c)$
, check whether there exist
$b_1$
and K satisfying (6.3) and
$d+2v_2(K) = 32-2a-2b-c$
. Here, we use a more convenient expression for K, namely
$K=(a_2-b_2)^2+(a_1-b_1)(a_1b_2-a_2b_1)$
.
The cases with large
$2a+c$
are the easiest to consider, and the cases with small
$2a+c$
are the longest ones (many subcases, etc.). Let us illustrate the method in one of the easiest cases,
$(a,c)=(11,10)$
. Here, we have
$a_2=\pm 2^{11}$
and
$a_1=\pm 2^53$
. If
$b_2=\pm 1$
, then
$K=(2^{11}\pm 1)^2+(\pm 2^53-b_1)(\pm 2^53\pm 2^{11}b_1) = (2^{11}\pm 1)^2+2^5(\pm 2^53-b_1)(\pm 3\pm 2^{6}b_1) = \pm 1$
. Note that
$b_1$
is odd (otherwise
$d>0$
and
$2a+2b+c+d>32$
); hence, the second summand in K is of the form
$2^5s$
, with odd s. On the other hand, note that
$(2^{11}\pm 1)^2+1=2\times s_{\pm }$
, and
$(2^{11}\pm 1)^2-1=2^{12}\times t_{\pm }$
, with odd
$s_{\pm }$
and
$t_{\pm }$
, a contradiction. If
$b_2$
is even, then
$2a+2b+c>32$
, again a contradiction.
We will discuss smooth curves of genus
$2$
with exactly two rational Weierstrass points and no quadratic Weierstrass points separately.
7 Curves with exactly three rational Weierstrass points
In this section, we assume that C is a smooth projective curve of genus
$2$
over
${\mathbb Q}$
described by a globally minimal Weierstrass equation of the form
$E \colon y^2+Q(x)y=P(x)$
, where
$P(x),Q(x)\in {\mathbb Z}[x]$
,
$\deg Q(x)\le 2$
, and
$\deg P(x)= 5$
. Assume, moreover, that
$\Delta _E$
is an odd square-free integer. In particular, C has good reduction at the prime
$2$
. If, moreover, C has exactly three
${\mathbb Q}$
-rational Weierstrass points, then it follows from Lemma 3.1 that C is described by a Weierstrass equation of the form
$$ \begin{align*}E'\colon y^2=x(x-b)(x^3+dx^2+ex+f),\qquad b,d,e,f\in{\mathbb Z},\end{align*} $$
whose discriminant
$\Delta _{E'}=2^{40}\Delta _E$
, and such that
$x^3+dx^2+ex+f$
is irreducible. This implies that
$E'$
is minimal at every odd prime. In this section, we find explicitly all such genus
$2$
curves. In fact, we show that there are only two one-parameter families of the latter Weierstrass equations.
One has
$$ \begin{align} \Delta_{E'} = 2^8 b^2f^2(b^3+db^2+eb+f)^2 (d^2e^2-4e^3-4d^3f+18def-27f^2)=2^{40}\Delta_E, \end{align} $$
where
$\Delta $
is an odd square-free integer.
Setting
$\epsilon _i=\pm 1$
,
$i=1,2,3,4$
, one has:
-
(a)
$b=\epsilon _1 2^k$
,
$f=\epsilon _2 2^l$
, -
(b)
$b^3+db^2+eb+f = \epsilon _3 2^m$
, -
(c)
$d^2e^2-4e^3-4d^3f+18def-27f^2 = \epsilon _4 2^n\Delta _E$
,
where
$2k+2l+2m+n=32$
.
Theorem 7.1. Let C be a smooth projective curve of genus
$2$
defined over
${\mathbb Q}$
with good reduction at the prime
$2$
. Assume that C has exactly three
${\mathbb Q}$
-rational Weierstrass points. If C is described by a globally minimal Weierstrass equation of the form
$E\colon y^2+Q(x)y=P(x)$
,
$\deg Q(x)\le 2$
and
$ P(x)$
is monic of degree
$5$
, such that
$|\Delta _E|$
is a square-free odd integer, then E lies in one of the following two one-parameter globally minimal Weierstrass equations
-
(i)
$E_t\colon y^2 - x^2\,y = x^5 + 16 t\, x^4 + (16 + 8 t )\,x^3 + (8 + t)\,x^2 + x$
, -
(ii)
$F_t\colon y^2+(-x^2-x)\,y=x^5+(-1 + t)\,x^4 + (-2 - 2t)\,x^3+(2+ t)\,x^2 - x$
,
where
$t\in {\mathbb Z}$
.
Proof. As explained above, the curve C can be described by an integral Weierstrass equation of the form
$E'\colon y^2=x(x-b)(x^3+dx^2+ex+f)$
, where
$\Delta _{E'}=2^{40}\Delta _E$
; and conditions (a)–(c) are satisfied. The values of b and f are determined by (a). Condition (b) implies that
$m\ge \min (k,l)$
. If
$l\ge k$
, then
$e(t) = \epsilon _1\epsilon _3 2^{m-k}-\epsilon _1(2^{2k}\epsilon _1+2^{k}t+2^{l-k}\epsilon _2),$
where
$d=t$
. If
$l<k$
, then
$m=l$
; if
$\epsilon _2=\epsilon _3$
, then
$e(t)=-(2^{2k}+2^k\epsilon _1 t)$
and
$d=t$
; whereas if
$\epsilon _2=-\epsilon _3$
, then
$k=l+1$
,
$e(t)=-\epsilon _1\epsilon _2-\epsilon _1(2^{2k}\epsilon _1+2^kt)$
, and
$d=t$
. Therefore, in any case, the Weierstrass equation
$E_t'\colon =E'$
is described as follows:
$$ \begin{align}E^{\prime}_t \colon y^2=x(x-2^k\epsilon_1)(x^3+tx^2+e(t)x+2^l\epsilon_2),\quad t\in{\mathbb Z}.\end{align} $$
The strategy of the proof now is as follows. Given a fixed pair of positive integers
$(k,l)$
such that
$0\le k+l\le 16$
, m is chosen such that
$0\le m\le 16-k-l$
,
$m\ge \min (k,l)$
, and
$n=32-2k-2l-2m\ge 0$
. One checks now which of these tuples
$(k,l,m,n)$
yields a curve with good reduction at the prime
$2$
, given that condition (c) is satisfied; in particular,
$$ \begin{align}2^n||(d^2e^2-4e^3-4d^3f+18def-27f^2).\end{align} $$
Let
$E^{\prime }_t$
be the corresponding integral Weierstrass equation, and we first check whether it has potential good reduction at the prime 2. This can be accomplished using Theorem 3.2. If it has potential good reduction at
$2$
, then one checks for which congruence classes of t, condition (7.3) is satisfied.
In fact, the only Weierstrass equations
$E^{\prime }_t$
that describes a curve C with potential good reduction at
$2$
, that is,
$J_{2i}^5/J_{10}^i\in {\mathbb Z}_2$
, for every
$1\le i\le 5$
, and such that (7.3) is satisfied are the ones corresponding to the following tuples
$(k,l,m,n)$
:
$$ \begin{align*} (0,0,8,16),\, &\epsilon_1=-\epsilon_2,\quad t\equiv 3 \textrm{ mod }64,\\(2,5,5,8), & \quad t\equiv 2\textrm{ mod }4, \\(1,6,3,12),\, &\epsilon_1=\epsilon_3, \quad t\equiv 0 \textrm{ mod }8,\\(4,4,4,8),\, &\epsilon_2=\epsilon_3, \quad t\equiv 0 \textrm{ mod }4,\\(2,6,6,4),\, &\quad t\equiv 1 \textrm{ mod }2,\\(0,8,0,16),\, &\epsilon_1=\epsilon_3, \quad t\equiv 0 \textrm{ mod }64. \end{align*} $$
Any other tuple
$(k,l,m,n)$
will yield an integral Weierstrass equation for which
$J_{2i}^5/J_{10}^i\not \in {\mathbb Z}_2$
for some i,
$1\le i\le 5$
; or condition (7.3) is not satisfied by the corresponding Weierstrass equation. More precisely, any other tuple
$(k,l,m,n)$
that is not in the above list yields an integral Weierstrass equation for which there is some i,
$1\le i\le 5$
, such that
$J_{2i}^5/J_{10}^i=x_i(t)/y_i(t)$
where
$x_i(t)-x_i(0)\in 2{\mathbb Z}[t]$
,
$x_i(0)$
is an odd integer, and
$y_i(t)\in 2{\mathbb Z}[t]$
; or else it is impossible for
$2^n$
to exactly divide
$(d^2e^2-4e^3-4d^3f+18def-27f^2)$
for any choice of an integer value of t.
For the tuple
$(2,6,6,4)$
, the minimal discriminant equals
$(16t^2+56t+157)^2$
if
$(\epsilon _1,\epsilon _2,\epsilon _3)=(1,1,-1)$
, and it equals
$(16t^2-40t+133)^2$
if
$(\epsilon _1,\epsilon _2,\epsilon _3)=(-1,-1,1)$
(hence it is never square-free).
Note that the models
$Y^2=X(X-\epsilon _1)(4X^3+(4t+2)X^2+2(-2\epsilon _1 t-2-\epsilon _1-\epsilon _1\epsilon _2+\epsilon _1\epsilon _3)X+2\epsilon _2)$
for
$(2,5,5,8)$
and
$Y^2=X(4X-2\epsilon _1)(X^3+2X^2+(-\epsilon _1 t-2\epsilon _1\epsilon _2)X+\epsilon _2)$
for
$(1,6,3,12)$
have discriminants of the form
$2^{20}\times \textrm {odd}$
. Such models are minimal at
$2$
, since the polynomials on the right-hand side are twice a stable polynomial (root multiplicities
$< 3$
) and it is not congruent to a square modulo
$4$
(see [Reference Liu17, corollaire 2, p. 4594] and [Reference Müller and Stoll20]).
The tuple
$(4,4,4,8)$
, where
$\epsilon _2=\epsilon _3=1$
and
$t\equiv 0$
mod
$4$
, yields an integral Weierstrass equation
$E_t'$
that defines a curve with good reduction at
$2$
and
$2^{40}||\Delta _{E_t'}$
. Replacing t with
$4t$
and minimizing the equation
$E_t'$
yields the curve described by
$$ \begin{align*}E_t^1(\epsilon_1)\colon y^2-x\,y=x^5+(-4 \epsilon_1 + t)\,x^4+(-16 - 8\epsilon_1 t)\,x^3+(64\epsilon_1+ 16 t)\,x^2-\epsilon_1\,x, \end{align*} $$
with
$2\nmid \Delta _{E_t^1}$
for any integer t.
The tuple
$(0,8,0,16)$
, where
$\epsilon _1=\epsilon _3=-1$
and
$t\equiv 0$
mod
$64$
, yields an integral Weierstrass equation
$E_t'$
that defines a curve with good reduction at
$2$
and
$2^{40}||\Delta _{E_t'}$
. Replacing t with
$64t$
and minimizing the equation
$E_t'$
yields the equation
$$ \begin{align*}E_t^2(\epsilon_2)\colon y^2-x^2\,y=x^5+16 t\, x^4+(16 \epsilon_2 + 8 t )\,x^3+(8 \epsilon_2 + t)\,x^2+\epsilon_2\,x, \end{align*} $$
with
$2\nmid \Delta _{E_t^2}$
for any integer t.
The tuple
$(0,0,8,16)$
, where
$\epsilon _1=1$
and
$\epsilon _2=-1$
, gives rise to an integral Weierstrass equation
$E_t'$
that defines a curve with good reduction at
$2$
and
$2^{40}||\Delta _{E_t'}$
, when
$t\equiv 3$
mod
$64$
. Minimizing the equation
$E_t'$
yields
$$ \begin{align*}E_t^3(\epsilon_3)\colon y^2+(-x^2-1)\,y&=x^5+(-5+64\epsilon_3 - 16 t )\,x^4+ (9 - 208\epsilon_3 + 56 t )\,x^3\\& \quad +(-9 + 252 \epsilon_3- 73 t)\,x^2 + (4 - 135\epsilon_3 + 42 t)\,x + (-1 + 27 \epsilon_3 - 9 t), \end{align*} $$
such that
$2\nmid \Delta _{E_t^3}$
for any integer t.
Now, we can check, using MAGMA, that the following tuples of Weierstrass equations describe isomorphic genus 2 curves:
$$ \begin{align*}(E_t^2(1),\, E_{t-4}^2(-1),\, E_{t+4}^1(-1)); \quad (E_{t}^1(1),\, E_{-t}^1(-1)); \quad (E_{t}^3(1),\, E_{-t}^2(-1)); \quad (E_{t}^3(-1),\, E_{-t}^2(1)). \end{align*} $$
Similarly, for the tuple
$(2,6,6,4)$
when
$t\equiv 1$
mod
$2$
and
$(\epsilon _1,\epsilon _2,\epsilon _3)\not \in \{(1,1,-1),(-1,-1,1)\}$
, this yields
$E_t^4(\epsilon _1,\epsilon _2,\epsilon _3)$
:
$$ \begin{align*}y^2+(-x^2-x)\,y&=x^5+(-\epsilon_1 + t)\,x^4+(-3/2-\epsilon_1/2-\epsilon_1\epsilon_2 + \epsilon_1\epsilon_3 - 2\epsilon_1 t)\,x^3\\ & \quad +(\epsilon_1 +2 \epsilon_2 -\epsilon_3+ t)\,x^2-\epsilon_1\epsilon_2\,x \end{align*} $$
after minimization where
$2\nmid \Delta _{E_t^4(\epsilon _1,\epsilon _2,\epsilon _3)}$
for any integer t. Using MAGMA, one checks that the following pairs of equations describe isomorphic genus 2 curves:
$$ \begin{align*}E_t^4(1,-1,1) &\textrm{ and } E_{t+1}^4(1,1,1); \!\!\quad E_t^4(1,-1,-1) \textrm{ and } E_{t+2}^4(1,1,1); \!\!\quad E_t^4(-1,1,1) \textrm{ and } E_{t-3}^4(1,1,1);\\[3pt]&E_t^4(-1,1,-1) \textrm{ and } E_{t-2}^4(1,1,1); \quad E_t^4(-1,-1,-1) \textrm{ and } E_{t-1}^4(1,1,1). \end{align*} $$
Reasoning as in the cases of tuples
$(2,5,5,8)$
and
$(1,6,3,12)$
, we obtain that, in the remaining cases for the tuples
$(0,0,8,16)$
,
$(4,4,4,8)$
,
$(2,6,6,4)$
, and
$(0,8,0,16)$
, the minimal discriminants are of the form
$2^{20}\times \textrm {odd}$
.
After computing the discriminants for the above families of Weierstrass equations, one concludes that the Weierstrass equations for which the absolute value of the discriminant is a square-free odd integer lie only in the families
$E_t:=E_t^2(1)$
and
$F_t:=E_t^4(1,1,1)$
.
Corollary 7.2. The absolute discriminant
$|\Delta _{E_{t_0}}|$
(resp.
$|\Delta _{F_{t_0}}|$
),
$t_0\in {\mathbb Z}$
, of the minimal Weierstrass equation
$E_{t_0}$
(resp.
$F_{t_0}$
) is a square-free odd integer m if and only if
$|f(t_0)|=m$
(resp.
$|g(t_0)|=m$
) where
$f(t), g(t)\in {\mathbb Z}[t]$
are degree-
$4$
irreducible polynomials described as follows:
$$ \begin{align*} f(t) &= 256 t^4 - 2,064 t^3 + 4,192 t^2 + 384 t - 1,051; \\ g(t) &= 256 t^4 + 768 t^3 - 800 t^2 - 2,064 t - 6,343. \end{align*} $$
In particular,
$\Delta _{E_{t_0}}=\pm p$
(resp.
$\Delta _{F_{t_0}}=\pm p$
), p is an odd prime, if and only if
$f(t_0)=\pm p$
(resp.
$g(t_0)=\pm p$
). It follows that there are, conjecturally, infinitely many integer values t such that
$|\Delta _{E_{t}}|$
(resp.
$|\Delta _{F_t}|$
) is an odd prime.
Proof. This follows immediately as direct calculations show that
$\Delta _{E_t}=f(t)$
and
$\Delta _{F_t}=g(t)$
where
$E_t$
and
$F_t$
are defined as in Theorem 7.1. Moreover, the polynomials
$f(t)$
and
$g(t)$
satisfy the conditions of Bouniakovsky’ conjecture [Reference Bouniakovsky5] for the infinitude of prime values attained by an irreducible polynomial.
Recall that
$E_t^4(\epsilon _1,\epsilon _2,\epsilon _3)$
is the Weierstrass equation
$$ \begin{align*}y^2+(-x^2-x)\,y&=x^5+(-\epsilon_1 + t)\,x^4+(-3/2-\epsilon_1/2-\epsilon_1\epsilon_2 + \epsilon_1\epsilon_3 - 2\epsilon_1 t)\,x^3\\& \quad +(\epsilon_1 +2 \epsilon_2 -\epsilon_3+ t)\,x^2-\epsilon_1\epsilon_2\,x. \end{align*} $$
The following statement is a corollary of the proof above.
Corollary 7.3. Let
$ (\epsilon _1,\epsilon _2,\epsilon _3)\in \{(1,1,-1),(-1,-1,1)\}$
. There are, conjecturally, infinitely many integer values t such that
$|\Delta _{E^4_t}(\epsilon _1,\epsilon _2,\epsilon _3)|=p^2$
, p is an odd prime.
8 Curves with exactly two rational Weierstrass points and no quadratic Weierstrass points
Let C be described by a Weierstrass equation of the form
$$\begin{align*}E\colon y^2=x (x^4 + bx^3 + cx^2 + dx+e),\qquad b,c,d,e\in{\mathbb Z},\end{align*}$$
where the quartic is irreducible. Then the discriminant is given by
$$ \begin{align*} \Delta_E &= 2^8 e^2 (b^2 c^2 d^2 - 4 c^3 d^2 - 4 b^3 d^3 + 18 b c d^3 - 27 d^4 - 4 b^2 c^3 e \\ &\quad + 16 c^4 e + 18 b^3 c d e - 80 b c^2 d e - 6 b^2 d^2 e + 144 c d^2 e \\ &\quad - 27 b^4 e^2 + 144 b^2 c e^2 - 128 c^2 e^2 - 192 b d e^2 + 256 e^3). \end{align*} $$
In this section, although we were not able to utilize the methods used before to classify all such curves, we produce two one-parametric families of curves that will contain infinitely many curves with an odd prime absolute discriminant. It is worth mentioning that
$\Delta _E/(2^4e^2)$
is the discriminant of the elliptic curve described by
$E'\colon y^2=x^4+bx^3+cx^2+dx+e$
; therefore, classifying genus
$2$
curves with an odd prime absolute discriminant described by E is equivalent to finding elliptic curves with odd prime absolute discriminant defined by
$E'$
.
(i) Let
$f(t)=6,912t^4 + 6,912t^3 + 2,592t^2 + 432t - 65,509$
. The hyperelliptic curve
$C_t$
given by the (non-minimal) equation
$$ \begin{align*}y^2 = x(x^4+16(4t+1)x+256),\qquad t\in{\mathbb Z}, \end{align*} $$
has discriminant
$\pm p$
for some odd prime p if and only if
$f(t)=\pm p$
. One can easily check that for
$0 < t < 100$
,
$|f(t)|$
is prime exactly when
$$ \begin{align*}t\in\{1,2,14,15,16,29,41,47,52,57,69,71,80,81\},\end{align*} $$
and for such values of t, the discriminant
$\Delta _{C_t}=-f(t)$
. For instance, one has
$\Delta _{C_2}=-111,611$
,
$\Delta _{C_{14}}=-284,946,491$
,
$\Delta _{C_{15}}=-373,772,171$
,
$\Delta _{C_{16}}=-481,901,339$
,
$\Delta _{C_{29}}=-5,059,429,931$
, and
$\Delta _{C_{41}}=-20,012,351,339$
. In a general case,
$\Delta _{C_t}$
is an odd integer.
(ii) Let
$f(t)=6,912t^4 - 19,712t^3 + 167,968t^2 - 288,720t + 134,075$
. The hyperelliptic curve
$C_t$
given by the (non-minimal) equation
$$ \begin{align*}y^2 =x(x^4+(4t+1)x^3-80x^2+256x-256), \qquad t\in{\mathbb Z}, \end{align*} $$
has discriminant
$\pm p$
for some odd prime p if and only if
$f(t)=\pm p$
. One can easily check that for
$0 < t < 100$
,
$f(t)$
is a prime exactly when
$$ \begin{align*}t\in\{1,4,7,14,36,39,44,67,81,96,99\},\end{align*} $$
and for such values of t, the discriminant
$\Delta _{C_t}=-f(t)$
. For instance, one has
$\Delta _{C_1}=-523$
,
$\Delta _{C_{4}}=-2,174,587$
,
$\Delta _{C_{7}}=-16,177,963$
,
$\Delta _{C_{14}}=-240,455,387$
,
$\Delta _{C_{36}}=-10,897,249,403$
, and
$\Delta _{C_{39}}=-1,5065,561,387$
. In a general case,
$\Delta _{C_t}$
is an odd integer.
Conjecturally, the above families contain infinitely many genus
$2$
curves with an odd prime absolute discriminant.
Acknowledgments
The authors are very grateful to the anonymous referee for many corrections and valuable suggestions that improved the manuscript. The authors are also very grateful to Armand Brumer and Ken Kramer, John Cremona, Qing Liu, and Michael Stoll for useful correspondence and suggestions related to this work. All the calculations in this work were performed using MAGMA [Reference Bosma, Cannon and Playoust4], Mathematica [31], and PARI/GP [30]. This work started while the authors were invited to Friendly Workshop on Diophantine Equations and Related Problems, 2019, at the Department of Mathematics, Bursa Uludǎ University, Bursa-Turkey. The authors thank the colleagues of this institution for their hospitality and support. M. Sadek is partially supported by BAGEP Award of the Science Academy, Turkey, and The Scientific and Technological Research Council of Turkey, TÜBİTAK (research grant: ARDEB 1001/122F312).
Data availability statement
The data that support the findings of this study are available on request from the authors.
Open access
