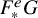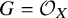1 Introduction
This work concerns the existence of (strong) generators in the bounded derived category of a noetherian scheme and, in particular, a commutative noetherian ring. The notion of a strong generator for an (essentially small) triangulated category
${\mathsf {T}}$
was introduced by Bondal and Van den Bergh [Reference Bondal and van den Bergh21]. Roughly speaking, an object G in
${\mathsf {T}}$
is a generator if each object A can be built from G using the operations in
${\mathsf {T}}$
: finite direct sums, summands, and mapping cones. When there is an an upper bound, independent of A, on the number of mapping cones required, G is said to be a strong generator; see 2.1.
Bondal and Van den Bergh [Reference Bondal and van den Bergh21] proved the existence of generators of derived categories of perfect complexes on quasi-separated and quasi-compact schemes. These are then generators for the bounded derived category of coherent sheaves when the scheme is smooth over a field. Rouquier [Reference Rouquier84] subsequently showed that the bounded derived category can have strong generators even in the singular case. Further work of Keller and Van den Bergh [Reference Keller, Murfet and Van den Bergh51], Lunts [Reference Lunts63], Iyengar and Takahashi [Reference Iyengar and Takahashi49], Neeman [Reference Neeman72], and Aoki [Reference Aoki3] focused on the existence of strong generators in growing generality.
While this settles the question of the existence of a generator for the bounded derived category of coherent sheaves quite broadly, there are few general results that identify them. Our motivation here is to identify, as canonically and explicitly as possible, generators. These will then immediately be strong whenever [Reference Aoki3] applies. We now survey the current literature.
We focus first on the affine situation: 
, where R is a commutative noetherian ring. In this case,
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
is equivalent to
${\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} R)$
, the bounded derived category of finitely generated R-modules. When R is regular and of finite Krull dimension, R itself is a strong generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} R)$
. In fact, any R-complex in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} R)$
having full support is a strong generator. The latter is a consequence of a theorem of Hopkins [Reference Hopkins45], and Neeman [Reference Neeman69]; see 2.5. One can also identify strong generators when R is a complete intersection ring with isolated singularities using a theorem of Stevenson [Reference Stevenson95]. When R is an artinian ring,
$R/J$
, where J is the Jacobson radical of R, is a strong generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} R)$
.
The situation is even more complicated in the global case. Perhaps the most comprehensive result is due to Orlov [Reference Orlov77] who proved that when X is quasi-projective, with very ample line bundle L, the direct sum
$\mathcal {O}_X \oplus L\oplus \cdots \oplus L^{\otimes d}$
, where
$d=\dim X$
, is a generator for
$\mathsf {Perf}\,X$
, the subcategory of perfect complexes. This gives strong generators for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
when X is regular. Outside this case, there are only a few results that identify explicit generators for the bounded derived category; see, for instance, the work of [Reference Ohkawa and Uehara73].
In light of these remarks, it is surprising that for any F-finite scheme of prime characteristic one can identify strong generators for the bounded derived category, at least in terms of generators for
$\mathsf {Perf}\,X$
. This is the content of the result below. The existence of a generator E, as below, for
$\mathsf {Perf}\,X$
is a result of Bondal and Van den Bergh [Reference Bondal and van den Bergh21, Theorem 3.1.1]. We emphasize that E need not be a strong generator for
$\mathsf {Perf}\,X$
. Indeed, the latter has no strong generators when X is singular; see [Reference Rouquier84, Reference Oppermann and Št’ovíček74]. As usual
$F^e_*G$
denotes the pushforward of a complex G in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
along
$F^e$
, the e-fold composition of the Frobenius map on X.
Theorem A. Let X be a noetherian F-finite scheme of prime characteristic p, and E a generator for
$\mathsf {Perf}\,X$
. For any G in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
with
$\operatorname {supp}_X G=X$
, the complex
$F^e_*(E\otimes ^{\operatorname {L}}_X G)$
is a generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
for any natural number
$e> \log _p(\operatorname {codepth} X)$
; it is a strong generator when X is separated.
This result is contained in Corollary 4.9. The invariant
$\operatorname {codepth} X$
is defined for any noetherian scheme X, in terms of the local rings at
$x\in X$
; see Section 4. When 
, the codepth of X is bounded above by the number of generators of the R-module
$F _*R$
; see Lemma 4.2, which also provides a better bound. In particular, the codepth is finite for any F-finite noetherian scheme. The codepth of X is equal to
$0$
if and only if X is regular, and so it can be viewed as a numerical measure of the singularity of X.
Two special cases are worth noting. When X is affine, the structure sheaf
$\mathcal {O}_X$
of X generates
$\mathsf {Perf}\,X$
, so the preceding result specializes to:
Corollary B. When R is an F-finite commutative noetherian ring of prime characteristic p, the R-module
$F^e_*R$
is a strong generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} R)$
for any natural number
$e>\log _p(\operatorname {codepth} R)$
.
In fact, one can take the Frobenius pushforward of any R-complex with coherent cohomology and full support; see Corollary 4.11. Here is another special case of Theorem A; it reappears as Corollary 4.10.
Corollary C. When X is a quasi-projective scheme over an F-finite field of prime characteristic p, and L a very ample line bundle,
$F^e_* \mathcal {O}_X \oplus F^e_* L \oplus \cdots \oplus F^e_* L^{\otimes \dim X}$
is a strong generator of
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
, for any natural number
$e> \log _p(\operatorname {codepth} X)$
.
It is not hard to deduce from these results that if for some G in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
with full support and integer
$n\ge 1$
, the complex
$F^n_*G$
is perfect, then X is regular; this recovers [Reference Avramov, Hochster, Iyengar and Yao8, Theorem 1.1]. Thus one can view Theorem A as a structural refinement of Kunz’s theorem [Reference Kunz55] that is the case
$G=\mathcal {O}_X$
. One can also deduce other results of this ilk, characterizing the singularity type of X in terms of homological properties of F; such as those from [Reference Avramov, Hochster, Iyengar and Yao8, Reference Herzog42, Reference Rodicio83, Reference Takahashi and Yoshino98, Reference Koh and Lee52] from our results.
There are two key ingredients that go into the proof of Theorem A. One is a local-to-global principle that says, roughly, that a complex G is a generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
if the stalk complex
$G_x$
is a generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} \mathcal {O}_x)$
for each
$x\in X$
; see Corollary 2.10. A subtle point here is that generation involves the structure of
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
as module over
$\mathsf {Perf}\,X$
viewed as a tensor-triangulated category. We deduce this local-to-global principle from a more general statement, involving the ind-completions of the categories. This builds on work of Stevenson [Reference Stevenson93], and is explained in Section 2.
Once we are down to the level of stalks, the main result concerns a nilpotence property of the Frobenius endomorphism on a local ring of prime characteristic. It implies that, under appropriate conditions involving support, high Frobenius pushforwards of any complex generates the finite length complexes in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} \mathcal {O}_x)$
. This is the content of Section 3.
Theorem A prompts a number of questions. One is what can be said, vis a vis generation, when
$F $
is not necessarily finite; see Theorem 4.6 for what we have to offer in this regard. Another question, prompted by Kunz’s theorem, is whether already the first Frobenius pushforward of some object generates the bounded derived category. Here is the most decisive result we prove concerning this question.
Theorem D. When X is F-finite and locally complete intersection, for any generator G of
$\mathsf {Perf}\,X$
, the complex
$F_*G$
is a strong generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
. In particular, if X is affine,
$F_*\mathcal {O}_X$
strongly generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
.
See Theorem 7.3, and also Theorem 7.5 for a more general statement. We also prove that Veronese subrings of
$k[x,y]$
have this property. The results for affine varieties raises the question: Does
$F_{*}R$
generate
${\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} R)$
for any commutative noetherian ring R? We do not know of any counterexamples.
In light of these results it is natural to ask for the smallest number e such that
$F^e_*\mathcal {O}_X$
strongly generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
. This is interesting even when
$X=\operatorname {Spec} R$
, for examples suggest that the upper bound for e given by Theorem A is far from optimal. Here are some results in this direction; see Sections 5 and 7.
-
•
$e\le \lceil \log _p(\mathrm {Loewy\,length}\, R)\rceil $
when R is an artinian local ring; -
•
$e\le \lceil \log _p(n+1)\rceil $
when
$X=\mathbb {P}^n$
; -
•
$e\le \lceil \log _p3\rceil $
with X the blowup of
$\mathbb {P}^2$
at
$\le 4$
points in general position; -
•
$e\le \lceil \log _pn\rceil $
for some smooth quadrics X of dimension n.
There may be no such e when, for instance, X is an F-finite smooth curve of positive genus; see Theorem 5.10. This prompts a definition: X is F-thick if
$F^e_*\mathcal {O}_X$
itself generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
for some
$e\ge 1$
. The class of F-thick schemes includes all affine schemes and overlaps significantly with varieties possessing a full exceptional collection. For smooth projective complete intersections F-thickness is tantamount to generation of the Kuznetsov component; see Theorem 5.16.
Shifting the focus from the full derived category to specific objects, recent and not so recent developments suggest considering the number of steps required to build
$\mathcal {O}_X$
from
$F^e_*\mathcal {O}_X$
, for some e. We are interested in this number partly because in the affine case it is one measure of a failure of the F-split property.
Corollary E. For any F-finite noetherian ring R one has that
$$\begin{align*}\inf\{n\mid \text{R is in } \operatorname{thick}^n(F^e_*R) \text{ for some e }\ge 1\} \end{align*}$$
is finite; it equals one if and only if R is F-split. It is bounded above by
$p^c$
when R is locally complete intersection and c is the codimension of R.
The finiteness is immediate from Corollary B, and the second part is essentially the definition of the F-split property. These results are proved in Section 6. Another reason for our interest in Corollary E is that it says, in the language of [Reference Dwyer, Greenlees and Iyengar28], that the R-module
$F^e_*R$
is proxy-small for
$e\gg 0$
. Among other things, this has consequences for the derived endomorphism ring of
$F^e_*R$
; see op. cit. and also [Reference Dwyer, Greenlees and Iyengar27].
2 Generators for triangulated categories
In this section we recall some basic notions and results concerning triangulated categories. The main examples of interest are various categories constructed from (quasi-)coherent sheaves on a noetherian scheme. We take Krause’s book [Reference Krause54] as our standard reference on triangulated categories; for constructions and results specific to schemes see Huybrecht’s book [Reference Huybrechts47] and the Stacks Project [Reference Johan de Jong26].
2.1. Let
${\mathsf {K}}$
be a triangulated category. A subcategory
${\mathsf {S}}$
of
${\mathsf {K}}$
is thick if it is a full triangulated subcategory closed under retracts. Given an object G (or a set of them) in
${\mathsf {K}}$
, we write
$\operatorname {thick}_{{\mathsf {K}}}(G)$
for the smallest thick subcategory, with respect to inclusion, containing G. The objects in
$\operatorname {thick}_{{\mathsf {K}}}(G)$
are referred to as being finitely built from G. This subcategory is also often denoted
$\langle G \rangle $
; see, for example, [Reference Bondal and van den Bergh21]. One can construct
$\operatorname {thick}_{{\mathsf {K}}}(G)$
inductively as follows: set
$\operatorname {thick}_{{\mathsf {K}}}^1(G)$
to be the smallest full subcategory of
${\mathsf {K}}$
containing G and closed under suspensions, finite sums, and retracts. For
$n> 1$
, let
$\operatorname {thick}_{{\mathsf {K}}}^n(G)$
be the smallest full subcategory of
${\mathsf {K}}$
containing all objects A that fit into a triangle
$$\begin{align*}A\to B\to C\to \mathsf{\Sigma} A\, \end{align*}$$
with B in
$\operatorname {thick}_{{\mathsf {K}}}^{n-1}(G)$
and C in
$\operatorname {thick}_{{\mathsf {K}}}^1 (G)$
, and which is closed under suspensions, finite sums, and retracts. One has a filtration
$$\begin{align*}\operatorname{thick}_{{\mathsf{K}}}(G) =\bigcup_{n\geqslant 1}\operatorname{thick}_{{\mathsf{K}}}^n(G)\,. \end{align*}$$
See [Reference Bondal and van den Bergh21], and also [Reference Avramov, Buchweitz, Iyengar and Miller7], for details. An object G is a (classical) generator for
${\mathsf {K}}$
if
$\operatorname {thick}_{{\mathsf {K}}}(G)={\mathsf {K}}$
; it is a strong generator provided that
$\operatorname {thick}_{{\mathsf {K}}}^d(G)={\mathsf {K}}$
for some integer d. Clearly, if
${\mathsf {K}}$
admits a strong generator, any generator is a strong generator.
Suppose
${\mathsf {K}}$
admits all coproducts. A triangulated subcategory of
${\mathsf {K}}$
is localizing when it is closed under small coproducts. We write
$\operatorname {Loc}_{{\mathsf {K}}}(G)$
for the smallest localizing subcategory containing G, and speak of objects in this category as being built from G. An object C in
${\mathsf {K}}$
is compact if
$\operatorname {Hom}_{{\mathsf {K}}}(C,-)$
commutes with coproducts in
${\mathsf {K}}$
, and
${\mathsf {K}}$
is compactly generated if there exists a set of compact objects G such that
$\operatorname {Loc}_{{\mathsf {K}}}(G)={\mathsf {K}}$
. We write
${{\mathsf {K}}}^{\mathrm c}$
for the compact objects in
${\mathsf {K}}$
; this is a thick subcategory of
${\mathsf {K}}$
. If G is a set of compact objects in
${\mathsf {K}}$
, then
$$ \begin{align} \operatorname{Loc}_{{\mathsf{K}}}(G) \cap {{\mathsf{K}}}^{\mathrm c}= \operatorname{thick}_{{\mathsf{K}}}(G)\,. \end{align} $$
This is proved by Neeman [Reference Neeman70, Theorem 2.1]; see also [Reference Krause54, Proposition 3.4.15].
Many of the triangulated categories of interest in this manuscript come equipped with an action of another triangulated category, and our proofs exploit this additional structure. The relevant notions are recalled below. For details see [Reference Stevenson93].
2.2. Let
$({\mathsf {T}},\otimes ,\mathbf {1})$
be a tensor triangulated category that acts on
${\mathsf {K}}$
(on the left), in the sense of Stevenson [Reference Stevenson93, Section 3]; see also [Reference Stevenson96]. We write
$\odot $
to denote this action. It is suggestive to think, and speak, of
${\mathsf {K}}$
as a
${\mathsf {T}}$
-module, as in [Reference Stevenson93, Reference Stevenson94]. Given an object G (or, as before, a set of them) in
${\mathsf {K}}$
, we denote
$\operatorname {thick}^{\odot }_{{\mathsf {K}}}(G)$
the thick
${\mathsf {T}}$
-submodule of
${\mathsf {K}}$
generated by G, that is to say, the smallest thick subcategory of
${\mathsf {K}}$
that is closed under the action of
${\mathsf {T}}$
.
When
${\mathsf {T}}$
and
${\mathsf {K}}$
admit all coproducts, we consider also
$\operatorname {Loc}^{\odot }_{{\mathsf {K}}}(G)$
, the localizing
${\mathsf {T}}$
-submodule of
${\mathsf {K}}$
generated by G. If
$\operatorname {Loc}_{{\mathsf {T}}}(U)={\mathsf {T}}$
for a set of objects U, then
$$ \begin{align} \operatorname{Loc}^{\odot}_{{\mathsf{K}}} (G)=\operatorname{Loc}_{{\mathsf{K}}}(A\odot B\mid A\in U \text{ and } B\in G)\,. \end{align} $$
In particular, if
$\operatorname {Loc}_{{\mathsf {T}}}(\mathbf {1})={\mathsf {T}}$
, then
$\operatorname {Loc}^{\odot }_{{\mathsf {K}}}(G)=\operatorname {Loc}_{{\mathsf {K}}}(G)$
; see [Reference Stevenson93, Lemma 3.13].
Suppose that
${\mathsf {T}}$
is compactly generated. Then Brown representability yields that
${\mathsf {T}}$
has an internal function object,
$\mathrm {hom}(-,-)$
, adjoint to
$-\otimes -$
; we assume that this is exact in each variable. An object D in
${\mathsf {T}}$
is rigid if for each E in
${\mathsf {T}}$
the natural map
$$\begin{align*}\mathrm{hom}(D,\mathbf{1})\otimes E \longrightarrow \mathrm{hom}(D,E) \end{align*}$$
is an isomorphism. The category
${\mathsf {T}}$
is rigidly compactly generated if it is compactly generated, and the set of compact objects and rigid objects coincide; see [Reference Stevenson93, Defintion 4.1]. In this case, the unit
$\mathbf {1}$
of
${\mathsf {T}}$
is compact. When a rigidly compactly generated category
${\mathsf {T}}$
acts on a compactly generated category
${\mathsf {K}}$
, the action restricts to compact objects, that is to say,
${{\mathsf {T}}}^{\mathrm c}$
acts on
${{\mathsf {K}}}^{\mathrm c}$
; see [Reference Stevenson93, Lemma 4.6].
These observations yield also a module version of (2.1.1), namely, when
${\mathsf {T}}$
is rigidly compactly generated and
${\mathsf {K}}$
is compactly generated, for any set G of compact objects in
${\mathsf {K}}$
, one has
$$ \begin{align} \operatorname{Loc}^{\odot}_{{\mathsf{K}}}(G) \cap {{\mathsf{K}}}^{\mathrm c}= \operatorname{thick}^{\odot}_{{\mathsf{K}}}(G)\,, \end{align} $$
where the category on the right is the
${\mathsf {T}}^{\mathrm c}$
-submodule of
${{\mathsf {K}}}^{\mathrm c}$
generated by G. This follows from (2.1.1), given (2.2.1).
2.3. Let X be a noetherian scheme and 
the derived category of quasi-coherent sheaves, viewed as a triangulated category with suspension functor
$\mathsf {\Sigma }$
. When
$X=\operatorname {Spec} R$
is affine, we identify 
with 
, the derived category of R-modules.
As a triangulated category 
admits arbitrary coproducts, and is compactly generated. The compact objects in 
are the bounded complexes of vector bundles; that is to say, perfect complexes. We write
$\mathsf {Perf}\,X$
for the full subcategory consisting of perfect complexes. Bondal and Van den Bergh [Reference Bondal and van den Bergh21, Theorem 3.1.1], see also [Reference Bondal and van den Bergh21, Theorem 3.1.3] or [Reference Johan de Jong26, Tag 09T4], proved that 
has a compact generator: a perfect complex G such that
It follows that 
; see (2.1.1).
Our main interest is in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
, the full subcategory of 
consisting of bounded complexes with coherent cohomology, and in finding strong generators for this triangulated category. Aoki [Reference Aoki3] proved that these exist whenever X is separated, quasi-excellent, and of finite Krull dimension.
2.4. The derived tensor product
$-\otimes ^{\operatorname {L}}_X -$
endows 
with a structure of a rigidly compactly generated tensor triangulated category. Moreover
$\mathsf {Perf}\,X$
is a tensor triangulated subcategory of 
and the derived tensor product gives an action of
$\mathsf {Perf}\,X$
on 
, in the sense of 2.2. One has
for any G in 
, where the category on the left is the localizing
$\mathsf {Perf}\,X$
-submodule of 
generated by G, and the category on the right is the localizing tensor ideal of 
. Moreover, when X is affine, the unit of the tensor product,
$\mathcal {O}_X$
, generates
$\mathsf {Perf}\,X$
as a thick subcategory, so
These observations will be used implicitly in the sequel.
The triangulated subcategory
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
of 
is not closed under the tensor product, unless X is regular; see 2.11. However, the tensor product on 
restricts to an action of
$\mathsf {Perf}\,X$
on
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
, so we are in the context of 2.2.
The next paragraph is a recap on some results involving support for objects in 
; for details see [Reference Iyengar, Lipman and Neeman48, Appendix A], or [Reference Johan de Jong26]. This builds on the theory of support for complexes over commutative noetherian rings developed by Foxby [Reference Foxby35].
2.5. Let X be a noetherian scheme as before, and fix E in 
. Given
$x\in X$
we write
$E_x$
for the stalk of E at x, viewed as an object in the derived category of the local ring
$\mathcal {O}_{x}$
. Let
$k(x)$
denote the residue field of
$\mathcal {O}_{x}$
. We identify
$k(x)$
with the coherent sheaf on
$\operatorname {Spec} \mathcal {O}_{x}$
it defines, as well as with the pushforward of this coherent sheaf along the localizing immersion
$\operatorname {Spec}\mathcal {O}_{x}\to X$
. The support of the complex E is the subset of X prescribed by
This is sometimes referred to as the small support of E. When E is in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
its support coincides with the usual one:
$$\begin{align*}\operatorname{supp}_X E = \{x\in X\mid \operatorname{H}(E_x)\ne 0\}\,. \end{align*}$$
In particular, in this case it is a closed subset of X.
When
$X=\operatorname {Spec} R$
, with R a commutative noetherian ring and E is the sheafification
$\widetilde {M}$
of an R-complex M, this is the notion of support from [Reference Foxby35], denoted
$\operatorname {supp}_RM$
. When moreover M is in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} R)$
one has
$$\begin{align*}\operatorname{supp}_X E = \operatorname{supp}_RM = V(\operatorname{ann}_R\operatorname{H}(M))\,. \end{align*}$$
Our interest in support stems from the following result, proved by Neeman [Reference Neeman69] in the affine case, and extended to schemes by Alonso Tarrío, Jeremías López, and Souto Solario [Reference Tarrío, López and Salorio2]: Given objects
$E,G$
in 
, one has
Using this result and (2.1.1) one deduces that when
$E,G$
are in
$\mathsf {Perf}\,X$
one has
$$ \begin{align} E\in \operatorname{thick}^{\otimes}_{\mathsf{Perf}\,X}(G)\Longleftrightarrow \operatorname{supp}_XE\subseteq \operatorname{supp}_XG\,. \end{align} $$
This result was proved by Thomason [Reference Thomason99]. The affine case is a result of Hopkins [Reference Hopkins45] and Neeman [Reference Neeman69]. From (2.5.2) it follows, for example, that when E in
$\mathsf {Perf}\,X$
has full support then it generates
$\mathsf {Perf}\,X$
as a module over itself.
2.6. Given
$x\in X$
let K be the Koszul complex on a finite generating set for the maximal ideal of the local ring
$\mathcal {O}_{x}$
, and for each E in 
set
viewed as an element in 
. This notation is ambiguous, for it does not reflect the choice of a generating set for the maximal ideal. However, if
$K'$
is the Koszul complex on a different generating set, then
$\operatorname {thick}(K)=\operatorname {thick}(K')$
as subcategories of 
; this follows from (2.5.2), but can also be checked directly, as is done in [Reference Hovey, Palmieri and Strickland46, Lemma 6.0.9]. Consequently
$\operatorname {thick}({E}(x))$
is well-defined, and this is what is relevant in the statement below, and also later on. Observe that, since K is a perfect
$\mathcal {O}_{x}$
-complex, when E is in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X) $
, the complex
${E}(x)$
is in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} \mathcal {O}_{x})$
.
Theorem 2.7. Let X be a noetherian scheme. Fix objects
$E,G$
in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
. If
${E}(x)$
is in 
for each
$x\in X$
, then E is in 
.
A proof is given further below; a input in it is the work of Stevenson [Reference Stevenson95]. Observe that the converse also holds: if E is in the
$\mathsf {Perf}\,X$
-submodule generated by G, then since both
$(-)_x$
and
$-\otimes _{\mathcal {O}_x}K$
are exact,
${E}(x)$
is generated by
${G}(x)$
, and hence also by
$G_x$
, as
$\mathcal {O}_x$
finitely builds K.
2.8. Let
${\mathsf {K}}({\mathsf {Inj}}\, X)$
denote the homotopy category of quasi-coherent injective sheaves on X. This is a compactly generated triangulated category and restricting the natural localization functor
to the subcategory of compact objects induces an equivalence
$$ \begin{align} {\mathsf{K}}({\mathsf{Inj}}\, X)^{\mathsf c}\xrightarrow{\ \sim\ }{\mathsf{D}}^{\mathsf{b}}(\operatorname{coh} X)\,. \end{align} $$
See [Reference Krause53, Theorem 1.1], where these results are proved when X is separated, and [Reference Čoupek and Šťovíček101, Appendix B] for the general case.
The tensor triangulated category 
is rigidly compactly generated and acts on
${\mathsf {K}}({\mathsf {Inj}}\,X)$
, in the sense of 2.2. One can view this action as the ind-completion of the action of
${\mathsf {Perf}}(X)$
on
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
. Here is a concrete description of this action, following [Reference Stevenson95, Section 3].
Given a flat
$\mathcal {O}_X$
-module F and an injective
$\mathcal {O}_X$
-module I, the
$\mathcal {O}_X$
-module
$F\otimes _XI$
is injective since X is noetherian. Thus, the tensor product induces an action of the homotopy category of complexes of flat modules on
${\mathsf {K}}({\mathsf {Inj}}\,X)$
. When F is an acyclic complex of flat modules with flat syzygies (also known as a pure acyclic complex), and I is a complex of injectives,
$F\otimes _XI$
is contractible. Thus the said action factors through the Verdier quotient of the homotopy category of flats by the subcategory of pure acyclic complexes. This category, introduced by Murfet [Reference Murfet68, Reference Neeman71], is usually denoted
${\mathsf {N}}(X)$
and called the Neeman category of X. When X is affine this is equivalent to the homotopy category of projective modules. A complex F of
$\mathcal {O}_X$
-modules is K-flat if it consists of flat
$\mathcal {O}_X$
-modules and
$F\otimes _X-$
preserves quasi-isomorphisms. Taking K-flat resolutions gives a fully faithful embedding of 
into
${\mathsf {N}}(X)$
, compatible with tensor products and coproducts. Via this embedding one gets an action of 
on
${\mathsf {K}}({\mathsf {Inj}}\,X)$
.
In what follows, we write
$\operatorname {Loc}^{\odot }_{{\mathsf {K}}(X)}(G)$
, with
${\mathsf {K}}(X)$
in the subscript rather than
${\mathsf {K}}({\mathsf {Inj}}\,X)$
, for the localizing submodule of
${\mathsf {K}}({\mathsf {Inj}}\,X)$
generated by an object G.
Fix
$x\in X$
and let
$\varGamma _x$
denote the exact functor from 
to 
defined by the assignment
$$\begin{align*}E\longrightarrow \mathbf{R}\varGamma_{\overline{\{x\}}}(E_x)\,. \end{align*}$$
See [Reference Stevenson93, Definition 5.3]. The local-to-global principle [Reference Stevenson93, Theorem 6.9] yields that given
$E,G$
in
${\mathsf {K}}({\mathsf {Inj}}\,X)$
, viewed with the
$\mathsf {Perf}\,X$
-action, one has
$$ \begin{align} E\in \operatorname{Loc}^{\odot}_{{\mathsf{K}}(X)}(G) \Longleftrightarrow \varGamma_x E\in \operatorname{Loc}_{{\mathsf{K}}(\mathcal{O}_x)}(\varGamma_xG) \quad \text{for each } x\in X. \end{align} $$
The condition on the right is equivalent to
$\varGamma _xE$
being in the localizing subcategory generated by
$G_x$
, for the functor
$\varGamma _x(-)$
commutes with coproducts. For another version of this local-to-global principle see [Reference Benson, Iyengar and Krause14, Lemma 3.2].
Proof of Theorem 2.7
The basic idea is to apply the local-to-global principle. We use the equivalence (2.8.1) and identify E and G with their images in
${\mathsf {K}}({\mathsf {Inj}}\,X)$
. The desired conclusion is that E is in the localizing 
-submodule of
${\mathsf {K}}({\mathsf {Inj}}\,X)$
generated by G; the statement about thick submodules follows by (2.2.2). For any x in X one has that
$$\begin{align*}\operatorname{Loc}_{{\mathsf{K}}(\mathcal{O}_x)}({E}(x)) = \operatorname{Loc}_{{\mathsf{K}}(\mathcal{O}_x)}(\varGamma_xE)\,. \end{align*}$$
This holds because
${\mathcal {O}}(x)$
, the Koszul complex of the local ring
$\mathcal {O}_x$
, and
$\varGamma _x\mathcal {O}_x$
build each other in 
; indeed both objects in question are supported on
$\{x\}$
, so (2.5.1) applies. Thanks to the tensor action of 
on
${\mathsf {K}}({\mathsf {Inj}}\,\mathcal {O}_x)$
the equality above holds. One can also give a direct, elementary proof; see, for example, [Reference Benson, Iyengar and Krause14, Proposition 2.11]. Given this observation, the hypothesis implies
$$\begin{align*}\varGamma_xE\in \operatorname{Loc}_{{\mathsf{K}}(\mathcal{O}_x)}(G_x) \quad \text{for each }x\in X. \end{align*}$$
At this point we can invoke the local-to-global principle (2.8.2) to deduce that E is in the 
-submodule of
${\mathsf {K}}({\mathsf {Inj}}\,X)$
generated by G, as desired.
2.9. Fix
$x\in X$
, set 
and 
. We write
$\varGamma _x{\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} R)$
for the subcategory of
${\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} R)$
consisting of R-complexes M supported at the closed point x of
$\operatorname {Spec} R$
; equivalently, the R-module
$\operatorname {H}(M)$
has finite length. This subcategory contains
${E}(x)$
for all E in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
. The residue field
$k(x)$
of R generates
$\varGamma _x{\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} R)$
; see, for example, [Reference Dwyer, Greenlees and Iyengar28]. However
$k(x)$
is a strong generator for this category if and only if R is artinian; see, for instance, [Reference Rouquier84].
Given these observations the result below is a consequence of Theorem 2.7.
Corollary 2.10. Let X be a noetherian scheme and fix G in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
. If for each
$x\in X$
, the complex
$G_x$
finitely builds
$k(x)$
, then G generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
as a
$\mathsf {Perf}\,X$
-module.
One reason for our interest in finding generators of derived categories is that they are test objects for finiteness of various homological invariants. A sample result along these lines is provided in Lemma 2.12; see also [Reference Dwyer, Greenlees and Iyengar28]. To illustrate this point, we recall a classical characterization of regularity.
2.11. Let X be a noetherian scheme. Clearly
$\mathsf {Perf}\,X\subseteq {\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
. Equality holds precisely when X is regular, that is to say, the local rings
$\mathcal {O}_{x}$
are regular for x in X; equivalently, at each closed point x in X. This characterization of regularity is due to Auslander, Buchsbaum, and Serre, given the following observation: A complex E in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
is perfect if and only if
$E_x$
is perfect in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} \mathcal {O}_x)$
for each
$x\in X$
; equivalently, at each closed point
$x\in X$
. In the affine case, which implies the global version, this is due to Bass and Murthy [Reference Bass and Pavaman Murthy13]; see also [Reference Avramov, Iyengar and Lipman10, Theorem 4.1].
Here is a related result: Any compact generator for 
generates
$\mathsf {Perf}\,X$
, as a thick subcategory. However
$\mathsf {Perf}\,X$
has a strong generator if and only if X is regular and of finite Krull dimension; see [Reference Rouquier84, Proposition 7.25].
Lemma 2.12. Let X be a noetherian scheme and G a generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
. An object E in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
is perfect if and only if
$\operatorname {Ext}_X^i(E,G)=0$
for
$i\gg 0$
. In particular, if
$\operatorname {Ext}_X^i(G,G)=0$
for all
$i\gg 0$
, then X is regular.
Proof. The second assertion follows immediately from the first, where the only if direction is clear. Suppose
$\operatorname {Ext}_X^i(E,G)=0$
for
$i\gg 0$
. Since G generates the bounded derived category, for each closed point
$x\in X$
, the coherent sheaf
$k(x)$
is finitely built from G in 
, hence the hypothesis yields
$$\begin{align*}\operatorname{Ext}^i_{\mathcal{O}_x}(E_x,k(x)) \cong \operatorname{Ext}^i_{X}(E,k(x)) =0 \quad \text{for } i\gg 0. \end{align*}$$
It follows that the
$\mathcal {O}_x$
-module
$E_x$
is perfect. Thus E is perfect; see 2.11.
3 Local rings
In this section we establish a nilpotence-type result concerning the Frobenius endomorphism on a local ring. This is one of the key inputs into our arguments, in the next section concerning generators for the bounded derived category of a scheme over a field of positive characteristic.
Let R be a noetherian ring of prime characteristic p; that is to say, p is a prime number and R contains the field
$\mathbb {F}_p$
as a subring. Let
$$\begin{align*}F\colon R\to R\quad\text{given by}\quad r\mapsto r^{p} \end{align*}$$
be its Frobenius endomorphism. It is well-known that the action induced by the Frobenius on various homology modules is often trivial; this springs from the fact that the Frobenius endomorphism on any simplicial commutative ring induces the trivial map in homology; see [Reference Pirashvili78] and also [Reference Bhatt and Scholze18, Section 11]. The gist of the result below is that, on noetherian local rings, the Frobenius endomorphism is even essentially nilpotent; see also Proposition 3.7.
Theorem 3.1. Let R be a noetherian local ring of prime characteristic p. For any R-complex M and natural number
$e> \log _p(\operatorname {codepth} R)$
there is an isomorphism
In particular, the residue field k is in 
whenever
$\operatorname {H}(K^M)\ne 0$
.
In the statement, 
where K is the Koszul complex on minimal generating set for the maximal ideal of R, and
$F ^e_*$
is the restriction of scalars functor along
$F ^e$
. The codepth of R is the non-negative integer
The equality on the right is by the depth sensitivity of the Koszul complex. Let
$Q\twoheadrightarrow R$
be a Cohen presentation, meaning that Q is a regular local ring and the map is surjective. One has
$$ \begin{align} \operatorname{codepth} R \le \operatorname{proj\,dim}_Q R\,, \end{align} $$
and equality holds if (and only if)
$\operatorname {edim} Q=\operatorname {edim} R$
, that is to say, when
$Q\twoheadrightarrow R$
is a minimal Cohen presentation. This holds because of the formula of Auslander and Buchsbaum [Reference Bruns and Herzog24, Theorem 1.3.3].
Since complete local rings admit Cohen presentations, this remark can be applied after completing R at its maximal ideal, for the codepth of R coincides with that of its completion; indeed, both the embedding dimension and the depth remain unchanged in this process.
3.2. Compare the statement of Theorem 3.1 with [Reference Avramov, Iyengar and Miller9, Theorem 6.2.2] that gives the same conclusion but where the lower bound for e is the spread of R. This number can be computed in terms of the graded Betti-numbers of
$\mathrm {gr}_{\mathfrak {m}}(R)$
, the associated graded ring of R at its maximal ideal
$\mathfrak {m}$
, over the symmetric algebra on
$\mathfrak {m}/\mathfrak {m}^2$
, and is related to the regularity of
$\mathrm {gr}_{\mathfrak {m}}(R)$
. The spread is harder to control; for instance, when R is a (not necessarily local) noetherian ring essentially of finite type, we do not know whether there is a global bound on the spread of
$R_{\mathfrak {p}}$
as
$\mathfrak {p}$
varies over the prime ideals in R. Such a bound is clear for the codepth and this fact is important in the sequel.
A key difference between the techniques used in [Reference Avramov, Iyengar and Miller9, Theorem 6.2.2] and our technique in Theorem 3.1 is that we exploit the special properties of the Frobenius map by working in category of simplicial algebras and simplicial modules over them. This yields our codepth bound in Theorem 3.1. The pertinent constructions and results concerning simplicial algebras are recalled below; see [Reference Quillen80, Reference Schwede and Shipley88] for proofs.
3.3. Given a simplicial ring
$\mathcal A$
we write
$\mathrm {Simp}(\mathcal A)$
for the category of simplicial
$\mathcal A$
-modules, with the usual model structure, and
$\mathrm {Ho}(\mathcal A)$
for the corresponding homotopy category.
Viewing a commutative ring R as a simplicial ring in the standard way, by the Dold-Kan theorem one gets an equivalence of categories
where
$N(-)$
is the normalization functor. These are compatible with natural model structures on the source and target. In particular, N induces an equivalence on homotopy categories:
$$\begin{align*}N\colon \mathrm{Ho}(R) \xrightarrow{\ \sim\ } {\mathsf{D}}_{\geqslant 0}(R)\,. \end{align*}$$
Here
${\mathsf {D}}_{\geqslant 0}(R)$
is the derived category on non-negatively graded chain complexes, which can be identified with the full subcategory of 
consisting of R-complexes with homology concentrated in non-negative degrees. It is not a triangulated subcategory, for it is not closed under negative suspensions.
Thanks to the equivalence above, one can work with simplicial R-modules, at least for objects in
${\mathsf {D}}_{\geqslant 0}(R)$
.
For a general simplicial ring
$\mathcal A$
, its normalization
$N(\mathcal A)$
is a graded-commutative differential graded algebra, concentrated in non-negative degrees, and the Dold-Kan functor induces an equivalence between
$\mathrm {Ho}({\mathcal A})$
and
${\mathsf {D}}_{\geqslant 0}(N(\mathcal A))$
, the derived category of differential graded
$N(\mathcal A)$
-modules with homology concentrated in non-negative degrees. This subsumes the case
$\mathcal A=R$
discussed above.
3.4. Let R be a ring. An R-complex M is said to be formal if there is an isomorphism
$M\simeq \operatorname {H}(M)$
in 
. Given the Dold-Kan equivalence, we say a simplicial R-module is formal if its normalization is formal. For instance, when k is a field, any simplicial k-vector space is formal.
3.5. Given a simplicial ring
$\mathcal A$
and an integer
$n\ge 0$
, there is a simplicial ring
$\mathcal B$
and a map of simplicial rings
$\varphi \colon \mathcal A\to \mathcal B$
with the following properties:
-
(1)
$\operatorname {H}_i(\mathcal B)=0$
for
$i\ge n+1$
; -
(2)
$\operatorname {H}_i(\varphi )$
is bijective for
$i\le n$
.
The map can be obtained by a process of killing the homology in
$\mathcal A$
in degree
$n+1$
and higher; see also the discussion on [Reference Toën100, pp. 162] for the construction of
$\varphi $
. This is part of the data of a Postnikov tower for
$\mathcal A$
.
3.6. Given a map
${\varphi }\colon \mathcal A\to \mathcal B$
of simplicial rings, one has an adjoint pair of functors
where
${\varphi }_*$
is restriction along
${\varphi }$
, and
${\varphi }^*$
is induced by
$\mathcal B\otimes _{\mathcal A}-$
. When
${\varphi }$
is an equivalence,
${\varphi }^*$
and
${\varphi }_*$
are inverse equivalences of categories. The normalization
$N(\mathcal A)$
is a differential graded algebra, and the following diagram
commutes up to isomorphism of functors. This observation is used in recasting the statement in Theorem 3.1 in terms of simplicial algebras and modules.
Proof of Theorem 3.1
One has that
$\mathfrak {m}\cdot \operatorname {H}(K^M)=0$
, where
$\mathfrak {m}$
is the maximal ideal of R. Thus, with
$\widehat {R}$
the
$\mathfrak {m}$
-adic completion of R, the map
$$\begin{align*}K^M \longrightarrow \widehat{R}\otimes_R K^M \cong K^{\widehat R\otimes M} \end{align*}$$
induced by the natural map
$R\to \widehat {R}$
, is a quasi-isomorphism. Thus passing to
$\widehat R$
, we can assume R is complete in the
$\mathfrak {m}$
-adic topology. Let
$Q\to R$
be a minimal Cohen presentation.
We view R as a simplicial Q-algebra in the usual way, and take a simplicial R-algebra model for
$K^R$
. Let
$\rho \colon Q\{X\}\xrightarrow {\simeq }R$
and
$Q\{Y\}\xrightarrow {\simeq }k$
be simplicial free resolutions of R and k, respectively, as Q-algebras. Then
is a simplicial free resolution of
$K^R$
over
$Q\{X\}$
. Let
$F^e\colon Q\{X\}\to Q\{X\}$
be the Frobenius map applied degreewise. At this point we have constructed the top two squares of the following commutative diagram of simplicial Q-algebras:
The equivalence
$Q\{X,Y\}\xrightarrow {\simeq } k\{X\}$
is obtained by applying
$Q\{X\}\otimes _Q-$
to the equivalence
$Q\{Y\}\xrightarrow {\simeq } k$
. Next we construct the lower part of the diagram.
Let J be the kernel of the canonical augmentation
$k\{X\}\to k$
; this is a simplicial ideal in
$k\{X\}$
and satisfies
$\operatorname {H}_i(J)=0$
for
$i\le 0$
. Since
$k\{X\}$
is free, as a simplicial k-algebra, for each integer
$n\ge 0$
one has
$\operatorname {H}_i(J^{n+1})=0$
for
$i\le n$
, by Quillen’s theorem [Reference Quillen79, Theorem 6.12]. In particular the surjection
$ k\{X\} \to k\{X\}/J^{n+1}$
is bijective in homology in degrees
$\le n$
. Set 
; thus
$$\begin{align*}\operatorname{H}_i(k\{X\})\cong \operatorname{H}_i(K^R)=0 \quad\text{for } i>c. \end{align*}$$
Let
$k\{X\}/J^{c+1}\to \mathcal {A}$
be a map of simplicial rings such that the induced map in homology is bijective in degrees
$\le c$
and
$\operatorname {H}_i(\mathcal A)=0$
for
$i\ge c+1$
; see 3.5. The map
$\alpha $
in the diagram is the composition of maps
$$\begin{align*}k\{X\} \longrightarrow k\{X\}/J^{c+1} \longrightarrow \mathcal{A} \end{align*}$$
By construction
$\operatorname {H}(\alpha )\colon \operatorname {H}(k\{X\})\to \operatorname {H}(\mathcal {A})$
is an isomorphism; that is to say,
$\alpha $
is an equivalence. The map
$\Phi \colon Q\{X\}\to \mathcal A$
is defined to ensure that the upper triangle commutes. Let
$\varepsilon \colon Q\{X\}\to k$
be the canonical augmentation and set 
. Since
$p^e\ge c+1$
, the composition of maps
$$\begin{align*}Q\{X\}\xrightarrow{\ F ^e\ } Q\{X\}\longrightarrow Q\{X,Y\}\longrightarrow k\{X\} \end{align*}$$
takes I into
$J^{c+1}$
, so
$\Phi $
factors through
$\varepsilon $
yielding the map
$\Psi $
in the diagram. This completes the construction of the commutative diagram. Observe that
$k\{X\}$
, and hence also
$\mathcal A$
is a simplicial k-algebra, and that the map
$\Psi \colon k\to \mathcal A$
is the composition of
$F ^e\colon k\to k$
with the structure map
$k\to \mathcal A$
.
At this point, we complete the proof under the additional assumption that the R-complex M satisfies
$\operatorname {H}_i(M)=0$
for
$i<0$
, for we can then work entirely in the simplicial context, given the Dold-Kan equivalence between non-negatively graded R-complexes and simplicial R-modules; see 3.3 and 3.6. To tackle the case of a general M, one can apply the normalization functor and get a commutative diagram of differential graded algebras and argue as below, but in the context of differential graded algebras and modules.
Since k is a field, any simplicial k-module is formal, in the sense of 3.4. Thus, for any simplicial
$\mathcal A$
-module
$\mathcal M$
, the simplicial R-module 
is formal. It thus follows from the commutative diagram above that for any simplicial
$K^R$
-module
$\mathcal N$
, the simplicial R-module
$F ^e_*(\mathcal N)$
is formal. This applies in particular to the simplicial model for
$K^M$
, and so the argument is complete.
As to the last part, if
$\operatorname {H}(K^M)\ne 0$
, then
$\operatorname {H}(F ^e_*(K^M)) \cong F ^e_* \operatorname {H}(K^M)$
, has
$F ^e_*k$
, and hence k, as a direct summand.
The essence of the argument above is the existence of the commutative diagram of simplicial algebras, and this can be paraphrased as follows.
Proposition 3.7. Let R be a noetherian local ring of prime characteristic p. For any natural number
$e> \log _p(\operatorname {codepth} R)$
, in the homotopy category of simplicial commutative algebras, the composition
$$\begin{align*}R\xrightarrow{F ^e}R\to K^R \end{align*}$$
factors through the natural surjection
$R\to k$
to the residue field.
Given Theorem 3.1, and more so the result above, it follows that any property of the ring that can be characterized in terms of some homological property of k can often be characterized in terms of the corresponding homological property of the Frobenius pushforwards,
$F ^e_*M$
, for any M with the maximal ideal in its support. Kunz’s characterization of regularity [Reference Kunz55, Theorem 2.1] of R is the prototypical such result, where
$M=R$
. See also Corollary 4.13. While some of these consequences can be deduced using results already available in the literature, in particular those in [Reference Avramov, Iyengar and Miller9] or [Reference Koh and Lee52], the approach outlined above lays bare the underlying phenomenon.
4 Schemes
In this section we build on the results in Section 3 to establish statements concerning generation of bounded derived categories; see Theorem 4.5. The main new input is the local-to-global principle from Section 2. To state our result we extend the definition of codepth for a local ring from Section 3 to any noetherian scheme X as follows:
When X is quasi-compact, excellent and of finite Krull dimension, there is bound on the embedding dimensions of the local rings
$\mathcal {O}_x$
and so also on
$\operatorname {codepth} X$
; this follows from [Reference Schoutens87, Proposition 5.2]. However we get no concrete bounds from this source. We would like to have such a bound, at least for F-finite schemes; for this see Lemma 4.2 below. To begin with, we record the following observation that means that for a local ring the codepth in the sense above is the same as the one introduced earlier.
Lemma 4.1. For any noetherian local ring R, one has
$\operatorname {codepth} R \ge \operatorname {codepth} R_{\mathfrak {p}}$
for any prime ideal
$\mathfrak {p}$
in R.
Proof. The desired statement is clear when R has a Cohen presentation
$Q\to R$
, which one can arrange to be minimal, for then (3.1.1) yields (in)equalities
$$\begin{align*}\operatorname{codepth} R = \operatorname{proj\,dim}_QR \ge \operatorname{proj\,dim}_{Q_{\mathfrak{p}}}(R_{\mathfrak{p}}) \ge \operatorname{codepth} R_{\mathfrak{p}}\,, \end{align*}$$
which is the desired inequality.
We reduce to this case by passing to the completion,
$\widehat R$
, of R at its maximal ideal. Pick a prime ideal, say
$\mathfrak {p}'$
in
$\operatorname {Spec}\widehat R$
lying over
$\mathfrak {p}$
and minimal with that property. One then has
$$\begin{align*}\operatorname{edim} (\widehat R_{\mathfrak{p}'}) \ge \operatorname{edim} R_{\mathfrak{p}} \quad\text{and}\quad \operatorname{depth} (\widehat R_{\mathfrak{p}'}) = \operatorname{depth} R_{\mathfrak{p}}\,, \end{align*}$$
where the inequality holds by, for example, [Reference Lech60] and the equality by [Reference Bruns and Herzog24, Proposition 1.2.16]. This gives the last of the following inequalities
$$\begin{align*}\operatorname{codepth} R = \operatorname{codepth} \widehat R \ge \operatorname{codepth} (\widehat R_{\mathfrak{p}'}) \ge \operatorname{codepth} R_{\mathfrak{p}}\,. \end{align*}$$
The equality is clear, whereas the first inequality is by the discussion in the previous paragraph, for
$\widehat R$
has a Cohen presentation.
In the statement below, for any finitely generated R-module M we write
$\beta ^R(M)$
for the minimal number of elements required to generate M. When R contains a field of positive characteristic, we say R is F-finite if the Frobenius endomorphism
$F\colon R\to R$
is a finite map. We use often the observation that quotients, localizations, and completions of F-finite noetherian rings are F-finite, and that the Frobenius endomorphism commutes with localization and completion.
Lemma 4.2. Let R be a noetherian ring.
-
(1) When R is a quotient of a regular ring Q, one has
$$\begin{align*}\operatorname{codepth} R\le \operatorname{proj\,dim}_QR<\infty\,. \end{align*}$$
-
(2) When R contains a field of prime characteristic and is
$F $
-finite one has In particular,
$$\begin{align*}\operatorname{edim} R_{\mathfrak{p}} \le \beta^R(F _*R)\quad\text{for each } \mathfrak{p}\in\operatorname{Spec} R. \end{align*}$$
$\operatorname {codepth} R<\infty $
.
Proof. (1) When R is a quotient of a regular ring Q one has inequalities
$$\begin{align*}\operatorname{codepth} R_{\mathfrak{p}} \le \operatorname{proj\,dim}_{Q_{\mathfrak{p}\cap Q}}R_{\mathfrak{p}}\le \operatorname{proj\,dim}_Q R<\infty\,, \end{align*}$$
for each prime ideal
$\mathfrak {p}$
of R, where the first one is by (3.1.1), and the finiteness of
$\operatorname {proj\,dim}_QR$
is by [Reference Bass and Pavaman Murthy13]. Thus
$\operatorname {codepth} R$
is finite, and bounded above by
$\operatorname {proj\,dim}_Q R$
.
(2) We can deduce this from (1) for any
$F $
-finite ring is a quotient of an F-finite regular ring, as was proved by Gabber [Reference Gabber36, Remark 13.6]. Here is a direct argument, based on the proof of [Reference Krause56, Proposition 1.1].
Since the number of generators does not go up under localization, the desired result is that when
$(R,\mathfrak {m},k)$
is a noetherian local ring
$\beta ^R(F _*R)\ge \operatorname {edim} R$
. This follows from the computation:
$$ \begin{align*} \beta^R(F _*R) & = \operatorname{rank}_k (k\otimes_R F _*R) \\ & = \operatorname{rank}_k (F _*(R/\mathfrak{m}^{[p]}))\\ &\ge \operatorname{rank}_k(F _*k)\operatorname{rank}_k(R/\mathfrak{m}^{[p]}) \\ & \ge \operatorname{rank}_k(\mathfrak{m}/\mathfrak{m}^2)\,. \end{align*} $$
The (in)equalities are all standard.
The preceding result gives one family of schemes whose codepth is finite. This family includes schemes that may have infinite Krull dimension.
Corollary 4.3. If X is a scheme essentially of finite type over a regular scheme, then
$\operatorname {codepth} X$
is finite.
For the present, the more pertinent result is the one below.
Proposition 4.4. If X is a noetherian F-finite scheme, then
$\operatorname {codepth} X$
is finite.
Proof. Since X admits a finite open affine cover, and
$\operatorname {codepth} X$
is computed locally, we can assume X is affine. The desired result follows from Lemma 4.2(2).
These considerations are pertinent to the result below; it contains Theorem A. See Section 2 for notation and terminology.
Theorem 4.5. Let X be an F-finite noetherian scheme over a field of prime characteristic p. Fix a natural number
$e> \log _p(\operatorname {codepth} X)$
. If
$E,G$
belong to
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
with
$\operatorname {supp}_XE\subseteq \operatorname {supp}_XG$
, then
Hence, if
$\operatorname {supp}_X G=X$
, then
$F_*^eG$
generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
as a
$\mathsf {Perf}\,X$
-module.
Proof. By Theorem 2.7 it suffices to check that
${E}(x)$
is in the thick subcategory of 
generated by
$(F _*^eG)_x$
for
$x\in X$
. Fix a point
$x\in X$
.
If
$x\notin \operatorname {supp}_XG$
, then
$\operatorname {supp}_XE\subseteq \operatorname {supp}_XG$
implies
$E_x\cong 0$
, hence also that
${E}(x)\cong 0$
, so the desired inclusion is clear.
Suppose
$x\in \operatorname {supp}_XG$
. Set 
, let k be its residue field, and set 
; thus
$M\not \cong 0$
in 
. By the definition of
$\operatorname {codepth} X$
one has
$p^e> \operatorname {codepth} R$
so Theorem 3.1 applied to M yields that k is in the thick subcategory generated by
$F ^e_*(K^M)$
, and since
$F ^e_*(K^M)$
is finitely built by
$F^e_*(M)$
, it follows that k is finitely built by
$F^e_*(M)$
. This implies that any R-complex with homology of finite length, and in particular
${E}(x)$
, is in that thick subcategory as well. It remains to observe that
$F ^e_*(M)\cong F ^e_*(G)_x$
, as R-complexes.
Next we establish a result akin to Theorem 4.5 that deals with the case when X is not necessarily
$F $
-finite. It concerns the homotopy category of injectives that appeared already in 2.8. We need also the functor
that assigns to each complex its injective resolution; see [Reference Krause54, Section 4.3].
Theorem 4.6. Let X be a noetherian scheme over a field of prime characteristic p. Fix a natural number
$e> \log _p(\operatorname {codepth} X)$
and a complex G in 
with
$\operatorname {H}(G)$
bounded and
$\operatorname {supp}_XG=X$
. As
$\mathsf {Perf}\,X$
-modules one has
$$\begin{align*}\operatorname{Loc}^{\odot}_{{\mathsf{K}}(X)}(\boldsymbol{i} F ^e_*G)={\mathsf{K}}({\mathsf{Inj}}\,X)\,. \end{align*}$$
This statement is vacuous when the codepth of X is infinite. A construction of Hochster, see [Reference Hochster44, Proposition 1], produces affine noetherian schemes of infinite codepth. However, as noted before, codepth is finite for excellent schemes of finite Krull dimension. See also Corollary 4.3.
Proof. By the local-to-global principle (2.8.2) it suffices to verify that for each x in X the localizing
$\mathsf {Perf}\,X$
-submodule of
${\mathsf {K}}({\mathsf {Inj}}\,X)$
generated by
$(\boldsymbol {i} F ^e_*G)_x$
contains the objects of
${\mathsf {K}}({\mathsf {Inj}}\,X)$
supported at x. Moreover, since
$\operatorname {H}^i(G)=0$
for
$|i|\gg 0$
, one gets the first isomorphism below:
$$\begin{align*}(\boldsymbol{i} F ^e_*G)_x \cong \boldsymbol{i}((F ^e_*G)_x)\cong \boldsymbol{i} F ^e_*(G_x)\,. \end{align*}$$
The second one is standard. Thus passing to the local ring at x, we arrive in the situation where 
is a noetherian local ring, say with maximal ideal
$\mathfrak {m}$
, and G is an R-complex with
$\operatorname {H}(G)$
bounded and
$\operatorname {supp}_RG=\operatorname {Spec} R$
. The task is to verify that any R-complex in
${\mathsf {K}}({\mathsf {Inj}}\,R)$
supported at
$\mathfrak {m}$
is in the localizing subcategory of
${\mathsf {K}}({\mathsf {Inj}}\,R)$
generated by
$\boldsymbol {i} F ^e_*G$
. This is equivalent to checking that if an object M of
${\mathsf {K}}({\mathsf {Inj}}\,R)$
is supported at
$\mathfrak {m}$
and satisfies
$$\begin{align*}\operatorname{Hom}_{{\mathsf{K}}}^*(\boldsymbol{i} F ^e_*G , M)=0 \end{align*}$$
then
$M\cong 0$
in
${\mathsf {K}}({\mathsf {Inj}}\,R)$
; that is to say, all its syzygy modules are injective.
Since
$K^G$
is finitely built from G in 
, it follows that
$F ^e_*(K^G)$
is in the thick subcategory of 
generated by
$F ^e_*G$
. Then, given the lower bound on e, Theorem 3.1 yields that k, the residue field of R, and hence also any R-module of finite length, is in the thick subcategory generated by
$F ^e_*G$
. Since
$\boldsymbol {i}(-)$
is an exact functor, we conclude that for each finite length R-module L, its injective resolution
$\boldsymbol {i} L$
is in the thick subcategory of
${\mathsf {K}}({\mathsf {Inj}}\,R)$
generated by
$\boldsymbol {i} F ^e_*G$
. Thus the condition above implies that
$$\begin{align*}\operatorname{Hom}_{{\mathsf{K}}}^*(\boldsymbol{i} L, M)=0\,, \end{align*}$$
for all such L. The category of
$\mathfrak {m}$
-power torsion R-modules is a locally noetherian Grothendieck category with noetherian objects the finite length R-modules. Thus, since M is
$\mathfrak {m}$
-power torsion, applying [Reference Krause53, Lemma 2.2] we deduce from the condition above that
$M\cong 0$
in
${\mathsf {K}}({\mathsf {Inj}}\,R)$
; see also [Reference Krause54, Lemma 6.4.11].
4.7. One can deduce Theorem 4.5 from the result above: When X is
$F $
-finite, if G is in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
so is
$F ^e_*G$
and hence
$\boldsymbol {i} F ^e_*G$
is compact in
${\mathsf {K}}({\mathsf {Inj}}\,X)$
; see (2.8.1). The localizing submodule generated by
$\boldsymbol {i} F ^e_*G$
equals
${\mathsf {K}}({\mathsf {Inj}}\,R)$
, so by (2.2.2)
$$\begin{align*}\operatorname{thick}^{\odot}(\boldsymbol{i} F ^e_*G ) = {{\mathsf{K}}({\mathsf{Inj}}\,X)}^{\mathsf{c}}\,. \end{align*}$$
Applying the quotient functor
$\boldsymbol {q}$
to the previous equality yields the desired result, given the equivalence (2.8.1).
Next we discuss alternative formulations of the preceding results, in terms of strong generators of
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
.
Lemma 4.8. Let X be a noetherian scheme over a field of prime characteristic p. Let
$U\subseteq \mathsf {Perf}\,X$
be such that 
. For any G in 
and integer
$e\ge 0$
one has
Proof. It suffices to verify this when
$e=1$
; this eases up the notation a bit.
Let 
denote pullback along F. For any collection of objects C in 
with 
, adjunction yields 
. From this observation and the fact that
$F^*$
restricts to an endofunctor on
$\mathsf {Perf}\,X$
, one can apply (2.1.1) to conclude that
Now it remains to observe that
where the first equality is by (4.8.1), the second equality is the projection formula
$$\begin{align*}F _*(F ^*(-)\otimes G)\simeq (-)\otimes F _*G \end{align*}$$
on
$\mathsf {Perf}\,X$
, and the last equality is evident since 
.
Strong generation
Here is our main result concerning the existence of strong generators for the bounded derived category of X. By a result of Bondal and Van den Bergh, see 2.3, a perfect complex E as in the hypothesis always exists; when X is affine, one can take
$G=\mathcal {O}_X$
.
Corollary 4.9. Let X be an F-finite noetherian scheme of prime characteristic p, and assume E generates
$\mathsf {Perf}\,X$
. For each
$e>\log _p(\operatorname {codepth} X)$
and G in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
with
$\operatorname {supp}_XG=X$
, the complex
$F^e_*(E\otimes G)$
is a generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
; it is a strong generator when X is separated.
Proof. Since
$\operatorname {supp}_X G= X$
, Theorem 4.5 yields the first equality below:
The second equality is by Lemma 4.8, given that E generates
$\mathsf {Perf}\,X$
.
Since X is F-finite, it has finite Krull dimension, by [Reference Krause56, Proposition 1.1] – see also Lemma 4.2(2) – and is excellent, by [Reference Krause56, Theorem 2.5]. When X is separated, Aoki’s theorem [Reference Aoki3] yields that
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
has a strong generator, and as
$F^e_*(E\otimes G)$
is generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
, it must be a strong generator as well.
Here is a corollary of the preceding result.
Corollary 4.10. Let X be a quasi-projective scheme over an
$F $
-finite field of prime characteristic p, L a very ample line bundle, and set
Then
$F^e_*G$
strongly generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
for each
$e> \log _p(\operatorname {codepth} X)$
.
Proof. Since G generates
$\mathsf {Perf}\,X$
, see [Reference Orlov77, Theorem 4], Corollary 4.9 applies.
The result below is immediate from Corollary 4.9, as
$\mathsf {Perf}\,X$
is generated by the tensor unit
$\mathcal {O}_X$
in the affine case.
Corollary 4.11. If X is an F-finite affine scheme of prime characteristic p, then
$F^e_*\mathcal {O}_X$
strongly generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
for each
$e> \log _p(\operatorname {codepth} X)$
. In fact
$F^e_*G$
is a strong generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
whenever G is in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
with
$\operatorname {supp}_X G=X.$
4.12. It follows from the preceding result that for any
$F $
-finite normal toric ring R the isomorphism classes of conic modules generate
${\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} R)$
. This is because each R-module
$F ^e_*R$
decomposes as a direct sum of conic modules, see [Reference Faber, Muller and Smith32, Proposition 4.15] (or [Reference Bruns22, section 3]), and there are only finitely many conic modules up to isomorphism; cf. [Reference Faber, Muller and Smith32, Corollary 4.12], as well as [Reference Bruns and Gubeladze23, Proposition 3.6].
One consequence of the existence of generators is the following strengthening of Kunz’s theorem [Reference Kunz55, Theorem 2.1] characterizing regularity in terms of flatness of the Frobenius. The result below is, in turn, subsumed by [Reference Avramov, Hochster, Iyengar and Yao8, Theorem 1.1] but it seems worthwhile to state and prove the version below for it highlights one application of statements concerning the existence of generators.
Corollary 4.13. Let X be an F-finite scheme. If there exists an G in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
with
$\operatorname {supp}_XG=X$
such that
$F^n_*G$
is perfect for some
$n\ge 1$
, then X is regular.
Proof. A key observation is that given finite maps of schemes
$$\begin{align*}X"\xrightarrow{f'}X'\xrightarrow{f} X \end{align*}$$
and complexes
$G"$
and
$G'$
over
$X"$
and
$X'$
, respectively, with
$f^{\prime }_*G"$
and
$f_*G'$
are perfect, the complex
$(ff')_*({f'}^{*}G'\otimes ^{\operatorname {L}} G")$
is perfect; the maps being finite guarantee that
${f'}^{*}G'\otimes ^{\operatorname {L}} G"$
has coherent cohomology; see, for instance, [Reference Berthelot, Grothendieck and Illusie16, Corollary 3.4].
Given this observation it follows that if
$F^n_*G$
is perfect for some
$n\ge 1$
, then
$F^{2n}_*(F^{n,*}G\otimes ^{\operatorname {L}} G)$
is perfect. Since F is a homeomorphism on the underlying topological spaces, the support of
$F^{n,*}G\otimes ^{\operatorname {L}} G$
equals that of G. Thus, repeating this construction, we can make n arbitrarily large; in particular, bigger than
$\log _p(\operatorname {codepth} X)$
. Let E be a generator for
$\mathsf {Perf}\,X$
. Using once again the observation in the previous paragraph, one deduces that
$F^n_*(E\otimes G)$
is also perfect. Since the complex generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
, by Corollary 4.9, it remains to apply Lemma 2.12 to deduce that X is regular.
5 F-thickness
The results in Section 4 guarantee that for any F-finite (separated) noetherian scheme X, its bounded derived category is (strongly) generated by a high Frobenius pushforward of some perfect complex G. In this section we investigate when taking
$G=\mathcal {O}_X$
does the job. We refer the reader to [Reference Huybrechts47] regarding background on exceptional collections, semiorthogonal decompositions, and tilting generators.
Definition 5.1. Let X be a noetherian F-finite scheme. We say X is F-thick if
$F_*^e \mathcal {O}_X$
generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh}{X})$
, for some integer
$e\ge 1$
.
By Corollary 4.11, every affine scheme is F-thick. In this section, we present other examples of F-thick schemes, and examples of schemes that are not F-thick.
Relation to tilting
The more stringent requirement that
$F_*^e \mathcal {O}_X$
is a tilting generator has been studied in [Reference Langer59, Reference Raedschelders, Špenko and Van den Bergh81, Reference Samokhin85, Reference Samokhin86]. The class of F-thick schemes is strictly larger. Indeed for toric varieties there are obstructions to the existence of full exceptional collections, which prevents the tilting condition from being satisfied; see [Reference Efimov29, Theorem 1.3], as well as [Reference Hille and Perling43, Reference Michałek67]. The affine situation is simpler.
Proposition 5.2. Let R be a commutative noetherian ring. If G is a tilting generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} R)$
, then
$G\cong \mathsf {\Sigma }^s P$
, for some finitely generated, faithful, projective R-module P and integer s; moreover, the ring R is regular. Therefore
${\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} R)$
has a tilting generator if and only if R is regular.
Proof. Lemma 2.12 implies R is regular, and hence also that
$\operatorname {proj\,dim}_RG<\infty $
. Then Nakayama’s Lemma yields that
$$\begin{align*}\operatorname{Ext}_R^g(G,G) \ne 0 \text{ when } g=\operatorname{proj\,dim}_RG - \inf \operatorname{H}_*(G)\,. \end{align*}$$
This implies the desired result.
We record some examples of F-thick schemes.
Example 5.3. Let 
denote projective n-space over k. In this case X is F-thick and, moreover,
$F_*^e \mathcal {O}_X$
is a tilting generator whenever
$p^e>n.$
Indeed, [Reference Rao82, Lemma 2.1] yields, for each
$l\in \mathbb {Z}$
, a decomposition
$$\begin{align*}F_* ( \mathcal{O}_X(l)) \cong \bigoplus_{i\geq -l/p}\mathcal{O}_X (-i)^{\oplus \alpha(i,l)}\,, \end{align*}$$
where
$\alpha (i,l)$
is the number of monomials of degree
$l+ip$
that are not divisible by any
$p^{\text {th}}$
-power of a variable. Also, by [Reference Bernšteĭn, Gel’fand and Gel’fand15],
$$\begin{align*}G=\mathcal{O}_X\oplus\mathcal{O}_X (-1)\oplus\ldots\oplus \mathcal{O}_X(-n) \end{align*}$$
generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
. So combining these two facts yields that
$F_*^e \mathcal {O}_X$
generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
whenever
$p^e> n$
. Also, as
$\operatorname {Ext}_X^t(G,G)=0$
for
$t>0$
, it follows that
$F_*^e \mathcal {O}_X$
is a tilting generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
.
Fix
$p^e \leq n$
. For each l in
$\mathbb {Z}$
one has
Hence
$F_*^e \mathcal {O}_X$
does not generate
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
.
Example 5.4. Let
$\mathbf {G}$
be a semisimple algebraic group over an algebraically closed field of prime characteristic p. If
$p>h$
where h is the Coxeter number of
$\mathbf {G}$
, then
$F_* \mathcal {O}_{\mathbf {G}}$
is a generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh}{\mathbf {G}})$
. Furthermore, if
$\mathbf {P}$
is a parabolic subgroup of
$\mathbf {G}$
and
$p>h$
, then
$F_* \mathcal {O}_{\mathbf {G}/\mathbf {P}}$
is a generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh}{\mathbf {G}/\mathbf {P}})$
(see [Reference Bezrukavnikov, Mirković and Rumynin17] and [Reference Samokhin85, Corollary 1.1]). If X is a flag variety of type
$\mathbf {A}_2$
(or
$\mathbf {B}_2$
) and
$p>3$
(or
$p>5$
, respectively), then
$F_* \mathcal {O}_X$
is a tilting generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh}{X})$
; see [Reference Samokhin85, Corollary 3.2].
Example 5.5. The blowup X of
$\mathbb {P}^2$
at four points in general position is F-thick. By [Reference Hara41, Corollary 5.4 & Proposition 6.4], if
$e \geq \log _p 3$
, then
$F_*^e \mathcal {O}_X$
contains as direct summands bundles that form a full strong exceptional collection on X.
Example 5.6. Let
$\mathbb {G}=G(2,n)$
be the Grassmannian over an algebraically closed field of prime characteristic p. By [Reference Raedschelders, Špenko and Van den Bergh81, Corollary 16.11]
$F_* \mathcal {O}_{\mathbb {G}}$
contains a full exceptional collection as direct summands whenever
$p\geq n$
, and hence it is a generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} \mathbb {G})$
; in fact, it contains the full exceptional collection in [Reference Kaneda50, Reference Masaharu64]. By [Reference Raedschelders, Špenko and Van den Bergh81, Theorem 1.1]
$F_* \mathcal {O}_{\mathbb {G}}$
is a tilting generator if and only if
$n=4$
and
$p>3$
.
Example 5.7. If X is a Severi-Brauer variety over a perfect field k of prime characteristic, then it is F-thick. We can apply [Reference Gille and Szamuely37, Corollary 5.1.5] to obtain a finite Galois extension
$\ell /k$
such that
$X_{\ell }\cong \mathbb {P}^n_\ell $
for some integer
$n>0$
. The projection morphism
$\pi \colon X_{\ell } \to X$
ensures that the exact functor
$$\begin{align*}\pi_* \colon {\mathsf{D}}^{\mathsf{b}}(\operatorname{coh}{X_{\ell}}) \to {\mathsf{D}}^{\mathsf{b}}(\operatorname{coh}{X}) \end{align*}$$
is essentially surjective (see [Reference Sosna92] and [Reference Ballard, Duncan and McFaddin12]). There exists
$e \gg 0$
such that
$F_*^e \mathcal {O}_{X_{\ell }}$
generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh}{X}_\ell )$
. Therefore,
$\pi _* (F_*^e \mathcal {O}_{X_\ell })$
generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
. Notice that
$$\begin{align*}\pi_* F_*^e \mathcal{O}_{X_\ell} \cong F_*^e \pi_* \mathcal{O}_{X_\ell} \cong F_*^e \pi_* \pi^* \mathcal{O}_X \cong (F_*^e \mathcal{O}_X)^{\oplus g}\,, \end{align*}$$
where 
.
Example 5.8. If X is a smooth quadric
$X\subset \mathbb {P}^{n+1}$
over an algebraically closed field of odd characteristic p, then it follows from [Reference Samokhin86, Corollary 5.2] and [Reference Achinger1, Theorem 2] X is F-thick when n is even and
$n\geq 2(p+1)$
, or n is odd and
$n \geq 3p+2$
. The case where
$F_*^e \mathcal {O}_X$
is a tilting generator has been considered in [Reference Langer59, Theorem 0.1].
Example 5.9. In 2006, Bondal [Reference Bondal20] suggested that toric varieties are F-thick. Recently, the first author speculated the stronger statement that
$F_\ast ^e \mathcal {O}_X$
generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
in exactly
$\dim X$
steps for a toric variety X, provided that e is sufficiently large. The latter was recently confirmed by Favero and Huang [Reference Favero and Huang33], and Hanlon, Hicks, and Jeffs [Reference Hanlon, Hicks and Lazarev40].
Nonsingular curves
Here we focus on nonsingular projective curves, and prove that the only ones which are F-thick are those of genus zero, and in this case,
$F_*^e \mathcal {O}_X$
is a tilting generator; see Theorem 5.10. This is in sharp contrast with the affine case; see Corollary 4.11. First, a bit of terminology.
Fix a nonsingular projective curve X, and let E denote a vector bundle on X of rank r. The slope of E is 
where
$\deg (E)$
is its degree. We say E is semistable (respectively, stable) if for all subbundles of positive rank
$G \subseteq E $
defined over k, one has
$\mu (G)\leq \mu (E)$
(respectively,
$\mu (G) < \mu ( E)$
).
Theorem 5.10. A nonsingular projective curve over an infinite field of prime characteristic is F-thick if and only if its genus is zero.
Proof. The genus zero case is essentially Example 5.3.
Next, suppose that X is an F-thick projective curve, and take
$e>0$
so that
$F_*^e\mathcal {O}_X$
generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
. If X has nonzero genus, then
$F_*^e \mathcal {O}_X$
is semistable by [Reference Sun97, Corollary 4.4], and so [Reference Biswas, Hein and Hoffmann19, Theorem 1] ensures there exists a nontrivial vector bundle E such that
$$\begin{align*}\operatorname{H}^i(X, E\otimes^{\operatorname{L}}_{X} F_*^e \mathcal{O}_X) =0\quad\text{for all } i. \end{align*}$$
Denote by
$E^\vee $
the dual vector bundle of E. From Serre duality, one gets
$$\begin{align*}\operatorname{H}^i(X, E \otimes^{\operatorname{L}}_{X} F_*^e \mathcal{O}_X) = \operatorname{Ext}^i_X(E ^\vee,F_*^e \mathcal{O}_X)=0\,, \end{align*}$$
which is a contradiction for
$E^\vee $
is nontrivial and
$F_*^e \mathcal {O}_X$
generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
. Therefore, the genus of X must be zero.
5.11. A direct sum decomposition of
$F_*^e \mathcal {O}_X$
is known when X is an elliptic curve (that is, the genus of X is one). Namely, if X is ordinary, then
$F_*^e \mathcal {O}_X$
splits into
$p^e$
nonisomorphic
$p^e$
-torsion line bundles; cf. [Reference Ejiri and Sannai31, Theorem 5.5]. On the other hand, when X is supersingular,
$F_*^e \mathcal {O}_X$
is isomorphic to Atiyah’s indecomposable vector bundle
$\mathcal {F}_{p^e}$
of degree zero and rank
$p^e$
; see [Reference Atiyah4].
For smooth projective curves X of genus
$g\geq 2$
, it follows from [Reference Lange and Pauly58, Proposition 1.2] that the vector bundle
$F_*^e \mathcal {O}_X$
is stable and hence indecomposable.
Nonexamples and obstructions
Here is family of nonsingular projective varieties that are not F-thick.
Theorem 5.12. If
$\pi \colon X \to C$
is a nonsingular projective ruled surface with C a nonsingular projective curve with positive genus over an algebraically closed field of prime characteristic, then X is not F-thick.
Proof. Assume the contrary that
$F_*^e \mathcal {O}_X$
is a generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh}{X})$
for some
$e>0$
. We claim that C is F-thick, contradicting Theorem 5.10.
To this end, the base field being algebraically closed allows us to use [Reference Orlov75, Theorem 2.6] to obtain the following semiorthogonal decomposition
$$\begin{align*}{\mathsf{D}}^{\mathsf{b}}(\operatorname{coh}{X}) = \langle \pi^*{\mathsf{D}}^{\mathsf{b}}(\operatorname{coh}{C}), \mathcal{B} \rangle\,. \end{align*}$$
The corresponding projection
$$ \begin{align} {\mathsf{D}}^{\mathsf{b}}(\operatorname{coh}{X}) \to {\mathsf{D}}^{\mathsf{b}}(\operatorname{coh}{C}) \end{align} $$
induces the isomorphism
$\pi _* F_*^e \mathcal {O}_X \cong F_*^e \mathcal {O}_C$
since
$\pi _* \mathcal {O}_X \cong \mathcal {O}_C$
as coherent
$\mathcal {O}_C$
-modules, and all higher derived pushforwards of
$\pi _* \mathcal {O}_X$
vanish. Finally, as (5.12.1) is essentially surjective it follows that
$F_*^e \mathcal {O}_C$
is a generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh}{C})$
, yielding the desired contradiction.
The next result identifies obstructions to the F-thick property.
Proposition 5.13. Let X be a smooth projective variety over an F-finite field. If there exists a nonzero object E in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh}{X})$
such that
$F^{e,*}E$
is acyclic for some positive integer e, then
$F_*^e \mathcal {O}_X$
cannot generate
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh}{X})$
.
Proof. Standard isomorphisms using hom-tensor adjunction, the projection formula and Serre duality yield that
vanish for each
$n\in \mathbb {Z}$
, where d is the dimension of X. From these isomorphisms and the assumption on
$F^{e,*}E$
, we conclude that
$F_*^e \mathcal {O}_X$
does not generate
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
.
Let X be a smooth projective F-thick variety. From Proposition 5.13, it follows that for every E in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
and
$e \gg 0$
, the complex
$F^{e,*} E$
is not acyclic. In particular, we have the following constraint on the cohomology of line bundles.
Corollary 5.14. If X is F-thick, then there is a nonnegative integer n such that
$\operatorname {H}^*(X,L^n) \neq 0$
for any line bundle L.
Proof. Since
$F^{e,*} L = L^{p^e}$
, we can apply Proposition 5.13 along with the displayed isomorphism in the proof of Proposition 5.13.
Corollary 5.15. Abelian varieties over algebraically closed fields of prime characteristic are not F-thick.
Proof. Let X be an abelian variety and pick
$L \in \operatorname {Pic}^0(X)$
that is not p-torsion. As
$\mathcal {O}_X \neq L^{p^e}$
, we have
$\operatorname {H}^*(X,F^{e,*}L) = 0$
, so Corollary 5.14 applies.
Projective complete intersection varieties
All varieties considered in the rest of this section are assumed to be defined over a fixed F-finite field k of characteristic p. For a projective complete intersection variety
$X\subseteq \mathbb {P}_k^n$
of degree d, as is well-known, there is a semiorthogonal decomposition
$$ \begin{align} {\mathsf{D}}^{\mathsf{b}}(\operatorname{coh} X) = \langle \mathcal A_X, \mathcal{O}_X (d-n) ,\ldots,\mathcal{O}_X \rangle\,; \end{align} $$
$\mathcal A_X$
is often referred to as the Kuznetsov component of (5.15.1) due to the connection Kuznetsov [Reference Kuznetsov57] drew between the structure of
$\mathcal A_X$
and the rationality of X. The component was also studied by Orlov [Reference Orlov76, Theorem 2.3] where he related it to the category of graded singularities associated to X. A scheme X is said to be globally F-split if
$\mathcal {O}_X$
is a summand of
$F^e_*\mathcal {O}_X$
.
Theorem 5.16. Let
$X\subseteq \mathbb {P}^n_k$
be a projective complete intersection of degree at most n and such that X is globally F-split. Then X is F-thick if and only if
$F_*^e \mathcal {O}_X$
generates the Kuznetsov component of X for some
$e>0$
.
Contrast this with Theorem 7.3 where we prove
$F_*G$
generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
for some perfect complex G. Theorem 5.16 follows from the following stronger result, describing
$ F_*^e \mathcal {O}_X $
for such X. We thank Devlin Mallory for suggesting this formulation, and for supplying part of the proof.
Theorem 5.17. Let X be as in Theorem 5.16 and let d be its degree. If
$p^e> n-d$
then there is a direct sum decomposition
$$\begin{align*}F_*^e \mathcal{O}_X = M\oplus \bigoplus_{i\in\mathbb{Z}} \mathcal{O}_X(i)^{a_i}\,, \end{align*}$$
where M has no twists of
$\mathcal {O}_X$
as direct summands, and
$$\begin{align*}a_i= \begin{cases} 1 & \text{if } i=0 \\ \ge 1 & \text{if } d-n\le i\le -1\\ 0 &\text{otherwise}. \end{cases} \end{align*}$$
Moreover, no other line bundles show up in the direct sum decomposition of
$F_*^e\mathcal {O}_X$
when
$\dim X\ge 3$
.
5.18. Any X as in Theorem 5.17 is Fano. If X is smooth it is well-known that it is F-split for
$p \gg 0$
. More generally for any rational singularity
$\tilde {X}$
with a model over a finitely generated
$\mathbb {Z}$
-algebra, its reduction mod p is F-split for
$p \gg 0$
; see [Reference Smith90].
We fix the following notation for the rest of the section. Let 
where each
$x_i$
has degree one, and write
$\mathfrak {m}$
for the homogeneous maximal ideal
$(x_0,\ldots ,x_n)$
of S. Fix I a homogeneous ideal of S and set 
.
5.19. Write
$I^{[p^e]}$
for the ideal generated by all
$r^{p^e}$
where
$r\in I$
. The element
$F^e_*r$
of
$F^e_*R$
refers to the elements
$r \in R$
viewed in
$F^e_*R$
. We record a variation on Fedder’s criterion: For a homogeneous element s in S, with image r in R, and for any positive integer e, the inclusion of the cyclic R-submodule of
$F_*^eR$
generated by
$F_*^e (r)$
splits if and only if
$s ( I^{[p^e]}:I) \not \subseteq \mathfrak {m}^{[p^e]}$
. The argument is similar to that in [Reference Fedder34, Proposition 1.7]; see also [Reference Glassbrenner38].
Proposition 5.20. As graded R-modules
$R(-j)$
is a direct summand of
$F_*^e R$
if and only if there exists
$s \in S_{p^ej}$
such that
$$\begin{align*}s (I^{[p^e]} : I) \not\subseteq \mathfrak{m}^{[p^e]}\,. \end{align*}$$
Proof. We consider the
$\frac {1}{p^e}\mathbb {Z}$
-graded structure on
$F^e_*R$
: for a homogeneous
$r \in R$
, the corresponding element in
$F^e_*R$
has degree
$\frac {\text {deg}(r)}{p^e}$
. The direct sum of all
$\mathbb {Z}$
-graded components of
$F_*^e R$
is denoted
$(F_\ast ^e R)_{\mathbb {Z}}$
. It can be shown that a
$\mathbb {Z}$
-graded R-module M is a direct summand of
$(F_\ast ^e R)_{\mathbb {Z}}$
if and only if it is a direct summand of
$F_\ast ^e R$
.
Suppose that
$R(-j)$
is a direct summand of
$(F_*^e R)_{\mathbb {Z}}$
as a
$\mathbb {Z}$
-graded R-module, and let
$\phi \colon R(-j) \to (F_*^e R)_{\mathbb {Z}}$
be a splitting. The element
$r \in R$
where
$F^e_* r = \phi (1)$
has degree
$p^ej$
and from 5.19 any lift s of r satisfies
$s (I^{[p^e]} : I) \not \subseteq \mathfrak {m}^{[p^e]}$
.
Conversely, suppose that there exists an
$s \in S_{p^ej}$
such that
$s (I^{[p^e]} : I) \not \subseteq \mathfrak {m}^{[p^e]}.$
Write r for the image of s in
$R_{p^ej}$
. The element
$F_*^e (r)$
in
$(F_*^e R)_{\mathbb {Z}}$
has degree d, and so the map of R-modules
$R \to (F_*^e R)_{\mathbb {Z}}$
defined by
$1 \mapsto F_*^e (r)$
induces a
$\mathbb {Z}$
-graded R-module map
$\phi \colon R(-j) \to (F_*^e R)_{\mathbb {Z}}$
. The assumption on s, combined with 5.19 ensures that
$\phi $
splits in the category of (ungraded) R-modules. Hence it also splits in the category of graded modules.
Proof of Theorem 5.17
Assume 
. First we verify that
$\mathcal {O}_X(a)$
is a summand of
$F_*^e\mathcal {O}_X$
for each a such that
$d-n\le a\le 0$
; this part of the proof works also when X has degree
$n+1$
. Note
$\mathcal {O}_X(a)$
is a summand of
$F^e_*\mathcal {O}_X$
if and only if
$R(a)$
is an R-module summand of
$F^e_*R$
; see [Reference Smith91, Theorem 3.10]. We produce necessary R-module splittings using Proposition 5.20. Let
$f_1,\ldots , f_t$
be a regular sequence in S that generates I, and defines X in
$\mathbb {P}^n$
. Then
$$\begin{align*}(I^{[q]}: I)= (f^{q-1})+ I^{[q]} \quad \text{where} \,\, f= f_1\cdots f_t \,. \end{align*}$$
Since X, and hence also R, is F-split,
$f^{q-1} \notin m^{[q]}$
; see [Reference Fedder34, section 2], [Reference Smith89, Prop 4.10]. Let g be a nonzero monomial in S such that
$$\begin{align*}g f^{q-1} \notin m^{[q]}\quad \text{but}\quad x_igf^{q-1} \in m^{[q]} \quad\text{for each } i=0,\ldots,n\,. \end{align*}$$
Thus
$(x_0\cdots x_n)^{q-1}$
appears in the homogeneous polynomial
$g f^{q-1}$
, and so its degree is
$(q-1)(n+1)$
. For
$q> n-d$
, one has
$$\begin{align*}(n-d)q \leq \text{deg}(g)= (n+1)(q-1)- d(q-1) \,. \end{align*}$$
Thus for
$j=0,\ldots , n-d$
we can choose a monomial factor
$s_j$
of g of degree
$jq$
with
$s_jf^{q-1} \notin m^{[q]}$
. Then Proposition 5.20 yields that
$\mathcal {O}_X(-j)$
is a summand of
$F^e_*\mathcal {O}_X$
.
We verify, by an induction on t, that
$\oplus _{j=n-d-t}^{n-d} \mathcal {O}_X(-j)$
is a summand of
$F^e_*\mathcal {O}_X$
for
$t \geq 0$
; this holds when
$t=0$
by the argument above. Once we know
$$\begin{align*}F^e_*\mathcal{O}_X \cong E \oplus \bigoplus_{j=n-d-t}^{n-d}\mathcal{O}_X(-j) \,, \end{align*}$$
it follows that
$\mathcal {O}_X(n-d-t-1)$
is a summand of E since the former is a summand of
$F^e_* \mathcal {O}_X$
and does not admit any nonzero map to
$\oplus _{j=n-d-t}^{n-d}\mathcal {O}_X(-j)$
. This completes the proof of the claim about the twists of
$\mathcal {O}_X$
occurring in
$F^e_*\mathcal {O}_X$
.
We now show that
$\mathcal {O}_X(a)$
can appear in the direct sum decomposition of
$F_*^e\mathcal {O}_X$
only if
$d-n\le a\le 0$
and exactly one copy of
$\mathcal {O}_X$
splits. To that end, write
$$\begin{align*}F_*^e \mathcal{O}_X = M\oplus \bigoplus_{i\in\mathbb{Z}} \mathcal{O}_X(i)^{a_i} \end{align*}$$
where M is some coherent sheaf. Since X is F-split,
$\mathcal {O}_X$
is a summand of
$F^e_* \mathcal {O}_X$
. Since
$\operatorname {H}^0(X,\mathcal {O}_X)=\operatorname {H}^0(X,F_*^e \mathcal {O}_X)$
and the global sections on the right side are already accounted for by one
$\mathcal {O}_X$
summand,
$a_0=1$
and
$\mathcal {O}_X(a)$
cannot appear as a direct summand of
$F_*^e \mathcal {O}_X$
for
$a\ge 1$
. As to the other summands, since
$\omega _X$
is invertible one has the first isomorphism below:
$$\begin{align*}\mathcal{H}\kern -1pt o\kern -1 pt m\kern -1pt(F^e_*\omega_X, \mathcal{O}_X) \otimes \omega_X \cong \mathcal{H}\kern -1pt o\kern -1 pt m\kern -1pt(F^e_*\omega_X, \omega_X) \cong F^e_*\mathcal{H}\kern -1pt o\kern -1 pt m\kern -1pt(\omega_X, F^{e, !}\omega_X)\cong F^e_*\mathcal{O}_X \,. \end{align*}$$
The others are standard. So
$\mathcal {O}_X(b)$
appears as a summand of
$F^e_*\mathcal {O}_X$
if and only if
$$\begin{align*}\mathcal{O}_X(-b) \otimes \omega_X \cong \mathcal{O}_X(-b) \otimes \mathcal{O}_X(d-n-1) = \mathcal{O}_X(d-n-1-b) \end{align*}$$
is a summand of
$F^e_*\omega _X$
. Since
$\omega _X$
is anti-ample,
$F^e_*\omega _X$
has no nonzero global sections, whereas
$\mathcal {O}_X(a)$
does whenever
$a\ge 0$
. We conclude that if
$\mathcal {O}_X(b)$
is a summand of
$F^e_* \mathcal {O}_X$
then
$b\ge d-n$
.
It remains to note that when
$\dim X\ge 3$
the Picard group of X is
$\mathbb {Z}\cdot \mathcal {O}_X (1)$
.
6 Numerical invariants
Motivated by the work in Section 4 one can introduce new invariants coming from the derived category to measure singularity types. One such invariant is briefly studied in this section. Throughout R is an F-finite noetherian ring.
Definition 6.1. The Frobenius level (or simply F-level) of R is
Corollary 4.11 implies that this number is finite. A natural question arises: Does
$F_*R$
already generate R? That is to say, is
$F_*R$
proxy-small? See [Reference Dwyer, Greenlees and Iyengar27, Reference Dwyer, Greenlees and Iyengar28] for a discussion on proxy-smallness, and some consequences of this property.
6.2. In the terminology of [Reference Avramov, Buchweitz, Iyengar and Miller7], the level of an R-complex M with respect to an R-complex N, denoted 
, is the infimum of the set of integers n such that M is in 
. Therefore
$F\!\operatorname {-level}(R)$
is the least value of the level of R with respect to
$F_*^eR$
for a positive integer e.
A ring R is F-split if the Frobenius map
$F\colon R\to R$
is split in
$\operatorname {mod} R$
. The Frobenius level is a measure of the failure of F-splitness. This follows from the result below; it is well-known, we sketch a proof for lack of an adequate reference.
Proposition 6.3. For any finite map
$f\colon R\to S$
, with R commutative noetherian, the following conditions are equivalent:
-
(1)
$f\colon R\to S$
is split as R-modules; -
(2)
$f_*S$
has R as a direct summand; -
(3)
$(f_*S)^n$
has R as a direct summand for some
$n\ge 1$
; -
(4)
$\mathsf {level}^{f_*S}(R)\le 1$
.
Proof. Clearly (1)
$\Rightarrow $
(2)
$\Rightarrow $
(3)
$\Rightarrow $
(4). Moreover, (4) means that R is a direct summand of an object of the form
$$\begin{align*}\bigoplus_{n\in \mathbb{Z}} \mathsf{\Sigma}^n (f_*S)^{\oplus s_n}\,; \end{align*}$$
equivalently, R is a direct summand of
$(f_*S)^{\oplus s_0}$
; thus (4)
$\Rightarrow $
(3).
It remains to verify
$(3)\Rightarrow (1)$
. As (1) can be checked locally on
$\operatorname {Spec} R$
, so we can assume R is local. Then (3) implies
$(f_*S)^n$
, and hence also
$f_*S$
is a faithful R-module, and moreover that this remains so under base change. Thus
$R\to S$
is pure; since it is finite, we deduce that it is split; see, for instance, [Reference Matsumura66, Theorem 7.14].
Example 6.4. Let R be an artinian F-finite local ring with residue field k, and let
$\ell \ell (R)$
denote the Loewy length of R. For
$e\ge \log _p\ell \ell (R)$
it is easy to see that
$F_*^eR$
is a nonzero finite k-vectorspace and hence,
see, for example, [Reference Avramov, Buchweitz, Iyengar and Miller7, Theorem 6.2]. Thus
$F\!\operatorname {-level}(R)\le \ell \ell (R)$
.
Here is another family of rings for which we could bound F-levels. The bound is sharp, for the result below and Proposition 6.3, any F-finite non-F-split hypersurface over a field of characteristic two has Frobenius level exactly 2.
Proposition 6.5. If R is an F-finite locally complete intersection ring of prime characteristic p, then
$F\!\operatorname {-level}(R)\le p^{\operatorname {codepth} R}$
.
Proof. By [Reference Letz61, Corollary 3.4],
so we can assume R is a local complete intersection ring. Applying [Reference Letz61, Corollary 2.12], we can further assume R is a quotient of an F-finite regular local ring S by a regular sequence
$f_1,\ldots ,f_c$
. It suffices to show
$F\!\operatorname {-level}(R)$
is at most
$p^c.$
Factor F as
$R\to R'\to R$
where
$R'=S/(f_1^p,\ldots , f_c^p)$
and the first map is base change along the Frobenius of S. Since S is F-finite and regular,
$R'$
is a nonzero finite free R-module. By [Reference Avramov and Miller11, Remark 2], one has a filtration
$$\begin{align*}0=R^{\prime}_{p^c}\subseteq \ldots \subseteq R_1'\subseteq R_0'=R' \end{align*}$$
by
$R'$
-submodules where each subquotient is
$F_*R$
. In particular,
since
$R'$
is free over R.
6.6. It seems interesting to consider the F-level of dualizing complexes. Clearly, there are other invariants that one can introduce to study the singularity type, also in the global context. In future work, we hope to explore the relations between them and properties like finite Frobenius representation type and strong F-regularity.
7 The first Frobenius pushforward
The results from Section 4 also bring up the following question.
Question 7.1. Suppose X is F-finite. Is there a perfect complex G such that
$F_*G$
itself generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
?
We know this is so when X is regular. The main result of this section, Theorem 7.3, generalizes this to locally complete intersections schemes.
Question 7.1 also brings to mind the result below, due to Mathew [Reference Mathew65].
7.2. Let R be a noetherian ring of prime characteristic and
$F $
its Frobenius endomorphism. Assume
$F $
is finite. Since the kernel of
$F $
consists of nilpotent elements, it follows from [Reference Mathew65, Theorem 3.16], see also [Reference Bhatt and Scholze18, Section 11], that for any integer
$e\ge 1$
the R-module
$F ^e_*R$
generates 
as a tensor ideal thick subcategory:
Locally complete intersections
A scheme X is locally complete intersection if it is noetherian and the local ring
$\mathcal {O}_x$
is complete intersection for each
$x\in X$
. This condition means that the completion of
$\mathcal {O}_x$
at its maximal ideal can be presented as a regular ring modulo a regular sequence; see [Reference Bruns and Herzog24, Section 2.3] for details.
Theorem 7.3. When X is F-finite and locally complete intersection, for any perfect complex G that generates
$\mathsf {Perf}\,X$
, the complex
$F_*G$
is a generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
. In particular, if X is affine,
$F_*\mathcal {O}_X$
is a strong generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
.
The proof uses the theory of cohomological support varieties for complete intersection local rings. The results we need are recalled below; see [Reference Avramov5] and [Reference Avramov and Buchweitz6].
7.4. Let R be a local complete intersection ring of codimension c, and residue field k. For each M in
$ {\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} R)$
, one can associate a Zariski closed cone
$\operatorname {V}_R(M)$
in the homogeneous spectrum
$\operatorname {Spec}^* \mathcal {S}$
where
$\mathcal {S}$
is the symmetric algebra on the graded k-space
$\mathsf {\Sigma }^{-2}k^c$
; see [Reference Avramov5]. This is the ring of cohomology operators of Gulliksen [Reference Gulliksen39] and Eisenbud [Reference Eisenbud30]. The (Krull) dimension of
$\operatorname {V}_R(M)$
is the complexity of M:
$$\begin{align*}\operatorname{cx}_R(M)=\inf\{d\in \mathbb{N}: \operatorname{rank}_k \operatorname{Ext}_R^n(M,k)\le a n^{d-1}\text{ for some } a>0\ \mathrm{and\ all}\ n\}\,. \end{align*}$$
The relevance of these varieties to the problem at hand is because of [Reference Liu and Pollitz62, Theorem 3.1]: If R is locally complete intersection and
$M,N$
are in
$ {\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} R)$
, then
Theorem 7.3 follows from the result below with
$G=\mathcal {O}_X$
, and Lemma 4.8.
Theorem 7.5. Let X be an
$F $
-finite noetherian scheme. If X is locally complete intersection, each G in
${\mathsf {D}}^{\mathsf {b}}(\operatorname {coh} X)$
with
$\operatorname {supp}_X G= X$
satisfies
as a
$\mathsf {Perf}\,X$
-module.
Proof. Fix
$x\in X$
, set 
and 
. Given Corollary 2.10, it suffices to verify the R-complex
$F _*M$
generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} R)$
.
Let N be in
$ {\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} R)$
and
$\mathfrak {p}\in \operatorname {Spec} R$
. By [Reference Avramov, Iyengar and Miller9, Theorem 12.2.4],
$$\begin{align*}\operatorname{cx}_{R_{\mathfrak{p}}}(F _*(M_{\mathfrak{p}}))=\operatorname{cx}_{R_{\mathfrak{p}}}(k(\mathfrak{p})) =\mathrm{codim} R_{\mathfrak{p}}\,. \end{align*}$$
In particular,
$\operatorname {V}_{R_{\mathfrak {p}}}(N_{\mathfrak {p}})\subseteq \operatorname {V}_{R_{\mathfrak {p}}}(F _*(M_{\mathfrak {p}}))$
. Since
$(F _*M)_{\mathfrak {p}}$
is isomorphic to
$F _*(M_{\mathfrak {p}})$
we obtain that
$$\begin{align*}\operatorname{V}_{R_{\mathfrak{p}}}(N_{\mathfrak{p}})\subseteq \operatorname{V}_{R_{\mathfrak{p}}}((F _*M)_{\mathfrak{p}})\,. \end{align*}$$
As the previous equality holds for each
$\mathfrak {p}\in \operatorname {Spec} R$
we can apply 7.4 to conclude that N is in 
.
The next result produces examples of rings R which are not locally complete intersection, yet
$F _*R$
generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} R)$
.
Veronese subrings
Let k be an
$F $
-finite field of prime characteristic and let 
, the polynomial ring in indeterminates
$x_1,\dots ,x_d$
, each having degree one. The observation below is applied when R is a Veronese subring of S.
Lemma 7.6. Let
$\iota \colon R\to S$
be a finite extension that is split as a map of R-modules. Then 
.
Proof. It suffices to show that any finitely generated R-module M is in 
. Since S is regular,
$S \otimes _R M$
is in 
and hence in 
by restriction of scalars along
$\iota $
. Since
$\iota $
is split, M is an R-module summand of
$S \otimes _RM $
. Thus M is finitely built from
$\iota _* S$
in 
.
The minimal graded free resolution of the S-module
$S/(x_1, \ldots , x_d)^j$
has the form:
The resolution is linear after the first term. The integers
$b_i(j)$
are given by
$$\begin{align*}b_i(j) = \begin{cases} 1 & i=0\\ \frac{(j+d-1)!}{(j-1)!(d-i)!(i-1)!(j+i-1)} & i \leq d \\ 0 & i\ge d+1\,. \end{cases} \end{align*}$$
See, for instance, [Reference Buchsbaum and Eisenbud25]. Fix an integer
$\ell \ge 1$
. For each integer j, let
$G_j$
denote the k-vector space spanned by all monomials in S whose total degree is congruent to j modulo
$\ell $
. Note that each
$G_j$
is a finitely generated R-module. Taking strands of (7.6.1) yields exact sequences of R-modules
$$ \begin{align} 0 \rightarrow G_{\ell-d+1}^{\oplus b_d(j)} \rightarrow \cdots G_{l-1}^{\oplus b_2(j)}\rightarrow R^{\oplus b_1(j)} \rightarrow G_j \rightarrow 0 \end{align} $$
for
$1 \leq j \leq \ell -1$
.
Lemma 7.7. Let R be the
$\ell $
-th Veronese subring of
$k[x,y]$
. For each integer
$1\le j\le \ell -1$
the following equality holds
Proof. Given Lemma 7.6 and the isomorphism
$S \cong G_0\oplus \ldots \oplus G_{\ell -1}$
of R-modules, it suffices to verify that each
$G_i$
is in 
for
$0\le i\le \ell -1$
. This becomes clear by applying (7.6.2) with
$d=2$
.
Proposition 7.8. Let k be an
$F $
-finite field. If R is the
$\ell $
-th Veronese subring of
$k[x,y]$
, for some
$\ell \ge 1$
, then
$F _*R$
is a strong generator for
${\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} R)$
.
Proof. By Lemma 7.7 it suffices to verify that 
contains R and at least one
$G_j$
where
$1 \leq j \leq \ell -1$
. The first containment is satisfied as the Frobenius map
$R \rightarrow F _*R$
splits as an R-module, as R is a direct summand of a regular ring.
To show some
$G_j$
is in 
, we import results from the theory of conic modules over a toric ring; see, for example, [Reference Bruns and Gubeladze23, Reference Faber, Muller and Smith32]. Namely, the module
$F _*R$
is isomorphic to a direct sum of conic modules; see [Reference Faber, Muller and Smith32, Proposition 4.15] and [Reference Bruns22, Theorem 3.1]. On the other hand, any conic R-module is isomorphic to some
$G_i$
by [Reference Faber, Muller and Smith32, Remark 7.6]. Therefore since
$G_0\cong R$
and R is not regular,
$F _*R$
must have a summand isomorphic to
$G_j$
for some
$1\leq j\leq \ell -1.$
7.9. Let
$S= k[x,y]$
and R be the
$\ell $
-th Veronese subring of S. For
$\ell \geq 3$
, the ring R is not a complete intersection ring. Moreover, if
$\ell>p^2[k:k^p]$
, then
$F _*R$
cannot have S as a free R-module summand; indeed, the rank of S and
$F _*R$
as R-modules are
$\ell $
and
$p^2[k:k^p]$
respectively, cf. Lemma 7.6.
We end with a few observations regarding Question 7.1.
7.10. By the local-to-global principle from [Reference Letz61, Corollary 3.4], to settle Question 7.1 in the affine setting, it suffices to check that when R is local
$F_*R$
generates the residue field of R. When R is also Cohen-Macaulay, one can reduce to R artinian.
Suppose R is an artinian local ring. Question 7.1 has a positive answer when k is a direct summand of
$F _*R$
. This property holds if and only if the maximal ideal
$\mathfrak {m}$
of R satisfies
$(0:\mathfrak {m}^{[p]})\not \subseteq \mathfrak {m}^{[p]}$
. For example, if
$R=\mathbb {F}_2[x,y]/(x^4,x^2y^2,y^4)$
it is not immediately clear whether
$F _*R$
generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} R)$
since k is not a summand of
$F_*R$
; in this example,
$$\begin{align*}F _*R\cong (R/(x^2,xy,y^2))^{\oplus 3}\,. \end{align*}$$
However a direct analysis shows that even for this ring
$F_*R$
generates
${\mathsf {D}}^{\mathsf {b}}(\operatorname {mod} R).$
Acknowledgements
Iyengar thanks Greg Stevenson for conversations on Section 2. Mukhopadhyay thanks the University of Utah mathematics department for hospitality during formative stages of the work. The authors thank Devlin Mallory and Eamon Quinlan-Gallego for comments on the material in Section 5 and Section 6, respectively, and Roman Bezrukavnikov for pointing us to [Reference Bezrukavnikov, Mirković and Rumynin17]. Finally, we are grateful to the anonymous referees for their helpful comments and suggestions.
Competing interests
The authors have no competing interest to declare.
Financial support
This material is based on work supported by Simons Foundation: Collaboration Grant for Mathematicians #708132 (Ballard) and Grant #586594 (Lank) and work supported by the National Science Foundation under Grants No. DMS-1840190 (Pollitz), DMS-FRG-1952399, DMS-2101075 (Mukhopadhyay), DMS-2001368 (Iyengar), DMS-2002173 (Pollitz), DMS-2302567 (Pollitz), DMS-2302263 (Ballard). This was also funded by ERC Advanced Grant 101095900-TriCatApp (Lank). Part of it was done at the Hausdorff Research Institute for Mathematics, Bonn, when Iyengar and Pollitz were at the “Spectral Methods in Algebra, Geometry, and Topology” trimester, funded by the Deutsche Forschungsgemeinschaft under Germany’s Excellence Strategy–EXC-2047/1–390685813. Additionally, Ballard, Iyengar, and Lank were supported by the National Science Foundation under Grant No. DMS-1928930 while the authors were in residence at the Simons Laufer Mathematical Sciences Institute (formerly MSRI).
Open access
