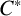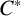1 Introduction
Inspired by and building on a series of papers by many different authors (see, for example, [Reference Bhowmick, Neshveyev and Sangha4, Reference Kasprzak22, Reference Kasprzak23, Reference Neshveyev and Tuset26, Reference Rieffel33, Reference Rieffel34]) on deformation of
![]() $C^*$
-algebras via actions and coactions of locally compact groups with deformation parameters given by
$C^*$
-algebras via actions and coactions of locally compact groups with deformation parameters given by
![]() $2$
-cocycles of these groups, we gave in [Reference Buss and Echterhoff7] a new description of such deformation by Borel cocycles of locally compact groups that works in a quite general setting.
$2$
-cocycles of these groups, we gave in [Reference Buss and Echterhoff7] a new description of such deformation by Borel cocycles of locally compact groups that works in a quite general setting.
Let us recall the basic ideas of this deformation procedure. Suppose that
![]() $\delta :A\to \mathcal M(A\otimes C^*(G))$
is a coaction of the locally compact group G on the
$\delta :A\to \mathcal M(A\otimes C^*(G))$
is a coaction of the locally compact group G on the
![]() $C^*$
-algebra A. Then the coaction crossed product
$C^*$
-algebra A. Then the coaction crossed product
![]() $B:=A\rtimes _{\delta }\widehat {G}$
is equipped with the dual action
$B:=A\rtimes _{\delta }\widehat {G}$
is equipped with the dual action
![]() $\beta :=\widehat {\delta }:G\curvearrowright B$
and a canonical nondegenerate
$\beta :=\widehat {\delta }:G\curvearrowright B$
and a canonical nondegenerate
![]() $\mathrm {rt}-\beta $
-equivariant inclusion
$\mathrm {rt}-\beta $
-equivariant inclusion
![]() $\phi :=j_{C_0(G)}:C_0(G)\to \mathcal M(B)$
, where
$\phi :=j_{C_0(G)}:C_0(G)\to \mathcal M(B)$
, where
![]() $\mathrm {rt}\colon G\curvearrowright C_0(G)$
denotes the action by right translations. The triple
$\mathrm {rt}\colon G\curvearrowright C_0(G)$
denotes the action by right translations. The triple
![]() $(B, \beta ,\phi )$
then provides a set of data that allows one to reconstruct the original cosystem
$(B, \beta ,\phi )$
then provides a set of data that allows one to reconstruct the original cosystem
![]() $(A,\delta )$
via an (exotic) version of Landstad duality. Now, if we deform the triple
$(A,\delta )$
via an (exotic) version of Landstad duality. Now, if we deform the triple
![]() $(B, \beta ,\phi )$
by certain parameters
$(B, \beta ,\phi )$
by certain parameters
![]() ${p}$
to a new Landstad triple
${p}$
to a new Landstad triple
![]() $(B_{{p}},\beta _{{p}},\theta _{{p}})$
, then applying Landstad duality to
$(B_{{p}},\beta _{{p}},\theta _{{p}})$
, then applying Landstad duality to
![]() $(B_{{p}},\beta _{{p}},\theta _{{p}})$
provides a deformed cosystem
$(B_{{p}},\beta _{{p}},\theta _{{p}})$
provides a deformed cosystem
![]() $(A^{{p}}, \delta ^{{p}})$
. The deformation parameters p can be certain group actions
$(A^{{p}}, \delta ^{{p}})$
. The deformation parameters p can be certain group actions
![]() $\alpha : G\curvearrowright A$
by
$\alpha : G\curvearrowright A$
by
![]() $^*$
-automorphisms, or Borel
$^*$
-automorphisms, or Borel
![]() $2$
-cocycles
$2$
-cocycles
![]() $\omega $
of G, or, related to the latter, central extensions
$\omega $
of G, or, related to the latter, central extensions
![]() $\sigma =(\mathbb T\hookrightarrow G_\sigma \twoheadrightarrow ~G)$
of G by the circle group
$\sigma =(\mathbb T\hookrightarrow G_\sigma \twoheadrightarrow ~G)$
of G by the circle group
![]() $\mathbb T$
. If we restrict ourselves to normal (or reduced) coactions, that is, those, for which the composition
$\mathbb T$
. If we restrict ourselves to normal (or reduced) coactions, that is, those, for which the composition
is faithful, a similar procedure has been given before by Bhowmick, Neshveyev and Sangha in [Reference Bhowmick, Neshveyev and Sangha4], using cocycles
![]() $\omega \in Z^2(G,\mathbb T)$
as deformation parameters. In that paper they also observed that for G discrete, deformation by
$\omega \in Z^2(G,\mathbb T)$
as deformation parameters. In that paper they also observed that for G discrete, deformation by
![]() $\omega $
can also be obtained via deformation of the underlying Fell bundle as studied by Yamashita in [Reference Yamashita36]. Recall from [Reference Ng27, Reference Quigg31] that for every normal coaction
$\omega $
can also be obtained via deformation of the underlying Fell bundle as studied by Yamashita in [Reference Yamashita36]. Recall from [Reference Ng27, Reference Quigg31] that for every normal coaction
![]() $\delta :A\to A\otimes C^*(G)$
of a discrete group G, there exists a unique Fell bundle
$\delta :A\to A\otimes C^*(G)$
of a discrete group G, there exists a unique Fell bundle
![]() $p:\mathcal A\to G$
such that the given coaction identifies with the dual coaction
$p:\mathcal A\to G$
such that the given coaction identifies with the dual coaction
![]() $\delta :C_r^*(\mathcal A)\to C_r^*(\mathcal A)\otimes C^*(G)$
on the reduced cross-sectional algebra
$\delta :C_r^*(\mathcal A)\to C_r^*(\mathcal A)\otimes C^*(G)$
on the reduced cross-sectional algebra
![]() $A:=C_r^*(\mathcal A)$
. Then, given any cocycle
$A:=C_r^*(\mathcal A)$
. Then, given any cocycle
![]() $\omega \in Z^2(G,\mathbb T)$
, the deformed Fell bundle
$\omega \in Z^2(G,\mathbb T)$
, the deformed Fell bundle
![]() ${\mathcal A}_\omega $
is constructed by introducing a twisted multiplication
${\mathcal A}_\omega $
is constructed by introducing a twisted multiplication
![]() $*_\omega $
on the original Fell bundle
$*_\omega $
on the original Fell bundle
![]() $\mathcal A$
via the formula
$\mathcal A$
via the formula
for
![]() $g,h\in G$
,
$g,h\in G$
,
![]() $a_g\in A_g$
,
$a_g\in A_g$
,
![]() $a_h\in A_h$
, where
$a_h\in A_h$
, where
![]() $a_ga_h$
denotes the product in
$a_ga_h$
denotes the product in
![]() $\mathcal A$
. Then the deformed coaction
$\mathcal A$
. Then the deformed coaction
![]() $(A^\omega ,\delta ^\omega )$
can be described as the dual coaction
$(A^\omega ,\delta ^\omega )$
can be described as the dual coaction
![]() $(C_r^*({\mathcal A}_\omega ), \delta _\omega )$
on the deformed Fell bundle
$(C_r^*({\mathcal A}_\omega ), \delta _\omega )$
on the deformed Fell bundle
![]() ${\mathcal A}_\omega $
.
${\mathcal A}_\omega $
.
If G is locally compact and
![]() $\omega \in Z^2(G,\mathbb T)$
is a continuous cocycle, then a similar deformation of a Fell bundle
$\omega \in Z^2(G,\mathbb T)$
is a continuous cocycle, then a similar deformation of a Fell bundle
![]() $\mathcal A$
over G makes perfect sense, and it is not too difficult to see that passing to reduced cross-sectional algebras in this setting will coincide with the deformation by
$\mathcal A$
over G makes perfect sense, and it is not too difficult to see that passing to reduced cross-sectional algebras in this setting will coincide with the deformation by
![]() $\omega $
of
$\omega $
of
![]() $A=C_r^*(\mathcal A)$
via the dual coaction
$A=C_r^*(\mathcal A)$
via the dual coaction
![]() $\delta : A\to \mathcal M(A\otimes C^*(G))$
in the sense of [Reference Bhowmick, Neshveyev and Sangha4] or [Reference Buss and Echterhoff7].
$\delta : A\to \mathcal M(A\otimes C^*(G))$
in the sense of [Reference Bhowmick, Neshveyev and Sangha4] or [Reference Buss and Echterhoff7].
The main objective of this paper is to describe a direct deformation procedure on the level of Fell bundles for groups of automorphisms
![]() $\alpha \colon G\curvearrowright \mathcal A$
, following an approach to deformation given by Abadie and Exel in [Reference Abadie and Exel1], and for twists
$\alpha \colon G\curvearrowright \mathcal A$
, following an approach to deformation given by Abadie and Exel in [Reference Abadie and Exel1], and for twists
![]() $\sigma =(\mathbb T\hookrightarrow G_\sigma \twoheadrightarrow G)$
for G, which then covers also the case of general Borel
$\sigma =(\mathbb T\hookrightarrow G_\sigma \twoheadrightarrow G)$
for G, which then covers also the case of general Borel
![]() $2$
-cocycles on G, and to compare the outcome with the deformation via dual coactions as studied for general duality crossed-product functors in [Reference Buss and Echterhoff7] (like, for instance, the dual coaction on the maximal cross-sectional algebra
$2$
-cocycles on G, and to compare the outcome with the deformation via dual coactions as studied for general duality crossed-product functors in [Reference Buss and Echterhoff7] (like, for instance, the dual coaction on the maximal cross-sectional algebra
![]() $C_{\mathrm \max }^*(\mathcal A)$
of the Fell bundle
$C_{\mathrm \max }^*(\mathcal A)$
of the Fell bundle
![]() $\mathcal A$
). This will provide a convenient direct deformation process in this situation. We then use continuity and K-theory results obtained in [Reference Buss and Echterhoff7] in the setting of deformation via coactions for the cross-sectional algebras of our deformed Fell bundles. In the special case of Fell bundles over discrete amenable groups G, we recover a beautiful result of Raeburn in [Reference Raeburn32], where he constructed a continuous bundle of deformed cross-sectional algebras
$\mathcal A$
). This will provide a convenient direct deformation process in this situation. We then use continuity and K-theory results obtained in [Reference Buss and Echterhoff7] in the setting of deformation via coactions for the cross-sectional algebras of our deformed Fell bundles. In the special case of Fell bundles over discrete amenable groups G, we recover a beautiful result of Raeburn in [Reference Raeburn32], where he constructed a continuous bundle of deformed cross-sectional algebras
![]() $C^*({\mathcal A}_\omega )$
over the second Borel cohomology group
$C^*({\mathcal A}_\omega )$
over the second Borel cohomology group
![]() $H^2(G,\mathbb T)$
.
$H^2(G,\mathbb T)$
.
2 Actions, coactions and their (exotic) crossed products
For terminology and notation concerning (co)actions, their (exotic) crossed products, and duality – particularly Landstad duality for coactions in terms of generalized fixed-point algebras – we refer the reader to our previous paper [Reference Buss and Echterhoff7].
Let us just recall some basic notation and terminology. Throughout the paper, G will usually denote a locally compact group, with a fixed Haar measure. Continuous actions of G on a
![]() $C^*$
-algebra B will usually be written as
$C^*$
-algebra B will usually be written as
![]() $\beta \colon G\curvearrowright B$
.
$\beta \colon G\curvearrowright B$
.
In what follows, by an (exotic) crossed product
![]() $B\rtimes _{\beta ,\mu }G$
for an action
$B\rtimes _{\beta ,\mu }G$
for an action
![]() $\beta :G\curvearrowright B$
we understand a
$\beta :G\curvearrowright B$
we understand a
![]() $C^*$
-completion of
$C^*$
-completion of
![]() $C_c(G,B)$
by a norm that satisfies
$C_c(G,B)$
by a norm that satisfies
![]() $\|f\|_r\leq \|f\|_\mu \leq \|f\|_{\mathrm \max }$
for all
$\|f\|_r\leq \|f\|_\mu \leq \|f\|_{\mathrm \max }$
for all
![]() $f\in C_c(G,B)$
, where the
$f\in C_c(G,B)$
, where the
![]() $\|\cdot \|_r$
(respectively,
$\|\cdot \|_r$
(respectively,
![]() $\|\cdot \|_{\mathrm \max }$
) denote the reduced (respectively, maximal) crossed-product norms on
$\|\cdot \|_{\mathrm \max }$
) denote the reduced (respectively, maximal) crossed-product norms on
![]() $C_c(G,B)$
. A crossed product
$C_c(G,B)$
. A crossed product
![]() $B\rtimes _{\beta ,\mu }G$
is called a duality crossed product if the dual coaction
$B\rtimes _{\beta ,\mu }G$
is called a duality crossed product if the dual coaction
![]() $\widehat {\beta }$
on
$\widehat {\beta }$
on
![]() $B\rtimes _{\beta ,\mathrm \max }G$
factors through a coaction
$B\rtimes _{\beta ,\mathrm \max }G$
factors through a coaction
![]() $\widehat {\beta }_\mu $
on
$\widehat {\beta }_\mu $
on
![]() $B\rtimes _{\beta ,\mu }G$
. A crossed-product functor is a functor
$B\rtimes _{\beta ,\mu }G$
. A crossed-product functor is a functor
![]() $(B,\beta )\mapsto B\rtimes _{\beta ,\mu }G$
from the category of G-algebras to the category of
$(B,\beta )\mapsto B\rtimes _{\beta ,\mu }G$
from the category of G-algebras to the category of
![]() $C^*$
-algebras that sends actions
$C^*$
-algebras that sends actions
![]() $\beta :G\curvearrowright B$
to crossed products
$\beta :G\curvearrowright B$
to crossed products
![]() $B\rtimes _{\beta ,\mu }G$
such that for any G-equivariant
$B\rtimes _{\beta ,\mu }G$
such that for any G-equivariant
![]() $^*$
-homomorphism
$^*$
-homomorphism
![]() $\Phi :(B,\beta )\to (B',\beta ')$
the associated
$\Phi :(B,\beta )\to (B',\beta ')$
the associated
![]() $^*$
-homomorphism
$^*$
-homomorphism
![]() $\Phi \rtimes _\mu G:B\rtimes _{\beta ,\mu }G\to B'\rtimes _{\beta ',\mu }G$
extends
$\Phi \rtimes _\mu G:B\rtimes _{\beta ,\mu }G\to B'\rtimes _{\beta ',\mu }G$
extends
![]() $\Phi \rtimes _{\mathrm {alg}}G: C_c(G,B)\to C_c(G,B'); f\mapsto \Phi \circ f$
. If all
$\Phi \rtimes _{\mathrm {alg}}G: C_c(G,B)\to C_c(G,B'); f\mapsto \Phi \circ f$
. If all
![]() $\rtimes _\mu $
-crossed products are duality crossed products, then
$\rtimes _\mu $
-crossed products are duality crossed products, then
![]() $\rtimes _\mu $
is called a duality crossed-product functor, which are the crossed-product functors we consider in this work. However, in Section 8 below, we need to restrict our attention to crossed-product functors that are also functorial with respect to (G-equivariant) correspondences. These are called correspondence crossed-product functors and include the maximal and reduced crossed products. It is shown in [Reference Buss, Echterhoff and Willett8, Theorem 5.6] that all correspondence crossed-product functors are duality functors.
$\rtimes _\mu $
is called a duality crossed-product functor, which are the crossed-product functors we consider in this work. However, in Section 8 below, we need to restrict our attention to crossed-product functors that are also functorial with respect to (G-equivariant) correspondences. These are called correspondence crossed-product functors and include the maximal and reduced crossed products. It is shown in [Reference Buss, Echterhoff and Willett8, Theorem 5.6] that all correspondence crossed-product functors are duality functors.
A coaction of G on a
![]() $C^*$
-algebra A will usually be denoted by the symbol
$C^*$
-algebra A will usually be denoted by the symbol
![]() $\delta \colon A\to \mathcal M(A\otimes C^*(G))$
and its crossed product will be denoted by
$\delta \colon A\to \mathcal M(A\otimes C^*(G))$
and its crossed product will be denoted by
![]() $A\rtimes _\delta \widehat {G}$
. Recall that
$A\rtimes _\delta \widehat {G}$
. Recall that
![]() $A\rtimes _\delta \widehat {G}$
can be realized as
$A\rtimes _\delta \widehat {G}$
can be realized as
where
![]() $M:C_0(G)\to \mathbb {B}(L^2(G))$
is the representation by multiplication operators. We often write
$M:C_0(G)\to \mathbb {B}(L^2(G))$
is the representation by multiplication operators. We often write
for the canonical morphisms from A and
![]() $C_0(G)$
into
$C_0(G)$
into
![]() $\mathcal M(A\rtimes _\delta \widehat {G})$
. The dual action
$\mathcal M(A\rtimes _\delta \widehat {G})$
. The dual action
![]() $\widehat {\delta }:G\curvearrowright A\rtimes _{\delta }\widehat {G}$
is then determined by the equation
$\widehat {\delta }:G\curvearrowright A\rtimes _{\delta }\widehat {G}$
is then determined by the equation
where
![]() $\mathrm {rt}:G\curvearrowright C_0(G)$
denotes the action by right translations.
$\mathrm {rt}:G\curvearrowright C_0(G)$
denotes the action by right translations.
It has been observed by Nilsen in [Reference Nilsen28, Corollary 2.6] that for every coaction
![]() $\delta :A\to \mathcal M(A\otimes C^*(G))$
there exists a canonical surjective
$\delta :A\to \mathcal M(A\otimes C^*(G))$
there exists a canonical surjective
![]() $^*$
-homomorphism
$^*$
-homomorphism
given as the integrated form of the covariant representation
![]() $(j_A\rtimes j_{C_0(G)}, 1\otimes \rho )$
. The coaction
$(j_A\rtimes j_{C_0(G)}, 1\otimes \rho )$
. The coaction
![]() $\delta $
is called maximal if
$\delta $
is called maximal if
![]() $\Psi _A$
is an isomorphism, and it is called normal if it factors through an isomorphism
$\Psi _A$
is an isomorphism, and it is called normal if it factors through an isomorphism
![]() $ A\rtimes _\delta \widehat {G}\rtimes _{\widehat \delta ,r}G\xrightarrow \sim A\otimes \mathbb K(L^2(G))$
. In general, it factors through an isomorphism
$ A\rtimes _\delta \widehat {G}\rtimes _{\widehat \delta ,r}G\xrightarrow \sim A\otimes \mathbb K(L^2(G))$
. In general, it factors through an isomorphism
for some (possibly exotic) duality crossed product
![]() $\rtimes _\mu $
. We then say that
$\rtimes _\mu $
. We then say that
![]() $(A,\delta )$
is a
$(A,\delta )$
is a
![]() $\mu $
-coaction to indicate that it satisfies Katayama duality for the
$\mu $
-coaction to indicate that it satisfies Katayama duality for the
![]() $\mu $
-crossed product.
$\mu $
-crossed product.
The triple
![]() $(A\rtimes _\delta \widehat {G},\widehat {\delta }, j_{C_0(G)})$
is what we call a weak
$(A\rtimes _\delta \widehat {G},\widehat {\delta }, j_{C_0(G)})$
is what we call a weak
![]() $G\rtimes G$
-algebra. More generally, a weak
$G\rtimes G$
-algebra. More generally, a weak
![]() $G\rtimes G$
-algebra is a triple
$G\rtimes G$
-algebra is a triple
![]() $(B, \beta , \phi )$
where:
$(B, \beta , \phi )$
where:
-
• B is a
 $C^*$
-algebra,
$C^*$
-algebra, -
•
 $\beta :G\curvearrowright B$
is an action of G on B,
$\beta :G\curvearrowright B$
is an action of G on B, -
•
 $\phi :C_0(G)\to \mathcal M(B)$
is a nondegenerate,
$\phi :C_0(G)\to \mathcal M(B)$
is a nondegenerate,
 $\mathrm {rt}-\beta $
-equivariant
$\mathrm {rt}-\beta $
-equivariant
 $*$
-homomorphism.
$*$
-homomorphism.
As a variant of the classical Landstad duality for reduced coactions [Reference Quigg30], it is shown in [Reference Buss and Echterhoff5] that for any given duality crossed product
![]() $B\rtimes _{\beta ,\mu }G$
, there exists a unique (up to isomorphism)
$B\rtimes _{\beta ,\mu }G$
, there exists a unique (up to isomorphism)
![]() $\mu $
-coaction
$\mu $
-coaction
![]() $(A_\mu , \delta _\mu )$
of G such that
$(A_\mu , \delta _\mu )$
of G such that
This provides the main tool for deformation by coactions, as introduced in [Reference Buss and Echterhoff7], which serves as the foundation for most of the results presented in this paper. The construction of
![]() $(A_\mu , \delta _\mu )$
is carried out using the theory of generalized fixed-point algebras and depends on the choice of the crossed product
$(A_\mu , \delta _\mu )$
is carried out using the theory of generalized fixed-point algebras and depends on the choice of the crossed product
![]() $B\rtimes _{\beta ,\mu }G$
. Moreover, if we start with a duality crossed-product functor
$B\rtimes _{\beta ,\mu }G$
. Moreover, if we start with a duality crossed-product functor
![]() $\rtimes _\mu $
on the category of G-
$\rtimes _\mu $
on the category of G-
![]() $C^*$
-algebras, it is shown in [Reference Buss and Echterhoff7, Proposition 2.9] (see also [Reference Buss and Echterhoff5, Lemma 7.1]) that the assignment
$C^*$
-algebras, it is shown in [Reference Buss and Echterhoff7, Proposition 2.9] (see also [Reference Buss and Echterhoff5, Lemma 7.1]) that the assignment
is functorial. More precisely, given weak
![]() $G\rtimes G$
-algebras
$G\rtimes G$
-algebras
![]() $(B,\beta ,\phi )$
and
$(B,\beta ,\phi )$
and
![]() $(B',\beta ',\phi ')$
, if
$(B',\beta ',\phi ')$
, if
![]() $\Psi :B\to B'$
is a
$\Psi :B\to B'$
is a
![]() $\beta -\beta '$
-equivariant
$\beta -\beta '$
-equivariant
![]() $*$
-homomorphism satisfying
$*$
-homomorphism satisfying
![]() $\Psi \circ \phi =\phi '$
, then
$\Psi \circ \phi =\phi '$
, then
![]() $\Psi $
induces a canonical
$\Psi $
induces a canonical
![]() $\delta _\mu -\delta ^{\prime }_\mu $
-equivariant
$\delta _\mu -\delta ^{\prime }_\mu $
-equivariant
![]() $*$
-homomorphism
$*$
-homomorphism
between the corresponding
![]() $\mu $
-fixed-point algebras. In particular, we obtain the following result.
$\mu $
-fixed-point algebras. In particular, we obtain the following result.
Proposition 2.1. Suppose that
![]() $(B,\beta ,\phi )$
and
$(B,\beta ,\phi )$
and
![]() $(B',\beta ',\phi ')$
are isomorphic weak
$(B',\beta ',\phi ')$
are isomorphic weak
![]() $G\rtimes G$
-algebras, and let
$G\rtimes G$
-algebras, and let
![]() $\rtimes _\mu $
be a duality crossed-product functor. Then the corresponding
$\rtimes _\mu $
be a duality crossed-product functor. Then the corresponding
![]() $\mu $
-coactions
$\mu $
-coactions
![]() $(A_\mu , \delta _\mu )$
and
$(A_\mu , \delta _\mu )$
and
![]() $(A^{\prime }_\mu ,\delta ^{\prime }_\mu )$
via Landstad duality are also isomorphic.
$(A^{\prime }_\mu ,\delta ^{\prime }_\mu )$
via Landstad duality are also isomorphic.
The above proposition will serve as our main tool for comparing different deformation procedures in this work.
3 Fell bundles
Recall from [Reference Doran and Fell12, Reference Doran and Fell13] that a Fell bundle
![]() $\mathcal A$
over the locally compact group G is a collection of Banach spaces
$\mathcal A$
over the locally compact group G is a collection of Banach spaces
![]() $\{A_s: s\in G\}$
together with a set of pairings (called multiplications)
$\{A_s: s\in G\}$
together with a set of pairings (called multiplications)
![]() $A_s\times A_t\to A_{st}: (a_s, a_t)\mapsto a_sa:t$
and involutions
$A_s\times A_t\to A_{st}: (a_s, a_t)\mapsto a_sa:t$
and involutions
![]() $A_s\to A_{s^{-1}}; a_s\mapsto a_s^*$
that are compatible with the linear structures in the usual sense known from
$A_s\to A_{s^{-1}}; a_s\mapsto a_s^*$
that are compatible with the linear structures in the usual sense known from
![]() $C^*$
-algebras, including the condition
$C^*$
-algebras, including the condition
![]() $\|a_sa:s^*\|=\|a_s\|^2$
for all
$\|a_sa:s^*\|=\|a_s\|^2$
for all
![]() $a_s\in A_s$
. In particular, it follows that the fibre
$a_s\in A_s$
. In particular, it follows that the fibre
![]() $A_e$
over the unit
$A_e$
over the unit
![]() $e\in G$
is a
$e\in G$
is a
![]() $C^*$
-algebra. If G is not discrete, the topological structure of
$C^*$
-algebra. If G is not discrete, the topological structure of
![]() $\mathcal A$
is determined by the set
$\mathcal A$
is determined by the set
![]() $C_c(\mathcal A)$
of compactly supported continuous sections
$C_c(\mathcal A)$
of compactly supported continuous sections
![]() $a: G\to \mathcal A$
,
$a: G\to \mathcal A$
,
![]() $s\mapsto a_s\in A_s$
. We refer to [Reference Doran and Fell12, Reference Doran and Fell13, Reference Exel15] for more details on this structure. The space
$s\mapsto a_s\in A_s$
. We refer to [Reference Doran and Fell12, Reference Doran and Fell13, Reference Exel15] for more details on this structure. The space
![]() $C_c(\mathcal A)$
becomes a
$C_c(\mathcal A)$
becomes a
![]() $^*$
-algebra when equipped with convolution and involution given by
$^*$
-algebra when equipped with convolution and involution given by
 $$ \begin{align*} (a*b)_t=\int_G a_sb:{s^{-1}t}\,\,d s\quad\text{and}\quad a^*_t=\Delta(t^{-1})a_{t^{-1}}^*, \quad a,b\in C_c(\mathcal A).\end{align*} $$
$$ \begin{align*} (a*b)_t=\int_G a_sb:{s^{-1}t}\,\,d s\quad\text{and}\quad a^*_t=\Delta(t^{-1})a_{t^{-1}}^*, \quad a,b\in C_c(\mathcal A).\end{align*} $$
A representation of
![]() $\mathcal A$
into
$\mathcal A$
into
![]() $\mathcal M(D)$
for some
$\mathcal M(D)$
for some
![]() $C^*$
-algebra D is a mapping
$C^*$
-algebra D is a mapping
![]() ${\pi :\mathcal A\to \mathcal M(D)}$
that preserves multiplication and involution, and such that for every
${\pi :\mathcal A\to \mathcal M(D)}$
that preserves multiplication and involution, and such that for every
![]() $d\in D$
and every
$d\in D$
and every
![]() $a\in C_c(\mathcal A)$
the map
$a\in C_c(\mathcal A)$
the map
![]() $G\to D; s\mapsto \pi (a_s)d$
is continuous. Such representation is nondegenerate if
$G\to D; s\mapsto \pi (a_s)d$
is continuous. Such representation is nondegenerate if
![]() $\pi (A_e)D=D$
, that is, the restriction of
$\pi (A_e)D=D$
, that is, the restriction of
![]() $\pi $
to the unit fibre
$\pi $
to the unit fibre
![]() $A_e$
of
$A_e$
of
![]() $\mathcal A$
is a nondegenerate representation of the
$\mathcal A$
is a nondegenerate representation of the
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $A_e$
. Every representation
$A_e$
. Every representation
![]() ${\pi :\mathcal A\to \mathcal M(D)}$
integrates to give a
${\pi :\mathcal A\to \mathcal M(D)}$
integrates to give a
![]() $^*$
-representation
$^*$
-representation
 $$ \begin{align*}\pi:C_c(\mathcal A)\to \mathcal M(D);\quad \pi(a)d:=\int_G \pi(a_s)d\, \,d s \quad\text{for all } a\in C_c(\mathcal A), d\in D,\end{align*} $$
$$ \begin{align*}\pi:C_c(\mathcal A)\to \mathcal M(D);\quad \pi(a)d:=\int_G \pi(a_s)d\, \,d s \quad\text{for all } a\in C_c(\mathcal A), d\in D,\end{align*} $$
which is nondegenerate (in the sense that
![]() $\overline {\operatorname {span}}\, \pi (C_c(\mathcal A))D=D$
) if and only if
$\overline {\operatorname {span}}\, \pi (C_c(\mathcal A))D=D$
) if and only if
![]() $\pi $
is nondegenerate. The maximal (or universal) cross-sectional
$\pi $
is nondegenerate. The maximal (or universal) cross-sectional
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $C^*(\mathcal A)$
is then defined as the completion of
$C^*(\mathcal A)$
is then defined as the completion of
![]() $C_c(\mathcal A)$
with respect to the
$C_c(\mathcal A)$
with respect to the
![]() $C^*$
-norm
$C^*$
-norm
where
![]() $\pi $
runs through all possible (nondegenerate) representations of
$\pi $
runs through all possible (nondegenerate) representations of
![]() $\mathcal A$
. Passing to the integrated form and extension to the completion
$\mathcal A$
. Passing to the integrated form and extension to the completion
![]() $C^*(\mathcal A)$
of
$C^*(\mathcal A)$
of
![]() $C_c(\mathcal A)$
then gives a one-to-one correspondence between nondegenerate representations of
$C_c(\mathcal A)$
then gives a one-to-one correspondence between nondegenerate representations of
![]() $\mathcal A$
and nondegenerate
$\mathcal A$
and nondegenerate
![]() $^*$
-representations of
$^*$
-representations of
![]() $C^*(\mathcal A)$
. We refer to [Reference Buss and Echterhoff6, Proposition 2.1] for a list of alternative characterizations of the representations of
$C^*(\mathcal A)$
. We refer to [Reference Buss and Echterhoff6, Proposition 2.1] for a list of alternative characterizations of the representations of
![]() $\mathcal A$
.
$\mathcal A$
.
At the other extreme we have the reduced cross-sectional
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $C_r^*(\mathcal A)$
, which can be described as the image of
$C_r^*(\mathcal A)$
, which can be described as the image of
![]() $C^*(\mathcal A)$
under the (left) regular representation
$C^*(\mathcal A)$
under the (left) regular representation
![]() $\Lambda _{\mathcal A}:C^{*}(\mathcal A)\to {\mathbb B}_{A_e}(L^2(\mathcal A))$
, with
$\Lambda _{\mathcal A}:C^{*}(\mathcal A)\to {\mathbb B}_{A_e}(L^2(\mathcal A))$
, with
![]() $\Lambda _{\mathcal A}(a)\xi =a^{*}\xi $
for
$\Lambda _{\mathcal A}(a)\xi =a^{*}\xi $
for
![]() $a\in {C_c}(\mathcal A)\subseteq C^{*}(\mathcal A)$
and
$a\in {C_c}(\mathcal A)\subseteq C^{*}(\mathcal A)$
and
![]() $\xi \in {C_c}(\mathcal A)\subseteq L^2(\mathcal A)$
, where
$\xi \in {C_c}(\mathcal A)\subseteq L^2(\mathcal A)$
, where
![]() $L^2(\mathcal A)$
denotes the Hilbert
$L^2(\mathcal A)$
denotes the Hilbert
![]() $A_e$
-module obtained as a completion of
$A_e$
-module obtained as a completion of
![]() $C_c(\mathcal A)$
by the
$C_c(\mathcal A)$
by the
![]() $A_e$
-valued inner product
$A_e$
-valued inner product
 $$ \begin{align*}\langle \xi, \eta\rangle_{A_e}=\int_G \xi(s)^{*} \eta(s)\,\,d s.\end{align*} $$
$$ \begin{align*}\langle \xi, \eta\rangle_{A_e}=\int_G \xi(s)^{*} \eta(s)\,\,d s.\end{align*} $$
There exists a dual coaction
given by the integrated form of the representation
![]() $s\mapsto a_s\otimes u_s$
, where, as above,
$s\mapsto a_s\otimes u_s$
, where, as above,
![]() $u:G\to U\mathcal M(C^*(G))$
denotes the universal representation of G and each
$u:G\to U\mathcal M(C^*(G))$
denotes the universal representation of G and each
![]() $a_s\in A_s$
acts as a multiplier of
$a_s\in A_s$
acts as a multiplier of
![]() $C^*(\mathcal A)$
by
$C^*(\mathcal A)$
by
![]() $(a_s\cdot f)(t):=a_sf(s^{-1}t)$
. It has been shown in [Reference Buss and Echterhoff6, Theorem 3.1] that
$(a_s\cdot f)(t):=a_sf(s^{-1}t)$
. It has been shown in [Reference Buss and Echterhoff6, Theorem 3.1] that
![]() $\delta _{\mathcal A}$
is a maximal coaction, that is, it satisfies Katayama duality (2-1) with respect to the maximal crossed product
$\delta _{\mathcal A}$
is a maximal coaction, that is, it satisfies Katayama duality (2-1) with respect to the maximal crossed product
![]() $\rtimes _{\mathrm \max }$
.
$\rtimes _{\mathrm \max }$
.
Now, similar to [Reference Buss and Echterhoff6, Definition 4.1], given any duality crossed-product functor
![]() $\rtimes _\mu $
, there is a unique quotient
$\rtimes _\mu $
, there is a unique quotient
![]() $C_\mu ^*(\mathcal A)$
of
$C_\mu ^*(\mathcal A)$
of
![]() $C^*(\mathcal A)$
such that
$C^*(\mathcal A)$
such that
![]() $\delta _{\mathcal A}$
factors through a coaction
$\delta _{\mathcal A}$
factors through a coaction
and such that
![]() $(C_\mu ^*(\mathcal A),\delta _\mu )$
satisfies Katayama duality for the
$(C_\mu ^*(\mathcal A),\delta _\mu )$
satisfies Katayama duality for the
![]() $\mu $
-crossed product as in (2-1). In particular, the dual coaction
$\mu $
-crossed product as in (2-1). In particular, the dual coaction
![]() $(C_r^*(\mathcal A), \delta _r)$
on the reduced cross-sectional algebra
$(C_r^*(\mathcal A), \delta _r)$
on the reduced cross-sectional algebra
![]() $C_r^*(\mathcal A)$
corresponds to the reduced crossed-product functor
$C_r^*(\mathcal A)$
corresponds to the reduced crossed-product functor
![]() $\rtimes _r$
in this way. It is the normalization of
$\rtimes _r$
in this way. It is the normalization of
![]() $(C^*(\mathcal A), \delta _{\mathcal A})$
in the sense of Quigg (see, for example, [Reference Buss and Echterhoff6]). We also have
$(C^*(\mathcal A), \delta _{\mathcal A})$
in the sense of Quigg (see, for example, [Reference Buss and Echterhoff6]). We also have
![]() $(C^*_{\mathrm \max }(\mathcal A),\delta _{\mathrm \max })=(C^*(\mathcal A),\delta _{\mathcal A})$
. In particular,
$(C^*_{\mathrm \max }(\mathcal A),\delta _{\mathrm \max })=(C^*(\mathcal A),\delta _{\mathcal A})$
. In particular,
![]() $C_\mu ^*(\mathcal A)$
is an ‘exotic’ completion of the cross-sectional
$C_\mu ^*(\mathcal A)$
is an ‘exotic’ completion of the cross-sectional
![]() $^*$
-algebra
$^*$
-algebra
![]() $C_c(\mathcal A)$
that sits between
$C_c(\mathcal A)$
that sits between
![]() $C^*(\mathcal A)$
and
$C^*(\mathcal A)$
and
![]() $C^*_r(\mathcal A)$
in the sense that the identity map on
$C^*_r(\mathcal A)$
in the sense that the identity map on
![]() $C_c(\mathcal A)$
extends to surjective
$C_c(\mathcal A)$
extends to surjective
![]() $^*$
-homomorphisms
$^*$
-homomorphisms
Combining this with [Reference Buss and Echterhoff5, Theorem 4.3] we obtain the following proposition.
Proposition 3.1. The coaction
![]() $(C_\mu ^*(\mathcal A),\delta _\mu )$
coincides with the coaction provided by applying
$(C_\mu ^*(\mathcal A),\delta _\mu )$
coincides with the coaction provided by applying
![]() $\mu $
-Landstad duality to the weak
$\mu $
-Landstad duality to the weak
![]() $G\rtimes G$
-algebra
$G\rtimes G$
-algebra
![]() $(C^*(\mathcal A)\rtimes _{\delta _{\mathcal A}}\widehat {G}, \widehat {\delta _{\mathcal A}}, j_{C_0(G)})$
.
$(C^*(\mathcal A)\rtimes _{\delta _{\mathcal A}}\widehat {G}, \widehat {\delta _{\mathcal A}}, j_{C_0(G)})$
.
3.1 The C*-algebra of kernels of a Fell bundle
We need to recall the realization of
![]() $C_r^*(\mathcal A)\rtimes _{\delta _r} \widehat {G}$
(and hence also of
$C_r^*(\mathcal A)\rtimes _{\delta _r} \widehat {G}$
(and hence also of
![]() $C_\mu ^*(\mathcal A)\rtimes _{\delta _\mu }\widehat {G}$
) as a completion of a certain
$C_\mu ^*(\mathcal A)\rtimes _{\delta _\mu }\widehat {G}$
) as a completion of a certain
![]() $^*$
-algebra of kernel functions
$^*$
-algebra of kernel functions
![]() $k:G\times G\to \mathcal A$
due to Abadie (see [Reference Abadie3, Section 5]). For this let
$k:G\times G\to \mathcal A$
due to Abadie (see [Reference Abadie3, Section 5]). For this let
In other words,
![]() $\Bbbk _c({\mathcal A})=C_c(\nu ^*(\mathcal A))$
, the space of compactly supported continuous sections of the pullback
$\Bbbk _c({\mathcal A})=C_c(\nu ^*(\mathcal A))$
, the space of compactly supported continuous sections of the pullback
![]() $\nu ^*(\mathcal A)$
of
$\nu ^*(\mathcal A)$
of
![]() $\mathcal A$
along
$\mathcal A$
along
![]() $\nu \colon G\times G\to G,\, (s,t)\mapsto st^{-1}$
. This is a
$\nu \colon G\times G\to G,\, (s,t)\mapsto st^{-1}$
. This is a
![]() $^*$
-algebra with convolution and involution given by
$^*$
-algebra with convolution and involution given by
 $$ \begin{align*} k*l(s,t)=\int_G k(s,r)l(r,t)\,d r\quad\text{and}\quad k^*(s,t)=k(t,s)^* \end{align*} $$
$$ \begin{align*} k*l(s,t)=\int_G k(s,r)l(r,t)\,d r\quad\text{and}\quad k^*(s,t)=k(t,s)^* \end{align*} $$
for all
![]() $k,l\in \Bbbk _c({\mathcal A})$
and
$k,l\in \Bbbk _c({\mathcal A})$
and
![]() $s,t\in G$
. By a continuous
$s,t\in G$
. By a continuous
![]() $^*$
-representation of
$^*$
-representation of
![]() $\Bbbk _c({\mathcal A})$
we understand a
$\Bbbk _c({\mathcal A})$
we understand a
![]() $^*$
-homomorphism
$^*$
-homomorphism
![]() $\pi : \Bbbk _c({\mathcal A})\to D$
for some
$\pi : \Bbbk _c({\mathcal A})\to D$
for some
![]() $C^*$
-algebra D such that
$C^*$
-algebra D such that
 $$ \begin{align*}\|\pi(k)\|\leq \|k\|_2:=\bigg(\int_{G\times G} \|k(s,t)\|^2\,\,d(s,t)\bigg)^{1/2}\end{align*} $$
$$ \begin{align*}\|\pi(k)\|\leq \|k\|_2:=\bigg(\int_{G\times G} \|k(s,t)\|^2\,\,d(s,t)\bigg)^{1/2}\end{align*} $$
for all
![]() $k\in \Bbbk _c({\mathcal A})$
. Let
$k\in \Bbbk _c({\mathcal A})$
. Let
![]() $\|k\|_u:=\sup _{\pi }\|\pi (k)\|$
, where
$\|k\|_u:=\sup _{\pi }\|\pi (k)\|$
, where
![]() $\pi $
runs through all continuous
$\pi $
runs through all continuous
![]() $^*$
-representations of
$^*$
-representations of
![]() $\Bbbk _c({\mathcal A})$
. Then the completion
$\Bbbk _c({\mathcal A})$
. Then the completion
![]() $\Bbbk ({\mathcal A})$
of
$\Bbbk ({\mathcal A})$
of
![]() $\Bbbk _c({\mathcal A})$
by this norm is a
$\Bbbk _c({\mathcal A})$
by this norm is a
![]() $C^*$
-algebra; this was introduced by Abadie in [Reference Abadie3]. As noticed there,
$C^*$
-algebra; this was introduced by Abadie in [Reference Abadie3]. As noticed there,
![]() $\Bbbk ({\mathcal A})$
can also be viewed as the enveloping
$\Bbbk ({\mathcal A})$
can also be viewed as the enveloping
![]() $C^*$
-algebra of the Banach
$C^*$
-algebra of the Banach
![]() $^*$
-algebra obtained as the completion of
$^*$
-algebra obtained as the completion of
![]() $\Bbbk _c({\mathcal A})$
with respect to
$\Bbbk _c({\mathcal A})$
with respect to
![]() $\|\cdot \|_2$
. We write
$\|\cdot \|_2$
. We write
![]() $\Bbbk _2 ({\mathcal A})$
for this
$\Bbbk _2 ({\mathcal A})$
for this
![]() $L^2$
-completion and note that it coincides with the
$L^2$
-completion and note that it coincides with the
![]() $L^2$
-completion of the space
$L^2$
-completion of the space
![]() $\Bbbk _{c,b} ({\mathcal A})$
of all bounded compactly supported measurable functions
$\Bbbk _{c,b} ({\mathcal A})$
of all bounded compactly supported measurable functions
![]() $k\colon G\times G\to \mathcal A$
that satisfy the condition
$k\colon G\times G\to \mathcal A$
that satisfy the condition
![]() $k(s,t)\in A_{st^{-1}}$
. The following result is due to Abadie [Reference Abadie3].
$k(s,t)\in A_{st^{-1}}$
. The following result is due to Abadie [Reference Abadie3].
Proposition 3.2. For every duality crossed-product functor
![]() $\rtimes _\mu $
, there is a canonical isomorphism
$\rtimes _\mu $
, there is a canonical isomorphism
![]() $C_\mu ^*(\mathcal A)\rtimes _{\delta _\mu }\widehat {G}\cong \Bbbk ({\mathcal A})$
that sends a typical element of the form
$C_\mu ^*(\mathcal A)\rtimes _{\delta _\mu }\widehat {G}\cong \Bbbk ({\mathcal A})$
that sends a typical element of the form
![]() $j_{C^*_\mu (\mathcal A)}(a) j_{C_0(G)}(f)$
with
$j_{C^*_\mu (\mathcal A)}(a) j_{C_0(G)}(f)$
with
![]() $a\in C_c(\mathcal A)$
and
$a\in C_c(\mathcal A)$
and
![]() $f\in C_c(G)$
to the kernel function
$f\in C_c(G)$
to the kernel function
Viewing
![]() $\Bbbk _c({\mathcal A})$
as a dense subalgebra of
$\Bbbk _c({\mathcal A})$
as a dense subalgebra of
![]() $C_\mu ^*(\mathcal A)\rtimes _{\delta _\mu }\widehat {G}$
using this isomorphism, the dual action
$C_\mu ^*(\mathcal A)\rtimes _{\delta _\mu }\widehat {G}$
using this isomorphism, the dual action
![]() $\widehat {\delta }_\mu $
of G is given on
$\widehat {\delta }_\mu $
of G is given on
![]() $\Bbbk _c({\mathcal A})$
by the formula
$\Bbbk _c({\mathcal A})$
by the formula
Moreover, we have
for all
![]() $k\in \Bbbk _c({\mathcal A})$
and
$k\in \Bbbk _c({\mathcal A})$
and
![]() $f\in C_0(G)$
.
$f\in C_0(G)$
.
Proof. Abadie only considers reduced coactions, that is, injective coactions of the reduced group
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $C^*_r(G)$
. It is well known that such coactions correspond bijectively (in a naturally functorial way) to normal coactions of
$C^*_r(G)$
. It is well known that such coactions correspond bijectively (in a naturally functorial way) to normal coactions of
![]() $C^*(G)$
in our sense (see, for example, [Reference Echterhoff, Kaliszewski, Quigg and Raeburn14, Appendix A.9]). Moreover, this bijective correspondence preserves crossed products and their representation theory. That said, what Abadie proves in [Reference Abadie3] is that there is an isomorphism
$C^*(G)$
in our sense (see, for example, [Reference Echterhoff, Kaliszewski, Quigg and Raeburn14, Appendix A.9]). Moreover, this bijective correspondence preserves crossed products and their representation theory. That said, what Abadie proves in [Reference Abadie3] is that there is an isomorphism
![]() $C^*_r(\mathcal A)\rtimes _{\delta _r}\widehat {G}\cong \Bbbk ({\mathcal A})$
that is given as in the statement (see the proof of Proposition 8.1 in [Reference Abadie3]). But this implies the general version as in the statement for every exotic
$C^*_r(\mathcal A)\rtimes _{\delta _r}\widehat {G}\cong \Bbbk ({\mathcal A})$
that is given as in the statement (see the proof of Proposition 8.1 in [Reference Abadie3]). But this implies the general version as in the statement for every exotic
![]() $C^*$
-norm associated to a duality crossed-product functor
$C^*$
-norm associated to a duality crossed-product functor
![]() $\rtimes _\mu $
by [Reference Buss and Echterhoff7, Theorem 2.4].
$\rtimes _\mu $
by [Reference Buss and Echterhoff7, Theorem 2.4].
The following result describes the representations of
![]() $\Bbbk ({\mathcal A})$
.
$\Bbbk ({\mathcal A})$
.
Proposition 3.3. Let D be a
![]() $C^*$
-algebra. A pair
$C^*$
-algebra. A pair
![]() $(\pi ,\kappa )\colon (C^*(\mathcal A),C_0(G))\to \mathcal M(D)$
of nondegenerate representations is covariant for a dual coaction
$(\pi ,\kappa )\colon (C^*(\mathcal A),C_0(G))\to \mathcal M(D)$
of nondegenerate representations is covariant for a dual coaction
![]() $\delta _{\mathcal A}$
of G on the cross-sectional
$\delta _{\mathcal A}$
of G on the cross-sectional
![]() $C^*$
-algebra of a Fell bundle
$C^*$
-algebra of a Fell bundle
![]() $\mathcal A$
, and hence extends to a nondegenerate representation
$\mathcal A$
, and hence extends to a nondegenerate representation
![]() $\pi \rtimes \kappa \colon C^*(\mathcal A)\rtimes _{\delta _{\mathcal A}}\widehat {G}\cong \Bbbk ({\mathcal A})\to \mathcal M(D)$
if and only if
$\pi \rtimes \kappa \colon C^*(\mathcal A)\rtimes _{\delta _{\mathcal A}}\widehat {G}\cong \Bbbk ({\mathcal A})\to \mathcal M(D)$
if and only if
where
![]() $_s f(t):=f(st)$
denotes left translation, and we use the same notation
$_s f(t):=f(st)$
denotes left translation, and we use the same notation
![]() $\pi \colon \mathcal A\to \mathcal M(D)$
for the disintegrated form of
$\pi \colon \mathcal A\to \mathcal M(D)$
for the disintegrated form of
![]() $\pi \colon C^*(\mathcal A)\to \mathcal M(D)$
.
$\pi \colon C^*(\mathcal A)\to \mathcal M(D)$
.
Proof. By definition,
![]() $(\pi ,\kappa )$
is covariant if and only if
$(\pi ,\kappa )$
is covariant if and only if
for all
![]() $a\in C^*(\mathcal A)$
, where
$a\in C^*(\mathcal A)$
, where
![]() $w_\kappa :=(\kappa \otimes \operatorname {{\mathrm {id}}})(w_G)$
and
$w_\kappa :=(\kappa \otimes \operatorname {{\mathrm {id}}})(w_G)$
and
![]() $w_G\in \mathcal M(C_0(G)\otimes C^*(G))$
is given by the universal representation
$w_G\in \mathcal M(C_0(G)\otimes C^*(G))$
is given by the universal representation
![]() $s\mapsto u_s$
. Since
$s\mapsto u_s$
. Since
![]() $\pi $
is nondegenerate, it extends to the multiplier algebra
$\pi $
is nondegenerate, it extends to the multiplier algebra
![]() $\mathcal M(C^*(\mathcal A))$
. Using the inclusion
$\mathcal M(C^*(\mathcal A))$
. Using the inclusion
![]() $A_s\hookrightarrow \mathcal M(C^*(\mathcal A))$
given by
$A_s\hookrightarrow \mathcal M(C^*(\mathcal A))$
given by
![]() $(a_s\cdot \xi )(t)=a_s\xi (s^{-1}t)$
, for
$(a_s\cdot \xi )(t)=a_s\xi (s^{-1}t)$
, for
![]() $a_s\in A_s$
,
$a_s\in A_s$
,
![]() $\xi \in C_c(\mathcal A)$
, and the formula
$\xi \in C_c(\mathcal A)$
, and the formula
![]() $\delta _{\mathcal A}(a_s)=a_s\otimes u_s$
, the covariance condition for
$\delta _{\mathcal A}(a_s)=a_s\otimes u_s$
, the covariance condition for
![]() $(\pi ,\kappa )$
is equivalent to
$(\pi ,\kappa )$
is equivalent to
Now we remark that if we view the Fourier algebra
![]() $A(G)\subseteq C_0(G)$
as a subalgebra of
$A(G)\subseteq C_0(G)$
as a subalgebra of
![]() $B(G)\cong C^*(G)'$
, the set of continuous linear functionals on
$B(G)\cong C^*(G)'$
, the set of continuous linear functionals on
![]() $C^*(G)$
, then
$C^*(G)$
, then
![]() $\kappa (f)=(\operatorname {{\mathrm {id}}}\otimes f)(w_\kappa )$
for all
$\kappa (f)=(\operatorname {{\mathrm {id}}}\otimes f)(w_\kappa )$
for all
![]() $f\in A(G)$
. Taking slices with
$f\in A(G)$
. Taking slices with
![]() $f\in A(G)$
, we see that the covariance condition is equivalent to
$f\in A(G)$
, we see that the covariance condition is equivalent to
But
 $$ \begin{align*} (\operatorname{{\mathrm{id}}}\otimes f)((1\otimes u_s)w_\kappa)&=(\kappa\otimes f)((1\otimes u_s)w_G)\\ &=(\kappa\otimes \operatorname{{\mathrm{id}}})(\operatorname{{\mathrm{id}}}\otimes f)((1\otimes u_s)w_G)=\kappa(f\cdot u_s), \end{align*} $$
$$ \begin{align*} (\operatorname{{\mathrm{id}}}\otimes f)((1\otimes u_s)w_\kappa)&=(\kappa\otimes f)((1\otimes u_s)w_G)\\ &=(\kappa\otimes \operatorname{{\mathrm{id}}})(\operatorname{{\mathrm{id}}}\otimes f)((1\otimes u_s)w_G)=\kappa(f\cdot u_s), \end{align*} $$
where
![]() $(f\cdot u_s)(x):=f(u_sx)$
for all
$(f\cdot u_s)(x):=f(u_sx)$
for all
![]() $x\in C^*(G)$
. Viewed as a function on G, this gives
$x\in C^*(G)$
. Viewed as a function on G, this gives
![]() $f\cdot u_s={_s}f$
. Therefore, the covariance condition is equivalent to
$f\cdot u_s={_s}f$
. Therefore, the covariance condition is equivalent to
Since
![]() $A(G)$
is dense in
$A(G)$
is dense in
![]() $C_0(G)$
, this is equivalent to (3-3).
$C_0(G)$
, this is equivalent to (3-3).
It was shown by Abadie [Reference Abadie3] that there exists a well-defined
![]() $^*$
-representation
$^*$
-representation
![]() $\Lambda _{\Bbbk ({\mathcal A})}:\Bbbk ({\mathcal A})\to {\mathbb B}_{A_e}(L^2(\mathcal A))$
, called the regular representation of
$\Lambda _{\Bbbk ({\mathcal A})}:\Bbbk ({\mathcal A})\to {\mathbb B}_{A_e}(L^2(\mathcal A))$
, called the regular representation of
![]() $\Bbbk ({\mathcal A})$
, given by
$\Bbbk ({\mathcal A})$
, given by
 $$ \begin{align*} (\Lambda_{\Bbbk ({\mathcal A})}(k)\xi)(t)=\int_G k(s,t)\xi(t)\,\,d t \quad\text{for }k\in \Bbbk_c({\mathcal A}),\xi\in C_c(\mathcal A).\end{align*} $$
$$ \begin{align*} (\Lambda_{\Bbbk ({\mathcal A})}(k)\xi)(t)=\int_G k(s,t)\xi(t)\,\,d t \quad\text{for }k\in \Bbbk_c({\mathcal A}),\xi\in C_c(\mathcal A).\end{align*} $$
It is stated in [Reference Abadie3, Theorem 5.1(2)] that
![]() $\Lambda _{\Bbbk ({\mathcal A})}$
is always faithful. But, unfortunately, this is not true in general (although it is true in several important cases, for example, if
$\Lambda _{\Bbbk ({\mathcal A})}$
is always faithful. But, unfortunately, this is not true in general (although it is true in several important cases, for example, if
![]() $\mathcal A$
is saturated). One can find more information about this in the arXiv version of the paper [Reference Abadie3] available at https://arxiv.org/pdf/math/0007109.pdf, where the incorrect statements have been fixed. As a counterexample let
$\mathcal A$
is saturated). One can find more information about this in the arXiv version of the paper [Reference Abadie3] available at https://arxiv.org/pdf/math/0007109.pdf, where the incorrect statements have been fixed. As a counterexample let
![]() $\mathcal A$
be the Fell bundle over
$\mathcal A$
be the Fell bundle over
![]() $\mathbb Z_2$
with fibres
$\mathbb Z_2$
with fibres
![]() ${\mathcal A}_0=\mathbb C$
and
${\mathcal A}_0=\mathbb C$
and
![]() ${\mathcal A}_1=0$
. Then
${\mathcal A}_1=0$
. Then
![]() $\Bbbk ({\mathcal A})=\mathbb C\oplus \mathbb C$
, while
$\Bbbk ({\mathcal A})=\mathbb C\oplus \mathbb C$
, while
![]() $L^2(\mathcal A)=\mathbb C$
.
$L^2(\mathcal A)=\mathbb C$
.
We now provide a different representation of
![]() $\Bbbk ({\mathcal A})$
that will be faithful in general. For this we use the fact that
$\Bbbk ({\mathcal A})$
that will be faithful in general. For this we use the fact that
![]() $\Bbbk ({\mathcal A})$
is isomorphic to the crossed product
$\Bbbk ({\mathcal A})$
is isomorphic to the crossed product
![]() $C^*(\mathcal A)\rtimes _{\delta _{\mathcal A}}\widehat {G}$
. Let
$C^*(\mathcal A)\rtimes _{\delta _{\mathcal A}}\widehat {G}$
. Let
denote the reduction of the dual coaction
![]() $\delta _{\mathcal A}$
of G on
$\delta _{\mathcal A}$
of G on
![]() $C^*(\mathcal A)$
(which factors through a genuine reduced coaction of
$C^*(\mathcal A)$
(which factors through a genuine reduced coaction of
![]() $C_r^*(G)$
on
$C_r^*(G)$
on
![]() $C_r^*(\mathcal A)$
). The algebra
$C_r^*(\mathcal A)$
). The algebra
![]() $\mathcal M(C_r^*(\mathcal A)\otimes C^*_r(G))$
is clearly represented faithfully on
$\mathcal M(C_r^*(\mathcal A)\otimes C^*_r(G))$
is clearly represented faithfully on
![]() $L^2(\mathcal A)\otimes L^2(G)$
via
$L^2(\mathcal A)\otimes L^2(G)$
via
![]() $\Lambda _{\mathcal A}\otimes \lambda $
. Now
$\Lambda _{\mathcal A}\otimes \lambda $
. Now
![]() $L^2(\mathcal A)\otimes L^2(G)$
can be identified with
$L^2(\mathcal A)\otimes L^2(G)$
can be identified with
![]() $L^2(\mathcal A\times G)$
if
$L^2(\mathcal A\times G)$
if
![]() $\mathcal A\times G$
denotes the Fell bundle over
$\mathcal A\times G$
denotes the Fell bundle over
![]() $G\times G$
given by the pullback of
$G\times G$
given by the pullback of
![]() $\mathcal A$
via the projection
$\mathcal A$
via the projection
![]() $G\times G\to G;(g,h)\mapsto g$
, so in what follows we regard
$G\times G\to G;(g,h)\mapsto g$
, so in what follows we regard
![]() $\Lambda _{\mathcal A}\otimes \lambda $
as a representation of
$\Lambda _{\mathcal A}\otimes \lambda $
as a representation of
![]() $\mathcal M(C_r^*(\mathcal A)\otimes C_r^*(G))$
into
$\mathcal M(C_r^*(\mathcal A)\otimes C_r^*(G))$
into
![]() $\mathbb B_{A_e}(L^2(\mathcal A\times G))$
. Then a short computation on the fibres
$\mathbb B_{A_e}(L^2(\mathcal A\times G))$
. Then a short computation on the fibres
![]() $A_s\subseteq \mathcal A$
shows (see [Reference Exel and Ng16, Lemma 2.9 and Proposition 2.10]) that
$A_s\subseteq \mathcal A$
shows (see [Reference Exel and Ng16, Lemma 2.9 and Proposition 2.10]) that
where
![]() $W_{\mathcal A}\in \mathbb B_{A_e}(L^2(\mathcal A\times G))$
is the unitary operator defined by
$W_{\mathcal A}\in \mathbb B_{A_e}(L^2(\mathcal A\times G))$
is the unitary operator defined by
Now recall that the crossed product
![]() $C^*(\mathcal A)\rtimes _{\delta _{\mathcal A}}\widehat {G}\cong C_r^*(\mathcal A)\rtimes _{\delta _r}\widehat {G}$
can be realized as
$C^*(\mathcal A)\rtimes _{\delta _{\mathcal A}}\widehat {G}\cong C_r^*(\mathcal A)\rtimes _{\delta _r}\widehat {G}$
can be realized as
A simple computation shows that
for all
![]() $f\in C_0(G)$
and
$f\in C_0(G)$
and
![]() $\zeta \in C_c(\mathcal A\times G)\subseteq L^2(\mathcal A\times G)$
. It follows that
$\zeta \in C_c(\mathcal A\times G)\subseteq L^2(\mathcal A\times G)$
. It follows that
Hence, conjugation by the unitary
![]() $W_{\mathcal A}$
yields an isomorphism
$W_{\mathcal A}$
yields an isomorphism
On the other hand, the operators
![]() $(\Lambda (a)\otimes 1)\tilde M_f$
can be computed as
$(\Lambda (a)\otimes 1)\tilde M_f$
can be computed as
 $$ \begin{align*} ((\Lambda(a)\otimes 1)\tilde M_f\zeta)(s,t)&=\int_G a(r)(\tilde M_f\zeta)(r^{-1}s,t)\,d r=\int_G a(r)f(r^{-1}st)\zeta(r^{-1}s,t)\,d r\\ &=\int_G a(sr^{-1})f(rt)\Delta(r)^{-1}\zeta(r,t)\,d r=\int_G \beta_t(k_{a,f})(s,r)\zeta(r,t)\,d r, \end{align*} $$
$$ \begin{align*} ((\Lambda(a)\otimes 1)\tilde M_f\zeta)(s,t)&=\int_G a(r)(\tilde M_f\zeta)(r^{-1}s,t)\,d r=\int_G a(r)f(r^{-1}st)\zeta(r^{-1}s,t)\,d r\\ &=\int_G a(sr^{-1})f(rt)\Delta(r)^{-1}\zeta(r,t)\,d r=\int_G \beta_t(k_{a,f})(s,r)\zeta(r,t)\,d r, \end{align*} $$
where
![]() $k_{a,f}(s,r):=a(sr^{-1})f(r)\Delta (r^{-1})$
as in (3-1), and
$k_{a,f}(s,r):=a(sr^{-1})f(r)\Delta (r^{-1})$
as in (3-1), and
![]() $\beta $
denotes the dual action of G on
$\beta $
denotes the dual action of G on
![]() $\Bbbk ({\mathcal A})$
as in Proposition 3.2. Using the isomorphism
$\Bbbk ({\mathcal A})$
as in Proposition 3.2. Using the isomorphism
![]() $\Bbbk ({\mathcal A})\cong C^*(\mathcal A)\rtimes _{\delta _{\mathcal A}}\widehat {G}$
provided by this proposition, we obtain the following proposition.
$\Bbbk ({\mathcal A})\cong C^*(\mathcal A)\rtimes _{\delta _{\mathcal A}}\widehat {G}$
provided by this proposition, we obtain the following proposition.
Proposition 3.4. Given a Fell bundle
![]() $\mathcal A$
over G, there exists a faithful representation
$\mathcal A$
over G, there exists a faithful representation
given on
![]() $\Bbbk _c({\mathcal A})$
(respectively,
$\Bbbk _c({\mathcal A})$
(respectively,
![]() $\Bbbk _{c,b} ({\mathcal A})$
) by the formula
$\Bbbk _{c,b} ({\mathcal A})$
) by the formula
 $$ \begin{align*}T_k\zeta(s,t):=\int_G \beta_t(k)(s,r)\zeta(r,t)\,d r=\int_G k(st,rt)\Delta(t)\zeta(r,t)\,d r.\end{align*} $$
$$ \begin{align*}T_k\zeta(s,t):=\int_G \beta_t(k)(s,r)\zeta(r,t)\,d r=\int_G k(st,rt)\Delta(t)\zeta(r,t)\,d r.\end{align*} $$
Corollary 3.5. The structural homomorphism
![]() $\phi \colon C_0(G)\to \mathcal M(\Bbbk ({\mathcal A}))$
extends to a G-equivariant faithful unital
$\phi \colon C_0(G)\to \mathcal M(\Bbbk ({\mathcal A}))$
extends to a G-equivariant faithful unital
![]() $^*$
-homomorphism
$^*$
-homomorphism
given by the formulas
![]() $(\bar \phi (f)k)(s,t){\kern-1pt}={\kern-1pt}f(s)k(s,t)$
,
$(\bar \phi (f)k)(s,t){\kern-1pt}={\kern-1pt}f(s)k(s,t)$
,
![]() $(k\bar \phi (f))(s,t){\kern-1pt}={\kern-1pt}k(s,t)f(t)$
for
$(k\bar \phi (f))(s,t){\kern-1pt}={\kern-1pt}k(s,t)f(t)$
for
![]() $f{\kern-1pt}\in{\kern-1pt} L^\infty (G), k\in \Bbbk _{c,b} ({\mathcal A})$
.
$f{\kern-1pt}\in{\kern-1pt} L^\infty (G), k\in \Bbbk _{c,b} ({\mathcal A})$
.
Proof. Consider the
![]() $*$
-representation
$*$
-representation
![]() $\Phi :L^\infty (G)\to {\mathbb B}_{A_e}(L^2(\mathcal A\times G))$
given by
$\Phi :L^\infty (G)\to {\mathbb B}_{A_e}(L^2(\mathcal A\times G))$
given by
![]() $(\Phi (f)\xi )(s,t)=f(s)\xi (s,t)$
for
$(\Phi (f)\xi )(s,t)=f(s)\xi (s,t)$
for
![]() $f\in L^\infty (G)$
and
$f\in L^\infty (G)$
and
![]() $\xi \in L^2(\mathcal A\times G)$
. We then compute
$\xi \in L^2(\mathcal A\times G)$
. We then compute
for all
![]() $f\in L^\infty (G)$
and
$f\in L^\infty (G)$
and
![]() $k\in \Bbbk _{c,b} ({\mathcal A})$
. This gives the result.
$k\in \Bbbk _{c,b} ({\mathcal A})$
. This gives the result.
4 Deformation
In [Reference Buss and Echterhoff7] we described a general process to deform
![]() $C^*$
-algebras via coactions as follows: if
$C^*$
-algebras via coactions as follows: if
![]() $\delta \colon A\to \mathcal M(A\otimes C^*(G))$
is a coaction of the locally compact group G on the
$\delta \colon A\to \mathcal M(A\otimes C^*(G))$
is a coaction of the locally compact group G on the
![]() $C^*$
-algebra A, we consider the associated weak
$C^*$
-algebra A, we consider the associated weak
![]() $G\rtimes G$
-algebra
$G\rtimes G$
-algebra
We assume that
![]() $(A,\delta )$
satisfies Katayama duality for a given duality crossed-product functor
$(A,\delta )$
satisfies Katayama duality for a given duality crossed-product functor
![]() $\rtimes _\mu $
for actions of G, as in (2-1). Given a suitable deformation parameter – such as a (Borel)
$\rtimes _\mu $
for actions of G, as in (2-1). Given a suitable deformation parameter – such as a (Borel)
![]() $2$
-cocycle on G or an action of G on A that commutes with
$2$
-cocycle on G or an action of G on A that commutes with
![]() $\delta $
– we deform the weak
$\delta $
– we deform the weak
![]() $G\rtimes G$
-algebra
$G\rtimes G$
-algebra
![]() $(B,\beta ,\phi )$
into another weak
$(B,\beta ,\phi )$
into another weak
![]() $G\rtimes G$
-algebra
$G\rtimes G$
-algebra
![]() $(B',\beta ',\phi ')$
accordingly. Applying Landstad duality to
$(B',\beta ',\phi ')$
accordingly. Applying Landstad duality to
![]() $(B',\beta ',\phi ')$
, as developed in [Reference Buss and Echterhoff5], with respect to the crossed-product functor
$(B',\beta ',\phi ')$
, as developed in [Reference Buss and Echterhoff5], with respect to the crossed-product functor
![]() $\rtimes _\mu $
, we obtain a deformed coaction
$\rtimes _\mu $
, we obtain a deformed coaction
![]() $(A',\delta ')$
such that
$(A',\delta ')$
such that
where
![]() $(A',\delta ')$
also satisfies Katayama duality with respect to
$(A',\delta ')$
also satisfies Katayama duality with respect to
![]() $\rtimes _\mu $
.
$\rtimes _\mu $
.
4.1 Abadie–Exel deformation
Following ideas of Abadie and Exel from [Reference Abadie and Exel1], we introduced in [Reference Buss and Echterhoff7, Section 3.2] a deformation process for a given coaction
![]() $\delta \colon A\to \mathcal M(A\otimes C^*(G))$
that uses a (strongly) continuous action
$\delta \colon A\to \mathcal M(A\otimes C^*(G))$
that uses a (strongly) continuous action
![]() $\alpha :G\curvearrowright A$
commuting with
$\alpha :G\curvearrowright A$
commuting with
![]() $\delta $
in the sense that
$\delta $
in the sense that
Given such an action
![]() $\alpha $
, the equation
$\alpha $
, the equation
determines an action
![]() $\tilde \alpha :G\curvearrowright B=A\rtimes _{\delta }\widehat {G}$
that commutes with the dual action
$\tilde \alpha :G\curvearrowright B=A\rtimes _{\delta }\widehat {G}$
that commutes with the dual action
![]() $\widehat {\delta }$
(meaning
$\widehat {\delta }$
(meaning
![]() $\tilde \alpha _s\circ \widehat {\delta }_t=\widehat {\delta }_t\circ \tilde \alpha _s$
for all
$\tilde \alpha _s\circ \widehat {\delta }_t=\widehat {\delta }_t\circ \tilde \alpha _s$
for all
![]() $s,t\in G$
) and fixes
$s,t\in G$
) and fixes
![]() $\phi =j_{C_0(G)}$
. Starting then from the weak
$\phi =j_{C_0(G)}$
. Starting then from the weak
![]() $G\rtimes G$
-algebra
$G\rtimes G$
-algebra
![]() $(B,\beta ,\phi )=(A\rtimes _\delta \widehat {G}, \widehat {\delta }, j_{C_0(G)})$
, we obtain a new weak
$(B,\beta ,\phi )=(A\rtimes _\delta \widehat {G}, \widehat {\delta }, j_{C_0(G)})$
, we obtain a new weak
![]() $G\rtimes G$
-algebra
$G\rtimes G$
-algebra
![]() $(B, \tilde \alpha \cdot \beta ,\phi )$
with
$(B, \tilde \alpha \cdot \beta ,\phi )$
with
![]() $(\tilde \alpha \cdot \beta )_s:=\tilde \alpha _s\circ \beta _s$
for all
$(\tilde \alpha \cdot \beta )_s:=\tilde \alpha _s\circ \beta _s$
for all
![]() $s\in G$
. Conversely, [Reference Buss and Echterhoff7, Lemma 3.3] shows that every action
$s\in G$
. Conversely, [Reference Buss and Echterhoff7, Lemma 3.3] shows that every action
![]() $\eta :G\curvearrowright B$
that commutes with
$\eta :G\curvearrowright B$
that commutes with
![]() $\beta =\widehat {\delta }$
and fixes
$\beta =\widehat {\delta }$
and fixes
![]() $\phi $
is equal to
$\phi $
is equal to
![]() $\tilde \alpha $
for some action
$\tilde \alpha $
for some action
![]() $\alpha :G\curvearrowright A$
commuting with
$\alpha :G\curvearrowright A$
commuting with
![]() $\delta $
.
$\delta $
.
Definition 4.1. Let
![]() $(A,\delta )$
be a
$(A,\delta )$
be a
![]() $\mu $
-coaction with respect to a duality crossed-product functor
$\mu $
-coaction with respect to a duality crossed-product functor
![]() $\rtimes _\mu $
and let
$\rtimes _\mu $
and let
![]() $\alpha :G\curvearrowright A$
be an action that commutes with
$\alpha :G\curvearrowright A$
be an action that commutes with
![]() $\delta $
as above. Let
$\delta $
as above. Let
![]() $(B,\beta , \phi )=(A\rtimes _\delta \widehat {G}, \widehat {\delta }, j_{C_0(G)})$
and let
$(B,\beta , \phi )=(A\rtimes _\delta \widehat {G}, \widehat {\delta }, j_{C_0(G)})$
and let
![]() $(A^\alpha , \delta ^\alpha )$
be the coaction obtained from the weak
$(A^\alpha , \delta ^\alpha )$
be the coaction obtained from the weak
![]() $G\rtimes G$
-algebra
$G\rtimes G$
-algebra
![]() $(B, \tilde \alpha \cdot \beta ,\phi )$
via Landstad duality with respect to
$(B, \tilde \alpha \cdot \beta ,\phi )$
via Landstad duality with respect to
![]() $\rtimes _\mu $
. Then we call
$\rtimes _\mu $
. Then we call
![]() $(A^\alpha , \delta ^\alpha )$
the Abadie–Exel deformation of
$(A^\alpha , \delta ^\alpha )$
the Abadie–Exel deformation of
![]() $(A,\delta )$
with respect to
$(A,\delta )$
with respect to
![]() $\alpha $
.
$\alpha $
.
We call this the Abadie–Exel deformation because it covers the deformation of cross-sectional algebras of Fell bundles as studied by Abadie and Exel in [Reference Abadie and Exel1], as we show in the next subsection.
4.2 Abadie–Exel deformation via Fell bundles
Let
![]() $\mathcal A=(A_s)_{s\in G}$
be a Fell bundle over the locally compact group G. Abadie and Exel considered in [Reference Abadie and Exel1] continuous actions
$\mathcal A=(A_s)_{s\in G}$
be a Fell bundle over the locally compact group G. Abadie and Exel considered in [Reference Abadie and Exel1] continuous actions
![]() $\alpha :G\curvearrowright \mathcal A$
of G by automorphisms of the Fell bundle
$\alpha :G\curvearrowright \mathcal A$
of G by automorphisms of the Fell bundle
![]() $\mathcal A$
. This means that for each
$\mathcal A$
. This means that for each
![]() $s,t\in G$
we get a Banach-space isomorphism
$s,t\in G$
we get a Banach-space isomorphism
such that:
-
(1)
 $\alpha ^t_s(a_t)\alpha ^r_s(a_r)=\alpha ^{tr}_s(a_ta_r)$
and
$\alpha ^t_s(a_t)\alpha ^r_s(a_r)=\alpha ^{tr}_s(a_ta_r)$
and
 $\alpha ^{t^{-1}}_s(a_t^*)=\alpha _s^t(a_t)^*$
for all
$\alpha ^{t^{-1}}_s(a_t^*)=\alpha _s^t(a_t)^*$
for all
 $a_t\in A_t, a_r\in A_r$
;
$a_t\in A_t, a_r\in A_r$
; -
(2) for each fixed section
 $a\in C_c(\mathcal A)$
the section
$a\in C_c(\mathcal A)$
the section
 $\alpha _s(a)$
defined by is continuous; and
$\alpha _s(a)$
defined by is continuous; and $$ \begin{align*}(\alpha_s(a))_t:=\alpha_s^t(a_t)\end{align*} $$
$$ \begin{align*}(\alpha_s(a))_t:=\alpha_s^t(a_t)\end{align*} $$
-
(3) the function
 $s\mapsto \alpha _s(a)$
is continuous with respect to
$s\mapsto \alpha _s(a)$
is continuous with respect to
 $\|\cdot \|_{\mathrm \max }$
, the universal norm on
$\|\cdot \|_{\mathrm \max }$
, the universal norm on
 $C_c(\mathcal A)$
(for this it suffices that the function
$C_c(\mathcal A)$
(for this it suffices that the function
 $s\mapsto \alpha _s(a)$
is continuous in the
$s\mapsto \alpha _s(a)$
is continuous in the
 $L^1$
-norm on
$L^1$
-norm on
 $C_c(\mathcal A)$
).
$C_c(\mathcal A)$
).
These properties imply that
![]() $\alpha $
induces an action (also called
$\alpha $
induces an action (also called
![]() $\alpha $
) of G on
$\alpha $
) of G on
![]() $C^*(\mathcal A)$
, which commutes with
$C^*(\mathcal A)$
, which commutes with
![]() $\delta _{\mathcal A}$
since
$\delta _{\mathcal A}$
since
![]() $\delta _{\mathcal A}\circ \alpha _s$
is the integrated form of the representation
$\delta _{\mathcal A}\circ \alpha _s$
is the integrated form of the representation
![]() $a_t\mapsto \alpha ^t_s(a_t)\otimes u_t$
that coincides with the representation
$a_t\mapsto \alpha ^t_s(a_t)\otimes u_t$
that coincides with the representation
![]() $(\alpha _s\otimes \operatorname {{\mathrm {id}}}_G)\circ \delta _{\mathcal A}$
.
$(\alpha _s\otimes \operatorname {{\mathrm {id}}}_G)\circ \delta _{\mathcal A}$
.
Now let
![]() $\rtimes _\mu $
be a duality crossed-product functor for G. Since
$\rtimes _\mu $
be a duality crossed-product functor for G. Since
it follows from [Reference Buss and Echterhoff7, Lemma 3.3] (using both directions of that lemma) that the action
![]() $\alpha $
factors through an action (still called
$\alpha $
factors through an action (still called
![]() $\alpha $
) on
$\alpha $
) on
![]() $C_\mu ^*(\mathcal A)$
, which commutes with
$C_\mu ^*(\mathcal A)$
, which commutes with
![]() $\delta _\mu $
. We then get the deformed cosystem
$\delta _\mu $
. We then get the deformed cosystem
![]() $(A^\alpha , \delta ^\alpha )$
as in Definition 4.1 starting from
$(A^\alpha , \delta ^\alpha )$
as in Definition 4.1 starting from
![]() $(A,\delta ):=(C_\mu ^*(\mathcal A), \delta _\mu )$
.
$(A,\delta ):=(C_\mu ^*(\mathcal A), \delta _\mu )$
.
On the other hand, using the action
![]() $\alpha $
on
$\alpha $
on
![]() $\mathcal A$
, we can now define a new multiplication and involution on the Fell bundle
$\mathcal A$
, we can now define a new multiplication and involution on the Fell bundle
![]() $\mathcal A$
by
$\mathcal A$
by
where from now on we simply write
![]() $\alpha _s(a_t)$
instead of
$\alpha _s(a_t)$
instead of
![]() $\alpha _s^t(a_t)$
. We write
$\alpha _s^t(a_t)$
. We write
![]() ${\mathcal A}_\alpha $
for the new Fell bundle obtained in this way. We write
${\mathcal A}_\alpha $
for the new Fell bundle obtained in this way. We write
![]() $\delta ^\alpha _\mu $
for the dual coaction on
$\delta ^\alpha _\mu $
for the dual coaction on
![]() $C_\mu ^*({\mathcal A}_\alpha )$
. Similar to our notation for the Fell bundle
$C_\mu ^*({\mathcal A}_\alpha )$
. Similar to our notation for the Fell bundle
![]() $\mathcal A$
, we write
$\mathcal A$
, we write
![]() $(C^*({\mathcal A}_\alpha ), \delta _{{\mathcal A}_\alpha })$
for the maximal coaction
$(C^*({\mathcal A}_\alpha ), \delta _{{\mathcal A}_\alpha })$
for the maximal coaction
![]() $(C_{\mathrm \max }^*({\mathcal A}_\alpha ), \delta ^\alpha _{\mathrm \max })$
.
$(C_{\mathrm \max }^*({\mathcal A}_\alpha ), \delta ^\alpha _{\mathrm \max })$
.
Theorem 4.2. There is a canonical isomorphism between the cosystems
![]() $(C_\mu ^*({\mathcal A}_\alpha ),\delta _\mu ^\alpha )$
and
$(C_\mu ^*({\mathcal A}_\alpha ),\delta _\mu ^\alpha )$
and
![]() $(A^\alpha ,\delta ^\alpha )$
as constructed above from the action
$(A^\alpha ,\delta ^\alpha )$
as constructed above from the action
![]() $\alpha :G\curvearrowright \mathcal A$
.
$\alpha :G\curvearrowright \mathcal A$
.
Remark 4.3. In [Reference Abadie and Exel1] Abadie and Exel define the deformed Fell bundles
![]() ${\mathcal A}_\alpha $
as above for arbitrary locally compact groups, but only discuss their cross-sectional
${\mathcal A}_\alpha $
as above for arbitrary locally compact groups, but only discuss their cross-sectional
![]() $C^*$
-algebras for discrete abelian groups. They then define the deformation of
$C^*$
-algebras for discrete abelian groups. They then define the deformation of
![]() $(A,\delta )$
via
$(A,\delta )$
via
![]() $\alpha :G\curvearrowright \mathcal A$
as the cosystem
$\alpha :G\curvearrowright \mathcal A$
as the cosystem
![]() $(C^*({\mathcal A}_\alpha ), \delta _{{\mathcal A}_\alpha })$
. The above construction extends this to arbitrary locally compact groups and other possible completions of
$(C^*({\mathcal A}_\alpha ), \delta _{{\mathcal A}_\alpha })$
. The above construction extends this to arbitrary locally compact groups and other possible completions of
![]() $C_c(\mathcal A)$
and
$C_c(\mathcal A)$
and
![]() $C_c({\mathcal A}_\alpha )$
, respectively.
$C_c({\mathcal A}_\alpha )$
, respectively.
Proof of Theorem 4.2.
Recall that we constructed
![]() $(A^\alpha , \delta ^\alpha )$
via Landstad duality for the weak
$(A^\alpha , \delta ^\alpha )$
via Landstad duality for the weak
![]() $G\rtimes G$
-algebra
$G\rtimes G$
-algebra
![]() $(B, \tilde \alpha \cdot \beta , \phi )$
with respect to
$(B, \tilde \alpha \cdot \beta , \phi )$
with respect to
![]() $\rtimes _\mu $
, with
$\rtimes _\mu $
, with
On the other hand, by Proposition 3.1, the cosystem
![]() $(C_\mu ^*({\mathcal A}_\alpha ),\delta _\mu ^\alpha )$
can be constructed similarly via the weak
$(C_\mu ^*({\mathcal A}_\alpha ),\delta _\mu ^\alpha )$
can be constructed similarly via the weak
![]() $G\rtimes G$
algebra
$G\rtimes G$
algebra
So the result will follow immediately from Proposition 2.1 if we can show that
as weak
![]() $G\rtimes G$
-algebras. Using Proposition 3.2, for this it suffices to show that there is an isomorphism between
$G\rtimes G$
-algebras. Using Proposition 3.2, for this it suffices to show that there is an isomorphism between
![]() $\Bbbk _c({\mathcal A})$
and
$\Bbbk _c({\mathcal A})$
and
![]() $\Bbbk _c({{\mathcal A}_\alpha })$
that is isometric for
$\Bbbk _c({{\mathcal A}_\alpha })$
that is isometric for
![]() $\|\cdot \|_2$
and that intertwines the relevant actions of G and
$\|\cdot \|_2$
and that intertwines the relevant actions of G and
![]() $C_0(G)$
, respectively. For this we define
$C_0(G)$
, respectively. For this we define
for all
![]() $k\in \Bbbk _c({{\mathcal A}_\alpha })$
. This is clearly a linear bijection that is isometric for the norm
$k\in \Bbbk _c({{\mathcal A}_\alpha })$
. This is clearly a linear bijection that is isometric for the norm
![]() $\|\cdot \|_2$
. But it is also a
$\|\cdot \|_2$
. But it is also a
![]() $^*$
-homomorphism: for
$^*$
-homomorphism: for
![]() $k,l\in \Bbbk _c({{\mathcal A}_\alpha })$
we compute
$k,l\in \Bbbk _c({{\mathcal A}_\alpha })$
we compute
 $$ \begin{align*} \Phi_\alpha(k*l)(s,t)&=\alpha_{s^{-1}}(k*l(s,t))=\alpha_{s^{-1}}\bigg(\int_G k(s,r)\alpha_{sr^{-1}}(l(r,t))\,d r\bigg)\\ &=\int_G\alpha_{s^{-1}}(k(s,r))\alpha_{r^{-1}}(l(r,t))\,d r\\ &=\Phi_\alpha(k)*\Phi_\alpha(l)(s,t), \end{align*} $$
$$ \begin{align*} \Phi_\alpha(k*l)(s,t)&=\alpha_{s^{-1}}(k*l(s,t))=\alpha_{s^{-1}}\bigg(\int_G k(s,r)\alpha_{sr^{-1}}(l(r,t))\,d r\bigg)\\ &=\int_G\alpha_{s^{-1}}(k(s,r))\alpha_{r^{-1}}(l(r,t))\,d r\\ &=\Phi_\alpha(k)*\Phi_\alpha(l)(s,t), \end{align*} $$
for all
![]() $s,t\in G$
. We also have
$s,t\in G$
. We also have
 $$ \begin{align*} \Phi_\alpha(k^*)(s,t)&=\alpha_{s^{-1}}(k^*(s,t))=\alpha_{s^{-1}}(k(t,s)^{*_\alpha})\\ &=\alpha_{t^{-1}}(k(t,s))^*=\Phi_\alpha(k(t,s))^*=\Phi_\alpha(k)^*(s,t). \end{align*} $$
$$ \begin{align*} \Phi_\alpha(k^*)(s,t)&=\alpha_{s^{-1}}(k^*(s,t))=\alpha_{s^{-1}}(k(t,s)^{*_\alpha})\\ &=\alpha_{t^{-1}}(k(t,s))^*=\Phi_\alpha(k(t,s))^*=\Phi_\alpha(k)^*(s,t). \end{align*} $$
This proves the existence of the isomorphism
![]() $\Phi _\alpha $
as stated in the theorem. It is trivial to check that
$\Phi _\alpha $
as stated in the theorem. It is trivial to check that
![]() $\Phi _\alpha $
intertwines the
$\Phi _\alpha $
intertwines the
![]() $C_0(G)$
-action
$C_0(G)$
-action
![]() $j_{C_0(G)}^\alpha $
with
$j_{C_0(G)}^\alpha $
with
![]() $j_{C_0(G)}$
and that it is
$j_{C_0(G)}$
and that it is
![]() ${\widehat {\delta _{{\mathcal A}_\alpha }}-\tilde \alpha \cdot \widehat {\delta }_{\mathcal A}}$
-equivariant. Hence, it preserves the weak
${\widehat {\delta _{{\mathcal A}_\alpha }}-\tilde \alpha \cdot \widehat {\delta }_{\mathcal A}}$
-equivariant. Hence, it preserves the weak
![]() $G\rtimes G$
-structures on both algebras. Since Landstad duality with respect to
$G\rtimes G$
-structures on both algebras. Since Landstad duality with respect to
![]() $\rtimes _\mu $
is functorial by [Reference Buss and Echterhoff5], this finishes the proof.
$\rtimes _\mu $
is functorial by [Reference Buss and Echterhoff5], this finishes the proof.
Example 4.4. Let A be a
![]() $C^*$
-algebra and consider the trivial Fell bundle
$C^*$
-algebra and consider the trivial Fell bundle
![]() $\mathcal A=A\times G$
over G with fibres
$\mathcal A=A\times G$
over G with fibres
![]() $A_t=A\times \{t\}\cong A$
for all
$A_t=A\times \{t\}\cong A$
for all
![]() $t\in G$
and with multiplication and involution given by
$t\in G$
and with multiplication and involution given by
![]() $(a,s)(b,t)=(ab,st)$
and
$(a,s)(b,t)=(ab,st)$
and
![]() $(a,s)^*=(a^*, s^{-1})$
. Any G-action
$(a,s)^*=(a^*, s^{-1})$
. Any G-action
![]() $\alpha \colon G\curvearrowright A$
extends to a G-action on
$\alpha \colon G\curvearrowright A$
extends to a G-action on
![]() $\mathcal A$
by
$\mathcal A$
by
![]() $\alpha ^t_s(a, t):=(\alpha _s(a),t)$
. The induced G-action on
$\alpha ^t_s(a, t):=(\alpha _s(a),t)$
. The induced G-action on
![]() $C^*(\mathcal A)\cong A\otimes _{\mathrm \max } C^*(G)$
is just
$C^*(\mathcal A)\cong A\otimes _{\mathrm \max } C^*(G)$
is just
![]() $\alpha \otimes \operatorname {{\mathrm {id}}}$
, and the dual G-coaction on
$\alpha \otimes \operatorname {{\mathrm {id}}}$
, and the dual G-coaction on
![]() $C^*(\mathcal A)$
corresponds to
$C^*(\mathcal A)$
corresponds to
![]() $\operatorname {{\mathrm {id}}}\otimes \delta _G$
. The
$\operatorname {{\mathrm {id}}}\otimes \delta _G$
. The
![]() $\alpha $
-deformed Fell bundle
$\alpha $
-deformed Fell bundle
![]() ${\mathcal A}_\alpha $
is easily seen to be isomorphic to the semidirect product Fell bundle
${\mathcal A}_\alpha $
is easily seen to be isomorphic to the semidirect product Fell bundle
![]() ${\mathcal A}_\alpha =A\times _\alpha G$
associated to the action
${\mathcal A}_\alpha =A\times _\alpha G$
associated to the action
![]() $\alpha \colon G\curvearrowright A$
. From our general Theorem 4.2 we get that the
$\alpha \colon G\curvearrowright A$
. From our general Theorem 4.2 we get that the
![]() $\alpha $
-deformation of the coaction
$\alpha $
-deformation of the coaction
![]() $(C^*(\mathcal A),\delta _{\mathcal A})\cong (A\otimes _{\mathrm \max } C^*(G),\operatorname {{\mathrm {id}}}\otimes \delta _G)$
is isomorphic to
$(C^*(\mathcal A),\delta _{\mathcal A})\cong (A\otimes _{\mathrm \max } C^*(G),\operatorname {{\mathrm {id}}}\otimes \delta _G)$
is isomorphic to
![]() $(C^*({\mathcal A}_\alpha ),\delta _{{\mathcal A}_\alpha })\cong (A\rtimes _{\alpha ,\mathrm \max }G,\widehat {\alpha })$
. Similarly, taking reduced norms, we get that
$(C^*({\mathcal A}_\alpha ),\delta _{{\mathcal A}_\alpha })\cong (A\rtimes _{\alpha ,\mathrm \max }G,\widehat {\alpha })$
. Similarly, taking reduced norms, we get that
![]() $(C^*_r(\mathcal A),\delta _{\mathcal A}^r)\cong (A\otimes C^*_r(G),\operatorname {{\mathrm {id}}}\otimes \delta _G^r)$
is deformed into
$(C^*_r(\mathcal A),\delta _{\mathcal A}^r)\cong (A\otimes C^*_r(G),\operatorname {{\mathrm {id}}}\otimes \delta _G^r)$
is deformed into
![]() $(A\rtimes _{\alpha ,r}G,\widehat {\alpha }_r)$
, and a similar result holds for exotic crossed products (where, in general,
$(A\rtimes _{\alpha ,r}G,\widehat {\alpha }_r)$
, and a similar result holds for exotic crossed products (where, in general,
![]() $A\rtimes _{\operatorname {{\mathrm {id}}},\mu }G$
has no obvious description as a ‘standard’ tensor product).
$A\rtimes _{\operatorname {{\mathrm {id}}},\mu }G$
has no obvious description as a ‘standard’ tensor product).
More generally, we can start with an arbitrary action
![]() $\beta \colon G\curvearrowright A$
on a fixed
$\beta \colon G\curvearrowright A$
on a fixed
![]() $C^*$
-algebra A, and then any other G-action
$C^*$
-algebra A, and then any other G-action
![]() $\alpha \colon G\curvearrowright A$
commuting with
$\alpha \colon G\curvearrowright A$
commuting with
![]() $\beta $
gives an action on the Fell bundle
$\beta $
gives an action on the Fell bundle
![]() ${\mathcal A}_\beta =A\times _\beta G$
with
${\mathcal A}_\beta =A\times _\beta G$
with
![]() $\alpha $
-deformed Fell bundle
$\alpha $
-deformed Fell bundle
![]() $({\mathcal A}_\beta )_\alpha ={\mathcal A}_{\beta \cdot \alpha }=A\times _{\beta \cdot \alpha }G$
, where
$({\mathcal A}_\beta )_\alpha ={\mathcal A}_{\beta \cdot \alpha }=A\times _{\beta \cdot \alpha }G$
, where
![]() $\beta \cdot \alpha \colon G\curvearrowright A$
is defined by
$\beta \cdot \alpha \colon G\curvearrowright A$
is defined by
![]() $(\beta \cdot \alpha )_t:=\beta _t\circ \alpha _t=\alpha _t\circ \beta _t$
. In this situation, given a duality crossed-product functor
$(\beta \cdot \alpha )_t:=\beta _t\circ \alpha _t=\alpha _t\circ \beta _t$
. In this situation, given a duality crossed-product functor
![]() $\rtimes _\mu $
for G, we deform the dual G-coaction on
$\rtimes _\mu $
for G, we deform the dual G-coaction on
![]() $C^*_\mu ({\mathcal A}_\beta )=A\rtimes _{\beta ,\mu }G$
into the dual G-coaction on
$C^*_\mu ({\mathcal A}_\beta )=A\rtimes _{\beta ,\mu }G$
into the dual G-coaction on
![]() $C^*_\mu ({\mathcal A}_{\beta \cdot \alpha })=A\rtimes _{\beta \cdot \alpha ,\mu }G$
.
$C^*_\mu ({\mathcal A}_{\beta \cdot \alpha })=A\rtimes _{\beta \cdot \alpha ,\mu }G$
.
Example 4.5. As a particular example, consider the trivial Fell bundle
![]() $C(\mathbb T)\times \mathbb Z$
and the action
$C(\mathbb T)\times \mathbb Z$
and the action
![]() $\alpha _\theta $
of
$\alpha _\theta $
of
![]() $\mathbb Z$
on
$\mathbb Z$
on
![]() $C(\mathbb T)$
by rotations for a fixed angle
$C(\mathbb T)$
by rotations for a fixed angle
![]() $\theta \in \mathbb R$
. In this case we deform
$\theta \in \mathbb R$
. In this case we deform
![]() $C(\mathbb T)\otimes C^*(\mathbb Z)\cong C(\mathbb T^2)$
with the dual
$C(\mathbb T)\otimes C^*(\mathbb Z)\cong C(\mathbb T^2)$
with the dual
![]() $\mathbb T$
-action (that is, a
$\mathbb T$
-action (that is, a
![]() $\mathbb Z$
-coaction) into the rotation algebra
$\mathbb Z$
-coaction) into the rotation algebra
![]() $C(\mathbb T^2_\theta ):=A\rtimes _{\alpha _\theta }\mathbb Z$
with its dual
$C(\mathbb T^2_\theta ):=A\rtimes _{\alpha _\theta }\mathbb Z$
with its dual
![]() $\mathbb T$
-action. It is interesting to notice that
$\mathbb T$
-action. It is interesting to notice that
![]() $\mathbb T$
-actions (that is,
$\mathbb T$
-actions (that is,
![]() $\mathbb Z$
-coactions) cannot be deformed using
$\mathbb Z$
-coactions) cannot be deformed using
![]() $2$
-cocycles (that is, twists) as in the next section because the group
$2$
-cocycles (that is, twists) as in the next section because the group
![]() $\mathbb Z$
carries no nontrivial
$\mathbb Z$
carries no nontrivial
![]() $2$
-cocycles. But we do get
$2$
-cocycles. But we do get
![]() $C(\mathbb T^2_\theta )$
as a cocycle deformation of
$C(\mathbb T^2_\theta )$
as a cocycle deformation of
![]() $C(\mathbb T^2)\cong C^*(\mathbb Z^2)$
, considering it endowed with its canonical (dual)
$C(\mathbb T^2)\cong C^*(\mathbb Z^2)$
, considering it endowed with its canonical (dual)
![]() $\mathbb T^2$
-action and deforming it with respect to the
$\mathbb T^2$
-action and deforming it with respect to the
![]() $2$
-cocycle on
$2$
-cocycle on
![]() $\mathbb Z^2$
given by
$\mathbb Z^2$
given by
![]() $\omega _\theta ((n,m),(k,l))=e^{2\pi i\theta mk}$
.
$\omega _\theta ((n,m),(k,l))=e^{2\pi i\theta mk}$
.
We see from the above family of examples that deformation of Fell bundles in the Abadie–Exel sense is quite general. In particular, we should not expect as many permanence results to hold in this setting, as we have for deformation by
![]() $2$
-cocycles as studied in [Reference Buss and Echterhoff7] or in Section 5 below.
$2$
-cocycles as studied in [Reference Buss and Echterhoff7] or in Section 5 below.
Of course, one can also combine Abadie–Exel deformations with cocycle deformations to obtain more examples. The numerous examples as discussed by Abadie and Exel in [Reference Abadie and Exel1] show that this theory has many interesting applications.
5 Deformation by twists
Here we recall the deformation of coactions via twists, following the approach introduced in [Reference Buss and Echterhoff7]. Let G be a locally compact group. We first recall that a twist over G is a central extension
of G by the circle group
![]() $\mathbb T$
. In what follows, we often omit the embedding
$\mathbb T$
. In what follows, we often omit the embedding
![]() $\iota $
in our notations by simply identifying
$\iota $
in our notations by simply identifying
![]() $\mathbb T$
as a (central) normal subgroup of
$\mathbb T$
as a (central) normal subgroup of
![]() $G_\sigma $
and q with the quotient map
$G_\sigma $
and q with the quotient map
![]() $G_\sigma \twoheadrightarrow G_\sigma /\mathbb T\cong G$
.
$G_\sigma \twoheadrightarrow G_\sigma /\mathbb T\cong G$
.
Given a Borel section
![]() $\mathfrak {s}\colon G\to G_\sigma $
for q which satisfies
$\mathfrak {s}\colon G\to G_\sigma $
for q which satisfies
![]() $\mathfrak {s}(e)=1$
, we obtain a (normalized) Borel cocycle
$\mathfrak {s}(e)=1$
, we obtain a (normalized) Borel cocycle
![]() $\omega =\omega _\sigma \in Z^2(G,\mathbb T)$
by
$\omega =\omega _\sigma \in Z^2(G,\mathbb T)$
by
![]() $\omega (g,h):=\mathfrak {s}(g)\mathfrak {s}(h)\mathfrak {s}(gh)^{-1}$
. The cohomology class
$\omega (g,h):=\mathfrak {s}(g)\mathfrak {s}(h)\mathfrak {s}(gh)^{-1}$
. The cohomology class
![]() $[\omega _\sigma ]\in H^2(G,\mathbb T)$
does not depend on the choice of the Borel section
$[\omega _\sigma ]\in H^2(G,\mathbb T)$
does not depend on the choice of the Borel section
![]() $\mathfrak {s}$
and we obtain an isomorphism
$\mathfrak {s}$
and we obtain an isomorphism
![]() $[\sigma ]\leftrightarrow [\omega _\sigma ]$
between the group
$[\sigma ]\leftrightarrow [\omega _\sigma ]$
between the group
![]() $\operatorname {{\mathrm {Twist}}}(G)$
of isomorphism classes
$\operatorname {{\mathrm {Twist}}}(G)$
of isomorphism classes
![]() $[\sigma ]$
of twists, equipped with the Baer multiplication of extensions, and the group
$[\sigma ]$
of twists, equipped with the Baer multiplication of extensions, and the group
![]() $H^2(G,\mathbb T)$
. We refer to [Reference Buss and Echterhoff7, Section 4] for a detailed discussion. There it is also shown that
$H^2(G,\mathbb T)$
. We refer to [Reference Buss and Echterhoff7, Section 4] for a detailed discussion. There it is also shown that
![]() $\operatorname {{\mathrm {Twist}}}(G)\cong H^2(G,\mathbb T)$
is isomorphic to the Brauer group
$\operatorname {{\mathrm {Twist}}}(G)\cong H^2(G,\mathbb T)$
is isomorphic to the Brauer group
![]() $\operatorname {{\mathrm {Br}}}(G)$
of Morita equivalence classes of actions
$\operatorname {{\mathrm {Br}}}(G)$
of Morita equivalence classes of actions
![]() $\alpha :G\curvearrowright \mathbb K({\mathcal H})$
on algebras of compact operators on some Hilbert space
$\alpha :G\curvearrowright \mathbb K({\mathcal H})$
on algebras of compact operators on some Hilbert space
![]() ${\mathcal H}$
. It sends a class
${\mathcal H}$
. It sends a class
![]() $[\omega ]\in H^2(G,\mathbb T)$
to the Morita equivalence class
$[\omega ]\in H^2(G,\mathbb T)$
to the Morita equivalence class
![]() $[\alpha ]$
of the action
$[\alpha ]$
of the action
![]() $\alpha =\text {Ad}\rho ^{\bar \omega }:G\curvearrowright \mathbb K(L^2(G))$
, where
$\alpha =\text {Ad}\rho ^{\bar \omega }:G\curvearrowright \mathbb K(L^2(G))$
, where
![]() ${\rho ^{\bar \omega }:G\curvearrowright \mathcal U(L^2(G))}$
is the
${\rho ^{\bar \omega }:G\curvearrowright \mathcal U(L^2(G))}$
is the
![]() $\bar \omega $
-twisted right regular representation of G given by the formula
$\bar \omega $
-twisted right regular representation of G given by the formula
![]() $(\rho ^{\bar \omega }_s\xi )(t)=\Delta (s)^{1/2}\bar \omega (t,s)\xi (ts)$
, and
$(\rho ^{\bar \omega }_s\xi )(t)=\Delta (s)^{1/2}\bar \omega (t,s)\xi (ts)$
, and
![]() $\bar \omega $
is the complex conjugate (that is, inverse) of
$\bar \omega $
is the complex conjugate (that is, inverse) of
![]() $\omega $
. In this paper we mostly use the picture of twists given by central extensions (5-1), and sometimes also use
$\omega $
. In this paper we mostly use the picture of twists given by central extensions (5-1), and sometimes also use
![]() $2$
-cocycles.
$2$
-cocycles.
Given a twist
![]() $G_\sigma $
over G, we can consider the Green twisted action of
$G_\sigma $
over G, we can consider the Green twisted action of
![]() $(G_\sigma ,\mathbb T)$
on
$(G_\sigma ,\mathbb T)$
on
![]() $\mathbb C$
given by the pair
$\mathbb C$
given by the pair
![]() $(\operatorname {{\mathrm {id}}}_{\mathbb C}, \iota ^\sigma )$
in which
$(\operatorname {{\mathrm {id}}}_{\mathbb C}, \iota ^\sigma )$
in which
![]() $\iota ^\sigma :\mathbb T\to \mathbb T=U(\mathbb C)$
denotes the identity map. Then, if
$\iota ^\sigma :\mathbb T\to \mathbb T=U(\mathbb C)$
denotes the identity map. Then, if
![]() $\beta :G\curvearrowright B$
is any action of G, we can twist
$\beta :G\curvearrowright B$
is any action of G, we can twist
![]() $\beta $
with
$\beta $
with
![]() $(\operatorname {{\mathrm {id}}}_{\mathbb C},\iota ^\sigma )$
by taking the diagonal twisted action
$(\operatorname {{\mathrm {id}}}_{\mathbb C},\iota ^\sigma )$
by taking the diagonal twisted action
where we identify
![]() $\beta $
with its inflation
$\beta $
with its inflation
![]() $\beta \circ q\colon G_\sigma \curvearrowright B$
. Note that in this setting we have
$\beta \circ q\colon G_\sigma \curvearrowright B$
. Note that in this setting we have
![]() $\iota ^\sigma _z b=zb$
for all
$\iota ^\sigma _z b=zb$
for all
![]() $z\in \mathbb T, b\in B$
.
$z\in \mathbb T, b\in B$
.
We now fix a duality crossed-product functor
![]() $\rtimes _\mu $
for G and a
$\rtimes _\mu $
for G and a
![]() $\mu $
-coaction
$\mu $
-coaction
![]() $(A,\delta )$
. Consider, as before, the corresponding weak
$(A,\delta )$
. Consider, as before, the corresponding weak
![]() $G\rtimes G$
-algebra
$G\rtimes G$
-algebra
We want to use this twisted action to construct a deformed weak
![]() $G\rtimes G$
-algebra
$G\rtimes G$
-algebra
![]() $(B_\sigma ,\beta _\sigma , \phi _\sigma )$
as follows. We first observe that the twist
$(B_\sigma ,\beta _\sigma , \phi _\sigma )$
as follows. We first observe that the twist
![]() $\sigma =(\mathbb T\hookrightarrow G_\sigma \stackrel q\twoheadrightarrow G)$
determines a complex line bundle
$\sigma =(\mathbb T\hookrightarrow G_\sigma \stackrel q\twoheadrightarrow G)$
determines a complex line bundle
![]() ${\mathcal L}_\sigma $
over G given by the quotient space
${\mathcal L}_\sigma $
over G given by the quotient space
with respect to the action
![]() $\mathbb T\curvearrowright G_\sigma \times \mathbb C; \;z\cdot (x, u)=(\bar zx, zu)$
. The
$\mathbb T\curvearrowright G_\sigma \times \mathbb C; \;z\cdot (x, u)=(\bar zx, zu)$
. The
![]() $C_0$
-sections of this bundle then naturally identify with the space of functions
$C_0$
-sections of this bundle then naturally identify with the space of functions
We observe in [Reference Buss and Echterhoff7, Remark 5.6] that
![]() $C_0(G_\sigma , \iota )$
becomes a
$C_0(G_\sigma , \iota )$
becomes a
![]() $C_0(G)-C_0(G)$
imprimitivity Hilbert bimodule and the right translation action
$C_0(G)-C_0(G)$
imprimitivity Hilbert bimodule and the right translation action
![]() $\mathrm {rt}^\sigma :G_\sigma \curvearrowright C_0(G_\sigma , \iota )$
implements a (Morita) equivalence between the right translation action
$\mathrm {rt}^\sigma :G_\sigma \curvearrowright C_0(G_\sigma , \iota )$
implements a (Morita) equivalence between the right translation action
![]() $\mathrm {rt}: G\curvearrowright C_0(G)$
on the left and the twisted right translation action
$\mathrm {rt}: G\curvearrowright C_0(G)$
on the left and the twisted right translation action
![]() $(\mathrm {rt},\iota ^\sigma ):(G_\sigma ,\mathbb T)\curvearrowright C_0(G)$
on the right. We then observe in [Reference Buss and Echterhoff7, Remark 5.11] that for the weak
$(\mathrm {rt},\iota ^\sigma ):(G_\sigma ,\mathbb T)\curvearrowright C_0(G)$
on the right. We then observe in [Reference Buss and Echterhoff7, Remark 5.11] that for the weak
![]() $G\rtimes G$
-algebra
$G\rtimes G$
-algebra
![]() $(B,\beta , \phi )$
, the internal tensor product
$(B,\beta , \phi )$
, the internal tensor product
is a full Hilbert B-module and the diagonal action
![]() $\mathrm {rt}^\sigma \otimes \beta $
of
$\mathrm {rt}^\sigma \otimes \beta $
of
![]() $G_\sigma $
on
$G_\sigma $
on
![]() ${\mathcal L}(G_\sigma ,B)$
is compatible with the twisted action
${\mathcal L}(G_\sigma ,B)$
is compatible with the twisted action
![]() $(\beta ,\iota ^\sigma ):(G_\sigma ,\mathbb T)\curvearrowright B$
as introduced in (5-2) above. The adjoint action
$(\beta ,\iota ^\sigma ):(G_\sigma ,\mathbb T)\curvearrowright B$
as introduced in (5-2) above. The adjoint action
![]() $\beta _\sigma :=\text {Ad}(\mathrm {rt}^\sigma \otimes \beta )$
then factors through an ordinary action of G on
$\beta _\sigma :=\text {Ad}(\mathrm {rt}^\sigma \otimes \beta )$
then factors through an ordinary action of G on
![]() $B_\sigma :=\mathbb K({\mathcal L}(G_\sigma ,B))$
and
$B_\sigma :=\mathbb K({\mathcal L}(G_\sigma ,B))$
and
![]() $({\mathcal L}(G_\sigma ,B), \mathrm {rt}^\sigma \otimes \beta )$
becomes a
$({\mathcal L}(G_\sigma ,B), \mathrm {rt}^\sigma \otimes \beta )$
becomes a
![]() $\beta _\sigma -(\beta , \iota ^\sigma )$
-equivariant Morita equivalence.
$\beta _\sigma -(\beta , \iota ^\sigma )$
-equivariant Morita equivalence.
Together with the left action of
![]() $\phi _\sigma : C_0(G)\to \mathbb B({\mathcal L}(G_\sigma ,B))\cong \mathcal M(B_\sigma )$
, which is induced from the left action of
$\phi _\sigma : C_0(G)\to \mathbb B({\mathcal L}(G_\sigma ,B))\cong \mathcal M(B_\sigma )$
, which is induced from the left action of
![]() $C_0(G)$
on
$C_0(G)$
on
![]() $C_0(G_\sigma ,\iota )$
, the triple
$C_0(G_\sigma ,\iota )$
, the triple
![]() $(B_\sigma , \beta _\sigma , \phi _\sigma )$
becomes a weak
$(B_\sigma , \beta _\sigma , \phi _\sigma )$
becomes a weak
![]() $G\rtimes G$
-algebra. The following definition is [Reference Buss and Echterhoff7, Definition 5.8].
$G\rtimes G$
-algebra. The following definition is [Reference Buss and Echterhoff7, Definition 5.8].
Definition 5.1. Let
![]() $(A,\delta )$
be a
$(A,\delta )$
be a
![]() $\mu $
-coaction for some duality crossed-product functor
$\mu $
-coaction for some duality crossed-product functor
![]() $\rtimes _\mu $
and let
$\rtimes _\mu $
and let
![]() $(B_\sigma ,\beta _\sigma , \phi _\sigma )$
be the weak
$(B_\sigma ,\beta _\sigma , \phi _\sigma )$
be the weak
![]() $G\rtimes G$
-algebra constructed from the twist
$G\rtimes G$
-algebra constructed from the twist
![]() $\sigma =(\mathbb T\hookrightarrow G_\sigma \twoheadrightarrow G)$
and from
$\sigma =(\mathbb T\hookrightarrow G_\sigma \twoheadrightarrow G)$
and from
![]() $(B,\beta , \phi ):=(A\rtimes _\delta \widehat {G}, \widehat {\delta }, j_{C_0(G)})$
as above. We then define the
$(B,\beta , \phi ):=(A\rtimes _\delta \widehat {G}, \widehat {\delta }, j_{C_0(G)})$
as above. We then define the
![]() $\sigma $
-deformation of
$\sigma $
-deformation of
![]() $(A,\delta )$
as the cosystem
$(A,\delta )$
as the cosystem
![]() $(A^\sigma _\mu , \delta ^\sigma _\mu )$
associated to
$(A^\sigma _\mu , \delta ^\sigma _\mu )$
associated to
![]() $(B_\sigma ,\beta _\sigma ,\phi _\sigma )$
and
$(B_\sigma ,\beta _\sigma ,\phi _\sigma )$
and
![]() $\rtimes _\mu $
via Landstad duality with respect to
$\rtimes _\mu $
via Landstad duality with respect to
![]() $\rtimes _\mu $
.
$\rtimes _\mu $
.
In other words,
![]() $(A^\sigma _\mu ,\delta ^\sigma _\mu )$
is the unique
$(A^\sigma _\mu ,\delta ^\sigma _\mu )$
is the unique
![]() $\mu $
-coaction for which there exists an isomorphism of weak
$\mu $
-coaction for which there exists an isomorphism of weak
![]() $G\rtimes G$
-algebras
$G\rtimes G$
-algebras
Remark 5.2. If we start with an arbitrary coaction
![]() $(A,\delta )$
and any possibly unrelated duality crossed-product functor
$(A,\delta )$
and any possibly unrelated duality crossed-product functor
![]() $\rtimes _\mu $
, it follows from
$\rtimes _\mu $
, it follows from
![]() $\mu $
-Landstad duality applied to
$\mu $
-Landstad duality applied to
![]() $(B,\beta ,\phi )=(A\rtimes _\delta \widehat {G},\widehat {\delta },j_{C_0(G)})$
that there is a unique (up to isomorphism)
$(B,\beta ,\phi )=(A\rtimes _\delta \widehat {G},\widehat {\delta },j_{C_0(G)})$
that there is a unique (up to isomorphism)
![]() $\mu $
-coaction
$\mu $
-coaction
![]() $(A_\mu ,\delta _\mu )$
such that
$(A_\mu ,\delta _\mu )$
such that
![]() $(B,\beta ,\phi )\cong (A_\mu \rtimes _{\delta _\mu }\widehat {G},\widehat {\delta _\mu },j_{C_0(G)})$
. The
$(B,\beta ,\phi )\cong (A_\mu \rtimes _{\delta _\mu }\widehat {G},\widehat {\delta _\mu },j_{C_0(G)})$
. The
![]() $\sigma $
-deformed coaction
$\sigma $
-deformed coaction
![]() $(A^\sigma _\mu ,\delta ^\sigma _\mu )$
associated to
$(A^\sigma _\mu ,\delta ^\sigma _\mu )$
associated to
![]() $(B_\sigma ,\beta _\sigma ,\phi _\sigma )$
is then the
$(B_\sigma ,\beta _\sigma ,\phi _\sigma )$
is then the
![]() $\sigma $
-deformation of
$\sigma $
-deformation of
![]() $(A_\mu ,\delta _\mu )$
.
$(A_\mu ,\delta _\mu )$
.
If the twist
![]() $\sigma =(\mathbb T\hookrightarrow G_\sigma \stackrel {q}\twoheadrightarrow G)$
splits via a continuous section
$\sigma =(\mathbb T\hookrightarrow G_\sigma \stackrel {q}\twoheadrightarrow G)$
splits via a continuous section
![]() $\mathfrak {s}\colon G\to G_\sigma $
, then
$\mathfrak {s}\colon G\to G_\sigma $
, then
![]() $\sigma $
is represented in
$\sigma $
is represented in
![]() $H^2(G,\mathbb T)$
by the class of the continuous
$H^2(G,\mathbb T)$
by the class of the continuous
![]() $2$
-cocycle
$2$
-cocycle
![]() $\omega (g,h)=\partial \mathfrak {s}(g,h)=\mathfrak {s}(g)\mathfrak {s}(h)\mathfrak {s}(gh)^{-1}$
. In this case the deformed weak
$\omega (g,h)=\partial \mathfrak {s}(g,h)=\mathfrak {s}(g)\mathfrak {s}(h)\mathfrak {s}(gh)^{-1}$
. In this case the deformed weak
![]() $G\rtimes G$
-algebra
$G\rtimes G$
-algebra
![]() $(B_\sigma ,\beta _\sigma ,\phi _\sigma )$
is isomorphic to the triple
$(B_\sigma ,\beta _\sigma ,\phi _\sigma )$
is isomorphic to the triple
![]() $(B, \beta ^\omega ,\phi )$
in which
$(B, \beta ^\omega ,\phi )$
in which
![]() $\beta ^\omega :G\curvearrowright B$
is given by the formula
$\beta ^\omega :G\curvearrowright B$
is given by the formula
where
![]() $U_\omega :G\to U\mathcal M(B)$
is defined by
$U_\omega :G\to U\mathcal M(B)$
is defined by
![]() $U_\omega (s)= \phi (u_\omega (s))$
, with
$U_\omega (s)= \phi (u_\omega (s))$
, with
![]() $u_\omega (s)\in C_b(G,\mathbb T)=U\mathcal M(C_0(G))$
given by
$u_\omega (s)\in C_b(G,\mathbb T)=U\mathcal M(C_0(G))$
given by
We refer to [Reference Buss and Echterhoff7, Section 3.3] for further details.
Indeed, for a general twist
![]() $\sigma =(\mathbb T\hookrightarrow G_\sigma \stackrel {q}\to G)$
, by [Reference Feldman and Greenleaf17, Theorem 1], we can always choose a Borel section
$\sigma =(\mathbb T\hookrightarrow G_\sigma \stackrel {q}\to G)$
, by [Reference Feldman and Greenleaf17, Theorem 1], we can always choose a Borel section
![]() $\mathfrak {s}\colon G\to G_\sigma $
for q with corresponding Borel cocycle
$\mathfrak {s}\colon G\to G_\sigma $
for q with corresponding Borel cocycle
![]() $\omega =\partial \mathfrak {s}$
and it may happen that the action (5-4) makes sense even if
$\omega =\partial \mathfrak {s}$
and it may happen that the action (5-4) makes sense even if
![]() $\omega $
is not continuous. This is the case, for example, if the structural homomorphism
$\omega $
is not continuous. This is the case, for example, if the structural homomorphism
![]() $\phi \colon C_0(G)\to \mathcal M(B)$
extends to a G-equivariant unital homomorphism
$\phi \colon C_0(G)\to \mathcal M(B)$
extends to a G-equivariant unital homomorphism
![]() $\bar \phi \colon L^\infty (G)\to \mathcal M(B)$
; this is the content of [Reference Buss and Echterhoff7, Proposition 5.13]. We will apply this in the next section to the kernel algebras
$\bar \phi \colon L^\infty (G)\to \mathcal M(B)$
; this is the content of [Reference Buss and Echterhoff7, Proposition 5.13]. We will apply this in the next section to the kernel algebras
![]() $\Bbbk ({\mathcal A})$
using Corollary 3.5 in order to deform dual coactions on cross-sectional
$\Bbbk ({\mathcal A})$
using Corollary 3.5 in order to deform dual coactions on cross-sectional
![]() $C^*$
-algebras of Fell bundles
$C^*$
-algebras of Fell bundles
![]() $\mathcal A$
over G.
$\mathcal A$
over G.
6 Deformation of Fell bundles by cocycles
Let
![]() $\rtimes _\mu $
be a duality crossed-product functor for a locally compact group G. Given a Fell bundle
$\rtimes _\mu $
be a duality crossed-product functor for a locally compact group G. Given a Fell bundle
![]() $\mathcal A$
over G, we consider its
$\mathcal A$
over G, we consider its
![]() $C^*$
-cross-sectional algebra
$C^*$
-cross-sectional algebra
![]() $C_\mu ^*(\mathcal A)$
, which comes equipped with the dual
$C_\mu ^*(\mathcal A)$
, which comes equipped with the dual
![]() $\mu $
-coaction
$\mu $
-coaction
![]() $\delta :C_\mu ^*(\mathcal A)\to \mathcal M(C_\mu ^*(\mathcal A)\otimes C^*(G))$
given by the integrated form of the map
$\delta :C_\mu ^*(\mathcal A)\to \mathcal M(C_\mu ^*(\mathcal A)\otimes C^*(G))$
given by the integrated form of the map
![]() $a_s\mapsto a_s\otimes u_s$
for
$a_s\mapsto a_s\otimes u_s$
for
![]() $a_s\in A_s$
.
$a_s\in A_s$
.
In this section we want to show that the deformation of
![]() $C_\mu ^*(\mathcal A)$
via this coaction and a twist
$C_\mu ^*(\mathcal A)$
via this coaction and a twist
![]() $\sigma =(\mathbb T\hookrightarrow G_\sigma \twoheadrightarrow G)$
can be described directly on the level of the Fell bundle
$\sigma =(\mathbb T\hookrightarrow G_\sigma \twoheadrightarrow G)$
can be described directly on the level of the Fell bundle
![]() $\mathcal A$
itself – similarly to what happened in Section 4.1 for the case of Abadie–Exel deformation. This result will generalize [Reference Buss and Echterhoff7, Proposition 5.16], which in turn generalizes [Reference Bhowmick, Neshveyev and Sangha4, Proposition 4.3], where a similar result has been shown for dual coactions of reduced crossed products, and also results from [Reference Yamashita36] for the case of reduced cross-sectional
$\mathcal A$
itself – similarly to what happened in Section 4.1 for the case of Abadie–Exel deformation. This result will generalize [Reference Buss and Echterhoff7, Proposition 5.16], which in turn generalizes [Reference Bhowmick, Neshveyev and Sangha4, Proposition 4.3], where a similar result has been shown for dual coactions of reduced crossed products, and also results from [Reference Yamashita36] for the case of reduced cross-sectional
![]() $C^*$
-algebras of Fell bundles over discrete groups.
$C^*$
-algebras of Fell bundles over discrete groups.
So in what follows let
![]() $\mathcal A=(A_g)_{g\in G}$
be a Fell bundle over G and
$\mathcal A=(A_g)_{g\in G}$
be a Fell bundle over G and
![]() $A=C_\mu ^*(\mathcal A)$
with respect to some duality crossed-product functor
$A=C_\mu ^*(\mathcal A)$
with respect to some duality crossed-product functor
![]() $\rtimes _\mu $
for G. We construct the deformed Fell bundle
$\rtimes _\mu $
for G. We construct the deformed Fell bundle
![]() ${\mathcal A}_\sigma $
via the twist
${\mathcal A}_\sigma $
via the twist
![]() $\sigma =(\mathbb T\stackrel {\iota }{\hookrightarrow } G_\sigma \stackrel {q}{\twoheadrightarrow } G)$
as follows. Consider the pullback Fell bundle over
$\sigma =(\mathbb T\stackrel {\iota }{\hookrightarrow } G_\sigma \stackrel {q}{\twoheadrightarrow } G)$
as follows. Consider the pullback Fell bundle over
![]() $G_\sigma $
that can be realized as
$G_\sigma $
that can be realized as
where
![]() $p\colon \mathcal A\to G$
denotes the bundle projection. The circle group
$p\colon \mathcal A\to G$
denotes the bundle projection. The circle group
![]() $\mathbb T$
acts ‘diagonally’ on
$\mathbb T$
acts ‘diagonally’ on
![]() $q^*(\mathcal A)$
via
$q^*(\mathcal A)$
via
Definition 6.1. We define the twisted Fell bundle
![]() ${\mathcal A}_\sigma $
as the quotient Fell bundle
${\mathcal A}_\sigma $
as the quotient Fell bundle
with respect to the diagonal
![]() $\mathbb T$
-action defined above. More concretely, this consists of equivalence classes
$\mathbb T$
-action defined above. More concretely, this consists of equivalence classes
![]() $[a,\tilde g]$
, with the bundle projection
$[a,\tilde g]$
, with the bundle projection
The algebraic operations on
![]() ${\mathcal A}_\sigma $
are also induced from those in
${\mathcal A}_\sigma $
are also induced from those in
![]() $q^*(\mathcal A)$
, that is,
$q^*(\mathcal A)$
, that is,
for all
![]() $\lambda \in \mathbb C$
,
$\lambda \in \mathbb C$
,
![]() $a,a'\in A_g$
,
$a,a'\in A_g$
,
![]() $b\in A_h, \tilde g,\tilde h\in G_\sigma $
,
$b\in A_h, \tilde g,\tilde h\in G_\sigma $
,
![]() $g=q(\tilde g)$
and
$g=q(\tilde g)$
and
![]() $h=q(\tilde h)$
.
$h=q(\tilde h)$
.
It is a well-known result that
![]() ${\mathcal A}_\sigma $
is a Fell bundle over G with respect to the above operations; see, for instance, [Reference Kaliszewski, Muhly, Quigg and Williams21, Corollary A.12].
${\mathcal A}_\sigma $
is a Fell bundle over G with respect to the above operations; see, for instance, [Reference Kaliszewski, Muhly, Quigg and Williams21, Corollary A.12].
Remark 6.2. The fibers of
![]() ${\mathcal A}_\sigma $
are
${\mathcal A}_\sigma $
are
![]() $A_{\sigma ,g}\cong A_g$
as Banach spaces for each
$A_{\sigma ,g}\cong A_g$
as Banach spaces for each
![]() $g\in G$
. Indeed, choosing
$g\in G$
. Indeed, choosing
![]() $\tilde g\in G_\sigma $
with
$\tilde g\in G_\sigma $
with
![]() $q(\tilde g)=g$
, the map
$q(\tilde g)=g$
, the map
![]() $a\mapsto [a,\tilde g]$
provides an isometric linear isomorphism
$a\mapsto [a,\tilde g]$
provides an isometric linear isomorphism
![]() $A_g\xrightarrow \sim A_{\sigma ,g}$
. However,
$A_g\xrightarrow \sim A_{\sigma ,g}$
. However,
![]() $\mathcal A$
and
$\mathcal A$
and
![]() ${\mathcal A}_\sigma $
are not isomorphic as topological bundles in general, as shown by the following special case.
${\mathcal A}_\sigma $
are not isomorphic as topological bundles in general, as shown by the following special case.
If we apply the above construction to the trivial Fell bundle
![]() $\mathcal A=\mathbb C\times G$
, we get the twisted Fell line bundle
$\mathcal A=\mathbb C\times G$
, we get the twisted Fell line bundle
![]() ${\mathcal L}_\sigma $
as in (5-3), and this is topologically trivial if and only if the twist
${\mathcal L}_\sigma $
as in (5-3), and this is topologically trivial if and only if the twist
![]() $\mathbb T\hookrightarrow G_\sigma \stackrel {q}\twoheadrightarrow G$
admits a continuous section
$\mathbb T\hookrightarrow G_\sigma \stackrel {q}\twoheadrightarrow G$
admits a continuous section
![]() $\mathfrak {s}\colon G\to G_\sigma $
. Moreover, every Fell line bundle over G is isomorphic to one of this form; see [Reference Doran and Fell13, VIII.16.2].
$\mathfrak {s}\colon G\to G_\sigma $
. Moreover, every Fell line bundle over G is isomorphic to one of this form; see [Reference Doran and Fell13, VIII.16.2].
One can show that, in general, the Fell bundle
![]() ${\mathcal A}_\sigma $
is isomorphic to the Fell bundle tensor product
${\mathcal A}_\sigma $
is isomorphic to the Fell bundle tensor product
![]() $\mathcal A\otimes _G {\mathcal L}_\sigma $
. Recall that if
$\mathcal A\otimes _G {\mathcal L}_\sigma $
. Recall that if
![]() $\mathcal A$
and
$\mathcal A$
and
![]() $\mathcal B$
are two Fell bundles over G, the (minimal) tensor product
$\mathcal B$
are two Fell bundles over G, the (minimal) tensor product
![]() $\mathcal A\otimes _G\mathcal B$
is the Fell bundle over G with fibres
$\mathcal A\otimes _G\mathcal B$
is the Fell bundle over G with fibres
![]() $A_g\otimes B_g$
for
$A_g\otimes B_g$
for
![]() $g\in G$
, where
$g\in G$
, where
![]() $\otimes $
here denotes the (external) minimal tensor product of Hilbert modules and multiplication and involution are given on elementary tensors in the obvious way. Since we do not need this description, we omit further details. Instead, we refer to [Reference Abadie2] where general tensor products of Fell bundles over groups are discussed, and [Reference Kaliszewski, Landstad and Quigg20, Section 3] where a similar construction of a (balanced) tensor product of Fell bundles over locally compact groups is used for maximal tensor products.
$\otimes $
here denotes the (external) minimal tensor product of Hilbert modules and multiplication and involution are given on elementary tensors in the obvious way. Since we do not need this description, we omit further details. Instead, we refer to [Reference Abadie2] where general tensor products of Fell bundles over groups are discussed, and [Reference Kaliszewski, Landstad and Quigg20, Section 3] where a similar construction of a (balanced) tensor product of Fell bundles over locally compact groups is used for maximal tensor products.
Applying the construction to the (semidirect product) Fell bundle
![]() $\mathcal A=A\times _\alpha G$
associated to a (continuous) action
$\mathcal A=A\times _\alpha G$
associated to a (continuous) action
![]() $\alpha $
of G on a
$\alpha $
of G on a
![]() $C^*$
-algebra A, the twisted Fell bundle
$C^*$
-algebra A, the twisted Fell bundle
![]() ${\mathcal A}_\sigma $
corresponds to a semidirect product Fell bundle
${\mathcal A}_\sigma $
corresponds to a semidirect product Fell bundle
![]() $A\times _{(\alpha ,\iota ^\sigma )}G$
for the Green twisted action
$A\times _{(\alpha ,\iota ^\sigma )}G$
for the Green twisted action
![]() $(\alpha , \iota ^\sigma )$
of
$(\alpha , \iota ^\sigma )$
of
![]() $(G_\sigma ,\mathbb T)$
similar to (5-2). It follows from [Reference Doran and Fell13, VIII.6] (see also [Reference Buss and Meyer10, Example 3.9]) that every Green twisted action of a pair
$(G_\sigma ,\mathbb T)$
similar to (5-2). It follows from [Reference Doran and Fell13, VIII.6] (see also [Reference Buss and Meyer10, Example 3.9]) that every Green twisted action of a pair
![]() $(H,N)$
, with
$(H,N)$
, with
![]() $N\trianglelefteq H$
a closed normal subgroup, corresponds to a Fell bundle over
$N\trianglelefteq H$
a closed normal subgroup, corresponds to a Fell bundle over
![]() $G=H/N$
.
$G=H/N$
.
We will now describe the space of sections of the twisted Fell bundle
![]() ${\mathcal A}_\sigma $
. We start with the following lemma.
${\mathcal A}_\sigma $
. We start with the following lemma.
Lemma 6.3. There is a bijection between the sections
![]() $\xi :G\to {\mathcal A}_\sigma $
and the set of sections
$\xi :G\to {\mathcal A}_\sigma $
and the set of sections
for
![]() $q^*\mathcal A$
that assigns to each section
$q^*\mathcal A$
that assigns to each section
![]() $\xi \in S(G_\sigma , \mathcal A,\iota )$
the section
$\xi \in S(G_\sigma , \mathcal A,\iota )$
the section
Moreover,
![]() $\xi $
is continuous (respectively, measurable, compactly supported) if and only if
$\xi $
is continuous (respectively, measurable, compactly supported) if and only if
![]() $\tilde \xi $
is continuous (respectively, measurable, compactly supported).
$\tilde \xi $
is continuous (respectively, measurable, compactly supported).
Proof. We first check that the section
![]() $\tilde \xi :G\to {\mathcal A}_\sigma $
as in (6-1) is well defined. Indeed, if
$\tilde \xi :G\to {\mathcal A}_\sigma $
as in (6-1) is well defined. Indeed, if
![]() ${\tilde {g}}, g'\in q^{-1}(g)\in G_{\sigma }$
, then there exists a unique
${\tilde {g}}, g'\in q^{-1}(g)\in G_{\sigma }$
, then there exists a unique
![]() $z\in \mathbb T$
such that
$z\in \mathbb T$
such that
![]() $g'={\tilde {g}} z$
, so that
$g'={\tilde {g}} z$
, so that
Thus
![]() $\tilde \xi $
sends the element
$\tilde \xi $
sends the element
![]() $g\in G$
to a well-defined element in the fibre
$g\in G$
to a well-defined element in the fibre
![]() $A_{\sigma ,g}$
of
$A_{\sigma ,g}$
of
![]() $A_\sigma $
. Conversely, if
$A_\sigma $
. Conversely, if
![]() $\tilde \xi :G\to {\mathcal A}_\sigma $
is any section, then for each
$\tilde \xi :G\to {\mathcal A}_\sigma $
is any section, then for each
![]() $g\in G$
there exist
$g\in G$
there exist
![]() $a_g\in A_g$
and
$a_g\in A_g$
and
![]() $g'\in q^{-1}(g)$
such that
$g'\in q^{-1}(g)$
such that
![]() $\tilde \xi (g)=[a_g, g']\in A_{\sigma ,g}$
. But then, for any
$\tilde \xi (g)=[a_g, g']\in A_{\sigma ,g}$
. But then, for any
![]() ${\tilde {g}}\in q^{-1}(g)$
, there is a unique
${\tilde {g}}\in q^{-1}(g)$
, there is a unique
![]() $z\in \mathbb T$
such that
$z\in \mathbb T$
such that
![]() $g'={\tilde {g}} z$
and then we get
$g'={\tilde {g}} z$
and then we get
It follows that
![]() $\xi ({\tilde {g}}):=za_g$
is the unique element in
$\xi ({\tilde {g}}):=za_g$
is the unique element in
![]() $A_g$
such that
$A_g$
such that
![]() $\tilde \xi (g)=[\xi ({\tilde {g}}), {\tilde {g}}]$
. We therefore obtain a well-defined element
$\tilde \xi (g)=[\xi ({\tilde {g}}), {\tilde {g}}]$
. We therefore obtain a well-defined element
![]() $\xi \in S(G_\sigma ,\mathcal A,\iota )$
that satisfies (6-1).
$\xi \in S(G_\sigma ,\mathcal A,\iota )$
that satisfies (6-1).
We now show that continuity of
![]() $\tilde \xi $
implies continuity of
$\tilde \xi $
implies continuity of
![]() $\xi $
. For this let
$\xi $
. For this let
![]() $({\tilde {g}}_i)$
be a net in
$({\tilde {g}}_i)$
be a net in
![]() $G_\sigma $
that converges to
$G_\sigma $
that converges to
![]() ${\tilde {g}}\in G_\sigma $
, and let us write
${\tilde {g}}\in G_\sigma $
, and let us write
![]() $g_i=q({\tilde {g}}_i)$
and
$g_i=q({\tilde {g}}_i)$
and
![]() $g={\tilde {g}}$
. Then
$g={\tilde {g}}$
. Then
![]() $g_i\to g$
and continuity of
$g_i\to g$
and continuity of
![]() $\tilde \xi $
implies that
$\tilde \xi $
implies that
![]() $\tilde \xi (g_i)=[\xi ({\tilde {g}}_i), {\tilde {g}}_i]\to [\xi ({\tilde {g}}), {\tilde {g}}]=\tilde \xi (g)$
. Since the quotient map
$\tilde \xi (g_i)=[\xi ({\tilde {g}}_i), {\tilde {g}}_i]\to [\xi ({\tilde {g}}), {\tilde {g}}]=\tilde \xi (g)$
. Since the quotient map
![]() $q^*(\mathcal A)\twoheadrightarrow q^*(\mathcal A)/\mathbb T={\mathcal A}_\sigma $
is open we may assume, after passing to a subnet if necessary, that there is a net
$q^*(\mathcal A)\twoheadrightarrow q^*(\mathcal A)/\mathbb T={\mathcal A}_\sigma $
is open we may assume, after passing to a subnet if necessary, that there is a net
![]() $(z_i)$
in
$(z_i)$
in
![]() $\mathbb T$
such that
$\mathbb T$
such that
![]() $z_i(\xi ({\tilde {g}}_i),{\tilde {g}}_i)= (\xi (z_i{\tilde {g}}_i), z_i{\tilde {g}}_i) \to (\xi ({\tilde {g}}),{\tilde {g}})$
in
$z_i(\xi ({\tilde {g}}_i),{\tilde {g}}_i)= (\xi (z_i{\tilde {g}}_i), z_i{\tilde {g}}_i) \to (\xi ({\tilde {g}}),{\tilde {g}})$
in
![]() $q^*(\mathcal A)$
. But since
$q^*(\mathcal A)$
. But since
![]() $\mathbb T$
is compact we may assume without loss of generality that
$\mathbb T$
is compact we may assume without loss of generality that
![]() $z_i\to z$
for some
$z_i\to z$
for some
![]() $z\in \mathbb T$
. But then it follows that
$z\in \mathbb T$
. But then it follows that
![]() ${\tilde {g}}_i\to \bar {z}{\tilde {g}}$
, and since
${\tilde {g}}_i\to \bar {z}{\tilde {g}}$
, and since
![]() ${\tilde {g}}_i\to {\tilde {g}}$
by assumption, we get
${\tilde {g}}_i\to {\tilde {g}}$
by assumption, we get
![]() $z=1$
and hence
$z=1$
and hence
![]() $\lim _i \xi ({\tilde {g}}_i)=\lim _i\xi (z_i{\tilde {g}}_i)=\xi ({\tilde {g}})$
, which proves continuity of
$\lim _i \xi ({\tilde {g}}_i)=\lim _i\xi (z_i{\tilde {g}}_i)=\xi ({\tilde {g}})$
, which proves continuity of
![]() $\xi $
.
$\xi $
.
Conversely, if
![]() $\xi $
is continuous and
$\xi $
is continuous and
![]() $g_i\to g$
in G, then using openness of
$g_i\to g$
in G, then using openness of
![]() $q:G_\sigma \twoheadrightarrow G$
, we may pass to a subnet to find a net
$q:G_\sigma \twoheadrightarrow G$
, we may pass to a subnet to find a net
![]() $({\tilde {g}}_i)$
in
$({\tilde {g}}_i)$
in
![]() $G_\sigma $
and
$G_\sigma $
and
![]() ${\tilde {g}}\in G_\sigma $
such that
${\tilde {g}}\in G_\sigma $
such that
![]() ${\tilde {g}}_i\to {\tilde {g}}$
and
${\tilde {g}}_i\to {\tilde {g}}$
and
![]() $q({\tilde {g}}_i)=g_i, q({\tilde {g}})=g$
. It then follows that
$q({\tilde {g}}_i)=g_i, q({\tilde {g}})=g$
. It then follows that
![]() $\tilde \xi (g_i)=[\xi ({\tilde {g}}_i), {\tilde {g}}_i]\to [\xi ({\tilde {g}}),{\tilde {g}}]=\tilde \xi (g)$
and therefore
$\tilde \xi (g_i)=[\xi ({\tilde {g}}_i), {\tilde {g}}_i]\to [\xi ({\tilde {g}}),{\tilde {g}}]=\tilde \xi (g)$
and therefore
![]() $\tilde \xi $
is continuous as well.
$\tilde \xi $
is continuous as well.
To see that
![]() $\tilde \xi $
is measurable if and only if
$\tilde \xi $
is measurable if and only if
![]() $\xi $
is measurable we recall from [Reference Doran and Fell12, Proposition 15.4] that
$\xi $
is measurable we recall from [Reference Doran and Fell12, Proposition 15.4] that
![]() $\xi $
is measurable if for every compact subset K of
$\xi $
is measurable if for every compact subset K of
![]() $G_\sigma $
there exists a sequence
$G_\sigma $
there exists a sequence
![]() $(\xi _n)$
of continuous sections such that
$(\xi _n)$
of continuous sections such that
![]() $\xi _n({\tilde {g}})\to \xi ({\tilde {g}})$
for almost all
$\xi _n({\tilde {g}})\to \xi ({\tilde {g}})$
for almost all
![]() ${\tilde {g}} \in K$
(and similarly for
${\tilde {g}} \in K$
(and similarly for
![]() $\tilde \xi $
). But
$\tilde \xi $
). But
![]() $\xi _n({\tilde {g}})\to \xi ({\tilde {g}})$
for almost all
$\xi _n({\tilde {g}})\to \xi ({\tilde {g}})$
for almost all
![]() ${\tilde {g}}\in K$
if and only if
${\tilde {g}}\in K$
if and only if
![]() $\tilde \xi _n(g)\to \tilde \xi (g)$
for almost all
$\tilde \xi _n(g)\to \tilde \xi (g)$
for almost all
![]() $g\in q(K)$
, and the result follows.
$g\in q(K)$
, and the result follows.
Finally, it follows from (6-1) that
![]() $\operatorname {{\mathrm {supp}}}\xi =q^{-1}(\operatorname {{\mathrm {supp}}}\tilde \xi )$
. Thus
$\operatorname {{\mathrm {supp}}}\xi =q^{-1}(\operatorname {{\mathrm {supp}}}\tilde \xi )$
. Thus
![]() $\xi $
has compact support if and only if
$\xi $
has compact support if and only if
![]() $\tilde \xi $
has compact support.
$\tilde \xi $
has compact support.
Lemma 6.4. The convolution algebra
![]() $C_c({\mathcal A}_\sigma )$
is isomorphic to the algebra
$C_c({\mathcal A}_\sigma )$
is isomorphic to the algebra
with convolution and involution given by
 $$ \begin{align*}(a*b)_{{\tilde{g}}}=\int_{G} a_{\tilde h} b_{\tilde{h}^{-1}{\tilde{g}}}\, \,d h\quad\text{and}\quad a^*_{{\tilde{g}}}=\Delta({\tilde{g}}) (a_{{\tilde{g}}^{-1}})^*,\end{align*} $$
$$ \begin{align*}(a*b)_{{\tilde{g}}}=\int_{G} a_{\tilde h} b_{\tilde{h}^{-1}{\tilde{g}}}\, \,d h\quad\text{and}\quad a^*_{{\tilde{g}}}=\Delta({\tilde{g}}) (a_{{\tilde{g}}^{-1}})^*,\end{align*} $$
where
![]() $\tilde {h}\in G_\sigma $
with
$\tilde {h}\in G_\sigma $
with
![]() $h=q(\tilde h)$
. Moreover, every section
$h=q(\tilde h)$
. Moreover, every section
![]() $a\in C_c(G_\sigma ,\mathcal A,\iota )$
can be written as a finite linear combination of functions of the form
$a\in C_c(G_\sigma ,\mathcal A,\iota )$
can be written as a finite linear combination of functions of the form
![]() ${\tilde {g}}\mapsto f({\tilde {g}})\tilde {a}_g$
,
${\tilde {g}}\mapsto f({\tilde {g}})\tilde {a}_g$
,
![]() $g=q({\tilde {g}})$
, with
$g=q({\tilde {g}})$
, with
![]() $f\in C_c(G_\sigma , \iota )$
and
$f\in C_c(G_\sigma , \iota )$
and
![]() $\tilde {a}\in C_c(\mathcal A)$
.
$\tilde {a}\in C_c(\mathcal A)$
.
Proof. It follows from Lemma 6.3 that
is a linear bijection. We need to check that it preserves convolution and involution. We first observe that by the conditions on the elements in
![]() $S(G_\sigma , \mathcal A, \iota )$
the integrand in the convolution integral in the lemma is constant on
$S(G_\sigma , \mathcal A, \iota )$
the integrand in the convolution integral in the lemma is constant on
![]() $\mathbb T$
-cosets in
$\mathbb T$
-cosets in
![]() $G_\sigma $
. Therefore, the integral makes sense. Now, if
$G_\sigma $
. Therefore, the integral makes sense. Now, if
![]() $\tilde {a}:G\to {\mathcal A}_\sigma $
is given by
$\tilde {a}:G\to {\mathcal A}_\sigma $
is given by
![]() $\tilde {a}_g=[a_{{\tilde {g}}}, {\tilde {g}}]$
for
$\tilde {a}_g=[a_{{\tilde {g}}}, {\tilde {g}}]$
for
![]() ${\tilde {g}}\in G_\sigma $
with
${\tilde {g}}\in G_\sigma $
with
![]() $q({\tilde {g}})=g$
, and similarly for b, we compute
$q({\tilde {g}})=g$
, and similarly for b, we compute
 $$ \begin{align*} (\tilde{a}*\tilde{b})_g&=\int_G \tilde{a}_h\tilde{b}_{h^{-1}g}\,\,d h = \int_G [a_{\tilde{h}}, \tilde{h}][b_{\tilde{h}^{-1}{\tilde{g}}}, \tilde{h}^{-1}{\tilde{g}}]\,\,d h\\ &=\int_G [a_{\tilde{h}}b_{\tilde{h}^{-1}{\tilde{g}}},{\tilde{g}}]\,\,d h =[(a*b)_{{\tilde{g}}},{\tilde{g}}], \end{align*} $$
$$ \begin{align*} (\tilde{a}*\tilde{b})_g&=\int_G \tilde{a}_h\tilde{b}_{h^{-1}g}\,\,d h = \int_G [a_{\tilde{h}}, \tilde{h}][b_{\tilde{h}^{-1}{\tilde{g}}}, \tilde{h}^{-1}{\tilde{g}}]\,\,d h\\ &=\int_G [a_{\tilde{h}}b_{\tilde{h}^{-1}{\tilde{g}}},{\tilde{g}}]\,\,d h =[(a*b)_{{\tilde{g}}},{\tilde{g}}], \end{align*} $$
which settles the claim on the convolution. We leave it as an exercise to check that the involution is preserved as well.
For the final assertion we use the fact that by Gleason’s theorem [Reference Gleason18, Theorem 4.1] there always exists a local continuous section for the quotient map
![]() $q:G_\sigma \to G$
. Thus, given an element
$q:G_\sigma \to G$
. Thus, given an element
![]() $a\in C_c(G_\sigma ,\mathcal A,\iota )$
, we can find a finite open cover
$a\in C_c(G_\sigma ,\mathcal A,\iota )$
, we can find a finite open cover
![]() $U_1,\ldots , U_l$
of
$U_1,\ldots , U_l$
of
![]() $K:=q(\operatorname {{\mathrm {supp}}} a)\subseteq G$
together with continuous maps
$K:=q(\operatorname {{\mathrm {supp}}} a)\subseteq G$
together with continuous maps
![]() $\mathfrak {s}_i:U_i\to q^{-1}(U_i)$
such that
$\mathfrak {s}_i:U_i\to q^{-1}(U_i)$
such that
![]() $q\circ \mathfrak {s}_i=\operatorname {{\mathrm {id}}}_{U_i}$
for all
$q\circ \mathfrak {s}_i=\operatorname {{\mathrm {id}}}_{U_i}$
for all
![]() $1\leq i\leq l$
. Let
$1\leq i\leq l$
. Let
![]() $\{\chi _i: 1\leq i\leq l\}\subseteq C_c^+(G)$
be a partition of the unit of K subordinate to
$\{\chi _i: 1\leq i\leq l\}\subseteq C_c^+(G)$
be a partition of the unit of K subordinate to
![]() $\{U_i: 1\leq i\leq l\}$
. For each
$\{U_i: 1\leq i\leq l\}$
. For each
![]() ${\tilde {g}}\in q^{-1}(U_i)$
there exists a unique element
${\tilde {g}}\in q^{-1}(U_i)$
there exists a unique element
![]() $z_{{\tilde {g}},i}\in \mathbb T$
such that
$z_{{\tilde {g}},i}\in \mathbb T$
such that
![]() ${\tilde {g}}=z_{{\tilde {g}},i}\mathfrak {s}_i(g)$
, with
${\tilde {g}}=z_{{\tilde {g}},i}\mathfrak {s}_i(g)$
, with
![]() $g=q({\tilde {g}})$
. We use this to define
$g=q({\tilde {g}})$
. We use this to define
![]() $f_i:G_\sigma \to \mathbb C$
by
$f_i:G_\sigma \to \mathbb C$
by
![]() $f_i({\tilde {g}})=\bar {z}_{{\tilde {g}},i}\sqrt {\chi _i(g)}$
for
$f_i({\tilde {g}})=\bar {z}_{{\tilde {g}},i}\sqrt {\chi _i(g)}$
for
![]() ${\tilde {g}}=z_{{\tilde {g}},i}\mathfrak {s}_i(g)\in q^{-1}(U_i)$
and
${\tilde {g}}=z_{{\tilde {g}},i}\mathfrak {s}_i(g)\in q^{-1}(U_i)$
and
![]() $0$
otherwise. Moreover, we define
$0$
otherwise. Moreover, we define
![]() $\tilde {a}_i\in C_c(\mathcal A)$
by
$\tilde {a}_i\in C_c(\mathcal A)$
by
![]() $\tilde {a}_i(g)=\sqrt {\chi _i(g)}a_{\mathfrak {s}_i(g)}$
for all
$\tilde {a}_i(g)=\sqrt {\chi _i(g)}a_{\mathfrak {s}_i(g)}$
for all
![]() $g\in U_i$
and
$g\in U_i$
and
![]() $0$
otherwise. Then for all
$0$
otherwise. Then for all
![]() ${\tilde {g}}\in G_\sigma $
we obtain, with
${\tilde {g}}\in G_\sigma $
we obtain, with
![]() $g=q({\tilde {g}})$
,
$g=q({\tilde {g}})$
,
 $$ \begin{align*} a({{\tilde{g}}})&=\sum_{i=1}^l\chi_i(g)a({{\tilde{g}}})=\sum_{g\in U_i}\chi_i(g)a({z_{{\tilde{g}},i}\mathfrak{s}_i(g)})\\ &=\sum_{g\in U_i} \bar{z}_{{\tilde{g}},i}\sqrt{\chi_i(g)}\sqrt{\chi_i(g)}a({\mathfrak{s}_i(g)}) =\sum_{i=1}^l f_i({\tilde{g}})\tilde{a}_i(g) \end{align*} $$
$$ \begin{align*} a({{\tilde{g}}})&=\sum_{i=1}^l\chi_i(g)a({{\tilde{g}}})=\sum_{g\in U_i}\chi_i(g)a({z_{{\tilde{g}},i}\mathfrak{s}_i(g)})\\ &=\sum_{g\in U_i} \bar{z}_{{\tilde{g}},i}\sqrt{\chi_i(g)}\sqrt{\chi_i(g)}a({\mathfrak{s}_i(g)}) =\sum_{i=1}^l f_i({\tilde{g}})\tilde{a}_i(g) \end{align*} $$
and the result follows.
In the special case where the extension
![]() $\sigma =(\mathbb T\hookrightarrow G_\sigma \stackrel {q}{\twoheadrightarrow } G)$
admits a continuous section
$\sigma =(\mathbb T\hookrightarrow G_\sigma \stackrel {q}{\twoheadrightarrow } G)$
admits a continuous section
![]() $\mathfrak {s}:G\to G_\sigma $
for the quotient map q with
$\mathfrak {s}:G\to G_\sigma $
for the quotient map q with
![]() $\mathfrak {s}(e)=e$
, the twisted Fell bundle
$\mathfrak {s}(e)=e$
, the twisted Fell bundle
![]() ${\mathcal A}_\sigma $
has a much more direct description as follows. Let
${\mathcal A}_\sigma $
has a much more direct description as follows. Let
![]() $\omega =\partial \mathfrak {s}\in Z^2(G,\mathbb T)$
denote the cocycle corresponding to
$\omega =\partial \mathfrak {s}\in Z^2(G,\mathbb T)$
denote the cocycle corresponding to
![]() $\sigma $
and
$\sigma $
and
![]() $\mathfrak {s}$
. Since
$\mathfrak {s}$
. Since
![]() $\mathfrak {s}$
is continuous,
$\mathfrak {s}$
is continuous,
![]() $\omega $
is continuous as well. We may then define an
$\omega $
is continuous as well. We may then define an
![]() $\omega $
-twisted multiplication on the Banach bundle
$\omega $
-twisted multiplication on the Banach bundle
![]() $\mathcal A$
by the formulas
$\mathcal A$
by the formulas
This gives a new Fell bundle structure on the Banach bundle
![]() $\mathcal A$
, which we denote by
$\mathcal A$
, which we denote by
![]() ${\mathcal A}_\omega $
. For the following proposition recall that for any fixed element
${\mathcal A}_\omega $
. For the following proposition recall that for any fixed element
![]() ${\tilde {g}}\in q^{-1}(G)\subseteq G_\sigma $
the elements in the fibre
${\tilde {g}}\in q^{-1}(G)\subseteq G_\sigma $
the elements in the fibre
![]() $A_{\sigma ,g}$
have a unique representative of the form
$A_{\sigma ,g}$
have a unique representative of the form
![]() $(a_g, {\tilde {g}})\in q^*\mathcal A$
. In particular, if we apply this to
$(a_g, {\tilde {g}})\in q^*\mathcal A$
. In particular, if we apply this to
![]() ${\tilde {g}}=\mathfrak {s}(g)$
we can identify
${\tilde {g}}=\mathfrak {s}(g)$
we can identify
![]() $A_g$
with
$A_g$
with
![]() $A_{\sigma ,g}$
via
$A_{\sigma ,g}$
via
![]() $a_g\mapsto [a_g, \mathfrak {s}(g)]$
.
$a_g\mapsto [a_g, \mathfrak {s}(g)]$
.
Proposition 6.5. Let
![]() $\mathcal A$
,
$\mathcal A$
,
![]() $\sigma $
and
$\sigma $
and
![]() $\omega $
be as above. Then the map
$\omega $
be as above. Then the map
is an isomorphism of Fell bundles.
Proof. As observed above, the map
![]() $\Theta $
is a bijection on each fibre, so we only need to see that it is a homeomorphism and preserves multiplication and involution. Indeed, arguments similar to those given in the proof of Lemma 6.3 show that
$\Theta $
is a bijection on each fibre, so we only need to see that it is a homeomorphism and preserves multiplication and involution. Indeed, arguments similar to those given in the proof of Lemma 6.3 show that
![]() $\Theta $
is a homeomorphism.
$\Theta $
is a homeomorphism.
To check that
![]() $\Theta $
is multiplicative let
$\Theta $
is multiplicative let
![]() $[a_g, \mathfrak {s}(g)]\in A_{\sigma , g}$
and
$[a_g, \mathfrak {s}(g)]\in A_{\sigma , g}$
and
![]() $[b_h, \mathfrak {s}(h)]\in A_{\sigma ,h}$
. Then
$[b_h, \mathfrak {s}(h)]\in A_{\sigma ,h}$
. Then
 $$ \begin{align*} \Theta(a_g\cdot_{\omega}b_h)&=\Theta(\overline{\omega(g,h)}a_gb_h)\\ &=[\overline{\omega(g,h)}a_gb_h, \mathfrak{s}(gh)]=[a_gb_h, \omega(g,h)\mathfrak{s}(gh)]\\ &=[a_gb_h, \mathfrak{s}(g)\mathfrak{s}(h)]=[a_g, \mathfrak{s}(g)][b_h, \mathfrak{s}(h)]. \end{align*} $$
$$ \begin{align*} \Theta(a_g\cdot_{\omega}b_h)&=\Theta(\overline{\omega(g,h)}a_gb_h)\\ &=[\overline{\omega(g,h)}a_gb_h, \mathfrak{s}(gh)]=[a_gb_h, \omega(g,h)\mathfrak{s}(gh)]\\ &=[a_gb_h, \mathfrak{s}(g)\mathfrak{s}(h)]=[a_g, \mathfrak{s}(g)][b_h, \mathfrak{s}(h)]. \end{align*} $$
A similar computation shows that
![]() $\Theta $
also preserves involution.
$\Theta $
also preserves involution.
In what follows, if
![]() $\mathcal A$
is a Fell bundle over G, and
$\mathcal A$
is a Fell bundle over G, and
![]() $\sigma =(\mathbb T\hookrightarrow G_\sigma \stackrel {q}\twoheadrightarrow G)$
is a twist for G, then we want to prove that the algebras of kernels
$\sigma =(\mathbb T\hookrightarrow G_\sigma \stackrel {q}\twoheadrightarrow G)$
is a twist for G, then we want to prove that the algebras of kernels
![]() $\Bbbk ({\mathcal A})$
and
$\Bbbk ({\mathcal A})$
and
![]() $\Bbbk ({{\mathcal A}_\sigma })$
are isomorphic. Recall that
$\Bbbk ({{\mathcal A}_\sigma })$
are isomorphic. Recall that
![]() $\Bbbk ({\mathcal A})\cong C^*(\mathcal A)\rtimes _{\delta _{\mathcal A}}\widehat {G}$
and that under this isomorphism the structural homomorphism
$\Bbbk ({\mathcal A})\cong C^*(\mathcal A)\rtimes _{\delta _{\mathcal A}}\widehat {G}$
and that under this isomorphism the structural homomorphism
![]() $j_{C_0(G)}$
and the dual action
$j_{C_0(G)}$
and the dual action
![]() $\widehat {\delta _{\mathcal A}}$
are given by
$\widehat {\delta _{\mathcal A}}$
are given by
Thus the dual weak
![]() $G\rtimes G$
-algebra
$G\rtimes G$
-algebra
![]() $(C^*(\mathcal A)\rtimes _{\delta _{\mathcal A}}\widehat {G}, \widehat {\delta _{\mathcal A}}, j_{C_0(G)})$
is given by
$(C^*(\mathcal A)\rtimes _{\delta _{\mathcal A}}\widehat {G}, \widehat {\delta _{\mathcal A}}, j_{C_0(G)})$
is given by
Similarly, the dual weak
![]() $G\rtimes G$
-algebra for
$G\rtimes G$
-algebra for
![]() $(C^*({\mathcal A}_\sigma ), \delta _{{\mathcal A}_\sigma })$
is given by the triple
$(C^*({\mathcal A}_\sigma ), \delta _{{\mathcal A}_\sigma })$
is given by the triple
We aim to show that the
![]() $\sigma $
-twisted weak
$\sigma $
-twisted weak
![]() $G\rtimes G$
-algebra
$G\rtimes G$
-algebra
![]() $(B_\sigma ,\beta _\sigma ,\phi _\sigma )$
of Definition 5.1 is isomorphic to
$(B_\sigma ,\beta _\sigma ,\phi _\sigma )$
of Definition 5.1 is isomorphic to
![]() $(C,\gamma ,\psi )$
. This will then show that for
$(C,\gamma ,\psi )$
. This will then show that for
![]() $(A,\delta )=(C_\mu ^*(\mathcal A), \delta _\mu )$
and any duality crossed-product functor
$(A,\delta )=(C_\mu ^*(\mathcal A), \delta _\mu )$
and any duality crossed-product functor
![]() $\rtimes _\mu $
the deformed cosystem
$\rtimes _\mu $
the deformed cosystem
![]() $(A^\sigma , \delta ^\sigma )$
is isomorphic to
$(A^\sigma , \delta ^\sigma )$
is isomorphic to
![]() $(C_\mu ^*({\mathcal A}_\sigma ), \delta ^\sigma _\mu )$
.
$(C_\mu ^*({\mathcal A}_\sigma ), \delta ^\sigma _\mu )$
.
We start with a description of
![]() $\Bbbk _c({{\mathcal A}_\sigma })$
and
$\Bbbk _c({{\mathcal A}_\sigma })$
and
![]() $\Bbbk _{c,b} ({{\mathcal A}_\sigma })$
as follows.
$\Bbbk _{c,b} ({{\mathcal A}_\sigma })$
as follows.
Lemma 6.6. The algebra
![]() $\Bbbk _c({{\mathcal A}_\sigma })$
can be identified with the space of continuous compactly supported functions
$\Bbbk _c({{\mathcal A}_\sigma })$
can be identified with the space of continuous compactly supported functions
![]() $k: G_\sigma \times G_\sigma \to \mathcal A$
satisfying the relations
$k: G_\sigma \times G_\sigma \to \mathcal A$
satisfying the relations
Under this identification, convolution and involution are given by the formulas
 $$ \begin{align} \begin{aligned} k*l({\tilde{g}}, {\tilde{h}})&=\int_{G} k({\tilde{g}},{\tilde{r}})\cdot l({\tilde{r}},{\tilde{h}})\,d r\quad\text{and}\\ k^*({\tilde{g}}, {\tilde{h}})&=k({\tilde{h}}, {\tilde{g}})^*, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} k*l({\tilde{g}}, {\tilde{h}})&=\int_{G} k({\tilde{g}},{\tilde{r}})\cdot l({\tilde{r}},{\tilde{h}})\,d r\quad\text{and}\\ k^*({\tilde{g}}, {\tilde{h}})&=k({\tilde{h}}, {\tilde{g}})^*, \end{aligned} \end{align} $$
where
![]() $r=q({\tilde {r}})$
and the product
$r=q({\tilde {r}})$
and the product
![]() $\cdot $
and involution
$\cdot $
and involution
![]() $^*$
are taken from
$^*$
are taken from
![]() $\mathcal A$
. Similarly, the algebra
$\mathcal A$
. Similarly, the algebra
![]() $\Bbbk _{c,b} ({{\mathcal A}_\sigma })$
can be identified with the bounded measurable compactly supported functions satisfying (6-2).
$\Bbbk _{c,b} ({{\mathcal A}_\sigma })$
can be identified with the bounded measurable compactly supported functions satisfying (6-2).
Note that it follows from (6-2) that the integrand in the convolution integral only depends on
![]() $r=q({\tilde {r}})$
, so the formula makes sense.
$r=q({\tilde {r}})$
, so the formula makes sense.
Proof. The proof can be done similarly to the proof of Lemma 6.3. If
![]() $\tilde {k}\in \Bbbk _c({{\mathcal A}_\sigma })$
, then for
$\tilde {k}\in \Bbbk _c({{\mathcal A}_\sigma })$
, then for
![]() $(t,g)\in G\times G$
and
$(t,g)\in G\times G$
and
![]() $({\tilde {g}},{\tilde {h}})\in q^{-1}(g)\times q^{-1}(h)$
we have
$({\tilde {g}},{\tilde {h}})\in q^{-1}(g)\times q^{-1}(h)$
we have
![]() $\tilde {k}(g,h)=A_{\sigma , gh^{-1}}$
. Hence, there is a unique element
$\tilde {k}(g,h)=A_{\sigma , gh^{-1}}$
. Hence, there is a unique element
![]() $k({\tilde {g}}, {\tilde {h}})\in A_{gh^{-1}}$
such that
$k({\tilde {g}}, {\tilde {h}})\in A_{gh^{-1}}$
such that
![]() $\tilde {k}(g,h)=[k({\tilde {g}},{\tilde {h}}), {\tilde {g}}{\tilde {h}}^{-1}]$
. Exactly as in the proof of Lemma 6.3 we can check that
$\tilde {k}(g,h)=[k({\tilde {g}},{\tilde {h}}), {\tilde {g}}{\tilde {h}}^{-1}]$
. Exactly as in the proof of Lemma 6.3 we can check that
![]() $\tilde {k}\leftrightarrow k$
gives a bijection between sections of
$\tilde {k}\leftrightarrow k$
gives a bijection between sections of
![]() ${\mathcal A}_\sigma $
and functions as in (6-2), and that
${\mathcal A}_\sigma $
and functions as in (6-2), and that
![]() $\tilde {k}$
is continuous (with compact support) if and only if k is. It is then straightforward to check the formulas for convolution and involution as in (6-3).
$\tilde {k}$
is continuous (with compact support) if and only if k is. It is then straightforward to check the formulas for convolution and involution as in (6-3).
Remark 6.7. Using Lemma 6.3, it follows from (3-1) that the kernel
![]() $k_{a,f}$
for
$k_{a,f}$
for
![]() $a\in C_c({\mathcal A}_\sigma )$
and
$a\in C_c({\mathcal A}_\sigma )$
and
![]() $f\in C_c(G)$
can be identified with the function
$f\in C_c(G)$
can be identified with the function
![]() $k_{a,f}:G_\sigma \times G_\sigma \to \mathcal A$
given by
$k_{a,f}:G_\sigma \times G_\sigma \to \mathcal A$
given by
Since
![]() $(z\tilde g)(u\tilde h)^{-1}=z\overline u \tilde g\tilde h^{-1}$
and
$(z\tilde g)(u\tilde h)^{-1}=z\overline u \tilde g\tilde h^{-1}$
and
![]() $a(z\tilde g)=\overline z a(\tilde g)\in A_g$
, these kernels satisfy (6-2).
$a(z\tilde g)=\overline z a(\tilde g)\in A_g$
, these kernels satisfy (6-2).
From now on, we always identify
![]() $\Bbbk _c({{\mathcal A}_\sigma })$
with the set of functions
$\Bbbk _c({{\mathcal A}_\sigma })$
with the set of functions
![]() $k:G_\sigma \times G_\sigma \to \mathcal A$
as in Lemma 6.6 above. In the following proposition let
$k:G_\sigma \times G_\sigma \to \mathcal A$
as in Lemma 6.6 above. In the following proposition let
![]() $\mathfrak {s}:G\to G_\sigma $
be any Borel cross-section for the quotient map
$\mathfrak {s}:G\to G_\sigma $
be any Borel cross-section for the quotient map
![]() $q:G_\sigma \to G$
, and let
$q:G_\sigma \to G$
, and let
![]() $\omega =\partial \mathfrak {s}\in Z^2(G,\mathbb T)$
be the associated Borel cocycle.
$\omega =\partial \mathfrak {s}\in Z^2(G,\mathbb T)$
be the associated Borel cocycle.
Proposition 6.8. Given a twist
![]() $\sigma =(\mathbb T\hookrightarrow G_\sigma \twoheadrightarrow G)$
and a Fell bundle
$\sigma =(\mathbb T\hookrightarrow G_\sigma \twoheadrightarrow G)$
and a Fell bundle
![]() $\mathcal A$
over G, with associated twisted Fell bundle
$\mathcal A$
over G, with associated twisted Fell bundle
![]() ${\mathcal A}_\sigma $
, we have an isomorphism of kernel
${\mathcal A}_\sigma $
, we have an isomorphism of kernel
![]() $C^*$
-algebras
$C^*$
-algebras
The isomorphism
![]() $\Phi $
commutes with the canonical structural homomorphisms from
$\Phi $
commutes with the canonical structural homomorphisms from
![]() $C_0(G)$
and sends the dual G-action
$C_0(G)$
and sends the dual G-action
![]() $\widehat {\delta _{{\mathcal A}_\sigma }}$
on
$\widehat {\delta _{{\mathcal A}_\sigma }}$
on
![]() $\Bbbk ({{\mathcal A}_\sigma })$
to the G-action
$\Bbbk ({{\mathcal A}_\sigma })$
to the G-action
![]() $\widehat {\delta }^\omega $
on
$\widehat {\delta }^\omega $
on
![]() $\Bbbk ({\mathcal A})$
given by
$\Bbbk ({\mathcal A})$
given by
for all
![]() $k\in \Bbbk _{c,b} ({\mathcal A})$
,
$k\in \Bbbk _{c,b} ({\mathcal A})$
,
![]() $t,g,h\in G$
.
$t,g,h\in G$
.
Proof. The discussion preceding Proposition 3.2 shows that we can regard
![]() $\Bbbk ({\mathcal A})$
also as the enveloping
$\Bbbk ({\mathcal A})$
also as the enveloping
![]() $C^*$
-algebra of the Banach
$C^*$
-algebra of the Banach
![]() $^*$
-algebra
$^*$
-algebra
![]() $\Bbbk _2 ({\mathcal A})$
, the completion of the space
$\Bbbk _2 ({\mathcal A})$
, the completion of the space
![]() $\Bbbk _{c,b} ({\mathcal A})$
with respect to the
$\Bbbk _{c,b} ({\mathcal A})$
with respect to the
![]() $L^2$
-norm
$L^2$
-norm
![]() $\|k\|_2=(\int _{G\times G} \| k(g,h)\|^2\,\,d g\,d h)^{1/2}$
. Now given the Borel section
$\|k\|_2=(\int _{G\times G} \| k(g,h)\|^2\,\,d g\,d h)^{1/2}$
. Now given the Borel section
![]() $\mathfrak {s}\colon G\to G_\sigma $
, we define
$\mathfrak {s}\colon G\to G_\sigma $
, we define
Straightforward computations show that this map preserves convolution and involution, and is isometric for
![]() $\|\cdot \|_2$
. To see that it is surjective, observe that for every
$\|\cdot \|_2$
. To see that it is surjective, observe that for every
![]() $l\in \Bbbk _{c,b} ({\mathcal A})$
we can define
$l\in \Bbbk _{c,b} ({\mathcal A})$
we can define
![]() $k\in \Bbbk _{c,b} ({{\mathcal A}_\sigma })$
by
$k\in \Bbbk _{c,b} ({{\mathcal A}_\sigma })$
by
![]() $k(\mathfrak {s}(g)z, \mathfrak {s}(h)u):=\bar {z}ul(g,h)$
, and then
$k(\mathfrak {s}(g)z, \mathfrak {s}(h)u):=\bar {z}ul(g,h)$
, and then
![]() $l=\Phi (k)$
.
$l=\Phi (k)$
.
It follows that
![]() $\Phi $
extends to an isometric isomorphism between
$\Phi $
extends to an isometric isomorphism between
![]() $\Bbbk _2 ({{\mathcal A}_\sigma })$
and
$\Bbbk _2 ({{\mathcal A}_\sigma })$
and
![]() $\Bbbk _2 ({\mathcal A})$
, and hence to their enveloping
$\Bbbk _2 ({\mathcal A})$
, and hence to their enveloping
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $\Bbbk ({{\mathcal A}_\sigma })$
and
$\Bbbk ({{\mathcal A}_\sigma })$
and
![]() $\Bbbk ({\mathcal A})$
. It follows from (3-2) that this isomorphism preserves the structure maps
$\Bbbk ({\mathcal A})$
. It follows from (3-2) that this isomorphism preserves the structure maps
![]() $j_{C_0(G)}$
and
$j_{C_0(G)}$
and
![]() $j_{C_0(G)}^\sigma $
. Finally, for the dual actions we compute
$j_{C_0(G)}^\sigma $
. Finally, for the dual actions we compute
 $$ \begin{align*} \Phi(\widehat{\delta^\sigma}_t(k))(g,h)&=\widehat{\delta^\sigma}_t(\mathfrak{s}(g),\mathfrak{s}(h))=\Delta(t)k(\mathfrak{s}(g)\mathfrak{s}(t),\mathfrak{s}(h)\mathfrak{s}(t))\\ &=\Delta(t)k(\omega(g,t)\mathfrak{s}(gt),\omega(h,t)\mathfrak{s}(h,t))=\Delta(t)\overline{\omega(g,t)}\omega(h,t)k(gt,ht). \end{align*} $$
$$ \begin{align*} \Phi(\widehat{\delta^\sigma}_t(k))(g,h)&=\widehat{\delta^\sigma}_t(\mathfrak{s}(g),\mathfrak{s}(h))=\Delta(t)k(\mathfrak{s}(g)\mathfrak{s}(t),\mathfrak{s}(h)\mathfrak{s}(t))\\ &=\Delta(t)k(\omega(g,t)\mathfrak{s}(gt),\omega(h,t)\mathfrak{s}(h,t))=\Delta(t)\overline{\omega(g,t)}\omega(h,t)k(gt,ht). \end{align*} $$
This yields the final assertion involving the dual actions.
The above proposition provides the main step of the proof of the following theorem.
Theorem 6.9. Let
![]() $\mathcal A\to G$
be a Fell bundle and let
$\mathcal A\to G$
be a Fell bundle and let
![]() $\sigma =(\mathbb T\hookrightarrow G_\sigma \twoheadrightarrow G)$
be a twist over G. Then the deformation
$\sigma =(\mathbb T\hookrightarrow G_\sigma \twoheadrightarrow G)$
be a twist over G. Then the deformation
![]() $(B_\sigma , \beta _\sigma , \phi _\sigma )$
of the weak
$(B_\sigma , \beta _\sigma , \phi _\sigma )$
of the weak
![]() $G\rtimes G$
-algebra
$G\rtimes G$
-algebra
![]() $(B, \beta ,\phi )=(\Bbbk ({\mathcal A}), \widehat {\delta _{\mathcal A}}, j_{C_0(G)})$
is isomorphic to
$(B, \beta ,\phi )=(\Bbbk ({\mathcal A}), \widehat {\delta _{\mathcal A}}, j_{C_0(G)})$
is isomorphic to
![]() $(\Bbbk ({{\mathcal A}_\sigma }), \widehat {\delta _{{\mathcal A}_\sigma }}, j_{C_0(G)}^\sigma )$
. Hence, for every duality crossed-product functor
$(\Bbbk ({{\mathcal A}_\sigma }), \widehat {\delta _{{\mathcal A}_\sigma }}, j_{C_0(G)}^\sigma )$
. Hence, for every duality crossed-product functor
![]() $\rtimes _\mu $
for G the dual G-coaction
$\rtimes _\mu $
for G the dual G-coaction
![]() $(C^*_\mu ({\mathcal A}_\sigma ), \delta ^\sigma _\mu )$
is isomorphic to the deformation
$(C^*_\mu ({\mathcal A}_\sigma ), \delta ^\sigma _\mu )$
is isomorphic to the deformation
![]() $(A^\sigma , \delta ^\sigma )$
of
$(A^\sigma , \delta ^\sigma )$
of
![]() $(A,\delta )=(C_\mu ^*(\mathcal A), \delta _\mu )$
.
$(A,\delta )=(C_\mu ^*(\mathcal A), \delta _\mu )$
.
Proof. We know from Corollary 3.5 that the structural homomorphism
![]() $\phi \colon C_0(G)\to \mathcal M(\Bbbk ({\mathcal A}))$
extends to
$\phi \colon C_0(G)\to \mathcal M(\Bbbk ({\mathcal A}))$
extends to
![]() $\bar \phi \colon L^\infty (G)\to \mathcal M(\Bbbk ({\mathcal A}))$
. It follows from [Reference Buss and Echterhoff7, Proposition 5.15] that the deformed
$\bar \phi \colon L^\infty (G)\to \mathcal M(\Bbbk ({\mathcal A}))$
. It follows from [Reference Buss and Echterhoff7, Proposition 5.15] that the deformed
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $B_\sigma =\Bbbk ({\mathcal A})_\sigma $
is isomorphic to
$B_\sigma =\Bbbk ({\mathcal A})_\sigma $
is isomorphic to
![]() $B=\Bbbk ({\mathcal A})$
, which is also isomorphic to
$B=\Bbbk ({\mathcal A})$
, which is also isomorphic to
![]() $\Bbbk ({{\mathcal A}_\sigma })$
by Proposition 6.8. All these isomorphisms preserve the structural homomorphism from
$\Bbbk ({{\mathcal A}_\sigma })$
by Proposition 6.8. All these isomorphisms preserve the structural homomorphism from
![]() $C_0(G)$
, and the dual G-action on
$C_0(G)$
, and the dual G-action on
![]() $\Bbbk ({{\mathcal A}_\sigma })$
is sent to the action
$\Bbbk ({{\mathcal A}_\sigma })$
is sent to the action
![]() $\widehat {\delta }^\omega \colon G\curvearrowright \Bbbk ({\mathcal A})$
given by (6-5). This also equals the G-action
$\widehat {\delta }^\omega \colon G\curvearrowright \Bbbk ({\mathcal A})$
given by (6-5). This also equals the G-action
![]() $\text {Ad} U_\omega (t)\circ \widehat {\delta }$
, where
$\text {Ad} U_\omega (t)\circ \widehat {\delta }$
, where
![]() $U_\omega (t)=\bar \phi (u_\omega (t))$
, with
$U_\omega (t)=\bar \phi (u_\omega (t))$
, with
![]() $u_\omega (t)(g)=\overline {\omega (g,t)}$
. This is precisely the action that appears in [Reference Buss and Echterhoff7, Proposition 5.15]. It follows that
$u_\omega (t)(g)=\overline {\omega (g,t)}$
. This is precisely the action that appears in [Reference Buss and Echterhoff7, Proposition 5.15]. It follows that
![]() $(B_\sigma , \beta _\sigma , \phi _\sigma )\cong (\Bbbk ({{\mathcal A}_\sigma }), \widehat {\delta _{{\mathcal A}_\sigma }}, j_{C_0(G)}^\sigma )$
. The final assertion follows from Proposition 3.1 in combination with Proposition 2.1.
$(B_\sigma , \beta _\sigma , \phi _\sigma )\cong (\Bbbk ({{\mathcal A}_\sigma }), \widehat {\delta _{{\mathcal A}_\sigma }}, j_{C_0(G)}^\sigma )$
. The final assertion follows from Proposition 3.1 in combination with Proposition 2.1.
For use in the next section, we now want to give an alternative description of the isomorphism
![]() $(B_\sigma ,\beta _\sigma ,\phi _\sigma )\cong (\Bbbk ({{\mathcal A}_\sigma }), \widehat {\delta _{{\mathcal A}_\sigma }}, j_{C_0(G)}^\sigma )$
of the above theorem, which does not depend on a choice of a Borel section
$(B_\sigma ,\beta _\sigma ,\phi _\sigma )\cong (\Bbbk ({{\mathcal A}_\sigma }), \widehat {\delta _{{\mathcal A}_\sigma }}, j_{C_0(G)}^\sigma )$
of the above theorem, which does not depend on a choice of a Borel section
![]() $\mathfrak {s}:G\to G_\sigma $
. The need for this comes from the fact that in general, if
$\mathfrak {s}:G\to G_\sigma $
. The need for this comes from the fact that in general, if
is a continuous family of twists
![]() $\sigma _x=(\mathbb T\hookrightarrow G_{\sigma _x}\twoheadrightarrow G)$
,
$\sigma _x=(\mathbb T\hookrightarrow G_{\sigma _x}\twoheadrightarrow G)$
,
![]() $x\in X$
, as introduced in [Reference Buss and Echterhoff7] to study continuity properties of our deformation process, we do not know whether there exists a global Borel cross-section
$x\in X$
, as introduced in [Reference Buss and Echterhoff7] to study continuity properties of our deformation process, we do not know whether there exists a global Borel cross-section
![]() $\mathfrak {S}:X\times G\to \mathcal G_\Sigma $
that induces Borel cross-sections
$\mathfrak {S}:X\times G\to \mathcal G_\Sigma $
that induces Borel cross-sections
![]() $\mathfrak {s}_x:G\to G_{\sigma _x}$
in the fibres.
$\mathfrak {s}_x:G\to G_{\sigma _x}$
in the fibres.
To overcome this problem, if
![]() $(B,\beta ,\phi )=(\Bbbk ({\mathcal A}), \widehat {\delta _{\mathcal A}}, j_{C_0(G)})$
as above, recall the Hilbert B-module
$(B,\beta ,\phi )=(\Bbbk ({\mathcal A}), \widehat {\delta _{\mathcal A}}, j_{C_0(G)})$
as above, recall the Hilbert B-module
Given a section
![]() $\mathfrak {s}:G\to G_\sigma $
, it follows from Corollary 3.5, [Reference Buss and Echterhoff7, Proposition 5.15] and (3-2) that
$\mathfrak {s}:G\to G_\sigma $
, it follows from Corollary 3.5, [Reference Buss and Echterhoff7, Proposition 5.15] and (3-2) that
![]() ${\mathcal L}(G_\sigma ,B)\cong B$
as Hilbert B-modules with isomorphism given by
${\mathcal L}(G_\sigma ,B)\cong B$
as Hilbert B-modules with isomorphism given by
In order to provide an alternative description of
![]() ${\mathcal L}(G_\sigma ,B)$
, we let
${\mathcal L}(G_\sigma ,B)$
, we let
![]() $\mathcal X_c(\mathcal A)$
denote the set of compactly supported continuous functions
$\mathcal X_c(\mathcal A)$
denote the set of compactly supported continuous functions
for all
![]() $z\in \mathbb T$
,
$z\in \mathbb T$
,
![]() $\tilde g\in G_\sigma , h\in G$
with
$\tilde g\in G_\sigma , h\in G$
with
![]() $g=q(\tilde g)$
. Define a
$g=q(\tilde g)$
. Define a
![]() $\Bbbk _c({\mathcal A})$
-valued inner product on
$\Bbbk _c({\mathcal A})$
-valued inner product on
![]() $\mathcal X_c(\mathcal A)$
by
$\mathcal X_c(\mathcal A)$
by
 $$ \begin{align*} \langle\xi\!\mid\!\eta\rangle_{\Bbbk_c({\mathcal A})}(g,h)= \int_{G} \xi({\tilde{r}}, g)^*\eta({\tilde{r}}, h)\,d r. \end{align*} $$
$$ \begin{align*} \langle\xi\!\mid\!\eta\rangle_{\Bbbk_c({\mathcal A})}(g,h)= \int_{G} \xi({\tilde{r}}, g)^*\eta({\tilde{r}}, h)\,d r. \end{align*} $$
with
![]() $r=q({\tilde {r}})$
. As before, one checks that the integrand only depends on
$r=q({\tilde {r}})$
. As before, one checks that the integrand only depends on
![]() $r=q({\tilde {r}})\in G$
, so the integral makes sense. On the other hand, we have a
$r=q({\tilde {r}})\in G$
, so the integral makes sense. On the other hand, we have a
![]() $\Bbbk _c({{\mathcal A}_\sigma })$
-valued left inner product on
$\Bbbk _c({{\mathcal A}_\sigma })$
-valued left inner product on
![]() $\mathcal X_c(\mathcal A)$
given by the formula
$\mathcal X_c(\mathcal A)$
given by the formula
 $$ \begin{align*}{_{\Bbbk_c({{\mathcal A}_\sigma})}\langle\xi\!\mid\!\eta\rangle}({\tilde{g}}, {\tilde{h}})=\int_G \xi({\tilde{g}}, r)\eta({\tilde{h}}, r)^*\,d r.\end{align*} $$
$$ \begin{align*}{_{\Bbbk_c({{\mathcal A}_\sigma})}\langle\xi\!\mid\!\eta\rangle}({\tilde{g}}, {\tilde{h}})=\int_G \xi({\tilde{g}}, r)\eta({\tilde{h}}, r)^*\,d r.\end{align*} $$
One easily checks that
![]() ${_{\Bbbk _c({{\mathcal A}_\sigma })}\langle \xi , \eta \rangle }$
satisfies (6-2). Moreover, we have left and right actions of
${_{\Bbbk _c({{\mathcal A}_\sigma })}\langle \xi , \eta \rangle }$
satisfies (6-2). Moreover, we have left and right actions of
![]() $\Bbbk _c({{\mathcal A}_\sigma })$
and
$\Bbbk _c({{\mathcal A}_\sigma })$
and
![]() $\Bbbk _c({\mathcal A})$
on
$\Bbbk _c({\mathcal A})$
on
![]() $\mathcal X_c(\mathcal A)$
given on kernels by
$\mathcal X_c(\mathcal A)$
given on kernels by
 $$ \begin{align*} k\cdot\xi({\tilde{g}}, t)=\int_{G}k({\tilde{g}}, {\tilde{h}})\xi({\tilde{h}}, t)\,d h \end{align*} $$
$$ \begin{align*} k\cdot\xi({\tilde{g}}, t)=\int_{G}k({\tilde{g}}, {\tilde{h}})\xi({\tilde{h}}, t)\,d h \end{align*} $$
and
 $$ \begin{align*} \xi\cdot l({\tilde{g}}, t)=\int_{G}\xi({\tilde{g}}, r) l(r,t)\,d r. \end{align*} $$
$$ \begin{align*} \xi\cdot l({\tilde{g}}, t)=\int_{G}\xi({\tilde{g}}, r) l(r,t)\,d r. \end{align*} $$
One checks that these formulas satisfy the usual algebraic compatibility conditions for a pre-equivalence bimodule, as for instance the relation
![]() $_{\Bbbk _c({{\mathcal A}_\sigma })}\langle \xi \!\mid \!\eta \rangle \cdot \zeta =\xi \cdot \langle \eta \!\mid \!\zeta \rangle _{\Bbbk _c({\mathcal A})}$
for all
$_{\Bbbk _c({{\mathcal A}_\sigma })}\langle \xi \!\mid \!\eta \rangle \cdot \zeta =\xi \cdot \langle \eta \!\mid \!\zeta \rangle _{\Bbbk _c({\mathcal A})}$
for all
![]() $\xi ,\eta ,\zeta \in \mathcal X_c(\mathcal A)$
. Finally, we define an action
$\xi ,\eta ,\zeta \in \mathcal X_c(\mathcal A)$
. Finally, we define an action
![]() $\gamma :G_\sigma \curvearrowright \chi _c(\mathcal A)$
by
$\gamma :G_\sigma \curvearrowright \chi _c(\mathcal A)$
by
An easy computation shows that it is compatible with (the inflations to
![]() $G_\sigma $
of) the dual actions
$G_\sigma $
of) the dual actions
![]() $\widehat {\delta _{{\mathcal A}_\sigma }}$
on
$\widehat {\delta _{{\mathcal A}_\sigma }}$
on
![]() $\Bbbk _c({{\mathcal A}_\sigma })$
on the left and the Green twisted action
$\Bbbk _c({{\mathcal A}_\sigma })$
on the left and the Green twisted action
![]() $(\widehat {\delta _{\mathcal A}},\iota ^\sigma )$
on
$(\widehat {\delta _{\mathcal A}},\iota ^\sigma )$
on
![]() $\Bbbk ({\mathcal A})$
on the right.
$\Bbbk ({\mathcal A})$
on the right.
Proposition 6.10. The
![]() $\Bbbk _c({{\mathcal A}_\sigma })-\Bbbk _c({\mathcal A})$
-pre-equivalence bimodule
$\Bbbk _c({{\mathcal A}_\sigma })-\Bbbk _c({\mathcal A})$
-pre-equivalence bimodule
![]() $\mathcal X_c(\mathcal A)$
completes to give a
$\mathcal X_c(\mathcal A)$
completes to give a
![]() $\widehat {\delta _{{\mathcal A}_\sigma }}-(\widehat {\delta _{\mathcal A}}, \iota ^\sigma )$
-equivariant
$\widehat {\delta _{{\mathcal A}_\sigma }}-(\widehat {\delta _{\mathcal A}}, \iota ^\sigma )$
-equivariant
![]() $\Bbbk ({{\mathcal A}_\sigma })-\Bbbk ({\mathcal A})$
-equivalence bimodule
$\Bbbk ({{\mathcal A}_\sigma })-\Bbbk ({\mathcal A})$
-equivalence bimodule
![]() $(\mathcal X(\mathcal A), \gamma )$
. Moreover, the map
$(\mathcal X(\mathcal A), \gamma )$
. Moreover, the map
extends to an
![]() $(\mathrm {rt}^{\sigma }\otimes \widehat {\delta _{\mathcal A}})-\gamma $
-equivariant isomorphism of right Hilbert
$(\mathrm {rt}^{\sigma }\otimes \widehat {\delta _{\mathcal A}})-\gamma $
-equivariant isomorphism of right Hilbert
![]() $\Bbbk ({\mathcal A})$
-modules
$\Bbbk ({\mathcal A})$
-modules
![]() ${\mathcal L}(G_\sigma ,\Bbbk ({\mathcal A}))\xrightarrow \sim \mathcal X(\mathcal A)$
, which then induces an isomorphism of weak
${\mathcal L}(G_\sigma ,\Bbbk ({\mathcal A}))\xrightarrow \sim \mathcal X(\mathcal A)$
, which then induces an isomorphism of weak
![]() $G\rtimes G$
-algebras
$G\rtimes G$
-algebras
![]() $(B_\sigma ,\beta _\sigma ,\phi _\sigma )\cong (\Bbbk ({{\mathcal A}_\sigma }), \widehat {\delta _{{\mathcal A}_\sigma }}, j_{C_0(G)}^\sigma )$
for
$(B_\sigma ,\beta _\sigma ,\phi _\sigma )\cong (\Bbbk ({{\mathcal A}_\sigma }), \widehat {\delta _{{\mathcal A}_\sigma }}, j_{C_0(G)}^\sigma )$
for
![]() $(B,\beta ,\phi ):=(\Bbbk ({\mathcal A}), \widehat {\delta _{\mathcal A}}, j_{C_0(G)})$
.
$(B,\beta ,\phi ):=(\Bbbk ({\mathcal A}), \widehat {\delta _{\mathcal A}}, j_{C_0(G)})$
.
Proof. We use the second assertion for the proof of the first. Indeed, it is straightforward to check that
![]() $\Psi $
preserves the right inner product and actions and an argument as in the proof of Lemma 6.4, using continuous local sections and partitions of the unit, shows that it is also surjective. This implies that
$\Psi $
preserves the right inner product and actions and an argument as in the proof of Lemma 6.4, using continuous local sections and partitions of the unit, shows that it is also surjective. This implies that
![]() $\mathcal X_c(\mathcal A)$
is a right pre-Hilbert
$\mathcal X_c(\mathcal A)$
is a right pre-Hilbert
![]() $\Bbbk ({\mathcal A})$
-module and that
$\Bbbk ({\mathcal A})$
-module and that
![]() $\Psi $
extends to an isomorphism
$\Psi $
extends to an isomorphism
![]() $\Psi : {\mathcal L}(G_\sigma ,\Bbbk ({\mathcal A}))\xrightarrow \sim \mathcal X(\mathcal A)$
of right Hilbert
$\Psi : {\mathcal L}(G_\sigma ,\Bbbk ({\mathcal A}))\xrightarrow \sim \mathcal X(\mathcal A)$
of right Hilbert
![]() $\Bbbk ({\mathcal A})$
-modules. By the compatibility conditions of the pairings for
$\Bbbk ({\mathcal A})$
-modules. By the compatibility conditions of the pairings for
![]() $\mathcal X_c(\mathcal A)$
we further see that
$\mathcal X_c(\mathcal A)$
we further see that
![]() $B_\sigma :=\Bbbk ({\mathcal A})_\sigma =\mathbb K({\mathcal L}(G_\sigma ,\Bbbk ({\mathcal A})))\cong \mathbb K(\mathcal X(\mathcal A))$
is a
$B_\sigma :=\Bbbk ({\mathcal A})_\sigma =\mathbb K({\mathcal L}(G_\sigma ,\Bbbk ({\mathcal A})))\cong \mathbb K(\mathcal X(\mathcal A))$
is a
![]() $C^*$
-completion of
$C^*$
-completion of
![]() $\Bbbk _c({{\mathcal A}_\sigma })$
. We need to show that it coincides with
$\Bbbk _c({{\mathcal A}_\sigma })$
. We need to show that it coincides with
![]() $\Bbbk ({{\mathcal A}_\sigma })$
. For this it suffices to show that the left action of
$\Bbbk ({{\mathcal A}_\sigma })$
. For this it suffices to show that the left action of
![]() $\Bbbk _c({{\mathcal A}_\sigma })$
on
$\Bbbk _c({{\mathcal A}_\sigma })$
on
![]() $\mathcal X_c(\mathcal A)$
extends faithfully to a left action of
$\mathcal X_c(\mathcal A)$
extends faithfully to a left action of
![]() $\Bbbk ({{\mathcal A}_\sigma })$
on
$\Bbbk ({{\mathcal A}_\sigma })$
on
![]() $\mathcal X(\mathcal A)$
. For this we choose a Borel section
$\mathcal X(\mathcal A)$
. For this we choose a Borel section
![]() $\mathfrak {s}:G\to G_\sigma $
and recall the isomorphism
$\mathfrak {s}:G\to G_\sigma $
and recall the isomorphism
![]() $\Theta : {\mathcal L}(G_\sigma , \Bbbk ({\mathcal A}))\xrightarrow \sim \Bbbk ({\mathcal A})$
as right Hilbert
$\Theta : {\mathcal L}(G_\sigma , \Bbbk ({\mathcal A}))\xrightarrow \sim \Bbbk ({\mathcal A})$
as right Hilbert
![]() $\Bbbk ({\mathcal A})$
-modules as in (6-6). Then the composition of isomorphisms
$\Bbbk ({\mathcal A})$
-modules as in (6-6). Then the composition of isomorphisms
sends a function
![]() $\xi \in \mathcal X_c(\mathcal A)$
to the function
$\xi \in \mathcal X_c(\mathcal A)$
to the function
![]() $\tilde \xi \in \Bbbk _c({\mathcal A})$
given by
$\tilde \xi \in \Bbbk _c({\mathcal A})$
given by
![]() $\tilde \xi (g,h):=\xi (\mathfrak {s}(g),h)$
. A simple computation then shows that
$\tilde \xi (g,h):=\xi (\mathfrak {s}(g),h)$
. A simple computation then shows that
where
![]() $\Phi :\Bbbk ({{\mathcal A}_\sigma })\xrightarrow \sim \Bbbk ({\mathcal A})$
is the isomorphism of (6-4). This proves that the left action is bounded and extends faithfully to a left action of
$\Phi :\Bbbk ({{\mathcal A}_\sigma })\xrightarrow \sim \Bbbk ({\mathcal A})$
is the isomorphism of (6-4). This proves that the left action is bounded and extends faithfully to a left action of
![]() $\Bbbk ({{\mathcal A}_\sigma })$
on
$\Bbbk ({{\mathcal A}_\sigma })$
on
![]() $\mathcal X(\mathcal A)$
. To complete the proof, we need to check that
$\mathcal X(\mathcal A)$
. To complete the proof, we need to check that
![]() $\Psi $
is
$\Psi $
is
![]() $\gamma -\mathrm {rt}^\sigma \otimes \widehat {\delta _{\mathcal A}}$
-equivariant and that it intertwines the left structure maps
$\gamma -\mathrm {rt}^\sigma \otimes \widehat {\delta _{\mathcal A}}$
-equivariant and that it intertwines the left structure maps
![]() $j_{C_0(G)}^\sigma :C_0(G)\to {\mathbb B}_{\Bbbk ({\mathcal A})}(\chi (\mathcal A))$
with the left action
$j_{C_0(G)}^\sigma :C_0(G)\to {\mathbb B}_{\Bbbk ({\mathcal A})}(\chi (\mathcal A))$
with the left action
![]() $\phi _\sigma :C_0(G)\to {\mathbb B}_{\Bbbk ({\mathcal A})}({\mathcal L}(G_\sigma ,\Bbbk ({\mathcal A})))$
induced from the left action of
$\phi _\sigma :C_0(G)\to {\mathbb B}_{\Bbbk ({\mathcal A})}({\mathcal L}(G_\sigma ,\Bbbk ({\mathcal A})))$
induced from the left action of
![]() $C_0(G)$
on
$C_0(G)$
on
![]() $C_0(G_\sigma ,\iota )$
by pointwise multiplication. We do the first and leave the second to the reader: for all
$C_0(G_\sigma ,\iota )$
by pointwise multiplication. We do the first and leave the second to the reader: for all
![]() $f\in C_0(G_\sigma )$
and
$f\in C_0(G_\sigma )$
and
![]() $k\in \Bbbk _c({\mathcal A})$
we compute
$k\in \Bbbk _c({\mathcal A})$
we compute
 $$ \begin{align*} \Psi((\mathrm{rt}^{\sigma}\otimes\widehat{\delta_{\mathcal A}})_{{\tilde{g}}}(f\otimes k))({\tilde{h}}, r)&= \Psi(\mathrm{rt}^\sigma_{{\tilde{g}}}(f)\otimes \widehat{\delta_{\mathcal A}}_{{\tilde{g}}}(k))({\tilde{h}},r)\\ &=f({\tilde{h}}{\tilde{g}})\Delta(g)k(hg,rg)\\ &=\Delta(g)(f({\tilde{h}}{\tilde{g}})k(hg, rg))\\ &=\gamma_{{\tilde{g}}}(\Psi(f\otimes k))({\tilde{h}},r) \end{align*} $$
$$ \begin{align*} \Psi((\mathrm{rt}^{\sigma}\otimes\widehat{\delta_{\mathcal A}})_{{\tilde{g}}}(f\otimes k))({\tilde{h}}, r)&= \Psi(\mathrm{rt}^\sigma_{{\tilde{g}}}(f)\otimes \widehat{\delta_{\mathcal A}}_{{\tilde{g}}}(k))({\tilde{h}},r)\\ &=f({\tilde{h}}{\tilde{g}})\Delta(g)k(hg,rg)\\ &=\Delta(g)(f({\tilde{h}}{\tilde{g}})k(hg, rg))\\ &=\gamma_{{\tilde{g}}}(\Psi(f\otimes k))({\tilde{h}},r) \end{align*} $$
for all
![]() ${\tilde {g}},{\tilde {h}}\in G_\sigma $
,
${\tilde {g}},{\tilde {h}}\in G_\sigma $
,
![]() $r\in G$
such that
$r\in G$
such that
![]() $g=q({\tilde {g}}), h=q({\tilde {h}})$
. This finishes the proof.
$g=q({\tilde {g}}), h=q({\tilde {h}})$
. This finishes the proof.
7 Continuous fields
In this section we study continuity properties of deformation of cross-sectional algebras of Fell bundles with respect to a continuous family of twists. Our results extend results of Raeburn in [Reference Raeburn32] who considered deformation of Fell bundles by continuous families of circle-valued
![]() $2$
-cocycles of discrete amenable groups G. Recall from [Reference Buss and Echterhoff7] that by a continuous family of twists of G over a locally compact Hausdorff space X, or simply a twist over
$2$
-cocycles of discrete amenable groups G. Recall from [Reference Buss and Echterhoff7] that by a continuous family of twists of G over a locally compact Hausdorff space X, or simply a twist over
![]() $X\times G$
, we understand a groupoid central extension
$X\times G$
, we understand a groupoid central extension
of the trivial group bundle
![]() $X\times G$
by the central trivial group bundle
$X\times G$
by the central trivial group bundle
![]() $X\times \mathbb T$
. Then for each
$X\times \mathbb T$
. Then for each
![]() $x\in X$
, we obtain a central extension
$x\in X$
, we obtain a central extension
![]() $\sigma _x:=(\mathbb T\hookrightarrow G_{\sigma _x}\twoheadrightarrow G)$
of G by
$\sigma _x:=(\mathbb T\hookrightarrow G_{\sigma _x}\twoheadrightarrow G)$
of G by
![]() $\mathbb T$
. For ease of notation, we denote the elements in
$\mathbb T$
. For ease of notation, we denote the elements in
![]() $\mathcal G$
generally by
$\mathcal G$
generally by
![]() $\tilde g$
, indicate by
$\tilde g$
, indicate by
![]() $(x,\tilde g)$
that
$(x,\tilde g)$
that
![]() $\tilde g$
lies in the fibre
$\tilde g$
lies in the fibre
![]() $G_{\sigma _x}=q^{-1}(\{x\}\times G)\subseteq \mathcal G$
over
$G_{\sigma _x}=q^{-1}(\{x\}\times G)\subseteq \mathcal G$
over
![]() $x\in X$
, and write
$x\in X$
, and write
![]() $(x, g)$
for its image in
$(x, g)$
for its image in
![]() $X\times G$
under the quotient map.
$X\times G$
under the quotient map.
As explained in [Reference Buss and Echterhoff7], continuous families of twists of G over X are closely related to
![]() $C_0(X)$
-linear actions on continuous trace
$C_0(X)$
-linear actions on continuous trace
![]() $C^*$
-algebras. More precisely, the following construction provides natural examples of continuous families of twists.
$C^*$
-algebras. More precisely, the following construction provides natural examples of continuous families of twists.
Example 7.1. Let
![]() $\mathbb K=\mathbb K({\mathcal H})$
for a Hilbert space
$\mathbb K=\mathbb K({\mathcal H})$
for a Hilbert space
![]() ${\mathcal H}$
and suppose that
${\mathcal H}$
and suppose that
![]() $\alpha :G\curvearrowright C_0(X,\mathbb K)$
is a
$\alpha :G\curvearrowright C_0(X,\mathbb K)$
is a
![]() $C_0(X)$
-linear (that is, fibrewise) action of G on
$C_0(X)$
-linear (that is, fibrewise) action of G on
![]() $C_0(X,\mathbb K)$
as considered in [Reference Buss and Echterhoff7, Definition 4.23]. For all
$C_0(X,\mathbb K)$
as considered in [Reference Buss and Echterhoff7, Definition 4.23]. For all
![]() $x\in X$
let
$x\in X$
let
![]() $\alpha ^x:G\curvearrowright \mathbb K$
denote the action on the fibre at x. Then
$\alpha ^x:G\curvearrowright \mathbb K$
denote the action on the fibre at x. Then
together with the embedding
![]() $X\times \mathbb T\hookrightarrow \mathcal G_\alpha; (x,z)\mapsto (x,e, \bar {z}1_{{\mathcal H}})$
and the quotient map
$X\times \mathbb T\hookrightarrow \mathcal G_\alpha; (x,z)\mapsto (x,e, \bar {z}1_{{\mathcal H}})$
and the quotient map
![]() $\mathcal G_\alpha \twoheadrightarrow X\times G; (x,g,v)\mapsto (x,g)$
defines a groupoid central extension
$\mathcal G_\alpha \twoheadrightarrow X\times G; (x,g,v)\mapsto (x,g)$
defines a groupoid central extension
as above. We refer to [Reference Buss and Echterhoff7, Lemma 4.28] for further details of this construction.
Remark 7.2. Conversely, every twist
![]() $\Sigma =(X\times \mathbb T\stackrel {\iota }{\hookrightarrow } \mathcal G\stackrel {q}\twoheadrightarrow X\times G)$
gives rise to a fibrewise action of G on a continuous field of compact operators over X. If G and X are second countable, this precisely inverts the construction of the above example. For the construction let
$\Sigma =(X\times \mathbb T\stackrel {\iota }{\hookrightarrow } \mathcal G\stackrel {q}\twoheadrightarrow X\times G)$
gives rise to a fibrewise action of G on a continuous field of compact operators over X. If G and X are second countable, this precisely inverts the construction of the above example. For the construction let
![]() $C_c(\mathcal G,\iota )$
denote the space of compactly supported continuous functions
$C_c(\mathcal G,\iota )$
denote the space of compactly supported continuous functions
![]() $\xi $
on
$\xi $
on
![]() $\mathcal G$
that satisfy the relation
$\mathcal G$
that satisfy the relation
We define a
![]() $C_0(X)$
-valued inner product on
$C_0(X)$
-valued inner product on
![]() $C_c(\mathcal G,\iota )$
by
$C_c(\mathcal G,\iota )$
by
 $$ \begin{align*} \langle\xi\!\mid\!\eta\rangle_{C_0(X)}(x)=\int_G \overline{\xi(x,{\tilde{g}})}\eta(x,{\tilde{g}})\,d g \end{align*} $$
$$ \begin{align*} \langle\xi\!\mid\!\eta\rangle_{C_0(X)}(x)=\int_G \overline{\xi(x,{\tilde{g}})}\eta(x,{\tilde{g}})\,d g \end{align*} $$
and we let
![]() $L^2(\mathcal G,\iota )$
denote the completion of
$L^2(\mathcal G,\iota )$
denote the completion of
![]() $C_c(\mathcal G,\iota )$
with respect to this inner product. Then the right translation action
$C_c(\mathcal G,\iota )$
with respect to this inner product. Then the right translation action
![]() $\rho _{\mathcal G}:\mathcal G\curvearrowright L^2(\mathcal G, \iota )$
is given fibrewise by the right translation action
$\rho _{\mathcal G}:\mathcal G\curvearrowright L^2(\mathcal G, \iota )$
is given fibrewise by the right translation action
![]() $\rho ^{\sigma _x}:G\curvearrowright L^2(G_{\sigma _x}, \iota )$
given by
$\rho ^{\sigma _x}:G\curvearrowright L^2(G_{\sigma _x}, \iota )$
given by
![]() $(\rho ^{\sigma _x}_{\tilde {g}}\xi )({\tilde {h}})=\sqrt {\Delta (g)}\xi ({\tilde {h}}{\tilde {g}})$
for
$(\rho ^{\sigma _x}_{\tilde {g}}\xi )({\tilde {h}})=\sqrt {\Delta (g)}\xi ({\tilde {h}}{\tilde {g}})$
for
![]() ${\tilde {g}},{\tilde {h}}\in G_{\sigma _x}$
and
${\tilde {g}},{\tilde {h}}\in G_{\sigma _x}$
and
![]() $g=q_x({\tilde {g}})$
. The adjoint action
$g=q_x({\tilde {g}})$
. The adjoint action
![]() $\text {Ad}\rho _{\mathcal G}$
then provides a
$\text {Ad}\rho _{\mathcal G}$
then provides a
![]() $C_0(X)$
-linear action
$C_0(X)$
-linear action
![]() $\alpha :G\curvearrowright \mathbb K(L^2(\mathcal G,\iota ))$
with fibre actions
$\alpha :G\curvearrowright \mathbb K(L^2(\mathcal G,\iota ))$
with fibre actions
![]() $\alpha ^x=\text {Ad}\rho ^{\sigma _x}:G\curvearrowright \mathbb K(L^2(G_{\sigma _x}, \iota ))$
. It has been shown in [Reference Buss and Echterhoff7, Lemma 4.33] that if
$\alpha ^x=\text {Ad}\rho ^{\sigma _x}:G\curvearrowright \mathbb K(L^2(G_{\sigma _x}, \iota ))$
. It has been shown in [Reference Buss and Echterhoff7, Lemma 4.33] that if
![]() $\Sigma =\Sigma _{\alpha '}$
for some continuous family of actions
$\Sigma =\Sigma _{\alpha '}$
for some continuous family of actions
![]() $\alpha ':G\curvearrowright C_0(X,\mathbb K)$
as in the above example, then
$\alpha ':G\curvearrowright C_0(X,\mathbb K)$
as in the above example, then
![]() $( \mathbb K(L^2(\mathcal G,\iota )), \alpha )$
and
$( \mathbb K(L^2(\mathcal G,\iota )), \alpha )$
and
![]() $(C_0(X,\mathbb K),\alpha ')$
are
$(C_0(X,\mathbb K),\alpha ')$
are
![]() $X\times G$
-equivariantly Morita equivalent.
$X\times G$
-equivariantly Morita equivalent.
Another source of examples for continuous families of twists is given via continuous families of
![]() $2$
-cocycles.
$2$
-cocycles.
Example 7.3. Suppose G is a second countable locally compact group. By a continuous family of Borel
![]() $2$
-cocycles
$2$
-cocycles
![]() $x\mapsto \omega _x$
over the second countable locally compact space X we understand a Borel
$x\mapsto \omega _x$
over the second countable locally compact space X we understand a Borel
![]() $2$
-cocycle
$2$
-cocycle
![]() $\Omega \colon G\times G\to C(X,\mathbb T)$
, where the trivial G-module
$\Omega \colon G\times G\to C(X,\mathbb T)$
, where the trivial G-module
![]() $C(X,\mathbb T)$
is equipped with the topology of uniform convergence on compact subsets of X, such that
$C(X,\mathbb T)$
is equipped with the topology of uniform convergence on compact subsets of X, such that
![]() $\omega _x:=\Omega (\cdot ,\cdot )(x)\in Z^2(G,\mathbb T)$
for all
$\omega _x:=\Omega (\cdot ,\cdot )(x)\in Z^2(G,\mathbb T)$
for all
![]() $x\in X$
. It follows then from [Reference Hurder, Olesen, Raeburn and Rosenberg19, Proposition 3.1] together with [Reference Crocker, Kumjian, Raeburn and Williams11, Theorem 5.1(3)] that
$x\in X$
. It follows then from [Reference Hurder, Olesen, Raeburn and Rosenberg19, Proposition 3.1] together with [Reference Crocker, Kumjian, Raeburn and Williams11, Theorem 5.1(3)] that
![]() $\Omega $
induces a
$\Omega $
induces a
![]() $C_0(X)$
-linear action
$C_0(X)$
-linear action
![]() $\alpha :G\curvearrowright C_0(X,\mathbb K(L^2(G)))$
by defining
$\alpha :G\curvearrowright C_0(X,\mathbb K(L^2(G)))$
by defining
![]() $\alpha ^x:=\text {Ad} \rho ^{\bar \omega _x}$
for all
$\alpha ^x:=\text {Ad} \rho ^{\bar \omega _x}$
for all
![]() $x\in X$
, where
$x\in X$
, where
![]() $\rho ^{\bar \omega _x} :G\to \mathcal U(L^2(G))$
denotes the
$\rho ^{\bar \omega _x} :G\to \mathcal U(L^2(G))$
denotes the
![]() $\bar \omega _x$
-right regular representation of G (see [Reference Buss and Echterhoff7, Remark 4.19]). By the construction in Example 7.1 we then obtain a twist
$\bar \omega _x$
-right regular representation of G (see [Reference Buss and Echterhoff7, Remark 4.19]). By the construction in Example 7.1 we then obtain a twist
![]() $\Sigma _{\Omega }:=\Sigma _\alpha $
and it follows from [Reference Buss and Echterhoff7, Theorem 4.14.] that for all
$\Sigma _{\Omega }:=\Sigma _\alpha $
and it follows from [Reference Buss and Echterhoff7, Theorem 4.14.] that for all
![]() $x\in X$
the twist
$x\in X$
the twist
![]() $\sigma _x=(\mathbb T\hookrightarrow G_x\twoheadrightarrow G)$
at x is isomorphic to the twist
$\sigma _x=(\mathbb T\hookrightarrow G_x\twoheadrightarrow G)$
at x is isomorphic to the twist
![]() $\sigma _{\omega _x}=(\mathbb T\hookrightarrow G_{\omega _x}\twoheadrightarrow G)$
corresponding to the cocycle
$\sigma _{\omega _x}=(\mathbb T\hookrightarrow G_{\omega _x}\twoheadrightarrow G)$
corresponding to the cocycle
![]() $\omega _x$
.
$\omega _x$
.
Notice that if
![]() $\Omega :G\times G\to C(X,\mathbb T)$
is a continuous cocycle (for example, if G is discrete), then
$\Omega :G\times G\to C(X,\mathbb T)$
is a continuous cocycle (for example, if G is discrete), then
![]() $\Sigma _{\Omega }$
can be constructed directly as
$\Sigma _{\Omega }$
can be constructed directly as
![]() $\Sigma _{\Omega }:=(X\times \mathbb T\hookrightarrow \mathcal G_{\Omega }\twoheadrightarrow X\times G)$
where
$\Sigma _{\Omega }:=(X\times \mathbb T\hookrightarrow \mathcal G_{\Omega }\twoheadrightarrow X\times G)$
where
![]() $\mathcal G_{\Omega }=G\times X\times \mathbb T$
is equipped with the product topology, multiplication defined by
$\mathcal G_{\Omega }=G\times X\times \mathbb T$
is equipped with the product topology, multiplication defined by
![]() $(g_1, x, z_1)(g_2, x, z_2)=(g_1g_2, x, \Omega (x)(g_1, g_2) z_1z_2)$
, and the obvious inclusion of
$(g_1, x, z_1)(g_2, x, z_2)=(g_1g_2, x, \Omega (x)(g_1, g_2) z_1z_2)$
, and the obvious inclusion of
![]() $X\times \mathbb T$
and projection onto
$X\times \mathbb T$
and projection onto
![]() $X\times G$
. This construction does not need any second countability assumptions. If
$X\times G$
. This construction does not need any second countability assumptions. If
![]() $\Omega $
is not continuous, it is not clear to us how to topologize
$\Omega $
is not continuous, it is not clear to us how to topologize
![]() $G\times X\times \mathbb T$
in this construction.
$G\times X\times \mathbb T$
in this construction.
A third class of important examples comes from central group extensions. The following example is [Reference Buss and Echterhoff7, Proposition 4.35].
Example 7.4. Let
![]() $Z\stackrel {\iota _Z}{\hookrightarrow } H\stackrel {q_H}{\twoheadrightarrow } G$
be a central extension of G by the abelian group Z. Then Z acts freely and properly on the product space
$Z\stackrel {\iota _Z}{\hookrightarrow } H\stackrel {q_H}{\twoheadrightarrow } G$
be a central extension of G by the abelian group Z. Then Z acts freely and properly on the product space
![]() $\widehat {Z}\times H\times \mathbb T$
by
$\widehat {Z}\times H\times \mathbb T$
by
and there is a twist
with
![]() $\mathcal G_H:=(\widehat {Z}\times H\times \mathbb T)/Z$
and inclusion and quotient maps given by
$\mathcal G_H:=(\widehat {Z}\times H\times \mathbb T)/Z$
and inclusion and quotient maps given by
Here e denotes the neutral element of H.
For each
![]() $\chi \in \widehat {Z}$
the fibre
$\chi \in \widehat {Z}$
the fibre
![]() $\sigma _\chi =(\mathbb T\stackrel {\iota _\chi }\hookrightarrow G_\chi \stackrel {q_\chi }\twoheadrightarrow G)$
at
$\sigma _\chi =(\mathbb T\stackrel {\iota _\chi }\hookrightarrow G_\chi \stackrel {q_\chi }\twoheadrightarrow G)$
at
![]() $\chi $
is then given by
$\chi $
is then given by
![]() $G_\chi :={(H\times \mathbb T)/Z}$
with respect to the action
$G_\chi :={(H\times \mathbb T)/Z}$
with respect to the action
![]() $z(h,w)=(zh, \chi (z)w)$
for
$z(h,w)=(zh, \chi (z)w)$
for
![]() $z\in Z, (h,w)\in H\times \mathbb T$
. The inclusion and quotient maps are given by
$z\in Z, (h,w)\in H\times \mathbb T$
. The inclusion and quotient maps are given by
![]() $\iota _\chi :w\mapsto [e,w]$
and
$\iota _\chi :w\mapsto [e,w]$
and
![]() $q_\chi :[h,w]\mapsto q_H(h)$
, respectively.
$q_\chi :[h,w]\mapsto q_H(h)$
, respectively.
Notation 7.5. If the locally compact group G admits a central extension
![]() $Z\stackrel {\iota _Z}{\hookrightarrow } H\stackrel {q_H}{\twoheadrightarrow } G$
as above such that the transgression map
$Z\stackrel {\iota _Z}{\hookrightarrow } H\stackrel {q_H}{\twoheadrightarrow } G$
as above such that the transgression map
![]() $\mathrm {tg}:\widehat {Z}\to \operatorname {{\mathrm {Twist}}}(G); \chi \mapsto [\sigma _\chi ]$
is bijective (hence an isomorphism of groups), we call
$\mathrm {tg}:\widehat {Z}\to \operatorname {{\mathrm {Twist}}}(G); \chi \mapsto [\sigma _\chi ]$
is bijective (hence an isomorphism of groups), we call
![]() $Z\stackrel {\iota _Z}{\hookrightarrow } H\stackrel {q_H}{\twoheadrightarrow } G$
a representation group for G. We say G is smooth if such a representation group exists.
$Z\stackrel {\iota _Z}{\hookrightarrow } H\stackrel {q_H}{\twoheadrightarrow } G$
a representation group for G. We say G is smooth if such a representation group exists.
This notation was introduced by Calvin Moore in [Reference Moore25] in the case of second countable locally compact groups, where he uses a Borel cross-section
![]() $\mathfrak {s}:G\to H$
in order to define a transgression map
$\mathfrak {s}:G\to H$
in order to define a transgression map
![]() $\mathrm {tg}:\widehat {Z}\to H^2(G,\mathbb T)$
. In that case, Moore’s transgression map can be obtained from ours by composing with the isomorphism
$\mathrm {tg}:\widehat {Z}\to H^2(G,\mathbb T)$
. In that case, Moore’s transgression map can be obtained from ours by composing with the isomorphism
![]() $\operatorname {{\mathrm {Twist}}}(G)\cong H^2(G,\mathbb T)$
. Note that our construction does not need a Borel section, which may not exist if G is not second countable. Notice that many (but by no means all) groups are smooth in the above sense, among them all discrete groups, all semisimple Lie groups, the group
$\operatorname {{\mathrm {Twist}}}(G)\cong H^2(G,\mathbb T)$
. Note that our construction does not need a Borel section, which may not exist if G is not second countable. Notice that many (but by no means all) groups are smooth in the above sense, among them all discrete groups, all semisimple Lie groups, the group
![]() $\mathbb R^n$
, and many more. We refer to [Reference Buss and Echterhoff7, Section 4] for a more detailed discussion and for concrete examples.
$\mathbb R^n$
, and many more. We refer to [Reference Buss and Echterhoff7, Section 4] for a more detailed discussion and for concrete examples.
7.1 Deformation via continuous families of twists
Suppose that
![]() $(B, \beta , \phi )$
is a weak
$(B, \beta , \phi )$
is a weak
![]() $G\rtimes G$
-algebra and that
$G\rtimes G$
-algebra and that
![]() $\rtimes _\mu $
is a duality crossed-product functor for G. Given a twist
$\rtimes _\mu $
is a duality crossed-product functor for G. Given a twist
![]() $\Sigma =(X\times \mathbb T\hookrightarrow \mathcal G\twoheadrightarrow X\times G)$
over
$\Sigma =(X\times \mathbb T\hookrightarrow \mathcal G\twoheadrightarrow X\times G)$
over
![]() $X\times G$
with fibres
$X\times G$
with fibres
![]() $\sigma _x=(\mathbb T\hookrightarrow G_x\twoheadrightarrow G)$
, our general deformation process of [Reference Buss and Echterhoff7, Section 6] (see Section 5 above) provides for all
$\sigma _x=(\mathbb T\hookrightarrow G_x\twoheadrightarrow G)$
, our general deformation process of [Reference Buss and Echterhoff7, Section 6] (see Section 5 above) provides for all
![]() $x\in X$
the weak
$x\in X$
the weak
![]() $G\rtimes G$
-algebras
$G\rtimes G$
-algebras
![]() $(B_{\sigma _x},\beta _{\sigma _x},\phi _{\sigma _x})$
and then, via Landstad duality, the cosystems
$(B_{\sigma _x},\beta _{\sigma _x},\phi _{\sigma _x})$
and then, via Landstad duality, the cosystems
![]() $(A^{\sigma _x}_\mu ,\delta ^{\sigma _x}_\mu )$
. In [Reference Buss and Echterhoff7, Theorem 6.16] we prove that the
$(A^{\sigma _x}_\mu ,\delta ^{\sigma _x}_\mu )$
. In [Reference Buss and Echterhoff7, Theorem 6.16] we prove that the
![]() $(B_{\sigma _x},\beta _{\sigma _x},\phi _{\sigma _x})$
are fibres of a continuous field
$(B_{\sigma _x},\beta _{\sigma _x},\phi _{\sigma _x})$
are fibres of a continuous field
![]() $(\mathcal B_\Sigma ,\beta _\Sigma ,\Phi _\Sigma )$
of weak
$(\mathcal B_\Sigma ,\beta _\Sigma ,\Phi _\Sigma )$
of weak
![]() $G\rtimes G$
-algebras over X, and from this we obtain, depending on certain properties of the given crossed-product functor
$G\rtimes G$
-algebras over X, and from this we obtain, depending on certain properties of the given crossed-product functor
![]() $\rtimes _\mu $
, continuity properties of the field of coactions
$\rtimes _\mu $
, continuity properties of the field of coactions
![]() $X\ni x\mapsto (A^{\sigma _x}_\mu ,\delta ^{\sigma _x}_\mu )$
over X.
$X\ni x\mapsto (A^{\sigma _x}_\mu ,\delta ^{\sigma _x}_\mu )$
over X.
We need to explain in more detail how
![]() $(\mathcal B_\Sigma ,\beta _\Sigma ,\Phi _\Sigma )$
is constructed and in what way it can be regarded as a continuous field of weak
$(\mathcal B_\Sigma ,\beta _\Sigma ,\Phi _\Sigma )$
is constructed and in what way it can be regarded as a continuous field of weak
![]() $G\rtimes G$
-algebras. For this we consider the function space
$G\rtimes G$
-algebras. For this we consider the function space
![]() $C_0(\mathcal G,\iota )$
consisting of
$C_0(\mathcal G,\iota )$
consisting of
![]() $C_0$
-functions
$C_0$
-functions
![]() $\xi \colon \mathcal G\to \mathbb C$
satisfying (7-1). Then
$\xi \colon \mathcal G\to \mathbb C$
satisfying (7-1). Then
![]() $C_0(\mathcal G,\iota )$
becomes an imprimitivity Hilbert bimodule over
$C_0(\mathcal G,\iota )$
becomes an imprimitivity Hilbert bimodule over
![]() $C_0(X\times G)$
with respect to the inner products
$C_0(X\times G)$
with respect to the inner products
We then consider
![]() $\mathcal B:=C_0(X,B)$
, viewed as a
$\mathcal B:=C_0(X,B)$
, viewed as a
![]() $C_0(X)$
-algebra with constant fibre B. We define the (balanced) tensor product of Hilbert modules,
$C_0(X)$
-algebra with constant fibre B. We define the (balanced) tensor product of Hilbert modules,
where
![]() $L^2(\mathcal G,\iota )^*$
denotes the
$L^2(\mathcal G,\iota )^*$
denotes the
![]() $C_0(X)-\mathbb K(L^2(\mathcal G,\iota ))$
equivalence bimodule dual to the right
$C_0(X)-\mathbb K(L^2(\mathcal G,\iota ))$
equivalence bimodule dual to the right
![]() $C_0(X)$
-Hilbert module
$C_0(X)$
-Hilbert module
![]() $L^2(\mathcal G,\iota )$
as constructed in Remark 7.2. It is shown in [Reference Buss and Echterhoff7] (see the discussion preceding [Reference Buss and Echterhoff7, Theorem 6.16]) that the
$L^2(\mathcal G,\iota )$
as constructed in Remark 7.2. It is shown in [Reference Buss and Echterhoff7] (see the discussion preceding [Reference Buss and Echterhoff7, Theorem 6.16]) that the
![]() $\mathcal G$
-action
$\mathcal G$
-action
for the right translation action
![]() $\mathrm {rt}_{\mathcal G}:\mathcal G\curvearrowright C_0(\mathcal G,\iota )$
and action
$\mathrm {rt}_{\mathcal G}:\mathcal G\curvearrowright C_0(\mathcal G,\iota )$
and action
![]() $\rho _{\mathcal G}:\mathcal G\curvearrowright L^2(\mathcal G,\iota )$
as in Remark 7.2 is trivial on
$\rho _{\mathcal G}:\mathcal G\curvearrowright L^2(\mathcal G,\iota )$
as in Remark 7.2 is trivial on
![]() $X\times \mathbb T$
and therefore factors through a well-defined
$X\times \mathbb T$
and therefore factors through a well-defined
![]() $C_0(X)$
-linear action
$C_0(X)$
-linear action
![]() $\gamma _\Sigma :G\curvearrowright \mathcal E_\Sigma (C_0(X,B))$
. We denote by
$\gamma _\Sigma :G\curvearrowright \mathcal E_\Sigma (C_0(X,B))$
. We denote by
![]() $\Phi _\Sigma :C_0(X\times G)\to \mathcal M(\mathbb K(\mathcal E_\Sigma (\mathcal G, B)))$
the nondegenerate
$\Phi _\Sigma :C_0(X\times G)\to \mathcal M(\mathbb K(\mathcal E_\Sigma (\mathcal G, B)))$
the nondegenerate
![]() $^*$
-homomorphism induced from the left action of
$^*$
-homomorphism induced from the left action of
![]() $C_0(X\times G)$
on
$C_0(X\times G)$
on
![]() $C_0(\mathcal G,\iota )$
. We then define
$C_0(\mathcal G,\iota )$
. We then define
It is then easy to check that for all
![]() $x\in X$
the quotient maps
$x\in X$
the quotient maps
![]() $q_x:\mathcal B_\Sigma \to B_{\sigma _x}$
induce surjective morphisms of weak
$q_x:\mathcal B_\Sigma \to B_{\sigma _x}$
induce surjective morphisms of weak
![]() $G\rtimes G$
-algebras
$G\rtimes G$
-algebras
Alternatively, we can also consider the right Hilbert
![]() $\mathcal B$
-module
$\mathcal B$
-module
equipped with the diagonal action
![]() $\epsilon _\Sigma :=\mathrm {rt}_{\mathcal G}\otimes _{C_0(X\times G)}\beta $
of
$\epsilon _\Sigma :=\mathrm {rt}_{\mathcal G}\otimes _{C_0(X\times G)}\beta $
of
![]() $\mathcal G$
. Since
$\mathcal G$
. Since
![]() $L^2(\mathcal G,\iota )$
is an imprimitivity bimodule, we also have
$L^2(\mathcal G,\iota )$
is an imprimitivity bimodule, we also have
where, similar to
![]() $\Phi _\Sigma $
, the
$\Phi _\Sigma $
, the
![]() $^*$
-homomorphism
$^*$
-homomorphism
![]() $\Psi _\Sigma :C_0(X\times G)\to \mathcal M(\mathbb K({\mathcal L}_\Sigma (\mathcal G,B)))$
is also induced from the left action of
$\Psi _\Sigma :C_0(X\times G)\to \mathcal M(\mathbb K({\mathcal L}_\Sigma (\mathcal G,B)))$
is also induced from the left action of
![]() $C_0(X\times G)$
on
$C_0(X\times G)$
on
![]() $C_0(\mathcal G,\iota )$
. We refer to [Reference Buss and Echterhoff7, Theorem 6.16] for more details.
$C_0(\mathcal G,\iota )$
. We refer to [Reference Buss and Echterhoff7, Theorem 6.16] for more details.
7.2 Deformation of Fell bundles via continuous families of twists
We want to apply the above deformation procedure to the dual weak
![]() $G\rtimes G$
-algebra
$G\rtimes G$
-algebra
![]() $(B, \beta ,\phi )=(C^*(\mathcal A)\rtimes _{\delta _{\mathcal A}}\widehat {G}, \widehat {\delta _{\mathcal A}}, j_{C_0(G)})$
of a Fell bundle
$(B, \beta ,\phi )=(C^*(\mathcal A)\rtimes _{\delta _{\mathcal A}}\widehat {G}, \widehat {\delta _{\mathcal A}}, j_{C_0(G)})$
of a Fell bundle
![]() $\mathcal A$
over G and we want to show that, similar to deformation by a twist
$\mathcal A$
over G and we want to show that, similar to deformation by a twist
![]() $\sigma =(\mathbb T\hookrightarrow G\twoheadrightarrow G)$
as considered in the previous section, the construction of
$\sigma =(\mathbb T\hookrightarrow G\twoheadrightarrow G)$
as considered in the previous section, the construction of
![]() $(\mathcal B_\Sigma , \beta _\Sigma , \Phi _\Sigma )$
can then be done completely on the level of Fell bundles. Given a Fell bundle
$(\mathcal B_\Sigma , \beta _\Sigma , \Phi _\Sigma )$
can then be done completely on the level of Fell bundles. Given a Fell bundle
![]() $p:\mathcal A\to G$
and a twist
$p:\mathcal A\to G$
and a twist
![]() $\Sigma =(X\times \mathbb T\hookrightarrow \mathcal G\twoheadrightarrow X\times ~G)$
, we construct a Fell bundle
$\Sigma =(X\times \mathbb T\hookrightarrow \mathcal G\twoheadrightarrow X\times ~G)$
, we construct a Fell bundle
![]() ${\mathcal A}_\Sigma $
over
${\mathcal A}_\Sigma $
over
![]() $X\times G$
as
$X\times G$
as
where
![]() $\mathcal A\times _{(X\times G)}\mathcal G=\{(a, (x,{\tilde {g}}))\in \mathcal A\times \mathcal G: p(a)=q_x({\tilde {g}})\}$
and where
$\mathcal A\times _{(X\times G)}\mathcal G=\{(a, (x,{\tilde {g}}))\in \mathcal A\times \mathcal G: p(a)=q_x({\tilde {g}})\}$
and where
![]() $\sim $
denotes the equivalence relation
$\sim $
denotes the equivalence relation
 $$ \begin{align*} &(a, (x,{\tilde{g}}))\sim (b, (y,{\tilde{h}}))\Longleftrightarrow x=y\quad\text{and}\nonumber\\ &\quad\text{there exists } z\in \mathbb T\;\text{such that}\; (b, (x,{\tilde{h}}))=(\bar{z}a, (x, z{\tilde{g}})). \end{align*} $$
$$ \begin{align*} &(a, (x,{\tilde{g}}))\sim (b, (y,{\tilde{h}}))\Longleftrightarrow x=y\quad\text{and}\nonumber\\ &\quad\text{there exists } z\in \mathbb T\;\text{such that}\; (b, (x,{\tilde{h}}))=(\bar{z}a, (x, z{\tilde{g}})). \end{align*} $$
The projection
![]() $p_\Sigma :{\mathcal A}_\Sigma \to X\times G$
is given by
$p_\Sigma :{\mathcal A}_\Sigma \to X\times G$
is given by
![]() $p_\Sigma ([a, (x,{\tilde {g}})])=(x, g)$
if
$p_\Sigma ([a, (x,{\tilde {g}})])=(x, g)$
if
![]() $g=q({\tilde {g}})$
. Observe that the restriction
$g=q({\tilde {g}})$
. Observe that the restriction
![]() ${\mathcal A}_\Sigma |_{\{x\}\times G_{\sigma _x}}$
coincides with the deformed Fell bundle
${\mathcal A}_\Sigma |_{\{x\}\times G_{\sigma _x}}$
coincides with the deformed Fell bundle
![]() ${\mathcal A}_{\sigma _x}$
with respect to the fibre
${\mathcal A}_{\sigma _x}$
with respect to the fibre
![]() $\sigma _x=(\mathbb T\hookrightarrow G_{\sigma _x}\twoheadrightarrow G)$
at
$\sigma _x=(\mathbb T\hookrightarrow G_{\sigma _x}\twoheadrightarrow G)$
at
![]() $x\in X$
as defined in the previous section. As usual we write
$x\in X$
as defined in the previous section. As usual we write
![]() $C_c({\mathcal A}_\Sigma )$
for the space of continuous sections
$C_c({\mathcal A}_\Sigma )$
for the space of continuous sections
![]() $a:X\times G\to {\mathcal A}_\Sigma $
with compact supports. Note that it becomes a
$a:X\times G\to {\mathcal A}_\Sigma $
with compact supports. Note that it becomes a
![]() $^*$
-algebra with respect to the convolution
$^*$
-algebra with respect to the convolution
 $$ \begin{align*}a*b(x,g)=\int_G a(x,h)b(x,h^{-1}g)\, \,d h\quad\text{and}\quad a^*(x,g)=\Delta(g^{-1})a_{(x,g^{-1})}^*\end{align*} $$
$$ \begin{align*}a*b(x,g)=\int_G a(x,h)b(x,h^{-1}g)\, \,d h\quad\text{and}\quad a^*(x,g)=\Delta(g^{-1})a_{(x,g^{-1})}^*\end{align*} $$
for
![]() $a,b\in C_c({\mathcal A}_\Sigma )$
. The following lemma is then a complete analogue of Lemma 6.4 above and we omit the proof.
$a,b\in C_c({\mathcal A}_\Sigma )$
. The following lemma is then a complete analogue of Lemma 6.4 above and we omit the proof.
Lemma 7.6. There is a bijection between the elements of
![]() $C_c({\mathcal A}_\Sigma )$
and the set of compactly supported continuous functions
$C_c({\mathcal A}_\Sigma )$
and the set of compactly supported continuous functions
![]() $a:\mathcal G\to \mathcal A$
satisfying
$a:\mathcal G\to \mathcal A$
satisfying
Under this identification, convolution and involution are given by the formulas
 $$ \begin{align*} a*b(x, {\tilde{g}})=\int_G a(x,{\tilde{h}})b(x,{\tilde{h}}^{-1}{\tilde{g}})\, \,d h\quad\text{and}\quad a^*(x,{\tilde{g}})=\Delta(g^{-1})a(x,{\tilde{g}}^{-1})^* \end{align*} $$
$$ \begin{align*} a*b(x, {\tilde{g}})=\int_G a(x,{\tilde{h}})b(x,{\tilde{h}}^{-1}{\tilde{g}})\, \,d h\quad\text{and}\quad a^*(x,{\tilde{g}})=\Delta(g^{-1})a(x,{\tilde{g}}^{-1})^* \end{align*} $$
where, as usual, we write
![]() $h=q_x({\tilde {h}})$
,
$h=q_x({\tilde {h}})$
,
![]() $g=q_x({\tilde {g}})$
for
$g=q_x({\tilde {g}})$
for
![]() $q_x:G_{\sigma _x}\to G$
.
$q_x:G_{\sigma _x}\to G$
.
There are constructions of full and reduced cross-sectional algebras of Fell bundles over groupoids, but in our situation these constructions can be reduced to the situation of Fell bundles over the group G by associating to
![]() ${\mathcal A}_\Sigma $
a Fell bundle, say
${\mathcal A}_\Sigma $
a Fell bundle, say
![]() $\widetilde {\mathcal A}_\Sigma $
, over G as follows: the fibres
$\widetilde {\mathcal A}_\Sigma $
, over G as follows: the fibres
![]() $\tilde {A}_g$
are given as the
$\tilde {A}_g$
are given as the
![]() $C_0$
-sections
$C_0$
-sections
![]() $C_0({\mathcal A}_\Sigma |_{X\times \{g\}})$
of the restriction
$C_0({\mathcal A}_\Sigma |_{X\times \{g\}})$
of the restriction
![]() ${\mathcal A}_\Sigma |_{X\times \{g\}}$
of
${\mathcal A}_\Sigma |_{X\times \{g\}}$
of
![]() ${\mathcal A}_\Sigma $
to
${\mathcal A}_\Sigma $
to
![]() $X\times \{g\}$
and multiplication and involution are defined pointwise over X.
$X\times \{g\}$
and multiplication and involution are defined pointwise over X.
Notation 7.7. Let
![]() ${\mathcal A}_\Sigma $
and
${\mathcal A}_\Sigma $
and
![]() $\widetilde {\mathcal A}_\Sigma $
be as above and let
$\widetilde {\mathcal A}_\Sigma $
be as above and let
![]() $\rtimes _\mu $
be any duality crossed-product functor for G. We then write
$\rtimes _\mu $
be any duality crossed-product functor for G. We then write
![]() $C^*({\mathcal A}_\Sigma ):=C^*(\widetilde {\mathcal A}_\Sigma )$
, and similarly
$C^*({\mathcal A}_\Sigma ):=C^*(\widetilde {\mathcal A}_\Sigma )$
, and similarly
![]() $C_\mu ^*({\mathcal A}_\Sigma ):=C^*_\mu (\widetilde {\mathcal A}_\Sigma )$
. Then
$C_\mu ^*({\mathcal A}_\Sigma ):=C^*_\mu (\widetilde {\mathcal A}_\Sigma )$
. Then
![]() $C^*({\mathcal A}_\Sigma )$
is equipped with a dual coaction
$C^*({\mathcal A}_\Sigma )$
is equipped with a dual coaction
![]() $\delta _{{\mathcal A}_\Sigma }: C^*({\mathcal A}_\Sigma )\to \mathcal M(C^*({\mathcal A}_\Sigma )\otimes C^*(G))$
, which factors through a coaction
$\delta _{{\mathcal A}_\Sigma }: C^*({\mathcal A}_\Sigma )\to \mathcal M(C^*({\mathcal A}_\Sigma )\otimes C^*(G))$
, which factors through a coaction
![]() $\delta ^\Sigma _\mu $
on
$\delta ^\Sigma _\mu $
on
![]() $C_\mu ^*({\mathcal A}_\Sigma )$
.
$C_\mu ^*({\mathcal A}_\Sigma )$
.
Note that there is an obvious inclusion
and one can show that this map induces an isomorphism of the usually defined full (or reduced) cross-sectional algebra
![]() $C^*({\mathcal A}_\Sigma )$
(respectively,
$C^*({\mathcal A}_\Sigma )$
(respectively,
![]() $C_r^*({\mathcal A}_\Sigma )$
) in the general setting of Fell bundles over groupoids and
$C_r^*({\mathcal A}_\Sigma )$
) in the general setting of Fell bundles over groupoids and
![]() $C^*(\widetilde {\mathcal A}_\Sigma )$
(respectively,
$C^*(\widetilde {\mathcal A}_\Sigma )$
(respectively,
![]() $C_r^*(\widetilde {\mathcal A}_\Sigma )$
), so our definition makes sense; indeed the case of full cross-sectional
$C_r^*(\widetilde {\mathcal A}_\Sigma )$
), so our definition makes sense; indeed the case of full cross-sectional
![]() $C^*$
-algebras is a special case of [Reference Buss and Meyer9, Theorem 6.2] and the reduced case a special case of [Reference LaLonde24, Proposition 5.1]. From now on, we simply identify
$C^*$
-algebras is a special case of [Reference Buss and Meyer9, Theorem 6.2] and the reduced case a special case of [Reference LaLonde24, Proposition 5.1]. From now on, we simply identify
![]() ${\mathcal A}_\Sigma $
with the Fell bundle
${\mathcal A}_\Sigma $
with the Fell bundle
![]() $\widetilde {\mathcal A}_\Sigma $
over G whenever it seems convenient.
$\widetilde {\mathcal A}_\Sigma $
over G whenever it seems convenient.
The crossed product
![]() $C^*({\mathcal A}_\Sigma )\rtimes _{\delta _{{\mathcal A}_\Sigma }}\widehat {G}$
comes with the dual action
$C^*({\mathcal A}_\Sigma )\rtimes _{\delta _{{\mathcal A}_\Sigma }}\widehat {G}$
comes with the dual action
![]() $\widehat {\delta _{{\mathcal A}_\Sigma }}$
of G and the inclusion
$\widehat {\delta _{{\mathcal A}_\Sigma }}$
of G and the inclusion
![]() $\Psi _G=j_{C_0(G)}:C_0(G)\to \mathcal M(C^*({\mathcal A}_\Sigma )\rtimes _{\delta _{{\mathcal A}_\Sigma }}\widehat {G})$
. We also have a canonical nondegenerate
$\Psi _G=j_{C_0(G)}:C_0(G)\to \mathcal M(C^*({\mathcal A}_\Sigma )\rtimes _{\delta _{{\mathcal A}_\Sigma }}\widehat {G})$
. We also have a canonical nondegenerate
![]() $^*$
-homomorphism
$^*$
-homomorphism
![]() $\Psi _X:C_0(X)\to Z\mathcal M(C^*({\mathcal A}_\Sigma )\rtimes _{\delta _{{\mathcal A}_\Sigma }}\widehat {G})$
, which is induced by pointwise multiplication
$\Psi _X:C_0(X)\to Z\mathcal M(C^*({\mathcal A}_\Sigma )\rtimes _{\delta _{{\mathcal A}_\Sigma }}\widehat {G})$
, which is induced by pointwise multiplication
![]() $(\varphi a)(x,{\tilde {g}})=\varphi (x)a(x,{\tilde {g}})$
of functions
$(\varphi a)(x,{\tilde {g}})=\varphi (x)a(x,{\tilde {g}})$
of functions
![]() $\varphi \in C_0(X)$
with sections
$\varphi \in C_0(X)$
with sections
![]() $a\in C_c({\mathcal A}_{\Sigma })$
. It is easily checked that it commutes with
$a\in C_c({\mathcal A}_{\Sigma })$
. It is easily checked that it commutes with
![]() $j_{C_0(G)}$
. We therefore obtain a well-defined structure map
$j_{C_0(G)}$
. We therefore obtain a well-defined structure map
Theorem 7.8. Let
![]() $(B, \beta ,\phi )=(C^*(\mathcal A)\rtimes _{\delta _{\mathcal A}}\widehat {G}, \widehat {\delta _{\mathcal A}}, j_{C_0(G)})$
be the dual weak
$(B, \beta ,\phi )=(C^*(\mathcal A)\rtimes _{\delta _{\mathcal A}}\widehat {G}, \widehat {\delta _{\mathcal A}}, j_{C_0(G)})$
be the dual weak
![]() $G\rtimes G$
-algebra for a Fell bundle
$G\rtimes G$
-algebra for a Fell bundle
![]() $\mathcal A$
over G. Let
$\mathcal A$
over G. Let
![]() $\Sigma =(X\times \mathbb T\hookrightarrow \mathcal G\twoheadrightarrow X\times G)$
be a twist for
$\Sigma =(X\times \mathbb T\hookrightarrow \mathcal G\twoheadrightarrow X\times G)$
be a twist for
![]() $X\times G$
and let
$X\times G$
and let
![]() $(\mathcal B_\Sigma ,\beta _\Sigma , \Phi _\Sigma )$
be the deformation of
$(\mathcal B_\Sigma ,\beta _\Sigma , \Phi _\Sigma )$
be the deformation of
![]() $(B,\beta ,\phi )$
by
$(B,\beta ,\phi )$
by
![]() $\Sigma $
as in Section 7.1. Then
$\Sigma $
as in Section 7.1. Then
![]() $(B_\Sigma ,\beta _\Sigma , \Phi _\Sigma )$
is isomorphic to the triple
$(B_\Sigma ,\beta _\Sigma , \Phi _\Sigma )$
is isomorphic to the triple
Proof. Arguing similarly to the proof of Proposition 6.10, we use the descriptions of
![]() $B=C^*(\mathcal A)\rtimes _{\delta _{\mathcal A}}\widehat {G}\cong \Bbbk ({\mathcal A})$
and
$B=C^*(\mathcal A)\rtimes _{\delta _{\mathcal A}}\widehat {G}\cong \Bbbk ({\mathcal A})$
and
![]() $C^*({\mathcal A}_\Sigma )\rtimes _{\delta _{{\mathcal A}_\Sigma }}\widehat {G}\cong \Bbbk ({{\mathcal A}_\Sigma })$
in order to construct the desired isomorphism. Let
$C^*({\mathcal A}_\Sigma )\rtimes _{\delta _{{\mathcal A}_\Sigma }}\widehat {G}\cong \Bbbk ({{\mathcal A}_\Sigma })$
in order to construct the desired isomorphism. Let
![]() ${\mathcal A}_X=X\times \mathcal A$
be the pullback of
${\mathcal A}_X=X\times \mathcal A$
be the pullback of
![]() $\mathcal A$
to
$\mathcal A$
to
![]() $X\times G$
via the projection
$X\times G$
via the projection
![]() $X\times G\to G$
(this can be regarded as a special case of the construction of
$X\times G\to G$
(this can be regarded as a special case of the construction of
![]() ${\mathcal A}_\Sigma $
for the trivial twist
${\mathcal A}_\Sigma $
for the trivial twist
![]() $X\times \mathbb T\hookrightarrow X\times (G\times \mathbb T)\twoheadrightarrow X\times G$
). We then have
$X\times \mathbb T\hookrightarrow X\times (G\times \mathbb T)\twoheadrightarrow X\times G$
). We then have
![]() $C^*({\mathcal A}_X)\cong C_0(X,C^*(\mathcal A))$
and
$C^*({\mathcal A}_X)\cong C_0(X,C^*(\mathcal A))$
and
We write
![]() $\Bbbk _c({{\mathcal A}_\Sigma })$
for the compactly supported functions
$\Bbbk _c({{\mathcal A}_\Sigma })$
for the compactly supported functions
![]() $k:\mathcal G\times _X\mathcal G\to \mathcal A$
satisfying
$k:\mathcal G\times _X\mathcal G\to \mathcal A$
satisfying
and observe that
![]() $\Bbbk _c({{\mathcal A}_\Sigma })$
can be regarded as a dense subalgebra of
$\Bbbk _c({{\mathcal A}_\Sigma })$
can be regarded as a dense subalgebra of
![]() $\Bbbk ({{\mathcal A}_\Sigma })$
in a canonical way.
$\Bbbk ({{\mathcal A}_\Sigma })$
in a canonical way.
We follow ideas similar to those in the proof of Proposition 6.10 and realize the right Hilbert
![]() $\mathcal B$
-module
$\mathcal B$
-module
![]() ${\mathcal L}(\mathcal G,\mathcal B)$
of (7-2) as a completion of the space
${\mathcal L}(\mathcal G,\mathcal B)$
of (7-2) as a completion of the space
![]() $\mathcal X_c( {\mathcal A}_X)$
of all compactly supported continuous functions
$\mathcal X_c( {\mathcal A}_X)$
of all compactly supported continuous functions
![]() $\xi \colon \mathcal G\times G\to \mathcal A$
satisfying
$\xi \colon \mathcal G\times G\to \mathcal A$
satisfying
We can mimic the formulas of the previous section and define inner products and left and right actions of
![]() $\Bbbk _c({{\mathcal A}_\Sigma })$
and
$\Bbbk _c({{\mathcal A}_\Sigma })$
and
![]() $\Bbbk _c({{\mathcal A}_X})$
by the following formulas for
$\Bbbk _c({{\mathcal A}_X})$
by the following formulas for
![]() $\xi ,\eta \in \mathcal X_c({\mathcal A}_X)$
,
$\xi ,\eta \in \mathcal X_c({\mathcal A}_X)$
,
![]() $k\in \Bbbk _c({{\mathcal A}_\Sigma })$
and
$k\in \Bbbk _c({{\mathcal A}_\Sigma })$
and
![]() $l\in \Bbbk _c({{\mathcal A}_X})$
:
$l\in \Bbbk _c({{\mathcal A}_X})$
:
 $$ \begin{align*}\langle\xi\!\mid\!\eta\rangle_{\Bbbk_c({{\mathcal A}_X})}(x,s,t):=\int_{G_x}\xi(g,s)^*\eta(g,t)\,d g,\end{align*} $$
$$ \begin{align*}\langle\xi\!\mid\!\eta\rangle_{\Bbbk_c({{\mathcal A}_X})}(x,s,t):=\int_{G_x}\xi(g,s)^*\eta(g,t)\,d g,\end{align*} $$
 $$ \begin{align*}_{\Bbbk_c({{\mathcal A}_\Sigma})}\langle\xi\!\mid\!\eta\rangle(x,\tilde g,\tilde h):=\int_G\xi(x,\tilde g,t)\eta(x,\tilde h,t)^*\,d t, \end{align*} $$
$$ \begin{align*}_{\Bbbk_c({{\mathcal A}_\Sigma})}\langle\xi\!\mid\!\eta\rangle(x,\tilde g,\tilde h):=\int_G\xi(x,\tilde g,t)\eta(x,\tilde h,t)^*\,d t, \end{align*} $$
 $$ \begin{align*}(k\cdot\xi)(x,\tilde g,t):=\int_{G_x}k(x,\tilde g,\tilde h)\xi(x,\tilde h,t)\,d \tilde h,\end{align*} $$
$$ \begin{align*}(k\cdot\xi)(x,\tilde g,t):=\int_{G_x}k(x,\tilde g,\tilde h)\xi(x,\tilde h,t)\,d \tilde h,\end{align*} $$
 $$ \begin{align*}(\xi\cdot l)(x,\tilde g,t):=\int_G\xi(x,\tilde g,h)l(h,t)\,d h.\end{align*} $$
$$ \begin{align*}(\xi\cdot l)(x,\tilde g,t):=\int_G\xi(x,\tilde g,h)l(h,t)\,d h.\end{align*} $$
The module
![]() ${\mathcal L}(\mathcal G,\mathcal B)$
is
${\mathcal L}(\mathcal G,\mathcal B)$
is
![]() $C_0(X)$
-linear with fibres
$C_0(X)$
-linear with fibres
where
![]() $\sigma _x=(\mathbb T\hookrightarrow G_{\sigma _x}\twoheadrightarrow G)$
is the fibre of
$\sigma _x=(\mathbb T\hookrightarrow G_{\sigma _x}\twoheadrightarrow G)$
is the fibre of
![]() $\Sigma $
at
$\Sigma $
at
![]() $x\in X$
. We know from Proposition 6.10 that the algebra of compact operators of this module is isomorphic to
$x\in X$
. We know from Proposition 6.10 that the algebra of compact operators of this module is isomorphic to
![]() $\Bbbk ({{\mathcal A}_{\sigma _x}})$
, where
$\Bbbk ({{\mathcal A}_{\sigma _x}})$
, where
![]() ${\mathcal A}_{\sigma _x}$
is the Fell bundle deformed from
${\mathcal A}_{\sigma _x}$
is the Fell bundle deformed from
![]() $\mathcal A$
via
$\mathcal A$
via
![]() $\sigma _x$
.
$\sigma _x$
.
We need to show that
![]() $\mathcal B_\Sigma =\mathbb K({\mathcal L}(\mathcal G,\mathcal B))$
is isomorphic to
$\mathcal B_\Sigma =\mathbb K({\mathcal L}(\mathcal G,\mathcal B))$
is isomorphic to
![]() $\Bbbk ({{\mathcal A}_\Sigma })$
, and that this isomorphism intertwines the actions and structure maps. Notice that
$\Bbbk ({{\mathcal A}_\Sigma })$
, and that this isomorphism intertwines the actions and structure maps. Notice that
![]() $C^*({\mathcal A}_\Sigma )$
is a
$C^*({\mathcal A}_\Sigma )$
is a
![]() $C_0(X)$
-algebra with fibres
$C_0(X)$
-algebra with fibres
![]() $C^*({\mathcal A}_{\sigma _x})$
: this follows from the fact that full cross-sectional
$C^*({\mathcal A}_{\sigma _x})$
: this follows from the fact that full cross-sectional
![]() $C^*$
-algebras of Fell bundles preserve exact sequences (see, for example, [Reference Exel15, Proposition 21.15], which proves this statement for Fell bundles over discrete groups; a similar proof applies for locally compact groups). It follows then from [Reference Nilsen29, Theorem 4.3] that
$C^*$
-algebras of Fell bundles preserve exact sequences (see, for example, [Reference Exel15, Proposition 21.15], which proves this statement for Fell bundles over discrete groups; a similar proof applies for locally compact groups). It follows then from [Reference Nilsen29, Theorem 4.3] that
![]() $\Bbbk ({{\mathcal A}_\Sigma })=C_0({\mathcal A}_\Sigma )\rtimes _{\delta _{{\mathcal A}_\Sigma }}\widehat {G}$
is also a
$\Bbbk ({{\mathcal A}_\Sigma })=C_0({\mathcal A}_\Sigma )\rtimes _{\delta _{{\mathcal A}_\Sigma }}\widehat {G}$
is also a
![]() $C_0(X)$
-algebra with fibres
$C_0(X)$
-algebra with fibres
Now observe that we have a canonical map
As in the case of a single twist, one checks that this preserves the structures of right modules over
![]() $\Bbbk _c({{\mathcal A}_X})$
, so that
$\Bbbk _c({{\mathcal A}_X})$
, so that
![]() $\Psi _X$
induces an isomorphism of right Hilbert
$\Psi _X$
induces an isomorphism of right Hilbert
![]() $\Bbbk ({{\mathcal A}_X})$
-modules
$\Bbbk ({{\mathcal A}_X})$
-modules
where
![]() $\mathcal X({\mathcal A}_X)$
denotes the completion of
$\mathcal X({\mathcal A}_X)$
denotes the completion of
![]() $\mathcal X_c({\mathcal A}_X)$
with respect to the right
$\mathcal X_c({\mathcal A}_X)$
with respect to the right
![]() $\mathcal B$
-module structure (recall that
$\mathcal B$
-module structure (recall that
![]() $\mathcal B=\Bbbk ({{\mathcal A}_X})$
). So again, as in the case of a single twist, to show that
$\mathcal B=\Bbbk ({{\mathcal A}_X})$
). So again, as in the case of a single twist, to show that
![]() $\Bbbk ({{\mathcal A}_\Sigma })=\mathcal B_\Sigma =\mathbb K({\mathcal L}(\mathcal G,\mathcal B))$
it is enough to see that the left action of
$\Bbbk ({{\mathcal A}_\Sigma })=\mathcal B_\Sigma =\mathbb K({\mathcal L}(\mathcal G,\mathcal B))$
it is enough to see that the left action of
![]() $\Bbbk _c({{\mathcal A}_\Sigma })$
on
$\Bbbk _c({{\mathcal A}_\Sigma })$
on
![]() $\mathcal X_c({\mathcal A}_X)$
extends to a
$\mathcal X_c({\mathcal A}_X)$
extends to a
![]() $^*$
-homomorphism (that is, a left action by adjointable operators)
$^*$
-homomorphism (that is, a left action by adjointable operators)
But since both the algebra and the module involved carry
![]() $C_0(X)$
-linear structures that are preserved by the left action of
$C_0(X)$
-linear structures that are preserved by the left action of
![]() $\Bbbk _c({{\mathcal A}_{\Sigma }})$
on
$\Bbbk _c({{\mathcal A}_{\Sigma }})$
on
![]() $\mathcal X({\mathcal A}_X)\cong {\mathcal L}(\mathcal G,\mathcal B)$
, and we already know that the fibrewise left action of
$\mathcal X({\mathcal A}_X)\cong {\mathcal L}(\mathcal G,\mathcal B)$
, and we already know that the fibrewise left action of
![]() $\Bbbk _c({{\mathcal A}_{\sigma _x}})$
on the fibre
$\Bbbk _c({{\mathcal A}_{\sigma _x}})$
on the fibre
![]() ${\mathcal L}(G_{\sigma _x},B)$
of
${\mathcal L}(G_{\sigma _x},B)$
of
![]() ${\mathcal L}(\mathcal G,\mathcal B)$
over x extends to an action by adjointable operators
${\mathcal L}(\mathcal G,\mathcal B)$
over x extends to an action by adjointable operators
the result follows. Finally, notice that by Proposition 6.10 we know that the isomorphism
![]() $\Bbbk ({{\mathcal A}_{\sigma _x}})\to {\mathbb B}_{B}({\mathcal L}(G_x,B))$
intertwines the actions and structure maps and therefore induces an isomorphism of weak
$\Bbbk ({{\mathcal A}_{\sigma _x}})\to {\mathbb B}_{B}({\mathcal L}(G_x,B))$
intertwines the actions and structure maps and therefore induces an isomorphism of weak
![]() $G\rtimes G$
-algebras
$G\rtimes G$
-algebras
Since the
![]() $C_0(X)$
-linear actions and structure maps for
$C_0(X)$
-linear actions and structure maps for
![]() $\mathcal B_\Sigma $
and
$\mathcal B_\Sigma $
and
![]() $\Bbbk ({{\mathcal A}_\Sigma })$
induce these actions and structure maps on the fibres, we can finally conclude the desired isomorphism
$\Bbbk ({{\mathcal A}_\Sigma })$
induce these actions and structure maps on the fibres, we can finally conclude the desired isomorphism
Recall that
![]() $C^*({\mathcal A}_\Sigma )$
is a
$C^*({\mathcal A}_\Sigma )$
is a
![]() $C_0(X)$
-algebra by extending pointwise multiplication of functions in
$C_0(X)$
-algebra by extending pointwise multiplication of functions in
![]() $C_0(X)$
with sections in
$C_0(X)$
with sections in
![]() $C_c({\mathcal A}_\Sigma )$
. The same holds true for
$C_c({\mathcal A}_\Sigma )$
. The same holds true for
![]() $C^*_\mu ({\mathcal A}_\Sigma )$
for every duality crossed-product functor
$C^*_\mu ({\mathcal A}_\Sigma )$
for every duality crossed-product functor
![]() $\rtimes _\mu $
. Recall that for any
$\rtimes _\mu $
. Recall that for any
![]() $C_0(X)$
-algebra D, the (maximal) fibre
$C_0(X)$
-algebra D, the (maximal) fibre
![]() $D_x$
of D over x is defined as the quotient
$D_x$
of D over x is defined as the quotient
![]() $D_x:=D/I_x$
with
$D_x:=D/I_x$
with
![]() $I_x=C_0(X\setminus \{x\})D$
. Thus we have the fibres
$I_x=C_0(X\setminus \{x\})D$
. Thus we have the fibres
![]() $C_\mu ^*({\mathcal A}_\Sigma )_x$
for each
$C_\mu ^*({\mathcal A}_\Sigma )_x$
for each
![]() $x\in X$
.
$x\in X$
.
On the other hand, it is clear that evaluation at
![]() $x\in X$
induces
$x\in X$
induces
![]() $\delta ^\Sigma _\mu -\delta ^{\sigma _x}_\mu $
-equivariant quotient maps
$\delta ^\Sigma _\mu -\delta ^{\sigma _x}_\mu $
-equivariant quotient maps
![]() $Q_x:C^*_\mu ({\mathcal A}_\Sigma )\twoheadrightarrow C^*_\mu ({\mathcal A}_{\sigma _x})$
, and the obvious question arises, under what conditions do the
$Q_x:C^*_\mu ({\mathcal A}_\Sigma )\twoheadrightarrow C^*_\mu ({\mathcal A}_{\sigma _x})$
, and the obvious question arises, under what conditions do the
![]() $Q_x$
factor through isomorphisms
$Q_x$
factor through isomorphisms
![]() $C_\mu ^*({\mathcal A}_\Sigma )_x \cong C^*_\mu ({\mathcal A}_{\sigma _x})$
? By [Reference Williams35, Theorem C.26], this is equivalent to saying that
$C_\mu ^*({\mathcal A}_\Sigma )_x \cong C^*_\mu ({\mathcal A}_{\sigma _x})$
? By [Reference Williams35, Theorem C.26], this is equivalent to saying that
![]() $C_\mu ^*({\mathcal A}_\Sigma )$
is an upper semicontinuous bundle of
$C_\mu ^*({\mathcal A}_\Sigma )$
is an upper semicontinuous bundle of
![]() $C^*$
-algebras with fibres
$C^*$
-algebras with fibres
![]() $C_\mu ^*({\mathcal A}_{\sigma ^x})$
. Indeed, as a direct application of the above theorem together with [Reference Buss and Echterhoff7, Theorem 6.16] we now get the following result.
$C_\mu ^*({\mathcal A}_{\sigma ^x})$
. Indeed, as a direct application of the above theorem together with [Reference Buss and Echterhoff7, Theorem 6.16] we now get the following result.
Theorem 7.9. Let
![]() $\mathcal A$
be a Fell bundle over G and let
$\mathcal A$
be a Fell bundle over G and let
![]() $\Sigma =(X\times \mathbb T\hookrightarrow \mathcal G\twoheadrightarrow X\times G)$
be a twist over
$\Sigma =(X\times \mathbb T\hookrightarrow \mathcal G\twoheadrightarrow X\times G)$
be a twist over
![]() $X\times G$
with fibres
$X\times G$
with fibres
![]() $\sigma _x=(\mathbb T\hookrightarrow G_{\sigma _x}\twoheadrightarrow G)$
. Then the following assertions hold.
$\sigma _x=(\mathbb T\hookrightarrow G_{\sigma _x}\twoheadrightarrow G)$
. Then the following assertions hold.
-
(1) If
 $\rtimes _\mu $
is an exact duality crossed-product functor (which always holds for
$\rtimes _\mu $
is an exact duality crossed-product functor (which always holds for
 $\rtimes _{\mathrm \max }$
) then
$\rtimes _{\mathrm \max }$
) then
 $Q_x:C^*_\mu ({\mathcal A}_\Sigma )\twoheadrightarrow C^*_\mu ({\mathcal A}_{\sigma _x})$
factors through an isomorphism
$Q_x:C^*_\mu ({\mathcal A}_\Sigma )\twoheadrightarrow C^*_\mu ({\mathcal A}_{\sigma _x})$
factors through an isomorphism
 $C_\mu ^*({\mathcal A}_\Sigma )_x \cong C^*_\mu ({\mathcal A}_{\sigma _x})$
.
$C_\mu ^*({\mathcal A}_\Sigma )_x \cong C^*_\mu ({\mathcal A}_{\sigma _x})$
. -
(2) If G is an exact group, then
 $C_r^*({\mathcal A}_\Sigma )$
is a continuous bundle of
$C_r^*({\mathcal A}_\Sigma )$
is a continuous bundle of
 $C^*$
-algebras over X with fibres
$C^*$
-algebras over X with fibres
 $C_r^*({\mathcal A}_{\sigma _x})$
.
$C_r^*({\mathcal A}_{\sigma _x})$
.
In the special case where G is a discrete amenable group, item (2) of the above theorem can be derived from the results in the paper [Reference Raeburn32, Section 6] by Iain Raeburn. Using the fact that every discrete group admits a representation group in the sense of Moore (see also Notation 7.5 above), he used this result to show that for every discrete amenable group G and Fell bundle
![]() $\mathcal A$
over G, there exists a kind of universal continuous bundle of
$\mathcal A$
over G, there exists a kind of universal continuous bundle of
![]() $C^*$
-algebras over
$C^*$
-algebras over
![]() $X=H^2(G,\mathbb T)$
(which, in this case, carries a canonical compact Hausdorff topology) with fibres
$X=H^2(G,\mathbb T)$
(which, in this case, carries a canonical compact Hausdorff topology) with fibres
![]() $C^*({\mathcal A}_\omega )$
, the (unique) cross-sectional algebra of the deformed Fell bundle
$C^*({\mathcal A}_\omega )$
, the (unique) cross-sectional algebra of the deformed Fell bundle
![]() ${\mathcal A}_\omega $
for
${\mathcal A}_\omega $
for
![]() $\omega \in Z^2(G,\mathbb T)$
as considered in Proposition 6.5 above. This result can now be generalized as follows.
$\omega \in Z^2(G,\mathbb T)$
as considered in Proposition 6.5 above. This result can now be generalized as follows.
Theorem 7.10. Suppose that G is smooth in the sense of Notation 7.5 and that
![]() $Z\hookrightarrow H\twoheadrightarrow G$
is a representation group for G. Let
$Z\hookrightarrow H\twoheadrightarrow G$
is a representation group for G. Let
![]() $\Sigma _H$
be the twist for
$\Sigma _H$
be the twist for
![]() $\widehat {Z} \times G$
constructed in Example 7.4.
$\widehat {Z} \times G$
constructed in Example 7.4.
Identifying
![]() $\operatorname {{\mathrm {Twist}}}(G)$
with
$\operatorname {{\mathrm {Twist}}}(G)$
with
![]() $\widehat {Z}$
via the transgression map
$\widehat {Z}$
via the transgression map
![]() $\mathrm {tg}:\chi \mapsto [\sigma _\chi ]$
, we obtain that
$\mathrm {tg}:\chi \mapsto [\sigma _\chi ]$
, we obtain that
![]() $C^*({\mathcal A}_{\Sigma _H})$
forms an upper semicontinuous bundle of
$C^*({\mathcal A}_{\Sigma _H})$
forms an upper semicontinuous bundle of
![]() $C^*$
-algebras over
$C^*$
-algebras over
![]() $\operatorname {{\mathrm {Twist}}}(G)$
, with fibres isomorphic to
$\operatorname {{\mathrm {Twist}}}(G)$
, with fibres isomorphic to
![]() $C^*({\mathcal A}_{\sigma })$
for
$C^*({\mathcal A}_{\sigma })$
for
![]() $[\sigma ] \in \operatorname {{\mathrm {Twist}}}(G)$
.
$[\sigma ] \in \operatorname {{\mathrm {Twist}}}(G)$
.
Furthermore, if G is exact, then
![]() $C_r^*({\mathcal A}_{\Sigma _H})$
is a continuous bundle of
$C_r^*({\mathcal A}_{\Sigma _H})$
is a continuous bundle of
![]() $C^*$
-algebras over
$C^*$
-algebras over
![]() $\operatorname {{\mathrm {Twist}}}(G)$
, with fibres isomorphic to
$\operatorname {{\mathrm {Twist}}}(G)$
, with fibres isomorphic to
![]() $C_r^*({\mathcal A}_{\sigma })$
for
$C_r^*({\mathcal A}_{\sigma })$
for
![]() $[\sigma ] \in \operatorname {{\mathrm {Twist}}}(G)$
.
$[\sigma ] \in \operatorname {{\mathrm {Twist}}}(G)$
.
8 K-theory
In this final section, we derive some consequences of our results in [Reference Buss and Echterhoff7] concerning the K-theory of deformed
![]() $C^*$
-algebras, applying them in the context of Fell bundles. Since we use results from
$C^*$
-algebras, applying them in the context of Fell bundles. Since we use results from
![]() $KK$
-theory, we need to restrict our considerations in this section to correspondence crossed-product functors
$KK$
-theory, we need to restrict our considerations in this section to correspondence crossed-product functors
![]() $\rtimes _\mu $
and assume from now on that G is a second-countable locally compact group and that
$\rtimes _\mu $
and assume from now on that G is a second-countable locally compact group and that
![]() $\mathcal A$
is a separable Fell bundle over G.
$\mathcal A$
is a separable Fell bundle over G.
We say that two twists
![]() $\sigma _0,\sigma _1$
of G are homotopic if there exists a twist
$\sigma _0,\sigma _1$
of G are homotopic if there exists a twist
![]() $\Sigma =([0,1]\times \mathbb T\hookrightarrow \mathcal G\twoheadrightarrow [0,1]\times G)$
such that the fibres of
$\Sigma =([0,1]\times \mathbb T\hookrightarrow \mathcal G\twoheadrightarrow [0,1]\times G)$
such that the fibres of
![]() $\Sigma $
at
$\Sigma $
at
![]() $0$
(respectively,
$0$
(respectively,
![]() $1$
) are
$1$
) are
![]() $\sigma _0$
(respectively,
$\sigma _0$
(respectively,
![]() $\sigma _1$
).
$\sigma _1$
).
Theorem 8.1. Let G and
![]() $\mathcal A$
be as above and assume that G satisfies the Baum–Connes conjecture with coefficients (for example, amenable groups or, more generally, groups with the Haagerup property). Let
$\mathcal A$
be as above and assume that G satisfies the Baum–Connes conjecture with coefficients (for example, amenable groups or, more generally, groups with the Haagerup property). Let
![]() $\sigma _0$
and
$\sigma _0$
and
![]() $\sigma _1$
be two homotopic twists for G. Then
$\sigma _1$
be two homotopic twists for G. Then
If, in addition, G is K-amenable, then
for any correspondence crossed-product functor
![]() $\rtimes _\mu $
.
$\rtimes _\mu $
.
The theorem is a direct consequence of [Reference Buss and Echterhoff7, Corollary 7.6] together with our identification
![]() $C_\mu ^*(A_\sigma )\cong A^\sigma _\mu $
for any twist
$C_\mu ^*(A_\sigma )\cong A^\sigma _\mu $
for any twist
![]() $\sigma $
for G and the cosystem
$\sigma $
for G and the cosystem
![]() $(A,\delta )=(C^*(\mathcal A), \delta _{\mathcal A})$
. Indeed, if G is K-amenable, we even have that
$(A,\delta )=(C^*(\mathcal A), \delta _{\mathcal A})$
. Indeed, if G is K-amenable, we even have that
![]() $C^*_\mu ({\mathcal A}_{\sigma })$
is
$C^*_\mu ({\mathcal A}_{\sigma })$
is
![]() $KK$
-equivalent to
$KK$
-equivalent to
![]() $C_r^*({\mathcal A}_\sigma )$
for every correspondence crossed-product functor
$C_r^*({\mathcal A}_\sigma )$
for every correspondence crossed-product functor
![]() $\rtimes _\mu $
and for every twist
$\rtimes _\mu $
and for every twist
![]() $\sigma $
for G. Moreover, if G satisfies the strong Baum–Connes conjecture (see [Reference Buss and Echterhoff7, Section 7] for the notation), then all K-theory isomorphisms in the above theorem come from
$\sigma $
for G. Moreover, if G satisfies the strong Baum–Connes conjecture (see [Reference Buss and Echterhoff7, Section 7] for the notation), then all K-theory isomorphisms in the above theorem come from
![]() $KK$
-equivalences.
$KK$
-equivalences.
In order to compare Theorem 8.1 with previous results on cocycle deformation, if
![]() $\omega _0,\omega _1\in Z^2(G,\mathbb T)$
are homotopic
$\omega _0,\omega _1\in Z^2(G,\mathbb T)$
are homotopic
![]() $2$
-cocycles in the sense that there is a
$2$
-cocycles in the sense that there is a
![]() $2$
-cocycle
$2$
-cocycle
![]() $\Omega \in Z^2(G,C([0,1],\mathbb T))$
whose point evaluations at
$\Omega \in Z^2(G,C([0,1],\mathbb T))$
whose point evaluations at
![]() $0,1\in [0,1]$
give
$0,1\in [0,1]$
give
![]() $\Omega _0=\omega _0$
and
$\Omega _0=\omega _0$
and
![]() $\Omega _1=\omega _1$
, then it follows from Example 7.3 that the corresponding twists
$\Omega _1=\omega _1$
, then it follows from Example 7.3 that the corresponding twists
![]() $\sigma _{\omega _1}$
and
$\sigma _{\omega _1}$
and
![]() $\sigma _{\omega _2}$
are homotopic as well. We therefore obtain analogous results for the Fell bundles
$\sigma _{\omega _2}$
are homotopic as well. We therefore obtain analogous results for the Fell bundles
![]() ${\mathcal A}_{\omega _i}:={\mathcal A}_{\sigma _{\omega _i}}$
,
${\mathcal A}_{\omega _i}:={\mathcal A}_{\sigma _{\omega _i}}$
,
![]() $i=1,2$
.
$i=1,2$
.
Acknowledgements
Both authors wish to express their deep gratitude for the profound insights they have gained from Iain Raeburn’s mathematical legacy. The second author had the pleasure of many stimulating joint projects with Iain from which he not only learned some deep mathematics, but also took away the desire to write the papers in a style which should be understandable to a large readership. Unfortunately, he never succeeded in reaching Iain’s mastery in this respect (and in others). Iain’s death is a huge loss for the operator algebras community!
Most of this work was written while the first author was visiting the University of Münster, and he is deeply grateful to the entire group – especially the second author – for their warm hospitality.