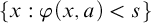1 Introduction
Ever since the discovery of the inconsistency of full comprehension principles at the turn of the last century, there have been various efforts to rescue the idea and formulate systems in which the entire domain of discourse is meaningfully represented as an element of the domain of discourse itself.
Neo-naïve set theories commonly take one of two approaches to repairing full comprehension. One is to weaken the comprehension principle while maintaining full classical logic, and the other is to weaken the underlying logic while maintaining the full comprehension principle. Extensionality is often weakened or abandoned entirely. While there have been many investigations into such theories, there are approximately three in particular we will be occasionally comparing to ours: Quine’s New Foundations,
![]() $\mathsf {NF}$
, and Jensen’s “slight (?) modification” thereof,
$\mathsf {NF}$
, and Jensen’s “slight (?) modification” thereof,
![]() $\mathsf {NFU}$
; the positive topological set theory
$\mathsf {NFU}$
; the positive topological set theory
![]() $\mathsf {GPK}^+$
, studied most prominently by Esser; and Cantor–Łukasiewicz set theory, originally isolated by Skolem but named by Hájek, which consists simply of the full comprehension scheme interpreted in the
$\mathsf {GPK}^+$
, studied most prominently by Esser; and Cantor–Łukasiewicz set theory, originally isolated by Skolem but named by Hájek, which consists simply of the full comprehension scheme interpreted in the
![]() $[0,1]$
-valued Łukasiewicz predicate logic.
$[0,1]$
-valued Łukasiewicz predicate logic.
![]() $\mathsf {NF}(\mathsf {U})$
and
$\mathsf {NF}(\mathsf {U})$
and
![]() $\mathsf {GPK}^+$
fall under the first approach mentioned above, and Cantor–Łukasiewicz set theory, abbreviated
$\mathsf {GPK}^+$
fall under the first approach mentioned above, and Cantor–Łukasiewicz set theory, abbreviated ![]() by Hájek, falls under the second.
by Hájek, falls under the second.
![]() $\mathsf {NF}$
and
$\mathsf {NF}$
and
![]() $\mathsf {GPK}^+$
have full extensionality, but
$\mathsf {GPK}^+$
have full extensionality, but ![]() is entirely inconsistent with it and
is entirely inconsistent with it and
![]() $\mathsf {NFU}$
weakens it by allowing urelements. To keep this introduction short, we will point the reader to [Reference Randall Holmes and Zalta18] for an overview of
$\mathsf {NFU}$
weakens it by allowing urelements. To keep this introduction short, we will point the reader to [Reference Randall Holmes and Zalta18] for an overview of
![]() $\mathsf {NF}(\mathsf {U})$
and
$\mathsf {NF}(\mathsf {U})$
and
![]() $\mathsf {GPK}^+$
and to [Reference Montagna17, Chapter 4.5] for an overview of Cantor–Łukasiewicz set theory. In particular, Hájek’s result [Reference Montagna17, Theorem 4.17] that
$\mathsf {GPK}^+$
and to [Reference Montagna17, Chapter 4.5] for an overview of Cantor–Łukasiewicz set theory. In particular, Hájek’s result [Reference Montagna17, Theorem 4.17] that ![]() has no
has no
![]() $\omega $
-models will be relevant, in that we will find a similar real-valued failure of induction in our theory (Theorem 5.10), although for us the failure may occur at arbitrarily large ordinals (Theorem 7.15), rather than necessarily at
$\omega $
-models will be relevant, in that we will find a similar real-valued failure of induction in our theory (Theorem 5.10), although for us the failure may occur at arbitrarily large ordinals (Theorem 7.15), rather than necessarily at
![]() $\omega $
.
$\omega $
.
In this article, we introduce a new set theory,
![]() $\mathsf {MSE}$
, which takes a combined approach to repairing comprehension: We weaken the comprehension scheme and weaken (or, more charitably, generalize) the underlying logic by working in a real-valued logic. For the sake of presentation, we will work in an ad hoc formalism, heavily based on first-order continuous logic, that capitalizes on the fact that our theory is a theory of sets that are actually sets of elements, rather than arbitrary
$\mathsf {MSE}$
, which takes a combined approach to repairing comprehension: We weaken the comprehension scheme and weaken (or, more charitably, generalize) the underlying logic by working in a real-valued logic. For the sake of presentation, we will work in an ad hoc formalism, heavily based on first-order continuous logic, that capitalizes on the fact that our theory is a theory of sets that are actually sets of elements, rather than arbitrary
![]() $[0,1]$
-valued predicates on some domain. In particular, our formalism will take bounded quantification as primitive, which is not possible to do in continuous logic, introduced in its modern form in [Reference Yaacov, Alexander Berenstein, Henson and Usvyatsov25].
$[0,1]$
-valued predicates on some domain. In particular, our formalism will take bounded quantification as primitive, which is not possible to do in continuous logic, introduced in its modern form in [Reference Yaacov, Alexander Berenstein, Henson and Usvyatsov25].
Models of
![]() $\mathsf {MSE}$
are triples
$\mathsf {MSE}$
are triples ![]() , where
, where
![]() $(M,d)$
is a complete metric space and
$(M,d)$
is a complete metric space and ![]() is a closed binary relation. Such a structure is a model of
is a closed binary relation. Such a structure is a model of
![]() $\mathsf {MSE}$
if it satisfies a strong metric form of extensionality and a weak approximation of comprehension. The strong form of extensionality, which we refer to as
$\mathsf {MSE}$
if it satisfies a strong metric form of extensionality and a weak approximation of comprehension. The strong form of extensionality, which we refer to as
![]() $\mathrm {H}$
-extensionality, requires that for any
$\mathrm {H}$
-extensionality, requires that for any
![]() $a,b \in M$
,
$a,b \in M$
, ![]() , where
, where
![]() $d_{\mathrm {H}}$
is the Hausdorff metric on sets (Definition 2.2). We refer to
$d_{\mathrm {H}}$
is the Hausdorff metric on sets (Definition 2.2). We refer to
![]() $\mathrm {H}$
-extensional structures
$\mathrm {H}$
-extensional structures ![]() as metric set structures.
as metric set structures.
The weak form of comprehension is the following principle: For any real-valued formula
![]() $\varphi (x,\bar {y})$
, any real numbers
$\varphi (x,\bar {y})$
, any real numbers
![]() $r < s$
, and any tuple of parameters
$r < s$
, and any tuple of parameters
![]() $\bar {a} \in M$
, there is a set
$\bar {a} \in M$
, there is a set
![]() $b \in M$
such that for any c, if
$b \in M$
such that for any c, if ![]() , then
, then ![]() and if
and if ![]() , then
, then
![]() $\varphi (c,\bar {a}) < s$
(Definition 2.7). Crucially, we make no guarantees about membership of those c’s for which
$\varphi (c,\bar {a}) < s$
(Definition 2.7). Crucially, we make no guarantees about membership of those c’s for which
![]() $\varphi (c,\bar {a})$
falls in the gap between r and s and so in this sense the principle is non-deterministic.
$\varphi (c,\bar {a})$
falls in the gap between r and s and so in this sense the principle is non-deterministic.
The word that we find most accurately captures this principle is excision, the idea being that we are only able to cut out a desired set somewhat crudely. From this we get the initialism
![]() $\mathsf {MSE}$
, for Metric Sets with Excision. Of course the nature of this principle depends entirely on what is meant by ‘real-valued formula,’ which is formalized in Section 2.2, but what matters is that these formulas are automatically uniformly continuous with regards to the metric. In particular, we have no direct access to the relation
$\mathsf {MSE}$
, for Metric Sets with Excision. Of course the nature of this principle depends entirely on what is meant by ‘real-valued formula,’ which is formalized in Section 2.2, but what matters is that these formulas are automatically uniformly continuous with regards to the metric. In particular, we have no direct access to the relation ![]() as a
as a
![]() $\{0,1\}$
-valued predicate and instead can only use it in instances of bounded quantification, such as
$\{0,1\}$
-valued predicate and instead can only use it in instances of bounded quantification, such as ![]() .
.
After defining
![]() $\mathsf {MSE}$
and developing some techniques for constructing particular sets, we will establish that
$\mathsf {MSE}$
and developing some techniques for constructing particular sets, we will establish that
![]() $\mathsf {MSE}$
is sufficiently strong and expressive by showing that it (with an axiom of infinity) interprets classical
$\mathsf {MSE}$
is sufficiently strong and expressive by showing that it (with an axiom of infinity) interprets classical
![]() $\mathsf {TSTI}$
Footnote
1
(or, equivalently, full
$\mathsf {TSTI}$
Footnote
1
(or, equivalently, full
![]() $\omega $
th-order arithmetic or the theory of a Boolean topos with a natural numbers object), which is well-known to be more than sufficient for the majority of everyday mathematics. In particular, we do this by considering uniformly discrete sets, which are better behaved than arbitrary sets in models of
$\omega $
th-order arithmetic or the theory of a Boolean topos with a natural numbers object), which is well-known to be more than sufficient for the majority of everyday mathematics. In particular, we do this by considering uniformly discrete sets, which are better behaved than arbitrary sets in models of
![]() $\mathsf {MSE}$
. We then build canonical representatives of internal well-order types in models of
$\mathsf {MSE}$
. We then build canonical representatives of internal well-order types in models of
![]() $\mathsf {MSE}$
(which we call ordinals). We show that
$\mathsf {MSE}$
(which we call ordinals). We show that
![]() $\mathsf {MSE}$
has no ultrametric
$\mathsf {MSE}$
has no ultrametric
![]() $\beta $
-models (i.e., models that are correct about well-foundedness) by showing that the class of ordinals of any such model M admits an external map s to
$\beta $
-models (i.e., models that are correct about well-foundedness) by showing that the class of ordinals of any such model M admits an external map s to
![]() $(0,1]$
that is non-increasing and has dense image (implying that the preimage of
$(0,1]$
that is non-increasing and has dense image (implying that the preimage of
![]() $(0,1)$
under s has no least element). When we eventually construct models of
$(0,1)$
under s has no least element). When we eventually construct models of
![]() $\mathsf {MSE}$
by using a non-standard modification of the ordinary construction of models of
$\mathsf {MSE}$
by using a non-standard modification of the ordinary construction of models of
![]() $\mathsf {GPK}^+$
, we show that they can have arbitrarily large standard ordinals (Theorem 7.15). This is of course similar to the situation with
$\mathsf {GPK}^+$
, we show that they can have arbitrarily large standard ordinals (Theorem 7.15). This is of course similar to the situation with
![]() $\mathsf {NF}$
and
$\mathsf {NF}$
and
![]() $\mathsf {NFU}$
, which has no true
$\mathsf {NFU}$
, which has no true
![]() $\beta $
-models yet can have arbitrarily large well-founded parts,Footnote
2
but the mode of failure is more conceptually similar to the mechanism that prevents
$\beta $
-models yet can have arbitrarily large well-founded parts,Footnote
2
but the mode of failure is more conceptually similar to the mechanism that prevents ![]() from having
from having
![]() $\omega $
-models in that it involves the difficulty of robustly formalizing induction for real-valued predicates. We also construct a pseudo-finite model of our theory (without infinity). This establishes that
$\omega $
-models in that it involves the difficulty of robustly formalizing induction for real-valued predicates. We also construct a pseudo-finite model of our theory (without infinity). This establishes that
![]() $\mathsf {MSE}$
without infinity has an incredibly low consistency strength, lower than Robinson arithmetic, in contrast to
$\mathsf {MSE}$
without infinity has an incredibly low consistency strength, lower than Robinson arithmetic, in contrast to
![]() $\mathsf {NFU}$
and
$\mathsf {NFU}$
and
![]() $\mathsf {GPK}^+$
without infinity.Footnote
3
We also show that any complete metric space of diameter at most
$\mathsf {GPK}^+$
without infinity.Footnote
3
We also show that any complete metric space of diameter at most
![]() $1$
can be embedded as an internal set of Quine atoms in a model of
$1$
can be embedded as an internal set of Quine atoms in a model of
![]() $\mathsf {MSE}$
, which in particular shows that not all models of
$\mathsf {MSE}$
, which in particular shows that not all models of
![]() $\mathsf {MSE}$
are ultrametric. Nevertheless, all models we are able to construct admit the map s as before, so we conjecture that this is in fact always the case.
$\mathsf {MSE}$
are ultrametric. Nevertheless, all models we are able to construct admit the map s as before, so we conjecture that this is in fact always the case.
Finally, we show how to formalize our theory in either continuous logic or Łukasiewicz predicate logic. In these contexts, we consider structures (without a given metric) of the form
![]() $(M,e)$
, where e is a binary
$(M,e)$
, where e is a binary
![]() $[0,1]$
-valued predicate on M. The intended interpretation of
$[0,1]$
-valued predicate on M. The intended interpretation of
![]() $e(x,y)$
is the quantity
$e(x,y)$
is the quantity ![]() . Our strong form of extensionality ensures that the metric
. Our strong form of extensionality ensures that the metric
![]() $d(x,y)$
can be recovered from
$d(x,y)$
can be recovered from
![]() $e(x,y)$
by the formula
$e(x,y)$
by the formula ![]() . The
. The
![]() $\mathrm {H}$
-extensionality axiom now takes the form
$\mathrm {H}$
-extensionality axiom now takes the form
and the axiom scheme of excision consists of
for each restricted
![]() $\mathcal {L}_e$
-formula
$\mathcal {L}_e$
-formula
![]() $\varphi (x,\bar {y})$
, where
$\varphi (x,\bar {y})$
, where
![]() $\varepsilon _\varphi $
is a certain rational number directly computable from
$\varepsilon _\varphi $
is a certain rational number directly computable from
![]() $\varphi $
. We show that models of the above theory are precisely pre-models of
$\varphi $
. We show that models of the above theory are precisely pre-models of
![]() $\mathsf {MSE}$
in the sense that the completion with regards to
$\mathsf {MSE}$
in the sense that the completion with regards to
![]() $d_e$
yields a model of
$d_e$
yields a model of
![]() $\mathsf {MSE}$
(by taking
$\mathsf {MSE}$
(by taking ![]() to be the relation
to be the relation
![]() $e(x,y) = 0$
). Furthermore, all models of
$e(x,y) = 0$
). Furthermore, all models of
![]() $\mathsf {MSE}$
arise in this way.
$\mathsf {MSE}$
arise in this way.
In Łukasiewicz logic, we use the predicateFootnote
4
![]() $x \mathrel{\hat{\epsilon }} y$
instead of
$x \mathrel{\hat{\epsilon }} y$
instead of
![]() $e(x,y)$
, with the intended meaning being that
$e(x,y)$
, with the intended meaning being that
![]() $(x \mathrel{\hat{\epsilon }} y) = 1-e(x,y)$
. The
$(x \mathrel{\hat{\epsilon }} y) = 1-e(x,y)$
. The
![]() $\mathrm {H}$
-extensionality axiom is directly translated as
$\mathrm {H}$
-extensionality axiom is directly translated as
where
![]() $x=_ey$
is the formula
$x=_ey$
is the formula ![]() (which is the same as
(which is the same as
![]() $1-d_e(x,y)$
), and the axiom scheme of excision is shown to be equivalent to the scheme
$1-d_e(x,y)$
), and the axiom scheme of excision is shown to be equivalent to the scheme
for each Łukasiewicz formula
![]() $\varphi (x,\bar {y})$
, where
$\varphi (x,\bar {y})$
, where
![]() $\# \varphi $
is the number of instances of
$\# \varphi $
is the number of instances of
![]() $\mathrel{\hat{\epsilon }}$
in
$\mathrel{\hat{\epsilon }}$
in
![]() $\varphi $
.
$\varphi $
.
2 Specification of MSE
2.1 H-extensionality and metric set structures
The structures we will be considering will be of the form ![]() , where
, where
![]() $(M,d)$
is a complete metric space, and
$(M,d)$
is a complete metric space, and ![]() is a closed binary relation. As is suggested by the notation,
is a closed binary relation. As is suggested by the notation, ![]() is meant to be interpreted as a set membership relation, and, as such, we would like for it to be extensional. Obviously we could just require extensionality of
is meant to be interpreted as a set membership relation, and, as such, we would like for it to be extensional. Obviously we could just require extensionality of ![]() as a binary relation in the standard sense, but for a few different reasons, we will opt to place a stronger condition on
as a binary relation in the standard sense, but for a few different reasons, we will opt to place a stronger condition on ![]() . To define this condition, recall one of many equivalent definitions of the Hausdorff distance between subsets of a metric space.
. To define this condition, recall one of many equivalent definitions of the Hausdorff distance between subsets of a metric space.
Definition 2.1. The Hausdorff distance between A and B, written
![]() $d_{\mathrm {H}}(A,B)$
, is the unique smallest element of
$d_{\mathrm {H}}(A,B)$
, is the unique smallest element of
![]() $[0,\infty ]$
such that for any
$[0,\infty ]$
such that for any
![]() $r> d_{\mathrm {H}}(A,B)$
,
$r> d_{\mathrm {H}}(A,B)$
,
-
• for every
 $a \in A$
, there is a
$a \in A$
, there is a
 $b \in B$
such that
$b \in B$
such that
 $d(a,b) < r$
, and
$d(a,b) < r$
, and -
• for every
 $b \in B$
, there is an
$b \in B$
, there is an
 $a \in A$
such that
$a \in A$
such that
 $d(a,b) < r$
.
$d(a,b) < r$
.
On the full power set of a metric space M,
![]() $d_{\mathrm {H}}$
is an extended pseudo-metric, but on the collection of close subsets of M, it is an extended metric. We will be concerned exclusively with
$d_{\mathrm {H}}$
is an extended pseudo-metric, but on the collection of close subsets of M, it is an extended metric. We will be concerned exclusively with
![]() $[0,1]$
-valued metrics. In this context, it makes sense to modify the above definition to take
$[0,1]$
-valued metrics. In this context, it makes sense to modify the above definition to take
![]() $d_{\mathrm {H}}$
to be
$d_{\mathrm {H}}$
to be
![]() $[0,1]$
-valued as well. This only changes the distance between the empty set and non-empty sets. In particular,
$[0,1]$
-valued as well. This only changes the distance between the empty set and non-empty sets. In particular,
![]() $d_{\mathrm {H}}(\varnothing , A) = 1$
for any non-empty A. This is the definition of the Hausdorff distance we will actually use.
$d_{\mathrm {H}}(\varnothing , A) = 1$
for any non-empty A. This is the definition of the Hausdorff distance we will actually use.
The form of Definition 2.1 above makes it clear that
![]() $d_{\mathrm {H}}$
is a direct metric generalization of extensional equality of sets.
$d_{\mathrm {H}}$
is a direct metric generalization of extensional equality of sets.
![]() $A=B$
if and only if for every
$A=B$
if and only if for every
![]() $a \in A$
, there is a
$a \in A$
, there is a
![]() $b \in B$
such that
$b \in B$
such that
![]() $a=b$
and for every
$a=b$
and for every
![]() $b \in B$
, there is an
$b \in B$
, there is an
![]() $a \in A$
such that
$a \in A$
such that
![]() $a=b$
. In this way, we take as our extensionality axiom a direct translation of the statement ‘
$a=b$
. In this way, we take as our extensionality axiom a direct translation of the statement ‘
![]() $A = B$
if and only if A and B are coextensive.’
$A = B$
if and only if A and B are coextensive.’
Definition 2.2. Given a metric space
![]() $(M,d)$
and a binary relation
$(M,d)$
and a binary relation ![]() , we say that
, we say that ![]() is
is
![]() $\mathrm {H}$
-extensional if for any
$\mathrm {H}$
-extensional if for any
![]() $a,b \in M$
,
$a,b \in M$
, ![]() .
.
We say that ![]() is a metric set structure if
is a metric set structure if
![]() $(M,d)$
is a complete metric space, d is
$(M,d)$
is a complete metric space, d is
![]() $[0,1]$
-valued, and
$[0,1]$
-valued, and ![]() is closed and
is closed and
![]() $\mathrm {H}$
-extensional.
$\mathrm {H}$
-extensional.
Metric set structures are a generalization of extensional digraphs (i.e., discrete models of the extensionality axiom). If
![]() $\delta $
is a
$\delta $
is a
![]() $\{0,1\}$
-valued metric on V, then
$\{0,1\}$
-valued metric on V, then
![]() $(V,\delta ,E)$
is a metric set structure if and only if
$(V,\delta ,E)$
is a metric set structure if and only if
![]() $(V,E)$
is an extensional digraph.
$(V,E)$
is an extensional digraph.
We should note that the definition of
![]() $\mathrm {H}$
-extensionality contains a somewhat arbitrary choice. After all, we could have just as easily required that
$\mathrm {H}$
-extensionality contains a somewhat arbitrary choice. After all, we could have just as easily required that ![]() . That said, the choice we have made is reasonable and seems to work well, so we have not investigated other possibilities in this article. Also, we should note that this notion of extensionality appears in a previous paper of the author [Reference Hanson9, Definition 6.4].
. That said, the choice we have made is reasonable and seems to work well, so we have not investigated other possibilities in this article. Also, we should note that this notion of extensionality appears in a previous paper of the author [Reference Hanson9, Definition 6.4].
A commonly cited benefit of extensionality is that it allows one to take
![]() $\in $
as the only primitive notion, with
$\in $
as the only primitive notion, with
![]() $x=y$
being defined as
$x=y$
being defined as ![]() . It seems unlikely that we will be able to do something similar with
. It seems unlikely that we will be able to do something similar with ![]() , but we can do something similar with the natural
, but we can do something similar with the natural
![]() $[0,1]$
-valued version of
$[0,1]$
-valued version of ![]() , which is the distance from x to the elements of Y, commonly written
, which is the distance from x to the elements of Y, commonly written
![]() $\operatorname {\mathrm {dist}}(x,Y)$
or
$\operatorname {\mathrm {dist}}(x,Y)$
or
![]() $d(x,Y)$
. In the context of a set theory,
$d(x,Y)$
. In the context of a set theory,
![]() $d(x,Y)$
is entirely unacceptable, being tantamount to writing
$d(x,Y)$
is entirely unacceptable, being tantamount to writing
![]() $x = Y$
to mean
$x = Y$
to mean
![]() $x \in Y$
.
$x \in Y$
.
![]() $\operatorname {\mathrm {dist}}(x,Y)$
is too long to use frequently, so we will use the following notation (which is used similarly in [Reference Chang3, Reference Fenstad4]).
$\operatorname {\mathrm {dist}}(x,Y)$
is too long to use frequently, so we will use the following notation (which is used similarly in [Reference Chang3, Reference Fenstad4]).
Definition 2.3. We write
![]() $e(x,y)$
for
$e(x,y)$
for ![]() .
.
Another useful characterization of the Hausdorff metric is this:
![]() $d_{\mathrm {H}}(A,B) = \sup _z|\operatorname {\mathrm {dist}}(z,A)-\operatorname {\mathrm {dist}}(z,B)|$
. This means that if
$d_{\mathrm {H}}(A,B) = \sup _z|\operatorname {\mathrm {dist}}(z,A)-\operatorname {\mathrm {dist}}(z,B)|$
. This means that if ![]() is a metric set structure, we have that
is a metric set structure, we have that
![]() $d(x,y) = \sup _z|e(z,x)-e(z,y)|$
. Since
$d(x,y) = \sup _z|e(z,x)-e(z,y)|$
. Since ![]() if and only if
if and only if
![]() $e(x,y) = 0$
, it should be possible to take
$e(x,y) = 0$
, it should be possible to take
![]() $e(x,y)$
as our only primitive notion. This is essentially the approach taken in the formalization of
$e(x,y)$
as our only primitive notion. This is essentially the approach taken in the formalization of ![]() (see [Reference Hájek8] and [Reference Montagna17, Chapter 4.5]) and this is the approach we will take in the ‘official’ continuous logic formulation of
(see [Reference Hájek8] and [Reference Montagna17, Chapter 4.5]) and this is the approach we will take in the ‘official’ continuous logic formulation of
![]() $\mathsf {MSE}$
, which we will discuss in Section 6.
$\mathsf {MSE}$
, which we will discuss in Section 6.
2.2 Formulas
Our formalism will be a small modification of first-order continuous logic, introduced in its modern form in [Reference Yaacov, Alexander Berenstein, Henson and Usvyatsov25]. Our only predicate symbol will be the metric,
![]() $d(x,y)$
, but we will take bound quantifiers of the form
$d(x,y)$
, but we will take bound quantifiers of the form ![]() as a primitive notion. Note though that we cannot access
as a primitive notion. Note though that we cannot access ![]() as a formula directly.
as a formula directly.
Definition 2.4. Our set of formulas, written ![]() , is the smallest non-empty set of expressions satisfying the following: For any
, is the smallest non-empty set of expressions satisfying the following: For any ![]() , variables x and y, and
, variables x and y, and
![]() $r \in \mathbb {R}$
,
$r \in \mathbb {R}$
, ![]() contains the expressions:
contains the expressions:

When we need to be more specific, we will refer to elements of ![]() as
as ![]() -formulas.
-formulas.
We refer to quantifiers of the form ![]() or
or ![]() as bounded. The free variables of a formula
as bounded. The free variables of a formula
![]() $\varphi $
are defined in the obvious way. We write
$\varphi $
are defined in the obvious way. We write
![]() $\varphi (\bar {x})$
to indicate that the free variables of
$\varphi (\bar {x})$
to indicate that the free variables of
![]() $\varphi $
are included in
$\varphi $
are included in
![]() $\bar {x}$
.
$\bar {x}$
.
For bookkeeping purposes, we will need the inductively defined quantity given by
-
•
 $v(1) = v(d(x,y)) = 1$
,
$v(1) = v(d(x,y)) = 1$
, -
•
 $v(\varphi + \psi )=v(\varphi )+v(\psi )$
,
$v(\varphi + \psi )=v(\varphi )+v(\psi )$
, -
•
 $v(\max (\varphi ,\psi ))=v(\min (\varphi ,\psi ))=\max (v(\varphi ),v(\psi ))$
,
$v(\max (\varphi ,\psi ))=v(\min (\varphi ,\psi ))=\max (v(\varphi ),v(\psi ))$
, -
•
 $v(r \cdot \varphi ) = |r|v(\varphi )$
,
$v(r \cdot \varphi ) = |r|v(\varphi )$
, -
•
 .
.
We are allowing ourselves arbitrary real numbers in Definition 2.4 because it will be convenient in several places. This convenience comes at a cost later in Section 6, however.
The intended interpretation of a given formula is clear, although we do need to specify the behavior of bounded quantifiers over empty sets. This is the first of two reasons why we defined the quantity
![]() $v(\varphi )$
.
$v(\varphi )$
.
Definition 2.5. Given a metric set structure ![]() we define real-valued functions
we define real-valued functions
![]() $\varphi ^M$
for
$\varphi ^M$
for ![]() inductively:
inductively:
-
•
 $1^M = 1$
.
$1^M = 1$
. -
•
 $(d(a,b))^M = d(a,b)$
for all
$(d(a,b))^M = d(a,b)$
for all
 $a,b \in M$
.
$a,b \in M$
. -
•
 $(\varphi +\psi )^M=\varphi ^M+\psi ^M$
. We define
$(\varphi +\psi )^M=\varphi ^M+\psi ^M$
. We define
 $(\max (\varphi ,\psi ))^M$
,
$(\max (\varphi ,\psi ))^M$
,
 $(\min (\varphi ,\psi ))^M$
, and
$(\min (\varphi ,\psi ))^M$
, and
 $(r\cdot \varphi )^M$
similarly.
$(r\cdot \varphi )^M$
similarly. -
•
 $(\sup _x\varphi (x,\bar {a}))^M = \sup \{\varphi ^M(b,\bar {a}) : b \in M\}$
. We define
$(\sup _x\varphi (x,\bar {a}))^M = \sup \{\varphi ^M(b,\bar {a}) : b \in M\}$
. We define
 $(\inf _x\varphi (x,\bar {a}))^M$
similarly.
$(\inf _x\varphi (x,\bar {a}))^M$
similarly. -
•
 if
if  for some
for some
 $c \in M$
.
$c \in M$
.  is defined similarly if
is defined similarly if  for some
for some
 $c \in M$
.
$c \in M$
. -
•
 if
if  for all
for all
 $c \in M$
.
$c \in M$
. -
•
 if
if  for all
for all
 $c \in M$
.
$c \in M$
.
We write expressions such as ![]() to mean that
to mean that ![]() . We may also write expressions like
. We may also write expressions like
![]() $M \models \varphi (\bar {a}) = r$
.
$M \models \varphi (\bar {a}) = r$
.
The conventions regarding suprema and infima of empty sets were chosen so that formulas would always be real-valued (rather than taking on values in
![]() $\mathbb {R}\cup \{\pm \infty \}$
) and so that
$\mathbb {R}\cup \{\pm \infty \}$
) and so that
![]() $\sup $
and
$\sup $
and
![]() $\inf $
are monotonic with regards to set inclusion, although we have to prove that this is actually the case.
$\inf $
are monotonic with regards to set inclusion, although we have to prove that this is actually the case.
We will often use commonsensical shorthand, such as
![]() $\varphi +\psi +\theta $
for
$\varphi +\psi +\theta $
for
![]() $\varphi +(\psi +\theta )$
,
$\varphi +(\psi +\theta )$
,
![]() $\varphi - \psi $
for
$\varphi - \psi $
for
![]() $\varphi + (-1)\cdot \psi $
, and
$\varphi + (-1)\cdot \psi $
, and
![]() $|\varphi |$
for
$|\varphi |$
for
![]() $\max (\varphi ,-\varphi )$
. We will abbreviate consecutive quantifiers with expressions such as
$\max (\varphi ,-\varphi )$
. We will abbreviate consecutive quantifiers with expressions such as
![]() $\sup _{xy}$
. By an abuse of notation, we will also write
$\sup _{xy}$
. By an abuse of notation, we will also write
![]() $e(x,y)$
as shorthand for the formula
$e(x,y)$
as shorthand for the formula ![]() .
.
In the context of a metric set structure M, we may often refer to formulas with parameters, such as
![]() $\varphi (\bar {x},\bar {a})$
for some
$\varphi (\bar {x},\bar {a})$
for some
![]() $\bar {a} \in M$
, as formulas and write them with parameters suppressed.
$\bar {a} \in M$
, as formulas and write them with parameters suppressed.
Two important properties of formulas in continuous logic are that they only take on values in some bounded interval and that they are always uniformly continuous. The relevant interval and modulus of uniform continuity can be determined by the formula alone. We will need similar facts here.
Lemma 2.6. For any metric set structure ![]() and formula
and formula
![]() $\varphi (\bar {x})$
,
$\varphi (\bar {x})$
,
-
(1)
 $\varphi ^M(\bar {a}) \in [-v(\varphi ),v(\varphi )]$
for all
$\varphi ^M(\bar {a}) \in [-v(\varphi ),v(\varphi )]$
for all
 $\bar {a} \in M$
and
$\bar {a} \in M$
and -
(2)
 $\varphi ^M : M^{|\bar {x}|} \to \mathbb {R}$
is
$\varphi ^M : M^{|\bar {x}|} \to \mathbb {R}$
is
 $2v(\varphi )$
-Lipschitz in the sense that for any
$2v(\varphi )$
-Lipschitz in the sense that for any
 $\bar {a},\bar {b} \in M$
,
$\bar {a},\bar {b} \in M$
,  (where
(where
 $d(\bar {a},\bar {b})$
is the max metric on tuples).
$d(\bar {a},\bar {b})$
is the max metric on tuples).
Proof. 1 follows by an easy induction argument and the fact that d is
![]() $[0,1]$
-valued. 2 follows similarly from the fact that
$[0,1]$
-valued. 2 follows similarly from the fact that
![]() $(x,y) \mapsto d(x,y)$
is
$(x,y) \mapsto d(x,y)$
is
![]() $2$
-Lipschitz.
$2$
-Lipschitz.
2.3 Excision
Our comprehension scheme is better defined in terms of its important consequence, rather than directly, as it takes a proof to establish that this property is even axiomatizable. The principle can be informally justified like this:
Suppose that we run a chalk factory and we are contractually obligated to produce pieces of chalk that are no longer than 7.62 cm in length. (The chalk is boxed by another company and needs to fit in their boxes.) Of course, our machine, being cheap, actually produces pieces that are anywhere between roughly 7.4 cm and 7.8 cm. To deal with this, we add a second machine that measures length and rejects pieces that are too long. To maximize our output, we might say that we want it to reject a piece if and only if its length is strictly longer than 7.62 cm, but the realities of physical measurement mean that this is impossible to actually accomplish. Since the penalties for violating the contract are quite harsh, we need to give ourselves some leeway, but we also want to make sure we aren’t throwing away too many acceptable pieces of chalk. So we configure the machine to accept chalk if it measures it to be no longer than 7.6 cm. We know that the error of the machine is no more than 0.01 cm, so we can guarantee that we will accept any piece of length at most 7.58 cm and reject any piece of length 7.62 cm or more, but we do not make any promises about the behavior of the machine in the gap between these bounds.Footnote 5
This is the manner in which we will approximate comprehension. Given a formula
![]() $\varphi (x,\bar {y})$
(i.e., a ‘measurable quantity’), bounds
$\varphi (x,\bar {y})$
(i.e., a ‘measurable quantity’), bounds
![]() $r < s$
, and parameters
$r < s$
, and parameters
![]() $\bar {a}$
, we promise that we can deliver a set b such that for any c, if
$\bar {a}$
, we promise that we can deliver a set b such that for any c, if ![]() , then
, then ![]() , and if
, and if
![]() $\varphi (c,\bar {a}) \geq s$
, then
$\varphi (c,\bar {a}) \geq s$
, then ![]() , but we make no commitment about those c’s for which
, but we make no commitment about those c’s for which
![]() $r < \varphi (c,\bar {a}) < s$
.
$r < \varphi (c,\bar {a}) < s$
.
Definition 2.7.
![]() satisfies excision if for any formula
satisfies excision if for any formula
![]() $\varphi (x,\bar {y})$
, reals
$\varphi (x,\bar {y})$
, reals
![]() $r < s$
, and
$r < s$
, and
![]() $\bar {a} \in M$
, there is a
$\bar {a} \in M$
, there is a
![]() $b \in M$
such that for any
$b \in M$
such that for any
![]() $c \in M$
, if
$c \in M$
, if ![]() , then
, then ![]() , and if
, and if ![]() , then
, then
![]() $\varphi (c,\bar {a}) < s$
.
$\varphi (c,\bar {a}) < s$
.
It is straightforward but worthwhile to see how this principle avoid Russell’s paradox. We can consider a set
![]() $a_r$
satisfying that if
$a_r$
satisfying that if ![]() , then
, then ![]() and if
and if ![]() , then
, then
![]() $1-e(b,b) < 1$
. As we pick r closer and closer to
$1-e(b,b) < 1$
. As we pick r closer and closer to
![]() $1$
, we get better and better approximations of the Russell class, but for each r, we consistently have that
$1$
, we get better and better approximations of the Russell class, but for each r, we consistently have that
![]() $0 < e(a_r,a_r) < 1-r$
. So we see that while our theory is strictly speaking a
$0 < e(a_r,a_r) < 1-r$
. So we see that while our theory is strictly speaking a
![]() $[0,1]$
-valued set theory like
$[0,1]$
-valued set theory like ![]() , there is something of a qualitative difference in its avoidance of Russell’s paradox. While
, there is something of a qualitative difference in its avoidance of Russell’s paradox. While ![]() is possiblyFootnote
6
able to avoid Russell’s paradox by Brouwer’s fixed point theorem, our theory avoids it by virtue of the required gap between r and s (although these are not unrelated phenomena).
is possiblyFootnote
6
able to avoid Russell’s paradox by Brouwer’s fixed point theorem, our theory avoids it by virtue of the required gap between r and s (although these are not unrelated phenomena).
We are now finally able to define the class of models of our theory directly before defining the theory itself.
Definition 2.8. We say that ![]() is a model of
is a model of
![]() $\mathsf {MSE}$
, written
$\mathsf {MSE}$
, written ![]() or
or
![]() $M \models \mathsf {MSE}$
, if it is a metric set structure that satisfies excision.
$M \models \mathsf {MSE}$
, if it is a metric set structure that satisfies excision.
![]() $\mathsf {MSE}$
stands for Metric Sets with Excision.
$\mathsf {MSE}$
stands for Metric Sets with Excision.
The following notation will be useful.
Definition 2.9. Given a metric set structure M, a formula
![]() $\varphi (x,\bar {y})$
, tuple
$\varphi (x,\bar {y})$
, tuple
![]() $\bar {a} \in M$
, and reals
$\bar {a} \in M$
, and reals
![]() $r < s$
, we write
$r < s$
, we write
to mean that for any c, if ![]() , then
, then ![]() and if
and if ![]() , then
, then
![]() $\varphi ^M(c,\bar {a}) < s$
.
$\varphi ^M(c,\bar {a}) < s$
.
Note of course that ![]() is not a uniquely specified object, but if M satisfies excision, it always exists.
is not a uniquely specified object, but if M satisfies excision, it always exists.
It is immediate to show that models of
![]() $\mathsf {MSE}$
contain some of the familiar sets one expects to see in a set theory with a universal set.
$\mathsf {MSE}$
contain some of the familiar sets one expects to see in a set theory with a universal set.
Proposition 2.10. For any
![]() $M \models \mathsf {MSE}$
, there are
$M \models \mathsf {MSE}$
, there are
![]() $a,b \in M$
such that for all
$a,b \in M$
such that for all
![]() $c \in M$
,
$c \in M$
, ![]() and
and ![]() .
.
Proof. Let ![]() and
and ![]() .
.
Since these sets are unique by
![]() $\mathrm {H}$
-extensionality, we will write
$\mathrm {H}$
-extensionality, we will write
![]() $\varnothing ^M$
for
$\varnothing ^M$
for ![]() and
and
![]() $V^M$
for
$V^M$
for ![]() . We may drop the superscript M if no confusion will arise.
. We may drop the superscript M if no confusion will arise.
3 Derived forms of comprehension
In this section we will show that models of
![]() $\mathsf {MSE}$
automatically satisfy certain instances of exact comprehension.
$\mathsf {MSE}$
automatically satisfy certain instances of exact comprehension.
3.1 Relative excision
An important common construction in set theory is separation, i.e., comprehension relative to a given set. Ordinarily, separation is an easy consequence of comprehension—
![]() $\{x \in A: \varphi (x)\}$
is the same as the set
$\{x \in A: \varphi (x)\}$
is the same as the set
![]() $\{x : x \in A \wedge \varphi (x)\}$
—but seeing that excision is merely an approximate form of comprehension, one might worry that we will only be able to find sets that are approximately subsets of other given sets. In other words, if B is a rough approximation of
$\{x : x \in A \wedge \varphi (x)\}$
—but seeing that excision is merely an approximate form of comprehension, one might worry that we will only be able to find sets that are approximately subsets of other given sets. In other words, if B is a rough approximation of
![]() $\{x : x \in A \wedge \varphi (x)\}$
, then it would only be the case that
$\{x : x \in A \wedge \varphi (x)\}$
, then it would only be the case that ![]() for some small but positive r. Fortunately, we are able to build exact subsets of a given set and thereby perform relative excision.
for some small but positive r. Fortunately, we are able to build exact subsets of a given set and thereby perform relative excision.
Definition 3.1. For any
![]() $a,b \in M$
, a metric set structure, we write
$a,b \in M$
, a metric set structure, we write
![]() $a \sqsubseteq b$
to mean that for all
$a \sqsubseteq b$
to mean that for all
![]() $c \in M$
, if
$c \in M$
, if ![]() , then
, then ![]() .
.
The following is a special case of relative excision, but we state it first because it is the only form of relative excision we will actually use and it is much easier to prove.
Proposition 3.2 (Discrete separation).
Fix
![]() $M \models \mathsf {MSE}$
and
$M \models \mathsf {MSE}$
and
![]() $\bar {a}$
and b in M. For any formula
$\bar {a}$
and b in M. For any formula
![]() $\varphi (x,\bar {a})$
and
$\varphi (x,\bar {a})$
and
![]() $r<s$
, if for all
$r<s$
, if for all ![]() ,
, ![]() or
or
![]() $\varphi ^M(c,\bar {a}) \geq s$
, then there is an
$\varphi ^M(c,\bar {a}) \geq s$
, then there is an
![]() $f \sqsubseteq b$
such that
$f \sqsubseteq b$
such that ![]() .
.
Proof. If ![]() for each
for each
![]() $n \in \mathbb {N}$
, then
$n \in \mathbb {N}$
, then
![]() $(f_n)_{n \in \mathbb {N}}$
is a Cauchy sequence that limits to the required set.
$(f_n)_{n \in \mathbb {N}}$
is a Cauchy sequence that limits to the required set.
Lemma 3.3. Fix
![]() $M \models \mathsf {MSE}$
. For any
$M \models \mathsf {MSE}$
. For any
![]() $a,b \in M$
and
$a,b \in M$
and
![]() $\varepsilon> 0$
, there is a
$\varepsilon> 0$
, there is a
![]() $c \sqsubseteq a$
such that
$c \sqsubseteq a$
such that
Proof. Fix
![]() $\varepsilon> 0$
. Let
$\varepsilon> 0$
. Let
![]() $c_0 = b$
. For any n, let
$c_0 = b$
. For any n, let ![]() . At stage n, given
. At stage n, given
![]() $c_n$
, let
$c_n$
, let
Note that for any
![]() $f \in M$
, if
$f \in M$
, if ![]() and
and
![]() $e(f,c_n) < t_n + 2^{-n-4}\varepsilon $
, then
$e(f,c_n) < t_n + 2^{-n-4}\varepsilon $
, then ![]() , and if
, and if ![]() , then
, then
![]() $e(f,a) < 2^{-n-4}\varepsilon $
and
$e(f,a) < 2^{-n-4}\varepsilon $
and
![]() $e(f,c_n) < t_n + 2^{-n-3}\varepsilon $
. In particular,
$e(f,c_n) < t_n + 2^{-n-3}\varepsilon $
. In particular, ![]() . Note also that by the definition of
. Note also that by the definition of
![]() $t_n$
, we have that for any
$t_n$
, we have that for any ![]() , there is an
, there is an ![]() such that
such that
![]() $d(f,g) < t_n + 2^{-n-4}\varepsilon $
. Such a g must be an element of
$d(f,g) < t_n + 2^{-n-4}\varepsilon $
. Such a g must be an element of
![]() $c_{n+1}$
. Since we can do this for any
$c_{n+1}$
. Since we can do this for any ![]() , we have that
, we have that ![]() . Hence, for any
. Hence, for any
![]() $n> 0$
, we have that
$n> 0$
, we have that ![]() . Therefore
. Therefore
![]() $(c_n)_{n\in \mathbb {N}}$
is a Cauchy sequence. Let
$(c_n)_{n\in \mathbb {N}}$
is a Cauchy sequence. Let ![]() .
.
Since
![]() $t_n \to 0$
as
$t_n \to 0$
as
![]() $n \to \infty $
, we have that
$n \to \infty $
, we have that
![]() $c \sqsubseteq a$
. Now we just need to verify that
$c \sqsubseteq a$
. Now we just need to verify that ![]() . Our estimates give that
. Our estimates give that

as required.
Proposition 3.4 (Relative excision).
If
![]() $M\models \mathsf {MSE}$
, then for any real-valued formula
$M\models \mathsf {MSE}$
, then for any real-valued formula
![]() $\varphi (x,\bar {y})$
,
$\varphi (x,\bar {y})$
,
![]() $\bar {a},b \in M$
, and reals
$\bar {a},b \in M$
, and reals
![]() $r < s$
, there is a
$r < s$
, there is a
![]() $c \in M$
with
$c \in M$
with
![]() $c \sqsubseteq b$
such that for any
$c \sqsubseteq b$
such that for any ![]() , if
, if ![]() , then
, then ![]() , and if
, and if ![]() , then
, then
![]() $\varphi (c,\bar {a}) < s$
.
$\varphi (c,\bar {a}) < s$
.
Proof. Fix ![]() ,
,
![]() $\bar {a}$
and b in M, and
$\bar {a}$
and b in M, and
![]() $\delta> 0$
with
$\delta> 0$
with
![]() $\delta < \frac {1}{4v(\varphi )}$
.
$\delta < \frac {1}{4v(\varphi )}$
.
Let ![]() . Note that
. Note that ![]() . Apply Lemma 3.3 to c to get an
. Apply Lemma 3.3 to c to get an
![]() $f \sqsubseteq b$
such that
$f \sqsubseteq b$
such that
![]() $d(c,f) < \delta $
. We now have that for any g, if
$d(c,f) < \delta $
. We now have that for any g, if ![]() and
and ![]() , then
, then
![]() $e(g,f) < \delta $
and if
$e(g,f) < \delta $
and if ![]() , then
, then ![]() and so
and so
![]() $\varphi (g,\bar {a}) < 2v(\varphi )\frac {1}{2v(\varphi )}$
.
$\varphi (g,\bar {a}) < 2v(\varphi )\frac {1}{2v(\varphi )}$
.
Since we can do this for any
![]() $\varphi (x,\bar {y})$
and
$\varphi (x,\bar {y})$
and
![]() $\bar {a} \in M$
, we have that M satisfies Definition 6.5 relative to the set b. The proposition then follows by repeating the proofs of Lemma 6.6 and Proposition 6.7 relative to the set b.
$\bar {a} \in M$
, we have that M satisfies Definition 6.5 relative to the set b. The proposition then follows by repeating the proofs of Lemma 6.6 and Proposition 6.7 relative to the set b.
In light of Propositions 3.2 and 3.4, we will write
to mean that for any
![]() $f \in M$
, if
$f \in M$
, if ![]() and
and ![]() , then
, then ![]() and if
and if ![]() , then
, then ![]() and
and
![]() $\varphi ^M(f,\bar {a}) < s$
.
$\varphi ^M(f,\bar {a}) < s$
.
3.2 Comprehension for definable classes
Given Proposition 3.4, one might be tempted to ask whether we can just outright show that models of
![]() $\mathsf {MSE}$
satisfy a more conventional form of comprehension. Suppose we have a formula
$\mathsf {MSE}$
satisfy a more conventional form of comprehension. Suppose we have a formula
![]() $\varphi (x)$
and we wish to form the set
$\varphi (x)$
and we wish to form the set
![]() $\{x \in M : \varphi ^M(x) = 0\}$
. Could we not just form the sequence
$\{x \in M : \varphi ^M(x) = 0\}$
. Could we not just form the sequence ![]() and take the limit? While we are perfectly able to form this sequence externally, the difficulty is that it will in general fail to be a Cauchy sequence.
and take the limit? While we are perfectly able to form this sequence externally, the difficulty is that it will in general fail to be a Cauchy sequence.
Regardless, there are times when such a sequence of approximations does actually converge in the Hausdorff metric, giving us an instance of exact comprehension. This happens precisely when
![]() $\{x \in M: \varphi ^M(x) = 0\}$
is a definable set in the sense of continuous logic, although in the context of a set theory it would be more appropriate to refer to these as definable classes.
$\{x \in M: \varphi ^M(x) = 0\}$
is a definable set in the sense of continuous logic, although in the context of a set theory it would be more appropriate to refer to these as definable classes.
Definition 3.5. A closed subset
![]() $D \subseteq M^n$
is a definable class if the function
$D \subseteq M^n$
is a definable class if the function
![]() $\bar {x} \mapsto \inf _{\bar {a} \in D}d(\bar {x},\bar {a})$
is a uniformly convergent limit of functions of the form
$\bar {x} \mapsto \inf _{\bar {a} \in D}d(\bar {x},\bar {a})$
is a uniformly convergent limit of functions of the form
![]() $\varphi ^M(\bar {x},\bar {b})$
for
$\varphi ^M(\bar {x},\bar {b})$
for ![]() and
and
![]() $\bar {b} \in M$
. D is definable without parameters if its definability is witnessed by formulas without parameters.
$\bar {b} \in M$
. D is definable without parameters if its definability is witnessed by formulas without parameters.
D is an explicitly definable class
Footnote
7
if there is a ![]() and a tuple
and a tuple
![]() $\bar {b}$
such that
$\bar {b}$
such that
![]() $\inf _{\bar {a} \in D}d(\bar {x},\bar {a}) = \varphi ^M(\bar {x},\bar {b})$
.
$\inf _{\bar {a} \in D}d(\bar {x},\bar {a}) = \varphi ^M(\bar {x},\bar {b})$
.
![]() $\bar {x} \mapsto \inf _{\bar {a} \in D}d(\bar {x},\bar {a})$
is called the distance predicate of D, which we may also write as
$\bar {x} \mapsto \inf _{\bar {a} \in D}d(\bar {x},\bar {a})$
is called the distance predicate of D, which we may also write as
![]() $e(\bar {x},D)$
.
$e(\bar {x},D)$
.
This definition is perhaps most strongly motivated by the fact that definable classes are precisely those that admit relative quantification.
Lemma 3.6. For any metric set structure M and
![]() $\bar {a} \in M$
, if
$\bar {a} \in M$
, if
![]() $\varphi (\bar {x},\bar {a})$
is the distance predicate of a definable class
$\varphi (\bar {x},\bar {a})$
is the distance predicate of a definable class
![]() $D \subseteq M^n$
, then for any
$D \subseteq M^n$
, then for any
![]() $\psi (\bar {x},\bar {y},\bar {z})$
and
$\psi (\bar {x},\bar {y},\bar {z})$
and
![]() $\bar {c} \in M$
,
$\bar {c} \in M$
,

where
![]() $\inf \varnothing $
is understood to be
$\inf \varnothing $
is understood to be
![]() $v(\psi )$
.
$v(\psi )$
.
Proof. Let
![]() $r = \inf _{\bar {x}}\min (\psi (\bar {x},\bar {c},\bar {b}) + 2v(\psi ) \varphi (\bar {x},\bar {a}),v(\psi ))$
and
$r = \inf _{\bar {x}}\min (\psi (\bar {x},\bar {c},\bar {b}) + 2v(\psi ) \varphi (\bar {x},\bar {a}),v(\psi ))$
and
![]() $s = \inf \{\psi ^M (\bar {f},\bar {c},\bar {b}) : \bar {f} \in D\}$
.
$s = \inf \{\psi ^M (\bar {f},\bar {c},\bar {b}) : \bar {f} \in D\}$
.
If D is empty, then
![]() $\varphi (\bar {x},\bar {a}) = 1$
and the result holds.
$\varphi (\bar {x},\bar {a}) = 1$
and the result holds.
If D is not empty, then we clearly have that ![]() since
since
![]() $\psi (\bar {x},\bar {c},\bar {b}) \in [-v(\psi ),v(\psi )]$
by Lemma 2.6. For the other direction, fix
$\psi (\bar {x},\bar {c},\bar {b}) \in [-v(\psi ),v(\psi )]$
by Lemma 2.6. For the other direction, fix
![]() $\bar {g} \in M$
. For any
$\bar {g} \in M$
. For any
![]() ${\varepsilon> 0}$
, there is an
${\varepsilon> 0}$
, there is an
![]() $\bar {f} \in D$
such that
$\bar {f} \in D$
such that
![]() $d(\bar {f},\bar {g}) < e(\bar {g},D)+ \varepsilon $
. By Lemma 2.6,
$d(\bar {f},\bar {g}) < e(\bar {g},D)+ \varepsilon $
. By Lemma 2.6,
![]() $\bar {x}\mapsto \psi (\bar {x},\bar {c},\bar {b})$
is
$\bar {x}\mapsto \psi (\bar {x},\bar {c},\bar {b})$
is
![]() $2v(\psi )$
-Lipschitz, so
$2v(\psi )$
-Lipschitz, so
![]() $\psi (\bar {g},\bar {c},\bar {b})+2v(\psi )\varphi (\bar {g},\bar {a}) \geq \psi (\bar {f},\bar {c},\bar {b})$
and therefore
$\psi (\bar {g},\bar {c},\bar {b})+2v(\psi )\varphi (\bar {g},\bar {a}) \geq \psi (\bar {f},\bar {c},\bar {b})$
and therefore
![]() $\min (\psi (\bar {g},\bar {c},\bar {b})+2v(\psi )\varphi (\bar {g},\bar {a}),v(\psi )) \geq \psi (\bar {f},\bar {c},\bar {b})$
. Since we can do this for any
$\min (\psi (\bar {g},\bar {c},\bar {b})+2v(\psi )\varphi (\bar {g},\bar {a}),v(\psi )) \geq \psi (\bar {f},\bar {c},\bar {b})$
. Since we can do this for any
![]() $\bar {g} \in M$
, we have that
$\bar {g} \in M$
, we have that
![]() $r \geq s$
and we are done.
$r \geq s$
and we are done.
In continuous logic generally, definable classes can be characterized as those sets that admit relative quantification in the same sense as Lemma 3.6. In models of
![]() $\mathsf {MSE}$
moreover, definable classes of
$\mathsf {MSE}$
moreover, definable classes of
![]() $1$
-tuples correspond precisely to sets. In particular, every definable class is explicitly definable by
$1$
-tuples correspond precisely to sets. In particular, every definable class is explicitly definable by
![]() $e(x,a)$
for some a.
$e(x,a)$
for some a.
Proposition 3.7. Let
![]() $M \models \mathsf {MSE}$
. A closed set
$M \models \mathsf {MSE}$
. A closed set
![]() $D \subseteq M$
is a definable class if and only if there is an
$D \subseteq M$
is a definable class if and only if there is an
![]() $a \in M$
such that
$a \in M$
such that ![]() .
.
Proof. The ![]() direction is obvious. To show the
direction is obvious. To show the
![]() $\Rightarrow $
direction, find a formula
$\Rightarrow $
direction, find a formula
![]() $\varphi _n(x,\bar {a}_n)$
for each
$\varphi _n(x,\bar {a}_n)$
for each
![]() $n \in \mathbb {N}$
such that
$n \in \mathbb {N}$
such that
![]() $\sup _x|\varphi _n(x,\bar {a}_n)-e(x,D)| < 2^{-n}$
. Let
$\sup _x|\varphi _n(x,\bar {a}_n)-e(x,D)| < 2^{-n}$
. Let ![]() . Note that if
. Note that if
![]() $c \in D$
, then
$c \in D$
, then ![]() and if
and if ![]() , then
, then
![]() $e(c,D) < 2^{-n+1}+2^{-n} < 2^{-n+1}$
. This implies that
$e(c,D) < 2^{-n+1}+2^{-n} < 2^{-n+1}$
. This implies that ![]() , and so the sequence
, and so the sequence
![]() $(b_n)_{n \in \mathbb {N}}$
is a Cauchy sequence and
$(b_n)_{n \in \mathbb {N}}$
is a Cauchy sequence and ![]() has the property that
has the property that ![]() if and only if
if and only if
![]() $c \in D$
.
$c \in D$
.
Proposition 3.7 allows us to answer some very basic questions that we haven’t resolved yet.
Corollary 3.8. Fix
![]() $M \models \mathsf {MSE}$
.
$M \models \mathsf {MSE}$
.
-
(1) (Singletons) For any
 $a \in M$
, there is a
$a \in M$
, there is a
 $b \in M$
such that
$b \in M$
such that  if and only if
if and only if
 $c = a$
.
$c = a$
. -
(2) (Finite unions) For any
 $a,b \in M$
, there is a
$a,b \in M$
, there is a
 $c \in M$
such that
$c \in M$
such that  if and only if
if and only if  or
or  .
. -
(3) (Finite sets) For any
 $a_0,\dots ,a_{n-1} \in M$
, there is a
$a_0,\dots ,a_{n-1} \in M$
, there is a
 $b \in M$
such that
$b \in M$
such that  if and only if
if and only if
 $c=a_i$
for some
$c=a_i$
for some
 $i<n$
.
$i<n$
. -
(4) (Closure-of-unions) For any
 $a \in M$
, there is a
$a \in M$
, there is a
 $b \in M$
such that
$b \in M$
such that  if and only if b is in the metric closure of
if and only if b is in the metric closure of  .
.
Proof.
-
(1) This is witnessed by the formula
 $d(x,a)$
.
$d(x,a)$
. -
(2) This is witnessed by the formula
 $\min (e(x,a),e(x,b))$
.
$\min (e(x,a),e(x,b))$
. -
(3) This follows from 1 and 2 by induction.
-
(4) This is witnessed by the formula
 .
.
Unfortunately, however, it is generally not the case that the distance to the intersection of two sets X and Y can be computed from the distances to X and Y. As such, we cannot establish the existence of intersections in general, and indeed as demonstrated in Proposition B.1 such intersections do not always exist. We do, however, get a kind of approximate intersection in the form of ![]() .
.
A minor corollary of Corollary 3.8 is that models of
![]() $\mathsf {MSE}$
satisfy
$\mathsf {MSE}$
satisfy
![]() $d(x,y) = \sup _{z}|e(x,z)-e(y,z)|$
, as witnessed by the singleton
$d(x,y) = \sup _{z}|e(x,z)-e(y,z)|$
, as witnessed by the singleton
![]() $\{x\}$
. In
$\{x\}$
. In
![]() $[0,1]$
-valued set theories, the quantity
$[0,1]$
-valued set theories, the quantity
![]() $1-\sup _z|e(x,z)-e(y,z)|$
is often referred to a Leibniz equality, as it represents the degree to which x and y cannot be discerned from each other.
$1-\sup _z|e(x,z)-e(y,z)|$
is often referred to a Leibniz equality, as it represents the degree to which x and y cannot be discerned from each other.
In light of Corollary 3.8, we will write
![]() $\{a_0,a_1,\dots ,a_{n-1}\}$
for the finite set containing
$\{a_0,a_1,\dots ,a_{n-1}\}$
for the finite set containing
![]() $a_0,a_1,\dots ,a_{n-1}$
,
$a_0,a_1,\dots ,a_{n-1}$
,
![]() $a \sqcup b$
for the union of a and b, and
$a \sqcup b$
for the union of a and b, and
![]() $\overline {\bigsqcup a}$
for the closure of the union of the elements of a.
$\overline {\bigsqcup a}$
for the closure of the union of the elements of a.
Now that we have the ability to form finite sets by Corollary 3.8, we are free to code ordered pairs. While we certainly could use the standard Kuratowski ordered pair, Wiener’s earlier definition is actually preferable to us for technical reasons.Footnote
8
As such, we will write ![]() for
for
![]() $\{\{\{a\},\varnothing \},\{\{b\}\}\}$
. Recall that
$\{\{\{a\},\varnothing \},\{\{b\}\}\}$
. Recall that ![]() .
.
Lemma 3.9. Let
![]() $M\models \mathsf {MSE}$
. For any
$M\models \mathsf {MSE}$
. For any
![]() $a,b,c,f \in M$
,
$a,b,c,f \in M$
,
Proof. Let
![]() $A = \{\{a\},\varnothing \}$
,
$A = \{\{a\},\varnothing \}$
,
![]() $B = \{\{b\}\}$
,
$B = \{\{b\}\}$
,
![]() $C = \{\{c\},\varnothing \}$
, and
$C = \{\{c\},\varnothing \}$
, and
![]() $F = \{\{f\}\}$
. We have that
$F = \{\{f\}\}$
. We have that
For any x,
![]() $d(\{x\},\varnothing ) = 1$
. This implies that
$d(\{x\},\varnothing ) = 1$
. This implies that
![]() $d(\{\{x\},\varnothing \},\{\{y\}\}) = 1$
for any x and y as well. This implies, for instance, that
$d(\{\{x\},\varnothing \},\{\{y\}\}) = 1$
for any x and y as well. This implies, for instance, that
This together with similar facts for the other three terms implies that
 $$ \begin{align*} d(\{A,B\},\{C,F\}) &= \max(d(A,C),d(B,F),d(C,A),d(F,B)) \\ &= \max(d(A,C),d(B,F)). \end{align*} $$
$$ \begin{align*} d(\{A,B\},\{C,F\}) &= \max(d(A,C),d(B,F),d(C,A),d(F,B)) \\ &= \max(d(A,C),d(B,F)). \end{align*} $$
Finally,
![]() $d(\{\{x\}\},\{\{y\}\}) = d(x,y)$
and
$d(\{\{x\}\},\{\{y\}\}) = d(x,y)$
and
![]() $d(\{\{x\},\varnothing \},\{\{y\},\varnothing \}) = d(x,y)$
for any x and y, so we have that
$d(\{\{x\},\varnothing \},\{\{y\},\varnothing \}) = d(x,y)$
for any x and y, so we have that ![]() , as required.
, as required.
Lemma 3.9 means that a sequence of ordered pairs can only converge to an ordered pair and that convergence of sequences of ordered pairs behaves in the expected way. In particular, the class of ordered pairs is closed. (Note that at the moment we don’t know that the collection of ordered pairs is a set, but we will show this later in Corollary 3.15.)
With a little more work we can establish the existence of power sets.
Proposition 3.10. (Power sets).
For any
![]() $a \in M$
, there is a
$a \in M$
, there is a
![]() $b \in M$
such that
$b \in M$
such that ![]() if and only if
if and only if
![]() $c \sqsubseteq a$
.
$c \sqsubseteq a$
.
Proof. First note that by basic properties of the Hausdorff metric, the class ![]() is necessarily closed. By Lemma 3.3, we know that for any
is necessarily closed. By Lemma 3.3, we know that for any
![]() $f \in M$
,
$f \in M$
,
On the other hand, for any
![]() $g \in \mathcal {P}(a)$
, we must have that
$g \in \mathcal {P}(a)$
, we must have that
by monotonicity of
![]() $\inf $
. Therefore,
$\inf $
. Therefore,
and so the two quantities are actually equal. Hence
![]() $\mathcal {P}(a)$
is a definable class and is coextensive with some element
$\mathcal {P}(a)$
is a definable class and is coextensive with some element
![]() $b\in M$
by Proposition 3.7.
$b\in M$
by Proposition 3.7.
We will write
![]() $\mathcal {P}(a)$
for the power set of a.
$\mathcal {P}(a)$
for the power set of a.
3.3 Definable functions and replacement
Now that we are confident that ordered pairs exist, the next natural thing to consider is Cartesian products. In order to show that the class ![]() is definable and therefore a set, what we would like to be able to do is write a real-valued formula like this:
is definable and therefore a set, what we would like to be able to do is write a real-valued formula like this:
If we did have this formula,
![]() $\varphi (x)$
would of course be the point-set distance from x to the class
$\varphi (x)$
would of course be the point-set distance from x to the class
![]() $a \times b$
. The issue is that the functions
$a \times b$
. The issue is that the functions
![]() $x \mapsto \{x\}$
and
$x \mapsto \{x\}$
and
![]() $(x,y) \mapsto \{x,y\}$
and the constant
$(x,y) \mapsto \{x,y\}$
and the constant
![]() $\varnothing $
are not formally part of our logic.
$\varnothing $
are not formally part of our logic.
Practically, however, it is commonly understood in the context of discrete logic that it is safe to pretend that certain functions—namely the definable functions—are formally part of the language in the following sense: Given a discrete structure M, a function
![]() $f:M^n \to M$
is definable if and only if for every formula
$f:M^n \to M$
is definable if and only if for every formula
![]() $\varphi (\bar {x},y,\bar {z})$
, there is a formula
$\varphi (\bar {x},y,\bar {z})$
, there is a formula
![]() $\psi (\bar {x},\bar {z})$
such that for any
$\psi (\bar {x},\bar {z})$
such that for any
![]() $\bar {a},\bar {b} \in M$
,
$\bar {a},\bar {b} \in M$
,
![]() $M \models \varphi (\bar {a},f(\bar {a}),\bar {b})$
if and only if
$M \models \varphi (\bar {a},f(\bar {a}),\bar {b})$
if and only if
![]() $M \models \psi (\bar {a},\bar {b})$
. It is easy to show that this is equivalent to the graph of f being a definable subset of
$M \models \psi (\bar {a},\bar {b})$
. It is easy to show that this is equivalent to the graph of f being a definable subset of
![]() $M^{n+1}$
.
$M^{n+1}$
.
In continuous logic, a similar thing can be done.
Definition 3.11. Given a set
![]() $X \subseteq M^n$
, a function
$X \subseteq M^n$
, a function
![]() $f : X \to M$
is definable if for every
$f : X \to M$
is definable if for every
![]() $\varepsilon> 0$
, there is a
$\varepsilon> 0$
, there is a ![]() and a
and a
![]() $\bar {c} \in M$
such that for any
$\bar {c} \in M$
such that for any
![]() $\bar {a} \in X$
and
$\bar {a} \in X$
and
![]() $b \in M$
,
$b \in M$
,
![]() $|d(f(\bar {a}),b) - \varphi ^M(\bar {a},b,\bar {c})| < \varepsilon $
.
$|d(f(\bar {a}),b) - \varphi ^M(\bar {a},b,\bar {c})| < \varepsilon $
.
f is explicitly definable if there is a ![]() and a tuple
and a tuple
![]() $\bar {c}$
such that
$\bar {c}$
such that
![]() $d(f(\bar {a}),b) = \varphi ^M(\bar {a},b,\bar {c})$
for every
$d(f(\bar {a}),b) = \varphi ^M(\bar {a},b,\bar {c})$
for every
![]() $\bar {a} \in X$
and
$\bar {a} \in X$
and
![]() $b \in M^{n+1}$
.
$b \in M^{n+1}$
.
If
![]() $X = M^n$
, we say that f is an (explicitly) definable total function. Otherwise it is an (explicitly) definable partial function.Footnote
9
$X = M^n$
, we say that f is an (explicitly) definable total function. Otherwise it is an (explicitly) definable partial function.Footnote
9
Given a function
![]() $g : M^n \to M$
, we say that g is (explicitly) definable on X if
$g : M^n \to M$
, we say that g is (explicitly) definable on X if
![]() $g {\upharpoonright } X$
is (explicitly) definable.
$g {\upharpoonright } X$
is (explicitly) definable.
When X is itself definable, it is not too hard to show that f is definable if and only if it is uniformly continuous and its graph is definable (in the sense of Definition 3.5 relative to the max metric on tuples).
While more general statements can be made (see [Reference Yaacov, Alexander Berenstein, Henson and Usvyatsov25, Section 9]), we really only need explicitly definable functions in this article.Footnote 10
Lemma 3.12. For any metric set structure M, formula
![]() $\varphi (\bar {x},y,\bar {z})$
, and explicitly definable function
$\varphi (\bar {x},y,\bar {z})$
, and explicitly definable function
![]() $f(\bar {x})$
with domain
$f(\bar {x})$
with domain
![]() $X \subseteq M^n$
, there is a formula
$X \subseteq M^n$
, there is a formula
![]() $\psi (\bar {x},\bar {z})$
(possibly with parameters) such that for all
$\psi (\bar {x},\bar {z})$
(possibly with parameters) such that for all
![]() $\bar {a} \in X$
and
$\bar {a} \in X$
and
![]() $\bar {b} \in M$
,
$\bar {b} \in M$
,
![]() $\psi ^M(\bar {a},\bar {b}) = \varphi ^M(\bar {a},f(\bar {a}),\bar {b})$
.
$\psi ^M(\bar {a},\bar {b}) = \varphi ^M(\bar {a},f(\bar {a}),\bar {b})$
.
Proof. Let
![]() $f(\bar {x})$
be defined on X by
$f(\bar {x})$
be defined on X by
![]() $\chi (\bar {x},y)$
(possibly with parameters). By the same argument as in the proof of Lemma 3.6, the formula
$\chi (\bar {x},y)$
(possibly with parameters). By the same argument as in the proof of Lemma 3.6, the formula
![]() $\inf _y\varphi (\bar {x},y,\bar {z}) + 2v(\varphi ) \chi (\bar {x},y)$
is the required
$\inf _y\varphi (\bar {x},y,\bar {z}) + 2v(\varphi ) \chi (\bar {x},y)$
is the required
![]() $\psi (\bar {x},\bar {z})$
.
$\psi (\bar {x},\bar {z})$
.
A corollary of Lemma 3.12 is that compositions of explicitly definable functions are explicitly definable. (This is also true of definable functions, but we will not need it.)
It is fairly immediate that the operations we established in Section 3.2 are in fact definable.
Proposition 3.13. Let
![]() $M \models \mathsf {MSE}$
. The following functions are explicitly definable:
$M \models \mathsf {MSE}$
. The following functions are explicitly definable:
-
(1)
 $()\mapsto \varnothing ^M$
.
$()\mapsto \varnothing ^M$
. -
(2)
 $()\mapsto V^M$
.
$()\mapsto V^M$
. -
(3)
 $(x_0,x_1,\dots ,x_{n-1}) \mapsto \{x_0,x_1,\dots ,x_{n-1}\}$
.
$(x_0,x_1,\dots ,x_{n-1}) \mapsto \{x_0,x_1,\dots ,x_{n-1}\}$
. -
(4)
 $(x,y) \mapsto x\sqcup y$
.
$(x,y) \mapsto x\sqcup y$
. -
(5)
 $x \mapsto \overline {\bigsqcup x}$
.
$x \mapsto \overline {\bigsqcup x}$
. -
(6)
 .
. -
(7)
 $x \mapsto \mathcal {P}(x)$
.
$x \mapsto \mathcal {P}(x)$
.
Proof. The definability of these functions other than (6) are witnessed by the following formulas:
-
(1)
 .
. -
(2)
 $d(y,V) = \sup _{z}e(z,y)$
.
$d(y,V) = \sup _{z}e(z,y)$
. -
(3)
 $d(y,\{x_0,x_1,\dots ,x_{n-1}\}) = \sup _{z}|e(z,y) - \min (d(z,x_0),\dots ,d(z,x_{n-1}))|$
.
$d(y,\{x_0,x_1,\dots ,x_{n-1}\}) = \sup _{z}|e(z,y) - \min (d(z,x_0),\dots ,d(z,x_{n-1}))|$
. -
(4)
 $d(z,x\sqcup y) = \sup _{w}|e(w,z) - \min (e(w,x),e(w,y))|$
.
$d(z,x\sqcup y) = \sup _{w}|e(w,z) - \min (e(w,x),e(w,y))|$
. -
(5)
 .
. -
(7)
 .
.
(6) follows from the fact that ![]() is a composition of other explicitly definable functions.
is a composition of other explicitly definable functions.
Now finally we can return to the question of forming a Cartesian product of two sets. The relevant fact is this:
Proposition 3.14. (Images of definable functions).
Let
![]() $M \models \mathsf {MSE}$
. For any definable function
$M \models \mathsf {MSE}$
. For any definable function
![]() $f: X \to M$
and any
$f: X \to M$
and any
![]() $a_0,\dots ,a_{n-1} \in M$
, if
$a_0,\dots ,a_{n-1} \in M$
, if
![]() $\bar {b} \in X$
for any tuple
$\bar {b} \in X$
for any tuple
![]() $\bar {b}$
satisfying
$\bar {b}$
satisfying ![]() for each
for each
![]() $i<n$
, then the metric closure of
$i<n$
, then the metric closure of ![]() is a definable class.
is a definable class.
Proof.
![]() is clearly the distance predicate of the class in question. By Lemma 3.12, this is equivalent to a formula.
is clearly the distance predicate of the class in question. By Lemma 3.12, this is equivalent to a formula.
Corollary 3.15. (Cartesian products).
Let
![]() $M \models \mathsf {MSE}$
. For any
$M \models \mathsf {MSE}$
. For any
![]() $a,b \in M$
, there is a
$a,b \in M$
, there is a
![]() $c \in M$
such that
$c \in M$
such that ![]() if and only if
if and only if ![]() for some
for some ![]() and
and ![]() .
.
Proof. By Proposition 3.14, the metric closure of ![]() is a definable class. By the discussion at the end of Section 3.2,
is a definable class. By the discussion at the end of Section 3.2,
![]() $a \times b$
is already metrically closed, so we have that it is a definable class. By Proposition 3.7, we have that the required c exists.
$a \times b$
is already metrically closed, so we have that it is a definable class. By Proposition 3.7, we have that the required c exists.
We will write
![]() $a \times b$
for the set whose existence is established in Corollary 3.15.
$a \times b$
for the set whose existence is established in Corollary 3.15.
One thing to note is that the proof of Corollary 3.15 actually establishes that the function
![]() $(x,y) \mapsto x \times y$
is explicitly definable as witnessed by the formula
$(x,y) \mapsto x \times y$
is explicitly definable as witnessed by the formula ![]()
It is occasionally useful to be able to project sets of ordered pairs onto their coordinates. Since the projection function ![]() is only partially defined, this is the first time we need the added generality of being able to talk about definable partial functions.
is only partially defined, this is the first time we need the added generality of being able to talk about definable partial functions.
Proposition 3.16. Let
![]() $M \models \mathsf {MSE}$
. Let
$M \models \mathsf {MSE}$
. Let
![]() $\pi _0$
and
$\pi _0$
and
![]() $\pi _1$
be the functions on the class of ordered pairs defined by
$\pi _1$
be the functions on the class of ordered pairs defined by ![]() and
and ![]() .
.
![]() $\pi _0$
and
$\pi _0$
and
![]() $\pi _1$
are explicitly definable.
$\pi _1$
are explicitly definable.
Proof. This is witnessed by the formulas ![]() and
and ![]() .
.
The following facts will also be useful.
Lemma 3.17. Fix closed sets
![]() $X \subseteq M^n$
and
$X \subseteq M^n$
and
![]() $Y\subseteq M^{n+1}$
. Suppose that there is a formula
$Y\subseteq M^{n+1}$
. Suppose that there is a formula
![]() $\varphi (\bar {x},y)$
such that for every
$\varphi (\bar {x},y)$
such that for every
![]() $\bar {a} \in X$
and
$\bar {a} \in X$
and
![]() $b \in M$
,
$b \in M$
,
![]() $\varphi ^M(\bar {a},b) = e(b,\{y : (\bar {a},y) \in Y\})$
. Then there is an explicitly definable function
$\varphi ^M(\bar {a},b) = e(b,\{y : (\bar {a},y) \in Y\})$
. Then there is an explicitly definable function
![]() $f: X \to M$
such that for every
$f: X \to M$
such that for every
![]() $\bar {a} \in X$
,
$\bar {a} \in X$
,
![]() $f(\bar {a})$
is coextensive with
$f(\bar {a})$
is coextensive with
![]() $\{y : (\bar {a},y) \in Y\}$
.
$\{y : (\bar {a},y) \in Y\}$
.
Proof. The formula
![]() $\psi (\bar {x},z) = \inf _{y}|e(y,z)-\varphi (\bar {x},y)|$
witnesses that the required function is explicitly definable.
$\psi (\bar {x},z) = \inf _{y}|e(y,z)-\varphi (\bar {x},y)|$
witnesses that the required function is explicitly definable.
Lemma 3.18. If
![]() $f: a \to M$
is an explicitly definable partial function on some set a, then the map
$f: a \to M$
is an explicitly definable partial function on some set a, then the map ![]() is an explicitly definable partial function on the set
is an explicitly definable partial function on the set
![]() $\mathcal {P}(a)$
.
$\mathcal {P}(a)$
.
Proof. Let
![]() $\varphi (y,z)$
be a formula (possibly with parameters) such that
$\varphi (y,z)$
be a formula (possibly with parameters) such that
![]() $\varphi ^M(b,c) = d(b,f(c))$
for all
$\varphi ^M(b,c) = d(b,f(c))$
for all ![]() and
and
![]() $c \in M$
. We now have that for any
$c \in M$
. We now have that for any
![]() $g\sqsubseteq a$
,
$g\sqsubseteq a$
, ![]() is the distance predicate of
is the distance predicate of ![]() . Therefore the required function is definable by Lemma 3.17.
. Therefore the required function is definable by Lemma 3.17.
3.4 Quotients by discrete equivalence relations
A commonly used operation is passing from an equivalence relation to its set of equivalence classes. We are able to do this for discrete equivalence relations.
Definition 3.19. Fix a metric set structure M. Given a set
![]() $a \in M$
, a formula
$a \in M$
, a formula
![]() $\varphi (x,y)$
is a discrete equivalence relation on a if for all
$\varphi (x,y)$
is a discrete equivalence relation on a if for all ![]() ,
,
![]() $\varphi ^M(b,c)$
is either
$\varphi ^M(b,c)$
is either
![]() $0$
or
$0$
or
![]() $1$
and
$1$
and
![]() $\varphi ^M(x,y) = 1$
is an equivalence relation on
$\varphi ^M(x,y) = 1$
is an equivalence relation on ![]() .
.
Given a discrete equivalence relation
![]() $\varphi (x,y)$
, we will refer to the equivalence classes of the equivalence relation
$\varphi (x,y)$
, we will refer to the equivalence classes of the equivalence relation
![]() $\varphi (x,y) = 1$
as
$\varphi (x,y) = 1$
as
![]() $\varphi $
-equivalence classes.
$\varphi $
-equivalence classes.
We need a small observation.
Lemma 3.20. Let
![]() $M \models \mathsf {MSE}$
. If
$M \models \mathsf {MSE}$
. If
![]() $\varphi (x,y)$
is a discrete equivalence relation on
$\varphi (x,y)$
is a discrete equivalence relation on
![]() $a \in M$
, then for any
$a \in M$
, then for any ![]() ,
,
is the distance predicate of the
![]() $\varphi $
-equivalence class of b.
$\varphi $
-equivalence class of b.
Proposition 3.21. Let
![]() $M \models \mathsf {MSE}$
. If
$M \models \mathsf {MSE}$
. If
![]() $\varphi (x,y)$
is a discrete equivalence relation on
$\varphi (x,y)$
is a discrete equivalence relation on
![]() $a \in M$
, then there is a
$a \in M$
, then there is a
![]() $b \in M$
containing precisely the
$b \in M$
containing precisely the
![]() $\varphi $
-equivalence classes of a.
$\varphi $
-equivalence classes of a.
Moreover, if c is a set such that
![]() $\varphi (x,y)$
is a discrete equivalence relation on every
$\varphi (x,y)$
is a discrete equivalence relation on every ![]() , then the map taking a to the set of
, then the map taking a to the set of
![]() $\varphi $
-equivalence classes of a is an explicitly definable partial function on c.
$\varphi $
-equivalence classes of a is an explicitly definable partial function on c.
Proof. The formula in Lemma 3.20 defines a partial function on a that maps elements to their
![]() $\varphi $
-equivalence classes. Therefore, by Proposition 3.14, the closure of the class of
$\varphi $
-equivalence classes. Therefore, by Proposition 3.14, the closure of the class of
![]() $\varphi $
-equivalence classes of a is a set in M. By Lemma 3.20, the class of
$\varphi $
-equivalence classes of a is a set in M. By Lemma 3.20, the class of
![]() $\varphi $
-equivalence classes is closed, so we are done.
$\varphi $
-equivalence classes is closed, so we are done.
The ‘Moreover’ statement follows from Lemma 3.17.
4 Uniformly discrete sets and ordinary mathematics
A common feature of models of set theories that implement some kind of nearly unrestricted comprehension is that they have a class of tame sets in which unrestricted separation is consistent. In
![]() $\mathsf {NF}$
and
$\mathsf {NF}$
and
![]() $\mathsf {NFU}$
, the strongly Cantorian sets are well behaved in this way, and in
$\mathsf {NFU}$
, the strongly Cantorian sets are well behaved in this way, and in
![]() $\mathsf {GPK}^+_\infty $
, the closed sets of isolated points are likewise well behaved. In the context of
$\mathsf {GPK}^+_\infty $
, the closed sets of isolated points are likewise well behaved. In the context of
![]() $\mathsf {MSE}$
, the analogously well-behaved class seems to be that of the uniformly discrete sets.
$\mathsf {MSE}$
, the analogously well-behaved class seems to be that of the uniformly discrete sets.
Definition 4.1. In a metric set structure M, an element
![]() $a \in M$
is
$a \in M$
is
![]() $\varepsilon $
-discrete if for any
$\varepsilon $
-discrete if for any ![]() , either
, either
![]() $b=c$
or
$b=c$
or
![]() $d(b,c) \geq \varepsilon $
. a is uniformly discrete if it is
$d(b,c) \geq \varepsilon $
. a is uniformly discrete if it is
![]() $\varepsilon $
-discrete for some
$\varepsilon $
-discrete for some
![]() $\varepsilon> 0$
.
$\varepsilon> 0$
.
While it might make sense to simply use the term ‘discrete’ for sets that are
![]() $\varepsilon $
-discrete for some
$\varepsilon $
-discrete for some
![]() $\varepsilon> 0$
, ‘discrete’ has a pre-existing topological meaning (i.e., that each element is topologically isolated) which is weaker than what we are considering here.
$\varepsilon> 0$
, ‘discrete’ has a pre-existing topological meaning (i.e., that each element is topologically isolated) which is weaker than what we are considering here.
Definition 4.2. For any a and b, the disjoint union of a and b, written
![]() $a \boxplus b$
, is
$a \boxplus b$
, is
![]() $(a\times \{\varnothing \})\sqcup (b\times \{\{\varnothing \}\})$
.
$(a\times \{\varnothing \})\sqcup (b\times \{\{\varnothing \}\})$
.
Note that it is immediate that
![]() $(x,y) \mapsto x\boxplus y$
is an explicitly definable function, as it is a composition of explicitly definable functions.
$(x,y) \mapsto x\boxplus y$
is an explicitly definable function, as it is a composition of explicitly definable functions.
Lemma 4.3. Let
![]() $M \models \mathsf {MSE}$
. If
$M \models \mathsf {MSE}$
. If
![]() $a,b \in M$
are
$a,b \in M$
are
![]() $\varepsilon $
-discrete, then
$\varepsilon $
-discrete, then
![]() $a \boxplus b$
,
$a \boxplus b$
,
![]() $a \times b$
, and
$a \times b$
, and
![]() $\mathcal {P}(a)$
are
$\mathcal {P}(a)$
are
![]() $\varepsilon $
-discrete.
$\varepsilon $
-discrete.
Proof. If a is empty, then the statements in the lemma are trivial, and if b is empty, then the statements for
![]() $a \boxplus b$
and
$a \boxplus b$
and
![]() $a \times b$
are trivial, so assume that a and b are both non-empty. Fix
$a \times b$
are trivial, so assume that a and b are both non-empty. Fix ![]() and
and ![]() .
.
For the disjoint union, we have that ![]() . Furthermore,
. Furthermore, ![]() and
and ![]() , so
, so
![]() $a \boxplus b$
is
$a \boxplus b$
is
![]() $\varepsilon $
-discrete.
$\varepsilon $
-discrete.
For the Cartesian product, if ![]() , then either
, then either
![]() $c\neq f$
or
$c\neq f$
or
![]() $g \neq h$
. In either case we have that
$g \neq h$
. In either case we have that ![]() .
.
For the power set, if
![]() $c \neq f$
, then we may assume without loss of generality that there is a g such that
$c \neq f$
, then we may assume without loss of generality that there is a g such that ![]() but
but ![]() . Since
. Since
![]() $g \neq h$
for all
$g \neq h$
for all ![]() , we have that
, we have that
![]() $e(g,h) \geq \varepsilon $
(since a is
$e(g,h) \geq \varepsilon $
(since a is
![]() $\varepsilon $
-discrete). Therefore
$\varepsilon $
-discrete). Therefore
![]() $d(c,f) \geq \varepsilon $
.
$d(c,f) \geq \varepsilon $
.
Note that Lemma 4.3 relies on our use of Wiener pairs over Kuratowski pairs. While seemingly a cosmetic issue, this matters in the treatment of uniformly discrete sets in the rest of this section and for much of the analysis of the global structure of models of
![]() $\mathsf {MSE}$
in Section 5.
$\mathsf {MSE}$
in Section 5.
Within uniformly discrete sets, we are generally able to reason in a familiar discrete manner. In order to do this, we will use a typed language for ‘discrete formulas,’ which we define next.
Definition 4.4. Given a tuple
![]() $\bar {a}$
of formal type variables, we write
$\bar {a}$
of formal type variables, we write
![]() $\bar {a}^\ast $
for the smallest collection of expressions containing
$\bar {a}^\ast $
for the smallest collection of expressions containing
![]() $\{a_0,a_1,\dots \}$
and containing (the formal expressions)
$\{a_0,a_1,\dots \}$
and containing (the formal expressions)
![]() $b\times c$
and
$b\times c$
and
![]() $\mathcal {P}(b)$
for any
$\mathcal {P}(b)$
for any
![]() $b,c \in \bar {a}^\ast $
.
$b,c \in \bar {a}^\ast $
.
We will assume that we have a sufficient collection of variable symbols assigned to each formal expression in
![]() $\bar {a}^\ast $
, which are to be regarded as types.
$\bar {a}^\ast $
, which are to be regarded as types.
Definition 4.5. We write
![]() $\mathcal {L}_{\mathrm {dis}}(\bar {a})$
for the smallest collection of formulas satisfying the following (where b and c are elements of
$\mathcal {L}_{\mathrm {dis}}(\bar {a})$
for the smallest collection of formulas satisfying the following (where b and c are elements of
![]() $\bar {a}^\ast $
):
$\bar {a}^\ast $
):
-
• For any x of type b and y of type c,
 $x=y$
is in
$x=y$
is in
 $\mathcal {L}_{\mathrm {dis}}(\bar {a})$
.
$\mathcal {L}_{\mathrm {dis}}(\bar {a})$
. -
• For any x of type b, y of type c, and z of type
 $b\times c$
,
$b\times c$
,  is in
is in
 $\mathcal {L}_{\mathrm {dis}}(\bar {a})$
.
$\mathcal {L}_{\mathrm {dis}}(\bar {a})$
. -
• For any x of type b and y of type
 $\mathcal {P}(b)$
,
$\mathcal {P}(b)$
,  is in
is in
 $\mathcal {L}_{\mathrm {dis}}(\bar {a})$
.
$\mathcal {L}_{\mathrm {dis}}(\bar {a})$
. -
• For
 $\Phi ,\Psi \in \mathcal {L}_{\mathrm {dis}}(\bar {a})$
,
$\Phi ,\Psi \in \mathcal {L}_{\mathrm {dis}}(\bar {a})$
,
 $\Phi \wedge \Psi $
,
$\Phi \wedge \Psi $
,
 $\Phi \vee \Psi $
,
$\Phi \vee \Psi $
,
 $\Phi \to \Psi $
, and
$\Phi \to \Psi $
, and
 $\neg \Phi $
are in
$\neg \Phi $
are in
 $\mathcal {L}_{\mathrm {dis}}(\bar {a})$
.
$\mathcal {L}_{\mathrm {dis}}(\bar {a})$
. -
• For
 $\Phi \in \mathcal {L}_{\mathrm {dis}}(\bar {a})$
and x of type b,
$\Phi \in \mathcal {L}_{\mathrm {dis}}(\bar {a})$
and x of type b,  and
and  are in
are in
 $\mathcal {L}_{\mathrm {dis}}(\bar {a})$
.
$\mathcal {L}_{\mathrm {dis}}(\bar {a})$
.
If we wish to specify the variables and formal type variables of a formula
![]() $\Phi \in \mathcal {L}_{\mathrm {dis}}(\bar {a})$
, we will write
$\Phi \in \mathcal {L}_{\mathrm {dis}}(\bar {a})$
, we will write
![]() $\Phi (\bar {x};\bar {a})$
(where the free variables of
$\Phi (\bar {x};\bar {a})$
(where the free variables of
![]() $\Phi $
are among
$\Phi $
are among
![]() $\bar {x}$
).
$\bar {x}$
).
To distinguish discrete formulas from real-valued formulas, we will usually write discrete formulas with capital Greek letters.
The formal type variables in a formula of
![]() $\mathcal {L}_{\mathrm {dis}}(\bar {a})$
are intended to be interpreted as uniformly discrete sets in a model of
$\mathcal {L}_{\mathrm {dis}}(\bar {a})$
are intended to be interpreted as uniformly discrete sets in a model of
![]() $\mathsf {MSE}$
, in which case a variable of type a is allowed to take on values in a. The interpretation of a formula is then clear.
$\mathsf {MSE}$
, in which case a variable of type a is allowed to take on values in a. The interpretation of a formula is then clear.
Definition 4.6. Fix
![]() $M \models \mathsf {MSE}$
. Given a formula
$M \models \mathsf {MSE}$
. Given a formula
![]() $\Phi (\bar {x};\bar {a}) \in \mathcal {L}_{\mathrm {dis}}(\bar {a})$
, a tuple
$\Phi (\bar {x};\bar {a}) \in \mathcal {L}_{\mathrm {dis}}(\bar {a})$
, a tuple
![]() $\bar {b} \in M$
of the same length as
$\bar {b} \in M$
of the same length as
![]() $\bar {a}$
, and a tuple
$\bar {a}$
, and a tuple
![]() $\bar {c}$
of the same length as
$\bar {c}$
of the same length as
![]() $\bar {x}$
, we say that
$\bar {x}$
, we say that
![]() $\Phi (\bar {c};\bar {b})$
is well-typed if for each
$\Phi (\bar {c};\bar {b})$
is well-typed if for each
![]() $c_i \in \bar {c}$
, if
$c_i \in \bar {c}$
, if
![]() $x_i$
is a variable of type
$x_i$
is a variable of type
![]() $t(\bar {a})$
(where
$t(\bar {a})$
(where
![]() $t(\bar {a})$
is a formal type expression), then
$t(\bar {a})$
is a formal type expression), then ![]() (where t is now interpreted as a literal expression involving the functions
(where t is now interpreted as a literal expression involving the functions
![]() $\times $
and
$\times $
and
![]() $\mathcal {P}$
in M).
$\mathcal {P}$
in M).
If
![]() $\Phi (\bar {c};\bar {b})$
is well-typed, we write
$\Phi (\bar {c};\bar {b})$
is well-typed, we write
![]() $M \models \Phi (\bar {c};\bar {b})$
to mean that
$M \models \Phi (\bar {c};\bar {b})$
to mean that ![]() satisfies
satisfies
![]() $\Phi (\bar {c};\bar {b})$
as a discrete structure (where quantifiers, such as
$\Phi (\bar {c};\bar {b})$
as a discrete structure (where quantifiers, such as ![]() are interpreted as
are interpreted as ![]() ).
).
Now, we will see that as long as the sets in
![]() $\bar {b}$
are
$\bar {b}$
are
![]() $\varepsilon $
-discrete, we can express these kinds of discrete formulas as real-valued formulas in a mostly uniform way.
$\varepsilon $
-discrete, we can express these kinds of discrete formulas as real-valued formulas in a mostly uniform way.
Definition 4.7. Given a tuple
![]() $\bar {a}$
of formal type variables, a formula
$\bar {a}$
of formal type variables, a formula
![]() $\Phi (\bar {x}) \in \mathcal {L}_{\mathrm {dis}}(\bar {a})$
, and
$\Phi (\bar {x}) \in \mathcal {L}_{\mathrm {dis}}(\bar {a})$
, and
![]() $\varepsilon> 0$
, we write
$\varepsilon> 0$
, we write ![]() for the real-valued formula defined by the following inductive procedure:
for the real-valued formula defined by the following inductive procedure:
-
•
 .
. -
•
 .
. -
•
 .
. -
•
 .
. -
•
 .
. -
•
 .
.
The other Boolean connectives and the universal quantifier are defined from the above in the typical way.
Proposition 4.8. Fix
![]() $M\models \mathsf {MSE}$
. For any formal tuple
$M\models \mathsf {MSE}$
. For any formal tuple
![]() $\bar {a}$
of type variable and any formula
$\bar {a}$
of type variable and any formula
![]() $\Phi (\bar {x};\bar {a}) \in \mathcal {L}_{\mathrm {dis}}(\bar {a})$
, we have for any
$\Phi (\bar {x};\bar {a}) \in \mathcal {L}_{\mathrm {dis}}(\bar {a})$
, we have for any
![]() $\varepsilon $
-discrete sets
$\varepsilon $
-discrete sets
![]() $\bar {b} \in M$
and any
$\bar {b} \in M$
and any
![]() $\bar {c} \in M$
such that
$\bar {c} \in M$
such that
![]() $\Phi (\bar {b};\bar {c})$
is well-typed,
$\Phi (\bar {b};\bar {c})$
is well-typed,
![]() $M \models \Phi (\bar {b};\bar {c})$
if and only if
$M \models \Phi (\bar {b};\bar {c})$
if and only if ![]() and
and
![]() $M \models \neg \Phi (\bar {b};\bar {c})$
if and only if
$M \models \neg \Phi (\bar {b};\bar {c})$
if and only if ![]() .
.
Proof. This follows immediately by induction on the construction of formulas in
![]() $\mathcal {L}_{\mathrm {dis}}(\bar {a})$
.
$\mathcal {L}_{\mathrm {dis}}(\bar {a})$
.
Given Proposition 4.8, we can now confidently talk about familiar discrete concepts in the context of uniformly discrete sets. In particular, we can develop the notion of cardinalities.
Definition 4.9. Given a uniformly discrete sets
![]() $a,b \in M \models \mathsf {MSE}$
, we write
$a,b \in M \models \mathsf {MSE}$
, we write
![]() $M \models a \approx b$
to mean that there is a
$M \models a \approx b$
to mean that there is a
![]() $c \sqsubseteq a \times b$
that is the graph of a bijection between a and b.
$c \sqsubseteq a \times b$
that is the graph of a bijection between a and b.
It is clear that there is an
![]() $\mathcal {L}_{\operatorname {\mathrm {dis}}}(a,b)$
-formula
$\mathcal {L}_{\operatorname {\mathrm {dis}}}(a,b)$
-formula
![]() $\eta (x,y)$
with the property that if a and b are
$\eta (x,y)$
with the property that if a and b are
![]() $\varepsilon $
-discrete,
$\varepsilon $
-discrete,
![]() $c \sqsubseteq a$
, and
$c \sqsubseteq a$
, and
![]() $f \sqsubseteq b$
, then
$f \sqsubseteq b$
, then ![]() if and only if
if and only if
![]() $M \models c \approx f$
. We will write
$M \models c \approx f$
. We will write
![]() $x \approx _{a,b}y$
for this formula. We will write
$x \approx _{a,b}y$
for this formula. We will write
![]() $\approx _a$
for
$\approx _a$
for
![]() $\approx _{a,a}$
. It is immediate that
$\approx _{a,a}$
. It is immediate that ![]() is an equivalence relation on
is an equivalence relation on
![]() $\mathcal {P}(a)$
whenever a is
$\mathcal {P}(a)$
whenever a is
![]() $\varepsilon $
-discrete.
$\varepsilon $
-discrete.
Definition 4.10. Given an
![]() $\varepsilon $
-discrete set a, a cardinal of a is a
$\varepsilon $
-discrete set a, a cardinal of a is a ![]() -equivalence class of subsets of a. We write
-equivalence class of subsets of a. We write
![]() $\operatorname {\mathrm {Card}}_a$
for the collection of cardinals of a.
$\operatorname {\mathrm {Card}}_a$
for the collection of cardinals of a.
Given
![]() $b \sqsubseteq a$
, we write
$b \sqsubseteq a$
, we write
![]() $|b|_a$
for the
$|b|_a$
for the ![]() -equivalence class of b.
-equivalence class of b.
It follows immediately from the above discussion and Proposition 3.21 that
![]() $\operatorname {\mathrm {Card}}_a$
is a set for any uniformly discrete
$\operatorname {\mathrm {Card}}_a$
is a set for any uniformly discrete
![]() $a\in M \models \mathsf {MSE}$
. Furthermore,
$a\in M \models \mathsf {MSE}$
. Furthermore,
![]() $x \mapsto |x|_a$
is a definable function on
$x \mapsto |x|_a$
is a definable function on
![]() $\mathcal {P}(a)$
.
$\mathcal {P}(a)$
.
Definition 4.11. Given a uniformly discrete set a and a set
![]() $b \sqsubseteq \mathcal {P}(a)$
, we write
$b \sqsubseteq \mathcal {P}(a)$
, we write
![]() $\operatorname {\mathrm {succ}}_a(b)$
for the collection
$\operatorname {\mathrm {succ}}_a(b)$
for the collection ![]() .
.
It follows from Proposition 3.2 that
![]() $\operatorname {\mathrm {succ}}_a(b)$
is a set for any uniformly discrete a and
$\operatorname {\mathrm {succ}}_a(b)$
is a set for any uniformly discrete a and
![]() $b \sqsubseteq a$
. Note that
$b \sqsubseteq a$
. Note that
![]() $\operatorname {\mathrm {succ}}_a$
is an explicitly definable function by Lemma 3.17. Furthermore, if
$\operatorname {\mathrm {succ}}_a$
is an explicitly definable function by Lemma 3.17. Furthermore, if
![]() $b \in \operatorname {\mathrm {Card}}_a$
, then either
$b \in \operatorname {\mathrm {Card}}_a$
, then either
![]() $\operatorname {\mathrm {succ}}_a(b) \in \operatorname {\mathrm {Card}}_a$
or
$\operatorname {\mathrm {succ}}_a(b) \in \operatorname {\mathrm {Card}}_a$
or
![]() $\operatorname {\mathrm {succ}}_a(b) = \varnothing $
.
$\operatorname {\mathrm {succ}}_a(b) = \varnothing $
.
Definition 4.12. We write
![]() $0$
for the set
$0$
for the set
![]() $\{\varnothing \}$
. (Note that
$\{\varnothing \}$
. (Note that
![]() $0$
is always an element of
$0$
is always an element of
![]() $\operatorname {\mathrm {Card}}_a$
.)
$\operatorname {\mathrm {Card}}_a$
.)
We write
![]() $\operatorname {\mathrm {ind}}_a(x)$
for the
$\operatorname {\mathrm {ind}}_a(x)$
for the
![]() $\mathcal {L}_{\operatorname {\mathrm {dis}}}(a)$
-formula
$\mathcal {L}_{\operatorname {\mathrm {dis}}}(a)$
-formula ![]() . If
. If
![]() $\operatorname {\mathrm {ind}}_a(x)$
holds, we say that x is an inductive set.
$\operatorname {\mathrm {ind}}_a(x)$
holds, we say that x is an inductive set.
We write
![]() $\mathbb {N}_a$
for the set
$\mathbb {N}_a$
for the set ![]() .
.
It is clear that
![]() $\operatorname {\mathrm {ind}}_a(\operatorname {\mathrm {Card}}_a)$
always holds and so
$\operatorname {\mathrm {ind}}_a(\operatorname {\mathrm {Card}}_a)$
always holds and so
![]() $\mathbb {N}_a \sqsubseteq \operatorname {\mathrm {Card}}_a$
for any uniformly discrete a.
$\mathbb {N}_a \sqsubseteq \operatorname {\mathrm {Card}}_a$
for any uniformly discrete a.
Now we can finally state the local version of the axiom of infinity.
Definition 4.13. We write
![]() $\mathsf {Inf}(a)$
for the
$\mathsf {Inf}(a)$
for the
![]() $\mathcal {L}_{\operatorname {\mathrm {dis}}}(a)$
-sentence
$\mathcal {L}_{\operatorname {\mathrm {dis}}}(a)$
-sentence ![]() .
.
It is easy to show that
![]() $\mathsf {Inf}(a)$
holds if and only if
$\mathsf {Inf}(a)$
holds if and only if
![]() $\mathbb {N}_a \neq \operatorname {\mathrm {Card}}_a$
.
$\mathbb {N}_a \neq \operatorname {\mathrm {Card}}_a$
.
Now provided that one can find a uniformly discrete
![]() $a \in M \models \mathsf {MSE}$
such that
$a \in M \models \mathsf {MSE}$
such that
![]() $M \models \mathsf {Inf}(a)$
, we have that
$M \models \mathsf {Inf}(a)$
, we have that
![]() $(\mathbb {N}_a,\mathcal {P}(\mathbb {N}_a),\mathcal {P}^2(\mathbb {N}_a),\dots )$
is a model of full
$(\mathbb {N}_a,\mathcal {P}(\mathbb {N}_a),\mathcal {P}^2(\mathbb {N}_a),\dots )$
is a model of full
![]() $\omega $
th-order arithmetic, which is sufficient to develop the majority of ordinary mathematics.
$\omega $
th-order arithmetic, which is sufficient to develop the majority of ordinary mathematics.
Given the local nature of our development here, one might worry that there could be uniformly discrete
![]() $a,b \in M \models \mathsf {MSE}$
for which
$a,b \in M \models \mathsf {MSE}$
for which
![]() $\mathsf {Inf}(a)$
and
$\mathsf {Inf}(a)$
and
![]() $\mathsf {Inf}(b)$
both hold but
$\mathsf {Inf}(b)$
both hold but
![]() $\mathbb {N}_a$
and
$\mathbb {N}_a$
and
![]() $\mathbb {N}_b$
are not internally isomorphic. Fortunately, since our theory is fully impredicative, this cannot happen.
$\mathbb {N}_b$
are not internally isomorphic. Fortunately, since our theory is fully impredicative, this cannot happen.
Proposition 4.14. Fix
![]() $M \models \mathsf {MSE}$
and uniformly discrete
$M \models \mathsf {MSE}$
and uniformly discrete
![]() $a\sqsubseteq b \in M$
.
$a\sqsubseteq b \in M$
.
-
(1) The equivalence relation
 $\approx _a$
is the restriction of the equivalence relation
$\approx _a$
is the restriction of the equivalence relation
 $\approx _b$
to
$\approx _b$
to
 $\mathcal {P}(a)\times \mathcal {P}(a)$
. Write
$\mathcal {P}(a)\times \mathcal {P}(a)$
. Write
 $\iota $
for the induced map from
$\iota $
for the induced map from
 $\operatorname {\mathrm {Card}}_a$
to
$\operatorname {\mathrm {Card}}_a$
to
 $\operatorname {\mathrm {Card}}_b$
.
$\operatorname {\mathrm {Card}}_b$
. -
(2) If
 $M \models \mathsf {Inf}(a)$
, then
$M \models \mathsf {Inf}(a)$
, then
 $M \models \mathsf {Inf}(b)$
and
$M \models \mathsf {Inf}(b)$
and
 $\mathbb {N}_b$
is the image of
$\mathbb {N}_b$
is the image of
 $\mathbb {N}_a$
under
$\mathbb {N}_a$
under
 $\iota $
.
$\iota $
. -
(3) For any uniformly discrete c, if
 $M \models \mathsf {Inf}(a) \wedge \mathsf {Inf}(c)$
, then
$M \models \mathsf {Inf}(a) \wedge \mathsf {Inf}(c)$
, then
 $\mathbb {N}_a \approx \mathbb {N}_c$
.
$\mathbb {N}_a \approx \mathbb {N}_c$
.
Proof. 1 follows from the fact that any bijection between subsets of a that exists as a subset of
![]() $b \times b$
is already a subset of
$b \times b$
is already a subset of
![]() $a \times a$
. 2 and 3 follow from 1.
$a \times a$
. 2 and 3 follow from 1.
5 Global structure of models of
 $\mathsf {MSE}$
$\mathsf {MSE}$
While Section 4 gives a satisfactory picture of the local structure of a model of
![]() $\mathsf {MSE}$
around some collection of uniformly discrete sets, the axiom of infinity is a global statement in that it says that there is some set, somewhere, that is infinite.
$\mathsf {MSE}$
around some collection of uniformly discrete sets, the axiom of infinity is a global statement in that it says that there is some set, somewhere, that is infinite.
It is clear that we can take a more global view of cardinality for uniformly discrete sets in a model of
![]() $\mathsf {MSE}$
.
$\mathsf {MSE}$
.
![]() $\approx $
is a perfectly well-defined equivalence relation externally and it would make sense to call its equivalence classes cardinals, but we cannot write it as a formula. While
$\approx $
is a perfectly well-defined equivalence relation externally and it would make sense to call its equivalence classes cardinals, but we cannot write it as a formula. While
![]() $0 = \{\varnothing \}$
and the class of all singletons,
$0 = \{\varnothing \}$
and the class of all singletons,
![]() $1$
, are both sets, the class of doubletons in a model of
$1$
, are both sets, the class of doubletons in a model of
![]() $\mathsf {MSE}$
is never closed, which precludes it from being a set.Footnote
11
That said, the class of sets of size
$\mathsf {MSE}$
is never closed, which precludes it from being a set.Footnote
11
That said, the class of sets of size
![]() $1$
or
$1$
or
![]() $2$
(or more generally the class of non-empty sets of size at most n for any (externally) finite n) is a set by Propositions 3.7 and 3.14. Something similar to this observation is used in Definition 5.13 and Theorem 5.14 in order to construct canonical representatives of ordinals in
$2$
(or more generally the class of non-empty sets of size at most n for any (externally) finite n) is a set by Propositions 3.7 and 3.14. Something similar to this observation is used in Definition 5.13 and Theorem 5.14 in order to construct canonical representatives of ordinals in
![]() $\mathsf {MSE}$
.
$\mathsf {MSE}$
.
Suppose that there is a
![]() $\frac {1}{2}$
-discrete set a such that
$\frac {1}{2}$
-discrete set a such that
![]() $M \models \mathsf {Inf}(a)$
. Does this necessarily imply that there is a
$M \models \mathsf {Inf}(a)$
. Does this necessarily imply that there is a
![]() $1$
-discrete set b such that
$1$
-discrete set b such that
![]() $M \models \mathsf {Inf}(b)$
? Can we somehow scale a set up in this way? We will see in Theorem 5.10 that the answer is no, and so in order to state the axiom of infinity in a global way, we will need to specify the scale at which infinity is to first appear.
$M \models \mathsf {Inf}(b)$
? Can we somehow scale a set up in this way? We will see in Theorem 5.10 that the answer is no, and so in order to state the axiom of infinity in a global way, we will need to specify the scale at which infinity is to first appear.
5.1 Collecting
 $\varepsilon $
-discrete sets and ‘the’ axiom of infinity
$\varepsilon $
-discrete sets and ‘the’ axiom of infinity
But before we can formalize that, we need to deal with another subtlety we have been ignoring up until now. How do we even know that we can find any uniformly discrete sets? Clearly
![]() $\varnothing $
is uniformly discrete, and likewise all hereditarily finite sets are, but it is not clear that the class of hereditarily finite sets is even a set.
$\varnothing $
is uniformly discrete, and likewise all hereditarily finite sets are, but it is not clear that the class of hereditarily finite sets is even a set.
What we would like to be able to do is make a formula
![]() $\varphi (x)$
that returns
$\varphi (x)$
that returns ![]() , but
, but
![]() $\operatorname {\mathrm {dis}}(x)$
is not a continuous function and so cannot possibly be a formula. If
$\operatorname {\mathrm {dis}}(x)$
is not a continuous function and so cannot possibly be a formula. If
![]() $(a_n)_{n \in \mathbb {N}}$
is a Cauchy sequence limiting to a with
$(a_n)_{n \in \mathbb {N}}$
is a Cauchy sequence limiting to a with
![]() $a_n \neq a$
for all
$a_n \neq a$
for all
![]() $n \in \mathbb {N}$
, then
$n \in \mathbb {N}$
, then
![]() $(\{a_n,a\})_{n\in \mathbb {N}}$
will be
$(\{a_n,a\})_{n\in \mathbb {N}}$
will be
![]() $d(a_n,a)$
-discrete but no better for every n, yet the limit,
$d(a_n,a)$
-discrete but no better for every n, yet the limit,
![]() $\{a\}$
, will be
$\{a\}$
, will be
![]() $1$
-discrete. (This is just the fact that the class of doubletons is not closed again.)
$1$
-discrete. (This is just the fact that the class of doubletons is not closed again.)
This makes it seem unlikely that we will be able to even approximately collect the r-discrete sets into a class. Nevertheless, we are able to do something nearly as good.
Fix
![]() $r> 0$
and consider the formula
$r> 0$
and consider the formula
Note that ![]() if and only if for every
if and only if for every ![]() , either
, either ![]() or
or
![]() $d(y,z) \geq r -\varepsilon $
. If moreover
$d(y,z) \geq r -\varepsilon $
. If moreover
![]() $\varepsilon < \frac {1}{3}r$
, this implies that the formula
$\varepsilon < \frac {1}{3}r$
, this implies that the formula
defines a discrete equivalence relation on the elements of a. If a is already r-discrete, then this equivalence relation is equality. For any
![]() $\varepsilon> 0$
with
$\varepsilon> 0$
with
![]() $\varepsilon < \frac {1}{3}r$
, let
$\varepsilon < \frac {1}{3}r$
, let
and let
![]() $f_{r} : X_{r} \to M$
be the function that takes a to the set of
$f_{r} : X_{r} \to M$
be the function that takes a to the set of
![]() $E_r$
-equivalence classes of a. By Lemma 3.17 and Proposition 3.21,
$E_r$
-equivalence classes of a. By Lemma 3.17 and Proposition 3.21,
![]() $f_{r}$
is an explicitly definable partial function. Let
$f_{r}$
is an explicitly definable partial function. Let
![]() $\psi _{r}(x,y)$
be a formula defining it (i.e., for any
$\psi _{r}(x,y)$
be a formula defining it (i.e., for any
![]() $a \in X_{r}$
and
$a \in X_{r}$
and
![]() $b \in M$
,
$b \in M$
,
![]() $\psi _{r}^M(a,b) = d(f_{r}(a),b)$
). Note that
$\psi _{r}^M(a,b) = d(f_{r}(a),b)$
). Note that
![]() $\psi _{r}(x,y)$
does not need any parameters. Note moreover that for any
$\psi _{r}(x,y)$
does not need any parameters. Note moreover that for any
![]() $a \in X_{r}$
,
$a \in X_{r}$
,
![]() $f_{r}(a)$
is
$f_{r}(a)$
is
![]() $\frac {1}{3}r$
-discrete.
$\frac {1}{3}r$
-discrete.
Definition 5.1. For any
![]() $r,\varepsilon> 0$
with
$r,\varepsilon> 0$
with
![]() $\varepsilon < \frac {1}{3}r$
, we let
$\varepsilon < \frac {1}{3}r$
, we let
![]() $\mathsf {Inf}_{r,\varepsilon }$
denote the condition
$\mathsf {Inf}_{r,\varepsilon }$
denote the condition
where ![]() means
means ![]() .
.
We let
![]() $\mathsf {Inf}$
denote the collection of conditions
$\mathsf {Inf}$
denote the collection of conditions
![]() $\{\mathsf {Inf}_{1,\varepsilon } : 0<\varepsilon < \frac {1}{3}\}$
.
$\{\mathsf {Inf}_{1,\varepsilon } : 0<\varepsilon < \frac {1}{3}\}$
.
Proposition 5.2. Fix
![]() $M \models \mathsf {MSE}$
.
$M \models \mathsf {MSE}$
.
-
(1) For any
 $r,\varepsilon> 0$
with
$r,\varepsilon> 0$
with
 $\varepsilon < \frac {1}{3}r$
,
$\varepsilon < \frac {1}{3}r$
,
 $M \models \mathsf {Inf}_{r,\varepsilon }$
if and only if for every
$M \models \mathsf {Inf}_{r,\varepsilon }$
if and only if for every
 $s \in (0,r-\varepsilon )$
, there is an s-discrete set
$s \in (0,r-\varepsilon )$
, there is an s-discrete set
 $a \in M$
such that
$a \in M$
such that
 $M \models \mathsf {Inf}(a)$
.
$M \models \mathsf {Inf}(a)$
. -
(2)
 $M \models \mathsf {Inf}$
if and only if for every
$M \models \mathsf {Inf}$
if and only if for every
 $r \in (0,1)$
, there is an r-discrete set
$r \in (0,1)$
, there is an r-discrete set
 $a \in M$
such that
$a \in M$
such that
 $M \models \mathsf {Inf}(a)$
.
$M \models \mathsf {Inf}(a)$
.
Proof. 2 follows immediately from 1. For the
![]() $\Rightarrow $
direction of
$\Rightarrow $
direction of
![]() $1$
, assume that
$1$
, assume that
![]() $M \models \mathsf {Inf}_{r,\varepsilon }$
. This implies that for any
$M \models \mathsf {Inf}_{r,\varepsilon }$
. This implies that for any
![]() $\delta> 0$
, there is a
$\delta> 0$
, there is a
![]() $b \in M$
such that
$b \in M$
such that
![]() $M \models 1 + \varepsilon - \varphi _r(b)> 1 - \delta $
and
$M \models 1 + \varepsilon - \varphi _r(b)> 1 - \delta $
and ![]() . The first condition implies that
. The first condition implies that
![]() $\varphi _r^M(b) < \varepsilon +\delta $
. For
$\varphi _r^M(b) < \varepsilon +\delta $
. For
![]() $\delta < \frac {1}{3}r - \varepsilon $
, this implies that b is in
$\delta < \frac {1}{3}r - \varepsilon $
, this implies that b is in
![]() $X_{r}$
and so
$X_{r}$
and so
![]() $f_r(b)$
is
$f_r(b)$
is
![]() $(r-\varepsilon -\delta )$
-discrete. Since
$(r-\varepsilon -\delta )$
-discrete. Since
![]() $b \in X_r$
, the second condition is equivalent to
$b \in X_r$
, the second condition is equivalent to ![]() , which is equivalent to
, which is equivalent to
![]() $M \models \mathsf {Inf}(f_r(b))$
and we can take
$M \models \mathsf {Inf}(f_r(b))$
and we can take
![]() $f_r(b)$
to be the required a. Since we can do this for any
$f_r(b)$
to be the required a. Since we can do this for any
![]() $\delta> 0$
(and since an s-discrete set is t-discrete for any
$\delta> 0$
(and since an s-discrete set is t-discrete for any
![]() $t < s$
), we have the required statement.
$t < s$
), we have the required statement.
For the ![]() direction, fix
direction, fix
![]() $s \in (\frac {2}{3}r,r-\varepsilon )$
and let a be an s-discrete set such that
$s \in (\frac {2}{3}r,r-\varepsilon )$
and let a be an s-discrete set such that
![]() $M \models \mathsf {Inf}(a)$
. Now we clearly have that
$M \models \mathsf {Inf}(a)$
. Now we clearly have that ![]() . Therefore
. Therefore
![]() $f_r(a)$
is defined (and equal to
$f_r(a)$
is defined (and equal to ![]() ). Since
). Since
![]() $M \models \mathsf {Inf}(a)$
,
$M \models \mathsf {Inf}(a)$
,
![]() $M \models \mathsf {Inf}(f_r(a))$
as well. (There is an obviously definable bijection between a and
$M \models \mathsf {Inf}(f_r(a))$
as well. (There is an obviously definable bijection between a and
![]() $f_r(a)$
. This exists as an element of
$f_r(a)$
. This exists as an element of
![]() $\mathcal {P}(a\times f_r(a))$
.) Since we can do this for any sufficiently large
$\mathcal {P}(a\times f_r(a))$
.) Since we can do this for any sufficiently large
![]() $s < r-\varepsilon $
, we’re done.
$s < r-\varepsilon $
, we’re done.
By the discussion in Section 4, any of the axioms
![]() $\mathsf {Inf}_{r,\varepsilon }$
is a sufficient form of the axiom of infinity for the purposes of developing standard mathematics. Nevertheless, we propose the scheme
$\mathsf {Inf}_{r,\varepsilon }$
is a sufficient form of the axiom of infinity for the purposes of developing standard mathematics. Nevertheless, we propose the scheme
![]() $\mathsf {Inf}$
as a canonical choice for ‘the axiom of infinity’ in the context of
$\mathsf {Inf}$
as a canonical choice for ‘the axiom of infinity’ in the context of
![]() $\mathsf {MSE}$
. One objection to this proposal might be that it is a scheme, rather than a single axiom, but as discussed in [Reference Hanson10, Section 6.1], the concept of finite axiomatizability is murky in continuous logic.
$\mathsf {MSE}$
. One objection to this proposal might be that it is a scheme, rather than a single axiom, but as discussed in [Reference Hanson10, Section 6.1], the concept of finite axiomatizability is murky in continuous logic.
For most of the models we construct in Section 7, there is a
![]() $1$
-discrete set a for which
$1$
-discrete set a for which
![]() $\mathsf {Inf}(a)$
holds. This is obviously a more comfortable condition than
$\mathsf {Inf}(a)$
holds. This is obviously a more comfortable condition than
![]() $M\models \mathsf {Inf}$
, but it is unclear whether it is actually axiomatizable. We could achieve it by adding a constant for some such a, but this is unsatisfying. Thus we have the following question.
$M\models \mathsf {Inf}$
, but it is unclear whether it is actually axiomatizable. We could achieve it by adding a constant for some such a, but this is unsatisfying. Thus we have the following question.
Question 5.3. Is the class
![]() $\{M \models \mathsf {MSE} : (\exists a \in M)a~\mathrm {is}~1\text{-}\mathrm{discrete,}~M\models \mathsf {Inf}(a)\}$
elementary in the sense of continuous logic?
$\{M \models \mathsf {MSE} : (\exists a \in M)a~\mathrm {is}~1\text{-}\mathrm{discrete,}~M\models \mathsf {Inf}(a)\}$
elementary in the sense of continuous logic?
General pessimism leads us to believe that the answer to this is no, but we do not see an approach to resolving this question. One candidate might be the existence of the von Neumann ordinal
![]() $\omega $
, which is necessarily
$\omega $
, which is necessarily
![]() $1$
-discrete if it exists in an
$1$
-discrete if it exists in an
![]() $\omega $
-standard model of
$\omega $
-standard model of
![]() $\mathsf {MSE}$
, but it is not clear that any model with a
$\mathsf {MSE}$
, but it is not clear that any model with a
![]() $1$
-discrete infinite set has
$1$
-discrete infinite set has
![]() $\omega $
as an element. It is also not clear whether it’s possible to axiomatize the existence of
$\omega $
as an element. It is also not clear whether it’s possible to axiomatize the existence of
![]() $\omega $
in a satisfactory way.
$\omega $
in a satisfactory way.
5.2 Ordinals
Rather than develop the global structure of cardinals in models of
![]() $\mathsf {MSE}$
, we will focus on ordinals. We do this for a couple of reasons. Many of the technical details for cardinals and ordinals are similar but not quite similar enough to develop simultaneously in an expeditious way. Furthermore, more can be said about the structure of ordinals than of cardinals without assuming some form of the axiom of choice.
$\mathsf {MSE}$
, we will focus on ordinals. We do this for a couple of reasons. Many of the technical details for cardinals and ordinals are similar but not quite similar enough to develop simultaneously in an expeditious way. Furthermore, more can be said about the structure of ordinals than of cardinals without assuming some form of the axiom of choice.
Definition 5.4. Fix
![]() $M \models \mathsf {MSE}$
. A chain in M is a set a such that for any
$M \models \mathsf {MSE}$
. A chain in M is a set a such that for any
![]() $b,c \in a$
, either
$b,c \in a$
, either
![]() $b \sqsubseteq c$
or
$b \sqsubseteq c$
or
![]() $c \sqsubseteq b$
.
$c \sqsubseteq b$
.
Two uniformly discrete chains a and b are order-isomorphic if there is a bijection
![]() $f \in \mathcal {P}(a\times b)$
such that for any
$f \in \mathcal {P}(a\times b)$
such that for any ![]() , it holds that
, it holds that
![]() $g \sqsubseteq h$
if and only if
$g \sqsubseteq h$
if and only if
![]() $f(g) \sqsubseteq f(h)$
. We write
$f(g) \sqsubseteq f(h)$
. We write
![]() $a \cong b$
to signify that a and b are order-isomorphic. The order type of a is the
$a \cong b$
to signify that a and b are order-isomorphic. The order type of a is the
![]() $\cong $
-class of a, written
$\cong $
-class of a, written
![]() $\operatorname {\mathrm {otp}}(a)$
.
$\operatorname {\mathrm {otp}}(a)$
.
A uniformly discrete chain a is well-ordered if for any non-empty
![]() $b \sqsubseteq a$
, there is a
$b \sqsubseteq a$
, there is a
![]() $\sqsubseteq $
-least element of b.
$\sqsubseteq $
-least element of b.
The
![]() $\cong $
-classes of uniformly discrete well-ordered chains in M are referred to as the ordinals of M, and the collection of such is written
$\cong $
-classes of uniformly discrete well-ordered chains in M are referred to as the ordinals of M, and the collection of such is written
![]() $\operatorname {\mathrm {Ord}}^M$
.
$\operatorname {\mathrm {Ord}}^M$
.
Note that we will typically use the term well-ordered to mean internally well-ordered. We will use the word ‘externally’ if we wish to emphasize that something is externally well-ordered.
Given a more general sort of linear order, namely a pair
![]() $(a,b)$
with a uniformly discrete and
$(a,b)$
with a uniformly discrete and
![]() $b \sqsubseteq a\times a$
the graph of a linear order, we can find a uniformly discrete chain c such that
$b \sqsubseteq a\times a$
the graph of a linear order, we can find a uniformly discrete chain c such that
![]() $(a,b)$
and
$(a,b)$
and
![]() $(c,{\sqsubseteq }{\upharpoonright } c\times c)$
are internally order-isomorphic. We just need to map each element f of a to the set
$(c,{\sqsubseteq }{\upharpoonright } c\times c)$
are internally order-isomorphic. We just need to map each element f of a to the set ![]() (i.e., the c-initial segment with largest element f). In this way we can see that uniformly discrete chains are sufficient to represent all uniformly discrete linear order types in models of
(i.e., the c-initial segment with largest element f). In this way we can see that uniformly discrete chains are sufficient to represent all uniformly discrete linear order types in models of
![]() $\mathsf {MSE}$
.
$\mathsf {MSE}$
.
We denote order types of uniformly discrete well-ordered chains with lowercase Greek letters near the beginning of the alphabet, such as
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. We write
$\beta $
. We write ![]() to mean that for any a with
to mean that for any a with
![]() $\operatorname {\mathrm {otp}}(a) = \alpha $
and any b with
$\operatorname {\mathrm {otp}}(a) = \alpha $
and any b with
![]() $\operatorname {\mathrm {otp}}(b) = \beta $
, a is order-isomorphic to some initial segment of b. We write
$\operatorname {\mathrm {otp}}(b) = \beta $
, a is order-isomorphic to some initial segment of b. We write
![]() $\alpha < \beta $
to mean that
$\alpha < \beta $
to mean that ![]() and
and
![]() $\alpha \neq \beta $
. By a completely standard argument, we have that for any ordinals
$\alpha \neq \beta $
. By a completely standard argument, we have that for any ordinals
![]() $\alpha ,\beta \in \operatorname {\mathrm {Ord}}^M$
, either
$\alpha ,\beta \in \operatorname {\mathrm {Ord}}^M$
, either
![]() $\alpha < \beta $
,
$\alpha < \beta $
,
![]() $\beta < \alpha $
, or
$\beta < \alpha $
, or
![]() $\alpha = \beta $
.
$\alpha = \beta $
.
It’s important to emphasize that the objects in
![]() $\operatorname {\mathrm {Ord}}^M$
are not internal sets in M, but rather externally defined equivalence classes of the equivalence relation
$\operatorname {\mathrm {Ord}}^M$
are not internal sets in M, but rather externally defined equivalence classes of the equivalence relation
![]() $\cong $
. To what extent can we get around this and approximate the class of well-ordered uniformly discrete chains with a set? As is typically the case in set theories with a universal set, something fishy needs to happen with regards to the class of ordinals, on pain of the Burali–Forti paradox. In particular, it is immediate that there cannot be a uniformly discrete set containing representatives of all ordinals of M.
$\cong $
. To what extent can we get around this and approximate the class of well-ordered uniformly discrete chains with a set? As is typically the case in set theories with a universal set, something fishy needs to happen with regards to the class of ordinals, on pain of the Burali–Forti paradox. In particular, it is immediate that there cannot be a uniformly discrete set containing representatives of all ordinals of M.
Using techniques similar to those in Section 5.1, we are able to collect representatives of all well-order types occurring below a certain scale. Just as there, we can’t easily form sets that consist solely of r-discrete chains, only things that are in some sense ‘approximate chains.’ We can use a similar trick, however, to turn these into order-isomorphic chains.
Definition 5.5. Let ![]() . Let
. Let ![]() .
.
Note that
![]() $\sigma (a,b) = 0$
if and only if
$\sigma (a,b) = 0$
if and only if
![]() $a \sqsubseteq b$
. Note also that
$a \sqsubseteq b$
. Note also that
![]() $d(a,b) = \max (\sigma (a,b),\sigma (b,a))$
. Furthermore,
$d(a,b) = \max (\sigma (a,b),\sigma (b,a))$
. Furthermore,
![]() $\operatorname {\mathrm {chn}}(a) = 0$
if and only if a is a chain. Let
$\operatorname {\mathrm {chn}}(a) = 0$
if and only if a is a chain. Let
![]() $\varphi _r $
,
$\varphi _r $
,
![]() $E_r$
,
$E_r$
,
![]() $X_r$
, and
$X_r$
, and
![]() $f_r$
be defined as they were in Section 5.1.
$f_r$
be defined as they were in Section 5.1.
Lemma 5.6 (Trichotomy for approximate chains).
For any
![]() $r> 0$
and
$r> 0$
and
![]() $a \in M \models \mathsf {MSE}$
, if
$a \in M \models \mathsf {MSE}$
, if
![]() $\varphi _r(a)< \frac {1}{3}r$
and
$\varphi _r(a)< \frac {1}{3}r$
and
![]() $\operatorname {\mathrm {chn}}(a) < \frac {1}{3}r$
, then for any
$\operatorname {\mathrm {chn}}(a) < \frac {1}{3}r$
, then for any ![]() , precisely one of the following holds:
, precisely one of the following holds:
![]() $d(a,b) < \frac {1}{3}r$
,
$d(a,b) < \frac {1}{3}r$
,
![]() $\sigma (a,b)> \frac {2}{3}r$
, or
$\sigma (a,b)> \frac {2}{3}r$
, or
![]() $\sigma (b,a)> \frac {2}{3}$
.
$\sigma (b,a)> \frac {2}{3}$
.
Proof. Since
![]() $\varphi _r(a) < \frac {1}{3}r$
, we have that for any
$\varphi _r(a) < \frac {1}{3}r$
, we have that for any ![]() , either
, either
![]() $d(b,c) < \frac {1}{3}r$
or
$d(b,c) < \frac {1}{3}r$
or
![]() $d(b,c)> \frac {2}{3}r$
. Since
$d(b,c)> \frac {2}{3}r$
. Since
![]() $\operatorname {\mathrm {chn}}(a) < \frac {1}{3}r$
, we have that for any
$\operatorname {\mathrm {chn}}(a) < \frac {1}{3}r$
, we have that for any ![]() , either
, either
![]() $\sigma (b,c) < \frac {1}{3}r$
or
$\sigma (b,c) < \frac {1}{3}r$
or
![]() $\sigma (c,b) < \frac {1}{3}r$
. If
$\sigma (c,b) < \frac {1}{3}r$
. If
![]() $d(b,c) \not < \frac {1}{3}r$
, then we must have either
$d(b,c) \not < \frac {1}{3}r$
, then we must have either
![]() $\sigma (b,c)\geq \frac {1}{3}r$
or
$\sigma (b,c)\geq \frac {1}{3}r$
or
![]() $\sigma (c,b) \geq \frac {1}{3}r$
, whence either
$\sigma (c,b) \geq \frac {1}{3}r$
, whence either
![]() $\sigma (b,c)> \frac {2}{3}r$
and
$\sigma (b,c)> \frac {2}{3}r$
and
![]() $\sigma (c,b) < \frac {1}{3}r$
or
$\sigma (c,b) < \frac {1}{3}r$
or
![]() $\sigma (c,b)> \frac {2}{3}r$
and
$\sigma (c,b)> \frac {2}{3}r$
and
![]() $\sigma (b,c) < \frac {1}{3}r$
.
$\sigma (b,c) < \frac {1}{3}r$
.
Define the formula
While
![]() $\sigma (x,y)$
measures how close x is to being a subset of y,
$\sigma (x,y)$
measures how close x is to being a subset of y,
![]() $\sigma ^\star (x,y)$
measures how close every element of x is to being a subset of every element of y. Lemma 5.6 implies that if
$\sigma ^\star (x,y)$
measures how close every element of x is to being a subset of every element of y. Lemma 5.6 implies that if
![]() $\varphi _r(a) < \frac {1}{3}r$
and
$\varphi _r(a) < \frac {1}{3}r$
and
![]() $\operatorname {\mathrm {chn}}(a) < \frac {1}{3}$
, then for any
$\operatorname {\mathrm {chn}}(a) < \frac {1}{3}$
, then for any
![]() $E_r$
-equivalence classes b and c of a, either
$E_r$
-equivalence classes b and c of a, either ![]() or
or ![]() . Furthermore, if both of these hold, then
. Furthermore, if both of these hold, then
![]() $b = c$
.
$b = c$
.
Let
![]() $C_r$
be the class
$C_r$
be the class
![]() $\{x \in X_r : \operatorname {\mathrm {chn}}(x) < \frac {1}{3}r\}$
. By the above observations, we have that the function
$\{x \in X_r : \operatorname {\mathrm {chn}}(x) < \frac {1}{3}r\}$
. By the above observations, we have that the function
![]() $g_r : C_r \to M$
defined by
$g_r : C_r \to M$
defined by
is explicitly definable (without parameters). (Note that we do not need to take closures as
![]() $f_r(a)$
is
$f_r(a)$
is
![]() $\frac {1}{3}r$
-discrete.) Furthermore, it is immediate that
$\frac {1}{3}r$
-discrete.) Furthermore, it is immediate that
![]() $g_r(a)$
is a
$g_r(a)$
is a
![]() $\frac {1}{3}r$
-discrete chain for any
$\frac {1}{3}r$
-discrete chain for any
![]() $a \in C_r$
and if
$a \in C_r$
and if
![]() $a \in C_r$
is a chain, then
$a \in C_r$
is a chain, then ![]() and moreover a and
and moreover a and
![]() $g_r(a)$
are order-isomorphic as chains.
$g_r(a)$
are order-isomorphic as chains.
With this machinery, we are finally in a position to examine the global structure of ordinals in models of
![]() $\mathsf {MSE}$
.
$\mathsf {MSE}$
.
Definition 5.7. For any ordinal
![]() $\alpha $
of
$\alpha $
of
![]() $M \models \mathsf {MSE}$
, we write
$M \models \mathsf {MSE}$
, we write
![]() $s(\alpha )$
for the quantity
$s(\alpha )$
for the quantity
It is easy to see that if ![]() , then
, then
![]() $s(\alpha ) \geq s(\beta )$
, so for any
$s(\alpha ) \geq s(\beta )$
, so for any
![]() $M \models \mathsf {MSE}$
, s is a non-increasing map from
$M \models \mathsf {MSE}$
, s is a non-increasing map from
![]() $\operatorname {\mathrm {Ord}}^M$
to
$\operatorname {\mathrm {Ord}}^M$
to
![]() $(0,1]$
. Furthermore, it is always the case that
$(0,1]$
. Furthermore, it is always the case that
![]() $s(0) = 1$
. By using Hartogs numbers, it is easy to show that for any ordinal
$s(0) = 1$
. By using Hartogs numbers, it is easy to show that for any ordinal
![]() $\alpha \in \operatorname {\mathrm {Ord}}^M$
, there is an ordinal
$\alpha \in \operatorname {\mathrm {Ord}}^M$
, there is an ordinal
![]() $\beta \in \operatorname {\mathrm {Ord}}^M$
of strictly larger cardinality, namely the Hartogs number of
$\beta \in \operatorname {\mathrm {Ord}}^M$
of strictly larger cardinality, namely the Hartogs number of
![]() $\mathcal {P}(a)$
, where
$\mathcal {P}(a)$
, where
![]() $\operatorname {\mathrm {otp}}(a) = \alpha $
. By an abuse of notation, we’ll write this as
$\operatorname {\mathrm {otp}}(a) = \alpha $
. By an abuse of notation, we’ll write this as
![]() $\aleph (\mathcal {P}(\alpha ))$
. Note that by Lemma 4.3 and the fact that the Hartogs number of X always embeds into
$\aleph (\mathcal {P}(\alpha ))$
. Note that by Lemma 4.3 and the fact that the Hartogs number of X always embeds into
![]() $\mathcal {P}^3(X)$
, we have that
$\mathcal {P}^3(X)$
, we have that
![]() $s(\alpha ) = s(\aleph (\mathcal {P}(\alpha )))$
. This means that if
$s(\alpha ) = s(\aleph (\mathcal {P}(\alpha )))$
. This means that if
![]() $s(\beta ) < s(\alpha )$
, then
$s(\beta ) < s(\alpha )$
, then
![]() $\beta $
has much larger cardinality than
$\beta $
has much larger cardinality than
![]() $\alpha $
.
$\alpha $
.
We’ll write
![]() $\omega ^M$
for the first limit ordinal in M, if it exists. The value of
$\omega ^M$
for the first limit ordinal in M, if it exists. The value of
![]() $s(\omega ^M)$
is directly related to the axiom of infinity.
$s(\omega ^M)$
is directly related to the axiom of infinity.
Proposition 5.8. Fix
![]() $M\models \mathsf {MSE}$
. For any
$M\models \mathsf {MSE}$
. For any
![]() $r \in (0,1]$
and
$r \in (0,1]$
and
![]() $\varepsilon \in (0,\frac {1}{3}r)$
,
$\varepsilon \in (0,\frac {1}{3}r)$
,
![]() $M \models \mathsf {Inf}_{r,\varepsilon }$
if and only if
$M \models \mathsf {Inf}_{r,\varepsilon }$
if and only if
![]() $\omega ^M$
exists and
$\omega ^M$
exists and ![]() . In particular,
. In particular,
![]() $M \models \mathsf {Inf}$
if and only if
$M \models \mathsf {Inf}$
if and only if
![]() $\omega ^M$
exists and
$\omega ^M$
exists and
![]() $s(\omega ^M) = 1$
.
$s(\omega ^M) = 1$
.
Proof. Let
![]() $\mathbb {N}_a^i$
be the set of initial segments of
$\mathbb {N}_a^i$
be the set of initial segments of
![]() $\mathbb {N}_a$
for some uniformly discrete a. It is immediate that
$\mathbb {N}_a$
for some uniformly discrete a. It is immediate that
![]() $\mathbb {N}_a^i$
is a well-ordered chain. If a is r-discrete, then we have by Lemma 4.3 that
$\mathbb {N}_a^i$
is a well-ordered chain. If a is r-discrete, then we have by Lemma 4.3 that
![]() $\mathbb {N}_a^i$
is r-discrete as well. It is easy to show that
$\mathbb {N}_a^i$
is r-discrete as well. It is easy to show that
![]() $\operatorname {\mathrm {otp}}(\mathbb {N}_a^i) = \omega ^M$
if and only if
$\operatorname {\mathrm {otp}}(\mathbb {N}_a^i) = \omega ^M$
if and only if
![]() $M \models \mathsf {Inf}(a)$
. Conversely, if
$M \models \mathsf {Inf}(a)$
. Conversely, if
![]() $\operatorname {\mathrm {otp}}(b) = \omega ^M$
for some well-ordered uniformly discrete chain b, then
$\operatorname {\mathrm {otp}}(b) = \omega ^M$
for some well-ordered uniformly discrete chain b, then
![]() $M \models \mathsf {Inf}(b)$
. The result now follows from Proposition 5.2.
$M \models \mathsf {Inf}(b)$
. The result now follows from Proposition 5.2.
Lemma 5.9. Let a and b be r-discrete chains in some
![]() $M\models \mathsf {MSE}$
. If
$M\models \mathsf {MSE}$
. If
![]() $d(a,b) < \frac {1}{2}r$
, then
$d(a,b) < \frac {1}{2}r$
, then
![]() $a \cong b$
. Furthermore, if
$a \cong b$
. Furthermore, if
![]() $(M,d)$
is an ultrametric space, it is enough to assume that
$(M,d)$
is an ultrametric space, it is enough to assume that
![]() $d(a,b) < r$
.
$d(a,b) < r$
.
Proof. Fix s such that
![]() $d(a,b) < s < \frac {1}{2}r$
. Since a and b are r-discrete, we have that the class
$d(a,b) < s < \frac {1}{2}r$
. Since a and b are r-discrete, we have that the class ![]() is a set and is the graph of a bijection between a and b. Now we need to show that f is actually an order isomorphism between a and b. Suppose that we have
is a set and is the graph of a bijection between a and b. Now we need to show that f is actually an order isomorphism between a and b. Suppose that we have ![]() with
with
![]() $c \sqsubseteq c'$
and
$c \sqsubseteq c'$
and ![]() with
with
![]() $d(c,g) < s$
and
$d(c,g) < s$
and
![]() $d(c',g') < s$
. If
$d(c',g') < s$
. If
![]() $c = c'$
, then
$c = c'$
, then
![]() $g = g'$
, so assume that
$g = g'$
, so assume that
![]() $c \sqsubset c'$
. Since
$c \sqsubset c'$
. Since
![]() $d(c,c') \geq r$
, we can find an
$d(c,c') \geq r$
, we can find an ![]() such that
such that
![]() $e(h,c)> 2s$
(as
$e(h,c)> 2s$
(as
![]() $2s < r$
). Since
$2s < r$
). Since
![]() $d(c',g') < s$
, we can find an
$d(c',g') < s$
, we can find an ![]() such that
such that
![]() $d(h,i) < s$
. The triangle inequality implies that
$d(h,i) < s$
. The triangle inequality implies that
![]() $e(i,g) \geq e(h,c) - d(h,i) - d(c,g)> 2s - s - s = 0.$
Therefore
$e(i,g) \geq e(h,c) - d(h,i) - d(c,g)> 2s - s - s = 0.$
Therefore ![]() and it must be the case that
and it must be the case that
![]() $g \sqsubset g'$
, as required.
$g \sqsubset g'$
, as required.
The proof in the ultrametric case is essentially the same.
Theorem 5.10. Fix
![]() $M \models \mathsf {MSE}$
and
$M \models \mathsf {MSE}$
and
![]() $r \in \{s(\gamma ) : \gamma \in \operatorname {\mathrm {Ord}}^M \}$
. Let
$r \in \{s(\gamma ) : \gamma \in \operatorname {\mathrm {Ord}}^M \}$
. Let
![]() $t = r$
if d is an ultrametric and let
$t = r$
if d is an ultrametric and let
![]() $t = \frac {1}{2}r$
otherwise.
$t = \frac {1}{2}r$
otherwise.
For any
![]() $s < t$
, there is an ordinal
$s < t$
, there is an ordinal
![]() $\alpha \in \operatorname {\mathrm {Ord}}^M$
with
$\alpha \in \operatorname {\mathrm {Ord}}^M$
with ![]() such that for any
such that for any
![]() $\beta \in \operatorname {\mathrm {Ord}}^M$
, if
$\beta \in \operatorname {\mathrm {Ord}}^M$
, if
![]() $s(\beta ) \geq r$
, then
$s(\beta ) \geq r$
, then
![]() $\beta < \alpha $
.
$\beta < \alpha $
.
In particular, if d is an ultrametric, then
![]() $\{s(\alpha ) : \alpha \in \operatorname {\mathrm {Ord}}^M\}$
is dense in
$\{s(\alpha ) : \alpha \in \operatorname {\mathrm {Ord}}^M\}$
is dense in
![]() $(0,1]$
and
$(0,1]$
and
![]() $\{\alpha \in \operatorname {\mathrm {Ord}}^M : s(\alpha ) < 1\}$
has no least element.
$\{\alpha \in \operatorname {\mathrm {Ord}}^M : s(\alpha ) < 1\}$
has no least element.
Proof. Fix positive
![]() $s < t$
and let
$s < t$
and let
![]() $\delta = 1-\frac {s}{t}$
(implying that
$\delta = 1-\frac {s}{t}$
(implying that
![]() $s=t(1-\delta )$
). Assume without loss of generality that
$s=t(1-\delta )$
). Assume without loss of generality that
![]() $t\delta < \frac {1}{3}r$
. Let
$t\delta < \frac {1}{3}r$
. Let
Note that every element of a is an element of
![]() $C_r$
. Let
$C_r$
. Let ![]() . Note that since the collection of chains in M is
. Note that since the collection of chains in M is
![]() $\{x \in M : \operatorname {\mathrm {chn}}^M(x) = 0\}$
, it is metrically closed. Hence every element of b is a chain. It is also easy to see that every element of b is
$\{x \in M : \operatorname {\mathrm {chn}}^M(x) = 0\}$
, it is metrically closed. Hence every element of b is a chain. It is also easy to see that every element of b is
![]() $r(1-\delta )$
-discrete (regardless of whether d is an ultrametric).
$r(1-\delta )$
-discrete (regardless of whether d is an ultrametric).
Let ![]() . Note that c is a set in M. Also note that for any
. Note that c is a set in M. Also note that for any
![]() $\beta \in \operatorname {\mathrm {Ord}}^M$
, if
$\beta \in \operatorname {\mathrm {Ord}}^M$
, if
![]() $s(\beta ) \geq r$
, then some element of c has order type
$s(\beta ) \geq r$
, then some element of c has order type
![]() $\beta $
. The equivalence relation
$\beta $
. The equivalence relation
![]() $\cong $
is discretely definable on c, so we can form the set
$\cong $
is discretely definable on c, so we can form the set ![]() . By Lemma 5.9, the set f is
. By Lemma 5.9, the set f is
![]() $t(1-\delta )$
-discrete (regardless of whether d is an ultrametric) or, in other words, s-discrete. We can find a formula
$t(1-\delta )$
-discrete (regardless of whether d is an ultrametric) or, in other words, s-discrete. We can find a formula
![]() $\varphi (x,y)$
with the property that for any
$\varphi (x,y)$
with the property that for any ![]() ,
,
![]() $\varphi (x,y) \in \{0,1\}$
and
$\varphi (x,y) \in \{0,1\}$
and
![]() $\varphi (x,y) = 0$
if and only
$\varphi (x,y) = 0$
if and only ![]() . This formula defines a linear order on f which by a standard argument is a well-order. Let
. This formula defines a linear order on f which by a standard argument is a well-order. Let
Since f contains representatives of all ordinals
![]() $\beta $
with
$\beta $
with
![]() $s(\beta ) \geq r$
, we must have that
$s(\beta ) \geq r$
, we must have that
![]() $\alpha $
is larger than any such
$\alpha $
is larger than any such
![]() $\beta $
. Therefore it cannot be the case that
$\beta $
. Therefore it cannot be the case that
![]() $s(\alpha ) \geq r$
. On the other hand, since f is s-discrete, it follows that
$s(\alpha ) \geq r$
. On the other hand, since f is s-discrete, it follows that
![]() $s(\alpha ) \geq s$
, as required.
$s(\alpha ) \geq s$
, as required.
The last statements in the theorem obviously follow from the rest of it.
Corollary 5.11. If
![]() $M\models \mathsf {MSE}$
has no infinite, uniformly discrete sets, then M has non-standard naturals.
$M\models \mathsf {MSE}$
has no infinite, uniformly discrete sets, then M has non-standard naturals.
Proof. By Corollary 3.8 and induction, any model of
![]() $\mathsf {MSE}$
contains hereditarily finite sets of every externally finite cardinality. Therefore for any standard natural n,
$\mathsf {MSE}$
contains hereditarily finite sets of every externally finite cardinality. Therefore for any standard natural n,
![]() $n \in \operatorname {\mathrm {Ord}}^M$
and
$n \in \operatorname {\mathrm {Ord}}^M$
and
![]() $s(n) = 1$
. Theorem 5.10 implies that there are ordinals
$s(n) = 1$
. Theorem 5.10 implies that there are ordinals
![]() $\alpha $
in M (which must be internally finite) such that
$\alpha $
in M (which must be internally finite) such that
![]() $s(\alpha ) < 1$
.
$s(\alpha ) < 1$
.
The behavior of ultrametric models of
![]() $\mathsf {MSE}$
in Theorem 5.10 is reminiscent of the behavior of
$\mathsf {MSE}$
in Theorem 5.10 is reminiscent of the behavior of
![]() $\omega $
in models of Cantor–Łukasiewicz set theory, as discovered by Hájek [Reference Montagna17, Theorem 4.17]. In particular, they both exhibit a manifestation of the sorites paradox: an inability to formalize an induction principle of the form
$\omega $
in models of Cantor–Łukasiewicz set theory, as discovered by Hájek [Reference Montagna17, Theorem 4.17]. In particular, they both exhibit a manifestation of the sorites paradox: an inability to formalize an induction principle of the form

for a real-valued predicate
![]() $\varphi (x)$
on some class of ordinals. For
$\varphi (x)$
on some class of ordinals. For ![]() , this induction principle cannot hold even for
, this induction principle cannot hold even for
![]() $\omega $
, but, as we will see in Theorem 7.15, models of
$\omega $
, but, as we will see in Theorem 7.15, models of
![]() $\mathsf {MSE}$
can have arbitrarily large standard ordinals. Theorem 5.10 is also of course similar to the non-existence of
$\mathsf {MSE}$
can have arbitrarily large standard ordinals. Theorem 5.10 is also of course similar to the non-existence of
![]() $\beta $
-models of
$\beta $
-models of
![]() $\mathsf {NFU}$
, although the mechanism by which models of
$\mathsf {NFU}$
, although the mechanism by which models of
![]() $\mathsf {NFU}$
are ill-founded is different. One might idly wonder what could happen if we were to restrict excision to stratified formulas.
$\mathsf {NFU}$
are ill-founded is different. One might idly wonder what could happen if we were to restrict excision to stratified formulas.
What is unclear at the moment is the status of non-ultrametric models of
![]() $\mathsf {MSE}$
. Theorem 5.10 does not preclude the possibility of
$\mathsf {MSE}$
. Theorem 5.10 does not preclude the possibility of
![]() $\beta $
-models of
$\beta $
-models of
![]() $\mathsf {MSE}$
(i.e., models in which
$\mathsf {MSE}$
(i.e., models in which
![]() $\operatorname {\mathrm {Ord}}^M$
is externally well-founded), but it seems unlikely that they exist. Every model of
$\operatorname {\mathrm {Ord}}^M$
is externally well-founded), but it seems unlikely that they exist. Every model of
![]() $\mathsf {MSE}$
we know how to produce contains a set that is an ultrametric model of
$\mathsf {MSE}$
we know how to produce contains a set that is an ultrametric model of
![]() $\mathsf {MSE}$
, whereby Theorem 5.10 applies. This leaves the following question.
$\mathsf {MSE}$
, whereby Theorem 5.10 applies. This leaves the following question.
Question 5.12. Does
![]() $\mathsf {MSE}$
have any
$\mathsf {MSE}$
have any
![]() $\beta $
-models? Is it true that for any
$\beta $
-models? Is it true that for any
![]() $M \models \mathsf {MSE}$
,
$M \models \mathsf {MSE}$
,
![]() $\{s(\alpha ) : \alpha \in \operatorname {\mathrm {Ord}}^M\}$
is dense in
$\{s(\alpha ) : \alpha \in \operatorname {\mathrm {Ord}}^M\}$
is dense in
![]() $(0,1]$
?
$(0,1]$
?
Given the behavior of the models constructed in Section 7, we conjecture that
![]() $\mathsf {MSE}$
has no
$\mathsf {MSE}$
has no
![]() $\beta $
-models and
$\beta $
-models and
![]() $\{s(\alpha ) : \alpha \in \operatorname {\mathrm {Ord}}^M\}$
is always dense in
$\{s(\alpha ) : \alpha \in \operatorname {\mathrm {Ord}}^M\}$
is always dense in
![]() $(0,1]$
.
$(0,1]$
.
Finally, although this is more or less a cosmetic nicety, we would like to show that we can build canonical ‘tokens’ representing well-order types, i.e., elements of M that somehow canonically represent a well-order type
![]() $\alpha $
. In
$\alpha $
. In
![]() $\mathsf {NFU}$
, this is accomplished by taking
$\mathsf {NFU}$
, this is accomplished by taking
![]() $\{x : \operatorname {\mathrm {otp}}(x) = \alpha \}$
. In
$\{x : \operatorname {\mathrm {otp}}(x) = \alpha \}$
. In
![]() $\mathsf {ZF}$
and
$\mathsf {ZF}$
and
![]() $\mathsf {GPK}^+_\infty $
, this is accomplished by taking the von Neumann ordinal of that order type. Neither of these approaches will work for
$\mathsf {GPK}^+_\infty $
, this is accomplished by taking the von Neumann ordinal of that order type. Neither of these approaches will work for
![]() $\mathsf {MSE}$
, so we will have to do something new.
$\mathsf {MSE}$
, so we will have to do something new.
Definition 5.13. Given a uniformly discrete set a, a set
![]() $b \sqsubseteq a \times V^M$
, and an element
$b \sqsubseteq a \times V^M$
, and an element ![]() , we write
, we write
![]() $b[c]$
for the class
$b[c]$
for the class ![]() . For any chain
. For any chain
![]() $a \in M \models \mathsf {MSE}$
and any set
$a \in M \models \mathsf {MSE}$
and any set
![]() $b \sqsubseteq a \times V^M$
, the closed chain union of b is
$b \sqsubseteq a \times V^M$
, the closed chain union of b is

In other words,
![]() $\chi (b)$
is the (not necessarily uniformly discrete) chain constructed out of the image of b as a many-valued function on a.
$\chi (b)$
is the (not necessarily uniformly discrete) chain constructed out of the image of b as a many-valued function on a.
Given a uniformly discrete chain
![]() $a \in M \models \mathsf {MSE}$
, the order token of a is the class
$a \in M \models \mathsf {MSE}$
, the order token of a is the class
So
![]() $\operatorname {\mathrm {otok}}(a)$
is roughly speaking the class (which we will shortly show is a set) of all chains that can be realized as a surjective order-preserving image of a. Thinking of
$\operatorname {\mathrm {otok}}(a)$
is roughly speaking the class (which we will shortly show is a set) of all chains that can be realized as a surjective order-preserving image of a. Thinking of
![]() $\operatorname {\mathrm {otok}}(a)$
as a canonical token representing the ordinal of a is analogous to thinking of
$\operatorname {\mathrm {otok}}(a)$
as a canonical token representing the ordinal of a is analogous to thinking of
![]() $\{\{a,b\} : a,b \in V\}$
(i.e., the set of sets of size
$\{\{a,b\} : a,b \in V\}$
(i.e., the set of sets of size
![]() $1$
or
$1$
or
![]() $2$
) as a canonical token representing the cardinal
$2$
) as a canonical token representing the cardinal
![]() $2$
, as discussed at the beginning of Section 5.
$2$
, as discussed at the beginning of Section 5.
Theorem 5.14. Fix
![]() $M \models \mathsf {MSE.}$
$M \models \mathsf {MSE.}$
-
(1)
 $\operatorname {\mathrm {otok}}(a)$
is a set for any uniformly discrete chain a.
$\operatorname {\mathrm {otok}}(a)$
is a set for any uniformly discrete chain a. -
(2) For any
 $r> 0$
, the map
$r> 0$
, the map
 $x \mapsto \operatorname {\mathrm {otok}}(x)$
is explicitly definable on the class of r-discrete chains.
$x \mapsto \operatorname {\mathrm {otok}}(x)$
is explicitly definable on the class of r-discrete chains. -
(3) If a and b are well-ordered uniformly discrete chains, then
 if and only if
if and only if
 $\operatorname {\mathrm {otok}}(a) \sqsubseteq \operatorname {\mathrm {otok}}(b)$
.
$\operatorname {\mathrm {otok}}(a) \sqsubseteq \operatorname {\mathrm {otok}}(b)$
.
Proof. 1 and 2 follow from Proposition 3.13 and Lemma 3.18.
For 3, assume that ![]() . Let this be witnessed by an order isomorphism
. Let this be witnessed by an order isomorphism
![]() $f: a \to b$
to some initial segment of b. For any
$f: a \to b$
to some initial segment of b. For any
![]() $c \sqsubseteq a \times V^M$
, we can form the set
$c \sqsubseteq a \times V^M$
, we can form the set ![]() (because the map
(because the map ![]() is definable) and we immediately have that
is definable) and we immediately have that
![]() $\chi (c) = \chi (c_f)$
. Therefore
$\chi (c) = \chi (c_f)$
. Therefore
![]() $\operatorname {\mathrm {otok}}(a) \sqsubseteq \operatorname {\mathrm {otok}}(b)$
.
$\operatorname {\mathrm {otok}}(a) \sqsubseteq \operatorname {\mathrm {otok}}(b)$
.
Conversely, assume that
![]() $\operatorname {\mathrm {otok}}(a) \sqsubseteq \operatorname {\mathrm {otok}}(b)$
. Let r be such that a and b are r-discrete. Find
$\operatorname {\mathrm {otok}}(a) \sqsubseteq \operatorname {\mathrm {otok}}(b)$
. Let r be such that a and b are r-discrete. Find
![]() $c \sqsubseteq b \times V^M$
such that
$c \sqsubseteq b \times V^M$
such that
![]() $d(a,\chi (c)) < \frac {1}{2}r$
. By Lemma 5.9, we have that a and
$d(a,\chi (c)) < \frac {1}{2}r$
. By Lemma 5.9, we have that a and
![]() $\chi (c)$
are order-isomorphic as chains. Let this be witnessed by
$\chi (c)$
are order-isomorphic as chains. Let this be witnessed by
![]() $f : a \to \chi (c)$
. For any
$f : a \to \chi (c)$
. For any ![]() , let
, let
![]() $g(x)$
be the smallest element of b such that
$g(x)$
be the smallest element of b such that ![]() . (This is a set by Proposition 3.2 and the fact that a and b are r-discrete.) g is an injective order-preserving map from a to b, so by a standard argument, we have that
. (This is a set by Proposition 3.2 and the fact that a and b are r-discrete.) g is an injective order-preserving map from a to b, so by a standard argument, we have that ![]() .
.
Now of course, given
![]() $\operatorname {\mathrm {otok}}(a)$
, we can build a canonical well-ordered chain with the same order type as a, namely
$\operatorname {\mathrm {otok}}(a)$
, we can build a canonical well-ordered chain with the same order type as a, namely
One can show that
![]() $x \mapsto \operatorname {\mathrm {ord}}(x)$
is explicitly definable on the class of r-discrete well-ordered chains for any
$x \mapsto \operatorname {\mathrm {ord}}(x)$
is explicitly definable on the class of r-discrete well-ordered chains for any
![]() $r> 0$
.
$r> 0$
.
Naturally, as discussed before, we could attempt to do something similar to Definition 5.13 with cardinalities, but without some form of the axiom of choice, we only seem to be able to build tokens representing equivalence classes of the
![]() $\approx ^\ast $
relation (where
$\approx ^\ast $
relation (where ![]() if there is a surjection from some subset of y onto x and
if there is a surjection from some subset of y onto x and
![]() $x \approx ^\ast y$
if
$x \approx ^\ast y$
if ![]() and
and ![]() ). Specifically, if we define
). Specifically, if we define ![]() , we then have that
, we then have that
![]() $a \approx ^\ast b$
if and only if
$a \approx ^\ast b$
if and only if
![]() $\operatorname {\mathrm {ctok}}^\ast (a) = \operatorname {\mathrm {ctok}}^\ast (b)$
for any uniformly discrete a and b. This raises an obvious question.
$\operatorname {\mathrm {ctok}}^\ast (a) = \operatorname {\mathrm {ctok}}^\ast (b)$
for any uniformly discrete a and b. This raises an obvious question.
Question 5.15. Is there a function
![]() $\operatorname {\mathrm {ctok}}(x)$
that is definable on the class of r-discrete sets for each
$\operatorname {\mathrm {ctok}}(x)$
that is definable on the class of r-discrete sets for each
![]() $r> 0$
such that for any uniformly discrete a and b,
$r> 0$
such that for any uniformly discrete a and b,
![]() $a \approx b$
if and only if
$a \approx b$
if and only if
![]() $\operatorname {\mathrm {ctok}}(a) = \operatorname {\mathrm {ctok}}(b)$
?
$\operatorname {\mathrm {ctok}}(a) = \operatorname {\mathrm {ctok}}(b)$
?
6 Formalizing
 $\mathsf {MSE}$
in continuous logic
$\mathsf {MSE}$
in continuous logic
Given a metric set structure ![]() , we can build a corresponding general structure
Footnote
12
, we can build a corresponding general structure
Footnote
12
![]() $(M,e)$
by taking the function
$(M,e)$
by taking the function
![]() $e:M^2 \to [0,1]$
to be the sole predicate. After doing so, the original structure can be recovered by taking
$e:M^2 \to [0,1]$
to be the sole predicate. After doing so, the original structure can be recovered by taking
![]() $d(x,y) = \sup _z|e(z,x)-e(z,y)|$
and
$d(x,y) = \sup _z|e(z,x)-e(z,y)|$
and ![]() . Our goal in this section is to characterize the structures that arise in this way and show that they form an elementary class in the sense of continuous logic.
. Our goal in this section is to characterize the structures that arise in this way and show that they form an elementary class in the sense of continuous logic.
Let
![]() $\mathcal {L}_e$
be the language with a single
$\mathcal {L}_e$
be the language with a single
![]() $[0,1]$
-valued predicate symbol e. Given any
$[0,1]$
-valued predicate symbol e. Given any
![]() $\mathcal {L}_e$
-structure
$\mathcal {L}_e$
-structure
![]() $(M,e)$
, we can define a pseudo-metric
$(M,e)$
, we can define a pseudo-metric
Since this is a formula in the sense of continuous logic,
![]() $d_e$
is a definable predicate on any
$d_e$
is a definable predicate on any
![]() $\mathcal {L}_e$
-structure. Note that by construction, for any
$\mathcal {L}_e$
-structure. Note that by construction, for any
![]() $\mathcal {L}_e$
-structure
$\mathcal {L}_e$
-structure
![]() $(M,e)$
and
$(M,e)$
and
![]() $a \in M$
, the function
$a \in M$
, the function
![]() $y \mapsto e(a,y)$
is
$y \mapsto e(a,y)$
is
![]() $1$
-Lipschitz with regards to
$1$
-Lipschitz with regards to
![]() $d_e$
.
$d_e$
.
The first thing we need to do is write out an axiom that guarantees that
![]() $e(x,b)$
is a distance predicate with regards to
$e(x,b)$
is a distance predicate with regards to
![]() $d_e$
for any choice of b. This is done for non-empty definable sets in [Reference Yaacov, Alexander Berenstein, Henson and Usvyatsov25, Theorem 9.12], but we need to allow for the possibility of empty definable sets here (where we take the distance predicate of
$d_e$
for any choice of b. This is done for non-empty definable sets in [Reference Yaacov, Alexander Berenstein, Henson and Usvyatsov25, Theorem 9.12], but we need to allow for the possibility of empty definable sets here (where we take the distance predicate of
![]() $\varnothing $
to be the constant function
$\varnothing $
to be the constant function
![]() $1$
). This is possible to add in by hand, but we will give a single axiom that covers both cases in Appendix 1. Specifically, we show that a formula
$1$
). This is possible to add in by hand, but we will give a single axiom that covers both cases in Appendix 1. Specifically, we show that a formula
![]() $\varphi (x)$
is a distance predicate (of a possibly empty set) if and only if
$\varphi (x)$
is a distance predicate (of a possibly empty set) if and only if
![]() $\sup _x |\varphi (x) - \inf _y\min (d(x,y) + 2\varphi (y), 1)| = 0$
.
$\sup _x |\varphi (x) - \inf _y\min (d(x,y) + 2\varphi (y), 1)| = 0$
.
Definition 6.1. The
![]() $\mathrm {H}$
-extensionality axiom is the
$\mathrm {H}$
-extensionality axiom is the
![]() $\mathcal {L}_e$
-condition
$\mathcal {L}_e$
-condition
We say that an
![]() $\mathcal {L}_e$
-structure M is
$\mathcal {L}_e$
-structure M is
![]() $\mathrm {H}$
-extensional if it satisfies the
$\mathrm {H}$
-extensional if it satisfies the
![]() $\mathrm {H}$
-extensionality axiom.
$\mathrm {H}$
-extensionality axiom.
Note that the
![]() $\mathrm {H}$
-extensionality axiom could more conventionally be written
$\mathrm {H}$
-extensionality axiom could more conventionally be written
Given an
![]() $\mathcal {L}_e$
-structure
$\mathcal {L}_e$
-structure
![]() $(M,e)$
, we write
$(M,e)$
, we write
![]() $M/e$
for the
$M/e$
for the
![]() $d_e=0$
quotient of M and we write
$d_e=0$
quotient of M and we write
![]() $\overline {M/e}$
for the completion of this under
$\overline {M/e}$
for the completion of this under
![]() $d_e$
. Given
$d_e$
. Given
![]() $a \in M$
, we write
$a \in M$
, we write
![]() $[a]_e$
for the corresponding element of
$[a]_e$
for the corresponding element of
![]() $M/e$
, which we regard as a subset of
$M/e$
, which we regard as a subset of
![]() $\overline {M/e}$
.
$\overline {M/e}$
.
Lemma 6.2. An
![]() $\mathcal {L}_e$
-structure
$\mathcal {L}_e$
-structure
![]() $(M,e)$
satisfies the
$(M,e)$
satisfies the
![]() $\mathrm {H}$
-extensionality axiom if and only if for any
$\mathrm {H}$
-extensionality axiom if and only if for any
![]() $b \in M$
, the function
$b \in M$
, the function
![]() $x \mapsto e(x,b)$
is
$x \mapsto e(x,b)$
is
![]() $1$
-Lipschitz with regards to
$1$
-Lipschitz with regards to
![]() $d_e$
and if
$d_e$
and if
![]() $f(x)$
is the extension of
$f(x)$
is the extension of
![]() $e(x,b)$
to
$e(x,b)$
to
![]() $\overline {M/e}$
, then for any
$\overline {M/e}$
, then for any
![]() $a \in \overline {M/e}$
,
$a \in \overline {M/e}$
,
![]() $f(a) = \inf \{d_e(a,c) : c \in \overline {M/e},~f(c) = 0\}$
, where
$f(a) = \inf \{d_e(a,c) : c \in \overline {M/e},~f(c) = 0\}$
, where
![]() $\inf \varnothing = 1$
.
$\inf \varnothing = 1$
.
Proof. For the
![]() $\Rightarrow $
direction, suppose that M satisfies the
$\Rightarrow $
direction, suppose that M satisfies the
![]() $\mathrm {H}$
-extensionality axiom and fix
$\mathrm {H}$
-extensionality axiom and fix
![]() $b \in M$
. We have by the
$b \in M$
. We have by the
![]() $\mathrm {H}$
-extensionality axiom that
$\mathrm {H}$
-extensionality axiom that
![]() $e(x,b) = \inf _z \min (d_e(x,z)+2e(z,b),1)$
for all x. The function
$e(x,b) = \inf _z \min (d_e(x,z)+2e(z,b),1)$
for all x. The function
![]() $x \mapsto \min (d_e(x,z)+2e(z,b),1)$
is
$x \mapsto \min (d_e(x,z)+2e(z,b),1)$
is
![]() $1$
-Lipschitz with regards to
$1$
-Lipschitz with regards to
![]() $d_e$
for any z, therefore
$d_e$
for any z, therefore
![]() $e(x,b)$
is as well (since it is the infimum of a family of
$e(x,b)$
is as well (since it is the infimum of a family of
![]() $1$
-Lipschitz functions). Let
$1$
-Lipschitz functions). Let
![]() $f(x)$
be the extension of
$f(x)$
be the extension of
![]() $e(x,b)$
to
$e(x,b)$
to
![]() $\overline {M/e}$
. It is immediate that
$\overline {M/e}$
. It is immediate that
![]() $\overline {M/e}$
satisfies
$\overline {M/e}$
satisfies
By Proposition A.1, we have that
![]() $f(x)$
is the distance predicate of its zero set, which is precisely the last condition in the statement of the lemma.
$f(x)$
is the distance predicate of its zero set, which is precisely the last condition in the statement of the lemma.
For the ![]() direction, suppose that
direction, suppose that
![]() $e(x,b)$
is
$e(x,b)$
is
![]() $1$
-Lipschitz with regards to
$1$
-Lipschitz with regards to
![]() $d_e$
for any
$d_e$
for any
![]() $b \in M$
and that for any
$b \in M$
and that for any
![]() $a \in \overline {M/e}$
,
$a \in \overline {M/e}$
,
![]() $f(a) = \inf \{d_e(a,x):f(x)= 0\}$
, where
$f(a) = \inf \{d_e(a,x):f(x)= 0\}$
, where
![]() $f(x)$
is the unique continuous extension of
$f(x)$
is the unique continuous extension of
![]() $e(x,b)$
to
$e(x,b)$
to
![]() $\overline {M/e}$
. Fix
$\overline {M/e}$
. Fix
![]() $a \in M$
and let
$a \in M$
and let
![]() $r = e(a,b) = f([a]_e)$
. Fix
$r = e(a,b) = f([a]_e)$
. Fix
![]() $\varepsilon> 0$
. Find
$\varepsilon> 0$
. Find
![]() $c \in \overline {M/e}$
such that
$c \in \overline {M/e}$
such that
![]() $f(c) = 0$
and
$f(c) = 0$
and
![]() $d([a]_e,c) < r + \frac {1}{4}\varepsilon $
. Find
$d([a]_e,c) < r + \frac {1}{4}\varepsilon $
. Find
![]() $c' \in M$
such that
$c' \in M$
such that
![]() $d(c,[c']_e) < \frac {1}{4}\varepsilon $
. Since
$d(c,[c']_e) < \frac {1}{4}\varepsilon $
. Since
![]() $f(x)$
is
$f(x)$
is
![]() $1$
-Lipschitz, we have that
$1$
-Lipschitz, we have that
![]() $f([c']_e)=e(c',b) < \frac {1}{4}\varepsilon $
. Note also that
$f([c']_e)=e(c',b) < \frac {1}{4}\varepsilon $
. Note also that
![]() $d_e(a,c') < r + \frac {2}{4}\varepsilon $
. We now have that
$d_e(a,c') < r + \frac {2}{4}\varepsilon $
. We now have that

Since we can do this for any
![]() $\varepsilon> 0$
, we have that
$\varepsilon> 0$
, we have that
For the other direction of the inequality, let
![]() $s = \inf _z \min (d_e(a,z)+2e(z,b),1)$
. If
$s = \inf _z \min (d_e(a,z)+2e(z,b),1)$
. If
![]() $s = 1$
, then the above implies that
$s = 1$
, then the above implies that
![]() $f(x) = 1$
for all
$f(x) = 1$
for all
![]() $x \in \overline {M/e}$
, so the
$x \in \overline {M/e}$
, so the
![]() $\mathrm {H}$
-extensionality axiom is satisfied. Otherwise assume that
$\mathrm {H}$
-extensionality axiom is satisfied. Otherwise assume that
![]() $s < 1$
and fix
$s < 1$
and fix
![]() $\varepsilon> 0$
with
$\varepsilon> 0$
with
![]() $s + \varepsilon < 1$
. Find
$s + \varepsilon < 1$
. Find
![]() $c \in M$
such that
$c \in M$
such that
![]() $\min (d_e(a,c)+2e(c,b),1) < s + \varepsilon $
. We must have that
$\min (d_e(a,c)+2e(c,b),1) < s + \varepsilon $
. We must have that
![]() $d_e(a,c) + 2e(c,b) < s+\varepsilon $
. By assumption,
$d_e(a,c) + 2e(c,b) < s+\varepsilon $
. By assumption,
![]() $e(c,b) = f([c]_e) = \inf \{d_e([c]_e,x) : f(x) = 0\}$
. Therefore
$e(c,b) = f([c]_e) = \inf \{d_e([c]_e,x) : f(x) = 0\}$
. Therefore

Since we can do this for any
![]() $\varepsilon> 0$
, we have that
$\varepsilon> 0$
, we have that ![]() . Therefore
. Therefore
![]() $e(a,b) = \inf _z\min (d_e(a,z) + 2e(z,b)),1$
for any
$e(a,b) = \inf _z\min (d_e(a,z) + 2e(z,b)),1$
for any
![]() $a,b \in M$
and the
$a,b \in M$
and the
![]() $\mathrm {H}$
-extensionality axiom holds.
$\mathrm {H}$
-extensionality axiom holds.
Note that since
![]() $y \mapsto e(a,y)$
is automatically
$y \mapsto e(a,y)$
is automatically
![]() $1$
-Lipschitz with regards to
$1$
-Lipschitz with regards to
![]() $d_e$
, the
$d_e$
, the
![]() $\mathrm {H}$
-extensionality axiom implies that
$\mathrm {H}$
-extensionality axiom implies that
![]() $(x,y) \mapsto e(x,y)$
is
$(x,y) \mapsto e(x,y)$
is
![]() $2$
-Lipschitz with regards to
$2$
-Lipschitz with regards to
![]() $d_e$
. This means that
$d_e$
. This means that
![]() $e(x,y)$
extends to a unique continuous function on
$e(x,y)$
extends to a unique continuous function on
![]() $\overline {M/e}$
. By an abuse of notation we will also denote this as e. Note that in this case,
$\overline {M/e}$
. By an abuse of notation we will also denote this as e. Note that in this case,
![]() $(\overline {M/e},e)$
still satisfies the
$(\overline {M/e},e)$
still satisfies the
![]() $\mathrm {H}$
-extensionality axiom (and is in fact elementarily equivalent to
$\mathrm {H}$
-extensionality axiom (and is in fact elementarily equivalent to
![]() $(M,e)$
as an
$(M,e)$
as an
![]() $\mathcal {L}_e$
-structure). In particular, by Lemma 6.2 applied to the structure
$\mathcal {L}_e$
-structure). In particular, by Lemma 6.2 applied to the structure
![]() $(\overline {M/e},e)$
, we have that
$(\overline {M/e},e)$
, we have that
![]() $x\mapsto e(x,b)$
is a distance predicate for any
$x\mapsto e(x,b)$
is a distance predicate for any
![]() $b \in \overline {M/e}$
.
$b \in \overline {M/e}$
.
Given an
![]() $\mathcal {L}_e$
-structure M for which
$\mathcal {L}_e$
-structure M for which
![]() $e(x,y)$
extends to
$e(x,y)$
extends to
![]() $\overline {M/e}$
, write
$\overline {M/e}$
, write ![]() for the relation
for the relation
![]() $\{(x,y) \in (\overline {M/e})^2 : e(x,y) = 0\}$
. Now we will see the manner in which the
$\{(x,y) \in (\overline {M/e})^2 : e(x,y) = 0\}$
. Now we will see the manner in which the
![]() $\mathrm {H}$
-extensionality axiom characterizes metric set structures.
$\mathrm {H}$
-extensionality axiom characterizes metric set structures.
Proposition 6.3. Fix an
![]() $\mathcal {L}_e$
-structure
$\mathcal {L}_e$
-structure
![]() $(M,e)$
.
$(M,e)$
.
![]() $(M,e)$
satisfies the
$(M,e)$
satisfies the
![]() $\mathrm {H}$
-extensionality axiom if and only if
$\mathrm {H}$
-extensionality axiom if and only if ![]() exists and is a metric set structure.
exists and is a metric set structure.
Proof. This follows from Lemma 6.2 and the fact that ![]() for all
for all
![]() $a,b \in \overline {M/e}$
.
$a,b \in \overline {M/e}$
.
Axiomatizing excision will be more technical. For convenience, we’ll take restricted
![]() $\mathcal {L}_e$
-formulas to be defined as in [Reference Hanson11, Section 1.3]: the only atomic formulas are those of the form
$\mathcal {L}_e$
-formulas to be defined as in [Reference Hanson11, Section 1.3]: the only atomic formulas are those of the form
![]() $e(x,y)$
and we take as connectives
$e(x,y)$
and we take as connectives
![]() $\varphi +\psi $
,
$\varphi +\psi $
,
![]() $\max (\varphi ,\psi )$
,
$\max (\varphi ,\psi )$
,
![]() $\min (\varphi ,\psi )$
, the constant
$\min (\varphi ,\psi )$
, the constant
![]() $1$
, and
$1$
, and
![]() $r\cdot \varphi $
for rational r. We should note though that the scheme described here would be sufficient with any definition of restricted formula, such as the one in [Reference Yaacov, Alexander Berenstein, Henson and Usvyatsov25, Section 3].
$r\cdot \varphi $
for rational r. We should note though that the scheme described here would be sufficient with any definition of restricted formula, such as the one in [Reference Yaacov, Alexander Berenstein, Henson and Usvyatsov25, Section 3].
Given a restricted
![]() $\mathcal {L}_e$
-formula
$\mathcal {L}_e$
-formula
![]() $\varphi $
, we can form a corresponding
$\varphi $
, we can form a corresponding ![]() -formula by replacing each instance of
-formula by replacing each instance of
![]() $e(x,y)$
with the
$e(x,y)$
with the ![]() -formula
-formula ![]() where z is taken to be any variable distinct from x and y. We write
where z is taken to be any variable distinct from x and y. We write ![]() for the formula resulting from this translation. By an abuse of notation, we will write
for the formula resulting from this translation. By an abuse of notation, we will write
![]() $v(\varphi )$
for
$v(\varphi )$
for ![]() .
.
Later on, we will also need a way to translate ![]() -formulas back to restricted
-formulas back to restricted
![]() $\mathcal {L}_e$
-formulas. The difficulty here is that we allowed real coefficients in
$\mathcal {L}_e$
-formulas. The difficulty here is that we allowed real coefficients in ![]() -formulas but only rational coefficients in
-formulas but only rational coefficients in
![]() $\mathcal {L}_e$
-formulas. With this issue in mind say that an
$\mathcal {L}_e$
-formulas. With this issue in mind say that an ![]() -formula is rational if all coefficients occurring in it are rational numbers. We define the
-formula is rational if all coefficients occurring in it are rational numbers. We define the
![]() $\mathcal {L}_e$
-formula
$\mathcal {L}_e$
-formula
![]() $\varphi _e$
corresponding to a rational
$\varphi _e$
corresponding to a rational ![]() -formula
-formula
![]() $\varphi $
inductively as follows:
$\varphi $
inductively as follows:
-
•
 $(d(x,y))_e = d_e(x,y)$
,
$(d(x,y))_e = d_e(x,y)$
, -
•
 , and
, and -
•
 ,
,
with the other elements of the translation defined in the obvious way. The following facts are either standard results in continuous logic or easily verified.
Fact 6.4. Fix an
![]() $\mathrm {H}$
-extensional
$\mathrm {H}$
-extensional
![]() $\mathcal {L}_e$
-structure
$\mathcal {L}_e$
-structure
![]() $(M,e)$
with
$(M,e)$
with
![]() $(M,d_e)$
complete.
$(M,d_e)$
complete.
-
(1) For any
 $\mathcal {L}_e$
-formula
$\mathcal {L}_e$
-formula
 $\varphi (\bar {x})$
and any
$\varphi (\bar {x})$
and any
 $\bar {a} \in M$
,
$\bar {a} \in M$
,  .
. -
(2) For any rational
 -formula
-formula
 $\varphi (\bar {x})$
and any
$\varphi (\bar {x})$
and any
 $\bar {a} \in M$
,
$\bar {a} \in M$
,  .
. -
(3) For any
 -formula
-formula
 $\varphi (\bar {x})$
and
$\varphi (\bar {x})$
and
 $\varepsilon> 0$
, there is a rational
$\varepsilon> 0$
, there is a rational  -formula
-formula
 $\psi (\bar {x})$
such that
$\psi (\bar {x})$
such that  for all
for all
 $\bar {a} \in M$
.
$\bar {a} \in M$
.
It follows from Lemma 2.6 and Fact 6.4 that if
![]() $(M,e)$
is
$(M,e)$
is
![]() $\mathrm {H}$
-extensional with
$\mathrm {H}$
-extensional with
![]() $(M,d_e)$
complete, then for any restricted
$(M,d_e)$
complete, then for any restricted
![]() $\mathcal {L}_e$
-formula
$\mathcal {L}_e$
-formula
![]() $\varphi (\bar {x})$
, the function
$\varphi (\bar {x})$
, the function
![]() $\bar {x} \mapsto \varphi ^M(\bar {x})$
is
$\bar {x} \mapsto \varphi ^M(\bar {x})$
is
![]() $2v(\varphi )$
-Lipschitz with regards to the max metric on tuples induced by
$2v(\varphi )$
-Lipschitz with regards to the max metric on tuples induced by
![]() $d_e$
. By passing to the completion
$d_e$
. By passing to the completion
![]() $(\overline {M/e},d_e)$
, this implies the same for any
$(\overline {M/e},d_e)$
, this implies the same for any
![]() $\mathrm {H}$
-extensional
$\mathrm {H}$
-extensional
![]() $(M,e)$
.
$(M,e)$
.
For any formula
![]() $\varphi \in \mathcal {L}_e$
, we define
$\varphi \in \mathcal {L}_e$
, we define
Note that for any
![]() $\mathrm {H}$
-extensional
$\mathrm {H}$
-extensional
![]() $(M,e)$
, if
$(M,e)$
, if
![]() $|\varphi ^M(\bar {a}) - \varphi ^M(\bar {b})| \geq \frac {1}{2}$
, then
$|\varphi ^M(\bar {a}) - \varphi ^M(\bar {b})| \geq \frac {1}{2}$
, then
![]() $d_e(\bar {a},\bar {b})> \varepsilon _\varphi $
.
$d_e(\bar {a},\bar {b})> \varepsilon _\varphi $
.
Definition 6.5. The axiom scheme of excision is the collection of
![]() $\mathcal {L}_e$
-conditions of the form
$\mathcal {L}_e$
-conditions of the form
for each restricted
![]() $\mathcal {L}_e$
-formula
$\mathcal {L}_e$
-formula
![]() $\varphi (x,\bar {y})$
(not containing z as a free variable).
$\varphi (x,\bar {y})$
(not containing z as a free variable).
Given an
![]() $\mathrm {H}$
-extensional
$\mathrm {H}$
-extensional
![]() $\mathcal {L}_e$
-structure M, we say that M satisfies
$\mathcal {L}_e$
-structure M, we say that M satisfies
![]() $\mathcal {L}_e$
-excision to mean that M satisfies the axiom scheme of excision.
$\mathcal {L}_e$
-excision to mean that M satisfies the axiom scheme of excision.
The axiom scheme of excision can be more conventionally stated like this: For all
![]() $\bar {y}$
,
$\bar {y}$
,
![]() $\delta> 0$
, and
$\delta> 0$
, and
![]() $\varphi (x,\bar {y}) \in \mathcal {L}_e$
, there is a z such that for all x,
$\varphi (x,\bar {y}) \in \mathcal {L}_e$
, there is a z such that for all x,
-
• if
 , then
, then
 $e(x,z) < \delta $
and
$e(x,z) < \delta $
and -
• if
 , then
, then
 $\varphi (x,\bar {y}) < 1+\delta $
.
$\varphi (x,\bar {y}) < 1+\delta $
.
It is also sufficient to assume merely that this holds for sufficiently small
![]() $\delta> 0$
. This is clearly an approximation of a certain case of the excision principle in
$\delta> 0$
. This is clearly an approximation of a certain case of the excision principle in
![]() $\mathsf {MSE}$
, but we will now show that in
$\mathsf {MSE}$
, but we will now show that in
![]() $\mathrm {H}$
-extensional M with
$\mathrm {H}$
-extensional M with
![]() $(M,d_e)$
complete, the axiom scheme of excision is enough to imply full excision.
$(M,d_e)$
complete, the axiom scheme of excision is enough to imply full excision.
Lemma 6.6. Fix an
![]() $\mathrm {H}$
-extensional
$\mathrm {H}$
-extensional
![]() $\mathcal {L}_e$
-structure M with
$\mathcal {L}_e$
-structure M with
![]() $(M,d_e)$
complete. Suppose that M satisfies
$(M,d_e)$
complete. Suppose that M satisfies
![]() $\mathcal {L}_e$
-excision. For any
$\mathcal {L}_e$
-excision. For any
![]() $a \in M$
and
$a \in M$
and
![]() $r,s \in [0,1]$
with
$r,s \in [0,1]$
with
![]() $r<s$
, there is a
$r<s$
, there is a
![]() $b \in M$
such that for any
$b \in M$
such that for any
![]() $c \in M$
, if
$c \in M$
, if ![]() , then
, then ![]() , and if
, and if ![]() , then
, then
![]() $e(c,a) < s$
.
$e(c,a) < s$
.
Proof. For readability, we will write d for
![]() $d_e$
and
$d_e$
and ![]() for
for ![]() .
.
Let
![]() $r_0 = \frac {2}{3}r+\frac {1}{3}s$
,
$r_0 = \frac {2}{3}r+\frac {1}{3}s$
,
![]() $s_0 = \frac {1}{3}r + \frac {2}{3}s$
, and
$s_0 = \frac {1}{3}r + \frac {2}{3}s$
, and
![]() $b_0 = a$
. For any n, let
$b_0 = a$
. For any n, let
![]() $\varphi _n(x,y) = \frac {e(x,y) - r_n}{s_n - r_n}$
.
$\varphi _n(x,y) = \frac {e(x,y) - r_n}{s_n - r_n}$
.
At stage n, suppose we are given
![]() $b_n$
and rationals
$b_n$
and rationals
![]() $r_n$
and
$r_n$
and
![]() $s_n$
with
$s_n$
with
![]() $0 < r_n < s_n$
. Since M satisfies
$0 < r_n < s_n$
. Since M satisfies
![]() $\mathcal {L}_e$
-excision, we have that for any
$\mathcal {L}_e$
-excision, we have that for any
![]() $\gamma> 0$
, there is an
$\gamma> 0$
, there is an
![]() $f \in M$
such that
$f \in M$
such that
Let
![]() $b_{n+1}$
be such an f with
$b_{n+1}$
be such an f with

We have that for any
![]() $c \in M$
, if
$c \in M$
, if ![]() (i.e., if
(i.e., if ![]() ), then
), then
![]() $e(c,b_{n+1}) < \delta _n$
. A fortiori, this implies that if
$e(c,b_{n+1}) < \delta _n$
. A fortiori, this implies that if ![]() , then
, then
![]() $e(c,b_{n+1}) < \delta _n$
.
$e(c,b_{n+1}) < \delta _n$
.
On the other hand, if
![]() $\varepsilon _{\varphi _n} - e(c,b_{n+1}) \geq \delta _n$
(i.e., if
$\varepsilon _{\varphi _n} - e(c,b_{n+1}) \geq \delta _n$
(i.e., if ![]() ), then
), then
![]() $\frac {e(c,b_n)-r_n}{s_n-r_n} - 1 < \delta _n$
and so
$\frac {e(c,b_n)-r_n}{s_n-r_n} - 1 < \delta _n$
and so
![]() $e(c,b_n) < r_n + (1+\delta _n)(s_n-r_n)$
. Since
$e(c,b_n) < r_n + (1+\delta _n)(s_n-r_n)$
. Since ![]() , this implies that if
, this implies that if ![]() , then
, then
![]() $e(c,b_n) < r_n + 2s_n$
.
$e(c,b_n) < r_n + 2s_n$
.
Finally, pick
![]() $r_{n+1}$
and
$r_{n+1}$
and
![]() $s_{n+1}$
so that
$s_{n+1}$
so that
![]() $2\delta _n < r_{n+1} < s_{n+1} < 3\delta _n$
, and move to the next stage of the construction.
$2\delta _n < r_{n+1} < s_{n+1} < 3\delta _n$
, and move to the next stage of the construction.
Claim.
![]() $(b_n)_{n<\omega }$
is a Cauchy sequence.
$(b_n)_{n<\omega }$
is a Cauchy sequence.
Proof of claim. For any
![]() $n> 0$
and
$n> 0$
and
![]() $c \in M$
, we have that if
$c \in M$
, we have that if ![]() , then
, then ![]() and also that if
and also that if ![]() , then
, then ![]() . Therefore, by
. Therefore, by
![]() $\mathrm {H}$
-extensionality,
$\mathrm {H}$
-extensionality, ![]() . Since we can do this for any positive n, the claim follows.
. Since we can do this for any positive n, the claim follows.
Let ![]() . b is an element of M since
. b is an element of M since
![]() $(M,d)$
is complete.
$(M,d)$
is complete.
Claim. For any
![]() $c \in M$
, if
$c \in M$
, if ![]() , then
, then ![]() .
.
Proof of claim. Since ![]() and since
and since ![]() , we have that
, we have that
![]() $e(c,b_0) = e(c,a) < r_0 - \delta _0$
. Therefore,
$e(c,b_0) = e(c,a) < r_0 - \delta _0$
. Therefore,
![]() $r(c,b_1) < \delta _0$
. For any n, suppose that we know that
$r(c,b_1) < \delta _0$
. For any n, suppose that we know that
![]() $e(c,b_{n+1}) < \delta _{n}$
. We then have that
$e(c,b_{n+1}) < \delta _{n}$
. We then have that

Hence, ![]() .
.
Therefore
![]() $e(c,b) < \frac {2^{-n-1}}{27}(s-r) + d(b_{n+2},b)$
for every n by induction. Since
$e(c,b) < \frac {2^{-n-1}}{27}(s-r) + d(b_{n+2},b)$
for every n by induction. Since
![]() $b_n \to b$
we have that
$b_n \to b$
we have that
![]() $e(c,b) = 0$
, i.e.,
$e(c,b) = 0$
, i.e., ![]() .
.
Finally we just need to verify that if ![]() , then
, then
![]() $e(c,a)< s$
. By the above estimate, we know that
$e(c,a)< s$
. By the above estimate, we know that ![]() . We have
. We have

Therefore,
So if ![]() , then there is an
, then there is an ![]() such that
such that
![]() $d(c,f) < s$
, implying that
$d(c,f) < s$
, implying that
![]() $e(c,a) < s$
, as required.
$e(c,a) < s$
, as required.
Proposition 6.7. Let
![]() $(M,e)$
be an
$(M,e)$
be an
![]() $\mathrm {H}$
-extensional
$\mathrm {H}$
-extensional
![]() $\mathcal {L}_e$
-structure with
$\mathcal {L}_e$
-structure with
![]() $(M,d_e)$
complete.
$(M,d_e)$
complete. ![]() if and only if
if and only if
![]() $(M,e)$
satisfies
$(M,e)$
satisfies
![]() $\mathcal {L}_e$
-excision.
$\mathcal {L}_e$
-excision.
Furthermore, all models of
![]() $\mathsf {MSE}$
arise in this manner.
$\mathsf {MSE}$
arise in this manner.
Proof. Let
![]() $\chi (x,\bar {y},z) \kern1.4pt{=}\kern1.4pt \max (\min (e(x,z),-\varphi (x,\bar {y})),\min (\varepsilon _\varphi \kern1.4pt{-}\kern1.4pt e(x,z),\varphi (x,\bar {y})))$
. Suppose that
$\chi (x,\bar {y},z) \kern1.4pt{=}\kern1.4pt \max (\min (e(x,z),-\varphi (x,\bar {y})),\min (\varepsilon _\varphi \kern1.4pt{-}\kern1.4pt e(x,z),\varphi (x,\bar {y})))$
. Suppose that ![]() . Fix a restricted
. Fix a restricted
![]() $\mathcal {L}_e$
-formula
$\mathcal {L}_e$
-formula
![]() $\varphi (x,\bar {y})$
. Fix a tuple of parameters
$\varphi (x,\bar {y})$
. Fix a tuple of parameters
![]() $\bar {a}$
. Let
$\bar {a}$
. Let ![]() . Now for any c, we have that if
. Now for any c, we have that if ![]() , then
, then
![]() $e(c,b) =0$
. So
$e(c,b) =0$
. So ![]() . Moreover, if
. Moreover, if
![]() $\varphi (c,\bar {a}) \geq 1$
, then
$\varphi (c,\bar {a}) \geq 1$
, then
![]() $d_e(c,f)> \varepsilon _\varphi $
for all
$d_e(c,f)> \varepsilon _\varphi $
for all ![]() (since these all satisfy
(since these all satisfy
![]() $\varphi ^M(f,\bar {a}) < \frac {1}{2}$
). Therefore
$\varphi ^M(f,\bar {a}) < \frac {1}{2}$
). Therefore
![]() $e(c,b) \geq \varepsilon _\varphi $
. So
$e(c,b) \geq \varepsilon _\varphi $
. So ![]() . Since we can do this for any
. Since we can do this for any
![]() $c \in M$
, we have that
$c \in M$
, we have that ![]() , whereby
, whereby ![]() . Since we can do this for any
. Since we can do this for any
![]() $\bar {a} \in M$
, we have that
$\bar {a} \in M$
, we have that
![]() $(M,e) \models \sup _{\bar {y}}\inf _z\sup _x\chi (x,\bar {y},z)$
. Finally since this holds for any restricted
$(M,e) \models \sup _{\bar {y}}\inf _z\sup _x\chi (x,\bar {y},z)$
. Finally since this holds for any restricted
![]() $\mathcal {L}_e$
-formula, we have that
$\mathcal {L}_e$
-formula, we have that
![]() $(M,e)$
satisfies
$(M,e)$
satisfies
![]() $\mathcal {L}_e$
-excision.
$\mathcal {L}_e$
-excision.
Now assume that
![]() $(M,e)$
satisfies
$(M,e)$
satisfies
![]() $\mathcal {L}_e$
-excision. Fix an
$\mathcal {L}_e$
-excision. Fix an ![]() -formula
-formula
![]() $\varphi (x,\bar {y})$
,
$\varphi (x,\bar {y})$
,
![]() $\bar {a} \in M$
, and
$\bar {a} \in M$
, and
![]() $r < s$
. By passing to
$r < s$
. By passing to
![]() $r'$
and
$r'$
and
![]() $s'$
with
$s'$
with
![]() $r < r' < s' < s$
if necessary, we may assume that r and s are rational. By Fact 6.4, we can fix a rational
$r < r' < s' < s$
if necessary, we may assume that r and s are rational. By Fact 6.4, we can fix a rational ![]() -formula
-formula
![]() $\psi (x,\bar {y})$
such that
$\psi (x,\bar {y})$
such that ![]() for all x and
for all x and
![]() $\bar {y}$
. Fix
$\bar {y}$
. Fix
![]() $\delta> 0$
with
$\delta> 0$
with
![]() $\delta < \frac {1}{2}\varepsilon _{3\psi -1}$
. Note that
$\delta < \frac {1}{2}\varepsilon _{3\psi -1}$
. Note that
![]() $\delta < \frac {1}{2}$
. Apply
$\delta < \frac {1}{2}$
. Apply
![]() $\mathcal {L}_e$
-excision to the restricted
$\mathcal {L}_e$
-excision to the restricted
![]() $\mathcal {L}_e$
-formula
$\mathcal {L}_e$
-formula
![]() $3\psi _e(x,\bar {a})-1$
to get
$3\psi _e(x,\bar {a})-1$
to get
![]() $b \in M$
such that for all
$b \in M$
such that for all
![]() $c \in M$
, if
$c \in M$
, if ![]() , then
, then
![]() $e(c,b) < \delta $
and if
$e(c,b) < \delta $
and if
![]() $e(c,b) < \varepsilon _{3\psi -1}-\delta $
, then
$e(c,b) < \varepsilon _{3\psi -1}-\delta $
, then
![]() $\psi _e(c,\bar {a}) < \frac {2}{3}+\frac {1}{3}\delta $
. Apply Lemma 6.6 to b to get a set f such that if
$\psi _e(c,\bar {a}) < \frac {2}{3}+\frac {1}{3}\delta $
. Apply Lemma 6.6 to b to get a set f such that if ![]() , then
, then ![]() and if
and if ![]() , then
, then ![]() .
.
For any
![]() $c \in M$
, suppose that
$c \in M$
, suppose that ![]() . We then have that
. We then have that
![]() $\psi (c,\bar {a}) = \psi _e(c,\bar {a}) < \frac {1}{6} < \frac {1}{3}-\frac {1}{3}\delta .$
Therefore,
$\psi (c,\bar {a}) = \psi _e(c,\bar {a}) < \frac {1}{6} < \frac {1}{3}-\frac {1}{3}\delta .$
Therefore,
![]() $e(c,b) < \delta $
and so
$e(c,b) < \delta $
and so ![]() . On the other hand, suppose that
. On the other hand, suppose that ![]() . We then have that
. We then have that
![]() $e(c,b) < \varepsilon _{3\psi -1}-\delta $
. Therefore
$e(c,b) < \varepsilon _{3\psi -1}-\delta $
. Therefore
![]() $\psi _e(c,\bar {a}) < \frac {2}{3}+\frac {1}{3}\delta $
, implying that
$\psi _e(c,\bar {a}) < \frac {2}{3}+\frac {1}{3}\delta $
, implying that
![]() $\frac {\varphi (c,\bar {a})-r}{s-r} < \frac {2}{3}+\frac {1}{3}\delta + \frac {1}{6} < 1$
and so
$\frac {\varphi (c,\bar {a})-r}{s-r} < \frac {2}{3}+\frac {1}{3}\delta + \frac {1}{6} < 1$
and so
![]() $\varphi (c,\bar {a}) < s$
.
$\varphi (c,\bar {a}) < s$
.
Since we can do this for any
![]() $\varphi (x,\bar {a})$
and
$\varphi (x,\bar {a})$
and
![]() $r < s$
, we have that
$r < s$
, we have that ![]() .
.
The ‘Furthermore’ statement follows from the fact that if ![]() , then
, then
![]() $(M,e)$
(where e is defined from
$(M,e)$
(where e is defined from ![]() and d) is
and d) is
![]() $\mathrm {H}$
-extensional and satisfies
$\mathrm {H}$
-extensional and satisfies
![]() $\mathcal {L}_e$
-excision.
$\mathcal {L}_e$
-excision.
Given Proposition 6.7, we will also use
![]() $\mathsf {MSE}$
to denote the
$\mathsf {MSE}$
to denote the
![]() $\mathcal {L}_e$
-theory consisting of the
$\mathcal {L}_e$
-theory consisting of the
![]() $\mathrm {H}$
-extensionality axiom and the axiom scheme of excision.
$\mathrm {H}$
-extensionality axiom and the axiom scheme of excision.
7 Constructing models of
 $\textsf{MSE}$
$\textsf{MSE}$
In order to construct models of
![]() $\mathsf {MSE}$
, we need to borrow techniques from the construction of models of
$\mathsf {MSE}$
, we need to borrow techniques from the construction of models of
![]() $\mathsf {GPK}$
. The construction also has something of the flavor of the construction of models of
$\mathsf {GPK}$
. The construction also has something of the flavor of the construction of models of
![]() $\mathsf {NFU}$
in that it involves non-standard models of another set theory. In order to show that arbitrary metric spaces can be a set of Quine atomsFootnote
13
in a model of
$\mathsf {NFU}$
in that it involves non-standard models of another set theory. In order to show that arbitrary metric spaces can be a set of Quine atomsFootnote
13
in a model of
![]() $\mathsf {MSE}$
, we will use a construction that combines elements of the tree structures in [Reference Weydert23] and the construction presented at the end of [Reference Forti and Honsell6, Section 2]. The construction we give here could be generalized to allow certain other metric set structures to be embedded in models of
$\mathsf {MSE}$
, we will use a construction that combines elements of the tree structures in [Reference Weydert23] and the construction presented at the end of [Reference Forti and Honsell6, Section 2]. The construction we give here could be generalized to allow certain other metric set structures to be embedded in models of
![]() $\mathsf {MSE}$
, in the same vein as [Reference Forti and Honsell6, Section 2], but we have not pursued this here. We work in the context of
$\mathsf {MSE}$
, in the same vein as [Reference Forti and Honsell6, Section 2], but we have not pursued this here. We work in the context of
![]() $\mathsf {ZF}$
(with a particular eye towards avoiding the axiom of choice in order to establish its independence from
$\mathsf {ZF}$
(with a particular eye towards avoiding the axiom of choice in order to establish its independence from
![]() $\mathsf {MSE}$
).
$\mathsf {MSE}$
).
In the following definition, Q is intended to be a set of Quine atoms in our resulting model, although the models we construct here always have precisely one additional Quine atom.
Definition 7.1. Fix a set Q and a
![]() $[0,1]$
-valued metric d on Q. Assume that Q does not contain any ordinal-indexed sequences. For any ordinal
$[0,1]$
-valued metric d on Q. Assume that Q does not contain any ordinal-indexed sequences. For any ordinal
![]() $\alpha $
, we let
$\alpha $
, we let
![]() $\mathcal {T}_\alpha (Q)$
be the set of all
$\mathcal {T}_\alpha (Q)$
be the set of all
![]() $\alpha $
-sequences x satisfying that:
$\alpha $
-sequences x satisfying that:
-
• for every
 $\beta <\alpha $
,
$\beta <\alpha $
,
 $x(\beta ) \subseteq Q \cup \mathcal {T}_\beta (Q)$
and
$x(\beta ) \subseteq Q \cup \mathcal {T}_\beta (Q)$
and -
• for every
 $\beta < \gamma < \alpha $
,
$\beta < \gamma < \alpha $
,
 $x(\beta )\cap Q = x(\gamma )\cap Q$
and
$x(\beta )\cap Q = x(\gamma )\cap Q$
and
 $x(\beta )\setminus Q = \{y{\upharpoonright } \beta : y \in x(\gamma )\setminus Q\}$
.
$x(\beta )\setminus Q = \{y{\upharpoonright } \beta : y \in x(\gamma )\setminus Q\}$
.
Let ![]() be a binary relation such that:
be a binary relation such that:
-
• for
 $x \in \mathcal {T}_\alpha (Q)$
and
$x \in \mathcal {T}_\alpha (Q)$
and
 $y \in Q$
,
$y \in Q$
,  holds if and only if
holds if and only if
 $x=y$
,
$x=y$
, -
• for
 $x \in Q$
and
$x \in Q$
and  ,
,  holds if and only if
holds if and only if
 $x\in y(\beta )$
for every
$x\in y(\beta )$
for every
 $b<\alpha $
, and
$b<\alpha $
, and -
• for
 $x \in \mathcal {T}_\alpha (Q) \setminus Q$
and
$x \in \mathcal {T}_\alpha (Q) \setminus Q$
and
 $y \in \mathcal {T}_\alpha (Q)\setminus Q$
,
$y \in \mathcal {T}_\alpha (Q)\setminus Q$
,  if and only if
if and only if
 $x {\upharpoonright } \beta \in y(\beta )$
for every
$x {\upharpoonright } \beta \in y(\beta )$
for every
 $\beta < \alpha $
.
$\beta < \alpha $
.
Note that
![]() $\mathcal {T}_\alpha (Q)$
is well-defined, as
$\mathcal {T}_\alpha (Q)$
is well-defined, as
![]() $\mathcal {T}_0(Q) = Q \cup \{\varnothing \}$
.
$\mathcal {T}_0(Q) = Q \cup \{\varnothing \}$
.
For any
![]() $x \in \mathcal {T}_\alpha (Q)$
, we write
$x \in \mathcal {T}_\alpha (Q)$
, we write
![]() $\operatorname {\mathrm {tc}}(x)$
for the smallest subset of
$\operatorname {\mathrm {tc}}(x)$
for the smallest subset of
![]() $\mathcal {T}_\alpha (Q)$
such that
$\mathcal {T}_\alpha (Q)$
such that ![]() and if
and if ![]() , then
, then
![]() $z \in \operatorname {\mathrm {tc}}(x)$
. For any
$z \in \operatorname {\mathrm {tc}}(x)$
. For any
![]() $x,y \in \mathcal {T}_\alpha (Q)$
, we define
$x,y \in \mathcal {T}_\alpha (Q)$
, we define

for all
![]() $\beta $
and limit
$\beta $
and limit ![]() , where
, where
![]() $\sup \varnothing = 0$
and
$\sup \varnothing = 0$
and
![]() $\inf \varnothing = 1$
.
$\inf \varnothing = 1$
.
We will often suppress the superscript
![]() $^{Q,\alpha }$
. Since the supremum of a family of pseudo-metrics is always a pseudo-metric, an easy inductive argument shows that
$^{Q,\alpha }$
. Since the supremum of a family of pseudo-metrics is always a pseudo-metric, an easy inductive argument shows that
![]() $\rho _\beta $
is a pseudo-metric for every
$\rho _\beta $
is a pseudo-metric for every
![]() $\beta \in \operatorname {\mathrm {Ord}}\cup \{\infty \}$
. It is also immediate that for any
$\beta \in \operatorname {\mathrm {Ord}}\cup \{\infty \}$
. It is also immediate that for any
![]() $x \in Q$
,
$x \in Q$
,
![]() $\operatorname {\mathrm {tc}}(x) = \{x\}$
, and so for
$\operatorname {\mathrm {tc}}(x) = \{x\}$
, and so for
![]() $x,y \in Q$
,
$x,y \in Q$
,
![]() $\rho _\beta (x,y) = d(x,y)$
for every
$\rho _\beta (x,y) = d(x,y)$
for every
![]() $\beta $
. Finally, it can be shown that if
$\beta $
. Finally, it can be shown that if
![]() $x(\gamma ) = y(\gamma )$
for all
$x(\gamma ) = y(\gamma )$
for all ![]() , then
, then
![]() $\rho _\beta (x,y) = 0$
.
$\rho _\beta (x,y) = 0$
.
Also, while we will not need it, we should note that
![]() $\mathcal {T}_\alpha (\varnothing )$
is precisely the tree structure of height
$\mathcal {T}_\alpha (\varnothing )$
is precisely the tree structure of height
![]() $\alpha $
of [Reference Weydert23] and in this case,
$\alpha $
of [Reference Weydert23] and in this case,
![]() $\rho _\beta (x,y)$
is
$\rho _\beta (x,y)$
is
![]() $0$
if and only if
$0$
if and only if
![]() $x{\upharpoonright } \beta = y {\upharpoonright } \beta $
and is
$x{\upharpoonright } \beta = y {\upharpoonright } \beta $
and is
![]() $1$
otherwise.
$1$
otherwise.
![]() $\rho _\beta $
is of course also closely related to the
$\rho _\beta $
is of course also closely related to the
![]() $\sim _\beta $
relation of [Reference Malitz15].
$\sim _\beta $
relation of [Reference Malitz15].
Lemma 7.2. For any
![]() $a,b \in \mathcal {T}_\alpha $
,
$a,b \in \mathcal {T}_\alpha $
,
![]() $\beta \mapsto \rho _\beta (a,b)$
and
$\beta \mapsto \rho _\beta (a,b)$
and
![]() $\beta \mapsto e_\beta (a,b)$
are both non-decreasing functions of
$\beta \mapsto e_\beta (a,b)$
are both non-decreasing functions of
![]() $\beta $
.
$\beta $
.
Proof. Proceed by induction on
![]() $\beta $
. Limit stages are obvious, so assume that we know that
$\beta $
. Limit stages are obvious, so assume that we know that
![]() $\gamma \mapsto \rho _\gamma (a,b)$
and
$\gamma \mapsto \rho _\gamma (a,b)$
and
![]() $\gamma \mapsto e_\gamma (a,b)$
are increasing functions for any
$\gamma \mapsto e_\gamma (a,b)$
are increasing functions for any
![]() $a,b \in \mathcal {T}_\alpha $
on the interval
$a,b \in \mathcal {T}_\alpha $
on the interval
![]() $[0,\beta ]$
and consider
$[0,\beta ]$
and consider
![]() $\rho _{\beta +1}(x,y)$
.
$\rho _{\beta +1}(x,y)$
.
If
![]() $\beta = 0$
, then we just need to argue that
$\beta = 0$
, then we just need to argue that
![]() $\rho _1(a,b) \geq \rho _0(a,b) = d_{\mathrm {H}}(\operatorname {\mathrm {tc}}(a) \cap Q, \operatorname {\mathrm {tc}}(b) \cap Q)$
. Suppose that
$\rho _1(a,b) \geq \rho _0(a,b) = d_{\mathrm {H}}(\operatorname {\mathrm {tc}}(a) \cap Q, \operatorname {\mathrm {tc}}(b) \cap Q)$
. Suppose that
![]() $\rho _0(a,b)> r$
. Without loss of generality, this implies that there is a
$\rho _0(a,b)> r$
. Without loss of generality, this implies that there is a
![]() $c \in \operatorname {\mathrm {tc}}(a)\cap Q$
such that
$c \in \operatorname {\mathrm {tc}}(a)\cap Q$
such that
![]() $\inf \{d(c,z) : z \in \operatorname {\mathrm {tc}}(b) \cap Q\}> r$
. Since
$\inf \{d(c,z) : z \in \operatorname {\mathrm {tc}}(b) \cap Q\}> r$
. Since
![]() $c \in \operatorname {\mathrm {tc}}(a)$
and
$c \in \operatorname {\mathrm {tc}}(a)$
and ![]() , there is an
, there is an ![]() such that
such that
![]() $c \in \operatorname {\mathrm {tc}}(f)$
. Since
$c \in \operatorname {\mathrm {tc}}(f)$
. Since
![]() $c \in \operatorname {\mathrm {tc}}(f)\cap Q$
and since
$c \in \operatorname {\mathrm {tc}}(f)\cap Q$
and since
![]() $\operatorname {\mathrm {tc}}(g) \subseteq \operatorname {\mathrm {tc}}(b)$
for any
$\operatorname {\mathrm {tc}}(g) \subseteq \operatorname {\mathrm {tc}}(b)$
for any ![]() , we have that
, we have that
![]() $\rho _0(f,g)> r$
for any
$\rho _0(f,g)> r$
for any ![]() . Therefore
. Therefore
![]() $\rho _1(a,b) \geq r$
. Since we can do this for any r, we have that
$\rho _1(a,b) \geq r$
. Since we can do this for any r, we have that
![]() $\rho _1(a,b) \geq \rho _0(a,b)$
.
$\rho _1(a,b) \geq \rho _0(a,b)$
.
If
![]() $\beta> 0$
, then for any
$\beta> 0$
, then for any ![]() , we have that
, we have that ![]() by the induction hypothesis, so
by the induction hypothesis, so

and therefore ![]() , as required. The fact that
, as required. The fact that
![]() $e_{\beta +1}(a,b) \geq e_\beta (a,b)$
is immediate. here
$e_{\beta +1}(a,b) \geq e_\beta (a,b)$
is immediate. here
Lemma 7.3. For any
![]() $(Q,d)$
and ordinals
$(Q,d)$
and ordinals
![]() $\alpha <\beta $
, there is a unique
$\alpha <\beta $
, there is a unique
![]() $v_\alpha \in \mathcal {T}_\beta (Q)$
such that
$v_\alpha \in \mathcal {T}_\beta (Q)$
such that ![]() and
and
![]() $(V_\alpha ,\in )$
are isomorphic and for any
$(V_\alpha ,\in )$
are isomorphic and for any
![]() $\gamma \in (\alpha ,\beta )$
and distinct
$\gamma \in (\alpha ,\beta )$
and distinct ![]() ,
,
![]() $\rho _\gamma (a,b) = 1$
.
$\rho _\gamma (a,b) = 1$
.
Proof. Fix an ordinal
![]() $\beta $
. We will prove this for all
$\beta $
. We will prove this for all
![]() $\alpha < \beta $
by induction. For
$\alpha < \beta $
by induction. For
![]() $V_0 = \varnothing $
, the statement is witnessed by the sequence
$V_0 = \varnothing $
, the statement is witnessed by the sequence
![]() $v_0(\gamma ) = \varnothing $
in
$v_0(\gamma ) = \varnothing $
in
![]() $\mathcal {T}_\beta (Q)$
.
$\mathcal {T}_\beta (Q)$
.
Now assume that for some
![]() $\alpha < \beta $
, the statement is known for all
$\alpha < \beta $
, the statement is known for all
![]() $\delta < \alpha $
. If
$\delta < \alpha $
. If
![]() $\alpha $
is a successor and equal to
$\alpha $
is a successor and equal to
![]() $\gamma + 1$
, let
$\gamma + 1$
, let
![]() $v_\alpha $
be defined by
$v_\alpha $
be defined by
![]() $v_\alpha (0) = \{\varnothing \}$
,
$v_\alpha (0) = \{\varnothing \}$
,
![]() $v_\alpha (\sigma +1) = \mathcal {P}(v_\gamma (\sigma ))$
, and
$v_\alpha (\sigma +1) = \mathcal {P}(v_\gamma (\sigma ))$
, and ![]() for any limit ordinal
for any limit ordinal ![]() . Since the statement holds for
. Since the statement holds for
![]() $\gamma $
, we have that
$\gamma $
, we have that
![]() $\rho _\gamma $
is
$\rho _\gamma $
is
![]() $\{0,1\}$
-valued on the
$\{0,1\}$
-valued on the ![]() -elements of
-elements of
![]() $v_\gamma $
, we get that
$v_\gamma $
, we get that
![]() $\rho _\alpha =\rho _{\gamma +1}$
is
$\rho _\alpha =\rho _{\gamma +1}$
is
![]() $\{0,1\}$
-valued on the
$\{0,1\}$
-valued on the ![]() -elements of
-elements of
![]() $v_\alpha $
. Furthermore, since
$v_\alpha $
. Furthermore, since ![]() is isomorphic to
is isomorphic to
![]() $(V_\gamma ,\in )$
, it follows immediately that
$(V_\gamma ,\in )$
, it follows immediately that ![]() is isomorphic to
is isomorphic to
![]() $(V_\alpha ,\in )$
.
$(V_\alpha ,\in )$
.
If
![]() $\alpha $
is a limit, then let
$\alpha $
is a limit, then let
![]() $v_\alpha (\sigma ) = \bigcup _{\gamma < \alpha }v_\gamma (\sigma )$
for every
$v_\alpha (\sigma ) = \bigcup _{\gamma < \alpha }v_\gamma (\sigma )$
for every
![]() $\sigma < \beta $
. The required statements are obvious.
$\sigma < \beta $
. The required statements are obvious.
Definition 7.4. For any Q and
![]() $\alpha $
, we let
$\alpha $
, we let
![]() $\tau _{Q,\alpha }$
be the topology on
$\tau _{Q,\alpha }$
be the topology on
![]() $\mathcal {T}_\alpha (Q)$
generated by sets of the form
$\mathcal {T}_\alpha (Q)$
generated by sets of the form
![]() $\{y \in \mathcal {T}_\alpha (Q) : \rho _\beta (x,y) < \varepsilon \}$
for
$\{y \in \mathcal {T}_\alpha (Q) : \rho _\beta (x,y) < \varepsilon \}$
for
![]() $x \in \mathcal {T}_\alpha (Q)$
,
$x \in \mathcal {T}_\alpha (Q)$
,
![]() $\beta <\alpha $
, and
$\beta <\alpha $
, and
![]() $\varepsilon> 0$
.
$\varepsilon> 0$
.
It is immediate from basic topological facts that for any
![]() $X \subseteq \mathcal {T}_\alpha (Q)$
, there is a unique smallest closed set
$X \subseteq \mathcal {T}_\alpha (Q)$
, there is a unique smallest closed set
![]() $\overline {X}$
containing X. More importantly, we have the following.
$\overline {X}$
containing X. More importantly, we have the following.
Proposition 7.5. For any Q, limit
![]() $\alpha $
, and
$\alpha $
, and
![]() $\tau _{Q,\alpha }$
-closed
$\tau _{Q,\alpha }$
-closed
![]() $F \subseteq \mathcal {T}_\alpha (Q)$
, there is an
$F \subseteq \mathcal {T}_\alpha (Q)$
, there is an
![]() $x \in \mathcal {T}_\alpha (Q)$
such that
$x \in \mathcal {T}_\alpha (Q)$
such that ![]() .
.
Proof. For any
![]() $\beta <\alpha $
, let
$\beta <\alpha $
, let ![]() . x is clearly an element of
. x is clearly an element of
![]() $\mathcal {T}_\alpha (Q)$
. Furthermore, we clearly have that if
$\mathcal {T}_\alpha (Q)$
. Furthermore, we clearly have that if
![]() $y \in F$
, then
$y \in F$
, then ![]() . So now we just need to show the converse.
. So now we just need to show the converse.
Suppose that ![]() . We would like to show that y is in the closure of F and therefore is in F. In order to do this, it is sufficient to show that
. We would like to show that y is in the closure of F and therefore is in F. In order to do this, it is sufficient to show that
![]() $\inf \{\rho _\beta (y,z) : z \in F\} = 0$
for each
$\inf \{\rho _\beta (y,z) : z \in F\} = 0$
for each
![]() $\beta < F$
. For each
$\beta < F$
. For each
![]() $\beta < \alpha $
, find
$\beta < \alpha $
, find
![]() $z \in F$
such that
$z \in F$
such that
![]() $y(\beta +1)$
is an initial segment of z. We now have that
$y(\beta +1)$
is an initial segment of z. We now have that
![]() $\rho _\beta (y,z) = 0$
. Since we can do this for any
$\rho _\beta (y,z) = 0$
. Since we can do this for any
![]() $\beta < \alpha $
, we have that y is in the closure of F.
$\beta < \alpha $
, we have that y is in the closure of F.
What will ultimately be relevant to us is that the above facts are first-order properties of the structure ![]() (assuming
(assuming
![]() $\mathcal {T}_\alpha (Q)$
is an element of
$\mathcal {T}_\alpha (Q)$
is an element of
![]() $V_{\alpha +\omega }$
). This is part of the motivation for Definition 7.7.
$V_{\alpha +\omega }$
). This is part of the motivation for Definition 7.7.
We will also need the following.
Lemma 7.6. Fix a metric space
![]() $(Q,d)$
and a limit ordinal
$(Q,d)$
and a limit ordinal
![]() $\alpha $
. Let
$\alpha $
. Let
![]() $\overline {Q}$
be the
$\overline {Q}$
be the
![]() $\tau _{Q,\alpha }$
-closure of
$\tau _{Q,\alpha }$
-closure of
![]() $Q \subset \mathcal {T}_\alpha (Q)$
. For any
$Q \subset \mathcal {T}_\alpha (Q)$
. For any
![]() $z \in \overline {Q}$
, there is an
$z \in \overline {Q}$
, there is an
![]() $x \in Q$
such that
$x \in Q$
such that
![]() $\rho _\beta (x,z) = 0$
for all
$\rho _\beta (x,z) = 0$
for all
![]() $\beta < \alpha $
.
$\beta < \alpha $
.
Proof. First we need to show that if
![]() $x \in \overline {Q}$
, then
$x \in \overline {Q}$
, then
![]() $|\operatorname {\mathrm {tc}}(x)\cap Q| = 1$
. Suppose that
$|\operatorname {\mathrm {tc}}(x)\cap Q| = 1$
. Suppose that
![]() $\operatorname {\mathrm {tc}}(x) \cap Q$
has more than one element. Let y and z be distinct elements of
$\operatorname {\mathrm {tc}}(x) \cap Q$
has more than one element. Let y and z be distinct elements of
![]() $\operatorname {\mathrm {tc}}(x) \cap Q$
. Suppose that
$\operatorname {\mathrm {tc}}(x) \cap Q$
. Suppose that
![]() $d(y,z)> r$
. We now immediately have that
$d(y,z)> r$
. We now immediately have that
![]() $\rho _0(x,w)> \frac {1}{2}r$
for any
$\rho _0(x,w)> \frac {1}{2}r$
for any
![]() $w \in Q$
. Therefore
$w \in Q$
. Therefore
![]() $x \notin \overline {Q}$
. On the other hand, suppose that
$x \notin \overline {Q}$
. On the other hand, suppose that
![]() $\operatorname {\mathrm {tc}}(x) \cap Q = \varnothing $
. Then likewise,
$\operatorname {\mathrm {tc}}(x) \cap Q = \varnothing $
. Then likewise,
![]() $\rho _0(x,w) = 1$
for any
$\rho _0(x,w) = 1$
for any
![]() $w \in Q$
. Therefore
$w \in Q$
. Therefore
![]() $x \notin \overline {Q}$
.
$x \notin \overline {Q}$
.
Now we need to argue that if
![]() $x \in \overline {Q}$
, then for any
$x \in \overline {Q}$
, then for any ![]() ,
,
![]() $y \in \overline {Q}$
as well. Suppose
$y \in \overline {Q}$
as well. Suppose ![]() and
and
![]() $y \notin \overline {Q}$
. By definition, this implies that there is a
$y \notin \overline {Q}$
. By definition, this implies that there is a
![]() $\beta < \alpha $
such that
$\beta < \alpha $
such that ![]() , but this implies that
, but this implies that
![]() $\rho _{\beta +1}(x,w) \geq r $
for all
$\rho _{\beta +1}(x,w) \geq r $
for all
![]() $w \in Q$
and so
$w \in Q$
and so
![]() $x \notin \overline {Q}$
.
$x \notin \overline {Q}$
.
For any
![]() $x \in \overline {Q}$
, let
$x \in \overline {Q}$
, let
![]() $\pi (x)$
denote the unique element of Q that is in
$\pi (x)$
denote the unique element of Q that is in
![]() $\operatorname {\mathrm {tc}}(x)$
. We need to show that
$\operatorname {\mathrm {tc}}(x)$
. We need to show that
![]() $\rho _\beta (x,\pi (x)) = 0$
for all
$\rho _\beta (x,\pi (x)) = 0$
for all
![]() $\beta < \alpha $
. Clearly
$\beta < \alpha $
. Clearly
![]() $\rho _0(y,\pi (x)) = 0$
for any
$\rho _0(y,\pi (x)) = 0$
for any
![]() $y \in \overline {Q}$
with
$y \in \overline {Q}$
with
![]() $\pi (y) = \pi (x)$
. Suppose that
$\pi (y) = \pi (x)$
. Suppose that
![]() $\rho _\gamma (y,\pi (x)) = 0$
for all
$\rho _\gamma (y,\pi (x)) = 0$
for all
![]() $\gamma < \beta $
and
$\gamma < \beta $
and
![]() $y \in \overline {Q}$
with
$y \in \overline {Q}$
with
![]() $\pi (y) = \pi (x)$
. If
$\pi (y) = \pi (x)$
. If
![]() $\beta $
is a limit, then
$\beta $
is a limit, then
![]() $\rho _\beta (x,\pi (x)) = 0$
. Assume that
$\rho _\beta (x,\pi (x)) = 0$
. Assume that
![]() $\beta = \delta +1$
for some
$\beta = \delta +1$
for some
![]() $\delta $
. Fix y with
$\delta $
. Fix y with
![]() $\pi (y) = \pi (x)$
. Fix
$\pi (y) = \pi (x)$
. Fix ![]() . We clearly have that
. We clearly have that
![]() $\operatorname {\mathrm {tc}}(z) \cap Q \subseteq \operatorname {\mathrm {tc}}(y) \cap Q$
. It also must be the case that
$\operatorname {\mathrm {tc}}(z) \cap Q \subseteq \operatorname {\mathrm {tc}}(y) \cap Q$
. It also must be the case that
![]() $z \in \overline {Q}$
. Therefore we must have that
$z \in \overline {Q}$
. Therefore we must have that
![]() $\pi (z) = \pi (y) = \pi (x)$
as well, so by the induction hypothesis, we have that
$\pi (z) = \pi (y) = \pi (x)$
as well, so by the induction hypothesis, we have that
![]() $\rho _\delta (z,\pi (x)) = 0$
. Since we can do this for any
$\rho _\delta (z,\pi (x)) = 0$
. Since we can do this for any ![]() , we have that
, we have that
![]() $\rho _{\delta +1}(y,\pi (x)) = 0$
, as required.
$\rho _{\delta +1}(y,\pi (x)) = 0$
, as required.
Definition 7.7. Fix a tuple ![]() as in Definition 7.1 and an infinite ordinal
as in Definition 7.1 and an infinite ordinal
![]() $\alpha $
such that
$\alpha $
such that
![]() $\mathcal {T}_\alpha (Q)$
is an element of
$\mathcal {T}_\alpha (Q)$
is an element of
![]() $V_{\alpha +\omega }$
. We will assume that restricted
$V_{\alpha +\omega }$
. We will assume that restricted
![]() $\mathcal {L}_e$
-formulas are elements of
$\mathcal {L}_e$
-formulas are elements of
![]() $V_{\alpha +\omega }$
.
$V_{\alpha +\omega }$
.
Let ![]() be a (discrete) structure elementarily equivalent to
be a (discrete) structure elementarily equivalent to ![]() .Footnote
14
We write
.Footnote
14
We write
![]() $\rho ^M_\beta (x,y)$
and
$\rho ^M_\beta (x,y)$
and
![]() $e^M_\beta (x,y)$
for the functions in M given by Definition 7.1 computed internally.
$e^M_\beta (x,y)$
for the functions in M given by Definition 7.1 computed internally.
Given any
![]() $r \in \mathbb {R}^M$
satisfying
$r \in \mathbb {R}^M$
satisfying ![]() for some standard natural n, the standard part of r, written
for some standard natural n, the standard part of r, written
![]() ${\text {st}}(r)$
, is the unique standard real satisfying
${\text {st}}(r)$
, is the unique standard real satisfying
![]() $r \geq t$
if and only if
$r \geq t$
if and only if
![]() ${\text {st}}(r) \geq t$
for all standard rationals t.
${\text {st}}(r) \geq t$
for all standard rationals t.
A gauge on M is a non-increasing function
![]() $s: \alpha ^M \to [0,1]$
(where
$s: \alpha ^M \to [0,1]$
(where
![]() $[0,1]$
is the standard unit interval) with
$[0,1]$
is the standard unit interval) with
![]() $s(0) = 1$
. An internal gauge on M is a non-increasing function
$s(0) = 1$
. An internal gauge on M is a non-increasing function
![]() $s \in M$
from
$s \in M$
from
![]() $\alpha ^M$
to
$\alpha ^M$
to
![]() $[0,1]^M$
with
$[0,1]^M$
with
![]() $s(0) = 1$
. An internal gauge on M is
$s(0) = 1$
. An internal gauge on M is
![]() $\varepsilon $
-smooth if:
$\varepsilon $
-smooth if:
-
•
 $s(0) = s(1)$
,
$s(0) = s(1)$
, -
•
 $s(\beta ) = 0$
for all sufficiently large
$s(\beta ) = 0$
for all sufficiently large
 $\beta \in \alpha ^M$
,
$\beta \in \alpha ^M$
, -
• for every
 $\beta \in \alpha ^M$
,
$\beta \in \alpha ^M$
,
 $s(\beta ) < s(\beta +1) + \varepsilon $
, and
$s(\beta ) < s(\beta +1) + \varepsilon $
, and -
• for any limit
 , there is a
, there is a  such that
such that  .
.
Given an internal gauge s on M, the standard part of s, written
![]() $s^{\text {st}}$
, is
$s^{\text {st}}$
, is
![]() ${\text {st}} \circ s$
.
${\text {st}} \circ s$
.
Given a gauge s on M, we define the functions
and ![]() . For any internal gauge s we write
. For any internal gauge s we write
![]() $\rho _s$
and
$\rho _s$
and
![]() $e_s$
for the corresponding quantities computed internally in M and we write
$e_s$
for the corresponding quantities computed internally in M and we write
![]() $\rho _s^{\text {st}}$
and
$\rho _s^{\text {st}}$
and
![]() $e_s^{\text {st}}$
for their corresponding standard parts.
$e_s^{\text {st}}$
for their corresponding standard parts.
Given two gauges
![]() $s_0$
and
$s_0$
and
![]() $s_1$
on M, we write
$s_1$
on M, we write ![]() for the quantity
for the quantity
![]() $\sup _{\beta \in \alpha ^M}|s_0(\beta ) - s_1(\beta )|$
.
$\sup _{\beta \in \alpha ^M}|s_0(\beta ) - s_1(\beta )|$
.
Note that
![]() $\rho ^{\text {st}}_s = \rho _{s^{\text {st}}}$
and
$\rho ^{\text {st}}_s = \rho _{s^{\text {st}}}$
and
![]() $e^{\text {st}}_s = e_{s^{\text {st}}}$
for any M as in Definition 7.7. Since
$e^{\text {st}}_s = e_{s^{\text {st}}}$
for any M as in Definition 7.7. Since
![]() $\rho _s(x,y)$
is the supremum of a family of pseudo-metrics, it is itself a pseudo-metric. Finally, it is trivial that for any gauge s on M,
$\rho _s(x,y)$
is the supremum of a family of pseudo-metrics, it is itself a pseudo-metric. Finally, it is trivial that for any gauge s on M,
![]() $(\mathcal {T}^M,e_s)$
is an
$(\mathcal {T}^M,e_s)$
is an
![]() $\mathcal {L}_e$
-structure.
$\mathcal {L}_e$
-structure.
In the statements of lemmas in the rest of this section, we will write ‘(M as in Definition 7.7.)’ to mean that the structure
![]() $M = (\mathcal {T}^M,\alpha ^M,\mathbb {R}^M)$
satisfies the conditions in Definition 7.7.
$M = (\mathcal {T}^M,\alpha ^M,\mathbb {R}^M)$
satisfies the conditions in Definition 7.7.
Lemma 7.8 (M as in Definition 7.7).
Fix a restricted
![]() $\mathcal {L}_e$
-formula
$\mathcal {L}_e$
-formula
![]() $\varphi (\bar {x})$
and a tuple
$\varphi (\bar {x})$
and a tuple
![]() $\bar {a} \in \mathcal {T}^M$
.
$\bar {a} \in \mathcal {T}^M$
.
-
(1) For any gauges s and t on M,

-
(2) For any internal gauge s on M,
where $$\begin{align*}\text{st}((\varphi^{(\mathcal{T}^M,e_s)}(\bar{a}))^M) = \varphi^{(\mathcal{T}^M,e_s^{\text{st}})}(\bar{a}), \end{align*}$$
$$\begin{align*}\text{st}((\varphi^{(\mathcal{T}^M,e_s)}(\bar{a}))^M) = \varphi^{(\mathcal{T}^M,e_s^{\text{st}})}(\bar{a}), \end{align*}$$
 $(\varphi ^{(\mathcal {T}^M,e_s)}(\bar {a}))^M$
is the value of
$(\varphi ^{(\mathcal {T}^M,e_s)}(\bar {a}))^M$
is the value of
 $\varphi ^{(\mathcal {T}^M,e_s)}(\bar {a})$
computed internally in M.
$\varphi ^{(\mathcal {T}^M,e_s)}(\bar {a})$
computed internally in M.
Proof. It is straightforward to show that for any
![]() $a,b \in \mathcal {T}^M$
,
$a,b \in \mathcal {T}^M$
, ![]() . This implies likewise that for any
. This implies likewise that for any
![]() $a,b \in \mathcal {T}^M$
,
$a,b \in \mathcal {T}^M$
, ![]() . From this, 1 follows by an induction argument. 2 also follows from an easy induction argument.
. From this, 1 follows by an induction argument. 2 also follows from an easy induction argument.
Lemma 7.9. (M as in Definition 7.7).
For any
![]() $\beta \in \alpha ^M$
,
$\beta \in \alpha ^M$
,
Proof. This follows immediately from the fact that
![]() $\rho _\beta ^M$
is a pseudo-metric on
$\rho _\beta ^M$
is a pseudo-metric on
![]() $\mathcal {T}^M$
and
$\mathcal {T}^M$
and
![]() $\rho _{\beta +1}^M(x,y)$
is precisely the Hausdorff distance between
$\rho _{\beta +1}^M(x,y)$
is precisely the Hausdorff distance between ![]() and
and ![]() with respect to
with respect to
![]() $\rho _{\beta +1}^M$
.
$\rho _{\beta +1}^M$
.
Lemma 7.10. (M as in Definition 7.7).
Fix
![]() $\varepsilon \in (0,1]^M$
and an
$\varepsilon \in (0,1]^M$
and an
![]() $\varepsilon $
-smooth internal gauge s on M. Let
$\varepsilon $
-smooth internal gauge s on M. Let ![]() . The following statements hold internally in M:
. The following statements hold internally in M:
-
(1)
 for all
for all
 $a,b \in \mathcal {T}^M$
.
$a,b \in \mathcal {T}^M$
. -
(2)
 for all
for all
 $a,b \in \mathcal {T}^M$
.
$a,b \in \mathcal {T}^M$
.
Proof. First note that by definition,
![]() $d_{e,s}(x,y)$
is the Hausdorff pseudo-metric induced by the pseudo-metric
$d_{e,s}(x,y)$
is the Hausdorff pseudo-metric induced by the pseudo-metric
![]() $\rho _s(x,y)$
. So in particular we also have that
$\rho _s(x,y)$
. So in particular we also have that

For 1, fix a and b in
![]() $\mathcal {T}$
. If a and b are both
$\mathcal {T}$
. If a and b are both ![]() -empty, then
-empty, then
![]() $d_{e,s}(a,b) = \rho _s(a,b) = 0$
. If one of them is
$d_{e,s}(a,b) = \rho _s(a,b) = 0$
. If one of them is ![]() -empty and the other isn’t, then
-empty and the other isn’t, then
![]() $d_{e,s}(a,b) = \rho _s(a,b) = 1$
. So assume that they are both non-
$d_{e,s}(a,b) = \rho _s(a,b) = 1$
. So assume that they are both non-![]() -empty.
-empty.
Suppose that
![]() $\rho _s(a,b)> r$
. This implies that there is a
$\rho _s(a,b)> r$
. This implies that there is a
![]() $\beta \in \alpha ^M$
such that
$\beta \in \alpha ^M$
such that
![]() $\min (\rho _\beta (a,b),s(\beta ))> r$
, which implies that
$\min (\rho _\beta (a,b),s(\beta ))> r$
, which implies that
![]() $\rho _\beta (a,b)> r$
. If
$\rho _\beta (a,b)> r$
. If
![]() $\beta $
is a limit ordinal, then
$\beta $
is a limit ordinal, then
![]() $\rho _\beta (a,b) = \sup _{\gamma < \beta }\rho _\gamma (a,b)$
, so, since s is non-increasing, we may assume that
$\rho _\beta (a,b) = \sup _{\gamma < \beta }\rho _\gamma (a,b)$
, so, since s is non-increasing, we may assume that
![]() $\beta $
is not a limit ordinal. Since
$\beta $
is not a limit ordinal. Since
![]() $s(0) = s(1)$
, we may assume that
$s(0) = s(1)$
, we may assume that
![]() $\beta> 0$
by Lemma 7.2. So let
$\beta> 0$
by Lemma 7.2. So let
![]() $\gamma + 1 = \beta $
. We may now assume without loss of generality that there is a
$\gamma + 1 = \beta $
. We may now assume without loss of generality that there is a ![]() such that
such that
![]() $e_\gamma (c,b)> r$
, implying that
$e_\gamma (c,b)> r$
, implying that
![]() $\rho _\gamma (c,f)> r$
for all
$\rho _\gamma (c,f)> r$
for all ![]() . Therefore we have that
. Therefore we have that
![]() $\rho _s(c,f) \geq \min (\rho _s(c,f),s(\gamma ))> r$
for all
$\rho _s(c,f) \geq \min (\rho _s(c,f),s(\gamma ))> r$
for all ![]() , whence
, whence
![]() $e_s(c,b) \geq r$
and
$e_s(c,b) \geq r$
and
![]() $d_{e,s}(a,b) \geq r$
. Since we can do this for any
$d_{e,s}(a,b) \geq r$
. Since we can do this for any
![]() $r < \rho _s(a,b)$
, we have that
$r < \rho _s(a,b)$
, we have that
![]() $d_{e,s}(a,b) \geq \rho _s(a,b)$
.
$d_{e,s}(a,b) \geq \rho _s(a,b)$
.
Now suppose that
![]() $d_{e,s}(a,b)> r$
for some
$d_{e,s}(a,b)> r$
for some
![]() $r> 0$
. We may assume without loss of generality that there is a
$r> 0$
. We may assume without loss of generality that there is a ![]() such that
such that
![]() $e_s(c,b)> r$
. So in particular,
$e_s(c,b)> r$
. So in particular,
![]() $\rho _s(c,f)> r$
for all
$\rho _s(c,f)> r$
for all ![]() . Therefore, for any such f, there is a
. Therefore, for any such f, there is a
![]() $\beta _f \in \alpha ^M$
such that
$\beta _f \in \alpha ^M$
such that
![]() $\min (\rho _{\beta _f}(c,f),s(\beta _f))> r$
. Since s is
$\min (\rho _{\beta _f}(c,f),s(\beta _f))> r$
. Since s is
![]() $\varepsilon $
-smooth, there is a largest
$\varepsilon $
-smooth, there is a largest
![]() $\gamma \in \alpha ^M$
such that
$\gamma \in \alpha ^M$
such that
![]() $s(\gamma )> r$
. Note that we must have
$s(\gamma )> r$
. Note that we must have
![]() $\gamma \geq \beta _f$
for all
$\gamma \geq \beta _f$
for all ![]() . So now we actually know that
. So now we actually know that
![]() $\rho _\gamma (c,f)> r$
for all
$\rho _\gamma (c,f)> r$
for all ![]() . Therefore
. Therefore
![]() $e_\gamma (c,b) \geq r$
and so
$e_\gamma (c,b) \geq r$
and so
![]() $\rho _{\gamma +1}(a,b) \geq r$
, whence
$\rho _{\gamma +1}(a,b) \geq r$
, whence
![]() $\rho _s(a,b) \geq \min (\rho _{\gamma +1}(a,b),s(\gamma +1))> r - \varepsilon $
. Since we can this for any
$\rho _s(a,b) \geq \min (\rho _{\gamma +1}(a,b),s(\gamma +1))> r - \varepsilon $
. Since we can this for any
![]() $r < d_{e,s}(a,b)$
, we have that
$r < d_{e,s}(a,b)$
, we have that
![]() $\rho _s(a,b) \geq d_{e,s}(a,b)-\varepsilon $
, as required.
$\rho _s(a,b) \geq d_{e,s}(a,b)-\varepsilon $
, as required.
For 2, it follows from the ![]() direction of the proof of Lemma 6.2 that
direction of the proof of Lemma 6.2 that
![]() $e_s(a,b) = \inf _z \min (\rho _s(a,z) + 2e_2(z,b), 1)$
for all
$e_s(a,b) = \inf _z \min (\rho _s(a,z) + 2e_2(z,b), 1)$
for all
![]() $a,b \in \mathcal {T}^M$
. It is immediate from part 1 that
$a,b \in \mathcal {T}^M$
. It is immediate from part 1 that
for all
![]() $a,b \in \mathcal {T}^M$
, so the required result follows.
$a,b \in \mathcal {T}^M$
, so the required result follows.
Lemma 7.11 (M as in Definition 7.7).
Fix
![]() $\varepsilon \in (0,1]^M$
and let s be an
$\varepsilon \in (0,1]^M$
and let s be an
![]() $\varepsilon $
-smooth internal gauge on M. For anyFootnote
15
$\varepsilon $
-smooth internal gauge on M. For anyFootnote
15
![]() $\mathcal {L}_e$
-formula
$\mathcal {L}_e$
-formula
![]() $\varphi (\bar {a},\bar {b})$
and any
$\varphi (\bar {a},\bar {b})$
and any
![]() $\bar {a},\bar {b} \in \mathcal {T}^M$
, it holds internally in M that
$\bar {a},\bar {b} \in \mathcal {T}^M$
, it holds internally in M that
where
![]() $d_{e,s}(\bar {a},\bar {b}) = \max _{i<|\bar {a}|}d_{e,s}(a_i,b_i)$
.
$d_{e,s}(\bar {a},\bar {b}) = \max _{i<|\bar {a}|}d_{e,s}(a_i,b_i)$
.
Proof. We prove this by induction on formulas. If
![]() $\varphi $
is
$\varphi $
is
![]() $e(x,y)$
, then we have
$e(x,y)$
, then we have

by Lemma 7.10. The argument for connectives and quantifiers the same as in Lemma 2.6.
Lemma 7.12. (M as in Definition 7.7).
Fix
![]() $\varepsilon \in (0,1]^M$
and let s be an
$\varepsilon \in (0,1]^M$
and let s be an
![]() $\varepsilon $
-smooth internal gauge on M. For any
$\varepsilon $
-smooth internal gauge on M. For any
![]() $\mathcal {L}_e$
-formula
$\mathcal {L}_e$
-formula
![]() $\varphi (x,\bar {y})$
, it holds internally in M that
$\varphi (x,\bar {y})$
, it holds internally in M that

Proof. For any
![]() $\mathcal {L}_e$
-formula
$\mathcal {L}_e$
-formula
![]() $\varphi (x,\bar {y})$
and any
$\varphi (x,\bar {y})$
and any
![]() $\bar {a} \in M$
, let
$\bar {a} \in M$
, let ![]() . We need to argue that
. We need to argue that
![]() $B_0$
is closed in the topology on
$B_0$
is closed in the topology on
![]() $\mathcal {T}^M$
given in Definition 7.4. Suppose that
$\mathcal {T}^M$
given in Definition 7.4. Suppose that
![]() $c \notin B_0$
. This means that
$c \notin B_0$
. This means that
![]() $\varphi ^{(\mathcal {T}^M,e_s)}(c,\bar {a})> 0$
. Since
$\varphi ^{(\mathcal {T}^M,e_s)}(c,\bar {a})> 0$
. Since
![]() $e_s$
is
$e_s$
is
![]() $2$
-Lipschitz with regards to
$2$
-Lipschitz with regards to
![]() $\rho _s$
, this implies that there is a
$\rho _s$
, this implies that there is a
![]() $\delta> 0$
such that for any
$\delta> 0$
such that for any
![]() $c' \in \mathcal {T}^M$
with
$c' \in \mathcal {T}^M$
with
![]() $\rho _s(c,c') < \delta $
,
$\rho _s(c,c') < \delta $
,
![]() $\varphi ^{(\mathcal {T}^M,e_s)}(c',\bar {a})> 0$
as well. Since s is
$\varphi ^{(\mathcal {T}^M,e_s)}(c',\bar {a})> 0$
as well. Since s is
![]() $\varepsilon $
-smooth, there is a
$\varepsilon $
-smooth, there is a
![]() $\gamma \in \alpha ^M$
such that
$\gamma \in \alpha ^M$
such that
![]() $s(\gamma ) = 0$
. By Lemma 7.2, we know that if
$s(\gamma ) = 0$
. By Lemma 7.2, we know that if
![]() $\rho _\gamma (c,c') < \frac {1}{2} \delta $
, then
$\rho _\gamma (c,c') < \frac {1}{2} \delta $
, then
![]() $\rho _s(c,c') < \delta $
. Therefore we have that the set
$\rho _s(c,c') < \delta $
. Therefore we have that the set
![]() $\{x : \rho _{\gamma }(x,c) < \frac {1}{2}\delta \}$
is disjoint from
$\{x : \rho _{\gamma }(x,c) < \frac {1}{2}\delta \}$
is disjoint from
![]() $B_0$
. Since we can do this for any
$B_0$
. Since we can do this for any
![]() $c \notin B_0$
, we have that
$c \notin B_0$
, we have that
![]() $B_0$
is closed.
$B_0$
is closed.
Let b be the unique element of
![]() $\mathcal {T}^M$
coextensive with
$\mathcal {T}^M$
coextensive with
![]() $B_0$
(which exists by Proposition 7.5). For any
$B_0$
(which exists by Proposition 7.5). For any
![]() $c \in \mathcal {T}^M$
, if
$c \in \mathcal {T}^M$
, if ![]() , then
, then ![]() by our choice of c and so
by our choice of c and so
![]() $e_s(c,b) = 0$
. Therefore
$e_s(c,b) = 0$
. Therefore ![]() for all
for all
![]() $c \in \mathcal {T}^M$
. On the other hand, if
$c \in \mathcal {T}^M$
. On the other hand, if ![]() , then there is an
, then there is an ![]() such that
such that
![]() $\rho _s(c,f) < \varepsilon _\varphi + \sigma $
for any
$\rho _s(c,f) < \varepsilon _\varphi + \sigma $
for any
![]() $\sigma> 0$
. Therefore,
$\sigma> 0$
. Therefore,
![]() $\varphi (c,\bar {a}) < 2v(\varphi )d_{e,s}(c,f) < 2v(\varphi )(\varepsilon _\varphi +\sigma +\varepsilon )$
by Lemmas 7.10 and 7.11. Since
$\varphi (c,\bar {a}) < 2v(\varphi )d_{e,s}(c,f) < 2v(\varphi )(\varepsilon _\varphi +\sigma +\varepsilon )$
by Lemmas 7.10 and 7.11. Since
![]() $2v(\varphi )\varepsilon _\varphi < 1$
and since we can do this for any
$2v(\varphi )\varepsilon _\varphi < 1$
and since we can do this for any
![]() $\sigma> 0$
, we have that
$\sigma> 0$
, we have that ![]() . Therefore
. Therefore ![]() for any
for any
![]() $c \in \mathcal {T}^M$
.
$c \in \mathcal {T}^M$
.
Lemma 7.13 (M as in Definition 7.7).
For any (external) gauge s on M with dense image in
![]() $[0,1]$
and (standard) rational
$[0,1]$
and (standard) rational
![]() $\varepsilon \in (0,1]$
, there is an
$\varepsilon \in (0,1]$
, there is an
![]() $\varepsilon $
-smooth internal gauge t such that
$\varepsilon $
-smooth internal gauge t such that ![]() .
.
Proof. Find standard n large enough that
![]() $\frac {1}{n} < \frac {1}{2}\varepsilon $
. For each
$\frac {1}{n} < \frac {1}{2}\varepsilon $
. For each
![]() $i<n$
, find
$i<n$
, find
![]() $\beta _i \in \alpha ^M$
such that
$\beta _i \in \alpha ^M$
such that ![]() . Note that since the range of s is dense, none of the
. Note that since the range of s is dense, none of the
![]() $\beta _i$
’s are
$\beta _i$
’s are
![]() $0$
or
$0$
or
![]() $1$
. Also note that
$1$
. Also note that
![]() $(\beta _i)_{i<n}$
is a decreasing sequence of ordinals. For any
$(\beta _i)_{i<n}$
is a decreasing sequence of ordinals. For any
![]() $\gamma \in \alpha ^M$
, let
$\gamma \in \alpha ^M$
, let
 $$\begin{align*}t(\gamma) = \begin{cases} 0 & \gamma \geq \beta_0 \\ \frac{i}{n} & 0<i< n,~\beta_{i-1}>\gamma \geq \beta_i \\ 1 & \beta_{n-1} > \gamma \end{cases}. \end{align*}$$
$$\begin{align*}t(\gamma) = \begin{cases} 0 & \gamma \geq \beta_0 \\ \frac{i}{n} & 0<i< n,~\beta_{i-1}>\gamma \geq \beta_i \\ 1 & \beta_{n-1} > \gamma \end{cases}. \end{align*}$$
Clearly
![]() $t(\gamma ) = 0$
for all sufficiently large
$t(\gamma ) = 0$
for all sufficiently large
![]() $\gamma $
. We also have that
$\gamma $
. We also have that
![]() $s(\gamma ) < s(\gamma +1) + \frac {2}{n} < s(\gamma +1) + \varepsilon $
for all
$s(\gamma ) < s(\gamma +1) + \frac {2}{n} < s(\gamma +1) + \varepsilon $
for all
![]() $\gamma \in \alpha ^M$
. Finally, the limit ordinal condition in the definition of
$\gamma \in \alpha ^M$
. Finally, the limit ordinal condition in the definition of
![]() $\varepsilon $
-smooth is clearly met, so t is
$\varepsilon $
-smooth is clearly met, so t is
![]() $\varepsilon $
-smooth.
$\varepsilon $
-smooth.
Now for any
![]() $\gamma $
, we have that if
$\gamma $
, we have that if
![]() $t(\gamma ) = 0$
, then
$t(\gamma ) = 0$
, then
![]() $\gamma \geq \beta _0$
and so
$\gamma \geq \beta _0$
and so ![]() . If
. If
![]() $t(\gamma ) \in (0,1)$
, then there is a positive
$t(\gamma ) \in (0,1)$
, then there is a positive
![]() $i<n$
such that
$i<n$
such that
![]() $\beta _{i-1}> \gamma \geq \beta _i$
, implying that
$\beta _{i-1}> \gamma \geq \beta _i$
, implying that ![]() , so
, so
![]() $|s(\gamma ) - t(\gamma )| = |s(\gamma ) - \frac {i}{n}| < \varepsilon $
. And if
$|s(\gamma ) - t(\gamma )| = |s(\gamma ) - \frac {i}{n}| < \varepsilon $
. And if
![]() $t(\gamma ) = 1$
, then
$t(\gamma ) = 1$
, then
![]() $s(\gamma ) \geq s(\beta _{n-1}) \geq \frac {n-1}{n}$
, so
$s(\gamma ) \geq s(\beta _{n-1}) \geq \frac {n-1}{n}$
, so ![]() . Therefore
. Therefore ![]() , as required.
, as required.
In order to proceed we will need a fact from model theory. This is similar to the approach typically used to build partially standard models of
![]() $\mathsf {NFU}$
.
$\mathsf {NFU}$
.
Lemma 7.14. For any ordinal
![]() $\sigma $
, there is an
$\sigma $
, there is an
![]() $\alpha> \sigma $
and a structure
$\alpha> \sigma $
and a structure
![]() $(M,\alpha ^M) \equiv (V_{\alpha +\omega },\alpha )$
such that:
$(M,\alpha ^M) \equiv (V_{\alpha +\omega },\alpha )$
such that:
-
•
 $V_\sigma ^M$
is isomorphic to
$V_\sigma ^M$
is isomorphic to
 $V_\sigma $
and
$V_\sigma $
and -
• there is a set of M-ordinals less than
 $\alpha ^M$
that is order-isomorphic to
$\alpha ^M$
that is order-isomorphic to
 $\mathbb {Q}$
.
$\mathbb {Q}$
.
Proof. Let
![]() $\kappa = |V_{\sigma }|$
. Let
$\kappa = |V_{\sigma }|$
. Let
![]() $\alpha = \beth _{(2^\kappa )^+}$
. Expand
$\alpha = \beth _{(2^\kappa )^+}$
. Expand
![]() $(V_{\alpha +\omega },\in )$
by Skolem functions. By [Reference Tent and Ziegler21, Lemma 7.2.12], we can find a
$(V_{\alpha +\omega },\in )$
by Skolem functions. By [Reference Tent and Ziegler21, Lemma 7.2.12], we can find a
![]() $V_{\sigma }$
-indiscernible sequence I with order type
$V_{\sigma }$
-indiscernible sequence I with order type
![]() $\mathbb {Q}$
in some elementary extension N of
$\mathbb {Q}$
in some elementary extension N of
![]() $(V_{\alpha +\omega },\in ,\alpha ,\text {Skolem functions})$
such that for any increasing sequence
$(V_{\alpha +\omega },\in ,\alpha ,\text {Skolem functions})$
such that for any increasing sequence
![]() $a_0<\dots < a_{n-1}$
in I, there are ordinals
$a_0<\dots < a_{n-1}$
in I, there are ordinals
![]() $\delta _0,\dots ,\delta _{n-1} < \alpha $
with
$\delta _0,\dots ,\delta _{n-1} < \alpha $
with
![]() $\operatorname {\mathrm {tp}}(\bar {a} / V_{\sigma }) = \operatorname {\mathrm {tp}}(\bar {\delta }/V_{\sigma })$
. Let M be the Skolem hull of
$\operatorname {\mathrm {tp}}(\bar {a} / V_{\sigma }) = \operatorname {\mathrm {tp}}(\bar {\delta }/V_{\sigma })$
. Let M be the Skolem hull of
![]() $V_{\sigma } \cup I$
. For any element a of
$V_{\sigma } \cup I$
. For any element a of
![]() $V_\sigma ^M$
, there is a Skolem function f and tuples
$V_\sigma ^M$
, there is a Skolem function f and tuples
![]() $\bar {b} \in V_\sigma $
and
$\bar {b} \in V_\sigma $
and
![]() $\bar {c} \in I$
such that
$\bar {c} \in I$
such that
![]() $a = f(\bar {b},\bar {c})$
. By construction, there is a tuple
$a = f(\bar {b},\bar {c})$
. By construction, there is a tuple
![]() $\bar \delta \in V_\alpha $
such that
$\bar \delta \in V_\alpha $
such that
![]() $\operatorname {\mathrm {tp}}(\bar {c}/V_{\sigma }) = \operatorname {\mathrm {tp}}(\bar \delta /V_{\sigma })$
. Since
$\operatorname {\mathrm {tp}}(\bar {c}/V_{\sigma }) = \operatorname {\mathrm {tp}}(\bar \delta /V_{\sigma })$
. Since
![]() $f(\bar {b},\bar \delta ) \in V_{\sigma }$
, we have that
$f(\bar {b},\bar \delta ) \in V_{\sigma }$
, we have that
![]() $f(\bar {b},\bar {c}) = f(\bar {b},\bar \delta )$
. Therefore
$f(\bar {b},\bar {c}) = f(\bar {b},\bar \delta )$
. Therefore
![]() $V_\sigma ^M = V_\sigma $
, as required.
$V_\sigma ^M = V_\sigma $
, as required.
Theorem 7.15. For any complete metric space
![]() $(Q,d)$
with
$(Q,d)$
with
![]() $[0,1]$
-valued metric and any ordinal
$[0,1]$
-valued metric and any ordinal
![]() $\sigma $
, there is a model N of
$\sigma $
, there is a model N of
![]() $\mathsf {MSE}$
such that N contains:
$\mathsf {MSE}$
such that N contains:
-
• a set of Quine atoms isometric to
 $(Q,d)$
,
$(Q,d)$
, -
• all closed subsets of Q as elements, and
-
• a
 $1$
-discrete set v such that
$1$
-discrete set v such that  is isomorphic to
is isomorphic to
 $(V_\sigma ,\in )$
(implying that
$(V_\sigma ,\in )$
(implying that
 $\operatorname {\mathrm {Ord}}^N$
has standard part of length at least
$\operatorname {\mathrm {Ord}}^N$
has standard part of length at least
 $\sigma $
and if
$\sigma $
and if
 $\sigma $
is infinite,
$\sigma $
is infinite,
 $N \models \mathsf {Inf}(v)$
).
$N \models \mathsf {Inf}(v)$
).
In particular,
![]() $\mathsf {MSE}$
is consistent.
$\mathsf {MSE}$
is consistent.
Proof. Fix
![]() $(Q,d)$
as in Definition 7.1. Fix some ordinal
$(Q,d)$
as in Definition 7.1. Fix some ordinal
![]() $\sigma $
. We may assume that
$\sigma $
. We may assume that
![]() $(Q,d)$
and the full power set of Q are in
$(Q,d)$
and the full power set of Q are in
![]() $V_\sigma $
. We may also assume that
$V_\sigma $
. We may also assume that
![]() $\sigma $
is a limit ordinal. Apply Lemma 7.14 to get a structure M elementarily equivalent to
$\sigma $
is a limit ordinal. Apply Lemma 7.14 to get a structure M elementarily equivalent to
![]() $V_{\alpha +\omega }$
for some
$V_{\alpha +\omega }$
for some
![]() $\alpha> \sigma $
such that the standard part of M contains
$\alpha> \sigma $
such that the standard part of M contains
![]() $V_\sigma $
. Let J be a set of M-ordinals less than
$V_\sigma $
. Let J be a set of M-ordinals less than
![]() $\alpha ^M$
order-isomorphic to
$\alpha ^M$
order-isomorphic to
![]() $\mathbb {Q}$
. Since
$\mathbb {Q}$
. Since
![]() $\mathcal {T}_\alpha (Q)$
is definable from Q and
$\mathcal {T}_\alpha (Q)$
is definable from Q and
![]() $\alpha $
, there is an element
$\alpha $
, there is an element
![]() $\mathcal {T}^M$
in M realizing the same type over Q and
$\mathcal {T}^M$
in M realizing the same type over Q and
![]() $\alpha ^M$
. In this way we can regard M as a structure satisfying the conditions of Definition 7.7.
$\alpha ^M$
. In this way we can regard M as a structure satisfying the conditions of Definition 7.7.
J is also order-isomorphic to
![]() $(0,1)\cap \mathbb {Q}$
. Let f be an order isomorphism witnessing this. Define
$(0,1)\cap \mathbb {Q}$
. Let f be an order isomorphism witnessing this. Define
![]() $s : \operatorname {\mathrm {Ord}}^M \to [0,1]$
by
$s : \operatorname {\mathrm {Ord}}^M \to [0,1]$
by ![]() with
with
![]() $\inf \varnothing = 1$
. This is clearly a gauge on M. Let
$\inf \varnothing = 1$
. This is clearly a gauge on M. Let
![]() $N = (\mathcal {T}^M,e_s)$
.
$N = (\mathcal {T}^M,e_s)$
.
We need to show that for any axiom
![]() $\varphi $
of
$\varphi $
of
![]() $\mathsf {MSE}$
(i.e., those listed in Definitions 6.1 and 6.5) and any
$\mathsf {MSE}$
(i.e., those listed in Definitions 6.1 and 6.5) and any
![]() $\varepsilon> 0$
,
$\varepsilon> 0$
, ![]() . If
. If
![]() $\varphi $
is the
$\varphi $
is the
![]() $\mathrm {H}$
-extensionality axiom, we can find with Lemma 7.13 a
$\mathrm {H}$
-extensionality axiom, we can find with Lemma 7.13 a
![]() $\frac {1}{2}\varepsilon $
-smooth internal gauge t such that
$\frac {1}{2}\varepsilon $
-smooth internal gauge t such that ![]() . By Lemmas 7.8 and 7.10, we have that
. By Lemmas 7.8 and 7.10, we have that ![]() . If
. If
![]() $\varphi $
is the excision axiom for the formula
$\varphi $
is the excision axiom for the formula
![]() $\psi $
, then we can do the same with a
$\psi $
, then we can do the same with a
![]() $\frac {1}{2v(\psi )}\varepsilon $
-smooth internal gauge t by Lemma 7.12. Since we can do this for any
$\frac {1}{2v(\psi )}\varepsilon $
-smooth internal gauge t by Lemma 7.12. Since we can do this for any
![]() $\varphi \in \mathsf {MSE}$
and
$\varphi \in \mathsf {MSE}$
and
![]() $\varepsilon> 0$
, we have that
$\varepsilon> 0$
, we have that
![]() $N \models \mathsf {MSE}$
.
$N \models \mathsf {MSE}$
.
Finally we just need to verify that the set of Quine atoms isomorphic to
![]() $(Q,d)$
, arbitrary closed subsets of Q, and the set isomorphic to
$(Q,d)$
, arbitrary closed subsets of Q, and the set isomorphic to
![]() $V_\sigma $
exist in N. Let q be the element of
$V_\sigma $
exist in N. Let q be the element of
![]() $\mathcal {T}^M$
coextensive with the set
$\mathcal {T}^M$
coextensive with the set
![]() $Q^\ast $
defined in Lemma 7.6. We have that Q is a dense subset of q and furthermore
$Q^\ast $
defined in Lemma 7.6. We have that Q is a dense subset of q and furthermore
![]() $\rho _\beta $
agrees with d on Q for all
$\rho _\beta $
agrees with d on Q for all
![]() $\beta < \alpha $
, therefore
$\beta < \alpha $
, therefore
![]() $(q,\rho _s)$
is isometric to
$(q,\rho _s)$
is isometric to
![]() $(Q,d)$
, since Q is metrically complete. Since
$(Q,d)$
, since Q is metrically complete. Since
![]() $\sigma $
is a limit ordinal, the fact that arbitrary closed subsets of Q are coextensive with elements of N follows from Proposition 7.5.
$\sigma $
is a limit ordinal, the fact that arbitrary closed subsets of Q are coextensive with elements of N follows from Proposition 7.5.
Finally, let
![]() $v = v_\sigma $
as defined in the proof of Lemma 7.3. Since
$v = v_\sigma $
as defined in the proof of Lemma 7.3. Since
![]() $\sigma (\sigma ) = 1$
, we have that v is
$\sigma (\sigma ) = 1$
, we have that v is
![]() $1$
-discrete. The relation
$1$
-discrete. The relation ![]() (i.e.,
(i.e.,
![]() $e(x,y) = 0$
) agrees with
$e(x,y) = 0$
) agrees with ![]() for
for ![]() -elements of v, so we have that
-elements of v, so we have that ![]() is isomorphic to
is isomorphic to
![]() $(V_\sigma ,\in )$
.
$(V_\sigma ,\in )$
.
One thing to note with regards to Theorem 7.15 is that if M satisfies the axiom of choice, then the resulting structure N will satisfy the axiom of choice in all of its uniformly discrete sets. Conversely, if there is a set
![]() $x \in V_\alpha ^M$
witnessing the failure of the axiom of choice, then the axiom of choice will fail for the corresponding
$x \in V_\alpha ^M$
witnessing the failure of the axiom of choice, then the axiom of choice will fail for the corresponding
![]() $1$
-discrete set in N. Since we did not use the axiom of choice at any point in our construction, this establishes that choice for uniformly discrete sets is independent of
$1$
-discrete set in N. Since we did not use the axiom of choice at any point in our construction, this establishes that choice for uniformly discrete sets is independent of
![]() $\mathsf {MSE}$
.
$\mathsf {MSE}$
.
Recall that an
![]() $\mathcal {L}_e$
-structure M is pseudo-finite if for every restricted
$\mathcal {L}_e$
-structure M is pseudo-finite if for every restricted
![]() $\mathcal {L}_e$
-sentence
$\mathcal {L}_e$
-sentence
![]() $\varphi $
and r, if
$\varphi $
and r, if
![]() $M \models \varphi < r$
, then there is a finite
$M \models \varphi < r$
, then there is a finite
![]() $\mathcal {L}_e$
-structure N such that
$\mathcal {L}_e$
-structure N such that
![]() $N \models \varphi < r$
.
$N \models \varphi < r$
.
Theorem 7.16. There is a pseudo-finite model of
![]() $\mathsf {MSE}$
.
$\mathsf {MSE}$
.
Proof. Consider the structure
![]() $M = (V_{\omega +\omega },\omega ,\varnothing ,\dots )$
. For each
$M = (V_{\omega +\omega },\omega ,\varnothing ,\dots )$
. For each
![]() $n \in \mathbb {N}$
, let
$n \in \mathbb {N}$
, let
![]() $s_n$
be the scale on M defined by
$s_n$
be the scale on M defined by
![]() $s_n(i) = \min (\max (1-\frac {i-1}{n},0),1)$
. This is easily seen to be
$s_n(i) = \min (\max (1-\frac {i-1}{n},0),1)$
. This is easily seen to be
![]() $\frac {1}{n}$
-smooth. The quotient of
$\frac {1}{n}$
-smooth. The quotient of
![]() $\mathcal {T}_\omega (\varnothing )$
by the pseudo-metric
$\mathcal {T}_\omega (\varnothing )$
by the pseudo-metric
![]() $\rho _{s_n}$
is finite, so any ultraproduct of the sequence
$\rho _{s_n}$
is finite, so any ultraproduct of the sequence
![]() $(\mathcal {T}_\omega (\varnothing )/\rho _{s_n},e_{s_n})_{n \in \mathbb {N}}$
is a pseudo-finite model of
$(\mathcal {T}_\omega (\varnothing )/\rho _{s_n},e_{s_n})_{n \in \mathbb {N}}$
is a pseudo-finite model of
![]() $\mathsf {MSE}$
by Lemmas 7.10 and 7.12.
$\mathsf {MSE}$
by Lemmas 7.10 and 7.12.
It is straightforward to show that no pseudo-finite model of
![]() $\mathsf {MSE}$
can satisfy
$\mathsf {MSE}$
can satisfy
![]() $\mathsf {Inf}$
, as no pseudo-finite structure can interpret Robinson arithmetic.
$\mathsf {Inf}$
, as no pseudo-finite structure can interpret Robinson arithmetic.
8 Formalizing
 $\mathsf {MSE}$
in Łukasiewicz logic
$\mathsf {MSE}$
in Łukasiewicz logic
It was observed in [Reference Caicedo and Iovino2] that there is a strong connection between continuous logic and Łukasiewicz–Pavelka predicate logic. This logic extends Łukasiewicz logic with
![]() $0$
-ary connectives for each rational
$0$
-ary connectives for each rational
![]() $r \in [0,1]$
. Since every unary connective
$r \in [0,1]$
. Since every unary connective
![]() $f(x)$
in rational Pavelka logic is piecewise linear and has that
$f(x)$
in rational Pavelka logic is piecewise linear and has that
![]() $\frac {\mathrm {d}}{\mathrm {d}x}f(x) \in \mathbb {Z}$
for all but finitely many
$\frac {\mathrm {d}}{\mathrm {d}x}f(x) \in \mathbb {Z}$
for all but finitely many
![]() $x \in [0,1]$
, it is immediate that
$x \in [0,1]$
, it is immediate that
![]() $\frac {x}{2}$
is not a connective that can be formed in it. One might think that this would prevent rational Pavelka logic from being logically complete in the sense of continuous logic, but as pointed out in [Reference Caicedo and Iovino2, Proposition 1.18], the connective
$\frac {x}{2}$
is not a connective that can be formed in it. One might think that this would prevent rational Pavelka logic from being logically complete in the sense of continuous logic, but as pointed out in [Reference Caicedo and Iovino2, Proposition 1.18], the connective
![]() $x \mapsto \frac {1}{2}x$
is a uniform limit of connectives in rational Pavelka logic:
$x \mapsto \frac {1}{2}x$
is a uniform limit of connectives in rational Pavelka logic:

uniformly for all
![]() $x \in [0,1]$
. This implies that all
$x \in [0,1]$
. This implies that all
![]() $[0,1]$
-valued formulas in continuous logic are uniform limits of Łukasiewicz–Pavelka formulas.
$[0,1]$
-valued formulas in continuous logic are uniform limits of Łukasiewicz–Pavelka formulas.
Beyond this, it follows from results in [Reference Hájek, Paris and Shepherdson7] and was shown explicitly in [Reference Caicedo and Iovino1, Theorem 6.3 and Corollary 6.4] via a Lindström’s theorem argument that on the level of conditions rather than formulas, ordinary Łukasiewicz logic is already logically complete relative to continuous logic.Footnote
16
As a consequence of this, any continuous first-order theory or type (in a language with
![]() $[0,1]$
-valued predicates) can be axiomatized entirely in Łukasiewicz logic. We will give an elementary proof of this via a syntactic transformation here.
$[0,1]$
-valued predicates) can be axiomatized entirely in Łukasiewicz logic. We will give an elementary proof of this via a syntactic transformation here.
Definition 8.1. A restricted formula
![]() $\varphi $
is a rational affine literal if it is a rational affine combination of atomic formulas. A quantifier-free formula is in maximal affine normal form or max ANF if it is
$\varphi $
is a rational affine literal if it is a rational affine combination of atomic formulas. A quantifier-free formula is in maximal affine normal form or max ANF if it is
![]() $\max _{n<N}\min _{m<M_n}\varphi _{nm}$
, where each
$\max _{n<N}\min _{m<M_n}\varphi _{nm}$
, where each
![]() $\varphi _{nm}$
is a rational affine literal. A formula
$\varphi _{nm}$
is a rational affine literal. A formula
![]() $\varphi $
is in prenex max ANF if it is a string of quantifiers followed by a max ANF formula.
$\varphi $
is in prenex max ANF if it is a string of quantifiers followed by a max ANF formula.
It is not too hard to show (and is written out explicitly in [Reference Hanson11, Proposition 1.4.12]) that every restricted formula is equivalent to a formula in prenex max ANF.
Proposition 8.2. Fix a continuous language
![]() $\mathcal {L}$
in which all predicates are
$\mathcal {L}$
in which all predicates are
![]() $[0,1]$
-valued. For every restricted
$[0,1]$
-valued. For every restricted
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
![]() $\varphi (\bar {x})$
(in either the sense of [Reference Yaacov, Alexander Berenstein, Henson and Usvyatsov25, Section 3] or the more permissive sense of [Reference Hanson11, Section 1.3]), there is a formula
$\varphi (\bar {x})$
(in either the sense of [Reference Yaacov, Alexander Berenstein, Henson and Usvyatsov25, Section 3] or the more permissive sense of [Reference Hanson11, Section 1.3]), there is a formula
![]() $\psi (\bar {x})$
using only the connectives
$\psi (\bar {x})$
using only the connectives
![]() $1$
and
$1$
and ![]() such that for any metric structure M and tuple
such that for any metric structure M and tuple
![]() $\bar {a} \in M$
,
$\bar {a} \in M$
, ![]() if and only if
if and only if ![]() .
.
Proof. By McNaughton’s theorem [Reference McNaughton16, Theorem 1], for any integers a and
![]() $b_0,\dots ,b_{n-1}$
, the function
$b_0,\dots ,b_{n-1}$
, the function
![]() $M(\bar {x};a,\bar {b}) = \min (\max (a+b_0x_0+b_1x_1+\dots +b_{n-1}x_{n-1},0),1)$
can be expressed using the connectives of Łukasiewicz logic.
$M(\bar {x};a,\bar {b}) = \min (\max (a+b_0x_0+b_1x_1+\dots +b_{n-1}x_{n-1},0),1)$
can be expressed using the connectives of Łukasiewicz logic.
Let ![]() be a restricted closed condition. We may assume without loss of generality that
be a restricted closed condition. We may assume without loss of generality that
![]() $r = 0$
. By the above discussion we can rewrite
$r = 0$
. By the above discussion we can rewrite
![]() $\varphi $
as an equivalent prenex max ANF formula
$\varphi $
as an equivalent prenex max ANF formula

where each
![]() $\operatorname *{\mathrm {qnt}}$
is either
$\operatorname *{\mathrm {qnt}}$
is either
![]() $\inf $
or
$\inf $
or
![]() $\sup $
and each
$\sup $
and each
![]() $\chi _{nmk}$
is an atomic formula. Let
$\chi _{nmk}$
is an atomic formula. Let
![]() $\ell $
some number larger than the denominators of the coefficients in
$\ell $
some number larger than the denominators of the coefficients in
![]() $\psi $
. Consider now the formula
$\psi $
. Consider now the formula
![]() $\psi ^\dagger (\bar {x})$
defined as
$\psi ^\dagger (\bar {x})$
defined as
Note that
![]() $\psi ^\dagger $
is equivalent to
$\psi ^\dagger $
is equivalent to
![]() $\min (\max (\ell !\cdot \psi ,0),1)$
. We clearly have that in any structure M,
$\min (\max (\ell !\cdot \psi ,0),1)$
. We clearly have that in any structure M, ![]() if and only if
if and only if ![]() , but this latter condition can be expressed in Łukasiewicz logic by McNaughton’s theorem. In particular, if we interpret
, but this latter condition can be expressed in Łukasiewicz logic by McNaughton’s theorem. In particular, if we interpret
![]() $M(-;\ell !\cdot a_{nm},\ell !\cdot b_{n,m,0},\dots ,\ell !\cdot b_{n,m,K_{nm}-1})$
as an expression in Łukasiewicz logic, then we have that
$M(-;\ell !\cdot a_{nm},\ell !\cdot b_{n,m,0},\dots ,\ell !\cdot b_{n,m,K_{nm}-1})$
as an expression in Łukasiewicz logic, then we have that
![]() $M \models \psi (\bar {a}) \geq 0$
if and only if M satisfies
$M \models \psi (\bar {a}) \geq 0$
if and only if M satisfies
where
![]() $Qx_i$
is
$Qx_i$
is
![]() $\exists x_i$
if
$\exists x_i$
if
![]() $\operatorname *{\mathrm {qnt}}_{x_i}$
is
$\operatorname *{\mathrm {qnt}}_{x_i}$
is
![]() $\sup _{x_i}$
and
$\sup _{x_i}$
and
![]() $\forall x_i$
if
$\forall x_i$
if
![]() $\operatorname *{\mathrm {qnt}}_{x_i}$
is
$\operatorname *{\mathrm {qnt}}_{x_i}$
is
![]() $\inf _{x_i}$
.
$\inf _{x_i}$
.
There are some minor differences in the treatment of equality (i.e., the metric) in continuous logic and Łukasiewicz logic and, relatedly, the intended semantics of continuous logic is more specific than that of Łukasiewicz logic, but for structures without equality (i.e., general structures such as our
![]() $\mathcal {L}_e$
-structures) there is no difference in expressive power.
$\mathcal {L}_e$
-structures) there is no difference in expressive power.
While the above discussion is sufficient to prove that it exists, we will now give an explicit axiomatization of
![]() $\mathsf {MSE}$
in Łukasiewicz logic. For the sake of compatibility with the existing Łukasiewicz logic literature, we will switch to the convention of regarding
$\mathsf {MSE}$
in Łukasiewicz logic. For the sake of compatibility with the existing Łukasiewicz logic literature, we will switch to the convention of regarding
![]() $1$
as true. As such, we will write
$1$
as true. As such, we will write
![]() $x \mathrel{\hat{\epsilon }} y$
for
$x \mathrel{\hat{\epsilon }} y$
for
![]() $1-e(x,y)$
. We will write
$1-e(x,y)$
. We will write
![]() $A \to B$
for connective
$A \to B$
for connective ![]() and
and
![]() $\bot $
for
$\bot $
for
![]() $0$
. Formulas are formed from
$0$
. Formulas are formed from
![]() $x \mathrel{\hat{\epsilon }} y$
using the connectives
$x \mathrel{\hat{\epsilon }} y$
using the connectives
![]() $\to $
and
$\to $
and
![]() $\bot $
and the quantifiers
$\bot $
and the quantifiers
![]() $\exists $
and
$\exists $
and
![]() $\forall $
. We’ll write
$\forall $
. We’ll write ![]() for this set of formulas, which we will regard as a subset of the set of restricted
for this set of formulas, which we will regard as a subset of the set of restricted
![]() $\mathcal {L}_e$
-formulas (where we interpret
$\mathcal {L}_e$
-formulas (where we interpret
![]() $\exists x$
as
$\exists x$
as
![]() $\sup _x$
and
$\sup _x$
and
![]() $\forall x$
as
$\forall x$
as
![]() $\inf _x$
). For an
$\inf _x$
). For an
![]() $\mathcal {L}_e$
-structure M, a tuple
$\mathcal {L}_e$
-structure M, a tuple
![]() $\bar {a} \in M$
, and a formula
$\bar {a} \in M$
, and a formula ![]() , we say that M satisfies
, we say that M satisfies
![]() $\varphi (\bar {a})$
if
$\varphi (\bar {a})$
if
![]() $M \models \varphi (\bar {a}) = 1$
.
$M \models \varphi (\bar {a}) = 1$
.
It is a basic fact that the connectives
![]() $\to $
and
$\to $
and
![]() $\bot $
can be used to define the following:
$\bot $
can be used to define the following: ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
First we need to define extensional equality: We will write
![]() $x =_e y$
as shorthand for the formula
$x =_e y$
as shorthand for the formula ![]() . (This is the same thing as
. (This is the same thing as
![]() $1-d_e(x,y)$
.) With this we can now write the
$1-d_e(x,y)$
.) With this we can now write the
![]() $\mathrm {H}$
-extensionality axiom as
$\mathrm {H}$
-extensionality axiom as
It is easy to verify that this is a literal transcription of Definition 6.1.
Given any formula ![]() , let
, let
![]() $\#\varphi $
be the number of instances of
$\#\varphi $
be the number of instances of
![]() $\mathrel{\hat{\epsilon }}$
in
$\mathrel{\hat{\epsilon }}$
in
![]() $\varphi $
.Footnote
17
For the axiom scheme of excision, we have
$\varphi $
.Footnote
17
For the axiom scheme of excision, we have
for every formula ![]() that does not contain z as a free variable. As this is not a literal transcription of the axiom scheme of excision given in Definition 6.5, we need to prove that it is equivalent.
that does not contain z as a free variable. As this is not a literal transcription of the axiom scheme of excision given in Definition 6.5, we need to prove that it is equivalent.
Proposition 8.3. An
![]() $\mathcal {L}_e$
-structure M is
$\mathcal {L}_e$
-structure M is
![]() $\mathrm {H}$
-extensional and satisfies
$\mathrm {H}$
-extensional and satisfies
![]() $\mathcal {L}_e$
-excision if and only if it satisfies (1) and (2
$\mathcal {L}_e$
-excision if and only if it satisfies (1) and (2
![]() $_\varphi $
) for all
$_\varphi $
) for all ![]() .
.
Proof. We clearly have that M is
![]() $\mathrm {H}$
-extensional if and only if it satisfies (1). Therefore we may assume without loss of generality that
$\mathrm {H}$
-extensional if and only if it satisfies (1). Therefore we may assume without loss of generality that
![]() $(M,d_e)$
is a complete metric space.
$(M,d_e)$
is a complete metric space.
An easy inductive argument shows that for any ![]() ,
,
![]() $v(\varphi ) = \#\varphi $
. In particular, any such
$v(\varphi ) = \#\varphi $
. In particular, any such
![]() $\varphi $
is
$\varphi $
is
![]() $(2\cdot \#\varphi )$
-Lipschitz relative to
$(2\cdot \#\varphi )$
-Lipschitz relative to
![]() $d_e$
.
$d_e$
.
For the
![]() $\Rightarrow $
direction, by Proposition 6.7,
$\Rightarrow $
direction, by Proposition 6.7, ![]() . Fix a formula
. Fix a formula ![]() and a tuple
and a tuple
![]() $\bar {a} \in M$
. If
$\bar {a} \in M$
. If
![]() $\#\varphi = 0$
, then
$\#\varphi = 0$
, then
![]() $\varphi (x,\bar {a})$
is a constant that does not depend on
$\varphi (x,\bar {a})$
is a constant that does not depend on
![]() $\bar {a}$
, so (2
$\bar {a}$
, so (2
![]() $_\varphi $
) is witnessed either by
$_\varphi $
) is witnessed either by
![]() $\varnothing ^M$
or by
$\varnothing ^M$
or by
![]() $V^M$
. If
$V^M$
. If
![]() $\#\varphi> 0$
, consider the set
$\#\varphi> 0$
, consider the set ![]() . For any
. For any
![]() $c \in M$
, we have that if
$c \in M$
, we have that if
![]() $\varphi ^M(c,\bar {a}) \geq \frac {2}{3}$
, then
$\varphi ^M(c,\bar {a}) \geq \frac {2}{3}$
, then
![]() $(c \mathrel{\hat{\epsilon }} b)^M = 1$
and if
$(c \mathrel{\hat{\epsilon }} b)^M = 1$
and if
![]() $(c \mathrel{\hat{\epsilon }} b)^M = 1$
, then
$(c \mathrel{\hat{\epsilon }} b)^M = 1$
, then
![]() $\varphi ^M(c,\bar {a})> \frac {1}{3}$
. In particular, this implies that if
$\varphi ^M(c,\bar {a})> \frac {1}{3}$
. In particular, this implies that if ![]() , then
, then ![]() (which implies that M satisfies
(which implies that M satisfies
![]() $\neg f \mathrel{\hat{\epsilon }} b \mathbin{\&} \cdots \mathbin{\&} \neg f \mathrel{\hat{\epsilon }} b$
with
$\neg f \mathrel{\hat{\epsilon }} b \mathbin{\&} \cdots \mathbin{\&} \neg f \mathrel{\hat{\epsilon }} b$
with
![]() $6\cdot \#\varphi $
instances of
$6\cdot \#\varphi $
instances of
![]() $\neg f \mathrel{\hat{\epsilon }} b$
). Furthermore M satisfies
$\neg f \mathrel{\hat{\epsilon }} b$
). Furthermore M satisfies
and
Since we can do this for any ![]() and any
and any
![]() $\bar {a} \in M$
, we have that M satisfies (2
$\bar {a} \in M$
, we have that M satisfies (2
![]() $_\varphi $
) for all
$_\varphi $
) for all ![]() .
.
For the ![]() direction, assume that M satisfies (1) and (2
direction, assume that M satisfies (1) and (2
![]() $_\varphi $
) for all
$_\varphi $
) for all ![]() . Fix a restricted
. Fix a restricted
![]() $\mathcal {L}_e$
-formula
$\mathcal {L}_e$
-formula
![]() $\varphi (x,\bar {y})$
. Assume without loss of generality that
$\varphi (x,\bar {y})$
. Assume without loss of generality that
![]() $\varphi (x,\bar {y})$
contains an instance of the predicate e and that
$\varphi (x,\bar {y})$
contains an instance of the predicate e and that
![]() $\varphi (x,\bar {y})$
is in prenex max ANF. Pick a sufficiently large
$\varphi (x,\bar {y})$
is in prenex max ANF. Pick a sufficiently large
![]() $\ell> 1$
and let
$\ell> 1$
and let
![]() $\varphi ^\dagger (x,\bar {y})$
be defined as above. In particular, we may think of
$\varphi ^\dagger (x,\bar {y})$
be defined as above. In particular, we may think of
![]() $\varphi ^\dagger (x,\bar {y})$
as a formula in
$\varphi ^\dagger (x,\bar {y})$
as a formula in ![]() which has the property that for any M and
which has the property that for any M and
![]() $a,\bar {b} \in M$
,
$a,\bar {b} \in M$
,
![]() $(\varphi ^\dagger )^M(a,\bar {b}) = \min (\max (\varphi ^M(a,\bar {b}),0),1)$
.
$(\varphi ^\dagger )^M(a,\bar {b}) = \min (\max (\varphi ^M(a,\bar {b}),0),1)$
.
Fix some
![]() $\bar {a} \in M$
and
$\bar {a} \in M$
and
![]() $\delta> 0$
with
$\delta> 0$
with
![]() $\delta < 1$
and apply (2
$\delta < 1$
and apply (2
![]() $_{\neg \varphi ^\dagger }$
) to
$_{\neg \varphi ^\dagger }$
) to
![]() $\bar {a}$
to get a
$\bar {a}$
to get a
![]() $b \in M$
such that for every
$b \in M$
such that for every
![]() $x \in M$
,
$x \in M$
,
-
• either
 $(x \mathrel{\hat{\epsilon }} b)^M> 1-\delta $
or
$(x \mathrel{\hat{\epsilon }} b)^M> 1-\delta $
or
 $(\neg \neg \varphi ^\dagger )^M(x,\bar {a})> \frac {1-\delta }{3}$
and
$(\neg \neg \varphi ^\dagger )^M(x,\bar {a})> \frac {1-\delta }{3}$
and -
• either
 $(\neg x \mathrel{\hat{\epsilon }} b)^M> \frac {1-\delta }{6\cdot \#\varphi ^\dagger }$
or
$(\neg x \mathrel{\hat{\epsilon }} b)^M> \frac {1-\delta }{6\cdot \#\varphi ^\dagger }$
or
 $(\neg \varphi ^\dagger )^M(x,\bar {a})> \frac {1-\delta }{3}$
.
$(\neg \varphi ^\dagger )^M(x,\bar {a})> \frac {1-\delta }{3}$
.
This means that for every
![]() $x \in M$
,
$x \in M$
,
-
• if
 , then
, then
 $e(x,b) < \delta $
and
$e(x,b) < \delta $
and -
• if
 $e(x,b) = 0$
, then
$e(x,b) = 0$
, then
 $\varphi (x,\bar {a}) < \frac {2+\delta }{3\cdot \ell !}$
.
$\varphi (x,\bar {a}) < \frac {2+\delta }{3\cdot \ell !}$
.
The first of these clearly implies that if ![]() , then
, then
![]() $e(x,z) < \delta $
. Now suppose that for some
$e(x,z) < \delta $
. Now suppose that for some
![]() $c \in M$
,
$c \in M$
, ![]() . We then have that there is an
. We then have that there is an
![]() $f \in M$
with
$f \in M$
with
![]() $(f \mathrel{\hat{\epsilon }} b)^M = 1$
such that
$(f \mathrel{\hat{\epsilon }} b)^M = 1$
such that
![]() $d(c,f)< \varepsilon _\varphi $
. Since
$d(c,f)< \varepsilon _\varphi $
. Since
![]() $(f\mathrel{\hat{\epsilon }} b)^M = 1$
, we have that
$(f\mathrel{\hat{\epsilon }} b)^M = 1$
, we have that
![]() $e(f,b) = 0$
, so
$e(f,b) = 0$
, so
![]() $\varphi (f,\bar {a}) < \frac {2+\delta }{3\cdot \ell !}$
and therefore
$\varphi (f,\bar {a}) < \frac {2+\delta }{3\cdot \ell !}$
and therefore
 $ \varphi (c,\bar {a}) < \varphi (f,\bar {a}) + 2v(\varphi )d(c,f) < \frac {2+\delta }{3\cdot \ell !} + 2v(\varphi )\varepsilon _\varphi < \frac {1}{\ell !} + \frac {2v(\varphi )}{6v(\varphi )} < \frac {1}{2} + \frac {1}{3} < 1 < 1 + \delta .$
Since we can do this for any sufficiently small
$ \varphi (c,\bar {a}) < \varphi (f,\bar {a}) + 2v(\varphi )d(c,f) < \frac {2+\delta }{3\cdot \ell !} + 2v(\varphi )\varepsilon _\varphi < \frac {1}{\ell !} + \frac {2v(\varphi )}{6v(\varphi )} < \frac {1}{2} + \frac {1}{3} < 1 < 1 + \delta .$
Since we can do this for any sufficiently small
![]() $\delta> 0$
, we have that M satisfies the excision axiom for
$\delta> 0$
, we have that M satisfies the excision axiom for
![]() $\varphi (x,\bar {y})$
. So since we can do this for any
$\varphi (x,\bar {y})$
. So since we can do this for any
![]() $\varphi (x,\bar {y}) \in \mathcal {L}_e$
, we have that M satisfies
$\varphi (x,\bar {y}) \in \mathcal {L}_e$
, we have that M satisfies
![]() $\mathcal {L}_e$
-excision.
$\mathcal {L}_e$
-excision.
It is of course also possible to translate our axioms of infinity and other sentences described in this article to Łukasiewicz logic, but doing so is more involved.
8.1 Comparison to 
While we have been primarily conceptualizing
![]() $\mathsf {MSE}$
as a theory that describes closed subsets of a metric space, it is also of course a
$\mathsf {MSE}$
as a theory that describes closed subsets of a metric space, it is also of course a
![]() $[0,1]$
-valued set theory in the same vein as
$[0,1]$
-valued set theory in the same vein as ![]() . As such it makes sense to compare them. In set theory without a primitive equality notion, extensionality is often formalized as
. As such it makes sense to compare them. In set theory without a primitive equality notion, extensionality is often formalized as
where ![]() is Leibniz equality (see [Reference Hájek8] and [Reference Montagna17, Chapter 4.5]). (Ext) is inconsistent with
is Leibniz equality (see [Reference Hájek8] and [Reference Montagna17, Chapter 4.5]). (Ext) is inconsistent with ![]() . It is also easy to see semantically that our
. It is also easy to see semantically that our
![]() $\mathrm {H}$
-extensionality axiom is strictly stronger than it. When rendered in continuous logic, (Ext) says that
$\mathrm {H}$
-extensionality axiom is strictly stronger than it. When rendered in continuous logic, (Ext) says that
![]() $\sup _z|e(x,z)-e(y,z)| = \sup _z|e(z,x)-e(z,y)|$
for any x and y. The
$\sup _z|e(x,z)-e(y,z)| = \sup _z|e(z,x)-e(z,y)|$
for any x and y. The
![]() $\mathrm {H}$
-extensionality axiom is equivalent to (Ext) plus the additional requirement that for any a,
$\mathrm {H}$
-extensionality axiom is equivalent to (Ext) plus the additional requirement that for any a,
![]() $x \mapsto e(x,a)$
is a distance predicate relative to the metric defined by
$x \mapsto e(x,a)$
is a distance predicate relative to the metric defined by ![]() . (Although, as evidenced by the structure of this article, we find the presentation of it in Definition 2.2 preferable.)
. (Although, as evidenced by the structure of this article, we find the presentation of it in Definition 2.2 preferable.)
Uniform continuity is ultimately responsible for the fact that ![]() is inconsistent with (Ext). Comprehension says that for any formula
is inconsistent with (Ext). Comprehension says that for any formula
![]() $\varphi (x)$
, we can find a set a such that
$\varphi (x)$
, we can find a set a such that
![]() $e(x,a) = \varphi (x)$
for any x. Coincidence implies that
$e(x,a) = \varphi (x)$
for any x. Coincidence implies that
![]() $x\mapsto e(x,a)$
is always a
$x\mapsto e(x,a)$
is always a
![]() $1$
-Lipschitz function with regards to the metric, but
$1$
-Lipschitz function with regards to the metric, but
![]() $\varphi (x)$
easily fails to be
$\varphi (x)$
easily fails to be
![]() $1$
-Lipschitz. The results of this article, and in particular Proposition 3.7, have demonstrated that when restricted to a certain natural class of
$1$
-Lipschitz. The results of this article, and in particular Proposition 3.7, have demonstrated that when restricted to a certain natural class of
![]() $1$
-Lipschitz formulas (namely distance predicates of definable classes), comprehension is consistent with (Ext) (in that it is consistent with the strong
$1$
-Lipschitz formulas (namely distance predicates of definable classes), comprehension is consistent with (Ext) (in that it is consistent with the strong
![]() $\mathrm {H}$
-extensionality axiom). This prompted an anonymous referee to suggest the following question.
$\mathrm {H}$
-extensionality axiom). This prompted an anonymous referee to suggest the following question.
Question 8.4. For which classes of
![]() $1$
-Lipschitz formulas is (Ext) consistent with the full comprehension scheme
$1$
-Lipschitz formulas is (Ext) consistent with the full comprehension scheme ![]() (i.e.,
(i.e.,
![]() $\inf _y \sup _x |e(x,y) - \varphi (x)|$
)?
$\inf _y \sup _x |e(x,y) - \varphi (x)|$
)?
To the best of our knowledge, there are no limitative results in this area. It’s possible that (Ext) is consistent with comprehension for arbitrary
![]() $1$
-Lipschitz formulas. That said, it seems unlikely that the techniques of this article could easily be adapted to prove this, as they’re fairly specialized to the case of
$1$
-Lipschitz formulas. That said, it seems unlikely that the techniques of this article could easily be adapted to prove this, as they’re fairly specialized to the case of
![]() $x \mapsto e(x,a)$
being a distance predicate.
$x \mapsto e(x,a)$
being a distance predicate.
Appendix A A single axiom for distance predicates in continuous logic.
Here we will give a single condition axiomatizing distance predicates of possibly non-empty sets in continuous logic. It is a slight modification of the condition
![]() $E_2$
in [Reference Yaacov, Alexander Berenstein, Henson and Usvyatsov25, Chapter 9] that obviates the need for
$E_2$
in [Reference Yaacov, Alexander Berenstein, Henson and Usvyatsov25, Chapter 9] that obviates the need for
![]() $E_1$
and covers the case of empty definable sets (where the distance predicate of
$E_1$
and covers the case of empty definable sets (where the distance predicate of
![]() $\varnothing $
in a
$\varnothing $
in a
![]() $[0,1]$
-valued metric is the constant function
$[0,1]$
-valued metric is the constant function
![]() $1$
).
$1$
).
It is possible to prove the following proposition using [Reference Yaacov, Alexander Berenstein, Henson and Usvyatsov25, Theorem 9.12], but doing so seems to roughly as hard as proving the equivalence directly, so we will do this for the sake of making this article more self-contained.
Proposition A.1. In any metric structure M with a
![]() $[0,1]$
-valued metric, a formula
$[0,1]$
-valued metric, a formula
![]() $\varphi (x)$
is the distance predicate of a (possibly empty) definable set if and only if
$\varphi (x)$
is the distance predicate of a (possibly empty) definable set if and only if
Proof. First suppose that
![]() $\varphi (x)$
is the distance predicate of a definable set D in the structure M. If D is empty, then
$\varphi (x)$
is the distance predicate of a definable set D in the structure M. If D is empty, then
![]() $\varphi (x) = r$
for all x and so
$\varphi (x) = r$
for all x and so
![]() $\min (d(x,y) + 2\varphi (y),1) = r$
for any x and y, implying that
$\min (d(x,y) + 2\varphi (y),1) = r$
for any x and y, implying that
![]() $|\varphi (x) - \inf _y \min (d(x,y) + 2\varphi (y),1)| = 0$
for every x.
$|\varphi (x) - \inf _y \min (d(x,y) + 2\varphi (y),1)| = 0$
for every x.
If D is not empty, fix
![]() $x \in M$
. Let
$x \in M$
. Let
![]() $t = \inf _y \min (d(x,y) + 2\varphi (y),1)$
. We need to show that
$t = \inf _y \min (d(x,y) + 2\varphi (y),1)$
. We need to show that
![]() $t = \varphi (x)$
. Fix an
$t = \varphi (x)$
. Fix an
![]() $\varepsilon> 0$
and
$\varepsilon> 0$
and
![]() $z \in D$
such that
$z \in D$
such that
![]() $d(x,z) < \varphi (x) + \varepsilon = \inf _{w \in D} d(x,w) + \varepsilon $
. Clearly
$d(x,z) < \varphi (x) + \varepsilon = \inf _{w \in D} d(x,w) + \varepsilon $
. Clearly
Since this is true for any
![]() $\varepsilon> 0$
, we have that
$\varepsilon> 0$
, we have that ![]() .
.
On the other hand, fix some
![]() $y \in M$
and consider the quantity
$y \in M$
and consider the quantity
![]() $\min (d(x,y) + 2\varphi (y),1)$
. Find a
$\min (d(x,y) + 2\varphi (y),1)$
. Find a
![]() $w \in D$
such that
$w \in D$
such that
![]() $d(y,w) < \varphi (y) + \varepsilon $
. We now have that
$d(y,w) < \varphi (y) + \varepsilon $
. We now have that
Since this is true for any
![]() $\varepsilon> 0$
, we have that
$\varepsilon> 0$
, we have that ![]() for any
for any
![]() $y \in M$
. Therefore
$y \in M$
. Therefore ![]() , whereby
, whereby
![]() $t = \varphi (x)$
.
$t = \varphi (x)$
.
Now suppose that M satisfies the condition in the statement of the proposition. If
![]() $\varphi (x) = 1$
for all x, then
$\varphi (x) = 1$
for all x, then
![]() $\varphi (x)$
is the distance predicate of the empty set. So assume that there is an
$\varphi (x)$
is the distance predicate of the empty set. So assume that there is an
![]() $a \in M$
such that
$a \in M$
such that
![]() $\varphi (a) < 1$
.
$\varphi (a) < 1$
.
Note that for any x, we have that
Therefore it cannot be the case that
![]() $\varphi (x) < 0$
, whereby we must have that
$\varphi (x) < 0$
, whereby we must have that
![]() $\varphi (x) \geq 0$
for all x.
$\varphi (x) \geq 0$
for all x.
Let D be the zero set of
![]() $\varphi (x)$
. For any
$\varphi (x)$
. For any
![]() $x\in M$
and
$x\in M$
and
![]() $y \in D$
, we have that
$y \in D$
, we have that ![]() . Therefore
. Therefore
![]() $\varphi (x)$
is upper bounded by the distance to the set D. We now just need to show that for any
$\varphi (x)$
is upper bounded by the distance to the set D. We now just need to show that for any
![]() $x \in M$
with
$x \in M$
with
![]() $\varphi (x) < 1$
and any
$\varphi (x) < 1$
and any
![]() $\varepsilon> 0$
, there is a
$\varepsilon> 0$
, there is a
![]() $y \in D$
such that
$y \in D$
such that
![]() $d(x,y) < \varphi (x) + \varepsilon $
.
$d(x,y) < \varphi (x) + \varepsilon $
.
Fix some
![]() $x \in M$
with
$x \in M$
with
![]() $\varphi (x) < 1$
and some
$\varphi (x) < 1$
and some
![]() $\varepsilon> 0$
. Find
$\varepsilon> 0$
. Find
![]() $\delta> 0$
such that
$\delta> 0$
such that
![]() ${\varphi (x) + \delta < 1}$
and
${\varphi (x) + \delta < 1}$
and
![]() $\delta < \varepsilon $
. Find
$\delta < \varepsilon $
. Find
![]() $y_0$
such that
$y_0$
such that ![]() . Since
. Since
![]() $\varphi (x) + \delta < 1$
, we actually have that
$\varphi (x) + \delta < 1$
, we actually have that
We will construct a sequence
![]() $(y_n)_{n \in \mathbb {N}}$
inductively. Our induction hypothesis will be that
$(y_n)_{n \in \mathbb {N}}$
inductively. Our induction hypothesis will be that
This holds in the
![]() $n = 0$
case.
$n = 0$
case.
Given
![]() $y_n$
satisfying the induction hypothesis, find a
$y_n$
satisfying the induction hypothesis, find a
![]() $\gamma> 0$
small enough that
$\gamma> 0$
small enough that
![]() $\gamma < 2^{-n}$
and
$\gamma < 2^{-n}$
and
![]() $\varphi (y_n) + \gamma < 1$
and
$\varphi (y_n) + \gamma < 1$
and
Find a
![]() $y_{n+1}$
such that
$y_{n+1}$
such that ![]() . Since
. Since
![]() $\varphi (y_n) + \gamma < 1$
, we actually have that
$\varphi (y_n) + \gamma < 1$
, we actually have that
Clearly we get
 $$ \begin{align*} &d(x,y_0) + \sum_{i < n+1}( d(y_i,y_{i+1}) + \varphi(y_i)) + 2\varphi(y_{n+1}) \\ ={}&d(x,y_0) + \sum_{i < n}( d(y_i,y_{i+1}) + \varphi(y_i)) + \varphi(y_n) + d(y_n,y_{n+1}) + 2\varphi(y_{n+1}) \\ <{}&d(x,y_0) + \sum_{i < n}( d(y_i,y_{i+1}) + \varphi(y_i)) + \varphi(y_n) + \varphi(y_n) + \gamma \\ <{}&\varphi(x) + \delta, \end{align*} $$
$$ \begin{align*} &d(x,y_0) + \sum_{i < n+1}( d(y_i,y_{i+1}) + \varphi(y_i)) + 2\varphi(y_{n+1}) \\ ={}&d(x,y_0) + \sum_{i < n}( d(y_i,y_{i+1}) + \varphi(y_i)) + \varphi(y_n) + d(y_n,y_{n+1}) + 2\varphi(y_{n+1}) \\ <{}&d(x,y_0) + \sum_{i < n}( d(y_i,y_{i+1}) + \varphi(y_i)) + \varphi(y_n) + \varphi(y_n) + \gamma \\ <{}&\varphi(x) + \delta, \end{align*} $$
and so the induction hypothesis holds for
![]() $n+1$
. Note also that
$n+1$
. Note also that ![]() .
.
Since ![]() and since
and since
![]() $\varphi (y_{n+1}) < \frac {1}{2}\varphi (y_n)$
for each n,
$\varphi (y_{n+1}) < \frac {1}{2}\varphi (y_n)$
for each n,
![]() $(y_n)_{n \in \mathbb {N}}$
is a Cauchy sequence. Let y be its limit. Since
$(y_n)_{n \in \mathbb {N}}$
is a Cauchy sequence. Let y be its limit. Since ![]() , we must have that
, we must have that
![]() $\varphi (y) = 0$
or in other words that
$\varphi (y) = 0$
or in other words that
![]() $y \in D$
. By construction, we have that
$y \in D$
. By construction, we have that
Since we can do this for any
![]() $\varepsilon> 0$
, we are done.
$\varepsilon> 0$
, we are done.
For
![]() $[0,r]$
-valued metrics more generally, it is immediate that
$[0,r]$
-valued metrics more generally, it is immediate that
![]() $\sup _{x}|\varphi (x) - \inf _y \min (d(x,y) + 2\varphi (y),r)| = 0$
is equivalent to
$\sup _{x}|\varphi (x) - \inf _y \min (d(x,y) + 2\varphi (y),r)| = 0$
is equivalent to
![]() $\varphi (x)$
being a distance predicate (where in this case the distance predicate of
$\varphi (x)$
being a distance predicate (where in this case the distance predicate of
![]() $\varnothing $
is the constant function r).
$\varnothing $
is the constant function r).
Appendix B A model of
 $\mathsf {MSE}$
in which the intersection of two sets is not a set.
$\mathsf {MSE}$
in which the intersection of two sets is not a set.
Here we will give an example of a model
![]() $\mathsf {MSE}$
in which the intersection of two sets is not always a set. This construction is an easy example in continuous logic of two definable sets with undefinable intersection.
$\mathsf {MSE}$
in which the intersection of two sets is not always a set. This construction is an easy example in continuous logic of two definable sets with undefinable intersection.
Proposition B.1. There is a model
![]() $M \models \mathsf {MSE}$
with
$M \models \mathsf {MSE}$
with
![]() $A,B \in M$
such that no element of M is coextensive with the intersection of A and B.
$A,B \in M$
such that no element of M is coextensive with the intersection of A and B.
Proof. Let
![]() $(Q,d)$
be a metric space consisting of an infinite sequence
$(Q,d)$
be a metric space consisting of an infinite sequence
![]() $(a_n,b_n)_{n \in \mathbb {N}}$
of pairs with
$(a_n,b_n)_{n \in \mathbb {N}}$
of pairs with
![]() $d(a_n,b_n) = 2^{-n}$
and
$d(a_n,b_n) = 2^{-n}$
and
![]() $d(a_n,b_m) = 1$
for
$d(a_n,b_m) = 1$
for
![]() $n \neq m$
. Let
$n \neq m$
. Let
![]() $A = \{a_n : n \in \mathbb {N}\}$
and
$A = \{a_n : n \in \mathbb {N}\}$
and
![]() $B = \{b_n : n \in \mathbb {N}\}$
. By Theorem 7.15, we can build a model
$B = \{b_n : n \in \mathbb {N}\}$
. By Theorem 7.15, we can build a model
![]() $N \models \mathsf {MSE}$
containing Q as a set of Quine atoms and containing A and B as sets. Let M be an
$N \models \mathsf {MSE}$
containing Q as a set of Quine atoms and containing A and B as sets. Let M be an
![]() $\aleph _0$
-saturated (in the sense of
$\aleph _0$
-saturated (in the sense of
![]() $\mathcal {L}_e$
-structures) elementary extension of N.
$\mathcal {L}_e$
-structures) elementary extension of N.
First we need to show that the intersection of ![]() and
and ![]() is non-empty in M. The partial type
is non-empty in M. The partial type
![]() $\Sigma (x,y)$
generated by the conditions
$\Sigma (x,y)$
generated by the conditions ![]() ,
, ![]() , and
, and ![]() for each
for each
![]() $n \in \mathbb {N}$
is finitely satisfiable in N and is therefore realized in M. Therefore, by
$n \in \mathbb {N}$
is finitely satisfiable in N and is therefore realized in M. Therefore, by
![]() $\aleph _0$
-saturation, there exists an
$\aleph _0$
-saturation, there exists an
![]() $f \in M$
such that
$f \in M$
such that ![]() and
and ![]() . Now let
. Now let
![]() $C \in M$
be an element satisfying that for any
$C \in M$
be an element satisfying that for any
![]() $f \in M$
, if
$f \in M$
, if ![]() , then
, then ![]() and
and ![]() . Clearly it must be the case that for any
. Clearly it must be the case that for any
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $M \models e(a_n,C) = 1$
and
$M \models e(a_n,C) = 1$
and
![]() $M \models e(b_n,C) = 1$
. Therefore the partial type
$M \models e(b_n,C) = 1$
. Therefore the partial type
![]() $\Pi (x,y)$
generated by the condition
$\Pi (x,y)$
generated by the condition ![]() ,
, ![]() ,
,
![]() $e(x,C) = 1$
,
$e(x,C) = 1$
,
![]() $e(y,C) = 1$
, and
$e(y,C) = 1$
, and ![]() for each
for each
![]() $n \in \mathbb {N}$
is finitely satisfiable in M. By
$n \in \mathbb {N}$
is finitely satisfiable in M. By
![]() $\aleph _0$
-saturation, it is realized in M, whereby there is a
$\aleph _0$
-saturation, it is realized in M, whereby there is a
![]() $g \in M$
such that
$g \in M$
such that ![]() and
and ![]() but
but ![]() .
.
Since we can do this for any such C in M, the class ![]() is not a set in M.
is not a set in M.
What’s unclear at the moment is whether this is possible in an
![]() $\omega $
-model.
$\omega $
-model.
Question B.2. Is there an
![]() $\omega $
-model of
$\omega $
-model of
![]() $\kern2pt\mathsf {MSE}$
containing two sets with no intersection?
$\kern2pt\mathsf {MSE}$
containing two sets with no intersection?





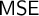
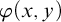
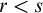
 and contained in the class
and contained in the class