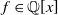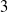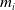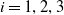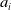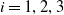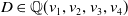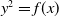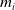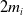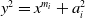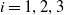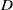1. Introduction
Given an abelian variety
![]() $A$
defined over a number field
$A$
defined over a number field
![]() $K$
, the Mordell–Weil theorem asserts that the abelian group of rational points
$K$
, the Mordell–Weil theorem asserts that the abelian group of rational points
![]() $A(K)$
is finitely generated. This implies that
$A(K)$
is finitely generated. This implies that
![]() $A(K)$
is isomorphic to
$A(K)$
is isomorphic to
![]() $\mathbb{T}\times \mathbb{Z}^r$
, where
$\mathbb{T}\times \mathbb{Z}^r$
, where
![]() $\mathbb T$
is the torsion subgroup of
$\mathbb T$
is the torsion subgroup of
![]() $A(K)$
and
$A(K)$
and
![]() $r$
is a non-negative integer, called the Mordell–Weil rank of
$r$
is a non-negative integer, called the Mordell–Weil rank of
![]() $A(K)$
. In this article, we are interested in the following question. Fix an integer
$A(K)$
. In this article, we are interested in the following question. Fix an integer
![]() $n\ge 2$
. Given (hyper)elliptic curves
$n\ge 2$
. Given (hyper)elliptic curves
![]() $C_i$
defined over
$C_i$
defined over
![]() $\mathbb{Q}$
of genus
$\mathbb{Q}$
of genus
![]() $g_i$
, and tuples of positive integers
$g_i$
, and tuples of positive integers
![]() $r_i$
,
$r_i$
,
![]() $i=1,\ldots ,n$
, is there a twist of
$i=1,\ldots ,n$
, is there a twist of
![]() $C_i$
such that the Mordell–Weil rank of the Jacobian of this twist is at least
$C_i$
such that the Mordell–Weil rank of the Jacobian of this twist is at least
![]() $r_i$
,
$r_i$
,
![]() $i=1,\ldots ,n?$
$i=1,\ldots ,n?$
The problem was initially discussed in [Reference Kuwata and Wang4] where it was proved that for a pair of elliptic curves
![]() $E_1$
and
$E_1$
and
![]() $E_2$
over
$E_2$
over
![]() $\mathbb{Q}$
whose
$\mathbb{Q}$
whose
![]() $j$
-invariants are not simultaneously
$j$
-invariants are not simultaneously
![]() $0$
or
$0$
or
![]() $1728$
, there exist infinitely many square-free rational numbers
$1728$
, there exist infinitely many square-free rational numbers
![]() $d$
such that the quadratic twists of
$d$
such that the quadratic twists of
![]() $E_1$
and
$E_1$
and
![]() $E_2$
by
$E_2$
by
![]() $d$
are both of positive Mordell–Weil rank. In [Reference Alaa and Sadek1], it was proved that there exist families of pairs of elliptic curves
$d$
are both of positive Mordell–Weil rank. In [Reference Alaa and Sadek1], it was proved that there exist families of pairs of elliptic curves
![]() $E_1$
and
$E_1$
and
![]() $E_2$
and infinitely many square-free rationals
$E_2$
and infinitely many square-free rationals
![]() $d$
such that the quadratic twists of
$d$
such that the quadratic twists of
![]() $E_1$
and
$E_1$
and
![]() $E_2$
by
$E_2$
by
![]() $d$
are both of Mordell–Weil rank at least
$d$
are both of Mordell–Weil rank at least
![]() $2$
. The positivity of the Mordell–Weil rank of families of twists of triples and quadruples of elliptic curves with
$2$
. The positivity of the Mordell–Weil rank of families of twists of triples and quadruples of elliptic curves with
![]() $j$
-invariants
$j$
-invariants
![]() $0$
or
$0$
or
![]() $1728$
was established in [Reference Ulas8, Reference Ulas9]. This motivates the investigation of the positivity of Mordell–Weil rank of families of twists of higher-dimensional abelian varieties.
$1728$
was established in [Reference Ulas8, Reference Ulas9]. This motivates the investigation of the positivity of Mordell–Weil rank of families of twists of higher-dimensional abelian varieties.
Given non-zero rational numbers
![]() $a, b, c$
, it was proved that there exists a polynomial
$a, b, c$
, it was proved that there exists a polynomial
![]() $d(t) \in \mathbb{Q}[t]$
such that the Jacobians of the curves given by
$d(t) \in \mathbb{Q}[t]$
such that the Jacobians of the curves given by
![]() $y^2 = x^n + ad(t)$
,
$y^2 = x^n + ad(t)$
,
![]() $y^2 = x^n + bd(t)$
,
$y^2 = x^n + bd(t)$
,
![]() $y^2=x^n+cd(t)$
, and
$y^2=x^n+cd(t)$
, and
![]() $n\ge 3$
, both have positive Mordell–Weil rank over
$n\ge 3$
, both have positive Mordell–Weil rank over
![]() $\mathbb{Q}(t)$
, see [Reference Jȩdrzejak, Top and Ulas5]. The latter result was extended to four such hyperelliptic curves when
$\mathbb{Q}(t)$
, see [Reference Jȩdrzejak, Top and Ulas5]. The latter result was extended to four such hyperelliptic curves when
![]() $n$
is odd. If
$n$
is odd. If
![]() $f \in \mathbb{Q}[x]$
is a square-free polynomial of degree at least
$f \in \mathbb{Q}[x]$
is a square-free polynomial of degree at least
![]() $3$
, it was proved in [Reference Jȩdrzejak and Ulas6] that there exists a function
$3$
, it was proved in [Reference Jȩdrzejak and Ulas6] that there exists a function
![]() $D \in \mathbb{Q}(u, v, w)$
such that the Jacobians of the curves
$D \in \mathbb{Q}(u, v, w)$
such that the Jacobians of the curves
![]() $Dy^2 = f(x)$
,
$Dy^2 = f(x)$
,
![]() $y^2 = Dx^m + b$
, and
$y^2 = Dx^m + b$
, and
![]() $C$
all have positive Mordell–Weil ranks over
$C$
all have positive Mordell–Weil ranks over
![]() $\mathbb{Q}(u, v, w)$
where
$\mathbb{Q}(u, v, w)$
where
![]() $C$
is either
$C$
is either
![]() $y^2=Dx^m+c$
or
$y^2=Dx^m+c$
or
![]() $y^2=x^m+cD$
, and
$y^2=x^m+cD$
, and
![]() $m\ge 3$
is odd. The question was investigated for other families of quadruples of hyperelliptic curves in [Reference Buğday and Sadek3].
$m\ge 3$
is odd. The question was investigated for other families of quadruples of hyperelliptic curves in [Reference Buğday and Sadek3].
In this work, we extend the latter results to include several families of quadruples of twisted hyperelliptic curves. Namely, we consider the following sets of hyperelliptic curves:
or
or
where
![]() $f(x)\in \mathbb{Q}[x]$
is a square-free polynomial of degree at least
$f(x)\in \mathbb{Q}[x]$
is a square-free polynomial of degree at least
![]() $3$
, and
$3$
, and
![]() $m_i\ge 3$
is an odd integer,
$m_i\ge 3$
is an odd integer,
![]() $i=1,2,3,4$
. We prove that if
$i=1,2,3,4$
. We prove that if
![]() $a$
,
$a$
,
![]() $b$
, and
$b$
, and
![]() $c$
are non-zero rational squares, then
$c$
are non-zero rational squares, then
![]() $D$
can be chosen to be a rational function in
$D$
can be chosen to be a rational function in
![]() $\mathbb{Q}(u,v_1,v_2,v_3)$
such that the Mordell–Weil ranks of all four hyperelliptic curves over
$\mathbb{Q}(u,v_1,v_2,v_3)$
such that the Mordell–Weil ranks of all four hyperelliptic curves over
![]() $\mathbb{Q}(u,v_1,v_2,v_3)$
are positive. The proof depends on associating a system of Diophantine equations to these quadruples of hyperelliptic curves. Finding such a rational
$\mathbb{Q}(u,v_1,v_2,v_3)$
are positive. The proof depends on associating a system of Diophantine equations to these quadruples of hyperelliptic curves. Finding such a rational
![]() $D$
corresponds to finding a rational solution to this system of equations.
$D$
corresponds to finding a rational solution to this system of equations.
As a byproduct, fixing an odd integer
![]() $m\ge 3$
, we show that there exists a rational
$m\ge 3$
, we show that there exists a rational
![]() $D\in \mathbb{Q}(u,v_1,v_2,v_3)$
such that the Mordell–Weil rank of the Jacobian of
$D\in \mathbb{Q}(u,v_1,v_2,v_3)$
such that the Mordell–Weil rank of the Jacobian of
![]() $Dy^2=f(x)$
is positive and the Mordell–Weil rank of the Jacobian of
$Dy^2=f(x)$
is positive and the Mordell–Weil rank of the Jacobian of
![]() $C$
is at least
$C$
is at least
![]() $3$
, where
$3$
, where
![]() $C$
is either
$C$
is either
![]() $y^2=Dx^m+a^2$
if
$y^2=Dx^m+a^2$
if
![]() $\deg f$
is at least
$\deg f$
is at least
![]() $3$
or
$3$
or
![]() $y^2=x^m+a^2D$
if
$y^2=x^m+a^2D$
if
![]() $f(x)$
is of degree
$f(x)$
is of degree
![]() $3$
or
$3$
or
![]() $4$
.
$4$
.
2. A quadratic twist and three higher-degree twists
Let
![]() $f(x)\in \mathbb{Q}[x]$
be a square-free polynomial of degree at least
$f(x)\in \mathbb{Q}[x]$
be a square-free polynomial of degree at least
![]() $3$
. Fix odd integers
$3$
. Fix odd integers
![]() $m_1,m_2,m_3\ge 3$
. We are investigating the existence of non-square rational numbers
$m_1,m_2,m_3\ge 3$
. We are investigating the existence of non-square rational numbers
![]() $D$
such that the Jacobians of the (hyperelliptic) curves
$D$
such that the Jacobians of the (hyperelliptic) curves
are of positive Mordell–Weil rank over
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
We set
![]() $M=\textrm {lcm}(m_1,m_2,m_3)$
and
$M=\textrm {lcm}(m_1,m_2,m_3)$
and
![]() $M_{i}=M/m_i$
,
$M_{i}=M/m_i$
,
![]() $i=1,2,3$
. The rational number
$i=1,2,3$
. The rational number
![]() $D$
can be found by solving the following system of equations:
$D$
can be found by solving the following system of equations:
More precisely, we are looking for solutions
![]() $x_i,y_i$
,
$x_i,y_i$
,
![]() $i=1,2,3,4$
, for the system (2.1) where
$i=1,2,3,4$
, for the system (2.1) where
In what follows, we suggest how one can obtain a family of parametric solutions to (2.1). We set
where
![]() $u,v_1,v_2,v_3$
are rational parameters. We observe that
$u,v_1,v_2,v_3$
are rational parameters. We observe that
 \begin{eqnarray*} T&=&\frac {f(u)}{v_3^{2m_3}(r^2-c)},\\ v_1^{2m_1}T^M(p^2-a)&=&v_2^{2m_2}T^M(q^2-b)=v_3^{2m_3}T^M(r^2-c). \end{eqnarray*}
\begin{eqnarray*} T&=&\frac {f(u)}{v_3^{2m_3}(r^2-c)},\\ v_1^{2m_1}T^M(p^2-a)&=&v_2^{2m_2}T^M(q^2-b)=v_3^{2m_3}T^M(r^2-c). \end{eqnarray*}
In other words, the system (2.1) can be simplified to
Geometrically, the second equation defines an intersection
![]() $\mathcal{C}_{a,b,c}$
of two quadratic surfaces in
$\mathcal{C}_{a,b,c}$
of two quadratic surfaces in
![]() $\mathbb{P}^3$
over
$\mathbb{P}^3$
over
![]() $\mathbb{Q}(v_1,v_2,v_3)$
. Since
$\mathbb{Q}(v_1,v_2,v_3)$
. Since
![]() $[p\,:\,q\,:\,r\,:\,s]=[\pm v_2^{m_2}v_3^{m_3}\,:\,\pm v_1^{m_1}v_3^{m_3}\,:\,\pm v_1^{m_1}v_2^{m_2}\,:\,0]$
are rational points on
$[p\,:\,q\,:\,r\,:\,s]=[\pm v_2^{m_2}v_3^{m_3}\,:\,\pm v_1^{m_1}v_3^{m_3}\,:\,\pm v_1^{m_1}v_2^{m_2}\,:\,0]$
are rational points on
![]() $\mathcal{C}_{a,b,c}$
, it follows that
$\mathcal{C}_{a,b,c}$
, it follows that
![]() $\mathcal{C}_{a,b,c}$
is an elliptic curve over
$\mathcal{C}_{a,b,c}$
is an elliptic curve over
![]() $\mathbb{Q}(v_1,v_2,v_3)$
. One may check that the latter four projective rational points form a subgroup isomorphic to
$\mathbb{Q}(v_1,v_2,v_3)$
. One may check that the latter four projective rational points form a subgroup isomorphic to
![]() $\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$
.
$\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$
.
We now assume, further, that
![]() $a$
,
$a$
,
![]() $b$
, and
$b$
, and
![]() $c$
are non-zero rational squares. After a transformation, the curve
$c$
are non-zero rational squares. After a transformation, the curve
![]() $\mathcal C_{a,b,c}$
is defined by
$\mathcal C_{a,b,c}$
is defined by
where
![]() $T_1=av_1^{m_1}$
,
$T_1=av_1^{m_1}$
,
![]() $T_2=bv_2^{m_2}$
, and
$T_2=bv_2^{m_2}$
, and
![]() $T_3=cv_3^{m_3}$
.
$T_3=cv_3^{m_3}$
.
Proposition 2.1.
Let
![]() $C_{T_1,T_2,T_3}$
be the elliptic curve defined by
$C_{T_1,T_2,T_3}$
be the elliptic curve defined by
over
![]() $\mathbb{Q}(T_1,T_2,T_3)$
. The curve
$\mathbb{Q}(T_1,T_2,T_3)$
. The curve
![]() $C_{T_1,T_2,T_3}$
has positive Mordell–Weil rank over
$C_{T_1,T_2,T_3}$
has positive Mordell–Weil rank over
![]() $\mathbb{Q}(T_1,T_2,T_3)$
. In particular, except for a thin set of triples
$\mathbb{Q}(T_1,T_2,T_3)$
. In particular, except for a thin set of triples
![]() $(t_1,t_2,t_3)\in \mathbb{Q}\times \mathbb{Q}\times \mathbb{Q}$
, the curve
$(t_1,t_2,t_3)\in \mathbb{Q}\times \mathbb{Q}\times \mathbb{Q}$
, the curve
![]() $C_{t_1,t_2,t_3}$
has positive Mordell–Weil rank over
$C_{t_1,t_2,t_3}$
has positive Mordell–Weil rank over
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
Proof.
The point
![]() $[T_1\,:\,T_2\,:\,T_3\,:\,1]\in C_{T_1,T_2,T_3}(\mathbb{Q}(T_1,T_2,T_3))$
. In addition, it specializes to a point of infinite order on
$[T_1\,:\,T_2\,:\,T_3\,:\,1]\in C_{T_1,T_2,T_3}(\mathbb{Q}(T_1,T_2,T_3))$
. In addition, it specializes to a point of infinite order on
![]() $C_{1,2,3}$
when
$C_{1,2,3}$
when
![]() $[1\,:\,1\,:\,1\,:\,0]$
is regarded as the identity element, Magma [Reference Bosma, Cannon and Playoust2]. For the convenience of the reader, we include the code as it will be used later.
$[1\,:\,1\,:\,1\,:\,0]$
is regarded as the identity element, Magma [Reference Bosma, Cannon and Playoust2]. For the convenience of the reader, we include the code as it will be used later.

Now the statement follows from Silverman’s specialization theorem [Reference Silverman7, Section 20, Theorem 20.1].
One remarks that when the point
![]() $[w_1\,:\,w_2\,:\,w_3\,:\,1]$
is a point of infinite order in
$[w_1\,:\,w_2\,:\,w_3\,:\,1]$
is a point of infinite order in
![]() $\mathcal C_{a,b,c}$
, then any of its multiples can be used to generate a solution to the system (2.1).
$\mathcal C_{a,b,c}$
, then any of its multiples can be used to generate a solution to the system (2.1).
Doubling the point
![]() $P\ {:}{=}\ [a\,:\,b\,:\,c\,:\,1]\in \mathcal{C}_{a^2,b^2,c^2}(\mathbb{Q}(v_1,v_2,v_3))$
yields that
$P\ {:}{=}\ [a\,:\,b\,:\,c\,:\,1]\in \mathcal{C}_{a^2,b^2,c^2}(\mathbb{Q}(v_1,v_2,v_3))$
yields that
![]() $2P=[w_1\,:\,w_2\,:\,w_3\,:\,1]$
is given by
$2P=[w_1\,:\,w_2\,:\,w_3\,:\,1]$
is given by
 \begin{eqnarray*} \bigg [ \frac {a^2 b^2 v_1^{2m_1} v_2^{2m_2} + a^2 c^2 v_1^{2m_1} v_3^{2m_3} - b^2 c^2 v_2^{2m_2} v_3^{2m_3}}{2a b c v_1^{2m_1} v_2^{m_2} v_3^{m_3}}&:&\frac {a^2 b^2 v_1^{2m_1} v_2^{2m_2} - a^2 c^2 v_1^{2m_1} v_3^{2m_3} + b^2 c^2 v_2^{2m_2} v_3^{2m_3}}{2a b c v_1^{m_1} v_2^{2m_2} v_3^{m_3}}\\ &:& \frac {-a^2 b^2 v_1^{2m_1} v_2^{2m_2} + a^2 c^2 v_1^{2m_1} v_3^{2m_3} + b^2 c^2 v_2^{2m_2} v_3^{2m_3}}{2 a b c v_1^{m_1} v_2^{m_2} v_3^{2m_3}}\,:\,1 \bigg ]. \end{eqnarray*}
\begin{eqnarray*} \bigg [ \frac {a^2 b^2 v_1^{2m_1} v_2^{2m_2} + a^2 c^2 v_1^{2m_1} v_3^{2m_3} - b^2 c^2 v_2^{2m_2} v_3^{2m_3}}{2a b c v_1^{2m_1} v_2^{m_2} v_3^{m_3}}&:&\frac {a^2 b^2 v_1^{2m_1} v_2^{2m_2} - a^2 c^2 v_1^{2m_1} v_3^{2m_3} + b^2 c^2 v_2^{2m_2} v_3^{2m_3}}{2a b c v_1^{m_1} v_2^{2m_2} v_3^{m_3}}\\ &:& \frac {-a^2 b^2 v_1^{2m_1} v_2^{2m_2} + a^2 c^2 v_1^{2m_1} v_3^{2m_3} + b^2 c^2 v_2^{2m_2} v_3^{2m_3}}{2 a b c v_1^{m_1} v_2^{m_2} v_3^{2m_3}}\,:\,1 \bigg ]. \end{eqnarray*}
We now set
We consider the following twists of hyperelliptic curves:
Now, the points
![]() $P_i\ {:}{=}\ (x_i,y_i)=\big(\frac {1}{v_i^2T^{M_i}},w_i\big)$
are
$P_i\ {:}{=}\ (x_i,y_i)=\big(\frac {1}{v_i^2T^{M_i}},w_i\big)$
are
![]() $\mathbb{Q}(v_1,v_2,v_3)$
-rational points in
$\mathbb{Q}(v_1,v_2,v_3)$
-rational points in
![]() $C_i$
,
$C_i$
,
![]() $i=1,2,3$
, whereas
$i=1,2,3$
, whereas
![]() $P\ {:}{=}\ (x_4,y_4)=\big (u,\frac {1}{T^{(M-1)/2}}\big )$
is a
$P\ {:}{=}\ (x_4,y_4)=\big (u,\frac {1}{T^{(M-1)/2}}\big )$
is a
![]() $\mathbb{Q}(u,v_1,v_2,v_3)$
-rational point in
$\mathbb{Q}(u,v_1,v_2,v_3)$
-rational point in
![]() $C$
.
$C$
.
In [Reference Ulas8, Reference Ulas9], explicit constructions of families of triples and quadruples of elliptic curves with
![]() $j$
-invariants
$j$
-invariants
![]() $0$
or
$0$
or
![]() $1728$
were given such that there is a rational function
$1728$
were given such that there is a rational function
![]() $D$
for which the twists of the curves in each tuple by
$D$
for which the twists of the curves in each tuple by
![]() $D$
are of positive Mordell–Weil rank. This was extended to pairs and triples of Jacobians of hyperelliptic curves of the same genus in [Reference Jȩdrzejak, Top and Ulas5, Reference Jȩdrzejak and Ulas6]. Following the argument above, we obtain the following theorem which can be considered as an extension of the aforementioned results to quadruples of Jacobians of hyperelliptic curves that are not necessarily of the same genus.
$D$
are of positive Mordell–Weil rank. This was extended to pairs and triples of Jacobians of hyperelliptic curves of the same genus in [Reference Jȩdrzejak, Top and Ulas5, Reference Jȩdrzejak and Ulas6]. Following the argument above, we obtain the following theorem which can be considered as an extension of the aforementioned results to quadruples of Jacobians of hyperelliptic curves that are not necessarily of the same genus.
Theorem 2.2.
Let
![]() $f \in \mathbb{Q}[x]$
be a square-free polynomial of degree at least
$f \in \mathbb{Q}[x]$
be a square-free polynomial of degree at least
![]() $3$
. Let
$3$
. Let
![]() $m_1,m_2,m_3\ge 3$
be odd integers. Consider the hyperelliptic curves
$m_1,m_2,m_3\ge 3$
be odd integers. Consider the hyperelliptic curves
where
![]() $a,b,c$
are non-zero rational numbers. Then there exists a rational function
$a,b,c$
are non-zero rational numbers. Then there exists a rational function
![]() $D_{2,m_1,m_2,m_3} \in \mathbb{Q}(u, v_1,v_2,v_3)$
such that the Jacobian of the quadratic twist of the curve
$D_{2,m_1,m_2,m_3} \in \mathbb{Q}(u, v_1,v_2,v_3)$
such that the Jacobian of the quadratic twist of the curve
![]() $E$
by
$E$
by
![]() $D_{2,m_1,m_2,m_3}$
and the Jacobians of the
$D_{2,m_1,m_2,m_3}$
and the Jacobians of the
![]() $m_i$
-twists of the curves
$m_i$
-twists of the curves
![]() $E_i$
,
$E_i$
,
![]() $i=1,2,3$
, by
$i=1,2,3$
, by
![]() $D_{2,m_1,m_2,m_3}$
have positive Mordell–Weil rank over
$D_{2,m_1,m_2,m_3}$
have positive Mordell–Weil rank over
![]() $\mathbb{Q}(u, v_1, v_2,v_3)$
.
$\mathbb{Q}(u, v_1, v_2,v_3)$
.
Proof.
Let
![]() $C$
and
$C$
and
![]() $C_i$
,
$C_i$
,
![]() $i=1,2,3$
, be the twists of
$i=1,2,3$
, be the twists of
![]() $E$
and
$E$
and
![]() $E_i$
,
$E_i$
,
![]() $i=1,2,3$
, described above. Let
$i=1,2,3$
, described above. Let
![]() $P_i$
,
$P_i$
,
![]() $i=1,2,3$
, and
$i=1,2,3$
, and
![]() $P$
be the rational points above. We set
$P$
be the rational points above. We set
![]() $J$
and
$J$
and
![]() $J_i$
to be the Jacobians of
$J_i$
to be the Jacobians of
![]() $C$
and
$C$
and
![]() $C_i$
,
$C_i$
,
![]() $i=1,2,3$
, respectively. We consider the rational divisors
$i=1,2,3$
, respectively. We consider the rational divisors
![]() $D=(P)-(\infty )$
on
$D=(P)-(\infty )$
on
![]() $C$
and
$C$
and
![]() $D_i= (P_i)-(\infty )$
,
$D_i= (P_i)-(\infty )$
,
![]() $i=1,2,3$
, on
$i=1,2,3$
, on
![]() $C_i$
. Since
$C_i$
. Since
![]() $C$
is a non-constant quadratic twist of a constant curve
$C$
is a non-constant quadratic twist of a constant curve
![]() $E$
, it follows that the divisor
$E$
, it follows that the divisor
![]() $D$
defines a rational point of infinite order in
$D$
defines a rational point of infinite order in
![]() $J(\mathbb{Q}(u, v_1, v_2,v_3))$
.
$J(\mathbb{Q}(u, v_1, v_2,v_3))$
.
Due to [Reference Jȩdrzejak, Top and Ulas5, Proposition 2.1], the divisor
![]() $D_i$
corresponds to a rational point of infinite order in
$D_i$
corresponds to a rational point of infinite order in
![]() $J_i(\mathbb{Q}(u, v_1, v_2,v_3))$
as
$J_i(\mathbb{Q}(u, v_1, v_2,v_3))$
as
![]() $P_i$
,
$P_i$
,
![]() $i=1,2,3$
, has non-constant coordinates with a non-zero
$i=1,2,3$
, has non-constant coordinates with a non-zero
![]() $y$
-coordinate.
$y$
-coordinate.
Example 2.3.
The curves
![]() $E\,{:}\, D y^2=x^5+x+1$
and
$E\,{:}\, D y^2=x^5+x+1$
and
![]() $E_i\,:\,y^2=D x^{4i+1}+i^2$
,
$E_i\,:\,y^2=D x^{4i+1}+i^2$
,
![]() $i=1,2,3$
, are of positive Mordell–Weil rank over
$i=1,2,3$
, are of positive Mordell–Weil rank over
![]() $\mathbb{Q}$
, where
$\mathbb{Q}$
, where
 \begin{eqnarray*} D\,:&=&D(u,v_1,v_2,v_3)=\frac {\big(u^5+u+1\big)^{585}\big(w_1^2-1\big)v_1^{10}}{v_3^{15210}(w_3^2-9)^{585}}\textrm { where} \\ w_1&=&\frac {3 v_3^{13}}{4 v_2^9} + v_2^9\left ( \frac {1}{3 v_3^{13}} - \frac {3 v_3^{13}}{v_1^{10}}\right)\!,\\ w_2&=&\frac {3 v_3^{13}}{v_1^5} + v_1^5\left ( \frac {1}{3 v_3^{13}} - \frac {3 v_3^{13}}{4v_2^{18}}\right)\!,\\ w_3&=&\frac {3 v_2^{9}}{v_1^5} + v_1^5\left ( \frac {3}{4 v_2^{9}} - \frac {v_2^{9}}{3v_3^{26}}\right)\!,\quad u,v_1,v_2,v_3\in \mathbb{Q}\setminus \{0\}. \end{eqnarray*}
\begin{eqnarray*} D\,:&=&D(u,v_1,v_2,v_3)=\frac {\big(u^5+u+1\big)^{585}\big(w_1^2-1\big)v_1^{10}}{v_3^{15210}(w_3^2-9)^{585}}\textrm { where} \\ w_1&=&\frac {3 v_3^{13}}{4 v_2^9} + v_2^9\left ( \frac {1}{3 v_3^{13}} - \frac {3 v_3^{13}}{v_1^{10}}\right)\!,\\ w_2&=&\frac {3 v_3^{13}}{v_1^5} + v_1^5\left ( \frac {1}{3 v_3^{13}} - \frac {3 v_3^{13}}{4v_2^{18}}\right)\!,\\ w_3&=&\frac {3 v_2^{9}}{v_1^5} + v_1^5\left ( \frac {3}{4 v_2^{9}} - \frac {v_2^{9}}{3v_3^{26}}\right)\!,\quad u,v_1,v_2,v_3\in \mathbb{Q}\setminus \{0\}. \end{eqnarray*}
Due to Silverman’s specialization theorem of abelian varieties, one knows that for all but a thin set of values of
![]() $u,v_1,v_2,v_3$
in
$u,v_1,v_2,v_3$
in
![]() $\mathbb{Q}$
, the points
$\mathbb{Q}$
, the points
![]() $\left (u,\frac {v_3^{7592}(w_3^2-9)^{292}}{(u^5+u+1)^{292}}\right )-(\infty )$
on the Jacobian of
$\left (u,\frac {v_3^{7592}(w_3^2-9)^{292}}{(u^5+u+1)^{292}}\right )-(\infty )$
on the Jacobian of
![]() $E$
and the point
$E$
and the point
![]() $(P_i)-(\infty )$
,
$(P_i)-(\infty )$
,
![]() $i=1,2,3$
, on the Jacobian of
$i=1,2,3$
, on the Jacobian of
![]() $E_i$
, where
$E_i$
, where
 \begin{equation*}P_i=\left (\frac {v_3^{26M_i}(w_3^2-9)^{M_i}}{v_i^2 (u^5+u+1)^{M_i}},w_i\right)\!, \,M_1=117,\,M_2=65,\,M_3=45,\end{equation*}
\begin{equation*}P_i=\left (\frac {v_3^{26M_i}(w_3^2-9)^{M_i}}{v_i^2 (u^5+u+1)^{M_i}},w_i\right)\!, \,M_1=117,\,M_2=65,\,M_3=45,\end{equation*}
are points of infinite order.
In Corollaries 3.2 and 4.2 of [Reference Jȩdrzejak and Ulas6], the authors established the existence of pairs of hyperelliptic curves
![]() $C_1$
and
$C_1$
and
![]() $C_2$
together with a rational function
$C_2$
together with a rational function
![]() $D$
such that the Mordell–Weil rank of the Jacobian of a twist of
$D$
such that the Mordell–Weil rank of the Jacobian of a twist of
![]() $C_1$
by
$C_1$
by
![]() $D$
is positive, whereas the Mordell–Weil rank of the Jacobian of a twist of
$D$
is positive, whereas the Mordell–Weil rank of the Jacobian of a twist of
![]() $C_2$
by
$C_2$
by
![]() $D$
is at least
$D$
is at least
![]() $2$
. In the following theorem, we present such examples of pairs of hyperelliptic curves where the Mordell–Weil rank of the Jacobian of a twist of
$2$
. In the following theorem, we present such examples of pairs of hyperelliptic curves where the Mordell–Weil rank of the Jacobian of a twist of
![]() $C_2$
by
$C_2$
by
![]() $D$
is at least
$D$
is at least
![]() $3$
.
$3$
.
Theorem 2.4.
Let
![]() $f \in \mathbb{Q}[x]$
be a square-free polynomial of degree at least
$f \in \mathbb{Q}[x]$
be a square-free polynomial of degree at least
![]() $3$
. Let
$3$
. Let
![]() $m\ge 3$
be an odd integer. Consider the hyperelliptic curves
$m\ge 3$
be an odd integer. Consider the hyperelliptic curves
Then there exists a rational function
![]() $D_{2,m} \in \mathbb{Q}(u, v_1,v_2,v_3)$
such that the Jacobian of the quadratic twist of the curve
$D_{2,m} \in \mathbb{Q}(u, v_1,v_2,v_3)$
such that the Jacobian of the quadratic twist of the curve
![]() $E$
by
$E$
by
![]() $D_{2,m}$
is of positive Mordell–Weil rank and the Mordell–Weil rank of the Jacobian of the
$D_{2,m}$
is of positive Mordell–Weil rank and the Mordell–Weil rank of the Jacobian of the
![]() $m$
-twist of the curve
$m$
-twist of the curve
![]() $E'$
by
$E'$
by
![]() $D_{2,m}$
over
$D_{2,m}$
over
![]() $\mathbb{Q}(u, v_1, v_2,v_3)$
is at least
$\mathbb{Q}(u, v_1, v_2,v_3)$
is at least
![]() $3$
.
$3$
.
Proof.
In Theorem 2.2, we set
![]() $a=b=c$
and
$a=b=c$
and
![]() $m\ {:}{=}\ m_1=m_2=m_3$
. Choosing
$m\ {:}{=}\ m_1=m_2=m_3$
. Choosing
![]() $(p,q,r)=(w_1,w_2,w_3)$
as defined above, we obtain the three rational points
$(p,q,r)=(w_1,w_2,w_3)$
as defined above, we obtain the three rational points
![]() $P_i=\left (\frac {1}{v_i^2},w_i\right )$
,
$P_i=\left (\frac {1}{v_i^2},w_i\right )$
,
![]() $i=1,2,3$
, in
$i=1,2,3$
, in
![]() $E'(\mathbb{Q})$
where
$E'(\mathbb{Q})$
where
![]() $E'$
is defined by
$E'$
is defined by
![]() $y^2=D x^m+a$
.
$y^2=D x^m+a$
.
We consider the automorphisms
![]() $\phi _{i}$
,
$\phi _{i}$
,
![]() $1\le i\le 3$
, of
$1\le i\le 3$
, of
![]() $K=\mathbb{Q}(u,v_1,v_2,v_3)$
defined by
$K=\mathbb{Q}(u,v_1,v_2,v_3)$
defined by
Since
![]() $\phi _i(T)=T$
and
$\phi _i(T)=T$
and
![]() $\phi _i(D)=D$
, the automorphism
$\phi _i(D)=D$
, the automorphism
![]() $\phi _i$
induces a map
$\phi _i$
induces a map
![]() $\Phi _i$
on
$\Phi _i$
on
![]() $E'$
and its Jacobian
$E'$
and its Jacobian
![]() $J$
. In particular,
$J$
. In particular,
We define the
![]() $K$
-rational divisors
$K$
-rational divisors
![]() $D_i\ {:}{=}\ (P_i)-(\infty )$
,
$D_i\ {:}{=}\ (P_i)-(\infty )$
,
![]() $i=1,2,3$
, on
$i=1,2,3$
, on
![]() $E'$
. In accordance with the proof of Theorem 2.2, the divisors
$E'$
. In accordance with the proof of Theorem 2.2, the divisors
![]() $D_i$
define rational points of infinite order in
$D_i$
define rational points of infinite order in
![]() $J$
. In addition, one has
$J$
. In addition, one has
We now assume that there are integers
![]() $\alpha ,\beta ,\gamma$
such that
$\alpha ,\beta ,\gamma$
such that
![]() $\alpha D_1 +\beta D_2+\gamma D_3\sim 0$
. Applying the automorphism
$\alpha D_1 +\beta D_2+\gamma D_3\sim 0$
. Applying the automorphism
![]() $\Phi _1$
, one gets
$\Phi _1$
, one gets
![]() $\alpha D_1-\beta D_2-\gamma D_3\sim 0$
. Adding the two linear equivalence relations, one obtains
$\alpha D_1-\beta D_2-\gamma D_3\sim 0$
. Adding the two linear equivalence relations, one obtains
![]() $2\alpha D_1\sim 0$
, hence
$2\alpha D_1\sim 0$
, hence
![]() $\alpha =0$
. Similarly, one applies the automorphism
$\alpha =0$
. Similarly, one applies the automorphism
![]() $\Phi _2$
and obtains
$\Phi _2$
and obtains
![]() $\beta =0$
. It follows that
$\beta =0$
. It follows that
![]() $D_1$
,
$D_1$
,
![]() $D_2$
, and
$D_2$
, and
![]() $D_3$
are linearly independent.
$D_3$
are linearly independent.
3. A quadratic twist and three twists of even degrees
Let
![]() $f(x)\in \mathbb{Q}[x]$
be a square-free polynomial of degree at least
$f(x)\in \mathbb{Q}[x]$
be a square-free polynomial of degree at least
![]() $3$
. Fix odd integers
$3$
. Fix odd integers
![]() $m_1,m_2,m_3\ge 3$
. We are investigating the existence of non-square rational numbers
$m_1,m_2,m_3\ge 3$
. We are investigating the existence of non-square rational numbers
![]() $D$
such that the Jacobians of the (hyperelliptic) curves
$D$
such that the Jacobians of the (hyperelliptic) curves
are of positive Mordell–Weil rank over
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
Setting
![]() $M=\textrm {lcm}(m_1,m_2,m_3)$
and
$M=\textrm {lcm}(m_1,m_2,m_3)$
and
![]() $M_{i}=M/m_i$
,
$M_{i}=M/m_i$
,
![]() $i=1,2,3$
. We find the rational number
$i=1,2,3$
. We find the rational number
![]() $D$
by solving the following system of equations
$D$
by solving the following system of equations
where the solutions
![]() $x_i,y_i$
,
$x_i,y_i$
,
![]() $i=1,2,3,4$
, satisfy
$i=1,2,3,4$
, satisfy
![]() $x_i y_i\ f(x_4)(y_1^2-x_1^{m_1})(y_2^2-x_2^{m_2})(y_3^2-x_3^{m_3})\ne 0$
. To produce a family of parametric solutions to the system (3.1), we set
$x_i y_i\ f(x_4)(y_1^2-x_1^{m_1})(y_2^2-x_2^{m_2})(y_3^2-x_3^{m_3})\ne 0$
. To produce a family of parametric solutions to the system (3.1), we set
 \begin{eqnarray*} x_1&=&v_1^{2}T^{M_1},\, x_2=v_2^2T^{M_2},\, x_3=v_3^2T^{M_3},\, x_4 =u,\\ y_1&=&pT^{(M-1)/2},\, y_2=qT^{(M-1)/2},\,y_3=rT^{(M-1)/2},\,y_4=\frac {1}{T^{(M-1)/2}}, \end{eqnarray*}
\begin{eqnarray*} x_1&=&v_1^{2}T^{M_1},\, x_2=v_2^2T^{M_2},\, x_3=v_3^2T^{M_3},\, x_4 =u,\\ y_1&=&pT^{(M-1)/2},\, y_2=qT^{(M-1)/2},\,y_3=rT^{(M-1)/2},\,y_4=\frac {1}{T^{(M-1)/2}}, \end{eqnarray*}
where
![]() $u,v_1,v_2,v_3$
are rational parameters. After simplification, one obtains
$u,v_1,v_2,v_3$
are rational parameters. After simplification, one obtains
It follows that solving the system (3.1) is equivalent to finding rational points on the curve
which is an intersection
![]() $\mathcal H_{a,b,c}$
of two quadratic surfaces in
$\mathcal H_{a,b,c}$
of two quadratic surfaces in
![]() $\mathbb{P}^3$
over
$\mathbb{P}^3$
over
![]() $\mathbb{Q}(v_1,v_2,v_3)$
. In addition, the curve
$\mathbb{Q}(v_1,v_2,v_3)$
. In addition, the curve
![]() $\mathcal H_{a,b,c}$
possesses the four projective rational points
$\mathcal H_{a,b,c}$
possesses the four projective rational points
![]() $[p\,:\,q\,:\,r\,:\,s]=[\!\pm v_1^{m_1}\,:\,\pm v_2^{m_2}\,:\,\pm v_3^{m_3}\,:\,0]$
. Thus,
$[p\,:\,q\,:\,r\,:\,s]=[\!\pm v_1^{m_1}\,:\,\pm v_2^{m_2}\,:\,\pm v_3^{m_3}\,:\,0]$
. Thus,
![]() $\mathcal H_{a,b,c}$
is an elliptic curve.
$\mathcal H_{a,b,c}$
is an elliptic curve.
Theorem 3.1.
Let
![]() $E$
be an elliptic curve defined by
$E$
be an elliptic curve defined by
![]() $y^2=f(x)$
where
$y^2=f(x)$
where
![]() $f \in \mathbb{Q}[x]$
is a polynomial of degree
$f \in \mathbb{Q}[x]$
is a polynomial of degree
![]() $3$
or
$3$
or
![]() $4$
. Assume, moreover, that the Mordell–Weil rank of
$4$
. Assume, moreover, that the Mordell–Weil rank of
![]() $E$
is positive. Let
$E$
is positive. Let
![]() $m_1,m_2,m_3\ge 3$
be odd integers. Consider the hyperelliptic curves
$m_1,m_2,m_3\ge 3$
be odd integers. Consider the hyperelliptic curves
where
![]() $a,b,c$
are non-zero rational numbers. Then there exists a rational function
$a,b,c$
are non-zero rational numbers. Then there exists a rational function
![]() $D_{2,2m_1,2m_2,2m_3} \in \mathbb{Q}( v_1,v_2,v_3)$
such that the quadratic twist of the curve
$D_{2,2m_1,2m_2,2m_3} \in \mathbb{Q}( v_1,v_2,v_3)$
such that the quadratic twist of the curve
![]() $E$
and the Jacobians of the
$E$
and the Jacobians of the
![]() $2m_i$
-twists of the curves
$2m_i$
-twists of the curves
![]() $E_i$
,
$E_i$
,
![]() $i=1,2,3$
, by
$i=1,2,3$
, by
![]() $D_{2,2m_1,2m_2,2m_3}$
have positive Mordell–Weil rank over
$D_{2,2m_1,2m_2,2m_3}$
have positive Mordell–Weil rank over
![]() $\mathbb{Q}(v_1, v_2,v_3)$
.
$\mathbb{Q}(v_1, v_2,v_3)$
.
Proof. Following the discussion above, one needs to find a rational point on the elliptic curve
Since
![]() $E$
is of positive Mordell–Weil rank, we choose
$E$
is of positive Mordell–Weil rank, we choose
![]() $u$
such that
$u$
such that
![]() $(u,y_u)\in E(\mathbb{Q})$
is of infinite order. Now, the elliptic curve
$(u,y_u)\in E(\mathbb{Q})$
is of infinite order. Now, the elliptic curve
![]() $\mathcal H_{a^2,b^2,c^2}$
is birational to
$\mathcal H_{a^2,b^2,c^2}$
is birational to
where
![]() $T_{1}=av_2^{m_2}v_3^{m_3}y_u$
,
$T_{1}=av_2^{m_2}v_3^{m_3}y_u$
,
![]() $T_{2}=bv_1^{m_1}v_3^{m_3}y_u$
, and
$T_{2}=bv_1^{m_1}v_3^{m_3}y_u$
, and
![]() $T_{3}=cv_1^{m_1}v_2^{m_2}y_u$
. According to Proposition2.1, the latter curve is of positive Mordell–Weil rank over
$T_{3}=cv_1^{m_1}v_2^{m_2}y_u$
. According to Proposition2.1, the latter curve is of positive Mordell–Weil rank over
![]() $\mathbb{Q}(T_1,T_2,T_3)$
. Now, the proof is similar to the proof of Theorem 2.2.
$\mathbb{Q}(T_1,T_2,T_3)$
. Now, the proof is similar to the proof of Theorem 2.2.
We remark that doubling the point of infinite order
![]() $[a y_u\,:\,by_u\,:\,cy_u\,:\,1]\in \mathcal H_{a^2,b^2,c^2}(\mathbb{Q}(v_1,v_2,v_3))$
yields the point
$[a y_u\,:\,by_u\,:\,cy_u\,:\,1]\in \mathcal H_{a^2,b^2,c^2}(\mathbb{Q}(v_1,v_2,v_3))$
yields the point
![]() $[w_1\,:\,w_2\,:\,w_3\,:\,1]$
given by
$[w_1\,:\,w_2\,:\,w_3\,:\,1]$
given by
 \begin{eqnarray*} \bigg [\frac {a^2 b^2 v_3^{2m_3} y_u + a^2 c^2 v_2^{2m_2} y_u - b^2 c^2 v_1^{2m_1} y_u}{2 a b c v_2^{m_2} v_3^{m_3}} &:& \frac {a^2 b^2 v_3^{2m_3} y_u - a^2 c^2 v_2^{2m_2}y_u + b^2 c^2 v_1^{2m_1} y_u}{2a b c v_1^{m_1}v_3^{m_3}} \\ &:& \frac {-a^2 b^2 v_3^{2m_3} y_u + a^2 c^2 v_2^{2m_2}y_u + b^2 c^2 v_1^{2m_1}y_u}{2a b c v_1^{m_1}v_2^{m_2}} \,:\, 1 \bigg ]\in \mathcal H_{a^2,b^2,c^2}(\mathbb{Q}(v_1,v_2,v_3)). \end{eqnarray*}
\begin{eqnarray*} \bigg [\frac {a^2 b^2 v_3^{2m_3} y_u + a^2 c^2 v_2^{2m_2} y_u - b^2 c^2 v_1^{2m_1} y_u}{2 a b c v_2^{m_2} v_3^{m_3}} &:& \frac {a^2 b^2 v_3^{2m_3} y_u - a^2 c^2 v_2^{2m_2}y_u + b^2 c^2 v_1^{2m_1} y_u}{2a b c v_1^{m_1}v_3^{m_3}} \\ &:& \frac {-a^2 b^2 v_3^{2m_3} y_u + a^2 c^2 v_2^{2m_2}y_u + b^2 c^2 v_1^{2m_1}y_u}{2a b c v_1^{m_1}v_2^{m_2}} \,:\, 1 \bigg ]\in \mathcal H_{a^2,b^2,c^2}(\mathbb{Q}(v_1,v_2,v_3)). \end{eqnarray*}
One obtains the following result.
Theorem 3.2.
Let
![]() $E$
be an elliptic curve defined by
$E$
be an elliptic curve defined by
![]() $y^2=f(x)$
where
$y^2=f(x)$
where
![]() $f \in \mathbb{Q}[x]$
is a polynomial of degree
$f \in \mathbb{Q}[x]$
is a polynomial of degree
![]() $3$
or
$3$
or
![]() $4$
. Assume, moreover, that the Mordell–Weil rank of
$4$
. Assume, moreover, that the Mordell–Weil rank of
![]() $E$
is positive. Let
$E$
is positive. Let
![]() $m\ge 3$
be an odd integer. Consider the hyperelliptic curves
$m\ge 3$
be an odd integer. Consider the hyperelliptic curves
![]() $E'\,:\,y^2=x^{m}+a^2$
, where
$E'\,:\,y^2=x^{m}+a^2$
, where
![]() $a$
is a non-zero rational number. Then there exists a rational function
$a$
is a non-zero rational number. Then there exists a rational function
![]() $D_{2,2m} \in \mathbb{Q}( v_1,v_2,v_3)$
such that the quadratic twist of the curve
$D_{2,2m} \in \mathbb{Q}( v_1,v_2,v_3)$
such that the quadratic twist of the curve
![]() $E$
by
$E$
by
![]() $D_{2,2m}$
is of positive Mordell–Weil rank and the Mordell–Weil rank of the Jacobian of the
$D_{2,2m}$
is of positive Mordell–Weil rank and the Mordell–Weil rank of the Jacobian of the
![]() $2m$
-twist of the curve
$2m$
-twist of the curve
![]() $E'$
by
$E'$
by
![]() $D_{2,2m}$
over
$D_{2,2m}$
over
![]() $\mathbb{Q}(v_1, v_2,v_3)$
is at least
$\mathbb{Q}(v_1, v_2,v_3)$
is at least
![]() $3$
.
$3$
.
Proof.
We set
![]() $m\ {:}{=}\ m_1=m_2=m_3$
and
$m\ {:}{=}\ m_1=m_2=m_3$
and
![]() $a=b=c$
in Theorem 3.1. The three
$a=b=c$
in Theorem 3.1. The three
![]() $\mathbb{Q}(v_1,v_2,v_3)$
-rational points
$\mathbb{Q}(v_1,v_2,v_3)$
-rational points
![]() $P_i\ {:}{=}\ \left (v_i^2, w_i T^{(m-1)/2}\right )$
,
$P_i\ {:}{=}\ \left (v_i^2, w_i T^{(m-1)/2}\right )$
,
![]() $i=1,2,3$
, on the curve
$i=1,2,3$
, on the curve
![]() $y^2=x^m+a D$
are of infinite order.
$y^2=x^m+a D$
are of infinite order.
We consider the automorphisms
![]() $\phi _{i}$
,
$\phi _{i}$
,
![]() $ i=1,2,3$
, of
$ i=1,2,3$
, of
![]() $\mathbb{Q}(v_1,v_2,v_3)$
defined by
$\mathbb{Q}(v_1,v_2,v_3)$
defined by
Now the proof follows as in the proof of Theorem 2.4.
4. One even-degree twist and three odd-degree twists
Given the curves
where
![]() $a,b,c,d$
are non-zero rationals and
$a,b,c,d$
are non-zero rationals and
![]() $m_i$
,
$m_i$
,
![]() $i=1,2,3,4$
, are odd integers, we investigate the existence of a rational function
$i=1,2,3,4$
, are odd integers, we investigate the existence of a rational function
![]() $D$
such that the Jacobians of the following twists are of positive Mordell–Weil rank:
$D$
such that the Jacobians of the following twists are of positive Mordell–Weil rank:
The rational
![]() $D$
can be obtained by solving the system:
$D$
can be obtained by solving the system:
where
![]() $x_iy_i(y_1^2-a)(y_2^2-b)(y_3^2-c)(y_4^2-x_4^{m_4})\ne 0$
. Let
$x_iy_i(y_1^2-a)(y_2^2-b)(y_3^2-c)(y_4^2-x_4^{m_4})\ne 0$
. Let
![]() $M=\textrm {lcm}(m_1,m_2,m_3,m_4)$
with
$M=\textrm {lcm}(m_1,m_2,m_3,m_4)$
with
![]() $M_i=M/m_i$
,
$M_i=M/m_i$
,
![]() $i=1,2,3,4$
. We set
$i=1,2,3,4$
. We set
 \begin{eqnarray*} x_1&=&\frac {1}{v_1^2T^{M_1}},\quad x_2=\frac {1}{v_2^2T^{M_2}},\quad x_3=\frac {1}{v_3^2T^{M_3}},\quad x_4=v_4^2 T^{m_4}, \\ y_1&=&p,\quad y_2=q,\quad y_3=r,\quad y_4=uT^{(M-1)/2} \end{eqnarray*}
\begin{eqnarray*} x_1&=&\frac {1}{v_1^2T^{M_1}},\quad x_2=\frac {1}{v_2^2T^{M_2}},\quad x_3=\frac {1}{v_3^2T^{M_3}},\quad x_4=v_4^2 T^{m_4}, \\ y_1&=&p,\quad y_2=q,\quad y_3=r,\quad y_4=uT^{(M-1)/2} \end{eqnarray*}
where
![]() $u,v_1,v_2,v_3,v_4$
are rational parameters. One now obtains that
$u,v_1,v_2,v_3,v_4$
are rational parameters. One now obtains that
In other words, one needs to solve the system:
We now obtain the following result.
Theorem 4.1.
Let
![]() $m_1,m_2,m_3,m_4\ge 3$
be odd integers. Consider the hyperelliptic curves
$m_1,m_2,m_3,m_4\ge 3$
be odd integers. Consider the hyperelliptic curves
where
![]() $a,b,c,d$
are non-zero rational numbers. Then there exists a rational function
$a,b,c,d$
are non-zero rational numbers. Then there exists a rational function
![]() $D_{m_1,m_2,m_3,2m_4} \in \mathbb{Q}(u, v_1,v_2,v_3)$
such that the Jacobian of the
$D_{m_1,m_2,m_3,2m_4} \in \mathbb{Q}(u, v_1,v_2,v_3)$
such that the Jacobian of the
![]() $m_i$
-twists of the curves
$m_i$
-twists of the curves
![]() $E_i$
,
$E_i$
,
![]() $i=1,2,3$
by
$i=1,2,3$
by
![]() $D_{m_1,m_2,m_3,2m_4}$
and the Jacobian of the
$D_{m_1,m_2,m_3,2m_4}$
and the Jacobian of the
![]() $2m_4$
-twist of
$2m_4$
-twist of
![]() $E_4$
by
$E_4$
by
![]() $D_{m_1,m_2,m_3,2m_4}$
have positive Mordell–Weil rank over
$D_{m_1,m_2,m_3,2m_4}$
have positive Mordell–Weil rank over
![]() $\mathbb{Q}(u, v_1, v_2,v_3)$
.
$\mathbb{Q}(u, v_1, v_2,v_3)$
.
Acknowledgements
The authors would like to thank the anonymous referee for many useful suggestions and comments that improved the manuscript. All the calculations in this work were performed using Magma [Reference Bosma, Cannon and Playoust2]. M. Sadek is supported by the Scientific and Technological Research Council of Turkey, TÜBİTAK, research grant ARDEB 1001/122F312.
Competing interests
The authors declare no conflicts of interest.