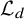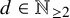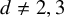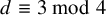1 Introduction
The arithmetic of K3 surfaces has been intensively studied and has witnessed great progress over the past 25 years. Two prominent and intertwined topics are (potential) Zariski density of rational points on K3 surfaces over nonalgebraically closed fields, and elliptic fibrations, in particular, the study of Mordell–Weil rank jumps among fibers of elliptic fibrations on K3 surfaces.
In this article, we study (potential) Mordell–Weil rank jumps for elliptic K3 surfaces. Our main result is the following.
Theorem 1.1. Let X be a K3 surface defined over a number field such that
$\operatorname {\mathrm {Pic}}(X)=U \oplus \langle -2d\rangle $
, for
$d\in \mathbb {N}$
, or equivalently a K3 surface defined over k admitting an elliptic fibration (possibly over a field extension of k) and with Picard number 3. Assume that
$d\neq 2,3$
. Then each elliptic fibration on X has the potential Mordell–Weil rank jump property and, moreover, if
$d\equiv 3\ \mod 4$
, then it has the Mordell–Weil rank jump property over its field of definition.
The innovation of our contribution is two-fold. Firstly, Theorem 1.1 presents the first instance of rank jump in a general context that does not involve a family of multisections but relies on the presence of a specific type of multisection, namely a saliently ramified multisection as introduced by Bogomolov and Tschinkel ([Reference Bogomolov and TschinkelBT98, Definition 2.3]) and adapted to the context of Mordell–Weil rank jumps by one of the authors with Pasten in [Reference Pasten and SalgadoPS24]. Secondly, to produce a saliently ramified multisection, we combine lattice theoretic and geometric methods, a technique used for the first time in that context. This geometric description allows one to control the field over which the jump property appears, and therefore we describe countable many families of K3 surfaces which have the rank jump property, and not just the potential one.
In what follows, we give a brief account of developments on (potential) density of rational points on K3 surfaces, and rank jumps on elliptic surfaces, leading to the motivation behind Theorem 1.1.
Throughout the text, we let k be a number field.
(Potential) Zariski density
In [Reference Bogomolov and TschinkelBT00, Theorem 1.1], Bogomolov and Tschinkel show that the rational points on K3 surfaces defined over k that admit either a genus 1 fibration or an infinite automorphism group are potentially dense in the Zariski topology, that is, there exists a finite extension
$l/k$
such that the l-points of the K3 surface are not contained in a finite union of proper subvarieties. One of the tools they introduce is the concept of saliently ramified multisections ([Reference Bogomolov and TschinkelBT98, Definition 2.3]), which are irreducible curves in the surface for which the restriction of the fibration map is of nonzero degree and ramified over at least one smooth fiber.
The relevance of saliently ramified rational or genus 1 multisections in the proof of potential density of rational points stems from the fact that they are nontorsion multisections on the associated jacobian fibration ([Reference Bogomolov and TschinkelBT00, Proposition 4.4], [Reference Bogomolov and TschinkelBT98, Proposition 2.4]). After a base change by such a multisection, the new fibration has positive Mordell–Weil rank and a specialization argument applied to the points on the image of the restriction map yields the desired Zariski density over the field of definition of the multisection.
Rank jumps
Given an elliptic fibration
$\pi : X \rightarrow C$
on a smooth projective algebraic surface X over k, denote by r the rank of the Mordell–Weil group of k-sections of
$\pi $
, that is, the rank of its generic fiber, and
$r_t$
the rank of the Mordell–Weil group of the fiber
$\pi ^{-1}(t)$
. We say that
$\pi $
has the (Mordell–Weil) rank jump property if the set
$\mathcal {R}(X, \pi , k):=\{t \in C(k); r_t> r \}$
is infinite. By a conjecture of Silverman ([Reference SilvermanSil85, p. 556]), it is expected that every nontrivial elliptic fibration over
$\mathbb {P}^1$
over k has the (Mordell–Weil) rank jump property. In particular, this is expected for elliptic K3 surfaces. In the remaining of the article we omit the reference to Mordell–Weil and refer to the rank jump property.
An immediate consequence of the aforementioned work by Bogomolov and Tschinkel is that an elliptic K3 surface with generic rank 0 Mordell–Weil group has the potential rank jump property; namely, there is a finite extension
$l/k$
such that
$\mathcal {R}(X,\pi , l)$
is infinite.
In [Reference SalgadoSal12a], the second-named author shows that certain K3 surfaces with two elliptic fibrations have the potential rank jump property. Recently, in a collaboration with Pasten ([Reference Pasten and SalgadoPS24]), they show a stronger result for certain doubly elliptic K3 surfaces; namely, that
$\mathcal {R}(X,\pi , l) \subset C \simeq \mathbb {P}^1(l)$
is not thin in the sense of Serre ([Reference SerreSer97, Section 9.1]), for some finite extension
$l/k$
.
In this context, the following questions arise:
Question 1:
Are there other examples of elliptic K3 surfaces that have the (potential) rank jump property, that is, the rank jump property over (a finite extension of) the ground field? In particular, are there examples with a nonfinite Mordell–Weil group and that are not doubly elliptic?
The main tool in [Reference Pasten and SalgadoPS24] is a modification of Bogomolov-Tschinkel’s saliently ramified multisections that allows one to control the subset of the base of the fibration where the restriction morphism is étale. The key observation which actually holds in the context of [Reference Bogomolov and TschinkelBT00] is that salient multisections not only are nontorsion but, moreover, are independent of the sections induced by the Mordell–Weil group of the original elliptic fibration in the base change ([Reference Pasten and SalgadoPS24, Lemma 3.3]). This gives us a potential tool to answer Question 1, namely by addressing the following:
Question 2:
Given a K3 surface with a genus 1 fibration, under which conditions are there saliently ramified rational multisections or singular genus 1 multisections?
In the previous question we allow both singular and smooth rational multisections, but we restrict to singular multisections of genus 1, since if there exists a smooth genus 1 multisection, then the surface is automatically doubly elliptic.
Main techniques
Given the discussion above, it is natural to search for a better understanding of multisections of elliptic, or more generally genus 1, fibrations on K3 surfaces, in particular with respect to the property of being saliently ramified. In what follows, we denote by
$\pi : X \rightarrow \mathbb {P}^1$
a genus 1 fibration on a K3 surface X. We show the following lattice theoretic results.
-
1a) The generic member in the 18-dimensional family of
$\langle 2\rangle \oplus \langle -2 \rangle $
–polarized K3 surfaces admits a saliently ramified smooth rational bisection (Proposition 3.4). -
1b) The generic member in the 18-dimensional family of
$U(2)$
–polarized K3 surfaces admits a saliently ramified smooth bisection of genus 1 (Proposition 3.6). -
1c) If a genus 1 fibration on a K3 surface admits a smooth bisection and it has Picard number 2, then it admits a smooth bisection of genus 0 or 1 (Corollary 3.3).
-
1d) Any generic member of the families in (1a) and (1b) admits a singular salient rational bisection (Remarks 3.5(c) and 3.7).
-
2a) The generic member of the family of
$\Lambda _d:=U\oplus \langle -2d \rangle $
-polarized K3 surfaces, for
$d\geq 4$
, admits a smooth bisection, which is of genus 0 if d is odd, and genus 1 if d is even. This bisection is saliently ramified. In particular, there are no generic members in the families that admit simultaneously smooth rational and smooth genus 1 bisections (Theorem 3.2). -
2b) The generic member of any of the families of
$\Lambda _d$
-polarized K3 surfaces, with
$d\leq 3$
, does not admit a smooth multisection of genus 0 or 1 (Corollary 4.3).
In particular, 2a) implies that each elliptic fibration on a generic member of the family of
$\Lambda _d$
-polarized K3 surfaces with
$d\geq 5$
,
$d\equiv 1\ \mod 2$
admits a saliently ramified smooth rational bisection and hence satisfies the potential rank jump property (Theorem 1.1). This yields three new 17-dimensional families of examples of K3 surfaces that satisfy the potential rank jump property (Theorem 1.1). In particular, this answers Questions 1 and 2 for the generic members of three 17-dimensional families of elliptic K3 surfaces. Moreover, the geometric construction of the bisection allows us to control the field on which it has rational points, and so to prove the rank jump property over the field of definition if
$d\equiv 3\ \mod 4$
.
Theorem 1.1 states the potential rank jump property for all the generic members of the families of elliptic K3 surfaces with a nontrivial Mordell–Weil group, with only two exceptions, and the rank jump property for countably many families among them. If
$d\geq 14$
or
$d=9$
the potential rank jump property for surfaces X with
$\operatorname {\mathrm {Pic}}(X)\simeq \Lambda _d$
follows from the fact that these surfaces are doubly elliptic, but we are also able to discuss the property of the field extension needed to have the rank jump.
We discuss the analogous properties for generic members of certain sub-families of dimension 16.
We provide explicit equations of K3 surfaces with Picard rank 3 which have the potential rank jump property; to compute their Picard numbers we combine the known techniques based on Tate’s conjecture with a more geometric and new approach that relies on the presence of an elliptic fibration.
Organization of the text
In Section 2, we cover the background on elliptic fibrations, multisections, base-change and rank jumps. We also cover the necessary background on K3 surfaces, lattice polarizations and their interplay with genus 1 fibrations. Section 3 focuses on the study of bisections via lattice theory and related geometric constructions. In particular, we show that elliptic K3 surfaces with Picard number 3 always admit a smooth bisection which is of genus 0 or 1, with the exception of 3 families (Theorem 3.2). We show, moreover, that for a generic such K3 the aforementioned bisection is saliently ramified. In order to prove that these bisections are saliently ramified, we give a realization of such a K3 surface as a double cover of the projective plane branched on a nodal sextic (Prop. 3.16) or of the quadric surface branched on a curve of bidegree
$(4,4)$
(Prop. 3.20), depending on the genus of the bisection and then we describe the elliptic fibration and the bisection in this model. Section 4 presents conditions on the polarization to guarantee the existence of a smooth rational curve which is a saliently ramified higher-degree multisection and gives a brief account of the geometric realization of K3 surfaces with such polarizations. Section 5 presents our contribution to the study of rank jumps on elliptic K3 surfaces. More precisely, given
$d>3$
and a
$U\oplus \langle 2d\rangle $
-polarized K3 surface, we show in Theorems 5.3 and 5.6 that it has the potential rank jump property and in Theorem 5.3 that it has the rank jump property if
$d\equiv 3\ \mod 4$
. In particular, Theorem 5.3 answers Question 1. We also extend the previous results to generic members of many subfamilies of codimension 1. Finally, Section 6 analyzes in detail examples of a K3 surface that admits a unique elliptic fibration with positive Mordell–Weil rank that was elusive to previous results and to which our results apply. We also consider an example in which the rank jump property can be proved by considering a rational multisection of degree 3, instead of a bisection. This provides an application of the results of Section 4.
2 Preliminaries
Let k be a number field. In what follows, curves and surfaces over a field are always assumed to be irreducible.
All divisors considered are on an algebraic surface, that is, are formal sums of curves. Let X be a smooth, projective, and geometrically integral surface over k. The intersection form is a bilinear pairing on
$\operatorname {\mathrm {Pic}}(X)$
, the group of divisors modulo linear equivalence. Given two divisors D and E in
$\operatorname {\mathrm {Pic}}(X)$
, we denote their intersection by
$DE$
. The divisor classes that are algebraically equivalent to 0 over
$\bar {k}$
form a group denoted by
$\operatorname {\mathrm {Pic}}^0(X)$
. The quotient
$\operatorname {\mathrm {Pic}} (X)/ \operatorname {\mathrm {Pic}}^0(X)$
is called the Néron–Severi group of X. Its rank is called the Picard number of X. For K3 surfaces,
$\operatorname {\mathrm {Pic}}^0$
is trivial, so
$\operatorname {\mathrm {NS}}(X) \simeq \operatorname {\mathrm {Pic}}(X)$
.
2.1 Genus 1 fibrations and elliptic surfaces
We cover the necessary background for this text on genus 1 and elliptic fibrations. The interested reader can consult [Reference MirandaMir89] for an account of the basic theory.
Definition 2.1. Given a smooth projective curve C over k, and a smooth projective surface X over k, we say that a morphism
$\pi :X\to C$
is an elliptic fibration if it is a genus 1 fibration with a distinguished section defined over k (these are sometimes called jacobian fibrations). The triple
$(X,\pi , C)$
, or simply X when
$\pi $
and C are clear from the context, is called an elliptic surface.
The set of k-sections of
$\pi $
is an abelian group which we denote by
$\operatorname {\mathrm {MW}}(X,\pi ,k)$
. We often omit k, if the field of definition is clear from the context. The fibration
$\pi :X\to C$
is called trivial if its generic fiber is isomorphic to
$E\otimes _k k(C)$
for some elliptic curve E over k.
Notation 2.2. In what follows, X always denotes a surface with a genus 1 fibration, not necessarily elliptic. We reserve the letter
$\pi $
for genus 1 fibrations, keeping in mind that there might be more than one such fibration on X. We denote by
$U_\pi $
the Zariski open of good reduction of
$\pi $
.
2.1.1 Multisections of genus 1 fibrations
Definition 2.3. Given a genus 1 fibration
$\pi : X \rightarrow C$
, a geometrically integral curve
$M \subset X$
is called a multisection of
$\pi $
if
$\pi |_{M}: M \rightarrow C$
is finite and of degree larger than 1.
Remark 2.4. Our definition is slightly different from that in [Reference Bogomolov and TschinkelBT00, Def. 3.2.]. We assume that the degree of the restriction of the fibration is larger than 1, while [Reference Bogomolov and TschinkelBT00] assumes that it is nonzero. So, in our definition, sections are not multisections. This modification is natural in our settings. Indeed, we are interested in the ramification of the restriction of the fibration of the multisection (Def. 2.5) which clearly only makes sense for maps of degree at least 2.
The presence of low genus multisections for elliptic fibrations has been explored both in the context of (potential) density of rational points on algebraic surfaces and of rank jump for elliptic fibrations. Indeed, in [Reference Bogomolov and TschinkelBT98] the authors observe that a torsion multisection T is such that
$\pi |_T: T \rightarrow C$
is étale over
$U_\pi $
. This motivated the following definition.
Definition 2.5. [Reference Bogomolov and TschinkelBT98, Definition 2.3].
A multisection M of
$\pi $
is called saliently ramified if
${\pi |M: M \rightarrow C}$
is ramified above at least one smooth fiber of
$\pi $
.
Building on the observation on torsion multisections above, they show that saliently ramified multisections yield nontorsion sections after base change ([Reference Bogomolov and TschinkelBT98, Prop. 2.10]).
Remark 2.6. Given M as in Def. 2.5, the map
$\pi |_M: M \rightarrow C$
is ramified at the points
$t\in C$
such that the intersection of M and
$\pi ^{-1}(t)$
is nonreduced. For fibrations for which all fiber components are reduced, these correspond to nontransverse intersections.
In situations where a nontorsion multisection M has infinitely many rational points over a given field l, one can conclude that the rational points are Zariski dense in X over l. Indeed, by a specialization argument on the base change
$X\times _C M$
followed by considering the fibers above the points in the image of
$\pi |_M: M \rightarrow C$
, there are infinitely many elliptic curves with positive Mordell–Weil rank over l.
2.2 Rank jump and base change
Let
$(X,\pi , C)$
be an elliptic surface defined over k. Let
$l/k$
be a finite extension of k.
Notation 2.7. For
$t\in C$
, we let
$X_t=\pi ^{-1}(t)$
, that is, the fiber of
$\pi $
above t. Denote by
$\mathcal {R}(X,\pi , l)$
the set
$$\begin{align*}\mathcal{R}(X,\pi, l):= \{t \in C(l); \mathrm{rank } \,X_t(l)> \mathrm{rank }\, \mathrm{MW }(X, \pi,l) \}. \end{align*}$$
Definition 2.8. We say that
$\pi $
has the rank jump property (resp. the potential rank jump property), if
$\mathcal {R}(X,\pi , k)$
(resp.
$\mathcal {R}(X,\pi , l)$
) is infinite.
Let
$M \subset X$
be a multisection of
$\pi $
defined over
$l/k$
. Let
$X_M$
be the relatively minimal elliptic surface obtained by resolving the singularities of
$X\times _C M$
. The projection onto M induces an elliptic fibration
$\pi _M: X_M \rightarrow M$
and we have an injection
$\alpha : \mathrm {MW }(X, \pi ,l) \hookrightarrow \mathrm {MW }(X_M,\pi _M,l)$
yielding
$$ \begin{align} \mathrm{rank}\, \operatorname{\mathrm{MW}}(X_M,\pi_M,l)\geq \mathrm{rank}\, \operatorname{\mathrm{MW}}(X,\pi,l). \end{align} $$
Let
$\iota :M\rightarrow X$
be the inclusion map and
$\mathrm {id: } M \rightarrow M$
, the identity map. Then
$(\iota , \mathrm {id}):M \rightarrow X \times _C M$
induces a section
$\sigma _M$
of
$\pi _M$
, namely the strict transform of
$(\iota , \mathrm {id})(M)$
under the birational map
$X_M\rightarrow X \times _{C} M$
. If the latter is linearly independent of the sections in the image of
$\alpha $
then the inequality in (2.1) is strict and, in particular, an application of Silverman’s Specialization Theorem ([Reference SilvermanSil83, Theorem C]) implies that
$\mathrm {rank}X_t(l)> \mathrm {rank}\, \operatorname {\mathrm {MW}}(X,\pi ,l)$
for all but finitely many t in the image of the l-points of the map
$\pi |_M: M \rightarrow C$
.
If, moreover,
$M(l)$
is infinite, then
$\mathcal {R}(X,\pi , l)$
is infinite.
There are several ways of checking that
$\sigma _M : M \rightarrow X_M$
induces a section which is linearly independent from the image of
$\operatorname {\mathrm {MW}}(X,\pi ,l)$
. For explicit
$(X, \pi , \operatorname {\mathrm {MW}}(X,\pi ,l))$
and M, one can compute the height matrix of M and the image of
$\operatorname {\mathrm {MW}}(X,\pi ,l)$
given the information of the intersection pairing for these divisors with each other and with the reducible components of the fibers of
$\pi $
. If this information is not available, alternative methods were given in [Reference SalgadoSal12b] and [Reference Pasten and SalgadoPS24]. We outline the latter for its relevance in the proof of Theorems 5.3 and 5.6.
The following statement is a slight simplification of [Reference Pasten and SalgadoPS24, Lemma 3.1], which we include here for the sake of self-containment.
Lemma 2.9. Let
$\pi :X \rightarrow C$
be an elliptic fibration and M a saliently ramified multisection defined over a field l. Let
$X_M$
and
$\pi _M: X_M \rightarrow M$
be as above. Then the section
$\sigma _M$
induced on
$X_M$
by
$(\iota , \mathrm {id}):M \rightarrow X \times _C M$
is linearly independent of the pull-back of the sections of
$\pi $
in
$\operatorname {\mathrm {MW}}(X_M,\pi _M,l)$
.
Proof. We observe that one can weaken the hypothesis of [Reference Pasten and SalgadoPS24, Lemma 3.1] and assume that the multisection B admits at least one ramification point in
$U_\pi $
. The proof is then taken verbatim from [Reference Pasten and SalgadoPS24] by considering T as the empty set.
Corollary 2.10. Let
$(X, \pi , C)$
and M be as above. Assume that M is defined over l and
$M(l)$
is infinite. Then
$$\begin{align*}\mathcal{R}(X, \pi, l) \text{ is infinite.} \end{align*}$$
In other words,
$\pi $
has the potential rank jump property.
In the remainder of this article, we focus on elliptic K3 surfaces. We take advantage of the lattice theoretic techniques available in this setting to prove that in all, except possibly two 17-dimensional families of elliptic K3 surfaces with non trivial Mordell–Weil group, the generic K3 surface admits at least one elliptic fibration with a multisection that satisfies the hypothesis of Corollary 2.10 over the field of definition of the elliptic fibration, that is, that have genus 0 or 1 and in the latter case, positive rank over the given field.
2.3 Lattice polarized K3 surfaces and genus 1 fibrations
One of the main tools in the study of families of K3 surfaces with prescribed geometric properties is the translation of such properties into lattice-theoretic conditions on the Picard group of surfaces and then the application of the theory of lattice polarized K3 surfaces described in [Reference DolgachevDo]. Here we give a short sketch of the main ideas in this theory.
The second cohomology group of any K3 surface is the unique (up to isometry) even unimodular lattice of signature
$(3,19)$
, often denoted by
$\Lambda _{K3}$
.
Let
$\Gamma $
be an even lattice of
$\mbox {rank}(\Gamma )=\gamma \leq 19$
and signature
$(1,\gamma -1)$
. Let us assume that there exists a primitive embedding of
$\Gamma $
in
$\Lambda _{K3}$
. Then, by the surjectivity of the period map of the K3 surfaces, there exists a K3 surface,
$X_0$
, defined over
$\mathbb {C}$
such that
$\operatorname {\mathrm {Pic}}(X_0)\simeq \Gamma $
.
Definition 2.11. A
$\Gamma $
-polarized K3 surface is a pair
$(X, j)$
where X is a K3 surface and
$j:\Gamma \hookrightarrow \operatorname {\mathrm {Pic}}(X)$
is a primitive embedding of lattices.
By considering the local deformations of the K3 surface
$X_0$
such that
$\operatorname {\mathrm {Pic}}(X_0)=\Gamma $
, one can construct a local moduli space
$\mathcal {X}_\Gamma $
of isomorphism classes of
$\Gamma $
-polarized K3 surfaces, see [Reference DolgachevDo]. Moreover, by gluing the local constructions and considering the restriction of the period map, one obtains a coarse moduli space of the
$\Gamma $
-polarized K3 surfaces. By this construction, one deduces that the family of the
$\Gamma $
-polarized K3 surfaces has dimension
$20-\gamma $
.
We observe that the Picard group of a very general K3 surface in the family of the
$\Gamma $
-polarized K3 surfaces is exactly
$\Gamma $
.
If a geometric property of a K3 surface can be completely described in terms of lattice polarized K3 surfaces, this, combined with the description of the moduli space of lattice polarized K3 surfaces, allows one to describe the family of K3 surfaces admitting the required geometric property.
The proposition below is an example of this phenomenon and is repeatedly used in what follows, hence even if it is well known, we recall here both the statement and the proof.
Proposition 2.12. A K3 surface X admits an elliptic fibration if, and only if, the lattice
$U\simeq \left [\begin {array}{ll}0&1\\1&0\end {array}\right ]$
is primitively embedded in
$\operatorname {\mathrm {Pic}}(X)$
. In particular, the family of K3 surfaces admitting an elliptic fibration is 18-dimensional and coincides with the family of U-polarized K3 surfaces.
Proof. This result is well known, cf. [Reference KondoKo, Lemma 2.1]. We briefly recall the idea of the proof. If a K3 surface admits an elliptic fibration, then there exists a smooth genus 1 curve, that is, a fiber of the fibration. We denote it by F and observe that
$F^2=0$
(by adjunction). Moreover, there exists a rational curve that is a section, denoted by
$\mathcal {O}$
. Then
$\mathcal {O}^2=-2$
(by adjunction) and
$F\mathcal {O}=1$
(since
$\mathcal {O}$
is a section). Therefore, the lattice
$U\simeq \langle F, F+\mathcal {O}\rangle $
is a sublattice of
$\operatorname {\mathrm {Pic}}(X)$
. Since U is a unimodular lattice, it does not have overlattices, so the embedding
$\langle F,F+\mathcal {O}\rangle \subset \operatorname {\mathrm {Pic}}(X)$
is primitive. The converse is more delicate; indeed, it is not true that each class with self-intersection 0 is necessarily the class of a smooth irreducible curve (and hence of a fiber of a genus 1 fibration). Nevertheless, given a primitive class in
$\operatorname {\mathrm {Pic}}(X)$
with self-intersection 0, it is true that up to reflections induced by smooth rational curves on the surface, one can assume that it is the class of a smooth irreducible curve, which necessarily has genus 1 by adjunction. So, let U be primitively embedded in
$\operatorname {\mathrm {Pic}}(X)$
. Considering (potentially) reflections in
$-2$
-curves, one can assume that one of the classes with self-intersection 0 is the class of a smooth irreducible curve of genus 1, say F, and then
$|F|$
defines a fibration onto
$\mathbb {P}(H^0(X,\mathcal {O}_X(F))^{\vee })=\mathbb {P}^1$
. Denoted
$\{F, v\}$
the base of U, with F as above,
$v-F$
is a
$-2$
-class with positive intersection with F, that is, it is an effective
$-2$
-class. Moreover, it intersects the fiber in one point and therefore it is either an irreducible curve, and in particular a section, or the union of several curves, among which there is a section. In both cases the fibration admits a section.
In the proof of the previous proposition we have that if there is a class of self-intersection 0 in the Picard group of a K3 surface X, then X admits a genus 1 fibration. This is true independently on the presence of a copy of U inside the Picard group, that is, a K3 surface admits a genus 1 fibration if and only if its Picard group contains a class with self-intersection 0. Since the lattice spanned by a class with self-intersection 0 is degenerate, it cannot be used to construct a family of lattice polarized K3 surfaces. This implies that a projective K3 surface which admits a genus 1 fibration is polarized with a rank 2 lattice which represents 0, that is, which contains at least one vector with self-intersection 0. There are infinitely many choices for these lattices, even up to isometries, which are classified and studied in [Reference van GeemenvG05].
2.3.1 K3 surfaces with more than one genus 1 fibration.
If a K3 surface contains two distinct genus 1 fibrations, then the class of the fiber of the first one, say
$F_1$
, and the one of the second one, say
$F_2$
, have a positive intersection
$F_1F_2=m>1$
. The intersection has to be larger than 1 since the base of a genus 1 fibration on a K3 surface is rational and so
$F_2$
cannot be a section. In particular,
$\langle F_1,F_2\rangle \simeq U(m)$
, with
$m>1$
, is primitively embedded in the Picard group of the surface. The generic K3 surface X such that
$\operatorname {\mathrm {Pic}}(X)\simeq U(m)$
admits two genus 1 fibrations whose classes of fibers meet in m points. Therefore the K3 surfaces that admit more than one genus 1 fibration are contained in the families of
$U(m)$
-polarized K3 surfaces for a certain
$m>1$
.
2.3.2 K3 surfaces with infinite automorphisms group and one genus 1 fibration.
Not only the properties of the elliptic fibrations, but also the ones of the automorphism group of a K3 surface can be studied by considering its Picard lattice, and therefore by using the theory of lattice polarized K3 surfaces. In a recent work, Brandhorst and Mezzedimi classified K3 surfaces that admit an infinite automorphism group and a unique genus 1 fibration ([Reference Brandhorst and MezzedimiBM24, Theorem 5.2]). Gvirtz-Chen and Mezzedimi compiled a list of all Picard lattices of such K3 surfaces, and a list of the Picard lattices that contain U as a sublattice, that is, for which the genus 1 fibration admits a section, making it an elliptic fibration (see the proof of [Reference Gvirtz-Chen and MezzedimiGM24, Theorem 4.5]). The list contains 49 lattices, among which 5 correspond to 17-dimensional families of elliptic K3 surfaces. The remaining 44 represent families of dimensions between 16 and 8 that arise as specializations of the 17-dimensional ones. The authors provide a magma code and a list of the 49 lattices on the website of the first author.
2.3.3 K3 surfaces with an elliptic fibration and low Picard number
Let
$(X,\pi ,\mathbb {P}^1)$
be an elliptic fibration on the K3 surface X. Then there are no multiple fibers of
$\pi $
, due to the presence of a section, nevertheless there can be reducible fibers which contain some nonreduced components. These are the fibers of type
$I_n^*$
,
$II^*$
,
$III^*$
or
$IV^*$
in the Kodaira classification of the singular fibers, see [Reference MirandaMir89] for notation. Each of these fibers has at least 5 components, and in particular at least 4 components which do not intersect the zero section. These components are independent in
$\operatorname {\mathrm {Pic}}(X)$
, and they are also independent with respect to the classes F and
$\mathcal {O}$
of the fiber and of the zero section of
$\pi $
, respectively. Hence, the presence of a fiber with nonreduced components forces the Picard number of the surface to be at least 6.
Let us now assume that
$(X,\pi ,\mathbb {P}^1)$
is an elliptic fibration on the K3 surface X that admits a torsion section of order n. The translation by this section is a symplectic automorphism of order n. By [Reference NikulinNik80] there cannot be symplectic automorphism of finite order on a K3 surface X if its Picard number is less than 8.
The previous observations give the following well-known result, which will be useful in the following.
Lemma 2.13. Let X be a K3 surface with
$\rho (X)< 6$
. Any elliptic fibration
$\pi :X\rightarrow \mathbb {P}^1$
admits neither fibers with nonreduced components nor torsion sections.
3 Bisections of genus 1 and elliptic fibrations
In what follows, we study bisections on elliptic K3 surfaces, with a focus on low-genus bisections and investigate, whenever possible, whether they are saliently ramified, due to their application to the rank jump problem (see Questions 1 and 2). Since the property of being saliently ramified is reflected in the local intersection behavior of the multisection with the elliptic fibers (Remark 2.6), we provide geometric realizations of the surface and the fibration that allow for the identification of the desired behavior, that is, nonreduced intersection with a smooth fiber.
Recall that K3 surfaces that admit an elliptic fibration
$\pi :X\rightarrow \mathbb {P}^1$
lie in the 18-dimensional space of U-polarized K3 surfaces (Proposition 2.12). In a generic member of this family, each smooth multisection M of
$\pi $
of degree
$m\geq 2$
has genus at least
$m^2+1$
. In fact,
$M\in \operatorname {\mathrm {Pic}}(X)=\langle F,\mathcal {O}\rangle $
can be written as
$M=aF+b\mathcal {O}$
. Then
$MF=m$
implies that
$b=m$
, while
$M\mathcal {O}=a-2m\geq 0$
, being the number of points at the intersection of two irreducible curves, so
$a\geq 2m$
. By adjunction,
$g(M)=(M^2+2)/2=am-m^2+1$
, so
$g(M)\geq m^2+1$
. To find lower genus smooth multisections we must consider elliptic fibrations on K3 surfaces with Picard rank at least 3. Then we study all the infinitely many 17-dimensional subfamilies of K3 surfaces admitting an elliptic fibration: these are indexed by
$d\in \mathbb {N}_{>0}$
and correspond to
$U\oplus \langle -2d \rangle $
-polarized K3 surfaces. We show that the generic members of all except three of these families admit a smooth low-genus bisection, that is, rational or of genus 1. The main results of this section are summarized in Theorem 3.2.
Notation 3.1. In what follows, we denote by
$\Lambda _d:=U\oplus \langle -2d\rangle $
and
$\mathcal {L}_d$
the family of the
$\Lambda _d$
-polarized K3 surfaces.
Theorem 3.2. Let X be a K3 surface with
$\rho (X)=3$
and
$X\in \mathcal {L}_d$
.
If
$d=1$
, then the unique elliptic fibration on X has a reducible fiber, its Mordell–Weil group is trivial and there are no smooth rational or genus 1 bisections.
For any other d, any elliptic fibration on X has no reducible fibers, the Mordell–Weil group of any elliptic fibration on X is isomorphic to
$\mathbb {Z}$
and admits a generator that intersects the zero section in
$d-2$
points.
Moreover, the following hold:
-
a) If
$d\leq 3$
, the unique elliptic fibration on X does not admit smooth multisections of genus
$g\leq 1$
. -
b) If
$d>3$
, then-
– any elliptic fibration on X admits a smooth rational bisection if, and only if,
$d\equiv 1\ \mod 2$
and this bisection is salient. -
– any elliptic fibration on X admits a smooth genus 1 bisection if, and only if,
$d\equiv 0 \ \mod 2$
and this bisection is salient.
-
We observe that by previous theorem, smooth rational and smooth genus 1 bisections of elliptic fibration cannot coexist, if
$\rho (X)\leq 3$
.
To prove this result we first consider the presence of specified bisections on K3 surfaces that admit a genus 1 fibration for which there are no sections, and then we extend the results to our context.
3.1 Bisections of genus 1 fibrations
Let X be a K3 surface that admits a genus 1 fibration
$\pi :X\rightarrow \mathbb {P}^1$
without a section. The class of the fiber F has trivial self-intersection, and there exists an ample class H with
$H^2=d>0$
among the generators of
$\operatorname {\mathrm {Pic}}(X)$
, whose rank is forced to be at least 2. In other words, a general K3 surface X with a genus 1 fibration and Picard number 2 has
$\operatorname {\mathrm {Pic}}(X)\simeq \Gamma _{b,c}$
, where
$\Gamma _{b,c}$
is the indefinite lattice of rank 2 defined as
$$ \begin{align} \Gamma_{b,c}:=\left\{\mathbb{Z}^2, (0,b,2c):= \begin{pmatrix} 0 & b \\ b & 2c \end{pmatrix}\right\}, \end{align} $$
where one can assume
$0\leq c<b$
, see [Reference van GeemenvG05, Remark 4.2]. Since
$\pi $
does not admit a section, the lattice
$\Gamma _{b,c}$
is not isometric to U. Since U is the unique hyperbolic even unimodular lattice of rank 2,
$\det (\Gamma _{b,c})\neq -1$
and so
$b\neq 1$
.
The presence of a bisection implies that
$b=2$
. Following [Reference van GeemenvG05], we observe that if
$b=2$
, there are two isomorphism classes of lattices
$\Gamma _{2,c}$
, namely
$\Gamma _{2,0}$
and
$\Gamma _{2,1}$
.
Corollary 3.3. Let X be a K3 surface with a genus 1 fibration
$\pi $
and
$\rho (X)=2$
. If
$\pi $
admits a smooth bisection then it admits a smooth bisection of genus 0 or 1 and the two possibilities are mutually exclusive.
Proof. If X admits a genus 1 fibration with a bisection and
$\rho (X)=2$
, then
$\operatorname {\mathrm {Pic}}(X)=\Gamma _{2,c}$
and by [Reference van GeemenvG05, Proposition 3.7], we can assume that
$c=0$
or
$c=1$
. Let
$D_1, D_2$
be two generators of
$\operatorname {\mathrm {Pic}}(X)$
with intersection matrix
$\Gamma _{2,c}$
. If
$c=0$
, then
$D_1$
and
$D_2$
are both classes of irreducible curves of genus 1 and
$D_i$
is a bisection for the genus 1 fibration given by
$D_j$
, for
$i,j\in \{1,2\}$
and
$i\neq j$
. If
$c=1$
, then one can assume that
$D_1$
is the class of a curve of genus 1. Since
$(D_2-D_1)^2=-2$
and
$(D_2-D_1)D_1>0$
,
$(D_2-D_1)$
is an effective class, which corresponds to a smooth rational curve on the surface or to a reducible curve with at least one component which is a smooth rational curve. Since there are exactly two classes of self-intersection
$-2$
in
$\Gamma _{2,1}$
(
$D_2-D_1$
and
$D_1-D_2$
) and only one of them is effective, we conclude that
$(D_2-D_1)$
is a smooth rational curve. Since
$(D_2-D_1)\cdot D_1=2$
, it is a rational bisection of the genus 1 fibration induced by
$D_1$
.
To show that the two possibilities are mutually exclusive, we prove that
$\pi $
admits a rational (resp. genus 1) bisection if and only if
$\operatorname {\mathrm {Pic}}(X)\simeq \Gamma _{2,1}$
(resp.
$\operatorname {\mathrm {Pic}}(X)\simeq \Gamma _{2,0})$
). We have already proven the only if condition. So now assume that
$\pi $
admits the required bisection B. Then
$\operatorname {\mathrm {Pic}}(X)$
contains the class F, of the fiber of
$\pi $
, and the class of B. Moreover,
$F^2=0$
and
$FB=2$
and
$B^2=-2$
(resp.
$B^2=0$
). Since there are no non trivial overlattices of finite index of
$\langle F,B\rangle $
which could appear as Picard group of a K3 surface, it follows that
$\pi $
admits a rational bisection if and only if
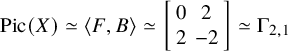$\operatorname {\mathrm {Pic}}(X)\simeq \langle F,B\rangle \simeq \left [\begin {array}{cc}0&2\\2&-2\end {array}\right ]\simeq \Gamma _{2,1}$
, where the isometry between the last two lattices was already proven (it suffices to compute the intersection form on
$\langle F,2F+B\rangle $
). Similarly,
$\pi $
admits a genus 1 bisection if and only if
$\operatorname {\mathrm {Pic}}(X)\simeq \langle F,B\rangle \simeq \Gamma _{2,0}$
. Since
$\Gamma _{2,0}$
does not contain classes with self intersect 2 and
$\Gamma _{2,1}$
does, they can not be isometric.
In what follows, we give a geometric realization of K3 surfaces with a genus 1 fibration that admits a smooth bisection, according to the genus of the bisection. Moreover, we show that, for a general K3 in the family, the smooth bisection described in Corollary 3.3 is saliently ramified for the genus 1 fibration.
Proposition 3.4. The family
$\mathcal {F}_{\mathrm {{rat}}}$
of K3 surfaces which admit a genus 1 fibration with a smooth rational bisection B is 18-dimensional and coincides with the family of the
$\langle 2\rangle \oplus \langle -2\rangle $
-polarized K3 surfaces, that is, with the family of the K3 surfaces which are double covers of
$\mathbb {P}^2$
branched on a sextic with a simple node.
For generic X in the family, the bisection B is saliently ramified.
Proof. Keeping the notation introduced in the proof of Corollary 3.3, the first part follows by considering
$\{D_2, D_2-D_1\}$
as base of the Picard group.
One can assume that the divisor
$D_2$
is nef and therefore
$\varphi _{|D_2|}:X\rightarrow \mathbb {P}^2$
is a
$2:1$
cover branched on a sextic
$C_6$
. Since
$D_2\cdot (D_2-D_1)=2-2=0$
,
$\varphi _{|D_2|}$
contracts the rational curve
$B=D_2-D_1$
to a singular point p of the branch sextic. The class of a fiber F is
$D_1=D_2-B$
, so it corresponds to the pencil
$\mathcal {P}$
of lines in
$\mathbb {P}^2$
passing through
$p=\varphi _{|D_2|}(B)$
. Each line
$\ell \in \mathcal {P}$
intersects the branch sextic
$C_6$
in p (with multiplicity 2) and in other 4 points. Hence
$\varphi _{|D_2|}$
restricted to
$\varphi _{|D_2|}^{-1}(\ell )$
is
$2:1$
cover of the rational curve
$\ell $
which is branched in 4 points; in particular it is a curve of genus 1, and indeed a fiber of
$\pi =\varphi _{|D_1|}$
.
The singular fibers of
$\pi $
are mapped by
$\varphi _{|D_2|}$
to lines of the pencil
$\mathcal {P}$
for which one intersection point with
$C_6-\{p\}$
has multiplicity higher than 1.
To construct the smooth surface X one first blows up
$\mathbb {P}^2$
in p and then considers the double cover branched on the strict transform of
$C_6$
. The exceptional divisor E of the blow-up is not in the branch locus. It intersects each line of
$\mathcal {P}$
in one point and hence its double cover B intersects the fiber corresponding to a line in
$\mathcal {P}$
in two points. In fact, B is a bisection. The double cover
$B\rightarrow E$
branches in the two points corresponding to the lines in
$\mathcal {P}$
that are the principal tangents of
$C_6$
through the node p. Since the exceptional divisor E parametrizes the lines in
$\mathcal {P}$
, we obtain that
$\pi :X\rightarrow \mathbb {P}^1\simeq E$
. The previous considerations show the following.
-
• The singular fibers of
$\pi $
are fibers over the points
$q\in E\simeq \mathbb {P}^1$
such that
$q=E\cap \widetilde {\ell _q}$
where
$\widetilde {\ell _q}$
is the strict transform of a line
$\ell _q\in \mathcal {P}$
and
$\ell _q$
is a line which intersects
$C_6-\{p\}$
in at least one point with multiplicity higher than 1; -
• The double cover
$B\rightarrow \mathbb {P}^1\simeq E$
branches on the points corresponding to the principal tangents of
$C_6$
in p.
Generically, each principal tangent to
$C_6$
in p intersects
$C_6$
in 3 other points with multiplicity 1, so generically it corresponds to a smooth fiber of the genus 1 fibration. Hence, generically, B branches on points corresponding to smooth fibers, and in particular it is saliently ramified.
Remark 3.5. In the setting of Proposition 3.4,
-
a) the result described on the genus 1 fibration induced by the pencil of the lines
$\mathcal {P}$
remains true on certain specializations of
$C_6$
. In particular, it remains true if the specialization
$C_6'$
of
$C_6$
is such that: the double cover of
$\mathbb {P}^2$
branched on
$C_6'$
is still a K3 surface X and the point p remains a simple node for
$C_6'$
; the latter condition guarantees that the K3 surface X admits a genus 1 fibration induced by
$\mathcal {P}$
and that
$B=\varphi _{|D_2|}^{-1}(p)$
is an irreducible smooth rational curve. One automatically obtains that B is a bisection of the genus 1 fibration. So, even under these specializations, B is a smooth rational bisection of a genus 1 fibration on a K3 surface and it is generically ramified on smooth fibers. -
b) There could be special sextic curves
$C_6$
for which a principal tangent in p intersects
$C_6$
in one point with multiplicity 1 and one point with multiplicity 2. If both principal tangents are of this type, then B is a smooth rational bisection that is not saliently ramified. -
c) Let
$\ell $
be a line not containing p and bitangent to
$C_6$
, then
$\varphi _{|D_2|}^{-1}(\ell )$
is a singular rational bisection of the fibration
$\varphi _{|D_1|}$
and it is generically saliently ramified.
Proposition 3.6. The family
$\mathcal {F}_{g=1}$
of K3 surfaces that admit a genus 1 fibration with a smooth genus 1 bisection B is 18-dimensional and coincides with the family of
$U(2)$
-polarized K3 surfaces, that is, with the family of the K3 surfaces which are double covers of
$\mathbb {P}^1\times \mathbb {P}^1$
branched on a curve of bidegree
$(4,4)$
.
The K3 surfaces in this family admit two elliptic fibrations with infinitely many smooth saliently ramified genus 1 bisections.
Proof. Let X be a K3 surface endowed with a genus 1 fibration
$\pi :X\rightarrow \mathbb {P}^1$
with a smooth genus 1 bisection. Denote by F the class of the fiber and B the class of the bisection, then the lattice
$\langle F, B\rangle $
is isometric to
$U(2)$
and the divisor
$F+B$
defines a map
$\varphi _{|F+B|}:X\rightarrow \mathbb {P}^1\times \mathbb {P}^1\subset \mathbb {P}^3$
that realizes X as a double cover of the quadric
$\mathbb {P}^1\times \mathbb {P}^1$
branched on a curve
$C_{4,4}$
of bidegree
$(4,4)$
. The equation of
$C_{4,4}$
is of the following type
$$ \begin{align*}x_0^4a_4(y_0:y_1)+x_0^3x_1b_4(y_0:y_1)+x_0^2x_1^2c_4(y_0:y_1)+x_0x_1^3d_4(y_0:y_1)+x_1^4e_4(y_0:y_1),\end{align*} $$
with
$a_4,b_4,c_4,d_4,e_4$
homogeneous polynomials of degree 4. The singular fibers correspond to the inverse image on X of the curves
$D_{(\alpha ,\beta )}=V(\alpha x_0-\beta x_1)$
of bidegree
$(1,0)$
, such that
$D_{(\alpha ,\beta )}\cap C_{4,4}$
contains at least one point with multiplicity greater than 1. There is a finite number of such curves, generically 24, which correspond to the 24 singular fibers of type
$I_1$
(that is, nodal) of a genus 1 fibration on X. Let us now consider a
$(0,1)$
-curve
$\ell _{(\gamma ,\delta )}$
with equation
$\gamma y_0-\delta y_1=0$
. For a generic choice of
$\gamma $
and
$\delta $
,
$\ell _{(\gamma ,\delta )}\cap C_{4,4}$
consists of 4 distinct points, so that the inverse image of
$\ell _{(\gamma ,\delta )}$
is a double cover of a rational curve branched in 4 points, that is, it is a smooth genus 1 curve on X. Since
$\ell _{(\gamma ,\delta )}$
is a section of the fibration
$\mathbb {P}^1_x\times \mathbb {P}^1_y\rightarrow \mathbb {P}^1_x$
, its inverse image in the double cover is a bisection of
$\pi :X\rightarrow \mathbb {P}^1_x$
. Again for a generic choice of
$\gamma $
and
$\delta $
, the points
$\ell _{(\gamma ,\delta )}\cap C_{4,4}$
are not contained in any curve
$D_{(\alpha , \beta )}$
corresponding to a singular fiber. This guarantees that the bisection which is the double cover of
$\ell _{(\gamma ,\delta )}$
is branched on smooth fibers, that is, is saliently ramified. So we find infinitely many saliently ramified genus 1 bisections of the genus 1 fibration on
$X\rightarrow \mathbb {P}^1_x$
.
Remark 3.7. Parallel to Remark 3.5(c), in the setting of the proof of Proposition 3.6, it is possible to specialize
$\ell _{(\gamma ,\delta )}$
in such a way that two of the intersection points with
$C_{4,4}$
coincide. In this case, its inverse image is a singular rational curve, which is still a bisection of
$\pi $
. For generic choice of
$C_{4,4}$
, this singular rational bisection is saliently ramified (with the same argument we used in the general context).
This specialization depends on the choice of
$\ell _{(\gamma ,\delta )}$
, and does not require a specialization of
$C_{4,4}$
, hence it appears on the general member of the family of K3 surfaces we are considering.
3.2 Elliptic K3 surfaces of Picard number 3
We specialize further in the families discussed in Subsection 3.1 and consider K3 surfaces with an elliptic fibration that admits a bisection. The coexistence of a section and of a bisection of low genus, implies that the Picard number of such K3 surfaces is at least 3, since both U and
$\Gamma _{2,c}$
have to be primitively embedded in the Picard lattice (see Propositions 2.12 and 3.4). We deal with the general case, that is, Picard number 3. We first present general results (Lemma 3.8) to later restrict to bisections.
Lemma 3.8. Let X be an elliptic K3 surface with Picard number 3. Then there exists
$d>0$
such that
$\operatorname {\mathrm {Pic}}(X)\simeq U\oplus \langle -2d\rangle $
. Moreover, for every elliptic fibration
$\pi :X\rightarrow \mathbb {P}^1$
,
-
•
$\mbox {rank}(\operatorname {\mathrm {MW}}(\pi ))=0$
if and only if
$d=1$
if and only if
$\pi $
admits a reducible fiber; -
•
$\mbox {rank}(\operatorname {\mathrm {MW}}(\pi ))=1$
if and only if
$d>1$
if and only if
$\pi $
has no reducible fiber. In this case
$\operatorname {\mathrm {MW}}(\pi )$
is generated by a section
$S_1$
that intersects the zero section in
$d-2$
points.
Proof. The result was already presented in [Reference GarbagnatiGar17, Sec. 4.3], but for the reader’s convenience we recap the key ideas. Since X admits an elliptic fibration, U has to be primitively embedded in its Picard group, see Proposition 2.12. Since the Picard number is 3, and the Picard lattice has signature
$(1,2)$
, the orthogonal complement of U in the Picard group is
$\langle -2d\rangle $
for a certain positive d, and
$\operatorname {\mathrm {Pic}}(X)$
is an overlattice of finite index of
$U\oplus \langle -2d\rangle $
. But there are no even lattices which are overlattices of finite nontrivial index of
$U\oplus \langle -2d\rangle $
in which
$\langle -2d\rangle $
is primitive, so
$\operatorname {\mathrm {Pic}}(X)\simeq U\oplus \langle -2d\rangle $
. This argument holds for every elliptic fibration on X, that is, every elliptic fibration on X is associated to an embedding of U in
$\operatorname {\mathrm {Pic}}(X)$
, whose orthogonal complement is
$\langle -2d\rangle $
. So all the geometric properties that depend only on the intersection numbers of classes in
$\operatorname {\mathrm {Pic}}(X)$
are common to all elliptic fibrations on X. We denote by
$u_1,u_2,b_3$
the base of
$\operatorname {\mathrm {Pic}}(X)$
on which the bilinear form is
$U\oplus \langle -2d\rangle $
, and we fix
$F:=u_1$
and
$\mathcal {O}=u_2-u_1$
. By Lemma 2.13, the torsion part of
$\operatorname {\mathrm {MW}}(\pi )$
is trivial.
If
$d=1$
, then the vector
$b_3$
is a
$(-2)$
-class and hence (up to a sign) the class of an irreducible component of a reducible fiber that does not intersect the zero section. By the Shioda–Tate formula, the presence of this reducible fiber is equivalent to
$\operatorname {\mathrm {MW}}(\pi )=\{1\}$
.
If
$d>1$
, then there are no
$(-2)$
-classes orthogonal to U and so
$\pi $
has no reducible fibers. Again by the Shioda–Tate formula, this is equivalent to
$\operatorname {\mathrm {MW}}(\pi )\simeq \mathbb {Z}$
. The classes of the sections of
$\pi $
are
$$ \begin{align*}S_n:=dn^2F+\mathcal{O}+nb_3\end{align*} $$
and the isomorphism
$\operatorname {\mathrm {MW}}(\pi )\simeq \mathbb {Z}$
maps
$\mathcal {O}$
to
$0$
and
$S_n$
to n. In particular, if
$\operatorname {\mathrm {Pic}}(X)\simeq U\oplus \langle -2d\rangle $
and
$d>1$
, then X admits an elliptic fibration without reducible fibers such that the generator
$S_1$
of
$\operatorname {\mathrm {MW}}(\pi )$
intersects the zero section in
$d-2$
, that is,
$S_1\mathcal {O}=d-2$
. Observe that
$S_1\mathcal {O}=S_{-1}\mathcal {O}$
and more in general
$S_n\mathcal {O}=S_{-n}\mathcal {O}$
.
Recalling Notation 3.1, by the previous discussion, if
$d>1$
the 17-dimensional family
$\mathcal {L}_d$
is the family whose general members are K3 surfaces that admit an elliptic fibration
$\pi $
without reducible fibers with
$\mbox {rank}(\operatorname {\mathrm {MW}}(\pi ))=1$
such that the generator of
$\operatorname {\mathrm {MW}}(\pi )$
intersects the zero section in
$d-2$
points.
Remark 3.9. As explained in the proof of Lemma 3.8, there could be more than one elliptic fibration on a K3 surface
$X\in \mathcal {L}_d$
for a determined values of d. Nevertheless, if X is general in its family, in particular if
$\rho (X)=3$
, then all these elliptic fibrations admit the same configurations of reducible fibers, their Mordell–Weil groups are isomorphic and the generator of the Mordell–Weil group intersects the zero section in the same number of points (briefly, their Mordell–Weil lattices are isometric).
As already recalled in Section 2, there is a classification of the K3 surfaces that admit a unique elliptic fibration given by Brandhorst and Mezzedimi ([Reference Brandhorst and MezzedimiBM24]) and Mezzedimi and Gvirtz-Chen ([Reference Gvirtz-Chen and MezzedimiGM24]).
Proposition 3.10. Let X be a K3 surface with
$\rho (X)=3$
, with a unique genus 1 fibration. Assume moreover that the genus 1 fibration admits at least one section, that is, it is an elliptic fibration. Then X belongs to one of the six families
$\mathcal {L}_d$
for
$d=1,2,3,5,7,13$
. Moreover,
$\mathrm {Aut}(X)$
is infinite if, and only if,
$d>1$
.
Proof. See the proof of [Reference Gvirtz-Chen and MezzedimiGM24, Theorem 4.5]. The authors provide a magma code and a list of the 49 lattices associated with K3 surfaces X with a unique genus 1 fibration in the website of the first author. The 49 lattices arise as specializations of at least one of the 6 lattices of rank 3 listed in the statement.
If
$X\in \mathcal {L}_d$
and
$d>1$
, then each elliptic fibration admits an infinite order section which yields, by translation, an automorphism of infinite order preserving the elliptic fibration. We discuss, in what follows, some properties of the automorphisms group of
$X\in \mathcal {L}_d$
.
3.2.1 Automorphisms of K3 surfaces in
$\mathcal {L}_d$
Let X be a general K3 surface in a family
$\mathcal {L}_d$
. Fix the base
$\{u_1,u_2,b_3\}$
of
$\Lambda _{d}$
considered in proof of Lemma 3.8. The elliptic involution on each fiber of
$\pi $
extends to an automorphism on X that acts on the chosen base of
$\Lambda _d$
as follows:
$$ \begin{align*}\varepsilon=\left[\begin{array}{rrr}1&0&0\\ 0&1&0\\ 0&0&-1\end{array}\right]\end{align*} $$
If
$d\geq 2$
, the translation by the section
$S_1$
is an automorphism of infinite order of the K3 surface, which acts on the base
$\{F,\mathcal {O},b_3\}$
as follows:
$$ \begin{align*}T_1=\left[\begin{array}{rrr}1&d&2d\\ 0&1&0\\ 0&1&1 \end{array}\right]\end{align*} $$
(indeed, by definition,
$T_1(F)=F$
,
$T_1(\mathcal {O})=S_1$
and
$T_1(S_1)=S_2$
).
If
$d=1$
, the previous matrix is still associated with an isometry of the lattice
$\Lambda _{d}$
, but this isometry cannot be associated with an automorphism since it maps
$F-b_3$
to
$-F-b_3$
. The former is an effective class corresponding to the component of
$I_2$
-fiber meeting the zero section. The latter is not effective since
$(-F-b_3)\mathcal {O}=-1$
.
If
$d>1$
, the group
$\langle T_1, \varepsilon \rangle $
is also generated by
$\varepsilon $
and
$ T_1\circ \varepsilon $
, and hence it is isomorphic to
$\left (\mathbb {Z}/2\mathbb {Z}\right )*\left ( \mathbb {Z}/2\mathbb {Z}\right )$
.
If
$d\neq 1,2,3,5,7,13$
, the surface X admits more than one elliptic fibration. Let
$\pi '$
be an elliptic fibration, then associated with
$\pi '$
there are two automorphisms
$\varepsilon '$
and
$T_1'$
that are respectively induced by the elliptic involution and by the translation on each fiber. If
$\pi $
and
$\pi '$
are not equivalent up to automorphisms,
$\varepsilon '$
and
$T_1'$
are not conjugate to
$\varepsilon $
and
$T_1$
in
$\mathrm {Aut}(X)$
.
Remark 3.11. If X is general in its family, then it is
$\mathrm {Aut}$
-general, that is, its automorphism group contains only symplectic automorphisms of infinite order (e.g.,
$T_1$
) and nonsymplectic automorphisms of order 2 (e.g.,
$\varepsilon $
). In particular, this implies that X does not admit isotrivial elliptic fibrations with j-invariant of the generic fiber equal to
$0$
or
$1728$
. Indeed, otherwise the complex multiplication on each fiber would induce an automorphism on the surface which is nonsymplectic and has order 3 or 4, respectively. If an elliptic fibration is isotrivial with a constant j-invariant not equal to 0 or 1728, then the reducible fibers are forced to be of type
$I_0^*$
, and in particular with non reduced components. By Lemma 2.13, these isotrivial fibrations cannot appear if the Picard number of X is at most 3, that is, for the surfaces considered in this paper.
In what follows, we continue the discussion on elliptic K3 surfaces with Picard number 3 that admit a smooth bisection. We present our results according to the genus of the smooth bisection.
3.3 Smooth rational bisections on elliptic K3 surfaces
Let X be a K3 surface with an elliptic fibration
$\pi :X\rightarrow \mathbb {P}^1$
and a smooth rational bisection B. Then, in particular X belongs to a subfamily of
$\mathcal {F}_{\mathrm {{rat}}}$
considered in Proposition 3.4 and, of course, to the family of K3 surfaces admitting an elliptic fibration.
Definition 3.12. Let
$\mathcal {F}_{\mathrm {{rat}}}^x$
be the family of K3 surfaces with an elliptic fibration admitting a smooth rational bisection which intersects the zero section in
$x\geq 0$
points (possibly counted with multiplicity).
Proposition 3.13. The family
$\mathcal {F}_{\mathrm {{rat}}}^x$
and the family
$\mathcal {L}_{2x+5}$
coincide.
Proof. Let X be a general K3 surface in
$\mathcal {F}_{\mathrm {{rat}}}^x$
and recall that
$x\geq 0$
since it is the intersection number of two irreducible distinct curves. The classes F, of the fiber of the fibration,
$\mathcal {O}$
, of the zero section of the fibration, and B, of the rational bisection, are contained in the Picard lattice of X. Let us denote
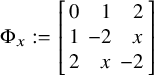$\Phi _x:=\left [\begin {array}{rrr}0&1&2\\1&-2&x\\2&x&-2\end {array}\right ]$
the lattice
$\langle F,\mathcal {O},B\rangle $
. By the base change
$\{F,\mathcal {O}, (-4-x)F-2\mathcal {O}+B\}$
, we obtain a lattice isometric to
$\Phi _x$
which is necessarily primitively embedded in
$\operatorname {\mathrm {Pic}}(X)$
. Indeed, we already observed that the sublattice
$\langle F,\mathcal {O}\rangle $
has to be primitively embedded in
$\operatorname {\mathrm {Pic}}(X)$
; the class
$(-4-x)F-2\mathcal {O}+B$
is not a divisible class in
$\operatorname {\mathrm {Pic}}(X)$
, since the coefficient of B is 1; there are no even overlattices of finite index of
$\langle F,\mathcal {O}, (-4-x)F-2\mathcal {O}+B\rangle $
in which both
$\langle F,\mathcal {O}\rangle $
and
$\langle (-4-x)F-2\mathcal {O}+B\rangle $
are primitively embedded. Hence, we proved that the family
$\mathcal {F}_{\mathrm {{rat}}}^x$
is the family of the
$\Phi _x$
-polarized K3 surfaces.
To compare the families
$\mathcal {F}_{\mathrm {{rat}}}^x$
and
$\mathcal {L}_{2x+5}$
, it suffices to show that the lattices
$\Phi _x$
and
$\Lambda _{2x+5}$
are isometric. We consider again the base
$\{F, F+\mathcal {O}, (-4-x)F-2\mathcal {O}+B\}$
of
$\Phi _x$
. The intersection form on this base is
$U\oplus \langle -2(2x+5)\rangle $
. This proves that
$\operatorname {\mathrm {Pic}}(X)$
is isometric to
$\Lambda _{d}$
if
$d=2x+5$
, with
$x\geq 0$
.
In the proof of Proposition 3.13, we give the base change from
$\{F,\mathcal {O}, B\}$
to
$\{u_1,u_2,b_3\}$
. The inverse base change gives
$B=b_3+(4+x)F+2\mathcal {O}=(2+x)u_1+2u_2+b_3$
. So if
$X\in \mathcal {L}_d$
with
$d\equiv 1\ \mod 2$
and
$d\geq 5$
, where
$2x+5=d$
, the class of the smooth rational bisection for
$\pi $
is
$$ \begin{align}B=\frac{d+3}{2}F+2\mathcal{O}+b_3.\end{align} $$
Remark 3.14. In the previous situation (i.e.,
$\operatorname {\mathrm {NS}}(X)\simeq \Lambda _d$
,
$d\equiv 1\ \mod 2$
,
$d\geq 5$
), we have shown that every elliptic fibration on X admits a smooth rational bisection B such that
$B\mathcal {O}=x=\frac {d-5}{2}$
, whose class is given in (3.2). The parity of
$B\mathcal {O}$
is the same as the one of
$BS_n$
for every
$n\in \mathbb {Z}$
and depends on d. More specifically,
$BS_n=\frac {d+3}{2}+2dn(n-1)-4\equiv \frac {d+3}{2}\ \mod 4$
, that is,
$BS_n\equiv x\ \mod 4$
. In particular:
$$ \begin{align} \begin{array}{c}B\mathcal{O}\equiv BS_n\equiv 0\quad \mod 2 \Leftrightarrow d\equiv 1\quad \mod 4\\ B\mathcal{O}\equiv BS_n\equiv 1\quad \mod 2 \Leftrightarrow d\equiv 3\quad \mod 4.\end{array} \end{align} $$
Remark 3.15. If
$\operatorname {\mathrm {NS}}(X)\simeq \Lambda _3$
(i.e.,
$d=3$
), then the class
$B=3F+2\mathcal {O}+b_3$
as in (3.2) is still a
$(-2)$
-class with intersection 2 with F, but it does not correspond to an irreducible curve, since
${B\mathcal {O}=-1<0}$
and
$\mathcal {O}$
is an irreducible curve. Indeed, the class B is not an irreducible bisection, but the sum of two sections, namely
$S_1=3F+\mathcal {O}+b_3$
and
$\mathcal {O}$
.
The automorphisms
$T_1$
and
$\varepsilon $
act as follows on the bisection B:
$$ \begin{align*}T_1(B)=6(x+2)F-4\mathcal{O}+3B,\ \ \varepsilon(B)=2(4+x)F+4\mathcal{O}-B \mbox{ and } T_1(\varepsilon(B))=B.\end{align*} $$
In particular, there is an involution of X that fixes the multisection B. We observe that
$T_1^n(B)$
and
$\varepsilon (B)$
are not equal to B, and since they are isometries and F is fixed by both of them, the curves
$T_1^n(B)$
and
$\varepsilon (B)$
are other rational bisections of the fibration.
By the proof of Proposition 3.4, K3 surfaces in
$\mathcal {F}_{rat}^x$
admit natural geometric realizations as a double cover of the plane branched on an irreducible nodal sextic. The presence of a section for the genus 1 fibration is equivalent to the splitting of a certain plane curve on the double cover. We discuss this in detail in what follows.
Proposition 3.16. Let
$X\in \mathcal {L}_{2x+5}$
, then there exists
$f:X\rightarrow \mathbb {P}^2$
a double cover of
$\mathbb {P}^2$
branched on a plane sextic
$C_6$
with a simple node at a point p, such that there exists a rational curve
$R\subset \mathbb {P}^2$
of degree
$x+1$
passing through p with multiplicity x that splits in the double cover.
The pencil of lines through p induces an elliptic fibration on X whose zero section is one of the components of
$f^{-1}(R)$
.
The cover involution of
$f:X\rightarrow \mathbb {P}^2$
is the involution
$T_1\circ\varepsilon$
and preserves the class of the bisection B.
Proof. For each
$x\geq 0$
,
$\mathcal {F}_{\mathrm {{rat}}}\supset \mathcal {F}_{\mathrm {{rat}}}^x$
and indeed
$\langle F,F+B\rangle $
is a copy of the lattice
$\Gamma _{2,1}$
primitively embedded in
$\Phi _x\simeq \Lambda _{2x+5}$
. By Proposition 3.4, the surfaces in the 18-dimensional family
$\mathcal {F}_{\mathrm {{rat}}}$
are realized as double covers of
$\mathbb {P}^2$
branched on a sextic
$C_6$
with a node at a point p, with a genus 1 fibration given by the pull-back of the pencil of lines through p; this realization holds for
$X\in \mathcal {F}_{\mathrm {{rat}}}^x$
. Indeed, the linear system of
$H=F+B$
gives the
$2:1$
map
$\varphi _{|H|}:X\rightarrow \mathbb {P}^2$
. As discussed in Proposition 3.4, B is contracted to the singular point p of
$C_6$
by the map
$\varphi _{|H|}$
.
The class of the zero section
$\mathcal {O}$
is such that
$\mathcal {O}H=1+x$
and
$\mathcal {O}B=x$
. Since
$\mathcal {O}$
intersects each fiber of
$\pi $
in exactly one point, its image
$R:=\varphi _{|H|}(\mathcal {O})\subset \mathbb {P}^2$
intersects each line at exactly one point different from p and R splits in the double cover, that is,
$(\varphi _{|H|})^{-1}(R)=\mathcal {O}\cup D$
where D is another section of the fibration
$\pi $
. Since
$\mathcal {O}H=x+1$
,
$\mathcal {O}B=x$
and R splits in the double cover, R is a plane curve of degree
$x+1$
which passes through p with multiplicity x.
We observe that
$\mathcal {O}\cap D$
are the inverse image of the points
$R\cap C_6$
different from p (since the point p was blown up). In particular,
$\mathcal {O}D=(6(x+1)-2x)/2=2x+3$
where we used that the degree of
$C_6$
is 6; the one of R is
$(x+1)$
; the multiplicity of
$C_6$
in p is 2; the one of R is x; each intersection point between
$C_6$
and R has multiplicity two when considered on X, so the number of intersection points on X is half of the intersection product considered in
$\mathbb {P}^2$
. Hence
$\mathcal {O}D=2x+3=(2x+5)-2=d-2$
, which is the intersection number between
$\mathcal {O}$
and either
$S_1$
or
$S_{-1}$
.
The cover involution of
$\varphi _{|H|}:X\rightarrow \mathbb {P}^2$
preserves the classes H and B. Recalling that
$H=F+B$
, we obtain that the cover involution preserves the classes F and B, and maps
$\mathcal {O}$
to D. In particular, it coincides with the involution
$ T_1\circ \varepsilon $
, which maps
$\mathcal {O}$
to
$S_{1}$
, which implies that
$D=S_{1}$
.
Since
$S_{n}H=2n^2d- 2nd+\frac {d-3}{2}$
and
$S_{n}B=2n^2d- 2nd+\frac {d-5}{2}$
, the sections
$S_{n}$
of the fibration
$\varphi _{|F|}$
are mapped by
$\varphi _{|H|}$
to plane curves of degree
$2n^2d- 2nd+\frac {d-3}{2}$
passing through p with multiplicity
$2n^2d- 2nd+\frac {d-5}{2}$
and splitting in the double cover
$\varphi _{|H|}:X\rightarrow \mathbb {P}^2$
.
Remark 3.17. In the case
$\operatorname {\mathrm {NS}}(X)\simeq \Lambda _3$
, we already observed that there is a class
$B=3F+2\mathcal {O}+b_3$
such that
$B^2=-2$
and
$BF=2$
, but it does not correspond to an irreducible curve. Similarly, one observes that the class
$H=F+B=4F+2\mathcal {O}+b_3$
is still associated to a
$2:1$
map
$\varphi _{|H|}:X\rightarrow \mathbb {P}^2$
, but in this case the branch locus of the double cover has a cusp and not a simple node, indeed
$H\mathcal {O}=HS_1=0$
and hence
$\varphi _{|H|}$
contracts two smooth irreducible curves which form an
$A_2$
-configuration to a point (see also [Reference Fortuna and MezzedimiFM21, Section 6.3]).
3.4 Smooth genus 1 bisections on elliptic K3 surfaces
Let X be a K3 surface which admits an elliptic fibration
$\pi :X\rightarrow \mathbb {P}^1$
and a genus 1 bisection B.
Definition 3.18. Let
$\mathcal {F}_{g=1}^x$
be the family of elliptic K3 surfaces admitting a smooth genus 1 bisection which intersects the zero section in x points (possibly counted with multiplicity).
Lemma 3.19. The family
$\mathcal {F}^x_{g=1}$
coincides with the family
$\mathcal {L}_{2x+4}$
.
Proof. The proof is analogous to the one of the case of rational bisection (see Proposition 3.13), by observing that the classes
$F,\ \mathcal {O},\ B$
have the following intersection properties
$F^2=B^2=0$
,
$F\mathcal {O}=1$
,
$FB=2$
and
$B\mathcal {O}=x$
and that there is a base change which gives
$u_1=F$
,
$u_2=F+\mathcal {O}$
and
$b_3=-(x+4)F-2O+B$
.
Hence the K3 surfaces which admit an elliptic fibration with a smooth genus 1 bisection which intersects the zero section in x points, correspond to the K3 surfaces that are
$\Lambda _{d}$
polarized with
$d\geq 4$
and
$d\equiv 0\ \mod 2$
.
The base change between
$\{F,\mathcal {O}, B\}$
and
$\{u_1,u_2,b_3\}$
gives
$B=b_3+(4+x)F+2\mathcal {O}=(2+x)u_1+2u_2+b_3$
, and this allows one to compute the image of B for the automorphisms
$T_1$
,
$\varepsilon $
and their composition:
$$ \begin{align*}T_1(B)=6(x+2)F-4\mathcal{O}+3B,\ \ \varepsilon(B)=2(4+x)F+4\mathcal{O}-B \mbox{ and } T_1(\varepsilon(B))=B.\end{align*} $$
In particular we observe that there is an involution of X which fixes the multisection B, and that the curves
$T_1^n(B)$
and
$\varepsilon (B)$
are other genus 1 bisections of the fibration.
Proposition 3.20. Let
$X\in \mathcal {L}_{2x+4}$
, then there exist
$f:X\rightarrow \mathbb {P}^1\times \mathbb {P}^1\subset \mathbb {P}^3$
, a double cover of
$\mathbb {P}^1 \times \mathbb {P}^1$
branched over a smooth curve
$C_{4,4}$
of bidegree
$(4,4)$
, and a rational curve
$R\subset \mathbb {P}^1 \times \mathbb {P}^1$
of bidegree
$(1,x)$
that splits in the double cover.
The pencil of
$(0,1)$
-curves induces an elliptic fibration on X whose zero section is one of the components of
$f^{-1}(R)$
.
The cover involution of
$f:X\rightarrow \mathbb {P}^1 \times \mathbb {P}^1$
is the involution
$T_1\circ\varepsilon$
. It preserves the class of the bisection B.
Proof. The proof is analogous to the one in the case of rational bisection (see Proposition 3.16).
Remark 3.21. We observe that if
$\operatorname {\mathrm {NS}}(X)\simeq \Lambda _2$
, the class
$B=3F+2\mathcal {O}+b_3$
is still a class such that
$B^2=0$
and
$BF=2$
, but it does not correspond to an irreducible curve of genus
$1$
since
$B\mathcal {O}=-1$
. Therefore, it is not a bisection, but the sum of two sections and a fiber, indeed
$B=S_1+\mathcal {O}+F$
. A geometric description of this surface is given in [Reference GarbagnatiGar17], where it is shown that the map
$\varphi _{|4F+2\mathcal {O}|}$
exhibits X as a double cover of a cone over the rational normal curve in
$\mathbb {P}^4$
. A Weierstrass equation of the elliptic fibration on this surface is given in [Reference Fortuna and MezzedimiFM21, Section 6.2].
Remark 3.22. Similarly to the Remark 3.14, we observe that
$B\mathcal {O}\equiv BS_n\equiv 1\ \mod 2$
if
$d\equiv 2\ \mod 4$
and
$B\mathcal {O}\equiv BS_n\equiv 0\ \mod 2$
if
$d\equiv 0\ \mod 4$
.
3.5 Proof of Theorem 3.2
We recap the previous results to give an explicit proof of Theorem 3.2.
In Lemma 3.8, we proved that the Picard lattice of a K3 surface with Picard number 3 admitting an elliptic fibration is isometric to
$\Lambda _d$
for a positive integer d and we described the properties of the elliptic fibrations on a K3 surface that is
$\Lambda _d$
-polarized.
Then we defined the families
$\mathcal {F}_{\mathrm {{rat}}}^x$
(resp.
$\mathcal {F}_{g=1}^x$
) as the families of K3 surfaces admitting an elliptic fibration with a smooth rational (resp. genus 1) bisection which intersects the zero section in x points. In particular, the set of the K3 surfaces admitting an elliptic fibration with a smooth rational (resp. genus 1) bisection is
$\bigcup _{x\in \mathbb {N}}\mathcal {F}_{\mathrm {{rat}}}^x$
(resp.
$\bigcup _{x\in \mathbb {N}}\mathcal {F}_{\mathrm {{g=1}}}^x$
).
By Proposition 3.13,
$\mathcal {F}_{\mathrm {{rat}}}^x$
coincides with the family
$\mathcal {L}_{2x+5}$
of the
$U\oplus \langle -2(2x+5)\rangle $
-polarized K3 surfaces. Hence, a K3 surface X with Picard number 3 admits a smooth rational bisection if and only if there exists
$x\in \mathbb {N}$
such that X is a general member of the family
$\mathcal {F}_{\mathrm {{rat}}}^x\simeq \mathcal {L}_{2x+5}$
, that is, if and only if its Picard lattice is
$U\oplus \langle -2d\rangle $
for
$d=2x+5$
and
$x\geq 0$
. This implies that
$d\equiv 1\ \mod 2$
and
$d\geq 5$
.
Similarly, by Lemma 3.19,
$\mathcal {F}_{\mathrm {{g=1}}}^x$
coincides with the family
$\mathcal {L}_{2x+4}$
of the
$U\oplus \langle -2(2x+4)\rangle $
-polarized K3 surfaces. Hence, a K3 surface X with Picard number 3 admits a smooth genus 1 bisection if and only if its Picard lattice is
$U\oplus \langle -2d\rangle $
for
$d=2x+4$
and
$x\geq 0$
. This implies that
$d\equiv 0\ \mod 2$
and
$d\geq 4$
. By Propositions 3.4 and 3.6 the described bisections are salient.
4 Higher degree multisections
We consider here multisections of degree higher than 2. The main ideas and the proofs are very similar to those in the previous section, where we considered multisections of degree 2. Indeed, as in that case, we discuss the 18-dimensional (resp. 17-dimensional) families of K3 surfaces with a genus 1 fibration (resp. elliptic fibration) admitting a smooth rational or genus 1 multisection of degree
$m>2$
. Moreover, for low values of m, namely
$m=3,4,5$
, one is also able to describe projective models of the generic K3 surface in the constructed families.
Lemma 4.1. Let X be a K3 surface with a genus 1 fibration
$\pi $
and
$\rho (X)=2$
. Then
$\operatorname {\mathrm {Pic}}(X)\simeq \Gamma _{m,c}:=\left [\begin {array}{cc}0&m\\m&2c\end {array}\right ]$
where m is the minimal degree of a multisection of
$\pi $
and
$-1\leq c\leq m-2$
. Moreover, the following hold.
-
i) The degree of any multisection of
$\pi $
is a multiple of m. -
ii) There is a smooth rational multisection of degree d of
$\pi $
if and only if
$d=m$
, where m is the minimal degree of a multisection of
$\pi $
, and
$\operatorname {\mathrm {Pic}}(X)\simeq \Gamma _{m,-1}$
. -
iii) If
$d=gcd(m,c)$
and
$m=dm'$
, then there is a smooth genus 1 multisection of degree
$mm'$
.
Proof. The class of the fiber of
$\pi $
, F, is primitive in
$\operatorname {\mathrm {Pic}}(X)$
, and hence there exists a basis of
$\operatorname {\mathrm {Pic}}(X)$
which is given by
$\{F,M\}$
with
$FM=m>0$
. In particular, chosen M to be the class of an irreducible curve, M is a multisection of degree m of
$\pi $
. The intersection form computed on these classes is
$\Gamma _{m,c}$
and the condition on c up to isometries of the lattices is given in [Reference van GeemenvG05, Proposition 3.7]. Each class in
$\operatorname {\mathrm {Pic}}(X)$
can be written as
$D=\alpha F+\beta M$
,
$\alpha ,\beta \in \mathbb {Z}$
. Therefore,
$FD=m\beta $
, which yields i). If D is an irreducible curve, and in particular a multisection, then
$FD=m\beta>0$
and it is m if and only if
$\beta =1$
. The self-intersection of D is
$2\beta (\alpha m+c\beta )$
. If D is the class of a smooth rational multisection, then
$\beta (\alpha m+c\beta )=-1$
, which implies
$\beta =1$
and
$c=-1-\alpha m$
. In particular,
$D=\alpha F+M$
, which is not irreducible unless
$\alpha =0$
. The irreducible rational multisection is then obtained for
$\alpha =0$
and so
$c=-1$
. So D coincides with M and D has degree
$FM=m$
. Viceversa, if
$\operatorname {\mathrm {Pic}}(X)\simeq \Gamma _{m,-1}$
, then M (the second generator of the basis of
$\operatorname {\mathrm {Pic}}(X)$
) is a rational multisection. This concludes the proof of ii).
Finally, for iii), if D is the class of a smooth genus 1 multisection, then
$\alpha m+c\beta =0$
. In particular, if
$c=dc'$
, the class
$-c'F+m'M$
has self intersection 0 and is primitive. Hence, it corresponds to the fiber of a genus 1 fibration, whose smooth fibers are infinitely many genus 1 multisections of
$\pi $
, of degree
$(-c'F+m'M)F=m'm$
.
We observe that if
$m=3$
, that is, X is a K3 surface admitting a genus 1 fibration with a trisection, X can be polarized with three nonisometric lattices that are
$\left [\begin {array}{cc}0&3\\3&2c\end {array}\right ]$
, with
$c=-1,0,1$
. They correspond to the cases in which the trisection M in the previous proof has genus 0,1 or 2, respectively. When m grows, more possibilities for the polarizing lattices appear, see [Reference van GeemenvG05, Proposition 3.7].
For low values of m, we give nice geometric models of the K3 surfaces and the genus 1 fibration (see [Reference van GeemenvG05, Paragraph 5.2]): let M be a smooth rational multisection of degree m of the genus 1 fibration whose class of the fiber is F, then
$H:=F+M$
is an ample divisor,
$\varphi _{|H|}(X)\subset \mathbb {P}^m$
and there is a pencil of hyperplanes in
$\mathbb {P}^m$
containing the degree
$m-2$
curve
$C:=\varphi _{|H|}(M)$
.
The fibers of the genus 1 fibration are given by the residual curves of the intersection of
$\varphi _{|H|}(X)$
with hyperplanes in the pencil of hyperplanes through C, indeed
$H-C\sim F+M-M=F$
. Specifically,
-
• if
$m=3$
,
$\varphi _{|H|}(X)$
is a quartic in
$\mathbb {P}^3$
containing a line C. The genus 1 fibration is given by the pencil of planes through C, which is the trisection. -
• if
$m=4$
,
$\varphi _{|H|}(X)$
is a complete intersection of type
$(2,3)$
in
$\mathbb {P}^4$
containing a smooth rational curve C of degree 2. There is a pencil of
$\mathbb {P}^3$
’s through C and each
$\mathbb {P}^3$
in the pencil intersects the surface at C and a genus 1 curve E. These two curves meet in 4 points (since
$E\sim (H-C)\sim F$
,
$C\sim M$
and
$FM=4$
): the pencil of residual genus 1 curves gives a genus 1 fibration on X, whose multisection of degree 4 is C. -
• if
$m=5$
,
$\varphi _{|H|}(X)$
is a complete intersection of type
$(2,2,2)$
in
$\mathbb {P}^5$
containing a smooth rational curve C of degree 3. There is a pencil of
$\mathbb {P}^4$
’s containing the curve C, and each
$\mathbb {P}^4$
cuts on the surface the curve C and a residual genus 1 curve E. These two curves meets in 5 points (since
$E\sim (H-C)\sim F$
,
$C\sim M$
and
$FM=5$
): the pencil of residual genus 1 curves gives a genus 1 fibration on X, whose multisection of degree 5 is C.
In all the cases above, the singular fibers of the fibration correspond to hyperplanes which cut on
$\varphi _{|H|}(X)$
the curve C and a singular curve. Since M is a multisection of the fibration, we have a map
$M\rightarrow \mathbb {P}^1$
to the base of the fibration. It is branched over fibers cut out by hyperplanes whose intersection with
$\varphi _{|H|}(X)$
consists of
$C=\varphi _{|H|}(M)$
and a curve which intersects C in at least one point with multiplicity higher than 1. For a general K3 surface, the hyperplanes corresponding to singular fibers and the ones corresponding to branch fibers for
$M\rightarrow \mathbb {P}^1$
do not coincide and hence the multisection M is generically a saliently ramified multisection.
Given a smooth genus 1 multisection M of degree
$m>2$
, the class
$H=F+M$
is still a very ample divisor, which embeds X in
$\mathbb {P}^m$
, and one has that the image is contained in a quadric of rank 4, as explained in [Reference van GeemenvG05, Paragraph 5.3].
We now specialize to the case of elliptic fibrations. For general m, the following holds.
Theorem 4.2. Let X be a K3 surface with
$\rho (X)=3$
and
$X\in \mathcal {L}_d$
. Then X admits an elliptic fibration
$\pi : X \rightarrow \mathbb {P}^1$
such that
-
•
$\pi $
admits a smooth rational multisection of degree m if, and only if,
$d\equiv 1\ \mod m$
and
$d\geq m^2+1$
; -
•
$\pi $
admits a smooth genus 1 multisection of degree m if, and only if,
$d\equiv 0\ \mod m$
and
$d\geq m^2$
.
Proof. Similarly to the proofs of Proposition 3.13 and Lemma 3.19, it suffices to look for an isometry between the lattice
$\langle F,\mathcal {O}, M\rangle $
and a lattice
$\Lambda _d$
for a certain integer d, where M is the class of an irreducible curve with
$FM=m$
,
$\mathcal {O}M=x\geq 0$
and
$M^2=-2$
, or
$M^2=0$
according to the genus of the multisection. More explicitly, if
$M^2=-2$
, then
$\langle F,\mathcal {O},M\rangle \simeq \langle F,\mathcal {O}, (-2m-x)F-m\mathcal {O}+M\rangle \simeq U\oplus \langle -2(m^2+mx+1)\simeq \Lambda _{(m^2+mx+1)}$
, which does not admit even finite index overlattices in which both
$\langle F,\mathcal {O}\rangle $
and
$\langle (-2m-x)F-m\mathcal {O}+M\rangle $
are primitively embedded. This implies that
$NS(X)\simeq \Lambda _{(m^2+mx+1)}$
, which forces
$d\equiv 1\ \mod m$
and
$d\geq m^2+1$
since
$x\geq 0$
. The argument is analogous if
$M^2=0$
, by observing that
$\langle F,\mathcal {O},M\rangle \simeq \langle F,\mathcal {O}, (-2m-x)F-2\mathcal {O}+M\rangle \simeq \Lambda _{(m^2+mx)}$
.
If X and
$\pi $
are as above,
$x=\mathcal {O}M$
and
$m=FM$
, then the previous models for
$m=3,4,5$
, specialize as follows: the surface
$\varphi _{|H|}(X)\subset \mathbb {P}^m$
contains a rational curve
$\varphi _{|H|}(\mathcal {O})$
of degree
$x+1$
that is a section of the fibration and intersects the curve
$C=\varphi _{|H|}(M)$
in x points.
In Theorem 3.2, we find smooth bisections of low genus (0 or 1) on the K3 surfaces in all the families
$\mathcal {L}_{d}$
with
$d\geq 4$
; the smooth multisections of low genus and degree
$m>2$
appear for higher values of d. So we do not find smooth saliently ramified multisections of degree
$m>2$
on elliptic fibrations that do not admit smooth saliently ramified bisections. We obtain the following result.
Corollary 4.3. The elliptic fibrations on a surface X such that
$\operatorname {\mathrm {Pic}}(X)\simeq \Lambda _d$
admit neither rational nor genus 1 smooth multisections if and only if
$d=1,2,3$
.
5 Rank jumps for K3 surfaces in
$\mathcal {L}_d$
Convention 5.1. In what follows,
$\pi : X\rightarrow \mathbb {P}^1$
is an elliptic fibration on a K3 surface X. The field of definition of
$\pi $
is the field over which the genus 1 fibration
$\pi $
admits a section. We denote it by k.
We combine the results of Subsections 2.2, 3.2 and [Reference Pasten and SalgadoPS24] to answer Question 1.
For the sake of completeness, we also deal with generic elliptic K3 surfaces with a smooth bisection of genus 1, that is, in
$\mathcal {L}_d$
for even d (Theorem 5.6), and we state a result for the general K3 surfaces in the family
$\mathcal {L}_1$
, that is a consequence of [Reference Bogomolov and TschinkelBT00]. As discussed in Subsection 3.2, the elliptic fibration on a K3 surface general member of
$\mathcal {L}_1$
admits a reducible fiber and has trivial Mordell–Weil group. By [Reference Bogomolov and TschinkelBT00, Theorem 1.1], its rational points are potentially dense. In particular, the following holds.
Theorem 5.2. Let X be a generic K3 in the family
$\mathcal {L}_1$
. Let k be the field of definition of the elliptic fibration on X. Then there is a finite extension
$l/k$
such that
$\mathcal {R}(X,\pi , l)$
is infinite. In other words,
$\pi $
has the potential rank jump property.
Theorem 5.3. Let
$(X, \pi )$
be a generic elliptic K3 surface with Picard number 3, that is, X is generic in a family
$\mathcal {L}_d$
. Let k be the field of definition of
$\pi $
, d odd and
$d>3$
.
-
• If
$d\equiv 1\ \mod 4$
, then there is an extension
$l/k$
of degree at most two such that the set is infinite. In particular, X has the potential rank jump property.
$$\begin{align*}\mathcal{R}(X,\pi, l)=\{t\in \mathbb{P}^1(l); \mathrm{rank} X_t(l)>\mathrm{rank} \operatorname{\mathrm{MW}}(X,\pi,l)\} \end{align*}$$
-
• If
$d\equiv 3\ \mod 4$
then the set is infinite. In particular, X has the rank jump property.
$$\begin{align*}\mathcal{R}(X,\pi, k)=\{t\in \mathbb{P}^1(k); \mathrm{rank} X_t(k)> \mathrm{rank} \operatorname{\mathrm{MW}}(X,\pi,k)\} \end{align*}$$
Proof. By Theorem 3.2, under the assumption that
$d>3$
is odd, for a generic X the fibration
$\pi $
admits a smooth salient bisection B that is of genus 0. By Lemma 2.9, B yields a section that is linearly independent from the sections induced by
$\pi $
on the base change.
Therefore, the only statement which has not yet been proved concerns the field of definition k (resp. l), namely, to show that the sets
$\mathcal {R}(X,\pi , k)$
(resp.
$\mathcal {R}(X,\pi , l)$
) are infinite if
$d\equiv 3\ \mod 4$
(resp.
$d\equiv 1\ \mod 4$
). In particular, we will verify that B is defined over k if d is odd, that it has infinitely many k-points if
$d\equiv 3\ \mod 4$
and that it has infinitely many l-points for a certain field extension l of degree two if
$d\equiv 1\ \mod 4$
.
Claim 1: The field of definition of the rational bisection from Theorem 3.2 is k.
Indeed, under the assumption that d is odd, a generic K3 surface in a family
$\mathcal {L}_d$
with Picard number 3 admits a realization as the double cover of
$\mathbb {P}^2_{k}$
branched on a sextic with a unique node (Proposition 3.16). The genus 1 fibration is defined by the pull-back of the pencil of lines through the node and thus the branch sextic and its node are defined over the same field k. The exceptional divisor above the node is isomorphic to a rational curve defined over k and is a bisection of
$\pi $
. In particular, the bisection is defined over the same field as
$\pi $
.
In particular, since X is a double cover of the blow-up of
$\mathbb {P}^2_{k}$
, and B is defined over k, it follows that B has infinitely many l-points for a certain degree two extension
$l/k$
.
Claim 2: The bisection B from Theorem 3.2 has infinitely many points over k if
$d\equiv 3\ \mod 4$
.
Since B is rational and defined over k, it suffices to show that there is at least one point of B defined over k to conclude that there are infinitely many.
The Galois group
$\operatorname {\mathrm {Gal}}(l/k)$
acts on the points of B by permuting the ones that are only defined over l (and not over k) and fixing the ones defined on k. If
$d\equiv 3 \ \mod 4$
, then there is an odd number of points in
$B\mathcal {O}$
, by Remark 3.14. Both the curves B and
$\mathcal {O}$
are defined over k, hence the Galois action preserves both of them. In particular it preserves the set of their intersection points. Since
$\operatorname {\mathrm {Gal}}(l/k)$
has order 2, if it acts on an odd number of points, then it fixes at least one of them, so there is a point in
$B\cap \mathcal {O}$
(and hence on B) which is defined over k. Therefore B can be embedded as a conic in the plane. The presence of a k-point allows us to take the projection away from it and conclude that B is isomorphic to
$\mathbb {P}^1$
over k.
Remark 5.4. Theorem 5.3 is of particular interest in the cases
$d=5,7,13$
since in all the other cases the K3 surface X admits at least two distinct genus 1 fibrations which yield potential density of rational points, and by [Reference Pasten and SalgadoPS24, Theorem 1.1], it has the potential rank jump property. Even for the other values of
$d\equiv 3\ \mod 4$
, in this level of generality, the result is stronger than the ones present in the literature so far since it shows the rank jump property over the field of definition of the elliptic fibration, without the need of a further finite field extension.
Remark 5.5. Let
$X\in \mathcal {L}_{d}$
with
$d\equiv 1 \ \mod 2$
and
$d\geq 5$
. If
$\rho (X)>3$
, then X admits an elliptic fibration that specializes
$\pi $
. The proof of the previous theorem goes through as long as the bisection B in Theorem 3.2 remains a bisection and does not split in the sum of two sections. If B splits, then the map
$\varphi _{|F+B|}$
exhibits X as double cover of
$\mathbb {P}^2$
branched on a sextic that admits a singularity that is worse than a simple node, cf. Remark 3.15. We discuss some of the cases with
$\rho (X)>3$
in Section 5.1.
Theorem 5.6. Let
$(X, \pi )$
be a generic elliptic K3 surface with Picard number 3, that is, X is generic in a family
$\mathcal {L}_d$
. Let k be the field of definition of
$\pi $
. If d is even and
$d>2$
then there is an extension
$l/k$
of degree at most two such that the set
$$\begin{align*}\mathcal{R}(X,\pi, l)=\{t\in \mathbb{P}^1(l); \mathrm{rank} X_t(l)>\mathrm{rank} \operatorname{\mathrm{MW}}(X,\pi,l)\} \end{align*}$$
is infinite. In particular, X has the potential rank jump property.
Proof. By Theorem 3.2, under the assumption that
$d>2$
is even, for a generic X the fibration
$\pi $
admits a smooth salient bisection B that is of genus 1. By Lemma 2.9, B yields a section that is linearly independent of the sections induced by
$\pi $
on the base change.
Since X is generic in
$\mathcal {L}_d$
, the elliptic fibration
$\pi $
is not isotrivial (see Section 2.3.3). Therefore, the base change by a multisection is a nontrivial elliptic fibration with an elliptic base and one can apply Silverman’s Specialization theorem ([Reference SilvermanSil83, Theorem C]) to the base change. In particular, the fibers of
$\pi $
above the points t in the image of
$\pi |_B$
verify
$r_t>r$
.
Therefore, the only statement which has not yet been proved concerns the field extension
$l/k$
over which B has infinitely many l-rational points and thus over which we have infinitely many t’s such that
$r_t>r$
.
Claim: There exists a field extension
$l/k$
of degree at most 2 such that the genus 1 bisection(s) from Theorem 3.2 have infinitely many l-rational points.
If
$d\geq 4$
is even then X admits a realization as a double cover of
$\mathbb {P}^1\times \mathbb {P}^1$
branched over a curve of bidegree
$(4,4)$
. In this case, the genus 1 fibration is given by the pull-back of the pencil of curves of bidegree
$(0,1)$
(resp.
$(1,0)$
) and there is a pencil of bisections, of which B is a member, given as the pull-back of the curves of bidegree
$(1,0)$
, (resp.
$(0,1)$
). Both pencils are clearly defined over the same field k. Moreover, the generic fibers of the two genus 1 pencils intersect in two geometric points that are (potentially) conjugate under
$\operatorname {\mathrm {Gal}}(\bar {k}(t)/k(t))$
and defined over an extension
$l(t)/k(t)$
of degree at most 2. In particular, B intersects each fiber
$\pi ^{-1}(t)$
in two
$\operatorname {\mathrm {Gal}}(\bar {k}(t)/k(t))$
-conjugate points
$p(t), p'(t)$
. Fix
$l=l(t)$
, for a t such that
$p(t)$
is of infinite order in the Mordell–Weil group of B. As the bisections belong to an infinite family, we can conclude that infinitely many of them are elliptic curves with a positive rank over l, proving the claim.
Remark 5.7. The final statement in Theorem 5.6 follows from [Reference Pasten and SalgadoPS24, Theorem 1.1] or, alternatively, by combining [Reference Gvirtz-Chen and MezzedimiGM24, Theorem 1.1] and [Reference Colliot-ThélèneCT20, Théorème 1.1]. In fact, both approaches imply a stronger result, namely that the set
$\mathcal {R}(X,\pi , l)$
is not thin in
$\mathbb {P}^1_l$
. An advantage of our point of view is that by providing a geometric realization of both genus 1 fibrations (Prop. 3.20), we are able to control the field extension
$l/k$
.
5.1 Rank jump properties for codimension one subfamilies
We discuss certain specializations of the surfaces considered above, in particular the ones which have Picard number 4 and appear in the list given by [Reference Gvirtz-Chen and MezzedimiGM24], since for these the potential rank jump property is still unknown.
First we observe that if a K3 surface has an elliptic fibration and Picard number 4, its Picard group is
$U\oplus \Gamma $
with base
$F,\mathcal {O}, b_3,b_4$
, and with respect to the fibration whose fiber is F one of the following three cases appears:
-
a)
$\Gamma $
does not contain vectors of self-intersection
$-2$
: in this case the elliptic fibration has no reducible fibers and the Mordell–Weil group has rank 2; -
b)
$\Gamma $
contains a class of self-intersection
$-2$
and the root lattice of
$\Gamma $
has rank 1: in this case there is exactly one reducible fiber, which has two components, and the Mordell–Weil group has rank 1; -
c)
$\Gamma $
is generated by roots: in this case the elliptic fibration has either two reducible fibers, each with two components, or it has one reducible fiber with three components. In both cases the Mordell–Weil group is trivial.
Since in case
$c)$
the Mordell–Weil group is trivial, we now focus on the other two cases.
In case
$a)$
,
$\Gamma $
is of type
$\left [\begin {array}{cc}-2\alpha &\beta \\ \beta &-2\gamma \end {array}\right ]$
with
$\alpha>1$
and
$\gamma>1$
. The Mordell–Weil group is isomorphic to
$\mathbb {Z}\times \mathbb {Z}$
and it contains the classes
$$ \begin{align}P_{n,m}:=(\alpha m^2-\beta m n+\gamma n^2)F+\mathcal{O}+mb_3+nb_4\end{align} $$
where the isomorphism between the groups is given by
$P_{(n,m)}\mapsto (n,m) $
and the section
$\mathcal {O}$
corresponds to
$(0,0)$
.
In case
$b)$
there are two possibilities, namely that the generator of the Mordell–Weil group intersects the same component of the reducible fiber as the section
$\mathcal {O}$
, or that it intersects in the other component. If the former holds, the Mordell–Weil lattice (see [Reference Schütt and ShiodaScS10, Section 11] for definition) has an integer discriminant and the lattice
$\Gamma $
is isometric to
$\langle -2\rangle \oplus \langle -2\gamma \rangle $
with
$\gamma>1$
; in this case the Mordell–Weil group is
$\mathbb {Z}$
and the classes of the sections are
$P_n=\gamma n^2 F+\mathcal {O}+nb_4$
. If the latter holds, the Mordell–Weil lattice has a noninteger discriminant and the lattice
$\Gamma $
is isometric to
$\left [\begin {array}{cc}-2&-1\\-1&-2\gamma \end {array}\right ]$
with
$\gamma>1$
; in this case the Mordell–Weil group is
$\mathbb {Z}$
; the classes of the sections corresponding to even integers are
$P_{-2n}=(4\gamma -1) n^2 F+\mathcal {O}+nb_3-2nb_4$
and the ones corresponding to odd integers are
$P_{-2n-1}=\left ((4\gamma -1) n^2+(4\gamma -1)n+\gamma \right ) F+\mathcal {O}+nb_3+(-2n-1)b_4$
.
We now consider the following special choice for
$\Gamma $
:
$\Gamma \simeq \langle -2d\rangle \oplus \langle -2c\rangle $
, that is,
$U\oplus \Gamma \simeq \Lambda _{d}\oplus \langle -2c\rangle $
.
Corollary 5.8. Let X be a K3 surface such that
$\operatorname {\mathrm {NS}}(X)\simeq \Lambda _{d}\oplus \langle -2c\rangle $
with
$c\geq 1$
and
$d\geq 5$
,
$d\equiv 3\ \mod 4$
. Then the elliptic fibration defined on X by the class of F (with the notation as above) has the rank jump property.
Proof. This follows as in Theorem 5.3, by applying Remark 5.5 to the class
$B=\frac {d+3}{2}F+2\mathcal {O}+b_3$
, which is such that
$B^2=-2$
,
$BF=2>0$
and
$B\mathcal {O}\equiv 1\ \mod 2$
. It is effective and, in the light of Remark 5.5, we now show that it cannot be written as the sum with non-negative coefficients of sections and components of fibers. In what follows, we give the details only in the case
$c>1$
, which corresponds to case a) in Section 5.1 above. In that case, the Mordell–Weil rank is 2 and all fibers are irreducible. Assume, by contradiction, that B can be written as a sum of fibers and sections. This implies that there are
$r,x,y\in \mathbb {N}$
such that
$B=rF+xP_{m,n}+yP_{p,q}$
. By the condition
$BF=2$
, it follows
$x+y=2$
; by the comparison of the coefficients of
$b_3$
(resp.
$b_4$
) in
$B=\frac {d+3}{2}F+2\mathcal {O}+b_3$
and in
$B=rF+xP_{m,n}+yP_{p,q}$
, one obtains
$xm+yp=1$
(resp.
$xn+yq=0$
). Therefore
$x=y=1$
,
$p=1-m$
and
$q=-n$
. By (5.1),
$P_{m,n}+P_{1-m,-n}=(2dm^2+2cn^2-2md+d)F+2\mathcal {O}+b_3$
with
$d\geq 5$
. The coefficient of F is larger than
$(d+3)/2$
for every choice of m and n, hence r is forced to be a negative number, yielding the desired contradiction.
The case where
$c=1$
, implies the existence of a vector of self-intersection
$-2$
which is orthogonal to the class of a fiber, yielding a fiber component. This corresponds to case b) in Section 5.1. One obtains a contradiction in a similar way: one considers the class
$B=\frac {d+3}{2}F+2\mathcal {O}+b_3$
and one shows that it is not possible that B can be also expressed as
$rF+xP_{m}+yP_{n}+zb_3$
with
$r,x,y,z\geq 0$
. One has to be careful since the expressions of
$P_m$
and
$P_n$
in terms of the basis
$\{F,\mathcal {O},b_3,b_4\}$
, depends on the parity of m and n, so one has to consider all the possible cases (i.e., m and n are both even, are both odd, one is odd and one is even).
We now restrict our attention to the families for which the potential rank jump property is not implied by the presence of a second genus 1 fibration, that is, the ones in the list provided in [Reference Gvirtz-Chen and MezzedimiGM24].
Proposition 5.9. The K3 surfaces whose Picard lattice is isometric to one of the lattices in Table 1 admit a unique elliptic fibration which has the potential rank jump property.
Table 1 Intersection form for Picard lattices of rank 4 of K3s with a unique elliptic fibration known to have the potentially rank jump property.
Proof. All the K3 surfaces in the statement admit a unique elliptic fibration by [Reference Brandhorst and MezzedimiBM24] and have Picard number 4. We now show that in all the cases but the last two, they are special members of the families
$\mathcal {L}_d$
with
$d\geq 5$
and
$d\equiv 1\ \mod 2$
and that their elliptic fibration admits a bisection B that satisfies Remark 5.5. This proves the statement for all the cases but the last two, which will be considered at the end of the proof.
We consider three different situations, according to the rank of the Mordell–Weil group.
First case: the Mordell–Weil group has rank 2 (case a)). This assumption corresponds to the first three lattices in the Table 1.
We first identify an effective class B such that
$BF=2$
and
$B^2=-2$
, and then we prove that it is supported on an irreducible curve (in particular it is not the sum of two sections and possibly some fibers). This guarantees that it indeed corresponds to an irreducible bisection and satisfies Remark 5.5.
For all the lattices considered here, one can prove that there exists a base
$\{b_3, b_4\}$
of
$\Gamma $
such that the bilinear form is
$\left [\begin {array}{rr}-2\alpha &\beta \\ \beta &-2\gamma \end {array}\right ]$
, with
$\gamma>0$
, and
$\alpha \geq 5$
,
$\alpha \equiv 1\ \mod 2$
. In particular
$\left [\begin {array}{cc}-6&-1\\ -1&-6\end {array}\right ]\simeq \left [\begin {array}{cc}-10&-5\\ -5&-6\end {array}\right ]$
and
$\left [\begin {array}{rr}-4&0\\ 0&-6\end {array}\right ]\simeq \left [\begin {array}{cc}-10&-4\\ -4&-4\end {array}\right ]$
.
Now one argues as in Corollary 5.8, by considering the element
$B:=\frac {\alpha +3}{2}F+2\mathcal {O}+b_3$
: if B were a reducible curve which is the union of two sections, say
$P_{m,n}$
and
$P_{p,q}$
, and possibly some components of fibers, then there would exist three non-negative integers
$x,y,z$
such that
$B=xF+yP_{m,n}+zP_{p,q}$
in
$\operatorname {\mathrm {Pic}}(X)$
. Considering the previous equations of B and
$P_{m,n}$
(see (5.1)), one obtains
$$ \begin{align*}&xF+y\left((\alpha m^2-\beta m n+\gamma n^2)F+\mathcal{O}+mb_3+nb_4\right)+z\left((\alpha p^2-\beta p q+\gamma q^2)F+\mathcal{O}+pb_3+qb_4\right)\\& \quad =\frac{\alpha+3}{2}F+2\mathcal{O}+b_3\end{align*} $$
which implies
$y+z=2$
,
$ym+zp=1$
,
$yn+zq=0$
, by comparing the coefficients of
$\mathcal {O}$
,
$b_3$
and
$b_4$
respectively. In particular, one obtains that
$y=z=1$
,
$p=1-m$
,
$q=-n$
and one concludes since
$x=\frac {\alpha +3}{2}-\left (2\alpha m^2-2\beta m n+2\gamma n^2+\alpha -2m\alpha +\beta n\right )$
is a negative number for any possible choice of
$(m,n)\in \mathbb {Z}\times \mathbb {Z}$
. Therefore B is irreducible.
Second case: the Mordell Weil group has rank 1 (case b)). The cases which appear in Table 1 are
$\Gamma =\left [\begin {array}{cc}-2&-1\\-1&-2\gamma \end {array}\right ]$
with
$\gamma =2,3,5$
. For
$\gamma =2,3,5$
, consider the class
$B=16F+2\mathcal {O}+b_3-4b_4$
,
$B=24F+2\mathcal {O}+b_3-4b_4$
and
$B=4F+2\mathcal {O}-b_4$
, respectively. It has the required properties (i.e.,
$BF=2$
,
$B^2=-2$
) and cannot be written as
$rF+xb_3+yP_{a}+zP_b$
with
$y+z=2$
and r and x non negative, where
$b_3$
is the class of an irreducible component of the reducible fiber and
$P_a$
and
$P_b$
are sections.
Third case: the Mordell–Weil group is trivial (case c)). This corresponds to the last two cases in Table 1. The fibration of each of these surfaces has no sections of infinite order, hence it is known to have the potential rank jump property, as mentioned in Theorem 5.2.
Remark 5.10. We now consider the four rank 4 lattices listed in [Reference Gvirtz-Chen and MezzedimiGM24], but not contained in Table 1.
If
$\Gamma \simeq \left [\begin {array}{rr}-4&-2\\-2&-4\end {array}\right ]$
, then it is not possible to find in
$\Gamma $
a class with self-intersection
$-2d$
such that d is odd, hence it is not possible to show the existence of a smooth rational bisection with the same method applied before. Moreover, since [Reference Gvirtz-Chen and MezzedimiGM24] guarantees that there are no more than one genus 1 fibration on the surface, the elliptic fibration does not admit a smooth genus 1 bisection.
If
$\Gamma \simeq \left [\begin {array}{rr}-2&0\\0&-4\end {array}\right ]$
in order to find a rational bisection, we need a class
$B=xF+y\mathcal {O}+z b_3+wb_4$
such that
$B^2=-2$
,
$BF=2$
,
$0\leq Bb_3\leq 2$
(since
$b_3$
is identified with the class of an irreducible component of a reducible fiber). This forces
$y=2$
,
$z=-1$
and hence
$x=2+w^2$
. So
$B=(2+w^2)F+2\mathcal {O}+b_3+wb_4$
, which is equal to
$2F+b_3+2P_{w/2}$
if w is even and to
$b_3+P_{v}+P_{v-1}$
if
$w=2v-1$
. In both cases B corresponds to the union of sections and components of fibers, and so it does not correspond to a smooth rational bisection. So for this choice of
$\Gamma $
the fibration does not admit a smooth bisection of genus either 0 or 1.
If
$\Gamma \simeq \left [\begin {array}{rr}-4&\mu \\\mu &-2\lambda \end {array}\right ]$
with
$(\mu ,\lambda )=(-2,3),(-1,2)$
we are not able to find a convenient B which represents an irreducible smooth rational bisection of the fibration (but we are not claiming that such B does not exist).
Finally, we observe that at least for some of the lattices in the Table 1, it is not possible to find a smooth rational bisection B such that
$B\mathcal {O}\equiv 1\ \mod 2$
, and hence to prove by this strategy the rank jump property, and not just the potential rank jump property. This is the case, for example, of the lattice
$U\oplus \langle -4\rangle \oplus \langle -6\rangle $
; indeed a class B such that
$B^2=-2$
,
$BF=2$
and
$\mathcal {O} B\mathcal \equiv 1 \ \mod 2$
is necessarily of the type
$B_{k,h}=(4k^2+6(h^2+h)+3)F+2\mathcal {O}+2kb_3+(2h+1)b_4$
,
$k,h\in \mathbb {Z}$
, but then
$B_{k,h}=P_{k,h}+P_{k,h+1}$
, so it splits in the union of two sections.
We observe that the similar strategies can be applied to consider subfamilies of
$\mathcal {L}_d$
with higher codimension.
6 Examples
In this section, we describe several examples for which we prove the potential rank jump property and/or the rank jump property on very explicit K3 surfaces with Picard number 3, for which we give an equation. We give two examples of elliptic K3 surfaces with Picard rank 3 over
$k=\mathbb {Q}(\sqrt {5})$
, realized as a double cover of a nodal sextic with principal tangents defined only over a degree 2 extension. In Example 6.1, the bisection above the node is
$\mathbb {P}^1_{\mathbb {Q}}$
. In Example 6.2, it is a conic without k-points. Therefore, by the proof of Theorem 5.3, the former admits the rank jump property over k, while the latter admits the property after a suitable degree 2 extension of k.
In the last example we use a trisection to prove the rank jump property on another K3 surface of Picard number 3.
In all these examples the geometric construction provides immediately the field of definition of the rational multisection and the field where it has rational points.
Example 6.1. Let C be the singular plane sextic curve given by the vanishing of the following polynomial:
$$ \begin{align*} f:=2x^4y^2 {\kern-1pt}+{\kern-1pt} 8x^4z^2 {\kern-1pt}+{\kern-1pt} x^3y^3 {\kern-1pt}+{\kern-1pt} x^3yz^2 + x^3z^3 + x^2y^4 + 5x^2y^2z^2 + 7x^2z^4 + xy^5+xy^4z +xy^3z^2 + 6xz^5 + 5y^4z^2. \end{align*} $$
Then C has a unique singularity, namely
$p=(1:0:0)$
, which is of type
$A_1$
. It admits a bitangent line
$L: x=0$
. As this line intersects the curve in only 2 points, namely
$(0:1:0)$
and
$(0:0:1)$
, with intersection multiplicities 2 and 4, respectively, it can be considered as a degenerate tritangent line. In particular, it splits in the double cover
$g:X\rightarrow \mathbb {P}^2$
branched on C. Indeed, if a curve D on a surface Y intersects the branch locus of a double cover
$g:X\rightarrow Y$
with an even multiplicity in a point q, then its inverse image
$g^{-1}(D)\subset X$
is singular in
$g^{-1}(q)$
but does not ramify in
$g^{-1}(q)$
(because of the splitting of the local equation of the double cover). So, for the double cover
$g:X\rightarrow \mathbb {P}^2$
branched on C, the inverse image of the line L does not contain ramification points but has two singular points (which are
$g^{-1}(0:1:0)$
and
$g^{-1}(0:0:1)$
). In particular, since L is rational and so simply connected, the inverse image
$g^{-1}(L)$
consists of two rational curves meeting in two points (one with multiplicity 2).
Let X be the K3 double cover of
$\mathbb {P}^2$
branched over C, then the geometric Picard number of X is at least 3. Indeed, its Picard lattice contains B, the rational curve above the exceptional divisor given by the desingularization of p, a genus 1 class F, given by the pull-back of any line through p, and the class
$\mathcal {O}$
given by one of the two irreducible rational curves above the line L. Since
$p\not \in L$
, their intersection matrix is as follows
$$ \begin{align*}\begin{pmatrix}-2&2&0\\ 2&0&1\\ 0&1&-2 \end{pmatrix} \end{align*} $$
and, with the same notation of Section 3.3, we have
$x=B\mathcal {O}=0$
, which implies
$d=5$
, that is, the Picard group contains a lattice isometric to
$\Lambda _{5}=U\oplus \langle -10\rangle $
.
We now prove that
$\rho (X)=3$
, which will imply that
$\operatorname {\mathrm {Pic}}(X)\simeq \Lambda _{5}$
and that L is the unique line in
$\mathbb {P}^2$
which splits in the double cover.
Our approach to determine the Picard number of X is based on Tate’s conjecture ([Reference Tate and SchillingTa65]). More precisely, we bound the geometric Picard number from above by the number of eigenvalues of the characteristic polynomial of Frobenius, for primes of good reduction, that are roots of unity (see [Reference van LuijkvL07, Corollary 2.3] for the statement and [Reference Elsenhans and JahnelEJ11, Sec. 4] for detailed examples of the approach in a similar setting).
In our case, a computation of the characteristic polynomial of the Frobenius for ordinary primes such as
$7, 11, 23, 31$
, and 37, done with the help of Magma ([Reference Bosma, Cannon and PlayoustMa]), yields a factor of degree 18 that is not cyclotomic. Since the characteristic polynomial of Frobenius has degree
$b_2=22$
, we obtain
$\rho \leq 22-18= 4$
.
We claim that
$\rho =3$
and verify it by exhibiting a class of a smooth rational curve that does not lift to characteristic 0.
For the prime
$7$
, the sextic C has two singularities of type
$A_1$
, namely
$p=(1:0:0)$
and
$q=(1:5:1)$
. The exceptional divisor above q is a smooth rational curve. So the Picard group for
$p=7$
is the lattice
$\Lambda _{5}\oplus \langle -2\rangle $
, where the last summand is spanned by the exceptional divisor over q. If this curve lifted over
$\mathbb {Q}$
, then the Picard group of X over
$\mathbb {Q}$
would be
$\Lambda _{5}\oplus \langle -2\rangle $
and in particular the elliptic fibration induced by the pencil of lines through p would have a fiber of type
$I_2$
. But one can directly check on the equation of the fibration (see, 6.1), that it does not admit any reducible fiber over
$\mathbb {Q}$
. Therefore the class which is defined for
$p=7$
as exceptional divisor over q does not lift over
$\mathbb {Q}$
and this implies that
$\rho =3$
over
$\mathbb {Q}$
.
Finally, we verify that the smooth bisection B is saliently ramified. Recall that the unique elliptic fibration on X is given by the pull-back of lines through p. Moreover, the restriction map
$\pi _B: B\rightarrow \mathbb {P}^1$
is branched over the fibers that are pull-backs of the two lines that are the principal tangents of C at the node p, namely
$y=2iz$
and
$y=-2iz$
. Since these intersect C transversally outside p, they pull-back to smooth fibers of
$\pi $
.
To be more explicit, the equation of the K3 surface X is
$w^2=f$
and the pencil of lines through p is given by
$y=tz$
, so the equation of the genus 1 fibration with fiber F is
$$ \begin{align} w^2=x^4(2t^2 + 8) + x^3z(t^3 + 3 + 1) + x^2z^2(t^4 + 5t^2 + 7) + xz^3(t^5+t^4 +t^3 + 6)+ 5t^4z^4.\end{align} $$
It intersects the inverse image of the line
$x=0$
in the curve
$w^2=5t^4z^4$
and if
$\sqrt {5}$
exists in the field of definition, this curve splits in the two curves
$w\pm \sqrt {5}z^2t^2=0$
and thus corresponds to the two sections
$(x(t),z(t),w(t))=(0,1,\pm \sqrt {5}t^2)$
. Therefore, the field of definition of the elliptic fibration (with section) is
$k=\mathbb {Q}(\sqrt {5})$
.
The elliptic fibration has no reducible fibers, as can be checked by the computation of its discriminant.
The bisection corresponds to the exceptional divisor over p, that is, to
$z=0$
and thus its equation is
$w^2=x^2(2t^2+8)$
which in particular describes a rational curve defined over
$\mathbb {Q}$
. It intersects the fiber above
$t=2$
at the
$\mathbb {Q}$
-points
$(x,z,w)=(1,0,\pm 4)$
, so it is isomorphic to
$\mathbb {P}^1_{\mathbb {Q}}$
and has infinitely many
$\mathbb {Q}$
-points, and, therefore, infinitely many k-rational points.
We observe that since the elliptic fibration has infinitely many sections, there are infinitely many irreducible curves in
$\mathbb {P}^2$
that split in the double cover. The section
$S_n$
comes from the splitting of a curve of degree
$10n^2-10n+1$
with a singular point of multiplicity
$10n^2+10n$
in p.
Example 6.2. We consider a slight modification of the coefficients of
$x^4y^2$
and
$x^4z^2$
in the sextic in Example 6.1. Let C be the singular plane sextic curve given by the vanishing of the following polynomial:
$$ \begin{align*} f:=-5x^4y^2 -6x^4z^2 + x^3y^3 + x^3yz^2 + x^3z^3 + x^2y^4 + 5x^2y^2z^2 + 7x^2z^4 + xy^5+xy^4z +xy^3z^2 + 6xz^5 + 5y^4z^2. \end{align*} $$
Then, as before, C has a unique singularity, namely
$p=(1:0:0)$
, which is of type
$A_1$
. It admits a degenerate tritangent line, namely
$L: x=0$
, which turns out to be unique, once one proved as above that
$\rho =3$
.
The same calculations as in Example 6.1 can be used to show that the Picard group is isometric to
$\Lambda _5$
. The upper bound on the geometric Picard number can be found by inspecting ordinary primes such as
$p=7,13,61$
. In fact, this K3 surface has the same reduction modulo 7 as in Example 6.1, so the same argument applies to show that the Picard group has indeed rank 3.
The bisection over k which corresponds to the exceptional divisor above p has equation
${w^2=x^2(-5t^2-6)}$
, which clearly admits no
$\mathbb {R}$
-points and, in particular, it has no k-points (but it has l-points where l is a field extension of degree 2 of k).
The next example is concerned with a
$\Lambda _d$
-polarized K3 surface, with an even d. In it, the rank jump property is realized over the field of definition of the elliptic fibration and is obtained by using a trisection (and not as above a bisection) as the ones described in Section 4. It is inspired by [Reference Nijgh and van LuijkNvL24, Theorem 3.3].
Example 6.3. Let X be the quartic K3 surface given by
$$ \begin{align} q_1f_1+q_2f_2+q_3f_3=0 \end{align} $$
where
$f_1, f_2, f_3$
are polynomials of degree 2 in
$\mathbb {Z}[x,y,z,w]$
given as follows:
$$\begin{align*}f_1:=x^2-xy;\, f_2:=z^2-zw; \, f_3:= yz-xw; \ \end{align*}$$
and
$q_1, q_2, q_3$
are also of degree 2 in
$\mathbb {Z}[x,y,z,w]$
and satisfy:
$$ \begin{align*}q_1 &\equiv y^2 +xw+xy +yw \quad \mod 2\\q_2 &\equiv xy +yz +yw+zw \quad \mod 2,\\ q_3 &\equiv xz +xw+z^2 +w^2 +y^2 \quad \mod 2, \end{align*} $$
and,
$$ \begin{align*}q_1 &\equiv y^2 +xw+2xz +2yz \quad \mod 3,\\q_2 &\equiv xy +yz +yw+x^2 +2xw \quad \mod 3,\\q_3 &\equiv xz +xw+z^2 +w^2 +2xy +2yw \quad \mod 3. \end{align*} $$
Then, by [Reference Nijgh and van LuijkNvL24, Thm. 3.3], X is a K3 surface with Picard number 3. Its Picard lattice is generated by the classes of
$H, L_0, L_1$
, where H corresponds to a hyperplane section,
$L_0$
is the class of the line given by
$x=z=0$
and
$L_1$
, the class of
$x-y=z-w=0$
. Moreover, it is
$U\oplus \langle -20 \rangle $
-polarized. In fact, the divisor
$D=6H-7L_0+3L_1$
is perpendicular to a copy of U, generated by
$H-L_0$
and
$L_1$
, and has self-intersection
$-20$
.
The surface X admits two evident elliptic fibrations. Indeed, the residual intersection of a hyperplane through any line is a genus 1 curve in X. Therefore, the pencil of hyperplanes through one of the lines
$L_0$
or
$L_1$
yields an elliptic fibration, which we denote by
$\pi _0, \pi _1$
, in reference to taking hyperplanes through
$L_0$
, or
$L_1$
, respectively, in what follows.
As a general hyperplane through
$L_0$
(resp.
$L_1$
) does not contain
$L_1$
(resp.
$L_0$
), the line
$L_1$
(resp.
$L_0$
) corresponds to a section of the elliptic fibration
$\pi _0$
(resp.
$\pi _1$
). On the other hand, the line
$L_0$
(resp.
$L_1$
) is a trisection of
$\pi _0$
(resp.
$\pi _1$
). From the construction, the fibers of
$\pi _0$
are smooth genus 1 bisections of
$\pi _1$
and vice versa.
We therefore have examples of elliptic fibrations that admit a rational trisection and a (family of) genus 1 bisection(s).
We claim that
$\pi _0$
and
$\pi _1$
have the rank jump property over
$\mathbb {Q}$
. To verify this claim, it suffices to show that the rational trisection of each fibration is saliently ramified. Alternatively, one can show that at least one of the infinitely many saliently ramified bisections of genus 1 has infinitely many
$\mathbb {Q}$
-points.
Let us choose
$q_i$
as follows
$$ \begin{align*}q_1 &= y^2 +xw+3xy +3yw +2xz+2yz,\\q_2 &= xy +yz +yw+4x^2+2xw+3zw,\\q_3 &= xz +xw+z^2 +w^2 +3y^2 +2xy+2yw. \end{align*} $$
Consider the line
$L_0$
and the pencil of planes
$x=tz$
through that line. The intersection of the quartic with
$x=tz$
contains the line
$L_0$
; the residual cubic is the fiber of the elliptic fibration
$\pi _0$
over the point t. One can directly check that for
$t=0$
the intersection between the line and the residual cubic consists of the points
$(0:0:0:1)$
and
$(0:1:0:0)$
and the first one has multiplicity two. In particular, the trisection (which corresponds to
$L_0$
) branches on the fiber over
$t=0$
. Nevertheless, one can also check that the intersection
$X\cap \{x=0\}$
consists of the line
$L_0$
and of a smooth cubic, so the trisection
$L_0$
branches over a smooth fiber of the fibration, that is, it is saliently ramified.
Acknowledgments
It is our pleasure to thank the referee for their helpful comments and for pointing out a mistake in the previous version of the paper, Bert van Geemen for reading and commenting on our manuscript, and Wim Nijgh for pointing out the quartic K3 that appears in Example 6.3 and for discussing details about it. The second author would also like to thank Brendan Hassett for a discussion on the ramification of trisections on elliptic K3 surfaces and the Institute for Advanced Study for their hospitality and stimulating atmosphere.
Competing interests
The authors have no competing interests to declare.
Financial support
The first author is a member of the INDAM-GNSAGA. Part of the second author’s work on this material is supported by the NWO XL grant Rational points: new dimensions, the James D. Wolfensohn Fund and the National Science Foundation under Grant No. DMS-1926686.
Open access
