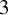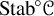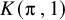1 Introduction
This paper provides a description of the entire stability manifold for a large class of finite-dimensional algebras, namely contraction algebras associated to
![]() $3$
-fold flops, in terms of their g-vector fans. To establish this purely algebraic result, which takes place in the derived category of a finite-dimensional algebra, requires both algebraic techniques through silting-discreteness and also, more remarkably, geometric techniques through Fourier–Mukai transforms. The main corollaries are algebraic, topological and geometric.
$3$
-fold flops, in terms of their g-vector fans. To establish this purely algebraic result, which takes place in the derived category of a finite-dimensional algebra, requires both algebraic techniques through silting-discreteness and also, more remarkably, geometric techniques through Fourier–Mukai transforms. The main corollaries are algebraic, topological and geometric.
1.1 Change of categories
In birational geometry,
![]() $3$
-fold flops play a vital role in the minimal model programme, providing a method to pass between the different minimal models of a given
$3$
-fold flops play a vital role in the minimal model programme, providing a method to pass between the different minimal models of a given
![]() $3$
-fold singularity. Contraction algebras [Reference Donovan and WemyssDW1, Reference Donovan and WemyssDW3] are an uncountable class of symmetric, finite-dimensional algebras introduced as a tool to study this geometry. To each
$3$
-fold singularity. Contraction algebras [Reference Donovan and WemyssDW1, Reference Donovan and WemyssDW3] are an uncountable class of symmetric, finite-dimensional algebras introduced as a tool to study this geometry. To each
![]() $3$
-fold flopping contraction
$3$
-fold flopping contraction
![]() $f\colon X\to \operatorname {Spec} R$
, where X has at worst Gorenstein terminal singularities, there is an associated contraction algebra
$f\colon X\to \operatorname {Spec} R$
, where X has at worst Gorenstein terminal singularities, there is an associated contraction algebra
![]() $\Lambda _{\mathrm {con}}$
, which recovers all known numerical invariants of the flop [Reference Donovan and WemyssDW1, Reference Hua and TodaHT, Reference WemyssW]. A common theme to which this paper contributes is that results for contraction algebras imply results for
$\Lambda _{\mathrm {con}}$
, which recovers all known numerical invariants of the flop [Reference Donovan and WemyssDW1, Reference Hua and TodaHT, Reference WemyssW]. A common theme to which this paper contributes is that results for contraction algebras imply results for
![]() $3$
-fold flops.
$3$
-fold flops.
To explain this connection, note that associated to f is the subcategory
of
![]() $\mathop {\mathrm {D}^b}(\operatorname {coh} X)$
. This subcategory is small enough in the sense that it has desirable properties such as finite-dimensional Hom-spaces and the 3-Calabi–Yau property whenever X is smooth, but it is large enough that many problems involving X, some of which are introduced in Section 1.3 below, can be solved by replacing
$\mathop {\mathrm {D}^b}(\operatorname {coh} X)$
. This subcategory is small enough in the sense that it has desirable properties such as finite-dimensional Hom-spaces and the 3-Calabi–Yau property whenever X is smooth, but it is large enough that many problems involving X, some of which are introduced in Section 1.3 below, can be solved by replacing
![]() $\mathop {\mathrm {D}^b}(\operatorname {coh} X)$
with
$\mathop {\mathrm {D}^b}(\operatorname {coh} X)$
with
.
The third (and easiest) category associated to this situation is the bounded derived category
![]() $\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
. This is very different from
$\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
. This is very different from
![]() , but the transfer between them is provided by noncommutative deformation theory, which gives a universal sheaf
, but the transfer between them is provided by noncommutative deformation theory, which gives a universal sheaf
![]() [Reference Donovan and WemyssDW3] and a functor
[Reference Donovan and WemyssDW3] and a functor
whose image lies in
![]() . The main idea is that establishing results on
. The main idea is that establishing results on
![]() $\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is in fact easier, and this in turn establishes results on
$\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is in fact easier, and this in turn establishes results on
![]() . To do this, we use the functor given by equation (1.1) twice: first to bring Fourier–Mukai transforms into algebra to prove the main result on
. To do this, we use the functor given by equation (1.1) twice: first to bring Fourier–Mukai transforms into algebra to prove the main result on
![]() $\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
and then to transfer the consequences back to
$\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
and then to transfer the consequences back to
![]() , and thus also X, in a series of corollaries.
, and thus also X, in a series of corollaries.
1.2 Main result
The change in category from
![]() to
to
![]() $\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
brings one major advantage, namely that
$\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
brings one major advantage, namely that
![]() $\Lambda _{\mathrm {con}}$
is silting-discrete [Reference AugustAu1, 4.12]. This fact has two happy consequences. First, we are able to describe the full space of stability conditions on
$\Lambda _{\mathrm {con}}$
is silting-discrete [Reference AugustAu1, 4.12]. This fact has two happy consequences. First, we are able to describe the full space of stability conditions on
![]() $\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
, not just a component. Second, it is known that all silting-discrete algebras have contractible stability manifolds [Reference Pauksztello, Saorín and ZvonarevaPSZ], and thus
$\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
, not just a component. Second, it is known that all silting-discrete algebras have contractible stability manifolds [Reference Pauksztello, Saorín and ZvonarevaPSZ], and thus
![]() $\operatorname {Stab}{}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is contractible before we even begin.
$\operatorname {Stab}{}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is contractible before we even begin.
Alas, the change in category also brings one major disadvantage. Whilst contractibility comes for free, moving to finite-dimensional algebras means that we lose the technology of Fourier–Mukai transforms, so controlling standard equivalences becomes significantly more difficult. An age-old algebraic problem rears its head: knowing whether a given autoequivalence that is the identity on simples is globally the identity functor. Happily, in our setting, we tame this problem by appealing to a commutative diagram that uses equation (1.1) to intertwine our algebraic equivalences with the geometric flop functors, where we can use a standard Fourier–Mukai argument (see Theorem 4.3).
The tilting theory of
![]() $\Lambda _{\mathrm {con}}$
is controlled by a real simplicial hyperplane arrangement
$\Lambda _{\mathrm {con}}$
is controlled by a real simplicial hyperplane arrangement
![]() [Reference AugustAu2], which can be described in many ways. On one hand,
[Reference AugustAu2], which can be described in many ways. On one hand,
![]() arises as the g-vector fan of
arises as the g-vector fan of
![]() $\Lambda _{\mathrm {con}}$
, and on the other, it arises naturally as the ample cone of
$\Lambda _{\mathrm {con}}$
, and on the other, it arises naturally as the ample cone of
![]() $f\colon X\to \operatorname {Spec} R$
. Our main result is the following.
$f\colon X\to \operatorname {Spec} R$
. Our main result is the following.
Theorem 1.1 (4.10).
If
![]() $\Lambda _{\mathrm {con}}$
is the contraction algebra of f, then the natural map
$\Lambda _{\mathrm {con}}$
is the contraction algebra of f, then the natural map
is a regular cover. Furthermore,
![]() $\operatorname {Stab}{}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is contractible, so this cover is universal.
$\operatorname {Stab}{}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is contractible, so this cover is universal.
The chambers of
![]() can be labelled by the contraction algebras of flopping contractions reached from f by iterated flops, and each path
can be labelled by the contraction algebras of flopping contractions reached from f by iterated flops, and each path
![]() $\unicode{x3b1} $
in the skeleton graph of
$\unicode{x3b1} $
in the skeleton graph of
![]() can be assigned a standard derived equivalence
can be assigned a standard derived equivalence
![]() $F_{\unicode{x3b1} }$
. With this notation, the Galois group for the cover in Theorem 1.1 is the image of a pure braid group under the group homomorphism
$F_{\unicode{x3b1} }$
. With this notation, the Galois group for the cover in Theorem 1.1 is the image of a pure braid group under the group homomorphism
![]() sending
sending
![]() $\unicode{x3b1} \mapsto F_{\unicode{x3b1} }$
.
$\unicode{x3b1} \mapsto F_{\unicode{x3b1} }$
.
1.3 Corollaries
The universality in Theorem 1.1 allows us to both extract new results and simplify others in the literature. The first consequence is the following, which gives a short proof of [Reference AugustAu2, 1.4].
Corollary 1.2 (5.2).
The homomorphism
![]() sending
sending
![]() $\unicode{x3b1} \mapsto F_{\unicode{x3b1} }$
is injective.
$\unicode{x3b1} \mapsto F_{\unicode{x3b1} }$
is injective.
Combining the topological Corollary 1.2 with the algebraic-geometric Theorem 4.3 allows us to side-step algebra automorphism issues and fully classify one-sided tilting complexes in
![]() $\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
. The following is a strengthening of [Reference AugustAu2, 7.2].
$\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
. The following is a strengthening of [Reference AugustAu2, 7.2].
Corollary 1.3 (5.3).
There is a bijection between morphisms in the Deligne groupoid of
![]() ending at the vertex associated to
ending at the vertex associated to
![]() $\Lambda _{\mathrm {con}}$
and the set of isomorphism classes of basic one-sided tilting complexes of
$\Lambda _{\mathrm {con}}$
and the set of isomorphism classes of basic one-sided tilting complexes of
![]() $\Lambda _{\mathrm {con}}$
.
$\Lambda _{\mathrm {con}}$
.
A more surprising consequence of the universality in Theorem 1.1 is the faithfulness of the geometric action
![]() from [Reference Donovan and WemyssDW3]. The logic is straightforward: given any element in the kernel of the geometric action, there is an element in the kernel of the algebraic action, and we can appeal directly to Corollary 1.2. As such, the following recovers the main result of the paper [Reference Hirano and WemyssHW1].
from [Reference Donovan and WemyssDW3]. The logic is straightforward: given any element in the kernel of the geometric action, there is an element in the kernel of the algebraic action, and we can appeal directly to Corollary 1.2. As such, the following recovers the main result of the paper [Reference Hirano and WemyssHW1].
Corollary 1.4 (5.5).
The homomorphism
![]() , which sends
, which sends
![]() $\unicode{x3b1} $
to the corresponding composition of Bridgeland-Chen flop functors, is injective.
$\unicode{x3b1} $
to the corresponding composition of Bridgeland-Chen flop functors, is injective.
We can further extend this to establish results on the stability manifold of the associated subcategory
. It was recently established in [Reference Hirano and WemyssHW2] that there is a component of the space of stability conditions,
and a regular covering map
with Galois group equal to the image of
. Given the faithfulness of this action from Corollary 1.4, which is implied from the silting-discrete contractibility theorem, we are also able to deduce that
is contractible. The logic again is straightforward: universal covers are unique. The proof of the following corollary is the only part of the paper where we use any prior results about
.
Corollary 1.5 (5.6).
![]() is contractible.
is contractible.
The original proof of Corollary 1.5 in [Reference Hirano and WemyssHW2] relies on knowing the universal cover of
![]() is contractible: in other words, knowing the
is contractible: in other words, knowing the
![]() $K(\unicode{x3c0} \,,1)$
-conjecture holds for
$K(\unicode{x3c0} \,,1)$
-conjecture holds for
![]() (or, more precisely, its associated braid group). Since the arrangement
(or, more precisely, its associated braid group). Since the arrangement
![]() associated to f can be obtained from the root system of an ADE Dynkin diagram by intersecting the reflecting hyperplanes with a certain subspace, it is always simplicial, and hence it is well-known that the
associated to f can be obtained from the root system of an ADE Dynkin diagram by intersecting the reflecting hyperplanes with a certain subspace, it is always simplicial, and hence it is well-known that the
![]() $K(\unicode{x3c0} \,,1)$
-conjecture holds in this case [Reference DeligneD1]. However, our approach via silting-discreteness allows us to bypass this result and actually reprove it without using [Reference BridgelandB3, Reference Brav and ThomasBT] or normal forms. For example, if
$K(\unicode{x3c0} \,,1)$
-conjecture holds in this case [Reference DeligneD1]. However, our approach via silting-discreteness allows us to bypass this result and actually reprove it without using [Reference BridgelandB3, Reference Brav and ThomasBT] or normal forms. For example, if
![]() $\Lambda _{\mathrm {con}}$
is a contraction algebra with associated
$\Lambda _{\mathrm {con}}$
is a contraction algebra with associated
![]() being an ADE root system, then
being an ADE root system, then
![]() , and it follows from Theorem 1.1 that the composition
, and it follows from Theorem 1.1 that the composition
is also a covering map.
Corollary 1.6 (5.1).
The
![]() $K(\unicode{x3c0} \,,1)$
-conjecture holds for all ADE braid groups.
$K(\unicode{x3c0} \,,1)$
-conjecture holds for all ADE braid groups.
We recall the
![]() $K(\unicode{x3c0} \,,1)$
-conjecture in Section 5 and remark that we actually reprove it for all intersection arrangements obtained from an ADE root system by intersecting the reflecting hyperplanes with a subspace generated by a choice of the coordinate vectors. This class of intersection arrangements is a bit eclectic: as a consequence, we prove
$K(\unicode{x3c0} \,,1)$
-conjecture in Section 5 and remark that we actually reprove it for all intersection arrangements obtained from an ADE root system by intersecting the reflecting hyperplanes with a subspace generated by a choice of the coordinate vectors. This class of intersection arrangements is a bit eclectic: as a consequence, we prove
![]() $K(\unicode{x3c0} \,,1)$
for the Coxeter groups
$K(\unicode{x3c0} \,,1)$
for the Coxeter groups
![]() $I_n$
for
$I_n$
for
![]() $n=3,4,5,6,8$
but none of the other n. The paper [Reference Iyama and WemyssIW2] describes in more detail the types of arrangements that can arise; see Remark 2.1.
$n=3,4,5,6,8$
but none of the other n. The paper [Reference Iyama and WemyssIW2] describes in more detail the types of arrangements that can arise; see Remark 2.1.
1.4 Conventions
Throughout, we work over the field of complex numbers. Given a noetherian ring A, modules will be right modules unless specified, and
![]() $\operatorname {mod} A$
denotes the category of finitely generated A-modules. We use the functional convention for composing arrows, so
$\operatorname {mod} A$
denotes the category of finitely generated A-modules. We use the functional convention for composing arrows, so
![]() $f\circ g$
means g then f. With this convention, given a ring R, an R-module M is a left
$f\circ g$
means g then f. With this convention, given a ring R, an R-module M is a left
![]() $\operatorname {End}_R(M)$
-module. Furthermore,
$\operatorname {End}_R(M)$
-module. Furthermore,
![]() $\operatorname {Hom}_R(M,N)$
is a right
$\operatorname {Hom}_R(M,N)$
is a right
![]() $\operatorname {End}_R(M)$
-module and a left
$\operatorname {End}_R(M)$
-module and a left
![]() $\operatorname {End}_R(N)$
-module, in fact a bimodule.
$\operatorname {End}_R(N)$
-module, in fact a bimodule.
2 Wall crossing and functorial composition
Throughout this paper,
![]() $f\colon X\to \operatorname {Spec} R$
is a fixed
$f\colon X\to \operatorname {Spec} R$
is a fixed
![]() $3$
-fold flopping contraction, where X has at worst Gorenstein terminal singularities and R is complete local. Necessarily, R is an isolated cDV singularity [Reference ReidR]. Associated to f is a rigid Cohen–Macaulay (=CM) module N, an algebra
$3$
-fold flopping contraction, where X has at worst Gorenstein terminal singularities and R is complete local. Necessarily, R is an isolated cDV singularity [Reference ReidR]. Associated to f is a rigid Cohen–Macaulay (=CM) module N, an algebra
![]() and a contraction algebra
and a contraction algebra
![]() $\Lambda _{\mathrm {con}}$
. We first briefly review these notions, mainly to set notation.
$\Lambda _{\mathrm {con}}$
. We first briefly review these notions, mainly to set notation.
2.1 Rigid modules
Since R is Gorenstein, recall that
For
![]() $M\in \operatorname {CM} R$
, we say that M is basic if there are no repetitions in its Krull–Schmidt decomposition into indecomposables. We call M a generator if one of these indecomposable summands is R, and we call M rigid if
$M\in \operatorname {CM} R$
, we say that M is basic if there are no repetitions in its Krull–Schmidt decomposition into indecomposables. We call M a generator if one of these indecomposable summands is R, and we call M rigid if
![]() $\operatorname {Ext}^1_R(M,M)=0$
. We say
$\operatorname {Ext}^1_R(M,M)=0$
. We say
![]() $M\in \operatorname {CM} R$
is maximal rigid if it is rigid, and furthermore it is maximal with respect to this property (see [Reference Iyama and WemyssIW1, 4.1]).
$M\in \operatorname {CM} R$
is maximal rigid if it is rigid, and furthermore it is maximal with respect to this property (see [Reference Iyama and WemyssIW1, 4.1]).
By the Auslander–McKay correspondence for cDV singularities, there is a one-to-one correspondence between flopping contractions
![]() $Y\to \operatorname {Spec} R$
, up to R-isomorphism, and basic rigid generators in
$Y\to \operatorname {Spec} R$
, up to R-isomorphism, and basic rigid generators in
![]() $\operatorname {CM} R$
[Reference WemyssW, 4.13]. In particular, both sets are finite. For our fixed flopping contraction
$\operatorname {CM} R$
[Reference WemyssW, 4.13]. In particular, both sets are finite. For our fixed flopping contraction
![]() $f\colon X\to \operatorname {Spec} R$
, the corresponding basic rigid CM generator across the bijection will be denoted N throughout this paper. The contraction algebra of f may then be defined as the stable endomorphism algebra
$f\colon X\to \operatorname {Spec} R$
, the corresponding basic rigid CM generator across the bijection will be denoted N throughout this paper. The contraction algebra of f may then be defined as the stable endomorphism algebra
![]() [Reference Donovan and WemyssDW1, Reference Donovan and WemyssDW3].
[Reference Donovan and WemyssDW1, Reference Donovan and WemyssDW3].
The set of basic rigid CM generators carries an operation called mutation. Indeed, given such an L, with indecomposable summand
![]() $L_i\ncong R$
, there is the so-called exchange sequence
$L_i\ncong R$
, there is the so-called exchange sequence
and
[Reference WemyssW, (A.A)]. Given the summand
![]() $K_i$
of
$K_i$
of
![]() $\unicode{x3bd} _iL$
, we can mutate again and obtain
$\unicode{x3bd} _iL$
, we can mutate again and obtain
![]() $\unicode{x3bd} _i\unicode{x3bd} _iL$
. It is a general fact for isolated cDV singularities that
$\unicode{x3bd} _i\unicode{x3bd} _iL$
. It is a general fact for isolated cDV singularities that
![]() $\unicode{x3bd} _i\unicode{x3bd} _iL\cong L$
[Reference WemyssW, 4.20(1)], and moreover in the second exchange sequence
$\unicode{x3bd} _i\unicode{x3bd} _iL\cong L$
[Reference WemyssW, 4.20(1)], and moreover in the second exchange sequence
we have
![]() $b_{ij}=c_{ij}$
for all
$b_{ij}=c_{ij}$
for all
![]() $i,j$
[Reference WemyssW, 5.22]. Furthermore, there are equivalences of derived categories
$i,j$
[Reference WemyssW, 5.22]. Furthermore, there are equivalences of derived categories

We will abuse notation and notate both as
and refer to them as the mutation functors.
Given our fixed basic rigid CM generator N corresponding to f, write
![]() $\operatorname {Mut}_0(N)$
for the set of basic rigid CM generators that can be obtained from N by iteratively mutating at indecomposable summands, noting that, in this paper, we will never mutate at the summand R. Geometrically, across the Auslander–McKay correspondence, this corresponds to all R-schemes that can be obtained from X by iteratively flopping curves.
$\operatorname {Mut}_0(N)$
for the set of basic rigid CM generators that can be obtained from N by iteratively mutating at indecomposable summands, noting that, in this paper, we will never mutate at the summand R. Geometrically, across the Auslander–McKay correspondence, this corresponds to all R-schemes that can be obtained from X by iteratively flopping curves.
2.2 Hyperplanes and labels
We fix a decomposition
![]() $N=R\oplus N_1\oplus \ldots \oplus N_n$
and will often implicitly declare
$N=R\oplus N_1\oplus \ldots \oplus N_n$
and will often implicitly declare
![]() $N_0=R$
. For every
$N_0=R$
. For every
![]() $L\in \operatorname {Mut}_0(N)$
and each indecomposable summand
$L\in \operatorname {Mut}_0(N)$
and each indecomposable summand
![]() $L_i$
of L, there is an exact sequence
$L_i$
of L, there is an exact sequence
 $$ \begin{align} 0\to \bigoplus_{j=0}^n N_j^{\oplus a_{ij}}\to \bigoplus_{j=0}^n N_j^{\oplus b_{ij}}\to L_i\to 0 , \end{align} $$
$$ \begin{align} 0\to \bigoplus_{j=0}^n N_j^{\oplus a_{ij}}\to \bigoplus_{j=0}^n N_j^{\oplus b_{ij}}\to L_i\to 0 , \end{align} $$
where the first and second terms do not share any indecomposable summands. In the setting where
![]() $N\in \operatorname {CM} R$
is maximal rigid, this fact is very well known; in the setting here for rigid generators, we rely instead on [Reference Iyama and WemyssIW2, 9.29, 5.6]. In any case, consider the cone
$N\in \operatorname {CM} R$
is maximal rigid, this fact is very well known; in the setting here for rigid generators, we rely instead on [Reference Iyama and WemyssIW2, 9.29, 5.6]. In any case, consider the cone

It is clear that
, which we denote throughout by
![]() $C_+$
. Furthermore, the chambers
$C_+$
. Furthermore, the chambers
![]() $C_L$
, as L varies over
$C_L$
, as L varies over
![]() $\operatorname {Mut}_0(N)$
, sweep out the chambers of a simplicial hyperplane arrangement
$\operatorname {Mut}_0(N)$
, sweep out the chambers of a simplicial hyperplane arrangement
[Reference Hirano and WemyssHW1, Reference Iyama and WemyssIW2].
Remark 2.1. The above arrangement has several equivalent descriptions; it can be obtained as the g-vector fan of
![]() $\Lambda _{\mathrm {con}}$
[Reference AugustAu2, 7.1] or as the moveable cone of the flopping contraction f [Reference Hirano and WemyssHW1, 4.6(3)] (where, as described in the following remark, both of these results are extended to the rigid setting using [Reference Iyama and WemyssIW2, 9.29]). Using this last description, HomMMP [Reference WemyssW, 5.24, 5.25] gives the description of
$\Lambda _{\mathrm {con}}$
[Reference AugustAu2, 7.1] or as the moveable cone of the flopping contraction f [Reference Hirano and WemyssHW1, 4.6(3)] (where, as described in the following remark, both of these results are extended to the rigid setting using [Reference Iyama and WemyssIW2, 9.29]). Using this last description, HomMMP [Reference WemyssW, 5.24, 5.25] gives the description of
![]() via intersecting a subspace of an ADE root system with the reflecting hyperplanes. In other words, all the
via intersecting a subspace of an ADE root system with the reflecting hyperplanes. In other words, all the
![]() above are intersection arrangements of ADE root systems and, as such, are both finite and simplicial.
above are intersection arrangements of ADE root systems and, as such, are both finite and simplicial.
Remark 2.2. The three key properties appearing here and later are the following:
-
1.
 $\unicode{x3bd} _i\unicode{x3bd} _iL \cong L$
for any basic rigid CM generator.
$\unicode{x3bd} _i\unicode{x3bd} _iL \cong L$
for any basic rigid CM generator. -
2. Moreover,
 $b_{ij}=c_{ij}$
in the corresponding exchange sequences.
$b_{ij}=c_{ij}$
in the corresponding exchange sequences. -
3. Every
 $L\in \operatorname {Mut}_0(N)$
has a two-term approximation by N, as in equation (2.2), ensuring that
$L\in \operatorname {Mut}_0(N)$
has a two-term approximation by N, as in equation (2.2), ensuring that
 $\operatorname {Hom}_R(L,N)$
is a tilting bimodule for
$\operatorname {Hom}_R(L,N)$
is a tilting bimodule for
 $\Lambda $
.
$\Lambda $
.
The first two follow as a consequence of HomMMP [Reference WemyssW, 4.20(1), 5.22], since flopping is an involution. In the maximal rigid setting, (3) is known, but to prove (3) in the general rigid setting requires a small part of [Reference Iyama and WemyssIW2]. Once (1)–(3) hold, [Reference AugustAu2, 4.9(2)] extends all the results of [Reference Hirano and WemyssHW1, Reference AugustAu2] to the setting of rigid modules, and this is what we use below. A reader wishing only to work in the maximal rigid setting or in the smooth setting may safely disregard references to [Reference Iyama and WemyssIW2].
As explained by the general Coxeter-style labelling of walls and chambers in [Reference Iyama and WemyssIW2, §9.7], the fixed decomposition
![]() $N=R\oplus N_1\oplus \ldots \oplus N_n$
induces an ordering on the summands of all other elements L of
$N=R\oplus N_1\oplus \ldots \oplus N_n$
induces an ordering on the summands of all other elements L of
![]() $\operatorname {Mut}_0(N)$
such that each local wall crossing has a label
$\operatorname {Mut}_0(N)$
such that each local wall crossing has a label
![]() $s_i$
and corresponds to mutation at the ith summand. In this way, there is a compatible labelling on the edges of the 1-skeleton of
$s_i$
and corresponds to mutation at the ith summand. In this way, there is a compatible labelling on the edges of the 1-skeleton of
![]() . We illustrate this in an example.
. We illustrate this in an example.
Example 2.3. There exists a two-curve flop over a
![]() $cD_4$
singularity with the simplicial hyperplane arrangement shown in Figure 1. Each local wall crossing is labelled by
$cD_4$
singularity with the simplicial hyperplane arrangement shown in Figure 1. Each local wall crossing is labelled by
![]() $s_i$
for
$s_i$
for
![]() $i=1,2$
, and under crossing wall
$i=1,2$
, and under crossing wall
![]() $s_i$
the ith summand is mutated. For clarity, in each chamber, we have not written the zeroth summand R. Note that
$s_i$
the ith summand is mutated. For clarity, in each chamber, we have not written the zeroth summand R. Note that
![]() $C_N=C_+$
is the top-right chamber.
$C_N=C_+$
is the top-right chamber.
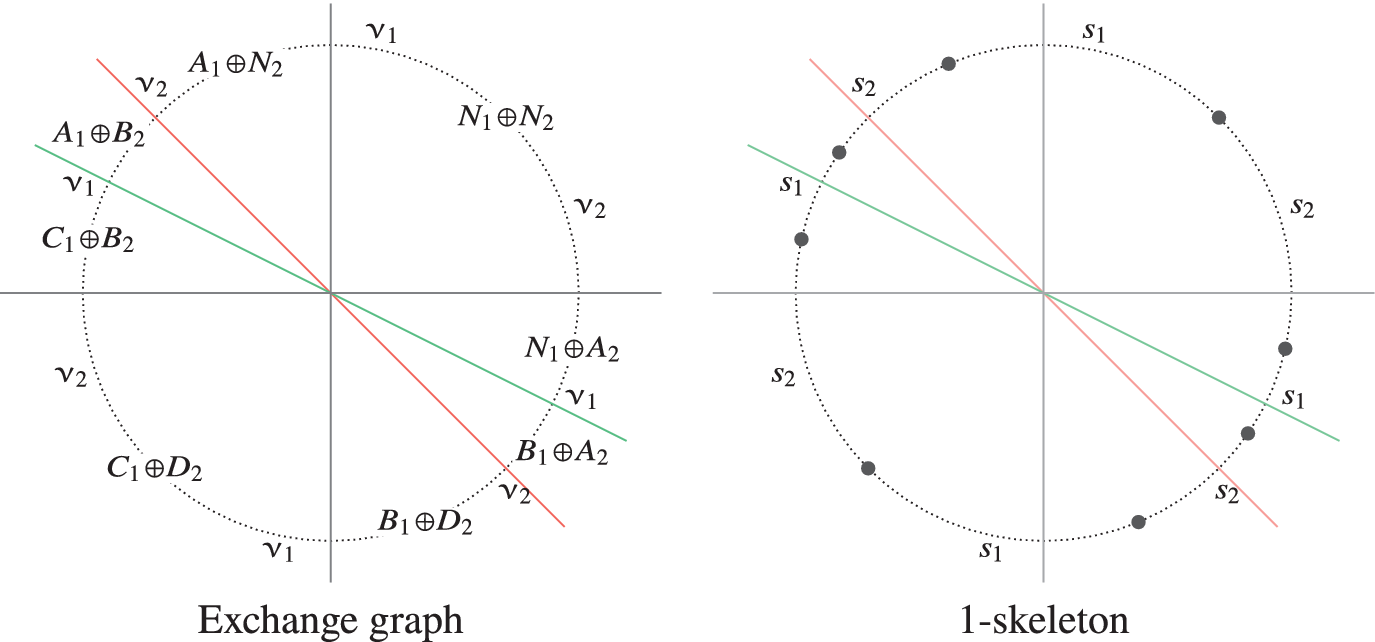
Figure 1 Exchange graph and
![]() $1$
-skeleton for a certain two-curve
$1$
-skeleton for a certain two-curve
![]() $cD_4$
singularity.
$cD_4$
singularity.
Fixing an ordering of the summands of N not only fixes an ordering of the projective modules
![]() of
of
![]() $\Lambda =\operatorname {End}_R(N)$
and, via the pairing between simples and projectives, an ordering of its simples
$\Lambda =\operatorname {End}_R(N)$
and, via the pairing between simples and projectives, an ordering of its simples
![]() , but also fixes an ordering on the projectives and simples of
, but also fixes an ordering on the projectives and simples of
![]() $\operatorname {End}_R(L)$
for all
$\operatorname {End}_R(L)$
for all
![]() $L\in \operatorname {Mut}_0(N)$
.
$L\in \operatorname {Mut}_0(N)$
.
To fix notation, for
![]() $L\in \operatorname {Mut}_0(N)$
, suppose that the induced ordering on the summands of L is
$L\in \operatorname {Mut}_0(N)$
, suppose that the induced ordering on the summands of L is
![]() $L=L_0\oplus L_1\oplus \ldots \oplus L_n$
, where
$L=L_0\oplus L_1\oplus \ldots \oplus L_n$
, where
![]() $L_0= R$
. There is an induced ordering on the projectives
$L_0= R$
. There is an induced ordering on the projectives
![]() of
of
![]() $\operatorname {End}_R(L)$
and again via the pairing between simples and projectives, an ordering of its simples
$\operatorname {End}_R(L)$
and again via the pairing between simples and projectives, an ordering of its simples
![]() . The simples for the contraction algebra
. The simples for the contraction algebra
![]() $\operatorname {\underline {End}}_R(L)$
are
$\operatorname {\underline {End}}_R(L)$
are
![]() .
.
2.3 Standard equivalences for simple wall crossings
Let
![]() $L\in \operatorname {Mut}_0(N)$
, with associated
$L\in \operatorname {Mut}_0(N)$
, with associated
![]() and contraction algebra
and contraction algebra
![]() . To ease notation, suppose that
. To ease notation, suppose that
![]() , with contraction algebra
, with contraction algebra
![]() $\mathrm {B}_{\mathrm {con}}$
, and consider the good truncation
$\mathrm {B}_{\mathrm {con}}$
, and consider the good truncation
which is a complex of
![]() $\mathrm {B}_{\mathrm {con}}$
-
$\mathrm {B}_{\mathrm {con}}$
-
![]() $\mathrm {A}_{\mathrm {con}}$
bimodules. In this basic rigid setting, it is already known that the complex
$\mathrm {A}_{\mathrm {con}}$
bimodules. In this basic rigid setting, it is already known that the complex
![]() is a two-sided tilting complex [Reference AugustAu2, 3.3].
is a two-sided tilting complex [Reference AugustAu2, 3.3].
Theorem 2.4. Suppose that
![]() $L,M \in \operatorname {Mut}_0(N)$
, which correspond to the flopping contractions
$L,M \in \operatorname {Mut}_0(N)$
, which correspond to the flopping contractions
![]() $X_L\to \operatorname {Spec} R$
and
$X_L\to \operatorname {Spec} R$
and
![]() $X_M\to \operatorname {Spec} R$
, say. Then the following are equivalent:
$X_M\to \operatorname {Spec} R$
, say. Then the following are equivalent:
-
1.
 $C_L$
and
$C_L$
and
 $C_M$
share a codimension one wall in
$C_M$
share a codimension one wall in
 .
. -
2.
 $M\cong \unicode{x3bd} _iL$
for some
$M\cong \unicode{x3bd} _iL$
for some
 $i\neq 0$
.
$i\neq 0$
. -
3.
 $X_L$
and
$X_L$
and
 $X_M$
are related by a flop at a single irreducible curve.
$X_M$
are related by a flop at a single irreducible curve.
In this case, set
,
and
,
. Then the mutation operations intertwine via the following commutative diagram

where
is the mutation functor,
![]() $\operatorname {\mathsf {Flop}}_i$
is the inverse of the Bridgeland–Chen flop functor [Reference BridgelandB1, Reference ChenC],
$\operatorname {\mathsf {Flop}}_i$
is the inverse of the Bridgeland–Chen flop functor [Reference BridgelandB1, Reference ChenC],
and
are the standard projective generators of zero perverse sheaves [Reference Van den BerghVdB] and
![]() $\operatorname {res}$
is restriction of scalars induced from the ring homomorphisms
$\operatorname {res}$
is restriction of scalars induced from the ring homomorphisms
![]() $\mathrm {A}\to \mathrm {A}_{\mathrm {con}}$
and
$\mathrm {A}\to \mathrm {A}_{\mathrm {con}}$
and
![]() $\mathrm {B}\to \mathrm {B}_{\mathrm {con}}$
.
$\mathrm {B}\to \mathrm {B}_{\mathrm {con}}$
.
Proof. The statement (1)
![]() $\Leftrightarrow $
(2) is clear; see also [Reference Hirano and WemyssHW2, 3.6]. The statement (2)
$\Leftrightarrow $
(2) is clear; see also [Reference Hirano and WemyssHW2, 3.6]. The statement (2)
![]() $\Leftrightarrow $
(3) is [Reference WemyssW, 4.13], where since we are mutating only at indecomposable summands and R is isolated, [Reference WemyssW, 4.20(1)] overrides the caveat in the latter part of [Reference WemyssW, 4.13]. The left-hand diagram commutes by [Reference AugustAu2, 1.1], and the right-hand diagram commutes by [Reference WemyssW, 4.2].
$\Leftrightarrow $
(3) is [Reference WemyssW, 4.13], where since we are mutating only at indecomposable summands and R is isolated, [Reference WemyssW, 4.20(1)] overrides the caveat in the latter part of [Reference WemyssW, 4.13]. The left-hand diagram commutes by [Reference AugustAu2, 1.1], and the right-hand diagram commutes by [Reference WemyssW, 4.2].
2.4 K-theory
Since
![]() $\Lambda _{\mathrm {con}}$
is a finite-dimensional algebra, consider the Grothendieck group
$\Lambda _{\mathrm {con}}$
is a finite-dimensional algebra, consider the Grothendieck group
which is well-known to be a free abelian group with basis given by the ordered simples
. The notation
![]() $\mathsf {G}_0$
is chosen since we are including in the Grothendieck group all modules, whereas
$\mathsf {G}_0$
is chosen since we are including in the Grothendieck group all modules, whereas
![]() $K_0$
often only deals with vector bundles and thus projectives.
$K_0$
often only deals with vector bundles and thus projectives.
Continuing the notation from Theorem 2.4, for any
![]() $L\in \operatorname {Mut}_0(N)$
, consider its associated contraction algebra
$L\in \operatorname {Mut}_0(N)$
, consider its associated contraction algebra
![]() $\mathrm {A}_{\mathrm {con}}=\operatorname {\underline {End}}_R(L)$
and its mutations
$\mathrm {A}_{\mathrm {con}}=\operatorname {\underline {End}}_R(L)$
and its mutations
. Abusing notation slightly, consider the standard equivalences

where the functor from right to left is induced by the mutation
![]() $\unicode{x3bd} _i L \to \unicode{x3bd} _i \unicode{x3bd} _i L \cong L$
. These and their inverses induce the following four isomorphisms on K-theory:
$\unicode{x3bd} _i L \to \unicode{x3bd} _i \unicode{x3bd} _i L \cong L$
. These and their inverses induce the following four isomorphisms on K-theory:

As in Subsection 2.2, write
![]() for the ordered simples of
for the ordered simples of
![]() $\mathrm {A}_{\mathrm {con}}$
. For lack of suitable alternatives, also write
$\mathrm {A}_{\mathrm {con}}$
. For lack of suitable alternatives, also write
![]() for the correspondingly ordered simples in
for the correspondingly ordered simples in
![]() $\unicode{x3bd} _i\mathrm {A}_{\mathrm {con}}$
.
$\unicode{x3bd} _i\mathrm {A}_{\mathrm {con}}$
.
Lemma 2.5. With the notation in equation (2.1),
![]() $\mathsf {F}_i\colon \mathsf {G}_0(\mathrm {A}_{\mathrm {con}})\to \mathsf {G}_0(\unicode{x3bd} _i\mathrm {A}_{\mathrm {con}})$
sends
$\mathsf {F}_i\colon \mathsf {G}_0(\mathrm {A}_{\mathrm {con}})\to \mathsf {G}_0(\unicode{x3bd} _i\mathrm {A}_{\mathrm {con}})$
sends

Proof. The fact that
![]() is [Reference WemyssW, 4.15]. Theorem 2.4 then implies that
is [Reference WemyssW, 4.15]. Theorem 2.4 then implies that
![]() maps, under restriction of scalars, to
maps, under restriction of scalars, to
![]() . It follows that
. It follows that
![]() in
in
![]() $\mathop {\mathrm {D}^b}(\mathrm {A}_{\mathrm {con}})$
; see, for example, [Reference AugustAu2, 6.6]. This establishes the top row.
$\mathop {\mathrm {D}^b}(\mathrm {A}_{\mathrm {con}})$
; see, for example, [Reference AugustAu2, 6.6]. This establishes the top row.
For the second row, applying
![]() $\operatorname {Hom}_R(L,-)$
to equation (2.1) and using the rigidity of L gives an exact sequence
$\operatorname {Hom}_R(L,-)$
to equation (2.1) and using the rigidity of L gives an exact sequence

Applying
to this, with
![]() $t\neq i$
, yields
$t\neq i$
, yields
Further, it is clear that
is zero if
![]() $j\neq t$
and equals
$j\neq t$
and equals
![]() $\mathbb {C}$
if
$\mathbb {C}$
if
![]() $j=t$
. Combining, we see that
$j=t$
. Combining, we see that
is a module, filtered by
![]() $b_{it}$
copies of
$b_{it}$
copies of
and one copy of
. Again, the left-hand side of the commutative diagram in Theorem 2.4 then shows that
must also be a module, filtered by
![]() $b_{it}$
copies of
$b_{it}$
copies of
and one copy of
. The second row follows.
Remark 2.6. Applying the above to
![]() $L=N$
, basing
$L=N$
, basing
![]() $\mathsf {G}_0(\Lambda _{\mathrm {con}})$
by the ordered simples
$\mathsf {G}_0(\Lambda _{\mathrm {con}})$
by the ordered simples
, the above transformation given by equation (2.5) assembles into an
![]() $n\times n$
matrix, with coefficients in
$n\times n$
matrix, with coefficients in
![]() $\mathbb {Z}$
, representing the map
$\mathbb {Z}$
, representing the map
![]() $\mathsf {F}_i\colon \mathbb {Z}^n\to \mathbb {Z}^n$
. As is standard in linear algebra, the dual map
$\mathsf {F}_i\colon \mathbb {Z}^n\to \mathbb {Z}^n$
. As is standard in linear algebra, the dual map
where
![]() $\mathsf {G}_0(\Lambda _{\mathrm {con}})^*$
has dual basis
$\mathsf {G}_0(\Lambda _{\mathrm {con}})^*$
has dual basis
![]() $\textbf {e}_1,\ldots ,\textbf {e}_n$
, say, is given by the transpose matrix. But the transpose is precisely the transformation
$\textbf {e}_1,\ldots ,\textbf {e}_n$
, say, is given by the transpose matrix. But the transpose is precisely the transformation
 $$\begin{align*}\textbf{e}_t\mapsto \left\{ \begin{array}{cl} \textbf{e}_t& \mbox{if } t\neq i,\\ -\textbf{e}_i+\sum_{j\neq i}b_{ij}\textbf{e}_j & \mbox{if } t=i, \end{array} \right. \end{align*}$$
$$\begin{align*}\textbf{e}_t\mapsto \left\{ \begin{array}{cl} \textbf{e}_t& \mbox{if } t\neq i,\\ -\textbf{e}_i+\sum_{j\neq i}b_{ij}\textbf{e}_j & \mbox{if } t=i, \end{array} \right. \end{align*}$$
which is precisely the transformation
seen in moduli tracking [Reference WemyssW, §5] or in K-theory of projectives in [Reference Hirano and WemyssHW2, 3.2]. In particular, it will be convenient to think of the dual basis
![]() $\textbf {e}_1,\ldots ,\textbf {e}_n$
as being the basis
$\textbf {e}_1,\ldots ,\textbf {e}_n$
as being the basis
of
, where
![]() $\operatorname {per}\Lambda $
is the full subcategory of
$\operatorname {per}\Lambda $
is the full subcategory of
![]() $\mathop {\mathrm {D}^b}(\Lambda )$
consisting of perfect complexes. Then the transformation
$\mathop {\mathrm {D}^b}(\Lambda )$
consisting of perfect complexes. Then the transformation
![]() $\mathsf {F}_i^*$
can be identified with these transformations elsewhere in the literature, and we can use those results freely. Note that the hyperplane arrangement
$\mathsf {F}_i^*$
can be identified with these transformations elsewhere in the literature, and we can use those results freely. Note that the hyperplane arrangement
from Subsection 2.2 is defined in terms of
![]() $\textbf {e}_i$
and so naturally lives in
$\textbf {e}_i$
and so naturally lives in
![]() $\mathsf {G}_0(\Lambda _{\mathrm {con}})^*$
.
$\mathsf {G}_0(\Lambda _{\mathrm {con}})^*$
.
By the above remark, the proof of the following does follow as the dual of [Reference Hirano and WemyssHW2, 3.2]. It is, however, instructive to give a direct proof.
Lemma 2.7. All four isomorphisms in equation (2.4) are given by the same matrix, namely the one from equation (2.5), and this matrix squares to the identity.
Proof. By equation (2.5), the matrices are controlled by the numbers
![]() $b_{ij}$
appearing in the relevant exchange sequences. Say the top
$b_{ij}$
appearing in the relevant exchange sequences. Say the top
![]() $\mathsf {F}_i$
is controlled by numbers
$\mathsf {F}_i$
is controlled by numbers
![]() $b_{ij}$
, and the bottom
$b_{ij}$
, and the bottom
![]() $\mathsf {F}_i$
is controlled by numbers
$\mathsf {F}_i$
is controlled by numbers
![]() $c_{ij}$
. That the two matrices labelled
$c_{ij}$
. That the two matrices labelled
![]() $\mathsf {F}_i$
are the same is simply the statement that
$\mathsf {F}_i$
are the same is simply the statement that
![]() $b_{ij}=c_{ij}$
, which has already been explained in Subsection 2.1. Given this fact that
$b_{ij}=c_{ij}$
, which has already been explained in Subsection 2.1. Given this fact that
![]() $b_{ij}=c_{ij}$
, we see that
$b_{ij}=c_{ij}$
, we see that
![]() $\mathsf {F}_i\mathsf {F}_i=\mathrm {Id}$
by simply observing
$\mathsf {F}_i\mathsf {F}_i=\mathrm {Id}$
by simply observing

which is clearly the identity. Applying
![]() $\mathsf {F}_i^{-1}$
to each side of the equation
$\mathsf {F}_i^{-1}$
to each side of the equation
![]() $\mathsf {F}_i\mathsf {F}_i=\mathrm {Id}$
gives
$\mathsf {F}_i\mathsf {F}_i=\mathrm {Id}$
gives
![]() $\mathsf {F}_i^{-1}=\mathsf {F}_i$
, and all statements follow.
$\mathsf {F}_i^{-1}=\mathsf {F}_i$
, and all statements follow.
2.5 Groupoids
As in Subsection 2.2, associated to every contraction algebra is a hyperplane arrangement
![]() . As is standard, there is an associated graph
. As is standard, there is an associated graph
![]() defined as follows.
defined as follows.
Definition 2.8. The vertices of
![]() are the chambers – that is, the connected components – of
are the chambers – that is, the connected components – of
![]() . There is a unique arrow
. There is a unique arrow
![]() $a \colon v_1\to v_2$
from chamber
$a \colon v_1\to v_2$
from chamber
![]() $v_1$
to chamber
$v_1$
to chamber
![]() $v_2$
if the chambers are adjacent; otherwise there is no arrow.
$v_2$
if the chambers are adjacent; otherwise there is no arrow.
By definition, if there is an arrow
![]() $a \colon v_1\to v_2$
, then there is a unique arrow
$a \colon v_1\to v_2$
, then there is a unique arrow
![]() $b\colon v_2\to v_1$
with the opposite direction of a. For an arrow
$b\colon v_2\to v_1$
with the opposite direction of a. For an arrow
![]() $a\colon v_1\to v_2$
, set
$a\colon v_1\to v_2$
, set
![]() and
and
![]() .
.
A positive path of length n in
is a formal symbol
whenever there exists a sequence of vertices
![]() $v_0,\ldots ,v_n$
of
$v_0,\ldots ,v_n$
of
and arrows
![]() $a_i\colon v_{i-1}\to v_i$
in
$a_i\colon v_{i-1}\to v_i$
in
. Set
,
,
, and write
![]() $p\colon s(p)\to t(p)$
. If
$p\colon s(p)\to t(p)$
. If
![]() $q=b_m\circ \ldots \circ b_2 \circ b_1$
is another positive path with
$q=b_m\circ \ldots \circ b_2 \circ b_1$
is another positive path with
![]() $t(p)=s(q)$
, we consider the formal symbol
$t(p)=s(q)$
, we consider the formal symbol
and call it the composition of p and q.
Definition 2.9. A positive path
![]() $\unicode{x3b1} $
is called minimal if there is no shorter positive path in
$\unicode{x3b1} $
is called minimal if there is no shorter positive path in
![]() with the same start and end points as
with the same start and end points as
![]() $\unicode{x3b1} $
.
$\unicode{x3b1} $
.
Following [Reference DelucchiD2, p7], let
![]() $\sim $
denote the smallest equivalence relation, compatible with morphism composition, that identifies all morphisms that arise as positive minimal paths with the same source and target. Then consider the free category
$\sim $
denote the smallest equivalence relation, compatible with morphism composition, that identifies all morphisms that arise as positive minimal paths with the same source and target. Then consider the free category
on the graph
, whose morphisms correspond to directed paths, and its quotient category
called the category of positive paths.
Definition 2.10. The Deligne groupoid
![]() is the groupoid defined as the groupoid completion of
is the groupoid defined as the groupoid completion of
![]() : that is, a formal inverse is added for every morphism in
: that is, a formal inverse is added for every morphism in
![]() .
.
It is a very well known fact [Reference DeligneD1, Reference ParisP1, Reference ParisP3, Reference SalvettiS] (see also [Reference ParisP2, 2.1]) that for any vertex
![]() , there is an isomorphism
, there is an isomorphism
![]() , where
, where
![]() . This fact is general and is significantly weaker and easier to establish than statements involving
. This fact is general and is significantly weaker and easier to establish than statements involving
![]() $K(\unicode{x3c0} \,,1)$
. We will use this fact implicitly throughout.
$K(\unicode{x3c0} \,,1)$
. We will use this fact implicitly throughout.
2.6 Composition and K-theory
For any
, say
![]() $\unicode{x3b1} ={s_{i_t}}\circ \ldots \circ {s_{i_1}}$
, consider
$\unicode{x3b1} ={s_{i_t}}\circ \ldots \circ {s_{i_1}}$
, consider

The following is known and easy to establish just using the tilting order, in the case when the modules are maximal rigid (e.g., if X is smooth). In our more general situation of rigid generators, the same proof works, but it relies on some recent advances in [Reference Iyama and WemyssIW2].
Proposition 2.11. Let
![]() $\unicode{x3b1} \colon C_L\to C_M$
be a positive minimal path. Set
$\unicode{x3b1} \colon C_L\to C_M$
be a positive minimal path. Set
![]() ,
,
![]() ,
,
![]() and
and
![]() . Then the following hold:
. Then the following hold:
-
1.
 is functorially isomorphic to
is functorially isomorphic to
 $\operatorname {{\textbf {R}}Hom}_{\mathrm {A}}(\operatorname {Hom}_R(L,M),-)$
.
$\operatorname {{\textbf {R}}Hom}_{\mathrm {A}}(\operatorname {Hom}_R(L,M),-)$
. -
2.
 $F_{\unicode{x3b1} }$
is functorially isomorphic to
$F_{\unicode{x3b1} }$
is functorially isomorphic to
 , where
, where
 is the two-sided tilting complex
is the two-sided tilting complex
 $ \unicode{x3c4} _{\scriptscriptstyle { \geq -1}} ( \mathrm {B}_{\mathrm {con}} \otimes ^{ \mathrm{\mathbf{L}}}_{\mathrm {B}} \operatorname {Hom}_R(L,M) \otimes ^{ \mathrm{\mathbf{L}}}_{\mathrm {A}} \mathrm {A}_{\mathrm {con}})$
.
$ \unicode{x3c4} _{\scriptscriptstyle { \geq -1}} ( \mathrm {B}_{\mathrm {con}} \otimes ^{ \mathrm{\mathbf{L}}}_{\mathrm {B}} \operatorname {Hom}_R(L,M) \otimes ^{ \mathrm{\mathbf{L}}}_{\mathrm {A}} \mathrm {A}_{\mathrm {con}})$
.
In particular, all positive minimal paths with the same start and end points are functorially isomorphic.
Proof. (1) When N is maximal rigid, this is precisely [Reference AugustAu2, 4.9(1)], [Reference Hirano and WemyssHW1, 4.6]. In the more general setting here with
![]() $L,M\in \operatorname {Mut}_0(N)$
, then certainly
$L,M\in \operatorname {Mut}_0(N)$
, then certainly
![]() $L\in \operatorname {Mut}_0(M)$
. Since R is isolated cDV, it follows from the combinatorial and geometric description of mutation of rigid modules in [Reference Iyama and WemyssIW2, 9.25, 9.29] that
$L\in \operatorname {Mut}_0(M)$
. Since R is isolated cDV, it follows from the combinatorial and geometric description of mutation of rigid modules in [Reference Iyama and WemyssIW2, 9.25, 9.29] that
![]() $\operatorname {Hom}_R(L,M)$
is a tilting
$\operatorname {Hom}_R(L,M)$
is a tilting
![]() $\operatorname {End}_R(M)$
-
$\operatorname {End}_R(M)$
-
![]() $\operatorname {End}_R(L)$
-bimodule of projective dimension one when viewed as a right
$\operatorname {End}_R(L)$
-bimodule of projective dimension one when viewed as a right
![]() $\operatorname {End}_R(L)$
-module. This is the key technical condition, explained in [Reference AugustAu2, 4.9(2)] and not available when [Reference Hirano and WemyssHW1] was written, that now allows us to use the main result [Reference Hirano and WemyssHW1, 4.6] freely in the more general setting here.
$\operatorname {End}_R(L)$
-module. This is the key technical condition, explained in [Reference AugustAu2, 4.9(2)] and not available when [Reference Hirano and WemyssHW1] was written, that now allows us to use the main result [Reference Hirano and WemyssHW1, 4.6] freely in the more general setting here.
(2) When N is maximal rigid, this is [Reference AugustAu2, 4.12]. The more general statement required here follows by (1) and, again, [Reference AugustAu2, 4.9(2)], which asserts, given (1), that we are able to apply the main result [Reference AugustAu2, 4.12] to the setting of rigid objects.
For any two positive minimal paths
![]() $\unicode{x3b1} $
and
$\unicode{x3b1} $
and
![]() $\unicode{x3b2} $
with the same start and end points, the above proposition shows that there is a functorial isomorphism
$\unicode{x3b2} $
with the same start and end points, the above proposition shows that there is a functorial isomorphism
![]() $F_{\unicode{x3b1} }\cong F_{\unicode{x3b2} }$
. Hence the association
$F_{\unicode{x3b1} }\cong F_{\unicode{x3b2} }$
. Hence the association
![]() $\unicode{x3b1} \mapsto F_{\unicode{x3b1} }$
descends to a functor from
$\unicode{x3b1} \mapsto F_{\unicode{x3b1} }$
descends to a functor from
![]() . Since
. Since
![]() $F_{\unicode{x3b1} }$
is already an equivalence, this in turn formally descends to a functor from
$F_{\unicode{x3b1} }$
is already an equivalence, this in turn formally descends to a functor from
![]() . Using the same logic, the assignment
. Using the same logic, the assignment
![]() also descends to a functor from
also descends to a functor from
![]() and then a functor from
and then a functor from
![]() .
.
Furthermore, for every
, using the notation from the second sentence in Proposition 2.11, the following diagram commutes

just by composition, since by [Reference AugustAu2, 1.1], respectively [Reference AugustAu2, 3.2], both of the following commute:

Later, the following is one of the crucial ingredients in establishing that
![]() $\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is a covering space. Recall that for the standard derived equivalence
$\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is a covering space. Recall that for the standard derived equivalence
![]() $F_{\unicode{x3b1} }$
associated to a path
$F_{\unicode{x3b1} }$
associated to a path
![]() $\unicode{x3b1} $
, the induced map on the K-theory is denoted
$\unicode{x3b1} $
, the induced map on the K-theory is denoted
![]() $\mathsf {F}_{\unicode{x3b1} }$
.
$\mathsf {F}_{\unicode{x3b1} }$
.
Proposition 2.12. Suppose that
![]() $\unicode{x3b2} \colon C\to D$
is a positive minimal path in
$\unicode{x3b2} \colon C\to D$
is a positive minimal path in
![]() .
.
-
1. If
 $\unicode{x3b1} \colon C\to D$
is any positive path, then
$\unicode{x3b1} \colon C\to D$
is any positive path, then
 $\mathsf {F}_{\unicode{x3b1} }=\mathsf {F}_{\unicode{x3b2} }$
.
$\mathsf {F}_{\unicode{x3b1} }=\mathsf {F}_{\unicode{x3b2} }$
. -
2. If
 , then
, then
 $\mathsf {F}_{\unicode{x3b1} }=\mathrm {Id}$
.
$\mathsf {F}_{\unicode{x3b1} }=\mathrm {Id}$
. -
3. If
 , then
, then
 $\mathsf {F}_{\unicode{x3b1} }=\mathsf {F}_{\unicode{x3b3} }$
.
$\mathsf {F}_{\unicode{x3b1} }=\mathsf {F}_{\unicode{x3b3} }$
.
Proof. Having established Lemma 2.7, this is now word-for-word identical to [Reference Hirano and WemyssHW2, 4.8]. Note that this proof is elementary and does not require Deligne normal form.
2.7 The dual composition
For each
![]() $L \in \operatorname {Mut}_0(N)$
, consider
$L \in \operatorname {Mut}_0(N)$
, consider
and recall that
. Choose a positive minimal path
![]() $\unicode{x3b2} \colon C_L \to C_+$
, which in turn gives rise to a derived equivalence
$\unicode{x3b2} \colon C_L \to C_+$
, which in turn gives rise to a derived equivalence
This derived equivalence is independent of the choice of positive minimal path, by Proposition 2.11. It induces an isomorphism
![]() $\mathsf {K}_0(\operatorname {per}\Lambda _L)\to \mathsf {K}_0(\operatorname {per}\Lambda )$
on the K-theory of perfect complexes, so write
$\mathsf {K}_0(\operatorname {per}\Lambda _L)\to \mathsf {K}_0(\operatorname {per}\Lambda )$
on the K-theory of perfect complexes, so write

in
![]() $\mathsf {K}_0(\operatorname {per}\Lambda )\cong \mathbb {Z}^{n+1}$
, where
$\mathsf {K}_0(\operatorname {per}\Lambda )\cong \mathbb {Z}^{n+1}$
, where
and
. Since
![]() $\unicode{x3b1} $
is a sequence of mutations that do not involve mutating the zeroth summand, the zeroth summand is fixed at each stage. Hence this isomorphism descends to an isomorphism
$\unicode{x3b1} $
is a sequence of mutations that do not involve mutating the zeroth summand, the zeroth summand is fixed at each stage. Hence this isomorphism descends to an isomorphism
Basing the first by
and the second by
, the matrix representing the isomorphism is
for
![]() $1\leq i,j\leq n$
. By Remark 2.6, later we will think of these bases as
$1\leq i,j\leq n$
. By Remark 2.6, later we will think of these bases as
![]() $\textbf {e}^{\prime }_1,\ldots ,\textbf {e}^{\prime }_n$
of
$\textbf {e}^{\prime }_1,\ldots ,\textbf {e}^{\prime }_n$
of
![]() $\mathsf {G}_0(\operatorname {\underline {End}}_R(L))^*$
and
$\mathsf {G}_0(\operatorname {\underline {End}}_R(L))^*$
and
![]() $\textbf {e}_1,\ldots ,\textbf {e}_n$
of
$\textbf {e}_1,\ldots ,\textbf {e}_n$
of
![]() $\mathsf {G}_0(\Lambda _{\mathrm {con}})^*$
, respectively.
$\mathsf {G}_0(\Lambda _{\mathrm {con}})^*$
, respectively.
Remark 2.13. The above description of
![]() is in terms of projectives of the ambient
is in terms of projectives of the ambient
![]() $\operatorname {End}_R(L)$
since this is convenient later. There is, however, a much more intrinsic description of
$\operatorname {End}_R(L)$
since this is convenient later. There is, however, a much more intrinsic description of
![]() that does not rely on this larger algebra, via the two-term tilting complexes of the contraction algebra
that does not rely on this larger algebra, via the two-term tilting complexes of the contraction algebra
![]() $\Lambda _{\mathrm {con}}$
. In particular, in the language of g-vectors,
$\Lambda _{\mathrm {con}}$
. In particular, in the language of g-vectors,
![]() , where
, where
![]() $g^{L_i}$
is the g-vector of the two-term complex of
$g^{L_i}$
is the g-vector of the two-term complex of
![]() $\Lambda _{\mathrm {con}}$
associated to the rigid object
$\Lambda _{\mathrm {con}}$
associated to the rigid object
![]() $L_i$
via the bijection [Reference AugustAu1, 2.18]. We do not use this description below.
$L_i$
via the bijection [Reference AugustAu1, 2.18]. We do not use this description below.
3 Stability and t-structures
3.1 Stability generalities
Throughout this subsection,
![]() denotes a triangulated category whose Grothendieck group
denotes a triangulated category whose Grothendieck group
![]() is a finitely generated free
is a finitely generated free
![]() $\mathbb {Z}$
-module.
$\mathbb {Z}$
-module.
Proposition 3.1 [Reference BridgelandB2, 5.3].
To give a stability condition on
is equivalent to giving a bounded t-structure
with heart
and a group homomorphism
, called the central charge, such that for all
, the complex number
![]() $Z(E)$
lies in the semi-closed upper half-plane
$Z(E)$
lies in the semi-closed upper half-plane
and where furthermore Z must satisfy the Harder–Narasimhan property.
Write
![]() for the set of locally-finite stability conditions on
for the set of locally-finite stability conditions on
![]() . We do not define these here, as below this condition is automatic for all stability conditions on
. We do not define these here, as below this condition is automatic for all stability conditions on
![]() $\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
, since all hearts of bounded t-structures will be equivalent to finite-dimensional modules on some finite-dimensional algebra.
$\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
, since all hearts of bounded t-structures will be equivalent to finite-dimensional modules on some finite-dimensional algebra.
Theorem 3.2 [Reference BridgelandB2, 1.2].
The space
has the structure of a complex manifold, and the forgetful map
is a local isomorphism onto an open subspace of
.
Any triangle equivalence
induces a natural map
defined by
, where
![]() $\unicode{x3c6} ^{-1}$
is the corresponding isomorphism on K-theory
$\unicode{x3c6} ^{-1}$
is the corresponding isomorphism on K-theory
induced by the functor
. In this way, the group
of isomorphism classes of autoequivalences of
acts on
.
3.2 t-structures for
 $\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
$\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
The contraction algebra
![]() $\Lambda _{\mathrm {con}}$
is a silting-discrete symmetric algebra [Reference AugustAu1, 3.3, 4.12]. Being symmetric, the technical condition of being silting-discrete is equivalent [Reference Aihara and MizunoAM, 2.11] to there being only finitely many basic tilting complexes between P and
$\Lambda _{\mathrm {con}}$
is a silting-discrete symmetric algebra [Reference AugustAu1, 3.3, 4.12]. Being symmetric, the technical condition of being silting-discrete is equivalent [Reference Aihara and MizunoAM, 2.11] to there being only finitely many basic tilting complexes between P and
![]() $P[1]$
(with respect to the silting order
$P[1]$
(with respect to the silting order
![]() $\leq $
), for every tilting complex P obtained by iterated irreducible left mutation from the free module
$\leq $
), for every tilting complex P obtained by iterated irreducible left mutation from the free module
![]() $\Lambda _{\mathrm {con}}$
. Geometrically, for each such P, this set is finite since it is in bijection with R-schemes obtained by iterated flops of irreducible curves starting from X, which is well-known to be finite.
$\Lambda _{\mathrm {con}}$
. Geometrically, for each such P, this set is finite since it is in bijection with R-schemes obtained by iterated flops of irreducible curves starting from X, which is well-known to be finite.
This fact has the following remarkable consequence.
Proposition 3.3. Suppose that
is the heart of a bounded t-structure on
![]() $\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
. Then
$\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
. Then
for some
![]() $L\in \operatorname {Mut}_0(M)$
and for some
$L\in \operatorname {Mut}_0(M)$
and for some
, where
and
![]() $F_{\unicode{x3b1} }$
is the derived equivalence from Subsection 2.6 associated to
$F_{\unicode{x3b1} }$
is the derived equivalence from Subsection 2.6 associated to
![]() $\unicode{x3b1} $
.
$\unicode{x3b1} $
.
Proof. Since
![]() $\Lambda _{\mathrm {con}}$
is silting-discrete, necessarily
$\Lambda _{\mathrm {con}}$
is silting-discrete, necessarily
![]() has finite length [Reference Pauksztello, Saorín and ZvonarevaPSZ]. Furthermore, by the bijections in [Reference Koenig and YangKY, §5], there exists a silting complex T in
has finite length [Reference Pauksztello, Saorín and ZvonarevaPSZ]. Furthermore, by the bijections in [Reference Koenig and YangKY, §5], there exists a silting complex T in
![]() $\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
such that, in the notation of [Reference Koenig and YangKY, §5.4],
$\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
such that, in the notation of [Reference Koenig and YangKY, §5.4],
Since
![]() $\Lambda _{\mathrm {con}}$
is symmetric, silting equals tilting, so T is a tilting complex. It is already known (see [Reference AugustAu1, 2.12]) that every tilting complex T in
$\Lambda _{\mathrm {con}}$
is symmetric, silting equals tilting, so T is a tilting complex. It is already known (see [Reference AugustAu1, 2.12]) that every tilting complex T in
![]() $\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
can be obtained as a composition of mutations from
$\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
can be obtained as a composition of mutations from
![]() $\Lambda _{\mathrm {con}}$
, so say
$\Lambda _{\mathrm {con}}$
, so say
![]() $T\cong \unicode{x3bc} _{\unicode{x3b2} }\Lambda _{\mathrm {con}}$
for some
$T\cong \unicode{x3bc} _{\unicode{x3b2} }\Lambda _{\mathrm {con}}$
for some
![]() . Set
. Set
![]() ; then [Reference AugustAu1, 3.10(1)] gives
; then [Reference AugustAu1, 3.10(1)] gives
![]() $F_{\unicode{x3b2} }(\unicode{x3bc} _{\unicode{x3b2} }\Lambda _{\mathrm {con}})\cong \mathrm {B}_{\mathrm {con}}$
, and hence
$F_{\unicode{x3b2} }(\unicode{x3bc} _{\unicode{x3b2} }\Lambda _{\mathrm {con}})\cong \mathrm {B}_{\mathrm {con}}$
, and hence
![]() $F_{\unicode{x3b2} }(T)\cong \mathrm {B}_{\mathrm {con}}$
.
$F_{\unicode{x3b2} }(T)\cong \mathrm {B}_{\mathrm {con}}$
.
Thus, applying
![]() $F_{\unicode{x3b2} }$
to equation (3.1),
$F_{\unicode{x3b2} }$
to equation (3.1),
so applying
![]() $F_{\unicode{x3b2} }^{-1}=F_{\unicode{x3b2} ^{-1}}$
shows that
$F_{\unicode{x3b2} }^{-1}=F_{\unicode{x3b2} ^{-1}}$
shows that
. Since
, the result follows.
Recall that inside
![]() $\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
are the simples
$\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
are the simples
![]() , which base the K-theory
, which base the K-theory
![]() $\mathsf {G}_0(\Lambda _{\mathrm {con}})$
. In a similar way, the simple modules
$\mathsf {G}_0(\Lambda _{\mathrm {con}})$
. In a similar way, the simple modules
![]() of
of
![]() $\operatorname {\underline {End}}_R(L)$
base its Grothendieck group.
$\operatorname {\underline {End}}_R(L)$
base its Grothendieck group.
Corollary 3.4. If
![]() $\unicode{x3c3} \in \operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
, then
$\unicode{x3c3} \in \operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
, then
![]() for some
for some
![]() and some Z satisfying
and some Z satisfying
![]() for all
for all
![]() $i=1,\ldots ,n$
.
$i=1,\ldots ,n$
.
Proof. By Proposition 3.3, every abelian heart is of the form
![]() for some
for some
![]() , and hence every point of
, and hence every point of
![]() is of the form
is of the form
![]() . To be a stability condition is equivalent to the map
. To be a stability condition is equivalent to the map
![]() sending all simples of
sending all simples of
![]() to
to
![]() $\mathbb {H}$
. Since the simples of
$\mathbb {H}$
. Since the simples of
![]() are of the form
are of the form
![]() , it follows that
, it follows that
![]() is a stability condition precisely when Z satisfies
is a stability condition precisely when Z satisfies
![]() for all i.
for all i.
The general action of
![]() $\operatorname {Auteq}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
on
$\operatorname {Auteq}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
on
![]() $\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
simplifies somewhat if we restrict to those standard equivalences given by
$\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
simplifies somewhat if we restrict to those standard equivalences given by
. The functorial assignment
![]() $\unicode{x3b1} \to F_{\unicode{x3b1} }$
defines a group homomorphism
$\unicode{x3b1} \to F_{\unicode{x3b1} }$
defines a group homomorphism
and we set
![]() $\mathop {\mathsf {PBr}}\nolimits $
to be the image of this homomorphism. Then using Corollary 3.4 to describe the points of
$\mathop {\mathsf {PBr}}\nolimits $
to be the image of this homomorphism. Then using Corollary 3.4 to describe the points of
![]() $\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
, the action of
$\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
, the action of
![]() $F_{\unicode{x3b2} }\in \mathop {\mathsf {PBr}}\nolimits $
on
$F_{\unicode{x3b2} }\in \mathop {\mathsf {PBr}}\nolimits $
on
![]() $\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is
$\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is
since
![]() $\mathsf {F}_{\unicode{x3b2} }=\mathop {\mathrm {Id}}\nolimits $
by Proposition 2.12(2).
$\mathsf {F}_{\unicode{x3b2} }=\mathop {\mathrm {Id}}\nolimits $
by Proposition 2.12(2).
4 Stability on contraction algebras as a universal cover
In order to realise
![]() $\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
as a universal cover, fix the isomorphism
$\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
as a universal cover, fix the isomorphism
given by
![]() , where
, where
![]() are the simples of
are the simples of
![]() $\Lambda _{\mathrm {con}}$
. Composing this with the forgetful map from Theorem 3.2, we thus obtain
$\Lambda _{\mathrm {con}}$
. Composing this with the forgetful map from Theorem 3.2, we thus obtain
Combining with Corollary 3.4, p sends an arbitrary point
![]() to
to
![]() . In this section, we will show that p is a regular covering map onto its image. To do this, it will be convenient to also consider the stability manifolds of the other contraction algebras of R and to track information between them.
. In this section, we will show that p is a regular covering map onto its image. To do this, it will be convenient to also consider the stability manifolds of the other contraction algebras of R and to track information between them.
Lemma 4.1. For any
, the following diagram commutes

where the topmost vertical arrows are the forgetful maps,
![]() $\mathsf {F}_{\unicode{x3b1} }^{-1}$
is the image in K-theory of the inverse of the functor
$\mathsf {F}_{\unicode{x3b1} }^{-1}$
is the image in K-theory of the inverse of the functor
![]() $F_{\unicode{x3b1} }$
defined in Subsection 2.6 and
$F_{\unicode{x3b1} }$
defined in Subsection 2.6 and
is defined in Subsection 2.7. The right-hand vertical composition is p.
Proof. The top square commutes by definition of
![]() $(\mathsf {F}_{\unicode{x3b1} })_*$
. For the bottom square, by Proposition 2.12(3) applied to
$(\mathsf {F}_{\unicode{x3b1} })_*$
. For the bottom square, by Proposition 2.12(3) applied to
![]() $\unicode{x3b1} ^{-1}$
, we have
$\unicode{x3b1} ^{-1}$
, we have
![]() $\mathsf {F}_{\unicode{x3b1} }^{-1}=\mathsf {F}_{\unicode{x3b1} ^{-1}}=\mathsf {F}_{\unicode{x3b2} }$
, where
$\mathsf {F}_{\unicode{x3b1} }^{-1}=\mathsf {F}_{\unicode{x3b1} ^{-1}}=\mathsf {F}_{\unicode{x3b2} }$
, where
![]() $\unicode{x3b2} $
is a positive minimal path
$\unicode{x3b2} $
is a positive minimal path
![]() $C_+ \to C_L$
. Writing
$C_+ \to C_L$
. Writing
![]() $\unicode{x3b2} =s_{i_t}\circ \ldots \circ s_{i_1}$
, then the middle map is the composition
$\unicode{x3b2} =s_{i_t}\circ \ldots \circ s_{i_1}$
, then the middle map is the composition
By Remark 2.6, each step is just the tracking of the projectives basing
under the mutation functors. Hence equation (4.2) is precisely
Consider the path
![]() $\overline {\unicode{x3b2} }=s_{i_1}\circ \ldots \circ s_{i_t}\colon C_L\to C_+$
. Being the opposite path to
$\overline {\unicode{x3b2} }=s_{i_1}\circ \ldots \circ s_{i_t}\colon C_L\to C_+$
. Being the opposite path to
![]() $\unicode{x3b2} $
, it follows that
$\unicode{x3b2} $
, it follows that
![]() $\overline {\unicode{x3b2} }$
is also positive minimal. But then, by Proposition 2.11, there is a functorial isomorphism
$\overline {\unicode{x3b2} }$
is also positive minimal. But then, by Proposition 2.11, there is a functorial isomorphism
Hence
, the image of this functor in
, realises equation (4.3).
As is standard, consider the subset of
![]() $\mathbb {C}^n$
$\mathbb {C}^n$

Corollary 4.2. For any point of
![]() $\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
, which is necessarily of the form
$\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
, which is necessarily of the form
for some
,

Proof. The first statement is Corollary 3.4. By definition,
, hence

The final statement that
again follows from Corollary 3.4.
4.1 A covering map
As in Section 3.2, let
![]() $\mathop {\mathsf {PBr}}\nolimits $
be the image of the homomorphism
$\mathop {\mathsf {PBr}}\nolimits $
be the image of the homomorphism
sending
![]() $\unicode{x3b2} \mapsto F_{\unicode{x3b2} }$
. Then
$\unicode{x3b2} \mapsto F_{\unicode{x3b2} }$
. Then
![]() $F_{\unicode{x3b2} }\in \mathop {\mathsf {PBr}}\nolimits $
acts on the space of stability conditions via the action in equation (3.2). In this subsection, we will establish that this action is free and properly discontinuous, so that
$F_{\unicode{x3b2} }\in \mathop {\mathsf {PBr}}\nolimits $
acts on the space of stability conditions via the action in equation (3.2). In this subsection, we will establish that this action is free and properly discontinuous, so that
![]() $\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}}) \to \operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})/\mathop {\mathsf {PBr}}\nolimits $
is a covering map.
$\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}}) \to \operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})/\mathop {\mathsf {PBr}}\nolimits $
is a covering map.
The following is one of our main technical results. It establishes a condition under which elements of
![]() $\mathop {\mathsf {PBr}}\nolimits $
, inside the autoequivalence group of
$\mathop {\mathsf {PBr}}\nolimits $
, inside the autoequivalence group of
![]() $\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
, are the identity. The proof is via Fourier–Mukai techniques. Forgetting the ambient geometry is thus a bad idea: it seems extremely difficult to establish the following result in a purely algebraic manner.
$\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
, are the identity. The proof is via Fourier–Mukai techniques. Forgetting the ambient geometry is thus a bad idea: it seems extremely difficult to establish the following result in a purely algebraic manner.
Theorem 4.3. Suppose that
![]() satisfies
satisfies
![]() $F_{\unicode{x3b1} }(\Lambda _{\mathrm {con}}) \cong \Lambda _{\mathrm {con}}$
. Then there is a functorial isomorphism
$F_{\unicode{x3b1} }(\Lambda _{\mathrm {con}}) \cong \Lambda _{\mathrm {con}}$
. Then there is a functorial isomorphism
![]() $F_{\unicode{x3b1} } \cong \mathop {\mathrm {Id}}\nolimits $
.
$F_{\unicode{x3b1} } \cong \mathop {\mathrm {Id}}\nolimits $
.
Proof. By the assumption, the standard equivalence
![]() $F_{\unicode{x3b1} }$
is induced by the one-sided tilting complex
$F_{\unicode{x3b1} }$
is induced by the one-sided tilting complex
![]() $\Lambda _{\mathrm {con}}$
. By the usual lifting argument (see, e.g., [Reference Rouquier and ZimmermannRZ, 2.3]), the bimodule complex defining
$\Lambda _{\mathrm {con}}$
. By the usual lifting argument (see, e.g., [Reference Rouquier and ZimmermannRZ, 2.3]), the bimodule complex defining
![]() $F_{\unicode{x3b1} }$
must be isomorphic to
$F_{\unicode{x3b1} }$
must be isomorphic to
![]() ${}_{1}({\Lambda _{\mathrm {con}}})_{\unicode{x3b6} }$
as bimodules, for some algebra automorphism
${}_{1}({\Lambda _{\mathrm {con}}})_{\unicode{x3b6} }$
as bimodules, for some algebra automorphism
![]() $\unicode{x3b6} \colon \Lambda _{\mathrm {con}}\to \Lambda _{\mathrm {con}}$
. Hence
$\unicode{x3b6} \colon \Lambda _{\mathrm {con}}\to \Lambda _{\mathrm {con}}$
. Hence
![]() $F_{\unicode{x3b1} }$
is induced by this algebra automorphism.
$F_{\unicode{x3b1} }$
is induced by this algebra automorphism.
Since
![]() $F_{\unicode{x3b1} }$
induces a Morita equivalence, it must take simples to simples. Furthermore, as
$F_{\unicode{x3b1} }$
induces a Morita equivalence, it must take simples to simples. Furthermore, as
![]() $F_{\unicode{x3b1} }$
is the identity on K-theory
$F_{\unicode{x3b1} }$
is the identity on K-theory
![]() $\mathsf {G}_0(\Lambda _{\mathrm {con}})$
by Proposition 2.12,
$\mathsf {G}_0(\Lambda _{\mathrm {con}})$
by Proposition 2.12,
![]() $F_{\unicode{x3b1} }$
must fix all simples.
$F_{\unicode{x3b1} }$
must fix all simples.
Now consider the commutative diagram

where the left-hand side is equation (2.6) and the right-hand side can be obtained by iterating the right-hand side of Theorem 2.4. Since
![]() $F_{\unicode{x3b1} }$
fixes simples, the left-hand commutative diagram implies that
$F_{\unicode{x3b1} }$
fixes simples, the left-hand commutative diagram implies that
fixes the simples
. By [Reference Van den BerghVdB, 3.5.8], across the right-hand commutative diagram, this in turn implies that
![]() $\operatorname {\mathsf {Flop}}_{\unicode{x3b1} }$
fixes the sheaves
$\operatorname {\mathsf {Flop}}_{\unicode{x3b1} }$
fixes the sheaves
, where each
![]() $\mathrm {C}_i\cong \mathbb {P}^1$
. Since the flop functor and its inverse both map
$\mathrm {C}_i\cong \mathbb {P}^1$
. Since the flop functor and its inverse both map
to
[Reference BridgelandB1, (4.4)] and commute with the pushdown to
![]() $\operatorname {Spec} R$
(see, e.g., [Reference Donovan and WemyssDW1, 7.16]), by the standard Fourier–Mukai argument (see [Reference WemyssW, 4.3], which itself is based on [Reference TodaT]),
$\operatorname {Spec} R$
(see, e.g., [Reference Donovan and WemyssDW1, 7.16]), by the standard Fourier–Mukai argument (see [Reference WemyssW, 4.3], which itself is based on [Reference TodaT]),
![]() $\operatorname {\mathsf {Flop}}_{\unicode{x3b1} }\cong h_*$
for some isomorphism
$\operatorname {\mathsf {Flop}}_{\unicode{x3b1} }\cong h_*$
for some isomorphism
![]() $h \colon X\to X$
that commutes with the pushdown. But this isomorphism is the identity on the dense open set obtained by removing the exceptional locus, and hence it must be the identity.
$h \colon X\to X$
that commutes with the pushdown. But this isomorphism is the identity on the dense open set obtained by removing the exceptional locus, and hence it must be the identity.
It follows that
![]() $\operatorname {\mathsf {Flop}}_{\unicode{x3b1} }\cong \mathop {\mathrm {Id}}\nolimits $
and hence
$\operatorname {\mathsf {Flop}}_{\unicode{x3b1} }\cong \mathop {\mathrm {Id}}\nolimits $
and hence
. Restricting the left-hand commutative diagram to
![]() $\operatorname {mod} \Lambda _{\mathrm {con}}$
, we obtain a commutative diagram
$\operatorname {mod} \Lambda _{\mathrm {con}}$
, we obtain a commutative diagram

where
![]() $\operatorname {mod} _{\{1,\ldots ,n\}}\Lambda $
denotes those
$\operatorname {mod} _{\{1,\ldots ,n\}}\Lambda $
denotes those
![]() $\Lambda $
-modules with a finite filtration by the simples
$\Lambda $
-modules with a finite filtration by the simples
. In particular,
![]() $F_{\unicode{x3b1} }$
restricted to
$F_{\unicode{x3b1} }$
restricted to
![]() $\operatorname {mod} \Lambda _{\mathrm {con}}$
is functorially isomorphic to the identity. Hence
$\operatorname {mod} \Lambda _{\mathrm {con}}$
is functorially isomorphic to the identity. Hence
![]() $\unicode{x3b6} $
is an inner automorphism (see, e.g., [Reference LinckelmannL, 2.8.16]), which in turn implies that
$\unicode{x3b6} $
is an inner automorphism (see, e.g., [Reference LinckelmannL, 2.8.16]), which in turn implies that
![]() $F_{\unicode{x3b1} }\cong \mathop {\mathrm {Id}}\nolimits $
.
$F_{\unicode{x3b1} }\cong \mathop {\mathrm {Id}}\nolimits $
.
Corollary 4.4. For each
![]() $x\in \operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
, there is an open neighbourhood
$x\in \operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
, there is an open neighbourhood
![]() of x such that
of x such that
![]() for all
for all
![]() $1\neq F_{\unicode{x3b2} }\in \mathop {\mathsf {PBr}}\nolimits $
.
$1\neq F_{\unicode{x3b2} }\in \mathop {\mathsf {PBr}}\nolimits $
.
Proof. Consider the open neighbourhood
of x defined by
where
![]() $d(-,-)$
is the metric on stability conditions introduced in [Reference BridgelandB2, Section 6]. Suppose that
$d(-,-)$
is the metric on stability conditions introduced in [Reference BridgelandB2, Section 6]. Suppose that
for some
![]() $F_{\unicode{x3b2} }\in \mathop {\mathsf {PBr}}\nolimits $
. We will show that
$F_{\unicode{x3b2} }\in \mathop {\mathsf {PBr}}\nolimits $
. We will show that
![]() $F_{\unicode{x3b2} }\cong \mathop {\mathrm {Id}}\nolimits $
.
$F_{\unicode{x3b2} }\cong \mathop {\mathrm {Id}}\nolimits $
.
As the two open balls of radius
![]() $\frac {1}{4}$
intersect, every
$\frac {1}{4}$
intersect, every
![]() must satisfy
must satisfy
![]() $d\bigl (y,(F_{\unicode{x3b2} })_*y\bigr )<1$
. Furthermore, the central charges of y and
$d\bigl (y,(F_{\unicode{x3b2} })_*y\bigr )<1$
. Furthermore, the central charges of y and
![]() $(F_{\unicode{x3b2} })_*y$
are equal by Proposition 2.12(2) and the top commutative diagram in Lemma 4.1. Using [Reference BridgelandB2, Lemma 6.4], it follows immediately that
$(F_{\unicode{x3b2} })_*y$
are equal by Proposition 2.12(2) and the top commutative diagram in Lemma 4.1. Using [Reference BridgelandB2, Lemma 6.4], it follows immediately that
![]() $y=(F_{\unicode{x3b2} })_*y$
, for every
$y=(F_{\unicode{x3b2} })_*y$
, for every
![]() .
.
In particular, by Corollary 3.4, say
![]() for some
for some
![]() . Since
. Since
![]() , the property
, the property
![]() $(F_{\unicode{x3b2} })_*(x)=x$
implies that
$(F_{\unicode{x3b2} })_*(x)=x$
implies that
![]() , so
, so
![]() $F_{\unicode{x3b2} }$
restricts to an equivalence
$F_{\unicode{x3b2} }$
restricts to an equivalence
![]() . In turn, this implies that the composition
. In turn, this implies that the composition
where
![]() , restricts to an equivalence
, restricts to an equivalence
![]() $\operatorname {mod} \Gamma _{\mathrm {con}}\to \operatorname {mod} \Gamma _{\mathrm {con}}$
. It follows that
$\operatorname {mod} \Gamma _{\mathrm {con}}\to \operatorname {mod} \Gamma _{\mathrm {con}}$
. It follows that
![]() $F_{\unicode{x3b1} ^{-1}\unicode{x3b2} \unicode{x3b1} }(\Gamma _{\mathrm {con}})$
must then be a basic tilting module, given that
$F_{\unicode{x3b1} ^{-1}\unicode{x3b2} \unicode{x3b1} }(\Gamma _{\mathrm {con}})$
must then be a basic tilting module, given that
![]() $\Gamma _{\mathrm {con}}$
is. Since
$\Gamma _{\mathrm {con}}$
is. Since
![]() $\Gamma _{\mathrm {con}}$
is symmetric, the only such module is
$\Gamma _{\mathrm {con}}$
is symmetric, the only such module is
![]() $\Gamma _{\mathrm {con}}$
, so
$\Gamma _{\mathrm {con}}$
, so
![]() $F_{\unicode{x3b1} ^{-1}\unicode{x3b2} \unicode{x3b1} }(\Gamma _{\mathrm {con}})\cong \Gamma _{\mathrm {con}}$
. By Proposition 4.3 applied to the contraction algebra
$F_{\unicode{x3b1} ^{-1}\unicode{x3b2} \unicode{x3b1} }(\Gamma _{\mathrm {con}})\cong \Gamma _{\mathrm {con}}$
. By Proposition 4.3 applied to the contraction algebra
![]() $\Gamma _{\mathrm {con}}$
, we conclude that
$\Gamma _{\mathrm {con}}$
, we conclude that
![]() $F_{\unicode{x3b1} ^{-1}\unicode{x3b2} \unicode{x3b1} }\cong \mathop {\mathrm {Id}}\nolimits $
, and hence
$F_{\unicode{x3b1} ^{-1}\unicode{x3b2} \unicode{x3b1} }\cong \mathop {\mathrm {Id}}\nolimits $
, and hence
![]() $F_{\unicode{x3b2} }\cong \mathop {\mathrm {Id}}\nolimits $
.
$F_{\unicode{x3b2} }\cong \mathop {\mathrm {Id}}\nolimits $
.
Corollary 4.5. The map
![]() $\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}}) \to \operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})/\mathsf {PBr}$
is the universal covering map, with Galois group
$\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}}) \to \operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})/\mathsf {PBr}$
is the universal covering map, with Galois group
![]() $\mathsf {PBr}$
.
$\mathsf {PBr}$
.
Proof.
![]() $\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is contractible since contraction algebras are silting-discrete [Reference AugustAu1, 4.12], and silting-discrete algebras have contractible stability manifolds [Reference Pauksztello, Saorín and ZvonarevaPSZ]. In particular,
$\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is contractible since contraction algebras are silting-discrete [Reference AugustAu1, 4.12], and silting-discrete algebras have contractible stability manifolds [Reference Pauksztello, Saorín and ZvonarevaPSZ]. In particular,
![]() $\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is path connected, so the given map is a regular covering map by Corollary 4.4 together with the standard [Reference HatcherH, 1.40(a)(b)]. The covering is clearly universal, since
$\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is path connected, so the given map is a regular covering map by Corollary 4.4 together with the standard [Reference HatcherH, 1.40(a)(b)]. The covering is clearly universal, since
![]() $\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is contractible and hence simply connected.
$\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is contractible and hence simply connected.
4.2 The regular cover to the complexified complement
In this subsection, we will establish that p induces an isomorphism
Combining with Corollary 4.5 will then prove that equation (4.1) is the universal covering map onto its image, with Galois group
![]() $\mathop {\mathsf {PBr}}\nolimits $
. We will establish equation (4.4) in two steps: first by showing that p has image
$\mathop {\mathsf {PBr}}\nolimits $
. We will establish equation (4.4) in two steps: first by showing that p has image
![]() , and then by establishing that equation (4.4) is well-defined and injective.
, and then by establishing that equation (4.4) is well-defined and injective.
Our proof makes use of the following key combinatorial result, which is folklore when
![]() is an ADE root system. In our mildly more general setting here, the proof, which is basically the same, can be found in [Reference Hirano and WemyssHW2, Appendix A].
is an ADE root system. In our mildly more general setting here, the proof, which is basically the same, can be found in [Reference Hirano and WemyssHW2, Appendix A].
Proposition 4.6. With notation as above, the following hold:
-
1. If
 $\unicode{x3b1} $
and
$\unicode{x3b1} $
and
 $\unicode{x3b2} $
terminate at
$\unicode{x3b2} $
terminate at
 $C_+$
, then
$C_+$
, then 
-
2. There is a disjoint union

The above combinatorics lead directly to the following. In the special case when
![]() is an ADE root system, the following result is already implicit in [Reference BridgelandB3] and [Reference TodaT].
is an ADE root system, the following result is already implicit in [Reference BridgelandB3] and [Reference TodaT].
Corollary 4.7. The image of p is
![]() .
.
Proof. By Proposition 4.6(2), all the sets
![]() avoid the complexified hyperplanes, so by Corollary 4.2, the image of p lies in
avoid the complexified hyperplanes, so by Corollary 4.2, the image of p lies in
![]() . Further, given any
. Further, given any
![]() , we may write
, we may write
![]() for some
for some
![]() $L \in \operatorname {Mut}_0(N)$
and some
$L \in \operatorname {Mut}_0(N)$
and some
![]() $h\in \mathbb {H}_+$
, again by Proposition 4.6(2). Since the standard heart in
$h\in \mathbb {H}_+$
, again by Proposition 4.6(2). Since the standard heart in
![]() $\mathop {\mathrm {D}^b}(\operatorname {\underline {End}}_R(L))$
has finite length, we can find a stability condition
$\mathop {\mathrm {D}^b}(\operatorname {\underline {End}}_R(L))$
has finite length, we can find a stability condition
![]() $\unicode{x3c3} \in \operatorname {Stab} \mathop {\mathrm {D}^b}(\operatorname {\underline {End}}_R(L) )$
, which maps to h via the left-hand vertical composition in Lemma 4.1. Then for any
$\unicode{x3c3} \in \operatorname {Stab} \mathop {\mathrm {D}^b}(\operatorname {\underline {End}}_R(L) )$
, which maps to h via the left-hand vertical composition in Lemma 4.1. Then for any
![]() , the commutative diagram in Lemma 4.1 shows that
, the commutative diagram in Lemma 4.1 shows that
![]() $(F_{\unicode{x3b1} })_*(\unicode{x3c3} )\in \operatorname {Stab} \mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}} )$
maps, under p, to z.
$(F_{\unicode{x3b1} })_*(\unicode{x3c3} )\in \operatorname {Stab} \mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}} )$
maps, under p, to z.
The following shows that equation (4.4) is both well-defined and injective.
Lemma 4.8. For
![]() $\unicode{x3c3} _1,\unicode{x3c3} _2\in \operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
, then
$\unicode{x3c3} _1,\unicode{x3c3} _2\in \operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
, then
Proof. Note that (
![]() $\Leftarrow $
) is clear since, by Proposition 2.12(2), the action in equation (3.2) of a pure braid does not affect the central charge of a stability condition.
$\Leftarrow $
) is clear since, by Proposition 2.12(2), the action in equation (3.2) of a pure braid does not affect the central charge of a stability condition.
For (
![]() $\Rightarrow $
), recall that by Corollary 3.4, we can assume that
$\Rightarrow $
), recall that by Corollary 3.4, we can assume that
![]() and
and
![]() , where
, where
![]() and
and
![]() . If
. If
![]() $p(\unicode{x3c3} _1)=p(\unicode{x3c3} _2)$
, then certainly
$p(\unicode{x3c3} _1)=p(\unicode{x3c3} _2)$
, then certainly
![]() $Z_1 =Z_2$
since p is simply the forgetful map followed by an isomorphism.
$Z_1 =Z_2$
since p is simply the forgetful map followed by an isomorphism.
Furthermore, by Corollary 4.2, we see that
, since the intersection contains
![]() $p(\unicode{x3c3} _1)=p(\unicode{x3c3} _2)$
. Hence by Proposition 4.6(1), it follows that
$p(\unicode{x3c3} _1)=p(\unicode{x3c3} _2)$
. Hence by Proposition 4.6(1), it follows that
![]() $s(\unicode{x3b1} )=s(\unicode{x3b2} )$
, and thus we can consider the composition
$s(\unicode{x3b1} )=s(\unicode{x3b2} )$
, and thus we can consider the composition
. Then
![]() $F_{\unicode{x3b3} }\in \mathop {\mathsf {PBr}}\nolimits $
and
$F_{\unicode{x3b3} }\in \mathop {\mathsf {PBr}}\nolimits $
and

proving the statement.
Corollary 4.9. The map
induces a homeomorphism
Proof. The map p is surjective by Corollary 4.7, and by Lemma 4.8 it induces the bijection in the statement. The induced map is itself a homeomorphism by the definition of the quotient topology and the fact that p is a local homeomorphism.
The following is our main result.
Corollary 4.10. The map
![]() is the universal cover, with Galois group
is the universal cover, with Galois group
![]() $\mathop {\mathsf {PBr}}\nolimits $
. Furthermore,
$\mathop {\mathsf {PBr}}\nolimits $
. Furthermore,
![]() $\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is contractible.
$\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is contractible.
Proof. The first statement is obtained by composing the universal cover from Corollary 4.5 with the homeomorphism from Corollary 4.9. As already stated, the second part follows from [Reference Pauksztello, Saorín and ZvonarevaPSZ] and [Reference AugustAu1, 4.12].
5 Corollaries
In this section, we prove the five main corollaries stated in the introduction. For an ADE root system, it is well-known [Reference BrieskornB4] that
![]() $\unicode{x3c0} _1(\mathfrak {h}_{\mathrm {reg}}/W)$
is isomorphic to the associated ADE braid group. Recall that the
$\unicode{x3c0} _1(\mathfrak {h}_{\mathrm {reg}}/W)$
is isomorphic to the associated ADE braid group. Recall that the
![]() $K(\unicode{x3c0} \,,1)$
-conjecture for ADE braid groups, which is already a theorem in this setting, asserts that the universal cover of
$K(\unicode{x3c0} \,,1)$
-conjecture for ADE braid groups, which is already a theorem in this setting, asserts that the universal cover of
![]() $\mathfrak {h}_{\mathrm {reg}}/W$
is contractible.
$\mathfrak {h}_{\mathrm {reg}}/W$
is contractible.
Corollary 5.1. The
![]() $K(\unicode{x3c0} \,,1)$
-conjecture holds for all ADE braid groups.
$K(\unicode{x3c0} \,,1)$
-conjecture holds for all ADE braid groups.
Proof. As in [Reference TodaT, §3] or [Reference Kollár and MoriKM, §4.3], we may choose a flopping contraction for which the hyperplane arrangement
is an ADE root system
![]() $\mathfrak {h}$
. It is well-known that the complexified complement
$\mathfrak {h}$
. It is well-known that the complexified complement
. Write W for the Weyl group, which is finite, and thus clearly the covering map
![]() $ \mathfrak {h}_{\mathrm {reg}}\to \mathfrak {h}_{\mathrm {reg}}/W$
has finite fibres. It follows that the composition
$ \mathfrak {h}_{\mathrm {reg}}\to \mathfrak {h}_{\mathrm {reg}}/W$
has finite fibres. It follows that the composition
is then also a covering map. As above, it is well-known that
![]() $\unicode{x3c0} _1(\mathfrak {h}_{\mathrm {reg}}/W)$
is the braid group. By Corollary 4.10, the fact that
$\unicode{x3c0} _1(\mathfrak {h}_{\mathrm {reg}}/W)$
is the braid group. By Corollary 4.10, the fact that
![]() $\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is contractible implies that it is simply connected. Hence the composition is the universal cover, and furthermore the universal cover is contractible.
$\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is contractible implies that it is simply connected. Hence the composition is the universal cover, and furthermore the universal cover is contractible.
Corollary 5.2. The homomorphism
![]() sending
sending
![]() $\unicode{x3b1} \mapsto F_{\unicode{x3b1} }$
is injective.
$\unicode{x3b1} \mapsto F_{\unicode{x3b1} }$
is injective.
Proof. As in Sections 3 and 4, by definition
![]() $\mathop {\mathsf {PBr}}\nolimits $
is the image of this homomorphism. Since p is a regular covering map, as is standard [Reference HatcherH, 1.40(c)], there is a short exact sequence of groups
$\mathop {\mathsf {PBr}}\nolimits $
is the image of this homomorphism. Since p is a regular covering map, as is standard [Reference HatcherH, 1.40(c)], there is a short exact sequence of groups
where
![]() as before takes
as before takes
![]() $\unicode{x3b1} \mapsto F_{\unicode{x3b1} }$
. However, since by Corollary 4.10
$\unicode{x3b1} \mapsto F_{\unicode{x3b1} }$
. However, since by Corollary 4.10
![]() $\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is contractible, its fundamental group is trivial.
$\operatorname {Stab}\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is contractible, its fundamental group is trivial.
For
![]() , set
, set
![]() , which is necessarily a tilting complex for
, which is necessarily a tilting complex for
![]() $\Lambda _{\mathrm {con}}$
since equivalences map tilting complexes to tilting complexes.
$\Lambda _{\mathrm {con}}$
since equivalences map tilting complexes to tilting complexes.
Corollary 5.3. The map
![]() $\unicode{x3b1} \mapsto T_{\unicode{x3b1} }$
is a bijection from morphisms in the Deligne groupoid ending at
$\unicode{x3b1} \mapsto T_{\unicode{x3b1} }$
is a bijection from morphisms in the Deligne groupoid ending at
![]() $C_+$
to the set of basic one-sided tilting complexes of
$C_+$
to the set of basic one-sided tilting complexes of
![]() $\Lambda _{\mathrm {con}}$
, up to isomorphism.
$\Lambda _{\mathrm {con}}$
, up to isomorphism.
Proof. Surjectivity is already known. Indeed, since
![]() $\Lambda _{\mathrm {con}}$
is silting-discrete, by [Reference AugustAu1, 3.16(2)], every standard derived equivalence from
$\Lambda _{\mathrm {con}}$
is silting-discrete, by [Reference AugustAu1, 3.16(2)], every standard derived equivalence from
![]() $\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is, up to algebra automorphism, isomorphic to
$\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
is, up to algebra automorphism, isomorphic to
![]() $F_{\unicode{x3b2} }$
for some
$F_{\unicode{x3b2} }$
for some
![]() . In particular, every one-sided tilting complex for
. In particular, every one-sided tilting complex for
![]() $\Lambda _{\mathrm {con}}$
is isomorphic to
$\Lambda _{\mathrm {con}}$
is isomorphic to
![]() $F_{\unicode{x3b2} }^{-1}(\operatorname {\underline {End}}_R(L))$
for some
$F_{\unicode{x3b2} }^{-1}(\operatorname {\underline {End}}_R(L))$
for some
![]() . Since
. Since
![]() and
and
![]() $F_{\unicode{x3b2} }^{-1}=F_{\unicode{x3b2} ^{-1}}$
, surjectivity of the map follows.
$F_{\unicode{x3b2} }^{-1}=F_{\unicode{x3b2} ^{-1}}$
, surjectivity of the map follows.
The content is that the map is also injective. Suppose that
![]() and
and
![]() are such that
are such that
![]() $T_{\unicode{x3b1} } \cong T_{\unicode{x3b2} }$
, where
$T_{\unicode{x3b1} } \cong T_{\unicode{x3b2} }$
, where
![]() $L,M \in \operatorname {Mut}_0(N)$
. Then by definition,
$L,M \in \operatorname {Mut}_0(N)$
. Then by definition,
and hence
![]() . In particular, choosing any central charge Z, we have
. In particular, choosing any central charge Z, we have
![]() and hence
and hence
![]() . But Corollary 4.2 then implies that
. But Corollary 4.2 then implies that
![]() and
and
![]() intersect, which by Proposition 4.6 implies that
intersect, which by Proposition 4.6 implies that
![]() $L \cong M$
.
$L \cong M$
.
Set
![]() . Applying
. Applying
![]() $F_{\unicode{x3b2} }^{-1}=F_{\unicode{x3b2} ^{-1}}$
to equation (5.2) gives
$F_{\unicode{x3b2} }^{-1}=F_{\unicode{x3b2} ^{-1}}$
to equation (5.2) gives
![]() $F_{\unicode{x3b2} ^{-1} \circ \unicode{x3b1} }(\mathrm {B}_{\mathrm {con}}) \cong \mathrm {B}_{\mathrm {con}}$
. Thus by applying Theorem 4.3 to the composition
$F_{\unicode{x3b2} ^{-1} \circ \unicode{x3b1} }(\mathrm {B}_{\mathrm {con}}) \cong \mathrm {B}_{\mathrm {con}}$
. Thus by applying Theorem 4.3 to the composition
![]() , we deduce that there is an isomorphism
, we deduce that there is an isomorphism
![]() $F_{\unicode{x3b2} ^{-1} \circ \unicode{x3b1} } \cong \mathop {\mathrm {Id}}\nolimits $
. Corollary 5.2 applied to the contraction algebra
$F_{\unicode{x3b2} ^{-1} \circ \unicode{x3b1} } \cong \mathop {\mathrm {Id}}\nolimits $
. Corollary 5.2 applied to the contraction algebra
![]() $\mathrm {B}_{\mathrm {con}}$
then shows that
$\mathrm {B}_{\mathrm {con}}$
then shows that
![]() $\unicode{x3b2} ^{-1} \circ \unicode{x3b1} $
must be the identity, and hence
$\unicode{x3b2} ^{-1} \circ \unicode{x3b1} $
must be the identity, and hence
![]() $\unicode{x3b1} =\unicode{x3b2} $
in the Deligne groupoid.
$\unicode{x3b1} =\unicode{x3b2} $
in the Deligne groupoid.
Remark 5.4. If we instead assign to a path
![]() $\unicode{x3b1} \colon C_+ \to C_L$
the tilting complex
$\unicode{x3b1} \colon C_+ \to C_L$
the tilting complex
![]() $F_{\unicode{x3b1} }^{-1}(\operatorname {\underline {End}}_R(L))$
, we equivalently obtain a bijection between the paths in the Deligne groupoid that start at
$F_{\unicode{x3b1} }^{-1}(\operatorname {\underline {End}}_R(L))$
, we equivalently obtain a bijection between the paths in the Deligne groupoid that start at
![]() $C_+$
and basic one-sided tilting complexes of
$C_+$
and basic one-sided tilting complexes of
![]() $\Lambda _{\mathrm {con}}$
.
$\Lambda _{\mathrm {con}}$
.
Corollary 5.5. The homomorphism
![]() sending
sending
![]() $\unicode{x3b1} \mapsto \operatorname {\mathsf {Flop}}_{\unicode{x3b1} }$
is injective.
$\unicode{x3b1} \mapsto \operatorname {\mathsf {Flop}}_{\unicode{x3b1} }$
is injective.
Proof. Suppose that
![]() $\unicode{x3b1} $
belongs to the kernel, so
$\unicode{x3b1} $
belongs to the kernel, so
![]() $\operatorname {\mathsf {Flop}}_{\unicode{x3b1} }=\mathop {\mathrm {Id}}\nolimits $
. Since
$\operatorname {\mathsf {Flop}}_{\unicode{x3b1} }=\mathop {\mathrm {Id}}\nolimits $
. Since
![]() is functorially isomorphic to
is functorially isomorphic to
![]() $\operatorname {\mathsf {Flop}}_{\unicode{x3b1} }$
after tilting by Theorem 2.4, necessarily
$\operatorname {\mathsf {Flop}}_{\unicode{x3b1} }$
after tilting by Theorem 2.4, necessarily
![]() . The left-hand part of the commutative diagram in Theorem 2.4 then implies that
. The left-hand part of the commutative diagram in Theorem 2.4 then implies that
![]() $F_{\unicode{x3b1} }(\Lambda _{\mathrm {con}})$
maps, under restriction of scalars, to
$F_{\unicode{x3b1} }(\Lambda _{\mathrm {con}})$
maps, under restriction of scalars, to
![]() $\Lambda _{\mathrm {con}}$
. It follows that
$\Lambda _{\mathrm {con}}$
. It follows that
![]() $F_{\unicode{x3b1} }(\Lambda _{\mathrm {con}})\cong \Lambda _{\mathrm {con}}$
in
$F_{\unicode{x3b1} }(\Lambda _{\mathrm {con}})\cong \Lambda _{\mathrm {con}}$
in
![]() $\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
; see, for example, [Reference AugustAu2, 6.6]. By Lemma 4.3, there is a functorial isomorphism
$\mathop {\mathrm {D}^b}(\Lambda _{\mathrm {con}})$
; see, for example, [Reference AugustAu2, 6.6]. By Lemma 4.3, there is a functorial isomorphism
![]() $F_{\unicode{x3b1} }\cong \mathop {\mathrm {Id}}\nolimits $
. By Corollary 5.2, we see that
$F_{\unicode{x3b1} }\cong \mathop {\mathrm {Id}}\nolimits $
. By Corollary 5.2, we see that
![]() $\unicode{x3b1} =1$
, proving the statement.
$\unicode{x3b1} =1$
, proving the statement.
Corollary 5.6. With the notation as in the introduction,
![]() is contractible.
is contractible.
Proof. By [Reference Hirano and WemyssHW2], there is a regular covering map
![]() with Galois group G equal to the image of
with Galois group G equal to the image of
![]() . But by Corollary 5.5, the map
. But by Corollary 5.5, the map
![]() is an isomorphism. By the corresponding version of equation (5.1),
is an isomorphism. By the corresponding version of equation (5.1),
![]() is trivial, so the cover is universal. Universal covers are unique, so by Corollary 4.10, it follows that
is trivial, so the cover is universal. Universal covers are unique, so by Corollary 4.10, it follows that
![]() is contractible.
is contractible.
Conflicts of Interest
None.
Financial support
During the research on this paper, J.A. was supported by the Carnegie Trust for the Universities of Scotland, and M.W. was supported by EPSRC grants EP/R009325/1 and EP/R034826/1. J.A. further acknowledges support from the Max Planck Institute for Mathematics and a DNRF Chair from the Danish National Research Foundation (grant no. DNRF156).