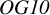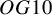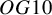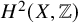1 Introduction
In recent years, there has been much progress in the study of symplectic automorphisms of irreducible holomorphic symplectic (IHS) manifolds. The model for this study is that of
![]() $K3$
surfaces; Mukai classifies symplectic automorphisms in his celebrated paper [Reference Mukai35]. This was later reproved by Xiao [Reference Xiao47], and a more streamlined approach was reached by Kondō [Reference Kondō and lattices23] using automorphisms of the Niemeier lattices. A full classification has been later provided by Hashimoto [Reference Hashimoto18] in terms of cohomological action. The techniques of Kondō were adapted to the classification of symplectic automorphisms of cubic fourfolds by Laza and Zheng in [Reference Laza and Zheng26]; here, an automorphism is symplectic if it induces a symplectic automorphism on the Fano variety of lines. In a similar vein, Mongardi obtained a classification of prime order symplectic automorphisms of IHS manifolds of
$K3$
surfaces; Mukai classifies symplectic automorphisms in his celebrated paper [Reference Mukai35]. This was later reproved by Xiao [Reference Xiao47], and a more streamlined approach was reached by Kondō [Reference Kondō and lattices23] using automorphisms of the Niemeier lattices. A full classification has been later provided by Hashimoto [Reference Hashimoto18] in terms of cohomological action. The techniques of Kondō were adapted to the classification of symplectic automorphisms of cubic fourfolds by Laza and Zheng in [Reference Laza and Zheng26]; here, an automorphism is symplectic if it induces a symplectic automorphism on the Fano variety of lines. In a similar vein, Mongardi obtained a classification of prime order symplectic automorphisms of IHS manifolds of
![]() $K3^{[n]}$
type [Reference Mongardi31, Reference Mongardi32], with similar results obtained by [Reference Huybrechts22]. Höhn and Mason [Reference Höhn and Mason20] completed the full classification of finite regular symplectic automorphisms for IHS manifolds of
$K3^{[n]}$
type [Reference Mongardi31, Reference Mongardi32], with similar results obtained by [Reference Huybrechts22]. Höhn and Mason [Reference Höhn and Mason20] completed the full classification of finite regular symplectic automorphisms for IHS manifolds of
![]() $K3^{[2]}$
type. In the case of O’Grady’s exceptional examples, the authors in [Reference Grossi, Onorati and Veniani17, Reference Giovenzana, Grossi, Onorati and Veniani15] show that for IHS manifolds of deformation type
$K3^{[2]}$
type. In the case of O’Grady’s exceptional examples, the authors in [Reference Grossi, Onorati and Veniani17, Reference Giovenzana, Grossi, Onorati and Veniani15] show that for IHS manifolds of deformation type
![]() $OG6$
and
$OG6$
and
![]() $OG10$
, any symplectic automorphism of finite order acts trivially on the second integral cohomology. In particular, IHS manifolds of
$OG10$
, any symplectic automorphism of finite order acts trivially on the second integral cohomology. In particular, IHS manifolds of
![]() $OG10$
type do not admit any nontrivial symplectic automorphism of finite order.
$OG10$
type do not admit any nontrivial symplectic automorphism of finite order.
For the two previous deformation types, the situation becomes richer if instead one considers symplectic birational transformations. The isometry classes of the invariant and coinvariant sublattices associated to symplectic birational transformations of finite order for IHS manifolds of
![]() $OG6$
type are classified in [Reference Grossi, Onorati and Veniani17]. A lattice classification of symplectic birational involutions for IHS manifolds of
$OG6$
type are classified in [Reference Grossi, Onorati and Veniani17]. A lattice classification of symplectic birational involutions for IHS manifolds of
![]() $OG10$
type was reached by the authors of the present paper in [Reference Marquand and Muller29]. Among them, three of the possible cases can be geometrically realised by involutions of a cubic fourfold via the construction of [Reference Laza, Saccà and Voisin25, Reference Saccà42] (see also [Reference Marquand28]). In this paper, we study finite groups of symplectic birational transformations of IHS manifolds of
$OG10$
type was reached by the authors of the present paper in [Reference Marquand and Muller29]. Among them, three of the possible cases can be geometrically realised by involutions of a cubic fourfold via the construction of [Reference Laza, Saccà and Voisin25, Reference Saccà42] (see also [Reference Marquand28]). In this paper, we study finite groups of symplectic birational transformations of IHS manifolds of
![]() $OG10$
type, and obtain a classification of (saturated) groups G.
$OG10$
type, and obtain a classification of (saturated) groups G.
For an IHS manifold X, we denote by
![]() $\mathrm {Bir}_s(X)$
the group of symplectic birational transformations of X. Let
$\mathrm {Bir}_s(X)$
the group of symplectic birational transformations of X. Let
![]() $(X,\eta , G)$
be a marked IHS manifold of
$(X,\eta , G)$
be a marked IHS manifold of
![]() $OG10$
type, and
$OG10$
type, and
![]() $G\leq \mathrm {Bir}_s(X)$
a finite subgroup. For such a triple, we obtain induced isometries of the second integral cohomology; that is,
$G\leq \mathrm {Bir}_s(X)$
a finite subgroup. For such a triple, we obtain induced isometries of the second integral cohomology; that is,
![]() $\eta _*(G)\leq O(\Lambda )$
, where
$\eta _*(G)\leq O(\Lambda )$
, where
![]() $\eta :H^2(X,\mathbb {Z})\cong \Lambda := U^3\oplus E_8^2\oplus A_2$
is an isometry. We can now state our main classification result.
$\eta :H^2(X,\mathbb {Z})\cong \Lambda := U^3\oplus E_8^2\oplus A_2$
is an isometry. We can now state our main classification result.
Theorem 1.1 (Theorem 5.1).
Let
![]() $(X, \eta , G)$
be a triple consisting of a marked IHS manifold
$(X, \eta , G)$
be a triple consisting of a marked IHS manifold
![]() $(X, \eta )$
of
$(X, \eta )$
of
![]() $OG10$
type and a finite group
$OG10$
type and a finite group
![]() $G\leq \mathrm {Bir}_s(X)$
. Then, up to conjugacy,
$G\leq \mathrm {Bir}_s(X)$
. Then, up to conjugacy,
![]() $\eta _\ast (G)\leq O(\Lambda )$
is contained in one of the 375 saturated groups of the dataset [Reference Marquand and Muller30].
$\eta _\ast (G)\leq O(\Lambda )$
is contained in one of the 375 saturated groups of the dataset [Reference Marquand and Muller30].
Moreover, Table 4 in the ancillary files gives information about each such conjugacy class. The strategy to obtain the classification in Theorem 5.1 follows three main steps.
First, we use the Global Torelli theorem to reduce the classification of groups of symplectic birational transformations of IHS manifolds of
![]() $OG10$
type to classifying subgroups
$OG10$
type to classifying subgroups
![]() $H\leq O^+(\Lambda )$
satisfying certain lattice-theoretic conditions. We recall that
$H\leq O^+(\Lambda )$
satisfying certain lattice-theoretic conditions. We recall that
![]() $O^+(\Lambda )\trianglelefteq O(\Lambda )$
denotes the normal subgroup consisting of orientation-preserving isometries. We classify such groups
$O^+(\Lambda )\trianglelefteq O(\Lambda )$
denotes the normal subgroup consisting of orientation-preserving isometries. We classify such groups
![]() $H\leq O^+(\Lambda )$
by distinguishing their induced action on the discriminant group
$H\leq O^+(\Lambda )$
by distinguishing their induced action on the discriminant group
![]() $D_\Lambda :=\Lambda ^\vee /\Lambda .$
Note that
$D_\Lambda :=\Lambda ^\vee /\Lambda .$
Note that
![]() $O(D_\Lambda )= \{\pm {id}_{D_\Lambda }\}$
, and let us denote by
$O(D_\Lambda )= \{\pm {id}_{D_\Lambda }\}$
, and let us denote by
![]() $O^\#(\Lambda )$
the kernel of the natural morphism
$O^\#(\Lambda )$
the kernel of the natural morphism
![]() $O(\Lambda )\to O(D_\Lambda )$
. We let, moreover,
$O(\Lambda )\to O(D_\Lambda )$
. We let, moreover,
![]() $O^{+, \#}(\Lambda ) := O^+(\Lambda )\cap O^\#(\Lambda )$
.
$O^{+, \#}(\Lambda ) := O^+(\Lambda )\cap O^\#(\Lambda )$
.
The second step of our proof of Theorem 5.1 consists of classifying finite subgroups
![]() $H\leq O^{+,\#}(\Lambda )$
; we say such a group H is stable.Footnote
1
A classical approach to classify stable groups is to realise H as an isometry group of the Leech lattice
$H\leq O^{+,\#}(\Lambda )$
; we say such a group H is stable.Footnote
1
A classical approach to classify stable groups is to realise H as an isometry group of the Leech lattice
![]() $\mathbb {L}$
, by embedding the coinvariant sublattice primitively into
$\mathbb {L}$
, by embedding the coinvariant sublattice primitively into
![]() $\mathbb {L}$
and extending the group of isometries. Unfortunately, this is no longer a sufficient strategy in the case of
$\mathbb {L}$
and extending the group of isometries. Unfortunately, this is no longer a sufficient strategy in the case of
![]() $OG10$
type manifolds X, due to the fact that
$OG10$
type manifolds X, due to the fact that
![]() $ H^2(X,\mathbb {Z})\cong \Lambda $
is not unimodular. Indeed, there exist stable groups
$ H^2(X,\mathbb {Z})\cong \Lambda $
is not unimodular. Indeed, there exist stable groups
![]() $H\leq O^{+, \#}(\Lambda )$
whose coinvariant sublattice does not primitively embed into
$H\leq O^{+, \#}(\Lambda )$
whose coinvariant sublattice does not primitively embed into
![]() $\mathbb {L}$
(see Example 4.12). Instead, we realise such stable groups H as subgroups of isometries of the Borcherds lattice
$\mathbb {L}$
(see Example 4.12). Instead, we realise such stable groups H as subgroups of isometries of the Borcherds lattice
![]() $\mathbb {B}:=U\oplus \mathbb {L}$
to obtain our classification. We obtain the following result:
$\mathbb {B}:=U\oplus \mathbb {L}$
to obtain our classification. We obtain the following result:
Theorem 1.2 (Theorem 4.1).
Let
![]() $(X, \eta , G)$
be a triple consisting of a marked IHS manifold
$(X, \eta , G)$
be a triple consisting of a marked IHS manifold
![]() $(X, \eta )$
of
$(X, \eta )$
of
![]() $OG10$
type and a finite group
$OG10$
type and a finite group
![]() $G\leq \mathrm {Bir}_s(X)$
such that
$G\leq \mathrm {Bir}_s(X)$
such that
![]() $H:=\eta _\ast (G)\leq O^{+, \#}(\Lambda )$
is stable. Then, up to conjugacy,
$H:=\eta _\ast (G)\leq O^{+, \#}(\Lambda )$
is stable. Then, up to conjugacy,
![]() $H\leq O^{+,\#}(\Lambda )$
is contained in one of the 192 stable groups of the dataset [Reference Marquand and Muller30].
$H\leq O^{+,\#}(\Lambda )$
is contained in one of the 192 stable groups of the dataset [Reference Marquand and Muller30].
Lastly, the final step in the proof of Theorem 5.1 is to classify the possible groups
![]() $H\leq O^+(\Lambda )$
with nontrivial action on
$H\leq O^+(\Lambda )$
with nontrivial action on
![]() $D_\Lambda $
. For such a group, there is a short exact sequence
$D_\Lambda $
. For such a group, there is a short exact sequence
where
![]() $H^\#$
is stable. Our approach to classify such possible groups H is to start with one of the 192 stable groups
$H^\#$
is stable. Our approach to classify such possible groups H is to start with one of the 192 stable groups
![]() $H^\#$
mentioned in Theorem 4.1, and classify all possible
$H^\#$
mentioned in Theorem 4.1, and classify all possible
![]() $\mu _2$
-extensions, along with their action on
$\mu _2$
-extensions, along with their action on
![]() $\Lambda $
. We then apply the Global Torelli theorem to extract those extensions that appear as groups of symplectic birational transformations of an IHS manifold of
$\Lambda $
. We then apply the Global Torelli theorem to extract those extensions that appear as groups of symplectic birational transformations of an IHS manifold of
![]() $OG10$
type.
$OG10$
type.
Our strategy to perform this extension classification is adapted from the original techniques of Brandhorst and Hashimoto [Reference Brandhorst and Hashimoto4], who classified maximal finite groups of automorphisms of
![]() $K3$
surfaces. In particular, such groups contain both symplectic and nonsymplectic automorphisms – we call such a group mixed. These techniques have been revisited by the independent works [Reference Comparin, Demelle and Mora9, Reference Wawak46] in the case of maximal mixed actions on IHS manifolds of
$K3$
surfaces. In particular, such groups contain both symplectic and nonsymplectic automorphisms – we call such a group mixed. These techniques have been revisited by the independent works [Reference Comparin, Demelle and Mora9, Reference Wawak46] in the case of maximal mixed actions on IHS manifolds of
![]() $K3^{[2]}$
type. Through a series of work [Reference Brandhorst and Hashimoto4, Reference Brandhorst, Hofmann and Manthe6, Reference Brandhorst and Veniani8], this classification approach culminated in the recent major algorithmic progress of Brandhorst and Hofmann [Reference Brandhorst and Hofmann5] where the authors completed a long-standing full classification work for finite mixed automorphisms on K3 surfaces.
$K3^{[2]}$
type. Through a series of work [Reference Brandhorst and Hashimoto4, Reference Brandhorst, Hofmann and Manthe6, Reference Brandhorst and Veniani8], this classification approach culminated in the recent major algorithmic progress of Brandhorst and Hofmann [Reference Brandhorst and Hofmann5] where the authors completed a long-standing full classification work for finite mixed automorphisms on K3 surfaces.
The algorithms developed in [Reference Brandhorst and Hofmann5] have been successfully implemented by the second author of the present paper on Oscar [Reference Decker, Eder, Fieker, Horn and Joswig12, QuadFormAndIsom], together with Nikulin’s theory on primitive extensions [Reference Nikulin36]. This package allows one to consider the classification of finite groups of symmetries of higher dimensional IHS manifolds. We develop an algorithmic procedure to complete the extension classification, and we obtain the classification of finite subgroups of symplectic birational transformations on IHS manifolds of
![]() $OG10$
type in Theorem 5.1.
$OG10$
type in Theorem 5.1.
A natural next step is to provide geometrical realisations for the groups H occuring in the classification developed in Theorem 5.1. For some of the groups with trivial action on
![]() $D_\Lambda ,$
this can be achieved by applying O’Grady’s original construction [Reference O’Grady37] to a
$D_\Lambda ,$
this can be achieved by applying O’Grady’s original construction [Reference O’Grady37] to a
![]() $K3$
surface with a specific group of automorphisms. In [Reference Marquand and Muller29], we provided geometric realisations for two of the symplectic birational involutions obtained as extensions of the trivial group
$K3$
surface with a specific group of automorphisms. In [Reference Marquand and Muller29], we provided geometric realisations for two of the symplectic birational involutions obtained as extensions of the trivial group
![]() $H^\#=1$
, via antisymplectic involutions of a cubic fourfold
$H^\#=1$
, via antisymplectic involutions of a cubic fourfold
![]() $V\subset \mathbb {P}^5$
. We briefly recall the construction. An antisymplectic involution
$V\subset \mathbb {P}^5$
. We briefly recall the construction. An antisymplectic involution
![]() $\phi \in \mathrm {Aut}(V)$
induces an antisymplectic birational involution
$\phi \in \mathrm {Aut}(V)$
induces an antisymplectic birational involution
![]() $\phi $
on a compactified intermediate Jacobian
$\phi $
on a compactified intermediate Jacobian
![]() $X_V$
, which is an IHS manifold of
$X_V$
, which is an IHS manifold of
![]() $OG10$
type as in [Reference Laza, Saccà and Voisin25, Reference Saccà42]. The manifold
$OG10$
type as in [Reference Laza, Saccà and Voisin25, Reference Saccà42]. The manifold
![]() $X_V$
has a Lagrangian fibration
$X_V$
has a Lagrangian fibration
![]() $\pi \colon X_V\to \mathbb {P}^5$
which admits a section, and it is equipped with another antisymplectic birational involution
$\pi \colon X_V\to \mathbb {P}^5$
which admits a section, and it is equipped with another antisymplectic birational involution
![]() $\tau \in \mathrm {Bir}(X_V)$
acting by
$\tau \in \mathrm {Bir}(X_V)$
acting by
![]() $-1$
on the smooth fibers. The composition
$-1$
on the smooth fibers. The composition
![]() $\tau \circ \phi $
is a symplectic birational involution of
$\tau \circ \phi $
is a symplectic birational involution of
![]() $X_V$
.
$X_V$
.
Let V be a cubic fourfold, and
![]() $\mathrm {Aut}_s(V)\leq \mathrm {Aut}(V)$
the subgroup of symplectic automorphisms. A group of symplectic automorphisms
$\mathrm {Aut}_s(V)\leq \mathrm {Aut}(V)$
the subgroup of symplectic automorphisms. A group of symplectic automorphisms
![]() $G_s\leq \mathrm {Aut}_s(V)$
will induce a group of symplectic birational transformations
$G_s\leq \mathrm {Aut}_s(V)$
will induce a group of symplectic birational transformations
![]() $G_s\leq \mathrm {Bir}_s(X_V)$
, acting trivially on the discriminant group. We show that if V exhibits in addition an antisymplectic automorphism (i.e., a nonsymplectic automorphism with symplectic square), then one can induce larger groups of symplectic birational transformations
$G_s\leq \mathrm {Bir}_s(X_V)$
, acting trivially on the discriminant group. We show that if V exhibits in addition an antisymplectic automorphism (i.e., a nonsymplectic automorphism with symplectic square), then one can induce larger groups of symplectic birational transformations
![]() $G\leq \mathrm {Bir}_s(X_V)$
that are
$G\leq \mathrm {Bir}_s(X_V)$
that are
![]() $\mu _2$
-extensions of
$\mu _2$
-extensions of
![]() $G_s$
. More precisely, we show the following:
$G_s$
. More precisely, we show the following:
Theorem 1.3 (Theorem 6.1).
Let X be an IHS manifold of
![]() $OG10$
type and let
$OG10$
type and let
![]() $G\leq \mathrm {Bir}_s(X)$
be a finite group of symplectic birational transformations. Suppose that
$G\leq \mathrm {Bir}_s(X)$
be a finite group of symplectic birational transformations. Suppose that
![]() $\Lambda ^G\cong U\oplus \Gamma $
holds, for some lattice
$\Lambda ^G\cong U\oplus \Gamma $
holds, for some lattice
![]() $\Gamma $
. Then there exists some smooth cubic fourfold V and an embedding
$\Gamma $
. Then there exists some smooth cubic fourfold V and an embedding
![]() $j\colon G\hookrightarrow \mathrm {Aut}(V)$
such that
$j\colon G\hookrightarrow \mathrm {Aut}(V)$
such that
-
1. either G acts trivially on the discriminant group
 $D_\Lambda $
, and
$D_\Lambda $
, and
 $j(G)\leq \mathrm {Aut}_s(V)$
;
$j(G)\leq \mathrm {Aut}_s(V)$
; -
2. or
 $G=\langle G_s, \phi \rangle $
with
$G=\langle G_s, \phi \rangle $
with
 $j(G_s)\leq \mathrm {Aut}_s(V)$
, and
$j(G_s)\leq \mathrm {Aut}_s(V)$
, and
 $j(\phi )\in \mathrm {Aut}(V)\setminus \mathrm {Aut}_s(V)$
is antisymplectic.
$j(\phi )\in \mathrm {Aut}(V)\setminus \mathrm {Aut}_s(V)$
is antisymplectic.
The pair
![]() $(G_s, \Lambda _{G_s})$
occurs in the classification of [Reference Laza and Zheng26].
$(G_s, \Lambda _{G_s})$
occurs in the classification of [Reference Laza and Zheng26].
Conversely, for any smooth cubic fourfold V, any LSV manifold
![]() $X_V$
associated to V and any finite subgroup
$X_V$
associated to V and any finite subgroup
![]() $G\leq \mathrm {Aut}(V)$
so that
$G\leq \mathrm {Aut}(V)$
so that
![]() $[G:G_s]\leq 2$
holds, there is an embedding of G into the group
$[G:G_s]\leq 2$
holds, there is an embedding of G into the group
![]() $\mathrm {Bir}_s(X_V)$
of symplectic birational transformations on
$\mathrm {Bir}_s(X_V)$
of symplectic birational transformations on
![]() $X_V$
.
$X_V$
.
Among the 375 groups mentioned in Theorem 5.1, we have that 77 of them can be realised via LSV manifolds associated to cubic fourfolds in the sense of Theorem 6.1. We also find that 34 of the pairs can be realised via the twisted LSV construction from a cubic fourfold as in [Reference Voisin45].
Remark 1.4. Note that even though we know the action of
![]() $G\leq \mathrm {Aut}(V)$
on
$G\leq \mathrm {Aut}(V)$
on
![]() $H^4(X,\mathbb {Z})_{prim}$
, we cannot (always) determine the action on
$H^4(X,\mathbb {Z})_{prim}$
, we cannot (always) determine the action on
![]() $H^2(X_V,\mathbb {Z})$
. The manifold
$H^2(X_V,\mathbb {Z})$
. The manifold
![]() $X_V$
admits a Lagrangian fibration
$X_V$
admits a Lagrangian fibration
![]() $\pi :X_V\rightarrow \mathbb {P}^5$
and has a distinguished divisor
$\pi :X_V\rightarrow \mathbb {P}^5$
and has a distinguished divisor
![]() $\Theta $
[Reference Laza, Saccà and Voisin25, Reference Saccà42]. There is a rational Hodge isometry between
$\Theta $
[Reference Laza, Saccà and Voisin25, Reference Saccà42]. There is a rational Hodge isometry between
![]() $\langle \Theta , \pi ^*\mathcal {O}_{\mathbb {P}^5}(1)\rangle ^\perp \subset H^2(X_V,\mathbb {Z})$
and
$\langle \Theta , \pi ^*\mathcal {O}_{\mathbb {P}^5}(1)\rangle ^\perp \subset H^2(X_V,\mathbb {Z})$
and
![]() $H^4(V,\mathbb {Z})_{prim}(-1)$
. The action of the induced group
$H^4(V,\mathbb {Z})_{prim}(-1)$
. The action of the induced group
![]() $G\leq \mathrm {Bir}_s(X_V)$
on
$G\leq \mathrm {Bir}_s(X_V)$
on
![]() $H^2(X_V,\mathbb {Z})$
could be determined if this isometry can be upgraded to an integral Hodge isometry. The conjectural action of the 77 groups above are indicated in Table 4 of the ancillary files.
$H^2(X_V,\mathbb {Z})$
could be determined if this isometry can be upgraded to an integral Hodge isometry. The conjectural action of the 77 groups above are indicated in Table 4 of the ancillary files.
Outline of the paper
In Section 2, we recall the definitions and known results surrounding lattices, isometries and primitive extensions. We also collect results regarding isometries of the Borcherds lattice. In Section 3, we recall the Global Torelli theorem for IHS manifolds of
![]() $OG10$
type and reduce the classification of finite groups of symplectic birational transformations to classifying certain isometry groups of the associated lattice. In Section 4, we classify finite groups of symplectic birational transformations acting trivially on
$OG10$
type and reduce the classification of finite groups of symplectic birational transformations to classifying certain isometry groups of the associated lattice. In Section 4, we classify finite groups of symplectic birational transformations acting trivially on
![]() $D_\Lambda $
, proving Theorem 4.1. In order to do so, we determine the isometry class of the coinvariant sublattices for some finite subgroups of isometries of
$D_\Lambda $
, proving Theorem 4.1. In order to do so, we determine the isometry class of the coinvariant sublattices for some finite subgroups of isometries of
![]() $\mathbb {B}$
: those are either primitively embedded into the Leech lattice, or they are displayed in Appendices A and B. The results of Theorem 4.1 are presented in Appendix C, Table 3. In Section 5, we explain our extension approach in order to classify finite groups of symplectic birational transformations acting nontrivially on
$\mathbb {B}$
: those are either primitively embedded into the Leech lattice, or they are displayed in Appendices A and B. The results of Theorem 4.1 are presented in Appendix C, Table 3. In Section 5, we explain our extension approach in order to classify finite groups of symplectic birational transformations acting nontrivially on
![]() $D_\Lambda $
. We implement the algorithms from Appendix D, and we prove Theorem 5.1. Finally, in Section 6, we provide geometric realisations for some of the groups in the classification via known constructions from either a
$D_\Lambda $
. We implement the algorithms from Appendix D, and we prove Theorem 5.1. Finally, in Section 6, we provide geometric realisations for some of the groups in the classification via known constructions from either a
![]() $K3$
surface, or a cubic fourfold. In particular, we prove Theorem 6.1 and apply it to our classification. Our work is computer aided: all the data supporting our proofs are contained in an external Zenodo dataset [Reference Marquand and Muller30], as well as several notebooks explaining our computations.
$K3$
surface, or a cubic fourfold. In particular, we prove Theorem 6.1 and apply it to our classification. Our work is computer aided: all the data supporting our proofs are contained in an external Zenodo dataset [Reference Marquand and Muller30], as well as several notebooks explaining our computations.
2 Preliminaries
In this section, we recall some preliminary results. In Section 2.1, we recall relevant notation and definitions regarding lattices and their isometries. In Section 2.2, we recall Nikulin’s theory of primitive embeddings, highlighting the equivariant analogue. In Section 2.3, we introduce the Borcherds lattice and recall the structure of its group of isometries.
2.1 Lattices and isometries
Let L be a lattice, which is a finitely generated free
![]() $\mathbb {Z}$
-module equipped with a nondegenerate, integer valued symmetric bilinear form. For two vectors
$\mathbb {Z}$
-module equipped with a nondegenerate, integer valued symmetric bilinear form. For two vectors
![]() $u,v\in L$
, we denote by
$u,v\in L$
, we denote by
![]() $u.v\in \mathbb {Z}$
the image by the bilinear form, and we let
$u.v\in \mathbb {Z}$
the image by the bilinear form, and we let
![]() $v^2 := v.v$
. We assume that L is even unless stated otherwise (i.e.,
$v^2 := v.v$
. We assume that L is even unless stated otherwise (i.e.,
![]() $v^2\in 2\mathbb {Z}$
for all
$v^2\in 2\mathbb {Z}$
for all
![]() $v\in L$
). Finally, we denote by
$v\in L$
). Finally, we denote by
![]() $O^+(L)\leq O(L)$
the group of orientiation-preserving isometries of L.
$O^+(L)\leq O(L)$
the group of orientiation-preserving isometries of L.
In what follows, all
![]() $ADE$
root lattices are assumed to be negative definite. The Leech lattice
$ADE$
root lattices are assumed to be negative definite. The Leech lattice
![]() $\mathbb {L}$
is the unique (up to isometry) negative definite even unimodular lattice of rank 24 that contains no
$\mathbb {L}$
is the unique (up to isometry) negative definite even unimodular lattice of rank 24 that contains no
![]() $(-2)$
-vectors. We denote by U the hyperbolic plane lattice, which is the unique even unimodular lattice of rank 2, up to isometry.
$(-2)$
-vectors. We denote by U the hyperbolic plane lattice, which is the unique even unimodular lattice of rank 2, up to isometry.
We denote by
![]() $D_L:=L^\vee /L$
the discriminant group of L. For any lattice isometry
$D_L:=L^\vee /L$
the discriminant group of L. For any lattice isometry
![]() $f\colon L\xrightarrow {\cong } L'$
, we denote by
$f\colon L\xrightarrow {\cong } L'$
, we denote by
![]() $D_f\colon D_L\xrightarrow {\cong } D_{L'}$
the induced isometry.
$D_f\colon D_L\xrightarrow {\cong } D_{L'}$
the induced isometry.
Definition 2.1. Let L be a lattice and let
![]() $G \leq O(L)$
be a group of isometries. We call the discriminant representation of G the morphism
$G \leq O(L)$
be a group of isometries. We call the discriminant representation of G the morphism
![]() $G\to O(D_L)$
. We denote by
$G\to O(D_L)$
. We denote by
![]() $\overline {G}$
its image and by
$\overline {G}$
its image and by
![]() $G^\#$
its kernel. Any element in
$G^\#$
its kernel. Any element in
![]() $G^\#$
is said to be stable, and we call G stable if
$G^\#$
is said to be stable, and we call G stable if
![]() $G = G^\#$
.
$G = G^\#$
.
Let
![]() $G\leq O(L)$
be a group of isometries. We denote by
$G\leq O(L)$
be a group of isometries. We denote by
![]() $L^G:=\{v\in L\mid g(v)=v, \,\, \forall g\in G\}$
and by
$L^G:=\{v\in L\mid g(v)=v, \,\, \forall g\in G\}$
and by
![]() $L_G:=(L^G)_L^\perp $
the associated invariant and coinvariant sublattices, respectively.
$L_G:=(L^G)_L^\perp $
the associated invariant and coinvariant sublattices, respectively.
Definition 2.2. Let L be a lattice, and let
![]() $H\leq G\leq O(L)$
be a chain of subgroups. We call the saturation of H in G, denoted
$H\leq G\leq O(L)$
be a chain of subgroups. We call the saturation of H in G, denoted
![]() $\mathrm {Sat}_G(H)$
, the largest subgroup
$\mathrm {Sat}_G(H)$
, the largest subgroup
![]() $H\leq \mathrm {Sat}_G(H)\leq G$
such that
$H\leq \mathrm {Sat}_G(H)\leq G$
such that
![]() $L^H = L^{\mathrm {Sat}_G(H)}$
. We say that H is saturated in G if
$L^H = L^{\mathrm {Sat}_G(H)}$
. We say that H is saturated in G if
![]() $\mathrm {Sat}_G(H) = H$
.
$\mathrm {Sat}_G(H) = H$
.
Lemma 2.3. Let L be a lattice and let
![]() $H\leq G\leq O(L)$
be a chain of subgroups. If H is saturated in G, then
$H\leq G\leq O(L)$
be a chain of subgroups. If H is saturated in G, then
![]() $H^\#$
is saturated in
$H^\#$
is saturated in
![]() $G^\#$
.
$G^\#$
.
Proof. Let
![]() $g\in G^\#$
such that g acts trivially on
$g\in G^\#$
such that g acts trivially on
![]() $L^{H^\#}$
. Since
$L^{H^\#}$
. Since
![]() $L^{H}\subseteq L^{H^\#}$
, we have that g is the identity on
$L^{H}\subseteq L^{H^\#}$
, we have that g is the identity on
![]() $L^H$
, and thus,
$L^H$
, and thus,
![]() $g\in \mathrm {Sat}_G(H) = H$
. Hence,
$g\in \mathrm {Sat}_G(H) = H$
. Hence,
![]() $g\in G^\#\cap H = H^\#$
, and
$g\in G^\#\cap H = H^\#$
, and
![]() $\mathrm {Sat}_{G^\#}(H^\#) = H^\#$
.
$\mathrm {Sat}_{G^\#}(H^\#) = H^\#$
.
Definition 2.4. We call a lattice with isometry any pair
![]() $(L, f)$
consisting of a lattice L and an isometry
$(L, f)$
consisting of a lattice L and an isometry
![]() $f\in O(L)$
. Two such pairs
$f\in O(L)$
. Two such pairs
![]() $(L_1, f_1)$
and
$(L_1, f_1)$
and
![]() $(L_2, f_2)$
are isomorphic if there exists an isometry
$(L_2, f_2)$
are isomorphic if there exists an isometry
![]() $\psi \colon L_1\xrightarrow {\cong } L_2$
such that
$\psi \colon L_1\xrightarrow {\cong } L_2$
such that
![]() $f_2 = \psi f_1\psi ^{-1}$
.
$f_2 = \psi f_1\psi ^{-1}$
.
Definition 2.5. Let L be a lattice and let
![]() $v\in L$
be a vector. We define the divisibility of v in L, which we denote
$v\in L$
be a vector. We define the divisibility of v in L, which we denote
![]() $\mathrm {div}_L(v)$
, the positive generator of the ideal
$\mathrm {div}_L(v)$
, the positive generator of the ideal
![]() $v.L$
.
$v.L$
.
2.2 Primitive extensions
For nondegenerate lattices, all morphisms are injective – we therefore talk about embeddings.
Definition 2.6. Let L be a lattice.
-
1. Any sublattice
 $S\subseteq L$
is called primitive if the quotient
$S\subseteq L$
is called primitive if the quotient
 $L/S$
is torsion-free.
$L/S$
is torsion-free. -
2. Any embedding
 $i\colon S\hookrightarrow L$
is called primitive if
$i\colon S\hookrightarrow L$
is called primitive if
 $i(S)\subseteq L$
is primitive.
$i(S)\subseteq L$
is primitive. -
3. Two primitive sublattices
 $S_1, S_2\subseteq L$
are said isomorphic if there exists an isometry
$S_1, S_2\subseteq L$
are said isomorphic if there exists an isometry
 $\psi \in O(L)$
such that
$\psi \in O(L)$
such that
 $\psi (S_1) = S_2$
.
$\psi (S_1) = S_2$
.
Given an even lattice S, the proof of [Reference Nikulin36, Proposition 1.15.1] describes a procedure to classify, up to isomorphism, primitive sublattices of an even lattice, with given signature and discriminant group, that are isometric to S. The proof makes use of the notion of primitive extensions, which we recall now.
Definition 2.7. For a lattice L and a sublattice
![]() $N\subseteq L$
, we say that L is an overlattice of N if L and N have the same rank, as
$N\subseteq L$
, we say that L is an overlattice of N if L and N have the same rank, as
![]() $\mathbb {Z}$
-modules.
$\mathbb {Z}$
-modules.
Let S and T be even lattices and let L be an overlattice of
![]() $S\oplus T$
. Such an overlattice
$S\oplus T$
. Such an overlattice
![]() $S\oplus T\subseteq L$
is called a primitive extension if both composite embeddings
$S\oplus T\subseteq L$
is called a primitive extension if both composite embeddings
![]() $S\hookrightarrow S\oplus T\hookrightarrow L$
and
$S\hookrightarrow S\oplus T\hookrightarrow L$
and
![]() $T\hookrightarrow S\oplus T\hookrightarrow L$
are primitive.
$T\hookrightarrow S\oplus T\hookrightarrow L$
are primitive.
Definition 2.8. We define a glue map between S and T to be an isomorphism of finite abelian groups
such that
![]() $x^2+\gamma (x)^2\in 2\mathbb {Z}$
for all
$x^2+\gamma (x)^2\in 2\mathbb {Z}$
for all
![]() $x\in H_S$
. We moreover call
$x\in H_S$
. We moreover call
![]() $H_S$
and
$H_S$
and
![]() $H_T$
the glue domains of
$H_T$
the glue domains of
![]() $\gamma $
.
$\gamma $
.
Proposition 2.9 [Reference Nikulin36, Proposition 1.4.1].
Glue maps
![]() $D_S\geq H_S\xrightarrow {\gamma } H_T\leq D_T$
correspond bijectively to even primitive extensions
$D_S\geq H_S\xrightarrow {\gamma } H_T\leq D_T$
correspond bijectively to even primitive extensions
![]() $S\oplus T\subseteq L_\gamma $
.
$S\oplus T\subseteq L_\gamma $
.
Definition 2.10. We call
![]() $L_\gamma $
the overlattice relative to
$L_\gamma $
the overlattice relative to
![]() $\gamma $
. In this situation, we also say that
$\gamma $
. In this situation, we also say that
![]() $H_S\leq D_S$
and
$H_S\leq D_S$
and
![]() $H_T\leq D_T$
are the glue domains of the primitive embeddings
$H_T\leq D_T$
are the glue domains of the primitive embeddings
![]() $S\hookrightarrow L$
and
$S\hookrightarrow L$
and
![]() $T\hookrightarrow L$
, respectively.
$T\hookrightarrow L$
, respectively.
Let
![]() $(S, s)$
and
$(S, s)$
and
![]() $(T, t)$
be two even lattices with isometry, where
$(T, t)$
be two even lattices with isometry, where
![]() $s\in O(S)$
and
$s\in O(S)$
and
![]() $t\in O(T)$
. Let
$t\in O(T)$
. Let
![]() $D_S\geq H_S\xrightarrow {\gamma } H_T\leq D_T$
be a glue map. The glue map
$D_S\geq H_S\xrightarrow {\gamma } H_T\leq D_T$
be a glue map. The glue map
![]() $\gamma $
is called
$\gamma $
is called
![]() $(s, t)$
-equivariant if
$(s, t)$
-equivariant if
![]() $H_S$
and
$H_S$
and
![]() $H_T$
are respectively
$H_T$
are respectively
![]() $D_s$
-stable and
$D_s$
-stable and
![]() $D_t$
-stable, and if it satisfies the equivariant gluing condition:
$D_t$
-stable, and if it satisfies the equivariant gluing condition:
Proposition 2.11 [Reference Nikulin36, Corollary 1.5.2].
The map
![]() $\gamma $
is
$\gamma $
is
![]() $(s, t)$
-equivariant if and only if
$(s, t)$
-equivariant if and only if
![]() $s\oplus t$
extends along the primitive extension
$s\oplus t$
extends along the primitive extension
![]() $S\oplus T\subseteq L_{\gamma }$
to an isometry
$S\oplus T\subseteq L_{\gamma }$
to an isometry
![]() $f_\gamma $
of
$f_\gamma $
of
![]() $L_{\gamma }.$
$L_{\gamma }.$
We call
![]() $(L_\gamma , f_\gamma )$
an equivariant primitive extension of
$(L_\gamma , f_\gamma )$
an equivariant primitive extension of
![]() $(S, s)$
and
$(S, s)$
and
![]() $(T, t)$
.
$(T, t)$
.
Definition 2.12. Let
![]() $(S_1, s_1)\oplus (T_1, t_1)\subseteq (L_1, f_1)$
and
$(S_1, s_1)\oplus (T_1, t_1)\subseteq (L_1, f_1)$
and
![]() $(S_2, s_2)\oplus (T_2, t_2)\subseteq (L_2, f_2)$
be two equivariant primitive extensions. They are said to be isomorphic if there exists an isomorphism
$(S_2, s_2)\oplus (T_2, t_2)\subseteq (L_2, f_2)$
be two equivariant primitive extensions. They are said to be isomorphic if there exists an isomorphism
![]() $\psi \colon (L_1, f_1)\to (L_2, f_2)$
which restricts to isomorphisms
$\psi \colon (L_1, f_1)\to (L_2, f_2)$
which restricts to isomorphisms
![]() $\psi _S\colon (S_1,s_2)\to (S_2, s_2)$
and
$\psi _S\colon (S_1,s_2)\to (S_2, s_2)$
and
![]() $\psi _T\colon (T_1, t_1)\to (T_2, t_2)$
.
$\psi _T\colon (T_1, t_1)\to (T_2, t_2)$
.
2.3 Borcherds lattice
A common technique to classify finite groups of symplectic birational transformations of IHS manifolds is to relate them to isometry groups of the Leech lattice
![]() $\mathbb {L}$
. Unfortunately, this lattice is too small for our purposes, and so we will require some results about isometries of the Borcherds lattice:
$\mathbb {L}$
. Unfortunately, this lattice is too small for our purposes, and so we will require some results about isometries of the Borcherds lattice:
Remark 2.13. In [Reference Brandhorst and Mezzedimi7], the authors define the notion of Borcherds lattices, which are a particular class of hyperbolic even lattices with infinitely many simple
![]() $(-2)$
-roots. They show that the Borcherds lattices of largest rank are isometric to
$(-2)$
-roots. They show that the Borcherds lattices of largest rank are isometric to
![]() $U\oplus \mathbb {L}$
, which motivates our definition. Note that our definition differs from the one given by Laza and Zheng in [Reference Laza and Zheng26], where they define
$U\oplus \mathbb {L}$
, which motivates our definition. Note that our definition differs from the one given by Laza and Zheng in [Reference Laza and Zheng26], where they define
![]() $U^2\oplus \mathbb {L}$
as Borcherds lattice, which is not a Borcherds lattice in the sense of Brandhorst and Mezzedimi.
$U^2\oplus \mathbb {L}$
as Borcherds lattice, which is not a Borcherds lattice in the sense of Brandhorst and Mezzedimi.
The lattice
![]() $\mathbb {B}$
is even unimodular, of signature
$\mathbb {B}$
is even unimodular, of signature
![]() $(1,25)$
, and unique in its genus. Let us fix a basis
$(1,25)$
, and unique in its genus. Let us fix a basis
![]() $\{e,s\}$
for
$\{e,s\}$
for
![]() $U\subset \mathbb {B}$
with
$U\subset \mathbb {B}$
with
![]() $e^2=0, s^2=-2$
and
$e^2=0, s^2=-2$
and
![]() $e. s=1$
.
$e. s=1$
.
The group of isometries of
![]() $\mathbb {B}$
is known and it has been studied for instance by Conway in [Reference Conway, Sloane, Bannai, Borcherds, Leech, Norton, Odlyzko, Parker, Queen and Venkov11, Chapter 27]. For the reader’s convenience, we recall Conway’s results, following an exposition of Brandhorst and Mezzedimi [Reference Brandhorst and Mezzedimi7].
$\mathbb {B}$
is known and it has been studied for instance by Conway in [Reference Conway, Sloane, Bannai, Borcherds, Leech, Norton, Odlyzko, Parker, Queen and Venkov11, Chapter 27]. For the reader’s convenience, we recall Conway’s results, following an exposition of Brandhorst and Mezzedimi [Reference Brandhorst and Mezzedimi7].
We denote by
![]() $\mathcal {P}$
one of the connected components of
$\mathcal {P}$
one of the connected components of
we call it the positive cone of
![]() $\mathbb {B}$
. Note that
$\mathbb {B}$
. Note that
![]() $O(\mathbb {B}) = \{\pm {id}\}\times O^+(\mathbb {B})$
and
$O(\mathbb {B}) = \{\pm {id}\}\times O^+(\mathbb {B})$
and
![]() $- {id}$
does not preserve
$- {id}$
does not preserve
![]() $\mathcal {P}$
– we can see that the group
$\mathcal {P}$
– we can see that the group
![]() $O^+(\mathbb {B})$
is the stabiliser of
$O^+(\mathbb {B})$
is the stabiliser of
![]() $\mathcal {P}$
in
$\mathcal {P}$
in
![]() $O(\mathbb {B})$
.
$O(\mathbb {B})$
.
Let us denote by
![]() $\Delta := \{r\in \mathbb {B}\;\mid \; r^2=-2\}$
the set of roots of
$\Delta := \{r\in \mathbb {B}\;\mid \; r^2=-2\}$
the set of roots of
![]() $\mathbb {B}$
and denote by
$\mathbb {B}$
and denote by
![]() $W(\mathbb {B})\leq O^+(\mathbb {B})$
the subgroup generated by the reflections in the roots
$W(\mathbb {B})\leq O^+(\mathbb {B})$
the subgroup generated by the reflections in the roots
![]() $r\in \Delta $
. The group
$r\in \Delta $
. The group
![]() $W(\mathbb {B})$
is the so-called Weyl group of
$W(\mathbb {B})$
is the so-called Weyl group of
![]() $\mathbb {B}$
, and it acts simply transitively on the set of connected components, or chambers, of
$\mathbb {B}$
, and it acts simply transitively on the set of connected components, or chambers, of
For any chamber
![]() $D\subseteq \Gamma $
, we let
$D\subseteq \Gamma $
, we let
![]() $P_D := \{v\in \mathbb {B}\;\mid \; v.x>0,\,\forall x\in \overline {D}\}$
, and moreover, we define
$P_D := \{v\in \mathbb {B}\;\mid \; v.x>0,\,\forall x\in \overline {D}\}$
, and moreover, we define
the set of simple roots of D [Reference Brandhorst and Mezzedimi7, §2.6].
Lemma 2.14. There exists a chamber
![]() $D_0\subset \Gamma $
such that
$D_0\subset \Gamma $
such that
![]() $e\in \overline {D_0}\cap \mathbb {B}$
and the set
$e\in \overline {D_0}\cap \mathbb {B}$
and the set
![]() $\{|e.r|\;\mid \; r\in \Delta _{D_0}\}$
is bounded. Moreover, the vector e is the unique isotropic vector in
$\{|e.r|\;\mid \; r\in \Delta _{D_0}\}$
is bounded. Moreover, the vector e is the unique isotropic vector in
![]() $\overline {D_0}\cap \mathbb {B}$
satisfying this property, and
$\overline {D_0}\cap \mathbb {B}$
satisfying this property, and
![]() $e.r=1$
for all
$e.r=1$
for all
![]() $r\in \Delta _{D_0}$
$r\in \Delta _{D_0}$
Proof. Existence of an isotropic element with the required properties follows from [Reference Conway, Sloane, Bannai, Borcherds, Leech, Norton, Odlyzko, Parker, Queen and Venkov11, Chapter 27]. Uniqueness follows from [Reference Brandhorst and Mezzedimi7, Theorem 3.7, Remark 3.8].
For the rest of the paper, we refer to e and
![]() $D_0$
as Conway’s vector and Conway’s chamber, respectively. We moreover denote by
$D_0$
as Conway’s vector and Conway’s chamber, respectively. We moreover denote by
![]() $\mathcal {D} := \overline {D_0}$
the closure of
$\mathcal {D} := \overline {D_0}$
the closure of
![]() $D_0$
in
$D_0$
in
![]() $\mathcal {P}$
, and we let
$\mathcal {P}$
, and we let
![]() $\mathrm {Aut}(\mathcal {D})$
be the subgroup of isometries of
$\mathrm {Aut}(\mathcal {D})$
be the subgroup of isometries of
![]() $O^+(\mathbb {B})$
preserving
$O^+(\mathbb {B})$
preserving
![]() $\mathcal {D}$
. Since
$\mathcal {D}$
. Since
![]() $\mathcal {D}$
is the closure of a fundamental domain for the action of
$\mathcal {D}$
is the closure of a fundamental domain for the action of
![]() $W(\mathbb {B})$
on
$W(\mathbb {B})$
on
![]() $\mathcal {P}$
, we can identify
$\mathcal {P}$
, we can identify
![]() $\mathrm {Aut}(\mathcal {D})$
with
$\mathrm {Aut}(\mathcal {D})$
with
![]() $O^+(\mathbb {B})/W(\mathbb {B})$
[Reference Brandhorst and Mezzedimi7, §2.6].
$O^+(\mathbb {B})/W(\mathbb {B})$
[Reference Brandhorst and Mezzedimi7, §2.6].
Lemma 2.15 [Reference Brandhorst and Mezzedimi7, Theorem 3.7].
The group
![]() $\mathrm {Aut}(\mathcal {D})$
is infinite, and any element
$\mathrm {Aut}(\mathcal {D})$
is infinite, and any element
![]() $h\in \mathrm {Aut}(\mathcal {D})$
fixes e.
$h\in \mathrm {Aut}(\mathcal {D})$
fixes e.
We would like to study finite subgroups of
![]() $\mathrm {Aut}(\mathcal {D})$
in order to determine their coinvariant sublattices. For this, we will need to understand the structure of
$\mathrm {Aut}(\mathcal {D})$
in order to determine their coinvariant sublattices. For this, we will need to understand the structure of
![]() $\mathrm {Aut}(\mathcal {D})$
.
$\mathrm {Aut}(\mathcal {D})$
.
Definition 2.16 (Eichler–Siegel transformation).
For any
![]() $\lambda \in \mathbb {L}$
, we define
$\lambda \in \mathbb {L}$
, we define
Note that
![]() $\psi _{\lambda }\in \mathrm {Aut}(\mathcal {D})$
by the proofs of [Reference Brandhorst and Mezzedimi7, Proposition 3.2, Theorem 4.7]. Further, the assignment
$\psi _{\lambda }\in \mathrm {Aut}(\mathcal {D})$
by the proofs of [Reference Brandhorst and Mezzedimi7, Proposition 3.2, Theorem 4.7]. Further, the assignment
is an injective group homomorphism (where we view
![]() $\mathbb {L}$
as a torsion free abelian group of finite rank under addition). By the definition of Conway’s vector e, which is isotropic, there is an exact sequence of lattices
$\mathbb {L}$
as a torsion free abelian group of finite rank under addition). By the definition of Conway’s vector e, which is isotropic, there is an exact sequence of lattices
inducing an isometry
![]() $\kappa \colon e^\perp /\mathbb {Z} e\xrightarrow {\cong }\mathbb {L}$
.
$\kappa \colon e^\perp /\mathbb {Z} e\xrightarrow {\cong }\mathbb {L}$
.
Lemma 2.17 [Reference Conway, Sloane, Bannai, Borcherds, Leech, Norton, Odlyzko, Parker, Queen and Venkov11, Chapter 27].
We have that
![]() $\mathrm {Aut}(\mathcal {D})=\mathbb {L}\rtimes O(\mathbb {L})$
.
$\mathrm {Aut}(\mathcal {D})=\mathbb {L}\rtimes O(\mathbb {L})$
.
Proof. Since any isometry in
![]() $\mathrm {Aut}(\mathcal {D})$
fixes e (Lemma 2.15), the isometry
$\mathrm {Aut}(\mathcal {D})$
fixes e (Lemma 2.15), the isometry
![]() $\kappa $
defines an orthogonal representation
$\kappa $
defines an orthogonal representation
which admits a section
![]() $\phi :O(\mathbb {L})\rightarrow \mathrm {Aut}(\mathcal {D})$
, given by extending an isometry of
$\phi :O(\mathbb {L})\rightarrow \mathrm {Aut}(\mathcal {D})$
, given by extending an isometry of
![]() $\mathbb {L}$
to one of
$\mathbb {L}$
to one of
![]() $\mathbb {B}$
acting as the identity on
$\mathbb {B}$
acting as the identity on
![]() $\mathbb {Z} e+\mathbb {Z} s\cong U.$
According to [Reference Brandhorst and Mezzedimi7, Proposition 3.2], the following sequence is exact:
$\mathbb {Z} e+\mathbb {Z} s\cong U.$
According to [Reference Brandhorst and Mezzedimi7, Proposition 3.2], the following sequence is exact:
Since all nontrivial elements of
![]() $\mathbb {L}$
have infinite order and
$\mathbb {L}$
have infinite order and
![]() $O(\mathbb {L})$
is of finite order, we have that
$O(\mathbb {L})$
is of finite order, we have that
![]() $\mathbb {L}\cap O(\mathbb {L})$
is trivial, as a subgroup of
$\mathbb {L}\cap O(\mathbb {L})$
is trivial, as a subgroup of
![]() $\mathrm {Aut}(\mathcal {D})$
, giving the claim.
$\mathrm {Aut}(\mathcal {D})$
, giving the claim.
Hence, any element
![]() $h\in \mathrm {Aut}(\mathcal {D})$
can be uniquely written in the form
$h\in \mathrm {Aut}(\mathcal {D})$
can be uniquely written in the form
![]() $\psi _\lambda \circ \phi (g)$
for some
$\psi _\lambda \circ \phi (g)$
for some
![]() $\lambda \in \mathbb {L}$
and some
$\lambda \in \mathbb {L}$
and some
![]() $g\in O(\mathbb {L})$
: we write
$g\in O(\mathbb {L})$
: we write
We record some properties of elements
![]() $h\in \mathrm {Aut}(\mathcal {D})$
for future use. The proof follows by direct calculation.
$h\in \mathrm {Aut}(\mathcal {D})$
for future use. The proof follows by direct calculation.
Proposition 2.18. Let
![]() $\lambda \in \mathbb {L}$
and let
$\lambda \in \mathbb {L}$
and let
![]() $g\in O(\mathbb {L})$
. The following hold:
$g\in O(\mathbb {L})$
. The following hold:
-
1.
 $\phi (g)\circ \psi _\lambda = \psi _{g(\lambda )}\circ \phi (g)$
;
$\phi (g)\circ \psi _\lambda = \psi _{g(\lambda )}\circ \phi (g)$
; -
2.
 $\psi ^{-1}_\lambda = \psi _{-\lambda }$
;
$\psi ^{-1}_\lambda = \psi _{-\lambda }$
; -
3.
 $h := (\lambda , g)$
is of finite order if and only if
$h := (\lambda , g)$
is of finite order if and only if
 $\lambda \in \mathbb {L}_g$
.
$\lambda \in \mathbb {L}_g$
.
Remark 2.19. A consequence of Proposition 2.18 (3) is that for any
![]() $h := (\lambda , g)\in \mathrm {Aut}(\mathcal {D})$
of finite order, then the order of h is the same as the order of g.
$h := (\lambda , g)\in \mathrm {Aut}(\mathcal {D})$
of finite order, then the order of h is the same as the order of g.
Theorem 2.20. Let
![]() $H\leq \mathrm {Aut}(\mathcal {D})$
be a subgroup, and let
$H\leq \mathrm {Aut}(\mathcal {D})$
be a subgroup, and let
![]() $G := \pi (H)\leq O(\mathbb {L})$
(Equation (2.1)). Then H is of finite order if and only if there exists
$G := \pi (H)\leq O(\mathbb {L})$
(Equation (2.1)). Then H is of finite order if and only if there exists
![]() $n \in \mathbb {Z}$
positive and
$n \in \mathbb {Z}$
positive and
![]() $v\in \mathbb {L}$
such that for all
$v\in \mathbb {L}$
such that for all
![]() $h = (\lambda , g)\in H$
,
$h = (\lambda , g)\in H$
,
Moreover, if H is of finite order, then
![]() $H\cong G$
, and n can be chosen to be
$H\cong G$
, and n can be chosen to be
![]() $\#(H\cdot s)$
.
$\#(H\cdot s)$
.
Proof. First remark that if H is of finite order, then
![]() $H\cap \mathbb {L}$
is the trivial subgroup of
$H\cap \mathbb {L}$
is the trivial subgroup of
![]() $\mathrm {Aut}(\mathcal {D})$
. In particular,
$\mathrm {Aut}(\mathcal {D})$
. In particular,
![]() $\pi $
restricts to an isomorphism between H and
$\pi $
restricts to an isomorphism between H and
![]() $G := \pi (H)$
. Note, moreover, that for any
$G := \pi (H)$
. Note, moreover, that for any
![]() $h = H\leq \mathrm {Aut}(\mathcal {D})$
, we have
$h = H\leq \mathrm {Aut}(\mathcal {D})$
, we have
![]() $h(e) = e$
(Lemma 2.15)
$h(e) = e$
(Lemma 2.15)
Suppose that H is of finite order, and denote by
![]() $n:= \#(H\cdot s)$
the length of the orbit of s under H. Since H is finite, we have that
$n:= \#(H\cdot s)$
the length of the orbit of s under H. Since H is finite, we have that
![]() $w := \sum _{r\in H\cdot s}r$
is fixed by H, and moreover
$w := \sum _{r\in H\cdot s}r$
is fixed by H, and moreover
![]() $e.w = n(e.s) = n$
. This implies that there exists
$e.w = n(e.s) = n$
. This implies that there exists
![]() $m\in \mathbb {Z}$
and
$m\in \mathbb {Z}$
and
![]() $v\in \mathbb {L}$
such that
$v\in \mathbb {L}$
such that
Since H fixes e and w, we have that H fixes
![]() $ns+v$
. In particular, for all
$ns+v$
. In particular, for all
![]() $h = (\lambda , g)\in H$
, we have
$h = (\lambda , g)\in H$
, we have
 $$ \begin{align} 0 = h(ns+v) - (ns+v) = (g(v)-v-n\lambda) + \left(\lambda.g(v)-n\frac{\lambda^2}{2}\right)e \in \mathbb{L}\oplus \mathbb{Z} e. \end{align} $$
$$ \begin{align} 0 = h(ns+v) - (ns+v) = (g(v)-v-n\lambda) + \left(\lambda.g(v)-n\frac{\lambda^2}{2}\right)e \in \mathbb{L}\oplus \mathbb{Z} e. \end{align} $$
This implies that
![]() $g(v)-v = n\lambda $
, and since this holds for any
$g(v)-v = n\lambda $
, and since this holds for any
![]() $h = (\lambda , g)\in H$
, we can conclude.
$h = (\lambda , g)\in H$
, we can conclude.
Conversely, suppose that such
![]() $n>0$
and
$n>0$
and
![]() $v\in \mathbb {L}$
exist, and let
$v\in \mathbb {L}$
exist, and let
![]() $h = (\lambda , g)\in H$
be arbitrary. Note that we have that
$h = (\lambda , g)\in H$
be arbitrary. Note that we have that
In particular, since
![]() $g(v)-v=n\lambda $
, we observe that
$g(v)-v=n\lambda $
, we observe that
According to Equation (2.2), we obtain that
![]() $ns+v\in \mathbb {B}^H$
. Since
$ns+v\in \mathbb {B}^H$
. Since
![]() $e\in \mathbb {B}^H$
too, one can find
$e\in \mathbb {B}^H$
too, one can find
![]() $m\in \mathbb {Z}_{\geq 0}$
large enough such that
$m\in \mathbb {Z}_{\geq 0}$
large enough such that
![]() $me+ns+v\in \mathbb {B}^H$
has positive norm. Since the lattice
$me+ns+v\in \mathbb {B}^H$
has positive norm. Since the lattice
![]() $\mathbb {B}$
is hyperbolic, we deduce that
$\mathbb {B}$
is hyperbolic, we deduce that
![]() $\mathbb {B}_H$
is negative definite and the group H acting faithfully on such a lattice must be finite.
$\mathbb {B}_H$
is negative definite and the group H acting faithfully on such a lattice must be finite.
Remark 2.21. Let
![]() $H\leq \mathrm {Aut}(\mathcal {D})$
be of finite order. Then the pair
$H\leq \mathrm {Aut}(\mathcal {D})$
be of finite order. Then the pair
![]() $(n, v)\in \mathbb {Z}_{>0}\times \mathbb {L}$
as in the statement of Theorem 2.20 is not unique: in fact, one can rescale simultaneously n and v by any nonzero integer, and v can be replaced by any element of
$(n, v)\in \mathbb {Z}_{>0}\times \mathbb {L}$
as in the statement of Theorem 2.20 is not unique: in fact, one can rescale simultaneously n and v by any nonzero integer, and v can be replaced by any element of
![]() $v+\Lambda ^G$
. In particular, we can always assume that
$v+\Lambda ^G$
. In particular, we can always assume that
![]() $n=\#H$
.
$n=\#H$
.
Remark 2.22. Let
![]() $H\leq \mathrm {Aut}(\mathcal {D})$
be finite, and let
$H\leq \mathrm {Aut}(\mathcal {D})$
be finite, and let
![]() $G := \pi (H)\leq O(\mathbb {L})$
where
$G := \pi (H)\leq O(\mathbb {L})$
where
![]() $\pi \colon \mathrm {Aut}(\mathcal {D})\to O(\mathbb {L})$
is the representation defined by the isometry
$\pi \colon \mathrm {Aut}(\mathcal {D})\to O(\mathbb {L})$
is the representation defined by the isometry
![]() $\kappa \colon e^\perp /\mathbb {Z} e\xrightarrow {\cong } \mathbb {L}$
. Since H fixes e, the lattice
$\kappa \colon e^\perp /\mathbb {Z} e\xrightarrow {\cong } \mathbb {L}$
. Since H fixes e, the lattice
![]() $\mathbb {B}_H\subseteq e^\perp $
and it does not contain
$\mathbb {B}_H\subseteq e^\perp $
and it does not contain
![]() $\mathbb {Z} e$
: we obtain, therefore, that
$\mathbb {Z} e$
: we obtain, therefore, that
![]() $\mathbb {B}_H$
embeds into
$\mathbb {B}_H$
embeds into
![]() $\mathbb {L}_G$
, and the two lattices have the same rank. However, this embedding is not necessarily primitive and,
$\mathbb {L}_G$
, and the two lattices have the same rank. However, this embedding is not necessarily primitive and,
![]() $\mathbb {B}_H$
and
$\mathbb {B}_H$
and
![]() $\mathbb {L}_G$
are not always isometric.
$\mathbb {L}_G$
are not always isometric.
Proposition 2.23. Let
![]() $H\leq \mathrm {Aut}(\mathcal {D})$
be a finite subgroup and let
$H\leq \mathrm {Aut}(\mathcal {D})$
be a finite subgroup and let
![]() $G := \pi (H)\cong H$
. Then
$G := \pi (H)\cong H$
. Then
![]() $\mathbb {B}_H$
and
$\mathbb {B}_H$
and
![]() $\mathbb {L}_G$
are isometric if and only if there exists
$\mathbb {L}_G$
are isometric if and only if there exists
![]() $v\in \mathbb {L}$
such that
$v\in \mathbb {L}$
such that
![]() $g(v)-v=\lambda $
for all
$g(v)-v=\lambda $
for all
![]() $(\lambda , g)\in H$
. If the previous does not hold, then there exists
$(\lambda , g)\in H$
. If the previous does not hold, then there exists
![]() $n>1$
such that
$n>1$
such that
holds.
Proof. According to the proof of Theorem 2.20, we know that there exists
![]() $n>0$
and
$n>0$
and
![]() $v\in \mathbb {L}$
such that
$v\in \mathbb {L}$
such that
and
![]() $g(v)-v = n\lambda $
for all
$g(v)-v = n\lambda $
for all
![]() $(\lambda , g)\in H$
. We define
$(\lambda , g)\in H$
. We define
![]() $H_v := \psi _v^{-1}\phi (G)\psi _v$
: by definition of
$H_v := \psi _v^{-1}\phi (G)\psi _v$
: by definition of
![]() $\phi \colon O(\mathbb {L})\to \mathrm {Aut}(\mathcal {D})$
and the fact that
$\phi \colon O(\mathbb {L})\to \mathrm {Aut}(\mathcal {D})$
and the fact that
![]() $g(v)-v=n\lambda $
for all
$g(v)-v=n\lambda $
for all
![]() $(\lambda , g)\in H$
, we see that elements of
$(\lambda , g)\in H$
, we see that elements of
![]() $H_v$
are of the form
$H_v$
are of the form
![]() $(n\lambda , g)$
, where
$(n\lambda , g)$
, where
![]() $(\lambda ,g)\in H$
. We therefore already note that if
$(\lambda ,g)\in H$
. We therefore already note that if
![]() $n=1$
(i.e.,
$n=1$
(i.e.,
![]() $g(v)-v=\lambda $
for all
$g(v)-v=\lambda $
for all
![]() $(\lambda ,g)\in H$
), then
$(\lambda ,g)\in H$
), then
![]() $H = H_v$
is conjugate to
$H = H_v$
is conjugate to
![]() $\phi (G)$
in
$\phi (G)$
in
![]() $\mathrm {Aut}(\mathcal {D})$
, and thus,
$\mathrm {Aut}(\mathcal {D})$
, and thus,
Furthermore, by direct computations, we infer that 𝔹 H v = (ℤe ⊕ 𝕃 G ) + ℤ(s + v). It hence follows that
holds. Since
![]() $\mathbb {B}$
is unimodular, and
$\mathbb {B}$
is unimodular, and
![]() $\mathbb {B}_{H_v} \cong \mathbb {L}_G$
, we also obtain that
$\mathbb {B}_{H_v} \cong \mathbb {L}_G$
, we also obtain that
holds too. From that, it is clear that if
![]() $\mathbb {B}_H\cong \mathbb {L}_G$
, then
$\mathbb {B}_H\cong \mathbb {L}_G$
, then
![]() $n=1$
and
$n=1$
and
![]() $g(v)-v=\lambda $
for all
$g(v)-v=\lambda $
for all
![]() $(\lambda ,g)\in H$
.
$(\lambda ,g)\in H$
.
3 Symplectic birational transformations of IHS manifolds of
 $OG10$
type
$OG10$
type
Our main aim is to classify finite groups of symplectic birational transformations of IHS manifolds of
![]() $OG10$
type. We recall the definition in Section 3.1, along with the period map for IHS manifolds of
$OG10$
type. We recall the definition in Section 3.1, along with the period map for IHS manifolds of
![]() $OG10$
type. In Section 3.2, we discuss birational transformations of such manifolds. Finally, in Section 3.3, we explain our strategy for completing this classification – namely, we relate the classification of finite groups of symplectic birational transformations to classifying certain isometry groups of an associated lattice.
$OG10$
type. In Section 3.2, we discuss birational transformations of such manifolds. Finally, in Section 3.3, we explain our strategy for completing this classification – namely, we relate the classification of finite groups of symplectic birational transformations to classifying certain isometry groups of an associated lattice.
3.1 IHS manifolds of
 $OG10$
type
$OG10$
type
An IHS manifold is a simply connected, compact, Kähler manifold X such that
![]() $H^0(X,\Omega ^2_X)$
is generated by a nowhere degenerate holomorphic
$H^0(X,\Omega ^2_X)$
is generated by a nowhere degenerate holomorphic
![]() $2$
-form
$2$
-form
![]() $\sigma _X$
. In this paper, we are focused on IHS manifolds that are deformation equivalent to O’Grady’s 10-dimensional exceptional example [Reference O’Grady37]. Such a manifold X is said to be of
$\sigma _X$
. In this paper, we are focused on IHS manifolds that are deformation equivalent to O’Grady’s 10-dimensional exceptional example [Reference O’Grady37]. Such a manifold X is said to be of
![]() $OG10$
type.
$OG10$
type.
It is well known that
![]() $H^2(X,\mathbb {Z})$
admits a quadratic form
$H^2(X,\mathbb {Z})$
admits a quadratic form
![]() $q_X$
, known as the Beauville–Bogomolov–Fujiki form. The form
$q_X$
, known as the Beauville–Bogomolov–Fujiki form. The form
![]() $q_X$
is integral and nondegenerate, and the isometry class of the lattice
$q_X$
is integral and nondegenerate, and the isometry class of the lattice
![]() $(H^2(X, \mathbb {Z}), q_X)$
is invariant under deformation. By [Reference Rapagnetta41], for an IHS manifold of
$(H^2(X, \mathbb {Z}), q_X)$
is invariant under deformation. By [Reference Rapagnetta41], for an IHS manifold of
![]() $OG10$
type, there is an isometry
$OG10$
type, there is an isometry
A choice of such an isometry
![]() $\eta $
is called a marking, and we say that
$\eta $
is called a marking, and we say that
![]() $(X, \eta )$
is a marked IHS manifold. Two such marked IHS manifolds
$(X, \eta )$
is a marked IHS manifold. Two such marked IHS manifolds
![]() $(X, \eta )$
and
$(X, \eta )$
and
![]() $(X', \eta ')$
are called equivalent if there exists an isomorphism
$(X', \eta ')$
are called equivalent if there exists an isomorphism
![]() $f\colon X\xrightarrow {\cong } X'$
such that
$f\colon X\xrightarrow {\cong } X'$
such that
![]() $\eta ' = \eta \circ f^\ast $
.
$\eta ' = \eta \circ f^\ast $
.
Marked IHS manifolds of
![]() $OG10$
type are classified up to equivalence in a coarse moduli space which we denote
$OG10$
type are classified up to equivalence in a coarse moduli space which we denote
![]() $\mathcal {M}_{OG10}$
. This space is neither Hausdorff nor connected, and two inseparable points in a same connected component define birational IHS manifolds of
$\mathcal {M}_{OG10}$
. This space is neither Hausdorff nor connected, and two inseparable points in a same connected component define birational IHS manifolds of
![]() $OG10$
type [Reference Huybrechts21, Theorem 4.3]. The period map
$OG10$
type [Reference Huybrechts21, Theorem 4.3]. The period map
relates a marked IHS manifold with its Hodge structure, where
![]() $\eta _{\mathbb {C}}$
denotes
$\eta _{\mathbb {C}}$
denotes
![]() $\eta $
extended over
$\eta $
extended over
![]() $\mathbb {C}$
. We have the following crucial result:
$\mathbb {C}$
. We have the following crucial result:
Theorem 3.1 [Reference Huybrechts21, Theorem 8.1].
The period map is a local homeomorphism, which is surjective onto
![]() $\Omega _{OG10}$
when restricted to any connected component of
$\Omega _{OG10}$
when restricted to any connected component of
![]() $\mathcal {M}_{OG10}$
.
$\mathcal {M}_{OG10}$
.
3.2 Global Torelli
Let X be an IHS manifold of
![]() $OG10$
type. We denote by
$OG10$
type. We denote by
![]() $\mathrm {Aut}(X) \leq \mathrm {Bir}(X)$
the groups of automorphisms and birational transformations of X, respectively. A birational transformation
$\mathrm {Aut}(X) \leq \mathrm {Bir}(X)$
the groups of automorphisms and birational transformations of X, respectively. A birational transformation
![]() $f\in \mathrm {Bir}(X)$
is well defined in codimension one, and so we obtain a Hodge isometry
$f\in \mathrm {Bir}(X)$
is well defined in codimension one, and so we obtain a Hodge isometry
![]() $f^*:H^2(X,\mathbb {Z})\rightarrow H^2(X,\mathbb {Z})$
.
$f^*:H^2(X,\mathbb {Z})\rightarrow H^2(X,\mathbb {Z})$
.
Definition 3.2. A birational transformation
![]() $f\in \mathrm {Bir}(X)$
is said to be symplectic if the induced action
$f\in \mathrm {Bir}(X)$
is said to be symplectic if the induced action
![]() $f^*:H^2(X,\mathbb {C})\rightarrow H^2(X,\mathbb {C})$
acts trivially on
$f^*:H^2(X,\mathbb {C})\rightarrow H^2(X,\mathbb {C})$
acts trivially on
![]() $\sigma _X$
. Otherwise, f is said to be nonsymplectic. If f is nonsymplectic with symplectic square, we say that f is antisymplectic.
$\sigma _X$
. Otherwise, f is said to be nonsymplectic. If f is nonsymplectic with symplectic square, we say that f is antisymplectic.
Let
![]() $(X, \eta )$
be a marked IHS manifold of
$(X, \eta )$
be a marked IHS manifold of
![]() $OG10$
type. The marking
$OG10$
type. The marking
![]() $\eta $
gives rise to an orthogonal representation
$\eta $
gives rise to an orthogonal representation
which is faithful [Reference Mongardi and Wandel34, Theorem 3.1]. By [Reference Onorati39, Theorem 5.4], the image of
![]() $\eta _{\ast }$
lies in
$\eta _{\ast }$
lies in
![]() $O^+(\Lambda )$
, the group of orientation-preserving isometries.
$O^+(\Lambda )$
, the group of orientation-preserving isometries.
Definition 3.3. We define the following:
-
1. A subgroup
 $H\leq O^+(\Lambda )$
is called symplectic if there exists a marked IHS manifold of
$H\leq O^+(\Lambda )$
is called symplectic if there exists a marked IHS manifold of
 $OG10$
type
$OG10$
type
 $(X, \eta )$
and a subgroup
$(X, \eta )$
and a subgroup
 $G\leq \mathrm {Bir}_s(X)$
such that
$G\leq \mathrm {Bir}_s(X)$
such that
 $\eta _{\ast }(G) = H$
.
$\eta _{\ast }(G) = H$
. -
2. Given a marked IHS manifold of
 $OG10$
type
$OG10$
type
 $(X, \eta )$
, we call a subgroup
$(X, \eta )$
, we call a subgroup
 $G\leq \mathrm {Bir}(X)$
stable or saturated if so is
$G\leq \mathrm {Bir}(X)$
stable or saturated if so is
 $\eta _{\ast }(G)\leq O^+(\Lambda )$
(see Definitions 2.1, 2.2).
$\eta _{\ast }(G)\leq O^+(\Lambda )$
(see Definitions 2.1, 2.2).
Remark 3.4. It is known that IHS manifolds of
![]() $OG10$
type admit no nontrivial symplectic automorphisms of finite order [Reference Giovenzana, Grossi, Onorati and Veniani15].
$OG10$
type admit no nontrivial symplectic automorphisms of finite order [Reference Giovenzana, Grossi, Onorati and Veniani15].
The aim of this paper is to classify finite groups of symplectic birational transformations of IHS manifolds of
![]() $OG10$
type. Using the surjectivity of the period map
$OG10$
type. Using the surjectivity of the period map
![]() $\mathcal {P}$
and the injectivity of
$\mathcal {P}$
and the injectivity of
![]() $\eta _{\ast }$
for any marked IHS manifolds of
$\eta _{\ast }$
for any marked IHS manifolds of
![]() $OG10$
type
$OG10$
type
![]() $(X, \eta )$
, our approach is to classify symplectic finite subgroups of
$(X, \eta )$
, our approach is to classify symplectic finite subgroups of
![]() $O^+(\Lambda )$
. We explain now how to determine whether a given finite subgroup of
$O^+(\Lambda )$
. We explain now how to determine whether a given finite subgroup of
![]() $O^+(\Lambda )$
is symplectic.
$O^+(\Lambda )$
is symplectic.
Let again
![]() $(X, \eta )$
be a marked IHS manifold of
$(X, \eta )$
be a marked IHS manifold of
![]() $OG10$
type. Any birational transformation of X preserves the birational Kähler cone
$OG10$
type. Any birational transformation of X preserves the birational Kähler cone
![]() $\mathcal {BK}(X)$
; the structure of this cone for a manifold of
$\mathcal {BK}(X)$
; the structure of this cone for a manifold of
![]() $OG10$
type is well understood [Reference Mongardi and Onorati33]. In particular, the walls of
$OG10$
type is well understood [Reference Mongardi and Onorati33]. In particular, the walls of
![]() $\overline {\mathcal {BK}(X)}$
are defined by the hyperplanes
$\overline {\mathcal {BK}(X)}$
are defined by the hyperplanes
![]() $D^\perp \subset \mathcal {C}(X)$
, where D is a stably prime exceptional divisor [Reference Markman27, §5], and
$D^\perp \subset \mathcal {C}(X)$
, where D is a stably prime exceptional divisor [Reference Markman27, §5], and
![]() $\mathcal {C}(X)$
denotes the connected component of the positive cone of X containing a Kähler class. We define the following set of vectors:
$\mathcal {C}(X)$
denotes the connected component of the positive cone of X containing a Kähler class. We define the following set of vectors:
Proposition 3.5 [Reference Mongardi and Onorati33, Proposition 3.1].
Let
![]() $(X, \eta )$
be a marked IHS manifold of
$(X, \eta )$
be a marked IHS manifold of
![]() $OG10$
type. Then
$OG10$
type. Then
![]() $D\in \mathrm {Pic}(X)$
is stably prime exceptional if and only if
$D\in \mathrm {Pic}(X)$
is stably prime exceptional if and only if
![]() $\eta (D)\in \mathcal {W}^{pex}.$
$\eta (D)\in \mathcal {W}^{pex}.$
It follows that
![]() $\mathcal {BK}(X)$
is contained in an exceptional chamber – that is, a component of
$\mathcal {BK}(X)$
is contained in an exceptional chamber – that is, a component of
(see [Reference Mongardi and Onorati33, Theorem 3.2]). Using this description, we can rephrase the Global Torelli theorem (due to Huybrechts, Markman and Verbitsky) in a way that is more suited for the study of symplectic birational transformations of X. This will provide us with criteria for when a finite group
![]() $H\leq O^+(\Lambda )$
is symplectic.
$H\leq O^+(\Lambda )$
is symplectic.
Lemma 3.6 [Reference Grossi, Onorati and Veniani17, Theorems 2.15 and 2.17].
Let
![]() $H\leq O^+(\Lambda )$
be finite. Then H is symplectic if and only if both of the following hold:
$H\leq O^+(\Lambda )$
be finite. Then H is symplectic if and only if both of the following hold:
-
1.
 $\Lambda _H$
is negative definite, and
$\Lambda _H$
is negative definite, and -
2.
 $\Lambda _H\cap \mathcal {W}^{pex}=\varnothing $
.
$\Lambda _H\cap \mathcal {W}^{pex}=\varnothing $
.
3.3 Classification problems
Recall that
![]() $\Lambda := U^3\oplus E_8^2\oplus A_2$
is the lattice isometric to the second integral cohomology lattice of any IHS manifold of
$\Lambda := U^3\oplus E_8^2\oplus A_2$
is the lattice isometric to the second integral cohomology lattice of any IHS manifold of
![]() $OG10$
type. We aim to classify finite groups
$OG10$
type. We aim to classify finite groups
![]() $H\leq O^+(\Lambda )$
that are symplectic (i.e., induced by a finite group G of symplectic birational transformations for IHS manifolds X of
$H\leq O^+(\Lambda )$
that are symplectic (i.e., induced by a finite group G of symplectic birational transformations for IHS manifolds X of
![]() $OG10$
type). By the discussion in Section 3.2, this is equivalent to classifying, up to conjugacy, finite subgroups
$OG10$
type). By the discussion in Section 3.2, this is equivalent to classifying, up to conjugacy, finite subgroups
![]() $H\leq O^+(\Lambda )$
with negative definite coinvariant sublattice, and such that
$H\leq O^+(\Lambda )$
with negative definite coinvariant sublattice, and such that
![]() $\Lambda _H\cap \mathcal {W}^{pex} = \varnothing $
.
$\Lambda _H\cap \mathcal {W}^{pex} = \varnothing $
.
Remark 3.7. According to [Reference Grossi, Onorati and Veniani17, Lemma 2.3], if
![]() $H\leq O(\Lambda )$
is such that
$H\leq O(\Lambda )$
is such that
![]() $\Lambda _H$
is negative definite, then
$\Lambda _H$
is negative definite, then
![]() $H\leq O^+(\Lambda )$
.
$H\leq O^+(\Lambda )$
.
Remark 3.8. For a classification purpose, it is enough to classify such groups H which are saturated in
![]() $O^+(\Lambda )$
. In fact, any finite subgroups of
$O^+(\Lambda )$
. In fact, any finite subgroups of
![]() $O^+(\Lambda )$
is a subgroup of a saturated group. Moreover, if a finite subgroup
$O^+(\Lambda )$
is a subgroup of a saturated group. Moreover, if a finite subgroup
![]() $H\leq O^+(\Lambda )$
is symplectic, then according to Definition 2.2 and Lemma 3.6, so is its saturation (see also [Reference Brandhorst and Hofmann5, Remark 3.18]).
$H\leq O^+(\Lambda )$
is symplectic, then according to Definition 2.2 and Lemma 3.6, so is its saturation (see also [Reference Brandhorst and Hofmann5, Remark 3.18]).
We use the action of such a group
![]() $H\leq O^+(\Lambda )$
on the discriminant group
$H\leq O^+(\Lambda )$
on the discriminant group
![]() $D_\Lambda $
in order to aid this classification. Note that, as abelian groups,
$D_\Lambda $
in order to aid this classification. Note that, as abelian groups,
![]() $D_\Lambda \cong \mathbb {Z}/3\mathbb {Z}$
, and in particular, there is an exact sequence
$D_\Lambda \cong \mathbb {Z}/3\mathbb {Z}$
, and in particular, there is an exact sequence
where
![]() $O(D_\Lambda )$
has order 2 generated by
$O(D_\Lambda )$
has order 2 generated by
![]() $- {id}$
. Hence, if
$- {id}$
. Hence, if
![]() $H\leq O^+(\Lambda )$
is a finite subgroup, we have an exact sequence
$H\leq O^+(\Lambda )$
is a finite subgroup, we have an exact sequence
where
![]() $H\to \mu _2$
is defined by the discriminant representation of H.
$H\to \mu _2$
is defined by the discriminant representation of H.
Corollary 3.9. Let
![]() $H\leq O^+(\Lambda )$
. Then one of the following is satisfied:
$H\leq O^+(\Lambda )$
. Then one of the following is satisfied:
-
1. either
 $H^\#$
is trivial and H is cyclic of order 2;
$H^\#$
is trivial and H is cyclic of order 2; -
2.
 $H = H^\#$
is nontrivial; or
$H = H^\#$
is nontrivial; or -
3.
 $H^\#$
is nontrivial and
$H^\#$
is nontrivial and
 $[H:H^\#] = 2$
.
$[H:H^\#] = 2$
.
Note that the classification of symplectic finite groups satisfying case (1) has already been completed by the same authors in [Reference Marquand and Muller29]. We treat the two other cases inductively. In what follows, we start by showing how to construct representatives of
![]() $O^+(\Lambda )$
-conjugacy classes of finite saturated subgroups of
$O^+(\Lambda )$
-conjugacy classes of finite saturated subgroups of
![]() $O^{+,\#}(\Lambda )$
, covering case (2). Then, we cover the last case (3) by adapting the extension approach of [Reference Brandhorst and Hashimoto4, Reference Brandhorst and Hofmann5] to Equation (3.1).
$O^{+,\#}(\Lambda )$
, covering case (2). Then, we cover the last case (3) by adapting the extension approach of [Reference Brandhorst and Hashimoto4, Reference Brandhorst and Hofmann5] to Equation (3.1).
4 Finite groups of stable symplectic isometries
In this section, we classify symplectic finite subgroups
![]() $H\leq O^+(\Lambda )$
, up to conjugacy in
$H\leq O^+(\Lambda )$
, up to conjugacy in
![]() $O^+(\Lambda )$
, that satisfy Corollary 3.9 case (2) (i.e., when the group
$O^+(\Lambda )$
, that satisfy Corollary 3.9 case (2) (i.e., when the group
![]() $H = H^\#$
is stable). More precisely, we prove the following:
$H = H^\#$
is stable). More precisely, we prove the following:
Theorem 4.1. Let
![]() $(X, \eta , G)$
be a triple consisting of a marked IHS manifold
$(X, \eta , G)$
be a triple consisting of a marked IHS manifold
![]() $(X, \eta )$
of
$(X, \eta )$
of
![]() $OG10$
type and a finite group of symplectic birational transformations
$OG10$
type and a finite group of symplectic birational transformations
![]() $G\leq \mathrm {Bir}(X)$
such that
$G\leq \mathrm {Bir}(X)$
such that
![]() $\eta _\ast (G)\leq O^+(\Lambda )$
is stable. Then, up to conjugacy,
$\eta _\ast (G)\leq O^+(\Lambda )$
is stable. Then, up to conjugacy,
![]() $\eta _\ast (G)\leq O^+(\Lambda )$
is contained in one of the 192 stable groups of the dataset [Reference Marquand and Muller30].
$\eta _\ast (G)\leq O^+(\Lambda )$
is contained in one of the 192 stable groups of the dataset [Reference Marquand and Muller30].
We outline the strategy to prove Theorem 4.1. Let
![]() $H\leq O^{+,\#}(\Lambda )$
be a stable symplectic finite subgroup that we aim to classify. In Section 4.1, we show that the group H is completely determined by the negative definite primitive sublattice
$H\leq O^{+,\#}(\Lambda )$
be a stable symplectic finite subgroup that we aim to classify. In Section 4.1, we show that the group H is completely determined by the negative definite primitive sublattice
![]() $C:=\Lambda _H\subseteq \Lambda $
, and H is identified with the group
$C:=\Lambda _H\subseteq \Lambda $
, and H is identified with the group
![]() $O^\#(C)$
, which fixes no nontrivial vector in C. Thus, we can classify such groups H by classifying instead primitive sublattices C of
$O^\#(C)$
, which fixes no nontrivial vector in C. Thus, we can classify such groups H by classifying instead primitive sublattices C of
![]() $\Lambda $
satisfying the above properties and which in addition satisfy
$\Lambda $
satisfying the above properties and which in addition satisfy
![]() $C\cap \mathcal {W}^{pex} =\varnothing .$
Such a lattice is called a heart of
$C\cap \mathcal {W}^{pex} =\varnothing .$
Such a lattice is called a heart of
![]() $\Lambda .$
In Section 4.2, we show that a heart
$\Lambda .$
In Section 4.2, we show that a heart
![]() $C\subseteq \Lambda $
primitively embeds into the Borcherds lattice, as a coinvariant lattice for a finite subgroup
$C\subseteq \Lambda $
primitively embeds into the Borcherds lattice, as a coinvariant lattice for a finite subgroup
![]() $H\leq \mathrm {Aut}(\mathcal {D})\leq O^+(\mathbb {B}).$
In Section 4.3, we determine the isometry class of the hearts that embed primitively into
$H\leq \mathrm {Aut}(\mathcal {D})\leq O^+(\mathbb {B}).$
In Section 4.3, we determine the isometry class of the hearts that embed primitively into
![]() $\mathbb {B}$
but not into
$\mathbb {B}$
but not into
![]() $\mathbb {L}$
, represented by the three lattices in Appendix B (see Corollary 4.17). Finally, in Section 4.4, we complete the classification of hearts of
$\mathbb {L}$
, represented by the three lattices in Appendix B (see Corollary 4.17). Finally, in Section 4.4, we complete the classification of hearts of
![]() $\Lambda $
and obtain 192
$\Lambda $
and obtain 192
![]() $O^+(\Lambda )$
-conjugacy classes of saturated symplectic finite subgroups of
$O^+(\Lambda )$
-conjugacy classes of saturated symplectic finite subgroups of
![]() $O^{+,\#}(\Lambda ),$
completing the proof of Theorem 4.1.
$O^{+,\#}(\Lambda ),$
completing the proof of Theorem 4.1.
4.1 Finite stable subgroups of
 $O^+(\Lambda )$
$O^+(\Lambda )$
Let
![]() $H\leq O^+(\Lambda )$
be a symplectic finite subgroup such that
$H\leq O^+(\Lambda )$
be a symplectic finite subgroup such that
![]() $H=H^\#$
. In particular, we assume
$H=H^\#$
. In particular, we assume
![]() ${H\leq O^{+,\#}(\Lambda )}$
. The following holds.
${H\leq O^{+,\#}(\Lambda )}$
. The following holds.
Lemma 4.2. Let
![]() $H\leq O^{+,\#}(\Lambda )$
be a nontrivial subgroup. Then
$H\leq O^{+,\#}(\Lambda )$
be a nontrivial subgroup. Then
![]() $H\to O(\Lambda _H)$
is injective with image lying in
$H\to O(\Lambda _H)$
is injective with image lying in
![]() $O^\#(\Lambda _H)$
. Moreover, H is saturated in
$O^\#(\Lambda _H)$
. Moreover, H is saturated in
![]() $O^{+,\#}(\Lambda )$
if and only if
$O^{+,\#}(\Lambda )$
if and only if
![]() $H = O^\#(\Lambda _H)$
holds, seeing H as a subgroup of
$H = O^\#(\Lambda _H)$
holds, seeing H as a subgroup of
![]() $O(\Lambda _H)$
.
$O(\Lambda _H)$
.
Proof. Let us embed
![]() $\Lambda $
primitively into the even unimodular lattice
$\Lambda $
primitively into the even unimodular lattice
![]() $M := U^5\oplus E_8^2$
, with orthogonal complement
$M := U^5\oplus E_8^2$
, with orthogonal complement
![]() $F\cong A_2(-1)$
. Since H is stable, we can extend it to a group of isometries
$F\cong A_2(-1)$
. Since H is stable, we can extend it to a group of isometries
![]() $\widetilde {H}\leq O(M)$
acting as the identity on F, in such a way that
$\widetilde {H}\leq O(M)$
acting as the identity on F, in such a way that
![]() $M_{\widetilde {H}} = \Lambda _H$
. Note, moreover, that
$M_{\widetilde {H}} = \Lambda _H$
. Note, moreover, that
![]() $F\oplus \Lambda ^H\subseteq M^{\widetilde {H}}$
is an overlattice. Since
$F\oplus \Lambda ^H\subseteq M^{\widetilde {H}}$
is an overlattice. Since
![]() $\widetilde {H}$
acts trivially on
$\widetilde {H}$
acts trivially on
![]() $M^{\widetilde {H}}$
, we see that
$M^{\widetilde {H}}$
, we see that
![]() $\widetilde {H}\to O(M_{\widetilde {H}})$
is injective. Moreover, since M is unimodular, the equivariant gluing condition Equation (EGC) tells us that
$\widetilde {H}\to O(M_{\widetilde {H}})$
is injective. Moreover, since M is unimodular, the equivariant gluing condition Equation (EGC) tells us that
![]() $\widetilde {H}$
maps into
$\widetilde {H}$
maps into
![]() $O^\#(M_{\widetilde {H}})$
. We therefore get an injective morphism
$O^\#(M_{\widetilde {H}})$
. We therefore get an injective morphism
Let
![]() $g\in O^\#(\Lambda _H) = O^\#(M_{\widetilde {H}})$
. We can extend g to an isometry
$g\in O^\#(\Lambda _H) = O^\#(M_{\widetilde {H}})$
. We can extend g to an isometry
![]() $\tilde {g}\in O(M)$
acting as the identity on
$\tilde {g}\in O(M)$
acting as the identity on
![]() $M^{\widetilde {H}}$
. Since
$M^{\widetilde {H}}$
. Since
![]() $F\oplus \Lambda ^H\subseteq M^{\widetilde {H}}$
, we have that
$F\oplus \Lambda ^H\subseteq M^{\widetilde {H}}$
, we have that
![]() $\widetilde {g}$
restricts to an isometry h of
$\widetilde {g}$
restricts to an isometry h of
![]() $\Lambda = F^\perp _M$
fixing pointwise
$\Lambda = F^\perp _M$
fixing pointwise
![]() $\Lambda ^H$
: h is the extension of g to
$\Lambda ^H$
: h is the extension of g to
![]() $O(\Lambda )$
with the identity on
$O(\Lambda )$
with the identity on
![]() $\Lambda ^H$
. Moreover,
$\Lambda ^H$
. Moreover,
![]() $h\in O^{+, \#}(\Lambda )$
according to Equation (EGC) and Remark 3.7. In particular, h lies in the saturation of H in
$h\in O^{+, \#}(\Lambda )$
according to Equation (EGC) and Remark 3.7. In particular, h lies in the saturation of H in
![]() $O^{+,\#}(\Lambda )$
.
$O^{+,\#}(\Lambda )$
.
Conversely, for any
![]() $h\in O^{+, \#}(\Lambda )$
fixing pointwise
$h\in O^{+, \#}(\Lambda )$
fixing pointwise
![]() $\Lambda ^H$
, we can extend h to an isometry
$\Lambda ^H$
, we can extend h to an isometry
![]() $\widetilde {h}$
of
$\widetilde {h}$
of
![]() $O(M)$
by extending with the identity on F. Similarly as before, the restrictions of h and
$O(M)$
by extending with the identity on F. Similarly as before, the restrictions of h and
![]() $\widetilde {h}$
to
$\widetilde {h}$
to
![]() $\Lambda _H = M_{\widetilde {H}}$
coincide, and they lie in
$\Lambda _H = M_{\widetilde {H}}$
coincide, and they lie in
![]() $O^\#(\Lambda _H)$
. We therefore conclude that the saturation of H in
$O^\#(\Lambda _H)$
. We therefore conclude that the saturation of H in
![]() $O^{+, \#}(\Lambda )$
coincides with the extension of
$O^{+, \#}(\Lambda )$
coincides with the extension of
![]() $O^\#(\Lambda _H)$
with the identity on
$O^\#(\Lambda _H)$
with the identity on
![]() $\Lambda ^H$
.
$\Lambda ^H$
.
Lemma 4.3. Suppose that
![]() $H\leq O^{+,\#}(\Lambda )$
is a nontrivial symplectic finite subgroup. Then the coinvariant sublattice
$H\leq O^{+,\#}(\Lambda )$
is a nontrivial symplectic finite subgroup. Then the coinvariant sublattice
![]() $C := \Lambda _H$
is even negative definite, it does not contain
$C := \Lambda _H$
is even negative definite, it does not contain
![]() $(-2)$
-vectors, and
$(-2)$
-vectors, and
![]() $O^\#(C)$
fixes no nontrivial vector in C.
$O^\#(C)$
fixes no nontrivial vector in C.
Proof. The two first statements follow from Lemma 3.6. For the last statement, we use Lemma 4.2 which tells us that H maps injectively into
![]() $O^\#(C)$
, and
$O^\#(C)$
, and
![]() $C^H = \{0\}$
by definition. Hence, in particular,
$C^H = \{0\}$
by definition. Hence, in particular,
![]() $O^\#(C)$
fixes no nontrivial vector in C.
$O^\#(C)$
fixes no nontrivial vector in C.
It follows that saturated symplectic finite subgroups H of
![]() $O^{+, \#}(\Lambda )$
are completely determined by some primitive sublattices
$O^{+, \#}(\Lambda )$
are completely determined by some primitive sublattices
![]() $C\subseteq \Lambda $
which are even negative definite, and such that
$C\subseteq \Lambda $
which are even negative definite, and such that
![]() $O^\#(C)$
fixes no nontrivial vector in C – here, H being defined as the extension of
$O^\#(C)$
fixes no nontrivial vector in C – here, H being defined as the extension of
![]() $O^\#(C)$
with the identity on
$O^\#(C)$
with the identity on
![]() $C^\perp _\Lambda $
. The fixed point free action of
$C^\perp _\Lambda $
. The fixed point free action of
![]() $O^\#(C)$
on the sublattice
$O^\#(C)$
on the sublattice
![]() $C\subseteq \Lambda $
is an additional tool in our classification. We thus make the following definition:
$C\subseteq \Lambda $
is an additional tool in our classification. We thus make the following definition:
Definition 4.4. Let C be an even lattice. We say that C is stable symplectic if it is negative definite, and
![]() $O^\#(C)$
fixes no nontrivial vector in C.
$O^\#(C)$
fixes no nontrivial vector in C.
By Lemma 4.3, in order to construct saturated symplectic finite subgroups H of
![]() $O^{+,\#}(\Lambda )$
, it suffices to construct primitive sublattices
$O^{+,\#}(\Lambda )$
, it suffices to construct primitive sublattices
![]() $ C\subseteq \Lambda $
where C is stable symplectic, and such that
$ C\subseteq \Lambda $
where C is stable symplectic, and such that
![]() $C\cap \mathcal {W}^{pex} = \varnothing $
. In order to ensure this last condition, we observe the following.
$C\cap \mathcal {W}^{pex} = \varnothing $
. In order to ensure this last condition, we observe the following.
Let us denote by
![]() $\Pi :=U^3\oplus E_8^3$
the unique even unimodular lattice of signature
$\Pi :=U^3\oplus E_8^3$
the unique even unimodular lattice of signature
![]() $(3,27)$
.
$(3,27)$
.
Proposition 4.5. Up to isomorphism,
![]() $\Pi $
admits a unique primitive sublattice isometric to
$\Pi $
admits a unique primitive sublattice isometric to
![]() $\Lambda $
.
$\Lambda $
.
Proof. We note that
![]() $E_6$
is the unique (up to isometry) lattice with signature
$E_6$
is the unique (up to isometry) lattice with signature
![]() $(0,6)$
and discriminant group
$(0,6)$
and discriminant group
![]() $D_{E_6}\cong D_\Lambda (-1)$
. Hence, there exists a primitive embedding of
$D_{E_6}\cong D_\Lambda (-1)$
. Hence, there exists a primitive embedding of
![]() $\Lambda $
into the unimodular lattice
$\Lambda $
into the unimodular lattice
![]() $\Pi $
, with orthogonal complement
$\Pi $
, with orthogonal complement
![]() $E_6$
. Since
$E_6$
. Since
![]() $O(E_6)\to O(D_{E_6})$
is surjective, by [Reference Nikulin36, Proposition 1.14.1], we see that such a primitive embedding is unique up to the action of
$O(E_6)\to O(D_{E_6})$
is surjective, by [Reference Nikulin36, Proposition 1.14.1], we see that such a primitive embedding is unique up to the action of
![]() $O(\Pi )$
and
$O(\Pi )$
and
![]() $O(\Lambda )$
.
$O(\Lambda )$
.
Lemma 4.6. Let
![]() $C\subseteq \Lambda $
be a stable symplectic primitive sublattice without
$C\subseteq \Lambda $
be a stable symplectic primitive sublattice without
![]() $(-2)$
-vectors. Then
$(-2)$
-vectors. Then
![]() ${C\cap \mathcal {W}^{pex}=\varnothing }$
.
${C\cap \mathcal {W}^{pex}=\varnothing }$
.
Proof. Let us consider the succession of inclusions
We will show that
![]() $C\cap \mathcal {W}^{pex} = \varnothing $
. First note that if C is trivial, then the result necessary holds. In what follows, we assume that C, and therefore
$C\cap \mathcal {W}^{pex} = \varnothing $
. First note that if C is trivial, then the result necessary holds. In what follows, we assume that C, and therefore
![]() $O^\#(C)$
, is nontrivial.
$O^\#(C)$
, is nontrivial.
Suppose that C has a vector v of square
![]() $-6$
such that
$-6$
such that
![]() $\mathrm {div}_\Lambda (v) = 3$
. Since the lattice C is stable symplectic, there exists an isometry
$\mathrm {div}_\Lambda (v) = 3$
. Since the lattice C is stable symplectic, there exists an isometry
![]() $g\in O^\#(C)$
such that
$g\in O^\#(C)$
such that
![]() $g(v)\neq v$
holds. Note that
$g(v)\neq v$
holds. Note that
![]() $g(v)\neq -v$
also holds: in fact, since g is stable, we have equalities
$g(v)\neq -v$
also holds: in fact, since g is stable, we have equalities
If
![]() $g(v) = -v$
were to hold, we would have that
$g(v) = -v$
were to hold, we would have that
![]() $\frac {2v}{3}\in C$
; however, this vector has square
$\frac {2v}{3}\in C$
; however, this vector has square
![]() $\frac {-8}{3}\notin \mathbb {Z}$
, contradicting that C is an even lattice. Hence,
$\frac {-8}{3}\notin \mathbb {Z}$
, contradicting that C is an even lattice. Hence,
![]() $v':=g(v)$
is not proportional to v, and it still has divisibility 3 in
$v':=g(v)$
is not proportional to v, and it still has divisibility 3 in
![]() $\Lambda $
(divisibility is preserved under isometry, and
$\Lambda $
(divisibility is preserved under isometry, and
![]() $g\in O^\#(C)$
being stable can be seen as an isometry of
$g\in O^\#(C)$
being stable can be seen as an isometry of
![]() $\Lambda $
). Similarly to the proof of [Reference Laza and Zheng26, Theorem 4.5,
$\Lambda $
). Similarly to the proof of [Reference Laza and Zheng26, Theorem 4.5,
![]() $(iii)\,{\Rightarrow}\, (i)$
], it follows that the primitive closure M of
$(iii)\,{\Rightarrow}\, (i)$
], it follows that the primitive closure M of
![]() $E_6+\mathbb {Z} v+\mathbb {Z} v'$
in
$E_6+\mathbb {Z} v+\mathbb {Z} v'$
in
![]() $\Pi $
is isometric to
$\Pi $
is isometric to
![]() $E_8$
. In particular, since
$E_8$
. In particular, since
![]() $E_8$
has a unique sublattice isometric to
$E_8$
has a unique sublattice isometric to
![]() $E_6$
(up to isometry), with orthogonal complement isometric to
$E_6$
(up to isometry), with orthogonal complement isometric to
![]() $A_2$
, one concludes that
$A_2$
, one concludes that
![]() $A_2\cong (E_6)^\perp _M$
embeds into C: this is a contradiction since C contains no
$A_2\cong (E_6)^\perp _M$
embeds into C: this is a contradiction since C contains no
![]() $(-2)$
-vectors. Hence,
$(-2)$
-vectors. Hence,
![]() $C\cap \mathcal {W}^{pex}=\varnothing $
.
$C\cap \mathcal {W}^{pex}=\varnothing $
.
By Lemma 4.6, we see that any stable symplectic primitive sublattice
![]() $C\subseteq \Lambda $
not containing
$C\subseteq \Lambda $
not containing
![]() $(-2)$
-vectors is the coinvariant sublattice of a symplectic finite subgroup
$(-2)$
-vectors is the coinvariant sublattice of a symplectic finite subgroup
![]() $H\leq O^{+, \#}(\Lambda )$
. We have therefore reduced our problem to constructing and classifying stable symplectic primitive sublattices of
$H\leq O^{+, \#}(\Lambda )$
. We have therefore reduced our problem to constructing and classifying stable symplectic primitive sublattices of
![]() $\Lambda $
not containing
$\Lambda $
not containing
![]() $(-2)$
-vectors.
$(-2)$
-vectors.
Definition 4.7. A heart is any stable symplectic primitive sublattice
![]() $C\subseteq \Lambda $
that does not contain any
$C\subseteq \Lambda $
that does not contain any
![]() $(-2)$
-vectors.
$(-2)$
-vectors.
In the following sections, we explain how to recover the abstract isometry class of such hearts. We then make use of the following theorem to eventually classify saturated symplectic finite subgroup
![]() $H\leq O^{+, \#}(\Lambda )$
up to conjugacy in
$H\leq O^{+, \#}(\Lambda )$
up to conjugacy in
![]() $O^+(\Lambda )$
.
$O^+(\Lambda )$
.
Theorem 4.8. Let C be a stable symplectic lattice. Then the set of
![]() $O^+(\Lambda )$
-conjugacy classes of saturated finite subgroups
$O^+(\Lambda )$
-conjugacy classes of saturated finite subgroups
![]() $H\leq O^{+, \#}(\Lambda )$
such that
$H\leq O^{+, \#}(\Lambda )$
such that
![]() $\Lambda _H\cong C$
is in bijection with the set of isomorphism classes of primitive sublattices
$\Lambda _H\cong C$
is in bijection with the set of isomorphism classes of primitive sublattices
![]() $C'\subseteq \Lambda $
such that
$C'\subseteq \Lambda $
such that
![]() $C'\cong C$
.
$C'\cong C$
.
Proof. First note that since
![]() $\Lambda $
has real signature
$\Lambda $
has real signature
![]() $(3, 21)$
, we have that
$(3, 21)$
, we have that
![]() $- {id}_\Lambda $
has negative real spinor norm [Reference Brandhorst and Cattaneo3, Example 4.1]. Hence,
$- {id}_\Lambda $
has negative real spinor norm [Reference Brandhorst and Cattaneo3, Example 4.1]. Hence,
![]() $O(\Lambda )/O^+(\Lambda )$
is generated by the coset of
$O(\Lambda )/O^+(\Lambda )$
is generated by the coset of
![]() $- {id}_\Lambda $
which is a central involution. In other terms, for any
$- {id}_\Lambda $
which is a central involution. In other terms, for any
![]() $f\in O(\Lambda )$
, we have that either f of
$f\in O(\Lambda )$
, we have that either f of
![]() $-f$
lies
$-f$
lies
![]() $O^+(\Lambda )$
. Since the conjugation actions on
$O^+(\Lambda )$
. Since the conjugation actions on
![]() $O(\Lambda )$
induced respectively by f and
$O(\Lambda )$
induced respectively by f and
![]() $-f$
are the same, we deduce that
$-f$
are the same, we deduce that
![]() $O^+(\Lambda )$
-conjugacy classes and
$O^+(\Lambda )$
-conjugacy classes and
![]() $O(\Lambda )$
-conjugacy classes of finite subgroups
$O(\Lambda )$
-conjugacy classes of finite subgroups
![]() $H\leq O^{+,\#}(\Lambda )$
coincide. The proof follows then from Lemma 4.2, which tells us that any saturated subgroup of
$H\leq O^{+,\#}(\Lambda )$
coincide. The proof follows then from Lemma 4.2, which tells us that any saturated subgroup of
![]() $O^{+, \#}(\Lambda )$
is uniquely determined by its coinvariant sublattice.
$O^{+, \#}(\Lambda )$
is uniquely determined by its coinvariant sublattice.
Remark 4.9. One may note that a consequence of Theorem 4.8 is that there might be several conjugacy classes of subgroups
![]() $H\leq O^{+,\#}(\Lambda )$
whose coinvariant sublattice is abstractly isometric to a fixed stable symplectic lattice C.
$H\leq O^{+,\#}(\Lambda )$
whose coinvariant sublattice is abstractly isometric to a fixed stable symplectic lattice C.
4.2 Isometry classes of hearts of
 $\Lambda $
$\Lambda $
Recall that
![]() $\mathbb {B} := U\oplus \mathbb {L}$
, where
$\mathbb {B} := U\oplus \mathbb {L}$
, where
![]() $\mathbb {L}$
is the Leech lattice, with fixed basis
$\mathbb {L}$
is the Leech lattice, with fixed basis
![]() $\{e,s\}$
for
$\{e,s\}$
for
![]() $U\subseteq \mathbb {B}$
such that
$U\subseteq \mathbb {B}$
such that
![]() $e^2 = 0$
,
$e^2 = 0$
,
![]() $s^2 = -2$
and
$s^2 = -2$
and
![]() $e.s = 1$
. We denote again by
$e.s = 1$
. We denote again by
![]() $\mathcal {D}$
the closure of Conway’s chamber
$\mathcal {D}$
the closure of Conway’s chamber
![]() $D_0$
.
$D_0$
.
Lemma 4.10. Let
![]() $C\subseteq \Lambda $
be a heart. Then C embeds primitively into
$C\subseteq \Lambda $
be a heart. Then C embeds primitively into
![]() $\mathbb {B}$
. Moreover, the group
$\mathbb {B}$
. Moreover, the group
![]() $O^\#(C)$
is isomorphic to a subgroup
$O^\#(C)$
is isomorphic to a subgroup
![]() $H\leq \mathrm {Aut}(\mathcal {D})$
so that
$H\leq \mathrm {Aut}(\mathcal {D})$
so that
![]() $\mathbb {B}_{H}\cong C$
.
$\mathbb {B}_{H}\cong C$
.
Proof. Since C is negative definite of rank at most 21, and since
[Reference Nikulin36, Proposition 1.15.1], we see that C embeds primitively into
![]() $\mathbb {B}$
[Reference Nikulin36, Corollary 1.12.3].
$\mathbb {B}$
[Reference Nikulin36, Corollary 1.12.3].
Let us fix
![]() $j\colon C\hookrightarrow \mathbb {B}$
such a primitive embedding. Since
$j\colon C\hookrightarrow \mathbb {B}$
such a primitive embedding. Since
![]() $\mathbb {B}$
is unimodular, Equation (EGC) tells us that we can extend
$\mathbb {B}$
is unimodular, Equation (EGC) tells us that we can extend
![]() $O^\#(C)$
with the identity on
$O^\#(C)$
with the identity on
![]() $N := j(C)^\perp _{\mathbb {B}}$
to a group
$N := j(C)^\perp _{\mathbb {B}}$
to a group
![]() $\widetilde {H}\leq O^+(\mathbb {B})$
. In particular,
$\widetilde {H}\leq O^+(\mathbb {B})$
. In particular,
![]() $\mathbb {B}_{\widetilde {H}} = j(C) \cong C$
. Since C does not contain
$\mathbb {B}_{\widetilde {H}} = j(C) \cong C$
. Since C does not contain
![]() $(-2)$
-vectors,
$(-2)$
-vectors,
![]() $N\otimes \mathbb {R}$
intersect a chamber D of the positive cone of
$N\otimes \mathbb {R}$
intersect a chamber D of the positive cone of
![]() $\mathbb {B}$
. The group
$\mathbb {B}$
. The group
![]() $\widetilde {H}$
acting trivially on N, we have that
$\widetilde {H}$
acting trivially on N, we have that
![]() $\widetilde {H}$
preserves a vector in D, and thus,
$\widetilde {H}$
preserves a vector in D, and thus,
![]() $\widetilde {H}$
preserves the entire chamber D. Hence,
$\widetilde {H}$
preserves the entire chamber D. Hence,
![]() $\widetilde {H}\leq \mathrm {Aut}(\overline {D})$
. Since both
$\widetilde {H}\leq \mathrm {Aut}(\overline {D})$
. Since both
![]() $\mathrm {Aut}(\overline {D})$
and
$\mathrm {Aut}(\overline {D})$
and
![]() $\mathrm {Aut}(\mathcal {D})$
are isomorphic to
$\mathrm {Aut}(\mathcal {D})$
are isomorphic to
![]() $O^+(\mathbb {B})/W(\mathbb {B})$
, we obtain that
$O^+(\mathbb {B})/W(\mathbb {B})$
, we obtain that
![]() $\widetilde {H}$
is
$\widetilde {H}$
is
![]() $O^+(\mathbb {B})$
-conjugate to a subgroup
$O^+(\mathbb {B})$
-conjugate to a subgroup
![]() $H\leq \mathrm {Aut}(\mathcal {D})$
. In particular,
$H\leq \mathrm {Aut}(\mathcal {D})$
. In particular,
![]() $\mathbb {B}_H\cong \mathbb {B}_{\widetilde {H}}\cong C$
.
$\mathbb {B}_H\cong \mathbb {B}_{\widetilde {H}}\cong C$
.
Remark 4.11. Let
![]() $H\leq \mathrm {Aut}(\mathcal {D})$
be a nontrivial subgroup. According to the proof of Theorem 2.20, the group H is finite if and only if
$H\leq \mathrm {Aut}(\mathcal {D})$
be a nontrivial subgroup. According to the proof of Theorem 2.20, the group H is finite if and only if
![]() $\mathbb {B}_H$
is stable symplectic and does not contain roots of
$\mathbb {B}_H$
is stable symplectic and does not contain roots of
![]() $\mathbb {B}$
.
$\mathbb {B}$
.
Therefore, as abstract lattices, we can view each heart
![]() $C\subseteq \Lambda $
as the coinvariant sublattice of a finite subgroup
$C\subseteq \Lambda $
as the coinvariant sublattice of a finite subgroup
![]() $H\leq \mathrm {Aut}(\mathcal {D})$
. As already noted in Proposition 2.23, in some cases, these are actually primitively embedded into the Leech lattice. Stable symplectic sublattices of the Leech lattice are known and well understood [Reference Höhn and Mason19]. Unfortunately, there exist hearts
$H\leq \mathrm {Aut}(\mathcal {D})$
. As already noted in Proposition 2.23, in some cases, these are actually primitively embedded into the Leech lattice. Stable symplectic sublattices of the Leech lattice are known and well understood [Reference Höhn and Mason19]. Unfortunately, there exist hearts
![]() $C\subset \Lambda $
that embed primitively into
$C\subset \Lambda $
that embed primitively into
![]() $\mathbb {B}$
, but not
$\mathbb {B}$
, but not
![]() $\mathbb {L}$
– we call such a hearts exceptional. In the next section, we describe a procedure to recover the abstract isometry class of such exceptional hearts. We then apply Theorem 4.8 to this list of abstract lattices, and to Höhn–Mason list of stable symplectic sublattices of
$\mathbb {L}$
– we call such a hearts exceptional. In the next section, we describe a procedure to recover the abstract isometry class of such exceptional hearts. We then apply Theorem 4.8 to this list of abstract lattices, and to Höhn–Mason list of stable symplectic sublattices of
![]() $\mathbb {L}$
, to classify conjugacy classes of hearts in
$\mathbb {L}$
, to classify conjugacy classes of hearts in
![]() $\Lambda $
.
$\Lambda $
.
4.3 Exceptional hearts
In this section, we aim to classify the remaining exceptional hearts: that is, the hearts
![]() $C'\subseteq \Lambda $
that embed primitively into
$C'\subseteq \Lambda $
that embed primitively into
![]() $\mathbb {B}$
but not into
$\mathbb {B}$
but not into
![]() $\mathbb {L}$
. In order to do so, we will use properties of isometries in
$\mathbb {L}$
. In order to do so, we will use properties of isometries in
![]() $\mathrm {Aut}(\mathcal {D})$
, discussed in Section 2.3. Example 4.12 proves that such exceptional hearts do in fact exist.
$\mathrm {Aut}(\mathcal {D})$
, discussed in Section 2.3. Example 4.12 proves that such exceptional hearts do in fact exist.
Example 4.12. See the Notebook ‘Counterexample’ in the dataset [Reference Marquand and Muller30] for explicit computations and proofs of the following statements. Let C be the negative definite even lattice with Gram matrix
 $$\begin{align*} \begin {pmatrix} -4 & 2 & 2 & -2 & -2 & 2 & -2 & 2 & 2 & 0 & 0 & 0 & 0 & 0 & 2 & 2 & -1 & 1 \\ 2 & -4 & -2 & 0 & 1 & -1 & 2 & -2 & -2 & -1 & -1 & 1 & 1 & -1 & -1 & -2 & -1 & -2 \\ 2 & -2 & -4 & 1 & 0 & -2 & 2 & -2 & -2 & -1 & -1 & -1 & 1 & -1 & 0 & -2 & 0 & -1 \\ -2 & 0 & 1 & -4 & -2 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & -1 & 1 & 0 & 2 & 0 & -1 \\ -2 & 1 & 0 & -2 & -4 & 1 & 0 & 0 & 0 & 1 & 1 & -1 & -1 & 1 & 2 & 2 & -1 & 1 \\ 2 & -1 & -2 & 0 & 1 & -4 & 2 & -2 & -2 & 0 & 0 & 0 & 0 & 0 & -2 & -1 & 1 & -1 \\ -2 & 2 & 2 & 0 & 0 & 2 & -4 & 2 & 2 & -1 & 1 & -1 & -1 & 1 & 0 & 0 & -1 & 2 \\ 2 & -2 & -2 & 0 & 0 & -2 & 2 & -4 & -1 & 1 & -1 & 1 & -1 & 1 & -1 & -1 & 0 & -1 \\ 2 & -2 & -2 & 0 & 0 & -2 & 2 & -1 & -4 & 0 & 1 & -1 & 0 & 0 & -1 & -1 & 0 & -1 \\ 0 & -1 & -1 & 1 & 1 & 0 & -1 & 1 & 0 & -4 & -1 & -1 & 2 & -2 & 0 & -2 & -1 & 0 \\ 0 & -1 & -1 & 1 & 1 & 0 & 1 & -1 & 1 & -1 & -4 & 2 & 2 & -1 & 1 & -1 & 0 & -1 \\ 0 & 1 & -1 & 0 & -1 & 0 & -1 & 1 & -1 & -1 & 2 & -4 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 1 & 1 & -1 & -1 & 0 & -1 & -1 & 0 & 2 & 2 & 0 & -4 & 2 & -1 & 1 & 0 & 1 \\ 0 & -1 & -1 & 1 & 1 & 0 & 1 & 1 & 0 & -2 & -1 & 0 & 2 & -4 & 1 & -1 & 0 & -1 \\ 2 & -1 & 0 & 0 & 2 & -2 & 0 & -1 & -1 & 0 & 1 & 0 & -1 & 1 & -4 & -1 & 1 & -1 \\ 2 & -2 & -2 & 2 & 2 & -1 & 0 & -1 & -1 & -2 & -1 & 0 & 1 & -1 & -1 & -4 & 0 & -1 \\ -1 & -1 & 0 & 0 & -1 & 1 & -1 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 1 & 0 & -4 & 1 \\ 1 & -2 & -1 & -1 & 1 & -1 & 2 & -1 & -1 & 0 & -1 & 1 & 1 & -1 & -1 & -1 & 1 & -4 \end {pmatrix}. \end{align*}$$
$$\begin{align*} \begin {pmatrix} -4 & 2 & 2 & -2 & -2 & 2 & -2 & 2 & 2 & 0 & 0 & 0 & 0 & 0 & 2 & 2 & -1 & 1 \\ 2 & -4 & -2 & 0 & 1 & -1 & 2 & -2 & -2 & -1 & -1 & 1 & 1 & -1 & -1 & -2 & -1 & -2 \\ 2 & -2 & -4 & 1 & 0 & -2 & 2 & -2 & -2 & -1 & -1 & -1 & 1 & -1 & 0 & -2 & 0 & -1 \\ -2 & 0 & 1 & -4 & -2 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & -1 & 1 & 0 & 2 & 0 & -1 \\ -2 & 1 & 0 & -2 & -4 & 1 & 0 & 0 & 0 & 1 & 1 & -1 & -1 & 1 & 2 & 2 & -1 & 1 \\ 2 & -1 & -2 & 0 & 1 & -4 & 2 & -2 & -2 & 0 & 0 & 0 & 0 & 0 & -2 & -1 & 1 & -1 \\ -2 & 2 & 2 & 0 & 0 & 2 & -4 & 2 & 2 & -1 & 1 & -1 & -1 & 1 & 0 & 0 & -1 & 2 \\ 2 & -2 & -2 & 0 & 0 & -2 & 2 & -4 & -1 & 1 & -1 & 1 & -1 & 1 & -1 & -1 & 0 & -1 \\ 2 & -2 & -2 & 0 & 0 & -2 & 2 & -1 & -4 & 0 & 1 & -1 & 0 & 0 & -1 & -1 & 0 & -1 \\ 0 & -1 & -1 & 1 & 1 & 0 & -1 & 1 & 0 & -4 & -1 & -1 & 2 & -2 & 0 & -2 & -1 & 0 \\ 0 & -1 & -1 & 1 & 1 & 0 & 1 & -1 & 1 & -1 & -4 & 2 & 2 & -1 & 1 & -1 & 0 & -1 \\ 0 & 1 & -1 & 0 & -1 & 0 & -1 & 1 & -1 & -1 & 2 & -4 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 1 & 1 & -1 & -1 & 0 & -1 & -1 & 0 & 2 & 2 & 0 & -4 & 2 & -1 & 1 & 0 & 1 \\ 0 & -1 & -1 & 1 & 1 & 0 & 1 & 1 & 0 & -2 & -1 & 0 & 2 & -4 & 1 & -1 & 0 & -1 \\ 2 & -1 & 0 & 0 & 2 & -2 & 0 & -1 & -1 & 0 & 1 & 0 & -1 & 1 & -4 & -1 & 1 & -1 \\ 2 & -2 & -2 & 2 & 2 & -1 & 0 & -1 & -1 & -2 & -1 & 0 & 1 & -1 & -1 & -4 & 0 & -1 \\ -1 & -1 & 0 & 0 & -1 & 1 & -1 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 1 & 0 & -4 & 1 \\ 1 & -2 & -1 & -1 & 1 & -1 & 2 & -1 & -1 & 0 & -1 & 1 & 1 & -1 & -1 & -1 & 1 & -4 \end {pmatrix}. \end{align*}$$
The lattice C lies in the genus
![]() $ {II}_{(0,18)}3^{-7}$
,
$ {II}_{(0,18)}3^{-7}$
,
![]() $O^\#(C)\cong C_3\times C_3$
fixes no nontrivial vector in C, and C contains no
$O^\#(C)\cong C_3\times C_3$
fixes no nontrivial vector in C, and C contains no
![]() $(-2)$
-vectors. Using [Reference Nikulin36, Proposition 1.15.1], one can check that the lattice C admits a primitive embedding into
$(-2)$
-vectors. Using [Reference Nikulin36, Proposition 1.15.1], one can check that the lattice C admits a primitive embedding into
![]() $\Lambda $
with orthogonal complement isometric to
$\Lambda $
with orthogonal complement isometric to
![]() $U(3)^{ 3}$
.
$U(3)^{ 3}$
.
However, we remark that
![]() $\text {rank}(C)+l(D_C) = 25$
: this implies that C does not embed primitively into the Leech lattice, but it does embed primitively into
$\text {rank}(C)+l(D_C) = 25$
: this implies that C does not embed primitively into the Leech lattice, but it does embed primitively into
![]() $\mathbb {B}$
.
$\mathbb {B}$
.
In order to determine, up to isometry, the stable symplectic sublattices of
![]() $\mathbb {B}$
not containing roots that do not embed primitively into the Leech lattice, we know from Proposition 2.23 that we need to look for finite subgroups
$\mathbb {B}$
not containing roots that do not embed primitively into the Leech lattice, we know from Proposition 2.23 that we need to look for finite subgroups
![]() $H\leq \mathrm {Aut}(\mathcal {D})$
such that there does not exist any
$H\leq \mathrm {Aut}(\mathcal {D})$
such that there does not exist any
![]() $v\in \mathbb {L}$
so that
$v\in \mathbb {L}$
so that
![]() $g(v)-v=\lambda $
for all
$g(v)-v=\lambda $
for all
![]() $(\lambda , g)\in H$
— we refer to such groups as exceptional. Note that since the isometry class of
$(\lambda , g)\in H$
— we refer to such groups as exceptional. Note that since the isometry class of
![]() $\mathbb {B}_H$
is preserved under conjugation of H by any element of
$\mathbb {B}_H$
is preserved under conjugation of H by any element of
![]() $O(\mathbb {B})$
, we describe a procedure to recover at least one representative for each
$O(\mathbb {B})$
, we describe a procedure to recover at least one representative for each
![]() $\mathrm {Aut}(\mathcal {D})$
-conjugacy class of finite exceptional subgroups of
$\mathrm {Aut}(\mathcal {D})$
-conjugacy class of finite exceptional subgroups of
![]() $\mathrm {Aut}(\mathcal {D})$
.
$\mathrm {Aut}(\mathcal {D})$
.
Recall from the proof of Lemma 2.17 that we have an exact sequence
where
![]() $\pi $
, which is induced by the isometry
$\pi $
, which is induced by the isometry
![]() $e^\perp /\mathbb {Z} e\cong \mathbb {L}$
, admits a section
$e^\perp /\mathbb {Z} e\cong \mathbb {L}$
, admits a section
![]() $\phi \colon O(\mathbb {L})\to \mathrm {Aut}(\mathcal {D})$
. Moreover, the same result tells us that
$\phi \colon O(\mathbb {L})\to \mathrm {Aut}(\mathcal {D})$
. Moreover, the same result tells us that
![]() $\mathrm {Aut}(\mathcal {D}) = \mathbb {L}\rtimes O(\mathbb {L})$
, so any element
$\mathrm {Aut}(\mathcal {D}) = \mathbb {L}\rtimes O(\mathbb {L})$
, so any element
![]() $h\in \mathrm {Aut}(\mathcal {D})$
of finite order can be written as a pair
$h\in \mathrm {Aut}(\mathcal {D})$
of finite order can be written as a pair
![]() $(\lambda , g)$
, where
$(\lambda , g)$
, where
![]() $g := \pi (h)$
and
$g := \pi (h)$
and
![]() $\lambda \in \mathbb {L}_g$
(Proposition 2.18). The section
$\lambda \in \mathbb {L}_g$
(Proposition 2.18). The section
![]() $\phi $
above sends any
$\phi $
above sends any
![]() $g\in O(\mathbb {L})$
to
$g\in O(\mathbb {L})$
to
![]() $\phi (g) := (0, g)\in \mathrm {Aut}(\mathcal {D})$
.
$\phi (g) := (0, g)\in \mathrm {Aut}(\mathcal {D})$
.
Let
![]() $G\leq O(\mathbb {L})$
be a subgroup. We define a
$G\leq O(\mathbb {L})$
be a subgroup. We define a
![]() $\mathbb {Z}$
-linear map
$\mathbb {Z}$
-linear map
 $$\begin{align*}p_G\colon \mathbb{L}\to\prod_{g\in G}\mathbb{L}_g,\; v\mapsto (g(v)-v)_{g\in G},\end{align*}$$
$$\begin{align*}p_G\colon \mathbb{L}\to\prod_{g\in G}\mathbb{L}_g,\; v\mapsto (g(v)-v)_{g\in G},\end{align*}$$
whose kernel is exactly
![]() $\mathbb {L}^G$
. Let us denote by m the order of G. We define moreover
$\mathbb {L}^G$
. Let us denote by m the order of G. We define moreover
 $$\begin{align*}\mathbb{L}\to \prod_{g\in G}\mathbb{L}_g/m\mathbb{L}_g,\; v\mapsto (g(v)-v+m\mathbb{L}_g)_{g\in G}\end{align*}$$
$$\begin{align*}\mathbb{L}\to \prod_{g\in G}\mathbb{L}_g/m\mathbb{L}_g,\; v\mapsto (g(v)-v+m\mathbb{L}_g)_{g\in G}\end{align*}$$
whose kernel is denoted by
![]() $K(G)$
. We observe that
$K(G)$
. We observe that
![]() $K(G)$
contains
$K(G)$
contains
![]() $\mathbb {L}^G+m\mathbb {L}$
. We denote by
$\mathbb {L}^G+m\mathbb {L}$
. We denote by
![]() $A(G) := K(G)/(m\mathbb {L}+\mathbb {L}^G)$
– it is a finite abelian group. We have seen in Theorem 2.20 and Remark 2.21 that for any finite subgroup
$A(G) := K(G)/(m\mathbb {L}+\mathbb {L}^G)$
– it is a finite abelian group. We have seen in Theorem 2.20 and Remark 2.21 that for any finite subgroup
![]() $H\leq \mathrm {Aut}(\mathcal {D})$
satisfying
$H\leq \mathrm {Aut}(\mathcal {D})$
satisfying
![]() $\pi (H) = G$
, there exists a vector
$\pi (H) = G$
, there exists a vector
![]() $v\in \mathbb {L}$
such that every element
$v\in \mathbb {L}$
such that every element
![]() $h = (\lambda , g)\in H$
satisfies
$h = (\lambda , g)\in H$
satisfies
and
![]() $\lambda \in \mathbb {L}_g$
. In particular,
$\lambda \in \mathbb {L}_g$
. In particular,
![]() $v\in K(G)$
, and it is uniquely determined by H, up to translation by a vector in
$v\in K(G)$
, and it is uniquely determined by H, up to translation by a vector in
![]() $\ker (p_G) = \mathbb {L}^G$
.
$\ker (p_G) = \mathbb {L}^G$
.
Lemma 4.13. Let
![]() $H, H'\leq \mathrm {Aut}(\mathcal {D})$
be finite subgroups such that
$H, H'\leq \mathrm {Aut}(\mathcal {D})$
be finite subgroups such that
![]() $\pi (H) = \pi (H') = G$
, and let
$\pi (H) = \pi (H') = G$
, and let
![]() $v,v'\in K(G)$
be associated vectors. Then the following items are equivalent:
$v,v'\in K(G)$
be associated vectors. Then the following items are equivalent:
-
1. the groups
 $H, H'$
are
$H, H'$
are
 $\mathbb {L}$
-conjugate in
$\mathbb {L}$
-conjugate in
 $\mathrm {Aut}(\mathcal {D})$
;
$\mathrm {Aut}(\mathcal {D})$
; -
2. the vectors v and
 $v'$
define the same class in
$v'$
define the same class in
 $A(G)$
.
$A(G)$
.
Proof. Let us suppose that there exists
![]() $\mu \in \mathbb {L}$
such that
$\mu \in \mathbb {L}$
such that
![]() $\psi _\mu H\psi _\mu ^{-1} = H'$
, where
$\psi _\mu H\psi _\mu ^{-1} = H'$
, where
![]() $\psi _{\mu }$
is the Eichler–Siegel transformation associated to
$\psi _{\mu }$
is the Eichler–Siegel transformation associated to
![]() $\mu $
(see Definition 2.16). Then, for all
$\mu $
(see Definition 2.16). Then, for all
![]() $g\in G$
, we have
$g\in G$
, we have
 $$\begin{align*}\psi_\mu\left(\frac{g(v)-v}{m}, g\right)\psi_\mu^{-1} = \left(\frac{g(v')-v'}{m}, g\right),\end{align*}$$
$$\begin{align*}\psi_\mu\left(\frac{g(v)-v}{m}, g\right)\psi_\mu^{-1} = \left(\frac{g(v')-v'}{m}, g\right),\end{align*}$$
which is equivalent to
Thus, we conclude that
![]() $v-v'-m\mu \in \mathbb {L}^g$
for all
$v-v'-m\mu \in \mathbb {L}^g$
for all
![]() $g\in G$
, meaning exactly that
$g\in G$
, meaning exactly that
![]() $v-v'\in \mathbb {L}^G+m\mathbb {L}$
. The converse holds similarly, by reversing the order of the arguments.
$v-v'\in \mathbb {L}^G+m\mathbb {L}$
. The converse holds similarly, by reversing the order of the arguments.
Corollary 4.14. The group
![]() $A(G)$
is trivial if and only if for all
$A(G)$
is trivial if and only if for all
![]() $H\leq \mathrm {Aut}(\mathcal {D})$
finite such that
$H\leq \mathrm {Aut}(\mathcal {D})$
finite such that
![]() $\pi (H) = G$
, the lattices
$\pi (H) = G$
, the lattices
![]() $\mathbb {B}_H$
and
$\mathbb {B}_H$
and
![]() $\mathbb {L}_G$
are isometric.
$\mathbb {L}_G$
are isometric.
Proof. If
![]() $A(G)$
is trivial, we know from Lemma 4.13 that any
$A(G)$
is trivial, we know from Lemma 4.13 that any
![]() $H\leq \mathrm {Aut}(\mathcal {D})$
finite such that
$H\leq \mathrm {Aut}(\mathcal {D})$
finite such that
![]() $\pi (H) = G$
is
$\pi (H) = G$
is
![]() $\mathbb {L}$
-conjugate to
$\mathbb {L}$
-conjugate to
![]() $\phi (G)$
: in particular,
$\phi (G)$
: in particular,
![]() $\mathbb {B}_H\cong \mathbb {B}_{\phi (G)} = \mathbb {L}_G$
.
$\mathbb {B}_H\cong \mathbb {B}_{\phi (G)} = \mathbb {L}_G$
.
Now, if
![]() $A(G)$
is nontrivial, then there is a vector
$A(G)$
is nontrivial, then there is a vector
![]() $v\in \mathbb {L}\setminus (\mathbb {L}^G+m\mathbb {L})$
such that, for all
$v\in \mathbb {L}\setminus (\mathbb {L}^G+m\mathbb {L})$
such that, for all
![]() $g\in G$
,
$g\in G$
,
![]() $\lambda _g := \frac {g(v)-v}{m}\in \mathbb {L}_g$
and,
$\lambda _g := \frac {g(v)-v}{m}\in \mathbb {L}_g$
and,
![]() $\{\lambda _g\}_{g\in G}$
does not lie in the image of
$\{\lambda _g\}_{g\in G}$
does not lie in the image of
![]() $\mathbb {L}$
by
$\mathbb {L}$
by
![]() $p_G$
. Therefore, according to Proposition 2.23, the finite subgroup
$p_G$
. Therefore, according to Proposition 2.23, the finite subgroup
![]() $H := \{(\lambda _g, g)\;\mid \; g\in G\}$
satisfies that
$H := \{(\lambda _g, g)\;\mid \; g\in G\}$
satisfies that
![]() $\mathbb {B}_H\not \cong \mathbb {L}_G$
.
$\mathbb {B}_H\not \cong \mathbb {L}_G$
.
Remark 4.15. Let
![]() $H'\leq \mathrm {Aut}(\mathcal {D})$
be finite such that
$H'\leq \mathrm {Aut}(\mathcal {D})$
be finite such that
![]() $G' := \pi (H')$
is
$G' := \pi (H')$
is
![]() $O(\mathbb {L})$
-conjugate to G. Let
$O(\mathbb {L})$
-conjugate to G. Let
![]() $f\in O(\mathbb {L})$
be such that
$f\in O(\mathbb {L})$
be such that
![]() $fG'f^{-1} = G$
. Then the group
$fG'f^{-1} = G$
. Then the group
is conjugate to
![]() $H'$
and satisfies
$H'$
and satisfies
![]() $\pi (H) = fG'f^{-1} = G$
.
$\pi (H) = fG'f^{-1} = G$
.
Therefore, in order to construct at least one representative for each
![]() $\mathrm {Aut}(\mathcal {D})$
-conjugacy class of finite exceptional subgroups H of
$\mathrm {Aut}(\mathcal {D})$
-conjugacy class of finite exceptional subgroups H of
![]() $\mathrm {Aut}(\mathcal {D})$
, we proceed as follows:
$\mathrm {Aut}(\mathcal {D})$
, we proceed as follows:
-
1. we start by fixing a stable symplectic sublattice C of the Leech lattice
 $\mathbb {L}$
[Reference Höhn and Mason19];
$\mathbb {L}$
[Reference Höhn and Mason19]; -
2. we compute a set
 $\mathcal {G}$
of representatives of
$\mathcal {G}$
of representatives of
 $O(\mathbb {L})$
-conjugacy classes of finite subgroups G of
$O(\mathbb {L})$
-conjugacy classes of finite subgroups G of
 $O^\#(C)$
such that
$O^\#(C)$
such that
 $C^G=\{0\}$
(Remark 4.15);
$C^G=\{0\}$
(Remark 4.15); -
3. for any
 $G\in \mathcal {G}$
, we compute
$G\in \mathcal {G}$
, we compute
 $A(G)$
: if this is trivial, we try a new group (Corollary 4.14);
$A(G)$
: if this is trivial, we try a new group (Corollary 4.14); -
4. for every
 $[v]\in A(G)$
nontrivial, we define
$[v]\in A(G)$
nontrivial, we define
 $H:= \left \{\left (\frac {g(v)-v}{\#G}, g\right )\;\mid \; g\in G\right \}\leq \mathrm {Aut}(\mathcal {D})$
.
$H:= \left \{\left (\frac {g(v)-v}{\#G}, g\right )\;\mid \; g\in G\right \}\leq \mathrm {Aut}(\mathcal {D})$
.
Note that according to Lemma 4.13, the
![]() $\mathrm {Aut}(\mathcal {D})$
-conjugacy class of H in step (4) does not depend on a choice of a representative for the nontrivial class
$\mathrm {Aut}(\mathcal {D})$
-conjugacy class of H in step (4) does not depend on a choice of a representative for the nontrivial class
![]() $[v]\in A(G)$
.
$[v]\in A(G)$
.
Theorem 4.16. Let
![]() $H\leq \mathrm {Aut}(\mathcal {D})$
be an exceptional finite subgroup so that
$H\leq \mathrm {Aut}(\mathcal {D})$
be an exceptional finite subgroup so that
![]() $\mathbb {B}_H$
has rank at most 21. Then,
$\mathbb {B}_H$
has rank at most 21. Then,
![]() $\mathbb {B}_H$
is abstractly isometric to one of the 101 stable symplectic lattices in the folder ‘exceptional’ of the dataset [Reference Marquand and Muller30].
$\mathbb {B}_H$
is abstractly isometric to one of the 101 stable symplectic lattices in the folder ‘exceptional’ of the dataset [Reference Marquand and Muller30].
Proof. We apply the previous procedure to the list of stable symplectic sublattices of the Leech lattice, of rank at most 21. For each such sublattice
![]() $C\leq \mathbb {L}$
, we enumerate conjugacy classes of subgroups
$C\leq \mathbb {L}$
, we enumerate conjugacy classes of subgroups
![]() $G\leq O^\#(C)$
so that
$G\leq O^\#(C)$
so that
![]() $C^G = \{0\}$
and
$C^G = \{0\}$
and
![]() $A(G)$
is nontrivial. By doing so, we obtain at least one representative for every
$A(G)$
is nontrivial. By doing so, we obtain at least one representative for every
![]() $\mathrm {Aut}(\mathcal {D})$
-conjugacy class of exceptional finite subgroups of
$\mathrm {Aut}(\mathcal {D})$
-conjugacy class of exceptional finite subgroups of
![]() $H\leq \mathrm {Aut}(\mathcal {D})$
satisfying
$H\leq \mathrm {Aut}(\mathcal {D})$
satisfying
![]() ${\pi (H) = G}$
(Lemma 4.13, Remark 4.15). We collect the coinvariant sublattices
${\pi (H) = G}$
(Lemma 4.13, Remark 4.15). We collect the coinvariant sublattices
![]() $\mathbb {B}_H$
associated to each such exceptional subgroup of
$\mathbb {B}_H$
associated to each such exceptional subgroup of
![]() $H\leq \mathrm {Aut}(\mathcal {D})$
, and we keep only one representative for each isometry class of lattices they represent. We record information about such lattices
$H\leq \mathrm {Aut}(\mathcal {D})$
, and we keep only one representative for each isometry class of lattices they represent. We record information about such lattices
![]() $\mathbb {B}_H$
in Appendix A, Table 2.
$\mathbb {B}_H$
in Appendix A, Table 2.
For our purposes, we only need those stable symplectic lattices of
![]() $\mathbb {B}$
that can embed into
$\mathbb {B}$
that can embed into
![]() $\Lambda $
. Thus, we conclude the following:
$\Lambda $
. Thus, we conclude the following:
Corollary 4.17. Let
![]() $C\subseteq \Lambda $
be an exceptional heart. Then C is abstractly isometric to one of the three stable symplectic lattices given in Appendix B.
$C\subseteq \Lambda $
be an exceptional heart. Then C is abstractly isometric to one of the three stable symplectic lattices given in Appendix B.
Proof. According to the proof of [Reference Nikulin36, Proposition 1.15.1], a stable symplectic lattice C embeds primitively into
![]() $\Lambda $
only if for all prime numbers p
$\Lambda $
only if for all prime numbers p
where
![]() $l(D_p)$
is the length of the p-Sylow subgroup of
$l(D_p)$
is the length of the p-Sylow subgroup of
![]() $D_C$
, and
$D_C$
, and
![]() $\delta _{3,p} = 1$
if
$\delta _{3,p} = 1$
if
![]() $p=3$
and 0 otherwise. In fact, it follows from the fact that
$p=3$
and 0 otherwise. In fact, it follows from the fact that
![]() $D_{\Lambda }$
has order 3 and any
$D_{\Lambda }$
has order 3 and any
![]() $\mathbb {Z}_3$
-lattice admits an orthogonal basis. We deduce from Table 2 that there are only three possible isometry classes of exceptional heart
$\mathbb {Z}_3$
-lattice admits an orthogonal basis. We deduce from Table 2 that there are only three possible isometry classes of exceptional heart
![]() $C\subseteq \Lambda $
.
$C\subseteq \Lambda $
.
Remark 4.18. If
![]() $C\subseteq \Lambda $
is an exceptional heart, Corollary 4.17 tells us what its isometry class can be. However, we have not proved yet that each of the three are realised as an exceptional heart of
$C\subseteq \Lambda $
is an exceptional heart, Corollary 4.17 tells us what its isometry class can be. However, we have not proved yet that each of the three are realised as an exceptional heart of
![]() $\Lambda $
.
$\Lambda $
.
One observes that for all sublattices
![]() $C\subseteq \mathbb {B}$
presented in Table 2, we have
$C\subseteq \mathbb {B}$
presented in Table 2, we have
![]() $\text {rank}(C)+l(D_C)>24$
. In particular, the following holds.
$\text {rank}(C)+l(D_C)>24$
. In particular, the following holds.
Corollary 4.19. Let C be a stable symplectic lattice of rank at most 21 and not containing
![]() $(-2)$
-vectors. Then C embeds primitively into the Leech lattice
$(-2)$
-vectors. Then C embeds primitively into the Leech lattice
![]() $\mathbb {L}$
so that
$\mathbb {L}$
so that
![]() $\mathbb {L}_{O^\#(C)} \cong C$
if and only if
$\mathbb {L}_{O^\#(C)} \cong C$
if and only if
Proof. Already note that if C embeds primitively into the Leech lattice, then according to [Reference Nikulin36, Corollary 1.12.3], we have that rank(C) + l(D C ) ≤rank(𝕃) = 24.
Now suppose that
![]() $\mathrm {rank}(C)+l(D_C)\leq 24$
. By this assumption, we know that C embeds primitively into
$\mathrm {rank}(C)+l(D_C)\leq 24$
. By this assumption, we know that C embeds primitively into
![]() $\mathbb {B}$
and this in a unique way up to the action
$\mathbb {B}$
and this in a unique way up to the action
![]() $O(\mathbb {B})$
[Reference Nikulin36, Proposition 1.14.1]. In particular, we can choose a primitive embedding
$O(\mathbb {B})$
[Reference Nikulin36, Proposition 1.14.1]. In particular, we can choose a primitive embedding
![]() $j\colon C\hookrightarrow \mathbb {B}$
such that the complement
$j\colon C\hookrightarrow \mathbb {B}$
such that the complement
![]() $N:= j(C)^\perp _{\mathbb {B}}$
intersects the interior of
$N:= j(C)^\perp _{\mathbb {B}}$
intersects the interior of
![]() $\mathcal {D}$
. Therefore, as in the proof of Lemma 4.10, we have that the finite group
$\mathcal {D}$
. Therefore, as in the proof of Lemma 4.10, we have that the finite group
![]() $H\leq O^+(\mathbb {B})$
obtained by extending
$H\leq O^+(\mathbb {B})$
obtained by extending
![]() $O^\#(C)$
with the identity on N preserves
$O^\#(C)$
with the identity on N preserves
![]() $\mathcal {D}$
. Thus, C is the coinvariant sublattice of a finite subgroup of
$\mathcal {D}$
. Thus, C is the coinvariant sublattice of a finite subgroup of
![]() $\mathrm {Aut}(\mathcal {D})$
. There are two cases: either H is exceptional or C is isometric to
$\mathrm {Aut}(\mathcal {D})$
. There are two cases: either H is exceptional or C is isometric to
![]() $\mathbb {L}_{\pi (H)}$
. However, the former is not possible since Table 2 tells us that the coinvariant sublattices N of exceptional finite subgroups of
$\mathbb {L}_{\pi (H)}$
. However, the former is not possible since Table 2 tells us that the coinvariant sublattices N of exceptional finite subgroups of
![]() $\mathrm {Aut}(\mathcal {D})$
satisfy
$\mathrm {Aut}(\mathcal {D})$
satisfy
4.4 Results and comments
Now that we have determined the possible isometry classes for the hearts of
![]() $\Lambda $
; we can conclude our classification by testing whether each such lattices embeds primitively into
$\Lambda $
; we can conclude our classification by testing whether each such lattices embeds primitively into
![]() $\Lambda $
, and in how many ways up to the action of
$\Lambda $
, and in how many ways up to the action of
![]() $O(\Lambda )$
(Theorem 4.8).
$O(\Lambda )$
(Theorem 4.8).
Proposition 4.20. There are exactly 192
![]() $O^+(\Lambda )$
-conjugacy classes of saturated symplectic finite subgroups
$O^+(\Lambda )$
-conjugacy classes of saturated symplectic finite subgroups
![]() $H\leq O^{+, \#}(\Lambda )$
.
$H\leq O^{+, \#}(\Lambda )$
.
Proof. According to Theorem 4.8 and Lemma 4.6, it suffices to compute representatives for the isomorphism classes of hearts
![]() $C\subseteq \Lambda $
. According to Lemma 4.10, Remark 4.11, Proposition 2.23 and Corollary 4.17, such a heart is abstractly isometric either to a stable symplectic sublattice of the Leech lattice
$C\subseteq \Lambda $
. According to Lemma 4.10, Remark 4.11, Proposition 2.23 and Corollary 4.17, such a heart is abstractly isometric either to a stable symplectic sublattice of the Leech lattice
![]() $\mathbb {L}$
, or to one of the three exceptional lattices in Appendix B. Recall that the former are classified in [Reference Höhn and Mason19]. We complete the classification by applying [Reference Nikulin36, Proposition 1.15.1] to each such lattice C. We use an implementation of the algorithm described in the proof of [Reference Nikulin36, Proposition 1.15.1] by the second author in [Reference Decker, Eder, Fieker, Horn and Joswig12, QuadFormAndIsom] to compute a representative for each isomorphism class of primitive sublattices of
$\mathbb {L}$
, or to one of the three exceptional lattices in Appendix B. Recall that the former are classified in [Reference Höhn and Mason19]. We complete the classification by applying [Reference Nikulin36, Proposition 1.15.1] to each such lattice C. We use an implementation of the algorithm described in the proof of [Reference Nikulin36, Proposition 1.15.1] by the second author in [Reference Decker, Eder, Fieker, Horn and Joswig12, QuadFormAndIsom] to compute a representative for each isomorphism class of primitive sublattices of
![]() $\Lambda $
isometric to C. The results of such computations are available in the folder ‘data’ of the dataset [Reference Marquand and Muller30]: we give an overview of this dataset in Appendix C, Table 3.
$\Lambda $
isometric to C. The results of such computations are available in the folder ‘data’ of the dataset [Reference Marquand and Muller30]: we give an overview of this dataset in Appendix C, Table 3.
In each case from Proposition 4.20, the groups
![]() $H\leq O^{+,\#}(\Lambda )$
are saturated in
$H\leq O^{+,\#}(\Lambda )$
are saturated in
![]() $O^{+,\#}(\Lambda )$
but they might not be saturated in
$O^{+,\#}(\Lambda )$
but they might not be saturated in
![]() $O^+(\Lambda )$
. Whether such a group H is saturated in
$O^+(\Lambda )$
. Whether such a group H is saturated in
![]() $O^+(\Lambda )$
can be tested as follows.
$O^+(\Lambda )$
can be tested as follows.
Lemma 4.21. Let
![]() $C\subseteq \Lambda $
be a negative definite primitive sublattice, and let
$C\subseteq \Lambda $
be a negative definite primitive sublattice, and let
![]() $P(C)$
be the largest subgroup of
$P(C)$
be the largest subgroup of
![]() $O(C)$
which can be extended with the identity on
$O(C)$
which can be extended with the identity on
![]() $C^\perp _\Lambda $
. Suppose that
$C^\perp _\Lambda $
. Suppose that
![]() $P(C)$
fixes no nontrivial vector in C. Then, for any subgroup
$P(C)$
fixes no nontrivial vector in C. Then, for any subgroup
![]() $H\leq P(C)$
fixing no nontrivial vector in C, we have that
$H\leq P(C)$
fixing no nontrivial vector in C, we have that
where we see H and
![]() $P(C)$
as subgroups of
$P(C)$
as subgroups of
![]() $O^+(\Lambda )$
by extending with the identity on
$O^+(\Lambda )$
by extending with the identity on
![]() $F:= C^\perp _\Lambda $
.
$F:= C^\perp _\Lambda $
.
Proof. Since H fixes no nontrivial vector in C, we have that
![]() $\Lambda _H = C$
– hence,
$\Lambda _H = C$
– hence,
![]() $\mathrm {Sat}_{O^+(\Lambda )}(H)$
is the pointwise stabiliser of
$\mathrm {Sat}_{O^+(\Lambda )}(H)$
is the pointwise stabiliser of
![]() $F:= C^\perp _\Lambda $
in
$F:= C^\perp _\Lambda $
in
![]() $O^+(\Lambda )$
. Now, by definition, any element f of
$O^+(\Lambda )$
. Now, by definition, any element f of
![]() $\mathrm {Sat}_{O^+(\Lambda )}(H)$
acts trivially on F, so its restriction
$\mathrm {Sat}_{O^+(\Lambda )}(H)$
acts trivially on F, so its restriction
![]() $f_{\mid C}$
to C lies in
$f_{\mid C}$
to C lies in
![]() $P(C)$
. Conversely, by definition, any element of
$P(C)$
. Conversely, by definition, any element of
![]() $P(C)$
extends to an isometry of
$P(C)$
extends to an isometry of
![]() $\Lambda $
with trivial spinor norm (Remark 3.7) and acting trivially on F.
$\Lambda $
with trivial spinor norm (Remark 3.7) and acting trivially on F.
Remark 4.22. With the notation from Lemma 4.21, let
![]() $ D_F\geq H_F\xrightarrow {\gamma } H_C\leq D_C$
be the glue map associated to the primitive extension
$ D_F\geq H_F\xrightarrow {\gamma } H_C\leq D_C$
be the glue map associated to the primitive extension
![]() $F\oplus C\subseteq \Lambda $
. Let us denote by
$F\oplus C\subseteq \Lambda $
. Let us denote by
![]() $\pi _C\colon O(C)\to O(D_C)$
the discriminant representation of
$\pi _C\colon O(C)\to O(D_C)$
the discriminant representation of
![]() $O(C)$
, whose image is denoted by
$O(C)$
, whose image is denoted by
![]() $G_C:= \pi _C(O(C))$
. Let moreover
$G_C:= \pi _C(O(C))$
. Let moreover
![]() $G_C(H_C)$
be the stabiliser of
$G_C(H_C)$
be the stabiliser of
![]() $H_C$
in
$H_C$
in
![]() $G_C$
, and let us finally denote
$G_C$
, and let us finally denote
![]() $K_C := \ker (G_C(H_C)\to O(H_C))$
. Then it follows from Equation (EGC) that
$K_C := \ker (G_C(H_C)\to O(H_C))$
. Then it follows from Equation (EGC) that
![]() $P(C) = \pi _C^{-1}(K_C)$
. In particular, since C is negative definite, we have that
$P(C) = \pi _C^{-1}(K_C)$
. In particular, since C is negative definite, we have that
In the case of nonsaturated groups, there is a way of characterising the saturation of
![]() $O^\#(C)$
in
$O^\#(C)$
in
![]() $O^+(\Lambda )$
.
$O^+(\Lambda )$
.
Proposition 4.23. Let
![]() $H \leq O^{+,\#}(\Lambda )$
be saturated, and let G be the saturation of H in
$H \leq O^{+,\#}(\Lambda )$
be saturated, and let G be the saturation of H in
![]() $O^+(\Lambda )$
. Then
$O^+(\Lambda )$
. Then
![]() $G^\#=H$
and
$G^\#=H$
and
![]() $[G:H] \leq 2$
.
$[G:H] \leq 2$
.
Proof. The fact that
![]() $G^\#=H$
follows from H being saturated in
$G^\#=H$
follows from H being saturated in
![]() $O^{+,\#}(\Lambda )$
. We conclude by remarking that
$O^{+,\#}(\Lambda )$
. We conclude by remarking that
![]() $G/H$
embeds into
$G/H$
embeds into
![]() $\text {im}(O(\Lambda )\to O(D_\Lambda ))$
which has order 2.
$\text {im}(O(\Lambda )\to O(D_\Lambda ))$
which has order 2.
Proof of Theorem 4.1.
This follows from Lemma 3.6 together with Proposition 4.20 for the list of conjugacy classes of groups, and Lemma 4.21 and Remark 4.22 for determining the saturated ones (Remark 3.8).
Let X be an IHS manifold of
![]() $OG10$
type and let
$OG10$
type and let
![]() $f\in \mathrm {Bir}_s(X)$
be of prime order p. It follows that
$f\in \mathrm {Bir}_s(X)$
be of prime order p. It follows that
![]() $\eta _*(f)$
acts trivially on the discriminant group
$\eta _*(f)$
acts trivially on the discriminant group
![]() $D_\Lambda $
unless
$D_\Lambda $
unless
![]() $p=2$
. Using the results of Theorem 4.1 and the classification of symplectic birational involutions [Reference Marquand and Muller29], we can extract a complete classification of prime order symplectic birational transformations of manifolds of
$p=2$
. Using the results of Theorem 4.1 and the classification of symplectic birational involutions [Reference Marquand and Muller29], we can extract a complete classification of prime order symplectic birational transformations of manifolds of
![]() $OG10$
type. We display for convenience of interested readers.
$OG10$
type. We display for convenience of interested readers.
Theorem 4.24. Let X be an IHS manifold of
![]() $OG10$
type,
$OG10$
type,
![]() $f\in \mathrm {Bir}_s(X)$
a symplectic birational transformation of prime order p. Then the induced action of
$f\in \mathrm {Bir}_s(X)$
a symplectic birational transformation of prime order p. Then the induced action of
![]() $H:=\langle \eta _*(f)\rangle $
on
$H:=\langle \eta _*(f)\rangle $
on
![]() $\Lambda $
appears in Table 1.
$\Lambda $
appears in Table 1.
Table 1 Classification of prime order symplectic birational transformations for IHS manifolds of
![]() $OG10$
type.
$OG10$
type.

Proof. The classification of such H for
![]() $p=2$
follows from [Reference Marquand and Muller29]. Suppose now that p is odd. In particular, we have that H is stable of prime order p, and therefore,
$p=2$
follows from [Reference Marquand and Muller29]. Suppose now that p is odd. In particular, we have that H is stable of prime order p, and therefore,
![]() $C:=\Lambda _H$
is p-elementary (see, for instance, [Reference Grossi, Onorati and Veniani17, Lemma 2.8]). Hence, by Proposition 4.20, we see that either C embeds primitively into the Leech lattice, or
$C:=\Lambda _H$
is p-elementary (see, for instance, [Reference Grossi, Onorati and Veniani17, Lemma 2.8]). Hence, by Proposition 4.20, we see that either C embeds primitively into the Leech lattice, or
![]() $p = 3$
and C is isometric to the lattice defined in Example 4.12.
$p = 3$
and C is isometric to the lattice defined in Example 4.12.
-
1. In the former case, we know that C embeds primitively into the Leech lattice, so we can use the classification of conjugacy classes of prime order isometries of the Leech lattice in [Reference Höhn and Mason19]. For each class of prime order isometries g of the Leech lattice, we know that
 $ \mathbb {L}_g$
is stable symplectic, and we moreover have that
$ \mathbb {L}_g$
is stable symplectic, and we moreover have that
 $(\mathbb {L}_g, g_{\mid \mathbb {L}_g})$
is unique up to isomorphism. Hence, we can infer from Table 3 whether
$(\mathbb {L}_g, g_{\mid \mathbb {L}_g})$
is unique up to isomorphism. Hence, we can infer from Table 3 whether
 $\mathbb {L}_g$
embeds primitively into
$\mathbb {L}_g$
embeds primitively into
 $\Lambda $
. If it does, then we know that
$\Lambda $
. If it does, then we know that
 $\Lambda $
has a prime order isometry
$\Lambda $
has a prime order isometry
 $f\in O^{+,\#}(\Lambda )$
with
$f\in O^{+,\#}(\Lambda )$
with
 $\Lambda _f\cong \mathbb {L}_g$
, and Table 3 also tells us what is the genus of
$\Lambda _f\cong \mathbb {L}_g$
, and Table 3 also tells us what is the genus of
 $F := \Lambda ^f$
. Note that one can apply [Reference Brandhorst and Hofmann5, Algorithm 2] to the triple of lattices with isometry
$F := \Lambda ^f$
. Note that one can apply [Reference Brandhorst and Hofmann5, Algorithm 2] to the triple of lattices with isometry
 $((F, {id}), (\mathbb {L}_g, g_{\mid \mathbb {L}_g}), (\Lambda , {id}))$
, with
$((F, {id}), (\mathbb {L}_g, g_{\mid \mathbb {L}_g}), (\Lambda , {id}))$
, with
 $k=p$
, to obtain the number of
$k=p$
, to obtain the number of
 $O^+(\Lambda )$
-conjugacy classes of such isometries f.
$O^+(\Lambda )$
-conjugacy classes of such isometries f. -
2. In the latter case, one can use an algorithm of Plesken–Souvignier [Reference Plesken and Souvignier40] to show that the stable symplectic lattice C defined in Example 4.12 admits a unique conjugacy class of fixed-point free isometry g of order 3. By applying again [Reference Brandhorst and Hofmann5, Algorithm 2] to the triple of lattices with isometry
 $((U(3)^{3}, {id}), (C, g), (\Lambda , {id}))$
with
$((U(3)^{3}, {id}), (C, g), (\Lambda , {id}))$
with
 $p=k=3$
, we obtain that there are two
$p=k=3$
, we obtain that there are two
 $O^+(\Lambda )$
-conjugacy classes of cyclic subgroups of
$O^+(\Lambda )$
-conjugacy classes of cyclic subgroups of
 $O^{+, \#}(\Lambda )$
generated by an isometry f of order 3 such that
$O^{+, \#}(\Lambda )$
generated by an isometry f of order 3 such that
 $\Lambda _f\cong C$
.
$\Lambda _f\cong C$
.
In all cases, since the lattices C we consider are stable symplectic without
![]() $(-2)$
-vectors, we know that the isometries
$(-2)$
-vectors, we know that the isometries
![]() $f\in O^{+, \#}(\Lambda )$
we have constructed are symplectic (Lemma 4.6). We refer to the Notebook ‘Prime’ in the folder ‘verification’ of the dataset [Reference Marquand and Muller30] for more details about the computations described in (1) and (2).
$f\in O^{+, \#}(\Lambda )$
we have constructed are symplectic (Lemma 4.6). We refer to the Notebook ‘Prime’ in the folder ‘verification’ of the dataset [Reference Marquand and Muller30] for more details about the computations described in (1) and (2).
Remark 4.25. We define the two following rank 2 even lattices:
 $$\begin{align*}K_7 := \begin{pmatrix} 4&-1\\-1&2 \end{pmatrix},\quad\quad H_5 := \begin{pmatrix} 2&1\\1&-2 \end{pmatrix}\end{align*}$$
$$\begin{align*}K_7 := \begin{pmatrix} 4&-1\\-1&2 \end{pmatrix},\quad\quad H_5 := \begin{pmatrix} 2&1\\1&-2 \end{pmatrix}\end{align*}$$
which are respectively positive definite and indefinite, of respective determinant 7 and
![]() $-5$
.
$-5$
.
For each finite cyclic group H as in Theorem 4.24, we display in Table 1 the invariant sublattice
![]() $\Lambda ^H$
and the genus of the coinvariant sublattice
$\Lambda ^H$
and the genus of the coinvariant sublattice
![]() $g(\Lambda _H)$
. Moreover, the number of
$g(\Lambda _H)$
. Moreover, the number of
![]() $O^+(\Lambda )$
-conjugacy classes of such a group, for fixed
$O^+(\Lambda )$
-conjugacy classes of such a group, for fixed
![]() $(\Lambda ^H, g(\Lambda _H))$
, is given in the last column of the table.
$(\Lambda ^H, g(\Lambda _H))$
, is given in the last column of the table.
5 From stable symplectic to symplectic
It remains to classify symplectic finite subgroups
![]() $H\leq O^+(\Lambda )$
that satisfy Corollary 3.9 case (3) (i.e., groups H where
$H\leq O^+(\Lambda )$
that satisfy Corollary 3.9 case (3) (i.e., groups H where
![]() $H^\#\leq H$
is an index 2 subgroup). In particular, there exists a short exact sequence (Equation (3.1))
$H^\#\leq H$
is an index 2 subgroup). In particular, there exists a short exact sequence (Equation (3.1))
where
![]() $H^\#\leq O^{+,\#}(\Lambda ).$
In this section, we adapt an extension approach of [Reference Brandhorst and Hashimoto4, Reference Brandhorst and Hofmann5] in order to classify those symplectic finite subgroups H whose subgroup
$H^\#\leq O^{+,\#}(\Lambda ).$
In this section, we adapt an extension approach of [Reference Brandhorst and Hashimoto4, Reference Brandhorst and Hofmann5] in order to classify those symplectic finite subgroups H whose subgroup
![]() $H^\#$
is contained in the classification of Section 4. More precisely, we prove the following:
$H^\#$
is contained in the classification of Section 4. More precisely, we prove the following:
Theorem 5.1. Let
![]() $(X, \eta , G)$
be a triple consisting of a marked IHS manifold
$(X, \eta , G)$
be a triple consisting of a marked IHS manifold
![]() $(X, \eta )$
of
$(X, \eta )$
of
![]() $OG10$
type and a finite group of symplectic birational transformations
$OG10$
type and a finite group of symplectic birational transformations
![]() $G\leq \mathrm {Bir}_s(X)$
. Then, up to conjugacy,
$G\leq \mathrm {Bir}_s(X)$
. Then, up to conjugacy,
![]() $\eta _\ast (G)\leq O(\Lambda )$
is contained in one of the 375 saturated groups of the dataset [Reference Marquand and Muller30].
$\eta _\ast (G)\leq O(\Lambda )$
is contained in one of the 375 saturated groups of the dataset [Reference Marquand and Muller30].
We outline our strategy to prove Theorem 5.1. In Section 5.1, we explain our adaptation of the Brandhorst–Hashimoto–Hofmann extension approach. Briefly, we develop a method to extend symplectic finite groups
![]() $H^\#$
that act trivially on the discriminant group
$H^\#$
that act trivially on the discriminant group
![]() $D_\Lambda $
by
$D_\Lambda $
by
![]() $\mu _2$
to obtain a subgroup
$\mu _2$
to obtain a subgroup
![]() $H\leq O^+(\Lambda )$
that is both symplectic and saturated. Note that for any generator
$H\leq O^+(\Lambda )$
that is both symplectic and saturated. Note that for any generator
![]() $hH^\#$
of
$hH^\#$
of
![]() $H/H^\#\cong \mu _2$
, the isometry h determines an equivariant primitive extension
$H/H^\#\cong \mu _2$
, the isometry h determines an equivariant primitive extension
Since the group H is generated by
![]() $H^\#$
and h, knowing
$H^\#$
and h, knowing
![]() $\Lambda _{H^\#}\subseteq \Lambda $
, the pair
$\Lambda _{H^\#}\subseteq \Lambda $
, the pair
![]() $(\Lambda ^{H^\#}, h|_{\Lambda ^{H^\#}})$
and the previous equivariant primitive extension, is enough to reconstruct
$(\Lambda ^{H^\#}, h|_{\Lambda ^{H^\#}})$
and the previous equivariant primitive extension, is enough to reconstruct
![]() $H\leq O^+(\Lambda )$
. The main result of the section is Theorem 5.9, which provides us with a way to construct all possible extensions of a symplectic finite subgroup
$H\leq O^+(\Lambda )$
. The main result of the section is Theorem 5.9, which provides us with a way to construct all possible extensions of a symplectic finite subgroup
![]() $H^\#\leq O^{+, \#}(\Lambda )$
starting from the primitive sublattice
$H^\#\leq O^{+, \#}(\Lambda )$
starting from the primitive sublattice
![]() $\Lambda _{H^\#}\subseteq \Lambda .$
In Appendix D, we explain the algorithms to undertake this procedure and prove that for a given primitive sublattice
$\Lambda _{H^\#}\subseteq \Lambda .$
In Appendix D, we explain the algorithms to undertake this procedure and prove that for a given primitive sublattice
![]() $\Lambda _{H^\#}\subseteq \Lambda $
they return a complete set of conjugacy classes of
$\Lambda _{H^\#}\subseteq \Lambda $
they return a complete set of conjugacy classes of
![]() $(\Lambda , H)$
with
$(\Lambda , H)$
with
![]() $H\leq O^+(\Lambda )$
symplectic finite subgroup extending
$H\leq O^+(\Lambda )$
symplectic finite subgroup extending
![]() $H^\#$
as in Equation (3.1). We prove Theorem 5.1 in Section 5.2 – our classification is contained in the folder ‘data’ of the dataset [Reference Marquand and Muller30].
$H^\#$
as in Equation (3.1). We prove Theorem 5.1 in Section 5.2 – our classification is contained in the folder ‘data’ of the dataset [Reference Marquand and Muller30].
5.1 Brandhorst–Hashimoto–Hofmann extension approach
In what follows, we adapt the extension approach as described in [Reference Brandhorst and Hashimoto4, Reference Brandhorst and Hofmann5] to our context. We do not expect that the reader is familiar with the content of the previously cited works. Our presentation of what follows is self contained.
Let again
![]() $\Lambda := U^3\oplus E_8^2\oplus A_2$
. Let
$\Lambda := U^3\oplus E_8^2\oplus A_2$
. Let
![]() $H\leq O^+(\Lambda )$
be finite such that
$H\leq O^+(\Lambda )$
be finite such that
![]() $H^\#$
is nontrivial and
$H^\#$
is nontrivial and
![]() $H\neq H^\#$
. Note that
$H\neq H^\#$
. Note that
![]() $\Lambda $
is unique in its genus, and for any lattice
$\Lambda $
is unique in its genus, and for any lattice
![]() $\Lambda '\cong \Lambda $
, we denote by
$\Lambda '\cong \Lambda $
, we denote by
![]() $\mathcal {W}^{pex}(\Lambda ')$
to be the set
$\mathcal {W}^{pex}(\Lambda ')$
to be the set
![]() $\varphi (\mathcal {W}^{pex})$
for any isometry
$\varphi (\mathcal {W}^{pex})$
for any isometry
![]() $\varphi \colon \Lambda \xrightarrow {\cong }\Lambda '$
. We have seen that there is an exact sequence (Equation (3.1))
$\varphi \colon \Lambda \xrightarrow {\cong }\Lambda '$
. We have seen that there is an exact sequence (Equation (3.1))
where the character
![]() $H\to \mu _2$
is induced by the discriminant representation
$H\to \mu _2$
is induced by the discriminant representation
![]() $H\to O(D_\Lambda )$
. In particular,
$H\to O(D_\Lambda )$
. In particular,
![]() $[H:H^\#] = 2$
and there exists a nonstable isometry
$[H:H^\#] = 2$
and there exists a nonstable isometry
![]() $h\in H\setminus H^\#$
such that
$h\in H\setminus H^\#$
such that
![]() $H/H^\#$
is generated by
$H/H^\#$
is generated by
![]() $hH^\#$
. The restriction a of h to
$hH^\#$
. The restriction a of h to
![]() $\Lambda ^{H^\#}$
has order
$\Lambda ^{H^\#}$
has order
![]() $2$
, except when
$2$
, except when
![]() $H^\#$
is not saturated in
$H^\#$
is not saturated in
![]() $O^+(\Lambda )$
and
$O^+(\Lambda )$
and
![]() $\Lambda ^{H^\#} = \Lambda ^{H}$
, in which case
$\Lambda ^{H^\#} = \Lambda ^{H}$
, in which case
![]() $a = {id}$
(see Proposition 4.23). In both cases, we observe that the definition of
$a = {id}$
(see Proposition 4.23). In both cases, we observe that the definition of
![]() $a\in O(\Lambda ^{H^\#})$
does not depend on a choice of a representative of
$a\in O(\Lambda ^{H^\#})$
does not depend on a choice of a representative of
![]() $hH^\#$
. However, for any
$hH^\#$
. However, for any
![]() $h'\in hH^\#$
, the restriction b of
$h'\in hH^\#$
, the restriction b of
![]() $h'$
to
$h'$
to
![]() $\Lambda _{H^\#}$
does depend on the choice of
$\Lambda _{H^\#}$
does depend on the choice of
![]() $h'$
, and it determines an equivariant primitive extension
$h'$
, and it determines an equivariant primitive extension
![]() $(\Lambda ^{H^\#}, a)\oplus (\Lambda _{H^\#}, b)\subseteq (\Lambda , h')$
with associated glue map
$(\Lambda ^{H^\#}, a)\oplus (\Lambda _{H^\#}, b)\subseteq (\Lambda , h')$
with associated glue map
![]() $\gamma $
.
$\gamma $
.
Remark 5.2. Even though the equivariant primitive extension
depends on the choice of
![]() $h'$
, the associated glue map
$h'$
, the associated glue map
![]() $\gamma $
does not depend on any
$\gamma $
does not depend on any
![]() $h'\in hH^\#$
or even on a. Indeed,
$h'\in hH^\#$
or even on a. Indeed,
![]() $\gamma $
is the glue map of the primitive extension
$\gamma $
is the glue map of the primitive extension
![]() $\Lambda ^{H^\#}\oplus \Lambda _{H^\#}\subseteq \Lambda $
.
$\Lambda ^{H^\#}\oplus \Lambda _{H^\#}\subseteq \Lambda $
.
Definition 5.3. Let H be a symplectic finite subgroup of
![]() $O^+(\Lambda )$
. We define
$O^+(\Lambda )$
. We define
-
1. the heart of H to be the stable symplectic lattice
 $\Lambda _{H^\#}$
;
$\Lambda _{H^\#}$
; -
2. the head of H to be the pair
 $(\Lambda ^{H^\#}, a)$
;
$(\Lambda ^{H^\#}, a)$
; -
3. the spine of H to be the glue map
 $\gamma $
.
$\gamma $
.
Remark 5.4. For a finite subgroup
![]() $H\leq O^+(\Lambda )$
, if H is saturated in
$H\leq O^+(\Lambda )$
, if H is saturated in
![]() $O^+(\Lambda )$
, then
$O^+(\Lambda )$
, then
![]() $H^\#$
is saturated
$H^\#$
is saturated
![]() $O^{+, \#}(\Lambda )$
(Lemma 2.3). In particular, the group
$O^{+, \#}(\Lambda )$
(Lemma 2.3). In particular, the group
![]() $H^\#$
is completely characterised by the primitive sublattice
$H^\#$
is completely characterised by the primitive sublattice
![]() $\Lambda _{H^\#}\subseteq \Lambda $
, and it is equal to
$\Lambda _{H^\#}\subseteq \Lambda $
, and it is equal to
![]() $O^\#(\Lambda _{H^\#})$
(Lemma 4.2). Moreover, the sublattice
$O^\#(\Lambda _{H^\#})$
(Lemma 4.2). Moreover, the sublattice
![]() $\Lambda _{H^\#}\subseteq \Lambda $
is a heart, as defined in Definition 4.7.
$\Lambda _{H^\#}\subseteq \Lambda $
is a heart, as defined in Definition 4.7.
Proposition 5.5. Let
![]() $H_1,H_2\leq O^+(\Lambda )$
be two symplectic finite subgroups and let
$H_1,H_2\leq O^+(\Lambda )$
be two symplectic finite subgroups and let
![]() $\psi \in O^+(\Lambda )$
conjugate
$\psi \in O^+(\Lambda )$
conjugate
![]() $H_1$
and
$H_1$
and
![]() $H_2$
. Then
$H_2$
. Then
-
1.
 $\psi $
restricts to an isometry between the respective hearts of
$\psi $
restricts to an isometry between the respective hearts of
 $H_1$
and
$H_1$
and
 $H_2$
;
$H_2$
; -
2.
 $\psi $
induces an isomorphism between the respective heads of
$\psi $
induces an isomorphism between the respective heads of
 $H_1$
and
$H_1$
and
 $H_2$
.
$H_2$
.
Proof. The first claim follows by definition of
![]() $\psi $
, and the second claim follows from the fact that the definition of the heads does not depend on the choice of a representative for the generators of
$\psi $
, and the second claim follows from the fact that the definition of the heads does not depend on the choice of a representative for the generators of
![]() $H_1/H_1^\#$
and
$H_1/H_1^\#$
and
![]() $H_2/H_2^\#$
respectively.
$H_2/H_2^\#$
respectively.
From Proposition 5.5, one sees that two conjugate symplectic finite subgroups of
![]() $O^+(\Lambda )$
share the same heart and head. We would like to measure to which extent the converse holds and describe an algorithm to compute representatives of conjugacy classes of such groups with given heart and head.
$O^+(\Lambda )$
share the same heart and head. We would like to measure to which extent the converse holds and describe an algorithm to compute representatives of conjugacy classes of such groups with given heart and head.
Definition 5.6. Let
![]() $C\subseteq \Lambda $
be a heart, and let
$C\subseteq \Lambda $
be a heart, and let
![]() $F := C^\perp _\Lambda $
. A head of C is a pair
$F := C^\perp _\Lambda $
. A head of C is a pair
![]() $(F,a)$
where the isometry
$(F,a)$
where the isometry
![]() $a\in O(F)$
has order
$a\in O(F)$
has order
![]() $n=1,2$
, and
$n=1,2$
, and
![]() $F_a$
is negative definite or trivial. We call
$F_a$
is negative definite or trivial. We call
![]() $n\in \{1,2\}$
the order of the head.
$n\in \{1,2\}$
the order of the head.
Now, for each head
![]() $(F,a)$
of a given heart C, we would like to classify isomorphism classes of equivariant primitive extensions
$(F,a)$
of a given heart C, we would like to classify isomorphism classes of equivariant primitive extensions
such that
![]() $b\notin O^\#(C)$
if
$b\notin O^\#(C)$
if
![]() $a= {id}_F$
. Indeed, we know that the extension of
$a= {id}_F$
. Indeed, we know that the extension of
![]() $O^\#(C)$
with the identity on F is stable.
$O^\#(C)$
with the identity on F is stable.
Definition 5.7. Let C be a heart and let
![]() $(F, a)$
be a head of C of order
$(F, a)$
be a head of C of order
![]() $n\in \{1,2\}$
. A spine between C and
$n\in \{1,2\}$
. A spine between C and
![]() $(F,a)$
is a glue map
$(F,a)$
is a glue map
such that
-
1.
 $D_aH_F \leq H_F$
;
$D_aH_F \leq H_F$
; -
2. there exists
 $b\in O(C)$
such that
$b\in O(C)$
such that
 $b\notin O^\#(C)$
if
$b\notin O^\#(C)$
if
 $a = {id}_F$
,
$a = {id}_F$
,
 $D_bH_C\leq H_C$
and
$D_bH_C\leq H_C$
and
 $\gamma $
is
$\gamma $
is
 $(a, b)$
-equivariant;
$(a, b)$
-equivariant; -
3. the equivariant primitive extension
 $(F, a)\oplus (C, b)\subseteq (\Lambda _\gamma , h)$
is such that
$(F, a)\oplus (C, b)\subseteq (\Lambda _\gamma , h)$
is such that-
(a)
 $\Lambda _\gamma \cong \Lambda $
;
$\Lambda _\gamma \cong \Lambda $
; -
(b)
 $h\in O^+(\Lambda _\gamma )\setminus O^\#(\Lambda _\gamma )$
;
$h\in O^+(\Lambda _\gamma )\setminus O^\#(\Lambda _\gamma )$
; -
(c)
 $(\Lambda _\gamma )_{H_\gamma }\cap \mathcal {W}^{pex}(\Lambda _\gamma ) = \varnothing $
where
$(\Lambda _\gamma )_{H_\gamma }\cap \mathcal {W}^{pex}(\Lambda _\gamma ) = \varnothing $
where
 $H_\gamma := \langle O^\#(C),\, h\rangle $
.
$H_\gamma := \langle O^\#(C),\, h\rangle $
.
-
If it exists, we call the isometry b a companion of a along
![]() $\gamma $
.
$\gamma $
.
It is not hard to see that the previous definitions are such that the heart
![]() $C := \Lambda _{H^\#}$
of any symplectic finite subgroup
$C := \Lambda _{H^\#}$
of any symplectic finite subgroup
![]() $H\leq O^+(\Lambda )$
is a heart and its head
$H\leq O^+(\Lambda )$
is a heart and its head
![]() $(\Lambda ^{H^\#}, a)$
is a head of C.
$(\Lambda ^{H^\#}, a)$
is a head of C.
For two lattices
![]() $L_1, L_2$
and two groups of isometries
$L_1, L_2$
and two groups of isometries
![]() $G_i\leq O(L_i)$
(
$G_i\leq O(L_i)$
(
![]() $i=1,2$
), we call the pairs
$i=1,2$
), we call the pairs
![]() $(L_1, G_1)$
and
$(L_1, G_1)$
and
![]() $(L_2, G_2)$
conjugate if there exists an isometry
$(L_2, G_2)$
conjugate if there exists an isometry
![]() $\psi \colon L_1\to L_2$
such that
$\psi \colon L_1\to L_2$
such that
![]() $G_2 = \psi G_1\psi ^{-1}$
. The following holds.
$G_2 = \psi G_1\psi ^{-1}$
. The following holds.
Theorem 5.8. Let C be a heart and let
![]() $(F, a)$
be a head of C of order
$(F, a)$
be a head of C of order
![]() $n\in \{1,2\}$
. Let
$n\in \{1,2\}$
. Let
![]() $D_F\geq H_F \xrightarrow {\gamma } H_C\leq D_C$
be a spine between C and
$D_F\geq H_F \xrightarrow {\gamma } H_C\leq D_C$
be a spine between C and
![]() $(F,a)$
, and let
$(F,a)$
, and let
![]() $b\in O(C)$
be a companion of a along
$b\in O(C)$
be a companion of a along
![]() $\gamma $
. Then
$\gamma $
. Then
-
1.
 $H_\gamma /O^\#(C)$
is a cyclic group of order 2;
$H_\gamma /O^\#(C)$
is a cyclic group of order 2; -
2.
 $H_\gamma \leq O^+(\Lambda _\gamma )$
is symplectic and
$H_\gamma \leq O^+(\Lambda _\gamma )$
is symplectic and
 $\overline {H_\gamma } \leq O(D_{\Lambda _\gamma })$
has order 2;
$\overline {H_\gamma } \leq O(D_{\Lambda _\gamma })$
has order 2; -
3. the definition of
 $H_\gamma $
is independent of the choice of b;
$H_\gamma $
is independent of the choice of b; -
4. the conjugacy class of
 $(\Lambda _\gamma , H_\gamma )$
is invariant under the action of
$(\Lambda _\gamma , H_\gamma )$
is invariant under the action of
 $O(C)$
and
$O(C)$
and
 $O(F, a)$
.
$O(F, a)$
.
Proof. We let
![]() $h := a\oplus b$
, where a is an isometry of F of order at most 2 and
$h := a\oplus b$
, where a is an isometry of F of order at most 2 and
![]() $b \notin O^\#(C)$
if
$b \notin O^\#(C)$
if
![]() $a = {id}_F$
. Since
$a = {id}_F$
. Since
![]() $O(D_{\Lambda _\gamma })$
has order 2, we have that
$O(D_{\Lambda _\gamma })$
has order 2, we have that
![]() $D_{h}^2$
is trivial. Thus,
$D_{h}^2$
is trivial. Thus,
![]() $h^2 = {id}_F\oplus b^2$
must lie in
$h^2 = {id}_F\oplus b^2$
must lie in
![]() $O^\#(C)$
because
$O^\#(C)$
because
![]() $O^\#(C)$
is saturated in
$O^\#(C)$
is saturated in
![]() $O^{+,\#}(\Lambda _\gamma )$
. By definition of a, we moreover know that h has negative definite coinvariant sublattice, which implies that
$O^{+,\#}(\Lambda _\gamma )$
. By definition of a, we moreover know that h has negative definite coinvariant sublattice, which implies that
![]() $h\in O^+(\Lambda _\gamma )$
by Remark 3.7. It follows that
$h\in O^+(\Lambda _\gamma )$
by Remark 3.7. It follows that
![]() $H_\gamma := \langle h,\, O^\#(C)\rangle \leq O^+(\Lambda _\gamma )$
also has negative definite coinvariant sublattice, and by definition of
$H_\gamma := \langle h,\, O^\#(C)\rangle \leq O^+(\Lambda _\gamma )$
also has negative definite coinvariant sublattice, and by definition of
![]() $\gamma $
, we obtain that
$\gamma $
, we obtain that
![]() $H_\gamma $
is symplectic (Lemma 3.6). Moreover,
$H_\gamma $
is symplectic (Lemma 3.6). Moreover,
![]() $O^\#(C) = H_\gamma ^\#$
is normal in
$O^\#(C) = H_\gamma ^\#$
is normal in
![]() $H_\gamma $
, so we have that
$H_\gamma $
, so we have that
![]() $H_\gamma /O^\#(C)=\langle hO^\#(C)\rangle $
has order 2.
$H_\gamma /O^\#(C)=\langle hO^\#(C)\rangle $
has order 2.
Now, if one had chosen
![]() $b\neq b'\in O(C)$
such that
$b\neq b'\in O(C)$
such that
![]() $H_C$
is
$H_C$
is
![]() $D_{b'}$
-stable and
$D_{b'}$
-stable and
![]() $\gamma \circ (D_a)_{\mid H_F} = (D_{b'})_{\mid H_C}\circ \gamma $
, giving rise to an isometry
$\gamma \circ (D_a)_{\mid H_F} = (D_{b'})_{\mid H_C}\circ \gamma $
, giving rise to an isometry
![]() $h'\in O(\Lambda _\gamma )$
, then
$h'\in O(\Lambda _\gamma )$
, then
![]() $h^{-1}h' = {id}_F\oplus b^{-1}b'$
would act trivially on F with
$h^{-1}h' = {id}_F\oplus b^{-1}b'$
would act trivially on F with
![]() $D_{h^{-1}h'} = D_{h^{-1}}D_{h'}$
trivial. Therefore,
$D_{h^{-1}h'} = D_{h^{-1}}D_{h'}$
trivial. Therefore,
![]() $b' \in bO^\#(C)$
since
$b' \in bO^\#(C)$
since
![]() $O^\#(C)$
is saturated in
$O^\#(C)$
is saturated in
![]() $O^{+, \#}(\Lambda _\gamma )$
, and thus,
$O^{+, \#}(\Lambda _\gamma )$
, and thus,
![]() $\langle O^\#(C),\, h\rangle = \langle O^\#(C),\, h'\rangle $
.
$\langle O^\#(C),\, h\rangle = \langle O^\#(C),\, h'\rangle $
.
Finally, let
![]() $\psi \in O(F, a)$
and let
$\psi \in O(F, a)$
and let
![]() $c\in O(C)$
. Then, for any spine
$c\in O(C)$
. Then, for any spine
between C and
![]() $(F, a)$
with companion b of a, the glue map
$(F, a)$
with companion b of a, the glue map
is a spine between C and
![]() $(F, a)$
, and
$(F, a)$
, and
![]() $cbc^{-1}$
is a companion of a along
$cbc^{-1}$
is a companion of a along
![]() $\gamma _2$
. By [Reference Nikulin36, Corollary 1.5.2],
$\gamma _2$
. By [Reference Nikulin36, Corollary 1.5.2],
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
indeed defines isomorphic equivariant primitive extensions, and since
$\gamma _2$
indeed defines isomorphic equivariant primitive extensions, and since
![]() $O^\#(C)$
is normal in
$O^\#(C)$
is normal in
![]() $O(C)$
, the corresponding resulting isometry
$O(C)$
, the corresponding resulting isometry
![]() $\psi ^{-1}\oplus c\colon L_{\gamma _1}\xrightarrow {\cong }L_{\gamma _2}$
conjugates
$\psi ^{-1}\oplus c\colon L_{\gamma _1}\xrightarrow {\cong }L_{\gamma _2}$
conjugates
![]() $\langle O^\#(C), a\oplus b\rangle \leq O^+(\Lambda _{\gamma _1})$
and
$\langle O^\#(C), a\oplus b\rangle \leq O^+(\Lambda _{\gamma _1})$
and
![]() $\langle O^\#(C), a\oplus cbc^{-1} \rangle \leq O^+(\Lambda _{\gamma _2})$
. The rest of the proof follows from the Definition 5.7.
$\langle O^\#(C), a\oplus cbc^{-1} \rangle \leq O^+(\Lambda _{\gamma _2})$
. The rest of the proof follows from the Definition 5.7.
Hence, the definitions of hearts, heads and spines are consistent with Definition 5.3. The following Theorem gives a converse to Proposition 5.5, and it is a stated in such a way that we can describe an effective algorithm out of it.
Theorem 5.9. Let C be a heart, let
![]() $(F,a)$
be a head of C of order
$(F,a)$
be a head of C of order
![]() $n\in \{1,2\}$
and let S be the set of spines between C and
$n\in \{1,2\}$
and let S be the set of spines between C and
![]() $(F, a)$
. Then the double cosets in
$(F, a)$
. Then the double cosets in
are in bijection with the conjugacy classes of pairs
![]() $(\Lambda _\gamma , H_\gamma )$
, where
$(\Lambda _\gamma , H_\gamma )$
, where
![]() $\Lambda _\gamma \cong \Lambda $
and
$\Lambda _\gamma \cong \Lambda $
and
![]() $H_\gamma \leq O^+(\Lambda _\gamma )$
is a symplectic finite subgroup such that
$H_\gamma \leq O^+(\Lambda _\gamma )$
is a symplectic finite subgroup such that
![]() $H_\gamma ^\#$
is saturated in
$H_\gamma ^\#$
is saturated in
![]() $O^{+, \#}(\Lambda _\gamma )$
, the subgroup
$O^{+, \#}(\Lambda _\gamma )$
, the subgroup
![]() $\overline {H_\gamma }\leq O(D_{\Lambda _\gamma })$
has order 2, the heart of
$\overline {H_\gamma }\leq O(D_{\Lambda _\gamma })$
has order 2, the heart of
![]() $H_\gamma $
is isometric to C and the head of
$H_\gamma $
is isometric to C and the head of
![]() $H_\gamma $
is isomorphic to
$H_\gamma $
is isomorphic to
![]() $(F, a)$
.
$(F, a)$
.
Proof. One direction follows from Theorem 5.8, while the other is a direct consequence of Proposition 5.5. The converse follows from Proposition 5.5 and Theorem 5.8.
Based on Theorem 5.9, the strategy behind the extension approach can be summarised in the following way.
-
1. Start with a given heart
 $C\subseteq \Lambda $
, as classified in Proposition 4.20.
$C\subseteq \Lambda $
, as classified in Proposition 4.20. -
2. Determine a set
 $\mathcal {F}_C(n)$
of representatives of isomorphism classes of heads
$\mathcal {F}_C(n)$
of representatives of isomorphism classes of heads
 $(F, a)$
of C of given order
$(F, a)$
of C of given order
 $n=1,2$
. Such pairs
$n=1,2$
. Such pairs
 $(F, a)$
must satisfy that
$(F, a)$
must satisfy that
 $F\cong C^\perp _\Lambda $
,
$F\cong C^\perp _\Lambda $
,
 $a\in O(F)$
has order n and
$a\in O(F)$
has order n and
 $F_a$
is negative definite or trivial.
$F_a$
is negative definite or trivial. -
3. For each heart C and candidate head
 $(F, a)\in \mathcal {F}_C(n)$
of order
$(F, a)\in \mathcal {F}_C(n)$
of order
 $n=1,2$
, compute and classify equivariant primitive extensions
$n=1,2$
, compute and classify equivariant primitive extensions
 $(F,a)\oplus (C, b)\subseteq (\Lambda ', h)$
, where
$(F,a)\oplus (C, b)\subseteq (\Lambda ', h)$
, where
 $\Lambda '\cong \Lambda $
,
$\Lambda '\cong \Lambda $
,
 $D_h\neq {id}$
and where
$D_h\neq {id}$
and where
 $b\notin O^\#(C)$
if
$b\notin O^\#(C)$
if
 $a= {id}_F$
.
$a= {id}_F$
.
Step (3) is done by constructing spines representing each of the double cosets described in Theorem 5.9.
Remark 5.10. From a technical point of view, the classification of hearts C in step (1) has been completed in Section 4. The classification of lattices with isometry
![]() $(F, a)$
in step (2) has been solved algorithmically by Brandhorst and Hofmann in their work [Reference Brandhorst and Hofmann5]. Finally, the computation and classification of spines for step (3) can also be carried out systematically thanks to Nikulin’s theory on primitive embeddings [Reference Nikulin36]. Both of these procedures have been implemented by the second author in [Reference Decker, Eder, Fieker, Horn and Joswig12, QuadFormAndIsom].
$(F, a)$
in step (2) has been solved algorithmically by Brandhorst and Hofmann in their work [Reference Brandhorst and Hofmann5]. Finally, the computation and classification of spines for step (3) can also be carried out systematically thanks to Nikulin’s theory on primitive embeddings [Reference Nikulin36]. Both of these procedures have been implemented by the second author in [Reference Decker, Eder, Fieker, Horn and Joswig12, QuadFormAndIsom].
5.2 Results and comments
We implement the extension procedure described in Theorem 5.9 to the list of hearts of
![]() $\Lambda $
determined in Theorem 4.1, and we obtain the following.
$\Lambda $
determined in Theorem 4.1, and we obtain the following.
Theorem 5.11. Let
![]() $\mathcal {H}$
be an
$\mathcal {H}$
be an
![]() $O^+(\Lambda )$
-conjugacy class of symplectic finite subgroups
$O^+(\Lambda )$
-conjugacy class of symplectic finite subgroups
![]() $H\leq O^+(\Lambda )$
. Then a representative of
$H\leq O^+(\Lambda )$
. Then a representative of
![]() $\mathcal {H}$
is computable. Moreover, the folder ‘data’ of the dataset [Reference Marquand and Muller30] contains representatives for each such conjugacy class.
$\mathcal {H}$
is computable. Moreover, the folder ‘data’ of the dataset [Reference Marquand and Muller30] contains representatives for each such conjugacy class.
Proof. This follows from Theorems 5.8 and 5.9. The representatives contained in the dataset [Reference Marquand and Muller30] have been computed using Algorithms 0.1 and 0.2, which have been implemented in Oscar [Reference Decker, Eder, Fieker, Horn and Joswig12]. See Appendix D for more details on the algorithmic aspect of the theorem.
From this, we can conclude our classification of finite subgroups of symplectic birational transformations for IHS manifolds of
![]() $OG10$
type.
$OG10$
type.
Proof of Theorem 5.1.
The classification follows from Theorem 5.11. We obtain 934 pairs
![]() $(\Lambda ',H)$
with
$(\Lambda ',H)$
with
![]() $\Lambda '\cong \Lambda $
and
$\Lambda '\cong \Lambda $
and
![]() $H^\#\leq O^{+, \#}(\Lambda ')$
saturated. These are contained in the dataset [Reference Marquand and Muller30]. We extract 375 pairs
$H^\#\leq O^{+, \#}(\Lambda ')$
saturated. These are contained in the dataset [Reference Marquand and Muller30]. We extract 375 pairs
![]() $(\Lambda ',H)$
with H saturated in
$(\Lambda ',H)$
with H saturated in
![]() $O^+(\Lambda ')$
using Remark 4.22, which are described in Table 5 of the ancillary files.
$O^+(\Lambda ')$
using Remark 4.22, which are described in Table 5 of the ancillary files.
According to the data compiled in the dataset [Reference Marquand and Muller30], we obtain the largest cohomological actions (i.e., groups with nontrivial action on second cohomology) for IHS manifolds of known deformation type. Recall that a finite group
![]() $G\leq \mathrm {Bir}(X)$
is mixed if it contains both nontrivial symplectic and nonsymplectic birational transformations.
$G\leq \mathrm {Bir}(X)$
is mixed if it contains both nontrivial symplectic and nonsymplectic birational transformations.
Proposition 5.12. The largest cohomological actions for IHS manifolds of all known deformation types have order 6531840 in the symplectic case, and 39191040 in the mixed case.
Proof. According to Tables 4 and 5 of the ancillary files, the largest symplectic finite subgroup
![]() $H\leq O^+(\Lambda )$
we have determined is isomorphic to a semidirect product
$H\leq O^+(\Lambda )$
we have determined is isomorphic to a semidirect product
![]() $\text {PSU}(4,3)\rtimes C_2$
(Id ‘163a.1’), and its order is
$\text {PSU}(4,3)\rtimes C_2$
(Id ‘163a.1’), and its order is
![]() $\#H=6531840$
. Note that this group is saturated in
$\#H=6531840$
. Note that this group is saturated in
![]() $O^+(\Lambda )$
. We prove that this group is maximal (in size) among all the finite groups of symplectic isometries of
$O^+(\Lambda )$
. We prove that this group is maximal (in size) among all the finite groups of symplectic isometries of
![]() $H^2(X, \mathbb {Z})$
for X an IHS manifold of known deformation type.
$H^2(X, \mathbb {Z})$
for X an IHS manifold of known deformation type.
By similar arguments as the ones used in this paper, the maximal order in the
![]() $K3^{[n]}$
cases (
$K3^{[n]}$
cases (
![]() $n\geq 1$
) is bounded above by 491520 ([Reference Höhn and Mason19, Table 2]). For an IHS manifold X of
$n\geq 1$
) is bounded above by 491520 ([Reference Höhn and Mason19, Table 2]). For an IHS manifold X of
![]() $Kum_n$
type (
$Kum_n$
type (
![]() $n\geq 2$
) or
$n\geq 2$
) or
![]() $OG6$
type, the negative signature of
$OG6$
type, the negative signature of
![]() $H^2(X, \mathbb {Z})$
is
$H^2(X, \mathbb {Z})$
is
![]() $k = 4$
or
$k = 4$
or
![]() $k=5$
, respectively. By the known bounds on the order of finite subgroups of
$k=5$
, respectively. By the known bounds on the order of finite subgroups of
![]() $\mathrm {GL}_k(\mathbb {Z})$
for
$\mathrm {GL}_k(\mathbb {Z})$
for
![]() $k=4,5$
, we know that the maximal orders in those cases is smaller than 200000.
$k=4,5$
, we know that the maximal orders in those cases is smaller than 200000.
Let
![]() $H= \text {PSU}(4,3)\rtimes C_2\leq O^+(\Lambda ).$
The invariant sublattice
$H= \text {PSU}(4,3)\rtimes C_2\leq O^+(\Lambda ).$
The invariant sublattice
![]() $F:= \Lambda ^H$
has Gram matrix
$F:= \Lambda ^H$
has Gram matrix
 $\scriptscriptstyle {\begin {pmatrix}2&-1&0\\-1&2&0\\0&0&4\end {pmatrix}}$
in its standard basis. This lattice admits an order 6 isometry
$\scriptscriptstyle {\begin {pmatrix}2&-1&0\\-1&2&0\\0&0&4\end {pmatrix}}$
in its standard basis. This lattice admits an order 6 isometry
![]() $a\in O(F)$
given by
$a\in O(F)$
given by
 $$ \begin{align*}\scriptscriptstyle{\begin{pmatrix}0&-1&0\\1&1&0\\0&0&1\end{pmatrix}},\end{align*} $$
$$ \begin{align*}\scriptscriptstyle{\begin{pmatrix}0&-1&0\\1&1&0\\0&0&1\end{pmatrix}},\end{align*} $$
with characteristic polynomial
![]() $\Phi _1\Phi _6$
. Using Equation (EGC), one can show that there exists an isometry
$\Phi _1\Phi _6$
. Using Equation (EGC), one can show that there exists an isometry
![]() $b\in O(\Lambda _H)$
such that we have an equivariant primitive extension
$b\in O(\Lambda _H)$
such that we have an equivariant primitive extension
where
![]() $\Lambda '\cong \Lambda $
. Since
$\Lambda '\cong \Lambda $
. Since
![]() $\Lambda _H$
is negative definite, such an isometry b is effectively computable using an algorithm of Plesken–Souvignier [Reference Plesken and Souvignier40]. The invariant sublattice
$\Lambda _H$
is negative definite, such an isometry b is effectively computable using an algorithm of Plesken–Souvignier [Reference Plesken and Souvignier40]. The invariant sublattice
![]() $(\Lambda ')^c$
has signature
$(\Lambda ')^c$
has signature
![]() $(1, \ast )$
and the isometry
$(1, \ast )$
and the isometry
![]() $c\in O^+(\Lambda ')$
. Moreover,
$c\in O^+(\Lambda ')$
. Moreover,
![]() $N := (\ker \Phi _1(c)\Phi _6(c))^\perp _{\Lambda '}\subseteq F^\perp _{\Lambda '} = \Lambda _H$
satisfies that
$N := (\ker \Phi _1(c)\Phi _6(c))^\perp _{\Lambda '}\subseteq F^\perp _{\Lambda '} = \Lambda _H$
satisfies that
![]() $N\cap \mathcal {W}^{pex}(\Lambda ')$
: in particular, similarly to [Reference Brandhorst and Hofmann5, Proposition 3.3], we can conclude that
$N\cap \mathcal {W}^{pex}(\Lambda ')$
: in particular, similarly to [Reference Brandhorst and Hofmann5, Proposition 3.3], we can conclude that
![]() $c\in O^+(\Lambda ')$
is effective and
$c\in O^+(\Lambda ')$
is effective and
![]() $\langle H, \,c\rangle $
is an effective finite subgroup of
$\langle H, \,c\rangle $
is an effective finite subgroup of
![]() $O^+(\Lambda ')$
(in the sense of [Reference Brandhorst and Hofmann5, Definition 3.2]). In particular, by the Strong Torelli theorem and the surjectivity of the period map,
$O^+(\Lambda ')$
(in the sense of [Reference Brandhorst and Hofmann5, Definition 3.2]). In particular, by the Strong Torelli theorem and the surjectivity of the period map,
![]() $\langle H, \,c\rangle $
has a faithful action by birational transformations on an IHS manifolds of
$\langle H, \,c\rangle $
has a faithful action by birational transformations on an IHS manifolds of
![]() $OG10$
type. As before, we claim that the action of this group on cohomology has maximal order for all known deformation types. See the Notebook ‘Maximal’ of the dataset [Reference Marquand and Muller30] for the computational details.
$OG10$
type. As before, we claim that the action of this group on cohomology has maximal order for all known deformation types. See the Notebook ‘Maximal’ of the dataset [Reference Marquand and Muller30] for the computational details.
Remark 5.13. The group
![]() $\text {PSU}(4,3)$
is a well-known group, and it appears to act faithfully on some other special objects. For instance, the authors in [Reference Ohashi and Schütt38] show that
$\text {PSU}(4,3)$
is a well-known group, and it appears to act faithfully on some other special objects. For instance, the authors in [Reference Ohashi and Schütt38] show that
![]() $\text {PSU}(4,3)$
is the largest finite group acting symplectically on a supersingular K3 surface of Artin invariant 1. Another recent occurrence of this group is in [Reference Yang, Yu and Zhu48], where it was shown that the automorphism group of the most symmetric sextic fourfold is a degree 2 extension of
$\text {PSU}(4,3)$
is the largest finite group acting symplectically on a supersingular K3 surface of Artin invariant 1. Another recent occurrence of this group is in [Reference Yang, Yu and Zhu48], where it was shown that the automorphism group of the most symmetric sextic fourfold is a degree 2 extension of
![]() $\text {PSU}(4, 3)$
(such sextic fourfold has been known since Todd [Reference Todd43], and it is intrinsically related to the Coxeter–Todd lattice
$\text {PSU}(4, 3)$
(such sextic fourfold has been known since Todd [Reference Todd43], and it is intrinsically related to the Coxeter–Todd lattice
![]() $K_{12}$
; see [Reference Conway and Sloane10]).
$K_{12}$
; see [Reference Conway and Sloane10]).
6 Geometrical Interpretations
In this section, we provide geometric realisations for some of the groups listed in the classification of Section 5. First, in Section 6.1, we investigate the possible groups that can be induced from a cubic fourfold via the LSV construction of [Reference Laza, Saccà and Voisin25], [Reference Saccà42]. In particular, we prove:
Theorem 6.1. Let X be an IHS manifold of
![]() $OG10$
type and let
$OG10$
type and let
![]() $G\leq \mathrm {Bir}_s(X)$
be a finite group of symplectic birational transformations. Suppose that
$G\leq \mathrm {Bir}_s(X)$
be a finite group of symplectic birational transformations. Suppose that
![]() $\Lambda ^G\cong U\oplus \Gamma $
holds, for some lattice
$\Lambda ^G\cong U\oplus \Gamma $
holds, for some lattice
![]() $\Gamma $
. Then there exists some smooth cubic fourfold V and an embedding
$\Gamma $
. Then there exists some smooth cubic fourfold V and an embedding
![]() $j\colon G\hookrightarrow \mathrm {Aut}(V)$
such that
$j\colon G\hookrightarrow \mathrm {Aut}(V)$
such that
-
1. either G acts trivially on the discriminant group
 $D_\Lambda $
, and
$D_\Lambda $
, and
 $j(G)\leq \mathrm {Aut}_s(V)$
;
$j(G)\leq \mathrm {Aut}_s(V)$
; -
2. or
 $G=\langle G_s, \phi \rangle $
with
$G=\langle G_s, \phi \rangle $
with
 $j(G_s)\leq \mathrm {Aut}_s(V)$
, and
$j(G_s)\leq \mathrm {Aut}_s(V)$
, and
 $j(\phi )\in \mathrm {Aut}(V)\setminus \mathrm {Aut}_s(V)$
is antisymplectic.
$j(\phi )\in \mathrm {Aut}(V)\setminus \mathrm {Aut}_s(V)$
is antisymplectic.
The pair
![]() $(G_s, \Lambda _{G_s})$
occurs in the classification of [Reference Laza and Zheng26].
$(G_s, \Lambda _{G_s})$
occurs in the classification of [Reference Laza and Zheng26].
Conversely, for any smooth cubic fourfold V, any LSV manifold
![]() $X_V$
associated to V and any finite subgroup
$X_V$
associated to V and any finite subgroup
![]() $G\leq \mathrm {Aut}(V)$
so that
$G\leq \mathrm {Aut}(V)$
so that
![]() $[G:G_s]\leq 2$
holds, there is an embedding of G into the group
$[G:G_s]\leq 2$
holds, there is an embedding of G into the group
![]() $\mathrm {Bir}_s(X_V)$
of symplectic birational transformations on
$\mathrm {Bir}_s(X_V)$
of symplectic birational transformations on
![]() $X_V$
.
$X_V$
.
In Section 6.2, we use similar techniques of [Reference Billi and Grossi2] to investigate when a group of symplectic birational transformations of an IHS manifold of
![]() $OG10$
type is induced from a cubic fourfold via the twisted LSV construction of [Reference Voisin45]. Such a group is isomorphic to a stable symplectic finite subgroup
$OG10$
type is induced from a cubic fourfold via the twisted LSV construction of [Reference Voisin45]. Such a group is isomorphic to a stable symplectic finite subgroup
![]() $H\leq O^{+,\#}(\Lambda )$
whose heart
$H\leq O^{+,\#}(\Lambda )$
whose heart
![]() $\Lambda _H$
embeds primitively into the Leech lattice, as in Section 4; we list the Id’s of the pairs from Table 3 that can be induced in this way in Corollary 6.11.
$\Lambda _H$
embeds primitively into the Leech lattice, as in Section 4; we list the Id’s of the pairs from Table 3 that can be induced in this way in Corollary 6.11.
Next, in Section 6.3, we apply the criteria developed recently in [Reference Felisetti, Giovenzana and Grossi13] to investigate when a group of symplectic birational transformations of an IHS manifold of
![]() $OG10$
type is induced from an underlying
$OG10$
type is induced from an underlying
![]() $K3$
surface. Such manifolds are necessarily numerical moduli spaces; that is, they are birational to a certain moduli space of sheaves on a
$K3$
surface. Such manifolds are necessarily numerical moduli spaces; that is, they are birational to a certain moduli space of sheaves on a
![]() $K3$
surface.
$K3$
surface.
6.1 LSV manifolds
Let
![]() $V\subset \mathbb {P}^5$
be a smooth cubic fourfold. By the construction of [Reference Laza, Saccà and Voisin25, Reference Saccà42], there exists an IHS manifold
$V\subset \mathbb {P}^5$
be a smooth cubic fourfold. By the construction of [Reference Laza, Saccà and Voisin25, Reference Saccà42], there exists an IHS manifold
![]() $X_V$
and a Lagrangian fibration
$X_V$
and a Lagrangian fibration
![]() $\pi :X_V\rightarrow (\mathbb {P}^5)^{\vee }$
that compactifies the intermediate Jacobian fibration associated to V. Further, the manifold
$\pi :X_V\rightarrow (\mathbb {P}^5)^{\vee }$
that compactifies the intermediate Jacobian fibration associated to V. Further, the manifold
![]() $X_V$
is an IHS manifold of
$X_V$
is an IHS manifold of
![]() $OG10$
type. We call such a manifold an LSV manifold associated to V.
$OG10$
type. We call such a manifold an LSV manifold associated to V.
Remark 6.2. Note that such a compactification
![]() $X_V$
may not be unique – indeed, if the cubic fourfold
$X_V$
may not be unique – indeed, if the cubic fourfold
![]() $V\subset \mathbb {P}^5$
is not general, then uniqueness is not guaranteed. In particular, a cubic fourfold with nontrivial automorphism group is not Hodge general.
$V\subset \mathbb {P}^5$
is not general, then uniqueness is not guaranteed. In particular, a cubic fourfold with nontrivial automorphism group is not Hodge general.
We prove Theorem 6.1 in a series of propositions. First, we establish the existence of cubic fourfolds with specified group actions.
Proposition 6.3. Let X be an IHS manifold of
![]() $OG10$
type and let
$OG10$
type and let
![]() $G\leq \mathrm {Bir}_s(X)$
be a finite group of symplectic birational transformations. Suppose that
$G\leq \mathrm {Bir}_s(X)$
be a finite group of symplectic birational transformations. Suppose that
![]() $\Lambda ^G\cong U\oplus \Gamma $
holds, for some lattice
$\Lambda ^G\cong U\oplus \Gamma $
holds, for some lattice
![]() $\Gamma $
. Then there exists some smooth cubic fourfold V and an embedding
$\Gamma $
. Then there exists some smooth cubic fourfold V and an embedding
![]() $j\colon G\hookrightarrow \mathrm {Aut}(V)$
such that
$j\colon G\hookrightarrow \mathrm {Aut}(V)$
such that
-
1. either G acts trivially on the discriminant group
 $D_\Lambda $
, and
$D_\Lambda $
, and
 $j(G)\leq \mathrm {Aut}_s(V)$
;
$j(G)\leq \mathrm {Aut}_s(V)$
; -
2. or
 $G=\langle G_s, \phi \rangle $
with
$G=\langle G_s, \phi \rangle $
with
 $j(G_s)\leq \mathrm {Aut}_s(V)$
, and
$j(G_s)\leq \mathrm {Aut}_s(V)$
, and
 $j(\phi )\in \mathrm {Aut}(V)\setminus \mathrm {Aut}_s(V)$
is antisymplectic.
$j(\phi )\in \mathrm {Aut}(V)\setminus \mathrm {Aut}_s(V)$
is antisymplectic.
The pair
![]() $(G_s, \Lambda _{G_s})$
occurs in the classification of [Reference Laza and Zheng26].
$(G_s, \Lambda _{G_s})$
occurs in the classification of [Reference Laza and Zheng26].
Proof. This follows a similar strategy as [Reference Marquand and Muller29, Theorems 4.1 and 5.1]. In what follows, we identify G with a subgroup of
![]() $O(\Lambda )$
by fixing a marking of X.
$O(\Lambda )$
by fixing a marking of X.
Let
![]() $U_1:=U$
be such that
$U_1:=U$
be such that
![]() $\Lambda ^G =U_1\oplus \Gamma \hookrightarrow \Lambda $
, and denote by
$\Lambda ^G =U_1\oplus \Gamma \hookrightarrow \Lambda $
, and denote by
![]() $L:=(U_1)^\perp _{\Lambda (-1)}$
. Then L is an even lattice of signature
$L:=(U_1)^\perp _{\Lambda (-1)}$
. Then L is an even lattice of signature
![]() $(20, 2)$
and (recalling that
$(20, 2)$
and (recalling that
![]() $ADE$
lattices are assumed negative definite),
$ADE$
lattices are assumed negative definite),
The group G restricts to
![]() $G\leq O(L)$
with
$G\leq O(L)$
with
We choose a weight 4 pure Hodge structure H of
![]() $K3$
type on L, such that
$K3$
type on L, such that
![]() $H^{2,2}\cap L = \Lambda _G(-1)$
. In particular,
$H^{2,2}\cap L = \Lambda _G(-1)$
. In particular,
![]() $H^{3,1}\subset L^G$
, and since
$H^{3,1}\subset L^G$
, and since
![]() $\Lambda _G\cap \mathcal {W}^{pex}=\varnothing $
, we can apply the Global Torelli Theorem for cubic fourfolds ([Reference Voisin44], [49, Prop 1.3]). We obtain a smooth cubic fourfold V with
$\Lambda _G\cap \mathcal {W}^{pex}=\varnothing $
, we can apply the Global Torelli Theorem for cubic fourfolds ([Reference Voisin44], [49, Prop 1.3]). We obtain a smooth cubic fourfold V with
![]() $H^4(V,\mathbb {Z})_{prim}\cong H$
as Hodge structures.
$H^4(V,\mathbb {Z})_{prim}\cong H$
as Hodge structures.
First, we assume that G acts trivially on
![]() $D_\Lambda $
, and hence on
$D_\Lambda $
, and hence on
![]() $D_L.$
In order to conclude that G embeds in
$D_L.$
In order to conclude that G embeds in
![]() $\mathrm {Aut}_s(V)$
, we need to extend G to a group of isometries of
$\mathrm {Aut}_s(V)$
, we need to extend G to a group of isometries of
![]() $H^4(V,\mathbb {Z})$
fixing the square of the hyperplane class
$H^4(V,\mathbb {Z})$
fixing the square of the hyperplane class
![]() $h^2\in H^4(V,\mathbb {Z})$
. We have that
$h^2\in H^4(V,\mathbb {Z})$
. We have that
![]() $L\oplus \langle h^2\rangle \subset H^4(V,\mathbb {Z})$
. Since G, seen as a subgroup of
$L\oplus \langle h^2\rangle \subset H^4(V,\mathbb {Z})$
. Since G, seen as a subgroup of
![]() $O(L)$
, is stable, we can extend G with
$O(L)$
, is stable, we can extend G with
![]() $ {id}_{\langle h^2\rangle }$
to an isometry group of
$ {id}_{\langle h^2\rangle }$
to an isometry group of
![]() $H^4(V,\mathbb {Z})$
; it follows by the Torelli theorem for cubic fourfolds that G embeds into
$H^4(V,\mathbb {Z})$
; it follows by the Torelli theorem for cubic fourfolds that G embeds into
![]() $\mathrm {Aut}(V)$
. Further, in this case, it follows that G acts faithfully symplectically on V.
$\mathrm {Aut}(V)$
. Further, in this case, it follows that G acts faithfully symplectically on V.
Next, we assume that G does not act trivially on
![]() $D_\Lambda $
. In other words, there exists a short exact sequence as in Equation (3.1):
$D_\Lambda $
. In other words, there exists a short exact sequence as in Equation (3.1):
We can conclude that
![]() $G=\langle G^\#, a\rangle $
, where
$G=\langle G^\#, a\rangle $
, where
![]() $a\in O(\Lambda )$
acts nontrivially on
$a\in O(\Lambda )$
acts nontrivially on
![]() $D_\Lambda $
. Here, a has even order and
$D_\Lambda $
. Here, a has even order and
![]() $\Lambda ^a$
splits
$\Lambda ^a$
splits
![]() $U_1$
as well, since
$U_1$
as well, since
![]() $\Lambda _a$
is negative definite. We can first embed
$\Lambda _a$
is negative definite. We can first embed
![]() $G^\#$
into
$G^\#$
into
![]() $\mathrm {Aut}_s(V)$
as above. It remains to extend the isometry a.
$\mathrm {Aut}_s(V)$
as above. It remains to extend the isometry a.
We restrict a to L to obtain an isometry of L, but acting nontrivially on the discriminant group
![]() $D_L$
. As in the proof of [Reference Marquand and Muller29, Theorem 4.3], we can instead extend the isometry
$D_L$
. As in the proof of [Reference Marquand and Muller29, Theorem 4.3], we can instead extend the isometry
![]() $-a\in O(L)$
to an isometry b of
$-a\in O(L)$
to an isometry b of
![]() $H^4(V,\mathbb {Z})$
, acting trivially on
$H^4(V,\mathbb {Z})$
, acting trivially on
![]() $\langle h^2\rangle ,$
and by the Torelli theorem, we conclude that b is induced by an automorphism of V, which we still denote by
$\langle h^2\rangle ,$
and by the Torelli theorem, we conclude that b is induced by an automorphism of V, which we still denote by
![]() $b\in \mathrm {Aut}(V)$
. However, this automorphism b is now antisymplectic: the isometry a acted trivially on
$b\in \mathrm {Aut}(V)$
. However, this automorphism b is now antisymplectic: the isometry a acted trivially on
![]() $H^{3,1};$
hence, b acts by
$H^{3,1};$
hence, b acts by
![]() $- {id}|_{H^{3,1}}$
. The group
$- {id}|_{H^{3,1}}$
. The group
![]() $\langle G_s, b\rangle \cong G$
is thus a subgroup of
$\langle G_s, b\rangle \cong G$
is thus a subgroup of
![]() $\mathrm {Aut}(V)$
, satisfying the statement of the Proposition.
$\mathrm {Aut}(V)$
, satisfying the statement of the Proposition.
Finally, since
![]() $G_s$
is a group of symplectic automorphisms of a cubic fourfold, the pair
$G_s$
is a group of symplectic automorphisms of a cubic fourfold, the pair
![]() $(G_s,\Lambda _{G_s})$
is a Leech pair and occurs in the classification of [Reference Laza and Zheng26].
$(G_s,\Lambda _{G_s})$
is a Leech pair and occurs in the classification of [Reference Laza and Zheng26].
Next, we investigate the birational transformations on an LSV induced from the associated cubic fourfold. It was observed in [Reference Saccà42, §3.1] (see also [Reference Laza, Pearlstein and Zhang24]) that any automorphism of the cubic fourfold V induces a birational transformation of any associated LSV manifold
![]() $X_V$
. Moreover, a symplectic automorphism of V induces a symplectic birational transformation of
$X_V$
. Moreover, a symplectic automorphism of V induces a symplectic birational transformation of
![]() $X_V$
.
$X_V$
.
Proposition 6.4. Let
![]() $V\subset \mathbb {P}^5$
be a smooth cubic fourfold, and
$V\subset \mathbb {P}^5$
be a smooth cubic fourfold, and
![]() $G\leq \mathrm {Aut}_s(V)$
be a finite subgroup of symplectic automorphisms of V. Then the group of symplectic birational transformations of any LSV manifold
$G\leq \mathrm {Aut}_s(V)$
be a finite subgroup of symplectic automorphisms of V. Then the group of symplectic birational transformations of any LSV manifold
![]() $X_V$
associated to V contains a finite subgroup isomorphic to G.
$X_V$
associated to V contains a finite subgroup isomorphic to G.
Proof. This is essentially the argument of [Reference Saccà42, §3.1] and [Reference Marquand and Muller29, Theorem 4.3] – we include the proof for completeness.
The automorphism group G acts on the universal family of hyperplane sections of V, and thus on the Donagi–Markman fibration
![]() $\mathcal {J}_U\rightarrow U$
, where
$\mathcal {J}_U\rightarrow U$
, where
![]() $U\subset (\mathbb {P}^5)^{\vee }$
parametrises smooth hyperplane sections of V. On a compactification, we obtain a group of birational transformations
$U\subset (\mathbb {P}^5)^{\vee }$
parametrises smooth hyperplane sections of V. On a compactification, we obtain a group of birational transformations
![]() $G\leq \mathrm {Bir}(X_V)$
that leaves the sublattice
$G\leq \mathrm {Bir}(X_V)$
that leaves the sublattice
![]() $\langle \Theta , \pi ^*\mathcal {O}_{\mathbb {P}^5}(1)\rangle \cong U$
invariant (here,
$\langle \Theta , \pi ^*\mathcal {O}_{\mathbb {P}^5}(1)\rangle \cong U$
invariant (here,
![]() $\Theta $
is the relative theta divisor). Since G acts symplectically on V, the group
$\Theta $
is the relative theta divisor). Since G acts symplectically on V, the group
![]() $G\leq \mathrm {Bir}(X_V)$
acts symplectically on
$G\leq \mathrm {Bir}(X_V)$
acts symplectically on
![]() $X_V$
by [Reference Saccà42, Lemma 3.2].
$X_V$
by [Reference Saccà42, Lemma 3.2].
Due to the presence of the Lagrangian fibration
![]() $\pi $
which always admits a section, an LSV manifold
$\pi $
which always admits a section, an LSV manifold
![]() $X_V$
always admits a birational involution
$X_V$
always admits a birational involution
![]() $\tau \in \mathrm {Bir}(X_V)$
that acts by
$\tau \in \mathrm {Bir}(X_V)$
that acts by
![]() $x\mapsto -x$
on the smooth fibers of
$x\mapsto -x$
on the smooth fibers of
![]() $\pi $
.
$\pi $
.
Remark 6.5. Note that
![]() $\tau \in \mathrm {Bir}(X_V)$
is moreover antisymplectic since it preserves the Lagrangian fibration and acts by
$\tau \in \mathrm {Bir}(X_V)$
is moreover antisymplectic since it preserves the Lagrangian fibration and acts by
![]() $-1$
on the
$-1$
on the
![]() $H^1$
of a smooth fiber of
$H^1$
of a smooth fiber of
![]() $\pi $
(compare with [Reference Flapan, Macrì, O’Grady and Saccà14, Proposition 3.1]).
$\pi $
(compare with [Reference Flapan, Macrì, O’Grady and Saccà14, Proposition 3.1]).
In [Reference Marquand and Muller29], we prove that an antisymplectic involution
![]() $\phi \in \mathrm {Bir}(X_V)$
induced from an antisymplectic involution of the underlying cubic fourfold V could be composed with
$\phi \in \mathrm {Bir}(X_V)$
induced from an antisymplectic involution of the underlying cubic fourfold V could be composed with
![]() $\tau $
, producing a symplectic birational involution
$\tau $
, producing a symplectic birational involution
![]() $\phi \circ \tau \in \mathrm {Bir}_s(X_V)$
which is nonstable.
$\phi \circ \tau \in \mathrm {Bir}_s(X_V)$
which is nonstable.
Remark 6.6. Note that
![]() $\tau \in \mathrm {Bir}(X_V)$
commutes with all transformations induced from
$\tau \in \mathrm {Bir}(X_V)$
commutes with all transformations induced from
![]() $\mathrm {Aut}(V)$
. Indeed,
$\mathrm {Aut}(V)$
. Indeed,
![]() $\tau $
acts trivially on the base
$\tau $
acts trivially on the base
![]() $(\mathbb {P}^5)^\vee $
, whereas any automorphism induced from
$(\mathbb {P}^5)^\vee $
, whereas any automorphism induced from
![]() $f\in \mathrm {Aut}(V)$
will either permute fibers or induce an automorphism of an invariant fiber that will commute with
$f\in \mathrm {Aut}(V)$
will either permute fibers or induce an automorphism of an invariant fiber that will commute with
![]() $\tau $
.
$\tau $
.
Proposition 6.7. Let
![]() $V\subset \mathbb {P}^5$
be a smooth cubic fourfold, and
$V\subset \mathbb {P}^5$
be a smooth cubic fourfold, and
![]() $G\leq \mathrm {Aut}(V)$
be a finite subgroup of automorphisms whose symplectic subgroup
$G\leq \mathrm {Aut}(V)$
be a finite subgroup of automorphisms whose symplectic subgroup
![]() $G_s := G\cap \mathrm {Aut}_s(V)$
has index 2 in G. Then the group of symplectic birational transformations of any LSV manifold
$G_s := G\cap \mathrm {Aut}_s(V)$
has index 2 in G. Then the group of symplectic birational transformations of any LSV manifold
![]() $X_V$
associated to V contains a finite subgroup isomorphic to G.
$X_V$
associated to V contains a finite subgroup isomorphic to G.
Proof. The proof is similar to the proof of Proposition 6.4; however, it is done in two steps. We have an exact sequence
where
![]() $G_s\leq \mathrm {Aut}_s(V).$
We apply Proposition 6.4 to the group
$G_s\leq \mathrm {Aut}_s(V).$
We apply Proposition 6.4 to the group
![]() $G_s$
and see that
$G_s$
and see that
![]() $G_s\leq \mathrm {Bir}_s(X_V)$
for any LSV manifold
$G_s\leq \mathrm {Bir}_s(X_V)$
for any LSV manifold
![]() $X_V$
associated to V. Next, we let
$X_V$
associated to V. Next, we let
![]() $g\in G\setminus G_s$
such that the quotient
$g\in G\setminus G_s$
such that the quotient
![]() $G/G_s$
is generated by
$G/G_s$
is generated by
![]() $gG_s$
. Then g has even order, and we denote
$gG_s$
. Then g has even order, and we denote
![]() $\widehat {g}\in \mathrm {Bir}(X_V)$
the antisymplectic transformation induced by g. Then
$\widehat {g}\in \mathrm {Bir}(X_V)$
the antisymplectic transformation induced by g. Then
![]() $\tau \circ \widehat {g}$
is a symplectic birational transformation of
$\tau \circ \widehat {g}$
is a symplectic birational transformation of
![]() $X_V$
with order the order of g. We can conclude that
$X_V$
with order the order of g. We can conclude that
![]() $(\tau \circ \widehat {g})^2=\widehat {g}^2$
lies in
$(\tau \circ \widehat {g})^2=\widehat {g}^2$
lies in
![]() $G_s\leq \mathrm {Bir}(X_V)$
and
$G_s\leq \mathrm {Bir}(X_V)$
and
![]() $G\cong \langle G_s, \tau \circ \widehat {g}\rangle \leq \mathrm {Bir}(X_V)$
.
$G\cong \langle G_s, \tau \circ \widehat {g}\rangle \leq \mathrm {Bir}(X_V)$
.
We see that as a consequence of Proposition 6.7, the LSV construction allows to realise larger groups using the extra involution
![]() $\tau $
. We illustrate the phenomenon described in Proposition 6.7 with the two following examples:
$\tau $
. We illustrate the phenomenon described in Proposition 6.7 with the two following examples:
Example 6.8 (The Clebsch cubic).
Let
![]() $V=\{x_0^3+x_1^3+x_2^3+x_3^3+x_4^3+x_5^3-(x_0+x_1+x_2+x_3+x_4+x_5)^3=0\}\subset \mathbb {P}^5$
be the Clebsch diagonal cubic fourfold. This has
$V=\{x_0^3+x_1^3+x_2^3+x_3^3+x_4^3+x_5^3-(x_0+x_1+x_2+x_3+x_4+x_5)^3=0\}\subset \mathbb {P}^5$
be the Clebsch diagonal cubic fourfold. This has
![]() $\mathrm {Aut}(V)=S_7$
, with group of symplectic automorphisms
$\mathrm {Aut}(V)=S_7$
, with group of symplectic automorphisms
![]() $H=A_7$
. In particular,
$H=A_7$
. In particular,
![]() $\mathrm {Aut}(V)/H\cong \mathbb {Z}/2$
, generated by the antisymplectic involution
$\mathrm {Aut}(V)/H\cong \mathbb {Z}/2$
, generated by the antisymplectic involution
![]() $\phi _1$
(in the notation of [Reference Marquand28]) given in these coordinates by exchanging
$\phi _1$
(in the notation of [Reference Marquand28]) given in these coordinates by exchanging
![]() $x_0, x_1$
.
$x_0, x_1$
.
Let
![]() $X_V$
be an associated LSV manifold and let
$X_V$
be an associated LSV manifold and let
![]() $\tau $
be the LSV involution. By Proposition 6.7, we see that
$\tau $
be the LSV involution. By Proposition 6.7, we see that
![]() $S_7\cong \langle \widehat {H}, \tau \circ \widehat {\phi _1}\rangle \leq \mathrm {Bir}_s(X_V)$
. This case appears under the Id ‘108a.1’ in the dataset [Reference Marquand and Muller30] (see also Tables 4 and 5 in the ancillary files).
$S_7\cong \langle \widehat {H}, \tau \circ \widehat {\phi _1}\rangle \leq \mathrm {Bir}_s(X_V)$
. This case appears under the Id ‘108a.1’ in the dataset [Reference Marquand and Muller30] (see also Tables 4 and 5 in the ancillary files).
As a further remark, since
![]() $\tau \in \mathrm {Bir}(X_V)$
is a nonsymplectic involution, the group
$\tau \in \mathrm {Bir}(X_V)$
is a nonsymplectic involution, the group
![]() $\langle \widehat {H}, \tau , \widehat {\phi _1}\rangle $
is a subgroup of
$\langle \widehat {H}, \tau , \widehat {\phi _1}\rangle $
is a subgroup of
![]() $\mathrm {Bir}(X_V)$
with mixed action, containing
$\mathrm {Bir}(X_V)$
with mixed action, containing
![]() $S_7\leq \mathrm {Bir}_s(X_V)$
as a subgroup of index two.
$S_7\leq \mathrm {Bir}_s(X_V)$
as a subgroup of index two.
Example 6.9 (The Fermat cubic).
Let
![]() $V=\{x_0^3+x_1^3+x_2^3+x_3^3+x_4^3+x_5^3=0\}\subset \mathbb {P}^5$
be the Fermat cubic fourfold. By [Reference Laza and Zheng26], the group of symplectic automorphisms of V is isomorphic to
$V=\{x_0^3+x_1^3+x_2^3+x_3^3+x_4^3+x_5^3=0\}\subset \mathbb {P}^5$
be the Fermat cubic fourfold. By [Reference Laza and Zheng26], the group of symplectic automorphisms of V is isomorphic to
![]() $H= C_3^4\rtimes A_6$
, and the quotient
$H= C_3^4\rtimes A_6$
, and the quotient
![]() $\mathrm {Aut}(V)/H=\langle \phi _1H, \psi H\rangle $
has order
$\mathrm {Aut}(V)/H=\langle \phi _1H, \psi H\rangle $
has order
![]() $6$
. Here,
$6$
. Here,
![]() $\phi _1$
is the antisymplectic involution exchanging
$\phi _1$
is the antisymplectic involution exchanging
![]() $x_0,x_1$
, and
$x_0,x_1$
, and
![]() $\psi $
is the order 3 nonsymplectic automorphism given by
$\psi $
is the order 3 nonsymplectic automorphism given by
![]() $x_0\mapsto \zeta _3 x_0$
.
$x_0\mapsto \zeta _3 x_0$
.
Let
![]() $X_V$
be an associated LSV manifold, and let
$X_V$
be an associated LSV manifold, and let
![]() $\tau $
be the LSV involution. By Proposition 6.7, we have that
$\tau $
be the LSV involution. By Proposition 6.7, we have that
![]() $C_3^4\rtimes S_6\cong \langle \widehat {H}, \tau \circ \widehat {\phi _1}\rangle \leq \mathrm {Bir}_s(X_V)$
. This case appears under the Id ‘101a.1’ in the dataset [Reference Marquand and Muller30] (see also Tables 4 and 5 in the ancillary files).
$C_3^4\rtimes S_6\cong \langle \widehat {H}, \tau \circ \widehat {\phi _1}\rangle \leq \mathrm {Bir}_s(X_V)$
. This case appears under the Id ‘101a.1’ in the dataset [Reference Marquand and Muller30] (see also Tables 4 and 5 in the ancillary files).
Again,
![]() $\tau \in \mathrm {Bir}(X_V)$
is an antisymplectic involution, and
$\tau \in \mathrm {Bir}(X_V)$
is an antisymplectic involution, and
![]() $\psi \in \mathrm {Aut}(V)$
induces a nonsymplectic birational transformation
$\psi \in \mathrm {Aut}(V)$
induces a nonsymplectic birational transformation
![]() $\widehat {\psi }\in \mathrm {Bir}(X_V)$
of order 3. The group
$\widehat {\psi }\in \mathrm {Bir}(X_V)$
of order 3. The group
![]() $G':=\langle \widehat {H}, \tau , \widehat {\phi _1}, \widehat {\psi } \rangle $
is a subgroup of the full birational group
$G':=\langle \widehat {H}, \tau , \widehat {\phi _1}, \widehat {\psi } \rangle $
is a subgroup of the full birational group
![]() $\mathrm {Bir}(X_V)$
with mixed action, and
$\mathrm {Bir}(X_V)$
with mixed action, and
![]() $G'$
contains
$G'$
contains
![]() $\langle \widehat {H}, \tau \circ \widehat {\phi _1}\rangle $
as a subgroup of index
$\langle \widehat {H}, \tau \circ \widehat {\phi _1}\rangle $
as a subgroup of index
![]() $6$
acting symplectically on
$6$
acting symplectically on
![]() $X_V$
. The group
$X_V$
. The group
![]() $G'$
has order
$G'$
has order
![]() $349920=2\cdot 174960$
, and it is the largest finite group acting faithfully by birational transformations on IHS manifolds of
$349920=2\cdot 174960$
, and it is the largest finite group acting faithfully by birational transformations on IHS manifolds of
![]() $OG10$
type we have been able to geometrically realise.
$OG10$
type we have been able to geometrically realise.
Note that the subgroup
![]() $\langle H, \phi _1. \psi \rangle $
of order 174960 acts on the Fano variety of lines
$\langle H, \phi _1. \psi \rangle $
of order 174960 acts on the Fano variety of lines
![]() $F(V)$
as shown in [Reference Wawak46]. The author realises this group as the largest finite group acting faithfully by regular automorphisms on an IHS manifold of
$F(V)$
as shown in [Reference Wawak46]. The author realises this group as the largest finite group acting faithfully by regular automorphisms on an IHS manifold of
![]() $K3^{[2]}$
type. This was also obtained independently by [Reference Comparin, Demelle and Mora9].
$K3^{[2]}$
type. This was also obtained independently by [Reference Comparin, Demelle and Mora9].
6.2 Twisted LSV manifolds
Let
![]() $V\subset \mathbb {P}^5$
be a smooth cubic fourfold. By the construction of [Reference Voisin45], there exists another IHS manifold
$V\subset \mathbb {P}^5$
be a smooth cubic fourfold. By the construction of [Reference Voisin45], there exists another IHS manifold
![]() $X_V^t$
of
$X_V^t$
of
![]() $OG10$
type, equipped with a Lagrangian fibration
$OG10$
type, equipped with a Lagrangian fibration
![]() $\pi ^t: X_V^t\rightarrow (\mathbb {P}^5)^\vee $
whose fiber over a general hyperplane section
$\pi ^t: X_V^t\rightarrow (\mathbb {P}^5)^\vee $
whose fiber over a general hyperplane section
![]() $Y_H:=V\cap H$
is the torsor
$Y_H:=V\cap H$
is the torsor
![]() $\mathrm {Jac}^1(Y_H)$
parametrising degree 1 cycles. We call such a manifold
$\mathrm {Jac}^1(Y_H)$
parametrising degree 1 cycles. We call such a manifold
![]() $X_V^t$
a twisted LSV manifold. Any automorphism of V induces a birational transformation of
$X_V^t$
a twisted LSV manifold. Any automorphism of V induces a birational transformation of
![]() $X_V^t$
acting trivially on the discriminant group of
$X_V^t$
acting trivially on the discriminant group of
![]() $\Lambda $
(see, for example, [Reference Billi and Grossi2, Remark 5.4]). In [Reference Billi and Grossi2], the authors investigate when an IHS manifold of
$\Lambda $
(see, for example, [Reference Billi and Grossi2, Remark 5.4]). In [Reference Billi and Grossi2], the authors investigate when an IHS manifold of
![]() $OG10$
type is birational to a twisted LSV manifold, and use their criterion to investigate when a nonsymplectic automorphism is induced from a cubic fourfold (in a similar manner to Proposition 6.4). By a small adaption of the arguments in [Reference Billi and Grossi2, Proposition 5.2], one obtains the following proposition.
$OG10$
type is birational to a twisted LSV manifold, and use their criterion to investigate when a nonsymplectic automorphism is induced from a cubic fourfold (in a similar manner to Proposition 6.4). By a small adaption of the arguments in [Reference Billi and Grossi2, Proposition 5.2], one obtains the following proposition.
Proposition 6.10. Let X be an IHS manifold of
![]() $OG10$
type, and
$OG10$
type, and
![]() $G\leq \mathrm {Bir}_s(X)$
be a finite group with
$G\leq \mathrm {Bir}_s(X)$
be a finite group with
![]() $H:=\eta _*(G)$
acting trivially
$H:=\eta _*(G)$
acting trivially
![]() $D_\Lambda $
. Suppose that there is a primitive embedding
$D_\Lambda $
. Suppose that there is a primitive embedding
![]() $U(3)\hookrightarrow \Lambda ^H$
such that the composition
$U(3)\hookrightarrow \Lambda ^H$
such that the composition
![]() $U(3)\hookrightarrow \Lambda $
has glue domain
$U(3)\hookrightarrow \Lambda $
has glue domain
![]() $\mathbb {Z}/3\mathbb {Z}$
. Then there exists a smooth cubic fourfold V with
$\mathbb {Z}/3\mathbb {Z}$
. Then there exists a smooth cubic fourfold V with
![]() $G\leq \mathrm {Aut}_s(V)$
such that
$G\leq \mathrm {Aut}_s(V)$
such that
![]() $(H, \Lambda _H)$
occurs in the classification of [Reference Laza and Zheng26].
$(H, \Lambda _H)$
occurs in the classification of [Reference Laza and Zheng26].
Proof. Consider the lattice
![]() $L:=U(3)^\perp \subset \Lambda ;$
this lattice is isometric to
$L:=U(3)^\perp \subset \Lambda ;$
this lattice is isometric to
![]() $U^2\oplus E_8(-1)^2\oplus A_2(-1)$
. Note that
$U^2\oplus E_8(-1)^2\oplus A_2(-1)$
. Note that
![]() $H:=\eta _*(G^\#)$
acts on L with
$H:=\eta _*(G^\#)$
acts on L with
![]() $L_H\cong \Lambda _H(-1)$
. We follow the proof of Proposition 6.3 to obtain a smooth cubic fourfold V with
$L_H\cong \Lambda _H(-1)$
. We follow the proof of Proposition 6.3 to obtain a smooth cubic fourfold V with
![]() $H^4(V,\mathbb {Z})_{prim}$
Hodge isomorphic to the lattice L with induced Hodge structure. Since H acts trivially on the discriminant group, we extend H to an isometry group of
$H^4(V,\mathbb {Z})_{prim}$
Hodge isomorphic to the lattice L with induced Hodge structure. Since H acts trivially on the discriminant group, we extend H to an isometry group of
![]() $H^4(V,\mathbb {Z})_{prim}$
as in Proposition 6.3 and conclude that
$H^4(V,\mathbb {Z})_{prim}$
as in Proposition 6.3 and conclude that
![]() $G\leq \mathrm {Aut}_s(V).$
It follows that the pair
$G\leq \mathrm {Aut}_s(V).$
It follows that the pair
![]() $(H, \Lambda _H)$
occurs in the classification of [Reference Laza and Zheng26].
$(H, \Lambda _H)$
occurs in the classification of [Reference Laza and Zheng26].
Corollary 6.11. A symplectic finite subgroup
![]() $H\leq O^+(\Lambda )$
can be realised by an induced action on a twisted LSV manifold associated to a cubic fourfold V if and only if H is stable, and the Id number, as listed in Table 3, is one of the following:
$H\leq O^+(\Lambda )$
can be realised by an induced action on a twisted LSV manifold associated to a cubic fourfold V if and only if H is stable, and the Id number, as listed in Table 3, is one of the following:
 $$ \begin{align*} {Id}\in \{&1, 2, 3, 4b, 7b, 9, 13, 15b, 18b, 19b, 20, 29b, 31, 35b, 39b, 44b, 46b, 47c,\\& 52, 53, 55, 68b, 72b, 77, 82b, 84,85b, 87,101b, 108b, 109b, 119, 120, 128b \}. \end{align*} $$
$$ \begin{align*} {Id}\in \{&1, 2, 3, 4b, 7b, 9, 13, 15b, 18b, 19b, 20, 29b, 31, 35b, 39b, 44b, 46b, 47c,\\& 52, 53, 55, 68b, 72b, 77, 82b, 84,85b, 87,101b, 108b, 109b, 119, 120, 128b \}. \end{align*} $$
Proof. Let X be an IHS manifold of
![]() $OG10$
type with
$OG10$
type with
![]() $G\leq \mathrm {Bir}_s(X)$
such that
$G\leq \mathrm {Bir}_s(X)$
such that
![]() $H:=\eta _*(G)$
is one of the Ids above. Then by Proposition 6.10, there exists a cubic fourfold V with
$H:=\eta _*(G)$
is one of the Ids above. Then by Proposition 6.10, there exists a cubic fourfold V with
![]() $G\leq \mathrm {Aut}_s(V).$
One then applies [Reference Billi and Grossi2, Proposition 5.6] to obtain a twisted LSV manifold
$G\leq \mathrm {Aut}_s(V).$
One then applies [Reference Billi and Grossi2, Proposition 5.6] to obtain a twisted LSV manifold
![]() $X_V$
associated to V with a compatible action of
$X_V$
associated to V with a compatible action of
![]() $G.$
$G.$
Conversely, if
![]() $H\leq O(\Lambda )$
is induced on a twisted LSV by a cubic fourfold, it must act trivially on the discriminant group, and is thus stable. The only groups H listed in Table 3 that satisfy the assumptions of Proposition 6.10 are those listed above, verified by direct computation.
$H\leq O(\Lambda )$
is induced on a twisted LSV by a cubic fourfold, it must act trivially on the discriminant group, and is thus stable. The only groups H listed in Table 3 that satisfy the assumptions of Proposition 6.10 are those listed above, verified by direct computation.
Remark 6.12. Let
![]() $V\subset \mathbb {P}^5$
be the Fermat cubic, and let
$V\subset \mathbb {P}^5$
be the Fermat cubic, and let
![]() $G=\mathrm {Aut}_s(V)\cong C_3^4\rtimes A_6.$
Then both
$G=\mathrm {Aut}_s(V)\cong C_3^4\rtimes A_6.$
Then both
![]() $X_V$
and
$X_V$
and
![]() $X_V^t$
inherit a group of symplectic birational automorphisms isomorphic to G, but the action on the second cohomology is different. Namely, the action on
$X_V^t$
inherit a group of symplectic birational automorphisms isomorphic to G, but the action on the second cohomology is different. Namely, the action on
![]() $H^2(X_V,\mathbb {Z})$
is given by the entry 101a in Table 3, whereas the action on
$H^2(X_V,\mathbb {Z})$
is given by the entry 101a in Table 3, whereas the action on
![]() $H^2(X_V^t, \mathbb {Z})$
is given by 101b. We point out that
$H^2(X_V^t, \mathbb {Z})$
is given by 101b. We point out that
![]() $X_V$
and
$X_V$
and
![]() $X_V^t$
are birational [Reference Billi and Grossi2, Remark 5.3], but the pairs
$X_V^t$
are birational [Reference Billi and Grossi2, Remark 5.3], but the pairs
![]() $(X_V, G)$
and
$(X_V, G)$
and
![]() $(X_V^t,G)$
are not birational conjugate.
$(X_V^t,G)$
are not birational conjugate.
6.3 Numerical moduli spaces
Using the close connection between cubic fourfolds and manifolds of
![]() $OG10$
type, we have geometrically realised certain group actions of symplectic birational transformations. Of course, it is natural to ask the same question using automorphisms of
$OG10$
type, we have geometrically realised certain group actions of symplectic birational transformations. Of course, it is natural to ask the same question using automorphisms of
![]() $K3$
surfaces.
$K3$
surfaces.
In [Reference Felisetti, Giovenzana and Grossi13], the authors develop a criterion for when an IHS manifold of
![]() $OG10$
type is birational to a moduli space of sheaves on a
$OG10$
type is birational to a moduli space of sheaves on a
![]() $K3$
surface. Further, they provide another criterion for when a group of birational transformations of such a manifold is induced by a group of automorphisms of an underlying
$K3$
surface. Further, they provide another criterion for when a group of birational transformations of such a manifold is induced by a group of automorphisms of an underlying
![]() $K3$
surface. In this subsection, we will apply these criteria to our classification of saturated birational effective groups G. We begin by recalling the relevant definitions of [Reference Felisetti, Giovenzana and Grossi13], and we refer to them for more details.
$K3$
surface. In this subsection, we will apply these criteria to our classification of saturated birational effective groups G. We begin by recalling the relevant definitions of [Reference Felisetti, Giovenzana and Grossi13], and we refer to them for more details.
Let S be a
![]() $K3$
surface. Recall that the Mukai lattice
$K3$
surface. Recall that the Mukai lattice
![]() $\tilde {H}(S,\mathbb {Z})= H^0(S,\mathbb {Z})\oplus H^2(S,\mathbb {Z})\oplus H^4(S,\mathbb {Z})$
. We have that
$\tilde {H}(S,\mathbb {Z})= H^0(S,\mathbb {Z})\oplus H^2(S,\mathbb {Z})\oplus H^4(S,\mathbb {Z})$
. We have that
![]() $\tilde {H}(S,\mathbb {Z})\cong \Lambda _{24}:=U^4\oplus E_8^2$
.
$\tilde {H}(S,\mathbb {Z})\cong \Lambda _{24}:=U^4\oplus E_8^2$
.
Definition 6.13 [Reference Felisetti, Giovenzana and Grossi13, Definition/Theorem 3.8].
A numerical moduli space of
![]() $OG10$
type is a marked IHS manifold of
$OG10$
type is a marked IHS manifold of
![]() $OG10$
type
$OG10$
type
![]() $(X,\eta )$
such that there exists a primitive class
$(X,\eta )$
such that there exists a primitive class
![]() $\sigma \in H^{1,1}(X)$
with
$\sigma \in H^{1,1}(X)$
with
![]() $\sigma ^2=-6$
and
$\sigma ^2=-6$
and
![]() $\mathrm {div}_{\Lambda }(\eta (\sigma ))=3$
, and the Hodge embedding
$\mathrm {div}_{\Lambda }(\eta (\sigma ))=3$
, and the Hodge embedding
![]() $\eta (\sigma )^\perp _\Lambda \hookrightarrow \Lambda _{24}$
embeds a copy of U in
$\eta (\sigma )^\perp _\Lambda \hookrightarrow \Lambda _{24}$
embeds a copy of U in
![]() $\Lambda _{24}^{1,1}$
as a direct summand.
$\Lambda _{24}^{1,1}$
as a direct summand.
Equivalently, a numerical moduli space is an IHS manifold X of
![]() $OG10$
type that is birational to
$OG10$
type that is birational to
![]() $\tilde {M}_V(S,\Theta )$
for some
$\tilde {M}_V(S,\Theta )$
for some
![]() $K3$
surface
$K3$
surface
![]() $S,$
a Mukai vector
$S,$
a Mukai vector
![]() $v=2w$
, where w is primitive of square
$v=2w$
, where w is primitive of square
![]() $2$
, and a v-generic polarisation
$2$
, and a v-generic polarisation
![]() $\theta .$
$\theta .$
Definition 6.14. Let
![]() $(X, \eta )$
be a marked IHS manifold of
$(X, \eta )$
be a marked IHS manifold of
![]() $OG10$
type and
$OG10$
type and
![]() $G\leq \mathrm {Bir}(X)$
a finite subgroup. We say the group G is
$G\leq \mathrm {Bir}(X)$
a finite subgroup. We say the group G is
-
•
 $K3$
-induced if there exists a
$K3$
-induced if there exists a
 $K3$
surface S with an injective group homomorphism
$K3$
surface S with an injective group homomorphism
 $i:G\hookrightarrow \mathrm {Aut}(S)$
, a G-invariant Mukai vector
$i:G\hookrightarrow \mathrm {Aut}(S)$
, a G-invariant Mukai vector
 $v\in \tilde {H}(S,\mathbb {Z})^G$
and a v-generic polarisation
$v\in \tilde {H}(S,\mathbb {Z})^G$
and a v-generic polarisation
 $\theta $
on S such that the action induced by G on
$\theta $
on S such that the action induced by G on
 $\tilde {M}_v(S,\theta )$
via i coincides with the given action of G on X.
$\tilde {M}_v(S,\theta )$
via i coincides with the given action of G on X. -
• numerically
 $K3$
-induced if there exists a G-invariant class
$K3$
-induced if there exists a G-invariant class
 $\sigma \in {NS}(X)$
with that
$\sigma \in {NS}(X)$
with that
 $\sigma ^2=-6$
and
$\sigma ^2=-6$
and
 $\mathrm {div}_{\Lambda }(\eta (\sigma ))=3$
such that given the Hodge embedding
$\mathrm {div}_{\Lambda }(\eta (\sigma ))=3$
such that given the Hodge embedding
 $\eta (\sigma )_\Lambda ^\perp \hookrightarrow \Lambda _{24}$
, the induced action of G on
$\eta (\sigma )_\Lambda ^\perp \hookrightarrow \Lambda _{24}$
, the induced action of G on
 $\Lambda _{24}$
is such that the
$\Lambda _{24}$
is such that the
 $(1,1)$
-part of
$(1,1)$
-part of
 $\Lambda _{24}^G$
contains U as a direct summand.
$\Lambda _{24}^G$
contains U as a direct summand.
Notice that if a group
![]() $G\leq \mathrm {Bir}_s(X)$
is
$G\leq \mathrm {Bir}_s(X)$
is
![]() $K3$
-induced, then its action on the discriminant group of
$K3$
-induced, then its action on the discriminant group of
![]() $H^2(X,\mathbb {Z})$
is necessarily trivial.
$H^2(X,\mathbb {Z})$
is necessarily trivial.
Let
![]() $\mathcal {S}$
denote the set of stable symplectic sublattices C of the Leech lattice
$\mathcal {S}$
denote the set of stable symplectic sublattices C of the Leech lattice
![]() $\mathbb {L}$
which embeds primitively into the
$\mathbb {L}$
which embeds primitively into the
![]() $K3$
lattice
$K3$
lattice
![]() $\Lambda _{K3} := U^3\oplus E_8^2$
(i.e., those that occur in [Reference Hashimoto18, Table 10.2]).
$\Lambda _{K3} := U^3\oplus E_8^2$
(i.e., those that occur in [Reference Hashimoto18, Table 10.2]).
Theorem 6.15. Let
![]() $(X, \eta )$
be a marked IHS manifold of
$(X, \eta )$
be a marked IHS manifold of
![]() $OG10$
type. Assume that
$OG10$
type. Assume that
![]() $(X, \eta )$
is a numerical moduli space. Then a finite subgroup
$(X, \eta )$
is a numerical moduli space. Then a finite subgroup
![]() $G\leq \mathrm {Bir}_s(X)$
is
$G\leq \mathrm {Bir}_s(X)$
is
![]() $K3$
-induced if and only if
$K3$
-induced if and only if
![]() $\Lambda _{G}$
is isometric to a lattice in the set
$\Lambda _{G}$
is isometric to a lattice in the set
![]() $\mathcal {S}.$
$\mathcal {S}.$
Proof. If
![]() $G\leq \mathrm {Bir}_s(X)$
is a
$G\leq \mathrm {Bir}_s(X)$
is a
![]() $K3$
-induced group of symplectic birational transformations, by definition, there exists a
$K3$
-induced group of symplectic birational transformations, by definition, there exists a
![]() $K3$
surface S with an injective group homomorphism
$K3$
surface S with an injective group homomorphism
![]() $i:G\hookrightarrow \mathrm {Aut}(X)$
. We use our classification of saturated groups of symplectic birational transformations. As the action of a
$i:G\hookrightarrow \mathrm {Aut}(X)$
. We use our classification of saturated groups of symplectic birational transformations. As the action of a
![]() $K3$
-induced automorphism on the discriminant group is trivial, we can restrict to our classification of finite groups of stable symplectic isometries as in Section 4.
$K3$
-induced automorphism on the discriminant group is trivial, we can restrict to our classification of finite groups of stable symplectic isometries as in Section 4.
If an action is
![]() $K3$
-induced, then it is numerically
$K3$
-induced, then it is numerically
![]() $K3$
-induced [Reference Felisetti, Giovenzana and Grossi13, Proposition 6.7], and in particular, there exists a primitive invariant class
$K3$
-induced [Reference Felisetti, Giovenzana and Grossi13, Proposition 6.7], and in particular, there exists a primitive invariant class
![]() $\sigma \in H^{1,1}(X,\mathbb {Z})$
with
$\sigma \in H^{1,1}(X,\mathbb {Z})$
with
![]() $\sigma ^2=-6$
and divisibility three; that is,
$\sigma ^2=-6$
and divisibility three; that is,
![]() $\eta (\sigma )\in \Lambda ^H$
, where
$\eta (\sigma )\in \Lambda ^H$
, where
![]() $H := \eta _\ast (G)$
. After embedding
$H := \eta _\ast (G)$
. After embedding
![]() $\eta (\sigma )^\perp _\Lambda \hookrightarrow \Lambda _{24}$
and extending the action of H, we obtain that
$\eta (\sigma )^\perp _\Lambda \hookrightarrow \Lambda _{24}$
and extending the action of H, we obtain that
![]() $\Lambda _H = (\Lambda _{24})_H$
. In particular, since G is numerically
$\Lambda _H = (\Lambda _{24})_H$
. In particular, since G is numerically
![]() $K3$
-induced, we know that H acts on
$K3$
-induced, we know that H acts on
![]() $\Lambda _{K3} = U^\perp _{\Lambda _{24}}$
in such a way that
$\Lambda _{K3} = U^\perp _{\Lambda _{24}}$
in such a way that
![]() $(\Lambda _{K3})_H = (\Lambda _{24})_H$
. Hence,
$(\Lambda _{K3})_H = (\Lambda _{24})_H$
. Hence,
![]() $\Lambda _H$
is isometric to a lattice in
$\Lambda _H$
is isometric to a lattice in
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
For the converse, we let G be a finite group of symplectic birational transformations of X such that
![]() $\Lambda _H$
is isometric to a lattice in
$\Lambda _H$
is isometric to a lattice in
![]() $\mathcal {S}$
, where
$\mathcal {S}$
, where
![]() $H=\eta _*(G)$
. We prove that G is numerically
$H=\eta _*(G)$
. We prove that G is numerically
![]() $K3$
-induced. Since by assumption
$K3$
-induced. Since by assumption
![]() $(X, \eta )$
is a numerical moduli space, there exists a class
$(X, \eta )$
is a numerical moduli space, there exists a class
![]() $\sigma \in {NS}(X)$
with
$\sigma \in {NS}(X)$
with
![]() $\sigma ^2=-6$
, and
$\sigma ^2=-6$
, and
![]() $\mathrm {div}_{\Lambda }(\eta (\sigma ))=3$
such that, given the Hodge embedding
$\mathrm {div}_{\Lambda }(\eta (\sigma ))=3$
such that, given the Hodge embedding
![]() $\eta (\sigma )_\Lambda ^\perp \hookrightarrow \Lambda _{24}$
, the lattice
$\eta (\sigma )_\Lambda ^\perp \hookrightarrow \Lambda _{24}$
, the lattice
![]() $\Lambda _{24}^{1,1}$
contains U as a direct summand. Such a copy of U must be contained in
$\Lambda _{24}^{1,1}$
contains U as a direct summand. Such a copy of U must be contained in
![]() $\Lambda ^H$
, since
$\Lambda ^H$
, since
![]() $\Lambda _H$
is negative definite. Notice also that
$\Lambda _H$
is negative definite. Notice also that
![]() $\eta (\sigma )\in \mathcal {W}^{pex}(X)$
; it follows from Lemma 3.6 that
$\eta (\sigma )\in \mathcal {W}^{pex}(X)$
; it follows from Lemma 3.6 that
![]() $\eta (\sigma )\not \in \Lambda _H$
. Thus,
$\eta (\sigma )\not \in \Lambda _H$
. Thus,
![]() $\eta (\sigma )$
must lie in
$\eta (\sigma )$
must lie in
![]() $\Lambda ^H$
; in other words, it is invariant, and we see that G is numerically
$\Lambda ^H$
; in other words, it is invariant, and we see that G is numerically
![]() $K3$
-induced. The result follows from [Reference Felisetti, Giovenzana and Grossi13, Theorem 6.8]
$K3$
-induced. The result follows from [Reference Felisetti, Giovenzana and Grossi13, Theorem 6.8]
A Exceptional stable symplectic sublattices of
 $\mathbb {B}$
$\mathbb {B}$
Each entry in Table 2 corresponds to an abstract isometry class of exceptional stable symplectic sublattices C of
![]() $\mathbb {B}$
without
$\mathbb {B}$
without
![]() $(-2)$
-vectors and of rank at most 21. For each entry we give
$(-2)$
-vectors and of rank at most 21. For each entry we give
-
• the rank of the lattice C;
-
• the length
 $l(D_C)$
of the discriminant group
$l(D_C)$
of the discriminant group
 $D_C$
of C;
$D_C$
of C; -
• the genus
 $g(C)$
of the lattice C;
$g(C)$
of the lattice C; -
• the order of the stable subgroup
 $O^\#(C)$
of isometries of C;
$O^\#(C)$
of isometries of C; -
• a description of the group
 $O^\#(C)$
, its Id in the Small Group Library [Reference Besche, Eick, O’Brien and Horn1], or nothing (—) if none of the previous are available.
$O^\#(C)$
, its Id in the Small Group Library [Reference Besche, Eick, O’Brien and Horn1], or nothing (—) if none of the previous are available.
Note that some of the lattices represented in Table 2 are in the same genus and have the same stable subgroup of isometries. However, the entries represent pairwise nonisometric lattices.
Table 2 Exceptional stable symplectic sublattices of
![]() $\mathbb {B}$
without
$\mathbb {B}$
without
![]() $(-2)$
-vectors.
$(-2)$
-vectors.

B Isometry classes of potential exceptional hearts of
 $\Lambda $
$\Lambda $
We display the Gram matrices for the exceptional stable symplectic sublattices of
![]() $\mathbb {B}$
without
$\mathbb {B}$
without
![]() $(-2)$
-vectors which could potentially embed primitively into the lattice
$(-2)$
-vectors which could potentially embed primitively into the lattice
![]() $\Lambda :=U^3\oplus E_8^2\oplus A_2$
. These are the only lattices represented in Table 2 for which
$\Lambda :=U^3\oplus E_8^2\oplus A_2$
. These are the only lattices represented in Table 2 for which
![]() $\text {rank}(-)+l(D_-) \leq 25$
.
$\text {rank}(-)+l(D_-) \leq 25$
.
 $$\begin{align*} E_{18} &:= {\begin {pmatrix} -4 & 2 & 2 & -2 & -2 & 2 & -2 & 2 & 2 & 0 & 0 & 0 & 0 & 0 & 2 & 2 & -1 & 1 \\ 2 & -4 & -2 & 0 & 1 & -1 & 2 & -2 & -2 & -1 & -1 & 1 & 1 & -1 & -1 & -2 & -1 & -2 \\ 2 & -2 & -4 & 1 & 0 & -2 & 2 & -2 & -2 & -1 & -1 & -1 & 1 & -1 & 0 & -2 & 0 & -1 \\ -2 & 0 & 1 & -4 & -2 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & -1 & 1 & 0 & 2 & 0 & -1 \\ -2 & 1 & 0 & -2 & -4 & 1 & 0 & 0 & 0 & 1 & 1 & -1 & -1 & 1 & 2 & 2 & -1 & 1 \\ 2 & -1 & -2 & 0 & 1 & -4 & 2 & -2 & -2 & 0 & 0 & 0 & 0 & 0 & -2 & -1 & 1 & -1 \\ -2 & 2 & 2 & 0 & 0 & 2 & -4 & 2 & 2 & -1 & 1 & -1 & -1 & 1 & 0 & 0 & -1 & 2 \\ 2 & -2 & -2 & 0 & 0 & -2 & 2 & -4 & -1 & 1 & -1 & 1 & -1 & 1 & -1 & -1 & 0 & -1 \\ 2 & -2 & -2 & 0 & 0 & -2 & 2 & -1 & -4 & 0 & 1 & -1 & 0 & 0 & -1 & -1 & 0 & -1 \\ 0 & -1 & -1 & 1 & 1 & 0 & -1 & 1 & 0 & -4 & -1 & -1 & 2 & -2 & 0 & -2 & -1 & 0 \\ 0 & -1 & -1 & 1 & 1 & 0 & 1 & -1 & 1 & -1 & -4 & 2 & 2 & -1 & 1 & -1 & 0 & -1 \\ 0 & 1 & -1 & 0 & -1 & 0 & -1 & 1 & -1 & -1 & 2 & -4 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 1 & 1 & -1 & -1 & 0 & -1 & -1 & 0 & 2 & 2 & 0 & -4 & 2 & -1 & 1 & 0 & 1 \\ 0 & -1 & -1 & 1 & 1 & 0 & 1 & 1 & 0 & -2 & -1 & 0 & 2 & -4 & 1 & -1 & 0 & -1 \\ 2 & -1 & 0 & 0 & 2 & -2 & 0 & -1 & -1 & 0 & 1 & 0 & -1 & 1 & -4 & -1 & 1 & -1 \\ 2 & -2 & -2 & 2 & 2 & -1 & 0 & -1 & -1 & -2 & -1 & 0 & 1 & -1 & -1 & -4 & 0 & -1 \\ -1 & -1 & 0 & 0 & -1 & 1 & -1 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 1 & 0 & -4 & 1 \\ 1 & -2 & -1 & -1 & 1 & -1 & 2 & -1 & -1 & 0 & -1 & 1 & 1 & -1 & -1 & -1 & 1 & -4 \end {pmatrix}} \\ E_{20} &:= {\begin {pmatrix} -4 & -2 & -1 & 1 & -1 & -1 & -1 & -1 & -1 & -1 & 1 & -1 & -2 & -2 & -1 & -2 & 1 & 1 & -1 & 0 \\ -2 & -4 & 1 & 2 & 1 & -2 & 1 & 1 & 1 & 1 & -1 & -2 & -1 & -2 & -1 & 0 & -1 & -1 & 0 & -1 \\ -1 & 1 & -4 & -2 & -2 & 2 & 0 & -2 & -2 & -2 & 0 & 1 & 0 & 0 & 1 & -1 & 0 & 2 & -2 & -1 \\ 1 & 2 & -2 & -4 & -2 & 2 & -1 & 0 & -2 & -2 & 1 & 2 & 0 & 0 & 0 & 1 & -1 & 2 & -1 & -1 \\ -1 & 1 & -2 & -2 & -4 & 0 & 0 & 0 & -1 & -1 & 2 & 2 & 0 & 0 & -1 & -1 & 0 & 2 & -2 & 0 \\ -1 & -2 & 2 & 2 & 0 & -4 & 1 & 2 & 2 & 2 & 1 & -1 & -1 & -1 & -2 & 0 & 0 & -1 & 0 & 1 \\ -1 & 1 & 0 & -1 & 0 & 1 & -4 & 0 & -1 & -1 & 1 & 1 & -2 & -1 & -1 & 0 & 1 & 1 & 0 & 1 \\ -1 & 1 & -2 & 0 & 0 & 2 & 0 & -4 & -2 & -2 & 0 & -1 & 1 & 1 & 2 & -2 & 1 & 1 & 0 & 0 \\ -1 & 1 & -2 & -2 & -1 & 2 & -1 & -2 & -4 & -2 & 1 & 0 & 0 & -1 & 1 & -1 & 1 & 1 & 0 & 0 \\ -1 & 1 & -2 & -2 & -1 & 2 & -1 & -2 & -2 & -4 & 0 & 1 & -1 & 0 & 1 & -1 & 0 & 2 & 0 & -1 \\ 1 & -1 & 0 & 1 & 2 & 1 & 1 & 0 & 1 & 0 & -4 & 0 & 0 & 0 & 1 & 1 & -1 & -1 & 1 & -1 \\ -1 & -2 & 1 & 2 & 2 & -1 & 1 & -1 & 0 & 1 & 0 & -4 & 0 & -1 & 0 & 0 & 0 & -1 & 1 & 0 \\ -2 & -1 & 0 & 0 & 0 & -1 & -2 & 1 & 0 & -1 & 0 & 0 & -4 & -2 & -2 & 0 & 0 & 1 & 0 & 0 \\ -2 & -2 & 0 & 0 & 0 & -1 & -1 & 1 & -1 & 0 & 0 & -1 & -2 & -4 & -2 & 0 & 0 & 0 & 0 & 0 \\ -1 & -1 & 1 & 0 & -1 & -2 & -1 & 2 & 1 & 1 & 1 & 0 & -2 & -2 & -4 & 1 & 0 & 0 & 0 & 0 \\ -2 & 0 & -1 & 1 & -1 & 0 & 0 & -2 & -1 & -1 & 1 & 0 & 0 & 0 & 1 & -4 & 1 & 1 & -1 & 1 \\ 1 & -1 & 0 & -1 & 0 & 0 & 1 & 1 & 1 & 0 & -1 & 0 & 0 & 0 & 0 & 1 & -4 & 0 & -1 & -1 \\ 1 & -1 & 2 & 2 & 2 & -1 & 1 & 1 & 1 & 2 & -1 & -1 & 1 & 0 & 0 & 1 & 0 & -4 & 2 & 1 \\ -1 & 0 & -2 & -1 & -2 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & -1 & -1 & 2 & -4 & 0 \\ 0 & -1 & -1 & -1 & 0 & 1 & 1 & 0 & 0 & -1 & -1 & 0 & 0 & 0 & 0 & 1 & -1 & 1 & 0 & -4 \end {pmatrix}}\\[6pt]E_{21} &:= {\begin {pmatrix} -4 & 2 & 2 & -1 & 2 & -2 & 2 & 1 & -1 & -2 & -2 & -2 & 1 & 0 & -2 & -2 & -1 & -2 & 2 & -2 & 2 \\ 2 & -4 & -2 & 2 & -1 & 0 & 0 & 1 & 2 & 1 & 2 & 2 & 1 & -1 & 1 & 2 & 2 & 2 & -2 & 1 & -1 \\ 2 & -2 & -4 & 2 & -2 & 1 & 0 & 1 & 0 & 0 & 2 & 1 & -1 & 1 & 0 & 1 & 0 & 0 & -1 & 2 & 0 \\ -1 & 2 & 2 & -4 & 0 & -1 & -1 & -1 & -1 & -1 & -2 & -1 & -1 & 1 & -1 & -2 & -1 & -1 & 1 & -2 & -1 \\ 2 & -1 & -2 & 0 & -4 & 2 & -2 & 1 & -1 & 0 & 0 & 0 & -1 & 0 & 1 & 1 & -1 & 0 & -2 & 1 & -2 \\ -2 & 0 & 1 & -1 & 2 & -4 & 1 & 1 & 1 & -1 & -1 & -1 & 1 & 0 & -1 & -1 & 0 & 0 & 1 & -1 & 1 \\ 2 & 0 & 0 & -1 & -2 & 1 & -4 & 0 & -1 & 0 & 0 & 1 & 0 & -1 & 2 & 1 & -1 & 1 & -1 & 0 & -2 \\ 1 & 1 & 1 & -1 & 1 & 1 & 0 & -4 & 0 & 2 & 1 & 1 & -1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & -1 \\ -1 & 2 & 0 & -1 & -1 & 1 & -1 & 0 & -4 & -2 & -1 & -1 & 0 & 1 & 0 & -1 & -2 & -2 & 1 & -1 & 0 \\ -2 & 1 & 0 & -1 & 0 & -1 & 0 & 2 & -2 & -4 & -2 & -1 & 0 & 0 & -1 & -1 & -2 & -2 & 2 & -2 & 1 \\ -2 & 2 & 2 & -2 & 0 & -1 & 0 & 1 & -1 & -2 & -4 & -2 & 0 & 0 & -1 & -1 & -2 & -1 & 1 & -2 & 0 \\ -2 & 2 & 1 & -1 & 0 & -1 & 1 & 1 & -1 & -1 & -2 & -4 & -1 & 1 & -1 & -2 & -2 & -1 & 1 & 0 & 1 \\ 1 & 1 & -1 & -1 & -1 & 1 & 0 & -1 & 0 & 0 & 0 & -1 & -4 & 2 & -1 & -1 & -1 & -1 & 0 & 1 & 0 \\ 0 & -1 & 1 & 1 & 0 & 0 & -1 & 1 & 1 & 0 & 0 & 1 & 2 & -4 & 2 & 1 & 0 & 1 & -1 & 0 & -1 \\ -2 & 1 & 0 & -1 & 1 & -1 & 2 & 0 & 0 & -1 & -1 & -1 & -1 & 2 & -4 & -1 & 0 & -2 & 1 & -1 & 2 \\ -2 & 2 & 1 & -2 & 1 & -1 & 1 & 0 & -1 & -1 & -1 & -2 & -1 & 1 & -1 & -4 & -1 & -1 & 2 & -1 & 1 \\ -1 & 2 & 0 & -1 & -1 & 0 & -1 & 1 & -2 & -2 & -2 & -2 & -1 & 0 & 0 & -1 & -4 & -1 & 1 & 0 & 0 \\ -2 & 2 & 0 & -1 & 0 & 0 & 1 & 0 & -2 & -2 & -1 & -1 & -1 & 1 & -2 & -1 & -1 & -4 & 1 & -1 & 1 \\ 2 & -2 & -1 & 1 & -2 & 1 & -1 & 0 & 1 & 2 & 1 & 1 & 0 & -1 & 1 & 2 & 1 & 1 & -4 & 2 & -2 \\ -2 & 1 & 2 & -2 & 1 & -1 & 0 & 0 & -1 & -2 & -2 & 0 & 1 & 0 & -1 & -1 & 0 & -1 & 2 & -4 & 0 \\ 2 & -1 & 0 & -1 & -2 & 1 & -2 & -1 & 0 & 1 & 0 & 1 & 0 & -1 & 2 & 1 & 0 & 1 & -2 & 0 & -4 \end {pmatrix}} \end{align*}$$
$$\begin{align*} E_{18} &:= {\begin {pmatrix} -4 & 2 & 2 & -2 & -2 & 2 & -2 & 2 & 2 & 0 & 0 & 0 & 0 & 0 & 2 & 2 & -1 & 1 \\ 2 & -4 & -2 & 0 & 1 & -1 & 2 & -2 & -2 & -1 & -1 & 1 & 1 & -1 & -1 & -2 & -1 & -2 \\ 2 & -2 & -4 & 1 & 0 & -2 & 2 & -2 & -2 & -1 & -1 & -1 & 1 & -1 & 0 & -2 & 0 & -1 \\ -2 & 0 & 1 & -4 & -2 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & -1 & 1 & 0 & 2 & 0 & -1 \\ -2 & 1 & 0 & -2 & -4 & 1 & 0 & 0 & 0 & 1 & 1 & -1 & -1 & 1 & 2 & 2 & -1 & 1 \\ 2 & -1 & -2 & 0 & 1 & -4 & 2 & -2 & -2 & 0 & 0 & 0 & 0 & 0 & -2 & -1 & 1 & -1 \\ -2 & 2 & 2 & 0 & 0 & 2 & -4 & 2 & 2 & -1 & 1 & -1 & -1 & 1 & 0 & 0 & -1 & 2 \\ 2 & -2 & -2 & 0 & 0 & -2 & 2 & -4 & -1 & 1 & -1 & 1 & -1 & 1 & -1 & -1 & 0 & -1 \\ 2 & -2 & -2 & 0 & 0 & -2 & 2 & -1 & -4 & 0 & 1 & -1 & 0 & 0 & -1 & -1 & 0 & -1 \\ 0 & -1 & -1 & 1 & 1 & 0 & -1 & 1 & 0 & -4 & -1 & -1 & 2 & -2 & 0 & -2 & -1 & 0 \\ 0 & -1 & -1 & 1 & 1 & 0 & 1 & -1 & 1 & -1 & -4 & 2 & 2 & -1 & 1 & -1 & 0 & -1 \\ 0 & 1 & -1 & 0 & -1 & 0 & -1 & 1 & -1 & -1 & 2 & -4 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 1 & 1 & -1 & -1 & 0 & -1 & -1 & 0 & 2 & 2 & 0 & -4 & 2 & -1 & 1 & 0 & 1 \\ 0 & -1 & -1 & 1 & 1 & 0 & 1 & 1 & 0 & -2 & -1 & 0 & 2 & -4 & 1 & -1 & 0 & -1 \\ 2 & -1 & 0 & 0 & 2 & -2 & 0 & -1 & -1 & 0 & 1 & 0 & -1 & 1 & -4 & -1 & 1 & -1 \\ 2 & -2 & -2 & 2 & 2 & -1 & 0 & -1 & -1 & -2 & -1 & 0 & 1 & -1 & -1 & -4 & 0 & -1 \\ -1 & -1 & 0 & 0 & -1 & 1 & -1 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 1 & 0 & -4 & 1 \\ 1 & -2 & -1 & -1 & 1 & -1 & 2 & -1 & -1 & 0 & -1 & 1 & 1 & -1 & -1 & -1 & 1 & -4 \end {pmatrix}} \\ E_{20} &:= {\begin {pmatrix} -4 & -2 & -1 & 1 & -1 & -1 & -1 & -1 & -1 & -1 & 1 & -1 & -2 & -2 & -1 & -2 & 1 & 1 & -1 & 0 \\ -2 & -4 & 1 & 2 & 1 & -2 & 1 & 1 & 1 & 1 & -1 & -2 & -1 & -2 & -1 & 0 & -1 & -1 & 0 & -1 \\ -1 & 1 & -4 & -2 & -2 & 2 & 0 & -2 & -2 & -2 & 0 & 1 & 0 & 0 & 1 & -1 & 0 & 2 & -2 & -1 \\ 1 & 2 & -2 & -4 & -2 & 2 & -1 & 0 & -2 & -2 & 1 & 2 & 0 & 0 & 0 & 1 & -1 & 2 & -1 & -1 \\ -1 & 1 & -2 & -2 & -4 & 0 & 0 & 0 & -1 & -1 & 2 & 2 & 0 & 0 & -1 & -1 & 0 & 2 & -2 & 0 \\ -1 & -2 & 2 & 2 & 0 & -4 & 1 & 2 & 2 & 2 & 1 & -1 & -1 & -1 & -2 & 0 & 0 & -1 & 0 & 1 \\ -1 & 1 & 0 & -1 & 0 & 1 & -4 & 0 & -1 & -1 & 1 & 1 & -2 & -1 & -1 & 0 & 1 & 1 & 0 & 1 \\ -1 & 1 & -2 & 0 & 0 & 2 & 0 & -4 & -2 & -2 & 0 & -1 & 1 & 1 & 2 & -2 & 1 & 1 & 0 & 0 \\ -1 & 1 & -2 & -2 & -1 & 2 & -1 & -2 & -4 & -2 & 1 & 0 & 0 & -1 & 1 & -1 & 1 & 1 & 0 & 0 \\ -1 & 1 & -2 & -2 & -1 & 2 & -1 & -2 & -2 & -4 & 0 & 1 & -1 & 0 & 1 & -1 & 0 & 2 & 0 & -1 \\ 1 & -1 & 0 & 1 & 2 & 1 & 1 & 0 & 1 & 0 & -4 & 0 & 0 & 0 & 1 & 1 & -1 & -1 & 1 & -1 \\ -1 & -2 & 1 & 2 & 2 & -1 & 1 & -1 & 0 & 1 & 0 & -4 & 0 & -1 & 0 & 0 & 0 & -1 & 1 & 0 \\ -2 & -1 & 0 & 0 & 0 & -1 & -2 & 1 & 0 & -1 & 0 & 0 & -4 & -2 & -2 & 0 & 0 & 1 & 0 & 0 \\ -2 & -2 & 0 & 0 & 0 & -1 & -1 & 1 & -1 & 0 & 0 & -1 & -2 & -4 & -2 & 0 & 0 & 0 & 0 & 0 \\ -1 & -1 & 1 & 0 & -1 & -2 & -1 & 2 & 1 & 1 & 1 & 0 & -2 & -2 & -4 & 1 & 0 & 0 & 0 & 0 \\ -2 & 0 & -1 & 1 & -1 & 0 & 0 & -2 & -1 & -1 & 1 & 0 & 0 & 0 & 1 & -4 & 1 & 1 & -1 & 1 \\ 1 & -1 & 0 & -1 & 0 & 0 & 1 & 1 & 1 & 0 & -1 & 0 & 0 & 0 & 0 & 1 & -4 & 0 & -1 & -1 \\ 1 & -1 & 2 & 2 & 2 & -1 & 1 & 1 & 1 & 2 & -1 & -1 & 1 & 0 & 0 & 1 & 0 & -4 & 2 & 1 \\ -1 & 0 & -2 & -1 & -2 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & -1 & -1 & 2 & -4 & 0 \\ 0 & -1 & -1 & -1 & 0 & 1 & 1 & 0 & 0 & -1 & -1 & 0 & 0 & 0 & 0 & 1 & -1 & 1 & 0 & -4 \end {pmatrix}}\\[6pt]E_{21} &:= {\begin {pmatrix} -4 & 2 & 2 & -1 & 2 & -2 & 2 & 1 & -1 & -2 & -2 & -2 & 1 & 0 & -2 & -2 & -1 & -2 & 2 & -2 & 2 \\ 2 & -4 & -2 & 2 & -1 & 0 & 0 & 1 & 2 & 1 & 2 & 2 & 1 & -1 & 1 & 2 & 2 & 2 & -2 & 1 & -1 \\ 2 & -2 & -4 & 2 & -2 & 1 & 0 & 1 & 0 & 0 & 2 & 1 & -1 & 1 & 0 & 1 & 0 & 0 & -1 & 2 & 0 \\ -1 & 2 & 2 & -4 & 0 & -1 & -1 & -1 & -1 & -1 & -2 & -1 & -1 & 1 & -1 & -2 & -1 & -1 & 1 & -2 & -1 \\ 2 & -1 & -2 & 0 & -4 & 2 & -2 & 1 & -1 & 0 & 0 & 0 & -1 & 0 & 1 & 1 & -1 & 0 & -2 & 1 & -2 \\ -2 & 0 & 1 & -1 & 2 & -4 & 1 & 1 & 1 & -1 & -1 & -1 & 1 & 0 & -1 & -1 & 0 & 0 & 1 & -1 & 1 \\ 2 & 0 & 0 & -1 & -2 & 1 & -4 & 0 & -1 & 0 & 0 & 1 & 0 & -1 & 2 & 1 & -1 & 1 & -1 & 0 & -2 \\ 1 & 1 & 1 & -1 & 1 & 1 & 0 & -4 & 0 & 2 & 1 & 1 & -1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & -1 \\ -1 & 2 & 0 & -1 & -1 & 1 & -1 & 0 & -4 & -2 & -1 & -1 & 0 & 1 & 0 & -1 & -2 & -2 & 1 & -1 & 0 \\ -2 & 1 & 0 & -1 & 0 & -1 & 0 & 2 & -2 & -4 & -2 & -1 & 0 & 0 & -1 & -1 & -2 & -2 & 2 & -2 & 1 \\ -2 & 2 & 2 & -2 & 0 & -1 & 0 & 1 & -1 & -2 & -4 & -2 & 0 & 0 & -1 & -1 & -2 & -1 & 1 & -2 & 0 \\ -2 & 2 & 1 & -1 & 0 & -1 & 1 & 1 & -1 & -1 & -2 & -4 & -1 & 1 & -1 & -2 & -2 & -1 & 1 & 0 & 1 \\ 1 & 1 & -1 & -1 & -1 & 1 & 0 & -1 & 0 & 0 & 0 & -1 & -4 & 2 & -1 & -1 & -1 & -1 & 0 & 1 & 0 \\ 0 & -1 & 1 & 1 & 0 & 0 & -1 & 1 & 1 & 0 & 0 & 1 & 2 & -4 & 2 & 1 & 0 & 1 & -1 & 0 & -1 \\ -2 & 1 & 0 & -1 & 1 & -1 & 2 & 0 & 0 & -1 & -1 & -1 & -1 & 2 & -4 & -1 & 0 & -2 & 1 & -1 & 2 \\ -2 & 2 & 1 & -2 & 1 & -1 & 1 & 0 & -1 & -1 & -1 & -2 & -1 & 1 & -1 & -4 & -1 & -1 & 2 & -1 & 1 \\ -1 & 2 & 0 & -1 & -1 & 0 & -1 & 1 & -2 & -2 & -2 & -2 & -1 & 0 & 0 & -1 & -4 & -1 & 1 & 0 & 0 \\ -2 & 2 & 0 & -1 & 0 & 0 & 1 & 0 & -2 & -2 & -1 & -1 & -1 & 1 & -2 & -1 & -1 & -4 & 1 & -1 & 1 \\ 2 & -2 & -1 & 1 & -2 & 1 & -1 & 0 & 1 & 2 & 1 & 1 & 0 & -1 & 1 & 2 & 1 & 1 & -4 & 2 & -2 \\ -2 & 1 & 2 & -2 & 1 & -1 & 0 & 0 & -1 & -2 & -2 & 0 & 1 & 0 & -1 & -1 & 0 & -1 & 2 & -4 & 0 \\ 2 & -1 & 0 & -1 & -2 & 1 & -2 & -1 & 0 & 1 & 0 & 1 & 0 & -1 & 2 & 1 & 0 & 1 & -2 & 0 & -4 \end {pmatrix}} \end{align*}$$
C Conjugacy classes of hearts of
 $\Lambda $
$\Lambda $
Each entry in Table 3 corresponds to an isomorphism class of hearts C of
![]() $\Lambda $
(Section 4). For each entry, we give
$\Lambda $
(Section 4). For each entry, we give
-
• the label of the associated lattice C. If C embeds primitively into the Leech lattice
 $\mathbb {L}$
, the Id corresponds to the one of the associated stable symplectic sublattice of
$\mathbb {L}$
, the Id corresponds to the one of the associated stable symplectic sublattice of
 $\mathbb {L}$
as given in [Reference Höhn and Mason19, Table 2]. Otherwise, if C is exceptional, the Id corresponds to the name of the associated lattice in Appendix B. In the case where
$\mathbb {L}$
as given in [Reference Höhn and Mason19, Table 2]. Otherwise, if C is exceptional, the Id corresponds to the name of the associated lattice in Appendix B. In the case where
 $\Lambda $
has several isomorphism classes of primitive sublattices abstractly isometric to C (Theorem 4.8), we add letters to distinguish each class;
$\Lambda $
has several isomorphism classes of primitive sublattices abstractly isometric to C (Theorem 4.8), we add letters to distinguish each class; -
• a description of the group
 $O^\#(C)$
, its Id in the Small Group Library [Reference Besche, Eick, O’Brien and Horn1], or its order;
$O^\#(C)$
, its Id in the Small Group Library [Reference Besche, Eick, O’Brien and Horn1], or its order; -
• the genus of the invariant sublattice
 $\Lambda ^{O^\#(C)}=C^\perp _\Lambda $
, following the convention of [Reference Conway, Sloane, Bannai, Borcherds, Leech, Norton, Odlyzko, Parker, Queen and Venkov11, Chapter 15];
$\Lambda ^{O^\#(C)}=C^\perp _\Lambda $
, following the convention of [Reference Conway, Sloane, Bannai, Borcherds, Leech, Norton, Odlyzko, Parker, Queen and Venkov11, Chapter 15]; -
• whether the group
 $O^\#(C)$
, which is saturated in
$O^\#(C)$
, which is saturated in
 $O^{+, \#}(\Lambda )$
, is saturated in
$O^{+, \#}(\Lambda )$
, is saturated in
 $O^+(\Lambda )$
.
$O^+(\Lambda )$
.
Remark C.1. For an IHS manifold X of deformation type
![]() $OG10$
, the wall divisors of X which are not prime exceptional correspond to vectors in
$OG10$
, the wall divisors of X which are not prime exceptional correspond to vectors in
![]() $H^{1,1}(X, \mathbb {R})\cap H^2(X, \mathbb {Z})$
which are of square
$H^{1,1}(X, \mathbb {R})\cap H^2(X, \mathbb {Z})$
which are of square
![]() $-4$
, or of square
$-4$
, or of square
![]() $-24$
and divisibility
$-24$
and divisibility
![]() $3$
[Reference Mongardi and Onorati33, Proposition 5.4]. Excluding the pairs
$3$
[Reference Mongardi and Onorati33, Proposition 5.4]. Excluding the pairs
all entries in the dataset [Reference Marquand and Muller30] are uniquely determined by
-
1. the isometry class of stable symplectic sublattice
 $C\subseteq \Lambda $
;
$C\subseteq \Lambda $
; -
2. the isometry class of the orthogonal complement of
 $C^\perp _\Lambda $
;
$C^\perp _\Lambda $
; -
3. the number of vectors of square
 $-4$
in C;
$-4$
in C; -
4. the number of vectors of square
 $-24$
in C which have divisibility 3 in
$-24$
in C which have divisibility 3 in
 $\Lambda $
.
$\Lambda $
.
Table 3 Hearts of
![]() $\Lambda $
.
$\Lambda $
.

D Extension approach – algorithms
In this section, we explain how to simplify the computations of representatives for the double cosets in Theorem 5.9. Let us observe the following:
Proposition D.1. Let C be a heart, and let
![]() $(F, a)$
be a head of C. One of the following two holds:
$(F, a)$
be a head of C. One of the following two holds:
-
• either
 $D_C$
embeds into
$D_C$
embeds into
 $D_F$
, as abelian groups;
$D_F$
, as abelian groups; -
• or
 $D_F$
embeds into
$D_F$
embeds into
 $D_C$
, as abelian groups.
$D_C$
, as abelian groups.
Proof. Let us see
![]() $C\subseteq \Lambda $
as the image of a primitive embedding
$C\subseteq \Lambda $
as the image of a primitive embedding
![]() $i\colon C\hookrightarrow \Lambda $
. According to [Reference Nikulin36, Proposition 1.15.1], the primitive embedding i determines an isomorphism between a subgroup
$i\colon C\hookrightarrow \Lambda $
. According to [Reference Nikulin36, Proposition 1.15.1], the primitive embedding i determines an isomorphism between a subgroup
![]() $I_C \leq D_C$
and a subgroup
$I_C \leq D_C$
and a subgroup
![]() $I_\Lambda \leq D_\Lambda $
. Now, since
$I_\Lambda \leq D_\Lambda $
. Now, since
![]() $D_\Lambda \cong \mathbb {Z}/3\mathbb {Z}$
as abelian group, then either
$D_\Lambda \cong \mathbb {Z}/3\mathbb {Z}$
as abelian group, then either
![]() $I_C$
is the trivial group, or
$I_C$
is the trivial group, or
![]() $I_C\cong D_\Lambda $
. In the former case, [Reference Nikulin36, Proposition 1.15.1] tells us that
$I_C\cong D_\Lambda $
. In the former case, [Reference Nikulin36, Proposition 1.15.1] tells us that
![]() $D_C$
is the glue domain of i, and thus,
$D_C$
is the glue domain of i, and thus,
![]() $D_C$
is identified with a subgroup of
$D_C$
is identified with a subgroup of
![]() $D_F$
. Similar arguments apply in the other case by exchanging the role of F and C.
$D_F$
. Similar arguments apply in the other case by exchanging the role of F and C.
Given a heart C, and given a head
![]() $(F, a)$
of C, we can easily decide in which case of Proposition D.1 the pair
$(F, a)$
of C, we can easily decide in which case of Proposition D.1 the pair
![]() $(C, F)$
fits, by comparing the determinant of C and F. In particular, we can already conclude the following.
$(C, F)$
fits, by comparing the determinant of C and F. In particular, we can already conclude the following.
Corollary D.2. Let C be a heart and let
![]() $(F, a)$
be a head of C. If
$(F, a)$
be a head of C. If
![]() $\det (C)$
divides
$\det (C)$
divides
![]() $\det (F)$
, then the image of
$\det (F)$
, then the image of
![]() $\{ {id}_F\}\times O^\#(C)$
along the primitive extension
$\{ {id}_F\}\times O^\#(C)$
along the primitive extension
![]() $F\oplus C\subseteq \Lambda $
is saturated in
$F\oplus C\subseteq \Lambda $
is saturated in
![]() $O^+(\Lambda )$
.
$O^+(\Lambda )$
.
Proof. According to Proposition D.1, we know that the glue map associated to
![]() $F\oplus C\subseteq \Lambda $
identifies
$F\oplus C\subseteq \Lambda $
identifies
![]() $D_C$
with a proper subgroup of
$D_C$
with a proper subgroup of
![]() $D_F$
. Thus, the result follows directly from Lemmas 4.2 and 4.21.
$D_F$
. Thus, the result follows directly from Lemmas 4.2 and 4.21.
Remark D.3. According to Corollary D.2, if C is a heart and
![]() $(F, a)$
is a head of C with
$(F, a)$
is a head of C with
![]() $\det (C)\mid \det (F)$
, then a must have order 2. In the case where
$\det (C)\mid \det (F)$
, then a must have order 2. In the case where
![]() $\det (F)$
divides
$\det (F)$
divides
![]() $\det (C)$
, we cannot conclude similarly (see Proposition 4.23)
$\det (C)$
, we cannot conclude similarly (see Proposition 4.23)
In what follows, we make Theorem 5.9 more explicit by separating these two cases from Proposition D.1. Indeed, we prove the following lemma.
Lemma D.4. Let C be a heart and let
![]() $(F, a)$
be a head of C. Let
$(F, a)$
be a head of C. Let
![]() $b\in O(C)$
and let
$b\in O(C)$
and let
![]() $\gamma $
be an
$\gamma $
be an
![]() $(a, b)$
-equivariant glue map. Then,
$(a, b)$
-equivariant glue map. Then,
![]() $a\oplus b\in O(\Lambda _\gamma )$
is non-stable if and only if
$a\oplus b\in O(\Lambda _\gamma )$
is non-stable if and only if
-
•
 $\det (C)\mid \det (F)$
and
$\det (C)\mid \det (F)$
and
 $D_a$
restricts to negative identity on the orthogonal complement of the glue domain of
$D_a$
restricts to negative identity on the orthogonal complement of the glue domain of
 $F\hookrightarrow \Lambda _{\gamma }$
;
$F\hookrightarrow \Lambda _{\gamma }$
; -
•
 $\det (F)\mid \det (C)$
and
$\det (F)\mid \det (C)$
and
 $D_b$
restricts to negative identity on the orthogonal complement of the glue domain of
$D_b$
restricts to negative identity on the orthogonal complement of the glue domain of
 $C\hookrightarrow \Lambda _\gamma $
.
$C\hookrightarrow \Lambda _\gamma $
.
Proof. Let
![]() $\gamma $
be an
$\gamma $
be an
![]() $(a,b)$
-equivariant glue map and let
$(a,b)$
-equivariant glue map and let
![]() $h := a\oplus b\in O(\Lambda _\gamma )$
. According to [Reference Nikulin36, Proposition 1.15.1],
$h := a\oplus b\in O(\Lambda _\gamma )$
. According to [Reference Nikulin36, Proposition 1.15.1],
![]() $D_{\Lambda _\gamma }$
is isometric to
$D_{\Lambda _\gamma }$
is isometric to
![]() $\Gamma ^\perp /\Gamma $
, where
$\Gamma ^\perp /\Gamma $
, where
![]() $\Gamma $
is the graph of
$\Gamma $
is the graph of
![]() $\gamma $
in
$\gamma $
in
![]() $D_F\oplus D_C$
, and the action of h on
$D_F\oplus D_C$
, and the action of h on
![]() $D_{\Lambda _\gamma }$
coincides with the one of
$D_{\Lambda _\gamma }$
coincides with the one of
![]() $a\oplus b$
on
$a\oplus b$
on
![]() $\Gamma ^\perp /\Gamma $
. Now
$\Gamma ^\perp /\Gamma $
. Now
-
• If
 $\det (C)\mid \det (F)$
, we write
$\det (C)\mid \det (F)$
, we write
 $D_F = S\oplus T$
, where
$D_F = S\oplus T$
, where
 $S\cong D_{\Lambda }$
and
$S\cong D_{\Lambda }$
and
 $T := S^{\perp }\cong D_C(-1)$
is the glue domain of
$T := S^{\perp }\cong D_C(-1)$
is the glue domain of
 $F\hookrightarrow \Lambda _\gamma $
. In that case, the action of
$F\hookrightarrow \Lambda _\gamma $
. In that case, the action of
 $a\oplus b$
on
$a\oplus b$
on
 $\Gamma ^\perp /\Gamma $
is given by
$\Gamma ^\perp /\Gamma $
is given by
 $(D_a)_{\mid S}$
;
$(D_a)_{\mid S}$
; -
• If
 $\det (F)\mid \det (C)$
, we write
$\det (F)\mid \det (C)$
, we write
 $D_C = S\oplus T$
, where
$D_C = S\oplus T$
, where
 $S\cong D_{\Lambda }$
and
$S\cong D_{\Lambda }$
and
 $T := S^{\perp }\cong D_F(-1)$
is the glue domain of
$T := S^{\perp }\cong D_F(-1)$
is the glue domain of
 $C\hookrightarrow \Lambda _\gamma $
. In that case, the action of
$C\hookrightarrow \Lambda _\gamma $
. In that case, the action of
 $a\oplus b$
on
$a\oplus b$
on
 $\Gamma ^{\perp }/\Gamma $
is given by
$\Gamma ^{\perp }/\Gamma $
is given by
 $(D_b)_{\mid S}$
.
$(D_b)_{\mid S}$
.
From a computational point of view, Lemma D.4 together with Theorem 5.8 allows us to decide at the level of hearts, heads and their companions which equivariant gluings will not give rise to spines. This is featured in Algorithms 0.1 and 0.2 to compute only the relevant equivariant primitive extensions (for our purpose).

Proposition D.5. For any heart C and any head
![]() $(F,a)$
of C such that
$(F,a)$
of C such that
![]() $\det (C)\mid \det (F)$
, Algorithm 0.1 returns the correct output.
$\det (C)\mid \det (F)$
, Algorithm 0.1 returns the correct output.
Proof. Since
![]() $\det (C)\mid \det (F)$
, Proposition D.1 tells us that for any primitive extensions
$\det (C)\mid \det (F)$
, Proposition D.1 tells us that for any primitive extensions
![]() $F\oplus C\subseteq \Lambda '$
with
$F\oplus C\subseteq \Lambda '$
with
![]() $\Lambda '\cong \Lambda $
, then the glue domain of
$\Lambda '\cong \Lambda $
, then the glue domain of
![]() $C\hookrightarrow \Lambda '$
is the discriminant group
$C\hookrightarrow \Lambda '$
is the discriminant group
![]() $D_C$
of C. Let
$D_C$
of C. Let
![]() $(\Lambda ', H)\in E$
be in the output of the algorithm. Since C and
$(\Lambda ', H)\in E$
be in the output of the algorithm. Since C and
![]() $F_a$
are negative definite, the condition in Line 22 ensures that H is symplectic (Lemma 3.6). Since it is generated by
$F_a$
are negative definite, the condition in Line 22 ensures that H is symplectic (Lemma 3.6). Since it is generated by
![]() $O^\#(C)$
and h where h lies in
$O^\#(C)$
and h where h lies in
![]() $O^+(\Lambda ')\setminus O^\#(\Lambda ')$
, we have that
$O^+(\Lambda ')\setminus O^\#(\Lambda ')$
, we have that
![]() $H^\# = O^\#(C)$
is saturated in
$H^\# = O^\#(C)$
is saturated in
![]() $O^{+, \#}(\Lambda ')$
. Note that here, we view
$O^{+, \#}(\Lambda ')$
. Note that here, we view
![]() $O^\#(C)$
as a saturated subgroup of
$O^\#(C)$
as a saturated subgroup of
![]() $O^{+, \#}(\Lambda ')$
after extending with the identity on F. Moreover, Line 7, together with Lemma D.4, ensures that
$O^{+, \#}(\Lambda ')$
after extending with the identity on F. Moreover, Line 7, together with Lemma D.4, ensures that
![]() $D_h$
acts by negative identity on
$D_h$
acts by negative identity on
![]() $D_{\Lambda '}\cong S$
. Therefore, together with the conditions in Lines 5 and 16, we know that
$D_{\Lambda '}\cong S$
. Therefore, together with the conditions in Lines 5 and 16, we know that
![]() $\gamma $
is a spine between C and
$\gamma $
is a spine between C and
![]() $(F, a)$
and b is companion to a. Moreover, Theorem 5.8 tells us that the definition of H does not depend on the choice of b in Line 18, and the conjugacy class of
$(F, a)$
and b is companion to a. Moreover, Theorem 5.8 tells us that the definition of H does not depend on the choice of b in Line 18, and the conjugacy class of
![]() $(\Lambda ', H)$
is independent on the choice of
$(\Lambda ', H)$
is independent on the choice of
![]() $(F, a)$
in its isomorphism class. Finally, by definition of H, we know that the heart of H is isometric to C, and
$(F, a)$
in its isomorphism class. Finally, by definition of H, we know that the heart of H is isometric to C, and
![]() $\overline {H}\leq D_{\Lambda '}$
is nontrivial by definition of h in Line 20.
$\overline {H}\leq D_{\Lambda '}$
is nontrivial by definition of h in Line 20.
Now, suppose that
![]() $H\leq O^+(\Lambda )$
is a symplectic finite subgroup, with
$H\leq O^+(\Lambda )$
is a symplectic finite subgroup, with
![]() $H^\#$
saturated in
$H^\#$
saturated in
![]() $O^{+, \#}(\Lambda )$
, with
$O^{+, \#}(\Lambda )$
, with
![]() $\overline {H}\leq D_\Lambda $
nontrivial, with heart isometric to C and with head isomorphic to
$\overline {H}\leq D_\Lambda $
nontrivial, with heart isometric to C and with head isomorphic to
![]() $(F, a)$
. Let
$(F, a)$
. Let
![]() $h\in H$
be such that
$h\in H$
be such that
![]() $H/O^\#(C)$
is generated by
$H/O^\#(C)$
is generated by
![]() $hO^\#(C)$
, and let b be the restriction of h to
$hO^\#(C)$
, and let b be the restriction of h to
![]() $\Lambda _{H^\#}\cong C$
. Then, by Theorems 5.8 and 5.9, up to the choice of a representative in the class of the glue domain for
$\Lambda _{H^\#}\cong C$
. Then, by Theorems 5.8 and 5.9, up to the choice of a representative in the class of the glue domain for
![]() $F\hookrightarrow \Lambda $
in Line 3, the choice of a representative in the double coset of the associated spines in Line 13 and the choice of a suitable companion
$F\hookrightarrow \Lambda $
in Line 3, the choice of a representative in the double coset of the associated spines in Line 13 and the choice of a suitable companion
![]() $b'$
of a in Line 18 with
$b'$
of a in Line 18 with
![]() $D_{b'} = D_b$
, we have that there exists
$D_{b'} = D_b$
, we have that there exists
![]() $(\Lambda ', H')\in E$
which is conjugate to
$(\Lambda ', H')\in E$
which is conjugate to
![]() $(\Lambda , H)$
. Note that the double cosets in Line 13 and in Theorem 5.9 are in bijection.
$(\Lambda , H)$
. Note that the double cosets in Line 13 and in Theorem 5.9 are in bijection.

Proposition D.6. For any heart C and any head
![]() $(F,a)$
of C such that
$(F,a)$
of C such that
![]() $\det (F)\mid \det (C)$
, Algorithm 0.1 returns the correct output.
$\det (F)\mid \det (C)$
, Algorithm 0.1 returns the correct output.
Proof. The proof is similar to the proof of Proposition D.5. Note that the main difference is that we do not start with a fixed isometry of C, so the translation of the double cosets from Theorem 5.9 to this context has to be adapted accordingly.
Let us note that if
![]() $a = {id}_F$
, it follows that H is the saturation of
$a = {id}_F$
, it follows that H is the saturation of
![]() $O^\#(C)$
in
$O^\#(C)$
in
![]() $O^+(\Lambda ')$
as described in Proposition 4.23. By definition of the saturation,
$O^+(\Lambda ')$
as described in Proposition 4.23. By definition of the saturation,
![]() $\Lambda ^{\prime }_H = C$
holds, and this implies that
$\Lambda ^{\prime }_H = C$
holds, and this implies that
![]() $\Lambda ^{\prime }_H\cap \mathcal {W}^{pex}(\Lambda ')$
is necessarily empty.
$\Lambda ^{\prime }_H\cap \mathcal {W}^{pex}(\Lambda ')$
is necessarily empty.
Remark D.7. The isometry b at Lines 18 and 17 of Algorithms 0.1 and 0.2, respectively, is computable in our setting since for us, the respective lattices C are definite: one can therefore effectively compute the discriminant representation
![]() $O(C)\to O(D_C)$
, and for each element in
$O(C)\to O(D_C)$
, and for each element in
![]() $\overline {O(C)}$
, one can compute a preimage. In the case where F is indefinite, then we do not compute
$\overline {O(C)}$
, one can compute a preimage. In the case where F is indefinite, then we do not compute
![]() $\overline {O(F, a)}$
through
$\overline {O(F, a)}$
through
![]() $O(F, a)$
, which might be in general infinite. However, the enumeration process described by Brandhorst and Hofmann features the computation of
$O(F, a)$
, which might be in general infinite. However, the enumeration process described by Brandhorst and Hofmann features the computation of
![]() $\overline {O(F, a)}$
by induction on gluing stabilisers along equivariant primitive extensions [Reference Brandhorst and Hofmann5, Algorithm 2].
$\overline {O(F, a)}$
by induction on gluing stabilisers along equivariant primitive extensions [Reference Brandhorst and Hofmann5, Algorithm 2].
Remark D.8. Each entry of Table 3 determines a pair
![]() $(C, F)$
, where C is a heart and F is its orthogonal complement in
$(C, F)$
, where C is a heart and F is its orthogonal complement in
![]() $\Lambda $
. In the cases where
$\Lambda $
. In the cases where
![]() $\det (C)\mid \det (F)$
and C has rank 21, then F is positive definite and it admits no nontrivial isometries with negative definite coinvariant sublattice. All the other cases are uniquely determined by C and F, up to isometry, except for the pair of cases 47a and 47b. In those cases,
$\det (C)\mid \det (F)$
and C has rank 21, then F is positive definite and it admits no nontrivial isometries with negative definite coinvariant sublattice. All the other cases are uniquely determined by C and F, up to isometry, except for the pair of cases 47a and 47b. In those cases,
![]() $F\in {II}_{(3,3)}2^{-2}3^29^1$
, and we have that
$F\in {II}_{(3,3)}2^{-2}3^29^1$
, and we have that
![]() $\det (F)\mid \det (C)$
. However, one can actually show that in this situation, the set
$\det (F)\mid \det (C)$
. However, one can actually show that in this situation, the set
![]() $\mathcal {H}_C$
, as defined in Algorithm 0.2, has actually cardinality 2 and which is why we obtain these two non-isomorphic primitive sublattices of
$\mathcal {H}_C$
, as defined in Algorithm 0.2, has actually cardinality 2 and which is why we obtain these two non-isomorphic primitive sublattices of
![]() $\Lambda $
. The upshot is the following. In our particular setting, for each pair
$\Lambda $
. The upshot is the following. In our particular setting, for each pair
![]() $(\Lambda ', H)$
in output of Algorithms 0.1 and 0.2, it is effectively possible to determine to which entry of Table 3 the stable sublattice
$(\Lambda ', H)$
in output of Algorithms 0.1 and 0.2, it is effectively possible to determine to which entry of Table 3 the stable sublattice
![]() $\Lambda ^{\prime }_{H^\#}\subseteq \Lambda '\cong \Lambda $
is isomorphic.
$\Lambda ^{\prime }_{H^\#}\subseteq \Lambda '\cong \Lambda $
is isomorphic.
Acknowledgements
The authors would like to thank Simon Brandhorst for his helpful comments and for his suggestion to use the Borcherds lattice, as in Section 2.3. Specifically, we thank him for the discussions about the proofs of Theorems 2.20 and 4.16. The authors would like to thank Simone Billi, Annalisa Grossi, Ljudmila Kamenova, Radu Laza and Giovanni Mongardi for helpful discussions and their comments. The authors would like to thank the OSCAR team for their support regarding the programming aspect of this project. Finally, the authors would like to thank the referee, whose comments greatly improved the manuscript.
Competing interest
The authors have no competing interests to declare.
Funding statement
The second author was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) [Gefördert durch die Deutsche Forschungsgemeinschaft (DFG) – Projektnummer 286237555 – TRR 195].
Data availability statement
The source code for OSCAR is available at https://github.com/oscar-system/Oscar.jl and the Zenodo dataset at [Reference Marquand and Muller30].