1. Introduction
The concept of the black hole goes back to Karl Schwarzschild’s point mass solution of Albert Einstein’s field equations of general relativity (Einstein Reference Einstein1916; Schwarzschild Reference Schwarzschild1916). The characteristic of a black hole is a horizon, a closed surface, from the inside of which escape would require superluminal motion and is hence not possible. As a consequence of general relativity, we expect such horizons to form for extremely compact objects, i.e. when the size of an object with mass M is smaller than its Schwarzschild radius,
![]() $r_\mathrm{s}=2GM/c^2 \approx 3\,$
km
$r_\mathrm{s}=2GM/c^2 \approx 3\,$
km
![]() $\,(M/M_\odot)$
, where G is the gravitational constant and c the speed of light. Rotating solutions to Einstein’s field equations have been found by Kerr (Reference Kerr1963). They also possess a horizon, if the spin angular momentum is below
$\,(M/M_\odot)$
, where G is the gravitational constant and c the speed of light. Rotating solutions to Einstein’s field equations have been found by Kerr (Reference Kerr1963). They also possess a horizon, if the spin angular momentum is below
![]() $J_\mathrm{max}=GM^2/c$
. Often, a spin parameter
$J_\mathrm{max}=GM^2/c$
. Often, a spin parameter
![]() $a=J/J_\mathrm{max}$
is used instead, where
$a=J/J_\mathrm{max}$
is used instead, where
![]() $a=1$
denotes a maximally rotating black hole.
$a=1$
denotes a maximally rotating black hole.
That such extremely compact configurations could indeed exist in nature was first hinted at by the huge energy requirements (Burbidge Reference Burbidge1956) to power extragalactic radio sources and jets from the nuclei of galaxies (Salpeter Reference Salpeter1964, also compare Blandford, Meier, & Readhead Reference Blandford, Meier and Readhead2019). This was corroborated when the high distances and therefore luminosities of active galactic nuclei were established (Schmidt Reference Schmidt1968). With optical luminosities in excess of a hundred times the luminosity of the Milky Way and energy requirements for radio sources that equated the conversion of sometimes more than a million times the mass of the Sun to energy, a single compact object of a mass comparable to the Sun was clearly insufficient as power source, and consequently, supermassive (
![]() $\gt10^6\,{\rm M}_\odot$
) black holes (SMBH) were postulated to explain the observations (Salpeter Reference Salpeter1964; Lynden-Bell Reference Lynden-Bell1969).
$\gt10^6\,{\rm M}_\odot$
) black holes (SMBH) were postulated to explain the observations (Salpeter Reference Salpeter1964; Lynden-Bell Reference Lynden-Bell1969).
Supermassive black holes influence their environment via their gravitational attraction. Their effect on the kinematics of surrounding stars has been measured in the nuclei of many galaxies (Kormendy & Richstone Reference Kormendy and Richstone1995; Magorrian et al. Reference Magorrian1998), most convincingly in the centre of our own galaxy (Ghez et al. Reference Ghez2008; Genzel, Eisenhauer, & Gillessen Reference Genzel, Eisenhauer and Gillessen2010). The Nobel prize to Andrea Ghez and Reinhard Genzel in 2020 marked the extensive work that has been done to constrain this object of four million solar masses (Genzel Reference Genzel2021).
The most direct evidence for black holes comes from gravitational waves. Gravitational waves are emitted when two compact objects orbit each other and, particularly, when they finally merge. The detection of gravitational waves thus implies the existence of binaries of compact objects. Gravitational waves were directly detected for the first time in 2015, from the merger of a stellar mass black hole binary (Abbott et al. Reference Abbott2016), for which a 2017 Nobel prize was awarded (Castelvecchi Reference Castelvecchi2017). Many events have been detected since, with the most massive black hole discovered in this way having a mass of
![]() $150\,{\rm M}_\odot$
(Abbott et al. Reference Abbott2020). The physical setup of Advanced LIGO detectors used in these observations is a Michelson interferometer with 4 km arm length. This limits the accessible frequency range and thus only stellar mass mergers can be observed. Direct detections of SMBHs will therefore have to wait for the space-borne LISA mission (Laser Interferometer Space Antenna, Amaro-Seoane et al. Reference Amaro-Seoane2023) with arm lengths of
$150\,{\rm M}_\odot$
(Abbott et al. Reference Abbott2020). The physical setup of Advanced LIGO detectors used in these observations is a Michelson interferometer with 4 km arm length. This limits the accessible frequency range and thus only stellar mass mergers can be observed. Direct detections of SMBHs will therefore have to wait for the space-borne LISA mission (Laser Interferometer Space Antenna, Amaro-Seoane et al. Reference Amaro-Seoane2023) with arm lengths of
![]() $\sim 2.5$
million km. In the meantime, pulsar timing arrays accurately monitor the arrival times of pulses from networks of nearby pulsars. Probing nanohertz frequencies they have the best chance to detect signals from the most massive supermassive black hole binaries (Section 8).
$\sim 2.5$
million km. In the meantime, pulsar timing arrays accurately monitor the arrival times of pulses from networks of nearby pulsars. Probing nanohertz frequencies they have the best chance to detect signals from the most massive supermassive black hole binaries (Section 8).
There are good reasons to believe that such supermassive binaries exist (e.g. Begelman, Blandford, & Rees Reference Begelman, Blandford and Rees1980). SMBHs are nowadays thought to be ubiquitous in galaxies. Their evolution is studied as an essential part of galaxy evolution, though still with considerable uncertainties (Section 2). When galaxies merge, which is cosmologically a frequent event, we expect their SMBHs to migrate towards the new centre and for many cases to merge well within the Hubble time (Section 3). This expectation is supported by a growing amount of direct observational evidence, obtained with similar techniques than the ones that have been used to establish the case for supermassive black holes in the first place (compare above). Activity of both black holes in such a system might be expected relatively frequently, as the merger event that brought in the secondary black hole might also bring in fresh gas. Dual active galactic nuclei with separations of the order of kiloparsec have been directly observed in X-rays, and highest resolution radio imaging has found a first good case of radio cores with parsec-scale separation (Section 4). Emission line signatures may reveal periodic kinematics in Doppler shifts in the future (Section 5). The direction of the black hole spin is the likely direction for jet ejection and likely parsec-scale SMBH binaries have been found to show dynamically changing jet features consistent with orbital motion (Sections 5.2). For such a close binary configuration, the relativistic geodetic precession effect would precess both spins on a much longer timescale. Corresponding precession features may have been seen on the
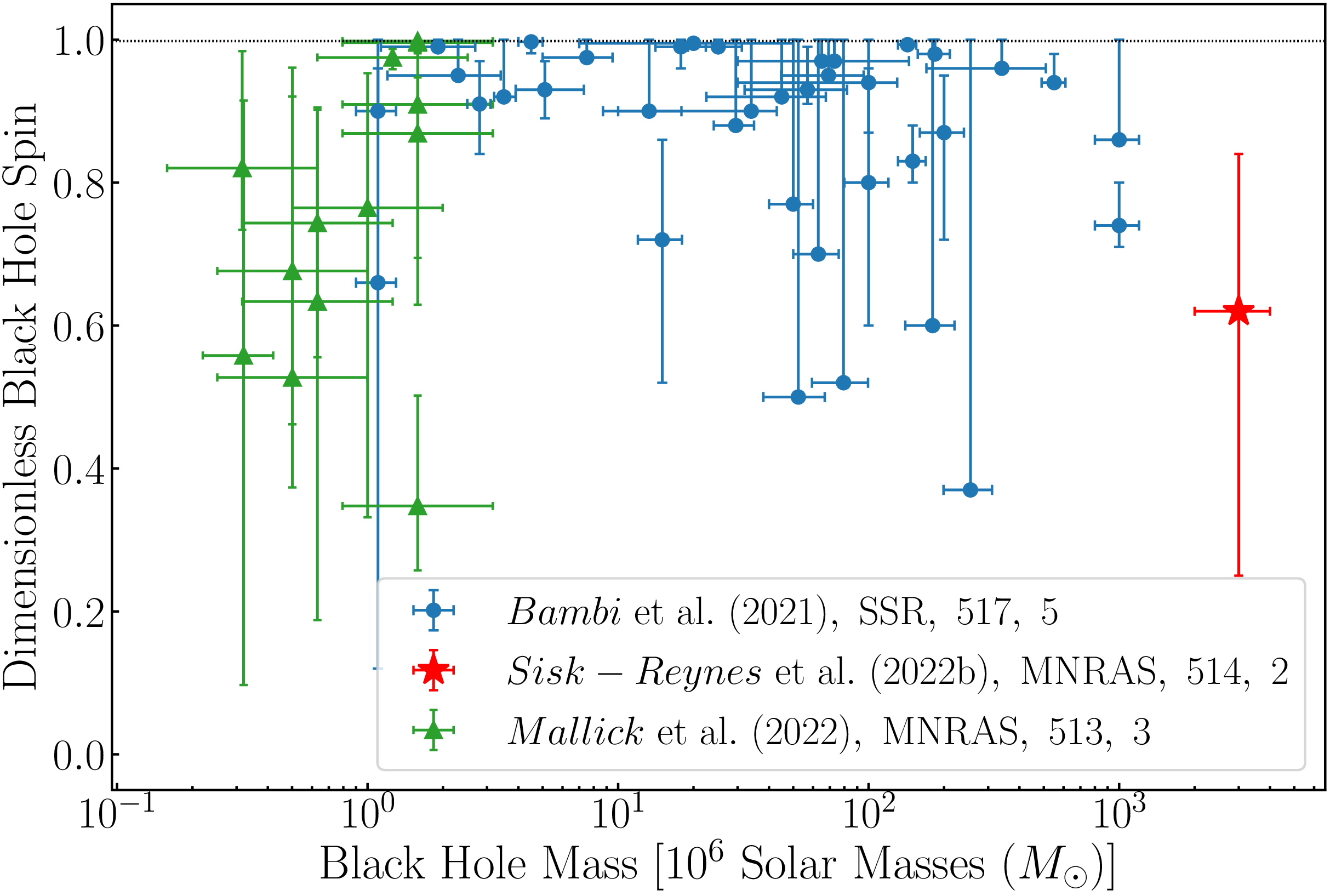
![]() $\approx 100$
kpc scale (Section 5.3). Cosmological simulations predict the magnitude of the black hole spins to be generally high from gas accretion, and to decrease after binary SMBH mergers. This can now be studied via X-ray spectroscopy for a number of accreting objects (Section 6). There are hints for spin-down at the higher masses, as expected from binary SMBH mergers. When black holes become gravitationally bound in a binary, the accretion flow becomes much more complex than single discs around each object (Section 7). This also influences the spin evolution and observational signatures of the double active galactic nucleus. The spin will also affect the signal shape of the gravitational waves in the eventual merger (Section 8). In the following sections, we review the state of these fields, starting with the area of perhaps greatest uncertainty.
$\approx 100$
kpc scale (Section 5.3). Cosmological simulations predict the magnitude of the black hole spins to be generally high from gas accretion, and to decrease after binary SMBH mergers. This can now be studied via X-ray spectroscopy for a number of accreting objects (Section 6). There are hints for spin-down at the higher masses, as expected from binary SMBH mergers. When black holes become gravitationally bound in a binary, the accretion flow becomes much more complex than single discs around each object (Section 7). This also influences the spin evolution and observational signatures of the double active galactic nucleus. The spin will also affect the signal shape of the gravitational waves in the eventual merger (Section 8). In the following sections, we review the state of these fields, starting with the area of perhaps greatest uncertainty.
2. The growth of supermassive black holes over cosmic time
Supermassive black holes are found in the centre of many, if not all, galaxies. In the local Universe, the diverse population of SMBHs encompasses objects with
![]() $\sim 10^{5}\, \rm M_{\odot}$
to SMBHs weighing up to
$\sim 10^{5}\, \rm M_{\odot}$
to SMBHs weighing up to
![]() $10^{9}-10^{10}\, \rm M_{\odot}$
in the largest galaxies (Greene, Strader, & Ho Reference Greene, Strader and Ho2020). At higher redshifts, still only accreting SMBHs (referred to as active galactic nuclei, AGN, and as quasars in their most powerful state) can be detected with current electromagnetic telescopes, though, progress in instrumentation is about to change this (Newman et al. Reference Newman2025). The discovery of quasars powered by extremely massive SMBHs with
$10^{9}-10^{10}\, \rm M_{\odot}$
in the largest galaxies (Greene, Strader, & Ho Reference Greene, Strader and Ho2020). At higher redshifts, still only accreting SMBHs (referred to as active galactic nuclei, AGN, and as quasars in their most powerful state) can be detected with current electromagnetic telescopes, though, progress in instrumentation is about to change this (Newman et al. Reference Newman2025). The discovery of quasars powered by extremely massive SMBHs with
![]() $10^{8-10}\, \rm M_{\odot}$
only 700 Myr after the Big Bang (e.g. Wang et al. Reference Wang2021) implies that SMBHs must originate from black hole seeds formed in the early Universe that have grown in mass efficiently over time by accretion of gas and stars, and mergers with other SMBHs (Fan, Bañados, & Simcoe Reference Fan, Bañados and Simcoe2023). Yet, the exact mechanism(s) of SMBH formation and the relative contributions of SMBH growth channels remain outstanding and unanswered questions in modern astrophysics.
$10^{8-10}\, \rm M_{\odot}$
only 700 Myr after the Big Bang (e.g. Wang et al. Reference Wang2021) implies that SMBHs must originate from black hole seeds formed in the early Universe that have grown in mass efficiently over time by accretion of gas and stars, and mergers with other SMBHs (Fan, Bañados, & Simcoe Reference Fan, Bañados and Simcoe2023). Yet, the exact mechanism(s) of SMBH formation and the relative contributions of SMBH growth channels remain outstanding and unanswered questions in modern astrophysics.
2.1 Supermassive black hole seeding
Most of today’s leading theoretical models form black hole seeds from the collapse of different massive stellar objects in metal-free or metal-poor halos (Inayoshi, Visbal, & Haiman Reference Inayoshi, Visbal and Haiman2020; Volonteri, Habouzit, & Colpi Reference Volonteri, Habouzit and Colpi2021, for recent reviews). Low-metallicity environments favour the formation of more massive seeds. The reason is twofold: the mass of the stellar object is set by the Jeans mass, the minimum mass a gas cloud must possess to overcome its gas pressure and collapse due to its own gravity, which increases with temperature. In the absence of efficient coolants (molecular hydrogen and metals), the Jeans mass of a collapsing gas cloud, which sets the mass of the stellar object that will form, remains high. Secondly, mass loss from that stellar object through winds is proportional to metallicity, and thus will remain small in metal-poor halos. A SMBH seed of similar mass will form. Based on the above, seeds could form from the collapse of the first-generation stars (Pop-III stars), from the collapse of very massive stars (VMS) formed by runaway mergers between stars or by hierarchical mergers of low-mass black holes in dense stellar clusters. Under rare conditions, Super Massive Stars (SMS) could form in atomic cooling halos and collapse into massive seeds. Rare major mergers of high-redshift and very massive galaxies (even in solar-metallicity environments) could both enhance gas inflow to the nuclear region and prevent cooling sufficiently to induce the formation of a SMS or a SMBH directly (Mayer et al. Reference Mayer, Kazantzidis, Escala and Callegari2010, Reference Mayer, Capelo, Zwick and Di Matteo2023). Finally, SMBHs could form well before the first stars and galaxies, potentially as early as inflation, if they originate from the collapse of high-contrast density perturbations in the primordial Universe (e.g. Carr & Kühnel Reference Carr and Kühnel2020). These SMBHs are referred to as primordial SMBHs. The channels mentioned above predict various ranges of initial masses (from tens of
![]() $\rm M_{\odot}$
to almost
$\rm M_{\odot}$
to almost
![]() $10^{6}\, \rm M_{\odot}$
) and different abundances of black hole seeds.
$10^{6}\, \rm M_{\odot}$
) and different abundances of black hole seeds.
2.2 Supermassive black hole growth
Not all seeds will blossom to become galaxies’ central engines, and not all SMBH formation models produce enough seeds to explain the presence of SMBHs in all galaxies. Light seeds with
![]() $\leqslant 10^{4-5}\, \rm M_{\odot}$
will struggle to achieve an efficient growth: they can form off the central gas reservoir of their host galaxies, and would then have a hard time sinking to the galaxy centre after galaxy mergers. This will limit both their accretion rates and their growth by SMBH mergers. Light seeds born in stellar clusters could alleviate these hurdles. Heavy seeds have the advantage to form massive but may be too rare to explain the bulk of the SMBH population (Habouzit et al. Reference Habouzit, Volonteri, Latif, Dubois and Peirani2016). The growth of SMBHs is a multi-faceted and complex problem due to their interplay with their host galaxies, and their galactic and large-scale environments (replenishment of gas from large-scale filaments, number of galaxy mergers, formation timescale of SMBH binaries set by galaxy properties, see Section 3 and Amaro-Seoane et al. Reference Amaro-Seoane2023, for a review).
$\leqslant 10^{4-5}\, \rm M_{\odot}$
will struggle to achieve an efficient growth: they can form off the central gas reservoir of their host galaxies, and would then have a hard time sinking to the galaxy centre after galaxy mergers. This will limit both their accretion rates and their growth by SMBH mergers. Light seeds born in stellar clusters could alleviate these hurdles. Heavy seeds have the advantage to form massive but may be too rare to explain the bulk of the SMBH population (Habouzit et al. Reference Habouzit, Volonteri, Latif, Dubois and Peirani2016). The growth of SMBHs is a multi-faceted and complex problem due to their interplay with their host galaxies, and their galactic and large-scale environments (replenishment of gas from large-scale filaments, number of galaxy mergers, formation timescale of SMBH binaries set by galaxy properties, see Section 3 and Amaro-Seoane et al. Reference Amaro-Seoane2023, for a review).
Over the last decade, the community has led a major effort to numerically address the formation and evolution of galaxies in a cosmological context with large-scale cosmological hydrodynamical simulations. The computational domain evolved in such simulations is typically a cube of
![]() $100\, \rm comoving \, Mpc$
side length such as e.g. Illustris (Sijacki et al. Reference Sijacki2015), Horizon-AGN (Dubois et al. Reference Dubois2016), or the recent Astrid (Ni et al. Reference Ni2022). They allow us to capture a large number of highly non-linear physical processes, diverse environments from dense regions to cosmic voids, and to track the cosmic evolution of thousands of galaxies with stellar masses in the range
$100\, \rm comoving \, Mpc$
side length such as e.g. Illustris (Sijacki et al. Reference Sijacki2015), Horizon-AGN (Dubois et al. Reference Dubois2016), or the recent Astrid (Ni et al. Reference Ni2022). They allow us to capture a large number of highly non-linear physical processes, diverse environments from dense regions to cosmic voids, and to track the cosmic evolution of thousands of galaxies with stellar masses in the range
![]() $10^{9}$
–
$10^{9}$
–
![]() $10^{12}\, \rm M_{\odot}$
. The resolution of these large-scale simulations is not sufficient to resolve processes across the entire dynamical range needed, from SMBH accretion discs to large-scale filaments. Processes related to SMBH formation, growth, and feedback, as well as any other baryonic processes taking place at small scales below the galactic scale, are modelled with sub-grid physics. Simulations all use different sub-grid models, e.g. different initial location and mass for SMBHs (the physical formation mechanisms described above are not modeled in these simulations, but see Habouzit, Volonteri, & Dubois Reference Habouzit, Volonteri and Dubois2017; Tremmel et al Reference Tremmel2017), different models to compute the accretion onto SMBHs (Rosas-Guevara et al. Reference Rosas-Guevara2015; Anglés-Alcázar et al. Reference Anglés-Alcázar2015, e.g. variations of the Bondi models or torque-limited accretion), different efficiencies and models to release energy from AGN, some models assuming that AGN feedback channels explicitly depend on SMBH mass (Weinberger et al. Reference Weinberger2017), some others assuming a uniform feedback (Schaye et al. Reference Schaye2015). Numerical difficulties persist to model accurately SMBH dynamics in these simulations of 1–2 kpc spatial resolution. Resolution of about
$10^{12}\, \rm M_{\odot}$
. The resolution of these large-scale simulations is not sufficient to resolve processes across the entire dynamical range needed, from SMBH accretion discs to large-scale filaments. Processes related to SMBH formation, growth, and feedback, as well as any other baryonic processes taking place at small scales below the galactic scale, are modelled with sub-grid physics. Simulations all use different sub-grid models, e.g. different initial location and mass for SMBHs (the physical formation mechanisms described above are not modeled in these simulations, but see Habouzit, Volonteri, & Dubois Reference Habouzit, Volonteri and Dubois2017; Tremmel et al Reference Tremmel2017), different models to compute the accretion onto SMBHs (Rosas-Guevara et al. Reference Rosas-Guevara2015; Anglés-Alcázar et al. Reference Anglés-Alcázar2015, e.g. variations of the Bondi models or torque-limited accretion), different efficiencies and models to release energy from AGN, some models assuming that AGN feedback channels explicitly depend on SMBH mass (Weinberger et al. Reference Weinberger2017), some others assuming a uniform feedback (Schaye et al. Reference Schaye2015). Numerical difficulties persist to model accurately SMBH dynamics in these simulations of 1–2 kpc spatial resolution. Resolution of about
![]() $10\, \rm pc$
would be needed to start resolving the dynamical friction from dark matter, gas, and stars, i.e. only the first phase in the long path of SMBH coalescence (Capelo et al. Reference Capelo2015; Pfister et al. Reference Pfister, Volonteri, Dubois, Dotti and Colpi2019). Such a fine resolution is only feasible in simulations that consider only individual galaxies or individual pairs of interacting galaxies (compare Section 3). Nonetheless, these fascinating multi-scale simulations have been able to reproduce a number of observed galaxy properties (e.g. realistic galaxy and halo stellar mass contents, star formation rates, galaxy morphologies). However, detailed analyses have shown that these simulations all produce different populations of SMBHs and AGN across cosmic times and highlighted differences with current observational constraints (e.g. with the AGN luminosity function beyond
$10\, \rm pc$
would be needed to start resolving the dynamical friction from dark matter, gas, and stars, i.e. only the first phase in the long path of SMBH coalescence (Capelo et al. Reference Capelo2015; Pfister et al. Reference Pfister, Volonteri, Dubois, Dotti and Colpi2019). Such a fine resolution is only feasible in simulations that consider only individual galaxies or individual pairs of interacting galaxies (compare Section 3). Nonetheless, these fascinating multi-scale simulations have been able to reproduce a number of observed galaxy properties (e.g. realistic galaxy and halo stellar mass contents, star formation rates, galaxy morphologies). However, detailed analyses have shown that these simulations all produce different populations of SMBHs and AGN across cosmic times and highlighted differences with current observational constraints (e.g. with the AGN luminosity function beyond
![]() $z=0$
, AGN fraction in low-mass galaxies,
$z=0$
, AGN fraction in low-mass galaxies,
![]() $M_{\rm MBH}-\sigma$
relation, Habouzit et al. Reference Habouzit2021, Reference Habouzit2022b; Li et al. Reference Li2020; Schirra et al. Reference Schirra2021; Haidar et al. Reference Haidar2022). In particular, there is no consensus among the simulations on the shape of the
$M_{\rm MBH}-\sigma$
relation, Habouzit et al. Reference Habouzit2021, Reference Habouzit2022b; Li et al. Reference Li2020; Schirra et al. Reference Schirra2021; Haidar et al. Reference Haidar2022). In particular, there is no consensus among the simulations on the shape of the
![]() $M_{\rm MBH}-M_{\star}$
relation, its scatter in
$M_{\rm MBH}-M_{\star}$
relation, its scatter in
![]() $M_{\rm MBH}$
at fixed
$M_{\rm MBH}$
at fixed
![]() $M_{\star}$
, and its evolution with redshift. The latter aspect has important implications: half of the large-scale simulations of the field predict that SMBHs are on average more massive with respect to their host galaxies at high redshift (e.g.
$M_{\star}$
, and its evolution with redshift. The latter aspect has important implications: half of the large-scale simulations of the field predict that SMBHs are on average more massive with respect to their host galaxies at high redshift (e.g.
![]() $z\geqslant 4$
) than they are in the local Universe, the other half predict under-massive SMBHs at high redshift. With the advent of the James Webb Space Telescope (JWST), the build-up of the
$z\geqslant 4$
) than they are in the local Universe, the other half predict under-massive SMBHs at high redshift. With the advent of the James Webb Space Telescope (JWST), the build-up of the
![]() $M_{\rm MBH}-M_{\star}$
relation can for the first time be constrained at
$M_{\rm MBH}-M_{\star}$
relation can for the first time be constrained at
![]() $z\geqslant 6$
with the observations of faint quasars (
$z\geqslant 6$
with the observations of faint quasars (
![]() $L_{\rm bol}=10^{44}$
–
$L_{\rm bol}=10^{44}$
–
![]() $10^{46}\, \rm erg/s$
) and their host galaxies (Habouzit et al. Reference Habouzit2022a; Maiolino et al. Reference Maiolino2024; Harikane Reference Harikane2025). JWST enables both the characterisation of the stellar component of high-redshift quasar hosts (Ding et al. Reference Ding2022, for the first detection) and more precise SMBH mass measurements. Such novel constraints will help improve our understanding and modeling of SMBH seeding, SMBH accretion (e.g. Negri & Volonteri Reference Negri and Volonteri2017), SMBH mergers, and the role of supernovae (e.g. Habouzit et al. Reference Habouzit, Volonteri and Dubois2017) and AGN feedback (e.g. Koudmani, Sijacki, & Smith Reference Koudmani, Sijacki and Smith2022) in cosmological simulations. This is crucial as those are all degenerate aspects of SMBH growth.
$10^{46}\, \rm erg/s$
) and their host galaxies (Habouzit et al. Reference Habouzit2022a; Maiolino et al. Reference Maiolino2024; Harikane Reference Harikane2025). JWST enables both the characterisation of the stellar component of high-redshift quasar hosts (Ding et al. Reference Ding2022, for the first detection) and more precise SMBH mass measurements. Such novel constraints will help improve our understanding and modeling of SMBH seeding, SMBH accretion (e.g. Negri & Volonteri Reference Negri and Volonteri2017), SMBH mergers, and the role of supernovae (e.g. Habouzit et al. Reference Habouzit, Volonteri and Dubois2017) and AGN feedback (e.g. Koudmani, Sijacki, & Smith Reference Koudmani, Sijacki and Smith2022) in cosmological simulations. This is crucial as those are all degenerate aspects of SMBH growth.
While comparing the large-scale cosmological simulations of the field, large discrepancies emerge on the number density and fraction of dual AGN that they predict (Puerto-Sánchez et al. Reference Puerto-Sánchez2025); reassuring that new observations are needed to constrain the AGN population in simulations. As described below dual AGN can be the precursors of SMBH binaries and the future events of the LISA gravitational wave antenna. LISA will provide a unique view of the merger history of black holes in the range
![]() $10^{4}$
–
$10^{4}$
–
![]() $10^{7}\, \rm M_{\odot}$
at any redshift.
$10^{7}\, \rm M_{\odot}$
at any redshift.
3. Black-hole migration within the remnants of galaxy mergers and the last-parsec problem
When galaxies with embedded SMBHs merge, the first phase of the orbital evolution of the black hole pair is dictated by the large-scale dynamics of the galaxy merger (Mayer et al. Reference Mayer2007; Capelo et al. Reference Capelo2015). Initially the orbital evolution is governed by dynamical friction between the two dark halos. This means that the gravitational interaction between the SMBHs and the dark matter leads to an exchange of energy and angular momentum. As the galaxies merge, the two black holes eventually end up in the remnant at some separation, forming a loose SMBH pair. The separation can vary between 100 pc and more than a kpc depending on the mass ratio between the galaxies, being larger for minor mergers (Callegari et al. Reference Callegari2009). In the latter the secondary galaxy, depending on its central density relative to that of the background galaxy, can be tidally disrupted before reaching the centre of the primary. If the latter happens, the secondary black hole can be left ‘naked’ at significant distance from the centre, which results in a long dynamical friction timescale (Callegari et al. Reference Callegari2009; Tremmel et al. Reference Tremmel, Governato, Volonteri, Pontzen and Quinn2018). The dynamics of the SMBH pair embedded in the merger remnant is then highly dependent on the structural properties of the host galaxy, in particular on the nature of the gaseous and stellar background providing the source of the drag onto the binary. The modelling uncertainties generally associated with baryonic processes in galaxy formation inevitably result in uncertainties in the effects of the gaseous background, while if the decay is governed by the interaction with stars the available models are much more robust. As a result, the timescale to form a bound binary, which forms at a separation of order 1–10 pc, depending on the mass of the black holes, can vary from less than a few tens of million years to several billion years. In the most extreme cases, the secondary black hole will be left wandering in the galaxy merger remnant (Bellovary et al. Reference Bellovary2010; Tremmel et al. Reference Tremmel, Governato, Volonteri, Pontzen and Quinn2018). In the following, we address the current knowledge and main open problems in understanding the entire evolution of SMBH pairs, from binary formation to coalescence.
3.1 Binary hardening on the last parsecs in gas-poor galaxy centres
The final parsec problem was first described by Begelman et al. (Reference Begelman, Blandford and Rees1980) who identified the fundamental timescales involved in SMBH mergers. It was subsequently seen in numerical N-Body simulations of massive black holes in gas-free spherically symmetric nuclei (Milosavljević & Merritt Reference Milosavljević and Merritt2001). The original models were constructed to mimic the mass distribution in the nuclei of early-type galaxies, the systems in which the largest black holes had been previously discovered. In this regime the two SMBHs first evolve as a result of dynamical friction against the stellar background, until they reach a separation at which their total mass supersedes the mass of the stars within their orbit. At this point, corresponding to a separation of 1–10 pc for black holes with masses exceeding a million solar masses, dynamical friction becomes inefficient. Instead, 3-body encounters between the loose SMBH binary and individual stars can drain orbital angular momentum and orbital energy, leading to a decrease of the orbital separation so that the binary becomes more tighly bound, i.e. a hardening of the binary. However, in spherical systems only a small region of the galactic nucleus comprises stars that can undergo close encounters with the binary. An important concept in this context is the loss cone, a term which describes the positions and velocities stars must have to be ejected by interaction with the supermassive binary. The reservoir of interacting stars steadily decreases as they are ejected after encounters, leading rapidly to an empty loss cone, hence to the stalling of the orbital decay. It is the latter occurrence that was originally referred to as the ‘last parsec problem’ (Milosavljević & Merritt Reference Milosavljević and Merritt2001)
Since these early studies, a number of ever more sophisticated N-Body simulations with increasingly high resolution have shown that, once the host potential is axisymmetric or triaxial, rather than spherically symmetric, the loss-cone remains filled owing to plentiful elongated plunging stellar orbits, such as tube/box orbits (Berczik et al. Reference Berczik, Merritt, Spurzem and Bischof2006; Khan et al. Reference Khan, Holley-Bockelmann, Berczik and Just2013), thus allowing the binary to harden further. The loss cone refilling is a purely collisionless phenomenon, and indeed N-body simulations with collisionless gravity solvers, such as tree codes, have nearly achieved convergence of loss cone refilling with increasing resolution (Gualandris et al. Reference Gualandris, Read, Dehnen and Bortolas2017). Finally, zoom-in cosmological simulations using particles to represent the different kinds of matter in the Universe, augmented with particle splitting to increase the mass and spatial resolution further in subsequent steps, have confirmed that the loss-cone is efficiently refilled in massive galaxies (Khan et al. Reference Khan, Fiacconi, Mayer, Berczik and Just2016). They have further pointed out that the hardening timescale below parsec separations, down to the milliparsec separation stage at which gravitational wave emission takes over, can be as short as a few tens of Myr for black holes with masses above
![]() $10^8$
solar masses in galactic nuclei with high central densities matching those of galaxies at
$10^8$
solar masses in galactic nuclei with high central densities matching those of galaxies at
![]() $z \gt 3$
. The hardening timescale is in the range
$z \gt 3$
. The hardening timescale is in the range
![]() $10^8$
–
$10^8$
–
![]() $10^9$
yr in the low density cores of present-day spiral galaxies, becoming strongly dependent on the orbital configuration of the galaxy merger (Khan et al. Reference Khan, Capelo, Mayer and Berczik2018). While more studies are required to best pin-down the range of hardening timescales for a realistic distribution of galaxy structural parameters and orbital configurations, it is fair to say that, generically, there is no last parsec problem when binary hardening is driven by stars. This is consistent with the recent determination of the gravitational wave background by pulsar timing arrays (discussed in more detail in Section 8, below), which is thought to be contributed by very large merging SMBHs hosted in early-type galaxies in which hardening is driven by stars.
$10^9$
yr in the low density cores of present-day spiral galaxies, becoming strongly dependent on the orbital configuration of the galaxy merger (Khan et al. Reference Khan, Capelo, Mayer and Berczik2018). While more studies are required to best pin-down the range of hardening timescales for a realistic distribution of galaxy structural parameters and orbital configurations, it is fair to say that, generically, there is no last parsec problem when binary hardening is driven by stars. This is consistent with the recent determination of the gravitational wave background by pulsar timing arrays (discussed in more detail in Section 8, below), which is thought to be contributed by very large merging SMBHs hosted in early-type galaxies in which hardening is driven by stars.
3.2 Binary hardening in gas-rich galaxy centres
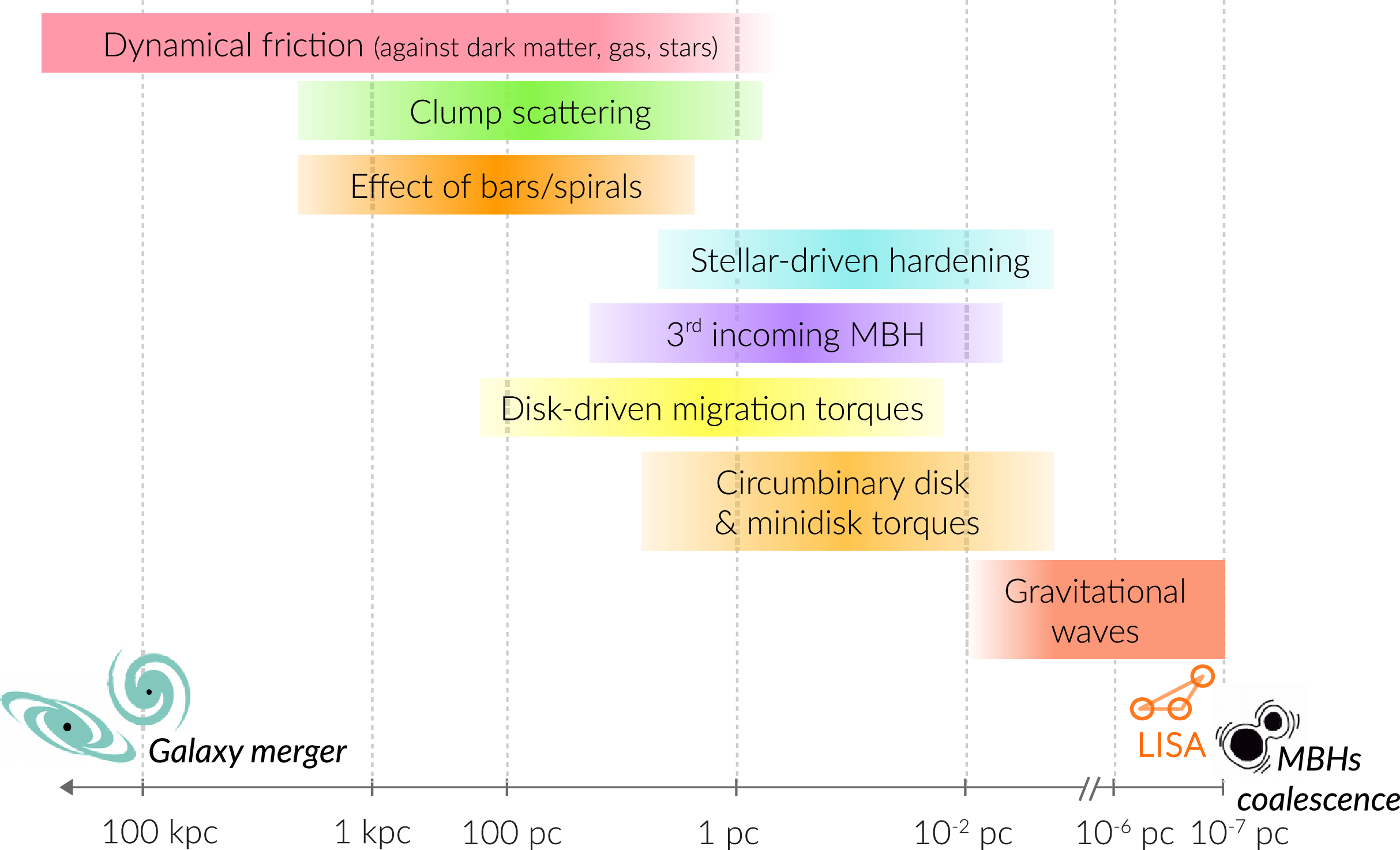
In gas-rich nuclei the phenomenology of orbital decay is much more complex. While initially it was believed that both SMBH binary formation by dynamical friction and hardening are more efficient in gaseous backgrounds rather than in stellar-dominated systems (Escala et al. Reference Escala, Larson, Coppi and Mardones2005; Mayer et al. Reference Mayer2007; Mayer Reference Mayer2013), numerical hydrodynamical simulations carried out at various scales have shown that this simple conclusion applies only to smooth gaseous galactic nuclei, such as axisymmetric nuclear discs or spherical clouds. Realistic gas-rich galactic nuclei have significant asymmetries, substructure and clumpiness that can hamper orbital decay at various stages (Amaro-Seoane et al. Reference Amaro-Seoane2023). In the following we summarise the main interaction mechanisms between the SMBH binary and the ambient medium, and how they affect its orbital evolution, eventually suppressing decay, starting with the scale between parsecs and a kiloparsec, and continuing with evolution at sub-pc scales (compare Figure 1). It is important to underline that the case of a SMBH pair interacting with a predominantly gaseous background is most relevant to LISA sources, since the SMBH mergers with the loudest signals in the LISA band are in a mass range,
![]() $10^5$
–
$10^5$
–
![]() $10^7$
solar masses and for such black holes the typical hosts are massive gas-rich spirals or (gas-rich) dwarf galaxies.
$10^7$
solar masses and for such black holes the typical hosts are massive gas-rich spirals or (gas-rich) dwarf galaxies.
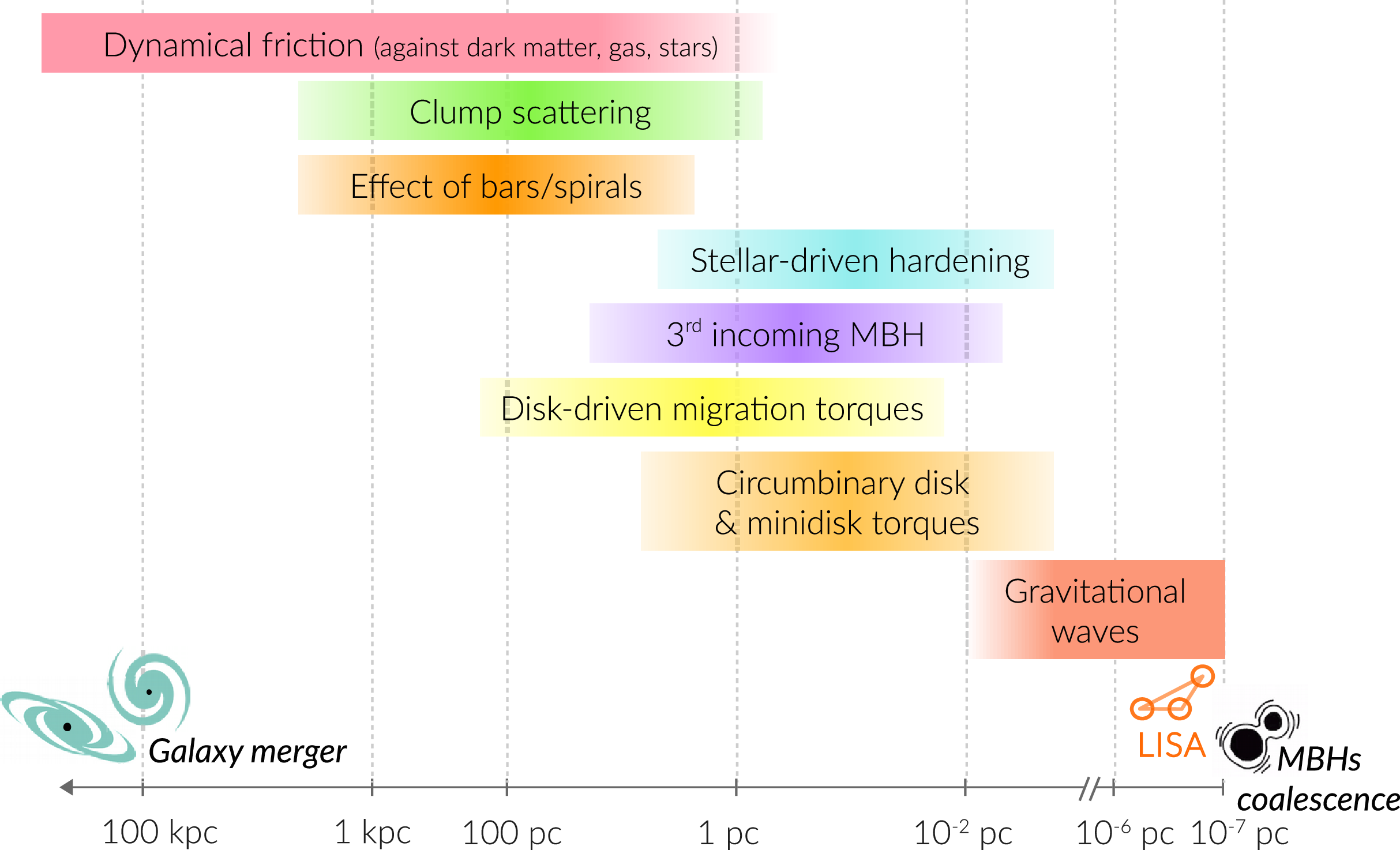
Figure 1. A summary of the various astrophysical mechanisms that contribute to drive the orbital evolution of massive black hole pairs from large to small scales, adapted from Amaro-Seoane et al. (Reference Amaro-Seoane2023) under Creative Commons license, https://creativecommons.org/licenses/by/4.0/.
Once the two black holes have formed a binary, they find themselves embedded in a dense circumnuclear disc of gas and stars, of order a hundred pc in size, whose properties can be inferred from observations of nearby galaxy merger remnants (Medling et al. Reference Medling2014). The gas in the circumnuclear disc is expected to cool radiatively to temperatures below
![]() $10^4$
K due to fine-structure line and molecular cooling. The radiated energy comes from out of the thermal energy reservoir. Slightly denser regions lose their pressure faster, cooling further. The disc is compressed in such regions, thus becoming overall inhomogeneous and clumpy. The dense clumpy phase corresponds to star forming giant molecular clouds (GMCs), weighing a million solar masses, consistent with the high specific star formation rates measured in such systems (Medling et al. Reference Medling2014). In this regime, scattering between the secondary lighter SMBH and the GMCs becomes dynamically important for SMBHs below
$10^4$
K due to fine-structure line and molecular cooling. The radiated energy comes from out of the thermal energy reservoir. Slightly denser regions lose their pressure faster, cooling further. The disc is compressed in such regions, thus becoming overall inhomogeneous and clumpy. The dense clumpy phase corresponds to star forming giant molecular clouds (GMCs), weighing a million solar masses, consistent with the high specific star formation rates measured in such systems (Medling et al. Reference Medling2014). In this regime, scattering between the secondary lighter SMBH and the GMCs becomes dynamically important for SMBHs below
![]() $10^7$
solar masses, namely those within the LISA band. As a result of scattering with GMC-sized clumps, the secondary SMBH can be ejected from the disc midplane, or undergo episodic outward migration (Fiacconi et al. Reference Fiacconi, Mayer, Roškar and Colpi2013; Roškar et al. Reference Roškar2015; Souza Lima et al. Reference Souza Lima, Mayer, Capelo and Bellovary2017). When it is ejected to several tens of parsecs dynamical friction becomes inefficient as the SMBH finds itself in a low density background (even when accounting for the stellar density of an embedding stellar bulge). As a result the SMBH binary formation timescale becomes long, of order a few 100 Myr as opposed to less than 10 Myr in a smooth disc (Roškar et al. Reference Roškar2015). In some cases, though, orbital decay can be accelerated relative to the smooth background case, because the net torque can still be negative by chance superposition of multiple torques components generated by multiple clumps and spiral density waves (Fiacconi et al. Reference Fiacconi, Mayer, Roškar and Colpi2013). Stochasticity in the outcome of orbital decay is the most general trait emerging from numerical simulations of SMBH pairs embedded in multi-phase circumnuclear discs. By stochasticity we mean that, under small changes of the orbital parameters of the black hole pair or of the physical parameters defining the properties of the environment (such as density, temperature, or other properties defining the background gravitational potential), the orbital evolution of the pair can change drastically. In other words, the trajectory of the black hole pair performs a random walk in parameter space, so that whether or not the separation of the pair increases or decreases, and what pace it does that, cannot be predicted.
$10^7$
solar masses, namely those within the LISA band. As a result of scattering with GMC-sized clumps, the secondary SMBH can be ejected from the disc midplane, or undergo episodic outward migration (Fiacconi et al. Reference Fiacconi, Mayer, Roškar and Colpi2013; Roškar et al. Reference Roškar2015; Souza Lima et al. Reference Souza Lima, Mayer, Capelo and Bellovary2017). When it is ejected to several tens of parsecs dynamical friction becomes inefficient as the SMBH finds itself in a low density background (even when accounting for the stellar density of an embedding stellar bulge). As a result the SMBH binary formation timescale becomes long, of order a few 100 Myr as opposed to less than 10 Myr in a smooth disc (Roškar et al. Reference Roškar2015). In some cases, though, orbital decay can be accelerated relative to the smooth background case, because the net torque can still be negative by chance superposition of multiple torques components generated by multiple clumps and spiral density waves (Fiacconi et al. Reference Fiacconi, Mayer, Roškar and Colpi2013). Stochasticity in the outcome of orbital decay is the most general trait emerging from numerical simulations of SMBH pairs embedded in multi-phase circumnuclear discs. By stochasticity we mean that, under small changes of the orbital parameters of the black hole pair or of the physical parameters defining the properties of the environment (such as density, temperature, or other properties defining the background gravitational potential), the orbital evolution of the pair can change drastically. In other words, the trajectory of the black hole pair performs a random walk in parameter space, so that whether or not the separation of the pair increases or decreases, and what pace it does that, cannot be predicted.
Simulations of massive clumpy galactic discs, which are common in star forming galaxies at high redshift (
![]() $z = 1-3$
), have shown that the same phenomenology can occur at larger scales, a few kpc, and for black holes with masses up to a few times
$z = 1-3$
), have shown that the same phenomenology can occur at larger scales, a few kpc, and for black holes with masses up to a few times
![]() $10^8\,{\rm M}_\odot$
. In the latter case the mass of the gaseous clumps is larger (even exceeding
$10^8\,{\rm M}_\odot$
. In the latter case the mass of the gaseous clumps is larger (even exceeding
![]() $10^8\,{\rm M}_\odot$
, Tamburello et al. Reference Tamburello, Capelo, Mayer, Bellovary and Wadsley2017), becoming thus comparable to that of even the most massive SMBHs. Since the timescales are longer in a galactic disc compared to a circumnuclear disc, indefinite stalling is a more likely outcome in these systems. Stochasticity, however, is the prevailing trait also in this case.
$10^8\,{\rm M}_\odot$
, Tamburello et al. Reference Tamburello, Capelo, Mayer, Bellovary and Wadsley2017), becoming thus comparable to that of even the most massive SMBHs. Since the timescales are longer in a galactic disc compared to a circumnuclear disc, indefinite stalling is a more likely outcome in these systems. Stochasticity, however, is the prevailing trait also in this case.
If a galactic or circumnuclear disc is not clumpy, the orbital decay of an SMBH pair is still subject to a complex interaction with the non-axisymmetric background. In particular, high-resolution cosmological simulations of star forming gas-rich disc galaxies have shown that, when the secondary SMBH is delivered at scale of order 0.5–1 kpc, a common occurrence of minor mergers, its further sinking can be hampered as well as promoted by large-scale structure in the merger remnant, such as spiral density waves and bars. The gravitational torque provided by the latter is found to dominate over the local effect of dynamical friction, resulting in a markedly stochastic orbital evolution (Bortolas et al. Reference Bortolas2020, Reference Bortolas2022).
In both circumnuclear discs and galactic discs the dynamical effect of clumps, spiral structure and bars is mediated by supernovae (SN) and AGN feedback, which, by heavily impacting both the local and the global density and temperature structure of the ambient medium via heating and wind/outflow driving, affects the magnitude and direction of the torques (del Valle & Volonteri Reference del Valle and Volonteri2018). In particular, under the simple assumption that the coupling of AGN feedback with the gas is mainly thermal, the dynamical friction wake can be washed away, leading to the stalling of the SMBH, a phenomenon that has been dubbed ‘wake evacuation effect’ (Souza Lima et al. Reference Souza Lima, Mayer, Capelo and Bellovary2017; Park & Bogdanović Reference Park and Bogdanović2017). Overall, among simulations of SMBHs embedded in clumpy discs, those in which both SN and AGN feedback are included have a higher occurrence of SMBH stalling.
If the SMBHs manage to reduce their separation below parsec scales in a gas-dominated galactic nucleus, the expectation is that, eventually, a cavity will form around the binary as the surrounding medium absorbs the excess orbital angular momentum and is torqued away. A circumbinary disc forms, and, in absence of self-gravity, the extraction of angular momentum which triggers the decay of the binary can be understood as resulting from a resonant interaction between the binary and the disc (Artymowicz & Lubow Reference Artymowicz and Lubow1994). Viscous and pressure forces act against cavity formation, and can partially refill the cavity, hence this stage is, like the others, dependent on the details of gas physics. Most of the work carried out in this regime assumes a locally isothermal or adiabatic medium, neglects self-gravity, accretion and/or feedback from the SMBHs (see the introductory section of Duffell et al. Reference Duffell2024). Most often a fixed binary orbit is assumed, and the mass ratio considered for the two SMBHs is in the range
![]() $0.1-1$
. These limitations in the physical modelling and parameter space call for caution in the generalisation of the results. A large variety of numerical hydro codes, from smooth particle hydrodanamics over static grid-based, to quasi-Lagrangian codes such as moving mesh and the meshless finite mass method (MFM), has been or is being employed in this regime. A major code comparison, initiated at KITP during the Spring 2022 (BINARY22 program) has been recently completed (Duffell et al. Reference Duffell2024).
$0.1-1$
. These limitations in the physical modelling and parameter space call for caution in the generalisation of the results. A large variety of numerical hydro codes, from smooth particle hydrodanamics over static grid-based, to quasi-Lagrangian codes such as moving mesh and the meshless finite mass method (MFM), has been or is being employed in this regime. A major code comparison, initiated at KITP during the Spring 2022 (BINARY22 program) has been recently completed (Duffell et al. Reference Duffell2024).
From the existing literature, some clear trends have emerged. As for the regimes at larger scales, torques acting on the black hole binary can be both negative and positive. First, in cold discs with low aspect ratio (
![]() $H/r \lt 0.05$
, where H is the disk scale height and r the radial scale length of the disk) migration of the black hole binary is generally inward (Tiede et al. Reference Tiede, Zrake, MacFadyen and Haiman2020; Franchini, Lupi, & Sesana Reference Franchini, Lupi and Sesana2022), while it can be outward otherwise (Muñoz, Miranda, & Lai Reference Muñoz, Miranda and Lai2019; Duffell et al. Reference Duffell2020). The outward migration occurs due to a positive torque predominantly generated by the mini-discs of gas surrounding the two SMBHs inside the cavity. This is also very sensitive to viscosity as the latter controls the amount of material flowing through the cavity, as well as the rate at which it flows (Heath & Nixon Reference Heath and Nixon2020; Franchini et al. Reference Franchini, Lupi and Sesana2022).
$H/r \lt 0.05$
, where H is the disk scale height and r the radial scale length of the disk) migration of the black hole binary is generally inward (Tiede et al. Reference Tiede, Zrake, MacFadyen and Haiman2020; Franchini, Lupi, & Sesana Reference Franchini, Lupi and Sesana2022), while it can be outward otherwise (Muñoz, Miranda, & Lai Reference Muñoz, Miranda and Lai2019; Duffell et al. Reference Duffell2020). The outward migration occurs due to a positive torque predominantly generated by the mini-discs of gas surrounding the two SMBHs inside the cavity. This is also very sensitive to viscosity as the latter controls the amount of material flowing through the cavity, as well as the rate at which it flows (Heath & Nixon Reference Heath and Nixon2020; Franchini et al. Reference Franchini, Lupi and Sesana2022).
When self-gravity is included, i.e. where the gas mass becomes non-negligible, the regime of the torques changes again (Cuadra et al. Reference Cuadra, Armitage, Alexander and Begelman2009). The torque is found to be negative because it is dominated by the direct gravitational pull of the circumbinary disc rather than by the interaction with gas in the mini-discs (Roedig et al. Reference Roedig2012; Franchini, Sesana, & Dotti Reference Franchini, Sesana and Dotti2021). More massive circumbinary discs drive faster inward migration as well as stronger eccentricity growth, which can have important consequences once they reach the GW-dominated regime. Moreover, when migration is outward in a non-self gravitating region of the disc, the radius at which the disc becomes self-gravitating will eventually be reached, at which point a reversal of the sign of migration occurs, and orbital decay can resume (Franchini et al. Reference Franchini, Sesana and Dotti2021; Bortolas et al. Reference Bortolas, Franchini, Bonetti and Sesana2021).
Finally, Bortolas et al. (Reference Bortolas, Franchini, Bonetti and Sesana2021) have investigated, with the aid of a semi-analytical model calibrated on numerical simulations, what would be the net outcome of the different concurrent torques once also the effect of stellar hardening in a typical stellar bulge is included. Even by assuming, very conservatively, that the gas torques resulting from the combination of circumbinary disc and mini-discs are positive until the binary reaches the self-gravitating radius, at which point it cancels out, they found that stellar hardening alone would drive the binary to coalescence always within less than a Gyr, and for a wide range of SMBH masses (
![]() $10^3$
–
$10^3$
–
![]() $10^8$
solar masses).
$10^8$
solar masses).
In conclusion, currently the results of simulations on various scales suggest that SMBH pairs evolving in stellar backgrounds are almost certainly going to merge, and likely do that on timescales much smaller than the age of the Universe. These should correspond to the high end of the SMBH mass distribution, which is accessible by Pulsar Timing Arrays (PTAs). Instead, for lower mass black holes evolving in predominantly gaseous backgrounds, which would be typical LISA sources, the jury is still out on the efficiency of the binary formation and hardening, with wandering SMBHs produced by stalling in various phases of the orbital evolution being a possible outcome. However, there are indications that also in this case stellar-driven hardening might come to rescue, at least if the SMBHs reach parsec-scale separations. Hence numerical models which can follow both the gas-driven and the stellar-driven torques self-consistently are needed to address this problem further.
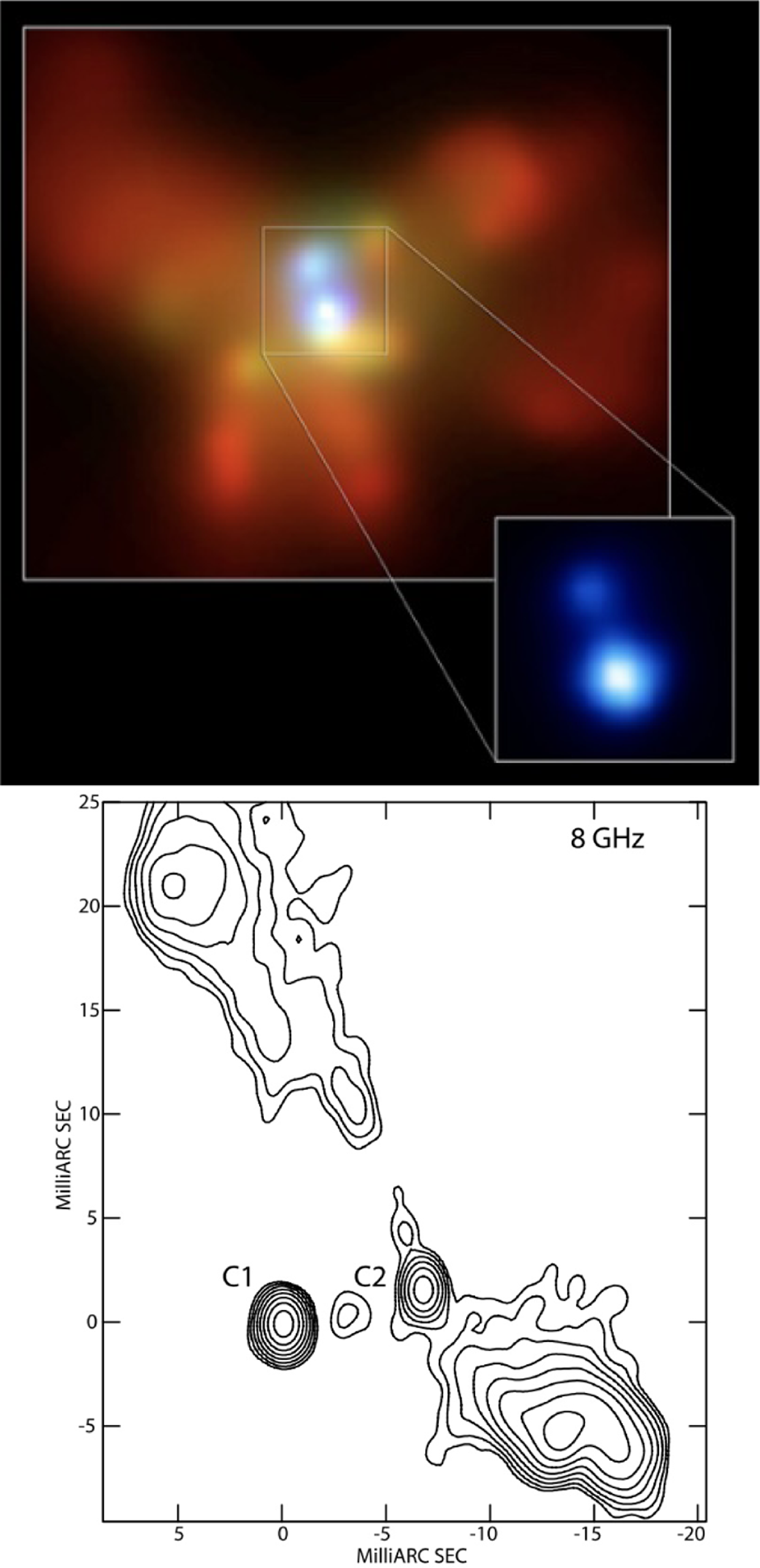
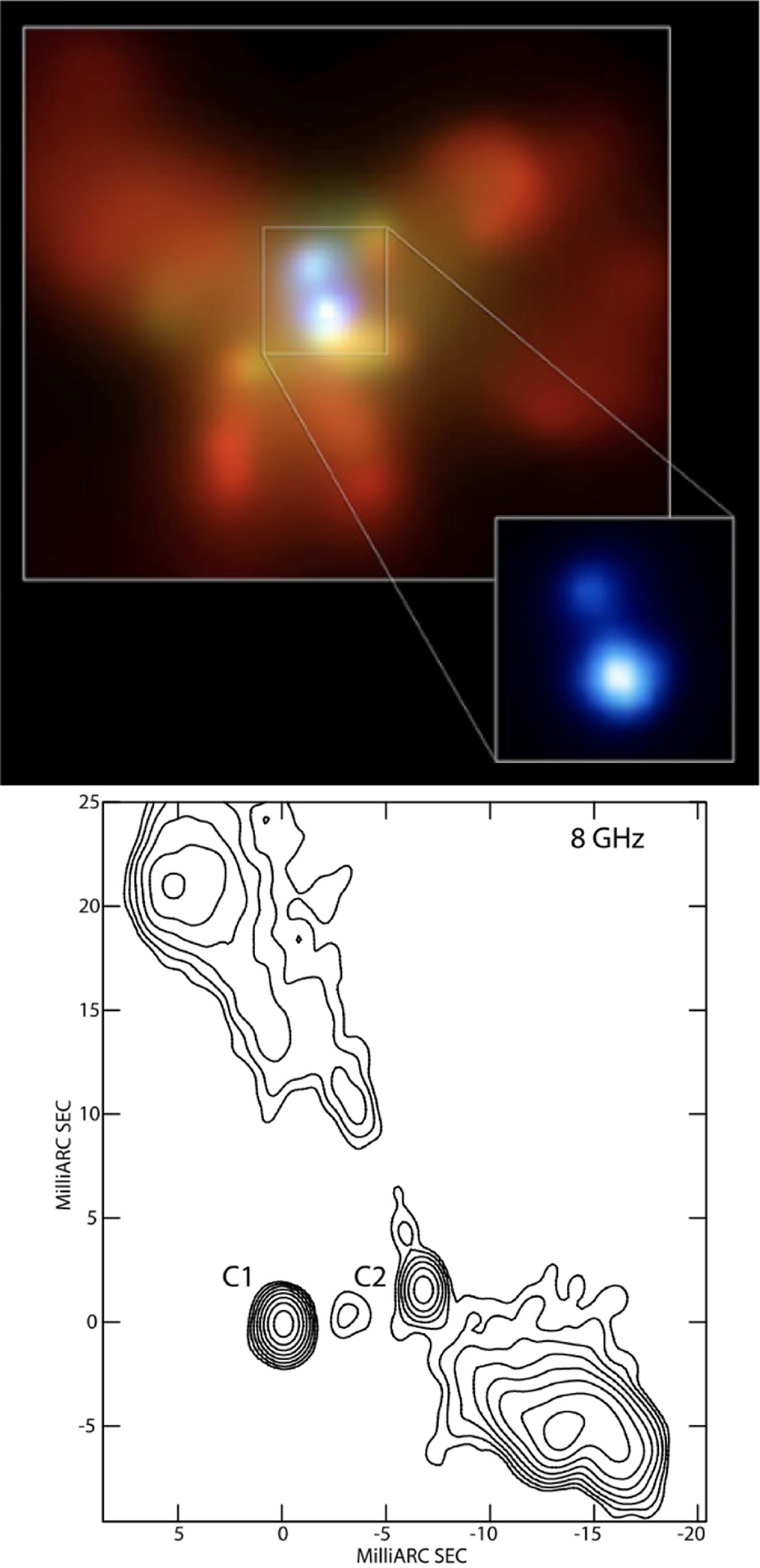
Figure 2. Directly resolved dual AGN. Top: X-ray maps of the merger remnant NGC 6240 obtained with Chandra. The large map in reddish colours shows the soft 0.5–1.5 keV band. The inset with blueish colours represent the hard 5–8 keV band. The X-ray detection confirms that both nuclei host active AGN and therefore supermassive black holes. Their separation is about 1 kpc in projection. The data was originally published by Komossa et al. (Reference Komossa2003). Bottom: Radio map at 8 GHz obtained with the Very Long Baseline Array radio telescope of the galaxy 0402+379 (Rodriguez et al. Reference Rodriguez2006). Two active galactic nuclei are directly detected at 7 pc separation. The weaker nucleus hosts a radio jet. Adopted under Creative Commons license, https://creativecommons.org/licenses/by/4.0/.
The length scales addressed in this section are well accessible with current state-of-the art observatories. The interaction of the black holes with the host galaxy’s gas distribution will quite possibly lead to activity of both black holes, though, likely, with different luminosities.
4. Observational evidence for dual active galactic nuclei
Dual AGN are systems of two actively accreting SMBHs, whose host galaxies are in the earliest process of merging. They are nominally defined as pairs with separations below 30 kpc, and SMBHs are not yet gravitationally bound (compare above). There exist many multi-wavelength techniques to detect dual AGN candidates. One of the earliest techniques was to use optical spectroscopy to search for double-peaked narrow line emission regions (which can sometimes be spatially resolved; see, e.g. Zhou et al. Reference Zhou, Wang, Zhang, Dong and Li2004; Gerke et al. Reference Gerke2007; Comerford et al. Reference Comerford2009; Liu et al. Reference Liu, Greene, Shen and Strauss2010; Fu et al. Reference Fu2012; Comerford et al. Reference Comerford2012; Comerford et al. Reference Comerford, Schluns, Greene and Cool2013; Barrows et al. Reference Barrows2013). Dual AGN systems can display two sets of narrow line emission regions, such as [O3]
![]() $\lambda$
5007, during the period of the merger when their narrow line regions (NLRs) are well separated in velocity (see below for a discussion of the broad line region). Here, the separation and width of each peak will depend on parameters such as the distance between the two AGNs. However, double-peaked emission features are known to originate from other processes, such as bipolar outflows and rotating discs (Greene & Ho Reference Greene and Ho2005; Rosario et al. Reference Rosario, Shields, Taylor, Salviander and Smith2010; Smith et al. Reference Smith2010; Nevin et al. Reference Nevin, Comerford, Müller-Sánchez, Barrows and Cooper2016).
$\lambda$
5007, during the period of the merger when their narrow line regions (NLRs) are well separated in velocity (see below for a discussion of the broad line region). Here, the separation and width of each peak will depend on parameters such as the distance between the two AGNs. However, double-peaked emission features are known to originate from other processes, such as bipolar outflows and rotating discs (Greene & Ho Reference Greene and Ho2005; Rosario et al. Reference Rosario, Shields, Taylor, Salviander and Smith2010; Smith et al. Reference Smith2010; Nevin et al. Reference Nevin, Comerford, Müller-Sánchez, Barrows and Cooper2016).
Confirmation of dual AGN systems requires spatially resolving each individual AGN; and beyond
![]() $z\gt0.05$
high-resolution imaging is necessary. Radio observations can resolve radio-emitting cores on the smallest spatial scales (see Rodriguez et al. Reference Rodriguez2006; Rosario et al. Reference Rosario, Shields, Taylor, Salviander and Smith2010; Tingay & Wayth Reference Tingay and Wayth2011; Fu et al. Reference Fu, Myers, Djorgovski and Yan2011, Reference Fu2015; Deane et al. Reference Deane2014; Gabányi et al. Reference Gabányi2014; Wrobel, Comerford, & Middelberg Reference Wrobel, Comerford and Middelberg2014a; Wrobel, Walker, & Fu Reference Wrobel, Walker and Fu2014b; Müller-Sánchez et al. Reference Müller-Sánchez2015; Kharb, Lal, & Merritt Reference Kharb, Lal and Merritt2017). The most closely separated dual AGN candidate to date, 0402+379, has a projected separation of approximately 7.3 pc and was discovered using VLBA and VLBI (Rodriguez et al. Reference Rodriguez2006; Bansal et al. Reference Bansal, Taylor, Peck, Zavala and Romani2017, Figure 2). However this technique is restricted to dual AGN where both AGN are radio bright (
$z\gt0.05$
high-resolution imaging is necessary. Radio observations can resolve radio-emitting cores on the smallest spatial scales (see Rodriguez et al. Reference Rodriguez2006; Rosario et al. Reference Rosario, Shields, Taylor, Salviander and Smith2010; Tingay & Wayth Reference Tingay and Wayth2011; Fu et al. Reference Fu, Myers, Djorgovski and Yan2011, Reference Fu2015; Deane et al. Reference Deane2014; Gabányi et al. Reference Gabányi2014; Wrobel, Comerford, & Middelberg Reference Wrobel, Comerford and Middelberg2014a; Wrobel, Walker, & Fu Reference Wrobel, Walker and Fu2014b; Müller-Sánchez et al. Reference Müller-Sánchez2015; Kharb, Lal, & Merritt Reference Kharb, Lal and Merritt2017). The most closely separated dual AGN candidate to date, 0402+379, has a projected separation of approximately 7.3 pc and was discovered using VLBA and VLBI (Rodriguez et al. Reference Rodriguez2006; Bansal et al. Reference Bansal, Taylor, Peck, Zavala and Romani2017, Figure 2). However this technique is restricted to dual AGN where both AGN are radio bright (
![]() $\approx 15\%$
of the AGN population is radio bright; Hooper et al. Reference Hooper, Impey, Foltz and Hewett1995), and individual AGNs can only be differentiated from jet components at radio frequencies if they are compact and fhave flat or inverted spectral indices (see, e.g. Burke-Spolaor Reference Burke-Spolaor2011; Hovatta et al. Reference Hovatta2014). Indeed, this is further complicated by the fact that regions of intense starbursts can mimic both compactness and brightness temperatures of AGNs; thus complementary IR data may be necessary to properly classify the source (see, e.g. Varenius et al. Reference Varenius2014).
$\approx 15\%$
of the AGN population is radio bright; Hooper et al. Reference Hooper, Impey, Foltz and Hewett1995), and individual AGNs can only be differentiated from jet components at radio frequencies if they are compact and fhave flat or inverted spectral indices (see, e.g. Burke-Spolaor Reference Burke-Spolaor2011; Hovatta et al. Reference Hovatta2014). Indeed, this is further complicated by the fact that regions of intense starbursts can mimic both compactness and brightness temperatures of AGNs; thus complementary IR data may be necessary to properly classify the source (see, e.g. Varenius et al. Reference Varenius2014).
4.1 Optical dual active galactic nuclei
There have been many optical searches for quasar pairs in the high-redshift Universe, where tens of candidates have been identified (
![]() $z\gt1$
; e.g. Hennawi et al. Reference Hennawi2006; Myers et al. Reference Myers2008; Hennawi et al. Reference Hennawi2010; Kayo & Oguri Reference Kayo and Oguri2012; Eftekharzadeh et al. Reference Eftekharzadeh2017). Most recently, optical spectroscopy and photometry aided in detecting the highest-z dual AGN candidates (
$z\gt1$
; e.g. Hennawi et al. Reference Hennawi2006; Myers et al. Reference Myers2008; Hennawi et al. Reference Hennawi2010; Kayo & Oguri Reference Kayo and Oguri2012; Eftekharzadeh et al. Reference Eftekharzadeh2017). Most recently, optical spectroscopy and photometry aided in detecting the highest-z dual AGN candidates (
![]() $z\gt5$
, Yue et al. Reference Yue, Fan, Yang and Wang2021, Reference Yue, Fan, Yang and Wang2023), as well as one of the closest dual AGN candidates (Koss et al. Reference Koss2023). For example, Stemo et al. (Reference Stemo2021) analysed a catalogue of 2585 AGN host galaxies observed with the Hubble Space Telescope and spanning a redshift range of
$z\gt5$
, Yue et al. Reference Yue, Fan, Yang and Wang2021, Reference Yue, Fan, Yang and Wang2023), as well as one of the closest dual AGN candidates (Koss et al. Reference Koss2023). For example, Stemo et al. (Reference Stemo2021) analysed a catalogue of 2585 AGN host galaxies observed with the Hubble Space Telescope and spanning a redshift range of
![]() $0.2 \lt z \lt 2.5$
. By identifying AGN host galaxies that have multiple stellar bulges, they find 204 offset and dual AGN candidates. Recently, new observational techniques that leverage the angular resolution of Gaia have been effective first steps for detecting the dual AGN population at high-z. Varstrometry techniques (see, e.g. Shen et al. Reference Shen, Hwang, Zakamska and Liu2019; Hwang et al. Reference Hwang, Shen, Zakamska and Liu2020; Shen et al. Reference Shen2021) combine variability with astrometry techniques. This technique exploits the empirical finding that the luminosity of any given AGN varies with time. If both SMBH of a binary are active, their fluxes will vary independently of each other. Thus, in a just unresolved dual AGN, the uncorrelated flux variability of the AGN will shift the astrometric centre, which leads to additional noise in the positions of the dual AGN as a function of time. Such observations have identified a
$0.2 \lt z \lt 2.5$
. By identifying AGN host galaxies that have multiple stellar bulges, they find 204 offset and dual AGN candidates. Recently, new observational techniques that leverage the angular resolution of Gaia have been effective first steps for detecting the dual AGN population at high-z. Varstrometry techniques (see, e.g. Shen et al. Reference Shen, Hwang, Zakamska and Liu2019; Hwang et al. Reference Hwang, Shen, Zakamska and Liu2020; Shen et al. Reference Shen2021) combine variability with astrometry techniques. This technique exploits the empirical finding that the luminosity of any given AGN varies with time. If both SMBH of a binary are active, their fluxes will vary independently of each other. Thus, in a just unresolved dual AGN, the uncorrelated flux variability of the AGN will shift the astrometric centre, which leads to additional noise in the positions of the dual AGN as a function of time. Such observations have identified a
![]() $z\gt2$
dual AGN (Chen et al. Reference Chen2023c) and the Gaia Multi-peak (GMP) method (Mannucci et al. Reference Mannucci2022) has detected further dual AGN candidates at
$z\gt2$
dual AGN (Chen et al. Reference Chen2023c) and the Gaia Multi-peak (GMP) method (Mannucci et al. Reference Mannucci2022) has detected further dual AGN candidates at
![]() $z\gt1$
(Ciurlo et al. Reference Ciurlo2020).
$z\gt1$
(Ciurlo et al. Reference Ciurlo2020).
4.2 X-ray dual active galactic nuclei
Optical selection techniques are affected by optical extinction and contamination from star formation, which is especially problematic when observing highly-obscured mergers (Kocevski et al. Reference Kocevski2015; Koss et al. Reference Koss2016; Ricci et al. Reference Ricci2017; Blecha et al. Reference Blecha, Snyder, Satyapal and Ellison2018; De Rosa et al. Reference De Rosa2018; Koss et al. Reference Koss2018; Lanzuisi et al. Reference Lanzuisi2018; Torres-Albà et al. Reference Torres-Albà2018). As a result, the confirmation of most AGN pairs have been made via X-ray observations as X-rays can more easily penetrate the dense obscuring gas (e.g. NGC 6240; Komossa et al. Reference Komossa2003, Figure 2), and most studies leverage Chandra’s superior angular resolution to discover closely-separated dual AGN (Koss et al. Reference Koss2012; Foord et al. Reference Foord2019, Reference Foord, Gültekin, Runnoe and Koss2021; Pfeifle et al. Reference Pfeifle2019). However, there are less than 50 directly detected pairs of X-ray AGN candidates to date (Chen et al. Reference Chen2022), as the majority of Chandra-detected dual AGN are restricted to the local universe (
![]() $z\lt0.1$
). High-z Chandra survey studies have resulted in non-detections (Sandoval et al. Reference Sandoval2023) due to the small field of view with high spatial resolution (
$z\lt0.1$
). High-z Chandra survey studies have resulted in non-detections (Sandoval et al. Reference Sandoval2023) due to the small field of view with high spatial resolution (
![]() $\lt1.5^{\prime\prime}$
) and sensitivity.
$\lt1.5^{\prime\prime}$
) and sensitivity.
4.3 The dual active galactic nucleus fraction
To date, most predictions of the dual AGN fraction at high-z have been carried out via cosmological simulations (compare Section 2 above, and particularly Steinborn et al. Reference Steinborn2016; Rosas-Guevara et al. Reference Rosas-Guevara, Bower, McAlpine, Bonoli and Tissera2019; Volonteri et al. Reference Volonteri2022; Chen et al. Reference Chen2023a). However, the observed dual AGN fraction remains relatively unconstrained and has been measured to be higher than cosmological simulations predict (Koss et al. Reference Koss2012; Barrows et al. Reference Barrows, Comerford, Greene and Pooley2017), which should not be surprising, given the large uncertainties in these simulations regarding the evolution of supermassive black holes. A handful of large surveys in the optical regime have yielded constraints on the high-z dual AGN fraction. Silverman et al. (Reference Silverman2020) analyse double quasars resolved by the Hyper Suprime-Cam (HSC) on the Subaru telescope, where
![]() $\sim$
100 dual AGN candidates were identified out to
$\sim$
100 dual AGN candidates were identified out to
![]() $z=4.5$
, and find no evidence for evolution across redshift. Shen et al. (Reference Shen2023) analyse 60 Gaia-resolved double quasars to measure quasar pair statistics at
$z=4.5$
, and find no evidence for evolution across redshift. Shen et al. (Reference Shen2023) analyse 60 Gaia-resolved double quasars to measure quasar pair statistics at
![]() $z\lt1.5$
, and similarly find no evolution across redshift. Most recently Sandoval et al. (Reference Sandoval2023) measure the X-ray fraction of dual AGN at
$z\lt1.5$
, and similarly find no evolution across redshift. Most recently Sandoval et al. (Reference Sandoval2023) measure the X-ray fraction of dual AGN at
![]() $2.5\lt z\lt3.5$
and find a non-detection among a sample of 66 AGN. This non-detection translates to an upper-limit of the dual AGN fraction of 4% at
$2.5\lt z\lt3.5$
and find a non-detection among a sample of 66 AGN. This non-detection translates to an upper-limit of the dual AGN fraction of 4% at
![]() $z=3$
.
$z=3$
.
4.4 Future surveys
In order to significantly expand the number of dual AGN, surveys with exceptional angular resolution, large field-of-views, and high effective areas are necessary. The next decade will be the golden age to observe SMBHs through cosmic times and in particular to detect them closer to the redshifts of their formation, and characterise their host galaxies. In addition to JWST, the Euclid and Roman telescopes will also image the first galaxies while detecting new accreting AGN and quasars. First results have been published very recently with dual and multiple AGN systems with separations from tens of kpc down to less then 1 kpc (Übler et al. Reference Übler2024; Perna et al. Reference Perna2025). New thirty-meter telescopes such as the Extremely Large Telescope (ELT), the Thirty Meter Telescope (TMT) and the Giant Magellan Telescope (GMT) will constrain the assembly of galaxies. Concept missions scanning the X-ray sky such as Athena (Nandra et al. Reference Nandra2013), Advanced X-ray Imaging Satellite (AXIS; Reynolds et al. Reference Reynolds, Siegmund and Hoadley2023), or Lynx (The Lynx Team 2018) could revolutionise our understanding of AGN activity before and during galaxy mergers by increasing substantially the number of X-ray-observed dual AGN all the way to cosmic dawn. For example, the probe-class AXIS (with baseline angular resolution of
![]() $1.5''$
half-power-diameter on-axis and
$1.5''$
half-power-diameter on-axis and
![]() $\sim 1.75''$
FoV-average) and the potential future flagship Lynx (
$\sim 1.75''$
FoV-average) and the potential future flagship Lynx (
![]() $\sim 0.5''$
FoV-average) aim at unprecedented sub-arc second angular resolution to uncover dual AGN with a separation down to a few kpc up to
$\sim 0.5''$
FoV-average) aim at unprecedented sub-arc second angular resolution to uncover dual AGN with a separation down to a few kpc up to
![]() $z=10$
(De Rosa et al. Reference De Rosa2019, for a review). On a shorter timescale from now, the Roman telescope with its near-IR wavelength large-sky coverage could probe dual AGN with luminosities down to
$z=10$
(De Rosa et al. Reference De Rosa2019, for a review). On a shorter timescale from now, the Roman telescope with its near-IR wavelength large-sky coverage could probe dual AGN with luminosities down to
![]() $L_{\rm bol}\geqslant 10^{42}\, \rm erg/s$
beyond
$L_{\rm bol}\geqslant 10^{42}\, \rm erg/s$
beyond
![]() $z\geqslant 1$
with an angular resolution of
$z\geqslant 1$
with an angular resolution of
![]() $\sim 0.13''$
(Haiman et al. Reference Haiman2023; Shen et al. Reference Shen2023, for two recent CSS white papers).
$\sim 0.13''$
(Haiman et al. Reference Haiman2023; Shen et al. Reference Shen2023, for two recent CSS white papers).
5. Observational evidence for sub-parsec binaries
Going down to sub-parsec separations we are approaching the distance where gravitational radiation drives their inspiral. Despite decades of observational effort, we do not yet have a sample of confirmed sub-parsec binary SMBHs. The closest pair that is often-cited as our best-case tight binary is at a separation of 7 pc and was already discussed above. Direct imaging of pairs rapidly grows prohibitive with currently available angular resolution. The most comprehensive search for black hole pairs at high angular resolution yielded no additional candidates (Burke-Spolaor Reference Burke-Spolaor2011).
5.1 Optical searches
Short of direct imaging, there are a number of additional techniques that have been attempted to uncover sub-pc pairs of (accreting) SMBHs. One, which we will not discuss in detail here, predicts quasi-periodic temporal variability linked to the orbital period of the two black holes. Here, the assumption is, based on hydrodynamic simulations, that the accretion rate onto the black holes, and thus their luminosities, would be modulated periodically with a period related to the orbital period of the binary (e.g. Charisi et al. Reference Charisi2016). A number of papers have searched for this signature and identified candidate sub-pc binaries (e.g. Graham et al. Reference Graham2015; Liu et al. Reference Liu2016; Charisi et al. Reference Charisi2016). However, because the survey lengths sample only
![]() $\sim $
1.5–3 orbital cycles, it can be easy to mistake the red-noise variability that characterises AGN lightcurves from true orbital variability (Vaughan et al. Reference Vaughan2016). Furthermore, the number of pairs is higher than would be expected from upper-limits on the gravitational-wave background (e.g. Sesana et al. Reference Sesana, Haiman, Kocsis and Kelley2018).
$\sim $
1.5–3 orbital cycles, it can be easy to mistake the red-noise variability that characterises AGN lightcurves from true orbital variability (Vaughan et al. Reference Vaughan2016). Furthermore, the number of pairs is higher than would be expected from upper-limits on the gravitational-wave background (e.g. Sesana et al. Reference Sesana, Haiman, Kocsis and Kelley2018).
The other approach looks for velocity shifts of broad optical emission lines from photo-ionised clouds in the vicinity of the black holes, the so-called broad line region, similar to spectroscopic binary stars (see nice review in Runnoe et al. Reference Runnoe2017). For many years, a small subset of AGN have been known to have two velocity peaks (e.g. Oke Reference Oke, Zensus and Pearson1987; Eracleous & Halpern Reference Eracleous and Halpern1994). One possible explanation for these two velocity components is a binary system (e.g. Gaskell Reference Gaskell1996), although far more likely in most cases based on the velocity structure and variability of the lines, is that we are seeing disc emission in these cases (e.g. Eracleous et al. Reference Eracleous, Halpern, Gilbert and Newman1997; Gezari, Halpern, & Eracleous Reference Gezari, Halpern and Eracleous2007). It is worth stating the caveat that this spectroscopic technique will only be sensitive to spatial scales larger than the size of the broad-line region (
![]() $\sim 0.01$
pc), when the two black holes can each sustain their own broad-line emission. In contrast, the quasi-periodic variability will in principle be sensitive to much more tightly bound objects with orbital periods of days to months.
$\sim 0.01$
pc), when the two black holes can each sustain their own broad-line emission. In contrast, the quasi-periodic variability will in principle be sensitive to much more tightly bound objects with orbital periods of days to months.
With the advent of the Sloan Digital Sky Survey, objects with dramatic velocity offsets between the broad and narrow lines emerged (e.g. Komossa, Zhou, & Lu Reference Komossa, Zhou and Lu2008; Shields, Bonning, & Salviander Reference Shields, Bonning and Salviander2009; Boroson & Lauer Reference Boroson and Lauer2009; Chornock et al. Reference Chornock2010). Boroson & Lauer (Reference Boroson and Lauer2010) initiated a systematic search through the SDSS for objects with large velocity shifts between broad and narrow lines, and Eracleous et al. (Reference Eracleous, Boroson, Halpern and Liu2012) began a long-term monitoring campaign of 88 candidate binaries from this sample. Thus far, after more than a decade of repeated spectroscopic observations, three of the 88 are still viable targets for binarity based on the radial velocity curves measured to date (Runnoe et al. Reference Runnoe2017). Indeed, a challenge with selecting objects showing 1 000 km/s velocity offsets between the broad and narrow emission lines is that if an orbiting black hole is implicated, then it will be at apocentre, and we will have to wait for a long time to measure changes.
A complementary spectroscopic approach is to simply search for radial velocity shifts in all AGN with multi-epoch spectroscopy, with the idea of observing radial velocity shifts corresponding to orbital motion (Ju et al. Reference Ju, Greene, Rafikov, Bickerton and Badenes2013; Shen et al. Reference Shen, Liu, Loeb and Tremaine2013). The main challenge with this approach, which otherwise should yield reliable constraints on the sub-pc binary fraction, is that velocity flickering in the broad-line region is a major source of noise. Ju et al. (Reference Ju, Greene, Rafikov, Bickerton and Badenes2013) identify candidate binary black holes from
![]() $\sim$
1–10 yr of spectroscopic monitoring by SDSS, but an additional epoch of follow-up for these targets shows that in all cases the velocities are varying in a stochastic way. Specifically, Wang et al. (Reference Wang2017) present a third epoch of spectroscopy for the seven candidates, and in no case is there a coherent radial velocity curve. Thus, this velocity flickering in single broad-line regions proves to be the primary contaminant to blind spectroscopic searches for binaries signalled by radial velocity shifts.
$\sim$
1–10 yr of spectroscopic monitoring by SDSS, but an additional epoch of follow-up for these targets shows that in all cases the velocities are varying in a stochastic way. Specifically, Wang et al. (Reference Wang2017) present a third epoch of spectroscopy for the seven candidates, and in no case is there a coherent radial velocity curve. Thus, this velocity flickering in single broad-line regions proves to be the primary contaminant to blind spectroscopic searches for binaries signalled by radial velocity shifts.
Real progress is on the horizon as time-domain imaging and spectroscopy become increasingly routine. Already SDSS-V have started working to characterize the temporal velocity structure of typical AGN from multi-epoch spectroscopy (Fries et al. Reference Fries2023). If we can characterize the power as a function of velocity coming from standard AGN, the hope is that we can filter out the rare systems with coherent radial velocity shifts. At the same time, the Rubin Observatory will soon launch the Legacy Survey of Space and Time (LSST, Ivezić et al. Reference Ivezić2019), which may finally realize the promise of quasi-periodic searches for AGN. With its high cadence of large-area deep optical suveys, LSST would allow studies of archival lightcurves of binary SMBH after detection of the gravitational waves with LISA (Xin & Haiman Reference Xin and Haiman2024) or identify the periodic signal from milli-parsec separation binary SMBH with large mass ratio (Cocchiararo et al. Reference Cocchiararo, Franchini, Lupi and Sesana2024).
5.2 Binary black hole jets in high-resolution radio imaging
So-called astrometric binaries might reveal themselves by precessing parsec-scale jets. Precession of AGN jets can be caused by either a misaligned binary SMBH system where for an SMBH with low spin, the jet direction is given by the disc angular momentum which is perturbed by the secondary (Abraham Reference Abraham2018) or the Lense-Thirring (LT) effect (misaligned disc around single black hole Lense & Thirring Reference Lense and Thirring1918; Thirring Reference Thirring1918). Another important effect, sometimes not subsumed under precession is a jet from an orbiting black hole (Fendt & Yardimci Reference Fendt and Yardimci2022), a case that is clearly observed in the source 0402+379 (Figure 2). The latter will cause a mirror-symmetric jet direction variability rather than point symmetry as for the other processes. However, as due to relativistic beaming, often only one jet is observed, orbital precession can be difficult to distinguish from the former two mechanisms. Precession is observed as periodic oscillation of the main jet ridge line and/or periodic patterns detectable in the light curve (e.g. Abraham & Carrara Reference Abraham and Carrara1998; Caproni & Abraham Reference Caproni and Abraham2004b, a; Britzen et al. Reference Britzen2010; Caproni, Abraham, & Monteiro Reference Caproni, Abraham and Monteiro2012; Britzen et al. Reference Britzen2017; Britzen et al. Reference Britzen2019; Britzen et al. Reference Britzen2021).
OJ 287 is considered to be one of the most promising candidates for harbouring a binary SMBH (e.g. Sillanpaa et al. Reference Sillanpaa, Haarala, Valtonen, Sundelius and Byrd1988; Valtonen et al. Reference Valtonen2009; Britzen et al. Reference Britzen2018), based on its characteristic periodicities in the optical light curve domain (
![]() $\sim$
11 yr). The most popular binary SMBH-model for OJ 287 (e.g. Lehto & Valtonen Reference Lehto and Valtonen1996; Valtonen et al. Reference Valtonen2009) explains the substructure inside the major outbursts with a model in which a smaller black hole crosses the accretion disc of a larger black hole during the binary orbit of the black holes about each other.
$\sim$
11 yr). The most popular binary SMBH-model for OJ 287 (e.g. Lehto & Valtonen Reference Lehto and Valtonen1996; Valtonen et al. Reference Valtonen2009) explains the substructure inside the major outbursts with a model in which a smaller black hole crosses the accretion disc of a larger black hole during the binary orbit of the black holes about each other.
Disturbances of the accretion disc should, however, also lead to corresponding disturbances of the radio jet, if the jet was produced by the larger black hole around which the accretion disc would be found, which are not observed (Britzen et al. Reference Britzen2018). Quite in contrast, according to Britzen et al. (Reference Britzen2018), the jet reveals the signature of continued precession on a timescale of 22–23 yr. As the authors demonstrate, also the radio light curve variability can be explained by the precession model. A binary SMBH or LT-precession seems to be required to explain the time scale of the precessing motion. Such a scenario intrinsically connects the radio and optical periods (radio period being twice the optical period) when viewed close to the rotation axis. The scenario would hence involve two accretion disc passages during one orbit of the smaller black hole, causing the optical brightenings (also compare Komossa et al. Reference Komossa2023, for more recent analysis of the binary SMBH system). The orbital motion would drive the disc and hence jet precession. Other explanations of the precession mechanism are possible. For example, the smaller black hole could also produce the jet. The precession would in this picture be caused by a largely ballistic motion, always driven away from the centre of the orbit and hence also produce one jet precession period for each full orbit of the smaller SMBH. Britzen et al. (Reference Britzen2023) most recently showed, that also the Spectral Energy Distribution (SED) can be directly related to the jet’s precession phase in OJ 287. This is due to the directional dependence of the Doppler effect. During the precession phase when the jet points towards the observer, the jet emission will be boosted, whereas the luminosity drops when the jet points away from the observer. This produces a periodic variation of the spectral components emitted by the jet. Zhao et al. (Reference Zhao2022) provided further support for the precession scenario in OJ 287. The first Global mm-VLBI Array (GMVA) and Atacama Large Millimeter/submillimeter Array (ALMA) observations observed at 3.5 mm show a radio structure resembling a precessing jet in projection. The modulating power of precession might more generally govern AGN structural as well as lightcurve variability in the cm-regime (Britzen et al. Reference Britzen2023).
5.3 Clues from precessing large-scale jets
Jets from supermassive black holes can extend for hundreds of kiloparsecs away from the galactic nucleus (Hardcastle & Croston Reference Hardcastle and Croston2020). When two or more SMBHs form a stable system in a single galaxy, periodic disturbances in the jet path are expected to arise from geodetic precession of the black hole spins around the total angular momentum vector, which is dominated by the orbital angular momentum (Begelman et al. Reference Begelman, Blandford and Rees1980). Geodetic precession is particularly useful for kpc-scale jet observations, as, even for sub-parsec SMBH binaries, the geodetic precession frequency can be of the order of millions of years, resulting in long-lasting, predictable morphological characteristics which can be used to identify suitable candidate galaxies for close binaries (Krause et al. Reference Krause2019).
Four morphological characteristics can be used to identify precession (Krause et al. Reference Krause2019, Figure 3, right): jets that are misaligned or at the edge of lobes (E); jets that show curvature (C); ‘S’-shaped symmetry between the two sides of the lobes (S), and ring-like, multiple or highly complex hotspot structures (R). All four structures can be reproduced easily with high-resolution numerical simulations (as demonstrated in the simulations on the left of Figure 3). Horton, Krause, & Hardcastle (Reference Horton, Krause and Hardcastle2020b) show that one or more of the E, C and S indicators are almost always visible in precessing jets, while the prevalence of false positives in non-precessing jets is low. The misalignment effect is a simple consequence of geometry. The velocity in the jet is usually much higher than the expansion speed of the lobe structure the jet lives in. This can be compared to the motion of the second hand of a wall clock. Take a photo at any given instance, and it will be very likely that it is not aligned with the 12-o-clock position. However, a non-precessing jet will have a strong tendency to point towards the symmetry axis of the lobe, which emerges roughly symmetrically around the jet as it propagates. This would correspond to a second hand fixed to the 12-o-clock position in the picture. Particularly for precessing jets that are aligned close to the line of sight, one expects to see curvature due to the change of ejection direction as a function of ejection time (Krause et al. Reference Krause2019; Giri et al. Reference Giri, Dubey, Rubinur, Vaidya and Kharb2022). Curvature is also expected where a precessing jet interacts with the lobe boundary. Indeed, this is particularly frequently seen for broad line radio galaxies or quasars, where the unobscured view towards the broad emission line regions around the AGN confirms the aligned jet orientation. Observing S-symmetry is significantly inhibited by the relativistic Doppler de-boosting of the counter jet. Hence, the counter hotspot will be the main piece of evidence for S-symmetry. Multiple hotspots were explored in Horton et al. (Reference Horton, Krause and Hardcastle2023) since hydrodynamic processes can produce multiple hotspots by several different mechanisms (also compare Figure 3, right). Some of these – such as hotspot complexes and dual jet paths – seem largely confined to precessing jets while others, such as hotspot splitting, can occur in non-precessing jets too. Backflow can push remnant hotspots into parts of the lobe where there has never been a primary flow. Overall multiple hotspots are confirmed as a signature of precessing jets. Precession may explain a number of complex radio structures, including re-starting, re-orienting, X-shaped and Z-shaped sources and possibly Odd Radio circles (Horton et al. Reference Horton, Krause and Hardcastle2020b; Nolting, Ball, & Nguyen Reference Nolting, Ball and Nguyen2023; Shabala et al. Reference Shabala2024).
Figure 3. 3D hydrodynamics simulations of precessing jets from Horton et al. (Reference Horton, Krause and Hardcastle2023), 3 examples towards the left with uniform black background and Very Large Array radio maps at 5 and 8 GHz of radio galaxies and quasars with jets that show signatures expected from a long-term driven precession, such as the relativistic geodetic spin precession in a binary SMBH (3 examples towards the right, each with their 3C ctalogue number). The three simulations had different precession parameters and form a variety of interactions with the lobe boundary and hotspot structures. Such features can be compared to observed radio galaxies and used to understand the properties of the driving system. For the observed radio maps towards the right, the projected sizes on the sky range between 70 and 330 kpc. Letters mark the occurrence of precession features discussed in more detail in the Section 5.3: E – jet detected towards the edge, rather than the middle of the lobe, S – S-symmetry, C – jet curvature, R – ring-like, extended or multiple hotspots. While the simulations on the left do not reproduce any particular system on the right, they do demonstrate that precessing jets may be curved, misaligned with the lobes and have multiple hotspots. Images adopted from Krause et al. (Reference Krause2019) who find strong indication for jet precession in 24 out of 33 powerful radio galaxies from a complete sample.
While precession has a clear impact on the jet path, the latter may not just be a simple ballistic trajectory of plasmons ejected from the vicinity of one SMBH. Horton et al. (Reference Horton, Hardcastle, Read and Krause2020a) used a Bayesian approach to fit a, relativistic, ballistic, precessing jet model (Gower et al. Reference Gower, Gregory, Unruh and Hutchings1982) to the well-studied radio galaxy Cygnus A. Cygnus A shows the presence of all four indicators to some degree. While it was possible to obtain probabilistic constraints on the binary separation using our approach, this was only possible for the case where at least one set of terminal hotspots were included at the end of the jet path. Without them, no fit could be found. This highlights the need to study jet paths including terminal hotspots with 3D hydrodynamical simulations. Horton et al. (Reference Horton, Krause and Hardcastle2023) found in such simulations that some mechanisms – such as large complexes with a high number of short-lived multiple hotspots – are dependent on more extreme forms of precession and if present may reveal additional information about the driving system.
Observed precession in powerful kpc-jets is likely due to geodetic precession. This is because the re-alignment timescale for LT-precession is relatively short, of the order of the precession period. Since the source ages are typically much greater than the likely precession period, disc-induced precession would require a co-incidental event that would have produced the disc misalignment just at the right time for the observation. The high incidence of kpc-scale precession at least in powerful sources (24 of 33 sources in the complete sample in Krause et al. Reference Krause2019) argues for a frequent occurrence of geodetic precession and hence, close binary SMBH. Horton et al. (Reference Horton, Hardcastle, Miley, Tasse and Shimwell2025) found 1 138 strong precessing jet candidates showing at least two precession indicatiors with the LOFAR Two-metre Sky Survey (LoTSS DR2), which will help to answer questions about host galaxy characteristics and the origins of different forms of precession (Figure 4). There are thus good prospects to address the prevalence of binary SMBH in specific types of galaxies.

Figure 4. Likely precessing 100 kpc-scale jets and therefore binary black hole candidates from LOFAR. Adopted from Horton et al. (Reference Horton, Hardcastle, Miley, Tasse and Shimwell2025). The image is a montage of representative precessing sources selected in Horton et al. (Reference Horton, Hardcastle, Miley, Tasse and Shimwell2025) to demonstrate the presence of precession indicators E, C and R discussed in Section 5.3. There is sometimes a striking similarity with the simulated images, compare, e.g. Figure 3, left.
In order to produce well-visible precession features, the precession period must be comparable to the age of the source. If it was much shorter, the jet would become unstable and would just produce fuzzy radio lobes. If it was much longer, the radio lobes have time to adjust and the radio source looks symmetrical again. The ages of well-resolved LOFAR radio sources are generally of the order of
![]() $10^8$
yr (Hardcastle et al. Reference Hardcastle2019). For geodetic precession with period
$10^8$
yr (Hardcastle et al. Reference Hardcastle2019). For geodetic precession with period
![]() $P_\mathrm{gp,8} \times 10^8\,$
yr in a supermassive binary of mass
$P_\mathrm{gp,8} \times 10^8\,$
yr in a supermassive binary of mass
![]() $M_9 \times 10^9 {\rm M}_\odot$
and of any mass ratio, the separation in parsec is limited by (Krause et al. Reference Krause2019):
$M_9 \times 10^9 {\rm M}_\odot$
and of any mass ratio, the separation in parsec is limited by (Krause et al. Reference Krause2019):
Probably the best case available for this method in the literature, which is Hydra A. For this radio source, dedicated hydrodynamic simulations have constrained the precession period to
![]() $10^6$
yr, with an accuracy of 50% (Nawaz et al. Reference Nawaz, Bicknell, Wagner, Sutherland and McNamara2016). The SMBH mass has been determined to
$10^6$
yr, with an accuracy of 50% (Nawaz et al. Reference Nawaz, Bicknell, Wagner, Sutherland and McNamara2016). The SMBH mass has been determined to
![]() $(5\pm4)\times 10^8\,{\rm M}_\odot$
(Rafferty et al. Reference Rafferty, McNamara, Nulsen and Wise2006). The long-term approximate stability of the precession is evident from the large-scale radio structure. Therefore, the precession is likely caused by geodetic precession in an SMBH binary with a separation less than 0.2 pc (compare Krause et al. Reference Krause2019). Hence, these sources might contain the tightest electromagnetic binary SMBH candidates so far.
$(5\pm4)\times 10^8\,{\rm M}_\odot$
(Rafferty et al. Reference Rafferty, McNamara, Nulsen and Wise2006). The long-term approximate stability of the precession is evident from the large-scale radio structure. Therefore, the precession is likely caused by geodetic precession in an SMBH binary with a separation less than 0.2 pc (compare Krause et al. Reference Krause2019). Hence, these sources might contain the tightest electromagnetic binary SMBH candidates so far.
6. Spin measurements of supermassive black holes from X-ray reflection
SMBH spin measurements can provide indirect evidence for binary SMBH mergers, and thus the existence of SMBH binaries. This is because coherent gas accretion tends to produce maximally spinning black holes, whereas SMBH mergers tend to produce more slowly spinning SMBH remnants. As we detail in this section, cosmological simulations have started tracking the SMBH spin evolution and including the effects of binary SMBH mergers. The observed distribution of SMBH spins over mass scales suggests higher spins at low SMBH masses and lower spins at very high SMBH masses. Informed by predictions from cosmological simulations, the observed distribution seems best explained by accretion (mergers) being important for low-mass (high-mass) SMBHs.
The magnitude of the black hole spin can be probed directly via X-ray emission from the innermost regions of the accretion disc. X-rays from the vicinity of the SMBH are reflected from a relatively cold accretion disc. The reflection produces an emission line that is redshifted gravitationally, such that from the distortion of the line profile one can infer the properties of the source of gravity, i.e. the SMBH, including the black hole spin magnitude.
Over recent decades, the application of relativistic reflection models to X-ray spectra have provided spin constraints for over 50 SMBHs across mass scales spanning
![]() $10^5 - 10^{10}\,{\rm M}_\odot$
(Figure 5). In addition to being one of the two fundamental properties of astrophysical black holes, the spin acts as a fossil record of their growth history. Specifically, the black hole spin provides an indicator of the relative contributions of coherent accretion, incoherent accretion, and SMBH mergers in powering the recent growth of SMBHs. This therefore suggests that tracing the magnitude of the black hole spin over cosmic time and mass scale may provide indirect evidence for the existence of SMBH binaries.
$10^5 - 10^{10}\,{\rm M}_\odot$
(Figure 5). In addition to being one of the two fundamental properties of astrophysical black holes, the spin acts as a fossil record of their growth history. Specifically, the black hole spin provides an indicator of the relative contributions of coherent accretion, incoherent accretion, and SMBH mergers in powering the recent growth of SMBHs. This therefore suggests that tracing the magnitude of the black hole spin over cosmic time and mass scale may provide indirect evidence for the existence of SMBH binaries.

Figure 5. Spin magnitude estimated from X-ray reflection as a function of mass for 51 SMBHs in AGN, compiled from the literature. The figure is adapted from the Reynolds (Reference Reynolds2021) and Bambi et al. (Reference Bambi2021) spin reviews with the inclusion of: the 13 SMBH spin estimates in low-mass AGN from Mallick et al. (Reference Mallick2022) (in green) and recent spin constraints for the SMBHs in H 1821+643 (Sisk-Reynés et al. Reference Sisk-Reynés, Reynolds, Matthews and Smith2022) and ESO 033-G002 (Walton et al. Reference Walton2021). Note some of the estimates from Bambi et al. (Reference Bambi2021) show a well-defined lower spin bound. We omit the following objects: IRAS 1339+2438 and 4C 74.26 (see Sec. 6 of Sisk-Reynés et al. Reference Sisk-Reynés, Reynolds, Matthews and Smith2022), Tons 180, and the sample of type-1 AGN from Mallick et al. (Reference Mallick2025). Error bars in spin/mass correspond to statistical uncertainties at the 68/90 per cent level, respectively. Comparing with predictions from cosmological models, the lower spins at the highest masses is best explained by binary SMBH merging. More measurements are needed to corroborate this result.
The power-law X-ray component that usually dominates the high-energy emission in AGN arises from direct emission of the X-ray corona, a magnetically-heated cloud of relativistic electrons which steadily illuminates the optically-thick accretion disc. The irradiating hard X-ray continuum from the corona is reprocessed in the surface layers of the disc and produces the ‘X-ray reflection spectrum’. This reflection spectrum contains a rich set of fluorescence and radiative recombination lines, with the most prominent being the K-shell lines of iron with rest-frame energy of 6.40–6.97 keV, depending on the ionisation state of the iron in the disc.
Reflection features from the inner disc are broadened and skewed due to the Doppler shifts of the mildly relativistic orbital motions in the disc, as well as gravitational redshift. Based on the dependence of the innermost stable circular orbit (ISCO) on the value of the black hole spin, (Eqs. 2–4 of Reynolds Reference Reynolds2021), reflection models can then predict the properties of the resulting irradiation profile if the inner disc radius is fixed at the ISCO (and thereby parametrized by BH spin; see García et al. Reference García2014; Dauser et al. Reference Dauser, Garcia, Parker, Fabian and Wilms2014). See Reynolds (Reference Reynolds2021) for a detailed discussion of the assumptions that underlie this method. We also note the discussion in (Barret & Cappi Reference Barret and Cappi2019) which explores the extent to which relativistic reflection signatures can be degenerate with absorption from fast ionized winds from the AGN.
The spin results shown in Figure 5 suggest an interesting, tentative dependence of the observed SMBH spins in the distribution as a function of SMBH mass. The population is dominated by rapidly spinning SMBHs in the mass range
![]() $10^{6-7.5}\,{\rm M}_\odot$
. However, a more slowly spinning population may be emerging both above and below this mass range. Interestingly, this pattern seems to naturally emerge from some state-of-the-art models of SMBH evolution. Bustamante & Springel (Reference Bustamante and Springel2019) incorporate a subgrid model to track the spin evolution of individual SMBHs into an extended version of the IllustrisTNG cosmological simulation of cosmic structure formation. Bustamante & Springel (Reference Bustamante and Springel2019) find that black holes of masses
$10^{6-7.5}\,{\rm M}_\odot$
. However, a more slowly spinning population may be emerging both above and below this mass range. Interestingly, this pattern seems to naturally emerge from some state-of-the-art models of SMBH evolution. Bustamante & Springel (Reference Bustamante and Springel2019) incorporate a subgrid model to track the spin evolution of individual SMBHs into an extended version of the IllustrisTNG cosmological simulation of cosmic structure formation. Bustamante & Springel (Reference Bustamante and Springel2019) find that black holes of masses
![]() $\lt10^8\,{\rm M}_\odot$
tend to grow via coherent accretion, since the typical accretion events can torque the (lower-mass) black holes into alignment (also compare Section 7). Hence these systems are readily spun up to close to maximum. More massive SMBHs (
$\lt10^8\,{\rm M}_\odot$
tend to grow via coherent accretion, since the typical accretion events can torque the (lower-mass) black holes into alignment (also compare Section 7). Hence these systems are readily spun up to close to maximum. More massive SMBHs (
![]() $\gt 10^8\,{\rm M}_\odot$
), on the other hand, cannot be torqued to alignment by the accretion flow and hence tend to grow in an incoherent mode (King, Pringle, & Hofmann Reference King, Pringle and Hofmann2008). The averaging of the incoming angular momentum tends to spin isolated, inividual black holes down. Furthermore, other cosmological models find that, in general, major mergers with other SMBHs are more important for more massive SMBHs compared to lower-mass SMBHs, and the result of a major merger between two SMBHs is typically a modestly spinning SMBH (Volonteri et al. Reference Volonteri, Madau, Quataert and Rees2005; Sesana et al. Reference Sesana, Barausse, Dotti and Rossi2014; Sala et al. Reference Sala, Valentini, Biffi and Dolag2024). The predictions from Bustamante & Springel (Reference Bustamante and Springel2019) are, however, in tension with those of the NEWHORIZONs simulation (Beckmann et al. Reference Beckmann2025), which includes a prescription to track the black hole spin evolution due to jet-driven spin-down episodes. Nevertheless, the importance of such episodes was also recently assessed by (Ricarte et al. Reference Ricarte, Natarajan, Narayan and Palumbo2025) from a semi-analytical model, concluding that the population shown in Figure 5 could point to jet-driven spin-down episodes for black holes which are initially growing at very low and very high specific accretion rates.
$\gt 10^8\,{\rm M}_\odot$
), on the other hand, cannot be torqued to alignment by the accretion flow and hence tend to grow in an incoherent mode (King, Pringle, & Hofmann Reference King, Pringle and Hofmann2008). The averaging of the incoming angular momentum tends to spin isolated, inividual black holes down. Furthermore, other cosmological models find that, in general, major mergers with other SMBHs are more important for more massive SMBHs compared to lower-mass SMBHs, and the result of a major merger between two SMBHs is typically a modestly spinning SMBH (Volonteri et al. Reference Volonteri, Madau, Quataert and Rees2005; Sesana et al. Reference Sesana, Barausse, Dotti and Rossi2014; Sala et al. Reference Sala, Valentini, Biffi and Dolag2024). The predictions from Bustamante & Springel (Reference Bustamante and Springel2019) are, however, in tension with those of the NEWHORIZONs simulation (Beckmann et al. Reference Beckmann2025), which includes a prescription to track the black hole spin evolution due to jet-driven spin-down episodes. Nevertheless, the importance of such episodes was also recently assessed by (Ricarte et al. Reference Ricarte, Natarajan, Narayan and Palumbo2025) from a semi-analytical model, concluding that the population shown in Figure 5 could point to jet-driven spin-down episodes for black holes which are initially growing at very low and very high specific accretion rates.
Finally, we note that there is an expectation that SMBHs with high-to-maximal spin are overrepresented in Figure 5 due to spin-dependence of the radiative efficiency (Brenneman et al. Reference Brenneman2011). That is, for a given accretion rate, SMBHs with higher spins will be brighter and more easily identifiable as potential good candidates from flux-limited AGN samples (see Fig. 3 of Reynolds Reference Reynolds2019). Moreover, other systematic effects must be accounted for, if the observed population in Figure 5 is used to compare with predictions from cosmological simulations, including the effects of disc thickness for SMBHs with sufficiently high Eddington fractions (Taylor & Reynolds Reference Taylor and Reynolds2018).
7. Accretion physics: Warping, breaking and spin evolution
The properties of gravitational waves and BH merger remnants are determined by the pre-merger BH properties–including masses and spins–as well as the orbital properties of the binary. Accretion prior to the merger can significantly alter BH spin, either via direct accretion of angular momentum or via gravitational torques between the BH and its accretion disc. For binaries in gas-rich environments, each BH’s accretion disc can be fed by gas streams from a larger circumbinary disc. The most general solution for this allows the BH spins, binary orbit, accretion discs and circumbinary disc to be freely oriented. Torques exerted on the binary by the gas not only drive binary evolution by modifying its angular momentum magnitude but also its orientation (e.g. Nixon, King, & Pringle Reference Nixon, King and Pringle2011). Further, if the accretion disc and BH spin are misaligned, Lense-Thirring precession, in combination with accretion disc viscosity leads to a warped disc where the disc orientation changes with radius. This process, known as the Bardeen-Petterson effect (Bardeen & Petterson Reference Bardeen and Petterson1975), torques the BH and (counter-) aligns the BH spin and accretion disc from the inner edge outwards (e.g. King et al. Reference King, Lubow, Ogilvie and Pringle2005). These processes strongly depend on the geometry, physical properties and thermodynamics of the system. How fast the BH spins align in these gas-rich binaries is thus a complex question.

Figure 6. Example circumbinary disc simulation in which the binary and disc are initially misaligned (full results presented in Bourne et al. Reference Bourne, Fiacconi, Sijacki, Piotrowska and Koudmani2024). The circumbinary disc, ‘minidiscs’ and binary evolution and interactions are resolved by the simulation, while the accretion disc and BH are modelled using the sub-grid accretion disc prescription of Fiacconi et al. (Reference Fiacconi, Sijacki and Pringle2018) to capture both the BH mass and spin evolution. (Image Credit: Martin A. Bourne, CC By 4.0)
Numerous simulation works have studied the evolution of BH binaries in circumbinary discs (e.g. Cuadra et al. Reference Cuadra, Armitage, Alexander and Begelman2009; Roedig et al. Reference Roedig2012; Duffell et al. Reference Duffell2020; Muñoz et al. Reference Muñoz, Miranda and Lai2019, Reference Muñoz, Lai, Kratter and Miranda2020; Franchini et al. Reference Franchini, Sesana and Dotti2021; Bourne et al. Reference Bourne, Fiacconi, Sijacki, Piotrowska and Koudmani2024; Siwek, Weinberger, & Hernquist Reference Siwek, Weinberger and Hernquist2023a, and discussion in Section 3), and some additionally resolve streams and discs around each BH in order to study their net affect on torquing the binary (e.g. Roedig et al. Reference Roedig2012; Duffell et al. Reference Duffell2020; Muñoz et al. Reference Muñoz, Miranda and Lai2019; Bourne et al. Reference Bourne, Fiacconi, Sijacki, Piotrowska and Koudmani2024). When BH growth is considered, preferential accretion onto the secondary is nearly universally observed (Farris et al. Reference Farris, Duffell, MacFadyen and Haiman2014; Duffell et al. Reference Duffell2020; Muñoz et al. Reference Muñoz, Lai, Kratter and Miranda2020; Siwek et al. Reference Siwek, Weinberger, Muñoz and Hernquist2023b), although this is possibly sensitive to gas thermodynamics and accretion modelling (see e.g. Roedig et al. Reference Roedig2012).
In addition to affecting the inward migration of the two SMBHs, the circumbinary disc can affect the alignment of the SMBH spins. This is of central importance to the question of whether ‘superkick’ configurations can be created that would eject the remnant SMBH from the galaxy post-merger. This problem was first examined by Bogdanović Reynolds, &Miller (2007) (Reference Bogdanović, Reynolds and Miller2007) who, using timescale arguments, suggested that SMBH spins would be readily aligned in gas-rich mergers thus avoiding superkicks. This was further developed by Gerosa et al. (Reference Gerosa, Veronesi, Lodato and Rosotti2015) who developed a semi-analytic model to predict BH-accretion disc-driven BH-spin alignment timescales in circumbinary discs assuming the binary, accretion discs and circumbinary disc are co-planar. They found that for high mass ratio binaries BH spins should align before the BHs merge, however, given their model assumes preferential accretion onto the secondary, reduced accretion onto the primary in systems with mass ratios
![]() $\lesssim0.2$
prevents it from aligning; leading to misaligned spins at merger and hence high expected recoil velocities (González et al. Reference González, Hannam, Sperhake, Brügmann and Husa2007; Lousto & Zlochower Reference Lousto and Zlochower2011). Bourne et al. (Reference Bourne, Fiacconi, Sijacki, Piotrowska and Koudmani2024) performed high-resolution simulations of binaries in gas-rich circumbinary discs for different setups that vary the binary mass ratio, eccentricity and inclination (including retrograde binaries), with an example setup shown in Figure 6. BH accretion and spin evolution due to accretion and the Bardeen-Petterson effect are modelled using the sub-grid model of Fiacconi et al. (Reference Fiacconi, Sijacki and Pringle2018). Therefore, it was possible to not only explore the evolution of the binary, which due to gas torques was found to shrink for all set-ups considered, but for the first time also track the BH spin evolution. Bourne et al. (Reference Bourne, Fiacconi, Sijacki, Piotrowska and Koudmani2024) found BH-accretion disc alignment timescales to generally be shorter than binary inspiral timescales even for low mass ratios, largely due to a lack of preferential accretion onto secondaries in their simulations, which is attributed to (i) using beta-cooling (where the cooling time is proportional to the local orbital time) combined with an adiabatic (opposed to locally-isothermal) equation of state, and (ii) calculating net inflow rates on the scale of the BH accretion disc as opposed to using a sink particle prescription. However, cases in which the binary and circumbinary disc are initially misaligned (as possibly observed in OJ 287, compare Section 5.2), show that the discs around each BH do not necessarily rapidly align with the circumbinary disc and sometimes precess. Hence, unless the system can evolve unperturbed for long timescales and processes such as disc breaking (see below) do not occur, even for rapid BH-accretion disc alignment, BH spins may remain misaligned at the time of merging. The situation may be even worse for other accretion disc geometries, such as thick or truncated discs, where alignment timescales are slower and precession may become important (Koudmani et al. Reference Koudmani2024).
$\lesssim0.2$
prevents it from aligning; leading to misaligned spins at merger and hence high expected recoil velocities (González et al. Reference González, Hannam, Sperhake, Brügmann and Husa2007; Lousto & Zlochower Reference Lousto and Zlochower2011). Bourne et al. (Reference Bourne, Fiacconi, Sijacki, Piotrowska and Koudmani2024) performed high-resolution simulations of binaries in gas-rich circumbinary discs for different setups that vary the binary mass ratio, eccentricity and inclination (including retrograde binaries), with an example setup shown in Figure 6. BH accretion and spin evolution due to accretion and the Bardeen-Petterson effect are modelled using the sub-grid model of Fiacconi et al. (Reference Fiacconi, Sijacki and Pringle2018). Therefore, it was possible to not only explore the evolution of the binary, which due to gas torques was found to shrink for all set-ups considered, but for the first time also track the BH spin evolution. Bourne et al. (Reference Bourne, Fiacconi, Sijacki, Piotrowska and Koudmani2024) found BH-accretion disc alignment timescales to generally be shorter than binary inspiral timescales even for low mass ratios, largely due to a lack of preferential accretion onto secondaries in their simulations, which is attributed to (i) using beta-cooling (where the cooling time is proportional to the local orbital time) combined with an adiabatic (opposed to locally-isothermal) equation of state, and (ii) calculating net inflow rates on the scale of the BH accretion disc as opposed to using a sink particle prescription. However, cases in which the binary and circumbinary disc are initially misaligned (as possibly observed in OJ 287, compare Section 5.2), show that the discs around each BH do not necessarily rapidly align with the circumbinary disc and sometimes precess. Hence, unless the system can evolve unperturbed for long timescales and processes such as disc breaking (see below) do not occur, even for rapid BH-accretion disc alignment, BH spins may remain misaligned at the time of merging. The situation may be even worse for other accretion disc geometries, such as thick or truncated discs, where alignment timescales are slower and precession may become important (Koudmani et al. Reference Koudmani2024).

Figure 7. Disc breaking in the presence of a binary BH, adapted from Nealon et al. (Reference Nealon, Ragusa, Gerosa, Rosotti and Barbieri2022). The colour here represents column density in code units. As the disc inclination is increased, the external torques from the BHs overcome the viscous stresses maintaining the disc and it breaks into independently precessing rings.
Gerosa et al. (Reference Gerosa, Rosotti and Barbieri2020) built on their earlier work by considering the impact of the binary companion on the BH spin and introduced a semi-analytic approach that solved the non-linear long-term dynamics of warped accretion discs in the presence of a misaligned binary. For a subset of the parameter space their results showed the accretion disc will become warped and align the BH spin on less than 10 times the analytic prediction for the disc and BH to realign (Scheuer & Feiler Reference Scheuer and Feiler1996). This analytic prediction is referred to as the ‘warp alignment timescale’ and is typically much faster than the accretion timescale but slower than the viscous timescale for typical AGN parameters (e.g. Gerosa et al. Reference Gerosa, Rosotti and Barbieri2020). However, for accretion discs with either steep warp profiles or low viscosities, the semi-analytic model of Gerosa et al. (Reference Gerosa, Rosotti and Barbieri2020) did not show convergence. For a given set of binary and accretion disc parameters, they named the inclination that marked the transition into a region of no solutions as the ‘critical obliquity’.
The misaligned binary scenario was subsequently explored by Nealon et al. (Reference Nealon, Ragusa, Gerosa, Rosotti and Barbieri2022) using 3D smoothed particle hydrodynamic simulations. They spanned the parameter space investigated by Gerosa et al. (Reference Gerosa, Rosotti and Barbieri2020) and broadly found excellent agreement with the semi-analytic model. Each of their simulations was classified into four outcomes: (i) warping, (ii) unsuccessful breaking, (iii) a single break and (iv) multiple breaking. In the latter two cases, the torque applied from the misaligned binary was able to overcome the viscous stresses maintaining the disc causing it to be torn into discrete discs that precessed independently – see Figure 7. Additionally, disc breaking occurred exclusively for parameters that corresponded to the regime above the ‘critical obliquity’ identified by Gerosa et al. (Reference Gerosa, Rosotti and Barbieri2020). At inclinations close to the critical obliquity, Nealon et al. (Reference Nealon, Ragusa, Gerosa, Rosotti and Barbieri2022) found examples of ‘unsuccessful breaking’, where the disc showed clear signatures of disc breaking (Doğan et al. 2018) but was unable to fully separate. In the event that gas assisted migration plays a strong role in the evolution of these binaries, we may thus expect discs to be either warped or broken into multiple discrete, precessing sub-discs.
When the disc is broken and precesses freely, as observed in the simulations of Nealon et al. (Reference Nealon, Ragusa, Gerosa, Rosotti and Barbieri2022), the back-reaction onto the primary BH was decreased. As a result BHs hosting broken discs did not align their spin as efficiently as those with continuous, warped discs. Using a combination of semi-analytic approaches Steinle & Gerosa (Reference Steinle and Gerosa2023) investigated the inspiral, coalescence and gravitational wave emission of such supermassive binaries taking the results of Nealon et al. (Reference Nealon, Ragusa, Gerosa, Rosotti and Barbieri2022) into account. Under the assumption that disc breaking prevents spin alignment, their results showed distinct sub-populations of aligned BHs that will be observable by LISA. While such observations will provide conclusive evidence for the Bardeen-Petterson effect, Steinle & Gerosa (Reference Steinle and Gerosa2023) also implied that the presence of disc breaking introduces an ambiguity as strongly misaligned BH mergers could be attributed to either a gas-poor environment or a gas-rich environment where disc breaking has occurred.
State of the art numerical calculations, such as those discussed above, provide a timely opportunity to make robust observational predictions for future missions such as LISA. The use of realistic accretion disc and circumbinary disc models, with the inclusion of warps and misalignments are vital to understand their impact on spin evolution and thus further work needs to be done to encompass the full, rich and complex behaviour of these systems.
8. Gravitational waves
The currently operating ground-based gravitational wave observatories, such as LIGO (LIGO Scientific Collaboration et al. Reference Scientific Collaboration2015), Virgo (Acernese et al. Reference Acernese2015), and KAGRA (Akutsu et al. Reference Akutsu2020) target frequencies at
![]() $\sim 10\,{\rm Hz}$
–
$\sim 10\,{\rm Hz}$
–
![]() $1\,{\rm kHz}$
. Ground-based facilities are not able to reach low enough gravitational-wave frequencies to detect supermassive black holes, instead detecting stellar-origin black hole and neutron star binaries (Abbott et al. Reference Abbott2023). The future space mission, LISA (Laser Interferometer Space Antenna Colpi et al. Reference Colpi2024), will observe the gravitational-wave sky at
$1\,{\rm kHz}$
. Ground-based facilities are not able to reach low enough gravitational-wave frequencies to detect supermassive black holes, instead detecting stellar-origin black hole and neutron star binaries (Abbott et al. Reference Abbott2023). The future space mission, LISA (Laser Interferometer Space Antenna Colpi et al. Reference Colpi2024), will observe the gravitational-wave sky at
![]() $0.1\,{\rm mHz}$
–
$0.1\,{\rm mHz}$
–
![]() $1\,{\rm Hz}$
. Until the arrival of the LISA space mission, the very-low frequency band (
$1\,{\rm Hz}$
. Until the arrival of the LISA space mission, the very-low frequency band (
![]() $\approx 1\,{\rm nHz}$
–
$\approx 1\,{\rm nHz}$
–
![]() $1\,\unicode{x03BC}{\rm Hz}$
) is therefore the exclusive domain of pulsar timing arrays (PTAs, e.g. Foster & Backer Reference Foster and Backer1990; Hobbs & Dai Reference Hobbs and Dai2017). While the frequency bands of LISA and PTA do not overlap, SMBH binaries at different stages of their evolution are accessible to both facilities.
$1\,\unicode{x03BC}{\rm Hz}$
) is therefore the exclusive domain of pulsar timing arrays (PTAs, e.g. Foster & Backer Reference Foster and Backer1990; Hobbs & Dai Reference Hobbs and Dai2017). While the frequency bands of LISA and PTA do not overlap, SMBH binaries at different stages of their evolution are accessible to both facilities.
Figure 8. Assuming the common-noise process observed by the PTAs originates from a population of SMBH binaries, we can make inferences on the properties of the population. Here we show posterior distributions for the merger rate per year per unit redshift for three different total mass ranges. The red and blue distributions show results for an agnostic and an astrophysically-informed model of the population, respectively. The solid lines indicate the median of the posterior, and the dark and light shading indicates the central 50% and 90% credible regions, respectively. The dotted line indicates the
![]() $99.5\%$
percentile of the astrophysically-informed prior. Reproduced from Steinle et al. (Reference Steinle2023).
$99.5\%$
percentile of the astrophysically-informed prior. Reproduced from Steinle et al. (Reference Steinle2023).
PTA observations consist of long-term radio observations of millisecond pulsars which are used to search for the imprint of gravitational waves in the pulse time of arrivals. Focusing on the gravitational-wave background produced by all the SMBH binaries in the entire Universe, theoretical predictions for signal amplitude are uncertain (Sesana Reference Sesana2013; Rosado, Sesana, & Gair Reference Rosado, Sesana and Gair2015; Kelley et al. Reference Kelley, Blecha, Hernquist, Sesana and Taylor2017; Chen, Yu, & Lu Reference Chen, Yu and Lu2020; Sykes et al. Reference Sykes2022), as one will expect after the above discussion. However, in the last few years, observations from the PTA consortia indicate the presence of a common-noise signal in the datasets of the International PTA (IPTA, Antoniadis et al. Reference Antoniadis2022), the European PTA (EPTA, Chen et al. Reference Chen2021), the Parkes PTA (PPTA, Goncharov et al. Reference Goncharov2021), and the North American Observatory for Gravitational waves (NANOGrav, Arzoumanian et al. Reference Arzoumanian2020). More recently, increased evidence that the observed signal has a gravitational-wave origin has been announced by the EPTA in collaboration with the Indian PTA (ETPA+InPTA EPTA Collaboration et al. Reference Collaboration2023; Tarafdar et al. Reference Tarafdar2022), the PPTA (Reardon et al. Reference Reardon2023), NANOGrav (Agazie et al. Reference Agazie2023c), the Chinese PTA (CPTA, Xu et al. Reference Xu2023; Lee Reference Lee, Qain and Li2016), and the MeerKAT PTA (MPTA Miles et al. Reference Miles2023, Reference Miles2025). Assuming a gravitational-wave origin, the significance of the reported signal is between
![]() $2\sigma$
and
$2\sigma$
and
![]() $4\sigma$
. If formed by gravitational waves, the signal could have a number of origins, including SMBH binaries, dark matter, and the early Universe (e.g. EPTA Collaboration et al. Reference Collaboration2024a; Agazie et al. Reference Agazie2023b; Afzal et al. Reference Afzal2023; Chen et al. Reference Chen, Yu and Lu2023b). Further study will be required to confirm the signal (e.g. Zic et al. Reference Zic2022) and the combined datasets of the IPTA will be used.
$4\sigma$
. If formed by gravitational waves, the signal could have a number of origins, including SMBH binaries, dark matter, and the early Universe (e.g. EPTA Collaboration et al. Reference Collaboration2024a; Agazie et al. Reference Agazie2023b; Afzal et al. Reference Afzal2023; Chen et al. Reference Chen, Yu and Lu2023b). Further study will be required to confirm the signal (e.g. Zic et al. Reference Zic2022) and the combined datasets of the IPTA will be used.
In addition to evidence for a gravitational-wave background, the PTA consortia also search for gravitational waves from individual SBHB binaries as continuous gravitational waves (Sesana, Vecchio, & Volonteri Reference Sesana, Vecchio and Volonteri2009; Rosado et al. Reference Rosado, Sesana and Gair2015; Kelley et al. Reference Kelley, Blecha, Hernquist, Sesana and Taylor2018; Bécsy, Cornish, & Kelley Reference Bécsy, Cornish and Kelley2022). Candidate signals have been investigated in the latest data sets (EPTA Collaboration et al. Reference Collaboration2024b; Agazie et al. Reference Agazie2023a), however further evidence will be required to confirm whether or not these signals originate from individual SBHB binaries. For the purpose of this work, we focus on the evidence for a gravitational-wave background and the population of SMBHs implied by it.
Throwing caution to the wind, one can make the assumption that the signal observed by the PTAs is indeed the signature of the gravitational-wave background and see what inferences can be placed on an associated population of inspiraling SMBH binaries via a Bayesian analysis. The results summarised here are presented in full in Steinle et al. (Reference Steinle2023). Following the methods in Steinle et al. (Reference Steinle2023), Middleton et al. (Reference Middleton2021), Chen, Sesana, & Conselice (Reference Chen, Sesana and Conselice2019), Chen et al. (Reference Chen, Middleton, Sesana, Del Pozzo and Vecchio2017), Middleton et al. (Reference Middleton, Del Pozzo, Farr, Sesana and Vecchio2016) which follow the formalism laid out in Phinney (Reference Phinney2001), we use two models of the population; an ‘agnostic’ model which makes minimal assumptions and a ‘astrophysically-informed’ model which uses information from simulation and observation to inform the priors. We note that the analysis in Steinle et al. (Reference Steinle2023) was carried out using the IPTA results in Antoniadis et al. (Reference Antoniadis2022), however they are consistent with the most recent announcements. Using the astrophysically-informed model, we can infer merger rate densities at the higher end of the astrophysical prior and shorter delay times between the galaxy merger and black hole binary merger (Figure 8, see Steinle et al. Reference Steinle2023; Middleton et al. Reference Middleton2021; Chen et al. Reference Chen, Sesana and Conselice2019, for full details).
Turning to future space-based observatories, the LISA mission (Amaro-Seoane et al. Reference Amaro-Seoane2017; Colpi et al. Reference Colpi2024) is expected to observe the merger itself for individual SMBH binaries in the gravitational-wave frequency band
![]() $0.1\,{\rm mHz}$
–
$0.1\,{\rm mHz}$
–
![]() $1\,{\rm Hz}$
, corresponding to short lived signals from mergers of lower mass SMBH binary systems (see for example Amaro-Seoane et al. Reference Amaro-Seoane2023). Parameter estimation studies of merging black hole binaries indicated that LISA inferences on the binary properties might be possible to within
$1\,{\rm Hz}$
, corresponding to short lived signals from mergers of lower mass SMBH binary systems (see for example Amaro-Seoane et al. Reference Amaro-Seoane2023). Parameter estimation studies of merging black hole binaries indicated that LISA inferences on the binary properties might be possible to within
![]() $\lt1\%$
in component mass, dependent on the system. For futher information see, for example Steinle et al. (Reference Steinle2023); Pratten et al. (Reference Pratten, Schmidt, Middleton and Vecchio2023b, Reference Pratten2023a), which uses the Balrog software package under development for LISA data analysis (Finch et al. Reference Finch2023; Klein et al. Reference Klein2022; Buscicchio et al. Reference Buscicchio2021; Roebber et al. Reference Roebber2020).
$\lt1\%$
in component mass, dependent on the system. For futher information see, for example Steinle et al. (Reference Steinle2023); Pratten et al. (Reference Pratten, Schmidt, Middleton and Vecchio2023b, Reference Pratten2023a), which uses the Balrog software package under development for LISA data analysis (Finch et al. Reference Finch2023; Klein et al. Reference Klein2022; Buscicchio et al. Reference Buscicchio2021; Roebber et al. Reference Roebber2020).
Finally, we consider how PTA and LISA observations will be complementary. Again making the assumption that the PTA signal originates from a gravitational-wave background from inspiraling SMBH binaries, we can extrapolate the inference described above to calculate the number of mergers per year of LISA operation as described in Steinle et al. (Reference Steinle2023). If the PTA signal does indeed have a SMBH binary origin, the implied population of inspiraling binaries should also provide merging sources in the LISA band. The posterior distribution for the merger rate per year per unit redshift is shown in Figure 6 for the agnostic and astrophysically-informed models in red and blue, respectively. Again using Balrog, we assess the detectability of these systems to provide an anticipated detection rate for LISA. Using the astrophysically-informed model, we predict a 95% upper limit on the detection rate of
![]() $\mathcal{R} \lt 134\,{\rm yr}^{-1}$
for binary masses in the range
$\mathcal{R} \lt 134\,{\rm yr}^{-1}$
for binary masses in the range
![]() $10^7$
–
$10^7$
–
![]() $10^8\,{\rm M_{\odot}}$
. For full details of this work see Steinle et al. (Reference Steinle2023). Another study using a semi-analytic galaxy formation model makes similar predictions (Barausse et al. Reference Barausse2023).
$10^8\,{\rm M_{\odot}}$
. For full details of this work see Steinle et al. (Reference Steinle2023). Another study using a semi-analytic galaxy formation model makes similar predictions (Barausse et al. Reference Barausse2023).
Further study is required. However, the next few years may well confirm that the PTA observation has a gravitational-wave origin, potentially from a population of SMBH binaries. Looking further ahead, space-based observatories will enable multi-band exploration of these systems through their gravitational waves.
9. Conclusions
We have reviewed the state of theoretical modelling and a variety of evidence for the different observable effects produced by binary SMBH, ranging from predictions for the cosmological evolution of SMBH, the physics of migration to the common centre after a galaxy merger, over binary SMBH accretion discs to electromagnetic and gravitational wave observations. While direct gravitational wave detections of supermassive black hole mergers are not yet available, the observation of the effects of SMBHs on their immediate environments as well the energetic requirements of active galactic nuclei provide strong arguments for the existence of SMBH in some, if not all centres of galaxies, most likely our own. Cosmological simulations then tell the story of SMBH growth via accretion and SMBH merging. However, uncertainties about the SMBH seeds, namely what the astrophysical processes involved actually are and what masses they produce, and limitations in resolution make the detailed prediction of SMBH evolution still uncertain. The spin is a key parameter here. While coherent gas accretion, which should occur typically for lower mass SMBH, would tend to produce rapidly spinning black holes, SMBH mergers are expected to produce a slowly spinning remnant. Spin observations via X-ray spectroscopy start informing the picture. With a sample of a few dozen SMBH a decline at the highest SMBH masses is seen, consistent with the cosmological expectation of mergers being important in this mass range. More, deep observations, especially towards the higher mass end would be highly desirable. Spin evolution and migration in the close binary state will be a result of the interaction with the accretion disc or discs, if one regards the circumbinary and individual accretion discs separately. Both is still uncertain and depending on modelling parameters like the assumed gas cooling processes. Angular momentum vectors of gas and SMBHs will in general not be aligned and for a binary SMBH embedded in a significant amount of gas, breaking of a warped disc can reduce the torques that would otherwise align the SMBH spins with the disc angular momentum vector. Large misalignments of SMBH spins at their merger can, however, produce kicks that may remove the merger remnant from the galactic centre.
An increasing number of dual AGN is detected in X-rays, radio and via a range of other methods. These observations support the idea that binary SMBH form during galaxy mergers, with X-ray imaging finding two active black holes within single galaxy structures. High-resolution radio imaging has revealed a good binary SMBH candidate with 7 pc projected separation. Similar discoveries and possibly tracking of orbits seem in reach (Wrobel & Lazio Reference Wrobel and Lazio2022). With longer timebases, candidates for sub-parsec binary SMBH are also being discovered from sinusoidal radio light curves (O’Neill et al. Reference O’Neill2022; Kiehlmann et al. Reference Kiehlmann2025). High-resolution optical as well as variability methods, while having to overcome significant issues with noise from unrelated astrophysical processes, have found candidates for sub-pc SMBH binaries.
Jet precession is a powerful tool here and might act as a magnifying glass for unresolved binaries, or ones where a weakly accreting secondary is only observable via the radio jet which may precess no matter which black hole produces it. OJ 287 is an observationally well studied example of a close binary SMBH that deserves further detailed modelling of the complex interplay of discs and parsec-scale jets. Large-scale jet morphologies consistent with geodetic precession expected from sub-parsec separation SMBH binaries have been observed in more than 1 000 radio sources. There is scope for combining AGN observations with future LISA gravitational wave observations (Steinle, Gerosa, & Krause Reference Steinle, Gerosa and Krause2024). Not only may radio emission from jets reveal morphological features even 100s of Myr after the source switched off (e.g. Shabala et al. Reference Shabala2024), thus providing for a fossil record of jet precession before a merger. Even sources where discs are actively re-aligning, with corresponding jet precession, might be detected with LISA (Steinle et al. Reference Steinle, Gerosa and Krause2024).
One expects a background of low-frequency gravitational waves produced by all the SMBH binaries in the Universe. A corresponding signal has been seen by pulsar timing arrays. The discussion if this signal is indeed due to the aforementioned SMBH binaries has to be informed by the astrophysics outlined above. A further confirmation would be the detection of the mergers of the putative SMBH population with LISA.
We have highlighted here some of the best pieces of evidence for binary supermassive black holes. Still more could have been mentioned, including the changes in stellar mass profile in a galaxy due to the inspiral (compare discussion in Krause et al. Reference Krause2019) and quasi-periodicities in gamma-ray lightcurves (Rieger Reference Rieger2007, Reference Rieger2019). Progress in instrumentation and data analysis methods suggest that all these methods have an exciting future.
Acknowledgements
This review was inspired by a discussion meeting hosted by the Royal Astronomical Society in London on 14 April 2023. J.M.S.R acknowledges support from the Science and Technology Facilities Council (STFC) under grant ST/V50659X/1 (project reference 2442592) and thanks Andy Fabian, Jiachen Jiang and Dom Walton for useful discussions. M.A.B acknowledges support from a UKRI Stephen Hawking Fellowship (EP/X04257X/1) and the Science and Technology Facilities Council (STFC), grant code ST/W000997/1. H. M. acknowledges the support of the UK Space Agency, Grant No. ST/V002813/1 and ST/X002071/1. RN acknowledges funding from UKRI/EPSRC through a Stephen Hawking Fellowship (EP/T017287/1). M.G.H.K acknowledges the hospitality of the Institute of Astronomy, University of Cambridge, UK for part of the writing of this manuscript.