Introduction
Although much thought has been given for over twenty years to the glacier sliding, bed–water–ice interface, problem, a detailed description of what that problem actually is conceived to be, at any given time, does not appear in the literature. Workers who have spent time trying to understand the glacier sliding process appear to have a clear picture of this ice–bed problem. Most of them are at this conference. Nevertheless, it may be useful even for them to take a step backwards in order to see the “big problem” before considering the newest theories and field observations. Doing so may be of help to those new to the field. Moreover, a review of the problem might reveal whether or not there is indeed at present a consensus as to what is the bed–water–ice interface, glacier sliding problem.
The theory of glacier sliding has now been developed by a number of investigators in many publications (Reference KambKamb, 1964, Reference Kamb1970; Reference Kamb and LaChapelleKamb and LaChapelle, 1963, Reference Kamb and LaChapelle1964; Reference LliboutryLliboutry, 1958[a], Reference Lliboutry[b], Reference Lliboutry1959, Reference Lliboutry1962, Reference Lliboutry1964, [a], Reference Lliboutry[b], Reference Lliboutry1964–65, Tom.2, p. 640–52 Reference Lliboutry1965, Reference Lliboutry1966, Reference Lliboutry1968[a], Reference Lliboutry[b], Reference Lliboutry1969, Reference Lliboutry1971, Reference Lliboutry1974, Reference Lliboutry1975; Reference HalletHallet, 1976; Reference MorlandMorland, 1976[a], Reference Morland[b]; Reference Morland and BoultonMorland and Boulton, 1975; National Academy of Sciences, 1976; Reference NyeNye, 1969, Reference Nye1970; Reference PatersonPaterson, 1969; Reference WeertmanWeertman, 1957, Reference Weertman1962, Reference Weertman1964[a], Reference Weertman[b], Reference Weertman1966[a], Reference Weertman[b], Reference Weertman1967[a], Reference Weertman[b], Reference Weertman1969, Reference Weertman1971[a], Reference Weertman[b], Reference Weertman1972). It is not the purpose of this paper to give a detailed review of all this theoretical work and of the disputes that have arisen in the past. Rather, one purpose of this paper is to present what still needs to be done before glacier sliding can be considered to be a phenomenon that is well understood. But a descriptive review of basic results that already have been established is needed in order to make more understandable what are the problems that remain to be solved. Of course, new problems of which we now have no hint may come to light during the solution of the outstanding problems.
The bed–water–ice interface problem
A glacier or ice sheet, of course, rests on the Earth’s crust. A glacier (or ice sheet) may lie directly on bed rock or on till. If the bottom surface of the glacier is at the melting temperature of ice, then ice may not be directly in contact with rock or till. A film of water may separate the ice from the rock (or till). Moreover, particularly if the overburden ice pressure is relatively small, air-filled cavities over limited regions of the bed can also separate the ice from the rock or the till. The ice of the glacier may contain rock fragments, silt, small water pockets, and similar “defects”.
Now consider any arbitrary block of ice that is within the glacier and which is just above the bed (Fig. 1). Let the dimensions of the block be small compared with the thickness of the glacier but large compared with the dimensions of irregularities in the bed surface. The bed–water–ice glacier sliding problem is simply the determination of the velocity U of this block of ice.
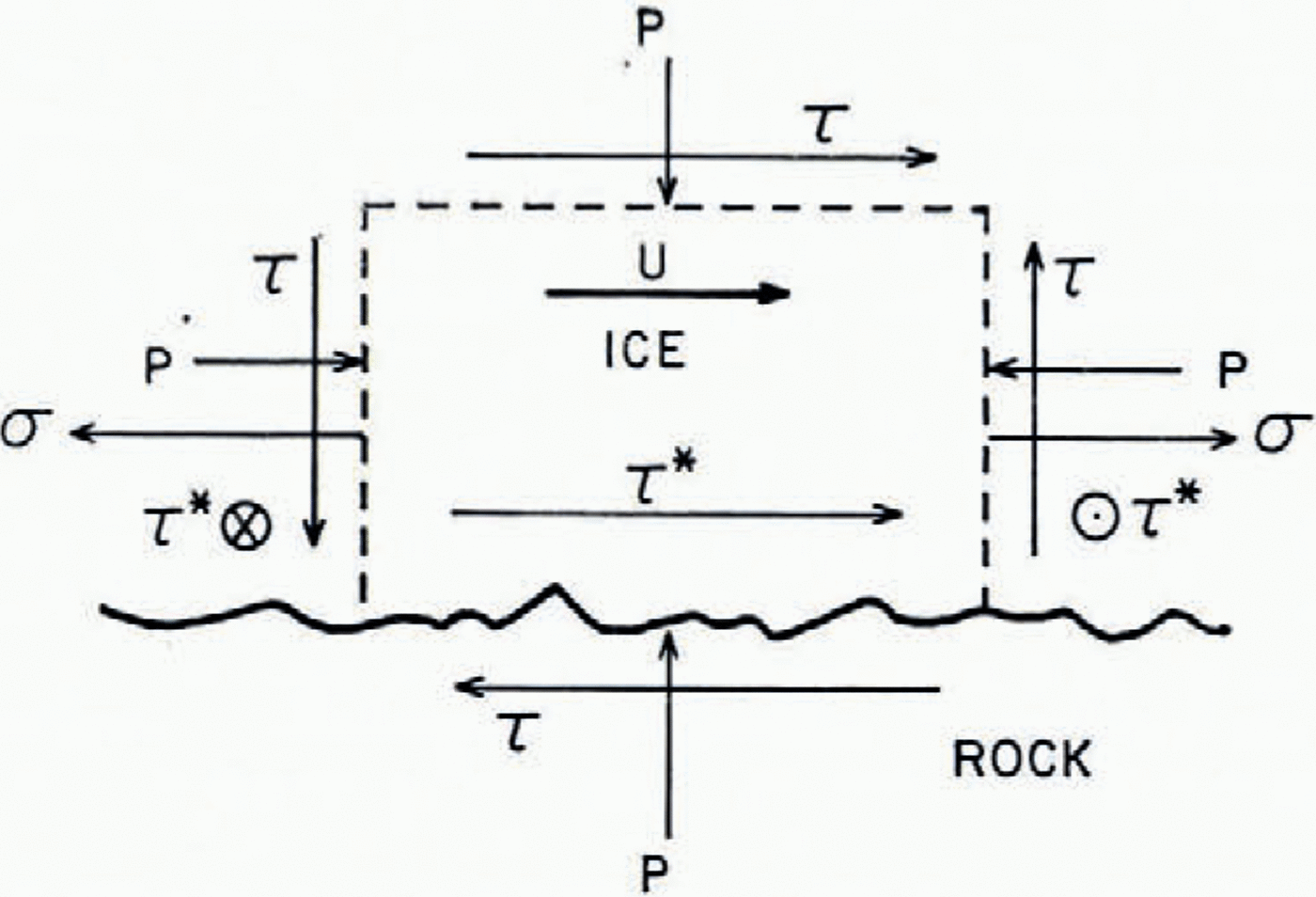
Fig. 1. Block of basal ice sliding over a glacier bed.
What factors determine the value of the ice-block velocity U? The following have been used in glacier sliding theories or have been suggested as having an influence on glacier sliding:
-
1. The average shear stress τ that acts parallel to the glacier bed (Fig. 1). Presumably the direction in which this basal shear stress acts is parallel to the average direction of the velocity U.
-
2. The average hydrostatic pressure P that acts on the ice block (Fig. 1).
-
3. The deviator stresses, one of which is indicated as the stress σ in Figure 1, that act normal to ice-block faces in Figure 1. The shear stress τ * that is indicated in Figure 1 that acts on the set of ice block sides that are all perpendicular to the bed should also be considered with the tensile or compressive deviator stresses.
-
4. The temperature of the ice as well as the bed.
-
5. The morphology of the bed surface.
-
6. The rheological properties of ice.
-
7. The rheological properties of the bed material.
-
8. The amount of water that is transported per unit time down the glacier within the bed–water–ice interface.
-
9. The amount of water that reaches in unit time the bed–water–ice interface through a permeable bed or escapes from this interface through a permeable bed.
-
10. The dissolved impurity content of the water at the bed–water–ice interface and the dissolved impurity content of the ice.
-
11. The amount of rock debris and silt within the ice.
-
12. The amount of geothermal heat transported to the glacier bed.
-
13. The amount of water that reaches the bottom surface of the glacier from the top surface of the glacier, either through moulins or crevasses that penetrate a glacier or down from the edge of a glacier.
Undoubtedly other factors will be added to this list in the future. The participants at this conference probably can suggest new ones.
If the sliding velocity U can be found as a function of all the variables that are mentioned above, then the boundary conditions needed to calculate a glacier profile can be specified at the base of a glacier or an ice sheet. Obviously, the dependence of the sliding velocity U on variables such as the basal shear stress must be known before accurate calculations can be made of time-dependent or steady-state profiles of glaciers and ice sheets. And obviously too, this boundary-value problem is more complicated than the usual ones. For example, if the sliding velocity is dependent upon the amount of water at the base of an ice mass and if the amount of water is partly determined by the amount of energy dissipated by the sliding process, because this energy causes ice to be melted, then the boundary value requires somewhat complicated feed-back specifications.
In the sections to follow a review is given as to why the sliding velocity of a glacier or an ice sheet might depend upon some of the factors that are listed above. But before entering this review, consider first the basic physical reasons why glaciers and ice sheets can slide over their beds.
The perfectly smooth interface
If the bed–ice interface or the bed–water–ice interface were perfectly smooth on an atomic scale what tangential shear stress could it support? Consider Figure 2 that shows a perfectly smooth rock–water–ice interface. The thickness of the water layer is equal to d. Let the ice velocity immediately above the water layer be equal to U. The velocity at the upper boundary of the water layer (at the ice–water contact) is thus equal to U. The velocity of water at the lower boundary (at the rock–water contact) is equal to zero. Thus the water layer is deformed in shear at a shear strain-rate of U/d. The shear stress τ that must be exerted across the ice–water contact surface and the rock–water contact surface to maintain such a shear-rate is equal to
where η is the viscosity of water. Taking a typical value of the sliding velocity (or U ≈ 10 to 100 m a-1 = 3.2 × 10-7 to 3.2 × 10-6 m s-1) and the value of the viscosity of water at 0°C (η = 0.018 poise = 0.001 8 Pa s) the shear stress τ is only of the order of 0.6 to 6 Pa (6 to 60 μbar) if the water layer thickness is as small as d = 10-9 m = 1 nm. Now the average shear stress at the base of a glacier is of the order of 0.1 MPa (1 bar) and thus is numerous orders of magnitude larger than the shear stress given by Equation (1). Hence for the glacier sliding problem to a very good approximation the perfectly smooth rock–water–ice interface can be considered to be incapable of supporting a tangential shear stress.

Fig. 2. Perfectly smooth ice–water–rock interface.
If the interface is below the freezing point so that no water layer exists, the interface will be able to support a tangential stress if ice can “wet” the solid. That is, it can if the surface energy of the interface is smaller than the sum of the surface energies of ice and the rock. Let γ represent the difference between the energy of (a unit area of) the interface and the sum of the surface energies of the rock and of ice and let b represent an atomic distance. The maximum tangential stress τ that the interface can support must be of the order of τ/b because the work done for a displacement of the order of b parallel to the boundary is certainly of the same magnitude as the work done in separating rock and ice by a distance b. The latter work is equal to γ.
Even if the value of γ is as small as 1/100th the value of the surface energy of ice the tangential stress τ has a value (τ ≈ 2 MPa = 20 bars) that is appreciably larger than the basal shear stress of glaciers and ice sheets. And of course laboratory experiments on ice adhesion demonstrate that a large stress is required to break an interface of ice frozen to a strong solid.
It is to be concluded, therefore, that a glacier whose bed temperature is below the melting point of ice should not slide. (If the bed is made up of some unusual material such as oil shale which ice cannot easily wet and were the bed perfectly smooth, sliding is possible.) And cold glaciers do not appear to slide over their beds. It is to be concluded further that temperate glaciers do not rest on perfectly smooth beds. Otherwise the basal shear stress would not be as large as it is.
Rough interface
Simple protuberance model
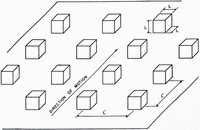
The first rough interface that was considered in glacier sliding theory is shown in Figure 3. Cubical bed protuberances key the ice and prevent fast slip from occurring despite the fact that any local area of the interface cannot support a tangential stress. This interface should not be taken too literally as a model of a glacier bed. However, with its use the basic glacier sliding mechanisms are easily understood.

Fig. 3. Simple idealized glacier bed. From Weertmart (1957).
For sliding to occur over the protuberance bed model of Figure 3, mass transport of ice must occur around the cubical protuberance. Because local areas of the interface cannot support tangential stresses concentrated stresses exist on the up-stream side of an obstacle and, if the hydrostatic pressure is sufficiently large to prevent cavitation, also on the down-stream side of an obstacle. If the average basal shear stress is equal to τ then tensile and compressive stresses will exist near each obstacle of the order of τ/R 2 where R = L/L’ is a measure of the roughness of the bed, L’ is the average separation of obstacles, and L is their average size. The stress concentrations around each obstacle will cause the ice to flow by creep around them. The creep-rate έ of ice can be expected to be a monotonically increasing function f of stress:
The stress concentration must die out at a distance from an obstacle of the order of the obstacle size. The average velocity with which ice flows around an obstacle is equal to the average creep-rate near an obstacle times the distance out to which this creep-rate is maintained. Thus creep flow permits ice to slide across the model bed of Figure 3 at a velocity Uc that is given by
where αc is a constant approximately equal to ½ if no cavitation occurs and is approximately equal to 1 if cavitation does occur. For the same value of roughness R the sliding velocity Uc is larger the larger are the obstacles.
Because the normal stress on the up-stream side and the down-stream side of an obstacle of Figure 3 differ by an amount equal to τ/R2 the melting temperature of ice is different on either side of an obstacle differ by an amount that is proportional to the stress term τ/R2 . If the ice at the bed is everywhere at the melting temperature then a temperature gradient must be set up across an obstacle. Heat must flow in a direction down this temperature gradient and cause ice to be melted on the up-stream of an obstacle and water to be refrozen on the down-stream side. If water that is produced by melting ice is free to flow to the down-stream side of an obstacle, then the regelation mechanism also permits mass transport of ice around an obstacle and thus is a sliding mechanism. The temperature gradient across an obstacle is proportional to L -1(τ/R 2). It is larger the smaller is an obstacle for a fixed value of the roughness R. The thickness of the ice layer melted off the up-stream side of an obstacle in a unit time is proportional to the temperature gradient across an obstacle in a well-behaved regelation process (but see below). The sliding velocity U r produced by the regelation mechanism is equal to the thickness of the ice layer melted off per unit time. Thus
where αr is a constant that contains such terms as the coefficient of thermal conduction of the material of an obstacle. The sliding velocity, for a fixed value of the roughness R, is larger the smaller are the obstacles.
The total sliding velocity U for the model bed of Figure 3 is equal to
and has a minimum value, for a fixed value of R, when L has a value given by
It should be noted that the controlling obstacle size L given by Equation (6) is a constant only if the flow-law function f is proportional to the stress. Since for power-law creep the function f increases with stress more rapidly than linearly, the controlling obstacle size L that is given by Equation (6) will decrease in value with increasing basal shear stress τ.
Because two sliding mechanisms operate that have qualitatively different relationships between sliding velocity and obstacle size, it is impossible to suppress sliding if R ≠ ∞.
An actual glacier bed has irregularities of various sizes, not just one. The simple analysis just given shows qualitatively why sliding can occur on a bed with a full spectrum of irregularities. The creep mechanism enables relatively fast flow to occur around the irregularities of large size and long wavelength and the regelation mechanism permits relatively fast motion past small irregularities of short wavelength. Provided that R is not a strong function of L and L’ most of the resistance to the sliding motion might be expected to be offered by obstacles or irregularities of intermediate size and wavelength, the so-called controlling obstacle size (or transition wavelength). The controlling size does depend upon the roughness R, the basal shear stress (except if the flow law is linear), the constants αr and αc, and the form of the function f.
Two unresolved problems
There are two unresolved problems in the glacier sliding problem that exist even for the simple model of Figure 3. The first of these is what is the form of the function f in Equation (2), which is the creep equation. The Glen creep equation for ice in steady-state creep has been used for Equation (2). The steady-state Glen creep equation is simply the power-law creep equation
where B is a temperature-dependent constant, the constant m ≈ 3, and σ is the stress used in an uniaxial test. (The power-law creep equation for steady-state creep can be generalized for the triaxial stress situation.) However, the ice that flows past irregularities at a glacier bed is not subjected to a constant stress, steady-state situation. The stress that deforms this ice can alternate between being compressive in character to being tensile in character. Thus the function f that appears in Equation (2) should be determined from cyclic creep tests rather than constant-stress creep tests. Definitive cyclic creep experiments on ice have yet to be carried out. Until such experiments are made, accurate quantitative predictions probably cannot be made for any glacier sliding theory although estimates of sliding velocities made with steady-state creep data probably are not unreasonable.
The second problem involves the regelation mechanism. Theoretical and experimental work at Bristol (Reference NyeNye, 1967, Reference Nye, Whalley, Whalley, Jones and Gold1973[a]; Reference FrankFrank, 1967; Reference Telford and TurnerTownsend and Vickery, 1967; Reference Nunn and RowellNunn and Rowell, 1967; Reference Chadbourne, Chadbourne, Cole, Tootill and WalfordChadbourne and others, 1975; Reference MorrisMorris, 1976), at UCLA (Reference Drake and ShreveDrake and Shreve, 1973) and elsewhere (Reference Hahne, Grigull, Riehl, Riehl, Bullemer and EngelhardtHahne and Grigull, 1969, Reference Hahne and Grigull1972; Reference Sugden and JohnTelford and Turner, 1963) have been carried out on the regelation mechanism in recent years. The general conclusion of this research is that the simple theory of regelation leads to predictions of velocities of wires pulled through ice that are up to about 5 000% larger than are measured. In one experiment that simulated a glacier-sliding situation (Reference MorrisMorris, 1976) the theoretical prediction was a factor of eight too large. Explanations and theories for the reduction of the regelation velocities include instabilities in the water film between the ice and a wire, the need for supercooling to obtain a finite rate of freezing, and change of freezing temperature of water because of the accumulation of dissolved impurity atoms in it as the regelation process proceeds. The latter effect may be quite important (Reference HalletHallet, 1976) for the glacier sliding regelation process because the basal water does contain dissolved impurities. Carbonates and silicates have been deposited on bedrock surfaces beneath glaciers (Reference HalletHallet, 1975, Reference Hallet1976, Reference Hallet1977; Reference Hallet, Hallet, Lorrain and SouchezHallet and others, 1978).
Although the basic physical process of regelation is clearly understood and there is no question that this process is involved in glacier sliding, the present theory of the process cannot be used at the moment to make accurate, quantitative predictions. Moreover, insufficient experiments exist whose results could be used in glacier sliding calculations in an empirical fashion to bypass regelation theory.
Glacier bed of general morphology
(Reference NyeNye 1969, Reference Nye1970) and Reference KambKamb (1970) independently set up the problem of ice sliding over a bed surface of arbitrary form. Figure 4 shows such a bed surface for the two-dimensional case. Nye and Kamb considered both the two-dimensional and the three-dimensional case. The bed morphology in their papers is described by Fourier series or integrals. They were able to obtain an exact solution for the problem after the following approximations and conditions had been made: 1. The difference between the mean bed slope and the actual bed slope at any point is a small quantity. (Thus the analysis does not treat a bed such as is shown in Figure 3.) 2. The deformation law for ice is taken to be a Newtonian one. That is, the creep-rate components are proportional to the deviator stress components. 3. Simple regelation theory is valid. 4. The water film between the bed and the ice is thin and therefore the lower ice surface has essentially an identical form to the bed surface. 5. The bed is water-tight.

Fig. 4. Two dimensional glacier bed surface of type used in Nye–Kamb theory.
The very elegant Nye–Kamb theory solved an outstanding problem in glacier sliding theory. How to make quantitative what is understood intuitively as the “roughness” of a glacier bed of arbitrary morphology.
For the case of a bed that is rough only in the direction of the sliding motion the Nye–Kamb relationship between sliding velocity U and the average basal shear stress τ is (Reference NyeNye, 1970)

where λ is the wavelength, k is the wave number (k = 2π/λ), η is the effective viscosity of ice, λ* = 2 π/k * where k * = (L*/4CKη)½ and L* is the latent heat of fusion of ice per unit volume of ice, C is the constant that relates the depression of the melting point with increase of pressure, K is the mean thermal conductivity of ice and rock, and S(k) is the spectral power-density function that is defined by the equation

where Z (k) is the Fourier transform of the bed profile. If z(x) represents the elevation of the bed at the horizontal position x then

As Reference NyeNye (1970) points out, the resistance or drag contribution of bed waves of different wavelength (or wave number) to the glacier sliding process has to be considered in a logarithmic sense. That is, the drag contribution in Equation (8) has to be considered over the interval δ(log λ) = δλ/λ (or the interval δ(log k) = δk/k) rather than the interval δλ (or δk). Thus waves of wavelength λ produce an increment of resistance δτ over a logarithmic wavelength interval δ (log λ) that is given by the equation
Reference KambKamb (1970) points out that the spectral power-density function S(k) = S (2π/λ) has dimensions of length cubed. Thus any bed that has the same roughness at different wavelengths must have a spectral function S that is proportional to λ3 or k-3 . Kamb calls such a bed that is equally rough at all wavelengths one of “white roughness”. When S∞λ3 then
and the maximum resistance to sliding is offered by waves of length equal to λ* (the transition wavelength).
The magnitude of the dimensionless ratio S/λ3 is a measure of the roughness of a glacier bed at the wavelength λ. The larger is this ratio the rougher is the bed at a wavelength λ. For a bed of white roughness this ratio has a constant value for all wavelengths.
If the functional dependence of S(2π/λ) can be approximated by S(2π/λ) ∝ λ n where n is a constant then the maximum resistance to sliding is offered by waves of length λ ’ (which now is the transition wavelength) given by
provided that n has a value such that 2 < n < 4. If n ≤ 2 or n ≥ 4 the integral of Equation (8) is infinite in value and thus for a finite basal shear stress the sliding velocity U = 0. (However, this is a mathematical result because the integral of Equation (8) has the limits 0 and ∞. For wavelengths that are smaller than the water-film thickness or an atomic dimension or for wavelengths longer than the length of a glacier clearly S = 0 and consequently the integral of Equation (8) actually must always be finite.) For n = 3, the case of white roughness, the length λ’ =λ*.
The wavelength λ’ that is given by Equation (13) is the analogue for the simple model of Figure 4 of the distance L’ = L/R which is the distance between obstacles of controlling size L, where L is given by Equation (6). In the Nye-Kamb theory the length λ*, and thus also the length λ’, is independent of the value of the basal shear stress and the roughness only because a linear flow law is used. The controlling obstacle size L likewise is independent of the value of the basal shear stress and the roughness if the flow law is linear. For the more realistic power-law flow law given by Equation (7) the equivalent transition wavelength λ* or λ’ will decrease in value the larger is the basal shear stress and the smoother is the bed.
The difficulties in solving exactly the Nye–Kamb equations for the case of non-linear flow of ice are so great that it is not realistic to expect that such a solution will ever be found. Although a Newtonian ice flow law is used because of its mathematical convenience, its usage is not a defect of too much significance to the Nye–Kamb theory. By adjusting the value of the viscosity, a Newtonian creep law can be made to approximate a more complicated flow law, at least over a limited range of stress. In fact, Reference KambKamb (1970) shows how a power-law creep equation can be approximated as a linear law in the Nye–Kamb theory. The Nye–Kamb theory should also be able to treat in at least an approximate manner more complicated regelation laws once these have been determined. Moreover, although the theory is developed rigorously under the assumption that the bed slope everywhere deviates only by a small amount from the mean bed slope, the theory should be able to give reasonable estimates of the sliding velocity for somewhat rougher beds.
With the completion of the work of Nye and Kamb, glacier sliding theory has been brought to the point that the problem essentially has been solved for the special case for which ice and bed are everywhere in intimate contact. The obvious problem now facing glaciologists is extending the Nye–Kamb theory for the case in which the bed and the ice at the bottom of a glacier are not everywhere in intimate contact.
Unsolved glacier-erosion, bed-roughness problem
The sliding motion of a glacier causes erosion of its bed (Reference RöthlisbergerRöthlisberger, 1968; Reference Boulton and CoatesBoulton, [c 1974]; Reference Embleton and KingEmbleton and King, 1975; Reference Sugden and JohnSugden and John, 1976). A simple calculation (Reference WeertmanWeertman, 1958) demonstrates that rocks and boulders, of small to huge size, that are imbedded in the basal ice are easily pushed along the bed of a sliding glacier. The resultant scraping of the bed must result in erosion. Thus a sliding glacier at least partly determines the shape of its bed and the roughness of its bed. Reference Nye and MartinNye and Martin (1968) have considered the erosional shaping of a glacier bed on a large scale and they have shown how large-scale waves can develop in the bed. Reference RöthlisbergerRöthlisberger (1968) points out that large waves can also be reduced in height by erosion. (These are waves of dimensions large compared with the ice thickness.)
A theory has yet to be developed as to how erosional processes at the bed determines the roughness ratio S/λ 3 at all wavelengths. Reference KambKamb (1970) and Reference Melosh and KambMelosh and Kamb (in press) have made the very plausible suggestion that a glacier will erode more quickly waves of lengths that offer the most resistance to glacier sliding. Thus if a glacier bed is originally white in roughness the amplitude of waves of length approximately equal to λ* should in time become reduced in amplitude.
Reference Melosh and KambMelosh and Kamb (in press) very recently have reported measurements of the roughness of exposed bedrock that had been covered by glaciers as well as measurements of the roughness of bedrock upon which a glacier never rested. The roughness was measured over wavelengths from 1 cm to 5 m. The roughness of the unglaciated terrain was found to be approximately white. For exposed bedrock near Blue Glacier on Mount Olympus, Washington, the constant n of Equation (12) was equal to 2.8 over wavelengths from about 0.015 to 1 m (average over 11 measured profiles) and was equal to about n = 4 (average over two measured profiles) at wavelengths between 1 to 6 m. Reference Melosh and KambMelosh and Kamb feel that their Blue Glacier data do indicate that the roughness-measure term S/λ3 does exhibit a minimum value at a wavelength near 0.6 m, which is a value that the transitional wavelength λ* might be expected to have. On formerly glaciated bedrock in the Sierra Nevada, California, the average value n for six profiles is 3.3 over wavelengths of about 0.1 to 2 m.
If many more measurements are made of the roughness of glacier beds over larger ranges of wavelengths it will be possible to use these empirical results as the boundary condition in glacier sliding calculations. Thus the theory of glacier erosion would not be needed. Nevertheless, a theory of how a glacier establishes the roughness of its bed would be very valuable, apart from the challenge of solving this problem. For example, is it certain that the roughness is constant in time? Is the roughness a function of sliding velocity? Such questions might be more easily answered once plausible theories have been developed.
Ice and bed not in intimate contact
The first treatment of glacier sliding in which the basal ice is not considered to be everywhere in intimate contact with the bed is that of Reference LliboutryLliboutry (1958[a]). Cavities are considered to exist on the lee side of bumps in the bed. Lliboutry considered cavities to occur for a two-dimensional bed but obviously they also can exist on the lee side of bumps of a three-dimensional bed (Reference WeertmanWeertman, 1964[a]). Cavities might be air- or water-filled where the ice is thin and the overburden pressure is small or they might be only water-filled where the overburden pressure is somewhat larger. Although Lliboutry’s analysis has been criticized and has been modified by him (Reference LliboutryLliboutry, 1968[a]) it seems clear enough that when cavities can form, the glacier sliding velocity is increased because the bed roughness “seen" by the glacier is actually smaller than the actual bed roughness. (The most up-to-date version of Lliboutry’s ideas on sliding and cavitation presumably will appear in his paper at this conference to which the reader is referred.) Because of the possibility of cavity formation the sliding velocity can even be a double-, or multiple-, valued function of the basal shear stress (Reference WeertmanWeertman, 1964[a]). Lliboutry’s conclusion that cavitation causes faster sliding velocities seems to be a very safe one. Both Reference NyeNye (1970) and Reference KambKamb (1970) have offered some qualitative considerations about cavity formation in their general theory.
Cavity formation is one mechanism by which basal ice is kept from direct contact everywhere with the bed. The water in the cavities plays a rather passive role in the separation process. Another mechanism that is qualitatively different from cavity formation is the formation of a water film of appreciable thickness between the basal ice and the bed (Reference WeertmanWeertman, 1962, Reference Weertman1966[a], Reference Weertman1969, Reference Weertman1972). In this mechanism water plays a very active role and the average thickness of the water film is determined by the amount of water flowing at the bed as well as pressure gradients that drive the flow. The effect of a water layer is also to make the effective bed seen by the basal ice smoother than the actual bed. Figure 5 shows why. This figure shows a cross-section of a three-dimensional bed but for simplicity indicates undulations of only two length scales. Also indicated is a water film. The water film thins out on the high-pressure, up-stream side of the larger undulations shown. Undulations of amplitude smaller than the water-layer thickness are “drowned" by the water layer. Hence the effect of the water film is to reduce drastically the value of the dimensionless ratio S/λ3, which is the measure of the roughness of a glacier bed at wavelength λ in the Nye–Kamb theory, for all wavelengths whose amplitude is smaller than or comparable to the average thickness of the water layer. Thus the value of the integral of Equation (8) is reduced and the sliding velocity is increased. If the functional dependence on λ of the spectral term S is one for which a transition wavelength λ’, such as is given by Equation (12), exists, then a very large increase in sliding velocity is expected to occur once the water-layer thickness is larger than the amplitude of waves of length equal to λ’ (or to the height of controlling obstacles in the simple theory of glacier sliding). Even if S has values that give no transition wavelength λ’ the sliding velocity will be increased. The magnitude of the increase will depend upon the thickness of the water layer and the variation of S with wavelength λ.

Fig. 5. Cross-section of a three-dimensional glacier bed that contains a water film of finite but variable thickness.
The unsolved general glacier sliding problem
I think that it is obvious now what is the general problem that must be solved to have a reasonably complete theory of glacier sliding. The Nye–Kamb analysis must be extended to the case in which the basal ice “sees” a bed that is smoother than the actual glacier bed. The effective bed is smoother because of cavity formation behind bumps and because a water layer of appreciable, but variable, thickness exists between the ice and bed. It is obvious also that this is a much more difficult problem to solve. The determination of the morphology of the effective bed is now an integral piece of the problem. The configuration of the effective bed seen by the basal ice is determined partly by the creep flow and regelation mass-transport mechanisms. It is also partly determined by the flow of the basal water which is determined in turn by the pressure gradients connected with the mass flow of the basal ice. It is highly likely that, even if the rate at which water is supplied to the bed is constant, the morphology of the effective bed is not time-independent. At one instant in time at one particular place at the bed the water layer may be thick but at another instant in time at the same place the layer may be thin. The general glacier sliding problem clearly is an intricately coupled ice-flow-water-flow problem whose solution is a challenge for the glaciologists of the coming decade.
Water-flow problem
One difficulty at present in solving the general glacier sliding problem arises from the fact that the solution of the water-flow problem, considered by itself, is by no means complete.
The source of the basal water generally is known. Some of this water must come from the ice that is melted off the bottom of a glacier or ice sheet by the geothermal heat that flows from the Earth’s interior. The work done in glacier sliding causes melting of basal ice too. The regelation cycle is actually a Carnot cycle. Consequently not all the ice that is melted during part of the cycle can be refrozen in the other part of the cycle and a net amount of water remains unfrozen. The work done in the creep flow of ice, both near the base of a glacier as well as higher up, also causes melting in the interior of the ice. This water is released at the base when the ice containing it is melted by the geothermal heat or it might flow directly to the base through the Nye–Frank intergranular veins in temperate glacier ice (Reference NyeNye and Frank, 1973). Surface melt water can descend to the base of a glacier through moulins or through Nye–Frank veins. As pointed out by Ward (quoted by Reference WeertmanWeertman, 1962), if the glacier bed is permeable, water can flow into the basal region through the bedrock (or conversely basal water can escape from the glacier bed through a permeable bedrock formation).
If all or a major fraction of the basal water cannot escape through a permeable bedrock formation, then it must escape from beneath a glacier by flowing along the bed. Ways it can do so are reviewed in Reference WeertmanShreve (1972), Reference WeertmanWeertman (1972), and Reference NyeNye (1976). The major question is whether most of the water flow is channeled or not. Two types of channels have been proposed. One type, Nye channels, are incised downwards into the bed (Reference NyeNye, 1973[b]). The other type, Röthlisberger or R-channels, are incised upwards into the basal ice (Reference RöthlisbergerRöthlisberger, 1972, Reference Röthlisberger1973). The conclusion in the Reference WeertmanWeertman (1972) review paper was that although channel water flow definitely occurs, sheet flow, in which the thickness of the sheet varies with position, is also likely to occur. However, whether water flows from a sheet into channels or vice versa is dependent upon the rheological properties of ice and the triaxial stress state at the base of a glacier. Thus a solution, or a partial solution, of the general glacier sliding problem could be very helpful in understanding the qualitative details of water flow at the base of a glacier. Such a solution might also be helpful in understanding the sometimes confusing results of experiments in which bore holes have been drilled to the base and the water level in the bore is measured. The water level in such a bore hole is not necessarily a simple expression of some sort of averaged water pressure at the base of a glacier (Reference HodgeHodge, 1976). The presence of the bore hole must modify the hydrological regime in its vicinity and must alter the dynamic water-flow pattern there.
Surging glacier problem
In this discussion one must not lose sight of the problem of explaining glacier surges. Two difficult problems involved with explaining surges are: (1) How is a surge initiated? (2) How do large surging glaciers maintain a sliding velocity that is several orders of magnitude larger than a normal sliding velocity. If a water layer is formed of average thickness that is comparable to or larger than the amplitude of waves of the transition wavelength λ’ then clearly a large increase in sliding velocity will occur. The thickness of the regelation layer can be used as a measure of this.
According to Reference KambKamb (1970): “Where the regelation layer has been measured in the field, the thickness found has been in the range 0 to 29 mm, averaging perhaps 5 mm”. Thus it seems the water-layer thickness need be only of the magnitude of 5 mm to explain large sliding-velocity changes. (Thicknesses of this magnitude were used to explain surge velocities by Reference WeertmanWeertman, (1962, Reference Weertman1969).)
If the lower limit on the integral in Equation (8) is set equal to λW where λW is the wavelength of the smallest waves that are not effectively “drowned” by a water film, and if the upper limit of the integral is set equal to λm where λm is the maximum physically reasonable wavelength, then the sliding velocity is given by

when the function S can be approximated by the relationship S = s 0(λ/λ 0) n where s0 is a constant of dimension length cubed and which is equal to the value of S at any arbitrarily chosen wavelength of λ = λ0. When λw > λ* Equation (14) reduces to
for n = 3,
for n = 4, and
for n = 2. Thus the smaller is the value of n the more sensitive should the glacier sliding velocity be to the presence of water. For n = 4 the sliding velocity should be virtually independent of the water content of the bed. (Of course, for a non-linear flow law of power larger than one the value of the effective viscosity η will decrease the larger is the value of λW.) Thus the second of the surge problems might be solved through a solution of the general glacier sliding problem provided that surging glaciers have beds with average values of n that are appreciably smaller than 4. A general glacier sliding solution clearly could make more quantitatively accurate calculations than have been made in the past of the increase of the sliding velocity when appreciable amounts of basal water are present.
The solution of the general problem also might solve the surge initiation problem. Reference Robin and WeertmanRobin and Weertman (1973) already have used the restricted Nye–Kamb theory solution to show that a surge might be started in a region where the average value of the basal shear stress varies rapidly with distance down a glacier. Other initiation mechanisms might fall out of the general solution.
Deformable bed problem
It has been assumed up to now in this paper that a glacier or ice sheet rests on a non-deformable bed. But a glacier or ice sheet, wholly or in part, may rest on glacial till. If the till does not deform but is permeable it will influence the sliding velocity by either allowing water to drain through it or by allowing additional water to reach the bed. If the basal shear stress and the pore pressure in the till is made sufficiently large the till itself will deform as suggested by Boulton and co-workers (Reference Boulton, Boulton, Dent and MorrisBoulton and others, 1974; Reference Boulton, Wright and MoseleyBoulton, [c1975]; Reference Boulton and PaulBoulton and Paul, 1976) and Reference IkenIken (1974). Recently Reference Boulton and JonesBoulton and Jones (1979) have made the first analysis of the deformation of a deformable bed and its effect on glacier profiles. They concluded that the basal shear stress will be much reduced in value and consequently a glacier or ice sheet resting on a deformable bed will be much thinner than a glacier or ice sheet that rests on a non-deformable bed. They point out that this thinning effect may have been important to the Pleistocene ice sheets. (Birchfield and Weertman (paper in preparation) are using this result of Boulton and Jones try to show that it is not necessary to have a large accumulation rate in order to build up a Pleistocene ice sheet of large horizontal extent in a relatively short time period.) The Boulton and Jones work undoubtedly will be followed up by other more ambitious analyses of glacier-ice movement over a deformable bed.
Englacial basal debris problem
Another problem that needs more study is the effect on sliding of rock debris that may be contained in the basal ice. The rheological properties of impure ice and of a two-component ice and debris mix is different from that of pure ice. Hence this change of the flow properties of the basal ice by itself must change the sliding velocity. Moreover the rock particles that are in contact with the bed (and which cause erosion of the bed) must hinder the sliding process.
Summary
This paper reviews the present status of glacier sliding theory without going into many specific details of various theories. It is pointed out that the analysis of glacier sliding of Nye and of Kamb has essentially completed the solution of this problem for the case in which basal ice is in intimate contact with a non-deformable bed of a given morphology. To apply this solution, however, requires that the rheological properties of ice (and of two component mixtures of ice and rock debris) and of impure ice under cyclic stress conditions be better known. In addition the regelation process needs to be better understood and experimental data need to be obtained on it that can be inserted into the sliding theory. The sliding velocity of a glacier is controlled by the bed roughness, but because the sliding motion causes bed erosion the bed roughness must be determined in turn by the sliding motion. Thus a complete theory of glacier sliding should include a sub-theory of how the actual roughness of a bed is developed by the sliding motion itself. This sub-theory does not exist at present.
The problem of a glacier sliding over a non-deformable bed in which the basal ice is not in intimate contact with the bed has not been completely solved. This very important problem is called the general glacier sliding problem in this paper. In this problem the water-flow process at the bed is intricately coupled with the sliding mechanisms. Basal ice that is not in intimate contact with the bed, because of the presence of cavities and water films of finite thickness, “sees” an effective bed that is smoother than the actual bed. Therefore the glacier sliding velocity is increased. Thus the solution of the general glacier sliding problem has obvious application to the glacier surge problem.
A new field of research in glacier sliding that is opening up is the motion of glaciers over deformable beds. As pointed out by Reference Boulton and JonesBoulton and Jones (1979) this problem may have important application to the Pleistocene ice sheets.
Discussion
J. Weertman: I should like to invite discussion on what others perceive as the important problems connected with glacier sliding.
W. B. Kamb: One important problem is that sliding theory has hardly at all been tested in the field, with actual observations of glacier sliding and of the parameters that theoretically control sliding. We cannot yet predict sliding reliably with theory. The transition wavelength, one of the most basic parameters of sliding theory, has been only estimated in the field once, to an order of magnitude (in the 1964 tunnel of LaChapelle and Kamb). Bed roughnesses, which are very important in controlling sliding, are practically unknown in general.
As to aspects of basal sliding that have not yet been fully considered, one that I think is particularly important, as I will discuss in the next paper, is the role of rock friction in basal sliding.
L. A. Lliboutry: You said that an extension of the Nye–Kamb theory in the case of cavitation is needed. In my opinion I have done it and shall not work again on this problem until it is proved that my theory is wrong. The actual problem to solve is to go from the local friction law to the global friction law which is necessary for the study of surges and glacier fluctuations.
Weertman: I did not make my position clear to you. Nye and Kamb in their theory took a glacier bed of arbitrary form. They obtained an exact solution for the sliding over this bed when classical regelation theory is valid and ice obeys the Newtonian law for the situation in which ice is in intimate contact with the bed. The generalization of this theory is to take the same bed, allow water to be created everywhere at the bed by melting ice with geothermal energy and sliding friction energy, add water from sources external to the bed, not to allow all this water to accumulate at the bed, and solve exactly the coupled water-flow problem and ice-sliding problem. The exact solution for this coupled problem is not in your papers, nor in my papers, nor in the papers of anyone else. This problem is the unsolved general glacier sliding problem discussed in my paper.
Now I am not saying that there are not valuable insights about the water problem and cavity problem of sliding in your papers (as well as in papers of Röthlisberger, Nye, Shreve, and, I hope, myself, as well as others). As far as the calculation on the effect of water on sliding goes, we are still in an almost back-of-the-envelope-calculation stage—the same stage we were in for the problem of ice sliding over a bed with which it is in intimate contact until the Nye–Kamb theory came along.
G. S. Boulton: Professor Weertman has spoken of the successes of glacier sliding theory. I would like to stress the dark side, where improvement is necessary. On the large scale, where we are concerned with the gross dynamics of glaciers, the theory may be very useful. On the small scale, where we are attempting to assess the variation of stress over an individual finite-slope, three-dimensional hump, an assessment necessary in developing a theory of erosion and deposition, the theory is not good. This is largely because the restrictions on the theory preclude its use in such local sites. Indeed the theory could be tested in such sites if a more realistic lower boundary were treated. As it is, the theory could be considered as a poor one if testability is used as the criterion of a good theory.
G. de Q. Robin: While we seem to have a fair understanding of the problems of internal deformation of glaciers, it seems that we still have a long way to go to understand processes in the bottom few metres of a glacier. In discussing the temperature at the ice-rock interface at the Burnaby symposium in 1975, I suggested cold patches—and hence locally high friction—may vary both spatially and with time. Professor Lliboutry has referred to one cause of cold patches, but a diffierent one to my suggested heat pump, while variation with time arising from variations of basal water pressure with time have not been discussed, although I believe such variations of basal water pressure with time are present and help explain jerky glacier motion.
May I suggest that the best people to say whether theoretical knowledge is satisfactory in glaciological research are those who work actively on glaciers in the field, and who therefore test theory against their own measurements.
Weertman: It works the other way around too. The theorists may be the best people to judge whether a measurement made can be used to judge a theory. A good example is given at this meeting. Someone pointed out that field measurements of sliding velocity versus basal shear stress do not agree with theory. But the theories that were implicitly referred to were those for which water plays no role (except in regelation). But sliding theory does predict that water can strongly influence the sliding velocity. Theory thus does predict correctly that there is no simple relationship between sliding velocity and basal shear stress for glaciers with appreciable amounts of water at their bases.
H. RÖthlisberger: Current sliding theories seem to treat almost exclusively the steady state. Transient periods can differ considerably from the steady state (see papers by Iken and others in this symposium); the transient phase during the formation of cavities appears to be another problem of glacier sliding that needs to be looked into more closely.
Weertman: I agree and would go even further. I made the guess in my paper “… that, even if the rate at which water is supplied to the bed is constant, the morphology of the effective bed is not time independent”.
T. J. Hughes: The main justification for glaciology is, in my opinion, to understand the interaction between glaciation and climate. In this case, the most important thrust of sliding theory is to understand the role of sliding in ice-stream flow, since ice streams drain most of present ice sheets and may have controlled much of the stability of former ice sheets. Is the rate-controlling mechanism in ice streams to be found at the ice-rock interface at the bed, or in the lateral shear zones alongside ice streams? For ice streams, at least, sliding theory should not be restricted to creep–regelation at the ice-rock interface. It should be expanded to include enhanced creep due to recrystallization and friction warming in the lateral shear zone, if the back-force there compares with or exceeds the back-force at the bed. What is the feed-back between ice–rock uncoupling at the bed due to basal melting and ice–ice uncoupling along the sides due to strain softening?
Weertman: Why ice streams move so fast is an outstanding problem. My own feeling is that there must be lots of “lubricating” water beneath them. If they slide easily over their beds the restraint at their sides may play an important role in their mechanics as you suggest.
I. M. Whillans: In order to best understand the sliding at the base of ice sheets, the problems of subglacial water flow and of the effect of bedrock irregularities need to be solved together.
M. F. Meier: Steve Hodge’s bore-hole experience at South Cascade Glacier suggests that the probability of intersecting a cavity which is connected to an R-channel or other connected drainage system is very low. Perhaps cavities in Lliboutry’s “autonomous” regime are intersected. Thus it may be difficult to develop an integrated ice–water–bed theory using existing N-channel, R-channel, or W-layer theory.
Weertman: I agree with you.
Lliboutry: The drainage system consists of minute glacial striae and rock joints, which cannot be found by drilling. It drains only a few centimetres of water per year. You cannot expect to have all the water stored in a bore hole emptied through this drainage system in a few minutes. You must put a pressure gauge at the bottom, seal the hole with a core of cold ice, and record the pressure over a long period. To distinguish the pressure fluctuations due to changes in the pressure p of the interconnected hydraulic system from the pressure fluctuations coming from different sites of the bedrock (up-stream or down-stream of an obstacle), several pressure gauges in neighbouring holes are needed. This has been done by Gillet on Glacier de Saint-Sorlin. In June there was a simultaneous increase of the pressure at all gauges, when superficial melt water invaded the ice–bedrock interface.
A. Dreimanis: As incorporation of large blocks (up to several square kilometres in area of bedrock of subglacial sediments) suggests that they were frozen to the base of cold-based ice sheets, then the sliding took place along shear planes in the bedrock or sediments underneath the ice, and not at the ice–bedrock interface. Has the theory of the sliding and friction related to these cases been worked out?
Lliboutry: No, not to my knowledge. Maybe the results obtained in soil mechanics for earth slides can be useful.
Weertman: Where freezing of water occurs under an ice sheet it would be possible to freeze ice underneath a block of rock. As more ice is frozen the block would be lifted higher into the ice sheet where it could be transported horizontally through the shear deformation of the ice.
R. H. Thomas: With the ever-growing requirements for a successful sliding theory I suspect that the final solution (if it is ever achieved) will be incomprehensible to most of us here and I mourn the apparent demise of Weertman’s original simple theory.
Lliboutry: If, instead of presenting in a hurry an invited paper, I had had the leisure to present four or five separate communications, with only one main idea in each one, you would have a quite different feeling. Weertman’s original theory was only a didactic way of doing dimensional analysis. His numerical factor is wrong by a full order of magnitude, and his double-valued friction comes from wrong reasoning. A sophisticated calculation is needed to prove this, but you may consider only my figure giving τ b as a function of U and N. I have simplified drastically Reference KambKamb’s (1970) very complicated calculations and shown that this theory is not valid for finite slopes. This theory was made for small sliding velocities over a vanishing microrelief. Now in this case, basal drift must be taken into account and Kamb’s new theory (which leads to Coulomb’s friction law) is much more convincing. For very high sliding velocities Coulomb’s law τ b = FN (F being a constant) may be adopted too. Coulomb’s law is still simpler than Weertman’s.
A more realistic law is

where s(t) is the shadowing function of the bedrock (which has a simple physical meaning), t = CtNn/U, and F is a simple function of t and s. For most bedrocks F is more or less constant, and for very large sliding velocities the third term is negligible. In this case the friction law becomes
This is only a little more complex than Weertman’s law τ b = kWU2/(n+1) , but it allows us to explain the seasonal fluctuations of velocity. For some bedrock surfaces, F may decrease at high sliding velocities, explaining the surges of some temperate glaciers. Since N becomes very small for tidal glaciers, the high velocities of the outlets of ice caps are also explained. Lastly, it shows the importance of studying the subglacial hydraulic system (a still open problem), whereas Weertman’s original law engendered the wrong feeling that the problem was definitely solved.
Weertman: My calculations (Reference WeertmanWeertman, 1971[a]) show that the simple theory disagrees with data by no more than a factor of two, not by the order of magnitude that you claim.
R. P. Goldthwait: Among the remaining important questions is there not the consideration of “turbulence”, by which I mean horizontal vortices of rotation, in a viscous plastic-like ice? How should we explain strong eroding currents at 90° to ice motion and in some cases downward, “scooping” a deep curving groove into the rock? Since it has never been observed in any tunnel known to me, it is presumably a deep-ice phenomenon exhibiting conditions under very deep (continental) ice, and not observable.
Weertman: Fast moving water in channels under an ice sheet clearly can be turbulent. I made some calculations on such turbulent flow in my 1972 paper.
D. J. Drewry: I would like to ask the opinion of both Weertman and Lliboutry on the question of scale effects on thesliding process. In most of the discussion we have heard, sliding has been approached at the level of temperate glaciers and, for instance, basal conditions treated with bumps separated by small zones of water, on the scale of a few metres. Beneath large ice sheets we may go up an order of magnitude and encounter water bodies of up to several thousand square kilometres in size (sub-ice lakes). Do these authors consider that at this large scale sliding characteristics and controls developed for small-scale beds are still applicable?
Weertman: They should not be applicable for sub-ice lakes of appreciable depth. The resistance to sliding motion should drop dramatically.
Lliboutry: In my opinion the characteristics and controls developed for small-scale beds do not necessarily apply to large-scale sliding characteristics. The local friction vanishes. A theory of friction at a scale of, say, 50 km must consider the temperatures within the ice sheet over a wavy surface: it has not been done.