1.1 Statement of the main results

We now give a more detailed description of the main results of this article. For simplicity, we explain this in the setting of unitary groups without similitude (whereas in the main body of this article we work with unitary similitude groups and PEL Shimura varieties). With notation as above, fix a CM type $\Psi $ of F and let $\tau _0 \in \Psi $ denote the place where W has signature $(1, 2n-1)$ . Let p be an odd prime which splits completely in $F/\mathbb {Q}$ and fix an identification $\iota _p \colon \mathbb {C} \cong \overline {\mathbb {Q}}_p$ . For any $\tau \in \Psi $ , let $\mathfrak {p}_{\tau }$ denote the prime of F lying above p determined by embedding $\iota _p \circ \tau $ , and let $\mathfrak {p}_{\bar {\tau }}$ denote its complex conjugate. Since p splits completely, we have an identification $\mathbf {G}_{0, \mathbb {Q}_p} = \prod _{\tau \in \Psi } \operatorname {GL}_{2n}$ .

Let $\pi $ be a cuspidal automorphic representation of $\mathbf {G}_0(\mathbb {A})$ such that its component $\pi _{\infty }$ at the infinite place lies in the discrete series L-packet parameterised by a self-dual dominant character $\lambda \in X^*(T)^+$ . More precisely, if $T \subset \mathbf {G}_{0, \mathbb {C}} = \prod _{\tau \in \Psi } \operatorname {GL}_{2n}$ denotes the standard diagonal torus, then $\lambda $ can be described as a tuple of integers $(\lambda _{1, \tau }, \dots , \lambda _{2n, \tau })$ with $\lambda _{1, \tau } \geq \lambda _{2, \tau } \geq \cdots \geq \lambda _{2n, \tau }$ and $\lambda _{i, \tau } = -\lambda _{2n+1-i, \tau }$ for all $i=1, \dots , 2n$ and $\tau \in \Psi $ . Consider the Levi subgroup $M = \left (\operatorname {GL}_1 \times \operatorname {GL}_{2n-1}\right ) \times \prod _{\tau \neq \tau _0} \operatorname {GL}_{2n} \subset \mathbf {G}_{0, \mathbb {C}}$ and let ${^MW}$ denote the set of minimal length representatives of the quotient $W_{M}\backslash W_{\mathbf {G}_0}$ of Weyl groups. We assume that the Harish-Chandra parameter of $\pi _{\infty }$ is of the form $w_n \cdot (\lambda + \rho )$ , where $\rho $ is the half-sum of the positive roots (with respect to the upper-triangular Borel) in $\mathbf {G}_{0, \mathbb {C}}$ , and $w_n$ is the unique element in ${^MW}$ of length n. Finally, we assume that $\pi $ is unramified at p and we fix a set S containing $\infty $ and all primes where $\pi $ is ramified (the primes where there does not exist a maximal special subgroup with nontrivial fixed points on the corresponding local component of $\pi $ ).

The main objects of study in this article are the following unitary Friedberg–Jacquet periods, namely, for any anticyclotomic algebraic Hecke character $\chi \colon F^{\times } \mathbb {A}_{F^+}^{\times } \backslash \mathbb {A}_F^{\times } \to \mathbb {C}^{\times }$ we set

(1.1.1)

where $\chi ' \colon \operatorname {Res}_{F^+/\mathbb {Q}}\operatorname {U}(1)(\mathbb {A}) \to \mathbb {C}^{\times }$ is the unique character satisfying $\chi (z) = \chi '(\bar {z}/z)$ for any $z \in \mathbb {A}_F^{\times }$ . Here $h_1$ (resp. $h_2$ ) denotes the component of h lying in the unitary group for $W_1$ (resp. $W_2=W_1^{\perp }$ ), and $dh$ denotes the Tamagawa measure. These periods are conjectured to be related to central values of the (standard) L-function $L(\Pi \otimes \chi , s)$ , where $\Pi $ denotes the base-change of $\pi $ to an automorphic representation of $\operatorname {GL}_{2n}(\mathbb {A}_F)$ . More precisely, one expects that $\mathscr {P}_{\pi , \chi } \neq 0$ if and only if $\Pi $ is of symplectic type, $\operatorname {Hom}_{\mathbf {H}_0(\mathbb {A}_f)}(\pi _f, \chi ' \boxtimes (\chi ')^{-1}) \neq 0$ , and $L(\Pi \otimes \chi , 1/2) \neq 0$ (see [Reference Chen and GanCG21, Conjecture 7.4]). Given this conjecture, it is therefore natural to study the periods $\mathscr {P}_{\pi , \chi }(\phi )$ (for suitable choices of test data $\phi \in \pi $ ) in lieu of the central L-values $L(\Pi \otimes \chi , 1/2)$ .

Firstly, we introduce the set of anticyclotomic characters over which we intend p-adically interpolate the unitary Friedberg–Jacquet periods. Let $\Sigma _{\pi }$ denote the set of anticyclotomic algebraic Hecke characters $\chi \colon F^{\times } \mathbb {A}_{F^+}^{\times } \backslash \mathbb {A}_F^{\times } \to \mathbb {C}^{\times }$ such that:

• • The $\infty $ -type of $\chi $ is equal to $(\lambda _{n, \tau _0} + 1 + j_{\tau _0}, -(\lambda _{n, \tau _0} + 1 + j_{\tau _0}))$ at the place $\tau _0$ , and equal to $(j_{\tau }, -j_{\tau })$ at any place $\tau \neq \tau _0$ , for some tuple of integers $j = (j_{\tau }) \in \prod _{\tau \in \Psi } \mathbb {Z}$ satisfying

  $$\begin{align*}0 \leq j_{\tau_0} \leq \lambda_{n-1, \tau_0} - \lambda_{n, \tau_0}, \quad \quad 0 \leq j_{\tau} \leq \lambda_{n, \tau} \; \; (\tau \neq \tau_0). \end{align*}$$

• • The conductor of $\chi $ is of the form $\prod _{\tau \in \Psi } (\mathfrak {p}_{\tau } \mathfrak {p}_{\bar {\tau }})^{c_{\tau }}$ with $c_{\tau _0} \geq 1$ . We let $e = (e_{\tau }) \in \prod _{\tau \in \Psi } \mathbb {Z}_{\geq 1}$ denote the tuple of integers given by $e_{\tau } = \operatorname {max}(1, c_{\tau })$ .

Let $F_{p^{\infty }} / F$ denote the maximal anticyclotomic abelian extension which is unramified away from p. For any $\chi \in \Sigma _{\pi }$ , we let $\hat {\chi } \colon \operatorname {\mathrm {Gal}}(F_{p^{\infty }}/F) \to \overline {\mathbb {Q}}_p^{\times }$ denote the corresponding continuous character via class field theory.

The test data we consider in this article is of the following form:

• • Let $K_{\infty } \subset \mathbf {G}_0(\mathbb {A})$ denote the maximal compact subgroup whose complexification equals $M(\mathbb {C})$ . We fix $\phi _{\infty } \in \pi _{\infty }$ a (nonzero) element in the minimal $K_{\infty }$ -type of $\pi _{\infty }$ which is an eigenvector under the action of $K_{\infty } \cap \mathbf {H}_0(\mathbb {A})$ .

• • Let $K \subset \mathbf {G}_0(\mathbb {A}_f)$ be a compact open subgroup of the form $K = K_S \cdot \prod _{\ell \not \in S} K_\ell $ , where

  $$\begin{align*}K_S \subset \prod_{\substack{\ell \in S \\ \text{ finite }}} \mathbf{G}_0(\mathbb{Q}_{\ell}), \quad \quad K_{\ell} \subset \mathbf{G}_0(\mathbb{Q}_{\ell}) \text{ maximal special, } \end{align*}$$
  such that $\pi _f^K \neq 0$ . We fix nonzero vectors $\phi _S \in \pi _{f, S}^{K_S}$ , and $\phi _{\ell } \in \pi _{\ell }^{K_{\ell }}$ for $\ell \notin S \cup \{ p \}$ , where $\pi _{f,S} = \bigotimes _{\substack {\ell \in S \\ \text { finite }}} \pi _{\ell }$ .

• • For any $\tau \in \Psi $ and $i =1, \dots , 2n$ , let $t_{p, i, \tau } \in \mathbf {G}_0(\mathbb {Q}_p)$ denote the diagonal matrix which is the identity outside the $\tau $ -component, and in the $\tau $ -component is given by $\operatorname {diag}(p, \dots , p, 1, \dots , 1)$ with i lots of p. We fix a p-stabilisation $\phi _p \in \pi _p$ , that is, an Iwahori-fixed vector which is an eigenvector for the action of the $U_p$ -Hecke operators associated with $t_{p, i, \tau }$ . Explicitly, $\phi _p$ is fixed by the standard upper-triangular Iwahori subgroup $\operatorname {Iw} \subset \mathbf {G}_0(\mathbb {Q}_p)$ , and there are (necessarily nonzero) complex numbers $\alpha _{i, \tau } \in \mathbb {C}^{\times }$ such that

  $$\begin{align*}[ \operatorname{Iw} \cdot t_{p, i, \tau} \cdot \operatorname{Iw}] \cdot \phi_p = \alpha_{i, \tau} \phi_p \end{align*}$$
  where $[ \operatorname {Iw} \cdot t_{p, i, \tau } \cdot \operatorname {Iw}]$ is the Hecke operator associated with $t_{p, i, \tau }$ . We assume that this eigensystem is small slope, that is, for any $\tau \in \Psi $ and $i = 1, \dots , 2n-1$ one has
  
  where $v_p$ denotes the p-adic valuation normalised such that $v_p(p) = 1$ .

For any $\chi \in \Sigma _{\pi }$ , we let $\phi ^{[j]}_e \in \pi $ denote the automorphic form given by

$$\begin{align*}\phi^{[j]}_e = (\Delta^{[j]}_{\kappa} \cdot \phi_{\infty}) \otimes \phi_S \otimes \bigotimes_{\ell \not\in S \cup \{p\}} \phi_{\ell} \otimes (u_{\operatorname{sph}} t_p^e \cdot \phi_p) \end{align*}$$

where $\Delta ^{[j]}_{\kappa } \in \mathcal {U}(\mathfrak {g}_{\mathbb {C}})$ is a certain differential operator depending on the tuple j and the weight ${\kappa = -w_M^{\operatorname {max}} [ w_n (\lambda + \rho ) - \rho ]}$ (see Definition A.1.5), $u_{\operatorname {sph}} \in \mathbf {G}_0(\mathbb {Q}_p)$ is a certain representative of the open orbit of the lower-triangular Borel subgroup of $\mathbf {G}_0(\mathbb {Q}_p)$ acting on $\mathbf {H}_0(\mathbb {Q}_p) \backslash \mathbf {G}_0(\mathbb {Q}_p)$ , and $t_p^e \in \mathbf {G}_0(\mathbb {Q}_p)$ denotes the diagonal matrix which in the $\tau $ -component is given by $\operatorname {diag}(p^{e_{\tau }(2n-1)}, p^{e_{\tau }(2n-2)}, \dots , p^{e_{\tau }}, 1)$ . Here $w_M^{\operatorname {max}} \in W_M$ denotes the longest Weyl element. One should view the operator $\Delta _{\kappa }^{[j]}$ as a higher-dimensional analogue of a certain power of the Maass–Shimura differential operator – indeed, if we identify $\mathfrak {g}_{\mathbb {C}} = \bigoplus _{\tau \in \Psi } \mathfrak {gl}_{2n}$ , then up to a nonzero rational number the operator $\Delta _{\kappa }^{[j]}$ in the $\tau $ -component is given by the $j_{\tau }$ -th power of the determinant operator

$$\begin{align*}\operatorname{det}_{\tau} = \sum_{\sigma \in S_n} \operatorname{sgn}(\sigma) \prod_{i=1}^n E_{i, n+\sigma(i)} \; \in \; \mathcal{U}(\mathfrak{gl}_{2n}) \end{align*}$$

where $E_{a, b} \in \mathfrak {gl}_{2n}$ denotes the elementary matrix with $1$ in the $(a, b)$ -th place. Furthermore, the local component $u_{\operatorname {sph}} t_p^e \cdot \phi _p$ is precisely the same element which appears in the study of twisted local zeta integrals associated with Shalika models (see [Reference Salazar, Dimitrov, Graham, Jorza and WilliamsBDG⁺22, Reference Salazar, Graham and WilliamsBGW25]).

We now state the first main result of this article.

Theorem A. There exists a locally analytic distribution $\mathscr {L}_{p, \phi }(\pi , -) \in \mathscr {D}^{\operatorname {la}}(\operatorname {\mathrm {Gal}}(F_{p^{\infty }}/F), L)$ such that for any $\chi \in \Sigma _{\pi }$

$$\begin{align*}\mathscr{L}_{p, \phi}(\pi, \hat{\chi}) = (\star) \cdot (2\pi i)^{-(n-1)} \cdot \mathscr{E}_p(\pi, \chi) \cdot \mathscr{P}_{\pi, \chi}(\phi_e^{[j]}) \end{align*}$$

where:

• • $L/\mathbb {Q}_p$ is a sufficiently large finite extension and $(\star )$ is a nonzero rational number independent of $\pi $ and $\chi $ ;

• • the factor $\mathscr {E}_p(\pi , \chi )$ is given by

  $$\begin{align*}\mathscr{E}_p(\pi, \chi) = p^{-e_{\tau_0}} \left( \frac{\alpha_{n, \tau_0}}{\alpha_{n-1, \tau_0}} \right)^{e_{\tau_0}} \chi_{\mathfrak{p}_{\bar{\tau}_0}}(-1) \chi_{\mathfrak{p}_{\bar{\tau}_0}}(p)^{-e_{\tau_0}} \mathscr{G}(\chi_{\mathfrak{p}_{\bar{\tau}_0}}) \left( \prod_{\tau \in \Psi} \chi_{\mathfrak{p}_{\bar{\tau}}}(-1)^n \right) (\alpha_p^e \delta_B(t_p^e))^{-1} \end{align*}$$
  where $\alpha _p^e$ is the eigenvalue corresponding to the action of $[\operatorname {Iw} \cdot t_p^e \cdot \operatorname {Iw}]$ on $\phi _p$ , $\delta _B$ denotes the modulus function associated with the upper-triangular Borel subgroup of $\mathbf {G}_0(\mathbb {Q}_p)$ , $\chi _{\mathfrak {p}_{\bar {\tau }}}$ denotes the restriction of $\chi $ to $F_{\mathfrak {p}_{\bar {\tau }}}^{\times } \cong \mathbb {Q}_p^{\times }$ , and $\mathscr {G}(\chi _{\mathfrak {p}_{\bar {\tau }_0}})$ is the Gauss sum associated with the character $\chi _{\mathfrak {p}_{\bar {\tau }_0}}$ .

Before describing the ingredients that go into the construction of $\mathscr {L}_{p, \phi }(\pi , -)$ , let us first make a few remarks.

Remark 1.1.5. For the locally analytic distribution $\mathscr {L}_{p, \phi }(\pi , -)$ to have a (potentially) nontrivial interpolation property, one should at the very least impose the additional conditions that $\Pi $ is of symplectic type, $\operatorname {Hom}_{\mathbf {H}_0(\mathbb {A}_f)}(\pi _f, \mathbb {C}) \neq 0$ , the Satake parameters for $\pi _p$ are distinct in each component indexed by $\Psi $ , and the choice of p-stablisation $\phi _p$ is spin (see [Reference Salazar, Dimitrov, Graham, Jorza and WilliamsBDG⁺22, §6]). Assuming these conditions hold, write

$$\begin{align*}\pi_p = \bigotimes_{\tau \in \Psi} \operatorname{Ind}(\theta_{\tau}) \end{align*}$$

where $\operatorname {Ind}(\theta _{\tau })$ denotes the smooth irreducible representation of $\operatorname {GL}_{2n}(\mathbb {Q}_p)$ obtained as the normalised induction of a smooth unramified character $\theta _{\tau } \colon (\mathbb {Q}_p^{\times })^{\oplus 2n} \to \mathbb {C}^{\times }$ . For any $i=1, \dots , 2n$ , let ${\theta _{i, \tau } \colon \mathbb {Q}_p^{\times } \to \mathbb {C}^{\times }}$ denote the i-th component of $\theta _{\tau }$ . We may assume that $\theta _{i, \tau } = \theta _{2n+1-i, \tau }^{-1}$ and that

$$\begin{align*}\alpha_{i, \tau} = \prod_{j=1}^i p^{n-j+\frac{1}{2}} \theta_{j, \tau}(p). \end{align*}$$

Similar to Waldspurger’s formula, it is expected that $|\mathscr {P}_{\pi , \chi }(\psi )|^2$ should decompose as a product of local zeta integrals for the automorphic representation $\Pi $ depending on the input vector $\psi $ . More precisely, one expects a decomposition of the following shape:

$$\begin{align*}\mathscr{L}_{p, \phi}(\pi, \hat{\chi})^2 = (\star) \cdot \mathscr{E}_p(\pi, \chi)^2 \cdot \left( \prod_{\tau \in \Psi} \zeta(\psi_{\tau}, \chi_{\mathfrak{p}_{\bar{\tau}}}^{-1}, 1/2) \cdot \zeta(\psi_{\tau}, \chi_{\mathfrak{p}_{\bar{\tau}}}, 1/2) \right) \cdot C^{(p)} \cdot L^{(p)}(\Pi \otimes \chi, 1/2) \end{align*}$$

where $\psi = \phi _{e}^{[j]}$ , $\psi _{\tau } \in \operatorname {Ind}(\theta _{\tau })$ denotes the component at p indexed by $\tau $ , $\zeta (\cdots )$ is the twisted local zeta integral associated with a Shalika model for a smooth representation of $\operatorname {GL}_{2n}(\mathbb {Q}_p)$ , $C^{(p)}$ is a product of factors depending on $\Pi $ away from p, and $L^{(p)}(\Pi \otimes \chi , 1/2)$ denotes the value of the L-function with Euler factors at p removed. Suppose that $c_{\tau } \geq 1$ for all $\tau \in \Psi $ for simplicity. Then the calculations in [Reference Salazar, Dimitrov, Graham, Jorza and WilliamsBDG⁺22, §5] show that

$$\begin{align*}\mathscr{E}_p(\pi, \chi)^2 \cdot \left( \prod_{\tau \in \Psi} \zeta(\psi_{\tau}, \chi_{\mathfrak{p}_{\bar{\tau}}}^{-1}, 1/2) \cdot \zeta(\psi_{\tau}, \chi_{\mathfrak{p}_{\bar{\tau}}}, 1/2) \right) \end{align*}$$

is (up to a constant only depending on the parity of $\chi _{\mathfrak {p}_{\bar {\tau }_0}}$ ) equal to

(1.1.6) $$ \begin{align} \varepsilon(\theta_{n, \tau_0}\chi_{\mathfrak{p}_{\bar{\tau}_0}}^{-1}, 1/2) \varepsilon(\theta_{n+1, \tau_0}\chi_{\mathfrak{p}_{\bar{\tau}_0}}, 1/2)^{-1} \prod_{\tau \in \Psi} \prod_{i=1}^n \varepsilon(\theta_{i, \tau}\chi_{\mathfrak{p}_{\bar{\tau}}}^{-1}, 1/2)^{-1} \varepsilon(\theta_{i, \tau}\chi_{\mathfrak{p}_{\bar{\tau}}}, 1/2)^{-1} \end{align} $$

where $\varepsilon (\eta , s) = \mathscr {G}(\eta ^{-1}) \cdot \eta (-p^c) p^{-cs}$ denotes the Langlands–Deligne local factor associated with any smooth character $\eta \colon \mathbb {Q}_p^{\times } \to \mathbb {C}^{\times }$ of conductor $p^c$ (see, e.g., [Reference Castella and HsiehCH18, p. 572]). Here we have used the calculation

$$ \begin{align*} \mathscr{E}_p(\pi, \chi) &= \varepsilon(\theta_{n, \tau_0} \chi_{\mathfrak{p}_{\bar{\tau}_0}}^{-1}, 1/2) \cdot \left( \prod_{\tau \in \Psi} \chi_{\mathfrak{p}_{\bar{\tau}}}(-1)^n \right) (\alpha_p^e \delta_B(t_p^e))^{-1} \\ &= \chi_{\mathfrak{p}_{\bar{\tau}_0}}(-1) \cdot \varepsilon(\theta_{n+1, \tau_0} \chi_{\mathfrak{p}_{\bar{\tau}_0}}, 1/2)^{-1} \cdot \left( \prod_{\tau \in \Psi} \chi_{\mathfrak{p}_{\bar{\tau}}}(-1)^n \right) (\alpha_p^e \delta_B(t_p^e))^{-1}. \end{align*} $$

The expression (1.1.6) is precisely of the shape predicted by Coates–Perrin-Riou [Reference Coates and Perrin-RiouCPR89, Reference CoatesCoa89] (note that $L(\eta , s) = 1$ when $\eta $ is ramified). In particular, we expect that the locally analytic distribution $\mathscr {L}_{p, \phi }(\pi , -)$ should be tempered, and a p-adic measure if $\phi _p$ is Borel-ordinary (i.e., $v_p(\alpha _{i, \tau }^{\circ }) = 0$ for all $\tau \in \Psi $ and $i=1, \dots , 2n-1$ ).Footnote ²

1.1.2 Expected relation with Euler systems

In analogy with the Heegner cycle setting, one expects that the p-adic L-functions in Theorems A and B should be related to Euler system classes outside the regions of interpolation. More precisely, suppose that $\pi $ is a cuspidal automorphic representation of $\mathbf {G}_0(\mathbb {A})$ satisfying the conditions in §1.1 including those in Remark 1.1.5. Furthermore, suppose that the sign of the functional equation of $L(\Pi , s)$ is $-1$ , and for simplicity, suppose that $\Pi $ is cuspidal and the eigensystem $\{ \alpha _{i, \tau } \}$ is Borel-ordinary. Let denote the square of the p-adic L-function in Theorem A with respect to a suitable choice of test data. Let $\rho _{\Pi } \colon \operatorname {\mathrm {Gal}}(\overline {F}/F) \to \operatorname {GL}_{2n}(L)$ denote the p-adic semisimple Galois representation associated with $\Pi $ , as constructed by Chenevier–Harris [Reference Chenevier and HarrisCH13].

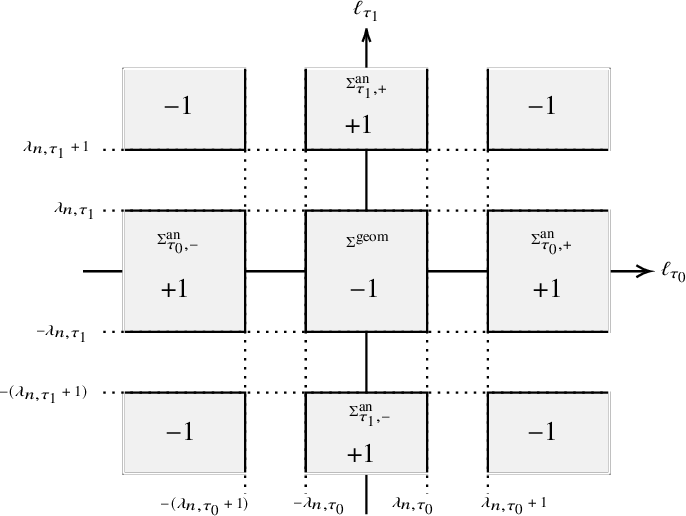
Then, continuing with Remark 1.1.5, one expects that $L_p(\Pi , -; \Sigma _{\tau _0,+}^{\operatorname {an}})$ is a p-adic measure on $\operatorname {\mathrm {Gal}}(F_{p^{\infty }}/F)$ which interpolates the central critical L-values $L(\Pi \otimes \chi , 1/2) = L(\rho _{\Pi }(n) \otimes \hat {\chi }, 0)$ as $\chi $ runs through the interpolating set:

Here we have changed notation slightly, and this interpolating set is larger than $\Sigma _{\pi }$ to include unramified characters and also the condition $-\lambda _{n, \tau } \leq j_{\tau } \leq 0$ for $\tau \neq \tau _0$ . By our assumptions, the sign of the functional equation for $L(\rho _{\Pi }(n) \otimes \hat {\chi }, s)$ is $+1$ for $\chi \in \Sigma _{\tau _0, +}^{\operatorname {an}}$ .

On the other hand, one can also consider the behaviour of the Galois representation $\rho _{\Pi }(n) \otimes \hat {\chi }$ for $\chi $ lying in a different ‘geometric’ region of twists

which is disjoint from $\Sigma _{\tau _0, +}^{\operatorname {an}}$ . In this region, the sign of the functional equation is $-1$ , and by generalising the construction in [Reference Graham and ShahGS23], one can construct split anticyclotomic Euler systems for $\rho _{\Pi }(n) \otimes \hat {\chi }$ with $\chi \in \Sigma ^{\operatorname {geom}}$ . The idea behind this construction is to consider the (p-adic) étale regulators of cycles arising from the pair of unitary Shimura varieties associated with $\mathbf {G}_0$ and $\mathbf {H}_0$ with appropriately chosen level subgroups. One can then extend this construction to all anticyclotomic characters by Soulé twisting. Let $z_{\chi } \in \operatorname {H}^1(F, \rho _{\Pi }(n) \otimes \hat {\chi })$ denote the bottom class of the Euler system (after inverting p); this class lies in the Bloch–Kato Selmer group if $\chi \in \Sigma ^{\operatorname {geom}}$ .

In this situation, one expects to be able to prove two kinds of explicit reciprocity laws:

• • If $\chi \in \Sigma ^{\operatorname {geom}}$ , then

  $$\begin{align*}L_p(\Pi, \hat{\chi}; \Sigma_{\tau_0, +}^{\operatorname{an}}) = (\star)_{\chi} \cdot \operatorname{log}_{\operatorname{BK}, \eta}(\operatorname{loc}_{\mathfrak{p}_{\tau_0}}(z_{\chi}))^2 , \end{align*}$$
  generalising [Reference Bertolini, Darmon and PrasannaBDP13, Theorem 5.13]. Here $\operatorname {log}_{\operatorname {BK}, \eta }$ is a certain linear functional on ${\operatorname {H}^1_f(F_{\mathfrak {p}_{\tau _0}}, \rho _{\Pi }(n) \otimes \hat {\chi })}$ constructed from the Bloch–Kato logarithm and a fixed choice $\eta \in \operatorname {Fil}^0\mathbf {D}_{\operatorname {dR}}(\rho _{\Pi }^*(1-n)|_{G_{F_{\mathfrak {p}_{\tau _0}}}})$ , and $(\star )_{\chi }$ is an explicit factor (involving the $\gamma $ -factors for $\theta _{n, \tau _0} \chi _{\mathfrak {p}_{\bar {\tau }_0}}^{-1}$ and $\theta _{n+1, \tau _0} \chi _{\mathfrak {p}_{\bar {\tau }_0}}$ ).

• • If $\chi \in \Sigma _{\tau _0, +}^{\operatorname {an}}$ , then

  $$\begin{align*}L_p(\Pi, \hat{\chi}; \Sigma_{\tau_0, +}^{\operatorname{an}}) = (\star)_{\chi} \cdot \operatorname{exp}^*_{\operatorname{BK}, \eta}(\operatorname{loc}_{\mathfrak{p}_{\tau_0}}(z_{\chi}))^2 , \end{align*}$$
  generalising [Reference Castella and HsiehCH18, Corollary 5.8]. Here $(\star )_{\chi }$ and $\eta $ are as in the previous bullet point, and $\operatorname {exp}^*_{\operatorname {BK}, \eta }$ is a certain linear functional on $\operatorname {H}^1(F_{\mathfrak {p}_{\tau _0}}, \rho _{\Pi }(n) \otimes \hat {\chi })$ built from the Bloch–Kato dual exponential map.

The key strategy for the first explicit reciprocity law will be to analyse the syntomic regulators of the cycles associated with the above pair of Shimura varieties (c.f., [Reference Loeffler and ZerbesLZ20] for an instance where this strategy is carried out for automorphic representations of $\operatorname {GSp}_4$ ). One will then be able to use p-adic deformation arguments to obtain the second explicit reciprocity law. For this latter step, the fact that the p-adic L-functions interpolate as one varies $\pi $ in a Coleman family (Theorem B) will be an important ingredient.

The benefit of establishing such explicit reciprocity laws is that one can obtain results towards the Bloch–Kato conjectures for anticyclotomic twists of $\rho _{\Pi }(n)$ . More precisely, using forthcoming work of Jetchev–Nekovář–Skinner [Reference Jetchev, Nekovář and SkinnerJNS]Footnote ³ (and the forthcoming work of Leslie–Xiao–Zhang [Reference Leslie, Xiao and ZhangLXZ]), and under the usual ‘big image’ assumptions on $\rho _{\Pi }(n)$ (see [Reference Alonso, Castella and RiveroACR23, §8.1]), one will be able to deduce that:

• • If $\chi \in \Sigma ^{\operatorname {geom}}$ and $L_p(\Pi , \hat {\chi }; \Sigma _{\tau _0, +}^{\operatorname {an}}) \neq 0$ , then the Bloch–Kato Selmer group

  $$\begin{align*}\operatorname{H}^1_f\left( F, \rho_{\Pi}(n) \otimes \hat{\chi} \right) \end{align*}$$
  is one-dimensional and generated by the class $z_{\chi }$ .

• • If $\chi \in \Sigma ^{\operatorname {an}}_{\tau _0, +}$ and the L-value $L(\rho _{\Pi }(n) \otimes \hat {\chi }, 0)$ is nonzero, then the Bloch–Kato Selmer group

  $$\begin{align*}\operatorname{H}^1_f\left( F, \rho_{\Pi}(n) \otimes \hat{\chi} \right) \end{align*}$$
  vanishes.

Indeed, for the first bullet point, the condition $L_p(\Pi , \hat {\chi }; \Sigma _{\tau _0, +}^{\operatorname {an}}) \neq 0$ and the first explicit reciprocity law implies that $z_{\chi } \neq 0$ ; hence [Reference Alonso, Castella and RiveroACR23, Theorem 8.3] implies that $\operatorname {H}^1_f\left ( F, \rho _{\Pi }(n) \otimes \hat {\chi } \right )$ is generated by $z_{\chi }$ . For the second bullet point, if $L(\rho _{\Pi }(n) \otimes \hat {\chi }, 0)$ is non zero, then the relation between unitary Friedberg–Jacquet periods and L-values, in combination with the interpolation property of the p-adic L-function, implies that $L_p(\Pi , \hat {\chi }; \Sigma _{\tau _0, +}^{\operatorname {an}}) \neq 0$ . Hence, the second explicit reciprocity law implies that $z_{\chi } \neq 0$ , and [Reference Alonso, Castella and RiveroACR23, Theorem 8.3] implies that a certain Selmer group $\operatorname {Sel}_{\operatorname {Gr}}(F, \rho _{\Pi }(n) \otimes \hat {\chi })$ (different from the Bloch–Kato Selmer group) is one-dimensional. One can then deduce that $\operatorname {H}^1_f\left ( F, \rho _{\Pi }(n) \otimes \hat {\chi } \right )$ vanishes from an argument involving the Poitou–Tate long exact sequence (c.f., [Reference Castella and HsiehCH18, Theorem 7.9] or [Reference Alonso, Castella and RiveroACR23, §9.2]).

We note that there is also some extra symmetry involved in the construction of the p-adic L-function in Theorem A. To be more precise, one could repeat the whole construction in this article to produce a p-adic L-function $L_p(\Pi , -; \Sigma _{\tau _0, -}^{\operatorname {an}})$ which interpolates the L-values $L(\rho _{\Pi }(n) \otimes \hat {\chi }, 0)$ for $\chi $ in the region

Furthermore, if we write $\Psi = \{ \tau _0, \dots , \tau _{d-1}\}$ with $d = [F^+:\mathbb {Q}]$ , then there is no reason to choose $\tau _0$ as the privileged place where the Hermitian space has signature $(1, 2n-1)$ ; one could also repeat the same construction to produce p-adic L-functions $L_p(\Pi , -; \Sigma _{\tau _i, \pm }^{\operatorname {an}})$ interpolating the L-values $L(\rho _{\Pi }(n) \otimes \hat {\chi }, 0)$ for $\chi $ in the regions

(note that, by switching the behaviour of the signatures at the places in $\Psi $ , the Hermitian space changes but the Galois representation $\rho _{\Pi }$ does not). With exactly the same methods, one should be able to prove explicit reciprocity laws for these extra p-adic L-functions and obtain similar applications to the Bloch–Kato conjecture. For example, when $d=2$ , one can produce p-adic L-functions in the four regions adjacent (horizontally and vertically) to $\Sigma ^{\operatorname {geom}}$ in Figure 1, and all of these should be related to Euler systems classes in $\Sigma ^{\operatorname {geom}}$ via an explicit reciprocity law.

Figure 1

Regions of twists when $[F^+:\mathbb {Q}] = 2$ .

Of course, there are many other regions of twists disjoint from $\Sigma ^{\operatorname {geom}}$ and $\Sigma _{\tau , \pm }^{\operatorname {an}}$ one could consider (depending on how the infinity-type of $\chi $ intertwines with the Hodge–Tate weights of $\rho _{\Pi }(n)$ ) – for example, the four regions in the corners of Figure 1. It would also be interesting to understand the behaviour of the Galois representation in these regions and whether one can construct Euler systems/p-adic L-functions for these twists.

Remark 1.1.7. One could also ask what happens when one instead imposes the condition that the sign of the functional equation for $L(\Pi , s)$ is $+1$ . In this setting, one expects to be able to produce a p-adic L-function which interpolates the values $L(\rho _{\Pi }(n) \otimes \hat {\chi }, 0)$ for $\chi \in \Sigma ^{\operatorname {geom}}$ by considering the p-adic variation of unitary Friedberg–Jacquet periods for a pair of definite unitary groups. This situation is more closely aligned with the formalism of bipartite Euler systems (generalising the strategy in [Reference Bertolini and DarmonBD05]) and will be studied in forthcoming work of Murilo Corato-Zanarella [Reference Corato-ZanarellaCor].

1.2 Method of proof

We now describe the main ingredients that go into the proofs of Theorem A and Theorem B. The first step is to reinterpret the unitary Friedberg–Jacquet periods as a pairing in the coherent cohomology of unitary Shimura varieties. For this, we work with the corresponding unitary similitude groups, since these give rise to PEL-type Shimura varieties. Let $\mathbf {G}$ denote the unitary similitude group associated with the Hermitian space W (with similitude in $\mathbb {G}_m$ ), and let $\mathbf {H} \subset \mathbf {G}$ denote the subgroup preserving the decomposition $W = W_1 \oplus W_2$ .

Let $\pi $ denote a cuspidal automorphic representation of $\mathbf {G}(\mathbb {A})$ satisfying the analogous hypotheses as in §1.1 (this is made precise in §9.1). It is also convenient to work with eigenvectors for the transpose $U_p$ -Hecke operators. More precisely, for an integer $\beta \geq 1$ , let $K^G_{\operatorname {Iw}}(p^{\beta }) \subset \mathbf {G}(\mathbb {Q}_p) = \mathbb {Q}_p^{\times } \times \prod _{\tau \in \Psi } \operatorname {GL}_{2n}(\mathbb {Q}_p)$ denote the upper-triangular modulo $p^{\beta }$ Iwahori subgroup. Then associated with the p-stabilisation $\phi _p$ , we can define eigenvectors $\psi _{p, \beta } \in \pi _p^{K^G_{\operatorname {Iw}}(p^{\beta })}$ satisfying the property:

$$\begin{align*}[K^G_{\operatorname{Iw}}(p^{\beta}) \cdot s_{p, i, \tau} \cdot K^G_{\operatorname{Iw}}(p^{\beta})] \cdot \psi_{p, \beta} = \alpha_{i, \tau} \psi_{p, \beta} \end{align*}$$

where $s_{p, i, \tau }$ denotes the conjugate of $t_{p, i, \tau }$ by the longest Weyl element of $\mathbf {G}(\mathbb {Q}_p)$ . Let $\psi _{\beta }^{[j]} = (\Delta ^{[j]}_{\kappa } \cdot \phi _{\infty }) \otimes \phi _S \otimes \bigotimes _{\ell \not \in S \cup \{p\}} \phi _{\ell } \otimes \hat {\gamma } \psi _{p, \beta } \in \pi $ , where $\hat {\gamma }$ is a certain representative of the Zariski open orbit of the upper-triangular Borel subgroup acting on $\mathbf {H}(\mathbb {Q}_p) \backslash \mathbf {G}(\mathbb {Q}_p)$ (see Definition 2.1.2). Then, up to an explicit nonzero rational number, the period $\mathscr {P}_{\pi , \chi }(\phi ^{[j]}_e)$ is equal to $\mathscr {P}_{\pi , \chi }(\psi ^{[j]}_{\beta })$ , provided that $\beta \geq \operatorname {max}_{\tau }(e_{\tau })$ . Therefore, it suffices to analyse these latter periods.

Let $S_{\mathbf {G}, \operatorname {Iw}}(p^{\beta })$ (resp. $S_{\mathbf {H}, \diamondsuit }(p^{\beta })$ ) denote the Shimura variety associated with $\mathbf {G}$ (resp. $\mathbf {H}$ ) of level $K^p K^G_{\operatorname {Iw}}(p^{\beta })$ (resp. $(K^p \cap \mathbf {H}(\mathbb {A}_f^p)) (\hat {\gamma } K^G_{\operatorname {Iw}}(p^{\beta }) \hat {\gamma }^{-1} \cap \mathbf {H}(\mathbb {Q}_p))$ ). There is a natural finite unramified morphism

$$\begin{align*}\hat{\iota} \colon S_{\mathbf{H}, \diamondsuit}(p^{\beta}) \to S_{\mathbf{G}, \operatorname{Iw}}(p^{\beta}) \end{align*}$$

induced from right-translation by $\hat {\gamma }$ . By the work of Su [Reference SuSu24], the test data $\psi _{\beta }^{[0]}$ can be encoded as a coherent cohomology class

$$\begin{align*}\eta_{\beta} \in \operatorname{H}^{n-1}\left( S_{\mathbf{G}, \operatorname{Iw}}(p^{\beta})(\mathbb{C}), \mathscr{M}_{G,\kappa^*} \right) \end{align*}$$

where $\mathscr {M}_{G, \kappa ^*}$ denotes the automorphic vector bundle with highest weight $\kappa ^* = w_n \cdot (\lambda + \rho ) - \rho $ . After possibly rescaling this test data, this cohomology class is defined over a finite extension of the reflex field of $S_{\mathbf {G}, \operatorname {Iw}}(p^{\beta })$ .

In general, to view the test data $\psi ^{[j]}_{\beta }$ as coherent cohomology classes, one needs to enlarge the automorphic vector bundle $\mathscr {M}_{G, \kappa ^*}$ to a sheaf of ‘nearly holomorphic forms’. More precisely, let $P_{\mathbf {G}}^{\operatorname {std}} \subset \operatorname {GL}_1 \times \prod _{\tau \in \Psi } \operatorname {GL}_{2n}$ denote the standard lower-triangular parabolic subgroup with Levi $M_{\mathbf {G}} = \operatorname {GL}_1 \times (\operatorname {GL}_{1} \times \operatorname {GL}_{2n-1}) \times \prod _{\tau \neq \tau _0} \operatorname {GL}_{2n}$ . Then there exists a $P_{\mathbf {G}}^{\operatorname {std}}$ -torsor

$$\begin{align*}\pi \colon P_{\mathbf{G}, \operatorname{dR}} \to S_{\mathbf{G}, \operatorname{Iw}}(p^{\beta}) \end{align*}$$

such that automorphic vector bundles arise as the associated sheaves of this torsor. Let and $\mathscr {N}_{G, \kappa ^*} = \left (\mathscr {N}_G \otimes V_{\kappa }^*\right )^{M_{\mathbf {G}}}$ , where $V_{\kappa }^*$ denotes the algebraic representation of $M_{\mathbf {G}}$ with highest weight $\kappa ^*$ . Then we have an embedding $\mathscr {M}_{G,\kappa ^*} \subset \mathscr {N}_{G, \kappa ^*}$ which identifies with the subspace of elements killed by the action of the Lie algebra of the unipotent radical of $P_{\mathbf {G}}^{\operatorname {std}}$ (obtained by differentiating the torsor structure). As explained in §5.2, the quasi-coherent sheaf $\mathscr {N}_G$ is in fact a $\mathcal {D}$ -module on $S_{\mathbf {G}, \operatorname {Iw}}(p^{\beta })$ , and carries an action of $(2n-1)$ commuting derivations $\{ \nabla _1, \dots , \nabla _{2n-1} \}$ which are algebraic interpretations of the Maass–Shimura differential operators on $S_{\mathbf {G}, \operatorname {Iw}}(p^{\beta })(\mathbb {C})$ . Furthermore, we can package these operators together into an $M_{\mathbf {G}}$ -equivariant algebra action

(1.2.1) $$ \begin{align} C^{\operatorname{pol}}(\mathbb{G}_a^{\oplus 2n-1}, \mathbb{G}_a) \otimes \mathscr{N}_G \to \mathscr{N}_G \end{align} $$

of polynomial functions, such that the projection to the i-th component acts through the operator $\nabla _i$ . The action of $M_{\mathbf {G}}$ on $C^{\operatorname {pol}}(\mathbb {G}_a^{\oplus 2n-1}, \mathbb {G}_a)$ is given by the adjoint action on the argument, by identifying $\mathbb {G}_a^{\oplus 2n-1}$ with the unipotent radical of $P_{\mathbf {G}}^{\operatorname {std}}$ . One can make similar definitions for the group $\mathbf {H}$ and there is an analogous $M_{\mathbf {H}}$ -equivariant action of polynomial functions on $\mathscr {N}_{H}$ .

With this formalism of sheaves of ‘nearly holomorphic forms’, we can reinterpret the period $\mathscr {P}_{\pi , \chi }(\psi _{\beta }^{[j]})$ algebraically as follows. Given $\chi \in \Sigma _{\pi }$ , one can construct a certain nonzero vector

$$\begin{align*}\delta_{\kappa, j} \in V_{\kappa} \otimes C^{\operatorname{pol}}(\mathbb{G}_a^{\oplus 2n-1}, \mathbb{G}_a) \end{align*}$$

which is an eigenvector for the action of $M_{\mathbf {H}}$ with eigencharacter given by a certain character $\sigma _{\kappa }^{[j], -1} \colon M_{\mathbf {H}} \to \mathbb {G}_m$ (see §2.2 for its definition) which, up to a shift by the sum of the positive roots of $\mathbf {H}$ not lying in $M_{\mathbf {H}}$ , encodes the infinity-type of $\chi $ . If we write $\delta _{\kappa , j} = \sum _{l} v_l \otimes p_l$ as a sum of pure tensors, then we can build a map

$$ \begin{align*} \mathscr{N}_{G, \kappa^*} = \operatorname{Hom}_{M_{\mathbf{G}}}(V_{\kappa}, \mathscr{N}_G) &\xrightarrow{\vartheta_{\kappa, j, \beta}} \operatorname{Hom}_{M_{\mathbf{H}}}(\sigma_{\kappa}^{[j], -1}, \hat{\iota}_*\mathscr{N}_H) = \hat{\iota}_*\mathscr{N}_{H, \sigma_{\kappa}^{[j]}} \\ F &\mapsto \left( 1 \mapsto \sum_l \hat{\iota}^*(p_l \star F(v_l)) \right) \end{align*} $$

where $\star $ denotes the action in (1.2.1) and $\hat {\iota }^*$ denotes the natural pullback map $\mathscr {N}_G \to \hat {\iota }_* \mathscr {N}_H$ . By analysing the representation theory and relevant branching laws for the pair of groups $(M_{\mathbf {G}}, M_{\mathbf {H}})$ , one can show that this morphism takes ‘holomorphic forms’ for $\mathbf {G}$ to ‘holomorphic forms’ for $\mathbf {H}$ , that is, one obtains an induced morphism $\vartheta _{\kappa , j, \beta } \colon \mathscr {M}_{G, \kappa ^*} \to \hat {\iota }_* \mathscr {M}_{H, \sigma _{\kappa }^{[j]}}$ . Finally, by Shimura reciprocity, the character $\chi $ can be interpreted as a cohomology class $[\chi ] \in \operatorname {H}^0\left ( S_{\mathbf {H}, \diamondsuit }(p^{\beta }), \mathscr {M}_{H, \sigma _{\kappa }^{[j]}}^{\vee } \right )$ , where $(-)^{\vee }$ denotes the Serre dual of a vector bundle. Therefore, for a sufficiently large finite extension $L/F$ , we can define an ‘evaluation map’:

$$ \begin{align*} \operatorname{Ev}_{\kappa, j, \chi, \beta} \colon \operatorname{H}^{n-1}\left( S_{\mathbf{G}, \operatorname{Iw}}(p^{\beta}), \mathscr{M}_{G, \kappa^*} \right) &\to L \\ \eta &\mapsto \langle \vartheta_{\kappa, j, \beta}(\eta), [\chi] \rangle. \end{align*} $$

Up to explicit nonzero factors, the automorphic period $\mathscr {P}_{\pi , \chi }(\psi _{\beta }^{[j]})$ is equal to the image of $\eta _{\beta }$ under the evaluation map $\operatorname {Ev}_{\kappa , j, \chi , \beta }$ , which is the desired algebraic interpretation of the unitary Friedberg–Jacquet periods.

The benefit of this reinterpretation is that we can study the p-adic behaviour of these evaluation maps, and hence the unitary Friedberg–Jacquet periods. In particular, if we (abusively) let $L/\mathbb {Q}_p$ denote the finite extension obtained as the completion of $\iota _p(L)$ and let $\mathcal {S}_{G, \operatorname {Iw}}(p^{\beta })$ denote the corresponding adic Shimura variety over L, then by rigid GAGA we can view $\eta _{\beta }$ (resp. $\operatorname {Ev}_{\kappa , j, \chi , \beta }$ ) as a cohomology class in (resp. linear form on) the cohomology group $\operatorname {H}^{n-1}\left ( \mathcal {S}_{G, \operatorname {Iw}}(p^{\beta }), \mathscr {M}_{G,\kappa ^*} \right )$ . Using the recently developed higher Coleman theory of Boxer–Pilloni [Reference Boxer and PilloniBP21], one can p-adically interpolate these cohomology groups and cohomology classes, so the strategy for p-adically interpolating $\operatorname {Ev}_{\kappa , j, \chi , \beta }$ is:

1. 1. to define overconvergent versions of $\mathscr {N}_G$ and $\mathscr {N}_H$ with actions of differential operators which can be p-adically iterated;

2. 2. construct a p-adic version of the map $\vartheta _{\kappa , j, \beta }$ by p-adically interpolating the eigenvectors $\delta _{\kappa , j}$ .

For (1), we generalise the results of [Reference Graham, Pilloni and JacintoGPR25] to the setting of unitary Shimura varieties, and for (2), we generalise the p-adic interpolation of branching laws appearing in [Reference GrahamGra24, Appendix A]. One then builds an overconvergent version of the morphism $\vartheta _{\kappa , j, \beta }$ in a similar way as above. This method can be described rather abstractly and we explain how to accomplish this in §2.3. To be able to p-adically interpolate the eigenvectors $\delta _{\kappa , j}$ one must first perform a certain ‘p-depletion’, and in §8.5 we explain how this is related to the appearance of the factor $\mathscr {E}_p(\pi , \chi )$ in the interpolation property in Theorem A. Additionally, this whole strategy can be extended to the setting where we allow the automorphic representation $\pi $ to vary in Coleman families, which leads to the construction of the p-adic L-function in Theorem B.

1.3 Structure of the article

This article comprises roughly of three parts. The material in §2–§4 is mostly preliminary and lays the foundations for the constructions of the evaluation maps. More precisely, in §2 we describe the abstract results from representation theory which generalise [Reference GrahamGra24, Appendix A], and give an overview for constructing the (p-adic versions of the) morphisms $\vartheta _{\kappa , j, \beta }$ . In §3, we summarise (and adapt to our setting) the main results on continuous operators on Banach spaces appearing in [Reference Graham, Pilloni and JacintoGPR25]. In §4, we describe a minor generalisation of the theory of Hecke operators and cohomology with support appearing in [Reference Boxer and PilloniBP21, Reference Boxer and PilloniBP], which is necessary for the (slightly more general) version of higher Coleman theory needed in this article.

The second part of this article (§5–§7) involves the study of the geometry and cohomology of unitary Shimura varieties and the construction of the (p-adic) evaluation maps. In §5, we introduce the Shimura varieties (and the associated moduli spaces of abelian varieties with extra structure), the sheaves of ‘nearly holomorphic forms’, and the evaluation maps $\operatorname {Ev}_{\kappa , j, \beta }$ (and their relation to unitary Friedberg–Jacquet periods). We then study the p-adic versions of the sheaves (the sheaves of ‘nearly overconvergent forms’) and the p-adic geometry of the adic Shimura varieties in §6, and describe how to p-adically interpolate the differential operators on these sheaves in §7. We end §7 by giving the construction of p-adic versions of the evaluation maps in families.

Finally, the third part of this article (§8–§9) describes the construction of the p-adic L-functions in Theorem A and Theorem B. More precisely, in §8 we introduce the action of Hecke operators on the cohomology groups appearing in higher Coleman theory, prove an interpolation property for the p-adic evaluation maps, and develop the abstract machinery for producing the p-adic L-function. In §9, we apply this general machinery to the relevant automorphic representations and prove Theorem A and Theorem B. To obtain the final interpolation formula, one also needs to incorporate some miscellaneous representation theoretic results on branching laws for general linear groups which we provide in Appendix A and Appendix B.

1.4 Notation and conventions

We fix the following notation and conventions throughout the article.

• • We let $F/F^+$ be a CM extension with maximal totally real subfield $F^+ \neq \mathbb {Q}$ . We assume that F contains an imaginary quadratic extension $E/\mathbb {Q}$ . We fix a CM type $\Psi $ of F and a distinguished place $\tau _0 \in \Psi $ (i.e., an embedding $\tau _0 \colon F \hookrightarrow \mathbb {C}$ ). We let $F^{\operatorname {cl}}$ denote the Galois closure of F in $\mathbb {C}$ via the embedding $\tau _0$ .

• • We fix an odd prime p which splits completely in $F/\mathbb {Q}$ and doesn’t divide the discriminant of $F/\mathbb {Q}$ . We will also impose Assumption 5.1.1 throughout the majority of the article.

• • We fix an identification $\iota _p \colon \mathbb {C} \cong \overline {\mathbb {Q}}_p$ , and for any embedding $\sigma \colon F \hookrightarrow \mathbb {C}$ we let $\mathfrak {p}_{\sigma }$ denote the prime of F lying above p determined by the embedding $\iota _p \circ \sigma \colon F \hookrightarrow \overline {\mathbb {Q}}_p$ .

• • We fix an integer $n \geq 1$ throughout the article (which will be half the dimension of the Hermitian space W). For convenience we assume that $n \geq 2$ , but note that, with suitable modifications, one can also adapt the methods in this article to treat the case $n=1$ .

• • For any number field $\Phi $ , we let $\mathbb {A}_{\Phi }$ (resp. $\mathbb {A}_{\Phi }^{\times }$ ) denote the adèles (resp. idèles) of $\Phi $ . If $\Phi = \mathbb {Q}$ , we will often omit this from the notation. If S is a finite set of places of $\Phi $ , we let $\mathbb {A}_{\Phi }^S$ (resp. $\mathbb {A}_{\Phi , S}$ ) denote the adèles away from S (resp. at S). We let $\mathbb {A}_{\Phi , f}$ denote the adèles at finite places.

• • Unless specified otherwise, we will use additive notation for the multiplication of characters. For a character $\kappa $ , we will often write .

• • By a ‘Tate affinoid algebra’ $(R, R^+)$ we mean a complete uniform Huber pair $(R, R^+)$ over $(\mathbb {Q}_p, \mathbb {Z}_p)$ . We will always assume that $(R, R^+)$ is sheafy, that is, $\operatorname {Spa}(R, R^+)$ is an adic space.

• • For a category $\mathcal {C}$ , let $\operatorname {Ind}\mathcal {C}$ denote the ind-category of $\mathcal {C}$ , that is, the category whose objects (which we refer to as ind-systems) are small filtered inductive systems $X = (X_i)_{i \in I}$ , and whose morphisms are

  
  where $Y = (Y_j)_{j \in J}$ and the transition maps are the obvious ones induced from pre-/postcomposition. By a representative of a morphism $f \in \operatorname {Hom}(X, Y)$ , we mean the data of a map $\alpha \colon I \to J$ , and morphisms $f_i \in \operatorname {Hom}(X_i, Y_{\alpha (i)})$ such that $f = (f_i)_{i \in I}$ (so in particular, for any $i' \geq i$ there exists $j \geq \alpha (i), \alpha (i')$ such that the morphisms $X_i \xrightarrow {f_i} Y_{\alpha (i)} \to Y_{j}$ and $X_i \to X_{i'} \xrightarrow {f_{i'}} Y_{\alpha (i')} \to Y_j$ coincide). If $F \colon \mathcal {C} \to \mathcal {D}$ is a functor, then we will also use the notation $F \colon \operatorname {Ind}\mathcal {C} \to \operatorname {Ind}\mathcal {D}$ to denote the natural functor given by . Whenever we say that a morphism $f \in \operatorname {Hom}(X, Y)$ satisfies an additional property (such as equivariance with respect to a group action) we mean that f has a representative $\{ f_i \}$ where each $f_i$ satisfy this property.

• • For a split reductive group G over a characteristic zero field, we let $w_G^{\operatorname {max}}$ denote the longest element of the Weyl group of G. If $G = \operatorname {GL}_d$ , we will usually take $w_{\operatorname {GL}_d}^{\operatorname {max}}$ to be the antidiagonal $(d \times d)$ -matrix with $1$ s along the antidiagonal.

• • We fix once and for all a choice $i = \sqrt {-1} \in \mathbb {C}$ . This determines a canonical choice of p-th power roots of unity $e^{2 \pi i/p^h} \in \mathbb {C}$ for $h \geq 0$ , and hence a system of p-th power roots of unity $\iota _p(e^{2 \pi i/p^h}) \in \overline {\mathbb {Q}}_p$ . Any construction depending on a choice of p-th power roots of unity will be with respect to this canonical choice (e.g., when defining Gauss sums associated with finite order characters of p-th power conductor).

• • If $s \geq 1$ is an integer, $(R, R^+)$ is a Tate affinoid algebra, and X is a p-adic manifold (that is, isomorphic to an open subset of $\mathbb {Q}_p^{r}$ for some $r \geq 1$ ), then we say that a continuous function $f \colon X \to R$ is s-analytic if: for every $\underline {a} = (a_1, \dots , a_r) \in X$ there exists $\alpha _{n_1, \dots , n_r} \in R$ with the property that $p^{s(n_1+ \cdots + n_r)} \alpha _{n_1, \dots , n_r} \to 0$ as $n_1+\cdots + n_r \to + \infty $ such that, for every $(x_1, \dots , x_r) \in X \cap B(\underline {a}, p^{-s})$ , one has

  $$\begin{align*}f(x_1, \dots, x_r) = \sum_{n_1, \dots, n_r \geq 0} \alpha_{n_1, \dots, n_r} (x_1 - a_1)^{n_1} \cdots (x_r - a_r)^{n_r} \end{align*}$$
  (c.f., [Reference UrbanUrb11, §3.2.1]). Here $B(\underline {a}, p^{-s}) \subset \mathbb {Q}_p^r$ denotes the ball of radius $p^{-s}$ with centre $\underline {a}$ . This is independent of the choice of identification of X with an open subset of $\mathbb {Q}_p^r$ .