Introduction
Almost 50 years after the first Apollo landing, it remains unclear how the Earth's Moon was formed. Since 1975 the leading model for the formation of the Moon is the classic giant impact hypothesis (GIH) (Hartmann & Davis, Reference Hartmann and Davis1975; Cameron & Ward, Reference Cameron and Ward1976). This hypothesis proposes that a Mars-sized planet impacted the Earth shortly after the Earth's formation, with debris from the collision accreting in orbit around the Earth to form the Moon. Until approximately 2012, the angular momentum associated with this collision was assumed to be equal to the angular momentum of the present-day Earth–Moon system, in the absence of viable mechanisms for losing angular momentum from the system after the Moon-forming event.
One robust result of hydrodynamic simulations of this type of collision (e.g. Canup, Reference Canup2008) is that the Moon consists mainly (~80%) of impactor-derived silicate material. As large bodies in the early solar system are known to be chemically distinct, this implies that there should be significant chemical differences between the Moon and the silicate Earth. In disagreement with these simulations, high-precision measurements of the chemical and isotopic composition of the Moon for several elements including oxygen (Wiechert et al., Reference Wiechert, Halliday, Lee, Snyder, Taylor and Rumble2001; Herwartz et al., Reference Herwartz, Pack, Friedrichs and Bischoff2014), silicon (Savage et al., Reference Savage, Georg, Armytage, Williams and Halliday2010; Armytage et al., Reference Armytage, Georg, Savage, Williams and Halliday2011), titanium (Zhang et al., Reference Zhang, Dauphas, Davis, Leya and Fedkin2012) and tungsten (Kruijer et al., Reference Kruijer, Kleine, Fischer-Goedde and Sprung2015; Touboul et al., Reference Touboul, Puchtel and Walker2015) show an unexpectedly high degree of similarity in composition of the silicate Earth and the Moon. Although recent new measurements of the oxygen isotopic composition of lunar rocks (Herwartz et al., Reference Herwartz, Pack, Friedrichs and Bischoff2014) suggest a very small difference in composition between the Moon and the silicate Earth, the observed difference can be explained straightforwardly by post-Moon-forming processes, such as the addition of a small amount of material via later impacts that is also required to explain the abundances of highly siderophile elements in lunar rocks (e.g. Rai & Van Westrenen, Reference Rai and Van Westrenen2014).
Fig. 1 schematically shows a comparison between the initial composition and angular momentum and the way the transition to the present situation is achieved for three Moon-formation models. The classic GIH can be made more consistent with the observed chemical similarities between silicate Earth and Moon by invoking complete chemical equilibration of the silicate Earth and the Moon after the giant impact (Pahlevan & Stevenson, Reference Pahlevan and Stevenson2007). As an alternative to the classic giant impact scenario, Cuk & Stewart (Reference Ćuk and Stewart2012) and Canup (Reference Canup2012) instead propose that the angular momentum of the proto-Earth–impactor system (L) was much higher than the angular momentum of the current Earth–Moon system (L 0). Hydrodynamic models of giant impacts show that in these cases material accreting to form the Moon is either sourced mostly from the impactor (Cuk & Stewart, Reference Ćuk and Stewart2012) or from a silicate rock reservoir that has been so well mixed that impactor and terrestrial material are chemically indistinguishable (Canup, Reference Canup2012). In both cases the required excess angular momentum in the system compared to the present-day value (L – L 0) has to be removed from the Earth–Moon system after the giant impact through an orbital resonance between the Sun and the Moon (Cuk & Stewart, Reference Ćuk and Stewart2012).
Schematic depiction of Moon formation models showing a comparison between the angular momentum of the resulting Earth–Moon system and the predicted lunar composition. The arrows and associated text indicate the processes invoked to reach the actual present-day Moon composition (= silicate Earth) and angular momentum (= 1).
Two other hypotheses of Moon formation yield similarities in composition between the Moon and the silicate Earth by deriving the Moon from the silicate Earth directly, without a giant impact: the fission hypothesis and the nuclear-explosion hypothesis. The fission hypothesis of Darwin (Reference Darwin1879), later refined by Ringwood (Reference Ringwood1960) and Wise (Reference Wise1963, Reference Wise1969) started with a fast-spinning (high angular momentum) proto-Earth with a homogeneous density. A combination of interior differentiation of the proto-Earth into metallic core and silicate shell, and tidal interaction of the proto-Earth with the Sun then leads to ejection of silicate rocks into orbit. This hypothesis provides no mechanism to remove the excess (with respect to the present-day Earth–Moon system) angular momentum (Fig. 1). In the hypothesis of De Meijer et al. (Reference De Meijer, Anisichkin and Van Westrenen2013), a shock wave triggered by an explosion of a natural nuclear georeactor near the core-mantle boundary (CMB) of the Earth ejected overlying silicate material into orbit (De Meijer & Van Westrenen, Reference De Meijer and Van Westrenen2008). This explosion could have been triggered by a supercritical reactor caused by natural concentration and/or compaction due to the impact of a small asteroid (De Meijer et al., Reference De Meijer, Anisichkin and Van Westrenen2013). This model assumes no change in angular momentum with time and therefore does not require loss of momentum after the Moon-forming event (Fig. 1).
In summary, Moon formation hypotheses that attempt to explain the observed chemical similarities between Moon and silicate Earth make very different assumptions about key physical properties of the system prior to the formation of the Moon, about the necessity and properties of an impactor colliding with the proto-Earth, and about property changes in the Earth–Moon system after Moon formation.
The aim of this work is to provide quantitative boundary conditions for the proto-Earth that are consistent with Moon formation, and to use them to assess the validity of the main assumptions made in the models mentioned above. To reach this aim, the integrity/stability of the proto-Earth is investigated for a range of parameters: mass, core-mantle density differentiation, shape and angular momentum. The criterion for stability is given by the rotation frequency of the proto-Earth. Additional boundary conditions are obtained from calculating the energy difference between an initial state with a proto-Earth that encapsulates a Moon mass, and a final state in which the Moon and the Earth are spherical bodies separated at a distance for which their summed potential and rotational energy is maximal.
Methodology
General approach
In our approach a transition is made between an initial state being a rotating single body with properties of the proto-Earth (i.e. the Earth before the formation of the Moon) to a final two-body state consisting of the Earth and the Moon. In the transition the total angular momentum is conserved, and it is assumed that after the Earth–Moon system is formed both bodies are spherical. The proto-Earth is assumed to have either a uniform density or a bimodal density distribution reflecting internal differentiation into a metallic core and silicate mantle. In our calculations the density distribution of the final state Earth after Moon formation corresponds to the density distribution of the proto-Earth in the initial state, i.e. when starting with a core-mantle differentiated proto-Earth the final state has a core-mantle differentiated Earth + Moon. We investigate the effects of the initial mass (m), the density distribution, the proto-Earth's shape and the value of the total angular momentum (L) in the initial state for this transition model.
In both cases we calculate (1) the moment of inertia as a function of initial mass and oblateness of the initial state to assess the proto-Earth's integrity/stability, and (2) the energy needed to place material with one lunar mass beyond the Roche limit. The Roche limit describes the minimum distance beyond which the self-gravitational force of an object is sufficient to prevent tidal disruption. It should be pointed out that this lunar mass does not need to consist of a single body – in the calculations only its centre of mass is considered. The energy required for the Moon material to be placed into an orbit beyond the Roche limit is calculated by subtracting the rotational energy of the ground state from the energy of the system with a Moon at the Roche limit (De Meijer et al., Reference De Meijer, Anisichkin and Van Westrenen2013).
Computational methods
To ensure the integrity/stability of a rotating proto-Earth with mass m and radius r, the centripetal acceleration at the surface should be larger than the centrifugal acceleration. In our case the centripetal acceleration is the gravitational acceleration:
$$\begin{equation}
\overrightarrow {{a_{\rm{g}}}} = -\gamma\frac{m}{r^{2}}\vec{u}
\end{equation}$$
In this equation γ represents the gravitational constant and 
$\vec u$ is a unit vector along the connecting radius. The centrifugal acceleration at the surface is given as:
$$\begin{equation}
\overrightarrow {{a_{\rm{c}}}} = {\omega ^{2}}r\vec{u}
\end{equation}$$where ω is the rotational frequency, related to the total angular momentum, L, and the moment of inertia, I, by:
$$\begin{equation}
L = I\omega
\end{equation}$$Consequently, the stability condition for a stable proto-Earth is:
$$\begin{equation}
\overrightarrow {{a_{\rm{g}}}} + \overrightarrow {{a_{\rm{c}}}} \le 0
\end{equation}$$Applying eqns 1–3 in eqn 4 leads to:
$$\begin{equation}
\omega = \frac{L}{I} \le \sqrt {\gamma \frac{m}{{{r^3}}}}
\end{equation}$$Eqn 5 presents the stability boundary conditions on ω and I for a given value of L.
The total energy T of the rotating proto-Earth is:
$$\begin{equation}
{T_{{\rm{tot}}}} = \frac{{{L^2}}}{{2I}}
\end{equation}$$In the final state the total energy of the Earth–Moon system (EM) is (according to De Meijer et al., Reference De Meijer, Anisichkin and Van Westrenen2013) given by:
$$\begin{equation}
T_{{\rm{tot}}}^{{\rm{EM}}} = \frac{1}{2}\left( {{I_{\rm{M}}}\omega _{\rm{M}}^2 + {I_{\rm{E}}}\omega _{\rm{E}}^2 - \gamma \frac{{{m_{\rm{M}}}{m_{\rm{E}}}}}{{{r_{{\rm{EM}}}}}}} \right),
\end{equation}$$Subscripts E and M refer to Earth and Moon, respectively, and ω M and ω E represent the rotation frequencies of Moon and Earth around their own axes, respectively.
Scenario 1: Uniform density proto-Earth
Consider the proto-Earth with mass m as an oblate, uniform density (ρ) body with long axes a = b and short axis c, rotating along its short axis. The body's volume and moment of inertia I(a) are given by:
$$\begin{equation}
V = \frac{4}{3}\pi {a^2}c = \frac{m}{\rho }
\end{equation}$$and
$$\begin{equation}
I\left( a \right) = \frac{2}{5}m{a^2}
\end{equation}$$For a given volume and a given ratio a/c the value of a can be determined:
$$\begin{equation}
a = {\left( {\frac{{3m}}{{4\pi \rho }}\frac{a}{c}} \right)^{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}}
\end{equation}$$Scenario 2: Two-layer differentiated proto-Earth
The second scenario is a two-layer, density differentiated proto-Earth with an iron-rich metallic core and a silicate mantle. In this scenario values are scaled to the total mass of the Earth, and the mass ratio of the mantle and core of the present-day Earth. The densities of the two reservoirs are variables. As the density of the core and/or the mantle changes, the volumes and radii of the two reservoirs also change to remain consistent with the total mass. The long radii of the proto-Earth, a, and its core, a c, depend on the ratio a/c, and on the mass and densities of the core (m cand ρ c) and of the mantle (m mand ρ m). Their values follow from eqn 8a as indicated in eqns 9a and 9b:
$$\begin{equation}
{a_{\rm{c}}} = {\left[ {\frac{{3{m_{\rm{c}}}}}{{4\pi {\rho _{\rm{c}}}}}\frac{a}{c}} \right]^{1/3}}
\end{equation}$$
$$\begin{equation}
{a^3} - {a_{\rm{c}}}^3 = \frac{{3{m_{\rm{m}}}}}{{4\pi {\rho _{\rm{m}}}}}\frac{a}{c}\ {\rm{or}}\ a = {\left[ {\frac{3}{{4\pi }}\left( {\frac{{{m_{\rm{m}}}}}{{{\rho _{\rm{m}}}}} + \frac{{{m_{\rm{c}}}}}{{{\rho _{\rm{c}}}}}} \right)\frac{a}{c}} \right]^{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}}
\end{equation}$$The corresponding moments of inertia for the core (I C) and the total body (I tot) are:
$$\begin{equation}
{I_{\rm{c}}} = \frac{2}{5}{m_{\rm{c}}}a_{\rm{c}}^2 = \frac{8}{{15}}\pi {\rho _{\rm{c}}}a_{\rm{c}}^5\frac{c}{a}
\end{equation}$$
$$\begin{equation}
{I_{{\rm{tot}}}} = \frac{8}{{15}}\pi {\rho _{\rm{m}}}{a^5}\frac{c}{a} - \frac{{{\rho _{\rm{m}}}}}{{{\rho _{\rm{c}}}}}{I_{\rm{c}}} + {I_{\rm{c}}} = \frac{8}{{15}}\pi {\rho _{\rm{m}}}{a^5}\frac{c}{a} + \frac{{{\rho _{\rm{c}}} - {\rho _{\rm{m}}}}}{{{\rho _{\rm{c}}}}}{I_{\rm{c}}}.
\end{equation}$$To facilitate the assessment of the radius and mass dependence of various quantities, eqns 10a and 10b have been given in terms of both radii and densities. In our calculations, density values are varied between 10,000 and 13,000 kg m–3 for the core and between 4000 and 5250 kg m–3 for the mantle, bracketing present-day values obtained from seismology (e.g. Dziewonski & Anderson, Reference Dziewonski and Anderson1981).
Energetics of Moon formation
The energy difference between the initial and final state follows from eqns 6 and 7. As shown in De Meijer et al. (Reference De Meijer, Anisichkin and Van Westrenen2013) the energy of the two-body state, being the sum of its rotational and potential energy, has a maximum value at an Earth–Moon distance of r max. The Moon mass has to be placed beyond r max and the required energy, termed the release energy, is calculated from the corresponding changes in rotational and potential energy, as given in De Meijer et al. (Reference De Meijer, Anisichkin and Van Westrenen2013):
$$\begin{equation}
{T_{{\rm{release}}}} = T_{{\rm{tot}}}^{{\rm{EM}}} - {T_{{\rm{tot}}}} + \gamma \frac{{{m_{\rm{M}}}{m_{\rm{E}}}}}{{a - {r_{\rm{M}}}}}
\end{equation}$$In eqn 11 the last term reflects the fact that the Moon material is near the surface of the proto-Earth before Moon formation.
In our approach we consider the Earth–Moon system to be a closed system in which angular momentum is conserved. In the classic GIH the release energy is supplied by the kinetic energy from a giant impact (e.g. Hartmann & Davis, Reference Hartmann and Davis1975; Cameron & Ward, Reference Cameron and Ward1976; Canup, Reference Canup2008). For the nuclear explosion model the release energy is supplied by nuclear fission of uranium and plutonium (De Meijer et al., Reference De Meijer, Anisichkin and Van Westrenen2013). In Darwin's fission model (Darwin, Reference Darwin1879; Ringwood, Reference Ringwood1960; Wise, Reference Wise1963, Reference Wise1969) the release energy is provided by tidal interaction between the proto-Earth and the Sun. In the calculations we perform in this study the source of the release energy is unspecified.
Results
Proto-Earth
Table 1 provides an overview of known values for various properties of the present-day Earth–Moon system. These values form the basis for the evaluation of our two scenarios (uniform density versus differentiated proto-Earth). With a mass m E = 5.97 × 1024 kg and a volume V E = 1.08 × 1020 m3, the average density of the Earth becomes ρ E = 5.52 × 103 kg m–3. This value will be used in Scenario 1. The present-day value for the angular momentum of the Earth–Moon system is L 0 = 3.53 × 1034 kg m2 s–1.
Present-day values of various Earth and Moon quantities.
Scenario 1: Uniform density proto-Earth
The solid lines in Fig. 2 show the relationship between rotation frequency for four values of the ratio a/c of an oblate proto-Earth with a uniform density and an angular momentum equal to the present-day value L 0. All values are considerably higher than the present-day ω E = 7.29 × 10–5 rad s–1 because at present the rotational properties of the Earth–Moon system are determined by the amount of angular momentum of the Moon and hence its distance from the Earth. With increasing m/m E the proto-Earth rotates, as to be expected, more slowly for a constant value of L. Fig. 2 shows that for a fixed value of m/m E the rotation frequency changes fastest around a/c = 1.0. Moreover it shows that ω is more sensitive to m/m E than to a/c. All ω values in Fig. 2 are within the stability region limits given by eqn 5: ω equals 12.4, 11.1, 10.1 and 8.8 × 10–4 rad s–1 for a/c = 1, 1.25, 1.5 and 2.0, respectively. These values correspond to rotation periods p = 1.41, 1.57, 1.72 and 1.99 h, respectively. Since ω is proportional to L the data in Fig. 2 also indicate at which L values the stability criterion is no longer valid. For m = 0.9m E the maximum L value ranges from 2.9 L 0 for a/c = 1 to 3.2 L 0 for a/c = 2; for m = 1.1m E the values range from L max/L 0 = 4.0–4.5.
Rotation frequency, ω, of an oblate proto-Earth with a uniform or a differentiated density as a function of its mass relative to the present Earth mass, and with an angular momentum L equal to its present-day value L 0. The dotted lines represent the rotation frequency of a differentiated proto-Earth with core and mantle densities taken from Table 1, for a/c = 1 and 2.
Scenario 2: Two-density layered proto-Earth
Compared to Scenario 1, this scenario offers a larger number of degrees of freedom. First, we again investigate the rotation frequency as a function of the mass ratio m/m E. As in Scenario 1 we assume that L = L 0, and additionally we assume that the ratio of the masses of core and mantle is fixed at the present-day value.
The dotted lines in Fig. 2 present for a/c = 1 and 2 the relation of the rotation frequency for a differentiated proto-Earth with core and mantle densities as presented in Table 1. Compared to the undifferentiated proto-Earth scenario, rotation frequency increases in accordance with the reduced momenta of inertia. The ω ratio for all corresponding values of m/m E and a/c is 1.16. This value is close to the value of 1.21 for the momenta of inertia of a uniform-density sphere at m/m E = 1 and a/c = 1 and the present-day value for the Earth. This indicates that the angular momentum of the Earth is slightly more reduced than modelled in this scenario due to a more complex density distribution compared to the simplified bimodal distribution we assume. For Scenario 2 the same stability limits apply as for Scenario 1 (see above); none of the presented rotation frequencies exceeds the limits of stability for L = L 0. The maximum allowed L values range from L max/L 0 = 2.5–3.9 for m/m E = 0.9 and a/c = 1 to m/m E = 1.1 and a/c = 2. For a proto-Earth differentiated in the same way as the present-day Earth with a moment of inertia ratio of 1.21, the range would be L max/L 0 = 2.4–3.7.
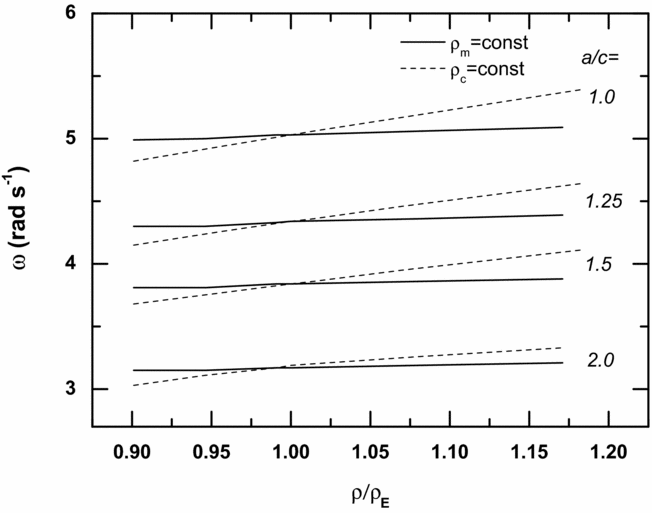
Fig. 3 shows that the rotation frequency only slightly depends on variations in core or mantle densities. This indicates that further refining of the density distribution will have a limited effect on the calculated rotation frequency. This confirms the conclusion in the previous paragraph. Again none of the rotation frequencies approach the integrity/stability limits given in eqn 5.
Rotation frequency as a function of variations in mantle and core densities relative to the present-day values, ρ E (see Table 1), for four values of the oblateness parameter a/c and a proto-Earth with a mass equal to 90% of the present-day mass. Solid lines: core density ρ c kept constant; dotted lines: mantle density ρ m kept constant.
In Fig. 4 the rotational energies are presented for both a uniform density and differentiated proto-Earth with m = 0.9m E for various values of a/c and two values of L (L/L 0 = 1 and 3), as well as the potential energy corresponding to the last term in eqn 7. Since the rotational energy scales with L/L 0 the curves for L = 3L 0 had to be scaled. The results presented in the figure show the expected decrease in rotation frequency for both T rot and T pot as function of a/c. This is in agreement with the earlier findings that the moment of inertia increases with a/c at constant mass.
Rotational energy, T rot, of an oblate proto-Earth with m = 0.9m E with a uniform or differentiated density as a function of the ratio of the length of equatorial and polar axes, a/c, for two values of L (L = L 0 and L = 3L 0). In addition the potential energy, T pot, for a Moon mass at the equatorial surface is presented.
Fig. 5 presents the rotation period as a function of the ratio a/c for m = m E and L/L 0 = 1 and 3. The difference in rotation period between the two L values is a factor of 3, as expected. For L/L 0 = 3 in a differentiated proto-Earth, the calculated rotation period is shorter than allowed by the stability criterion indicated by the red line for all a/c values. For a uniform density distribution, the moments of inertia are somewhat larger than for the differentiated scenario. In this case, proto-Earths of uniform density and a/c < 1.3 have rotation periods at which the proto-Earth would disintegrate, whereas the proto-Earth would be stable at larger a/c values. From this result it is obvious that at L/L 0 = 3 a proto-Earth needs little to no help to break up. For a differentiated proto-Earth with a density similar to the present-day situation the line of stability will be crossed at even lower L value.
Dependence on oblateness a/c of the proto-Earth rotation period for a uniform (blue line) and a differentiated density distribution and two values of angular momentum L (L = L 0 and L = 3L 0). The mass of the proto-Earth corresponds to the present-day value of the Earth. The red curve is the stability criterion line. Rotation periods lower than the stability line lead to spontaneous disintegration of the proto-Earth.
The stability of the proto-Earth for three values of a/c as a function of their angular momentum L is presented in Fig. 6. The curves show that with increasing a/c the stability increases but that at about L/L 0 = 2.5 a differentiated proto-Earth with a/c = 1 (as in the present-day Earth) becomes unstable. If a/c = 2, this maximum L/L 0 increases to approximately 2.8. Differentiation clearly contributes to instability as shown by the lowering of all curves in Fig. 6 when going from an undifferentiated to a differentiated scenario.
Rotation period (h) for the proto-Earth as function of the angular momentum ratio L/L 0 for three values of oblateness a/c. The solid and dashed curves indicate uniform and differentiated densities. The horizontal lines indicate the colour-corresponding lines of stability, below which spontaneous disintegration of the proto-Earth occurs.
Moon formation
On top of the boundary conditions related to the integrity and stability of the proto-Earth, there are additional limitations on the proto-Earth to be able to form a Moon. One is the so-called Roche limit condition. This condition states that for a stable object the material that is supposed to form a Moon should be positioned relative to the Earth in such a way that its own gravitational force, which keeps the object together, should exceed tidal forces exerted by the Earth. The distance at which the two forces are in equilibrium is called the Roche limit, r Roche, and depends on the rigidity of the orbiting object: a fully molten satellite is disrupted more easily than a solid rigid body with the same density. This is reflected in the coefficient α in eqn 12 for the Roche distance:
$$\begin{equation}
{r_{{\rm{Roche}}}} = \alpha {r_{\rm{E}}}{\left( {\frac{{{\rho _{\rm{E}}}}}{{{\rho _{\rm{M}}}}}} \right)^{\displaystyle\frac{1}{3}}}
\end{equation}$$The value of α ranges from 1.26 for a rigid body to 2.45 for a fully molten body. Eqn 12 shows that the Roche limit is related to the ratio of the densities of the Earth and the Moon. Using values listed in Table 1 the Roche limits for rigid and molten moonlike material orbiting the Earth are 9.5 × 106 and 1.8 × 107 m, respectively.
After Moon formation, the Earth–Moon system consists of two spherical differentiated bodies separated by a distance (from centre to centre) r EM. Their total energy as given in eqn 7 is dominated by the two latter terms since the rotational energy of the Moon is very small compared to these terms. The total energy is a function of their relative distance and the total angular momentum of the two-body system. Fig. 7 presents the total energy as a function of their distance for three L values. The figure shows a maximum value r max that has to be exceeded for the Earth–Moon system to become an energetically stable system. This maximum coincides with the Roche limit at L/L 0 = 0.9. At higher L values the maximum r max is within the Roche limit. This implies that the Moon can only be formed as a stable orbiting solid body after frictional forces cause the material to move from r max to beyond the Roche limit. For L/L 0 of 1.5 or higher, the maximum r max is positioned inside the proto-Earth (r max < r E), which is unphysical.
The total energy of the Earth–Moon system (eqn 7) as a function of their separation distance, r, for three values of L. The red chequered field encompasses the range of the Roche limit radius r Roche calculated assuming rigid Moon material (lower bound) and molten Moon material (upper bound) as end members.
This has some implications for Moon formation. After material has been brought into space beyond r max it will not fall back to Earth. At this relatively short Earth–Moon distance tidal forces will rapidly lock the material, leading to a synchronous orbit and continuously increasing Earth–Moon distance. If this material cools rapidly and forms a rigid body, the Roche limit will hardly be a limitation as it is very close to r max. If, due to the heat produced during the Moon formation process or due to the proto-Earth being very hot prior to Moon formation, Moon-forming materials were hot and dominated by molten materials, final coalescence of materials to a Moon must be delayed until the Earth–Moon distance has exceeded the Roche limit for the molten state, i.e. 1.8 × 107 m.
Release energy
The next criterion for the stability of the Earth–Moon system is that the energy to transform the proto-Earth to a two-body system is positive. As it is the most realistic scenario, used in all major Moon-forming models, our starting point for an assessment of this criterion is a differentiated proto-Earth. Table 2 presents the release energy for a set of L and a/c values. Negative energy values and cases where r max < 0.6 × 107 m are not physical. Hence the relevant values have been marked in bold face. This implies that for L/L 0 values larger than 1.5, Moon formation is not realistic.
Release energy (in Joule) needed to form an Earth–Moon system from a differentiated proto-Earth resulting from eqn 11, as a function of angular momentum ratio L/L 0, maximum Earth–Moon distance r max and oblateness a/c
Physically plausible values given in bold italic face.
Discussion and conclusions
In this paper we have examined various boundary conditions imposed by a proto-Earth and an Earth–Moon system to comply with basic physics. The stability/integrity of the proto-Earth is manifested by a maximum rotation frequency, ω max. We quantified how the differentiation of density resulting from core formation in the proto-Earth causes the moment of inertia of the proto-Earth to decrease, consequently speeding up its rotation. With increasing oblateness, the moment of inertia increases. Angular momentum has a significant effect on the stability of the proto-Earth. Since the rotation frequency depends linearly on the angular momentum of the system, the stability criterion limits the maximum L value. For the proto-Earth we noticed that the system becomes increasingly less stable with a maximum around L/L 0 = 2.5–2.8 for a differentiated proto-Earth, with the precise maximum dependent on the oblateness.
Further limitations are imposed by the Roche limit and the logical condition that the separated Earth–Moon system should be formed outside the proto-Earth. This further limits the L values to a maximum of about L/L 0 = 1.5. A final limitation is imposed by the requirement of a positive release energy, since negative release energy is unphysical. This limitation indicates that the proto-Earth had to be deformed with a/c ≥ 1.2. At this minimum a/c value the angular momentum is limited to L/L 0 = 1.1. For larger a/c values the L values are limited by the above limitations.
These results have consequences for the present models trying to explain the formation of the Moon from predominantly terrestrial materials as deduced from the similarity in chemical composition between silicate Earth and lunar rocks. The latest giant-impact models that yield a Moon with silicate Earth like composition (Canup, Reference Canup2012; Ćuk & Stewart, 2013) require L/L 0 > 2. Our work suggests that these models may not be physically relevant. In the nuclear explosion model (De Meijer et al., Reference De Meijer, Anisichkin and Van Westrenen2013) the model was demonstrated to produce a Moon with L/L 0 = 1 and assumed a/c = 2. The present work indicates that their model is physically relevant for a/c ≥ 1.2. At the limit of a/c = 1.2, the energy required to form the Moon is reduced to about 1029 J. This is an order of magnitude lower than the previous estimate of De Meijer et al. (Reference De Meijer, Anisichkin and Van Westrenen2013) based on a uniform density proto-Earth and a/c = 2. Consequently a smaller amount of fissionable material is needed for the nuclear explosion.
Based on the above we conclude that the recent attempts to salvage the classic giant impact hypothesis by studying systems with far higher values of L are not supported by the boundary condition calculations in this work. On the contrary, this work indicates that the nuclear explosion model requires less energy than originally estimated. Hence, in our view the nuclear explosion model is presently the model that best explains the formation of the Moon from terrestrial materials.
Acknowledgements
We would like to thank three anonymous reviewers for their constructive criticisms, which helped to improve the quality of this manuscript. WvW and RdM thank the late Prof. Rama Murthy for moral support. Financial support for part of this work was provided by the Netherlands Organisation for Scientific Research (NWO) through a Vici grant to WvW.
