1. Introduction
In this paper we study the Cramér type moderate deviations for random fields, in particular, linear random fields (often called spatial linear processes in statistics literature) with short or long memory (short- or long-range dependence). The study of moderate deviation probabilities in nonlogarithmic form for independent random variables goes back to the 1920s. The first theorem in this field was published by [Reference Khinchin23] who studied a particular case of the Bernoulli random variables. In his fundamental work, [Reference Cramér7] studied the estimation of the tail probability by the standard normal distribution under the condition that the random variable has moment generating function in a neighborhood of the origin (cf. (2.1) below). This condition has been referred to as the Cramér condition. Cramér’s work was improved by [Reference Petrov33] (see also [Reference Petrov35, Reference Petrov36]). Their works have stimulated a large amount of research on moderate and large deviations; see below for a brief (and incomplete) review on literature related to this paper. Nowadays, the area of moderate and large deviation deviations is not only important in probability but also plays an important role in many applied fields, for instance, the premium calculation problem, risk management in insurance (cf. [Reference Asmussen and Albrecher2]), nonparametric estimation in statistics (see, e.g. [Reference Bahadur and Rao5, Reference Van Der Vaart47, Reference Joutard21, Reference Joutard22]), and in network information theory (cf. [Reference Lee, Tan and Khisti26, Reference Lee, Tan and Khisti27]).
Let X, X 1, X 2, … be a sequence of independent and identically distributed (i.i.d.) random variables with mean 0 and variance σ 2. Let ![]() $S_{n}=\sum_{k=1}^n X_k (n\ge 1$) be the partial sums. By the central limit theorem,
$S_{n}=\sum_{k=1}^n X_k (n\ge 1$) be the partial sums. By the central limit theorem,
where Φ(x) is the probability distribution of the standard normal random variable. If, for a suitable sequence cn, we have
or ![]() $\mathbb P(S_{n}>x\sigma\sqrt{n})=(1-\Phi (x))(1+o(1))$ uniformly over x ∈ [0, cn], then (1.1) is called a moderate deviation probability or normal deviation probability for Sn since it can be estimated by the standard normal distribution. We refer to [0, cn] as a range for the moderate deviation. The most famous result of this kind is the Cramér type moderate deviation. Under Cramér’s condition, we have the following Cramér’s theorem [Reference Cramér7, Reference Petrov33], [Reference Petrov35, p. 218], or [Reference Petrov36, p. 178]): if x ≥ 0 and
$\mathbb P(S_{n}>x\sigma\sqrt{n})=(1-\Phi (x))(1+o(1))$ uniformly over x ∈ [0, cn], then (1.1) is called a moderate deviation probability or normal deviation probability for Sn since it can be estimated by the standard normal distribution. We refer to [0, cn] as a range for the moderate deviation. The most famous result of this kind is the Cramér type moderate deviation. Under Cramér’s condition, we have the following Cramér’s theorem [Reference Cramér7, Reference Petrov33], [Reference Petrov35, p. 218], or [Reference Petrov36, p. 178]): if x ≥ 0 and ![]() $x=o(\sqrt{n})$ then
$x=o(\sqrt{n})$ then
Here ![]() $\lambda (z)=\sum_{k=0}^{\infty }c_{k}z^{k}$ is a power series with coefficients depending on the cumulants of the random variable X. Equation (1.2) provides a more precise approximation than (1.1) which holds uniformly on the range [0, cn] for any
$\lambda (z)=\sum_{k=0}^{\infty }c_{k}z^{k}$ is a power series with coefficients depending on the cumulants of the random variable X. Equation (1.2) provides a more precise approximation than (1.1) which holds uniformly on the range [0, cn] for any ![]() $c_n = o(\sqrt{n})$. The moderate deviations under Cramér’s condition for independent nonidentically distributed random variables were obtained by [Reference Feller9, Reference Petrov33, Reference Statulevičius44]. The Cramér type moderate deviation has also been established for the sum of independent random variables with pth moment, p > 2. To name a few, see, for example, see [Reference Rubin and Sethuraman40, Reference Nagaev29, Reference Nagaev30, Reference Michel28, Reference Slastnikov43, Reference Amosova1, Reference Frolov10]. It should be pointed out that the ranges of the moderate deviations in these references are smaller (e.g.
$c_n = o(\sqrt{n})$. The moderate deviations under Cramér’s condition for independent nonidentically distributed random variables were obtained by [Reference Feller9, Reference Petrov33, Reference Statulevičius44]. The Cramér type moderate deviation has also been established for the sum of independent random variables with pth moment, p > 2. To name a few, see, for example, see [Reference Rubin and Sethuraman40, Reference Nagaev29, Reference Nagaev30, Reference Michel28, Reference Slastnikov43, Reference Amosova1, Reference Frolov10]. It should be pointed out that the ranges of the moderate deviations in these references are smaller (e.g. ![]() $c_n = O(\sqrt{\log n})$).
$c_n = O(\sqrt{\log n})$).
The Cramér type moderate deviations for dependent random variables have also been studied in the literature. Ghosh (Reference Ghosh1974), [Reference Heinrich18] studied the moderate deviation for m-dependent random variables. Ghosh and Babu (Reference Ghosh and Babu1977), [Reference Babu and Singh3] studied moderate deviation for mixing processes. Grama (Reference Grama1997), [Reference Fan, Grama and Liu8, Reference Grama and Haeusler14, Reference Grama and Haeusler15] investigated the large and moderate deviations for martingales. Babu and Singh (Reference Babu and Singh1978b) established moderate deviation results for linear processes with coefficients satisfying ![]() $\sum_{i=1}^\infty i|a_i|\lt\infty$. Wu and Zhao (Reference Wu and Zhao2008) studied moderate deviations for stationary processes under certain conditions in terms of the physical dependence measure. But it can be verified that the results from [Reference Wu and Zhao48] can only be applied to linear processes with short memory and their transformations. Recently, Peligrad et al. (2013) studied the exact moderate and large deviations for short or long memory linear processes. Sang and Xiao (Reference Sang and Xiao2018) studied exact moderate and large deviations for linear random fields and applied the moderate result to prove a Davis–Gut law of the iterated logarithm. Nevertheless, in the aforementioned works, the moderate deviations are studied for dependent random variables with pth moment, p > 2. The exact moderate deviation for random fields under Cramér’s condition has not been well studied. For example, the optimal range [0, cn] and the exact rate of convergence in (1.1) had been unknown in the random field setting.
$\sum_{i=1}^\infty i|a_i|\lt\infty$. Wu and Zhao (Reference Wu and Zhao2008) studied moderate deviations for stationary processes under certain conditions in terms of the physical dependence measure. But it can be verified that the results from [Reference Wu and Zhao48] can only be applied to linear processes with short memory and their transformations. Recently, Peligrad et al. (2013) studied the exact moderate and large deviations for short or long memory linear processes. Sang and Xiao (Reference Sang and Xiao2018) studied exact moderate and large deviations for linear random fields and applied the moderate result to prove a Davis–Gut law of the iterated logarithm. Nevertheless, in the aforementioned works, the moderate deviations are studied for dependent random variables with pth moment, p > 2. The exact moderate deviation for random fields under Cramér’s condition has not been well studied. For example, the optimal range [0, cn] and the exact rate of convergence in (1.1) had been unknown in the random field setting.
The main objective of this paper is to establish exact moderate deviation analogous to (1.2) for random fields under Cramér’s condition. Our main result is Theorem 2.1 below, whose proof is based on the conjugate method to change the probability measure as in the classical case (see, e.g. [Reference Petrov33, Reference Petrov34]). The extension of this method to the random field setting reveals the deep relationship between the tail probabilities and the properties of the cumulant generating functions of the random variables such as the analytic radius and the bounds, for x within some ranges related to the sum of the variances and the analytic radius of the cumulant generating functions of these random variables. Compared with the results in [Reference Sang and Xiao41] for linear random fields, Theorems 2.1 and 3.1 in this paper provide more precise convergence rates in the moderate deviations and explicit information on the range [0, cn], which is much bigger than the range in Theorem 2.1 of [Reference Sang and Xiao41]. In Section 3 we show that Theorem 2.1 is applicable to linear random fields with short or long memory and to nonparametric regression analysis. The results there can be applied to approximate the quantiles and tail conditional expectations for the partial sums of linear random fields.
In this paper we use the following notation. For two sequences {an} and {bn} of real numbers, an~bn means an/bn → 1 as n → ∞; an ∝ bn means that an/bn → C as n → ∞ for some constant C > 0; for positive sequences, the notation an ≪ bn or bn ≫ an means that an/bn is bounded. For d, m ∈ ℕ, denote ![]() $\Gamma^d_m=[-m, m]^d \cap \mathbb{Z}^d$. In Section 2 we give the main results. In Section 3 we study the application of the main results in linear random fields and nonparametric regression. All the proofs are presented in Section 4.
$\Gamma^d_m=[-m, m]^d \cap \mathbb{Z}^d$. In Section 2 we give the main results. In Section 3 we study the application of the main results in linear random fields and nonparametric regression. All the proofs are presented in Section 4.
2. Main results
Let {Xnj, n ∈ ℕ j ∈ ℤd } be a random field with zero means defined on a probability space (Ω, ![]() ${\mathcal F}, {\rm {\mathbb P}}$). Suppose that, for each n, the random variables Xnj, j ∈ ℤd are independent and satisfy the following Cramér condition: there is a positive constant Hn such that the cumulant generating function
${\mathcal F}, {\rm {\mathbb P}}$). Suppose that, for each n, the random variables Xnj, j ∈ ℤd are independent and satisfy the following Cramér condition: there is a positive constant Hn such that the cumulant generating function
Here Dn = {z ∈ ℂ: |z| < Hn} is the disc of radius Hn on the complex plane ℂ, and log denotes the principal value of the logarithm so that Lnj(0) = 0. This setting is convenient for applications to linear random fields in Section 3.
Without loss of generality, we assume in this section that ![]() $\mathop {\lim \sup }\limits_{n \to \infty } {H_n} \lt \infty $. Within the disc {z ∈ ℂ: |z| < Hn}, Lnj can be expanded in a convergent power series
$\mathop {\lim \sup }\limits_{n \to \infty } {H_n} \lt \infty $. Within the disc {z ∈ ℂ: |z| < Hn}, Lnj can be expanded in a convergent power series
 \begin{align*}
L_{nj}(z)=\sum_{k=1}^\infty \frac{\gamma_{knj}}{k!}z^{\,k},\end{align*}
\begin{align*}
L_{nj}(z)=\sum_{k=1}^\infty \frac{\gamma_{knj}}{k!}z^{\,k},\end{align*}
where γknj is the cumulant of order k of the random variable Xnj. We have ![]() $\gamma_{1nj}= {\rm {\mathbb E}} X_{nj}=0$ and
$\gamma_{1nj}= {\rm {\mathbb E}} X_{nj}=0$ and ![]() $\gamma_{2nj}= {\rm {\mathbb E}} X_{nj}^2=\sigma_{nj}^2$. By Taylor’s expansion, we can verify that a sufficient condition for (2.1) is the following moment condition:
$\gamma_{2nj}= {\rm {\mathbb E}} X_{nj}^2=\sigma_{nj}^2$. By Taylor’s expansion, we can verify that a sufficient condition for (2.1) is the following moment condition:
This condition has been used frequently in probability and statistics, see, for example, [Reference Petrov35, p. 55], [Reference Johnstone20, p. 64], [Reference Picard and Tribouley38, p. 301], [Reference Zhang and Wong49, p. 164], among others.
Denote
and assume that Sn is well defined and Bn < ∞ for each n ∈ℕ. The following theorem is the main result of this paper.
Theorem 2.1. Suppose that, for all n ∈ ℕ and j ∈ ℤd, there exist nonnegative constants cnj such that
and suppose that ![]() $B_n H_n^2\to \infty$ as n → ∞, and
$B_n H_n^2\to \infty$ as n → ∞, and
If x ≥ 0 and ![]() $x=o(H_n\sqrt{B_n})$, then
$x=o(H_n\sqrt{B_n})$, then
where
is a power series that stays bounded uniformly in n for sufficiently small values of |t| and the coefficients βkn only depend on the cumulants of Xnj (n ∈ ℤ, j ∈ ℤd).
For the rest of the paper, we only state the results for x ≥ 0. Since ![]() $\lambda_n(t)=\sum_{k=0}^\infty \beta_{kn}t^k$ stays bounded uniformly in n for sufficiently small values of |t| and β 0n = (Hn/6Bn) Σj∈ℤd γ3nj from the proof of Theorem 2.1, we have the following corollary.
$\lambda_n(t)=\sum_{k=0}^\infty \beta_{kn}t^k$ stays bounded uniformly in n for sufficiently small values of |t| and β 0n = (Hn/6Bn) Σj∈ℤd γ3nj from the proof of Theorem 2.1, we have the following corollary.
Corollary 2.1. Assume that the conditions of Theorem 2.1 hold. Then, for x ≥ 0 with ![]() $x=O((H_n\sqrt{B_n})^{1/3})$ we have
$x=O((H_n\sqrt{B_n})^{1/3})$ we have
 \begin{align*}\frac{1-F_n(x)}{1-\Phi(x)}=\exp\Big\{\frac{x^3}{6B_n^{3/2}}\sum_{j\in\mathbb{Z}^d}\gamma_{\,3nj}\Big\}\Big(1+O\Big(\frac{x+1}{H_n\sqrt{B_n}\,}\Big)\Big).\end{align*}
\begin{align*}\frac{1-F_n(x)}{1-\Phi(x)}=\exp\Big\{\frac{x^3}{6B_n^{3/2}}\sum_{j\in\mathbb{Z}^d}\gamma_{\,3nj}\Big\}\Big(1+O\Big(\frac{x+1}{H_n\sqrt{B_n}\,}\Big)\Big).\end{align*}
Note that ![]() $({x^3}/{6B_n^{3/2}})\sum_{j\in\mathbb{Z}^d}\gamma_{3nj}=O(1)$ under the condition
$({x^3}/{6B_n^{3/2}})\sum_{j\in\mathbb{Z}^d}\gamma_{3nj}=O(1)$ under the condition ![]() $x=O((H_n\sqrt{B_n})^{1/3})$. Also, taking into the account the fact that, for x > 0,
$x=O((H_n\sqrt{B_n})^{1/3})$. Also, taking into the account the fact that, for x > 0,
we obtain the following corollaries.
Corollary 2.2. Under the conditions of Theorem 2.1, we have, for x ≥ 0 with ![]() $x=O((H_n\sqrt{B_n})^{1/3})$,
$x=O((H_n\sqrt{B_n})^{1/3})$,
 \begin{align*}1-F_n(x)=(1-\Phi(x))\exp\Bigg\{\frac{x^3}{6B_n^{3/2}}\sum_{j\in\mathbb{Z}^d}\gamma_{\,3nj}\Bigg\}+O\Big(\frac{\text {e}^{-x^2/2}}{H_n\sqrt{B_n}\,}\Big).\end{align*}
\begin{align*}1-F_n(x)=(1-\Phi(x))\exp\Bigg\{\frac{x^3}{6B_n^{3/2}}\sum_{j\in\mathbb{Z}^d}\gamma_{\,3nj}\Bigg\}+O\Big(\frac{\text {e}^{-x^2/2}}{H_n\sqrt{B_n}\,}\Big).\end{align*}
Corollary 2.3. Assume that the conditions of Theorem 2.1 hold and Σj∈ℤd γ 3nj = 0 for all n ∈ ℕ Then, for x ≥ 0 with ![]() $x=O((H_n\sqrt{B_n})^{1/3})$, we have
$x=O((H_n\sqrt{B_n})^{1/3})$, we have
Also, ![]() $\text{as} \space 1-\Phi(x) \sim {\text {e}^{-x^2/2}}/{x\sqrt{2\pi}}$ as x → ∞, we have the following.
$\text{as} \space 1-\Phi(x) \sim {\text {e}^{-x^2/2}}/{x\sqrt{2\pi}}$ as x → ∞, we have the following.
Corollary 2.4. Under the conditions of Theorem 2.1, if ![]() $x\to\infty, x=o(H_n\sqrt{B_n})$, then
$x\to\infty, x=o(H_n\sqrt{B_n})$, then
for every positive constant c.
3. Applications
In this section we provide some applications of the main result given in Section 2. First, we derive a moderate deviation result for linear random fields with short or long memory. We then apply this result to risk measures and implement the same argument to study nonparametric regression.
3.1. Cramér-type moderate deviation for linear random fields
Let X = {Xj, j ∈ ℤd} be a linear random field defined on a probability space (Ω, ![]() $\mathcal F$, ℙ) by
$\mathcal F$, ℙ) by
where the innovations εi, i ∈ ℤd, are i.i.d. random variables with mean zero and finite variances σ 2, and where {ai, i ∈ ℤd} is a sequence of real numbers that satisfy ![]() $\sum_{i \in \mathbb{Z}^d} a_i^2 \lt \infty$.
$\sum_{i \in \mathbb{Z}^d} a_i^2 \lt \infty$.
Linear random fields have been extensively studied in probability and statistics. We refer to [Reference Sang and Xiao41] for a brief review on studies in limit theorems, large and moderate deviations for linear random fields, and to [Reference Koul, Mimoto and Surgailis24, Reference Lahiri and Robinson25], and the reference therein for recent developments in statistics.
By applying Theorem 2.1, we establish the following moderate deviation result for linear random fields with short or long memory, under Cramér’s condition on the innovations εi, i ∈ ℤd. Compared with the moderate deviation results in [Reference Sang and Xiao41], our Theorem 3.1 below gives a more precise convergence rate which holds on a much wider range for x.
Suppose that there is a disc centered at z = 0 within which the cumulant generating function ![]() $L(z) =L_{\varepsilon_i}(z)=\log {\rm {\mathbb E}} \text {e}^{z\varepsilon_i}$ of εi is analytic and can be expanded in a convergent power series
$L(z) =L_{\varepsilon_i}(z)=\log {\rm {\mathbb E}} \text {e}^{z\varepsilon_i}$ of εi is analytic and can be expanded in a convergent power series
 \begin{align*}
L(z)=\sum_{k=1}^\infty \frac{\gamma_k}{k!}z^{\,k},
\end{align*}
\begin{align*}
L(z)=\sum_{k=1}^\infty \frac{\gamma_k}{k!}z^{\,k},
\end{align*}
where γk is the cumulant of order k of the random variables εi, i ∈ ℤd. We have ![]() $\gamma_1= {\rm {\mathbb E}}\varepsilon_i=0$ and
$\gamma_1= {\rm {\mathbb E}}\varepsilon_i=0$ and ![]() $\gamma_2 = {\rm {\mathbb E}}\varepsilon_i^2=\sigma^2, i\in\mathbb{Z}^d$.
$\gamma_2 = {\rm {\mathbb E}}\varepsilon_i^2=\sigma^2, i\in\mathbb{Z}^d$.
We write
where ![]() $b_{nj}=\sum_{i\in\Gamma^d_n}a_{i-j}$. In the setting of Section 2, we have Xnj = bnjεj, j ∈ ℤd. Then it can be verified that, for all n ≥ 1 and j ∈ ℤd, Xnj satisfy condition (2.1) for suitably chosen Hn. In the notation of Section 2, we have
$b_{nj}=\sum_{i\in\Gamma^d_n}a_{i-j}$. In the setting of Section 2, we have Xnj = bnjεj, j ∈ ℤd. Then it can be verified that, for all n ≥ 1 and j ∈ ℤd, Xnj satisfy condition (2.1) for suitably chosen Hn. In the notation of Section 2, we have
Hence, we can apply Theorem 2.1 to prove the following theorem.
Theorem 3.1. Assume that the linear random field X = {Xj, j ∈ ℤd} has short memory, i.e.
or long memory with coefficients
where α ∈ (d/2, d) is a constant, l(·): [1, ∞) → ℝ is a slowly varying function at ∞, and b(·) is a continuous function defined on the unit sphere ![]() ${\mathbb S}_{d-1}$ Suppose that there exist positive constants H and C such that
${\mathbb S}_{d-1}$ Suppose that there exist positive constants H and C such that
in the disc |z| < H. Then, for all x ≥ 0 with x = o(nd /2), we have
where
is a power series that stays bounded uniformly in n for sufficiently small values of |t|, and the coefficients βkn only depend on the cumulants of εi and on the coefficients ai of the linear random field.
To the best of our knowledge, Theorem 3.1 is the first result that gives the exact tail probability for partial sums of random fields with dependence structure under the Cramér condition.
Due to its preciseness, Theorem 3.1 can be applied to evaluate the performance of approximation of the distribution of linear random fields by truncation. We often use the random variable ![]() $X_j^m=\sum_{i\in \Gamma_m^d} a_i \varepsilon_{j-i}$ with finite terms to approximate the linear random field
$X_j^m=\sum_{i\in \Gamma_m^d} a_i \varepsilon_{j-i}$ with finite terms to approximate the linear random field ![]() $X_j=\sum_{i\in \mathbb{Z}^d}a_i \varepsilon_{j-i}$ in practice. For example, the moving average with finite terms MA(m) is applied to approximate the linear process (moving average with infinite terms). In this case, Theorem 3.1 also applies to the partial sum
$X_j=\sum_{i\in \mathbb{Z}^d}a_i \varepsilon_{j-i}$ in practice. For example, the moving average with finite terms MA(m) is applied to approximate the linear process (moving average with infinite terms). In this case, Theorem 3.1 also applies to the partial sum ![]() $S_n^m = \sum_{j\in\Gamma^d_n }X_j^m=\sum_{j\in\mathbb{Z}^d} b_{nj}^m\varepsilon_j$. Here only finite terms
$S_n^m = \sum_{j\in\Gamma^d_n }X_j^m=\sum_{j\in\mathbb{Z}^d} b_{nj}^m\varepsilon_j$. Here only finite terms ![]() $b_{nj}^m$ are nonzero. Denote
$b_{nj}^m$ are nonzero. Denote
Then, for all x ≥ 0 with x = o(nd/ 2), we have
where
and where the coefficients ![]() $\beta_{kn}^m$have a similar definition as βkn. To see the difference between the two tail probabilities of the partial sums, we have
$\beta_{kn}^m$have a similar definition as βkn. To see the difference between the two tail probabilities of the partial sums, we have
 \begin{align*}
\frac{1-F_n(x)}{1-F_n^m(x)}&=\exp\Big\{\frac{x^3}{n^{d/2}}\Big[\lambda_n
\Big(\frac{x}{n^{d/2}}\Big)-\lambda_n^m\Big(\frac{x}{n^{d/2}}\Big)\Big]\Big\}
\Big(1+O\Big(\frac{x+1}{n^{d/2}}\Big)\Big)
\\
&=\exp\Big\{\frac{x^3}{n^{d/2}}\Big[\beta_{0n}-\beta_{0n}^m+\sum_{k=1}^\infty
(\beta_{kn}-\beta_{kn}^m)\Big(\frac{x}{n^{d/2}}\Big)^k\Big]\Big\}
\Big(1+O\Big(\frac{x+1}{n^{d/2}}\Big)\Big),
\end{align*}
\begin{align*}
\frac{1-F_n(x)}{1-F_n^m(x)}&=\exp\Big\{\frac{x^3}{n^{d/2}}\Big[\lambda_n
\Big(\frac{x}{n^{d/2}}\Big)-\lambda_n^m\Big(\frac{x}{n^{d/2}}\Big)\Big]\Big\}
\Big(1+O\Big(\frac{x+1}{n^{d/2}}\Big)\Big)
\\
&=\exp\Big\{\frac{x^3}{n^{d/2}}\Big[\beta_{0n}-\beta_{0n}^m+\sum_{k=1}^\infty
(\beta_{kn}-\beta_{kn}^m)\Big(\frac{x}{n^{d/2}}\Big)^k\Big]\Big\}
\Big(1+O\Big(\frac{x+1}{n^{d/2}}\Big)\Big),
\end{align*}
here, as in the proof of Theorem 3.1, we take Mn = maxj∈ℤd|bnj|, Hn = H/2Mn, ![]() $M_n^m=\max_{j\in\mathbb{Z}^d}|b_{nj}^m|$,
$M_n^m=\max_{j\in\mathbb{Z}^d}|b_{nj}^m|$, ![]() $H_n={H}/{2M_n^m}$,
$H_n={H}/{2M_n^m}$,
 \begin{align*}
\beta_{0n}&=\frac{H_n}{6B_n}\sum_{j\in\mathbb{Z}^d}\gamma_{\,3nj}
=\frac{H\gamma_3}{12M_nB_n}\sum_{j\in\mathbb{Z}^d}(b_{nj})^3,
\\
\beta_{0n}^m&=\frac{H_n^m}{6B_n^m}\sum_{j\in\mathbb{Z}^d}\gamma_{\,3nj}^m
=\frac{H\gamma_3}{12M_n^mB_n^m}\sum_{j\in\mathbb{Z}^d}(b_{nj}^m)^3.
\end{align*}
\begin{align*}
\beta_{0n}&=\frac{H_n}{6B_n}\sum_{j\in\mathbb{Z}^d}\gamma_{\,3nj}
=\frac{H\gamma_3}{12M_nB_n}\sum_{j\in\mathbb{Z}^d}(b_{nj})^3,
\\
\beta_{0n}^m&=\frac{H_n^m}{6B_n^m}\sum_{j\in\mathbb{Z}^d}\gamma_{\,3nj}^m
=\frac{H\gamma_3}{12M_n^mB_n^m}\sum_{j\in\mathbb{Z}^d}(b_{nj}^m)^3.
\end{align*}
If γ 3 ≠ 0, ![]() ${(1-F_n(x))}/{(1-F_n^m(x))}$ is dominated by exp
${(1-F_n(x))}/{(1-F_n^m(x))}$ is dominated by exp![]() $\{({x^3}/{n^{d/2}})(\beta_{0n}-\beta_{0n}^m)\}$. If γ 3 = 0, then
$\{({x^3}/{n^{d/2}})(\beta_{0n}-\beta_{0n}^m)\}$. If γ 3 = 0, then ![]() $\beta_{0n}=\beta_{0n}^m=0$ and
$\beta_{0n}=\beta_{0n}^m=0$ and ![]() ${(1-F_n(x))}/{(1-F_n^m(x))}$ can be dominated by exp
${(1-F_n(x))}/{(1-F_n^m(x))}$ can be dominated by exp![]() $\{({x^4}/{n^{d}})(\beta_{1n}-\beta_{1n}^m)\}$ which depends on whether γ 4 = 0. In general, Theorem 3.1 can be applied to evaluate whether the truncated version
$\{({x^4}/{n^{d}})(\beta_{1n}-\beta_{1n}^m)\}$ which depends on whether γ 4 = 0. In general, Theorem 3.1 can be applied to evaluate whether the truncated version ![]() $X_j^m$ is a good approximation to Xj in terms of the ratio
$X_j^m$ is a good approximation to Xj in terms of the ratio ![]() ${(1-F_n(x))}/{(1-F_n^m(x))}$ for x in different ranges which depends on the property of the innovation ε and the sequence {ai i ∈ ℤd }.
${(1-F_n(x))}/{(1-F_n^m(x))}$ for x in different ranges which depends on the property of the innovation ε and the sequence {ai i ∈ ℤd }.
Theorem 3.1 can be applied to calculate the tail probability of the partial sum of some well-known dependent models. For example, the autoregressive fractionally integrated moving average FARIMA(p, β, q) processes in the one-dimensional case introduced by [Reference Granger and Joyeux16, Reference Hosking19], which is defined as
Here p, q are nonnegative integers, ϕ(z) = 1 − ϕ 1 z − · · · − ϕ pz p is the AR polynomial, and θ(z) = 1 + θ 1 z + · · · + θqz q is the MA polynomial. Under the conditions that ϕ(z) and θ(z) have no common zeros, the zeros of ϕ(·) lie outside the closed unit disk and ![]() $-\tfrac12\lt\beta\lt\tfrac12$, the FARIMA(p, β, q) process has linear process form
$-\tfrac12\lt\beta\lt\tfrac12$, the FARIMA(p, β, q) process has linear process form ![]() ${X_n} = \sum\nolimits_{i = 0}^\infty {{a_i}{\varepsilon _{n - 1}}} $,
${X_n} = \sum\nolimits_{i = 0}^\infty {{a_i}{\varepsilon _{n - 1}}} $, ![]() $\;n\in\mathbb{N}$ with ai = θ(1)iβ −1/ϕ(1) Γ(β) + O(i −1). Here (·) is the gamma function.
$\;n\in\mathbb{N}$ with ai = θ(1)iβ −1/ϕ(1) Γ(β) + O(i −1). Here (·) is the gamma function.
3.2. Approximation of risk measures
Theorem 3.1 can be applied to approximate the risk measures such as quantiles and tail conditional expectations for the partial sums Sn in (3.1) of the linear random field X = {Xj, j ∈ ℤd }. Given the tail probability α ∈ (0, 1), let Qα,n be the upper αth quantile of Sn. Namely, ℙ(Sn ≥ Qα,n) = α. By Theorem 3.1, for all x ≥ 0 with x = o(nd /2),
We approximate Qα,n by ![]() $x_{\alpha}\sqrt{B_n}$ where x = xα = o(nd /2) can be solved numerically from
$x_{\alpha}\sqrt{B_n}$ where x = xα = o(nd /2) can be solved numerically from
The tail conditional expectation is computed as
 \begin{align}{\rm {\mathbb E}}(S_{n}\mid S_{n} \geq Q_{\alpha,n}) &= \frac{Q_{\alpha,n}{\rm {\mathbb P}} (S_{n}\geq
Q_{\alpha,n})+{\int_{Q_{\alpha,n}}^{\infty}{\rm {\mathbb P}}(S_{n}\geq w)\text d
w}}{{{\rm {\mathbb P}}(S_{n}\geq Q_{\alpha,n})}}
\\
&= Q_{\alpha,n}+\frac{\sqrt{B_n}}{\alpha}
{\int_{Q_{\alpha,n}/\sqrt{B_n}}^{\infty}\exp\Big\{\frac{y^3}{n^{d/2}}
\lambda_n\Big(\frac{y}{n^{d/2}}\Big)\Big\}(1-\Phi(y))\text d y},
\end{align}
\begin{align}{\rm {\mathbb E}}(S_{n}\mid S_{n} \geq Q_{\alpha,n}) &= \frac{Q_{\alpha,n}{\rm {\mathbb P}} (S_{n}\geq
Q_{\alpha,n})+{\int_{Q_{\alpha,n}}^{\infty}{\rm {\mathbb P}}(S_{n}\geq w)\text d
w}}{{{\rm {\mathbb P}}(S_{n}\geq Q_{\alpha,n})}}
\\
&= Q_{\alpha,n}+\frac{\sqrt{B_n}}{\alpha}
{\int_{Q_{\alpha,n}/\sqrt{B_n}}^{\infty}\exp\Big\{\frac{y^3}{n^{d/2}}
\lambda_n\Big(\frac{y}{n^{d/2}}\Big)\Big\}(1-\Phi(y))\text d y},
\end{align}
which can be solved numerically. The quantile and tail conditional expectations, which are also called value at risk (VaR) or expected shortfall (ES) in finance and risk theory, are important measures to model the extremal behavior of random variables in practice. The precise moderate deviation results in this paper provide a vehicle in the computation of these two measures of time series or spatial random fields. See [Reference Peligrad, Sang, Zhong and Wu31] for a brief review of VaR and ES in the literature, and a study of them when a linear process has pth moment p > 2 or has a regularly varying tail with exponent t > 2.
3.3. Nonparametric regression
Consider the regression model
where g is a bounded continuous function on ℝm, zn,j are fixed design points over ![]() $\Gamma_n^d \subseteq \mathbb{Z}^d$ with values in a compact subset of ℝm, and Xn,j = Σi∈ ℤd aiεn,j −i is a linear random field over ℤd,where the i.i.d. innovations εn,i satisfy the same conditions as in Subsection 3.1. The kernel regression estimation for the function g on the basis of sample pairs (zn,j, Yn,j),
$\Gamma_n^d \subseteq \mathbb{Z}^d$ with values in a compact subset of ℝm, and Xn,j = Σi∈ ℤd aiεn,j −i is a linear random field over ℤd,where the i.i.d. innovations εn,i satisfy the same conditions as in Subsection 3.1. The kernel regression estimation for the function g on the basis of sample pairs (zn,j, Yn,j), ![]() $j\in \Gamma_n^2 \subset \mathbb{Z}^2$ has been studied by [Reference Sang and Xiao41] under the condition that the i.i.d. innovations εn,i satisfy ‖εn,i‖ p < ∞ for some p > 2, and (or) the innovations have regularly varying right tail with index t > 2. See [Reference Sang and Xiao41] for more references in the literature for regression models with independent or weakly dependent random field errors.
$j\in \Gamma_n^2 \subset \mathbb{Z}^2$ has been studied by [Reference Sang and Xiao41] under the condition that the i.i.d. innovations εn,i satisfy ‖εn,i‖ p < ∞ for some p > 2, and (or) the innovations have regularly varying right tail with index t > 2. See [Reference Sang and Xiao41] for more references in the literature for regression models with independent or weakly dependent random field errors.
We study the kernel regression estimation for the function g on the basis of sample pairs (zn,j, Yn,j), ![]() $j\in \Gamma_n^d$, when the i.i.d. innovations εn,i satisfy the conditions as in Subsection 3.1. As in [Reference Sang and Xiao41] and the other references in the literature, the estimator that we consider is given by
$j\in \Gamma_n^d$, when the i.i.d. innovations εn,i satisfy the conditions as in Subsection 3.1. As in [Reference Sang and Xiao41] and the other references in the literature, the estimator that we consider is given by
where the weight functions wn,j(·) on ℝm have the form
Here K : ℝm → ℝ+ is a kernel function and hn is a sequence of bandwidths which goes to 0 as n → ∞. Note that the weight functions satisfy the condition ![]() $\sum_{j\in\Gamma_n^d} w_{n,j}(z) = 1$.
$\sum_{j\in\Gamma_n^d} w_{n,j}(z) = 1$.
For a fixed z ∈ ℝm, let
where ![]() $b_{n,j}(z)=\sum_{i\in\Gamma_n^d} w_{n,i}(z) a_{i-j}.$ Let
$b_{n,j}(z)=\sum_{i\in\Gamma_n^d} w_{n,i}(z) a_{i-j}.$ Let ![]() $B_n(z)=\sigma^2\sum_{j\in \mathbb{Z}^d}b_{n,j}^2(z)$ and
$B_n(z)=\sigma^2\sum_{j\in \mathbb{Z}^d}b_{n,j}^2(z)$ and ![]() $M_n(z)=\max_{j\in\mathbb{Z}^d}| b_{nj}(z)|$. By the same analysis as in the proof of Theorem 3.1, we take Hn ∝ Mn(z)−1 and derive a moderate deviation result for
$M_n(z)=\max_{j\in\mathbb{Z}^d}| b_{nj}(z)|$. By the same analysis as in the proof of Theorem 3.1, we take Hn ∝ Mn(z)−1 and derive a moderate deviation result for ![]() $S_n(z)=g_n(z)-\mathbb{E}g_n(z)$. That is, if
$S_n(z)=g_n(z)-\mathbb{E}g_n(z)$. That is, if ![]() $B_n (z)H_n^2\to \infty$ as n → ∞, x ≥ 0,
$B_n (z)H_n^2\to \infty$ as n → ∞, x ≥ 0, ![]() $x=o(H_n\sqrt{B_n(z)})$, then
$x=o(H_n\sqrt{B_n(z)})$, then
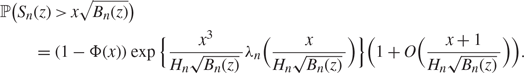 $$\matrix{ {{\rm {\mathbb P}}({S_n}(z) > x\sqrt {{B_n}(z)} )} \hfill \cr
{\quad \;\quad = \left( {1 - \Phi (x)} \right)\exp \left\{ {{{{x^3}} \over {{H_n}\sqrt {{B_n}(z)} {\kern 1pt} }}{\lambda _n}\left( {{x \over {{H_n}\sqrt {{B_n}(z)} {\kern 1pt} }}} \right)} \right\}\left( {1 + O\left( {{{x + 1} \over {{H_n}\sqrt {{B_n}(z)} {\kern 1pt} }}} \right)} \right).} \hfill \cr } $$
$$\matrix{ {{\rm {\mathbb P}}({S_n}(z) > x\sqrt {{B_n}(z)} )} \hfill \cr
{\quad \;\quad = \left( {1 - \Phi (x)} \right)\exp \left\{ {{{{x^3}} \over {{H_n}\sqrt {{B_n}(z)} {\kern 1pt} }}{\lambda _n}\left( {{x \over {{H_n}\sqrt {{B_n}(z)} {\kern 1pt} }}} \right)} \right\}\left( {1 + O\left( {{{x + 1} \over {{H_n}\sqrt {{B_n}(z)} {\kern 1pt} }}} \right)} \right).} \hfill \cr } $$
A similar bound can be derived for ![]() ${\rm {\mathbb P}}(|S_n(z)|>x\sqrt{B_n(z)} )$. Note that these tail probability estimates are more precise than those obtained in [Reference Sang and Xiao41], where an upper bound for the law of the iterated logarithm of
${\rm {\mathbb P}}(|S_n(z)|>x\sqrt{B_n(z)} )$. Note that these tail probability estimates are more precise than those obtained in [Reference Sang and Xiao41], where an upper bound for the law of the iterated logarithm of ![]() $g_n(z)-\mathbb{E}g_n(z)$ was derived. With the more precise bound on the tail probability in (3.5) and certain assumptions on g and the fixed design points {zn ,j} (cf. [Reference Gu and Tran17]), we can construct a confidence interval for g(z).
$g_n(z)-\mathbb{E}g_n(z)$ was derived. With the more precise bound on the tail probability in (3.5) and certain assumptions on g and the fixed design points {zn ,j} (cf. [Reference Gu and Tran17]), we can construct a confidence interval for g(z).
More interestingly, our method provides a way for constructing confidence bands for the function g(z) when z ∈ T, where T ∈ ℝm is a compact interval. Observe that, for any z, z′ ∈ T, we can write
Under certain regularity assumptions on g and the fixed design points {zn ,j} (cf. [Reference Gu and Tran17]), we can apply the argument in Subsection 3.1 to derive an exponential upper bound for the tail probability ![]() ${\rm {\mathbb P}} (|S_n(z) - S_n(z')|>x\sqrt{B_n(z, z')})$, where
${\rm {\mathbb P}} (|S_n(z) - S_n(z')|>x\sqrt{B_n(z, z')})$, where ![]() $B_n(z, z') = \sigma^2\sum_{j\in \mathbb{Z}^d}(b_{n,j}(z) - b_{n,j}(z'))^2$. Such a sharp upper bound, combined with the chaining argument (cf. [Reference Talagrand46]) would allow us to derive an exponential upper bound for
$B_n(z, z') = \sigma^2\sum_{j\in \mathbb{Z}^d}(b_{n,j}(z) - b_{n,j}(z'))^2$. Such a sharp upper bound, combined with the chaining argument (cf. [Reference Talagrand46]) would allow us to derive an exponential upper bound for
which can be applied to derive the uniform convergence rate of gn(z) → g(z) for all z ∈ T and to construct a confidence band for the function g(z), z ∈ T. It is nontrivial to carry out this project rigorously and the verification of the details is a little lengthy. Hence, we will have to consider it elsewhere.
4. Proofs
4.1. Proof of Theorem 2.1
Since γ 1nj = 0, the cumulant generating function Lnj(z) of Xnj can be written as
 \begin{align*}
L_{nj}(z)=\log {\rm {\mathbb E}} \text e^{z\:X_{nj}}=\sum_{k=2}^\infty
\frac{\gamma_{knj}}{k!}z^{\,k}.
\end{align*}
\begin{align*}
L_{nj}(z)=\log {\rm {\mathbb E}} \text e^{z\:X_{nj}}=\sum_{k=2}^\infty
\frac{\gamma_{knj}}{k!}z^{\,k}.
\end{align*}
Cauchy’s inequality for the derivatives of analytic functions together with the condition (2.2) yields
By following the conjugate method (cf. [Reference Petrov34, Reference Petrov35]), we now introduce an auxiliary sequence of independent random variables {X̅nj}, j ∈ ℤd, with the distribution functions
where Vnj(y) = ℙ(Xnj < y) and z ∈ (− Hn, Hn) is a real number whose value will be specified later.
Denote
 \begin{align*}
\overline{m}_{nj}= {\rm {\mathbb E}}\overline{X}_{nj}, \quad\quad \overline{\sigma}_{nj}^2=
{\rm {\mathbb E}}(\overline{X}_{nj}-\overline{m}_{nj})^2, \quad\quad
\overline{S}_{m,n}=\sum_{j\in\Gamma^d_m}\overline{X}_{nj},
\\
\overline{S}_n=\sum_{j\in\mathbb{Z}^d}\overline{X}_{nj}, \quad\quad
\overline{M}_{n}=\sum_{j\in\mathbb{Z}^d}\overline{m}_{nj}, \quad\quad
\overline{B}_{n}=\sum_{j\in\mathbb{Z}^d}\overline{\sigma}_{nj}^2
\end{align*}
\begin{align*}
\overline{m}_{nj}= {\rm {\mathbb E}}\overline{X}_{nj}, \quad\quad \overline{\sigma}_{nj}^2=
{\rm {\mathbb E}}(\overline{X}_{nj}-\overline{m}_{nj})^2, \quad\quad
\overline{S}_{m,n}=\sum_{j\in\Gamma^d_m}\overline{X}_{nj},
\\
\overline{S}_n=\sum_{j\in\mathbb{Z}^d}\overline{X}_{nj}, \quad\quad
\overline{M}_{n}=\sum_{j\in\mathbb{Z}^d}\overline{m}_{nj}, \quad\quad
\overline{B}_{n}=\sum_{j\in\mathbb{Z}^d}\overline{\sigma}_{nj}^2
\end{align*}
and
Note that, in the above and below, we have suppressed z for simplicity of notation.
We shall see in the later analysis that the quantities S̅n, M̅n, and B̅n are well defined for every n and z ∈ ℝ with |z| < aHn, where a < 1 is a positive constant which is independent of n. Throughout the proof we will obtain some estimates holding for the values of z satisfying |z| < bHn, where the positive constant b < 1 may vary but is always independent of n. We will then take a to be the smallest one among those constants b. The selection of the constants does not affect the proof since the z = zn we need in the later analysis has property z = o(Hn).
Also, the change of the order of summation of double series presented in the proof is justified by the absolute convergence of those series in the specified regions.
Step 1: Representation of ℙ(Sn < x) in terms of the conjugate measure. First note that by Equation (2.11) of [Reference Petrov35, p. 221], for any m ∈ ℕ, we have
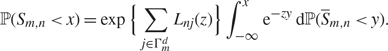 \begin{align}\label{partial}
{\rm {\mathbb P}}(S_{m,n}\lt x)=\exp\Big\{\sum_{j\in\Gamma^d_m}L_{nj}(z)\Big\}
\int_{-\infty}^{x}\text e^{-zy}\text d{\rm {\mathbb P}}(\overline{S}_{m,n}\lt y).
\end{align}
\begin{align}\label{partial}
{\rm {\mathbb P}}(S_{m,n}\lt x)=\exp\Big\{\sum_{j\in\Gamma^d_m}L_{nj}(z)\Big\}
\int_{-\infty}^{x}\text e^{-zy}\text d{\rm {\mathbb P}}(\overline{S}_{m,n}\lt y).
\end{align}
Note that the condition (2.3) implies that Cn < ∞, n ∈ ℕ. From (4.1), it follows that, for any w with ![]() $|w|\lt \tfrac{2}{3}H_n$ and for any m ∈ ℕ, we have
$|w|\lt \tfrac{2}{3}H_n$ and for any m ∈ ℕ, we have
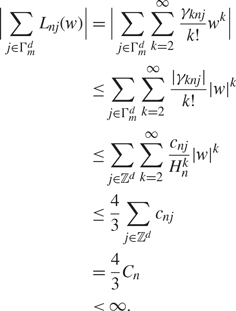 \begin{align}
\Big|\sum_{j\in\Gamma^d_m}L_{nj}(w)\Big| & =
\Big|\sum_{j\in\Gamma^d_m}\sum_{k=2}^\infty
\frac{\gamma_{knj}}{k!}w^k\Big|
\\
&\leq \sum_{j\in\Gamma^d_m}\sum_{k=2}^\infty
\frac{|\gamma_{knj}|}{k!}|w|^k\\
&\leq \sum_{j\in\mathbb{Z}^d}\sum_{k=2}^\infty
\frac{c_{nj}}{H_n^k}|w|^k
\\
&\leq
\frac{4}{3}\sum_{j\in\mathbb{Z}^d}c_{nj}
\\
&=\frac{4}{3}C_n
\\
&\lt \infty.\label{cgf partial}
\end{align}
\begin{align}
\Big|\sum_{j\in\Gamma^d_m}L_{nj}(w)\Big| & =
\Big|\sum_{j\in\Gamma^d_m}\sum_{k=2}^\infty
\frac{\gamma_{knj}}{k!}w^k\Big|
\\
&\leq \sum_{j\in\Gamma^d_m}\sum_{k=2}^\infty
\frac{|\gamma_{knj}|}{k!}|w|^k\\
&\leq \sum_{j\in\mathbb{Z}^d}\sum_{k=2}^\infty
\frac{c_{nj}}{H_n^k}|w|^k
\\
&\leq
\frac{4}{3}\sum_{j\in\mathbb{Z}^d}c_{nj}
\\
&=\frac{4}{3}C_n
\\
&\lt \infty.\label{cgf partial}
\end{align}
Therefore, for any v with ![]() $|v|\lt \tfrac{1}{2}H_n$ and z with
$|v|\lt \tfrac{1}{2}H_n$ and z with ![]() $|z|\lt \tfrac{1}{6}H_n$,
$|z|\lt \tfrac{1}{6}H_n$,
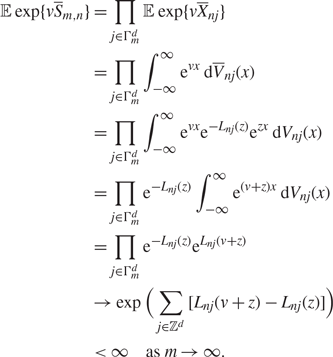 \begin{align}
{\rm {\mathbb E}} \exp\{v\overline{S}_{m,n}\} &= \prod_{j\in\Gamma^d_m} {\rm {\mathbb E}}\exp\{v
\overline{X}_{nj}\}
\\
&=\prod_{j\in\Gamma^d_m}\int_{-\infty}^{\infty}\text e^{vx}\text d
\overline{V}_{nj}(x)
\\
&= \prod_{j\in\Gamma^d_m}\int_{-\infty}^{\infty}\text e^{vx}\text e^{-L_{nj}(z)}
\text e^{zx}\text d V_{nj}(x)
\\
&=\prod_{j\in\Gamma^d_m}\text e^{-L_{nj}(z)}\int_{-\infty}^{\infty}
\text e^{(v+z)x}\text d V_{nj}(x)
\\
&= \prod_{j\in\Gamma^d_m}\text e^{-L_{nj}(z)}\text e^{L_{nj}(v+z)}
\\
&\rightarrow\exp\Big(\sum_{j\in\mathbb{Z}^d}
[L_{nj}(v+z)-L_{nj}(z)]\Big)
\\
&\lt \infty \quad\text{as } m\rightarrow \infty.\label{mgf partial}
\end{align}
\begin{align}
{\rm {\mathbb E}} \exp\{v\overline{S}_{m,n}\} &= \prod_{j\in\Gamma^d_m} {\rm {\mathbb E}}\exp\{v
\overline{X}_{nj}\}
\\
&=\prod_{j\in\Gamma^d_m}\int_{-\infty}^{\infty}\text e^{vx}\text d
\overline{V}_{nj}(x)
\\
&= \prod_{j\in\Gamma^d_m}\int_{-\infty}^{\infty}\text e^{vx}\text e^{-L_{nj}(z)}
\text e^{zx}\text d V_{nj}(x)
\\
&=\prod_{j\in\Gamma^d_m}\text e^{-L_{nj}(z)}\int_{-\infty}^{\infty}
\text e^{(v+z)x}\text d V_{nj}(x)
\\
&= \prod_{j\in\Gamma^d_m}\text e^{-L_{nj}(z)}\text e^{L_{nj}(v+z)}
\\
&\rightarrow\exp\Big(\sum_{j\in\mathbb{Z}^d}
[L_{nj}(v+z)-L_{nj}(z)]\Big)
\\
&\lt \infty \quad\text{as } m\rightarrow \infty.\label{mgf partial}
\end{align}
Hence, S̅n is well defined and S̅m,n converges to S̅n in distribution or, equivalently, in probability or almost surely as m→ ∞.
For the x in ℙ(Sn < x), let f (y) = exp{−zy}1{y < x} and M > 0. By Markov’s inequality, we have
 \begin{align*}
&{\rm {\mathbb E}} \{f(\overline{S}_{m,n})\textbf{1}\{ |f(\overline{S}_{m,n})|>M\}\}
\\
&\quad\quad\leq {\rm {\mathbb E}} \{\exp\{\!-z\overline{S}_{m,n}\} \textbf{1}\{
\exp\{\!-z\overline{S}_{m,n}\}>M\}\}
\\
&\quad\quad\leq\Big[{\rm {\mathbb E}} \Big\{\!\exp\{\!-2z\overline{S}_{m,n}\}\Big\}
\Big]^{{1}/{2}}\Big[{\rm {\mathbb E}} \Big\{ \textbf{1}\{
\exp\{\!-z\overline{S}_{m,n}\}>M\}\Big\} \Big]^{{1}/{2}}
\\
&\quad\quad\leq \Big[ \prod_{j\in\Gamma^d_m}\text e^{-L_{nj}(z)}\text e^{L_{nj}(\!-z)}
\Big]^{{1}/{2}}\Big[\frac{1}{M}{\rm {\mathbb E}}
\Big\{\!\exp\{\!-z\overline{S}_{m,n}\}\Big\}\Big]^{{1}/{2}}
\\
&\quad\quad=\frac{1}{\sqrt{M}\,}\Big[
\prod_{j\in\Gamma^d_m}\text e^{-L_{nj}(z)}\text e^{L_{nj}(\!-z)}\Big]^{{1}/{2}}
\Big[ \prod_{j\in\Gamma^d_m}\text e^{-L_{nj}(z)}
\text e^{L_{nj}(0)}\Big]^{{1}/{2}}.
\end{align*}
\begin{align*}
&{\rm {\mathbb E}} \{f(\overline{S}_{m,n})\textbf{1}\{ |f(\overline{S}_{m,n})|>M\}\}
\\
&\quad\quad\leq {\rm {\mathbb E}} \{\exp\{\!-z\overline{S}_{m,n}\} \textbf{1}\{
\exp\{\!-z\overline{S}_{m,n}\}>M\}\}
\\
&\quad\quad\leq\Big[{\rm {\mathbb E}} \Big\{\!\exp\{\!-2z\overline{S}_{m,n}\}\Big\}
\Big]^{{1}/{2}}\Big[{\rm {\mathbb E}} \Big\{ \textbf{1}\{
\exp\{\!-z\overline{S}_{m,n}\}>M\}\Big\} \Big]^{{1}/{2}}
\\
&\quad\quad\leq \Big[ \prod_{j\in\Gamma^d_m}\text e^{-L_{nj}(z)}\text e^{L_{nj}(\!-z)}
\Big]^{{1}/{2}}\Big[\frac{1}{M}{\rm {\mathbb E}}
\Big\{\!\exp\{\!-z\overline{S}_{m,n}\}\Big\}\Big]^{{1}/{2}}
\\
&\quad\quad=\frac{1}{\sqrt{M}\,}\Big[
\prod_{j\in\Gamma^d_m}\text e^{-L_{nj}(z)}\text e^{L_{nj}(\!-z)}\Big]^{{1}/{2}}
\Big[ \prod_{j\in\Gamma^d_m}\text e^{-L_{nj}(z)}
\text e^{L_{nj}(0)}\Big]^{{1}/{2}}.
\end{align*}
Hence, by (4.3) we have, for ![]() $|z|\lt \tfrac{1}{6}H_n$,
$|z|\lt \tfrac{1}{6}H_n$,
Applying Theorem 2.20 of [Reference Van Der Vaart47], we have
And taking into account that
and
we obtain, from (4.2),
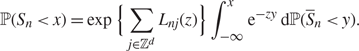 \begin{align} \label{cdf1}
{\rm {\mathbb P}}(S_n\lt x)=\exp\Big\{\sum_{j\in\mathbb{Z}^d}L_{nj}(z)\Big\}
\int_{-\infty}^{x}\text e^{-zy}\text d{\rm {\mathbb P}}(\overline{S}_n\lt y).
\end{align}
\begin{align} \label{cdf1}
{\rm {\mathbb P}}(S_n\lt x)=\exp\Big\{\sum_{j\in\mathbb{Z}^d}L_{nj}(z)\Big\}
\int_{-\infty}^{x}\text e^{-zy}\text d{\rm {\mathbb P}}(\overline{S}_n\lt y).
\end{align}
Step 2: Properties of the conjugate measure. From the calculation of (4.4), it follows that the cumulant generating function L̅nj(v) of the random variable X̅nj exists when |v| is sufficiently small and we have
j ∈ ℤd. Denoting by ![]() $\overline{\gamma}_{knj}$ the cumulant of order k of the random variable X̅nj, we obtain
$\overline{\gamma}_{knj}$ the cumulant of order k of the random variable X̅nj, we obtain
 \begin{align*}
\overline{\gamma}_{knj}=\Big[\frac{\text d^k\overline{L}_{nj}(v)} {\text d
v^k}\Big]_{v=0}=\frac{\text d^kL_{nj}(z)}{\text d z^{\,k}}.
\end{align*}
\begin{align*}
\overline{\gamma}_{knj}=\Big[\frac{\text d^k\overline{L}_{nj}(v)} {\text d
v^k}\Big]_{v=0}=\frac{\text d^kL_{nj}(z)}{\text d z^{\,k}}.
\end{align*}
Setting k = 1 and k = 2, we find that
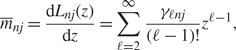 \begin{align} \label{Eq:mbar}
\overline{m}_{nj}=\frac{\text d L_{nj}(z)}{\text d z}= \sum_{\ell =2}^\infty
\frac{\gamma_{\ell nj}}{(\ell -1)!}z^{\ell-1},
\end{align}
\begin{align} \label{Eq:mbar}
\overline{m}_{nj}=\frac{\text d L_{nj}(z)}{\text d z}= \sum_{\ell =2}^\infty
\frac{\gamma_{\ell nj}}{(\ell -1)!}z^{\ell-1},
\end{align}
and
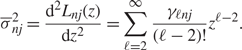 \begin{align} \label{Eq:sbar}
\overline{\sigma}_{nj}^2=\frac{\text d^2L_{nj}(z)}{\text d
z^2}=\sum_{\ell=2}^\infty \frac{\gamma_{\ell nj}}{(\ell-2)!}z^{\ell-2}.
\end{align}
\begin{align} \label{Eq:sbar}
\overline{\sigma}_{nj}^2=\frac{\text d^2L_{nj}(z)}{\text d
z^2}=\sum_{\ell=2}^\infty \frac{\gamma_{\ell nj}}{(\ell-2)!}z^{\ell-2}.
\end{align}
Hence, for ![]() $|z|\lt \tfrac{1}{2}H_n$, (4.7) implies that
$|z|\lt \tfrac{1}{2}H_n$, (4.7) implies that
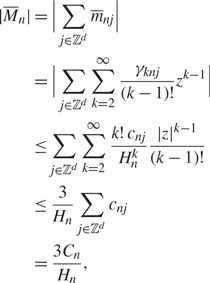 \begin{align} \label{M_nn}
|\overline{M}_{n}|&=\Big|\sum_{j\in\mathbb{Z}^d}\overline{m}_{nj} \Big
|
\\
&= \Big|\sum_{j\in\mathbb{Z}^d}\sum_{k=2}^\infty
\frac{\gamma_{knj}}{(k-1)!}z^{k-1}\Big|
\\
&\leq\sum_{j\in\mathbb{Z}^d}\sum_{k=2}^\infty
\frac{k!\,c_{nj}}{H_n^k}\frac{|z|^{k-1}}{(k-1)!}
\\
&\leq\frac{3}{H_n}\sum_{j\in\mathbb{Z}^d}c_{nj}
\\
&=\frac{3C_n}{H_n},
\end{align}
\begin{align} \label{M_nn}
|\overline{M}_{n}|&=\Big|\sum_{j\in\mathbb{Z}^d}\overline{m}_{nj} \Big
|
\\
&= \Big|\sum_{j\in\mathbb{Z}^d}\sum_{k=2}^\infty
\frac{\gamma_{knj}}{(k-1)!}z^{k-1}\Big|
\\
&\leq\sum_{j\in\mathbb{Z}^d}\sum_{k=2}^\infty
\frac{k!\,c_{nj}}{H_n^k}\frac{|z|^{k-1}}{(k-1)!}
\\
&\leq\frac{3}{H_n}\sum_{j\in\mathbb{Z}^d}c_{nj}
\\
&=\frac{3C_n}{H_n},
\end{align}
which means that M̅n is well defined and, as a function of z ∈ ℂ, is analytic in ![]() $|z|\lt \tfrac{1}{2}H_n$.
$|z|\lt \tfrac{1}{2}H_n$.
Also, without loss of generality, we assume that
By the definition of M̅n and (4.7), we have
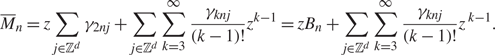 \begin{align}\label{sum for M_n}
\overline{M}_{n} =z\sum_{j\in\mathbb{Z}^d}
\gamma_{2nj}+\sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty
\frac{\gamma_{knj}}{(k-1)!}z^{k-1}
=zB_n+\sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty
\frac{\gamma_{knj}}{(k-1)!}z^{\,k-1}.
\end{align}
\begin{align}\label{sum for M_n}
\overline{M}_{n} =z\sum_{j\in\mathbb{Z}^d}
\gamma_{2nj}+\sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty
\frac{\gamma_{knj}}{(k-1)!}z^{k-1}
=zB_n+\sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty
\frac{\gamma_{knj}}{(k-1)!}z^{\,k-1}.
\end{align}
It follows from (4.1) that
 \begin{align*}
\Big|\sum_{k=3}^\infty \frac{\gamma_{knj}}{(k-1)!}z^{\,k-1}\Big| &\leq
|z|\sum_{k=3}^\infty \frac{k!\,c_{nj}}{H_n^k}\frac{|z|^{k-2}}{(k-1)!}
=\frac{|z|c_{nj}}{H_n^2}\sum_{k=3}^\infty k\Big| \frac{z}{H_n}\Big|^{k-2}
\leq \frac{|z|c_{nj}}{2H_n^2}
\end{align*}
\begin{align*}
\Big|\sum_{k=3}^\infty \frac{\gamma_{knj}}{(k-1)!}z^{\,k-1}\Big| &\leq
|z|\sum_{k=3}^\infty \frac{k!\,c_{nj}}{H_n^k}\frac{|z|^{k-2}}{(k-1)!}
=\frac{|z|c_{nj}}{H_n^2}\sum_{k=3}^\infty k\Big| \frac{z}{H_n}\Big|^{k-2}
\leq \frac{|z|c_{nj}}{2H_n^2}
\end{align*}
for |z| < b 1Hn and a suitable positive constant b 1 < 1 which is independent of j and n. This together with (4.11) implies that, for |z| < b 1Hn,
Taking into account condition (4.10), we obtain
Moreover, (4.11) implies that, for ![]() $|z|\lt \frac{1}{2}H_n$,
$|z|\lt \frac{1}{2}H_n$,
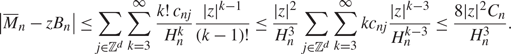 \begin{align}\label{M_n-zB_n}
\big|\overline{M}_{n}-zB_n \big|
\leq\sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty
\frac{k!\,c_{nj}}{H_n^k}\frac{|z|^{k-1}}{(k-1)!}\leq\frac{|z|^2}{H_n^3}\sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty
kc_{nj}\frac{|z|^{k-3}}{H_n^{k-3}}\leq
\frac{8|z|^2C_n}{H_n^3}.
\end{align}
\begin{align}\label{M_n-zB_n}
\big|\overline{M}_{n}-zB_n \big|
\leq\sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty
\frac{k!\,c_{nj}}{H_n^k}\frac{|z|^{k-1}}{(k-1)!}\leq\frac{|z|^2}{H_n^3}\sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty
kc_{nj}\frac{|z|^{k-3}}{H_n^{k-3}}\leq
\frac{8|z|^2C_n}{H_n^3}.
\end{align}
Also, by the definition of B̅n and (4.8), we have
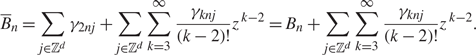 \begin{align}\label{sum for B_n}\overline{B}_{n} =\sum_{j\in{\rm \mathbb{Z}}^d}\gamma_{2nj}+\sum_{j\in{\rm \mathbb{Z}}^d}\sum_{k=3}^\infty\frac{\gamma_{knj}}{(k-2)!}z^{\,k-2}=B_n+\sum_{j\in{\rm \mathbb{Z}}^d}\sum_{k=3}^\infty\frac{\gamma_{knj}}{(k-2)!}z^{\,k-2}.\end{align}
\begin{align}\label{sum for B_n}\overline{B}_{n} =\sum_{j\in{\rm \mathbb{Z}}^d}\gamma_{2nj}+\sum_{j\in{\rm \mathbb{Z}}^d}\sum_{k=3}^\infty\frac{\gamma_{knj}}{(k-2)!}z^{\,k-2}=B_n+\sum_{j\in{\rm \mathbb{Z}}^d}\sum_{k=3}^\infty\frac{\gamma_{knj}}{(k-2)!}z^{\,k-2}.\end{align}
It follows from (4.1) that
 \begin{align*}
\Big|\sum_{k=3}^\infty \frac{\gamma_{knj}}{(k-2)!}z^{\,k-2}\Big|
\leq\sum_{k=3}^\infty \frac{k!\,
c_{nj}}{H_n^k}\frac{|z|^{k-2}}{(k-2)!}\leq\frac{c_{nj}}{2H_n^2}
\end{align*}
\begin{align*}
\Big|\sum_{k=3}^\infty \frac{\gamma_{knj}}{(k-2)!}z^{\,k-2}\Big|
\leq\sum_{k=3}^\infty \frac{k!\,
c_{nj}}{H_n^k}\frac{|z|^{k-2}}{(k-2)!}\leq\frac{c_{nj}}{2H_n^2}
\end{align*}
for |z| < b 2Hn and a suitable positive constant b 2 < 1 which is independent of j and n. This together with (4.14) implies that, for |z| < b 2 Hn, B̅n is well defined and
Condition (4.10) then implies that
Furthermore, (4.14) and (4.1) imply that, for ![]() $|z|\lt \frac{1}{2}H_n$,
$|z|\lt \frac{1}{2}H_n$,
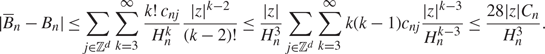 \begin{align} \label{B_n tail}
| \overline{B}_{n}-B_n| \leq\sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty
\frac{k!\,c_{nj}}{H_n^k}\frac{|z|^{k-2}}{(k-2)!}
\leq\frac{|z|}{H_n^3}\sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty
k(k-1)c_{nj}\frac{|z|^{k-3}}{H_n^{k-3}}\leq \frac{28|z|C_n}{H_n^3}.
\end{align}
\begin{align} \label{B_n tail}
| \overline{B}_{n}-B_n| \leq\sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty
\frac{k!\,c_{nj}}{H_n^k}\frac{|z|^{k-2}}{(k-2)!}
\leq\frac{|z|}{H_n^3}\sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty
k(k-1)c_{nj}\frac{|z|^{k-3}}{H_n^{k-3}}\leq \frac{28|z|C_n}{H_n^3}.
\end{align}
Step 3: Selection of z. Let z = zn be the real solution of
and let
Then
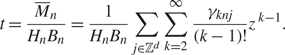 \begin{align}\label{t1}
t=\frac{\overline{M}_{n}}{H_nB_n}
=\frac{1}{H_nB_n}\sum_{j\in\mathbb{Z}^d}\sum_{k=2}^\infty
\frac{\gamma_{knj}}{(k-1)!}z^{\,k-1}.
\end{align}
\begin{align}\label{t1}
t=\frac{\overline{M}_{n}}{H_nB_n}
=\frac{1}{H_nB_n}\sum_{j\in\mathbb{Z}^d}\sum_{k=2}^\infty
\frac{\gamma_{knj}}{(k-1)!}z^{\,k-1}.
\end{align}
By (4.9), we know that M̅n/HnBn is analytic in a disc ![]() $|z|\lt \frac{1}{2}H_n$ and
$|z|\lt \frac{1}{2}H_n$ and
in that disc. It follows from Bloch’s theorem (see, e.g. [Reference Privalov39, p. 256]) that (4.19) has a real solution which can be written as
for
 \begin{align*}
|t|\lt \Biggl(\sqrt{\frac{1}{2}+\frac{3C_n}{H_n^2B_n}}-
\sqrt{\frac{3C_n}{H_n^2B_n}} \Biggr)^2.
\end{align*}
\begin{align*}
|t|\lt \Biggl(\sqrt{\frac{1}{2}+\frac{3C_n}{H_n^2B_n}}-
\sqrt{\frac{3C_n}{H_n^2B_n}} \Biggr)^2.
\end{align*}
Moreover, the absolute value of that sum in (4.20) is less than ![]() $\frac{1}{2}H_n$. Condition (2.3) implies that there exists a disc with center at t = 0 and radius R that does not depend on n within which the series on the right-hand side of (4.20) converges.
$\frac{1}{2}H_n$. Condition (2.3) implies that there exists a disc with center at t = 0 and radius R that does not depend on n within which the series on the right-hand side of (4.20) converges.
It can be checked from (4.19) and (4.20) that
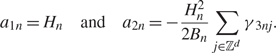 \begin{align}\label{a1a2}
a_{1n}=H_n \quad\text{and}\quad
a_{2n}=-\frac{H_n^2}{2B_n}\sum_{j\in\mathbb{Z}^d}\gamma_{\,3nj}.
\end{align}
\begin{align}\label{a1a2}
a_{1n}=H_n \quad\text{and}\quad
a_{2n}=-\frac{H_n^2}{2B_n}\sum_{j\in\mathbb{Z}^d}\gamma_{\,3nj}.
\end{align}
Cauchy’s inequality implies that, for every m ∈ ℕ,
Therefore, as t → 0, a 1nt becomes the dominant term of the series in (4.20). Hence, for sufficiently large n, we have
and taking into account (4.18) we obtain
It follows from (4.3) and (4.9) that for ![]() $z\lt \frac{1}{2}H_n$,
$z\lt \frac{1}{2}H_n$,
 \begin{align*}
\Big|z\overline{M}_{n}-\sum_{j\in\mathbb{Z}^d}L_{nj}(z)\Big|\leq
\frac{3|z|}{H_n}C_n+\frac{4}{3}C_n\lt 3C_n.
\end{align*}
\begin{align*}
\Big|z\overline{M}_{n}-\sum_{j\in\mathbb{Z}^d}L_{nj}(z)\Big|\leq
\frac{3|z|}{H_n}C_n+\frac{4}{3}C_n\lt 3C_n.
\end{align*}
For the solution z of (4.17), we also have
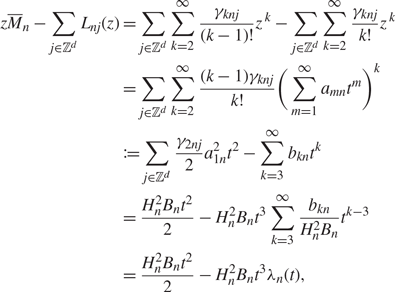 \begin{align}
z\overline{M}_{n}-\sum_{j\in\mathbb{Z}^d}L_{nj}(z)&=\sum_{j\in
\mathbb{Z}^d}\sum_{k=2}^\infty \frac{\gamma_{knj}}
{(k-1)!}z^{\,k}-\sum_{j\in\mathbb{Z}^d}\sum_{k=2}^\infty
\frac{\gamma_{knj}}{k!}z^{\,k}
\\
&=\sum_{j\in\mathbb{Z}^d} \sum_{k=2}^\infty
\frac{(k-1)\gamma_{knj}}{k!}\Bigg(\sum\limits_{m=1}^\infty a_{mn}t^m
\Bigg)^k
\\
&:= \sum_{j\in\mathbb{Z}^d}\frac{\gamma_{2nj}}{2}a_{1n}^2t^2-
\sum_{k=3}^\infty b_{kn}t^k
\\
& =\frac{H_n^2B_nt^2} {2}-H_n^2B_nt^3\sum_{k=3}^\infty\frac{
b_{kn}}{H_n^2B_n}t^{k-3}
\\
&=\frac{H_n^2B_nt^2}{2}-H_n^2B_nt^3\lambda_n(t),\label{lambda}
\end{align}
\begin{align}
z\overline{M}_{n}-\sum_{j\in\mathbb{Z}^d}L_{nj}(z)&=\sum_{j\in
\mathbb{Z}^d}\sum_{k=2}^\infty \frac{\gamma_{knj}}
{(k-1)!}z^{\,k}-\sum_{j\in\mathbb{Z}^d}\sum_{k=2}^\infty
\frac{\gamma_{knj}}{k!}z^{\,k}
\\
&=\sum_{j\in\mathbb{Z}^d} \sum_{k=2}^\infty
\frac{(k-1)\gamma_{knj}}{k!}\Bigg(\sum\limits_{m=1}^\infty a_{mn}t^m
\Bigg)^k
\\
&:= \sum_{j\in\mathbb{Z}^d}\frac{\gamma_{2nj}}{2}a_{1n}^2t^2-
\sum_{k=3}^\infty b_{kn}t^k
\\
& =\frac{H_n^2B_nt^2} {2}-H_n^2B_nt^3\sum_{k=3}^\infty\frac{
b_{kn}}{H_n^2B_n}t^{k-3}
\\
&=\frac{H_n^2B_nt^2}{2}-H_n^2B_nt^3\lambda_n(t),\label{lambda}
\end{align}
where ![]() $\lambda_n(t) =\sum_{k=0}^\infty \beta_{kn}t^k$ with
$\lambda_n(t) =\sum_{k=0}^\infty \beta_{kn}t^k$ with ![]() $ \beta_{kn} = b_{(k+3)n}(H_n^2B_n)^{-1}$.
$ \beta_{kn} = b_{(k+3)n}(H_n^2B_n)^{-1}$.
Recall that the series ![]() $\sum_{m=1}^\infty a_{mn} t^m$ converges in the disc centered at t = 0 with radius R > 0 that does not depend on n, and the absolute value of this sum is less than
$\sum_{m=1}^\infty a_{mn} t^m$ converges in the disc centered at t = 0 with radius R > 0 that does not depend on n, and the absolute value of this sum is less than ![]() $\frac{1}{2}H_n$. We see from (4.23) that the function λn(t) is obtained by the substitution of
$\frac{1}{2}H_n$. We see from (4.23) that the function λn(t) is obtained by the substitution of ![]() $\sum_{m=1}^\infty a_{mn}t^m$ in a series that converges on the interval
$\sum_{m=1}^\infty a_{mn}t^m$ in a series that converges on the interval ![]() $(-\frac{1}{2}H_n,\frac{1}{2}H_n)$. It follows from Cauchy’s inequality that
$(-\frac{1}{2}H_n,\frac{1}{2}H_n)$. It follows from Cauchy’s inequality that
which means that, for ![]() $|t|\lt \frac{1}{2}R, \lambda_n(t)$ stays bounded uniformly in n. In particular, by (4.21) and (4.23), we have β 0n = (Hn/6Bn) Σj∈ℤd γ 3nj.
$|t|\lt \frac{1}{2}R, \lambda_n(t)$ stays bounded uniformly in n. In particular, by (4.21) and (4.23), we have β 0n = (Hn/6Bn) Σj∈ℤd γ 3nj.
From now on we will assume that z is the unique real solution of (4.17).
Step 4: The 0 ≤ x ≤ 1 case. Now we prove the theorem for the 0 ≤ x ≤ 1 case using the method presented in [Reference Petrov and Robinson37]. Throughout the proof, C denotes a positive constant which may vary from line to line, but is independent of j, n, and z. If fn(s) is the characteristic function of ![]() $S_n/\sqrt{B_{n}}$ then, for
$S_n/\sqrt{B_{n}}$ then, for ![]() $|s|\lt H_n \sqrt{B_{n}}/2$,
$|s|\lt H_n \sqrt{B_{n}}/2$,
 \begin{align*}
f_n(s) =\int\limits_{-\infty}^\infty \text e^{isu}\text d{\rm {\mathbb P}}(S_n\leq
u\sqrt{B_{n}}) =\int_{-\infty}^\infty \text e^{isy/\sqrt{B_{n}}}\text d
{\rm {\mathbb P}}(S_n\leq y)
=\exp\Big\{\sum_{j\in\mathbb{Z}^d}L_{nj}\Big(\frac{is}{\sqrt{B_{n}}\,}\Big)\Big\}.
\end{align*}
\begin{align*}
f_n(s) =\int\limits_{-\infty}^\infty \text e^{isu}\text d{\rm {\mathbb P}}(S_n\leq
u\sqrt{B_{n}}) =\int_{-\infty}^\infty \text e^{isy/\sqrt{B_{n}}}\text d
{\rm {\mathbb P}}(S_n\leq y)
=\exp\Big\{\sum_{j\in\mathbb{Z}^d}L_{nj}\Big(\frac{is}{\sqrt{B_{n}}\,}\Big)\Big\}.
\end{align*}
Then
 \begin{align*}
\log f_n(s)&= \sum_{j\in\mathbb{Z}^d}L_{nj}\Big(\frac{is}{\sqrt{B_{n}}\,}\Big)
\\
&=\sum_{j\in\mathbb{Z}^d}\sum_{k=2}^\infty
\frac{\gamma_{knj}}{k!}\Big(\frac{is}{\sqrt{B_{n}}\,}\Big)^k
\\
&=-\sum_{j\in\mathbb{Z}^d}\frac{\gamma_{2nj}}{2}\frac{s^2}{B_{n}}+
\sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty
\frac{\gamma_{knj}}{k!}\Big(\frac{is}{\sqrt{B_{n}}\,}\Big)^k
\\
&=-\frac{s^2}{2}+\sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty
\frac{\gamma_{knj}}{k!}\Big(\frac{is}{\sqrt{B_{n}}\,}\Big)^k.
\end{align*}
\begin{align*}
\log f_n(s)&= \sum_{j\in\mathbb{Z}^d}L_{nj}\Big(\frac{is}{\sqrt{B_{n}}\,}\Big)
\\
&=\sum_{j\in\mathbb{Z}^d}\sum_{k=2}^\infty
\frac{\gamma_{knj}}{k!}\Big(\frac{is}{\sqrt{B_{n}}\,}\Big)^k
\\
&=-\sum_{j\in\mathbb{Z}^d}\frac{\gamma_{2nj}}{2}\frac{s^2}{B_{n}}+
\sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty
\frac{\gamma_{knj}}{k!}\Big(\frac{is}{\sqrt{B_{n}}\,}\Big)^k
\\
&=-\frac{s^2}{2}+\sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty
\frac{\gamma_{knj}}{k!}\Big(\frac{is}{\sqrt{B_{n}}\,}\Big)^k.
\end{align*}
Thus, using (4.1), we obtain, for ![]() $|s|\lt \delta H_n \sqrt{B_{n}}/2$ with 0 < δ < 1,
$|s|\lt \delta H_n \sqrt{B_{n}}/2$ with 0 < δ < 1,
 \begin{align*}\Big|\log f_n(s)+\frac{s^2}{2}\Big|\leq\sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty c_{nj}\Big(\frac{|s|}{H_n\sqrt{B_{n}}\,}\Big)^k\leq C_n\Big(\frac{|s|}{H_n\sqrt{B_{n}}\,}\Big)^3(1-\delta)^{-1}\end{align*}
\begin{align*}\Big|\log f_n(s)+\frac{s^2}{2}\Big|\leq\sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty c_{nj}\Big(\frac{|s|}{H_n\sqrt{B_{n}}\,}\Big)^k\leq C_n\Big(\frac{|s|}{H_n\sqrt{B_{n}}\,}\Big)^3(1-\delta)^{-1}\end{align*}
Then, for an appropriate choice of δ, we have
 \begin{align*}|f_n(s)-\text e^{-s^2/2}|\lt C\frac{\text e^{-s^2/4}|s|^3C_n}{H_n^3\sqrt{B_{n}}^3}
\lt C\frac{\text e^{-s^2/4}|s|^3}{H_n\sqrt{B_{n}}} \quad\text{for $|s|\lt \delta H_n \sqrt{B_{n}}/2$.}\end{align*}
\begin{align*}|f_n(s)-\text e^{-s^2/2}|\lt C\frac{\text e^{-s^2/4}|s|^3C_n}{H_n^3\sqrt{B_{n}}^3}
\lt C\frac{\text e^{-s^2/4}|s|^3}{H_n\sqrt{B_{n}}} \quad\text{for $|s|\lt \delta H_n \sqrt{B_{n}}/2$.}\end{align*} Now applying Theorem 5.1 of [Reference Petrov36] with b = 1/π and ![]() $T=\delta H_n \sqrt{B_{n}}/2$, we obtain
$T=\delta H_n \sqrt{B_{n}}/2$, we obtain
Since 0 ≤ x ≤ 1, ![]() $B_nH_n^2\rightarrow \infty$ as n → ∞, and
$B_nH_n^2\rightarrow \infty$ as n → ∞, and ![]() $\lambda_n({x}/{H_n\sqrt{B_n}})$ is bounded uniformly in n, we have
$\lambda_n({x}/{H_n\sqrt{B_n}})$ is bounded uniformly in n, we have
Together with condition (2.3), to have (2.4) in the 0 ≤ x ≤ 1 case, it is sufficient to show that 1
which is given by (4.24), since ![]() $\tfrac12\le \Phi(x)\le \Phi(1)$ for
$\tfrac12\le \Phi(x)\le \Phi(1)$ for ![]() $0\le x\le 1$.
$0\le x\le 1$.
So we will limit the proof of the theorem to the case x > 1, ![]() $x=o(H_n\sqrt{B_n})$.
$x=o(H_n\sqrt{B_n})$.
Step 5: The case x > 1, ![]() $x=o(H_n\sqrt{B_n})$}. Making a change of variables
$x=o(H_n\sqrt{B_n})$}. Making a change of variables ![]() $ y\rightsquigarrow \overline{M}_n+y\sqrt{\overline{B}_n}$ and applying (4.17), we can rewrite (4.5) as
$ y\rightsquigarrow \overline{M}_n+y\sqrt{\overline{B}_n}$ and applying (4.17), we can rewrite (4.5) as
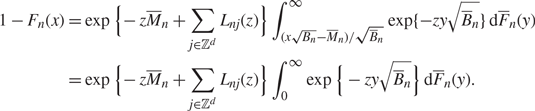 \begin{align}\label{cdf3}
1-F_n(x)&=\exp\Big\{\!-z\overline{M}_n+\sum_{j\in\mathbb{Z}^d}L_{nj}(z)
\Big\}\int_{(x\sqrt{B_n}-\overline{M}_n)/\sqrt{\overline{B}_n}}^{\infty}
\exp\{-zy\sqrt{\overline{B}_n}\}\text d\overline{F}_n(y)\notag
\\
&=\exp\Big\{\!-z\overline{M}_n+\sum_{j\in\mathbb{Z}^d}L_{nj}(z)\Big\}
\int_0^{\infty} \exp\Big\{-zy\sqrt{\overline{B}_n}\Big\}
\text d\overline{F}_n(y).
\end{align}
\begin{align}\label{cdf3}
1-F_n(x)&=\exp\Big\{\!-z\overline{M}_n+\sum_{j\in\mathbb{Z}^d}L_{nj}(z)
\Big\}\int_{(x\sqrt{B_n}-\overline{M}_n)/\sqrt{\overline{B}_n}}^{\infty}
\exp\{-zy\sqrt{\overline{B}_n}\}\text d\overline{F}_n(y)\notag
\\
&=\exp\Big\{\!-z\overline{M}_n+\sum_{j\in\mathbb{Z}^d}L_{nj}(z)\Big\}
\int_0^{\infty} \exp\Big\{-zy\sqrt{\overline{B}_n}\Big\}
\text d\overline{F}_n(y).
\end{align}
Denote rn(x) = F̅n(x) − Φ(x) and we show that, for sufficiently large n,
Let f̅n(s) be the characteristic function of ![]() $\[({\bar S_n} - {\bar M_n})/\sqrt {{{\bar B}_n}} \]$. We then have
$\[({\bar S_n} - {\bar M_n})/\sqrt {{{\bar B}_n}} \]$. We then have
 \begin{align*}
\overline{f}_n(s) &=\int_{-\infty}^\infty \text e^{isu}\text d
{\rm {\mathbb P}}(\overline{S}_n\leq u\sqrt{\overline{B}_{n}}+\overline{M}_{n})
\\
&=\int_{-\infty}^\infty \text e^{is(y-
\overline{M}_{n})/\sqrt{\overline{B}_{n}}} \text d{\rm {\mathbb P}}(\overline{S}_n\leq y)
\\
&=\exp\Big\{\!-\frac{is\overline{M}_{n}}{\sqrt{\overline{B}_{n}}\,}-
\sum_{j\in\mathbb{Z}^d}L_{nj}(z)\Big\}\int_{-\infty}^\infty
\text e^{(z+is/\sqrt{\overline{B}_{n}})y}\text d{\rm {\mathbb P}}(S_n\leq y)
\\
&=\exp\Big\{\!-\frac{is\overline{M}_{n}}{\sqrt{\overline{B}_{n}}\,}-
\sum_{j\in\mathbb{Z}^d}L_{nj}(z)+\sum_{j\in\mathbb{Z}^d}L_{nj}
\Big(z+\frac{is}{\sqrt{\overline{B}_{n}}\,}\Big)\Big\}.
\end{align*}
\begin{align*}
\overline{f}_n(s) &=\int_{-\infty}^\infty \text e^{isu}\text d
{\rm {\mathbb P}}(\overline{S}_n\leq u\sqrt{\overline{B}_{n}}+\overline{M}_{n})
\\
&=\int_{-\infty}^\infty \text e^{is(y-
\overline{M}_{n})/\sqrt{\overline{B}_{n}}} \text d{\rm {\mathbb P}}(\overline{S}_n\leq y)
\\
&=\exp\Big\{\!-\frac{is\overline{M}_{n}}{\sqrt{\overline{B}_{n}}\,}-
\sum_{j\in\mathbb{Z}^d}L_{nj}(z)\Big\}\int_{-\infty}^\infty
\text e^{(z+is/\sqrt{\overline{B}_{n}})y}\text d{\rm {\mathbb P}}(S_n\leq y)
\\
&=\exp\Big\{\!-\frac{is\overline{M}_{n}}{\sqrt{\overline{B}_{n}}\,}-
\sum_{j\in\mathbb{Z}^d}L_{nj}(z)+\sum_{j\in\mathbb{Z}^d}L_{nj}
\Big(z+\frac{is}{\sqrt{\overline{B}_{n}}\,}\Big)\Big\}.
\end{align*}
Then, by (4.6), for ![]() $|z|\lt \frac{1}{2} H_n$ and
$|z|\lt \frac{1}{2} H_n$ and ![]() $|s|\lt H_n \sqrt{\overline{B}_{n}}/6$, we have
$|s|\lt H_n \sqrt{\overline{B}_{n}}/6$, we have
 \begin{align*}
\log\overline{f}_n(s) &= -\frac{is\overline{M}_{n}}
{\sqrt{\overline{B}_{n}}\,}+
\sum_{j\in\mathbb{Z}^d}\overline{L}_{nj}(\frac{is}
{\sqrt{\overline{B}_{n}}\,})
\\
&= -\frac{1}{2}s^2+\frac{1}{6}\big(\frac{is}
{\sqrt{\overline{B}_{n}}\,}\big)^3
\Big[\frac{\text d^3\sum_{j\in\mathbb{Z}^d} \overline{L}_{nj}(y)}{\text d y^3}
\Big]_{y=\theta is/\sqrt{\overline{B}_{n}}},
\end{align*}
\begin{align*}
\log\overline{f}_n(s) &= -\frac{is\overline{M}_{n}}
{\sqrt{\overline{B}_{n}}\,}+
\sum_{j\in\mathbb{Z}^d}\overline{L}_{nj}(\frac{is}
{\sqrt{\overline{B}_{n}}\,})
\\
&= -\frac{1}{2}s^2+\frac{1}{6}\big(\frac{is}
{\sqrt{\overline{B}_{n}}\,}\big)^3
\Big[\frac{\text d^3\sum_{j\in\mathbb{Z}^d} \overline{L}_{nj}(y)}{\text d y^3}
\Big]_{y=\theta is/\sqrt{\overline{B}_{n}}},
\end{align*}
where 0 ≤ |θ| ≤ 1. For ![]() $|z|\lt \frac{1}{2} H_n$ and
$|z|\lt \frac{1}{2} H_n$ and ![]() $|s|\lt \delta H_n \sqrt{\overline{B}_{n}}/6$ with 0 < δ < 1, we have
$|s|\lt \delta H_n \sqrt{\overline{B}_{n}}/6$ with 0 < δ < 1, we have
 \begin{align*}
\Big|\Big[\frac{\text d^3\sum_{j\in\mathbb{Z}^d}\overline{L}_{nj}(y)} {\text d
y^3}\Big]_{y=\theta
is/\sqrt{\overline{B}_{n}}}\Big|&=\Big|\Big[\frac{\text d^3}{\text d y^3}
\sum_{j\in\mathbb{Z}^d}\sum_{k=1}^\infty
\frac{\overline{\gamma}_{knj}}{k!}y^k\Big]_{y=\theta
is/\sqrt{\overline{B}_{n}}}\Big|
\\
&=\Big|\sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty
\frac{\overline{\gamma}_{knj}}{(k-3)!}\Big(\frac{\theta
is}{\sqrt{\overline{B}_{n}}\,}\Big)^{k-3}\Big|
\\
&\leq \sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty
k(k-1)(k-2)\frac{c_{nj}}{(H_n/2)^k}
\Bigg(\frac{s}{\sqrt{\overline{B}_{n}}\,}\Bigg)^{k-3}
\\
&=\frac{48C_n}{H_n^3}\Big(1-\frac{s/\sqrt{\overline{B}_{n}}}{H_n/2}
\Big)^{-4}
\\
&\leq \frac{48C_n}{H_n^3}(1-\delta)^{-4}.
\end{align*}
\begin{align*}
\Big|\Big[\frac{\text d^3\sum_{j\in\mathbb{Z}^d}\overline{L}_{nj}(y)} {\text d
y^3}\Big]_{y=\theta
is/\sqrt{\overline{B}_{n}}}\Big|&=\Big|\Big[\frac{\text d^3}{\text d y^3}
\sum_{j\in\mathbb{Z}^d}\sum_{k=1}^\infty
\frac{\overline{\gamma}_{knj}}{k!}y^k\Big]_{y=\theta
is/\sqrt{\overline{B}_{n}}}\Big|
\\
&=\Big|\sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty
\frac{\overline{\gamma}_{knj}}{(k-3)!}\Big(\frac{\theta
is}{\sqrt{\overline{B}_{n}}\,}\Big)^{k-3}\Big|
\\
&\leq \sum_{j\in\mathbb{Z}^d}\sum_{k=3}^\infty
k(k-1)(k-2)\frac{c_{nj}}{(H_n/2)^k}
\Bigg(\frac{s}{\sqrt{\overline{B}_{n}}\,}\Bigg)^{k-3}
\\
&=\frac{48C_n}{H_n^3}\Big(1-\frac{s/\sqrt{\overline{B}_{n}}}{H_n/2}
\Big)^{-4}
\\
&\leq \frac{48C_n}{H_n^3}(1-\delta)^{-4}.
\end{align*}
Thus,
 \begin{align*}
\Big|\log\overline{f}_n(s)+\frac{s^2}{2}\Big|\lt \frac{8|s|^3C_n}{H_n^3
\sqrt{\overline{B}_{n}}^3}(1-\delta)^{-4}.
\end{align*}
\begin{align*}
\Big|\log\overline{f}_n(s)+\frac{s^2}{2}\Big|\lt \frac{8|s|^3C_n}{H_n^3
\sqrt{\overline{B}_{n}}^3}(1-\delta)^{-4}.
\end{align*}Then, for an appropriate choice of δ, we have
 \begin{align*}
|\overline{f}_n(s)-\text e^{-s^2/2}|\lt C\frac{\text e^{-s^2/4}|s|^3C_n}{H_n^3
\sqrt{\overline{B}_{n}}^3}\lt C\frac{\text e^{-s^2/4}|s|^3}{H_n
\sqrt{\overline{B}_{n}}} \quad\text{for $|s|\lt \delta H_n
\sqrt{\overline{B}_{n}}/6$.}
\end{align*}
\begin{align*}
|\overline{f}_n(s)-\text e^{-s^2/2}|\lt C\frac{\text e^{-s^2/4}|s|^3C_n}{H_n^3
\sqrt{\overline{B}_{n}}^3}\lt C\frac{\text e^{-s^2/4}|s|^3}{H_n
\sqrt{\overline{B}_{n}}} \quad\text{for $|s|\lt \delta H_n
\sqrt{\overline{B}_{n}}/6$.}
\end{align*}
Now applying (4.15) and Theorem 5.1 of [Reference Petrov36] with b = 1/π and ![]() $T=\delta H_n \sqrt{\overline{B}_{n}}/6$, we have (4.26).
$T=\delta H_n \sqrt{\overline{B}_{n}}/6$, we have (4.26).
By (4.26), we have
 \begin{align} \label{int}
&\int_0^{\infty}\exp\{-zy\sqrt{\overline{B}_n}\} \text d\overline{F}_n(y)
\\
&\quad\quad=\frac{1}{\sqrt{2\pi}\,} \int_0^{\infty}\exp
\biggl\{\!-zy\sqrt{\overline{B}_n} -\frac{y^2}{2}\biggr\}\text d
y-r_n(0)+z\sqrt{\overline{B}_n}\int_0^{\infty}r_n(y)\exp
\{\!-zy\sqrt{\overline{B}_n}\}\text d y
\\
&\quad\quad=\frac{1}{\sqrt{2\pi}\,}\int_0^{\infty}\exp
\Big\{\!-zy\sqrt{\overline{B}_n}-\frac{y^2}{2}\Big\}\text d y+\alpha_n,
\end{align}
\begin{align} \label{int}
&\int_0^{\infty}\exp\{-zy\sqrt{\overline{B}_n}\} \text d\overline{F}_n(y)
\\
&\quad\quad=\frac{1}{\sqrt{2\pi}\,} \int_0^{\infty}\exp
\biggl\{\!-zy\sqrt{\overline{B}_n} -\frac{y^2}{2}\biggr\}\text d
y-r_n(0)+z\sqrt{\overline{B}_n}\int_0^{\infty}r_n(y)\exp
\{\!-zy\sqrt{\overline{B}_n}\}\text d y
\\
&\quad\quad=\frac{1}{\sqrt{2\pi}\,}\int_0^{\infty}\exp
\Big\{\!-zy\sqrt{\overline{B}_n}-\frac{y^2}{2}\Big\}\text d y+\alpha_n,
\end{align}
where ![]() $|\alpha_n|\leq {C}/{H_n\sqrt{B_{n}}}$.
$|\alpha_n|\leq {C}/{H_n\sqrt{B_{n}}}$.
Denote
and
where
is the Mills ratio which is known to satisfy
Hence, by (4.22) and (4.15), we obtain
 \begin{align*}
\frac{\alpha_n}{xI_1} &=\frac{\alpha_nz\sqrt{\overline{B}_n}}{x}+
\frac{\alpha_n}{xz\sqrt{\overline{B}_n}\,}
\\
&\leq
C\Bigg(\frac{z\sqrt{B_n}}{xH_n\sqrt{B_n}\,}+\frac{1}{H_n\sqrt{B_n}xz
\sqrt{B_n}\,}\Bigg)
\\
&\leq C\Bigg(\frac{1}{H_n\sqrt{B_n}\,}+\frac{1}{H_n\sqrt{B_n}x^2}\Bigg)
\\
&\leq \frac{C}{H_n\sqrt{B_n}\,}.
\end{align*}
\begin{align*}
\frac{\alpha_n}{xI_1} &=\frac{\alpha_nz\sqrt{\overline{B}_n}}{x}+
\frac{\alpha_n}{xz\sqrt{\overline{B}_n}\,}
\\
&\leq
C\Bigg(\frac{z\sqrt{B_n}}{xH_n\sqrt{B_n}\,}+\frac{1}{H_n\sqrt{B_n}xz
\sqrt{B_n}\,}\Bigg)
\\
&\leq C\Bigg(\frac{1}{H_n\sqrt{B_n}\,}+\frac{1}{H_n\sqrt{B_n}x^2}\Bigg)
\\
&\leq \frac{C}{H_n\sqrt{B_n}\,}.
\end{align*}
Hence,
For every y 1 < y 2, we have ψ(y 2) − ψ(y 1) = (y 2 − y 1)ψ′(u), where y 1 < u < y 2. As for u > 0, |ψ′(u)| < u −2, then using (2.3), (4.12), (4.13), (4.15), (4.16), and (4.22), we obtain
 \begin{align*}
|I_2-I_1| &=|\psi '(u)||\overline{M}_{n}B^{-{1}/{2}}_n-z
\sqrt{\overline{B}_n}|
\\
&\leq \frac{1}{u^2\sqrt{B_n}\,}|\overline{M}_{n}-z\sqrt{B_n}
\sqrt{\overline{B}_n}|
\\
&\leq\frac{1}{u^2\sqrt{B_n}\,}\Big(|\overline{M}_{n}-zB_n|+
|zB_n-z\sqrt{B_n}\sqrt{\overline{B}_n}|\Big)
\\
&\leq \frac{C}{(x/{4})^2\sqrt{B_n}\,}\Big(\frac{z^2C_n}{H_n^3}+
z\sqrt{B}_n|\sqrt{B_n}-\sqrt{\overline{B}_n}|\Big)
\\
&\leq \frac{C}{x^2\sqrt{B_n}\,}\Big(\frac{x^2C_n}{B_nH_n^3}+\frac{x|B_n
-\overline{B}_n|}{\sqrt{B_n}+\sqrt{\overline{B}_n}\,}\Big)
\\
&\leq \frac{C}{x^2\sqrt{B_n}\,}\Big(\frac{x^2C_n}{B_nH_n^3}+\frac{xzC_n}
{H_n^3\sqrt{B_n}}\Big)
\\
&\leq \frac{C}{x^2\sqrt{B_n}}\Big(\frac{x^2C_n}{B_nH_n^3}+\frac{x^2C_n}
{H_n^3B_n}\Big)
\\
&=\frac{CC_n}{B_n^{{3}/{2}}H_n^3}
\\
&\leq \frac{C}{H_n\sqrt{B_n}\,}.
\end{align*}
\begin{align*}
|I_2-I_1| &=|\psi '(u)||\overline{M}_{n}B^{-{1}/{2}}_n-z
\sqrt{\overline{B}_n}|
\\
&\leq \frac{1}{u^2\sqrt{B_n}\,}|\overline{M}_{n}-z\sqrt{B_n}
\sqrt{\overline{B}_n}|
\\
&\leq\frac{1}{u^2\sqrt{B_n}\,}\Big(|\overline{M}_{n}-zB_n|+
|zB_n-z\sqrt{B_n}\sqrt{\overline{B}_n}|\Big)
\\
&\leq \frac{C}{(x/{4})^2\sqrt{B_n}\,}\Big(\frac{z^2C_n}{H_n^3}+
z\sqrt{B}_n|\sqrt{B_n}-\sqrt{\overline{B}_n}|\Big)
\\
&\leq \frac{C}{x^2\sqrt{B_n}\,}\Big(\frac{x^2C_n}{B_nH_n^3}+\frac{x|B_n
-\overline{B}_n|}{\sqrt{B_n}+\sqrt{\overline{B}_n}\,}\Big)
\\
&\leq \frac{C}{x^2\sqrt{B_n}\,}\Big(\frac{x^2C_n}{B_nH_n^3}+\frac{xzC_n}
{H_n^3\sqrt{B_n}}\Big)
\\
&\leq \frac{C}{x^2\sqrt{B_n}}\Big(\frac{x^2C_n}{B_nH_n^3}+\frac{x^2C_n}
{H_n^3B_n}\Big)
\\
&=\frac{CC_n}{B_n^{{3}/{2}}H_n^3}
\\
&\leq \frac{C}{H_n\sqrt{B_n}\,}.
\end{align*}
Hence,
which means that
Finally, combining (4.17), (4.18), (4.23), (4.25), (4.27), and (4.28), we obtain
 \begin{align*}
1-F_n(x)
&=\exp\Big\{\!-\frac{H_n^2B_nt^2}{2}+H_n^2B_nt^3\lambda_n(t)\Big\}
\int_{0}^{\infty}\exp\Big\{\!-zy\sqrt{\overline{B}_n}\Big\}
\text d\overline{F}_n(y)
\\
&=\exp\Big\{\!-\frac{x^2}{2}+\frac{x^3}{H_n\sqrt{B_n}\,}\lambda_n
\Big(\frac{x}{H_n\sqrt{B_n}\,}\Big)\Big\}\Big(\frac{1}{\sqrt{2\pi}\,}
I_1+\alpha_n\Big)
\\
&=\exp\Big\{\!-\frac{x^2}{2}+\frac{x^3}{H_n\sqrt{B_n}\,}\lambda_n
\Big(\frac{x}{H_n\sqrt{B_n}\,}\Big)\Big\}\frac{1}{\sqrt{2\pi}\,}I_1
\Big(1+O\Big(\frac{x}{H_n\sqrt{B_n}\,}\Big)\Big).
\end{align*}
\begin{align*}
1-F_n(x)
&=\exp\Big\{\!-\frac{H_n^2B_nt^2}{2}+H_n^2B_nt^3\lambda_n(t)\Big\}
\int_{0}^{\infty}\exp\Big\{\!-zy\sqrt{\overline{B}_n}\Big\}
\text d\overline{F}_n(y)
\\
&=\exp\Big\{\!-\frac{x^2}{2}+\frac{x^3}{H_n\sqrt{B_n}\,}\lambda_n
\Big(\frac{x}{H_n\sqrt{B_n}\,}\Big)\Big\}\Big(\frac{1}{\sqrt{2\pi}\,}
I_1+\alpha_n\Big)
\\
&=\exp\Big\{\!-\frac{x^2}{2}+\frac{x^3}{H_n\sqrt{B_n}\,}\lambda_n
\Big(\frac{x}{H_n\sqrt{B_n}\,}\Big)\Big\}\frac{1}{\sqrt{2\pi}\,}I_1
\Big(1+O\Big(\frac{x}{H_n\sqrt{B_n}\,}\Big)\Big).
\end{align*}
By (4.29) and the fact that I 2 = ψ(x), we see that
This proves (2.4). The proof of (2.5) follows the same pattern and is therefore omitted.
4.2. Proof of Theorem 3.1
Since γ 1 = 0, we see that the cumulant generating function Lnj(z) of the random variable bnjεj, j ∈ ℤd, is given by
 \begin{align*}
L_{nj}(z)=\log {\rm {\mathbb E}} \text e^{zb_{nj}\varepsilon_j}=\sum_{k=2}^\infty
\frac{\gamma_k b_{nj}^k}{k!}z^{\,k}.
\end{align*}
\begin{align*}
L_{nj}(z)=\log {\rm {\mathbb E}} \text e^{zb_{nj}\varepsilon_j}=\sum_{k=2}^\infty
\frac{\gamma_k b_{nj}^k}{k!}z^{\,k}.
\end{align*}
Cauchy’s inequality for the derivatives of analytic functions together with the condition (3.3) yields
Denote ![]() $M_n=\max\limits_{j\in\mathbb{Z}^d}| b_{nj}|$. Then by (4.30), for any Hn with 0 < Hn ≤ H/2Mn and for any z with |z| < Hn, we have
$M_n=\max\limits_{j\in\mathbb{Z}^d}| b_{nj}|$. Then by (4.30), for any Hn with 0 < Hn ≤ H/2Mn and for any z with |z| < Hn, we have
 \begin{align*}
\big|L_{nj}(z)\big| \leq\sum_{k=2}^\infty \frac{|\gamma_k||
b_{nj}|^k}{k!}|z|^k \leq C\sum_{k=2}^\infty \frac{| b_{nj}H_n|^k}{H^k} =
\frac{C}{H} \frac{b_{nj}^2H_n^2}{H-| b_{nj}H_n|} \leq
\frac{2Cb_{nj}^2H_n^2}{H^2}.
\end{align*}
\begin{align*}
\big|L_{nj}(z)\big| \leq\sum_{k=2}^\infty \frac{|\gamma_k||
b_{nj}|^k}{k!}|z|^k \leq C\sum_{k=2}^\infty \frac{| b_{nj}H_n|^k}{H^k} =
\frac{C}{H} \frac{b_{nj}^2H_n^2}{H-| b_{nj}H_n|} \leq
\frac{2Cb_{nj}^2H_n^2}{H^2}.
\end{align*}
Hence,
 \begin{align*}
C_n=\sum_{j\in\mathbb{Z}^d} \frac{2Cb_{nj}^2H_n^2}{H^2}=\frac{2CB_nH_n^2}{\sigma^2H^2}.
\end{align*}
\begin{align*}
C_n=\sum_{j\in\mathbb{Z}^d} \frac{2Cb_{nj}^2H_n^2}{H^2}=\frac{2CB_nH_n^2}{\sigma^2H^2}.
\end{align*}
Then by Theorem 2.1, if ![]() $B_n H_n^2\to \infty$ as n → ∞, we have
$B_n H_n^2\to \infty$ as n → ∞, we have
for x ≥ 0, ![]() $x=o(H_n\sqrt{B_n})$.
$x=o(H_n\sqrt{B_n})$.
If the linear random field has long memory then we have (see [Reference Surgailis45, Theorem 2]) Bn ∝ n 3d−2αl 2(n). As the function b(·) is bounded, then, for ![]() $j\in\Gamma^d_n$, we have
$j\in\Gamma^d_n$, we have
 \begin{align*}
|b_{nj}| \leq C_1\sum_{i\in\Gamma^d_n}l(|i-j|)|i-j|^{-\alpha}\leq
C_1\sum\limits_{k=1}^{2dn}k^{d-1}l(k)k^{-\alpha} \propto
n^{d-\alpha}l(n),
\end{align*}
\begin{align*}
|b_{nj}| \leq C_1\sum_{i\in\Gamma^d_n}l(|i-j|)|i-j|^{-\alpha}\leq
C_1\sum\limits_{k=1}^{2dn}k^{d-1}l(k)k^{-\alpha} \propto
n^{d-\alpha}l(n),
\end{align*}
where we have used the fact (see [Reference Bingham, Goldie and Teugels6] or [Reference Seneta42]) that, for a slowly varying function l(x) defined on [1, ∞) and for any θ > −1,
It follows from the definition of ai in (3.2) that (for sufficiently large n) ![]() $M_n=\max\limits_{j\in\mathbb{Z}^d}| b_{nj}|$ is attained at some
$M_n=\max\limits_{j\in\mathbb{Z}^d}| b_{nj}|$ is attained at some ![]() $j\in \Gamma^d_n$. Hence, Mn = O(nd −αl(n)). We take Hn ∝ n −d+αl −1(n) which yields
$j\in \Gamma^d_n$. Hence, Mn = O(nd −αl(n)). We take Hn ∝ n −d+αl −1(n) which yields
Then the result follows from (4.31).
If the linear random field has short memory, i.e. A := Σi∈ℤd |ai| < ∞, a := Σi∈ℤd ai ≠ 0, we can take Mn = A and Hn = H/2A. Moreover, we also have
and
which means that Σj∈ℤd |bnj| ∝ nd.
As for all n ∈ ℕ, we have |bnj| ≤ A by the definition of A, then
On the other hand, for ![]() $j\in\Gamma^d_{\left \lfloor{n/2}\right \rfloor}$, we have |bnj| > |a|/2 for sufficiently large n. Hence,
$j\in\Gamma^d_{\left \lfloor{n/2}\right \rfloor}$, we have |bnj| > |a|/2 for sufficiently large n. Hence,
 \begin{align*}
&\sum_{j\in\mathbb{Z}^d}b_{nj}^2\geq \sum_{j\in\Gamma^d_{\left
\lfloor{n/2}\right \rfloor }}b_{nj}^2\geq \frac{a^2}{4} \Big( 2\left
\lfloor{\frac{n}{2}}\right \rfloor+1\Big)^d.
\end{align*}
\begin{align*}
&\sum_{j\in\mathbb{Z}^d}b_{nj}^2\geq \sum_{j\in\Gamma^d_{\left
\lfloor{n/2}\right \rfloor }}b_{nj}^2\geq \frac{a^2}{4} \Big( 2\left
\lfloor{\frac{n}{2}}\right \rfloor+1\Big)^d.
\end{align*}
Thus, ![]() $\sum_{j\in\mathbb{Z}^d}b_{nj}^2\propto n^d$ and the result follows from (4.31).
$\sum_{j\in\mathbb{Z}^d}b_{nj}^2\propto n^d$ and the result follows from (4.31).
Acknowledgements
The authors are grateful to the referee and the Associate Editor for carefully reading the paper and for insightful suggestions that significantly improved the presentation of the paper. The research of Hailin Sang was supported by the Simons Foundation Grant 586789 and the College of Liberal Arts Faculty Grants for Research and Creative Achievement at the University of Mississippi. The research of Yimin Xiao was partially supported by NSF grants DMS-1612885 and DMS-1607089.

