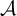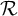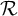1 Introduction
Linear cocycles consist of products of matrices driven by some dynamical system. A precise description of the asymptotics of these products is available for those orbits that are Lyapunov-Perron (or LP) regular. The multiplicative ergodic theorem of Oseledets says that the set
![]() $\mathcal {R}$
of LP-regular points is always large in a measure-theoretical sense: it has full measure with respect to any invariant probability measure. However, in many situations, the set
$\mathcal {R}$
of LP-regular points is always large in a measure-theoretical sense: it has full measure with respect to any invariant probability measure. However, in many situations, the set
![]() $\mathcal {R}$
is of first Baire category (i.e., meager) and so is small in a topological sense. Manifestations of this phenomenon in specific settings can be found in the works [Reference Tian60, Reference Ferreira and Varandas25, Reference Varandas and Dias61]. As for derivative cocycles, [Reference Abdenur, Bonatti and Crovisier1, Theorem 3.14] asserts that
$\mathcal {R}$
is of first Baire category (i.e., meager) and so is small in a topological sense. Manifestations of this phenomenon in specific settings can be found in the works [Reference Tian60, Reference Ferreira and Varandas25, Reference Varandas and Dias61]. As for derivative cocycles, [Reference Abdenur, Bonatti and Crovisier1, Theorem 3.14] asserts that
![]() $\mathcal {R}$
is a meager set for
$\mathcal {R}$
is a meager set for
![]() $C^1$
-generic diffeomorphisms.
$C^1$
-generic diffeomorphisms.
Our objective is to investigate the Baire category of the set
![]() $\mathcal {R}$
of Lyapunov-Perron regular points. More specifically, we aim to identify sufficient conditions under which
$\mathcal {R}$
of Lyapunov-Perron regular points. More specifically, we aim to identify sufficient conditions under which
![]() $\mathcal {R}$
is meager. We want these conditions to be as broadly applicable as possible.
$\mathcal {R}$
is meager. We want these conditions to be as broadly applicable as possible.
As a guiding principle, if the set
![]() $\mathcal {R}$
is non-meager, then some underlying rigid structure should account for this fact. Here is a result that corroborates this principle (Corollary 4.5): If the dynamics has the property that stable (or unstable) sets of periodic orbits are dense, then for every continuous cocycle, the set
$\mathcal {R}$
is non-meager, then some underlying rigid structure should account for this fact. Here is a result that corroborates this principle (Corollary 4.5): If the dynamics has the property that stable (or unstable) sets of periodic orbits are dense, then for every continuous cocycle, the set
![]() $\mathcal {R}$
of LP-regular points is meager, unless all periodic orbits have exactly the same Lyapunov spectrum. The hypothesis on the dynamics in Corollary 4.5 is quite general (allowing for nonuniformly hyperbolic maps, for instance), and there are no regularity assumptions on the cocycle other than continuity.
$\mathcal {R}$
of LP-regular points is meager, unless all periodic orbits have exactly the same Lyapunov spectrum. The hypothesis on the dynamics in Corollary 4.5 is quite general (allowing for nonuniformly hyperbolic maps, for instance), and there are no regularity assumptions on the cocycle other than continuity.
Under the strong assumption of minimality of the base dynamics, we obtain an even sharper dichotomy (Theorem 4.10): for every continuous cocycle, the set
![]() $\mathcal {R}$
of LP-regular points is either meager or it is the whole space. Furthermore, in the latter case, the cocycle will have extra properties that we call complete regularity.
$\mathcal {R}$
of LP-regular points is either meager or it is the whole space. Furthermore, in the latter case, the cocycle will have extra properties that we call complete regularity.
Given a continuous linear cocycle
![]() $\mathcal {A}$
over any topological dynamical system f, complete regularity is defined by two requirements. They are: (1) every trajectory of f is LP-regular, (2) the Lyapunov spectrum of
$\mathcal {A}$
over any topological dynamical system f, complete regularity is defined by two requirements. They are: (1) every trajectory of f is LP-regular, (2) the Lyapunov spectrum of
![]() $\mathcal {A}$
is independent of the point x. A restriction of a cocycle
$\mathcal {A}$
is independent of the point x. A restriction of a cocycle
![]() $\mathcal {A}$
to a periodic orbit of f is a simple example of a completely regular cocycle.
$\mathcal {A}$
to a periodic orbit of f is a simple example of a completely regular cocycle.
If a cocycle is completely regular, then the Oseledets splitting is defined everywhere. We prove (Corollary 3.3) that the Oseledets splitting is uniformly dominated and, in particular, continuous.
It becomes apparent that complete regularity is pertinent to our study of the Baire category of the set
![]() $\mathcal {R}$
of LP-regular points. Our most general criterion for meagerness of
$\mathcal {R}$
of LP-regular points. Our most general criterion for meagerness of
![]() $\mathcal {R}$
(Theorem 4.3) is actually formulated in terms of complete regularity. If the base dynamics f is hyperbolic and the cocycle
$\mathcal {R}$
(Theorem 4.3) is actually formulated in terms of complete regularity. If the base dynamics f is hyperbolic and the cocycle
![]() $\mathcal {A}$
is Hölder continuous, then we have a sharp dichotomy again (Theorem 4.8): either
$\mathcal {A}$
is Hölder continuous, then we have a sharp dichotomy again (Theorem 4.8): either
![]() $\mathcal {R}$
is meager or the cocycle is completely regular.
$\mathcal {R}$
is meager or the cocycle is completely regular.
Complete regularity can be characterized in terms of the Sacker–Sell spectrum of the cocycle: see [Reference Johnson and Zampogni35] and the discussion in Section 3.4 below.
Thus, motivated to understand the notion of complete regularity, we investigated whether the two requirements in the definition of complete regularity are independent. The short answer is yes: Section 5 exhibits examples of cocycles where one of the two conditions is satisfied but not the other. These examples may be of interest in other contexts.
2 Preliminaries
In this section, we recall some basic notions about linear cocycles and Lyapunov exponents.
Despite the fact that much of the material of this section makes sense in a measurable setting, we will assume continuity and compactness throughout.
2.1 Linear cocycles over continuous transformations
Let X be a topological space and
![]() $f: X\to X$
a homeomorphism. A function
$f: X\to X$
a homeomorphism. A function
![]() $\mathcal {A}=\mathcal {A}(x,n)$
,
$\mathcal {A}=\mathcal {A}(x,n)$
,
![]() $x\in X$
and
$x\in X$
and
![]() $n\in \mathbb {Z}$
with values in
$n\in \mathbb {Z}$
with values in
![]() $\mathrm {GL}(d,\mathbb {R})$
is called a continuous linear cocycle if the following properties hold:
$\mathrm {GL}(d,\mathbb {R})$
is called a continuous linear cocycle if the following properties hold:
-
1. for each
 $x\in X$
, we have
$x\in X$
, we have
 $\mathcal {A}(x,0)=\mathrm {Id}$
, and given
$\mathcal {A}(x,0)=\mathrm {Id}$
, and given
 $n,k\in \mathbb {Z}$
,
$n,k\in \mathbb {Z}$
,  $$\begin{align*}\mathcal{A}(x, n+k)=\mathcal{A}(f^k(x), n)\mathcal{A}(x, k); \end{align*}$$
$$\begin{align*}\mathcal{A}(x, n+k)=\mathcal{A}(f^k(x), n)\mathcal{A}(x, k); \end{align*}$$
-
2. for every
 $n\in \mathbb {Z}$
, the function
$n\in \mathbb {Z}$
, the function
 $\mathcal {A}(\cdot ,n)\colon X\to \mathrm {GL}(d,\mathbb {R})$
is continuous.
$\mathcal {A}(\cdot ,n)\colon X\to \mathrm {GL}(d,\mathbb {R})$
is continuous.
Given a continuous function
![]() $A\colon X\to \mathrm {GL}(d,\mathbb {R})$
, we define a cocycle by
$A\colon X\to \mathrm {GL}(d,\mathbb {R})$
, we define a cocycle by
 $$\begin{align*}\mathcal{A}(x, n) \mathrel{:=} \begin{cases} A(f^{n-1}(x))\cdots A(f(x))A(x) &\text{if } n>0\\ \text{Id} &\text{if } n=0,\\ {A(f^n(x))}^{-1}\cdots {A(f^{-2}(x))}^{-1}{A(f^{-1}(x))}^{-1} &\text{if } n<0. \end{cases} \end{align*}$$
$$\begin{align*}\mathcal{A}(x, n) \mathrel{:=} \begin{cases} A(f^{n-1}(x))\cdots A(f(x))A(x) &\text{if } n>0\\ \text{Id} &\text{if } n=0,\\ {A(f^n(x))}^{-1}\cdots {A(f^{-2}(x))}^{-1}{A(f^{-1}(x))}^{-1} &\text{if } n<0. \end{cases} \end{align*}$$
We call the map
![]() $A(x)$
the generator of the cocycle
$A(x)$
the generator of the cocycle
![]() $\mathcal {A}(x,n)$
and we say that the cocycle is generated by the function
$\mathcal {A}(x,n)$
and we say that the cocycle is generated by the function
![]() $A(x)$
. Every cocycle
$A(x)$
. Every cocycle
![]() $\mathcal {A}(x,n)$
is generated by the function
$\mathcal {A}(x,n)$
is generated by the function
![]() $A(x) \mathrel {:=} \mathcal {A}(x,1)$
.
$A(x) \mathrel {:=} \mathcal {A}(x,1)$
.
2.2 Lyapunov exponents and regularity of cocycles
Given a continuous cocycle
![]() $\mathcal {A}$
over the homeomorphism f, we say that a point
$\mathcal {A}$
over the homeomorphism f, we say that a point
![]() $x \in X$
is regular if there exist a list of numbers
$x \in X$
is regular if there exist a list of numbers
and a splitting
 $$ \begin{align} \mathbb{R}^d=\bigoplus_{i=1}^{s(x)}E_i(x) \end{align} $$
$$ \begin{align} \mathbb{R}^d=\bigoplus_{i=1}^{s(x)}E_i(x) \end{align} $$
such that the following conditions are satisfied:
-
• for every i with
 $1 \le i \le s(x)$
, the two-sided sequence converges to
$1 \le i \le s(x)$
, the two-sided sequence converges to $$\begin{align*}\frac1n \log\|\mathcal{A}(x,n)v\| \end{align*}$$
$$\begin{align*}\frac1n \log\|\mathcal{A}(x,n)v\| \end{align*}$$
 $\chi _i(x)$
as
$\chi _i(x)$
as
 $n \to \pm \infty $
uniformly in
$n \to \pm \infty $
uniformly in
 $v \in S^{d-1} \cap E_i(x)$
;
$v \in S^{d-1} \cap E_i(x)$
;
-
• for every partition of the set
 $\{1,\dots ,s(x)\}$
into two nonempty (disjoint) subsets I, J, we have where the angle
$\{1,\dots ,s(x)\}$
into two nonempty (disjoint) subsets I, J, we have where the angle $$\begin{align*}\lim_{n \to \pm \infty} \frac{1}{|n|} \log \measuredangle \left( \mathcal{A}(x,n) \left(\bigoplus_{i \in I} E_i(x)\right), \mathcal{A}(x,n) \left(\bigoplus_{j \in J} E_j(x)\right) \right) = 0 \, , \end{align*}$$
$$\begin{align*}\lim_{n \to \pm \infty} \frac{1}{|n|} \log \measuredangle \left( \mathcal{A}(x,n) \left(\bigoplus_{i \in I} E_i(x)\right), \mathcal{A}(x,n) \left(\bigoplus_{j \in J} E_j(x)\right) \right) = 0 \, , \end{align*}$$
 $\measuredangle (E,F)$
between two subspaces is defined as the least nonnegative angle between two vectors in the corresponding spaces.
$\measuredangle (E,F)$
between two subspaces is defined as the least nonnegative angle between two vectors in the corresponding spaces.
If x is a regular point, it can be shown that the Lyapunov exponents (2.1) and the Oseledets splitting (2.2) are uniquely defined. Let
![]() $\mathcal {R}$
denote the set of regular points. It can be shown that
$\mathcal {R}$
denote the set of regular points. It can be shown that
![]() $\mathcal {R}$
is a Borel set and that the number
$\mathcal {R}$
is a Borel set and that the number
![]() $s(x)$
, the Lyapunov exponents
$s(x)$
, the Lyapunov exponents
![]() $\chi _i(x)$
, and Oseledets spaces
$\chi _i(x)$
, and Oseledets spaces
![]() $E_i(x)$
all depend Borel measurably on x, and that they satisfy the invariance relations:
$E_i(x)$
all depend Borel measurably on x, and that they satisfy the invariance relations:
According to the Multiplicative Ergodic Theorem of Oseledets,
![]() $\mu (\mathcal {R})=1$
for every f-invariant Borel probability measure
$\mu (\mathcal {R})=1$
for every f-invariant Borel probability measure
![]() $\mu $
on X. If
$\mu $
on X. If
![]() $\mu $
is ergodic, then the Lyapunov exponent
$\mu $
is ergodic, then the Lyapunov exponent
![]() $\chi _i(x)$
is the same for
$\chi _i(x)$
is the same for
![]() $\mu $
-almost every x, and this common value is denoted
$\mu $
-almost every x, and this common value is denoted
![]() $\chi _i(\mu )$
.
$\chi _i(\mu )$
.
The notion of regularity as defined above is equivalent to Lyapunov-Perron regularity (or LP regularity). The latter requires that the cocycle
![]() $\mathcal A$
must be forward and backward regular. We refer the reader to [Reference Barreira and Pesin7] for these definitions. We note that our requirements (2.1) and (2.2) imply that every regular point is both forward and backwards regular; we stress that simultaneous forward and backward regularity does not imply regularity.
$\mathcal A$
must be forward and backward regular. We refer the reader to [Reference Barreira and Pesin7] for these definitions. We note that our requirements (2.1) and (2.2) imply that every regular point is both forward and backwards regular; we stress that simultaneous forward and backward regularity does not imply regularity.
Here are some other properties that we will need: if x is forward regular, then
where
is the co-norm of the linear map L. Furthermore, if
![]() $x \in \mathcal {R}$
,
$x \in \mathcal {R}$
,
Given a regular point
![]() $x \in \mathcal {R}$
, the dimension
$x \in \mathcal {R}$
, the dimension
![]() $d_i(x)$
of the subbundle
$d_i(x)$
of the subbundle
![]() $E_i(x)$
is called the multiplicity of the Lyapunov exponent
$E_i(x)$
is called the multiplicity of the Lyapunov exponent
![]() $\chi _i(x)$
. The collection
$\chi _i(x)$
. The collection
is called the Lyapunov spectrum of the cocycle
![]() $\mathcal {A}$
at x. Sometimes we will also use the list of values of the Lyapunov exponent
$\mathcal {A}$
at x. Sometimes we will also use the list of values of the Lyapunov exponent
in which distinct values
![]() $\chi _i(x)$
are repeated according to their multiplicities
$\chi _i(x)$
are repeated according to their multiplicities
![]() $d_i(x)$
,
$d_i(x)$
,
![]() $1\le i\le s(x)$
. When we want to stress the dependence on the cocycle, we use more explicit notations such as
$1\le i\le s(x)$
. When we want to stress the dependence on the cocycle, we use more explicit notations such as
![]() $\mathrm {Sp}(\mathcal {A},x)$
,
$\mathrm {Sp}(\mathcal {A},x)$
,
![]() $\chi _i(\mathcal {A},x)$
, etc.
$\chi _i(\mathcal {A},x)$
, etc.
2.3 Cohomology
Let
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
be two cocycles over the same homeomorphism f, and of the same dimension. We say that they are continuously cohomologous if there exists a continuous conjugacy between them, that is, a continuous map
$\mathcal {B}$
be two cocycles over the same homeomorphism f, and of the same dimension. We say that they are continuously cohomologous if there exists a continuous conjugacy between them, that is, a continuous map
![]() $C \colon X \to \mathrm {GL}(d,\mathbb R)$
such that
$C \colon X \to \mathrm {GL}(d,\mathbb R)$
such that
Since C is continuous, it is tempered, and hence continuously cohomologous cocycles have the same set of Lyapunov–Perron regular points, and the same Lyapunov spectra.
2.4 The exterior power of cocycles
Consider the vector space of all alternating i-forms on
![]() $\mathbb R^d$
, that is, the space of all multilinear maps from
$\mathbb R^d$
, that is, the space of all multilinear maps from
![]() $\mathbb R^d \times \cdots \times \mathbb R^d$
(with i copies) to
$\mathbb R^d \times \cdots \times \mathbb R^d$
(with i copies) to
![]() $\mathbb R$
which are alternating. The dual of this vector space is denoted
$\mathbb R$
which are alternating. The dual of this vector space is denoted
![]() $(\mathbb {R}^d)^{\wedge i}$
. There exists a canonical alternating multilinear map
$(\mathbb {R}^d)^{\wedge i}$
. There exists a canonical alternating multilinear map
called the exterior product. Given a linear operator L of
![]() $\mathbb {R}^d$
, we define the i-fold exterior power
$\mathbb {R}^d$
, we define the i-fold exterior power
![]() $L^{\wedge i}$
as the unique linear operator of
$L^{\wedge i}$
as the unique linear operator of
![]() $(\mathbb {R}^d)^{\wedge i}$
such that
$(\mathbb {R}^d)^{\wedge i}$
such that
Let
![]() $\mathcal {A}$
be a cocycle over a homeomorphism f of a topological space X. For each
$\mathcal {A}$
be a cocycle over a homeomorphism f of a topological space X. For each
![]() $i=1,\dots ,n$
consider the cocycle
$i=1,\dots ,n$
consider the cocycle
![]() $\mathcal {A}^{\wedge i} \colon X\times {\mathbb {Z}}\to \mathrm {GL}(n,\mathbb {R})^{\wedge i}$
defined by
$\mathcal {A}^{\wedge i} \colon X\times {\mathbb {Z}}\to \mathrm {GL}(n,\mathbb {R})^{\wedge i}$
defined by
![]() $\mathcal {A}^{\wedge i}(x,n) = \mathcal {A}(x,n)^{\wedge i}$
. We call
$\mathcal {A}^{\wedge i}(x,n) = \mathcal {A}(x,n)^{\wedge i}$
. We call
![]() $\mathcal {A}^{\wedge i}$
the i-fold exterior power cocycle of
$\mathcal {A}^{\wedge i}$
the i-fold exterior power cocycle of
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
One can show (see [Reference Arnold5, p. 211], [Reference Barreira and Pesin7, Section 3.1], or [Reference Raghunathan51]) that
-
1. if
 $x\in X$
is a LP-regular point for the cocycle
$x\in X$
is a LP-regular point for the cocycle
 $\mathcal {A}$
, then it is also a LP-regular point for the exterior power cocycle
$\mathcal {A}$
, then it is also a LP-regular point for the exterior power cocycle
 $\mathcal {A}^{\wedge i}$
;
$\mathcal {A}^{\wedge i}$
; -
2. the list of values of the Lyapunov exponents of the cocycle
 $\mathcal {A}^{\wedge i}$
is (2.7)in particular,
$\mathcal {A}^{\wedge i}$
is (2.7)in particular, $$ \begin{align} \{\widetilde\chi_k(\mathcal{A}^{\wedge i},x)\} = \big\{\widetilde\chi_{j_1}(\mathcal{A},x)+\cdots+\widetilde\chi_{j_i}(\mathcal{A},x) \ : \ j_1>\cdots >j_i \big\}; \end{align} $$
(2.8)
$$ \begin{align} \{\widetilde\chi_k(\mathcal{A}^{\wedge i},x)\} = \big\{\widetilde\chi_{j_1}(\mathcal{A},x)+\cdots+\widetilde\chi_{j_i}(\mathcal{A},x) \ : \ j_1>\cdots >j_i \big\}; \end{align} $$
(2.8) $$ \begin{align} \widetilde\chi_1(\mathcal{A}^{\wedge i},x) = \widetilde\chi_{1}(\mathcal{A},x)+\cdots+\widetilde\chi_{i}(\mathcal{A},x) \,. \end{align} $$
$$ \begin{align} \widetilde\chi_1(\mathcal{A}^{\wedge i},x) = \widetilde\chi_{1}(\mathcal{A},x)+\cdots+\widetilde\chi_{i}(\mathcal{A},x) \,. \end{align} $$
2.5 Uniform splittings
Let f be a homeomorphism of a compact metric space X. Let
![]() $\mathcal {A}$
be a continuous linear cocycle over f. Suppose that for each
$\mathcal {A}$
be a continuous linear cocycle over f. Suppose that for each
![]() $x \in X$
, we are given a splitting
$x \in X$
, we are given a splitting
 $$ \begin{align} \mathbb R^d=\bigoplus_{i=1}^s E_i(x) \end{align} $$
$$ \begin{align} \mathbb R^d=\bigoplus_{i=1}^s E_i(x) \end{align} $$
where each
![]() $\dim E_i(x)$
is independent of the point. Furthermore, assume that this splitting is
$\dim E_i(x)$
is independent of the point. Furthermore, assume that this splitting is
![]() $\mathcal {A}$
-invariant in the sense that
$\mathcal {A}$
-invariant in the sense that
![]() $\mathcal {A}(x,n) E_i(x) = E_i(f^n(x))$
. We say that splitting is dominated if there exists
$\mathcal {A}(x,n) E_i(x) = E_i(f^n(x))$
. We say that splitting is dominated if there exists
![]() $n_0>0$
such that for every point
$n_0>0$
such that for every point
![]() $x \in X$
and each i with
$x \in X$
and each i with
![]() $0 < i < s$
, we have:
$0 < i < s$
, we have:
Equivalently, for all choices of unit vectors
![]() $v_i\in E_i(x)$
, we have:
$v_i\in E_i(x)$
, we have:
We say that the subbundle
![]() $E_i$
dominates the subbundle
$E_i$
dominates the subbundle
![]() $E_{i+1}$
.
$E_{i+1}$
.
Let us emphasize that domination is a uniform property: the amount of time
![]() $n_0$
needed for the validity of the inequalities above is the same for every point x. In fact, this assumption is strong enough to force continuity (see [Reference Bonatti, Díaz and Viana12, Section B.1] or [Reference Crovisier and Potrie19, Section 2.1]):
$n_0$
needed for the validity of the inequalities above is the same for every point x. In fact, this assumption is strong enough to force continuity (see [Reference Bonatti, Díaz and Viana12, Section B.1] or [Reference Crovisier and Potrie19, Section 2.1]):
Proposition 2.1. If (2.9) is a dominated splitting, then each subbundle
![]() $E_i(x)$
depends continuously on
$E_i(x)$
depends continuously on
![]() $x \in X$
.
$x \in X$
.
In particular, the angle between different subbundles of a dominated splitting is bounded below. Actually, for every partition of the set
![]() $\{1,\dots ,s\}$
into two nonempty (disjoint) subsets I, J, we have
$\{1,\dots ,s\}$
into two nonempty (disjoint) subsets I, J, we have
 $$\begin{align*}\inf_{x \in X} \measuredangle \left( \bigoplus_{i \in I} E_i(x) , \bigoplus_{j \in J} E_j(x) \right)> 0 \,. \end{align*}$$
$$\begin{align*}\inf_{x \in X} \measuredangle \left( \bigoplus_{i \in I} E_i(x) , \bigoplus_{j \in J} E_j(x) \right)> 0 \,. \end{align*}$$
Let us introduce two other uniform notions related to domination. Again, let
![]() $\mathcal {A}$
be a continuous linear cocycle over f, and suppose we are given an
$\mathcal {A}$
be a continuous linear cocycle over f, and suppose we are given an
![]() $\mathcal {A}$
-invariant splitting (2.9) into subspaces of constant dimensions. We say that the splitting is absolutely dominated if there exists
$\mathcal {A}$
-invariant splitting (2.9) into subspaces of constant dimensions. We say that the splitting is absolutely dominated if there exists
![]() $n_0>0$
such that for all pairs of points
$n_0>0$
such that for all pairs of points
![]() $x,y \in X$
and each i with
$x,y \in X$
and each i with
![]() $0 < i < s$
,
$0 < i < s$
,
In particular, the splitting is dominated.
Finally, an
![]() $\mathcal {A}$
-invariant splitting
$\mathcal {A}$
-invariant splitting
![]() $\mathbb R^d = E^{\mathrm {u}}(x) \oplus E^{\mathrm {s}}(x)$
into two subbundles of constant dimensions is called uniformly hyperbolic if there exists
$\mathbb R^d = E^{\mathrm {u}}(x) \oplus E^{\mathrm {s}}(x)$
into two subbundles of constant dimensions is called uniformly hyperbolic if there exists
![]() $n_0>0$
such that for all point
$n_0>0$
such that for all point
![]() $x \in X$
,
$x \in X$
,
Note that a uniformly hyperbolic splitting is always absolutely dominated and, in particular, continuous.
We will need the following characterization of uniform hyperbolicity:
Proposition 2.2. Let f be a homeomorphism of a compact metric space X. Let
![]() $\mathcal {A}$
be a continuous linear cocycle over f. For each
$\mathcal {A}$
be a continuous linear cocycle over f. For each
![]() $x \in X$
, define subspaces
$x \in X$
, define subspaces

If these two subbundles have constant dimensions and form a splitting
![]() $\mathbb R^d = E^{\mathrm {u}}(x) \oplus E^{\mathrm {s}}(x)$
at every point
$\mathbb R^d = E^{\mathrm {u}}(x) \oplus E^{\mathrm {s}}(x)$
at every point
![]() $x \in X$
, then this splitting is uniformly hyperbolic.
$x \in X$
, then this splitting is uniformly hyperbolic.
The statement above corresponds to Mañé [Reference Mañé41, Corollary 1.2] specialized to bundles of constant dimensions. We note that related results were obtained by Sacker and Sell [Reference Sacker and Sell54] and Selgrade [Reference Selgrade58]; see [Reference Chicone and Latushkin18, Chapters 1 and 6], [Reference Wen64, Chapter 6], and [Reference Blumenthal and Latushkin8] for more information.
2.6 Vector bundle setting
If
![]() $\mathcal {A}$
is a d-dimensional linear cocycle over
$\mathcal {A}$
is a d-dimensional linear cocycle over
![]() $f \colon X \to X$
with generator A, we can consider the following transformation
$f \colon X \to X$
with generator A, we can consider the following transformation
![]() $T_{\mathcal {A}}$
of the product
$T_{\mathcal {A}}$
of the product
![]() $X \times \mathbb R^d$
:
$X \times \mathbb R^d$
:
This is a skew-product over f which is linear on fibers. The transformation
![]() $T_{\mathcal {A}}$
completely determines the cocycle.
$T_{\mathcal {A}}$
completely determines the cocycle.
This motivates considering the more general situation where the product space
![]() $X \times \mathbb R^d$
is replaced with a vector bundle over X of fiber dimension d, and the skew-product
$X \times \mathbb R^d$
is replaced with a vector bundle over X of fiber dimension d, and the skew-product
![]() $T_{\mathcal {A}}$
is replaced with a continuous vector bundle automorphism F that factors over f. The concepts discussed above can be extended to this setting in a straightforward manner.
$T_{\mathcal {A}}$
is replaced with a continuous vector bundle automorphism F that factors over f. The concepts discussed above can be extended to this setting in a straightforward manner.
The fiber bundle setting allows us, for example, to discuss derivative cocycles: in this case, f is a
![]() $C^1$
diffeomorphism and we consider the induced automorphism
$C^1$
diffeomorphism and we consider the induced automorphism
![]() $F=Df$
on the tangent bundle.
$F=Df$
on the tangent bundle.
For simplicity of presentation, in this paper we focus on linear cocycles (on trivial vector bundles
![]() $X \times \mathbb R^d$
), but actually the statements remain correct for general vector bundles, unless noted otherwise.
$X \times \mathbb R^d$
), but actually the statements remain correct for general vector bundles, unless noted otherwise.
2.7 Subadditivity
Recall that a sequence of functions
![]() $\varphi _n \colon X \to \mathbb R$
is called subadditive with respect to some dynamics
$\varphi _n \colon X \to \mathbb R$
is called subadditive with respect to some dynamics
![]() $f \colon X \to X$
if, for all
$f \colon X \to X$
if, for all
![]() $n,m \ge 1$
,
$n,m \ge 1$
,
A standard example is the sequence
![]() $\varphi _n(x) = \log \|\mathcal {A}(x,n)\|$
, where
$\varphi _n(x) = \log \|\mathcal {A}(x,n)\|$
, where
![]() $\mathcal {A}$
is cocycle over f.
$\mathcal {A}$
is cocycle over f.
Proposition 2.3 (Semi-uniform subadditive ergodic theorem [Reference Schreiber57, Theorem 1], [Reference Sturman and Stark59, Theorem 1.7]).
Let f be a continuous transformation of a compact metric space X. Consider a subadditive sequence of continuous functions
![]() $\varphi _n \colon X \to \mathbb R$
. Then:
$\varphi _n \colon X \to \mathbb R$
. Then:
 $$ \begin{align} \lim_{n \to \infty} \sup_{X} \frac{\varphi_n}{n} = \sup_{\mu \in \mathcal{M}_f} \lim_{n \to \infty} \int_X \frac{\varphi_n}{n} \, d\mu \, , \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \sup_{X} \frac{\varphi_n}{n} = \sup_{\mu \in \mathcal{M}_f} \lim_{n \to \infty} \int_X \frac{\varphi_n}{n} \, d\mu \, , \end{align} $$
where
![]() $\mathcal {M}_f$
denotes the set of f-invariant Borel probability measures. Furthermore, the supremum in the right hand side is attained at some ergodic measure.
$\mathcal {M}_f$
denotes the set of f-invariant Borel probability measures. Furthermore, the supremum in the right hand side is attained at some ergodic measure.
We note that variations of this result have been found by several authors (see, e.g., [Reference Furman27, § 3]). The most complete version is [Reference Morris45, Theorem A.3], which shows that upper-semicontinuity is sufficient, and provides other characterizations of the quantity (2.11).
Corollary 2.4. Let f be a continuous transformation of a compact metric space X. If
![]() $\varphi $
is a continuous function such that
$\varphi $
is a continuous function such that
![]() $\int \varphi \, d\mu = c$
for every
$\int \varphi \, d\mu = c$
for every
![]() $\mu \in \mathcal {M}_f$
, where c is a constant, then the Birkhoff averages of
$\mu \in \mathcal {M}_f$
, where c is a constant, then the Birkhoff averages of
![]() $\varphi $
with respect to f converge uniformly to c.
$\varphi $
with respect to f converge uniformly to c.
Corollary 2.4 follows directly from Proposition 2.3, or from the usual proof that unique ergodicity implies uniform convergence in the ergodic theorem.
3 Completely regular cocycles
3.1 Definition and basic properties
Let X be a compact metric space and
![]() $f:X\to X$
a homeomorphism. Let
$f:X\to X$
a homeomorphism. Let
![]() $\mathcal {A}\colon X\times \mathbb {Z}\to \mathrm {GL}(d,\mathbb {R})$
be a continuous cocycle over f. We say that
$\mathcal {A}\colon X\times \mathbb {Z}\to \mathrm {GL}(d,\mathbb {R})$
be a continuous cocycle over f. We say that
![]() $\mathcal {A}$
is completely regular if it satisfies the following two conditions:
$\mathcal {A}$
is completely regular if it satisfies the following two conditions:
-
1. every point
 $x\in X$
is LP-regular;
$x\in X$
is LP-regular; -
2. the Lyapunov exponents are independent of the point
 $x\in X$
; more precisely, there are numbers
$x\in X$
; more precisely, there are numbers
 $\chi _1>\cdots >\chi _s$
and positive integers
$\chi _1>\cdots >\chi _s$
and positive integers
 $d_1,\dots ,d_s$
with
$d_1,\dots ,d_s$
with
 $\sum _{i=1}^s d_i=d$
such that
$\sum _{i=1}^s d_i=d$
such that
 $\mathrm {Sp}(\mathcal {A},x)=\{(\chi _i,d_i), i=1,\dots ,s\}$
for every
$\mathrm {Sp}(\mathcal {A},x)=\{(\chi _i,d_i), i=1,\dots ,s\}$
for every
 $x\in X$
.
$x\in X$
.
Therefore, if a cocycle is completely regular, then at every x we have an Oseledets splitting
 $$ \begin{align} \mathbb R^d=\bigoplus_{i=1}^s E_i(x) \end{align} $$
$$ \begin{align} \mathbb R^d=\bigoplus_{i=1}^s E_i(x) \end{align} $$
where the number of subbundles and their dimensions are independent of the point. In general, the Oseledets splitting is only measurable and there is no a priori information on the speed of convergence in (2.5) and (2.6). However, under the assumption of complete regularity, we obtain better properties, as the following result shows.
Theorem 3.1. Let
![]() $\mathcal {A}$
be a completely regular cocycle over a homeomorphism f of a compact metric space X. Let (3.1) be its Oseledets splitting. Then for each i with
$\mathcal {A}$
be a completely regular cocycle over a homeomorphism f of a compact metric space X. Let (3.1) be its Oseledets splitting. Then for each i with
![]() $1 \le i \le s$
the following statements hold:
$1 \le i \le s$
the following statements hold:
-
1. the subspace
 $E_i(x)$
depends continuously on x;
$E_i(x)$
depends continuously on x; -
2. the limits in (2.5) and (2.6) are both uniform with respect to x; more precisely, for all
 $\varepsilon>0$
we can find N such that (3.2)for every
$\varepsilon>0$
we can find N such that (3.2)for every $$ \begin{align} \begin{aligned} \chi_i-\varepsilon&\le\frac1n\log m(\mathcal{A}(x,n)|E_i(x)) & \\ &\le\frac1n\log\|\mathcal{A}(x,n)|E_i(x)\|&\le \chi_i+\varepsilon \,. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \chi_i-\varepsilon&\le\frac1n\log m(\mathcal{A}(x,n)|E_i(x)) & \\ &\le\frac1n\log\|\mathcal{A}(x,n)|E_i(x)\|&\le \chi_i+\varepsilon \,. \end{aligned} \end{align} $$
 $|n|>N$
and
$|n|>N$
and
 $x\in X$
.
$x\in X$
.
Before proving the statement above in full generality, we establish first the case
![]() $s=1$
, where actually a weaker hypothesis suffices:
$s=1$
, where actually a weaker hypothesis suffices:
Proposition 3.2. Let
![]() $\mathcal {A}$
be a continuous linear cocycle over a homeomorphism f of a compact metric space X. Suppose that there exists a number
$\mathcal {A}$
be a continuous linear cocycle over a homeomorphism f of a compact metric space X. Suppose that there exists a number
![]() $\chi \in \mathbb R$
such that for every f-invariant Borel probability measure
$\chi \in \mathbb R$
such that for every f-invariant Borel probability measure
![]() $\mu $
on X, for
$\mu $
on X, for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $x\in X$
, all Lyapunov exponents at x are equal to
$x\in X$
, all Lyapunov exponents at x are equal to
![]() $\chi $
. Then, for all
$\chi $
. Then, for all
![]() $x \in X$
,
$x \in X$
,
and these limits are uniform with respect to x.
Proof. It is sufficient to consider positive times n, since negative times can be dealt with using the inverse cocycle. Consider the subadditive sequence of continuous functions
![]() $\varphi _n(x)=\log \|\mathcal {A}(x,n)\|$
. By assumption, the sequence
$\varphi _n(x)=\log \|\mathcal {A}(x,n)\|$
. By assumption, the sequence
![]() $\frac {\varphi _n(x)}{n}$
converges pointwise to the constant
$\frac {\varphi _n(x)}{n}$
converges pointwise to the constant
![]() $\chi $
. It follows from Proposition 2.3 that
$\chi $
. It follows from Proposition 2.3 that
Similarly, the sequence
![]() $\psi _n(x)=\log m(\mathcal {A}(x, n))$
is superadditive and
$\psi _n(x)=\log m(\mathcal {A}(x, n))$
is superadditive and
![]() $\frac {\psi _n(x)}{n}$
converges pointwise to the constant
$\frac {\psi _n(x)}{n}$
converges pointwise to the constant
![]() $\chi $
, implying that
$\chi $
, implying that
Since
![]() $\psi _n\le \varphi _n$
, we conclude that both limits
$\psi _n\le \varphi _n$
, we conclude that both limits
![]() $\frac {\varphi _n}{n}\to \chi $
and
$\frac {\varphi _n}{n}\to \chi $
and
![]() $\frac {\psi _n}{n}\to \chi $
are uniform.
$\frac {\psi _n}{n}\to \chi $
are uniform.
Proof of Theorem 3.1.
Let
![]() $\mathcal {A}$
be a completely regular cocycle, with Oseledets splitting
$\mathcal {A}$
be a completely regular cocycle, with Oseledets splitting
![]() $\mathbb R^d=\bigoplus _{i=1}^s E_i(x)$
. Let
$\mathbb R^d=\bigoplus _{i=1}^s E_i(x)$
. Let
![]() $\chi _1>\cdots >\chi _s$
be the Lyapunov exponents, which are independent of
$\chi _1>\cdots >\chi _s$
be the Lyapunov exponents, which are independent of
![]() $x \in X$
. The case
$x \in X$
. The case
![]() $s=1$
is covered by Proposition 3.2, so assume that
$s=1$
is covered by Proposition 3.2, so assume that
![]() $s \ge 2$
.
$s \ge 2$
.
Let us prove statement (1), that is, continuity of the subbundles
![]() $E_i(x)$
. Fix numbers
$E_i(x)$
. Fix numbers
![]() $c_1,\dots ,c_{s-1}$
such that
$c_1,\dots ,c_{s-1}$
such that
![]() $\chi _i>c_i>\chi _{i+1}$
. For each
$\chi _i>c_i>\chi _{i+1}$
. For each
![]() $i\in \{1,\dots ,s-1\}$
, consider the cocycle
$i\in \{1,\dots ,s-1\}$
, consider the cocycle
![]() $\widetilde {\mathcal {A}}_i=e^{-c_i}\mathcal {A}$
. This cocycle admits an invariant measurable splitting
$\widetilde {\mathcal {A}}_i=e^{-c_i}\mathcal {A}$
. This cocycle admits an invariant measurable splitting
![]() $E^{\mathrm {u}}_i(x)\oplus E^{\mathrm {s}}_i(x)$
, where
$E^{\mathrm {u}}_i(x)\oplus E^{\mathrm {s}}_i(x)$
, where
Note that all Lyapunov exponents along
![]() $E^{\mathrm {u}}_i(x)$
(respectively,
$E^{\mathrm {u}}_i(x)$
(respectively,
![]() $E^{\mathrm {s}}_i(x)$
) are positive (respectively, negative). An application of Proposition 2.2 shows that the splitting
$E^{\mathrm {s}}_i(x)$
) are positive (respectively, negative). An application of Proposition 2.2 shows that the splitting
![]() $E^{\mathrm {u}}_i \oplus E^{\mathrm {s}}_i$
is uniformly hyperbolic. In particular, the bundles
$E^{\mathrm {u}}_i \oplus E^{\mathrm {s}}_i$
is uniformly hyperbolic. In particular, the bundles
![]() $E_i^{\mathrm {u}}$
and
$E_i^{\mathrm {u}}$
and
![]() $E_i^{\mathrm {s}}$
are continuous. It follows that
$E_i^{\mathrm {s}}$
are continuous. It follows that
![]() $E_1 = E^{\mathrm {u}}_1$
and
$E_1 = E^{\mathrm {u}}_1$
and
![]() $E_s = E^{\mathrm {s}}_s$
are continuous. Furthermore, for each i, the bundle
$E_s = E^{\mathrm {s}}_s$
are continuous. Furthermore, for each i, the bundle
![]() $E_i$
is the transverse intersection of
$E_i$
is the transverse intersection of
![]() $E_i^{\mathrm {u}}$
and
$E_i^{\mathrm {u}}$
and
![]() $E_{i-1}^{\mathrm {s}}$
, and therefore, it is continuous as well. This completes the proof of statement (1).
$E_{i-1}^{\mathrm {s}}$
, and therefore, it is continuous as well. This completes the proof of statement (1).
Now we apply Proposition 3.2 (or actually its extension to the vector bundle setting) to the restrictions
![]() $\mathcal {A}(x, n)|E_i(x)$
. We then obtain the desired uniformity property, statement (2).
$\mathcal {A}(x, n)|E_i(x)$
. We then obtain the desired uniformity property, statement (2).
As an important consequence of Theorem 3.1, we obtain the property of absolute domination (defined in Section 2.5 above):
Corollary 3.3. Given a completely regular cocycle, its Oseledets splitting (3.1) is either trivial (i.e.,
![]() $s=1$
) or absolutely dominated.
$s=1$
) or absolutely dominated.
Proof. Let
![]() $\mathcal {A}$
be a completely regular cocycle with spectrum
$\mathcal {A}$
be a completely regular cocycle with spectrum
![]() $(\chi _i,d_i)_{i=1,\dots ,s}$
. Assume that
$(\chi _i,d_i)_{i=1,\dots ,s}$
. Assume that
![]() $s> 1$
. Fix a positive number
$s> 1$
. Fix a positive number
![]() $\varepsilon $
small enough so that
$\varepsilon $
small enough so that
![]() $\chi _i-\varepsilon> \chi _{i+1} + \varepsilon $
for each i with
$\chi _i-\varepsilon> \chi _{i+1} + \varepsilon $
for each i with
![]() $0< i < s$
. Let N be as in Statement (2) in Theorem 3.1. Then, for all
$0< i < s$
. Let N be as in Statement (2) in Theorem 3.1. Then, for all
![]() $n>N$
, all
$n>N$
, all
![]() $x,y \in X$
, and all i with
$x,y \in X$
, and all i with
![]() $0< i < s$
, we have
$0< i < s$
, we have
This proves absolute domination.
It is clear that complete regularity is invariant under continuous cohomology. Here is another basic property:
Proposition 3.4. The exterior power of a completely regular cocycle is completely regular.
Proof. This follows immediately from the discussion in Subsection 2.4.
3.2 Examples
We present some examples of completely regular cocycles.
Example 3.5. A one-dimensional continuous linear cocycle with generator A (which in this case takes values in
![]() $\mathbb R\setminus \{0\}$
) is completely regular if and only if the forward and backward limits of Birkhoff averages of the function
$\mathbb R\setminus \{0\}$
) is completely regular if and only if the forward and backward limits of Birkhoff averages of the function
![]() $\varphi (x) \mathrel {:=} \log |A(x)|$
exist everywhere and are equal to some constant c. Equivalently (see Corollary 2.4),
$\varphi (x) \mathrel {:=} \log |A(x)|$
exist everywhere and are equal to some constant c. Equivalently (see Corollary 2.4),
![]() $\int \varphi \, d \mu = c$
for every f-invariant Borel probability measure
$\int \varphi \, d \mu = c$
for every f-invariant Borel probability measure
![]() $\mu $
.
$\mu $
.
Another equivalent condition is that
![]() $\varphi -c$
is a uniform limit of continuous coboundaries (see [Reference Moulin Ollagnier and Pinchon46] or [Reference Bousch and Jenkinson13, Lemma 3]).
$\varphi -c$
is a uniform limit of continuous coboundaries (see [Reference Moulin Ollagnier and Pinchon46] or [Reference Bousch and Jenkinson13, Lemma 3]).
Example 3.6. If the space X is finite and
![]() $f \colon X \to X$
is a cyclic permutation, that is, if the dynamics consists of a single periodic trajectory, then any cocycle over f is completely regular.
$f \colon X \to X$
is a cyclic permutation, that is, if the dynamics consists of a single periodic trajectory, then any cocycle over f is completely regular.
Example 3.7. Now assume that f is a uniquely ergodic homeomorphism, and that the cocycle
![]() $\mathcal {A}$
takes values in
$\mathcal {A}$
takes values in
![]() $\mathrm {SL}^{\pm }(2,\mathbb R)$
(the subgroup of
$\mathrm {SL}^{\pm }(2,\mathbb R)$
(the subgroup of
![]() $\mathrm {GL}(2,\mathbb R)$
formed by matrices with determinant
$\mathrm {GL}(2,\mathbb R)$
formed by matrices with determinant
![]() $\pm 1$
). Let
$\pm 1$
). Let
![]() $\mu $
be the unique invariant probability measure for f, which is necessarily ergodic, and let
$\mu $
be the unique invariant probability measure for f, which is necessarily ergodic, and let
![]() $\chi _1 = \chi _1(\mu )$
and
$\chi _1 = \chi _1(\mu )$
and
![]() $\chi _2 = \chi _2(\mu )$
. By the hypothesis on the determinant,
$\chi _2 = \chi _2(\mu )$
. By the hypothesis on the determinant,
![]() $\chi _1 \ge 0 \ge \chi _2 = -\chi _1$
.
$\chi _1 \ge 0 \ge \chi _2 = -\chi _1$
.
There are three mutually exclusive cases:
-
1.
 $\chi _1 = 0 = \chi _2$
.
$\chi _1 = 0 = \chi _2$
. -
2.
 $\chi _1> 0 > \chi _2$
and the cocycle is uniformly hyperbolic.
$\chi _1> 0 > \chi _2$
and the cocycle is uniformly hyperbolic. -
3.
 $\chi _1> 0 > \chi _2$
and the cocycle is not uniformly hyperbolic.
$\chi _1> 0 > \chi _2$
and the cocycle is not uniformly hyperbolic.
Proposition 3.8. Consider a continuous
![]() $\mathrm {SL}^{\pm }(2,\mathbb R)$
-cocycle over a uniquely ergodic homeomorphism. Then, the cocycle is completely regular in cases (1) and (2) above, and it is not completely regular in case (3).
$\mathrm {SL}^{\pm }(2,\mathbb R)$
-cocycle over a uniquely ergodic homeomorphism. Then, the cocycle is completely regular in cases (1) and (2) above, and it is not completely regular in case (3).
Proof. Note that
![]() $m(\mathcal {A}(x,n)) = \|\mathcal {A}(x,n)\|$
, since determinants are
$m(\mathcal {A}(x,n)) = \|\mathcal {A}(x,n)\|$
, since determinants are
![]() $\pm 1$
. Consider case (1). By Proposition 3.2,
$\pm 1$
. Consider case (1). By Proposition 3.2,
![]() $\frac {1}{n}\log \|\mathcal {A}(x,n)\|$
converges uniformly to zero. It follows that every
$\frac {1}{n}\log \|\mathcal {A}(x,n)\|$
converges uniformly to zero. It follows that every
![]() $x\in X$
is LP-regular with zero Lyapunov exponents. In particular, the cocycle is completely regular.
$x\in X$
is LP-regular with zero Lyapunov exponents. In particular, the cocycle is completely regular.
Next, consider the uniformly hyperbolic case (2). The hyperbolic bundles are continuous, invariant, and one-dimensional. Unique ergodicity of the base dynamics then implies that the cocycle is completely regular.
Finally, consider the nonuniformly hyperbolic case (3). If the cocycle were completely regular, then, by Corollary 3.3, it would admit a dominated splitting into one-dimensional bundles. Since
![]() $|\det A(x)| \equiv 1$
, that splitting would actually be uniformly hyperbolic, contrary to our assumption. This shows that case (3) forbids complete regularity.
$|\det A(x)| \equiv 1$
, that splitting would actually be uniformly hyperbolic, contrary to our assumption. This shows that case (3) forbids complete regularity.
If f is an irrational rotation of the circle, simple examples of cocycles in situation (3) were obtained by Herman [Reference Herman30]. The existence of cocycles of type (3) for any uniquely ergodic dynamics with a nonatomic invariant measure was established only recently by Avila and Damanik [Reference Avila and Damanik6], answering a question of Walters [Reference Walters, Arnold and Wihstutz63].
We point out that Proposition 3.8 is essentially contained in [Reference Furman27]. For related results, see [Reference Damanik and Lenz20].
Remark 3.9. Given a cocycle
![]() $\mathcal {A}$
over a homeomorphism f, and an f-invariant and ergodic Borel probability measure
$\mathcal {A}$
over a homeomorphism f, and an f-invariant and ergodic Borel probability measure
![]() $\mu $
, we define the Lyapunov spectrum
$\mu $
, we define the Lyapunov spectrum
![]() $\mathrm {Sp}(\mathcal {A},\mu )$
as equal to
$\mathrm {Sp}(\mathcal {A},\mu )$
as equal to
![]() $\mathrm {Sp}(\mathcal {A},x)$
for
$\mathrm {Sp}(\mathcal {A},x)$
for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $x \in X$
. Proposition 3.2 shows that if
$x \in X$
. Proposition 3.2 shows that if
![]() $\mathrm {Sp}(\mathcal {A},\mu )$
is the same for all ergodic measures
$\mathrm {Sp}(\mathcal {A},\mu )$
is the same for all ergodic measures
![]() $\mu $
and consists of a single Lyapunov exponent, then the cocycle
$\mu $
and consists of a single Lyapunov exponent, then the cocycle
![]() $\mathcal {A}$
is completely regular. On the other hand, the condition in italics cannot be dropped: consider for instance any cocycle of type (3) in Proposition 3.8.
$\mathcal {A}$
is completely regular. On the other hand, the condition in italics cannot be dropped: consider for instance any cocycle of type (3) in Proposition 3.8.
Example 3.10. Let f be a homeomorphism of a compact metric space X,
![]() $c_1> \cdots > c_s$
a list of distinct real numbers, and
$c_1> \cdots > c_s$
a list of distinct real numbers, and
![]() $d_1, \dots , d_s$
positive integers such that
$d_1, \dots , d_s$
positive integers such that
![]() $d =d_1 + \dots + d_s$
. Suppose that
$d =d_1 + \dots + d_s$
. Suppose that
![]() $B : X \to \mathrm {GL}(d, \mathbb R)$
is a continuous block-diagonal matrix function
$B : X \to \mathrm {GL}(d, \mathbb R)$
is a continuous block-diagonal matrix function
 $$ \begin{align} B(x) = \begin{pmatrix} B_1(x) & & 0 \\ & \ddots & \\ 0 & & B_s(x) \end{pmatrix}, \end{align} $$
$$ \begin{align} B(x) = \begin{pmatrix} B_1(x) & & 0 \\ & \ddots & \\ 0 & & B_s(x) \end{pmatrix}, \end{align} $$
where each diagonal block
![]() $B_i(x)$
has dimension
$B_i(x)$
has dimension
![]() $d_i \times d_i$
and has block-triangular form
$d_i \times d_i$
and has block-triangular form
 $$ \begin{align} B_i(x) = e^{c_i} \, \begin{pmatrix} U_{i,1}(x) & * & & * \\ & U_{i,2}(x) & \ddots & \\ & & \ddots & * \\ 0 & & & U_{i,\ell_i}(x) \end{pmatrix}, \end{align} $$
$$ \begin{align} B_i(x) = e^{c_i} \, \begin{pmatrix} U_{i,1}(x) & * & & * \\ & U_{i,2}(x) & \ddots & \\ & & \ddots & * \\ 0 & & & U_{i,\ell_i}(x) \end{pmatrix}, \end{align} $$
where each matrix
![]() $U_{i,j}(x)$
is orthogonal.
$U_{i,j}(x)$
is orthogonal.
Consider the cocycle
![]() $\mathcal {B}(x,n)$
with generator
$\mathcal {B}(x,n)$
with generator
![]() $B(x)$
. Then, this cocycle is completely regular, with Lyapunov exponents
$B(x)$
. Then, this cocycle is completely regular, with Lyapunov exponents
![]() $c_1, \dots , c_s$
, and respective multiplicities
$c_1, \dots , c_s$
, and respective multiplicities
![]() $d_1, \dots , d_s$
.
$d_1, \dots , d_s$
.
Example 3.11. We extend the previous example. Let f be a homeomorphism of a compact metric space X, let
![]() $\mathcal {E}$
be a continuous vector bundle over X whose fibers
$\mathcal {E}$
be a continuous vector bundle over X whose fibers
![]() $\mathcal {E}(x)$
have dimension d, and let
$\mathcal {E}(x)$
have dimension d, and let
![]() $F \colon \mathcal {E} \to \mathcal {E}$
be an automorphism that factors over f. We say that F admits a continuous amenable reduction
Footnote
1
if there exist
$F \colon \mathcal {E} \to \mathcal {E}$
be an automorphism that factors over f. We say that F admits a continuous amenable reduction
Footnote
1
if there exist
-
• real numbers
 $c_1> \cdots > c_s$
;
$c_1> \cdots > c_s$
; -
• positive integers
 $d_1, \dots , d_s$
such that
$d_1, \dots , d_s$
such that
 $d =d_1 + \dots + d_s$
;
$d =d_1 + \dots + d_s$
; -
• a continuous family on inner products on the fibers
 $\mathcal {E}(x)$
(called a ‘metric’);
$\mathcal {E}(x)$
(called a ‘metric’); -
• a continuous F-invariant splitting
where each subbundle $$\begin{align*}\mathcal{E}_1(x) \oplus \cdots \oplus \mathcal{E}_s(x) = \mathcal{E}(x) \end{align*}$$
$$\begin{align*}\mathcal{E}_1(x) \oplus \cdots \oplus \mathcal{E}_s(x) = \mathcal{E}(x) \end{align*}$$
 $\mathcal {E}_i$
has dimension
$\mathcal {E}_i$
has dimension
 $d_i$
;
$d_i$
;
-
• for each
 $i \in \{1,\dots , s\}$
, a continuous F-invariant field of flags
$i \in \{1,\dots , s\}$
, a continuous F-invariant field of flags  $$\begin{align*}\{0\} = \mathcal{E}_{i,0}(x) \subset \mathcal{E}_{i,1}(x) \subset \cdots \subset \mathcal{E}_{i,\ell_i}(x)= \mathcal{E}_i(x) \end{align*}$$
$$\begin{align*}\{0\} = \mathcal{E}_{i,0}(x) \subset \mathcal{E}_{i,1}(x) \subset \cdots \subset \mathcal{E}_{i,\ell_i}(x)= \mathcal{E}_i(x) \end{align*}$$
such that, for each
![]() $i \in \{1,\dots , s\}$
and
$i \in \{1,\dots , s\}$
and
![]() $j \in \{1,\dots ,\ell _i\}$
, the action induced by F on the quotient bundle
$j \in \{1,\dots ,\ell _i\}$
, the action induced by F on the quotient bundle
![]() $\mathcal {E}_{i,j}/\mathcal {E}_{i,j-1}$
expands the (induced) metric by a constant factor
$\mathcal {E}_{i,j}/\mathcal {E}_{i,j-1}$
expands the (induced) metric by a constant factor
![]() $e^{c_i}$
.
$e^{c_i}$
.
In this case, the vector bundle automorphism F is completely regular, with Lyapunov exponents
![]() $c_1, \dots , c_s$
, and respective multiplicities
$c_1, \dots , c_s$
, and respective multiplicities
![]() $d_1, \dots , d_s$
.
$d_1, \dots , d_s$
.
Existence of a continuous amenable reduction is invariant with respect to continuous cohomology. The cocycle
![]() $\mathcal {B}$
in Example 3.10 admits a continuous amenable reduction where the spaces
$\mathcal {B}$
in Example 3.10 admits a continuous amenable reduction where the spaces
![]() $\mathcal {E}_{i,j}$
are independent of x. In particular, if a cocycle
$\mathcal {E}_{i,j}$
are independent of x. In particular, if a cocycle
![]() $\mathcal {A}$
is continuously cohomologous to a cocycle
$\mathcal {A}$
is continuously cohomologous to a cocycle
![]() $\mathcal {B}$
as in Example 3.10, then
$\mathcal {B}$
as in Example 3.10, then
![]() $\mathcal {A}$
admits a continuous amenable reduction. The converse is not true, since there is no guarantee that the subbundles
$\mathcal {A}$
admits a continuous amenable reduction. The converse is not true, since there is no guarantee that the subbundles
![]() $\mathcal {E}_{i,j}$
are trivializable.
$\mathcal {E}_{i,j}$
are trivializable.
Example 3.12. Consider any surface diffeomorphism of class
![]() $C^1$
admitting a homoclinic tangency, that is, a hyperbolic fixed point p whose stable and unstable manifolds are tangent at a point q. Let X be the closure of the orbit of q and consider the derivative cocycle
$C^1$
admitting a homoclinic tangency, that is, a hyperbolic fixed point p whose stable and unstable manifolds are tangent at a point q. Let X be the closure of the orbit of q and consider the derivative cocycle
![]() $Df$
restricted to X. This cocycle has a unique LP-regular point, namely p.
$Df$
restricted to X. This cocycle has a unique LP-regular point, namely p.
This example has the property that all points in X are both forward and backwards regular and the Lyapunov exponents for future and past agree, but nevertheless the cocycle is not completely regular.
3.3 Hölder continuous cocycles over hyperbolic dynamics
We will discuss a setting where it is possible to obtain a concrete description of all completely regular cocycles. The result is stated in terms of vector bundle automorphisms (see Section 2.6) and continuous amenable reduction (see Example 3.11). Actually, we will work with Hölder continuous vector bundles and their automorphisms (see [Reference Kalinin and Sadovskaya37, § 2.2], [Reference Bochi and Garibaldi10, § 2.2–2.3]).
Theorem 3.13. Assume that X is a compact smooth manifold and
![]() $f:X\to X$
is a transitive
$f:X\to X$
is a transitive
![]() $C^{1+\delta }$
Anosov diffeomorphism. Let
$C^{1+\delta }$
Anosov diffeomorphism. Let
![]() $\mathcal {E}$
be a Hölder vector bundle over X and let
$\mathcal {E}$
be a Hölder vector bundle over X and let
![]() $A \colon \mathcal {E} \to \mathcal {E}$
be a Hölder automorphism that factors over f. Then the following conditions are equivalent:
$A \colon \mathcal {E} \to \mathcal {E}$
be a Hölder automorphism that factors over f. Then the following conditions are equivalent:
-
1. F is completely regular;
-
2. F admits a continuous amenable reduction;
-
3.
 $\mathrm {Sp}(F,p) = \mathrm {Sp}(F,q)$
for all pairs of periodic points
$\mathrm {Sp}(F,p) = \mathrm {Sp}(F,q)$
for all pairs of periodic points
 $p,q$
.
$p,q$
.
Furthermore, if any of these conditions hold, then the subbundles and the metric composing the amenable reduction of F can be taken Hölder continuous, with the same Hölder exponent as the initial data.
Proof. The implications (2)
![]() $\Rightarrow $
(1)
$\Rightarrow $
(1)
![]() $\Rightarrow $
(3) are automatic (and independent of f being Anosov or F being Hölder). We are left to prove that (3)
$\Rightarrow $
(3) are automatic (and independent of f being Anosov or F being Hölder). We are left to prove that (3)
![]() $\Rightarrow $
(2).
$\Rightarrow $
(2).
So assume (3), that is, all periodic points have a common Lyapunov spectrum
![]() $(\chi _i,d_i)_{i=1}^s$
. As shown by Guysinsky [Reference Guysinsky29] and DeWitt–Gogolev [Reference DeWitt and Gogolev22, Theorems 1.2 and 3.10], the cocycle admits a dominated splitting
$(\chi _i,d_i)_{i=1}^s$
. As shown by Guysinsky [Reference Guysinsky29] and DeWitt–Gogolev [Reference DeWitt and Gogolev22, Theorems 1.2 and 3.10], the cocycle admits a dominated splitting
![]() $\mathcal {E}_1 \oplus \cdots \oplus \mathcal {E}_s$
where
$\mathcal {E}_1 \oplus \cdots \oplus \mathcal {E}_s$
where
![]() $\dim \mathcal {E}_i = d_i$
. In our setting, the subbundles
$\dim \mathcal {E}_i = d_i$
. In our setting, the subbundles
![]() $\mathcal {E}_i$
of a dominated splitting are Hölder continuous (see [Reference Brin and Katok14]). Consider the restriction of the automorphism F to one of these subbundles
$\mathcal {E}_i$
of a dominated splitting are Hölder continuous (see [Reference Brin and Katok14]). Consider the restriction of the automorphism F to one of these subbundles
![]() $\mathcal {E}_i$
. By a result of Kalinin and Sadovskaya [Reference Kalinin and Sadovskaya37, Theorem 3.9] (see also [Reference Sadovskaya and Damjanović56, § 13.7]), there exists a Hölder continuous metric (i.e., family of inner products) on
$\mathcal {E}_i$
. By a result of Kalinin and Sadovskaya [Reference Kalinin and Sadovskaya37, Theorem 3.9] (see also [Reference Sadovskaya and Damjanović56, § 13.7]), there exists a Hölder continuous metric (i.e., family of inner products) on
![]() $\mathcal {E}_i(x)$
and an invariant Hölder continuous field of flags
$\mathcal {E}_i(x)$
and an invariant Hölder continuous field of flags
such that the action induced by F on the quotient bundle
![]() $\mathcal {E}_{i,j}/\mathcal {E}_{i,j-1}$
expands the (induced) metric by a constant factor
$\mathcal {E}_{i,j}/\mathcal {E}_{i,j-1}$
expands the (induced) metric by a constant factor
![]() $e^{\varphi _i(x)}$
, where
$e^{\varphi _i(x)}$
, where
![]() $\varphi _i$
is a Hölder function on X. In our situation,
$\varphi _i$
is a Hölder function on X. In our situation,
![]() $\varphi _i$
has the same integral with respect to all invariant probability measures supported on periodic orbits, namely
$\varphi _i$
has the same integral with respect to all invariant probability measures supported on periodic orbits, namely
![]() $\chi _i$
. Therefore we can apply Livsic theorem and write
$\chi _i$
. Therefore we can apply Livsic theorem and write
![]() $\varphi _i = \chi _i + \psi _i \circ f - \psi _i$
, where
$\varphi _i = \chi _i + \psi _i \circ f - \psi _i$
, where
![]() $\psi _i$
is a Hölder continuous function. We rescale the Riemannian metric inside
$\psi _i$
is a Hölder continuous function. We rescale the Riemannian metric inside
![]() $\mathcal {E}_i(x)$
by multiplying it by
$\mathcal {E}_i(x)$
by multiplying it by
![]() $e^{-\psi _i(x)}$
, so that the new expansion factor is the constant
$e^{-\psi _i(x)}$
, so that the new expansion factor is the constant
![]() $e^{\chi _i}$
. Then we combine these metrics by declaring the subbundles
$e^{\chi _i}$
. Then we combine these metrics by declaring the subbundles
![]() $\mathcal {E}_i(x)$
to be orthogonal. This shows that F admits a Hölder continuous amenable reduction.
$\mathcal {E}_i(x)$
to be orthogonal. This shows that F admits a Hölder continuous amenable reduction.
Let us note that in dimension
![]() $d=1$
, Theorem 3.13 is equivalent to Livsic theorem for the group
$d=1$
, Theorem 3.13 is equivalent to Livsic theorem for the group
![]() $(\mathbb R,+)$
. Since Livsic theorem does not hold for functions that are merely continuous instead of Hölder (see [Reference Bousch and Jenkinson13, p. 215] or [Reference Kocsard38]), the regularity hypothesis on the automorphism is necessary for the validity of our statement.
$(\mathbb R,+)$
. Since Livsic theorem does not hold for functions that are merely continuous instead of Hölder (see [Reference Bousch and Jenkinson13, p. 215] or [Reference Kocsard38]), the regularity hypothesis on the automorphism is necessary for the validity of our statement.
On the other hand, we believe that Theorem 3.13 holds for (transitive) Anosov diffeomorphisms of class
![]() $C^1$
(instead of
$C^1$
(instead of
![]() $C^{1+\delta }$
), or even for (transitive) hyperbolic homeomorphisms (see, e.g., [Reference Ruelle53, Chapter 7], [Reference Alekseev and Yakobson4, Part II], [Reference Akin2, Chapter 11]).
$C^{1+\delta }$
), or even for (transitive) hyperbolic homeomorphisms (see, e.g., [Reference Ruelle53, Chapter 7], [Reference Alekseev and Yakobson4, Part II], [Reference Akin2, Chapter 11]).
We mention here the work [Reference Chen, Cao and Zou16] concerning the uniformity of the first Lyapunov exponent in a related setting.
3.4 Relation with Sacker–Sell theory
Let f be a homeomorphism of a compact metric space X. We assume that f is invariantly connected, that is, the only invariant clopen sets are
![]() $\emptyset $
and X. This condition is satisfied if f is transitive or X is connected.
$\emptyset $
and X. This condition is satisfied if f is transitive or X is connected.
Let
![]() $\mathcal {A}$
be a continuous linear d-dimensional cocycle over f. For each real number
$\mathcal {A}$
be a continuous linear d-dimensional cocycle over f. For each real number
![]() $\lambda $
, we define a cocycle
$\lambda $
, we define a cocycle
The Sacker–Sell spectrum of
![]() $\mathcal {A}$
is the set
$\mathcal {A}$
is the set
(Here hyperbolic subbundles are allowed to be
![]() $\{0\}$
.) According to [Reference Sacker and Sell55, Theorem 2] (see also [Reference Johnson and Zampogni35, Theorem 2.4]), the Sacker–Sell spectrum is a compact subset of
$\{0\}$
.) According to [Reference Sacker and Sell55, Theorem 2] (see also [Reference Johnson and Zampogni35, Theorem 2.4]), the Sacker–Sell spectrum is a compact subset of
![]() $\mathbb R$
with at most d connected components, that is,
$\mathbb R$
with at most d connected components, that is,
Furthermore, there exists an absolutely dominated splitting (see Section 2.5 above) into s bundles,
As a consequence of domination (recall Proposition 2.1), the subbundles vary continuously with x. As shown by Johnson, Palmer, and Sell [Reference Johnson, Palmer and Sell34, Theorem 2.3] the boundary points
![]() $\alpha _i$
,
$\alpha _i$
,
![]() $\beta _i$
of the connected components of the Sacker–Sell spectrum can be characterized in terms the Lyapunov exponents as follows. If we reindex the intervals in (3.5) so that
$\beta _i$
of the connected components of the Sacker–Sell spectrum can be characterized in terms the Lyapunov exponents as follows. If we reindex the intervals in (3.5) so that
![]() $\beta _1\ge \alpha _1> \dots > \beta _s\ge \alpha _s$
, then, for every i we have
$\beta _1\ge \alpha _1> \dots > \beta _s\ge \alpha _s$
, then, for every i we have
where
![]() $\mu $
runs on the set of ergodic measures; furthermore, each sup and each inf are attained. Using Proposition 2.3, we can characterize these numbers as:
$\mu $
runs on the set of ergodic measures; furthermore, each sup and each inf are attained. Using Proposition 2.3, we can characterize these numbers as:
 $$ \begin{align*} \beta_i &= \lim_{n \to \infty} \sup_{x\in X} \frac{1}{n} \log \| \mathcal{A}(x,n)|E_i\| \, , \\ \alpha_i &= \lim_{n \to \infty} \inf_{x\in X} \frac{1}{n} \log m(\mathcal{A}(x,n)|E_i) \,. \end{align*} $$
$$ \begin{align*} \beta_i &= \lim_{n \to \infty} \sup_{x\in X} \frac{1}{n} \log \| \mathcal{A}(x,n)|E_i\| \, , \\ \alpha_i &= \lim_{n \to \infty} \inf_{x\in X} \frac{1}{n} \log m(\mathcal{A}(x,n)|E_i) \,. \end{align*} $$
Note that the Sacker–Sell splitting (3.6) is actually the finest absolutely dominated splitting for the cocycle
![]() $\mathcal {A}$
, that is, the absolutely dominated splitting into the maximal number of subbundles.
$\mathcal {A}$
, that is, the absolutely dominated splitting into the maximal number of subbundles.
The Sacker–Sell spectrum is a discrete set if and only if
![]() $\alpha _i = \beta _i$
for each
$\alpha _i = \beta _i$
for each
![]() $i = 1,\dots ,s$
. Cocycles with discrete Sacker–Sell spectrum were studied by Johnson and Zampogni [Reference Johnson and Zampogni35]. It turns out that this property coincides with complete regularity:
$i = 1,\dots ,s$
. Cocycles with discrete Sacker–Sell spectrum were studied by Johnson and Zampogni [Reference Johnson and Zampogni35]. It turns out that this property coincides with complete regularity:
Theorem 3.14. A continuous cocycle
![]() $\mathcal {A}$
over an invariantly connected homeomorphism f has discrete Sacker–Sell spectrum if and only if it is completely regular.
$\mathcal {A}$
over an invariantly connected homeomorphism f has discrete Sacker–Sell spectrum if and only if it is completely regular.
Proof. The fact that discrete Sacker–Sell spectrum implies complete regularity is the content of [Reference Johnson and Zampogni35, Proposition 3.1]; it also follows directly from the fundamental facts listed above. For the converse implication, if
![]() $\mathcal {A}$
is completely regular with exponents
$\mathcal {A}$
is completely regular with exponents
![]() $\chi _1> \cdots > \chi _s$
, then by Corollary 3.3, its Oseledets splitting is the finest absolutely dominated splitting, and by relations (3.7), (3.8) we have
$\chi _1> \cdots > \chi _s$
, then by Corollary 3.3, its Oseledets splitting is the finest absolutely dominated splitting, and by relations (3.7), (3.8) we have
![]() $\beta _i = \chi _i = \alpha _i$
for each i, showing that
$\beta _i = \chi _i = \alpha _i$
for each i, showing that
![]() $\mathcal {A}$
has discrete Sacker–Sell spectrum.
$\mathcal {A}$
has discrete Sacker–Sell spectrum.
There is another classical object associated to a linear cocycle called the Mather spectrum (see [Reference Mather42], [Reference Pesin49, § 3.1]), which is directly related to the Sacker-Sell spectrum (see [Reference Chicone and Latushkin18, Corollary 6.45]).
4 The Baire category of sets of regular points
4.1 Baire category
Recall that a subset A in a topological space X is called nowhere dense if its closure
![]() $\bar {A}$
has empty interior. A subset
$\bar {A}$
has empty interior. A subset
![]() $A\subset X$
is said to be of the 1st Baire category if it can be represented as a union of a countable collection of nowhere dense sets, and of 2nd Baire category otherwise. Sets of 1st Baire category are also called meager. Note that any subset of a meager set is a meager set.
$A\subset X$
is said to be of the 1st Baire category if it can be represented as a union of a countable collection of nowhere dense sets, and of 2nd Baire category otherwise. Sets of 1st Baire category are also called meager. Note that any subset of a meager set is a meager set.
A subset
![]() $A \subset X$
is called residual if its complement is meager. If X is a complete metric space, then residual sets are of 2nd Baire category. In particular, X and every other dense
$A \subset X$
is called residual if its complement is meager. If X is a complete metric space, then residual sets are of 2nd Baire category. In particular, X and every other dense
![]() $G_\delta $
set are of the second category.
$G_\delta $
set are of the second category.
Like the collection of sets of probability zero, the collection of meager sets contains the empty set, is closed under countable unions, is hereditary, and is proper. Therefore, one can think of meager sets as being ‘small’. See [Reference Oxtoby48] for a full discussion.
4.2 Dynamically defined meager sets
We now describe a general mechanism for the occurrence of meager sets. Let X be a complete metric space and
![]() $(\varphi _n)_{n>0}$
a sequence of real-valued continuous functions on X. Given numbers
$(\varphi _n)_{n>0}$
a sequence of real-valued continuous functions on X. Given numbers
![]() $\alpha ,\beta \in \mathbb {R}$
, define the following sets
$\alpha ,\beta \in \mathbb {R}$
, define the following sets
 $$ \begin{align*} I_\alpha &\mathrel{:=} \big\{x\in X\colon\liminf\varphi_n(x)<\alpha\big\} \, ,\\ S_\beta &\mathrel{:=} \big\{x\in X\colon\limsup\varphi_n(x)>\beta\big\} \,. \end{align*} $$
$$ \begin{align*} I_\alpha &\mathrel{:=} \big\{x\in X\colon\liminf\varphi_n(x)<\alpha\big\} \, ,\\ S_\beta &\mathrel{:=} \big\{x\in X\colon\limsup\varphi_n(x)>\beta\big\} \,. \end{align*} $$
Theorem 4.1. Assume that there are real numbers
![]() $\alpha <\beta $
such that the sets
$\alpha <\beta $
such that the sets
![]() $I_\alpha $
and
$I_\alpha $
and
![]() $S_\beta $
are both dense in X. Then the set of points
$S_\beta $
are both dense in X. Then the set of points
![]() $x\in X$
for which
$x\in X$
for which
![]() $\lim _{n\to \infty }\varphi _n(x)$
exists is meager.
$\lim _{n\to \infty }\varphi _n(x)$
exists is meager.
Proof. Fix numbers
![]() $\alpha < \alpha ' < \alpha " < \beta " < \beta ' < \beta $
. Letting
$\alpha < \alpha ' < \alpha " < \beta " < \beta ' < \beta $
. Letting
 $$\begin{align*}\widetilde{I}_{\alpha'} \mathrel{:=} \bigcap_{m=1}^\infty\bigcup_{n=m}^\infty\{x\in X\colon \varphi_n(x)<\alpha'\} \, , \end{align*}$$
$$\begin{align*}\widetilde{I}_{\alpha'} \mathrel{:=} \bigcap_{m=1}^\infty\bigcup_{n=m}^\infty\{x\in X\colon \varphi_n(x)<\alpha'\} \, , \end{align*}$$
we have
![]() $I_\alpha \subset \widetilde {I}_{\alpha '} \subset I_{\alpha "}$
. The set
$I_\alpha \subset \widetilde {I}_{\alpha '} \subset I_{\alpha "}$
. The set
![]() $I_\alpha $
is dense, by assumption, and the set
$I_\alpha $
is dense, by assumption, and the set
![]() $\widetilde {I}_{\alpha '}$
is a
$\widetilde {I}_{\alpha '}$
is a
![]() $G_\delta $
. Therefore the set
$G_\delta $
. Therefore the set
![]() $I_{\alpha "}$
contains a dense
$I_{\alpha "}$
contains a dense
![]() $G_\delta $
, so it is residual. Similarly,
$G_\delta $
, so it is residual. Similarly,
![]() $S_{\beta "}$
is residual. Thus, the set
$S_{\beta "}$
is residual. Thus, the set
![]() $I_{\alpha "} \cap S_{\beta "}$
is residual, and for any point in this set,
$I_{\alpha "} \cap S_{\beta "}$
is residual, and for any point in this set,
![]() $\lim _{n\to \infty }\varphi _n(x)$
does not exist.
$\lim _{n\to \infty }\varphi _n(x)$
does not exist.
Without trying to be comprehensive, let us illustrate how Theorem 4.1 can be applied to a simple dynamical setting. Suppose that
![]() $f : X \to X$
is a continuous transformation of a compact metric space. Given a (say) continuous function
$f : X \to X$
is a continuous transformation of a compact metric space. Given a (say) continuous function
![]() $\varphi : X \to \mathbb R$
, consider the sequence of Birkhoff averages
$\varphi : X \to \mathbb R$
, consider the sequence of Birkhoff averages
 $$ \begin{align*} \varphi_n(x) \mathrel{:=} \frac{1}{n}\sum_{k=0}^{n-1}\varphi(f^k(x)) \end{align*} $$
$$ \begin{align*} \varphi_n(x) \mathrel{:=} \frac{1}{n}\sum_{k=0}^{n-1}\varphi(f^k(x)) \end{align*} $$
and let
![]() $\mathcal {R}_\varphi $
be the set of points
$\mathcal {R}_\varphi $
be the set of points
![]() $x\in X$
for which
$x\in X$
for which
![]() $\lim _{n\to \infty }\varphi _n(x)$
exists. By Birkhoff ergodic theorem, we know that this set has full measure with respect to any invariant probability measure and hence, is ‘large’ from the measure-theoretical point of view. But what can we say about the Baire category of this set?
$\lim _{n\to \infty }\varphi _n(x)$
exists. By Birkhoff ergodic theorem, we know that this set has full measure with respect to any invariant probability measure and hence, is ‘large’ from the measure-theoretical point of view. But what can we say about the Baire category of this set?
Following [Reference Akin, Auslander and Nagar3], a (perhaps noninvertible) continuous transformation f of a compact metric space X is called strongly transitive if the backward orbit
![]() $ \{f^{-n}(x) \colon n \ge 0\}$
of every point
$ \{f^{-n}(x) \colon n \ge 0\}$
of every point
![]() $x \in X$
is dense in X. Examples include any minimal homeomorphism, any transitive one-sided subshift of finite type, and the restriction of any rational map of
$x \in X$
is dense in X. Examples include any minimal homeomorphism, any transitive one-sided subshift of finite type, and the restriction of any rational map of
![]() $\bar {\mathbb {C}}$
to its Julia set (see [Reference Milnor44, Corollary 4.13]).
$\bar {\mathbb {C}}$
to its Julia set (see [Reference Milnor44, Corollary 4.13]).
Theorem 4.2. Let
![]() $f \colon X \to X$
be a strongly transitive map, and let
$f \colon X \to X$
be a strongly transitive map, and let
![]() $\varphi \colon X \to \mathbb R$
be a continuous function. Then the set
$\varphi \colon X \to \mathbb R$
be a continuous function. Then the set
![]() $\mathcal {R}_\varphi $
of points of convergence of Birkhoff averages is either a meager set or the whole space X. In the latter case, the Birkhoff averages of
$\mathcal {R}_\varphi $
of points of convergence of Birkhoff averages is either a meager set or the whole space X. In the latter case, the Birkhoff averages of
![]() $\varphi $
with respect to f converge uniformly to a constant.
$\varphi $
with respect to f converge uniformly to a constant.
Proof. Suppose that the Birkhoff averages do not converge uniformly to a constant. By Corollary 2.4, there exist two ergodic Borel probability measures
![]() $\mu _1$
and
$\mu _1$
and
![]() $\mu _2$
such that
$\mu _2$
such that
![]() $\int \varphi \, d\mu _1 \neq \int \varphi \, d\mu _2$
. For
$\int \varphi \, d\mu _1 \neq \int \varphi \, d\mu _2$
. For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $\mathcal {B}_i$
be the set of points x such that
$\mathcal {B}_i$
be the set of points x such that
![]() $\varphi _n(x) \to \int \varphi \, d\mu _i$
. These sets are nonempty and invariant. In particular, they contain full backward orbits. It follows from strong transitivity that both sets
$\varphi _n(x) \to \int \varphi \, d\mu _i$
. These sets are nonempty and invariant. In particular, they contain full backward orbits. It follows from strong transitivity that both sets
![]() $\mathcal {B}_1$
and
$\mathcal {B}_1$
and
![]() $\mathcal {B}_2$
are dense in X. It follows from Theorem 4.1 that the set of convergence
$\mathcal {B}_2$
are dense in X. It follows from Theorem 4.1 that the set of convergence
![]() $\mathcal {R}_\varphi $
is meager.
$\mathcal {R}_\varphi $
is meager.
The literature contains many related results; we mention [Reference Johnson33, Theorem 4.3.(2)], [Reference Akin2, Theorem 11, p. 166], and [Reference Carvalho and Varandas15]. The general message is that the set of points for which Birkhoff ergodic theorem holds, while large from a measure-theoretic viewpoint, is often meager.
As it is reasonable to expect, similar phenomena for the multiplicative ergodic theorem of Oseledets occur in a variety of contexts: see for instance [Reference Abdenur, Bonatti and Crovisier1, Theorem 3.14], [Reference Tian60], [Reference Micena and de la Llave43], [Reference Varandas and Dias61], and [Reference Lin and Tian40, Corollary C]. We now turn to our investigation of this matter, where the previously discussed concept of complete regularity will naturally enter into the picture. Our goal is to establish sufficient conditions under which the set
![]() $\mathcal {R}$
of LP-regular points is meager, thereby ensuring that the set of irregular points is topologically large. We note that the set of irregular points may also be large in terms of entropy [Reference Chen, Zang and Zou17] or Lebesgue measure [Reference Kiriki, Li, Nakano and Soma39].
$\mathcal {R}$
of LP-regular points is meager, thereby ensuring that the set of irregular points is topologically large. We note that the set of irregular points may also be large in terms of entropy [Reference Chen, Zang and Zou17] or Lebesgue measure [Reference Kiriki, Li, Nakano and Soma39].
4.3 A criterion for generic irregularity
We now come back to the setting of continuous linear cocycles. We will formulate a sufficient condition for the set of LP-regular points to be meager. Our condition uses the notion of complete regularity studied above.
Given a homeomorphism f of a compact metric space X and a nonempty subset
![]() $Y\subset X$
, we define the stable set of Y as
$Y\subset X$
, we define the stable set of Y as
Now we can state the following result:
Theorem 4.3. Let f be a homeomorphism of a compact metric space X and let
![]() $\mathcal {A}$
be a continuous linear cocycle over f. Assume that there exist two f-invariant disjoint compact subsets
$\mathcal {A}$
be a continuous linear cocycle over f. Assume that there exist two f-invariant disjoint compact subsets
![]() $X_1, X_2\subset X$
such that
$X_1, X_2\subset X$
such that
-
1. the stable sets
 $W^{\mathrm {s}}(X_1)$
and
$W^{\mathrm {s}}(X_1)$
and
 $W^{\mathrm {s}}(X_2)$
are both dense in X;
$W^{\mathrm {s}}(X_2)$
are both dense in X; -
2. the restrictions of the cocycle
 $\mathcal {A}$
to
$\mathcal {A}$
to
 $X_1$
and
$X_1$
and
 $X_2$
, denoted
$X_2$
, denoted
 $\mathcal {A}|X_1$
and
$\mathcal {A}|X_1$
and
 $\mathcal {A}|X_2$
, are both completely regular;
$\mathcal {A}|X_2$
, are both completely regular; -
3. the cocycles
 $\mathcal {A}|X_1$
and
$\mathcal {A}|X_1$
and
 $\mathcal {A}|X_2$
have different Lyapunov spectra, that is,
$\mathcal {A}|X_2$
have different Lyapunov spectra, that is,
 $\mathrm {Sp}(\mathcal {A}|X_1)\ne \mathrm {Sp}(\mathcal {A}|X_2)$
.
$\mathrm {Sp}(\mathcal {A}|X_1)\ne \mathrm {Sp}(\mathcal {A}|X_2)$
.
Then the set
![]() $\mathcal {FR}$
of points which are forward regular for the cocycle
$\mathcal {FR}$
of points which are forward regular for the cocycle
![]() $\mathcal {A}$
is meager and, in particular, so is the set
$\mathcal {A}$
is meager and, in particular, so is the set
![]() $\mathcal {R}$
of LP-regular points.
$\mathcal {R}$
of LP-regular points.
The proof of this theorem will use Theorem 4.1 above and also the following lemma:
Lemma 4.4. Let
![]() $Y\subset X$
be a compact f-invariant subset such that the restriction of the cocycle
$Y\subset X$
be a compact f-invariant subset such that the restriction of the cocycle
![]() $\mathcal {A}$
to Y is completely regular with Lyapunov exponents
$\mathcal {A}$
to Y is completely regular with Lyapunov exponents
![]() $\chi _1>\cdots >\chi _s$
. Then, for every
$\chi _1>\cdots >\chi _s$
. Then, for every
![]() $x\in W^{\mathrm {s}}(Y)$
,
$x\in W^{\mathrm {s}}(Y)$
,
Proof. It follows from the definition of complete regularity and property (2.3) that the desired conclusion (4.1) holds for every point in Y. Actually, it follows from Theorem 3.1 that the limit in (4.1) is uniform over Y. In particular, given
![]() $\varepsilon>0$
, we can find
$\varepsilon>0$
, we can find
![]() $N>0$
such that, for all
$N>0$
such that, for all
![]() $y \in Y$
,
$y \in Y$
,
By continuity, if
![]() $d(x,Y)$
is sufficiently small, then
$d(x,Y)$
is sufficiently small, then
Then, as a straightforward consequence of submultiplicativity of norms, we have
for all
![]() $x \in W^{\mathrm {s}}(Y)$
. Since
$x \in W^{\mathrm {s}}(Y)$
. Since
![]() $\varepsilon>0$
is arbitrary, the limsup above is actually
$\varepsilon>0$
is arbitrary, the limsup above is actually
![]() $\le \chi _1$
for all
$\le \chi _1$
for all
![]() $x \in W^{\mathrm {s}}(Y)$
.
$x \in W^{\mathrm {s}}(Y)$
.
In order to obtain an inequality in the reverse direction, fix
![]() $\varepsilon>0$
again. Using Theorem 3.1 we find
$\varepsilon>0$
again. Using Theorem 3.1 we find
![]() $N>0$
such that, for all points
$N>0$
such that, for all points
![]() $y \in Y$
and all unit vectors
$y \in Y$
and all unit vectors
![]() $u \in E_1(y)$
,
$u \in E_1(y)$
,
Since the cocycle
![]() $\mathcal {A}$
restricted to the compact invariant set Y admits a dominated splitting with dominating bundle
$\mathcal {A}$
restricted to the compact invariant set Y admits a dominated splitting with dominating bundle
![]() $E_1$
, we can define a family of cones
$E_1$
, we can define a family of cones
![]() $C(y) \subset \mathbb R^d$
depending continuously on
$C(y) \subset \mathbb R^d$
depending continuously on
![]() $y \in Y$
with the following properties: for every
$y \in Y$
with the following properties: for every
![]() $y \in Y$
, we have
$y \in Y$
, we have
![]() $E_1(y) \subset C(y)$
and
$E_1(y) \subset C(y)$
and
Such a cone field is easily constructed using an adapted metric: see [Reference Gourmelon28, Reference Crovisier and Potrie19]. The subbundle attracts vectors in the cone field in the following sense: for every
![]() $y \in Y$
and every unit vector
$y \in Y$
and every unit vector
![]() $u \in C(y)$
,
$u \in C(y)$
,
and this convergence is actually uniform with respect to y and u. We extend continuously the cone field to a neighbourhood U of Y so that the strict invariance property is satisfied for points in
![]() $U \cap f^{-1}(U)$
.
$U \cap f^{-1}(U)$
.
Fix
![]() $x\in W^{\mathrm {s}}(Y)$
. Replacing x by an iterate if necessary, we assume that
$x\in W^{\mathrm {s}}(Y)$
. Replacing x by an iterate if necessary, we assume that
![]() $f^n(x) \in U$
for every
$f^n(x) \in U$
for every
![]() $n \ge 0$
. Fix any unit vector
$n \ge 0$
. Fix any unit vector
![]() $v \in C(x)$
. It follows from property (4.3) that there exist a sequence of points
$v \in C(x)$
. It follows from property (4.3) that there exist a sequence of points
![]() $y_n\in Y$
and a sequence of unit vectors
$y_n\in Y$
and a sequence of unit vectors
![]() $u_n \in E_1(y_n)$
such that
$u_n \in E_1(y_n)$
such that
Inequality (4.2) applies to each pair
![]() $(y,u) = (y_n, u_n)$
. For every sufficiently large n, the pair
$(y,u) = (y_n, u_n)$
. For every sufficiently large n, the pair
![]() $\big (f^n(x),\frac {\mathcal {A}(x,n)v}{\|\mathcal {A}(x,n)v\|}\big )$
is close to
$\big (f^n(x),\frac {\mathcal {A}(x,n)v}{\|\mathcal {A}(x,n)v\|}\big )$
is close to
![]() $(y_n,u_n)$
, and therefore
$(y_n,u_n)$
, and therefore
Now it is straightforward to check that
Since
![]() $\varepsilon>0$
is arbitrary, the liminf above is actually
$\varepsilon>0$
is arbitrary, the liminf above is actually
![]() $\ge \chi _1$
for all
$\ge \chi _1$
for all
![]() $x \in W^{\mathrm {s}}(Y)$
. The proof of the lemma is completed.
$x \in W^{\mathrm {s}}(Y)$
. The proof of the lemma is completed.
Proof of Theorem 4.3.
For each
![]() $j=1,2$
, let
$j=1,2$
, let
![]() $\widetilde \chi _1^j\ge \cdots \ge \widetilde \chi _d^j$
be the list of values of the Lyapunov exponent of the cocycle
$\widetilde \chi _1^j\ge \cdots \ge \widetilde \chi _d^j$
be the list of values of the Lyapunov exponent of the cocycle
![]() $\mathcal {A}|X_j$
, where each value is repeated according to multiplicity. By assumption, these two lists are not identical.
$\mathcal {A}|X_j$
, where each value is repeated according to multiplicity. By assumption, these two lists are not identical.
We first assume that
![]() $\widetilde \chi _1^1\neq \widetilde \chi _1^2$
. For definiteness, assume that
$\widetilde \chi _1^1\neq \widetilde \chi _1^2$
. For definiteness, assume that
![]() $\widetilde \chi _1^1> \widetilde \chi _1^2$
. Consider the sequence of continuous functions
$\widetilde \chi _1^1> \widetilde \chi _1^2$
. Consider the sequence of continuous functions
By Lemma 4.4, for each
![]() $j=1,2$
, we have
$j=1,2$
, we have
![]() $\lim \varphi _n(x) = \widetilde \chi _1^j$
for all
$\lim \varphi _n(x) = \widetilde \chi _1^j$
for all
![]() $x \in W^{\mathrm {s}}(X_j)$
. Each of these stable sets is dense, by hypothesis. Applying Theorem 4.1 with
$x \in W^{\mathrm {s}}(X_j)$
. Each of these stable sets is dense, by hypothesis. Applying Theorem 4.1 with
![]() $\alpha =\widetilde \chi _1^2$
and
$\alpha =\widetilde \chi _1^2$
and
![]() $\beta =\widetilde \chi _1^1$
, we obtain that the set of points for which
$\beta =\widetilde \chi _1^1$
, we obtain that the set of points for which
![]() $\lim _{n\to \infty }\varphi _n(x)$
exists is meager and hence, so is its subset
$\lim _{n\to \infty }\varphi _n(x)$
exists is meager and hence, so is its subset
![]() $\mathcal {FR}$
of forward regular points (see [Reference Barreira and Pesin7]). This completes the proof of the theorem in the particular case when
$\mathcal {FR}$
of forward regular points (see [Reference Barreira and Pesin7]). This completes the proof of the theorem in the particular case when
![]() $\widetilde \chi _1^1 \neq \widetilde \chi _1^2$
.
$\widetilde \chi _1^1 \neq \widetilde \chi _1^2$
.
We now proceed with the general case and show how to reduce it to the previous one by using exterior powers. As explained in Subsection 2.4, a regular point
![]() $x\in X$
for the cocycle
$x\in X$
for the cocycle
![]() $\mathcal {A}$
is also a regular point for the exterior power cocycle
$\mathcal {A}$
is also a regular point for the exterior power cocycle
![]() $\mathcal {A}^{\wedge i}$
. Now let i be the smallest index such that
$\mathcal {A}^{\wedge i}$
. Now let i be the smallest index such that
![]() $\widetilde \chi _i^1\neq \widetilde \chi _i^2$
, that is,
$\widetilde \chi _i^1\neq \widetilde \chi _i^2$
, that is,
![]() $\widetilde \chi _i(\mathcal {A}|X_1)\ne \widetilde \chi _i(\mathcal {A}|X_2)$
. Then, by formula (2.8), we obtain that
$\widetilde \chi _i(\mathcal {A}|X_1)\ne \widetilde \chi _i(\mathcal {A}|X_2)$
. Then, by formula (2.8), we obtain that
Since the cocycle
![]() $\mathcal {A}$
is completely regular on subsets
$\mathcal {A}$
is completely regular on subsets
![]() $X_1$
and
$X_1$
and
![]() $X_2$
, the exterior power cocycle
$X_2$
, the exterior power cocycle
![]() $\mathcal {A}^{\wedge i}$
is also completely regular on these sets (see Proposition 3.4). By the previous case, the set of forward regular points for the cocycle
$\mathcal {A}^{\wedge i}$
is also completely regular on these sets (see Proposition 3.4). By the previous case, the set of forward regular points for the cocycle
![]() $\mathcal {A}^{\wedge i}$
is meager, and hence, so is the set of forward regular points for the cocycle
$\mathcal {A}^{\wedge i}$
is meager, and hence, so is the set of forward regular points for the cocycle
![]() $\mathcal {A}$
. This completes the proof of the theorem.
$\mathcal {A}$
. This completes the proof of the theorem.
4.4 Applications of the criterion
We present some corollaries of Theorem 4.3.
If p is a periodic point for f, let
![]() $O(p)$
denote the orbit of p. Given any linear cocycle
$O(p)$
denote the orbit of p. Given any linear cocycle
![]() $\mathcal {A}$
over f, the periodic point p is LP-regular, and its Lyapunov exponents can be computed from the eigenvalues of the matrix
$\mathcal {A}$
over f, the periodic point p is LP-regular, and its Lyapunov exponents can be computed from the eigenvalues of the matrix
![]() $\mathcal {A}(p,k)$
, where k is the period of p.
$\mathcal {A}(p,k)$
, where k is the period of p.
Corollary 4.5. Let f be a homeomorphism of a compact metric space X and let
![]() $\mathcal {A}$
be a continuous linear cocycle over f. Suppose there are two periodic points
$\mathcal {A}$
be a continuous linear cocycle over f. Suppose there are two periodic points
![]() $p,q\in X$
such that
$p,q\in X$
such that
-
1. the stable sets
 $W^{\mathrm {s}}(O(p))$
and
$W^{\mathrm {s}}(O(p))$
and
 $W^{\mathrm {s}}(O(q))$
are both dense in X;
$W^{\mathrm {s}}(O(q))$
are both dense in X; -
2.
 $\mathrm {Sp}(\mathcal {A},p)\ne \mathrm {Sp}(\mathcal {A},q)$
.
$\mathrm {Sp}(\mathcal {A},p)\ne \mathrm {Sp}(\mathcal {A},q)$
.
Then the set
![]() $\mathcal {FR}$
of points which are forward regular for the cocycle
$\mathcal {FR}$
of points which are forward regular for the cocycle
![]() $\mathcal {A}$
is meager and, in particular, so is the set
$\mathcal {A}$
is meager and, in particular, so is the set
![]() $\mathcal {R}$
of LP-regular points.
$\mathcal {R}$
of LP-regular points.
Proof. Recall from Example 3.6 that the restriction of the cocycle
![]() $\mathcal {A}$
to any periodic orbit is completely regular. The result now follows from Theorem 4.3.
$\mathcal {A}$
to any periodic orbit is completely regular. The result now follows from Theorem 4.3.
There are situations where Theorem 4.3 applies, but Corollary 4.5 does not. For example, suppose
![]() $\varphi ^t \colon M \to M$
is a transitive Anosov flow of a compact manifold. If
$\varphi ^t \colon M \to M$
is a transitive Anosov flow of a compact manifold. If
![]() $t_0>0$
is small enough, then
$t_0>0$
is small enough, then
![]() $f \mathrel {:=} \varphi ^{t_0}$
has no periodic points, so we are out of the scope of Corollary 4.5. Now, suppose
$f \mathrel {:=} \varphi ^{t_0}$
has no periodic points, so we are out of the scope of Corollary 4.5. Now, suppose
![]() $x_1$
and
$x_1$
and
![]() $x_2$
are periodic points for the flow, and let
$x_2$
are periodic points for the flow, and let
![]() $X_1$
and
$X_1$
and
![]() $X_2$
be the respective orbits. Then the restrictions
$X_2$
be the respective orbits. Then the restrictions
![]() $f|X_1$
and
$f|X_1$
and
![]() $f|X_2$
are conjugate to irrational rotations. If
$f|X_2$
are conjugate to irrational rotations. If
![]() $\mathcal {A}$
is any continuous cocycle over f whose restrictions
$\mathcal {A}$
is any continuous cocycle over f whose restrictions
![]() $\mathcal {A}|X_1$
and
$\mathcal {A}|X_1$
and
![]() $\mathcal {A}|X_2$
are completely regular but have different Lyapunov spectra, then its set
$\mathcal {A}|X_2$
are completely regular but have different Lyapunov spectra, then its set
![]() $\mathcal {R}$
of LP-regular points is meager in M. Indeed, the stable sets
$\mathcal {R}$
of LP-regular points is meager in M. Indeed, the stable sets
![]() $W^{\mathrm {s}}(X_1)$
and
$W^{\mathrm {s}}(X_1)$
and
![]() $W^{\mathrm {s}}(X_2)$
are dense (see, e.g., [Reference Fisher and Hasselblatt26, Theorem 2.6.10]), so Theorem 4.3 applies.
$W^{\mathrm {s}}(X_2)$
are dense (see, e.g., [Reference Fisher and Hasselblatt26, Theorem 2.6.10]), so Theorem 4.3 applies.
On the other hand, there is a particular setting of the dynamics in which the denseness hypothesis in Corollary 4.5 is naturally satisfied, namely homoclinic classes. We recall the definition.
Let
![]() $f: M\to M$
be a
$f: M\to M$
be a
![]() $C^1$
diffeomorphism of a compact smooth Riemannian manifold M. Let also
$C^1$
diffeomorphism of a compact smooth Riemannian manifold M. Let also
![]() $p,q\in M$
be two hyperbolic periodic points. We say that p and q are homoclinically related and write
$p,q\in M$
be two hyperbolic periodic points. We say that p and q are homoclinically related and write
![]() $q\sim p$
if the sets of transverse intersection points
$q\sim p$
if the sets of transverse intersection points
![]() $W^{\mathrm {u}}(O(p))\pitchfork W^{\mathrm {s}}(O(q))$
and
$W^{\mathrm {u}}(O(p))\pitchfork W^{\mathrm {s}}(O(q))$
and
![]() $W^{\mathrm {s}}(O(p))\pitchfork W^{\mathrm {u}}(O(q))$
are both nonempty. This turns out to be an equivalence relation (see [Reference Newhouse47, Proposition 2.1]), and every equivalence class is an invariant subset. The homoclinic class of p is defined to be the closure of the equivalence class of p. (We note that two homoclinic classes may intersect without being identical.) Furthermore (see [Reference Newhouse47, Corollary 2.7]),
$W^{\mathrm {s}}(O(p))\pitchfork W^{\mathrm {u}}(O(q))$
are both nonempty. This turns out to be an equivalence relation (see [Reference Newhouse47, Proposition 2.1]), and every equivalence class is an invariant subset. The homoclinic class of p is defined to be the closure of the equivalence class of p. (We note that two homoclinic classes may intersect without being identical.) Furthermore (see [Reference Newhouse47, Corollary 2.7]),
In particular, for any periodic point
![]() $q \sim p$
the set
$q \sim p$
the set
![]() $W^{\mathrm {s}}(O(q))$
is dense in
$W^{\mathrm {s}}(O(q))$
is dense in
![]() $H_p = H_q$
. Thus Corollary 4.5 implies the following result:
$H_p = H_q$
. Thus Corollary 4.5 implies the following result:
Corollary 4.6. Let f be a
![]() $C^1$
diffeomorphism, let p be a hyperbolic periodic point, and let
$C^1$
diffeomorphism, let p be a hyperbolic periodic point, and let
![]() $H_p$
be its homoclinic class. Let
$H_p$
be its homoclinic class. Let
![]() $\mathcal {A}$
be any continuous cocycle on
$\mathcal {A}$
be any continuous cocycle on
![]() $H_p$
. Assume that there exists another periodic point q which is homoclinically related to p such that
$H_p$
. Assume that there exists another periodic point q which is homoclinically related to p such that
![]() $\mathrm {Sp}(\mathcal {A}|O(p))\ne \mathrm {Sp}(\mathcal {A}|O(q))$
. Then the set
$\mathrm {Sp}(\mathcal {A}|O(p))\ne \mathrm {Sp}(\mathcal {A}|O(q))$
. Then the set
![]() $\mathcal {R}$
of LP-regular points for
$\mathcal {R}$
of LP-regular points for
![]() $\mathcal {A}$
is meager in the relative topology of
$\mathcal {A}$
is meager in the relative topology of
![]() $H_p$
.
$H_p$
.
Of course, the most natural application of the result above is for the derivative cocycle restricted to the homoclinic class.
For the sake of completeness, let us describe here a related result by Tian [Reference Tian60]. Let f be a homeomorphism of a compact metric space X. We say that f has exponential specification property with exponent
![]() $\lambda> 0$
if for any
$\lambda> 0$
if for any
![]() $\delta> 0$
there is
$\delta> 0$
there is
![]() $N=N(\delta )> 0$
such that for any
$N=N(\delta )> 0$
such that for any
![]() $k\ge 1$
, any k points
$k\ge 1$
, any k points
![]() $x_1,x_2,\dots ,x_k\in X$
, any integers
$x_1,x_2,\dots ,x_k\in X$
, any integers
![]() $a_1\le b_1 <a_2\le b_2 <\ldots <a_k\le b_k$
with
$a_1\le b_1 <a_2\le b_2 <\ldots <a_k\le b_k$
with
![]() $a_{i+1}-b_i\ge N$
, one can find a point
$a_{i+1}-b_i\ge N$
, one can find a point
![]() $y\in X$
such that
$y\in X$
such that
for
![]() $a_j\le i\le b_j$
and
$a_j\le i\le b_j$
and
![]() $1\le j\le k$
.
$1\le j\le k$
.
Theorem 4.7 (see [Reference Tian60, Theorem 1.4]).
Let
![]() $\mathcal {A}$
be a Hölder continuous cocycle over a homeomorphism f with the exponential specification property. Then either the set
$\mathcal {A}$
be a Hölder continuous cocycle over a homeomorphism f with the exponential specification property. Then either the set
![]() $\mathcal {R}$
of LP-regular points is meager in X or the cocycle has the same Lyapunov spectrum with respect to all ergodic f-invariant measures.
$\mathcal {R}$
of LP-regular points is meager in X or the cocycle has the same Lyapunov spectrum with respect to all ergodic f-invariant measures.
A homeomorphism f with the exponential specification property may fail to have periodic orbits (see [Reference Tian60, Example 2.4.(2)]). Thus we cannot use Corollary 4.5 to derive Theorem 4.7. Note that Theorem 4.3 and its corollaries apply to all continuous cocycles. In contrast, Theorem 4.7 requires Hölder continuity of the cocycle, since its proof employs estimates from [Reference Kalinin36] that rely crucially on this stronger regularity assumption.
4.5 All-or-meager results
Here is a related result, this time following from Corollary 4.5 combined with Theorem 3.13:
Theorem 4.8. Let
![]() $\mathcal {A}$
be a Hölder continuous cocycle over a transitive Anosov
$\mathcal {A}$
be a Hölder continuous cocycle over a transitive Anosov
![]() $C^{1+\delta }$
diffeomorphism f of a compact smooth manifold X. Then either the set
$C^{1+\delta }$
diffeomorphism f of a compact smooth manifold X. Then either the set
![]() $\mathcal {R}$
of LP-regular points is meager in X or
$\mathcal {R}$
of LP-regular points is meager in X or
![]() $\mathcal {R} = X$
and the cocycle is completely regular.
$\mathcal {R} = X$
and the cocycle is completely regular.
Notice the sharp contrast between the two alternatives: either the set
![]() $\mathcal {R}$
is the whole space, or it is a meager subset. We call statements with this type of conclusion all-or-meager results. Another example is Theorem 4.2.
$\mathcal {R}$
is the whole space, or it is a meager subset. We call statements with this type of conclusion all-or-meager results. Another example is Theorem 4.2.
Let us look for other results of this type. Optimistically, one could ask: are the conclusions of Theorem 4.8 valid for any continuous linear cocycle over any homeomorphism of a compact space? The answer is negative, as the following example shows.
Example 4.9. Let
![]() $g : Y \to Y$
be a homeomorphism of a compact metric space Y and let
$g : Y \to Y$
be a homeomorphism of a compact metric space Y and let
![]() $\mathcal {B}$
be a linear cocycle over g, with generator B. We assume two conditions: First, g admits a fully-supported Borel probability measure
$\mathcal {B}$
be a linear cocycle over g, with generator B. We assume two conditions: First, g admits a fully-supported Borel probability measure
![]() $\mu $
. Second, the set
$\mu $
. Second, the set
![]() $\mathcal {R}_{\mathcal {B}}$
of LP-regular points is not the whole space Y. Examples satisfying these conditions can be found using Theorem 4.8, for instance. Note that
$\mathcal {R}_{\mathcal {B}}$
of LP-regular points is not the whole space Y. Examples satisfying these conditions can be found using Theorem 4.8, for instance. Note that
![]() $\mu $
-almost every point in Y has alpha- and omega-limit sets both equal to Y. Fix a point
$\mu $
-almost every point in Y has alpha- and omega-limit sets both equal to Y. Fix a point
![]() $y_0$
with these properties which is also an element of the full-measure set
$y_0$
with these properties which is also an element of the full-measure set
![]() $\mathcal {R}_{\mathcal {B}}$
. Let
$\mathcal {R}_{\mathcal {B}}$
. Let
![]() $y_n \mathrel {:=} g^n(y_0)$
; then, for any
$y_n \mathrel {:=} g^n(y_0)$
; then, for any
![]() $N>0$
, the sets
$N>0$
, the sets
![]() $\{y_n : n> N\}$
and
$\{y_n : n> N\}$
and
![]() $\{y_n : n < -N\}$
are both dense in Y. Now fix an increasing two-sided sequence
$\{y_n : n < -N\}$
are both dense in Y. Now fix an increasing two-sided sequence
![]() $(t_n)_{n \in {\mathbb {Z}}}$
such that
$(t_n)_{n \in {\mathbb {Z}}}$
such that
![]() $t_n \to 0$
as
$t_n \to 0$
as
![]() $n \to -\infty $
and
$n \to -\infty $
and
![]() $t_n \to 1$
as
$t_n \to 1$
as
![]() $n \to +\infty $
. Define the following subsets of
$n \to +\infty $
. Define the following subsets of
![]() $Y \times [0,1]$
:
$Y \times [0,1]$
:
Then
![]() $\overline {Z} = X$
and in particular X is compact. Also note that each point in Z has a neighbourhood disjoint from
$\overline {Z} = X$
and in particular X is compact. Also note that each point in Z has a neighbourhood disjoint from
![]() $Y \times \{0,1\}$
and in particular Z is a relatively open subset of X. Define a map
$Y \times \{0,1\}$
and in particular Z is a relatively open subset of X. Define a map
![]() $f \colon X \to X$
as follows:
$f \colon X \to X$
as follows:
Then f is actually a homeomorphism of X, and the subset Z is the orbit of
![]() $(y_0,t_0)$
. Finally, define a cocycle
$(y_0,t_0)$
. Finally, define a cocycle
![]() $\mathcal {A}$
over f whose generator is
$\mathcal {A}$
over f whose generator is
![]() $\mathcal {A}(y,t) \mathrel {:=} B(y)$
. Then the set
$\mathcal {A}(y,t) \mathrel {:=} B(y)$
. Then the set
![]() $\mathcal {R}_{\mathcal {A}}$
of LP-regular points is not the whole space X, as its complement includes
$\mathcal {R}_{\mathcal {A}}$
of LP-regular points is not the whole space X, as its complement includes
![]() $(Y\setminus \mathcal {R}_{\mathcal {B}}) \times \{0,1\}$
. On the other hand, since the set
$(Y\setminus \mathcal {R}_{\mathcal {B}}) \times \{0,1\}$
. On the other hand, since the set
![]() $\mathcal {R}_{\mathcal {B}}$
contains the point
$\mathcal {R}_{\mathcal {B}}$
contains the point
![]() $y_0$
, the set
$y_0$
, the set
![]() $\mathcal {R}_{\mathcal {A}}$
contains the point
$\mathcal {R}_{\mathcal {A}}$
contains the point
![]() $(y_0,t_0)$
, as well as its orbit Z. Since Z is an open and dense subset of X, it follows that
$(y_0,t_0)$
, as well as its orbit Z. Since Z is an open and dense subset of X, it follows that
![]() $\mathcal {R}_{\mathcal {A}}$
is not a meager set. Thus, we have exhibited an example where the all-or-meager dichotomy fails.
$\mathcal {R}_{\mathcal {A}}$
is not a meager set. Thus, we have exhibited an example where the all-or-meager dichotomy fails.
The example above is somewhat unsatisfactory because the map f has wandering points.
Returning to the case of transitive Anosov diffeomorphisms, it is an open problem whether Theorem 4.8 extends to cocycles that are merely continuous rather than Hölder continuous.
On the other hand, if we assume that the dynamics is minimal, then we have the following all-or-meager dichotomy that applies to all continuous linear cocycles:
Theorem 4.10. Let
![]() $\mathcal {A}$
be a continuous cocycle over a minimal homeomorphism f of a compact metric space. Then either the set
$\mathcal {A}$
be a continuous cocycle over a minimal homeomorphism f of a compact metric space. Then either the set
![]() $\mathcal {R}$
of LP-regular points is meager in X or
$\mathcal {R}$
of LP-regular points is meager in X or
![]() $\mathcal {R} = X$
and the cocycle is completely regular.
$\mathcal {R} = X$
and the cocycle is completely regular.
The proof of this theorem is given in Section 4.7.
Theorem 4.10 extends some previous results such as [Reference Furman27, Theorem 4] and [Reference Hou, Lin and Tian32, Corollary 6.6].
Johnson and Zampogni asked a question in [Reference Johnson and Zampogni35, p. 104], which in our terminology is as follows: Assume that the dynamics f is minimal, and that for all points x and all nonzero vectors v, the forward Lyapunov exponent
![]() $\lim _{n \to \infty } \frac 1n \log \|\mathcal {A}(x,n)v\|$
is well-defined; does it follow that the cocycle is completely regular? Note that Theorem 4.10 provides a positive answer to this question under the stronger hypothesis that all points are LP-regular.
$\lim _{n \to \infty } \frac 1n \log \|\mathcal {A}(x,n)v\|$
is well-defined; does it follow that the cocycle is completely regular? Note that Theorem 4.10 provides a positive answer to this question under the stronger hypothesis that all points are LP-regular.
4.6 Singular values of cocycles
As a preparation for the proof of Theorem 4.10, we discuss the behaviour of the singular values of the cocycle. Furthermore, under assumption of minimality, we obtain new information about singular values in the absence of dominated splitting (Theorem 4.12).
The singular values of a linear operator
![]() $L \colon \mathbb R^d \to \mathbb R^d$
are the eigenvalues of
$L \colon \mathbb R^d \to \mathbb R^d$
are the eigenvalues of
![]() $\sqrt {L^* L}$
, which we list with multiplicity as
$\sqrt {L^* L}$
, which we list with multiplicity as
Each singular value
![]() $\sigma _k(L)$
depends continuously on L. The extreme singular values are the norm
$\sigma _k(L)$
depends continuously on L. The extreme singular values are the norm
![]() $\|L\| = \sigma _1(L)$
and the co-norm
$\|L\| = \sigma _1(L)$
and the co-norm
![]() $m(L) = \sigma _d(L)$
. More generally, by the Courant–Fischer principle [Reference Horn and Johnson31, Theorem 7.3.8], for any
$m(L) = \sigma _d(L)$
. More generally, by the Courant–Fischer principle [Reference Horn and Johnson31, Theorem 7.3.8], for any
![]() $k = 1, \dots , d$
,
$k = 1, \dots , d$
,
 $$\begin{align*}\sigma_k(L) &= \max \big\{ m(A|_E) \colon E \text{ is a subspace of dim. } k \big\} \\ &= \min \big\{ \|A|_F\|\ \ \ \colon F \text{ is a subspace of dim. } d-k+1 \big\} \,. \end{align*}$$
$$\begin{align*}\sigma_k(L) &= \max \big\{ m(A|_E) \colon E \text{ is a subspace of dim. } k \big\} \\ &= \min \big\{ \|A|_F\|\ \ \ \colon F \text{ is a subspace of dim. } d-k+1 \big\} \,. \end{align*}$$
As a simple consequence, we have the following useful bounds:
The list of singular values of the exterior power
![]() $L^{\wedge r}$
coincides with the list
$L^{\wedge r}$
coincides with the list
![]() $\sigma _{k_1}(L) + \cdots + \sigma _{k_r}(L)$
, where
$\sigma _{k_1}(L) + \cdots + \sigma _{k_r}(L)$
, where
![]() $1 \le k_1 < \cdots < k_r \le d$
, with repetitions being taken into account.
$1 \le k_1 < \cdots < k_r \le d$
, with repetitions being taken into account.
The Lyapunov exponents of a linear cocycle
![]() $\mathcal {A}$
are related to the singular values as follows: for every forward regular point x,
$\mathcal {A}$
are related to the singular values as follows: for every forward regular point x,
Dominated splittings (see Section 2.5) can be detected in terms of separation of singular values as follows:
Proposition 4.11 [Reference Bochi and Gourmelon11, Theorem A].
Let f be a homeomorphism of a compact metric space, and let
![]() $\mathcal {A}$
be a d-dimensional continuous linear cocycle over f. For every k with
$\mathcal {A}$
be a d-dimensional continuous linear cocycle over f. For every k with
![]() $0<k<d$
, the cocycle
$0<k<d$
, the cocycle
![]() $\mathcal {A}$
admits a dominated splitting with a nontrivial dominating bundle of dimension k if and only if there exist positive constants c and
$\mathcal {A}$
admits a dominated splitting with a nontrivial dominating bundle of dimension k if and only if there exist positive constants c and
![]() $\varepsilon $
such that
$\varepsilon $
such that
for all
![]() $x \in X$
and all
$x \in X$
and all
![]() $n>0$
.
$n>0$
.
In the result above, the ‘only if’ part is rather trivial. It is the ‘if’ part that is interesting: the exponential separation of singular values forces the existence of a dominated splitting.
Our next result can be seen as an improvement of Proposition 4.11 under the assumption of minimality:
Theorem 4.12. Let f be a minimal homeomorphism of a compact metric space, and let
![]() $\mathcal {A}$
be a d-dimensional continuous linear cocycle over f. Fix k with
$\mathcal {A}$
be a d-dimensional continuous linear cocycle over f. Fix k with
![]() $0<k<d$
. Then the cocycle
$0<k<d$
. Then the cocycle
![]() $\mathcal {A}$
does not admits a dominated splitting with a dominating bundle of dimension k if and only if there exists a residual subset G of X such that for every
$\mathcal {A}$
does not admits a dominated splitting with a dominating bundle of dimension k if and only if there exists a residual subset G of X such that for every
![]() $x \in G$
,
$x \in G$
,
Note that the minimality assumption cannot be dropped, as Example 3.12 shows.
Proof of Theorem 4.12.
The ‘if’ part is a direct consequence of (the trivial half of) Proposition 4.11. So let us prove the ‘only if’ part. Assume that the cocycle
![]() $\mathcal {A}$
admits no dominated splitting with dominating bundle of dimension k. By Proposition 4.11, for every
$\mathcal {A}$
admits no dominated splitting with dominating bundle of dimension k. By Proposition 4.11, for every
![]() $i>0$
there exists
$i>0$
there exists
![]() $x_i \in X$
and
$x_i \in X$
and
![]() $n_i> i$
such that
$n_i> i$
such that
Since X is compact and the cocycle is continuous, there exists
![]() $c>0$
such that
$c>0$
such that
for all
![]() $x\in X$
and
$x\in X$
and
![]() $n \in {\mathbb {Z}}$
. Consider the matrix identity
$n \in {\mathbb {Z}}$
. Consider the matrix identity
Using inequalities (4.6),
 $$\begin{align*}\frac{\sigma_k(\mathcal{A}(f^j(x), n))}{\sigma_{k+1}(\mathcal{A}(f^j(x), n))} \le e^{4c|j|} \, \frac{\sigma_k(\mathcal{A}(x,n))}{\sigma_{k+1}(\mathcal{A}(x, n))} \,. \end{align*}$$
$$\begin{align*}\frac{\sigma_k(\mathcal{A}(f^j(x), n))}{\sigma_{k+1}(\mathcal{A}(f^j(x), n))} \le e^{4c|j|} \, \frac{\sigma_k(\mathcal{A}(x,n))}{\sigma_{k+1}(\mathcal{A}(x, n))} \,. \end{align*}$$
In particular, if
![]() $|j|< \sqrt {n_i}$
, then
$|j|< \sqrt {n_i}$
, then

Note that
![]() $\varepsilon _i \to 0$
as
$\varepsilon _i \to 0$
as
![]() $i \to \infty $
.
$i \to \infty $
.
Now define a sequence of open sets
 $$\begin{align*}U_i \mathrel{:=} \left\{ x \in X \colon \frac{1}{n_i} \log \frac{\sigma_k(\mathcal{A}(x, n_i))}{\sigma_{k+1}(\mathcal{A}(x, n_i))} < \varepsilon_i \right\} \,. \end{align*}$$
$$\begin{align*}U_i \mathrel{:=} \left\{ x \in X \colon \frac{1}{n_i} \log \frac{\sigma_k(\mathcal{A}(x, n_i))}{\sigma_{k+1}(\mathcal{A}(x, n_i))} < \varepsilon_i \right\} \,. \end{align*}$$
By the previous observations,
![]() $U_i$
contains the orbit segment
$U_i$
contains the orbit segment
![]() $\{f^j(x_i) : |j| < \sqrt {n_i}\}$
. Since
$\{f^j(x_i) : |j| < \sqrt {n_i}\}$
. Since
![]() $n_i \to \infty $
and f is a minimal transformation, there exists a sequence
$n_i \to \infty $
and f is a minimal transformation, there exists a sequence
![]() $\delta _i \to 0$
such that each set
$\delta _i \to 0$
such that each set
![]() $U_i$
is
$U_i$
is
![]() $\delta _i$
-dense in X. It follows that, for each
$\delta _i$
-dense in X. It follows that, for each
![]() $m>0$
, the set
$m>0$
, the set
![]() $V_m \mathrel {:=} \bigcup _{i=m}^\infty U_i$
is open and dense. By Baire’s theorem, the set
$V_m \mathrel {:=} \bigcup _{i=m}^\infty U_i$
is open and dense. By Baire’s theorem, the set
![]() $G \mathrel {:=} \bigcap _{m=1}^\infty V_m$
is residual, and in particular dense.
$G \mathrel {:=} \bigcap _{m=1}^\infty V_m$
is residual, and in particular dense.
For every point x in G, there exists a sequence
![]() $i_j \to \infty $
such that
$i_j \to \infty $
such that
![]() $x \in U_{i_j}$
, and so
$x \in U_{i_j}$
, and so
 $$\begin{align*}\lim_{j \to \infty}\frac{1}{n_{i_j}} \log \frac{\sigma_k(\mathcal{A}(x, n_{i_j}))}{\sigma_{k+1}(\mathcal{A}(x, n_{i_j}))} = 0 \,.\\[-42pt] \end{align*}$$
$$\begin{align*}\lim_{j \to \infty}\frac{1}{n_{i_j}} \log \frac{\sigma_k(\mathcal{A}(x, n_{i_j}))}{\sigma_{k+1}(\mathcal{A}(x, n_{i_j}))} = 0 \,.\\[-42pt] \end{align*}$$
Let us highlight a consequence of Theorem 4.12 in the particular context discussed in Example 3.7, Section 3.2:
Corollary 4.13. Let f be a uniquely ergodic homeomorphism of a compact metric space and let
![]() $\mathcal {A}$
be a continuous
$\mathcal {A}$
be a continuous
![]() $\mathrm {SL}^{\pm }(2,\mathbb R)$
-cocycle over f. If the cocycle
$\mathrm {SL}^{\pm }(2,\mathbb R)$
-cocycle over f. If the cocycle
![]() $\mathcal {A}$
is not uniformly hyperbolic, then there exists a residual subset
$\mathcal {A}$
is not uniformly hyperbolic, then there exists a residual subset
![]() $G_0$
of X such that for all
$G_0$
of X such that for all
![]() $x\in G_0$
, the set of accumulation points of the sequence
$x\in G_0$
, the set of accumulation points of the sequence
![]() $\frac {1}{n}\log \|\mathcal {A}(x,n)\|$
is the interval
$\frac {1}{n}\log \|\mathcal {A}(x,n)\|$
is the interval
![]() $[0,\chi _1]$
, where
$[0,\chi _1]$
, where
![]() $\chi _1 = \chi _1(\mu )$
is the first Lyapunov exponent of the cocycle with respect to the unique f-invariant measure
$\chi _1 = \chi _1(\mu )$
is the first Lyapunov exponent of the cocycle with respect to the unique f-invariant measure
![]() $\mu $
.
$\mu $
.
Note that the result above improves some of the conclusions of [Reference Furman27, Theorem 4].
Proof. For each x, let
![]() $\Lambda _x$
be the set of accumulation points of the sequence
$\Lambda _x$
be the set of accumulation points of the sequence
![]() $\frac {1}{n}\log \|\mathcal {A}(x,n)\|$
. Then
$\frac {1}{n}\log \|\mathcal {A}(x,n)\|$
. Then
![]() $\Lambda _x$
is a compact interval (see, e.g., [Reference Walters, Arnold and Wihstutz63, Lemma 2.5]). Note that
$\Lambda _x$
is a compact interval (see, e.g., [Reference Walters, Arnold and Wihstutz63, Lemma 2.5]). Note that
![]() $\Lambda _x \subset [0,\infty )$
because
$\Lambda _x \subset [0,\infty )$
because
![]() $|\det \mathcal {A}| \equiv 1$
, and
$|\det \mathcal {A}| \equiv 1$
, and
![]() $\Lambda _x \subset [0,\chi _1]$
due to Proposition 2.3. If
$\Lambda _x \subset [0,\chi _1]$
due to Proposition 2.3. If
![]() $\chi _1 = 0$
, there is nothing to show. So, assume that
$\chi _1 = 0$
, there is nothing to show. So, assume that
![]() $\chi _1$
is positive. Since the cocycle is not uniformly hyperbolic, by Theorem 4.12 there is a dense set of points x for which
$\chi _1$
is positive. Since the cocycle is not uniformly hyperbolic, by Theorem 4.12 there is a dense set of points x for which
![]() $\liminf \frac {1}{n}\log \|\mathcal {A}(x,n)\| = 0$
. On the other hand, there is another dense set of points x for which
$\liminf \frac {1}{n}\log \|\mathcal {A}(x,n)\| = 0$
. On the other hand, there is another dense set of points x for which
![]() $\lim \frac {1}{n}\log \|\mathcal {A}(x,n)\| = \chi _1$
. The proof of Theorem 4.1 actually shows that if
$\lim \frac {1}{n}\log \|\mathcal {A}(x,n)\| = \chi _1$
. The proof of Theorem 4.1 actually shows that if
![]() $0<\alpha "<\beta "<\chi _1$
, then there is a residual subset of points x such that
$0<\alpha "<\beta "<\chi _1$
, then there is a residual subset of points x such that
and in particular
![]() $\Lambda _x \supset [\alpha ", \beta "]$
. Therefore, the set of points x such that
$\Lambda _x \supset [\alpha ", \beta "]$
. Therefore, the set of points x such that
![]() $\Lambda _x = [0,\chi _1]$
is residual.
$\Lambda _x = [0,\chi _1]$
is residual.
4.7 Proof of Theorem 4.10
Recall that, given an ergodic measure
![]() $\mu $
, its Lyapunov exponents, repeated according to their multiplicities, are denoted
$\mu $
, its Lyapunov exponents, repeated according to their multiplicities, are denoted
![]() $\widetilde {\chi }_1(\mathcal {A},\mu ) \ge \cdots \ge \widetilde \chi _d(\mathcal {A},\mu )$
.
$\widetilde {\chi }_1(\mathcal {A},\mu ) \ge \cdots \ge \widetilde \chi _d(\mathcal {A},\mu )$
.
Lemma 4.14. Let f be a minimal homeomorphism of a compact metric space X. Let
![]() $\mathcal {A}$
be a d-dimensional continuous linear cocycle over f and let
$\mathcal {A}$
be a d-dimensional continuous linear cocycle over f and let
![]() $\mathcal {R}$
be the set of its LP-regular points. Suppose that
$\mathcal {R}$
be the set of its LP-regular points. Suppose that
![]() $\mathcal {A}$
admits no dominated splitting into nontrivial subbundles. Then:
$\mathcal {A}$
admits no dominated splitting into nontrivial subbundles. Then:
-
1. either
 $\widetilde \chi _1(\mathcal {A},\mu ) = \widetilde \chi _d(\mathcal {A},\mu )$
for every f-ergodic Borel probability measure
$\widetilde \chi _1(\mathcal {A},\mu ) = \widetilde \chi _d(\mathcal {A},\mu )$
for every f-ergodic Borel probability measure
 $\mu $
, in which case the set
$\mu $
, in which case the set
 $\mathcal {R}$
equals X and the cocycle
$\mathcal {R}$
equals X and the cocycle
 $\mathcal {A}$
is completely regular;
$\mathcal {A}$
is completely regular; -
2. or
 $\widetilde \chi _1(\mathcal {A},\mu )> \widetilde \chi _d(\mathcal {A},\mu )$
for some f-ergodic Borel probability measure
$\widetilde \chi _1(\mathcal {A},\mu )> \widetilde \chi _d(\mathcal {A},\mu )$
for some f-ergodic Borel probability measure
 $\mu $
, in which case the set
$\mu $
, in which case the set
 $\mathcal {R}$
is meager in X.
$\mathcal {R}$
is meager in X.
Proof. As a first case, suppose that
![]() $\widetilde \chi _1(\mathcal {A},\mu ) = \widetilde \chi _d(\mathcal {A},\mu )$
for every f-ergodic Borel probability measure
$\widetilde \chi _1(\mathcal {A},\mu ) = \widetilde \chi _d(\mathcal {A},\mu )$
for every f-ergodic Borel probability measure
![]() $\mu $
. Consider the following ‘normalized’ cocycle
$\mu $
. Consider the following ‘normalized’ cocycle
whose determinants are
![]() $\pm 1$
. Our assumption ensures that all Lyapunov exponents of
$\pm 1$
. Our assumption ensures that all Lyapunov exponents of
![]() $\hat {\mathcal {A}}$
with respect to all ergodic measures are zero. By Proposition 3.2, the cocycle
$\hat {\mathcal {A}}$
with respect to all ergodic measures are zero. By Proposition 3.2, the cocycle
![]() $\hat {\mathcal {A}}$
is completely regular with zero spectrum.
$\hat {\mathcal {A}}$
is completely regular with zero spectrum.
Let
![]() $\varphi _n(x) \mathrel {:=} \log |\det \mathcal {A}(x,n)|$
, and let
$\varphi _n(x) \mathrel {:=} \log |\det \mathcal {A}(x,n)|$
, and let
![]() $\mathcal {D}$
be the set of
$\mathcal {D}$
be the set of
![]() $x \in X$
such that the following two limits exist and coincide:
$x \in X$
such that the following two limits exist and coincide:
We claim that
![]() $\mathcal {R}$
(the set of LP-regular points for
$\mathcal {R}$
(the set of LP-regular points for
![]() $\mathcal {A}$
) equals
$\mathcal {A}$
) equals
![]() $\mathcal {D}$
. Indeed, the inclusion
$\mathcal {D}$
. Indeed, the inclusion
![]() $\mathcal {R} \subset \mathcal {D}$
always holds, as for LP-regular points the limit (4.8) will be the sum of the Lyaponov exponents. On the other hand, since
$\mathcal {R} \subset \mathcal {D}$
always holds, as for LP-regular points the limit (4.8) will be the sum of the Lyaponov exponents. On the other hand, since
![]() $\hat {\mathcal {A}}$
is completely regular with zero exponents, it follows from (4.7) that
$\hat {\mathcal {A}}$
is completely regular with zero exponents, it follows from (4.7) that
for all
![]() $x \in X$
and all nonzero
$x \in X$
and all nonzero
![]() $v \in \mathbb R^d$
, showing the reverse inclusion
$v \in \mathbb R^d$
, showing the reverse inclusion
![]() $\mathcal {D} \subset \mathcal {R}$
.
$\mathcal {D} \subset \mathcal {R}$
.
Applying Theorem 4.2 to f and
![]() $f^{-1}$
, we see that the set
$f^{-1}$
, we see that the set
![]() $\mathcal {D}$
(that is,
$\mathcal {D}$
(that is,
![]() $\mathcal {R}$
) is either meager or equal to X and, in the latter case, the limits (4.8) equal some constant
$\mathcal {R}$
) is either meager or equal to X and, in the latter case, the limits (4.8) equal some constant
![]() $\chi $
. So, when
$\chi $
. So, when
![]() $\mathcal {R}=X$
, (4.9) says that all Lyapunov exponents of the cocycle
$\mathcal {R}=X$
, (4.9) says that all Lyapunov exponents of the cocycle
![]() $\mathcal {A}$
are equal to
$\mathcal {A}$
are equal to
![]() $\chi $
and, in particular, the cocycle is completely regular.
$\chi $
and, in particular, the cocycle is completely regular.
Now consider the second case, where there exists an ergodic Borel probability measure
![]() $\mu $
such that
$\mu $
such that
![]() $\widetilde \chi _1(\mathcal {A},\mu )> \widetilde \chi _d(\mathcal {A},\mu )$
. Then, for
$\widetilde \chi _1(\mathcal {A},\mu )> \widetilde \chi _d(\mathcal {A},\mu )$
. Then, for
![]() $\mu $
-almost every point y,
$\mu $
-almost every point y,
By minimality of f, the measure
![]() $\mu $
has full support, so the formula above holds for a dense set of points y. On the other hand, by Theorem 4.12, there is another dense set where the formula fails, and actually the liminf of the sequence is
$\mu $
has full support, so the formula above holds for a dense set of points y. On the other hand, by Theorem 4.12, there is another dense set where the formula fails, and actually the liminf of the sequence is
![]() $0$
. Now we can apply Theorem 4.1 and conclude that the set of points z for which
$0$
. Now we can apply Theorem 4.1 and conclude that the set of points z for which
exists is meager in X. In particular, the set
![]() $\mathcal {R}$
of LP-regular points is meager, as we wanted to show.
$\mathcal {R}$
of LP-regular points is meager, as we wanted to show.
At last, we can establish our general all-or-meager dichotomy for cocycles over minimal transformations:
Proof of Theorem 4.10.
Let
![]() $\mathcal {A}$
be an arbitrary continuous cocycle over the minimal dynamics f. Consider the finest dominated splitting of the cocycle (see [Reference Bonatti, Díaz and Viana12, Theorem B.2]; see also [Reference Selgrade58, Reference Blumenthal and Latushkin8]), that is, the invariant splitting
$\mathcal {A}$
be an arbitrary continuous cocycle over the minimal dynamics f. Consider the finest dominated splitting of the cocycle (see [Reference Bonatti, Díaz and Viana12, Theorem B.2]; see also [Reference Selgrade58, Reference Blumenthal and Latushkin8]), that is, the invariant splitting
![]() $E_1 \oplus \cdots \oplus E_s$
which is dominated (i.e., satisfies inequalities (2.10) for some
$E_1 \oplus \cdots \oplus E_s$
which is dominated (i.e., satisfies inequalities (2.10) for some
![]() $n_0$
), and the number of bundles s is maximal. The case
$n_0$
), and the number of bundles s is maximal. The case
![]() $s=1$
corresponds to the situation where the cocycle admits no dominated splitting into nontrivial subbundles. The subbundles are continuous, by Proposition 2.1. For each i, let
$s=1$
corresponds to the situation where the cocycle admits no dominated splitting into nontrivial subbundles. The subbundles are continuous, by Proposition 2.1. For each i, let
![]() $\mathcal {R}_i$
be the set of LP-regular points of the restriction of the cocycle to the i
th bundle
$\mathcal {R}_i$
be the set of LP-regular points of the restriction of the cocycle to the i
th bundle
![]() $E_i$
. By Lemma 4.14, each
$E_i$
. By Lemma 4.14, each
![]() $\mathcal {R}_i$
is either a meager set or the whole X, and the latter alternative occurs only if the restricted cocycle
$\mathcal {R}_i$
is either a meager set or the whole X, and the latter alternative occurs only if the restricted cocycle
![]() $\mathcal {A}|E_i$
is completely regular. Note that the set of LP-regular points of
$\mathcal {A}|E_i$
is completely regular. Note that the set of LP-regular points of
![]() $\mathcal {A}$
is
$\mathcal {A}$
is
![]() $\mathcal {R} = \mathcal {R}_1 \cap \cdots \cap \mathcal {R}_k$
. Therefore,
$\mathcal {R} = \mathcal {R}_1 \cap \cdots \cap \mathcal {R}_k$
. Therefore,
![]() $\mathcal {R}$
is either a meager set or the whole X. Furthermore, if
$\mathcal {R}$
is either a meager set or the whole X. Furthermore, if
![]() $\mathcal {R} = X$
, then for every i we have
$\mathcal {R} = X$
, then for every i we have
![]() $\mathcal {R}_i = X$
, which implies that each
$\mathcal {R}_i = X$
, which implies that each
![]() $\mathcal {A}|E_i$
is completely regular, and therefore
$\mathcal {A}|E_i$
is completely regular, and therefore
![]() $\mathcal {A}$
itself is completely regular.
$\mathcal {A}$
itself is completely regular.
5 Further discussion of the notion of complete regularity
In this section, we return to our definition of complete regularity. Recall that a continuous d-dimensional linear cocycle over a homeomorphism of a compact metric space is completely regular when
-
1. every point is LP-regular, and
-
2. the Lyapunov spectra of all (LP-regular) points are the same.
In this section, we investigate the interdependency of these two conditions. We will construct examples showing that they are essentially independent – in a sense to be made precise.
5.1 All points being regular does not imply complete regularity
By Theorem 4.10, if the dynamics f is minimal, then Condition (1) in the definition of complete regularity does imply Condition (2), that is, if a cocycle has the property that all points are LP-regular, then the Lyapunov exponents do not depend on the point.
On the other hand, if f is non-minimal, then Condition (1) does not imply Condition (2). For example, let f be the automorphism of the two-torus
![]() $(\mathbb R/{\mathbb {Z}})^2$
induced by the matrix
$(\mathbb R/{\mathbb {Z}})^2$
induced by the matrix
![]() $\left ( \begin {smallmatrix} 1 & 1 \\ 0 & 1 \end {smallmatrix} \right )$
, that is,
$\left ( \begin {smallmatrix} 1 & 1 \\ 0 & 1 \end {smallmatrix} \right )$
, that is,
If we take a continuous cocycle of diagonal matrices, then every point will be LP-regular. But the Lyapunov exponents will not be constant, in general. This example was pointed out before in [Reference Johnson and Zampogni35, Example 4.1].
Let us exhibit an example where f is topologically transitive. Consider the group
![]() $G \mathrel {:=} \mathrm {SL}(2,\mathbb R)$
, the lattice
$G \mathrel {:=} \mathrm {SL}(2,\mathbb R)$
, the lattice
![]() $\Gamma \mathrel {:=} \mathrm {SL}(2,{\mathbb {Z}})$
, and the quotient
$\Gamma \mathrel {:=} \mathrm {SL}(2,{\mathbb {Z}})$
, and the quotient
![]() $N\mathrel {:=}{_\Gamma }\backslash ^G$
, that is, the set of right cosets
$N\mathrel {:=}{_\Gamma }\backslash ^G$
, that is, the set of right cosets
![]() $\Gamma g$
. Then N is a Hausdorff but noncompact space with respect to the quotient topology (actually it is the unit tangent bundle of the modular surface). Let
$\Gamma g$
. Then N is a Hausdorff but noncompact space with respect to the quotient topology (actually it is the unit tangent bundle of the modular surface). Let
![]() $X \mathrel {:=} N \cup \{\infty \}$
be the one-point compactification of N. Define
$X \mathrel {:=} N \cup \{\infty \}$
be the one-point compactification of N. Define
![]() $f \colon X \to X$
by
$f \colon X \to X$
by
![]() $f(\infty ) \mathrel {:=} \infty $
and
$f(\infty ) \mathrel {:=} \infty $
and
The map f is a homeomorphism and, like the previous example (5.1), is such the Birkhoff averages of every continuous function converge pointwise (see [Reference Dani21, Theorem 5.1]); furthermore, f is topologically transitive. Arguing as before, Condition (1) does not imply Condition (2) for this map f.
The following result provides a similar example with a derivative cocycle of a diffeomorphism.
Theorem 5.1. There exists a topologically transitive diffeomorphism
![]() $f: M\to M$
of a compact connected smooth Riemannian manifold M of dimension
$f: M\to M$
of a compact connected smooth Riemannian manifold M of dimension
![]() $11$
such that every point
$11$
such that every point
![]() $x\in M$
is LP-regular for the derivative cocycle and the set of Lyapunov vectors
$x\in M$
is LP-regular for the derivative cocycle and the set of Lyapunov vectors
has the power of the continuum.
For our construction we need the following objects:
-
1. The group
 $G \mathrel {:=} \mathrm {SL}(3,\mathbb {R})$
, which is a simple connected Lie group; we identify
$G \mathrel {:=} \mathrm {SL}(3,\mathbb {R})$
, which is a simple connected Lie group; we identify
 $\mathrm {SL}(2,\mathbb R)$
with the subgroup consisting of matrices of the form
$\mathrm {SL}(2,\mathbb R)$
with the subgroup consisting of matrices of the form
 $\left ( \begin {smallmatrix} * & * & 0 \\ * & * & 0 \\ 0 & 0 & 1 \end {smallmatrix} \right )$
.
$\left ( \begin {smallmatrix} * & * & 0 \\ * & * & 0 \\ 0 & 0 & 1 \end {smallmatrix} \right )$
. -
2. A co-compact lattice
 $\Gamma \subset G$
such that
$\Gamma \subset G$
such that
 $\Gamma \cap \mathrm {SL}(2,\mathbb R)$
is a co-compact lattice in
$\Gamma \cap \mathrm {SL}(2,\mathbb R)$
is a co-compact lattice in
 $\mathrm {SL}(2,\mathbb R)$
(see [Reference Witte Morris65, Exerc. 4, §18.6]).
$\mathrm {SL}(2,\mathbb R)$
(see [Reference Witte Morris65, Exerc. 4, §18.6]). -
3. The quotient
 $N\mathrel {:=}{_\Gamma }\backslash ^G$
, that is, the set of right cosets
$N\mathrel {:=}{_\Gamma }\backslash ^G$
, that is, the set of right cosets
 $\Gamma g$
; this is a compact smooth manifold of dimension
$\Gamma g$
; this is a compact smooth manifold of dimension
 $8$
; we denote by
$8$
; we denote by
 $m_N$
the normalized volume in N which is induced on N by the Haar measure on the group G.
$m_N$
the normalized volume in N which is induced on N by the Haar measure on the group G. -
4. The one-parameter subgroup of unipotent matrices
and the corresponding unipotent flow $$ \begin{align*} u^t \mathrel{:=} \begin{pmatrix} 1&t&0\\0&1&0\\0&0&1\end{pmatrix} \end{align*} $$
which preserves the volume measure
$$ \begin{align*} u^t \mathrel{:=} \begin{pmatrix} 1&t&0\\0&1&0\\0&0&1\end{pmatrix} \end{align*} $$
which preserves the volume measure $$ \begin{align*} \varphi^t \colon N &\to N \\ \Gamma g &\mapsto \Gamma g u^t \, , \end{align*} $$
$$ \begin{align*} \varphi^t \colon N &\to N \\ \Gamma g &\mapsto \Gamma g u^t \, , \end{align*} $$
 $m_N$
.
$m_N$
.
-
5. A
 $C^\infty $
strictly positive function
$C^\infty $
strictly positive function
 $\tau :N\to \mathbb {R}$
whose choice will be specified later.
$\tau :N\to \mathbb {R}$
whose choice will be specified later. -
6. The Anosov flow
 $\{\psi ^t\}$
which is a suspension flow with constant roof function
$\{\psi ^t\}$
which is a suspension flow with constant roof function
 $1$
over an Anosov automorphism of the two-dimensional torus
$1$
over an Anosov automorphism of the two-dimensional torus
 $\mathbb {T}^2$
given by the matrix
$\mathbb {T}^2$
given by the matrix
 $A= \left ( \begin {smallmatrix} 2&1\\1&1 \end {smallmatrix} \right )$
; we denote by S the
$A= \left ( \begin {smallmatrix} 2&1\\1&1 \end {smallmatrix} \right )$
; we denote by S the
 $3$
-dimensional suspension manifold; the flow
$3$
-dimensional suspension manifold; the flow
 $\{\psi ^t\}$
preserves volume in S which we denote by
$\{\psi ^t\}$
preserves volume in S which we denote by
 $m_S$
.
$m_S$
.
Denote
![]() $M \mathrel {:=} N\times S$
. Given
$M \mathrel {:=} N\times S$
. Given
![]() $\alpha>0$
, consider a skew-product map
$\alpha>0$
, consider a skew-product map
![]() $f_\alpha : M\to M$
given by:
$f_\alpha : M\to M$
given by:
For every
![]() $\alpha $
, the map
$\alpha $
, the map
![]() $f_\alpha $
is a
$f_\alpha $
is a
![]() $C^\infty $
diffeomorphism preserving a smooth measure on M. We will show that with an appropriate choice of the parameter
$C^\infty $
diffeomorphism preserving a smooth measure on M. We will show that with an appropriate choice of the parameter
![]() $\alpha $
and the function
$\alpha $
and the function
![]() $\tau $
, the map
$\tau $
, the map
![]() $f_\alpha $
has the desired properties.
$f_\alpha $
has the desired properties.
For every point
![]() $(x,y)\in M$
we have the following splitting of the tangent space
$(x,y)\in M$
we have the following splitting of the tangent space
where
are the one-dimensional stable and, respectively, the one-dimensional unstable subspaces and
By Ratner’s equidistribution theorem [Reference Ratner52, Theorem B], for every
![]() $x \in N$
, the future and past orbits
$x \in N$
, the future and past orbits
![]() $\{\varphi ^{\pm n} x\}_{n \ge 0}$
are equidistributed with respect to a probability measure
$\{\varphi ^{\pm n} x\}_{n \ge 0}$
are equidistributed with respect to a probability measure
![]() $m_x$
on N, that is, for every continuous function
$m_x$
on N, that is, for every continuous function
![]() $h \colon N \to \mathbb R$
, we have
$h \colon N \to \mathbb R$
, we have
 $$ \begin{align} \lim_{n \to \infty} \frac{1}{n} \sum_{j=0}^{n-1} h(\varphi^{\pm j} x) = \int_N h \, dm_x \,. \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \frac{1}{n} \sum_{j=0}^{n-1} h(\varphi^{\pm j} x) = \int_N h \, dm_x \,. \end{align} $$
Furthermore (see [Reference Ratner52, p. 255]), the measures
![]() $m_x$
are ergodic, and thus
$m_x$
are ergodic, and thus
![]() $\varphi $
is pointwise ergodic in the terminology of [Reference Downarowicz and Weiss23].
$\varphi $
is pointwise ergodic in the terminology of [Reference Downarowicz and Weiss23].
The desired properties of the map
![]() $f_\alpha $
follow immediately from the following three lemmas.
$f_\alpha $
follow immediately from the following three lemmas.
Lemma 5.2. There is a smooth strictly positive function
![]() $\tau : N\to \mathbb {R}$
such that the set
$\tau : N\to \mathbb {R}$
such that the set
has the power of continuum.
Lemma 5.3. For every smooth strictly positive function
![]() $\tau :N\to \mathbb {R}$
there exists a countable set
$\tau :N\to \mathbb {R}$
there exists a countable set
![]() $A \subset \mathbb R_+$
such that for every
$A \subset \mathbb R_+$
such that for every
![]() $\alpha \in \mathbb R_+ \setminus A$
, the map
$\alpha \in \mathbb R_+ \setminus A$
, the map
![]() $f_\alpha $
is topologically transitive.
$f_\alpha $
is topologically transitive.
Lemma 5.4. For any choice of a smooth function
![]() $\tau $
and any
$\tau $
and any
![]() $\alpha \in (0,1)$
the splitting (5.2) is continuous, invariant under
$\alpha \in (0,1)$
the splitting (5.2) is continuous, invariant under
![]() $df_\alpha $
, and for every
$df_\alpha $
, and for every
![]() $(x,y)\in M$
,
$(x,y)\in M$
,
where
![]() $\lambda>1$
is the top eigenvalue of the matrix A. In particular, every point
$\lambda>1$
is the top eigenvalue of the matrix A. In particular, every point
![]() $(x,y)\in M$
is LP-regular.
$(x,y)\in M$
is LP-regular.
We proceed with proofs of these three lemmas.
Proof of Lemma 5.2.
Let
![]() $\widetilde {G}$
be the subgroup of G consisting of the matrices of the form
$\widetilde {G}$
be the subgroup of G consisting of the matrices of the form
![]() $\left ( \begin {smallmatrix} * & * & 0 \\ * & * & 0 \\ 0 & 0 & 1 \end {smallmatrix} \right )$
, that is, the standard copy of
$\left ( \begin {smallmatrix} * & * & 0 \\ * & * & 0 \\ 0 & 0 & 1 \end {smallmatrix} \right )$
, that is, the standard copy of
![]() $\mathrm {SL}(2,\mathbb R)$
in
$\mathrm {SL}(2,\mathbb R)$
in
![]() $\mathrm {SL}(3,\mathbb R)$
. Let
$\mathrm {SL}(3,\mathbb R)$
. Let
![]() $\pi \colon G \to N$
be the quotient map
$\pi \colon G \to N$
be the quotient map
![]() $\pi (g) \mathrel {:=} \Gamma g$
and let
$\pi (g) \mathrel {:=} \Gamma g$
and let
![]() $N_0 \mathrel {:=} \pi (\widetilde G)$
. Since the unipotent subgroup
$N_0 \mathrel {:=} \pi (\widetilde G)$
. Since the unipotent subgroup
![]() $(u^t)$
is contained in
$(u^t)$
is contained in
![]() $\widetilde G$
, the set
$\widetilde G$
, the set
![]() $N_0$
is invariant under the unipotent flow
$N_0$
is invariant under the unipotent flow
![]() $\{\varphi ^t\}$
. Recall that our lattice
$\{\varphi ^t\}$
. Recall that our lattice
![]() $\Gamma < G$
was chosen so that
$\Gamma < G$
was chosen so that
![]() $\widetilde \Gamma \mathrel {:=} \Gamma \cap \widetilde G$
is a co-compact lattice in
$\widetilde \Gamma \mathrel {:=} \Gamma \cap \widetilde G$
is a co-compact lattice in
![]() $\widetilde G$
. Therefore, the quotient
$\widetilde G$
. Therefore, the quotient
![]() $\widetilde N\mathrel {:=}{_{\widetilde \Gamma }}\backslash ^{\widetilde G}$
is a compact
$\widetilde N\mathrel {:=}{_{\widetilde \Gamma }}\backslash ^{\widetilde G}$
is a compact
![]() $3$
-manifold which is actually the unit tangent bundle of a compact hyperbolic surface. We define a unipotent flow on
$3$
-manifold which is actually the unit tangent bundle of a compact hyperbolic surface. We define a unipotent flow on
![]() $\widetilde N$
by the formula
$\widetilde N$
by the formula
![]() $\widetilde {\varphi }^t (\widetilde \Gamma \widetilde g) \mathrel {:=} \widetilde \Gamma \widetilde g u^t$
; this is actually the horocycle flow on the unit tangent bundle. Define a map
$\widetilde {\varphi }^t (\widetilde \Gamma \widetilde g) \mathrel {:=} \widetilde \Gamma \widetilde g u^t$
; this is actually the horocycle flow on the unit tangent bundle. Define a map
![]() $\widetilde {N} \to N_0$
by
$\widetilde {N} \to N_0$
by
![]() $\widetilde \Gamma \widetilde {g} \mapsto \Gamma \widetilde {g}$
. This map is a homeomorphism, and it conjugates the flows
$\widetilde \Gamma \widetilde {g} \mapsto \Gamma \widetilde {g}$
. This map is a homeomorphism, and it conjugates the flows
![]() $\widetilde {\varphi }^t$
and
$\widetilde {\varphi }^t$
and
![]() $\varphi ^t|_{N_0}$
. By a theorem of Furstenberg, the horocycle flow
$\varphi ^t|_{N_0}$
. By a theorem of Furstenberg, the horocycle flow
![]() $\widetilde {\varphi }^t$
is strictly ergodic (i.e., minimal and uniquely ergodic); furthermore, the time-
$\widetilde {\varphi }^t$
is strictly ergodic (i.e., minimal and uniquely ergodic); furthermore, the time-
![]() $1$
map
$1$
map
![]() $\widetilde {\varphi }^1$
is also strictly ergodic: see [Reference Ellis and Perrizo24]. We conclude that the submanifold
$\widetilde {\varphi }^1$
is also strictly ergodic: see [Reference Ellis and Perrizo24]. We conclude that the submanifold
![]() $N_0$
of N supports a unique
$N_0$
of N supports a unique
![]() $\varphi ^1$
-invariant measure, which we call
$\varphi ^1$
-invariant measure, which we call
![]() $m_{N_0}$
.
$m_{N_0}$
.
Next, consider the one-parameter subgroup of G formed by the matrices of the form
 $$\begin{align*}a^s \mathrel{:=} \begin{pmatrix} e^s & 0 & 0 \\ 0 & e^s & 0 \\ 0 & 0 & e^{-2s} \end{pmatrix} \, , \quad s \in \mathbb R \,. \end{align*}$$
$$\begin{align*}a^s \mathrel{:=} \begin{pmatrix} e^s & 0 & 0 \\ 0 & e^s & 0 \\ 0 & 0 & e^{-2s} \end{pmatrix} \, , \quad s \in \mathbb R \,. \end{align*}$$
Note that
![]() $a^s \widetilde {g} = \widetilde {g} a^s$
for every
$a^s \widetilde {g} = \widetilde {g} a^s$
for every
![]() $\widetilde {g} \in \widetilde {G}$
, and in particular,
$\widetilde {g} \in \widetilde {G}$
, and in particular,
![]() $a^s u^t = u^t a^s$
. As a consequence, the flow
$a^s u^t = u^t a^s$
. As a consequence, the flow
 $$ \begin{align*} \zeta^s \colon N &\to N \\ \Gamma g &\mapsto \Gamma g a^s \,; \end{align*} $$
$$ \begin{align*} \zeta^s \colon N &\to N \\ \Gamma g &\mapsto \Gamma g a^s \,; \end{align*} $$
commutes with the unipotent flow, that is,
Therefore, the submanifold
![]() $N_s \mathrel {:=} \zeta ^s(N_0)$
supports a unique
$N_s \mathrel {:=} \zeta ^s(N_0)$
supports a unique
![]() $\varphi ^1$
-invariant measure, namely
$\varphi ^1$
-invariant measure, namely
![]() ${m_{N_s} \mathrel {:=} (\zeta ^s)_*(m_{N_0})}$
. For every point x in
${m_{N_s} \mathrel {:=} (\zeta ^s)_*(m_{N_0})}$
. For every point x in
![]() $N_s$
, the measure
$N_s$
, the measure
![]() $m_x$
defined by (5.5) coincides with
$m_x$
defined by (5.5) coincides with
![]() $m_{N_s}$
.
$m_{N_s}$
.
We have constructed a continuous curve
![]() $s \mapsto m_{N_s}$
in the space of
$s \mapsto m_{N_s}$
in the space of
![]() $\varphi ^1$
-invariant Borel probability measures on N (endowed with the weak topology). We will prove that this curve is nonconstant. Once we do that, the lemma will immediately follow, as it will be sufficient to take any
$\varphi ^1$
-invariant Borel probability measures on N (endowed with the weak topology). We will prove that this curve is nonconstant. Once we do that, the lemma will immediately follow, as it will be sufficient to take any
![]() $C^\infty $
strictly positive function
$C^\infty $
strictly positive function
![]() $\tau $
for which the function
$\tau $
for which the function
![]() $s \mapsto \int _{N}\tau \,dm_{N_s}$
is nonconstant.
$s \mapsto \int _{N}\tau \,dm_{N_s}$
is nonconstant.
Note that
![]() $a^s \not \in \widetilde G$
for all nonzero s. Since the projection
$a^s \not \in \widetilde G$
for all nonzero s. Since the projection
![]() $\pi \colon G \to N$
is a covering map and
$\pi \colon G \to N$
is a covering map and
![]() $\pi (\widetilde {G})$
is the compact set
$\pi (\widetilde {G})$
is the compact set
![]() $N_0$
, it follows that
$N_0$
, it follows that
![]() $\pi (a^s) \not \in N_0$
for all sufficiently small
$\pi (a^s) \not \in N_0$
for all sufficiently small
![]() $s \neq 0$
. But
$s \neq 0$
. But
![]() $\pi (a_s) \in N_s$
, and so
$\pi (a_s) \in N_s$
, and so
![]() $N_s \neq N_0$
for all sufficiently small
$N_s \neq N_0$
for all sufficiently small
![]() $s \neq 0$
. Since
$s \neq 0$
. Since
![]() $N_s$
is the support of the measure
$N_s$
is the support of the measure
![]() $m_{N_s}$
, this proves that the curve
$m_{N_s}$
, this proves that the curve
![]() $s \mapsto m_{N_s}$
is nonconstant, as we wanted to show.
$s \mapsto m_{N_s}$
is nonconstant, as we wanted to show.
Proof of Lemma 5.3.
Consider the following two dynamical systems on the manifold
![]() $M = N \times S$
:
$M = N \times S$
:
-
• the flow
 $\mathrm {id} \times \psi ^t$
whose time t map is
$\mathrm {id} \times \psi ^t$
whose time t map is
 $(x,y) \mapsto (x,\psi ^t(y))$
;
$(x,y) \mapsto (x,\psi ^t(y))$
; -
• the diffeomorphism
 $f_0 (x,y) = (\varphi ^1(x),\psi ^{\tau (x)} y)$
.
$f_0 (x,y) = (\varphi ^1(x),\psi ^{\tau (x)} y)$
.
Note that the flow and the diffeomorphism above commute. Therefore, we obtain an action of the group
![]() $\mathbb R \times {\mathbb {Z}}$
on M. Note that the action preserves the product measure
$\mathbb R \times {\mathbb {Z}}$
on M. Note that the action preserves the product measure
![]() $m_N \times m_S$
.
$m_N \times m_S$
.
We claim that the product measure is ergodic with respect to the
![]() $\mathbb R \times {\mathbb {Z}}$
-action. Indeed, if
$\mathbb R \times {\mathbb {Z}}$
-action. Indeed, if
![]() $h \colon M \to \mathbb R$
is an invariant bounded Borel measurable function, then it is also invariant under the flow
$h \colon M \to \mathbb R$
is an invariant bounded Borel measurable function, then it is also invariant under the flow
![]() $\mathrm {id} \times \psi ^t$
. Since the measure
$\mathrm {id} \times \psi ^t$
. Since the measure
![]() $m_S$
is ergodic for the flow
$m_S$
is ergodic for the flow
![]() $\psi ^t$
, there exists some bounded Borel measurable function
$\psi ^t$
, there exists some bounded Borel measurable function
![]() $h_1 \colon N \to \mathbb R$
such that
$h_1 \colon N \to \mathbb R$
such that
![]() $h(x,y) = h_1(x)$
for
$h(x,y) = h_1(x)$
for
![]() $m_N \times m_S$
-almost every
$m_N \times m_S$
-almost every
![]() $(x,y)$
. Since
$(x,y)$
. Since
![]() $h \circ f_0 = h$
, we have
$h \circ f_0 = h$
, we have
![]() $h_1 \circ \varphi ^1 = h_1 m_N$
-almost everywhere. Ergodicity implies that
$h_1 \circ \varphi ^1 = h_1 m_N$
-almost everywhere. Ergodicity implies that
![]() $h_1$
coincides with a constant
$h_1$
coincides with a constant
![]() $m_N$
-almost everywhere. Hence, h is constant
$m_N$
-almost everywhere. Hence, h is constant
![]() $m_N \times m_S$
-almost everywhere, completing the proof of ergodicity.
$m_N \times m_S$
-almost everywhere, completing the proof of ergodicity.
Note that the element
![]() $(\alpha ,1)$
of the
$(\alpha ,1)$
of the
![]() $\mathbb R \times {\mathbb {Z}}$
-action is the diffeomorphism
$\mathbb R \times {\mathbb {Z}}$
-action is the diffeomorphism
![]() $f_\alpha $
. Let A be the set of
$f_\alpha $
. Let A be the set of
![]() $\alpha \in \mathbb R_+$
such that
$\alpha \in \mathbb R_+$
such that
![]() $(f_\alpha , m_N \times m_S)$
is not ergodic. By a result of Pugh and Shub [Reference Pugh and Shub50, Theorem 2], the set A is countable. Since the measure
$(f_\alpha , m_N \times m_S)$
is not ergodic. By a result of Pugh and Shub [Reference Pugh and Shub50, Theorem 2], the set A is countable. Since the measure
![]() $m_N \times m_S$
is positive on open sets, the map
$m_N \times m_S$
is positive on open sets, the map
![]() $f_\alpha $
is topologically transitive whenever it is ergodic.
$f_\alpha $
is topologically transitive whenever it is ergodic.
Proof of Lemma 5.4.
Equality (5.6) follows from the definition of the map
![]() $f_\alpha $
, and the following two facts: (a) all the Lyapunov exponents of
$f_\alpha $
, and the following two facts: (a) all the Lyapunov exponents of
![]() $\varphi ^t$
are zero; and (b) the Lyapunov exponent of the Anosov flow in its flow direction is zero. Equality (5.9) follows from (5.4) and the fact that the function
$\varphi ^t$
are zero; and (b) the Lyapunov exponent of the Anosov flow in its flow direction is zero. Equality (5.9) follows from (5.4) and the fact that the function
![]() $\tau $
is bounded. To prove equality (5.7), observe that for every
$\tau $
is bounded. To prove equality (5.7), observe that for every
![]() $n>0$
,
$n>0$
,
where
![]() $\tau _n(x)=\sum _{k=0}^{n-1}\tau (\varphi ^k(x))$
. By property (5.5), for every
$\tau _n(x)=\sum _{k=0}^{n-1}\tau (\varphi ^k(x))$
. By property (5.5), for every
![]() $x \in N$
we have
$x \in N$
we have
The desired equality now follows from the fact that every
![]() $v\in E^{\mathrm {s}}(y)$
contracts under the Anosov flow by a constant factor
$v\in E^{\mathrm {s}}(y)$
contracts under the Anosov flow by a constant factor
![]() $\lambda ^t$
. The proof of equality (5.8) is similar.
$\lambda ^t$
. The proof of equality (5.8) is similar.
We proved the lemmas and, as explained before, this completes the proof of Theorem 5.1.
5.2 Agreement of Lyapunov spectra does not imply complete regularity
In this subsection we discuss the problem of whether Condition (2) alone is sufficient for complete regularity. Strictly speaking, as stated this condition subsumes the first and so the problem seems hollow. However, we may ask the following meaningful question: Suppose every two points that are LP-regular have the same Lyapunov spectrum. Does it follow that every point is LP-regular?
The answer is negative, as Example 3.12 illustrates. In that example, most points are wandering; in fact, there is no invariant Borel probability measure whose support is X. The next result provides a more interesting example:
Theorem 5.5. There exists a homeomorphism
![]() $f \colon X \to X$
of a compact space X admitting a fully-supported invariant Borel probability measure and there exists a
$f \colon X \to X$
of a compact space X admitting a fully-supported invariant Borel probability measure and there exists a
![]() $2$
-dimensional continuous linear cocycle
$2$
-dimensional continuous linear cocycle
![]() $\mathcal {A}$
over f with the following properties:
$\mathcal {A}$
over f with the following properties:
-
• all LP-regular points
 $x \in X$
have Lyapunov exponents
$x \in X$
have Lyapunov exponents
 $\chi _1(x) = c$
and
$\chi _1(x) = c$
and
 $\chi _2(x) = -c$
, where c is a positive constant;
$\chi _2(x) = -c$
, where c is a positive constant; -
• there exist points in X that are not LP-regular.
In fact, the map f in our example is uniquely ergodic, and so, by Theorem 4.10, points that are not LP-regular for the cocycle
![]() $\mathcal {A}$
form a residual subset of X.
$\mathcal {A}$
form a residual subset of X.
We do not know if there exist examples of cocycles over a hyperbolic base dynamics satisfying the conclusions of Theorem 5.5. If that is the case, the matrix maps cannot be Hölder continuous, by Theorem 3.13.
Another question is the following: Assuming Condition (1) in the definition of complete regularity, can Condition (2) be weakened to the following condition (2’)?
-
2’. all ergodic measures have the same Lyapunov spectrum.
We now turn to the proof of Theorem 5.5.
If
![]() $f \colon X \to X$
is a homeomorphism of a compact metric space X, we say that f is a Veech-like map if it is strictly ergodic (i.e., minimal and uniquely ergodic) and
$f \colon X \to X$
is a homeomorphism of a compact metric space X, we say that f is a Veech-like map if it is strictly ergodic (i.e., minimal and uniquely ergodic) and
![]() $f^2$
is minimal but not uniquely ergodic. Veech-like maps were first constructed by Veech [Reference Veech62].
$f^2$
is minimal but not uniquely ergodic. Veech-like maps were first constructed by Veech [Reference Veech62].
Walters [Reference Walters, Arnold and Wihstutz63] has shown that given a Veech-like map f, one can construct a nonuniformly hyperbolic cocycle with base f. We will construct a specific Walters cocycle with some additional properties which will be instrumental in our proof of Theorem 5.5. For this cocycle we need the base Veech-like map constructed in [Reference Bochi9, Sec. 4] (the idea of this construction is due to Scott Schmieding).
Proof of Theorem 5.5.
Let
![]() $e_1, e_2, \dots $
be words in the alphabet
$e_1, e_2, \dots $
be words in the alphabet
![]() $\mathsf {A} \mathrel {:=} \{ \mathord {\uparrow }, \mathord {\downarrow } , 0 \}$
, defined in a recursive manner as follows:
$\mathsf {A} \mathrel {:=} \{ \mathord {\uparrow }, \mathord {\downarrow } , 0 \}$
, defined in a recursive manner as follows:
 $$ \begin{align} \notag e_{1} &\mathrel{:=} \mathord{\uparrow} \mathord{\downarrow} \, , \\ e_{k+1} &\mathrel{:=} e_k^{k^2+1} \, 0 \, e_k \, \overline{e_k}^{k^2+1} \, 0 \, \overline{e_k} \, , \end{align} $$
$$ \begin{align} \notag e_{1} &\mathrel{:=} \mathord{\uparrow} \mathord{\downarrow} \, , \\ e_{k+1} &\mathrel{:=} e_k^{k^2+1} \, 0 \, e_k \, \overline{e_k}^{k^2+1} \, 0 \, \overline{e_k} \, , \end{align} $$
where
![]() $\overline {e_k}$
denotes the word obtained from
$\overline {e_k}$
denotes the word obtained from
![]() $e_k$
by switching the arrows. Let X be the subset of
$e_k$
by switching the arrows. Let X be the subset of
![]() $\mathsf {A}^{\mathbb {Z}}$
formed by those bi-infinite sequences
$\mathsf {A}^{\mathbb {Z}}$
formed by those bi-infinite sequences
![]() $\omega =(\omega _i)_{i\in {\mathbb {Z}}}$
such that for every
$\omega =(\omega _i)_{i\in {\mathbb {Z}}}$
such that for every
![]() $n> 0$
, the word
$n> 0$
, the word
![]() $\omega _{-n}\omega _{-n+1}\cdots \omega _n$
occurs as a subword (i.e., a factor) of some
$\omega _{-n}\omega _{-n+1}\cdots \omega _n$
occurs as a subword (i.e., a factor) of some
![]() $e_k$
. According to [Reference Bochi9, Theorem 4.1], X is a closed, shift-invariant subset of
$e_k$
. According to [Reference Bochi9, Theorem 4.1], X is a closed, shift-invariant subset of
![]() $\mathsf {A}^{\mathbb {Z}}$
, and if
$\mathsf {A}^{\mathbb {Z}}$
, and if
![]() $f \colon X \to X$
is the restricted shift, then f is a Veech-like map. Define a continuous matrix valued map
$f \colon X \to X$
is the restricted shift, then f is a Veech-like map. Define a continuous matrix valued map
 $$\begin{align*}A(\omega) \mathrel{:=} \begin{pmatrix} 0 & e^{\varphi(\omega)} \\ e^{-\varphi(\omega)} & 0 \end{pmatrix} \quad \text{where} \quad \varphi(\omega) \mathrel{:=} \begin{cases} \phantom{-}1 &\text{if } \omega_0 = \mathord{\uparrow} \, , \\ -1 &\text{if } \omega_0 = \mathord{\downarrow} \, , \\ \phantom{-}0 &\text{if } \omega_0 = 0 \,. \end{cases} \end{align*}$$
$$\begin{align*}A(\omega) \mathrel{:=} \begin{pmatrix} 0 & e^{\varphi(\omega)} \\ e^{-\varphi(\omega)} & 0 \end{pmatrix} \quad \text{where} \quad \varphi(\omega) \mathrel{:=} \begin{cases} \phantom{-}1 &\text{if } \omega_0 = \mathord{\uparrow} \, , \\ -1 &\text{if } \omega_0 = \mathord{\downarrow} \, , \\ \phantom{-}0 &\text{if } \omega_0 = 0 \,. \end{cases} \end{align*}$$
Then [Reference Bochi9, Theorem 4.11] states that the corresponding cocycle
![]() $\mathcal {A}$
has nonzero Lyapunov exponents (with respect to the unique f-invariant measure), and it is not uniformly hyperbolic. Note that for any
$\mathcal {A}$
has nonzero Lyapunov exponents (with respect to the unique f-invariant measure), and it is not uniformly hyperbolic. Note that for any
![]() $\omega \in X$
and
$\omega \in X$
and
![]() $n>0$
,
$n>0$
,
 $$ \begin{align*} \frac{1}{n}\log \left\|\mathcal{A}(\omega,n) \right\| &= \frac{1}{n} \left| \sum_{j=0}^{n-1}(-1)^j \varphi(f^j(\omega)) \right| \, , \\ \frac{1}{n} \log \left\|\mathcal{A}(\omega,-n) \right\| &= \frac{1}{n} \left| \sum_{j=-n}^{-1}(-1)^j \varphi(f^j(\omega)) \right| \,. \end{align*} $$
$$ \begin{align*} \frac{1}{n}\log \left\|\mathcal{A}(\omega,n) \right\| &= \frac{1}{n} \left| \sum_{j=0}^{n-1}(-1)^j \varphi(f^j(\omega)) \right| \, , \\ \frac{1}{n} \log \left\|\mathcal{A}(\omega,-n) \right\| &= \frac{1}{n} \left| \sum_{j=-n}^{-1}(-1)^j \varphi(f^j(\omega)) \right| \,. \end{align*} $$
If
![]() $\omega $
is a LP-regular point, then the two sequences above must converge to the same limit as
$\omega $
is a LP-regular point, then the two sequences above must converge to the same limit as
![]() $n \to \infty $
. However, according to [Reference Bochi9, Lemma 4.12], this common limit, whenever it exists, is a number
$n \to \infty $
. However, according to [Reference Bochi9, Lemma 4.12], this common limit, whenever it exists, is a number
![]() $c>0$
independent of
$c>0$
independent of
![]() $\omega $
. Therefore all LP-regular points of our Walters cocycle have the same Lyapunov exponents c and
$\omega $
. Therefore all LP-regular points of our Walters cocycle have the same Lyapunov exponents c and
![]() $-c$
.
$-c$
.
At the same time, since f is uniquely ergodic and
![]() $\mathcal {A}$
is not uniformly hyperbolic, we must be in case (3) of Proposition 3.8. Consequently,
$\mathcal {A}$
is not uniformly hyperbolic, we must be in case (3) of Proposition 3.8. Consequently,
![]() $\mathcal {A}$
cannot be completely regular (even though, as we saw above, all LP-regular points have the same spectra).
$\mathcal {A}$
cannot be completely regular (even though, as we saw above, all LP-regular points have the same spectra).
Acknowledgements
We express our thanks to Boris Kalinin and Federico Rodriguez Hertz for helpful discussions and to Matías Ures for pointing out the missing requirement of uniform convergence in the definition of regularity. We thank the referee for their careful revision and suggestions.
Competing interests
The authors have no competing interest to declare.
Funding statement
Y.P. was partially supported by NSF grant DMS 2153053. O.S. was partially supported by ISF grant 264/22 and by Minerva grant ‘Chaotic non-Anosov dynamical systems’.