1 Introduction
Defining abstractions that support both programming with and reasoning about side effects is a research question with a long and rich history. The goal is to define an abstract interface of (possibly) side-effecting operations together with equations describing their behavior, where the interface hides operational details about the operations and their side effects that are irrelevant for defining or reasoning about a program. Such encapsulation makes it easy to refactor, optimize, or even change the behavior of a program while preserving proofs, by changing the implementation of the interface.
Monads (Reference MoggiMoggi, 1989b ) have long been the preferred solution to this research question, but they lack modularity: given two computations defined in different monads, there is no canonical way to combine them that is both universally applicable and preserves modular reasoning. This presents a problem for scalability since, in practice, programs, and therefore proofs, are developed incrementally. Algebraic effects and handlers (Plotkin & Power, Reference Plotkin and Power2002; Plotkin & Pretnar, Reference Plotkin and Pretnar2009) provide a solution for this problem by defining a syntactic class of monads, which permits composition of syntax, equational theories, and proofs. Algebraic effects and handlers maintain a strict separation of syntax and semantics, where programs are only syntax, and semantics is assigned later on a per-effect basis using handlers.
Many common operations, however, cannot be expressed as syntax in this framework. Specifically, higher-order operations that take computational arguments, such as exception, catching or modifying environments in the reader monad. While it is possible to express higher-order operations by inlining handler applications within the definition of the operation itself, this effectively relinquishes key modularity benefits. The syntax, equational theories, and proofs of such inlined operations do not compose.
In this paper, we propose to address this problem by appealing to an overloading mechanism which postpones the choice of handlers to inline. As we demonstrate, this approach provides a syntax and semantics of higher-order operations with similar modularity benefits as traditional algebraic effects; namely syntax, equational theories, and proofs that compose. To realize this, we use a syntactic class of monads that supports higher-order operations (which we dub hefty trees). Algebras over this syntax (hefty algebras) let us modularly elaborate this syntax into standard algebraic effects and handlers. We show that a wide variety of higher-order operations can be defined and assigned a semantics this way. Crucially, program definitions using hefty trees enjoy the same modularity properties as programs defined with algebraic effects and handlers. Specifically, they support the composition of syntax, semantics, equational theories, and proofs. This demonstrates that overloading is not only syntactically viable but also supports the same modular reasoning as algebraic effects for programs with side effects that involve higher-order operations.
1.1 Background: Algebraic effects and handlers
To understand the modularity benefits of algebraic effects and handlers, and why this modularity breaks when defining operations that take computations as parameters, we give a brief introduction to algebraic effects. To this end, we will use informal examples using a simple calculus inspired by Pretnar’s calculus for algebraic effects (Pretnar, Reference Pretnar2015). Section 2 of this paper provides a semantics for algebraic effects and handlers in Agda which corresponds to this calculus.
1.1.1 Effect signatures
Say we want an effectful operation
![]() ${out}$
for printing output. Besides its side effect of printing output, the operation should take a string as an argument and return the unit value. Using algebraic effects, we can declare this operation using the following effect signature:
${out}$
for printing output. Besides its side effect of printing output, the operation should take a string as an argument and return the unit value. Using algebraic effects, we can declare this operation using the following effect signature:
We can use this operation in any program that has the
![]() ${Output}$
effect. For example, the following
${Output}$
effect. For example, the following
![]() ${hello}$
program:
${hello}$
program:
The type
![]() ${{()}}\mathop{!}{Output}$
indicates that
${{()}}\mathop{!}{Output}$
indicates that
![]() ${hello}$
is an effectful computation which returns a unit value, and which is allowed to call the operations in
${hello}$
is an effectful computation which returns a unit value, and which is allowed to call the operations in
![]() ${Output}$
(i.e., only the
${Output}$
(i.e., only the
![]() ${out}$
operation).
${out}$
operation).
More generally, computations of type
![]() ${A}\mathop{!}{\Delta}$
are allowed (but not required) to call any operation of any effect in
${A}\mathop{!}{\Delta}$
are allowed (but not required) to call any operation of any effect in
![]() $\Delta$
, where
$\Delta$
, where
![]() $\Delta$
is a row (i.e., unordered sequence) of effects. An effect is essentially a label associated with a set of operations. The association of labels to operations is declared using effect signatures, akin to the signature for
$\Delta$
is a row (i.e., unordered sequence) of effects. An effect is essentially a label associated with a set of operations. The association of labels to operations is declared using effect signatures, akin to the signature for
![]() ${Output}$
above.
${Output}$
above.
1.1.2 Effect theories
A crucial feature of algebraic effects and handlers is that it permits abstract reasoning about programs containing effects, such as
![]() ${hello}$
above. That is, each effect is associated with a set of laws that characterizes the behavior of its operations. Their purpose is to constrain an effect’s behavior without appealing to any specifics of the implementation of the effects. Consequently, program proofs derived from these equations remain valid for all handler implementations satisfying the laws of its equational theory.
${hello}$
above. That is, each effect is associated with a set of laws that characterizes the behavior of its operations. Their purpose is to constrain an effect’s behavior without appealing to any specifics of the implementation of the effects. Consequently, program proofs derived from these equations remain valid for all handler implementations satisfying the laws of its equational theory.
Importantly, these laws are purely syntactic, in the sense that they are part of the effect’s specification rather than representing universal truths about the behavior of effectful computation. Whether a law is “valid” depends entirely on how we handle the effects, and different handlers may satisfy different laws. Figuring out a suitable set of laws is part of the development process of (new) effects. Typically, the final specification of an effect is the result of a back-and-forth refinement between an effect’s specification and its handler implementations. This process ultimately converges to a definition that matches our intuitive understanding of what an effect should do.
For example, the
![]() ${Output}$
effect has a single law that characterizes the behavior of
${Output}$
effect has a single law that characterizes the behavior of
![]() ${out}$
:
${out}$
:
Here,
![]() $\mathrel{+\mkern-5mu+}$
is string concatenation. Using this law, we can prove that our
$\mathrel{+\mkern-5mu+}$
is string concatenation. Using this law, we can prove that our
![]() ${hello}$
program will print the string “Hello world!”. Crucially, this proof does not depend on operational implementation details of the
${hello}$
program will print the string “Hello world!”. Crucially, this proof does not depend on operational implementation details of the
![]() ${Output}$
effect. Instead, it uses the laws of the equational theory of the effect. While the program and effect discussed so far has been deliberately simple, the approach illustrates how algebraic effects let us reason about effectful programs in a way that abstracts from the concrete implementation of the underlying effects.
${Output}$
effect. Instead, it uses the laws of the equational theory of the effect. While the program and effect discussed so far has been deliberately simple, the approach illustrates how algebraic effects let us reason about effectful programs in a way that abstracts from the concrete implementation of the underlying effects.
1.1.3 Effect handlers
An alternative perspective is to view effects as interfaces that specify the parameter, return type, and laws of each operation. Implementations of such interfaces are given by effect handlers. An effect handler essentially defines how to interpret operations in the execution context they occur in. This interpretation must be consistent with the laws of the effect. (We will not dwell further on this consistency here; we return to this in Section 5.6.)
The type of an effect handler is
![]() ${A}\mathop{!}{\Delta}~\Rightarrow~{B}\mathop{!}{\Delta^\prime}$
, where
${A}\mathop{!}{\Delta}~\Rightarrow~{B}\mathop{!}{\Delta^\prime}$
, where
![]() $\Delta$
is the row of effects before applying the handler and
$\Delta$
is the row of effects before applying the handler and
![]() $\Delta^\prime$
is the row after. For example, here is a specific type of an effect handler for
$\Delta^\prime$
is the row after. For example, here is a specific type of an effect handler for
![]() ${Output}$
:Footnote
1
${Output}$
:Footnote
1
The
![]() ${Output}$
effect is being handled, so it is only present in the effect row on the left.Footnote
2
As the type suggests, this handler handles
${Output}$
effect is being handled, so it is only present in the effect row on the left.Footnote
2
As the type suggests, this handler handles
![]() ${out}$
operations by accumulating a string of output. Below is an example implementation of this handler:
${out}$
operations by accumulating a string of output. Below is an example implementation of this handler:
The
![]() $\mathbf{return}{}$
case of the handler says that, if the computation being handled terminates normally with a value x, then we return a pair of x and the empty string. The case for
$\mathbf{return}{}$
case of the handler says that, if the computation being handled terminates normally with a value x, then we return a pair of x and the empty string. The case for
![]() ${out}$
binds a variable s for the string argument of the operation, but also a variable k representing the execution context (or continuation). Invoking an operation suspends the program and its execution context up-to the nearest handler of the operation. The handler can choose to re-invoke the suspended execution context (possibly multiple times). The handler case for
${out}$
binds a variable s for the string argument of the operation, but also a variable k representing the execution context (or continuation). Invoking an operation suspends the program and its execution context up-to the nearest handler of the operation. The handler can choose to re-invoke the suspended execution context (possibly multiple times). The handler case for
![]() ${out}$
above always invokes k once. Since k represents an execution context that includes the current handler, calling k gives a pair of a value y and a string
${out}$
above always invokes k once. Since k represents an execution context that includes the current handler, calling k gives a pair of a value y and a string
![]() $s^\prime$
, representing the final value and output of the execution context. The result of handling
$s^\prime$
, representing the final value and output of the execution context. The result of handling
![]() ${out}~s$
is then y and the current output (s) plus the output of the rest of the program (
${out}~s$
is then y and the current output (s) plus the output of the rest of the program (
![]() $s^\prime$
).
$s^\prime$
).
In general, a computation
![]() $m : {A}\mathop{!}{\Delta}$
can only be run in a context that provides handlers for each effect in
$m : {A}\mathop{!}{\Delta}$
can only be run in a context that provides handlers for each effect in
![]() $\Delta$
. To this end, the expression
$\Delta$
. To this end, the expression
![]() $\textbf{with}~{h}~\textbf{handle}~{m}$
represents applying the handler h to handle a subset of effects of m. For example, we can run the
$\textbf{with}~{h}~\textbf{handle}~{m}$
represents applying the handler h to handle a subset of effects of m. For example, we can run the
![]() ${hello}$
program from earlier with the handler
${hello}$
program from earlier with the handler
![]() ${hOut}$
to compute the following result:
${hOut}$
to compute the following result:
The key benefit of algebraic effects and handlers is that programs such as
![]() ${hello}$
are defined independently of how the effectful operations they use are implemented. This makes it possible to reason about programs independently of how the underlying effects are implemented and also makes it possible to refine, refactor, and optimize the semantics of operations, without having to modify the programs that use them. For example, we could refine the meaning of
${hello}$
are defined independently of how the effectful operations they use are implemented. This makes it possible to reason about programs independently of how the underlying effects are implemented and also makes it possible to refine, refactor, and optimize the semantics of operations, without having to modify the programs that use them. For example, we could refine the meaning of
![]() ${out}$
without modifying the
${out}$
without modifying the
![]() ${hello}$
program or proofs derived from equations of the
${hello}$
program or proofs derived from equations of the
![]() ${Output}$
effect, by using a different handler which prints output to the console. However, some operations are challenging to express while retaining the same modularity benefits.
${Output}$
effect, by using a different handler which prints output to the console. However, some operations are challenging to express while retaining the same modularity benefits.
1.2 The modularity problem with higher-order operations
We discuss the problem with defining higher-order operations using effect signatures (Section 1.2.1) and potential workarounds (Sections 1.2.2 and 1.2.3).
1.2.1 The problem
Say we want to declare an operation
![]() ${censor}\, f\, m$
, which applies a censoring function
${censor}\, f\, m$
, which applies a censoring function
![]() $f : {String} \to {String}$
to the side-effectful output of the computation m. We might try to declare an effect
$f : {String} \to {String}$
to the side-effectful output of the computation m. We might try to declare an effect
![]() ${Censor}$
with a
${Censor}$
with a
![]() ${censor}$
operation by the following type:
${censor}$
operation by the following type:
However, using algebraic effects, we cannot declare
![]() ${censor}$
as an operation.
${censor}$
as an operation.
The problem is that effect signatures do not offer direct support for declaring operations with computation parameters. Effect signatures have the following shape:
Here, each operation parameter type
![]() $A_i$
is going to be typed as a value. While we may pass around computations as values, passing around computations as arguments of computations is not a desirable approach to defining higher-order operations in general. We will return to this point in Section 1.2.2.
$A_i$
is going to be typed as a value. While we may pass around computations as values, passing around computations as arguments of computations is not a desirable approach to defining higher-order operations in general. We will return to this point in Section 1.2.2.
The fact that effect signatures do not directly support operations with computational arguments is also evident from how handler cases are typed (Pretnar, Reference Pretnar2015, Fig. 6):
Here, A is the argument type of an operation, and B is the return type of an operation. The term c represents the code of the handler case, which must have type
![]() $C~!~\Delta^\prime$
.
$C~!~\Delta^\prime$
.
Observe how only the continuation k that is statically known to have computation type which matches the effects of the context in which the handler is applied. While the argument type A could be instantiated with a computation type
![]() $A~!~\Delta^{\prime\prime}$
, the effects of this computation are hardcoded in the definition of the operation. Because handlers are agnostic to the row
$A~!~\Delta^{\prime\prime}$
, the effects of this computation are hardcoded in the definition of the operation. Because handlers are agnostic to the row
![]() $\Delta^\prime$
of effects that they do not handle, and since in general
$\Delta^\prime$
of effects that they do not handle, and since in general
![]() $\Delta^\prime~\neq~\Delta^{\prime\prime}$
, we are forced, in a clear violation of modularity, to hardcode the handler for
$\Delta^\prime~\neq~\Delta^{\prime\prime}$
, we are forced, in a clear violation of modularity, to hardcode the handler for
![]() $\Delta^{\prime\prime}$
as well. As a result, the only option for defining operations with computation parameters that preserves modularity is to encode them in the continuation k.
$\Delta^{\prime\prime}$
as well. As a result, the only option for defining operations with computation parameters that preserves modularity is to encode them in the continuation k.
A consequence of this observation is that we can only define and modularly handle higher-order operations whose computation parameters are continuation-like. Following Plotkin & Power (Reference Plotkin and Power2003), such operations satisfy the following law, known as the algebraicity property. For any operation
![]() ${op} : {A}\mathop{!}{\Delta} \to \cdots \to {A}\mathop{!}{\Delta} \to {A}\mathop{!}{\Delta}$
and any
${op} : {A}\mathop{!}{\Delta} \to \cdots \to {A}\mathop{!}{\Delta} \to {A}\mathop{!}{\Delta}$
and any
![]() $m_1,\ldots,m_n$
and k,
$m_1,\ldots,m_n$
and k,
The law says that the computation parameter values
![]() $m_1,\ldots,m_n$
are only ever run in a way that directly passes control to k. Such operations can without loss of generality or modularity be encoded as operations without computation parameters;Footnote
3
i.e., as algebraic operations that match the handler typing in (*) above.
$m_1,\ldots,m_n$
are only ever run in a way that directly passes control to k. Such operations can without loss of generality or modularity be encoded as operations without computation parameters;Footnote
3
i.e., as algebraic operations that match the handler typing in (*) above.
Some higher-order operations obey the algebraicity property; many do not. Examples that do not obey algebraicity include:
-
• Exception handling: let
 ${catch}~m_1~m_2$
be an operation that handles exceptions thrown during evaluation of computation
${catch}~m_1~m_2$
be an operation that handles exceptions thrown during evaluation of computation
 $m_1$
by running
$m_1$
by running
 $m_2$
instead, and
$m_2$
instead, and
 ${throw}$
be an operation that throws an exception. These operations are not algebraic. For example,
${throw}$
be an operation that throws an exception. These operations are not algebraic. For example,  \[ \mathbf{do}~({catch}~m_1~m_2); {throw}\ \not\equiv\ {catch}~(\mathbf{do}~m_1; {throw})~(\mathbf{do}~m_2; {throw}) \]
\[ \mathbf{do}~({catch}~m_1~m_2); {throw}\ \not\equiv\ {catch}~(\mathbf{do}~m_1; {throw})~(\mathbf{do}~m_2; {throw}) \]
-
• Local binding (the reader monad Jones, Reference Jones1995): let
 ${ask}$
be an operation that reads a local binding, and
${ask}$
be an operation that reads a local binding, and
 ${local}~r~m$
be an operation that makes r the current binding in computation m. Observe:
${local}~r~m$
be an operation that makes r the current binding in computation m. Observe:  \[ \mathbf{do}~({local}~r~m); {ask} \ \not\equiv\ {local}~r~(\mathbf{do}~m; {ask}) \]
\[ \mathbf{do}~({local}~r~m); {ask} \ \not\equiv\ {local}~r~(\mathbf{do}~m; {ask}) \]
-
• Logging with censoring (an extension of the writer monad Jones, Reference Jones1995): let
 ${out}~s$
be an operation for logging a string, and
${out}~s$
be an operation for logging a string, and
 ${censor}~f~m$
be an operation for post-processing the output of computation m by applying
${censor}~f~m$
be an operation for post-processing the output of computation m by applying
 $f : {String} \to {String}$
.Footnote
4
Observe:
$f : {String} \to {String}$
.Footnote
4
Observe:  \[ \mathbf{do}~({censor}~f~m); {out}~s \ \not\equiv\ {censor}~f~(\mathbf{do}~m; {out}~s) \]
\[ \mathbf{do}~({censor}~f~m); {out}~s \ \not\equiv\ {censor}~f~(\mathbf{do}~m; {out}~s) \]
-
• Function abstraction as an effect: let
 ${abs}~x~m$
be an operation that constructs a function value binding x in computation m,
${abs}~x~m$
be an operation that constructs a function value binding x in computation m,
 ${app}~v~m$
be an operation that applies a function value v to an argument computation m, and
${app}~v~m$
be an operation that applies a function value v to an argument computation m, and
 ${var}~x$
be an operation that dereferences a bound x. Observe:
${var}~x$
be an operation that dereferences a bound x. Observe:  \[ \mathbf{do}~({abs}~x~m); {var}~x \ \not\equiv\ {abs}~x~(\mathbf{do}~m; {var}~x) \]
\[ \mathbf{do}~({abs}~x~m); {var}~x \ \not\equiv\ {abs}~x~(\mathbf{do}~m; {var}~x) \]
1.2.2 Potential workaround: Computations as arguments of operations
A tempting possible workaround to the issues summarized in Section 1.2.1 is to declare an effect signature with a parameter type
![]() $A_i$
that carries effectful computations. However, this workaround can cause operations to escape their handlers. Following Pretnar (Reference Pretnar2015), the semantics of effect handling obeys the following law.Footnote
5
If h handles operations other than
$A_i$
that carries effectful computations. However, this workaround can cause operations to escape their handlers. Following Pretnar (Reference Pretnar2015), the semantics of effect handling obeys the following law.Footnote
5
If h handles operations other than
![]() ${op}$
, then:
${op}$
, then:
This law tells us that effects in v will not be handled by h. This is problematic if h is the intended handler for one or more effects in v. The solution we describe in Section 1.3 does not suffer from this problem.
Nevertheless, for applications where it is known exactly which effects v contains, we can work around the issue by encoding computations as argument values of operations. We consider how and discuss the modularity problems that this workaround suffers from. The following
![]() ${Censor}$
effect declares the type of an operation
${Censor}$
effect declares the type of an operation
![]() ${censorOp}~(f,m)$
where f is a censoring function and m is a computation encoded as a value argument:Footnote
6
${censorOp}~(f,m)$
where f is a censoring function and m is a computation encoded as a value argument:Footnote
6
This effect can be handled as follows:

The handler case for
![]() ${censorOp}$
runs m with handlers for both the
${censorOp}$
runs m with handlers for both the
![]() ${Output}$
and
${Output}$
and
![]() ${Censor}$
effects, which yields a pair (x,s) where x represents the value returned by m, and s represents the (possibly sub-censored) output of m. We then output the result of applying the censoring function f to s, before passing x to the continuation k.
${Censor}$
effects, which yields a pair (x,s) where x represents the value returned by m, and s represents the (possibly sub-censored) output of m. We then output the result of applying the censoring function f to s, before passing x to the continuation k.
This handler lets us run programs such as the following:
Applying
![]() ${hCensor}$
and
${hCensor}$
and
![]() ${hOut}$
yields the printed output “Hello world!”, because
${hOut}$
yields the printed output “Hello world!”, because
:
As the example above illustrates, it is sometimes possible to encode higher-order effects as algebraic operations. However, encoding higher-order operations in this way suffers from a modularity problem. Say we want to extend our program with a new effect for throwing exceptions—i.e., an effect with a single operation
![]() ${throw}$
—and a new effect for catching exceptions—i.e., an effect with a single operation
${throw}$
—and a new effect for catching exceptions—i.e., an effect with a single operation
![]() ${catch}~m_1~m_2$
where exceptions thrown by
${catch}~m_1~m_2$
where exceptions thrown by
![]() $m_1$
are handled by running
$m_1$
are handled by running
![]() $m_2$
. The
$m_2$
. The
![]() ${Throw}$
effect is a plain algebraic effect, defined as follows.Footnote
7
${Throw}$
effect is a plain algebraic effect, defined as follows.Footnote
7
The
![]() ${Catch}$
effect is higher-order. We can again encode it as an operation with computations as value arguments.
${Catch}$
effect is higher-order. We can again encode it as an operation with computations as value arguments.

To support subcomputations with exception catching, we need to refine the computation type we use for
![]() ${Censor}$
. (This refinement could have been done modularly if we had used a more polymorphic type.)
${Censor}$
. (This refinement could have been done modularly if we had used a more polymorphic type.)
The modularity problem arises when we consider whether to handle
![]() ${Catch}$
or
${Catch}$
or
![]() ${Censor}$
first. If we handle
${Censor}$
first. If we handle
![]() ${Censor}$
first, then we get exactly the problem described earlier in connection with the law (†): the handler
${Censor}$
first, then we get exactly the problem described earlier in connection with the law (†): the handler
![]() ${hCensor}$
is not applied to sub-computations of
${hCensor}$
is not applied to sub-computations of
![]() ${catchOp}$
operations. Let us consider the consequences of this. Say we want to define a handler for
${catchOp}$
operations. Let us consider the consequences of this. Say we want to define a handler for
![]() ${catchOp}$
of the following type:
${catchOp}$
of the following type:
Any such handler which runs the sub-computation
![]() $m_1$
of an operation
$m_1$
of an operation
![]() ${catchOp}~m_1~m_2$
must hardcode a handler for the
${catchOp}~m_1~m_2$
must hardcode a handler for the
![]() ${Censor}$
effect. Otherwise the handler would allow effects to escape in a way that breaks the typing discipline of algebraic effects and handlers (Pretnar, Reference Pretnar2015). To illustrate why this is the case, consider the following program.
${Censor}$
effect. Otherwise the handler would allow effects to escape in a way that breaks the typing discipline of algebraic effects and handlers (Pretnar, Reference Pretnar2015). To illustrate why this is the case, consider the following program.
Per equation 12 of Pretnar (Reference Pretnar2015, Figure 7), this program is equivalent to:
Which means that
![]() ${hCatch}$
is now responsible for handling the remaining
${hCatch}$
is now responsible for handling the remaining
![]() ${Censor}$
effect in the first sub-computation of
${Censor}$
effect in the first sub-computation of
![]() ${catchOp}$
, otherwise it violates the promise of its type that the resulting computation does not have the
${catchOp}$
, otherwise it violates the promise of its type that the resulting computation does not have the
![]() ${Censor}$
effect. While for some applications it may be acceptable to hardcode handler invokations this way, it is non-modular and should not be—and, indeed, is not–necessary.
${Censor}$
effect. While for some applications it may be acceptable to hardcode handler invokations this way, it is non-modular and should not be—and, indeed, is not–necessary.
Before showing the solution, we propose which avoids this, we first consider a different workaround (Section 1.2.3) and previous solutions proposed in the literature (Section 1.2.4).
1.2.3 Potential workaround: Define higher-order operations as handlers
It is possible to define many higher-order operations in terms of algebraic effects and handlers. For example, instead of defining
![]() ${censor}$
as an operation, we could define it as a function which uses an inline handler application of
${censor}$
as an operation, we could define it as a function which uses an inline handler application of
![]() ${hOut}$
:
${hOut}$
:
Defining higher-order operations in terms of standard algebraic effects and handlers in this way is a key use case of effect handlers (Plotkin & Pretnar, Reference Plotkin and Pretnar2009). In fact, all other higher-order operations above (with the exception of function abstraction) can be defined in a similar manner.
However, it is unclear what the semantics is of composing syntax, equational theories, and proofs of programs with such functions occuring inline in programs. We address this gap by proposing notions of syntax and equational theories for programs with higher-order operations. The semantics of such programs and theories is given by elaborating them into standard algebraic effects and handlers.
1.2.4 Previous approaches to solving the modularity problem
The modularity problem of higher-order effects, summarized in Section 1.2.1, was first observed by Wu et al. (Reference Wu, Schrijvers and Hinze2014) who proposed scoped effects and handlers (Wu et al., Reference Wu, Schrijvers and Hinze2014; Piróg et al., Reference Piróg, Schrijvers, Wu and Jaskelioff2018; Yang et al., Reference Yang, Paviotti, Wu, van den Berg and Schrijvers2022) as a solution. Scoped effects and handlers work for a wide class of effects, including many higher-order effects, providing similar modularity benefits as algebraic effects and handlers when writing programs. Using parameterized algebraic theories (Lindley et al., Reference Lindley, Matache, Moss, Staton, Wu and Yang2024; Matache et al., Reference Matache, Lindley, Moss, Staton, Wu and Yang2025), it is possible reason about programs with scoped effects independently of how their effects are implemented.
Van den Berg et al. (Reference van den Berg, Schrijvers, Poulsen and Wu2021) recently observed, however, that operations that defer computation, such as evaluation strategies for
![]() $\lambda$
application or (multi-)staging (Taha & Sheard, Reference Taha and Sheard2000), are beyond the expressiveness of scoped effects. Therefore, van den Berg et al. (Reference van den Berg, Schrijvers, Poulsen and Wu2021) introduced another flavor of effects and handlers that they call latent effects and handlers. It remains an open question how to reason about latent effects and handlers independently of how effects are implemented.
$\lambda$
application or (multi-)staging (Taha & Sheard, Reference Taha and Sheard2000), are beyond the expressiveness of scoped effects. Therefore, van den Berg et al. (Reference van den Berg, Schrijvers, Poulsen and Wu2021) introduced another flavor of effects and handlers that they call latent effects and handlers. It remains an open question how to reason about latent effects and handlers independently of how effects are implemented.
In this paper, we demonstrate that an overloading-based approach provides a semantics of composition for effect theories that is comparable to standard algebraic effects and handlers, and, we expect, to parameterized algebraic theories. Furthermore, we demonstrate that the approach lets us model the syntax and semantics of key examples from the literature: optionally transactional exception catching, akin to scoped effect handlers (Wu et al., Reference Wu, Schrijvers and Hinze2014), and evaluation strategies for effectful
![]() $\lambda$
application (van den Berg et al., Reference van den Berg, Schrijvers, Poulsen and Wu2021). Formally relating the expressiveness of our approach with, e.g., scoped effects and parameterized algebraic theories, is future work.
$\lambda$
application (van den Berg et al., Reference van den Berg, Schrijvers, Poulsen and Wu2021). Formally relating the expressiveness of our approach with, e.g., scoped effects and parameterized algebraic theories, is future work.
1.3 Solution: Elaboration algebras
We propose to define operations such as
![]() ${censor}$
from Section 1.2 as modular elaborations from a syntax of higher-order effects into algebraic effects and handlers. To this end, we introduce a new type of computations with higher-order effects, which can be modularly translated into computations with only standard algebraic effects:
${censor}$
from Section 1.2 as modular elaborations from a syntax of higher-order effects into algebraic effects and handlers. To this end, we introduce a new type of computations with higher-order effects, which can be modularly translated into computations with only standard algebraic effects:
Here
![]() ${A}\mathop{!\kern-1pt!}{H}$
is a computation type where A is a return type and H is a row comprising both algebraic and higher-order effects. The key idea is that the higher-order effects in the row H are modularly elaborated into a computation with effects given by the row
${A}\mathop{!\kern-1pt!}{H}$
is a computation type where A is a return type and H is a row comprising both algebraic and higher-order effects. The key idea is that the higher-order effects in the row H are modularly elaborated into a computation with effects given by the row
![]() $\Delta$
. To achieve this, we define
$\Delta$
. To achieve this, we define
![]() ${elaborate}$
such that it can be modularly composed from separately defined elaboration cases, called elaboration algebras (for reasons explained in Section 3).
${elaborate}$
such that it can be modularly composed from separately defined elaboration cases, called elaboration algebras (for reasons explained in Section 3).
![]() ${A}\mathop{!\kern-1pt!}{H} \Rrightarrow {A}\mathop{!}{\Delta}$
as the type of elaboration algebras that elaborate the higher-order effects in H to
${A}\mathop{!\kern-1pt!}{H} \Rrightarrow {A}\mathop{!}{\Delta}$
as the type of elaboration algebras that elaborate the higher-order effects in H to
![]() $\Delta$
, we can modularly compose any pair of elaboration algebras
$\Delta$
, we can modularly compose any pair of elaboration algebras
![]() $e_1 : {A}\mathop{!\kern-1pt!}{{H_1}} \Rrightarrow{} {A}\mathop{!}{\Delta}$
and
$e_1 : {A}\mathop{!\kern-1pt!}{{H_1}} \Rrightarrow{} {A}\mathop{!}{\Delta}$
and
![]() $e_2 : {A}\mathop{!\kern-1pt!}{{H_2}} \Rrightarrow{} {A}\mathop{!}{\Delta}$
into an algebra
$e_2 : {A}\mathop{!\kern-1pt!}{{H_2}} \Rrightarrow{} {A}\mathop{!}{\Delta}$
into an algebra
![]() $e_{12} : {A}\mathop{!\kern-1pt!}{{H_1,H_2}} \Rrightarrow{} {A}\mathop{!}{\Delta}$
.Footnote
8
$e_{12} : {A}\mathop{!\kern-1pt!}{{H_1,H_2}} \Rrightarrow{} {A}\mathop{!}{\Delta}$
.Footnote
8
Elaboration algebras are as simple to define as non-modular elaborations such as
![]() ${censor}$
(Section 1.2.3). For example, here is the elaboration algebra for the higher-order
${censor}$
(Section 1.2.3). For example, here is the elaboration algebra for the higher-order
![]() ${Censor}$
effect whose only associated operation is the higher-order operation
${Censor}$
effect whose only associated operation is the higher-order operation
![]() ${censor_{op}} : ({String} \to {String}) \to {A}\mathop{!\kern-1pt!}{H} \to {A}\mathop{!\kern-1pt!}{H}$
:
${censor_{op}} : ({String} \to {String}) \to {A}\mathop{!\kern-1pt!}{H} \to {A}\mathop{!\kern-1pt!}{H}$
:
The implementation of
![]() ${eCensor}$
is essentially the same as
${eCensor}$
is essentially the same as
![]() ${censor}$
, with two main differences. First, elaboration happens in-context, so the value yielded by the elaboration is passed to the context (or continuation) k. Second, and most importantly, programs that use the
${censor}$
, with two main differences. First, elaboration happens in-context, so the value yielded by the elaboration is passed to the context (or continuation) k. Second, and most importantly, programs that use the
![]() ${censor_{op}}$
operation are now programmed against the interface given by
${censor_{op}}$
operation are now programmed against the interface given by
![]() ${Censor}$
, meaning programs do not (and cannot) make assumptions about how
${Censor}$
, meaning programs do not (and cannot) make assumptions about how
![]() ${censor_{op}}$
is elaborated. As a consequence, we can modularly refine the elaboration of higher-order operations such as
${censor_{op}}$
is elaborated. As a consequence, we can modularly refine the elaboration of higher-order operations such as
![]() ${censor_{op}}$
, without modifying the programs that use the operations. Similarly, we can define equational theories that constrain the behavior elaborations of higher-order operations and write proofs about programs using higher-order operations that are valid for any elaboration that satisfies these equations.
${censor_{op}}$
, without modifying the programs that use the operations. Similarly, we can define equational theories that constrain the behavior elaborations of higher-order operations and write proofs about programs using higher-order operations that are valid for any elaboration that satisfies these equations.
For example, here is again a program which censors and replaces “Hello” with “Goodbye”:Footnote 9
Say we have a handler
![]() ${hOut^\prime} : ({String} \to {String}) \to {A}\mathop{!}{{Output},\Delta} \Rightarrow {(A \times {String})}\mathop{!}{\Delta}$
which handles each operation
${hOut^\prime} : ({String} \to {String}) \to {A}\mathop{!}{{Output},\Delta} \Rightarrow {(A \times {String})}\mathop{!}{\Delta}$
which handles each operation
![]() ${out}~s$
by pre-applying a censor function (
${out}~s$
by pre-applying a censor function (
![]() ${String} \to {String}$
) to s before emitting it. Using this handler, we can give an alternative elaboration of
${String} \to {String}$
) to s before emitting it. Using this handler, we can give an alternative elaboration of
![]() ${censor_{op}}$
which post-processes output strings individually:
${censor_{op}}$
which post-processes output strings individually:
In contrast,
![]() ${eCensor}$
applies the censoring function (
${eCensor}$
applies the censoring function (
![]() ${String} \to {String}$
) to the batch output of the computation argument of a
${String} \to {String}$
) to the batch output of the computation argument of a
![]() ${censor_{op}}$
operation. The batch output of
${censor_{op}}$
operation. The batch output of
![]() ${hello}$
is “Hello world!” which is unequal to “Hello”, so
${hello}$
is “Hello world!” which is unequal to “Hello”, so
![]() ${eCensor}$
leaves the string unchanged. On the other hand,
${eCensor}$
leaves the string unchanged. On the other hand,
![]() ${eCensor^\prime}$
censors the individually output “Hello”:
${eCensor^\prime}$
censors the individually output “Hello”:
This gives higher-order operations the same modularity benefits as algebraic operations for defining programs. In Section 5, we show that these modularity benefits extend to program reasoning as well.
1.4 Contributions
This paper formalizes the ideas sketched in this introduction by shallowly embedding them in Agda. However, the ideas transcend Agda. Similar shallow embeddings can be implemented in other dependently typed languages, such as Idris (Reference BradyBrady, 2013a ); but also in less dependently typed languages like Haskell, OCaml, or Scala.Footnote 10 By working in a dependently typed language, we can state algebraic laws about interfaces of effectful operations, and prove that implementations of the interfaces respect the laws. We make the following technical contributions:
-
• Section 2 describes how to encode algebraic effects in Agda, revisits the modularity problem with higher-order operations, and summarizes how scoped effects and handlers address the modularity problem, for some (scoped operations) but not all higher-order operations.
-
• Section 3 presents our solution to the modularity problem with higher-order operations. Our solution is to (1) type programs as higher-order effect trees (which we dub hefty trees) and (2) build modular elaboration algebras for folding hefty trees into algebraic effect trees and handlers. The computations of type
 ${A}\mathop{!\kern-1pt!}{H}$
discussed in Section 1.3 correspond to hefty trees, and the elaborations of type
${A}\mathop{!\kern-1pt!}{H}$
discussed in Section 1.3 correspond to hefty trees, and the elaborations of type
 ${A}\mathop{!\kern-1pt!}{H} \Rrightarrow {A}\mathop{!}{\Delta}$
correspond to hefty algebras.
${A}\mathop{!\kern-1pt!}{H} \Rrightarrow {A}\mathop{!}{\Delta}$
correspond to hefty algebras. -
• Section 4 presents examples of how to define hefty algebras for common higher-order effects from the literature on effect handlers.
-
• Section 5 shows that hefty algebras support formal and modular reasoning on a par with algebraic effects and handlers, by developing reasoning infrastructure that supports verification of equational laws for higher-order effects such as exception catching. Crucially, proofs of correctness of elaborations are compositional. When composing two proven correct elaboration, correctness of the combined elaboration follows immediately without requiring further proof work.
Section 6 discusses related work and Section 7 concludes. The paper assumes a passing familiarity with dependent types. We do not assume familiarity with Agda: we explain Agda-specific syntax and features when we use them.
An artifact containing the code of the paper and a Haskell embedding of the same ideas is available online (van der Rest & Poulsen, Reference van der Rest and Poulsen2024). A subset of the contributions of this paper was previously published in a conference paper (Poulsen & van der Rest, Reference Poulsen and van der Rest2023). While that version of the paper too discusses reasoning about higher-order effects, the correctness proofs were non-modular, in that they make assumptions about the order in which the algebraic effects implementing a higher-order effect are handled. When combining elaborations, these assumptions are often incompatible, meaning that correctness proofs for the individual elaborations do not transfer to the combined elaboration. As a result, one would have to re-prove correctness for every combination of elaborations. For this extended version, we developed reasoning infrastructure to support modular reasoning about higher-order effects in Section 5 and proved that correctness of elaborations is preserved under composition of elaborations.
2 Algebraic effects and handlers in Agda
This section describes how to encode algebraic effects and handlers in Agda. We do not assume familiarity with Agda and explain Agda specific notation in footnotes. Sections 2.1 to 2.4 defines algebraic effects and handlers; Section 2.5 revisits the problem of defining higher-order effects using algebraic effects and handlers; and Section 2.6 discusses how scoped effects (Wu et al., Reference Wu, Schrijvers and Hinze2014; Piróg et al., Reference Piróg, Schrijvers, Wu and Jaskelioff2018; Yang et al., Reference Yang, Paviotti, Wu, van den Berg and Schrijvers2022) solves the problem for scoped operations but not all higher-order operations.
2.1 Algebraic effects and the free monad
We encode algebraic effects in Agda by representing computations as an abstract syntax tree given by the free monad over an effect signature. Such effect signatures are traditionally (Swierstra, Reference Swierstra2008; Awodey, Reference Awodey2010; Kammar et al., Reference Kammar, Lindley and Oury2013; Wu et al., Reference Wu, Schrijvers and Hinze2014; Kiselyov & Ishii, Reference Kiselyov and Ishii2015) given by a functor; i.e., a type of kind
![]() together with a (lawful) mapping function.Footnote
11
In our Agda implementation, effect signature functors are defined by giving a container (Abbott et al., Reference Abbott, Altenkirch and Ghani2003, Reference Abbott, Altenkirch and Ghani2005). Each container corresponds to a value of type
together with a (lawful) mapping function.Footnote
11
In our Agda implementation, effect signature functors are defined by giving a container (Abbott et al., Reference Abbott, Altenkirch and Ghani2003, Reference Abbott, Altenkirch and Ghani2005). Each container corresponds to a value of type
![]() that is both strictly positive
Footnote
12
and universe consistent
Footnote
13
(Martin-Löf, Reference Martin-Löf1984), meaning they are a constructive approximation of endofunctors on
that is both strictly positive
Footnote
12
and universe consistent
Footnote
13
(Martin-Löf, Reference Martin-Löf1984), meaning they are a constructive approximation of endofunctors on
![]() . Effect signatures are given by a (dependent) record type:
Footnote 14,Footnote 15
. Effect signatures are given by a (dependent) record type:
Footnote 14,Footnote 15

Here,
![]() is the set of operations, and
is the set of operations, and
![]() defines the return type for each operation in the set
defines the return type for each operation in the set
![]() . The extension of an effect signature,
. The extension of an effect signature,
![]() $[\![\_]\!]$
, reflects its input of type
$[\![\_]\!]$
, reflects its input of type
![]() as a value of type
as a value of type
![]() :Footnote
16
:Footnote
16

The extension of an effect
![]() $\Delta$
into
$\Delta$
into
![]() is indeed a functor, as witnessed by the following function:Footnote
17
is indeed a functor, as witnessed by the following function:Footnote
17

As discussed in the introduction, computations may use multiple different effects. Effect signatures are closed under co-products:Footnote 18 ,Footnote 19

We compute the co-product of two effect signatures by taking the disjoint sum of their operations and combining the return type mappings pointwise. We use co-products to encode effect rows. For example, the effect
![]() corresponds to the row union denoted as
corresponds to the row union denoted as
![]() $\Delta_{1},\Delta_{2}$
in the introduction.
$\Delta_{1},\Delta_{2}$
in the introduction.
The syntax of computations with effects
![]() $\Delta$
is given by the free monad over
$\Delta$
is given by the free monad over
![]() $\Delta$
. We encode the free monad as follows:
$\Delta$
. We encode the free monad as follows:

Here,
![]() is a computation with no side-effects, whereas
is a computation with no side-effects, whereas
![]() is an operation whose syntax is given by the functor
is an operation whose syntax is given by the functor
![]() . By applying this functor to
. By applying this functor to
![]() , we encode an operation whose continuation may contain more effectful operations.Footnote
20
To see in what sense, let us consider an example.
, we encode an operation whose continuation may contain more effectful operations.Footnote
20
To see in what sense, let us consider an example.
Example. The data type on the left below defines an operation for outputting a string. On the right is its corresponding effect signature.

The effect signature on the right says that
![]() returns a unit value (
returns a unit value (
![]() is the unit type). Using this, we can write a simple hello world corresponding to the
is the unit type). Using this, we can write a simple hello world corresponding to the
![]() ${hello}$
program from Section 1:
${hello}$
program from Section 1:

Section 2.1 shows how to make this program more readable by using monadic
![]() notation.
notation.
The
![]() program above makes use of just a single effect. Say we want to use another effect,
program above makes use of just a single effect. Say we want to use another effect,
![]() , with a single operation,
, with a single operation,
![]() , which represents throwing an exception (therefore having the empty type
, which represents throwing an exception (therefore having the empty type
![]() as its return type):
as its return type):

Programs that use multiple effects, such as
![]() and
and
![]() , are unnecessarily verbose. For example, consider the following program which prints two strings before throwing an exception:Footnote
21
, are unnecessarily verbose. For example, consider the following program which prints two strings before throwing an exception:Footnote
21

To reduce syntactic overhead, we use row insertions and smart constructors (Swierstra, Reference Swierstra2008).
2.2 Row insertions and smart constructors
A smart constructor constructs an effectful computation comprising a single operation. The type of this computation is polymorphic in what other effects the computation has. For example, the type of a smart constructor for the
![]() effect is
effect is
Here, the
![]() type declares the row insertion witness as an instance argument of
type declares the row insertion witness as an instance argument of
![]() . Instance arguments in Agda are conceptually similar to type class constraints in Haskell: when we call
. Instance arguments in Agda are conceptually similar to type class constraints in Haskell: when we call
![]() , Agda will attempt to automatically find a witness of the right type, and implicitly pass this as an argument.Footnote
22
Thus, calling
, Agda will attempt to automatically find a witness of the right type, and implicitly pass this as an argument.Footnote
22
Thus, calling
![]() will automatically inject the
will automatically inject the
![]() effect into some larger effect row
effect into some larger effect row
![]() $\Delta$
.
$\Delta$
.
We define the
![]() order on effect rows in terms of a different
order on effect rows in terms of a different
![]() which witnesses that any operation of
which witnesses that any operation of
![]() $\Delta$
is isomorphic to either an operation of
$\Delta$
is isomorphic to either an operation of
![]() $\Delta_{1}$
or an operation of
$\Delta_{1}$
or an operation of
![]() $\Delta_{2}$
:Footnote
23
,Footnote
24
$\Delta_{2}$
:Footnote
23
,Footnote
24

Using this, the
![]() order is defined as follows:
order is defined as follows:

It is straightforward to show that
![]() is a preorder; i.e., that it is a reflexive and transitive relation.
is a preorder; i.e., that it is a reflexive and transitive relation.
We can also define the following function, which uses a
![]() $\Delta_{1}$
$\Delta_{1}$
![]()
![]() $\Delta_{2}$
witness to coerce an operation of effect type
$\Delta_{2}$
witness to coerce an operation of effect type
![]() $\Delta_{1}$
into an operation of some larger effect type
$\Delta_{1}$
into an operation of some larger effect type
![]() $\Delta_{2}$
.Footnote
25
$\Delta_{2}$
.Footnote
25

Furthermore, we can freely coerce the operations of a computation from one effect row to a different effect row:Footnote 26 ,Footnote 27

Using this infrastructure, we can now implement a generic
![]() function which lets us define smart constructors for operations such as the
function which lets us define smart constructors for operations such as the
![]() operation discussed in the previous subsection.
operation discussed in the previous subsection.

2.3 Fold and monadic bind for

Since
![]() is a monad, we can sequence computations using monadic bind, which is naturally defined in terms of the fold over
is a monad, we can sequence computations using monadic bind, which is naturally defined in terms of the fold over
![]() .
.

Besides the input computation to be folded (last parameter), the fold is parameterized by a function
![]() (first parameter) which folds a
(first parameter) which folds a
![]() computation, and an algebra
computation, and an algebra
![]()
![]() $\Delta$
A (second parameter) which folds an
$\Delta$
A (second parameter) which folds an
![]() computation. We call the latter an algebra because it corresponds to an F-algebra (Arbib & Manes, Reference Arbib and Manes1975; Pierce, Reference Pierce1991) over the signature functor of
computation. We call the latter an algebra because it corresponds to an F-algebra (Arbib & Manes, Reference Arbib and Manes1975; Pierce, Reference Pierce1991) over the signature functor of
![]() , denoted
, denoted
![]() $F_{\Delta}$
. That is, a tuple
$F_{\Delta}$
. That is, a tuple
![]() $(A, \alpha)$
where A is an object called the carrier of the algebra, and
$(A, \alpha)$
where A is an object called the carrier of the algebra, and
![]() $\alpha$
a morphism
$\alpha$
a morphism
![]() $F_{\Delta}(A) \to A$
. Using
$F_{\Delta}(A) \to A$
. Using
![]() , monadic bind for the free monad is defined as follows:
, monadic bind for the free monad is defined as follows:
Intuitively,
![]() concatenates g to all the leaves in the computation m.
concatenates g to all the leaves in the computation m.
Example. The following defines a smart constructor for
![]() :
:
Using this and the definition of
![]() above, we can use do-notation in Agda to make the
above, we can use do-notation in Agda to make the
![]() program from Section 2.1 more readable:
program from Section 2.1 more readable:

This illustrates how we use the free monad to write effectful programs against an interface given by an effect signature. Next, we define effect handlers.
2.4 Effect handlers
An effect handler implements the interface given by an effect signature, interpreting the syntactic operations associated with an effect. Like monadic bind, effect handlers can be defined as a fold over the free monad. The following type of parameterized handlers (Leijen, Reference Leijen2017, §2.2) defines how to fold, respectively,
![]() and
and
![]() computations:Footnote
28
computations:Footnote
28

A handler of type
![]() is parameterized in the sense that it turns a computation of type
is parameterized in the sense that it turns a computation of type
![]() into a parameterized computation of type
into a parameterized computation of type
![]() . The following function does so by folding using
. The following function does so by folding using
![]() , and a
, and a
![]() function:Footnote
29
function:Footnote
29

Comparing with the syntax, we used to explain algebraic effects and handlers in the introduction, the
![]() field corresponds to the
field corresponds to the
![]() $\mathbf{return}{}$
case of the handlers from the introduction, and
$\mathbf{return}{}$
case of the handlers from the introduction, and
![]() corresponds to the cases that define how operations are handled. The parameterized handler type
corresponds to the cases that define how operations are handled. The parameterized handler type
![]() corresponds to the type
corresponds to the type
![]() ${A}\mathop{!}{\Delta,\Delta^\prime} \Rightarrow P \to {B}\mathop{!}{\Delta^\prime}$
, and
${A}\mathop{!}{\Delta,\Delta^\prime} \Rightarrow P \to {B}\mathop{!}{\Delta^\prime}$
, and
![]() h
h
![]() m corresponds to
m corresponds to
![]() $\textbf{with}~{h}~\textbf{handle}~{m}$
.
$\textbf{with}~{h}~\textbf{handle}~{m}$
.
Using this type of handler, the
![]() ${hOut}$
handler from the introduction can be defined as follows:
${hOut}$
handler from the introduction can be defined as follows:

The handler
![]() ${hOut}$
in Section 1.1 did not bind any parameters. However, since we are encoding it as a parameterized handler,
${hOut}$
in Section 1.1 did not bind any parameters. However, since we are encoding it as a parameterized handler,
![]() now binds a unit-typed parameter. Besides this difference, the handler is the same as in Section 1.1. We can use the
now binds a unit-typed parameter. Besides this difference, the handler is the same as in Section 1.1. We can use the
![]() handler to run computations. To this end, we introduce a
handler to run computations. To this end, we introduce a
![]() effect with no associated operations which we will use to indicate where an effect row ends:
effect with no associated operations which we will use to indicate where an effect row ends:

Using these, we can run a simple hello world program:Footnote 30

An example of parameterized (as opposed to unparameterized) handlers is the state effect. Figure 1 declares and illustrates how to handle such an effect with operations for reading (
![]() ) and changing (
) and changing (
![]() ) the state of a memory cell holding a natural number.
) the state of a memory cell holding a natural number.

Fig 1. A state effect (upper), its handler (
![]() below), and a simple test (
below), and a simple test (
![]() , also below) which uses (the elided) smart constructors for
, also below) which uses (the elided) smart constructors for
![]() and
and
![]() .
.
2.5 The modularity problem with higher-order effects, revisited
Section 1.2 described the modularity problem with higher-order effects, using a higher-order operation that interacts with output as an example. In this section, we revisit the problem, framing it in terms of the definitions introduced in the previous section. To this end, we use a different effect whose interface is summarized by the
![]() record below. The record asserts that the computation type M :
record below. The record asserts that the computation type M :
![]() has at least a higher-order operation
has at least a higher-order operation
![]() and a first-order operation
and a first-order operation
![]() :
:

The idea is that
![]() throws an exception, and
throws an exception, and
![]() m
m
![]() $_{1}$
m
$_{1}$
m
![]() $_{2}$
handles any exception thrown during evaluation of m
$_{2}$
handles any exception thrown during evaluation of m
![]() $_{1}$
by running m
$_{1}$
by running m
![]() $_{2}$
instead. The problem is that we cannot give a modular definition of operations such as
$_{2}$
instead. The problem is that we cannot give a modular definition of operations such as
![]() using algebraic effects and handlers alone. As discussed in Section 1.2, the crux of the problem is that algebraic effects and handlers provide limited support for higher-order operations. However, as also discussed in Section 1.2, we can encode
using algebraic effects and handlers alone. As discussed in Section 1.2, the crux of the problem is that algebraic effects and handlers provide limited support for higher-order operations. However, as also discussed in Section 1.2, we can encode
![]() in terms of more primitive effects and handlers, such as the following handler for the
in terms of more primitive effects and handlers, such as the following handler for the
![]() effect:
effect:

The handler modifies the return type of the computation by decorating it with a
![]() . If no exception is thrown,
. If no exception is thrown,
![]() wraps the yielded value in a
wraps the yielded value in a
![]() constructor. If an exception is thrown, the handler never invokes the continuation k and aborts the computation by returning
constructor. If an exception is thrown, the handler never invokes the continuation k and aborts the computation by returning
![]() instead. We can elaborate
instead. We can elaborate
![]() into an inline application of
into an inline application of
![]() . To do so, we make use of effect masking which lets us “weaken” the type of a computation by inserting extra effects in an effect row:
. To do so, we make use of effect masking which lets us “weaken” the type of a computation by inserting extra effects in an effect row:
Using this, the following elaboration defines a semantics for the
![]() operation:Footnote
31
,Footnote
32
operation:Footnote
31
,Footnote
32

If m
![]() $_{1}$
does not throw an exception, we return the produced value. If it does, m
$_{1}$
does not throw an exception, we return the produced value. If it does, m
![]() $_{2}$
is run.
$_{2}$
is run.
As observed by Wu et al. (Reference Wu, Schrijvers and Hinze2014), programs that use elaborations such as
![]() are less modular than programs that only use plain algebraic operations. In particular, the effect row of computations no longer represents the interface of operations that we use to write programs, since the
are less modular than programs that only use plain algebraic operations. In particular, the effect row of computations no longer represents the interface of operations that we use to write programs, since the
![]() elaboration is not represented in the effect type at all. So we have to rely on different machinery if we want to refactor, optimize, or change the semantics of
elaboration is not represented in the effect type at all. So we have to rely on different machinery if we want to refactor, optimize, or change the semantics of
![]() without having to change programs that use it.
without having to change programs that use it.
In the next subsection, we describe how to define effectful operations such as
![]() modularly using scoped effects and handlers and discuss how this is not possible for, e.g., operations representing
modularly using scoped effects and handlers and discuss how this is not possible for, e.g., operations representing
![]() $\lambda$
-abstraction.
$\lambda$
-abstraction.
2.6 Scoped effects and handlers
This subsection gives an overview of scoped effects and handlers. While the rest of the paper can be read and understood without a deep understanding of scoped effects and handlers, we include this overview to facilitate comparison with the alternative solution that we introduce in Section 3.
Scoped effects extend the expressiveness of algebraic effects to support a class of higher-order operations that Wu et al. (Reference Wu, Schrijvers and Hinze2014), Piróg et al. (Reference Piróg, Schrijvers, Wu and Jaskelioff2018), Yang et al. (Reference Yang, Paviotti, Wu, van den Berg and Schrijvers2022) call scoped operations. We illustrate how scoped effects work, using a freer monad encoding of the endofunctor algebra approach of Yang et al. (Reference Yang, Paviotti, Wu, van den Berg and Schrijvers2022). The work of Yang et al. (Reference Yang, Paviotti, Wu, van den Berg and Schrijvers2022) does not include examples of modular handlers, but the original paper on scoped effects and handlers by Wu et al. (Reference Wu, Schrijvers and Hinze2014) does. We describe an adaptation of the modular handling techniques due to Wu et al. (Reference Wu, Schrijvers and Hinze2014) to the endofunctor algebra approach of Yang et al. (Reference Yang, Paviotti, Wu, van den Berg and Schrijvers2022).
2.6.1 Scoped programs
Scoped effects extend the free monad data type with an additional row for scoped operations. The
![]() and
and
![]() constructors of
constructors of
![]() below correspond to the
below correspond to the
![]() and
and
![]() constructors of the free monad, whereas
constructors of the free monad, whereas
![]() is new:
is new:

Here, the
![]() constructor represents a higher-order operation with sub-scopes; i.e., computations that themselves return computations:
constructor represents a higher-order operation with sub-scopes; i.e., computations that themselves return computations:

This type represents scoped computations in the sense that outer computations can be handled independently of inner ones, as we illustrate in sec:scoped-effect-handlers. One way to think of inner computations is as continuations (or join-points) of sub-scopes.
Using
![]() , the catch operation can be defined as a scoped operation:
, the catch operation can be defined as a scoped operation:

The effect signature indicates that
![]() has two scopes since
has two scopes since
![]() has two inhabitants. Following Yang et al. (Reference Yang, Paviotti, Wu, van den Berg and Schrijvers2022), scoped operations are handled using a structure-preserving fold over
has two inhabitants. Following Yang et al. (Reference Yang, Paviotti, Wu, van den Berg and Schrijvers2022), scoped operations are handled using a structure-preserving fold over
![]() :
:

The first argument represents the case where we are folding a
![]() node; the second and third correspond to, respectively,
node; the second and third correspond to, respectively,
![]() and
and
![]() .
.
2.6.2 Scoped effect handlers
The following defines a type of parameterized scoped effect handlers:

A handler of type
![]() handles operations of
handles operations of
![]() $\Delta$
and
$\Delta$
and
![]() $\gamma$
simultaneously and turns a computation
$\gamma$
simultaneously and turns a computation
![]() into a parameterized computation of type
into a parameterized computation of type
![]() . The
. The
![]() and
and
![]() cases are similar to the
cases are similar to the
![]() and
and
![]() cases from sec:effect-handlers. The crucial addition that adds support for higher-order operations is the
cases from sec:effect-handlers. The crucial addition that adds support for higher-order operations is the
![]() case.
case.
The
![]() field is given by an
field is given by an
![]() case. This case takes as input a scoped operation whose outer and inner computation have been folded into a parameterized computation of type
case. This case takes as input a scoped operation whose outer and inner computation have been folded into a parameterized computation of type
![]() and returns as output an interpretation of that operation as a computation of type
and returns as output an interpretation of that operation as a computation of type
![]() . The
. The
![]() function is used for modularly weaving (Wu et al., Reference Wu, Schrijvers and Hinze2014) side effects of handlers through sub-scopes of yet-unhandled operations.
function is used for modularly weaving (Wu et al., Reference Wu, Schrijvers and Hinze2014) side effects of handlers through sub-scopes of yet-unhandled operations.
2.6.3 Weaving
To see why
![]() is needed, it is instructional to look at how the fields in the record type above are used to fold over
is needed, it is instructional to look at how the fields in the record type above are used to fold over
![]() :
:

The second to last line above shows how
![]() is used. Because
is used. Because
![]() eagerly folds the current handler over scopes (sc), there is a mismatch between the type that the continuation expects (B) and the type that the scoped computation returns (G B). The
eagerly folds the current handler over scopes (sc), there is a mismatch between the type that the continuation expects (B) and the type that the scoped computation returns (G B). The
![]() function fixes this mismatch for the particular return type modification G :
function fixes this mismatch for the particular return type modification G :
![]() of a parameterized scoped effect handler.
of a parameterized scoped effect handler.
The scoped effect handler for exception catching is thus:

The
![]() field for the
field for the
![]() operation first runs m
operation first runs m
![]() $_{1}$
. If no exception is thrown, the value produced by m
$_{1}$
. If no exception is thrown, the value produced by m
![]() $_{1}$
is forwarded to k. Otherwise, m
$_{1}$
is forwarded to k. Otherwise, m
![]() $_{2}$
is run and its value is forwarded to k, or its exception is propagated. The
$_{2}$
is run and its value is forwarded to k, or its exception is propagated. The
![]() field of
field of
![]() says that, if an unhandled exception is thrown during evaluation of a scope, the continuation is discarded and the exception is propagated; and if no exception is thrown the continuation proceeds normally.
says that, if an unhandled exception is thrown during evaluation of a scope, the continuation is discarded and the exception is propagated; and if no exception is thrown the continuation proceeds normally.
2.6.4 Discussion and limitations
As observed by Berg et al. (2021), some higher-order effects do not correspond to scoped operations. In particular, the
![]() record shown below is not a scoped operation:
record shown below is not a scoped operation:

The
![]() field represents an operation that constructs a
field represents an operation that constructs a
![]() $\lambda$
value. The
$\lambda$
value. The
![]() field represents an operation that will apply the function value in the first parameter position to the argument computation in the second parameter position. The
field represents an operation that will apply the function value in the first parameter position to the argument computation in the second parameter position. The
![]() operation has a computation as its second parameter so that it remains compatible with different evaluation strategies.
operation has a computation as its second parameter so that it remains compatible with different evaluation strategies.
To see why the operations summarized by the
![]() record above are not scoped operations, let us revisit the
record above are not scoped operations, let us revisit the
![]() constructor of
constructor of
![]() :
:

As summarized earlier in this subsection,
![]() lets us represent higher-order operations (specifically, scoped operations), whereas
lets us represent higher-order operations (specifically, scoped operations), whereas
![]() does not (only algebraic operations). Just like we defined the computational parameters as scopes (given by the outer
does not (only algebraic operations). Just like we defined the computational parameters as scopes (given by the outer
![]() in the type of
in the type of
![]() ), we might try to define the body of a lambda as a scope in a similar way. However, whereas the
), we might try to define the body of a lambda as a scope in a similar way. However, whereas the
![]() operation always passes control to its continuation (the inner
operation always passes control to its continuation (the inner
![]() ), the
), the
![]() effect is supposed to package the body of the lambda into a value and pass this value to the continuation (the inner computation). Because the inner computation is nested within the outer computation, the only way to gain access to the inner computation (the continuation) is by first running the outer computation (the body of the lambda). This does not give us the right semantics.
effect is supposed to package the body of the lambda into a value and pass this value to the continuation (the inner computation). Because the inner computation is nested within the outer computation, the only way to gain access to the inner computation (the continuation) is by first running the outer computation (the body of the lambda). This does not give us the right semantics.
It is possible to elaborate the
![]() operations into more primitive effects and handlers, but as discussed in Sections 1.2 and 2.5, such elaborations are not modular. In the next section, we show how to make such elaborations modular.
operations into more primitive effects and handlers, but as discussed in Sections 1.2 and 2.5, such elaborations are not modular. In the next section, we show how to make such elaborations modular.
3 Hefty trees and algebras
As observed in Section 2.5, operations such as
![]() can be elaborated into more primitive effects and handlers. However, these elaborations are not modular. We solve this problem by factoring elaborations into interfaces of their own to make them modular.
can be elaborated into more primitive effects and handlers. However, these elaborations are not modular. We solve this problem by factoring elaborations into interfaces of their own to make them modular.
To this end, we first introduce a new type of abstract syntax trees (Sections 3.1–3.3) representing computations with higher-order operations, which we dub hefty trees (an acronymic pun on higher-order effects). We then define elaborations as algebras (hefty algebras; sec:hefty-algebras) over these trees. The following pipeline summarizes the idea, where H is a higher-order effect signature:
For the categorically inclined reader,
![]() conceptually corresponds to the initial algebra of the functor
conceptually corresponds to the initial algebra of the functor
![]() ${HeftyF}~H~A~R = A + H~R~(R~A)$
where
${HeftyF}~H~A~R = A + H~R~(R~A)$
where
![]() defines the signature of higher-order operations and is a higher-order functor, meaning we have both the usual functorial
defines the signature of higher-order operations and is a higher-order functor, meaning we have both the usual functorial
![]() ${map} : (X \to Y) \to H~F~X \to H~F~Y$
for any functor F as well as a function
${map} : (X \to Y) \to H~F~X \to H~F~Y$
for any functor F as well as a function
![]() ${hmap} : \mathrm{Nat}(F, G) \to \mathrm{Nat}(H~F, H~G)$
which lifts natural transformations between any F and G to a natural transformation between
${hmap} : \mathrm{Nat}(F, G) \to \mathrm{Nat}(H~F, H~G)$
which lifts natural transformations between any F and G to a natural transformation between
![]() $H~F$
and
$H~F$
and
![]() $H~G$
. A hefty algebra is then an F-algebra over a higher-order signature functor H. The notion of elaboration that we introduce in Section 3.4 is an F-algebra whose carrier is a “first-order” effect tree (
$H~G$
. A hefty algebra is then an F-algebra over a higher-order signature functor H. The notion of elaboration that we introduce in Section 3.4 is an F-algebra whose carrier is a “first-order” effect tree (
![]()
![]() $\Delta$
).
$\Delta$
).
In this section, we encode this conceptual framework in Agda using a container-inspired approach to represent higher-order signature functors H as a strictly positive type. We discuss and compare our approach with previous work in Section 3.5.
3.1 Generalizing Free to support higher-order operations
As summarized in Section 2.1,
![]()
![]() $\Delta$
A is the type of abstract syntax trees representing computations over the effect signature
$\Delta$
A is the type of abstract syntax trees representing computations over the effect signature
![]() $\Delta$
. Our objective is to arrive at a more general type of abstract syntax trees representing computations involving (possibly) higher-order operations. To realize this objective, let us consider how to syntactically represent this variant of the
$\Delta$
. Our objective is to arrive at a more general type of abstract syntax trees representing computations involving (possibly) higher-order operations. To realize this objective, let us consider how to syntactically represent this variant of the
![]() ${censor}$
operation (Section 1.2), where M is the type of abstract syntax trees whose type we wish to define:
${censor}$
operation (Section 1.2), where M is the type of abstract syntax trees whose type we wish to define:
We call the second parameter of this operation a computation parameter. Using
![]() , computation parameters can only be encoded as continuations. But the computation parameter of
, computation parameters can only be encoded as continuations. But the computation parameter of
![]() is not a continuation, since
is not a continuation, since
The crux of the issue is how signature functors
![]() are defined. Since this is an endofunctor on
are defined. Since this is an endofunctor on
![]() , the only suitable option in the
, the only suitable option in the
![]() constructor is to apply the functor to the type of continuations:
constructor is to apply the functor to the type of continuations:
A more flexible approach would be to allow signature functors to build computation trees with an arbitrary return type, including the return type of the continuation. A higher-order signature functor of some higher-order signature H, written
![]() would fit that bill. Using such a signature functor, we could define the
would fit that bill. Using such a signature functor, we could define the
![]() case as follows:
case as follows:

Here,
![]() is the type of the free monad using higher-order signature functors instead. In the rest of this subsection, we consider how to define higher-order signature functors H, their higher-order functor extensions
is the type of the free monad using higher-order signature functors instead. In the rest of this subsection, we consider how to define higher-order signature functors H, their higher-order functor extensions
![]() , and the type of
, and the type of
![]() trees.
trees.
Recall how we defined plain algebraic effects in terms of containers:

Here,
![]() is the type of operations, and
is the type of operations, and
![]() defines the return type of each operation. In order to allow operations to have sub-computations, we generalize this type to allow each operation to be associated with a number of sub-computations, where each sub-computation can have a different return type. The following record provides this generalization:
defines the return type of each operation. In order to allow operations to have sub-computations, we generalize this type to allow each operation to be associated with a number of sub-computations, where each sub-computation can have a different return type. The following record provides this generalization:

The set of operations is still given by a type field (
![]() ), and each operation still has a return type (
), and each operation still has a return type (
![]() ).
).
![]() associates each operation with a type that indicates how many sub-computations (or forks) an operation has, and
associates each operation with a type that indicates how many sub-computations (or forks) an operation has, and
![]() indicates the return type of each such fork. For example, say we want to encode an operation op with two sub-computations with different return types, and whose return type is of a unit type. That is, using M as our type of computations:
indicates the return type of each such fork. For example, say we want to encode an operation op with two sub-computations with different return types, and whose return type is of a unit type. That is, using M as our type of computations:
The following signature declares a higher-order effect signature with a single operation with return type
![]() , and with two forks (we use
, and with two forks (we use
![]() to encode this fact), and where each fork has, respectively,
to encode this fact), and where each fork has, respectively,
![]() and
and
![]() as return types.
as return types.

The extension of higher-order effect signatures implements the intuition explained above:

Let us unpack this definition.

The extension of a higher-order signature functor is given by (1) the sum of operations of the signature, where each operation has (2) a continuation (of type M X) that expects to be passed a value of the operation’s return type, and (3) a set of forks where each fork is (4) a computation that returns the expected type for each fork.
Using the higher-order signature functor and its extension above, our generalized free monad becomes:

This type of
![]() trees can be used to define higher-order operations with an arbitrary number of computation parameters, with arbitrary return types. Using this type, and using a co-product for higher-order effect signatures (
trees can be used to define higher-order operations with an arbitrary number of computation parameters, with arbitrary return types. Using this type, and using a co-product for higher-order effect signatures (
![]() ) which is analogous to the co-product for algebraic effect signatures in Section 2.2, Figure 2 represents the syntax of the
) which is analogous to the co-product for algebraic effect signatures in Section 2.2, Figure 2 represents the syntax of the
![]() operation.
operation.

Fig 2. A higher-order censor effect and operation, with a single computation parameter (declared with
![]() in the effect signature top right) with return type
in the effect signature top right) with return type
![]() (declared with
(declared with
![]() top right).
top right).
Just like
![]() trees can be sequenced using monadic bind. Unlike for
trees can be sequenced using monadic bind. Unlike for
![]() , the monadic bind of
, the monadic bind of
![]() is not expressible in terms of the standard fold over
is not expressible in terms of the standard fold over
![]() trees. The difference between
trees. The difference between
![]() and
and
![]() is that
is that
![]() is a regular data type, whereas
is a regular data type, whereas
![]() is a nested datatype (Bird & Paterson, Reference Bird and Paterson1999). The fold of a nested data type is limited to describe natural transformations. As Bird & Paterson (Reference Bird and Paterson1999) show, this limitation can be overcome by using a generalized fold, but for the purpose of this paper, it suffices to define monadic bind as a recursive function:
is a nested datatype (Bird & Paterson, Reference Bird and Paterson1999). The fold of a nested data type is limited to describe natural transformations. As Bird & Paterson (Reference Bird and Paterson1999) show, this limitation can be overcome by using a generalized fold, but for the purpose of this paper, it suffices to define monadic bind as a recursive function:

The bind behaves similarly to the bind for
![]() ; i.e.,
; i.e.,
![]() concatenates g to all the leaves in the continuations (but not computation parameters) of m.
concatenates g to all the leaves in the continuations (but not computation parameters) of m.
In Section 3.4, we show how to modularly elaborate higher-order operations into more primitive algebraic effects and handlers (i.e., computations over
![]() ), by folding modular elaboration algebras (hefty algebras) over
), by folding modular elaboration algebras (hefty algebras) over
![]() trees. First, we show (in Section 3.2) how
trees. First, we show (in Section 3.2) how
![]() trees support programming against an interface of both algebraic and higher-order operations. We also address (in Section 3.3) the question of how to encode effect signatures for higher-order operations whose computation parameters have polymorphic return types, such as the highlighted
trees support programming against an interface of both algebraic and higher-order operations. We also address (in Section 3.3) the question of how to encode effect signatures for higher-order operations whose computation parameters have polymorphic return types, such as the highlighted
![]() below:
below:
3.2 Programs with algebraic and higher-order effects
Any algebraic effect signature can be lifted to a higher-order effect signature with no fork (i.e., no computation parameters):

Using this effect signature and using higher-order effect row insertion witnesses analogous to the ones we defined and used in Section 2.2, the following smart constructor lets us represent any algebraic operation as a
![]() computation:
computation:
Using this notion of lifting,
![]() trees can be used to program against interfaces of both higher-order and plain algebraic effects.
trees can be used to program against interfaces of both higher-order and plain algebraic effects.
3.3 Higher-order operations with polymorphic return types
Let us consider how to define
![]() as a higher-order effect. Ideally, we would define an operation that is parameterized by a return type of the branches of a particular catch operation, as shown on the left, such that we can define the higher-order effect signature on the right:Footnote
33
as a higher-order effect. Ideally, we would define an operation that is parameterized by a return type of the branches of a particular catch operation, as shown on the left, such that we can define the higher-order effect signature on the right:Footnote
33

The
![]() field on the right says that
field on the right says that
![]() has two sub-computations (since
has two sub-computations (since
![]() has two constructors), and that each computation parameter has some return type A. However, the signature on the right above is not well defined!
has two constructors), and that each computation parameter has some return type A. However, the signature on the right above is not well defined!
The problem is that, because
![]() has a constructor that quantifies over a type (
has a constructor that quantifies over a type (
![]() ), the
), the
![]() type lives in
type lives in
![]() . Consequently, it does not fit the definition of
. Consequently, it does not fit the definition of
![]() , whose operations live in
, whose operations live in
![]() . There are two potential solutions to this problem: (1) increase the universe level of
. There are two potential solutions to this problem: (1) increase the universe level of
![]() to allow
to allow
![]() to live in
to live in
![]() or (2) use a universe of types (Martin-Löf, Reference Martin-Löf1984). Either solution is applicable here; we choose type universes.
or (2) use a universe of types (Martin-Löf, Reference Martin-Löf1984). Either solution is applicable here; we choose type universes.
A universe of types is a (dependent) pair of a syntax of types (
![]() ) and a semantic function (
) and a semantic function (
![]() ) defining the meaning of the syntax by reflecting it into Agda’s
) defining the meaning of the syntax by reflecting it into Agda’s
![]() :
:

Section 4.1 contains a concrete example usage this notion of type universe. Using type universes, we can parameterize the
![]() constructor on the left below by a syntactic type
constructor on the left below by a syntactic type
![]() of some universe u and use the meaning of this type (
of some universe u and use the meaning of this type (
![]() ) as the return type of the computation parameters in the effect signature on the right below:
) as the return type of the computation parameters in the effect signature on the right below:

While the universe of types encoding restricts the kind of type that catch can have as a return type, the effect signature is parametric in the universe. Thus the implementer of the
![]() effect signature (or interface) is free to choose a sufficiently expressive universe of types.
effect signature (or interface) is free to choose a sufficiently expressive universe of types.
3.4 Hefty algebras
As shown in Section 2.5, the higher-order catch operation can be encoded as a non-modular elaboration:
We can make this elaboration modular by expressing it as an algebra over
![]() trees containing operations of the
trees containing operations of the
![]() signature. To this end, we will use the following notion of hefty algebra (
signature. To this end, we will use the following notion of hefty algebra (
![]() ) and fold (or catamorphism Meijer et al., Reference Meijer, Fokkinga and Paterson1991,
) and fold (or catamorphism Meijer et al., Reference Meijer, Fokkinga and Paterson1991,
![]() ) for
) for
![]() :
:

Here,
![]() defines how to transform an
defines how to transform an
![]() node of type
node of type
![]() H A into a value of type F A, assuming we have already folded the computation parameters and continuation into F values. A nice property of algebras is that they are closed under higher-order effect signature sums:
H A into a value of type F A, assuming we have already folded the computation parameters and continuation into F values. A nice property of algebras is that they are closed under higher-order effect signature sums:

By defining elaborations as hefty algebras (below) we can compose them using
![]() .
.

An
![]() H
H
![]() $\Delta$
elaborates higher-order operations of signature H into algebraic operations of signature
$\Delta$
elaborates higher-order operations of signature H into algebraic operations of signature
![]() $\Delta$
. Given an elaboration, we can generically transform any hefty tree into more primitive algebraic effects and handlers:
$\Delta$
. Given an elaboration, we can generically transform any hefty tree into more primitive algebraic effects and handlers:
Example 1 (Elaboration for Output Censoring). Let us return to the example from the introduction. Here is the elaboration of the
![]() effect from Figure 2.
effect from Figure 2.

This elaboration matches the
![]() ${eCensor}$
elaboration discussed in sec:solving-the-modularity-problem.
${eCensor}$
elaboration discussed in sec:solving-the-modularity-problem.
Example 2 (Elaboration for Exception Catching). We can also elaborate exception catching analogously to the non-modular
![]() elaboration discussed in Section 2.5 and in the beginning of this subsection:
elaboration discussed in Section 2.5 and in the beginning of this subsection:

The elaboration is essentially the same as its non-modular counterpart, except that it now uses the universe of types encoding discussed in Section 3.3, and that it now transforms syntactic representations of higher-order operations instead. Using this elaboration, we can, for example, run the following example program involving the state effect from Figure 1, the throw effect from Section 2.1, and the catch effect defined here:

The program first sets the state to 1; then to 2; and then throws an exception. The exception is caught, and control is immediately passed to the final operation in the program which gets the state. By also defining elaborations for
![]() and
and
![]() , we can elaborate and run the program:
, we can elaborate and run the program:

The program in Example 2 uses a so-called global interpretation of state, where the
![]() operation in the “try block” of
operation in the “try block” of
![]() causes the state to be updated globally. In Section 4.2.2, we return to this example and show how we can modularly change the elaboration of the higher-order effect
causes the state to be updated globally. In Section 4.2.2, we return to this example and show how we can modularly change the elaboration of the higher-order effect
![]() to yield a so-called transactional interpretation of state where the
to yield a so-called transactional interpretation of state where the
![]() operation in the try block is rolled back when an exception is thrown.
operation in the try block is rolled back when an exception is thrown.
3.5 Discussion and limitations
Which (higher-order) effects can we describe using hefty trees and algebras? Since the core mechanism of our approach is modular elaboration of higher-order operations into more primitive effects and handlers, it is clear that hefty trees and algebras are at least as expressive as standard algebraic effects. The crucial benefit of hefty algebras over algebraic effects is that higher-order operations can be declared and implemented modularly. In this sense, hefty algebras provide a modular abstraction layer over standard algebraic effects that, although it adds an extra layer of indirection by requiring both elaborations and handlers to give a semantics to hefty trees, is comparatively cheap and implemented using only standard techniques such as F-algebras. As we show in Section 5, hefty algebras also let us define higher-order effect theories, akin to algebraic effect theories.
Conceptually, we expect that hefty trees can capture any monadic higher-order effect whose signature is given by a higher-order functor on
![]() . Filinski (Reference Filinski1999) showed that any monadic effect can be represented using continuations, and given that we can encode the continuation monad using algebraic effects (Schrijvers et al., Reference Schrijvers, Piróg, Wu and Jaskelioff2019) in terms of the sub/jump operations (Section 4.2.2) by Thielecke (Reference Thielecke1997), Fiore & Staton (Reference Fiore and Staton2014), it is possible to elaborate any monadic effect into algebraic effects using hefty algebras. The current Agda implementation, though, is slightly more restrictive. The type of effect signatures,
. Filinski (Reference Filinski1999) showed that any monadic effect can be represented using continuations, and given that we can encode the continuation monad using algebraic effects (Schrijvers et al., Reference Schrijvers, Piróg, Wu and Jaskelioff2019) in terms of the sub/jump operations (Section 4.2.2) by Thielecke (Reference Thielecke1997), Fiore & Staton (Reference Fiore and Staton2014), it is possible to elaborate any monadic effect into algebraic effects using hefty algebras. The current Agda implementation, though, is slightly more restrictive. The type of effect signatures,
![]() , approximates the set of higher-order functors by constructively enforcing that all occurrences of the computation type are strictly positive. Hence, there may be higher-order effects that are well-defined semantically, but which cannot be captured in the Agda encoding presented here.
, approximates the set of higher-order functors by constructively enforcing that all occurrences of the computation type are strictly positive. Hence, there may be higher-order effects that are well-defined semantically, but which cannot be captured in the Agda encoding presented here.
Recent work by Berg & Schrijvers (2023) introduced a higher-order free monad that coincides with our
![]() type. Their work shows that hefty trees are, in fact, a free monad. Furthermore, they demonstrate that a range of existing effects frameworks from the literature can be viewed as instances of hefty trees.
type. Their work shows that hefty trees are, in fact, a free monad. Furthermore, they demonstrate that a range of existing effects frameworks from the literature can be viewed as instances of hefty trees.
When comparing hefty trees to scoped effects, we observe two important differences. The first difference is that the syntax of programs with higher-order effects is fundamentally more restrictive when using scoped effects. Specifically, as discussed at the end of Section 2.6.4, scoped effects impose a restriction on operations that their computation parameters must pass control directly to the continuation of the operation. Hefty trees, on the other hand, do not restrict the control flow of computation parameters, meaning that they can be used to define a broader class of operations. For instance, in Section 4.1, we define a higher-order effect for function abstraction, which is an example of an operation where control does not flow from the computation parameter to the continuation.
The second difference is that hefty algebras and scoped effects and handlers are modular in different ways. Scoped effects are modular because we can modularly define, compose, and handle scoped operations, by applying scoped effect handlers in sequence; i.e.:
As discussed in Section 2.6.3, each handler application modularly “weaves” effects through sub-computations, using a dedicated
![]() function.applying different scoped effect handlers in different orders.
function.applying different scoped effect handlers in different orders.
Hefty algebras, on the other hand, work by applying an elaboration algebra assembled from modular components in one go. The program resulting from elaboration can then be handled using standard algebraic effect handlers; i.e.:
The algebraic effect handlers
![]() $h_1,\ldots,h_k$
in (§) serve the same purpose as the scoped effect handlers
$h_1,\ldots,h_k$
in (§) serve the same purpose as the scoped effect handlers
![]() $h_1',\ldots,h_n'$
in (
$h_1',\ldots,h_n'$
in (
![]() $\dagger$
); namely, to provide a semantics of operations. The order of handling is significant for both algebraic effect handlers and for scoped effect handlers: applying the same handlers in different orders may give a different semantics.
$\dagger$
); namely, to provide a semantics of operations. The order of handling is significant for both algebraic effect handlers and for scoped effect handlers: applying the same handlers in different orders may give a different semantics.
In contrast, the order that elaborations (
![]() $E_1,\ldots,E_m$
) are composed in (§) does not matter. Hefty algebras merely mediate higher-order operations into “first-order” effect trees that then must be handled, using standard effect handlers. While scoped effects supports “weaving”, standard algebraic effect handlers do not. This might suggest that scoped effects and handlers are generally more expressive. However, many scoped effects and handlers can be emulated using algebraic effects and hanlders, by encoding scoped operations as algebraic operations whose continuations encode a kind of scoped syntax, inspired by Wu et al. (Reference Wu, Schrijvers and Hinze2014, §7-9).Footnote
34
We illustrate how in Section 4.2.2.
$E_1,\ldots,E_m$
) are composed in (§) does not matter. Hefty algebras merely mediate higher-order operations into “first-order” effect trees that then must be handled, using standard effect handlers. While scoped effects supports “weaving”, standard algebraic effect handlers do not. This might suggest that scoped effects and handlers are generally more expressive. However, many scoped effects and handlers can be emulated using algebraic effects and hanlders, by encoding scoped operations as algebraic operations whose continuations encode a kind of scoped syntax, inspired by Wu et al. (Reference Wu, Schrijvers and Hinze2014, §7-9).Footnote
34
We illustrate how in Section 4.2.2.
4 Examples
As discussed in Section 2.5, there is a wide range of examples of higher-order effects that cannot be defined as algebraic operations directly and are typically defined as non-modular elaborations instead. In this section, we give examples of such effects and show to define them modularly using hefty algebras. The artifact (van der Rest & Poulsen, Reference van der Rest and Poulsen2024) contains the full examples.
4.1
 $\lambda$
as a higher-order operation
$\lambda$
as a higher-order operation
As recently observed by van den Berg et al. (Reference van den Berg, Schrijvers, Poulsen and Wu2021), the (higher-order) operations for
![]() $\lambda$
abstraction and application are neither algebraic nor scoped effects. We demonstrate how hefty algebras allow us to modularly define and elaborate an interface of higher-order operations for
$\lambda$
abstraction and application are neither algebraic nor scoped effects. We demonstrate how hefty algebras allow us to modularly define and elaborate an interface of higher-order operations for
![]() $\lambda$
abstraction and application, inspired by Levy’s call-by-push-value (Levy, Reference Levy2006). The interface we will consider is parametric in a universe of types given by the following record:
$\lambda$
abstraction and application, inspired by Levy’s call-by-push-value (Levy, Reference Levy2006). The interface we will consider is parametric in a universe of types given by the following record:

The
![]() field represents a function type, whereas
field represents a function type, whereas
![]() is the type of thunk values. Distinguishing thunks in this way allows us to assign either a call-by-value or call-by-name semantics to the interface for
is the type of thunk values. Distinguishing thunks in this way allows us to assign either a call-by-value or call-by-name semantics to the interface for
![]() $\lambda$
abstraction, given by the higher-order effect signature in Figure 3 and summarized by the following smart constructors:
$\lambda$
abstraction, given by the higher-order effect signature in Figure 3 and summarized by the following smart constructors:

Fig 3. Higher-order effect signature of
![]() $\lambda$
abstraction and application.
$\lambda$
abstraction and application.

Here,
![]() is a higher-order operation with a function typed computation parameter and whose return type is a function value (
is a higher-order operation with a function typed computation parameter and whose return type is a function value (
![]() ). The
). The
![]() operation accepts a thunk value as argument and yields a value of a matching type. The
operation accepts a thunk value as argument and yields a value of a matching type. The
![]() operation is also a higher-order operation: its first parameter is a function value type, whereas its second parameter is a computation parameter whose return type matches that of the function value parameter type.
operation is also a higher-order operation: its first parameter is a function value type, whereas its second parameter is a computation parameter whose return type matches that of the function value parameter type.
The interface above defines a kind of higher-order abstract syntax (Pfenning & Elliott, Reference Pfenning and Elliott1988), which piggy-backs on Agda functions for name binding. However, unlike most Agda functions, the constructors above represent functions with side effects. The representation in principle supports functions with arbitrary side effects since it is parametric in what the higher-order effect signature H is. Furthermore, we can assign different operational interpretations to the operations in the interface without having to change the interface or programs written against the interface. To illustrate we give two different implementations of the interface: one that implements a call-by-value evaluation strategy, and one that implements call-by-name.
4.1.1 Call-by-value
We give a call-by-value interpretation of
![]() by generically elaborating to algebraic effect trees with any set of effects
by generically elaborating to algebraic effect trees with any set of effects
![]() $\Delta$
. Our interpretation is parametric in proof witnesses that the following isomorphisms hold for value types (
$\Delta$
. Our interpretation is parametric in proof witnesses that the following isomorphisms hold for value types (
![]() is the type of isomorphisms from the Agda standard library):
is the type of isomorphisms from the Agda standard library):

The first isomorphism says that a function value type corresponds to a function which accepts a value of type t
![]() $_{1}$
and produces a computation whose return type matches that of the function type. The second says that thunk types coincide with value types. Using these isomorphisms, the following defines a call-by-value elaboration of functions:
$_{1}$
and produces a computation whose return type matches that of the function type. The second says that thunk types coincide with value types. Using these isomorphisms, the following defines a call-by-value elaboration of functions:

The
![]() case passes the function body given by the sub-tree
case passes the function body given by the sub-tree
![]() $\psi$
as a value to the continuation, where the
$\psi$
as a value to the continuation, where the
![]() function mediates the sub-tree of type
function mediates the sub-tree of type
![]() to a value type
to a value type
![]() , using the isomorphism
, using the isomorphism
![]() . The
. The
![]() case uses the
case uses the
![]() function to mediate a
function to mediate a
![]() value to a
value to a
![]() value, using the isomorphism
value, using the isomorphism
![]() . The
. The
![]() case first eagerly evaluates the argument expression of the application (in the sub-tree
case first eagerly evaluates the argument expression of the application (in the sub-tree
![]() $\psi$
) to an argument value and then passes the resulting value to the function value of the application. The resulting value is passed to the continuation.
$\psi$
) to an argument value and then passes the resulting value to the function value of the application. The resulting value is passed to the continuation.
Using the elaboration above, we can evaluate programs such as the following which uses both the higher-order lambda effect, the algebraic state effect, and assumes that our universe has a number type
![]() :
:

The program first sets the state to
![]() . Then it constructs a function that binds a variable x, dereferences the variable twice, and adds the two resulting values together. Finally, the application in the second-to-last line applies the function with an argument expression which increments the state by
. Then it constructs a function that binds a variable x, dereferences the variable twice, and adds the two resulting values together. Finally, the application in the second-to-last line applies the function with an argument expression which increments the state by
![]() and returns the resulting value. Running the program produces
and returns the resulting value. Running the program produces
![]() since the state increment expression is eagerly evaluated before the function is applied.
since the state increment expression is eagerly evaluated before the function is applied.

4.1.2 Call-by-name
The key difference between the call-by-value and the call-by-name interpretation of our
![]() $\lambda$
operations is that we now assume that thunks are computations. That is, we assume that the following isomorphisms hold for value types:
$\lambda$
operations is that we now assume that thunks are computations. That is, we assume that the following isomorphisms hold for value types:

Using these isomorphisms, the following defines a call-by-name elaboration of functions:

The case for
![]() is the same as the call-by-value elaboration. The case for
is the same as the call-by-value elaboration. The case for
![]() now needs to force the thunk by running the computation and passing its result to k. The case for
now needs to force the thunk by running the computation and passing its result to k. The case for
![]() passes the argument sub-tree (
passes the argument sub-tree (
![]() $\psi$
) as an argument to the function f, runs the computation resulting from doing so, and then passes its result to k. Running the example program
$\psi$
) as an argument to the function f, runs the computation resulting from doing so, and then passes its result to k. Running the example program
![]() from above now produces
from above now produces
![]() as result, since the state increment expression in the argument of
as result, since the state increment expression in the argument of
![]() is thunked and run twice during the evaluation of the called function.
is thunked and run twice during the evaluation of the called function.

4.2 Optionally transactional exception catching
A feature of scoped effect handlers (Wu et al., Reference Wu, Schrijvers and Hinze2014; Piróg et al., Reference Piróg, Schrijvers, Wu and Jaskelioff2018; Yang et al., Reference Yang, Paviotti, Wu, van den Berg and Schrijvers2022) is that changing the order of handlers makes it possible to obtain different semantics of effect interaction. A classical example of effect interaction is the interaction between state and exception catching that we briefly considered at the end of sec:hefty-algebras in connection with this
![]() program:
program:

The state and exception catching effect can interact to give either of these two semantics:
1. Global interpretation of state, where the
![]() program returns
program returns
![]() since the
since the
![]() operation in the “try” block causes the state to be updated globally.
operation in the “try” block causes the state to be updated globally.
2. Transactional interpretation of state, where the
![]() program returns
program returns
![]() since the state changes of the
since the state changes of the
![]() operation are rolled back when the “try” block throws an exception.
operation are rolled back when the “try” block throws an exception.
With monad transformers (Cenciarelli & Moggi, Reference Cenciarelli and Moggi1993; Liang et al., Reference Liang, Hudak and Jones1995), we can recover either of these semantics by permuting the order of monad transformers. With scoped effect handlers, we can also recover either by permuting the order of handlers. However, the
![]() elaboration in Section 3.4 always gives us a global interpretation of state. In this section, we demonstrate how we can recover a transactional interpretation of state by using a different elaboration of the
elaboration in Section 3.4 always gives us a global interpretation of state. In this section, we demonstrate how we can recover a transactional interpretation of state by using a different elaboration of the
![]() operation into an algebraically effectful program with the
operation into an algebraically effectful program with the
![]() operation and the off-the-shelf sub/jump control effects due to Thielecke (Reference Thielecke1997), Fiore & Staton (Reference Fiore and Staton2014). The different elaboration is modular in the sense that we do not have to change the interface of the catch operation nor any programs written against the interface.
operation and the off-the-shelf sub/jump control effects due to Thielecke (Reference Thielecke1997), Fiore & Staton (Reference Fiore and Staton2014). The different elaboration is modular in the sense that we do not have to change the interface of the catch operation nor any programs written against the interface.
4.2.1 Sub/Jump
We recall how to define two operations, sub and jump, due to Thielecke (Reference Thielecke1997), Fiore & Staton (Reference Fiore and Staton2014). We define these operations as algebraic effects following Schrijvers et al. (Reference Schrijvers, Piróg, Wu and Jaskelioff2019). The algebraic effect signature of
![]() Ref is given in Figure 4 and is summarized by the following smart constructors:
Ref is given in Figure 4 and is summarized by the following smart constructors:

Fig 4. Effect signature of the sub/jump effect.

An operation
![]() f g gives a computation f access to the continuation g via a reference value Ref t which represents a continuation expecting a value of type
f g gives a computation f access to the continuation g via a reference value Ref t which represents a continuation expecting a value of type
![]() . The
. The
![]() operation invokes such continuations.
operation invokes such continuations.
The operations and their handler (abbreviated to
![]() ) satisfy the following laws:
) satisfy the following laws:

The last law asserts that
![]() and
and
![]() are algebraic operations, since their computational sub-terms behave as continuations. Thus, we encode
are algebraic operations, since their computational sub-terms behave as continuations. Thus, we encode
![]() and its handler as an algebraic effect.
and its handler as an algebraic effect.
4.2.2 Optionally transactional exception catching
By using the
![]() and
and
![]() operations in our elaboration of
operations in our elaboration of
![]() , we get a semantics of exception catching whose interaction with state depends on the order that the state effect and sub/jump effect is handled.
, we get a semantics of exception catching whose interaction with state depends on the order that the state effect and sub/jump effect is handled.

The elaboration uses
![]() to capture the continuation of a higher-order
to capture the continuation of a higher-order
![]() operation. If no exception is raised, then control flows to the continuation k without invoking the continuation of
operation. If no exception is raised, then control flows to the continuation k without invoking the continuation of
![]() . Otherwise, we jump to the continuation of
. Otherwise, we jump to the continuation of
![]() , which runs
, which runs
![]() ${m_{2}}$
before passing control to k. Capturing the continuation in this way interacts with state because the continuation of
${m_{2}}$
before passing control to k. Capturing the continuation in this way interacts with state because the continuation of
![]() may have been pre-applied to a state handler that only knows about the “old” state. This happens when we handle the state effect before the sub/jump effect: in this case, we get the transactional interpretation of state, so running
may have been pre-applied to a state handler that only knows about the “old” state. This happens when we handle the state effect before the sub/jump effect: in this case, we get the transactional interpretation of state, so running
![]() gives
gives
![]() . Otherwise, if we run the sub/jump handler before the state handler, we get the global interpretation of state and the result
. Otherwise, if we run the sub/jump handler before the state handler, we get the global interpretation of state and the result
![]() .
.
The sub/jump elaboration above is more involved than the scoped effect handler that we considered in Section 2.6. However, the complicated encoding does not pollute the higher-order effect interface and only turns up if we strictly want or need effect interaction.
4.3 Logic programming
Following Schrijvers et al. (Reference Schrijvers, Wu, Desouter and Demoen2014), Wu et al. (Reference Wu, Schrijvers and Hinze2014), Yang et al. (Reference Yang, Paviotti, Wu, van den Berg and Schrijvers2022), we can define a nondeterministic choice operation (
![]() ) as an algebraic effect, to provide support for expressing the kind of non-deterministic search for solutions that is common in logic programming. We can also define a
) as an algebraic effect, to provide support for expressing the kind of non-deterministic search for solutions that is common in logic programming. We can also define a
![]() operation that indicates that the search in the current branch was unsuccessful. The effect signature for
operation that indicates that the search in the current branch was unsuccessful. The effect signature for
![]() is given in Figure 5. The following smart constructors are the lifted higher-order counterparts to the
is given in Figure 5. The following smart constructors are the lifted higher-order counterparts to the
![]() and
and
![]() operations:
operations:

Fig 5. Effect signature of the choice effect.

A useful operator for cutting non-deterministic search short when a solution is found is the
![]() operator. The
operator. The
![]() operator, whose higher-order effect signature is given in Figure 6, is not an algebraic effect, but a scoped (and thus higher-order) effect.
operator, whose higher-order effect signature is given in Figure 6, is not an algebraic effect, but a scoped (and thus higher-order) effect.

Fig 6. Higher-order effect signature of the once effect.
We can define the meaning of the
![]() operator as the following elaboration:
operator as the following elaboration:

The elaboration runs the branch (
![]() $\psi$
) of
$\psi$
) of
![]() under the
under the
![]() handler to compute a list of all solutions of
handler to compute a list of all solutions of
![]() $\psi$
. It then tries to choose the first solution and pass that to the continuation k. If the branch has no solutions, we fail. Under a strict evaluation order, the elaboration computes all possible solutions which is doing more work than needed. Agda 2.6.2.2 does not have a specified evaluation strategy, but does compile to Haskell which is lazy. In Haskell, the solutions would be lazily computed, such that the
$\psi$
. It then tries to choose the first solution and pass that to the continuation k. If the branch has no solutions, we fail. Under a strict evaluation order, the elaboration computes all possible solutions which is doing more work than needed. Agda 2.6.2.2 does not have a specified evaluation strategy, but does compile to Haskell which is lazy. In Haskell, the solutions would be lazily computed, such that the
![]() operator cuts search short as intended.
operator cuts search short as intended.
4.4 Concurrency
Finally, we consider how to define higher-order operations for concurrency, inspired by Yang et al.’s (Reference Yang, Paviotti, Wu, van den Berg and Schrijvers2022) resumption monad (Schmidt, Reference Schmidt1986; Claessen, Reference Claessen1999; Piróg & Gibbons, Reference Piróg and Gibbons2014) defined using scoped effects. We summarize our encoding and compare it with the resumption monad. The goal is to define the two operations, whose higher-order effect signature is given in Figure 7, and summarized by these smart constructors:

The operation
![]()
![]() ${m_{1}}~{m_{2}}$
spawns two threads that run concurrently, and returns the value produced by
${m_{1}}~{m_{2}}$
spawns two threads that run concurrently, and returns the value produced by
![]() ${m}_{1}$
after both have finished. The operation
${m}_{1}$
after both have finished. The operation
![]() m represents a block to be executed atomically; i.e., no other threads run before the block finishes executing.
m represents a block to be executed atomically; i.e., no other threads run before the block finishes executing.
We elaborate
![]() by interleaving the sub-trees of its computations. To this end, we use a dedicated function that interleaves the operations in two trees and yields as output the value of the left input tree (the first computation parameter):
by interleaving the sub-trees of its computations. To this end, we use a dedicated function that interleaves the operations in two trees and yields as output the value of the left input tree (the first computation parameter):

Here, the
![]() effect is the sub/jump effect that we also used in Section 4.2.2. The
effect is the sub/jump effect that we also used in Section 4.2.2. The
![]() function ensures atomic execution by only interleaving code that is not wrapped in a
function ensures atomic execution by only interleaving code that is not wrapped in a
![]() operation. We elaborate
operation. We elaborate
![]() into
into
![]() as follows, where the
as follows, where the
![]() and
and
![]() functions use the row insertion witness w
functions use the row insertion witness w
![]() $_a$
to move the
$_a$
to move the
![]() effect to the front of the row and back again:
effect to the front of the row and back again:

The elaboration uses
![]() as a delimiter for blocks that should not be interleaved, such that the
as a delimiter for blocks that should not be interleaved, such that the
![]() function only interleaves code that does not reside in atomic blocks. At the end of an
function only interleaves code that does not reside in atomic blocks. At the end of an
![]() block, we
block, we
![]() to the (possibly interleaved) computation context, k. By using
to the (possibly interleaved) computation context, k. By using
![]() to explicitly delimit blocks that should not be interleaved, we have encoded what Wu et al. (Reference Wu, Schrijvers and Hinze2014, § 7) call scoped syntax.
to explicitly delimit blocks that should not be interleaved, we have encoded what Wu et al. (Reference Wu, Schrijvers and Hinze2014, § 7) call scoped syntax.
Example. Below is an example program that spawns two threads that use the
![]() effect. The first thread prints
effect. The first thread prints
![]() , and
, and
![]() ; the second prints
; the second prints
![]() and
and
![]() .
.

Since the
![]() effect is elaborated to interleave the effects of the two threads, the printed output appears in interleaved order:
effect is elaborated to interleave the effects of the two threads, the printed output appears in interleaved order:

The following program spawns an additional thread with an
![]() block
block

Inspecting the output, we see that the additional thread indeed computes atomically:

The example above is inspired by the resumption monad, and in particular by the scoped effects definition of concurrency due to Yang et al. (Reference Yang, Paviotti, Wu, van den Berg and Schrijvers2022). Yang et al. do not (explicitly) consider how to define the concurrency operations in a modular style. Instead, they give a direct semantics that translates to the resumption monad which we can encode as follows in Agda (assuming resumptions are given by the free monad):

We could elaborate into this type using a hefty algebra
![]() but that would be incompatible with our other elaborations which use the free monad. For that reason, we emulate the resumption monad using the free monad instead of using the
but that would be incompatible with our other elaborations which use the free monad. For that reason, we emulate the resumption monad using the free monad instead of using the
![]() type directly.
type directly.
5 Modular reasoning for higher-order effects
A key aspect of algebraic effects and handlers is the ability to state and prove equational laws as part of an effect’s specification that characterize correct implementations. Usually, an effect is associated with several laws that govern its behavior. An effect, together with its laws, constitutes an effect theory (Plotkin & Power, Reference Plotkin and Power2002, Reference Plotkin and Power2003; Hyland et al., Reference Hyland, Plotkin and Power2006; Yang & Wu, Reference Yang and Wu2021). Equational reasoning within an effect theory can be used to derive syntactic equalities between effectful programs without appealing to the effect’s implementation. Such equalities remain true in the semantic domain for any handler that respects the laws of the theory.
The concept of effect theory extends to higher-order effect theories, which describe the intended behavior of higher-order effects. In this section, we first discuss how to define theories for algebraic effects in Agda by adapting the exposition of Yang &Wu (Reference Yang and Wu2021), and show how correctness of implementations with respect to a given theory can be stated and proved. We then extend this reasoning infrastructure to higher-order effects, which allows for the derivation of syntactic equalities between programs with higher-order effects and modular reasoning about the correctness of elaborations.
5.1 Effect theories and implementation correctness
Let us consider the state effect as an example, which comprises the
![]() and
and
![]() operations. With the state effect, we typically associate a set of equations (or laws) that specify how its implementations ought to behave. One such law is the get-get law, which captures the intuition that the state returned by two subsequent
operations. With the state effect, we typically associate a set of equations (or laws) that specify how its implementations ought to behave. One such law is the get-get law, which captures the intuition that the state returned by two subsequent
![]() operations does not change if we do not use the
operations does not change if we do not use the
![]() operation in between:
operation in between:
We can define equational laws for higher-order effects in a similar fashion. For example, the following catch-return law for the
![]() operation of the
operation of the
![]() effect, stating that catching exceptions in a computation that only returns a value does nothing.
effect, stating that catching exceptions in a computation that only returns a value does nothing.
Correctness of an implementation of an algebraic effect with respect to a given theory is defined by comparing the implementations of programs that are equal under that theory. That is, if we can show that two programs are equal using the equations of a theory for its effects, handling the effects should produce equal results. For instance, a way to implement the state effect is by mapping programs to functions of the form
![]() ${S}~\to~{S}\times{A}$
. Such an implementation would be correct if programs that are equal with respect to a theory of the state effect are mapped to functions that give the same value and output state for every input state.
${S}~\to~{S}\times{A}$
. Such an implementation would be correct if programs that are equal with respect to a theory of the state effect are mapped to functions that give the same value and output state for every input state.
For higher-order effects, correctness is defined in a similar manner. However, since we define higher-order effects by elaborating them into algebraic effects, correctness of elaborations with respect to a higher-order effect theory is defined by comparing the elaborated programs. Crucially, the elaborated programs do not have to be syntactically equal, but rather we should be able to prove them equal using a theory of the algebraic effects used to implement a higher-order effect.
Effect theories are known to be closed under the co-product of effects, by combining the equations into a new theory that contains all equations for both effects (Hyland et al., Reference Hyland, Plotkin and Power2006). Similarly, theories of higher-order effects are closed under sums of higher-order effect signatures. In Section 5.9, we show that composing two elaborations preserves their correctness, with respect to the sum of their respective theories.
5.2 Theories of algebraic effects
Theories of effects are collections of equations, so we start defining the type of equations in Agda. At its core, an equation for an effect
![]() $\Delta$
is given by a pair of effect trees of type
$\Delta$
is given by a pair of effect trees of type
![]() , that define the left- and right-hand side of the equation. However, looking at the get-get law above, we see that this equation contains a term metavariable; i.e.,
, that define the left- and right-hand side of the equation. However, looking at the get-get law above, we see that this equation contains a term metavariable; i.e.,
![]() ${k}$
. Furthermore, when considering the type of
${k}$
. Furthermore, when considering the type of
![]() ${k}$
, which is
${k}$
, which is
![]() , we see that it refers to a type metavariable; i.e.,
, we see that it refers to a type metavariable; i.e.,
![]() ${A}$
. Generally speaking, an equation may refer to any number of term metavariables, which, in turn, may depend on any number of type metavariables. Moreover, the type of the value returned by the left-hand side and right-hand side of an equation may depend on these type metavariables as well, as is the case for the get-get law above. This motivates the following definition of equations in Agda.
${A}$
. Generally speaking, an equation may refer to any number of term metavariables, which, in turn, may depend on any number of type metavariables. Moreover, the type of the value returned by the left-hand side and right-hand side of an equation may depend on these type metavariables as well, as is the case for the get-get law above. This motivates the following definition of equations in Agda.

An equation consists of five components. The field
![]() defines the number of type metavariables used in the equation. Then, the fields
defines the number of type metavariables used in the equation. Then, the fields
![]() and
and
![]() , respectively, define the term metavariables (
, respectively, define the term metavariables (
![]() ) and return type (
) and return type (
![]() ) of the equation.
) of the equation.
Example. To illustrate how the
![]() record captures equational laws of effects, we consider how to define the get-get as a value of type
record captures equational laws of effects, we consider how to define the get-get as a value of type
![]() .
.

The fields
![]() and
and
![]() define the left- and right-hand sides of the equation. Both sides only use a single term metavariable, representing a continuation of type
define the left- and right-hand sides of the equation. Both sides only use a single term metavariable, representing a continuation of type
![]() . The field
. The field
![]() declares this term meta-variable. For equations with more than
declares this term meta-variable. For equations with more than
![]() $n>1$
metavariables, we would define
$n>1$
metavariables, we would define
![]() as an n-ary product instead.
as an n-ary product instead.
5.3 Modal necessity
The current definition of equations is too weak, in the sense that it does not apply in many situations where it should. The issue is that it fixes the set of effects that can be used in the left- and right-hand side. To illustrate why this is problematic, consider the following equality:
We might expect to be able to prove this equality using the get-get law, but using the embedding of the law defined above—i.e.,
![]() —this is not possible. The reason for this is that we cannot pick an appropriate instantiation for the term metavariable k: it ranges over values of type
—this is not possible. The reason for this is that we cannot pick an appropriate instantiation for the term metavariable k: it ranges over values of type
![]() , inhibiting all references to effectful operation that are not part of the state effect, such as
, inhibiting all references to effectful operation that are not part of the state effect, such as
![]() .
.
Given an equation for the effect
![]() $\Delta$
, the solution to this problem is to view
$\Delta$
, the solution to this problem is to view
![]() $\Delta$
as a lower bound on the effects that might occur in the left-hand and right-hand side of the equation, rather than an exact specification. Effectively, this means that we close over all posible contexts of effects in which the equation can occur. This pattern of closing over all possible extensions of a type index is well-known (Allais et al., Reference Allais, Atkey, Chapman, McBride and McKinna2021; van der Rest et al., Reference van der Rest, Poulsen, Rouvoet, Visser and Mosses2022), and corresponds to a shallow embedding of the Kripke semantics of the necessity modality from modal logic. We can define it in Agda as follows.Footnote
35
$\Delta$
as a lower bound on the effects that might occur in the left-hand and right-hand side of the equation, rather than an exact specification. Effectively, this means that we close over all posible contexts of effects in which the equation can occur. This pattern of closing over all possible extensions of a type index is well-known (Allais et al., Reference Allais, Atkey, Chapman, McBride and McKinna2021; van der Rest et al., Reference van der Rest, Poulsen, Rouvoet, Visser and Mosses2022), and corresponds to a shallow embedding of the Kripke semantics of the necessity modality from modal logic. We can define it in Agda as follows.Footnote
35

Intuitively, the
![]() modality transforms, for any effect-indexed type (P :
modality transforms, for any effect-indexed type (P :
![]() ), an exact specification of the set of effects to a lower bound on the set of effects. For equations, the difference between terms of type
), an exact specification of the set of effects to a lower bound on the set of effects. For equations, the difference between terms of type
![]() and
and
![]() amounts to the former defining an equation relating programs that have exactly effects
amounts to the former defining an equation relating programs that have exactly effects
![]() $\Delta$
, while the latter defines an equation relating programs that have at least the effects
$\Delta$
, while the latter defines an equation relating programs that have at least the effects
![]() $\Delta$
but potentially more. The
$\Delta$
but potentially more. The
![]() modality is a comonad: the counit (
modality is a comonad: the counit (
![]() below) witnesses that we can always transform a lower bound on effects to an exact specification, by instantiating the extension witness with a proof of reflexivity.
below) witnesses that we can always transform a lower bound on effects to an exact specification, by instantiating the extension witness with a proof of reflexivity.

We can now redefine the get-get law such that it applies to all programs that have the
![]() effect, but potentially other effects too.
effect, but potentially other effects too.

The above definition of the get-get law now lets us prove the equality in Equation (5.1); the term metavariable k ranges ranges over all continuations that return a tree of type
![]() , for all
, for all
![]() ${\Delta^\prime}$
such that
${\Delta^\prime}$
such that
![]() . This way, we can instantiate
. This way, we can instantiate
![]() ${\Delta^\prime}$
with an effect signature that subsumes both the
${\Delta^\prime}$
with an effect signature that subsumes both the
![]() and the
and the
![]() , which in turn allows us to instantiate k with
, which in turn allows us to instantiate k with
![]() .
.
5.4 Effect theories
Equations for an effect
![]() $\Delta$
can be combined into a theory for
$\Delta$
can be combined into a theory for
![]() $\Delta$
. A theory for the effect
$\Delta$
. A theory for the effect
![]() $\Delta$
is simply a collection of equations, transformed using the
$\Delta$
is simply a collection of equations, transformed using the
![]() modality to ensure that term metavariables can range over programs that include more effects than just
modality to ensure that term metavariables can range over programs that include more effects than just
![]() $\Delta$
.
$\Delta$
.

An effect theory consists of an
![]() that defines the number of equations in the theory, and a function that maps arities to equations. We can think of effect theories as defining a specification for how implementations of an effect ought to behave. Although implementations may vary, depending for example on whether they are tailored to readability or efficiency, they should at least respect the equations of the theory of the effect they implement. We will make precise what it means for an implementation to respect an equation in sec:handler-correctness.
that defines the number of equations in the theory, and a function that maps arities to equations. We can think of effect theories as defining a specification for how implementations of an effect ought to behave. Although implementations may vary, depending for example on whether they are tailored to readability or efficiency, they should at least respect the equations of the theory of the effect they implement. We will make precise what it means for an implementation to respect an equation in sec:handler-correctness.
Effect theories are closed under several composition operations that allow us to combine the equations of different theories into single theory. The most basic way of combining effect theories is by summing their arities.

This way of combining effects is somewhat limiting, as it imposes that the theories we are combining are theories for the exact same effect. It is more likely, however, that we would want to combine theories for different effects. This requires that we can weaken effect theories with respect to the
![]() relation.
relation.

Categorically speaking, the observation that for a given effect-indexed type P we can transform a value of type
![]() $P\ {\Delta_{1}}$
to a value of type
$P\ {\Delta_{1}}$
to a value of type
![]() $P\ {\Delta_{2}}$
if we know that
$P\ {\Delta_{2}}$
if we know that
![]() is equivalent to saying that P is a functor from the category of containers and container morphisms to the category of sets. From this perspective, the existence of weakening for free
is equivalent to saying that P is a functor from the category of containers and container morphisms to the category of sets. From this perspective, the existence of weakening for free
![]() , as witnessed by the
, as witnessed by the
![]() operation discussed in Section 3, implies that it too is a such a functor.
operation discussed in Section 3, implies that it too is a such a functor.
With weakening for theories at our disposal, we can combine effect theories for different effects into a theory of the coproduct of their respective effects. This requires us to first define appropriate witnesses relating coproducts to effect inclusion.

It is now straightforward to show that effect theories are closed under the coproduct of effect signatures, by summing the weakened theories.

While this operation is in principle sufficient for our purposes, it forces a specific order on the effects of the combined theories. We can further generalize the operation above to allow for the effects of the combined theory to appear in any order. This requires the following instances.

We show that effect theories are closed under coproducts up to reordering by, again, summing the weakened theories.

Since equations are defined by storing the syntax trees that define their left-hand and right-hand side, and effect trees are weakenable, we would expect equations to be weakenable too. Indeed, we can define the following function witnessing weakenability of equations.
This begs the question: why would we opt to use weakenability of the
![]() modality (or, bother with the
modality (or, bother with the
![]() modality at all) to show that theories are weakenable, rather than using
modality at all) to show that theories are weakenable, rather than using
![]() directly? Although the latter approach would indeed allow us to define the composition operations for effect theories defined above, the possible ways in which we can instantiate term metavariables remains too restrictive. That is, we would still not be able to prove the equality in Equation (5.1), despite the fact that we can weaken the get-get law so that it applies to programs that use the
directly? Although the latter approach would indeed allow us to define the composition operations for effect theories defined above, the possible ways in which we can instantiate term metavariables remains too restrictive. That is, we would still not be able to prove the equality in Equation (5.1), despite the fact that we can weaken the get-get law so that it applies to programs that use the
![]() effect as well. Instantiations of the term metavariable k will be limited to weakened effect trees, precluding any instantiation that use operations of effects other than
effect as well. Instantiations of the term metavariable k will be limited to weakened effect trees, precluding any instantiation that use operations of effects other than
![]() , such as
, such as
![]() .
.
Finally, we define the following predicate to witness that an equation is part of a theory.
We construct a proof
![]() that an equation
that an equation
![]() ${eq}$
is part of a theory
${eq}$
is part of a theory
![]() ${T}$
by providing an arity together with a proof that
${T}$
by providing an arity together with a proof that
![]() ${T}$
maps to
${T}$
maps to
![]() ${eq}$
for that arity.
${eq}$
for that arity.
5.5 Syntactic equivalence of effectful programs
Propositional equality of effectful programs is too strict, as it precludes us from proving equalities that rely on a semantic understanding of the effects involved, such as the equality in Equation (5.1). The solution is to define an inductive relation that captures syntactic equivalence modulo some effect theory. We base our definition of syntactic equality of effectful programs on the relation defining equivalent computations by Yang &Wu (Reference Yang and Wu2021), Definition 3.1, adapting their definition where necessary to account for the use of modal necessity in the definition of
![]() .
.

A value of type
![]() witnesses that programs
witnesses that programs
![]() ${m_{1}}$
and
${m_{1}}$
and
![]() ${m_{2}}$
are equal modulo the equations of theory
${m_{2}}$
are equal modulo the equations of theory
![]() ${T}$
. The first three constructors ensure that it is an equivalence relation.
${T}$
. The first three constructors ensure that it is an equivalence relation.

Then, we add the following congruence rule, which establishes that we can prove equality of two programs starting with the same operation by proving that the continuations yield equal programs for every possible value.

The final constructor allows to prove equality of programs by reifying equations of an effect theory.

Since the equations of a theory are wrapped in the
![]() modality, we cannot refer to its components directly, but we must first provide a suitable extension witness.
modality, we cannot refer to its components directly, but we must first provide a suitable extension witness.
With the
![]() constructor, we can prove equivalence between the left-hand and right-hand side of an equation, sequenced with an arbitrary continuation
constructor, we can prove equivalence between the left-hand and right-hand side of an equation, sequenced with an arbitrary continuation
![]() ${k}$
. For convenience, we define the following lemma that allows us to apply an equation where the sides of the equation do not have a continuation.
${k}$
. For convenience, we define the following lemma that allows us to apply an equation where the sides of the equation do not have a continuation.

The definition of
![]() follows readily from the right-identity law for monads, i.e.,
follows readily from the right-identity law for monads, i.e.,
![]() , which allows us to instantiate
, which allows us to instantiate
![]() with
with
![]() .
.
To construct proofs of equality, it is convenient to use the following set of combinators to write proof terms in an equational style. They are completely analogous to the combinators commonly used to construct proofs of Agda’s propositional equality, for example, as found in PLFA (Wadler et al., Reference Wadler, Kokke and Siek2020).

We now have all the necessary tools to prove syntactic equality of programs modulo a theory of their effect. To illustrate, we consider how to prove the equation in Equation (5.1). First, we define a theory for the
![]() effect containing the
effect containing the
![]() law. While this is not the only law typically associated with
law. While this is not the only law typically associated with
![]() , for this example it is enough to only have the
, for this example it is enough to only have the
![]() law.
law.

Now to prove the equality in Equation (5.1) is simply a matter of invoking the
![]() law.
law.

5.6 Handler correctness
A handler is correct with respect to a given theory if handling syntactically equal programs yields equal results. Since handlers are defined as algebras over effect signatures, we start by defining what it means for an algebra of an effect
![]() $\Delta$
to respect an equation of the same effect, adapting Definition 2.1 from the exposition of Yang & Wu (Reference Yang and Wu2021).
$\Delta$
to respect an equation of the same effect, adapting Definition 2.1 from the exposition of Yang & Wu (Reference Yang and Wu2021).

An algebra
![]() ${alg}$
respects an equation
${alg}$
respects an equation
![]() ${eq}$
if folding with that algebra produces propositionally equal results for the left- and right-hand side of the equation, for all possible instantiations of its type and term metavariables, and continuations k.
${eq}$
if folding with that algebra produces propositionally equal results for the left- and right-hand side of the equation, for all possible instantiations of its type and term metavariables, and continuations k.
A handler
![]() ${H}$
is correct with respect to a given theory
${H}$
is correct with respect to a given theory
![]() ${T}$
if its algebra respects all equations of
${T}$
if its algebra respects all equations of
![]() ${T}$
(Yang & Wu, Reference Yang and Wu2021, Definition 4.3).
${T}$
(Yang & Wu, Reference Yang and Wu2021, Definition 4.3).

We can now show that the handler for the
![]() effect defined in Figure 1 is correct with respect to
effect defined in Figure 1 is correct with respect to
![]() . The proof follows immediately by reflexivity.
. The proof follows immediately by reflexivity.

5.7 Theories of higher-order effects
For the most part, equations and theories for higher-order effects are defined in the same way as for first-order effects and support many of the same operations. Indeed, the definition of equations ranging over higher-order effects is exactly the same as its first-order counterpart, the most major difference being that the left-hand and right-hand side are now defined as Hefty trees. To ensure compatibility with the use of type universes to avoid size-issues, we must also allow type metavariables to range over the types in a universe in addition to
![]() . For this reason, the set of type metavariables is no longer described by a natural number, but rather by a list of kinds, which stores for each type metavariable whether it ranges over a types in a universe, or an Agda
. For this reason, the set of type metavariables is no longer described by a natural number, but rather by a list of kinds, which stores for each type metavariable whether it ranges over a types in a universe, or an Agda
![]() .
.
A
![]() carries unapplied substitutions for a given set of type metavariables and is defined by induction over a list of kinds.Footnote
36
carries unapplied substitutions for a given set of type metavariables and is defined by induction over a list of kinds.Footnote
36

Equations of higher-order effects are then defined as follows.

This definition of equations suffers the same problem when it comes to term metavariables, which here too can only range over programs that exhibit the exact effect that the equation is defined for. Again, we address the issue using an embedding of modal necessity to close over all possible extensions of this effect. The definition is analogous to the one in sec:modal-necessity, but this time we use higher-order effect subtyping as the modal accessibility relation:

To illustrate: we can define the catch-return law from the introduction of this section as a value of type
![]() a follows. Since the
a follows. Since the
![]() operation relies on a type universe to avoid size issues, the sole type metavariable of this equation must range over the types in this universe as well.
operation relies on a type universe to avoid size issues, the sole type metavariable of this equation must range over the types in this universe as well.

Theories of higher-order effects bundle extensible equations. The setup is the same as for theories of first-order effects.

The following predicate establishes that an equation is part of a theory. We prove this fact by providing an arity whose corresponding equation is equal to
![]() ${eq}$
.
${eq}$
.

Weakenability of theories of higher-order effects then follows from weakenability of its equations.

Theories of higher-order effects can be combined using the following sum operation. The resulting theory contains all equations of both argument theories.

Theories of higher-order effects are closed under sums of higher-order effect theories as well. This operation is defined by appropriately weakening the respective theories, for which we need the following lemmas witnessing that higher-order effect signatures can be injected in a sum of signatures.

The operation that combines theories under signature sums is then defined like so.

5.8 Equivalence of programs with higher-order effects
We define the following inductive relation to capture equivalence of programs with higher-order effects modulo the equations of a given theory.

To ensure that it is indeed an equivalence relation, we include constructors for reflexivity, symmetry, and transitivity.

Furthermore, we include the following congruence rule that equates two program trees that have the same operation at the root, if their continuations are equivalent for all inputs.

Finally, we include a constructor that equates two programs using an equation of the theory.

We can define the same reasoning combinators as in Section 5.5 to construct proofs of equivalence for programs with higher-order effects.

To illustrate, we can prove that the programs
![]() are equal under a theory for the afCatch effect that contains the catch-return law.
are equal under a theory for the afCatch effect that contains the catch-return law.

The equivalence proof above makes, again, essential use of modal necessity. That is, by closing over all possible extensions of the
![]() effe, the term metavariable in the catch-return law to range over programs that have higher-order effects other than
effe, the term metavariable in the catch-return law to range over programs that have higher-order effects other than
![]() , which is needed to apply the law if the second branch of the
, which is needed to apply the law if the second branch of the
![]() operation contains the
operation contains the
![]() operation.
operation.
5.9 Correctness of elaborations
As the first step toward defining correctness of elaborations, we must specify what it means for an algebra over a higher-order effect signature
![]() ${H}$
to respect an equation. The definition is broadly similar to its counterpart for first-order effects in Section 5.6, with the crucial difference that the definition of “being equation respecting” for algebras over higher-order effect signatures is parameterized over a binary relation
${H}$
to respect an equation. The definition is broadly similar to its counterpart for first-order effects in Section 5.6, with the crucial difference that the definition of “being equation respecting” for algebras over higher-order effect signatures is parameterized over a binary relation ![]() between first-order effect trees. In practice, this binary relation will be instantiated with the inductive equivalence relation defined in Section 5.5; propositional equality would be too restrictive, since that does not allow us prove equivalence of programs using equations of the first-order effect(s) that we elaborate into.
between first-order effect trees. In practice, this binary relation will be instantiated with the inductive equivalence relation defined in Section 5.5; propositional equality would be too restrictive, since that does not allow us prove equivalence of programs using equations of the first-order effect(s) that we elaborate into.

Since elaborations are composed in parallel, the use of necessity in the definition of equations has additional consequences for the definiton of elaboration correctness. That is, correctness of an elaboration is defined with respect to a theory whose equations have left-hand and right-hand sides that may contain term metavariables that range over programs with more higher-order effects than those the elaboration is defined for. Therefore, to state correctness, we must also close over all possible ways these additional effects are elaborated. For this, we define the following binary relation on extensible elaborations.Footnote 37

A proof of the form
![]() ${e_{1}}~\mathbin{\sqsubseteq}~{e_{2}}$
witnesses that the elaboration
${e_{1}}~\mathbin{\sqsubseteq}~{e_{2}}$
witnesses that the elaboration
![]() ${e_{1}}$
is included in
${e_{1}}$
is included in
![]() ${e_{2}}$
. Informally, this means that
${e_{2}}$
. Informally, this means that
![]() ${e_{2}}$
may elaborate a bigger set of higher-order effects, for which it may need to refer to a bigger set of first-order effects, but for those higher-order effects that both
${e_{2}}$
may elaborate a bigger set of higher-order effects, for which it may need to refer to a bigger set of first-order effects, but for those higher-order effects that both
![]() ${e_{1}}$
and
${e_{1}}$
and
![]() ${e_{2}}$
know how to elaborate, they should agree on how those effects are elaborated.
${e_{2}}$
know how to elaborate, they should agree on how those effects are elaborated.
We then define correctness of elaborations as follows.

Which is to say that an elaboration is correct with respect to a theory of the higher-order effects it elaborates (
![]() ${Th}$
) and a theory of the first-order effects it elaborates into (
${Th}$
) and a theory of the first-order effects it elaborates into (
![]() ${T}$
), if all possible extensions of said elaboration respect all equations of the higher-order theory, modulo the equations of the first-order theory.
${T}$
), if all possible extensions of said elaboration respect all equations of the higher-order theory, modulo the equations of the first-order theory.
Crucially, correctness of elaborations is preserved under composition of elaborations. Figure 8 shows the type of the corresponding correctness theorem in Agda; for the full details of the proof we refer to the Agda formalization accompanying this paper (van der Rest & Poulsen, Reference van der Rest and Poulsen2024). We remark that correctness of a composed elaboration is defined with respect to the composition of the theories of the first-order effects that the respective elaborations use. Constructing a handler that is correct with respect to this composed first-order effect theory is a separate concern; a solution based on fusion is detailed in the work by Yang & Wu (Reference Yang and Wu2021).

Fig 7. Higher-order effect signature of the concur effect.

Fig 8. The central correctness theorem, which establishes that correctness of elaborations is preserved under composition.
5.10 Proving correctness of elaborations
To illustrate how the reasoning infrastructure build up in this section can be applied to verify correctness of elaborations, we show how to verify the catch-return law for the elaboration
![]() defined in Section 3.4. First, we define the following syntax for invoking a known elaboration.
defined in Section 3.4. First, we define the following syntax for invoking a known elaboration.

When opening the module
![]() ${Elab}$
, we can use the syntax
${Elab}$
, we can use the syntax
![]() for elaborating m with some known elaboration, which helps to simplify and improve readability of equational proofs for higher-order effects.
for elaborating m with some known elaboration, which helps to simplify and improve readability of equational proofs for higher-order effects.
Now, to prove that
![]() is correct with respect to a higher-order theory for the
is correct with respect to a higher-order theory for the
![]() effect containing the catch-return law, we must produce a proof that the programs
effect containing the catch-return law, we must produce a proof that the programs
![]() are equal (in the sense of the inductive equivalence relation defined in Section 5.5) with respect to some first-order theory for the
are equal (in the sense of the inductive equivalence relation defined in Section 5.5) with respect to some first-order theory for the
![]() effect. In this instance, we do not need any equations from this underlying theory to prove the equality, but sometimes it is necessary to invoke equations of the underlying first-order effects to prove correctness of an elaboration.
effect. In this instance, we do not need any equations from this underlying theory to prove the equality, but sometimes it is necessary to invoke equations of the underlying first-order effects to prove correctness of an elaboration.

In the Agda formalization accompanying this paper (van der Rest & Poulsen, Reference van der Rest and Poulsen2024), we verify correctness of elaborations for the higher-order operations that are part of the 3MT library by Delaware et al. (Reference Delaware, Keuchel and Schrijvers2013). Table 1 shows an overview of first-order and higher-order effects included in the development, and the laws which we prove about their handlers respectively elaborations.
Table 1 Overview of effects, their operations, and verified laws in the Agda code

5.11 Discussion
In the introduction, we discussed the desired degrees of modularity that hefty algebras and their reasoning infrastructure should support. That is, they should support the modular composition of syntax, semantics, equational theories, and proofs.
Composability of the syntax and semantics of higher order effects follows readily from the fact that we define higher-order effect signatures and elaborations as higher-order functors and their algebras respectively (Section 3.1), which are closed under coproducts.
For proofs, we demonstrate in Section 5.3 that equational proofs for programs with higher-order effects are similarly modular. For instance, the proof of the
![]() law can be reused to reason about larger programs even if they involve additional (higher-order) effects. Crucially, correctness proofs of elaborations also compose: combining two correct elaborations automatically yields a proof of correctness for the composite elaboration (Section 5.9). This demonstrates that hefty trees enjoy the same, if not more, modularity properties than algebraic effects, which require sophisticated reasoning about fusion to compose proofs of handler correctness (Yang & Wu, Reference Yang and Wu2021).
law can be reused to reason about larger programs even if they involve additional (higher-order) effects. Crucially, correctness proofs of elaborations also compose: combining two correct elaborations automatically yields a proof of correctness for the composite elaboration (Section 5.9). This demonstrates that hefty trees enjoy the same, if not more, modularity properties than algebraic effects, which require sophisticated reasoning about fusion to compose proofs of handler correctness (Yang & Wu, Reference Yang and Wu2021).
Finally, we remark that elaborations and their correctness proofs support a more fine-grained composition than coproducts. Building on techniques developped by van der Rest et al. (Reference van der Rest, Poulsen, Rouvoet, Visser and Mosses2022), composition operators consume a separation witness, which act as a specification of which equations to identify across theories. This way, we avoid indiscriminate summation of effect theories. For more details we refer to the artifact accompanying this paper (van der Rest & Poulsen, Reference van der Rest and Poulsen2024).
6 Related work
As stated in the introduction of this paper, defining abstractions for programming constructs with side effects is a research question with a long and rich history, which we briefly summarize here. Reference MoggiMoggi (1989a ) introduced monads as a means of modeling side effects and structuring programs with side effects; an idea which Wadler (Reference Wadler1992) helped popularize. A problem with monads is that they do not naturally compose. A range of different solutions have been developed to address this issue (Cenciarelli & Moggi, Reference Cenciarelli and Moggi1993; Jones & Duponcheel, Reference Jones and Duponcheel1993; Steele, Reference Steele1994; Filinski, Reference Filinski1999). Of these solutions, monad transformers (Cenciarelli & Moggi, Reference Cenciarelli and Moggi1993; Liang et al., Reference Liang, Hudak and Jones1995; Jaskelioff, Reference Jaskelioff2008) is the more widely adopted solution. However, more recently, algebraic effects (Plotkin & Power, Reference Plotkin and Power2002) was proposed as an alternative solution which offers some modularity benefits over monads and monad transformers. In particular, whereas monads and monad transformers may “leak” information about the implementation of operations, algebraic effects enforce a strict separation between the interface and implementation of operations. Furthermore, monad transformers commonly require glue code to “lift” operations between layers of monad transformer stacks. While the latter problem is addressed by the Monatron framework of Jaskelioff (Reference Jaskelioff2008), algebraic effects have a simple composition semantics that does not require intricate liftings.
However, some effects, such as exception catching, did not fit into the framework of algebraic effects. Effect handlers (Plotkin & Pretnar, Reference Plotkin and Pretnar2009) were introduced to address this problem. Algebraic effects and handlers has since been gaining traction as a framework for modeling and structuring programs with side effects in a modular way. Several libraries have been developed based on the idea such as Handlers in Action (Kammar et al., Reference Kammar, Lindley and Oury2013), the freer monad (Kiselyov & Ishii, Reference Kiselyov and Ishii2015), or Idris’ Effects DSL (Reference BradyBrady, 2013b ); but also standalone languages such as Eff (Bauer & Pretnar, Reference Bauer and Pretnar2015), Koka (Leijen, Reference Leijen2017), Frank (Lindley et al., Reference Lindley, McBride and McLaughlin2017), and Effekt (Brachthäuser et al., Reference Brachthäuser, Schuster and Ostermann2020). Footnote 38
As discussed in Sections 1.2 and 2.5, some modularity benefits of algebraic effects and handlers do not carry over to higher-order effects. Scoped effects and handlers (Wu et al., Reference Wu, Schrijvers and Hinze2014; Piróg et al., Reference Piróg, Schrijvers, Wu and Jaskelioff2018; Yang et al., Reference Yang, Paviotti, Wu, van den Berg and Schrijvers2022) address this shortcoming for scoped operations, as we summarized in Section 2.6. This paper provides a different solution to the modularity problem with higher-order effects. Our solution is to provide modular elaborations of higher-order effects into more primitive effects and handlers. We can, in theory, encode any effect in terms of algebraic effects and handlers. However, for some effects, the encodings may be complicated. While the complicated encodings are hidden behind a higher-order effect interface, complicated encodings may hinder understanding the operational semantics of higher-order effects, and may make it hard to verify algebraic laws about implementations of the interface. Our framework would also support elaborating higher-order effects into scoped effects and handlers, which might provide benefits for verification. We leave this as a question to explore in future work.
Existing languages for algebraic effects and handlers, such as Eff (Bauer & Pretnar, Reference Bauer and Pretnar2015), Frank (Lindley et al., Reference Lindley, McBride and McLaughlin2017), Koka (Leijen, Reference Leijen2017), Effekt (Brachthäuser et al., Reference Brachthäuser, Schuster and Ostermann2020), or Flix (Lutze & Madsen, Reference Lutze and Madsen2024) offer indirect support for higher-order effects, via the encoding discussed in Section 1.2.2, As also discussed in Section 1.2.2. this encoding suffers from a modularity problem. Nevertheless, the encoding may suffice for applications in practice.
Whereas most languages (e.g., Eff, Koka, Flix, and Effekt) use so-called deep handlers, Frank (Lindley et al., Reference Lindley, McBride and McLaughlin2017) uses shallow handlers (Hillerström & Lindley, Reference Hillerström and Lindley2018). The difference between shallow effect and deep effect handlers is in how continuations are typed. A deep handler of type
![]() ${X}\mathop{!}{\Delta} \Rightarrow {C}\mathop{!}{\Delta^\prime}$
is typed as follows, where
${X}\mathop{!}{\Delta} \Rightarrow {C}\mathop{!}{\Delta^\prime}$
is typed as follows, where
![]() ${op} : A \to B$
is an operation of the effect row
${op} : A \to B$
is an operation of the effect row
![]() $\Delta$
:
$\Delta$
:
In contrast, shallow handlers are typed as follows:
Following Hillerström & Lindley (Reference Hillerström and Lindley2018), shallow handlers can emulate deep handlers by always invoking their continuations in the scope of a recursive call to the handler being defined (assuming a language with recursive functions). Hillerström & Lindley (Reference Hillerström and Lindley2018) also shows how deep handlers can emulate shallow handlers. As far as we are aware, shallow handlers support higher-order effects on a par with deep handlers, using the same encoding as we discussed in Section 1.2.2.
A recent paper by van den Berg et al. (Reference van den Berg, Schrijvers, Poulsen and Wu2021) introduced a generalization of scoped effects that they call latent effects, which supports a broader class of effects, including
![]() $\lambda$
abstraction. While the framework appears powerful, it currently lacks a denotational model, and seems to require similar weaving glue code as scoped effects. The solution we present in this paper does not require weaving glue code and is given by a modular but simple mapping onto algebraic effects and handlers.
$\lambda$
abstraction. While the framework appears powerful, it currently lacks a denotational model, and seems to require similar weaving glue code as scoped effects. The solution we present in this paper does not require weaving glue code and is given by a modular but simple mapping onto algebraic effects and handlers.
Another recent paper by van den Berg & Schrijvers (Reference van den Berg and Schrijvers2023) presents a unified framework for describing higher-order effects, which can be specialized to recover several instances such as Scoped Effects (Wu et al., Reference Wu, Schrijvers and Hinze2014) or Latent Effects (van den Berg et al., Reference van den Berg, Schrijvers, Poulsen and Wu2021). They present a generic free monad generated from higher-order signatures that coincides with the type of
![]() trees that we present in Section 3. Their approach relies on a Generalized Fold (Bird & Paterson, Reference Bird and Paterson1999) for describing semantics of handling operations, in contrast to the approach in this paper, where we adopt a two-stage process of elaboration and handling that can be expressed using the standard folds of first-order and higher-order free monads. To explore how the use of generalized folds versus standard folds affects the relative expressivity of approaches to higher-order effects is a subject of further study.
trees that we present in Section 3. Their approach relies on a Generalized Fold (Bird & Paterson, Reference Bird and Paterson1999) for describing semantics of handling operations, in contrast to the approach in this paper, where we adopt a two-stage process of elaboration and handling that can be expressed using the standard folds of first-order and higher-order free monads. To explore how the use of generalized folds versus standard folds affects the relative expressivity of approaches to higher-order effects is a subject of further study.
The equational framework we present in Section 5 is inspired by the work of Yang &Wu (Reference Yang and Wu2021). Specifically, the notion of higher-order effect theory we formalized in Agda is an extension of the notion of (first-order) effect theory they use. In closely related recent work by Kidney et al. (Reference Kidney, Yang and Wu2024), they present a formalization of first-order effect theories in Cubical Agda (Vezzosi et al., Reference Vezzosi, Mörtberg and Abel2021). Whereas our formalization requires extrinsic verification of the equalities of an effect theory, they use quotient types as provided by homotopy type theory (Program, Reference Program2013) and cubical type theory (Angiuli et al., Reference Angiuli, Brunerie, Coquand, Harper, (Favonia) and Licata2021; Cohen et al., Reference Cohen, Coquand, Huber and Mörtberg2017) to verify that handlers intrinsically respect their effect theories. They also present a Hoare logic for verifying pre- and post-conditions. An interesting question for future work is whether this logic and the framework of Kidney et al. (Reference Kidney, Yang and Wu2024) could be extended to higher-order effect theories.
In other recent work, Matache et al. (Reference Matache, Lindley, Moss, Staton, Wu and Yang2025) developed an equational reasoning system for scoped effects. The work builds on previous work by Staton on parameterized algebraic theories (Staton, Reference Staton2013a,b) which provide a syntactic framework for modeling computational effects with notions of locality (or, in scoped effects terminology, scope). Matache et al. (Reference Matache, Lindley, Moss, Staton, Wu and Yang2025) show that scoped effects translate into a variant of parameterized algebraic theories and demonstrate that such theories provide algebraic characterizations of key examples from the literature on scoped effects: nondeterminism with semi-determinism, catching exceptions, and local state.
Whereas Matache et al. use parameterized algebraic theories as their underlying abstraction, Section 5 of this paper develops a notion of algebraic theory (
![]() in Section 5.7) over the higher-order free monad—i.e., a free monad construction that uses higher-order functors, given by a suitably generalized notion of container, instead of usual plain functors and containers (Abbott et al., Reference Abbott, Altenkirch and Ghani2005)—in Agda’s
in Section 5.7) over the higher-order free monad—i.e., a free monad construction that uses higher-order functors, given by a suitably generalized notion of container, instead of usual plain functors and containers (Abbott et al., Reference Abbott, Altenkirch and Ghani2005)—in Agda’s
![]() . The equations of our higher-order effect theories are validated by elaborations into free ordinary effect theories. An interesting question for future work is to study the relationship between and compare the expressiveness of our proposed notion of higher-order effect theory and parameterized algebraic theories+scoped effects.
. The equations of our higher-order effect theories are validated by elaborations into free ordinary effect theories. An interesting question for future work is to study the relationship between and compare the expressiveness of our proposed notion of higher-order effect theory and parameterized algebraic theories+scoped effects.
As discussed in the introduction, this paper explores a formal semantics for overloading-based definitions of higher-order effects. We formalized this semantics using an initial algebra semantics. An alternative approach would have been to use a so-called final tagless (Carette et al., Reference Carette, Kiselyov and Shan2009) encoding. That is, instead of declaring syntax as an inductive datatype, we declare it as a record type, and program against that record. A benefit of the final tagless approach is that we do not have to explicitly fold over syntax. The idea is to program against interfaces given by record types; e.g.:

Using this final tagless encoding, the semantics of
![]() will be given by passing two concrete implementations of
will be given by passing two concrete implementations of
![]() and
and
![]() . In contrast, with the initial algebra semantics approach we use in Section 5, we would define
. In contrast, with the initial algebra semantics approach we use in Section 5, we would define
![]() in terms of an inductive data type for
in terms of an inductive data type for
![]() ; and then give its semantics by folding algebras over the abstract syntax tree. A benefit of final tagless is that it tends to have a have a lower interpretive overhead (Carette et al., Reference Carette, Kiselyov and Shan2009), since it avoids the need to iterate over syntax trees. These benefits extend to effects (Devriese, Reference Devriese2019). On the other hand, the inductive data types of initial encodings support induction, whereas final tagless encodings generally do not. We do not make extensive use of inductive reasoning in this paper, and we expect that it should be possible to port most of the definitions in our paper to use final tagless encodings. Our main reason for using an initial encoding for our hefty trees and algebras is that it follows the tradition of modeling algebraic effects and handlers using initial encodings, and that we expect induction to be useful for some applications.
; and then give its semantics by folding algebras over the abstract syntax tree. A benefit of final tagless is that it tends to have a have a lower interpretive overhead (Carette et al., Reference Carette, Kiselyov and Shan2009), since it avoids the need to iterate over syntax trees. These benefits extend to effects (Devriese, Reference Devriese2019). On the other hand, the inductive data types of initial encodings support induction, whereas final tagless encodings generally do not. We do not make extensive use of inductive reasoning in this paper, and we expect that it should be possible to port most of the definitions in our paper to use final tagless encodings. Our main reason for using an initial encoding for our hefty trees and algebras is that it follows the tradition of modeling algebraic effects and handlers using initial encodings, and that we expect induction to be useful for some applications.
Looking beyond purely functional models of semantics and effects, there are also lines of work on modular support for side effects in operational semantics (Plotkin, Reference Plotkin2004). Mosses’ Modular Structural Operational Semantics (Mosses, Reference Mosses2004) (MSOS) defines small-step rules that implicitly propagate an open-ended set of auxiliary entities which encode common classes of effects, such as reading or emitting data, stateful mutation, and even control effects (Sculthorpe et al., Reference Sculthorpe, Torrini and Mosses2015). The K Framework (Rosu & Serbanuta, Reference Rosu and Serbanuta2010) takes a different approach but provides many of the same benefits. These frameworks do not encapsulate operational details but instead make it notationally convenient to program (or specify semantics) with side-effects.
7 Conclusion
In this paper, we presented a semantics for higher-order effects based on overloading, by defining higher-order effects in terms of elaborations to algebraic effect trees. In this setup, we program against an interface of higher-order effects in a way that provides effect encapsulation. This means we can modularly change the implementation of effects without changing programs written against the interface, and without changing the definition of any interface implementations. Crucially, hefty trees and their elaborations support modular reasoning. Equational proofs about programs with higher-order effects inherit this modularity: they can be reused in the context of larger programs, even if those rely on additional effects. Most significantly, correctness proofs of elaborations are themselves modular. As a result, correctness proofs can be lifted to proofs over composite elaborations, something which is generally not possible for algebraic effect handlers without appealing to fusion theorems.
While we have made use of Agda and dependent types throughout this paper, the framework should be portable to less dependently-typed functional languages, such as Haskell, OCaml, or Scala. An interesting direction for future work is to explore whether the framework could provide a denotational model for handling higher-order effects in standalone languages with support for effect handlers.
Acknowledgments
We thank the anonymous reviewers for their comments that helped improve the exposition of the paper. Furthermore, we thank Nicolas Wu, Andrew Tolmach, Peter Mosses, and Jaro Reinders for feedback on earlier drafts. This research was partially funded by the NWO VENI Composable and Safe-by-Construction Programming Language Definitions project (VI.Veni.192.259).
Data availability statement
The code and proofs supporting this paper are publically available (van der Rest & Bach Poulsen, Reference van der Rest and Bach Poulsen2025).
Competing interests
The authors report no conflict of interest.



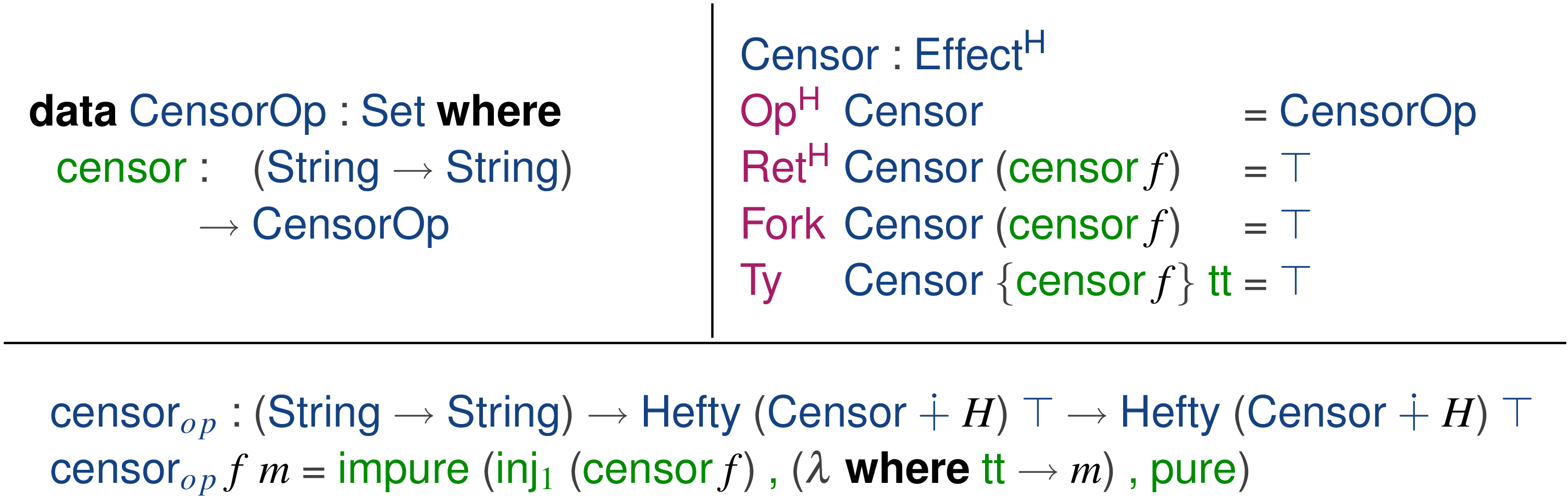








Discussions
No Discussions have been published for this article.